মাধ্যমিক গণিত – বৃত্ত সম্পর্কিত উপপাদ্য – উপপাদ্য

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের তৃতীয় অধ্যায়, ‘বৃত্ত সম্পর্কিত উপপাদ্য’ -এর উপপাদ্যমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

উপপাদ্য – 31. তিনটি অসমরেখ বিন্দু দিয়ে একটি মাত্র বৃত্ত অঙ্কন সম্ভব।

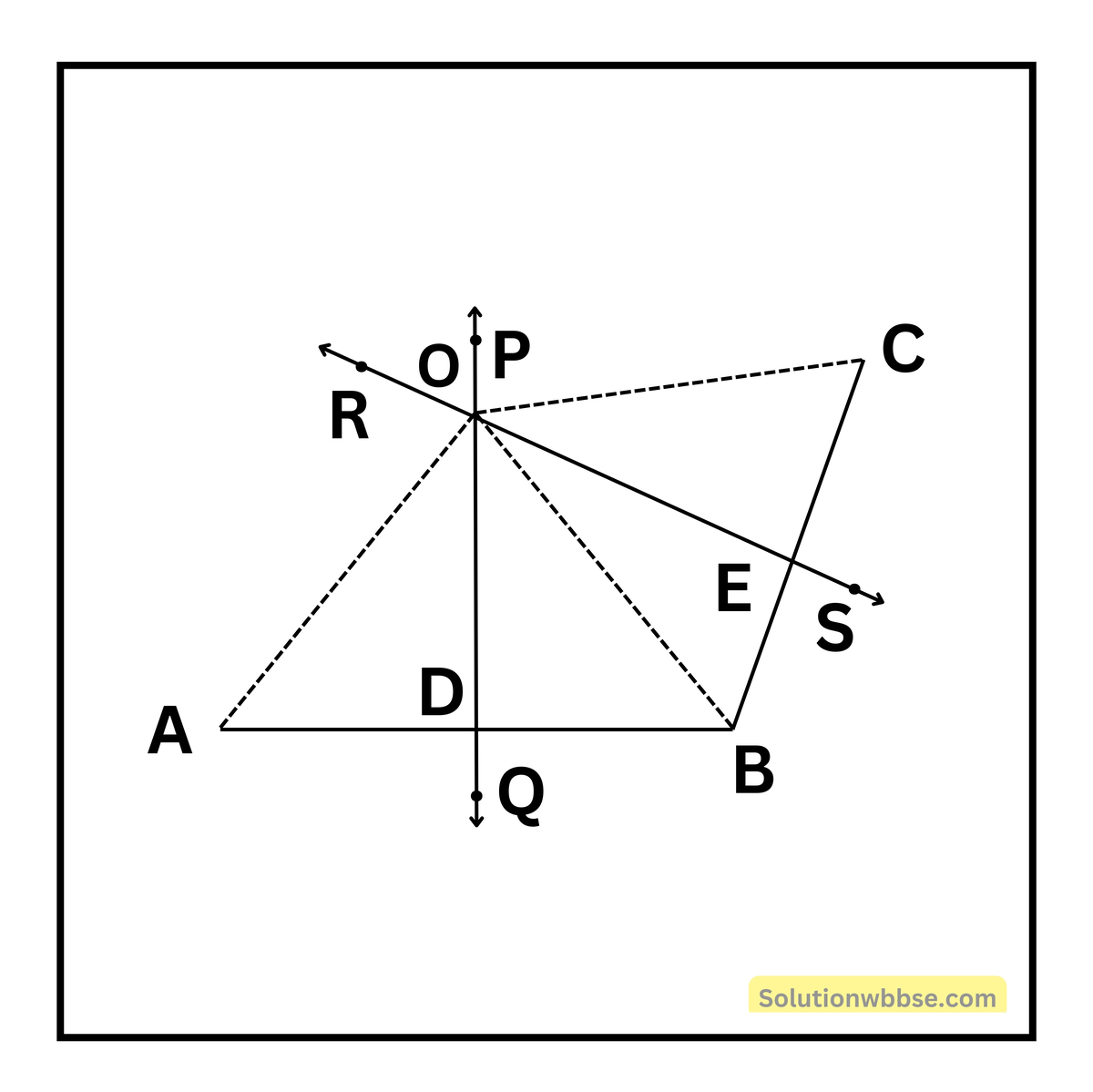
প্রদত্ত – A, B, C তিনটি অসমরেখ বিন্দু।

প্রমাণ করতে হবে – A, B, C তিনটি অসমরেখ বিন্দু দিয়ে একটি মাত্র বৃত্ত অঙ্কন সম্ভব।

অঙ্কন – A, B বিন্দুদ্বয় ও B, C বিন্দুদ্বয় যুক্ত করি। AB ও BC সরলরেখাংশ দুটির লম্বসমদ্বিখণ্ডক অঙ্কন করি এবং তারা যথাক্রমে PQ ও RS সরলরেখা।

যেহেতু AB ও BC সরলরেখাংশ দুটি সমান্তরাল নয়, সুতরাং তাদের লম্বসমদ্বিখণ্ডক দুটি PQ ও RS সরলরেখা বিন্দুতে ছেদ করে। PQ এবং RS সরলরেখা AB ও BC সরলরেখাংশদ্বয়কে যথাক্রমে D ও E বিন্দুতে ছেদ করে। O, A বিন্দুদ্বয়; O, B বিন্দুদ্বয় এবং O, C বিন্দুদ্বয় যুক্ত করি।

প্রমাণ – ΔOAD এবং ΔOBD-এর মধ্যে

AD = BD (∵ OD, AB সরলরেখাংশের লম্বসমদ্বিখণ্ডক)

∠ODA = ∠ODB (∵ প্রত্যেকটি কোণ সমকোণ)

OD সাধারণ বাহু ∴ ΔOAD ≅ ΔOBD (S-A-S সর্বসমতা অনুসারে)

সুতরাং OA = OB (সর্বসম ত্রিভুজের অনুরূপ অংশ)

অনুরূপে, ΔOBE ≅ ΔОСЕ

∴ OB = OC

সুতরাং OA = OB = OC

∴ O বিন্দুকে কেন্দ্র করে OA দৈর্ঘ্যের ব্যাসার্ধ নিয়ে বৃত্ত অঙ্কন করলে বৃত্তটি A, B, C বিন্দুগামী হবে।

সুতরাং তিনটি অসমরেখ বিন্দু দিয়ে একটি বৃত্ত অঙ্কন সম্ভব।

A, B, C বিন্দু তিনটি নির্দিষ্ট। অতএব, AB ও BC সরলরেখাংশ দুটি নির্দিষ্ট।

সুতরাং AB ও BC সরলরেখাংশ দুটির লম্বসমদ্বিখণ্ডক যথাক্রমে PQ ও RS সরলরেখা নির্দিষ্ট।

যেহেতু PQ ও RS সরলরেখা নির্দিষ্ট, সুতরাং তাদের ছেদবিন্দু O নির্দিষ্ট।

আবার যেহেতু O এবং A বিন্দুদ্বয় নির্দিষ্ট, সুতরাং OA সরলরেখাংশের দৈর্ঘ্য নির্দিষ্ট।

অতএব নির্দিষ্ট বিন্দু O-কে কেন্দ্র করে এবং নির্দিষ্ট দৈর্ঘ্যের ব্যাসার্ধ নিয়ে একটি মাত্র বৃত্ত অঙ্কন সম্ভব।

∴ তিনটি অসমরেখ বিন্দু A, B, C দিয়ে একটি মাত্র বৃত্ত অঙ্কন সম্ভব।

উপপাদ্য – 32. ব্যাস নয় এরূপ কোনো জ্যা-এর উপর বৃত্তের কেন্দ্র থেকে লম্ব অঙ্কন করা হলে, ওই লম্ব জ্যাটিকে সমদ্বিখণ্ডিত করে।

উপপাদ্য – 32. ব্যাস নয় এরূপ কোনো জ্যা-এর উপর বৃত্তের কেন্দ্র থেকে লম্ব অঙ্কন করা হলে, ওই লম্ব জ্যাটিকে সমদ্বিখণ্ডিত করে।

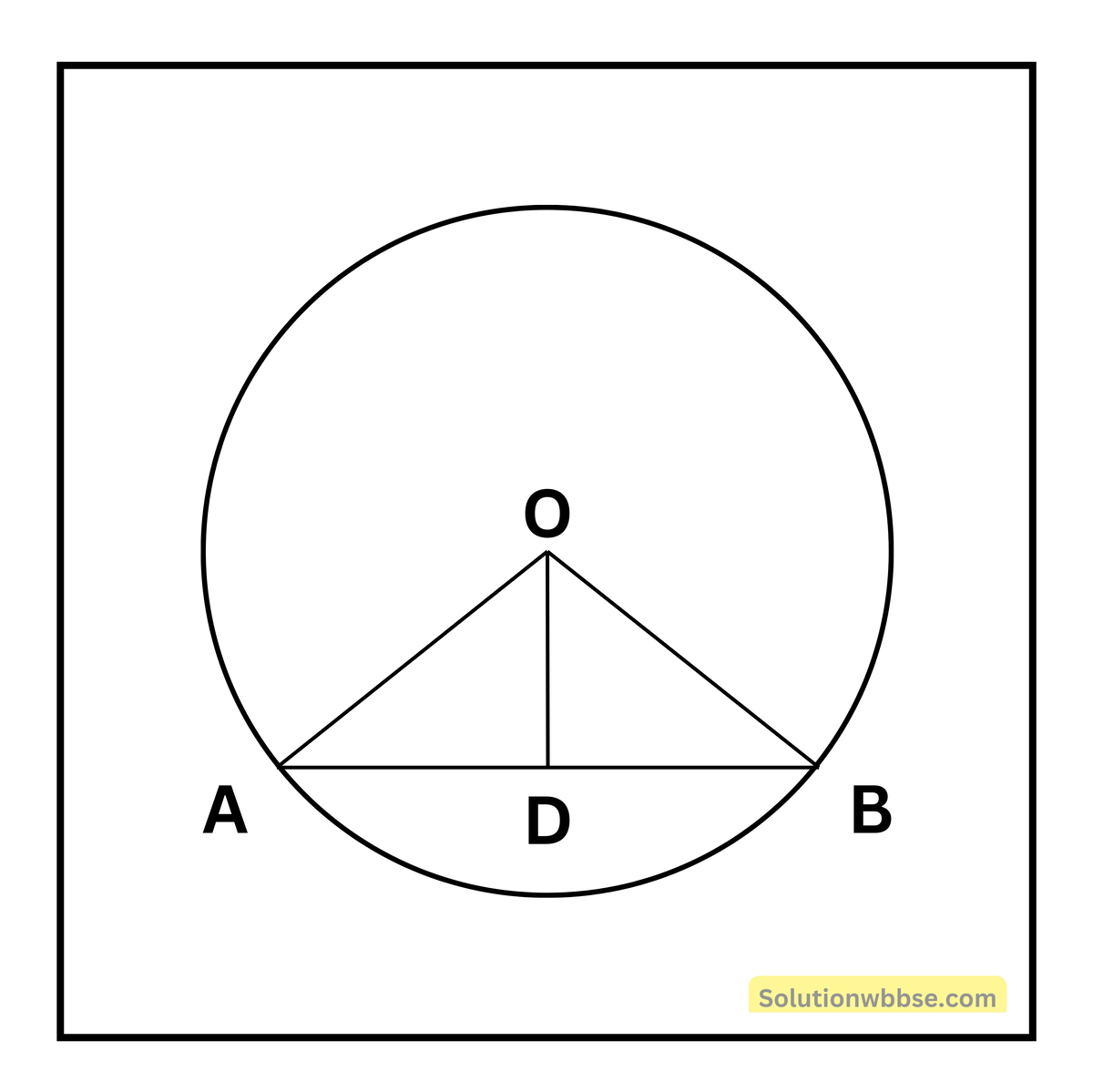
প্রদত্ত – O কেন্দ্রীয় বৃত্তের AB ব্যাস নয় এরূপ একটি জ্যা এবং OD, AB জ্যা-এর উপর লম্ব।

প্রমাণ করতে হবে – OD, AB জ্যাকে সমদ্বিখণ্ডিত করেছে অর্থাৎ AD = DB

অঙ্কন – O, A এবং O, B যুক্ত করি।

প্রমাণ – OD, AB জ্যা-এর উপর লম্ব।

সুতরাং, ΔODA ও ΔODB সমকোণী।

∴ সমকোণী ΔODA ও ΔODB তে ∠ODA = ∠ODB (প্রত্যেকটি কোণ সমকোণ)

অতিভুজ OA = অতিভুজ OB [একই বৃত্তের ব্যাসার্ধ], এবং OD সাধারণ বাহু

∴ ΔODA ≅ ΔODB [R-H-S সর্বসমতার শর্তানুসারে]

∴ AD = DB [সর্বসম ত্রিভুজের অনুরূপ অংশ] [প্রমাণিত]

উপপাদ্য – 33. প্রমাণ করি যে ব্যাস নয় এরূপ কোনো জ্যা-কে যদি বৃত্তের কেন্দ্রবিন্দুগামী কোনো সরলরেখা সমদ্বিখণ্ডিত করে, তাহলে ওই সরলরেখা ওই জ্যা-এর উপর লম্ব হবে।

উপপাদ্য – 33. প্রমাণ করি যে ব্যাস নয় এরূপ কোনো জ্যা-কে যদি বৃত্তের কেন্দ্রবিন্দুগামী কোনো সরলরেখা সমদ্বিখন্ডিত করে, তাহলে ওই সরলরেখা ওই জ্যা-এর উপর লম্ব হবে।

প্রদত্ত – ধরি, O কেন্দ্রীয় বৃত্তের ব্যাস নয় এরূপ একটি জ্যা AB এবং D, AB-এর মধ্যবিন্দু অর্থাৎ AD = DB

প্রমাণ করতে হবে – OD ⊥ AB অর্থাৎ OD, AB জ্যা-এর উপর লম্ব।

অঙ্কন – O, A এবং O, B যুক্ত করি।

প্রমাণ – ΔOAD ও ΔOBD তে

OA = OB [একই বৃত্তের ব্যাসার্ধ]

AD = DB [প্রদত্ত] [D, AB-এর মধ্যবিন্দু]

এবং OD সাধারণ বাহু

∴ ΔOAD ≅ ΔODB [সর্বসমতার বাহু-বাহু-বাহু (S-S-S) শর্তানুসারে]

∴ ∠ODA = ∠ODB [সর্বসম ত্রিভুজের অনুরূপ অংশ]

যেহেতু, OD, AB জ্যা-এর উপর দণ্ডায়মান হয়ে সমান কোণ উৎপন্ন করেছে,

সুতরাং, ∠ODA = ∠ODB = 1 সমকোণ

∴ OD ⊥ AB [প্রমাণিত]

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের তৃতীয় অধ্যায়, ‘বৃত্ত সম্পর্কিত উপপাদ্য’ -এর উপপাদ্যমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।

আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।