এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের অষ্টম অধ্যায়, ‘লম্ব বৃত্তাকার চোঙ’ -এর ‘কষে দেখি – 8’ বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

1. পাশের চিত্রের ঘনবস্তুটি দেখি ও নীচের প্রশ্নের উত্তর লিখি।
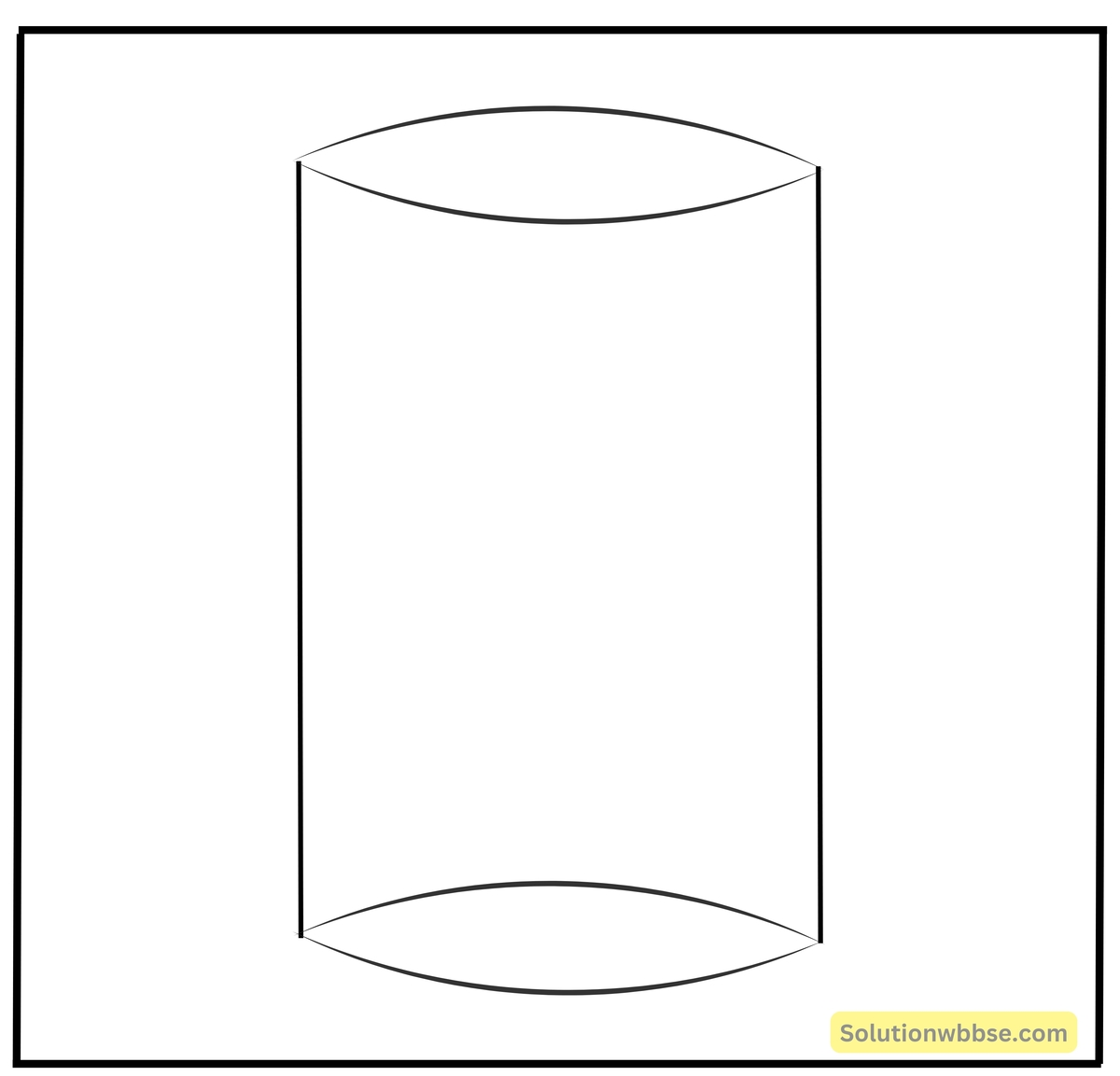
(i) ছবির ঘনবস্তুটির ___ টি তল।
উত্তর – ছবির ঘনবস্তুটির 3টি তল।
(ii) ছবির ঘনবস্তুটির ___ টি বক্রতল ও ___ টি সমতল।
উত্তর – 1টি বক্রতল এবং 2টি সমতল।
2. আমার বাড়ির 5টি ঘনবস্তুর নাম লিখি যাদের আকার লম্ব বৃত্তাকার চোঙ।
উত্তর – তেলের ড্রাম, কলের পাইপ, গ্যাস সিলিন্ডার, লম্ব বৃত্তাকার পিলার, টিউব লাইট।
3. স্টিলের পাতলা চাদর দিয়ে তৈরি ঢাকনাসমেত একটি ড্রামের ব্যাসের দৈর্ঘ্য 28 সেমি.। ড্রামটি তৈরি করতে যদি 2816 বর্গ সেমি, চাদর লাগে, তবে ড্রামটির উচ্চতা হিসাব করে লিখি।
ষ্টীলের পাতলা চাদর দিয়ে তৈরি ঢাকনাসহ একটি ড্রামের ব্যাসের দৈর্ঘ্য 28 সেমি.
∴ ড্রামটির ব্যাসার্ধ (r) = \(\frac{28}{2}\) সেমি. = 14 সেমি.
ধরি, ড্রামটির উচ্চতা \(h\) সেমি.
∴ ঢাকনাসহ ড্রামটির সমগ্রতলের ক্ষেত্রফল = \(2\pi r(h + r)\) বর্গ সেমি.
= \(2 \times \frac{22}{7} \times 14 \times (h + 14)\) বর্গ সেমি.
= \(88 \times (h + 14)\) বর্গ সেমি.
ড্রামটির সমগ্রতলের ক্ষেত্রফল এবং ড্রামটি তৈরি করতে যে পরিমাণ চাদর লাগে তা সমান
∴ \(88(h + 14) = 2816\)
বা, \(h + 14 = \frac{2816}{88}\)
বা, \(h + 14 = 32\)
বা, \(h = 32 – 14\)
বা, \(h = 18\)
∴ ড্রামটির উচ্চতা 18 সেমি.।
4. একটি ঘরের বারান্দায় 5.6 ডেসিমি. ব্যাসের এবং 2.5 মিটার লম্বা দুটি লম্ব বৃত্তাকার পিলার ঢালাই করতে কত ঘন ডেসিমি. মশলা লাগবে হিসাব করে লিখি। প্রতি বর্গ মিটার 125 টাকা হিসাবে পিলার দুটি প্লাস্টার করতে কত খরচ হবে হিসাব করি।
দুটি সমান মাপের পিলারের প্রত্যেকটির ব্যাস = 5.6 ডেসিমি.
∴ প্রত্যেকটি পিলারের ভূমির ব্যাসার্ধ (\(r\)) = \(\frac{5.6}{2}\) ডেসিমি. = 2.8 ডেসিমি.
প্রত্যেকটি পিলারের উচ্চতা (\(h\)) = 2.5 মিটার = 25 ডেসিমি.
পিলার দুটি তৈরি করতে যে পরিমাণ মশলা লাগবে তা পিলার দুটির আয়তনের সাথে সমান
পিলার দুটির আয়তন = \(2 \times \pi \times r^2 \times h\) ঘন ডেসিমি.
= \(2 \times \frac{22}{7} \times (2.8)^2 \times 25\) ঘন ডেসিমি.
= \(2 \times \frac{22}{7} \times \frac{28}{10} \times \frac{28}{10} \times 25\) ঘন ডেসিমি.
= 1232 ঘন ডেসিমি.
∴ পিলার দুটি তৈরি করতে যে মশলা লাগবে তার পরিমাণ 1232 ঘন ডেসিমি.
এখন দুটি পিলারের বক্রতলের ক্ষেত্রফল = \(2 \times 2 \times \pi \times r \times h\) বর্গ ডেসিমি.
= \(2 \times 2 \times \frac{22}{7} \times 2.8 \times 25\) বর্গ ডেসিমি.
= \(2 \times 2 \times \frac{22}{7} \times \frac{28}{10} \times 25\) বর্গ ডেসিমি.
= \(2 \times 2 \times \frac{22}{7} \times \frac{28}{10} \times 25 \times \frac{1}{100}\) বর্গ ডেসিমি.
= 8.8 বর্গ মিটার
প্রতি বর্গ মিটার প্লাস্টার করতে 125 টাকা হিসাবে দুটি পিলারে মোট খরচ হবে
= \(8.8 \times 125\) টাকা
= 1100 টাকা।
5. 2.8 ডেসিমি. দৈর্ঘ্যের অন্তর্ব্যাসবিশিষ্ট এবং 7.5 ডেসিমি. লম্বা একটি জ্বালানি গ্যাস সিলিন্ডারে 15.015 কিগ্রা, গ্যাস থাকলে, প্রতি ঘন ডেসিমি. গ্যাসের ওজন হিসাব করে লিখি।
গ্যাস সিলিন্ডার টির অন্তর্ব্যাস = 2.8 ডেসিমি
∴ অন্তর্ব্যাসার্ধ (\(r\)) = \(\frac{2.8}{2}\) ডেসিমি. = 1.4 ডেসিমি.
সিলিন্ডারের দৈর্ঘ্য (\(h\)) = 7.5 ডেসিমি.
∴ সিলিন্ডারটির আয়তন = \(\pi r^2 h\) ঘন ডেসিমি.
= \(\frac{22}{7}\times\left(1.4\right)^2\times 7.5\) ঘন ডেসিমি.
= \(\frac{22}{7}\times1.4\times1.4\times7.5\) ঘন ডেসিমি.
= \(\frac{22}{7}\times\frac{14}{10}\times\frac{14}{10}\times\frac{75}{10}\) ঘন ডেসিমি.
= 46.2 ঘন ডেসিমি.
সিলিন্ডারে গ্যাসের পরিমাণ = 15.015 কিগ্রা।
∴ 46.2 ঘন ডেসিমি. আয়তনের সিলিন্ডারে গ্যাসের পরিমাণ 15.015 কিগ্রা।
∴ 1 ঘন ডেসিমি. আয়তনের সিলিন্ডারে গ্যাসের পরিমাণ
= \(\frac{15.015}{46.2}\) কিগ্রা
= 0.325 কিগ্রা
= 325 গ্রাম।
6. সমান ব্যাস ও সমান উচ্চতাবিশিষ্ট তিনটি জারের প্রথমটির \(\frac{2}{3}\) অংশ, দ্বিতীয়টির \(\frac{5}{6}\) অংশ এবং তৃতীয়টির \(\frac{7}{9}\) অংশ লঘু সালফিউরিক অ্যাসিডে পূর্ণ ছিল। ওই তিনটি জারের অ্যাসিড যদি 2.1 ডেসিমি. দৈর্ঘ্যের ব্যাসের একটি জারে রাখা হয়, তবে জারে অ্যাসিডের উচ্চতা 4.1 ডেসিমি. হয়। প্রথম তিনটি জারের ব্যাসের দৈর্ঘ্য 1.4 ডেসিমি. হলে, তাদের উচ্চতা হিসাব করে লিখি।
প্রথম তিনটি জারের ব্যাসের দৈর্ঘ্য 1.4 ডেসিমি.
∴ প্রত্যেকটি জারের ব্যাসার্ধ (\(r\)) = \(\frac{1.4}{2}\) ডেসিমি = 0.7 ডেসিমি.
ধরি, তিনটি জারের প্রত্যেকটির উচ্চতা \(h\) ডেসিমি.
সমান তিনটি জারের মোট অ্যাসিডের আয়তন
= \(\left[\frac{2}{3}\pi r^2 h + \frac{5}{6}\pi r^2 h + \frac{7}{9}\pi r^2 h\right]\) ঘন ডেসিমি.
= \(\pi r^2 h \left(\frac{2}{3} + \frac{5}{6} + \frac{7}{9}\right)\) ঘন ডেসিমি.
= \(\frac{22}{7}\times\left(0.7\right)^2\times h\times\left(\frac{12+15+14}{18}\right)\) ঘন ডেসিমি.
= \(\frac{22}{7}\times\frac{7}{10}\times\frac{7}{10}\times h\times\frac{41}{18}\) ঘন ডেসিমি.
আবার, বড় জারের ব্যাস = 2.1 ডেসিমি.
∴ ব্যাসার্ধ (\(r\)) = \(\frac{2.1}{2}\) ডেসিমি. = \(\frac{21}{20}\) ডেসিমি.
বড় জারে অ্যাসিড এর উচ্চতা (\(h\)) = 4.1 ডেসিমি.
এখন, বড় জারে অ্যাসিডের আয়তন
= \(\pi r^2 h\) ঘন ডেসিমি.
= \(\frac{22}{7}\times\left(\frac{21}{20}\right)^2\times 4.1\) ঘন ডেসিমি.
= \(\frac{22}{7}\times\frac{21}{20}\times\frac{21}{20}\times\frac{41}{10}\) ঘন ডেসিমি.
যেহেতু, সমান তিনটি জারের সমগ্র অ্যাসিড বড় জারে ঢালা হয়েছে
∴ তিনটি জারের মোট অ্যাসিডের আয়তন = বড় জারের অ্যাসিডের আয়তন
বা, \(\frac{22}{7}\times\frac{7}{10}\times\frac{7}{10}\times h\times\frac{41}{18} = \frac{22}{7}\times\frac{21}{20}\times\frac{21}{20}\times\frac{41}{10}\) ঘন ডেসিমি.
বা, \(\frac{7}{10}\times\frac{7}{10}\times h\times\frac{41}{18} = \frac{21}{20}\times\frac{21}{20}\times\frac{41}{10}\) ঘন ডেসিমি.
বা, \(h = \frac{21 \times 21 \times 41 \times 10 \times 10 \times 18}{7 \times 7 \times 41 \times 20 \times 20 \times 10}\) ঘন ডেসিমি.
= 4.05 ঘন ডেসিমি.
∴ তিনটি জারের প্রত্যেকটির উচ্চতা 4.05 ডেসিমি.।
7. একমুখ খোলা একটি লম্ব বৃত্তাকার পাত্রের সমগ্রতলের ক্ষেত্রফল 2002 বর্গ সেমি.। পাত্রটির ভূমির ব্যাসের দৈর্ঘ্য 14 সেমি. হলে, পাত্রটিতে কত লিটার জল ধরবে হিসাব করে লিখি।
একমুখ খোলা একটি লম্ব বৃত্তাকার পাত্রের ভূমির ব্যাসের দৈর্ঘ্য 14 সেমি.
ব্যাসার্ধ (\(r\)) = \(\frac{14}{2}\) সেমি. = 7 সেমি.
ধরি, লম্ব বৃত্তাকার পাত্রের উচ্চতা = \(h\) সেমি.
একমুখ খোলা পাত্রটির সমগ্রতলের ক্ষেত্রফল = \(2\pi rh + \pi r^2\) বর্গ সেমি.
= \(2\times\frac{22}{7}\times 7\times h + \frac{22}{7}\times\left(7\right)^2\) বর্গ সেমি.
= 44h + 154 বর্গ সেমি.
শর্তানুসারে,
44h + 154 = 2002
বা, 44h = 2002 – 154
বা, 44h = 1848
বা, h = 42
∴ পাত্রটির উচ্চতা 42 সেমি.।
∴ পাত্রটির আয়তন = \(\pi r^2 h\) ঘন সেমি.
= \(\frac{22}{7}\times 7^2\times 42\) ঘন সেমি.
= \(\frac{22}{7}\times 49\times 42\) ঘন সেমি.
= 6468 ঘন সেমি,
= \(\frac{6468}{1000}\) ঘন ডেসিমি. [যেহেতু, 1 ঘন ডেসিমি. = 1000 ঘন সেমি.]
= 6.468 লিটার [যেহেতু, 1 ঘন ডেসিমি. = 1 লিটার]
∴ পাত্রটিতে জল ধরে 6.468 লিটার।
8. যদি 14 সেমি. ব্যাসের পাইপযুক্ত একটি পাম্পসেট মিনিটে 2500 মিটার জল সেচ করতে পারে, তাহলে ওই পাম্পটি 1 ঘণ্টায় কত কিলো লিটার জলসেচ করবে, হিসাব করে লিখি। [1 লিটার = 1 ঘন ডেসিমি.]
পাম্পটির ব্যাস 14 সেমি.
∴ পাম্পটির ব্যাসার্ধ (\(r\)) = \(\frac{14}{2}\) সেমি.
= 7 সেমি.
= \(\frac{7}{100}\) মিটার
পাম্পটি মিনিটে 2500 মিটার জলসেচ করতে পারে
\(h = 2500\) মিটার।
পাম্পটি 1 মিনিটে যে পরিমান জলসেচ করে তার আয়তন = \(\pi r^2 h\) ঘন মিটার
= \(\frac{22}{7}\times\left(3.5\right)^2\times h\) ঘন মিটার
= \(\frac{22}{7}\times\frac{35}{10}\times\frac{35}{10}\times h\) ঘন মিটার
= 38.5 ঘন মিটার
= 38.5 কিলোলিটার [যেহেতু, 1 ঘন মিটার = 1 কিলোলিটার।]
∴ 1 মিনিটে পাম্পটি জলসেচ করে 38.5 কিলো লিটার
∴ 1 ঘণ্টা = 60 মিনিটে পাম্পটি জলসেচ করে
= 60 × 38.5 কিলো লিটার
= 2310 কিলো লিটার
∴ পাম্পটি 1 ঘণ্টায় জলসেচ করে 2310 কিলো লিটার।
9. 7 সেমি. ব্যাসের একটি লম্বা গ্যাসজারে কিছু জল আছে। ওই জলে যদি 5.6 সেমি. দৈর্ঘ্যের ব্যাসের 5 সেমি. লম্বা একটি নিরেট লোহার লম্ব বৃত্তাকার চোঙাকৃতি টুকরো সম্পূর্ণ ডোবানো হয়, তবে জলতল কতটুকু উপরে উঠবে হিসাব করে লিখি।
গ্যাসজারের ব্যাস = 7 সেমি.
∴ গ্যাস জারের ব্যাসার্ধ (\(r\)) = \(\frac{7}{2}\) সেমি. = 3.5 সেমি.
ধরি, নিরেট লম্ব বৃত্তাকার চোঙটি ডোবানর পর জলতল \(h\) সেমি. উঠবে।
∴ অপসারিত জলের আয়তন = \(\pi r^2 h\) ঘন সেমি.
= \(\frac{22}{7}\times\left(3.5\right)^2\times h\) ঘন সেমি.
= \(\frac{22}{7}\times\frac{35}{10}\times\frac{35}{10}\times h\) ঘন সেমি.
নিরেট লম্ববৃত্তাকার চোঙের ব্যাস = 5.6 সেমি.
∴ ব্যাসার্ধ (\(r_1\)) = \(\frac{5.6}{2}\) সেমি. = 2.8 সেমি,
নিরেট লম্ববৃত্তাকার চোঙের উচ্চতা (\(h_1\)) = 5 সেমি.
নিরেট লম্ববৃত্তাকার চোঙের আয়তন = \(\pi r_1^2 h_1\) ঘন সেমি.
= \(\frac{22}{7}\times\left(2.8\right)^2\times5\) ঘন সেমি.
= \(\frac{22}{7}\times\frac{28}{10}\times\frac{28}{10}\times5\) ঘন সেমি.
শর্তানুসারে,
\(\frac{22}{7}\times\frac{35}{10}\times\frac{35}{10}\times h = \frac{22}{7}\times\frac{28}{10}\times\frac{28}{10}\times5\)বা, \(h = \frac{28\times28\times5}{35\times35}\)
বা, \(h = \frac{80}{25}\)
বা, \(h = 3.2\)
∴ জলতল 3.2 সেমি. উঠে আসবে।
10. একটি লম্ব বৃত্তাকার স্তম্ভের বক্রতলের ক্ষেত্রফল 264 বর্গ মিটার এবং আয়তন 924 ঘন মিটার হলে, এই স্তম্ভের ব্যাসের দৈর্ঘ্য ও উচ্চতা হিসাব করে লিখি।
ধরি, লম্ববৃত্তাকার স্তম্ভের ব্যাসার্ধের দৈর্ঘ্য \(r\) মিটার এবং উচ্চতা \(h\) মিটার।
∴ \(\pi r^2 h = 924 \quad \text{—(i)}\)
এবং, \(2\pi rh = 264 \quad \text{—(ii)}\)
(i) নং সমীকরণ কে (ii) নং সমীকরণ দ্বারা ভাগ করে পাই,
\(\frac{\pi r^2 h}{2\pi r h} = \frac{924}{264}\)বা, \(\frac{r}{2} = 3.5\)
বা, \(r = 7\)
∴ ব্যাসার্ধ 7 মিটার।
∴ ব্যাস = 2 × 7 = 14 মিটার
r এর মান (ii) নং সমীকরণে বসিয়ে পাই,
\(2\pi(7)h = 264\)বা, \(2 \times \frac{22}{7} \times 7 \times h = 264\)
বা, \(h = \frac{264}{2 \times 22}\)
বা, \(h = 6\)
∴ উচ্চতা = 6 মিটার
∴ স্তম্ভের ব্যাস 14 মিটার এবং উচ্চতা 6 মিটার।
11. 9 মিটার উচ্চতা বিশিষ্ট একটি লম্ব বৃত্তাকার চোঙাকৃতি ট্যাঙ্ক জলপূর্ণ আছে। 6 সেমি দীর্ঘের ব্যাসের একটি পাইপ দিয়ে মিনিটে 225 মিটার বেগে জল বের হয়, তাহলে 36 মিনিটে ট্যাঙ্কটির সব জল বেরিয়ে যায়। ট্যাঙ্কটির ব্যাসের দৈর্ঘ্য হিসাব করে লিখি।
ট্যাঙ্কটির উচ্চতা (\(h\)) = 9 মিটার।
ধরি, ট্যাঙ্কটির ব্যাসার্ধ (\(r\)) মিটার।
∴ ট্যাঙ্ক এর আয়তন = \(\pi r^2 h\) ঘন মিটার
= \(\pi r^2 (9)\) ঘন মিটার
= \(9\pi r^2\) ঘন মিটার
এখন, পাইপের ব্যাস 6 সেমি।
∴ পাইপের ব্যাসার্ধ = \(\frac{6}{2}\) সেমি. = 3 সেমি. = \(\frac{3}{100}\) মিটার = 0.03 মিটার
1 মিনিটে ওই পাইপ দিয়ে যে পরিমান জল নির্গত হয় তার আয়তন
= \(\pi \times (0.03)^2 \times 225\) ঘন মিটার
∴ 36 মিনিটে নির্গত জলের পরিমাণ
= \(36 \times \pi \times \frac{3}{100} \times \frac{3}{100} \times 225\) ঘন মিটার
36 মিনিটে ট্যাঙ্কের সমস্ত জল বেরিয়ে যায় অর্থাৎ 36 মিনিটে নির্গত জলের পরিমাণ এবং ট্যাঙ্কের মোট আয়তন সমান
∴ \(9 \times \pi \times r^2 = 36 \times \pi \times \frac{3}{100} \times \frac{3}{100} \times 225\)
বা, \(9r^2 = 36 \times \frac{3}{100} \times \frac{3}{100} \times 225\)
বা, \(r^2 = \frac{36}{9} \times \frac{3}{100} \times \frac{3}{100} \times 225\)
বা, \(r^2 = 4 \times \frac{3}{100} \times \frac{3}{100} \times 225\)
বা, \(r^2 = 4 \times \frac{3}{100} \times \frac{3}{100} \times 15 \times 15\)
বা, \(r^2 = 2 \times 2 \times \frac{3}{100} \times \frac{3}{100} \times 15 \times 15\)
বা, \(r^2 = \left(\frac{2 \times 3 \times 15}{100}\right)^2\)
বা, \(r^2 = \left(\frac{90}{100}\right)^2\)
বা, \(r = 0.9\)
বা, 2r = 1.8
∴ ট্যাঙ্কটির ব্যাস = 1.8 মিটার = 180 সেমি।
12. সমান ঘনত্বের একটি লম্ব বৃত্তাকার কাঠের গুড়ির বক্রতলের ক্ষেত্রফল 440 বর্গ ডেসিমি.। এক ঘন ডেসিমি. কাঠের গুড়ির ওজন 1.5 কিগ্রা. এবং গুঁড়িটির ওজন 9.24 কুইন্টাল হলে, গুঁড়িটির ব্যাসের দৈর্ঘ্য ও উচ্চতা হিসাব করে লিখি।
এক ঘন ডেসিমি. কাঠের গুড়ির ওজন 1.5 কিগ্রা. এবং গুঁড়িটির ওজন 9.24 কুইন্টাল।
9.24 কুইন্টাল = 9.24 × 100 কিগ্রা. = 924 কিগ্রা. [যেহেতু, 1 কুইন্টাল= 100 কিগ্রা.]
∴ কাঠের গুঁড়ির আয়তন = \(\frac{924}{1.5}\) ঘন ডেসিমি.
= 616 ঘন ডেসিমি.
ধরি, গুঁড়িটির ব্যাসার্ধ \(r\) সেমি. এবং গুঁড়িটির উচ্চতা \(h\) সেমি
∴ \(\pi r^2 h = 616 \quad \text{—(i)}\)
এবং, \(2\pi r h = 440 \quad \text{—(ii)}\)
(i) নং সমীকরণকে (ii) নং সমীকরণ দ্বারা ভাগ করে পাই,
বা, \(\frac{\pi r^2 h}{2\pi r h} = \frac{616}{440}\)
বা, \(\frac{r}{2} = 1.4\)
বা, \(r = 2.8\)
বা, 2r = 5.6
∴ কাঠের গুঁড়িটির ব্যাসের দৈর্ঘ্য 5.6 ডেসিমি.
এখন, \(r\) এর প্রাপ্ত মান (ii) নং সমীকরণে বসিয়ে পাই,
\(2\pi(2.8)h = 440\)বা, \(2 \times \frac{22}{7} \times 2.8 \times h = 440\)
বা, \(h = \frac{440}{2 \times 22 \times 0.4}\)
বা, \(h = \frac{440 \times 10}{2 \times 22 \times 4}\)
বা, \(h = 25\)
∴ কাঠের গুঁড়িটির উচ্চতা 25 ডেসিমি.
13. দুই মুখ খোলা একটি লম্ব বৃত্তাকার লোহার পাইপের মুখের বহ্যিাসের দৈর্ঘ্য 30 সেমি. অন্তর্ব্যাসের দৈর্ঘ্য 26 সেমি. এবং পাইপটির দৈর্ঘ্য 14.7 মিটার। প্রতি বর্গডেসিমি. 2.25 টাকা হিসাবে ওই পাইপটির সমগ্রতলে আলকাতরার প্রলেপ দিতে কত খরচ হবে, হিসাব করে লিখি।
পাইপটির বহ্যিাস = 30 সেমি,
∴ পাইপটির বহ্যিাসার্ধ (\(R\)) = \(\frac{30}{2}\) সেমি = 15 সেমি.
পাইপটির অন্তর্ব্যাস = 26 সেমি.
পাইপটির অন্তর্ব্যাসার্ধ (\(r\)) = \(\frac{26}{2}\) সেমি. = 13 সেমি.
পাইপটির দৈর্ঘ্য (\(h\)) = 14.7 মিটার = 1470 সেমি.
পাইপটির বাইরের তলের ক্ষেত্রফল = \(2\pi R h\) বর্গ সেমি
= \(2 \times \frac{22}{7} \times 15 \times 1470\) বর্গ সেমি.
= 138600 বর্গ সেমি.
= 1386 বর্গ ডেসিমি,
পাইপটির ভিতরের তলের ক্ষেত্রফল = \(2\pi r h\) বর্গ সেমি
= \(2 \times \frac{22}{7} \times 13 \times 1470\) বর্গ সেমি.
= 120120 বর্গ সেমি.
= 1201.20 বর্গ ডেসিমি,
পাইপটির দুইপাশের দুটি বলয় অংশের ক্ষেত্রফল
= \(2 \times \pi \times (R^2 – r^2)\) বর্গ সেমি.
= \(2 \times \frac{22}{7} \times \left( (15)^2 – (13)^2 \right)\) বর্গ সেমি.
= \(2 \times \frac{22}{7} \times 56\) বর্গ সেমি.
= 352 বর্গ সেমি.
= 3.52 বর্গ ডেসিমি.
∴ সমগ্রতলের ক্ষেত্রফল = (1386 + 1201.20 + 3.52) বর্গ ডেসিমি.
= 2590.72 বর্গ ডেসিমি.
প্রতি বর্গ ডেসিমি. 2.25 টাকা হিসাবে আলকাতরার প্রলেপ দিতে মোট খরচ হবে = 2590.72 × 2.25 টাকা
= 5829.12 টাকা
∴ সমগ্রতল আলকাতরার প্রলেপ দিতে মোট খরচ হবে 5829.12 টাকা।
14. দুই মুখ খোলা লোহার লম্ব বৃত্তাকার ফাঁপা চোঙের উচ্চতা 2.8 মিটার। চোঙটির অন্তর্ব্যাসের দৈর্ঘ্য 4.6 ডেসিমি. এবং চোঙটি 84.48 ঘন ডেসিমি. লোহা দিয়ে তৈরি হলে, চোঙটির বহির্ব্যাসের দৈর্ঘ্য নির্ণয় করি।
দুই মুখ খোলা লোহার লম্ব বৃত্তাকার ফাঁপা চোঙের উচ্চতা 2.8 মিটার
∴ \(h = 2.8\) মিটার = 28 ডেসিমি.।
চোঙটির অন্তর্ব্যাসের দৈর্ঘ্য 4.6 ডেসিমি.
অন্তর্ব্যাসার্ধ \(r_1 = \frac{4.6}{2}\) ডেসিমি. = 2.3 ডেসিমি.
ধরি, চোঙটির বহির্ব্যাসার্ধ \(r_2\) ডেসিমি.
∴ চোঙটির আয়তন = \(\pi\left(r_2^2 – r_1^2\right)h\) ঘন ডেসিমি.
= \(\frac{22}{7} \times \left( r_2^2 – 2.3^2 \right) \times 28\) ঘন ডেসিমি.
= 88 × \((r_2^2 – 2.3^2)\) ঘন ডেসিমি.
আবার ফাঁপা চোঙটি তৈরি করতে 84.48 ঘন ডেসিমি. লোহা লেগেছে।
∴ 88 × \((r_2^2 – 2.3^2) = 84.48\)
বা, \((r_2^2 – 2.3^2) = 0.96\)
বা, \(r_2^2 – 5.29 = 0.96\)
বা, \(r_2^2 = 6.26\)
বা, \(r_2 = 2.5\)
বা, \(2r_2 = 5\)
∴ ফাঁপা চোঙটির বহির্ব্যাস = 5 ডেসিমি.
15. একটি লম্ব বৃত্তাকার চোঙের উচ্চতা উহার ব্যাসার্ধের দ্বিগুন। যদি উচ্চতা 6 গুন হত তবে চোঙটির আয়তন 539 ঘন ডেসিমি বেশি হত। চোঙটির উচ্চতা হিসাব করে লিখি।
ধরি, লম্ব বৃত্তাকার চোঙের ব্যাসার্ধ \(r\) ডেসিমি.
∴ চোঙটির উচ্চতা (\(h\)) = 2r ডেসিমি. [যেহেতু, উচ্চতা ব্যাসার্ধের দ্বিগুন]
চোঙটির আয়তন = \(\pi r^2 h\) ঘন ডেসিমি.
= \(\pi r^2 (2r)\) ঘন ডেসিমি.
= \(2\pi r^3\) ঘন ডেসিমি.
এখন, চোঙের উচ্চতা 6 গুন হলে,
\(h = 6 \times r = 6r\) ডেসিমি.
∴ চোঙের আয়তন = \(\pi r^2 h\) ঘন ডেসিমি.
= \(\pi r^2 (6r)\) ঘন ডেসিমি.
= \(6\pi r^3\) ঘন ডেসিমি.
শর্তানুসারে,
\(6\pi r^3 = 2\pi r^3 + 539\)বা, \(4\pi r^3 = 539\)
বা, \(r^3 = \frac{539}{4\pi}\)
বা, \(r^3 = \frac{539 \times 7}{88}\)
বা, \(r^3 = 42.875\)
বা, \(r^3 = 3.5 \times 3.5 \times 3.5\)
বা, \(r^3 = (3.5)^3\)
বা, \(r = 3.5\)
∴ ব্যাসার্ধ = 3.5 সেমি.
∴ উচ্চতা = 2r ডেসিমি.
= 2 × 3.5 ডেসিমি.
= 7 ডেসিমি.
∴ চোঙটির উচ্চতা 7 ডেসিমি.।
16. ফায়ার ব্রিগেড এর কোনো একটি দল একটি জল ভর্তি লম্ব বৃত্তাকার ট্যাংকারের জল 2 সেমি. দীর্ঘ ব্যাসের তিনটি হোস পাইপ দিয়ে মিনিটে 420 মিটার বেগে ঢেলে 40 মিনিটে আগুন নেভাল। যদি ট্যাংকারটির ব্যাসের দৈর্ঘ্য 2.8 মিটার হয় এবং দৈর্ঘ্য 6 মিটার হয় তবে (i) আগুন নেভাতে কত জল খরচ হয়েছে? (ii) ট্যাঙ্কে আর কত জল রয়েছে নির্ণয় করি।
প্রত্যেকটি পাইপের ব্যাস 2 সেমি.
∴ প্রত্যেকটি পাইপের ব্যাসার্ধ (\(r\)) = \(\frac{2}{2}\) সেমি.
= 1 সেমি.
= \(\frac{1}{100}\) মিটার
= 0.01 মিটার।
প্রতি মিনিটে প্রতিটি পাইপের মধ্যে দিয়ে যে পরিমান জল নির্গত হয় তার আয়তন
= \(\pi r^2 h\) ঘন মিটার
= \(\frac{22}{7} \times (0.01)^2 \times 420\) ঘন মিটার
= 22 × 60 × 0.01 × 0.01 ঘন মিটার
= 0.132 ঘন মিটার
∴ 1 মিনিটে প্রতিটি পাইপের মধ্যে দিয়ে নির্গত জলের পরিমান 0.132 ঘন মিটার
∴ 40 মিনিটে 3টি পাইপের মধ্যে দিয়ে নির্গত জলের পরিমান = 40 × 0.132 × 3 ঘন মিটার
= 15.84 ঘন মিটার
= 15.84 × 1000 ঘন ডেসিমি,
= 15840 লিটার [যেহেতু 1 ঘনডেসিমি = 1 লিটার]
∴ আগুন নেভাতে যে জল খরচ হয়েছে তার আয়তন 15840 লিটার।
ট্যাংকারটির ব্যাসের দৈর্ঘ্য 2.8 মিটার
ব্যাসার্ধ (\(r\)) = \(\frac{2.8}{2}\) মিটার = 1.4 মিটার
দৈর্ঘ্য (\(h\)) = 6 মিটার
লম্ব বৃত্তাকার ট্যাংকারের আয়তন
= \(\pi r^2 h\) ঘন মিটার
= \(\pi \times (1.4)^2 \times 6\) ঘন মিটার
= \(\frac{22}{7} \times 1.4 \times 1.4 \times 6\) ঘন মিটার
= 36.96 ঘন মিটার
= 36960 ঘন ডেসিমি.
= 36960 লিটার [যেহেতু 1 ঘন ডেসিমি = 1 লিটার]
∴ ট্যাঙ্কে অবশিষ্ট জলের পরিমান
= (36960 – 15840) লিটার
= 21120 লিটার
∴ (i) আগুন নেভাতে যে জল খরচ হয়েছে তার আয়তন 15840 লিটার।
(ii) ট্যাঙ্কে অবশিষ্ট জলের পরিমান 21120 লিটার।
17. 17.5 সেমি. ব্যাসের 4টি লম্ব বৃত্তাকার চালাই পিলারের চারপাশে 3.5 সেমি. পুরু বালি-সিমেন্টের প্লাস্টার করতে হবে।
(i) প্রতিটি পিলার যদি 3 মিটার লম্বা হয়, তবে কত ঘন ডেসিমি মশলা লাগবে হিসাব করে লিখি।
(ii) প্লাস্টারের মশলা তৈরি করতে যদি 4 : 1 অনুপাতে বালি-সিমেন্ট মেশাতে হয়, তবে কত ঘন ডেসিমি সিমেন্টের প্রয়োজন, হিসাব করে লিখি।
প্রতিটি লম্ব বৃত্তাকার পিলারের ব্যাস 17.5 সেমি।
∴ অন্তর্ব্যাসার্ধ \(\left(r_1\right)=\frac{17.5}2\) সেমি. = 8.75 সেমি।
প্লাস্টারের পুরুত্ব = 3.5 সেমি।
∴ লম্ব বৃত্তাকার পিলারের বহিব্যাসার্ধ \(\left(r_2\right) = 8.75 + 3.5 = 12.25\) সেমি।
(i) প্রতিটি পিলারের উচ্চতা (h) = 3 মিটার = 300 সেমি।
∴ প্রতিটি পিলারে মশলার আয়তন
= π{\(r_1^2 – (r_2)^2\)}h ঘন সেমি।
= \(\frac{22}{7} \times \left( \left( 12.25 \right)^2 – \left( 8.75 \right)^2 \right) \times 300\)
= \(\frac{22}7 \times \left(12.25 + 8.75\right) \times \left(12.25 – 8.75\right) \times 300\)
= \(\frac{22}7 \times 21 \times 0.5 \times 300\)
= 22 × 21 × 0.5 × 300 ঘন সেমি।
= 69300 ঘন সেমি।
= 69.3 ঘন ডেসিমি,
∴ 4টি পিলারে প্রয়োজনীয় মশলার আয়তন = 4 × 69.3 ঘন ডেসিমি = 277.2 ঘন ডেসিমি।
(ii) প্লাস্টারের মশলা তৈরি করতে যদি 4 : 1 অনুপাতে বালি-সিমেন্ট মেশাতে হয়
∴ সিমেন্ট প্রয়োজন = \(\frac{1}{4+1} \times 277.2\) ঘন ডেসিমি।
= \(\frac{1}{5} \times 277.2\) ঘন ডেসিমি।
∴ (i) 4টি পিলারে প্রয়োজনীয় মশলার আয়তন 277.2 ঘন ডেসিমি।
(ii) 4টি পিলার প্লাস্টার করতে প্রয়োজনীয় সিমেন্টের পরিমান 55.44 ঘন ডেসিমি।
18. একটি লম্ব বৃত্তাকার ফাঁপা চোঙের বহির্ব্যাসের দৈর্ঘ্য 16 সেমি. এবং অন্তর্ব্যাসের দৈর্ঘ্য 12 সেমি.। চোঙটির উচ্চতা 36 সেমি.। চোঙটিকে গলিয়ে 2 সেমি. ব্যাস বিশিষ্ট এবং 6 সেমি. দীর্ঘের কতগুলি নিরেট চোঙ তৈরি করা যাবে হিসাব করে লিখি।
একটি লম্ব বৃত্তাকার ফাঁপা চোঙের বহির্ব্যাসের দৈর্ঘ্য 16 সেমি।
∴ বহির্ব্যাসার্ধ \(\left(r_2\right) = \frac{16}{2}\) সেমি. = 8 সেমি।
এবং অন্তর্ব্যাসের দৈর্ঘ্য 12 সেমি।
∴ অন্তর্ব্যাসার্ধ \(\left(r_1\right) = \frac{12}{2}\) সেমি. = 6 সেমি।
চোঙটির উচ্চতা (h1) = 36 সেমি।
নিরেট চোঙের ব্যাস = 2 সেমি।
∴ ব্যাসার্ধ (r) = 1 সেমি
নিরেট চোঙের দৈর্ঘ্য (h2) = 6 সেমি।
ধরি, লম্ব বৃত্তাকার ফাঁপা চোঙটিকে গলিয়ে xটি নিরেট চোঙ তৈরি করা যাবে।
∴ ফাঁপা চোঙের আয়তন = xটি নিরেট চোঙের আয়তন
∴ \(\pi \left( \left( r_2 \right)^2 – \left( r_1 \right)^2 \right) h_1 = x \times \pi r^2 h_2\)
বা, \((8^2 – 6^2) \times 36 = x \times (1)^2 \times 6\)
বা, (64 – 36) × 6 = x
বা, x = 168
∴ ফাঁপা চোঙটিকে গলিয়ে 168টি নিরেট চোঙ তৈরি করা যাবে।
19. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) –
(i) দুটি লম্ব বৃত্তাকার নিরেট চোঙের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত 2 : 3 এবং উচ্চতার অনুপাত 5 : 3 হলে, তাদের বক্রতলের ক্ষেত্রফলের অনুপাত
(a) 2 : 5
(b) 8 : 7
(c) 10 : 9
(d) 16 : 9
উত্তর – (c) 10 : 9
সমাধান,
ধরা যাক, নিরেট লম্ব বৃত্তাকার চোঙ দুটির ব্যাসার্ধের দৈর্ঘ্য যথাক্রমে, \(r_1\) একক এবং \(r_2\) একক এবং উচ্চতা যথাক্রমে \(h_1\) একক এবং \(h_2\) একক।
∴ \(r_1 : r_2 = 2 : 3\)
এবং \(h_1 : h_2 = 5 : 3\)
∴ তাদের বক্রতলের ক্ষেত্রফলের অনুপাত
= \(2 \pi r_1 h_1 : 2 \pi r_2 h_2\)
= \(\frac{2 \pi r_1 h_1}{2 \pi r_2 h_2}\)
= \(\frac{r_1}{r_2} \times \frac{h_1}{h_2}\)
= \(\frac{2}{3} \times \frac{5}{3}\)
= \(10 : 9\)
(ii) দুটি লম্ব বৃত্তাকার নিরেট চোঙের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত 2 : 3 এবং উচ্চতার অনুপাত 5 : 3 হলে, তাদের আয়তনের অনুপাত
(a) 27 : 20
(b) 20 : 27
(c) 4 : 9
(d) 9 : 4
উত্তর – (b) 20 : 27
সমাধান,
ধরি, দুটি লম্ব বৃত্তাকার নিরেট চোঙের ব্যাসার্ধ যথাক্রমে r1 একক এবং r2 একক।
আরও ধরাযাক, দুটি লম্ব বৃত্তাকার নিরেট চোঙের উচ্চতা যথাক্রমে h1 একক এবং h2 একক।
∴ r1 : r2 = 2 : 3
এবং h1 : h2 = 5 : 3
চোঙদুটির আয়তনের অনুপাত
∴ π(r1)2h1 : π(r2)2h2
= \(\frac{2\mathrm\pi\left({\mathrm r}_1\right)^2{\mathrm h}_1}{2\mathrm\pi\left({\mathrm r}_2\right)^2{\mathrm h}_2}\)
= \(\left(\frac23\right)^2\times\frac53\)
= \(\left(\frac{{\mathrm r}_1}{{\mathrm r}_2}\right)^2\times\frac{{\mathrm h}_1}{{\mathrm h}_2}\)
= \(\frac49\times\frac53\)
= \(\frac{20}{27}\)
= 20 : 27
(iii) দুটি লম্ব বৃত্তাকার নিরেট চোঙের আয়তন সমান এবং তাদের উচ্চতার অনুপাত 1 : 2 হলে, তানে ব্যাসার্ধের দৈর্ঘ্যের অনুপাত
(a) \(1:\sqrt2\)
(b) \(\sqrt2:1\)
(c) 1 : 2
(d) 2 : 1
উত্তর – (b) \(\sqrt2:1\)
সমাধান,
ধরাযাক, লম্ব বৃত্তাকার চোঙ দুটির ব্যাসার্ধ যথাক্রমে r1 একক এবং r2 একক এবং উচ্চতা যথাক্রমে h1 একক এবং h2 একক।
h1 : h2 = 1 : 2
বা, h2 : h1 = 2 : 1
শর্তানুসারে,
π(г1)2h1 = π(r2)2h2
বা, \(\left(\frac{r_1}{r_2}\right)^2=\frac{h_2}{h_1}\)
বা, \(\left(\frac{r_1}{r_2}\right)^2=\frac21\)
বা, \(\left(\frac{r_1}{r_2}\right)=\sqrt{\frac21}\)
বা, \(r_1:r_2=\sqrt2:1\)
∴ ব্যাসার্ধের অনুপাত = \(\sqrt2:1\)
(iv) একটি লম্ব বৃত্তাকার চোঙের ব্যাসার্ধের দৈর্ঘ্য অর্ধেক এবং উচ্চতা দ্বিগুণ হলে, চোঙটির আয়তন হবে পূর্বের চোঙের আয়তনের
(a) সমান
(b) দ্বিগুণ
(c) অর্ধেক
(d) 4 গুণ
উত্তর – (c) অর্ধেক
সমাধান,
ধরি, লম্ব বৃত্তাকার চোঙের ব্যাসার্ধ r একক এবং উচ্চতা h একক
∴ আয়তন = πr2h ঘন একক
এখন, ব্যাসার্ধ পূর্বের অর্ধেক হলে, পরিবর্তিত ব্যাসার্ধ হবে \(\frac r2\) একক।
উচ্চতা দ্বিগুন হলে, পরিবর্তিত উচ্চতা হবে 2h একক।
∴ পরিবর্তিত আয়তন
= \(\mathrm\pi\times\left(\frac{\mathrm r}2\right)^2\times2\mathrm h\) ঘন একক
= \(\mathrm\pi\times\frac{\mathrm r^2}4\times2\mathrm h\) ঘন একক
= \(\frac12\times\mathrm{πr}^2\mathrm h\) ঘন একক
= \(\frac12\) × পূর্বের চোঙের আয়তন
অর্থাৎ, পরিবর্তিত চোঙের আয়তন পূর্বের চোঙের আয়তনের অর্ধেক।
(v) একটি লম্ব বৃত্তাকার চোঙের ব্যাসার্ধের দৈর্ঘ্য দ্বিগুণ এবং উচ্চতা অর্ধেক করা হলে, বক্রতলের ক্ষেত্রফল পূর্বের চোঙের বক্রতলের ক্ষেত্রফলের
(a) সমান
(b) দ্বিগুণ
(c) অর্ধেক
(d) 4 গুণ
উত্তর – (a) সমান
সমাধান,
ধরি, লম্ব বৃত্তাকার চোঙের ব্যাসার্ধের দৈর্ঘ্য r একক এবং উচ্চতার দৈর্ঘ্য h একক।
∴ বক্রতলের ক্ষেত্রফল = 2πrh বর্গ একক
ব্যাসার্ধের দৈর্ঘ্য দ্বিগুন এবং উচ্চতা অর্ধেক করা হলে পরিবর্তিত ব্যাসার্ধ ও উচ্চতা যথাক্রমে 2r একক ও \(\frac{\mathrm h}2\) একক।
∴ পরিবর্তিত লম্ব বৃত্তাকার চোঙের বক্রতলের ক্ষেত্রফল = \(2\mathrm\pi\times\left(2\mathrm r\right)\times\frac{\mathrm h}2\) বর্গ একক = 2πrh বর্গ একক
সুতরাং পূর্বের চোঙ ও পরিবর্তিত চোঙের বক্রতলের ক্ষেত্রফল সমান হবে।
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি –
(i) একটি লম্ব চোঙাকৃতি ড্রামের ব্যাসার্ধের দৈর্ঘ্য r সেমি. এবং উচ্চতা h সেমি.। ড্রামের অর্ধেক জলপূর্ণ থাকলে, জলের আয়তন হবে πr2h ঘন সেমি.।
উত্তর – মিথ্যা।
(ii) একটি লম্ব বৃত্তাকার চোঙের ব্যাসার্ধের দৈর্ঘ্য 2 একক হলে, চোঙটির যে-কোনো উচ্চতার জন্য চোঙটির আয়তন এবং বক্রতলের ক্ষেত্রফলের সাংখ্যমান সমান হবে।
উত্তর – সত্য।
সমাধান,
ধরি, যেকোনো উচ্চতা h একক
তাহলে আয়তন হবে
= πr2h ঘন একক
= π(2)2h ঘন একক
= 4πh ঘন একক
এবং বক্রতলের ক্ষেত্রফল
= 2πrh বর্গ একক
= 2π(2)h বর্গ একক
= 4πh বর্গ একক
∴ যেকোনো উচ্চতার জন্য চোঙটির আয়তন ও বক্রতলের ক্ষেত্রফলের সাংখ্যমান সমান।
(C) শূন্যস্থান পূরণ করি –
(i) একটি আয়তক্ষেত্রাকার কাগজের দৈর্ঘ্য l একক এবং প্রস্থ b একক। আয়তক্ষেত্রাকার কাগজটিকে মুড়ে একটি লম্ব বৃত্তাকার চোঙ তৈরি করা হলো যার পরিধি কাগজটির দৈর্ঘ্যের সমান। চোঙটির বক্রতলের ক্ষেত্রফল ___ বর্গ একক।
উত্তর – lb
(ii) একটি লম্ব বৃত্তাকার চোঙের ব্যাসের দৈর্ঘ্য 3 সেমি. এবং উচ্চতা 4 সেমি. হলে, চোঙটির ভিতর সর্বাপেক্ষা লম্বা যে দণ্ড রাখা যাবে তার দৈর্ঘ্য ___ সেমি.।
উত্তর – 5 সেমি.
সমাধান,
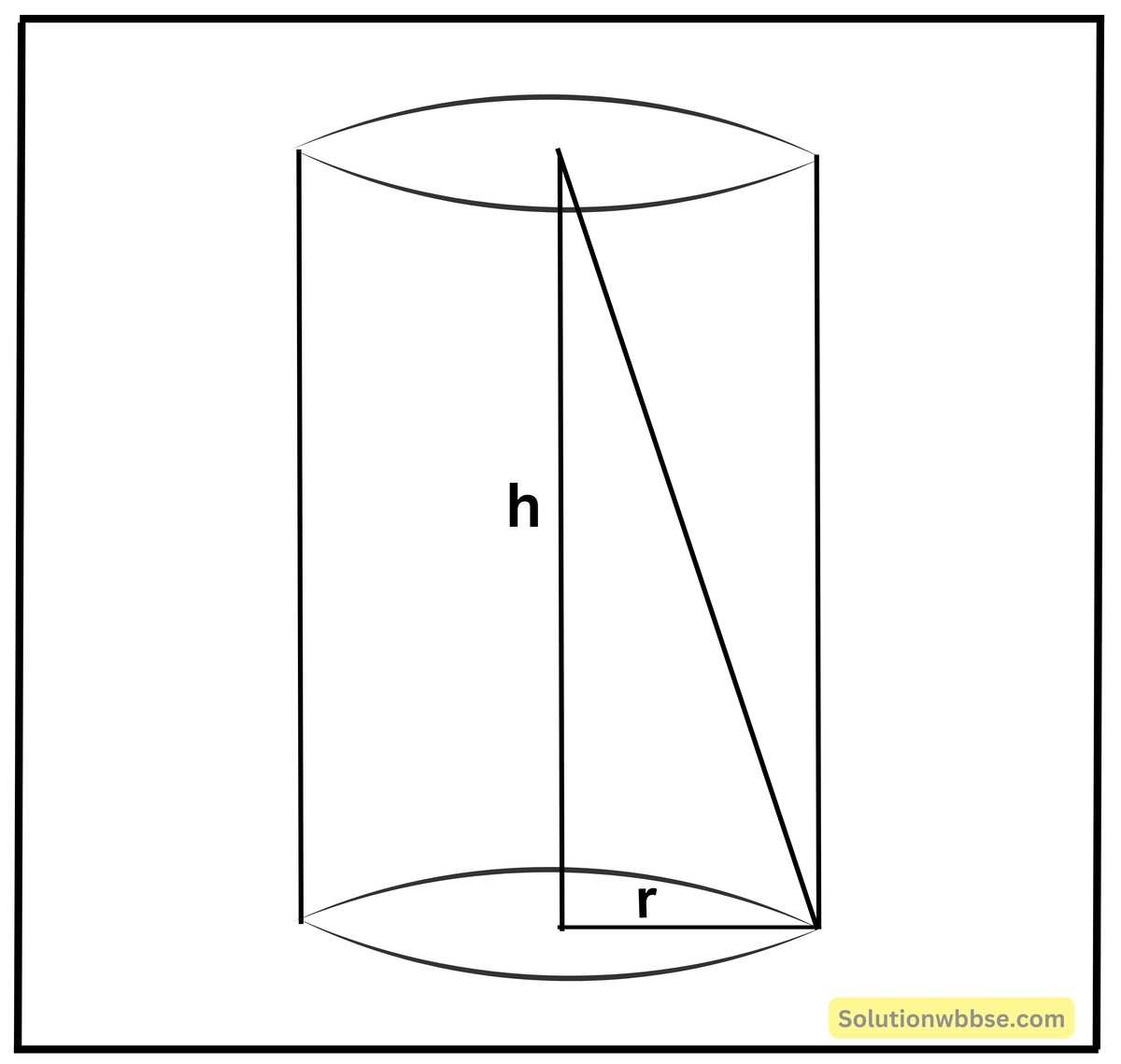
এক্ষেত্রে 3 সেমি. ব্যাসার্ধ ও 4 সেমি. উচ্চতা বিশিষ্ট যে সমকোণী ত্রিভুজ তৈরি হবে তার অতিভুজের দৈর্ঘ্য হল সর্বাপেক্ষা লম্বা দণ্ডের দৈর্ঘ্য যা চোঙের মধ্যে রাখা যেতে পারে।
অতিভুজের দৈর্ঘ্য
= \(\sqrt{3^2+4^2}\) সেমি. [পিথাগোরাসের উপপাদ্যের সাহায্যে।
= \(\sqrt{9+16}\) সেমি.
= \(\sqrt{25}\) সেমি.
= 5 সেমি.
(iii) একটি লম্ব বৃত্তাকার চোঙের আয়তন এবং বক্রতলের ক্ষেত্রফলের সাংখ্যমান সমান হলে, চোঙটির ব্যাসের দৈর্ঘ্য ___ একক।
উত্তর – 4 একক।
সমাধান,
ধরি, লম্ব বৃত্তাকার চোঙের ব্যাসার্ধ r একক এবং উচ্চতা h একক।
লম্ব বৃত্তাকার চোঙের আয়তন = πr2h ঘন একক
লম্ব বৃত্তাকার চোঙের বক্রতলের ক্ষেত্রফল = 2πrh বর্গ একক
∴ শর্তানুসারে,
πr2h = 2πrh
বা, r = 2
বা, 2r = 4
∴ চোঙটির ব্যাসের দৈর্ঘ্য 4 একক।
20. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
(i) একটি লম্ব বৃত্তাকার চোঙাকৃতি স্তম্ভের বক্রতলের ক্ষেত্রফল 264 বর্গ মিটার এবং আয়তন 924 ঘন মিটার হলে, স্তম্ভের ভূমির ব্যাসার্ধের দৈর্ঘ্য কত লিখি।
ধরি, লম্ব বৃত্তাকার চোঙের ভূমির ব্যাসার্ধের দৈর্ঘ্য \(r\) মিটার এবং উচ্চতা \(h\) মিটার।
শর্তানুসারে,
\(2\pi rh = 264 \quad \text{—(i)}\)এবং \(\pi r^2 h = 924 \quad \text{—(ii)}\)
(ii) নং সমীকরণকে (i) নং সমীকরণ দ্বারা ভাগ করে পাই,
\(\frac{\pi r^2 h}{2 \pi r h} = \frac{924}{264}\)বা, \(\frac{r}{2} = 3.5\)
বা, \(r = 7\)
∴ লম্ব বৃত্তাকার চোঙের ভূমির ব্যাসার্ধ \(7\) সেমি.।
(ii) একটি লম্ব বৃত্তাকার চোঙের বক্রতলের ক্ষেত্রফল \(c\) বর্গ একক, ভূমির ব্যাসার্ধের দৈর্ঘ্য \(r\) একক এবং আয়তন \(v\) একক হলে, \(\frac{cr}{v}\) -এর মান কত তা লিখি।
সমাধান,
ধরি, লম্ব বৃত্তাকার চোঙের উচ্চতা \(h\) একক।
∴ \(C = 2\pi rh\)
\(V = \pi r^2 h\)∴ \(\frac{cr}{v} = \frac{2 \pi r h \times r}{\pi r^2 h} = \frac{2 \pi r^2 h}{\pi r^2 h} = 2\)
∴ \(\frac{cr}{v}\) এর মান \(2\)।
(iii) একটি লম্ব বৃত্তাকার চোঙের উচ্চতা 14 সেমি. এবং বক্রতলের ক্ষেত্রফল 264 বর্গ সেমি. হলে, চোঙটির আয়তন কত তা লিখি।
ধরি, লম্ব বৃত্তাকার চোঙের ব্যাসার্ধ \(r\) সেমি.
লম্ব বৃত্তাকার চোঙের উচ্চতা \(h = 14\) সেমি.
শর্তানুসারে,
\(2\pi rh = 264\)বা, \(2 \times \frac{22}{7} \times r \times 14 = 264\)
বা, \(88r = 264\)
বা, \(r = \frac{264}{88}\)
বা, \(r = 3\)
∴ ব্যাসার্ধ = \(3\) সেমি।
লম্ব বৃত্তাকার চোঙের আয়তন = \(\pi r^2 h\) ঘন সেমি.
= \(\frac{22}{7} \times (3)^2 \times 14\) ঘন সেমি.
= \(\frac{22}{7} \times 9 \times 14\) ঘন সেমি.
= \(396\) ঘন সেমি.
∴ চোঙটির আয়তন \(396\) ঘন সেমি.।
(iv) দুটি লম্ব বৃত্তাকার চোঙের উচ্চতার অনুপাত 1 : 2 এবং ভূমির পরিধির অনুপাত 3 : 4 হলে, তাদের আয়তনের অনুপাত কত তা লিখি।
ধরি, লম্ব বৃত্তাকার চোঙ দুটির ব্যাসার্ধ যথাক্রমে \(r_1\) একক এবং \(r_2\) একক ও চোঙ দুটির উচ্চতা যথাক্রমে \(h_1\) একক এবং \(h_2\) একক।
শর্তানুসারে,
\(h_1 : h_2 = 1 : 2\) এবং \(2\pi r_1 : 2\pi r_2 = 3 : 4\)
∴ \(r_1 : r_2 = 3 : 4\)
লম্ব বৃত্তাকার চোঙ দুটির আয়তনের অনুপাত
\(\pi (r_1)^2 h_1 : \pi (r_2)^2 h_2\)= \(\frac{\pi (r_1)^2 h_1}{\pi (r_2)^2 h_2}\)
= \(\frac{(r_1)^2}{(r_2)^2} \times \frac{h_1}{h_2}\)
= \(\left(\frac{r_1}{r_2}\right)^2 \times \frac{h_1}{h_2}\)
= \(\left(\frac{3}{4}\right)^2 \times \frac{1}{2}\)
= \(\frac{9}{16} \times \frac{1}{2}\)
= \(\frac{9}{32}\)
= \(9 : 32\)
∴ চোঙ দুটির আয়তনের অনুপাত \(9 : 32\)।
(v) একটি লম্ব বৃত্তাকার চোঙের ব্যাসার্ধের দৈর্ঘ্য 50% হ্রাস করা হলো এবং উচ্চতা 50% বৃদ্ধি করা হলো। চোঙটির আয়তনের শতকরা কত পরিবর্তন হবে তা লিখি।
ধরি, একটি লম্ব বৃত্তাকার চোঙের ব্যাসার্ধ \(r\) একক এবং উচ্চতা \(h\) একক।
∴ লম্ব বৃত্তাকার চোঙের আয়তন = \(\pi r^2 h\) ঘন একক
ব্যাসার্ধের দৈর্ঘ্য 50% হ্রাস করা হলে, পরিবর্তিত ব্যাসার্ধ
= \(r – \frac{50}{100} \times r\) একক
= \(r – \frac{r}{2}\) একক
= \(\frac{r}{2}\) একক
চোঙের উচ্চতা 50% বৃদ্ধি করা হলে, পরিবর্তিত উচ্চতা
= \(h + \frac{50}{100} \times h\) একক
= \(h + \frac{h}{2}\) একক
= \(\frac{3h}{2}\) একক
∴ পরিবর্তিত চোঙের আয়তন
= \(\pi \left(\frac{r}{2}\right)^2 \times \frac{3h}{2}\) ঘন একক
= \(\pi \times \frac{r^2}{4} \times \frac{3h}{2}\) ঘন একক
= \(\frac{3}{8} \pi r^2 h\) ঘন একক
চোঙটির আয়তন শতকরা পরিবর্তন
= \(\frac{\pi r^2 h – \frac{3}{8} \pi r^2 h}{\pi r^2 h} \times 100%\)
= \(\frac{5 \pi r^2 h}{8 \pi r^2 h} \times 100%\)
= \(\frac{500}{8}%\)
= \(\frac{125}{2}%\)
= \(62 \frac{1}{2}%\)
∴ চোঙটির আয়তন শতকরা \(62 \frac{1}{2}%\) পরিবর্তিত হবে।
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের অষ্টম অধ্যায়, ‘লম্ব বৃত্তাকার চোঙ’ -এর ‘কষে দেখি – 8’ বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment