মাধ্যমিক গণিত – বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য – উপপাদ্য

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের দশম অধ্যায়, ‘বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য’ -এর উপপাদ্যমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

উপপাদ্য 38. বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক।

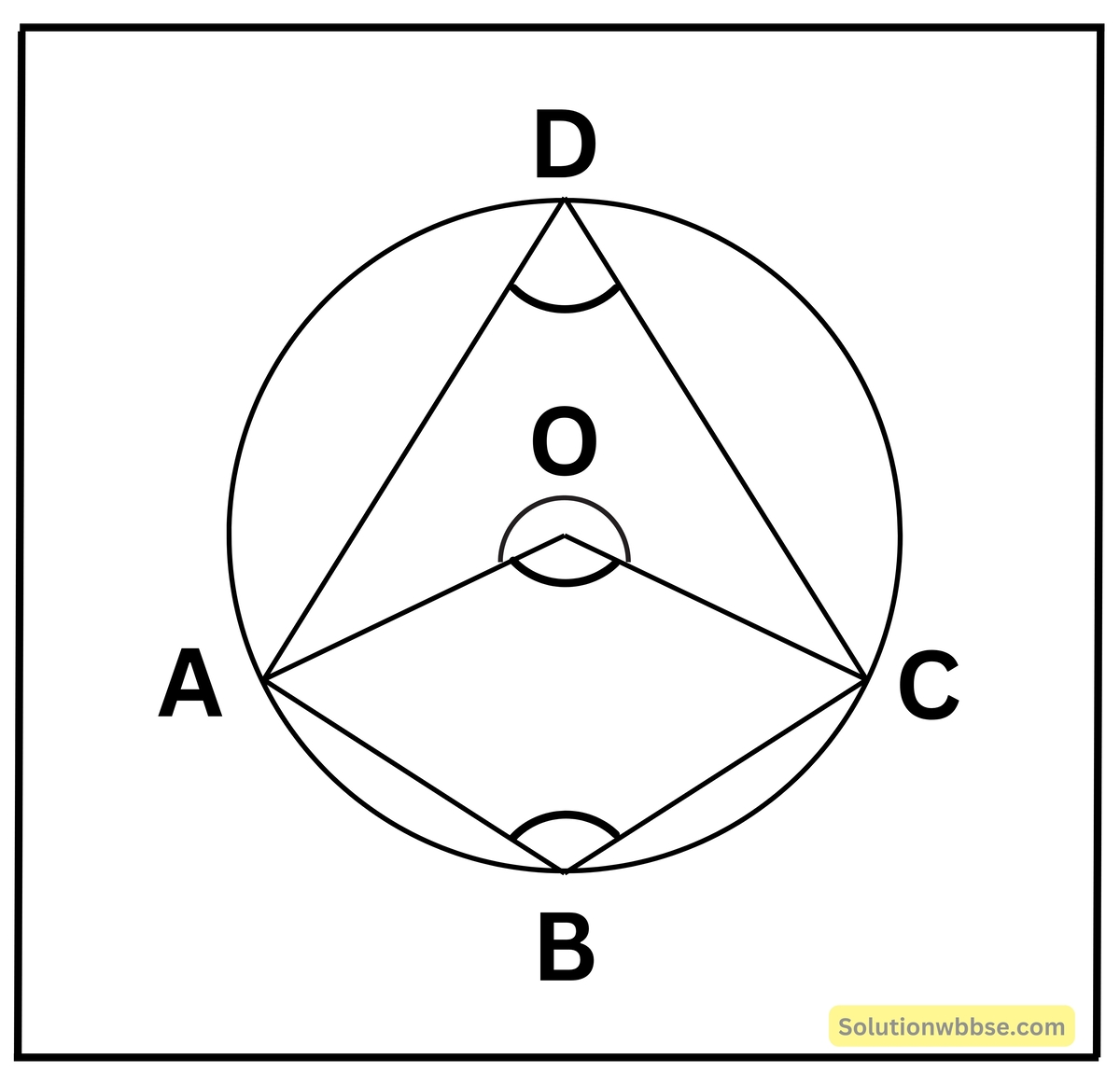
প্রদত্ত – O কেন্দ্রীয় বৃত্তে ABCD একটি বৃত্তস্থ চতুর্ভুজ।

প্রমাণ করতে হবে যে – ∠ABC+ ∠ADC = 2 সমকোণ এবং ∠BAD + ∠BCD = 2 সমকোণ

অঙ্কন – A, O এবং C, O যোগ করলাম।

প্রমাণ: – ADC বৃত্তচাপের দ্বারা গঠিত কেন্দ্রস্থ কোণ প্রবৃদ্ধ ∠AOC এবং বৃত্তস্থ কোণ ∠ABC

∴ প্রবৃদ্ধ ∠AOC = 2∠ABC

∴ ∠ABC = \(\frac12\)প্রবৃদ্ধ∠AOC —(i)

আবার ABC বৃত্তচাপের দ্বারা গঠিত কেন্দ্রস্থ কোণ ∠AOC এবং বৃত্তস্থ কোণ ∠ADC

∴ ∠AOC = 2∠ADC

∠ADC = \(\frac12\)∠AOC —(ii)

∴ (i) ও (ii) হইতে পাই, ∠ABC + ∠ADC = \(\frac12\)প্রবৃদ্ধ∠AOC + \(\frac12\)∠AOC

= \(\frac12\)(প্রবৃদ্ধ∠AOC + ∠AOC)

= \(\require{cancel}\frac1{\cancel2}\times\overset2{\cancel4}\) সমকোণ

= 2 সমকোণ

অনুরূপে B, O এবং D, O যোগ করে প্রমাণ করতে পারি যে, ∠BAD + ∠BCD = 2 সমকোণ [প্রমাণিত]

বিকল্প প্রমাণ

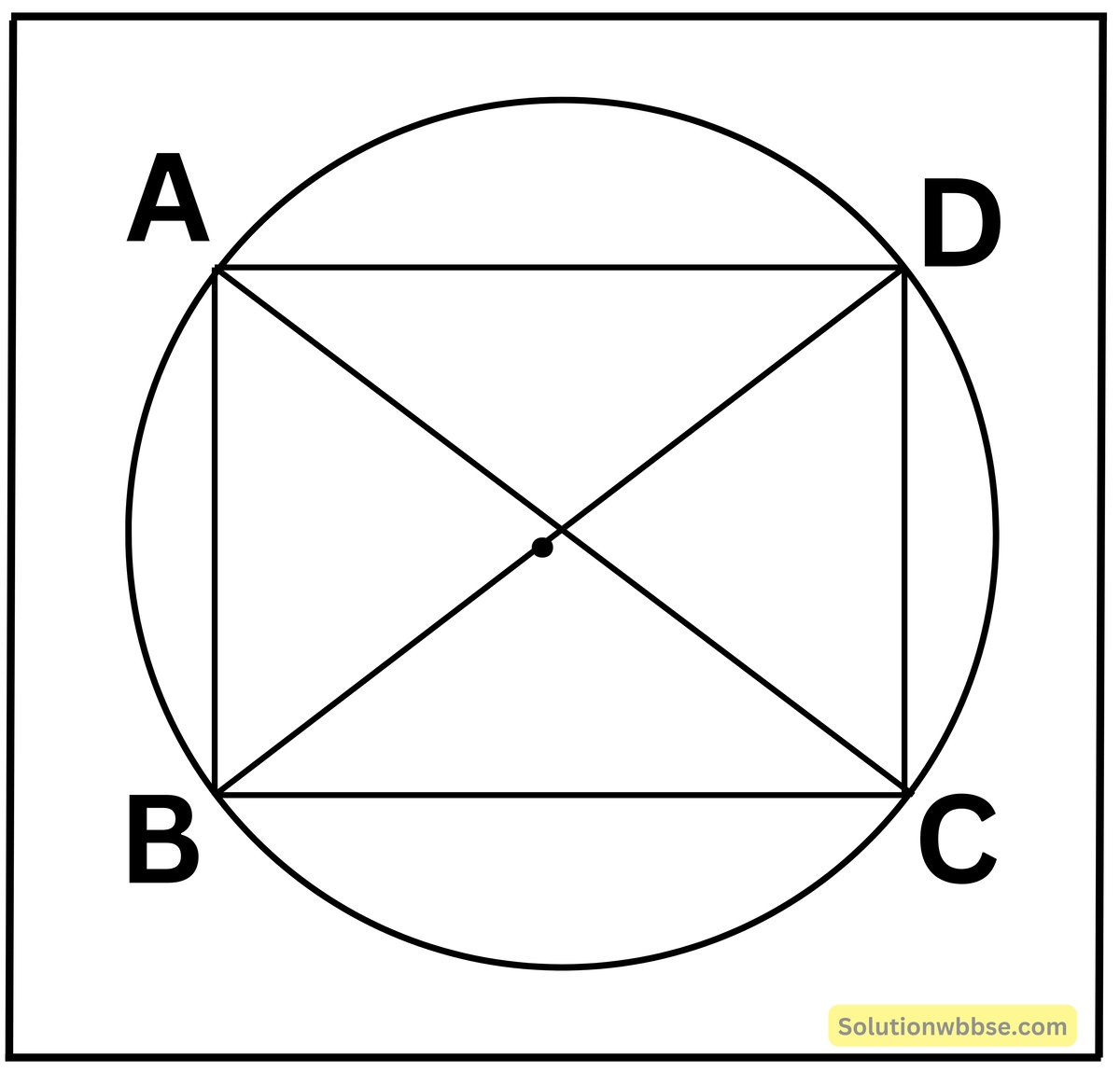
প্রদত্ত – ABCD একটি বৃত্তস্থ চতুর্ভুজ।

প্রমাণ করতে হবে যে – ∠ABC + ∠ADC = 2 সমকোণ এবং ∠BAD + ∠BCD = 2 সমকোণ

অঙ্কন – AC ও BD দুটি কর্ণ টানলাম।

প্রমাণ – ∠ADB = ∠ACB [একই বৃত্তাংশস্থ কোণ]

আবার ∠BAC = ∠BDC [একই বৃত্তাংশস্থ কোণ]

আবার ∠ADC = ∠ADB + ∠BDC

= ∠ACB + ∠BAC

∴ ∠ADC + ∠ABC = ∠ACB + ∠BAC + ∠ABC

∴ ∠ADC + ∠ABC = 2 সমকোণ [∵ ত্রিভুজের তিনটি কোণের সমষ্টি 2 সমকোণ]

অনুরূপে প্রমাণ করতে পারি যে, ∠BAD + ∠BCD = 2 সমকোণ [প্রমাণিত]

উপপাদ্য 39. কোনো চতুর্ভুজের বিপরীত কোণ পরস্পর সম্পূরক হলে, চতুর্ভুজটির শীর্ষবিন্দুগুলি সমবৃত্তস্থ হবে।

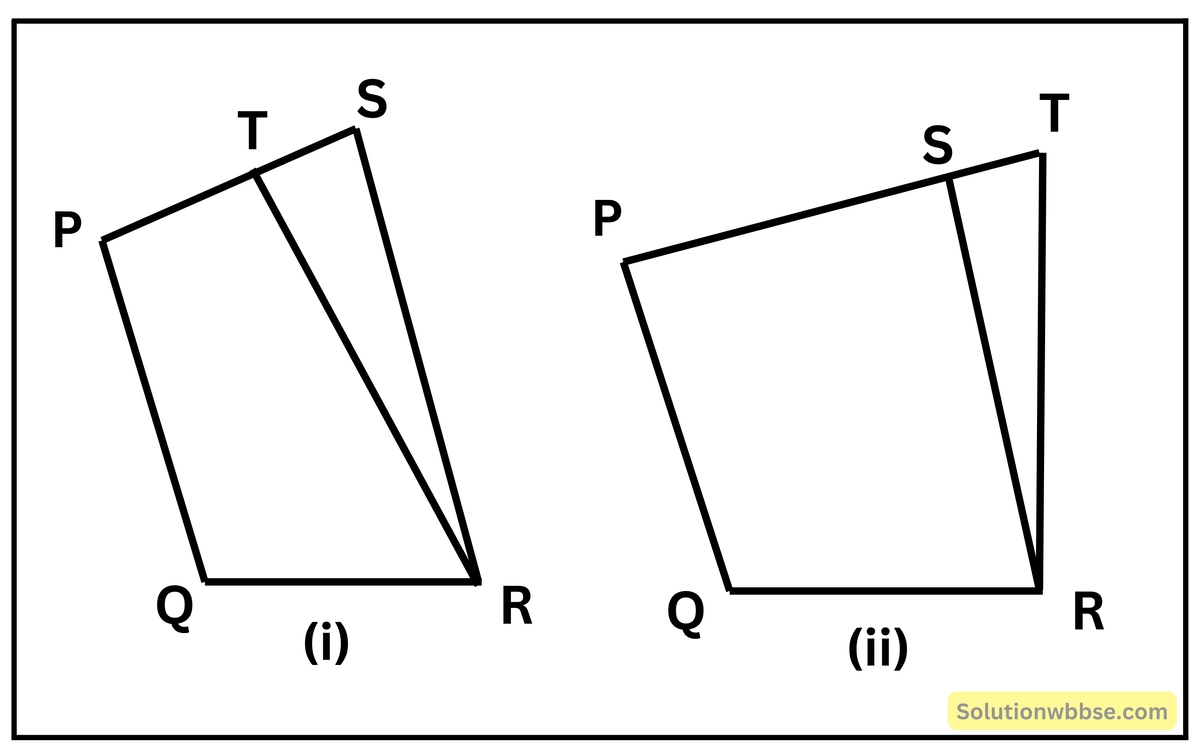
প্রদত্ত – ধরি, PQRS একটি চতুর্ভুজ যার ∠PQR এবং ∠PSR পরস্পর সম্পূরক, এক, অর্থাৎ

∠PQR + ∠PSR = 2 সমকোণ

প্রমাণ করতে হবে যে – চতুর্ভুজটির শীর্ষবিন্দুগুলি অর্থাৎ P, Q, R, S বিন্দু চারটি সমবৃত্তস্থ।

অঙ্কন – P, Q, R তিনটি অসমরেখ বিন্দু দিয়ে একটি মাত্র বৃত্ত অঙ্কন করা যায়। ধরি, অঙ্কিত বৃত্তটি S বিন্দুগামী নয়। বৃত্তটি PS বা PS -এর বর্ধিতাংশকে T বিন্দুতে ছেদ করে। T ও R যুক্ত করলাম।

প্রমাণ – অঙ্কন অনুসারে, PQRT একটি বৃত্তস্থ চতুর্ভুজ

∴ ∠PQR + ∠PTR = 2 সমকোণ —(1)

কিন্তু ∠PQR + ∠PSR = 2 সমকোণ [প্রদত্ত] —(2)

(1) নং ও (2) নং থেকে পাই, ∠PQR + ∠PTR = ∠PQR + ∠PSR

∴ ∠PTR = ∠PSR

একটি ত্রিভুজের বহিঃস্থকোণ ত্রিভুজের বিপরীত অন্তঃস্থ কোণের সমান হতে পারে না।

∴ ∠PTR = ∠PSR হবে যখন S ও T বিন্দুদ্বয় সমাপতিত হবে।

∴ P, Q, R বিন্দুগামী বৃত্তটি অবশ্যই S বিন্দু দিয়ে যাবে।

∴ P, Q, R, S বিন্দু চারটি সমবৃত্তস্থ।

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের দশম অধ্যায়, ‘বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য’ -এর উপপাদ্যমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।

আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।