এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের একাদশ অধ্যায়, ‘সম্পাদ্য: ত্রিভুজের পরিবৃত্ত ও অন্তবৃত্ত অঙ্কন’ -এর সম্পাদ্যমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

5 সেমি., 6 সেমি., 7 সেমি. বাহুবিশিষ্ট একটি ত্রিভুজ অঙ্কন করে ত্রিভুজটির পরিবৃত্ত অঙ্কন করি।
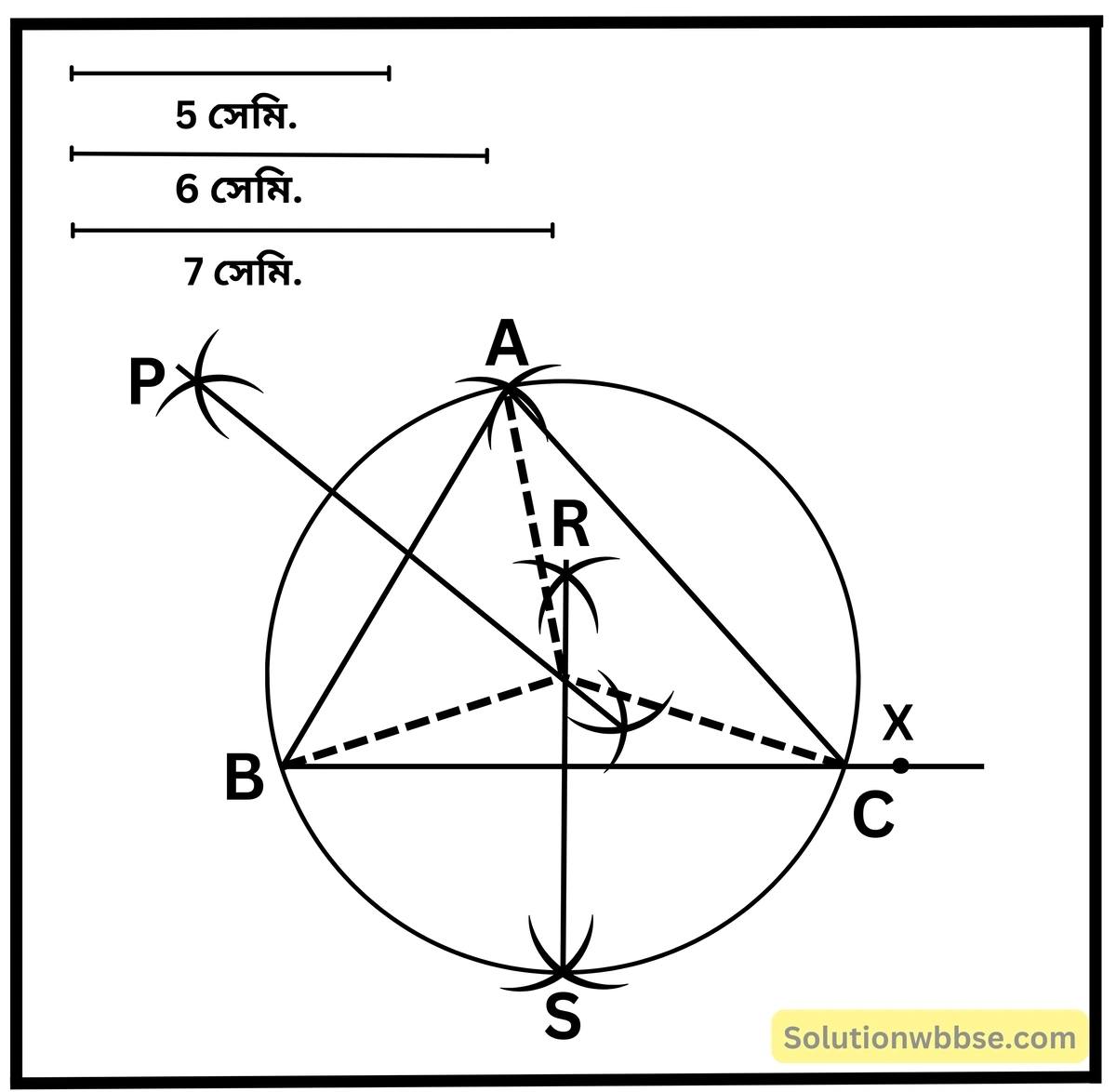
অঙ্কন প্রণালী –
(i) প্রথমে 5 সেমি., 6সেমি. ও 7 সেমি. বাহুবিশিষ্ট ∆ABC অঙ্কন করি।
(ii) [∆ABC -এর পরিবৃত্ত অঙ্কনের জন্য প্রথমেই পরিবৃত্তের কেন্দ্র নির্ণয় করব। তাই ∆ABC -এর যে-কোনো দুটি বাহুর লম্বসমদ্বিখণ্ডক অঙ্কন করব।]
∆ABC -এর AB ও BC বাহুর দুটি লম্ব সমদ্বিখণ্ডক যথাক্রমে PQ ও RS অঙ্কন করলাম যারা পরস্পরকে বিন্দুতে ছেদ করল।
(iii) O বিন্দুটি AB ও BC-এর লম্বসমদ্বিখণ্ডকের ছেদবিন্দু।
∴ O বিন্দুটি A, B ও C থেকে সমদূরবর্তী।
O বিন্দুকে কেন্দ্র করে OA অথবা OB অথবা OC দৈর্ঘ্যের ব্যাসার্ধ নিয়ে একটি বৃত্ত অঙ্কন করলাম। যা ∆ABC -এর পরিবৃত্ত।
প্রমাণ – O, A; O, B; O, C যোগ করলাম।
O, AB -এর লম্বসমদ্বিখণ্ডকের উপর একটি বিন্দু।
∴ O থেকে A ও B বিন্দুদ্বয় সমদূরবর্তী অর্থাৎ OA = OB
অনুরূপে প্রমাণ করা যায় যে, OB = OC
∴ OA = OB = OC.
O -কে কেন্দ্র করে OA দৈর্ঘ্যের ব্যাসার্ধ নিয়ে যে বৃত্ত অঙ্কন করব সেই বৃত্ত B ও C বিন্দুগামী হবে অর্থাৎ বৃত্তটি ∆ABC -এর তিনটি শীর্ষবিন্দু A, B ও C দিয়ে যাবে।
∴ ওই বৃত্তটিই ∆ABC -এর পরিবৃত্ত।
ABC একটি ত্রিভুজ অঙ্কন করি, যার BC= 6 সেমি., CA = 5.5 সেমি. এবং AB = 4.5 সেমি.। ∆ABC -এর অন্তবৃত্ত অঙ্কন করি।
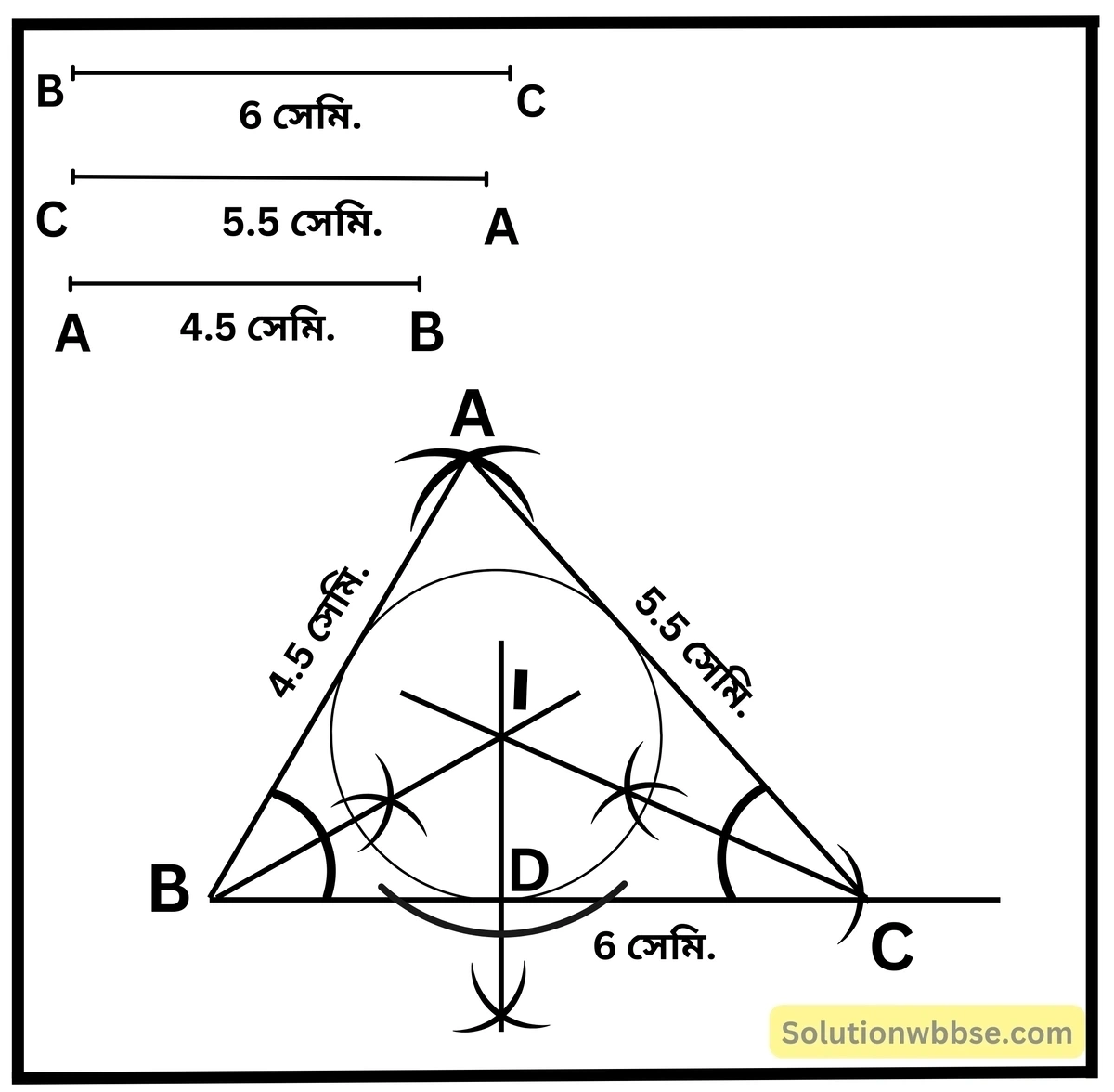
অঙ্কন প্রণালী –
(i) ∠ABCও ∠ACB -এর অন্তসমদ্বিখণ্ডক যথাক্রমে BI ও CI অঙ্কন করলাম যারা পরস্পরকে I বিন্দুতে ছেদ করল।
(ii) I বিন্দু থেকে BC বাহুর উপর লম্ব অঙ্কন করলাম যা BC বাহুকে D বিন্দুতে ছেদ করল।
(ii) I বিন্দুকে কেন্দ্র করে ID দৈর্ঘ্যের ব্যাসার্ধ নিয়ে একটি বৃত্ত অঙ্কন করলাম। ওই বৃত্তই হলো △ABC -এর অন্তবৃত্ত।
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের একাদশ অধ্যায়, ‘সম্পাদ্য: ত্রিভুজের পরিবৃত্ত ও অন্তবৃত্ত অঙ্কন’ -এর সম্পাদ্যমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment