আজকের আর্টিকেলে আমরা নবম শ্রেণীর ভৌতবিজ্ঞান বইয়ের দ্বিতীয় অধ্যায় “বল ও গতি” এর “গতির সমীকরণ” থেকে সহজ ও সংক্ষিপ্ত প্রশ্ন-উত্তর শেয়ার করবো। এই প্রশ্নগুলো নবম শ্রেণির ইউনিট টেস্ট থেকে বার্ষিক পরীক্ষা এর জন্য যেমন গুরুত্বপূর্ণ, তেমনি চাকরি বা বিভিন্ন প্রতিযোগিতার পরীক্ষাতেও কাজে লাগবে। এই অধ্যায় থেকে স্কুল পরীক্ষা থেকে শুরু করে চাকরির পরীক্ষায় প্রায়ই প্রশ্ন আসে, তাই এই প্রশ্নোত্তরগুলো সবাইকে সাহায্য করবে। প্রতিটি প্রশ্নের উত্তর সহজ ভাষায় লেখা হয়েছে, যাতে সবাই বুঝতে পারেন। পড়ার শেষে এই অধ্যায়ের মুখ্য বিষয়গুলো আপনার আয়ত্তে চলে আসবে এবং যেকোনো পরীক্ষায় আত্মবিশ্বাসের সঙ্গে লিখতে পারবেন।

জ্ঞানমূলক প্রশ্নোত্তর
অতিক্রান্ত দূরত্ব ও সরণ বলতে কী বোঝায়?
অতিক্রান্ত দূরত্ব (Distance) – কোনো গতিশীল বস্তুকণা সরল বা বক্র যে-কোনো পথে যে পথদৈর্ঘ্য অতিক্রম করে, তাকেই অতিক্রান্ত দূরত্ব বা সংক্ষেপে দূরত্ব বলে। নির্দিষ্ট কোনো অভিমুখ না থাকায় দূরত্ব একটি স্কেলার রাশি।
সরণ (Displacement) – নির্দিষ্ট অভিমুখে কোনো বস্তুকণার অবস্থানের পরিবর্তনকে ওই বস্তুকণার সরণ বলা হয়। কণার প্রাথমিক ও অন্তিম অবস্থানের মধ্যে সরলরৈখিক দূরত্বের মানই হল সরণের পরিমাপ এবং সরলরেখায় ব্যবহৃত তিরচিহ্নটি নির্দেশ করে সরণের অভিমুখ। মান ও অভিমুখ দুই-ই নির্দিষ্ট হওয়ায় সরণ একটি ভেক্টর রাশি।
সরণের পরিমাপ করবে কীভাবে?
সরণের পরিমাপ – কোনো গতিশীল বস্তুর প্রথম ও শেষ অবস্থানের মাঝের সরলরৈখিক দূরত্বই হল ওই বস্তুর সরণের পরিমাপ এবং ওই সরলরেখা বরাবর প্রথম অবস্থান থেকে শেষ অবস্থানের দিকই হল সরণের দিক বা অভিমুখ। যেমন – নীচের চিত্রে একটি গতিশীল বস্তু A থেকে B বিন্দুর দিকে যাচ্ছে। বস্তুটি a, b, c, d ইত্যাদি পথে A থেকে B -তে যেতে পারে। কিন্তু সরণ বলতে b পথে স্থান পরিবর্তনকে বোঝায়। কারণ – b পথই হল A ও B বিন্দুর মধ্যে সরলরৈখিক (ন্যূনতম) দূরত্ব।
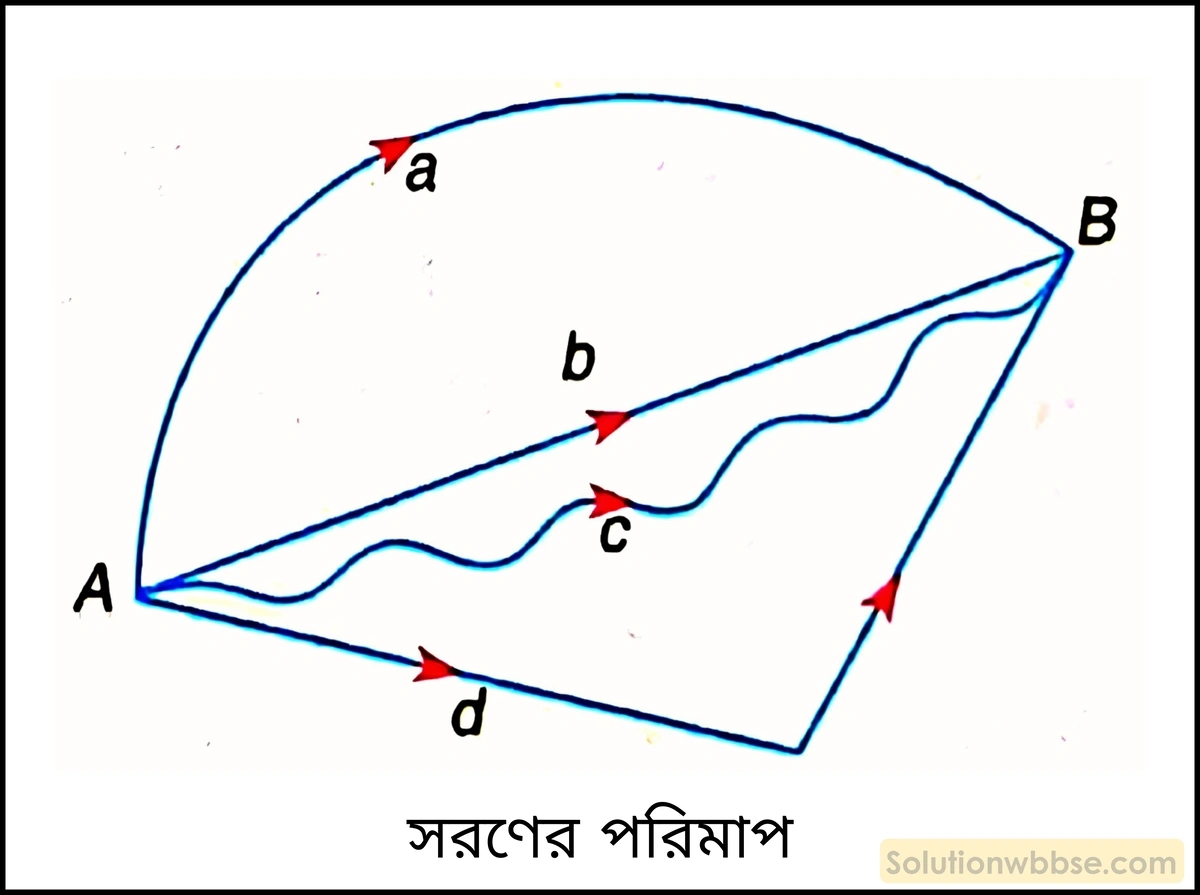
সরণের একক ও মাত্রীয় সংকেত লেখো।
CGS পদ্ধতিতে সরণের একক সেন্টিমিটার (cm) এবং SI -তে একক হল মিটার (m)।
সরণের মাত্রীয় সংকেত হল = [L]।
দ্রুতি কাকে বলে? এর CGS ও SI -তে একক ও মাত্রীয় সংকেত লেখো।
দ্রুতি (Speed) – একক সময়ে কোনো গতিশীল বস্তু যে দূরত্ব অতিক্রম করে, তাকে দ্রুতি বলে। এই দূরত্ব সরলপথ বা বক্রপথ বরাবর হতে পারে। ধরি, t সময় অবকাশে কোনো কণা s দূরত্ব অতিক্রম করলে দ্রুতি হয়, \(v=\frac st\)
∴
যেহেতু, দ্রুতি হল দুটি স্কেলার রাশির অনুপাত, তাই এটি একটি স্কেলার রাশি।
CGS পদ্ধতিতে দ্রুতির একক সেন্টিমিটার/সেকেন্ড (cm/s) এবং SI -তে একক মিটার/সেকেন্ড (m/s)।
দ্রুতির মাত্রীয় সংকেত = ]বেগ বলতে কী বোঝায়? CGS ও SI -তে বেগের একক ও মাত্রীয় সংকেত লেখো।
বেগ (Velocity) – কোনো বস্তু একক সময়ে একটি নির্দিষ্ট দিকে যে দূরত্ব অতিক্রম করে, তাকে ওই বস্তুর বেগ বলা হয়। অথবা, একক সময়ে কোনো গতিশীল বস্তুর সরণকে অর্থাৎ, কণার সরণের হারকে ওই বস্তুর বেগ বলে।
ধরি, t সময় অবকাশে কোনো কণার সরণ \(\overrightarrow s\) হলে, ওর বেগ হয়, \(\overrightarrow v=\frac{\overrightarrow s}t\)
∴
একটি ভেক্টর ও একটি স্কেলার রাশির অনুপাত হওয়ায় বেগ হল ভেক্টর রাশি। এর অভিমুখ সরণের অভিমুখের সঙ্গে অভিন্ন। CGS পদ্ধতিতে বেগের একক সেন্টিমিটার/সেকেন্ড (cm⋅s-1) এবং SI -তে একক মিটার/সেকেন্ড (m⋅s-1)।
ত্বরণ কাকে বলে? CGS ও SI -তে ত্বরণের একক ও মাত্রীয় সংকেত লেখো।
অথবা, কোনো বস্তুর ওপর t সময় ধরে কিছু পরিমাণ বল প্রযুক্ত হওয়ায় বস্তুর বেগ v1 থেকে v2 হল, যেখানে v2 > v1। বস্তুটির ত্বরণ কত?
ত্বরণ (Acceleration) – কোনো গতিশীল বস্তুর বেগ যদি ক্রমশ বাড়তে থাকে, তবে সময়ের সাপেক্ষে বস্তুটির বেগ বৃদ্ধির হারকে ত্বরণ বেগ বৃদ্ধি বলে। ধরি, \(\overrightarrow u\) প্রাথমিক বেগসহ গতিশীল একটি কণা t সময়ে \(\overrightarrow v\) চূড়ান্ত বেগ অর্জন করে, তবে ত্বরণ \(\overrightarrow a=\frac{\overrightarrow v-\overrightarrow u}t\)
∴
CGS পদ্ধতিতে ত্বরণের একক সেন্টিমিটার/সেকেন্ড2 (cm.s-2) এবং SI -তে ত্বরণের একক মিটার/সেকেন্ড2 (m.s-2)।
।
∴ ত্বরণের মাত্রীয় সংকেত =
মন্দন কাকে বলে? এর মাত্রীয় সংকেত এবং CGS ও SI -তে এককগুলি লেখো।
মন্দন (Retardation) – কোনো গতিশীল বস্তুর বেগ যদি সময়ের সাপেক্ষে ক্রমাগত কমতে থাকে, তবে বস্তুটির বেগ হ্রাসের হারকে মন্দন বা ঋণাত্মক ত্বরণ বলে। ধরি, কোনো গতিশীল কণার প্রাথমিক বেগ, \( \overrightarrow u \), t সময় অবকাশে ওর বেগ হ্রাস পেয়ে \( \overrightarrow v \) হলে, মন্দন হবে \( \overrightarrow a’=\left(\frac{\overrightarrow v‐\overrightarrow u}t\right) \) (এক্ষেত্রে u > v হয়)।
মন্দনের মাত্রীয় সংকেত এবং CGS ও SI -তে এককগুলি ত্বরণের সঙ্গে অভিন্ন।
সমদ্রুতি ও অসমদ্রুতি বলতে কী বোঝায়?
সমদ্রুতি (Uniform speed) – কোনো গতিশীল বস্তুকণা যদি একই সময়ের ব্যবধানে সরল বা বক্র যে-কোনো পথে সর্বদা একই পরিমাণ দূরত্ব অতিক্রম করে, তবে ওই বস্তুকণার গতি হল সমদ্রুতিসম্পন্ন এবং সংশ্লিষ্ট দ্রুতিকে বলে সমদ্রুতি।
সমদ্রুতির উদাহরণ – ঘর্ষণহীন তল বরাবর সুষমভাবে গতিশীল বল।
অসমদ্রুতি (Non-uniform speed) – কোনো বস্তুকণা যদি একই সময়ের অবকাশে ভিন্ন ভিন্ন পথদৈর্ঘ্য অতিক্রম করে তবে ওই গতিকে অসমদ্রুতিসম্পন্ন এবং সংশ্লিষ্ট দ্রুতিকে বলা হয় অসমদ্রুতি।
অসমদ্রুতির উদাহরণ – অমসৃণ তলে গতিশীল বল বা ভিড় রাস্তায় গতিশীল মোটরগাড়ি ইত্যাদি। প্রকৃতপক্ষে যে-কোনো বাস্তব গতিই অসমদ্রুতিযুক্ত গতির উদাহরণ।
সমবেগ ও অসমবেগ কাকে বলে?
সমবেগ (Uniform velocity) – কোনো বস্তুকণা নির্দিষ্ট অভিমুখে যদি সর্বদা একই মানের বেগ নিয়ে চলে, তবে ওই গতিকে সমবেগযুক্ত গতি এবং বস্তুকণার ওই বেগকে সমবেগ বলা হয়।
সমবেগের উদাহরণ – পতনশীল বৃষ্টির ফোঁটার গতি।
অসমবেগ (Non-uniform velocity) – সময়ের সঙ্গে যদি কোনো গতিশীল বস্তুকণার বেগের মান বা দিক অথবা উভয়ই পরিবর্তিত হয় তবে ওই গতিকে অসমবেগযুক্ত বলা হয় এবং সংশ্লিষ্ট কণার বেগকে বলা হয় অসমবেগ।
অসমবেগের উদাহরণ – নির্দিষ্ট উচ্চতা থেকে খাড়া উল্লম্বরেখায় অবাধে পতনশীল বস্তু অথবা বৃত্তপথে সুষম বা অসম গতিতে চলমান বস্তুকণার গতি ইত্যাদি। প্রকৃতপক্ষে যে-কোনো ত্বরণ বা মন্দনযুক্ত গতিই অসমবেগসম্পন্ন গতির উদাহরণ।
পতনশীল বৃষ্টি ফোঁটার গতির শুরুতে অভিকর্ষজ ত্বরণের প্রভাবে বেগের কী পরিবর্তন ঘটে?
পতনশীল বৃষ্টি ফোঁটার গতির শুরুতে অভিকর্ষজ ত্বরণের প্রভাবে বেগ বৃদ্ধি পেতে শুরু করলেও বায়ুর প্লবতা ও সান্দ্রতা বলের প্রভাবে বেগ বৃদ্ধির হার ক্রমশ কমে এবং যে মুহূর্তে অভিকর্ষ বল বিপরীত অভিমুখে ক্রিয়াশীল প্লবতা ও সান্দ্র বলের যৌথ ক্রিয়ায় সম্পূর্ণ প্রতিমিত হয়, সেই মুহূর্তে বারিবিন্দু একটি স্থির মানের বেগ (সীমান্ত বা প্রান্তীয় বেগ) অর্জন করে এবং ওই বেগসহ ভূ-পৃষ্ঠে পৌঁছোয়।
গড়দ্রুতি ও গড়বেগ কাকে বলে?
গড়দ্রুতি (Average speed) – কোনো বস্তুকণা ভিন্ন ভিন্ন সময়ের অবকাশে ভিন্ন ভিন্ন দূরত্ব অতিক্রম করলে অর্থাৎ, অসমদ্রুতিতে গতিশীল কোনো বস্তুকণা দ্বারা মোট অতিক্রান্ত দূরত্ব ও মোট অতিবাহিত সময়ের অনুপাতকে বলা হয় কণাটির গড়দ্রুতি।
যদি কণাটি \( t_{1,}t_{2,}t_3 … t_n \) ইত্যাদি সময় অবকাশে যথাক্রমে \( d_{1,}d_{2,}d_3 … d_n \) দূরত্ব অতিক্রম করে,
তবে তার গড়দ্রুতি, \( v_{av}=\frac{d_1+d_1+d_1+…d_n}{t_1+t_1+t_1+…t_n} \)
গড়বেগ (Average velocity) – ভিন্ন ভিন্ন সময় অবকাশে কোনো গতিশীল বস্তুকণার সরণ বিভিন্ন হলে কণার মোট সরণ ও মোট অতিবাহিত সময়ের অনুপাতকে বলা হয় গড়বেগ।
যদি \( t_1,\;t_2,t_3….t_n \) ইত্যাদি সময়ান্তরে কণার সরণ যথাক্রমে \( \overrightarrow{s_1},\overrightarrow{s_2},\overrightarrow{s_3} … \overrightarrow{s_n} \) হয় তবে কণার গড় বেগকে লেখা যায়,
\(\overrightarrow{V_{av}}=\frac{\overrightarrow{s_1}+\overrightarrow{s_2}+\overrightarrow{s_3}+…\overrightarrow{s_n}}{t_1+t_2+t_3+…t_n} \\\)তাৎক্ষণিক দ্রুতই বা তাৎক্ষণিক বেগ বলতে কি বোঝায়? তাৎক্ষণিক ত্বরণ কাকে বলে?
তাৎক্ষণিক মুক্তি বা তাৎক্ষণিক বেগ (Instanteneous speed or velocity) – কোনো গতিশীল বস্তুকণার গতির যে-কোনো নির্দিষ্ট মুহূর্তে দ্রুতি বা বেগের মানকে ওই বস্তুকণার তাৎক্ষণিক দ্রুতি বা তাৎক্ষণিক বেগ বলে। যেমন – একটি মোটরগাড়ির স্পিডোমিটারের কাঁটার পাঠ তার তাৎক্ষণিক দ্রুতি নির্দেশ করে।
তাৎক্ষণিক ত্বরণ (Instanteneous accelaration) – বস্তুকণার গতির যে-কোনো নির্দিষ্ট মুহূর্তে ক্ষুদ্র সময় অবকাশে বেগের যে পরিবর্তন বা বেগ বৃদ্ধি হয়, সেই বেগ বৃদ্ধি ও সময় অবকাশের অনুপাতকে ওই বস্তুকণার ওই মুহূর্তের তাৎক্ষণিক ত্বরণ বলে।
সমত্বরণের উদাহরণসহ সংজ্ঞা দাও।
সমত্বরণ (Uniform acceleration) – একই সময়ের ব্যবধানে কোনো বস্তুকণার বেগ যদি একই পরিমাণে বৃদ্ধি পায়, তবে ওই বস্তুকণার ত্বরণকে সমত্বরণ বলা হয়।
উদাহরণ – অভিকর্ষের ক্রিয়ায় অবাধে পতনশীল কোনো বস্তুর বেগ নির্দিষ্ট সময় অবকাশে সুষম হারে বৃদ্ধি পায়, এটি সমত্বরণযুক্ত গতির উদাহরণ।
অসমত্বরণের উদাহরণসহ সংজ্ঞা দাও।
অসমত্বরণ (Non-uniform acceleration) – একই সময়ের ব্যবধানে কোনো বস্তুকণার বেগের বৃদ্ধি যদি ভিন্ন ভিন্ন ক্ষেত্রে পৃথক হয়, তবে সংশ্লিষ্ট ত্বরণকে অসমত্বরণ বলে।
উদাহরণ – দোলক ঘড়ির পিণ্ড অথবা সরল দোলগতিযুক্ত যে-কোনো বস্তুকণার ত্বরণ মধ্যবিন্দু বা সাম্য অবস্থানে শূন্য ও দুই প্রান্তিক অবস্থানে সর্বোচ্চ। সুতরাং, এক্ষেত্রে কণার গতি অসমত্বরণ-যুক্ত গতির উদাহরণ।
ধনাত্মক ও ঋণাত্মক ত্বরণের ধারণার ব্যাবহারিক দৃষ্টান্ত উল্লেখ করো।
ধনাত্মক ও ঋণাত্মক স্বরণের ব্যাবহারিক দৃষ্টান্ত – কোনো গতিশীল বস্তু বা বস্তুকণার বেগ সময় সাপেক্ষে বৃদ্ধি পেলে তার ত্বরণকে ধনাত্মক ও হ্রাস পেলে সংশ্লিষ্ট ত্বরণকে ঋণাত্মক ত্বরণ বলা হয়। যেমন – গাড়ির অ্যাকসিলারেটরে চাপ দিলে গাড়ির বেগ বাড়ে। এক্ষেত্রে, গাড়ির ত্বরণ ধনাত্মক হয়। আবার, ব্রেক কষে গাড়ি থামানোর সময় গাড়ির ত্বরণ ঋণাত্মক হয়।
গতীয় সমীকরণ বলতে কী বোঝায়? এর গুরুত্ব লেখো।
গতীয় সমীকরণ (Equation of motion) – গতি নিয়ন্ত্রক চলরাশিগুলি (সরণ, বেগ, ত্বরণ ইত্যাদি) দ্বারা গঠিত যে সমীকরণগুলির সাহায্যে কোনো বস্তুকণার গতিকে গাণিতিকভাবে বর্ণনা করা যায়, তাদের গতীয় সমীকরণ বলে।
গতীয় সমীকরণের গুরুত্ব – এই সমীকরণগুলির সাহায্যে সমবেগে বা সমত্বরণসহ গতিশীল বস্তুকণার গতীয় আচরণের নিখুঁত বর্ণনা পাওয়া যায়। যে-কোনো সমীকরণে উপস্থিত চলরাশিসমূহের একটি অজ্ঞাত হলে অন্যান্য রাশিগুলির দেওয়া মান ব্যবহার করে সেটি নির্ণয় করা যায়।
সমবেগযুক্ত গতির ক্ষেত্রে প্রযোজ্য গতীয় সমীকরণটি বীজগাণিতিক পদ্ধতিতে প্রতিষ্ঠা করো।
ধরা যাক, কোনো বস্তুকণা মানের নির্দিষ্ট বেগসহ সরলরেখায় গতিশীল হয়ে t সময়ে s দূরত্ব অতিক্রম করে।
সংজ্ঞানুসারে, কণার বেগ v =
∴ s = vt
এটি হল সমবেগযুক্ত গতির ক্ষেত্রে গতীয় সমীকরণ।
v = u + at -সমত্বরণযুক্ত গতির ক্ষেত্রে প্রমাণ করো।
v = u + at -এর বীজগাণিতিক প্রমাণ –
ধরা যাক, কোনো বস্তুর প্রাথমিক গতিবেগ = u
t সময় ধরে a সমত্বরণে চলার পর বস্তুটির অন্তিম গতিবেগ = v
∴ t সময়ে গতিবেগের পরিবর্তন = v – u
∴ একক সময়ে গতিবেগের পরিবর্তন \( =\frac{v-u}t \)
∴ ত্বরণ = একক সময়ে গতিবেগের পরিবর্তন,
∴ \( a=\frac{v-u}t \)
বা, \( at=v-u \)
বা, \( v=u+at \)
∴ \( v = u + at \) (প্রমাণিত)।
\( s=ut+\frac12at^2 \) -সমত্বরণযুক্ত গতির ক্ষেত্রে প্রমাণ করো।
\( s=ut+\frac12at^2 \) -এর বীজগাণিতিক প্রমাণ –
ত্বরণ থাকার দরুন গতিশীল কণার প্রতি মুহূর্তে বেগ পরিবর্তিত হয়। সুতরাং, মোট অতিক্রান্ত দূরত্ব নির্ণয় করতে হলে এক্ষেত্রে সংশ্লিষ্ট গতির গড়বেগ বিবেচনা করা প্রয়োজন।
গতি শুরুর 1 সেকেন্ড পরে কণার বেগ,
v1 = u + a⋅1
বা, v1 = u + a
গতি শেষ হওয়ার 1 সেকেন্ড আগে কণার বেগ,
v2 = u + a (t – 1)
বা, v2 = u + at – a
বা, v2 = u – a [∵ t সময় পর কণাটির বেগ, v = u + at]
∴ কণাটির গড় বেগ \( \left(v_{ab}\right)=\frac{v_1+v_2}2\)
বা, \(v_{ab}=\frac{u+a+v-a}2\)
বা, \(v_{ab}=\frac{u+v}2\)
গড়বেগের রাশিমালায় ত্বরণ অনুপস্থিত হওয়ায় সর্বত্র গতিবেগের এই মান নির্দিষ্ট বা ধ্রুবক।
সুতরাং, সমত্বরণযুক্ত গতিটি এক্ষেত্রে vab মানবিশিষ্ট সমবেগযুক্ত গতির সঙ্গে তুলনীয়।
∴ t সময়ে কণার দ্বারা অতিক্রান্ত দূরত্ব, \( s=v_{ab}\times t\)
বা, \( s=\frac{u+v}2\times t\)
বা, \( s=\frac{u+u+at}2\times t \) [v = u + at ব্যবহার করে পাই]
∴ \( s=\frac{2ut+at^2}2 \)
∴ \( s=ut+\frac12at^2 \)
∴ \( s=ut+\frac12at^2 \) (প্রমাণিত)
\( v^2=u^2+2as \) -সমত্বরণযুক্ত গতির ক্ষেত্রে প্রমাণ করো।
\( v^2=u^2+2as \) -এর বীজগাণিতিক প্রমাণ –
সমত্বরণযুক্ত গতির ক্ষেত্রে চূড়ান্ত বেগ, \(v=u+at\) ___(1)
(1) নং সমীকরণকে উভয় দিকে বর্গ করে পাই, \( v^2=\left(u+at\right)^2\)
বা, \(v^2=u^2+2uat+a^2t^2\)
বা, \(v^2=u^2+2a\left(ut+\frac12at^2\right)\)
বা, \(v^2=u^2+2as\) [∵ \(s=ut+\frac12at^2\)]
∴ \(v^2=u^2+2as\) (প্রমাণিত)।
\( s_t=u+\frac12a(2t-1) \) -সমত্বরণযুক্ত গতির ক্ষেত্রে প্রমাণ করো।
\( s_t=u+\frac12a\left(2t-1\right) \) -এর বীজগাণিতিক প্রমান –
t -তম সেকেন্ড বলতে (t – 1) সেকেন্ড ও t সেকেন্ডের মধ্যে অবস্থিত 1 সেকেন্ড ব্যাপী একটি সময়ান্তর বোঝায়।
t – তম সেকেন্ডে অতিক্রান্ত দূরত্ব = t সেকেন্ডে অতিক্রান্ত দূরত্ব (s)-(t-1) সেকেন্ডে অতিক্রান্ত দূরত্ব (s’)
বা, \( s_t=\left(ut+\frac12at^2\right)-\left[u\left(t-1\right)+\frac12a\left(t-1\right)^2\right]\)
বা, \( s_t=ut+\frac12at^2-ut+u-\frac12at^2+at-\frac12a\)
বা, \( s_t=u+at-\frac12a \)
বা, \( s_t=u+\frac12a\left(2t-1\right) \)
∴ \( s_t=u+\frac12a(2t-1) \) (প্রমাণিত)
গতির ক্ষেত্রে প্রযোজ্য গতি সমীকরণগুলি লিখো।
যেহেতু মন্দনকে ঋণাত্মক ত্বরণ হিসেবে গণ্য করা হয়, তাই উপরোক্ত সমীকরণগুলিতে ত্বরণ a -এর পরিবর্তে -a লেখা হলে, সেগুলি সমমন্দনযুক্ত গতির ক্ষেত্রে প্রযোজ্য গতি সমীকরণগুলি নির্দেশ করে।
∴ সমমন্দনযুক্ত গতির জন্য –
v = u – at, \( s=ut+\frac12at^2 \), v2 = u2 – 2as, এবং \( s_t=u-\frac12a(2t-1) \)
যদি বস্তুটি স্থির অবস্থা থেকে চলতে শুরু করে, তবে u = 0।
∴ v = at2, \( s_t=u-\frac12a(2t-1) \) (সমত্বরণযুক্ত গতির ক্ষেত্রে)।
যদি বস্তুটির ত্বরণ না থাকে, তবে a = 0
∴ v = u অর্থাৎ, বস্তুটি সমবেগে চলছে।
গতীয় লেখচিত্র বলতে কী বোঝায়? এই লেখচিত্রের প্রকারভেদগুলি কী কী?
গতীয় লেখচিত্র (Graphs of motion) – X অক্ষ বরাবর সময় এবং Y অক্ষ বরাবর গতি নিয়ন্ত্রক রাশিগুলি, যেমন – বেগ, সরণ, ত্বরণ ইত্যাদির পরিবর্তন বিবেচনা করে যে দ্বিমাত্রিক লেখচিত্র অঙ্কন করা যায়, তাকে গতীয় লেখচিত্র বলা হয়।
গতীয় লেখচিত্র মূলত তিন প্রকার হয়, যথা –
- বেগ-সময় (v-t) লেখ
- সরণ-সময় (s-t) লেখ
- ত্বরণ-সময় (a-t) লেখ।
তাত্ত্বিকভাবে ত্বরণ-সময় লেখচিত্র অঙ্কন সম্ভব হলেও ব্যবহারিক ক্ষেত্রে এই লেখচিত্রের উপযোগিতা খুব বেশি নেই কেন?
তাত্ত্বিকভাবে ত্বরণ-সময় লেখচিত্র অঙ্কন সম্ভব হলেও ব্যবহারিক ক্ষেত্রে এই লেখচিত্রের উপযোগিতা খুব বেশি নেই। কারণ দ্বিমাত্রিক গতি সম্পর্কিত যে – কোনো তথ্যই প্রত্যক্ষ বা পরোক্ষভাবে v-t বা s-t লেখ থেকে পাওয়া যায়।
সমবেগে গতিশীল কণার বেগ-সময় লেখচিত্র অঙ্কন করো এবং লেখচিত্রের বৈশিষ্ট্য উল্লেখ করো।
সমবেগে গতিশীল কণা –
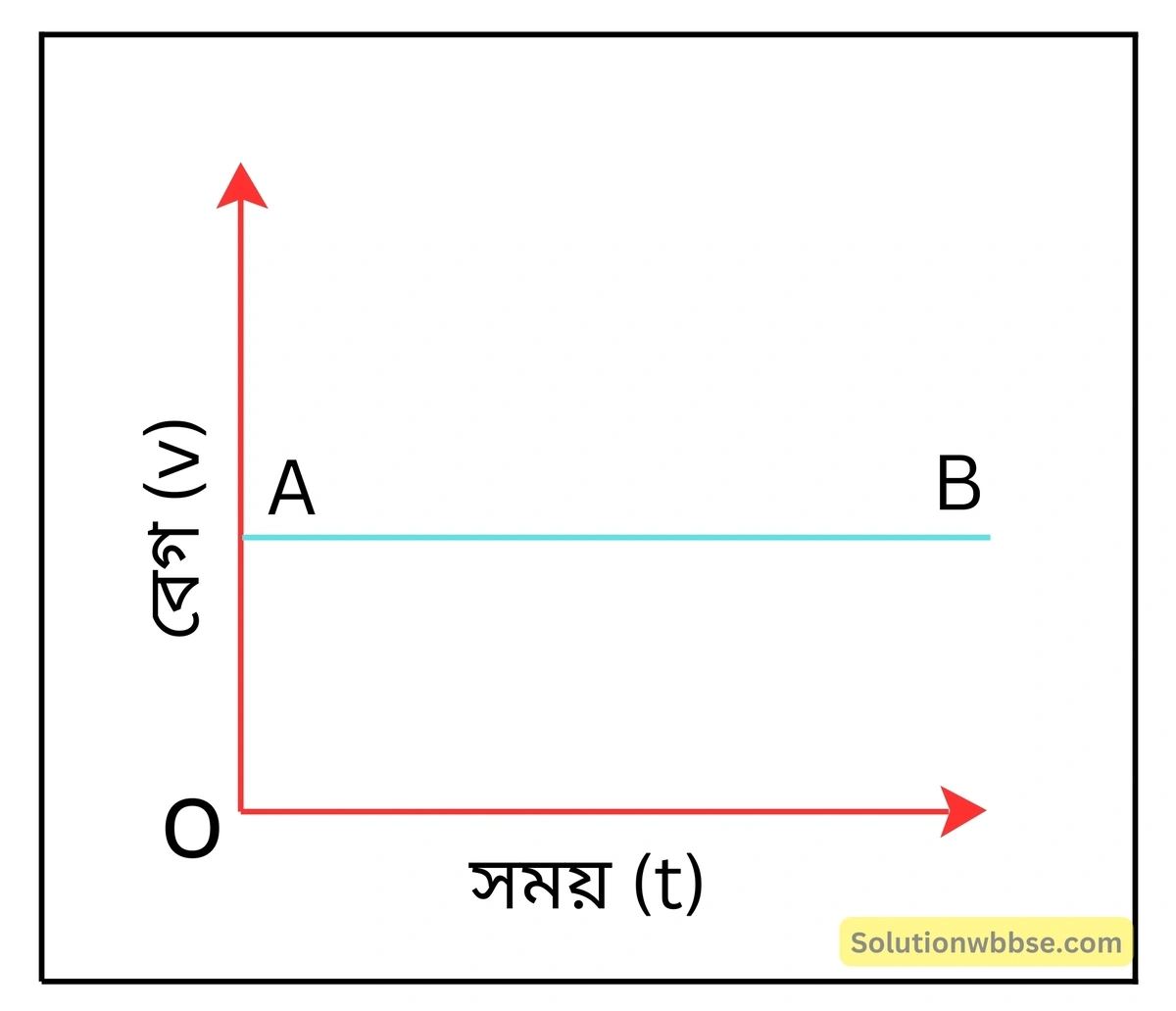
বৈশিষ্ট্য – এক্ষেত্রে বেগ-সময় লেখ (AB) সময় অক্ষের সমান্তরাল সরলরেখা হয়।
সমত্বরণসহ গতিশীল কণার বেগ-সময় লেখচিত্র অঙ্কন করো এবং লেখচিত্রের বৈশিষ্ট্য উল্লেখ করো।
সমত্বরণসহ গতিশীল কণা –
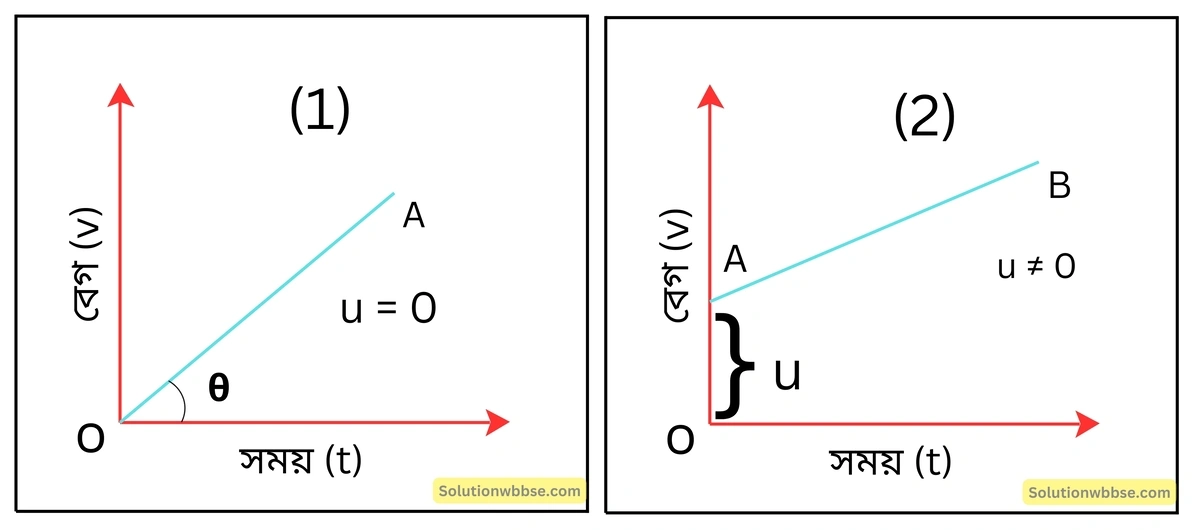
বৈশিষ্ট্য – উভয়ক্ষেত্রেই (1 ও 2) বেগ-সময় লেখ সময় অক্ষের সঙ্গে নির্দিষ্ট কোণে নত সরলরেখা।
সমমন্দনযুক্ত গতিশীল কণার বেগ-সময় লেখচিত্র অঙ্কন করো এবং লেখচিত্রের বৈশিষ্ট্য উল্লেখ করো।
সমমন্দনযুক্ত গতিশীল কণা –
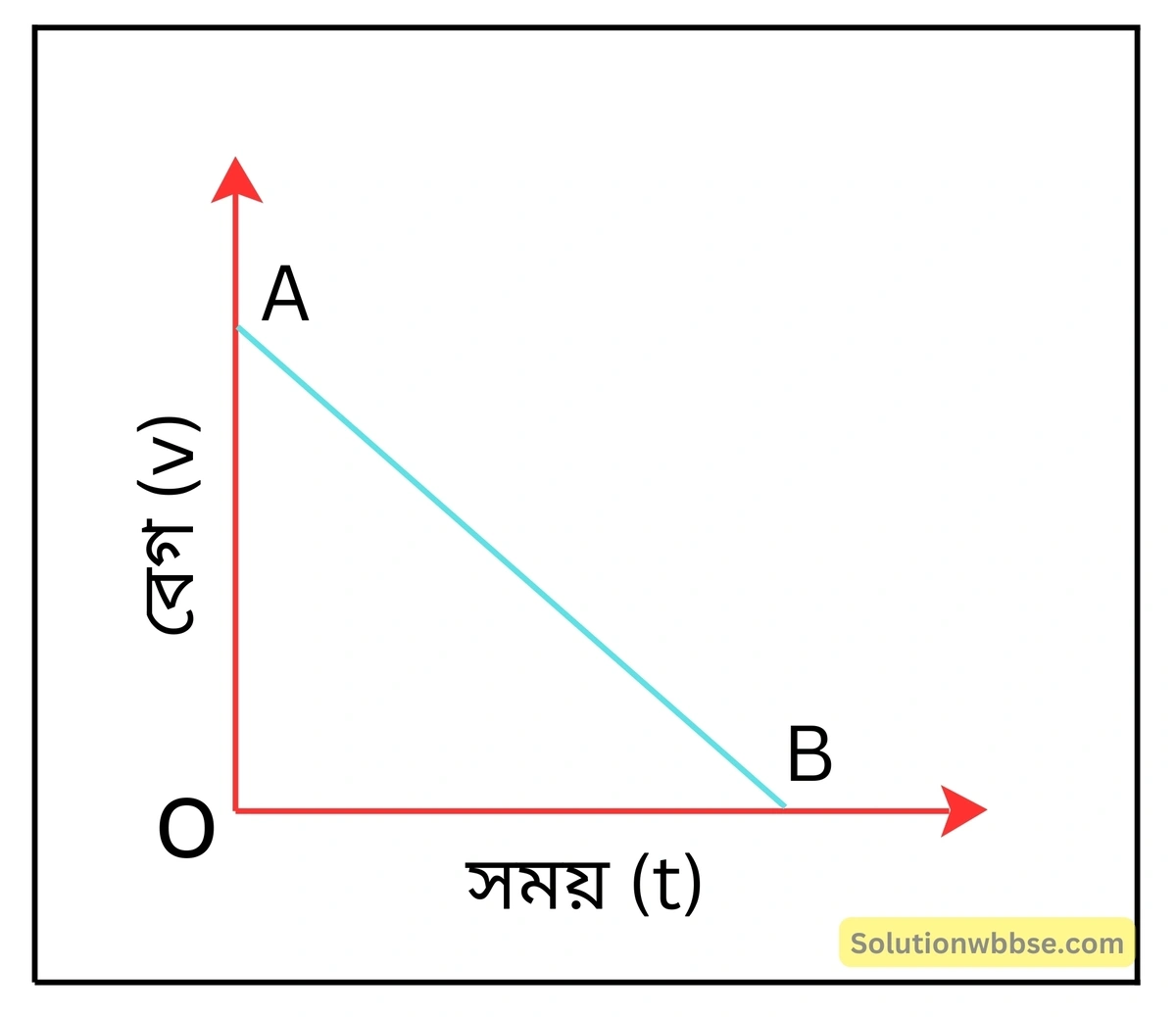
বৈশিষ্ট্য – এক্ষেত্রে বেগ-সময় লেখ ঋণাত্মক নতিযুক্ত একটি সরলরেখা (AB) হয়।
সরণ-সময় লেখচিত্র কাকে বলে?
সরণ-সময় লেখচিত্র – X অক্ষ বরাবর সময় এবং Y অক্ষ বরাবর সরণের পরিবর্তন বিবেচনা করে যে লেখচিত্র অঙ্কন করা যায়, তাকে সরণ-সময় (s-t) লেখ বলে।
সমবেগে গতিশীলর সরণ-সময় (s-t) লেখ অঙ্কন করো এবং প্রত্যেক ক্ষেত্রে লেখচিত্রের বৈশিষ্ট্য উল্লেখ করো।
অথবা, উপরের সরণ-সময় লেখচিত্রটিতে OA লেখ থেকে তুমি বস্তুটির বেগ সম্পর্কে কী ধারণা করতে পারো?
বিভিন্ন ক্ষোভ সরণ-সময় (st) লেখচিত্র –
সমবেগে গতিশীল বস্তু –
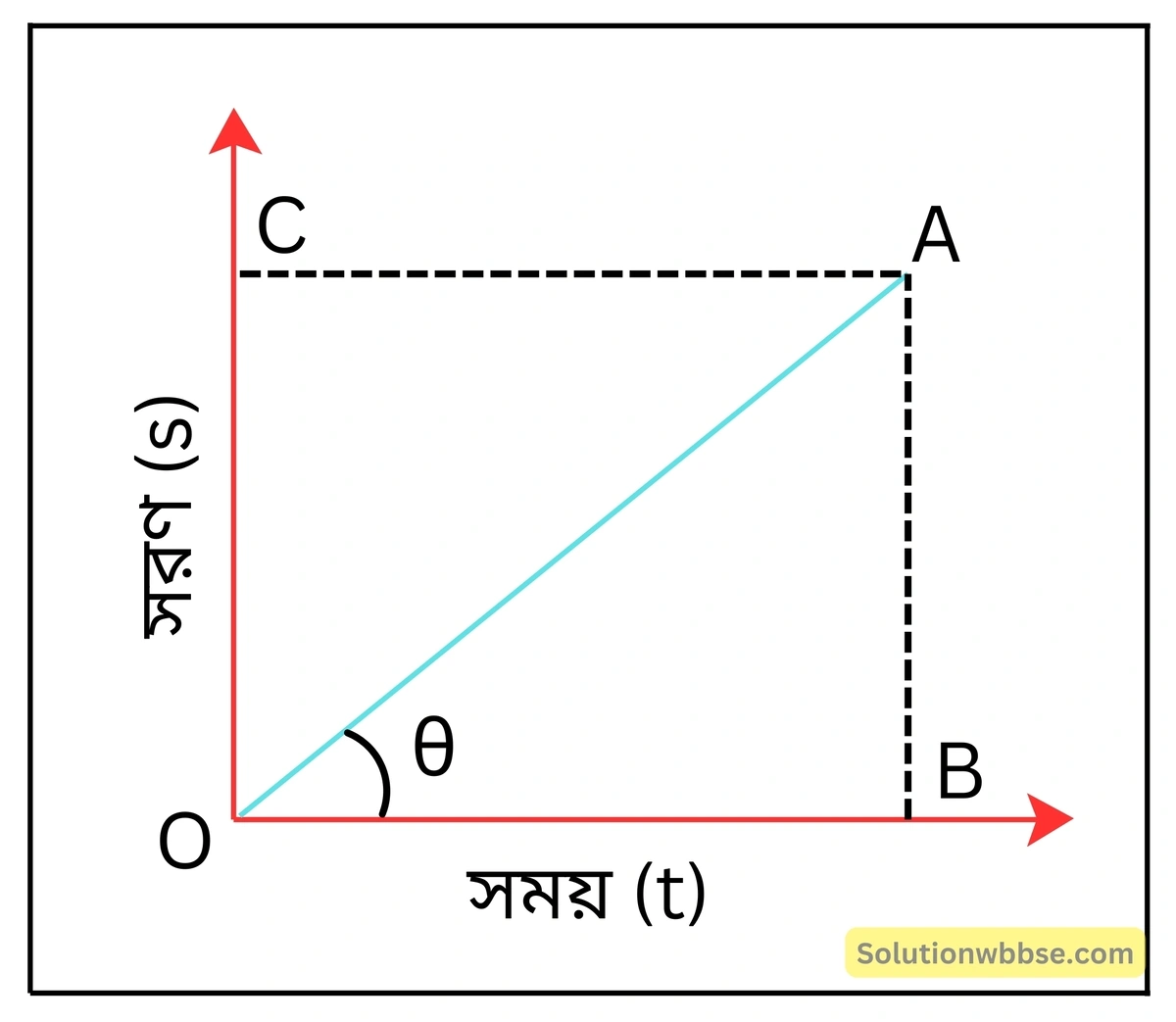
বৈশিষ্ট্য – এক্ষেত্রে (s-t) লেখ OA সময় অক্ষের সঙ্গে θ কোণে নত একটি সরলরেখা।
সমত্বরণে গতিশীল বস্তুর সরণ-সময় (s-t) লেখ অঙ্কন করো এবং প্রত্যেক ক্ষেত্রে লেখচিত্রের বৈশিষ্ট্য উল্লেখ করো।
সমত্বরণে গতিশীল বস্তু –
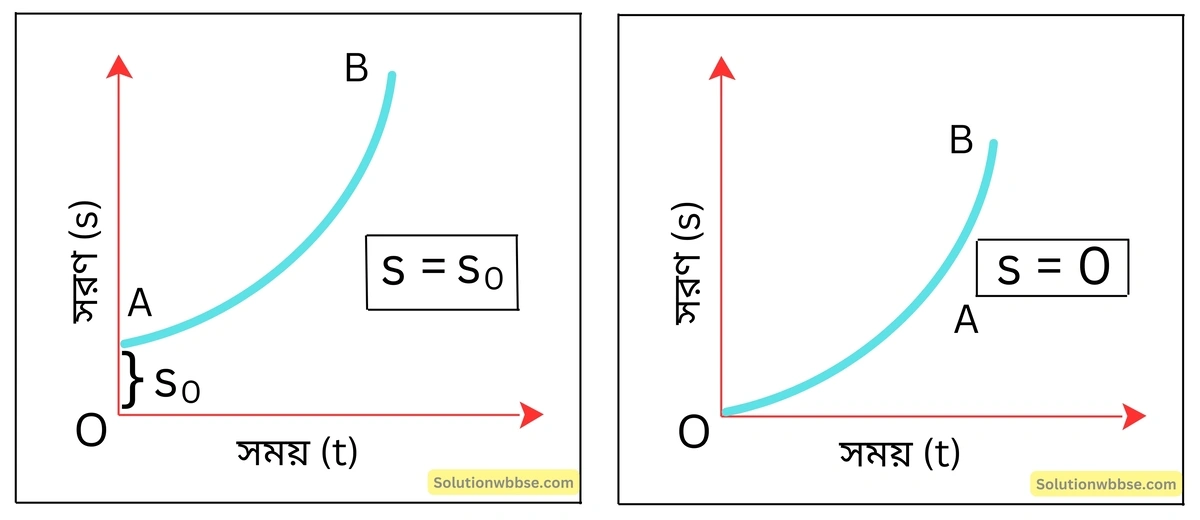
বৈশিষ্ট্য – এক্ষেত্রে (s-t) লেখ হল মূলবিন্দুগামী অধিবৃত্তাকার বক্ররেখা OAB (যখন s = 0) এবং AB (যখন S = S0) লেখর যে – কোনো বিন্দুতে অঙ্কিত স্পর্শকের নতি হল এখানে কণার তাৎক্ষণিক বেগের পরিমাপ।
অসমত্বরণযুক্ত বস্তুর সরণ-সময় (s-t) লেখ অঙ্কন করো এবং প্রত্যেক ক্ষেত্রে লেখচিত্রের বৈশিষ্ট্য উল্লেখ করো।
অসমত্বরণযুক্ত বস্তু –
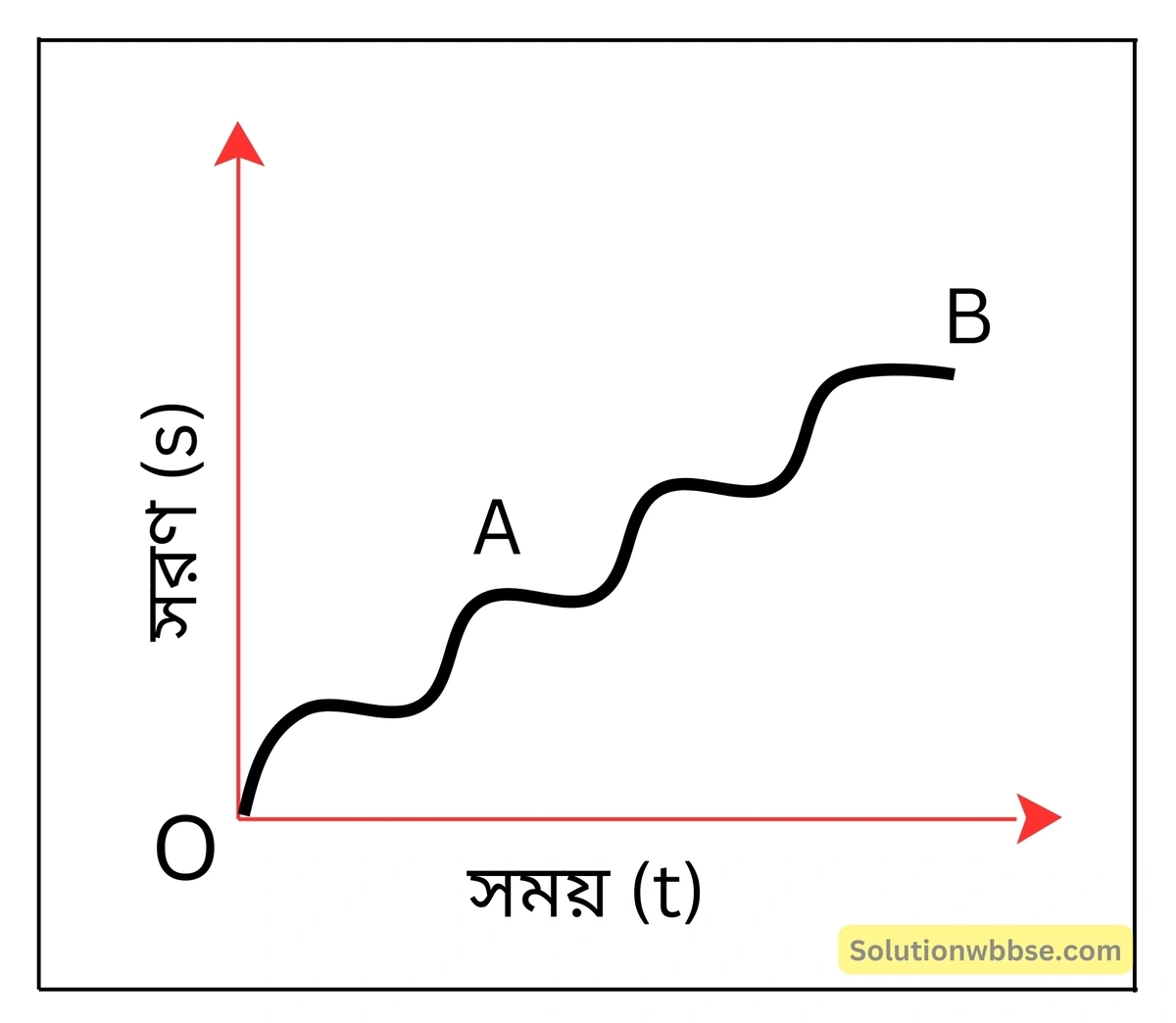
বৈশিষ্ট্য – এক্ষেত্রে সরণ-সময় (s-t) লেখ একটি অনির্দিষ্ট বক্ররেখা হয়।
গতির লেখচিত্র অঙ্কন করার পদ্ধতি সংক্ষেপে ব্যাখ্যা করো।
লেখচিত্র অঙ্কনের পদ্ধতি – ছক কাগজের ওপর পরস্পর লম্বভাবে অবস্থিত দুটি সরলরেখা X’OX ও Y’OY -কে লেখচিত্রের দুটি অক্ষ (যথাক্রমে X ও Y অক্ষ) এবং অক্ষদ্বয়ের ছেদবিন্দুকে (O) মূলবিন্দু বিবেচনা করা হয়। মূলবিন্দু এক্ষেত্রে নির্দেশবিন্দুর ভূমিকা পালন করে। উপযুক্ত একক (ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের দৈর্ঘ্য বা প্রয়োজনমতো অপর কোনো দৈর্ঘ্য) ব্যবহার করে X অক্ষ বরাবর সময় ও Y অক্ষ বরাবর সংশ্লিষ্ট বস্তু বা বস্তুকণার গতি সম্পর্কিত প্রয়োজনীয় রাশি, যেমন – সরণ, বেগ, ত্বরণ ইত্যাদির মান নির্দেশক বিন্দুগুলি স্থাপন করা হয়। সংশ্লিষ্ট বিন্দুগুলিকে সংযুক্ত করে যে সরল বা বক্ররেখা পাওয়া যায় সেটিই গতির লেখচিত্র [(s-t), (v-t), (a-t)] প্রকাশ করে।
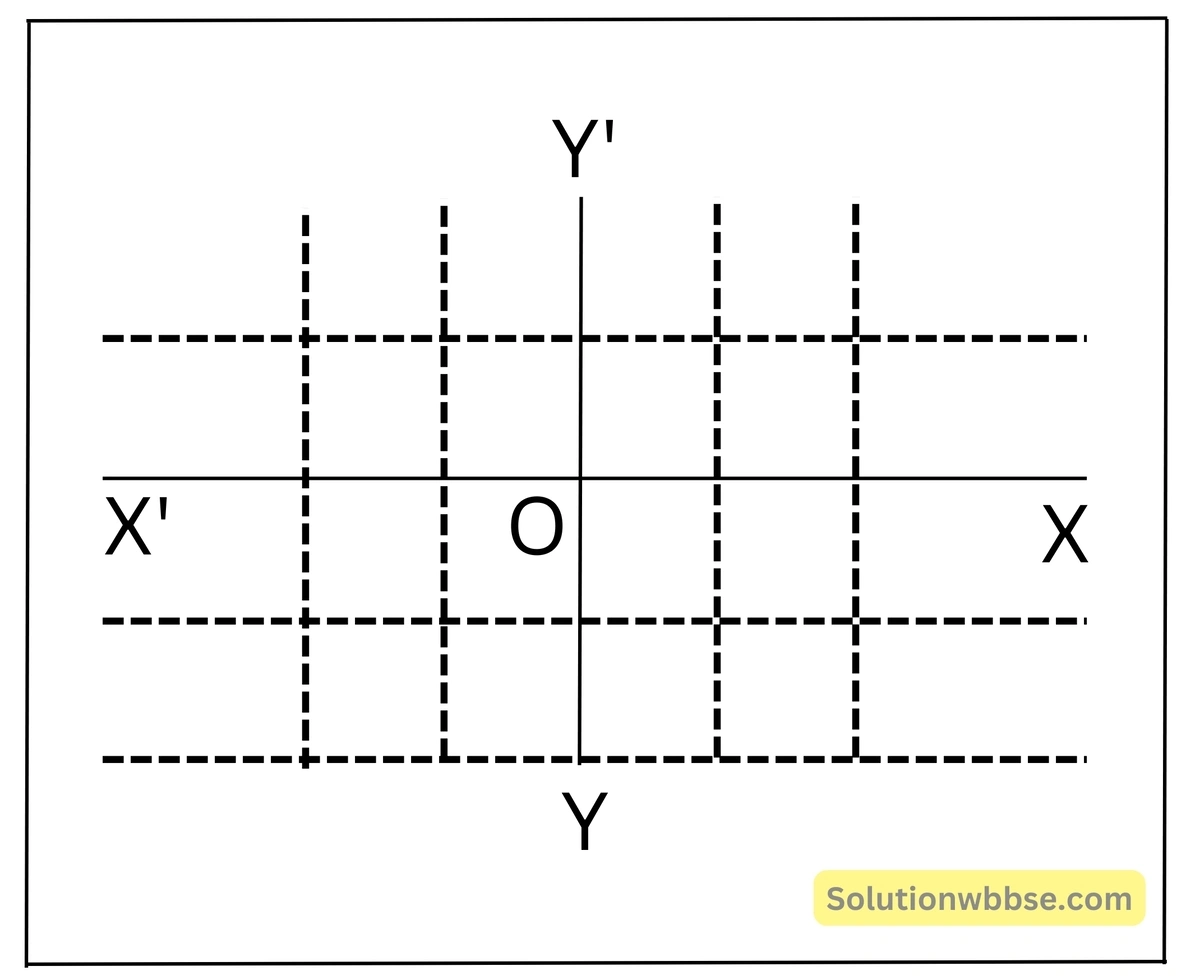
একটি গাড়ির সময়ের সাপেক্ষে দূরত্বের পরিবর্তন সম্পর্কিত প্রয়োজনীয় তথ্য নীচের দুটি সারণিতে (table) দেওয়া হল। প্রত্যেক ক্ষেত্রে দূরত্ব-সময় (s-t) লেখ অঙ্কন করো এবং তা থেকে যে যে তথ্যগুলি পাওয়া সম্ভব তা নির্ণয় করে দেখাও।
| সারণি (a) | সময় (t) | 0 | 2 | 5 | 7 | 8 |
| সারণি (a) | সরণ (s)(m) | 25 | 25 | 25 | 25 | 25 |
| সারণি b) | সময় (t) | 0 | 1 | 2 | 3 | 4 | 5 |
| সারণি (b) | সরণ (s)(m) | 0 | 10 | 20 | 30 | 40 | 50 |
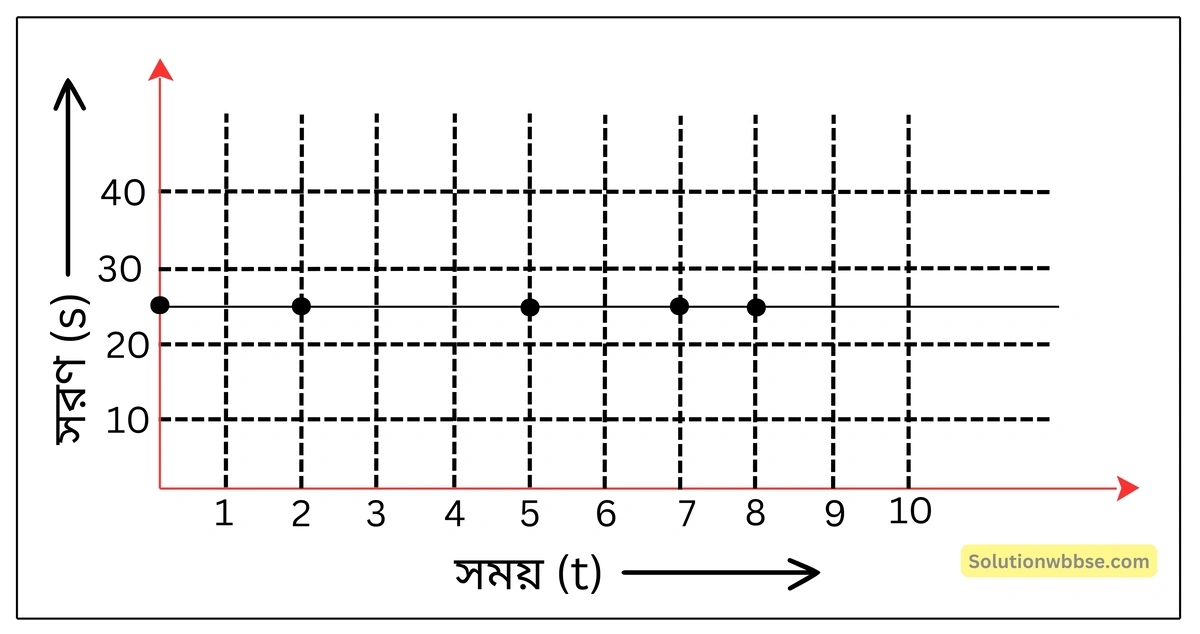
প্রথম (a) সারণিতে দেওয়া তথ্য সরণ-সময় লেখচিত্রে স্থানাঙ্ক অর্থাৎ, বিন্দুর আকারে স্থাপন করে বিন্দুগুলিকে সংযুক্ত করলে সময় অক্ষের সমান্তরাল একটি সরলরেখা পাওয়া যায়। লেখচিত্র থেকে স্পষ্ট হয় যে, সময় সাপেক্ষে সরণের মান অপরিবর্তিত থাকছে অর্থাৎ, গাড়িটি এক্ষেত্রে স্থির অবস্থায় আছে। OP দূরত্বের মান (25 m) মূলবিন্দু সাপেক্ষে গাড়িটির অবস্থান নির্দেশ করছে।
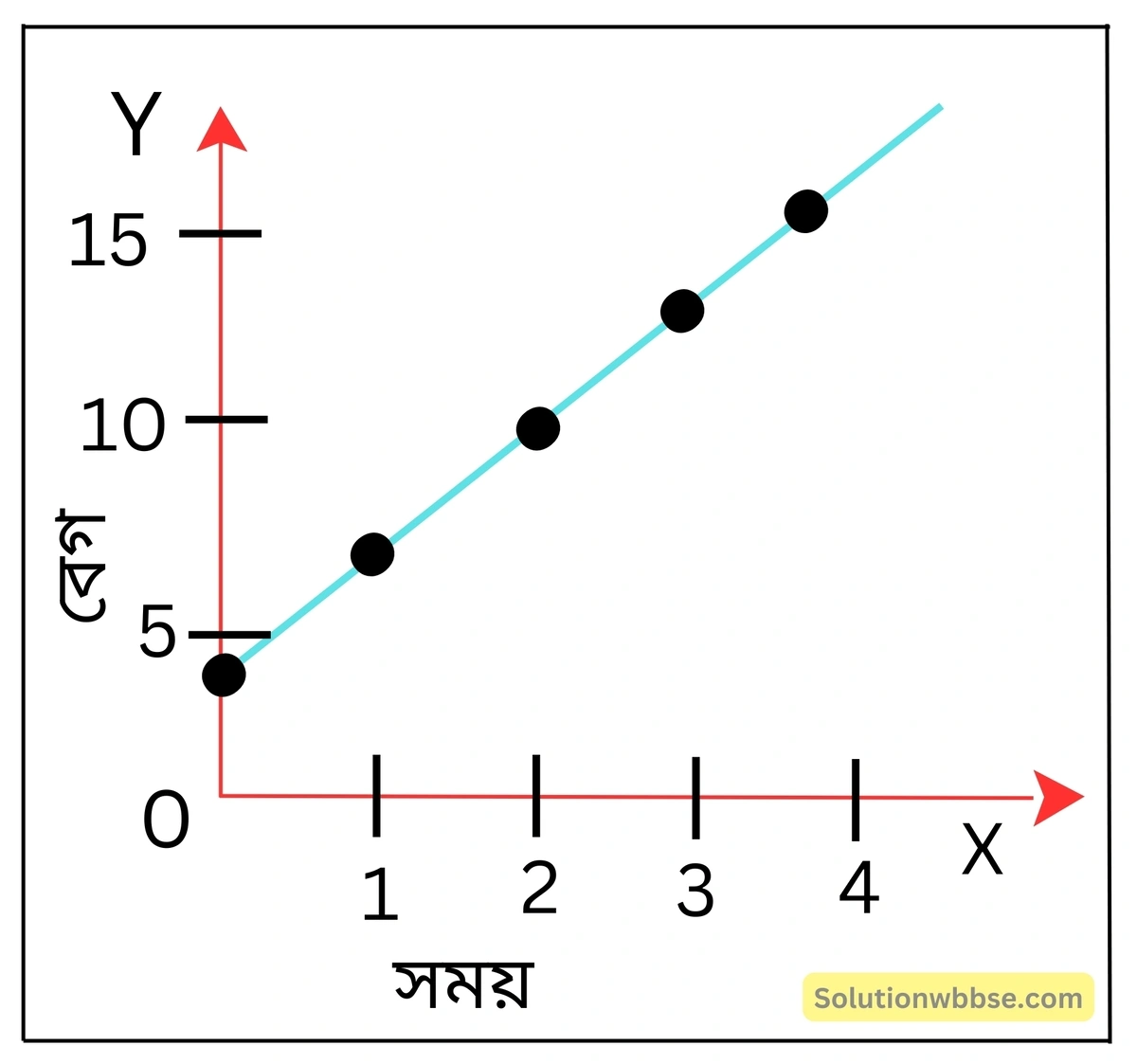
দ্বিতীয় (b) সারণিতে এক্ষেত্রে নির্দিষ্ট সময়ে গাড়ির সরণের মান নির্দেশক বিন্দুগুলি ছক কাগজে স্থাপন করে বিন্দুগুলি সংযুক্ত করলে মূলবিন্দুগামী একটি সরলরেখা OP পাওয়া যায়। লেখচিত্রের রৈখিক প্রকৃতি নির্দেশ করে যে, এক্ষেত্রে সরণ সময়ের সমানুপাতিক (s ∝ t)। OP সরলরেখার নতি গতিশীল গাড়িটির বেগের মান নির্দেশ করে।
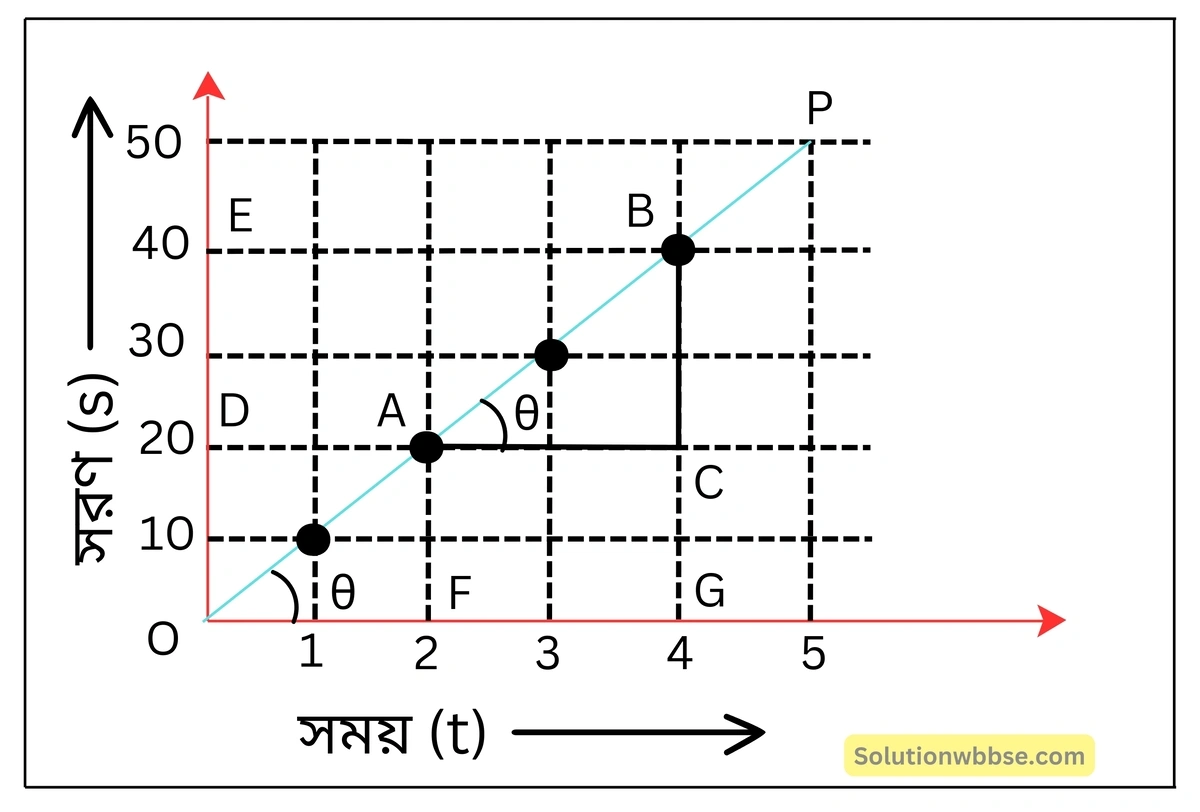
চিত্র থেকে পাওয়া যায়, লেখচিত্রের নতি
\( \tan\theta=\frac{BC}{AC}=\frac{ED}{GF}\\\)= \(\frac{\left(40-20\right)}{\left(4-2\right)}m/s\)
= \(\frac{20}2m/s\)
= \(10\;m\cdot s^{-1}\)
যেখানে, θ হল সময় অক্ষের সঙ্গে লেখচিত্রের নতিকোণ। নতির মান যত বেশি হয় (অর্থাৎ, লেখচিত্রটি যত বেশি খাড়া হয়) বেগের মান তত বৃদ্ধি পায়।
বেগ-সময় লেখচিত্র ব্যবহার করে s = vt গতীয় সমীকরণটি প্রমাণ করো।
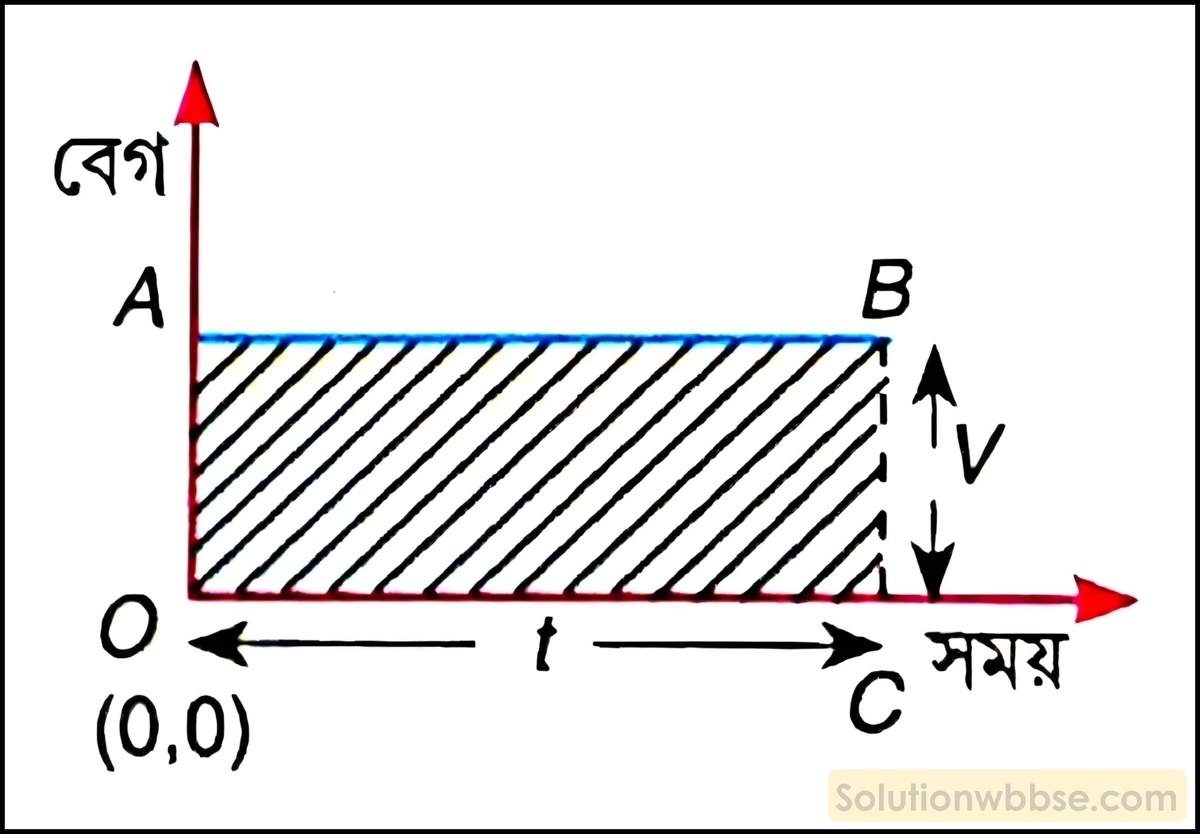
ধরা যাক, একটি বস্তু t সময় ধরে v সমবেগে চলছে।
এক্ষেত্রে বেগকে Y অক্ষ এবং সময়কে X অক্ষ বরাবর ধরলে বেগ-সময় লেখচিত্র, সময় অক্ষ অর্থাৎ, X অক্ষের সঙ্গে সমান্তরাল হবে।
প্রদত্ত চিত্রে এটি AB সরলরেখা দ্বারা প্রকাশ করা হয়েছে।
∴ বস্তুটি দ্বারা t সময়ে অতিক্রান্ত দূরত্ব s হলে,
s = AB ও স্থানাঙ্ক অক্ষ দ্বারা আবদ্ধ আয়তক্ষেত্রের ক্ষেত্রফল
বা, s = ABCO – এর ক্ষেত্রফল
বা, s = AB × CB (∵ আয়তক্ষেত্রের ক্ষেত্রফল = দৈর্ঘ্য × প্রস্থ)
বা, s = t × v (AB = t, CB = V)
বা, s = vt
∴ s = vt (প্রমাণিত)।
বেগ-সময় লেখচিত্র ব্যবহার করে v = u + at গতীয় সমীকরণটি প্রমাণ করো।
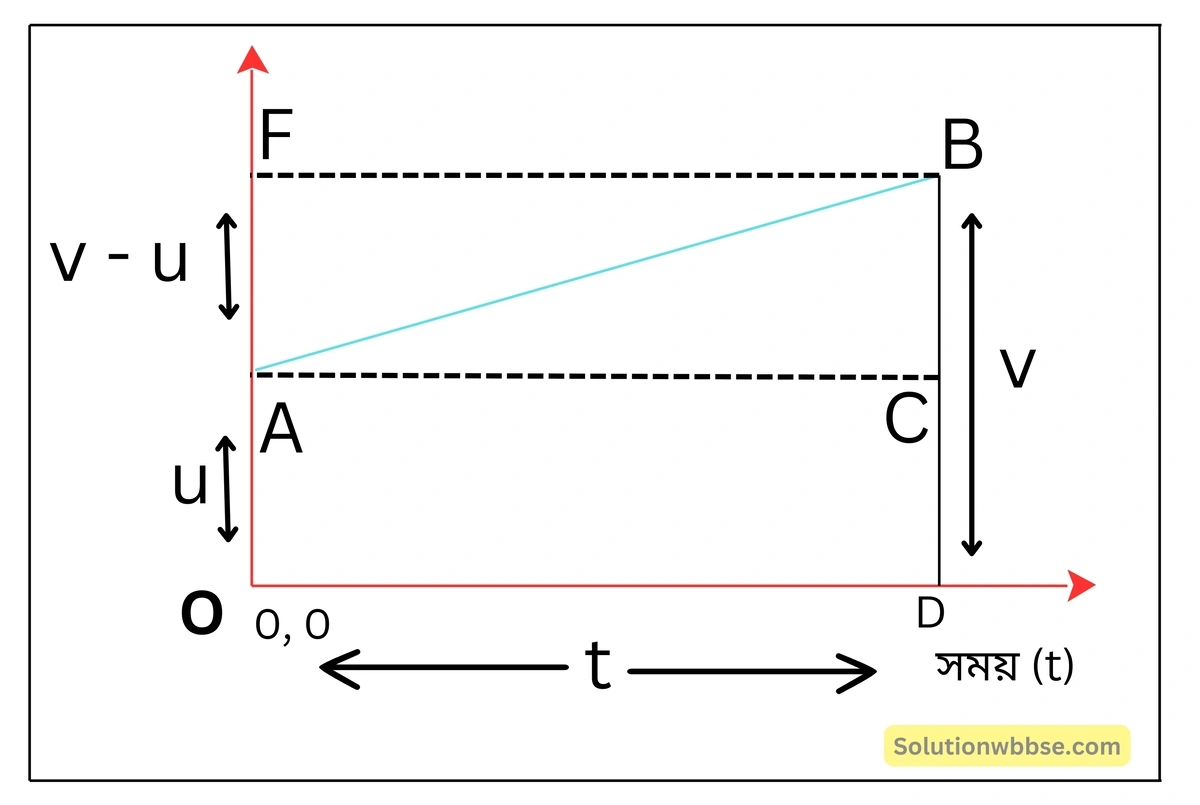
ধরা যাক, একটি বস্তুর প্রাথমিক গতিবেগ = u।
লেখচিত্রে A (0, u) বিন্দু দ্বারা এটি বোঝানো হয়েছে।
এরপর বস্তুটির বেগ ক্রমশ বাড়তে থাকে এবং t সময় পরে বেগ হয় v, লেখচিত্রে B (t, v) বিন্দু দ্বারা এটি বোঝানো হয়েছে।
লেখচিত্র অনুযায়ী, DB = DC + CB
বা, OF = OA + AF [∵ DB = OF, CB = AF, DC = OA]
বা, v = (v – u) + u [∵ OF = v, AF = OF – AO = v – u, AO = u]
বা, v = at + u [∵ a = ত্বরণ = \( \frac{v-u}t \) ∴ at = v – u]
∴ v = u + at (প্রমাণিত)।
বেগ-সময় লেখচিত্র ব্যবহার করে \(s=\frac12at^2 \) গতীয় সমীকরণটি প্রমাণ করো।
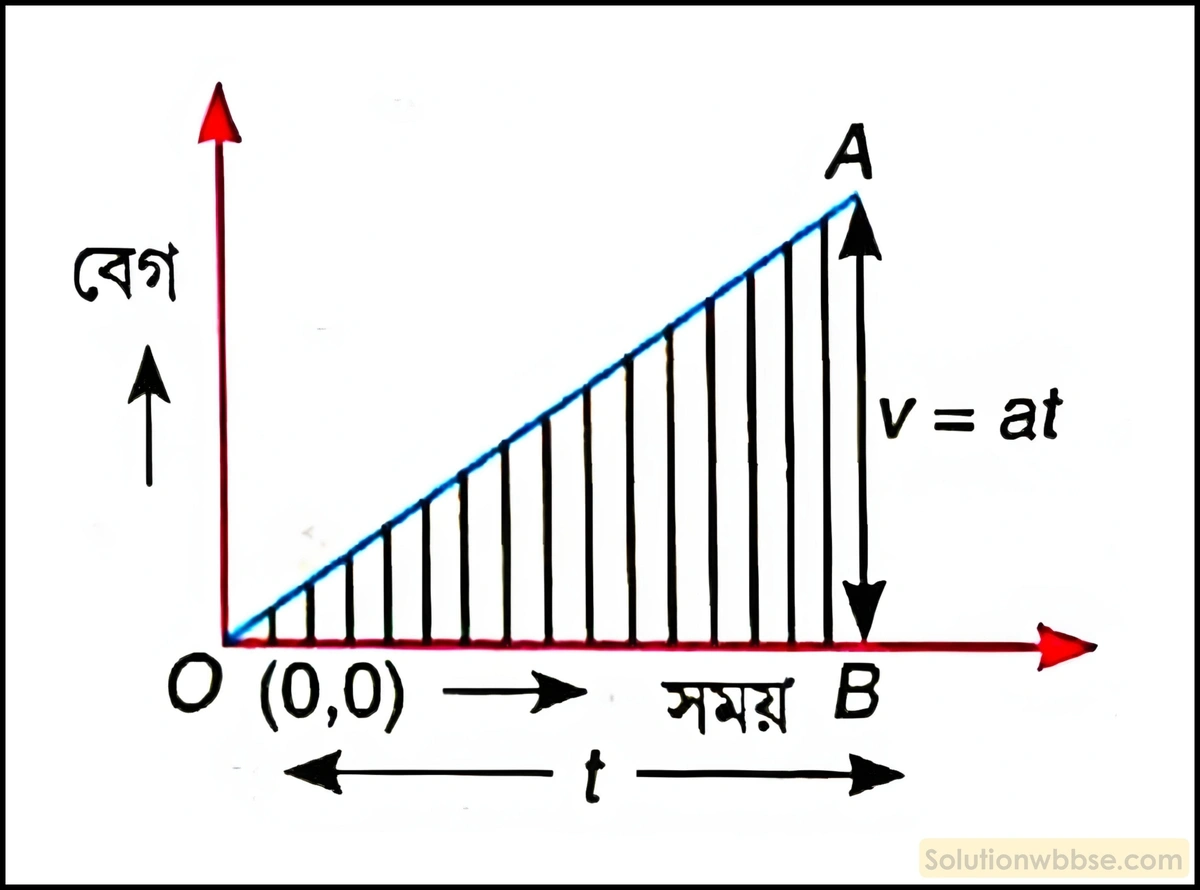
একটি বস্তুর প্রাথমিক গতিবেগ = 0, অর্থাৎ সময় = 0 হলে, বেগ = 0। O (0,0) বিন্দু দ্বারা এটি বোঝানো হয়েছে। এরপর বস্তুটির গতিবেগ ক্রমশ বাড়তে থাকে এবং সময় = t হলে বেগ = v হয়। A (t, v) বিন্দু দ্বারা এটি বোঝানো হয়েছে।
এখন বস্তুটি দ্বারা t সময়ে অতিক্রান্ত দূরত্ব s হলে
s = OAB অংশের ক্ষেত্রফল
বা, s = [∵ OAB একটি ত্রিভুজ]]
বা, \(s = \frac12\times OB\times AB\)
বা, \(s = \frac12\times t\times at\)
বা, \(s=\frac12at^2\) [∵ OB = t এবং AB = v = u + at = at (∵ u = 0)]
∴ \( s=\frac12at^2 \) (প্রমাণিত)
বেগ-সময় লেখচিত্র ব্যবহার করে \(s=ut+\frac12at^2 \) গতীয় সমীকরণটি প্রমাণ করো।
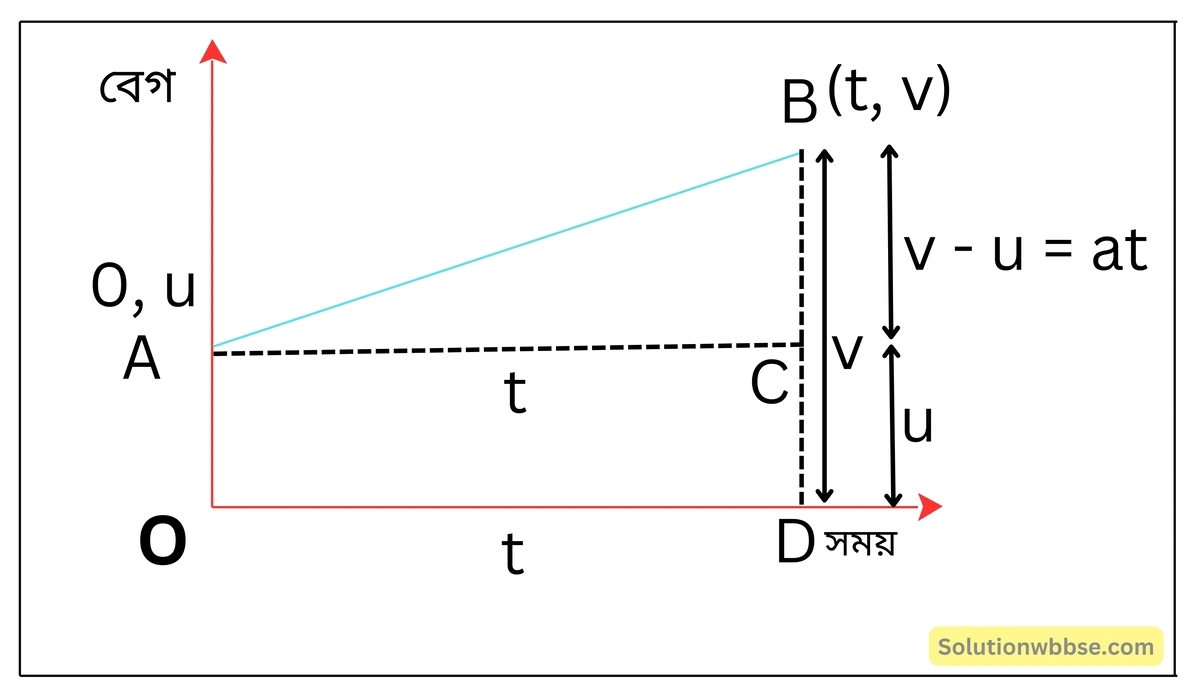
একটি বস্তুর প্রাথমিক গতিবেগ = u অর্থাৎ, সময় = 0 হলে বেগ = u।
চিত্রে, A(0, u) বিন্দু দ্বারা এটি বোঝানো হয়েছে।
এরপর বস্তুটির বেগ ক্রমশ বাড়তে থাকে এবং বস্তুটি a ত্বরণে চলতে থাকে। ফলে, t সময় পরে বেগ হয় v।
লেখচিত্রে B(t, v) বিন্দু দ্বারা এটি বোঝানো হয়েছে।
এখন বস্তুটি দ্বারা t সময়ে অতিক্রান্ত দূরত্ব s হলে,
s = ABDOA ট্রাপিজিয়ামের ক্ষেত্রফল
বা, s = ABC ত্রিভুজের ক্ষেত্রফল + ACDO আয়তক্ষেত্রের ক্ষেত্রফল
বা, \(s =\left(\frac12\times AC\times CB\right)+\left(AC\times CD\right) \) [∵ ত্রিভুজের ক্ষেত্রফল = \(\frac12\) × ভূমি × উচ্চতা]
বা, \(s=\left(\frac12\times t\times at\right)+\left(t\times u\right)\) [∵ AC = t, CB = at, CD = u]
বা, \( s=\frac12at^2+ut \)
∴ \( s=ut+\frac12at^2 \) (প্রমাণিত)।
বেগ-সময় লেখচিত্র ব্যবহার করে v2 = u2 + 2as গতীয় সমীকরণটি প্রমাণ করো।
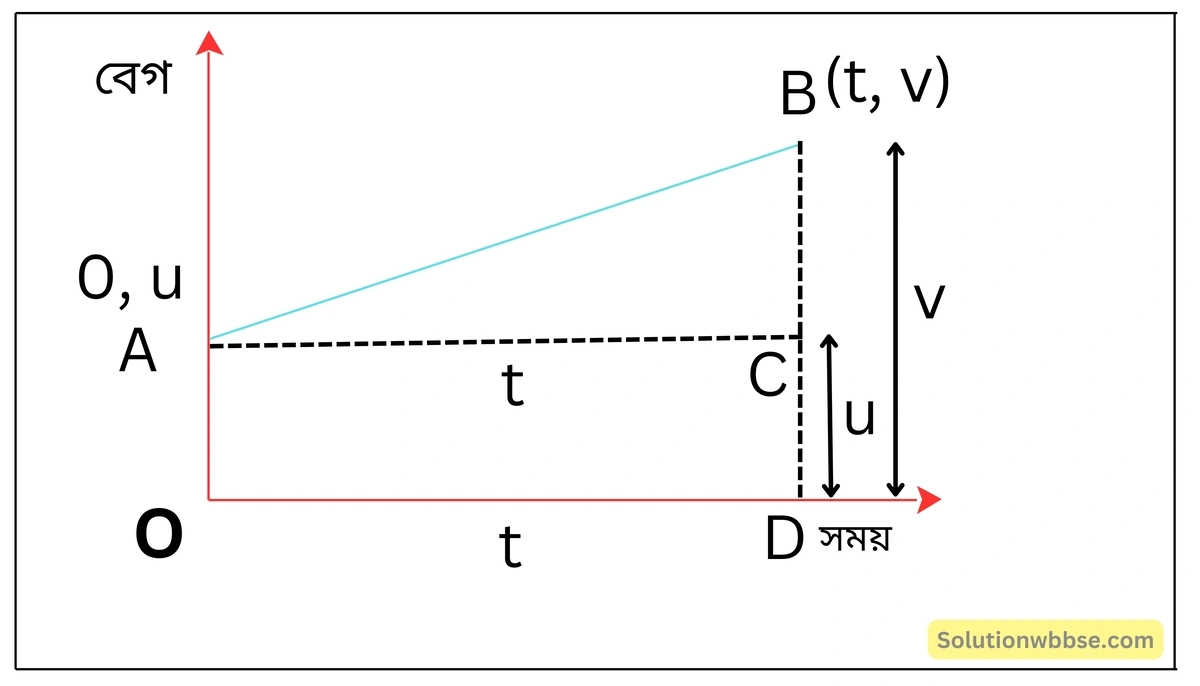
একটি বস্তুর প্রাথমিক গতিবেগ = u অর্থাৎ, সময় = 0 হলে বেগ = u।
চিত্রে A (0, u) বিন্দু দ্বারা এটি বোঝানো হয়েছে।
এরপর বস্তুটির বেগ ক্রমশ বাড়তে থাকে এবং বস্তুটি a ত্বরণে চলতে থাকে। ফলে, t সময় পরে বেগ হয় v।
চিত্রে B (t, v) বিন্দু দ্বারা এটি বোঝানো হয়েছে।
এখন বস্তুটি দ্বারা t সময়ে অতিক্রান্ত দূরত্ব ও হলে,
s = OABDO ট্রাপিজিয়ামের ক্ষেত্রফল
বা, (ট্রাপিজিয়ামের সমান্তরাল বাহু দুটির যোগফল) × বাহু দুটির মধ্যে লম্ব দূরত্ববা, \( s=\frac12\times\left(OA+BD\right)\times OD \)
বা, \( s=\frac12\times\left(u+v\right)\times t \) \( \left[∵ OA=CD=u,\;BD=v,\;OD=t\right] \)
বা, \( s=\frac12\times\left(u+v\right)\times\frac{at}a \)
বা, \( s=\frac12\times\left(u+v\right)\times\frac{v-u}a \) [∵ \(a=\frac{v-u}t\) ∴ \(at=\left(u-v\right)\)]
বা, \( s=\frac12\times\frac{\left(v+u\right)\left(v-u\right)}a \)
বা, \( s=\frac12\times\frac{\left(v^2-u^2\right)}a \)
∴ 2as = v2 – u2
∴ v2 = u2 + 2as (প্রমাণিত)।
বেগ-সময় লেখচিত্রের ব্যবহারগুলি লেখো।
বেগ-সময় লেখচিত্রের ব্যবহারগুলি হল –
- বস্তু দ্বারা অতিক্রান্ত দূরত্ব নির্ণয় করা।
- বস্তুর তাৎক্ষণিক বেগ নির্ণয় করা।
- বস্তুর ত্বরণ নির্ণয় করা।
নিম্নলিখিত পাঁচটি মান থেকে বেগ-সময় লেখচিত্র অঙ্কন করো।
বেগ ধ্রুবক (অর্থাৎ, সময় পরিবর্তনে বেগের পরিবর্তন হয় না)
বেগ ধ্রুবক হলে বেগ-সময় লেখচিত্র –
| বেগ | 3 | 3 | 3 | 3 | 3 |
| সময় | 0 | 1 | 2 | 3 | 4 |
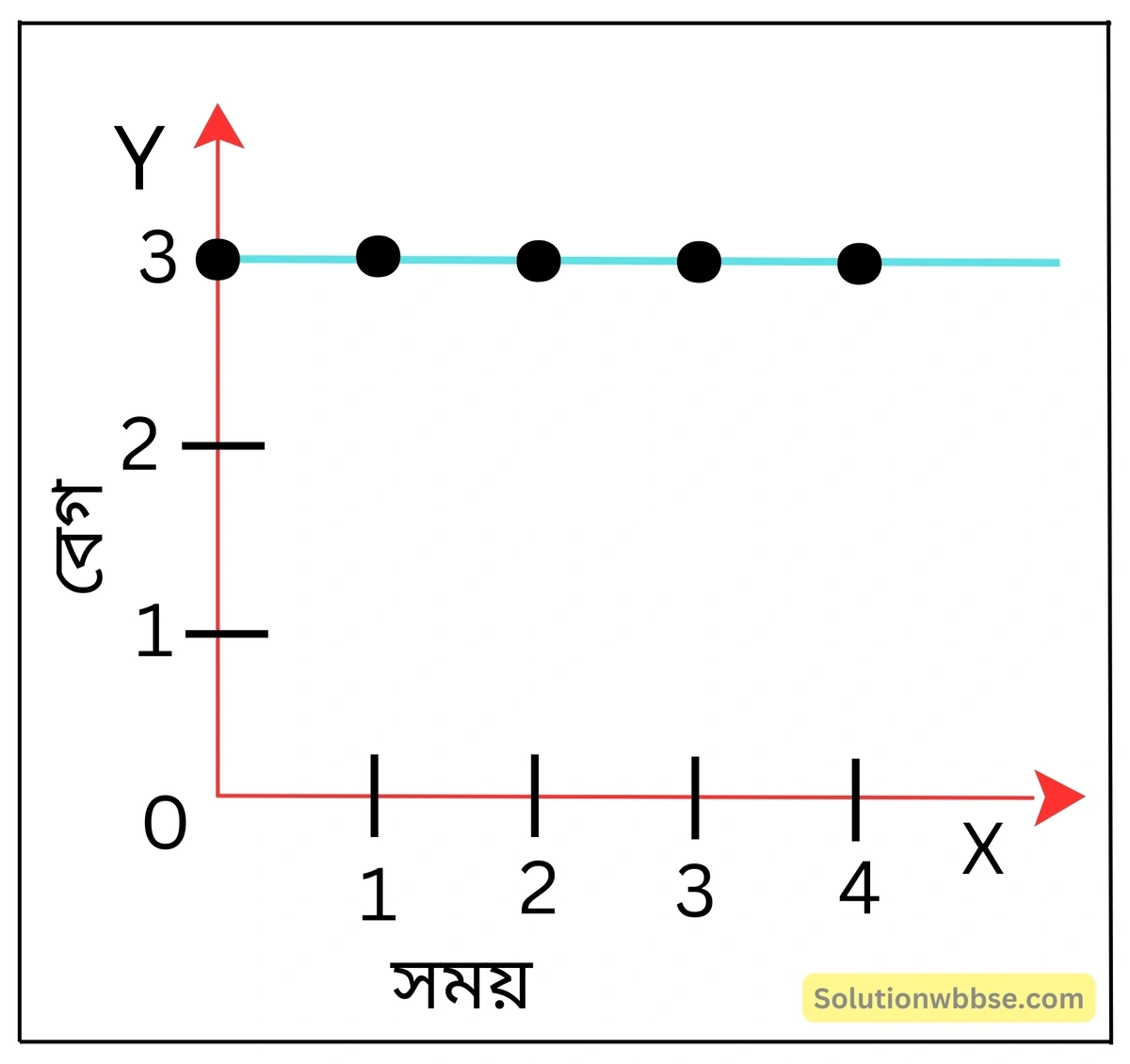
ত্বরণ ধ্রুবক প্রতিক্ষেত্রে \( \frac{v-u}t \) – এর মান ধ্রুবক অর্থাৎ ত্বরণ ধ্রুবক, যেমন – \( \frac{6-3}1=3,\frac{9-3}2=3,\frac{12-3}3=3,\frac{15-3}43 \) (চিহ্নগুলি প্রচলিত অর্থবহ)
| বেগ | 3 | 6 | 9 | 12 | 15 |
| সময় | 0 | 1 | 2 | 3 | 4 |
ত্বরণ ধ্রুবক হলে বেগ-সময় লেখচিত্র –
দেখাও যে, সমত্বরণ বা সমমন্দনযুক্ত গতির v-t লেখচিত্রের প্রকৃতি সরলরেখা হয়।
ধরা যাক, একটি বস্তুকণা প্রাথমিক বেগসহ t সময় ধরে a সমত্বরণে যাত্রা করে s দূরত্ব অতিক্রম করে। t সময় অবকাশে কণার চূড়ান্ত বেগ হয় v । কণাটির বেগ-সময় লেখচিত্র AB সরলরেখা দ্বারা নির্দেশিত হয়।
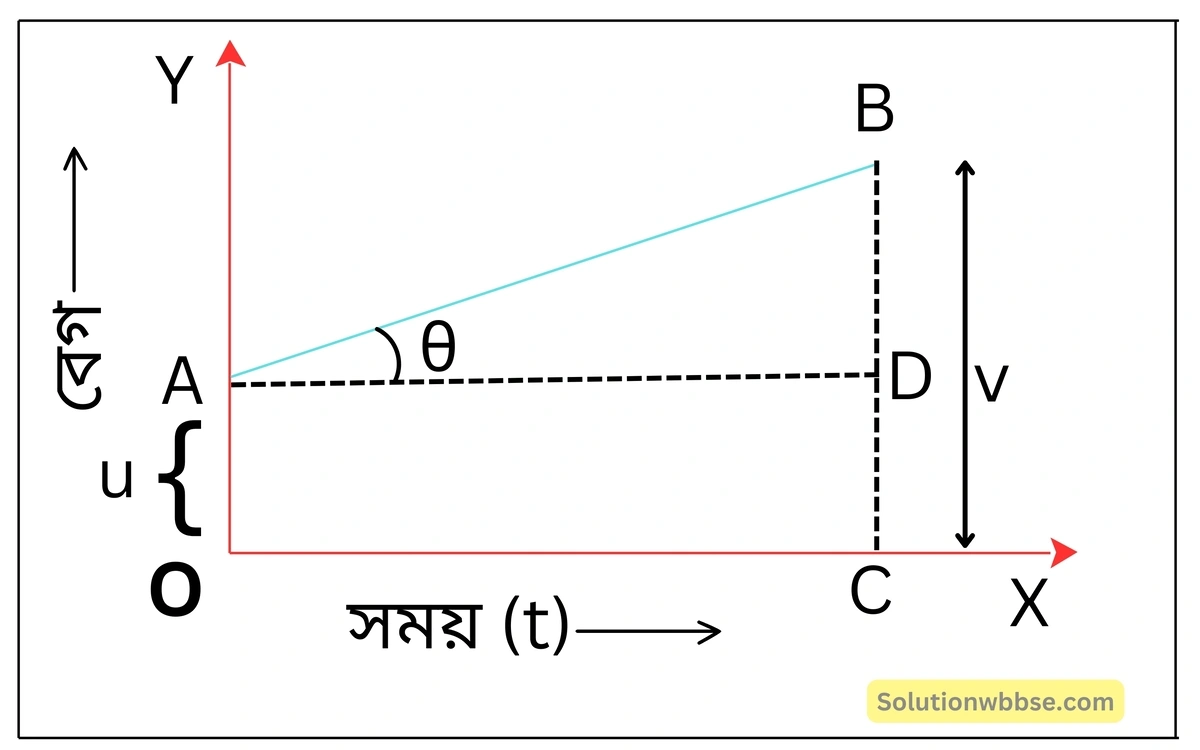
এই লেখচিত্রে, OC = t (অতিবাহিত সময়)।
CB = v (চূড়ান্ত বেগ), OA = CD = u (প্রাথমিক বেগ) সময় অক্ষ ও বেগ-সময় লেখর অন্তর্বর্তী কোণ θ
লেখচিত্রের ∆ABD অংশ থেকে পাই,
লেখচিত্রের নতি \( =\frac{BD}{AD} \)
বা, \( \tan\angle BAD=\frac{BD}{AD}\)
বা, \( \tan\angle BAD=\frac{CB-CD}{OC} \) \( \left[AD=OC=t,OA=CD=u\right] \)
বা, \( \tan\theta=\frac{v-u}t=a \)
∴ \( a=\tan\;\theta \)
∴ এখন সমত্বরণ বা সমমন্দনযুক্ত গতির ক্ষেত্রে a = ধ্রুবক, অর্থাৎ, tan θ = ধ্রুবক।
বা, θ = ধ্রুবক অর্থাৎ, গতিশীল কণার বেগ-সময় লেখচিত্র একটি সরলরেখা।
বোধমূলক প্রশ্নোত্তর
সমবেগযুক্ত গতি অবশ্যই সমদ্রুতিসম্পন্ন কিন্তু সমদ্রুতিসম্পন্ন কোনো বস্তু সমবেগযুক্ত নাও হতে পারে – ব্যাখ্যা করো।
কোনো বস্তুকণা বা বিস্তৃত বস্তু সমবেগে গতিশীল হলে গতিবেগের মান ও অভিমুখ দুই-ই অপরিবর্তনীয় থাকে। তাই, সমবেগযুক্ত গতি অবশ্যই সমদ্রুতিসম্পন্ন।
কিন্তু সমদ্রুতিসহ গতিশীল বস্তুর গতির অভিমুখ সময়ের সাপেক্ষে অপরিবর্তনীয় থাকতেও পারে, নাও পারে। ফলে গতির অভিমুখ যদি পালটে যায়, তবে সেক্ষেত্রে বেগ ভেক্টর রাশি হওয়ায় বেগ ভেক্টরের অভিমুখ ভিন্ন ভিন্ন বিন্দুতে বিভিন্ন হয়। এক্ষেত্রে, সমদ্রুতিসম্পন্ন গতি সমবেগযুক্ত একথা বলা সম্ভব নয়। যেমন – সুষম বৃত্তপথে গতিশীল কণা সমদ্রুতিযুক্ত হলেও ভিন্ন ভিন্ন বিন্দুতে বেগের অভিমুখ ভিন্ন হওয়ার কারণে একে সমবেগযুক্ত গতি বলা যায় না।
তাৎক্ষণিক দ্রুতি, সমদ্রুতি ও গড় দ্রুতির মধ্যে ব্যাবহারিক ক্ষেত্রে কোনটি বেশি প্রাসঙ্গিক?
বাস্তব জীবনের অভিজ্ঞতা থেকেই আমরা দেখতে পাই যে, চলমান কোনো যানবাহনের পক্ষে প্রযুক্তিগত বা পরিস্থিতিগত কারণেই দীর্ঘসময় ধরে একই অবকাশে একই দূরত্ব অতিক্রম করা সম্ভব হয় না। একইভাবে গতির বর্ণনায় কোনো নির্দিষ্ট মুহূর্তে দ্রুতির তুলনায় নির্দিষ্ট অবকাশে অতিক্রান্ত দূরত্বের একটি গড় হিসাবই আমরা বেশি ব্যবহার করি। তাই গড় দ্রুতির ধারণা, ব্যাবহারিক দিক থেকে বেশি উপযোগী।
ঘূর্ণায়মান বৈদ্যুতিক পাখার একটি ব্লেডের ঘূর্ণাক্ষের নিকটবর্তী অংশ ও প্রান্তীয় অংশের গতিবেগ একই হয় কি?
বৈদ্যুতিক পাখার ব্লেডের গতি হল ঘূর্ণন গতি। এক্ষেত্রে পাখার কেন্দ্রাস্থিত অক্ষের সাপেক্ষে ব্লেডের ঘূর্ণন হয়। ঘূর্ণায়মান পাখার ব্লেডের প্রতি অংশের আবর্তনের কৌণিক বেগ সমান হলেও ব্লেডের ভিতরের (ঘূর্ণাক্ষের নিকটবর্তী) ও প্রান্তীয় অংশের রৈখিক বেগ সমান হয় না। এর কারণ আবর্তনরত বস্তুর কোনো অংশের রৈখিক বেগ, ওই অংশ যে বৃত্তপথে আবর্তন করে তার ব্যাসার্ধের সমানুপাতিক হয়। ঘূর্ণাক্ষের নিকটবর্তী অংশটি প্রান্তীয় অংশের তুলনায় কম ব্যাসার্ধের বৃত্তপথে ঘোরে। ফলে, ওই অংশের রৈখিক বেগ অপেক্ষাকৃত কম হয়।

সমবৃত্তীয় গতিকে সমবেগসম্পন্ন গতি বলা যায় না কেন?
কোনো বস্তু যখন সমবৃত্তীয় গতিতে চলে তখন বস্তুটির বেগের অভিমুখ প্রতি মুহূর্তে পালটায়। কিন্তু বেগের মান পালটায় না। তবে কোনো বস্তু যখন সমবেগে চলে তখন বস্তুটির বেগের মান ও অভিমুখ সর্বদা একই থাকে।
এটি হল সমবৃত্তীয় ও সমবেগসম্পন্ন গতির মধ্যে পার্থক্য। এই পার্থক্যের জন্যই সমবৃত্তীয় গতিকে সমবেগসম্পন্ন গতি বলা যায় না।
সমবৃত্তীয় গতি কাকে বলে?
কোনো বস্তুকণা যদি বৃত্তপথে সমদ্রুতিতে গতিশীল থাকে তবে সেই গতিকে সমবৃত্তীয় গতি বলে।
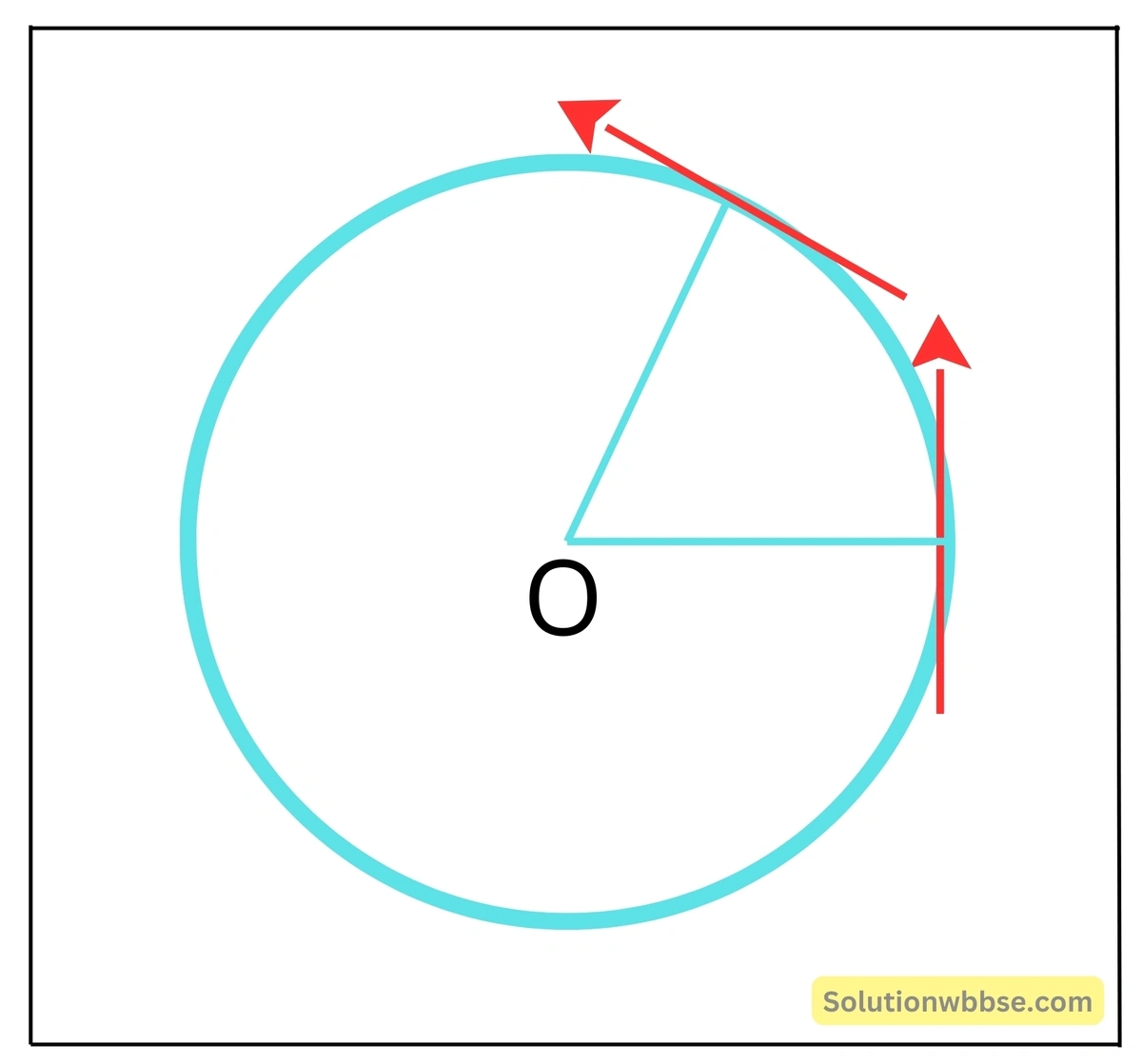
বৃত্তপথে গতিশীল অবস্থায় কণার বেগ যে-কোনো মুহূর্তে ওই বিন্দুতে বৃত্তের স্পর্শক বরাবর ক্রিয়াশীল হয়।
একটি বস্তু কিছুটা দূরত্ব অতিক্রম করল। এর সরণ শূন্য হতে পারে কি?
কোনো গতিশীল বস্তুকণা কোনো নির্দিষ্ট বিন্দু থেকে যাত্রা শুরু করে যে-কোনো পথ অনুসরণ করে আবার প্রারম্ভিক বিন্দুতে ফিরে এলে সে নির্দিষ্ট দূরত্ব অতিক্রম করে। কিন্তু এক্ষেত্রে, প্রারম্ভিক ও অন্তিম বিন্দু অভিন্ন হয় বলে এদের মধ্যেকার সরলরৈখিক দূরত্ব বা সরণ শূন্য হয়।
মন্দনকে ঋণাত্মক ত্বরণ বলা হয় কেন?
মন্দনকে ঋণাত্মক ত্বরণ বলার কারণ – ত্বরণযুক্ত গতির ক্ষেত্রে বস্তুর বেগ বাড়লেও মন্দনের ক্ষেত্রে বেগ কমে অর্থাৎ, বৈশিষ্ট্যগতভাবে মন্দন ত্বরণের বিপরীত। তাই একে ঋণাত্মক ত্বরণ বলা হয়। ধারণাটি গাণিতিকভাবেও প্রতিষ্ঠা করা যায় –
বস্তুর প্রাথমিক বেগ u ও t সময় অবকাশে চূড়ান্ত বেগ v-u হলে তার ত্বরণ – \( a=\frac{v-u}t \) (যখন v > u)
এবং মন্দন (a’) \( =\frac{v-u}t \) (যখন v < u)
এখন \( a’=\frac{u-v}t=-\left(\frac{v-u}t\right)=-a \)
সুতরাং, মন্দন ত্বরণের বিপরীত রাশি।
ত্বরণের এককে প্রতি সেকেন্ড কথাটি দুবার ব্যবহৃত হওয়ার কারণ কী?
আমরা জানি,
বা,
বা, ত্বরণের একক =
বা, ত্বরণের একক =
সুতরাং, ত্বরণের বা মন্দনের এককে প্রতি সেকেন্ড কথাটি দুবার আসে – একবার বেগ বোঝানোর জন্য এবং আর একবার বেগ পরিবর্তনের হার বোঝানোর জন্য।
বৃত্তপথে সমদ্রুতিসহ গতিশীল কোনো কণার গতি ত্বরণযুক্ত হয় কি?
অথবা, কোনো গতিশীল কণার ত্বরণ আছে, কিন্তু বেগের মান ধ্রুবক হতে পারে কি?
কোনো বস্তুকণা বৃত্তাকার পথে সমদ্রুতিসহ গতিশীল হলে বৃত্তপথের যে-কোনো বিন্দুতে অঙ্কিত স্পর্শক ওই বিন্দুতে কণার বেগের অভিমুখ নির্দেশ করে।
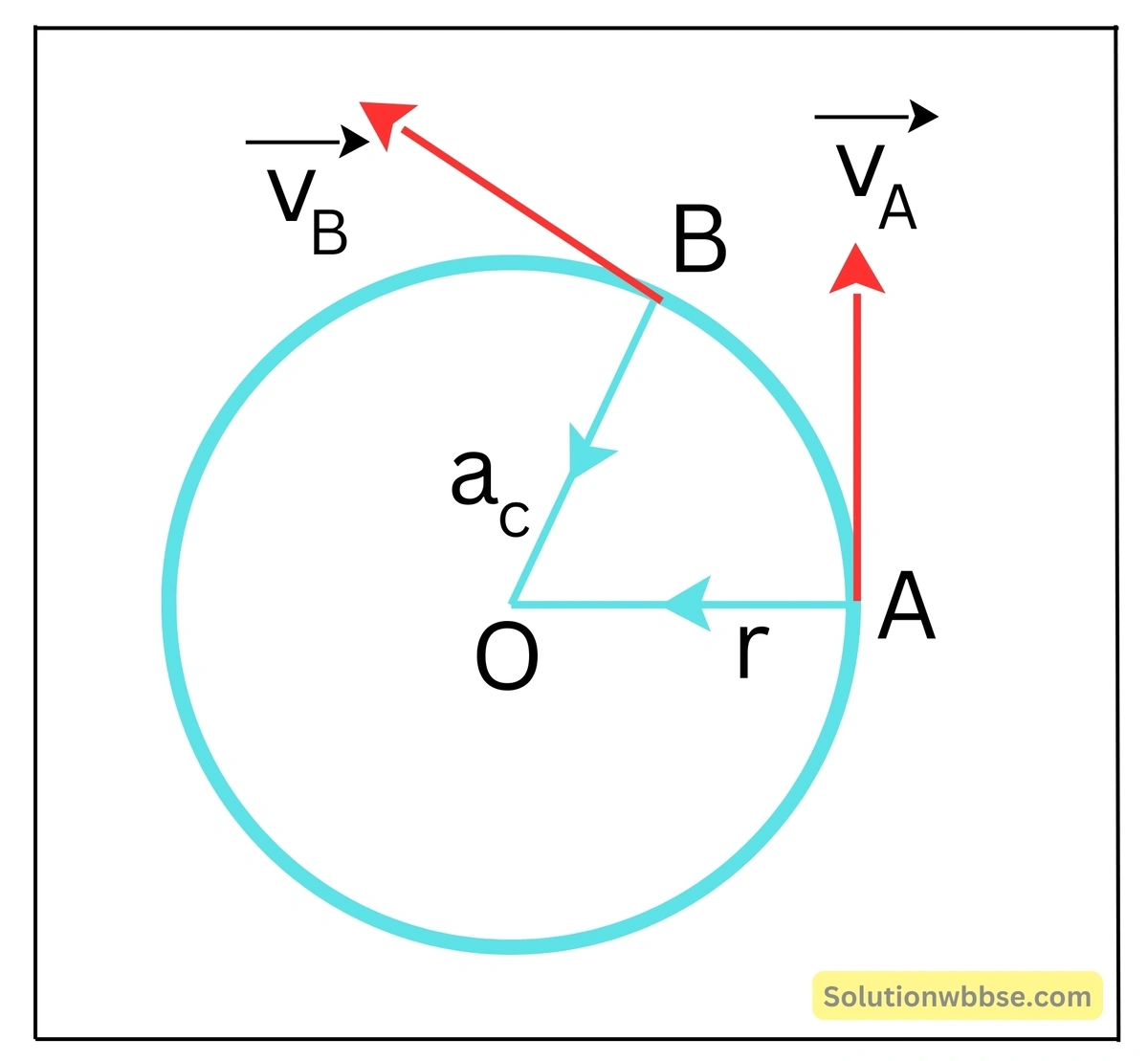
এক্ষেত্রে প্রত্যেক বিন্দুতে কণার দ্রুতি সমান হলেও অভিমুখ পরিবর্তনের জন্য A, B ইত্যাদি ভিন্ন ভিন্ন বিন্দুতে তাৎক্ষণিক বেগ \(\overrightarrow{v_A},\;\overrightarrow{v_B}\) ইত্যাদি বিভিন্ন হয়। নিরবচ্ছিন্নভাবে বেগ পরিবর্তনের জন্য বৃত্তপথের যে-কোনো বিন্দুতে বৃত্তের ব্যাসার্ধ বরাবর কেন্দ্র অভিমুখী একটি বিশেষ ত্বরণ \(\left(a_c\right)\) উৎপন্ন হয়। একে অভিকেন্দ্র ত্বরণ বলে। তাই, সমদ্রুতিসম্পন্ন বৃত্তগতির ক্ষেত্রেও বস্তুকণার ত্বরণের অস্তিত্ব থাকে।
গতিবেগ ও ত্বরণ বিপরীতমুখী হতে পারে কি?
চলমান বস্তুর বেগ যখন প্রাথমিক বেগের তুলনায় কমতে থাকে সেই অবস্থায় ওর গতিবেগ ও ত্বরণ ভেক্টরের অভিমুখ পরস্পর বিপরীত হয় যখন –
- কোনো ট্রেন স্টেশনে প্রবেশ করে।
- সরল দোলকের পিণ্ড সাম্যাবস্থান থেকে যে-কোনো প্রান্ত অভিমুখে গতিশীল হয়।
- উল্লম্বরেখায় খাড়া উঁচুতে নিক্ষিপ্ত বস্তুর বেগ ঊর্ধ্বমুখী কিন্তু বস্তুটির উপর ক্রিয়াশীল অভিকর্ষ বল এবং তার প্রভাবে উৎপন্ন অভিকর্ষজ ত্বরণ খাড়া নীচের দিকে ক্রিয়া করে।
চালকদের শেখানো হয় যে, গাড়ির গতি দ্বিগুণ হলে থামানোর দূরত্ব চারগুণ হতে হবে। – কেন?
ধরা যাক, একটি গাড়ি u বেগে গতিশীল। ব্রেক কষে গাড়িটিকে a মন্দনে থামানো হয়। ফলে s দূরত্ব গিয়ে গাড়িটি থেমে যায়। অর্থাৎ, অন্তিম গতিবেগ (v) = 0।
আমরা জানি, v2 = u2 – 2as [∵ মন্দন ঘটেছে]
বা, 0 = u2 – 2as
বা, u2 = 2as
বা, \( s=\frac{u^2}{2a} \)
বা, s ∝ u2 [∵ মন্দন (-a) = ধ্রুবক]
অর্থাৎ, গাড়ির গতি দ্বিগুণ হলে থামানোর দূরত্ব = (2)2 = 4 গুণ হবে।
তাই চালকদের শেখানো হয় যে, গাড়ির গতি দ্বিগুণ হলে থামানোর দূরত্ব চারগুণ হতে হবে।
সরণের মান অতিক্রান্ত দূরত্বের চেয়ে বেশি হতে পারে কি?
অথবা, কোন্ শর্তে সরণের মান ও অতিক্রান্ত দূরত্ব সমান হবে?
দুটি নির্দিষ্ট বিন্দুর একটি থেকে অন্যটিতে কোনো বস্তু বা কণা বিভিন্ন সম্ভাব্য পথে পৌঁছোতে পারে অর্থাৎ অতিক্রান্ত দূরত্বের একাধিক সম্ভাব্য মান থাকতে পারে। এখন, দুটি নির্দিষ্ট বিন্দুর মধ্যে নির্দিষ্ট অভিমুখে অর্থাৎ সরলরৈখিক পথে অতিক্রান্ত দূরত্বকেই বলা হয় সরণ। যেহেতু সরলরৈখিক দূরত্বই হল অতিক্রান্ত দূরত্বের সর্বনিম্ন মান, তাই সরণ ≤ অতিক্রান্ত দূরত্ব। সুতরাং, সরণের মান কখনোই অতিক্রান্ত দূরত্ব অপেক্ষা বেশি হতে পারে না।
একটি বাস্তব উদাহরণ উল্লেখ করো যেখানে সমবেগযুক্ত, ত্বরণযুক্ত ও মন্দনযুক্ত গতি একই সঙ্গে উপস্থিত থাকে।
দুটি স্টেশনের মধ্যে ট্রেনের গতির ক্ষেত্রে সমবেগযুক্ত, ত্বরণযুক্ত ও মন্দনযুক্ত গতি একই সঙ্গে উপস্থিত থাকে। ট্রেনটি একটি স্টেশন ছেড়ে বেরিয়ে এলে ত্বরণ থাকার জন্য তার বেগ বাড়ে। এরপর ত্বরণ শূন্য হয় ও কিছু সময়ের জন্য ট্রেনটি সমবেগে চলে। অবশেষে ব্রেক কষে ট্রেনে মন্দন সৃষ্টি করা হলে এর বেগ ধীরে ধীরে কমে ও একসময় সেটি পরবর্তী স্টেশনে এসে স্থির হয়।
বেগ শূন্য অথচ ত্বরণ বর্তমান এমন একটি ঘটনার উদাহরণ দাও।
খাড়া বা উল্লম্বভাবে নিক্ষিপ্ত বস্তুর গতির সর্বোচ্চ অবস্থানে বেগ শূন্য হলেও বস্তুটির উপর ত্বরণ (অভিকর্ষজ ত্বরণ) ক্রিয়াশীল থাকে। অথবা, সরল দোলগতি নির্বাহকারী কণার যে-কোনো প্রান্তিক অবস্থানে বেগ শূন্য হলেও ওই বিন্দুতে অবস্থানকালে কণাটির ওপর দোলগতির সাম্যাবস্থান অভিমুখে একটি প্রত্যানয়ক ত্বরণ ক্রিয়া করে।
ত্বরণ শূন্য অথচ বেগ আছে এমন পরিস্থিতির উদাহরণ দাও।
সমবেগে গতিশীল কণার বেগ শূন্য না হলেও বেগের মান বা অভিমুখের কোনো পরিবর্তন না হওয়ায় ত্বরণ শূন্য হয়। অথবা, সরল দোলগতিতে দোলনরত কোনো বস্তুকণার সাম্যাবস্থানে বেগের অস্তিত্ব থাকলেও ত্বরণ শূন্য হয়।
বস্তুর গড়বেগ কখন গড়দ্রুতির সমান হয়?
একমাত্র রৈখিক চলন গতির ক্ষেত্রে বস্তু সমদ্রুতিতে গতিশীল হলে গড়বেগ ও গড়দ্রুতির মান সমান হতে পারে। এক্ষেত্রে মান ও অভিমুখ দুই-ই অপরিবর্তিত থাকে বলে এমনটা হয়।
গতির লেখচিত্রগুলিতে (s-t, v-t, a-t) সবক্ষেত্রেই X অক্ষ বরাবর সময়ের পরিবর্তন বিবেচনা করা হয় কেন?
লেখচিত্রে X অক্ষ বরাবর সর্বদা স্বাধীন চলরাশি ও Y অক্ষ বরাবর নির্ভরশীল চলরাশির পরিবর্তন বিবেচনা করা হয়। গতির লেখচিত্রে ব্যবহৃত চলরাশিগুলির মধ্যে সময় স্বাধীন চলরাশি এবং অন্যান্য রাশিগুলি, যেমন – সরণ, বেগ, ত্বরণ ইত্যাদি প্রত্যক্ষভাবে সময়ের ওপর নির্ভরশীল। এই কারণেই, X অক্ষ বরাবর সর্বদা সময়ের পরিবর্তন বিবেচনা করা হয়।
একই বেগ-সময় লেখচিত্রে সমত্বরণ, ক্রমবর্ধমান ত্বরণ ও ক্রমহ্রাসমান ত্বরণ কীভাবে নির্দেশিত হয়?
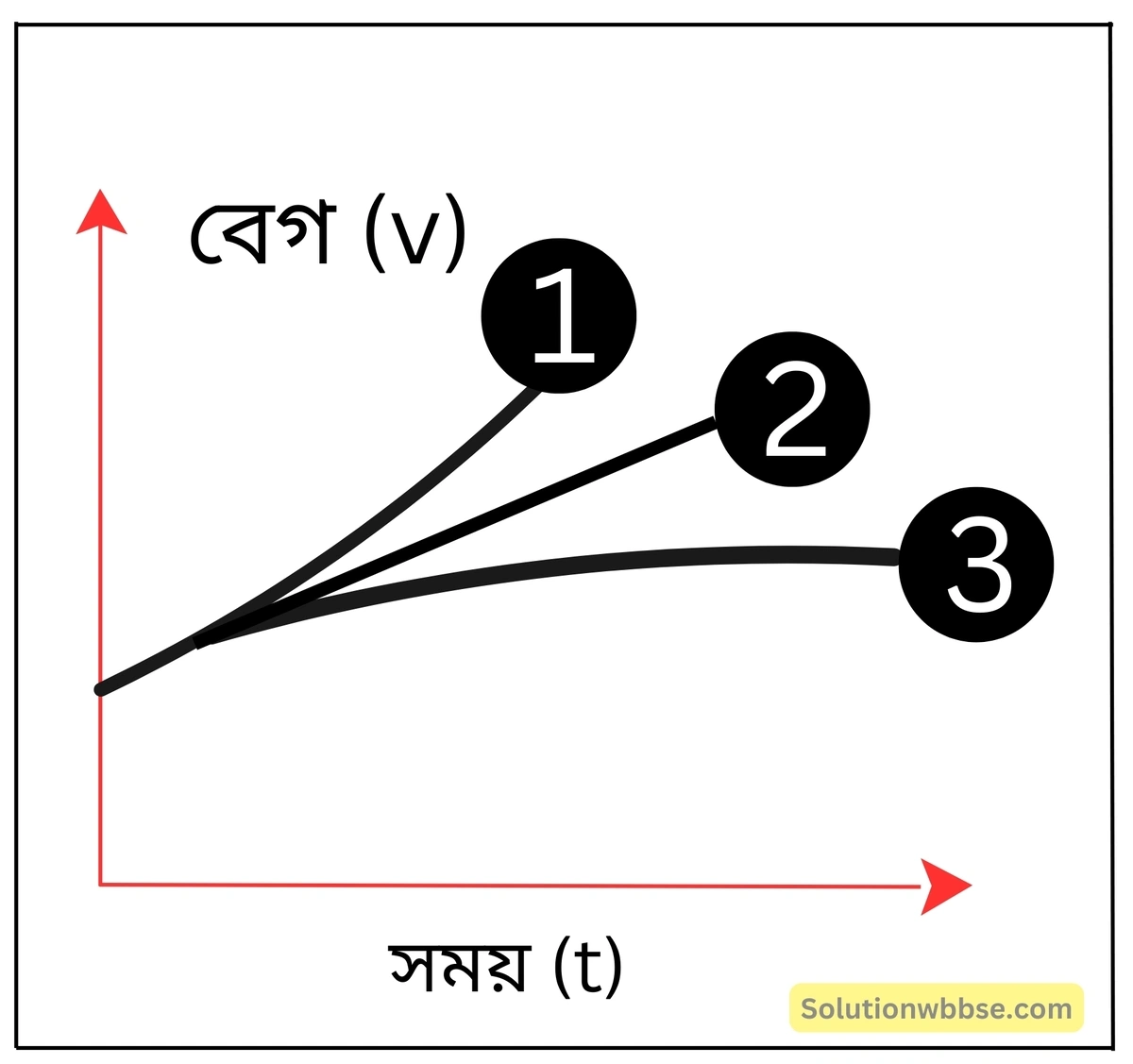
- 1 নং লেখ দ্বারা ক্রমবর্ধমান ত্বরণ
- 2 নং লেখ দ্বারা সমত্বরণ এবং
- 3 নং লেখ দ্বারা ক্রমহ্রাসমান ত্বরণ নির্দেশিত হয়।
একই বেগ-সময় লেখচিত্রে সমমন্দন, ক্রমহ্রাসমান মন্দন ও ক্রমবর্ধমান মন্দন কীভাবে নির্দেশিত হয়?
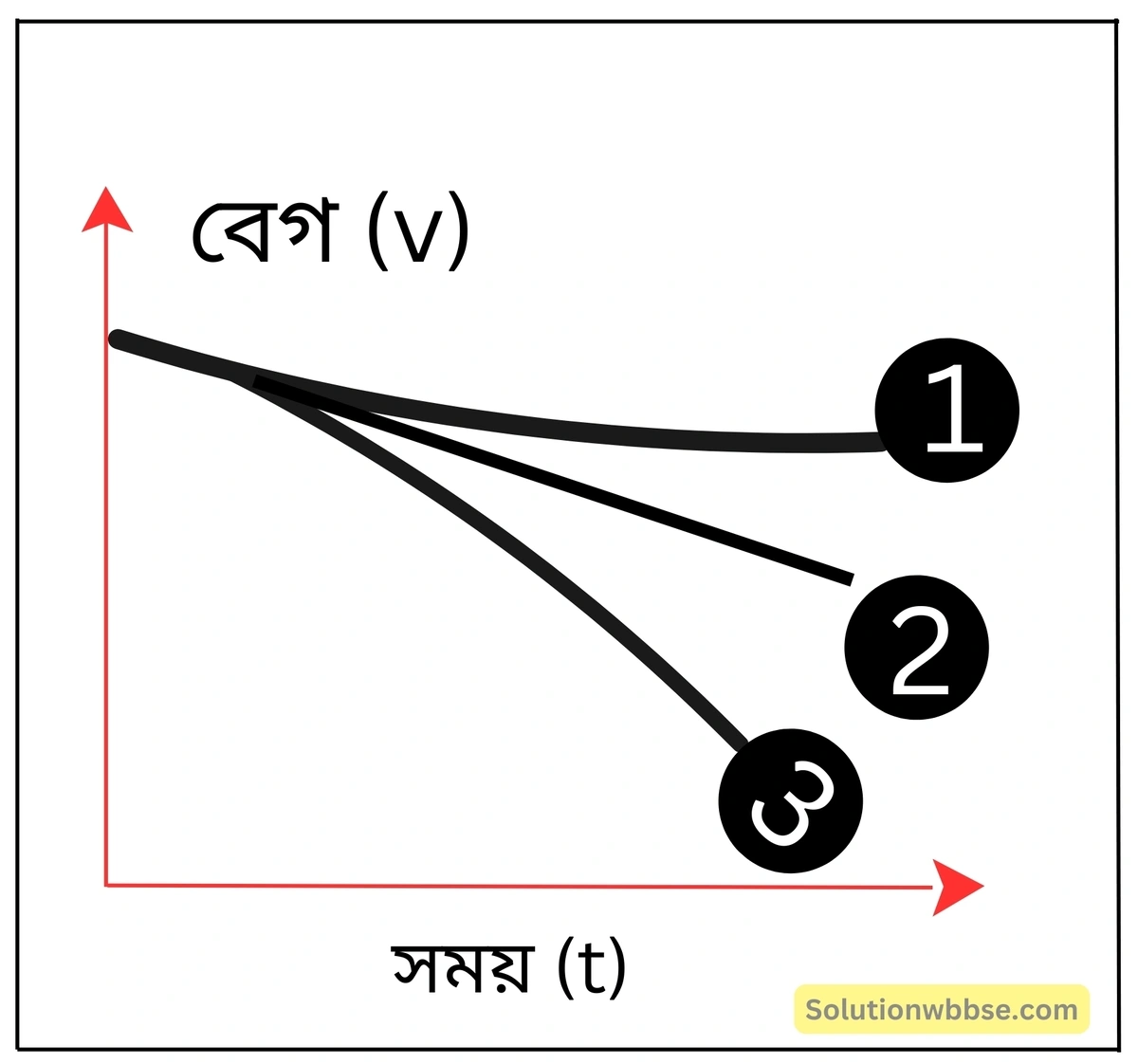
- 1 নং লেখ দ্বারা ক্রমহ্রাসমান মন্দন,
- 2 নং দ্বারা সমমন্দন এবং
- 3 নং লেখ দ্বারা ক্রমবর্ধমান মন্দন নির্দেশিত হয়।
একটি সরলরেখা বরাবর গতিশীল কণার সরণ-সময় (s-t) লেখচিত্রে দেখানো হয়েছে। কণাটির গতির প্রকৃতি সংক্ষেপে বিবৃত করো।
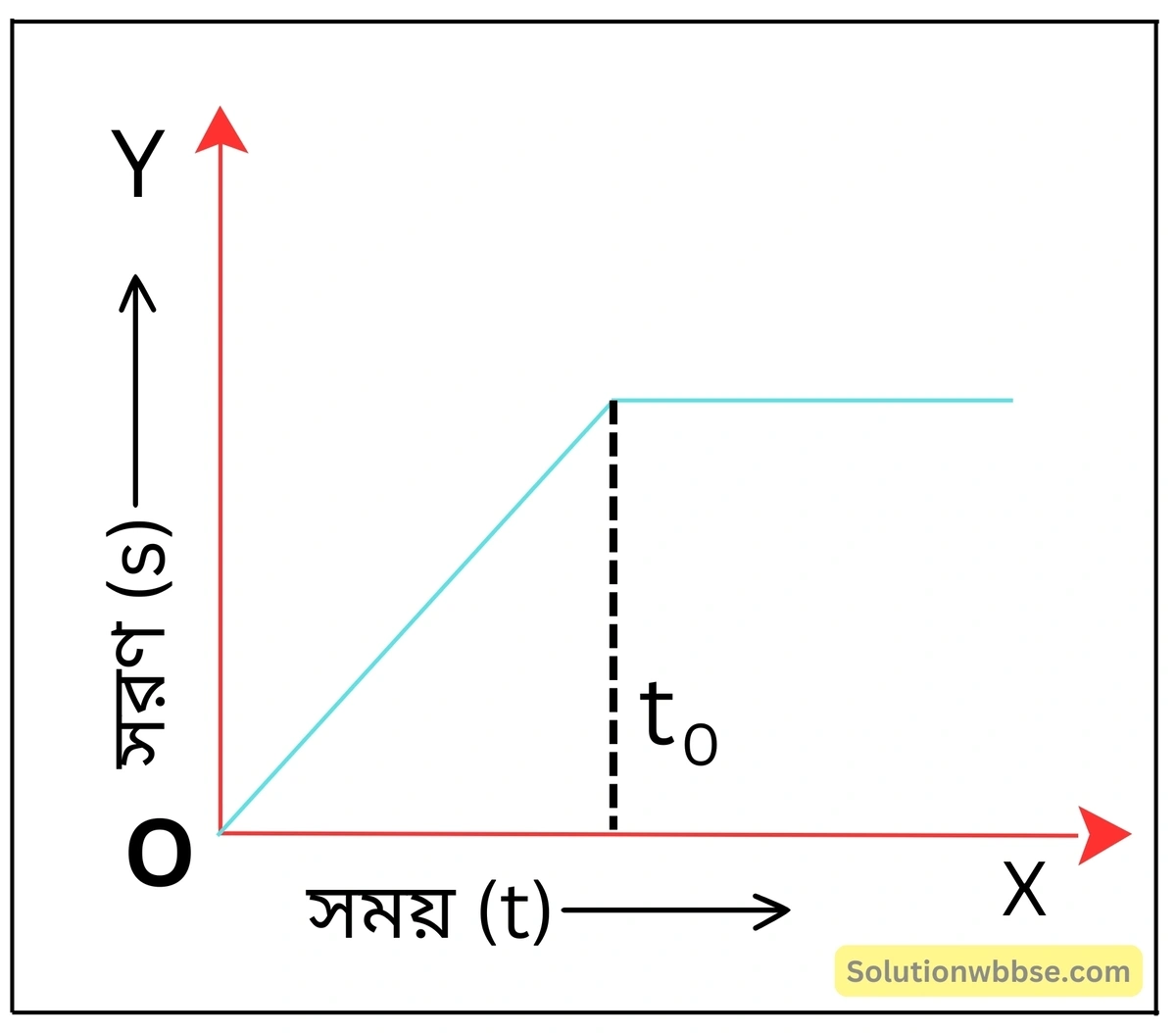
লেখচিত্র থেকে বোঝা যায় যে, কণাটি t0 সময় পর্যন্ত সমবেগে গতিশীল থাকে এবং t > t0 সময়ে স্থিরাবস্থা প্রাপ্ত হয় এবং ওই অবস্থা বজায় রাখে।
বাস্তবে কোনো কণার সরণের সাপেক্ষে সময়ের পরিবর্তন প্রদত্ত লেখচিত্রের মতো হতে পারে কি?
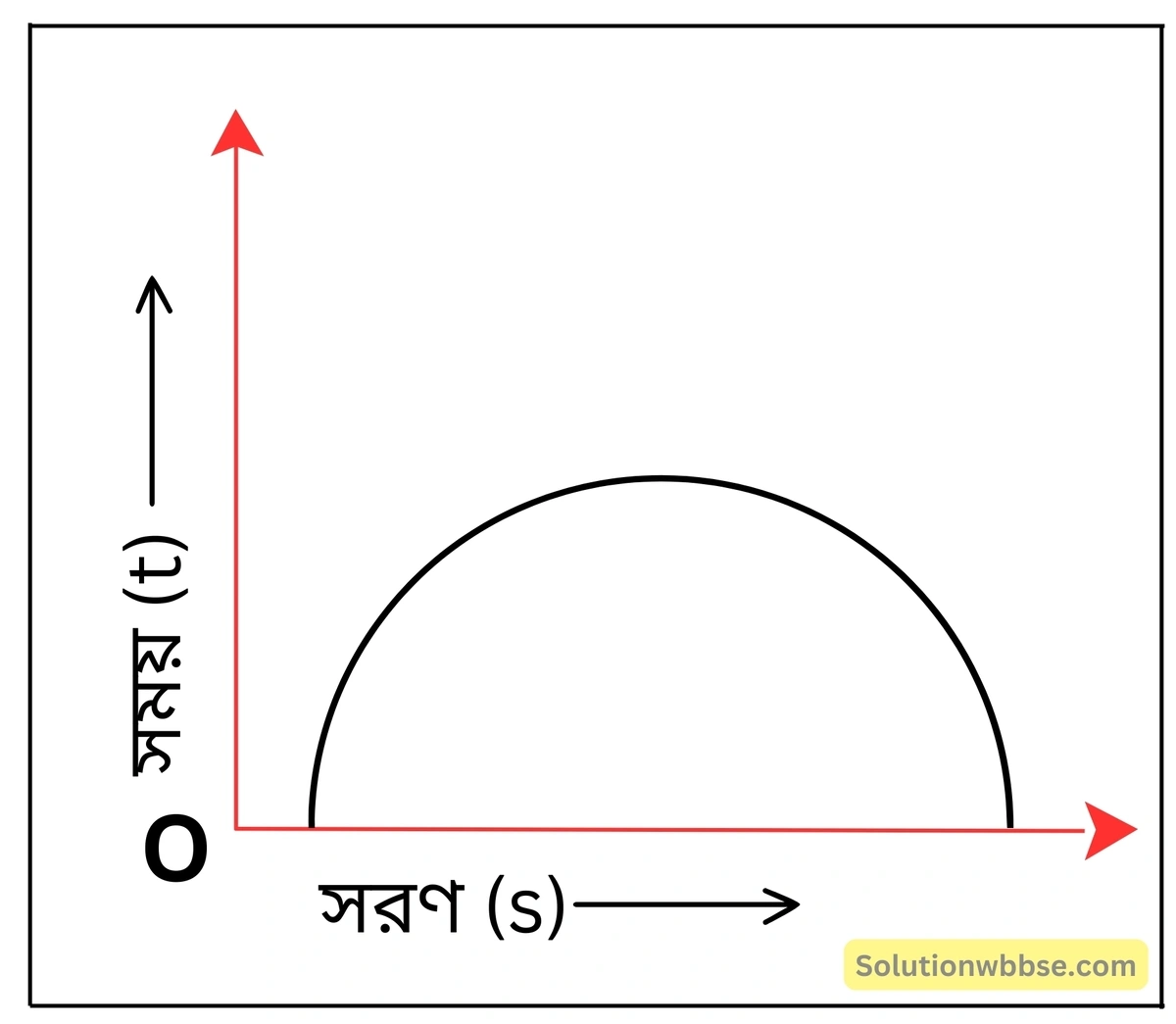
বাস্তবে এরূপ লেখচিত্র পাওয়া সম্ভব নয়। সময়ের গতি সর্বদা একমুখী, তা সর্বদাই বৃদ্ধি পায় এবং কখনোই বিপরীতমুখী হয় না অর্থাৎ, কমে না। কিন্তু চিত্র অনুসারে সরণের মান বৃদ্ধির সঙ্গে সময় প্রথমে বাড়ে এবং পরে কমে। সুতরাং, এরকম লেখচিত্রের কোনো বাস্তব অস্তিত্ব নেই।
পাশের লেখচিত্রে দুটি গাড়ি A ও B -এর জন্য দূরত্ব-সময় (s-t) লেখ প্রদর্শিত হয়েছে। কোন্ গাড়িটির দ্রুতি বেশি?
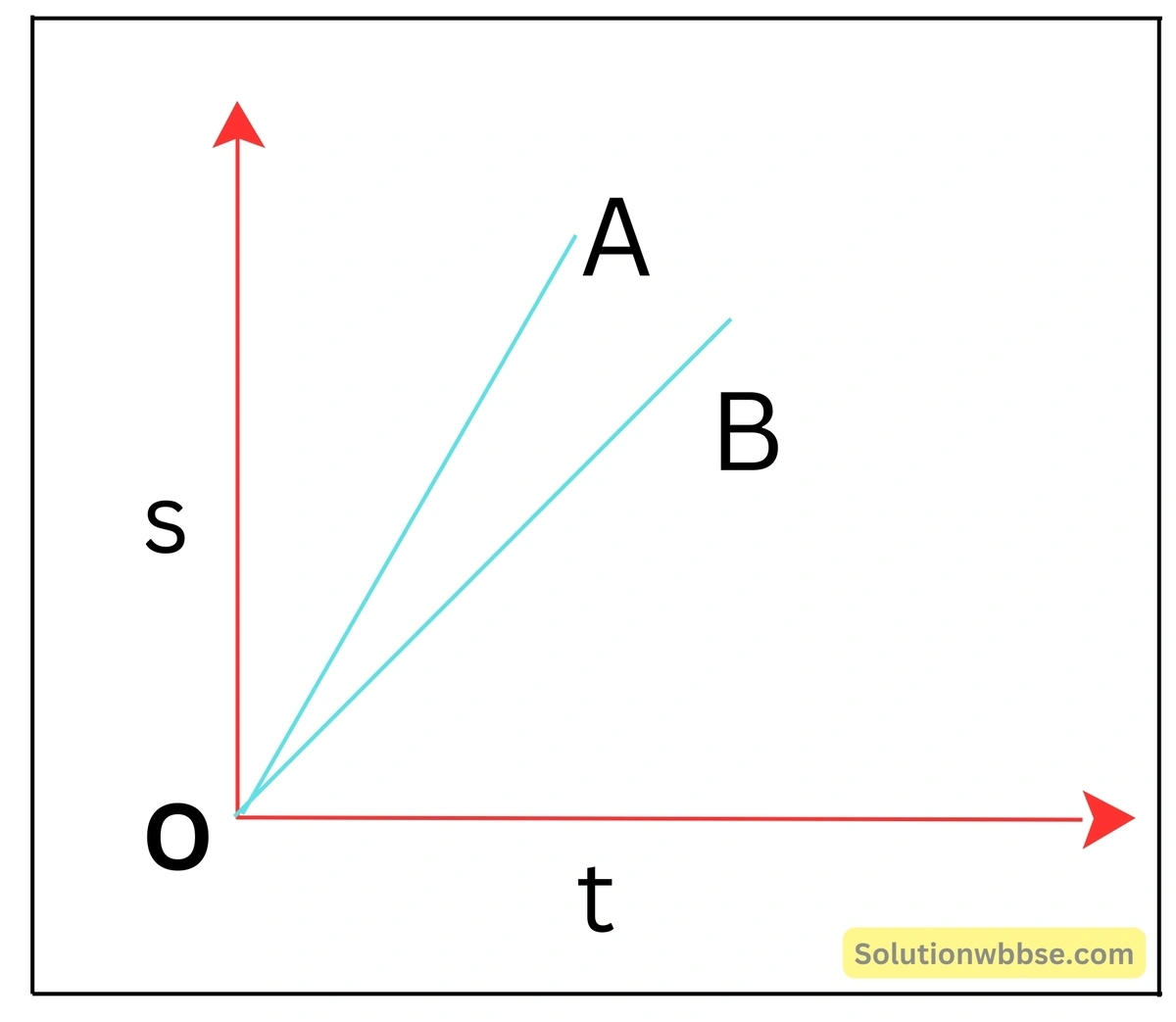
লেখচিত্র থেকে দেখা যায় যে, কোনো নির্দিষ্ট মুহূর্তে সময় অক্ষের উপর অবস্থিত নির্দিষ্ট বিন্দু C -তে অঙ্কিত লম্ব B ও A গাড়ির লেখকে যথাক্রমে E ও Fবিন্দুতে ছেদ করে।
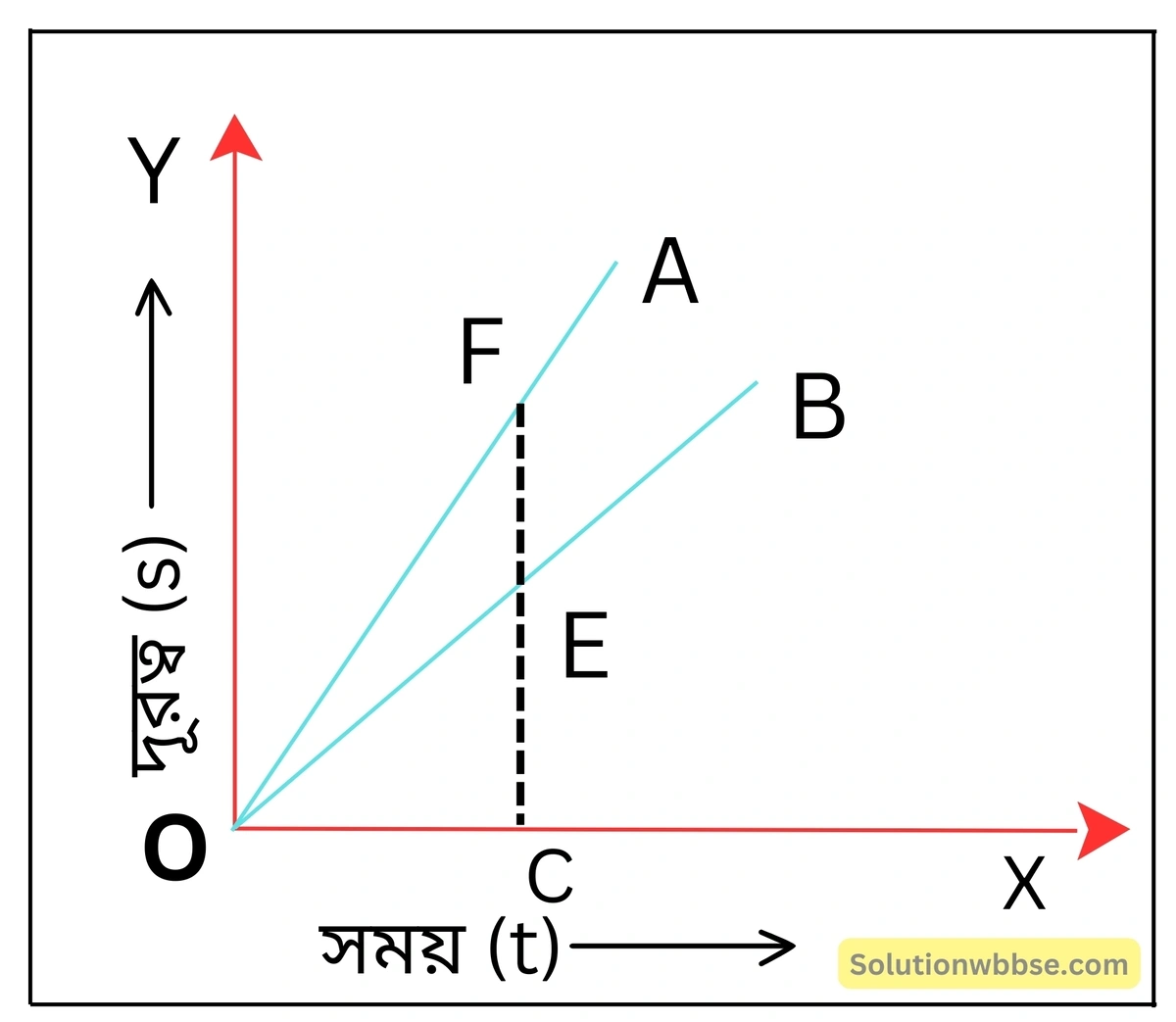
∵ CF > CE, তাই একই সময় অবকাশে A গাড়ি দ্বারা অতিক্রান্ত দূরত্ব B গাড়ি কর্তৃক অতিক্রান্ত দূরত্ব অপেক্ষা বেশি। সুতরাং, A গাড়ির দ্রুতি বেশি।
একটি গাড়ির দূরত্ব-সময় লেখচিত্র পাশের ছবিতে দেখানো হয়েছে। এটি ব্যবহার করে গাড়িটির দ্রুতি-সময় লেখচিত্র অঙ্কন করো।
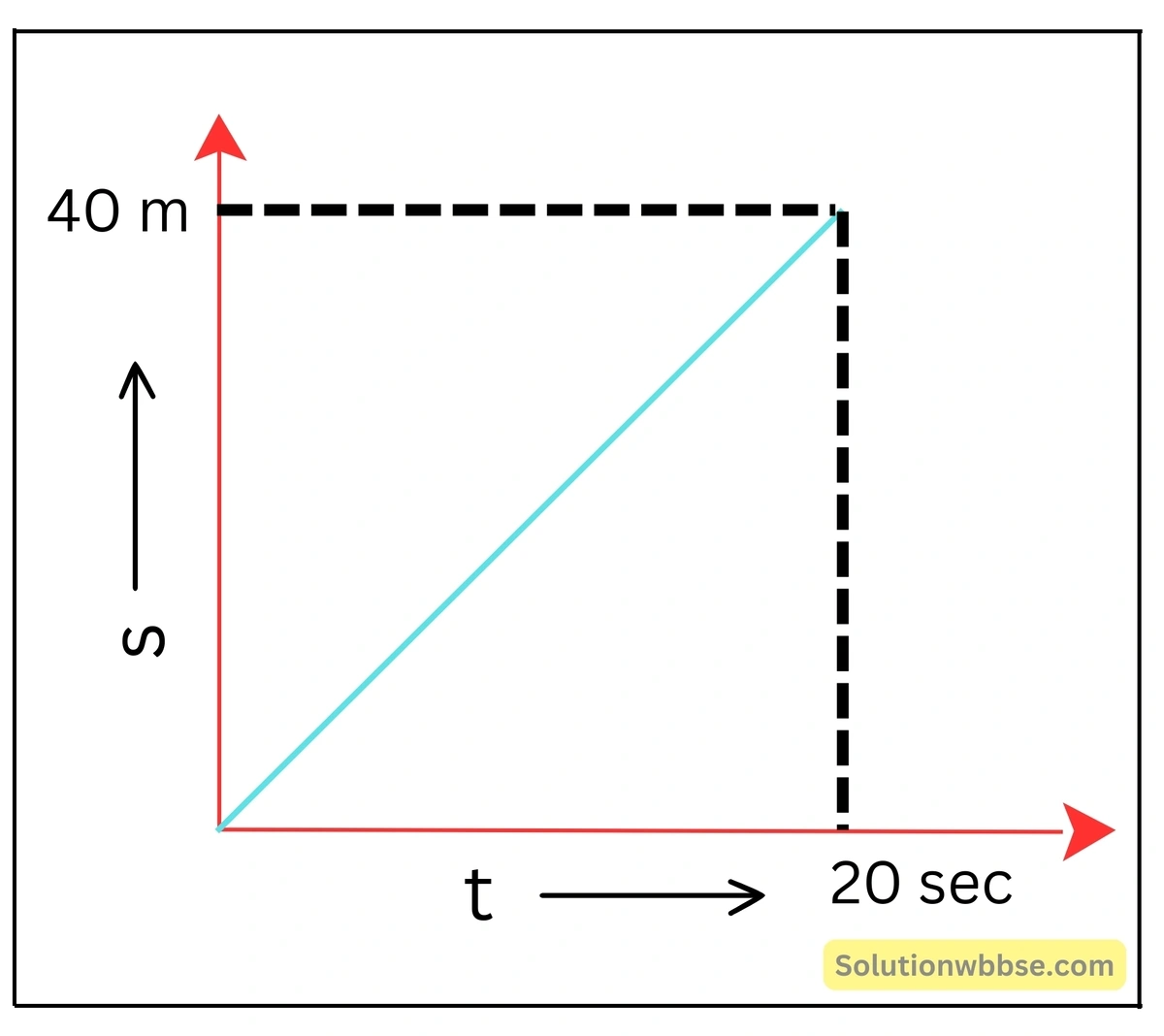
লেখচিত্রের সরলরৈখিক প্রকৃতি নির্দেশ করে গাড়িটি সমদ্রুতিসহ গতিশীল।
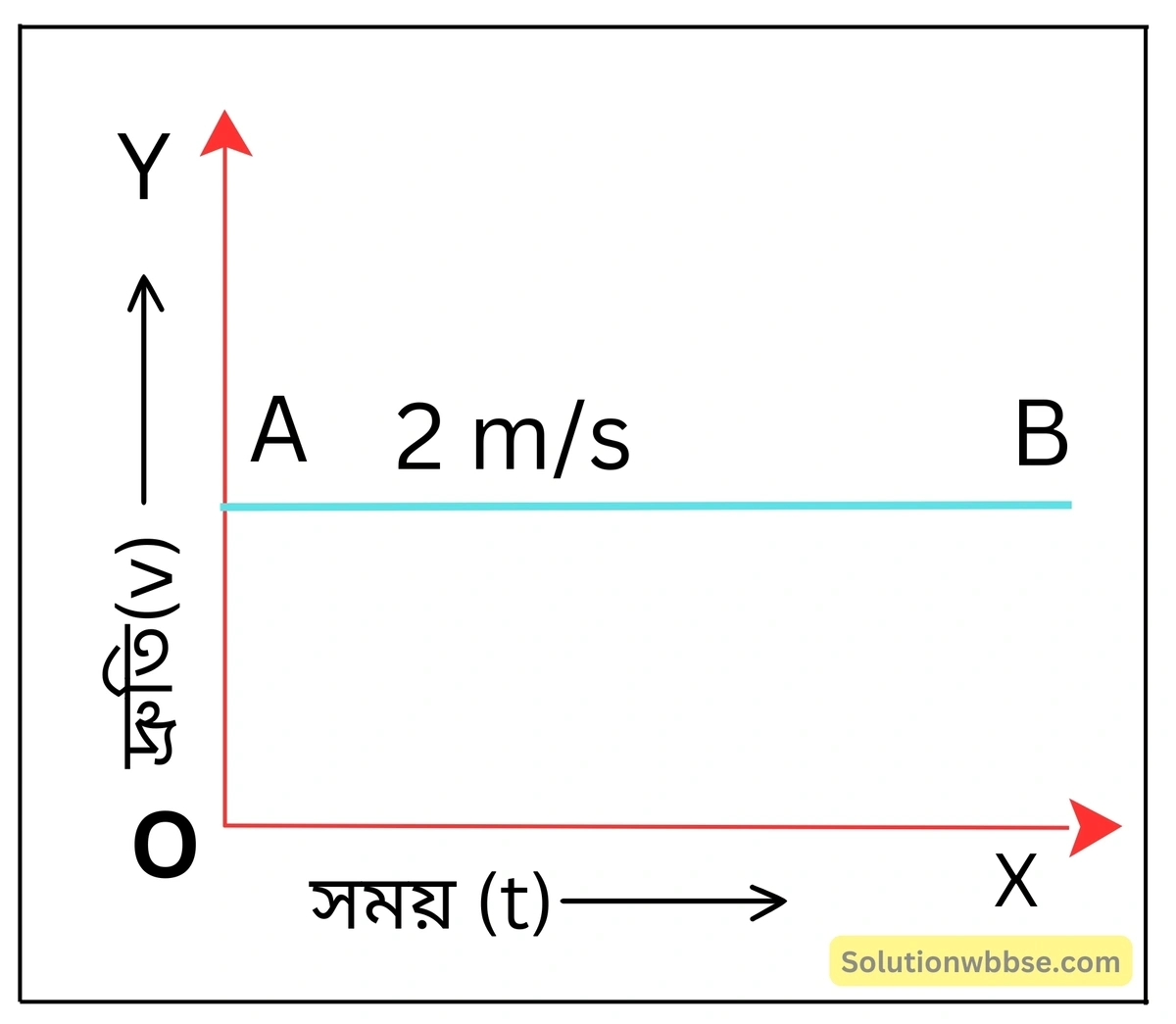
গাড়ির দ্রুতি = v
= \(\frac{40}{20}\) মি/সে
= 2 মি/সে
∴ গাড়িটির দ্রুতি-সময় লেখচিত্রটি হবে সময়-অক্ষের সমান্তরাল একটি সরলরেখা।
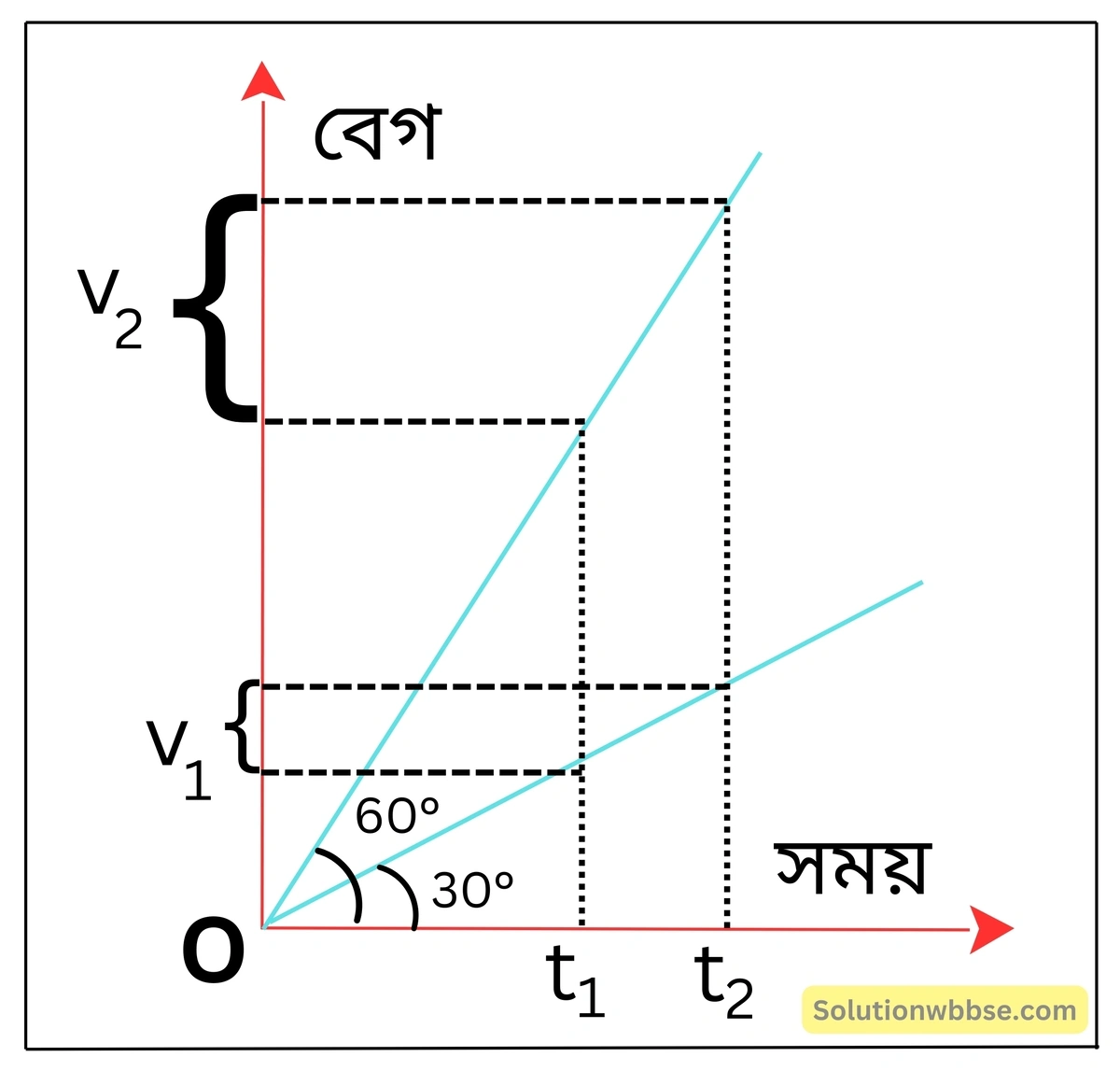
দুটি গতিশীল বস্তুর বেগ-সময় লেখ দুটির নতি যথাক্রমে 30° ও 60°; কোনটির ত্বরণ বেশি?
আমরা জানি, ত্বরণ = বেগ বৃদ্ধির হার। অর্থাৎ, একই সময়ে যে গতিশীল বস্তুর বেগ বৃদ্ধি বেশি, তার ত্বরণও বেশি। পাশের লেখচিত্র থেকে দেখা যায় ( t2 – t1) সময়ে গতিশীল বস্তুদুটির বেগের পরিবর্তন যথাক্রমে v1 ও v2 এবং v2 > v1। অর্থাৎ, 60° নতিবিশিষ্ট কণাটির ত্বরণ বেশি। কারণ – এর বেগ বৃদ্ধির পরিমাণ বেশি।
কোনো বস্তুর গড়বেগ শূন্য কিন্তু গড়দ্রুতি শূন্য নাও হতে পারে কি?
ধরা যাক, একটি বস্তুকণা একটি নির্দিষ্ট স্থান থেকে যাত্রা শুরু করে, ভিন্ন ভিন্ন দ্রুতি নিয়ে চলতে থাকে এবং কিছু সময় পর পুনরায় ওই প্রারম্ভিক স্থানে ফিরে আসে। এক্ষেত্রে বস্তুকণার প্রারম্ভিক ও অন্তিম অবস্থান একই হওয়ায় সরণ শূন্য হয়, তথা কণাটির গড়বেগ শূন্য হয়। এখন মোট অতিক্রান্ত দূরত্বকে সময় দিয়ে ভাগ করলে যেহেতু গড়দ্রুতি পাওয়া যায়, তাই এই বস্তুকণাটির ক্ষেত্রে গড়দ্রুতি বর্তমান। সুতরাং, কোনো বস্তুর গড়বেগ শূন্য হলেও গড় দ্রুতি শূন্য নাও হতে পারে।
একটি বলকে উপরে ছুড়ে দেওয়া হল -এর বেগ-সময় লেখচিত্র অঙ্কন করো।
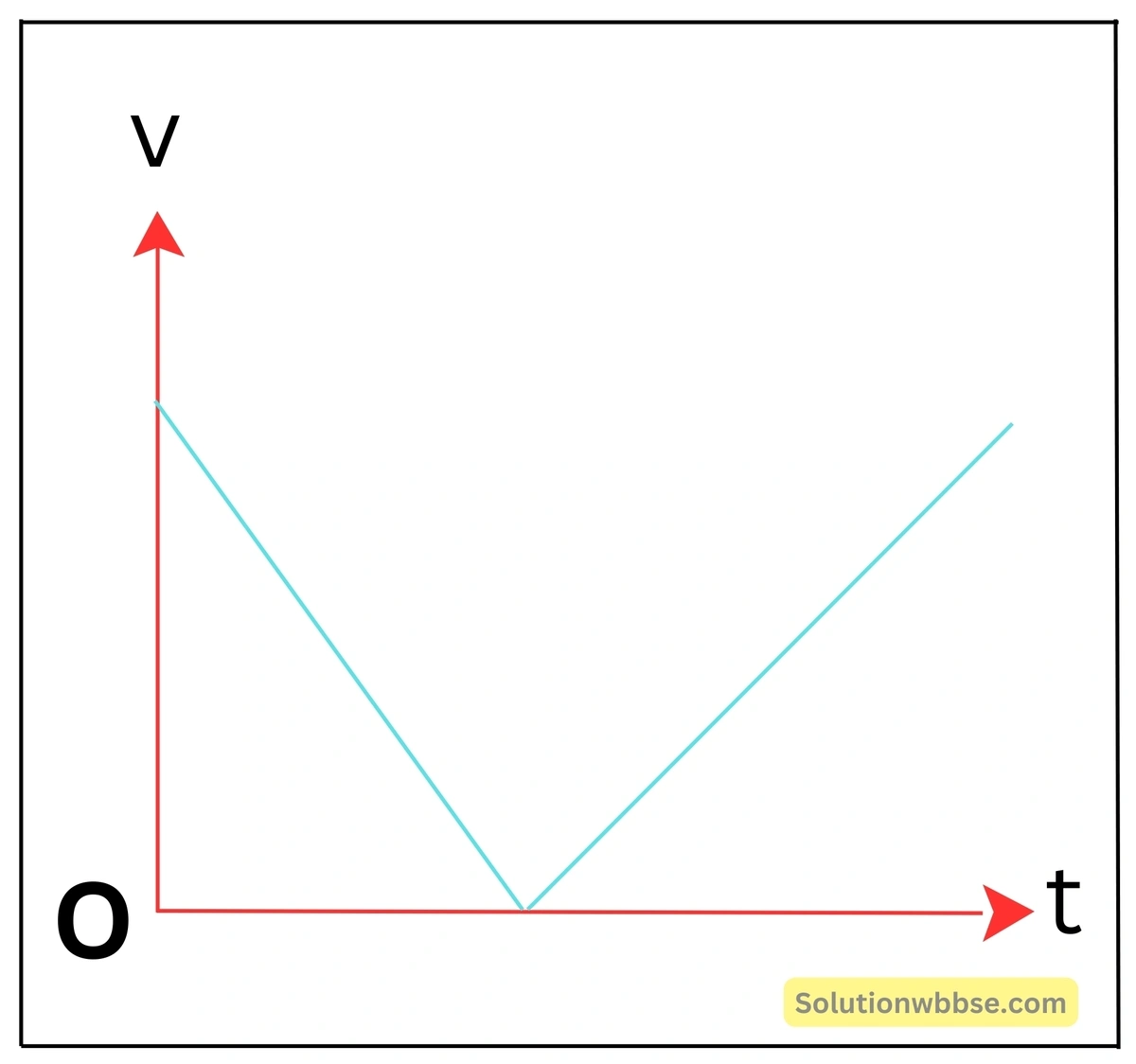
বলকে উপরে ছুড়ে দিলে প্রথমে তার গতিবেগ সর্বোচ্চ থাকে। অর্থাৎ, t = 0 হলে V = Vmax। এরপর গতিবেগ ক্রমশ কমে শূন্য হয়। তারপর বেগ আবার বাড়ে ও বস্তুটি নীচে নেমে আসে।
একটি ট্রেন স্টেশন থেকে যাত্রা শুরু করে প্রথমে কিছুটা পথ ত্বরণসহ গেল, তারপর সমবেগে কিছুটা পথ গেল, তারপর মন্দনসহ কিছু দূরত্ব অতিক্রম করে স্টেশনে থামল -এর বেগ-সময় লেখচিত্র অঙ্কন করো।
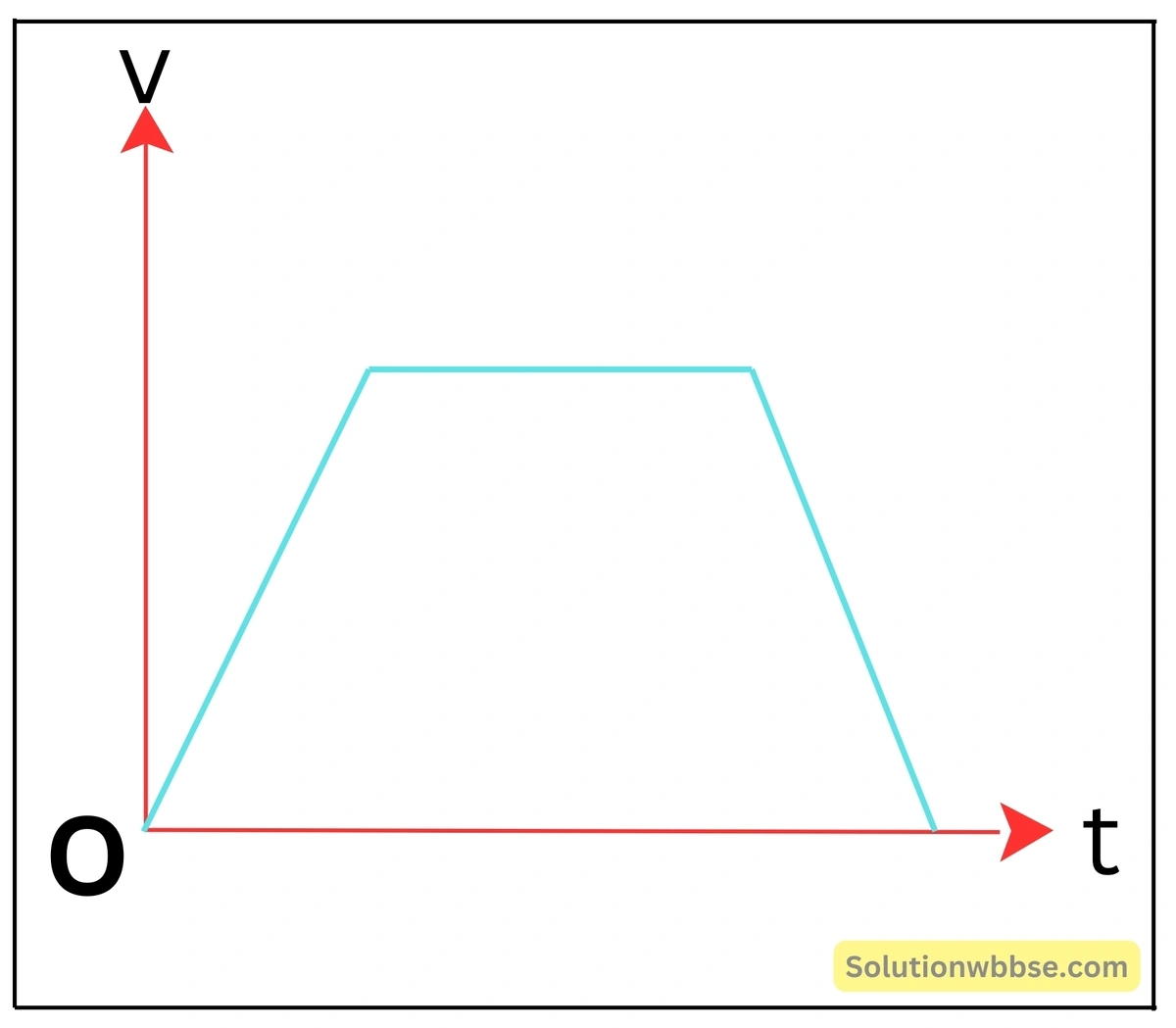
ট্রেনটি প্রথমে ত্বরণসহ যায়। তাই সময় বাড়লে বেগ বাড়ে। এরপর ট্রেনটি সমবেগে যায়। শেষে ট্রেনটি সমমন্দনে যায় ও স্টেশনে থামে। তাই বেগ ক্রমশ কমে শূন্য হয়।
একটি গাড়ি সমবেগে চলার কিছু সময় পর লাল সিগন্যাল দেখে থামল -এর বেগ-সময় লেখচিত্র অঙ্কন করো।
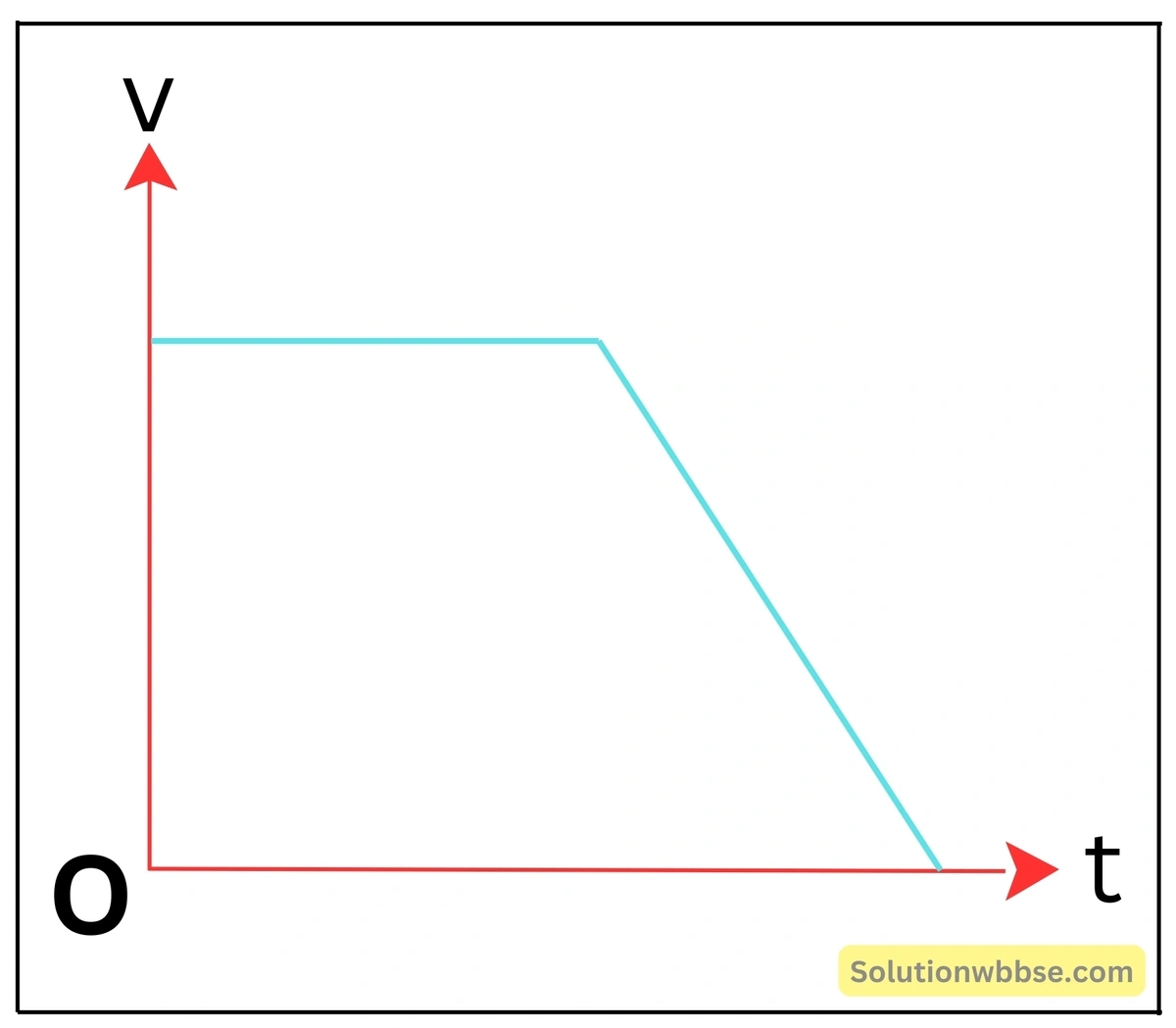
প্রথমে গাড়িটি সমবেগে চলে। তাই সময় বাড়লে গতিবেগ একই থাকে। এরপর গাড়িটি সিগন্যাল দেখে থামার জন্য মন্দনসহ চলে। তাই বেগ ক্রমশ কমে শূন্য হয়।
পার্থক্যধর্মী প্রশ্নোত্তর
সরণ ও অতিক্রান্ত দূরত্বের মধ্যে পার্থক্য লেখো।
সরণ ও অতিক্রান্ত দূরত্বের মধ্যে পার্থক্যগুলি হল –
| বিষয় | সরণ (Displacement) | অতিক্রান্ত দূরত্ব (Distance) |
| রাশির প্রকৃতি | অভিমুখ নির্দিষ্ট হওয়ায় এটি ভেক্টর রাশি। | অভিমুখ অনির্দিষ্ট তাই এটি স্কেলার রাশি। |
| অতিক্রান্ত পথের ওপর নির্ভরশীলতা | এর মান অতিক্রান্ত পথের দৈর্ঘ্য ও প্রকৃতির ওপর নির্ভর করে না। | এর মান বস্তুকণা দ্বারা অতিক্রান্ত পথের প্রকৃতি ও দৈর্ঘ্যের ওপর নির্ভরশীল। |
| মান | সরণের মান সর্বদা অতিক্রান্ত দূরত্ব অপেক্ষা কম বা তার সমান হয়। | অতিক্রান্ত দূরত্বের মান সরণের মানের সমান বা তার থেকে বেশিও হতে পারে। |
| চিহ্ন | অভিমুখের ওপর নির্ভর করে এটি ধনাত্মক বা ঋণাত্মক হতে পারে। | অতিক্রান্ত দূরত্ব সর্বদাই ধনাত্মক হয়। |
| শূন্য মান | অতিক্রান্ত দূরত্ব শূন্য না হলেও সরণের মান শূন্য হওয়া সম্ভব, যদি প্রাথমিক ও অন্তিম অবস্থান অভিন্ন হয়। | সরণের মান যাই হোক না কেন অতিক্রান্ত দূরত্ব কখনোই শূন্য হতে পারে না। |
দ্রুতি (Speed) ও বেগ (Velocity) -এর মধ্যে পার্থক্য লেখো।
দ্রুতি (Speed) ও বেগ (Velocity) -এর মধ্যে পার্থক্যগুলি হল –
| বিষয় | দ্রুতি (Speed) | বেগ (Velocity) |
| সংজ্ঞা | গতিশীল বস্তুকণা দ্বারা একক সময়ে অতিক্রান্ত দূরত্বকে দ্রুতি বলা হয়। | গতিশীল বস্তুকণা দ্বারা একক সময়ে নির্দিষ্ট অভিমুখে অতিক্রান্ত দূরত্ব বা সরণের হারকে বেগ বলা হয়। |
| রাশির প্রকৃতি | নির্দিষ্ট অভিমুখ নেই বলে এটি স্কেলার রাশি। | নির্দিষ্ট অভিমুখ থাকায় এটি ভেক্টর রাশি। |
| চিহ্ন | অভিমুখ বিবেচনা করতে হয় না বলে দ্রুতি সর্বদা ধনাত্মক। | গতির অভিমুখের ওপর নির্ভর করে বেগ ধনাত্মক ও ঋণাত্মক দুই-ই হতে পারে। |
| বৃত্তগতির ক্ষেত্রে গড় মান | বৃত্তীয় পথে একবার সম্পূর্ণ আবর্তনের ফলে কণার গড় দ্রুতি শূন্য না হলেও গড় বেগ সর্বদা শূন্য হয়। | বৃত্তপথে একবার সম্পূর্ণ আবর্তনের ক্ষেত্রে কণার গড়বেগ শূন্য হলেও গড় দ্রুতি কখনো শূন্য হয় না। |
ত্বরণ (Acceleration) ও মন্দন (Retardation) -এর মধ্যে পার্থক্য লেখো।
ত্বরণ (Acceleration) ও মন্দন (Retardation) -এর মধ্যে পার্থক্যগুলি হল –
| বিষয় | ত্বরণ (Acceleration) | মন্দন (Retardation) |
| সংজ্ঞা | সময়ের সাপেক্ষে গতিশীল বস্তু বা কণার বেগ বৃদ্ধির তাহারই হল ত্বরণ। | সময়ের সাপেক্ষে গতিশীল বস্তু বা কণার বেগ হ্রাসের হারকে বলা হয় মন্দন। |
| বলের ক্রিয়া | ত্বরণসহ গতিশীল বস্তুর গতির অভিমুখে কার্যকরী বা লব্ধিবল ক্রিয়া করে। | সরলরেখায় মন্দনসহ গতিশীল বস্তুর গতির অভিমুখের বিপরীতে লব্ধিবল ক্রিয়াশীল হয়। |
| স্থির অবস্থায় আসার সম্ভাবনা | ত্বরণসহ গতিশীল বস্তুর পক্ষে কখনোই স্থিরাবস্থায় আসা সম্ভব নয়। | মন্দনসহ গতিশীল বস্তু স্থিরাবস্থায় আসতেও পারে, নাও আসতে পারে। |
| প্রাথমিক বেগের অস্তিত্ব | গতিশীল বস্তুর প্রাথমিক বেগ শূন্য হলেও সেটি ত্বরণসহ গতিশীল হতে পারে। | প্রাথমিক বেগ শূন্য হলে বস্তু কখনোই মন্দনসহ গতিশীল হতে সক্ষম হবে না। |
গাণিতিক প্রশ্নাবলি
প্রয়োজনীয় সূত্রাবলি
সরণ = নির্দিষ্ট দিকে অতিক্রান্ত দূরত্ব।
\(v=u\pm at\\\)\(s=ut\pm\frac12at^2\\\)\(v^2=u^2\pm2as\\\)
এক ব্যক্তি সোজা পূর্বদিকে 8 km যাওয়ার পর দিক পরিবর্তন করে উত্তর দিকে 6 km গেল। ওই ব্যক্তির সরণ কত?
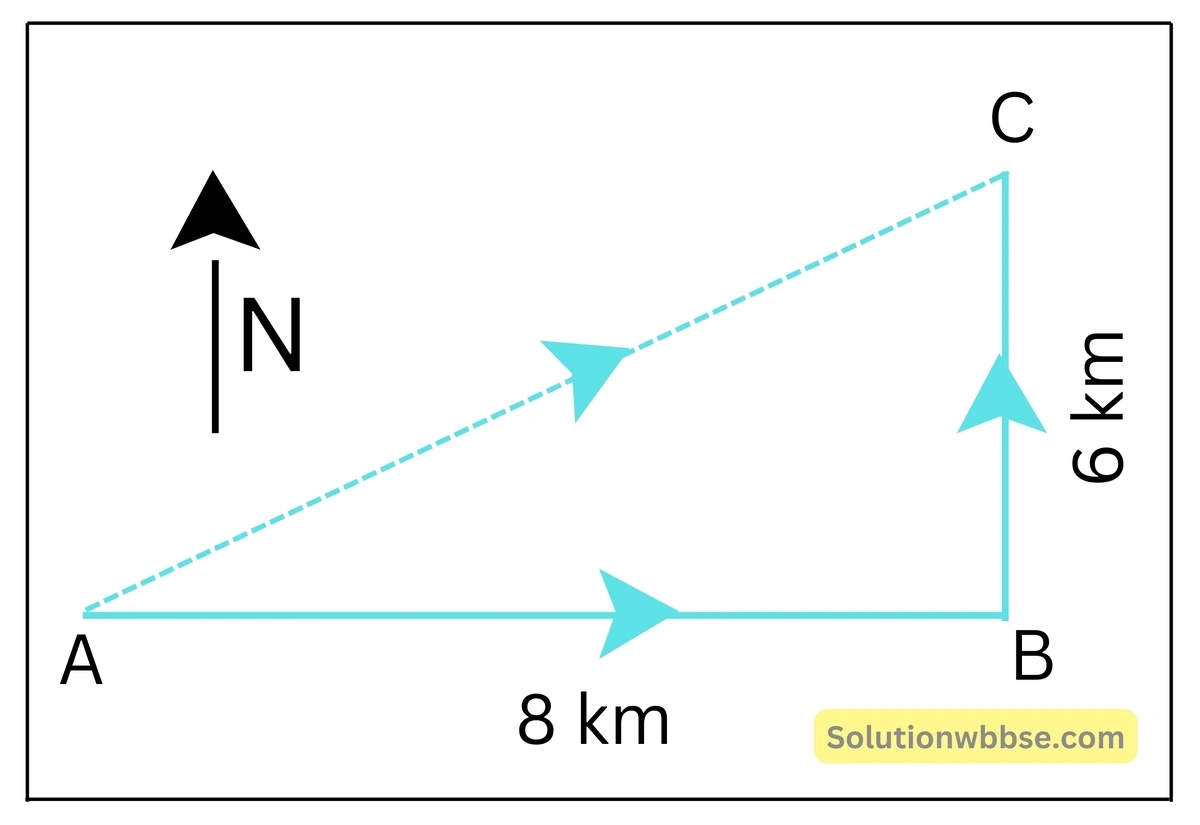
ওই ব্যক্তি পূর্বদিকে অর্থাৎ A থেকে B -এর দিকে প্রথমে 8 কিমি যাওয়ার পর B থেকে C পর্যন্ত (উত্তর দিকে) 6 km গেল।
সুতরাং, ব্যক্তির সরণ AC
AC2 = AB2 + BC2
বা, AC2 = 82 + 62
বা, AC2 = 100
∴ AC = 10
∴ সরণের মান 10 km এবং সরণের অভিমুখ হল A থেকে C -এর দিকে অর্থাৎ, উত্তর-পূর্ব দিকে।
একটি চাকা অনুভূমিক তলের উপর দিয়ে অর্ধপাক ঘুরে গেল। চাকার ব্যাসার্ধ 28 cm হলে ভূমিসংলগ্ন বিন্দুর সরণের মান কত?
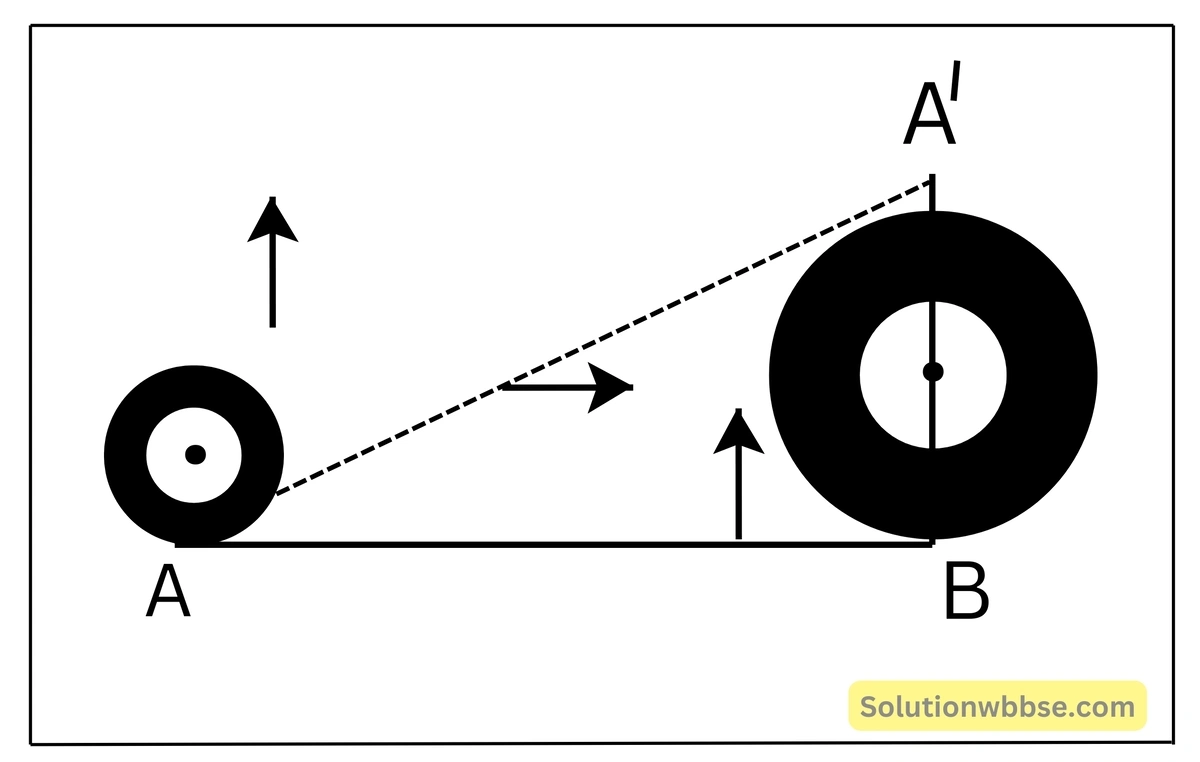
প্রথমে ভূমিসংলগ্ন বিন্দুর অবস্থান = A
চাকাটি অনুভূমিক তলের উপর দিয়ে অর্ধপাক ঘুরে গেলে অবস্থান হয় A’
AB = π × 28
বা, \(AB=\frac{22}7\times28=88\mathrm{cm}\)
এবং A’B = 2 × 28 = 56 cm
∴ নির্ণেয় সরণ = A থেকে A’ -এর সরলরৈখিক দূরত্ব (AA’)
= \(\sqrt{AB^2+A’B^2}\)
= \(\sqrt{\left(88\right)^2+\left(56\right)^2}\)
= \(\sqrt{10880}\)
= 104.31 cm
∴ ভূমিসংলগ্ন বিন্দুর সরণের মান 104.31 cm।
একটি গাড়ি 5 min -এ 2.7 km পথ অতিক্রম করল। গাড়িটির দ্রুতি কত?
অতিক্রান্ত দূরত্ব = 2.7 km = 2700 m
সময় = 5 × 60 = 300 s
বা, দ্রুতি = \(\frac{2700}{300}m/s\)
বা, দ্রুতি = 9 m/s
∴ গাড়িটির দ্রুতি 9 m/s।
একটি গাড়ি তার গতির অর্ধেক সময় 30 km/hr দ্রুতিতে এবং অবশিষ্ট অর্ধেক সময় 40 km/hr দ্রুতিতে চলে। গাড়ির গড় দ্রুতি কত?
ধরি, মোট সময় 2t hr
প্রথম t hr -এ গাড়ি যায় 30 × t km পথ।
পরের t hr -এ গাড়ি যায় 40 × t km পথ।
∴ মোট অতিক্রান্ত দূরত্ব = (30t + 40t) = 70t km
বা, গাড়িটির গড় দ্রুতি = \(\frac{70t}{2t}\)
∴ গাড়িটির গড় দ্রুতি = 35 km/hr।
একটি উড়োজাহাজের উত্তর দিকে 324 km যেতে 20 min সময় লাগল। উড়োজাহাজটির গতিবেগ কত?
উড়োজাহাজটির সরণ = 324 km
সময় = \(20\;min=\frac{20}{60}hr=\frac13hr\)
∴
বা, গতিবেগ = \(\frac{324\;km}{{\displaystyle\frac13}\;hr}\)
∴ গতিবেগ = 972 km/hr (উত্তর দিকে)।
একটি ট্রেন দুই স্টেশনের মাঝের দূরত্বের প্রথম অর্ধেক 20 km/hr বেগে এবং শেষ অর্ধেক দূরত্ব 60 km/hr বেগে অতিক্রম করে। ট্রেনটির গড় বেগ কত?
ধরি, দুই স্টেশনের মাঝের দূরত্ব = 2x km
প্রথম অর্ধেক অর্থাৎ, x km দূরত্ব অতিক্রম করতে সময় = \(\frac X{20}hr\)
পরের অর্ধেক x km দূরত্ব অতিক্রম করে = \(\frac X{60}hr\) -এ।
∴ মোট সময় = \(\frac X{20}+\frac X{60}hr=\frac X{15}hr\)
∴
বা, গড়বেগ = \(\frac{2X}{\displaystyle\frac X{15}}km/hr\)
বা, গড়বেগ = 30 km/hr
∴ ট্রেনটির গড় বেগ 30 km/hr
এক ব্যক্তি 84 m ব্যাসবিশিষ্ট বৃত্তাকার পার্কে 2 min -এ দৌড় শেষ করল। তার দ্রুতি ও বেগের মান কত?
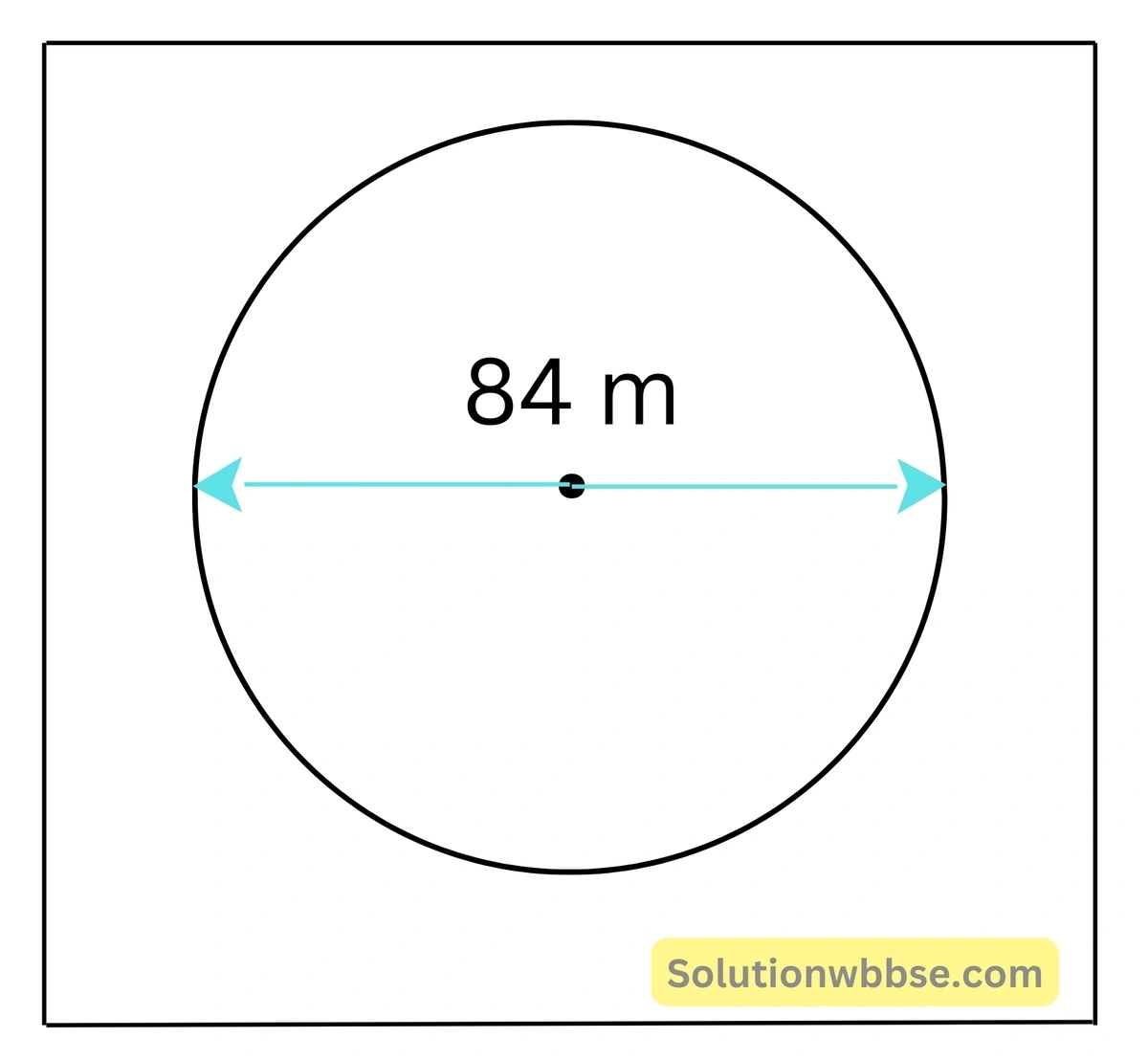
বৃত্তাকার পার্কের ব্যাস = 84 m।
∴ ব্যাসার্ধ (r) = \(\frac{84}2\) m = 42 m
বৃত্তাকার পথের মোট দৈর্ঘ্য
= 2πr
= \(2\times\frac{22}7\times42\)
= 264 m
সময় = 2 min = 2 × 60 s
∴
বা, দ্রুতি = \(\frac{264}{2\times60}\)
বা, দ্রুতি = 2.2 m/s
এক্ষেত্রে, ব্যক্তিটির প্রাথমিক অবস্থান ও শেষ অবস্থান একই। সুতরাং সরণ = 0।
∴
বা, বেগ = \(\frac0{2\times60}\) m/s
বা, বেগ = 0
∴ তার দ্রুতি ও বেগের মান 2.2 m/s ও 0।
এক ব্যক্তি পূর্বদিকে 12 km গিয়ে সেখান থেকে উত্তর দিকে 5 km গেল। ওই দূরত্ব অতিক্রম করতে তার 1 hr সময় লাগলে ওই ব্যক্তির সরণ, দ্রুতি ও বেগ নির্ণয় – করো।
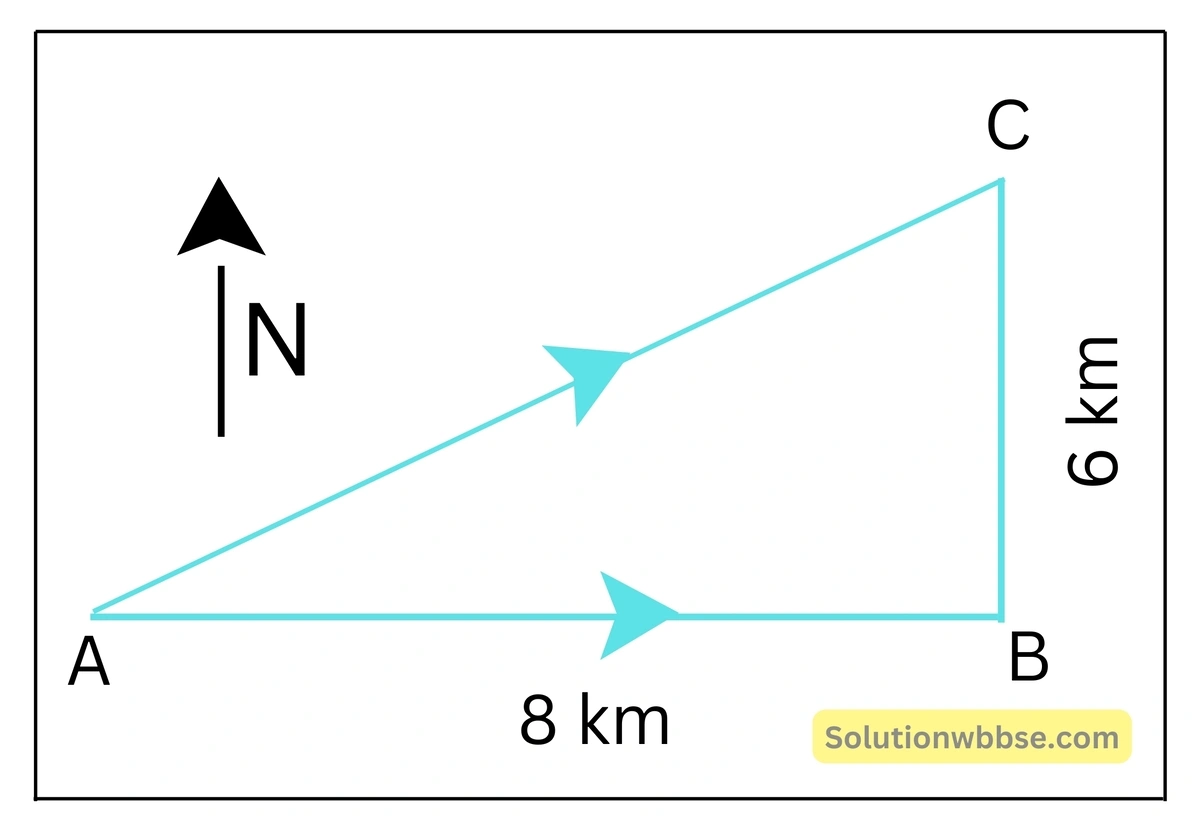
প্রশ্নানুযায়ী, AB = 12 km এবং BC = 5 km
∴ মোট অতিক্রান্ত পথ
= (AB + BC)
= (12 + 5) km
= 17 km
= 17 × 1000 m
= 17000 m
সময় = 1 hr = 60 × 60 s
∴ ব্যক্তির সরণ = AC
= \(AC=\sqrt{AB^2+BC^2}\)
= \(\sqrt{12^2+5^2}\)
= \(\sqrt{144+25}\)
= \(\sqrt{169}\)
= 13 km
= 13000 m উত্তর-পূর্ব দিকে।
∴
= \(\frac{17000}{60\times60}\) m/s
= 4.72 m/s
∴
= \(\frac{13000}{60\times60}\) m/s
= 3.61 m/s
স্থির অবস্থায় একটি বস্তুর ওপর বল প্রয়োগ করলে বস্তুটি 8 cm/s² সমত্বরণে চলতে শুরু করে। 12 s পরে চূড়ান্ত বেগ কত হবে?
প্রশ্নানুযায়ী, প্রাথমিক বেগ = u = 0
ত্বরণ = a = 8 cm/s²,
সময় = t = 12 s,
অন্তিম বেগ = v = ?
আমরা জানি, v = u + at
বা, v = 0 + (8 × 12)
বা, v = 96 cm/s
∴ 12 s পরে চূড়ান্ত বেগ 96 cm/s হবে।
একটি বস্তুর বেগ 5 min -এ 10 m/s থেকে 25 m/s হলে এর ত্বরণ নির্ণয় করো।
প্রাথমিক বেগ = u = 10 m/s
অন্তিম বেগ = v = 25 m/s
সময় (t) = 5 min = 300 s
ত্বরণ = a = ?
সূত্রানুযায়ী, v = u + at
বা, 25 = 10 + (a × 300)
বা, 300a = 15
বা, \(a=\frac{15}{300}\)
বা, \(a=\frac1{20}\)
বা, a = 0.05 m/s2
∴ ত্বরণ = 0.05 m/s2
ঘণ্টায় 36 কিমি/ঘণ্টা বেগে চলন্ত একটি গাড়িকে ব্রেকের সাহায্যে 5 সেকেন্ডে থামানো হল। গাড়িটির মন্দন কত?
এখানে প্রাথমিক বেগ (u) = 36 km/s।
= \(\frac{36\times1000}{3600}\) m/s
= 10 m/s
সময় = t = 5 s। অন্তিম বেগ = v = 0
v = u – at সমীকরণ থেকে পাই,
বা, 0 = 10 – (a × 5)
বা, 5a = 10
বা, \(a=\frac{10}5\)
বা, a = 2 m/s2
∴ গাড়িটির মন্দন 2 m/s2
36 km/hr বেগে চলন্ত একটি গাড়িকে ব্রেকের সাহায্যে থামানো হল। গাড়িটির মন্দন যদি 5 m/s2 হয় তবে গাড়িটিকে থামাতে কত সময় লাগবে?
গাড়ির প্রাথমিক গতিবেগ (u) = 36 km/hr
= \(\frac{36000}{3600}\) m/s
= 10 m/s
মন্দন = – a = 5 m/s², অন্তিম গতিবেগ = v = 0, সময় = t = ?
আমরা জানি, v = u + at
বা, 0 = 10 – 5t
বা, \(t=\frac{10}5=2s\)
বা, t = 2 s
∴ গাড়িটিকে থামাতে 2 s সময় লাগবে।
দৌড় প্রতিযোগিতায় একজন প্রতিযোগী প্রতিযোগিতা শুরুর পরবর্তী 4 সেকেন্ড সময় ধরে 2.5 m/s² ত্বরণসহ যাচ্ছে। এই সময়ের মধ্যে সে কতটা দূরত্ব অতিক্রম করতে পারবে?
প্রশ্নানুযায়ী, প্রাথমিক বেগ (u) = 0, ত্বরণ (a) = 2.5 m/s2, সময় (t) = 4 s, অতিক্রান্ত দূরত্ব = s =?
আমরা জানি, \(s=ut+\frac12at^2\)
= \(0\times4+\frac12\times2.5\times\left(4\right)^2\) m
= \(\frac12\times2.5\times4\times4\) m
= 20 m
∴ 20 m দূরত্ব অতিক্রম করতে পারবে
একটি কণা স্থিরাবস্থা থেকে সমত্বরণে যাত্রা শুরু করে প্রথম 2 সেকেন্ডে x একক দূরত্ব এবং পরবর্তী 3 সেকেন্ডে আরও y একক দূরত্ব গেল। x ও y – এর মধ্যে সম্পর্ক নির্ণয় করো।
প্রথম 2 সেকেন্ডে কণাটি স্থিরাবস্থা থেকে a সমত্বরণ নিয়ে যাত্রা শুরু করে x দূরত্ব যায়।
এক্ষেত্রে, \(s=ut+\frac12at^2\) সূত্রটি প্রয়োগ করে পাই –
\(x=0+\frac12\times a\times2^2\\\)বা, \(x=2a\)
বা, \(a=\frac x2\)
পরবর্তী ও সেকেন্ডে কণাটি আরও y দূরত্ব যায়। অর্থাৎ, (2 + 3) সেকেন্ডে (x + y) দূরত্ব অতিক্রম করেছে।
∴ \(x+y=0+\frac12\times a\times5^2\)
বা, \(x+y=\frac{25a}2\)
বা, \(x+y=\frac{25}2\cdot\frac x2\)
বা, \(y=\frac{25x}4-x\)
বা, \(y=\frac{21x}4\)
বা, \(21y=4y\) -এটিই \(x\) ও \(y\) -এর মধ্যে নির্ণেয় সম্পর্ক।
একটি মোটরগাড়িতে ব্রেক কষে 6 m/s² মন্দন উৎপন্ন হয়। গাড়িটি 2 sec পর স্থির হল। এই সময়ে গাড়িটি কতটা দূরত্ব যাবে?
গাড়ির মন্দন (- a) = 6 m/s² ।
সময় (t) = 2 sec, অন্তিম বেগ (v) = 0
ধরা যাক, গাড়িটি s দূরত্ব অতিক্রম করে এবং প্রাথমিক বেগ = u
v = u + at সমীকরণ থেকে পাই –
0 = u – 6 × 2
বা, u = 12 m/s²
আবার, \(s=ut-\frac12at^2\) সূত্রটি ব্যবহার করে পাই –
বা, \(s=12\times2-\frac12\times6\times2^2\)
বা, s = 24 – 12
বা, s = 12
∴ মোটরগাড়িটি 12 m দূরত্ব অতিক্রম করে।
স্থিরাবস্থা থেকে 8 m/s² সমত্বরণে চলার 12 s পর একটি কণার চূড়ান্ত বেগ কত হবে? ওই সময়ের মধ্যে কণাটি কতদূর যাবে?
এক্ষেত্রে প্রাথমিক বেগ (u) = 0, সমত্বরণ a = 8 m/s² সময় t = 12 s, চূড়ান্ত বেগ v = ?, s = ?
চূড়ান্ত বেগ v = u + at
= 0 + 8 × 12
= 96 m/s
অতিক্রান্ত দূরত্ব \(s=ut+\frac12at^2\)
বা, \(s=0\times12+\frac12\times8\times12^2\)
বা, s = 576 m
∴ কণাটি 576 m দূরত্ব যাবে।
একটি বস্তুকণা 2 সেকেন্ডে 200 সেমি ও পরবর্তী 4 সেকেন্ডে 220 সেমি দূরত্ব সরলরেখায় অতিক্রম করে। যাত্রা শুরুর 7 sec পর কণাটির বেগ কত হবে?
ধরা যাক কণার প্রাথমিক বেগ ও সমত্বরণ যথাক্রমে u cm/s ও a cm/s²।
2s সময়ে কণাটি দ্বারা অতিক্রান্ত সরলরৈখিক দূরত্ব
\(s=200=2u+\frac12a\times2^2\\\)বা, u + a = 100 ___(1)
আবার (2 + 4) = 6 s সময়ে অতিক্রান্ত দূরত্ব
বা, s’ = (200 + 220)
বা, s’ = \(6u+\frac12a\times6^2\)
বা, 6u + 18a = 420
বা, u + 3a = 70 ___(2)
সমাধান করে পাই,
(u + 3a) – (u + a) = 70 – 100
বা, 2a = – 30
বা, a = – 15 cm/s²
এবং u = (100 + 15) = 115 cm/s
∴ 7 s পর কণার বেগ = u + at
= 115 + 7 × (- 15)
= 10 cm/s
∴ কণাটির বেগ 10 cm/s হবে।
সমত্বরণসম্পন্ন একটি কণা প্রথম 6 সেকেন্ডে 30 মিটার ও পরবর্তী 6 সেকেন্ডে 80 মিটার পথ অতিক্রম করে। কণাটি 18 সেকেন্ড সময়ে মোট কতটা পথ অতিক্রম করবে?
ধরা যাক, কণাটির প্রাথমিক বেগ ও সমত্বরণ যথাক্রমে u cm/s এবং a cm/s²।
6 sec -এ কণা দ্বারা অতিক্রান্ত সরলরৈখিক দূরত্ব,
\(s’=30=6u+\frac12a\times6^2\\\)বা, u + 3a = 5 ___(1)
আবার, (6 + 6) = 12 sec -এ অতিক্রান্ত দূরত্ব,
\(s”=30+80=12u+\frac12a\times12^2\\\)বা, 6u + 36a = 55 ___(2)
(1) ও (2) সমাধান করে পাই,
6u + 36a – 6u – 18a = 55 – 30
বা, 18a = 25
বা, \(a=\frac{25}{18}\) m/s2
(1) নং সমীকরণ থেকে পাই – \(u+3\times\frac{25}{18}=5\)
বা, \(u=\frac56\) m/s
∴ 18 সেকেন্ডে কণাটি দ্বারা অতিক্রান্ত পথ –
\(s=ut+\frac12at^2\) সূত্র ব্যবহার করে পাই
\(s=\frac56\times18+\frac12\times\frac{25}{18}\times18^2\\\)= 15 + 225 m
= 240 m
∴ কণাটি 18 সেকেন্ড সময়ে মোট 240 m পথ অতিক্রম করবে।
একটি কণা সমত্বরণে সরলরেখা বরাবর গতিশীল। t সেকেন্ডে কণার বেগ 10 m/s থেকে পরিবর্তিত হয়ে 20 m/s হয় এবং উক্ত সময় অবকাশে কণাটি 13500 cm দূরত্ব অতিক্রম করে। t -এর মান কত?
কণাটির প্রাথমিক বেগ, u = 10 m/s, অন্তিম বেগ, v = 20 m/s, অতিক্রান্ত দূরত্ব, s = 13500 cm = 135 m
\(s=ut+\frac12at^2\) ব্যবহার করে পাই –
\(10t+\frac12at^2=135\) ___(1)
আবার, v = u + at থেকে পাই –
20 = 10 + at
বা, at = 10 ___(2)
(1) ও (2) সমাধান করে পাই
\(10t+\frac1210t=135\\\)বা, 15t = 135
বা, t = 9 sec
∴ t -এর মান 9 sec
সুষম ত্বরণসহ গতিশীল একটি কণা সরলরেখায় ষষ্ঠ ও দশম সেকেন্ডে যথাক্রমে 41 ও 49 cm দূরত্ব অতিক্রম করে। 15 সেকেন্ড সময়ে কণাটি দ্বারা অতিক্রান্ত দূরত্ব নির্ণয় করো।
ধরা যাক, কণাটির প্রাথমিক বেগ u ও সমত্বরণ a
∴ ষষ্ঠ সেকেন্ডে অতিক্রান্ত দূরত্ব,
\(s_6=u+\frac12a\times\left(2\times6-1\right)\\\)বা, \(u+\frac{11}2a=41\) ___(1)
এবং দশম সেকেন্ডে অতিক্রান্ত দূরত্ব,
\(s_{10}=u+\frac12a\times\left(2\times10-1\right)\\\)বা, \(u+\frac{19}2a=49\) ___(2)
(1) ও (2) সমাধান করে পাই,
\(u+\frac{19}2a-u-\frac{11}2a=49-41\\\)বা, 4a = 8
বা, a = 2
এবং \(u+\frac{11}2\times2=41\)
বা, u = 30
∴ 15 সেকেন্ডে অতিক্রান্ত দূরত্ব –
\(s=30\times15+\frac12\times2\times15^2\\\)বা, s = (450 + 225)
বা, s = 675 cm
∴ 15 সেকেন্ড সময়ে কণাটি দ্বারা অতিক্রান্ত দূরত্ব 675 cm
স্থিরাবস্থা থেকে একটি গাড়ি সমত্বরণে 27s ধরে চলে 40 km/hr বেগ অর্জন করে। এরপর গাড়িটি 3 min সমবেগে গেল। অবশেষে ব্রেক কষায় গাড়িটি সমমন্দনে চলে 18 sec -এ স্থির হল। গাড়িটি মোট কত দূরত্ব অতিক্রম করল।
সমত্বরণে গতির ক্ষেত্রে – \(t_1=27\) s,
\(v=40\) km/hr
বা, \(v=\frac{40\times1000}{3600}\) m/s
বা, \(v=\frac{100}9\) m/s
\(v=0+\;a_1t_1\),
বা, \(a_1t_1=\frac{100}9\) ___(1)
∴ অতিক্রান্ত দূরত্ব \(s_1=0\times t_1+\frac12a_1t_1^2\)
বা,\(s_1=\frac12a_1t_1\cdot t_1\)
বা, \(s_1=\left(\frac12\times\frac{100}9\times27\right)\) m
বা, \(s_1=150\) m
সমবেগে গতির ক্ষেত্রে – অতিক্রান্ত দূরত্ব,
\(s_2=v\times t_2\\\)বা, \(s_2=\left(\frac{100}9\times3\times60\right)\)
বা, \(s_2=2000\) m
সমমন্দনে গতির ক্ষেত্রে – সমমন্দন a2 হলে,
\(0=v-a_2t_3\\\)বা, \(v=a_2t_3\)
বা, \(a_2t_3=\frac{100}9\) ___(2)
∴ অতিক্রান্ত দূরত্ব \(s_3=vt_3-\frac12a_2t_3^2\)
বা, \(s_3=a_2t_3\cdot t_3-\frac12a_2t_3^2\)
বা, \(s_3=\frac12a_2t_3^2\)
বা, \(s_3=\frac12a_2t_3\cdot t_3\)
বা, \(s_3=\frac12\times\frac{100}9\times10\)
বা, \(s_3=100\) m
গাড়িটি দ্বারা অতিক্রান্ত মোট দূরত্ব, s = s1 + s2 + s3
= (150 + 2000 + 100) m
= 2250 m
= 2.25 km
∴ গাড়িটি মোট 2.25 km দূরত্ব অতিক্রম করল।
একটি খেলনা গাড়ি 20 cm/s বেগে চলছিল। 1 m দূরত্ব যাবার পরে ওই গাড়ির বেগ দাড়ালো 50 cm/s। গাড়ির ত্বরণ নির্ণয় করো।
প্রশ্নানুযায়ী,
প্রাথমিক বেগ (u) = 20 cm/s,
অন্তিম বেগ (v) = 50 cm/s,
অতিক্রান্ত দূরত্ব (s) = 1 m = 100 cm,
ত্বরণ (a) = ?
আমরা জানি,
v2 = u2 + 2as
বা, \(a=\frac{u^2-v^2}{2s}\)
বা, \(a=\frac{\left(50\right)^2-\left(20\right)^2}{2\times100}\) cm/s2
বা, a = 10.5 cm/s2
∴গাড়ির ত্বরণ = 10.5 cm/s2
একটি ট্রেন 90 কিমি/ঘণ্টা সমবেগে যেতে যেতে ব্রেক কষল এবং 0.5 মি/সে2 সমমন্দনে চলতে শুরু করল। কতদূর যাওয়ার পর ট্রেনটি থেমে যাবে?
প্রশ্নানুযায়ী, প্রাথমিক বেগ (u) = 90 km/hr
= \(\frac{90\times1000}{60\times60}\) m/s
= 25 m/s
অন্তিম গতিবেগ (v) = 0, মন্দন (- a) = 0.5 m/s2, অতিক্রান্ত দূরত্ব = s =?
আমরা জানি,
v2 = u2 + 2as
বা, \(s=\frac{u^2-v^2}{2a}\)
বা, \(s=\frac{25^2-0^2}{2\times0.5}\) m
বা, s = 625 m
∴ 625 m যাওয়ার পর ট্রেনটি থেমে যাবে।
একটি গাড়ি 0.5 km দূরত্ব যাওয়ার পর তার বেগ 18 km/hr থেকে বৃদ্ধি পেয়ে 54 km/hr হয়। গাড়িটি সমত্বরণসহ গতিশীল হলে 90 km/hr বেগ অর্জন করতে কত দূরত্ব অতিক্রম করবে?
প্রাথমিক বেগ, u = 18 km/hr = \(\frac{18\times1000}{3600}\) = 5 m/s
অন্তিম বেগ, v = 54 km/hr = \(\frac{54\times1000}{3600}\) = 15 m/s
অতিক্রান্ত দূরত্ব, s = 0.5 km = 500 m
গাড়িটি a সমত্বরণসহ গতিশীল হলে v2 = u2 + 2as সমীকরণ থেকে পাই –
152 = 52 + 2a × 500
বা, 1000a = 200
বা, a = 0.2 m/s2
গাড়িটির চূড়ান্ত বেগ v1 = 90 km/hr
বা, \(v_1=\frac{90\times1000}{3600}\)
বা, \(v_1=25\) m/s
অতিক্রান্ত দূরত্ব \(s_1\) হলে, \(v_1^2=u_1^2+2as_1\)
বা, \(\left(25\right)^2=5^2+2\times0.2\times s_1\)
বা, \(s_1=\frac{600}{2\times0.2}=1500\) m
∴ 90 km/hr বেগ অর্জন করতে \( 1500\) m দূরত্ব অতিক্রম করবে।
একটি কাঠের ব্লকের 3 cm ভেদ করে একটি বুলেটের বেগ অর্ধেক কমে যায়। বুলেটটি ওই কাঠের ব্লকে আর কতটা প্রয়োগ করে থেমে যায়?
ধরা যাক, বুলেটে সৃষ্ট গড় মন্দন a এবং বুলেটের প্রাথমিক বেগ u। 3 cm ভেদ করার পর বুলেটের বেগ হল \(\frac u2\)।
\(\left(\frac u2\right)^2=u^2-2a\times3\\\)বা, \(u^2=4u^2-24a\)
বা, \(24a=3u^2\)
বা, \(a=\frac{u^2}8\)
ধরা যাক, আরও x cm দূরত্ব কাঠের ব্লকে প্রবেশ করে বুলেটটি থেমে যাবে।
∴ \(0^2=\left(\frac u2\right)^2-2xa\)
বা, \(\frac{u^2}4=2x\cdot\frac{u^2}8\)
বা, x = 1
∴ কাঠের ব্লকে 1 cm প্রবেশ করে বুলেটটি থেমে যাবে।
একটি বস্তু প্রথম 5 সেকেন্ড সময়ে 2 মিটার/সেকেন্ড সমবেগে গেল। পরবর্তী 5 সেকেন্ডে তার গতিবেগ বেড়ে 10 মিটার/সেকেন্ড হল। এরপর বস্তুটি সমমন্দনে গেল এবং 10 সেকেন্ড পরে স্থির অবস্থায় এল –
(1) বস্তুটির বেগ-সময় লেখচিত্র অঙ্কন করো।
(2) লেখচিত্রে দেখাও কোন্ অংশে বস্তু সমবেগে এবং কোন্ অংশে অসম বেগ নিয়ে চলে?
লেখচিত্রে X অক্ষ বরাবর সময় এবং Y অক্ষ বরাবর বেগ ধরা হল। এরপর নিম্নলিখিত বিন্দুগুলি বসিয়ে সরলরেখা দ্বারা যুক্ত করা হল।
| বেগ | 2 | 2 | 10 | 0 |
| সময় | 0 | 5 | 10 | 20 |
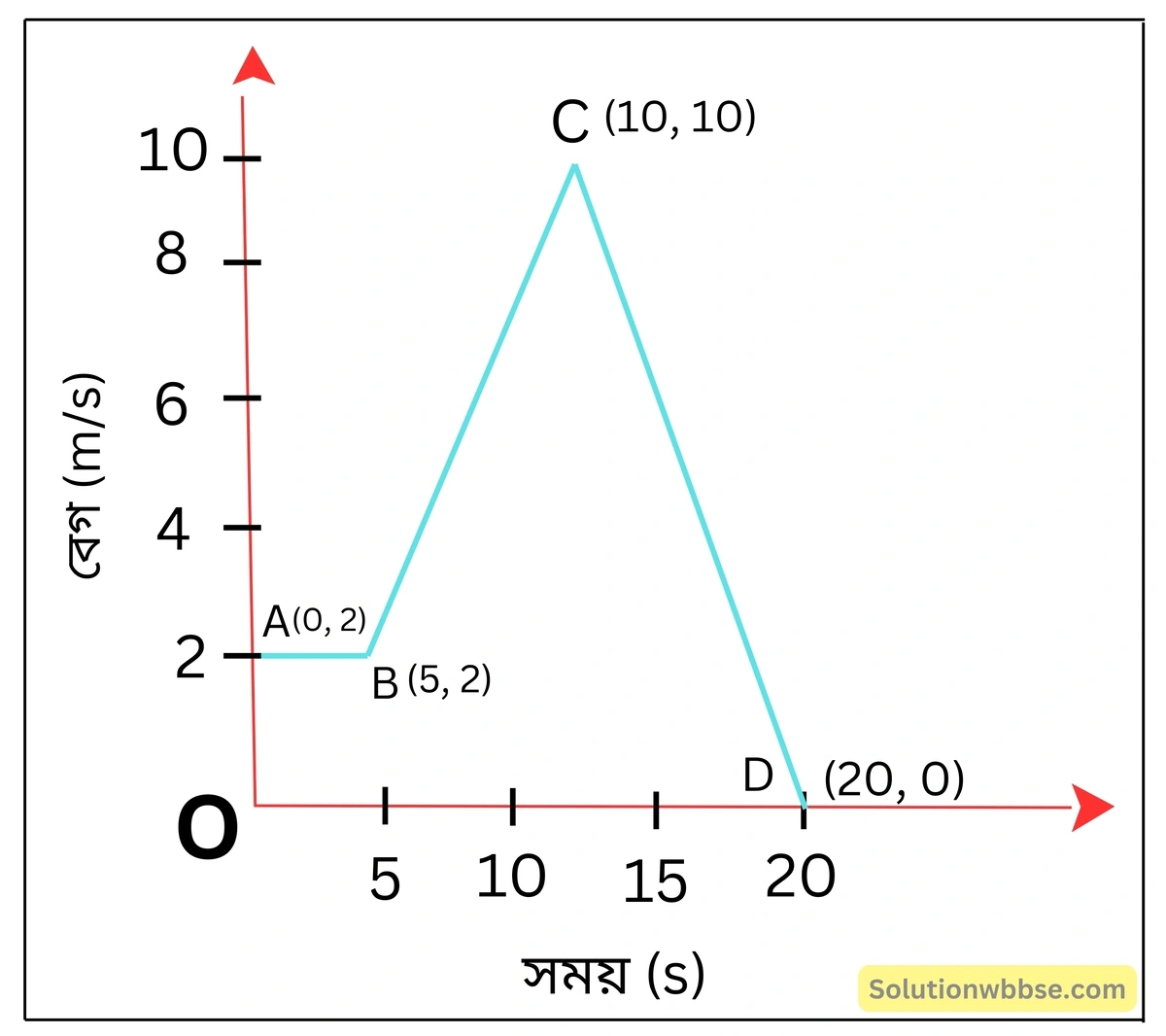
(2) লেখচিত্রের AB অংশে বস্তুটি সমবেগ নিয়ে চলে। লেখচিত্রের BC ও CD অংশে বস্তুটি অসমবেগ নিয়ে চলে।
একটি বস্তুকণার বেগ-সময় লেখচিত্র নিম্নরূপ –
(1) লেখচিত্র থেকে বলো PQ, QR, RS অংশে বস্তুকণার গতি কেমন?
(2) P থেকে Q -তে যেতে বস্তুকণার ত্বরণ কত?
(3) Q থেকে R -এ যেতে বস্তুকণার ত্বরণ কত?
(4) R থেকে S -এ যেতে বস্তুকণার ত্বরণ কত?
(5) লেখচিত্রের কোন্ অংশে বস্তুকণার বেগ বদলায় না?
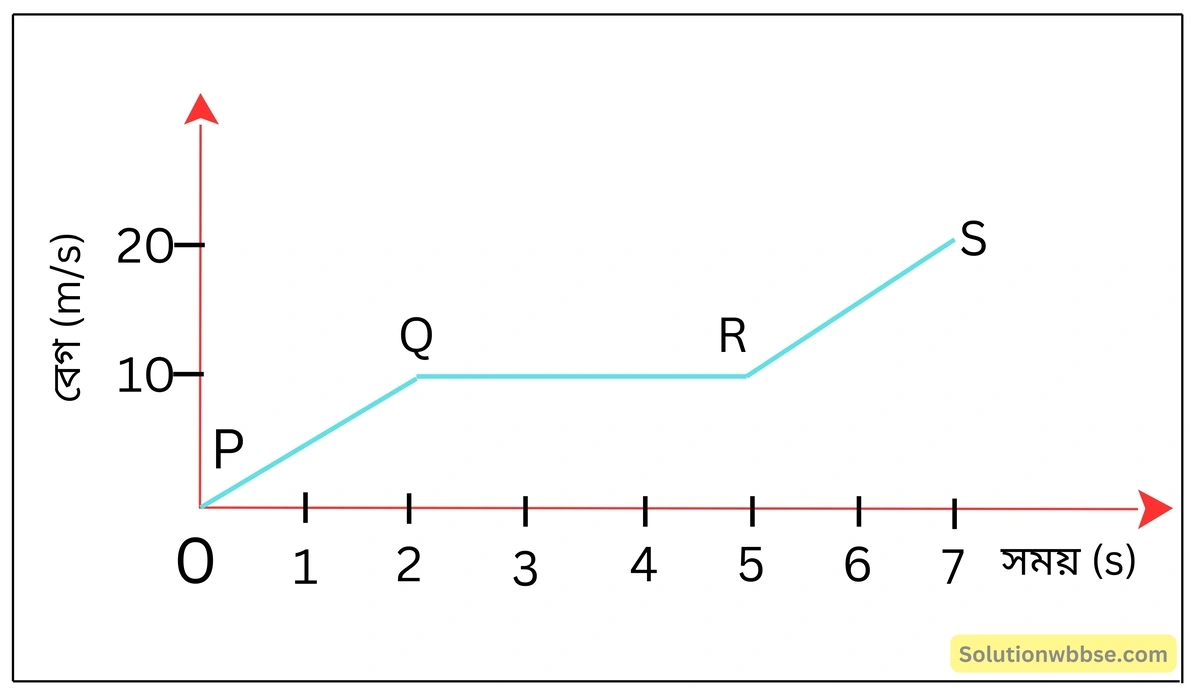
- PQ অংশে বস্তুকণাটি সমত্বরণে চলে। QR অংশে বস্তুকণাটি সমবেগে চলে। RS অংশে বস্তুকণাটি আবার সমত্বরণে চলে।
- P থেকে Q -তে যেতে ত্বরণ \(=\frac{10-0}{2-0}=5\) m/s2
- Q থেকে R -এ যেতে ত্বরণ = 0
- R থেকে S -এ যেতে ত্বরণ \(=\frac{20-10}{7-5}=5\) m/s2
- লেখচিত্রের QR অংশে বস্তুকণার বেগ বদলায় না।
একটি বস্তুকণা 5 m/s গতিবেগে যাত্রা শুরু করে এবং 10 সেকেন্ড পরে তার বেগ হয় 20 m/s। এই সময়ে কণাটি কত দূরত্ব যাবে তা বেগ-সময় লেখচিত্র থেকে নির্ণয় করো।
প্রদত্ত বস্তুকণার বেগ-সময় লেখচিত্র হল –
| বেগ | 5 | 20 |
| সময় | 0 | 10 |
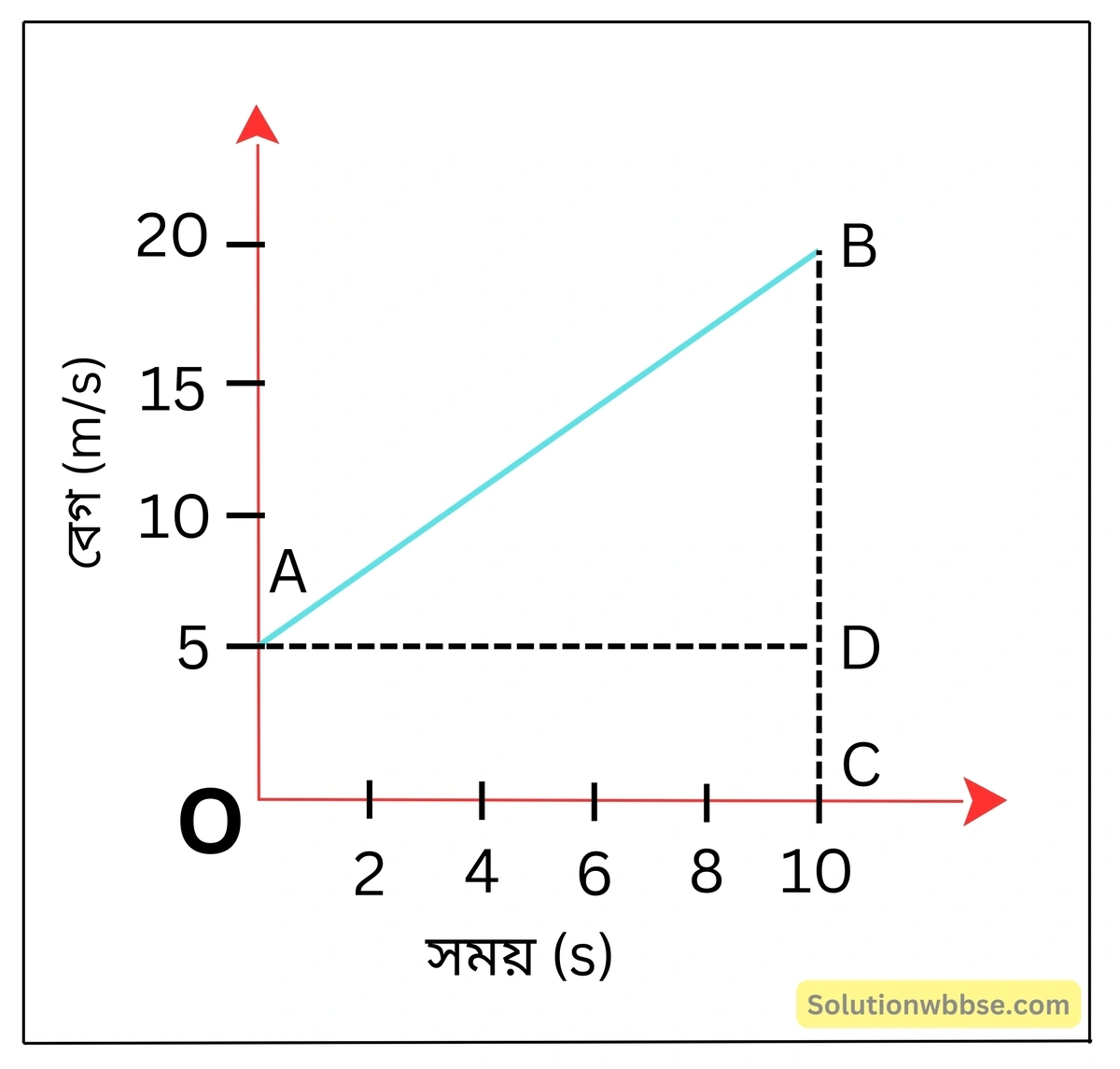
বস্তু দ্বারা অতিক্রান্ত দূরত্ব লেখচিত্র ও সময় অক্ষ দ্বারা আবদ্ধ অংশের ক্ষেত্রফল = OABC ট্রাপিজিয়ামের ক্ষেত্রফল।
= \(\frac12\left(OA+BC\right)\times OC\)
= \(\frac12\left(5+20\right)\times10\)
= 125 m
একটি বস্তুকণার বেগ-সময় লেখচিত্রটি নিম্নরূপ। নিম্নলিখিত বিষয়গুলি নির্ণয় করো।
(1) সমবেগে অতিক্রান্ত দূরত্ব
(2) 7 sec সময়ে অতিক্রান্ত মোট দূরত্ব।
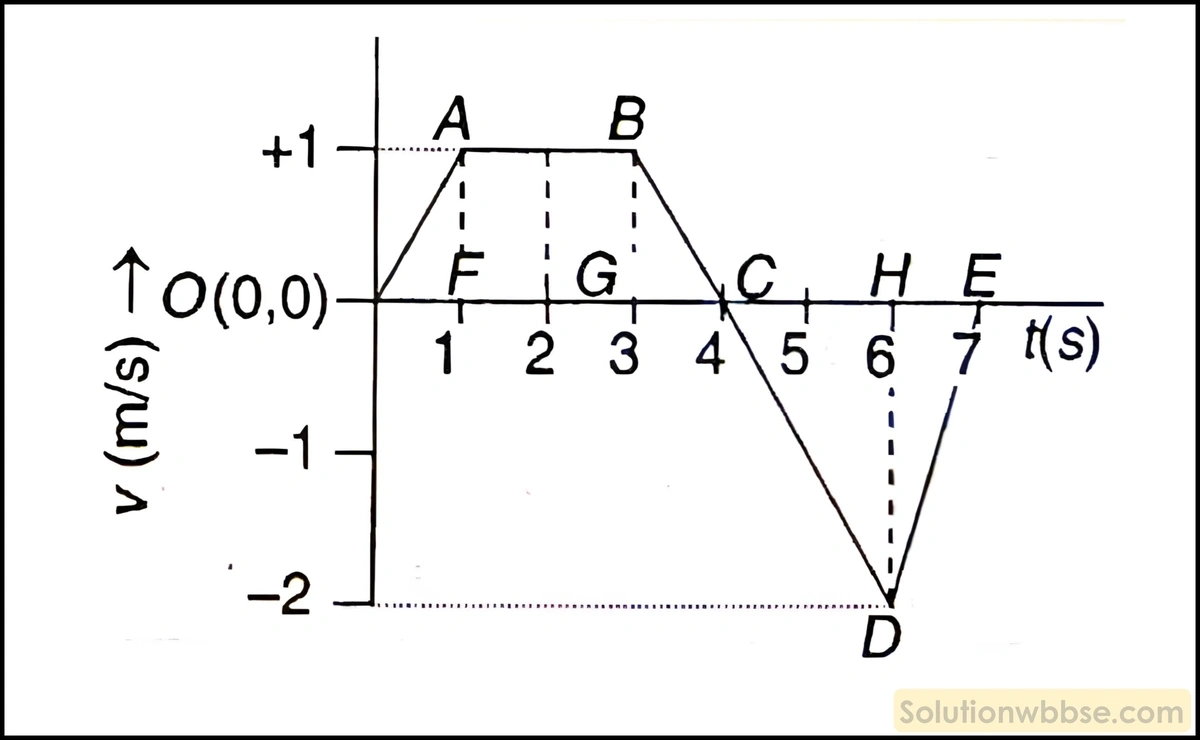
1. সমবেগে অতিক্রান্ত দূরত্ব
সমবেগে বস্তুকণাটি দ্বারা অতিক্রান্ত দূরত্ব,
= ABGF আয়তক্ষেত্রের ক্ষেত্রফল
= AB × AF
= (OG – OF) × AF [∵ AB = GF]
= (3 – 1) × 1 m
= 2m
2. 7 sec সময়ে অতিক্রান্ত মোট দূরত্ব
7 sec -এ কণাটি দ্বারা অতিক্রান্ত দূরত্ব = লেখচিত্র ও সময় অক্ষ দ্বারা আবদ্ধ অংশের ক্ষেত্রফল,
= ABCO ট্রাপিজিয়ামের ক্ষেত্রফল + CDE ত্রিভুজের ক্ষেত্রফল
= \(\frac12\left(OC+AB\right)\times AF+\frac12CE\times HD\)
= \(\frac12\left(4+2\right)\times1+\frac12\times3\times2\)
= 3 + 3
= 6 m
∴ 7 sec সময়ে কণাটি দ্বারা অতিক্রান্ত মোট দূরত্ব 6 m।
নীচের চিত্রটি একটি গতিশীল বস্তুকণার বেগ-সময় লেখচিত্র। এটি থেকে –
(1) বস্তুর প্রাথমিক গতিবেগ,
(2) বস্তু দ্বারা অতিক্রান্ত দূরত্ব,
(3) ত্বরণ নির্ণয় করো।
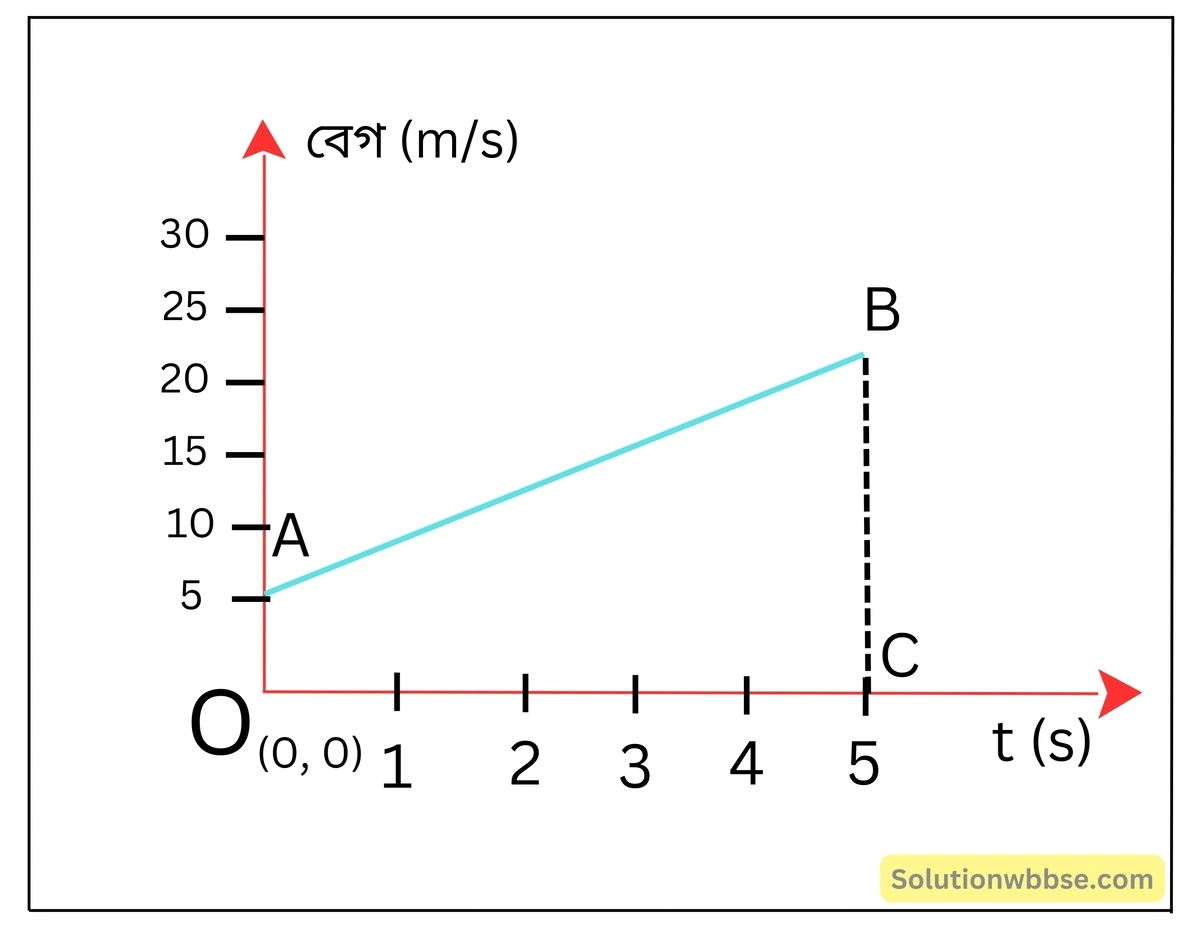
বস্তুর প্রাথমিক গতিবেগ
লেখচিত্র থেকে বোঝা যায় বস্তুটির প্রাথমিক গতিবেগ v = 5 m/s।
বস্তু দ্বারা অতিক্রান্ত দূরত্ব
বস্তু দ্বারা অতিক্রান্ত দূরত্ব = OABC ট্রাপিজিয়ামের ক্ষেত্রফল
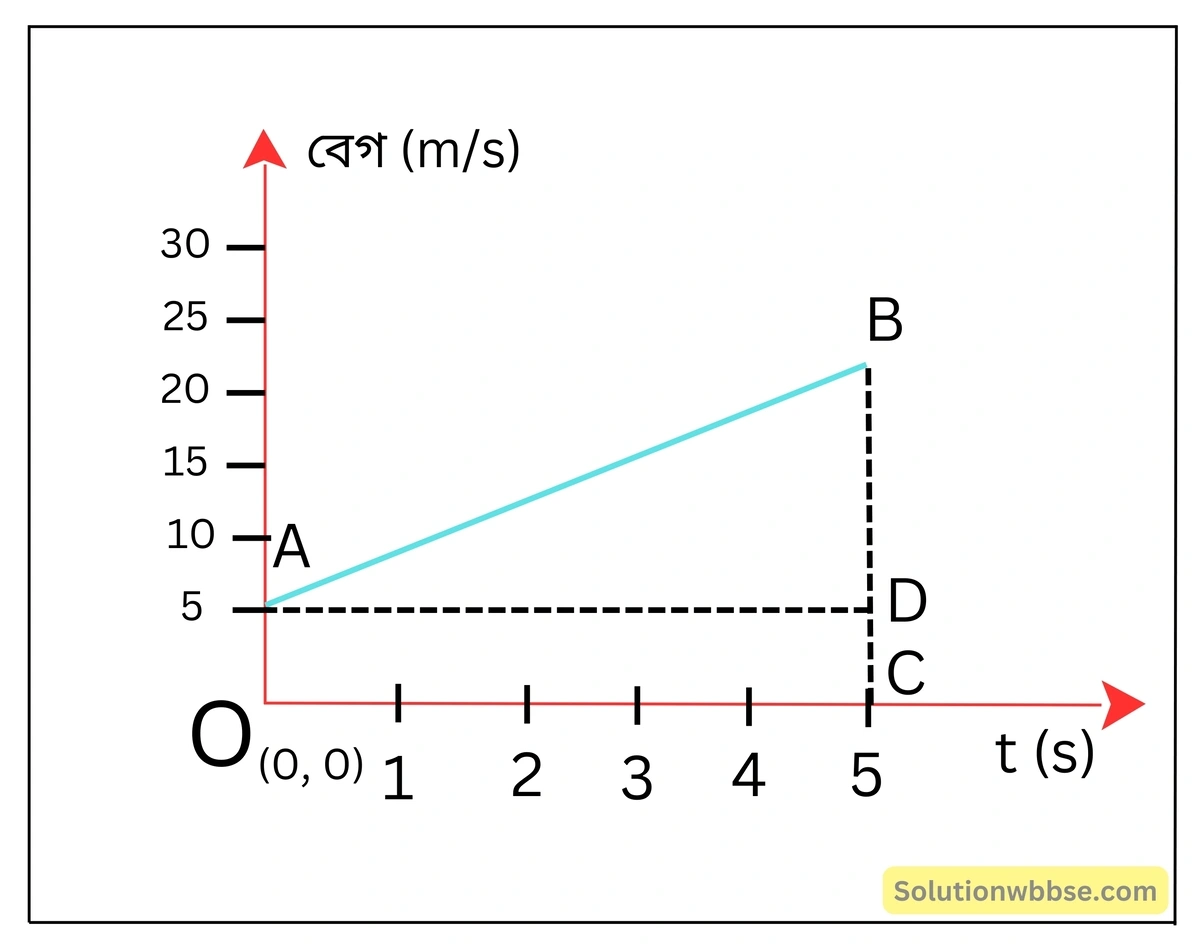
= \(\frac12\times\left(OA+BC\right)\times OC\)
= \(\frac12\times\left(5+25\right)\times5\)
= 75 মিটার।
ত্বরণ নির্ণয়
ত্বরণ = লেখচিত্রের নতি
= tanθ
= \(\frac{BD}{AD}\)
= \(\frac{BC-CD}{OC}\)
= \(\frac{25-5}5\)
= 4 m/s2
একটি গাড়ি রাস্তা দিয়ে সমত্বরণে গতিশীল। বিভিন্ন সময়ে গাড়ির বেগের তালিকা দেওয়া হল। বেগ-সময় লেখচিত্র আঁকো এবং লেখচিত্র থেকে
(1) গাড়ির ত্বরণ এবং
(2) 10 sec -এ অতিক্রান্ত দূরত্ব নির্ণয় করো।
| সময় | 0 | 2 | 4 | 6 | 8 | 10 |
| বেগ | 4 | 8 | 12 | 16 | 20 | 24 |
গাড়িটির বেগ-সময় লেখচিত্র নিম্নরূপ –
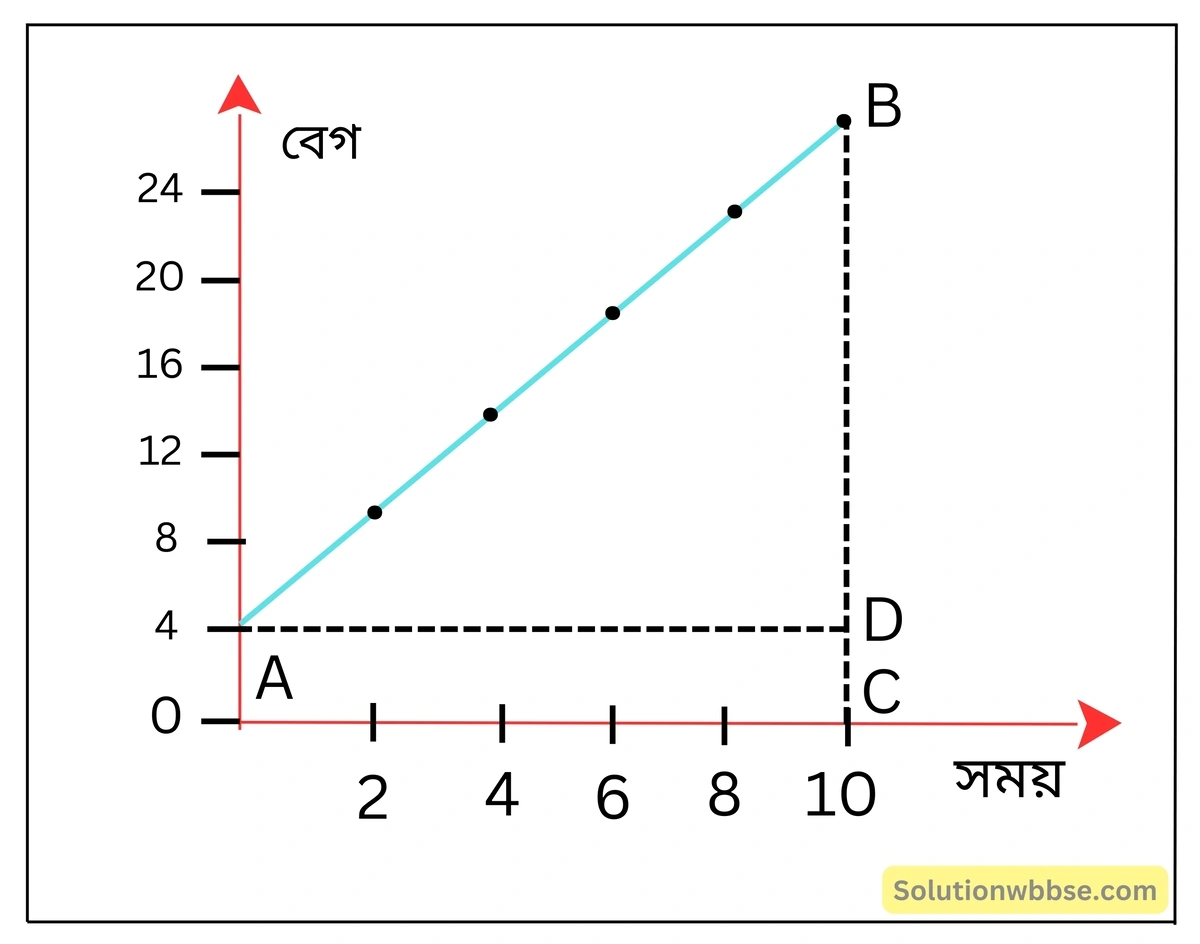
গাড়ির ত্বরণ
গাড়িটির ত্বরণ a = বেগ-সময় লেখচিত্রের নতি
= tanθ
= \(\frac{BD}{AD}\)
= \(\frac{BC-CD}{OC}\)
= \(\frac{24-4}{10}\)
= \(\frac{20}{10}\)
= 2 m/s2
10 sec -এ অতিক্রান্ত দূরত্ব নির্ণয় –
10 sec -এ অতিক্রান্ত দূরত্ব s = OABC ট্রাপিজিয়ামের ক্ষেত্রফল
= \(\frac12\left(OA+BC\right)\times OC\)
= \(\frac12\left(4+24\right)\times10\)
= 140 m
প্রদত্ত লেখচিত্র থেকে বস্তুকণা দ্বারা 6 সেকেন্ডে অতিক্রান্ত দূরত্বের মান নির্ণয় করো।
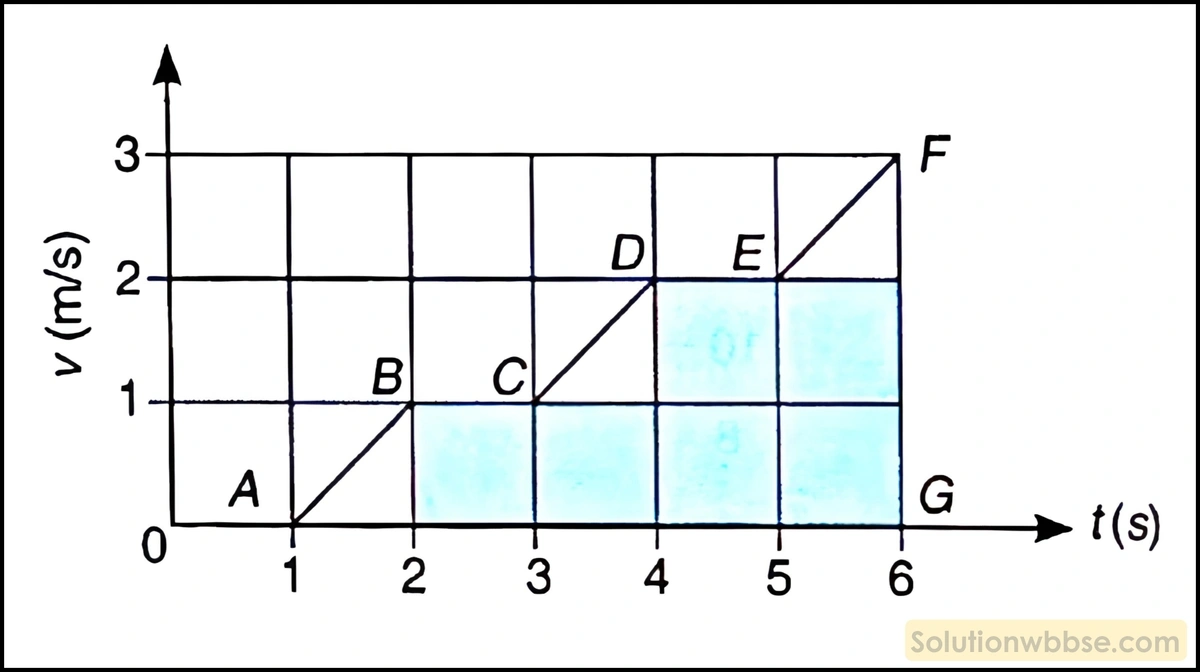
কণাটি দ্বারা 6 সেকেন্ডে অতিক্রান্ত দূরত্ব = 3 × (সাদা অংশের ত্রিভুজের ক্ষেত্রফল) + 6 × (রঙিন বর্গক্ষেত্রের ক্ষেত্রফল)
= \(\left\{3\times\left(\frac12\times1\times1\right)+6\times\left(1\times1\right)\right\}\) মিটার।
= \(\frac32+6\) মিটার
= 7.5 মিটার।
একটি গতিশীল বস্তুর বেগ-সময় লেখচিত্র দেখানো হল –
(1) 2 sec সময় পরে কণার বেগ,
(2) 7 sec -এ মোট অতিক্রান্ত দূরত্ব নির্ণয় করো এবং
(3) কণাটি কত সময় ধরে সমবেগে চলছে?
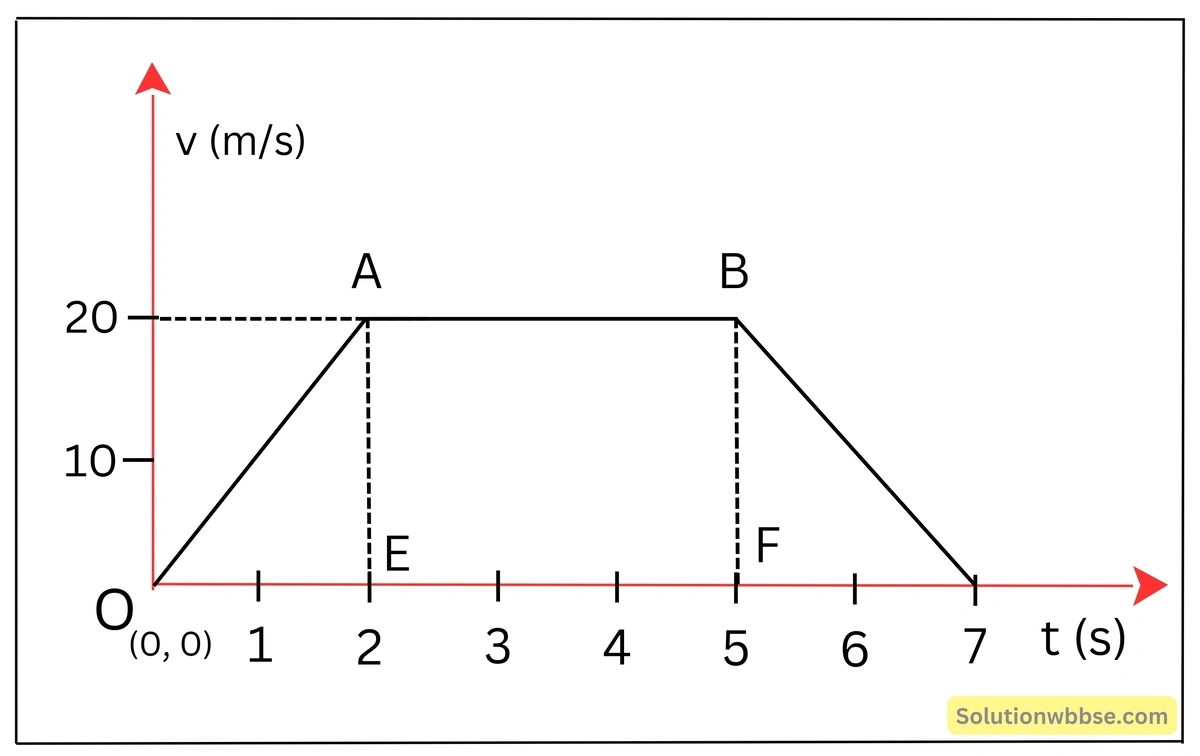
2 sec সময় পরে কণার বেগ
2 sec পর কণার বেগ = EA = 20 m/s
7 sec -এ মোট অতিক্রান্ত দূরত্ব নির্ণয়
7 sec -এ কণাটি দ্বারা অতিক্রান্ত মোট দূরত্ব,
= OABC ট্রাপিজিয়ামের ক্ষেত্রফল
= \(\frac12\left(AB+OC\right)\times AE\)
= \(\frac12\left(3+7\right)\times20\)
= 100 m
কণাটি কত সময় ধরে সমবেগে চলছে
লেখ থেকে পাই, কণাটি AB অর্থাৎ (5 – 2) s = 3 s সময় ধরে সমবেগে চলে।
একটি কণার বেগ-সময় লেখচিত্র পাশে দেখানো হয়েছে।
(1) কণাটি দ্বারা অতিক্রান্ত মোট দূরত্ব কত?
(2) কণাটির মোট সরণের মান কত হবে?
(3) কণাটির গড়দ্রুতি ও গড়বেগ নির্ণয় করো।
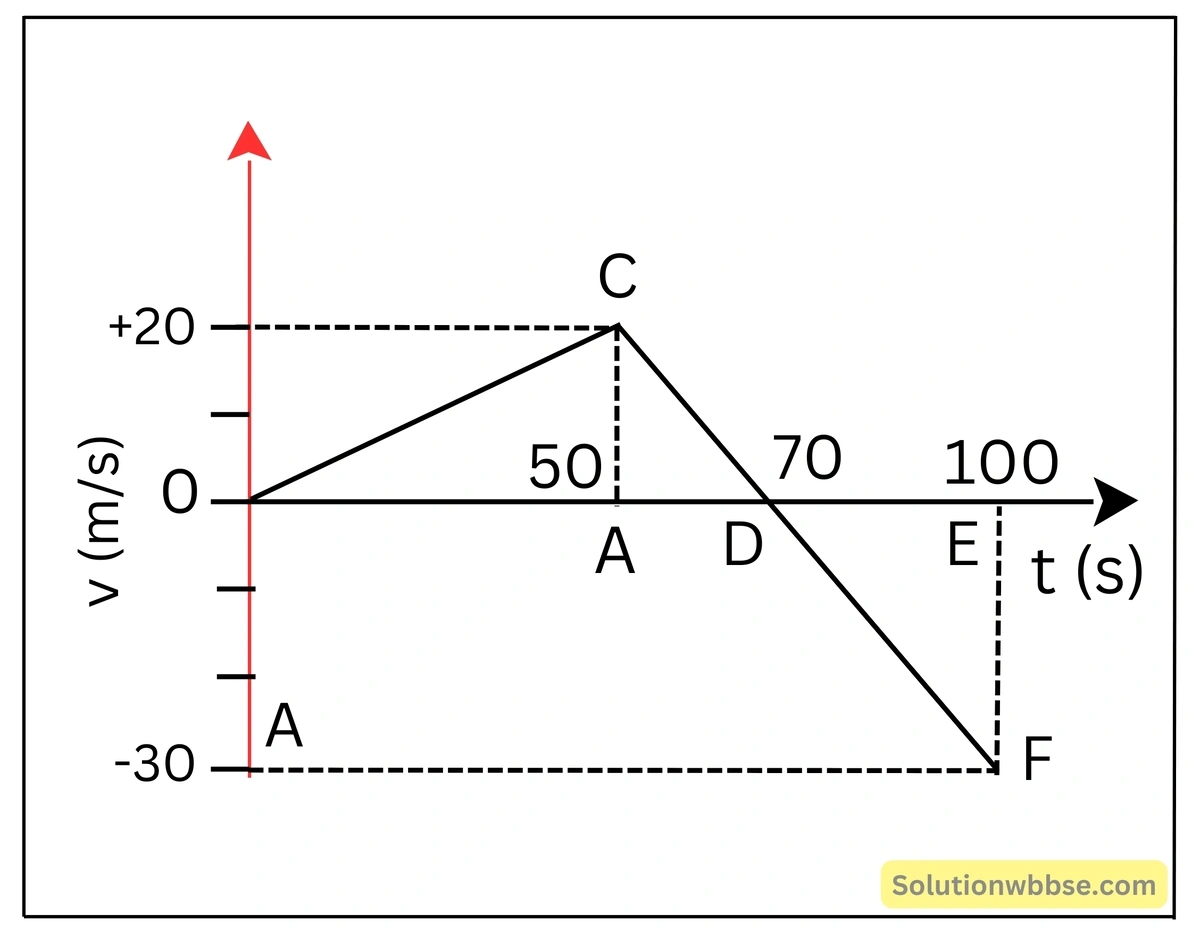
কণাটি দ্বারা অতিক্রান্ত মোট দূরত্ব
লেখচিত্র থেকে পাই কণাটি দ্বারা অতিক্রান্ত মোট দূরত্ব,
s = △OCD -এর ক্ষেত্রফল + △DEF -এর ক্ষেত্রফল
বা, s = \(\frac12\left(AC+OD\right)+\frac12\left(DE\times FE\right)\)
বা, s = \(\frac12\left(20\times70+30\times30\right)\)
বা, s = \(\frac{2300}2\) m
বা, s = 1150 m
কণাটির মোট সরণের মান
মোট সরণ \(\left(\overrightarrow s\right)\) -এর মান,
\(\left|\overrightarrow s\right|=△OCD\) -এর ক্ষেত্রফল △DEF -এর ক্ষেত্রফল (∵ DE সময় অবকাশে সরণ ঋণাত্মক)
বা, \(\left|\overrightarrow s\right|=\frac12\left(20\times70-30\times30\right)\)
বা, \(\left|\overrightarrow s\right|=\frac{500}2\) m
বা, \(\left|\overrightarrow s\right|=500\) m
কণাটির গড়দ্রুতি ও গড়বেগ নির্ণয়
মোট অতিবাহিত সময় (t) = 100 s,
অতিক্রান্ত দূরত্ব s = 1150 m
∴ কণার দ্রুতি \(v=\frac{1150}{100}m/s=11.5m/s\)
কণার বেগ \(\left(\overrightarrow v\right)\) -এর মান \(\left|\overrightarrow v\right|\)
=
= \(\frac{250}{100}\) m/s
= 2.5 m/s
নীচের লেখচিত্র থেকে নির্ণয় করো।
(1) কণাটি কখন সমবেগে গতিশীল?
(2) দশম সেকেন্ডে কণার বেগ কত?
(3) কণার গতির CD অংশের ত্বরণের মান নির্ণয় করো।
(4) গতির শেষ 2 সেকেন্ডে কণাটি কত পথ অতিক্রম করেছে?
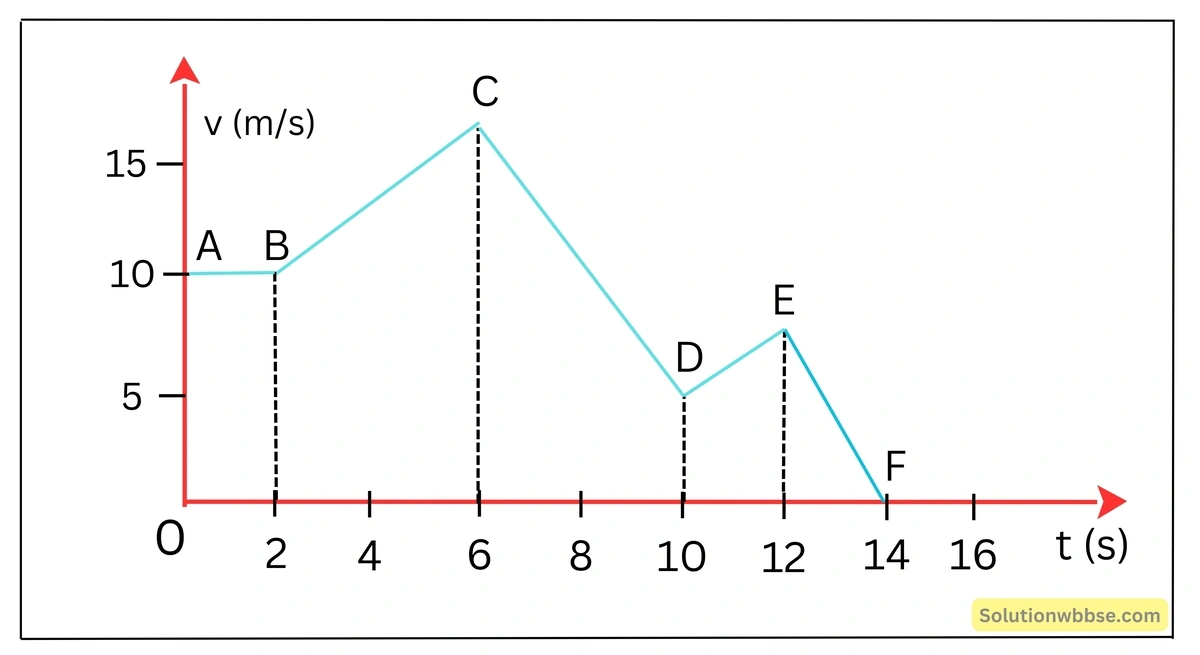
কণাটি কখন সমবেগে গতিশীল –
কণাটি যাত্রা শুরুর প্রথম 2 sec (AB লেখ) সমবেগে গতিশীল থাকবে।
দশম সেকেন্ডে কণার বেগ
দশম সেকেন্ডে কণার বেগ 5 m/s
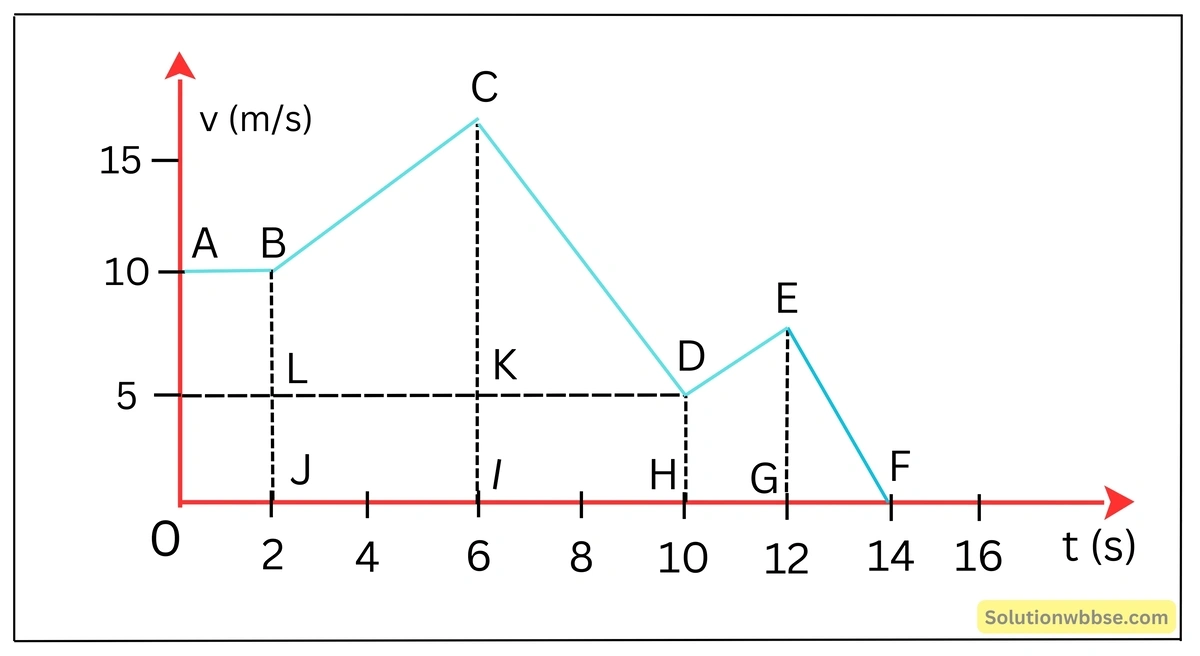
কণার গতির CD অংশের ত্বরণের মান নির্ণয়
কণার গতির CD অংশের ত্বরণ,
= CD অংশের লেখচিত্রের নতি
= tanθ
= – latex]\left(\frac{CK}{KD}\right)[/latex]
= – latex]\left(\frac{Cl-lK}{lH}\right)[/latex]
= – latex]\frac{15-5}4[/latex]
= 2.5 m/s2
এক্ষেত্রে সময়ের সঙ্গে বেগ হ্রাস পাওয়ায় কণার গতিতে মন্দন অর্থাৎ, ঋণাত্মক ত্বরণ দেখা যাবে।
গতির শেষ 2 সেকেন্ডে কণাটি পথ অতিক্রম
গতির শেষ 2 sec -এ কণাটি দ্বারা অতিক্রান্ত পথ = ∆EFG -এর ক্ষেত্রফল
= \(\frac12\times GF\times EG\)
= \(\frac12\times2\times10\) m
= 10 m
Class 9 Physical Science – Notes for All Chapters
| Chapter Name | Tropics |
|---|---|
| পরিমাপ | পরিমাপ ও একক বিভিন্ন মাপের একক মাত্রা পরিমাপ |
| বল ও গতি | স্থিতি ও গতি গতির সমীকরণ নিউটনের প্রথম গতিসূত্র নিউটনের দ্বিতীয় গতি সূত্র নিউটনের তৃতীয় গতিসূত্র বিভিন্ন ধরনের বল রৈখিক ভরবেগ রৈখিক ভরবেগ সংরক্ষণ |
| পদার্থ : গঠন ও ধর্ম | তরল ও বায়ুর চাপ আর্কিমিডিসের নীতি পৃষ্ঠটান সান্দ্রতা বার্নোলির নীতি স্থিতিস্থাপকতা |
| পদার্থ : পরমাণুর গঠন ও পদার্থের ভৌত ও রাসায়নিক ধর্মসমূহ | পরমাণুর গঠন মোলের ধারণা দ্রবণ অ্যাসিড, ক্ষার, লবণ মিশ্রণের উপাদানের পৃথকীকরণ জল |
| শক্তির ক্রিয়া , কার্য, ক্ষমতা | শক্তির ক্রিয়া , কার্য, ক্ষমতা |
| তাপ | ক্যালোরিমিতি কার্য ও তাপের তুল্যতা লীনতাপ সম্পৃক্ত ও অসম্পৃক্ত বাষ্প জলের ব্যতিক্রান্ত প্রসারণ |
| শব্দ | শব্দের উৎস : কম্পন শব্দের বিস্তার : তরঙ্গ শব্দের কয়েকটি ধর্ম শব্দের বৈশিষ্ট্য মানুষের কান ও শব্দ শোনার কৌশল শব্দদূষণ |
আজকের আর্টিকেলে আমরা নবম শ্রেণির ভৌতবিজ্ঞান বইয়ের দ্বিতীয় অধ্যায় “বল ও গতি” এর “গতির সমীকরণ” থেকে পরীক্ষায় আসা গুরুত্বপূর্ণ প্রশ্ন ও উত্তরগুলো আলোচনা করেছি। এই প্রশ্নোত্তরগুলো নবম শ্রেণির বার্ষিক পরীক্ষা, এমনকি চাকরি বা যেকোনো প্রতিযোগিতামূলক পরীক্ষার জন্যও উপযোগী। কারণ, এই অধ্যায়ের প্রশ্ন প্রায়ই বিভিন্ন পরীক্ষায় কমন আসে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সাহায্য করবে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন কিংবা টেলিগ্রামে যোগাযোগ করুন—আপনাদের প্রশ্নের উত্তর দিতে আমি সর্বদা প্রস্তুত।
ধন্যবাদ সবাইকে।






Leave a Comment