ত্রিভুজের ক্ষেত্রফল বের করার জন্য সাধারণত দুইটি পদ্ধতি বেশি ব্যবহৃত হয়। এখানে এই দুই পদ্ধতি উদাহরণসহ ব্যাখ্যা করা হয়েছে। আপনি নিজের প্রয়োজন অনুযায়ী যে কোনো পদ্ধতি ব্যবহার করতে পারেন।
পদ্ধতি ১ – যখন ত্রিভুজের ভিত্তি এবং উচ্চতা দেওয়া থাকে।
ত্রিভুজের ক্ষেত্রফল বের করার সূত্র: \( A = \frac{b \times h}{2} \)
এখানে,
- A হলো ত্রিভুজের ক্ষেত্রফল।
- b হলো ত্রিভুজের ভিত্তি।
- h হলো ত্রিভুজের উচ্চতা।
উদাহরণ:
একটি ত্রিভুজের ভিত্তি 12 সেমি এবং উচ্চতা 8 সেমি। ত্রিভুজের ক্ষেত্রফল বের করতে হবে।
ত্রিভুজের ক্ষেত্রফল, \( A = \frac{b \times h}{2} \)
এখানে, b=12 এবং h=8 ।
∴ \( A = \frac{12 \times 8}{2} = \frac{96}{2} = 48\) বর্গ সেমি
উত্তর: ত্রিভুজের ক্ষেত্রফল 48 বর্গ সেমি
পদ্ধতি ২ – যখন ত্রিভুজের তিন বাহুর দৈর্ঘ্য দেওয়া থাকে।
হেরনের সূত্র ব্যবহার করে ক্ষেত্রফল বের করার পদ্ধতি –
\( A = \sqrt{s(s-a)(s-b)(s-c)} \)এখানে,
- a,b,c হলো ত্রিভুজের তিন বাহুর দৈর্ঘ্য।s হলো ত্রিভুজের আধা-পরিধি।
আধা-পরিধি (s) বের করার সূত্র –
উদাহরণ:
একটি ত্রিভুজের তিন বাহুর দৈর্ঘ্য যথাক্রমে 7 সেমি, 8 সেমি, এবং 9 সেমি। ত্রিভুজের ক্ষেত্রফল বের করতে হবে।
সমাধান:
ধাপ ১ – আধা-পরিধি (s) বের করা
\( s = \frac{a + b + c}{2} \)এখানে, a=7, b=8, এবং c=9।
গণনা:
\( s = \frac{7 + 8 + 9}{2} = \frac{24}{2} = 12 \)সেমি
ধাপ ২ – হেরনের সূত্র ব্যবহার করা
ত্রিভুজের ক্ষেত্রফল,
\( A = \sqrt{s(s-a)(s-b)(s-c)} \)
এখানে, s=12, a=7, b=8, এবং c=9।
গণনা:
\( A = \sqrt{12(12-7)(12-8)(12-9)} \)
\( A = \sqrt{12 \times 5 \times 4 \times 3} \)
\( A = \sqrt{720} \)
ধাপ ৩ – 720-এর বর্গমূল বের করা
\( A \approx 26.83 \) বর্গসেমি
উত্তর: ত্রিভুজের ক্ষেত্রফল 26.83 বর্গ সেমি।
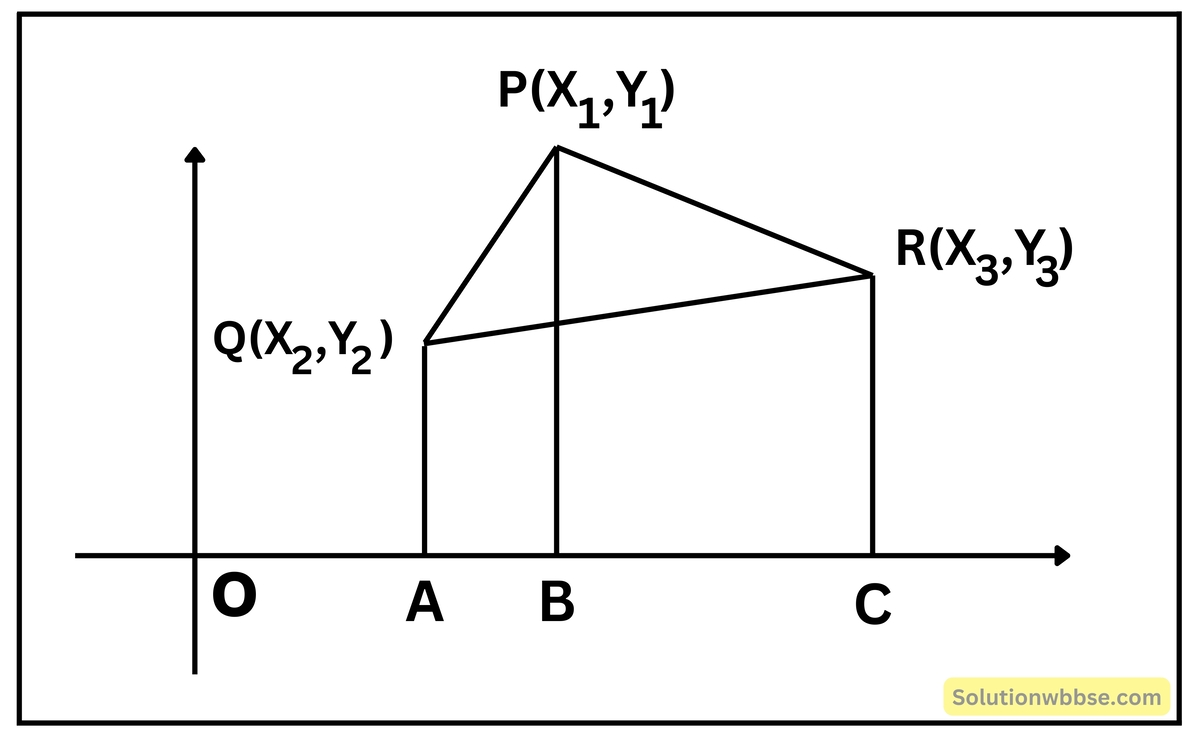
পদ্ধতি ৩ – স্থানাঙ্ক জ্যামিতিতে ত্রিভুজের ক্ষেত্রফল নির্ণয়ের পদ্ধতি
ধরা যাক, একটি ত্রিভুজের শীর্ষবিন্দু হল \([
P(x_1, y_1), \, Q(x_2, y_2), \, R(x_3, y_3)
]\)। এই বিন্দুগুলোর সাহায্যে ত্রিভুজের ক্ষেত্রফল বের করার জন্য আমরা নিচের সূত্রটি ব্যবহার করব:
A = \frac{1}{2} \left| x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2) \right|
\)
এখানে –
• \(
x_1, y_1; \, x_2, y_2; \, x_3, y_3\) হলো শীর্ষবিন্দুগুলোর স্থানাঙ্ক।
• A ত্রিভুজের ক্ষেত্রফল।
বিশেষ নিয়মাবলী:
- যদি ক্ষেত্রফল 0 হয়, তাহলে তিনটি বিন্দু সমরেখ (একই সরলরেখায়)।
- ক্ষেত্রফল সর্বদা ধনাত্মক নিতে হবে।
উদাহরণ:
ধরা যাক, ত্রিভুজ ABC -এর শীর্ষবিন্দুগুলি হল A(1,2), B(4,2), এবং C(3,5)। এর ক্ষেত্রফল নির্ণয় করব।
ধাপ ১: সূত্রে মান বসানো –
\(A = \frac{1}{2} \left| x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2) \right|
\)
এখানে -\[
x_1 = 1, \, y_1 = 2,\quad \\
x_2 = 4, \, y_2 = 2,\quad \\
x_3 = 3, \, y_3 = 5
\]
ধাপ ২: সূত্র প্রয়োগ:
\(A = \frac{1}{2} \left| 1(2-5) + 4(5-2) + 3(2-2) \right|
\)
\(
A = \frac{1}{2} \left| 1(-3) + 4(3) + 3(0) \right|
\)
\(
A = \frac{1}{2} \left| -3 + 12 + 0 \right|
\)
\(
A = \frac{1}{2} \times 9 = \frac{9}{2}
\)
উত্তর: ত্রিভুজ ABC -এর ক্ষেত্রফল 92 বর্গ একক।
এই আর্টিকেলে আমরা ত্রিভুজের তিনটি ক্ষেত্রফল নির্ণয়ের পদ্ধতি সম্পর্কে আলোচনা করেছি। এই পদ্ধতি তোমাদের বিভিন্ন অংক করার কাজে লাগবে, তাছাড়া এখান থেকে প্রশ্ন প্রায়ই চাকরির পরীক্ষায় দেখা যায়, ত্রিভুজের ক্ষেত্রফল নির্ণয় কোন জায়গায় কোন অসুবিধা হলে অবশ্যই আমাদের টেলিগ্রামে জানাবেন আমরা উত্তর দেওয়ার চেষ্টা করব, টেলিগ্রাম মেল লিংক নিচে দেওয়া আছে। ধন্যবাদ






Leave a Comment