পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) দশম শ্রেণির গণিত পাঠ্যবইয়ের বিংশতম অধ্যায় হলো ‘স্থানাঙ্ক জ্যামিতি : ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল’। এই পোস্টে ‘কষে দেখি – 20‘-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. নিচের শীর্ষবিন্দু বিশিষ্ট ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল প্রতিক্ষেত্রে নির্ণয় করি
(i) \((2, -2)\), \((4, 2)\) এবং \((-1, 3)\)
সমাধান –
\((2,-2)\), \((4,2)\) এবং \((-1,3)\) শীর্ষবিন্দুবিশিষ্ট ত্রিভুজের ক্ষেত্রফল –
= \( \frac{1}{2} |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)|\) বর্গএকক
= \( \frac{1}{2} |2(2-3) + 4(3-(-2)) + (-1)(-2-2)|\) বর্গএকক [ এক্ষেত্রে, \((x_1, y_1) = (2,-2)\), \((x_2, y_2) = (4,2)\) এবং \((x_3, y_3) = (-1,3)\) ]
= \( \frac{1}{2} |\{2 \times (-1)\} + (4 \times 5) + \{(-1) \times (-4)\}|\) বর্গএকক
= \( \frac{1}{2} |-2 + 20 + 4|\) বর্গএকক
= \( \frac{1}{2} \times 22\) বর্গএকক
= \( 11\) বর্গএকক [উত্তর]
(ii) \((8, 9)\), \((2, 6)\) এবং \((9, 2)\)
সমাধান –
\((8,9)\), \((2,6)\) এবং \((9,2)\) স্থানাঙ্কবিশিষ্ট ত্রিভুজের ক্ষেত্রফল
= \( \frac{1}{2} |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)|\) বর্গএকক
= \( \frac{1}{2} |8(6-2) + 2(2-9) + 9(9-6)|\) বর্গএকক [এক্ষেত্রে, \((x_1, y_1) = (8,9)\), \((x_2, y_2) = (2,6)\) এবং \((x_3, y_3) = (9,2)\) ]
= \( \frac{1}{2} |32 – 14 + 27|\) বর্গএকক
= \( \frac{1}{2} \times 45\) বর্গএকক
= \( 22 \frac{1}{2}\) বর্গএকক [উত্তর]
(iii) \((1, 2)\), \((3, 0)\) এবং মূলবিন্দু
সমাধান –
প্রদত্ত বিন্দুগুলি হল – \((1,2)\), \((3,0)\) এবং মূলবিন্দু
অর্থাৎ \((1,2)\), \((3,0)\) এবং \((0,0)\) স্থানাঙ্কবিশিষ্ট ত্রিভুজের ক্ষেত্রফল
= \( \frac{1}{2} |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)|\) বর্গএকক
= \( \frac{1}{2} |1(0-0) + 3(0-2) + 0(2-0)|\) বর্গএকক [ এক্ষেত্রে, \((x_1, y_1) = (1,2)\), \((x_2, y_2) = (3,0)\) এবং \((x_3, y_3) = (0,0)\) ]
= \( \frac{1}{2} |-6|\) বর্গএকক
= \( \frac{1}{2} \times 6\) বর্গএকক
= \( 3\) বর্গএকক [উত্তর]
2. প্রমাণ করি যে, \((3, -2)\), \((-5, 4)\) এবং \((-1, 1)\) বিন্দু তিনটি সমরেখ।
সমাধান –
\((3,-2)\), \((-5,4)\) এবং \((-1,1)\) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল
= \( \frac{1}{2} |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)|\) বর্গএকক
= \( \frac{1}{2} |3(4-1) + (-5)\{1-(-2)\} + (-1)(-2-4)|\) বর্গএকক [এক্ষেত্রে, \((x_1, y_1) = (3,-2)\), \((x_2, y_2) = (-5,4)\) এবং \((x_3, y_3) = (-1,1)\) ]
= \( \frac{1}{2} |(3 \times 3) + (-5) \times (3) + \{(-1) \times (-6)\}|\) বর্গএকক
= \( \frac{1}{2} |9 – 15 + 6|\) বর্গএকক
= \( 0\)
যেহেতু, \((3,-2)\), \((-5,4)\) এবং \((-1,1)\) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল 0
\(\therefore\) বিন্দু তিনটি সমরেখ [প্রমাণিত]।
3. K –এর মান কত হলে, \((1, -1)\), \((2, -1)\) এবং \((K, -1)\) বিন্দু তিনটি সমরেখ।
সমাধান –
\((1,-1)\), \((2,-1)\) এবং \((K,-1)\) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজটির ক্ষেত্রফল
\(\therefore \frac{1}{2} |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)|\) বর্গএকক
= \( \frac{1}{2} |1(-1-(-1)) + 2(-1-(-1)) + (K)(-1-(-1))|\) বর্গএকক [ এক্ষেত্রে \((x_1, y_1) = (1,-1)\), \((x_2, y_2) = (2,-1)\) এবং \((x_3, y_3) = (K,-1)\) ]
= \( \frac{1}{2} |1(-1+1) + 2(-1+1) + K(-1+1)|\) বর্গএকক
= \( 0\)
\(\therefore\) K –এর যেকোনো বাস্তব মানের জন্য প্রদত্ত বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল শূন্য।
\(\therefore\) K –এর যেকোনো বাস্তব মানের জন্য প্রদত্ত বিন্দু তিনটি সমরেখ হবে।
4. প্রমাণ করি যে, \((1, 2)\) এবং \((-2, -4)\) বিন্দুদ্বয়ের সংযোজক সরলরেখা মূলবিন্দুগামী।
সমাধান –
\((1,2)\), \((-2,-4)\) এবং মূলবিন্দু \((0,0)\) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল
= \( \frac{1}{2} |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)|\) বর্গএকক
= \( \frac{1}{2} | 1(-4-0) + (-2)(0 – 2) + 0\{2-(-4)\}|\) বর্গএকক [এক্ষেত্রে, \((x_1, y_1) =(1,2)\), \((x_2, y_2) = (-2,-4)\) এবং \((x_3, y_3) = (0,0)\) ]
= \( \frac{1}{2} | (-4 + 4) |\) বর্গএকক
= \( 0\)
যেহেতু, \((1,2)\), \((-2 , -4)\) এবং মূলবিন্দু \((0,0)\) দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল 0।
\(\therefore\) \((1,2)\), \((-2 , -4)\) এবং \((0,0)\) বিন্দুগুলি সমরেখ।
\(\therefore\) \((1,2)\) এবং \((-2 , -4)\) বিন্দুদ্বয়ের সংযোজক সরলরেখা মূলবিন্দুগামী [প্রমাণিত]।
5. প্রমাণ করি যে, \((2, 1)\) এবং \((6, 5)\) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশের মধ্যবিন্দু \((-4, -5)\) ও \((9, 8)\) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশের উপর অবস্থিত।
সমাধান –
\((2,1)\) এবং \((6,5)\) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশের মধ্যবিন্দুর স্থানাঙ্ক \(\left( \frac{2+6}{2} , \frac{1+5}{2} \right) = (4, 3)\)
\(\therefore\) \((-4,-5)\), \((9,8)\) এবং \((4,3)\) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল
= \( \frac{1}{2} |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)|\)
= \( \frac{1}{2} |-4 (8-3) + 9\{3-(-5)\} + 4 (-5 – 8)|\) বর্গএকক [এক্ষেত্রে, \((x_1, y_1) = (-4,-5)\), \((x_2, y_2) = (9,8)\) এবং \((x_3, y_3) = (4,3)\) ]
= \( \frac{1}{2} | (-4)(5) + 9(8) + 4(-13)|\) বর্গএকক
= \( \frac{1}{2} | -20 + 72 – 52 |\) বর্গএকক
= \( \frac{1}{2} |-72 + 72|\) বর্গএকক
= \( \frac{1}{2} |0|\) বর্গএকক
= \( 0\)
\(\therefore\) \((-4,-5)\), \((9,8)\) এবং \((4,3)\) বিন্দু তিনটি সমরেখ।
\(\therefore\) \((2,1)\) এবং \((6,5)\) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশের মধ্যবিন্দু \((-4,-5)\) ও \((9,8)\) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশের উপর অবস্থিত।
6. নিচের প্রতিক্ষেত্রে প্রদত্ত বিন্দু চারটির সংযোগে গঠিত চতুর্ভুজাকার ক্ষেত্রের ক্ষেত্রফল নির্ণয় করি
(i) \((1,1)\), \((3,4)\), \((5,-2)\), \((4,-7)\)
সমাধান –
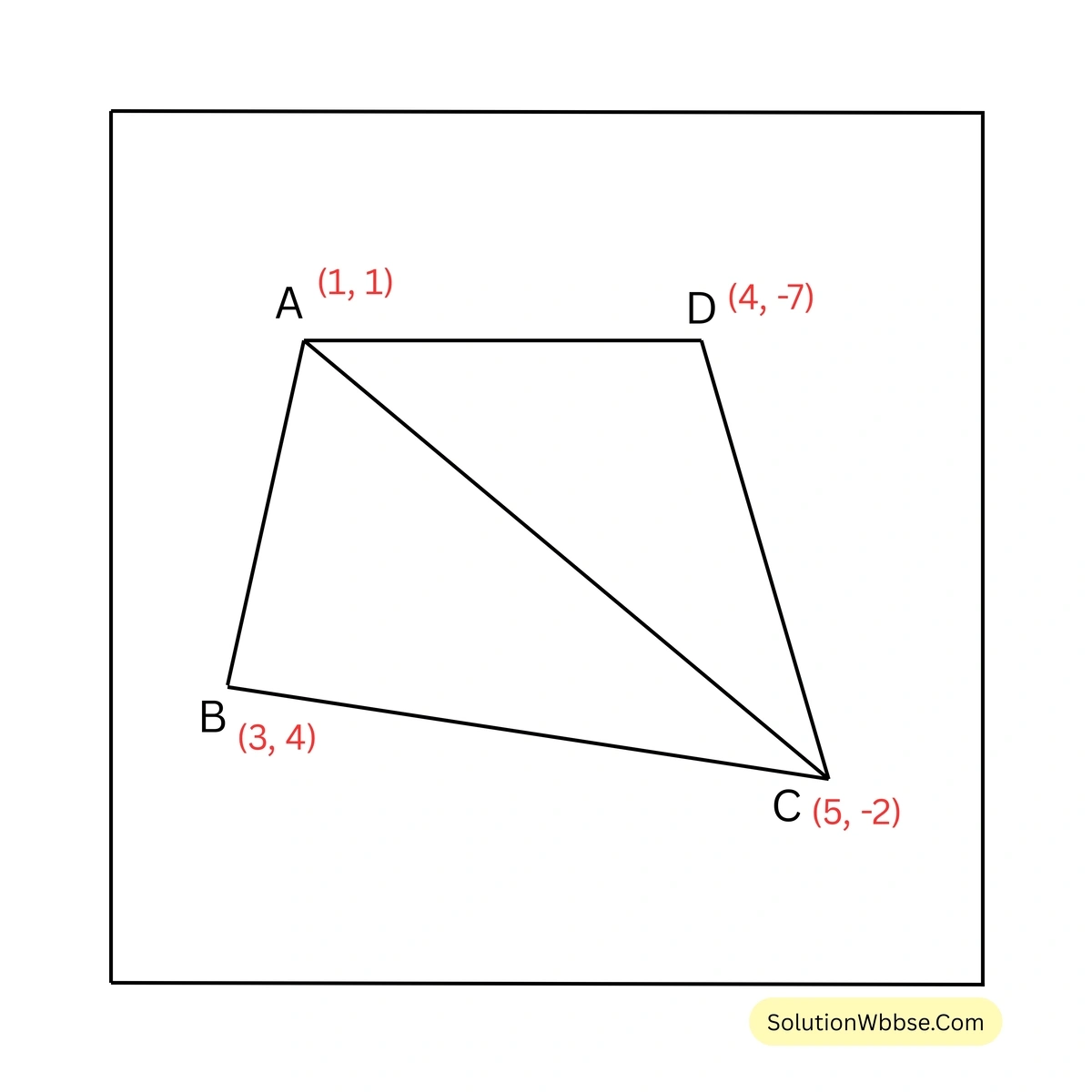
ধরি, ABCD চতুর্ভুজের A, B, C এবং D বিন্দুগুলির স্থানাঙ্ক যথাক্রমে \((1,1)\), \((3,4)\), \((5,-2)\) এবং \((4,-7)\)।
এখন, AC কর্ণ টানা হল যার ফলে চতুর্ভুজটি দুটি ত্রিভুজ \(\Delta ABC\) এবং \(\Delta ACD\) –তে বিভক্ত হল।
ABC ত্রিভুজের ক্ষেত্রফল –
= \( \frac{1}{2} |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)|\) বর্গএকক
= \( \frac{1}{2} |1\{4-(-2)\} + 3(-2-1) + 5(1-4)|\) বর্গএকক [এক্ষেত্রে, \((x_1, y_1) = (1,1)\), \((x_2, y_2) = (3,4)\), \((x_3, y_3) = (5,-2)\)]
= \( \frac{1}{2} |(6 – 9 – 15)|\) বর্গএকক
= \( \frac{1}{2} |-18|\) বর্গএকক
= \( \frac{1}{2} \times 18\) বর্গএকক
= \( 9\) বর্গএকক
ACD ত্রিভুজের ক্ষেত্রফল –
= \( \frac{1}{2} |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)|\) বর্গএকক
= \( \frac{1}{2} |1\{-2-(-7)\} + 5(-7-1) + 4\{1-(-2)\}|\) বর্গএকক
[এক্ষেত্রে, \((x_1, y_1) = (1,1)\), \((x_2, y_2) = (5,-2)\), \((x_3, y_3) = (4,-7)\)]
= \( \frac{1}{2} |(5 – 40 + 12)|\) বর্গএকক
= \( \frac{1}{2} |-23|\) বর্গএকক
= \( \frac{1}{2} \times 23\) বর্গএকক
= \( \frac{23}{2}\) বর্গএকক
\(\therefore\) ABCD চতুর্ভুজের ক্ষেত্রফল
= \( \Delta ABC\) –এর ক্ষেত্রফল + \(\Delta ACD\) এর ক্ষেত্রফল
= \( (9 + \frac{23}{2})\) বর্গএকক
= \( \frac{18+23}{2}\) বর্গএকক
= \( \frac{41}{2}\) বর্গএকক
= \( 20 \frac{1}{2}\) বর্গএকক [উত্তর]
(ii) \((1,4)\), \((-2,1)\), \((2,-3)\), \((3,3)\)
সমাধান –
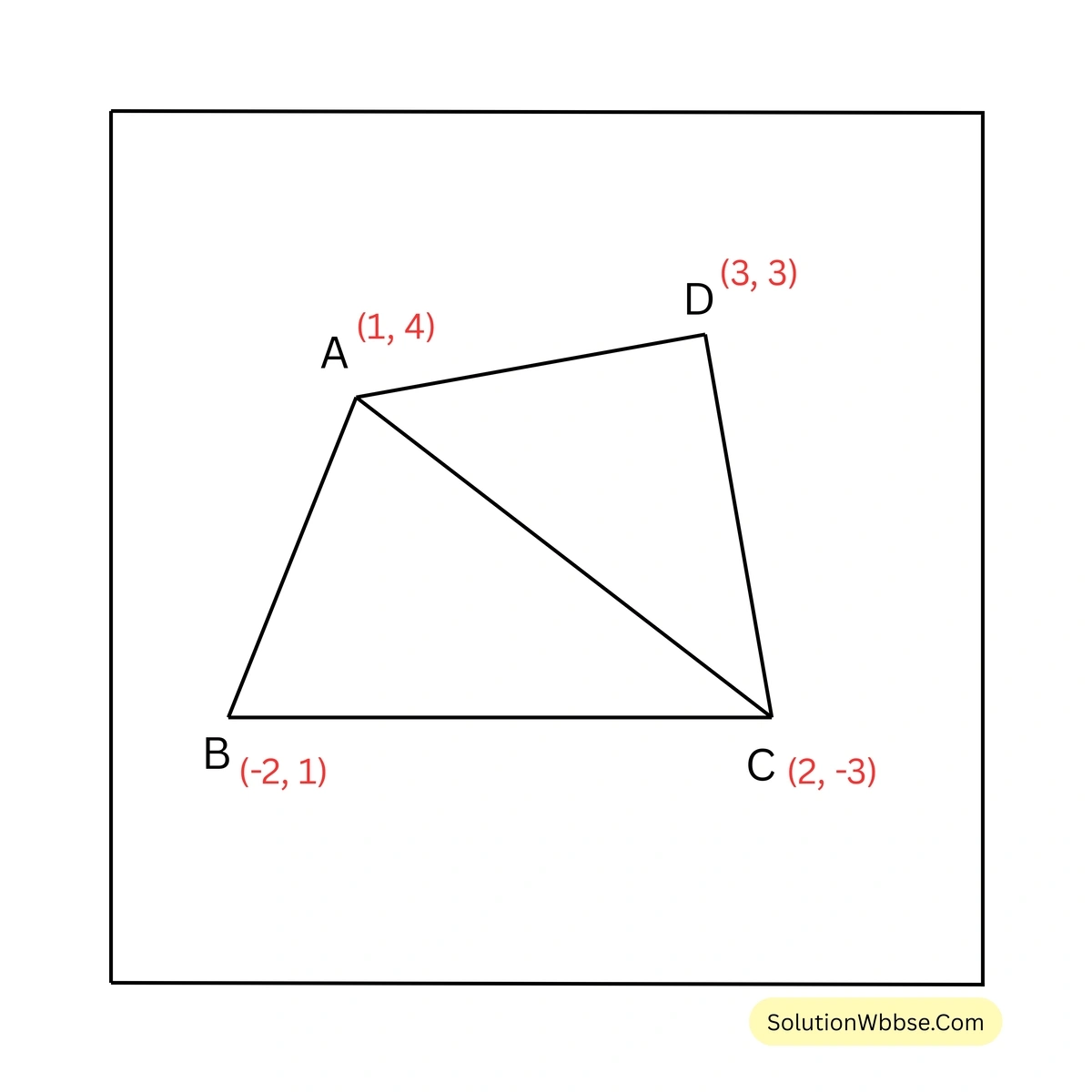
ধরি, ABCD চতুর্ভুজের A, B, C এবং D বিন্দুগুলির স্থানাঙ্ক যথাক্রমে \((1,4)\), \((-2,1)\), \((2,-3)\) এবং \((3,3)\)।
এখন, AC কর্ণ টানা হল যার ফলে চতুর্ভুজটি দুটি ত্রিভুজ \(\Delta ABC\) এবং \(\Delta ACD\) –তে বিভক্ত হল।
\(\Delta ABC\) ত্রিভুজের ক্ষেত্রফল –
= \( \frac{1}{2} |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)|\) বর্গএকক
= \( \frac{1}{2} |1\{1-(-3)\} + (-2)(-3-4) + 2(4-1)|\) বর্গএকক
[এক্ষেত্রে, \((x_1, y_1) = (1,4)\), \((x_2, y_2) = (-2,1)\), \((x_3, y_3) = (2,-3)\)]
= \( \frac{1}{2} |(4 + 14 + 6)|\) বর্গএকক
= \( \frac{1}{2} |24|\) বর্গএকক
= \( 12\) বর্গএকক
\(\Delta ACD\) ত্রিভুজের ক্ষেত্রফল –
= \( \frac{1}{2} |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)|\) বর্গএকক
= \( \frac{1}{2} |1(-3-3) + 2(3-4) + 3\{4-(-3)\}|\) বর্গএকক
[এক্ষেত্রে, \((x_1, y_1) = (1,4)\), \((x_2, y_2) = (2,-3)\), \((x_3, y_3) = (3,3)\)]
= \( \frac{1}{2} |(-6 -2 + 21)|\) বর্গএকক
= \( \frac{1}{2} |13|\) বর্গএকক
= \( \frac{1}{2} \times 13\) বর্গএকক
= \( \frac{13}{2}\) বর্গএকক
\(\therefore\) ABCD চতুর্ভুজের ক্ষেত্রফল
= \( \Delta ABC\) –এর ক্ষেত্রফল + \(\Delta ACD\) এর ক্ষেত্রফল
= \( (12 + \frac{13}{2})\) বর্গএকক
= \( \frac{24+13}{2}\) বর্গএকক
= \( \frac{37}{2}\) বর্গএকক
= \( 18 \frac{1}{2}\) বর্গএকক [উত্তর]
7. A, B, C বিন্দু তিনটির স্থানাঙ্ক যথাক্রমে \((3,4)\), \((-4,3)\) এবং \((8,-6)\); ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল নির্ণয় করি এবং A বিন্দু থেকে BC বাহুর উপর লম্বের দৈর্ঘ্য নির্ণয় করি।
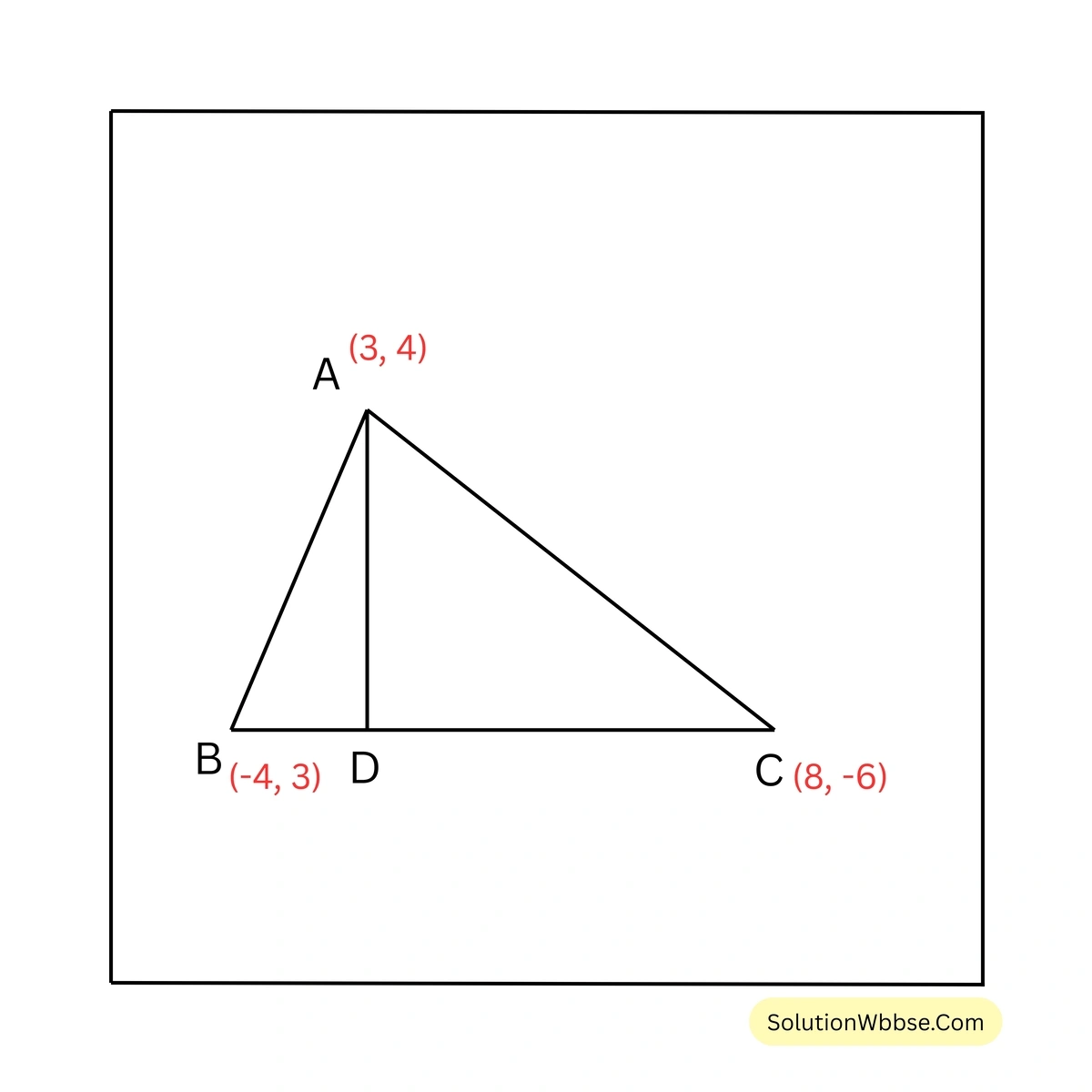
সমাধান –
ABC ত্রিভুজের ক্ষেত্রফল –
= \( \frac{1}{2} |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)|\) বর্গএকক
= \( \frac{1}{2} |3\{3-(-6)\} + (-4)(-6-4) + 8(4-3)|\) বর্গএকক
= \( \frac{1}{2} |3(3+6) + (-4)(-10) + 8(1)|\) বর্গএকক
= \( \frac{1}{2} |27 + 40 + 8|\) বর্গএকক
= \( \frac{1}{2} |75|\) বর্গএকক
= \( \frac{75}{2}\) বর্গএকক
= \( 37 \frac{1}{2}\) বর্গএকক
এখন, A বিন্দু থেকে BC বাহুর উপর AD লম্ব টানা হল।
ABC-ত্রিভুজের BC বাহুর দৈর্ঘ্য –
= \( \sqrt{[8-(-4)]^2 + (-6-3)^2}\) একক
= \( \sqrt{(12)^2 + (-9)^2}\) একক
= \( \sqrt{144 + 81}\) একক
= \( \sqrt{225}\) একক
= \( 15\) একক
\(\therefore \Delta ABC\) –এর ক্ষেত্রফল \(= \frac{1}{2} \times\) ভূমি \(\times\) উচ্চতা \(= \frac{1}{2} \times BC \times AD = \frac{1}{2} \times 15 \times AD\)
\(\therefore \frac{1}{2} \times 15 \times AD = \frac{75}{2}\)বা, \(15 \times AD = 75\)
বা, \(AD = \frac{75}{15}\)
বা, \(AD = 5\)
\(\therefore\) ABC –এর A বিন্দু থেকে বিপরীত বাহু BC-এর উপর লম্বের দৈর্ঘ্য \(5\) একক। [উত্তর]
8. ABC ত্রিভুজের A বিন্দুর স্থানাঙ্ক \((2,5)\) এবং ত্রিভুজটির ভরকেন্দ্রের স্থানাঙ্ক \((-2,1)\) হলে, BC বাহুর মধ্যবিন্দুর স্থানাঙ্ক নির্ণয় করি।
সমাধান –
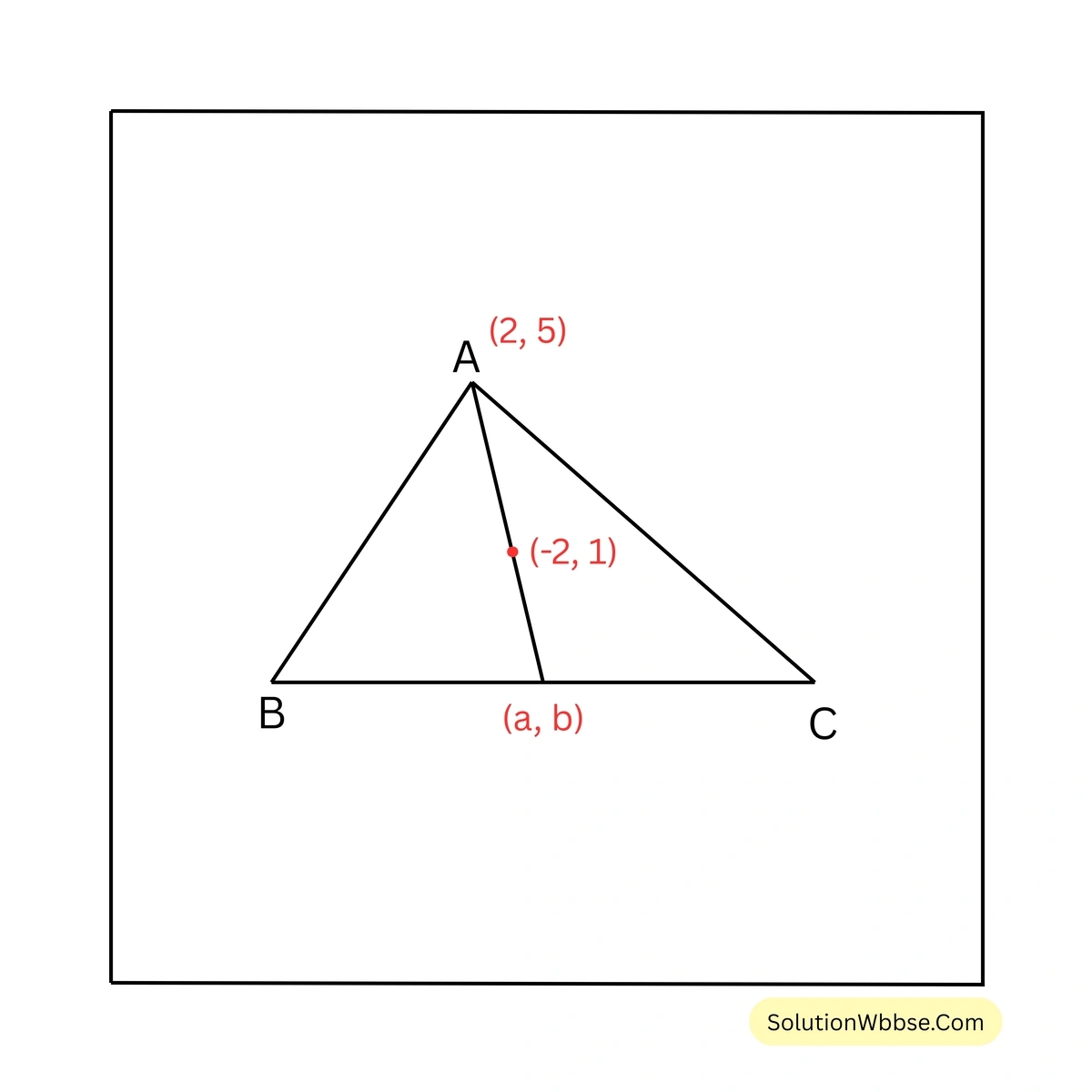
ধরি, BC বাহুর মধ্যবিন্দুর স্থানাঙ্ক \((a,b)\)। ABC ত্রিভুজের A বিন্দুর স্থানাঙ্ক \((2,5)\) এবং ত্রিভুজটির ভরকেন্দ্রের স্থানাঙ্ক \((-2,1)\)।
আমরা জানি, কোনো ত্রিভুজের ভরকেন্দ্র ওই ত্রিভুজের মধ্যমাকে \(2:1\) অনুপাতে বিভক্ত করে।
\(\therefore\) ভরকেন্দ্রের স্থানাঙ্ক = \( \left(\frac{2a+2}{2+1}, \frac{2b+5}{2+1}\right)\)
\(\therefore (-2,1) = \left(\frac{2a+2}{3}, \frac{2b+5}{3}\right)\)\(\therefore \frac{2a+2}{3} = -2\)বা, \(2a + 2 = -6\)
বা, \(2a = -6-2\)
বা, \(2a = -8\)
বা, \(a = \frac{-8}{2}\)
বা, \(a = -4\)
এবং, \(\frac{2b+5}{3} = 1\)
বা, \(2b+5 = 3\)
বা, \(2b = 3-5\)
বা, \(2b = -2\)
বা, \(b = \frac{-2}{2}\)
বা, \(b = -1\)
\(\therefore\) মধ্যবিন্দুর স্থানাঙ্ক \((-4, -1)\)। [উত্তর]
9. একটি ত্রিভুজের তিনটি শীর্ষবিন্দুর স্থানাঙ্ক \((4,-3)\), \((-5,2)\) এবং \((x,y)\); যদি ত্রিভুজটির ভরকেন্দ্র মূলবিন্দু হয়, তাহলে x ও y এর মান নির্ণয় করি।
সমাধান –
ত্রিভুজের তিনটি শীর্ষবিন্দুর স্থানাঙ্ক \((4,-3)\), \((-5,2)\) এবং \((x,y)\)।
\(\therefore\) ত্রিভুজটির ভরকেন্দ্রের স্থানাঙ্ক = \( \left(\frac{4-5+x}{3}, \frac{-3+2+y}{3}\right) = \left(\frac{x-1}{3}, \frac{y-1}{3}\right)\)
যেহেতু ত্রিভুজটির ভরকেন্দ্র মূলবিন্দু \((0,0)\)
\(\therefore \left(\frac{x-1}{3}, \frac{y-1}{3}\right) = (0,0)\)বা, \(\frac{x-1}{3} = 0\)
বা, \(x-1 = 0\)
বা, \(x = 1\)
আবার, \(\frac{y-1}{3} = 0\)
বা, \(y-1 = 0\)
বা, \(y = 1\)
\(\therefore x\) এর মান \(1\) এবং \(y\) –এর মান \(1\)। [উত্তর]
10. \(A(-1,5)\), \(B(3,1)\) এবং \(C(5,7)\) ত্রিভুজ ABC –এর শীর্ষবিন্দু। D, E, F যথাক্রমে BC, CA এবং AB বাহুর মধ্যবিন্দু। DEF ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল নির্ণয় করি এবং দেখাই যে \(\Delta ABC = 4 \Delta DEF\)
সমাধান –
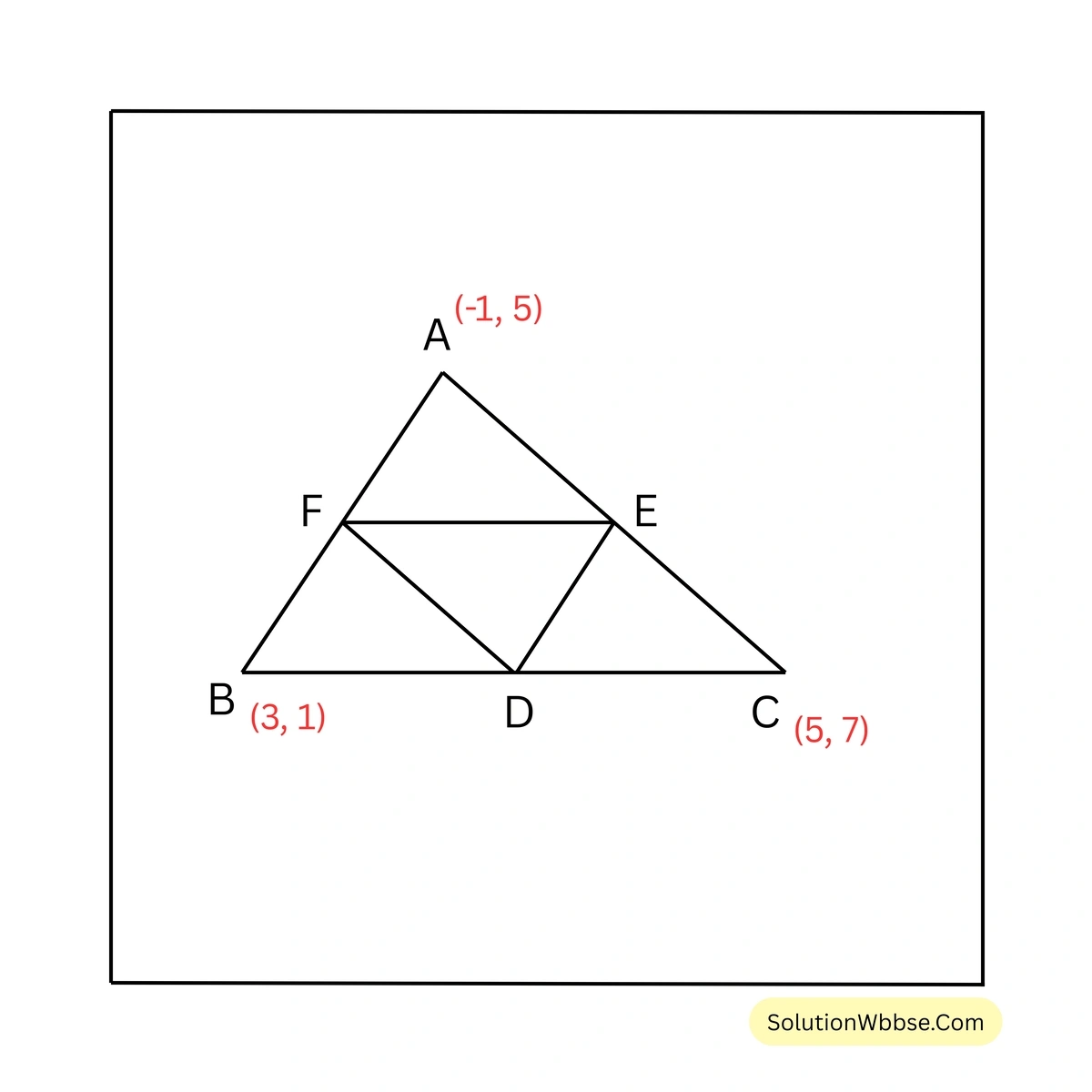
\(A(-1,5)\), \(B(3,1)\) এবং \(C(5,7)\) ত্রিভুজ ABC –এর শীর্ষবিন্দু।
BC বাহুর মধ্যবিন্দু D।
\(\therefore\) D বিন্দুর স্থানাঙ্ক = \( \left( \frac{3+5}{2}, \frac{1+7}{2} \right) = \left( \frac{8}{2}, \frac{8}{2} \right) = (4,4)\)
E, CA বাহুর মধ্যবিন্দু।
\(\therefore\) E বিন্দুর স্থানাঙ্ক = \( \left( \frac{5+(-1)}{2}, \frac{7+5}{2} \right) = \left( \frac{4}{2}, \frac{12}{2} \right) = (2,6)\)
এবং, F, AB বাহুর মধ্যবিন্দু।
\(\therefore\) F বিন্দুর স্থানাঙ্ক = \( \left( \frac{-1+3}{2}, \frac{5+1}{2} \right) = \left( \frac{2}{2}, \frac{6}{2} \right) = (1,3)\)
ABC ত্রিভুজের ক্ষেত্রফল –
= \( \frac{1}{2} |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)|\) বর্গএকক
= \( \frac{1}{2} |-1(1-7) + 3(7-5) + 5(5-1)|\) বর্গএকক [এক্ষেত্রে, \((x_1, y_1) = (-1,5)\), \((x_2, y_2) = (3,1)\) এবং \((x_3, y_3) = (5,7)\)]
= \( \frac{1}{2} |(-1)(-6) + 3(2) + 5(4)|\) বর্গএকক
= \( \frac{1}{2} |6 + 6 + 20|\) বর্গএকক
= \( \frac{1}{2} \times 32\) বর্গএকক
= \( 16\) বর্গএকক
DEF ত্রিভুজের ক্ষেত্রফল –
= \( \frac{1}{2} |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)|\) বর্গএকক
= \( \frac{1}{2} |4(6-3) + 2(3-4) + 1(4-6)|\) বর্গএকক [এক্ষেত্রে, \((x_1, y_1) = (4,4)\), \((x_2, y_2) = (2,6)\) এবং \((x_3, y_3) = (1,3)\)]
= \( \frac{1}{2} |4(3) + 2(-1) + 1(-2)|\) বর্গএকক
= \( \frac{1}{2} |12 – 2 – 2|\) বর্গএকক
= \( \frac{1}{2} \times 8\) বর্গএকক
= \( 4\) বর্গএকক
\(\therefore\) ABC এর ক্ষেত্রফল = \( 4 \times\) DEF এর ক্ষেত্রফল [প্রমাণিত]
11. বহুবিকল্পীয় প্রশ্ন –
(i) \((0,4)\), \((0,0)\) এবং \((-6,0)\) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(a) 24 বর্গএকক
(b) 12 বর্গএকক
(c) 6 বর্গএকক
(d) 8 বর্গএকক
Ans – (b) 12 বর্গএকক
সমাধান –
\((0,4)\), \((0,0)\) এবং \((-6,0)\) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল –
= \( \frac{1}{2} |0(0-0) + 0(0-4) + (-6)\{0-(-4)\}|\) বর্গএকক
= \( \frac{1}{2} |24|\) বর্গএকক
= \( \frac{1}{2} \times 24\) বর্গএকক
= \( 12\) বর্গএকক
(ii) \((7,-5)\), \((-2,5)\) এবং \((4,6)\) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ভরকেন্দ্রের স্থানাঙ্ক
(a) \((3,-2)\)
(b) \((2,3)\)
(c) \((3,2)\)
(d) \((2,-3)\)
Ans – (c) \((3,2)\)
সমাধান –
\((7,-5)\), \((-2,5)\) এবং \((4,6)\) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ভরকেন্দ্রের স্থানাঙ্ক –
\(\left(\frac{7-2+4}{3}, \frac{-5+5+6}{3}\right)\)= \( \left(\frac{9}{3}, \frac{6}{3}\right)\)
= \( (3,2)\)
(iii) ABC সমকোণী ত্রিভুজের \(\angle ABC = 90^\circ\); A ও C বিন্দুর স্থানাঙ্ক যথাক্রমে \((0,4)\) এবং \((3,0)\) হলে, ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(a) 12 বর্গএকক
(b) 6 বর্গএকক
(c) 24 বর্গএকক
(d) 8 বর্গএকক
Ans – (b) 6 বর্গএকক
সমাধান – ABC সমকোণী ত্রিভুজের \(\angle ABC = 90^\circ\); A ও C বিন্দুর স্থানাঙ্ক যথাক্রমে \((0,4)\) এবং \((3,0)\) হলে, B বিন্দুর স্থানাঙ্ক হবে \((0,0)\)।
\(\therefore\) ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল –
= \( \frac{1}{2} |0(0-0) + 0(0-4) + 3(4-0)|\) বর্গএকক
= \( \frac{1}{2} \times 12\) বর্গএকক
= \( 6\) বর্গএকক
(iv) \((0,0)\), \((4,-3)\) এবং \((x,y)\) বিন্দু তিনটি সমরেখ হলে
(a) \(x=8, y=-6\)
(b) \(x=8, y=6\)
(c) \(x=4, y=-6\)
(d) \(x=-8, y=-6\)
Ans – (a) \(x=8, y=-6\)
সমাধান – \((0,0)\), \((4,-3)\) এবং \((x,y)\) বিন্দু তিনটি সমরেখ হলে বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল শূন্য হবে।
\(\therefore \frac{1}{2} |0(-3-y) + 4(y-0) + x(0+3)| = 0\)বা, \(\frac{1}{2} |4y + 3x| = 0\)
বা, \(4y + 3x = 0\) —(i)
এখন, \(y = -6\) এবং \(x = 8\) (i) নং সমীকরণকে সিদ্ধ করে।
\(\therefore y = -6\) এবং \(x = 8\)
(v) ত্রিভুজ ABC এর A শীর্ষবিন্দুর স্থানাঙ্ক \((7,-4)\) এবং ত্রিভুজটির ভরকেন্দ্রের স্থানাঙ্ক \((1,2)\) হলে, BC বাহুর মধ্যবিন্দুর স্থানাঙ্ক
(a) \((-2,-5)\)
(b) \((-2,5)\)
(c) \((2,-5)\)
(d) \((5,-2)\)
Ans – (b) \((-2,5)\)
সমাধান – ত্রিভুজ ABC এর A শীর্ষবিন্দুর স্থানাঙ্ক \((7,-4)\)
ধরি, BC বাহুর মধ্যবিন্দুর স্থানাঙ্ক \((x ,y)\)
\(\therefore\) ত্রিভুজটির ভরকেন্দ্রের স্থানাঙ্ক – \(\left(\frac{1(7)+2(x)}{2+1}, \frac{1(-4)+2(y)}{2+1}\right) = \left(\frac{7+2x}{3}, \frac{-4+2y}{3}\right)\)
[যেহেতু, ভরকেন্দ্র ত্রিভুজের মধ্যমাকে 2:1 অনুপাতে বিভক্ত করে]
শর্তানুসারে,
\(\left(\frac{7+2x}{3}, \frac{-4+2y}{3}\right) = (1,2)\)\(\therefore \frac{7+2x}{3} = 1\)বা, \(7+2x = 3\)
বা, \(2x = 3-7\)
বা, \(2x = -4\)
বা, \(x = \frac{-4}{2}\)
বা, \(x = -2\)
এবং \(\frac{-4+2y}{3} = 2\)
বা, \(-4 + 2y = 6\)
বা, \(2y = 6+4\)
বা, \(2y = 10\)
বা, \(y = \frac{10}{2}\)
বা, \(y = 5\)
\(\therefore\) BC বাহুর মধ্যবিন্দুর স্থানাঙ্ক \((-2,5)\)।
12. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন
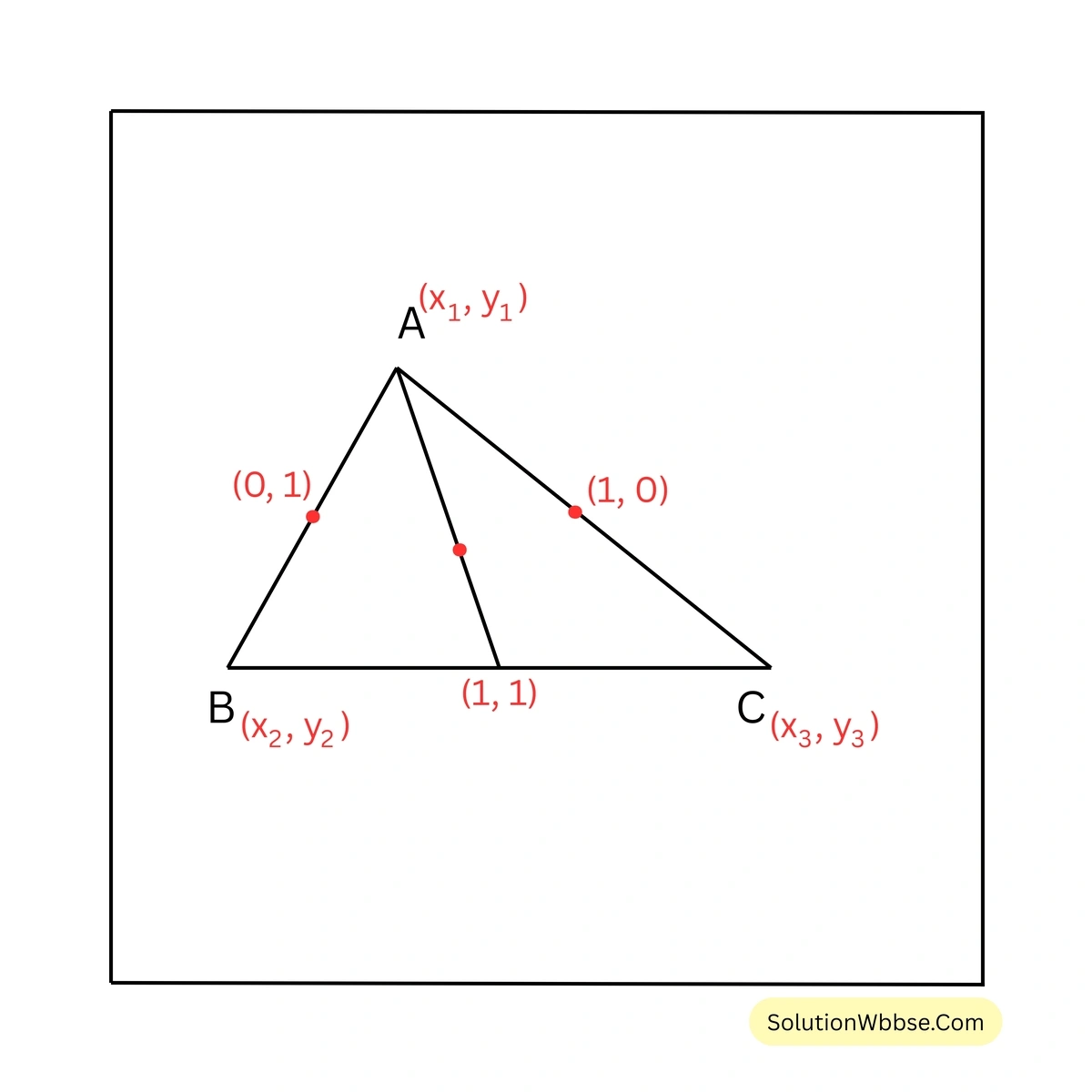
(i) ABC ত্রিভুজের বাহুগুলির মধ্যবিন্দুর স্থানাঙ্ক \((0,1)\), \((1,1)\) এবং \((1,0)\); ত্রিভুজের ভরকেন্দ্রের স্থানাঙ্ক নির্ণয় করি।
সমাধান –
সমাধান –
ধরা যাক, ABC ত্রিভুজের A, B এবং C শীর্ষবিন্দুগুলির স্থানাঙ্ক যথাক্রমে \((x_1, y_1)\), \((x_2, y_2)\) এবং \((x_3, y_3)\)।
ABC ত্রিভুজের AB, BC এবং CA বাহুর মধ্যবিন্দুর স্থানাঙ্ক যথাক্রমে \((0,1)\), \((1,1)\) এবং \((1,0)\)
\(\therefore \left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right) = (0,1)\)\(\therefore \frac{x_1+x_2}{2} = 0\)বা, \(x_1+x_2 = 0\) — (i)
এবং, \(\frac{y_1+y_2}{2} = 1\)
বা, \(y_1+y_2 = 2\) — (ii)
এবং, \(\left(\frac{x_2+x_3}{2}, \frac{y_2+y_3}{2}\right) = (1,1)\)
\(\therefore \frac{x_2+x_3}{2} = 1\)বা, \(x_2+x_3 = 2\) — (iii)
এবং, \(\frac{y_2+y_3}{2} = 1\)
বা, \(y_2+y_3 = 2\) — (iv)
আবার, \(\left(\frac{x_3+x_1}{2}, \frac{y_3+y_1}{2}\right) = (1,0)\)
\(\therefore \frac{x_3+x_1}{2} = 1\)বা, \(x_3+x_1 = 2\) — (v)
এবং, \(\frac{y_3+y_1}{2} = 0\)
বা, \(y_3+y_1 = 0\) — (vi)
এখন, (i), (iii) এবং (v) নং সমীকরণ যোগ করে পাই,
\(x_1+x_2 + x_2+x_3 + x_3+x_1 = 4\)বা, \(2(x_1+x_2+x_3) = 4\)
বা, \(x_1+x_2+x_3 = \frac{4}{2}\)
বা, \(x_1+x_2+x_3 = 2\) — (vii)
(ii), (iv) এবং (vi) নং সমীকরণ যোগ করে পাই,
\(y_1+y_2 + y_2+y_3 + y_3+y_1 = 4\)বা, \(2(y_1+y_2+y_3) = 4\)
বা, \(y_1+y_2+y_3 = 2\) — (viii)
(vii) নং সমীকরণ থেকে (iii) নং সমীকরণ বিয়োগ করে পাই,
\(x_1+x_2+x_3 – (x_2+x_3) = 2 – 2\)বা, \(x_1 = 0\)
আবার, (viii) নং সমীকরণ থেকে (iv) নং সমীকরণ বিয়োগ করে পাই,
\(y_1+y_2+y_3 – (y_2+y_3) = 2 – 2\)বা, \(y_1 = 0\)
\(\therefore\) A বিন্দুর স্থানাঙ্ক \((0,0)\)
আবার, BC বাহুর মধ্যবিন্দুর স্থানাঙ্ক \((1,1)\)।
\(\therefore\) ভরকেন্দ্রের স্থানাঙ্ক = \(\left(\frac{2(1)+1(0)}{2+1}, \frac{2(1)+1(0)}{2+1}\right) = \left(\frac{2}{3}, \frac{2}{3}\right)\) [যেহেতু ত্রিভুজের ভরকেন্দ্র মধ্যমাকে 2:1 অনুপাতে বিভক্ত করে]
\(\therefore\) ভরকেন্দ্রের স্থানাঙ্ক \(\left(\frac{2}{3}, \frac{2}{3}\right)\)।
(ii) একটি ত্রিভুজের ভরকেন্দ্রের স্থানাঙ্ক \((6,9)\) এবং দুটি শীর্ষবিন্দুর স্থানাঙ্ক \((15,0)\) এবং \((0,10)\) তৃতীয় শীর্ষবিন্দুর স্থানাঙ্ক নির্ণয় করি।
সমাধান –
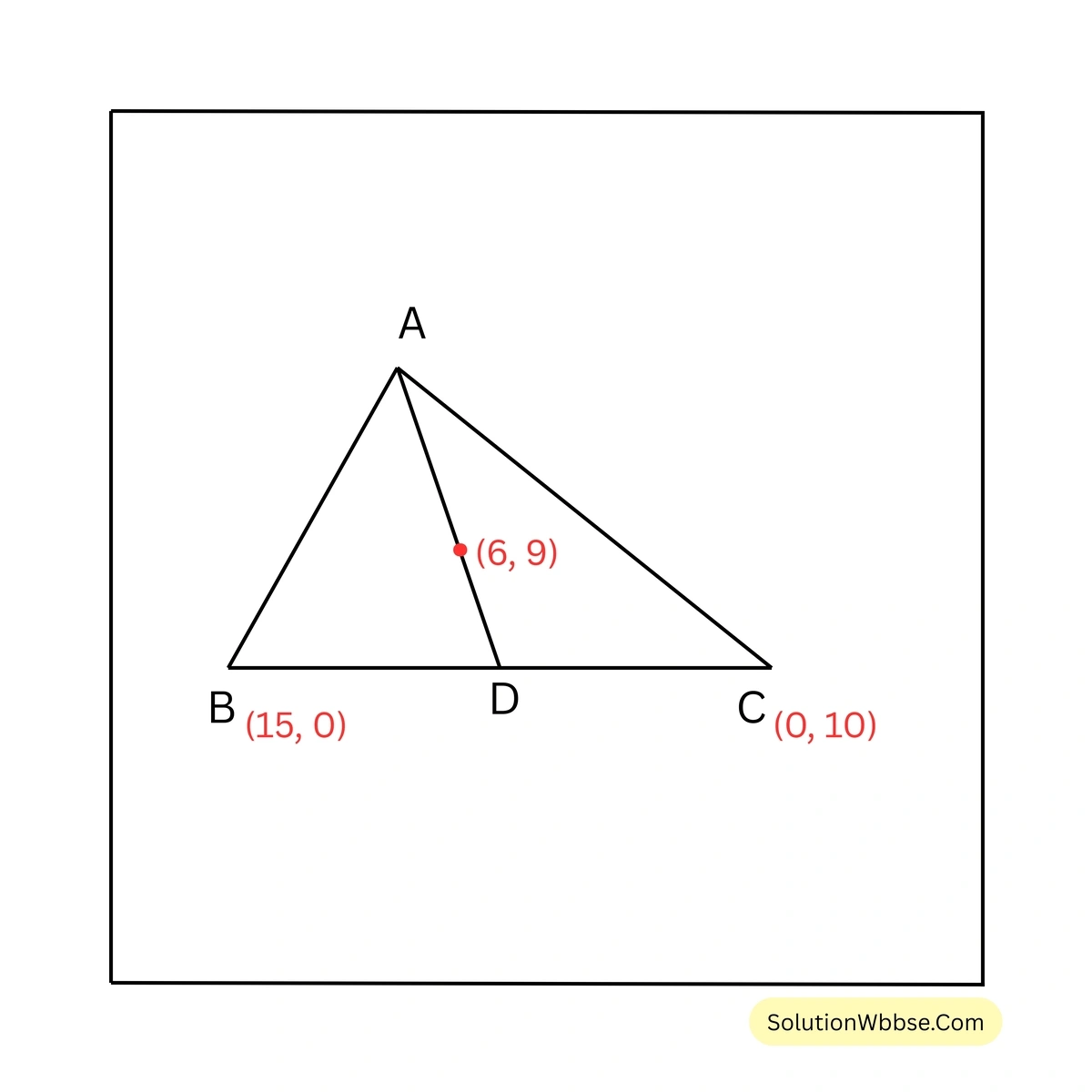
ধরা যাক, ABC একটি ত্রিভুজ যার ভরকেন্দ্রের স্থানাঙ্ক \((6,9)\) এবং B ও C বিন্দুর স্থানাঙ্ক যথাক্রমে \((15,0)\) এবং \((0,10)\)। ধরি, A বিন্দুর স্থানাঙ্ক \((x,y)\) এবং BC বাহুর মধ্যবিন্দু D।
BC বাহুর মধ্যবিন্দু (D) এর স্থানাঙ্ক = \( \left(\frac{15+0}{2}, \frac{0+10}{2}\right) = \left(\frac{15}{2}, 5\right)\)
ভরকেন্দ্র AD মধ্যমাকে 2:1 অনুপাতে বিভক্ত করে।
\(\therefore\) ভরকেন্দ্রের স্থানাঙ্ক = \(\left(\frac{2 \cdot \frac{15}{2} + 1 \cdot x}{2+1}, \frac{2 \cdot 5 + 1 \cdot y}{2+1}\right) = \left(\frac{15+x}{3}, \frac{10+y}{3}\right)\)
\(\therefore \left(\frac{15+x}{3}, \frac{10+y}{3}\right) = (6,9)\)\(\therefore \frac{15+x}{3} = 6\)বা, \(15+x = 18\)
বা, \(x = 18-15\)
বা, \(x = 3\)
এবং, \(\frac{10+y}{3} = 9\)
বা, \(10+y = 27\)
বা, \(y = 27-10\)
বা, \(y = 17\)
\(\therefore\) A বিন্দুর স্থানাঙ্ক \((3,17)\)।
(iii) \((a,0)\), \((0,b)\) এবং \((1,1)\) বিন্দু তিনটি সমরেখ হলে দেখাই যে, \(\frac{1}{a} + \frac{1}{b} = 1\)
সমাধান –
\((a,0)\), \((0,b)\) এবং \((1,1)\) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল =
= \( \frac{1}{2} |a(b-1) + 0(1-0) + 1(0-b)|\) বর্গএকক
= \( \frac{1}{2} |ab – a – b|\) বর্গএকক
\(\because\) যেহেতু, \((a,0)\), \((0,b)\) এবং \((1,1)\) বিন্দু তিনটি সমরেখ
\(\therefore \frac{1}{2} |ab – a – b| = 0\)বা, \(ab – a – b = 0\)
বা, \(ab = a + b\)
বা, \(\frac{ab}{ab} = \frac{a}{ab} + \frac{b}{ab}\)
বা, \(1 = \frac{1}{b} + \frac{1}{a}\)
বা, \(\frac{1}{a} + \frac{1}{b} = 1\) [প্রমাণিত]
(iv) \((1,4)\), \((-1,2)\) এবং \((-4,1)\) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল নির্ণয় করো।
সমাধান –
\((1,4)\), \((-1,2)\) এবং \((-4,1)\) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল =
= \( \frac{1}{2} |1(2-1) + (-1)(1-4) + (-4)(4-2)|\) বর্গএকক
= \( \frac{1}{2} |1 + 3 – 8|\) বর্গএকক
= \( \frac{1}{2} |-4|\) বর্গএকক
= \( \frac{1}{2} \times 4\) বর্গএকক
= \( 2\) বর্গএকক
\(\therefore\) \((1,4)\), \((-1,2)\) এবং \((-4,1)\) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল 2 বর্গএকক।
(v) \((x-y, y-z)\), \((-x, -y)\) এবং \((y, z)\) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ভরকেন্দ্রের স্থানাঙ্ক লিখি।
সমাধান –
\((x-y, y-z)\), \((-x, -y)\) এবং \((y, z)\) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ভরকেন্দ্রের স্থানাঙ্ক =
= \( \left(\frac{(x-y) + (-x) + y}{3}, \frac{(y-z) + (-y) + z}{3}\right)\)
= \( \left(\frac{x-y-x+y}{3}, \frac{y-z-y+z}{3}\right)\)
= \( (0,0)\)
\(\therefore\) \((x-y, y-z)\), \((-x, -y)\) এবং \((y, z)\) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ভরকেন্দ্রের স্থানাঙ্ক \((0,0)\)।
এই আর্টিকেলে নবম শ্রেণির গণিতের ‘স্থানাঙ্ক জ্যামিতি : ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল‘ অধ্যায়ের ‘কষে দেখি – 20’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।
কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন