নবম শ্রেণী গণিত – ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল – কষে দেখি – 15.1

পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) দশম শ্রেণির গণিত পাঠ্যবইয়ের পঞ্চদশ অধ্যায় হলো ‘ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল’। এই পোস্টে ‘কষে দেখি – 15.1‘-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. আমি কামালদের বাড়ির ছবি দেখি ও উত্তর খুঁজি।

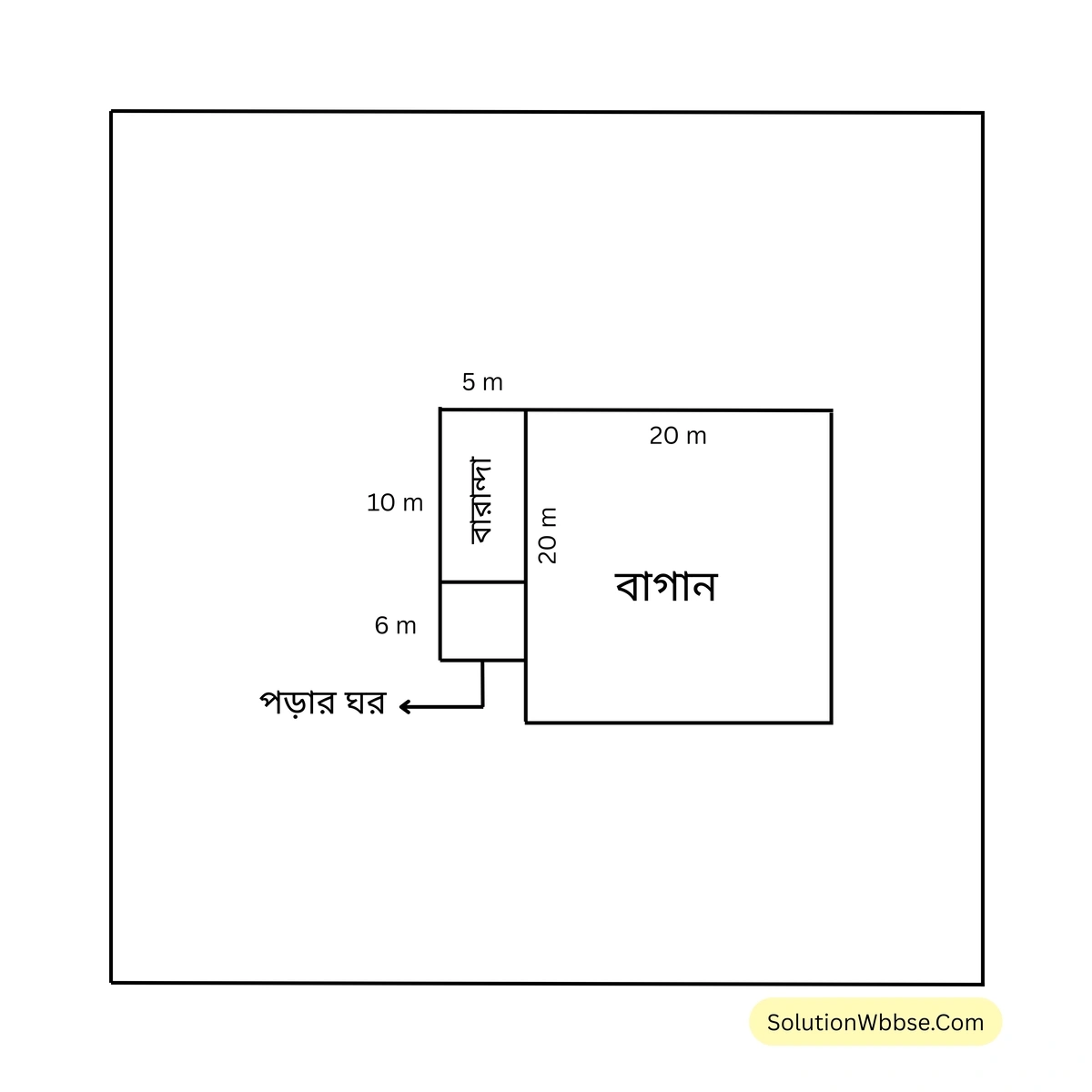
(i) কামালদের বাগানের ক্ষেত্রফল হিসাব করে লিখি।
(ii) প্রতি বর্গমিটার 30 টাকা হিসাবে কামালদের বারান্দার মেঝে মেরামত করতে কত খরচ হবে হিসাব করে লিখি।
(iii) কামাল তাঁর পড়ার ঘরের মেঝেতে টালি বসাতে চায়। যদি প্রতিটি টালি 25 সেমি. \(\times\) 25 সেমি. হয়, তাহলে তাঁর পড়ার ঘরের মেঝেতে টালি বসাতে কতগুলি টালি লাগবে হিসাব করে লিখি।

সমাধান –

(i) কামালদের বাগানের ক্ষেত্রফল হিসাব করে লিখি।

কামালদের বাগানের দৈর্ঘ্য 20 মি. এবং প্রস্থ 20 মি.

\(\therefore\) কামালদের বাগানের ক্ষেত্রফল = \(\) দৈর্ঘ্য \(\times\) প্রস্থ = \( (20 \times 20)\) বর্গমিটার = \( 400\) বর্গমিটার। [উত্তর]

(ii) প্রতি বর্গমিটার 30 টাকা হিসাবে কামালদের বারান্দার মেঝে মেরামত করতে কত খরচ হবে হিসাব করে লিখি।

কামালদের বারান্দার মেঝের দৈর্ঘ্য 10 মিটার এবং প্রস্থ 5 মিটার।

\(\therefore\) কামালদের মেঝের ক্ষেত্রফল = \( (10 \times 5)\) বর্গমিটার = \( 50\) বর্গমিটার।

প্রতি বর্গমিটার 30 টাকা হিসাবে মেঝেটি মেরামত করতে খরচ হবে = \( (50 \times 30)\) টাকা = \( 1500\) টাকা। [উত্তর]

(iii) কামালদের পড়ার ঘরের দৈর্ঘ্য 6 মিটার এবং প্রস্থ 5 মিটার।

\(\therefore\) পড়ার ঘরের ক্ষেত্রফল = \( (6 \times 5)\) বর্গমিটার = \( 30\) বর্গমিটার = \( (30 \times 100 \times 100)\) বর্গসেমি. = \( 300000\) বর্গসেমি.

একটি টালির ক্ষেত্রফল = \( (25 \times 25)\) বর্গসেমি. = \( 625\) বর্গসেমি.

\(\therefore\) পড়ার ঘরের মেঝেতে বসানো টালির সংখ্যা = \( 300000 \div 625 = 480\) টি। [উত্তর]

2. নীচের ছবি দেখি ও রঙিন অংশের ক্ষেত্রফল হিসাব করে লিখি।

(i)

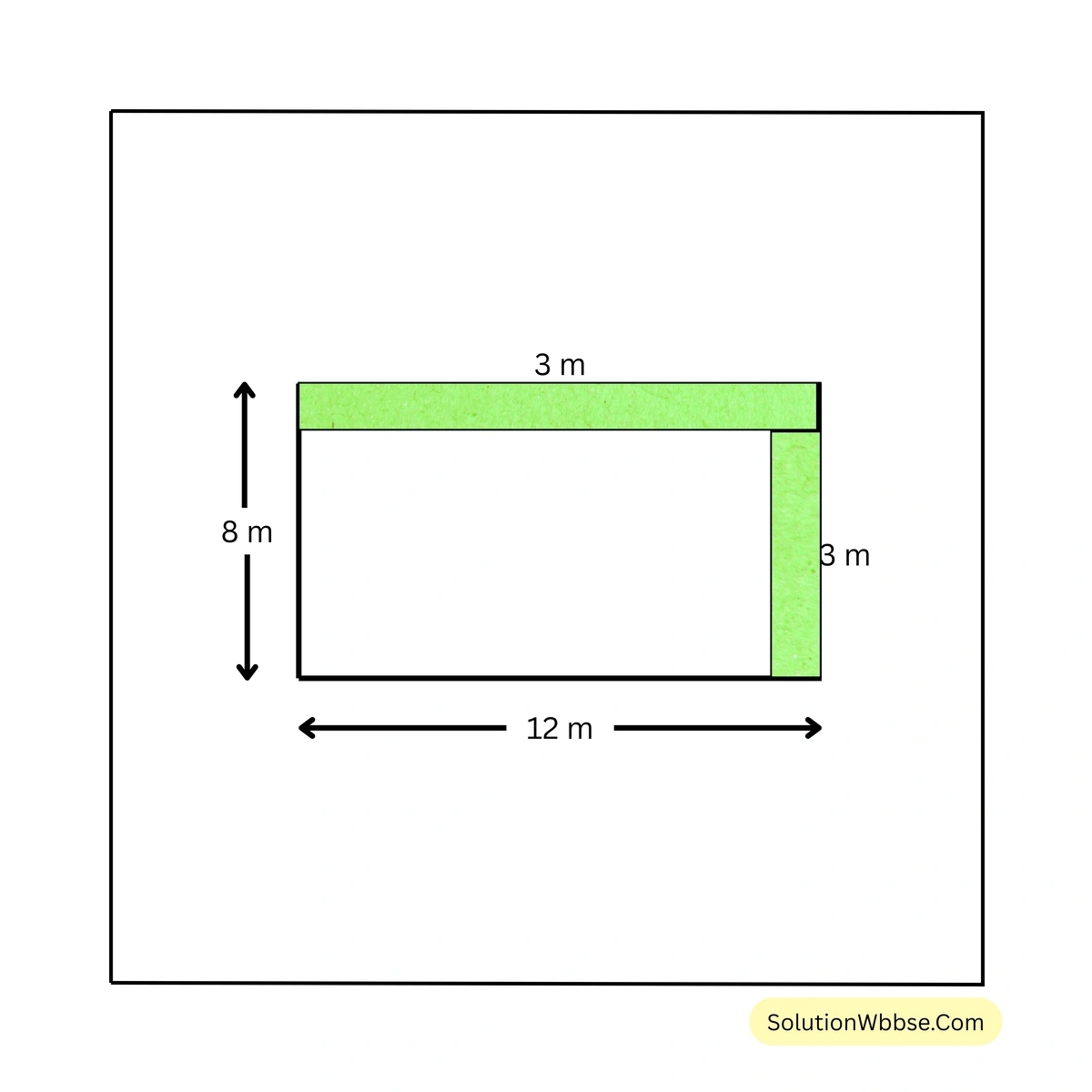
সমাধান – \(ABCD\) আয়তক্ষেত্রের দৈর্ঘ্য 12 মিটার এবং প্রস্থ 8 মিটার।

\(\therefore\) \(ABCD\) আয়তক্ষেত্রের ক্ষেত্রফল = \( (12 \times 8)\) বর্গমিটার = \( 96\) বর্গমিটার।

আবার, \(BEFG\) আয়তক্ষেত্রের দৈর্ঘ্য = \( (12 – 3)\) মিটার = \( 9\) মিটার এবং প্রস্থ = \( (8 – 3)\) মিটার = \( 5\) মিটার।

\(\therefore\) \(BEFG\) আয়তক্ষেত্রের ক্ষেত্রফল = \( (9 \times 5)\) বর্গমিটার = \( 45\) বর্গমিটার।

\(\therefore\) রঙিন অংশের ক্ষেত্রফল = \( (ABCD\) অংশের ক্ষেত্রফল \(– BEFG\) অংশের ক্ষেত্রফল) = \( (96 – 45)\) বর্গমিটার = \( 51\) বর্গমিটার। [উত্তর]

(ii)

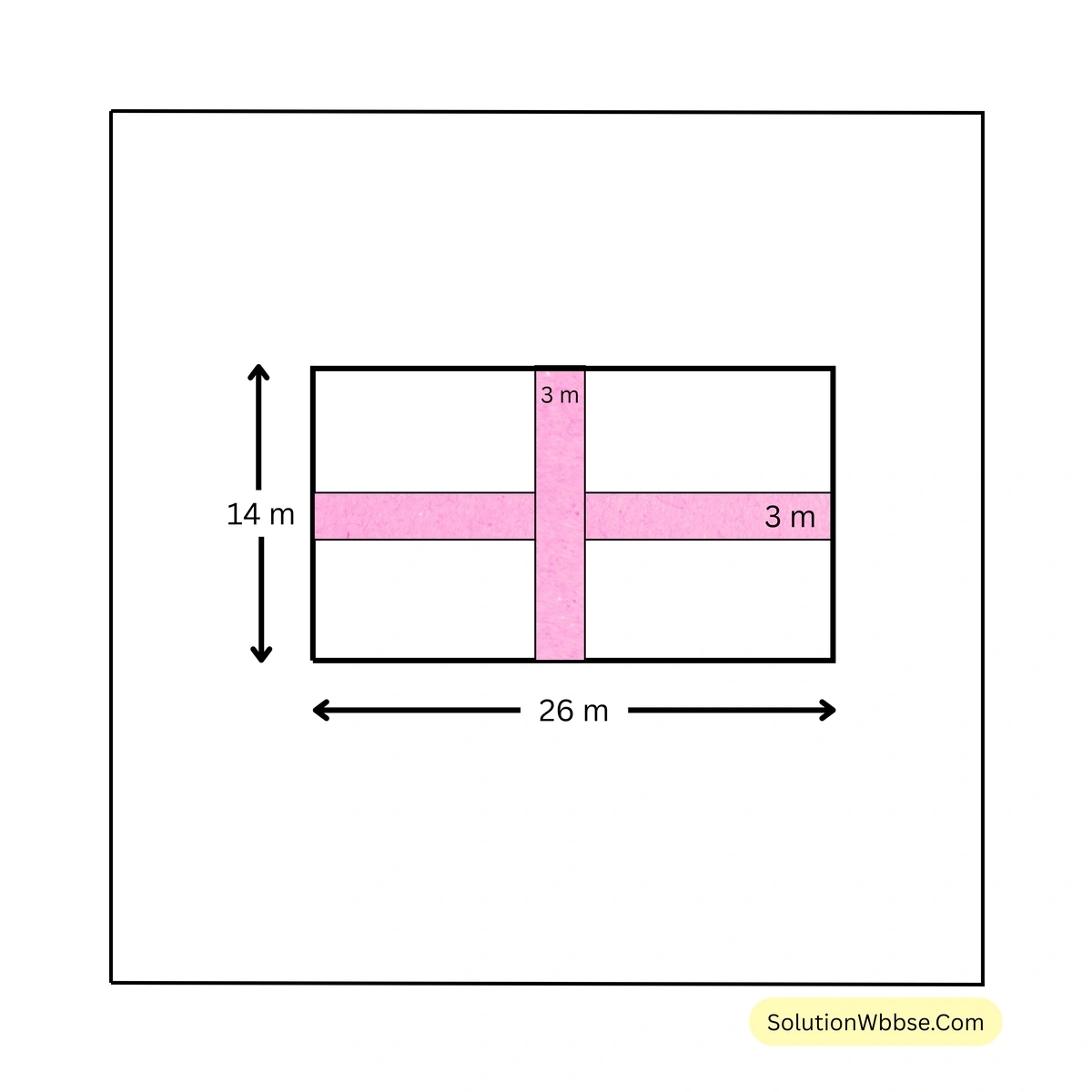
সমাধান – দৈর্ঘ্যের সমান্তরালে রঙিন আয়তকার পট্টির ক্ষেত্রফল = \( (26 \times 3)\) বর্গমিটার = \( 78\) বর্গমিটার।

প্রস্থের সমান্তরালে রঙিন আয়তকার পট্টির ক্ষেত্রফল = \( (14 \times 3)\) বর্গমিটার = \( 42\) বর্গমিটার।

\(\therefore\) সমগ্র রঙিন অংশের ক্ষেত্রফল = \( \{ 78 + 42 – (3 \times 3) \}\) বর্গমিটার = \( (78 + 42 – 9)\) বর্গমিটার = \( (120 – 9)\) বর্গমিটার = \( 111\) বর্গমিটার। [উত্তর]

(iii)

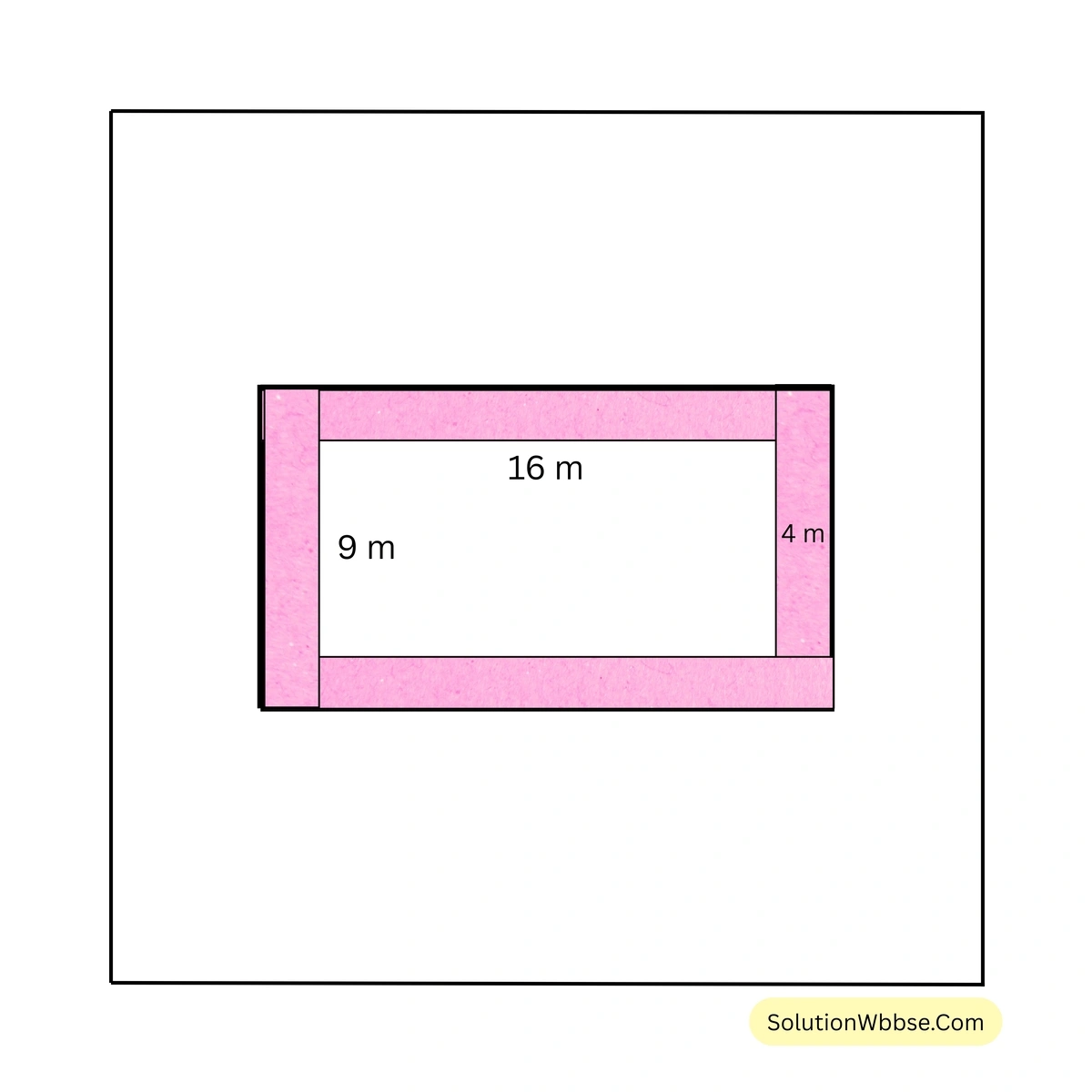
সমাধান – রঙিন অংশ সহ আয়তক্ষেত্রের দৈর্ঘ্য \((16 + 4 + 4)\) মিটার = \( 24\) মিটার।

রঙিন অংশ সহ আয়তক্ষেত্রের প্রস্থ = \( (9 + 4 + 4)\) মিটার = \( 17\) মিটার।

\(\therefore\) রঙিন অংশ সহ আয়তক্ষেত্রের ক্ষেত্রফল = \( (24 \times 17)\) বর্গমিটার = \( 408\) বর্গমিটার।

রঙিন অংশ বাদে আয়তক্ষেত্রের ক্ষেত্রফল = \( (16 \times 9)\) বর্গমিটার = \( 144\) বর্গমিটার।

\(\therefore\) রঙিন অংশের ক্ষেত্রফল = \( (408 – 144)\) বর্গমিটার = \( 264\) বর্গমিটার। [উত্তর]

(iv)

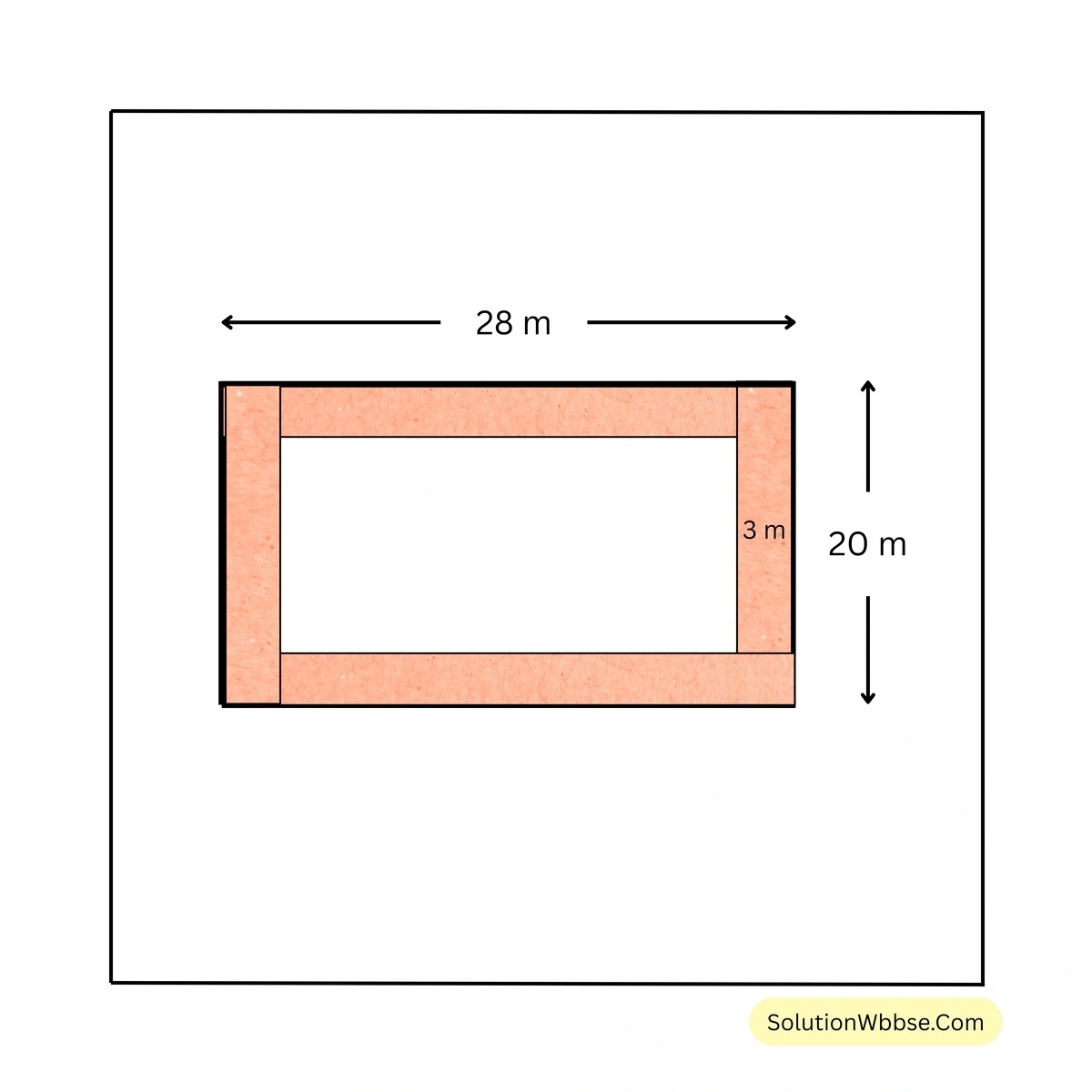
সমাধান – রঙিন অংশ সহ আয়তক্ষেত্রের দৈর্ঘ্য 28 মিটার এবং প্রস্থ 20 মিটার।

\(\therefore\) রঙিন অংশ সহ আয়তক্ষেত্রের ক্ষেত্রফল = \( (28 \times 20)\) বর্গমিটার = \( 560\) বর্গমিটার।

রঙিন অংশ বাদে আয়তক্ষেত্রের দৈর্ঘ্য = \( (28 – 3 – 3)\) মিটার = \( 22\) মিটার।

রঙিন অংশ বাদে আয়তক্ষেত্রের প্রস্থ = \( (20 – 3 – 3)\) মিটার = \( 14\) মিটার।

\(\therefore\) রঙিন অংশ বাদে আয়তক্ষেত্রের ক্ষেত্রফল = \( (22 \times 14)\) বর্গমিটার = \( 308\) বর্গমিটার।

সুতরাং রঙিন অংশের ক্ষেত্রফল = \( (560 – 308)\) বর্গমিটার = \( 252\) বর্গমিটার। [উত্তর]

(v)

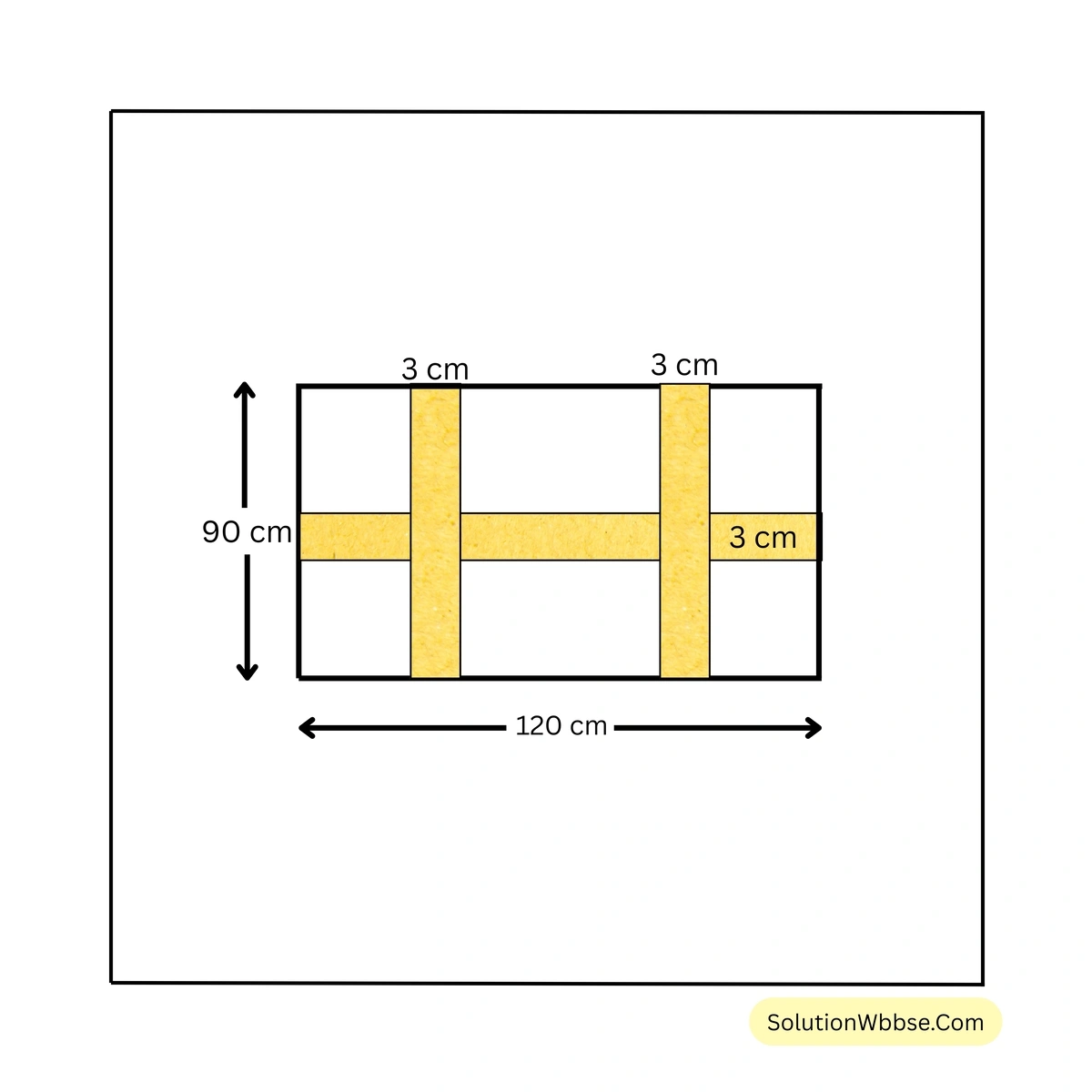
সমাধান – দৈর্ঘ্যের সমান্তরালে রঙিন আয়তকার পট্টির ক্ষেত্রফল = \( (120 \times 3)\) বর্গমিটার = \( 360\) বর্গমিটার।

প্রস্থের সমান্তরালে 2 টি রঙিন আয়তকার পট্টির ক্ষেত্রফল = \( 2 \times (90 \times 3)\) বর্গমিটার = \( 540\) বর্গমিটার।

\(\therefore\) সমগ্র রঙিন অংশের ক্ষেত্রফল = \( \{ (360 + 540) – 2 \times (3 \times 3) \}\) বর্গমিটার = \( (900 – 18)\) বর্গমিটার = \( 882\) বর্গমিটার। [উত্তর]

3. বিরাটি মহাজাতি সঙ্ঘের আয়তাকার মাঠের দৈর্ঘ্য ও প্রস্থের অনুপাত \(4:3\); মাঠটির চারিদিকে একবার হেঁটে এলে 336 মিটার পথ অতিক্রম করা যায়। মাঠের ক্ষেত্রফল হিসাব করে লিখি।

সমাধান – বিরাটি মহাজাতি সঙ্ঘের আয়তাকার মাঠের দৈর্ঘ্য ও প্রস্থের অনুপাত \(4:3\)।

ধরি, আয়তাকার মাঠের দৈর্ঘ্য \(4x\) মিটার এবং প্রস্থ \(3x\) মিটার।

\(\therefore\) আয়তাকার মাঠের পরিসীমা = \( \{2 \times (4x + 3x)\}\) মিটার = \( 14x\) মিটার।

\(\therefore 14x = 336\)

বা, \(x = \frac{336}{14}\)

বা, \(x = 24\)

\(\therefore\) মাঠটির দৈর্ঘ্য \(4x = (4 \times 24)\) মিটার = \( 96\) মিটার এবং প্রস্থ \(3x = (3 \times 24)\) মিটার = \( 72\) মিটার।

\(\therefore\) মাঠটির ক্ষেত্রফল = \( (96 \times 72)\) বর্গমিটার = \( 6912\) বর্গমিটার। [উত্তর]

4. প্রতি বর্গমিটারে 3.50 টাকা হিসাবে সমরদের একটি বর্গাকার জমি চাষ করতে খরচ হয় 1400 টাকা। প্রতি মিটারে 8.50 টাকা হিসাবে সমরদের জমিটির চারধারে একই উচ্চতার বেড়া দিতে কত খরচ হবে হিসাব করে লিখি।

সমাধান – প্রতি বর্গমিটারে 3.50 টাকা হিসাবে সমরদের একটি বর্গাকার জমি চাষ করতে খরচ হয় 1400 টাকা।

\(\therefore\) বর্গাকার জমির ক্ষেত্রফল = \( (1400 \div 3.50)\) বর্গমিটার = \( 400\) বর্গমিটার।

\(\therefore\) বর্গাকার জমির প্রতিটি বাহুর দৈর্ঘ্য = \( \sqrt{400}\) মিটার = \( 20\) মিটার।

\(\therefore\) বর্গাকার জমির পরিসীমা = \( (20 \times 4)\) মিটার = \( 80\) মিটার।

এখন, প্রতি মিটারে 8.50 টাকা হিসাবে সমরদের জমিটির চারধারে একই উচ্চতার বেড়া দিতে খরচ হবে = \( (80 \times 8.50)\) টাকা = \( 680\) টাকা। [উত্তর]

5. সুহাসদের আয়তাকার জমির ক্ষেত্রফল 500 বর্গমিটার। জমিটির দৈর্ঘ্য 3 মিটার কমালে এবং প্রস্থ 2 মিটার বাড়ালে জমিটি বর্গাকার হয়। সুহাসদের জমির দৈর্ঘ্য ও প্রস্থ হিসাব করে লিখি।

সমাধান – ধরি, সুহাসদের জমির দৈর্ঘ্য \(x\) মিটার এবং প্রস্থ \(y\) মিটার।

শর্তানুসারে, \(xy = 500\) — (i)

এবং \(x – 3 = y + 2\) — (ii) [যেহেতু, বর্গাকার জমির প্রতিটি বাহুর দৈর্ঘ্য সমান]

(ii) নং সমীকরণ থেকে পাই,

\(x – y = 3 + 2\)

বা, \(x – y = 5\) — (iii)

এখন, \((x + y)^2 = (x – y)^2 + 4xy\)

বা, \((x + y)^2 = (5)^2 + 4 \times 500\) [(i) ও (iii) নং সমীকরণ থেকে যথাক্রমে \(xy\) এবং \((x – y)\) এর মান বসিয়ে পাই]

বা, \((x + y)^2 = 25 + 2000\)

বা, \((x + y)^2 = 2025\)

বা, \((x + y)^2 = (45)^2\)

বা, \(x + y = 45\) — (iv)

(iii) নং ও (iv) নং সমীকরণ যোগ করে পাই,

\(x + y + x – y = 45 + 5\)

বা, \(2x = 50\)

বা, \(x = \frac{50}{2}\)

বা, \(x = 25\)

\(x\)-এর মান (iv) নং সমীকরণে বসিয়ে পাই,

\(25 + y = 45\)

বা, \(y = 45 – 25\)

বা, \(y = 20\)

\(\therefore\) সুহাসদের জমির দৈর্ঘ্য 25 মিটার এবং প্রস্থ 20 মিটার। [উত্তর]

6. আমাদের গ্রামে একটি বর্গাকার জমির প্রতিটি বাহুর দৈর্ঘ্য 300 মিটার। এই বর্গাকার জমির চারধারে একই উচ্চতার 3 ডেসিমি. দেওয়াল দিয়ে ঘিরব। হিসাব করে দেখি প্রতি 100 বর্গমিটার জমিতে 5000 টাকা হিসাবে দেওয়ালের জন্য কত খরচ পড়বে।

সমাধান – বর্গাকার জমির প্রতিটি বাহুর দৈর্ঘ্য 300 মিটার।

বর্গাকার জমির ক্ষেত্রফল = \( (300)^2\) বর্গমিটার = \( 90000\) বর্গমিটার।

এই বর্গাকার জমির চারধারে একই উচ্চতার 3 ডেসিমি. = \( 0.3\) মিটার চওড়া একটি দেওয়াল আছে।

দেওয়াল বাদে বর্গাকার জমির প্রতিটি বাহুর দৈর্ঘ্য = \( (300 – 0.3 – 0.3)\) মিটার = \( (300 – 0.6)\) মিটার = \( 299.4\) মিটার।

দেওয়াল বাদে বর্গাকার জমির ক্ষেত্রফল = \( (299.4)^2\) বর্গমিটার = \( 89640.36\) বর্গমিটার।

দেওয়ালের ক্ষেত্রফল = \( (90000 – 89640.36)\) বর্গমিটার = \( 359.64\) বর্গমিটার।

এখন, দেওয়ালের জন্য প্রতি 100 বর্গমিটার জমিতে খরচ হয় 5000 টাকা।

\(359.64\) বর্গমিটার জমির জন্য খরচ হবে = \( \left(\frac{359.64}{100} \times 5000\right)\) টাকা = \( 17982\) টাকা।

দেওয়াল তৈরি করতে মোট খরচ হবে 17982 টাকা।

7. রেহানাদের আয়তাকার বাগানের দৈর্ঘ্য 14 মিটার এবং প্রস্থ 12 মিটার। বাগানটির ভিতরের চারিদিকে সমান চওড়া একটি রাস্তা তৈরি করতে প্রতি বর্গমিটারে 20 টাকা হিসাবে মোট 1380 টাকা খরচ হলে, রাস্তাটি কত মিটার চওড়া হিসাব করে লিখি।

সমাধান – রেহানাদের আয়তাকার বাগানের দৈর্ঘ্য 14 মিটার এবং প্রস্থ 12 মিটার।

রেহানাদের আয়তাকার বাগানের ক্ষেত্রফল = \( (14 \times 12)\) বর্গমিটার = \( 168\) বর্গমিটার।

বাগানটির ভিতরের চারিদিকে সমান চওড়া একটি রাস্তা তৈরি করতে প্রতি বর্গমিটারে 20 টাকা হিসাবে মোট 1380 টাকা খরচ হলে, রাস্তার ক্ষেত্রফল = \( \frac{1380}{20}\) বর্গমিটার = \( 69\) বর্গমিটার।

ধরি, রাস্তাটি \(x\) মিটার চওড়া।

রাস্তা বাদে আয়তাকার বাগানের দৈর্ঘ্য \((14 – x – x)\) মিটার = \( (14 – 2x)\) মিটার।

এবং রাস্তা বাদে আয়তাকার বাগানের প্রস্থ \((12 – x – x)\) মিটার = \( (12 – 2x)\) মিটার।

রাস্তা বাদে আয়তাকার বাগানের ক্ষেত্রফল = \( (14 – 2x)(12 – 2x)\) বর্গমিটার।

শর্তানুসারে,

\(168 – (14 – 2x)(12 – 2x) = 69\)

বা, \((14 – 2x)(12 – 2x) = 168 – 69\)

বা, \((14 – 2x)(12 – 2x) = 99\)

বা, \(168 – 28x – 24x + 4x^2 = 99\)

বা, \(4x^2 – 52x + 168 = 99\)

বা, \(4x^2 – 52x + 168 – 99 = 0\)

বা, \(4x^2 – 52x + 69 = 0\)

বা, \(x = \frac{52 \pm \sqrt{(-52)^2 – 4 \cdot 4 \cdot 69}}{2 \cdot 4}\)

বা, \(x = \frac{52 \pm \sqrt{2704 – 1104}}{8}\)

বা, \(x = \frac{52 \pm \sqrt{1600}}{8}\)

বা, \(x = \frac{52 \pm 40}{8}\)

\(\therefore x = \frac{52 + 40}{8} = \frac{92}{8} = 11.5\) অথবা \(x = \frac{52 – 40}{8} = \frac{12}{8} = 1.5\)

এক্ষেত্রে \(x = 11.5\) মিটার গ্রহণযোগ্য নয়, কারণ বাগানের দৈর্ঘ্য বা প্রস্থের চেয়ে বেশি।

সুতরাং রাস্তাটি \(1.5\) মিটার চওড়া। [উত্তর]

8. 1200 বর্গসেমি ক্ষেত্রফল বিশিষ্ট একটি আয়তক্ষেত্রাকার জমির দৈর্ঘ্য 40 সেমি. হলে, তার কর্ণের ওপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি।

সমাধান –

40 সেমি দৈর্ঘ্য বিশিষ্ট একটি আয়তক্ষেত্রের ক্ষেত্রফল 1200 বর্গসেমি.।

\(\therefore\) আয়তক্ষেত্রটির প্রস্থ = \((1200 \div 40)\) সেমি. = 30 সেমি.

$\begin{array}{l}\therefore \text{কর্ণের দৈর্ঘ্য =}\sqrt{{\left(\mathrm{দৈর্ঘ্য}\right)}^2+{\left(\mathrm{প্রস্থ}\right)}^2}\\ =\sqrt{{\left(40\right)}^2+{\left(30\right)}^2}\text{সেমি.}\\ =\sqrt{1600+900}\text{সেমি.}\\ =\sqrt{2500}\text{সেমি.}\\ =50\text{সেমি.}\end{array}$

\(\therefore\) কর্ণের দৈর্ঘ্যের ওপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল = \((50)^2\) বর্গসেমি. = 2500 বর্গসেমি.। [উত্তর]

9. একটি হলঘরের দৈর্ঘ্য 4 মিটার, প্রস্থ 6 মিটার এবং উচ্চতা 4 মিটার। ঘরটিতে তিনটি দরজা আছে যাদের প্রত্যেকটি 1.5 মি. × 1 মি. এবং চারটি জানালা আছে যাদের প্রত্যেকটি 1.2 মি. × 1 মি.। ঘরটির চার দেওয়াল প্রতি বর্গমিটারে 70 টাকা হিসাবে রঙিন কাগজ দিয়ে ঢাকতে কত খরচ পড়বে হিসাব করে লিখি।

সমাধান –

হলঘরের দৈর্ঘ্য 4 মিটার, প্রস্থ 6 মিটার এবং উচ্চতা 4 মিটার।

$\begin{array}{l}\therefore \text{কর্ণের দৈর্ঘ্য =}\sqrt{{\left(\mathrm{দৈর্ঘ্য}\right)}^2+{\left(\mathrm{প্রস্থ}\right)}^2}\\ =\sqrt{{\left(40\right)}^2+{\left(30\right)}^2}\text{সেমি.}\\ =\sqrt{1600+900}\text{সেমি.}\\ =\sqrt{2500}\text{সেমি.}\\ =50\text{সেমি.}\end{array}$

প্রতিটি দরজার ক্ষেত্রফল = \((1.5 \times 1)\) বর্গমিটার = 1.5 বর্গমিটার।

\(\therefore\) 3 টি দরজার ক্ষেত্রফল = \((3 \times 1.5)\) বর্গমিটার = 4.5 বর্গমিটার।

প্রতিটি জানালার ক্ষেত্রফল = \((1.2 \times 1)\) বর্গমিটার = 1.2 বর্গমিটার।

\(\therefore\) 4 টি জানালার ক্ষেত্রফল = \((4 \times 1.2)\) বর্গমিটার = 4.8 বর্গমিটার।

\(\therefore\) 3 টি দরজা ও 4 টি জানালা বাদে চার দেওয়ালের ক্ষেত্রফল = \((80 – 4.5 – 4.8)\) বর্গমিটার = 70.70 বর্গমিটার।

এখন, চার দেওয়ালে প্রতি বর্গমিটারে 70 টাকা হিসাবে রঙিন কাগজ দিয়ে ঢাকতে খরচ পড়বে = \((70.70 \times 70)\) টাকা = 4949 টাকা। [উত্তর]

10. একটি ঘরের চার দেওয়ালের ক্ষেত্রফল 42 বর্গমিটার এবং মেঝের ক্ষেত্রফল 12 বর্গমিটার। ঘরটির দৈর্ঘ্য 4 মিটার হলে ঘরটির উচ্চতা হিসাব করে লিখি।

সমাধান –

ধরি, ঘরটির উচ্চতা x মিটার।

মেঝের ক্ষেত্রফল 12 বর্গমিটার এবং ঘরটির দৈর্ঘ্য 4 মিটার।

\(\therefore\) ঘরটির প্রস্থ = \(12 / 4\) মিটার = 3 মিটার।

$\therefore \text{ঘরটির চার দেওয়ালের ক্ষেত্রফল}$
$=2\times (\text{দৈর্ঘ্য}+\text{প্রস্থ})\times \text{উচ্চতা}$
$=(2\times (4+3)\times x)\text{বর্গমিটার}$
$=14x\text{বর্গমিটার।}$\(14x = 42\)

বা, \(x = 42 / 14\)

বা, \(x = 3\)

\(\therefore\) ঘরটির উচ্চতা 3 মিটার। [উত্তর]

11. সুজাতা 84 বর্গসেমি ক্ষেত্রফল বিশিষ্ট একটি আয়তকার কাগজে ছবি আঁকবে। কাগজটির দৈর্ঘ্য ও প্রস্থের অন্তর 5 সেমি.। সুজাতার কাগজটির পরিসীমা হিসাব করি।

সমাধান –

ধরি, আয়তকার কাগজের দৈর্ঘ্য x সেমি. এবং প্রস্থ y সেমি.।

শর্তানুসারে, \(xy = 84\) —(i)

এবং \(x – y = 5\) —(ii)

এখন, \((x + y)^2 = (x – y)^2 + 4xy\)

বা, \((x+y)^2 = (5)^2 + 4(84)\) [(i) ও (ii) থেকে যথাক্রমে xy এবং (x-y) এর মান বসিয়ে পাই]

বা, \((x+y)^2 = 25 + 336\)

বা, \((x+y)^2 = 361\)

বা, \((x+y)^2 = (19)^2\)

বা, \((x+y) = 19\)

বা, \(2(x+y) = 2 \times 19\)

বা, \(2(x+y) = 38\)

সুতরাং, আয়তকার ছবির পরিসীমা 38 সেমি.। [উত্তর]

12. সিরাজদের বাগানের বাইরে চারদিকে 2.5 মিটার চওড়া একটি রাস্তা আছে। রাস্তাটির ক্ষেত্রফল 165 বর্গমিটার। বাগানটির ক্ষেত্রফল এবং কর্ণের দৈর্ঘ্য হিসাব করি। (\(\sqrt{2} = 1.414\))।

সমাধান – ধরি, বর্গাকার বাগানের প্রতিটি বাহুর দৈর্ঘ্য x মিটার।

\(\therefore\) বর্গাকার বাগানের ক্ষেত্রফল = \(x^2\) বর্গমিটার।

রাস্তাসহ বর্গাকার বাগানের প্রতিটি বাহুর দৈর্ঘ্য = (x+2.5+2.5) মিটার = (x+5) মিটার।

\(\therefore\) রাস্তাসহ বর্গাকার বাগানের ক্ষেত্রফল = \((x+5)^2\) বর্গমিটার।

\(\therefore\) রাস্তার ক্ষেত্রফল = \(\{(x+5)^2 – x^2\}\) বর্গমিটার

শর্তানুসারে,

\((x+5)^2 – x^2 = 165\)

বা, \(x^2 + 10x + 25 – x^2 – 165 = 0\)

বা, \(10x – 140 = 0\)

বা, \(x = 140 / 10\)

বা, \(x = 14\)

\(\therefore\) বর্গাকার বাগানের ক্ষেত্রফল \((14 \times 14)\) বর্গমিটার = 196 বর্গমিটার।[উত্তর]

এবং বর্গাকার বাগানের কর্ণের দৈর্ঘ্য = \(14\sqrt{2}\) মিটার = \((14 \times 1.414)\) মিটার = 19.796 মিটার।[উত্তর]

13. যে বর্গাকার জমির কর্ণের দৈর্ঘ্য \(20\sqrt{2}\) মিটার তার চারধার পাঁচিল দিয়ে ঘিরতে কত মিটার লম্বা পাঁচিল লাগবে হিসাব করে লিখি। প্রতি বর্গমিটারে 20 টাকা হিসাবে ঘাস বসাতে কত খরচ হবে হিসাব করে লিখি।

সমাধান – ধরি, বর্গাকার জমির বাহুর দৈর্ঘ্য a মিটার।

\(\therefore\) বর্গাকার জমির কর্ণের দৈর্ঘ্য \(a\sqrt{2}\) মিটার।

শর্তানুসারে,

\(a\sqrt{2} = 20\sqrt{2}\)\(\Rightarrow a = 20\)

\(\therefore\) বর্গাকার জমির বাহুর দৈর্ঘ্য 20 মিটার।

\(\therefore\) বর্গাকার জমির পরিসীমা \((4 \times 20)\) মিটার = 80 মিটার।

\(\therefore\) বর্গাকার জমিটিকে পাঁচিল দিয়ে ঘিরতে 80 মিটার দৈর্ঘ্যের পাঁচিলের প্রয়োজন হবে।[উত্তর]

বর্গাকার জমির ক্ষেত্রফল \((20)^2\) বর্গমিটার = 400 বর্গমিটার

\(\therefore\) প্রতিবর্গমিটারে 20 টাকা হিসাবে ঘাস বসাতে খরচ হবে = \((400 \times 20)\) টাকা = 8000 টাকা।[উত্তর]

14. আমাদের আয়তকার বাগানের একটি কর্ণ বরাবর একটি বেড়া দেব। আয়তকার বাগানের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 12 মিটার ও 7 মিটার হলে, বেড়ার দৈর্ঘ্য হিসাব করে লিখি। বেড়াটি আয়তকার বাগানটিকে যে দুটি ত্রিভুজে ভাগ করবে তাদের পরিসীমা লিখি।

সমাধান – আয়তকার বাগানের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 12 মিটার ও 7 মিটার।

$\therefore \text{ আয়তকার বাগানের কর্ণের দৈর্ঘ্য}$ $=\sqrt{{\left(\text{দৈর্ঘ্য}\right)}^2+{\left(\text{প্রস্থ}\right)}^2}$$=\sqrt{{\left(12\right)}^2+{\left(7\right)}^2}\text{মিটার}$$=\sqrt{144+49}\text{মিটার}$$=\sqrt{193}\text{মিটার}$

\(\therefore\) আয়তকার বাগানের কর্ণ বরাবর বেড়ার দৈর্ঘ্য \(\sqrt{193}\) মিটার।

বেড়াটি আয়তকার বাগানটিকে যে দুটি ত্রিভুজে ভাগ করেছে তাদের প্রত্যেকটির পরিসীমা = \((12+7+\sqrt{193})\) মিটার = \((19+\sqrt{193})\) মিটার।

\(\therefore\) বেড়ার দৈর্ঘ্য \(\sqrt{193}\) মিটার এবং প্রত্যেকটি ত্রিভুজের পরিসীমা \((19+\sqrt{193})\) মিটার।[উত্তর]

15. মৌসুমীদের বাড়ির আয়তকার বড় হলঘরের দৈর্ঘ্য ও প্রস্থের অনুপাত 9:5 এবং পরিসীমা 140 মিটার। মৌসুমীরা হলঘরের মেঝেতে 25 সেমি. \(\times\) 20 সেমি. আকারের আয়তকার টালি বসাতে চায়। প্রতি 100 টালির দাম 500 টাকা হলে, মৌসুমীদের হলঘরের মেঝেতে টালি বসাতে কত খরচ হবে হিসাব করে লিখি।

সমাধান – মৌসুমীদের বাড়ির আয়তকার বড় হলঘরের দৈর্ঘ্য ও প্রস্থের অনুপাত 9:5।

ধরি, মৌসুমীদের বাড়ির আয়তকার হল ঘরের দৈর্ঘ্য 9x মিটার এবং প্রস্থ 5x মিটার।

শর্তানুসারে,

\(2(9x+5x) = 140\)

বা, \(28x = 140\)

বা, \(x = 140 / 28\)

বা, \(x = 5\)

\(\therefore\) মৌসুমীদের বাড়ির আয়তকার হল ঘরের দৈর্ঘ্য = \((9 \times 5)\) মিটার = 45 মিটার এবং প্রস্থ = \((5 \times 5)\) মিটার = 25 মিটার।

\(\therefore\) মৌসুমীদের বাড়ির আয়তকার হল ঘরের ক্ষেত্রফল = \((45 \times 25)\) বর্গমিটার = 1125 বর্গমিটার = \((1125 \times 100 \times 100)\) বর্গসেমি. = 11250000 বর্গসেমি.।

মৌসুমীরা হলঘরের মেঝেতে 25 সেমি.\(\times\)20 সেমি. আকারের আয়তকার টালি বসাতে চায়।

$\therefore \text{টালির সংখ্যা}$ $=\frac{\text{হলঘরের মেঝের ক্ষেত্রফল}}{\text{একটি টালির ক্ষেত্রফল}}$$=\frac{11250000}{25\times 20}$$=22500\text{টি।}$

এখন, 100 টি টালির দাম 500 টাকা

1 টি টালির দাম \(\frac{500}{100}\) টাকা

22500 টি টালির দাম \(\frac{500 \times 22500}{100}\) টাকা

= 1,12,500 টাকা।

\(\therefore\) মৌসুমীদের হলঘরের আয়তকার ঘরের মেঝেতে টালি বসাতে খরচ হবে 1,12,500 টাকা।[উত্তর]

16. 18 মিটার দৈর্ঘ্য বিশিষ্ট একটি বড় হলঘরে কার্পেট দিয়ে মুড়তে 2160 টাকা খরচ হয়। যদি প্রস্থ 4 মিটার কম হত তাহলে 1620 টাকা খরচ হত। হলঘরের ক্ষেত্রফল হিসাব করে লিখি।

সমাধান – ধরি, হলঘরের প্রস্থ x মিটার।

\(\therefore\) হলঘরের ক্ষেত্রফল 18x বর্গমিটার।

আবার, হলঘরের প্রস্থ (x-4) মিটার হলে হলঘরের ক্ষেত্রফল 18(x-4) বর্গমিটার।

এখন, 18x ক্ষেত্রফল বিশিষ্ট হলঘর কার্পেট দিয়ে মুড়তে খরচ হয় 2160 টাকা।

\(\therefore\) 18(x-4) ক্ষেত্রফল বিশিষ্ট হলঘর কার্পেট দিয়ে মুড়তে খরচ হবে

\(= \frac{2160 \times 18(x-4)}{18x}\) টাকা

\(= \frac{2160 \times (x-4)}{x}\) টাকা

শর্তানুসারে,

\(\frac{2160 \times (x-4)}{x} = 1620\)

বা, \(2160x – 8640 = 1620x\)

বা, \(2160x – 1620x = 8640\)

বা, \(540x = 8640\)

বা, \(x = 8640/540\)

বা, \(x = 16\)

\(\therefore\) হলঘরের প্রস্থ 16 মিটার।

\(\therefore\) হলঘরের ক্ষেত্রফল = \((18 \times 16)\) বর্গমিটার = 288 বর্গমিটার।[উত্তর]

17. একটি আয়তকার জমির কর্ণের দৈর্ঘ্য 15 মিটার এবং দৈর্ঘ্য ও প্রস্থের অন্তর 3 মিটার। জমিটির পরিসীমা ও ক্ষেত্রফল নির্ণয় করি।

সমাধান –

ধরি, আয়তকার জমির দৈর্ঘ্য x মিটার এবং প্রস্থ y মিটার।

\(\therefore \sqrt{x^2+y^2} = 15\) —(i)

এবং, \(x-y = 3\) —(ii)

(i) নং সমীকরণ থেকে পাই,

\(x^2 + y^2 = 225\) [উভয়পক্ষে বর্গ করে]

বা, \((x-y)^2 + 2xy = 225\)

বা, \((3)^2 + 2xy = 225\) [যেহেতু, \(x-y=3\)]

বা, \(9 + 2xy = 225\)

বা, \(2xy = 225-9\)

বা, \(2xy = 216\)

বা, \(xy = 108\) —(iii)

\(\therefore\) আয়তকার জমির ক্ষেত্রফল 108 বর্গমিটার। [উত্তর]

আবার, \((x+y)^2 = (x-y)^2 + 4xy\)

বা, \((x+y)^2 = (3)^2 + 4(108)\) [(ii) ও (iii) নং সমীকরণ থেকে যথাক্রমে \((x-y)\) এবং \(xy\)-এর মান বসিয়ে পাই]

বা, \((x+y)^2 = 9 + 432\)

বা, \((x+y)^2 = 441\)

বা, \((x+y)^2 = (21)^2\)

বা, \((x+y) = 21\)

বা, \(2(x+y) = 42\)

\(\therefore\) আয়তকার জমির পরিসীমা 42 মিটার। [উত্তর]

18. 385 মিটার \(\times\) 60 মিটার পরিমাপের একটি আয়তকার চাতাল পাকা করতে সর্ববৃহৎ কত মাপের বর্গাকার টাইলস ব্যবহার করা যাবে এবং সেক্ষেত্রে টাইলসের সংখ্যা কত হবে হিসাব করে লিখি।

সমাধান –

আয়তকার চাতালের দৈর্ঘ্য = 385 মিটার = (\(5\times7\times11\)) মিটার এবং প্রস্থ = 60 মিটার = (\(2\times2\times3\times5\)) মিটার।

\(\therefore\) আয়তকার চাতালের দৈর্ঘ্য ও প্রস্থের গসাগু 5 মিটার।

\(\therefore\) সর্ববৃহৎ বর্গাকার টাইলসের মাপ হবে = 5 মিটার \(\times\) 5 মিটার [উত্তর]

এবং টাইলসের সংখ্যা হবে = \(\frac{385 \times 60}{5 \times 5}\) টি = 924 টি।

\(\therefore\) চাতাল পাকা করতে সর্ববৃহৎ 5 মিটার \(\times\) 5 মিটার মাপের বর্গাকার টাইলস ব্যবহার করা যাবে এবং সেক্ষেত্রে টাইলসের সংখ্যা হবে 924 টি। [উত্তর]

19. বহু বিকল্পীয় প্রশ্ন (M.C.Q):

(i) একটি বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য \(12\sqrt{2}\) সেমি.। বর্গক্ষেত্রটির ক্ষেত্রফল

(a) 288 বর্গসেমি.
(b) 144 বর্গসেমি.
(c) 72 বর্গসেমি.
(d) 18 বর্গসেমি.

Ans: (b) 144 বর্গসেমি.

সমাধান –

(বাহুর দৈর্ঘ্য) \(\times \sqrt{2} = 12\sqrt{2}\)

বা, বাহুর দৈর্ঘ্য = 12

$\therefore \text{বর্গক্ষেত্রটির ক্ষেত্রফল}={\left(\text{বাহুর দৈর্ঘ্য}\right)}^2={\left(12\right)}^2\text{বর্গসেমি.}=144\text{বর্গসেমি.}।$

(ii) যদি একটি বর্গক্ষেত্রের ক্ষেত্রফল \(A_1\) বর্গ একক এবং ওই বর্গক্ষেত্রের কর্ণের ওপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল \(A_2\) বর্গএকক হয়, তাহলে \(A_1 : A_2\) হবে –

(a) 1 : 2
(b) 2 : 1
(c) 1 : 4
(d) 4 : 1

Ans: (a) 1 : 2

সমাধান –

বর্গক্ষেত্রের ক্ষেত্রফল \(A_1\) বর্গএকক।

\(\therefore\) বর্গক্ষেত্রের বাহুর দৈর্ঘ্য \(\sqrt{A_1}\) একক।

\(\therefore\) বর্গক্ষেত্রটির কর্ণের দৈর্ঘ্য \(= (\sqrt{A_1} \times \sqrt{2})\) একক \(= \sqrt{2A_1}\) একক।

\(\therefore\) বর্গক্ষেত্রটির কর্ণের ওপর অবস্থিত বর্গক্ষেত্রের ক্ষেত্রফল \(= (\sqrt{2A_1})^2\) বর্গএকক \(= 2A_1\) বর্গএকক।

\(\therefore 2A_1 = A_2\)

বা, \(A_1 : A_2 = 1:2\)

(iii) 6 মিটার লম্বা ও 4 মিটার চওড়া একটি আয়তকার জায়গা 2 ডেসিমি. বর্গ টালি দিয়ে বাঁধাতে হলে টালি লাগবে

(a) 1200
(b) 2400
(c) 600
(d) 1800

Ans: (c) 600

সমাধান –

6 মিটার লম্বা ও 4 মিটার চওড়া একটি আয়তকার জায়গার ক্ষেত্রফল \(= (6 \times 4)\) বর্গমিটার = 24 বর্গমিটার = 2400 বর্গডেসিমি.

আয়তকার জায়গাটি 2 ডেসিমি. বর্গ টালি দিয়ে সাজাতে প্রয়োজনীয় টালির সংখ্যা \(= (2400 \div (2)^2) = 600\) টি।

(iv) সমান পরিসীমা বিশিষ্ট একটি বর্গক্ষেত্র এবং একটি আয়তক্ষেত্রের ক্ষেত্রফল যথাক্রমে \(S\) এবং \(R\) হলে,

(a) \(S = R\)
(b) \(S > R\)
(c) \(S < R\)

Ans: (b) \(S > R\)

সমাধান –

ধরি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য \(a\) একক এবং আয়তক্ষেত্রের দৈর্ঘ্য ও প্রস্থ যথাক্রমে \(x\) একক ও \(y\) একক।

\(\therefore\) বর্গক্ষেত্রের পরিসীমা \(= 4a\) একক এবং আয়তক্ষেত্রের পরিসীমা \(= 2(x+y)\) একক।

শর্তানুসারে,

\(4a = 2(x+y)\)

বা, \(2a = (x+y)\)

বা, \(a = \frac{x+y}{2}\)

\(\therefore a^2 = \left(\frac{x+y}{2}\right)^2 = \frac{(x-y)^2 + 4xy}{4} = \frac{(x-y)^2}{4} + xy\)

স্পষ্টতই, \(\frac{(x-y)^2}{4} > 0\)

\(\therefore a^2 > xy\)

\(\therefore\) বর্গক্ষেত্রের ক্ষেত্রফল > আয়তক্ষেত্রের ক্ষেত্রফল

\(\therefore S > R\)

(v) একটি আয়তক্ষেত্রের কর্ণের দৈর্ঘ্য 10 সেমি. এবং ক্ষেত্রফল 62.5 বর্গসেমি. হলে, আয়তক্ষেত্রটির দৈর্ঘ্য ও প্রস্থের সমষ্টি

(a) 12 সেমি.
(b) 15 সেমি.
(c) 20 সেমি.
(d) 25 সেমি.

Ans: (b) 15 সেমি.

সমাধান –

ধরি, আয়তক্ষেত্রের দৈর্ঘ্য x সেমি. ও প্রস্থ y সেমি.

\(\therefore \sqrt{(x^2+y^2)} = 10\) —(i)

এবং, \(xy = 62.5\) —(ii)

(i) নং সমীকরণের উভয়দিকে বর্গ করে পাই,

\(x^2+y^2= 100\)

বা, \((x+y)^2 -2xy = 100\)

বা, \((x+y)^2 – 2(62.5) = 100\) [যেহেতু, \(xy =62.5\)]

বা, \((x+y)^2 – 125 =100\)

বা, \((x+y)^2 = 225\)

বা, \((x+y)^2 = (15)^2\)

বা, \((x+y) = 15\)

\(\therefore\) দৈর্ঘ্য ও প্রস্থের সমষ্টি 15 সেমি.।

20. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন

(i) একটি বর্গক্ষেত্রের বাহুর দৈর্ঘ্য 10% বৃদ্ধি করলে, বর্গক্ষেত্রটির ক্ষেত্রফল শতকরা কত বৃদ্ধি পাবে?

সমাধান –

ধরি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য 100 একক।

\(\therefore\) বর্গক্ষেত্রটির ক্ষেত্রফল \(= (100)^2\) বর্গএকক \(= 10000\) বর্গএকক

বর্গক্ষেত্রটির বাহুর দৈর্ঘ্য 10% বৃদ্ধি করলে পরিবর্তিত বাহুর দৈর্ঘ্য \(= (100+10)\) একক \(= 110\) একক

এখন, বর্গক্ষেত্রটির ক্ষেত্রফল \(= (110)^2\) বর্গএকক \(= 12100\) বর্গএকক

বর্গক্ষেত্রটির ক্ষেত্রফল বৃদ্ধি পেল \(= (12100 – 10000)\) বর্গএকক \(= 2100\) বর্গএকক।

\(\therefore\) বর্গক্ষেত্রটির ক্ষেত্রফল শতকরা বৃদ্ধি পেল \(= (\frac{2100}{10000} \times 100)\% = 21\%\)।

\(\therefore\) বর্গক্ষেত্রের ক্ষেত্রফল শতকরা 21% বৃদ্ধি পাবে।

(ii) একটি আয়তক্ষেত্রের দৈর্ঘ্য 10% বৃদ্ধি এবং প্রস্থ 10% হ্রাস করা হলে, ক্ষেত্রফল শতকরা কত বৃদ্ধি বা হ্রাস পাবে হিসাব করে লিখি।

সমাধান –

ধরি, আয়তক্ষেত্রের দৈর্ঘ্য 100 একক এবং প্রস্থও 100 একক।

সুতরাং আয়তক্ষেত্রের ক্ষেত্রফল \(= (100 \times 100)\) বর্গএকক \(= 10000\) বর্গএকক।

আয়তক্ষেত্রের দৈর্ঘ্য 10% বৃদ্ধি এবং প্রস্থ 10% হ্রাস করা হলে পরিবর্তিত দৈর্ঘ্য ও প্রস্থ যথাক্রমে 110 একক এবং 90 একক হবে।

এখন আয়তক্ষেত্রের ক্ষেত্রফল \(= (110 \times 90)\) বর্গএকক \(= 9900\) বর্গএকক।

\(\therefore\) ক্ষেত্রফল হ্রাস পেল \(= (10000 – 9900)\) বর্গএকক \(= 100\) বর্গএকক।

\(\therefore\) ক্ষেত্রফল শতকরা হ্রাস পেল \(= (\frac{100}{10000} \times 100)\% = 1\%\)।

\(\therefore\) আয়তক্ষেত্রের ক্ষেত্রফল শতকরা 1% হ্রাস পাবে।

(iii) একটি আয়তক্ষেত্রের কর্ণের দৈর্ঘ্য 5 সেমি.। কর্ণদ্বয়ের ছেদবিন্দু থেকে আয়তক্ষেত্রের ওপর লম্বের দৈর্ঘ্য 2 সেমি.। আয়তক্ষেত্রের প্রস্থের দৈর্ঘ্য কত?

সমাধান –

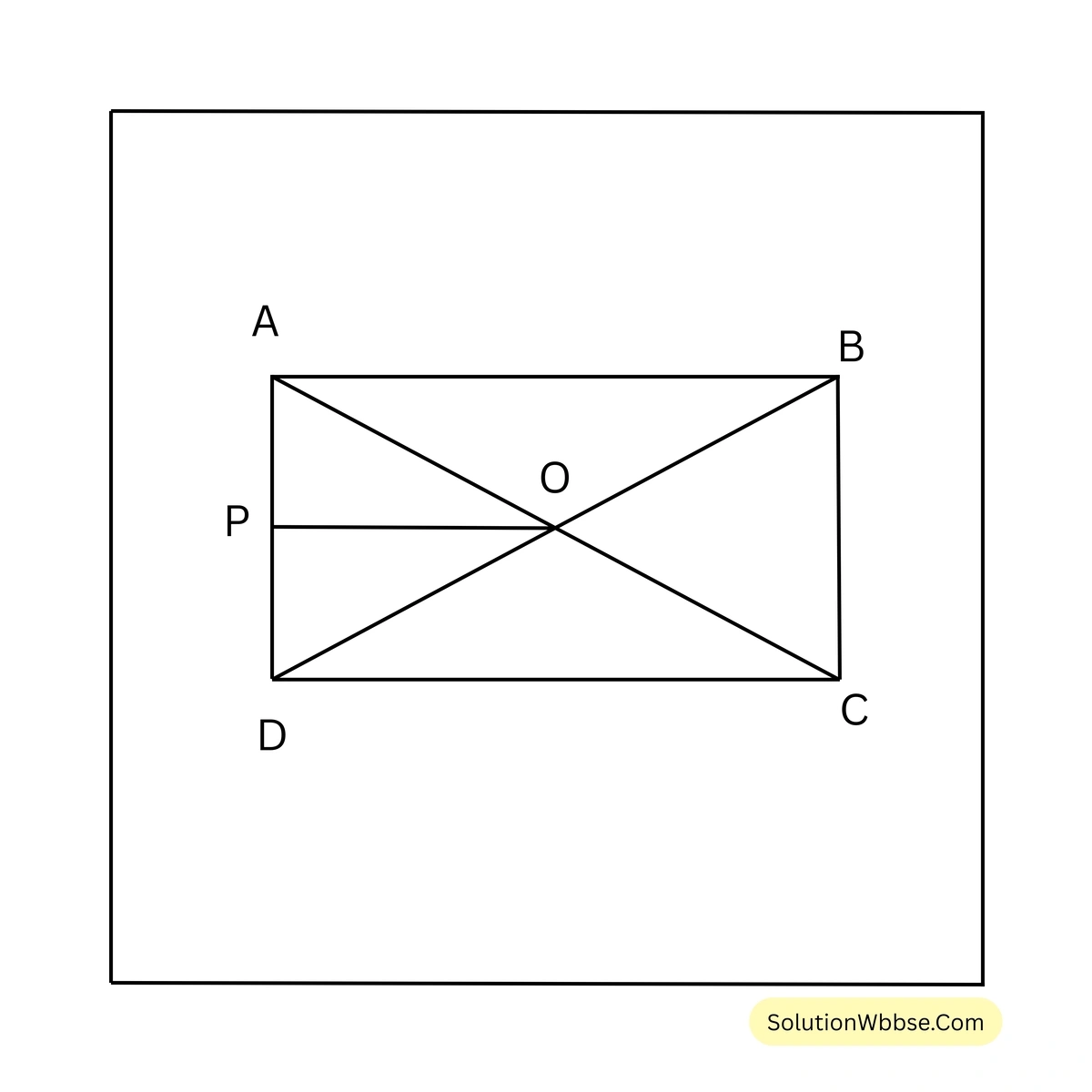
ধরা যাক, ABCD একটি আয়তক্ষেত্র যার AC ও BD দুটি কর্ণ পরস্পরকে O বিন্দুতে ছেদ করেছে। O বিন্দু থেকে AD এর ওপর OP লম্ব।

\(\therefore \text{AC} = \text{BD} = 5\) সেমি. এবং \(\text{OP} = 2\) সেমি.

\(\therefore \text{AB} = 2 \times \text{OP} = (2 \times 2)\) সেমি. \(= 4\) সেমি.।

সমকোণী ত্রিভুজ ABD থেকে পাই,

\(\text{AB}^2 + \text{AD}^2 = \text{BD}^2\)

বা, \((4)^2 + \text{AD}^2 = (5)^2\)

বা, \(\text{AD}^2 = 25 – 16\)

বা, \(\text{AD}^2 = 9\)

বা, \(\text{AD}^2 = (3)^2\)

বা, \(\text{AD} = 3\)

\(\therefore\) আয়তক্ষেত্রের প্রস্থ 3 সেমি.।

(iv) একটি বর্গক্ষেত্রের কর্ণদ্বয়ের ছেদবিন্দু থেকে তার যেকোনো একটি বাহুর ওপর অঙ্কিত লম্বের দৈর্ঘ্য \(2\sqrt{2}\) সেমি. হলে, বর্গক্ষেত্রটির প্রতিটি কর্ণের দৈর্ঘ্য কত?

সমাধান – বর্গক্ষেত্রের কর্ণদ্বয়ের ছেদবিন্দু থেকে তার যেকোনো একটি বাহুর ওপর অঙ্কিত লম্বের দৈর্ঘ্য \(2\sqrt{2}\) সেমি.।

\(\therefore\) বর্গক্ষেত্রের প্রতিটি বাহুর দৈর্ঘ্য \(= (2 \times 2\sqrt{2})\) সেমি. \(= 4\sqrt{2}\) সেমি.

\(\therefore\) বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য \(= (4\sqrt{2} \times \sqrt{2})\) সেমি. \(= 8\) সেমি.

\(\therefore\) বর্গক্ষেত্রের প্রতিটি কর্ণের দৈর্ঘ্য 8 সেমি.।

(v) একটি আয়তক্ষেত্রের পরিসীমা 34 সেমি. এবং ক্ষেত্রফল 60 বর্গসেমি.। আয়তক্ষেত্রের প্রতিটি কর্ণের দৈর্ঘ্য কত?

সমাধান – ধরি, আয়তক্ষেত্রের দৈর্ঘ্য \(x\) সেমি. এবং প্রস্থ \(y\) সেমি.।

\(\therefore\) আয়তক্ষেত্রের পরিসীমা \(= 2(x+y)\) সেমি. এবং ক্ষেত্রফল \(xy\) বর্গসেমি.

\(\therefore 2(x+y) = 34\)

বা, \(x+y = \frac{34}{2}\)

বা, \(x+y = 17\) —(i)

এবং, \(xy = 60\) —(ii)

এখন, \(x^2 + y^2 = (x+y)^2 – 2xy = (17)^2 – 2(60) = 289 – 120 = 169\)

বা, \(\sqrt{x^2 + y^2} = \sqrt{169}\)

বা, \(\sqrt{x^2 + y^2} = 13\)

\(\therefore\) আয়তক্ষেত্রের কর্ণের দৈর্ঘ্য 13 সেমি.।

---

এই আর্টিকেলে নবম শ্রেণির গণিতের ‘ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল‘ অধ্যায়ের ‘কষে দেখি – 15.1’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।

কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করতে পারেন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।