পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) দশম শ্রেণির গণিত পাঠ্যবইয়ের পঞ্চদশ অধ্যায় হলো ‘ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল’। এই পোস্টে ‘কষে দেখি – 15.2‘-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. নিচের ছবিগুলির ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি।
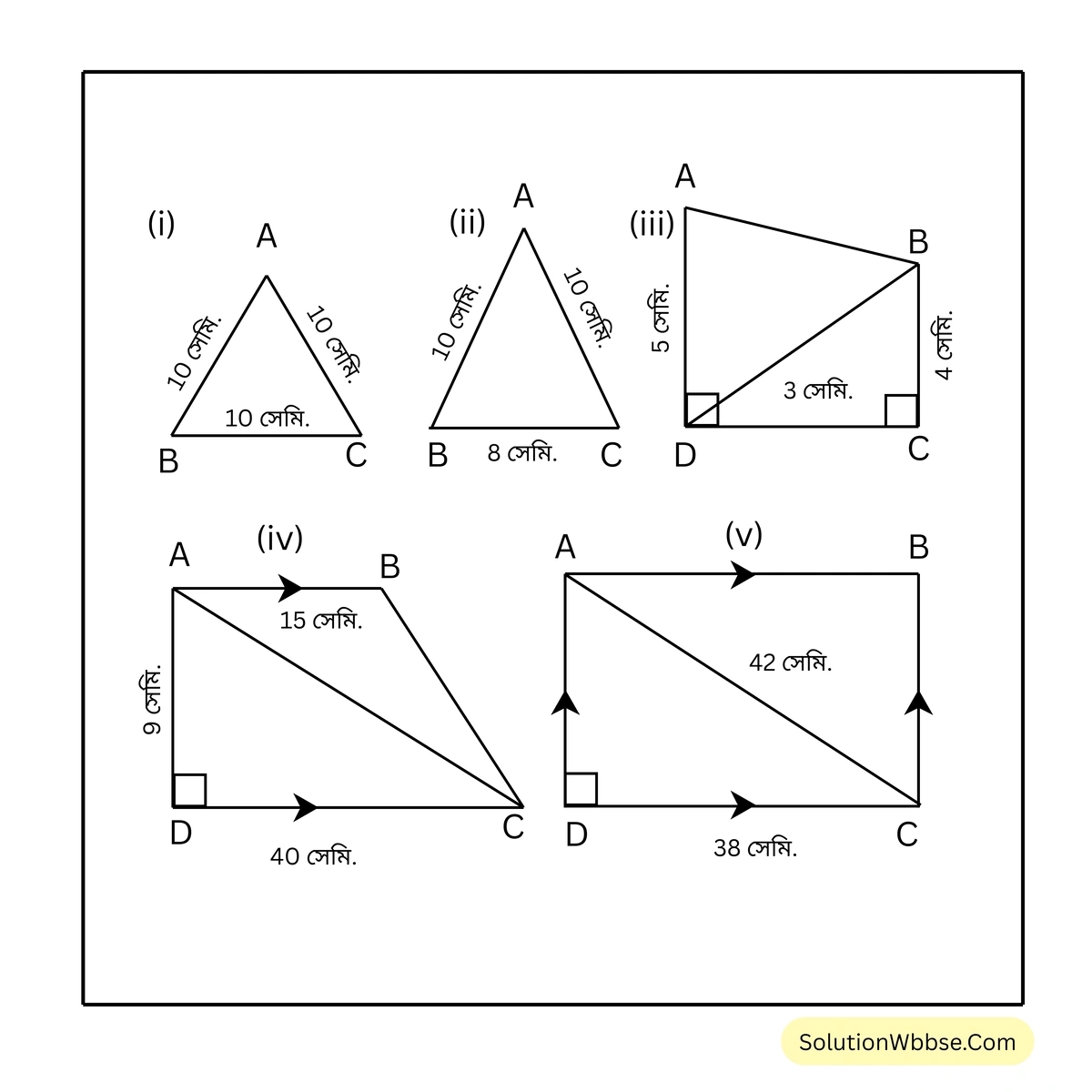
(i) \(\triangle ABC\) ত্রিভুজের \(AB = BC = CA = 10\) সেমি.
\(\therefore \triangle ABC\) একটি সমবাহু ত্রিভুজ
(ii) \(\triangle ABC\) ত্রিভুজের \(AB = AC = 10\) সেমি. এবং \(BC = 8\) সেমি.
\(\therefore \triangle ABC\) একটি সমদ্বিবাহু ত্রিভুজ।
\(A\) বিন্দু থেকে \(BC\) বাহুর ওপর \(AD\) লম্ব অঙ্কন করা হল।
\(\therefore AD\), \(\triangle ABC\) ত্রিভুজের একটি মধ্যমা।
\(\therefore CD = \frac{8}{2}\) সেমি. = \(4\) সেমি.
এখন \(\triangle ADC\) সমকোণী ত্রিভুজ থেকে পাই,
বা, \((10)^2 = AD^2 + (4)^2\)
বা, \(100 = AD^2 + 16\)
বা, \(AD^2 = 100 – 16\)
বা, \(AD^2 = 84\)
বা, \(AD = \sqrt{84}\)
বা, \(AD = 2\sqrt{21}\)
(iii) \(ABCD\) চতুর্ভুজের \(AD \parallel BC\)
\(\therefore ABCD\) একটি ট্রাপিজিয়াম।
আবার, \(CD \perp AD\) এবং \(CD \perp BC\)
\(\therefore CD\), \(ABCD\) ট্রাপিজিয়ামের উচ্চতা।
ABCD ট্রাপিজিয়ামের ক্ষেত্রফল= \(\frac{1}{2} \times (AD + BC) \times CD\)
= \(\left\{ \frac{1}{2} \times (5+4) \times 3 \right\}\) বর্গ সেমি.
= \(\frac{27}{2}\) বর্গ সেমি.
= \(13.5\) বর্গ সেমি.
(iv) \(ABCD\) চতুর্ভুজের \(AB \parallel DC\) এবং \(AD \perp BC\)
\(\therefore ABCD\) একটি ট্রাপিজিয়াম যার উচ্চতা \(AD\)
ABCD ট্রাপিজিয়ামের ক্ষেত্রফল= \(\frac{1}{2} \times (AB+DC) \times AD\)
= \(\left\{ \frac{1}{2} \times (15+40) \times 9 \right\}\) বর্গ সেমি.
= \(247.50 \) বর্গ সেমি.
(v) \(ABCD\) চতুর্ভুজের \(AB \parallel DC\) এবং \(AD \parallel BC\), অর্থাৎ বিপরীত বাহুগুলি পরস্পর সমান্তরাল এবং \(\angle ADC = 90^\circ\)
\(\therefore ABCD\) একটি আয়তক্ষেত্র
এখন, \(\triangle ADC\) সমকোণী ত্রিভুজ থেকে পাই,
\(AD^2 + CD^2 = AC^2\)বা, \(AD^2 + (38)^2 = (42)^2\)
বা, \(AD^2 = (42)^2 – (38)^2\)
বা, \(AD^2 = (42+38) (42-38)\)
বা, \(AD^2 = 80 \times 4\)
বা, \(AD^2 = 320\)
বা, \(AD = 8\sqrt{5}\)
\(\therefore ABCD\) আয়তক্ষেত্রের ক্ষেত্রফল = \(AD \times DC = (8\sqrt{5} \times 38)\) বর্গ সেমি. = \(304\sqrt{5}\) বর্গ সেমি.
2. কোনো সমবাহু ত্রিভুজের পরিসীমা 48 সেমি. হলে তার ক্ষেত্রফল হিসাব করে লিখি।
সমাধান –
ধরি, সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য \(a\) সেমি।
\(\therefore\) সমবাহু ত্রিভুজের পরিসীমা = \(3a\) সেমি।
শর্তানুসারে,
\(3a = 48\)বা, \(a = 48/3\)
বা, \(a = 16\)
\(\therefore\) সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য 16 সেমি।
এবং সমবাহু ত্রিভুজটির ক্ষেত্রফল
= \(\frac{\sqrt{3}}{4} \times (\text{বাহু})^2\)
= \(\frac{\sqrt{3}}{4} \times (16)^2\) বর্গ সেমি.
= \(\left( \frac{\sqrt{3}}{4} \times 16 \times 16 \right)\) বর্গ সেমি.
= \(64\sqrt{3}\) বর্গ সেমি.
\(\therefore\) সমবাহু ত্রিভুজের ক্ষেত্রফল \(64\sqrt{3}\) বর্গ সেমি।
3. \(ABC\) সমবাহু ত্রিভুজের উচ্চতা \(5\sqrt{3}\) সেমি. হলে, ত্রিভুজটির পরিসীমা ও ক্ষেত্রফল হিসাব করে লিখি।
সমাধান –
ধরি, সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য \(a\) সেমি।
\(\therefore\) সমবাহু ত্রিভুজের উচ্চতা = \(\left( \frac{\sqrt{3}}{2} \times a \right)\) সেমি.
\(\therefore \frac{\sqrt{3}}{2} \times a = 5\sqrt{3}\)বা, \(a = 10\)
\(\therefore\) সমবাহু ত্রিভুজটির বাহুর দৈর্ঘ্য 10 সেমি।
\(\therefore\) ত্রিভুজটির পরিসীমা = \(3 \times\) বাহুর দৈর্ঘ্য = \((3 \times 10)\) সেমি. = \(30\) সেমি.
এবং ত্রিভুজটির ক্ষেত্রফল = \(\frac{\sqrt{3}}{4} \times a^2\) বর্গ সেমি. = \(\frac{\sqrt{3}}{4} \times (10)^2\) বর্গ সেমি. = \(25\sqrt{3}\) বর্গ সেমি।
4. \(ABC\) সমদ্বিবাহু ত্রিভুজের সমান বাহুদুটির প্রত্যেকটির দৈর্ঘ্য 10 সেমি. এবং ভূমির দৈর্ঘ্য 4 সেমি হলে, \(ABC\) এর ক্ষেত্রফল হিসাব করে লিখি।

সমাধান –
ধরা যাক, \(ABC\) সমদ্বিবাহু ত্রিভুজের \(AB = AC = 10\) সেমি. এবং \(BC = 4\) সেমি.। এখন \(A\) বিন্দু থেকে \(BC\) বাহুর ওপর \(AD\) লম্ব অঙ্কন করা হল।
\(\therefore \angle ADB = \angle ADC = 90^{\circ}\) এবং \(D\), \(BC\) এর মধ্যবিন্দু।
\(\therefore BD = DC = 4/2\) সেমি. = \(2\) সেমি.
সমকোণী ত্রিভুজ \(ADC\) থেকে পাই,
\(AC^2 = AD^2 + CD^2\)বা, \((10)^2 = AD^2 + (2)^2\)
বা, \(100 = AD^2 + 4\)
বা, \(AD^2 = 96\)
বা, \(AD = \sqrt{96} = \sqrt{16 \times 6} = 4\sqrt{6}\)
\(\therefore\) \(ABC\) সমদ্বিবাহু ত্রিভুজের উচ্চতা \(4\sqrt{6}\) সেমি।
\(\therefore\) \(ABC\) সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল
= \(\frac{1}{2} \times \text{ভূমি} \times \text{উচ্চতা}\)
= \(\frac{1}{2} \times BC \times AD\)
= \(\left( \frac{1}{2} \times 4 \times 4\sqrt{6} \right)\) বর্গ সেমি.
= \(8\sqrt{6}\) বর্গ সেমি.
\(\therefore\) \(ABC\) সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল \(8\sqrt{6}\) বর্গ সেমি।
5. যদি কোনো সমদ্বিবাহু ত্রিভুজের ভূমির দৈর্ঘ্য 12 সেমি. এবং সমান বাহুর প্রত্যেকটির দৈর্ঘ্য 10 সেমি. হয়, তবে ওই সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল হিসাব করে লিখি।

সমাধান –
ধরা যাক, \(ABC\) একটি সমদ্বিবাহু ত্রিভুজ যার \(AB = AC = 10\) সেমি. এবং ভূমি \(BC = 12\) সেমি.। এখন \(A\) বিন্দু থেকে \(BC\) বাহুর ওপর \(AD\) লম্ব অঙ্কন করা হল।
\(\therefore \angle ADB = \angle ADC = 90^{\circ}\) এবং \(D\), \(BC\) এর মধ্যবিন্দু।
\(\therefore BD = DC = \frac{12}{2}\) সেমি. = \(6\) সেমি.
সমকোণী ত্রিভুজ \(ADC\) থেকে পাই,
\(AC^2 = AD^2 + CD^2\)বা, \((10)^2 = AD^2 + (6)^2\)
বা, \(100 = AD^2 + 36\)
বা, \(AD^2 = 64\)
বা, \(AD = \sqrt{64} = 8\)
\(\therefore\) \(ABC\) সমদ্বিবাহু ত্রিভুজের উচ্চতা \(8\) সেমি.
\(\therefore\) \(ABC\) সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল
= \(\frac{1}{2} \times BC \times AD\)
= \(\left( \frac{1}{2} \times 12 \times 8 \right)\) বর্গ সেমি.
= \(48\) বর্গ সেমি.
\(\therefore\) \(ABC\) সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল \(48\) বর্গ সেমি.
6. কোনো সমদ্বিবাহু ত্রিভুজের পরিসীমা 544 সেমি. এবং সমান বাহুর প্রত্যেকটির দৈর্ঘ্য ভূমির দৈর্ঘ্যের \(\frac{5}{6}\) অংশ; ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি।
সমাধান –
ধরা যাক, সমদ্বিবাহু ত্রিভুজটির ভূমির দৈর্ঘ্য \(x\) সেমি.
\(\therefore\) সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য \(\frac{5x}{6}\) সেমি.
শর্তানুসারে,
\(\frac{5x}{6} + \frac{5x}{6} + x = 544\)বা, \(\frac{5x + 5x + 6x}{6} = 544\)
বা, \(16x = 3264\)
বা, \(x = \frac{3264}{16}\)
বা, \(x = 204\)
\(\therefore\) ভূমির দৈর্ঘ্য \(204\) সেমি. এবং সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য \(\frac{5x}{6}\) সেমি. = \(\left( \frac{5}{6} \times 204 \right)\) সেমি. = \(170\) সেমি.
যেখানে: a = সমান বাহুর দৈর্ঘ্য, b = ভূমির দৈর্ঘ্য
= \(\frac{1}{2} \times 204 \times \sqrt{(170)^2 – (102)^2}\) বর্গ সেমি.
= \(102 \times \sqrt{28900 – 10404}\) বর্গ সেমি.
= \(102 \times \sqrt{18496}\) বর্গ সেমি.
= \(102 \times 136\) বর্গ সেমি.
= \(13872\) বর্গ সেমি.
\(\therefore\) সমদ্বিবাহু ত্রিভুজটির ক্ষেত্রফল \(13872\) বর্গ সেমি.
8. পৃথা একটি সামান্তরিক এঁকেছে যার কর্ণদ্বয়ের দৈর্ঘ্য যথাক্রমে \(6\) সেমি. ও \(8\) সেমি. এবং কর্ণদ্বয়ের মধ্যবর্তী কোণগুলির প্রত্যেকটি \(90^\circ\); সামান্তরিকের বাহুগুলির দৈর্ঘ্য লিখি এবং সামান্তরিকটির বৈশিষ্ট্য লিখি।

সমাধান –
ধরা যাক, \(ABCD\) একটি সামান্তরিক যার কর্ণদ্বয় \(AC\) ও \(BD\) পরস্পরকে \(O\) বিন্দুতে \(90^\circ\) কোণে ছেদ করেছে। \(\therefore ABCD\) একটি রম্বস।
আরও ধরা যাক, \(AC = 6\) সেমি. এবং \(BD = 8\) সেমি.।
যেহেতু, রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে,
\(\therefore AO = OC = \frac{6}{2} = 3\) সেমি. এবং \(OB = OD = \frac{8}{2} = 4\) সেমি.
এখন, \(\triangle AOD\) সমকোণী ত্রিভুজ থেকে পাই,
\(AD^2 = OA^2 + OD^2\)বা, \(AD^2 = (3)^2 + (4)^2\)
বা, \(AD^2 = 9 + 16\)
বা, \(AD^2 = 25\)
বা, \(AD^2 = (5)^2\)
বা, \(AD = 5\)
\(\therefore AB = BC = CD = DA = 5\) সেমি. [যেহেতু, রম্বসের প্রতিটি বাহুর দৈর্ঘ্য সমান]
\(\therefore\) সামান্তরিকটির প্রতিটি বাহুর দৈর্ঘ্য \(5\) সেমি. এবং সামান্তরিকটি একটি রম্বস।
9. আমাদের পাড়ার ত্রিভুজাকৃতি একটি পার্কের বাহুগুলির দৈর্ঘ্যের অনুপাত \(2:3:4\); পার্কটির পরিসীমা \(216\) মিটার।
(i) হিসাব করে পার্কটির ক্ষেত্রফল লিখি।
(ii) পার্কটির বৃহত্তম বাহুর বিপরীত বিন্দু থেকে ওই বাহুতে সোজাসুজি যেতে কত পথ হাঁটতে হবে হিসাব করে লিখি।
সমাধান –
ধরি, ত্রিভুজাকৃতি পার্কের বাহুগুলির দৈর্ঘ্য যথাক্রমে \(2x\) মিটার, \(3x\) মিটার এবং \(4x\) মিটার।
শর্তানুসারে,
\(2x + 3x + 4x = 216\)বা, \(9x = 216\)
বা, \(x = \frac{216}{9}\)
বা, \(x = 24\)
\(\therefore\) ত্রিভুজাকৃতি পার্কের বাহুর দৈর্ঘ্য যথাক্রমে \((2 \times 24)\) মিটার = \(48\) মিটার, \((3 \times 24)\) মিটার = \(72\) মিটার এবং \((4 \times 24)\) মিটার = \(96\) মিটার।
(i) ত্রিভুজাকৃতি পার্কের ক্ষেত্রফল –
ত্রিভুজাকৃতি পার্কের পরিসীমা = \((48+72+96)\) মিটার = \(216\) মিটার।
\(\therefore\) ত্রিভুজাকৃতি পার্কের অর্ধ পরিসীমা \((s) = \frac{216}{2}\) মিটার = \(108\) মিটার।
\(\therefore\) ত্রিভুজাকৃতি পার্কের ক্ষেত্রফল
= \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{108(108-48)(108-72)(108-96)}\) বর্গ মিটার [যেখানে, \(a = 48\) মিটার, \(b = 72\) মিটার এবং \(c = 96\) মিটার]
= \(\sqrt{108 \times 60 \times 36 \times 12}\) বর্গ মিটার
= \(2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3 \sqrt{3 \times 5}\) বর্গ মিটার
= \(432\sqrt{15}\) বর্গ মিটার
\(\therefore\) ত্রিভুজাকৃতি পার্কের ক্ষেত্রফল \(432\sqrt{15}\) বর্গ মিটার।
(ii) ধরা যাক, \(\triangle ABC\) হল ত্রিভুজাকৃতি পার্ক এবং \(BC\) হল বৃহত্তম বাহু।
এখন, \(A\) থেকে \(BC\) বাহুর ওপর \(AD\) লম্ব টানা হল।
অর্থাৎ \(AD\) হল পার্কের বৃহত্তম বাহু থেকে বিপরীত কৌণিক বিন্দু \(A\) পর্যন্ত লম্ব দূরত্ব।
শর্তানুসারে,
\(\frac{1}{2} \times BC \times AD = 432\sqrt{15}\)বা, \(\frac{1}{2} \times 96 \times AD = 432\sqrt{15}\)
বা, \(AD = \frac{432\sqrt{15} \times 2}{96}\)
বা, \(AD = 9\sqrt{15}\)
অর্থাৎ, পার্কের বৃহত্তম বাহু থেকে বিপরীত কৌণিক বিন্দু পর্যন্ত হাঁটতে হলে \(9\sqrt{15}\) মিটার দূরত্ব অতিক্রম করতে হবে।
10. পহলমপুর গ্রামের ত্রিভুজাকৃতি মাঠের তিনদিকের দৈর্ঘ্য যথাক্রমে 26 মিটার, 28 মিটার ও 30 মিটার।
(i) প্রতি বর্গমিটার 5 টাকা হিসাবে ত্রিভুজাকৃতি মাঠে ঘাস লাগাতে মোট কত টাকা খরচ হবে হিসাব করে লিখি।
(ii) ওই ত্রিভুজাকৃতি মাঠে প্রবেশের গেট তৈরির জন্য 5 মিটার জায়গা ছেড়ে বাকি চারধার বেড়া দিয়ে ঘিরতে প্রতি মিটার 18 টাকা হিসাবে মোট কত টাকা খরচ হবে হিসাব করে লিখি।
সমাধান –
ত্রিভুজাকৃতি মাঠের পরিসীমা = \((26+28+30)\) মিটার = \(84\) মিটার
\(\therefore\) অর্ধ পরিসীমা \((s) = \frac{84}{2}\) মিটার = \(42\) মিটার।
\(\therefore\) ত্রিভুজাকৃতি মাঠের ক্ষেত্রফল
= \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{42 (42 – 26)(42 – 28)(42 – 30)}\) বর্গ মিটার [যেখানে, \(a = 26\) মিটার, \(b = 28\) মিটার এবং \(c = 30\) মিটার]
= \(\sqrt{42 \times 16 \times 14 \times 12}\) বর্গ মিটার
= \(\sqrt{3 \times 2 \times 7 \times 2 \times 2 \times 2 \times 2 \times 7 \times 2 \times 3 \times 2 \times 2}\) বর্গ মিটার
= \((3 \times 2 \times 2 \times 2 \times 2 \times 7)\) বর্গ মিটার
= \(336\) বর্গ মিটার
\(\therefore\) প্রতি বর্গ মিটার 5 টাকা হিসাবে ঘাস লাগাতে খরচ হবে = \((336 \times 5)\) টাকা = \(1680\) টাকা।
(ii) ওই ত্রিভুজাকৃতি মাঠে প্রবেশের গেট তৈরির জন্য 5 মিটার জায়গা ছেড়ে বাকি চারধার বেড়া দিয়ে ঘিরতে, যে দৈর্ঘ্যের বেড়া লাগবে তা হল –
(ত্রিভুজাকৃতি মাঠের পরিসীমা – গেটের জন্য ছেড়ে রাখা জায়গার পরিমাণ)
= \((84 – 5)\) মিটার
= \(79\) মিটার
\(\therefore\) প্রতি মিটার 18 টাকা হিসাবে বেড়া দিতে খরচ হবে = \((79 \times 18)\) টাকা = \(1422\) টাকা।
11. শাকিল একটি সমবাহু ত্রিভুজ PQR এঁকেছে। আমি ওই সমবাহু ত্রিভুজের অন্তঃস্থ কোনো বিন্দু থেকে ত্রিভুজের বাহুগুলির ওপর তিনটি লম্ব অঙ্কন করেছি যাদের দৈর্ঘ্য যথাক্রমে 10 সেমি., 12 সেমি. এবং 8 সেমি.। হিসাব করে PQR ত্রিভুজের ক্ষেত্রফল লিখি।
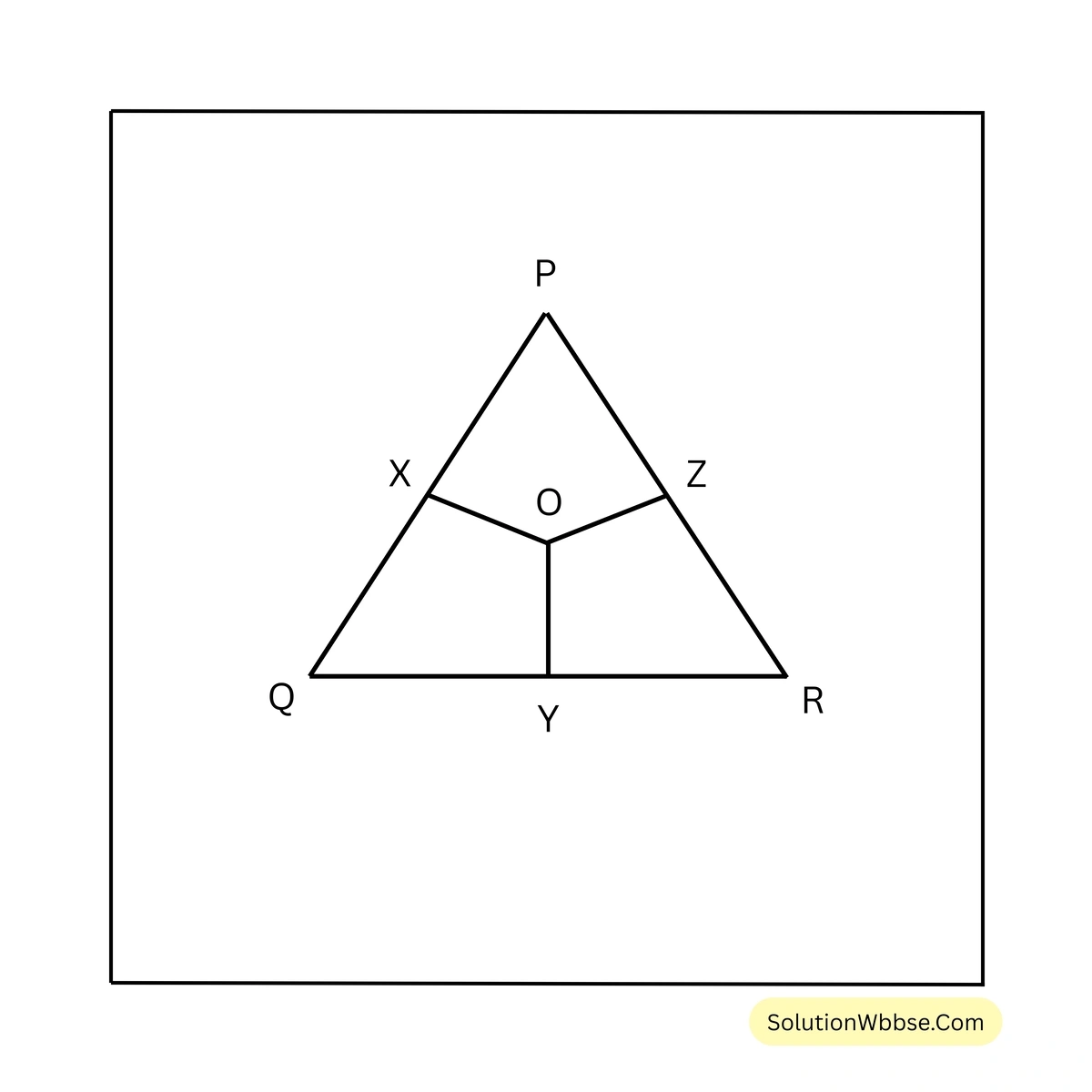
সমাধান –
ধরি, PQR সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য \(a\) সেমি.।
\(\therefore PQ = QR = RP = a\) সেমি.।
আরও ধরা যাক, PQR ত্রিভুজের অন্তঃস্থ বিন্দু O থেকে PQ, QR এবং PR বাহুগুলির ওপর লম্ব তিনটি যথাক্রমে OX, OY এবং OZ এবং \(OX = 10\) সেমি., \(OY = 12\) সেমি. এবং \(OZ = 8\) সেমি.।
স্পষ্টতই, \(\triangle PQR = \triangle OPQ + \triangle OQR + \triangle ORP\)
বা, \(\frac{\sqrt{3}}{4} \times a^2 = \left( \frac{1}{2} \times a \times 10 + \frac{1}{2} \times a \times 12 + \frac{1}{2} \times a \times 8 \right)\)
বা, \(\frac{\sqrt{3}}{4} \times a^2 = 5a + 6a + 4a\)
বা, \(\frac{\sqrt{3}}{4} \times a^2 = 15a\)
বা, \(\frac{\sqrt{3}}{4} \times a = 15\)
বা, \(a = \frac{60}{\sqrt{3}}\)
\(\therefore\) PQR সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য \(\frac{60}{\sqrt{3}}\) সেমি.।
\(\therefore\) PQR সমবাহু ত্রিভুজের ক্ষেত্রফল = \(\frac{\sqrt{3}}{4} \times \left( \frac{60}{\sqrt{3}} \right)^2\) বর্গ সেমি. = \(\frac{\sqrt{3}}{4} \times \frac{3600}{3}\) বর্গ সেমি. = \(300\sqrt{3}\) বর্গ সেমি.
\(\therefore\) PQR সমবাহু ত্রিভুজের ক্ষেত্রফল \(300\sqrt{3}\) বর্গ সেমি.।
12. একটি সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য 20 সেমি. এবং ওই বাহুদ্বয়ের অন্তর্ভুক্ত কোণ \(45^{\circ}\) হলে, ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি।
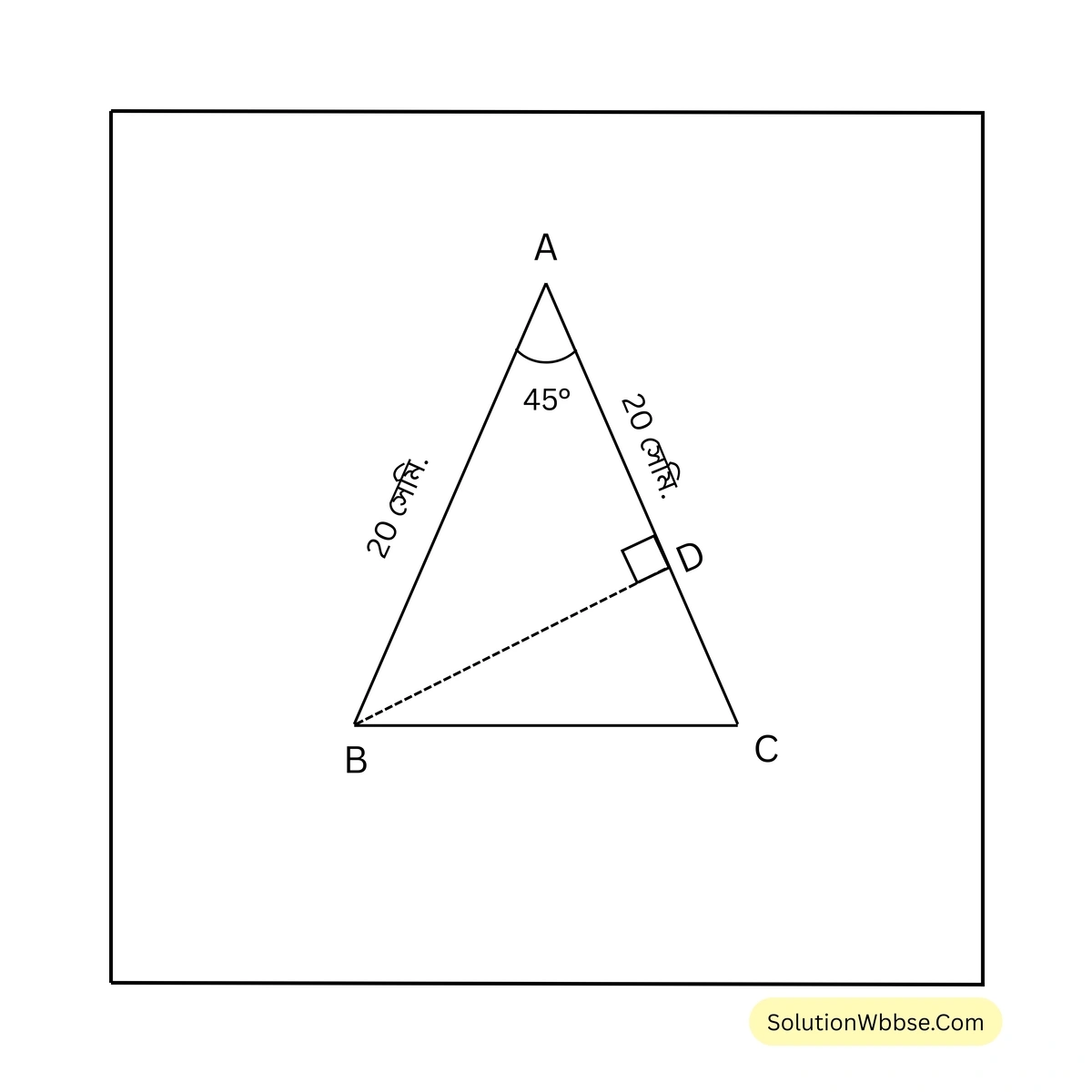
ধরি, \(\triangle ABC\) ত্রিভুজের সমান বাহুদ্বয় হল \(AB\) এবং \(BC\)। অর্থাৎ \(AB = BC = 20\) সেমি. এবং \(\angle ABC = 45^{\circ}\)।
অঙ্কন – \(\triangle ABC\) ত্রিভুজটির \(A\) বিন্দু থেকে \(BC\) বাহুর ওপর লম্ব \(AD\) অঙ্কন করা হল।
\(\triangle ABD\) ত্রিভুজের \(\angle ABD = 45^{\circ}\) এবং \(\angle ADB = 90^{\circ}\)
\(\therefore \angle BAD = 180^{\circ} – (\angle ADB + \angle ABD) \)= \(180^{\circ} – (90^{\circ}+45^{\circ}) \)
= \(180^{\circ} – 135^{\circ} \)
= \(45^{\circ}\)
\(\therefore \triangle ABD\) ত্রিভুজের \(\angle BAD = \angle ABD = 45^{\circ}\)
\(\therefore AD = BD\)ধরি, \(AD = BD = x\) সেমি.
এখন সমকোণী ত্রিভুজ \(ABD\) থেকে পাই,
\(AB^2 = AD^2 + BD^2\)বা, \(20^2 = 2x^2\)
বা, \(2x^2 = 400\)
বা, \(x^2 = 200\)
বা, \(x^2 = 2 \times 100\)
বা, \(x = 10\sqrt{2}\)
\(\therefore \triangle ABC\) ত্রিভুজের ভূমি \(BC = 20\) সেমি. এবং উচ্চতা = \(10\sqrt{2}\) সেমি.
\(\therefore \triangle ABC\) ত্রিভুজের ক্ষেত্রফল = \(\frac{1}{2} \times\) ভূমি \(\times\) উচ্চতা
= \(\left( \frac{1}{2} \times 20 \times 10\sqrt{2} \right)\) বর্গ সেমি.
= \(100\sqrt{2}\) বর্গ সেমি.
বিকল্প পদ্ধতি (ত্রিকোণমিতি প্রয়োগ করে)

ধরা যাক, \(\triangle ABC\) একটি সমদ্বিবাহু ত্রিভুজ যার \(AB = AC = 20\) সেমি. এবং \(\angle BAC = 45^{\circ}\); \(B\) বিন্দু থেকে \(AC\) এর ওপর \(BD\) লম্ব অঙ্কন করা হল।
এখন, \(\triangle BAD\) সমকোণী ত্রিভুজ থেকে পাই,
\(\sin 45^{\circ} = \frac{BD}{AB}\)বা, \(\frac{1}{\sqrt{2}} = \frac{BD}{AB}\)
বা, \(\frac{1}{\sqrt{2}} = \frac{BD}{20}\)
বা, \(BD = \frac{20}{\sqrt{2}}\)
\(\therefore \triangle ABC\) সমদ্বিবাহু ত্রিভুজের উচ্চতা \(\frac{20}{\sqrt{2}}\) সেমি.
\(\therefore \triangle ABC\) এর ক্ষেত্রফল = \(\frac{1}{2} \times\) ভূমি \(\times\) উচ্চতা
= \(\frac{1}{2} \times AC \times BD \)
= \( \left( \frac{1}{2} \times 20 \times \frac{20}{\sqrt{2}} \right)\) বর্গ সেমি.
= \(\frac{200}{\sqrt{2}}\) বর্গ সেমি.
= \(\left( \frac{200}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} \right)\) বর্গ সেমি.
= \(100\sqrt{2}\) বর্গ সেমি.।
13. একটি সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য 20 সেমি. এবং ওই বাহুদ্বয়ের অন্তর্ভুক্ত কোণ \(30^{\circ}\) হলে, ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি।
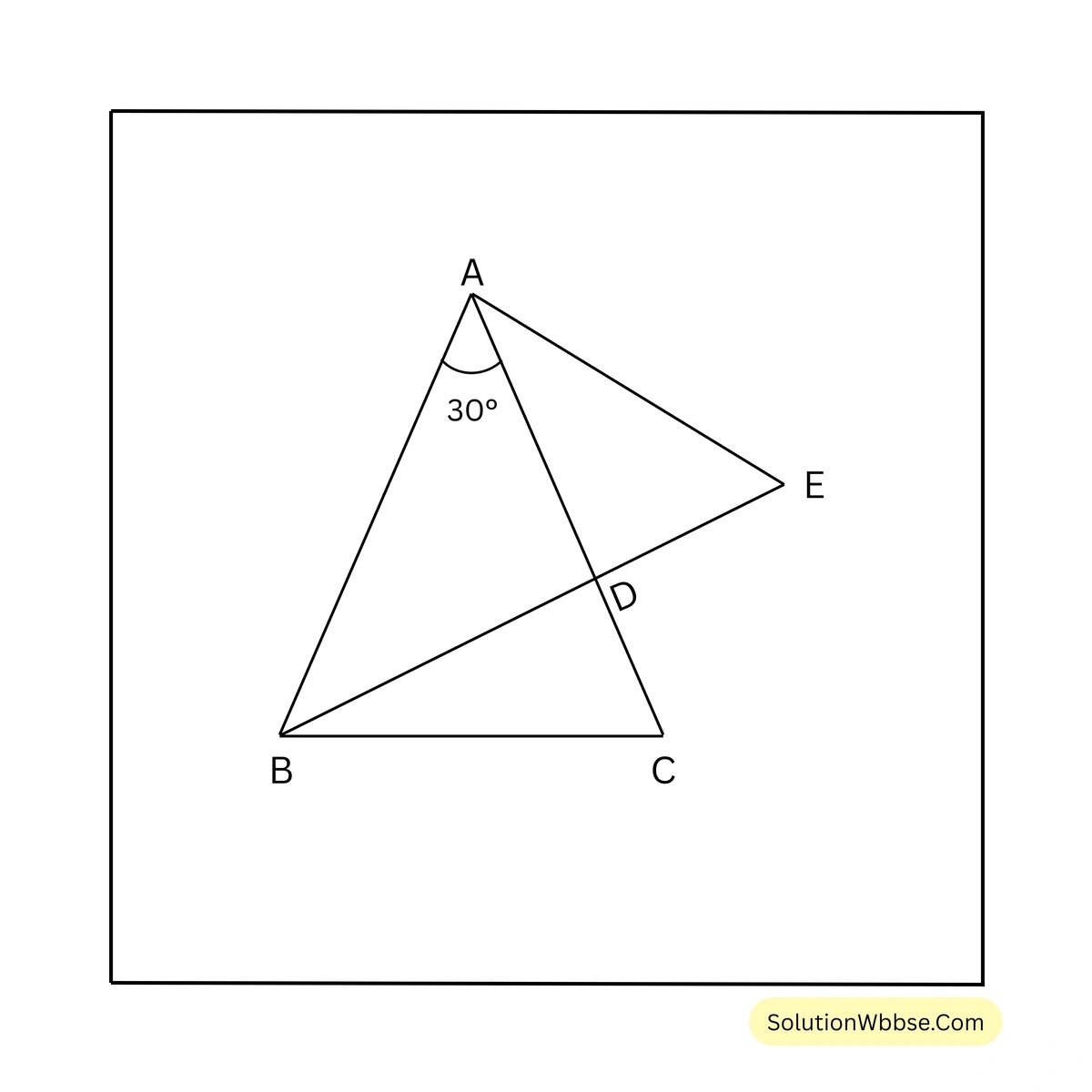
সমাধান –
ধরি, \(\triangle ABC\) ত্রিভুজের সমান বাহুদ্বয় হল \(AB\) এবং \(BC\)। অর্থাৎ \(AB = BC = 20\) সেমি. এবং \(\angle ABC = 30^{\circ}\)।
অঙ্কন – এখন, \(\triangle ABC\) এর \(A\) বিন্দু থেকে \(BC\) বাহুর ওপর \(AD\) লম্ব অঙ্কন করা হল। \(AD\) কে \(E\) পর্যন্ত এমনভাবে বর্ধিত করা হল যেন \(AD = DE\) হয়।
এখন ত্রিভুজ \(ABD\) এবং ত্রিভুজ \(BDE\) এর ক্ষেত্রে,
\(AD = DE\) [অঙ্কনানুসারে]
\(\angle ADB = \angle BDE = 90^{\circ}\)\(BD\) সাধারণ বাহু
\(\therefore \triangle ABD \cong \triangle BDE\) (S-A-S শর্তানুসারে)
\(\therefore \angle ABD = \angle DBE = 30^{\circ}\)আবার, \(\angle BAD = \angle BED\)
ত্রিভুজ \(ABD\)-এর
\(\angle BAD + \angle ABD + \angle BDA = 180^{\circ}\)বা, \(\angle BAD + 30^{\circ} + 90^{\circ} = 180^{\circ}\)
বা, \(\angle BAD = 180^{\circ} – 120^{\circ}\)
বা, \(\angle BAD = 60^{\circ}\)
\(\therefore \angle BED = 60^{\circ}\)এখন ত্রিভুজ \(ABE\)-এর,
\(\angle ABE = \angle ABD + \angle DBE = 30^{\circ} + 30^{\circ} = 60^{\circ}\)আবার, \(\angle BAD = \angle BAE = 60^{\circ}\) এবং \(\angle BED = \angle BEA = 60^{\circ}\)
\(\therefore\) ত্রিভুজ \(ABE\) একটি সমবাহু ত্রিভুজ।
\(\therefore AB = BE = AE = 20\) সেমি.
আবার, \(AD = DE\)
\(\therefore AD = 10\) সেমি.
∴= \(\frac{1}{2} \times 20 \times 10\) বর্গ সেমি.
= \(100\) বর্গ সেমি.
বিকল্প পদ্ধতি (ত্রিকোণমিতি প্রয়োগ করে) –
13. একটি সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য 20 সেমি. এবং ওই বাহুদ্বয়ের অন্তর্ভুক্ত কোণ \(30^{\circ}\) হলে, ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি।

সমাধান –
ধরা যাক, \(\triangle ABC\) একটি সমদ্বিবাহু ত্রিভুজ যার \(AB = AC = 20\) সেমি. এবং \(\angle BAC = 30^{\circ}\); \(B\) বিন্দু থেকে \(AC\) এর ওপর \(BD\) লম্ব অঙ্কন করা হল।
এখন, \(\triangle BAD\) সমকোণী ত্রিভুজ থেকে পাই,
\(\sin 30^{\circ} = \frac{BD}{AB}\)বা, \(\frac{1}{2} = \frac{BD}{AB}\)
বা, \(\frac{1}{2} = \frac{BD}{20}\)
বা, \(BD = \frac{20}{2}\)
\(\therefore\) \(\triangle ABC\) সমদ্বিবাহু ত্রিভুজের উচ্চতা \(10\) সেমি.
∴= \(\frac{1}{2} \times AC \times BD \)
= \(\left( \frac{1}{2} \times 20 \times 10 \right)\) বর্গ সেমি.
= \(100\) বর্গ সেমি.।
14. একটি সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমা \((\sqrt{2}+1)\) সেমি. হলে, ত্রিভুজটির অতিভুজের দৈর্ঘ্য ও ক্ষেত্রফল হিসাব করে লিখি।
সমাধান –
ধরি, সমকোণী সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য \(a\) সেমি. এবং অতিভুজের দৈর্ঘ্য \(b\) সেমি.।
\(\therefore a+a+b = (\sqrt{2}+1)\)বা, \(2a+b = (\sqrt{2}+1)\) — (i)
এখন, পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই,
\(a^2+a^2=b^2\)বা, \(2a^2=b^2\)
বা, \(b = a\sqrt{2}\)
(i) নং সমীকরণ থেকে পাই,
\(a+a+a\sqrt{2} = \sqrt{2}+1\)বা, \(2a+a\sqrt{2} = \sqrt{2}+1\)
বা, \(a(2+\sqrt{2}) = \sqrt{2}+1\)
বা, \(a = \frac{\sqrt{2}+1}{2+\sqrt{2}}\)
লব ও হরকে \((2-\sqrt{2})\) দিয়ে গুণ করে,
\(a = \frac{(\sqrt{2}+1)(2-\sqrt{2})}{(2+\sqrt{2})(2-\sqrt{2})}\)\(a = \frac{2\sqrt{2}-2+2-\sqrt{2}}{4-2}\)\(a = \frac{\sqrt{2}}{2}\)\(a = \frac{1}{\sqrt{2}}\)\(\therefore\) অতিভুজের দৈর্ঘ্য \(b = a\sqrt{2} = \frac{1}{\sqrt{2}} \times \sqrt{2} = 1\) সেমি.।
এবং, ত্রিভুজটির ক্ষেত্রফল = \(\frac{1}{2} \times\) ভূমি \(\times\) উচ্চতা
= \(\left( \frac{1}{2} \times \frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}} \right)\) বর্গ সেমি.
= \(\frac{1}{4}\) বর্গ সেমি.
= \(0.25\) বর্গ সেমি.।
15. মারিয়া ঘণ্টায় 18 কিমি. বেগে সাইকেল চালিয়ে 10 মিনিটে একটি সমবাহু ত্রিভুজাকার মাঠের পরিসীমা বরাবর ঘুরে এল। ত্রিভুজটির একটি কৌণিক বিন্দু থেকে বিপরীত বাহুর মধ্যবিন্দু পর্যন্ত সোজা যেতে মারিয়ার কত সময় লাগবে হিসাব করে লিখি। (\(\sqrt{3} \approx 1.732\))
সমাধান –
18 কিমি. = \(18000\) মিটার।
মারিয়া 60 মিনিটে যায় \(18000\) মিটার
1 মিনিটে যায় \(\frac{18000}{60}\) মিটার = \(300\) মিটার
10 মিনিটে যায় \((300 \times 10)\) মিটার = \(3000\) মিটার।
যেহেতু, 10 মিনিটে মারিয়া সমবাহু ত্রিভুজাকার মাঠের পরিসীমা বরাবর ঘুরে এল।
\(\therefore\) সমবাহু ত্রিভুজাকৃতি মাঠের পরিসীমা = \(3000\) মিটার।
\(\therefore\) সমবাহু ত্রিভুজাকৃতি মাঠের প্রতিটি বাহুর দৈর্ঘ্য = \(\frac{3000}{3}\) মিটার = \(1000\) মিটার।
\(\therefore\) সমবাহু ত্রিভুজাকৃতি মাঠের একটি কৌণিক বিন্দু থেকে বিপরীত বাহুর মধ্যবিন্দু পর্যন্ত লম্ব দূরত্ব = \(\left( \frac{\sqrt{3}}{2} \times 1000 \right)\) মিটার
= \(500\sqrt{3}\) মিটার = \((500 \times 1.732)\) মিটার
= \(866\) মিটার (প্রায়)।
মারিয়া, \(18000\) মিটার যায় \(60\) মিনিটে
\(\quad \quad \quad 1\) মিটার যায় \(\frac{60}{18000}\) মিনিটে
\(\quad \quad \quad 866\) মিটার যায় \(\frac{60 \times 866}{18000}\) মিনিটে = \(2.89\) মিনিটে (প্রায়)
\(\therefore\) সমবাহু ত্রিভুজাকার মাঠের একটি কৌণিক বিন্দু থেকে বিপরীত বাহুর মধ্যবিন্দু পর্যন্ত যেতে মারিয়ার সময় লাগবে \(2.89\) মিনিট।
16. একটি সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য 1 মিটার বৃদ্ধি করলে ত্রিভুজটির ক্ষেত্রফল \(\sqrt{3}\) বর্গ মিটার বৃদ্ধি পায়। সমবাহু ত্রিভুজটির বাহুর দৈর্ঘ্য হিসাব করি।
সমাধান –
ধরা যাক, সমবাহু ত্রিভুজটির বাহুর দৈর্ঘ্য \(a\) মিটার।
\(\therefore\) সমবাহু ত্রিভুজের ক্ষেত্রফল = \(\left( \frac{\sqrt{3}}{4} \times a^2 \right)\) বর্গ মিটার
সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য 1 মিটার বৃদ্ধি করলে ত্রিভুজটির বাহুর দৈর্ঘ্য হয় \((a+1)\) মিটার। তখন সমবাহু ত্রিভুজের ক্ষেত্রফল = \(\frac{\sqrt{3}}{4} \times (a+1)^2\) বর্গ মিটার।
শর্তানুসারে,
\(\frac{\sqrt{3}}{4} \times (a+1)^2 – \frac{\sqrt{3}}{4} \times a^2 = \sqrt{3}\)বা, \(\frac{\sqrt{3}}{4} \times (a^2 + 2a + 1 – a^2) = \sqrt{3}\)
বা, \(2a+1 = \sqrt{3} \times \frac{4}{\sqrt{3}}\)
বা, \(2a+1 = 4\)
বা, \(2a = 4-1\)
বা, \(2a = 3\)
বা, \(a = \frac{3}{2}\)
বা, \(a = 1.5\)
\(\therefore\) সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য \(1.5\) মিটার।
17. একটি সমবাহু ত্রিভুজ এবং বর্গক্ষেত্রের ক্ষেত্রফলের অনুপাত \(\sqrt{3} : 2\); বর্গক্ষেত্রটির কর্ণের দৈর্ঘ্য \(60\) সেমি. হলে, সমবাহু ত্রিভুজের পরিসীমা হিসাব করে লিখি।
সমাধান –
ধরি, সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য \(a\) সেমি. এবং বর্গক্ষেত্রের প্রতিটি বাহুর দৈর্ঘ্য \(b\) সেমি.।
\(\therefore\) সমবাহু ত্রিভুজের ক্ষেত্রফল = \(\frac{\sqrt{3}}{4} \times a^2\) বর্গ সেমি. এবং বর্গক্ষেত্রের ক্ষেত্রফল = \(b^2\) বর্গ সেমি.
শর্তানুসারে,
\(\frac{\sqrt{3}}{4} \times a^2 : b^2 = \sqrt{3} : 2\)বা, \(\frac{a^2\sqrt{3}}{4b^2} = \frac{\sqrt{3}}{2}\)
বা, \(a^2 = 2b^2\)
বা, \(a = \sqrt{2}b\) — (i)
আবার যেহেতু বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য \(60\) সেমি.
\(\therefore b\sqrt{2} = 60\)বা, \(b = \frac{60}{\sqrt{2}}\)
(i) নং সমীকরণে \(b\)-এর মান বসিয়ে পাই,
\(a = \sqrt{2} \times b\)বা, \(a = \sqrt{2} \times \frac{60}{\sqrt{2}}\)
বা, \(a = 60\)
\(\therefore\) সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য \(60\) সেমি.।
\(\therefore\) সমবাহু ত্রিভুজের পরিসীমা = \((3 \times 60)\) সেমি. = \(180\) সেমি.। [উত্তর]
18. একটি সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য এবং পরিসীমা যথাক্রমে \(13\) সেমি. এবং \(30\) সেমি.। ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি।
সমাধান –
ধরা যাক, সমকোণী ত্রিভুজটির সমকোণ সংলগ্ন বাহুগুলির দৈর্ঘ্য যথাক্রমে \(a\) সেমি. এবং \(b\) সেমি.।
\(\therefore a+b =\) ত্রিভুজটির পরিসীমা – অতিভুজের দৈর্ঘ্য = \((30 – 13)\) সেমি. = \(17\) সেমি.।
আবার, \(a^2 + b^2 = (13)^2\)
বা, \((a+b)^2 – 2ab = 169\)
বা, \((17)^2 – 2ab = 169\)
বা, \(289 – 2ab = 169\)
বা, \(2ab = 289 – 169\)
বা, \(2ab = 120\)
বা, \(ab = 60\)
\(\therefore\) সমকোণী ত্রিভুজটির ক্ষেত্রফল = \(\frac{1}{2} \times\) ভূমি \(\times\) উচ্চতা = \(\frac{1}{2} \times 60\) বর্গ সেমি. = \(30\) বর্গ সেমি.।
\(\therefore\) ত্রিভুজটির ক্ষেত্রফল \(30\) বর্গ সেমি.।
19. একটি সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহু দুটির দৈর্ঘ্য যথাক্রমে \(12\) সেমি. ও \(5\) সেমি.। সমকৌণিক বিন্দু থেকে অতিভুজের ওপর লম্বের দৈর্ঘ্য হিসাব করে লিখি। (\(3\) দশমিক স্থান পর্যন্ত আসন্নমান)।
সমাধান –
সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য
= \(\sqrt{12^2 + 5^2}\) সেমি.
= \(\sqrt{144 + 25}\) সেমি.
= \(\sqrt{169}\) সেমি.
= \(13\) সেমি.
যেহেতু, সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহুর দৈর্ঘ্য যথাক্রমে \(12\) সেমি. ও \(5\) সেমি.
\(\therefore\) সমকোণী ত্রিভুজের ক্ষেত্রফল = \(\frac{1}{2} \times\) ভূমি \(\times\) উচ্চতা = \(\left( \frac{1}{2} \times 12 \times 5 \right)\) বর্গ সেমি. = \(30\) বর্গ সেমি.।
ধরি, সমকোণী ত্রিভুজটির সমকৌণিক বিন্দু থেকে অতিভুজের ওপর অঙ্কিত লম্বের দৈর্ঘ্য \(x\) সেমি.।
\(\therefore \frac{1}{2} \times 13 \times x = 30\)বা, \(x = \frac{30 \times 2}{13}\)
বা, \(x = \frac{60}{13}\)
বা, \(x = 4.615\) (প্রায়)
\(\therefore\) সমকৌণিক বিন্দু থেকে অতিভুজের ওপর লম্বের দৈর্ঘ্য \(4.615\) সেমি. (প্রায়)।
20. 3 সেমি., 4 সেমি. ও 5 সেমি. দৈর্ঘ্যের বাহুবিশিষ্ট একটি সমকোণী ত্রিভুজাকার ক্ষেত্র থেকে একটি সর্ববৃহৎ বর্গাকারক্ষেত্র এমনভাবে কেটে নেওয়া হলো যার একটি শীর্ষবিন্দু ত্রিভুজটির অতিভুজের ওপর অবস্থিত। বর্গাকার ক্ষেত্রটির বাহুর দৈর্ঘ্যের হিসাব করে লিখি।
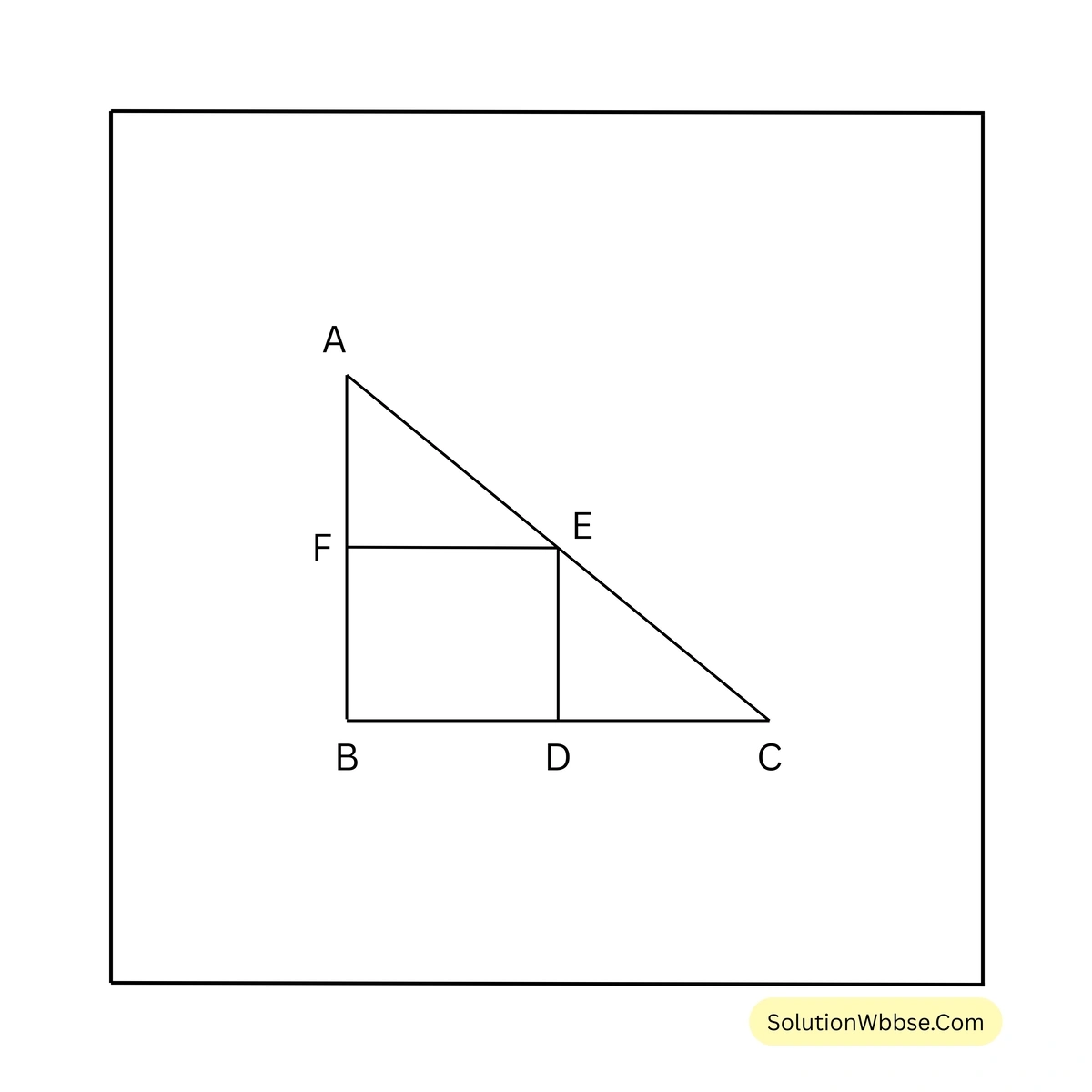
সমাধান –
ধরি, সমকোণী ত্রিভুজ \(ABC\)-এর \(AB = 3\) সেমি., \(BC = 4\) সেমি. এবং \(AC = 5\) সেমি.।
সমকোণী ত্রিভুজাকার ক্ষেত্র থেকে একটি সর্ববৃহৎ বর্গাকার ক্ষেত্র \(BDEF\) কেটে নেওয়া হল যার একটি শীর্ষবিন্দু \(E\) ত্রিভুজটির অতিভুজ \(AC\)-এর ওপর অবস্থিত। ধরি, বর্গাকার ক্ষেত্রটির বাহুর দৈর্ঘ্য \(a\) সেমি.।
\(\therefore AF = (3-a)\) সেমি. এবং \(DC = (4-a)\) সেমি.।
বা, \(\frac{1}{2} \times FE \times AF + \frac{1}{2} \times DC \times DE + BD^2 = \frac{1}{2} \times 4 \times 3\)
বা, \(\frac{1}{2} [a(3-a) +(4-a)a ] + a^2 = \frac{1}{2} \times 4 \times 3\)
বা, \(\frac{1}{2} [3a-a^2 +4a -a^2 ] +a^2 =6\)
বা, \(\frac{7a}{2} – a^2 +a^2 = 6\)
বা, \(7a = 12\)
বা, \(a = \frac{12}{7} = 1\frac{5}{7}\)
\(\therefore\) বর্গাকার ক্ষেত্রটির বাহুর দৈর্ঘ্য \(1\frac{5}{7}\) সেমি.।
21. বহু বিকল্পীয় প্রশ্ন (M.C.Q)
(i) একটি সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য 4 সেমি. হলে ত্রিভুজটির উচ্চতার পরিমাপ
(a) \(4\sqrt{3}\) সেমি.
(b) \(16\sqrt{3}\) সেমি.
(c) \(8\sqrt{3}\) সেমি.
(d) \(2\sqrt{3}\) সেমি.
Ans – (d) \(2\sqrt{3}\) সেমি.
সমাধান –
সমবাহু ত্রিভুজটির উচ্চতা = \(\frac{\sqrt{3}}{2} \times\) (বাহুর দৈর্ঘ্য) = \(\left( \frac{\sqrt{3}}{2} \times 4 \right)\) সেমি. = \(2\sqrt{3}\) সেমি.।
(ii) একটি সমকোণী সমদ্বিবাহু ত্রিভুজ যার সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য a একক। ত্রিভুজটির পরিসীমা
(a) \((1+\sqrt{2})a\) একক
(b) \((2+\sqrt{2})a\) একক
(c) \(3a\) একক
(d) \((3+2\sqrt{2})a\) একক
Ans – (b) \((2+\sqrt{2})a\) একক
সমাধান – অতিভুজের দৈর্ঘ্য = \(\sqrt{a^2 + a^2}\) একক = \(\sqrt{2a^2}\) একক = \(a\sqrt{2}\) একক
\(\therefore\) ত্রিভুজটির পরিসীমা = \((a+a+ a\sqrt{2})\) একক = \((2a+a\sqrt{2})\) একক = \(a(2+\sqrt{2})\) একক।
(iii) একটি সমবাহু ত্রিভুজের ক্ষেত্রফল, পরিসীমা এবং উচ্চতা যথাক্রমে a, s এবং h হলে, \(\frac{2a}{sh}\) এর মান
(a) 1
(b) \(\frac{1}{2}\)
(c) \(\frac{1}{3}\)
(d) \(\frac{1}{4}\)
Ans – (c) \(\frac{1}{3}\)
সমাধান – ধরি, সমবাহু ত্রিভুজটির প্রতিটি বাহুর দৈর্ঘ্য x একক।
\(\therefore\) ত্রিভুজটির ক্ষেত্রফল \(a = \frac{\sqrt{3}}{4} \times x^2\) বর্গ একক
পরিসীমা \(s = 3x\) একক
এবং, উচ্চতা \(h = \left( \frac{\sqrt{3}}{2} \times x \right)\) একক
\(\therefore \frac{2a}{sh} = \frac{2 \times \frac{\sqrt{3}}{4} \times x^2}{3x \times \frac{\sqrt{3}}{2} \times x}\)= \(\frac{\frac{\sqrt{3}}{2} x^2}{\frac{3\sqrt{3}}{2} x^2}\)
= \(\frac{\sqrt{3}}{2} \times \frac{2}{3\sqrt{3}}\)
= \(\frac{1}{3}\)
(iv) একটি সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের দৈর্ঘ্য 5 সেমি. এবং ভূমির দৈর্ঘ্য 6 সেমি.। ত্রিভুজটির ক্ষেত্রফল
(a) 18 বর্গ সেমি.
(b) 12 বর্গ সেমি.
(c) 15 বর্গ সেমি.
(d) 30 বর্গ সেমি.
Ans – (b) 12 বর্গ সেমি.
সমাধান –
= \(\frac{1}{2} \times 6 \times \sqrt{(5)^2 – (3)^2}\) বর্গ সেমি.
= \(3 \times \sqrt{25 – 9}\) বর্গ সেমি.
= \(3 \times \sqrt{16}\) বর্গ সেমি.
= \(3 \times 4\) বর্গ সেমি.
= \(12\) বর্গ সেমি.
(v) \(\triangle ABC\) ত্রিভুজের \(AC\) বাহুর ওপর \(D\) এমন একটি বিন্দু যে \(AD : DC = 3:2\); \(\triangle ABC\) ত্রিভুজের ক্ষেত্রফল 40 বর্গ সেমি. হলে \(\triangle BDC\) ত্রিভুজের ক্ষেত্রফল
(a) 16 বর্গ সেমি.
(b) 24 বর্গ সেমি.
(c) 30 বর্গ সেমি.
(d) 36 বর্গ সেমি.
Ans – (a) 16 বর্গ সেমি.
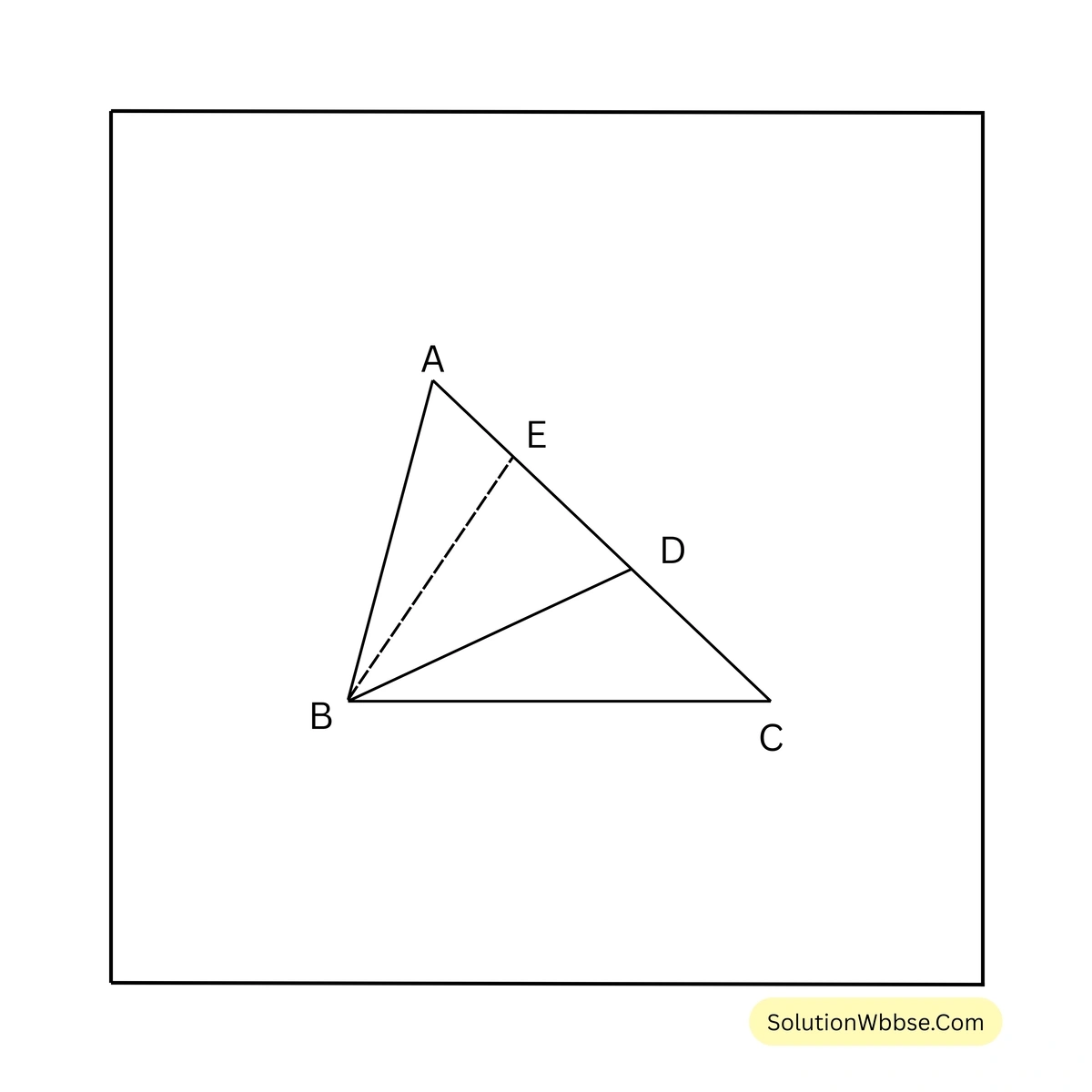
\(B\) বিন্দু থেকে \(AC\)-এর ওপর \(BE\) লম্ব টানা হল।
আবার, \(AD : DC = 3:2\) [প্রদত্ত]
\(\therefore \triangle ABD : \triangle BDC = \frac{1}{2} \times AD \times BE : \frac{1}{2} \times DC \times BE = AD : DC = 3:2\)
বা, \(2\triangle ABD = 3 \triangle BDC\)
বা, \(\triangle ABD = \frac{3}{2} \triangle BDC\)
\(\therefore \triangle ABC = \triangle ABD + \triangle BDC\)বা, \( 40 = \frac{3}{2} \triangle BDC + \triangle BDC\)
বা, \( 40 = \frac{5}{2} \triangle BDC\)
বা, \( \triangle BDC = 16\)
\(\therefore\) \(\triangle BDC\) ত্রিভুজের ক্ষেত্রফল 16 বর্গ সেমি.।
(vi) একটি ত্রিভুজের অর্ধ পরিসীমা থেকে প্রতিটি বাহুর দৈর্ঘ্যের অন্তর যথাক্রমে 8 সেমি., 7 সেমি. ও 5 সেমি.। ত্রিভুজটির ক্ষেত্রফল
(a) \(20\sqrt{7}\) বর্গ সেমি.
(b) \(10\sqrt{14}\) বর্গ সেমি.
(c) \(20\sqrt{14}\) বর্গ সেমি.
(d) 140 বর্গ সেমি.
Ans – (c) \(20\sqrt{14}\) বর্গ সেমি.
সমাধান –
ধরা যাক, ত্রিভুজটির অর্ধ পরিসীমা \(s\) সেমি.
\(\therefore (s-a) = 8\) সেমি., \((s-b) = 7\) সেমি., \((s-c) = 5\) সেমি.
\(\therefore (s-a)+(s-b)+(s-c) = 20\)বা, \(3s – (a+b+c) = 20\)
বা, \(3 \times \frac{a+b+c}{2} – (a+b+c) = 20\)
বা, \(3(a+b+c) – 2(a+b+c) = 40\)
বা, \((a+b+c) = 40\)
বা, \(\frac{a+b+c}{2} = 20\)
বা, \(s = 20\)
\(\therefore \sqrt{s(s-a)(s-b)(s-c)}\) বর্গ সেমি.
= \(\sqrt{20 \times 8 \times 7 \times 5}\) বর্গ সেমি.
= \(\sqrt{2 \times 2 \times 5 \times 2 \times 2 \times 2 \times 7 \times 5}\) বর্গ সেমি.
= \(2 \times 2 \times 5 \sqrt{2 \times 7}\) বর্গ সেমি.
= \(20 \sqrt{14}\) বর্গ সেমি.
22. সংক্ষিপ্ত উত্তর ভিত্তিক প্রশ্ন
(i) একটি সমবাহু ত্রিভুজের ক্ষেত্রফল ও উচ্চতার সাংখ্যমান সমান। ত্রিভুজের বাহুর দৈর্ঘ্য কত?
সমাধান – ধরি, সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য \(a\) একক।
\(\therefore\) সমবাহু ত্রিভুজটির ক্ষেত্রফল = \(\frac{\sqrt{3}}{4} a^2\) বর্গ একক এবং সমবাহু ত্রিভুজটির উচ্চতা = \(\frac{\sqrt{3}}{2} a\) একক।
শর্তানুসারে,
\(\frac{\sqrt{3}}{4} a^2 = \frac{\sqrt{3}}{2} a\)বা, \(a = 2\)
\(\therefore\) সমবাহু ত্রিভুজটির বাহুর দৈর্ঘ্য \(2\) একক।
(ii) একটি সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য দ্বিগুণ করলে, ত্রিভুজটির ক্ষেত্রফল শতকরা কত বৃদ্ধি পাবে?
সমাধান – ধরা যাক, সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য \(a\) একক।
\(\therefore\) ত্রিভুজটির ক্ষেত্রফল \(A = \frac{\sqrt{3}}{4} a^2\) বর্গ একক।
আবার, সমবাহু ত্রিভুজটির প্রতিটি বাহুকে দ্বিগুণ করলে পরিবর্তিত বাহুর দৈর্ঘ্য \(2a\) একক।
\(\therefore\) ক্ষেত্রফল \(A’ = \frac{\sqrt{3}}{4} (2a)^2\) বর্গ একক
= \(\frac{\sqrt{3}}{4} \times 4a^2\) বর্গ একক
= \(4 \times \frac{\sqrt{3}}{4} a^2\) বর্গ একক
= \(4A\) বর্গ একক।
\(\therefore\) ত্রিভুজের ক্ষেত্রফল শতকরা বৃদ্ধি পাবে = \(\left( \frac{A’ – A}{A} \times 100 \right)\%\)
= \(\left( \frac{4A – A}{A} \times 100 \right)\%\)
= \(300\%\)
\(\therefore\) ত্রিভুজটির ক্ষেত্রফল শতকরা \(300\%\) বৃদ্ধি পাবে।
(iii) একটি সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য তিনগুণ করলে, ত্রিভুজটির ক্ষেত্রফল শতকরা কত বৃদ্ধি হয়?
সমাধান – ধরা যাক, সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য \(a\) একক।
\(\therefore\) ত্রিভুজটির ক্ষেত্রফল \(A = \frac{\sqrt{3}}{4} a^2\) বর্গ একক।
আবার, সমবাহু ত্রিভুজটির প্রতিটি বাহুকে তিনগুণ করলে পরিবর্তিত বাহুর দৈর্ঘ্য \(3a\) একক।
\(\therefore\) ক্ষেত্রফল \(A’ = \frac{\sqrt{3}}{4} (3a)^2\) বর্গ একক
= \(\left( \frac{\sqrt{3}}{4} \times 9a^2 \right)\) বর্গ একক
= \(9 \times \left( \frac{\sqrt{3}}{4} a^2 \right)\) বর্গ একক
= \(9A\) বর্গ একক।
\(\therefore\) ত্রিভুজের ক্ষেত্রফল শতকরা বৃদ্ধি পাবে = \(\left( \frac{A’ – A}{A} \times 100 \right)\% = \left( \frac{9A – A}{A} \times 100 \right)\% = 800\%\)
\(\therefore\) ত্রিভুজটির ক্ষেত্রফল শতকরা \(800\%\) বৃদ্ধি পাবে।
(iv) একটি সমকোণী ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য \((x-2)\) সেমি., \(x\) সেমি. এবং \((x+2)\) সেমি.। ত্রিভুজটির অতিভুজের দৈর্ঘ্য কত?
সমাধান – একটি সমকোণী ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য \((x-2)\) সেমি., \(x\) সেমি. এবং \((x+2)\) সেমি.।
সমকোণী ত্রিভুজে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই,
\((x+2)^2 = x^2 + (x-2)^2\)বা, \(x^2 + 4x + 4 = x^2 + x^2 – 4x + 4\)
বা, \(x^2 + 4x + 4 – x^2 – x^2 + 4x – 4 = 0\)
বা, \(-x^2 + 8x = 0\)
বা, \(-x (x – 8) = 0\)
বা, \(x (x – 8) = 0\)
দুটি রাশির গুণফল শূন্য।
\(\therefore x = 0\) অথবা \((x-8) = 0 \Rightarrow x = 8\)
কিন্তু, \(x = 0\) এক্ষেত্রে অসম্ভব।
\(\therefore x = 8\)সুতরাং ত্রিভুজটির অতিভুজের দৈর্ঘ্য \((x+2)\) সেমি. = \((8+2)\) সেমি. = \(10\) সেমি.।
(v) একটি সমবাহু ত্রিভুজের উচ্চতার ওপর একটি বর্গক্ষেত্র অঙ্কন করা হল। ত্রিভুজ ও বর্গক্ষেত্রের ক্ষেত্রফলের অনুপাত কত?
সমাধান – ধরি, সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য \(a\) একক।
\(\therefore\) সমবাহু ত্রিভুজের ক্ষেত্রফল = \(\frac{\sqrt{3}}{4} a^2\) বর্গ একক এবং সমবাহু ত্রিভুজের উচ্চতা = \(\frac{\sqrt{3}}{2} a\) একক।
সমবাহু ত্রিভুজটির উচ্চতার ওপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল
= \(\left( \frac{\sqrt{3}}{2} a \right)^2\) বর্গ একক
= \(\frac{3}{4} a^2\) বর্গ একক
\(\therefore\) ত্রিভুজ ও বর্গক্ষেত্রের ক্ষেত্রফলের অনুপাত
= \(\frac{\sqrt{3}}{4} a^2 : \frac{3}{4} a^2\)
= \(1 : \sqrt{3}\) [উত্তর]
ই আর্টিকেলে নবম শ্রেণির গণিতের ‘ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল‘ অধ্যায়ের ‘কষে দেখি – 15.2’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।
কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন