পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) দশম শ্রেণির গণিত পাঠ্যবইয়ের পঞ্চদশ অধ্যায় হলো ‘ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল’। এই পোস্টে ‘কষে দেখি – 15.3‘-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. রাতুল একটি সামান্তরিক অঙ্কন করেছে যার ভূমির দৈর্ঘ্য 5 সেমি. এবং উচ্চতা 4 সেমি.। রাতুলের আঁকা সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি।
সমাধান –
রাতুল একটি সামান্তরিক এঁকেছে যার ভূমির দৈর্ঘ্য 5 সেমি. এবং উচ্চতা 4 সেমি.।
\(\therefore\) রাতুলের আঁকা সামান্তরিক আঁকা ক্ষেত্রের ক্ষেত্রফল = ভূমি \(\times\) উচ্চতা = (5 \(\times\) 4) বর্গ সেমি. = 20 বর্গ সেমি.।
2. একটি সামান্তরিকের ভূমি তার উচ্চতার দ্বিগুণ। যদি সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল 98 বর্গ সেমি. হয়, তাহলে সামান্তরিকের দৈর্ঘ্য ও উচ্চতার পরিমাপ হিসাব করে লিখি।
সমাধান –
ধরি, সামান্তরিকের উচ্চতা x সেমি.।
\(\therefore\) সামান্তরিকের ভূমি 2x সেমি.।
শর্তানুসারে,
2x.x = 98
বা, \(2x^2\) = 98
বা, \(x^2\) = 98/2
বা, \(x^2\) = 49
বা, \(x^2\) = \(7^2\)
বা, x = 7
\(\therefore\) সামান্তরিকের উচ্চতা 7 সেমি. এবং ভূমি 2x = (2\(\times\)7) সেমি. = 14 সেমি.।
3. আমাদের বাড়ির পাশে একটি সামান্তরিক আকারের জমি আছে যার সন্নিহিত বাহুদ্বয়ের দৈর্ঘ্য যথাক্রমে 15 মিটার ও 13 মিটার। যদি এই জমির একটি কর্ণের দৈর্ঘ্য 14 মিটার হয়, তবে হিসাব করে সামান্তরিক আকারের জমির ক্ষেত্রফল লিখি।
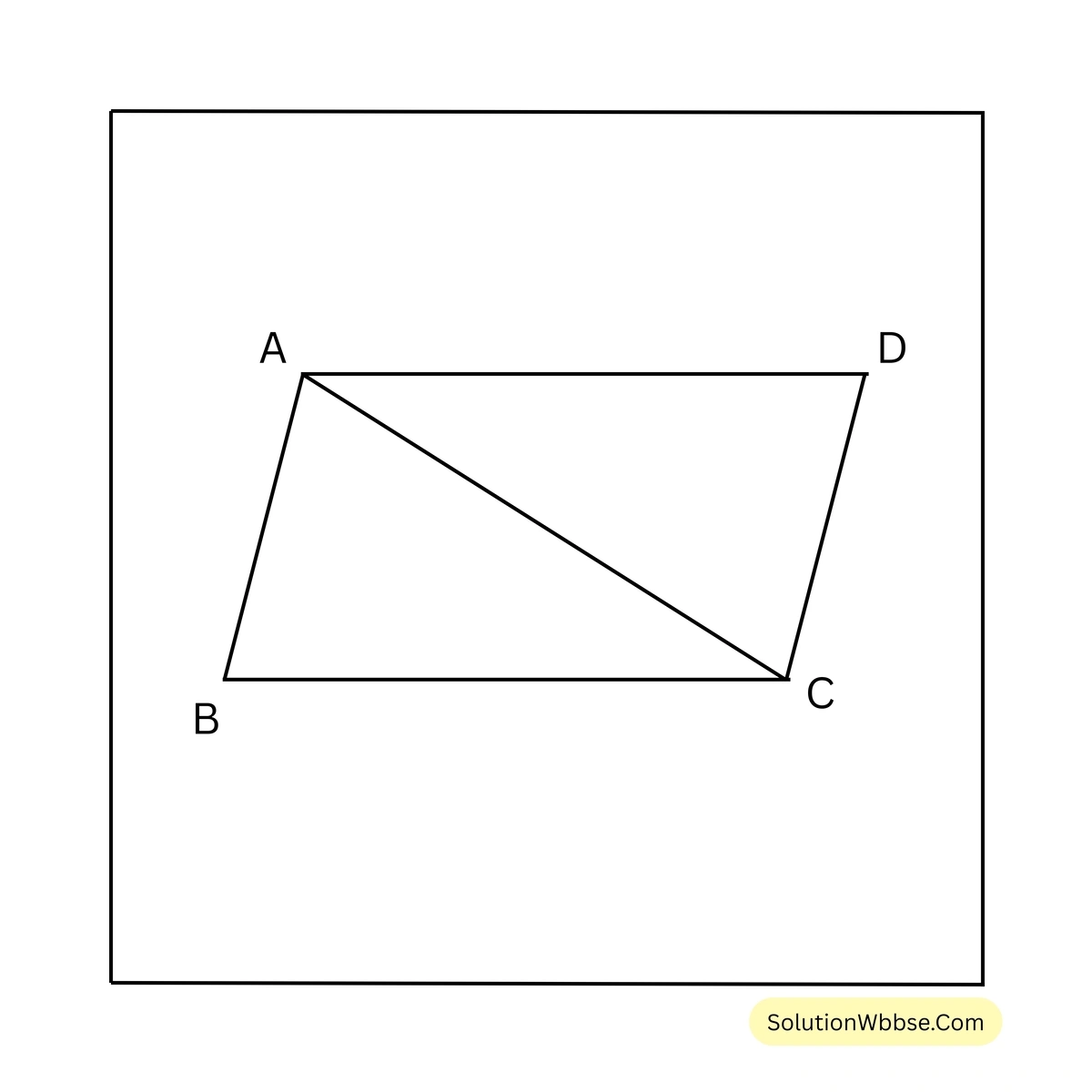
সমাধান –
ধরা যাক, ABCD হল সামান্তরিক আকারের জমি যার সন্নিহিত বাহুদ্বয় AB এবং BC -এর দৈর্ঘ্য যথাক্রমে 15 মিটার এবং 13 মিটার এবং কর্ণ AC -এর দৈর্ঘ্য 14 মিটার।
\(\therefore\) ABC ত্রিভুজের পরিসীমা = (15 + 13 + 14) মিটার = 42 মিটার।
\(\therefore\) অর্ধপরিসীমা (s) = 42/2 মিটার = 21 মিটার।
\(\therefore\) ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
= \(\sqrt{21(21 – 15)(21 – 13)(21 – 14)}\) বর্গ মিটার
= \(\sqrt{21 \times 6 \times 8 \times 7}\) বর্গ মিটার
= \(\sqrt{3 \times 7 \times 3 \times 2 \times 2 \times 2 \times 2 \times 7}\) বর্গমিটার
= (2\(\times\)2\(\times\)3\(\times\)7) বর্গ মিটার
= 84 বর্গমিটার
\(\therefore\) ABCD সামান্তরিকের ক্ষেত্রফল
= 2 \(\times\) \(\Delta\)ABC-এর ক্ষেত্রফল [যেহেতু সামান্তরিকের কর্ণ সামান্তরিকটিকে দুটি সর্বসম ত্রিভুজে বিভক্ত করে]
= (2\(\times\)84) বর্গ মিটার
= 168 বর্গ মিটার [উত্তর]
4. পৃথা একটি সামান্তরিক এঁকেছে যার সন্নিহিত বাহুগুলির দৈর্ঘ্য 25 সেমি. ও 15 সেমি. এবং একটি কর্ণের দৈর্ঘ্য 20 সেমি.। হিসাব করে 25 সেমি. বাহুর ওপর সামান্তরিকের উচ্চতা হিসাব করে লিখি।
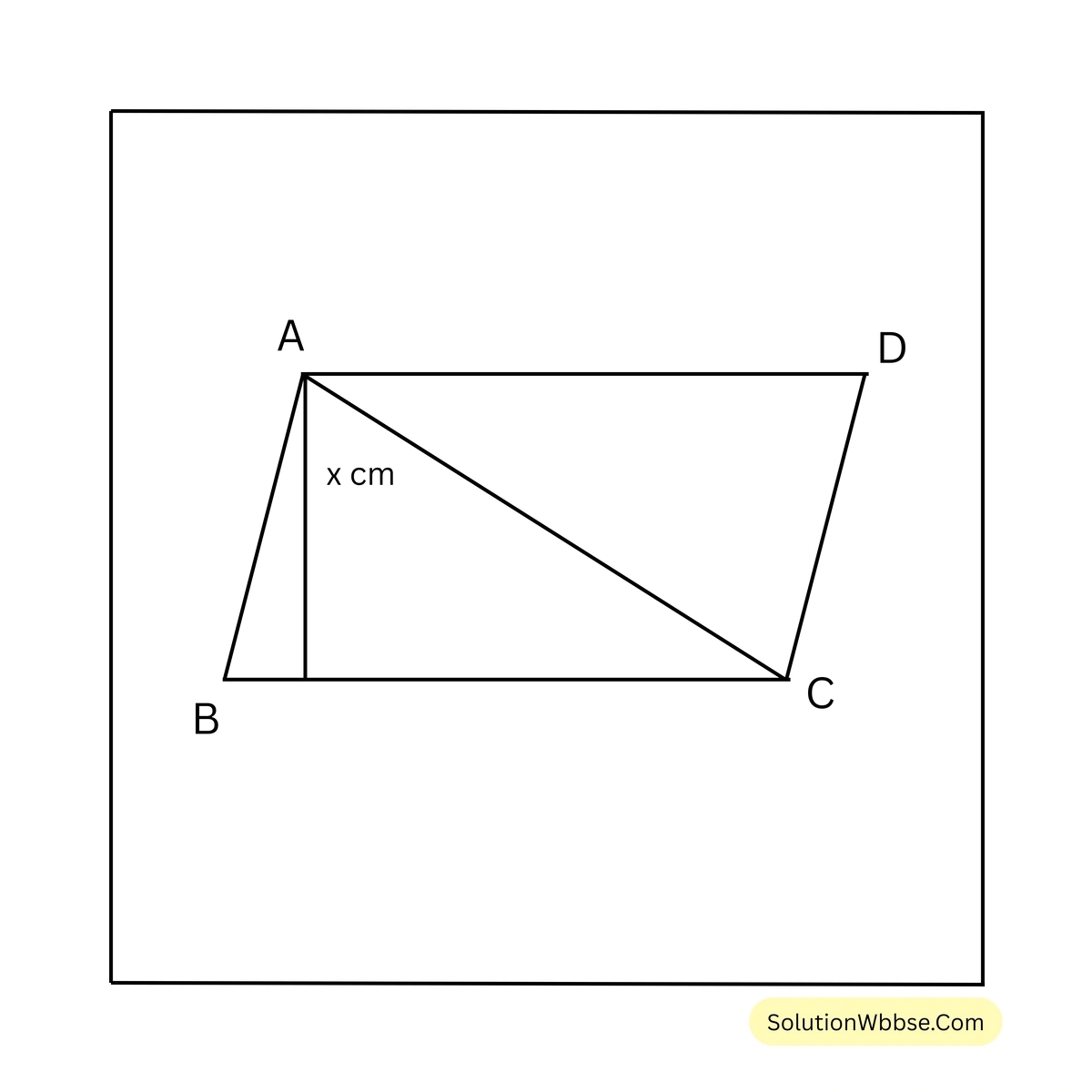
সমাধান –
ধরা যাক, পৃথার আঁকা সামান্তরিকটি হল ABCD যার, AB = 15 সেমি. এবং BC = 25 সেমি. এবং AC কর্ণ = 20 সেমি.।
\(\therefore\) ABC ত্রিভুজের অর্ধপরিসীমা \((s) = (15+25+20)/2\) সেমি. \(= 60/2\) সেমি. \(= 30\) সেমি.
\(\therefore\) ABC ত্রিভুজের ক্ষেত্রফল
\(= \sqrt{30 \times (30 – 25) \times (30 – 15) \times (30 – 20)}\) বর্গ সেমি.
\(= \sqrt{30 \times 5 \times 15 \times 10}\) বর্গ সেমি.
\(= \sqrt{2 \times 3 \times 5 \times 5 \times 3 \times 5 \times 5 \times 2}\) বর্গ সেমি.
\(= 2 \times 3 \times 5 \times 5\) বর্গ সেমি.
\(= 150\) বর্গ সেমি.
ধরি, 25 সেমি. বাহুর \((BC)\) – এর ওপর অঙ্কিত লম্বের দৈর্ঘ্য \(x\) সেমি.।
\(\therefore \frac{1}{2} \times \text{BC} \times x = 150\)বা, \(\frac{1}{2} \times 25 \times x = 150\)
বা, \(25x = 150 \times 2\)
বা, \(25x = 300\)
বা, \(x = 300/25\)
বা, \(x = 12\)
\(\therefore\) 25 সেমি. বাহুর ওপর সামান্তরিকের উচ্চতা 12 সেমি.।
5. একটি সামান্তরিকের দুটি সন্নিহিত বাহুর দৈর্ঘ্য 15 সেমি. ও 12 সেমি.। ক্ষুদ্রতর বাহু দুটির মধ্যে দূরত্ব 7.5 সেমি. হলে, বৃহত্তর বাহু দুটির মধ্যে দূরত্ব হিসাব করি।
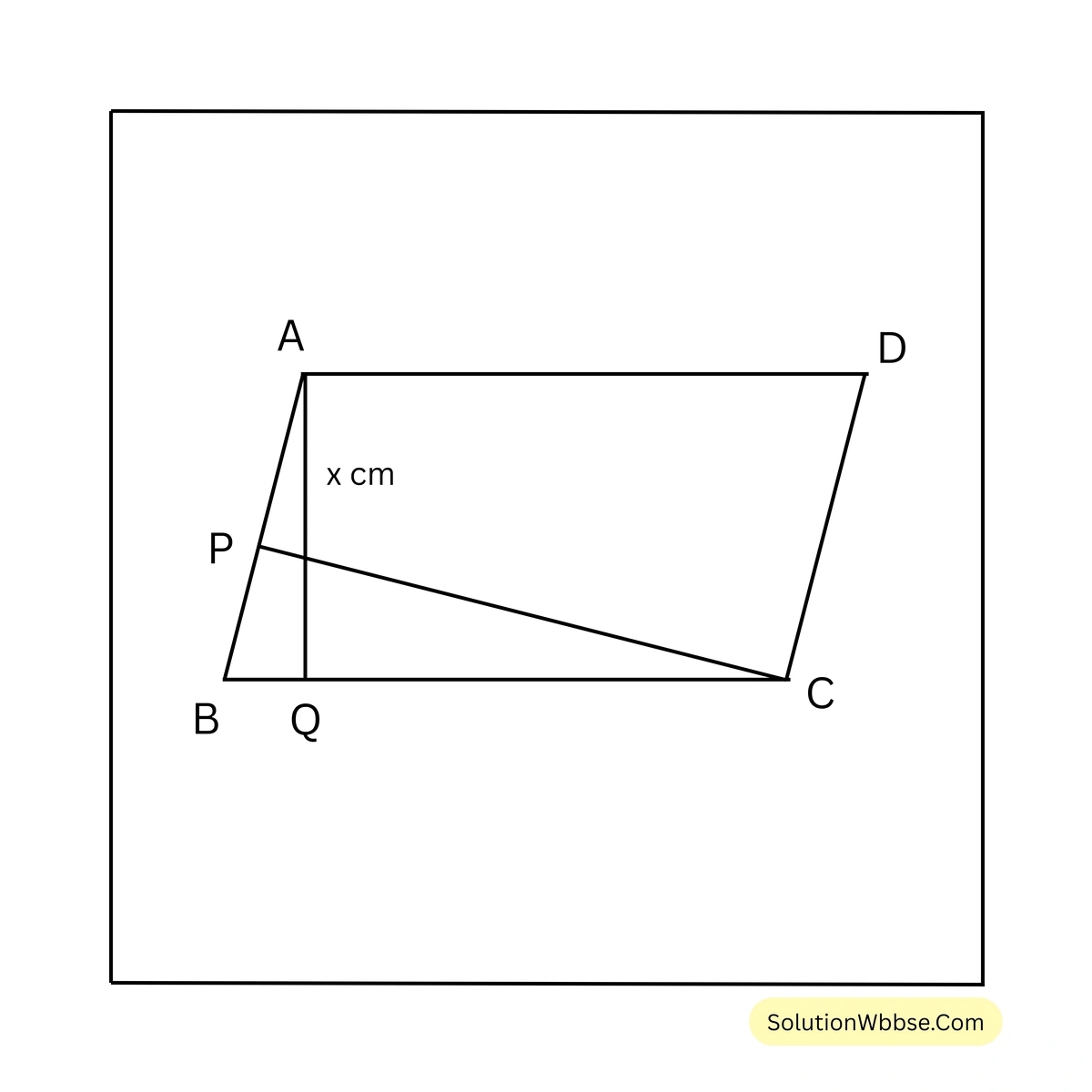
সমাধান –
ধরি, ABCD সামান্তরিকের দুটি সন্নিহিত বাহুর দৈর্ঘ্য BC = 15 সেমি. এবং AB = 12 সেমি.। ক্ষুদ্রতর বাহু দুটি AB ও CD এর মধ্যে দূরত্ব CP = 7.5 সেমি. এবং বৃহত্তর বাহু দুটি AD ও BC এর মধ্যে দূরত্ব AQ।
\(\therefore \frac{1}{2} \times \text{AB} \times \text{CP} = \frac{1}{2} \times \text{BC} \times \text{AQ}\)বা, \(\frac{1}{2} \times 15 \times \text{AQ} = \frac{1}{2} \times 12 \times 7.5\)
বা, \(\text{AQ} = \frac{12 \times 7.5}{15}\)
বা, \(\text{AQ} = 6\)
\(\therefore\) বৃহত্তর বাহু দুটির মধ্যে দূরত্ব 6 সেমি.।
6. একটি রম্বসের কর্ণদ্বয়ের পরিমাপ 15 মিটার ও 20 মিটার হলে, উহার পরিসীমা, ক্ষেত্রফল ও উচ্চতা হিসাব করে লিখি।
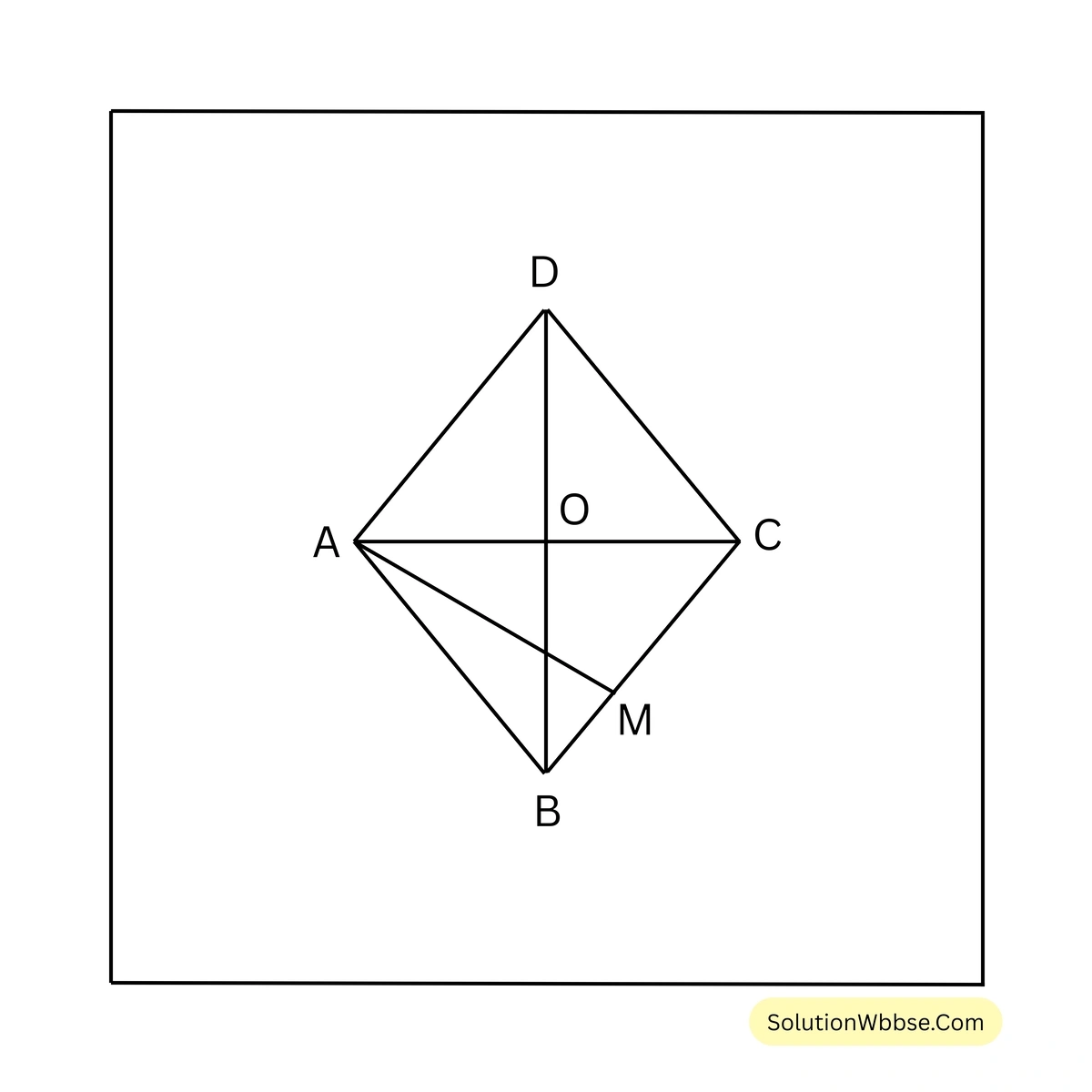
সমাধান –
ধরি, ABCD রম্বসের কর্ণদ্বয়ের পরিমাপ AC = 15 মিটার ও BD = 20 মিটার এবং AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করেছে।
যেহেতু, রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে,
\(\therefore\) সমকোণী ত্রিভুজ AOB এর \(AO = \frac{1}{2} AC = 15/2\) মিটার এবং \(BO = \frac{1}{2} BD = 20/2\) মিটার = 10 মিটার
\(\therefore\) AOB সমকোণী ত্রিভুজ থেকে পাই,
\(AB^2 = AO^2 + BO^2\)বা, \( AB^2 = (10)^2 + (15/2)^2\)
বা, \( AB^2 = 100 + \frac{225}{4}\)
বা, \( AB^2 = \frac{400+225}{4}\)
বা, \( AB^2 = \frac{625}{4}\)
বা, \( AB^2 = (\frac{25}{2})^2\)
বা, \( AB = \frac{25}{2}\)
\(\therefore\) রম্বসের প্রতিটি বাহুর দৈর্ঘ্য \(\frac{25}{2}\) মিটার।
\(\therefore\) রম্বসের পরিসীমা = \((4 \times \frac{25}{2}) = 50\) মিটার।
ধরি, রম্বসটির উচ্চতা \(AM = x\) মিটার
\(\therefore BC \times AM = 150\) [যেহেতু, রম্বসের ক্ষেত্রফল = ভূমি \(\times\) উচ্চতা]
বা, \( \frac{25}{2} \times AM = 150\)
বা, \( AM = \frac{150 \times 2}{25}\)
বা, \( AM = 12\)
\(\therefore\) রম্বসটির পরিসীমা 50 মিটার, ক্ষেত্রফল 150 বর্গমিটার এবং উচ্চতা 12 মিটার।
7. একটি রম্বসের পরিসীমা 400 মিটার এবং সমান্তরাল বাহু দুটির মধ্যে দূরত্ব 22 মিটার হলে, রম্বসাকার ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি।
সমাধান –
রম্বসের পরিসীমা = 400 মিটার।
\(\therefore\) রম্বসের প্রতিটি বাহুর দৈর্ঘ্য = \(\frac{400}{4}\) মিটার = 100 মিটার।
সমান্তরাল বাহু দুটির মধ্যে দূরত্ব 22 মিটার। অর্থাৎ, রম্বসের উচ্চতা = 22 মিটার।
আমরা জানি, রম্বসাকার ক্ষেত্রের ক্ষেত্রফল = ভূমি \(\times\) উচ্চতা।
সুতরাং, নির্ণেয় ক্ষেত্রফল = \((100 \times 22)\) বর্গমিটার
\(= 2200\) বর্গমিটার।
8. যদি একটি রম্বসের পরিসীমা 20 সেমি. এবং একটি কর্ণের দৈর্ঘ্য 6 সেমি. হয়, তবে ওই রম্বসের ক্ষেত্রফল হিসাব করে লিখি।
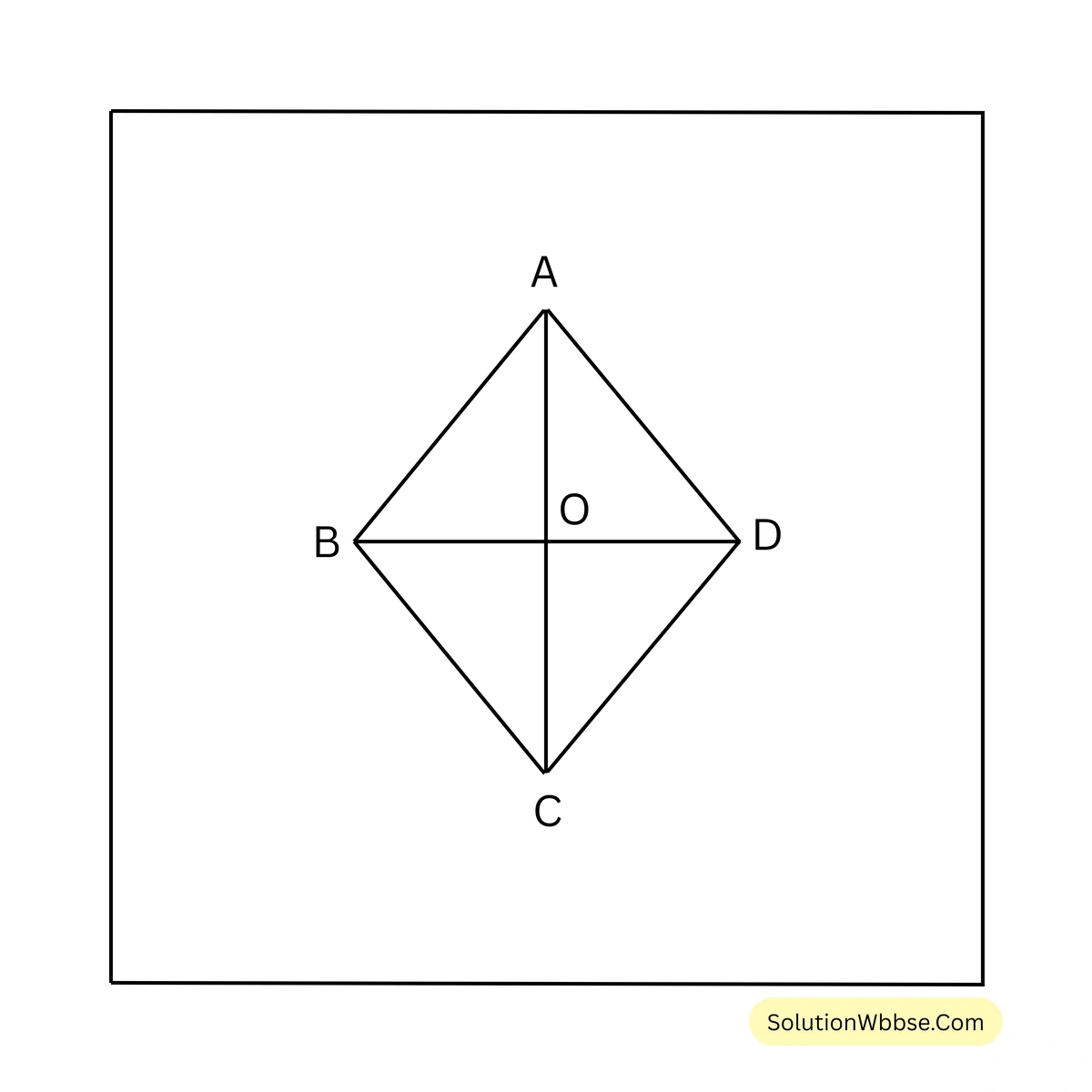
সমাধান –
রম্বসের পরিসীমা 20 সেমি,
\(\therefore\) রম্বসের একটি বাহুর দৈর্ঘ্য \(20/4\) সেমি. \(= 5\) সেমি. এবং রম্বসের একটি কর্ণের দৈর্ঘ্য 6 সেমি.।
ধরা যাক, ABCD হল প্রদত্ত রম্বস যার \(AB = BC = CD = DA = 5\) সেমি. এবং \(AC\) কর্ণ \(= 6\) সেমি.।
\(AC\) ও \(BD\) কর্ণ পরস্পরকে \(O\) বিন্দুতে সমকোণে সমদ্বিখণ্ডিত করে।
\(\therefore OA = 6/2\) সেমি. \(= 3\) সেমি.
এখন, \(AOB\) সমকোণী ত্রিভুজ থেকে পাই,
\(OA^2 + OB^2 = AB^2\)বা, \((3)^2 + OB^2 = (5)^2\)
বা, \(9 + OB^2 = 25\)
বা, \(OB^2 = 25 – 9\)
বা, \(OB^2 = 16\)
বা, \(OB^2 = (4)^2\)
বা, \(OB = 4\)
\(\therefore\) \(BD\) কর্ণের দৈর্ঘ্য \((2 \times 4)\) সেমি. \(= 8\) সেমি.।
\(\therefore\) \(ABCD\) রম্বসের ক্ষেত্রফল = \(\frac{1}{2} \times\) (কর্ণদ্বয়ের গুণফল) = \((\frac{1}{2} \times 8 \times 6)\) বর্গ সেমি.
\(= 24\) বর্গ সেমি.।
9. একটি ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল 1400 বর্গ ডেকামিটার। উহার সমান্তরাল বাহুদ্বয়ের মধ্যে লম্ব দূরত্ব 20 ডেকামিটার এবং সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্যের অনুপাত 3:4 হলে, ওই বাহুদ্বয়ের দৈর্ঘ্য হিসাব করে লিখি।
সমাধান –
ধরি, ট্রাপিজিয়াম আকার ক্ষেত্রের সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য যথাক্রমে \(3x\) ডেকামিটার এবং \(4x\) ডেকামিটার।
\(\therefore\) ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল = \(\frac{1}{2} \times\) (সমান্তরাল বাহুদ্বয়ের যোগফল) \(\times\) উচ্চতা = \(\left\{\frac{1}{2} \times (3x+4x) \times 20\right\}\) বর্গ ডেকামিটার
প্রশ্নানুসারে,
\(\frac{1}{2} \times (3x+4x) \times 20 = 1400\)বা, \(\frac{1}{2} \times 7x \times 20 = 1400\)
বা, \(140x = 2800\)
বা, \(x = 2800 / 140\)
বা, \(x = 20\)
\(\therefore\) সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য যথাক্রমে \(3x = (3 \times 20)\) ডেকামিটার = 60 ডেকামিটার এবং \(4x = (4 \times 20)\) ডেকামিটার = 80 ডেকামিটার।
10. 8 সেমি. বাহু বিশিষ্ট সুষম ষড়ভুজাকার ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি (সংকেত: সুষম ষড়ভুজের কর্ণ গুলি আঁকা হলে ছয়টি সর্বসম সমবাহু ত্রিভুজ পাব)
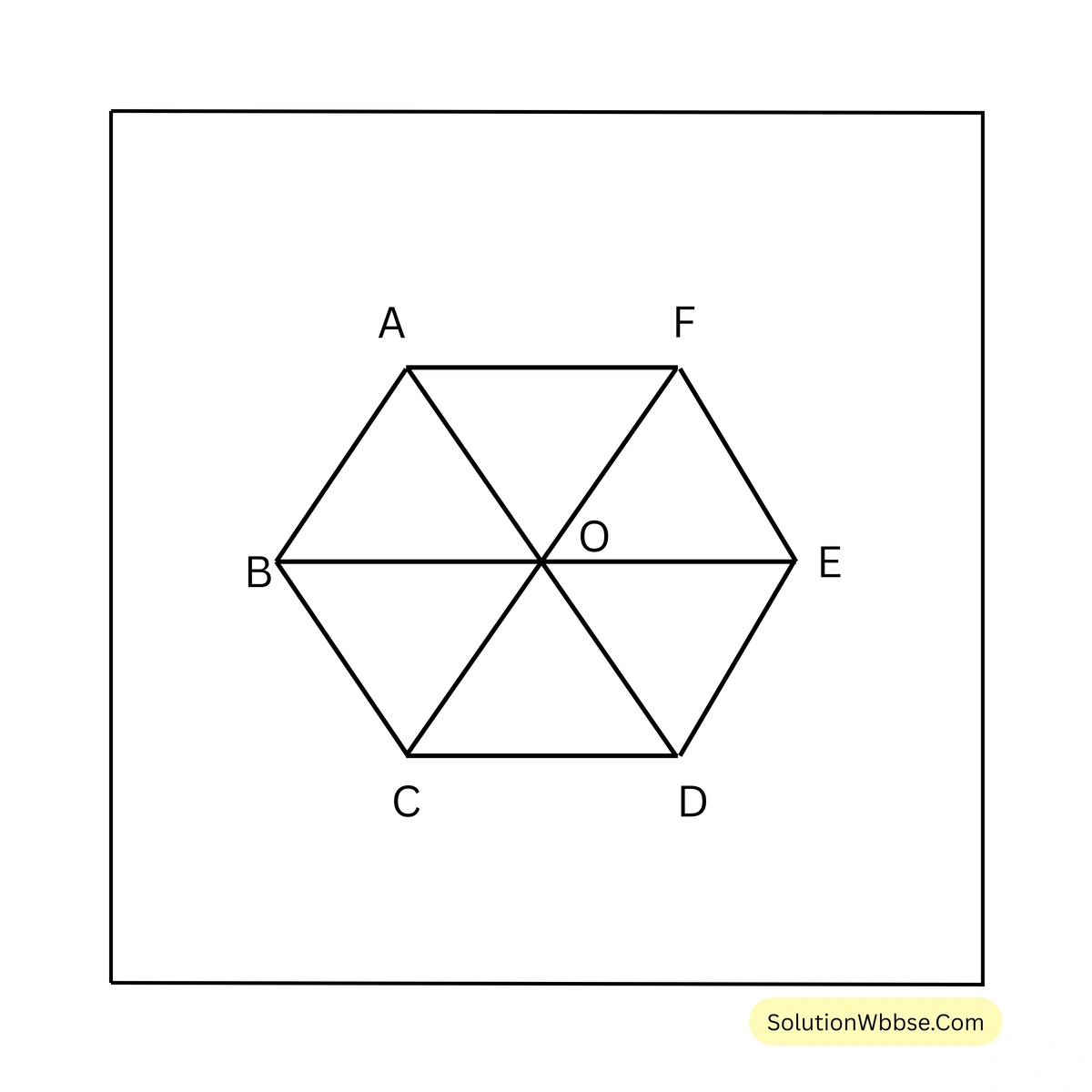
সমাধান – সুষম ষড়ভুজাকার ক্ষেত্রের কর্ণগুলি ষড়ভুজটিকে 6 টি সর্বসম ত্রিভুজে বিভক্ত করেছে।
\(\therefore\) 8 সেমি বাহুবিশিষ্ট সমবাহু ত্রিভুজের ক্ষেত্রফল
\(= \frac{\sqrt{3}}{4} \times (8)^2\) বর্গ সেমি.
\(= (\frac{\sqrt{3}}{4} \times 64)\) বর্গ সেমি.
\(= 16\sqrt{3}\) বর্গ সেমি.
\(\therefore\) সুষম ষড়ভুজাকার ক্ষেত্রের ক্ষেত্রফল = \((6 \times 16\sqrt{3})\) বর্গ সেমি. = \(96\sqrt{3}\) বর্গ সেমি.। [উত্তর]
11. ABCD চতুর্ভুজের AB =5 মিটার, BC =12 মিটার, CD =14 মিটার, DA = 15 মিটার এবং ABC = 90 হলে ABCD চতুর্ভুজাকার ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি।
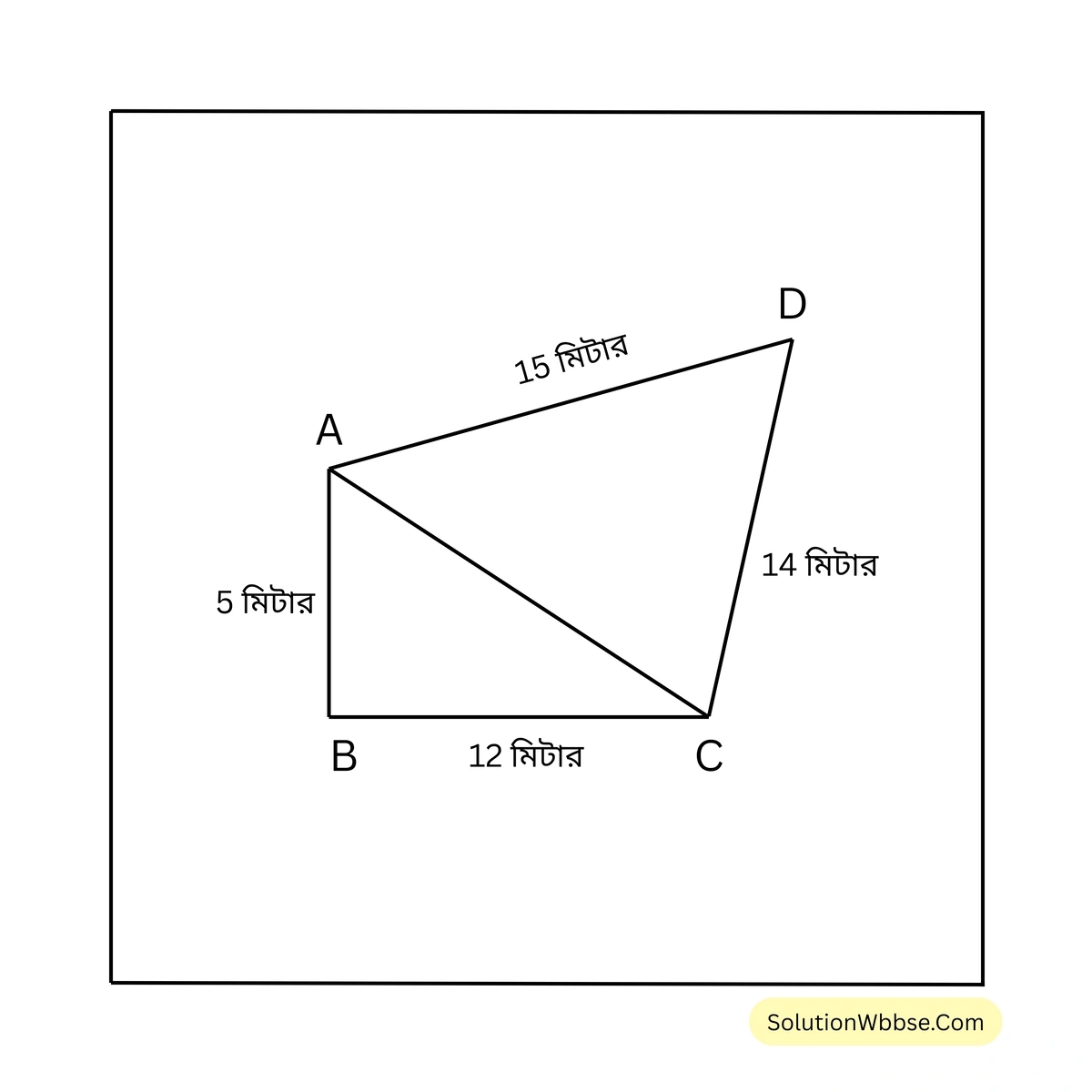
সমাধান –
ABCD চতুর্ভুজের AC কর্ণ এবং \(\angle ABC = 90^\circ\)
\(\therefore\) সমকোণী ত্রিভুজ ABC এর ক্ষেত্রফল = \(\frac{1}{2} \times BC \times AB = \frac{1}{2} \times 12 \times 5\) বর্গ মিটার = 30 বর্গমিটার
আবার, সমকোণী ত্রিভুজ ABC থেকে পাই,
\(AC^2 = AB^2 + BC^2\)বা, \(AC^2 = (5)^2 + (12)^2\)
বা, \(AC^2 = 25+144\)
বা, \(AC^2 = 169\)
বা, \(AC^2 = (13)^2\)
বা, \(AC = 13\)
\(\therefore\) ADC ত্রিভুজের পরিসীমা = (15+14+13) মিটার = 42 মিটার।
\(\therefore\) ADC ত্রিভুজের অর্ধ-পরিসীমা \((s) = 42 /2\) মিটার = 21 মিটার।
\(\therefore\) ADC ত্রিভুজের ক্ষেত্রফল
\(= \sqrt{21(21 – 15)(21 – 14)(21 – 13)}\) বর্গ মিটার
\(= \sqrt{21 \times 6 \times 7 \times 8}\) বর্গ মিটার
\(= \sqrt{3 \times 7 \times 3 \times 2 \times 7 \times 2 \times 2 \times 2}\) বর্গ মিটার
\(= (3 \times 2 \times 2 \times 7)\) বর্গ মিটার
\(= 84\) বর্গ মিটার
\(\therefore\) ABCD চতুর্ভুজের ক্ষেত্রফল = (\(\Delta ABC + \Delta ADC\)) -এর ক্ষেত্রফল = (30 + 84) বর্গ মিটার = 114 বর্গ মিটার। [উত্তর]
12. সাহির ABCD একটি ট্রাপিজিয়াম এঁকেছে, যার BD কর্ণের দৈর্ঘ্য 11 সেমি. এবং A ও C বিন্দু থেকে BD কর্ণের ওপর দুটি লম্ব এঁকেছে যাদের দৈর্ঘ্য যথাক্রমে 5 সেমি. ও 11 সেমি.। হিসাব করে ট্রাপিজিয়াম আকার ক্ষেত্র ABCD-এর ক্ষেত্রফল লিখি।
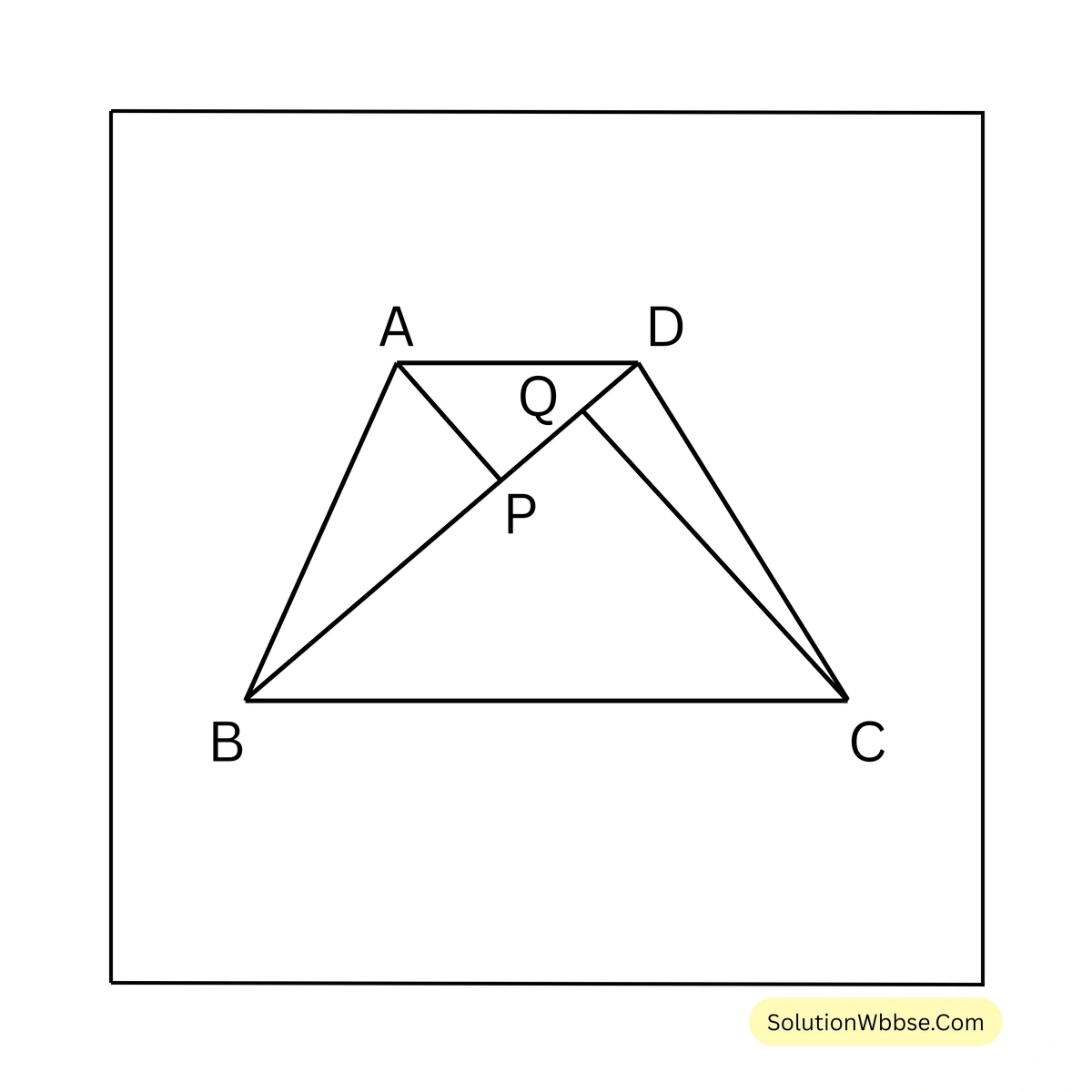
সমাধান –
ABCD ট্রাপিজিয়ামের BD কর্ণের দৈর্ঘ্য 11 সেমি.।
ধরি, A ও C বিন্দু থেকে BD কর্ণের ওপর অঙ্কিত লম্বের দৈর্ঘ্য যথাক্রমে AP ও CQ এবং AP = 5 সেমি. এবং CQ = 11 সেমি.।
\(\therefore\) ABCD ট্রাপিজিয়ামের ক্ষেত্রফল
\(= \frac{1}{2} \times (AP+CQ) \times BD\)\(= \left\{\frac{1}{2} \times (5+11) \times 11\right\}\) বর্গ সেমি.
\(= \left\{\frac{1}{2} \times 16 \times 11\right\}\) বর্গ সেমি.
\(= 88\) বর্গ সেমি.
\(\therefore\) ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল 88 বর্গ সেমি.।
13. ABCDE একটি পঞ্চভুজ যার BC বাহুটি AD কর্ণের সমান্তরাল। EP, BC এর ওপর লম্ব এবং EP, AD -কে Q বিন্দুতে ছেদ করেছে। BC = 7 সেমি., AD = 13 সেমি., PE = 9 সেমি. এবং \(PQ = \frac{4}{9} PE\) হলে, ABCDE পঞ্চভুজাকার ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি।
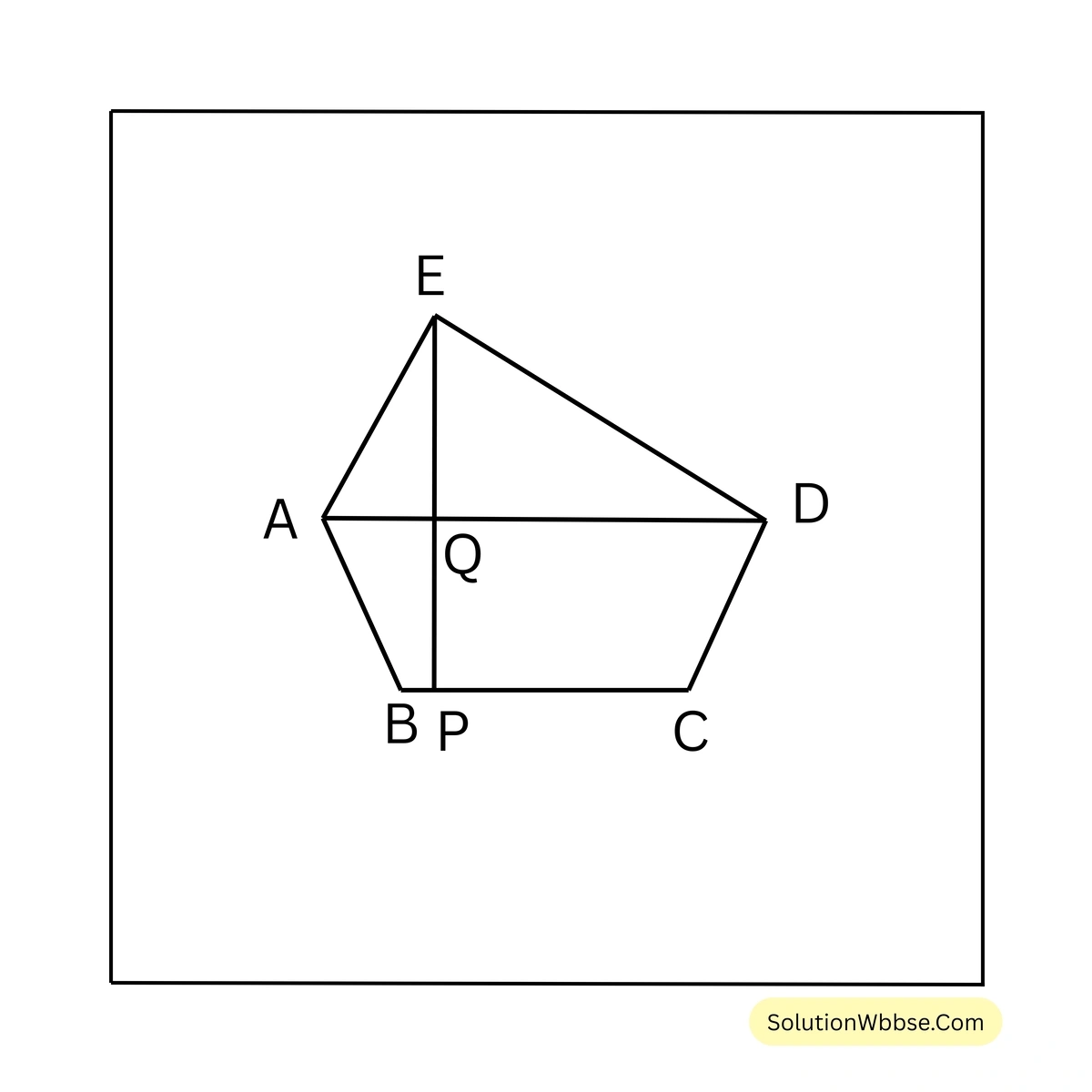
সমাধান –
ABCDE একটি পঞ্চভুজ যার BC বাহুটি AD কর্ণের সমান্তরাল। EP, BC এর ওপর লম্ব এবং EP, AD -কে Q বিন্দুতে ছেদ করেছে। BC = 7 সেমি., AD = 13 সেমি., PE = 9 সেমি. এবং \(PQ = \frac{4}{9} PE = (\frac{4}{9} \times 9)\) সেমি. = 4 সেমি.।
\(EQ = (PE – PQ) = (9-4)\) সেমি. = 5 সেমি.
এখন, ABCD ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল \(= \frac{1}{2} \times (AD+BC) \times PQ\)
\(= \frac{1}{2} \times (13+7) \times 4\) বর্গ সেমি.
\(= \frac{1}{2} \times 20 \times 4\) বর্গ সেমি.
\(= 40\) বর্গ সেমি.
এখন যেহেতু \(BC \parallel AD\) এবং \(EP \perp BC\),
\(\therefore EQ \perp AD\)।
\(\therefore \Delta EAD\) এর ক্ষেত্রফল \(= \frac{1}{2} \times AD \times EQ = (\frac{1}{2} \times 13 \times 5)\) বর্গ সেমি. \(= 32.5\) বর্গ সেমি.।
\(\therefore ABCDE\) পঞ্চভুজের ক্ষেত্রফল = ABCD ট্রাপিজিয়ামের ক্ষেত্রফল + EAD ত্রিভুজের ক্ষেত্রফল \(= 40\) বর্গ সেমি. + \(32.5\) বর্গ সেমি. \(= 72.5\) বর্গ সেমি.। [উত্তর]
14. একটি রম্বসের বাহুর দৈর্ঘ্য ও একটি বর্গক্ষেত্রের বাহুর দৈর্ঘ্য সমান এবং বর্গক্ষেত্রটির কর্ণের দৈর্ঘ্য \(40\sqrt{2}\) সেমি.। যদি রম্বসের কর্ণদ্বয়ের দৈর্ঘ্যের অনুপাত 3:4 হয়, তাহলে রম্বস আকার ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি।
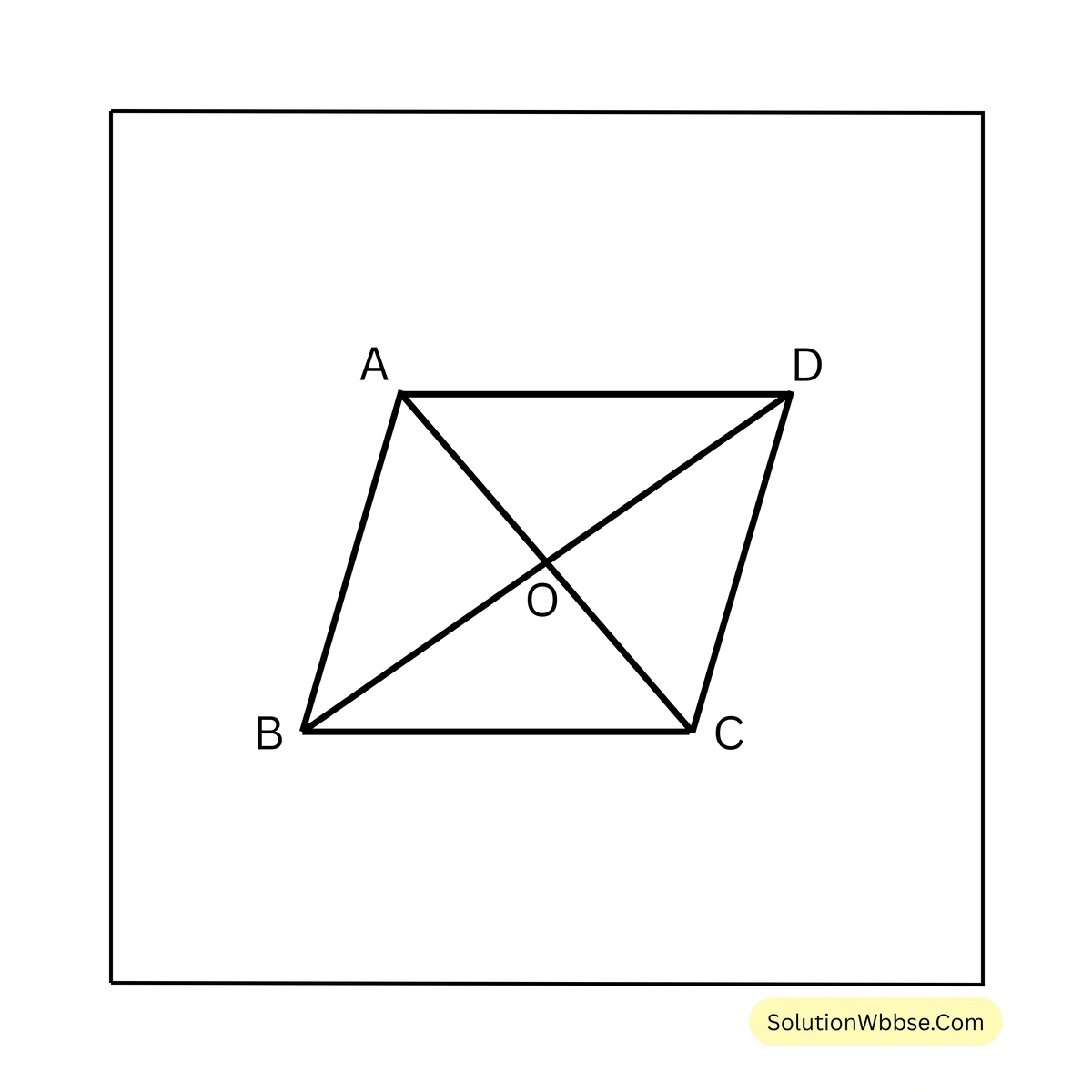
সমাধান –
ধরি, ABCD একটি রম্বস যার প্রতিটি বাহুর দৈর্ঘ্য a সেমি.।
\(\therefore\) বর্গক্ষেত্রের বাহুর দৈর্ঘ্য a সেমি.। [যেহেতু, রম্বস ও বর্গক্ষেত্রের বাহুর দৈর্ঘ্য পরস্পর সমান]
\(\therefore a\sqrt{2} = 40\sqrt{2}\)বা, \(a = 40\)।
\(\therefore\) রম্বসের বাহুর দৈর্ঘ্য 40 সেমি.।
ধরি, রম্বসের কর্ণদ্বয় \(AC = 3x\) সেমি. এবং \(BD = 4x\) সেমি.। এবং রম্বস ABCD এর কর্ণদ্বয় পরস্পরকে O বিন্দুতে সমকোণে সমদ্বিখণ্ডিত করে।
\(\therefore\) সমকোণী ত্রিভুজ AOB থেকে পাই,
\(AO^2 + BO^2 = AB^2\)বা, \( (\frac{3x}{2})^2 + (\frac{4x}{2})^2 = 40^2\)
বা, \( \frac{9x^2}{4} + 4x^2 = 1600\)
বা, \( \frac{9x^2 + 16x^2}{4} = 1600\)
বা, \( \frac{25x^2}{4} = 1600\)
বা, \( x^2 = \frac{1600 \times 4}{25}\)
বা, \( x^2 = 256\)
বা, \( x^2 = (16)^2\)
বা, \( x = 16\)
\(\therefore AC\) কর্ণের দৈর্ঘ্য \(= 3x\) সেমি. \(= (3 \times 16)\) সেমি. \(= 48\) সেমি. এবং \(BD\) কর্ণের দৈর্ঘ্য \(= 4x\) সেমি. \(= (4 \times 16)\) সেমি. \(= 64\) সেমি.।
\(\therefore ABCD\) রম্বসের ক্ষেত্রফল \(= \frac{1}{2} \times 48 \times 64\) বর্গ সেমি. \(= 1536\) বর্গ সেমি.।
\(\therefore\) রম্বসটির ক্ষেত্রফল 1536 বর্গ সেমি.।
15. একটি সমদ্বিবাহু ট্রাপিজিয়ামের তির্যক বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য 10 সেমি. এবং সমান্তরাল বাহুদুটির দৈর্ঘ্য যথাক্রমে 5 সেমি. ও 17 সেমি.। ট্রাপিজিয়াম আকার ক্ষেত্রের কর্ণের দৈর্ঘ্য ও ক্ষেত্রফল হিসাব করে লিখি।
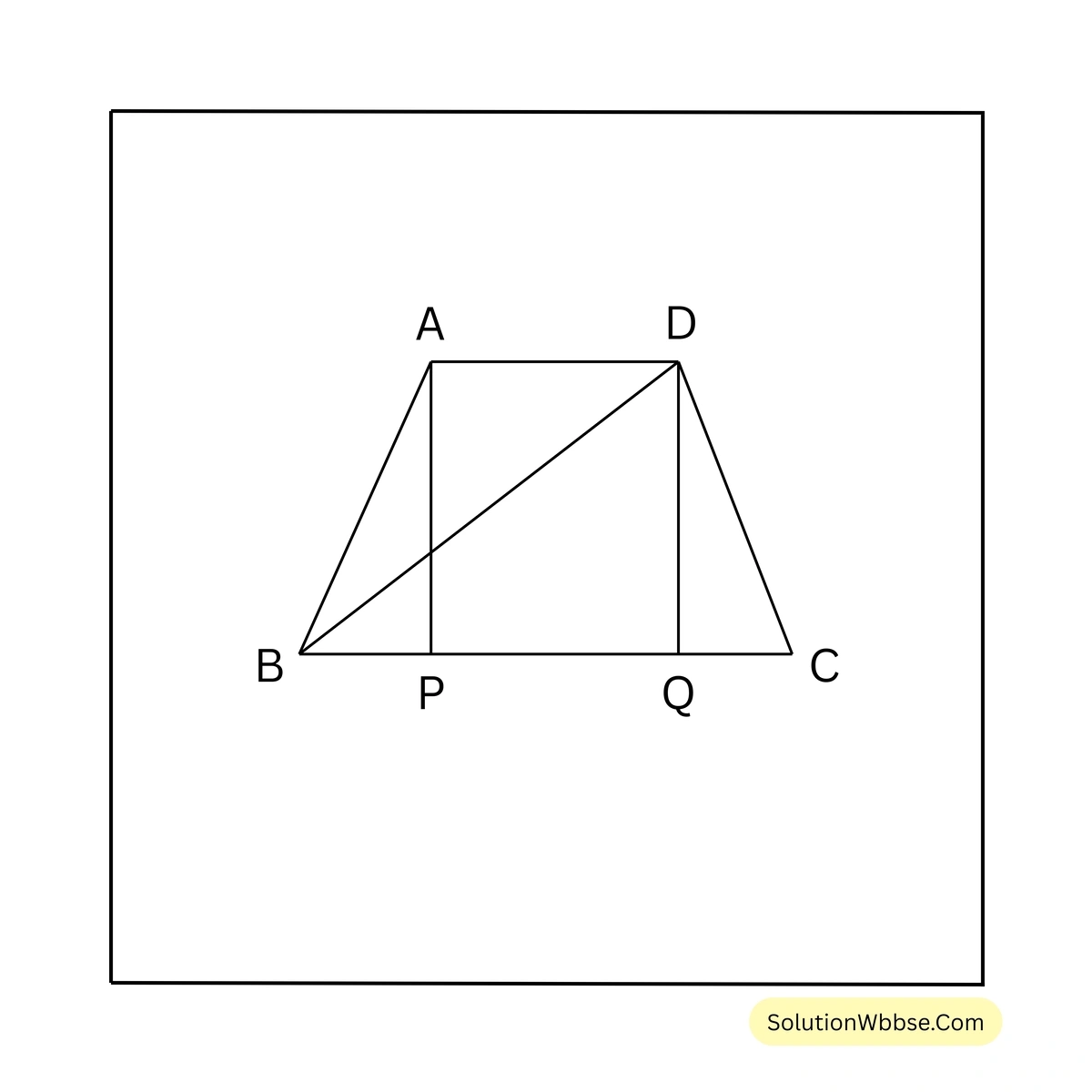
সমাধান –
ধরি, ABCD সমদ্বিবাহু ট্রাপিজিয়ামের তির্যক বাহুদ্বয় AB = CD = 10 সেমি. এবং সমান্তরাল বাহু দুটির দৈর্ঘ্য যথাক্রমে AD = 5 সেমি. ও BC = 17 সেমি.।
A ও D বিন্দু থেকে BC বাহুর ওপর যথাক্রমে AP ও DQ লম্ব টানা হল।
\(\therefore\) AD || BC
\(\therefore\) PQ = AD = 5 সেমি.
আবার যেহেতু, AB = CD
সুতরাং BP = CQ = \(\frac{1}{2} (17 – 5)\) সেমি. = 6 সেমি.
এখন সমকোণী ত্রিভুজ ABP এর,
\(AP^2 = AB^2 – BP^2\)বা, \(AP^2 = 10^2 – 6^2\)
বা, \(AP^2 = 100 – 36\)
বা, \(AP^2 = 64\)
বা, \(AP^2 = 8^2\)
বা, AP = 8
\(\therefore\) ট্রাপিজিয়ামের উচ্চতা 8 সেমি.।
এখন সমকোণী ত্রিভুজ DBQ এর,
BQ = BP + PQ = (6+5) সেমি. = 11 সেমি. এবং DQ = AP = 8 সেমি.।
\(\therefore BD^2 = BQ^2 + DQ^2\)বা, \(BD^2 = 11^2 + 8^2\)
বা, \(BD^2 = 121 + 64\)
বা, \(BD^2 = 185\)
বা, \(BD = \sqrt{185}\)
\(\therefore\) ট্রাপিজিয়ামটির কর্ণের দৈর্ঘ্য \(\sqrt{185}\) সেমি.।
এবং ABCD ট্রাপিজিয়ামের ক্ষেত্রফল = \(\left\{\frac{1}{2} \times (17+5) \times 8\right\}\) বর্গ সেমি. = 88 বর্গ সেমি.
\(\therefore\) ABCD ট্রাপিজিয়ামের ক্ষেত্রফল 88 বর্গ সেমি. এবং কর্ণের দৈর্ঘ্য \(\sqrt{185}\) সেমি.।
16. একটি ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য 19 সেমি. ও 9 সেমি. এবং তির্যক বাহুদ্বয়ের দৈর্ঘ্য 8 সেমি. ও 6 সেমি.। ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল হিসাব করি।
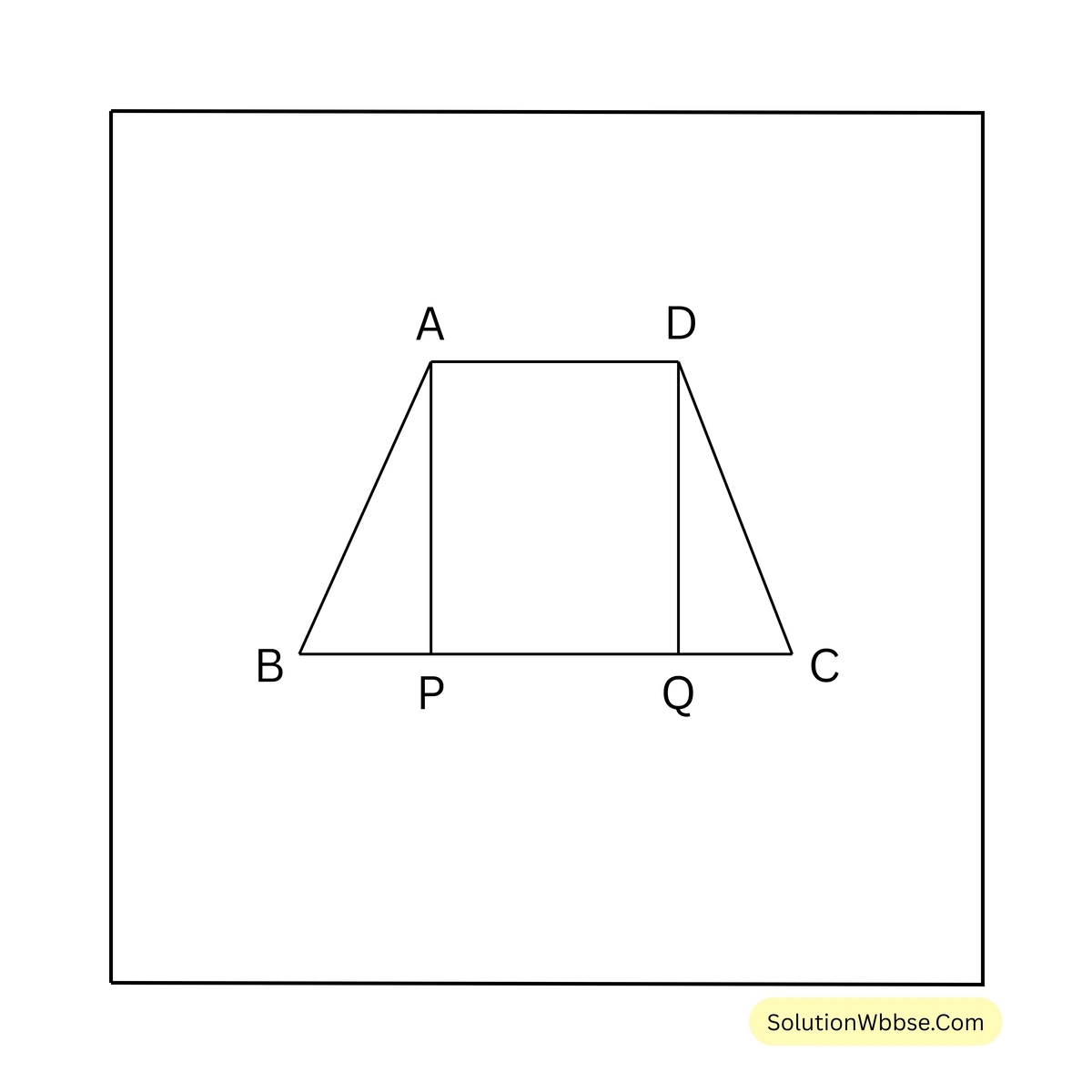
সমাধান –
ধরি, ABCD ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য BC = 19 সেমি. ও AD = 9 সেমি. এবং তির্যক বাহুদ্বয়ের দৈর্ঘ্য AB = 8 সেমি. এবং CD = 6 সেমি.।
A ও D বিন্দু থেকে BC বাহুর ওপর যথাক্রমে AP ও DQ লম্ব টানা হল।
\(\therefore\) AD || BC
\(\therefore\) PQ = AD = 9 সেমি.
\(\therefore\) BP = BC – (PQ+CQ) = 19 – (9+CQ) = 10-CQ
এখন, সমকোণী ত্রিভুজ ABP –এর,
\(BP^2 = AB^2 – AP^2\)বা, \(AP^2 = 64 – BP^2\) — (i)
আবার, সমকোণী ত্রিভুজ DCQ এর,
\(DQ^2 = DC^2 – CQ^2\)বা, \(DQ^2 = 6^2 – CQ^2\)
বা, \(DQ^2 = 36 – CQ^2\) — (ii)
আবার, AP = DQ
\(\therefore AP^2 = DQ^2\)বা, \(64 – BP^2 = 36 – CQ^2\)
বা, \(64 – (10-CQ)^2 = 36 – CQ^2\)
বা, \(64 – (100 – 20CQ + CQ^2) = 36 – CQ^2\)
বা, \(64 – 100 + 20CQ – CQ^2 = 36 – CQ^2\)
বা, \(20CQ = 36 – 64 + 100\)
বা, \(CQ = 72/20\)
বা, \(CQ = 18/5\)
(ii) নং সমীকরণে \(CQ = \frac{18}{5}\) বসিয়ে পাই,
\(DQ^2 = 36 – (\frac{18}{5})^2\)বা, \(DQ^2 = 36 – \frac{324}{25}\)
বা, \(DQ^2 = \frac{900-324}{25}\)
বা, \(DQ = \sqrt{\frac{576}{25}}\)
বা, \(DQ = \frac{24}{5}\)
বা, DQ = 4.8
\(\therefore\) ট্রাপিজিয়ামটির উচ্চতা AP = DQ = 4.8 সেমি.।
\(\therefore\) ট্রাপিজিয়ামটির ক্ষেত্রফল = \(\frac{1}{2} \times (19+9) \times 4.8\) বর্গ সেমি. = \(\frac{1}{2} \times 28 \times 4.8\) বর্গ সেমি. = 67.2 বর্গ সেমি.। [উত্তর]
17. বহু বিকল্পীয় প্রশ্ন (M.C.Q)
(i) একটি সামান্তরিকের উচ্চতা ভূমির একতৃতীয়াংশ। সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল 192 বর্গ সেমি. হলে, সামান্তরিকের উচ্চতা
(a) 4 সেমি.
(b) 8 সেমি.
(c) 16 সেমি.
(d) 24 সেমি.
Ans: (b) 8 সেমি.
সমাধান –
ধরি, সামান্তরিকের ভূমি \(x\) সেমি.।
\(\therefore\) সামান্তরিকের উচ্চতা \(\frac{x}{3}\) সেমি.।
শর্তানুসারে,
\(x \times \frac{x}{3} = 192\)বা, \( x^2 = 3 \times 192\)
বা, \( x^2 = 576\)
বা, \( x^2 = 24^2\)
বা, \( x = 24\)
\(\therefore\) সামান্তরিকের উচ্চতা \(\frac{x}{3}\) সেমি. = \(\frac{24}{3}\) সেমি. = 8 সেমি.।
(ii) একটি রম্বসের একটি বাহুর দৈর্ঘ্য 6 সেমি. এবং একটি কোণের পরিমাপ \(60^{\circ}\) হলে, রম্বস আকার ক্ষেত্রের ক্ষেত্রফল
(a) \(9\sqrt{3}\) বর্গ সেমি.
(b) \(18\sqrt{3}\) বর্গ সেমি.
(c) \(36\sqrt{3}\) বর্গ সেমি.
(d) \(6\sqrt{3}\) বর্গ সেমি.
Ans – (b) \(18\sqrt{3}\) বর্গ সেমি.
সমাধান –
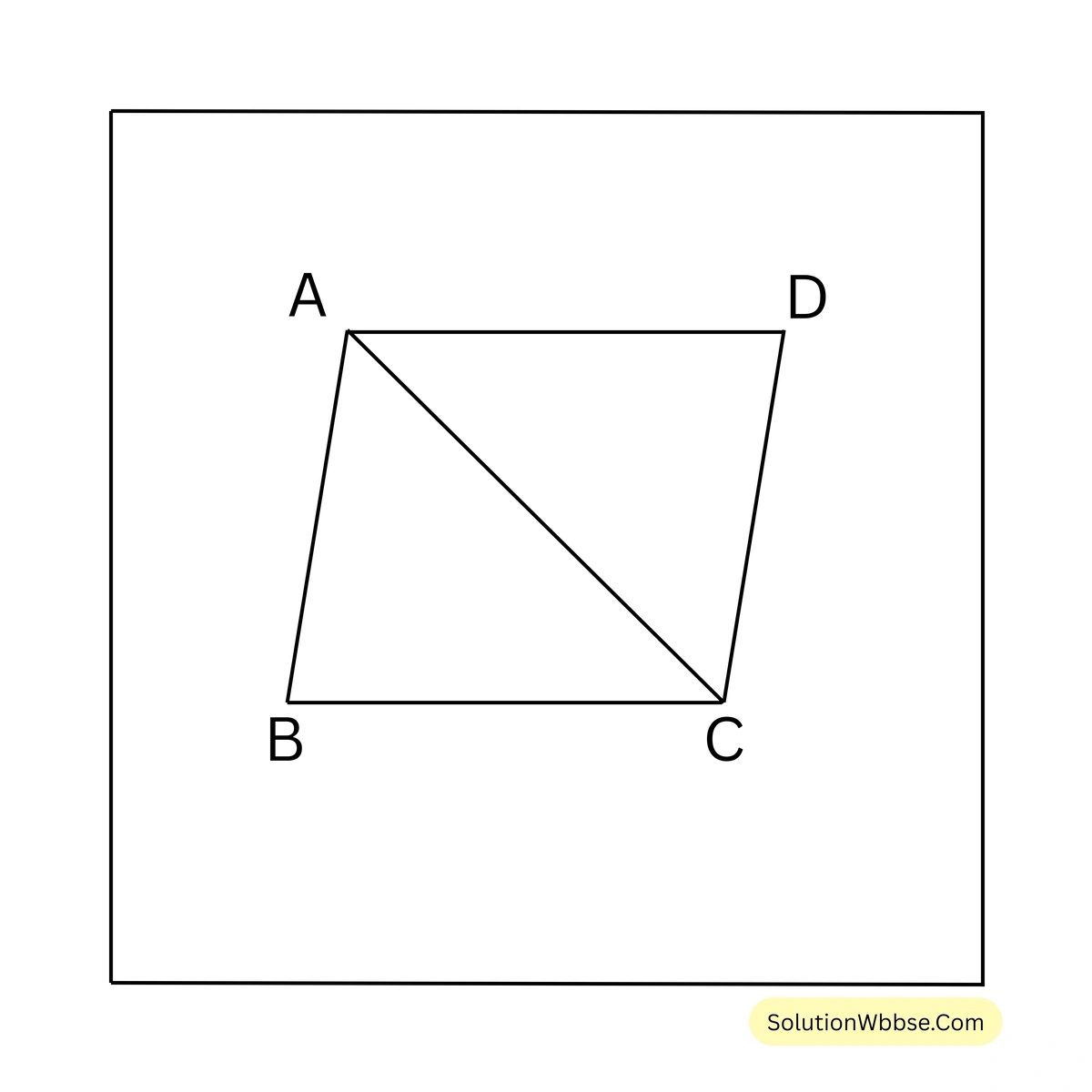
ABCD রম্বসের বাহুর দৈর্ঘ্য 6 সেমি. এবং \(\angle ABC = 60^{\circ}\)। AC কর্ণ যোগ করে পাই, \(\angle BAC = \angle BCA = (180^{\circ} – 60^{\circ}) / 2 = 60^{\circ}\)
\(\because\) AC কর্ণ ABCD রম্বসকে দুটি 6 সেমি. বাহু বিশিষ্ট সমবাহু ত্রিভুজে বিভক্ত করেছে।
\(\therefore\) ABCD রম্বসের ক্ষেত্রফল = \(2 \times \frac{\sqrt{3}}{4} \times 6^2\) বর্গ সেমি. = \(18\sqrt{3}\) বর্গ সেমি.
(iii) একটি রম্বসের একটি কর্ণের দৈর্ঘ্য অপর কর্ণটির দৈর্ঘ্যের তিনগুণ। যদি রম্বস আকার ক্ষেত্রের ক্ষেত্রফল 96 বর্গ সেমি. হয় তাহলে বড় কর্ণটির দৈর্ঘ্য
(a) 8 সেমি.
(b) 12 সেমি.
(c) 16 সেমি.
(d) 24 সেমি.
Ans: (d) 24 সেমি.
সমাধান –
ধরি, একটি কর্ণের দৈর্ঘ্য \(x\) সেমি.
\(\therefore\) অপর কর্ণের দৈর্ঘ্য হবে \(3x\) সেমি.।
প্রশ্নানুসারে,
\(\frac{1}{2} \times x \times 3x = 96\)বা, \(3x^2 = 96 \times 2\)
বা, \(3x^2 = 192\)
বা, \(x^2 = 192/3\)
বা, \(x^2 = 64\)
বা, \(x^2 = 8^2\)
বা, \(x = 8\)
\(\therefore\) বড় কর্ণটির দৈর্ঘ্য \(3x\) সেমি. = \((3 \times 8)\) সেমি. = 24 সেমি.।
(iv) একটি রম্বস ও একটি বর্গক্ষেত্র একই ভূমির উপর অবস্থিত। বর্গক্ষেত্রের ক্ষেত্রফল \(x^2\) বর্গ একক এবং রম্বস আকার ক্ষেত্রের ক্ষেত্রফল \(y\) বর্গ একক হলে,
(a) \(y > x^2\)
(b) \(y < x^2\)
(c) \(y = x^2\)
Ans: (b) \(y < x^2\)
সমাধান –
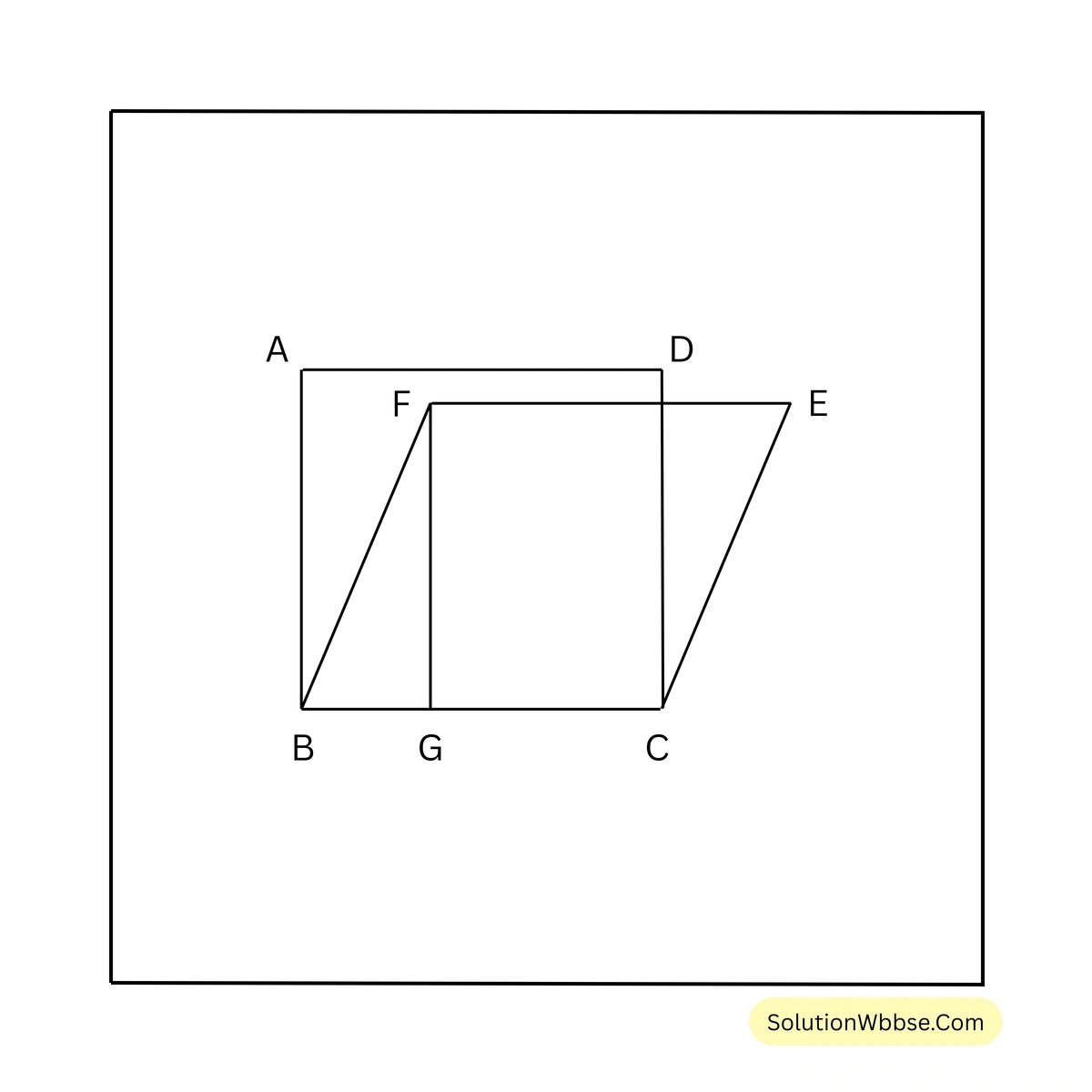
বর্গক্ষেত্রের ক্ষেত্রফল \(x^2\) বর্গ একক।
\(\therefore\) বর্গক্ষেত্রের প্রতিটি বাহুর দৈর্ঘ্য \(x\) একক।
\(\therefore\) রম্বসের প্রতিটি বাহুর দৈর্ঘ্য \(x\) একক।
ধরি, রম্বসের উচ্চতা \(h\) একক।
\(\therefore\) রম্বসের ক্ষেত্রফল \(xh\) বর্গ একক।
\(\therefore y = xh\)স্পষ্টতই, \(h < x\) [\(\because\) BFG সমকোণী ত্রিভুজের উচ্চতা (FG) < অতিভুজ (BF)]
\(\therefore hx < x^2\)\(\therefore y < x^2\)(v) একটি ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল 162 বর্গ সেমি. এবং উচ্চতা 6 সেমি.। ট্রাপিজিয়ামটির একটি সমান্তরাল বাহুর দৈর্ঘ্য 23 সেমি. হলে, অপর সমান্তরাল বাহুর দৈর্ঘ্য
(a) 29 সেমি.
(b) 31 সেমি.
(c) 32 সেমি.
(d) 33 সেমি.
Ans: (b) 31 সেমি.
সমাধান –
ধরি, ট্রাপিজিয়ামটির অপর বাহুর দৈর্ঘ্য \(x\) সেমি.।
\(\therefore \frac{1}{2} \times (x + 23) \times 6 = 162\)বা, \(x + 23 = \frac{162 \times 2}{6}\)
বা, \(x + 23 = 54\)
বা, \(x = 54 – 23\)
বা, \(x = 31\)
\(\therefore\) অপর বাহুটির দৈর্ঘ্য 31 সেমি.।
18. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন
(i) ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল \(96\) বর্গ সেমি. ও BD কর্ণের দৈর্ঘ্য \(12\) সেমি.। A বিন্দু থেকে BD কর্ণের ওপর লম্বের দৈর্ঘ্য কত?
সমাধান –
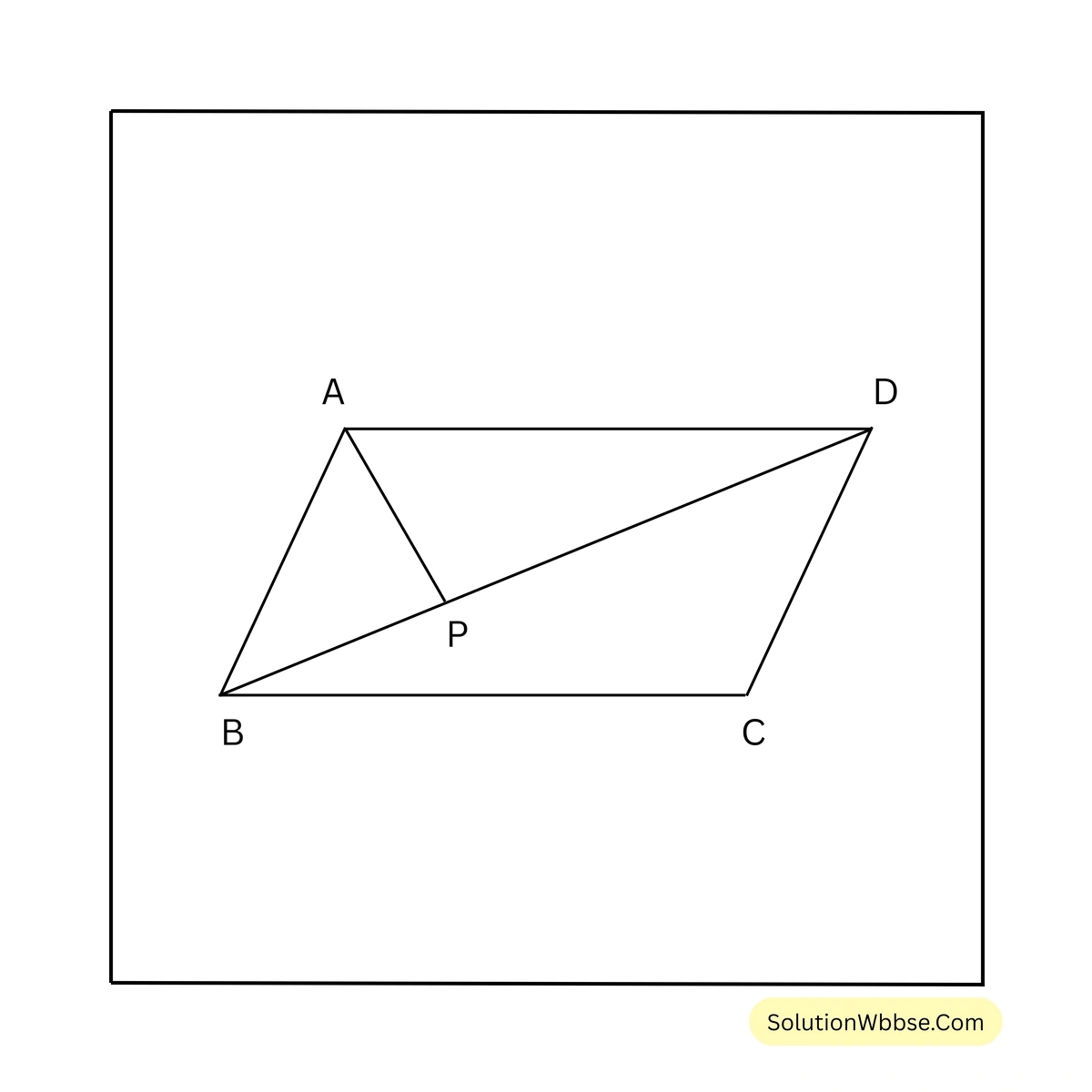
ধরা যাক, ABCD সামান্তরিকের A বিন্দু থেকে BD কর্ণের ওপর AP লম্ব টানা হল।
সামান্তরিকের কর্ণ সামান্তরিককে দুটি সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজে বিভক্ত করে।
\(\therefore\) ABD এর ক্ষেত্রফল = \(\frac{1}{2} \times 96\) বর্গ সেমি. = \(48\) বর্গ সেমি.
আবার ABD এর ক্ষেত্রফল = \(\frac{1}{2} \times BD \times AP = \frac{1}{2} \times 12 \times AP = 6AP\)
\(\therefore 6AP = 48\)বা, \(AP = \frac{48}{6}\)
বা, \(AP = 8\)
\(\therefore\) A বিন্দু থেকে BD কর্ণের ওপর লম্বের দৈর্ঘ্য \(8\) সেমি.।
(ii) একটি সামান্তরিকের সন্নিহিত বাহুর দৈর্ঘ্য \(5\) সেমি. এবং \(3\) সেমি.। বৃহত্তর বাহুর মধ্যে দূরত্ব \(2\) সেমি. হলে ক্ষুদ্রতর বাহুর মধ্যে দূরত্ব কত?
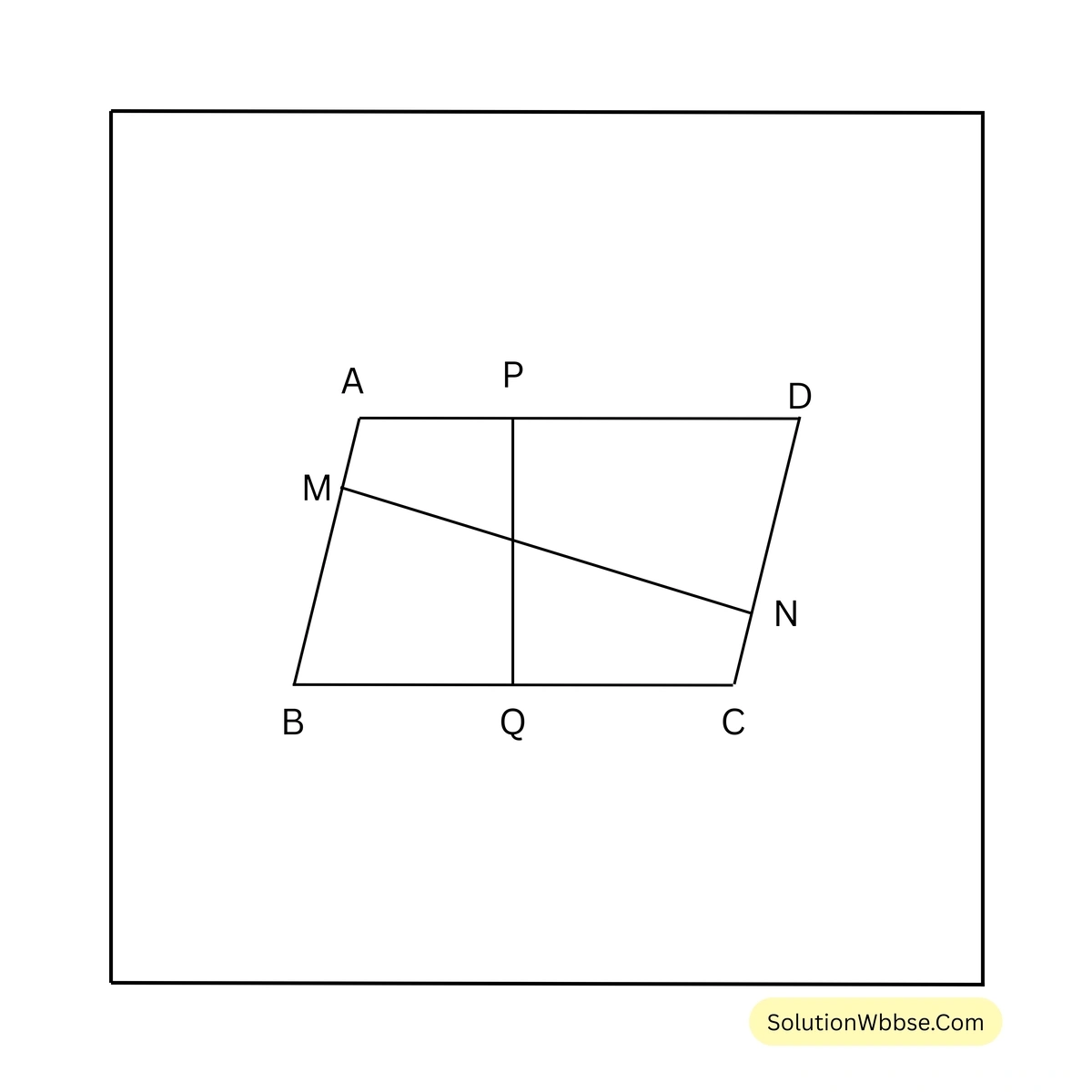
সমাধান –
ধরি, ABCD সামান্তরিকের সন্নিহিত বাহুদ্বয়ের দৈর্ঘ্য \(AB = 5\) সেমি. এবং \(BC = 3\) সেমি.। বৃহত্তর বাহুদ্বয়ের মধ্যে দূরত্ব \(MN = 2\) সেমি. এবং ক্ষুদ্রতর বাহুদ্বয়ের মধ্যে দূরত্ব \(PQ\)।
\(\therefore 3 \times PQ = 5 \times MN\)বা, \( PQ = \frac{5 \times 2}{3}\)
বা, \( PQ = \frac{10}{3}\)
বা, \( PQ = 3\frac{1}{3}\)
\(\therefore\) ক্ষুদ্রতর বাহুদ্বয়ের মধ্যে দূরত্ব \(3\frac{1}{3}\) সেমি.।
(iii) একটি রম্বসের উচ্চতা \(4\) সেমি. এবং বাহুর দৈর্ঘ্য \(5\) সেমি.। রম্বস আকার ক্ষেত্রের ক্ষেত্রফল কত?
সমাধান – রম্বসের ক্ষেত্রফল = (ভূমি \(\times\) উচ্চতা) = \((5 \times 4)\) বর্গ সেমি. = \(20\) বর্গ সেমি.।
(iv) একটি সমদ্বিবাহু ট্রাপিজিয়ামের যেকোনো সমান্তরাল বাহু সংলগ্ন একটি কোণ \(45^\circ\), ট্রাপিজিয়ামের তীর্যক বাহুর দৈর্ঘ্য \(62\) সেমি. হলে, সমান্তরাল বাহুদ্বয়ের মধ্যে দূরত্ব কত?
সমাধান –
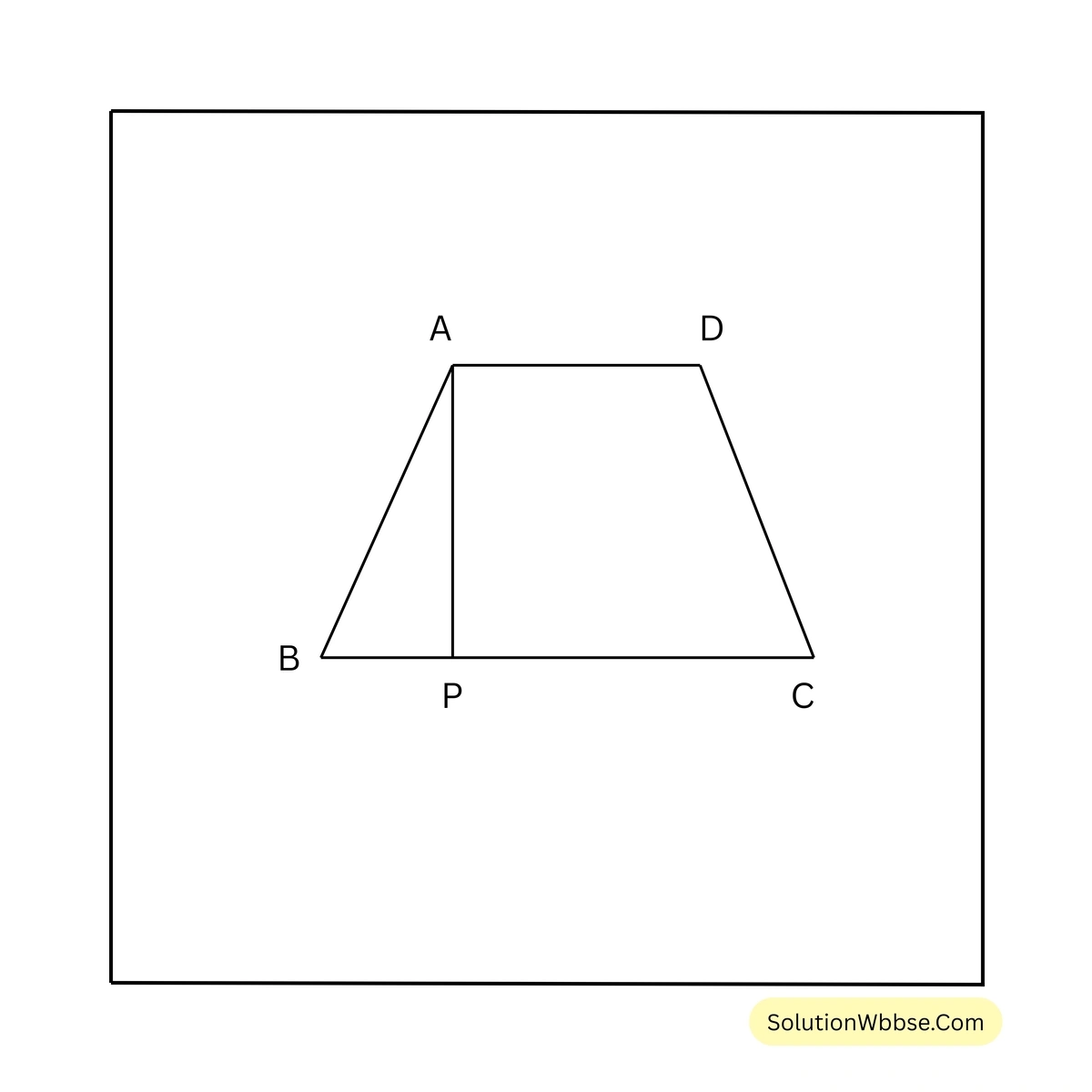
ধরি, ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম যার \(AD \parallel BC\) এবং সমান্তরাল বাহু সংলগ্ন একটি কোণ \(\angle ABC = 45^\circ\)। ধরি, ট্রাপিজিয়ামের তীর্যক বাহু AB এর দৈর্ঘ্য \(62\) সেমি. এবং A বিন্দু থেকে BC-এর ওপর অঙ্কিত লম্ব \(AP = a\) সেমি.
\(\Delta ABP\)-এর \(\angle ABC = 45^\circ\), \(\angle APB = 90^\circ\)
\(\therefore \angle BAP = 180^\circ – (90^\circ + 45^\circ) = 45^\circ\)\(\therefore ABP\) একটি সমকোণী সমদ্বিবাহু ত্রিভুজ যার \(AP = BP\)
\(AP^2 + BP^2 = AB^2\)বা, \(a^2 + a^2 = 62^2\)
বা, \(2a^2 = 62 \times 62\)
বা, \(a^2 = \frac{62 \times 62}{2}\)
বা, \(a = 31\sqrt{2}\)
\(\therefore\) সমান্তরাল বাহুদ্বয়ের মধ্যে দূরত্ব \(31\sqrt{2}\) সেমি.।
(v) ABCD সামান্তরিকের \(AB = 4\) সেমি., \(BC = 6\) সেমি. এবং \(\angle ABC = 30^\circ\) হলে ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল কত?
সমাধান –
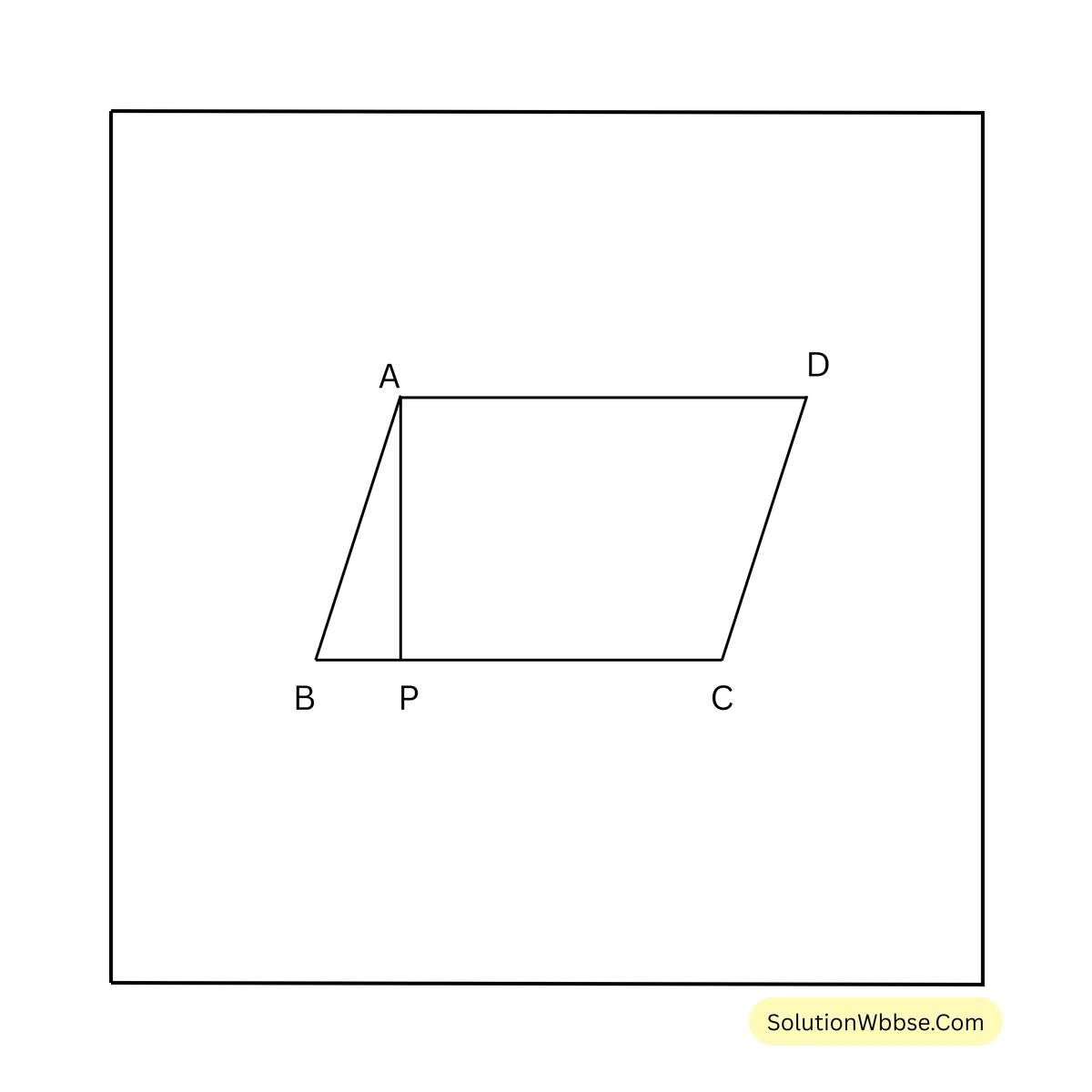
ABCD সামান্তরিকের \(AB = 4\) সেমি. \(BC = 6\) সেমি. এবং \(\angle ABC = 30^\circ\)
ধরি, A বিন্দু থেকে BC এর ওপর অঙ্কিত লম্ব AP সমকোণী ত্রিভুজ ABP থেকে পাই,
\(\frac{AP}{AB} = \sin 30^\circ\)বা, \(\frac{AP}{4} = \frac{1}{2}\)
বা, \(AP = 2\)
\(\therefore\) সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল = \((6 \times 2)\) বর্গ সেমি. = \(12\) বর্গ সেমি.।
এই আর্টিকেলে নবম শ্রেণির গণিতের ‘ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল‘ অধ্যায়ের ‘কষে দেখি – 15.3’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।
কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন