নবম শ্রেণী গণিত – বাস্তব সংখ্যা – কষে দেখি – 1.1

পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) নবম শ্রেণির গণিত পাঠ্যবইয়ের প্রথম অধ্যায় হলো ‘বাস্তব সংখ্যা’। এই পোস্টে ‘কষে দেখি – 1.1’-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. মূলদ সংখ্যা কাকে বলে লিখি। 4 টি মূলদ সংখ্যা লিখি।

উত্তর – যেসব বাস্তব সংখ্যাদের \(\frac pq\) আকারে প্রকাশ করা যায়, যেখানে p,q উভয়ই পূর্ণসংখ্যা এবং p ≠ 0 তাদের মূলদ সংখ্যা বলা হয়।

2. 0 কি একটি মূলদ সংখ্যা? 0-কে \(\frac pq\) [যেখানে p ও q পূর্ণসংখ্যা এবং q ≠ 0 এবং p ও q এর মধ্যে 1 ছাড়া কোনো সাধারণ উৎপাদক না থাকে] আকারে প্রকাশ করি।

উত্তর – 0 একটি মূলদ সংখ্যা।

0 = \(\frac 0q\) (q ≠ 0) আকারে প্রকাশ করা যায়।

3. নীচের মূলদ সংখ্যাগুলি সংখ্যারেখায় স্থাপন করি। (i) 7 (ii) -4 (iii) \(\frac35\) (iv) \(\frac92\) (v) \(\frac29\) (vi) \(\frac{11}2\) (vii) –\( \frac{13}2\)

(i) 7

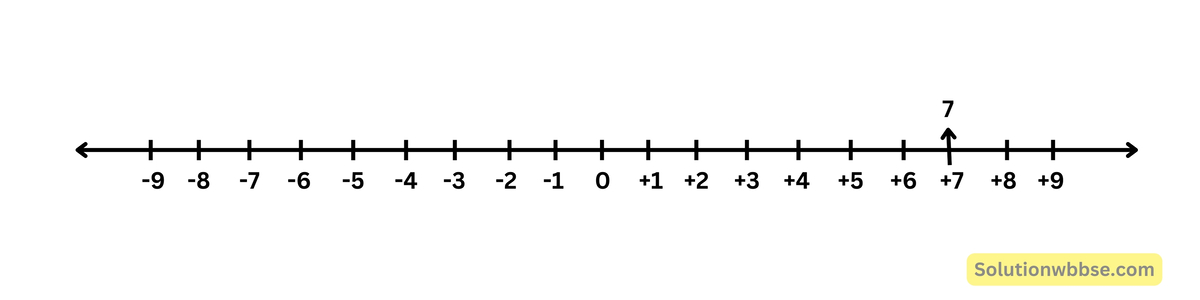
(ii) -4

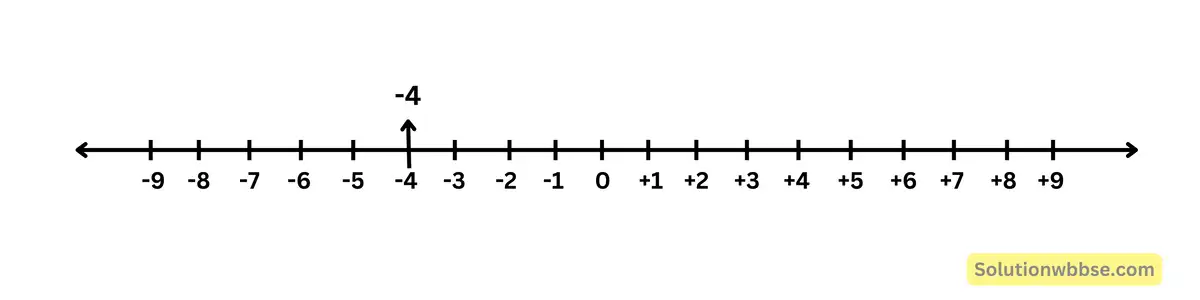
(iii) \(\frac35\)

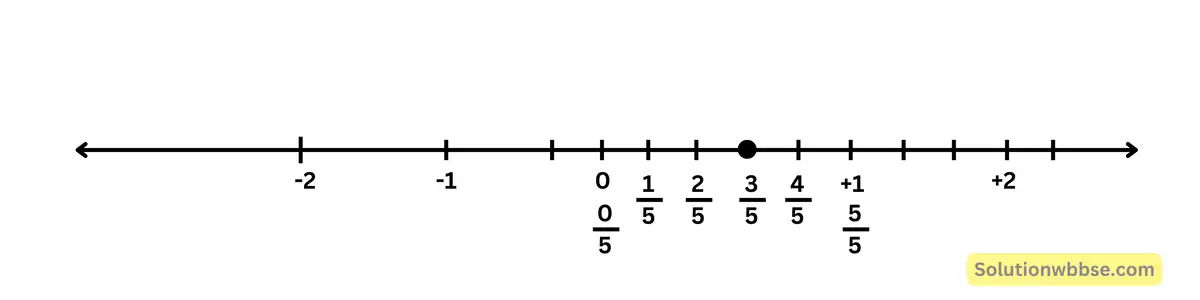
(iv) \(\frac92\)

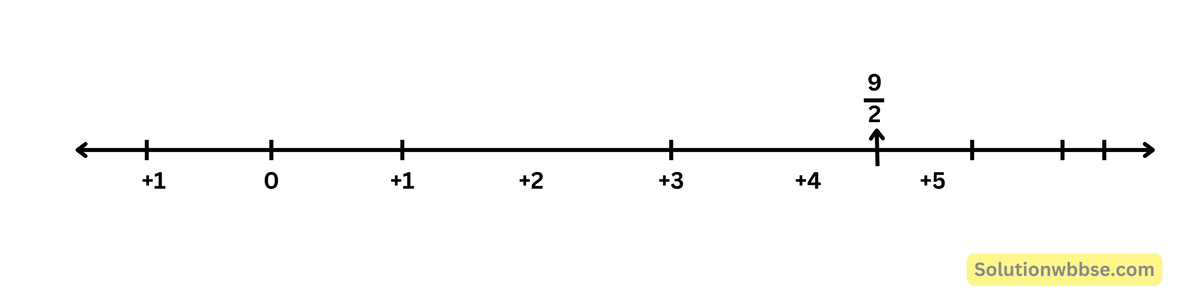
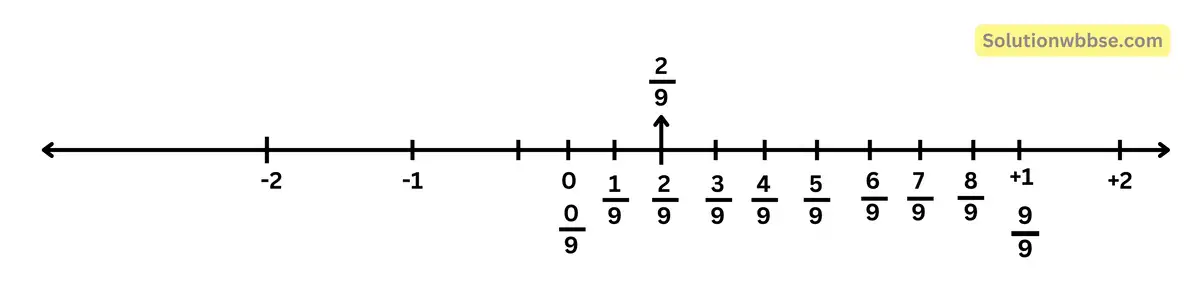
(v) \(\frac29\)

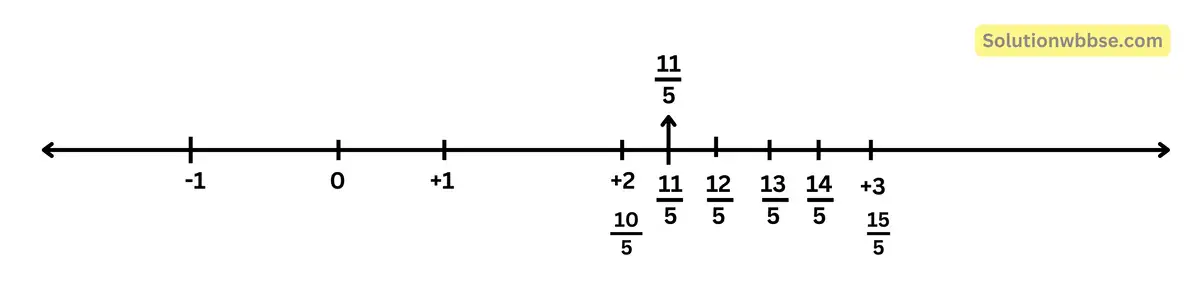
(vi) \(\frac{11}5\)

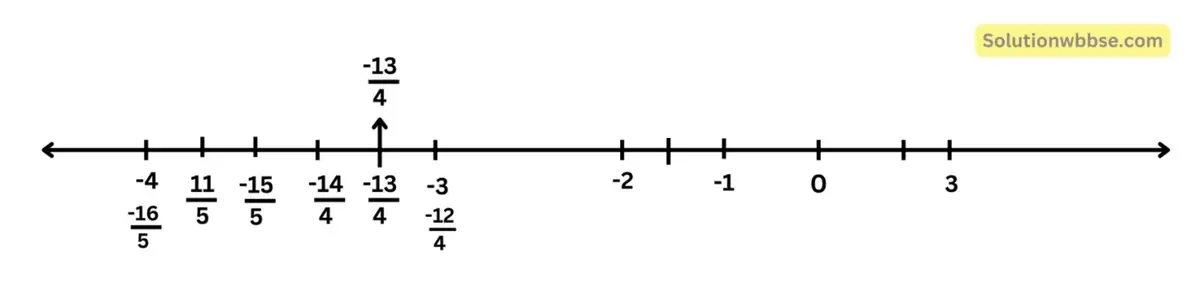
(vii) –\(\frac{13}4\)

4. নীচের প্রতিটি ক্ষেত্রে মূলদ সংখ্যা দুটির মধ্যে একটি মূলদ সংখ্যা লিখি ও সংখ্যারেখায় বসাই। (i) 4 ও 5 (ii) 1 ও 2 (iii) \(\frac14\) ও \(\frac12\) (iv) -1 ও \(\frac12\) (v) \(\frac14\) ও \(\frac13\) (vii) -2 ও -1

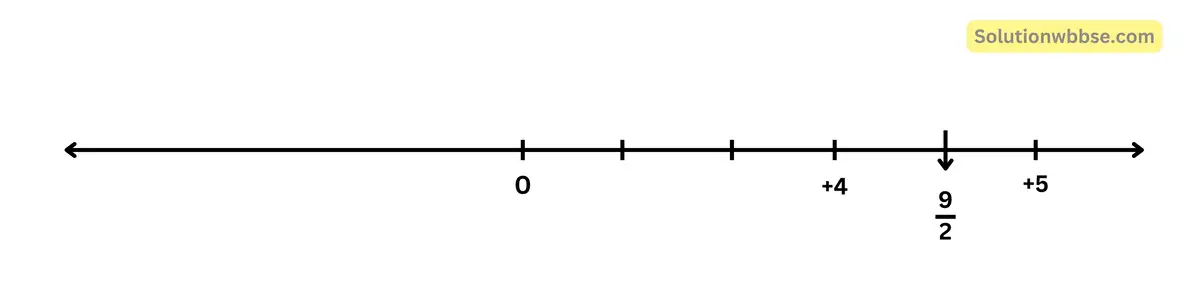
(i) 4 ও 5

উত্তর – \(\frac12\left(4+5\right)=\frac94\)

(ii) 1 ও 2

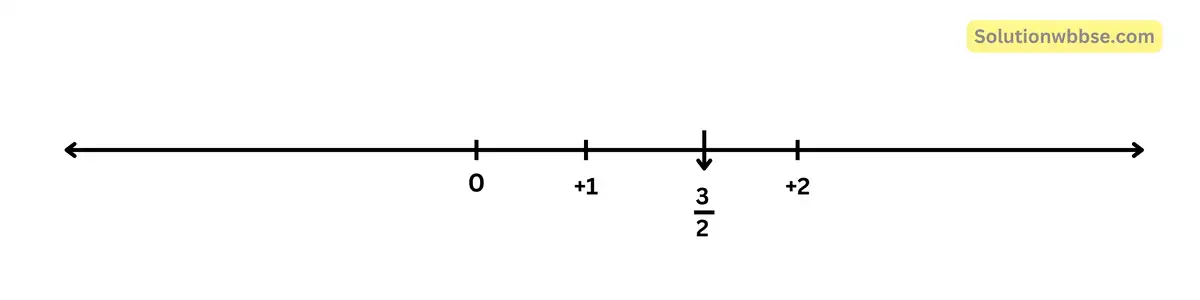
উত্তর – \(\frac12\left(1+2\right)=\frac32\), 1 ও 2 -এর মধ্যবর্তী মূলদ সংখ্যা।

(iii) \(\frac14\) ও \(\frac12\)

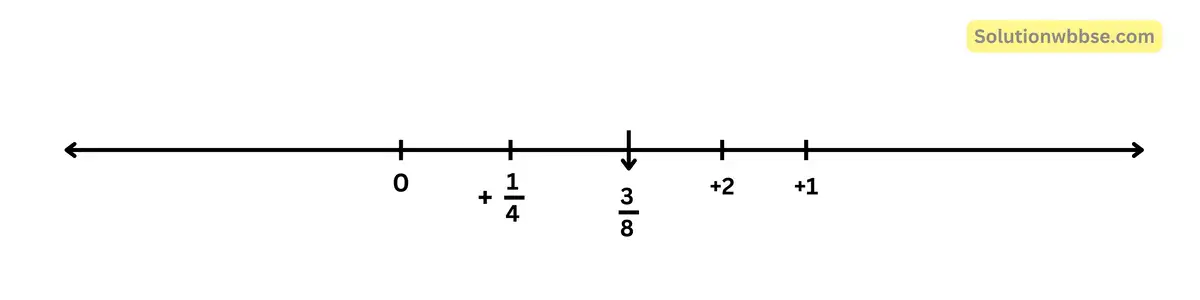
উত্তর – \(\frac12\left(\frac14+\frac12\right)=\frac38\)

(iv) -1 ও \(\frac12\)

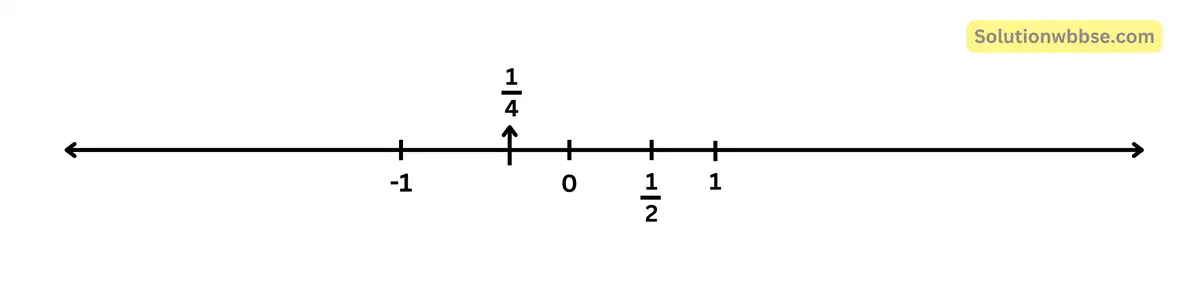
উত্তর – \(\frac12\left(-1+\frac12\right)=-\frac14\)

(v) \(\frac14\) ও \(\frac13\)

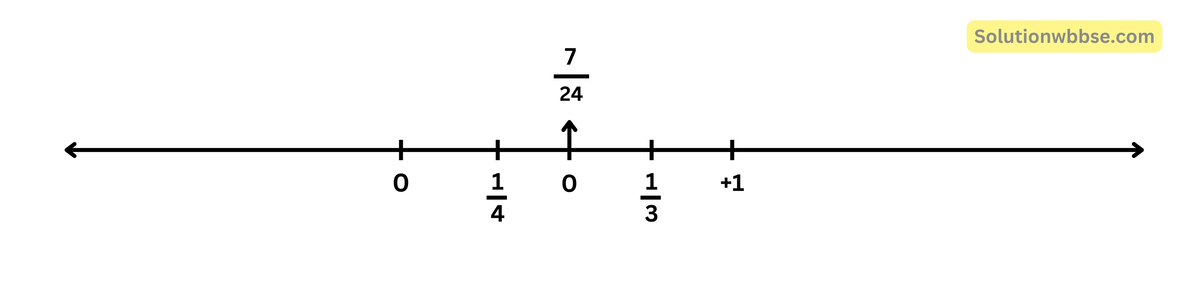
উত্তর – \(\frac12\left(\frac14+\frac12\right)=\frac7{24}\)

(vii) -2 ও -1

উত্তর – \(\frac12\left\{-2+\left(-1\right)\right\}=-\frac32\)

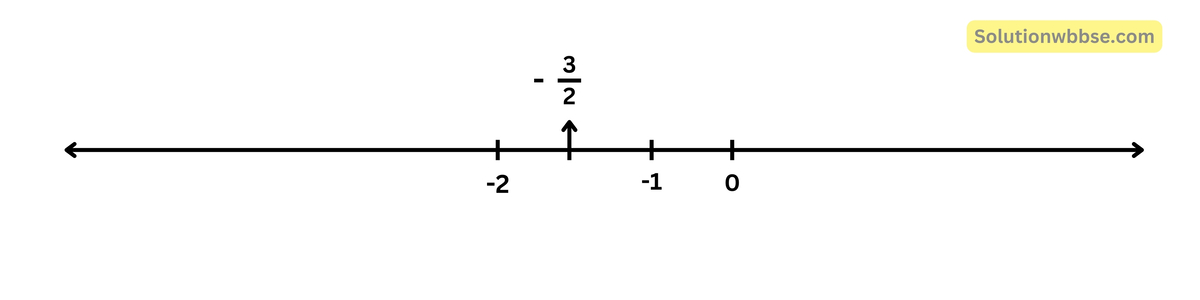
5. 4 ও 5-এর মধ্যে 3 টি মূলদ সংখ্যা লিখি ও সংখ্যারেখায় বসাই।

উত্তর – \(\frac12\left(4+5\right)=\frac92\)

\(\frac12\left(4+\frac92\right)=\frac{17}4\\\)\(\frac12\left(5+\frac92\right)=\frac{19}4\)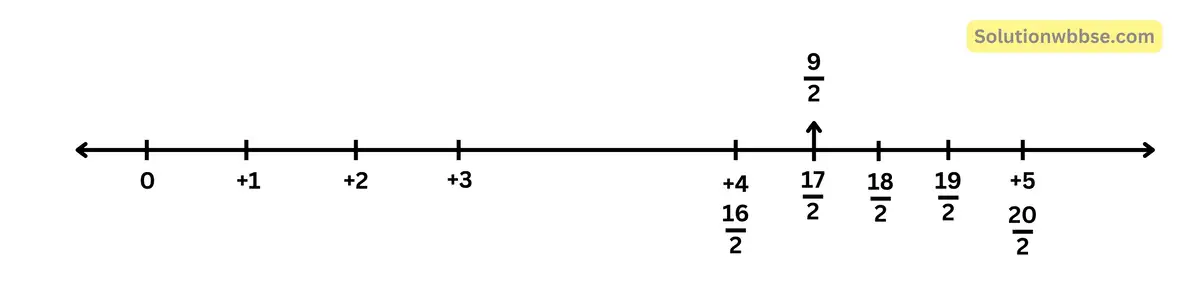

6. 1 ও 2-এর মধ্যে 6 টি মূলদ সংখ্যা লিখি ও সংখ্যারেখায় বসাই।

(i) \(\frac12\left(1+2\right)=\frac32\)

(ii) \(\frac12\left(1+\frac32\right)=\frac54\)

(iii) \(\frac12\left(\frac32+2\right)=\frac74\)

(iv) \(\frac12\left(\frac32+\frac74\right)=\frac12\left(\frac{13}4\right)=\frac{13}8\)

(v) \(\frac12\left(\frac74+\frac{13}8\right)=\frac12\left(\frac{27}8\right)=\frac{27}{16}\)

(vi) \(\frac12\left(\frac54+\frac{13}8\right)=\frac{23}{16}\)

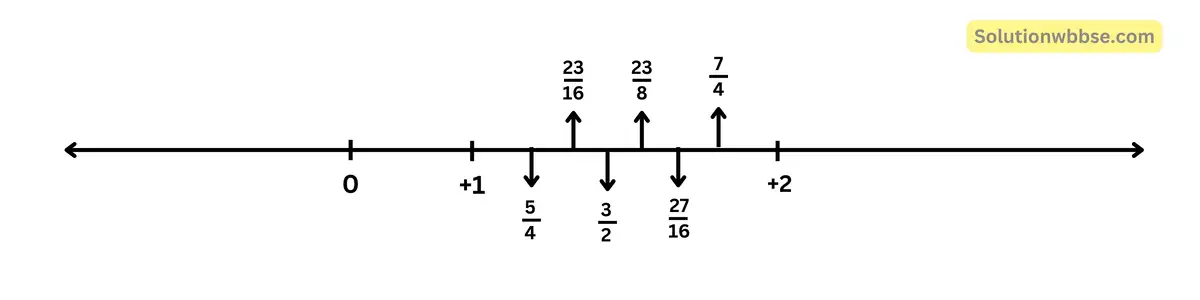
7. \(\frac15\) ও \(\frac14\) -এর মধ্যে 3টি মূলদ সংখ্যা লিখি।

উত্তর – \(\frac12\left(\frac15+\frac14\right)=\frac9{40}\)

\(\frac12\left(\frac15+\frac9{40}\right)=\frac{17}{80}\\\)\(\frac12\left(\frac9{40}+\frac14\right)=\frac{19}{80}\\\)

∴ \(\frac15\) ও \(\frac14\) -এর মধ্যে 3টি \(\frac9{40},\frac{17}{80},\frac{19}{80}\) মূলদ সংখ্যা।

8. বক্তব্যটি সত্য হলে (T) ও মিথ্যা হলে (F) পাশে বসাই।

(i) দুটি পূর্ণসংখ্যা যোগ, বিয়োগ ও গুণ করে পূর্ণসংখ্যা পাই।

উত্তর – সত্য (T)

(ii) দুটি পূর্ণসংখ্যা ভাগ করে সর্বদাই পূর্ণসংখ্যা পাই।

উত্তর – মিথ্যা (F)

9. দুটি মূলদ সংখ্যার যোগ, বিয়োগ, গুণ ও ভাগ (ভাজক শূন্য নয়) করলে কী সংখ্যা পাবো লিখি।

উত্তর – মনে করি, \(x=\frac pq\), \(y=\frac rx\) দুটি মূলদ সংখ্যা।

\(x+y=\frac pq+\frac rs=\frac{ps+rq}{qs}\) মূলদ সংখ্যা।

\(x-y=\frac pq-\frac rs=\frac{ps-rq}{qs}\) মূলদ সংখ্যা।

\(xy=\frac pq\times\frac rs=\frac{pr}{qs}\) মূলদ সংখ্যা।

\(\frac xy=\frac pq\div\frac rs=\frac pq\times\frac sr=\frac{ps}{qr}\) মূলদ সংখ্যা।

---

এই আর্টিকেলে নবম শ্রেণির গণিতের ‘বাস্তব সংখ্যা’ অধ্যায়ের ‘কষে দেখি – 1.1’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।

কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করতে পারেন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।