পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) নবম শ্রেণির গণিত পাঠ্যবইয়ের প্রথম অধ্যায় হলো ‘বাস্তব সংখ্যা’। এই পোস্টে ‘কষে দেখি – 1.3’-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. ভাগ না করে নীচের কোন সংখ্যাগুলির দশমিক বিস্তার সসীম হবে লিখি
(i) \( \frac{17}{80} \)
সমাধান –
কোনো মূলদ সংখ্যার হরের উৎপাদক যদি শুধুমাত্র 2 এবং 5 হয় তবে সংখ্যাটিকে দশমিক বিস্তার করলে সসীম সংখ্যা পাওয়া যাবে।
\( \frac{17}{80} \) এর হর \( = 80 = 2 \times 2 \times 2 \times 2 \times 5 \)
অর্থাৎ হরের উৎপাদক শুধুমাত্র 2 এবং 5।
\( \therefore \) \( \frac{17}{80} \) সংখ্যাটির দশমিক বিস্তার সসীম হবে।
(ii) \( \frac{13}{24} \)
সমাধান –
কোনো মূলদ সংখ্যার হরের উৎপাদক যদি শুধুমাত্র 2 এবং 5 হয় তবে সংখ্যাটিকে দশমিক বিস্তার করলে সসীম সংখ্যা পাওয়া যাবে। \( \frac{13}{24} \) এর হর \( = 24 = 2 \times 2 \times 2 \times 3 \) অর্থাৎ হরের উৎপাদক শুধুমাত্র 2 এবং 3।
\( \therefore \) \( \frac{13}{24} \) সংখ্যাটির দশমিক বিস্তার অসীম হবে।
(iii) \( \frac{17}{12} \)
সমাধান –
কোনো মূলদ সংখ্যার হরের উৎপাদক যদি শুধুমাত্র 2 এবং 5 হয় তবে সংখ্যাটিকে দশমিক বিস্তার করলে সসীম সংখ্যা পাওয়া যাবে।
\( \frac{17}{12} \) এর হর \( = 12 = 2 \times 2 \times 3 \)
অর্থাৎ হরের উৎপাদক শুধুমাত্র 2 এবং 3।
\( \therefore \) \( \frac{17}{12} \) সংখ্যাটির দশমিক বিস্তার অসীম হবে।
(iv) \( \frac{16}{125} \)
সমাধান –
কোনো মূলদ সংখ্যার হরের উৎপাদক যদি শুধুমাত্র 2 এবং 5 হয় তবে সংখ্যাটিকে দশমিক বিস্তার করলে সসীম সংখ্যা পাওয়া যাবে।
\( \frac{16}{125} \) এর হর \( = 125 = 5 \times 5 \times 5 \)
অর্থাৎ হরের উৎপাদক শুধুমাত্র 5।
\( \therefore \) \( \frac{16}{125} \) সংখ্যাটির দশমিক বিস্তার সসীম হবে।
(v) \( \frac{4}{35} \)
সমাধান –
কোনো মূলদ সংখ্যার হরের উৎপাদক যদি শুধুমাত্র 2 এবং 5 হয় তবে সংখ্যাটিকে দশমিক বিস্তার করলে সসীম সংখ্যা পাওয়া যাবে।
\( \frac{4}{35} \) এর হর \( = 35 = 5 \times 7 \)
অর্থাৎ হরের উৎপাদক শুধুমাত্র 5 এবং 7।
\( \therefore \) \( \frac{4}{35} \) সংখ্যাটির দশমিক বিস্তার অসীম হবে।
2. নীচের প্রত্যেক সংখ্যার দশমিক বিস্তার করি ও কি ধরনের দশমিক বিস্তার পাব লিখি।
(i) \( \frac{1}{11} \)
(ii) \( \frac{5}{8} \)
(iii) \( \frac{3}{13} \)
(iv) \( 3\frac{1}{8} \)
(v) \( \frac{2}{11} \)
(vi) \( \frac{7}{25} \)
(i) \( \frac{1}{11} \)
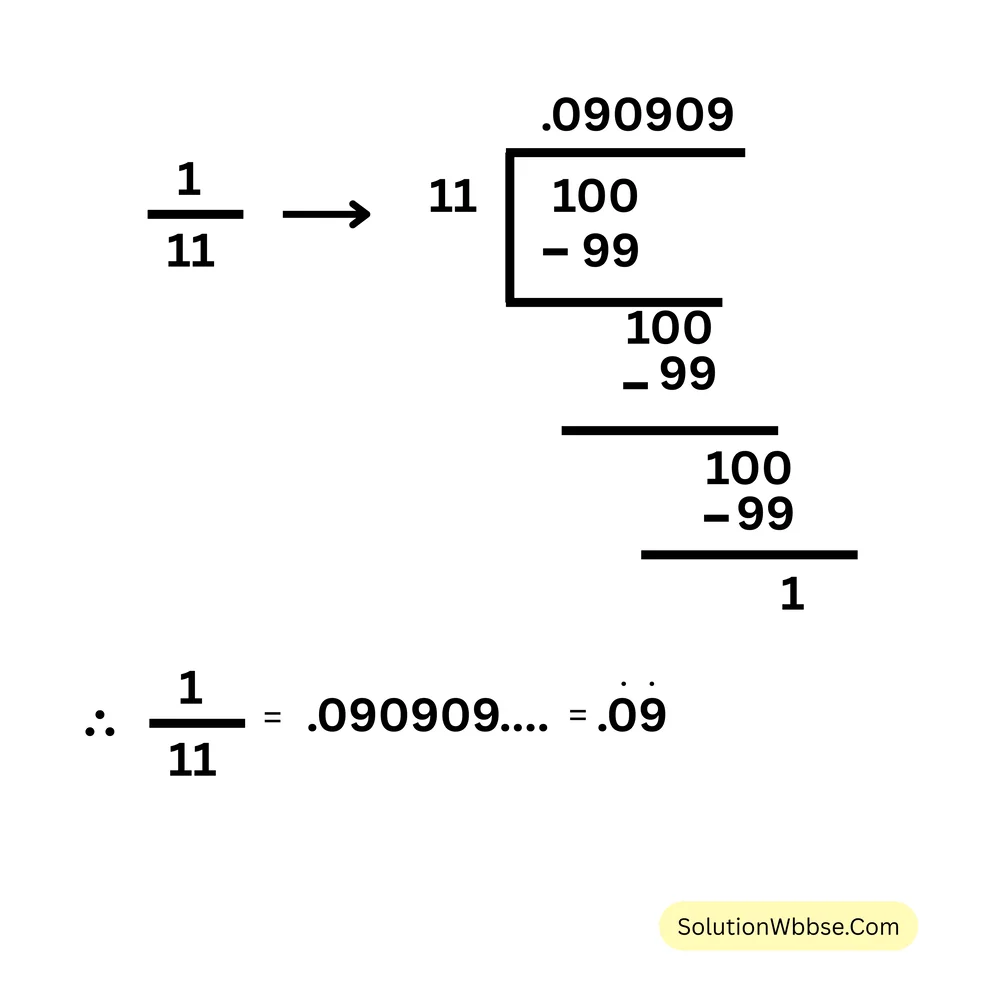
(ii) \( \frac{5}{8} \)
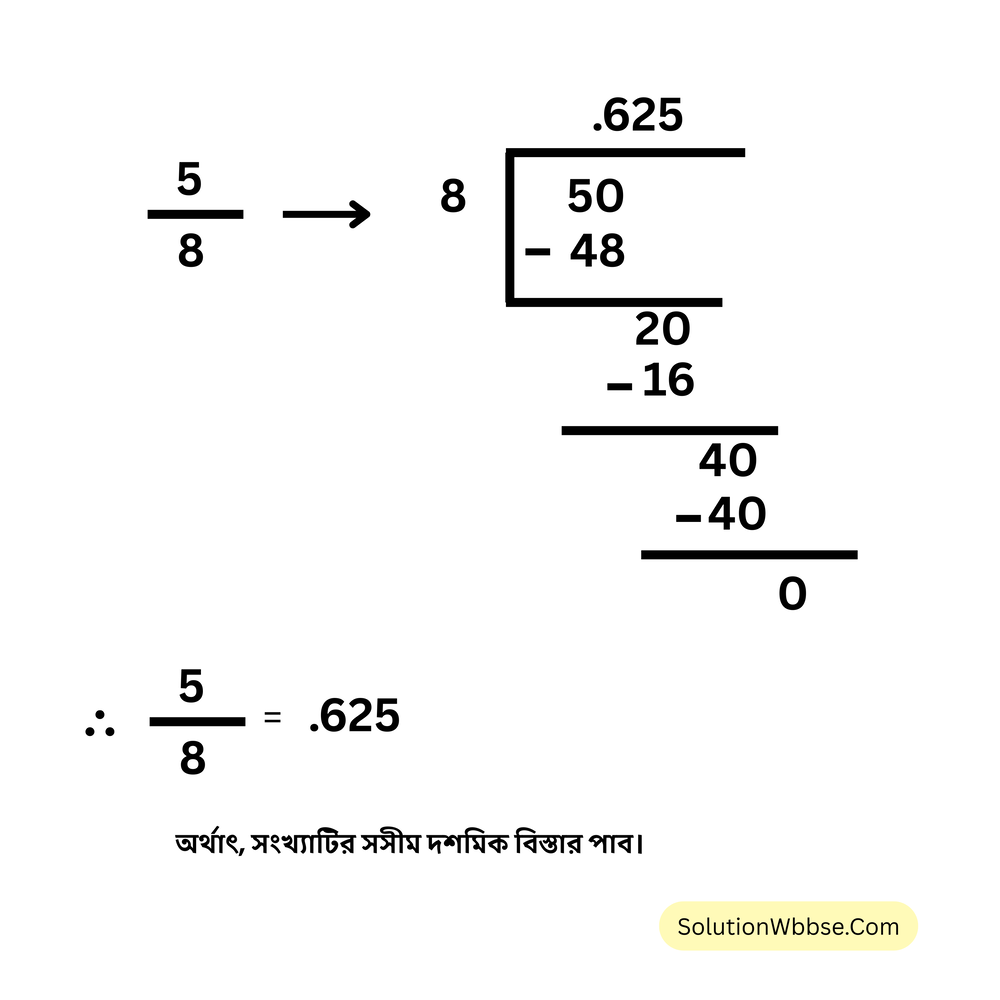
(iii) \( \frac{3}{13} \)
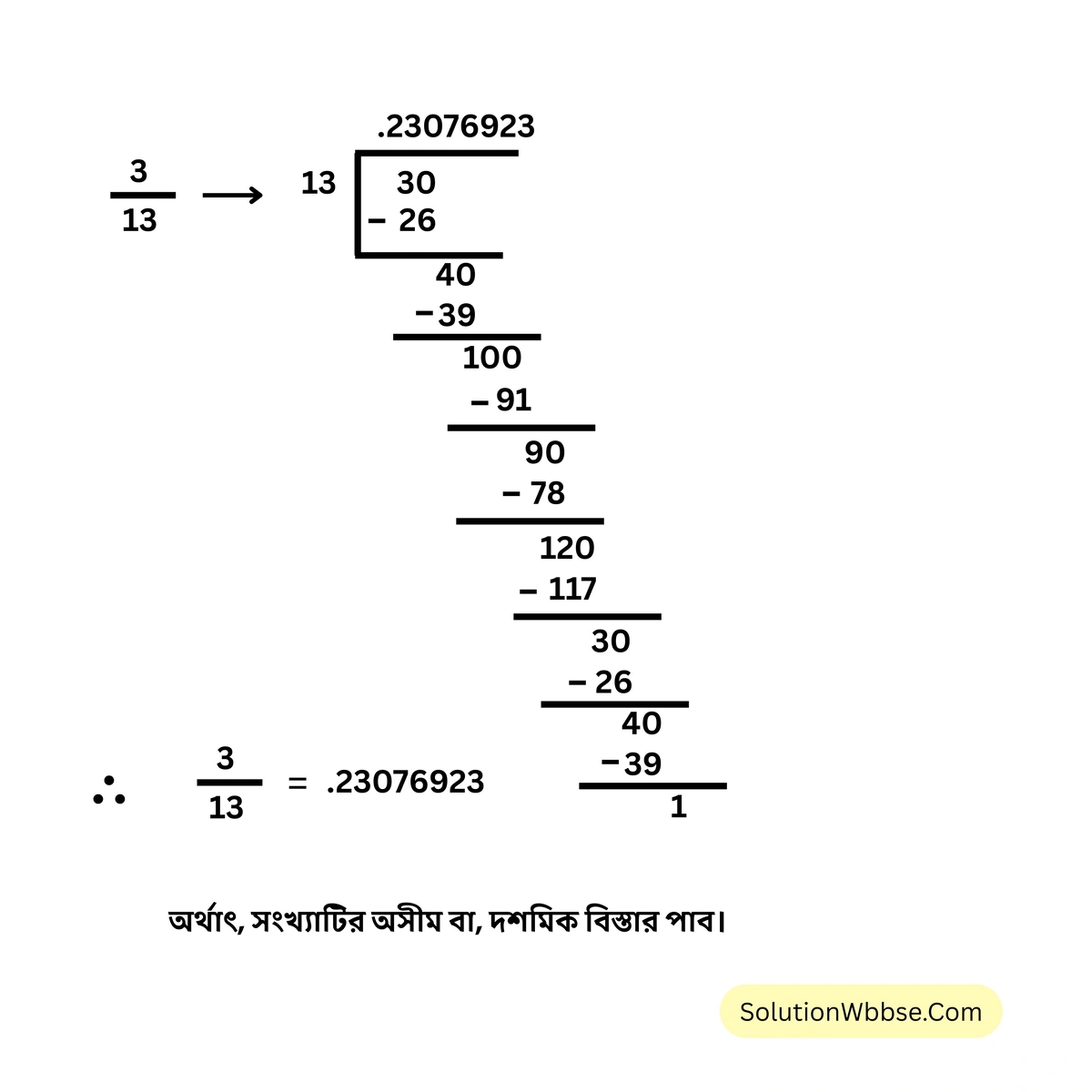
(iv) \( 3\frac{1}{8} \)
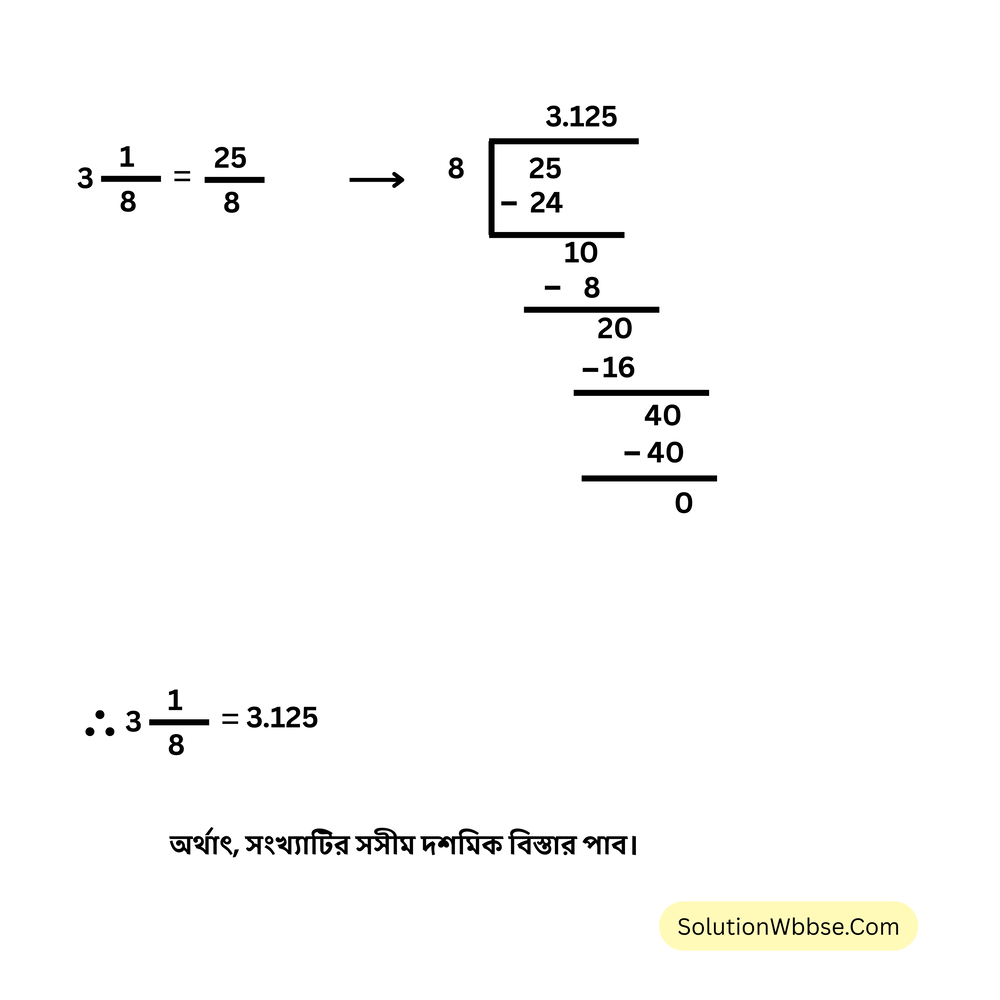
(v) \( \frac{2}{11} \)
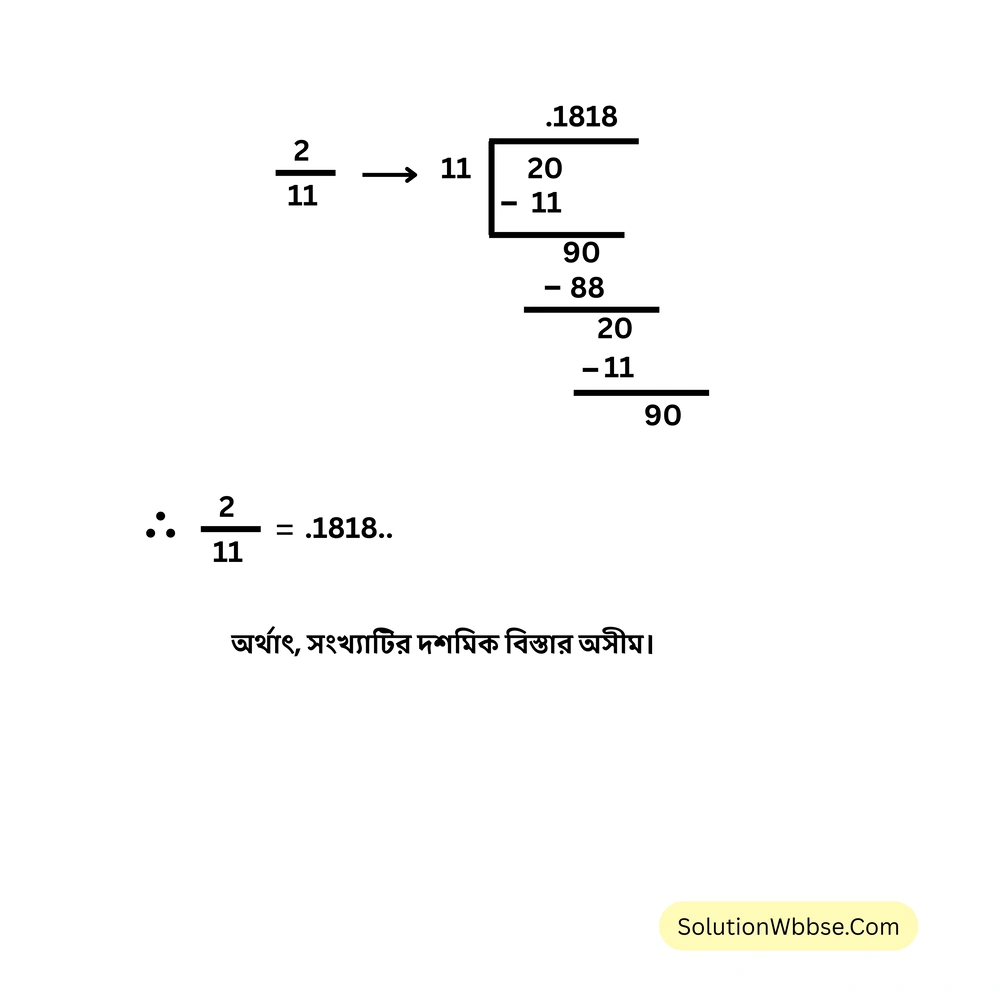
(vi) \( \frac{7}{25} \)
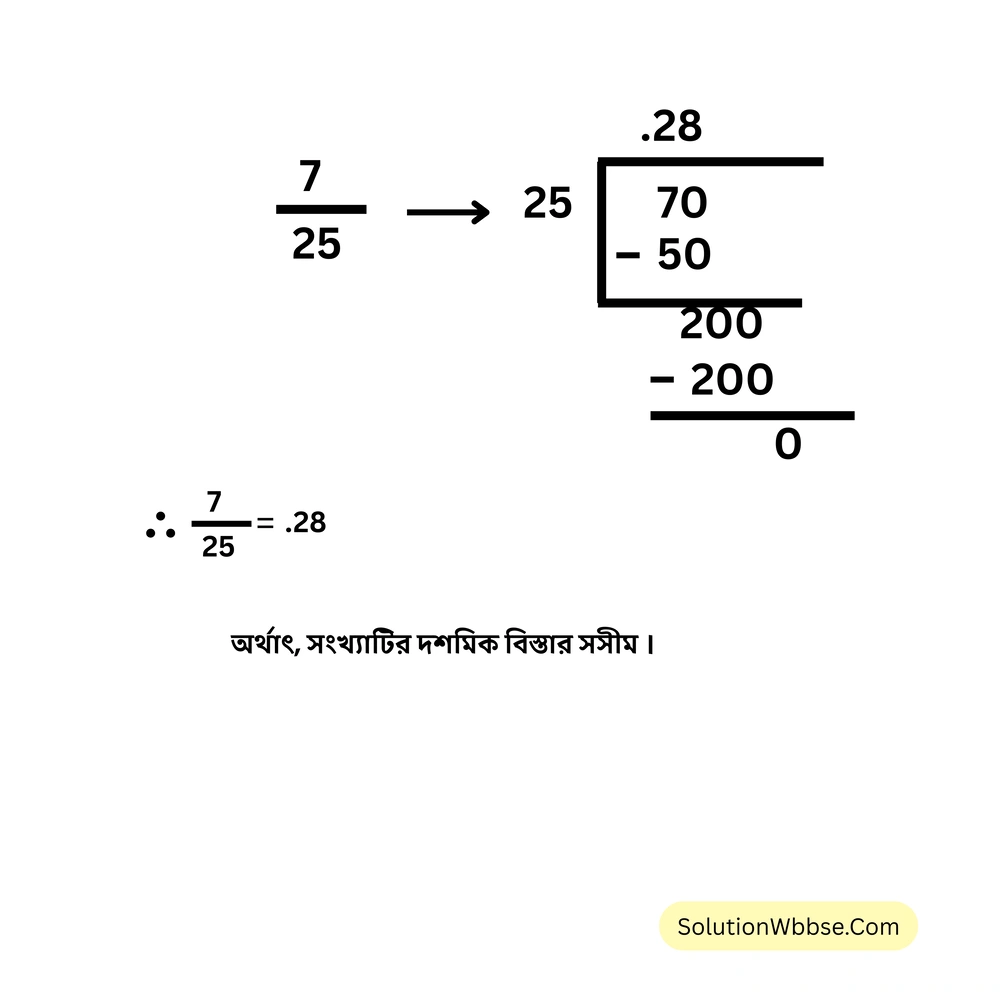
3. নিচের প্রতিটি সংখ্যা p/q আকারে প্রকাশ করি যেখানে p ও q পূর্ণ সংখ্যা এবং q ≠ 0 ।
(i) \(0.\dot{3}\)
(ii) \(1.\dot{3}\)
(iii) \(0.5\dot{4}\)
(iv) \(0.\dot{3}\dot{4}\)
(v) \(3.\dot{1}\dot{4}\)
(vi) \(0.1\dot{7}\)
(vii) \(0.4\dot{7}\)
(viii) \(0.\dot{5}\dot{4}\)
(ix) \(0.\dot{0}0\dot{1}\)
(x) \(0.\dot{1}6\dot{3}\)
সমাধান –
(i) \(0.\dot{3}\)
সমাধান – ধরি, \(0.\dot{3}=x\)
\(x= 0.3333… ——— (i)\)\(\therefore 10x=3.3333… ———(ii)\)(ii) থেকে (i) বিয়োগ করে পাই,
\(10x-x=3.000… – 0.333…\)বা, \(9x=3\)
বা, \(x = \frac{3}{9} = \frac{1}{3}\)
\(\therefore 0.\dot{3} = \frac{3}{9} = \frac{1}{3}\)(ii) \(1.\dot{3}\)
সমাধান –
ধরি, \(1.\dot{3}=x\)
\(\therefore x=1.3333… ——- (i)\)\(\therefore 10x=13.333… ——- (ii)\)(ii) থেকে (i) বিয়োগ করে পাই,
\(10x-x=13.333… – 1.333…\)বা, \(9x=12\)
বা, \(x= \frac{12}{9} = \frac{4}{3}\)
\(\therefore 1.\dot{3} = \frac{4}{3}\)(iii) \(0.5\dot{4}\)
সমাধান –
ধরি, \(0.5\dot{4} = x\)
\(\therefore x=0.5444… ——- (i)\)\(\therefore 10x=5.444… ——- (ii)\)এবং \(100x=5.444… ——- (iii)\)
(iii) থেকে (ii) বিয়োগ করে পাই,
\(100x- 10x =54.444… – 5.444…\)বা, \(90x=49\)
বা, \(x= \frac{49}{90}\)
(iv) \(0.\dot{3}\dot{4}\)
সমাধান –
ধরি, \(0.\dot{3}\dot{4}=x\)
\(\therefore x=0.343434… ——- (i)\)\(\therefore 100x=34.3434… ——- (ii)\)(ii) থেকে (i) বিয়োগ করে পাই,
\(100x- x =34.3434… – 0.3434…\)বা, \(99x=34\)
বা, \(x= \frac{34}{99}\)
(v) \(3.\dot{1}\dot{4}\)
সমাধান –
ধরি, \(3.\dot{1}\dot{4}=x\)
\(\therefore x=3.141414… ——- (i)\)\(\therefore 100x=314.141414… ——- (ii)\)(ii) থেকে (i) বিয়োগ করে পাই,
\(100x-x= 314.141414….. – 0.141414…\)বা, \(99x = 314\)
বা, \(x= \frac{314}{99}\)
(vi) \(0.1\dot{7}\)
সমাধান –
ধরি, \(0.1\dot{7} =x\)
\(\therefore x= 0.177777…… –(i)\)\(\therefore 10x= 1.77777….. –(ii)\)এবং \(100x = 17.77777…. –(iii)\)
(iii) থেকে (ii) বিয়োগ করে পাই,
\(100x-10x=17.77777…. – 1.77777….\)বা, \(90x= 16\)
বা, \(x = \frac{16}{90}\)
বা, \(x = \frac{8}{45}\)
\(\therefore 0.1\dot{7} = \frac{8}{45}\)(vii) \(0.4\dot{7}\)
সমাধান –
ধরি, \(0.4\dot{7} =x\)
\(\therefore x = 0.477777…. –(i)\)\(\therefore 10x= 4.77777….. –(ii)\)এবং \(100x =47.77777…. –(iii)\)
(iii) থেকে (ii) বিয়োগ করে পাই,
\(100x-10x= 47.77777…. – 4.77777….\)বা, \(90x = 43\)
বা, \(x = \frac{43}{90}\)
\(\therefore 0.4\dot{7} = \frac{43}{90}\)(viii) \(0.\dot{5}\dot{4}\)
সমাধান –
ধরি, \(0.\dot{5}\dot{4}=x\)
\(\therefore x=0.545454… ——- (i)\)\(\therefore 100x=54.545454… ——- (ii)\)(ii) থেকে (i) বিয়োগ করে পাই,
\(100x- x =54.545454… – 0.545454…\)বা, \(99x=54\)
বা, \(x= \frac{54}{99}\)
\(\therefore 0.\dot{5}\dot{4} = \frac{54}{99} = \frac{6}{11}\)(ix) \(0.\dot{0}0\dot{1}\)
সমাধান – ধরি, \(x=0.\dot{0}0\dot{1}\)
\(\therefore x=0.001001001… ——- (i)\)\(1000x=1.001001001… ——- (ii)\)(ii) থেকে (i) বিয়োগ করে পাই,
বা, \(999x=1\)
বা, \(x= \frac{1}{999}\)
(x) \(0.\dot{1}6\dot{3}\)
সমাধান –
ধরি, \(x=0.\dot{1}6\dot{3}\)
\(\therefore x= .163163163… ——- (i)\)\(1000x=163.163163… ——- (ii)\)(ii) থেকে (i) বিয়োগ করে পাই,
বা, \(999x=163\)
বা, \(x= \frac{163}{999}\)
4. 4 টি সংখ্যা লিখি যাদের দশমিক বিস্তার অসীম ও অনাবৃত [ non recurring and non terminating] ।
উত্তর – \(\sqrt{3}, \sqrt{5}, \sqrt{7}, \sqrt{17}\) সংখ্যাগুলির দশমিক বিস্তার অসীম ও অনাবৃত ।
5. 5/7 ও 9/7 এর মধ্যে 3 টি ভিন্ন অমূলদ সংখ্যা লিখি।
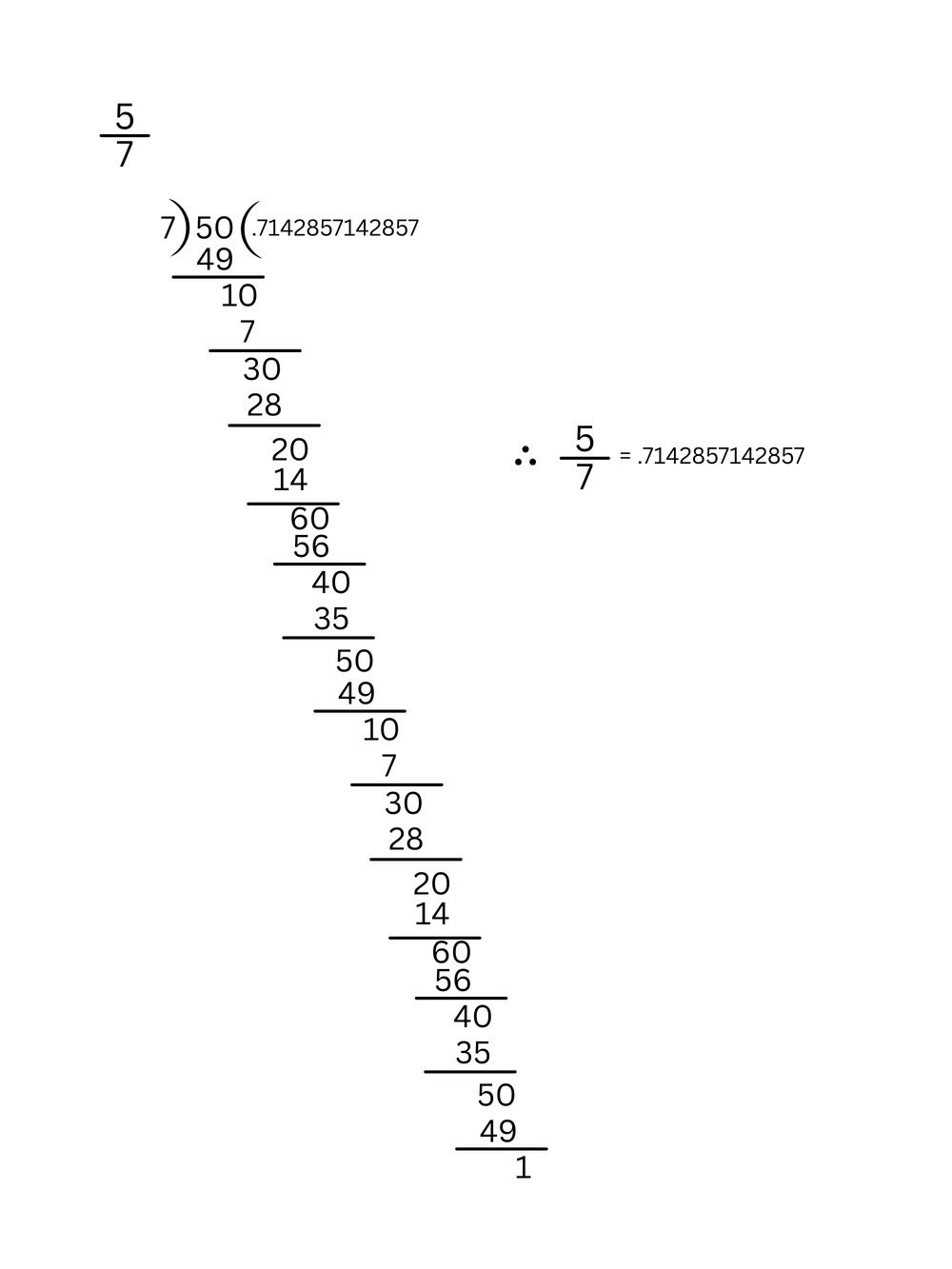
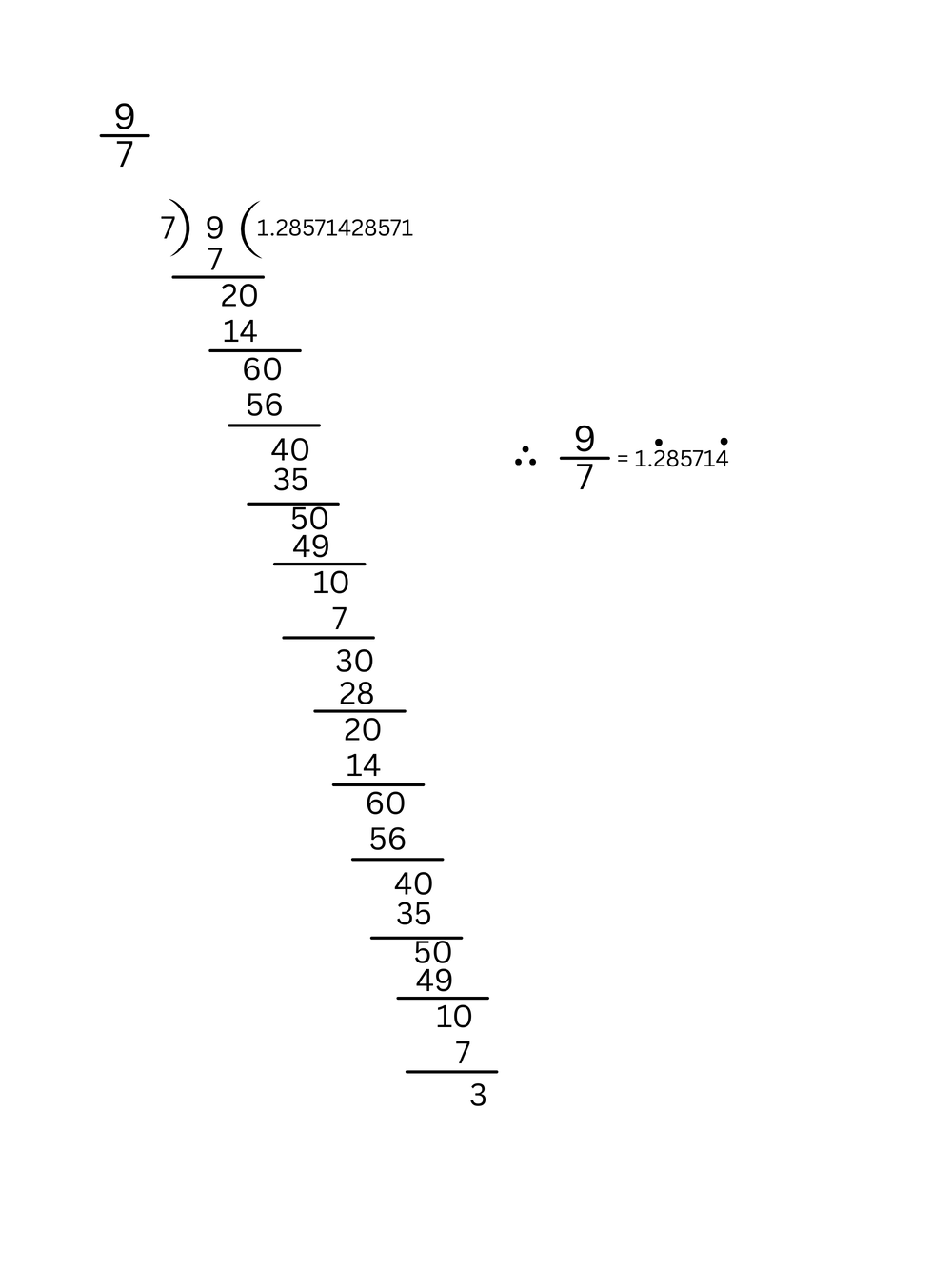
\(\therefore \frac{5}{7}\) এবং \(\frac{9}{7}\) এর মধ্যবর্তী তিনটি ভিন্ন অমূলদ সংখ্যা হল
(i) \(0.808008000………\)
(ii) \(0.909009000………\)
(iii) \(0.959559555………\)
6. 3/7 ও 1/11 এর মধ্যে 2 টি ভিন্ন অমূলদ সংখ্যা লিখি।
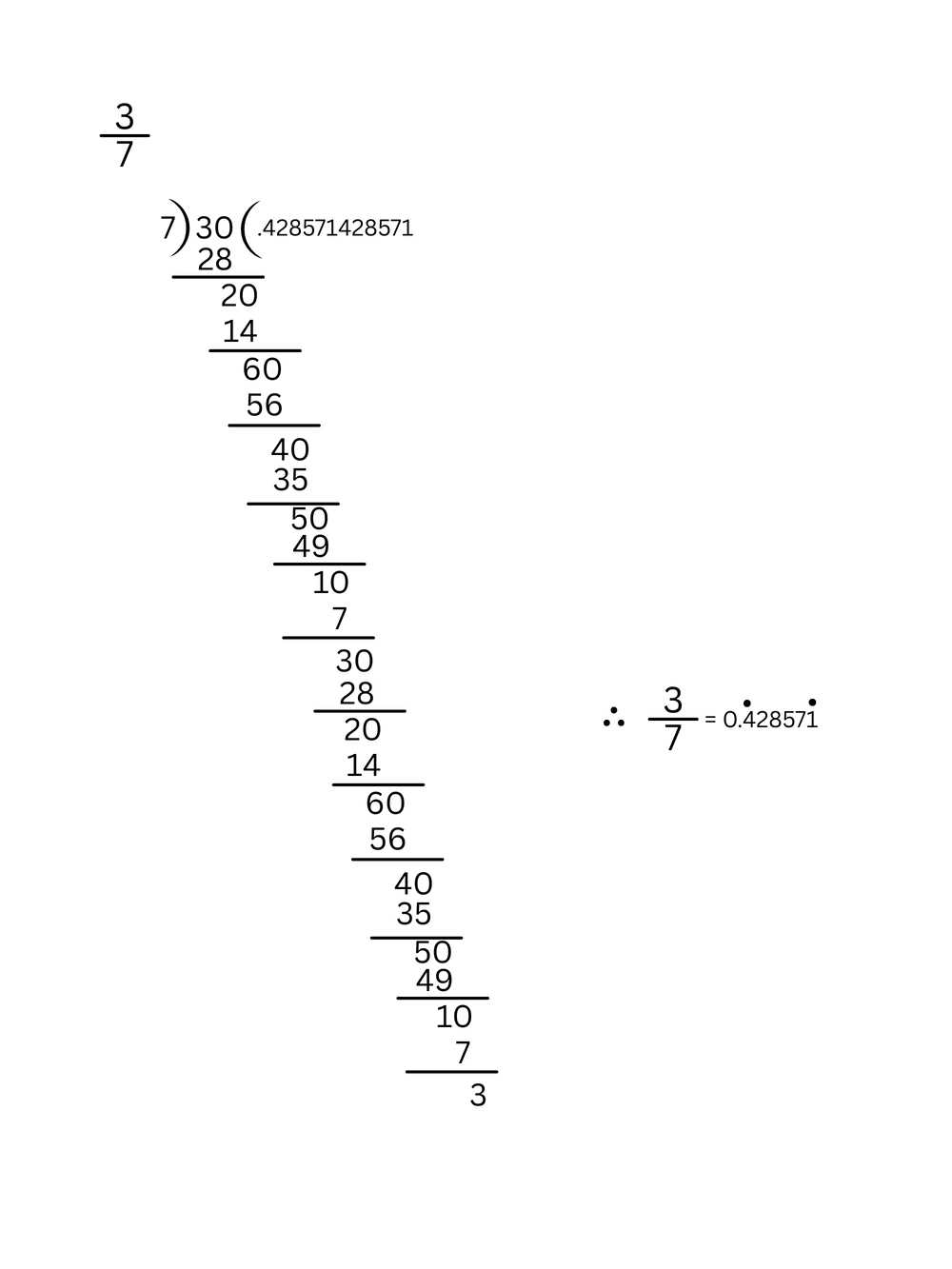
\(\therefore\) \(\frac{3}{7}\) এবং \(\frac{1}{11}\) এর মধ্যে দুটি ভিন্ন অমূলদ সংখ্যা হল ——
(i) \(0.101001000………\)
(ii) \(0.202002000………\)
7. নীচের সংখ্যা গুলির মধ্যে কোনটি মূলদ সংখ্যা ও কোনটি অমূলদ সংখ্যা লিখি ।
(i) \(\sqrt{47}\)
উত্তর – অমূলদ
(ii) \(\sqrt{625}\)
উত্তর – \(\sqrt{625} = 25\) , মূলদ সংখ্যা ।
(iii) \(6.5757…\)
উত্তর – প্রদত্ত সংখ্যাটি একটি আবৃত সংখ্যা তাই এটি একটি মূলদ সংখ্যা ।
(iv) \(1.1010010001..\)
উত্তর – প্রদত্ত সংখ্যাটি একটি অনাবৃত দশমিক সংখ্যা তাই এটি একটি অমূলদ সংখ্যা ।
8. সংখ্যারেখায় নীচের সংখ্যা গুলি স্থাপন করি।
(i) 5.762
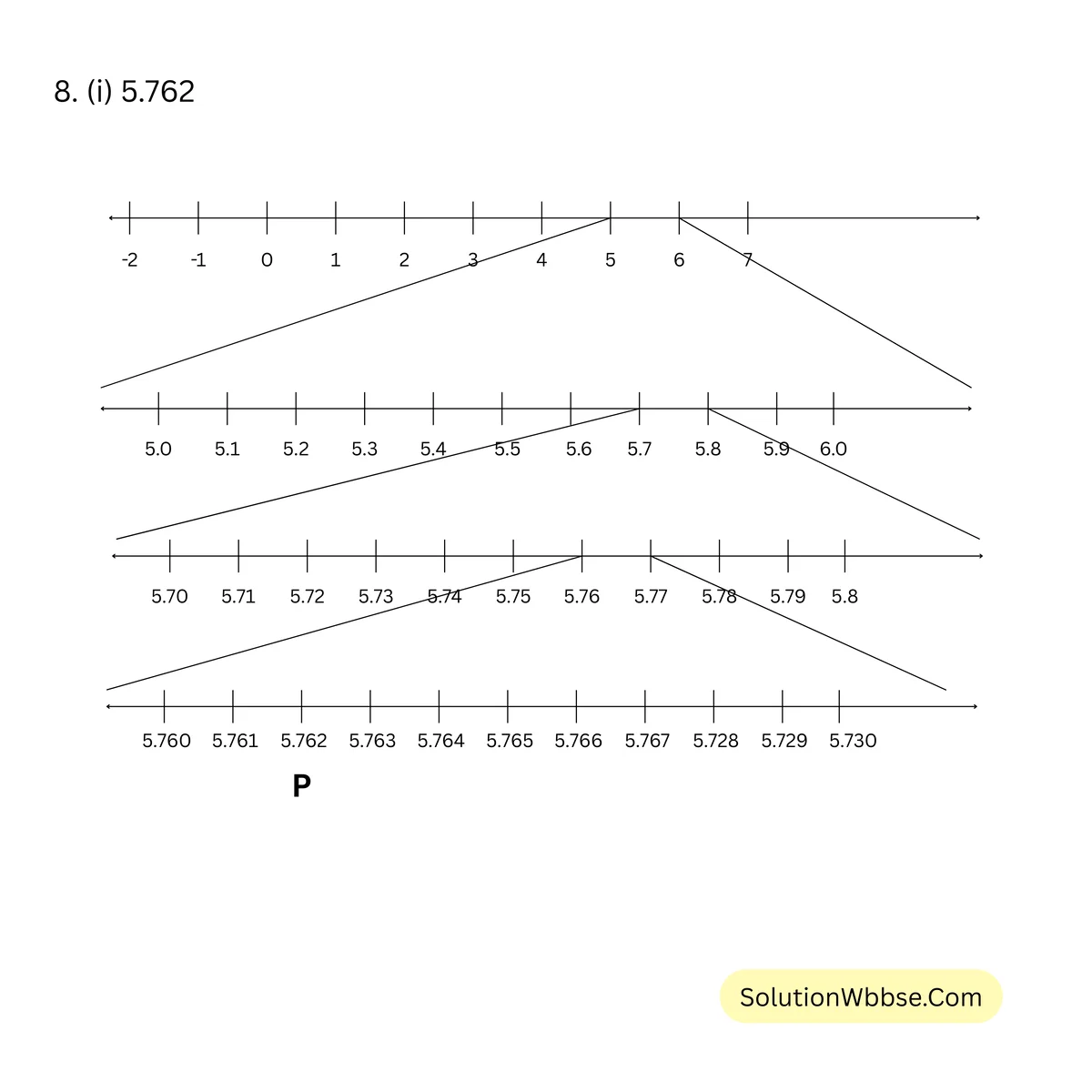
(ii) 2.321
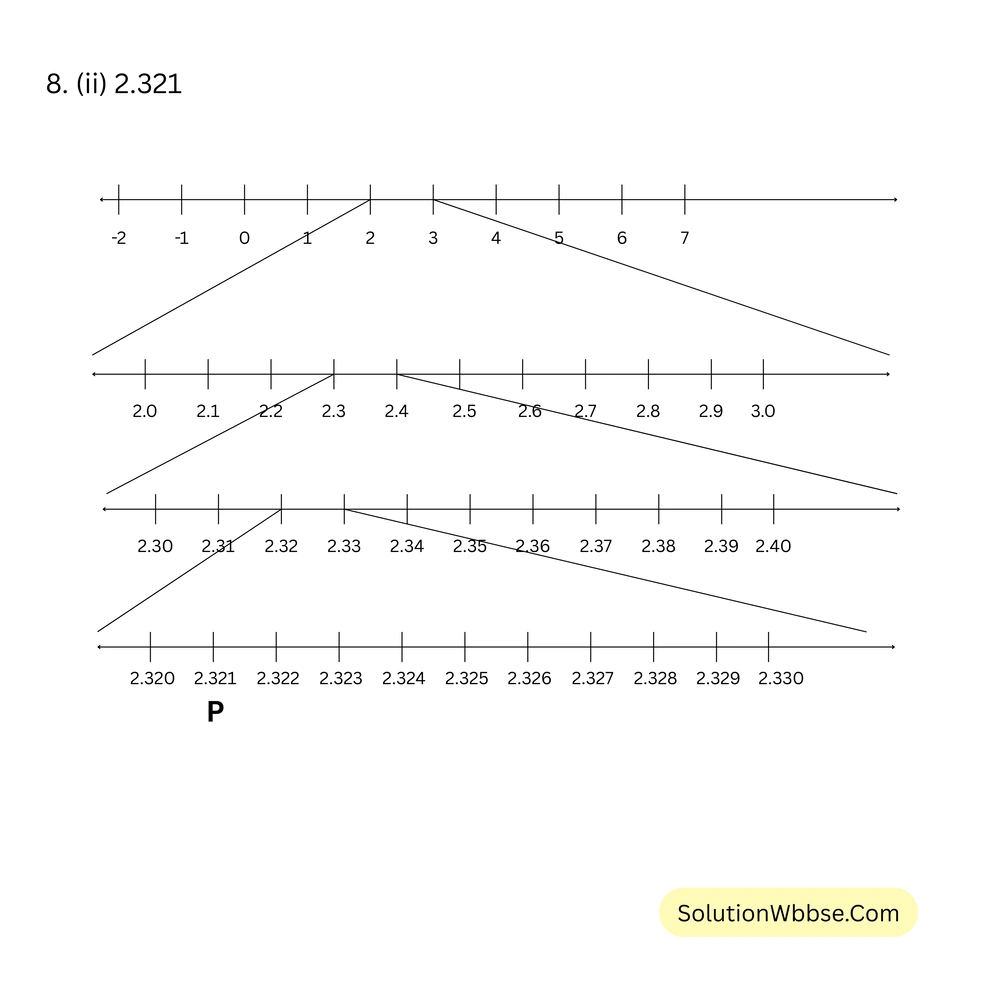
8. (iii) 1.052
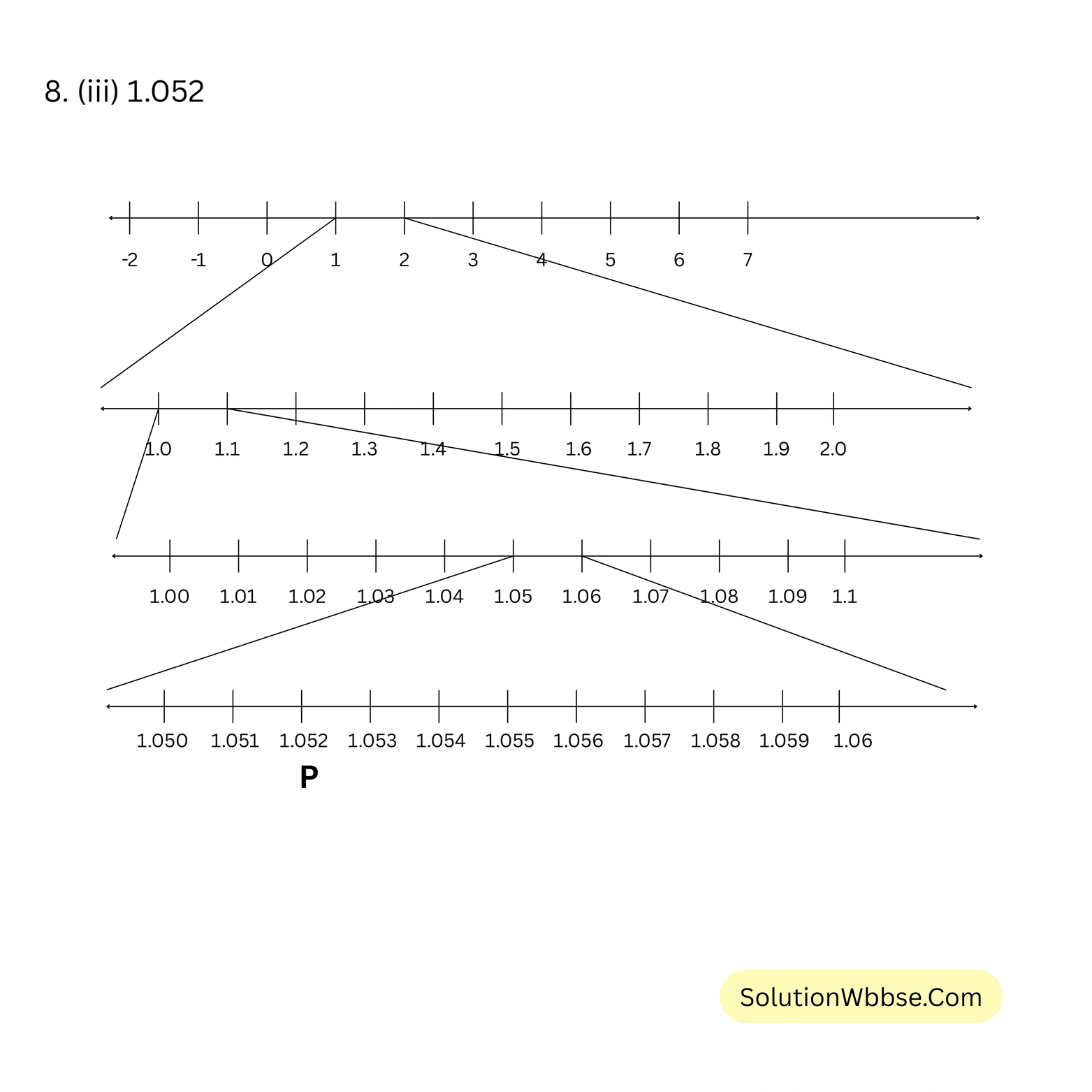
8. (iv) 4.178
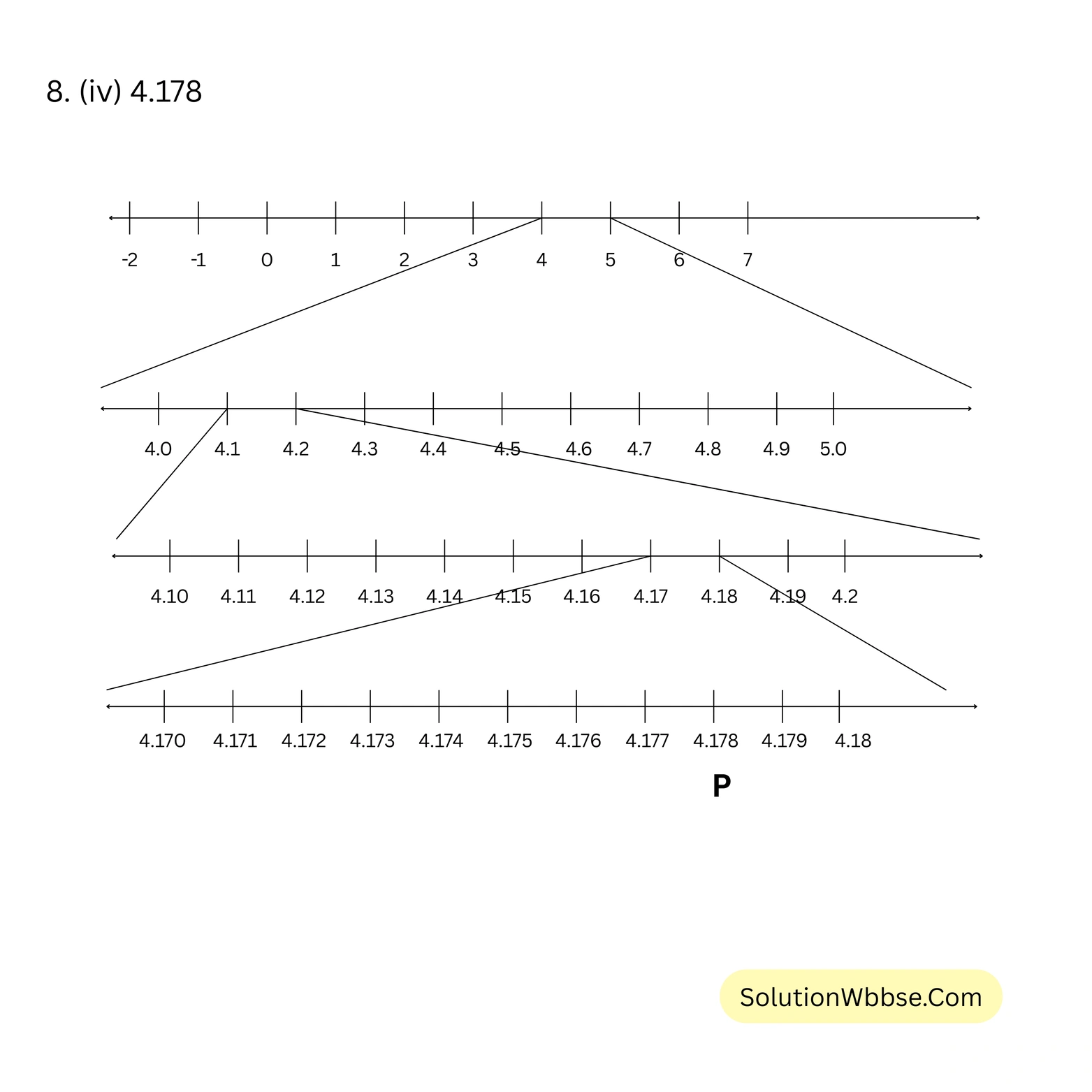
9. \(2.\dot{2}\dot{6}\) ও \(5.5\dot{4}\) সংখ্যাদুটি 4 দশমিক স্থান পর্যন্ত সংখ্যারেখায় স্থাপন করি।
\(2.\dot{2}\dot{6}\) = 2.262626
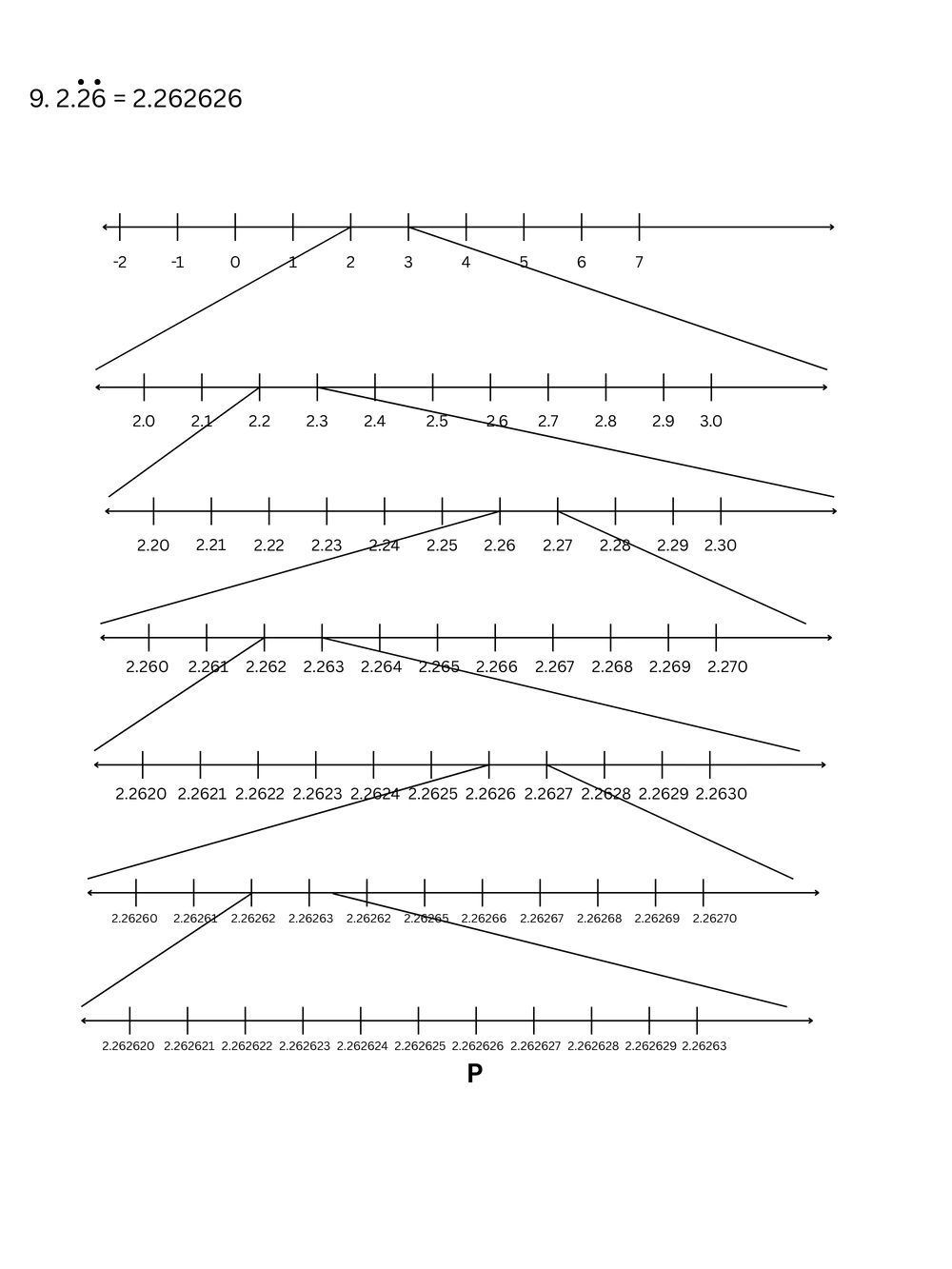
\(5.5\dot{4}\) = 5.5444
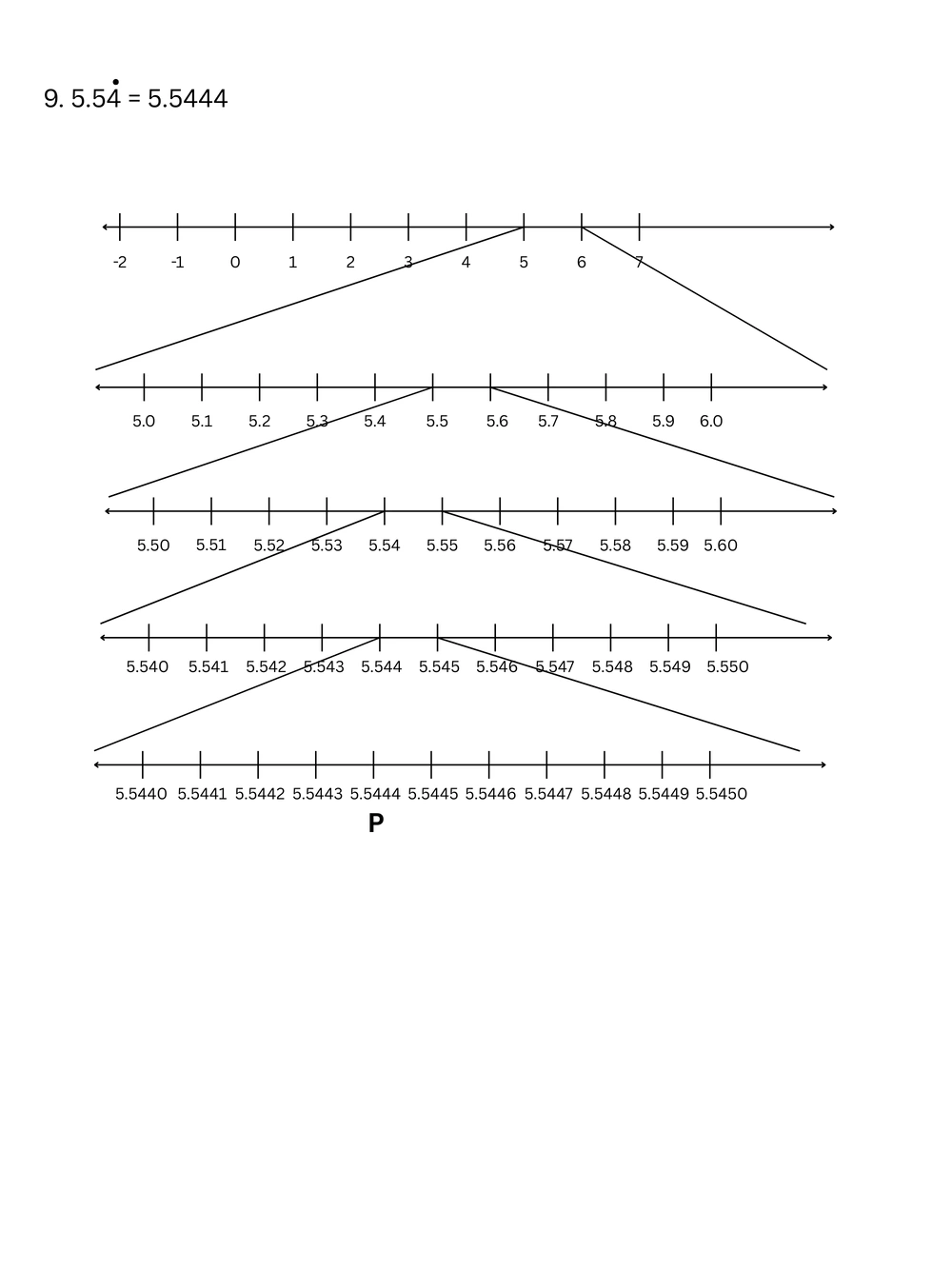
10. \(0.232332333233332…\) এবং \(0.212112111211112…\) সংখ্যা দুটির মধ্যে দুটি মূলদ সংখ্যা লিখি।
উত্তর – \(0.232332333233332…\) এবং \(0.212112111211112…\) সংখ্যা দুটির মধ্যে দুটি মূলদ সংখ্যা হলো \(0.22\) এবং \(0.23\)।
11. \(0.2101\) এবং \(0.2222…\) বা \(0.\dot{2}\) এর মধ্যে দুটি মূলদ সংখ্যা লিখি।
উত্তর – \(0.2101\) এবং \(0.2222…\) বা \(0.\dot{2}\) – এর মধ্যে দুটি মূলদ সংখ্যা হল \(0.215\) এবং \(0.22\)।
12. স্বাভাবিক সংখ্যা, অখণ্ড সংখ্যা , পূর্ণ সংখ্যা, মূলদ সংখ্যা ,অমূলদ সংখ্যা ও বাস্তব সংখ্যা নিয়ে দশটি সত্য বক্তব্য ও দশটি মিথ্যা বক্তব্য লিখি।
উত্তর –
10 টি সত্য বক্তব্য
- 0 একটি স্বাভাবিক সংখ্যা নয় ।
- 1 হল ক্ষুদ্রতম স্বাভাবিক সংখ্যা ।
- বাস্তব সংখ্যা সসীম ।
- দুটি অখণ্ড সংখ্যার গুণফল অখণ্ড সংখ্যা হবে ।
- শূন্য অপেক্ষা বড় পূর্ণসংখ্যা কে ধনাত্মক পূর্ণসংখ্যা বলে এবং শূন্য অপেক্ষা ছোটো পূর্ণসংখ্যা কে ঋণাত্মক পূর্ণসংখ্যা বলে ।
- যে সকল সংখ্যা কে \(\frac{p}{q}\) আকারে প্রকাশ করা যায় যেখানে \(p\) এবং \(q\) পূর্ণসংখ্যা এবং \(q \neq 0\), তাদের মূলদ সংখ্যা বলে।
- সকল পূর্ণসংখ্যাই মূলদ সংখ্যা ।
- যে সকল সংখ্যা কে \(\frac{p}{q}\) আকারে প্রকাশ করা যায় না যেখানে \(p\) এবং \(q\) পূর্ণসংখ্যা এবং \(q \neq 0\), তাদের অমূলদ সংখ্যা বলে।
- সকল মূলদ এবং অমূলদ সংখ্যাই বাস্তব সংখ্যা ।
- দুটি অমূলদ সংখ্যার বিয়োগফল সর্বদা অমূলদ সংখ্যা হয় না ।
10 টি মিথ্যা বক্তব্য
- দুটি অমূলদ সংখ্যার গুনফল সর্বদা অমূলদ সংখ্যা হবে ।
- দুটি অমূলদ সংখ্যার যোগফল সর্বদা অমূলদ সংখ্যা হবে ।
- সকল বাস্তব সংখ্যার দশমিকে বিস্তার সম্ভব নয় ।
- প্রতিটি বাস্তব সংখ্যাই অমূলদ সংখ্যা ।
- 0 একটি স্বাভাবিক সংখ্যা ।
- মূলদ সংখ্যা সসীম ।
- \(\sqrt{47}\) একটি মূলদ সংখ্যা ।
- দুটি অমূলদ সংখ্যার মধ্যে একটি মাত্র অমূলদ সংখ্যা আছে ।
- দুটি মূলদ সংখ্যার মধ্যে কোনো মূলদ সংখ্যা নেই ।
- \(\sqrt{3}\) এর দশমিক বিস্তার একটি সসীম অথবা আবৃত দশমিক ।
13. একটি গুণ করতে 2 টাকা ও একটি যোগ করতে 1 টাকা লাগলে নীচের সংখ্যামালাগুলির মান নির্ণয় করতে কত টাকা লাগবে এবং কী নিয়ম ব্যবহার করে সবচেয়ে কম কত টাকায় সংখ্যামালাটির মান বের করা যায় দেখি।
(i) \(3x^2+2x+1\), যখন \(x=5\)
(ii) \(2x^3+3x^2+2x+3\), যখন \(x=7\)
সমাধান –
(i) \(3x^2+2x+1\), যখন \(x=5\)
\(3(5)^2+2(5)+1=3 \times 5 \times 5 + 2 \times 5 + 1\),
এখানে 3টি গুণ এবং 2টি যোগ করতে হচ্ছে তাই \((3 \times 2+2 \times 1)=8\) টাকা লাগবে।
কিন্তু যদি বিচ্ছেদ নিয়ম প্রয়োগ করি তবে \(3x^2+2x+1=x(3x+2)+1\), এখানে দুটি গুণ এবং দুটি যোগ করতে হচ্ছে তাই
\((2 \times 2+2 \times 1)=6\) টাকা লাগবে।
সুতরাং এক্ষেত্রে বিচ্ছেদ নিয়ম ব্যবহার করলে সবচেয়ে কম টাকা লাগবে।
(ii) \(2x^3+3x^2+2x+3\), যখন \(x=7\)
\(2(7)^3+3(7)^2+2 \times 7 +3 = 2 \times 7 \times 7 \times 7 + 3 \times 7 \times 7 + 2 \times 7+3\)এক্ষেত্রে 6টি গুণ এবং 3টি যোগ করতে হচ্ছে তাই \((6 \times 2+3 \times 1)=15\) টাকা লাগবে।
আবার,
\(2x^3+3x^2+2x+3\)= \(2x^3+2x+3x^2+3\)
= \(2x(x^2+1)+3(x^2+1)\)
= \((x^2+1)(2x+3)\)
= \((7 \times 7+1) \times (2 \times 7+3)\)
এক্ষেত্রে বিচ্ছেদ নিয়ম প্রয়োগ করলে 3টি গুণ ও 2টি যোগ করতে হচ্ছে।
\(\therefore 3 \times 2+2 \times 1=8\) টাকা লাগবে।
সুতরাং এক্ষেত্রে বিচ্ছেদ নিয়ম ব্যবহার করলে সবচেয়ে কম টাকা লাগবে।
14. বহু বিকল্পীয় প্রশ্ন (M.C.Q.)
(i) \(\sqrt{5}\) এর দশমিক বিস্তার
(a) একটি সসীম দশমিক
(b) একটি সসীম অথবা আবৃত দশমিক
(c) একটি অসীম এবং অনাবৃত দশমিক
(d) কোনোটিই নয়
উত্তর – (c) একটি অসীম এবং অনাবৃত দশমিক
(ii) দুটি অমূলদ সংখ্যার গুণফল
(a) সর্বদাই অমূলদ সংখ্যা
(b) সর্বদাই মূলদ সংখ্যা
(c) সর্বদা একটি পূর্ণ সংখ্যা
(d) মূলদ কিংবা অমূলদ সংখ্যা
উত্তর – (d) মূলদ কিংবা অমূলদ সংখ্যা
(iii) \(\pi\) এবং \(\frac{22}{7}\)
(a) সর্বদাই মূলদ সংখ্যা
(b) সর্বদাই অমূলদ সংখ্যা
(c) \(\pi\) মূলদ সংখ্যা এবং \(\frac{22}{7}\) অমূলদ সংখ্যা
(d) \(\pi\) অমূলদ সংখ্যা এবং \(\frac{22}{7}\) মূলদ সংখ্যা
উত্তর – (d) \(\pi\) অমূলদ সংখ্যা এবং \(\frac{22}{7}\) মূলদ সংখ্যা
(iv) দুটি মূলদ সংখ্যার মধ্যে
(a) কোনও মূলদ সংখ্যা নেই
(b) একটি মাত্র মূলদ সংখ্যা আছে
(c) অসংখ্য মূলদ সংখ্যা আছে
(d) কোনো অমূলদ সংখ্যা নেই
উত্তর – (c) অসংখ্য মূলদ সংখ্যা আছে
(v) দুটি অমূলদ সংখ্যার মধ্যে
(a) কোনও মূলদ সংখ্যা নেই
(b) একটি মাত্র অমূলদ সংখ্যা আছে
(c) অসংখ্য অমূলদ সংখ্যা আছে
(d) কোনো অমূলদ সংখ্যা নেই
উত্তর – (c) অসংখ্য অমূলদ সংখ্যা আছে
(vi) 0 সংখ্যাটি
(a) অখণ্ড সংখ্যা কিন্তু পূর্ণ সংখ্যা নয়
(b) পূর্ণ সংখ্যা কিন্তু মূলদ সংখ্যা নয়
(c) মূলদ সংখ্যা কিন্তু বাস্তব সংখ্যা নয়
(d) অখণ্ড সংখ্যা, পূর্ণ সংখ্যা, মূলদ সংখ্যা এবং বাস্তব সংখ্যা কিন্তু অমূলদ সংখ্যা নয়
উত্তর – (d) অখণ্ড সংখ্যা, পূর্ণ সংখ্যা, মূলদ সংখ্যা এবং বাস্তব সংখ্যা কিন্তু অমূলদ সংখ্যা নয়
15.
(i) একটি সংখ্যা লিখি যেখানে দুটি অমূলদ সংখ্যার যোগফল একটি মূলদ সংখ্যা।
উত্তর – \((7+\sqrt{3})\) এবং \((7-\sqrt{3})\) দুটি অমূলদ সংখ্যা।
এদের যোগফল = \((7+\sqrt{3})+(7-\sqrt{3})=7+\sqrt{3}+7-\sqrt{3}=14\), একটি মূলদ সংখ্যা।
(ii) একটি সংখ্যা লিখি যেখানে দুটি অমূলদ সংখ্যার বিয়োগফল একটি মূলদ সংখ্যা।
উত্তর – \((5+\sqrt{2})\) এবং \((-5+\sqrt{2})\) দুটি অমূলদ সংখ্যা।
এদের বিয়োগফল = \((5+\sqrt{2})-(-5+\sqrt{2})=5+\sqrt{2}+5-\sqrt{2}=10\), একটি মূলদ সংখ্যা।
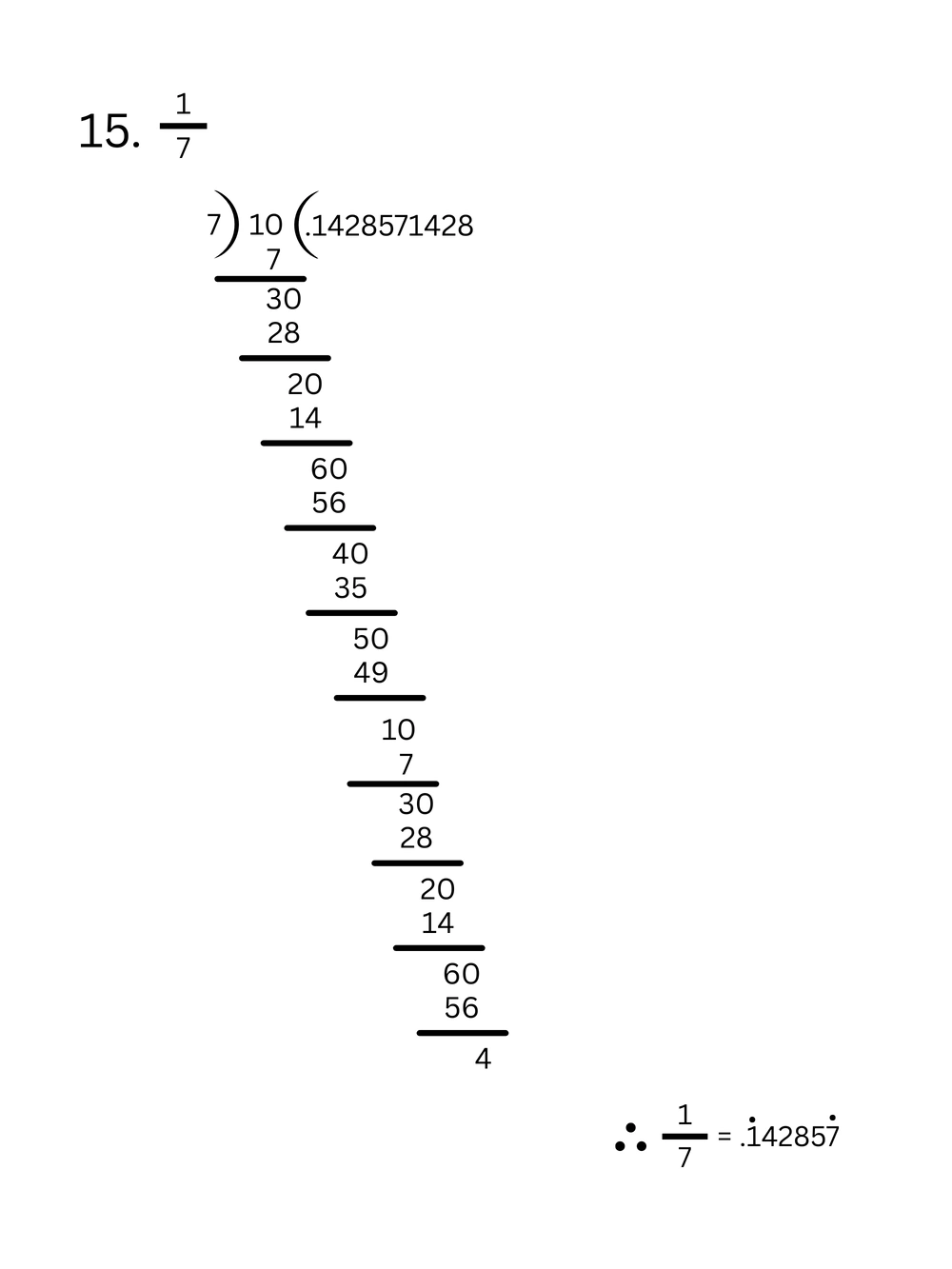
(iii) \(\frac{1}{7}\) ও \(\frac{2}{7}\) এর মধ্যে একটি মূলদ সংখ্যা লিখি।
উত্তর – \(\frac{1}{7}\) ও \(\frac{2}{7}\) এর মধ্যে একটি মূলদ সংখ্যা
= \(\frac{1}{2}\left(\frac{1}{7}+\frac{2}{7}\right)\)
= \(\frac{1}{2}\times\frac{3}{7}\)
= \(\frac{3}{14}\) (Answer)
(iv) 1/7 ও 2/7 এর মধ্যে একটি অমূলদ সংখ্যা লিখি।
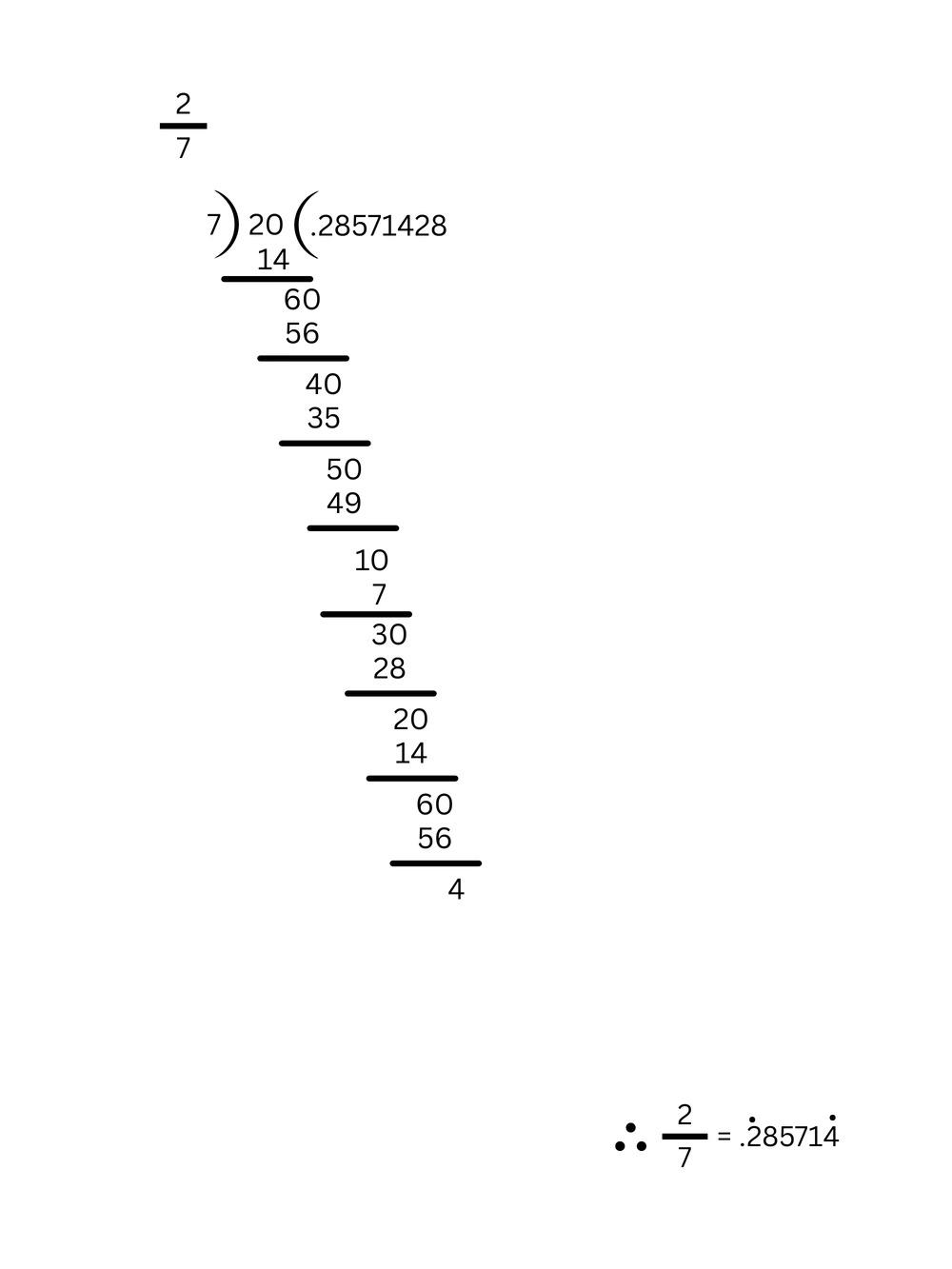
\(\therefore\) \(\frac{1}{7}\) এবং \(\frac{2}{7}\) এর মধ্যবর্তী একটি অমূলদ সংখ্যা হলো \(0.20200200020000…\)
(v) \(0.012\dot{3}\) আবৃত দশমিক সংখ্যাকে সামান্য ভগ্নাংশে লিখি।
সমাধান –
\(x = 0.012\dot{3}\)বা, \(x = 0.0123333333\dots\)
বা, \(1000x = 12.3333333\dots\) — (i)
বা, \(10000x = 123.3333333\dots\) — (ii)
(ii) নং এবং (i) নং সমীকরণ বিয়োগ করে পাই,
বা, \(10000x – 1000x = 111\)
বা, \(9000x = 111\)
বা, \(x = \frac{111}{9000}\)
বা, \(x = \frac{37}{3000}\)
\(\therefore 0.012\dot{3} = \frac{37}{3000}\) [উত্তর]
এই আর্টিকেলে নবম শ্রেণির গণিতের ‘বাস্তব সংখ্যা’ অধ্যায়ের ‘কষে দেখি – 1.3’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।
কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন