পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) নবম শ্রেণির গণিত পাঠ্যবইয়ের নবম অধ্যায় হলো ‘ভেদক ও মধ্যবিন্দু সংক্রান্ত উপপাদ্য’। এই পোস্টে ‘কষে দেখি – 9‘-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D; D বিন্দু দিয়ে CA এবং BA বাহুর সমান্তরাল সরলরেখাংশ BA এবং CA বাহুকে যথাক্রমে E ও F বিন্দুতে ছেদ করে। প্রমাণ করি যে, EF = \(\frac12\)BC
উত্তর –
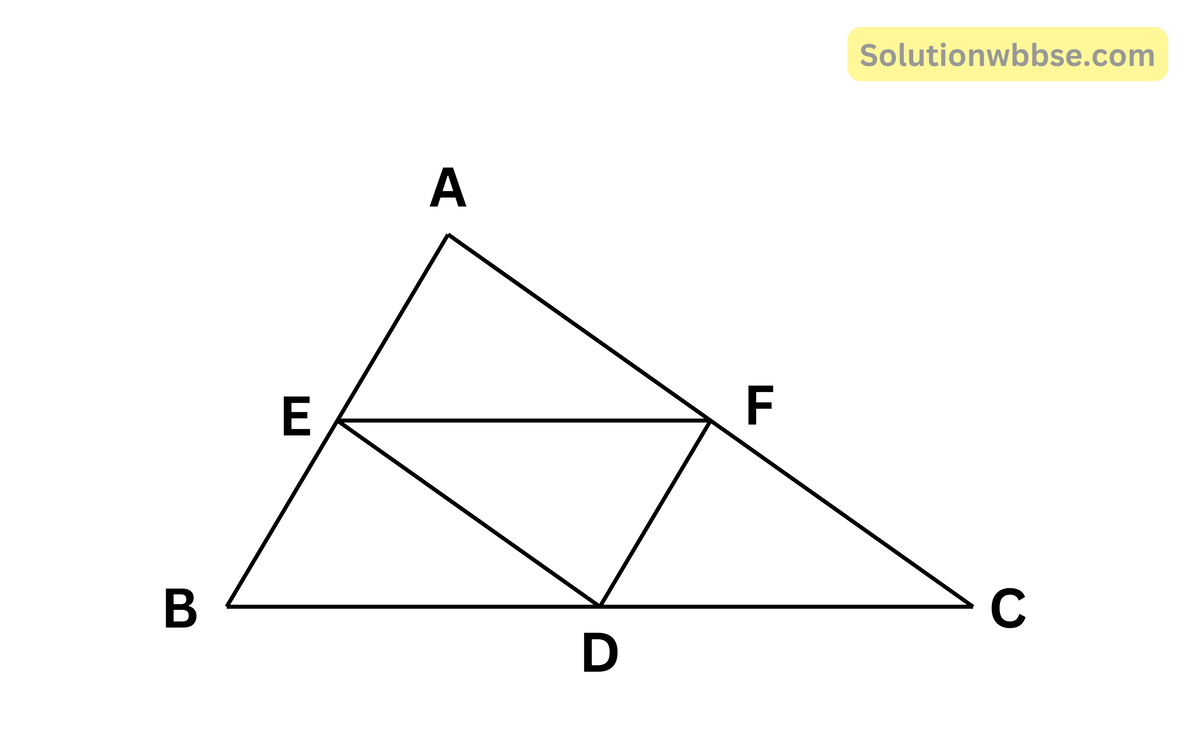
ধরা যাক, ∆ABC -এর BC বাহুর মধ্যবিন্দু D; D থেকে CA ও BA -এর সমান্তরাল সরলরেখা দুটি যথাক্রমে BA ও CA কে E ও F বিন্দুতে ছেদ করে।
প্রামাণ্য – EF = \(\frac12\)BC
প্রমাণ – DF || BA (অঙ্কনানুসারে), আবার D, BC -এর মধ্যবিন্দু
∴ F, AC -এর মধ্যবিন্দু।
আবার DE || CA (অঙ্কনানুসারে) এবং D, BC -এর মধ্যবিন্দু
∴ E, AB -এর মধ্যবিন্দু।
এখন E ও F যথাক্রমে ∆ABC -এর AB ও AC বাহুর মধ্যবিন্দু।
∴ EF = \(\frac12\)BC (প্রমাণিত)
2. D এবং E যথাক্রমে ABC ত্রিভুজের উপর এমনভাবে অবস্থিত যে, AD = \(\frac14\)AB এবং AE = \(\frac14\)AC; প্রমাণ করি যে, DE || BC এবং DE = \(\frac14\)BC
উত্তর –
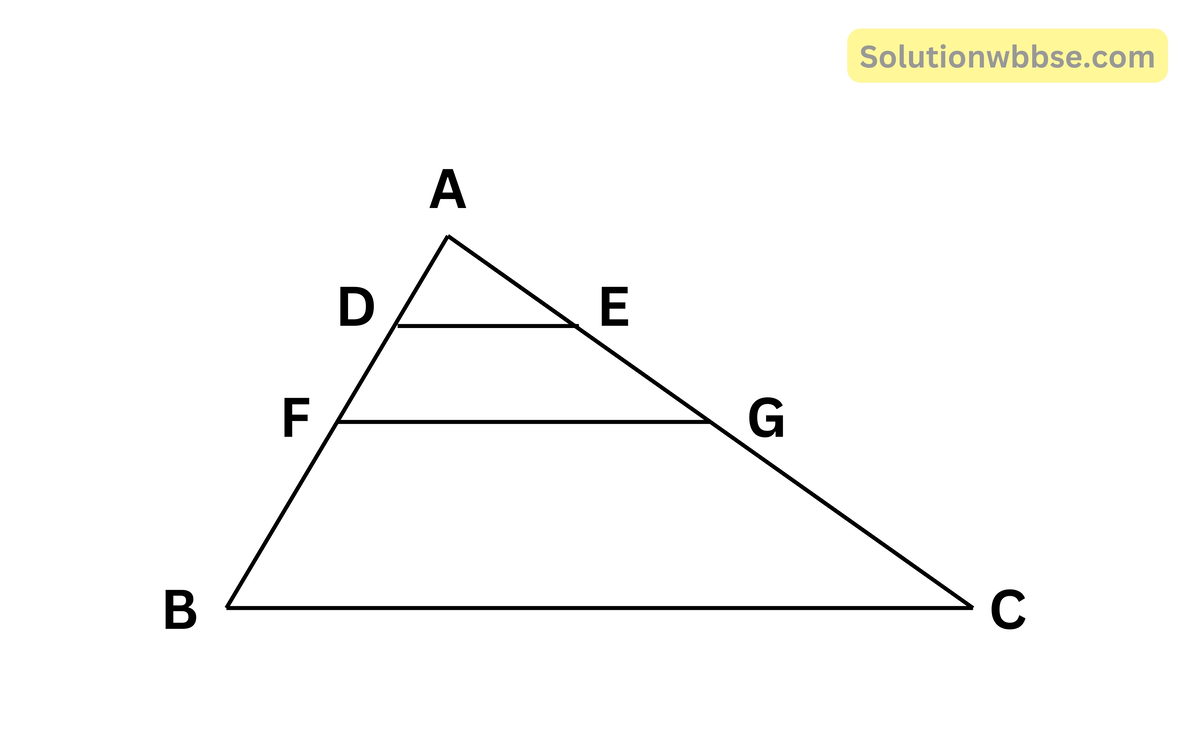
ধরা যাক, D এবং E যথাক্রমে ABC ত্রিভুজের উপর এমনভাবে অবস্থিত যে, AD = \(\frac14\)AB এবং AE = \(\frac14\)AC
প্রামাণ্য – DE || BC এবং DE = \(\frac14\)BC
অঙ্কন – AB বাহুর মধ্যবিন্দু F এবং AC বাহুর মধ্যবিন্দু G নেওয়া হল। F, G যুক্ত করা হল।
প্রমাণ – এখন ∆ABC -এর AB ও AC বাহুর মধ্যবিন্দু যথাক্রমে F এবং G
∴ FG || BC এবং FG = \(\frac12\)BC
আবার যেহেতু F, AB -এর মধ্যবিন্দু এবং AD = \(\frac14\)AB
∴ D, AF -এর মধ্যবিন্দু
আবার যেহেতু G, AC -এর মধ্যবিন্দু এবং AE = \(\frac14\)AC
∴ E, AG -এর মধ্যবিন্দু।
সুতরাং ∆AFG -এর AF ও AG বাহুর মধ্যবিন্দু যথাক্রমে D ও E
∴ DE || FG আবার FG || BC
∴ DE || BC
এবং DE = \(\frac12\)FG
= \(\frac12\times\frac12\)BC [∵ FG = \(\frac12\)BC]
∴ DE = \(\frac12\)BC (প্রমাণিত)
3. X এবং Z যথাক্রমে PQR ত্রিভুজের QR এবং QP বাহুর মধ্যবিন্দু। QP বাহুকে S বিন্দু পর্যন্ত এমনভাবে বর্ধিত করা হলো যাতে PS = ZP হয়। SX, PR বাহুকে Y বিন্দুতে ছেদ করে। প্রমাণ করি যে, PY = \(\frac14\)PR
উত্তর –
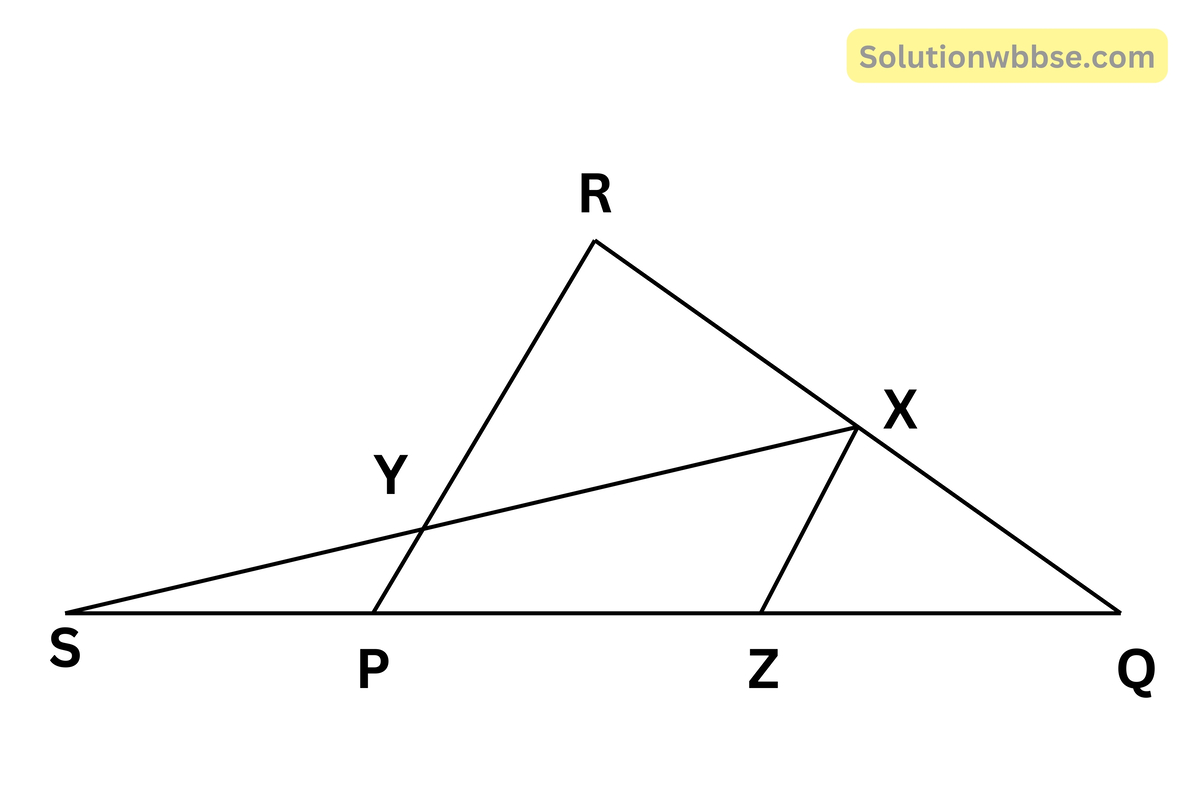
ধরা যাক, PQR -এর QR ও PQ বাহুর মধ্যবিন্দু যথাক্রমে X ও Z
QP কে S পর্যন্ত এমনভাবে বর্ধিত করা হল যাতে PS = ZP হয়।
SX, PR বাহুর Y বিন্দুতে ছেদ করে।
প্রামাণ্য – PY = \(\frac14\)PR
অঙ্কন – X, Z যুক্ত করা হল।
প্রমাণ – QP ও QR বাহুদ্বয়ের মধ্যবিন্দু যথাক্রমে Z ও X
∴ ZX || PR এবং ZX = \(\frac12\)PR
আবার ∆SZX -এর
SZ বাহুর মধ্যবিন্দু P এবং PY || ZX
∴ SX বাহুর মধ্যবিন্দু Y
∴ PY = \(\frac12\)ZX
= \(\frac12\times\frac12\)PR [∵ ZX = \(\frac12\)PR]
∴ PY = \(\frac12\)PR (প্রমাণিত)
4. প্রমাণ করি যে, একটি সামান্তরিকের বাহুগুলির মধ্যবিন্দুগুলি যুক্ত করে যে চতুর্ভুজ গঠিত হয় সেটি একটি সামান্তরিক।
উত্তর –
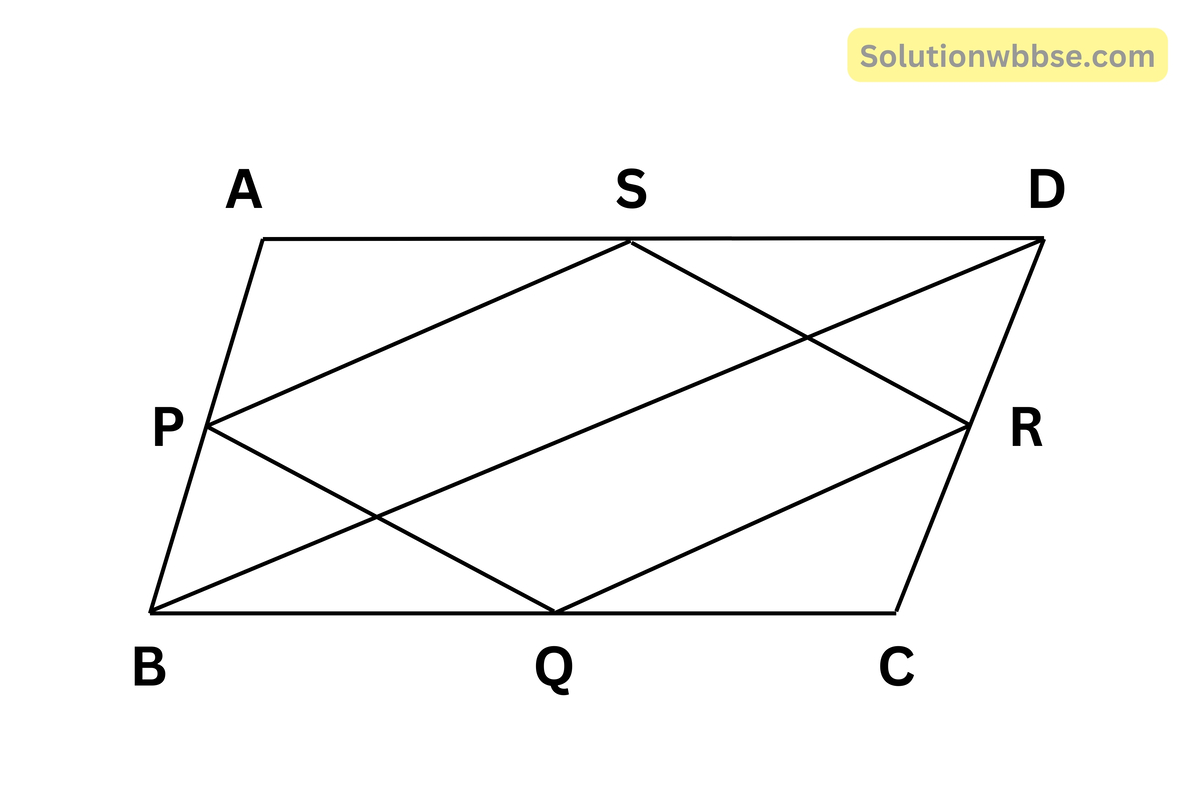
ধরা যাক, ABCD একটি সামান্তরিক যার AB, BC, CD ও DA বাহুগুলির মধ্যবিন্দু যথাক্রমে P, Q, R ও S;
এখন, P, Q; Q, R; R, S ও S, P যুক্ত করলাম
প্রামাণ্য – PQRS একটি সামান্তরিক।
অঙ্কন – BD কর্ণ অঙ্কন করলাম।
প্রমাণ – ΔABD -এর AB ও AD বাহুর মধ্যবিন্দু যথাক্রমে P ও S;
∴ PS || BD এবং PS = \(\frac12\)BD
একইভাবে ΔCBD -এর CB ও CD বাহুর মধ্যবিন্দু যথাক্রমে Q ও R
∴ QR || BD ও QR = \(\frac12\)BD
যেহেতু PS || BD এবং QR || BD, সুতরাং PS || QR
PS = \(\frac12\)BD এবং QR = \(\frac12\)BD সুতরাং PS = QR
এখন PQRS চতুর্ভুজের PS || QR এবং PS = QR
সুতরাং PQRS একটি সামান্তরিক। (প্রমাণিত)
5. প্রমাণ করি যে, একটি আয়তাকার চিত্রের বাহুগুলির মধ্যবিন্দুগুলি যুক্ত করে যে চতুর্ভুজটি গঠিত হয় সেটি একটি রম্বস কিন্তু বর্গাকার চিত্র নয়।
উত্তর –
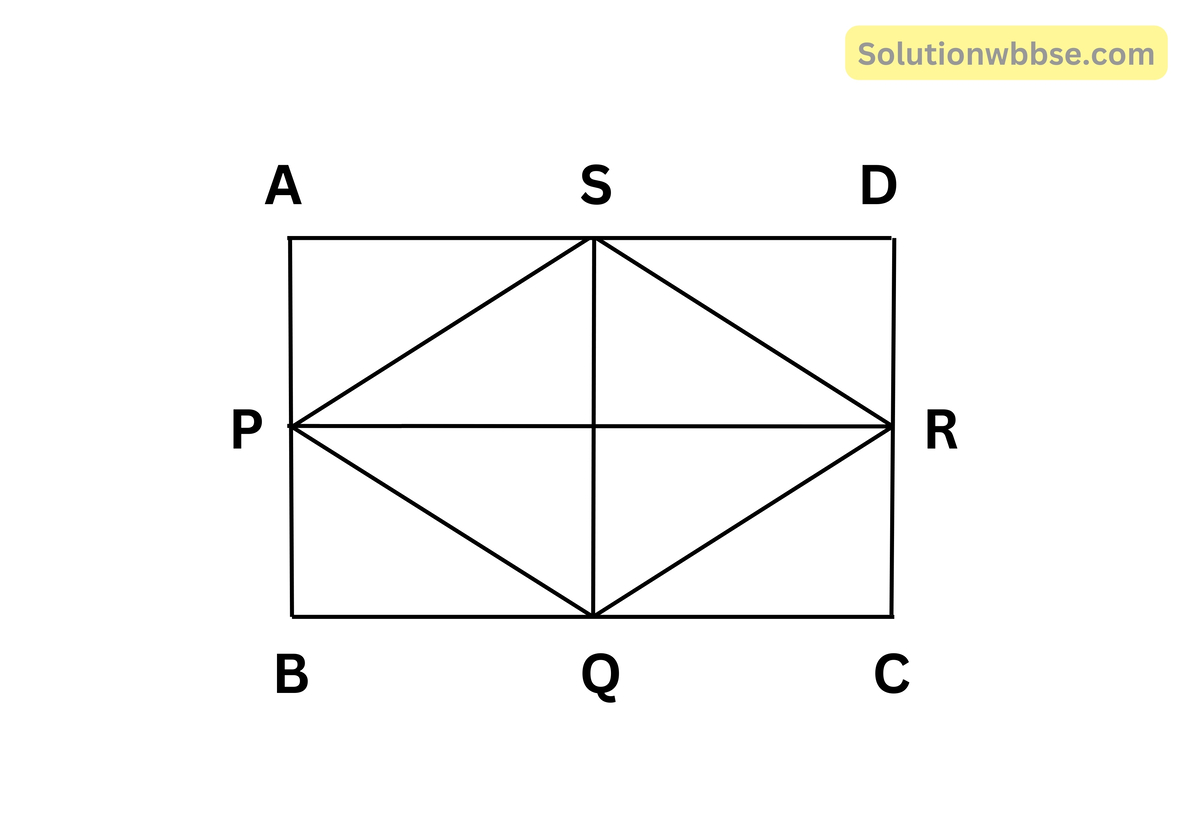
ধরা যাক, ABCD একটি আয়তক্ষেত্র। AB, BC, CD, DA বাহুগুলির মধ্যবিন্দু যথাক্রমে P, Q, R, S
P, Q; Q, R; R, S এবং S, P যুক্ত করা হল।
প্রামাণ্য – PQRS একটি রম্বস কিন্তু বর্গক্ষেত্র নয়।
অঙ্কন – P, R ও S, Q যুক্ত করা হল।
প্রমাণ – ∆APS ও ∆PBQ -এর
AP = BP [কল্পনানুসারে]
AS = BQ [কল্পনানুসারে]
∠PAS = ∠PBQ [উভয়েই সমকোণ]
∴ ∆ΑΡS ≅ ∆ΡBQ
∴ PS = PQ
অনুরূপে, ∆PBQ ও ∆RCQ হতে থেকে PQ = QR
∆QRC ও ∆RSD হতে থেকে QR = RS
∆RSD ও ∆APS হতে থেকে RS = PS
∴ PQ = QR = RS = SP
এখন PQRS চতুর্ভুজের PQ = QR = RS = SP
কিন্তু PR > SQ [∵ PQ = BC ≠ AB = SQ]
∴ PQRS চতুর্ভুজের চারটি বাহু সমান এবং কর্ণদ্বয় অসমান সুতরাং PQRS একটি রম্বস কিন্তু বর্গক্ষেত্র নয়।
6. প্রমাণ করি যে, একটি বর্গাকার চিত্রের বাহুগুলির মধ্যবিন্দুগুলি যুক্ত করলে যে চতুর্ভুজটি গঠিত হয় সেটি একটি বর্গাকার চিত্র।
উত্তর –
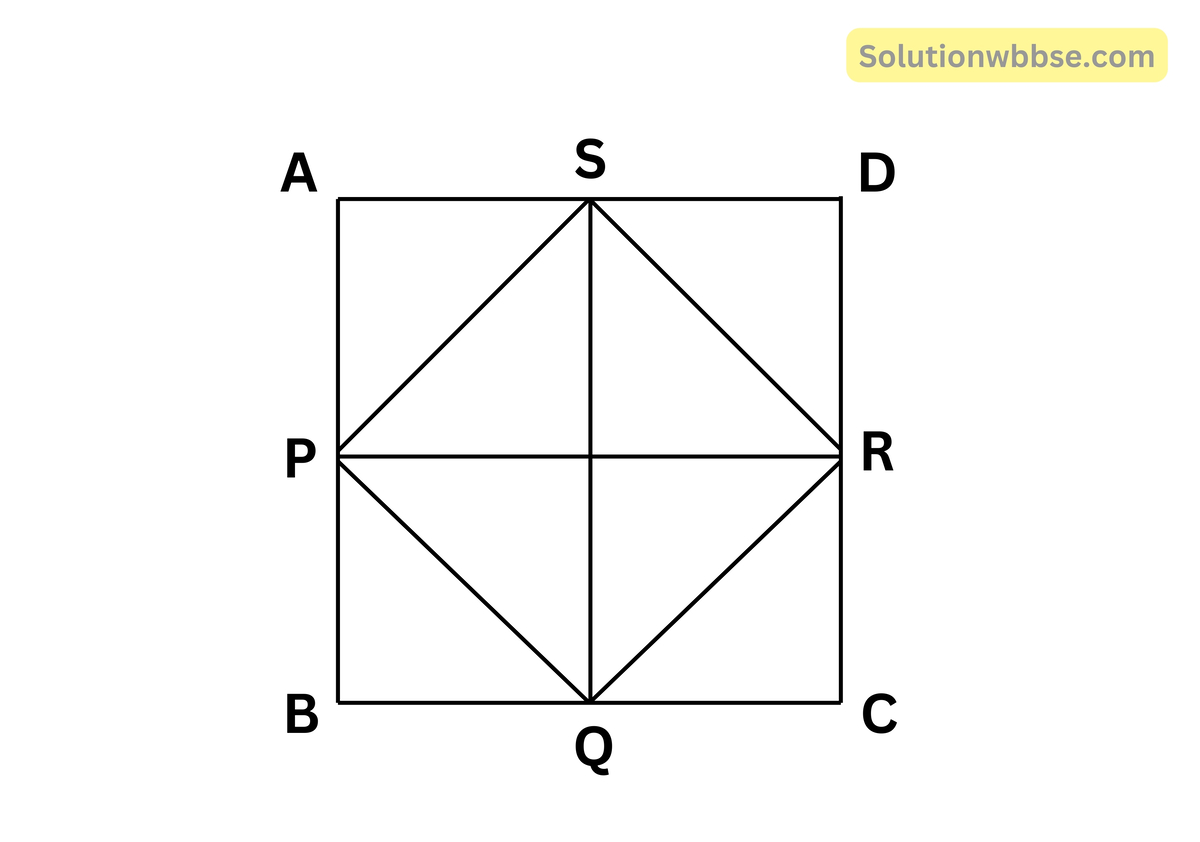
ধরা যাক, ABCD একটি বর্গক্ষেত্র। AB, BC, CD, DA বাহুগুলির মধ্যবিন্দু যথাক্রমে P, Q, R ও S
P, Q; Q, R; R, S এবং S, P যুক্ত করা হল।
প্রামাণ্য – PQRS একটি বর্গক্ষেত্র।
অঙ্কন – P, R ও S, Q যুক্ত করা হল।
প্রমাণ – ∆APS ও ∆PBQ-এর
AP = BP [কল্পনানুসারে]
AS = BQ [কল্পনানুসারে]
∠PAS = ∠PBQ [উভয়েই সমকোণ]
∴ ∆APS ≅ ∆PBQ
∴ PS = PQ
অনুরূপে, ∆PBQ ও ∆RCQ থেকে পাই, PQ = QR
∆QRC ও ∆RSD থেকে পাই, QR = RS
∆RSD ও ∆APS থেকে পাই, RS = PS
∴ PQ = QR = RS = SP
এখন PQRS চতুর্ভুজের চারটি বাহুর সমান।
আবার PR = QS [∵ AB = SQ = BC = PR]
যেহেতু PQRS চতুর্ভুজের চারটি বাহু সমান এবং কর্ণদ্বয়ের মানও সমান।
সুতরাং PQRS একটি বর্গক্ষেত্র।
7. প্রমাণ করি যে, একটি রম্বসের বাহুগুলির মধ্যবিন্দুগুলি যুক্ত করে যে চতুর্ভুজটি গঠিত হয় সেটি একটি আয়তাকার চিত্র।
উত্তর –
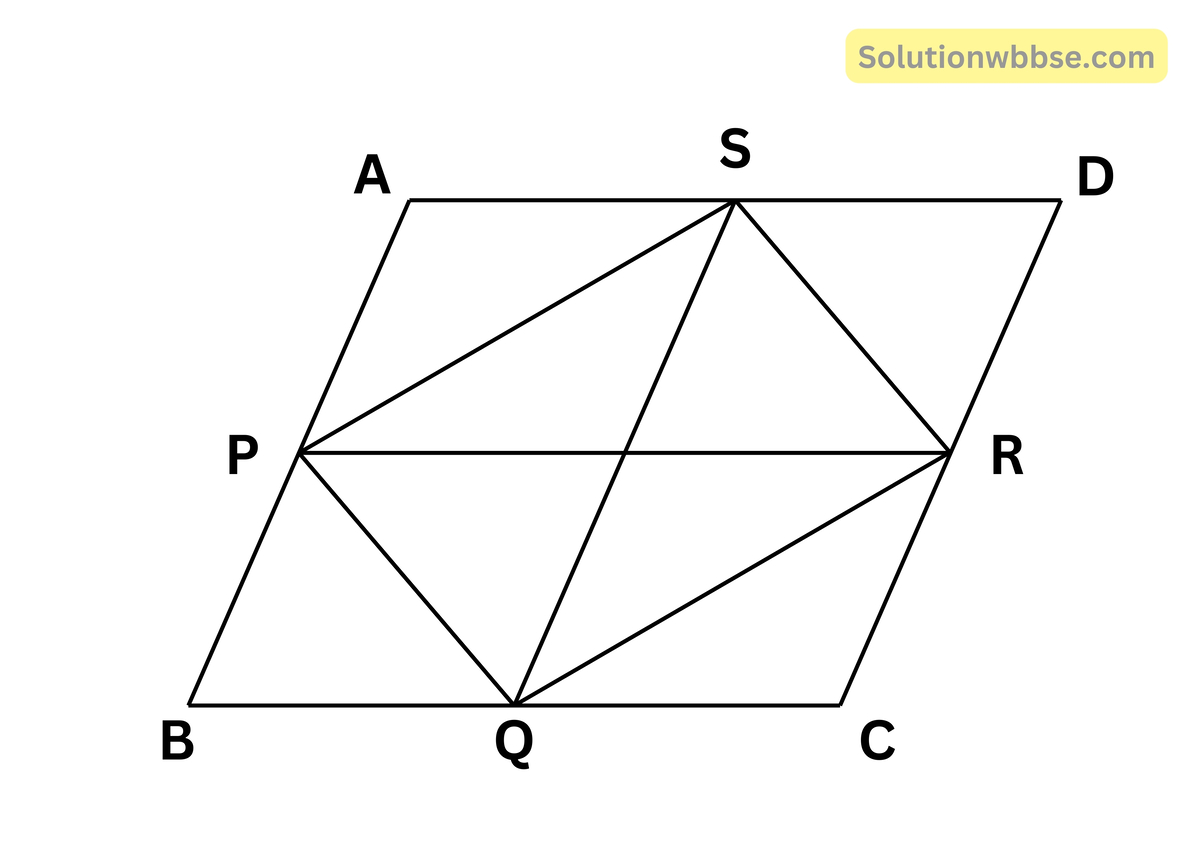
ধরা যাক, ABCD একটি রম্বস। AB, BC, CD, DA বাহুগুলির মধ্যবিন্দু যথাক্রমে P, Q, R ও S
P, Q; Q, R; R, S এবং S, P যুক্ত করা হল।
প্রামাণ্য – PQRS একটি আয়তক্ষেত্র।
প্রমাণ – ∆APS ও ∆CRQ -এর AP = CR [কল্পনানুসারে)
AS = QC [কল্পনানুসারে)
∠PAS = ∠QCR [রম্বসের বিপরীত কোণ]
∆APS ≅ ∆CQR
∴ PS = QR [সর্বসম ত্রিভুজের অনুরূপ বাহু]
অনুরূপে, ∆BPQ ও ∆DSR থেকে প্রমাণ করা যায় PQ = SR
এখন PQRS চতুর্ভুজের PQ = SR এবং PS = QR
আবার PR = SQ [∵ BC = PR = QS = AB]
সুতরাং PQRS একটি আয়তক্ষেত্র।
8. ABC ত্রিভুজের AB এবং AC বাহুর মধ্যবিন্দু যথাক্রমে D এবং E; P এবং Q যথাক্রমে CD ও BD -এর মধ্যবিন্দু। প্রমাণ করি যে, BE এবং PQ পরস্পরকে সমদ্বিখণ্ডিত করে।
উত্তর –
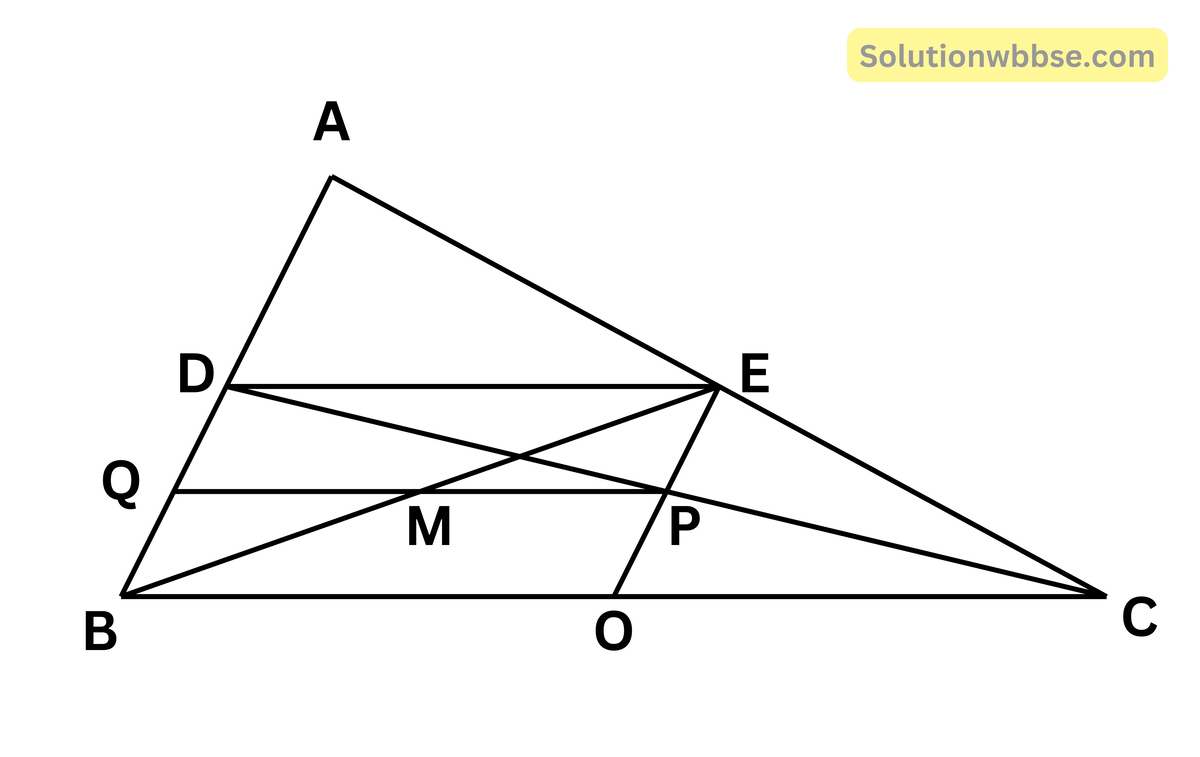
ধরা যাক ∆ABC- এর AB ও AC বাহুর মধ্যবিন্দু যথাক্রমে D এবং E। P এবং Q যথাক্রমে CD ও BD -এর মধ্যবিন্দু।
প্রামাণ্য – BE এবং QP পরস্পরকে সমদ্বিখণ্ডিত করেছে।
অঙ্কন – D ও E বিন্দুদ্বয় যুক্ত করা হল। E ও P বিন্দু যুক্ত করা হল এবং বর্ধিত করা হল যা BC -কে O বিন্দুতে ছেদ করেছে।
প্রমাণ – ∆ABC -এর AB ও AC বাহুর মধ্যবিন্দু যথাক্রমে D ও E
∴ DE = \(\frac12\)BC
এখন ∆ABC -এর AC বাহুর মধ্যবিন্দু E এবং EP || AB [∵ AC ও DC বাহুর মধ্যবিন্দু যথাক্রমে E ও P]
∴ BC বাহুর মধ্যবিন্দু O
∴ BO = OC
এখন BOED চতুর্ভুজের DE || BO এবং DE = BO
∴ BOED চতুর্ভুজটি একটি সামান্তরিক
এখন ∆BDE -এর BD বাহুর মধ্যবিন্দু Q
এবং QM || DE [∵ ∆BDC -এর BD এর মধ্যবিন্দু Q এবং DC-এর মধ্যবিন্দু P]
∴ BE বাহুর মধ্যবিন্দু M
∴ QM = \(\frac12\)DE
আবার ∆BOE -এর BE বাহুর মধ্যবিন্দু M এবং MP || BO
∴ MP = \(\frac12\)BO = \(\frac12\)DE [∵ BO = DE]
∴ QM = EM
আবার BE বাহুর মধ্যবিন্দু M
∴ BE ও QP পরস্পরকে সমদ্বিখণ্ডিত করেছে। (প্রমাণিত)
9. ABC ত্রিভুজের ∠ABC -এর সমদ্বিখন্ডকের উপর AD লম্ব। D বিন্দু দিয়ে BC বাহুর সমান্তরাল সরলরেখাংশ DE টানা হল যা AC বাহুকে E বিন্দুতে ছেদ করে। প্রমাণ করি যে, AE = EC
উত্তর –
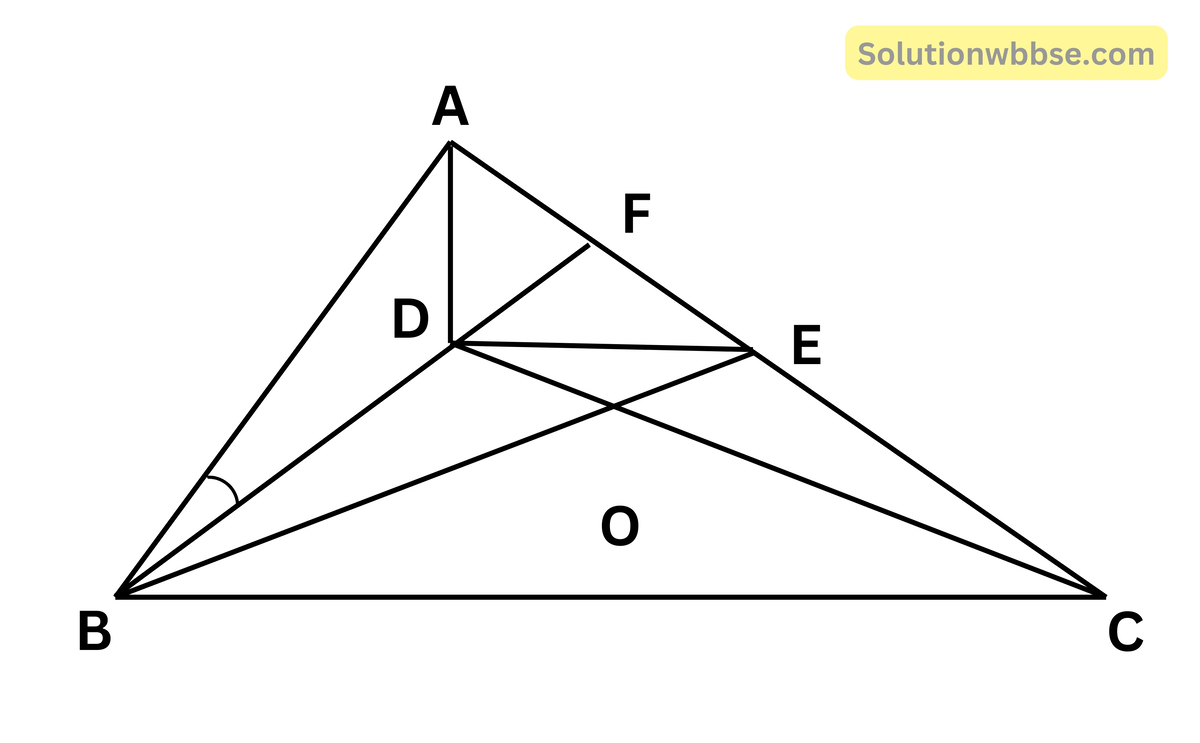
ধরা যাক ABC ত্রিভুজের ∠ABC -এর সমদ্বিখন্ডকের উপর AD লম্ব। D বিন্দু দিয়ে BC বাহুর সমান্তরাল DE টানা হল যা AC -কে E বিন্দুতে ছেদ করে।
প্রামাণ্য – AE = EC
অঙ্কন – D, C ও B, E যুক্ত করা হল। যারা O বিন্দুতে ছেদ করে।
প্রমাণ – ∆BOD ও ∆EOC -এর
∠DOB = বিপ্রতীপ ∠EOC
অবশিষ্ট ∠ODB = অবশিষ্ট ∠OEC
∴ ∆BOD ≅ ∆EOC
∴ BD = EC ও DO = EO [সর্বসম ত্রিভুজের অনুরূপ বাহু]
∆ABD ও ∆BED -এর
∠BAD = ∠DEB
AB = BE
AD সাধারণ বাহু
∆ΑΒΟ ≅ ∆ΒED
∴ AD = DE
অর্থাৎ ADE একটি সমদ্বিবাহু ত্রিভুজ
∆ADB ও ∆EDC -এর
AD = DE (প্রমাণিত)
BD = EC (প্রমাণিত)
∴ AB = CD
∴ ∆ADB ≅ ∆EDC
∴ AE = EC (প্রমাণিত)
10. ABC ত্রিভুজের AD মধ্যমা। B ও C বিন্দু দিয়ে AD -এর সমান্তরল সরলরেখাংশ BR এবং CT টানা হল যারা বর্ধিত BA এবং CA বাহুর সাথে যথাক্রমে T এবং R বিন্দুতে মিলিত হয়। প্রমাণ করি যে, \(\frac1{AD}=\frac1{RB}+\frac1{TC}\)
উত্তর –
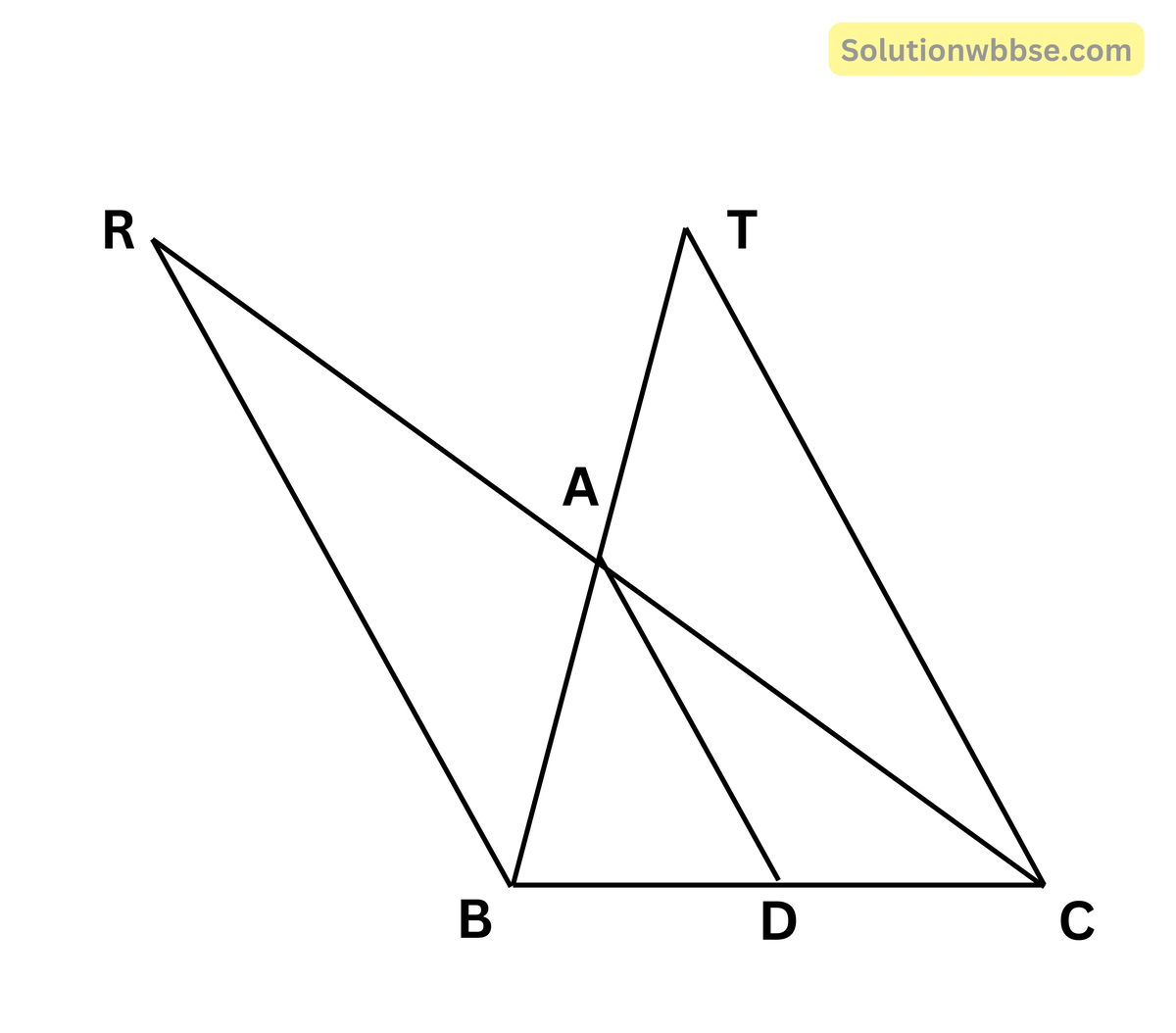
ধরা যাক, ABC ত্রিভুজের AD মধ্যমা। B ও C বিন্দু দিয়ে AD -এর সমান্তরাল সরলরেখা BR এবং CT টানা হল যা বর্ধিত BA এবং CA বাহুর সাথে যথাক্রমে T এবং R বিন্দুতে মিলিত হয়।
প্রামাণ্য – \(\frac1{AD}=\frac1{RB}+\frac1{TC}\)
প্রমাণ – ∆BCR এর D, BC বাহুর মধ্যবিন্দু
এবং AD || RB
সুতরাং A, CR-এর মধ্যবিন্দু এবং AD = \(\frac12\)BR
অনুরূপে, D; BC এর মধ্যবিন্দু এবং AD || TC
∴ AD = \(\frac12\)TC
∴ \(\frac12\)BR = \(\frac12\)TC
∴ BR = TC
∴ \(\frac1{AD}=\frac1{{\displaystyle\frac12}BR}=\frac2{BR}=\frac1{BR}+\frac1{BR}\)
∴ \(\frac1{AD}=\frac1{RB}+\frac1{TC}\) [∵ BR = TC] (প্রমাণিত)
11. ABCD ট্রাপিজিয়ামের AB || DC এবং AB > DC; E ও F যথাক্রমে কর্ণদ্বয় AC ও BD -এর মধ্যবিন্দু। প্রমাণ করি যে, EF = \(\frac12\)(AB – DC)
উত্তর –
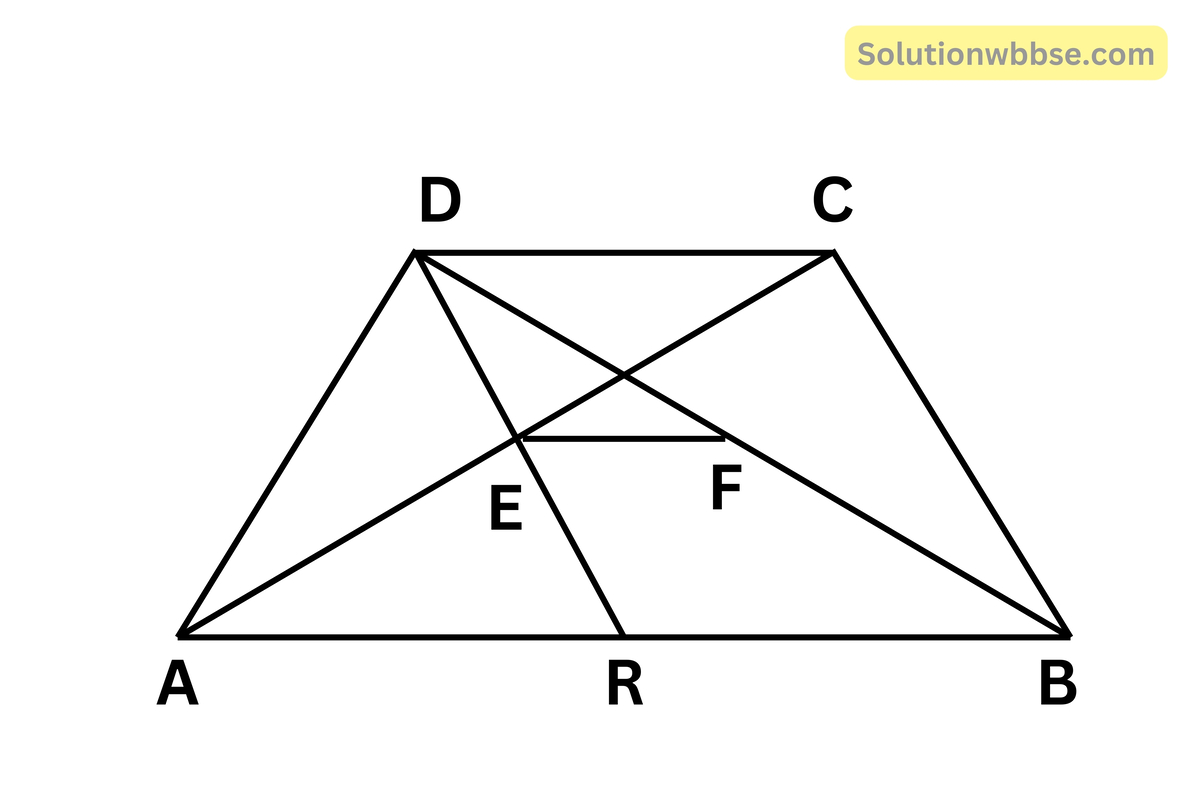
মনে করি, ABCD ট্রাপিজিয়ামের AB || DC যেখানে AB > DC
AC ও BD কর্ণের মধ্যবিন্দু যথাক্রমে E ও F।
প্রামাণ্য – প্রমাণ করতে হবে যে, EF = \(\frac12\)(AB – DC)
অঙ্কন – D, E যোগ করি যার বর্ধিতাংশ AB -কে R বিন্দুতে ছেদ করেছে।
প্রমাণ – ∆AER ও ∆DEC -এ
∠AER = ∠DEC
∠EAR = ∠ECD [∵ CD || AB এবং AC ছেদক]
এবং AE = EC [∵ E, AC -এর মধ্যবিন্দু]
∴ ∆AER ≅ ∆DEC
এখন AR = CD [অনুরূপ বাহু]
ER = ED [অনুরূপ বাহু]
E, DR -এর মধ্যবিন্দু।
এখন, ∆DRB -এ E, DR -এর মধ্যবিন্দু এবং F, BD -এর মধ্যবিন্দু
সুতরাং EF || RB এবং EF = \(\frac12\)RB
∴ ER = \(\frac12\)(AB – AR)
= \(\frac12\)(AB – CD) (প্রমাণিত)
12. AB সরলরেখাংশের মধ্যবিন্দু C এবং PQ যে-কোনো একটি সরলরেখা। A, B এবং C বিন্দু থেকে PQ সরলরেখার ক্ষুদ্রতম দূরত্ব যথাক্রমে AR, BS এবং CT; প্রমাণ করি যে, AR + BS = 2CT
উত্তর –
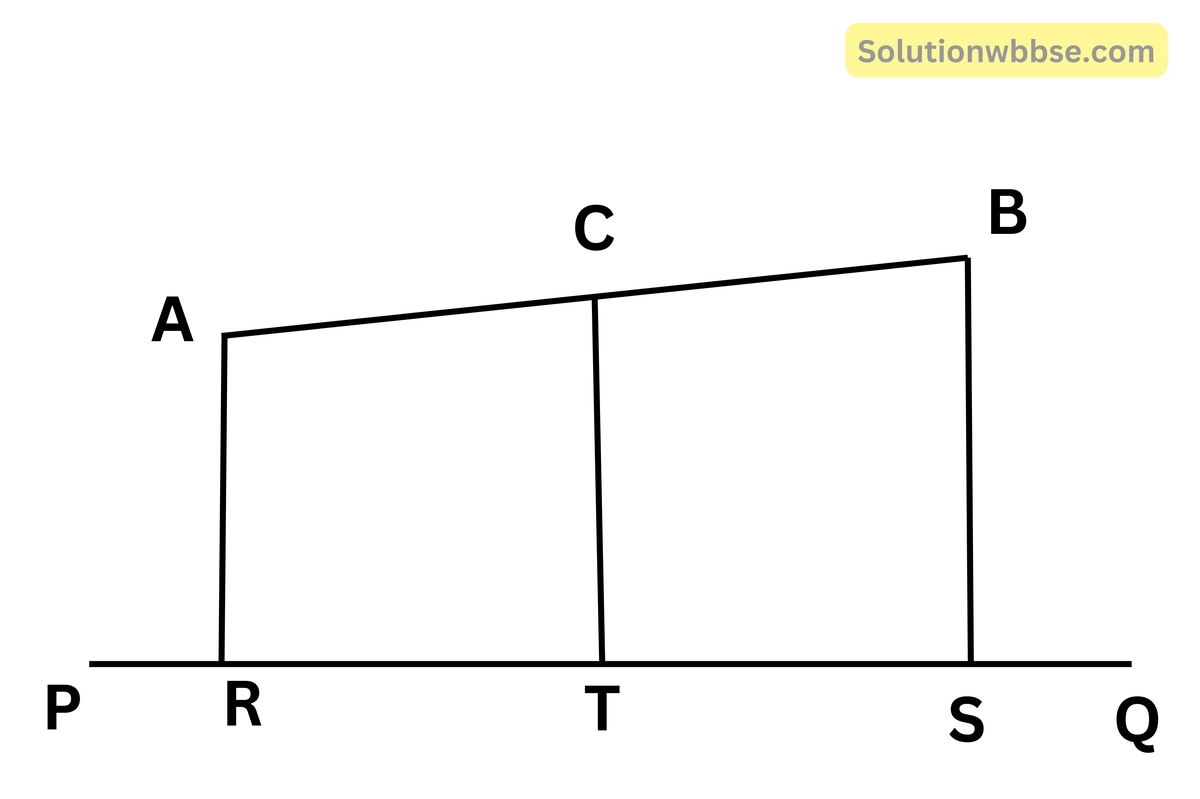
মনে করি, AB রেখাংশের মধ্যবিন্দু C এবং PQ যে-কোনো একটি সরলরেখা।
A, B, C বিন্দুগুলি থেকে PQ-এর ন্যূনতম দূরত্ব যথাক্রমে AR, BS ও CT
প্রমাণ করতে হবে যে, AR + BS = 2CT
প্রমাণ – যেহেতু AR, BS এবং CT সরলরেখাগুলি যথাক্রমে A, B ও C বিন্দু থেকে PQ সরলরেখার ক্ষুদ্রতম দূরত্ব।
∴ AR, BS, CT এরা প্রত্যেকেই PQ-এর উপর লম্ব এবং পরস্পর সমান্তরাল।
এখন RABS চতুর্ভুজের AR || BS এবং RS ও AB তির্যক বাহু
∴ RASB একটি ট্রাপিজিয়ম।
আবার AB বাহুর মধ্যবিন্দু C এবং CT || AR ও CT || BS
∴ T, RS বাহুর মধ্যবিন্দু।
∴ CT = (AR + BS)
∴ AR + BS = 2CT (প্রমাণিত)
13. ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D; A বিন্দু দিয়ে PQ যে-কোনো একটি সরলরেখা। B, C এবং D বিন্দু থেকে PQ সরলরেখার উপর লম্ব যথাক্রমে BL, CM এবং DN; প্রমাণ করি যে, DL = DM.
উত্তর –
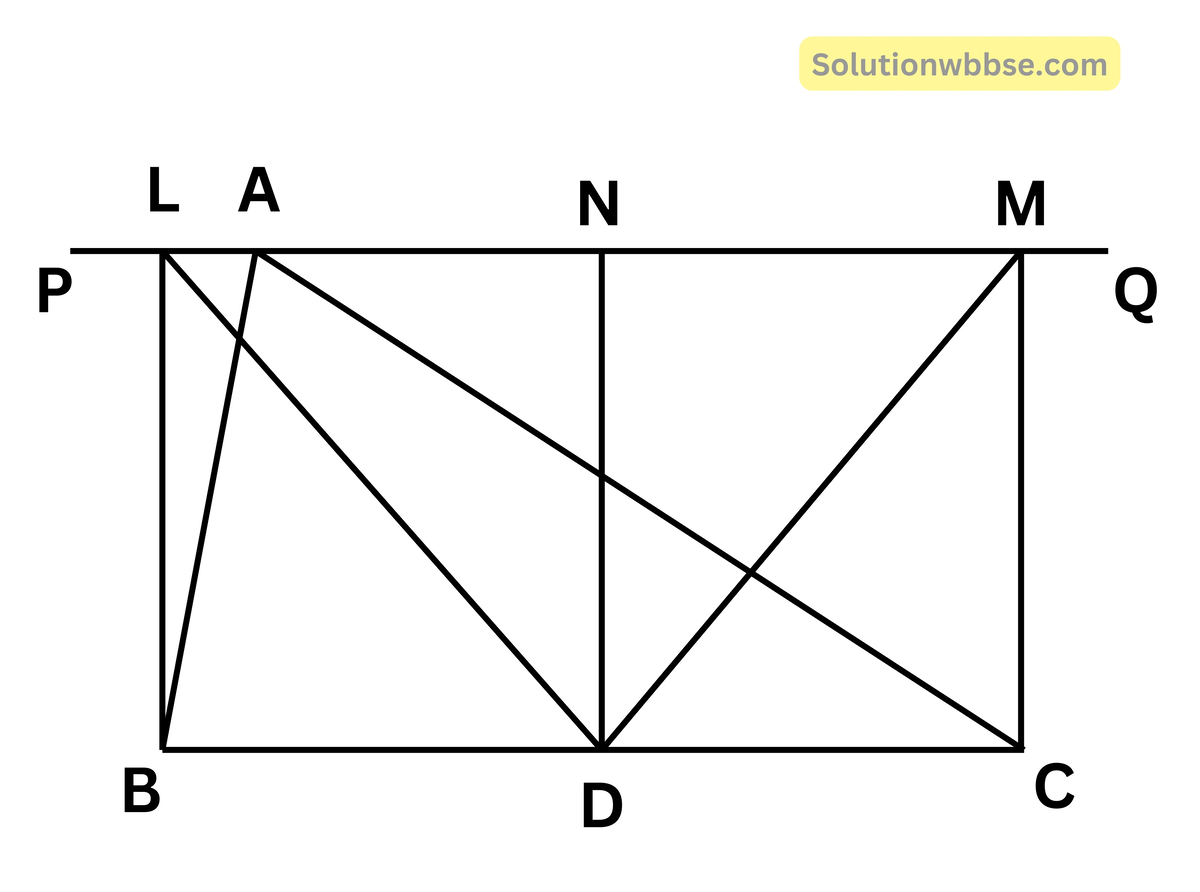
প্রমাণ – যেহেতু, BL, DN ও CM এর প্রত্যেকেই PQ সরলরেখার উপর লম্ব, সুতরাং তারা পরস্পর সমান্তরাল।
যেহেতু, BL || DN || CM এবং BD = DC
∴ LN = NM
এবার, ∆DLN ও ∆DMN -এর
LN = MN (প্রমাণিত)
DN সাধারণ বাহু।
এবং অন্তর্ভূত ∠DNL = অন্তর্ভূত ∠DNM [∵ DN ⊥ PQ]
∴ ∆DLN ≅ ∆DMN
∴ DL = DM (অনুরূপ)।
14. ABCD একটি বর্গাকার চিত্র। AC এবং BD কর্ণদ্বয় O বিন্দুতে ছেদ করে। ∠BAC-এর সমদ্বিখণ্ডক BO-কে P বিন্দুতে এবং BC -কে Q বিন্দুতে ছেদ করে। প্রমাণ করি যে, OP = \(\frac12\)CQ
উত্তর –
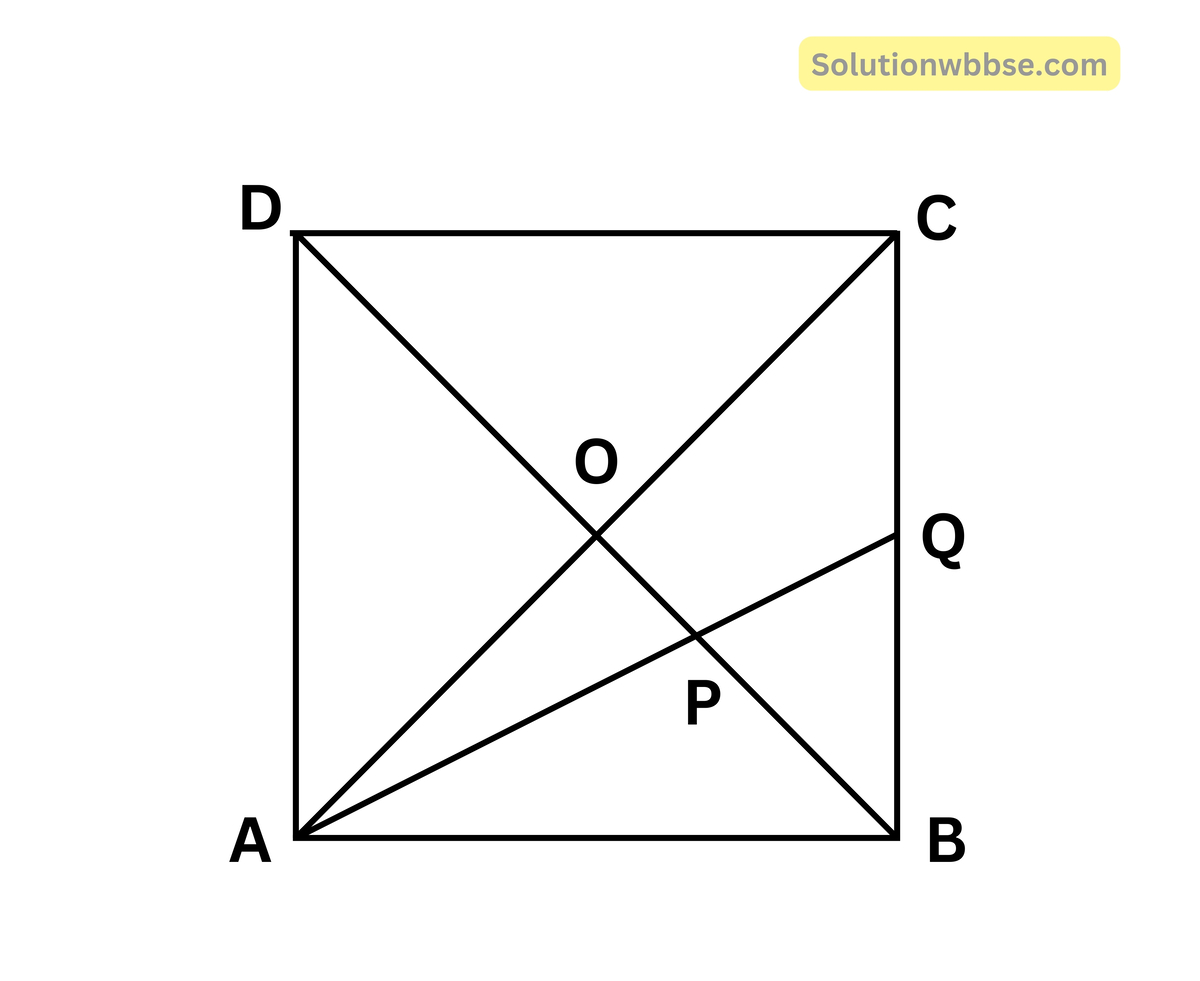
মনে করি, ABCD বর্গাকার চিত্রের AC এবং BD কর্ণদ্বয় পরস্পর ০ বিন্দুতে ছেদ করে এবং ∠BAC -এর সমদ্বিখণ্ডক OB -কে P বিন্দুতে এবং CB -কে Q বিন্দুতে ছেদ করেছে।
প্রামাণ্য – প্রমাণ করতে হবে যে, OP = \(\frac12\)CQ
প্রমাণ – ∠BAC -এর সমদ্বিখন্ডক BO
∠BAC = ∠BOA + ∠BOC
P, OB -এর মধ্যবিন্দু
∴ OP = \(\frac12\)CQ
15. বহু বিকল্পীয় প্রশ্ন (M. C. Q.) :
(i) PQR ত্রিভুজে ∠PQR = 90° এবং PR = 10 সেমি। PR বাহুর মধ্যবিন্দু S হলে QS -এর দৈর্ঘ্য
(a) 4 সেমি
(b) 5 সেমি
(c) 6 সেমি
(d) 3 সেমি
উত্তর – (b) 5 সেমি
সমাধান –
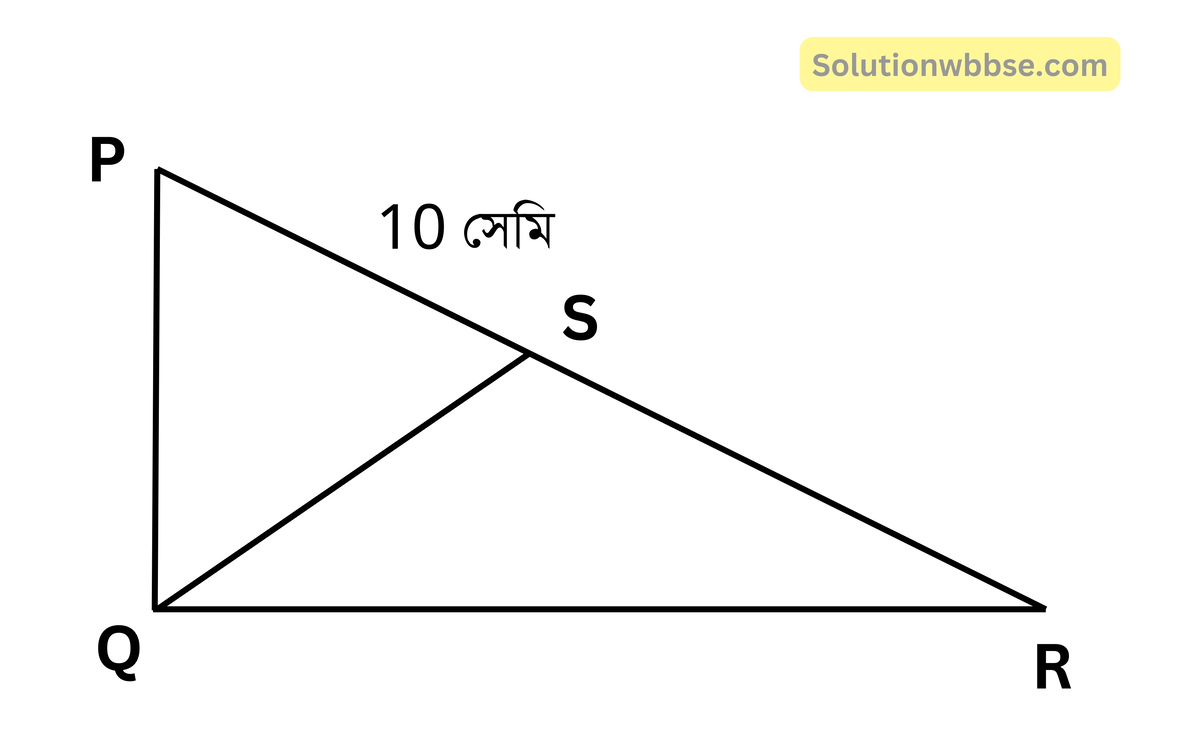
PR = 10 সেমি
∴ PS = SR = 5 সেমি [∵ S, PR এর মধ্যবিন্দু]
∵ ∠PQR = 90° এবং S, PR-এর মধ্যবিন্দু
∴ PSQ একটি সমদ্বিবাহু ত্রিভুজ
∴ QS = PS = 5 সেমি
(ii) ABCD ট্রাপিজিয়ামের AB || DC এবং AB = 7 সেমি ও DC = 5 সেমি। AD ও BC বাহুর মধ্যবিন্দু যথাক্রমে E ও F হলে EF -এর দৈর্ঘ্য
(a) 5 সেমি
(b) 7 সেমি
(c) 6 সেমি
(d) 12 সেমি
উত্তর – (c) 6 সেমি
সমাধান –
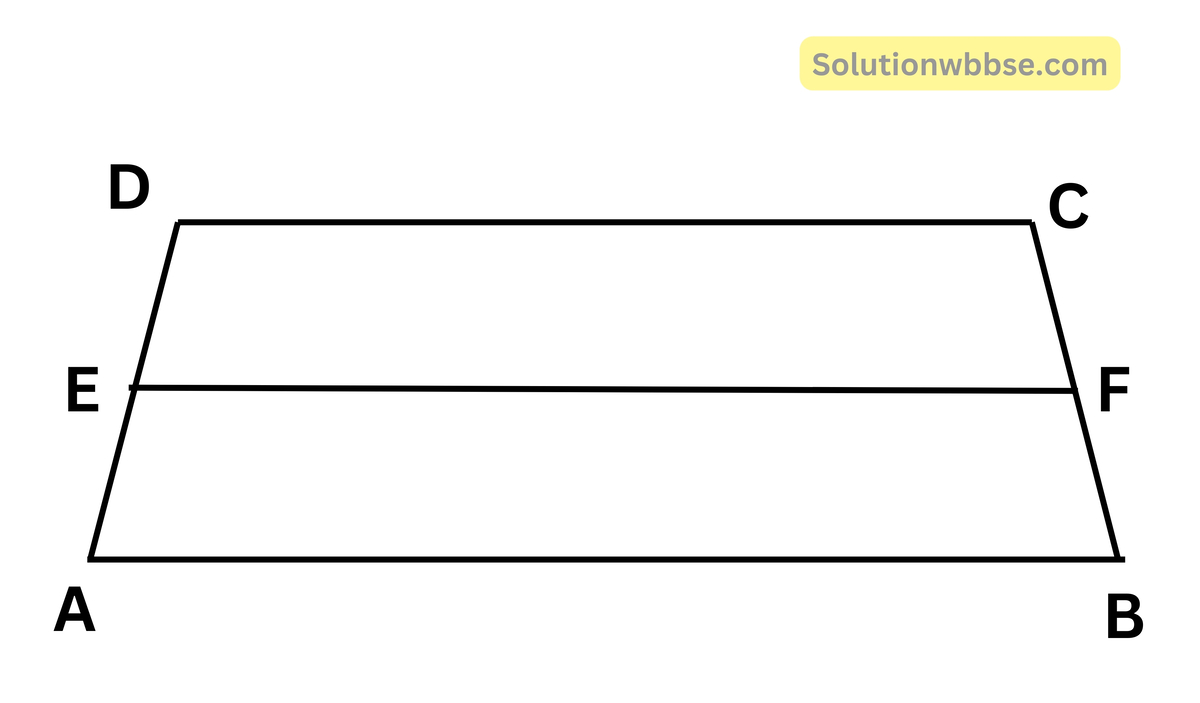
যেহেতু, E ও F যথাক্রমে AD ও BC বাহুর মধ্যবিন্দু
∴ EF = \(\frac12\)(AB + DC)
= \(\frac12\left(7+5\right)\)
= 6
∴ EF -এর দৈর্ঘ্য 6 সেমি.
(iii) ABC ত্রিভুজের AD মধ্যমার মধ্যবিন্দু E; বর্ধিত BE, AC কে F বিন্দুতে ছেদ করে। AC = 10.5 সেমি হলে AF -এর দৈর্ঘ্য
(a) 3 সেমি
(b) 5 সেমি
(c) 2.5 সেমি
(d) 3.5 সেমি
উত্তর – (d) 3.5 সেমি
সমাধান –
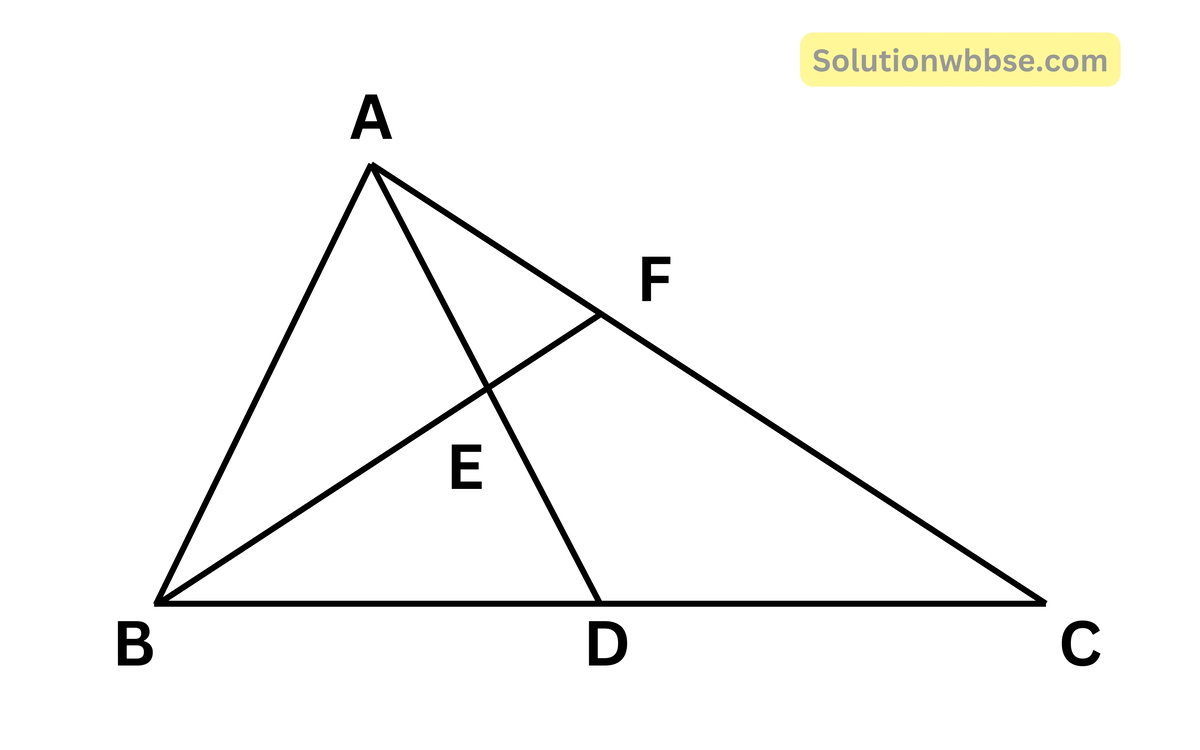
যেহেতু, AD মধ্যমার মধ্যবিন্দু F এবং বর্ধিত BE, AC -কে F বিন্দুতে ছেদ করে।
∴ AF = \(\frac13\)AC
= \(\left(\frac12\times10.5\right)\) সেমি
= 3.5 সেমি
(iv) ABC ত্রিভুজের BC, CA ও AB বাহুর মধ্যবিন্দু যথাক্রমে D, E ও F; BE ও DF, X বিন্দুতে এবং CF ও DE, Y বিন্দুতে ছেদ করলে XY -এর দৈর্ঘ্য সমান
(a) \(\frac12\)BC
(b) \(\frac14\)BC
(c) \(\frac13\)BC
(d) \(\frac18\)BC
উত্তর – (b) \(\frac14\)BC
(v) ABCD সামান্তরিকের BC বাহুর মধ্যবিন্দু E; DE এবং বর্ধিত AB, F বিন্দুতে মিলিত হয়। AF -এর দৈর্ঘ্য সমান
(a) \(\frac32\)AB
(b) 2AB
(c) 3AB
(d) \(\frac54\)AB
উত্তর – (b) 2AB
সমাধান –
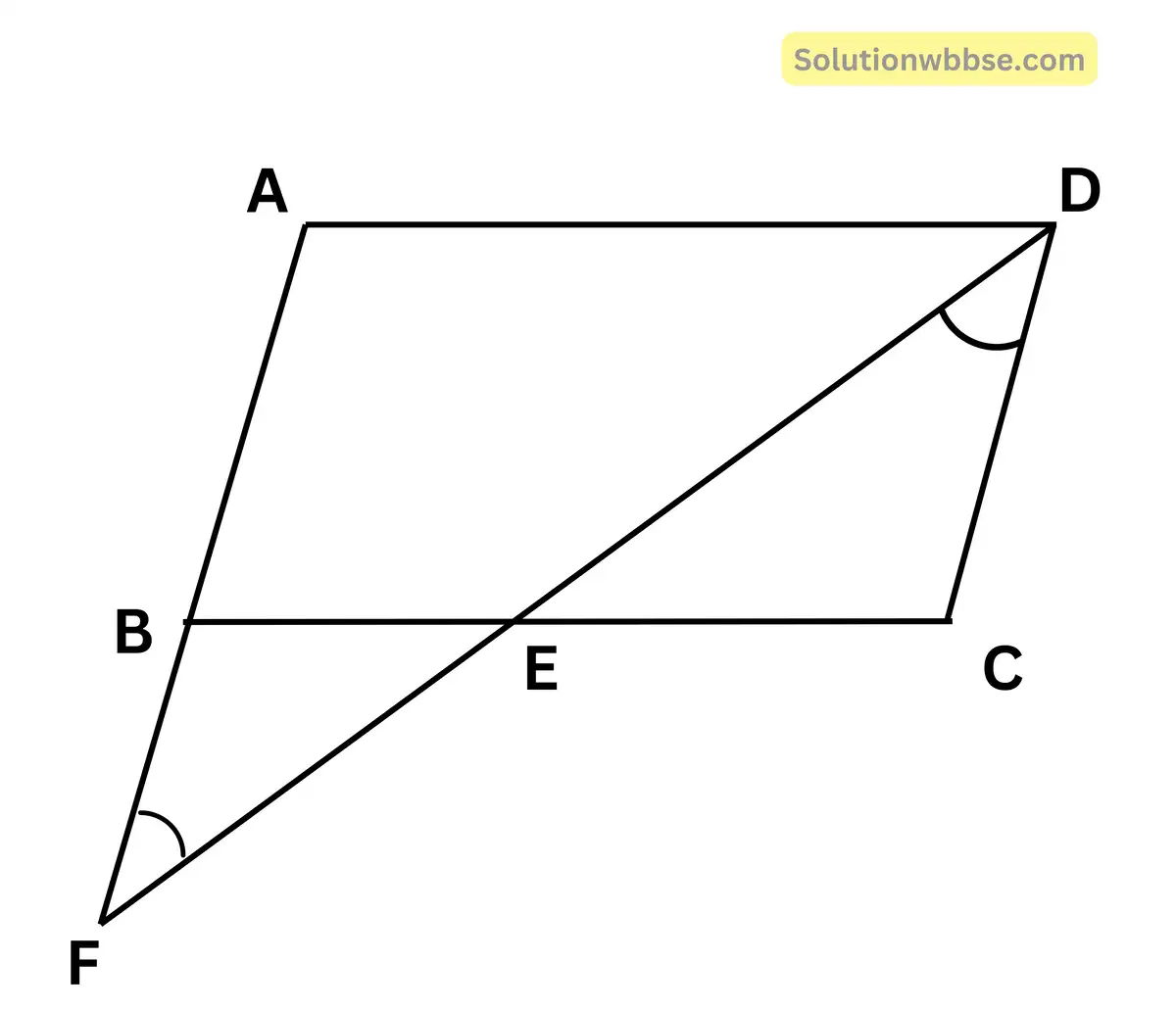
∆BEF ও ∆DCE -এর
BE = EC
∠BEF = ∠DEC
∠BFE = ∠EDC
∴ ∆BEF ≅ ∆DCE
∴ BF = CD
আবার CD = AB
∴ BF = AB
∴ AF = AB + BF = AB + AB = 2AB
16. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন
(i) ABC ত্রিভুজের AD এবং BE মধ্যমা এবং BE -এর সমান্তরাল সরলরেখা DF, AC বাহুর সাথে F বিন্দুতে মিলিত হয়। AC বাহুর দৈর্ঘ্য 8 সেমি হলে CF বাহুর দৈর্ঘ্য কত তা লিখি।
উত্তর –
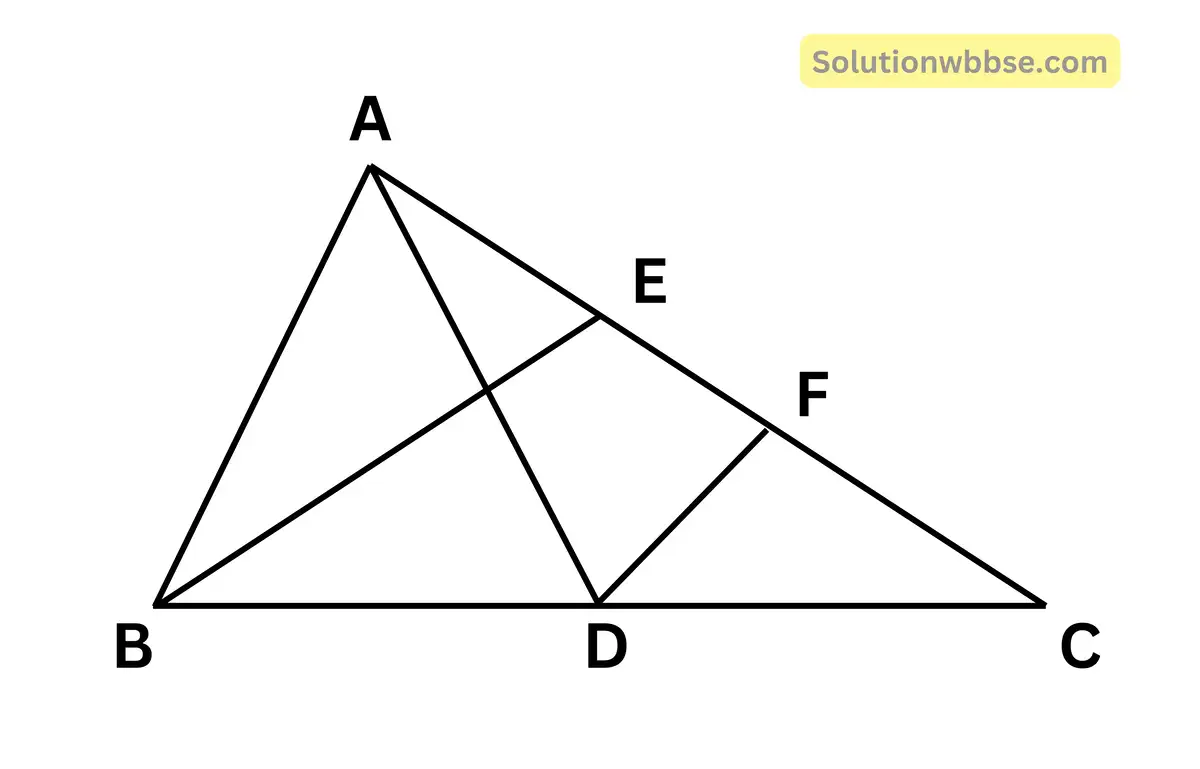
যেহেতু, E, AC এর মধ্যবিন্দু
∴ AE = EC
আবার যেহেতু BE || DF
∴ F, EC -এর মধ্যবিন্দু
∴ EF = FC
∴ CF = \(\frac12\)EC = \(\frac12\times\frac12\)AC
= \(\frac14\)AC = \(\frac12\times8\) = 2 সেমি।
∴ CF বাহুর দৈর্ঘ্য 2 সেমি।
(ii) ABC ত্রিভুজের BC, CA এবং AB বাহুর মধ্যবিন্দু যথাক্রমে P, Q, R; যদি AC = 21 সেমি, BC = 29 সেমি এবং AB = 30 সেমি হয়, তাহলে ARPQ চতুর্ভুজের পরিসীমা লিখি।
উত্তর –
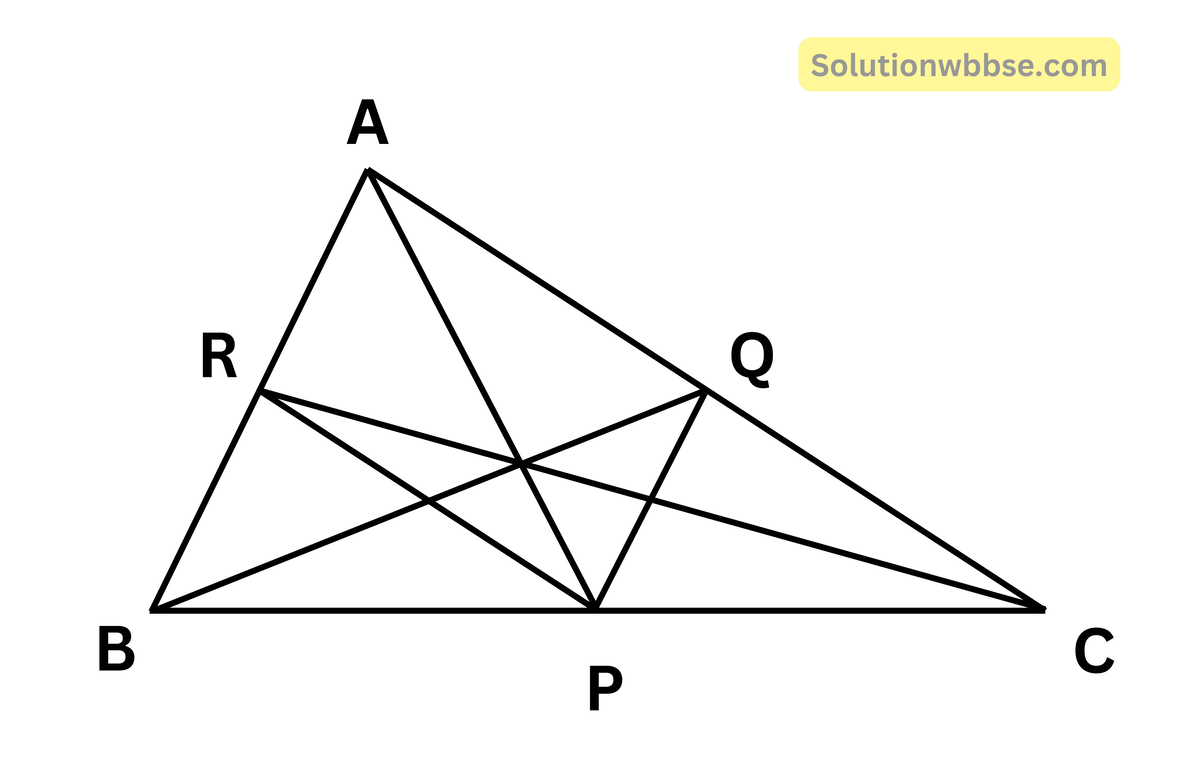
AC = 21 সেমি., BC 24 সেমি., AB = 30 সেমি.
∴ AQ = \(\frac{21}2\) সেমি.
এবং AR = \(\frac{30}2\) সেমি.
∴ ARPQ চতুর্ভুজের পরিসীমা
= \(\left\{\left(\frac{21}2\times2\right)+\left(\frac{30}2\times2\right)\right\}\) সেমি.
= (21 + 30) সেমি = 51 সেমি।
(iii) ABC ত্রিভুজের AC বাহুর উপর D যে-কোনো একটি বিন্দু। P, Q, X, Y, যথাক্রমে AB, BC, AD এবং DC -এর মধ্যবিন্দু। PX = 5 সেমি. হলে QY -এর দৈর্ঘ্য কত তা লিখি।
উত্তর –
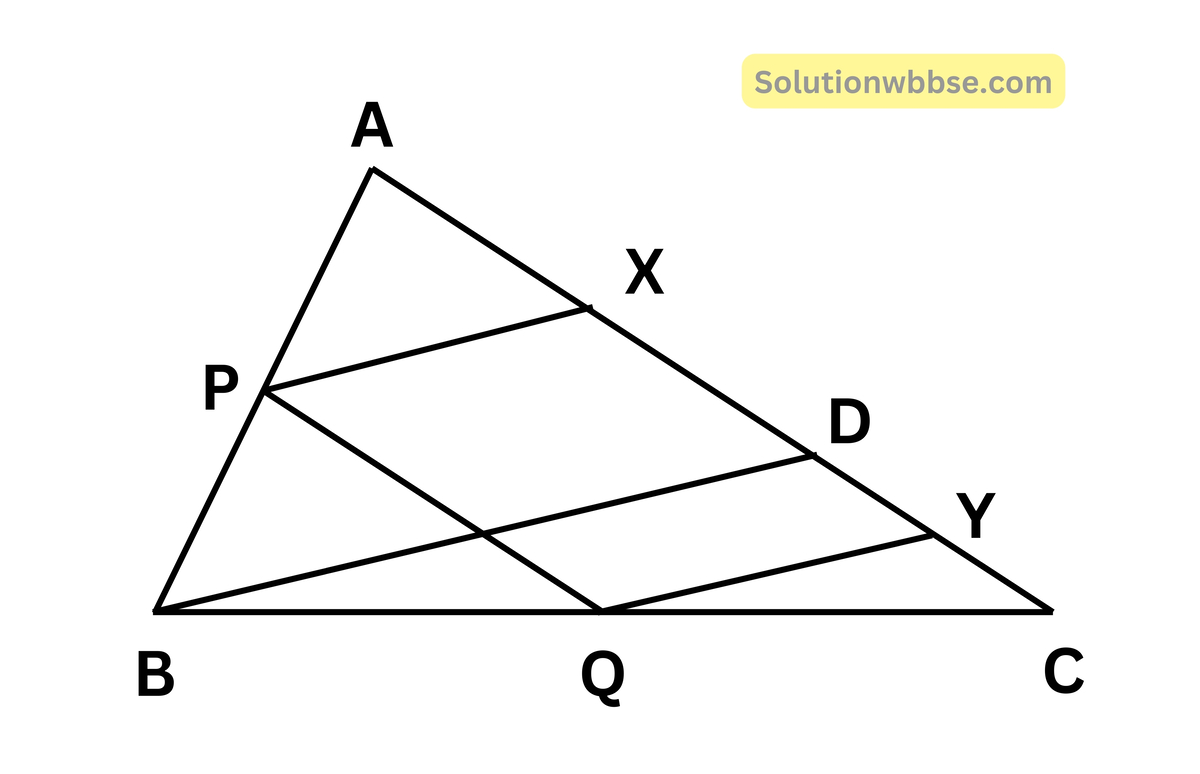
যেহেতু, P, Q বিন্দুদুটি যথাক্রমে AB ও BC বাহুর মধ্যবিন্দু
∴ PQ || AC এবং PQ = \(\frac12\)AC
আবার ∆ABD থেকে পাই, PX || BD
এবং ∆BDC থেকে পাই, QY || BD
∴ PX || QY
এখন PXCQ চতুর্ভুজের, PX || QY
এবং PQ || XY [∵ PQ || AC]
∴ PXYQ একটি সামান্তরিক।
∴ PX = QY = 5 সেমি।
(iv) ABC ত্রিভুজের BE ও CF মধ্যমা G বিন্দুতে ছেদ করে। P এবং Q যথাক্রমে BG এবং CG -এর মধ্যবিন্দু। PQ = 3 সেমি হলে BC -এর দৈর্ঘ্য কত তা লিখি।
উত্তর –
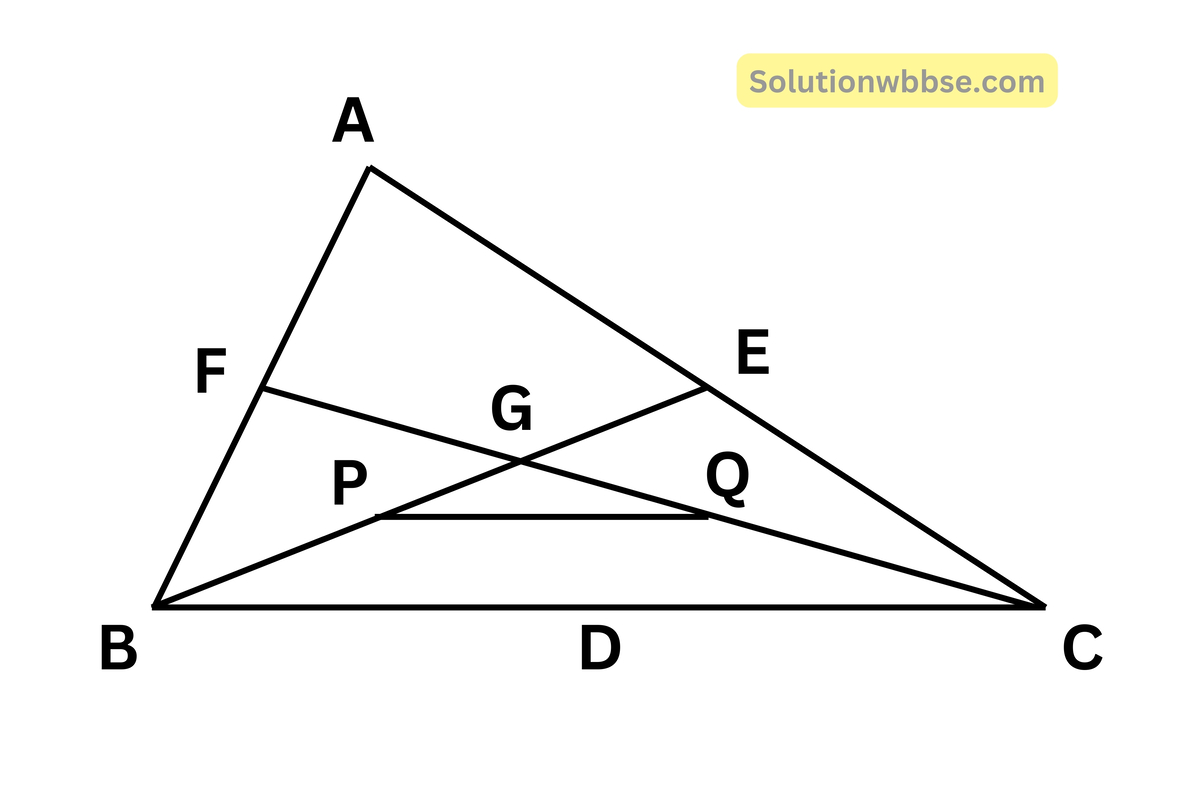
PQ = 3 সেমি
∆GBC থেকে পাই,
P এবং Q যথাক্রমে GBC এর GB ও GC বাহুর মধ্যবিন্দু
∴ PQ || BC এবং PQ = \(\frac12\)BC
∴ BC = 2PQ = (2 × 3) সেমি
= 6 সেমি
∴ BC -এর দৈর্ঘ্য 6 সেমি।
(v) ABC ত্রিভুজের BC, CA ও AB বাহুর মধ্যবিন্দু যথাক্রমে D, E ও F; EF, AD -কে O বিন্দুতে ছেদ করে। AD = 6 সেমি. হলে, AO -এর দৈর্ঘ্য কত তা লিখি।
উত্তর –
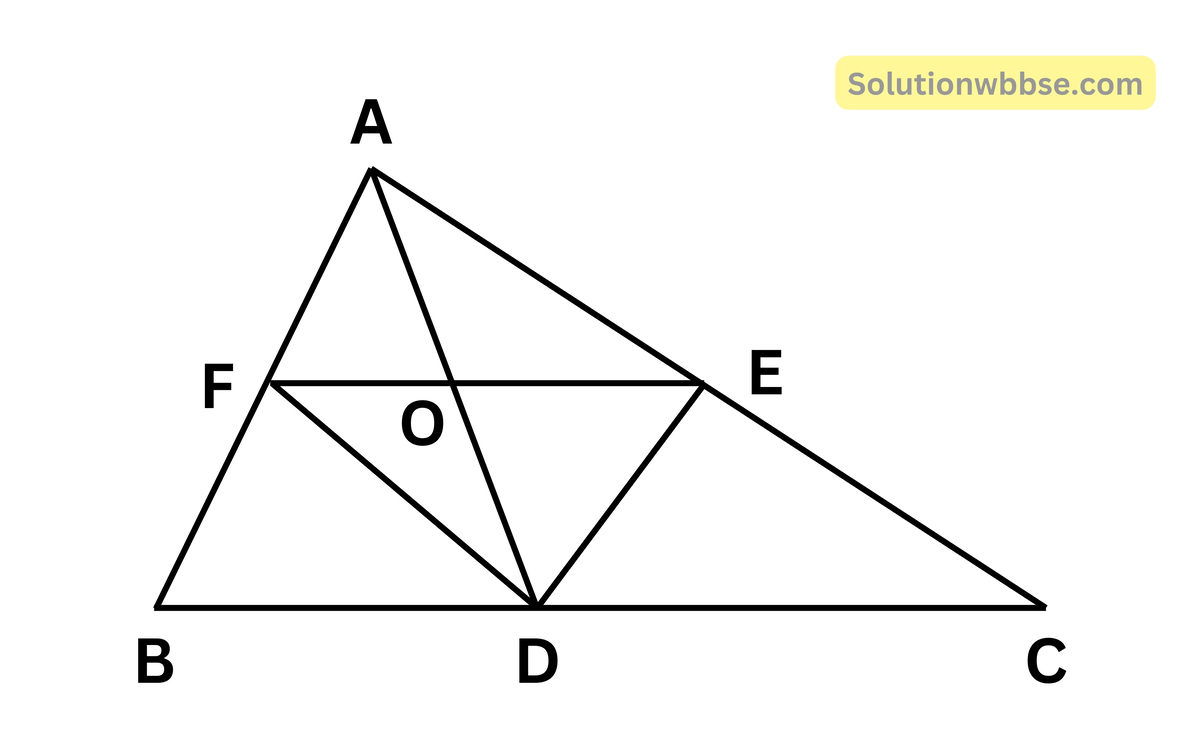
∆ABC থেকে পাই,
FD || AC [∵ F, D যথাক্রমে AB ও BC বাহুর মধ্যবিন্দু]
∴ FD || AE
আবার ∆ABC থেকে লিখতে পারি
ED || AB [∵ E, D যথাক্রমে AC ও BC বাহুর মধ্যবিন্দু]
∴ ED || AF
এখন AFDE চতুর্ভুজের FD || AE এবং ED || AF
∴ AFDE একটি সামান্তরিক।
আবার AD ও FE সামান্তরিক AFDE -এর কর্ণ
আমরা জানি, সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।
∴ AO = OD
∴ AO = \(\frac62\) = 3 সেমি।
এই আর্টিকেলে নবম শ্রেণির গণিতের ‘ভেদক ও মধ্যবিন্দু সংক্রান্ত উপপাদ্য‘ অধ্যায়ের ‘কষে দেখি – 9’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।
কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন