পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) নবম শ্রেণির গণিত পাঠ্যবইয়ের নবম অধ্যায় হলো ‘ভেদক ও মধ্যবিন্দু সংক্রান্ত উপপাদ্য’। এই পোস্টে ‘উপপাদ্য‘-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

উপপাদ্য 20. কোনো ত্রিভুজের দুটি বাহুর মধ্যবিন্দুদ্বয়ের সংযোজক সরলরেখাংশ তৃতীয় বাহুর সমান্তরাল ও অর্ধেক। আমি যুক্তি দিয়ে প্রমাণ করি।
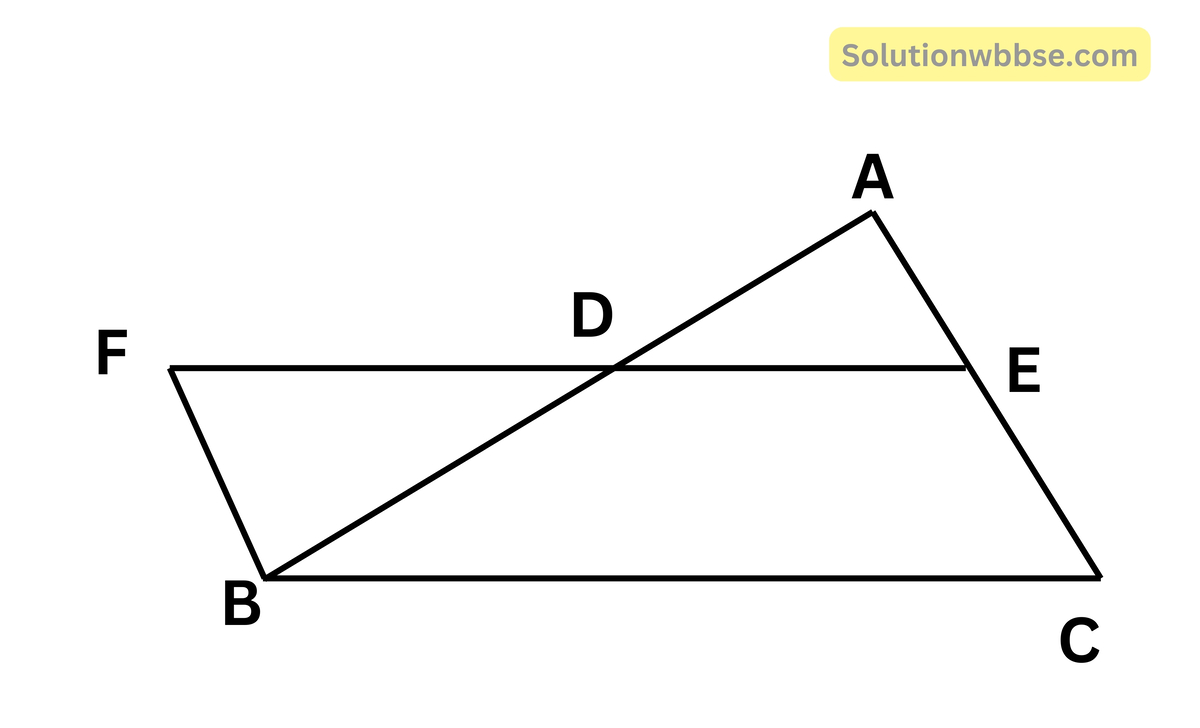
প্রদত্ত – ধরা যাক, ABC ত্রিভুজের AB বাহুর মধ্যবিন্দু D এবং AC বাহুর মধ্যবিন্দু E; D ও E যুক্ত করলাম।
প্রমাণ করতে হবে যে – (i) DE || BC এবং (ii) DE = \(\frac12\)BC
অঙ্কন – ED কে F বিন্দু পর্যন্ত এমনভাবে বর্ধিত করলাম যেন ED = DF হয়। B ও F বিন্দুদ্বয় যোগ করলাম।
প্রমাণ – ∆ADE এবং ∆BDF -এ AD = BD [স্বীকার]
∠ADE = ∠BDF [বিপ্রতীপ কোণ]
DE = DF [অঙ্কনানুসারে)
∴ ∆ADE ≅ ∆BDF [S-A-S শর্তানুসারে]
∴ AE = BF [সর্বসম ত্রিভুজের অনুরূপ বাহু]
কিন্তু, AE = CE [স্বীকার]
∴ BF = CE
এবং ∠DAE = ∠DBF; কিন্তু এরা একান্তর কোণ।
∴ BF || AE; অর্থাৎ, BF || CE
BCEF চতুর্ভুজের BF || CE এবং BF = CE
∴ BCEF একটি সামান্তরিক [BCEF চতুর্ভুজের একজোড়া বিপরীত বাহু সমান ও সমান্তরাল।
∴ FE || BC; অর্থাৎ, DE || BC (প্রমাণিত)
এবং, BC = EF = DE + DF = DE + DE = 2DE (∵ DE = DF)
∴ DE = \(\frac12\)BC (প্রমাণিত)।
উপপাদ্য 21. কোনো ত্রিভুজের যে কোনো একটি বাহুর মধ্যবিন্দু দিয়ে অঙ্কিত দ্বিতীয় একটি বাহুর সমান্তরাল সরলরেখা তৃতীয় বাহুকে সমদ্বিখণ্ডিত করবে এবং ত্রিভুজের বাহুগুলির দ্বারা সমান্তরাল সরলরেখার খণ্ডিতাংশ দ্বিতীয় বাহুর অর্ধেক হবে।

প্রদত্ত – ধরা যাক, ∆ABC এর AB বাহুর মধ্যবিন্দু D দিয়ে BC এর সমান্তরাল DE টানা হল যা AC বাহুকে E বিন্দুতে ছেদ করল।
প্রমাণ করতে হবে যে – AE = CE এবং DE = \(\frac12\)BC
অঙ্কন – ED কে F বিন্দু পর্যন্ত এমনভাবে বর্ধিত করলাম, যেন ED = DF হয়। B ও F বিন্দুদ্বয় যোগ করলাম।
প্রমাণ – ∆ADE এবং ∆BDF -এর মধ্যে
AD = BD [স্বীকার]
∠ADE = ∠BDF [বিপ্রতীপ কোণ]
DE = DF [অঙ্কন অনুসারে]
∴ ∆ADE ≅ ∆BDF [S-A-S শর্তানুসারে]
∴ AE = FB [সর্বসম ত্রিভুজের অনুরূপ বাহু]
এবং ∠DAE = ∠DBF, কিন্তু এরা একান্তর কোণ।
∴ AE || BF বা CE || BF
আবার, EF || BC [স্বীকার]
∴ BCEF চতুর্ভুজটি একটি সামান্তরিক।
সুতরাং, BC = FE এবং BF = CE; কিন্তু FB = AE
∴ AE = CE (প্রমাণিত)
আবার, BC = EF = DF + DE
= DE + DE
= 2DE [∵ DF = DE]
∴ DE = \(\frac12\)BC (প্রমাণিত)।
উপপাদ্য 21. প্রমাণ করো যে, ত্রিভুজের যে কোনো দুটি বাহুর মধ্যবিন্দুদ্বয়ের সংযোজক সরলরেখাংশ তৃতীয় বাহুর সমান্তরাল ও অর্ধেক।
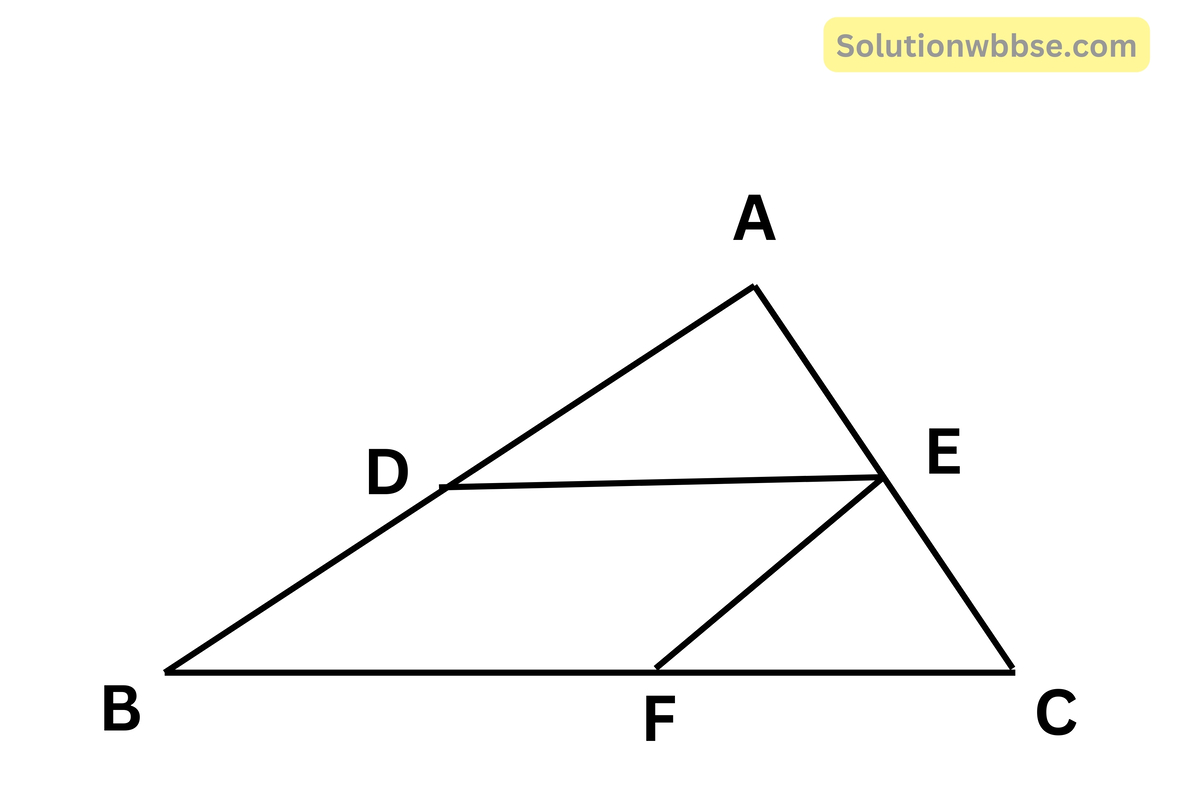
প্রদত্ত – ∆ABC -এর AB ও AC বাহুর মধ্যবিন্দু দুটি যথাক্রমে D ও E; D, E যুক্ত করা হলো।
প্রমাণ করতে হবে যে – (i) DE || BC (ii) DE = \(\frac12\)BC
অঙ্কন – AC বাহুর মধ্যবিন্দু E দিয়ে AB বাহুর সমান্তরাল সরলরেখাংশ টানলাম যা BC -কে F বিন্দুতে ছেদ করল।
প্রমাণ – E, AC -এর মধ্যবিন্দু এবং EF || AB [অঙ্কনানুসারে]
∴ F., BC -এর মধ্যবিন্দু। অর্থাৎ BF = \(\frac12\)BC এবং EF = \(\frac12\)AB
সুতরাং, EF = \(\frac12\)AB = DB [∵ D, AB -এর মধ্যবিন্দু]
চতুর্ভুজ DBFE -এর
EF = DB এবং EF || DB [অঙ্কনানুযায়ী]
∴ DBFE একটি সামান্তরিক।
সুতরাং, DE || BF; অর্থাৎ DE || BC [(i) নং প্রমাণিত]
DE = BF = \(\frac12\)BC [(ii) নং প্রমাণিত]
উপপাদ্য 22. যদি তিনটি বা তার বেশি সমান্তরাল সরলরেখা যে-কোনো ভেদক থেকে সমান সমান অংশ খণ্ডিত করে তাহলে তারা অপর যে-কোনো ভেদক থেকেও সমান সমান অংশ খণ্ডিত করবে।
প্রদত্ত – AB, CD এবং EF সমান্তরাল সরলরেখা তিনটি PQ ভেদক থেকে GH ও HI দুটি সমান অংশ খণ্ডিত করেছে। অর্থাৎ GH = HI; ওই সমান্তরাল সরলরেখা তিনটি অপর একটি ভেদক XY থেকেও JK ও KL দুটি অংশ খণ্ডিত করেছে।
প্রমাণ করতে হবে যে – JK = KL
অঙ্কন – G ও L বিন্দু দুটি যোগ করলাম যা CD সরলরেখাকে T বিন্দুতে ছেদ করল।
প্রমাণ – ∆GIL -এর, H, GI -এর মধ্যবিন্দু [∵ GH = HI, প্রদত্ত]
এবং HT || IL [প্রদত্ত]
∴ T, GL -এর মধ্যবিন্দু।
আবার, ∆GLJ -এর, T, GL -এর মধ্যবিন্দু এবং TK || GJ [প্রদত্ত]
∴ K, JL -এর মধ্যবিন্দু।
∴ JK = KL (প্রমাণিত)
PQR ত্রিভুজের PQ এবং PR -বাহু দুটির মধ্যবিন্দু যথাক্রমে X এবং Y; X, Y বিন্দু দুটি যোগ করলাম। আমি যুক্তি দিয়ে প্রমাণ করি যে, XY || QR এবং XY = \(\frac12\)QR
উত্তর –
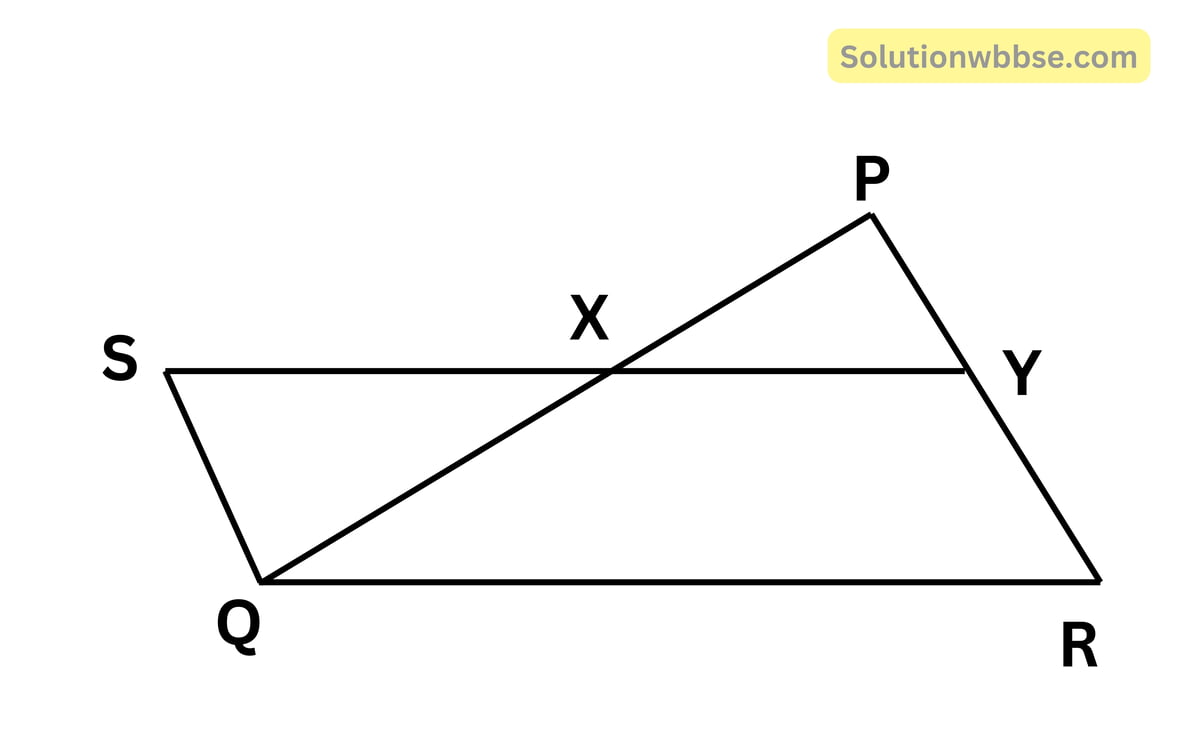
প্রদত্ত – ধরা যাক, PQR ত্রিভুজের PQ বাহুর মধ্যবিন্দু X এবং PQ বাহুর মধ্যবিন্দু Y; X ও Y যুক্ত করলাম।
প্রামাণ্য – (i) XY || QR এবং (ii) XY = \(\frac12\)QR
অঙ্কন – XY -কে S বিন্দু পর্যন্ত এমনভাবে বর্ধিত করলাম যেন XY = XS হয়। S, ও Q বিন্দুদ্বয় যোগ করলাম।
প্রমাণ – ∆PXY এবং ∆XSQ -এ
PX = XQ [প্রদত্ত]
∠PXY = ∠SXQ [বিপ্রতীপ কোণ]
এবং XY = SX [অঙ্কনানুসারে]
∴ ∆PXY ≅ ∆SXQ [S-A-S শর্তানুসারে]
∴ PY = SQ [সর্বসম ত্রিভুজের অনুরূপ বাহু]
কিন্তু PY = YR [প্রদত্ত]
∴ SQ = YR
এবং ∠XPY = ∠XQS; কিন্তু এরা একান্তর কোণ।
∴ SQ || PY অর্থাৎ SQ || YR
∴ QRYS একটি সামান্তরিক [সেহেতু QRYS চতুর্ভুজের একজোড়া বিপরীত বাহু সমান ও সমান্তরাল]
∴ SY || QR অর্থাৎ XY || QR (প্রমাণিত) —-(i)
এবং QR = SY = SX + XY = XY + XY = 2XY
∴ XY = \(\frac12\)QR (প্রমাণিত) —-(ii)
এই আর্টিকেলে নবম শ্রেণির গণিতের ‘ভেদক ও মধ্যবিন্দু সংক্রান্ত উপপাদ্য‘ অধ্যায়ের ‘উপপাদ্য’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।
কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন