পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) দশম শ্রেণির গণিত পাঠ্যবইয়ের অষ্টাদশ অধ্যায় হলো ‘বৃত্তের ক্ষেত্রফল’। এই পোস্টে ‘কষে দেখি – 18‘-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. আমিনাবিবি আজ 2.1 মিটার লম্বা একটি দড়ি দিয়ে তার গোরুটিকে ফাঁকা মাঠে খুঁটির সঙ্গে বাঁধলেন। হিসাব করে দেখি গোরুটি সবথেকে বেশি কতটা জমির ঘাস খেতে পারবে।
সমাধান –
2.1 মিটার ব্যাসার্ধ বিশিষ্ট বৃত্তাকার অংশের ক্ষেত্রফল
= \( \pi r^2\) বর্গ মিটার
= \( \frac{22}{7} \times (2.1)^2\) বর্গ মিটার
= \( \frac{22}{7} \times 2.1 \times 2.1\) বর্গ মিটার
= \( 22 \times 0.3 \times 2.1\) বর্গ মিটার
= \( 13.86\) বর্গ মিটার
উত্তর – গোরুটি 13.86 বর্গ মিটার জমির ঘাস খেতে পারবে।
2. সুহানা একটি বৃত্ত আঁকবে যার পরিধি 35.2 সেমি। হিসাব করে দেখি সুহানা যে বৃত্ত আঁকবে তার ব্যাসার্ধের দৈর্ঘ্য কত নেবে এবং বৃত্তাকার ক্ষেত্রের ক্ষেত্রফল কত হবে।
সমাধান –
ধরি, সুহানা যে বৃত্ত আঁকবে তার ব্যাসার্ধ হবে \(r\) সেমি.।
প্রশ্নানুসারে,
\(2\pi r = 35.2\)বা, \(2 \times \frac{22}{7} \times r = 35.2\)
বা, \(r = \frac{35.2 \times 7}{22 \times 2}\)
বা, \(r = 5.6\)
\(\therefore\) সুহানা যে বৃত্ত আঁকবে তার ব্যাসার্ধের দৈর্ঘ্য নেবে 5.6 সেমি.।
সুহানার আঁকা বৃত্তের ক্ষেত্রফল = \( \pi r^2\) বর্গ সেমি.
= \( \frac{22}{7} \times (5.6)^2\) বর্গ সেমি.
= \( \frac{22}{7} \times 5.6 \times 5.6\) বর্গ সেমি.
= \( 98.56\) বর্গ সেমি.
উত্তর – সুহানার আঁকা বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5.6 সেমি. এবং বৃত্তাকার ক্ষেত্রের ক্ষেত্রফল 98.56 বর্গ সেমি.।
3. রেখার দিদিমা একটি গোলাকার টেবিলের ঢাকনা তৈরি করেছেন যার ক্ষেত্রফল 5544 বর্গ সেমি। তিনি এই টেবিলের ঢাকনার চারদিকে রঙিন ফিতে লাগাতে চান। হিসাব করে দেখি দিদিমাকে কত দৈর্ঘ্যের রঙিন ফিতে কিনতে হবে।
সমাধান –
ধরি, গোলাকার টেবিলের ব্যাসার্ধ \(r\) সেমি.।
\(\therefore \pi r^2 = 5544\)বা, \(\frac{22}{7} \times r^2 = 5544\)
বা, \(r^2 = \frac{5544 \times 7}{22}\)
বা, \(r^2 = 1764\)
বা, \(r^2 = 42^2\)
বা, \(r = 42\)
এখন গোলাকার টেবিলের পরিসীমা = \( 2\pi r\) সেমি.
= \( 2 \times \frac{22}{7} \times 42\) সেমি.
= \( 22 \times 12\) সেমি.
= \( 264\) সেমি.
\(\therefore\) টেবিলের চারদিকে রঙিন ফিতে লাগাতে হলে 264 সেমি. দৈর্ঘ্যের ফিতের প্রয়োজন।
উত্তর – দিদিমাকে 264 সেমি. দৈর্ঘ্যের ফিতে কিনতে হবে।
4. আমাদের পাড়ার বৃত্তাকার খেলার মাঠটি বেড়া দিয়ে ঘিরতে প্রতি মিটার 21 টাকা হিসাবে 924 টাকা খরচ হয়েছে। মাঠটি ত্রিপল দিয়ে ঢেকে দেওয়ার জন্য কত বর্গ মিটার ত্রিপল কিনতে হবে হিসাব করে লিখি।
সমাধান –
আমাদের পাড়ার বৃত্তাকার খেলার মাঠটি বেড়া দিয়ে ঘিরতে প্রতি মিটার 21 টাকা হিসাবে 924 টাকা খরচ হয়েছে।
\(\therefore\) বেড়ার দৈর্ঘ্য = \( \frac{924}{21}\) মিটার = \( 44\) মিটার
\(\therefore\) খেলার মাঠটির পরিসীমা = \( 44\) মিটার
ধরি, গোলাকার খেলার মাঠের ব্যাসার্ধ \(r\) মিটার
\(\therefore 2\pi r = 44\)বা, \(2 \times \frac{22}{7} \times r = 44\)
বা, \(r = \frac{44 \times 7}{22 \times 2}\)
বা, \(r = 7\)
\(\therefore\) বৃত্তাকার খেলার মাঠের ব্যাসার্ধ 7 মিটার।
\(\therefore\) খেলার মাঠটি ত্রিপল দিয়ে ঢাকার জন্য যে পরিমাণ ত্রিপল লাগবে তা হল মাঠটির ক্ষেত্রফলের সমান = \( \pi r^2\) বর্গ মিটার
= \( \frac{22}{7} \times (7)^2\) বর্গ মিটার
= \( \frac{22}{7} \times 7 \times 7\) বর্গ মিটার
= \( 154\) বর্গ মিটার
উত্তর – মাঠটি ত্রিপল দিয়ে ঢাকার জন্য 154 বর্গমিটারের ত্রিপল লাগবে।
5. ফারুক একটি বৃত্ত আঁকবে যার ক্ষেত্রের ক্ষেত্রফল হবে 616 বর্গ সেমি। হিসাব করে দেখি ফারুক যে বৃত্ত আঁকবে তার ব্যাসার্ধের দৈর্ঘ্য কত নেবে এবং বৃত্তটির পরিধি কত পাবে।
সমাধান –
ধরি, ফারুকের আঁকা বৃত্তের ব্যাসার্ধের দৈর্ঘ্য \(r\) সেমি.।
প্রশ্নানুসারে,
\(\pi r^2 = 616\)বা, \(\frac{22}{7} \times r^2 = 616\)
বা, \(r^2 = \frac{616 \times 7}{22}\)
বা, \(r^2 = 28 \times 7\)
বা, \(r^2 = 2 \times 2 \times 7 \times 7\)
বা, \(r^2 = (2 \times 7)^2\)
বা, \(r^2 = 14^2\)
বা, \(r = 14\)
\(\therefore\) বৃত্তের পরিধি = \( 2\pi r\) সেমি. = \( 2 \times \frac{22}{7} \times 14\) সেমি.
= \( 88\) সেমি.
উত্তর – ফারুক যে বৃত্ত আঁকবে তার ব্যাসার্ধ 14 সেমি. এবং পরিধি 88 সেমি.।
6. পলাশ ও পিয়ালী দুটি বৃত্ত এঁকেছে যাদের ব্যাসার্ধের দৈর্ঘ্য অনুপাত 4:5; হিসাব করে দুজনের আঁকা বৃত্তাকার ক্ষেত্র দুটির ক্ষেত্রফলের অনুপাত লিখি।
সমাধান –
ধরি, পলাশ ও পিয়ালির আঁকা বৃত্তের ব্যাসার্ধ যথাক্রমে \(4r\) একক এবং \(5r\) একক।
\(\therefore\) দুজনের আঁকা বৃত্তাকার ক্ষেত্র দুটির ক্ষেত্রফলের অনুপাত = \( \pi(4r)^2 : \pi(5r)^2\)
= \( 16r^2 : 25r^2\)
= \( 16:25\)
উত্তর – পলাশ ও পিয়ালির আঁকা বৃত্তাকার ক্ষেত্রের ক্ষেত্রফলের অনুপাত \(16:25\)।
7. সুমিত ও রেবা একই দৈর্ঘ্যের দুটি তামার তার এনেছে। সুমিত ওই তারটি বেঁকিয়ে আয়তাকার চিত্র তৈরি করেছে যার দৈর্ঘ্য 48 সেমি এবং প্রস্থ 40 সেমি। কিন্তু রেবা একই দৈর্ঘ্যের তামার তারটি বেঁকিয়ে বৃত্ত তৈরি করল। হিসাব করে দেখি সুমিতের তৈরি আয়তাকার চিত্র এবং রেবার তৈরি বৃত্তের মধ্যে কোনটি বেশি জায়গা জুড়ে থাকবে।
সমাধান –
সুমিতের তৈরি আয়তাকার চিত্রের পরিসীমা = 2(দৈর্ঘ্য + প্রস্থ) সেমি. = \(2 \times (48 + 40)\) সেমি. = \(176\) সেমি.।
যেহেতু দুটি তারের দৈর্ঘ্য সমান, সুতরাং সুমিতের তৈরি আয়তাকার চিত্রের পরিসীমা = রেবার তৈরি বৃত্তের পরিধি = \(176\) সেমি.।
ধরি, রেবার তৈরি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য \(r\) সেমি.।
শর্তানুসারে,
\(2\pi r = 176\)বা, \(2 \times \frac{22}{7} \times r = 176\)
বা, \(\frac{44}{7} r = 176\)
বা, \(r = 176 \times \frac{7}{44}\)
বা, \(r = 28\)
\(\therefore\) বৃত্তের ব্যাসার্ধ \(28\) সেমি.।
\(\therefore\) বৃত্তের ক্ষেত্রফল
= \( \pi r^2\) বর্গ সেমি.
= \( \frac{22}{7} \times 28^2\) বর্গ সেমি.
= \( \frac{22}{7} \times 28 \times 28\) বর্গ সেমি.
= \( 2464\) বর্গ সেমি.
আবার সুমিতের তৈরি আয়তাকার চিত্রের ক্ষেত্রফল = \(48 \times 40\) বর্গ সেমি. = \(1920\) বর্গ সেমি.।
উত্তর – সুমিতের তৈরি আয়তাকার চিত্র ও রেবার তৈরি বৃত্তাকার চিত্রের মধ্যে রেবার তৈরি বৃত্তাকার চিত্রটি বেশি জায়গা জুড়ে আছে।
8. পাইওনিয়ার অ্যাথলেটিক ক্লাবের আয়তাকার মাঠের মাঝখানে একটি বৃত্তাকার জলাশয় আছে যার ব্যাসার্ধের দৈর্ঘ্য 14 মিটার। আয়তাকার মাঠের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 60 মিটার ও 42 মিটার। জলাশয় বাদে আয়তাকার মাঠের বাকি জায়গায় ঘাস লাগাতে প্রতি বর্গমিটার 75 টাকা হিসাবে কত খরচ হবে হিসাব করে দেখি।
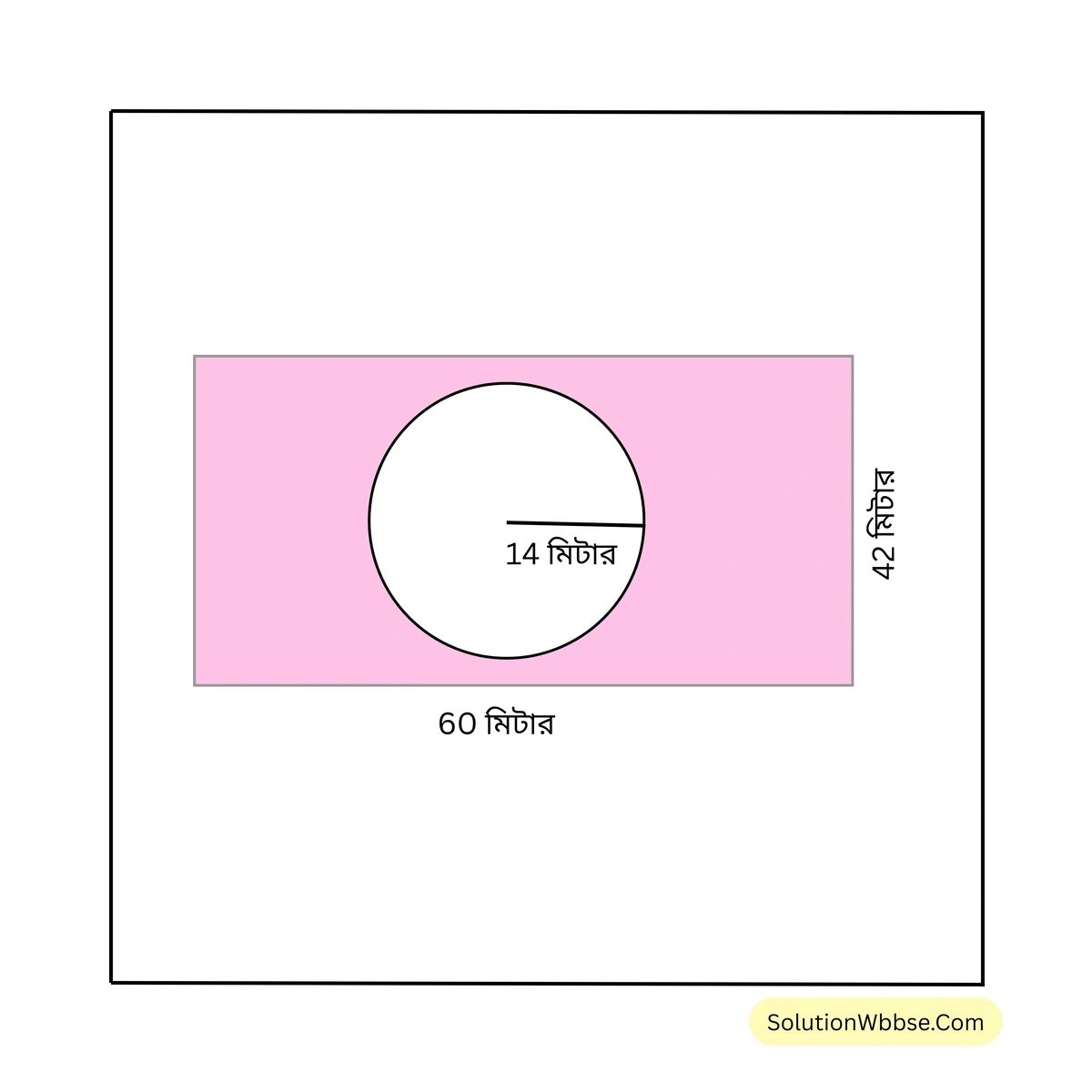
সমাধান –
বৃত্তাকার জলাশয়ের ব্যাসার্ধ \(r = 14\) মিটার।
\(\therefore\) বৃত্তাকার জলাশয়ের ক্ষেত্রফল = \( \pi r^2\) বর্গ মিটার
= \( \frac{22}{7} \times (14)^2\) বর্গ মিটার
= \( \frac{22}{7} \times 14 \times 14\) বর্গ মিটার
= \( 44 \times 14\) বর্গ মিটার
= \( 616\) বর্গ মিটার
আয়তাকার মাঠটির ক্ষেত্রফল = \(60 \times 42\) বর্গ মিটার = \(2520\) বর্গ মিটার।
\(\therefore\) জলাশয় বাদে আয়তাকার মাঠের ক্ষেত্রফল = \((2520 – 616)\) বর্গ মিটার = \(1904\) বর্গ মিটার।
\(\therefore\) প্রতি বর্গমিটার 75 টাকা হিসাবে মাঠের বাকি জায়গায় ঘাস লাগাতে খরচ পড়বে = \(1904 \times 75\) টাকা = \(142800\) টাকা।
উত্তর – জলাশয় বাদে আয়তাকার মাঠের বাকি জায়গায় ঘাস লাগাতে খরচ পড়বে 142800 টাকা।
9. ইটালগাছা ফ্রেন্ডস অ্যাসোসিয়েশন ক্লাবের বৃত্তাকার পার্কের বাইরের দিকে পরিধি বরাবর একটি 7 মিটার চওড়া রাস্তা আছে। বৃত্তাকার পার্কের পরিধি 352 মিটার হলে, রাস্তাটির ক্ষেত্রফল হিসাব করে লিখি। প্রতি বর্গ মিটার 20 টাকা হিসাবে রাস্তাটি বাঁধাতে কত টাকা খরচ হবে হিসাব করে লিখি।
সমাধান –
ধরি, বৃত্তাকার পার্কের ব্যাসার্ধ \(r\) মিটার।
\(\therefore 2\pi r = 352\)বা, \(2 \times \frac{22}{7} \times r = 352\)
বা, \(\frac{44}{7} r = 352\)
বা, \(r = 352 \times \frac{7}{44}\)
বা, \(r = 56\)
\(\therefore\) বৃত্তাকার পার্কের ব্যাসার্ধ \(56\) মিটার।
7 মিটার চওড়া রাস্তা সহ বৃত্তাকার পার্কের ব্যাসার্ধ = \((56 + 7)\) মিটার = \(63\) মিটার।
\(\therefore\) রাস্তাসহ পার্কের ক্ষেত্রফল = \( \pi r^2\) বর্গ মিটার
= \( \frac{22}{7} \times (63)^2\) বর্গ মিটার
= \( \frac{22}{7} \times 63 \times 63\) বর্গ মিটার
= \( 12474\) বর্গ মিটার।
এবং রাস্তা বাদে পার্কটির ক্ষেত্রফল = \( \frac{22}{7} \times (56)^2\) বর্গ মিটার
= \( \frac{22}{7} \times 56 \times 56\) বর্গ মিটার
= \( 22 \times 8 \times 56\) বর্গ মিটার
= \( 9856\) বর্গ মিটার।
\(\therefore\) শুধু রাস্তার ক্ষেত্রফল = \((12474 – 9856)\) বর্গ মিটার = \(2618\) বর্গ মিটার। এবং প্রতি বর্গ মিটার 20 টাকা হিসাবে রাস্তাটি বাঁধাতে খরচ পড়বে = \(2618 \times 20\) টাকা = \(52360\) টাকা।
উত্তর – শুধু রাস্তার ক্ষেত্রফল 2618 বর্গ মিটার এবং প্রতি বর্গ মিটার 20 টাকা হিসাবে রাস্তাটি বাঁধাতে খরচ পড়বে 52360 টাকা।
10. আনোয়ারা বিবি তার অর্ধবৃত্তাকার জমির চারদিকে প্রতি মিটার 18.50 টাকা হিসাবে বেড়া দিতে 2664 টাকা খরচ করেছেন। তিনি যদি তার ওই অর্ধবৃত্তাকার জমি প্রতি বর্গ মিটার 32 টাকা হিসাবে চাষ করান, তাহলে মোট কত টাকা খরচ করবেন হিসাব করে লিখি।
সমাধান –
আনোয়ারা বিবি তার অর্ধবৃত্তাকার জমির চারদিকে প্রতি মিটার 18.50 টাকা হিসাবে বেড়া দিতে 2664 টাকা খরচ করেছেন।
\(\therefore\) বৃত্তাকার জমির পরিধি = \(\frac{2664}{18.50}\) মিটার = \(144\) মিটার।
ধরি, অর্ধবৃত্তাকার জমির ব্যাসার্ধ \(r\) মিটার।
শর্তানুসারে,
\(\pi r + 2r = 144\)বা, \(\frac{22}{7} r + 2r = 144\)
বা, \(\frac{22r + 14r}{7} = 144\)
বা, \(\frac{36r}{7} = 144\)
বা, \(r = 144 \times \frac{7}{36}\)
বা, \(r = 28\)
\(\therefore\) অর্ধবৃত্তাকার জমির ব্যাসার্ধ \(28\) মিটার।
ওই জমির ক্ষেত্রফল = \(\frac{\pi r^2}{2}\) বর্গ মিটার = \(\frac{\frac{22}{7} \times 28 \times 28}{2}\) বর্গ মিটার = \(1232\) বর্গ মিটার।
ওই অর্ধবৃত্তাকার জমি প্রতি বর্গ মিটার 32 টাকা হিসাবে চাষ করতে মোট খরচ হবে = \(1232 \times 32\) টাকা = \(39424\) টাকা।
উত্তর – আনোয়ারা বিবি চাষ করতে মোট 39424 টাকা খরচ করলেন।
11. আজ আমার বন্ধু রজত একই বেগে দৌড়ে স্কুলের বৃত্তাকার মাঠটি যে সময়ে একবার প্রদক্ষিণ করল, একই বেগে মাঠের ব্যাস বরাবর দৌড়তে 30 সেকেন্ড কম সময় নিল। তার গতিবেগ 9 মিটার/সেকেন্ড হলে, স্কুলের মাঠের ক্ষেত্রফল হিসাব করে লিখি।
সমাধান – রজতের গতিবেগ 9 মিটার/সেকেন্ড।
\(\therefore\) রজত 1 সেকেন্ডে যায় 9 মিটার।
\(\therefore\) রজত 30 সেকেন্ডে যায় \(30 \times 9 = 270\) মিটার।
\(\therefore\) মাঠের পরিধি ও ব্যাসের দৈর্ঘ্যের অন্তর 270 মিটার।
শর্তানুসারে,
\(2\pi r – 2r = 270\)বা, \(2r(\pi – 1) = 270\)
বা, \(2r \left( \frac{22}{7} – 1 \right) = 270\)
বা, \(2r \left( \frac{22-7}{7} \right) = 270\)
বা, \(2r \times \frac{15}{7} = 270\)
বা, \(2r = \frac{270 \times 7}{15}\)
বা, \(2r = 126\)
বা, \(r = 63\)
\(\therefore\) স্কুলের মাঠের ক্ষেত্রফল = \( \pi r^2\) বর্গ মিটার
= \( \frac{22}{7} \times 63^2\) বর্গ মিটার
= \( \frac{22}{7} \times 63 \times 63\) বর্গ মিটার
= \( 12474\) বর্গ মিটার
উত্তর – স্কুলের মাঠের ক্ষেত্রফল \(12474\) বর্গ মিটার।
12. বকুলতলার বৃত্তাকার মাঠের বাইরের চারদিকে একটি সমপরিসরের রাস্তা আছে। রাস্তাটির বাইরের সীমারেখার দৈর্ঘ্য ভিতরের সীমারেখার দৈর্ঘ্য অপেক্ষা 132 মিটার বেশি। পথটির ক্ষেত্রফল 14190 বর্গ মি. হলে, বৃত্তাকার মাঠটির ক্ষেত্রফল হিসাব করে লিখি।
সমাধান –
ধরি, বৃত্তাকার মাঠের ব্যাসার্ধ \(r\) মিটার এবং রাস্তা সহ বৃত্তাকার মাঠের ব্যাসার্ধ \(R\) মিটার।
শর্তানুসারে,
\(2\pi R – 2\pi r = 132\)বা, \(2\pi(R – r) = 132\)
বা, \(2 \times \frac{22}{7} \times (R – r) = 132\)
বা, \((R – r) = \frac{132 \times 7}{2 \times 22}\)
বা, \(R – r = 21\) —(i)
এবং, \(\pi R^2 – \pi r^2 = 14190\)
বা, \(\pi (R^2 – r^2) = 14190\)
বা, \(\frac{22}{7} (R+r) (R-r) = 14190\)
বা, \((R+r) (R-r) = \frac{14190 \times 7}{22}\)
বা, \((R+r) (R-r) = 4515\)
বা, \((R+r) \times 21 = 4515\) [\(\because\) \(R-r = 21\)]
বা, \((R+r) = \frac{4515}{21}\)
বা, \((R+r) = 215\) —(ii)
(i) নং ও (ii) নং সমীকরণ যোগ করে পাই,
\(R+r + R -r = 215 + 21\)বা, \(2R = 236\)
বা, \(R = \frac{236}{2}\)
বা, \(R = 118\)
(ii) নং সমীকরণে \(R\) এর মান বসিয়ে পাই,
\(118 + r = 215\)বা, \(r = 215 – 118\)
বা, \(r = 97\)
\(\therefore\) বৃত্তাকার মাঠটির ক্ষেত্রফল = \( \pi r^2\) বর্গ মিটার
= \( \pi(97)^2\) বর্গ মিটার
= \( \frac{22}{7} \times 97 \times 97\) বর্গ মিটার
= \( \frac{266998}{7}\) বর্গ মিটার
= \( 29571 \frac{1}{7}\) বর্গ মিটার
উত্তর – বৃত্তাকার মাঠের ক্ষেত্রফল \(29571 \frac{1}{7}\) বর্গ মিটার।
13. নিচের ছবির রেখাঙ্কিত অঞ্চলের ক্ষেত্রফল হিসাব করে লিখি।
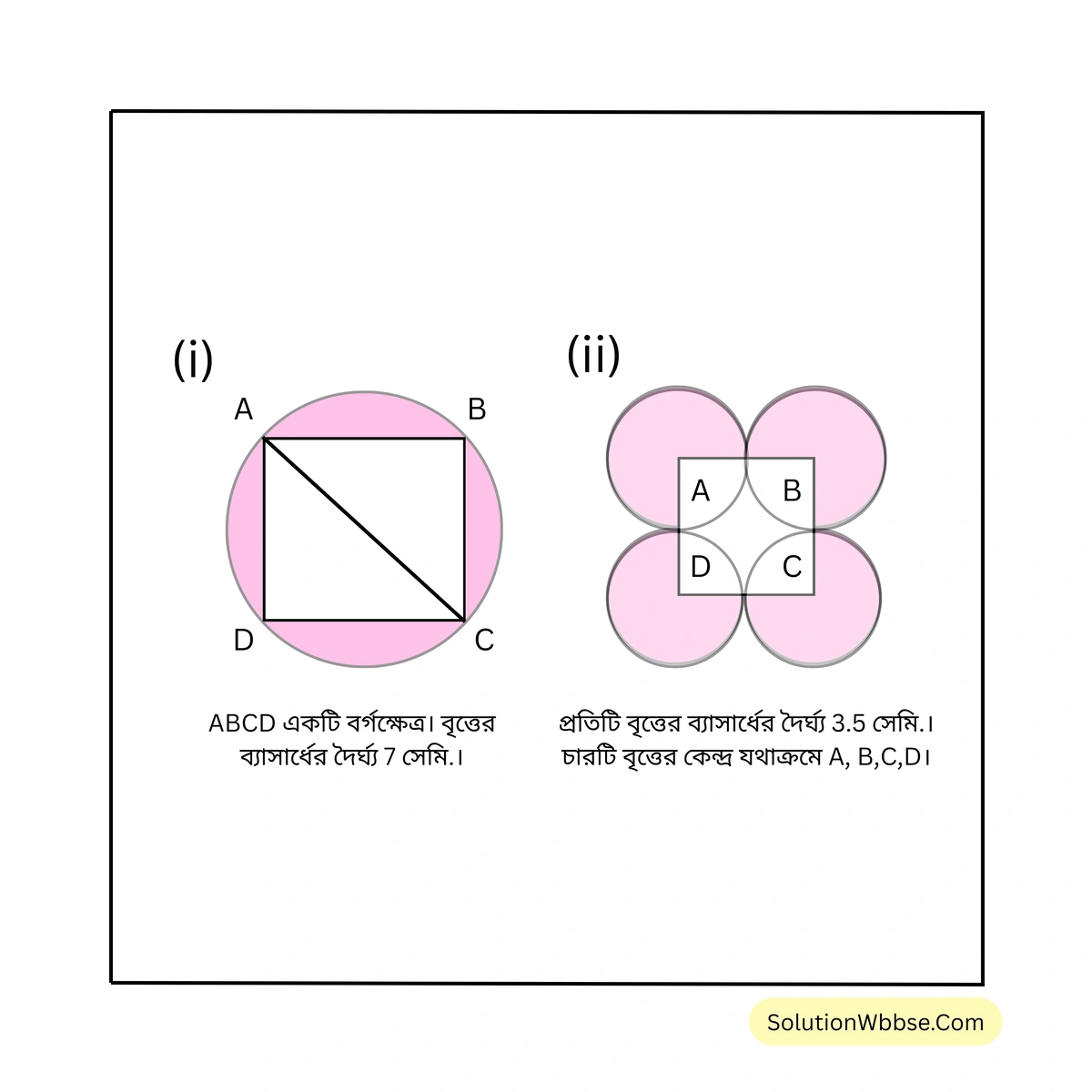
(i) ABCD একটি বর্গক্ষেত্র। বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 7 সেমি।
সমাধানঃ AC = বৃত্তের ব্যাস = 14 সেমি।
ধরি, বর্গক্ষেত্রের প্রতিটি বাহুর দৈর্ঘ্য \(a\) সেমি।
শর্তানুসারে,
\(a\sqrt{2} = 14\)বা, \(a = \frac{14}{\sqrt{2}}\)
এখন, বৃত্তের ক্ষেত্রফল
= \( \pi(7)^2\) বর্গ সেমি
= \( \frac{22}{7} \times 7 \times 7\) বর্গ সেমি
= \( 154\) বর্গ সেমি
এবং, বর্গক্ষেত্রের ক্ষেত্রফল
= \( \left( \frac{14}{\sqrt{2}} \right)^2\) বর্গ সেমি
= \( \frac{14 \times 14}{2}\) বর্গ সেমি
= \( 98\) বর্গ সেমি
\(\therefore\) রেখাঙ্কিত অংশের ক্ষেত্রফল = \((154 – 98)\) বর্গ সেমি = \(56\) বর্গ সেমি
উত্তর – রেখাঙ্কিত অংশের ক্ষেত্রফল \(56\) বর্গ সেমি।
(ii) প্রতিটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 3.5 সেমি। চারটি বৃত্তের কেন্দ্র যথাক্রমে A, B, C এবং D।
সমাধান – প্রতিটি বৃত্তের ক্ষেত্রফল
= \( \pi r^2\) বর্গ সেমি
= \( \frac{22}{7} \times (3.5)^2\) বর্গ সেমি
= \( \frac{22}{7} \times 3.5 \times 3.5\) বর্গ সেমি
= \( 22 \times 0.5 \times 3.5\) বর্গ সেমি
= \( 38.5\) বর্গ সেমি
\(\therefore\) 4টি বৃত্তের ক্ষেত্রফল = \((4 \times 38.5)\) বর্গ সেমি = \(154\) বর্গ সেমি
প্রতিটি বৃত্তকলার ক্ষেত্রফল
= \( \frac{90^{\circ}}{360^{\circ}} \times\) একটি বৃত্তের ক্ষেত্রফল
= \( \frac{90^{\circ}}{360^{\circ}} \times 38.5\) বর্গ সেমি
= \( \frac{1}{4} \times 38.5\) বর্গ সেমি
= \( 9.625\) বর্গ সেমি
\(\therefore\) 4টি বৃত্তকলার ক্ষেত্রফল = \((4 \times 9.625)\) বর্গ সেমি = \(38.5\) বর্গ সেমি
সুতরাং, রেখাঙ্কিত অংশের ক্ষেত্রফল = (4টি বৃত্তের ক্ষেত্রফল – 4টি বৃত্তকলার ক্ষেত্রফল) = \((154 – 38.5)\) বর্গ সেমি = \(115.5\) বর্গ সেমি
উত্তর – রেখাঙ্কিত অংশের ক্ষেত্রফল \(115.5\) বর্গ সেমি।
14. দীনেশ তাদের শ্রেণির কতজন কোন খেলা খেলতে ভালোবাসে তার একটা পাই-চিত্র তৈরি করেছে। সে বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 3.5 নিয়েছে। হিসাব করে প্রতিটি বৃত্তকলার পরিসীমা ও ক্ষেত্রফল লিখি।
সমাধান – ধরি, দীনেশের শ্রেণির মোট ছাত্রসংখ্যা 60 জন।
এই 60 জন ছাত্রের কতজন কোন খেলা খেলতে ভালবাসে তা নীচের ছকের মাধ্যমে দেখানো হল –
কেন্দ্রীয় কোণ নির্ণয় –
- ক্রিকেট খেলতে ভালবাসে এমন ছাত্র সংখ্যার কেন্দ্রীয় কোণ \( = \frac{26}{60} \times 360^\circ = 156^\circ \)
- ফুটবল খেলতে ভালবাসে এমন ছাত্র সংখ্যার কেন্দ্রীয় কোণ \( = \frac{20}{60} \times 360^\circ = 120^\circ \)
- টেনিস খেলতে ভালবাসে এমন ছাত্র সংখ্যার কেন্দ্রীয় কোণ \( = \frac{8}{60} \times 360^\circ = 48^\circ \)
- ভলিবল খেলতে ভালবাসে এমন ছাত্র সংখ্যার কেন্দ্রীয় কোণ \( = \frac{6}{60} \times 360^\circ = 36^\circ \)
বৃত্তকলার পরিসীমা নির্ণয় –
\(156^\circ\) কেন্দ্রীয় কোণ সম্পন্ন বৃত্তকলার পরিসীমা
= \( \left( \frac{156}{360} \times 2 \times \frac{22}{7} \times 3.5 \right) + 2 \times 3.5\) সেমি. [ ব্যাসার্ধ 3.5 সেমি. ]
= \( \left( \frac{156}{360} \times 2 \times \frac{22}{7} \times \frac{7}{2} \right) + 7\) সেমি.
= \( \left( \frac{156}{360} \times 22 \right) + 7\) সেমি.
= \( \frac{156 \times 22}{360} + 7\) সেমি.
= \( \frac{3432}{360} + 7\) সেমি.
= \( \frac{286}{30} + 7\) সেমি.
= \( \frac{143}{15} + 7\) সেমি.
= \( \frac{143 + 105}{15}\) সেমি.
= \( \frac{248}{15}\) সেমি.
= \( 16\frac{8}{15}\) সেমি.
\(120^\circ\) কেন্দ্রীয় কোণ সম্পন্ন বৃত্তকলার পরিসীমা
= \( \left( \frac{120}{360} \times 2 \times \frac{22}{7} \times 3.5 \right) + 2 \times 3.5\) সেমি. [ ব্যাসার্ধ 3.5 সেমি. ]
= \( \left( \frac{120}{360} \times 2 \times \frac{22}{7} \times \frac{7}{2} \right) + 7\) সেমি.
= \( \left( \frac{120}{360} \times 22 \right) + 7\) সেমি.
= \( \frac{120 \times 22}{360} + 7\) সেমি.
= \( \frac{2640}{360} + 7\) সেমি.
= \( \frac{22}{3} + 7\) সেমি.
= \( \frac{22 + 21}{3}\) সেমি.
= \( \frac{43}{3}\) সেমি.
= \( 14\frac{1}{3}\) সেমি.
\(48^\circ\) কেন্দ্রীয় কোণ সম্পন্ন বৃত্তকলার পরিসীমা
= \( \left( \frac{48}{360} \times 2 \times \frac{22}{7} \times 3.5 \right) + 2 \times 3.5\) সেমি. [ ব্যাসার্ধ 3.5 সেমি. ]
= \( \left( \frac{48}{360} \times 2 \times \frac{22}{7} \times \frac{7}{2} \right) + 7\) সেমি.
= \( \left( \frac{48}{360} \times 22 \right) + 7\) সেমি.
= \( \frac{48 \times 22}{360} + 7\) সেমি.
= \( \frac{1056}{360} + 7\) সেমি.
= \( \frac{88}{30} + 7\) সেমি.
= \( \frac{44}{15} + 7\) সেমি.
= \( \frac{44 + 105}{15}\) সেমি.
= \( \frac{149}{15}\) সেমি.
= \( 9\frac{14}{15}\) সেমি.
\(36^\circ\) কেন্দ্রীয় কোণ সম্পন্ন বৃত্তকলার পরিসীমা
= \( \left( \frac{36}{360} \times 2 \times \frac{22}{7} \times 3.5 \right) + 2 \times 3.5\) সেমি. [ ব্যাসার্ধ 3.5 সেমি. ]
= \( \left( \frac{36}{360} \times 2 \times \frac{22}{7} \times \frac{7}{2} \right) + 7\) সেমি.
= \( \left( \frac{36}{360} \times 22 \right) + 7\) সেমি.
= \( \frac{36 \times 22}{360} + 7\) সেমি.
= \( \frac{792}{360} + 7\) সেমি.
= \( \frac{22}{10} + 7\) সেমি.
= \( \frac{11}{5} + 7\) সেমি.
= \( \frac{11 + 35}{5}\) সেমি.
= \( \frac{46}{5}\) সেমি.
= \( 9\frac{1}{5}\) সেমি.
বৃত্তকলার ক্ষেত্রফল নির্ণয় –
\(156^\circ\) কেন্দ্রীয় কোণ সম্পন্ন বৃত্তকলার ক্ষেত্রফল
= \( \frac{156}{360} \times \frac{22}{7} \times (3.5)^2\) বর্গ সেমি. [ ব্যাসার্ধ 3.5 সেমি. ]
= \( \frac{156}{360} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) বর্গ সেমি.
= \( \frac{156}{360} \times 22 \times \frac{7}{4}\) বর্গ সেমি.
= \( \frac{156}{360} \times \frac{154}{4}\) বর্গ সেমি.
= \( \frac{156 \times 154}{360 \times 4}\) বর্গ সেমি.
= \( \frac{24024}{1440}\) বর্গ সেমি.
= \( \frac{1001}{60}\) বর্গ সেমি.
= \( 16\frac{41}{60}\) বর্গ সেমি.
\(120^\circ\) কেন্দ্রীয় কোণ সম্পন্ন বৃত্তকলার ক্ষেত্রফল
= \( \frac{120}{360} \times \frac{22}{7} \times (3.5)^2\) বর্গ সেমি. [ ব্যাসার্ধ 3.5 সেমি. ]
= \( \frac{120}{360} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) বর্গ সেমি.
= \( \frac{120}{360} \times 22 \times \frac{7}{4}\) বর্গ সেমি.
= \( \frac{120}{360} \times \frac{154}{4}\) বর্গ সেমি.
= \( \frac{120 \times 154}{360 \times 4}\) বর্গ সেমি.
= \( \frac{18480}{1440}\) বর্গ সেমি.
= \( \frac{77}{6}\) বর্গ সেমি.
= \( 12\frac{5}{6}\) বর্গ সেমি.
\(48^\circ\) কেন্দ্রীয় কোণ সম্পন্ন বৃত্তকলার ক্ষেত্রফল
= \( \frac{48}{360} \times \frac{22}{7} \times (3.5)^2\) বর্গ সেমি. [ ব্যাসার্ধ 3.5 সেমি. ]
= \( \frac{48}{360} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) বর্গ সেমি.
= \( \frac{48}{360} \times 22 \times \frac{7}{4}\) বর্গ সেমি.
= \( \frac{48}{360} \times \frac{154}{4}\) বর্গ সেমি.
= \( \frac{48 \times 154}{360 \times 4}\) বর্গ সেমি.
= \( \frac{7392}{1440}\) বর্গ সেমি.
= \( \frac{154}{30}\) বর্গ সেমি.
= \( \frac{77}{15}\) বর্গ সেমি.
= \( 5\frac{2}{15}\) বর্গ সেমি.
\(36^\circ\) কেন্দ্রীয় কোণ সম্পন্ন বৃত্তকলার ক্ষেত্রফল
= \( \frac{36}{360} \times \frac{22}{7} \times (3.5)^2\) বর্গ সেমি. [ ব্যাসার্ধ 3.5 সেমি. ]
= \( \frac{36}{360} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) বর্গ সেমি.
= \( \frac{36}{360} \times 22 \times \frac{7}{4}\) বর্গ সেমি.
= \( \frac{36}{360} \times \frac{154}{4}\) বর্গ সেমি.
= \( \frac{36 \times 154}{360 \times 4}\) বর্গ সেমি.
= \( \frac{5544}{1440}\) বর্গ সেমি.
= \( \frac{231}{60}\) বর্গ সেমি.
= \( \frac{77}{20}\) বর্গ সেমি.
= \( 3\frac{17}{20}\) বর্গ সেমি.
15. নীতু একটি বর্গক্ষেত্র ABCD এঁকেছে যার প্রতিটি বাহুর দৈর্ঘ্য 12 সেমি। আমার বোন পাশের ছবির মতো A, B, C ও D বিন্দুকে কেন্দ্র করে 6 সেমি দৈর্ঘ্যের ব্যাসার্ধের চারটি বৃত্তচাপ এঁকেছে এবং কিছু জায়গায় নকশা আঁকা ক্ষেত্রের পরিসীমা ও ক্ষেত্রফল লিখি।
সমাধান –
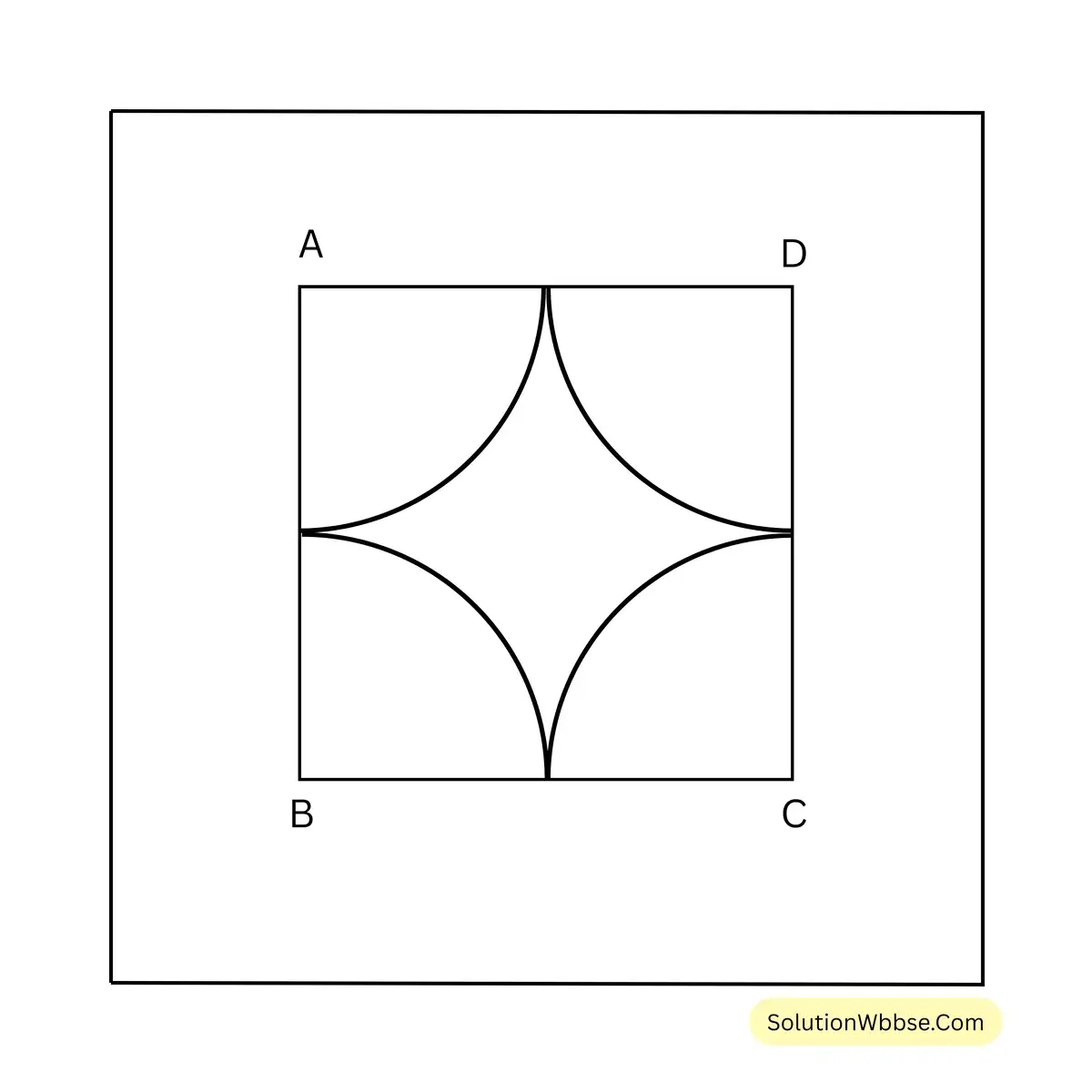
বৃত্তচাপের ব্যাসার্ধের দৈর্ঘ্য (\(r\)) = \(6\) সেমি.।
প্রতিটি বৃত্তচাপের দৈর্ঘ্য = \( \left( \frac{90^{\circ}}{360^{\circ}} \times 2\pi r \right)\) সেমি.
= \( \frac{1}{4} \times 2 \times \frac{22}{7} \times 6\) সেমি.
= \( \frac{1}{4} \times \frac{264}{7}\) সেমি.
\(\therefore\) নকশা আঁকা অংশের পরিসীমা
= \( 4 \times \frac{1}{4} \times \frac{264}{7}\) সেমি.
= \( \frac{264}{7}\) সেমি.
= \( 37\frac{5}{7}\) সেমি.
প্রতিটি বৃত্তকলার ক্ষেত্রফল = \( \frac{90^{\circ}}{360^{\circ}} \times \pi r^2\) বর্গ সেমি.
= \( \frac{1}{4} \times \frac{22}{7} \times 6^2\) বর্গ সেমি.
= \( \frac{1}{4} \times \frac{22 \times 36}{7}\) বর্গ সেমি.
\(\therefore\) 4টি বৃত্তচাপের ক্ষেত্রফল = \( 4 \times \frac{1}{4} \times \frac{22 \times 36}{7}\) বর্গ সেমি.
= \( \frac{22 \times 36}{7}\) বর্গ সেমি.
= \( \frac{792}{7}\) বর্গ সেমি.
এখন, ABCD বর্গক্ষেত্রের ক্ষেত্রফল = \((12)^2\) বর্গ সেমি. = \(144\) বর্গ সেমি.।
\(\therefore\) নকশা আঁকা ক্ষেত্রের ক্ষেত্রফল = \(\left(144 – \frac{792}{7}\right)\) বর্গ সেমি. = \(\frac{1008 – 792}{7}\) বর্গ সেমি. = \(\frac{216}{7}\) বর্গ সেমি. = \(30\frac{6}{7}\) বর্গ সেমি.।
উত্তর – নকশা আঁকা ক্ষেত্রের পরিসীমা \(37\frac{5}{7}\) সেমি. এবং নকশা আঁকা ক্ষেত্রের ক্ষেত্রফল \(30\frac{6}{7}\) বর্গ সেমি.।
16. একটি বৃত্তাকার মাঠের ক্ষেত্রফল 154 বর্গসেমি। বৃত্তাকার মাঠটির পরিলিখিত বর্গক্ষেত্রের পরিসীমা ও ক্ষেত্রফল হিসাব করে লিখি। যদি বর্গক্ষেত্রটি বৃত্তাকার মাঠের অন্তরলিখিত হতো, তাহলে বর্গক্ষেত্রটির পরিসীমা ও ক্ষেত্রফল কত হতো তা হিসাব করে লিখি।
সমাধান –
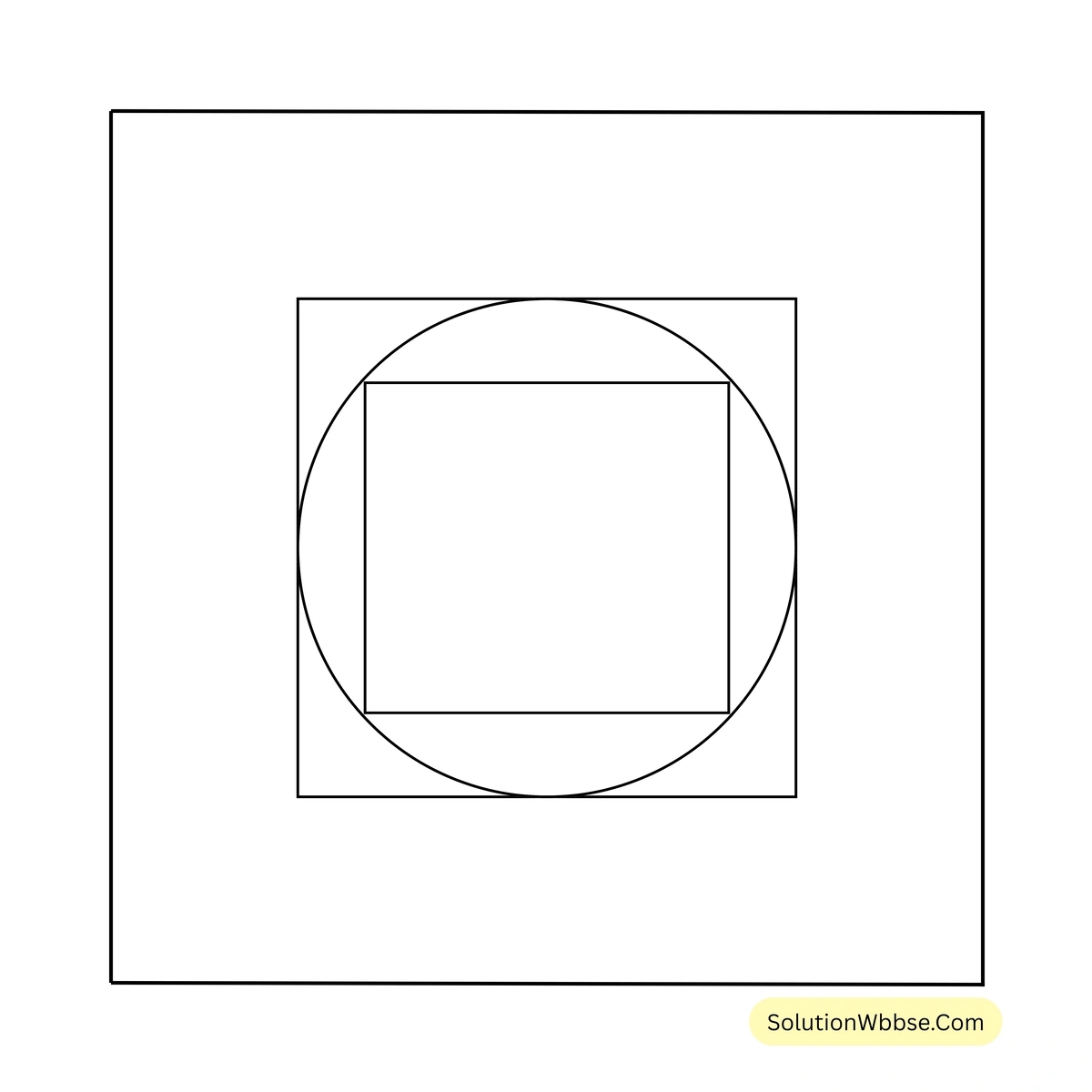
ধরি, বৃত্তাকার মাঠটির ব্যাসার্ধ \(r\) সেমি.।
\(\therefore\) শর্তানুসারে,
\(\pi r^2 = 154\)বা, \(\frac{22}{7} \times r^2 = 154\)
বা, \(r^2 = \frac{154 \times 7}{22}\)
বা, \(r^2 = 7 \times 7\)
বা, \(r^2 = (7)^2\)
বা, \(r = 7\)
\(\therefore\) বৃত্তের ব্যাসার্ধ \(7\) সেমি.।
\(\therefore\) বৃত্তের ব্যাসের দৈর্ঘ্য \((2 \times 7)\) সেমি. = \(14\) সেমি.।
\(\therefore\) বৃত্তাকার মাঠটির পরিলিখিত বর্গক্ষেত্রটির বাহুর দৈর্ঘ্য = বৃত্তের ব্যাসের দৈর্ঘ্য = \(14\) সেমি.।
\(\therefore\) বর্গক্ষেত্রের পরিসীমা = \( (4 \times 14)\) সেমি.
= \( 56\) সেমি. এবং ক্ষেত্রফল
= \( (14)^2\) বর্গ সেমি.
= \( 196\) বর্গ সেমি.। [উত্তর]
যদি বর্গক্ষেত্রটি বৃত্তের অন্তরলিখিত হত, তাহলে বর্গক্ষেত্রটির কর্ণের দৈর্ঘ্য এবং বৃত্তের ব্যাসের দৈর্ঘ্য সমান হত।
\(\therefore \sqrt{2} \times\) বাহুর দৈর্ঘ্য = \(14\)
বা, বাহুর দৈর্ঘ্য = \( \frac{14}{\sqrt{2}} = \frac{14 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} = 7\sqrt{2}\)
\(\therefore\) বর্গক্ষেত্রটির পরিসীমা = \( (4 \times 7\sqrt{2})\) সেমি. = \( 28\sqrt{2}\) সেমি.। [উত্তর]
বর্গক্ষেত্রটির ক্ষেত্রফল = \( (7\sqrt{2})^2\) বর্গ সেমি. = \(98\) বর্গ সেমি.। [উত্তর]
17. নিচের বৃত্তকলাগুলির রেখাঙ্কিত অঞ্চলের পরিসীমা ও ক্ষেত্রফল লিখি।
(i)
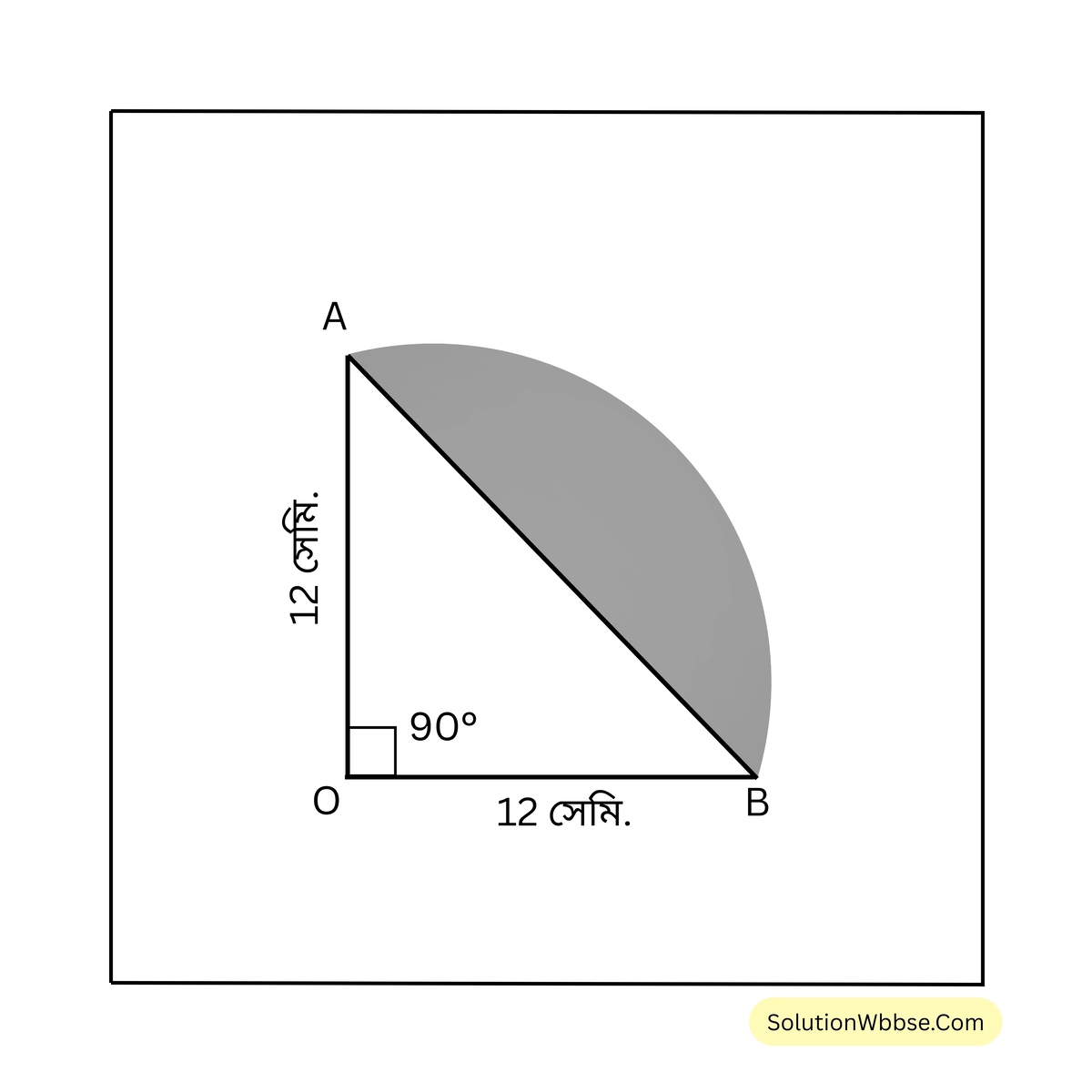
সমাধান –
(i) সমকোণী ত্রিভুজের অতিভুজ AB-এর দৈর্ঘ্য
\(\sqrt{12^2 + 12^2} = \sqrt{144 + 144} = \sqrt{288} = 12\sqrt{2}\) সেমি. = \( 12 \times 1.414\) সেমি.
= \( 16.968\) সেমি.।
AB বৃত্তচাপের দৈর্ঘ্য = \( \frac{90^{\circ}}{360^{\circ}} \times\) বৃত্তের পরিধি
= \( \frac{1}{4} \times 2 \pi \times 12\) সেমি.
= \( 6\pi\) সেমি.
= \( 6 \times \frac{22}{7}\) সেমি.
= \( 18.857\) সেমি.।
\(\therefore\) রেখাঙ্কিত অংশের পরিসীমা = \( (16.968 + 18.857)\) সেমি. = \( 35.83\) সেমি. (প্রায়)।
সমকোণী ত্রিভুজের ক্ষেত্রফল = \( \frac{1}{2} \times 12 \times 12\) বর্গ সেমি.
= \( 72\) বর্গ সেমি.।
সমগ্র বৃত্তকলাটির ক্ষেত্রফল = \( \frac{90^{\circ}}{360^{\circ}} \times\) বৃত্তের ক্ষেত্রফল
= \( \frac{1}{4} \times \pi \times (12)^2\) বর্গ সেমি.
= \( \frac{1}{4} \times \frac{22}{7} \times 12 \times 12\) বর্গ সেমি.
= \( \frac{792}{7}\) বর্গ সেমি.।
\(\therefore\) রেখাঙ্কিত অংশের ক্ষেত্রফল = \( \left( \frac{792}{7} – 72 \right)\) বর্গ সেমি.
= \( \frac{792 – 504}{7}\) বর্গ সেমি.
= \( \frac{288}{7}\) বর্গ সেমি.
= \( 41\frac{1}{7}\) বর্গ সেমি.।
উত্তর – রেখাঙ্কিত অংশের পরিসীমা \(35.83\) সেমি. এবং ক্ষেত্রফল \(41\frac{1}{7}\) বর্গ সেমি.।
ii.
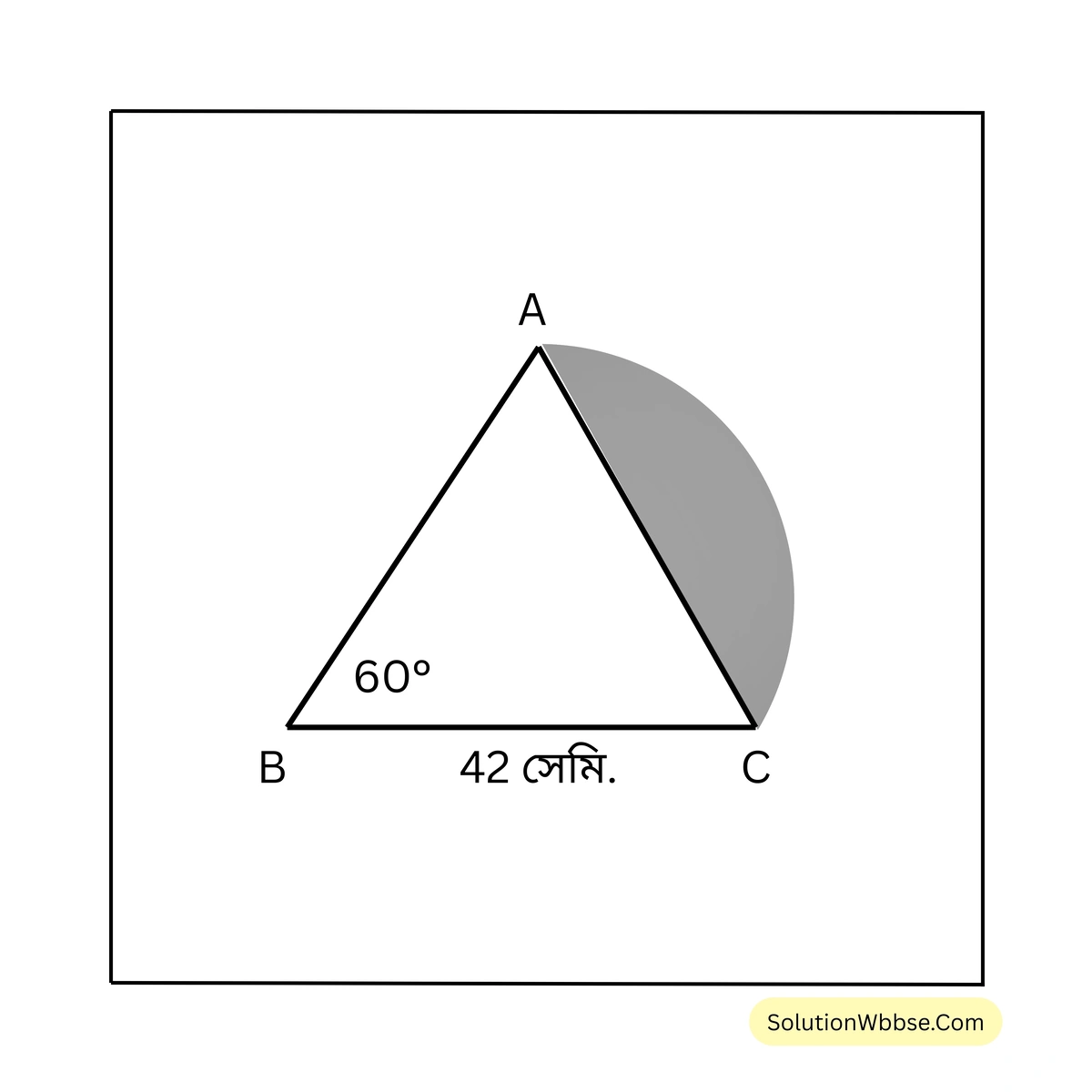
(ii) AC বৃত্তচাপের দৈর্ঘ্য
= \( \frac{60^{\circ}}{360^{\circ}} \times\) বৃত্তের পরিধি
= \( \frac{1}{6} \times 2 \pi \times 42\) সেমি.
= \( 14\pi\) সেমি.
= \( 14 \times \frac{22}{7}\) সেমি.
= \( 44\) সেমি.।
রেখাঙ্কিত অংশের পরিসীমা = \( (44 + 42)\) সেমি. = \( 86\) সেমি.।
\(\triangle ABC\) সমবাহু ত্রিভুজের ক্ষেত্রফল = \( \frac{\sqrt{3}}{4} \times (42)^2\) বর্গ সেমি.
= \( \frac{\sqrt{3}}{4} \times 42 \times 42\) বর্গ সেমি.
= \( \sqrt{3} \times 21 \times 21\) বর্গ সেমি.
= \( 763.834\) বর্গ সেমি.।
ABC বৃত্তকলার ক্ষেত্রফল = \( \frac{60^{\circ}}{360^{\circ}} \times \pi\) বর্গ সেমি.
= \( \frac{1}{6} \times \frac{22}{7} \times (42)^2\) বর্গ সেমি.
= \( \frac{1}{6} \times \frac{22}{7} \times 42 \times 42\) বর্গ সেমি.
= \( 924\) বর্গ সেমি.।
\(\therefore\) রেখাঙ্কিত অংশের ক্ষেত্রফল = \( (924 – 763.834)\) বর্গ সেমি. = \( 160.166\) বর্গ সেমি.।
উত্তর – রেখাঙ্কিত অংশের পরিসীমা \(86\) সেমি. এবং ক্ষেত্রফল \(160.166\) বর্গ সেমি.।
18. লীনা মেলা থেকে একটি বালা কিনে হাতে পরেছে। বালাটিতে 269.5 বর্গ সেমি ধাতু আছে। বালাটির বহির্ব্যাসের দৈর্ঘ্য 28 সেমি হলে, অন্তর্ব্যাসের দৈর্ঘ্য কত হিসাব করে লিখি।
সমাধান –
ধরি, বালাটির অন্তর্ব্যাসার্ধের দৈর্ঘ্য \(r\) সেমি.।
বালাটির বহির্ব্যাসার্ধের দৈর্ঘ্য = \(\frac{28}{2}\) সেমি. = \(14\) সেমি.
শর্তানুসারে,
\(\pi(14)^2 – \pi r^2 = 269.5\)বা, \(\frac{22 \times 196}{7} – \frac{22r^2}{7} = 269.5\)
বা, \(22 \times 28 – \frac{22r^2}{7} = 269.5\)
বা, \(616 – 269.5 = \frac{22r^2}{7}\)
বা, \(\frac{22r^2}{7} = 346.5\)
বা, \(r^2 = \frac{346.5 \times 7}{22}\)
বা, \(r^2 = 110.25\)
বা, \(r^2 = (10.5)^2\)
বা, \(r = 10.5\)
\(\therefore\) অন্তর্ব্যাসার্ধের দৈর্ঘ্য \(10.5\) সেমি.।
\(\therefore\) অন্তর্ব্যাসের দৈর্ঘ্য = \((2 \times 10.5)\) সেমি. = \(21\) সেমি.।
উত্তর – অন্তর্ব্যাসের দৈর্ঘ্য \(21\) সেমি.।
19. প্রতুল পাশের ছবির মতো একটি সমবাহু ত্রিভুজ ABC এঁকেছে যার প্রতিটি বাহুর দৈর্ঘ্য 10 সেমি। সুমিতা A, B ও C বিন্দুকে কেন্দ্র করে 5 সেমি দৈর্ঘ্যের ব্যাসার্ধের তিনটি বৃত্তচাপ এঁকেছে এবং মাঝের কিছু জায়গা রঙিন করেছে। হিসাব করে রঙিন জায়গার ক্ষেত্রফল লিখি। [\(\sqrt{3} = 1.732\) (প্রায়)]
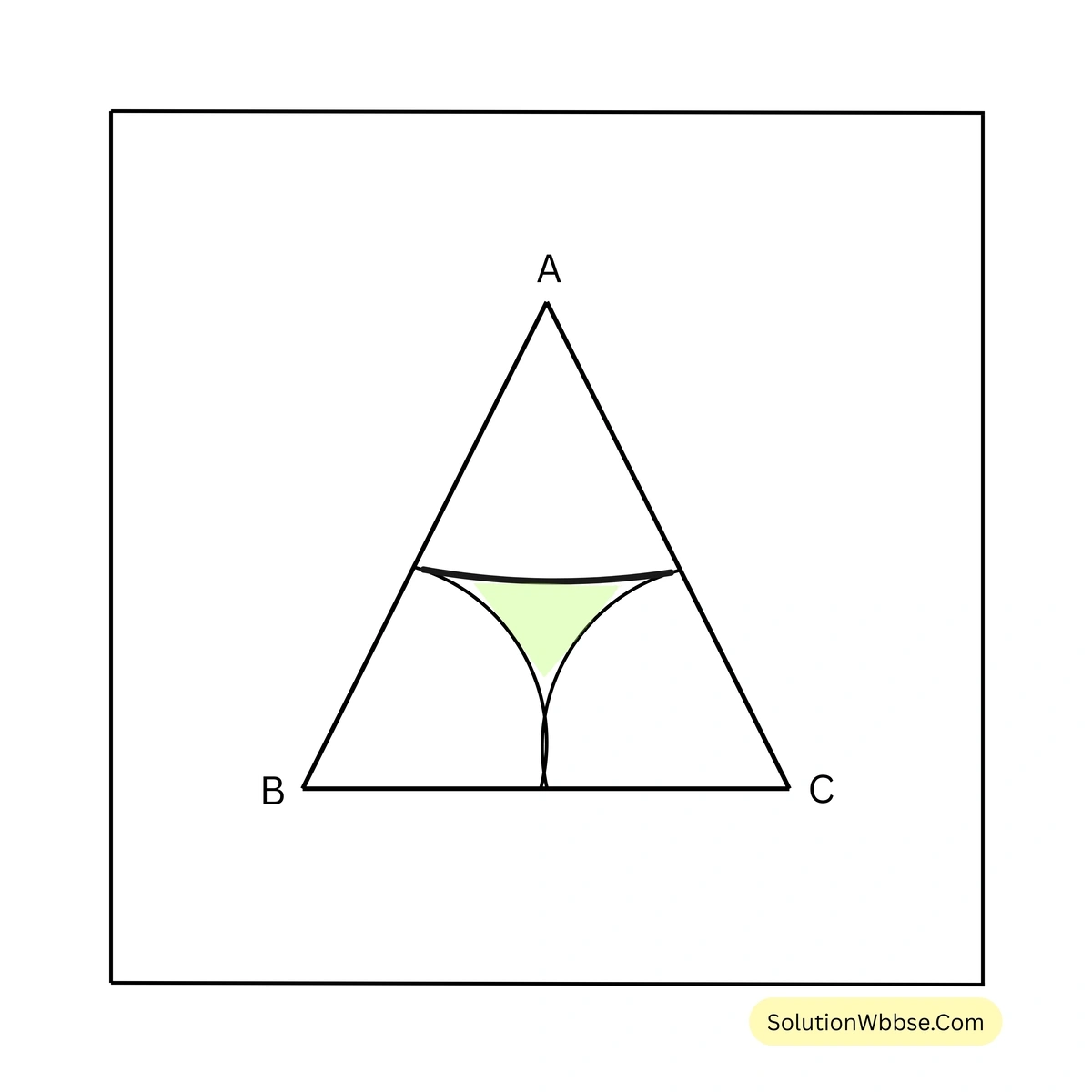
সমাধান –
সমবাহু ত্রিভুজ ABC-এর প্রতিটি কোণের মান \(60^\circ\)।
\(\therefore\) প্রতিটি বৃত্তকলার ক্ষেত্রফল = \( \frac{60^\circ}{360^\circ} \times\) বৃত্তের ক্ষেত্রফল = \( \frac{60^\circ}{360^\circ} \pi r^2\)
= \( \frac{1}{6} \times \pi \times (5)^2\) বর্গ সেমি.
= \( \frac{1}{6} \times \frac{22}{7} \times 25\) বর্গ সেমি.
= \( \frac{275}{21}\) বর্গ সেমি.
\(\therefore\) তিনটি বৃত্তকলার ক্ষেত্রফল
= \( 3 \times \frac{275}{21}\) বর্গ সেমি.
= \( \frac{275}{7}\) বর্গ সেমি.
= \( 39.28\) বর্গ সেমি.
ABC ত্রিভুজের ক্ষেত্রফল
= \( \frac{\sqrt{3}}{4} \times 10 \times 10\) বর্গ সেমি.
= \( 25\sqrt{3}\) বর্গ সেমি.
= \( 25 \times 1.732\) বর্গ সেমি.
= \( 43.3\) বর্গ সেমি.
\(\therefore\) রঙিন অংশের ক্ষেত্রফল = \((43.3 – 39.28)\) বর্গ সেমি. = \(4.02\) বর্গ সেমি.।
20. রাবেয়া একটি বড়ো কাগজে 21 সেমি বাহুবিশিষ্ট সমবাহু ত্রিভুজ আঁকল। ওই সমবাহু ত্রিভুজের একটি অন্তর্বৃত্ত অঙ্কন করে বৃত্তাকার জায়গাটি রঙিন করল। আমি রঙিন জায়গার ক্ষেত্রফল হিসাব করে লিখি।
সমাধান –
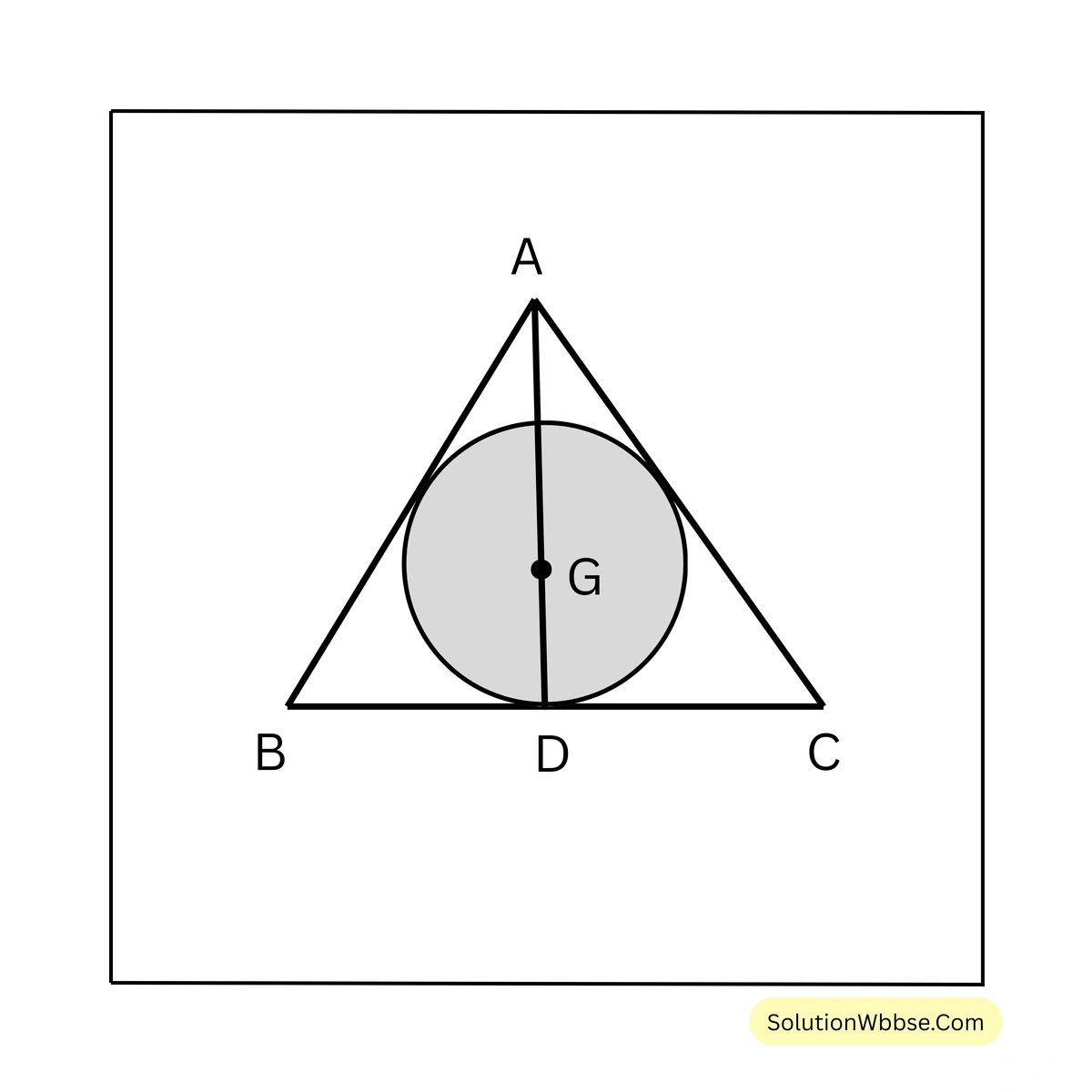
সমবাহু ত্রিভুজের উচ্চতা = \( \frac{\sqrt{3}}{2} \times\) বাহুর দৈর্ঘ্য
= \( \frac{\sqrt{3}}{2} \times 21\) সেমি.
= \( 21 \times \frac{\sqrt{3}}{2}\) সেমি.।
\(\therefore\) সমবাহু ত্রিভুজের মধ্যমা \(21 \times \frac{\sqrt{3}}{2}\) সেমি.। আমরা জানি, ভরকেন্দ্র ত্রিভুজের মধ্যমাকে 2:1 অনুপাতে বিভক্ত করে। আবার, সমবাহু ত্রিভুজের ভরকেন্দ্র ও অন্তর্বৃত্তের কেন্দ্র একই বিন্দু। অর্থাৎ উপরের চিত্রে GD হল অন্তর্বৃত্তের ব্যাসার্ধ এবং AG হল পরিবৃত্তের ব্যাসার্ধ।
\(\therefore\) অন্তর্বৃত্তের ব্যাসার্ধ (GD) = \( \frac{1}{3} \times \frac{21\sqrt{3}}{2}\) সেমি.
= \( \frac{7\sqrt{3}}{2}\) সেমি.।
\(\therefore\) অন্তর্বৃত্তের ক্ষেত্রফল = \( \pi \left( \frac{7\sqrt{3}}{2} \right)^2\) বর্গ সেমি.
= \( \frac{22}{7} \times \frac{49 \times 3}{4}\) বর্গ সেমি.
= \( \frac{21 \times 11}{2}\) বর্গ সেমি.
= \( \frac{231}{2}\) বর্গ সেমি.
= \( 115.5\) বর্গ সেমি.।
\(\therefore\) রঙিন অংশের ক্ষেত্রফল \(115.5\) বর্গ সেমি.।
উত্তর – রঙিন অংশের ক্ষেত্রফল 115.5 বর্গ সেমি.।
21. একটি সমবাহু ত্রিভুজের পরিবৃত্তের ক্ষেত্রের ক্ষেত্রফল 462 বর্গ সেমি। ত্রিভুজটির প্রতিটি বাহুর দৈর্ঘ্য হিসাব করে লিখি।
সমাধান –
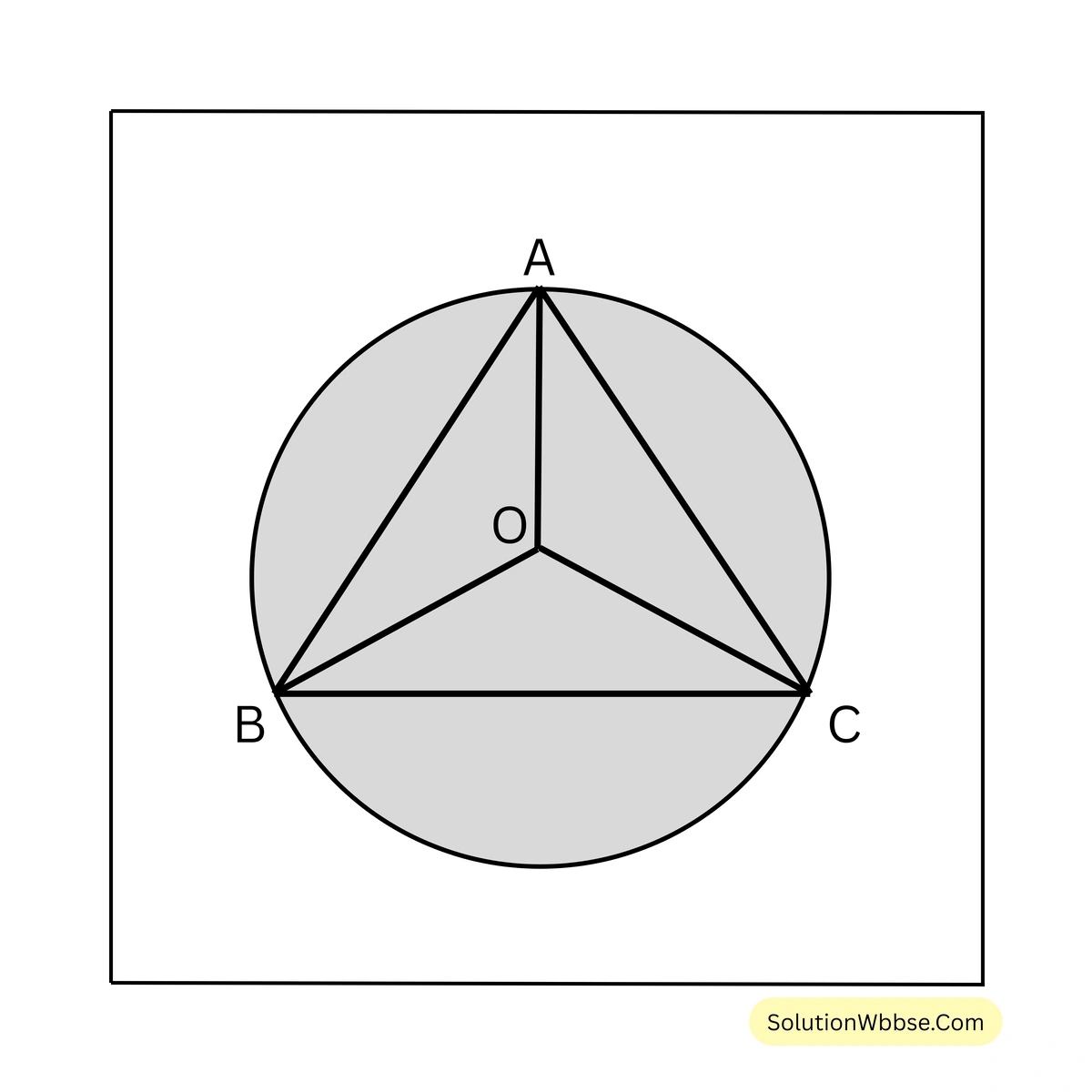
ধরি, সমবাহু ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ \(r\) সেমি.।
শর্তানুসারে,
\(\pi r^2 = 462\)বা, \( \frac{22}{7} \times r^2 = 462\)
বা, \( 22r^2 = 7 \times 462\)
বা, \( 22r^2 = 3234\)
বা, \( r^2 = \frac{3234}{22}\)
বা, \( r^2 = 147\)
বা, \( r^2 = 7 \times 7 \times 3\)
বা, \( r = 7\sqrt{3}\)
\(\therefore\) পরিবৃত্তের ব্যাসার্ধ = \( 7\sqrt{3}\) সেমি.।
সমবাহু ত্রিভুজের উচ্চতা = \( \frac{\sqrt{3}}{2} \times\) বাহু।আ
বার সমবাহু ত্রিভুজের পরিবৃত্তের ব্যাসার্ধের দৈর্ঘ্য = \( \frac{2}{3} \times\) উচ্চতা।
\(\therefore \frac{2}{3} \times\) উচ্চতা = \( 7\sqrt{3}\)
বা, \( \frac{2}{3} \times \frac{\sqrt{3}}{2} \times\) বাহু = \( 7\sqrt{3}\)
বা, \(\) বাহু = \( \frac{7\sqrt{3} \times 3 \times 2}{2 \times \sqrt{3}}\)
বা, \(\) বাহু = \( 21\)
\(\therefore\) সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য 21 সেমি.।
উত্তর – সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য 21 সেমি.।
22. একটি ত্রিভুজের পরিসীমা 32 সেমি এবং ত্রিভুজটির অন্তর্বৃত্তের ক্ষেত্রের ক্ষেত্রফল 38.5 বর্গসেমি। ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি।
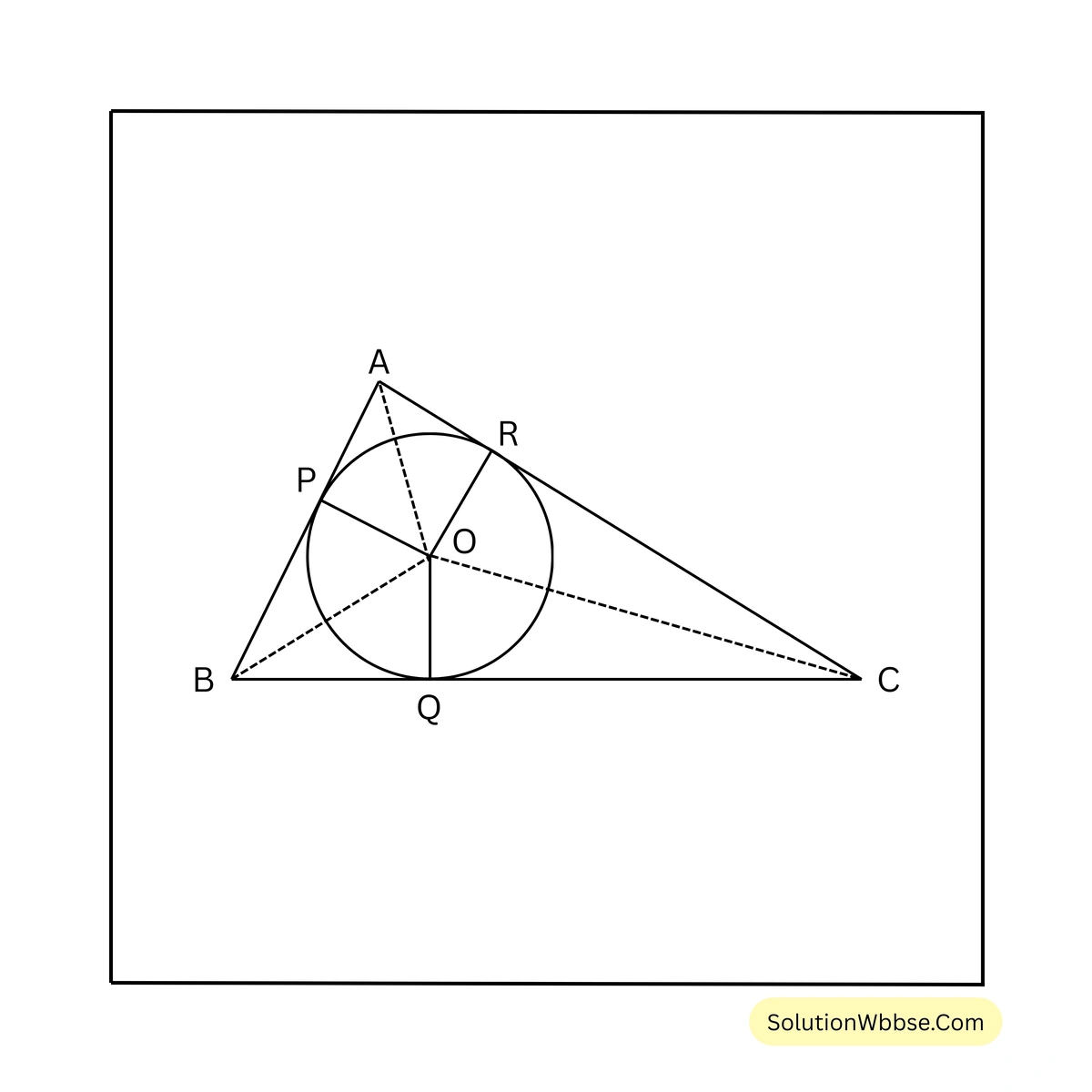
সমাধান –
ধরি, ABC ত্রিভুজের পরিসীমা 32 সেমি. এবং O কেন্দ্রীয় অন্তর্বৃত্তের ক্ষেত্রফল 38.5 বর্গ সেমি.।
\(\therefore AB + BC + CA = 32\) সেমি.।
ধরি, অন্তর্বৃত্তের ব্যাসার্ধ \(OP = OQ = OR = r\) সেমি.।
\(\therefore\) শর্তানুসারে,
\(\pi r^2 = 38.5\)বা, \( \frac{22}{7} r^2 = 38.5\)
বা, \( r^2 = 38.5 \times \frac{7}{22}\)
বা, \( r^2 = 12.25\)
বা, \( r^2 = (3.5)^2\)
বা, \( r = 3.5\)
এখন, ABC ত্রিভুজের ক্ষেত্রফল
= \( \Delta AOB \text{ –এর ক্ষেত্রফল } + \Delta BOC \text{ –এর ক্ষেত্রফল } + \Delta AOC \text{ –এর ক্ষেত্রফল}\)
= \( \frac{1}{2} \times AB \times OP + \frac{1}{2} \times BC \times OQ + \frac{1}{2} \times AC \times OR\)
= \( \frac{1}{2} \times AB \times r + \frac{1}{2} \times BC \times r + \frac{1}{2} \times AC \times r\)
= \( \frac{r}{2} \times (AB+BC+CA)\)
= \( \frac{3.5}{2} \times 32\)
= \( 56\)
\(\therefore\) ত্রিভুজটির ক্ষেত্রফল 56 বর্গ সেমি.।
উত্তর – ত্রিভুজটির ক্ষেত্রফল 56 বর্গ সেমি.।
23. 20 সেমি, 15 সেমি এবং 25 সেমি বাহুবিশিষ্ট ত্রিভুজের অন্তর্বৃত্ত ও পরিবৃত্তের ব্যাসার্ধের দৈর্ঘ্য হিসাব করে লিখি। অন্তর্বৃত্ত ও পরিবৃত্তের ক্ষেত্রের ক্ষেত্রফল হিসাব করে নির্ণয় করি।
সমাধান –
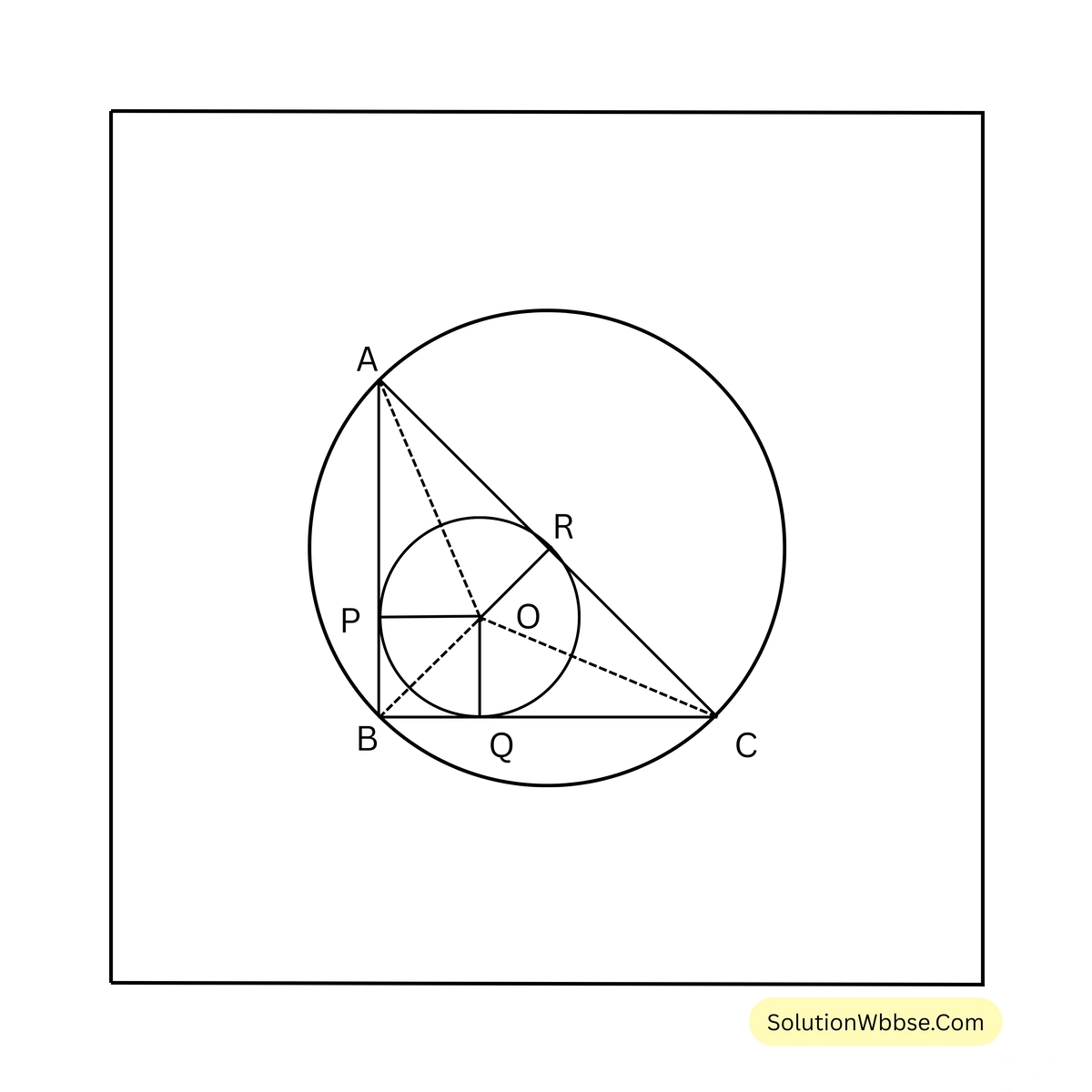
যেহেতু, \(20^2 + 15^2 = 25^2\), সেহেতু বলা যায় ত্রিভুজটি একটি সমকোণী ত্রিভুজ যার সমকোণ সংলগ্ন বাহুর দৈর্ঘ্য 15 সেমি. ও 20 সেমি. এবং অতিভুজের দৈর্ঘ্য 25 সেমি.।
\(\therefore\) ত্রিভুজটির ক্ষেত্রফল = \( \frac{1}{2} \times 20 \times 15\) বর্গ সেমি. = \( 150\) বর্গ সেমি.।
ধরি, অন্তর্বৃত্তের ব্যাসার্ধ \(OP = OQ = OR = r\) সেমি.।
এখন, ABC –এর ক্ষেত্রফল = \( \Delta AOB\) –এর ক্ষেত্রফল \(+ \Delta BOC\) –এর ক্ষেত্রফল \(+ \Delta AOC\) –এর ক্ষেত্রফল
= \( \frac{1}{2} \times AB \times OP + \frac{1}{2} \times BC \times OQ + \frac{1}{2} \times AC \times OR\)
= \( \frac{1}{2} \times AB \times r + \frac{1}{2} \times BC \times r + \frac{1}{2} \times AC \times r\)
= \( \frac{r}{2} \times (AB + BC + CA)\)
= \( \frac{r}{2} \times 60\)
= \( 30r\)
শর্তানুসারে,
\(30r = 150\)বা, \( r = \frac{150}{30}\)
বা, \( r = 5\)
\(\therefore\) অন্তর্বৃত্তের ব্যাসার্ধ 5 সেমি. এবং সমকোণী ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ সমকোণী ত্রিভুজের অতিভুজের অর্ধেক।
\(\therefore\) ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ = \( \frac{25}{2}\) সেমি. = \( 12.5\) সেমি.।
ত্রিভুজটির অন্তর্বৃত্তের ক্ষেত্রফল = \( \pi(5)^2\) বর্গ সেমি.
= \( \frac{22}{7} \times 25\) বর্গ সেমি.
= \( \frac{550}{7}\) বর্গ সেমি.
= \( 78\frac{4}{7}\) বর্গ সেমি.।
ত্রিভুজটির পরিবৃত্তের ক্ষেত্রফল = \( \pi (12.5)^2\) বর্গ সেমি.
= \( \frac{22}{7} \times \frac{125}{10} \times \frac{125}{10}\) বর্গ সেমি.
= \( \frac{6875}{14}\) বর্গ সেমি.
= \( 491 \frac{1}{14}\) বর্গ সেমি.।
\(\therefore\) ত্রিভুজটির অন্তর্বৃত্তের ক্ষেত্রফল \(78\frac{4}{7}\) বর্গ সেমি. এবং পরিবৃত্তের ক্ষেত্রফল \(491 \frac{1}{14}\) বর্গ সেমি.।
24. জয়া একটি বর্গক্ষেত্রের অন্তর্বৃত্ত অঙ্কন করল। ওই বৃত্তটি আবার একটি সমবাহু ত্রিভুজের পরিবৃত্ত যার প্রত্যেক বাহুর দৈর্ঘ্য \(4\sqrt{3}\) সেমি। বর্গক্ষেত্রটির একটি কর্ণের দৈর্ঘ্য হিসাব করে লিখি।
সমাধান –
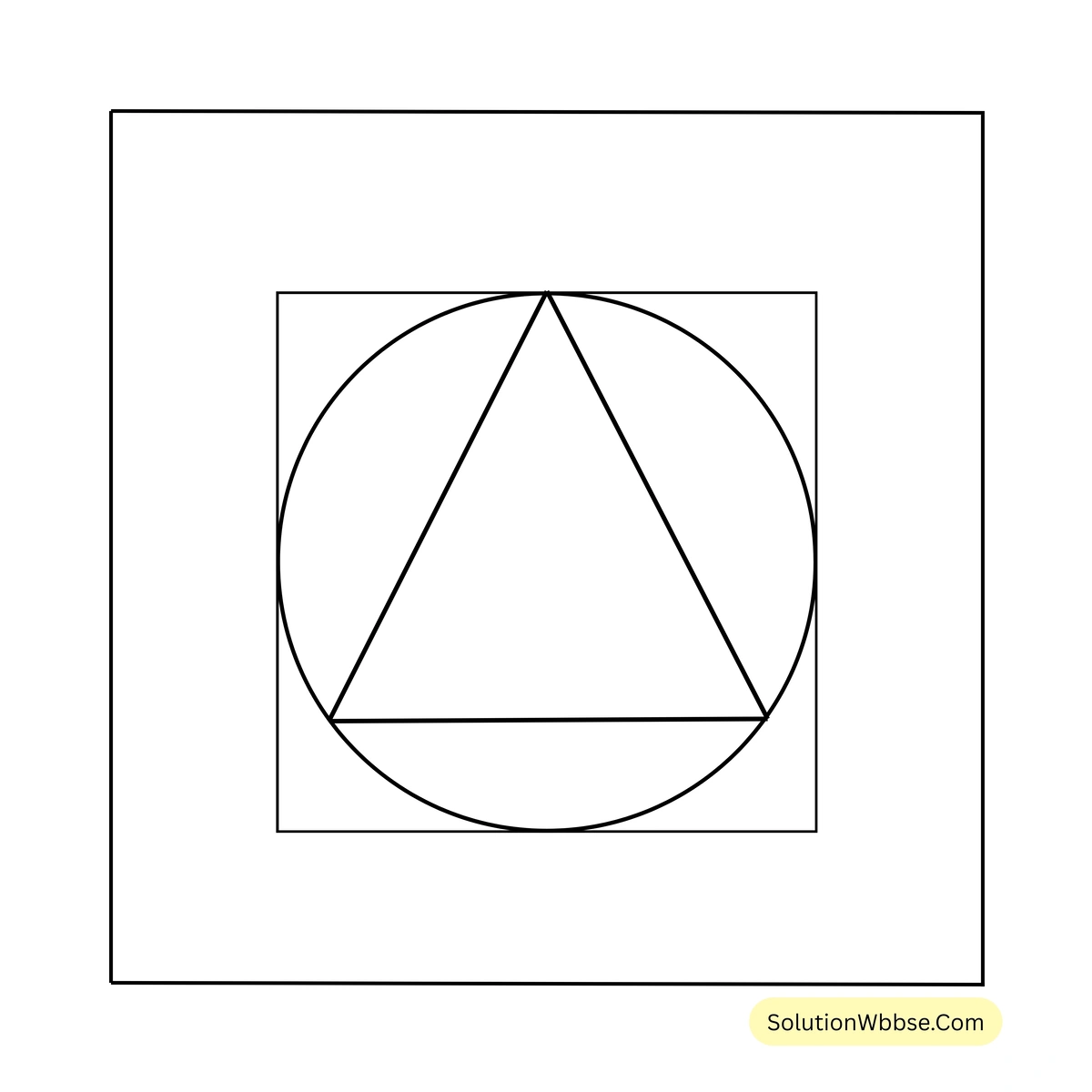
সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য \(4\sqrt{3}\) সেমি.।
\(\therefore\) সমবাহু ত্রিভুজের উচ্চতা = \( \frac{\sqrt{3}}{2} \times\) বাহুর দৈর্ঘ্য
= \( \frac{\sqrt{3}}{2} \times 4\sqrt{3}\) সেমি.
= \( 6\) সেমি.।
সমবাহু ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ = \( 6 \times \frac{2}{3}\) সেমি.
= \( 4\) সেমি.।
\(\therefore\) বৃত্তটির ব্যাস = \( (2 \times 4)\) সেমি. = \( 8\) সেমি.।
\(\therefore\) বৃত্তটির ব্যাসের দৈর্ঘ্য = \(\) বর্গক্ষেত্রের বাহুর দৈর্ঘ্য
= \( 8\) সেমি.।
\(\therefore\) বর্গক্ষেত্রটির কর্ণের দৈর্ঘ্য = \( 8\sqrt{2}\) সেমি.।
উত্তর – বর্গক্ষেত্রের একটি কর্ণের দৈর্ঘ্য \(8\sqrt{2}\) সেমি.।
25. সুমিত একটি তারকে দুটি সমান অংশে কাটল। একটি অংশকে বর্গাকারে ও অপর অংশটিকে বৃত্তাকারে বাঁকাল। বৃত্তাকার তারটি বর্গাকার তারটির থেকে 33 বর্গ সেমি বেশি জায়গা নিলে তারটির প্রকৃত দৈর্ঘ্য হিসাব করে লিখি।
সমাধান – ধরি, বৃত্তাকার তারের ব্যাসার্ধ \(r\) সেমি.।
\(\therefore\) বৃত্তাকার অংশের ক্ষেত্রফল = \( \pi r^2\) বর্গ সেমি.।
\(\therefore\) বর্গাকার তারের ক্ষেত্রফল = \( (\pi r^2 – 33)\) বর্গ সেমি.।
\(\therefore\) বর্গাকার তারের বাহুর দৈর্ঘ্য = \( \sqrt{\pi r^2 – 33}\)
\(\therefore\) বর্গাকার তারের পরিসীমা = \( 4\sqrt{\pi r^2 – 33}\)
শর্তানুসারে,
\(4\sqrt{\pi r^2 – 33} = 2\pi r\)বা, \( 2\sqrt{\pi r^2 – 33} = \pi r\)
বা, \( 4 \left( \pi r^2 – 33 \right) = \pi^2 r^2\)
বা, \( 4\pi r^2 – 132 = \pi^2 r^2\)
বা, \( r^2 \left( 4\pi – \pi^2 \right) = 132\)
বা, \( r^2 \left( \frac{88}{7} – \frac{484}{49} \right) = 132\)
বা, \( r^2 \left( \frac{616 – 484}{49} \right) = 132\)
বা, \( r^2 \times \frac{132}{49} = 132\)
বা, \( r^2 = 49\)
বা, \( r = 7\)
\(\therefore\) বৃত্তের পরিধি = \( 2 \times \frac{22}{7} \times 7\) সেমি. = \( 44\) সেমি. = \(\) বর্গক্ষেত্রের পরিসীমা।
\(\therefore\) তারটির দৈর্ঘ্য = \( (44 + 44)\) সেমি. = \( 88\) সেমি.।
উত্তর – তারটির দৈর্ঘ্য 88 সেমি.।
26. বহু বিকল্পীয় প্রশ্ন (M.C.Q.)
(i) একটি বৃত্তাকার ক্ষেত্রের ক্ষেত্রফল x বর্গ একক, পরিধি y একক ও ব্যাসের দৈর্ঘ্য z একক হলে, \(x/yz\) এর মান
(a) \(1/2\)
(b) \(1/4\)
(c) \(1\)
(d) \(1/8\)
উত্তর – (b) \(\frac{1}{4}\)
সমাধান –
ধরি, বৃত্তাকার ক্ষেত্রের ব্যাসার্ধ \(r\) একক।
\(\therefore\) বৃত্তাকার ক্ষেত্রের ক্ষেত্রফল = \( \pi r^2\) বর্গ একক = \( x\) বর্গ একক
বৃত্তাকার ক্ষেত্রের পরিধি = \( 2\pi r\) একক = \( y\) একক
ব্যাসের দৈর্ঘ্য = \( 2r\) একক = \( z\) একক
(ii) একটি বৃত্তের পরিলিখিত ও অন্তরলিখিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের অনুপাত
(a) \(4:1\)
(b) \(1:4\)
(c) \(2:1\)
(d) \(1:2\)
উত্তর – (c) \(2:1\)
সমাধান –
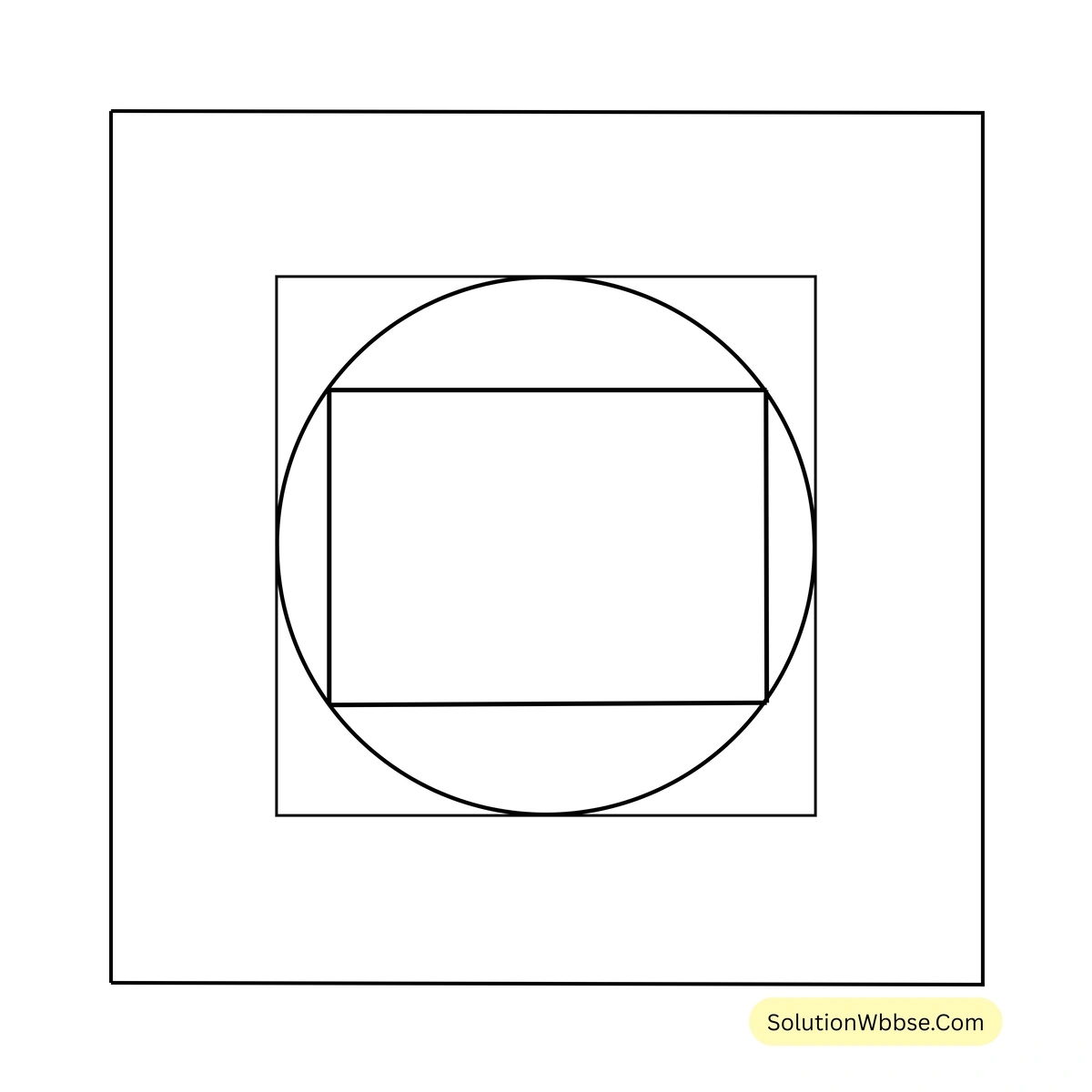
ধরি, বৃত্তের ব্যাসার্ধ \(a\) একক।
\(\therefore\) বৃত্তের ব্যাস = \( 2a\) একক
\(\therefore\) পরিলিখিত বর্গক্ষেত্রের বাহুর দৈর্ঘ্য = \( 2a\) একক
\(\therefore\) পরিলিখিত বর্গক্ষেত্রের ক্ষেত্রফল = \( (2a)^2\) বর্গএকক = \( 4a^2\) বর্গএকক
আবার, বৃত্তের ব্যাস = \( 2a\) একক
\(\therefore\) অন্তরলিখিত বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য = \( 2a\) একক
\(\therefore\) অন্তরলিখিত বর্গক্ষেত্রের বাহুর দৈর্ঘ্য = \( \frac{2a}{\sqrt{2}}\) একক = \( a\sqrt{2}\) একক
\(\therefore\) অন্তরলিখিত বর্গক্ষেত্রের ক্ষেত্রফল = \( (a\sqrt{2})^2\) বর্গ একক = \( 2a^2\) বর্গ একক
\(\therefore\) বৃত্তে পরিলিখিত ও অন্তরলিখিত বর্গক্ষেত্রের ক্ষেত্রফলের অনুপাত = \( 4a^2 : 2a^2 = 2:1\)
(iii) একটি বৃত্তাকার ক্ষেত্রের পরিধি ও ক্ষেত্রফলের সাংখ্যমান সমান। ওই বৃত্তের পরিলিখিত বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য
(a) \(4\) একক
(b) \(2\) একক
(c) \(4\sqrt{2}\) একক
(d) \(2\sqrt{2}\) একক
উত্তর – (c) \(4\sqrt{2}\) একক
সমাধান – ধরি, বৃত্তাকার ক্ষেত্রের ব্যাসার্ধ \(r\) একক।
প্রশ্নানুসারে,
\(2\pi r = \pi r^2\)বা, \( r = 2\)
\(\therefore\) বৃত্তের ব্যাস = \( (2 \times 2)\) একক = \( 4\) একক।
\(\therefore\) বৃত্তের পরিলিখিত বর্গক্ষেত্রের বাহুর দৈর্ঘ্য \(4\) একক।
\(\therefore\) বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য \(4\sqrt{2}\) একক।
(iv) একটি সমবাহু ত্রিভুজের পরিলিখিত ও অন্তরলিখিত বৃত্তাকার ক্ষেত্রের ক্ষেত্রফলের অনুপাত
(a) \(4:1\)
(b) \(1:4\)
(c) \(2:1\)
(d) \(1:2\)
উত্তর – (a) \(4:1\)
সমাধান –
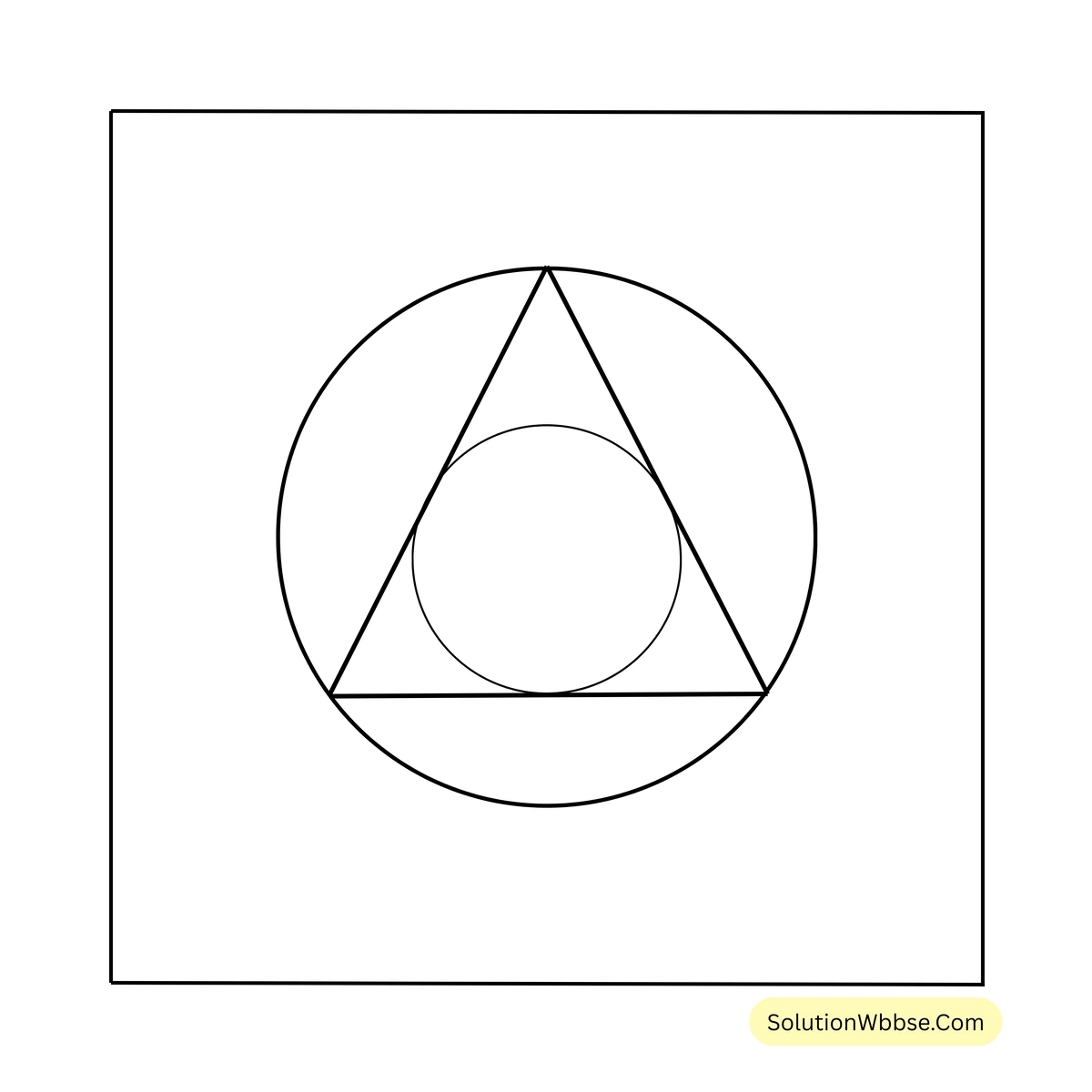
ধরি, সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য \(a\) একক।
\(\therefore\) সমবাহু ত্রিভুজের উচ্চতা বা মধ্যমা = \( \frac{\sqrt{3}}{2} \times a\) একক
\(\therefore\) সমবাহু ত্রিভুজের অন্তর্বৃত্তের ব্যাসার্ধ = \( \frac{1}{3} \times \frac{\sqrt{3}}{2} \times a\) একক = \( \frac{a}{2\sqrt{3}}\) একক
এবং সমবাহু ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ = \( \frac{2}{3} \times \frac{\sqrt{3}}{2} \times a\) একক = \( \frac{a}{\sqrt{3}}\) একক
\(\therefore\) অন্তর্বৃত্তের ক্ষেত্রফল = \( \pi \left( \frac{a}{2\sqrt{3}} \right)^2\) বর্গ একক
= \( \pi \times \frac{a^2}{12}\) বর্গ একক
= \( \frac{\pi a^2}{12}\) বর্গ একক
এবং পরিবৃত্তের ক্ষেত্রফল = \( \pi \left( \frac{a}{\sqrt{3}} \right)^2\) বর্গ একক
= \( \frac{\pi a^2}{3}\) বর্গ একক
\(\therefore\) পরিবৃত্তের ক্ষেত্রফল ও অন্তর্বৃত্তের ক্ষেত্রফলের অনুপাত = \( \frac{\pi a^2}{3} : \frac{\pi a^2}{12}\)
= \( \frac{1}{3} : \frac{1}{12}\)
= \( 4:1\)
(v) একটি বলয়াকৃতি লোহার পাতের অন্তর্ব্যাস 20 সেমি এবং বহির্ব্যাস 22 সেমি। বলয়টিতে লোহার পাত আছে
(a) \(22\) বর্গ সেমি
(b) \(44\) বর্গ সেমি
(c) \(66\) বর্গ সেমি
(d) \(88\) বর্গ সেমি
উত্তর – (c) \(66\) বর্গ সেমি
সমাধান – বলয়াকৃতি লোহার পাতের অন্তর্ব্যাস 20 সেমি এবং বহির্ব্যাস 22 সেমি।
\(\therefore\) অন্তর্ব্যাসার্ধ \((r) = \frac{20}{2}\) সেমি. = \( 10\) সেমি.
এবং বহির্ব্যাসার্ধ \((R) = \frac{22}{2}\) সেমি. = \( 11\) সেমি.
\(\therefore\) বলয়টিতে লোহার পাতের ক্ষেত্রফল
= \( \pi(R^2 – r^2)\) বর্গ সেমি.
= \( \pi(11^2 – 10^2)\) বর্গ সেমি.
= \( \pi(121 – 100)\) বর্গ সেমি.
= \( \frac{22}{7} \times 21\) বর্গ সেমি.
= \( 66\) বর্গ সেমি.
এই আর্টিকেলে নবম শ্রেণির গণিতের ‘বৃত্তের ক্ষেত্রফল‘ অধ্যায়ের ‘কষে দেখি – 18’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।
কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন