পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) দশম শ্রেণির গণিত পাঠ্যবইয়ের ষোড়শ অধ্যায় হলো ‘বৃত্তের পরিধি’। এই পোস্টে ‘কষে দেখি – 16‘-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. নীচের ছবিগুলির পরিসীমা হিসাব করে লিখি –
(i)
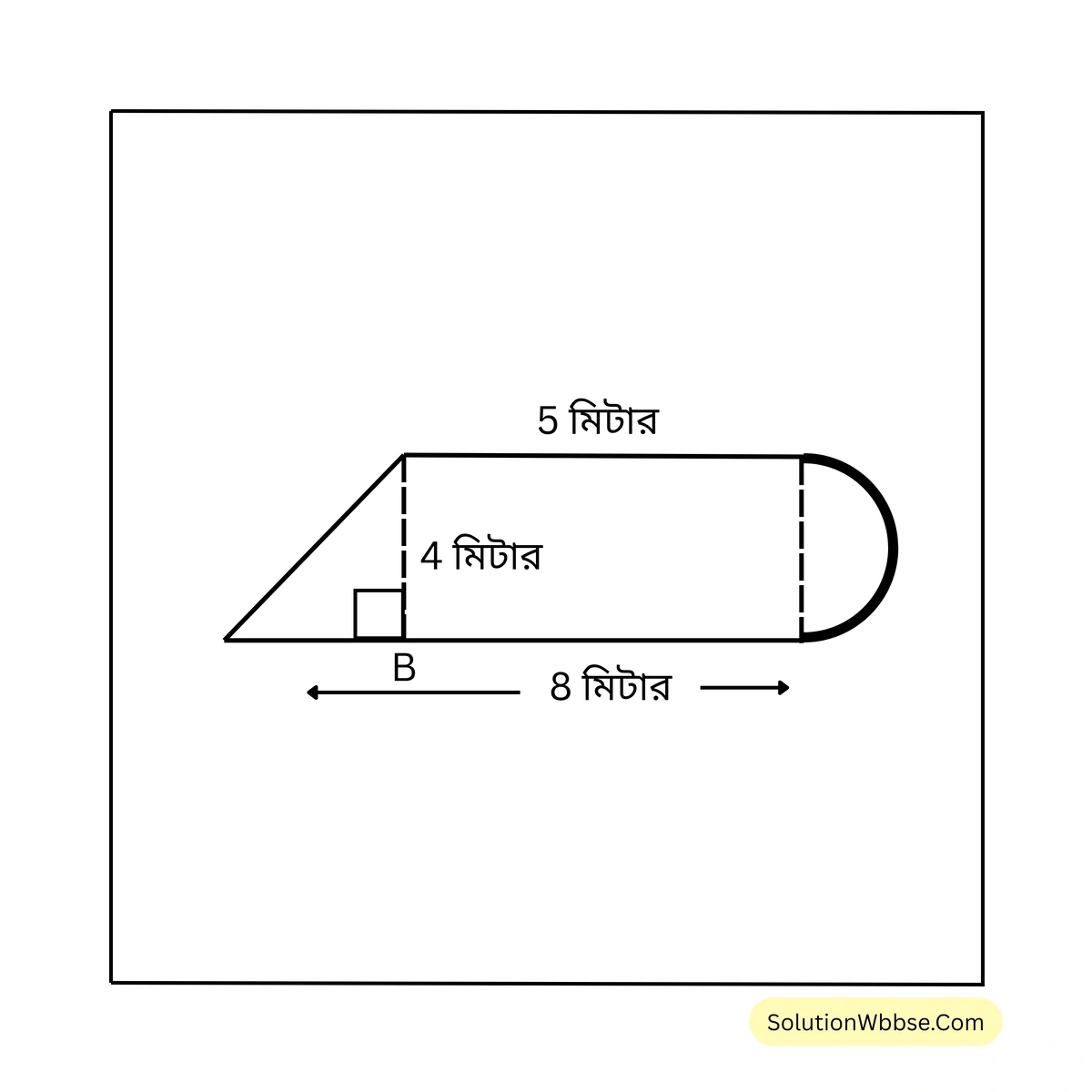
সমাধান –
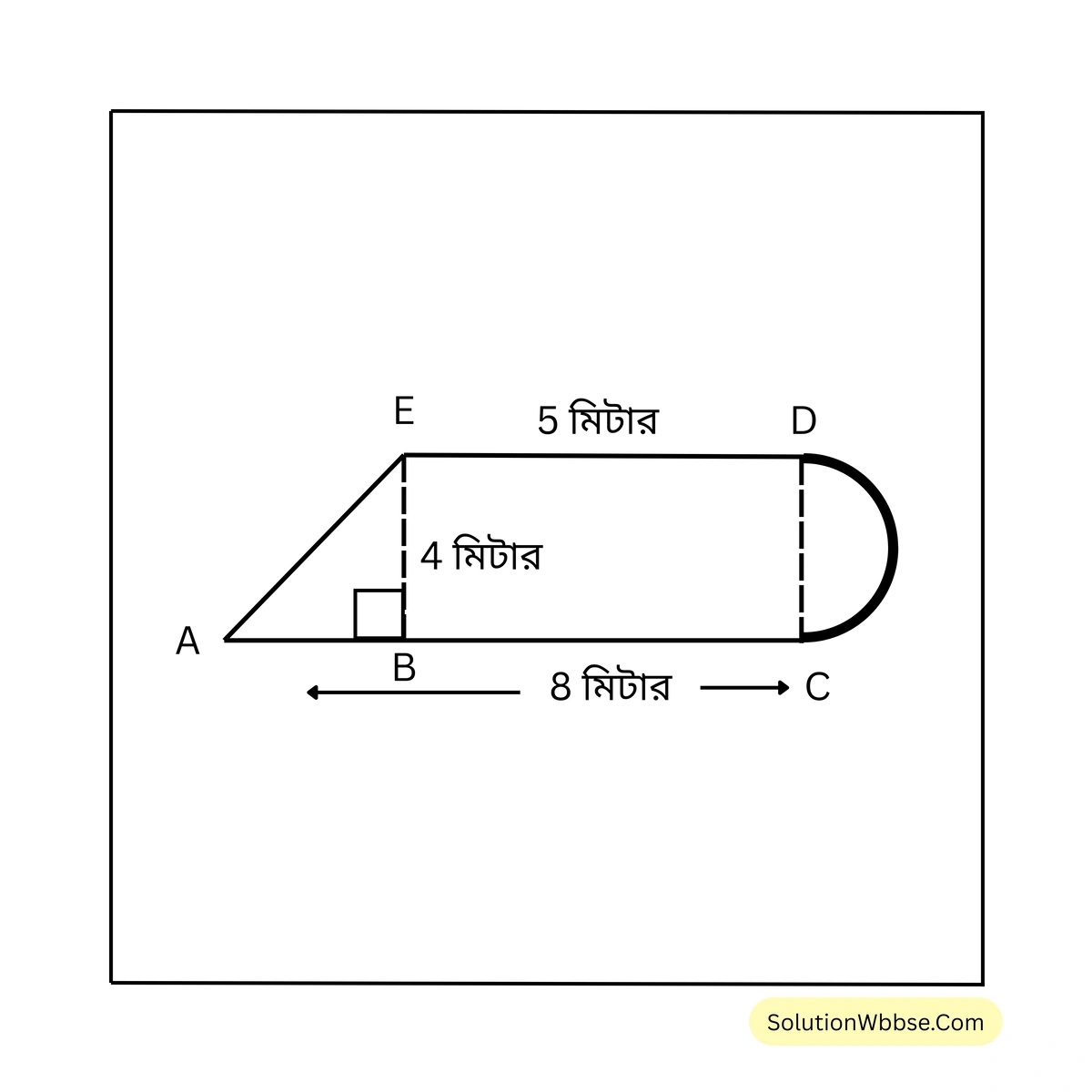
চিত্রে \(AC = 8\) মিটার; \(ED = 5\) মিটার; \(BE = DC = 4\) মিটার
\(\therefore AB = AC – BC = AC – ED = (8-5)\) মিটার = \( 3\) মিটার।
সমকোণী ত্রিভুজ ABC থেকে পাই,
\(AE = \sqrt{AB^2 + BE^2} = \sqrt{3^2 + 4^2} = \sqrt{9+16} = \sqrt{25} = 5\)বৃত্তাকার অংশের পরিসীমা = \( \pi r\) মিটার = \( \frac{22}{7} \times \frac{4}{2}\) সেমি. = \( \frac{44}{7}\) সেমি.
\(\therefore ABCDE\) – এর পরিসীমা
= \( AC +\) (অর্ধবৃত্ত CD) + DE + AE
= \( (8 + \frac{44}{7} + 5 + 5)\) মিটার
= \( (\frac{56+44+35+35}{7})\) মিটার
= \( \frac{170}{7}\) মিটার
= \( 24\frac{2}{7}\) মিটার [উত্তর]
(ii)
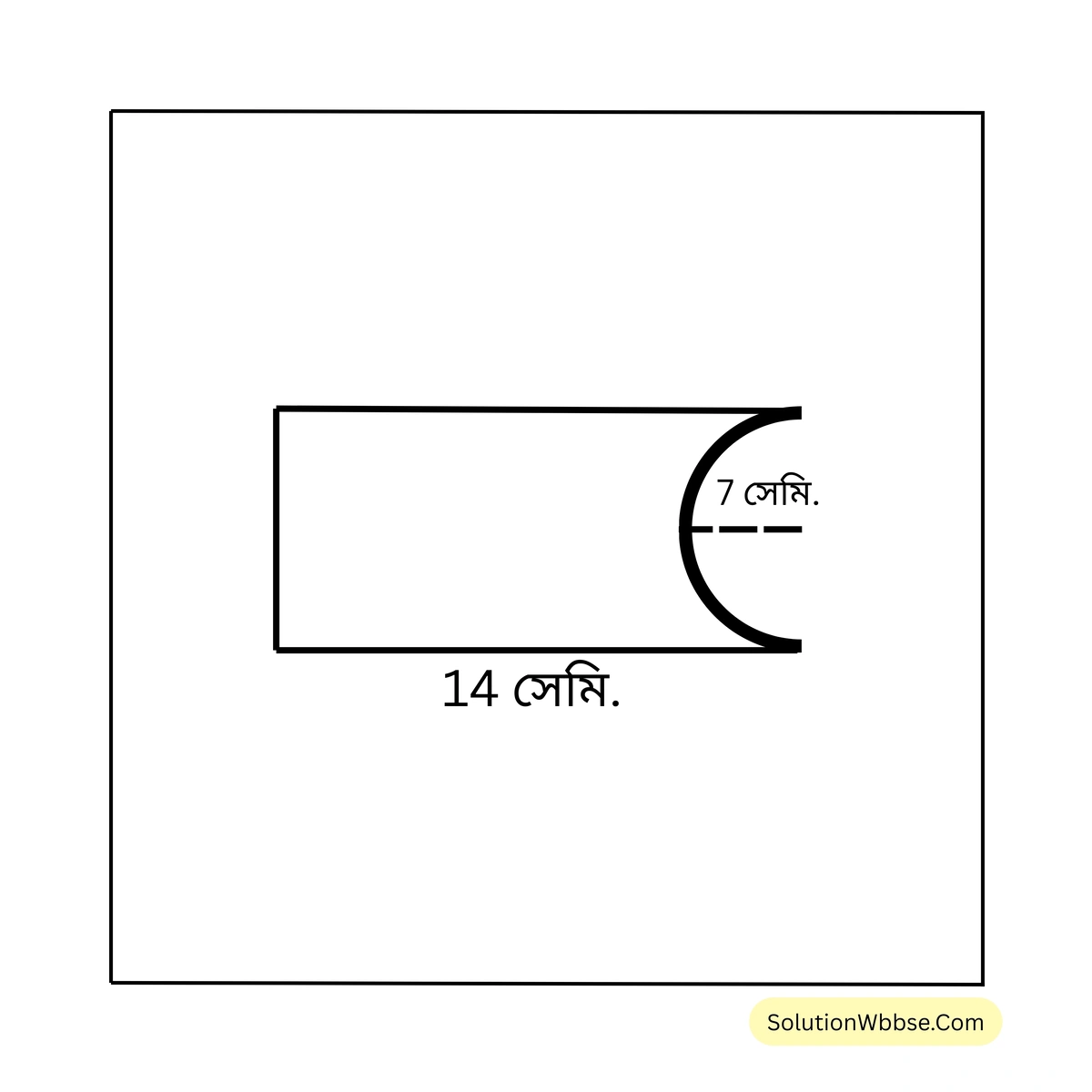
সমাধান –
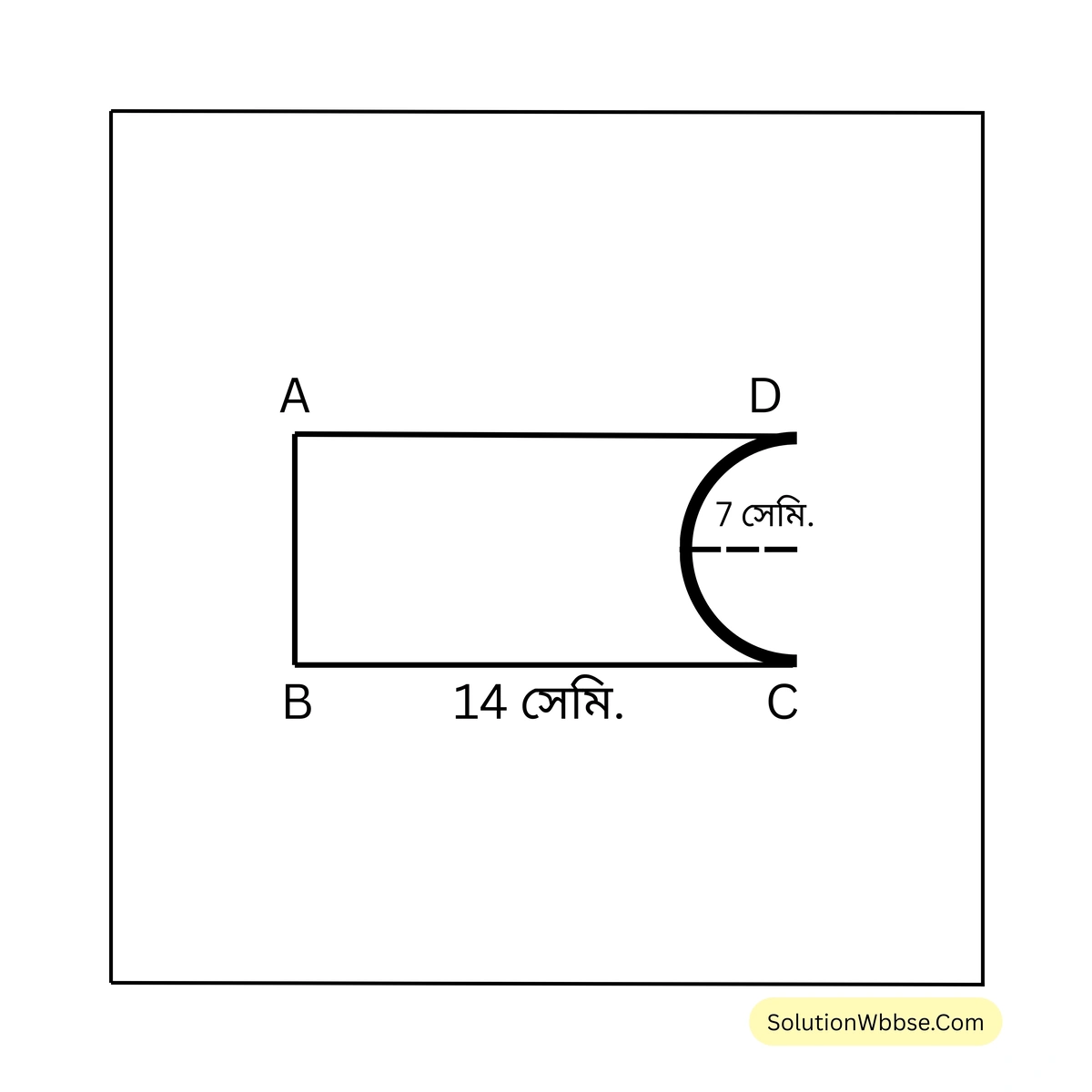
\(AB = 14\) মিটার, \(BC = 14\) মিটার, \(AD = 14\) মিটার, \(CD\) বৃত্তচাপের
পরিধি = \( \pi r\) মিটার = \( \frac{22}{7} \times 7\) মিটার = \( 22\) মিটার।
\(\therefore ABCD\) এর পরিসীমা = \( (AB + BC + CD + DA)\) সেমি. = \( (14+14+22+14)\) সেমি. = \( 64\) সেমি. (উত্তর)
2. 35 মিটার দৈর্ঘ্যের ব্যাসার্ধ বিশিষ্ট একটি বৃত্তাকার তারের রিং তৈরি করতে কত লম্বা তার নেব হিসাব করে লিখি।
সমাধান –
বৃত্তাকার রিংয়ের ব্যাসার্ধ \((r)\) = 35 মিটার।
\(\therefore\) বৃত্তাকার রিংয়ের পরিধি = \(2\pi r\) মিটার = \(2 \times \frac{22}{7} \times 35\) মিটার = 220 মিটার।
\(\therefore\) বৃত্তাকার রিং তৈরি করতে 220 মিটার তার লাগবে।
3. একটি ট্রেনের চাকার ব্যাসার্ধের দৈর্ঘ্য 0.35 মিটার। 1 মিনিটে চাকাটি 450 বার ঘুরলে ট্রেনটির গতিবেগ ঘন্টায় কত কিমি হিসাব করে লিখি।
সমাধান –
ট্রেনের চাকার ব্যাসার্ধের দৈর্ঘ্য \((r)\) = 0.35 মিটার।
\(\therefore\) ট্রেনের চাকার পরিধি
= \( 2\pi r\) মিটার
= \( 2 \times \frac{22}{7} \times 0.35\) মিটার
= \( 44 \times 0.05\) মিটার
= \( 2.2\) মিটার।
\(\therefore\) 1 বার চাকাটি পূর্ণ আবর্তন করলে 2.2 মিটার পথ অতিক্রম করে।
\(\therefore\) 450 বার চাকাটি পূর্ণ আবর্তন করলে \((2.2 \times 450)\) মিটার = 990 মিটার পথ অতিক্রম করে।
\(\therefore\) ট্রেনটি 1 মিনিটে 990 মিটার পথ অতিক্রম করে।
\(\therefore\) ট্রেনটি 60 মিনিটে \((990 \times 60)\) মিটার = 59400 মিটার = 59.4 কিমি পথ অতিক্রম করে।
\(\therefore\) ট্রেনটির গতিবেগ 59.4 কিমি প্রতি ঘণ্টা।
4. আমোদপুর গ্রামের একটি বৃত্তাকার মাঠের ব্যাসার্ধের দৈর্ঘ্য 280 মিটার। চৈতালি প্রতি ঘণ্টায় 5.5 কিমি বেগে হেঁটে মাঠটি পরিক্রমা করতে চায়। হিসাব করে দেখি মাঠটি একবার প্রদক্ষিণ করতে চৈতালির কত সময় লাগবে?
সমাধান –
বৃত্তাকার মাঠটির ব্যাসার্ধের দৈর্ঘ্য 280 মিটার।
\(\therefore\) মাঠটির পরিধি = \(2 \times \frac{22}{7} \times 280\) মিটার = 1760 মিটার।
5.5 কিমি = 5500 মিটার।
চৈতালি 5500 মিটার পথ অতিক্রম করে 60 মিনিটে।
1 মিটার পথ অতিক্রম করে \(\frac{60}{5500}\) মিনিটে।
1760 মিটার পথ অতিক্রম করে \(\frac{60 \times 1760}{5500}\) মিনিটে = \(\frac{96}{5}\) মিনিটে = \(19\frac{1}{5}\) মিনিটে = 19 মিনিট \((\frac{1}{5} \times 60)\) সেকেন্ডে = 19 মিনিট 12 সেকেন্ডে।
\(\therefore\) মাঠটি একবার প্রদক্ষিণ করতে চৈতালির সময় লাগবে 19 মিনিট 12 সেকেন্ড।
5. তথাগত একটি তামার তার আয়তাকারে বেঁকিয়েছে যার দৈর্ঘ্য 18 সেমি. এবং প্রস্থ 15 সেমি.। আমি ওই তামার তারটি বেঁকিয়ে বৃত্ত তৈরি করলাম। হিসাব করে ওই বৃত্তাকার তামার তারটির ব্যাসার্ধ লিখি।
সমাধান –
তথাগতের তৈরি আয়তক্ষেত্রের পরিসীমা = \(2(18+15)\) সেমি. = \(66\) সেমি.
\(\therefore\) বৃত্তাকার তারের পরিধিও হবে \(66\) সেমি.।
ধরি, বৃত্তাকার তারটির ব্যাসার্ধ \(r\) সেমি.
\(\therefore 2\pi r = 66\)বা, \(2 \times \frac{22}{7} \times r = 66\)
বা, \(r = \frac{66 \times 7}{44}\)
বা, \(r = \frac{21}{2}\)
বা, \(r = 10.5\)
\(\therefore\) বৃত্তাকার তারটির ব্যাসার্ধ হবে \(10.5\) সেমি.।
6. একটি অর্ধবৃত্তাকার মাঠের পরিসীমা 108 মিটার হলে, মাঠের ব্যাসার্ধের দৈর্ঘ্য হিসাব করে লিখি।
সমাধান –
ধরি, মাঠটির ব্যাসার্ধের দৈর্ঘ্য \(r\) মিটার।
\(\therefore\) অর্ধবৃত্তাকার মাঠের পরিসীমা = \((\frac{2\pi r}{2} + 2r)\) মিটার = \((\pi r + 2r)\) মিটার।
প্রশ্নানুসারে,
\(\pi r + 2r = 108\)বা, \(\frac{22}{7} \times r + 2r = 108\)
বা, \(r (\frac{22}{7} + 2) = 108\)
বা, \(r \times \frac{36}{7} = 108\)
বা, \(r = \frac{108 \times 7}{36}\)
বা, \(r = 21\)
\(\therefore\) অর্ধবৃত্তাকার মাঠটির ব্যাস = \(2 \times 21\) মিটার = \(42\) মিটার।
7. একটি চাকার পরিধি ও ব্যাসের দৈর্ঘ্যের অন্তর 75 সেমি. হলে ওই চাকার ব্যাসার্ধের দৈর্ঘ্য হিসাব করে লিখি।
সমাধান –
ধরি, চাকার ব্যাসার্ধ \(r\) সেমি.
\(\therefore 2\pi r – 2r = 75\)বা, \(2r (\pi – 1) = 75\)
বা, \(2r (\frac{22}{7} – 1) = 75\)
বা, \(2r \times \frac{22-7}{7} = 75\)
বা, \(2r \times \frac{15}{7} = 75\)
বা, \(2r = \frac{75 \times 7}{15}\)
বা, \(2r = 35\)
বা, \(r = \frac{35}{2}\)
বা, \(r = 17.5\)
\(\therefore\) ওই চাকার ব্যাসার্ধের দৈর্ঘ্য \(17.5\) সেমি.।
8. 28 মিটার দৈর্ঘ্যের ব্যাস বিশিষ্ট বৃত্তাকার ট্র্যাকে পূজা ও জাকির একই জায়গা থেকে প্রতিযোগিতা শুরু করে। পূজা যখন 4 পাক ঘুরে প্রতিযোগিতা শেষ করে জাকির তখন 1 পাক পিছনে থাকে। প্রতিযোগিতাটি কত মিটারের ছিল এবং পূজা জাকিরকে কত মিটারে পরাজিত করেছে হিসাব করে লিখি।
সমাধান –
বৃত্তাকার ট্র্যাকের ব্যাস 28 মিটার।
\(\therefore\) ট্র্যাকটির ব্যাসার্ধ \((r) = \frac{28}{2}\) মিটার।
\(\therefore\) বৃত্তাকার ট্র্যাকের পরিধি = \( 2\pi r\) মিটার = \( 2 \times \frac{22}{7} \times \frac{28}{2}\) মিটার = \( 88\) মিটার।
\(\therefore\) পূজা 4 পাক ঘুরে প্রতিযোগিতাটি শেষ করলে প্রতিযোগিতাটি ছিল মোট \((88 \times 4)\) মিটারের = \( 352\) মিটারের।
জাকির পূজার চেয়ে 1 পাক পিছনে থাকলে পূজা জাকিরকে 88 মিটারে পরাজিত করে।
9. আমাদের পাড়ার একটি পাতকুয়োর পরিধি 440 সেমি.। এই পাতকুয়োর চার ধারে সমান চওড়া একটি পাথরের পাড় আছে। যদি বেদ সমেত পাতকুয়োর পরিধি 616 সেমি. হয়, তবে পাথরের পাড় কত চওড়া হিসাব করে লিখি।
সমাধান –
ধরি, পাতকুয়োর ব্যাসার্ধ \(r\) সেমি. এবং পাথরের চওড়া পাড় সহ পাতকুয়োর ব্যাসার্ধ \(R\) সেমি.
প্রশ্নানুসারে,
\(2\pi r = 440\) —-(i)
\(2\pi R = 616\) —(ii)
(ii) নং সমীকরণ থেকে (i) নং সমীকরণ বিয়োগ করে পাই,
\(2\pi R – 2\pi r = 616 – 440\)বা, \(2\pi(R-r) = 176\)
বা, \(2 \times \frac{22}{7} \times (R-r) = 176\)
বা, \(\frac{44}{7} \times (R-r) = 176\)
বা, \((R-r) = \frac{176 \times 7}{44}\)
বা, \((R-r) = 28\)
\(\therefore\) পাথরের তৈরি পাড়টি 28 সেমি. চওড়া ছিল।
10. গ্রামের নিয়ামত চাচা একটি মোটরের চাকার সঙ্গে বেল্ট দিয়ে একটি মেশিনের চাকা যুক্ত করেছেন। মোটরের চাকার ব্যাসের দৈর্ঘ্য 14 সেমি. এবং মেশিনের চাকার ব্যাসের দৈর্ঘ্য 94.5 সেমি.। মোটরের চাকা যদি প্রতি সেকেন্ডে 27 বার ঘোরে, তবে মেশিনের চাকা ঘণ্টায় কতবার ঘুরবে হিসাব করে লিখি।
সমাধান –
মোটরের চাকার ব্যাসের দৈর্ঘ্য 14 সেমি.।
\(\therefore\) মোটরের চাকার ব্যাসার্ধ \((r) = \frac{14}{2}\) সেমি. = \( 7\) সেমি.
মোটরের চাকার পরিধি = \( 2\pi r\) সেমি. = \( 2 \times \frac{22}{7} \times 7\) সেমি. = \( 44\) সেমি.
মোটরের চাকা প্রতি সেকেন্ডে 27 বার ঘোরে।
\(\therefore\) মোটরের চাকা 1 সেকেন্ডে অতিক্রম করে = \( (44 \times 27)\) সেমি. = \( 1188\) সেমি.
মেশিনের চাকার ব্যাস 94.5 সেমি.।
\(\therefore\) মেশিনের চাকার ব্যাসার্ধ \((R) = \frac{94.5}{2}\) সেমি.
মেশিনের চাকার পরিধি = \( 2\pi R\) সেমি. = \( 2 \times \frac{22}{7} \times \frac{94.5}{2}\) সেমি. = \( 297\) সেমি.
\(\therefore\) মেশিনের চাকা 1 সেকেন্ডে ঘোরে = \( \frac{1188}{297} = 4\) বার।
\(\therefore\) মেশিনের চাকা 1 ঘণ্টা অর্থাৎ 3600 সেকেন্ডে ঘোরে = \( 4 \times 3600\) বার = \( 14400\) বার।
\(\therefore\) মেশিনের চাকা ঘণ্টায় 14400 বার ঘুরবে।
11. আমাদের ক্লাব ঘরের ঘড়িটির ঘণ্টার কাঁটা ও মিনিটের কাঁটার দৈর্ঘ্য যথাক্রমে 8.4 সেমি. ও 14 সেমি.। একদিনে প্রতিটি কাঁটা কতটা দূরত্ব অতিক্রম করবে হিসাব করে লিখি।
সমাধান –
ঘণ্টার কাঁটা 12 ঘণ্টায় একবার প্রদক্ষিণ করে।
\(\therefore\) একদিনে অর্থাৎ 24 ঘণ্টায় কাঁটাটি 2 বার ঘড়ির সমগ্র পথ অতিক্রম করে।
\(\therefore\) একদিনে ঘণ্টার কাঁটা যে পথ অতিক্রম করে তা হল –
= \( 2 \times\) ঘড়ির পরিধি
= \( 2 \times 2\pi r\)
= \( 2 \times 2 \times \frac{22}{7} \times 8.4\) সেমি.
= \( 105.6\) সেমি.
মিনিটের কাঁটা 1 ঘণ্টায় একবার প্রদক্ষিণ করে।
\(\therefore\) একদিনে অর্থাৎ 24 ঘণ্টায় কাঁটাটি 24 বার ঘড়ির সমগ্র পথ অতিক্রম করে।
\(\therefore\) একদিনে মিনিটের কাঁটা যে পথ অতিক্রম করে তা হল –
= \( 24 \times\) ঘড়ির পরিধি
= \( 24 \times 2\pi r\) সেমি.
= \( 24 \times 2 \times \frac{22}{7} \times 14\) সেমি.
= \( 2112\) সেমি.
\(\therefore\) একদিনে ঘণ্টার কাঁটা 105.6 সেমি. এবং মিনিটের কাঁটা 2112 সেমি. পথ অতিক্রম করবে।
12. আমি ও বন্ধু মিহির দুটি বৃত্ত এঁকেছি যাদের ব্যাসের দৈর্ঘ্যের অনুপাত [ ] : [ ] । হিসাব করে দেখছি আমাদের বৃত্তের পরিধির অনুপাত হয় [ ] : [ ] । [নিজে করি]
13. রহিমের একটি বৃত্তাকার মাঠের পুরোটা একবার দৌড়াতে যে সময় লাগে, ব্যাস বরাবর এক প্রান্ত থেকে আর এক প্রান্তে যেতে তার থেকে \(40\) সেকেন্ড কম সময় লাগে। রহিমের গতিবেগ \(90\) মিটার প্রতি মিনিট হলে, মাঠের ব্যাসের দৈর্ঘ্য হিসাব করে লিখি।
সমাধান –
রহিম \(60\) সেকেন্ডে যায় \(90\) মিটার।
\(1\) সেকেন্ডে যায় \(\frac{90}{60}\) মিটার।
\(40\) সেকেন্ডে যায় \(\frac{90 \times 40}{60}\) মিটার \(= 60\) মিটার।
\(\therefore\) মাঠের ব্যাসটি মাঠের পরিধি অপেক্ষা \(60\) মিটার ছোটো।
ধরি, মাঠের ব্যাসার্ধ \(r\) মিটার।
শর্তানুসারে,
\(2\pi r – 2r = 60\)বা, \(2r (\pi – 1) = 60\)
বা, \(2r (\frac{22}{7} – 1) = 60\)
বা, \(2r \times (\frac{22-7}{7}) = 60\)
বা, \(2r = \frac{60 \times 7}{15}\)
বা, \(2r = 28\)
\(\therefore\) মাঠের ব্যাসের দৈর্ঘ্য \(28\) মিটার।
14. দুটি বৃত্তের পরিধির অনুপাত \(2:3\) এবং তাদের ব্যাসার্ধের দৈর্ঘ্যের অন্তর \(2\) সেমি.। বৃত্ত দুটির ব্যাসের দৈর্ঘ্য হিসাব করে লিখি।
সমাধান –
ধরি, বড় বৃত্তের ব্যাসার্ধের দৈর্ঘ্য \(R\) সেমি. এবং ছোটো বৃত্তের ব্যাসার্ধের দৈর্ঘ্য \(r\) সেমি.।
\(\therefore R – r = 2\) —(i)
এবং \(2\pi r : 2\pi R = 2:3\) —-(ii)
(ii) নং সমীকরণ থেকে পাই,
\(\frac{2\pi r}{2\pi R} = \frac{2}{3}\)বা, \(\frac{r}{R} = \frac{2}{3}\)
বা, \(\frac{R}{3} = \frac{r}{2} = k\) [ধরা হল]
\(\therefore R = 3k\) এবং \(r = 2k\) [\(k \neq 0\) একটি আনুপাতিক ধ্রুবক]
(i) নং সমীকরণ থেকে পাই,
\(R – r = 2\)বা, \(3k – 2k = 2\)
বা, \(k = 2\)
\(\therefore R = 3k = (3 \times 2)\) সেমি. \(= 6\) সেমি. এবং \(r = 2k = (2 \times 2)\) সেমি. \(= 4\) সেমি.।
\(\therefore 2R = 12\) সেমি. এবং \(2r = 8\) সেমি.।
সুতরাং, বৃত্ত দুটির ব্যাসের দৈর্ঘ্য যথাক্রমে \(12\) সেমি. এবং \(8\) সেমি.।
15. 196 বর্গ সেমি. ক্ষেত্রফলের একটি পাত থেকে চারটি সর্ব বৃহৎ বৃত্তাকার পাত কেটে নেওয়া হলো। প্রতিটি বৃত্তাকার পাতের পরিধি হিসাব করে লিখি।
সমাধান –
বর্গাকার পেতলের পাতের ক্ষেত্রফল = \(196\) বর্গ সেমি.
\(\therefore\) বর্গাকার পেতলের পাতটির বাহুর দৈর্ঘ্য = \(\sqrt{196}\) সেমি. = \(14\) সেমি.
\(14\) সেমি বাহুবিশিষ্ট বর্গাকার পাত থেকে কেটে নেওয়া চারটি সর্ব বৃহৎ বৃত্তাকার পাতের প্রতিটির ব্যাস হবে \(14 / 2\) সেমি. = \(7\) সেমি.
\(\therefore\) প্রতিটি পাতের পরিধি হবে = \(2 \times \frac{22}{7} \times \frac{7}{2}\) সেমি. = \(22\) সেমি.
\(\therefore\) প্রতিটি বৃত্তাকার পাতের পরিধি \(22\) সেমি. হবে।
16. একটি বৃত্তাকার মাঠের বৃত্ত বরাবর একপ্রান্ত থেকে অপর প্রান্তে যেতে নাসিফার যে সময় লাগে, মাঠের ব্যাস বরাবর অতিক্রম করতে তার থেকে 45 সেকেন্ড সময় কম লাগে। নাসিফার গতিবেগ মিনিটে 80 মিটার হলে, মাঠটির ব্যাসের দৈর্ঘ্য হিসাব করে লিখি।
সমাধান –
নাসিফা 60 সেকেন্ডে যায় 80 মিটার।
1 সেকেন্ডে যায় \(\frac{80}{60}\) মিটার।
45 সেকেন্ডে যায় \(\frac{80 \times 45}{60}\) মিটার = \(60\) মিটার।
\(\therefore\) মাঠের ব্যাসটি মাঠের পরিধি অপেক্ষা 60 মিটার ছোটো।
ধরি, মাঠের ব্যাসার্ধ \(r\) মিটার।
শর্তানুসারে,
\(2\pi r – 2r = 60\)বা, \(2r (\pi – 1) = 60\)
বা, \(2r (\frac{22}{7} – 1) = 60\)
বা, \(2r \times (\frac{22-7}{7}) = 60\)
বা, \(2r \times \frac{15}{7} = 60\)
বা, \(2r = \frac{60 \times 7}{15}\)
বা, \(2r = 28\)
\(\therefore\) মাঠটির ব্যাসের দৈর্ঘ্য 28 মিটার।
17. মহিম সাইকেলে চেপে 7 মিটার 5 ডেসিমি. চওড়া একটি বৃত্তাকার পথের বাইরের ও ভিতরের ধার বরাবর সম্পূর্ণ একবার ঘুরতে যথাক্রমে 46 সেকেন্ড ও 44 সেকেন্ড নেয়। ভিতরের ধার বরাবর বৃত্তটির ব্যাসের দৈর্ঘ্য হিসাব করি।
সমাধান –
7 মিটার 5 ডেসিমি. = \(7.5\) মিটার।
ধরি, বৃত্তটির ব্যাসার্ধ \(r\) মিটার।
\(\therefore\) রাস্তা সমেত বৃত্তটির ব্যাসার্ধ = \((r + 7.5)\) মিটার।
রাস্তার ভিতরের দিকের পরিধি = \(2\pi r\) মিটার এবং বাইরের দিকের পরিধি = \(2\pi (r+7.5)\) মিটার।
মহিম, \(2\pi r\) মিটার যায় 44 সেকেন্ডে।
1 মিটার যায় \(\frac{44}{2\pi r}\) সেকেন্ডে।
\(2\pi (r+7.5)\) মিটার যায় \(\frac{44 \times 2\pi (r+7.5)}{2\pi r}\) সেকেন্ডে
\(= \frac{44(r+7.5)}{r}\) সেকেন্ডে।
প্রশ্নানুসারে,
\(\frac{44(r+7.5)}{r} = 46\)বা, \(44r + 330 = 46r\)
বা, \(2r = 330\)
\(\therefore\) ভিতরের ধার বরাবর বৃত্তটির ব্যাসের দৈর্ঘ্য 330 মিটার।
18. একজন সাইকেল আরোহীর একটি বৃত্তাকার পথে বাইরের ও ভিতরের ধার বরাবর সম্পূর্ণ একবার ঘুরতে সময়ের অনুপাত 20:19; যদি পথটি 5 মিটার চওড়া হয়, তবে ভিতরের বৃত্তের ব্যাসের দৈর্ঘ্য লিখি।
সমাধান –
ধরি, একজন সাইকেল আরোহীর বাইরের ধার বরাবর ঘুরতে \(20t\) সেকেন্ড এবং ভিতরের ধার বরাবর ঘুরতে \(19t\) সেকেন্ড সময় লাগে। আরো ধরি, রাস্তাটির ভিতরের ব্যাসার্ধ \(r\) মিটার।
\(\therefore\) রাস্তার বাইরের ব্যাসার্ধ = \((r + 5)\) মিটার।
\(\therefore\) রাস্তার ভিতরের দিকের পরিধি = \(2\pi r\) মিটার এবং বাইরের দিকের পরিধি = \(2\pi (r+5)\) মিটার।
সাইকেল আরোহী \(2\pi (r+5)\) মিটার যায় \(20t\) সেকেন্ডে।
1 মিটার যায় \(\frac{20t}{2\pi (r+5)}\) সেকেন্ডে।
\(2\pi r\) মিটার যায় \(\frac{20t \times 2\pi r}{2\pi (r+5)}\) সেকেন্ডে \(= \frac{20tr}{r+5}\) সেকেন্ডে।
প্রশ্নানুসারে,
\(\frac{20tr}{r+5} = 19t\)বা, \(\frac{20r}{r+5} = 19\)
বা, \(20r = 19r + 95\)
বা, \(20r – 19r = 95\)
বা, \(r = 95\)
বা, \(2r = 190\)
\(\therefore\) ভিতরের বৃত্তের ব্যাসের দৈর্ঘ্য 190 মিটার।
19. বহু বিকল্পীয় প্রশ্ন (M.C.Q.)
(i) একটি ঘড়ির ঘণ্টার কাঁটা ও মিনিটের কাঁটার গতিবেগের অনুপাত
(a) \(1:12\)
(b) \(12:1\)
(c) \(1:24\)
(d) \(24:1\)
উত্তর – (a) \(1:12\)
সমাধান –
ধরি, ঘড়ির ব্যাসার্ধ \(r\) একক।
\(\therefore\) ঘড়ির পরিধি \(2\pi r\) একক।
\(\therefore\) ঘড়ির ঘণ্টার কাঁটা \(12\) ঘণ্টায় অতিক্রম করে \(2\pi r\) একক।
ঘড়ির ঘণ্টার কাঁটা \(1\) ঘণ্টায় অতিক্রম করে \(\frac{2\pi r}{12}\) একক \(= \frac{\pi r}{6}\) একক।
\(\therefore\) ঘণ্টার কাঁটার বেগ \(\frac{\pi r}{6}\) একক প্রতি ঘণ্টা।
আবার, ঘড়ির মিনিটের কাঁটা \(1\) ঘণ্টায় অতিক্রম করে ঘড়ির পরিধি \(= 2\pi r\) একক।
\(\therefore\) মিনিটের কাঁটার বেগ \(2\pi r\) একক প্রতি ঘণ্টা।
কাঁটা দুটির গতিবেগের অনুপাত \(= \frac{\pi r}{6} : 2\pi r = \frac{1}{6} : 2 = 1 : 12\)
(ii) একটি বৃত্তাকার পার্ক সম্পূর্ণ একবার পরিক্রমা করতে সোমার \(\frac{\pi x}{100}\) মিনিট সময় লাগে। পার্কটি সোজাসুজি ব্যাস বরাবর অতিক্রম করতে সোমার সময় লাগবে
(a) \(\frac{x}{200}\) মিনিট
(b) \(\frac{x}{100}\) মিনিট
(c) \(\frac{\pi}{100}\) মিনিট
(d) \(\frac{\pi}{200}\) মিনিট
উত্তর – (b) \(\frac{x}{100}\) মিনিট
সমাধান –
\(2\pi r\) একক দূরত্ব অতিক্রম করতে সময় লাগে \(\frac{\pi x}{100}\) মিনিট।
\(1\) একক দূরত্ব অতিক্রম করতে সময় লাগে \(\frac{\pi x}{2\pi r \times 100}\) মিনিট।
\(2r\) একক দূরত্ব অতিক্রম করতে সময় লাগে \(\frac{\pi x \times 2r}{2\pi r \times 100}\) মিনিট।
\(= \frac{x}{100}\) মিনিট।
\(\therefore\) পার্কটি সোজাসুজি ব্যাস বরাবর অতিক্রম করতে সোমার সময় লাগবে \(\frac{x}{100}\) মিনিট।
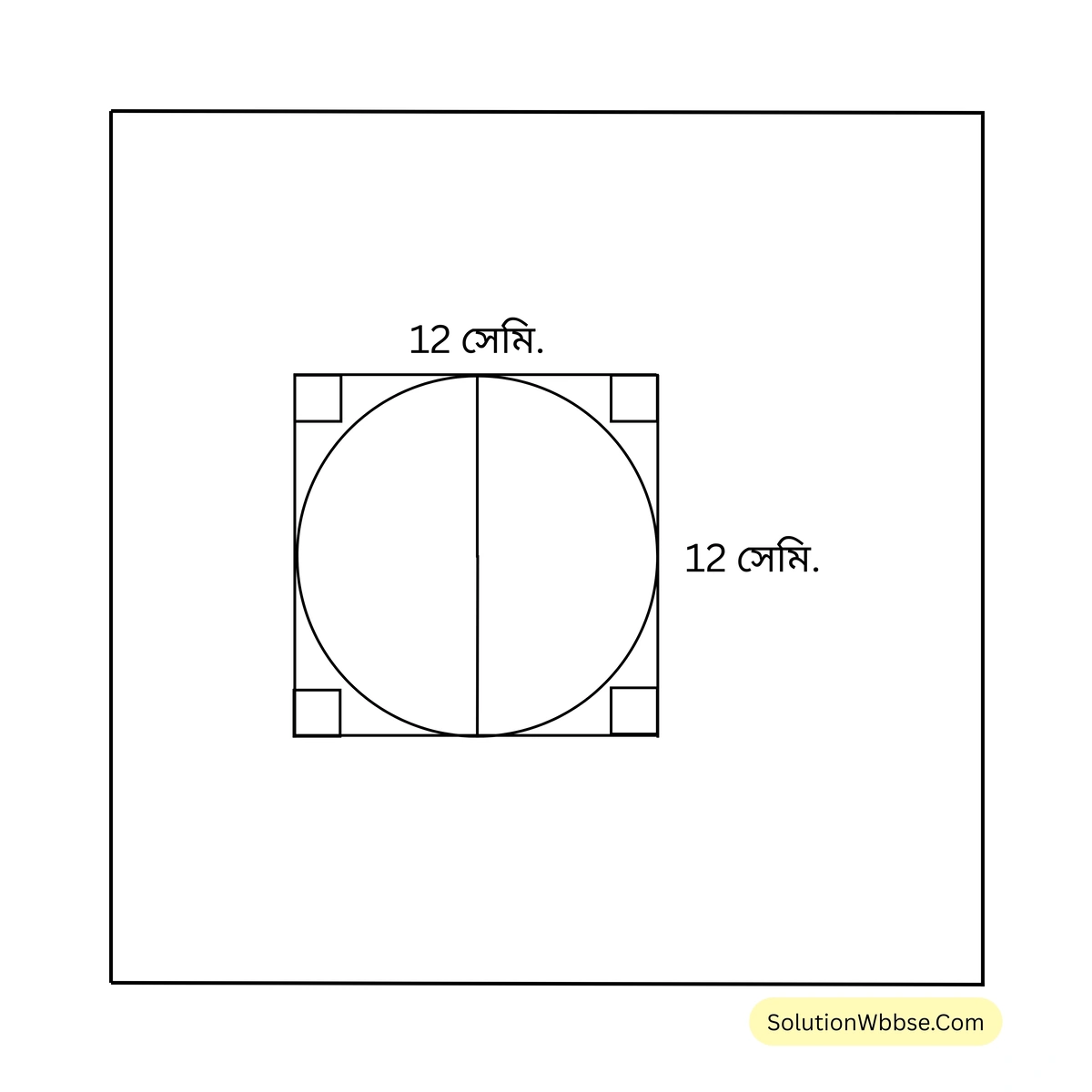
(iii) একটি বৃত্ত একটি বর্গক্ষেত্রের অন্তর্লিখিত। বর্গক্ষেত্রের বাহুর দৈর্ঘ্য 10 সেমি হলে বৃত্তের ব্যাসের দৈর্ঘ্য
(a) \(10\) সেমি
(b) \(5\) সেমি
(c) \(20\) সেমি
(d) \(10\sqrt{2}\) সেমি
উত্তর – (a) \(10\) সেমি
সমাধান –
যেহেতু বৃত্তটি বর্গক্ষেত্রে অন্তর্লিখিত।
\(\therefore\) বর্গক্ষেত্রের বাহুর দৈর্ঘ্য = বৃত্তের ব্যাসের দৈর্ঘ্য।
\(\therefore\) বৃত্তের ব্যাসের দৈর্ঘ্য \(10\) সেমি।
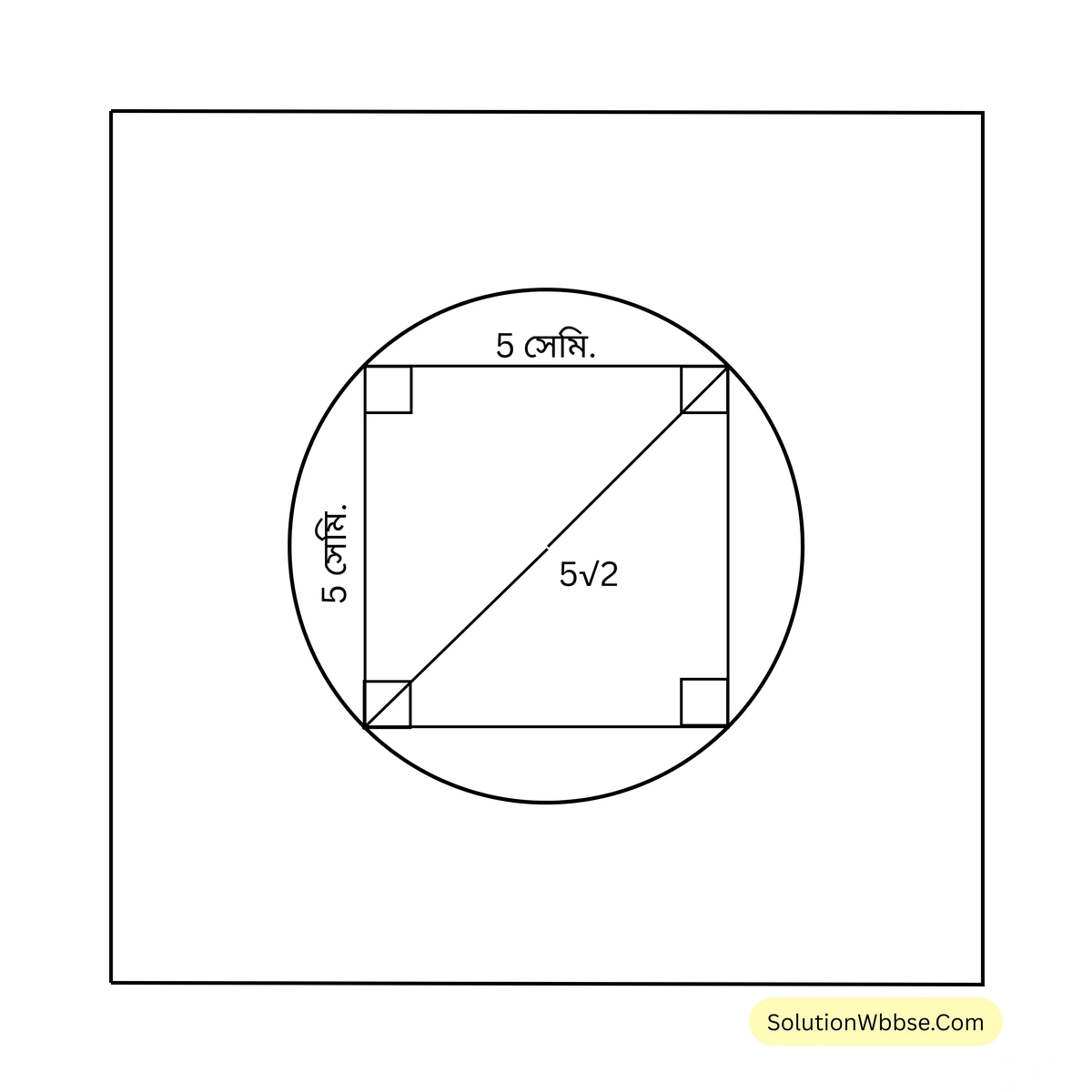
(iv) একটি বৃত্ত একটি বর্গক্ষেত্রের পরিলিখিত। বর্গক্ষেত্রের বাহুর দৈর্ঘ্য 5 সেমি হলে, বৃত্তের ব্যাসের দৈর্ঘ্য
(a) \(5\sqrt{2}\) সেমি
(b) \(10\sqrt{2}\) সেমি
(c) \(5\) সেমি
(d) \(10\) সেমি
উত্তর – (a) \(5\sqrt{2}\) সেমি
সমাধান –
বৃত্তটি বর্গক্ষেত্রে পরিলিখিত এবং বর্গক্ষেত্রের বাহুর দৈর্ঘ্য \(5\) সেমি।
এক্ষেত্রে, বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য = বৃত্তের ব্যাসের দৈর্ঘ্য।
\(\therefore\) বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য \(5\sqrt{2}\) সেমি।
\(\therefore\) বৃত্তের ব্যাসের দৈর্ঘ্য \(5\sqrt{2}\) সেমি।
(v) একটি বৃত্তাকার বলয় 5 সেমি চওড়া। বৃত্তের বহির্ব্যাসার্ধের দৈর্ঘ্য ও অন্তর্ব্যাসার্ধের দৈর্ঘ্যের অন্তর
(a) \(5\) সেমি
(b) \(2.5\) সেমি
(c) \(10\) সেমি
(d) কোনোটিই নয়।
উত্তর – (a) \(5\) সেমি
সমাধান –
যেহেতু বলয়টি 5 সেমি. চওড়া।
\(\therefore\) বৃত্তের বহির্ব্যাসার্ধের দৈর্ঘ্য ও অন্তর্ব্যাসার্ধের দৈর্ঘ্যের অন্তর = \(5\) সেমি।
20. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন –
(i) একটি অর্ধবৃত্তের পরিসীমা 36 সেমি হলে, অর্ধবৃত্তের ব্যাসের দৈর্ঘ্য কত?
সমাধান –
ধরি, অর্ধবৃত্তের ব্যাসার্ধের দৈর্ঘ্য \(r\) সেমি।
\(\therefore \pi r + 2r = 36\)বা, \(r (\frac{22}{7} + 2) = 36\)
বা, \(r (\frac{22+14}{7}) = 36\)
বা, \(r \times \frac{36}{7} = 36\)
বা, \(r = \frac{36 \times 7}{36}\)
বা, \(r = 7\)
\(\therefore\) অর্ধবৃত্তের ব্যাসের দৈর্ঘ্য \(2r\) সেমি. \(= (2 \times 7)\) সেমি. \(= 14\) সেমি. [উত্তর]
(ii) একটি ঘড়ির মিনিটের কাঁটার দৈর্ঘ্য 7 সেমি। \(90^{\circ}\) কোণ ঘুরতে মিনিটের কাঁটা কত দৈর্ঘ্য ঘুরবে?
সমাধান –
ঘড়ির মিনিটের কাঁটার দৈর্ঘ্য 7 সেমি।
\(\therefore\) ঘড়িটির ব্যাসার্ধ 7 সেমি।
\(\therefore\) পরিধি \(= 2\pi r\) সেমি. \(= 2 \times \frac{22}{7} \times 7\) সেমি. \(= 44\) সেমি.
\(\therefore\) ঘড়ির কাঁটাটি একবার অর্থাৎ \(360^{\circ}\) ঘুরতে অতিক্রম করে 44 সেমি.
\(\therefore 90^{\circ}\) ঘুরতে অতিক্রম করে \(= (44 \times \frac{90}{360})\) সেমি. \(= 11\) সেমি. [উত্তর]
(iii) কোনো বর্গক্ষেত্রের অন্তর্বৃত্ত ও পরিবৃত্তের ব্যাসার্ধের অনুপাত কত?
সমাধান –
ধরি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য \(a\) একক।
\(\therefore\) বর্গক্ষেত্রের অন্তর্বৃত্তের ব্যাস = বর্গক্ষেত্রের বাহুর দৈর্ঘ্য \(= a\) একক।
এবং বর্গক্ষেত্রের পরিবৃত্তের ব্যাস = বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য \(= a\sqrt{2}\) একক।
\(\therefore\) বর্গক্ষেত্রের অন্তর্বৃত্ত ও পরিবৃত্তের ব্যাসার্ধের অনুপাত \(= \frac{a}{2} : \frac{a\sqrt{2}}{2}\) \(= 1 : \sqrt{2}\) [উত্তর]
(iv) কোনো ঘড়ির মিনিটের কাঁটার দৈর্ঘ্য 7 সেমি। 15 মিনিটে কাঁটাটি কত দৈর্ঘ্য ঘুরবে?
সমাধান –
ঘড়ির মিনিটের কাঁটার দৈর্ঘ্য 7 সেমি।
\(\therefore\) ঘড়িটির ব্যাসার্ধ 7 সেমি।
\(\therefore\) পরিধি \(= 2\pi r\) সেমি. \(= 2 \times \frac{22}{7} \times 7\) সেমি. \(= 44\) সেমি.
\(\therefore\) ঘড়ির কাঁটাটি 60 মিনিটে অতিক্রম করে 44 সেমি.
\(\therefore\) ঘড়ির কাঁটাটি 15 মিনিটে অতিক্রম করে \(= (44 \times \frac{15}{60})\) সেমি. \(= 11\) সেমি. [উত্তর]
(v) একটি বৃত্তের ব্যাসের দৈর্ঘ্য এবং একটি বর্গক্ষেত্রের বাহুর দৈর্ঘ্য সমান হলে, তাদের পরিসীমার অনুপাত কত?
সমাধান –
ধরি, বৃত্তের ব্যাসার্ধ \(r\) একক।
\(\therefore\) বৃত্তের ব্যাস \(= 2r\) একক।
\(\therefore\) বর্গক্ষেত্রের বাহুর দৈর্ঘ্য \(2r\) একক।
\(\therefore\) বৃত্তের এবং বর্গক্ষেত্রের পরিসীমার অনুপাত = \( 2\pi r : 4 \times 2r\)
= \( 2\pi r : 8r\)
= \( \pi : 4\)
= \( \frac{22}{7} : 4\)
\(= 22 : 28 = 11 : 14\) [উত্তর]
এই আর্টিকেলে নবম শ্রেণির গণিতের ‘বৃত্তের পরিধি‘ অধ্যায়ের ‘কষে দেখি – 16′-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।
কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন