পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) দশম শ্রেণির গণিত পাঠ্যবইয়ের সপ্তদশ অধ্যায় হলো ‘সমবিন্দু সংক্রান্ত উপপাদ্য’। এই পোস্টে ‘কষে দেখি 17‘-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. ABC ত্রিভুজের B ও C এর অন্তঃসমদ্বিখণ্ডক I বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, \(\angle BIC = 90^\circ + \frac{\angle BAC}{2}\)
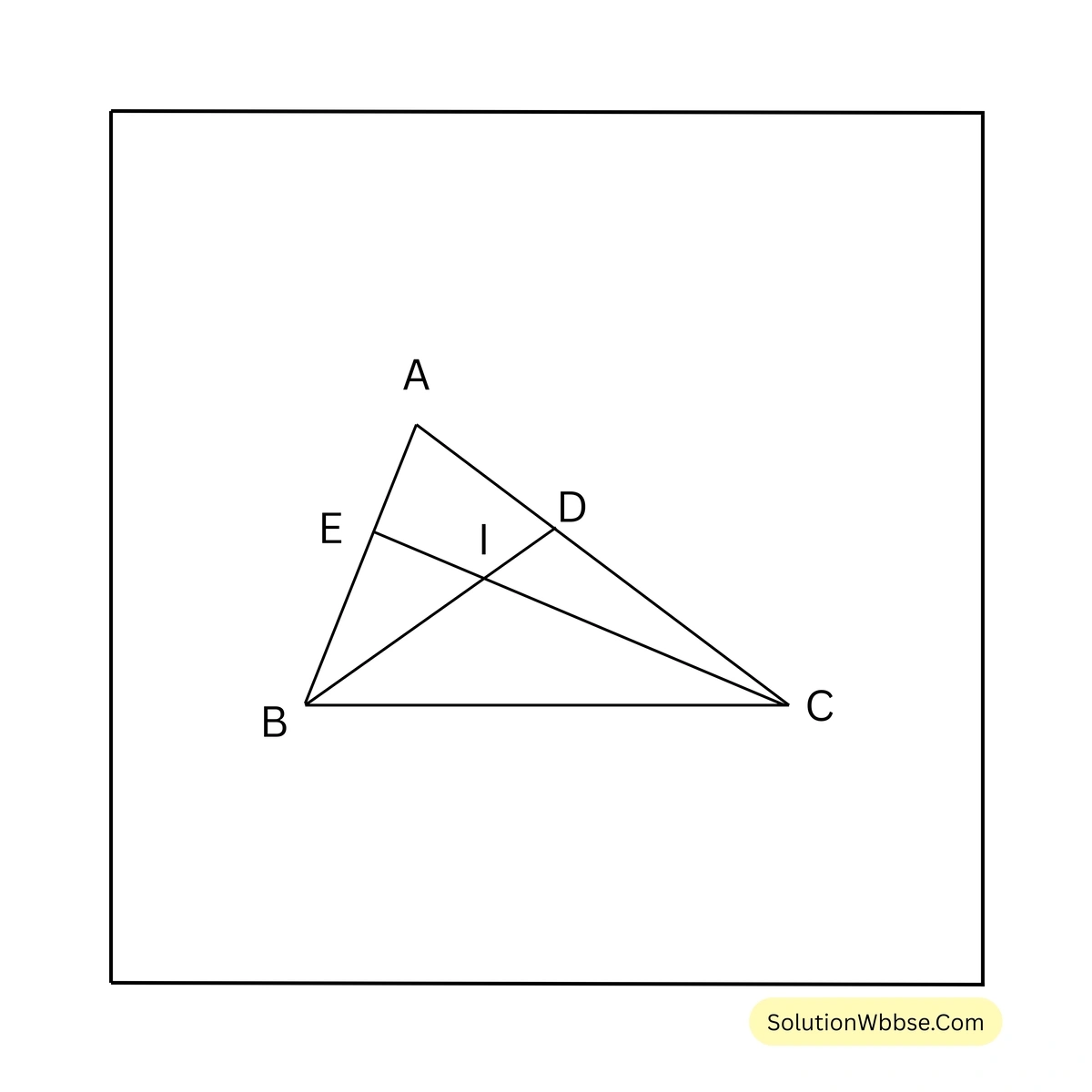
ধরি, ABC ত্রিভুজের B -এর অন্তঃসমদ্বিখণ্ডক BD ও C -এর অন্তঃসমদ্বিখণ্ডক CE পরস্পরকে I বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে, \(\angle BIC = 90^\circ + \frac{\angle BAC}{2}\)।
প্রমাণ –
যেহেতু BD, B এর সমদ্বিখণ্ডক,
\(\therefore \angle ABI = \angle IBC\)আবার যেহেতু, CE, C-এর সমদ্বিখণ্ডক,
\(\therefore \angle ACI = \angle ICB\)\(\therefore \angle IBC + \angle ICB = \angle ABI + \angle ACI \dots (i)\)এখন, IBC ত্রিভুজের ক্ষেত্রে,
\(\angle IBC + \angle ICB = 180^\circ – \angle BIC \dots (ii)\)\(\therefore \angle ABI + \angle ACI = 180^\circ – \angle BIC\) [(i) ও (ii) থেকে পাই]
আবার, \(\angle ABI + \angle ACI\)
= \( \frac{1}{2} \angle ABC + \frac{1}{2} \angle ACB\)
= \( \frac{1}{2} (\angle ABC + \angle ACB)\)
= \( \frac{1}{2} (180^\circ – \angle BAC)\)
= \( 90^\circ – \frac{\angle BAC}{2} \dots (iii)\)
\(\therefore 180^\circ – \angle BIC = 90^\circ – \frac{\angle BAC}{2}\) [(ii) ও (iii) থেকে পাই]
বা, \(-\angle BIC = 90^\circ – \frac{\angle BAC}{2} – 180^\circ\)
বা, \(-\angle BIC = -90^\circ – \frac{\angle BAC}{2}\)
বা, \(\angle BIC = 90^\circ + \frac{\angle BAC}{2}\) [প্রমাণিত]
2. একটি ত্রিভুজের তিনটি মধ্যমার দৈর্ঘ্য সমান হলে প্রমাণ করি যে, ত্রিভুজটি সমবাহু।
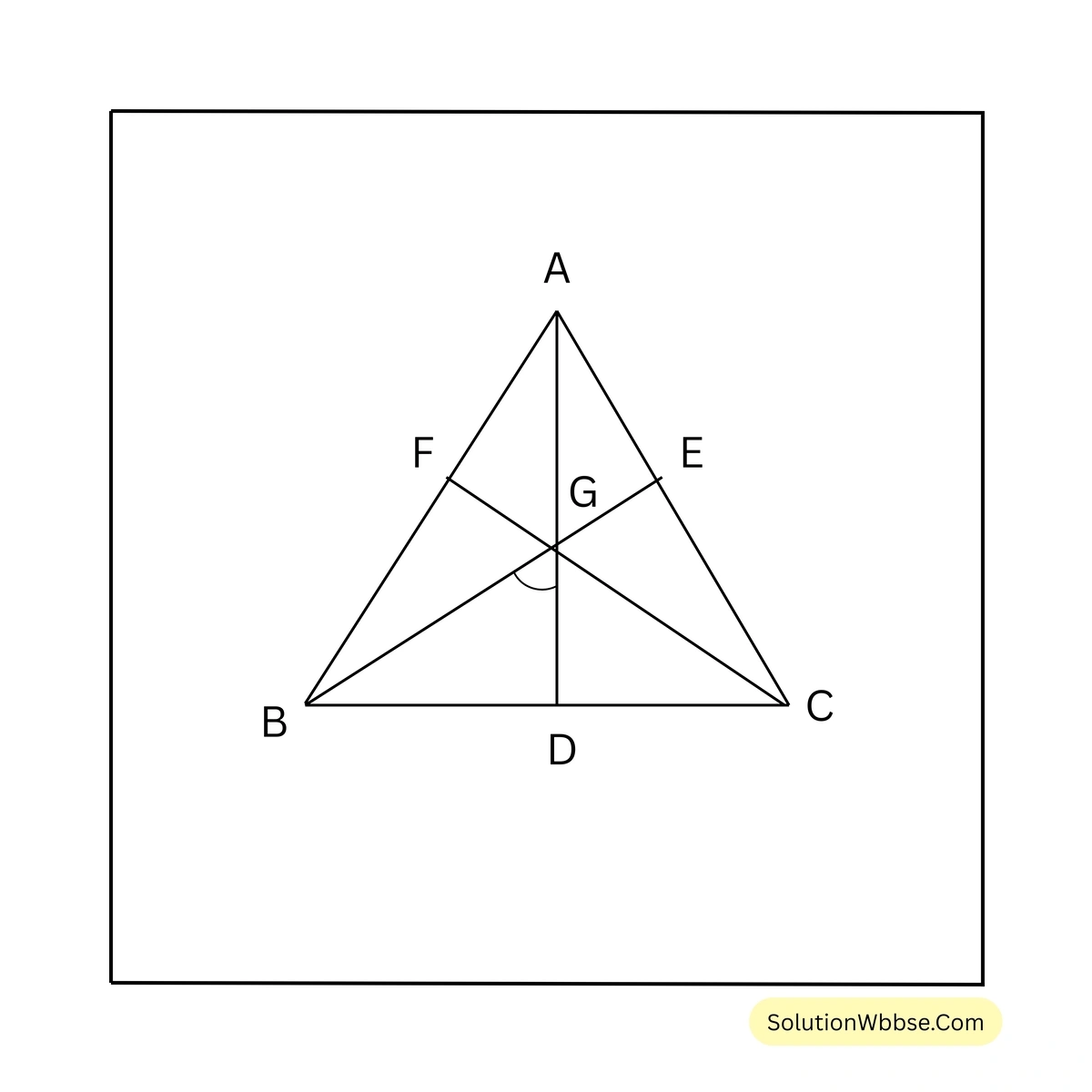
ABC ত্রিভুজের AD, BE ও CF তিনটি মধ্যমা। \(AD = BE = CF\)। প্রমাণ করতে হবে ABC একটি সমবাহু ত্রিভুজ। AD, BE, CF মধ্যমাত্রয় পরস্পর G বিন্দুতে ছেদ করেছে।
\(\therefore\) G ত্রিভুজটির ভরকেন্দ্র।
প্রমাণ –
ত্রিভুজের প্রত্যেক মধ্যমা ভরকেন্দ্রে সমত্রিখণ্ডিত হয়।
\(\therefore BG = \frac{2}{3} BE\), এবং \(GE = \frac{1}{3} BE\)।
\(CG = \frac{2}{3} CF, GF = \frac{1}{3} CF, AG = \frac{2}{3} AD, GD = \frac{1}{3} AD\)।
\(\because AD = BE = CF\),
\(\therefore \frac{2}{3} AD = \frac{2}{3} BE = \frac{2}{3} CF\),
\(\therefore AG = BG = CG\),
অনুরূপে, \(GE = GF = GD\)।
\(\Delta GBF\) ও \(\Delta GCE\) -এর \(GB = GC, GF = GE, \angle BGF =\) বিপ্রতীপ \(\angle CGE\),
\(\therefore \Delta GBF \cong \Delta GCE\), \(\therefore BF = CE\), \(\therefore 2BF = 2CE\), \(\therefore AB = AC\)।
অনুরূপে \(\Delta GBD\) ও \(\Delta AGE\) ত্রিভুজদ্বয় সর্বসম।
\(\therefore BD = AE \therefore BC = AC, \therefore AB = BC = AC\),
\(\therefore\) ABC একটি সমবাহু ত্রিভুজ।
3. প্রমাণ করি সমবাহু ত্রিভুজের পরিকেন্দ্র, অন্তঃকেন্দ্র, ভরকেন্দ্র ও লম্ববিন্দু সমপাতিত হয়।
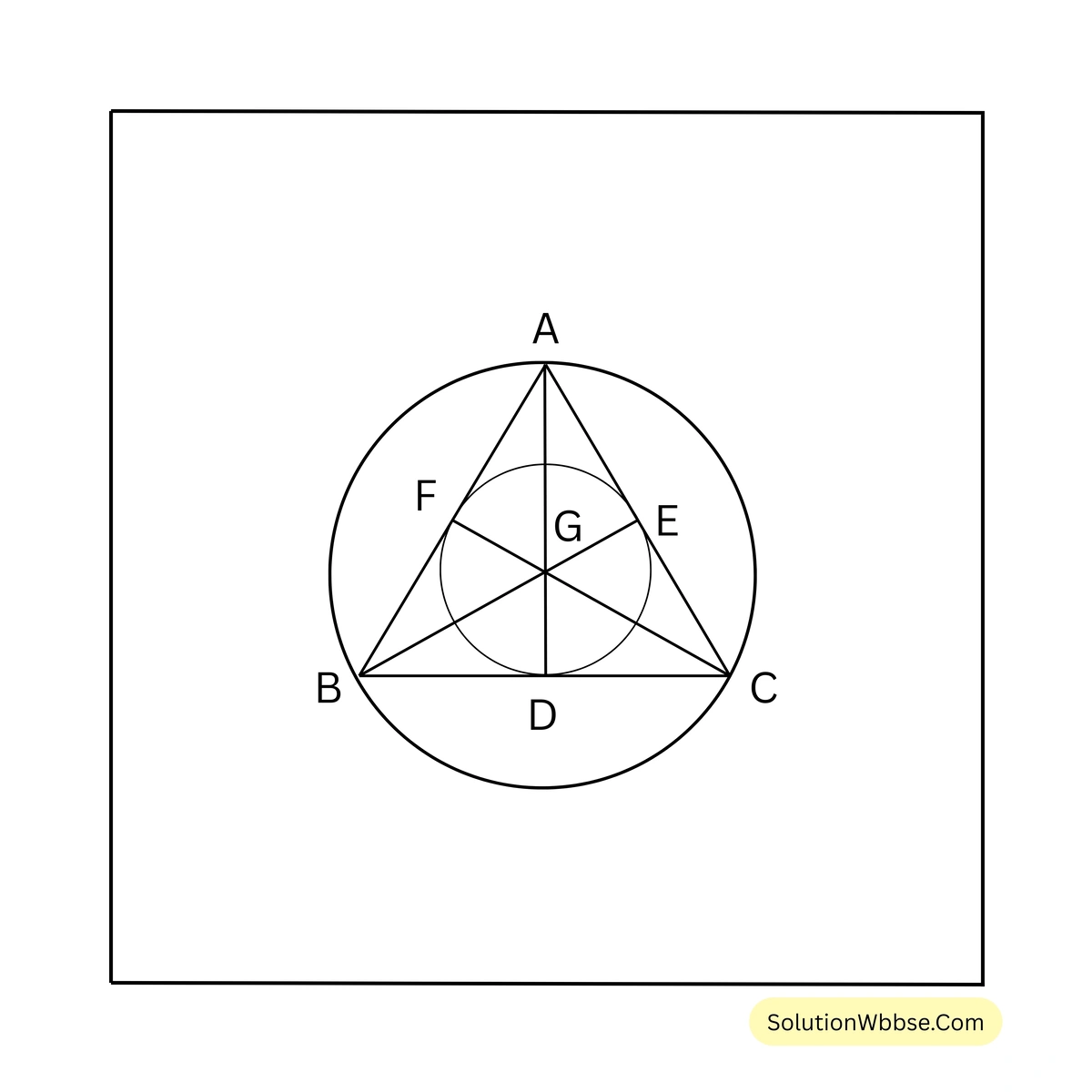
ধরি, সমবাহু ত্রিভুজ ABC-এর মধ্যমা ত্রয় AD, BE এবং CF পরস্পরকে G বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে যে, সমবাহু ত্রিভুজটির পরিকেন্দ্র, অন্তঃকেন্দ্র, ভরকেন্দ্র ও লম্ববিন্দু সমপাতিত হয়েছে।
প্রমাণ –
\(\Delta ABC\) -এর মধ্যমা ত্রয় AD, BE এবং CF পরস্পরকে G বিন্দুতে ছেদ করেছে।
\(\therefore \Delta ABC\) -এর ভরকেন্দ্র G।
আবার আমরা জানি সমবাহু ত্রিভুজের উচ্চতাই হল মধ্যমা।
\(\therefore \Delta ABC\) -এর লম্ববিন্দু G।
আমরা জানি, সমবাহু ত্রিভুজের অন্তঃবৃত্তের ব্যাসার্ধ তার উচ্চতার দৈর্ঘ্যের এক-তৃতীয়াংশ।
\(\therefore GD = GE = GF =\) অন্তঃবৃত্তের ব্যাসার্ধ।
\(\therefore\) অন্তঃবৃত্তের কেন্দ্র হল G।
আমরা জানি, সমবাহু ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ তার উচ্চতার দুই-তৃতীয়াংশ।
\(\therefore AG = BG = CG =\) পরিবৃত্তের ব্যাসার্ধ।
\(\therefore\) পরিবৃত্তের কেন্দ্রটি হল G।
\(\therefore\) সমবাহু ত্রিভুজের পরিকেন্দ্র, অন্তঃকেন্দ্র, ভরকেন্দ্র ও লম্ববিন্দু সমপাতিত হয়। [প্রমাণিত]
4. ABC ত্রিভুজের AD, BE এবং CF মধ্যমা। প্রমাণ করি যে, ABC ও DEF ত্রিভুজের ভরকেন্দ্র একই বিন্দু।
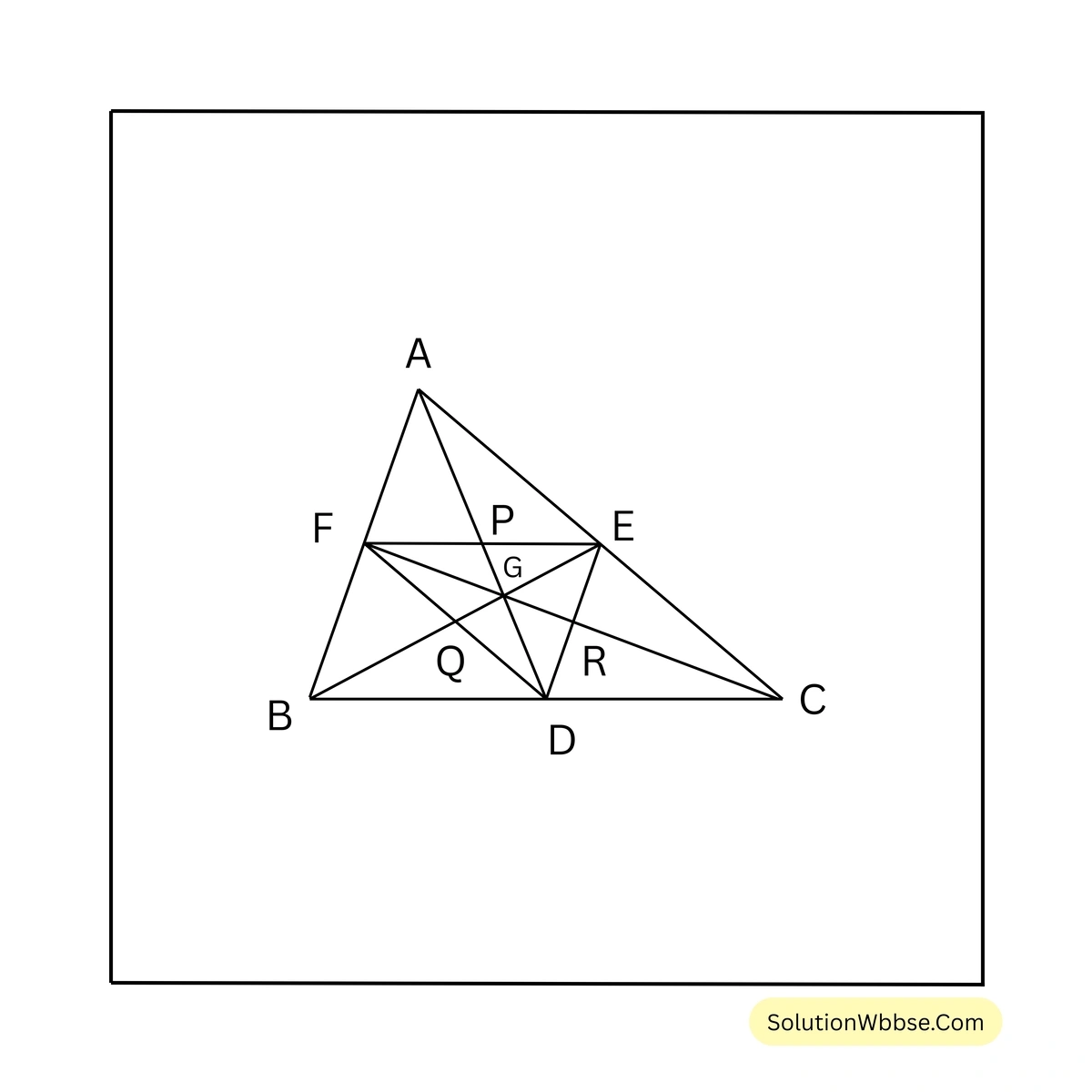
ধরি, ABC এর AD, BE এবং CF মধ্যমা ত্রয় পরস্পরকে G বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে, ABC ও DEF ত্রিভুজের ভরকেন্দ্র একই বিন্দু। অর্থাৎ, \(\Delta DEF\) -এর ভরকেন্দ্র G প্রমাণ করলেই হবে, \(\Delta ABC\) এবং \(\Delta DEF\) -এর ভরকেন্দ্র একই বিন্দু।
প্রমাণ –
\(\Delta ABC\) -এর AB এবং AC বাহুর মধ্যবিন্দু যথাক্রমে F এবং E।
\(\therefore FE \parallel BC\) এবং \(EF = \frac{1}{2} BC\)।
আবার D, BC এর মধ্যবিন্দু।
\(\therefore EF = BD\)।
এখন BDEF চতুর্ভুজের, \(FE \parallel BD\) \([\because FE \parallel BC]\) এবং \(FE = BD\),
\(\therefore BDEF\) একটি সামান্তরিক।
অনুরূপভাবে প্রমাণ করা যায় যে, DCEF এবং AFDE উভয়ই সামান্তরিক।
আমরা জানি সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।
\(\therefore BDEF\) সামান্তরিক থেকে পাই,
\(FQ = QD\), \(\therefore Q\), FD এর মধ্যবিন্দু।
\(DCEF\) সামান্তরিক থেকে পাই,
\(DR = RE\), \(\therefore R\), DE এর মধ্যবিন্দু।
এবং \(AFDE\) সামান্তরিক থেকে পাই,
\(FP = PE\), \(\therefore P\), FE এর মধ্যবিন্দু।
\(\therefore \Delta DEF\) -এর মধ্যমা তিনটি হল DP, EQ এবং FR, যারা পরস্পরকে G বিন্দুতে ছেদ করেছে।
\(\therefore \Delta DEF\) -এর ভরকেন্দ্র G।
\(\therefore\) ABC ও DEF ত্রিভুজের ভরকেন্দ্র একই বিন্দু। [প্রমাণিত]
5. প্রমাণ করি যে একটি ত্রিভুজের দুটি মধ্যমার দৈর্ঘ্যের সমষ্টি তৃতীয় মধ্যমার দৈর্ঘ্য অপেক্ষা বৃহত্তর।
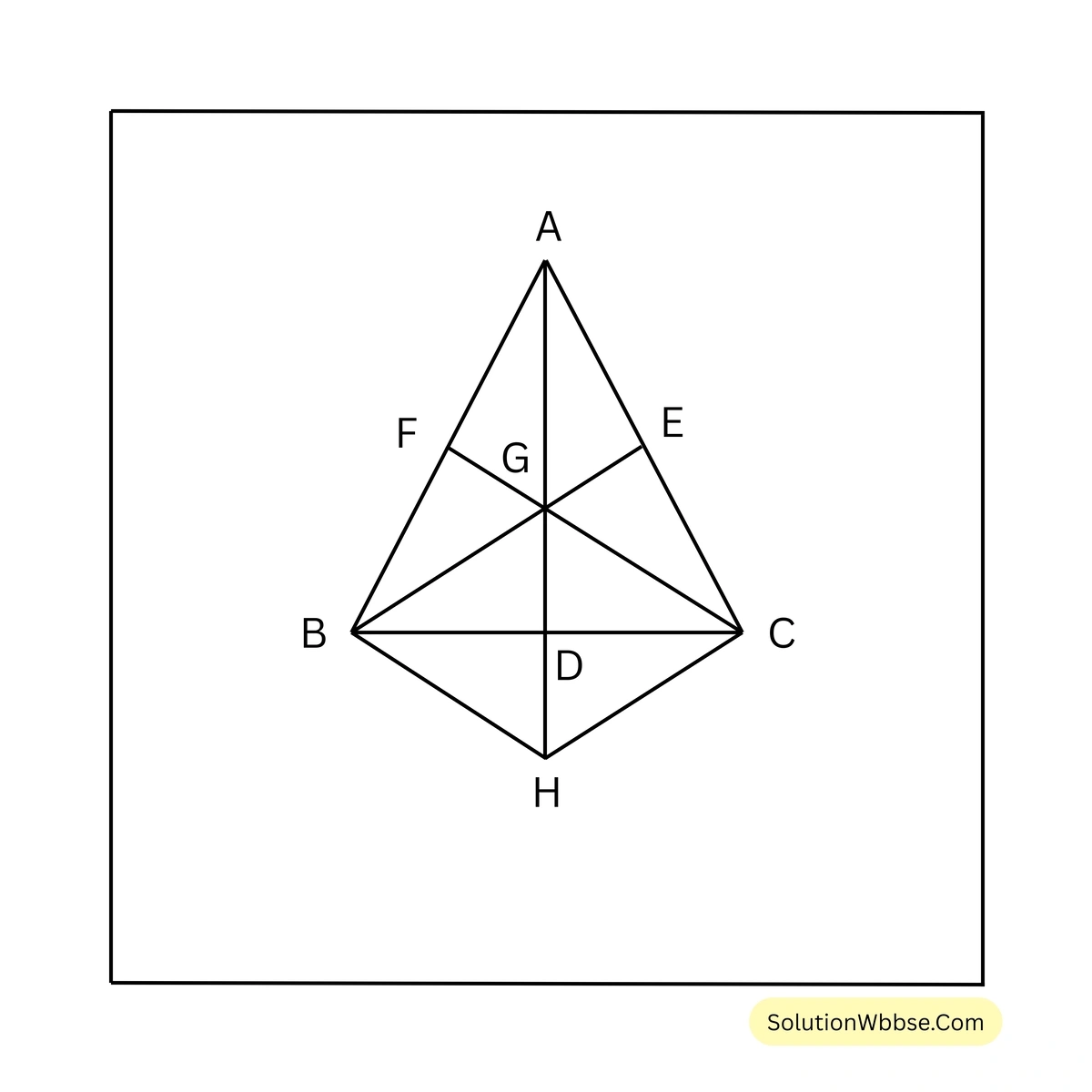
ABC ত্রিভুজের AD, BE, CF মধ্যমা G বিন্দুতে মিলিত হয়েছে। G ত্রিভুজটির ভরকেন্দ্র। প্রমাণ করতে হবে যে, এর যেকোন মধ্যমাদ্বয়ের সমষ্টি তৃতীয় মধ্যমা থেকে বৃহত্তর।
অঙ্কন –
GD কে H পর্যন্ত এরূপভাবে বর্ধিত করা হল যেন \(GD = DH\) হয়। CH যুক্ত করা হল।
প্রমাণ –
\(\Delta ABH\) এর AB ও AH বাহু দুটির মধ্যবিন্দু যথাক্রমে F ও G, \(\therefore FG \parallel BH\), অর্থাৎ, \(GC \parallel BH\)।
আবার, \(\Delta AHC\) এর AH ও CA বাহুর মধ্যবিন্দু যথাক্রমে G ও E, \(\therefore GE \parallel HC\)। অর্থাৎ, \(BG \parallel HC\), \(\therefore BGCH\) একটি সামান্তরিক।
\(\therefore BH = GC\), G ভরকেন্দ্র, \(\therefore GB = \frac{2}{3} BE\), \(GC = \frac{2}{3} CF\), \(BH = \frac{2}{3} CF\)।
\(GD = \frac{1}{3} AD\), \(\therefore GH = 2GD = \frac{2}{3} AD\)। \(\Delta GBH\) এর, \(GB + BH > GH\),
\(\therefore \frac{2}{3} BE + \frac{2}{3} CF > \frac{2}{3} AD\)। \(\therefore BE + CF > AD\), অনুরূপ প্রমাণ করা যায়,
\(AD + BE > CF\) এবং \(AD + CF > BE\)।
6. ABC ত্রিভুজের AD, BE ও CF মধ্যমা। প্রমাণ করি যে, (i) \(4(AD+BE+CF) > 3(AB+BC+CA)\) ; (ii) \(3(AB+BC+CA) > 2(AD+BE+CF)\)
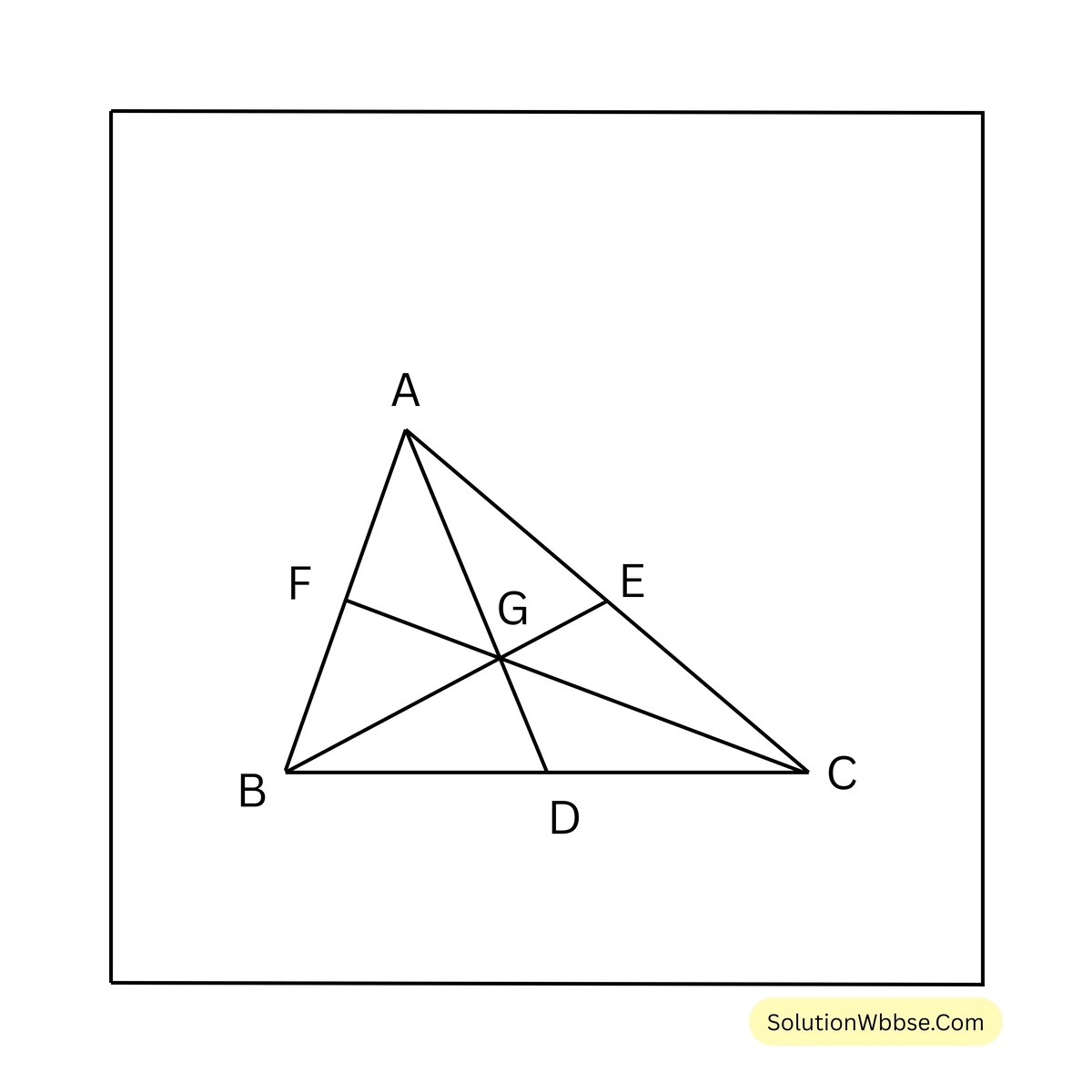
ধরি, ABC এর AD, BE এবং CF মধ্যমাত্রয় পরস্পরকে G বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে,
(i) \(4(AD+BE+CF) > 3(AB+BC+CA)\) ;
(ii) \(3(AB+BC+CA) > 2(AD+BE+CF)\)
প্রমাণ –
যেহেতু ত্রিভুজের ভরকেন্দ্র মধ্যমাকে 2:1 অনুপাতে বিভক্ত করে,
\(\therefore AG = \frac{2}{3} AD, BG = \frac{2}{3} BE\) এবং \(CG = \frac{2}{3} CF\)
এখন BGC থেকে পাই,
\(BG+GC > BC\)বা, \(\frac{2}{3} BE + \frac{2}{3} CF > BC\)
বা, \(2BE + 2CF > 3BC\) —(i)
অনুরূপভাবে AGC থেকে পাই,
\(2AD+2CF > 3AC\) —(ii)
এবং AGB থেকে পাই,
\(2AD + 2BE > 3AB\) —(iii)
(i), (ii) ও (iii) নং সমীকরণ যোগ করে পাই,
2BE+2CF+2AD+2CF+2AD+2BE > 3BC+3AC+3AB
বা, \(4(AD+BE+CF) > 3(AB+BC+CA)\) [(i) নং প্রমাণিত]
\(\Delta ACD\) থেকে পাই,
\(AC + CD > AD\)বা, \(AC + \frac{1}{2} BC > AD\) — (iv) [\(\because\) D, BC এর মধ্যবিন্দু]
একইভাবে \(\Delta ABE\) থেকে পাই, \(AB + \frac{1}{2} AC > BE\) —(v)
এবং \(\Delta BFC\) থেকে পাই, \(BC + \frac{1}{2} AB > CF\) —(vi)
(iv), (v) এবং (vi) নং সমীকরণ যোগ করে পাই,
\(AC+ \frac{1}{2} BC + AB+ \frac{1}{2} AC + BC + \frac{1}{2} AB > AD+BE+CF\)বা, \(\frac{3}{2} AB + \frac{3}{2} BC + \frac{3}{2} AC > AD+BE+CF\)
বা, \(3(AB+BC+AC) > 2(AD+BE+CF)\) [(ii) নং প্রমাণিত]
7. ABC এর AD, BE এবং CF মধ্যমা তিনটি G বিন্দুতে পরস্পরকে ছেদ করেছে। \(\Delta ABC\)-এর ক্ষেত্রফল 36 বর্গসেমি. হলে (i) \(\Delta AGB\)-এর ক্ষেত্রফল (ii) \(\Delta CGE\)-এর ক্ষেত্রফল (iii) চতুর্ভুজ BDGF এর ক্ষেত্রফল নির্ণয় করো।

ABC ত্রিভুজের AD মধ্যমা,
\(\therefore\) কোনো ত্রিভুজের মধ্যমা ত্রিভুজটিকে সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজে বিভক্ত করে।
\(\therefore \Delta ABD = \Delta ADC\)আবার, \(\Delta BGC\) ত্রিভুজে GD মধ্যমা,
\(\therefore \Delta BGD = \Delta CGD\)\(\therefore \Delta ABD – \Delta BGD = \Delta ADC – \Delta CGD\)বা, \(\Delta ABG = \Delta AGC\) — (i)
অনুরূপভাবে দেখানো যায় যে, \(\Delta AGC = \Delta BGC\) — (ii)
এবং \(\Delta BGC = \Delta AGB\) —-(iii)
\(\therefore\) (i), (ii) এবং (iii) নং সমীকরণ থেকে পাই,
\(\Delta ABG = \Delta AGC = \Delta BGC\)\(\therefore \Delta ABG = \Delta AGC = \Delta BGC = \frac{1}{3} \Delta ABC\)\(\therefore \Delta AGB\) ত্রিভুজের ক্ষেত্রফল = \(\frac{1}{3}\) (\(\Delta ABC\) এর ক্ষেত্রফল)
(i) \(\Delta AGB\) ত্রিভুজের ক্ষেত্রফল = (\(\frac{1}{3} \times 36\)) বর্গসেমি. = 12 বর্গসেমি. [উত্তর]
(ii) AGC এর GE মধ্যমা।
\(\therefore \Delta CGE = \frac{1}{2} \Delta AGC = \frac{1}{2} (\frac{1}{3} \Delta ABC) = \frac{1}{6} \Delta ABC\)\(\therefore \Delta CGE\) এর ক্ষেত্রফল = (\(\frac{1}{6} \times 36\)) বর্গসেমি. = 6 বর্গসেমি. [উত্তর]
(iii) চতুর্ভুজ BDGF–এর ক্ষেত্রফল
= \(\Delta BGD + \Delta BGF\)
= \(\frac{1}{2} \Delta BGC + \frac{1}{2} \Delta ABG\)
= \(\frac{1}{2} (\frac{1}{3} \Delta ABC) + \frac{1}{2} (\frac{1}{3} \Delta ABC)\)
= \(\frac{1}{6} \Delta ABC + \frac{1}{6} \Delta ABC\)
= (\(\frac{1}{6} \times 36 + \frac{1}{6} \times 36\)) বর্গসেমি.
= (6+6) বর্গসেমি.
= 12 বর্গসেমি. [উত্তর]
8. ABC ত্রিভুজের AD, BE ও CF মধ্যমা। যদি \(\frac{2}{3} AD = BC\) হয়, তাহলে প্রমাণ করি যে, অপর দুটি মধ্যমা BE এবং CF-এর অন্তর্ভুক্ত কোণের পরিমাপ \(90^\circ\)।

ধরি, \(\Delta ABC\) এর AD, BE এবং CF মধ্যমাত্রয় পরস্পরকে G বিন্দুতে ছেদ করেছে এবং \(\frac{2}{3} AD = BC\)। প্রমাণ করতে হবে যে, অপর দুটি মধ্যমা BE এবং CF-এর অন্তর্ভুক্ত কোণ \(\angle BGC = 90^\circ\)।
প্রমাণ –
যেহেতু \(\Delta ABC\) এর ভরকেন্দ্র G,
\(\therefore DG = \frac{1}{3} AD\)আবার, \(BC = \frac{2}{3} AD \Rightarrow AD = \frac{3}{2} BC\)
\(\therefore DG = \frac{1}{3} \cdot \frac{3}{2} BC = \frac{1}{2} BC\)\(\therefore DG = \frac{1}{2} BC\) —(i)
আবার যেহেতু D, BC-এর মধ্যবিন্দু,
\(\therefore BD = DC = \frac{1}{2} BC\) —(ii)
(i) ও (ii) থেকে পাই,
\(\therefore DG = BD = DC\)এখন \(\Delta BGD\) এর \(BD = DG\),
\(\therefore \angle DBG = \angle DGB\)এবং \(\Delta CGD\) এর \(CD = DG\),
\(\therefore \angle DCG = \angle DGC\)যেহেতু ত্রিভুজের তিনটি কোণের সমষ্টি \(180^\circ\),
\(\therefore \Delta BGD\) থেকে পাই,
\(\angle DBG + \angle DGB + \angle BDG = 180^\circ\) —(iii)
এবং \(\Delta CGD\) থেকে পাই,
\(\angle DCG + \angle DGC + \angle CDG = 180^\circ\) —(iv)
(iii) ও (iv) নং সমীকরণ থেকে পাই,
\(\angle DBG + \angle DGB + \angle BDG + \angle DCG + \angle DGC + \angle CDG = 180^\circ + 180^\circ\)
বা, \(2\angle DGB + \angle BDG + 2\angle DGC + \angle CDG = 360^\circ\)
বা, \(2(\angle DGB + \angle DGC) + \angle BDG + \angle CDG = 360^\circ\)
\(\because\) BC বাহুর ওপর DG দণ্ডায়মান,
\(\therefore \angle BDG + \angle CDG = 180^\circ\)\(\therefore 2(\angle DGB + \angle DGC) + 180^\circ = 360^\circ\)বা, \(2\angle BGC = 180^\circ\)
বা, \(\angle BGC = 90^\circ\)
\(\therefore \angle BGC = 90^\circ\) [প্রমাণিত]
9. ABCD সামান্তরিকের BC ও CD বাহুর মধ্যবিন্দু যথাক্রমে P এবং Q; AP এবং AQ কর্ণ BD-কে যথাক্রমে K ও L বিন্দুতে ছেদ করে। প্রমাণ করি যে, BK = KL = LD।
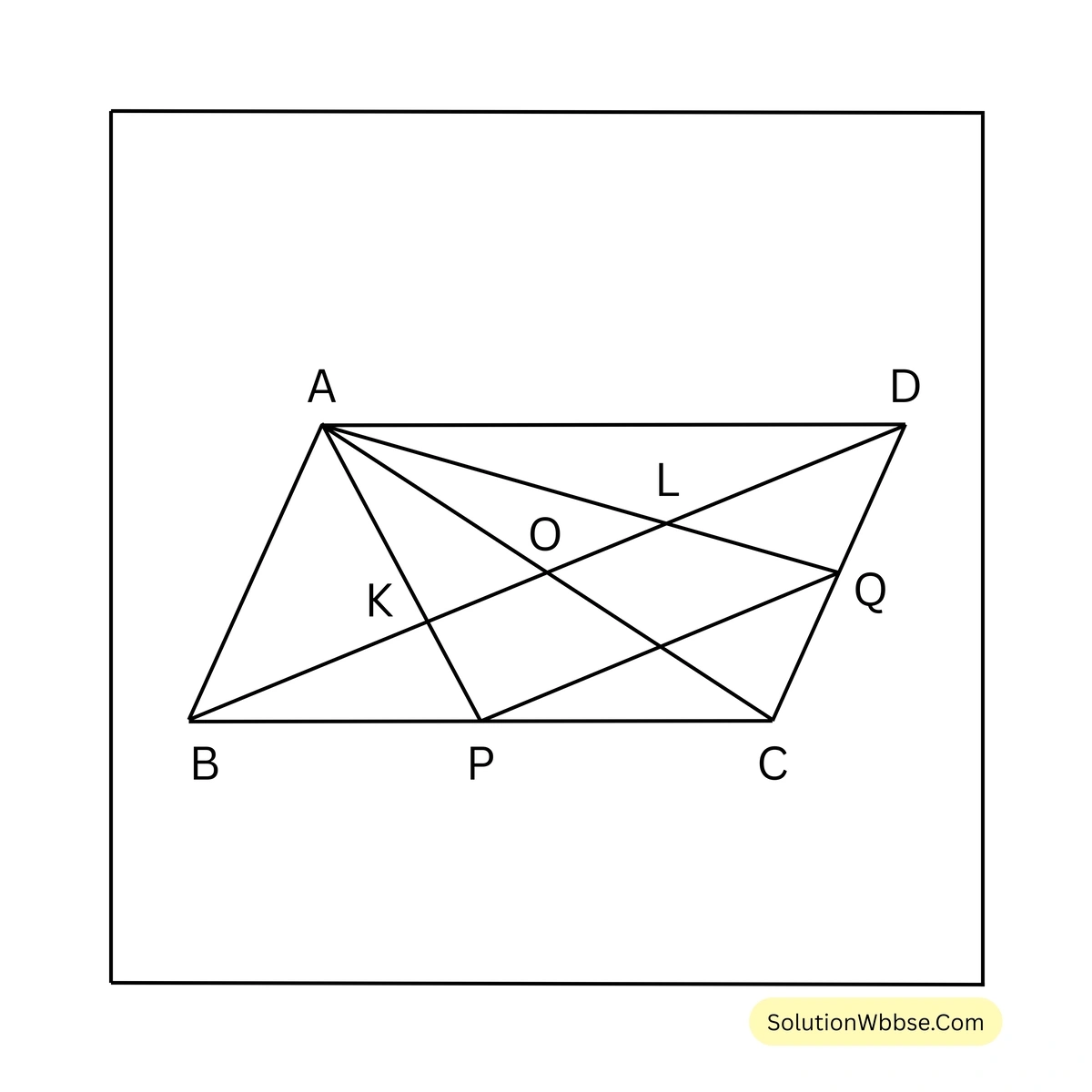
ধরি, ABCD সামান্তরিকের BC এবং CD বাহুর মধ্যবিন্দু যথাক্রমে P এবং Q; AP এবং AQ কর্ণ BD-কে যথাক্রমে K ও L বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে, BK = KL = LD।
অঙ্কন – A, C যুক্ত করলাম।
প্রমাণ –
যেহেতু সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে, \(\therefore\) O, AC-এর মধ্যবিন্দু এবং \(OB = OD\)।
এখন \(\Delta ABC\)-এর AC এবং BC বাহুর মধ্যবিন্দু যথাক্রমে O এবং P,
\(\therefore \Delta ABC\)-এর AP এবং BO মধ্যমা পরস্পরকে K বিন্দুতে ছেদ করেছে।
\(\therefore\) K, \(\Delta ABC\)-এর ভরকেন্দ্র।
\(\therefore BK = \frac{2}{3} OB\) —(i)
এবং \(KO = \frac{1}{3} OB\)
অনুরূপভাবে, L, \(\Delta ADC\)-এর ভরকেন্দ্র,
\(\therefore LD = \frac{2}{3} OD = \frac{2}{3} OB\) [\(\because\) OB = OD] —(ii)
এবং \(OL = \frac{1}{3} OD\)
এখন, \(KL = KO + OL\)
\(\Rightarrow KL = \frac{1}{3} OB + \frac{1}{3} OD\)\(\Rightarrow KL = \frac{1}{3} OB + \frac{1}{3} OB\) [\(\because\) OB = OD]
\(\therefore KL = \frac{2}{3} OB\) —-(iii)
(i), (ii) ও (iii) নং সমীকরণ থেকে পাই,
BK = KL = LD [প্রত্যেকের মান \(\frac{2}{3} OB\)]
\(\therefore\) BK = KL = LD [প্রমাণিত]
10. বহু বিকল্পীয় প্রশ্ন (M.C.Q)
(i) ABC ত্রিভুজের পরিকেন্দ্র O; \(\angle BOC = 60^\circ\) হলে, \(\angle BAC\)-এর পরিমাপ
(a) \(30^\circ\)
(b) \(45^\circ\)
(c) \(60^\circ\)
(d) \(90^\circ\)
Ans – (a) \(30^\circ\)
সমাধান –
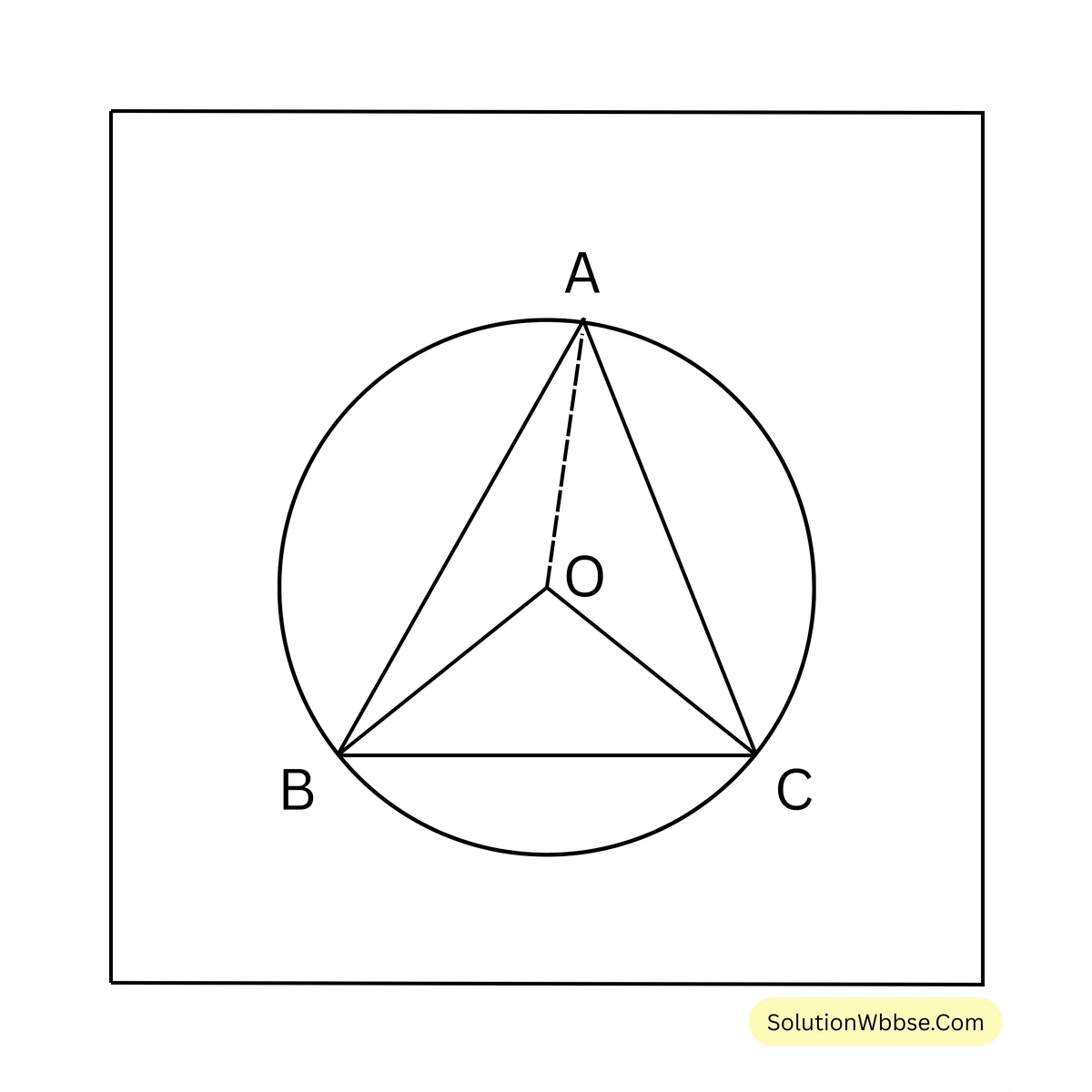
ABC ত্রিভুজের পরিকেন্দ্র O, \(\therefore OA = OB = OC\) [একই বৃত্তের ব্যাসার্ধ]।
ধরি, \(\angle BAC = x\) এবং \(\angle ABC = y\)।
এখন, ABC ত্রিভুজ থেকে পাই,
\(\angle BAC + \angle ABC + \angle ACB = 180^\circ\)বা, \(x + y + \angle ACB = 180^\circ\)
\(\because \Delta OBC\) এ \(OB = OC\), \(\therefore \angle OBC = \angle OCB = \frac{1}{2}(180^\circ – 60^\circ) = 60^\circ\)
\(\therefore \angle OBC = 60^\circ\), কিন্তু \(\angle OBC = \angle ABC = y\)
অতএব, \(y = 60^\circ\)
তাহলে, \(x + 60^\circ + \angle ACB = 180^\circ\)
এবং \(\angle ACB = \angle BOC/2 = 30^\circ\) [পরিধিস্থ কোণ কেন্দ্রস্থ কোণের অর্ধেক]
সুতরাং, \(x = 180^\circ – 60^\circ – 30^\circ = 90^\circ\)? না, আসুন ঠিকভাবে করি:
বিকল্প পদ্ধতি –
ABC ত্রিভুজের পরিকেন্দ্র O হলে, \(\angle BOC = 2\angle BAC\) [যেহেতু, একই বৃত্তচাপের ওপর কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুণ]
\(\Rightarrow \angle BAC = \frac{1}{2} \times 60^\circ = 30^\circ\)(ii) ABC ত্রিভুজের লম্ববিন্দু O; \(\angle BOC = 120^\circ\) হলে \(\angle BAC\)-এর পরিমাপ
(a) \(30^\circ\)
(b) \(60^\circ\)
(c) \(90^\circ\)
(d) \(120^\circ\)
Ans: (b) \(60^\circ\)
সমাধান –
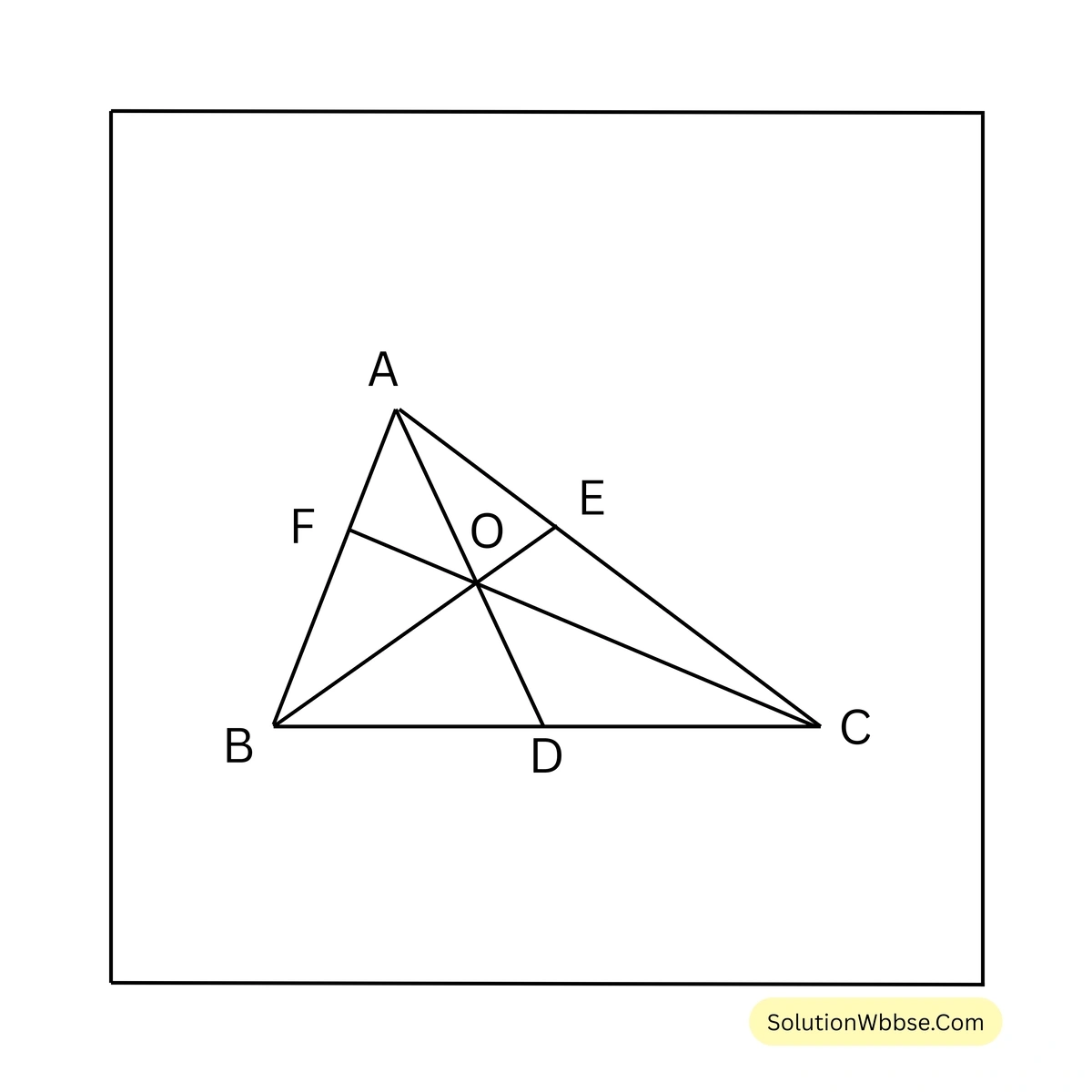
চতুর্ভুজ AFOE–এর \(\angle AFO = 90^\circ\) এবং \(\angle AEO = 90^\circ\)
\(\therefore \angle FOE = 180^\circ – \angle BAC\)\(\Rightarrow \angle BOC = 180^\circ – \angle BAC\) [যেহেতু, \(\angle FOE\) ও \(\angle BOC\) একই কোণ]
\(\Rightarrow 120^\circ = 180^\circ – \angle BAC\)\(\Rightarrow \angle BAC = 180^\circ – 120^\circ = 60^\circ\)(iii) ABC ত্রিভুজের অন্তঃকেন্দ্র O; \(\angle BOC = 120^\circ\) হলে \(\angle BAC\)-এর পরিমাপ
(a) \(30^\circ\)
(b) \(60^\circ\)
(c) \(90^\circ\)
(d) \(120^\circ\)
Ans – (b) \(60^\circ\)
সমাধান –
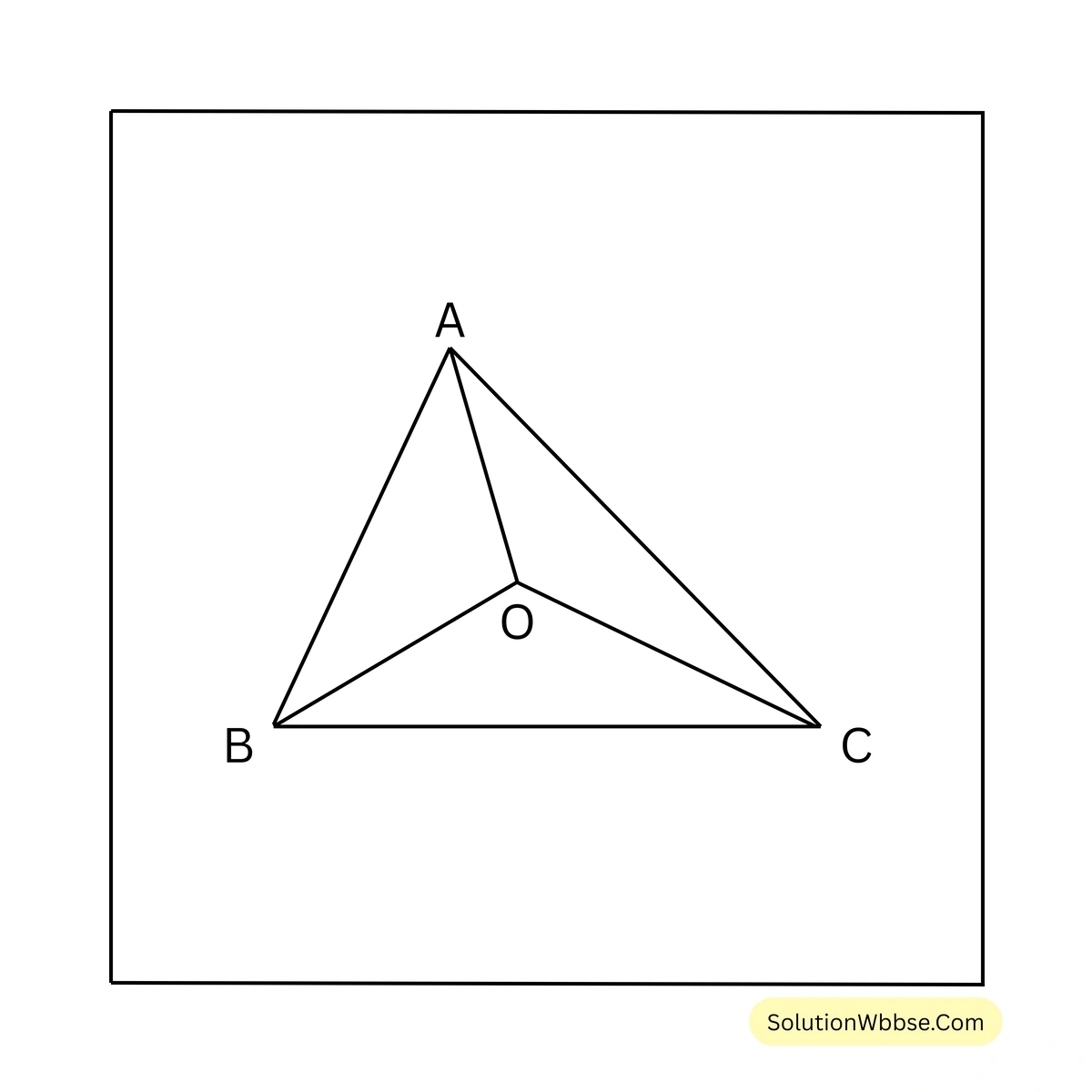
ABC ত্রিভুজের অন্তঃকেন্দ্র O।
\(BO\) এবং \(CO\) যথাক্রমে B এবং C–এর সমদ্বিখণ্ডক।
\(\Delta ABC\)–এর \(\angle BAC + \angle ABC + \angle ACB = 180^\circ\)
বা, \(\angle ABC + \angle ACB = 180^\circ – \angle BAC\)
\(\angle OBC = \frac{1}{2} \angle ABC\), \(\angle OCB = \frac{1}{2} \angle ACB\)
\(\Delta OBC\)–এর \(\angle OBC + \angle OCB + \angle BOC = 180^\circ\)
বা, \(\frac{1}{2} \angle ABC + \frac{1}{2} \angle ACB + 120^\circ = 180^\circ\)
বা, \(\frac{1}{2} (\angle ABC + \angle ACB) = 180^\circ – 120^\circ = 60^\circ\)
বা, \(\angle ABC + \angle ACB = 120^\circ\)
এখন \(\Delta ABC\) থেকে পাই, \(\angle BAC = 180^\circ – (\angle ABC + \angle ACB) = 180^\circ – 120^\circ = 60^\circ\)
(iv) ABC ত্রিভুজের ভরকেন্দ্র G; GBC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল 12 বর্গ সেমি. হলে ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(a) 24 বর্গ সেমি.
(b) 6 বর্গ সেমি.
(c) 36 বর্গ সেমি.
(d) কোনোটিই নয়।
Ans – (c) 36 বর্গ সেমি.

সমাধান –
\(\Delta GBC\)-এর ক্ষেত্রফল = \(\frac{1}{3} \Delta ABC\)-এর ক্ষেত্রফল = \(12 \times 3\) বর্গ সেমি. = \(36\) বর্গ সেমি.।
(v) ABC সমকোণী ত্রিভুজের পরিব্যাসার্ধের দৈর্ঘ্য 5 সেমি. হলে অতিভুজের দৈর্ঘ্য
(a) 25 সেমি.
(b) 10 সেমি.
(c) 5 সেমি.
(d) কোনোটিই নয়।
Ans: (b) 10 সেমি.
সমাধান –
সমকোণী ত্রিভুজের পরিব্যাসার্ধের দৈর্ঘ্য তার অতিভুজের দৈর্ঘ্যের অর্ধেক।
সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য = \(2 \times 5\) সেমি. = \(10\) সেমি.।
11. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন
(i) একটি ত্রিভুজের বাহুর দৈর্ঘ্য 6 সেমি., 8 সেমি. ও 10 সেমি. হলে ত্রিভুজটির পরিকেন্দ্র ত্রিভুজাকার ক্ষেত্রের কোথায় অবস্থিত তা লিখি।
সমাধান –
একটি ত্রিভুজের বাহুর দৈর্ঘ্য 6 সেমি., 8 সেমি. ও 10 সেমি.।
এখন, \(8^2 + 6^2 = 64 + 36 = 100 = (10)^2\)
\(\therefore\) ত্রিভুজটি একটি সমকোণী ত্রিভুজ। আমরা জানি সমকোণী ত্রিভুজের ক্ষেত্রে ত্রিভুজের পরিকেন্দ্র ত্রিভুজটির অতিভুজের মধ্যবিন্দুতে অবস্থিত।
\(\therefore\) ত্রিভুজটির পরিকেন্দ্র ত্রিভুজাকার ক্ষেত্রের 10 সেমি. বাহুর মধ্যবিন্দুতে অবস্থিত।
(ii) ABC সমবাহু ত্রিভুজের AD মধ্যমা এবং G ভরকেন্দ্র। ত্রিভুজটির বাহুর দৈর্ঘ্য \(3\sqrt{3}\) সেমি. হলে AG-এর দৈর্ঘ্য কত তা লিখি।
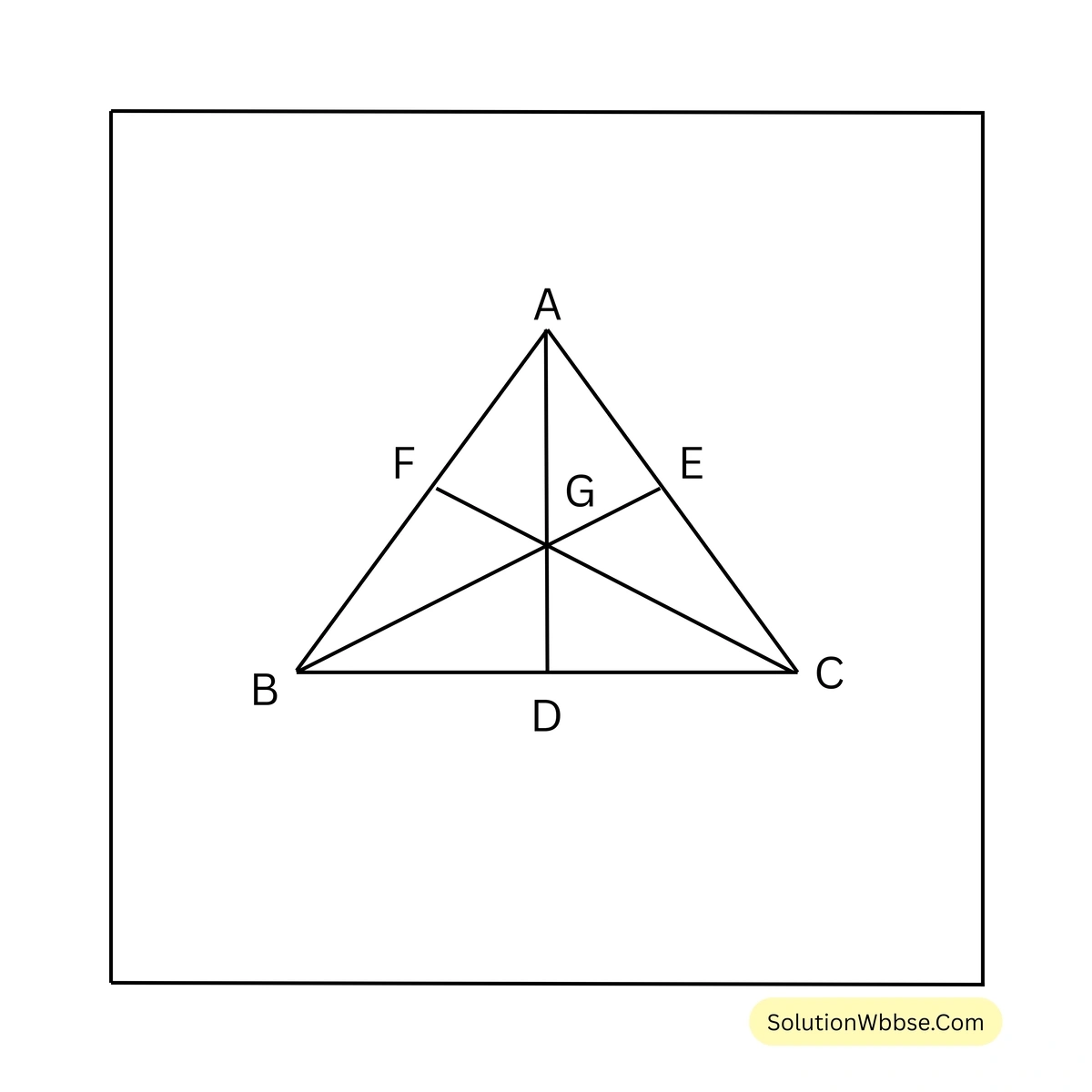
সমাধান –
সমবাহু ত্রিভুজের মধ্যমার দৈর্ঘ্য তার উচ্চতার সমান হয়।
\(\therefore\) সমবাহু ত্রিভুজটির উচ্চতা = \( \frac{\sqrt{3}}{2} \times\) বাহুর দৈর্ঘ্য = \( \frac{\sqrt{3}}{2} \times 3\sqrt{3}\) সেমি. = \( \frac{9}{2}\) সেমি. = \( 4.5\) সেমি.।
\(\because\) ত্রিভুজের ভরকেন্দ্র ত্রিভুজের মধ্যমাকে 2:1 অনুপাতে ভাগ করে।
সুতরাং \(AG = \frac{2}{3} AD = \frac{2}{3} \times 4.5\) সেমি. = \( 3\) সেমি.।
\(\therefore\) AG-এর দৈর্ঘ্য 3 সেমি.।
(iii) একটি ত্রিভুজের কয়টি বিন্দু ত্রিভুজের বাহুগুলি থেকে সমদূরবর্তী তা লিখি।
সমাধান – একটি অন্তঃকেন্দ্র (অন্তর্বৃত্তের কেন্দ্র) এবং তিনটি বহিঃকেন্দ্র (বহির্বৃত্তের কেন্দ্র) ত্রিভুজের বাহুগুলি থেকে সমদূরবর্তী।
\(\therefore\) একটি ত্রিভুজের চারটি বিন্দু ত্রিভুজের বাহুগুলি থেকে সমদূরবর্তী।
(iv) ABC সমবাহু ত্রিভুজের পাদ ত্রিভুজ \(\Delta DEF\); \(\angle FDA\)-এর পরিমাপ কত তা লিখি।
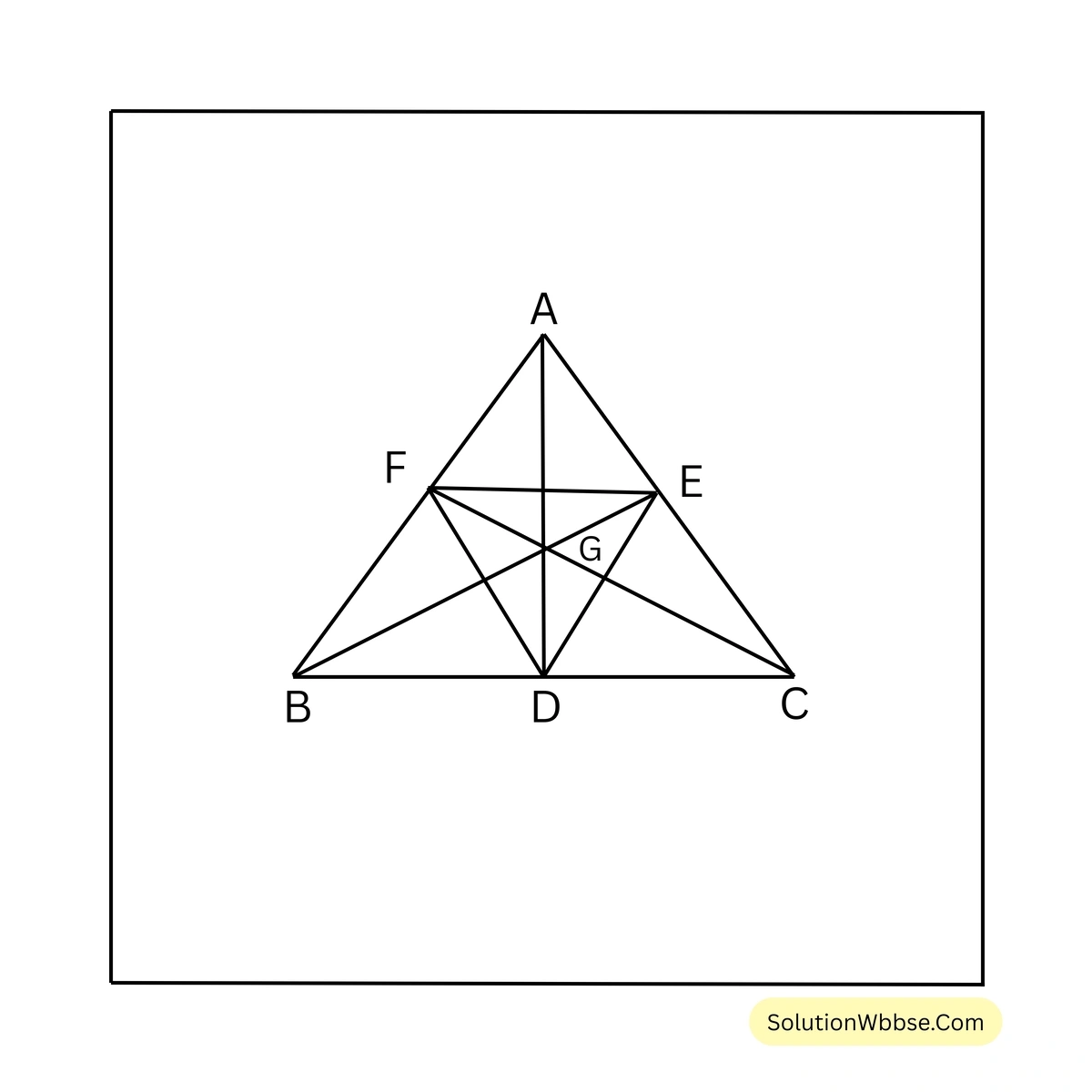
সমাধান –
সমবাহু ত্রিভুজের পাদ ত্রিভুজও সমবাহু ত্রিভুজ হবে।
\(\therefore\) DEF একটি সমবাহু ত্রিভুজ, সুতরাং এর প্রতিটি কোণ \(60^{\circ}\)।
যেহেতু AB এবং AC-এর মধ্যবিন্দু যথাক্রমে F এবং E,
\(\therefore FE = \frac{1}{2} BC = \frac{1}{2} AC = \frac{1}{2} AB\) \(\because AB=BC=CA\)
\(\therefore\) AEF একটি সমবাহু ত্রিভুজ, সুতরাং এর প্রতিটি কোণ \(60^{\circ}\)।
\(\Delta ADF\)-এর \(FD = AF\),
\(\therefore \angle FDA = \angle FAD\)।
\(\therefore \angle FDA + \angle FAD + \angle AFD = 180^{\circ}\)বা, \(\angle FDA + \angle FDA + [ \angle AFE + \angle DFE ] = 180^{\circ}\)
বা, \(2\angle FDA + [60^{\circ}+60^{\circ}] = 180^{\circ}\)
বা, \(2\angle FDA = 180^{\circ}-120^{\circ}\)
বা, \(2\angle FDA = 60^{\circ}\)
বা, \(\angle FDA = 30^{\circ}\)
\(\therefore \angle FDA = 30^{\circ}\)(v) ABC সমদ্বিবাহু ত্রিভুজের \(\angle ABC = \angle ACB\) এবং মধ্যমা \(AD = \frac{1}{2} BC\)। যদি \(AB = \sqrt{2}\) সেমি. হয়, তাহলে ত্রিভুজটির পরিব্যাসার্ধের দৈর্ঘ্য কত তা লিখি।
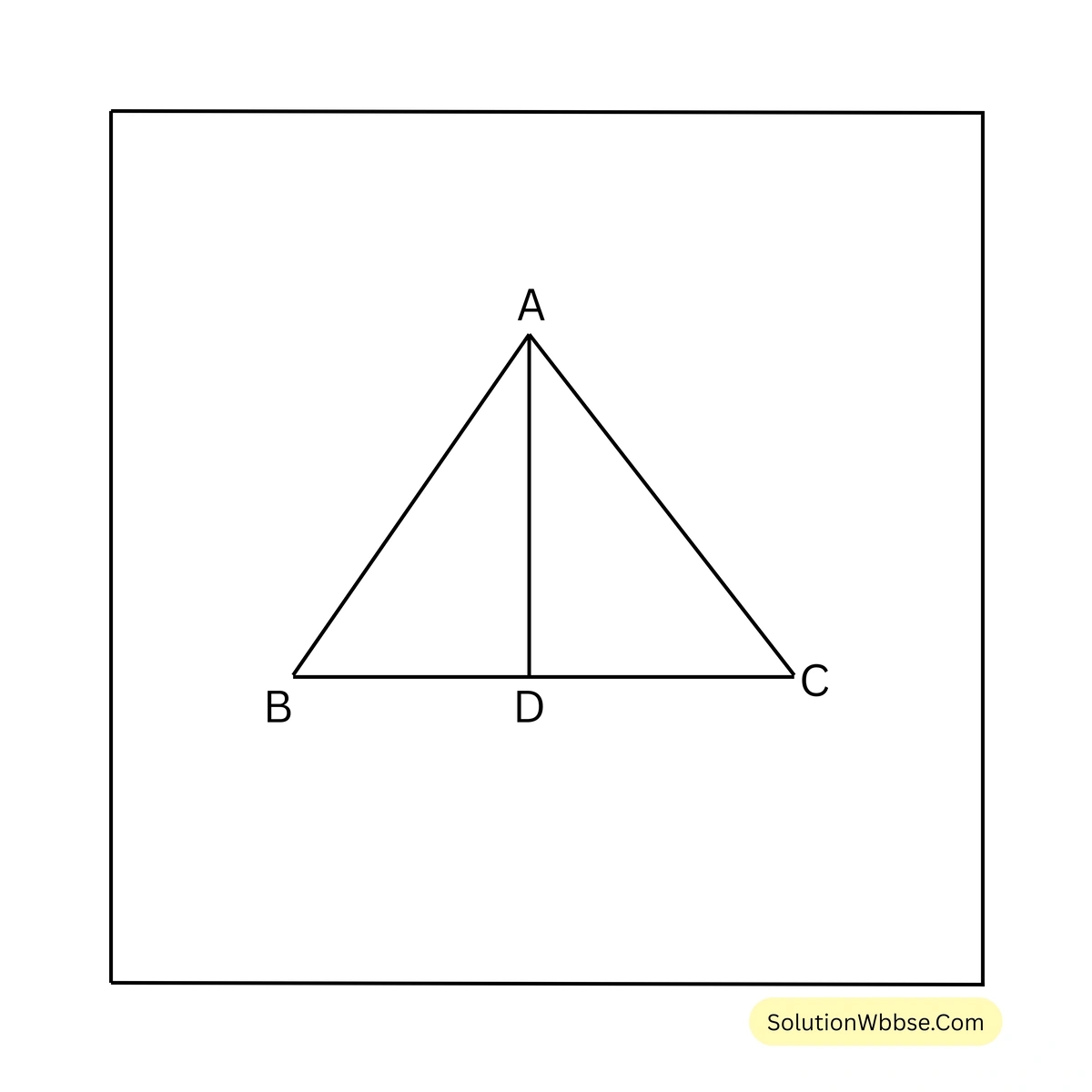
সমাধান –
ABC সমদ্বিবাহু ত্রিভুজের D, BC বাহুর মধ্যবিন্দু এবং \(AD = \frac{1}{2} BC\),
\(\therefore \angle BAC = 90^{\circ}\), সুতরাং, ABC একটি সমকোণী ত্রিভুজ।
আবার, ABC সমদ্বিবাহু ত্রিভুজের \(\angle ABC = \angle ACB\),
\(\therefore AB = AC = \sqrt{2}\) সেমি.।
ABC সমকোণী সমদ্বিবাহু ত্রিভুজের \(AB^2 + AC^2 = BC^2\),
\(\therefore BC = \sqrt{(\sqrt{2})^2 + (\sqrt{2})^2}\) সেমি. = \( \sqrt{4}\) সেমি. = \( 2\) সেমি.।
আমরা জানি, সমকোণী ত্রিভুজের পরিব্যাসার্ধের দৈর্ঘ্য অতিভুজের অর্ধেক,
\(\therefore\) ত্রিভুজটির পরিব্যাসার্ধের দৈর্ঘ্য \(\frac{2}{2}\) সেমি. = \( 1\) সেমি.।
এই আর্টিকেলে নবম শ্রেণির গণিতের ‘সমবিন্দু সংক্রান্ত উপপাদ্য‘ অধ্যায়ের ‘কষে দেখি – 17’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।
কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন