পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) নবম শ্রেণির গণিত পাঠ্যবইয়ের ষষ্ঠ অধ্যায় হলো ‘সামান্তরিকের ধর্ম’। এই পোস্টে ‘কষে দেখি – 6‘-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. প্রমাণ করো যে, একটি সামান্তরিকের কর্ণদ্বয় সমান হলে সামান্তরিকটি একটি আয়তকার চিত্র।
মনে কর, \(ABCD\) সামান্তরিকের \(AC\) ও \(BD\) কর্ণদ্বয় সমান। প্রমাণ করতে হবে যে, \(ABCD\) একটি আয়তক্ষেত্র।
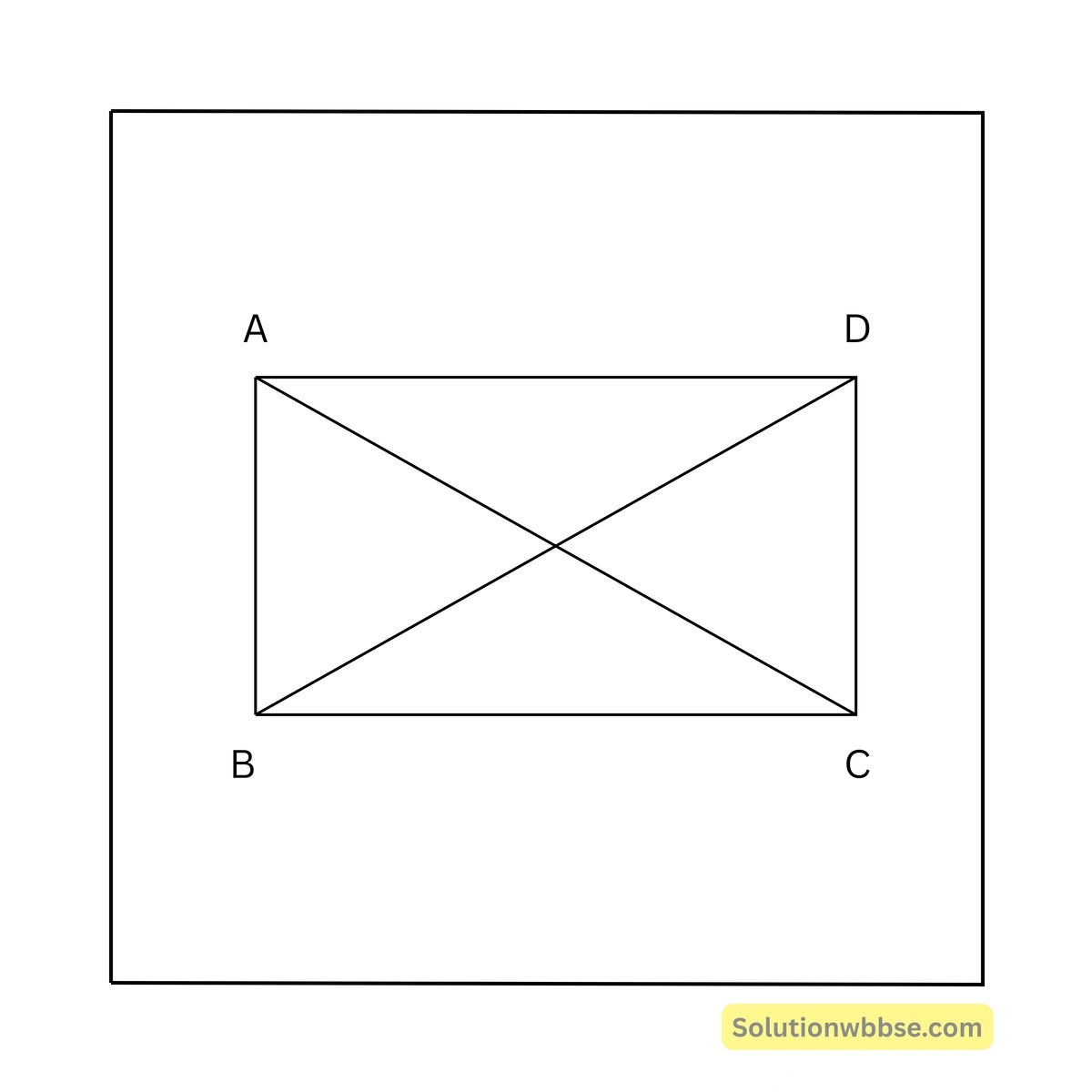
প্রমাণ –
\(\triangle ABC\) এবং \(\triangle BCD\)-এর মধ্যে,
\(AB = CD\), \(AC = BD\) এবং \(BC\) সাধারণ বাহু।
এখন \(AB \parallel CD\) এবং \(BC\) ছেদক।
অতএব, \(\angle ABC + \angle BCD = 180^{\circ}\);
\(\therefore \angle ABC = 90^{\circ}\)।
\(\therefore ABCD\) একটি আয়তক্ষেত্র।
2. প্রমাণ করি যে, একটি সামান্তরিকের কর্ণদ্বয়ের দৈর্ঘ্য সমান হলে এবং কর্ণদ্বয় পরস্পরকে লম্বভাবে ছেদ করলে, সামান্তরিকটি একটি বর্গাকার চিত্র।
মনে কর, \(ABCD\) চতুর্ভুজের \(AC\) ও \(BD\) কর্ণদ্বয় সমান এবং তারা পরস্পরকে লম্বভাবে \(O\) বিন্দুতে সমদ্বিখণ্ডিত করেছে।
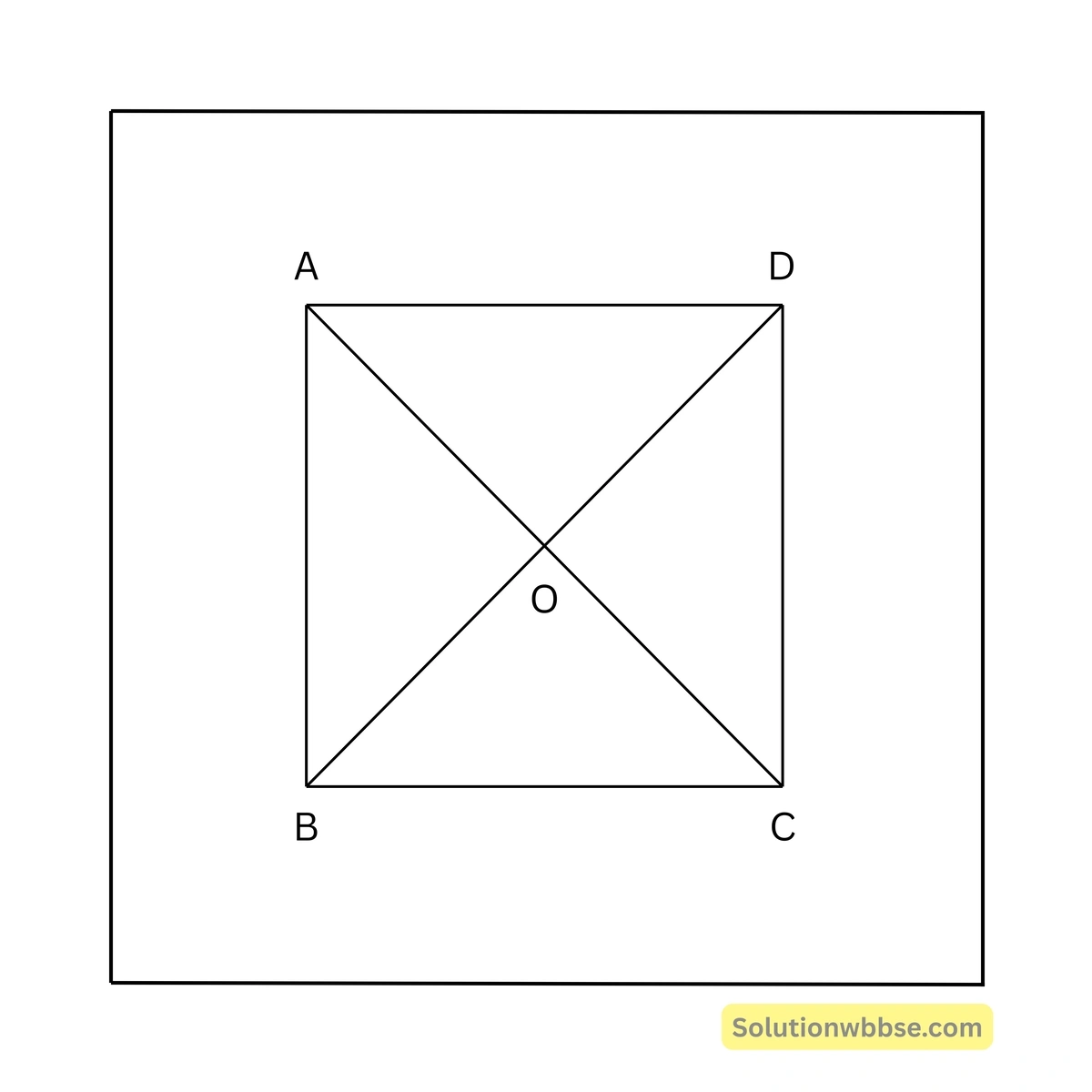
প্রমাণ করতে হবে যে, \(ABCD\) একটি বর্গক্ষেত্র।
প্রমাণ –
\(AO = OC; BO = OD\) \(\therefore ABCD\) একটি সামান্তরিক।
এখন, \(\triangle ADC\) ও \(\triangle BDC\)-এর মধ্যে, \(AD = BC\), \(AC = BD\) এবং \(CD\) সাধারণ বাহু।
\(\therefore \triangle ADC \cong \triangle BDC\)\(\therefore \angle ADC = \angle BCD\)কিন্তু, \(\angle ADC + \angle BCD = 2\) সমকোণ।
\(\therefore \angle ADC + \angle ADC = 2\) সমকোণ,
\(\therefore 2\angle ADC = 2\) সমকোণ।
\(\therefore \angle ADC = 1\) সমকোণ।
\(\therefore ABCD\) একটি আয়তক্ষেত্র।
আবার, \(\triangle AOD\) এবং \(\triangle AOB\)-এর মধ্যে, \(DO = BO\), \(\angle AOD = \angle AOB\) এবং \(AO\) সাধারণ বাহু। সুতরাং, ত্রিভুজদ্বয় সর্বসম,
\(\therefore AD = AB\)\(\therefore ABCD\) একটি বর্গক্ষেত্র।
3. প্রমাণ করি যে, একটি সামান্তরিকের কর্ণদ্বয় পরস্পরকে লম্বভাবে ছেদ করলে, সামান্তরিকটি একটি রম্বস।
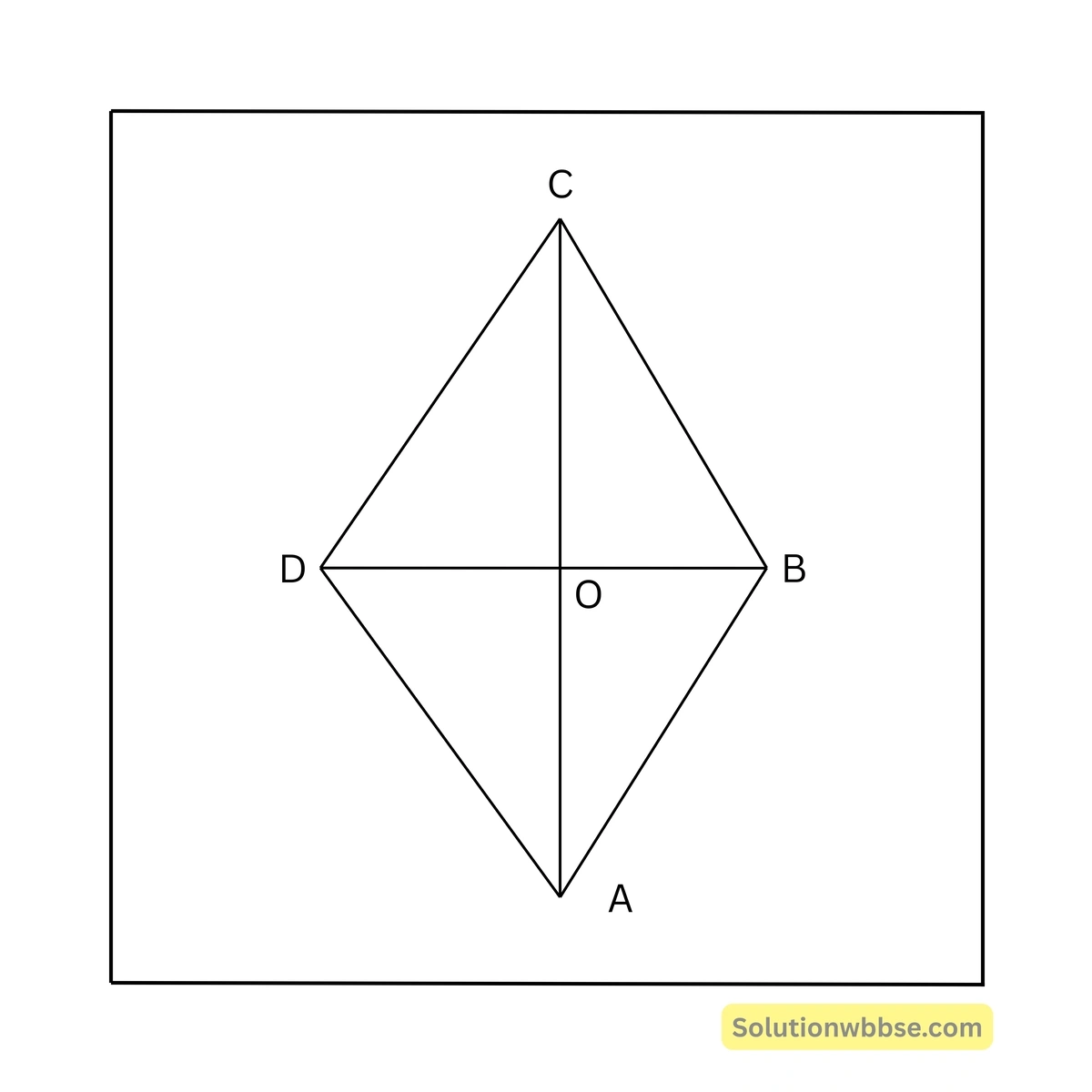
ধরা যাক, \(ABCD\) একটি সামান্তরিক যার \(AC\) ও \(BD\) কর্ণদ্বয় পরস্পরকে \(O\) বিন্দুতে লম্বভাবে ছেদ করেছে।
\(\therefore \angle AOB = \angle BOC = \angle COD = \angle DOA = 90^\circ\)প্রমাণ করতে হবে যে, \(ABCD\) একটি রম্বস।
প্রমাণ –
\(\triangle AOB\) ও \(\triangle BOC\)-এর মধ্যে,
\(OB\) সাধারণ বাহু।
\(\angle AOB = \angle BOC\) [প্রত্যেকে \(1\) সমকোণ]
এবং \(OA = OC\) [যেহেতু সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে]
\(\therefore \triangle BOC \cong \triangle BOA\)\(\therefore BC = AB\)অনুরূপে প্রমাণ করা যায়, \(BC = AD\) এবং \(AD = CD\)
\(\therefore AB = BC = CD = DA\)\(\therefore ABCD\) সামান্তরিকের \(AB = BC = CD = DA\)
\(\therefore ABCD\) একটি রম্বস।
4. \(ABCD\) সামান্তরিকের \(AC\) ও \(BD\) কর্ণদ্বয় পরস্পরকে \(O\) বিন্দুতে ছেদ করেছে। \(O\) বিন্দুগামী যেকোনো সরলরেখা \(AB\) ও \(DC\) বাহুকে যথাক্রমে \(P\) ও \(Q\) বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে \(OP = OQ\)।
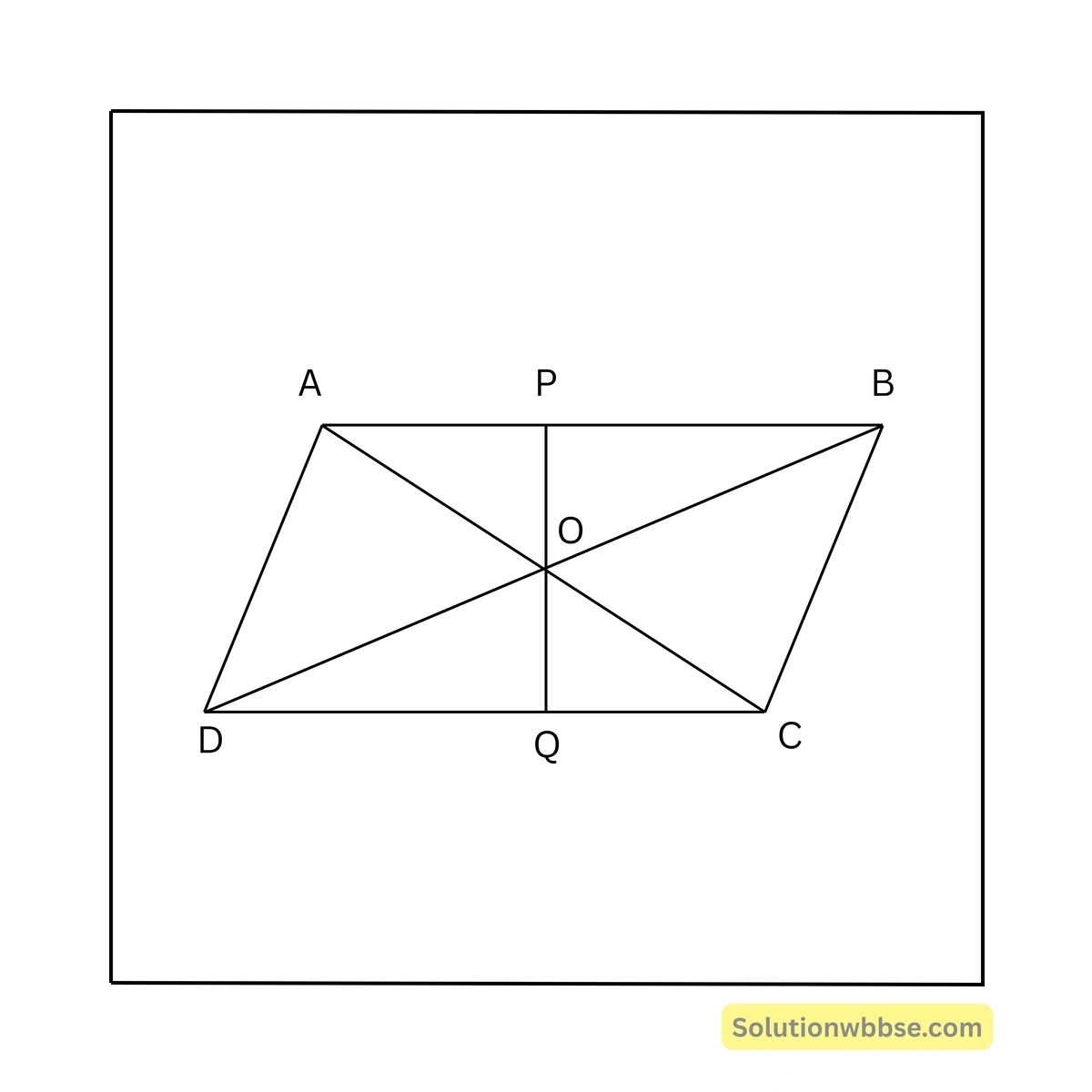
\(ABCD\) সামান্তরিকের \(AC\) ও \(BD\) কর্ণদ্বয় পরস্পরকে \(O\) বিন্দুতে ছেদ করেছে। \(O\) বিন্দুগামী একটি সরলরেখা \(AB\) ও \(DC\) বাহুকে যথাক্রমে \(P\) ও \(Q\) বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে, \(OP = OQ\)।
প্রমাণ –
\(\Delta AOP\) ও \(\Delta COQ\)-এর মধ্যে,
\(\angle AOP = \angle COQ\) [বিপ্রতীপ কোণ]
\(OA = OC\) [যেহেতু সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে]
\(\angle OAP = \angle OCQ\) [একান্তর কোণ, যেহেতু, \(AB \parallel DC\) এবং \(AC\) ভেদক]
\(\therefore \Delta AOP \cong \Delta COQ\) [কোণ-বাহু-কোণ শর্তানুসারে]
\(\therefore OP = OQ\) [প্রমাণিত]।
5. প্রমাণ করি যে একটি সমদ্বিবাহু ট্রাপিজিয়ামের যেকোনো সমান্তরাল বাহু সংলগ্ন দুটি কোণ পরস্পর সমান।
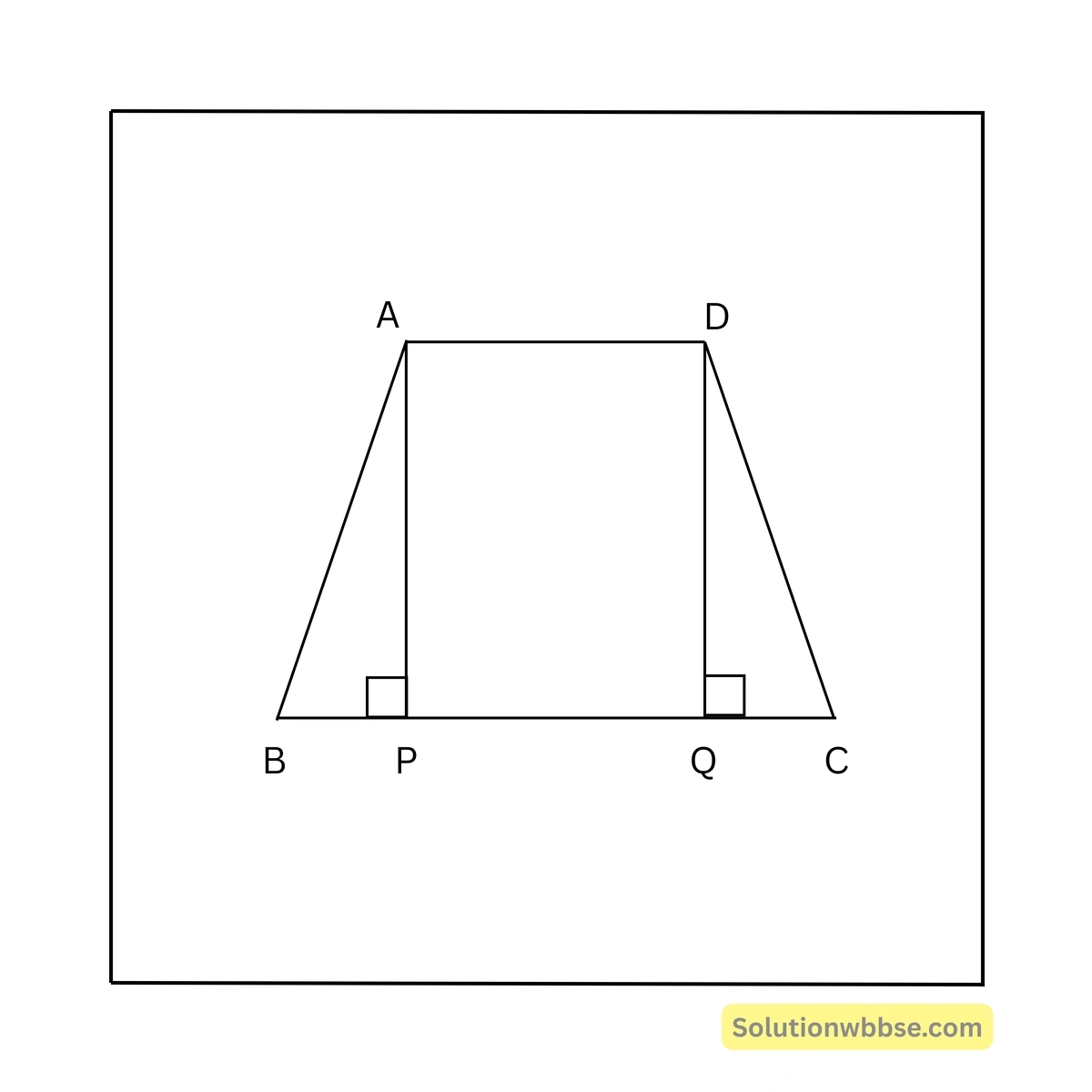
ধরা যাক, \(ABCD\) একটি সমদ্বিবাহু ট্রাপিজিয়াম যার \(AD \parallel BC\), প্রমাণ করতে হবে যে, \(\angle ABC = \angle DCB\)।
অঙ্কন –
\(A\) ও \(D\) বিন্দু থেকে \(BC\)–এর ওপর যথাক্রমে \(AP\) ও \(DQ\) লম্ব অঙ্কন করা হল।
প্রমাণ –
\(\triangle APB\) ও \(\triangle CQD\)–এর মধ্যে,
\(\angle APB = \angle DQC\) [প্রত্যেকে \(90^{\circ}\)]
\(AP = DQ\) [যেহেতু, \(AD \parallel BC\) এবং \(AP\) ও \(DQ\) উভয়েই \(BC\)-এর উপর লম্ব]
\(AB = DC\) [কল্পনানুসারে]
\(\therefore \triangle APB \cong \triangle CQD\) [R-H-S শর্তানুসারে]
\(\therefore \angle ABP = \angle DCQ\)\(\therefore \angle ABC = \angle DCB\) [প্রমাণিত]।
6. \(ABCD\) বর্গাকার চিত্রের \(BC\) বাহুর উপর \(P\) যেকোনো একটি বিন্দু। \(B\) বিন্দু থেকে \(AP\)–এর উপর অঙ্কিত লম্ব \(DC\) বাহুকে \(Q\) বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, \(AP = BQ\)।
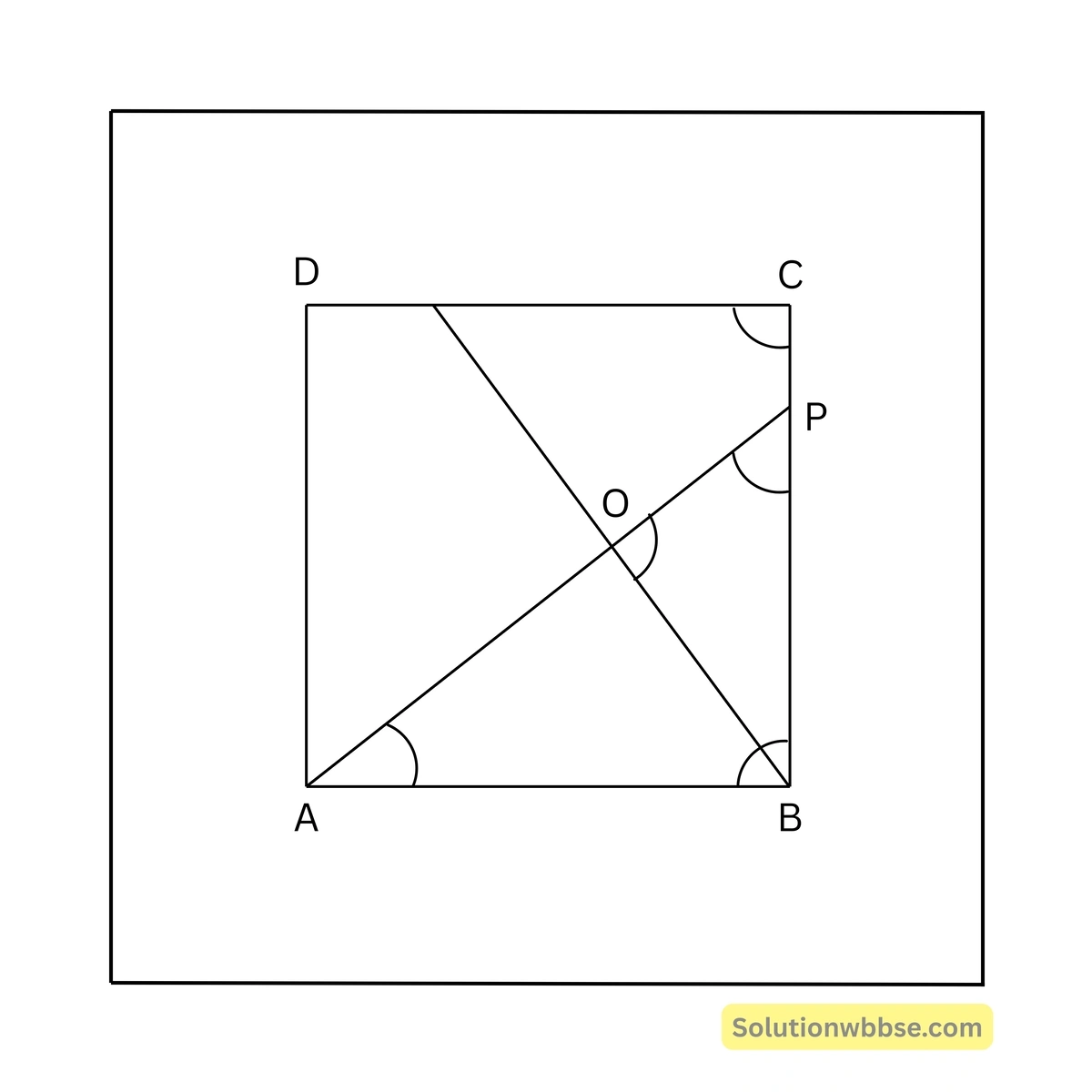
মনে কর, \(ABCD\) বর্গক্ষেত্রের \(BC\) বাহুর উপর \(P\) একটি যেকোনো বিন্দু। \(B\) বিন্দু থেকে \(AP\)–এর উপর অঙ্কিত লম্ব \(DC\)–কে \(Q\) এবং \(AP\)–কে \(O\) বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে, \(AP = BQ\)।
প্রমাণ –
\(\triangle ABP\) এবং \(\triangle BOP\)-এর মধ্যে,
\(\angle ABP = \angle BOP\) (প্রত্যেকে সমকোণ)
\(\angle APB = \angle OPB\) (সাধারণ কোণ)
\(\therefore\) অবশিষ্ট \(\angle BAP\) = অবশিষ্ট \(\angle OBP\)
\(\therefore \angle BAP = \angle CBQ\)এখন, \(\triangle ABP\) এবং \(\triangle CBQ\)-এর মধ্যে,
\(\angle ABP = \angle QCB\) (প্রত্যেকে সমকোণ),
\(\angle BAP = \angle CBQ\)এবং \(AB = BC\)।
\(\therefore \triangle ABP \cong \triangle CBQ\)\(\therefore AP = BQ\) (প্রমাণিত)।
7. প্রমাণ করি যে, একটি চতুর্ভুজের দুটি বিপরীত কোণ পরস্পর সমান ও দুটি বিপরীত বাহু পরস্পর সমান্তরাল হলে, চতুর্ভুজটি একটি সামান্তরিক।
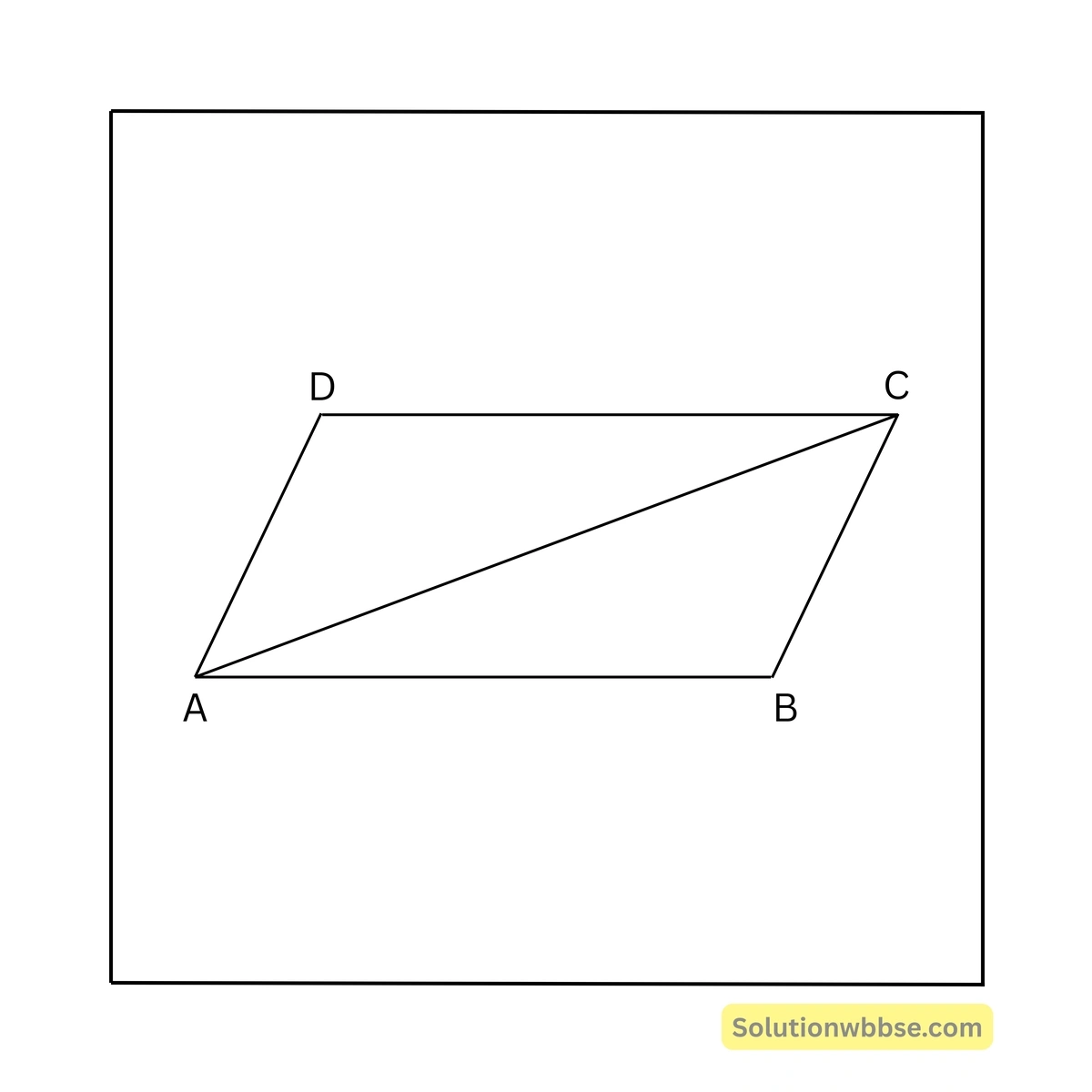
মনে কর, \(ABCD\) একটি চতুর্ভুজ, যার \(\angle ABC = \angle ADC\) এবং \(AB \parallel DC\)।
প্রমাণ করতে হবে, \(ABCD\) একটি সামান্তরিক।
অঙ্কন – \(AC\) অঙ্কন করা হল।
প্রমাণ –
\(\triangle ABC\) এবং \(\triangle ADC\)-এর মধ্যে,
\(\angle ABC = \angle ADC\), \(\angle BAC =\) একান্তর \(\angle ACD\)
(\(\because AB \parallel DC\))
\(\therefore\) অবশিষ্ট \(\angle ACB =\) অবশিষ্ট \(\angle CAD\); কিন্তু এরা একান্তর কোণ।
\(\therefore BC \parallel AD \quad \therefore ABCD\) একটি সামান্তরিক।
8. \(\triangle ABC\)-এর \(BP\) ও \(CQ\) মধ্যমা দুটি যথাক্রমে \(R\) ও \(S\) বিন্দু পর্যন্ত এমনভাবে বর্ধিত করা হল যে, \(BP = PR\) এবং \(CQ = QS\) হয়। প্রমাণ করি যে, \(S, A, R\) বিন্দু তিনটি সমরেখ।
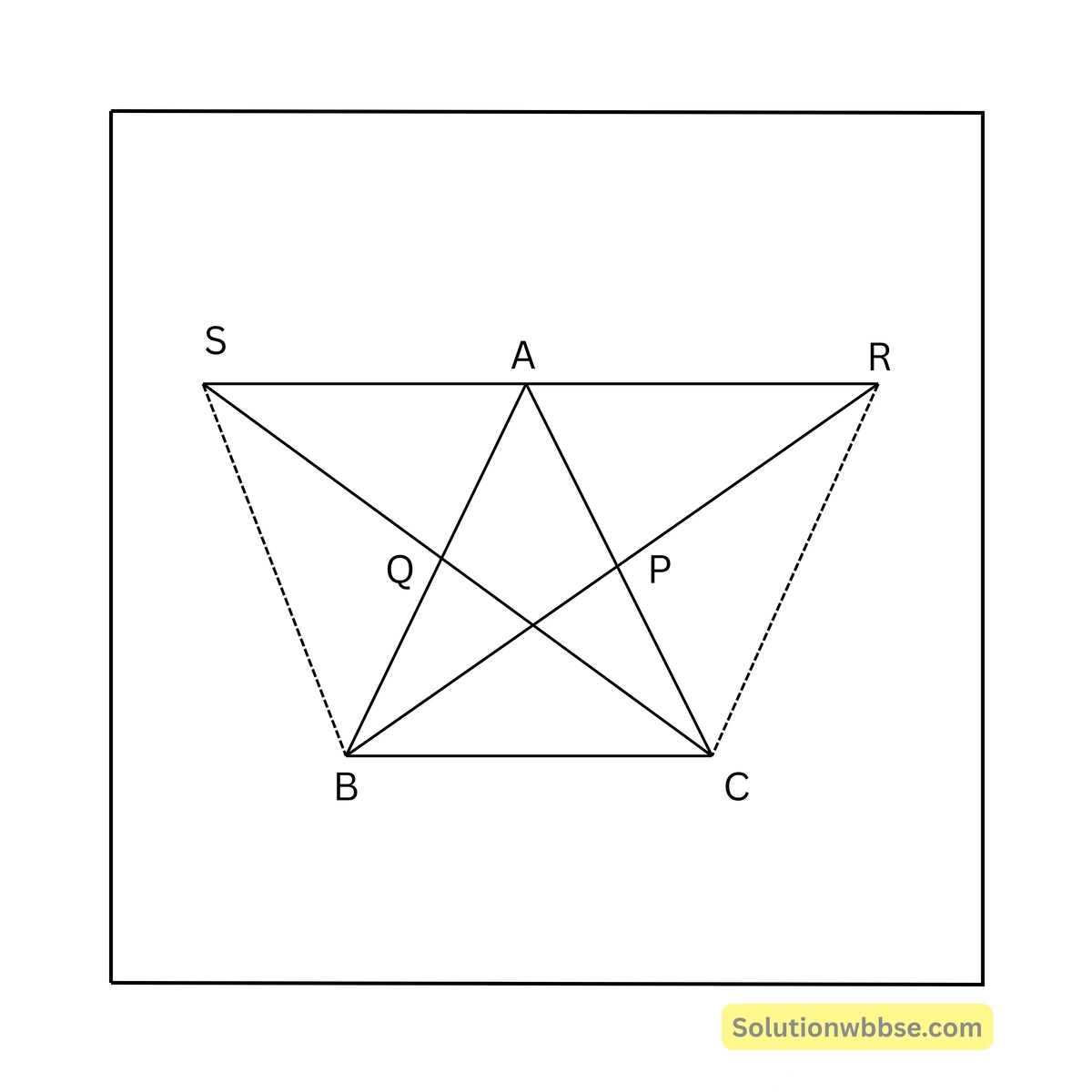
\(\triangle ABC\)-এর \(BP\) ও \(CQ\) মধ্যমা দুটি যথাক্রমে \(R\) ও \(S\) বিন্দু পর্যন্ত এমনভাবে বর্ধিত করা হল যে, \(BP = PR\) এবং \(CQ = QS\) হয়। প্রমাণ করতে হবে যে, \(S, A, R\) বিন্দু তিনটি সমরেখ।
অঙ্কন –
\(B, S\); \(C, R\) যুক্ত করা হল।
প্রমাণ –
\(\triangle ABC\) ত্রিভুজের \(BP\) মধ্যমা।
\(\therefore AP = PC\)আবার, \(BP = PR\) [প্রদত্ত]
\(\therefore ABCR\) চতুর্ভুজের \(AC\) ও \(BR\) কর্ণদ্বয় পরস্পরকে \(P\) বিন্দুতে সমদ্বিখণ্ডিত করে।
\(\therefore ABCR\) একটি সামান্তরিক।
\(\therefore AR \parallel BC\) [যেহেতু সামান্তরিকের বিপরীত বাহুগুলি পরস্পর সমান্তরাল]
\(\therefore \angle RAC = \angle ACB\) [একান্তর কোণ]
\(\triangle ABC\) ত্রিভুজের \(CQ\) মধ্যমা।
\(\therefore AB\) বাহুর মধ্যবিন্দু \(Q\)
আবার, \(CQ = QS\)
\(\therefore ACBS\) চতুর্ভুজের \(AB\) ও \(CS\) কর্ণদ্বয় \(Q\) বিন্দুতে পরস্পরকে সমদ্বিখণ্ডিত করে।
\(\therefore ACBS\) একটি সামান্তরিক।
\(\therefore SA \parallel BC\) [যেহেতু সামান্তরিকের বিপরীত বাহুগুলি পরস্পর সমান্তরাল]
\(\therefore \angle SAB = \angle ABC\) [একান্তর কোণ]
\(\triangle ABC\)-এর
\(\angle ABC + \angle ACB = 180^\circ – \angle BAC\)বা, \(\angle SAB + \angle RAC = 180^\circ – \angle BAC\)
বা, \(\angle SAB + \angle RAC + \angle BAC = 180^\circ\)
বা, \(\angle SAR = 180^\circ\)
\(\therefore S, A, R\) বিন্দু তিনটি সমরেখ।
9. PQRS সামান্তরিকের SQ কর্ণ K ও L বিন্দুতে সমান তিনভাগে বিভক্ত হয়েছে। PK, SR-কে M বিন্দুতে এবং RL, PQ-কে N বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, PMRN একটি সামান্তরিক।
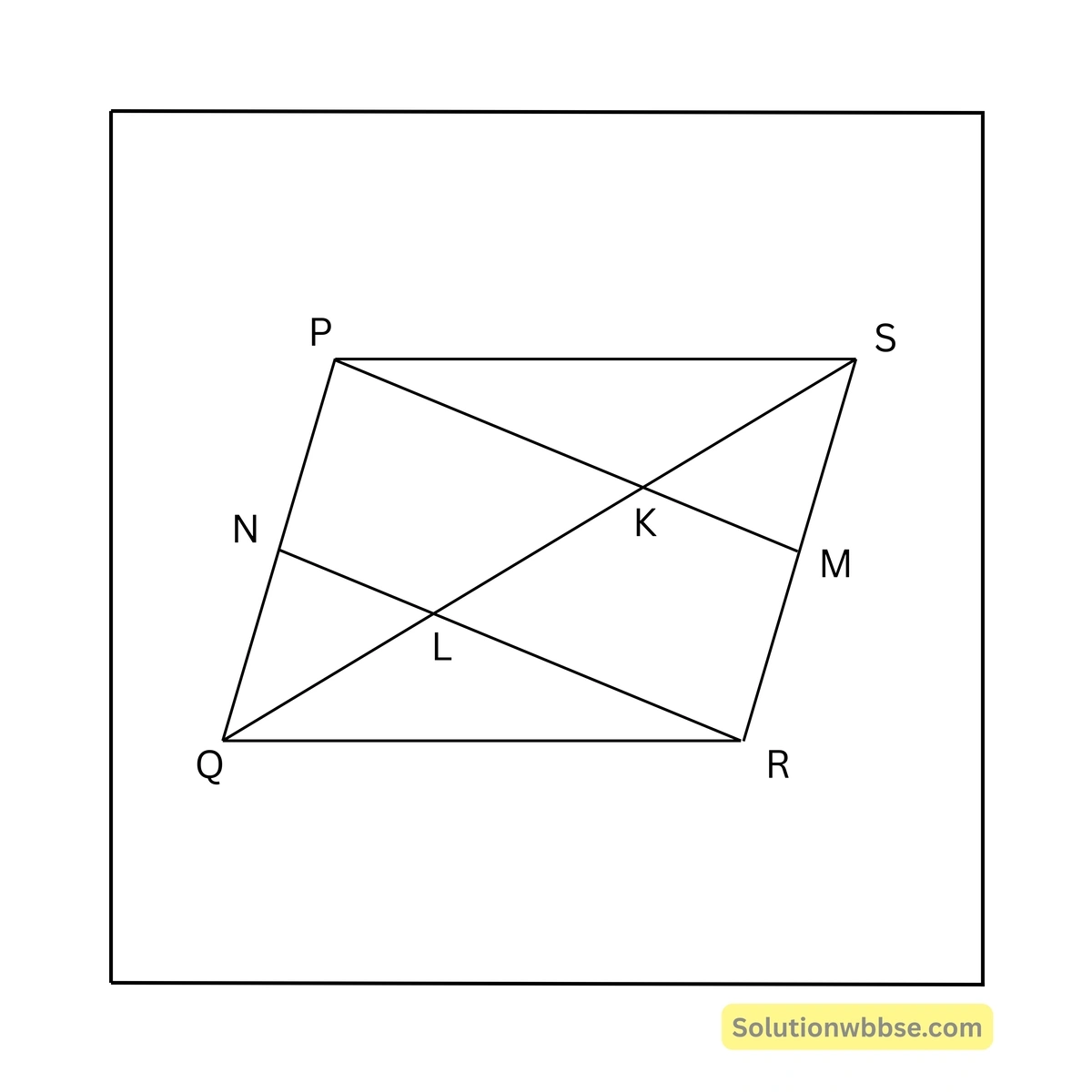
ধরা যাক, PQRS একটি সামান্তরিক। PQRS সামান্তরিকের SQ কর্ণ K ও L বিন্দুতে সমান তিনভাগে বিভক্ত হয়েছে।
\(\therefore SK = KL = LQ\)আবার, PK, SR-কে M বিন্দুতে এবং RL, PQ-কে N বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে, PMRN একটি সামান্তরিক।
প্রমাণ –
\(\triangle PKS\) এবং \(\triangle QLR\)-এর ক্ষেত্রে,
\(PS = QR\) [সামান্তরিকের বিপরীত বাহু]
\(SK = QL\) [প্রদত্ত]
\(\angle LQR = \angle KSP\) [একান্তর কোণ, কারণ \(PS \parallel QR\) এবং \(QS\) ভেদক]
\(\therefore \triangle PKS \cong \triangle QLR\)\(\therefore \angle SPK = \angle LRQ\) [সর্বসম ত্রিভুজের অনুরূপ কোণ]
আবার, \(\triangle SPM\) এবং \(\triangle QRN\)-এর ক্ষেত্রে,
\(SP = QR\) [সামান্তরিকের বিপরীত বাহু]
\(\angle SPM = \angle QRN\) [পূর্বে প্রমাণিত]
\(\angle NQR = \angle MSP\) [সামান্তরিকের বিপরীত কোণ]
\(\therefore \triangle RNQ \cong \triangle SPM\)\(\therefore QN = SM\) [সর্বসম ত্রিভুজের অনুরূপ বাহু]
আবার, \(PQ = SR\) [সামান্তরিকের বিপরীত বাহু]
\(\therefore PQ – QN = SR – SM\)\(\therefore PN = MR\)আবার, \(PN \parallel MR\) [যেহেতু, \(PQ \parallel SR\)]
\(\therefore PNRM\) চতুর্ভুজের একজোড়া বিপরীত বাহু (\(PN\) এবং \(RM\)) পরস্পর সমান ও সমান্তরাল।
সুতরাং, PNRM চতুর্ভুজটি একটি সামান্তরিক। [প্রমাণিত]
10. ABCD ও AECF দুটি সামান্তরিকেরই AC একটি কর্ণ। B, E, D এবং F সমরেখ না হলে, প্রমাণ করি যে, BEDF একটি সামান্তরিক।
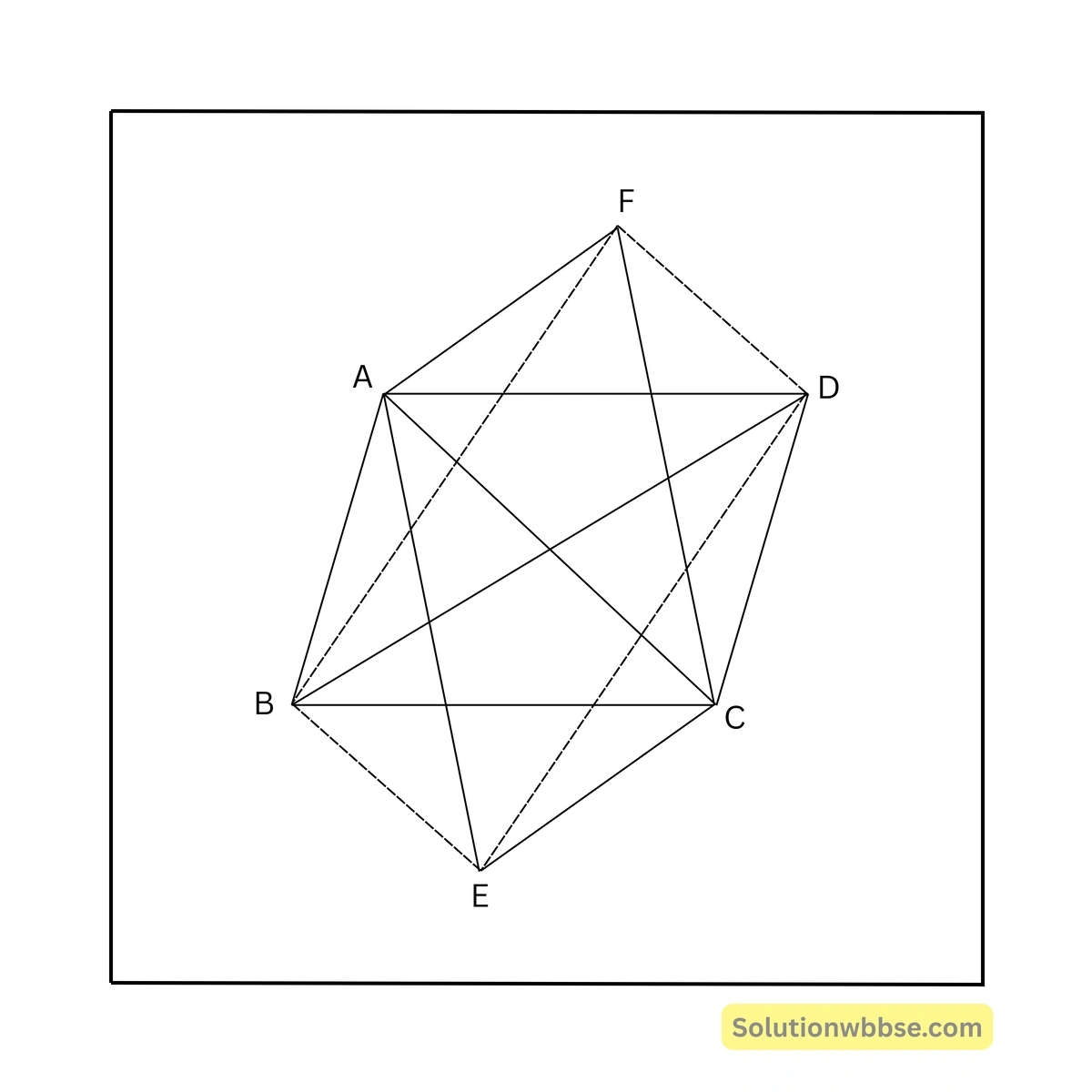
ধরা যাক, ABCD ও AECF দুটি সামান্তরিক। দুটি সামান্তরিকেরই AC একটি কর্ণ। B, E, D এবং F বিন্দুগুলি সমরেখ নয়। প্রমাণ করতে হবে যে, BEDF একটি সামান্তরিক।
প্রমাণ –
\(\triangle BAF\) এবং \(\triangle ECD\) এর মধ্যে,
\(AB = CD\) [\(ABCD\) সামান্তরিকের বিপরীত বাহু]—(i)
\(AF = EC\) [\(AECF\) সামান্তরিকের বিপরীত বাহু] —(ii)
আবার, \(\angle ACE = \angle CAF\) [একান্তর কোণ কারণ \(AF \parallel EC\) এবং \(AC\) ভেদক]
এবং \(\angle ACD = \angle BAC\) [একান্তর কোণ কারণ \(AB \parallel CD\) এবং \(AC\) ভেদক]
\(\therefore \angle ACE + \angle ACD = \angle CAF + \angle BAC\)\(\therefore \angle ECD = \angle BAF\) —(iii)
(i), (ii) ও (iii) থেকে পাই,
\(\triangle BAF \cong \triangle ECD\)\(\therefore BF = ED\) [সর্বসম ত্রিভুজের অনুরূপ বাহু]
\(\triangle ABE\) এবং \(\triangle CDF\) এর মধ্যে
\(CD = AB\) [\(ABCD\) সামান্তরিকের বিপরীত বাহু]—(iv)
\(CF = AE\) [\(AECF\) সামান্তরিকের বিপরীত বাহু] —(v)
এবং \(\angle BAC = \angle ACD\) [একান্তর কোণ কারণ \(AB \parallel DC\), \(AC\) ভেদক]
আবার, \(\angle EAC = \angle ACF\) [একান্তর কোণ কারণ \(AE \parallel FC\), \(AC\) ভেদক]
\(\therefore \angle BAC – \angle EAC = \angle ACD – \angle ACF\)\(\angle BAE = \angle DCF\) —(vi)
\(\therefore\) (iv), (v) এবং (vi) থেকে পাই,
\(\triangle ABE \cong \triangle CDF\)\(\therefore BE = FD\) [সর্বসম ত্রিভুজের অনুরূপ বাহু]
\(\therefore BEDF\) চতুর্ভুজের \(BF = ED\) এবং \(BE = FD\), অর্থাৎ বিপরীত বাহুগুলি পরস্পর সমান।
\(\therefore BEDF\) একটি সামান্তরিক। [প্রমাণিত]
11. \(ABCD\) একটি চতুর্ভুজ। \(ABCE\) ও \(BADF\) দুটি সামান্তরিক অঙ্কন করা হলো। প্রমাণ করি যে, \(CD\) ও \(EF\) পরস্পরকে সমদ্বিখণ্ডিত করে।
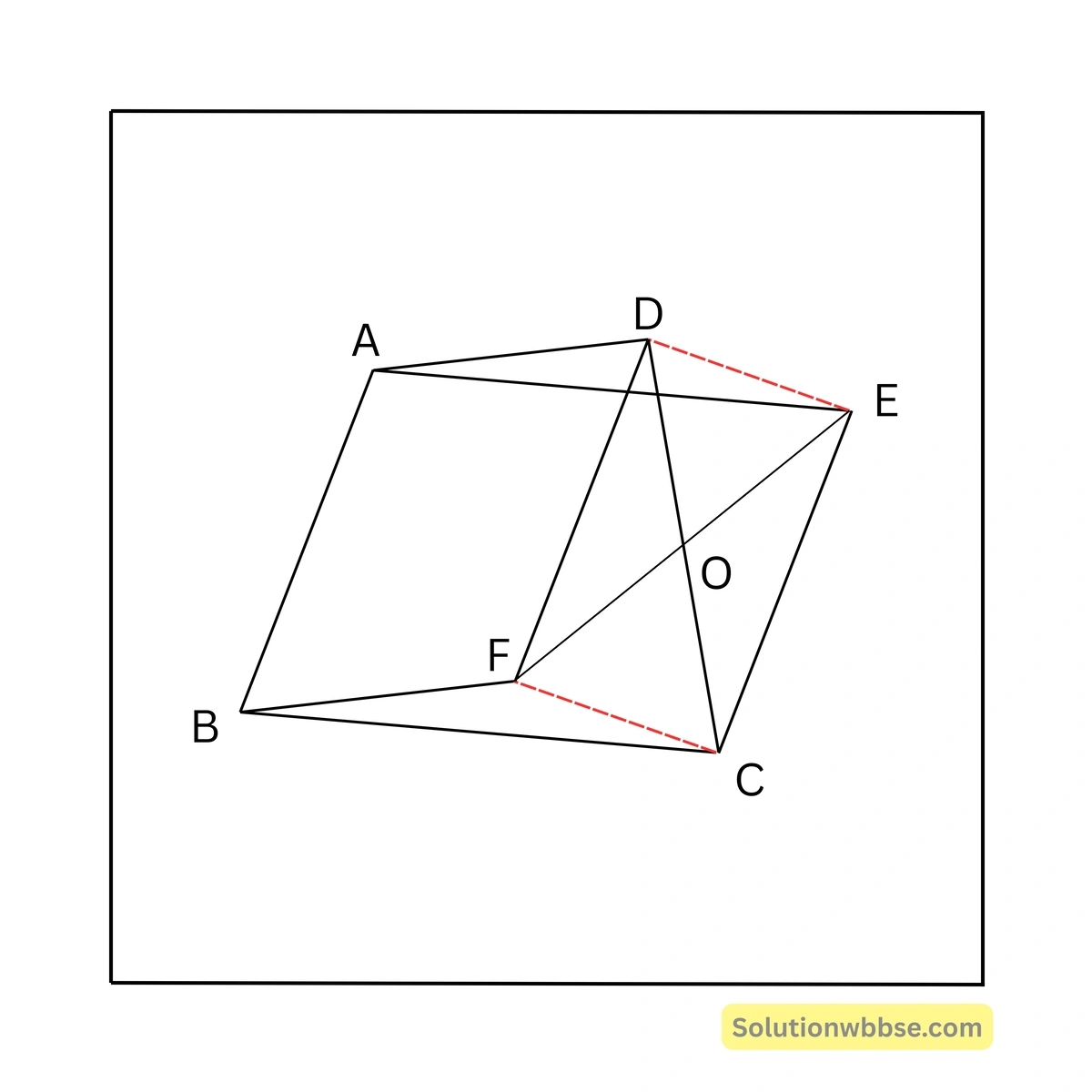
\(ABCD\) একটি চতুর্ভুজ। \(ABCE\) ও \(BADF\) দুটি সামান্তরিক। \(CD\) ও \(EF\) পরস্পরকে সমদ্বিখণ্ডিত করে। \(C\), \(D\) যুক্ত করাতে তা \(EF\) কে \(O\) বিন্দুতে ছেদ করল।
প্রমাণ করতে হবে যে, \(CD\) ও \(EF\) পরস্পরকে \(O\) বিন্দুতে সমদ্বিখণ্ডিত করে।
অঙ্কন – \(D\), \(E\) এবং \(C\), \(F\) যুক্ত করা হল।
প্রমাণ – \(ABCE\) একটি সামান্তরিক।
\(\therefore AB = CE\) এবং \(AB \parallel CE\) —(i)
আবার, \(BADF\) একটি সামান্তরিক।
\(\therefore AB = DF\) এবং \(AB \parallel DF\) —(ii)
(i) ও (ii) থেকে পাই,
\(DF = EC\) এবং \(DF \parallel EC\)
\(\therefore DFCE\) চতুর্ভুজের একজোড়া বিপরীত বাহু পরস্পর সমান ও সমান্তরাল।
\(\therefore DFCE\) চতুর্ভুজটি একটি সামান্তরিক।
আমরা জানি সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।
\(\therefore CD\) ও \(EF\) পরস্পরকে \(O\) বিন্দুতে সমদ্বিখণ্ডিত করেছে। [প্রমাণিত]
12. \(ABCD\) সামান্তরিকের \(AB = 2AD\); প্রমাণ করি যে, \(\angle BAD\) ও \(\angle ABC\) এর সমদ্বিখণ্ডকদ্বয় \(DC\) বাহুর মধ্যবিন্দুতে সমকোণে মিলিত হয়।
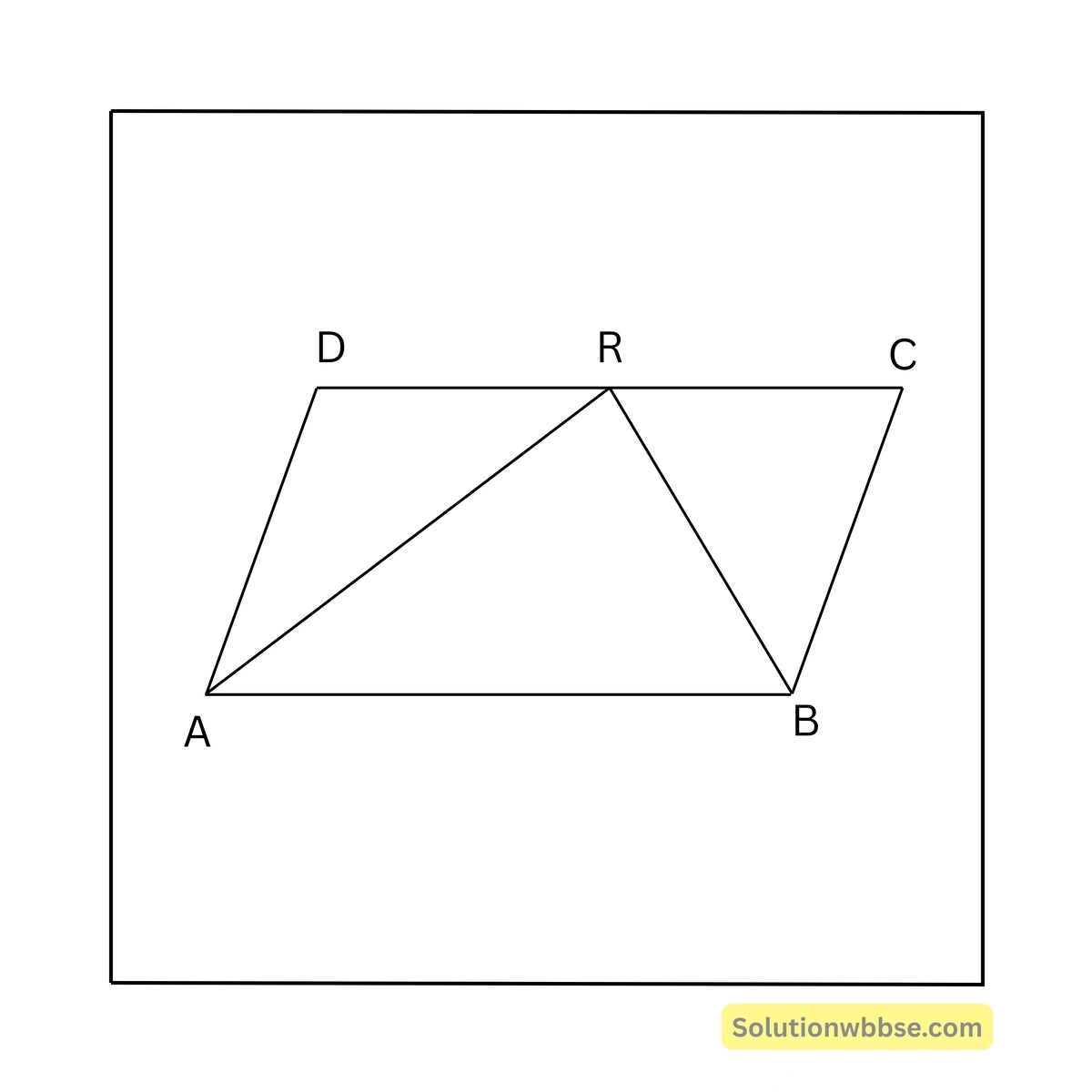
\(ABCD\) একটি সামান্তরিক যার \(AB = 2AD\); প্রমাণ করতে হবে যে, \(\angle BAD\) ও \(\angle ABC\) এর সমদ্বিখণ্ডকদ্বয় \(DC\) বাহুর মধ্যবিন্দুতে সমকোণে মিলিত হয়।
প্রমাণ –
\(ABCD\) সামান্তরিকের \(DC \parallel AB\), \(AR\) ভেদক
\(\therefore \angle ARD = \angle RAB\) [একান্তর কোণ]—(i)
আবার, \(AR\) হল কোণ \(\angle BAD\) এর সমদ্বিখণ্ডক।
\(\therefore \angle DAR = \angle RAB\) —(ii)
(i) ও (ii) থেকে পাই,
\(\angle ARD = \angle DAR\)\(\therefore \triangle ADR\)-এর \(AD = DR\) —(iii)
আবার \(AB = 2AD\)
বা, \(AD = \frac{1}{2} AB = \frac{1}{2} DC\) [যেহেতু \(AB = DC\) (সামান্তরিকের বিপরীত বাহু)]
\(\therefore DR = \frac{1}{2} DC\) [যেহেতু (iii) নং থেকে পাই \(AD = DR\)]
\(\therefore R\), \(DC\) এর মধ্যবিন্দু। —(iv)
আবার, \(\angle DAB + \angle ABC = 180^\circ\) [যেহেতু ভেদকের একই পার্শ্বস্থ অন্তঃকোণের সমষ্টি \(180^\circ\)]
বা, \(2\angle RAB + 2\angle RBA = 180^\circ\) [যেহেতু, \(RA\) এবং \(RB\) যথাক্রমে \(\angle BAD\) এবং \(\angle ABC\) এর সমদ্বিখণ্ডক]
বা, \(2(\angle RAB + \angle RBA) = 180^\circ\)
বা, \(\angle RAB + \angle RBA = \frac{180^\circ}{2}\)
বা, \(\angle RAB + \angle RBA = 90^\circ\)
\(\therefore \triangle ABR\)-এর,
\(\angle RAB + \angle RBA + \angle ARB = 180^\circ\)বা, \(90^\circ + \angle ARB = 180^\circ\) [যেহেতু, \(\angle RAB + \angle RBA = 90^\circ\)]
বা, \(\angle ARB = 180^\circ – 90^\circ\)
বা, \(\angle ARB = 90^\circ\) —(v)
\(\therefore\) (iv) ও (v) থেকে পাই, \(\angle BAD\) ও \(\angle ABC\) এর সমদ্বিখণ্ডকদ্বয় \(DC\) বাহুর মধ্যবিন্দুতে সমকোণে মিলিত হয়। [প্রমাণিত]
13. ABCD সামান্তরিকের AB ও AD বাহুর উপর যথাক্রমে ABPQ ও ADRS বর্গাকার চিত্র অঙ্কন করা হল যারা সামান্তরিকের বাইরে অবস্থিত। প্রমাণ করি যে, PRC ত্রিভুজটি সমদ্বিবাহু।

মনে কর, \(ABCD\) সামান্তরিকের \(AB\) ও \(AD\) বাহুর উপর যথাক্রমে \(ABPQ\) ও \(ADRS\) বর্গক্ষেত্র অঙ্কন করা হল যা সামান্তরিকের বাইরে অবস্থিত।
প্রমাণ করতে হবে যে, \(PRC\) সমদ্বিবাহু ত্রিভুজ।
প্রমাণ –
\(RD = AD\) [কারণ \(ADRS\) বর্গক্ষেত্র]
আবার, \(AD = BC\) [কারণ \(ABCD\) সামান্তরিক]
\(\therefore RD = BC\)অনুরূপে, \(DC = AB\) [কারণ \(ABCD\) সামান্তরিক]
আবার, \(AB = BP\) [কারণ \(ABPQ\) বর্গক্ষেত্র]
\(\therefore DC = BP\)আমরা জানি, কোনো বিন্দুর চারদিকে উৎপন্ন কোণগুলির সমষ্টি \(= 360^{\circ}\)
\(\therefore D\) বিন্দুর ক্ষেত্রে, \(\angle ADR + \angle ADC + \angle RDC = 360^{\circ}\)
বা, \(90^{\circ} + \angle ADC + \angle RDC = 360^{\circ}\)
বা, \(\angle RDC = 360^{\circ} – (90^{\circ} + \angle ADC)\) ………(i)
আবার, \(B\) বিন্দুর ক্ষেত্রে, \(\angle ABP + \angle ABC + \angle PBC = 360^{\circ}\)
বা, \(90^{\circ} + \angle ABC + \angle PBC = 360^{\circ}\)
বা, \(90^{\circ} + \angle ADC + \angle PBC = 360^{\circ}\) [কারণ \(\angle ABC = \angle ADC\)]
বা, \(\angle PBC = 360^{\circ} – (90^{\circ} + \angle ADC)\) ………(ii)
এখন, (i) ও (ii) থেকে পাই, \(\angle RDC = \angle PBC\)
এখন, \(\triangle RDC\) ও \(\triangle PBC\)-এর মধ্যে \(RD = BC\), \(DC = BP\) এবং \(\angle RDC = \angle PBC\)
\(\therefore \triangle RDC \cong \triangle PBC\) (বাহু-কোণ-বাহু সমতা অনুসারে)
\(\therefore RC = PC\) (সর্বসম ত্রিভুজের অনুরূপ বাহু)
সুতরাং, \(\triangle PRC\) সমদ্বিবাহু ত্রিভুজ। [প্রমাণিত]
14. ABCD সামান্তরিকের BAD স্থূলকোণ; AB ও AD বাহুর উপর দুটি সমবাহু ত্রিভুজ \(\triangle ABP\) ও \(\triangle ADQ\) অঙ্কন করা হল যারা সামান্তরিকের বাইরে অবস্থিত। প্রমাণ করি যে, \(\triangle CPQ\) একটি সমবাহু ত্রিভুজ।
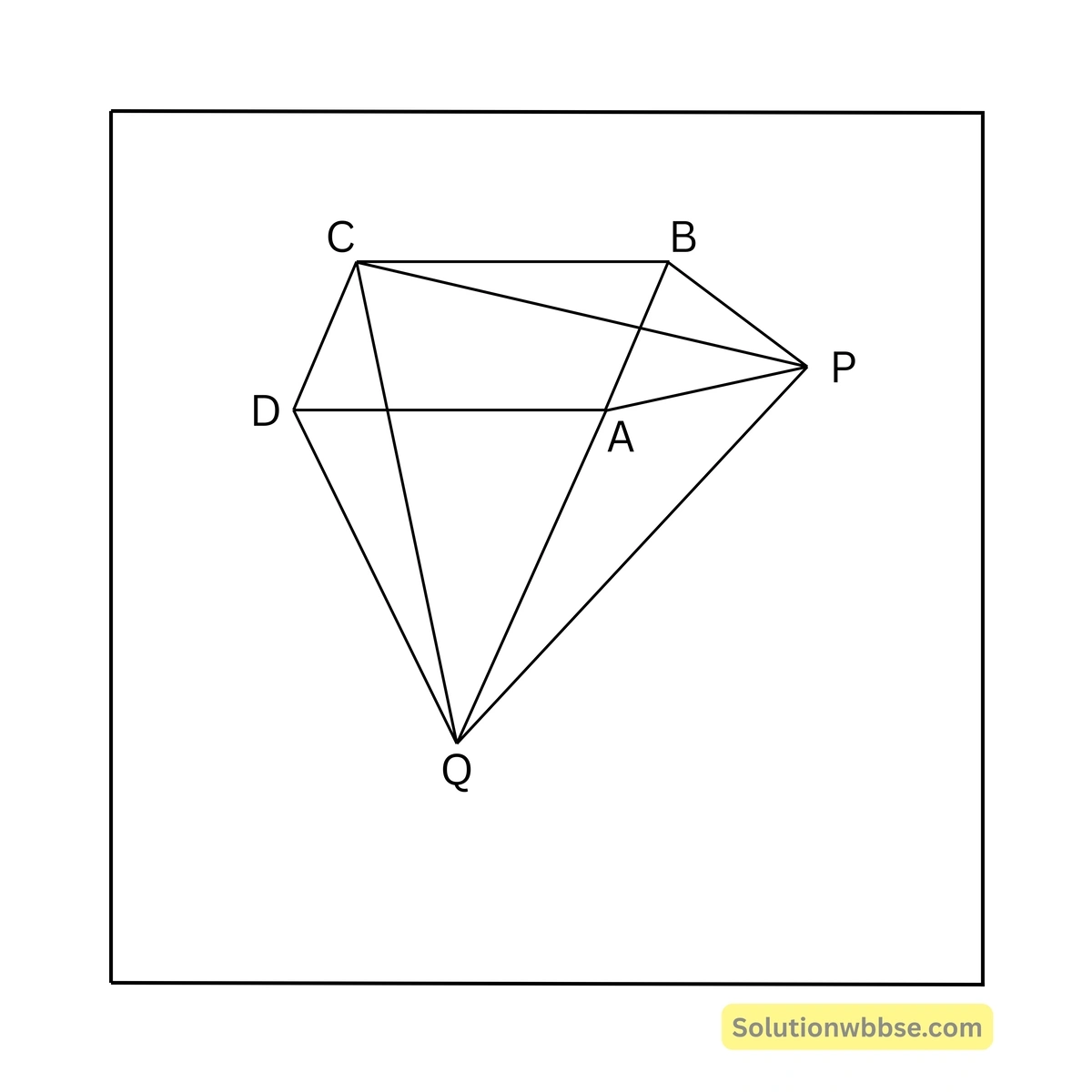
\(ABCD\) সামান্তরিকের \(\angle BAD\) স্থূলকোণ; AB ও AD বাহুর উপর দুটি সমবাহু ত্রিভুজ \(\triangle ABP\) ও \(\triangle ADQ\) অঙ্কন করা হল যারা সামান্তরিকের বাইরে অবস্থিত। প্রমাণ করতে হবে যে, \(\triangle CPQ\) একটি সমবাহু ত্রিভুজ।
প্রমাণ –
\(\triangle CDQ\) ও \(\triangle PBC\)-এর মধ্যে,
\(CD = AB\) [\(ABCD\) সামান্তরিকের বিপরীত বাহু] —(i)
\(DQ = AD\) [যেহেতু, \(\triangle ADQ\) সমবাহু ত্রিভুজ]
আবার, \(AD = BC\) [\(ABCD\) সামান্তরিকের বিপরীত বাহু]
\(\therefore DQ = BC\) —(ii)
\(\angle ADQ = \angle ABP = 60^{\circ}\)এবং \(\angle ADC = \angle ABC\) [\(ABCD\) সামান্তরিকের বিপরীত কোণ]
\(\therefore \angle ADQ + \angle ADC = \angle ABP + \angle ABC\)বা, \(\angle CDQ = \angle PBC\) —(iii)
(i), (ii) ও (iii) থেকে পাই, \(\triangle CDQ \cong \triangle PBC\) (বাহু-কোণ-বাহু সমতা অনুসারে)
\(\therefore CQ = PC\) [সর্বসম ত্রিভুজের অনুরূপ বাহু] —(iv)
\(\angle DAQ = \angle BAP = 60^{\circ}\) [যেহেতু, \(\triangle DAQ\) এবং \(\triangle BAP\) প্রত্যেকে সমবাহু ত্রিভুজ]
\(\therefore \angle BAD + \angle PAQ = 360^{\circ} – 120^{\circ}\)বা, \(\angle BAD + \angle PAQ = 240^{\circ}\)
বা, \(\angle PAQ = 240^{\circ} – \angle BAD\)
বা, \(\angle PAQ = 240^{\circ} – (180^{\circ} – \angle ABC)\) [যেহেতু, \(ABCD\) সামান্তরিকের \(\angle ABC + \angle BAD = 180^{\circ}\)]
বা, \(\angle PAQ = 240^{\circ} – 180^{\circ} + \angle ABC\)
বা, \(\angle PAQ = 60^{\circ} + \angle ABC\)
বা, \(\angle PAQ = \angle PBA + \angle ABC\) [যেহেতু, \(\angle PBA = 60^{\circ}\)]
বা, \(\angle PAQ = \angle PBC\) —(v)
\(AQ = AD\) [যেহেতু, \(\triangle ADQ\) সমবাহু ত্রিভুজ]
আবার, \(AD = BC\) [সামান্তরিকের বিপরীত বাহু]
\(\therefore AQ = BC\) —(vi)
আবার, \(AP = PB\) [যেহেতু, \(\triangle PAB\) সমবাহু ত্রিভুজ] —(vii)
\(\therefore\) (v), (vi) এবং (vii) থেকে পাই,
\(\triangle PBC \cong \triangle AQP\) (বাহু-কোণ-বাহু সমতা অনুসারে)
\(\therefore CP = PQ\) —(viii)
(iv) ও (viii) থেকে পাই,
\(CQ = CP = PQ\)\(\therefore \triangle PCQ\) একটি সমবাহু ত্রিভুজ। [প্রমাণিত]
15. \(OP, OQ\) ও \(OR\) তিনটি সরলরেখাংশ। \(OPAQ, OQBR\) এবং \(ORCP\) সামান্তরিক তিনটি অঙ্কন করা হল। প্রমাণ করতে হবে যে, \(AR, BP\) ও \(CQ\) পরস্পরকে সমদ্বিখণ্ডিত করে।
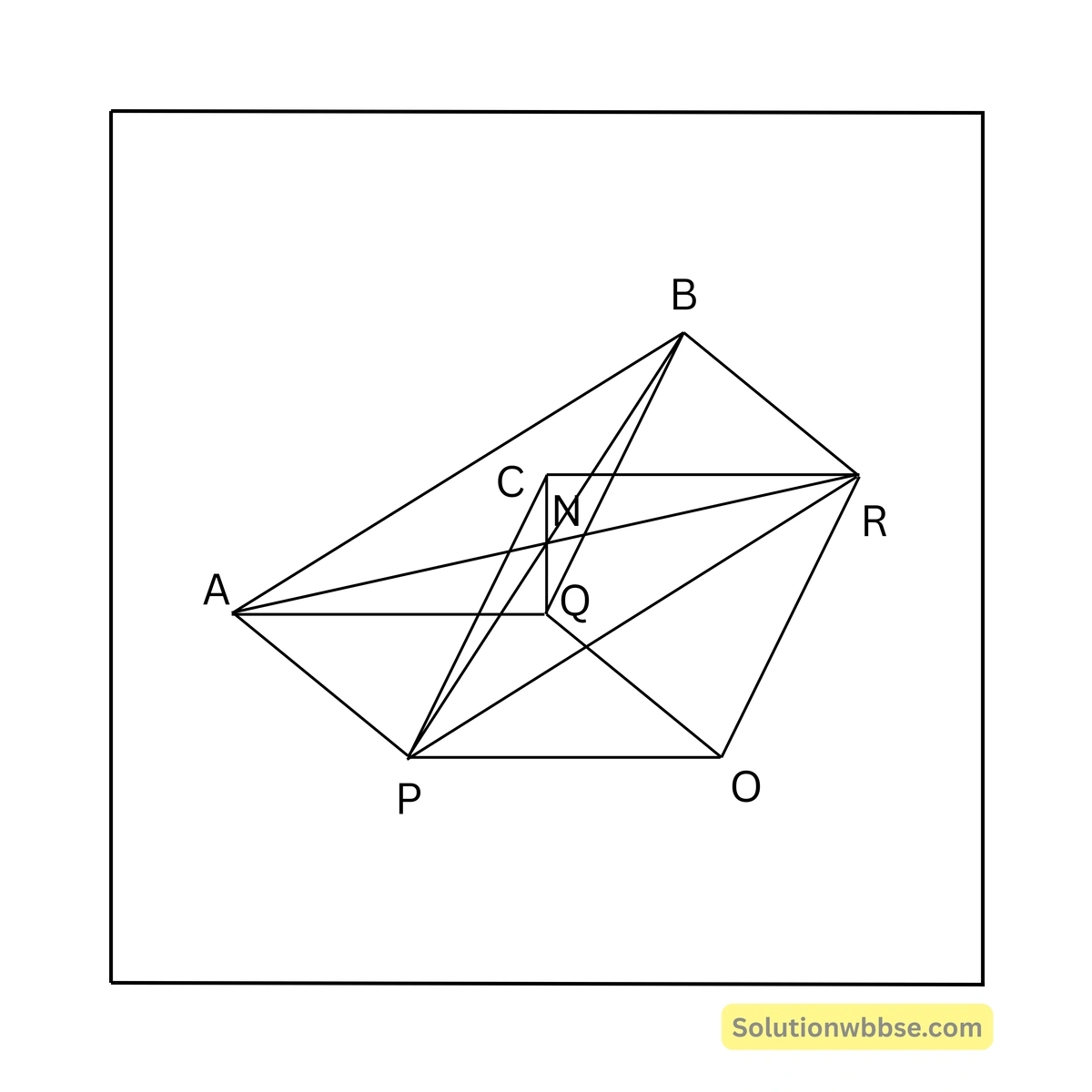
মনে করি, \(OP, OQ\) ও \(OR\) তিনটি সরলরেখাংশ। \(OPAQ, OQBR\) এবং \(ORCP\) তিনটি সামান্তরিক অঙ্কন করা হয়েছে। \(AR, BP\) ও \(CQ\) সরলরেখা তিনটি পরস্পরকে \(N\) বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে, \(AR, BP\) ও \(CQ\) সরলরেখা তিনটি পরস্পরকে সমদ্বিখণ্ডিত করে।
অঙ্কন –
\(A, B\) এবং \(P, R\) যুক্ত করা হল।
প্রমাণ –
যেহেতু, \(OPAQ\) একটি সামান্তরিক,
সুতরাং, \(AP \parallel QO\) এবং \(AP = QO\)
আবার যেহেতু \(OQBR\) একটি সামান্তরিক,
সুতরাং, \(OQ \parallel BR\) এবং \(BR = QO\)
\(\therefore AP \parallel BR\) এবং \(AP = BR\)
\(\therefore APRB\) একটি সামান্তরিক, যার \(AR\) এবং \(BP\) দুটি কর্ণ।
যেহেতু, সামান্তরিকের কর্ণ পরস্পরকে সমদ্বিখণ্ডিত করে, সুতরাং \(AR\) ও \(BP\) সরলরেখা দুটি পরস্পরকে সমদ্বিখণ্ডিত করে।
\(\therefore N\), \(AR\) ও \(BP\) সরলরেখা দুটির মধ্যবিন্দু।
এখন \(\triangle AQN\) এবং \(\triangle CRN\) এর মধ্যে
\(\angle ANQ =\) বিপ্রতীপ \(\angle CNR\) এবং \(\angle AQN =\) একান্তর \(\angle NCR\) [ যেহেতু, \(AQ \parallel PO \parallel CR\) ]
এবং \(AN = NR\)
\(\therefore \triangle AQN \cong \triangle CRN\)\(\therefore NQ = CN\) [অনুরূপ বাহু]
\(\therefore N\), \(CQ\)-এর মধ্যবিন্দু।
\(\therefore AR, BP\) ও \(CQ\) সরলরেখা তিনটি পরস্পরকে সমদ্বিখণ্ডিত করে। [প্রমাণিত]
16. বহু বিকল্পীয় প্রশ্ন (M.C.Q) –
(i) ABCD সামান্তরিকের \(\angle BAD = 75^\circ\) এবং \(\angle CBD = 60^\circ\) হলে, \(\angle BDC\)-এর পরিমাপ
(a) \(60^\circ\)
(b) \(75^\circ\)
(c) \(45^\circ\)
(d) \(50^\circ\)
উত্তর – (c) \(45^\circ\)
সমাধান –
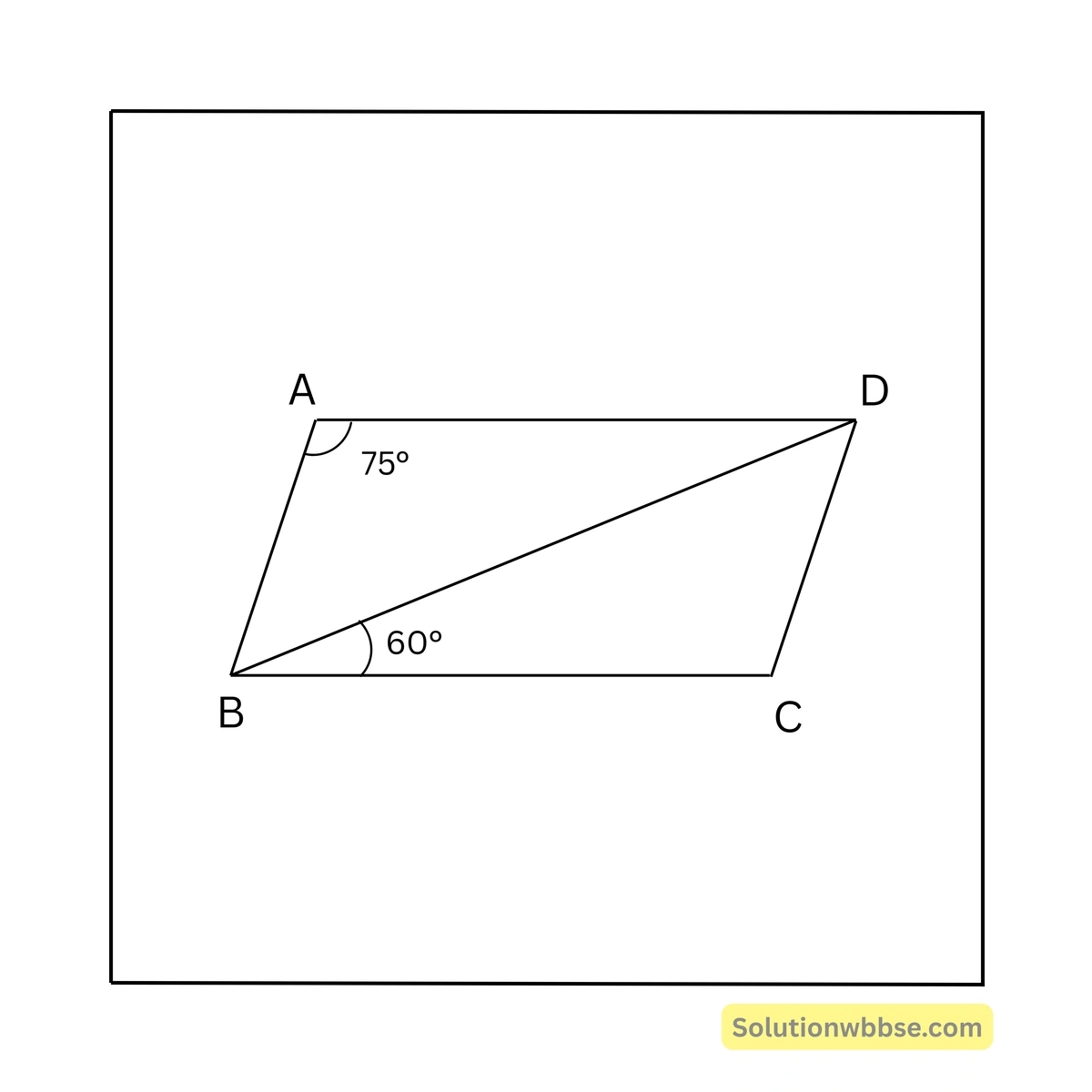
\(\therefore \angle BCD = 75^\circ\) [যেহেতু সামান্তরিকের বিপরীত কোণগুলি পরস্পর সমান]
এখন, \(\triangle BCD\)-এর,
\(\angle BCD + \angle CBD + \angle BDC = 180^\circ\)বা, \(75^\circ + 60^\circ + \angle BDC = 180^\circ\)
বা, \(\angle BDC = 180^\circ – 75^\circ – 60^\circ\)
বা, \(\angle BDC = 180^\circ – 135^\circ\)
বা, \(\angle BDC = 45^\circ\)
(ii) নিম্নলিখিত জ্যামিতিক চিত্রগুলির মধ্যে কোনটির কর্ণদ্বয়ের দৈর্ঘ্য সমান তা লিখি।
(a) সামান্তরিক
(b) রম্বস
(c) ট্রাপিজিয়াম
(d) আয়তকার চিত্র
উত্তর – (d) আয়তকার চিত্র
(iii) ABCD সামান্তরিকের \(\angle BAD = \angle ABC\) হলে, ABCD সামান্তরিকটি
(a) রম্বস
(b) ট্রাপিজিয়াম
(c) আয়তকার চিত্র
(d) কোনোটিই নয়
উত্তর – (c) আয়তকার চিত্র
সমাধান –
ABCD সামান্তরিকের \(\angle BAD = \angle ABC\)
যেহেতু, ভেদকের একই পার্শ্বস্থ অন্তঃস্থ কোণের সমষ্টি \(180^\circ\),
\(\therefore \angle BAD + \angle ABC = 180^\circ\)বা, \(\angle BAD + \angle BAD = 180^\circ\)
বা, \(2\angle BAD = 180^\circ\)
বা, \(\angle BAD = \frac{180^\circ}{2}\)
বা, \(\angle BAD = 90^\circ\)
\(\therefore\) ABCD সামান্তরিকের একটি কোণের মান \(90^\circ\)
\(\therefore\) ABCD একটি আয়তক্ষেত্র।
(iv) ABCD সামান্তরিকের BD কর্ণের মধ্যবিন্দু M; BM, \(\angle ABC\)-কে সমদ্বিখণ্ডিত করলে, \(\angle AMB\)-এর পরিমাপ
(a) \(45^\circ\)
(b) \(60^\circ\)
(c) \(90^\circ\)
(d) \(75^\circ\)
উত্তর – (c) \(90^\circ\)
সমাধান –
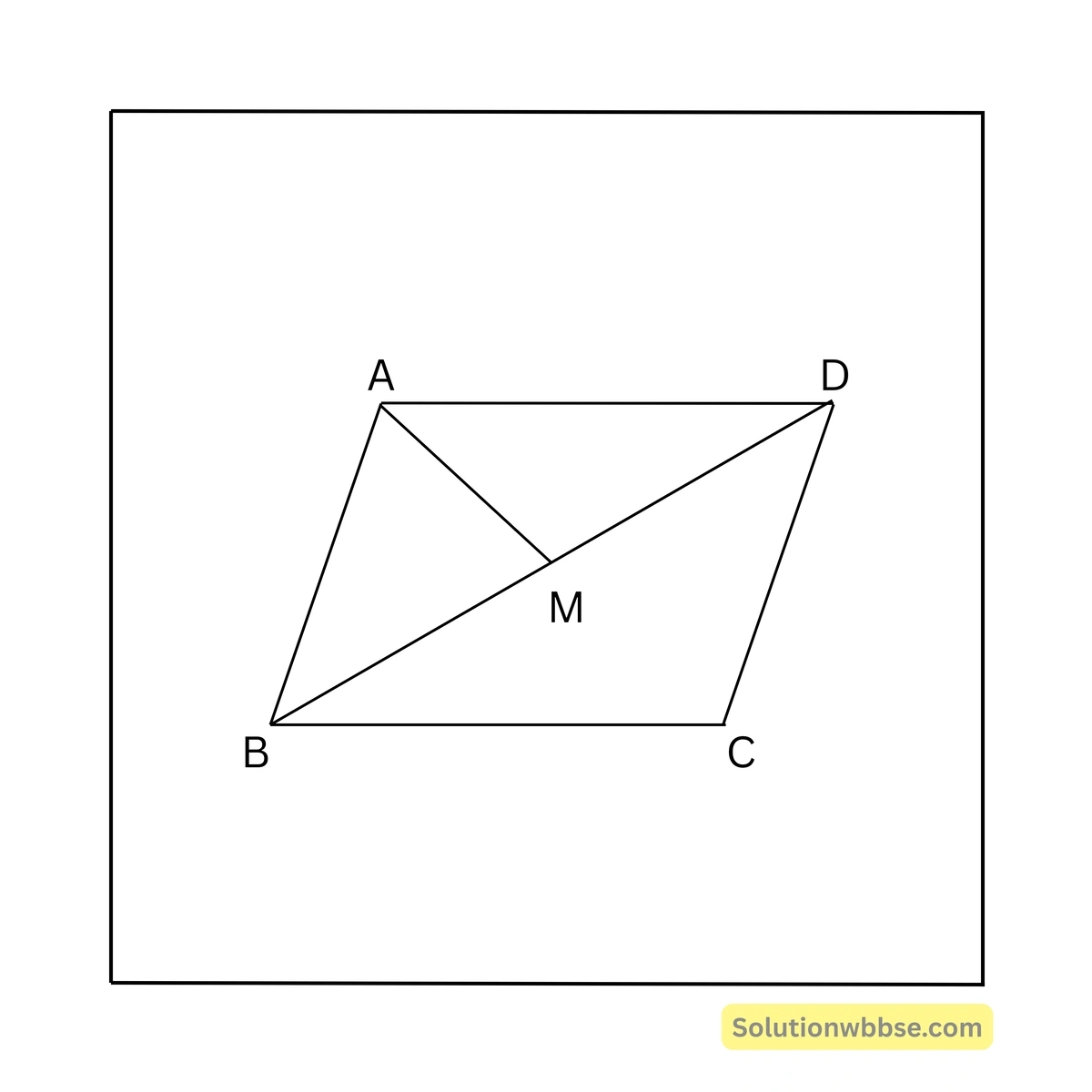
\(\angle CBD = \angle ADB\) [একান্তর কোণ]
আবার, \(\angle ABD = \angle CBD\) [যেহেতু, BD, \(\angle ABC\)-এর সমদ্বিখণ্ডক]
\(\therefore \angle ADB = \angle ABD\)\(\therefore AB = AD\)\(\therefore\) ABCD সামান্তরিকের \(AB = AD\)
\(\therefore\) ABCD একটি রম্বস।
যেহেতু, রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে,
\(\therefore \angle AMB = 90^\circ\)(v) ABCD রম্বসের \(\angle ACB = 40^\circ\) হলে, \(\angle ADB\)-এর পরিমাপ
(a) \(50^\circ\)
(b) \(110^\circ\)
(c) \(90^\circ\)
(d) \(120^\circ\)
Ans: (a) \(50^\circ\)
সমাধান –

ABCD রম্বসের AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করেছে।
\(\therefore \angle AOD = 90^\circ\)\(\angle ACB = 40^\circ\)\(\therefore \angle ACB = \angle CAD = 40^\circ\) [একান্তর কোণ, যেহেতু, \(BC \parallel AD\) এবং AC ভেদক]
\(\triangle AOD\)-এর ক্ষেত্রে,
\(\angle AOD + \angle OAD + \angle ODA = 180^\circ\)বা, \(90^\circ + 40^\circ + \angle ODA = 180^\circ\)
বা, \(\angle ODA = 180^\circ – 90^\circ – 40^\circ\)
বা, \(\angle ODA = 50^\circ\)
\(\therefore \angle ADB = 50^\circ\)17. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন –
(i) ABCD সামান্তরিকের \(\angle A : \angle B = 3:2\) হলে, সামান্তরিকটির কোণগুলির পরিমাপ লিখি।
সমাধান –
ধরি, \(\angle A = 3x\) এবং \(\angle B = 2x\) [\(x (\neq 0)\) একটি আনুপাতিক ধ্রুবক]।
ABCD সামান্তরিকের,
\(\angle A + \angle B = 180^\circ\) [যেহেতু, ভেদকের একই পার্শ্বস্থ অন্তঃকোণের সমষ্টি \(180^\circ\)]
বা, \(3x + 2x = 180^\circ\)
বা, \(5x = 180^\circ\)
বা, \(x = \frac{180^\circ}{5}\)
বা, \(x = 36^\circ\)
\(\therefore \angle A = 3 \times 36^\circ = 108^\circ\) এবং \(\angle B = 2 \times 36^\circ = 72^\circ\)
যেহেতু, সামান্তরিকের বিপরীত কোণগুলির পরিমাপ সমান,
\(\therefore \angle C = 108^\circ\) এবং \(\angle D = 72^\circ\)।
(ii) ABCD সামান্তরিকের \(\angle A\) ও \(\angle B\)-এর সমদ্বিখণ্ডকদ্বয় \(CD\) বাহুর উপর \(E\) বিন্দুতে মিলিত হয়। \(BC\) বাহুর দৈর্ঘ্য 2 সেমি. হলে, \(AB\) বাহুর দৈর্ঘ্য কত তা লিখি।
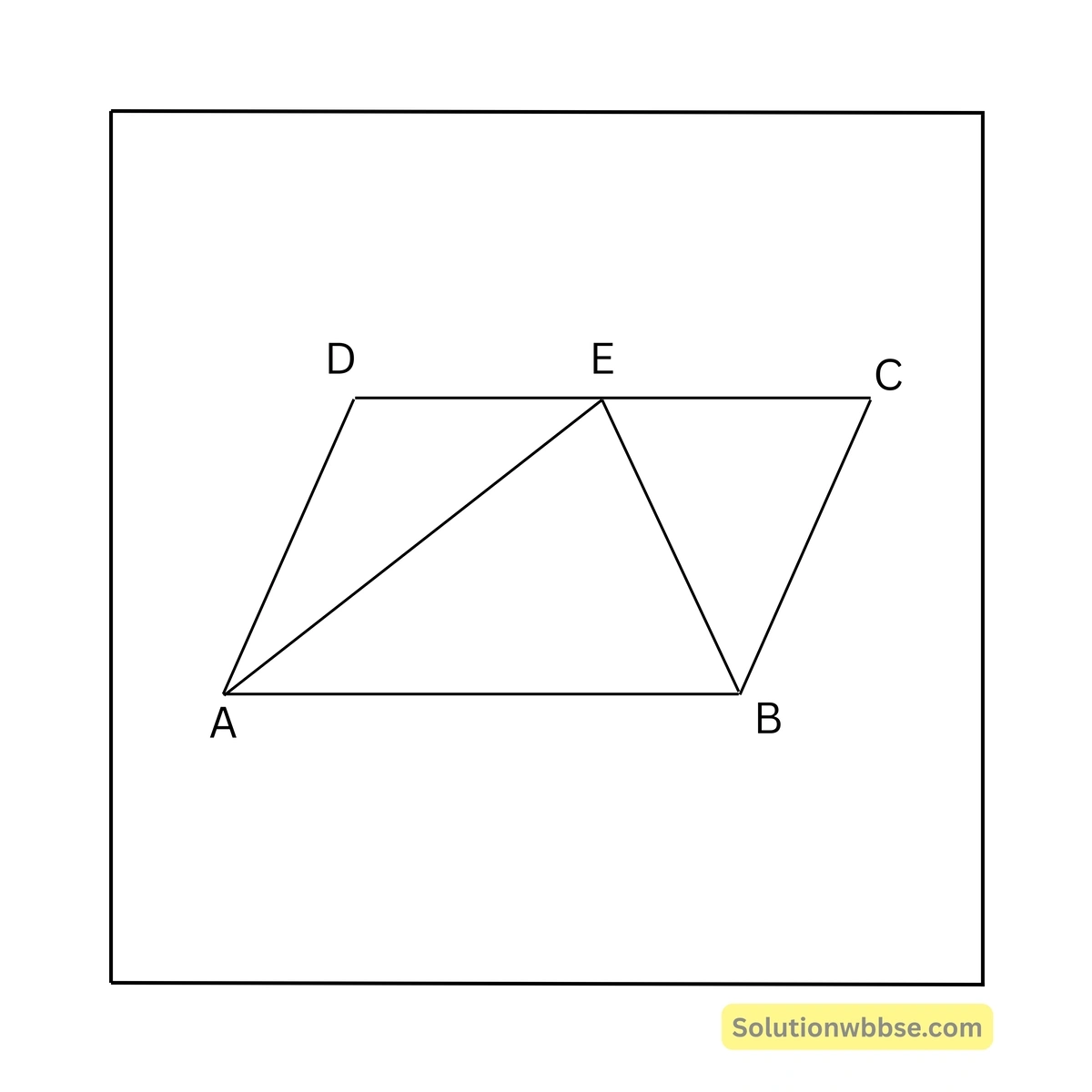
সমাধান –
\(ABCD\) সামান্তরিকের \(\angle A\) ও \(\angle B\) কোণের সমদ্বিখণ্ডকদ্বয় পরস্পর \(CD\) বাহুর উপর \(E\) বিন্দুতে মিলিত হয়।
\(\therefore \angle BAE = \angle DAE\) —(i)
এবং \(\angle BAE = \angle AED\) [একান্তর কোণ] —(ii)
(i) ও (ii) থেকে পাই,
\(\angle DAE = \angle AED\)\(\therefore AD = DE\)আবার, \(AD = BC = 2\) সেমি. [সামান্তরিকের বিপরীত বাহু]
আবার, \(\angle ABE = \angle CBE\) [যেহেতু, \(BE\), \(\angle ABC\)-এর সমদ্বিখণ্ডক] –(iii)
আবার, \(\angle ABE = \angle BEC\) [একান্তর কোণ] —(iv)
(iii) ও (iv) থেকে পাই,
\(\angle CBE = \angle BEC\)\(\therefore CE = CB\)\(\therefore CE = 2\) সেমি.
\(\therefore CD = CE + DE = (2 + 2)\) সেমি. \(= 4\) সেমি.
\(\therefore AB = 4\) সেমি. [যেহেতু, \(AB\) এবং \(CD\) পরস্পর \(ABCD\) সামান্তরিকের বিপরীত বাহু]
(iii) ABCD বর্গাকার চিত্রের ভিতর সমবাহু ত্রিভুজ \(\triangle AOB\) অবস্থিত। \(\angle COD\)-এর পরিমাণ লিখি।
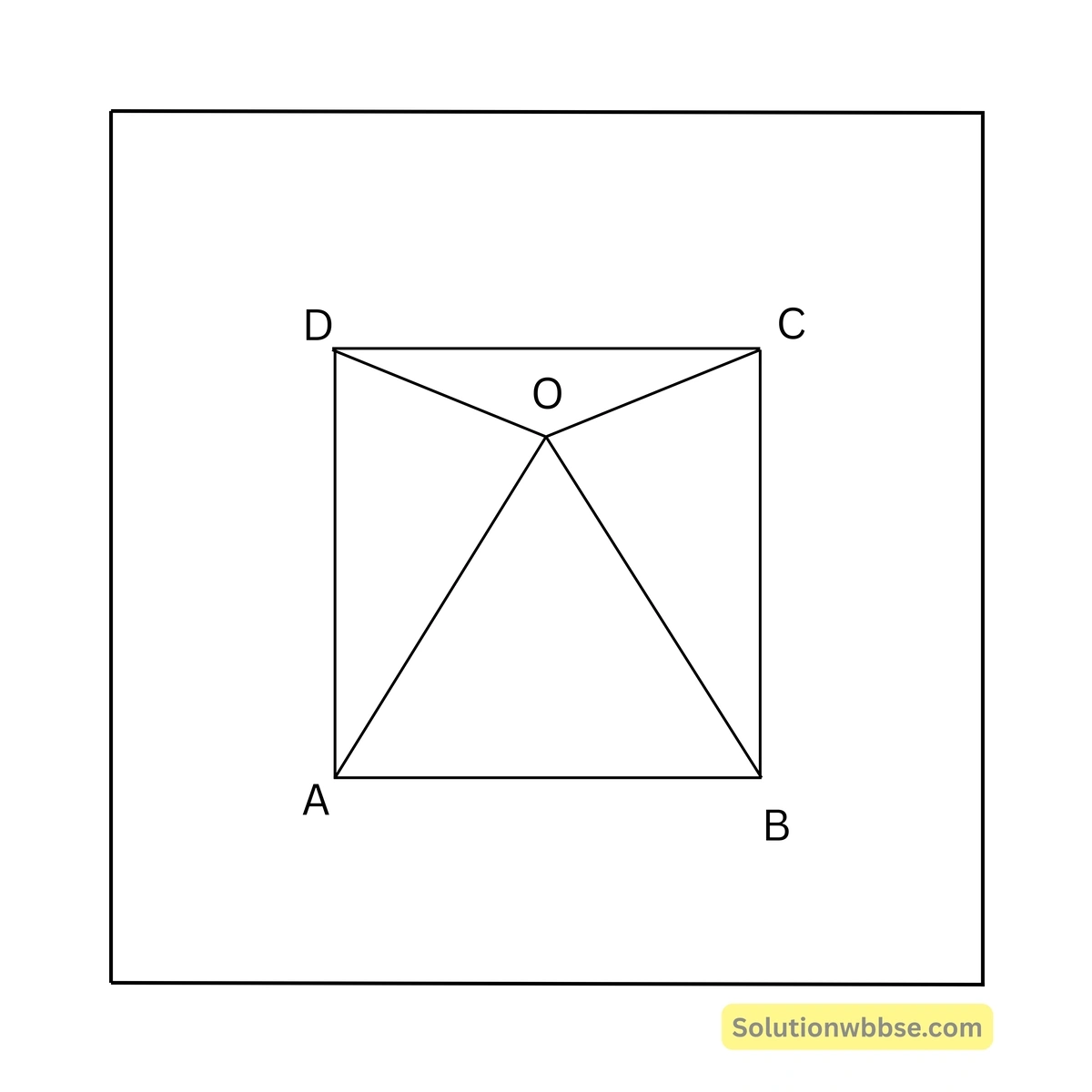
সমাধান –
ABCD বর্গক্ষেত্রের ভিতরে \(\triangle AOB\) সমবাহু ত্রিভুজ।
\(\therefore \angle AOB = \angle OBA = \angle OAB = 60^{\circ}\)\(\therefore \angle OBC = 90^{\circ} – \angle OBA = 90^{\circ} – 60^{\circ} = 30^{\circ}\)এবং \(OA = AB = OB = BC\)
যেহেতু, \(OB = BC\)
\(\therefore \angle BOC = \angle BCO = (180^{\circ} – \angle OBC)/2 = (180^{\circ} – 30^{\circ})/2 = 150^{\circ}/2 = 75^{\circ}\)অনুরূপে, \(\angle AOD = 75^{\circ}\)
\(\therefore \angle COD = 360^{\circ} – (\angle AOB + \angle AOD + \angle BOC) = 360^{\circ} – (60^{\circ} + 75^{\circ} + 75^{\circ}) = 360^{\circ} – 210^{\circ} = 150^{\circ}\)(iv) ABCD বর্গাকার চিত্রের AD বাহুর উপর M একটি বিন্দু যাতে \(\angle CMD = 30^{\circ}\) হয়। কর্ণ BD, CM কে P বিন্দুতে ছেদ করলে, \(\angle DPC\)-এর পরিমাণ কত তা লিখি।
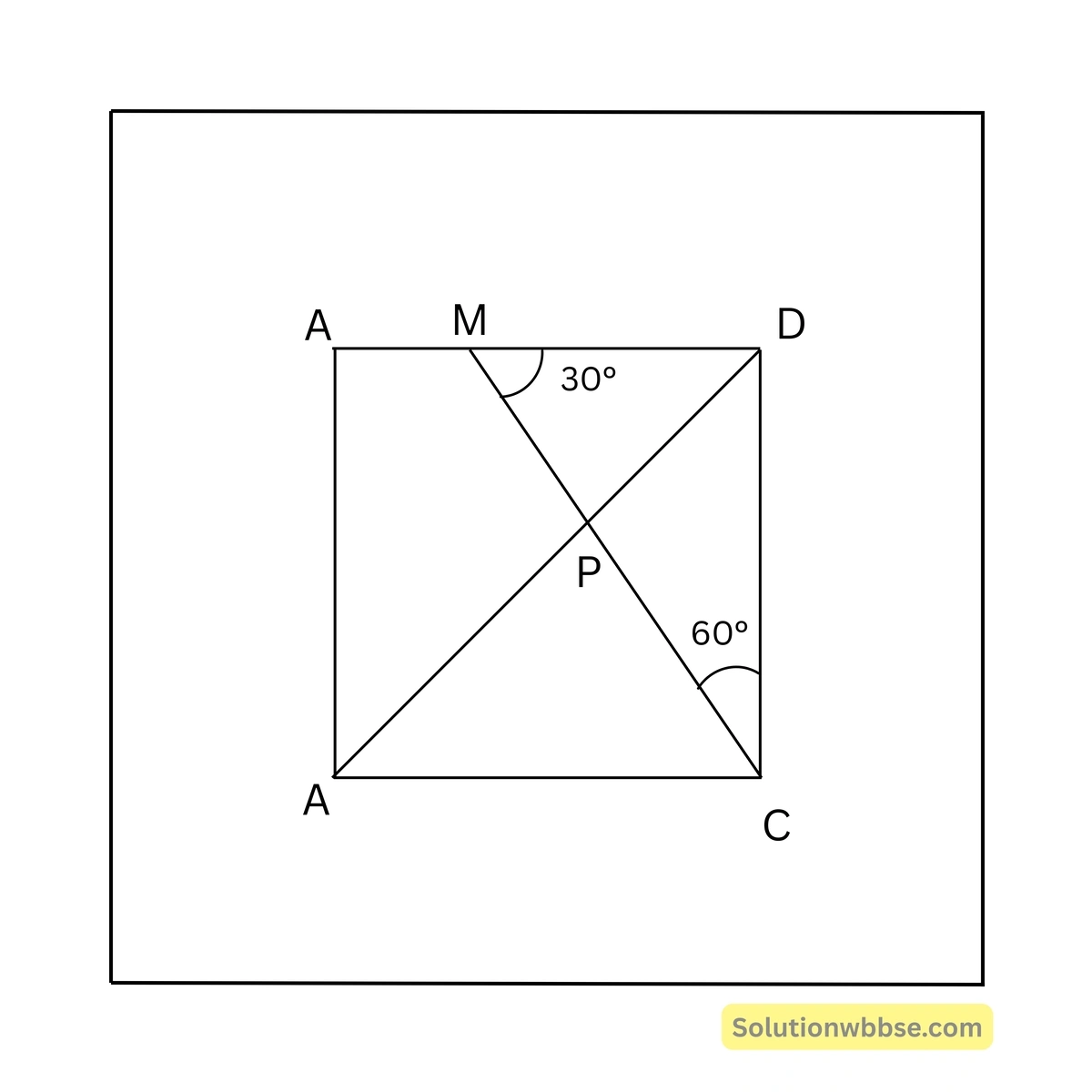
সমাধান –
\(\angle CMD = 30^{\circ}\) [প্রদত্ত]
\(\angle CDM = 90^{\circ}\)\(\therefore \angle MCD = 180^{\circ} – (\angle CMD + \angle CDM) = 180^{\circ} – (30^{\circ} + 90^{\circ}) = 180^{\circ} – 120^{\circ} = 60^{\circ}\)আবার, ABCD বর্গক্ষেত্রের BD কর্ণ।
\(\therefore \angle BDC = \angle DBC = 45^{\circ}\)এখন, \(\triangle CPD\) এর ক্ষেত্রে,
\(\angle CPD = 180^{\circ} – (\angle PCD + \angle PDC) = 180^{\circ} – (60^{\circ} + 45^{\circ}) = 180^{\circ} – 105^{\circ} = 75^{\circ}\)(v) ABCD রম্বসের AB বাহুর দৈর্ঘ্য 4 সেমি. এবং \(\angle BCD = 60^{\circ}\) হলে, কর্ণ BD-এর দৈর্ঘ্য কত তা লিখি।

সমাধান –
ABCD রম্বসের \(AB = 4\) সেমি.।
\(\therefore AB = BC = CD = DA = 4\) সেমি.
\(\triangle BCD\) ত্রিভুজের ক্ষেত্রে,
\(\angle BCD = 60^{\circ}\)এবং \(BC = CD\)
\(\therefore \angle CBD = \angle CDB = 60^{\circ}\)\(\therefore \triangle CBD\) একটি সমবাহু ত্রিভুজ।
\(\therefore BC = CD = BD = 4\) সেমি.
এই আর্টিকেলে নবম শ্রেণির গণিতের ‘সামান্তরিকের ধর্ম’ অধ্যায়ের ‘কষে দেখি – 6’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।
কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন