নবম শ্রেণী গণিত – লাভ ও ক্ষতি – কষে দেখি – 10.1

পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) দশম শ্রেণির গণিত পাঠ্যবইয়ের দশম অধ্যায় হলো ‘লাভ ও ক্ষতি’। এই পোস্টে ‘কষে দেখি – 10.1‘-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. নীচের ছক  পূরণ করি

ক্রয়মূল্য (Cost Price)	বিক্রয়মূল্য (Selling Price)	লাভ / ক্ষতি (Profit / Loss)	শতকরা লাভ / ক্ষতি (Percentage Profit/Loss)
\(500\) টাকা	বিক্রয়মূল্য = ক্রয়মূল্য + লাভ = \((500 + 125)\) টাকা = \(625\) টাকা	লাভ = শতকরা লাভ × ক্রয়মূল্য বা, লাভ = \(\frac{25}{100} \times 500\) টাকা = \(125\) টাকা	\(25\%\) লাভ
\(300\) টাকা	বিক্রয়মূল্য = ক্রয়মূল্য – ক্ষতি = \((300 – 21)\) টাকা = \(279\) টাকা	ক্ষতি = শতকরা ক্ষতি × ক্রয়মূল্য বা, ক্ষতি = \(\frac{7}{100} \times 300\) টাকা = \(21\) টাকা	\(7\%\) ক্ষতি
\(1250\) টাকা	বিক্রয়মূল্য = ক্রয়মূল্য – ক্ষতি = \((1250 – 100)\) টাকা = \(1150\) টাকা	ক্ষতি = শতকরা ক্ষতি × ক্রয়মূল্য বা, ক্ষতি = \(\frac{8}{100} \times 1250\) টাকা = \(100\) টাকা	\(8\%\) ক্ষতি
যেহেতু, ক্রয়মূল্য + লাভ = বিক্রয়মূল্য বা, \(x + 0.15x = 23000\) বা, \(1.15x = 23000\) বা, \(x = \frac{23000}{1.15}\) ক্রয়মূল্য = \(20,000\) টাকা	\(23000\) টাকা	ধরি, ক্রয়মূল্য \(x\) টাকা লাভ = শতকরা লাভ × ক্রয়মূল্য বা, লাভ = \(\frac{15}{100} \times x\) টাকা = \(0.15x\) টাকা লাভ = বিক্রয়মূল্য – ক্রয়মূল্য = \(23000 – x\) টাকা সুতরাং, \(0.15x = 23000 – x\) বা, \(1.15x = 23000\) বা, \(x = 20000\) লাভ = \(23000 – 20000 = 3000\) টাকা	\(15\%\) লাভ

2. লেখচিত্রটি থেকে নীচের প্রশ্নের উত্তর খুঁজি।

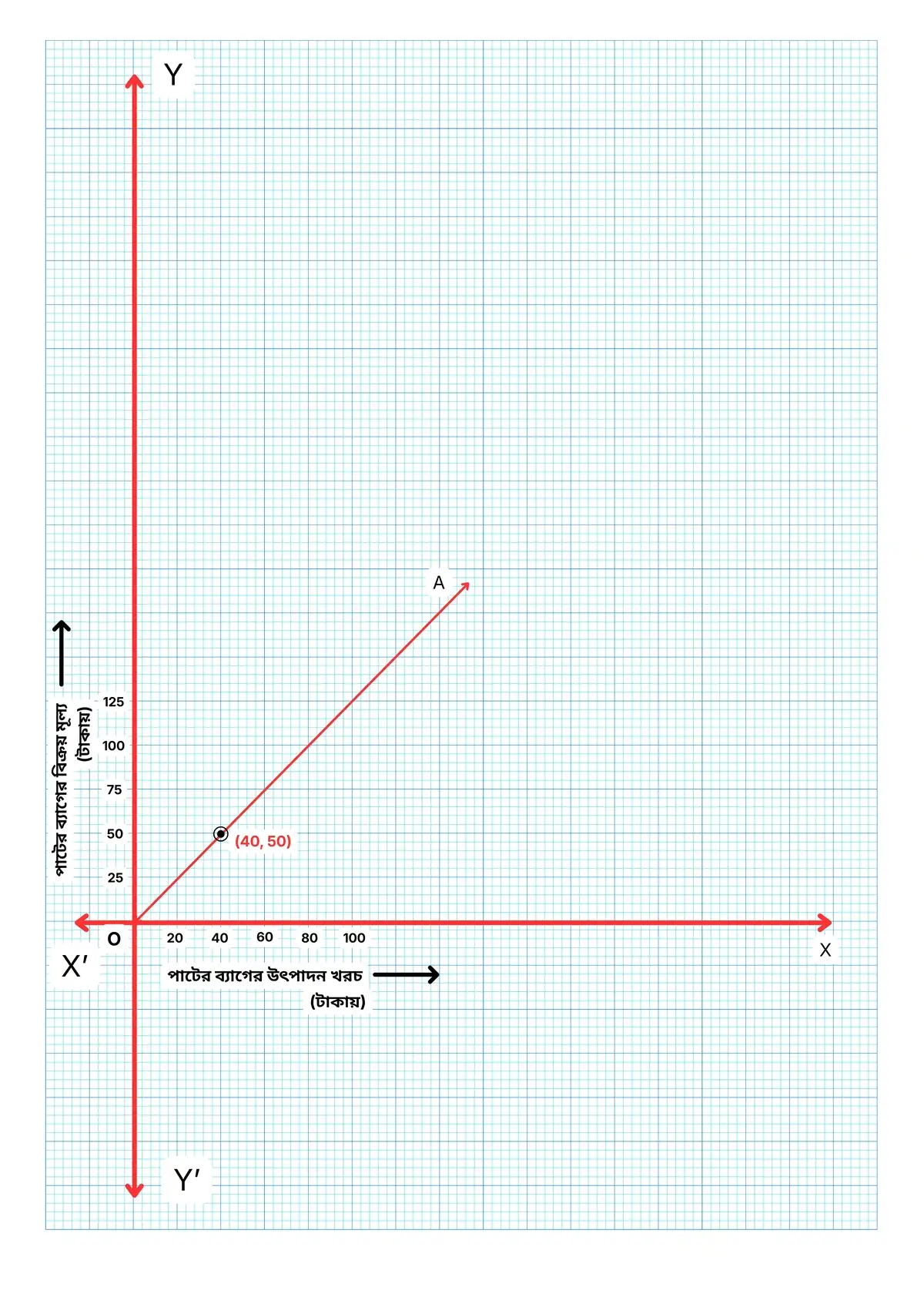
(a) লেখচিত্র দেখে ক্রয়মূল্য ও বিক্রয়মূল্যের সম্পর্ক লিখি।

(b) যে পাটের ব্যাগের উৎপাদন খরচ 60 টাকা তার বিক্রয়মূল্য কত হবে?

(c) যে পাটের ব্যাগের বিক্রয়মূল্য 125 টাকা তার উৎপাদন খরচ কী হবে লেখচিত্র দেখে লিখি।

(d) লেখচিত্র থেকে শতকরা লাভ বা ক্ষতি হিসাব করে লিখি।

(e) লেখচিত্র থেকে বিক্রয়মূল্যের ওপর শতকরা লাভ বা ক্ষতি লিখি।

সমাধান –

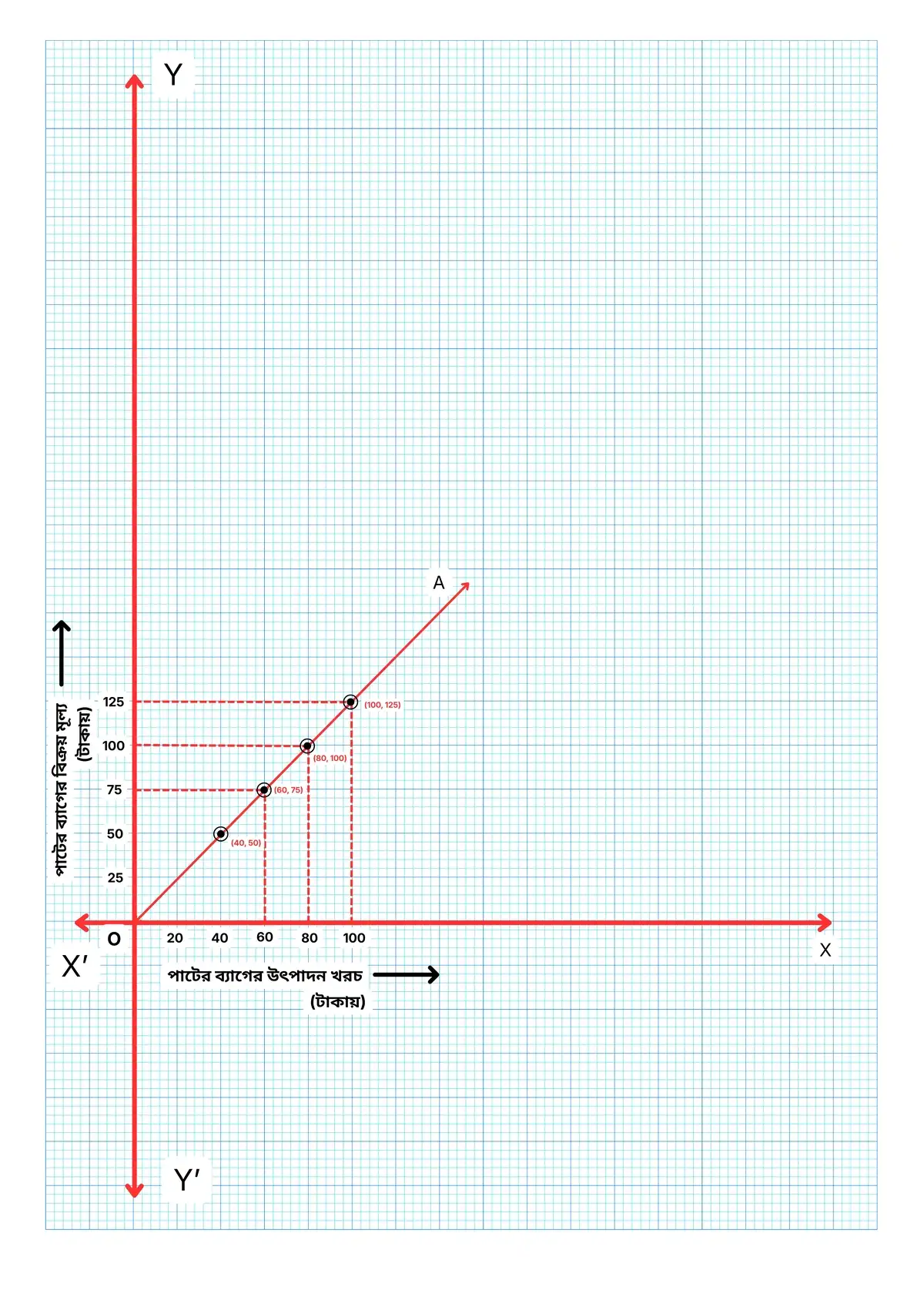
(a) লেখচিত্র থেকে স্পষ্টতই, ক্রয়মূল্য ও বিক্রয়মূল্যের সম্পর্ক সরল সমানুপাতী।

(b) লেখচিত্র থেকে দেখা যায়, যে পাটের ব্যাগের উৎপাদন খরচ 60 টাকা তার বিক্রয়মূল্য 75 টাকা।

(c) যে পাটের ব্যাগের বিক্রয়মূল্য 125 টাকা তার উৎপাদন খরচ 100 টাকা।

(d) লেখচিত্র থেকে দেখা যাচ্ছে, যে পাটের ব্যাগের উৎপাদন খরচ 100 টাকা হলে বিক্রয়মূল্য হয় 125 টাকা।

∴ 100 টাকায় লাভ হয় (125 – 100) টাকা = 25 টাকা।

∴ লাভের শতকরা হার 25%।

(e) লেখচিত্র থেকে দেখা যাচ্ছে, যে পাটের ব্যাগের বিক্রয়মূল্য 100 টাকা হয় তার উৎপাদন খরচ হয় 80 টাকা।

∴ 100 টাকা বিক্রয়মূল্যে লাভ হয় (100 – 80) = 20 টাকা।

∴ বিক্রয়মূল্যের উপর শতকরা লাভ 20%।

3. সুবীর কাকা 176 টাকা মূল্যে একটি ঘড়ি বিক্রি করেছেন। যদি ঘড়িটি বিক্রি করে সুবীর কাকার 12% ক্ষতি হয়, তাহলে হিসাব করে দেখি তিনি কত টাকায় ঘড়িটি কিনেছিলেন?

সমাধান –

যেহেতু ঘড়িটি বিক্রি করে সুবীর কাকার 12% ক্ষতি হয়েছে।

ধরি, ঘড়িটির ক্রয়মূল্য 100 টাকা।

\(\therefore\) ঘড়িটির বিক্রয়মূল্য = (100-12) টাকা = 88 টাকা।

\(\therefore\) 88 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য 100 টাকা।

1 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\frac{100}{88}\) টাকা।

176 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\frac{100 \times 176}{88}\) টাকা = 200 টাকা।

\(\therefore\) ঘড়িটি সুবীর কাকা 200 টাকায় কিনেছিলেন।

4. আনোয়ারা বিবি 10টি লেবু 30 টাকায় কিনে প্রতি ডজন 42 টাকায় বিক্রি করেছিলেন। হিসাব করে দেখি, আনোয়ারা বিবির শতকরা কত লাভ বা ক্ষতি হল?

সমাধান –

10টি লেবুর ক্রয়মূল্য 30 টাকা।

\(\therefore\) 1টি লেবুর ক্রয়মূল্য \(\frac{30}{10}\) টাকা = 3 টাকা।

আবার, 12টি লেবুর বিক্রয়মূল্য 42 টাকা।

\(\therefore\) 1টি লেবুর বিক্রয়মূল্য \(\frac{42}{12}\) টাকা = \(\frac{7}{2}\) টাকা।

\(\therefore\) লাভ = \((\frac{7}{2} – 3)\) টাকা = \((\frac{7-6}{2})\) টাকা = \(\frac{1}{2}\) টাকা।

\(\therefore\) শতকরা লাভ

= \( (\frac{\text{লাভ}}{\text{ক্রয়মূল্য}} \times 100)\%\)

= \( (\frac{\frac{1}{2}}{3} \times 100)\%\)

= \( (\frac{1}{6} \times 100)\%\)

= \( 16\frac{2}{3}\%\)।

\(\therefore\) শতকরা লাভ \(16\frac{2}{3}\%\)।

5. অমলবাবু একটি ছবি 20% ক্ষতিতে বিক্রয় করলেন। কিন্তু আরও 200 টাকা বেশি মূল্যে বিক্রয় করলে 5% লাভ করতেন। তিনি ছবিটি কত মূল্যে কিনেছিলেন হিসাব করে লিখি।

সমাধান –

ধরি, অমলবাবু ছবিটি \(x\) টাকায় ক্রয় করেছিলেন।

শতকরা ক্ষতি = 20%

\(\therefore\) ক্ষতি = \(\frac{20x}{100}\) টাকা = \(\frac{x}{5}\) টাকা।

\(\therefore\) বিক্রয়মূল্য = (ক্রয়মূল্য – ক্ষতি) = \((x – \frac{x}{5})\) টাকা = \(\frac{4x}{5}\) টাকা।

বিক্রয়মূল্য আরও 200 টাকা বেশি হলে পরিবর্তিত বিক্রয়মূল্য = \((\frac{4x}{5} + 200)\) টাকা।

তখন লাভ = \(\{(\frac{4x}{5} + 200) – x\}\) টাকা

= \( (\frac{4x}{5} – x + 200)\) টাকা

= \( (200 – \frac{x}{5})\) টাকা।

\(\therefore\) শতকরা লাভ

= \( (\frac{\text{লাভ}}{\text{ক্রয়মূল্য}} \times 100)\%\)

= \( \{\frac{(200 – \frac{x}{5})}{x} \times 100\}\%\)

শর্তানুসারে,

\(\{\frac{(200 – \frac{x}{5})}{x} \times 100\} = 5\)

বা, \(\frac{(200 – \frac{x}{5})}{x} = \frac{5}{100}\)

বা, \(\frac{(200 – \frac{x}{5})}{x} = \frac{1}{20}\)

বা, \(20(200 – \frac{x}{5}) = x\)

বা, \(4000 – 4x = x\)

বা, \(5x = 4000\)

বা, \(x = 800\)

\(\therefore\) অমলবাবু ছবিটি 800 টাকায় কিনেছিলেন।

6. সুপ্রিয়া একটি ঘড়ি কিনেছে। যদি সে ঘড়িটি 370 টাকায় বিক্রি করে, তখন তার যত টাকা লাভ হবে, 210 টাকায় বিক্রি করলে তত টাকা ক্ষতি হবে। হিসাব করে দেখি ঘড়িটির ক্রয়মূল্য কত?

সমাধান –

ধরি, ঘড়িটির ক্রয়মূল্য \(x\) টাকা।

370 টাকা বিক্রয়মূল্য হলে লাভ = (370 – \(x\)) টাকা।

আবার, 210 টাকা বিক্রয়মূল্য হলে ক্ষতি = (\(x\) – 210) টাকা।

শর্তানুসারে,

\(370 – x = x – 210\)

বা, \(x + x = 370 + 210\)

বা, \(2x = 580\)

বা, \(x = \frac{580}{2}\)

বা, \(x = 290\)

\(\therefore\) ঘড়িটির ক্রয়মূল্য 290 টাকা।

7. আমার দিদি অরুণ মামার দোকান থেকে 255 টাকার একটি ছাতা কিনল। অরুণ মামা যদি ছাতার ধার্যমূল্যের ওপর 15% ছাড় দিয়ে থাকেন, তবে ওই ছাতার ধার্যমূল্য কত ছিল হিসাব করে লিখি।

সমাধান –

ধরি, ছাতার ধার্যমূল্য ছিল 100 টাকা।

অরুণ মামা যদি ছাতার ধার্যমূল্যের ওপর 15% ছাড় দিয়ে থাকেন, তবে ছাতাটির বিক্রয়মূল্য = (100-15) টাকা = 85 টাকা।

\(\therefore\) 85 টাকা বিক্রয়মূল্য হলে ধার্যমূল্য 100 টাকা।

1 টাকা বিক্রয়মূল্য হলে ধার্যমূল্য \(\frac{100}{85}\) টাকা।

255 টাকা বিক্রয়মূল্য হলে ধার্যমূল্য \(\frac{100 \times 255}{85}\) টাকা = 300 টাকা।

\(\therefore\) ওই ছাতার ধার্যমূল্য ছিল 300 টাকা।

8. আমার বন্ধু একটি গল্পের বইয়ের লিখিত মূল্যের উপর \(25\%\) ছাড়ে কিনল। সে যদি বইটি লিখিত মূল্যেই বিক্রি করে, তবে সে শতকরা কত লাভ করবে হিসাব করে লিখি।

সমাধান – ধরি, গল্পের বইয়ের লিখিত মূল্য \(100\) টাকা।

লিখিত মূল্যের উপর ছাড় \(25\%\)

\(\therefore\) বিক্রয় মূল্য = \( (100-25)\) টাকা = \( 75\) টাকা।

\(\therefore\) আমার বন্ধু বইটি কিনল \(75\) টাকায়।

আমার বন্ধু বইটি বিক্রয় করে লিখিত মূল্যে অর্থাৎ \(100\) টাকায়।

\(\therefore\) বইটি বিক্রি করে বন্ধুর লাভ = \((100 -75)\) টাকা = \( 25\) টাকা।

∴ শতকরা লাভ $=\left(\frac{\mathrm{লাভ}}{\mathrm{ক্রয়মূল্য}}\times 100\right)$ টাকা

= \( \left(\frac{25}{75} \times 100\right)\) টাকা

= \( \frac{100}{3}\) টাকা

= \( 33\frac{1}{3}\) টাকা

\(\therefore\) বইটি বিক্রি করে আমার বন্ধুর লাভ শতকরা \(33\frac{1}{3}\) টাকা।

9. নিয়ামতচাচা প্রতিটি \(5\) টাকা দরে \(150\) টি ডিম কিনেছেন। কিন্তু দোকানে এনে দেখলেন \(8\) টি ডিম ফেটে গেছে এবং \(7\) টি ডিম পচা। প্রতিটি ডিম \(6\) টাকা দরে বিক্রি করলে, নিয়ামতচাচার শতকরা কত লাভ বা ক্ষতি হবে হিসাব করে লিখি।

সমাধান – নিয়ামতচাচা প্রতিটি \(5\) টাকা দরে \(150\) টি ডিম কিনেছেন।

\(\therefore\) \(150\) টি ডিমের ক্রয়মূল্য \((150 \times 5)\) টাকা = \( 750\) টাকা

\(150\) টি ডিমের মধ্যে \(8\) টি ডিম ফেটে গেছে এবং \(7\) টি ডিম পচা।

\(\therefore\) এখন ডিমের সংখ্যা = \( \{150-(8+7)\}\) টি = \( 135\) টি।

\(135\) টি ডিম প্রতিটি \(6\) টাকা দরে বিক্রয় করলে, \(135\) টি ডিমের বিক্রয়মূল্য = \( (135 \times 6)\) টাকা = \( 810\) টাকা

\(\therefore\) লাভ = \(\) বিক্রয়মূল্য – ক্রয়মূল্য = \( (810 – 750)\) টাকা = \( 60\) টাকা।

∴ শতকরা লাভ $=\left(\frac{\mathrm{লাভ}}{\mathrm{ক্রয়মূল্য}}\times 100\right)$ টাকা

= \( \left(\frac{60}{750} \times 100\right)\) টাকা

= \( 8\) টাকা

\(\therefore\) নিয়ামতচাচার শতকরা লাভ হবে \(8\) টাকা।

10. আসিফচাচা একটি খেলনা \(5\%\) লাভে বিক্রি করলেন। যদি খেলনাটির ক্রয়মূল্য \(20\%\) কম এবং বিক্রয়মূল্য \(34\) টাকা কম হত, তাহলে আসিফ চাচার \(10\%\) লাভ হত। খেলনাটির ক্রয়মূল্য হিসাব করে লিখি।

সমাধান – ধরি, খেলনাটির ক্রয়মূল্য \(x\) টাকা।

শতকরা লাভ = \( 5\%\)

\(\therefore\) লাভ = \( \frac{5x}{100}\) টাকা = \( \frac{x}{20}\) টাকা

\(\therefore\) বিক্রয়মূল্য

= \(\) ক্রয়মূল্য \(+\) লাভ

= \( \left(x + \frac{x}{20}\right)\) টাকা

= \( \frac{21x}{20}\) টাকা

ক্রয়মূল্য \(20\%\) কম হলে, পরিবর্তিত ক্রয়মূল্য –

= \( \left(x – \frac{20x}{100}\right)\) টাকা

= \( \left(x – \frac{x}{5}\right)\) টাকা

= \( \frac{4x}{5}\) টাকা

বিক্রয়মূল্য \(34\) টাকা কম হলে, পরিবর্তিত বিক্রয়মূল্য – \(\left(\frac{21x}{20} – 34\right)\) টাকা

\(\therefore\) লাভ = \(\) (বিক্রয়মূল্য – ক্রয়মূল্য)

= \( \left\{\left(\frac{21x}{20} – 34\right) – \frac{4x}{5}\right\}\) টাকা

= \( \left(\frac{21x}{20} – \frac{4x}{5} – 34\right)\) টাকা

= \( \left(\frac{21x – 16x – 680}{20}\right)\) টাকা

= \( \left(\frac{5x – 680}{20}\right)\) টাকা

= \( \left(\frac{x – 136}{4}\right)\) টাকা

∴ শতকরা লাভ $=\left(\frac{\mathrm{লাভ}}{\mathrm{ক্রয়মূল্য}}\times 100\right)$ টাকা

= \( \left(\frac{\frac{x-136}{4}}{\frac{4x}{5}} \times 100\right)\) টাকা

= \( \left(\frac{5x-680}{16x} \times 100\right)\) টাকা

শর্তানুসারে,

\(\left(\frac{5x-680}{16x} \times 100\right) = 10\)

বা, \(\frac{5x-680}{16x} = \frac{10}{100}\)

বা, \(\frac{5x-680}{16x} = \frac{1}{10}\)

বা, \(10 (5x – 680) = 16x\)

বা, \(50x – 6800 = 16x\)

বা, \(50x – 16x = 6800\)

বা, \(34x = 6800\)

বা, \(x = \frac{6800}{34}\)

বা, \(x = 200\)

\(\therefore\) খেলনাটির ক্রয়মূল্য \(200\) টাকা।

11. টাকায় \(12\) টি জিনিস বিক্রয় করে \(4\%\) ক্ষতি হয়। টাকায় কটি জিনিস বিক্রয় করলে \(44\%\) লাভ হবে?

সমাধান – \(12\) টি জিনিসের বিক্রয়মূল্য \(1\) টাকা।

\(\therefore\) \(1\) টি জিনিসের বিক্রয়মূল্য \(\frac{1}{12}\) টাকা।

\(12\) টি জিনিস বিক্রি করে \(4\%\) ক্ষতি হয়।

\(\therefore\) \(96\) টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(100\) টাকা

\(1\) টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\frac{100}{96}\) টাকা

এবং, \(\frac{1}{12}\) টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\left(\frac{100}{96} \times \frac{1}{12}\right)\) টাকা = \( \frac{25}{288}\) টাকা

\(44\%\) লাভ অর্থাৎ,

\(100\) টাকা ক্রয়মূল্য হলে বিক্রয়মূল্য \(144\) টাকা

\(1\) টাকা ক্রয়মূল্য হলে বিক্রয়মূল্য \(\frac{144}{100}\) টাকা

\(\frac{25}{288}\) টাকা ক্রয়মূল্য হলে বিক্রয়মূল্য \(\left(\frac{144}{100} \times \frac{25}{288}\right)\) টাকা

= \( \frac{1}{8}\) টাকা

\(\therefore \frac{1}{8}\) টাকায় পাওয়া যায় \(1\) টি জিনিস।

\(\therefore\) \(1\) টাকায় পাওয়া যায় \(\left(1 \div \frac{1}{8}\right)\) টি জিনিস

= \( (1 \times 8)\) টি জিনিস

= \( 8\) টি জিনিস।

\(\therefore\) টাকায় \(8\) টি জিনিস বিক্রয় করলে তার \(44\%\) লাভ হবে।

12. রমা পিসি দুটি শাড়ি তৈরি করে একটি \(15\%\) এবং অপরটি \(20\%\) লাভে বিক্রি করলেন। তার মোট লাভ হল \(262.50\) টাকা। শাড়ি দুটির উৎপাদন ব্যয় \(1:3\) হলে, শাড়ি দুটির প্রত্যেকটির উৎপাদন ব্যয় কত?

সমাধান –

ধরি, একটি শাড়ির উৎপাদন ব্যয় \(x\) টাকা

\(\therefore\) অন্য শাড়ির উৎপাদন ব্যয় \(3x\) টাকা। [যেহেতু, শাড়ি দুটির উৎপাদন ব্যয়ের অনুপাত \(1:3\)]

রমা পিসি প্রথম শাড়িতে লাভ করেন \(15\%\)

\(\therefore\) লাভ = \( \frac{15x}{100}\) টাকা।

রমা পিসি দ্বিতীয় শাড়িতে লাভ করেন \(20\%\)

\(\therefore\) লাভ = \( \frac{20 \times 3x}{100}\) টাকা = \( \frac{60x}{100}\) টাকা

শর্তানুসারে,

\(\frac{15x}{100} + \frac{60x}{100} = 262.50\)

বা, \(\frac{15x+60x}{100} = 262.50\)

বা, \(75x = 26250\)

বা, \(x = \frac{26250}{75}\)

বা, \(x = 350\)

\(\therefore 3x = 3 \times 350 = 1050\)

\(\therefore\) প্রথম শাড়ির উৎপাদন ব্যয় \(350\) টাকা এবং দ্বিতীয় শাড়ির উৎপাদন ব্যয় \(1050\) টাকা।

13. এক ব্যক্তি \(2\) টাকায় \(15\) টি হিসেবে কিছু লজেন্স কিনলেন। তিনি অর্ধেক টাকায় \(5\) টি দরে এবং বাকি অর্ধেক টাকায় \(10\) টি দরে বিক্রি করলেন। তার শতকরা কত লাভ বা ক্ষতি হল?

সমাধান – ধরি, ওই ব্যক্তি \(2x\) টি লজেন্স কিনেছেন।

\(\therefore\) \(15\) টি লজেন্সের দাম \(2\) টাকা

\(1\) টি লজেন্সের দাম \(\frac{2}{15}\) টাকা

\(2x\) টি লজেন্সের দাম \(\frac{2 \times 2x}{15}\) টাকা = \( \frac{4x}{15}\) টাকা

\(\therefore 2x\) টি লজেন্সের ক্রয়মূল্য \(\frac{4x}{15}\) টাকা

তিনি অর্ধেক টাকায় \(5\) টি দরে এবং বাকি অর্ধেক টাকায় \(10\) টি দরে বিক্রি করলেন।

\(\therefore x\) টি লজেন্স বিক্রি করেন টাকায় \(5\) টি দরে এবং বাকি \(x\) টি লজেন্স বিক্রি করেন টাকায় \(10\) টি দরে।

\(\therefore\) \(5\) টি লজেন্সের বিক্রয়মূল্য \(1\) টাকা

\(1\) টি লজেন্সের বিক্রয়মূল্য \(\frac{1}{5}\) টাকা

\(x\) টি লজেন্সের বিক্রয়মূল্য \(\frac{x}{5}\) টাকা

আবার,

\(10\) টি লজেন্সের বিক্রয়মূল্য \(1\) টাকা

\(1\) টি লজেন্সের বিক্রয়মূল্য \(\frac{1}{10}\) টাকা

\(x\) টি লজেন্সের বিক্রয়মূল্য \(\frac{x}{10}\) টাকা

\(\therefore\) মোট \(2x\) টি লজেন্সের বিক্রয়মূল্য

= \( \left(\frac{x}{5} + \frac{x}{10}\right)\) টাকা

= \( \frac{2x+x}{10}\) টাকা

= \( \frac{3x}{10}\) টাকা

\(\therefore 2x\) টি লজেন্স বিক্রয় করে লাভ = (বিক্রয়মূল্য – ক্রয়মূল্য) = \( \left(\frac{3x}{10} – \frac{4x}{15}\right)\) টাকা

= \( \frac{9x-8x}{30}\) টাকা

= \( \frac{x}{30}\) টাকা

∴ শতকরা লাভ$=\left(\frac{\mathrm{লাভ}}{\mathrm{ক্রয়মূল্য}}\times 100\right)$ টাকা

= \( \frac{\frac{x}{30}}{\frac{4x}{15}} \times 100\) টাকা

= \( \frac{x}{30} \div \frac{4x}{15} \times 100\) টাকা

= \( \frac{x}{30} \times \frac{15}{4x} \times 100\) টাকা

= \( \frac{100}{8}\) টাকা

= \( \frac{25}{2}\) টাকা

= \( 12\frac{1}{2}\) টাকা

উত্তর – তার শতকরা লাভ হল \(12\frac{1}{2}\) টাকা।

14. আফসারচাচা দুটি কাঠের চেয়ার একই দামে তৈরি করলেন এবং কাঠের চেয়ার দুটির প্রত্যেকটির ধার্যমূল্য ঠিক করলেন 1250 টাকা। তিনি একটি চেয়ার \(8\%\) ছাড়ে বিক্রি করে \(15\%\) লাভ করলেন। যদি তিনি দ্বিতীয় চেয়ারটি 1120 টাকায় বিক্রি করেন, তাহলে তার মোটের ওপর শতকরা কত লাভ বা ক্ষতি হল?

সমাধান –

প্রথম চেয়ারের ধার্যমূল্য 1250 টাকা।

ছাড় = \( 8\%\)

\(\therefore\) 100 টাকা ধার্যমূল্য হলে বিক্রয়মূল্য \((100-8)\) টাকা = \( 92\) টাকা।

100 টাকা ধার্যমূল্য হলে বিক্রয়মূল্য 92 টাকা।

1 টাকা ধার্যমূল্য হলে বিক্রয়মূল্য \(\frac{92}{100}\) টাকা।

1250 টাকা ধার্যমূল্য হলে বিক্রয়মূল্য \(\frac{92 \times 1250}{100}\) টাকা

= \( 1150\) টাকা।

\(\therefore\) প্রথম চেয়ারের বিক্রয়মূল্য 1150 টাকা।

প্রথম চেয়ার বিক্রি করে লাভ = \( 15\%\)

\(\therefore\) 115 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য 100 টাকা।

1 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\frac{100}{115}\) টাকা।

1150 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\frac{100 \times 1150}{115}\) টাকা

= \( 1000\) টাকা।

\(\therefore\) প্রথম এবং দ্বিতীয় চেয়ারের প্রত্যেকটির ক্রয়মূল্য 1000 টাকা করে।

\(\therefore\) দুটি চেয়ারের মোট ক্রয়মূল্য = \( (1000+1000)\) টাকা = \( 2000\) টাকা।

আবার দুটি চেয়ারের মোট বিক্রয়মূল্য = \( (1150+1120)\) টাকা = \( 2270\) টাকা।

\(\therefore\) লাভ = \(\) (বিক্রয়মূল্য – ক্রয়মূল্য) = \( (2270 – 2000)\) টাকা = \( 270\) টাকা।

∴ শতকরা লাভ $=\left(\frac{\mathrm{লাভ}}{\mathrm{ক্রয়মূল্য}}\times 100\right)$ টাকা

= \( \left(\frac{270}{2000} \times 100\right)\) টাকা

= \( \frac{27}{2}\) টাকা

= \( 13.5\) টাকা।

\(\therefore\) আফসারচাচা মোটের ওপর শতকরা \(13.5\%\) লাভ করে।

15. একটি বিশেষ ধরণের কলমের ধার্যমূল্য 36.50 টাকা। রফিকচাচা শুভমকে একটি পেনে 2.90 টাকা ছাড় দিয়ে বিক্রি করে \(12\%\) লাভ করলেন। যদি ওই ধরণের আরএকটি কলম মিতাকে 34.50 টাকায় বিক্রি করেন, তাহলে তার মোটের ওপর শতকরা কত লাভ বা ক্ষতি হল নির্ণয় করি।

সমাধান –

কলমটির ধার্যমূল্য 36.50 টাকা।

ছাড় = \( 2.90\) টাকা।

\(\therefore\) বিক্রয়মূল্য = \(\) (ধার্যমূল্য – ছাড়) = \( (36.50 – 2.90)\) টাকা = \( 33.60\) টাকা।

শতকরা লাভ = \( 12\%\)

1 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\frac{100}{112}\) টাকা।

33.60 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\frac{100 \times 33.60}{112}\) টাকা

= \( 30\) টাকা।

\(\therefore\) প্রথম কলমের ক্রয়মূল্য 30 টাকা।

\(\therefore\) একই প্রকারের দ্বিতীয় কলমের ক্রয়মূল্য = \( 30\) টাকা।

দ্বিতীয় কলমের বিক্রয়মূল্য = \( 34.50\) টাকা।

\(\therefore\) লাভ = (বিক্রয়মূল্য – ক্রয়মূল্য) = \( (34.50 – 30)\) টাকা = \( 4.50\) টাকা।

∴ শতকরা লাভ $=\left(\frac{\mathrm{লাভ}}{\mathrm{ক্রয়মূল্য}}\times 100\right)$ টাকা

= \( \left(\frac{4.50}{30} \times 100\right)\) টাকা

= \( 15\) টাকা।

\(\therefore\) দ্বিতীয় কলম বিক্রি করে তাঁর শতকরা লাভ \(15\%\)।

16. একটি পুস্তক প্রকাশক 2000 কপি বই ছাপার জন্য 3875 টাকার কাগজ কিনতে, 3315 টাকা ছাপাতে এবং 810 টাকা বাঁধনোর জন্য খরচ করেন। তিনি পুস্তক বিক্রেতাদের \(20\%\) ছাড় দিয়ে \(20\%\) লাভে বিক্রি করেন। প্রতিটি বইয়ের ধার্যমূল্য কত নির্ণয় করি।

সমাধান –

2000 কপি বই তৈরি করতে মোট খরচ = \( (3875+3315+810)\) টাকা = \( 8000\) টাকা।

\(\therefore\) একটি বইয়ের উৎপাদন খরচ = \( 8000 / 2000\) টাকা = \( 4\) টাকা।

লাভ = \( 20\%\)

\(\therefore\) 100 টাকা ক্রয়মূল্য হলে বিক্রয়মূল্য 120 টাকা।

1 টাকা ক্রয়মূল্য হলে বিক্রয়মূল্য \(\frac{120}{100}\) টাকা।

4 টাকা ক্রয়মূল্য হলে বিক্রয়মূল্য \(\frac{120 \times 4}{100}\) টাকা

= \( 4.80\) টাকা।

ছাড় = \( 20\%\)

\(\therefore\) 80 টাকা বিক্রয়মূল্য হলে ধার্যমূল্য 100 টাকা।

1 টাকা বিক্রয়মূল্য হলে ধার্যমূল্য \(\frac{100}{80}\) টাকা।

4.80 টাকা বিক্রয়মূল্য হলে ধার্যমূল্য \(\frac{100 \times 4.80}{80}\) টাকা

= \( 6\) টাকা।

\(\therefore\) প্রতিটি বইয়ের ধার্যমূল্য 6 টাকা।

17. হাসিমাবিবি দুটি হস্তশিল্পের প্রত্যেকটি 1248 টাকায় বিক্রি করেন। তিনি প্রথমটিতে \(4\%\) লাভ করেন, কিন্তু দ্বিতীয়টিতে \(4\%\) ক্ষতি হয়। তাঁর মোট লাভ বা ক্ষতি কত হল?

সমাধান –

প্রথম হস্তশিল্প বিক্রি করে \(4\%\) লাভ করেন।

\(\therefore\) 104 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য 100 টাকা।

1 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\frac{100}{104}\) টাকা।

1248 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\frac{100 \times 1248}{104}\) টাকা

= \( 1200\) টাকা।

আবার, দ্বিতীয় হস্তশিল্প বিক্রি করে \(4\%\) ক্ষতি হয়।

অর্থাৎ, 96 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য 100 টাকা।

1 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\frac{100}{96}\) টাকা।

1248 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\frac{100 \times 1248}{96}\) টাকা

= \( 1300\) টাকা।

\(\therefore\) মোট ক্রয়মূল্য = \( (1200+1300)\) টাকা = \( 2500\) টাকা।

এবং, মোট বিক্রয়মূল্য = \( (2 \times 1248)\) টাকা = \( 2496\) টাকা।

\(\therefore\) ক্ষতি = \(\) (ক্রয়মূল্য – বিক্রয়মূল্য) = \( (2500 – 2496)\) টাকা = \( 4\) টাকা।

\(\therefore\) তাঁর মোট ক্ষতি 4 টাকা।

18. করিম মোহনকে 4860 টাকার একটি মোবাইল ফোন বিক্রি করায় \(19\%\) ক্ষতি হয়, মোহন রহিমকে যে দামে বিক্রি করে সেই দামে করিম মোহনকে বিক্রি করলে করিমের \(17\%\) লাভ হয়। মোহনের শতকরা লাভ কত?

সমাধান: করিম মোহনকে 4860 টাকার একটি মোবাইল ফোন বিক্রি করায় \(19\%\) ক্ষতি হয়।

\(\therefore\) 81 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য 100 টাকা।

1 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\frac{100}{81}\) টাকা।

4860 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\frac{100 \times 4860}{81}\) টাকা

= \( 6000\) টাকা।

করিমের লাভ = \( 17\%\)

\(\therefore\) 100 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য 117 টাকা।

1 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\frac{117}{100}\) টাকা।

6000 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\frac{117 \times 6000}{100}\) টাকা

= \( 7020\) টাকা।

অর্থাৎ, মোহন করিমের থেকে মোবাইলটি ক্রয় করে 4860 টাকায় এবং মোহন রহিমকে মোবাইলটি বিক্রয় করে 7020 টাকায়।

\(\therefore\) মোহনের লাভ

= \(\) (বিক্রয়মূল্য – ক্রয়মূল্য)

= \( (7020 – 4860)\) টাকা

= \( 2160\) টাকা।

∴ শতকরা লাভ $=\left(\frac{\mathrm{লাভ}}{\mathrm{ক্রয়মূল্য}}\times 100\right)$ টাকা

= \( \left(\frac{2160}{4860} \times 100\right)\) টাকা

= \( 44 \frac{4}{9}\) টাকা।

\(\therefore\) মোহনের শতকরা লাভ \(44 \frac{4}{9}\%\)।

19. ফিরোজচাচা একটি প্যান্ট \(20\%\) লাভে এবং একটি জামা \(15\%\) লাভে বিক্রয় করে মোট 719.50 টাকা পেলেন। তিনি যদি প্যান্টটি \(25\%\) এবং জামাটি \(20\%\) লাভে বিক্রি করতেন, তাহলে তিনি আরও 30.50 টাকা বেশি পেতেন। প্যান্ট ও জামার ক্রয়মূল্য নির্ণয় করি।

সমাধান –

ধরি, প্যান্টের ক্রয়মূল্য \(x\) টাকা এবং জামার ক্রয়মূল্য \(y\) টাকা।

\(x + \frac{20x}{100} + y + \frac{15y}{100} = 719.50\)

বা, \(\frac{100x + 20x + 100y + 15y}{100} = 719.50\)

বা, \(120x + 115y = 71950\)

বা, \(24x + 23y = 14390\) — (i)

আবার,

\(x + \frac{25x}{100} + y + \frac{20y}{100} = 719.50 + 30.50\)

বা, \(\frac{100x + 25x + 100y + 20y}{100} = 750\)

বা, \(125x + 120y = 75000\)

বা, \(25x + 24y = 15000\) — (ii)

(i) নং ও (ii) নং সমীকরণকে বজ্রগুণন করে পাই,

\(\frac{x}{23(-15000) – 24(-14390)} = \frac{y}{25(-14390) – 24(-15000)} = \frac{1}{24(24) – 25(23)}\)

বা, \(\frac{x}{-345000 + 345360} = \frac{y}{-359750 + 360000} = \frac{1}{576 – 575}\)

বা, \(\frac{x}{360} = \frac{y}{250} = \frac{1}{1}\)

\(\therefore \frac{x}{360} = \frac{1}{1}\)

বা, \(x = 360\)

আবার, \(\frac{y}{250} = \frac{1}{1}\)

বা, \(y = 250\)

\(\therefore\) প্যান্টের দাম 360 টাকা এবং জামার দাম 250 টাকা।

20. রবীন কাকু 3000 টাকার চাল কিনলেন। তিনি \(\frac{1}{3}\) অংশ \(20\%\) ক্ষতিতে, \(\frac{2}{5}\) অংশ \(25\%\) লাভে বিক্রি করলেন। শতকরা কত লাভে তিনি বাকি অংশ বিক্রি করলে তাঁর মোটের ওপর \(10\%\) লাভ হবে।

সমাধান –

মোটের ওপর \(10\%\) লাভ হতে গেলে সমগ্র চালের বিক্রয়মূল্য হবে –

\(= (3000 + 3000 \times \frac{10}{100})\) টাকা

\(= (3000 + 300)\) টাকা

\(= 3300\) টাকা

\(\frac{1}{3}\) অংশ চালের ক্রয়মূল্য

\(= (3000 \times \frac{1}{3})\) টাকা

\(= 1000\) টাকা

\(\frac{1}{3}\) অংশ চাল \(20\%\) ক্ষতিতে বিক্রয় করলে বিক্রয়মূল্য

\(= (1000 – 1000 \times \frac{20}{100})\) টাকা

\(= (1000 – 200)\) টাকা

\(= 800\) টাকা

আবার, \(\frac{2}{5}\) অংশ চালের ক্রয়মূল্য

\(= (3000 \times \frac{2}{5})\) টাকা

\(= 1200\) টাকা

\(\frac{2}{5}\) অংশ চাল \(25\%\) লাভে বিক্রয় করলে বিক্রয়মূল্য

\(= (1200 + 1200 \times \frac{25}{100})\) টাকা

\(= (1200 + 300)\) টাকা

\(= 1500\) টাকা

\(\therefore\) অবশিষ্ট চালের ক্রয়মূল্য

\(= \{3000 – (1000 + 1200)\}\) টাকা

\(= (3000 – 2200)\) টাকা

\(= 800\) টাকা

অবশিষ্ট চালের বিক্রয়মূল্য হবে

\(= \{3300 – (800 + 1500)\}\) টাকা

\(= (3300 – 2300)\) টাকা

\(= 1000\) টাকা

\(\therefore\) অবশিষ্ট চাল বিক্রি করে লাভ \((1000 – 800)\) টাকা \(= 200\) টাকা

\(\therefore\) অবশিষ্ট চাল বিক্রি করে শতকরা লাভ

\(= (\frac{200}{800} \times 100)\) টাকা

\(= (\frac{1}{4} \times 100)\) টাকা

\(= 25\) টাকা

\(\therefore\) বাকি চাল তাকে \(25\%\) লাভে বিক্রয় করতে হবে।

21. এক ব্যবসায়ী এক ধরনের চা 80 টাকা প্রতি কিগ্রা দরে বিক্রি করে \(20\%\) ক্ষতি এবং অপর এক ধরনের চা 200 টাকা প্রতি কিগ্রা দরে বিক্রি করে \(25\%\) লাভ করেন। তিনি দুই ধরনের চা কী অনুপাতে মিশিয়ে প্রতি কিগ্রা 150 টাকা দরে বিক্রি করলে \(25\%\) লাভ হবে।

সমাধান –

ধরি, প্রথম প্রকারের \(x\) কেজি চা–এর সঙ্গে দ্বিতীয় প্রকারের \(y\) কেজি চা মেশাতে হবে।

\(\therefore\) মোট চা-এর পরিমাণ \((x+y)\) কেজি।

\(20\%\) ক্ষতি অর্থাৎ,

80 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য 100 টাকা।

\(25\%\) লাভ অর্থাৎ,

125 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য 100 টাকা।

1 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\frac{100}{125}\) টাকা।

200 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য \(\frac{100 \times 200}{125}\) টাকা

\(= 160\) টাকা।

\(\therefore (x+y)\) কেজি চা-এর ক্রয়মূল্য \((100x + 160y)\) টাকা।

\(25\%\) লাভ অর্থাৎ,

100 টাকা ক্রয়মূল্য হলে বিক্রয়মূল্য 125 টাকা।

1 টাকা ক্রয়মূল্য হলে বিক্রয়মূল্য \(\frac{125}{100}\) টাকা।

\((100x + 160y)\) টাকা ক্রয়মূল্য হলে বিক্রয়মূল্য \(\frac{125}{100} \times (100x + 160y)\) টাকা

\(= \frac{5}{4} \times (100x + 160y)\) টাকা।

প্রশ্নানুসারে,

\(\frac{5}{4} \times (100x + 160y) \text{টাকা} = 150 (x+y)\)

বা, \(500x + 800y = 600x + 600y\)

বা, \(500x – 600x = 600y – 800y\)

বা, \(-100x = -200y\)

বা, \(x = 2y\)

বা, \(\frac{x}{y} = \frac{2}{1}\)

বা, \(x:y = 2:1\)

\(\therefore\) দুই ধরনের চা \(2:1\) অনুপাতে মেশাতে হবে।

---

এই আর্টিকেলে নবম শ্রেণির গণিতের ‘লাভ ও ক্ষতি‘ অধ্যায়ের ‘কষে দেখি – 10.1’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।

কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করতে পারেন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।