পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) নবম শ্রেণির গণিত পাঠ্যবইয়ের তৃতীয় অধ্যায় হলো ‘লেখচিত্র’। এই পোস্টে ‘কষে দেখি – 3.2’-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।
1. নিম্নলিখিত বিন্দুগুলি ছক কাগজে স্থাপন করি ও কোথায় (অক্ষের উপর বা কোন পাদে) অবস্থিত তা লিখি।
(i) (3,0), (ii) (0,8), (iii) (-5,0), (iv) (0,-6), (v) (6,4), (vi) (-7,4), (vii) (9,-9), (viii) (-4,-5)
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে প্রদত্ত বিন্দুগুলি স্থাপন করা হল।
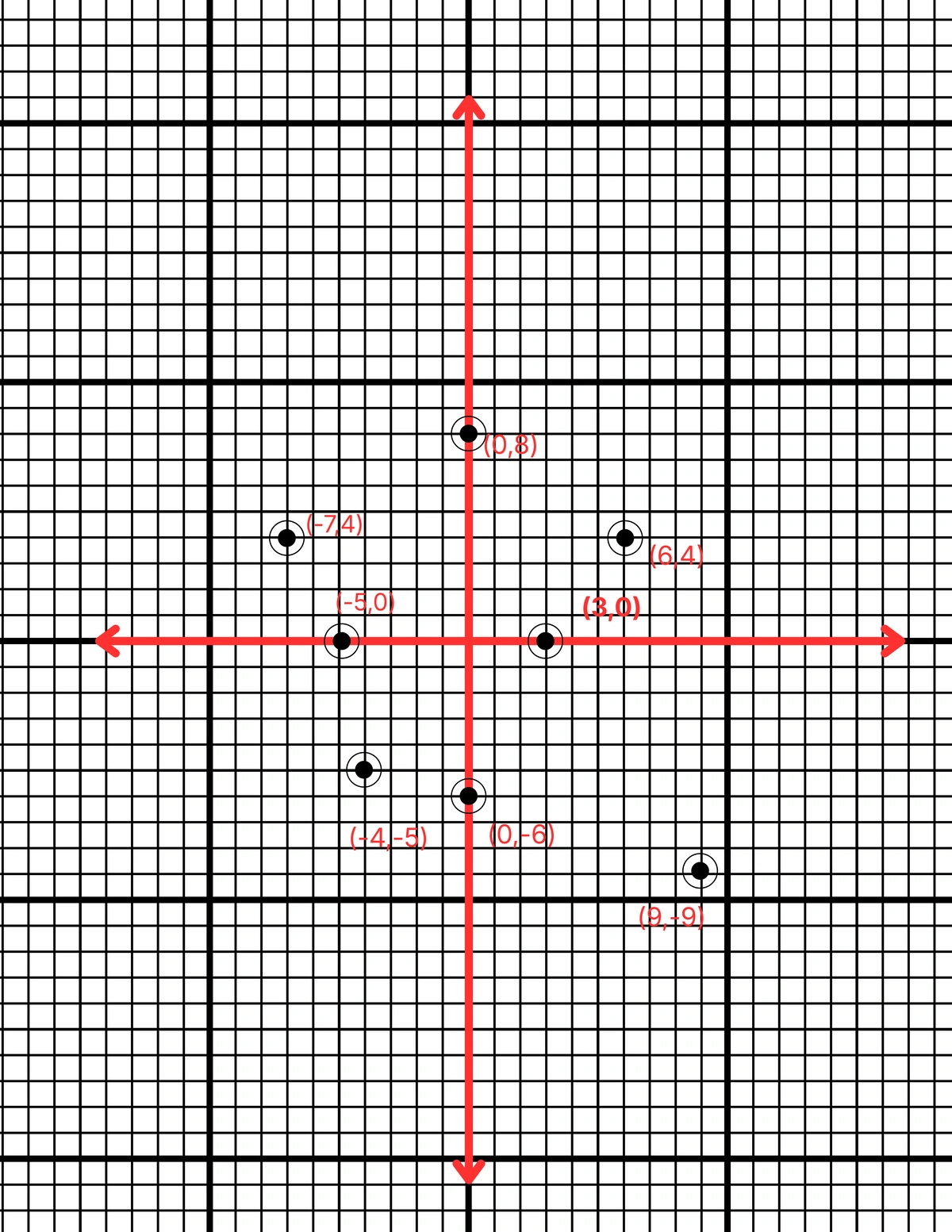
উত্তর –
(i) (3,0) বিন্দুটি x অক্ষের উপর অবস্থিত।
(ii) (0,8) বিন্দুটি y অক্ষের উপর অবস্থিত।
(iii) (-5,0) বিন্দুটি x অক্ষের উপর অবস্থিত।
(iv) (0,-6) বিন্দুটি y অক্ষের উপর অবস্থিত।
(v) (6,4) বিন্দুটি প্রথম পাদে অবস্থিত।
(vi) (-7,4) বিন্দুটি দ্বিতীয় পাদে অবস্থিত।
(vii) (9,-9) বিন্দুটি চতুর্থ পাদে অবস্থিত।
(viii) (-4,-5) বিন্দুটি তৃতীয় পাদে অবস্থিত।
2. ছক কাগজে XOX´ ও YOY´ পরস্পর লম্ব অক্ষ টেনে যেকোনো 5টি বিন্দু স্থাপন করি যারা তৃতীয় পাদে অবস্থিত।
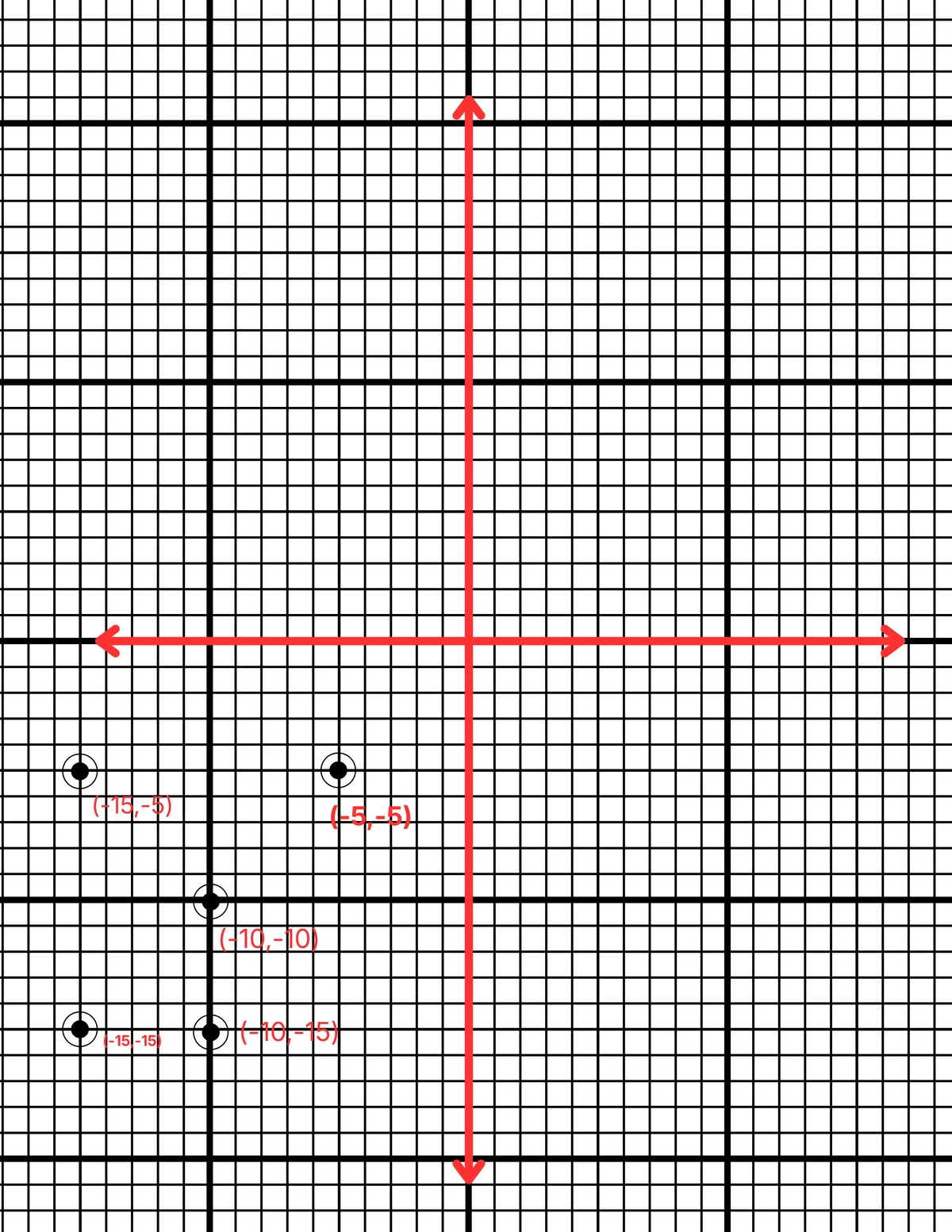
5টি বিন্দু হল (-15, -5), (-5, -5), (-10, -10), (-10, -15) এবং (-15, -15)।
3. নীচের বক্তব্যগুলি রৈখিক সমীকরণ আকারে প্রকাশ করি।
(i) 3 টি খাতা ও 2 টি পেনের দাম 55 টাকা এবং 4 টি খাতা ও 3 টি পেনের মোট দাম 75 টাকা।
সমাধান –
ধরি, একটি খাতার দাম x টাকা এবং একটি পেনের দাম y টাকা।
∴ 3 টি খাতা ও 2 টি পেনের মোট দাম = (3x+2y) টাকা এবং 4 টি খাতা ও 3 টি পেনের মোট দাম = (4x+3y) টাকা
শর্তানুসারে,
3x+2y = 55 — (i)
এবং 4x+3y = 75 — (ii)
(i) ও (ii) নং সমীকরণ দুটি হল প্রদত্ত সমস্যার নির্ণেয় রৈখিক সমীকরণ।
(ii) দুটি সংখ্যার যোগফল 80 এবং ওই দুটি সংখ্যার বিয়োগফলের 3 গুণ বড় সংখ্যাটির থেকে 20 বেশি।
সমাধান – ধরি, সংখ্যা দুটি হল x এবং y এবং x > y।
∴ x + y = 80 — (i)
এবং 3(x – y) = x + 20 — (ii)
(i) ও (ii) নং সমীকরণ দুটি হল প্রদত্ত সমস্যার নির্ণেয় রৈখিক সমীকরণ।
(iii) কোনো ভগ্নাংশের লব ও হরের প্রত্যেকটির সঙ্গে 2 যোগ করলে ভগ্নাংশটির মান হয় \(\frac{7}{9}\) এবং ভগ্নাংশের লব ও হর প্রত্যেকটি থেকে 3 বিয়োগ করলে ভগ্নাংশটির মান হয় \(\frac{1}{2}\) ।
সমাধান –
ধরি , ভগ্নাংশটি হল \(\frac{x}{y}\) ।
শর্তানুসারে ,
\(\frac{x+2}{y+2} = \frac{7}{9} \cdots (i)\)এবং,
\(\frac{x-3}{y-3} = \frac{1}{2} \cdots (ii)\)(i) ও (ii) নং সমীকরণ হল প্রদত্ত সমস্যাটির নির্ণেয় রৈখিক সমীকরণ ।
(iv) দুই অঙ্কবিশিষ্ট কোনো সংখ্যার দশকের অঙ্কটি এককের অঙ্কের দ্বিগুণ। অঙ্কদ্বয়কে উলটে লিখলে যে সংখ্যাটি পাওয়া যায় তা মূলসংখ্যা থেকে 27 কম।
সমাধান –
ধরি, দুই অঙ্কবিশিষ্ট সংখ্যার এককের ঘরের অঙ্ক \(x\) এবং দশকের ঘরের অঙ্ক \(y\)।
∴ সংখ্যাটি হবে – \(10y+x\)
অঙ্কদ্বয়কে উল্টে লিখলে সংখ্যাটি হবে – \(10x+y\)
শর্তানুসারে,
\(y = 2x\) —(i)
এবং \(10y+x – (10x+y) = 27\)
বা, \(10y + x – 10x – y = 27\)
বা, \(9y – 9x = 27\)
বা, \(9(y – x) = 27\)
বা, \(y – x = \frac{27}{9}\)
বা, \(y – x = 3\) —(ii)
∴ (i) ও (ii) নং সমীকরণ দুটি হল নির্ণেয় রৈখিক সমীকরণ।
4. নীচের বক্তব্যগুলি দুইচল বিশিষ্ট একঘাত সমীকরণ আকারে প্রকাশ করি ও সমীকরণগুলির লেখচিত্র অঙ্কন করি।
(i) বর্তমানে সুজাতার পিতার বয়স সুজাতার বয়স অপেক্ষা 26 বছর বেশি। [ ধরি, সুজাতার পিতার বয়স x বছর এবং সুজাতার বয়স y বছর ]
সমাধান –
যেহেতু সুজাতার বয়স y বছর এবং সুজাতার পিতার বয়স x বছর।
∴ \(x = y + 26\) —(i)
সুতরাং (i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 14 | 16 | 10 |
| y | -12 | -10 | -16 |
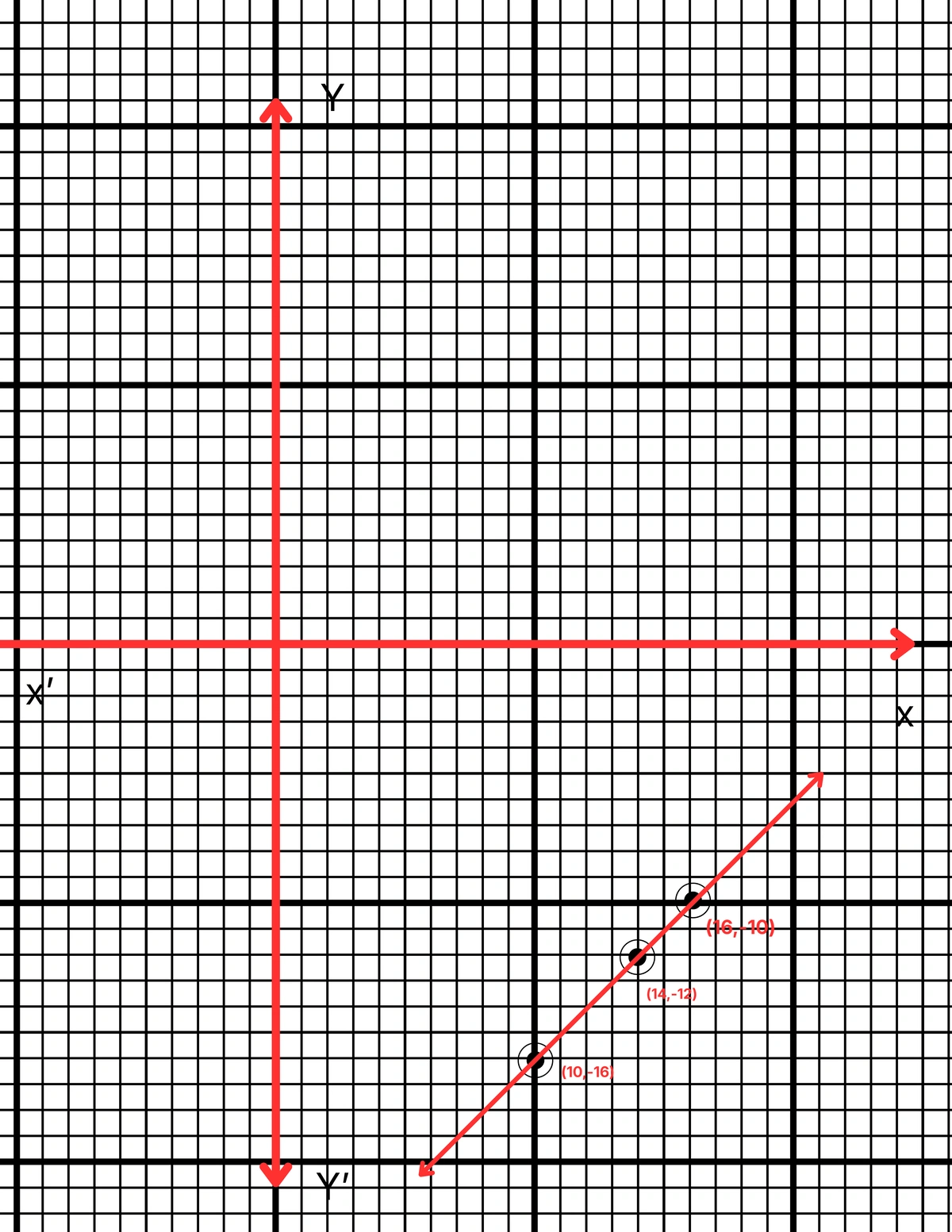
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে (14, -12), (16, -10) এবং (10, -16) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে সরলরেখা পেলাম। PQ সরলরেখা হল নির্ণেয় লেখচিত্র।
(ii) দুটি সংখ্যার সমষ্টি 15
সমাধানঃ ধরি, একটি সংখ্যা \(x\) এবং অপর সংখ্যাটি \(y\)।
∴ \(x + y = 15\)
বা, \(x = 15 – y\)
সুতরাং (i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
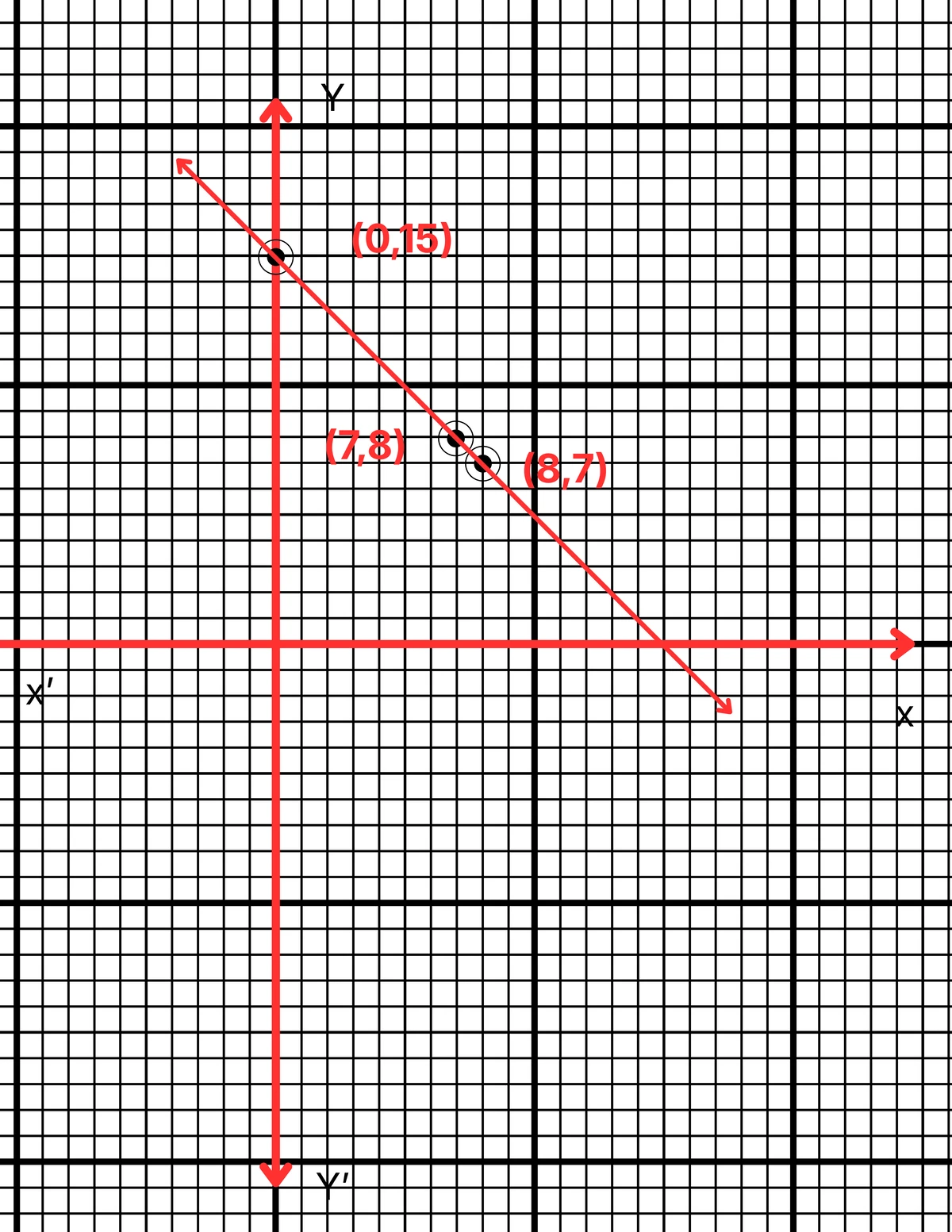
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে (0,15), (8,7) এবং (7,8) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে PQ সরলরেখা পেলাম। PQ সরলরেখা হল নির্ণেয় লেখচিত্র(iii) কোনো ভগ্নাংশের লব ও হরের প্রত্যেকটির সঙ্গে 2 যোগ করলে ভগ্নাংশটির মান 7/9 হয়।
(iii) কোনো ভগ্নাংশের লব ও হরের প্রত্যেকটির সঙ্গে 2 যোগ করলে ভগ্নাংশটির মান 7/9 হয়।
সমাধান –
ধরি, ভগ্নাংশটি হল \(\frac{x}{y}\)।
শর্তানুসারে,
\(\frac{x+2}{y+2} = \frac{7}{9}\)বা, \(9(x+2) = 7(y+2)\)
বা, \(9x + 18 = 7y + 14\)
বা, \(9x = 7y + 14 – 18\)
বা, \(9x = 7y – 4\)
বা, \(x = \frac{7y – 4}{9}\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 25 | 20 | 15 |
| y | 15 | 20 | 25 |
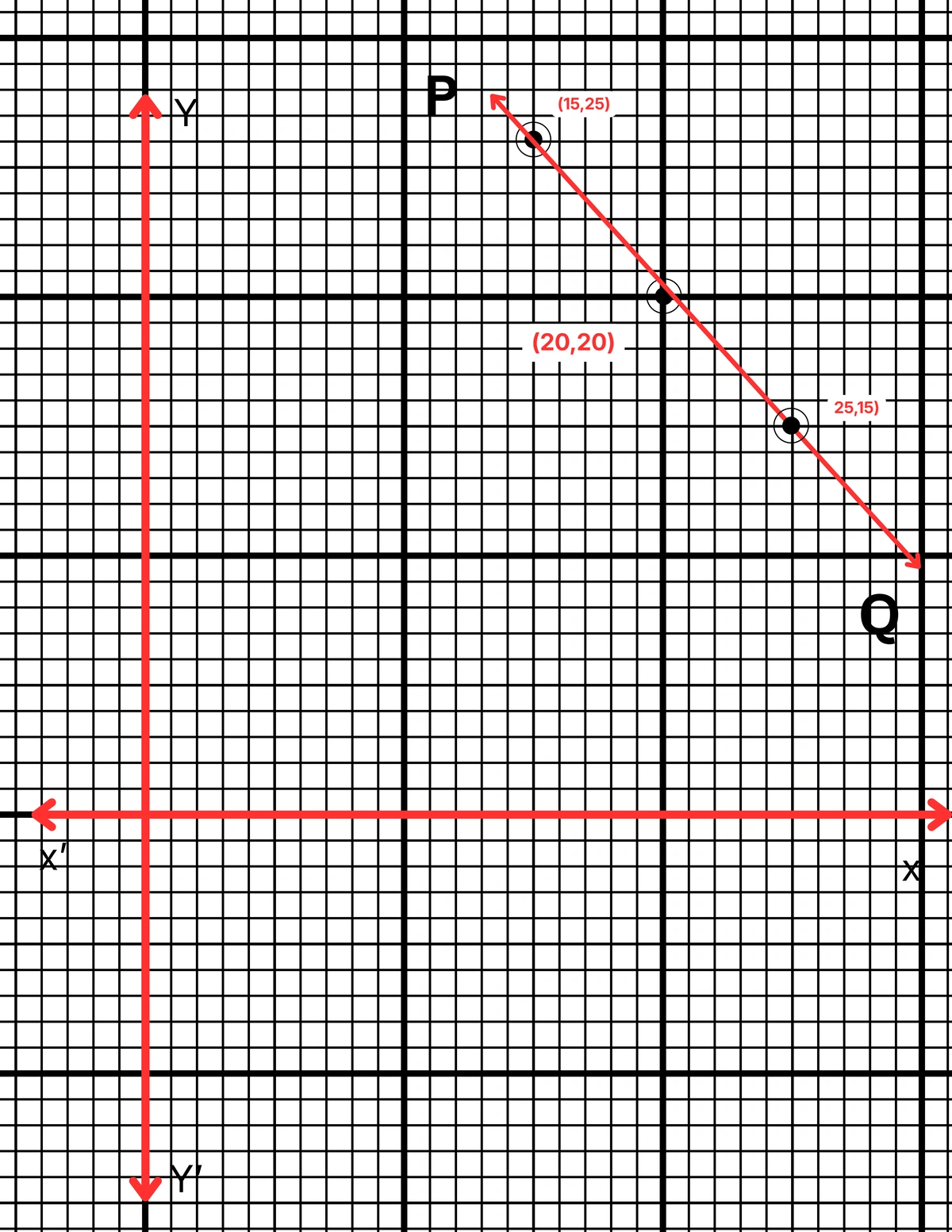
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((25,15)\), \((20,20)\) এবং \((15,25)\) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে PQ সরলরেখা পেলাম। PQ সরলরেখা হল নির্ণেয় লেখচিত্র।
(iv) আমাদের আয়তাকার বাগানের পরিসীমা 80 মিটার।
সমাধান –
ধরি, আয়তাকার বাগানের দৈর্ঘ্য \(x\) মিটার এবং প্রস্থ \(y\) মিটার।
শর্তানুসারে,
\(2(x+y) = 80\)বা, \(x+y = \frac{80}{2}\)
বা, \(x+y = 40\)
বা, \(x = 40-y\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 25 | 20 | 15 |
| y | 15 | 20 | 25 |
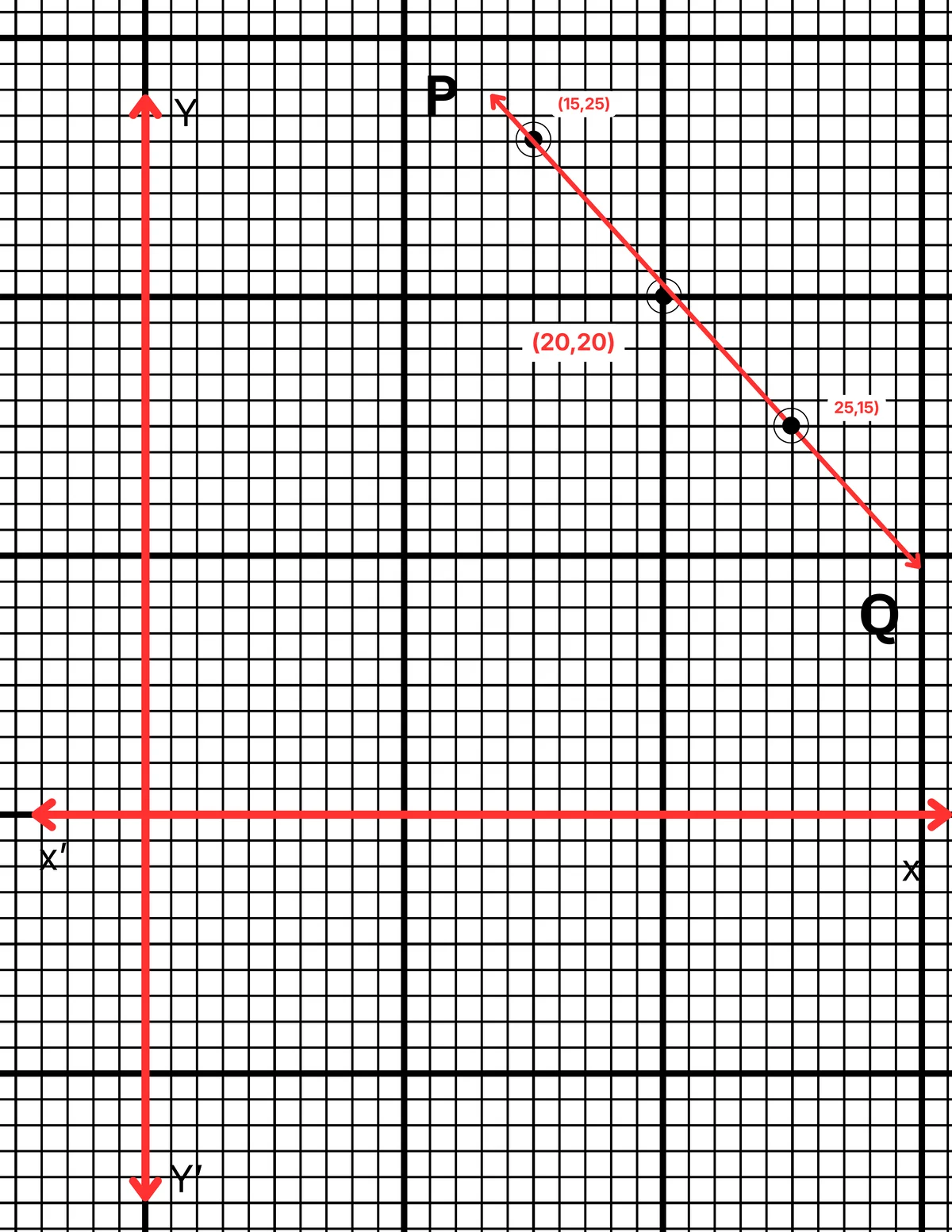
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((25,15)\), \((20,20)\) এবং \((15,25)\) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে PQ সরলরেখা পেলাম। PQ সরলরেখা হল নির্ণেয় লেখচিত্র।
(v) দুটি সংখ্যার বড়োটির 5 গুণ ছোটোটির 8 গুনের সমান।
সমাধান –
ধরি, বড়ো সংখ্যাটি \(x\) এবং ছোটো সংখ্যা \(y\)।
শর্তানুসারে, \(5x = 8y\)
বা, \(x = \frac{8y}{5}\) —(i)
(i) নং সমীকরণটির জন্য প্রয়োজনীয় ছকটি হল –
| x | 8 | 16 | 0 |
| y | 5 | 10 | 0 |
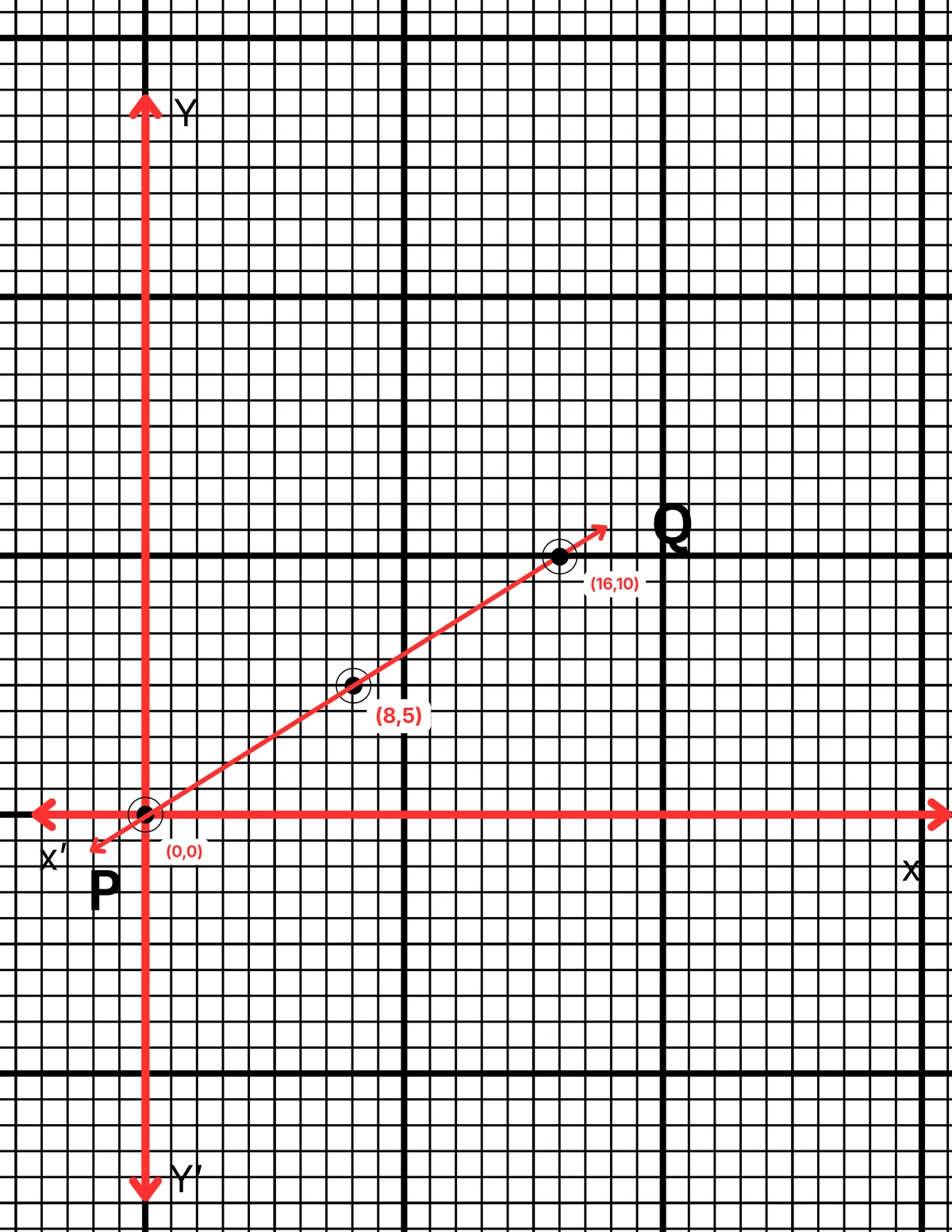
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((0,0)\), \((8,5)\) এবং \((16,10)\) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে PQ সরলরেখা পেলাম। PQ সরলরেখা হল নির্ণেয় লেখচিত্র।
5. নীচের সমীকরণগুলির লেখচিত্র অঙ্কন কর
(i) \(x = 5\)
সমাধান –
প্রদত্ত রৈখিক সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 5 | 5 | 5 |
| y | 5 | 7 | 10 |
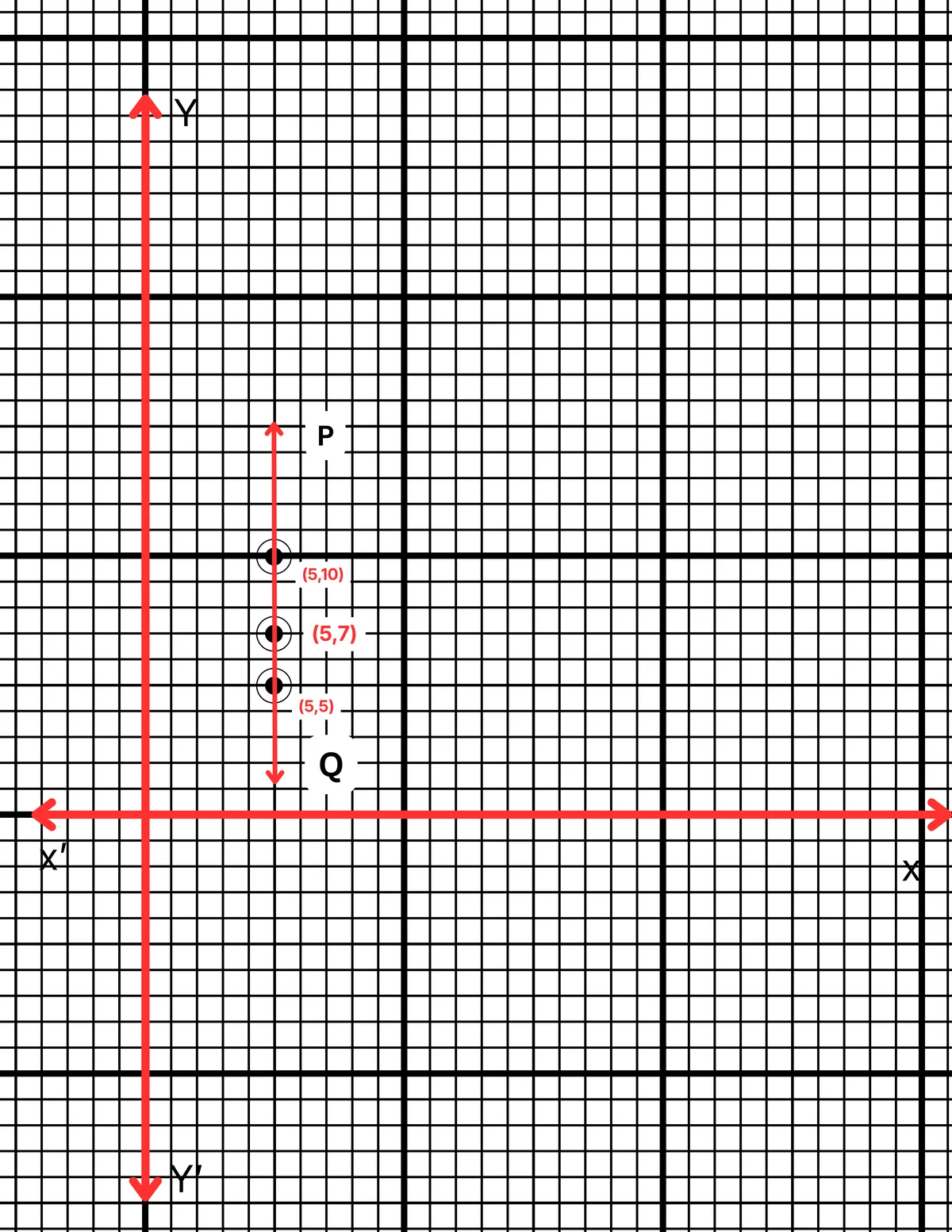
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((5,5)\), \((5,7)\) এবং \((5,10)\) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে PQ সরলরেখা পেলাম। PQ সরলরেখা হল নির্ণেয় লেখচিত্র।
(ii) y + 2 = 0
সমাধান –
y + 2 = 0
বা, y = -2 — (i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 3 | 5 | 7 |
| y | -2 | -2 | -2 |
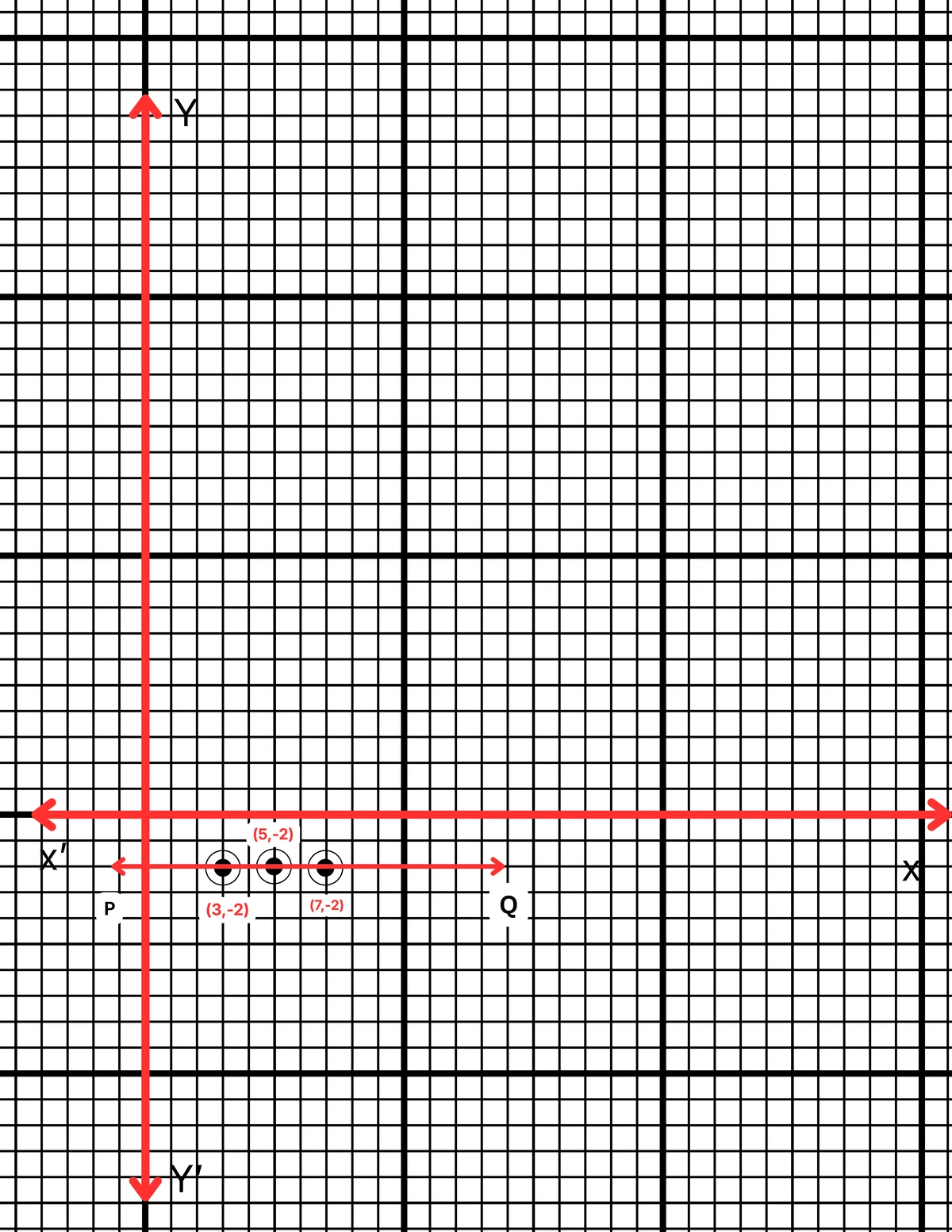
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে (3, -2), (5, -2) এবং (7, -2) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে PQ সরলরেখা পেলাম। PQ সরলরেখা হল নির্ণেয় লেখচিত্র।
(iii) \(x = 3 – 4y\)
সমাধান – \(x = 3 – 4y\)
প্রদত্ত সমীকরণটির জন্য প্রয়োজনীয় ছকটি হল –
| x | 3 | 15 | -5 |
| y | 0 | -3 | 2 |
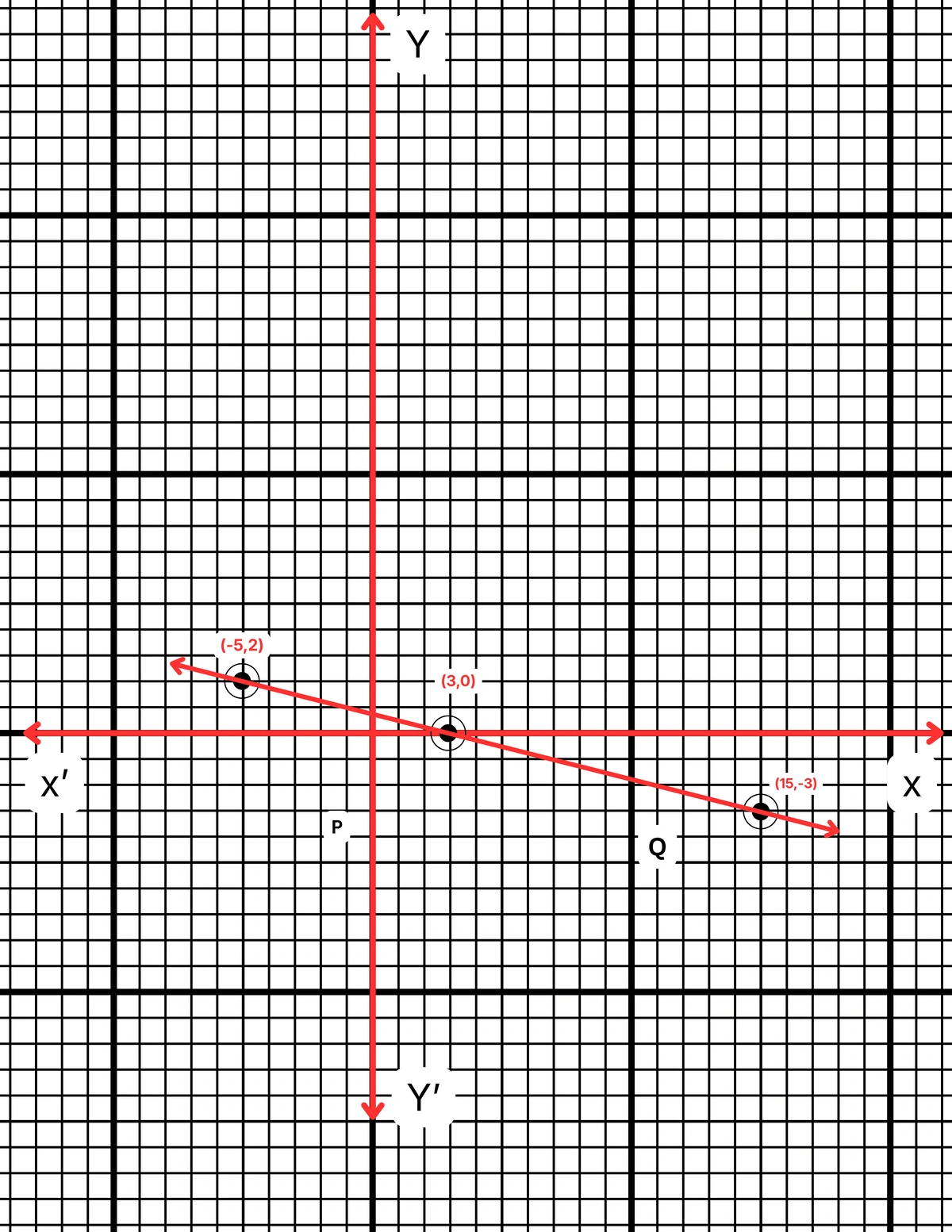
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((3,0)\), \((15,-3)\) এবং \((-5,2)\) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে PQ সরলরেখা পেলাম। PQ সরলরেখা হল নির্ণেয় লেখচিত্র।
(iv) \(3x – 7y = 21\)
সমাধান –
\(3x – 7y = 21\)বা, \(3x = 21 + 7y\)
বা, \(x = \frac{21 + 7y}{3}\) — (i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 7 | 0 | 14 |
| y | 0 | -3 | 3 |
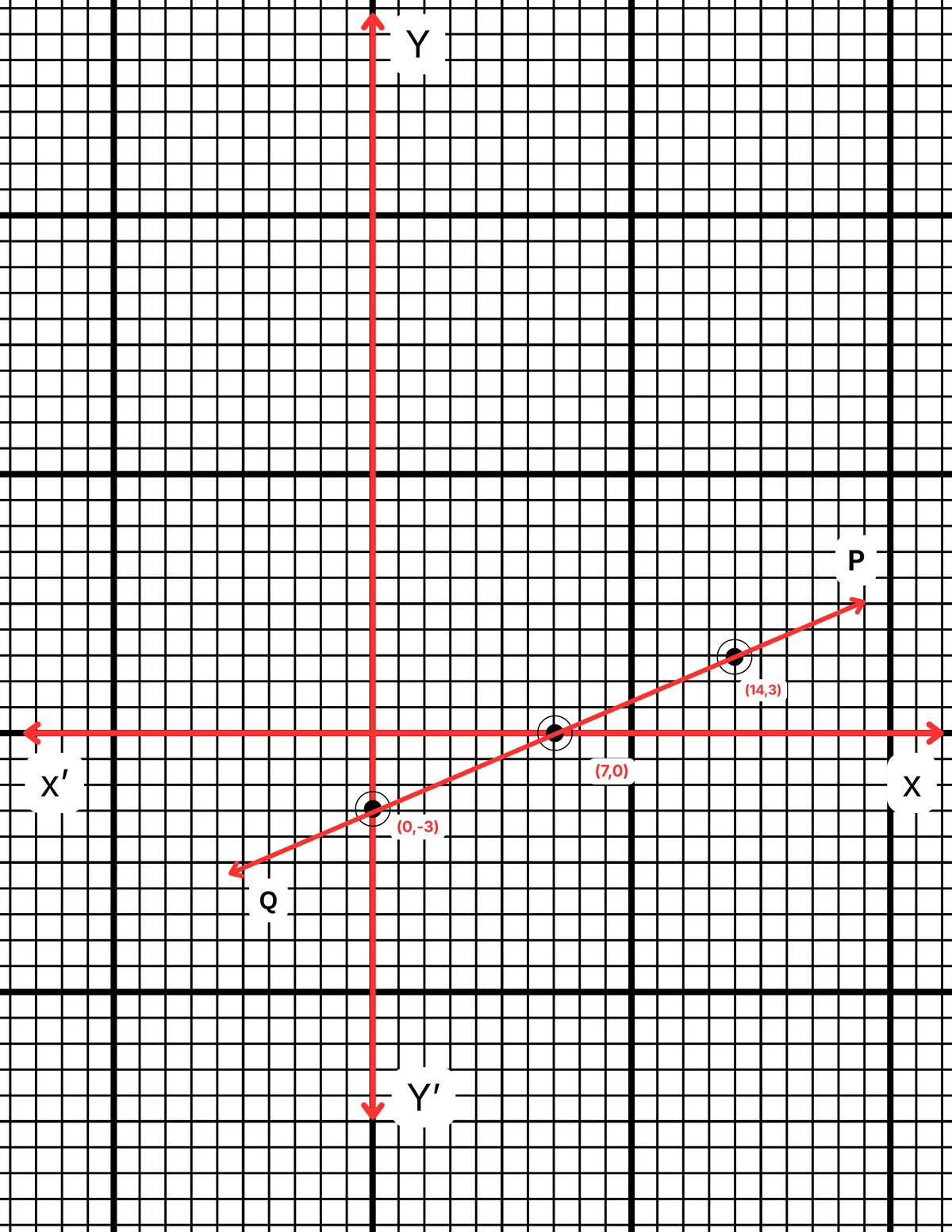
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((7,0)\), \((0,-3)\) এবং \((14,3)\) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে PQ সরলরেখা পেলাম। PQ সরলরেখা হল নির্ণেয় লেখচিত্র।
(v) \(5x-3y = 8\)
সমাধান –
\(5x-3y = 8\)বা, \(5x = 8 + 3y\)
বা, \(x = \frac{8 + 3y}{5}\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 4 | 7 | 1 |
| y | 4 | 9 | -1 |
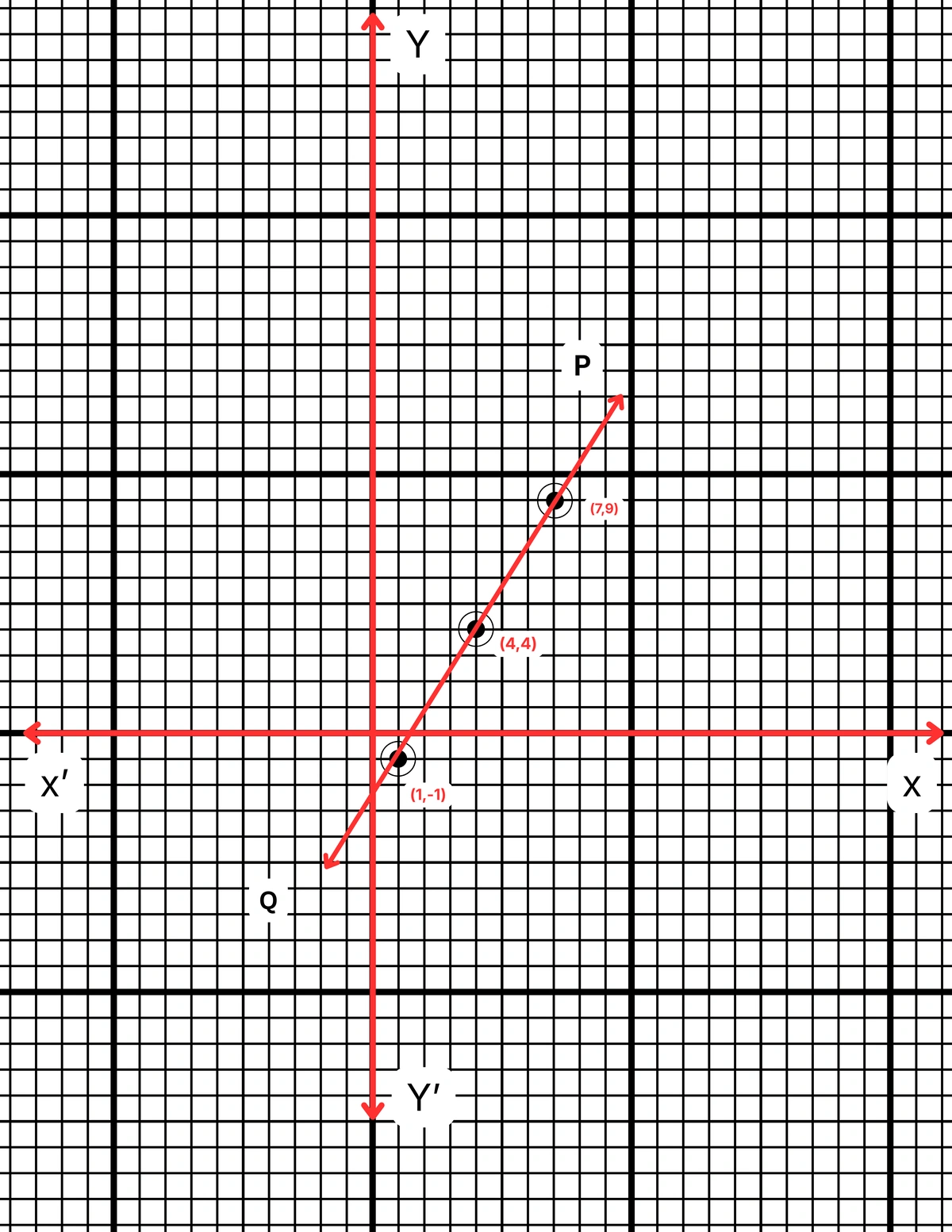
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((4,4)\), \((7,9)\) এবং \((1,-1)\) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে PQ সরলরেখা পেলাম। PQ সরলরেখা হল নির্ণেয় লেখচিত্র।
(vi) \(2x+3y = 11\)
সমাধান –
\(2x+3y = 11\)বা, \(2x = 11 – 3y\)
বা, \(x = \frac{11-3y}{2}\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 4 | 1 | -2 |
| y | 1 | 3 | 5 |
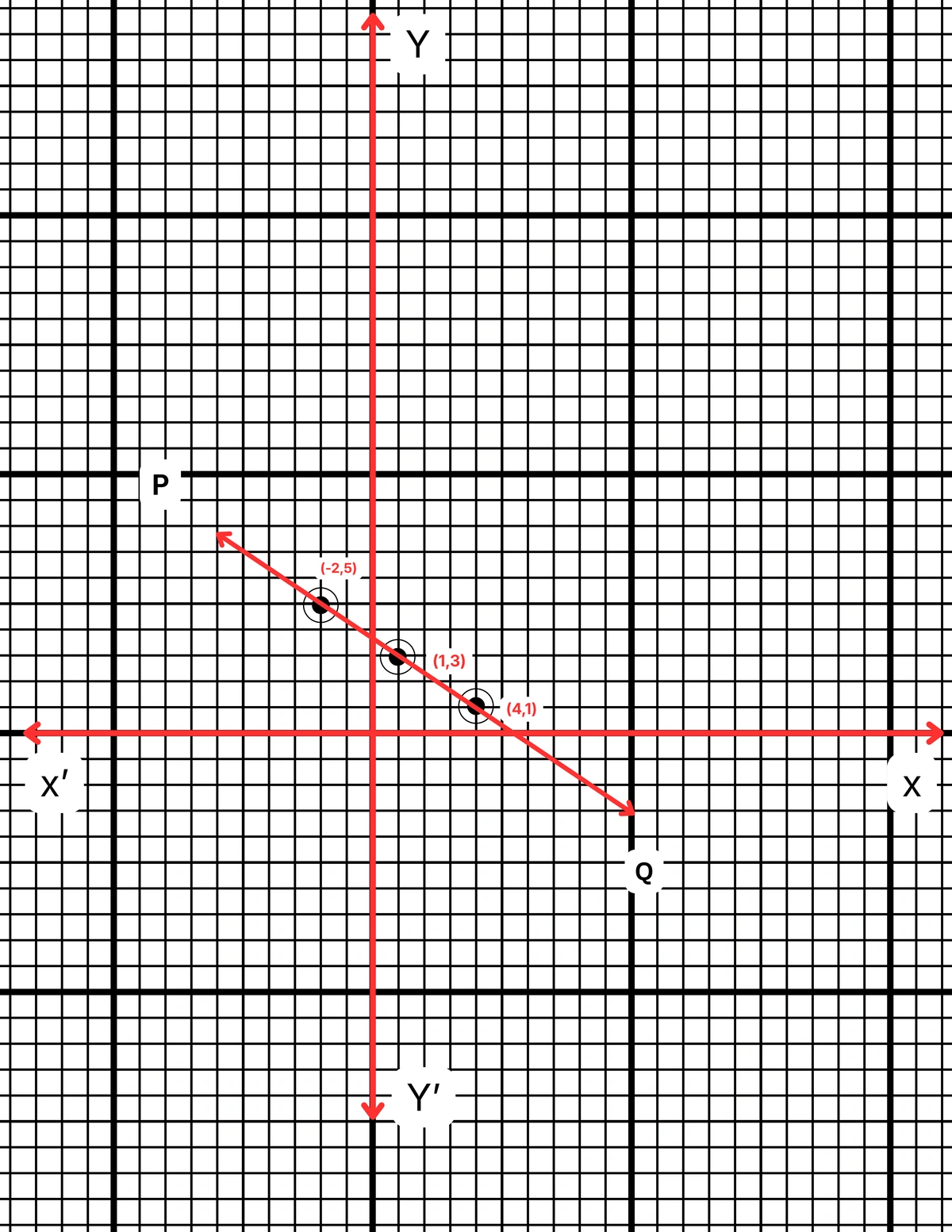
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((4,1)\), \((1,3)\) এবং \((-2,5)\) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে PQ সরলরেখা পেলাম। PQ সরলরেখা হল নির্ণেয় লেখচিত্র।
(vii) \(\frac{x}{3} + \frac{y}{4} = 0\)
সমাধান –
\(\frac{x}{3} + \frac{y}{4} = 0\)বা, \(\frac{x}{3} = – \frac{y}{4}\)
বা, \(x = \frac{-3y}{4}\) — (i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | -3 | -6 | 3 |
| y | 4 | 8 | -4 |
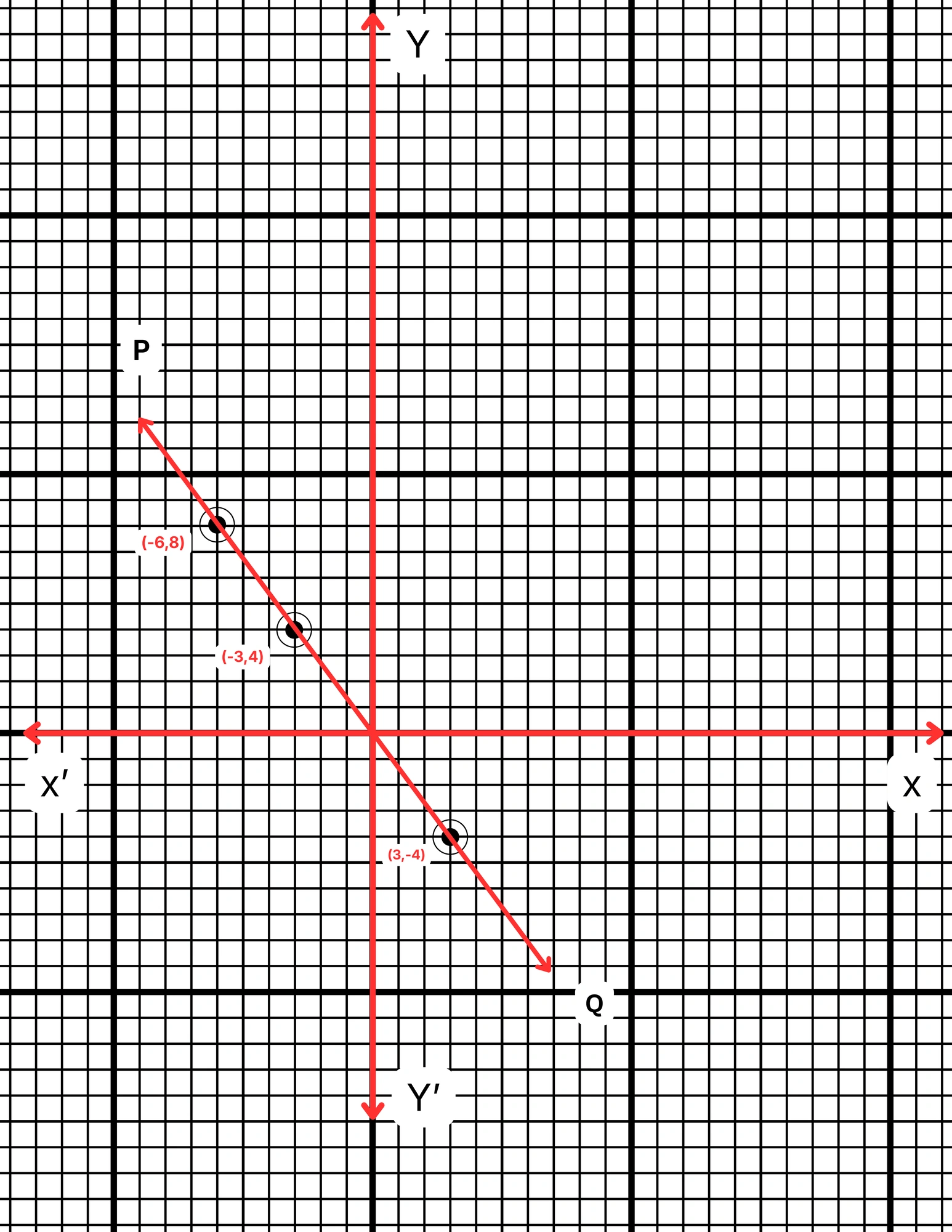
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((-3,4)\), \((-6,8)\) এবং \((3,-4)\) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে PQ সরলরেখা পেলাম। PQ সরলরেখা হল নির্ণেয় লেখচিত্র।
(viii) \(6x – 7y = 12\)
সমাধান –
\(6x – 7y = 12\)বা, \(6x = 7y + 12\)
বা, \(x = \frac{7y + 12}{6}\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 2 | 9 | -5 |
| y | 0 | 7 | -7 |
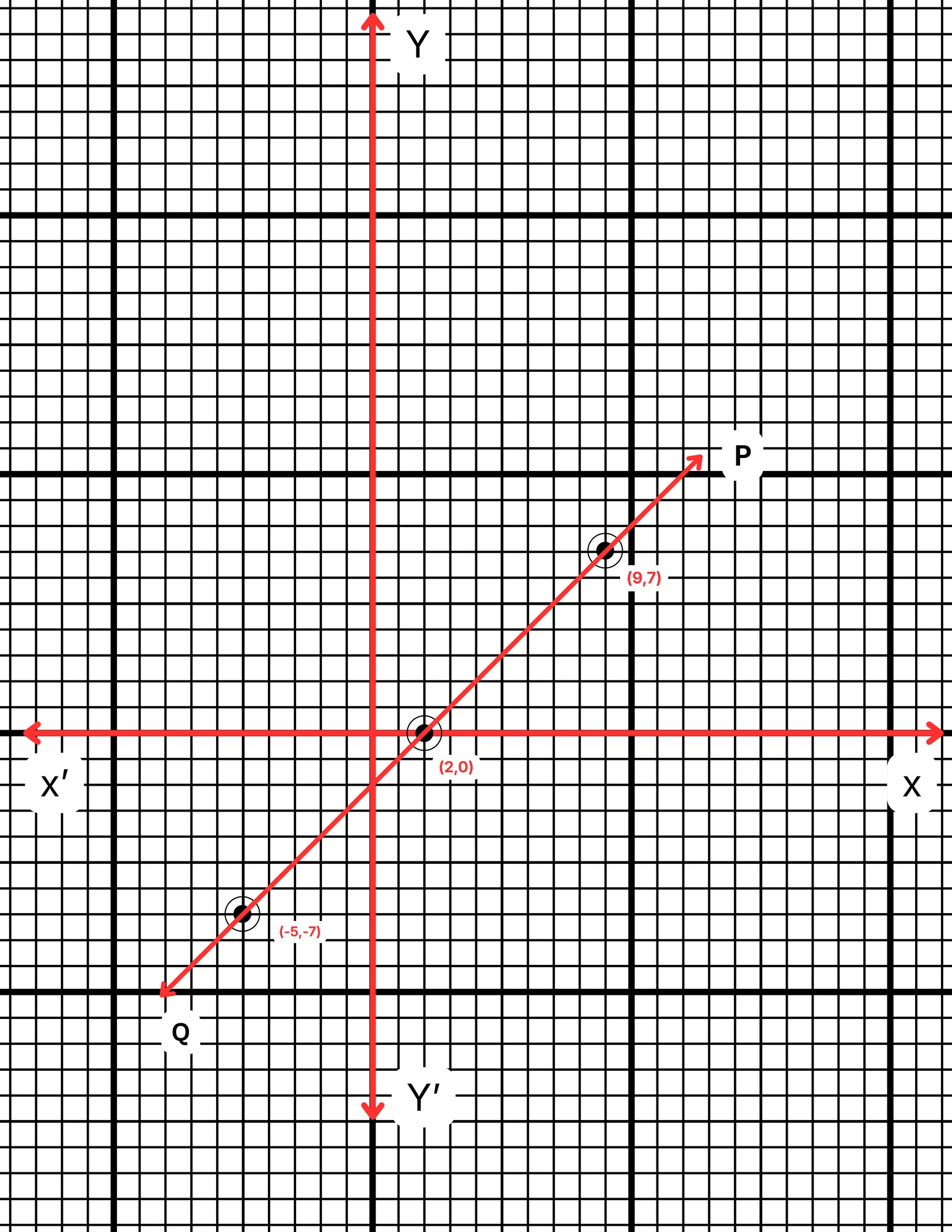
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((9,7)\), \((2,0)\) এবং \((-5,-7)\) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে PQ সরলরেখা পেলাম। PQ সরলরেখা হল নির্ণেয় লেখচিত্র।
(ix) \(x + y – 10 = 0\)
সমাধান –
\(x + y – 10 = 0\)বা, \(x = 10 – y\) — (i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 5 | 6 | 3 |
| y | 5 | 4 | 7 |
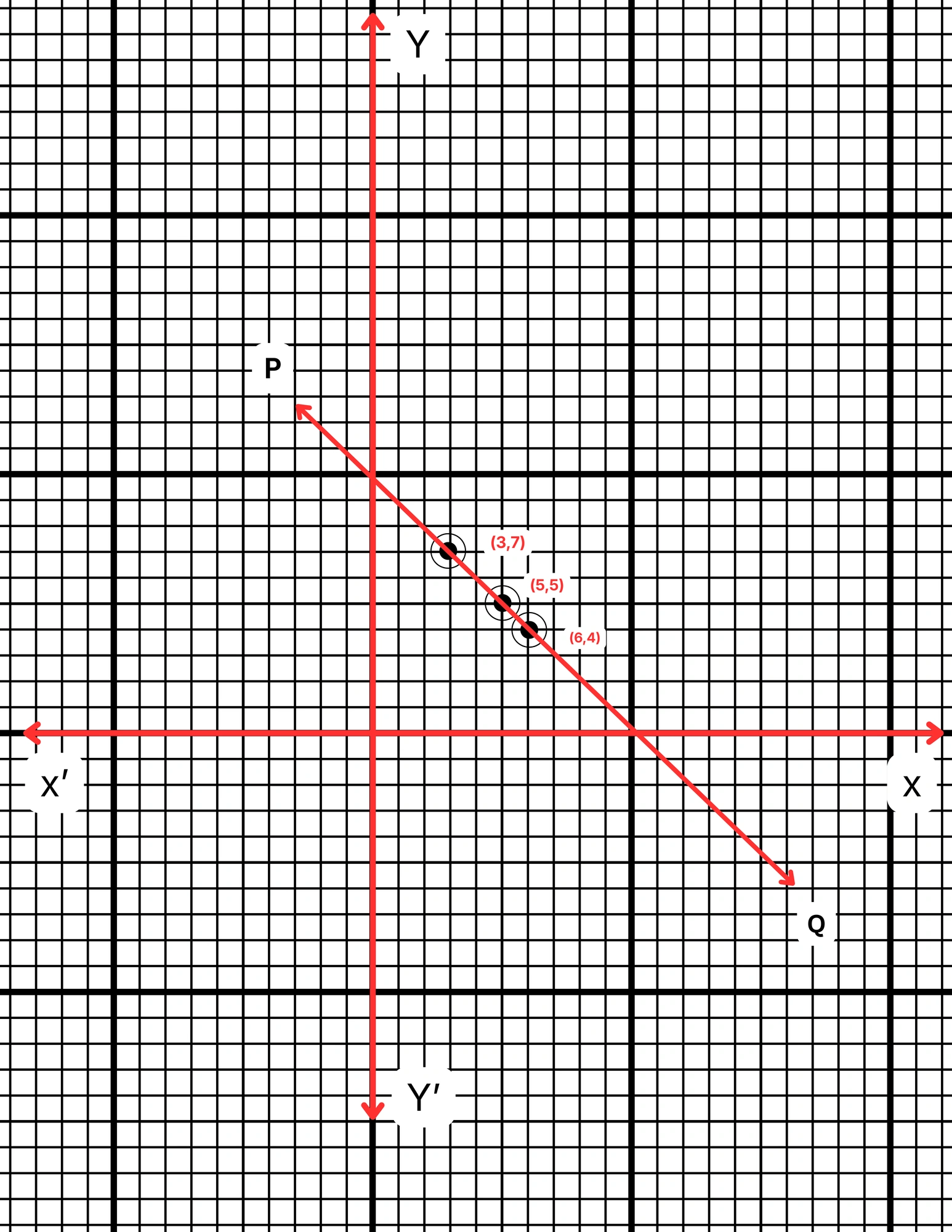
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((5,5)\), \((6,4)\) এবং \((3,7)\) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে PQ সরলরেখা পেলাম। PQ সরলরেখা হল নির্ণেয় লেখচিত্র।
(x) \(y = 5x – 3\)
সমাধান –
\(y = 5x – 3\)বা, \(5x = y + 3\)
বা, \(x = \frac{y + 3}{5}\) — (i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 2 | 3 | 0 |
| y | 7 | 12 | -3 |
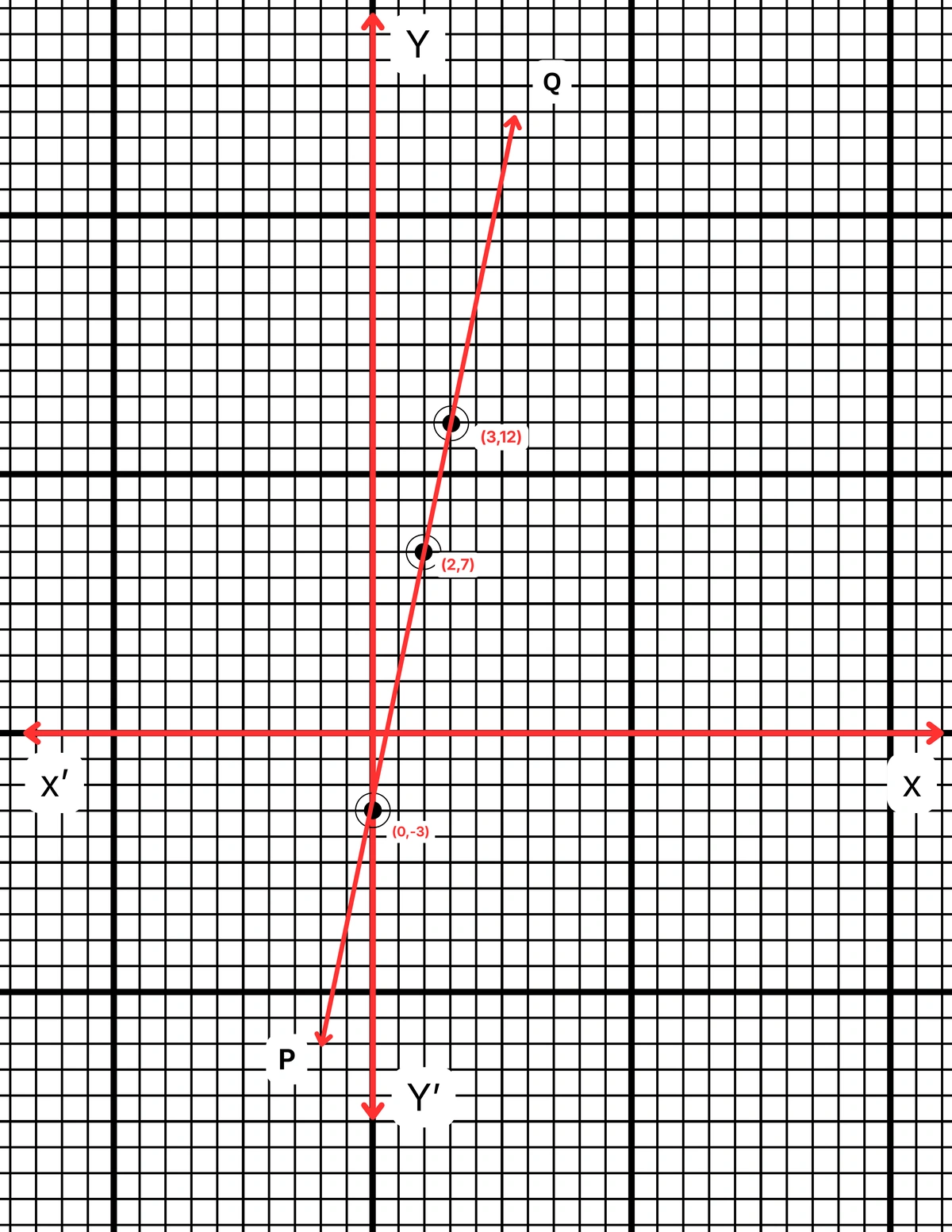
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((2, 7)\), \((3, 12)\) এবং \((0, -3)\) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে PQ সরলরেখা পেলাম। PQ সরলরেখা হল নির্ণেয় লেখচিত্র।
(xi) y = 0
সমাধান –
প্রদত্ত সমীকরনের জন্য প্রয়োজনীয় ছকটি হল –
| x | 5 | 10 | 14 |
| y | 0 | 0 | 0 |
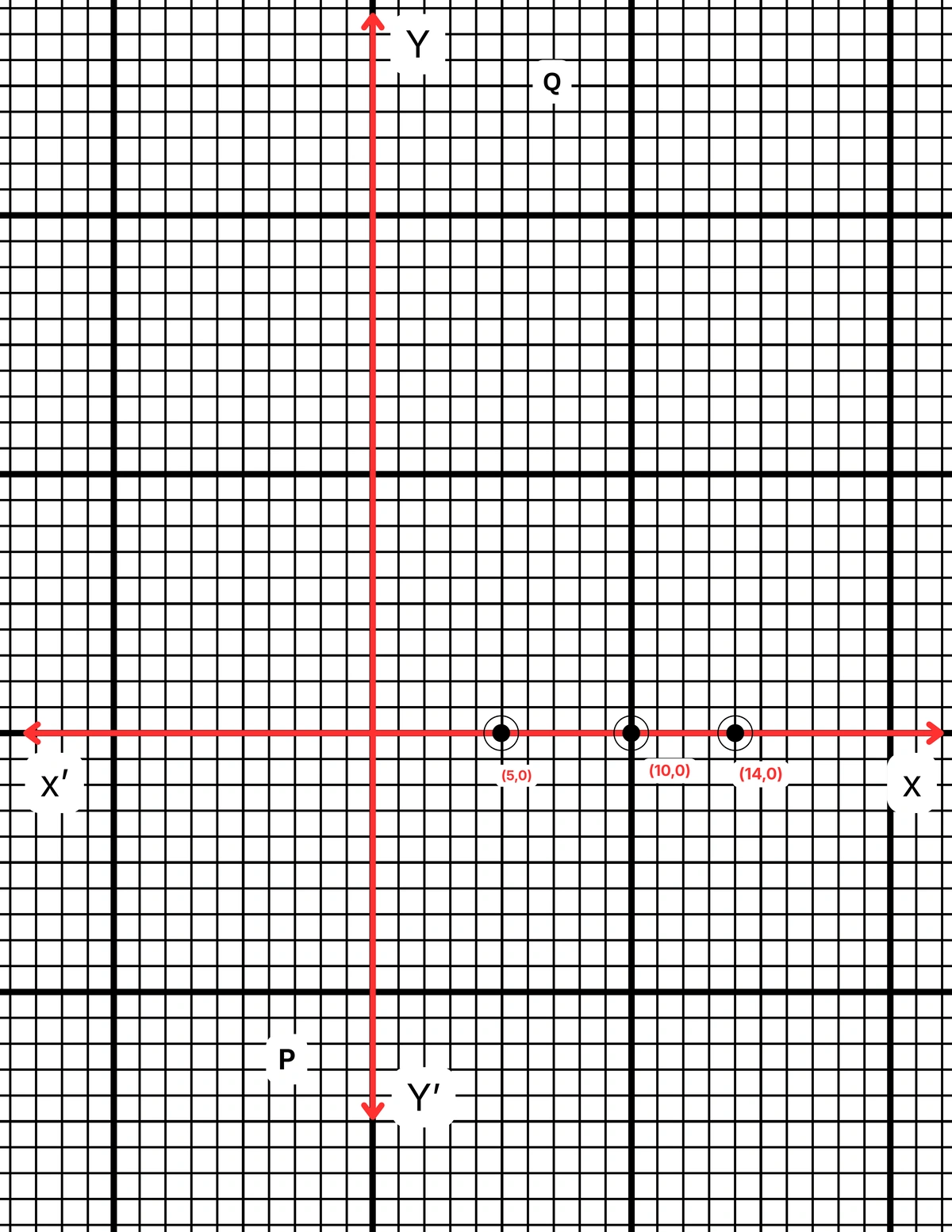
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে (5,0), (10,0) এবং (14,0) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে একটি সরলরেখা XOX´ পেলাম।
∴ y = 0 সমীকরণের লেখচিত্র হল XOX´ সরলরেখা বা X অক্ষ।
6. নীচের বক্তব্যগুলি রৈখিক সমীকরণ আকারে প্রকাশ করি ও সমীকরণগুলির লেখচিত্র অঙ্কন করে সমাধান করি।
(i) বর্তমানে রজতের মামা রজতের চেয়ে 16 বছরের বড়ো। 8 বছর পরে তার মামার বয়স তার বয়সের 2 গুণ হবে। বর্তমানে রজতের বয়স ও রজতের মামার বয়স লেখচিত্রের সাহায্যে প্রকাশ করো।
সমাধান –
ধরি, রজতের বয়স \(x\) বছর এবং রজতের মামার বয়স \(y\) বছর।
শর্তানুসারে,
\(y = x + 16\)বা, \(x = y – 16\) — (i)
এবং, \(y + 8 = 2(x + 8)\)
বা, \(y + 8 = 2x + 16\)
বা, \(y = 2x + 16 – 8\)
বা, \(y = 2x + 8\)
বা, \(2x = y – 8\)
বা, \(x = \frac{y – 8}{2}\) — (ii)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| X | 0 | -6 | 8 |
| Y | 16 | 10 | 24 |
(ii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 0 | -2 | 8 |
| y | 8 | 4 | 24 |
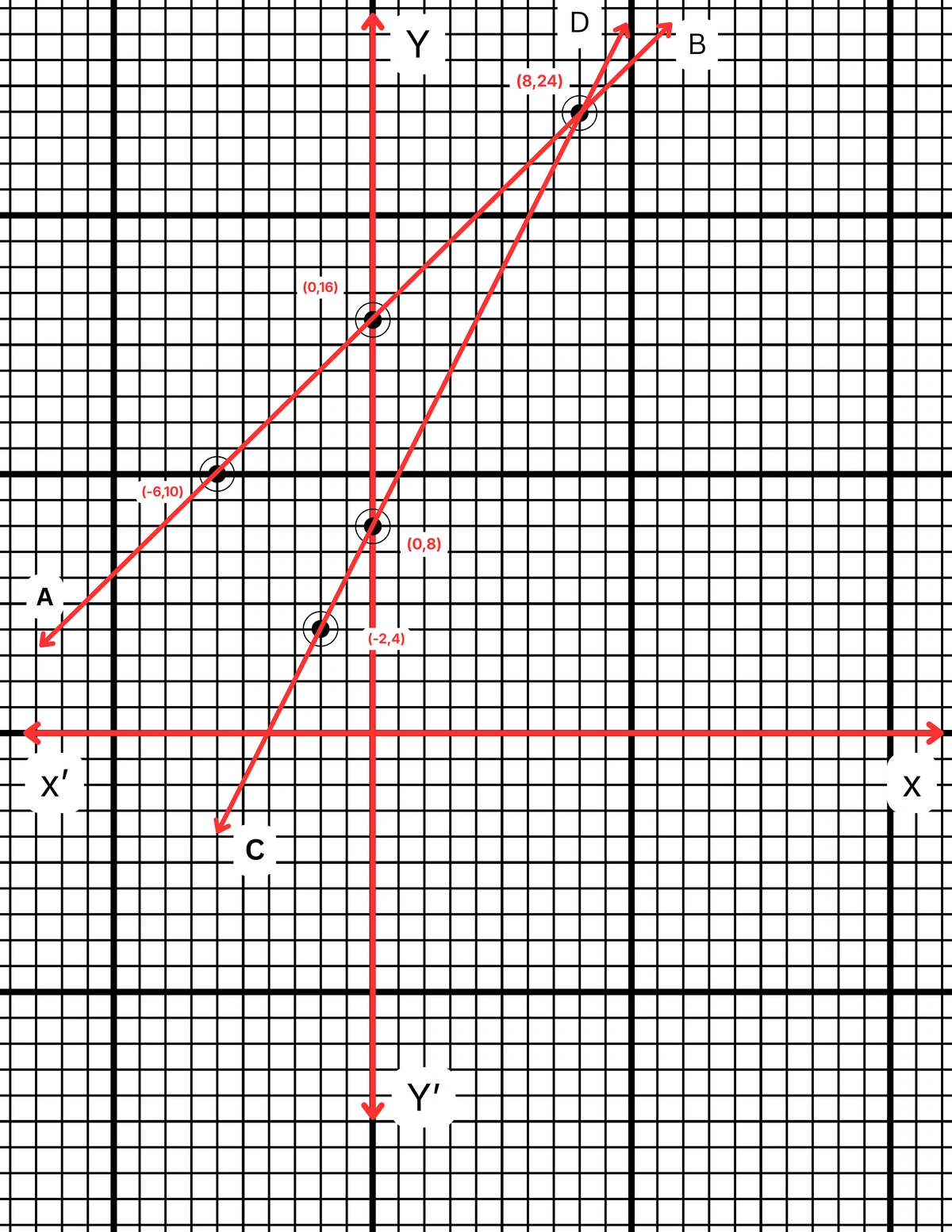
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((0,16)\), \((-6,10)\) এবং \((8,24)\) বিন্দুগুলি স্থাপন করে AB সরলরেখা এবং \((0,8)\), \((-2,4)\) এবং \((8,24)\) বিন্দুগুলি যোগ করে CD সরলরেখা পেলাম। AB ও CD সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করে। P বিন্দুর স্থানাঙ্ক \((8,24)\)।
∴ নির্ণেয় সমাধান \(x = 8\) এবং \(y = 24\)।
∴ রজতের বয়স 8 বছর এবং রজতের মামার বয়স 24 বছর।
(ii) দুটি সংখ্যার সমষ্টি 15 এবং অন্তর 3; লেখচিত্রের সাহায্যে সমীকরণগুলি সমাধান করে সংখ্যা দুটি লিখি।
সমাধান –
ধরি, দুটি সংখ্যা \(x\) এবং \(y\) (\(x > y\))।
শর্তানুসারে,
\(x + y = 15\)বা, \(x = 15 – y\) —(i)
এবং, \(x – y = 3\)
বা, \(x = 3 + y\) —(ii)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 0 | 8 | 9 |
| y | 15 | 7 | 6 |
(ii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 8 | 9 | 0 |
| y | 5 | 6 | -3 |
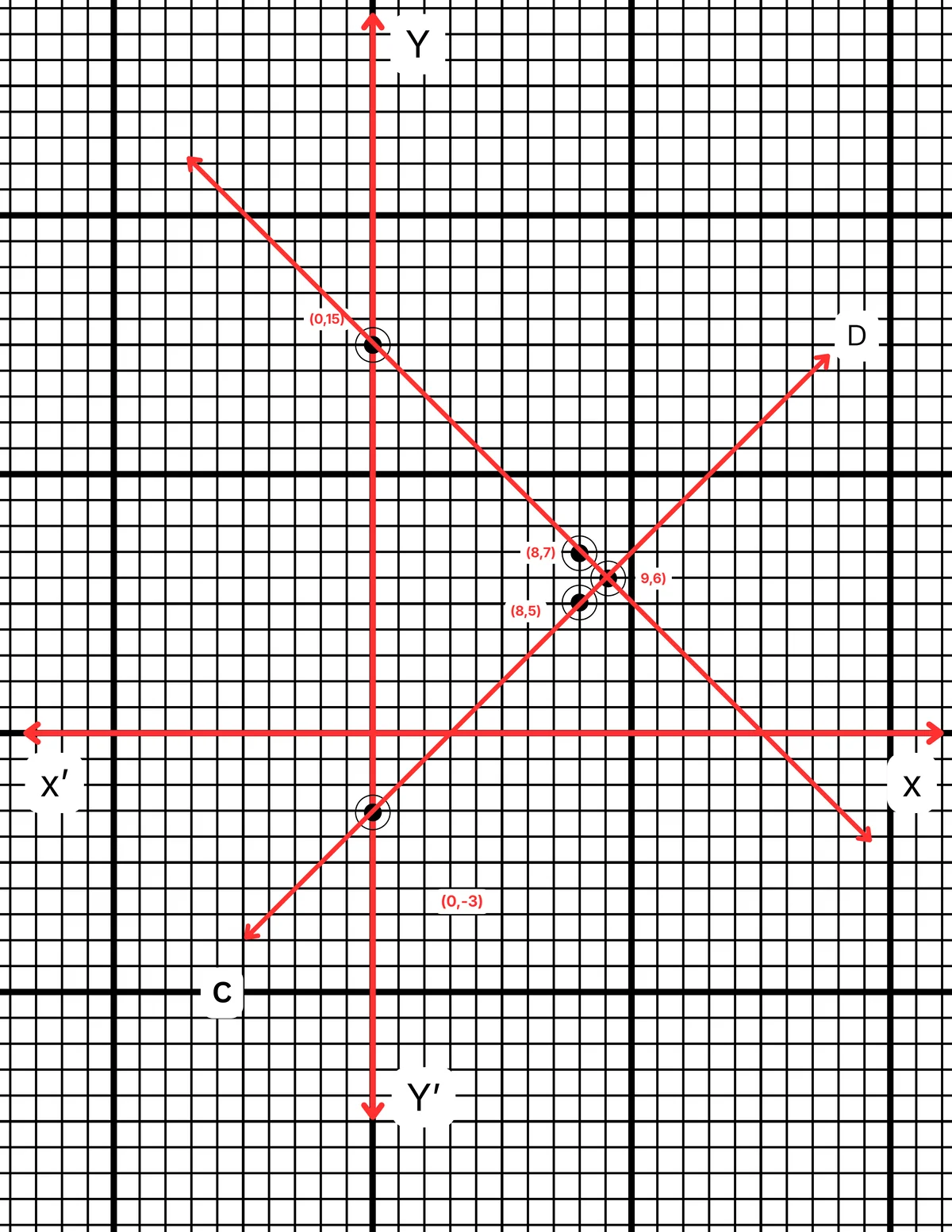
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((0,15)\), \((8,7)\) এবং \((9,6)\) বিন্দুগুলি স্থাপন করে AB সরলরেখা এবং \((8,5)\), \((9,6)\) এবং \((0,-3)\) বিন্দুগুলি যোগ করে CD সরলরেখা পেলাম। AB ও CD সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করে। P বিন্দুর স্থানাঙ্ক \((9,6)\)।
∴ নির্ণেয় সমাধান \(x = 9\) এবং \(y = 6\)।
∴ সংখ্যা দুটি হল 9 এবং 6।
(iii) একটি ভগ্নাংশের লব থেকে 3 বিয়োগ এবং হরের সঙ্গে 2 যোগ করলে ভগ্নাংশটি \(\frac{1}{3}\) হয় এবং লব থেকে 4 ও হর থেকে 2 বিয়োগ করলে ভগ্নাংশটি \(\frac{1}{2}\) হয়। বক্তব্যটির সমীকরণ গঠন করি ও লেখচিত্রের সাহায্যে সমাধান করে ভগ্নাংশটি লিখি।
সমাধান –
ধরি, ভগ্নাংশটি হল \(\frac{x}{y}\)।
শর্তানুসারে,
\(\frac{x-3}{y+2} = \frac{1}{3}\)বা, \(3(x-3) = y+2\)
বা, \(3x-9 = y+2\)
বা, \(3x = y+9+2\)
বা, \(x = \frac{y+11}{3}\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 5 | 4 | 6 |
| y | 4 | 1 | 7 |
এবং, \(\frac{x-4}{y-2} = \frac{1}{2}\)
বা, \(2(x-4) = y-2\)
বা, \(2x – 8 = y-2\)
বা, \(2x = 8+y-2\)
বা, \(2x = y+6\)
বা, \(x = \frac{y+6}{2}\) —(ii)
(ii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 4 | 5 | 0 |
| y | 2 | 4 | -6 |
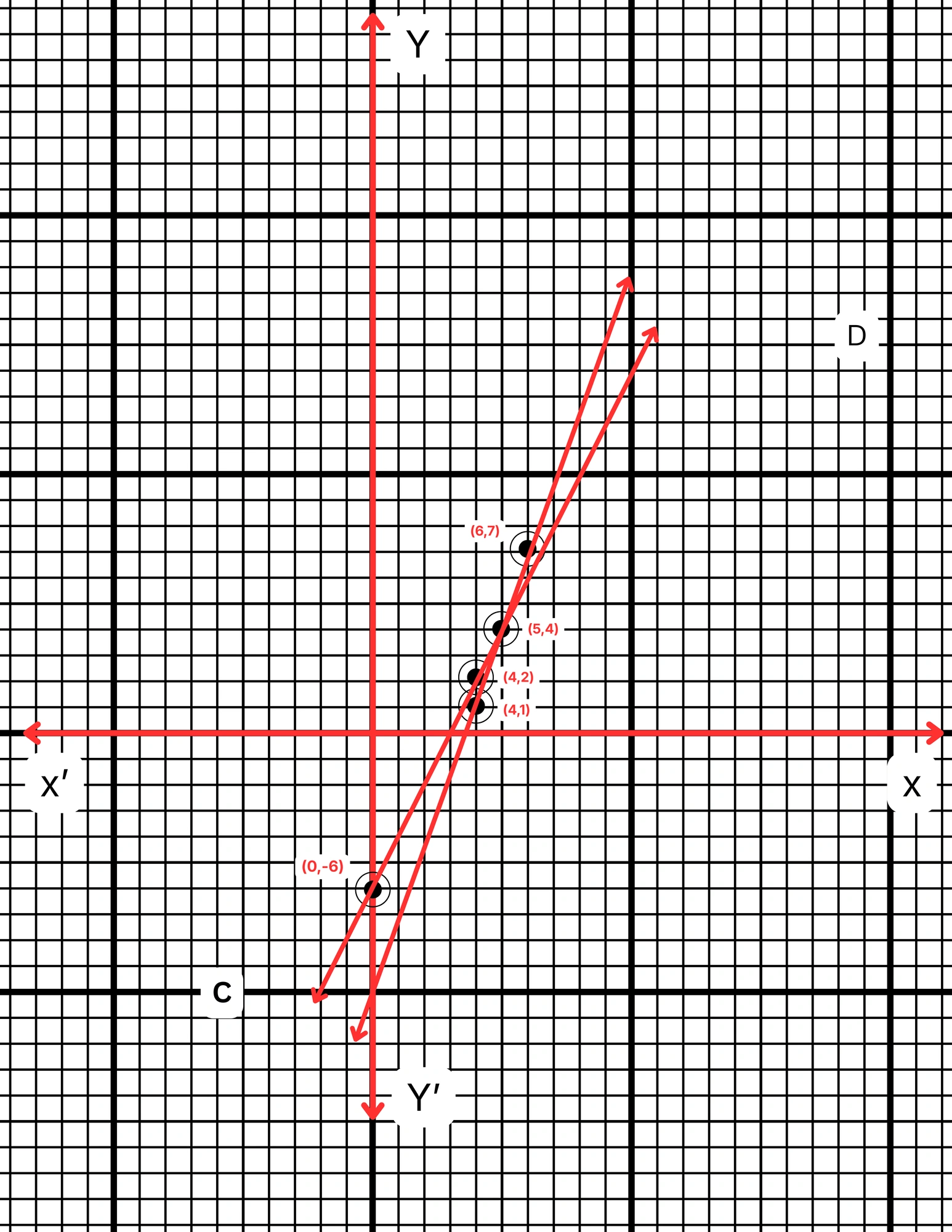
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((5,4)\), \((4,1)\) এবং \((6,7)\) বিন্দুগুলি স্থাপন করে AB সরলরেখা এবং \((4,2)\), \((5,4)\) এবং \((0,-6)\) বিন্দুগুলি যোগ করে CD সরলরেখা পেলাম। AB ও CD সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করে। P বিন্দুর স্থানাঙ্ক \((5,4)\)।
∴ নির্ণেয় সমাধান \(x = 5\) এবং \(y = 4\)।
∴ নির্ণেয় ভগ্নাংশ \(\frac{5}{4}\)।
(iv) রোহিতের আয়তাকার বাগানের পরিসীমা 60 মিটার। বাগানের দৈর্ঘ্য 2 মিটার বেশি ও প্রস্থ 2 মিটার কম হলে বাগানটির ক্ষেত্রফল 24 বর্গমিটার কম হয়। লেখচিত্রের সাহায্যে সমাধান করে আয়তাকার বাগানটির দৈর্ঘ্য ও প্রস্থ লিখি।
সমাধান –
ধরি, আয়তাকার বাগানের দৈর্ঘ্য \(x\) মিটার এবং প্রস্থ \(y\) মিটার।
শর্তানুসারে,
\(2(x+y) = 60\)বা, \(x + y = \frac{60}{2}\)
বা, \(x + y = 30\)
বা, \(x = 30 – y\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| X | 15 | 20 | 12 |
| y | 15 | 10 | 18 |
এবং \(xy – (x+2)(y-2) = 24\)
বা, \(xy – xy – 2y + 2x + 4 – 24 = 0\)
বা, \(2x – 2y – 20 = 0\)
বা, \(2(x-y) = 20\)
বা, \(x – y = \frac{20}{2}\)
বা, \(x – y = 10\)
বা, \(x = 10 + y\) —(ii)
(ii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 20 | 0 | 15 |
| y | 10 | -10 | 5 |
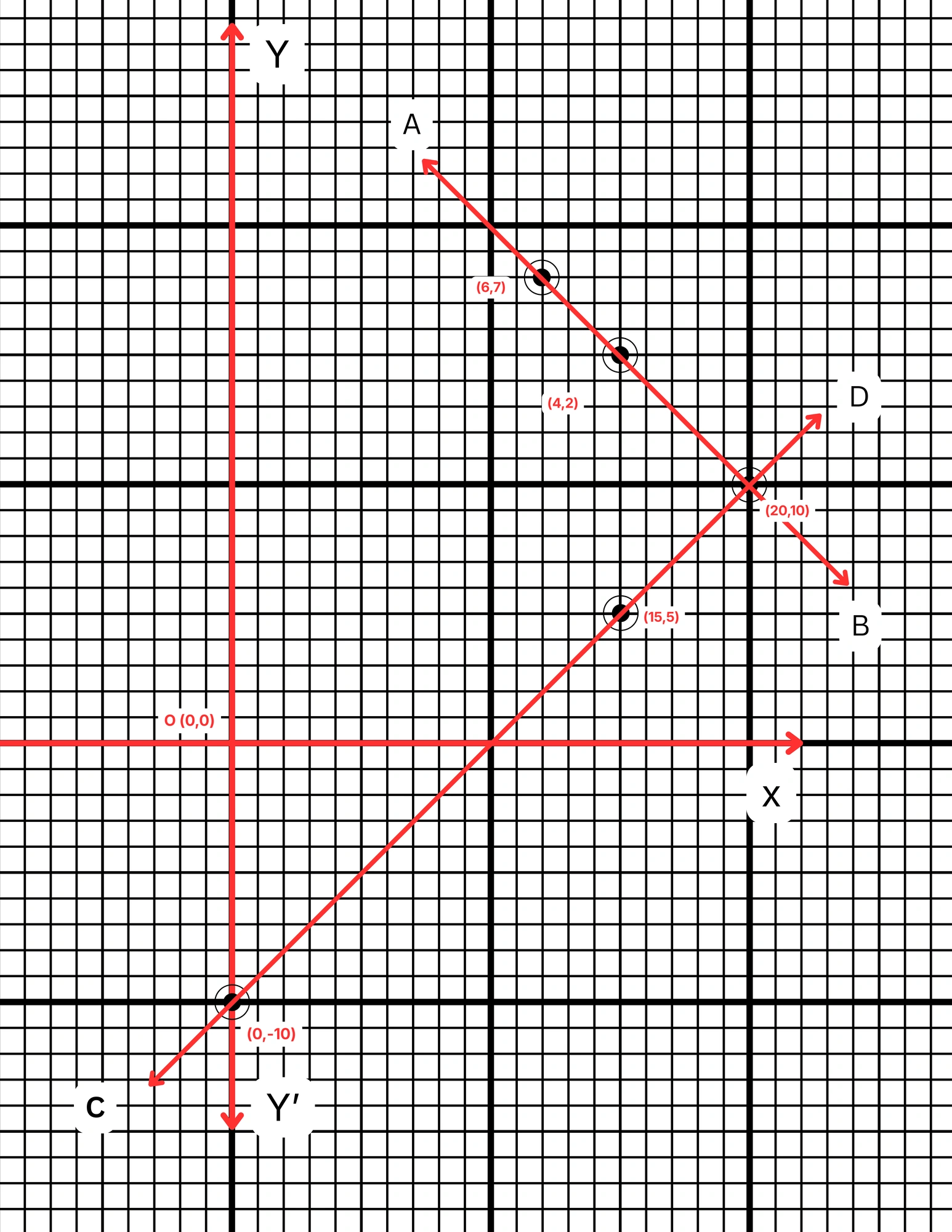
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((15,15)\), \((20,10)\) এবং \((12,18)\) বিন্দুগুলি স্থাপন করে AB সরলরেখা এবং \((20,10)\), \((0,-10)\) এবং \((15,5)\) বিন্দুগুলি যোগ করে CD সরলরেখা পেলাম। AB ও CD সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করে। P বিন্দুর স্থানাঙ্ক \((20,10)\)।
∴ নির্ণেয় সমাধান \(x = 20\) এবং \(y = 10\)।
অর্থাৎ আয়তাকার বাগানের দৈর্ঘ্য 20 মিটার এবং প্রস্থ 10 মিটার।
(v) একটি নৌকা স্রোতের অনুকূলে 16 ঘণ্টায় 96 কিমি. যায় এবং স্রোতের প্রতিকূলে 8 ঘণ্টায় 16 কিমি. যায়। লেখচিত্রের সাহায্যে সমাধান করে, স্থির জলে নৌকার বেগ ও স্রোতের বেগ লিখি।
সমাধান –
ধরি, নৌকার বেগ \(x\) কিমি/ঘণ্টা এবং স্রোতের বেগ \(y\) কিমি/ঘণ্টা।
\(\therefore\) স্রোতের অনুকূলে নৌকার বেগ \((x+y)\) কিমি/ঘণ্টা এবং স্রোতের প্রতিকূলে নৌকার বেগ \((x-y)\) কিমি/ঘণ্টা।
এখন, নৌকাটি স্রোতের অনুকূলে \((x+y)\) কিমি/ঘণ্টা গতিবেগ নিয়ে 96 কিমি. অতিক্রম করে \(\frac{96}{(x+y)}\) ঘণ্টায়।
\(\therefore \frac{96}{(x+y)} = 16\)বা, \(x+y = 96/16\)
বা, \(x+y = 6\)
বা, \(x = 6-y\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 0 | 4 | 8 |
| y | 6 | 2 | -2 |
আবার, নৌকাটি স্রোতের প্রতিকূলে \((x-y)\) কিমি/ঘণ্টা গতিবেগ নিয়ে 16 কিমি অতিক্রম করে \(\frac{16}{(x-y)}\) ঘণ্টায়।
\(\therefore \frac{16}{(x-y)} = 8\)বা, \(x-y = \frac{16}{8}\)
বা, \(x-y = 2\)
বা, \(x= y+2\) —(ii)
(ii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| X | 4 | 0 | 6 |
| y | 2 | -2 | 4 |
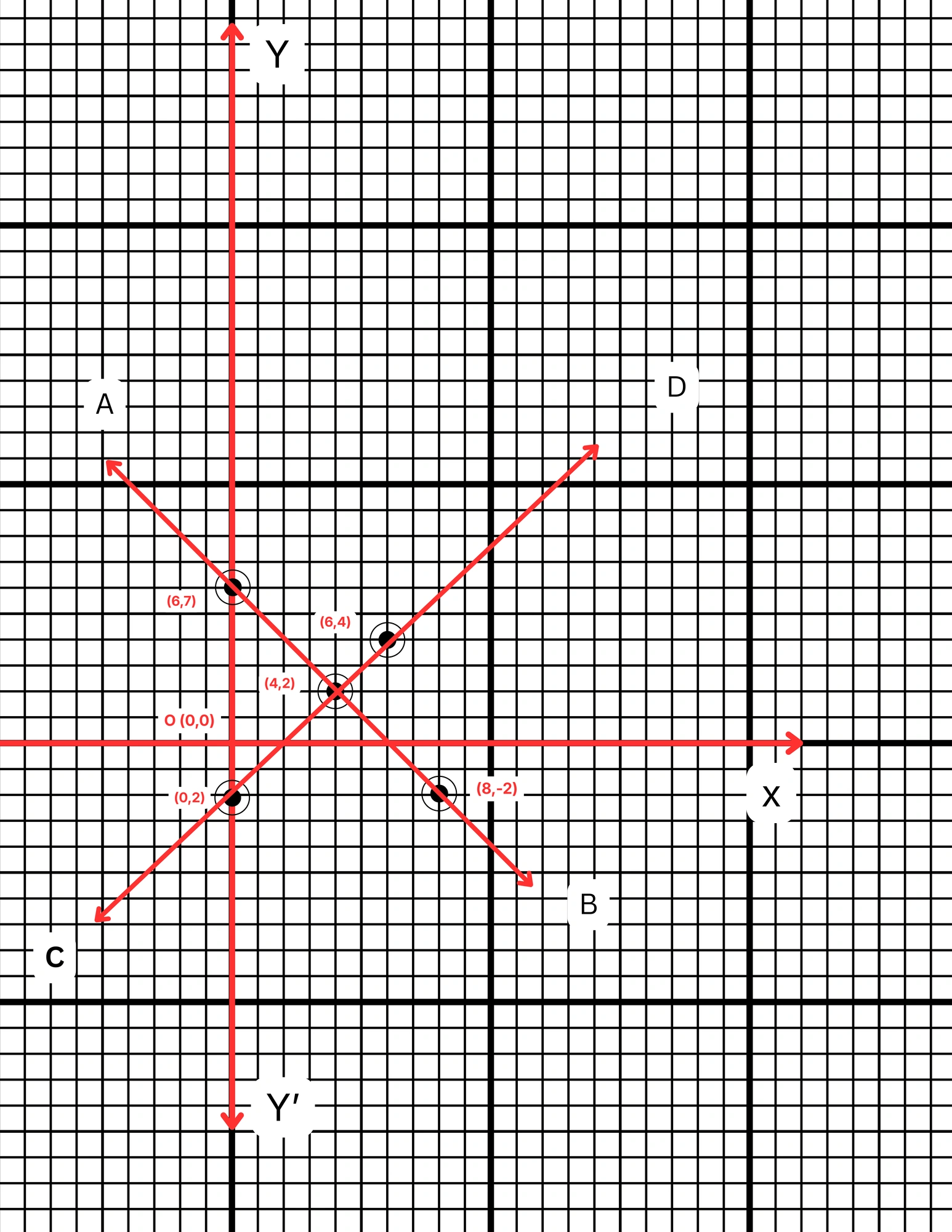
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((0,6)\), \((4,2)\) এবং \((8,-2)\) বিন্দুগুলি স্থাপন করে AB সরলরেখা এবং \((4,2)\), \((0,-2)\) এবং \((6,4)\) বিন্দুগুলি যোগ করে CD সরলরেখা পেলাম। AB ও CD সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করে। P বিন্দুর স্থানাঙ্ক \((4,2)\)।
\(\therefore\) নির্ণেয় সমাধান \(x = 4\) এবং \(y = 2\)।
অর্থাৎ স্রোতের বেগ 4 কিমি./ঘণ্টা এবং নৌকার বেগ 2 কিমি./ঘণ্টা।
7. নীচের সমীকরণগুলির লেখচিত্র অঙ্কন করি ও ছেদবিন্দুর স্থানাঙ্ক নির্ণয় করি।
(i) \(x = 0\) এবং \(2x+3y = 15\)
সমাধান –
\(x = 0\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 0 | 0 | 0 |
| y | 5 | 10 | 12 |
বা, \(x = \frac{15-3y}{2}\) —(ii)
(ii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 0 | -3 | -6 |
| y | 5 | 7 | 9 |
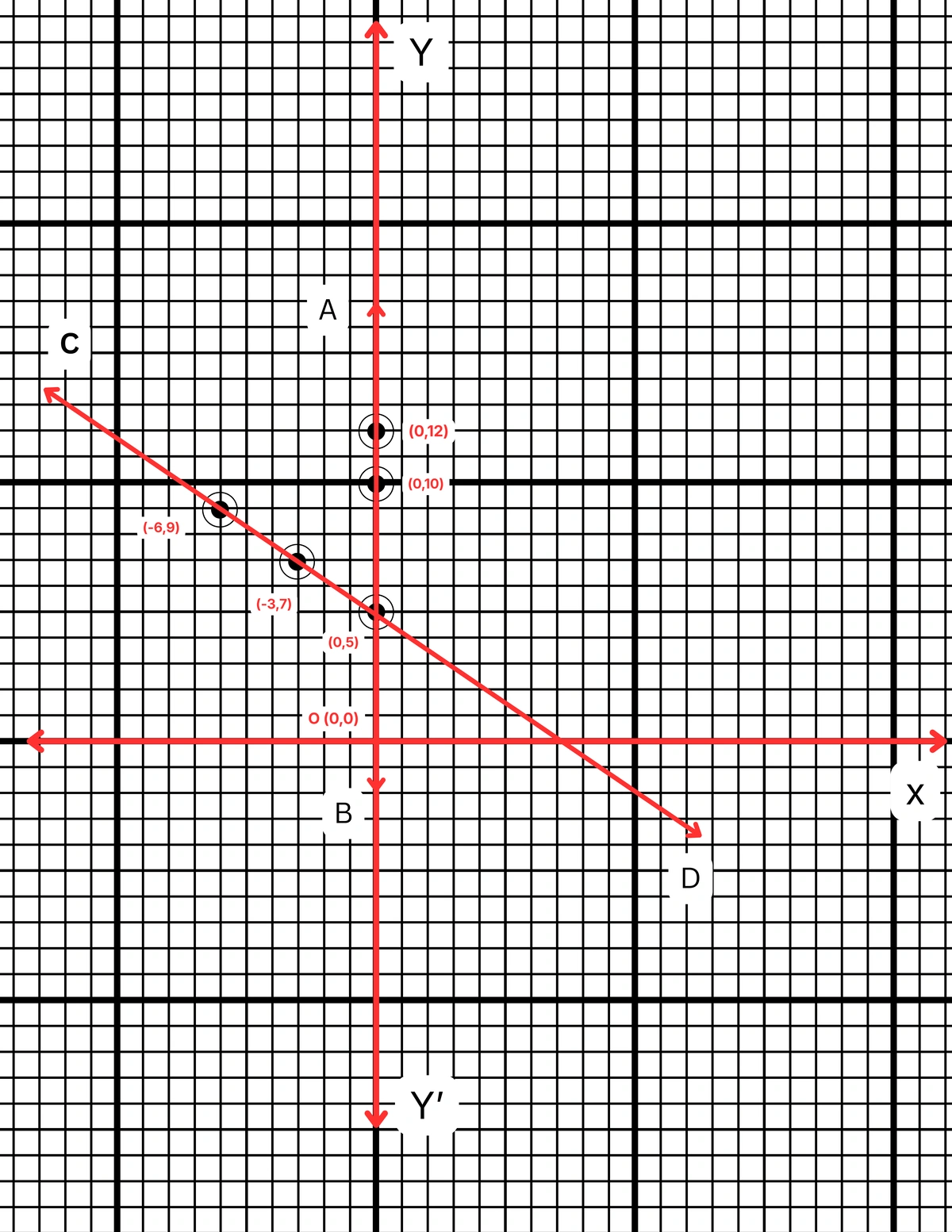
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((0,5)\), \((0,10)\) এবং \((0,12)\) বিন্দুগুলি স্থাপন করে AB সরলরেখা এবং \((0,5)\), \((-3,7)\) এবং \((-6,9)\) বিন্দুগুলি যোগ করে CD সরলরেখা পেলাম। AB ও CD সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করে। P বিন্দুর স্থানাঙ্ক \((0,5)\)।
\(\therefore\) লেখচিত্র দুটির ছেদবিন্দুর স্থানাঙ্ক \((0,5)\)।
(ii) \(y = 5\) এবং \(2x+3y = 11\)
সমাধান –
\(y = 5\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 10 | 5 | -10 |
| y | 5 | 5 | 5 |
বা, \(2x = 11-3y\)
বা, \(x = \frac{11-3y}{2}\) —(ii)
(ii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 1 | -2 | -8 |
| y | 3 | 5 | 9 |
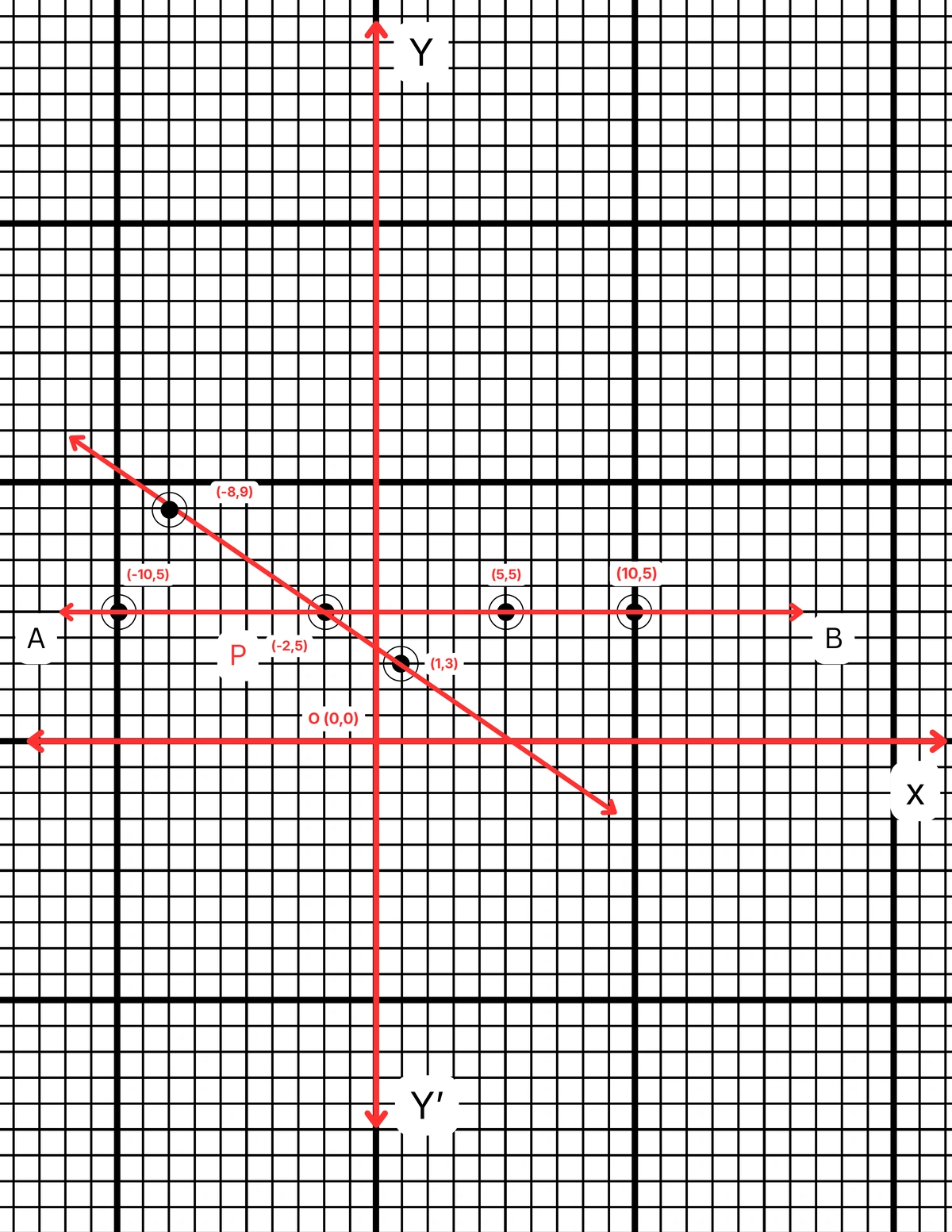
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((10,5)\), \((5,5)\) এবং \((-10,5)\) বিন্দুগুলি স্থাপন করে AB সরলরেখা এবং \((1,3)\), \((-2,5)\) এবং \((-8,9)\) বিন্দুগুলি যোগ করে CD সরলরেখা পেলাম। AB ও CD সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করে। P বিন্দুর স্থানাঙ্ক \((-2,5)\)।
\(\therefore\) লেখচিত্র দুটির ছেদবিন্দুর স্থানাঙ্ক \((-2,5)\)।
(iii) \(x+y = 12\) এবং \(x-y = 2\)
সমাধান –
\(x+y = 12\)বা, \(x = 12-y\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 6 | 2 | 10 |
| y | 6 | 10 | 2 |
বা, \(x = y+2\) —(ii)
(ii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল–
| x | 6 | 12 | 8 |
| y | 4 | 10 | 6 |
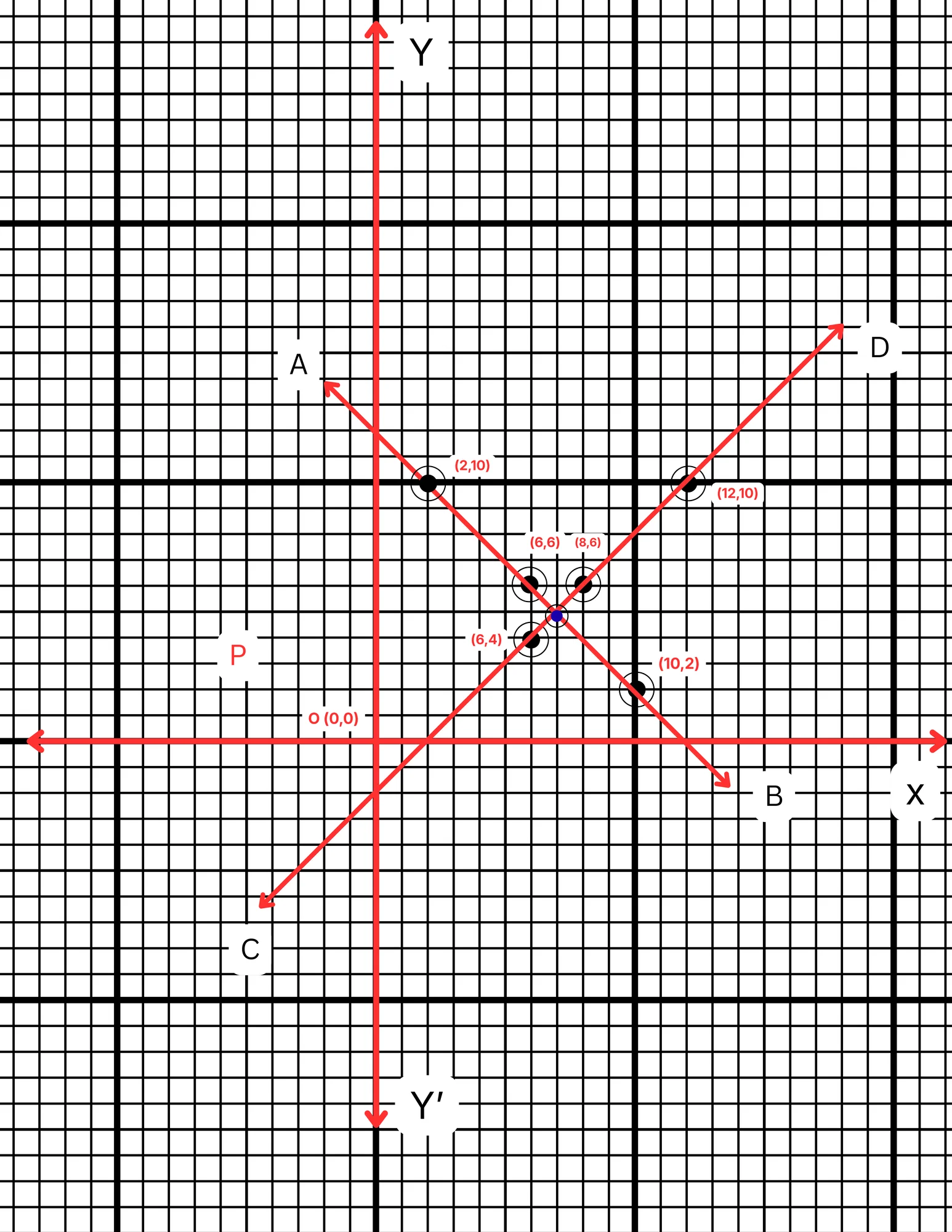
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((6,6)\), \((2,10)\) এবং \((10,2)\) বিন্দুগুলি স্থাপন করে AB সরলরেখা এবং \((6,4)\), \((12,10)\) এবং \((8,6)\) বিন্দুগুলি যোগ করে CD সরলরেখা পেলাম। AB ও CD সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করে। P বিন্দুর স্থানাঙ্ক \((7,5)\)।
∴ লেখচিত্র দুটির ছেদবিন্দুর স্থানাঙ্ক \((7,5)\)।
(iv) \(3x-5y = 16\) এবং \(2x-9y = 5\)
সমাধান –
\(3x-5y = 16\)বা, \(3x = 16+5y\)
বা, \(x = \frac{16+5y}{3}\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 7 | 2 | 12 |
| y | 1 | -2 | 4 |
বা, \(2x = 9y+5\)
বা, \(x = \frac{9y+5}{2}\) —(ii)
(ii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 7 | 16 | -2 |
| y | 1 | 3 | -1 |
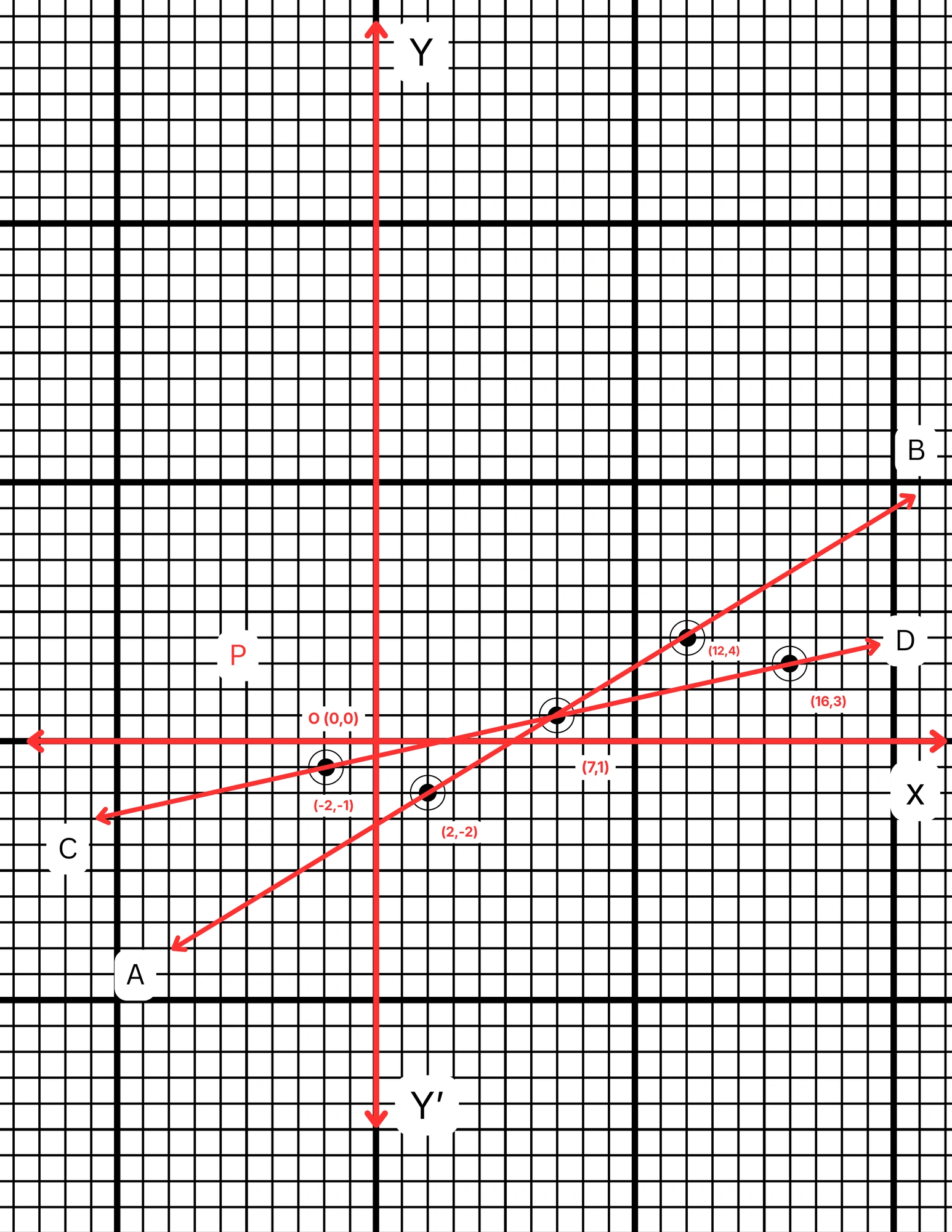
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((7,1)\), \((2,-2)\) এবং \((12,4)\) বিন্দুগুলি স্থাপন করে AB সরলরেখা এবং \((7,1)\), \((16,3)\) এবং \((-2,-1)\) বিন্দুগুলি যোগ করে CD সরলরেখা পেলাম। AB ও CD সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করে। P বিন্দুর স্থানাঙ্ক \((7,1)\)।
∴ লেখচিত্র দুটির ছেদবিন্দুর স্থানাঙ্ক \((7,1)\)।
8. লেখচিত্রের সাহায্যে নীচের সমীকরণগুলি সমাধান করি।
(i) \(4x-y = 3\) ; \(2x+3y = 5\)
সমাধান –
\(4x-y = 3\)বা, \(4x = y + 3\)
বা, \(x = \frac{y+3}{4}\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 2 | 0 | 3 |
| y | 5 | -3 | 9 |
বা, \(2x = 5 -3y\)
বা, \(x = \frac{5-3y}{2}\) —(ii)
(ii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | -2 | 4 | 7 |
| y | 3 | -1 | -3 |
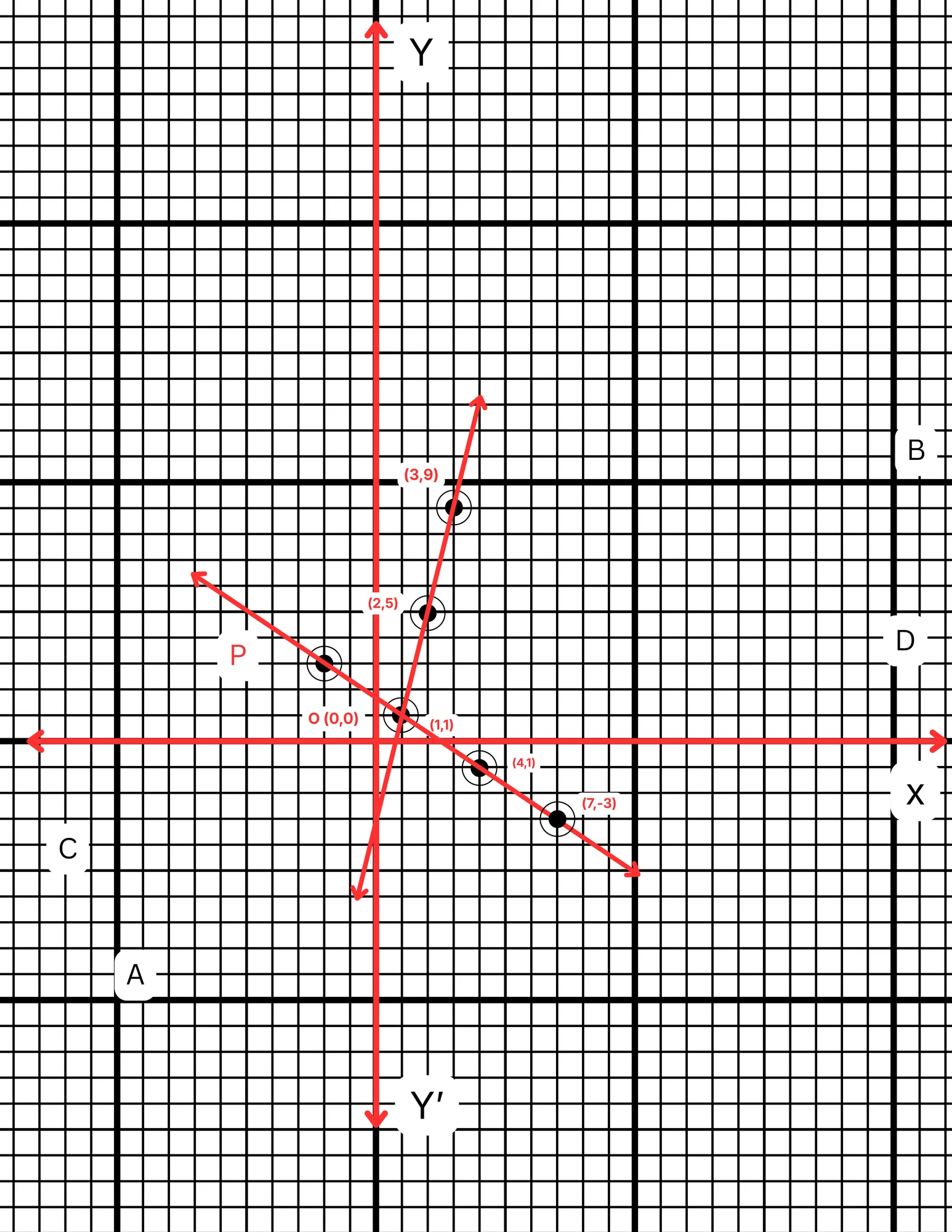
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((2,5)\), \((0,-3)\) এবং \((3,9)\) বিন্দুগুলি স্থাপন করে AB সরলরেখা এবং \((-2,3)\), \((4,-1)\) এবং \((7,-3)\) বিন্দুগুলি যোগ করে CD সরলরেখা পেলাম। AB ও CD সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করে। P বিন্দুর স্থানাঙ্ক \((1,1)\)।
∴ নির্ণেয় সমাধান \(x = 1\) এবং \(y = 1\)।
(ii) \(3x – y = 5\) ; \(4x + 3y = 11\)
সমাধান –
\(3x – y = 5\)বা, \(3x = y + 5\)
বা, \(x = \frac{y+5}{3}\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | -1 | -4 | 5 |
| y | 5 | 9 | -3 |
বা, \(4x = 11 – 3y\)
বা, \(x = \frac{11-3y}{4}\) —(ii)
(ii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 2 | 3 | 1 |
| y | 1 | 4 | -2 |
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে latex[/latex], latex[/latex] এবং latex[/latex] বিন্দুগুলি স্থাপন করে AB সরলরেখা এবং latex[/latex], latex[/latex] এবং latex[/latex] বিন্দুগুলি যোগ করে CD সরলরেখা পেলাম। AB ও CD সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করে। P বিন্দুর স্থানাঙ্ক latex[/latex]।
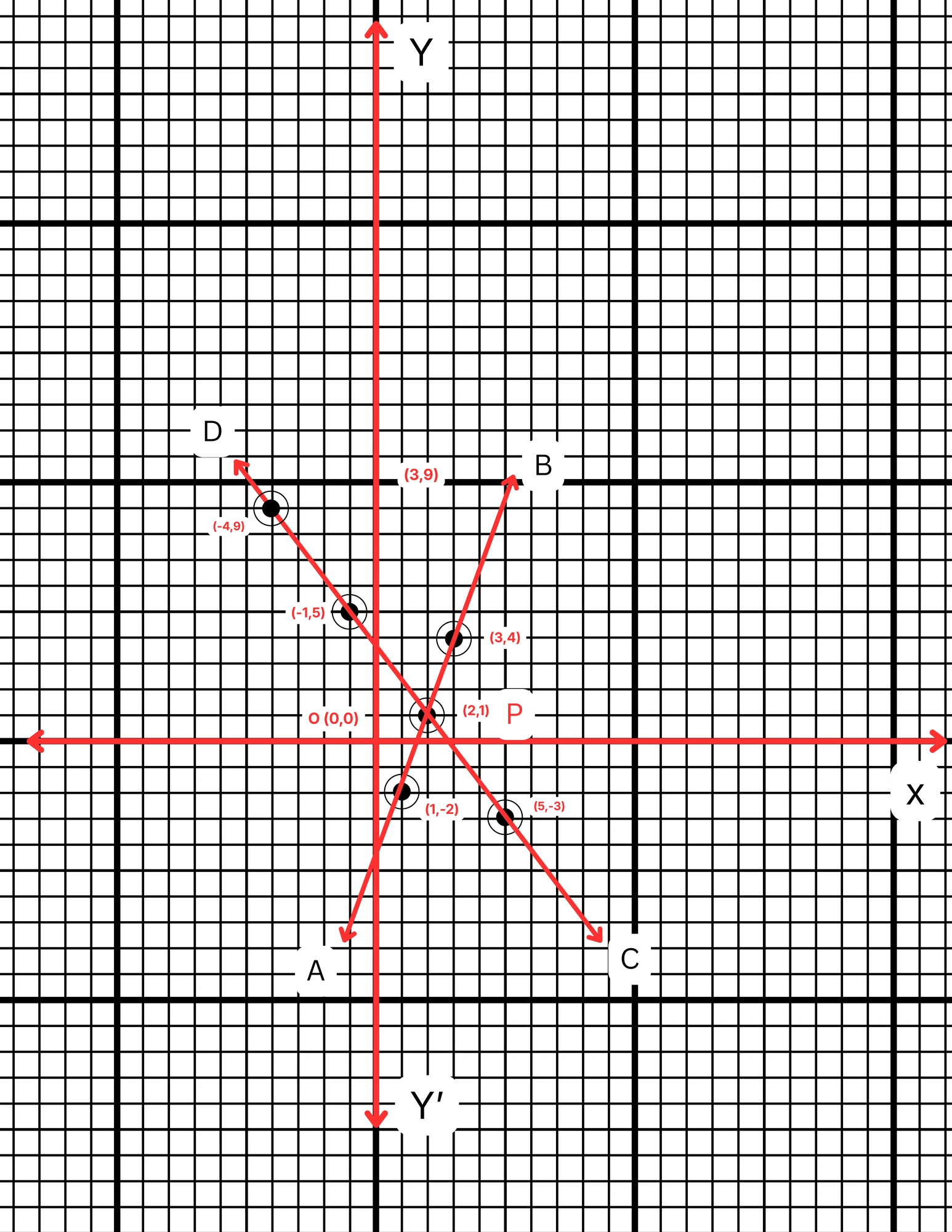
\(\therefore\) নির্ণেয় সমাধান \(x = 2\) এবং \(y = 1\)।
(iii) \(3x-2y = 1\) ; \(2x-y = 3\)
সমাধান –
\(3x-2y = 1\)বা, \(3x = 1+ 2y\)
বা, \(x = \frac{2y+1}{3}\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 1 | 3 | 5 |
| y | 1 | 4 | 7 |
এবং \(2x-y = 3\)
বা, \(2x = y+3\)
বা, \(x = \frac{y+3}{2}\) —(ii)
(ii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 6 | 4 | 5 |
| y | 9 | 5 | 7 |
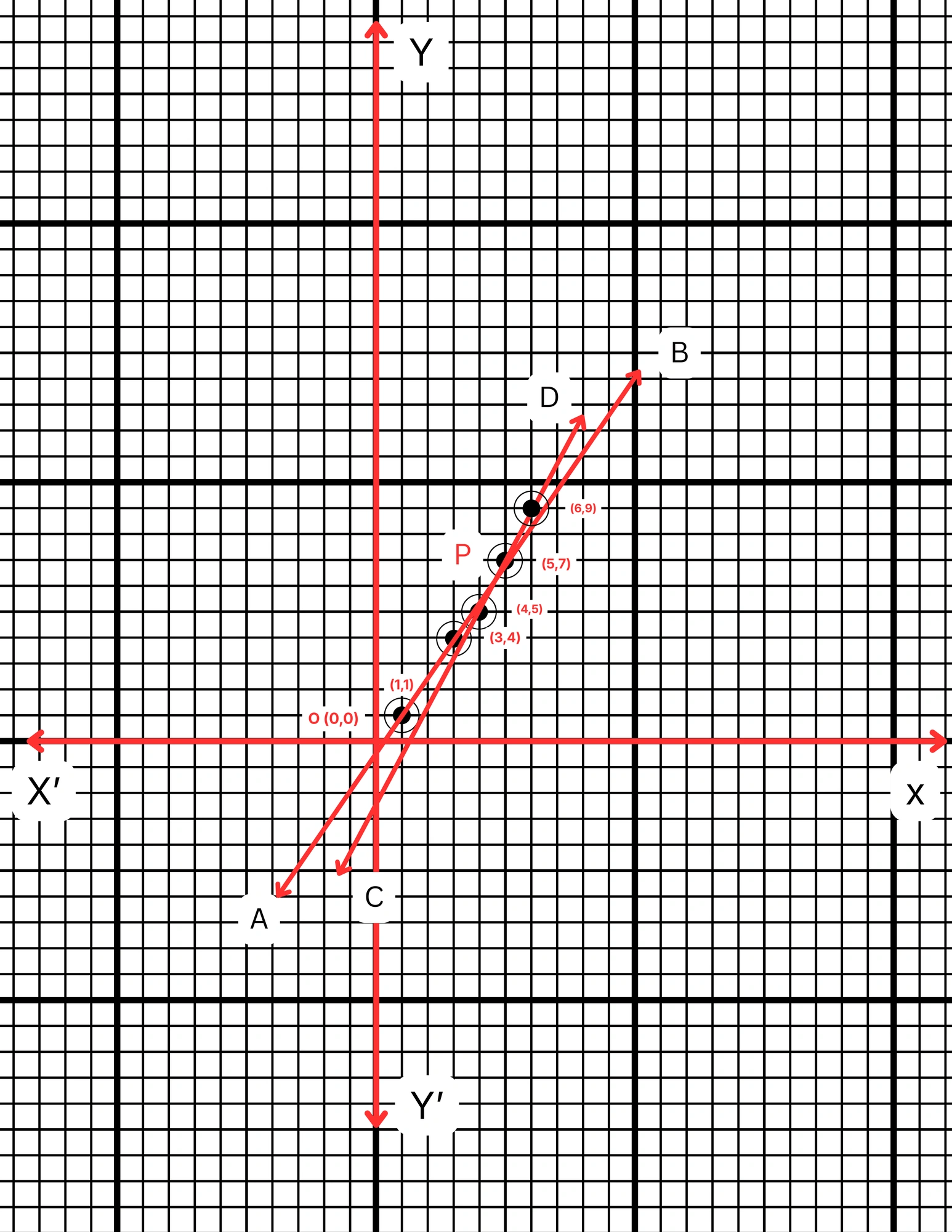
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((1,1)\), \((3,4)\) এবং \((5,7)\) বিন্দুগুলি স্থাপন করে AB সরলরেখা এবং \((2,1)\), \((4,5)\) এবং \((5,7)\) বিন্দুগুলি যোগ করে CD সরলরেখা পেলাম। AB ও CD সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করে। P বিন্দুর স্থানাঙ্ক \((5,7)\)।
∴ নির্ণেয় সমাধান \(x = 5\) এবং \(y = 7\)।
(iv) \(2x+3y = 12\) ; \(2x = 3y\)
সমাধান –
\(2x + 3y = 12\)বা, \(2x = 12 – 3y\)
বা, \(x = \frac{12 – 3y}{2}\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 6 | 3 | 0 |
| y | 0 | 2 | 4 |
বা, \(x = \frac{3y}{2}\) —(ii)
(ii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 3 | 9 | 15 |
| y | 2 | 6 | 10 |
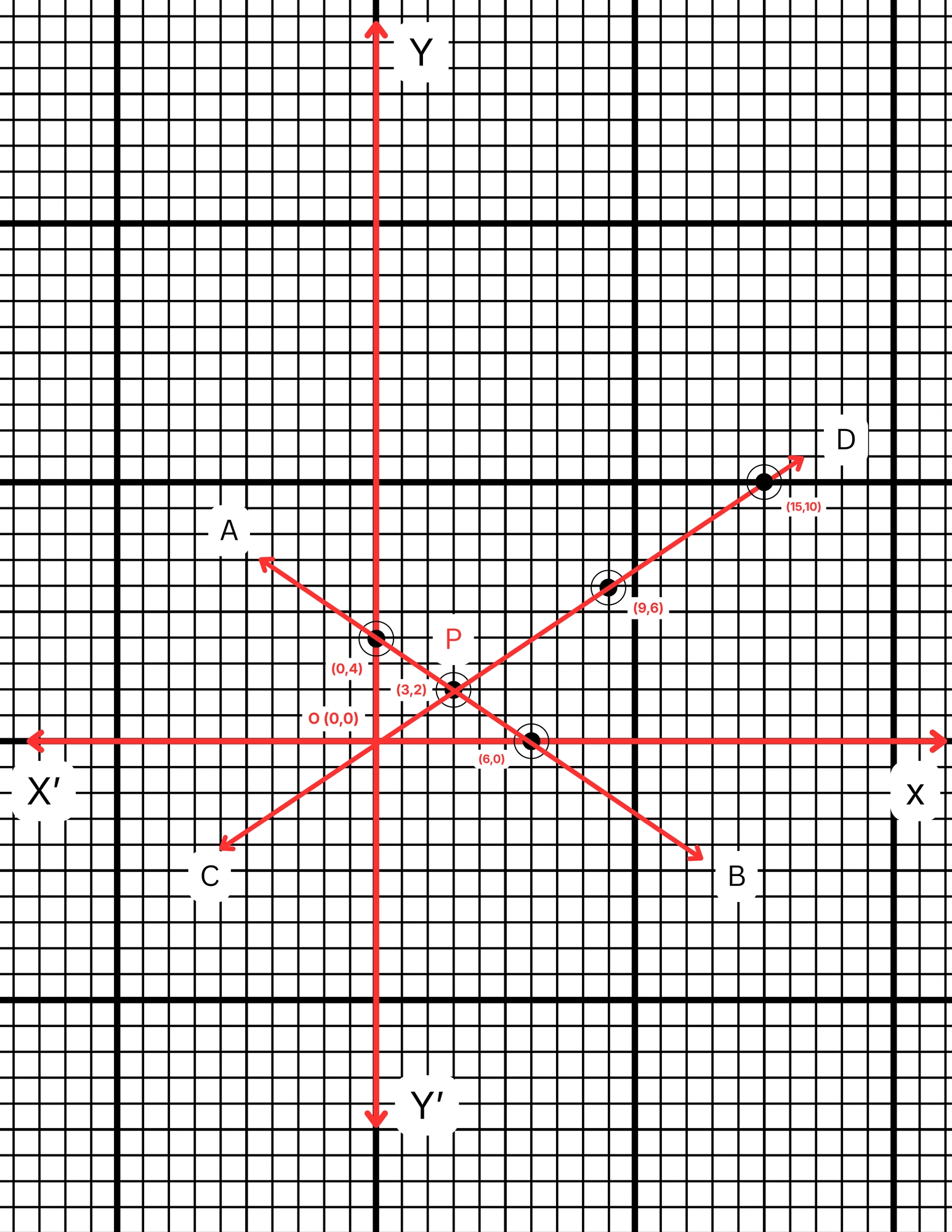
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((6,0)\), \((3,2)\) এবং \((0,4)\) বিন্দুগুলি স্থাপন করে AB সরলরেখা এবং \((3,2)\), \((9,6)\) এবং \((15,10)\) বিন্দুগুলি যোগ করে CD সরলরেখা পেলাম। AB ও CD সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করে। P বিন্দুর স্থানাঙ্ক \((3,2)\)।
\(\therefore\) নির্ণেয় সমাধান \(x = 3\) এবং \(y = 2\)।
(v) \(5x-2y = 1\) ; \(3x+5y = 13\)
সমাধান –
\(5x – 2y = 1\)বা, \(5x = 1 + 2y\)
বা, \(x = \frac{1+2y}{5}\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 1 | 3 | 5 |
| y | 2 | 7 | 12 |
বা, \(3x = 13 – 5y\)
বা, \(x = \frac{13-5y}{3}\) —(ii)
(ii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 1 | -4 | 6 |
| y | 2 | 5 | -1 |
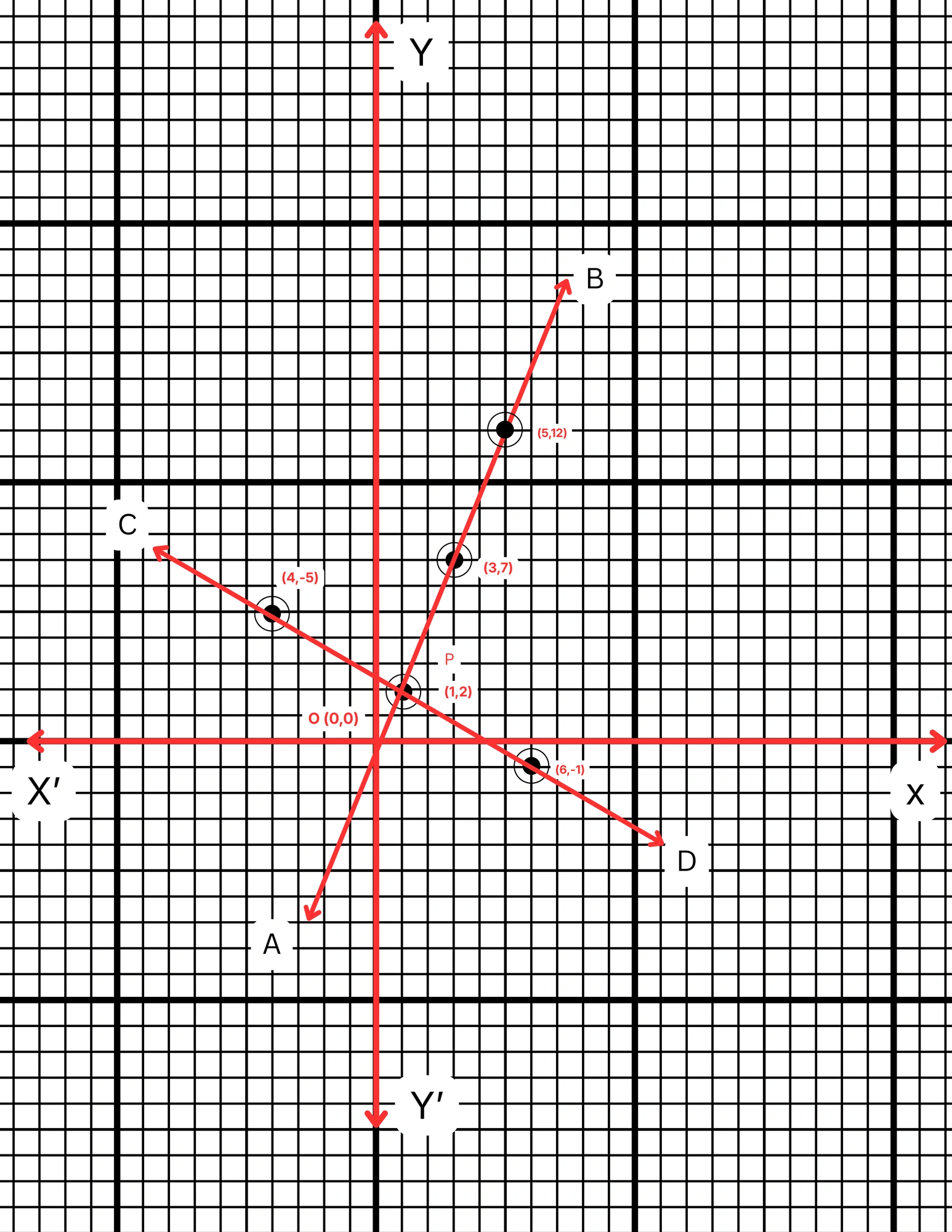
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((1,2)\), \((3,7)\) এবং \((5,12)\) বিন্দুগুলি স্থাপন করে AB সরলরেখা এবং \((1,2)\), \((-4,5)\) এবং \((6,-1)\) বিন্দুগুলি যোগ করে CD সরলরেখা পেলাম। AB ও CD সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করে। P বিন্দুর স্থানাঙ্ক \((1,2)\)।
\(\therefore\) নির্ণেয় সমাধান \(x = 1\) এবং \(y = 2\)।
9. লেখচিত্রের মাধ্যমে প্রদত্ত সমীকরণ দুটির সমাধান নির্ণয় করি।
\(3x+2y = 12\), \(12 = 9x -2y\)
সমাধান –
\(3x+2y = 12\)বা, \(3x = 12 -2y\)
বা, \(x = \frac{12-2y}{3}\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হবে –
| x | 0 | -2 | 4 |
| y | 6 | 9 | 0 |
বা, \(9x = 12 +2y\)
বা, \(x = \frac{12+2y}{9}\) —(ii)
(ii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 2 | 6 | -2 |
| y | 3 | 21 | -15 |
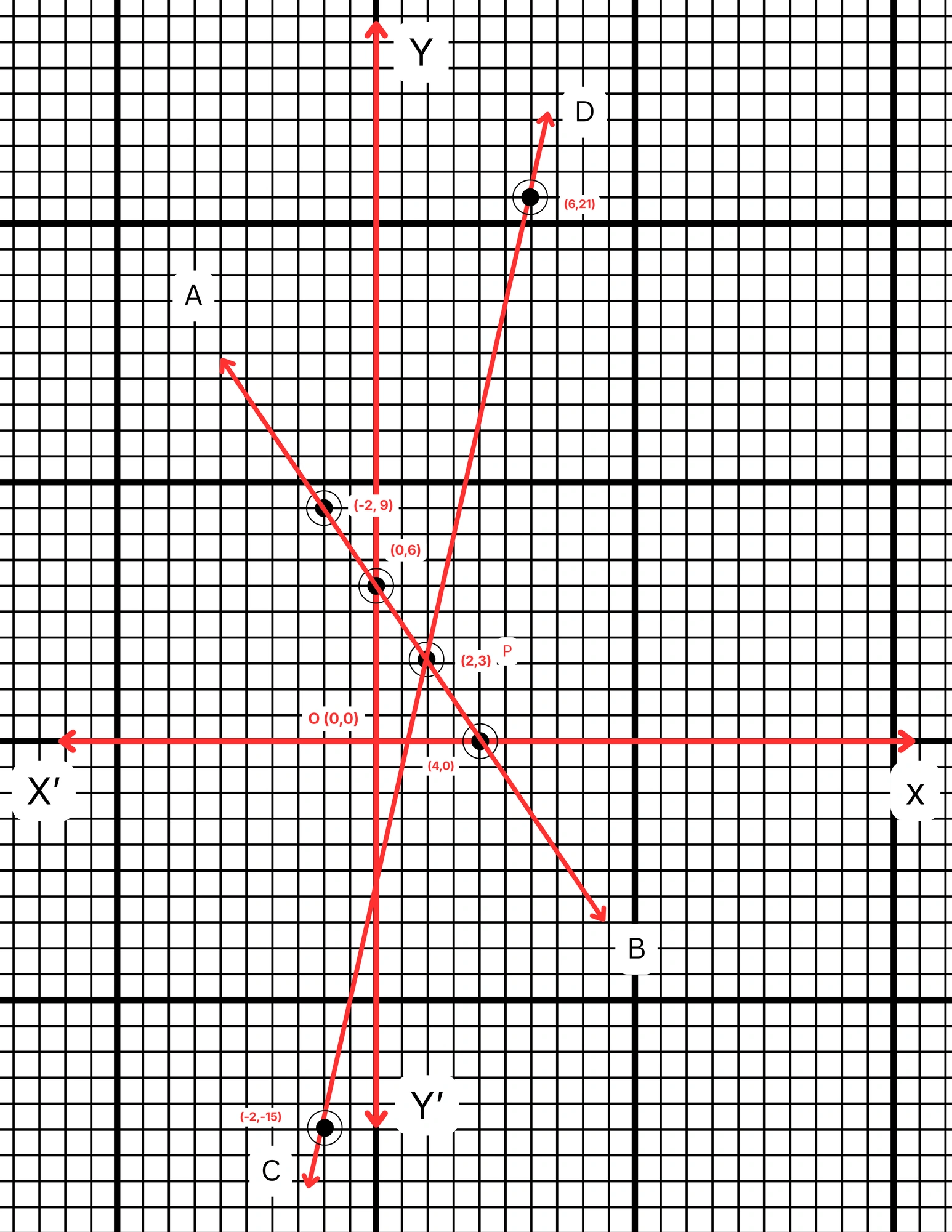
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((0,6)\), \((-2,9)\) এবং \((4,0)\) বিন্দুগুলি স্থাপন করে AB সরলরেখা এবং \((2,3)\), \((6,21)\) এবং \((-2,-15)\) বিন্দুগুলি যোগ করে CD সরলরেখা পেলাম। AB ও CD সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করে। P বিন্দুর স্থানাঙ্ক \((2,3)\)।
∴ নির্ণেয় সমাধান \(x = 2\) এবং \(y = 3\)।
10. \(\frac{x}{3} + \frac{y}{4} = 2\) সমীকরণটির লেখচিত্র অঙ্কন করি ও সমীকরণের লেখচিত্রটি অক্ষদ্বয়ের সঙ্গে যে ত্রিভুজ উৎপন্ন করেছে তার ক্ষেত্রফল হিসেব করে লিখি।
সমাধান –
প্রদত্ত সমীকরণটি হল–
\(\frac{x}{3} + \frac{y}{4} = 2\)বা, \(\frac{x}{3} = 2 – \frac{y}{4}\)
বা, \(\frac{x}{3} = \frac{8-y}{4}\)
বা, \(x = \frac{3(8-y)}{4}\)
বা, \(x = \frac{24-3y}{4}\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল–
| X | 6 | 0 | 3 |
| y | 0 | 8 | 4 |
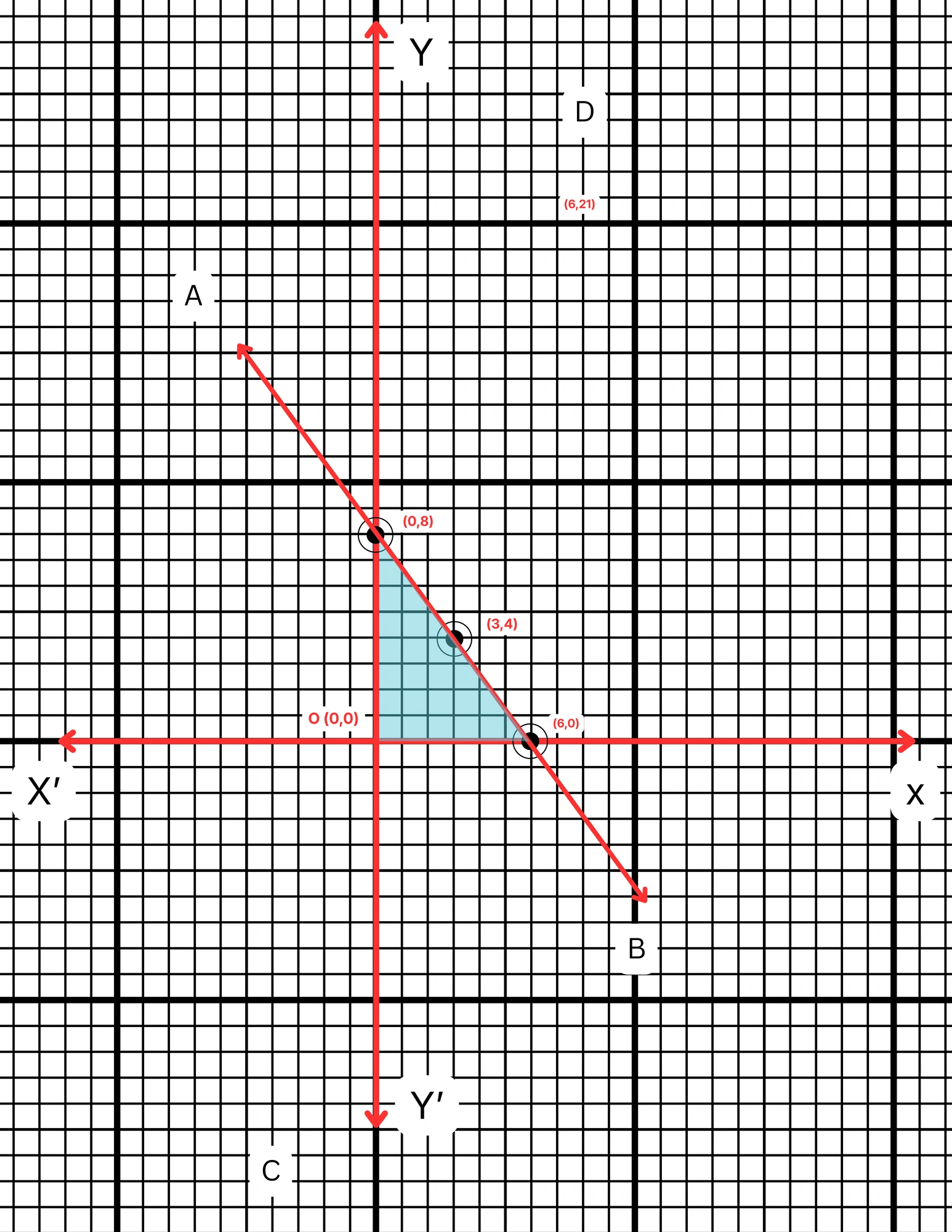
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((6,0)\), \((0,8)\) এবং \((3,4)\) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে PQ সরলরেখা পেলাম। PQ সরলরেখা X অক্ষকে M বিন্দুতে এবং Y অক্ষকে N বিন্দুতে ছেদ করেছে। সুতরাং, PQ লেখচিত্রটি অক্ষদ্বয়ের সাথে যে ত্রিভুজটি তৈরি করে তা হল \(\triangle OMN\) যার \(OM = 8\) একক এবং \(ON = 6\) একক। স্পষ্টতই \(\triangle OMN\) একটি সমকোণী ত্রিভুজ।
\(\triangle OMN\) ত্রিভুজের ক্ষেত্রফল \(= \frac{1}{2} \times \text{ভূমি} \times \text{উচ্চতা} = \frac{1}{2} \times 6 \times 8\) বর্গ একক \(= 24\) বর্গ একক।
11. \(x = 4\), \(y = 3\) এবং \(3x+4y = 12\) সমীকরণ তিনটির লেখচিত্র অঙ্কন করি এবং লেখচিত্র দ্বারা ত্রিভুজটির ক্ষেত্রফল নির্ণয় করি।
সমাধান –
\(x = 4\) —(i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 4 | 4 | 4 |
| y | 8 | 12 | 18 |
\(y = 3\) —(ii)
(ii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| X | -3 | 5 | 8 |
| y | 3 | 3 | 3 |
বা, \(3x = 12 – 4y\)
বা, \(x = \frac{12-4y}{3}\) —(iii)
(iii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল–
| x | 0 | -4 | 8 |
| y | 3 | 6 | -3 |
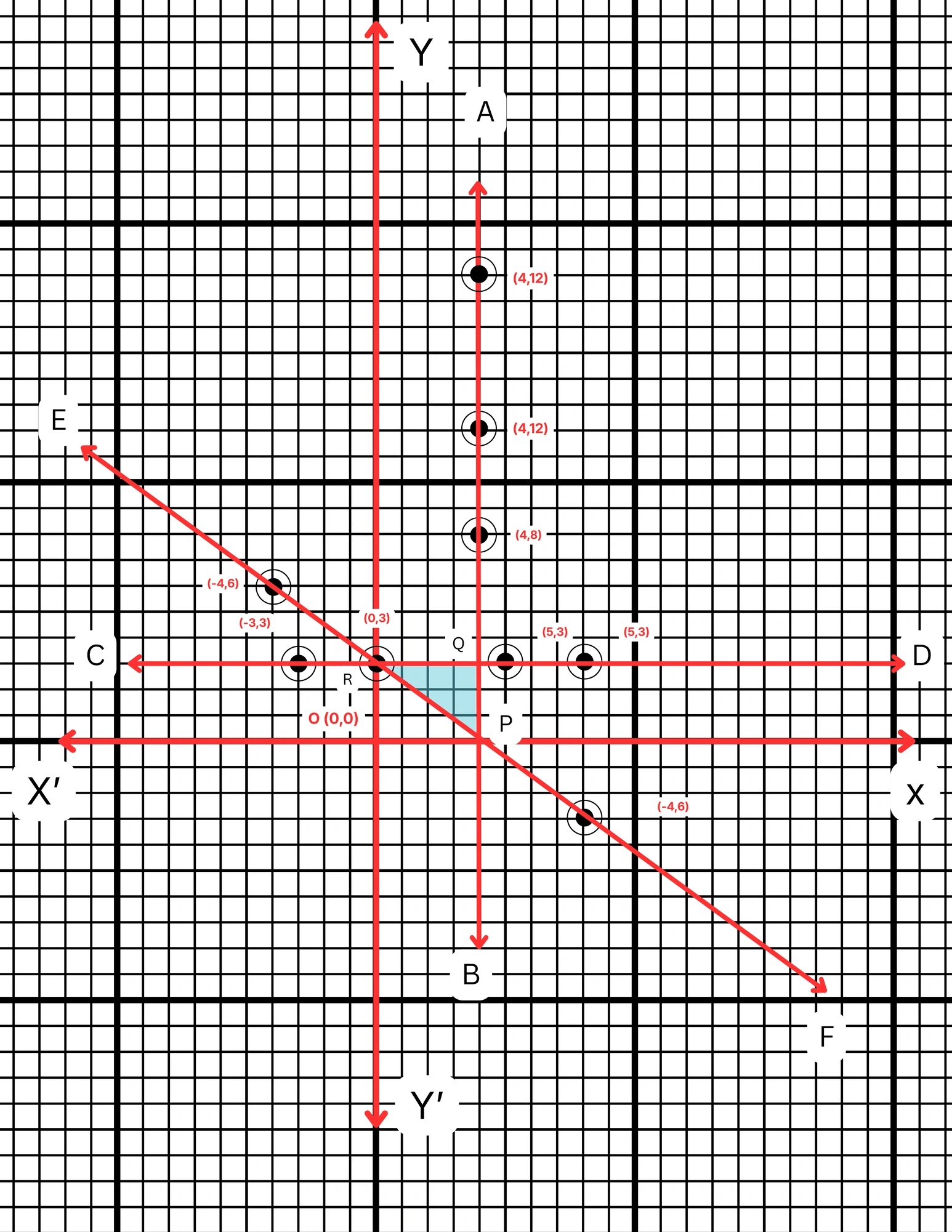
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((4,8)\), \((4,12)\) এবং \((4,18)\) বিন্দুগুলি স্থাপন করে AB সরলরেখা, \((-3,3)\), \((5,3)\) ও \((8,3)\) বিন্দুগুলি স্থাপন করে CD সরলরেখা এবং \((0,3)\), \((-4,6)\) এবং \((8,-3)\) বিন্দুগুলি স্থাপন করে EF সরলরেখা অঙ্কন করা হল। এখন, AB, CD এবং EF সরলরেখা তিনটি দ্বারা PQR ত্রিভুজ গঠিত হয়। স্পষ্টতই PQR একটি সমকোণী ত্রিভুজ, যার \(QP = OR = 4\) একক এবং \(QR = OP = 3\) একক।
∴ PQR ত্রিভুজের ক্ষেত্রফল \(= \frac{1}{2} \times \text{ভূমি} \times \text{উচ্চতা} = \frac{1}{2} \times QR \times PQ\) বর্গএকক \(= \left( \frac{1}{2} \times 3 \times 4 \right)\) বর্গএকক \(= 6\) বর্গএকক।
∴ লেখচিত্রগুলি দ্বারা গঠিত ত্রিভুজটির ক্ষেত্রফল \(6\) বর্গএকক।
12. y = (x+2)/3 সমীকরণের লেখচিত্র অঙ্কন করি। সেই লেখচিত্র থেকে x = -2 এর জন্য y এর মান এবং x-এর কোন মানের জন্য y এর মান 3 হবে তা নির্ণয় করি।
সমাধান –
y = (x+2)/3
বা, 3y = x+2
বা, x = 3y-2 — (i)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল–
| x | -2 | 10 | 7 |
| y | 0 | 4 | 3 |
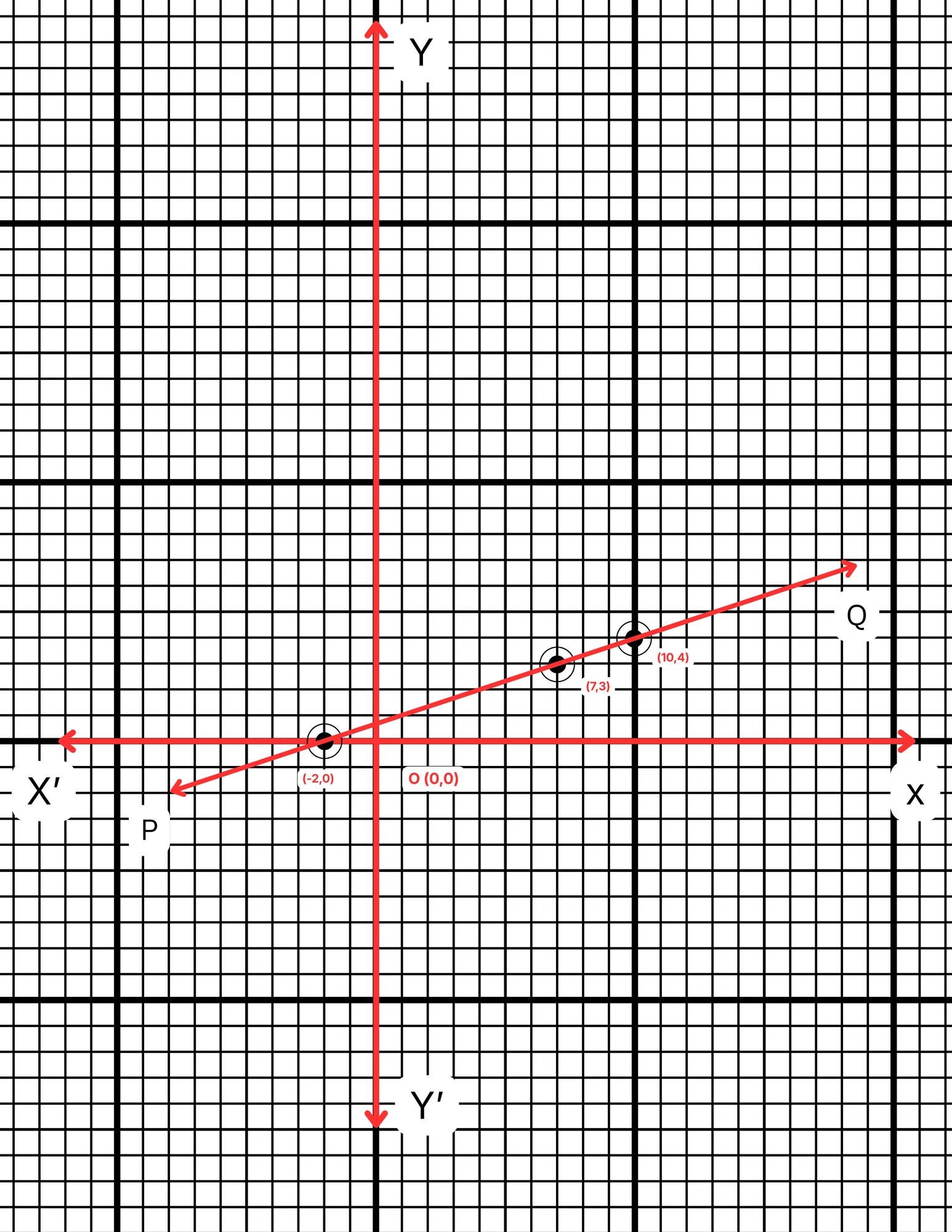
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে (-2,0), (10,4) এবং (7,3) বিন্দুগুলি স্থাপন করা হল এবং বিন্দুগুলি যোগ করে PQ সরলরেখা পেলাম। PQ সরলরেখা হল নির্ণেয় লেখচিত্র। এই লেখচিত্র থেকে স্পষ্টতই বলা যায়, x = -2 হলে, y = 0 এবং x এর মান 7 হলে, y = 3 হবে।
13. লেখচিত্রের সাহায্যে সমাধান করি –
\(\frac{3x-1}{2} = \frac{2x+6}{3}\)সমাধান –
ধরি, \(y = \frac{3x-1}{2} = \frac{2x+6}{3}\)
\(\therefore y = \frac{3x-1}{2}\)বা, \(2y = 3x-1\)
বা, \(3x = 2y+1\)
বা, \(x = \frac{2y+1}{3} \cdots (i)\)
(i) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 1 | 3 | 5 |
| y | 1 | 4 | 7 |
আবার, \(y = \frac{2x+6}{3}\)
বা, \(3y = 2x+6\)
বা, \(2x = 3y-6\)
বা, \(x = \frac{3y-6}{2}\) —(ii)
(ii) নং সমীকরণের জন্য প্রয়োজনীয় ছকটি হল –
| x | 0 | 3 | -6 |
| y | 2 | 4 | -2 |
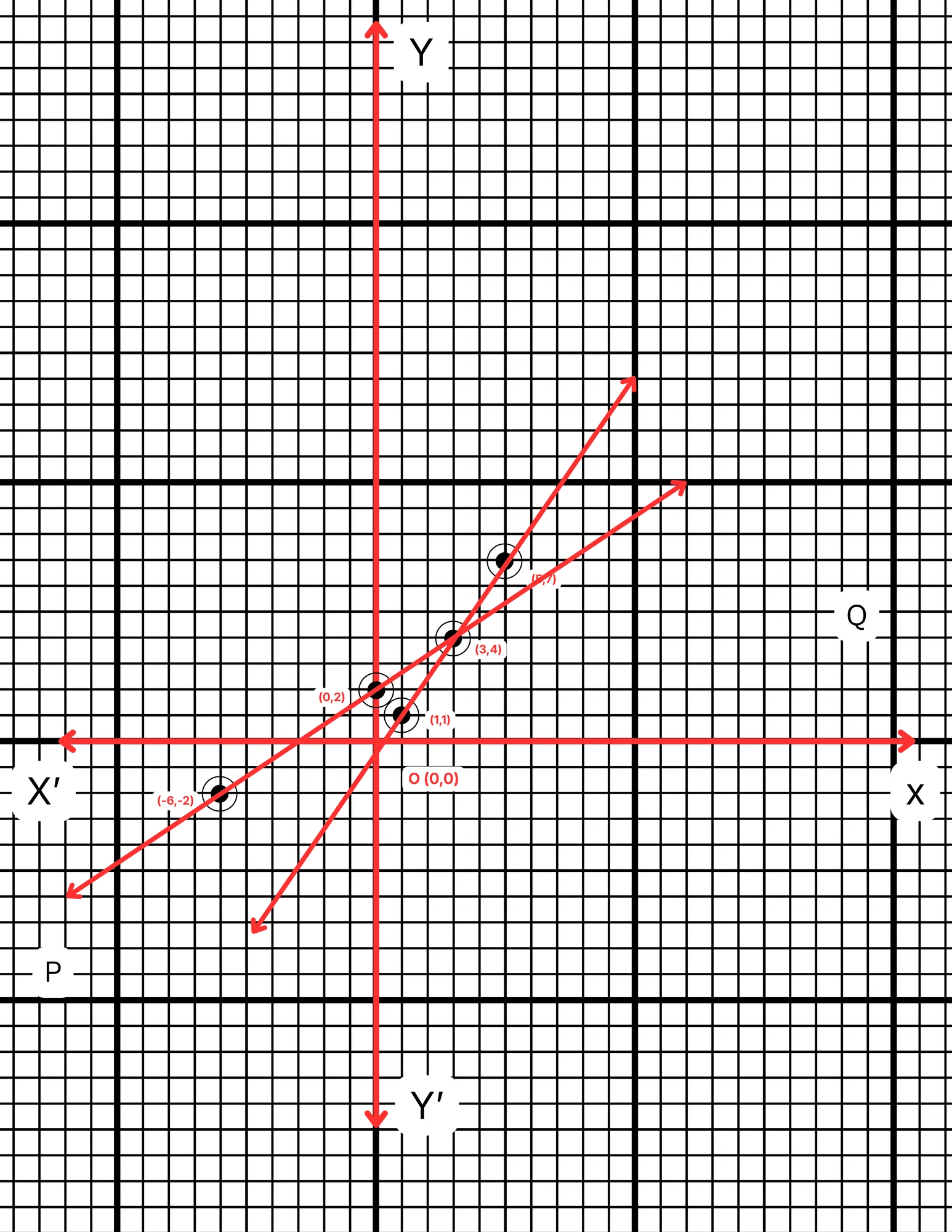
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((1,1)\), \((3,4)\) এবং \((5,7)\) বিন্দুগুলি স্থাপন করে AB সরলরেখা এবং \((0,2)\), \((3,4)\) এবং \((-6,2)\) বিন্দুগুলি যোগ করে CD সরলরেখা পেলাম। AB ও CD সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করে। P বিন্দুর স্থানাঙ্ক \((3,4)\)।
\(\therefore\) নির্ণেয় সমাধান \(x = 3\) এবং \(y = 4\)।
14. বহুমুখী বিকল্পীয় প্রশ্ন (M.C.Q)
(i) \(2x+3=0\) সমীকরণের লেখচিত্রটি
(a) x অক্ষের সমান্তরাল
(b) y অক্ষের সমান্তরাল
(c) কোনো অক্ষের সমান্তরাল নয়
(d) মূলবিন্দুগামী
উত্তর – (b) y অক্ষের সমান্তরাল।
সমাধান – \(2x+3=0\)
বা, \(2x=-3\)
বা, \(x=-\frac{3}{2}\), এটি y অক্ষের সমান্তরাল সরলরেখার সমীকরণ।
(ii) \(ay+b=0\) (a ও b ধ্রুবক এবং \(a \neq 0, b \neq 0\)) সমীকরণের লেখচিত্রটি
(a) x অক্ষের সমান্তরাল
(b) y অক্ষের সমান্তরাল
(c) কোনো অক্ষের সমান্তরাল নয়
(d) মূলবিন্দুগামী
উত্তর – (a) x অক্ষের সমান্তরাল।
সমাধান – \(ay+b=0\)
বা, \(ay=-b\)
বা, \(y=-\frac{b}{a}\), এই সমীকরণটি x অক্ষের সমান্তরাল সরলরেখার সমীকরণ।
(iii) \(2x+3y=0\) সমীকরণের লেখচিত্রটি
(a) x অক্ষের সমান্তরাল
(b) y অক্ষের সমান্তরাল
(c) মূলবিন্দুগামী
(d) \((2,0)\) বিন্দুগামী
উত্তর – (c) মূলবিন্দুগামী।
(iv) \(cx+d=0\) (c ও d ধ্রুবক, \(c \neq 0\)) সমীকরণের লেখচিত্রটি y অক্ষের সমীকরণ হবে যখন
(a) \(d=-c\)
(b) \(d=c\)
(c) \(d=0\)
(d) \(d=1\)
উত্তর – (c) \(d=0\)
সমাধান – y অক্ষের সমীকরণ \(x=0\)
∴ \(cx+d=0\)
বা, \(c \cdot 0 + d = 0\)
বা, \(d=0\)
(v) \(ay+b=0\) (a ও b ধ্রুবক, \(a \neq 0\)) সমীকরণের লেখচিত্রটি x অক্ষের সমীকরণ হবে যখন
(a) \(b=a\)
(b) \(b=-a\)
(c) \(b=2\)
(d) \(b=0\)
উত্তর – (d) \(b=0\)
সমাধান – x অক্ষের সমীকরণ \(y=0\)
∴ \(ay+b=0\)
বা, \(a \cdot 0 + b = 0\)
বা, \(b=0\)
15. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন
(i) \(2x+3y = 12\) সমীকরণের লেখচিত্রটি x অক্ষকে যে বিন্দুতে ছেদ করে তার স্থানাঙ্ক লিখি।
সমাধান –
\(2x+3y = 12\) সমীকরণের লেখচিত্রটি x অক্ষকে যে বিন্দুতে ছেদ করে তার y স্থানাঙ্ক বা কোটি সর্বদা শূন্য।
অর্থাৎ প্রদত্ত সমীকরণে y এর স্থানে 0 বসিয়ে পাই,
\(2x = 12\)বা, \(x = 6\)
সুতরাং নির্ণেয় বিন্দুটি হল \((6, 0)\)।
(ii) \(2x-3y = 12\) সমীকরণের লেখচিত্রটি y অক্ষকে যে বিন্দুতে ছেদ করে তার স্থানাঙ্ক লিখি।
সমাধান –
\(2x-3y = 12\) সমীকরণের লেখচিত্রটি y অক্ষকে যে বিন্দুতে ছেদ করে তার x স্থানাঙ্ক বা ভুজ শূন্য হবে।
∴ প্রদত্ত সমীকরণে \(x = 0\) বসিয়ে পাই,
\(-3y = 12\)বা, \(y = -\frac{12}{3}\)
বা, \(y = -4\)
সুতরাং বিন্দুটির স্থানাঙ্ক \((0, -4)\)।
(iii) \(3x+4y = 12\) সমীকরণের লেখচিত্রটি ও অক্ষদ্বয় দ্বারা গঠিত ত্রিভুজটির ক্ষেত্রফল কত তা লিখি।
সমাধান –
\(3x+4y = 12\) সমীকরণে \(x = 0\) বসিয়ে পাই,
\(4y = 12\)বা, \(y = \frac{12}{4}\)
বা, \(y = 3\)
সুতরাং সরলরেখাটি y অক্ষকে ছেদ করে \((0, 3)\) বিন্দুতে।
আবার, \(3x+4y = 12\) সমীকরণে \(y = 0\) বসিয়ে পাই,
\(3x = 12\)বা, \(x = \frac{12}{3}\)
বা, \(x = 4\)
সুতরাং সরলরেখাটি x অক্ষকে ছেদ করে \((4, 0)\) বিন্দুতে।
∴ যে ত্রিভুজটি উৎপন্ন হবে তার ভূমি 4 একক এবং উচ্চতা 3 একক। স্পষ্টতই ত্রিভুজটি একটি সমকোণী ত্রিভুজ।
সুতরাং ত্রিভুজটির ক্ষেত্রফল \(= \frac{1}{2} \times \text{ভূমি} \times \text{উচ্চতা} = \frac{1}{2} \times 4 \times 3\) বর্গএকক \(= 6\) বর্গএকক।
(iv) \((6, -8)\) বিন্দুটির x অক্ষ থেকে দূরত্ব ও y অক্ষ থেকে দূরত্ব কত তা লিখি।
সমাধান –
\((6, -8)\) বিন্দুটির x অক্ষ থেকে দূরত্ব 8 একক ও y অক্ষ থেকে দূরত্ব 6 একক।
(v) \(x = y\) সমীকরণের লেখচিত্র x অক্ষের সঙ্গে যে কোণ উৎপন্ন করে তার মান লিখি।
সমাধান –
প্রদত্ত সমীকরণটি হল, \(y = x\)
বা, \(y = 1 \cdot x + 0\) [ \(y = mx+c\) সরলরেখায় \(m\) হল সরলরেখার নতি এবং \(m = \tan \theta\) ]
এখানে, \(m = 1 = \tan 45^\circ\)
∴ \(x = y\) সমীকরণের লেখচিত্র x অক্ষের সঙ্গে যে কোণ উৎপন্ন করে তার মান \(45^\circ\)।
এই আর্টিকেলে নবম শ্রেণির গণিতের ‘লেখচিত্র’ অধ্যায়ের ‘কষে দেখি – 3.1’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।
কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করতে পারেন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।
মন্তব্য করুন