পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) নবম শ্রেণির গণিত পাঠ্যবইয়ের পঞ্চম অধ্যায় হলো ‘রৈখিক সহসমীকরণ (দুই চল বিশিষ্ট)’। এই পোস্টে ‘কষে দেখি – 5.1’-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. আমার দিদি ও আমার বাবার বর্তমান বয়সের সমষ্টি 55 বছর। হিসাব করে দেখছি 16 বছর পরে আমার বাবার বয়স আমার দিদির বয়সের দ্বিগুণ হবে।
(a) সহসমীকরণ গঠন করে লেখচিত্র অঙ্কন করি।
(b) লেখচিত্রের সাহায্যে দেখি সহসমীকরণ দুটির সাধারণ সমাধান পাওয়া যায় কিনা?
(c) লেখচিত্র থেকে আমার দিদি ও আমার বাবার বর্তমান বয়স লিখি।
সমাধান – ধরি, আমার দিদির বয়স \(x\) বছর এবং আমার বাবার বর্তমান বয়স \(y\) বছর।
শর্তানুসারে,
\(x+y = 55\) —(i)
এবং \(y+16 = 2(x+16)\)
বা, \(y+16 = 2x+32\)
বা, \(2x = y+16-32\)
বা, \(2x = y-16\) —(ii)
(i) নং সমীকরণ থেকে পাই,
| x | 14 | 10 | 6 |
| y | 0 | 3 | 6 |
আবার, (ii) নং সমীকরণ থেকে পাই,
\(2x = y-16\)বা, \(x = \frac{y-16}{2}\)
| x | 8 | 0 | 2 |
| y | 0 | 16 | 20 |
(a) ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অঙ্কন করে, ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((15,40)\), \((30,25)\) এবং \((25,30)\) বিন্দুগুলি স্থাপন করে AB এবং \((16,0)\), \((26,5)\) এবং \((36,10)\) বিন্দুগুলি স্থাপন করে CD সরলরেখা অঙ্কন করা হল।
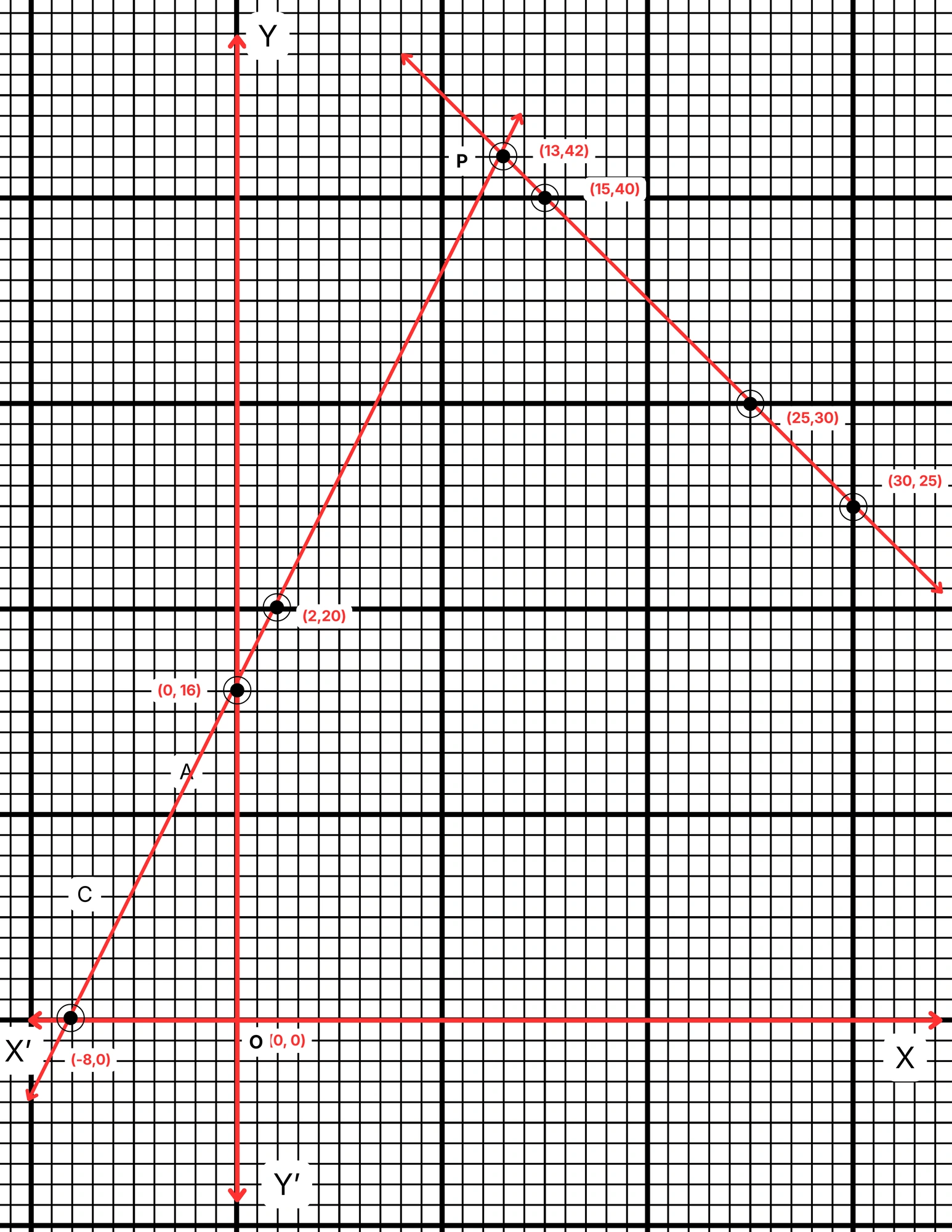
(b) AB ও CD সরলরেখাদ্বয় পরস্পরকে P বিন্দুতে ছেদ করে। P বিন্দুর স্থানাঙ্ক \((13,42)\)
∴ লেখচিত্র দুটির সাধারণ সমাধান, \(x = 13\), \(y = 42\)
(c) লেখচিত্র থেকে পাওয়া গেল, দিদির বয়স \(= 13\) বছর এবং বাবার বয়স \(= 42\) বছর।
2. মিতা যাদব কাকুর দোকান থেকে 42 টাকায় 3 টি পেন ও 4 টি পেনসিল কিনেছে। আমি বন্ধুদের দেওয়ার জন্য যাদবকাকুর দোকান থেকে একই মূল্যের 9 টি পেন ও 1 ডজন পেনসিল 126 টাকায় কিনলাম।
(a) সহসমীকরণ গঠন করে লেখচিত্র অঙ্কন করি।
(b) লেখচিত্রের সাহায্যে আরও দেখি যে সমীকরণ দুটির সাধারণ সমাধান পাওয়া যায় কিনা।
(c) 1 টি পেন ও 1 টি পেনসিলের আলাদা আলাদা দাম কী হবে লেখচিত্র থেকে পাই কিনা দেখি।
সমাধান –
ধরি, 1 টি পেনের দাম \(x\) টাকা এবং 1 টি পেনসিলের দাম \(y\) টাকা।
শর্তানুসারে,
\(3x+4y = 42\) —(i)
এবং, \(9x + 12y = 126\) —(ii)
(i) নং সমীকরণ থেকে পাই,
\(3x = 42 -4y\)বা, \(x = \frac{42-4y}{3}\)
| x | 14 | 10 | 6 |
| y | 0 | 3 | 6 |
(ii) নং সমীকরণ থেকে পাই,
\(9x + 12y = 126\)বা, \(3(3x+4y) = 126\)
বা, \(3x+4y = \frac{126}{3}\)
বা, \(3x+4y = 42\)
বা, \(x = \frac{42-4y}{3}\)
| x | 14 | 10 | 6 |
| y | 0 | 3 | 6 |
(a) ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অঙ্কন করে, ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((14,0)\), \((10,3)\) এবং \((6,6)\) বিন্দুগুলি স্থাপন করে (i) নং সমীকরণের লেখচিত্র এবং \((14,0)\), \((10,3)\) এবং \((6,6)\) বিন্দুগুলি স্থাপন করে (ii) নং সমীকরণের লেখচিত্র অঙ্কন করা হল।
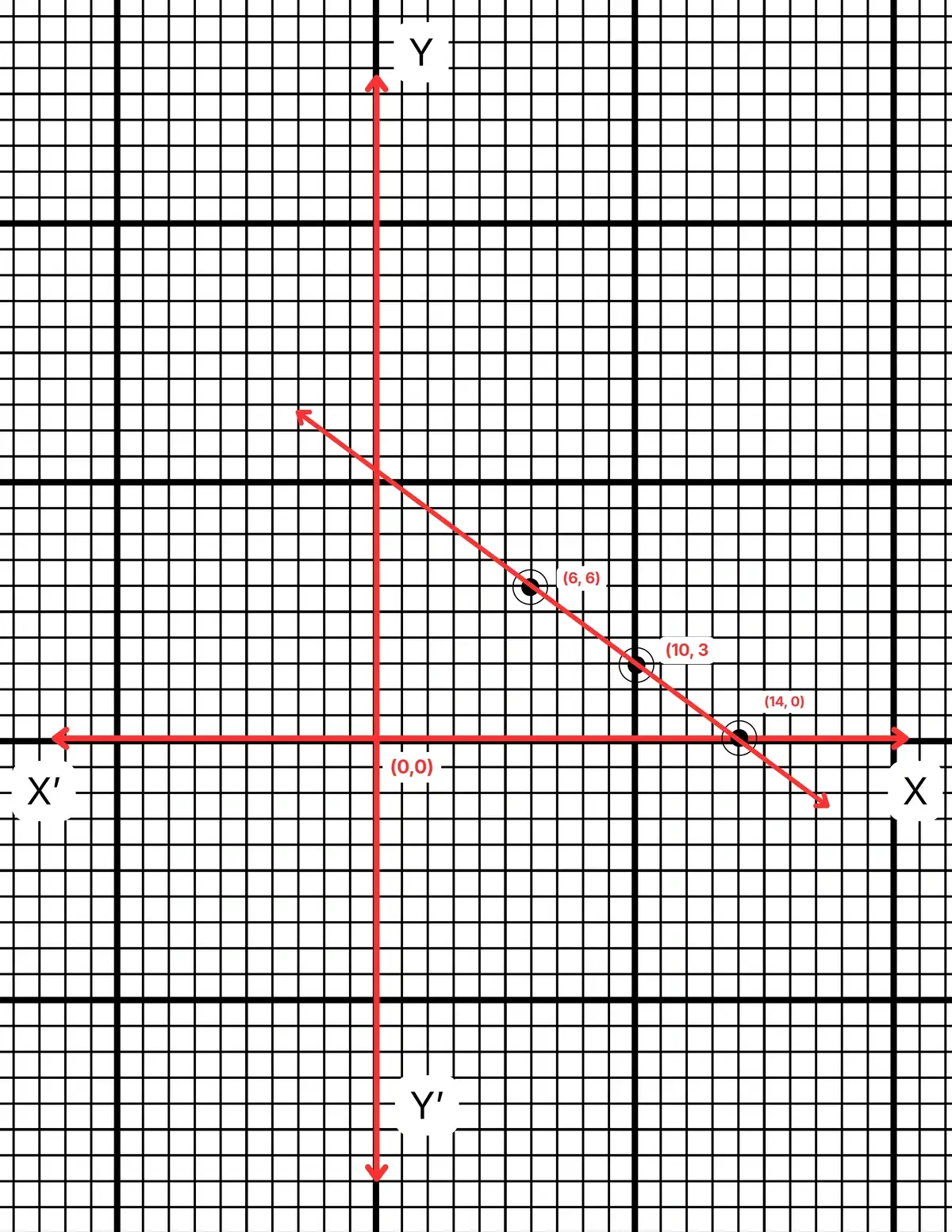
লেখচিত্রদ্বয় পরস্পরের ওপর সমপাতিত হয়েছে।
(b) যেহেতু লেখচিত্রদ্বয় পরস্পরের ওপর সমপাতিত হয়েছে, সুতরাং সমীকরণদ্বয়ের কোনো সাধারণ সমাধান পাওয়া যাবে না।
(c) লেখচিত্র থেকে 1 টি পেন ও 1 টি পেনসিলের আলাদা আলাদা দাম কী হবে, তা নির্দিষ্ট করে নির্ণয় করা যাবে না, পেন ও পেনসিলের মূল্য ভিন্ন হতে পারে।
3. আজ স্কুলে আমরা যেমন খুশি আঁকব। তাই আমি 2 টি আর্ট পেপার ও 5 টি স্কেচপেন 16 টাকায় কিনেছি। কিন্তু দোলা ওই একই দোকান থেকে একই মূল্যের 4 টি আর্ট পেপার ও 10 টি স্কেচ পেন 28 টাকায় কিনেছে।
(a) সমীকরণ গঠন করি ও লেখচিত্র আঁকি।
(b) লেখচিত্র থেকে সমীকরণ দুটির সাধারণ সমাধান পাওয়া যায় কিনা দেখি।
(c) 1 টি আর্ট পেপার ও 1 টি স্কেচপেনের দাম পাই কিনা লিখি।
সমাধান –
ধরি, 1 টি আর্টপেপারের দাম \(x\) টাকা এবং 1 টি স্কেচপেনের দাম \(y\) টাকা।
শর্তানুসারে,
\(2x+5y = 16\) —(i)
এবং, \(4x +10y = 28\) —(ii)
(i) নং সমীকরণ থেকে পাই,
\(2x =16-5y\)বা, \(x = \frac{16-5y}{2}\)
| x | 8 | -2 | 3 |
| y | 0 | 4 | 2 |
ii) নং সমীকরণ থেকে পাই,
\(4x = 28-10y\)বা, \(x = \frac{28-10y}{4}\)
| x | 7 | 2 | -3 |
| y | 0 | 2 | 4 |
(a) ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অঙ্কন করে, ক্ষুদ্রতম বর্গক্ষেত্রের বাহুকে 1 একক ধরে \((8,0)\), \((-2,4)\) এবং \((3,2)\) বিন্দুগুলি স্থাপন করে AB এবং \((7,0)\), \((2,2)\) এবং \((-3,4)\) বিন্দুগুলি স্থাপন করে CD সরলরেখা অঙ্কন করা হল।
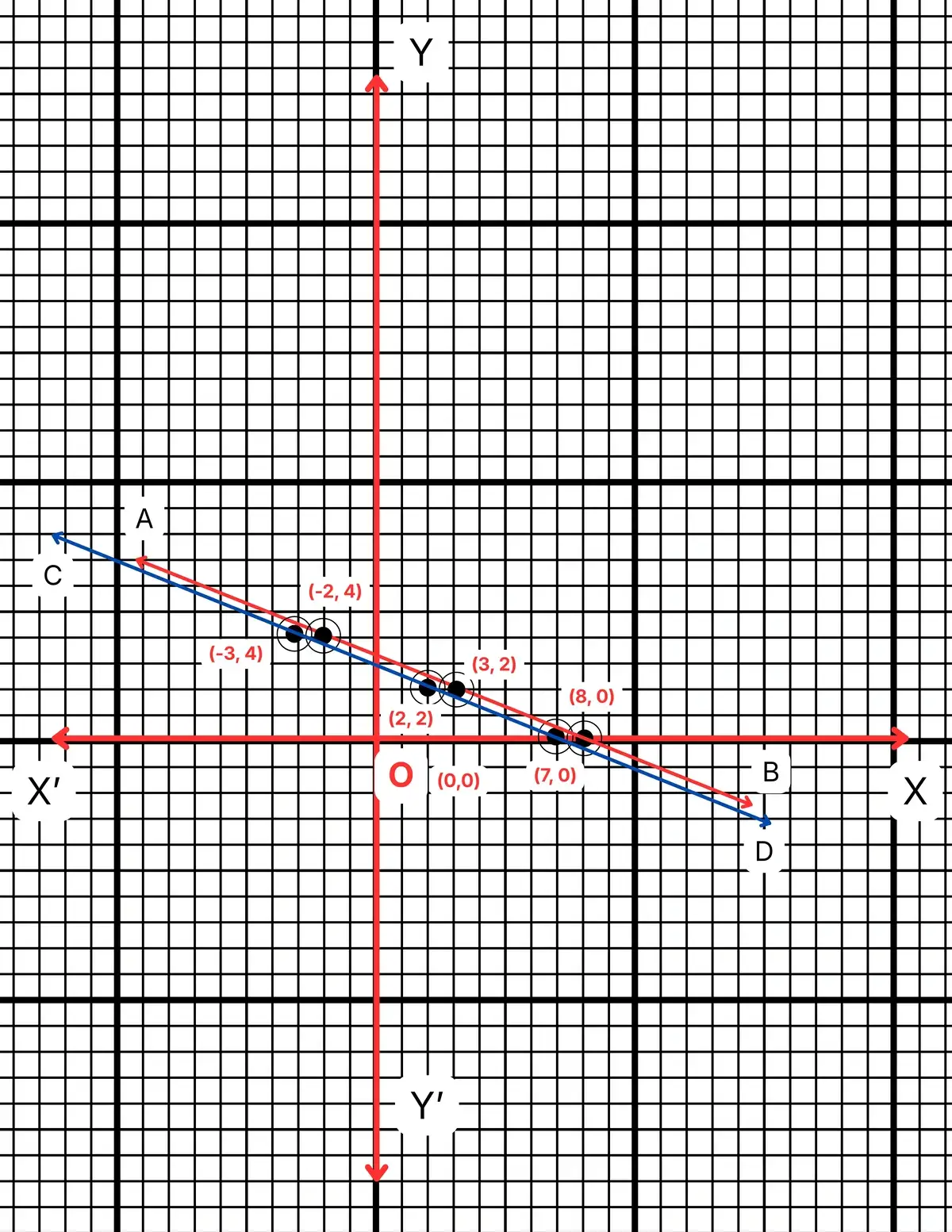
(b) AB এবং CD লেখচিত্রদ্বয় পরস্পর সমান্তরাল।
∴ (i) ও (ii) নং সমীকরণের কোনো সাধারণ সমাধান পাওয়া যাবে না।
(c) 1 টি আর্টপেপার ও 1 টি স্কেচপেনের দাম নির্ণয় করা সম্ভব নয়।
এই আর্টিকেলে নবম শ্রেণির গণিতের ‘রৈখিক সহসমীকরণ (দুই চল বিশিষ্ট)’ অধ্যায়ের ‘কষে দেখি – 5.1’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।
কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন