পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) দশম শ্রেণির গণিত পাঠ্যবইয়ের দ্বাদশ অধ্যায় হলো ‘ক্ষেত্রফল সংক্রান্ত উপপাদ্য’। এই পোস্টে ‘কষে দেখি – 12‘-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. ABCD সামান্তরিকের AB এবং DC বাহুর মধ্যবিন্দু যথাক্রমে P এবং Q; প্রমাণ করি যে, APCQ চতুর্ভুজাকার ক্ষেত্রের ক্ষেত্রফল = \(\frac{1}{2} \times\) ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল।
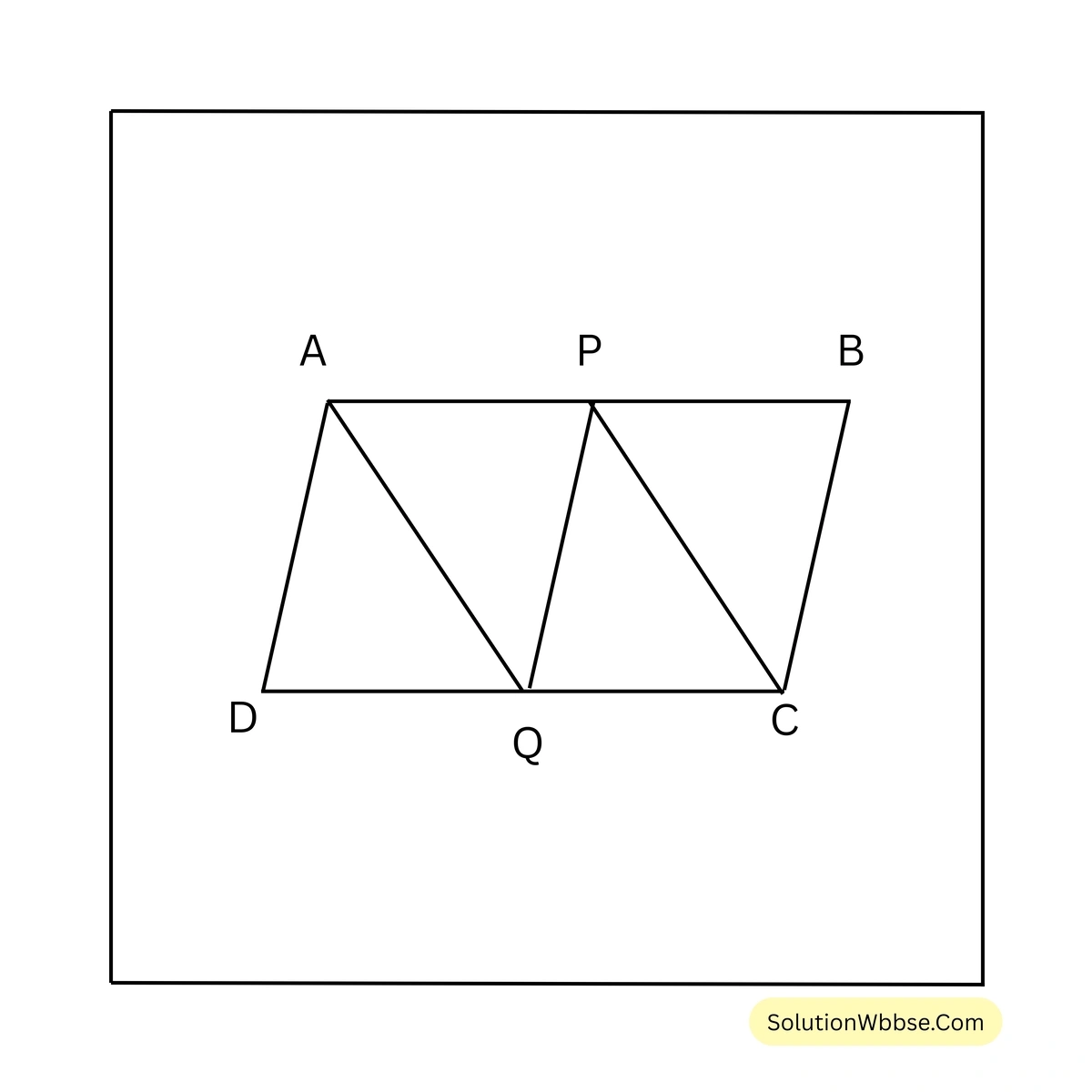
সমাধান –
ধরি, \(ABCD\) সামান্তরিকের \(AB\) এবং \(DC\) বাহুর মধ্যবিন্দু যথাক্রমে \(P\) ও \(Q\)। \(P,C\); \(A,Q\) এবং \(P,Q\) যুক্ত করা হল।
প্রমাণ করতে হবে যে, \(APCQ\) চতুর্ভুজাকার ক্ষেত্রের ক্ষেত্রফল \(= \frac{1}{2} \times ABCD\) সামান্তরিকাকার ক্ষেত্রের ক্ষেত্রফল।
\(\therefore \triangle APQ = \frac{1}{2}\) সামান্তরিক \(APQD\)
আবার, সামান্তরিক \(BPQC\) এবং ত্রিভুজ \(\triangle CPQ\) একই ভূমি \(QC\) এবং একই সমান্তরাল যুগল \(QC\) ও \(PB\) এর মধ্যে অবস্থিত।
\(\therefore \triangle APQ + \triangle CPQ = \frac{1}{2}\) সামান্তরিক \(APQD + \frac{1}{2}\) সামান্তরিক \(BPQC\)
বা, চতুর্ভুজ \(APCQ\) ক্ষেত্রের ক্ষেত্রফল \(= \frac{1}{2} \times\) সামান্তরিক \(ABCD\) [প্রমাণিত]
2. \(ABCD\) রম্বসের \(AB\) ও \(DC\) বাহুর মধ্যে দূরত্ব \(PQ\) এবং \(AD\) ও \(BC\) বাহুর মধ্যে দূরত্ব \(RS\); প্রমাণ করো যে, \(PQ = RS\)
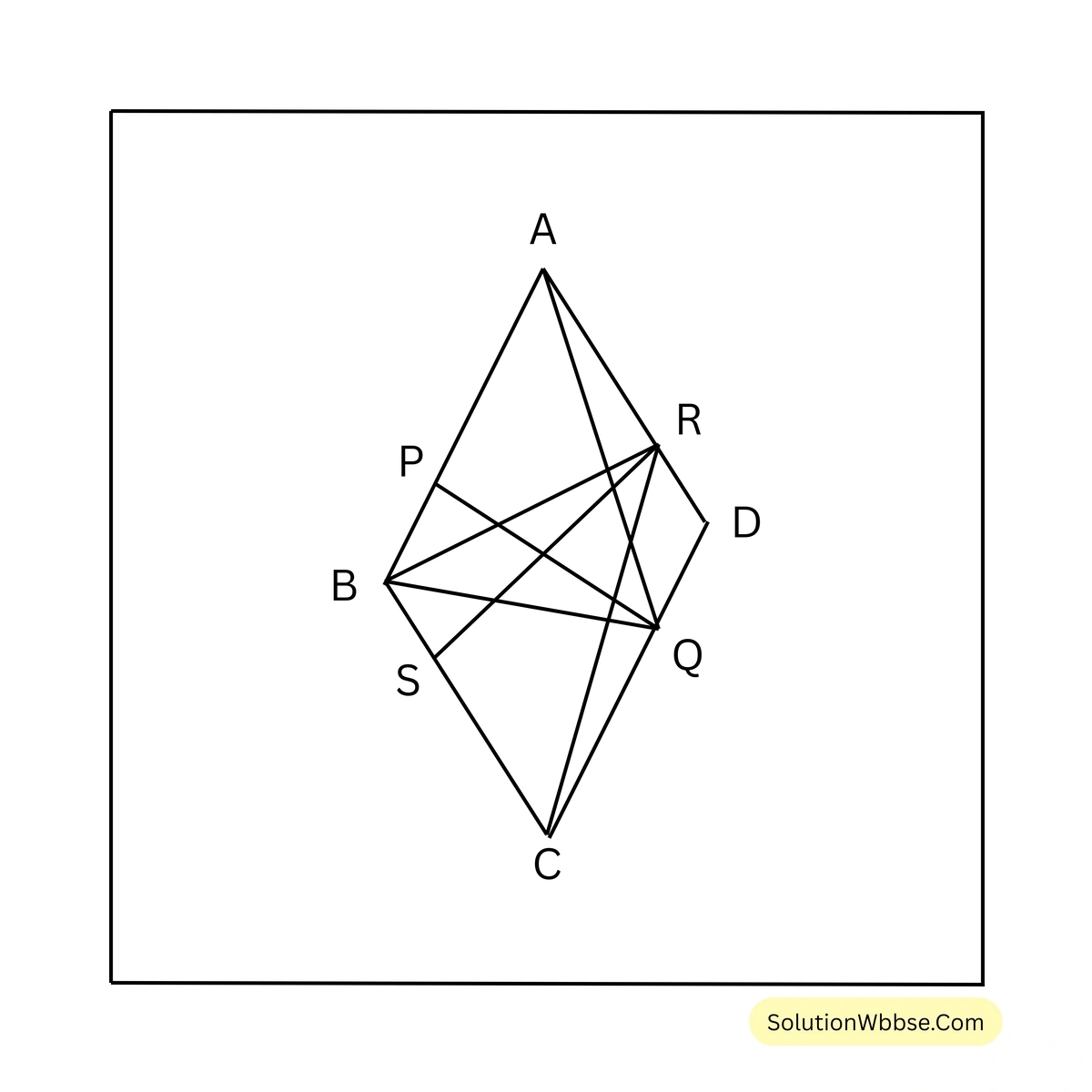
ধরি, \(ABCD\) রম্বসের \(AB\) ও \(DC\) বাহুর মধ্যে দূরত্ব \(PQ\) এবং \(AD\) ও \(BC\) বাহুর মধ্যে দূরত্ব \(RS\), প্রমাণ করতে হবে যে, \(PQ = RS\)।
অঙ্কন – \(A,Q\) ও \(B,Q\) যুক্ত করা হল। এবং \(B,R\) ও \(C,R\) যুক্ত করা হল।
প্রমাণ – যেহেতু রম্বস একটি সামান্তরিক
সামান্তরিক \(ABCD\) এবং \(\triangle ABQ\) এর একই ভূমি \(AB\) এবং একই সমান্তরাল যুগল \(AB\) ও \(CD\)-এর মধ্যে অবস্থিত।
\(\triangle ABQ = \frac{1}{2}\) সামান্তরিক \(ABCD\)
আবার, সামান্তরিক \(ABCD\) এবং \(\triangle BCR\) একই ভূমি \(BC\) এবং একই সমান্তরাল যুগল \(BC\) ও \(AD\) এর মধ্যে অবস্থিত।
\(\triangle BCR = \frac{1}{2}\) সামান্তরিক \(ABCD\)
\(\triangle ABQ = \triangle BCR\)বা, \(AB \cdot PQ = BC \cdot RS\) [যেহেতু, ত্রিভুজের ক্ষেত্রফল = ভূমি × উচ্চতা]
\(PQ = RS\) [যেহেতু, \(ABCD\) একটি রম্বস, \(AB = BC\)] [প্রমাণিত]
3. \(ABCD\) সামান্তরিকের \(AB\) ও \(DC\) বাহুর মধ্যবিন্দু যথাক্রমে \(P\) এবং \(Q\); প্রমাণ করতে হবে যে, (i) \(PBQD\) একটি সামান্তরিক (ii) \(\triangle PBC = \frac{1}{2}\) সামান্তরিক \(PBQD\)
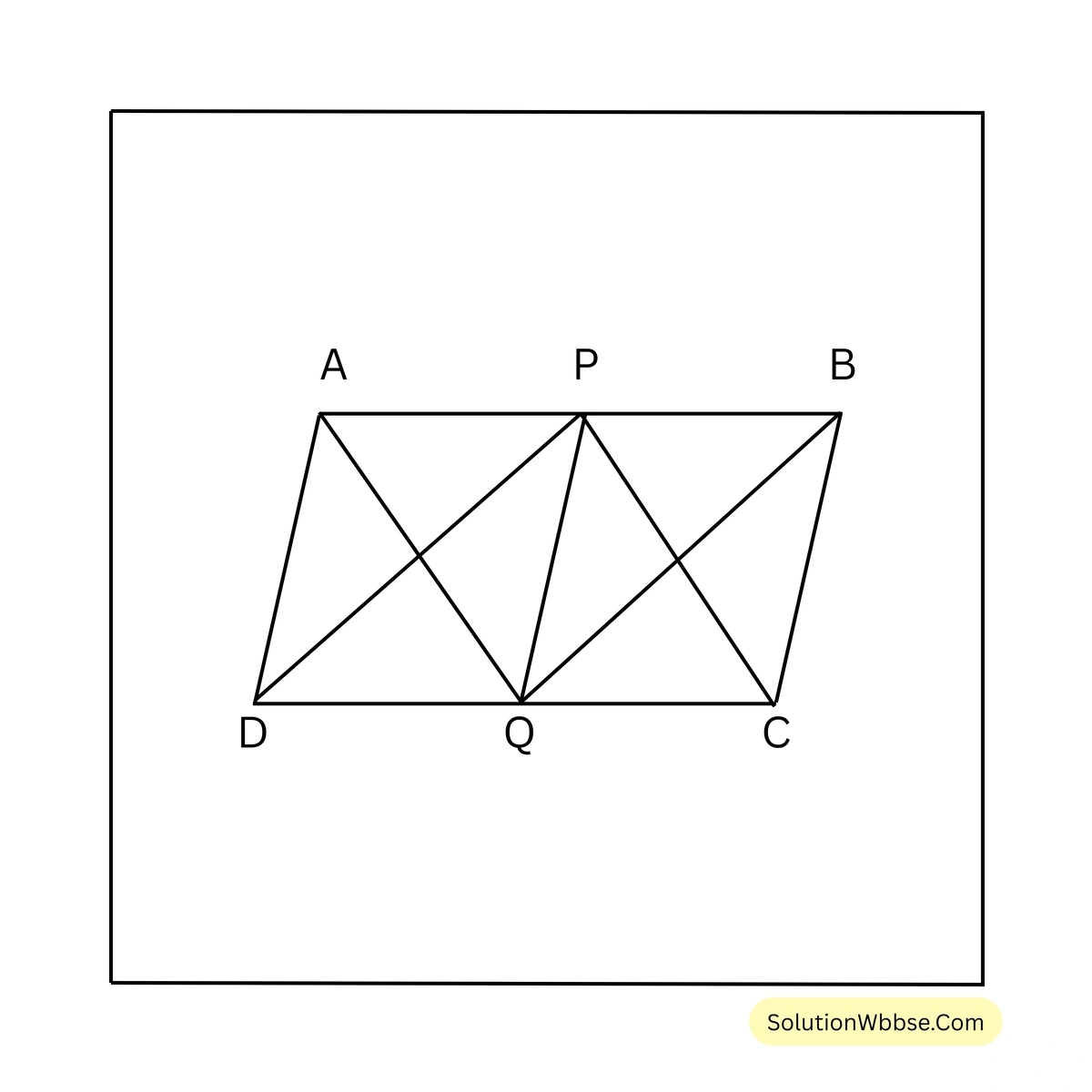
অঙ্কন – \(P,D\) ও \(B,Q\) এবং \(P,C\) যুক্ত করা হল।
প্রমাণ – \(ABCD\) একটি সামান্তরিক
\(PB = DQ\) [যেহেতু, \(P,Q\) যথাক্রমে \(AB\) ও \(CD\) এর মধ্যবিন্দু]
আবার, যেহেতু \(ABCD\) একটি সামান্তরিক
\(AB \parallel DC\)\(PB \parallel DQ\)এখন, চতুর্ভুজ \(PBQD\) এর \(PB \parallel DQ\) এবং \(PB = DQ\)
\(PBQD\) একটি সামান্তরিক [(i) নং প্রমাণিত]
এখন, \(\triangle PBC\) ও সামান্তরিক \(PBCQ\) একই ভূমি \(PB\) ও একই সমান্তরাল যুগল \(PB\) ও \(CD\) এর মধ্যে অবস্থিত।
\(\triangle PBC = \frac{1}{2}\) সামান্তরিক \(PBQD\) [(ii) নং প্রমাণিত]
4. \(ABC\) সমদ্বিবাহু ত্রিভুজের \(AB = AC\) এবং বর্ধিত \(BC\) বাহুর উপর \(P\) যেকোনো একটি বিন্দু। \(P\) বিন্দু থেকে \(AB\) এবং \(AC\) বাহুর ওপর যথাক্রমে \(PQ\) ও \(PR\) লম্ব। \(B\) বিন্দু থেকে \(AC\) বাহুর ওপর লম্ব \(BS\); প্রমাণ করি যে, \(PQ – PR = BS\)
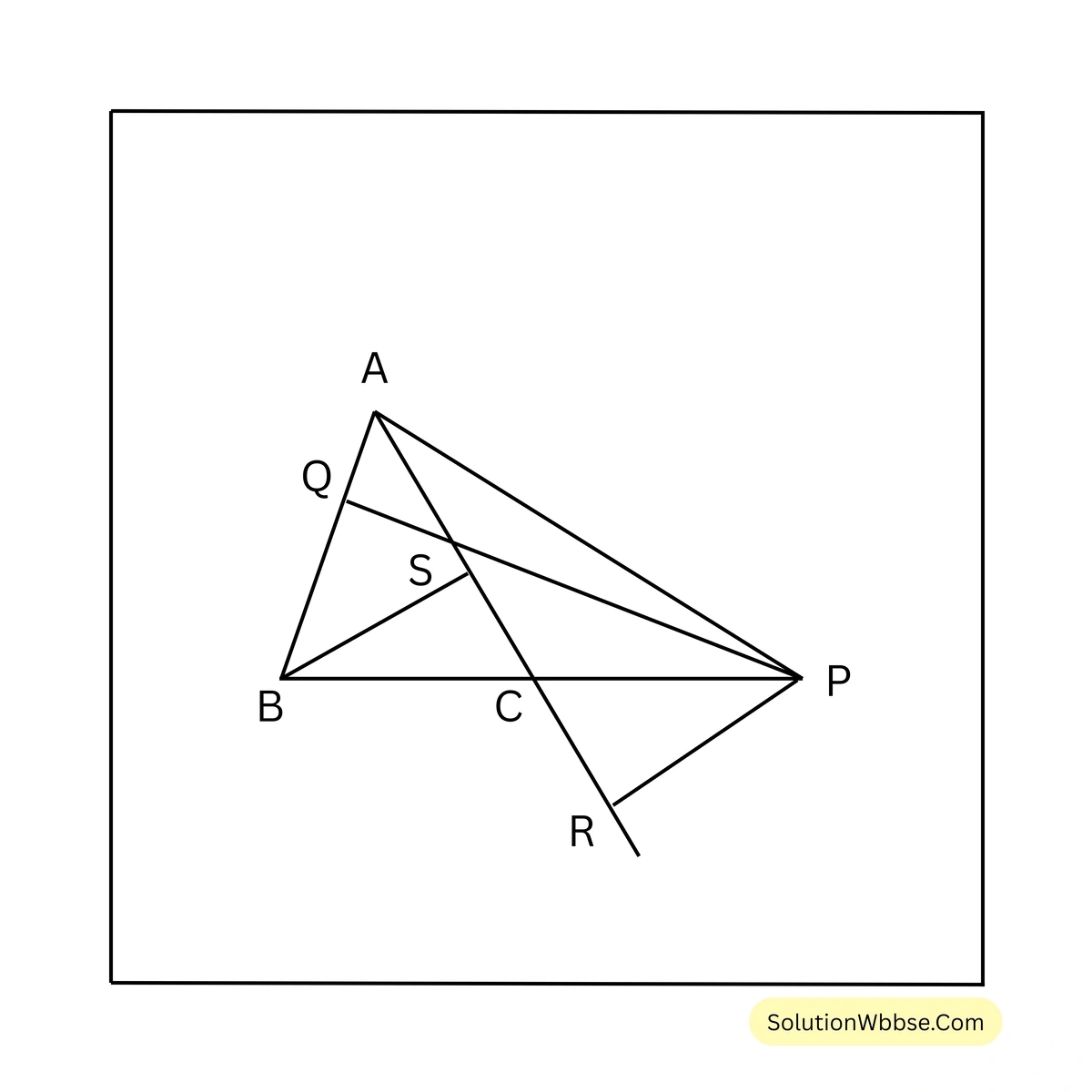
ধরি, \(ABC\) সমদ্বিবাহু ত্রিভুজের \(AB = AC\) এবং বর্ধিত \(BC\) বাহুর উপর \(P\) যেকোনো একটি বিন্দু। \(P\) থেকে বর্ধিত \(AB\) এবং \(AC\) বাহুর উপর যথাক্রমে \(PQ\) ও \(PR\) লম্ব। \(B\) বিন্দু থেকে \(AC\) বাহুর ওপর লম্ব \(BS\)
প্রমাণ করতে হবে যে, \(PQ – PR = BS\)
অঙ্কন – \(A,P\) যুক্ত করা হল।
প্রমাণ – \(\triangle ABC\)-এর ক্ষেত্রফল = \(\frac{1}{2} \times AC \times BS\) [যেহেতু, ত্রিভুজের ক্ষেত্রফল = \(\frac{1}{2} \times\) ভূমি \(\times\) উচ্চতা]
এবং \(\triangle ACP\)-এর ক্ষেত্রফল = \(\frac{1}{2} \times AC \times PR\) [যেহেতু, ত্রিভুজের ক্ষেত্রফল = \(\frac{1}{2} \times\) ভূমি \(\times\) উচ্চতা]
আবার, \(\triangle ABP = \triangle ABC + \triangle ACP\)
বা, \(\frac{1}{2} \times AB \times PQ = \frac{1}{2} \times AC \times BS + \frac{1}{2} \times AC \times PR\)
বা, \(\frac{1}{2} \times AC \times PQ = \frac{1}{2} \times AC \times (BS + PR)\) [যেহেতু, \(AB = AC\)]
বা, \(PQ = BS + PR\)
বা, \(PQ – PR = BS\) [প্রমাণিত]
5. \(ABC\) সমবাহু ত্রিভুজের বাইরে এবং \(ABC\) কৌণিক অঞ্চলের মধ্যে \(O\) যেকোনো একটি বিন্দু। \(O\) বিন্দু থেকে \(AB\), \(BC\) এবং \(CA\) বাহুর উপর লম্ব যথাক্রমে \(OP\), \(OQ\) এবং \(OR\); প্রমাণ করি যে, ত্রিভুজটির উচ্চতা = \(OP + OQ – OR\)
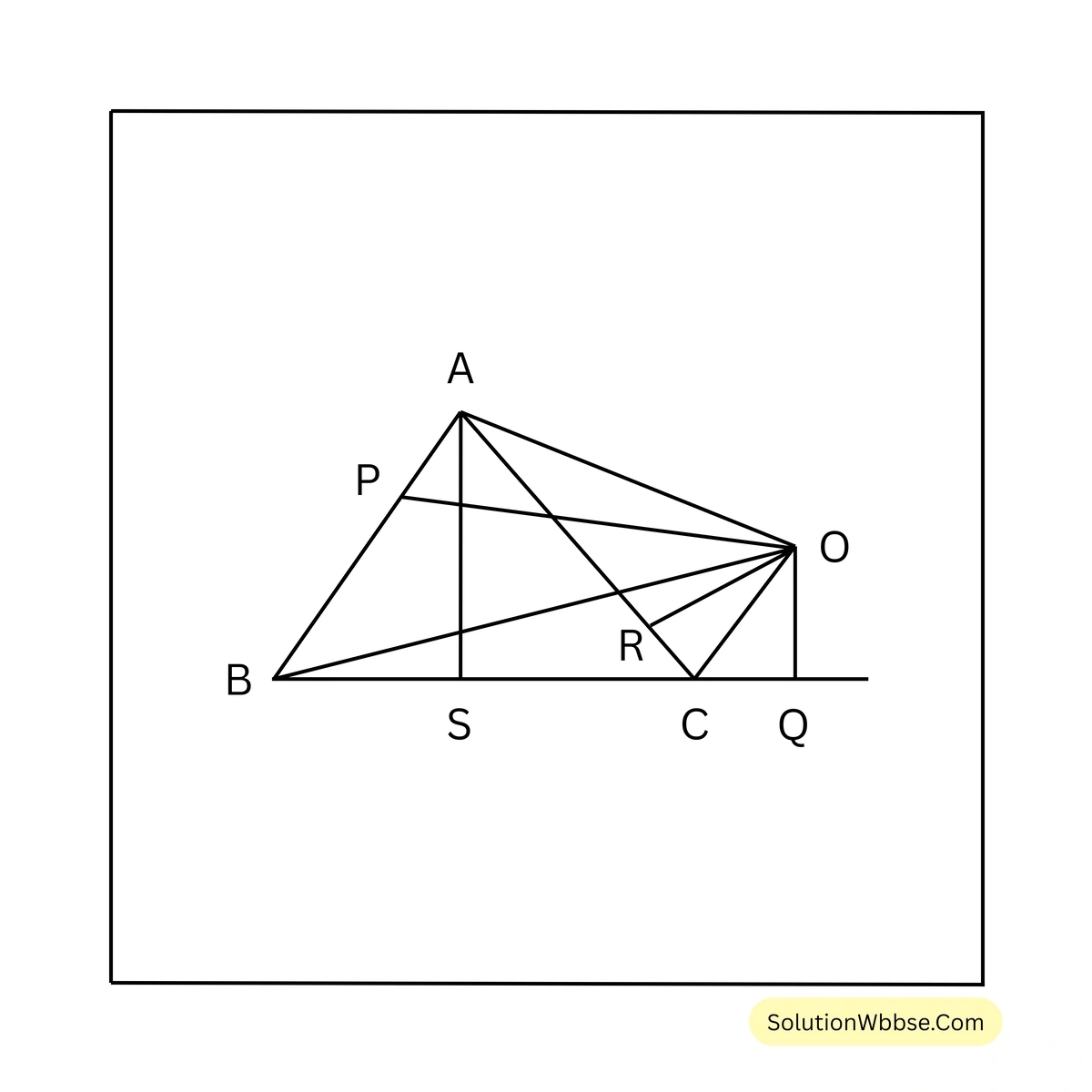
ধরি, \(ABC\) সমবাহু ত্রিভুজের বাইরে এবং \(ABC\) কৌণিক অঞ্চলের মধ্যে \(O\) যেকোনো একটি বিন্দু। \(O\) বিন্দু থেকে \(AB\), \(BC\) এবং \(CA\) বাহুর উপর লম্ব যথাক্রমে \(OP\), \(OQ\) এবং \(OR\)
প্রমাণ করতে হবে যে, ত্রিভুজটির উচ্চতা = \(OP + OQ – OR\)
অঙ্কন – \(A\) বিন্দু থেকে \(BC\)-এর ওপর \(AS\) লম্ব অঙ্কন করা হল। \(O,A\); \(O,B\) এবং \(O,C\) যুক্ত করা হল।
প্রমাণ – \(\triangle ABC = \triangle AOB + \triangle BOC – \triangle AOC\)
বা, \(\frac{1}{2} \times BC \times AS = \frac{1}{2} \times AB \times OP + \frac{1}{2} \times BC \times OQ – \frac{1}{2} \times AC \times OR\)
বা, \(BC \times AS = BC \times OP + BC \times OQ – BC \times OR\) [যেহেতু, \(AB = AC = BC\)]
বা, \(AS = OP + OQ – OR\)
\(\therefore\) ত্রিভুজটির উচ্চতা = \(OP + OQ – OR\) [প্রমাণিত]
6. \(ABCD\) সামান্তরিকের \(AB\) বাহুর সমান্তরাল সরলরেখা \(AD\), \(AC\) এবং \(BC\)–কে বা তাদের বর্ধিতাংশকে যথাক্রমে \(E\), \(F\) ও \(G\) বিন্দুতে ছেদ করে। প্রমাণ করি যে, \(\Delta AEG = \Delta AFD\)
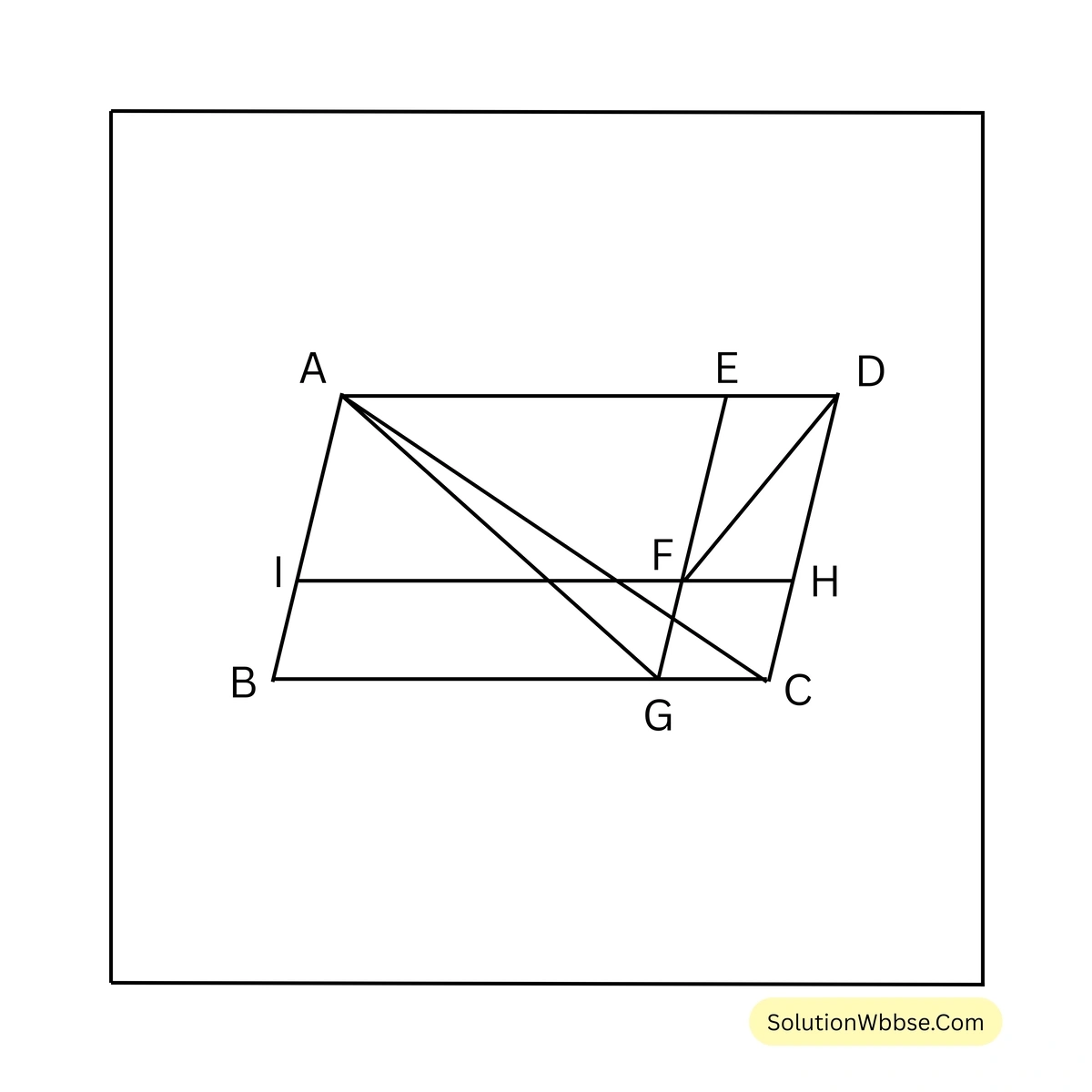
ধরি, \(ABCD\) সামান্তরিকের \(AB\) বাহুর সমান্তরাল সরলরেখা \(AD\), \(AC\) ও \(BC\) কে বা তাদের বর্ধিতাংশকে যথাক্রমে \(E\), \(F\) ও \(G\) বিন্দুতে ছেদ করে।
প্রমাণ করতে হবে যে, \(\Delta AEG = \Delta AFD\)
অঙ্কন – \(F\) বিন্দু দিয়ে \(AD\) এর সমান্তরাল সরলরেখা \(AB\) ও \(CD\) কে যথাক্রমে \(I\) এবং \(H\) বিন্দুতে ছেদ করে।
প্রমাণ – \(AIFE\), \(BIFG\), \(CGFH\) এবং \(DEFH\) প্রত্যেকেই সামান্তরিক।
\(ABCD\) সামান্তরিকের কর্ণ \(AC\)
\(\therefore \Delta ABC = \Delta ACD\)অনুরূপভাবে, \(\triangle AIF = \triangle AEF\)
এবং \(\triangle FGC = \triangle FHC\)
\(\therefore \Delta ABC – \Delta AIF – \Delta FGC = \Delta ACD – \Delta AEF – \Delta FHC\)\(\therefore\) সামান্তরিক \(BIFG =\) সামান্তরিক \(DEFH\)
\(\therefore\) সামান্তরিক \(BIFG +\) সামান্তরিক \(AIFE =\) সামান্তরিক \(DEFH +\) সামান্তরিক \(AIFE\)
\(\therefore\) সামান্তরিক \(ABGE =\) সামান্তরিক \(AIHD\)
যেহেতু \(\Delta AFD\) এবং সামান্তরিক \(AIHD\) এর একই ভূমি \(AD\) এবং একই সমান্তরাল যুগল \(AD\) ও \(IH\) এর মধ্যে অবস্থিত।
\(\therefore \Delta AFD = \frac{1}{2} \times\) সামান্তরিক \(AIHD\)
আবার সামান্তরিক \(ABGE\) এর মধ্যমা \(AG\)
\(\therefore \Delta AEG = \frac{1}{2} \times\) সামান্তরিক \(ABGE\)
যেহেতু, সামান্তরিক \(ABGE =\) সামান্তরিক \(AIHD\)
\(\therefore \Delta AEG = \Delta AFD\) [প্রমাণিত]
7. \(ABCD\) সামান্তরিকের \(DC\) বাহুর উপর \(E\) যেকোনো একটি বিন্দু। বর্ধিত \(AE\), বর্ধিত \(BC\) কে \(F\) বিন্দুতে ছেদ করে। \(D, F\) যুক্ত করা হল। প্রমাণ করি যে, (i) \(\Delta ADF = \Delta ABE\) (ii) \(\Delta DEF = \Delta BEC\)
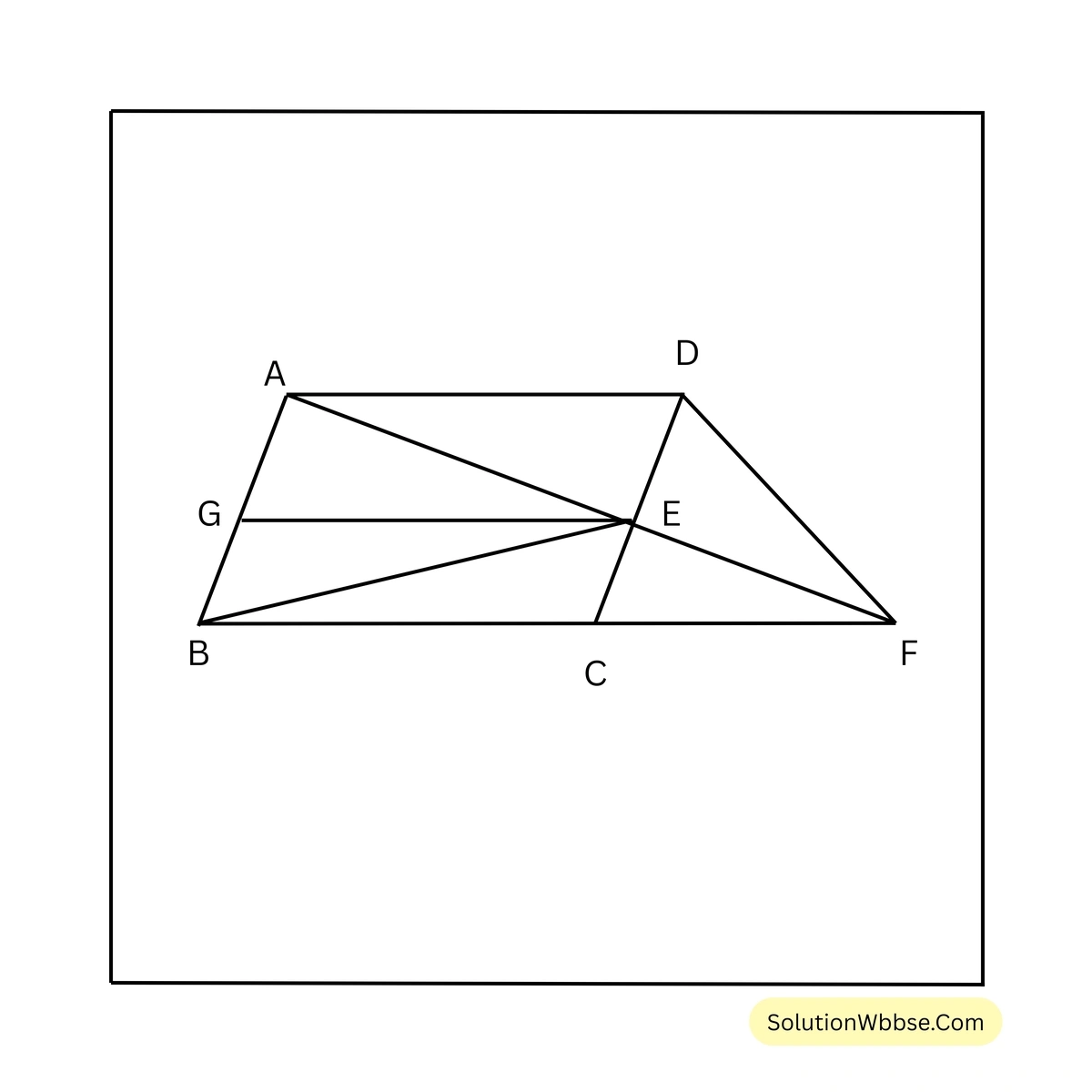
ধরি, \(ABCD\) সামান্তরিকের \(DC\) বাহুর উপর \(E\) যেকোনো বিন্দু। বর্ধিত \(AE\), বর্ধিত \(BC\) কে \(F\) বিন্দুতে ছেদ করে। \(D, F\) যুক্ত করা হল। প্রমাণ করতে হবে যে, (i) \(\Delta ADF = \Delta ABE\) (ii) \(\Delta DEF = \Delta BEC\)
অঙ্কন – \(E\) বিন্দু দিয়ে \(AD\) এর সমান্তরাল সরলরেখা \(AB\) কে \(G\) বিন্দুতে ছেদ করে।
প্রমাণ – \(\Delta ADF\) ও সামান্তরিক \(ABCD\) এর একই ভূমি \(AD\) এবং একই সমান্তরাল যুগল \(AD\) ও \(BF\) এর মধ্যে অবস্থিত।
\(\therefore \Delta ADF = \frac{1}{2} \times\) সামান্তরিক \(ABCD\)
আবার, \(\Delta ABE\) ও সামান্তরিক \(ABCD\) এর একই ভূমি \(AB\) এবং একই সমান্তরাল যুগল \(AB\) ও \(CD\) এর মধ্যে অবস্থিত।
\(\therefore \Delta ABE = \frac{1}{2} \times\) সামান্তরিক \(ABCD\)
\(\therefore \Delta ADF = \Delta ABE\) [(i) নং প্রমাণিত]
যেহেতু, \(\Delta ADF = \Delta ABE\)
\(\therefore \Delta DEF + \Delta ADE = \Delta AGE + \Delta BEG\)\(\therefore \Delta DEF + \Delta AGE = \Delta AGE + \Delta BEC\)[যেহেতু, \(AGED\) এর \(AE\) কর্ণ এবং \(BCEG\) এর \(BE\) কর্ণ]
\(\therefore \Delta DEF = \Delta BEC\) [(ii) নং প্রমাণিত]
8. সমান ক্ষেত্রফলবিশিষ্ট \(\triangle ABC\) এবং \(\triangle ABD\) দুটি ত্রিভুজাকার ক্ষেত্র \(AB\) বাহুর বিপরীত দিকে অবস্থিত। প্রমাণ করি যে, \(AB\), \(CD\) কে সমদ্বিখণ্ডিত করে।
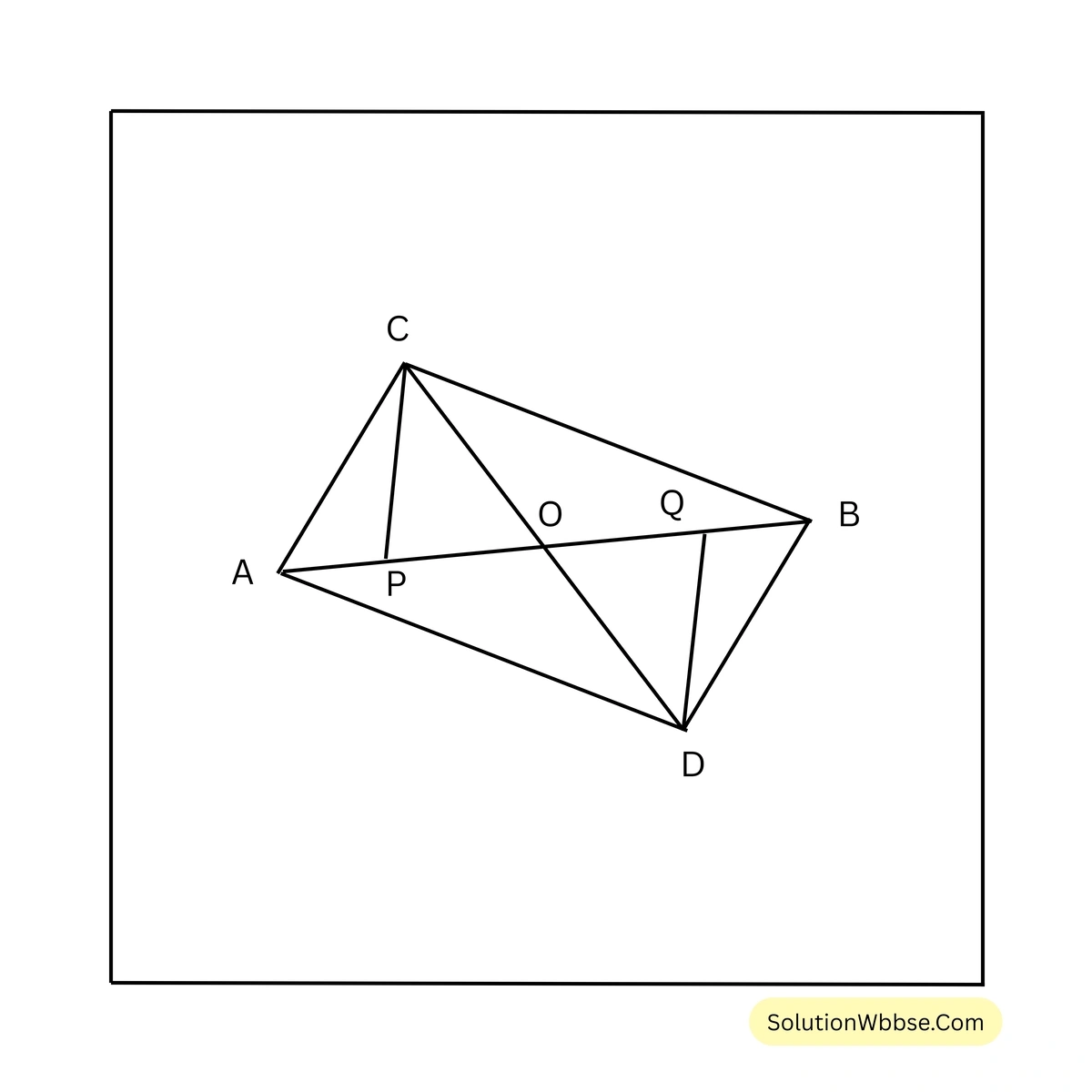
ধরি, সমান ক্ষেত্রফলবিশিষ্ট \(\triangle ABC\) এবং \(\triangle ABD\) দুটি ত্রিভুজাকার ক্ষেত্র \(AB\) বাহুর বিপরীত দিকে অবস্থিত। প্রমাণ করতে হবে যে, \(AB\), \(CD\)-কে সমদ্বিখণ্ডিত করে।
অঙ্কন – \(AB\) এর উপর \(C\) ও \(D\) বিন্দু থেকে যথাক্রমে \(CP\) এবং \(DQ\) লম্ব অঙ্কন করা হল।
প্রমাণ – যেহেতু, \(\triangle ABC = \triangle ABD\)
\(\therefore \frac{1}{2} \times AB \times CP = \frac{1}{2} \times AB \times DQ\)\(\therefore CP = DQ\)এখন \(\triangle CPO\) এবং \(\triangle DQO\) এর মধ্যে,
\(\angle CPO = \angle DQO\) [উভয়ই সমকোণ]
\(\angle COP = \angle DOQ\) [বিপ্রতীপ কোণ]
এবং \(CP = DQ\)
\(\therefore \triangle CPO \cong \triangle DQO\)\(\therefore CO = OD\)\(\therefore O\), \(CD\) এর মধ্যবিন্দু
\(\therefore AB\), \(CD\) কে সমদ্বিখণ্ডিত করে। [প্রমাণিত]
9. \(\triangle ABC\) ত্রিভুজের \(BC\) বাহুর মধ্যবিন্দু \(D\); সামান্তরিক \(CDEF\)টি \(BC\) বাহু এবং \(A\) বিন্দু দিয়ে \(BC\) বাহুর সমান্তরাল সরলরেখার মধ্যে অবস্থিত। প্রমাণ করি যে, \(\triangle ABC =\) সামান্তরিক \(CDEF\)।
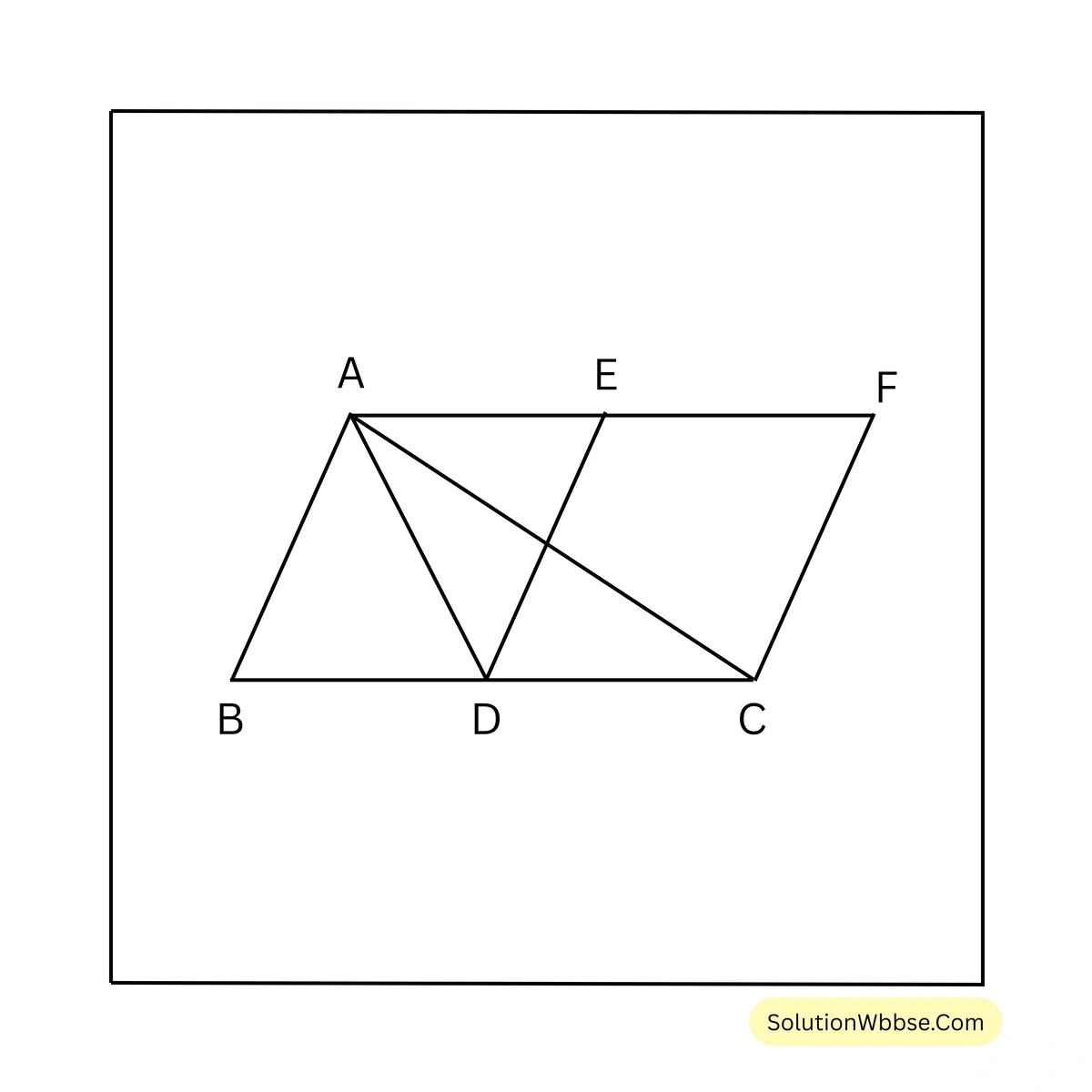
ধরি, \(\triangle ABC\) ত্রিভুজের \(BC\) বাহুর মধ্যবিন্দু \(D\); সামান্তরিক \(CDEF\)টি \(BC\) বাহু এবং \(A\) বিন্দু দিয়ে \(BC\) বাহুর সমান্তরাল সরলরেখার মধ্যে অবস্থিত।
প্রমাণ করতে হবে যে, \(\triangle ABC =\) সামান্তরিক \(CDEF\)।
অঙ্কন – \(A, D\) যুক্ত করা হল।
প্রমাণ – \(\triangle ADC\) এবং সামান্তরিক \(CDEF\) এর একই ভূমি \(CD\) এবং একই সমান্তরাল যুগল \(DC\) ও \(EF\) এর মধ্যে অবস্থিত।
\(\therefore \triangle ADC = \frac{1}{2}\) সামান্তরিক \(CDEF\)
আবার, \(BC\) বাহুর মধ্যবিন্দু \(D\)
\(\therefore AD\), \(\triangle ABC\) এর মধ্যমা
\(\therefore \triangle ADC = \frac{1}{2} \triangle ABC\)\(\therefore \frac{1}{2} \triangle ABC = \frac{1}{2}\) সামান্তরিক \(CDEF\)
\(\therefore \triangle ABC =\) সামান্তরিক \(CDEF\) [প্রমাণিত]
10. \(ABCD\) সামান্তরিকের \(BD\) কর্ণের উপর \(P\) যেকোনো একটি বিন্দু। প্রমাণ করি যে, \(\triangle APD = \triangle CPD\)।
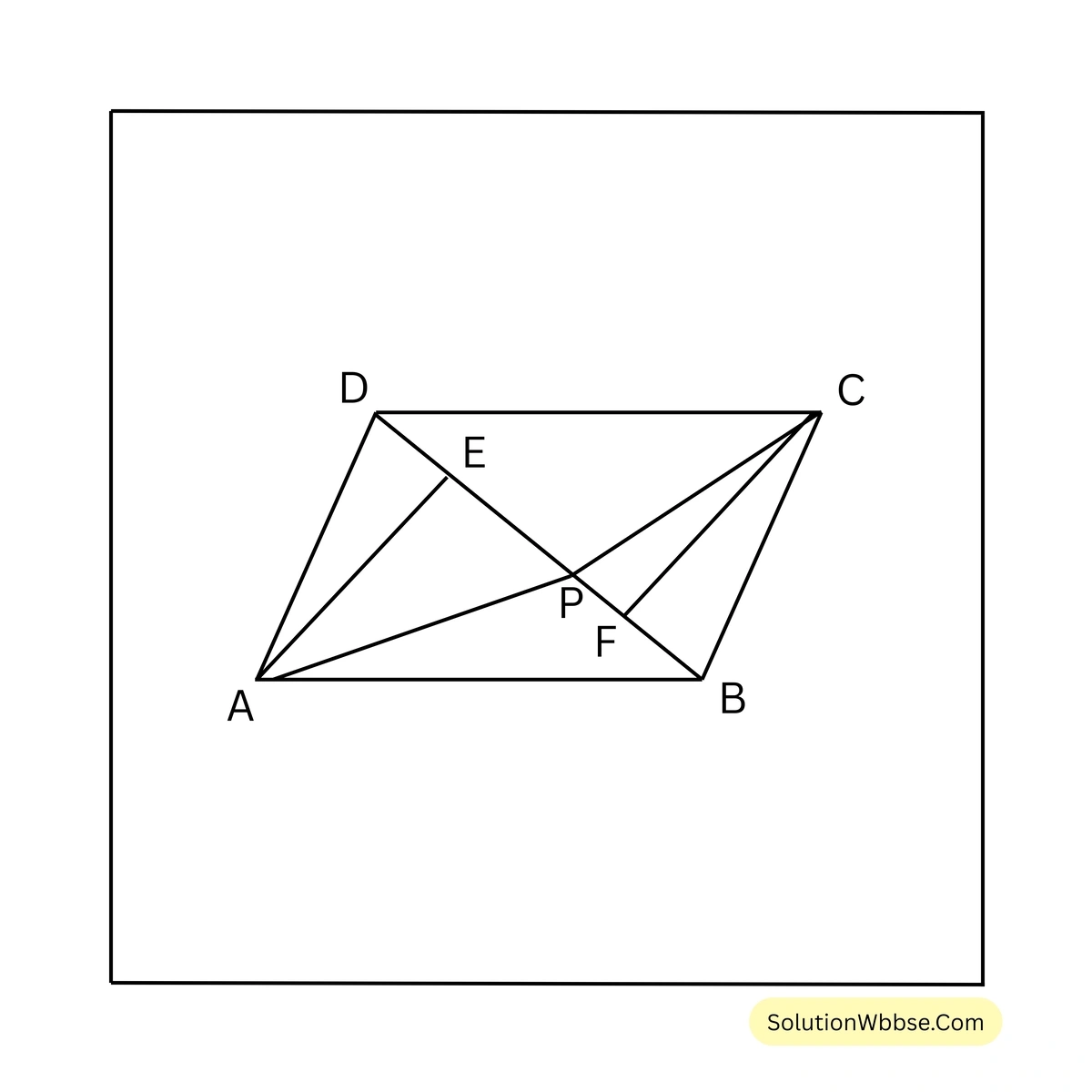
ধরি, \(ABCD\) সামান্তরিকের \(BD\) কর্ণের উপর \(P\) যেকোনো একটি বিন্দু। প্রমাণ করতে হবে যে, \(\triangle APD = \triangle CPD\)।
অঙ্কন – \(A\) ও \(C\) বিন্দু দিয়ে \(BD\) এর উপর যথাক্রমে \(AE\) ও \(CF\) লম্ব অঙ্কন করা হল।
প্রমাণ – \(\triangle ADE\) এবং \(\triangle BCF\)–এর মধ্যে
\(AD = BC\) [সামান্তরিকের বিপরীত বাহু]
\(\angle ADE = \angle CBF\) [একান্তর কোণ, যেহেতু \(AD \parallel BC\) এবং \(DB\) ভেদক]
এবং \(\angle AED = \angle BFC\) [উভয়ই সমকোণ]
\(\therefore \triangle ADE \cong \triangle BCF\)‘
\(\therefore AE = CF\) [অনুরূপ বাহু]
এখন \(\triangle APD\) ও \(\triangle CPD\) এর একই ভূমি \(DP\) এবং একই উচ্চতা বিশিষ্ট [যেহেতু, \(AE = CF\)]
\(\therefore \triangle APD = \triangle CPD\) [প্রমাণিত]
11. \(\triangle ABC\) ত্রিভুজের \(AD\) এবং \(BE\) মধ্যমা। প্রমাণ করি যে, \(\triangle ACD = \triangle BCE\)
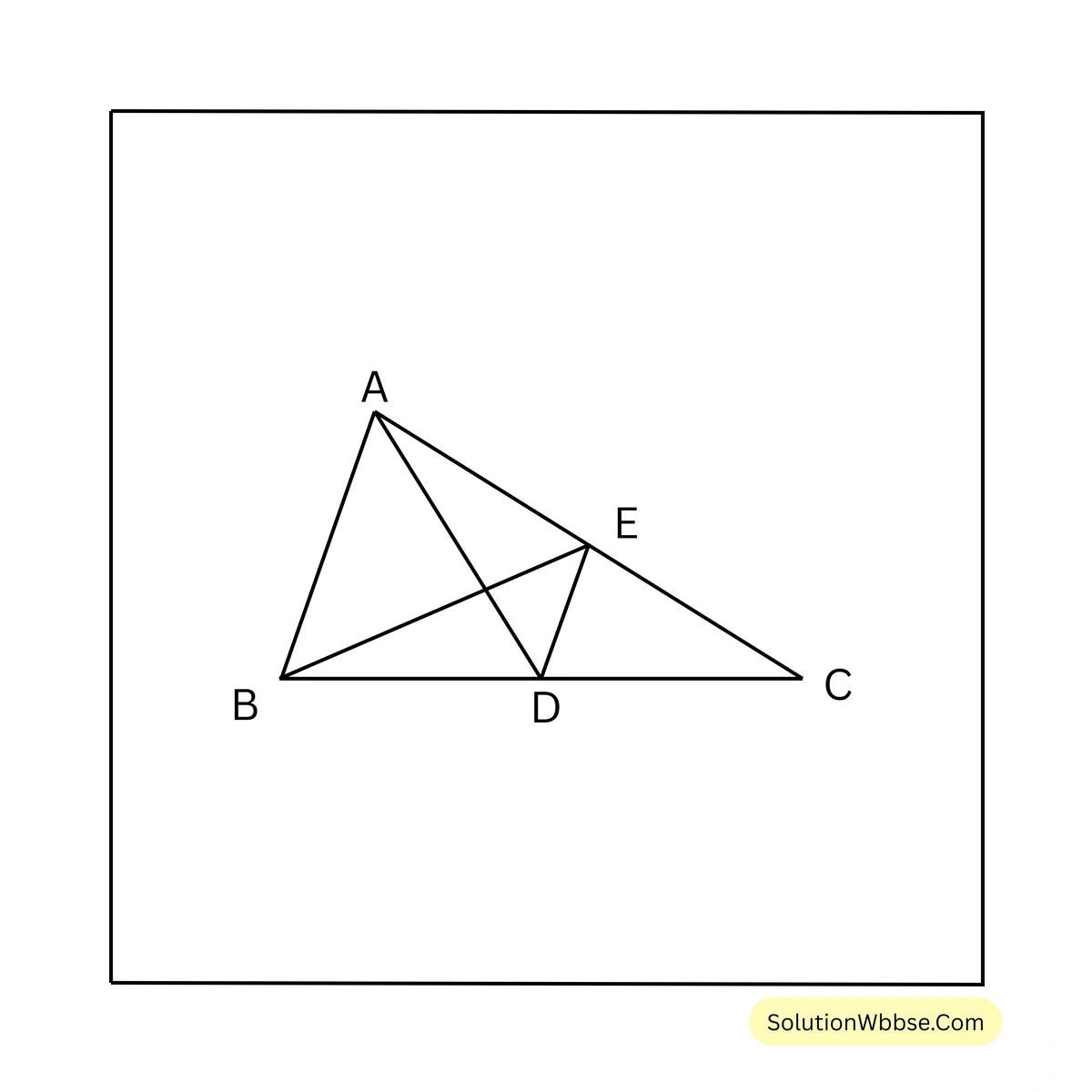
ধরি, \(\triangle ABC\) ত্রিভুজের \(AD\) এবং \(BE\) মধ্যমা। প্রমাণ করতে হবে যে, \(\triangle ACD = \triangle BCE\)।
অঙ্কন – \(D, E\) যুক্ত করা হল।
প্রমাণ – \(AD\) এবং \(BE\) উভয়ই \(\triangle ABC\)-এর মধ্যমা।
\(D\) ও \(E\) যথাক্রমে \(BC\) এবং \(AC\)-এর মধ্যবিন্দু।
\(ED \parallel AB\)এখন \(\triangle ADE\) এবং \(\triangle BDE\) ত্রিভুজদ্বয় একই ভূমি \(DE\) এবং একই সমান্তরাল যুগল \(ED\) ও \(AB\) এর মধ্যে অবস্থিত।
\(\triangle ADE = \triangle BDE\)উভয়পক্ষে \(\triangle DEC\) যোগ করে পাই,
\(\triangle ADE + \triangle DEC = \triangle BDE + \triangle DEC\)সুতরাং, \(\triangle ACD = \triangle BCE\) [প্রমাণিত]
12. \(\triangle ABC\) ত্রিভুজের \(BC\) বাহুর সমান্তরাল সরলরেখা \(AB\) এবং \(AC\) বাহুকে যথাক্রমে \(P\) এবং \(Q\) বিন্দুতে ছেদ করে। \(CP\) এবং \(BQ\) পরস্পরকে \(X\) বিন্দুতে ছেদ করে।
প্রমাণ করি যে, (i) \(\triangle BPQ = \triangle CPQ\)
(ii) \(\triangle BCP = \triangle BCQ\)
(iii) \(\triangle ACP = \triangle ABQ\)
(iv) \(\triangle BXP = \triangle CXQ\)
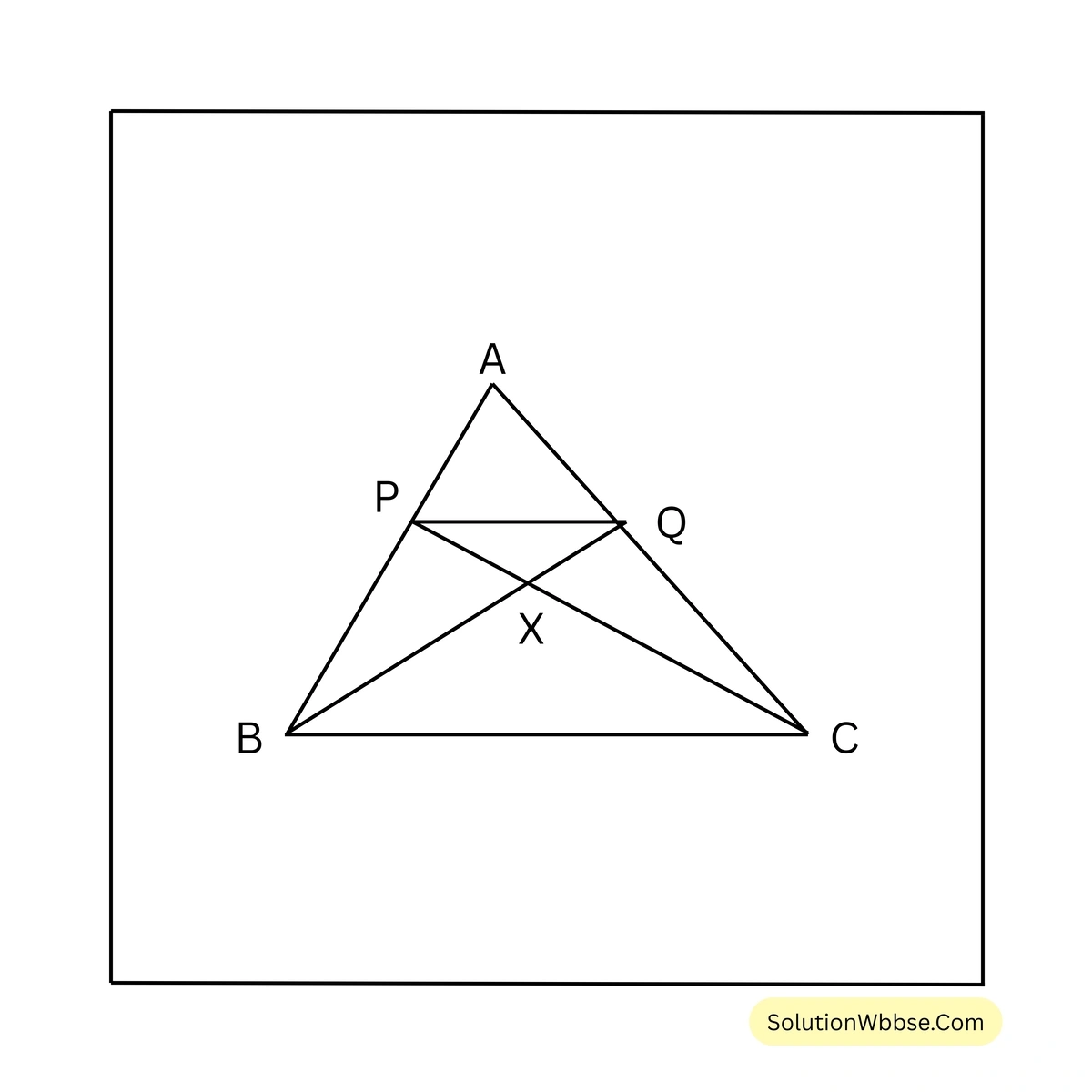
ধরি, \(\triangle ABC\) ত্রিভুজের \(BC\) বাহুর সমান্তরাল সরলরেখা \(AB\) ও \(AC\) বাহুকে যথাক্রমে \(P\) এবং \(Q\) বিন্দুতে ছেদ করে। \(CP\) এবং \(BQ\) পরস্পরকে \(X\) বিন্দুতে ছেদ করে।
প্রমাণ করতে হবে যে, (i) \(\triangle BPQ = \triangle CPQ\) (ii) \(\triangle BCP = \triangle BCQ\) (iii) \(\triangle ACP = \triangle ABQ\) (iv) \(\triangle BXP = \triangle CXQ\)
প্রমাণ –
\(\triangle BPQ\) ও \(\triangle CPQ\) এর একই ভূমি \(PQ\) এবং একই সমান্তরাল যুগল \(PQ\) ও \(BC\)-এর মধ্যে অবস্থিত।
\(\triangle BPQ = \triangle CPQ\) [(i) নং প্রমাণিত]
\(\triangle BCP\) ও \(\triangle BCQ\) এর একই ভূমি \(BC\) এবং একই সমান্তরাল যুগল \(PQ\) ও \(BC\) এর মধ্যে অবস্থিত।
\(\triangle BCP = \triangle BCQ\) [(ii) নং প্রমাণিত]
যেহেতু, \(\triangle CPQ = \triangle BPQ\)
\(\triangle CPQ + \triangle APQ = \triangle BPQ + \triangle APQ\)\(\triangle ACP = \triangle ABQ\) [(iii) নং প্রমাণিত]
যেহেতু, \(\triangle BPQ = \triangle CPQ\)
\(\triangle BPQ – \triangle PQX = \triangle CPQ – \triangle PQX\)\(\triangle BXP = \triangle CXQ\) [(iv) নং প্রমাণিত]
13. \(ABC\) ত্রিভুজের \(BC\) বাহুর মধ্যবিন্দু \(D\) এবং \(BC\) বাহুর উপর \(P\) যেকোনো একটি বিন্দু। \(P, A\) যুক্ত করি। \(D\) বিন্দু দিয়ে \(PA\) সরলরেখাংশের সমান্তরাল সরলরেখা \(AB\) বাহুকে \(Q\) বিন্দুতে ছেদ করে। প্রমাণ করি যে,
(i) \(\triangle ADQ = \triangle PDQ\)
(ii) \(\triangle BPQ = \frac{1}{2} \triangle ABC\)
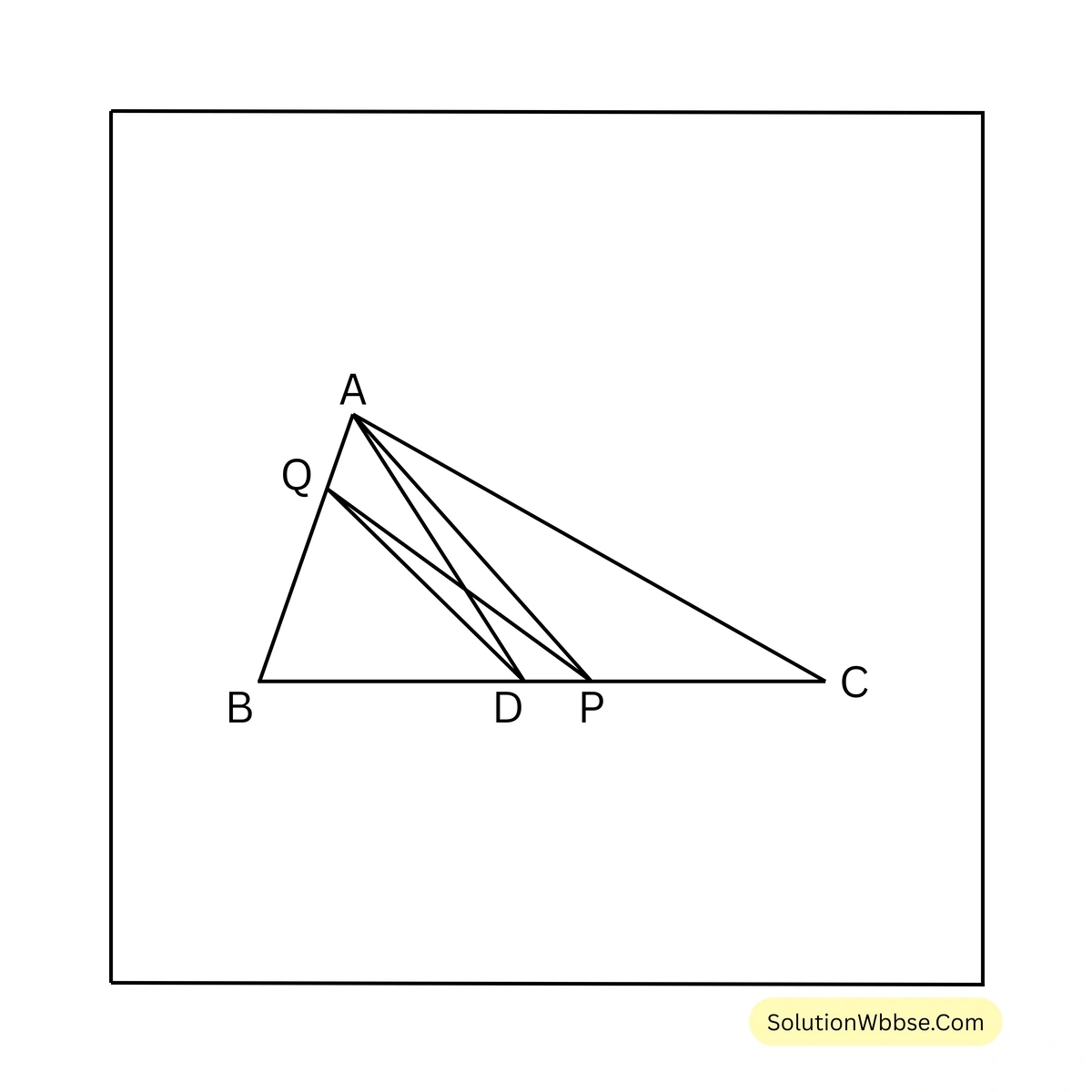
ধরি, \(ABC\) ত্রিভুজের \(BC\) বাহুর মধ্যবিন্দু \(D\) এবং \(BC\) বাহুর উপর \(P\) যেকোনো একটি বিন্দু। \(P, A\) যুক্ত করা হল। \(D\) বিন্দু দিয়ে \(PA\) সরলরেখাংশের সমান্তরাল সরলরেখা \(AB\) বাহুকে \(Q\) বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে, (i) \(\triangle ADQ = \triangle PDQ\) (ii) \(\triangle BPQ = \frac{1}{2} \triangle ABC\)
প্রমাণ – \(\triangle ADQ\) এবং \(\triangle PDQ\) ত্রিভুজদ্বয় একই ভূমি \(QD\) এবং একই সমান্তরাল যুগল \(QD\) ও \(AP\) এর মধ্যে অবস্থিত।
\(\therefore \triangle ADQ = \triangle PDQ\) [(i) নং প্রমাণিত]
\(\triangle BPQ = \triangle BDQ + \triangle PDQ\)বা, \(\triangle BPQ = \triangle BDQ + \triangle ADQ\) [যেহেতু, \(\triangle ADQ = \triangle PDQ\)]
বা, \(\triangle BPQ = \triangle ABD\)
বা, \(\triangle BPQ = \frac{1}{2} \triangle ABC\) [যেহেতু, \(AD\) মধ্যমা]
\(\therefore \triangle BPQ = \frac{1}{2} \triangle ABC\) [(ii) নং প্রমাণিত]
14. \(ABC\) ত্রিভুজে \(AB = AC\); \(B\) বিন্দু থেকে \(AC\) বাহুর উপর লম্ব এবং \(C\) বিন্দু থেকে \(AB\) বাহুর উপর লম্ব যথাক্রমে \(AC\) ও \(AB\) বাহুকে \(E\) ও \(F\) বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, \(FE \parallel BC\)
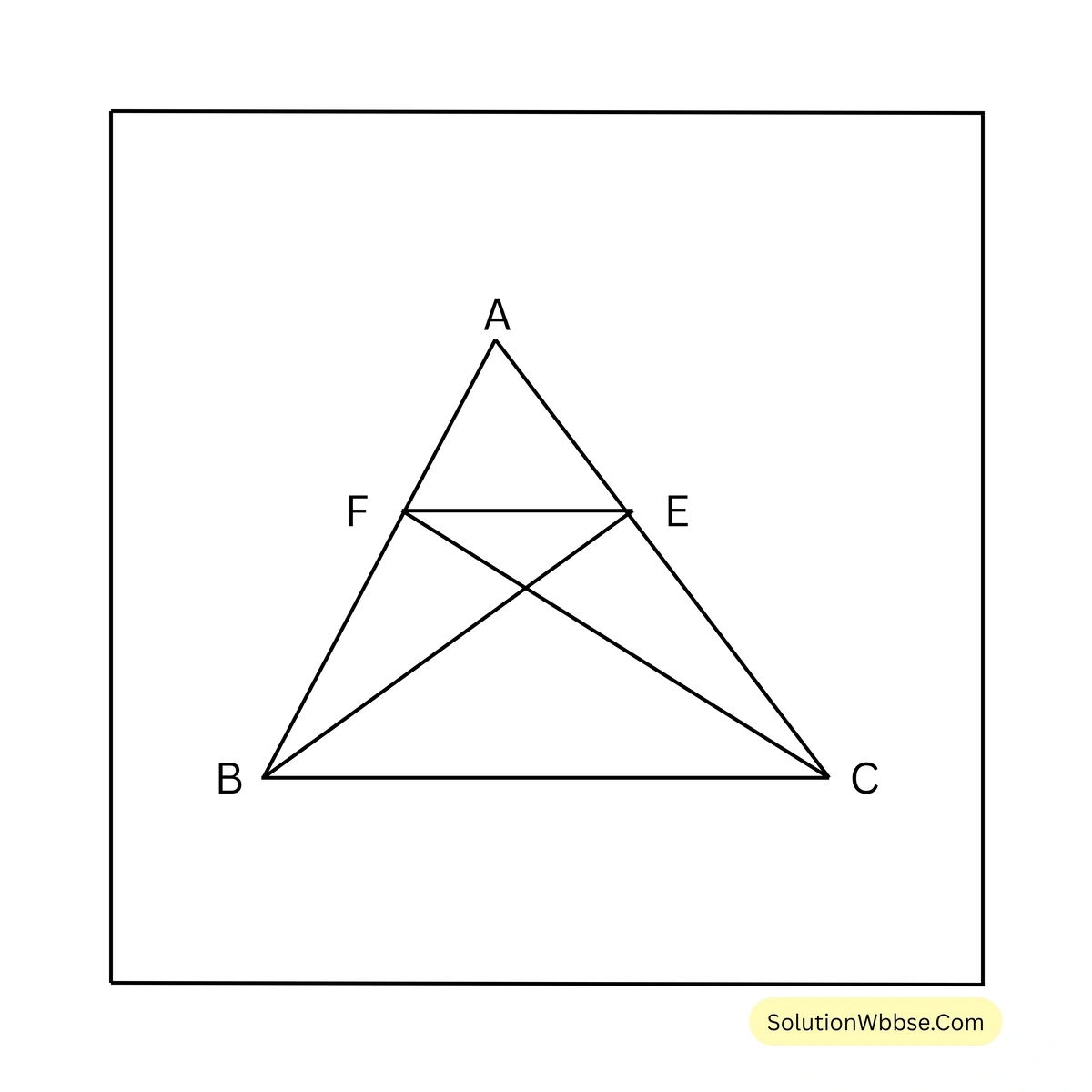
ধরি, \(ABC\) ত্রিভুজে \(AB = AC\); \(B\) বিন্দু থেকে \(AC\) বাহুর উপর লম্ব এবং \(C\) বিন্দু থেকে \(AB\) বাহুর উপর লম্ব যথাক্রমে \(AC\) ও \(AB\) বাহুকে \(E\) ও \(F\) বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে, \(FE \parallel BC\)
প্রমাণ – \(\triangle ABC = \frac{1}{2} \times AB \times CF\)
আবার, \(\triangle ABC = \frac{1}{2} \times AC \times BE\)
\(\therefore \frac{1}{2} \times AB \times CF = \frac{1}{2} \times AC \times BE\)বা, \(CF = BE\) [যেহেতু, \(AB = AC\)]
এখন \(\triangle BCE\) এবং \(\triangle BFC\) এর মধ্যে
\(\angle BEC = \angle BFC\) [উভয়ই সমকোণ]
\(CF = BE\)এবং \(BC\) সাধারণ বাহু
\(\therefore \triangle BEC \cong \triangle BFC\)এখন \(\triangle BEC\) এবং \(\triangle BFC\) এর একই ভূমি \(BC\) এবং তাদের ক্ষেত্রফল সমান, সুতরাং তারা \(BC\) ভূমির একই পার্শ্বে এবং একই সমান্তরাল যুগলের মধ্যে অবস্থিত।
\(\therefore FE \parallel BC\) [প্রমাণিত]
15. \(\triangle ABC\) ত্রিভুজে \(\angle ABC = \angle ACB\), \(\angle ABC\) ও \(\angle ACB\) কোণের সমদ্বিখণ্ডকদ্বয় \(AC\) এবং \(AB\) বাহুকে যথাক্রমে \(E\) ও \(F\) বিন্দুতে ছেদ করে। প্রমাণ করি যে, \(FE \parallel BC\)

ধরি, \(\triangle ABC\) ত্রিভুজে \(\angle ABC = \angle ACB\); \(\angle ABC\) ও \(\angle ACB\) কোণের সমদ্বিখণ্ডকদ্বয় \(AC\) এবং \(AB\) বাহুকে যথাক্রমে \(E\) ও \(F\) বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে, \(FE \parallel BC\)
অঙ্কন – \(E, F\) যুক্ত করা হল।
প্রমাণ – যেহেতু, \(BE\) ও \(CF\) যথাক্রমে \(\angle ABC\) ও \(\angle ACB\) কোণের সমদ্বিখণ্ডক এবং \(\angle ABC = \angle ACB\)
\(\therefore \angle EBC = \angle FCB\)এখন \(\triangle BEC\) এবং \(\triangle BFC\) এর মধ্যে
\(\angle EBC = \angle FCB\)\(\angle ECB = \angle BFC\) [যেহেতু, \(\angle ABC = \angle ACB\)]
এবং \(BC\) সাধারণ বাহু
\(\therefore \triangle BEC \cong \triangle BFC\)এখন \(\triangle BEC\) এবং \(\triangle BFC\) ত্রিভুজদ্বয়ের একই ভূমি \(BC\) এবং এদের ক্ষেত্রফল সমান এবং তারা \(BC\) ভূমির একই পার্শ্বে অবস্থিত।
\(\therefore FE \parallel BC\) [প্রমাণিত]
16. সমান ক্ষেত্রফলবিশিষ্ট \(ABCD\) ও \(AEFG\) সামান্তরিক আকারের ক্ষেত্র দুটির \(\angle A\) সাধারণ এবং \(E\), \(AB\) বাহুর উপর অবস্থিত। প্রমাণ করি যে, \(DE \parallel FC\)
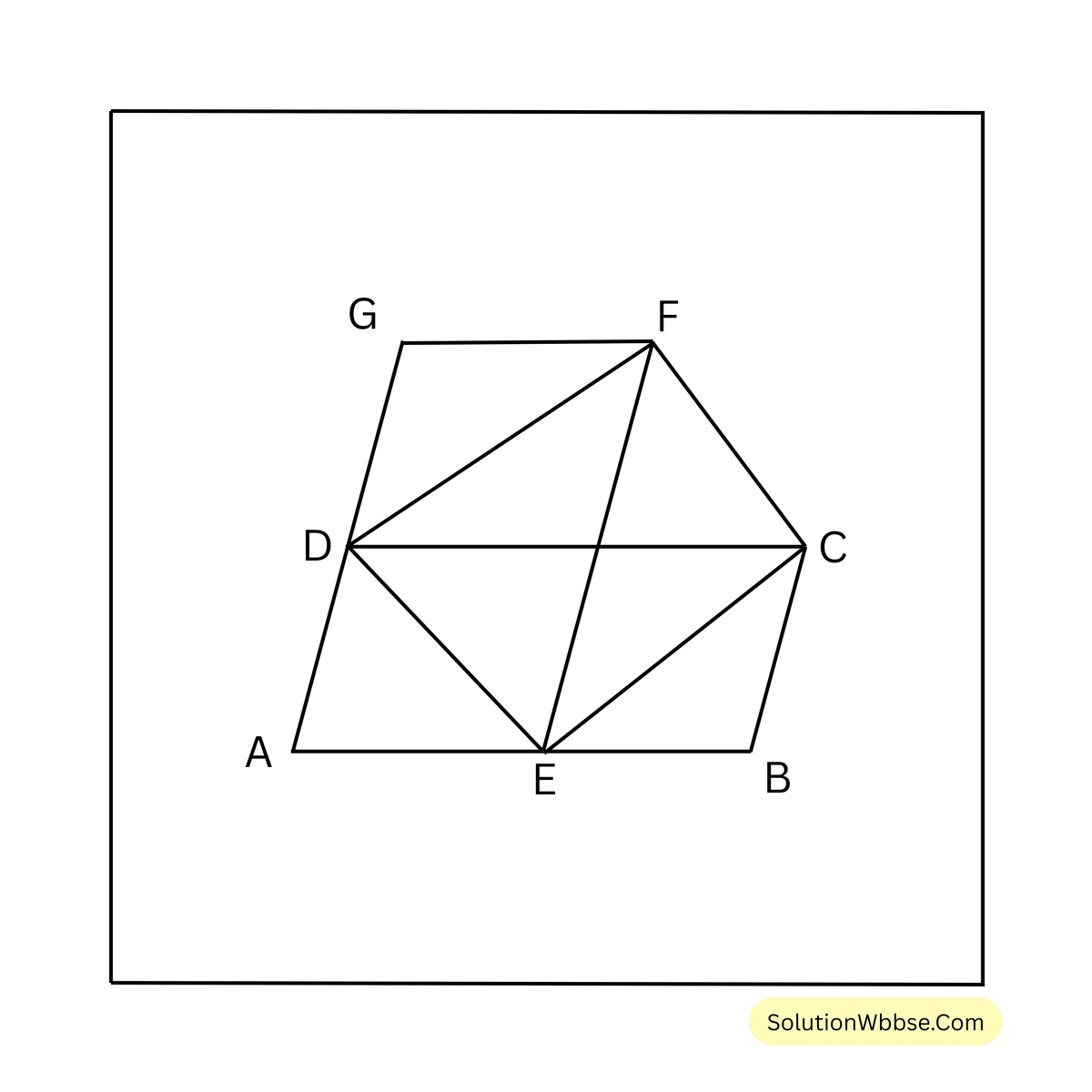
ধরি, সমান ক্ষেত্রফলবিশিষ্ট \(ABCD\) ও \(AEFG\) সামান্তরিক আকারের ক্ষেত্র দুটির \(\angle A\) সাধারণ এবং \(E\), \(AB\) বাহুর উপর অবস্থিত।
প্রমাণ করতে হবে যে, \(DE \parallel FC\)
অঙ্কন – \(D,E\) এবং \(C,E\) যুক্ত করা হল।
প্রমাণ – \(\triangle DEC\) এবং সামান্তরিক \(ABCD\) এর একই ভূমি \(DC\) এবং একই সমান্তরাল যুগল \(DC\) ও \(AB\) এর মধ্যে অবস্থিত।
\(\therefore \triangle DEC = \frac{1}{2}\) সামান্তরিক \(ABCD\)
আবার, \(\triangle DEF\) এবং সামান্তরিক \(AEFG\) এর একই ভূমি \(EF\) এবং একই সমান্তরাল যুগল \(EF\) ও \(AG\) এর মধ্যে অবস্থিত।
\(\therefore \triangle DEF = \frac{1}{2}\) সামান্তরিক \(AEFG\)
আবার যেহেতু \(ABCD\) ও \(AEFG\) সামান্তরিক আকারের ক্ষেত্র দুটির ক্ষেত্রফল সমান।
\(\therefore \triangle DEC = \triangle DEF\)এখন, \(\triangle DEC\) ও \(\triangle DEF\) এর একই ভূমি \(DE\) এবং ক্ষেত্রফল সমান এবং তারা \(DE\) এর একই পার্শ্বে অবস্থিত।
\(\therefore DE \parallel FC\) [প্রমাণিত]
17. \(ABCD\) একটি সামান্তরিক এবং \(ABCE\) একটি চতুর্ভুজ। \(AC\) কর্ণ \(ABCE\) চতুর্ভুজ আকারের ক্ষেত্রটিকে দুটি সমান অংশে বিভক্ত করে। প্রমাণ করি, \(AC \parallel DE\)
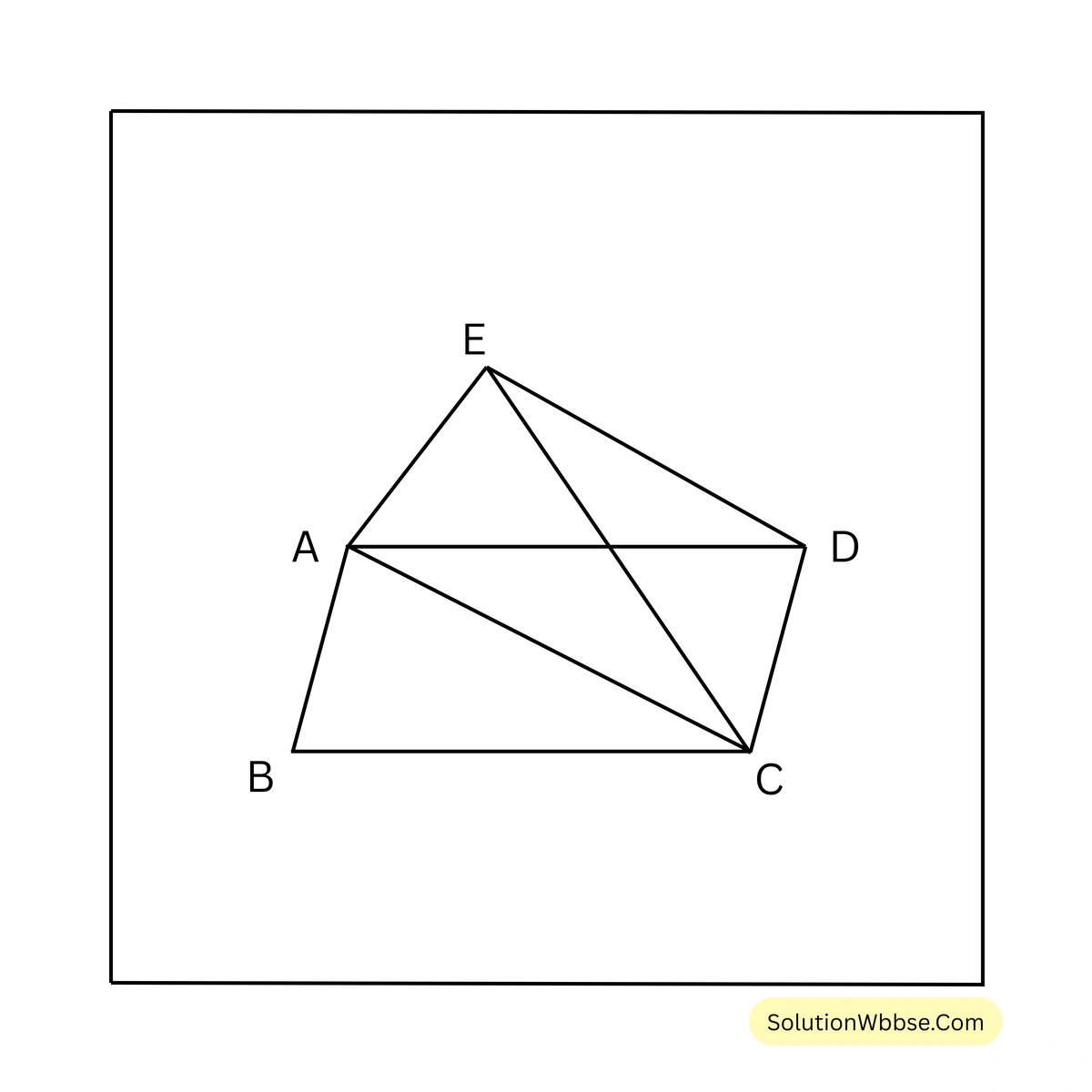
ধরি, \(ABCD\) একটি সামান্তরিক এবং \(ABCE\) একটি চতুর্ভুজ। \(AC\) কর্ণ \(ABCE\) চতুর্ভুজ আকারের ক্ষেত্রটিকে দুটি সমান অংশে বিভক্ত করে। প্রমাণ করতে হবে যে, \(AC \parallel DE\)
প্রমাণ – সামান্তরিক \(ABCD\) এর কর্ণ \(AC\)
\(\therefore \triangle ABC = \triangle ADC\)আবার যেহেতু \(AC\) কর্ণ \(ABCE\) চতুর্ভুজ আকারের ক্ষেত্রটিকে দুটি সমান অংশে বিভক্ত করে।
\(\therefore \triangle ABC = \triangle ACE\)\(\therefore \triangle ADC = \triangle ACE\)এখন \(\triangle ADC\) ও \(\triangle ACE\) এর একই ভূমি \(AC\) এবং তাদের ক্ষেত্রফল সমান এবং তারা \(AC\) এর একই পার্শ্বে অবস্থিত।
\(\therefore AC \parallel DE\) [প্রমাণিত]
18. \(\triangle ABC\) ত্রিভুজের \(BC\) বাহুর মধ্যবিন্দু \(D\); \(P\) এবং \(Q\) যথাক্রমে \(BC\) ও \(BA\) বাহুর উপর এমনভাবে অবস্থিত যে, \(\triangle BPQ = \frac{1}{2} \triangle ABC\); প্রমাণ করি যে, \(DQ \parallel PA\)

ধরি, \(\triangle ABC\) ত্রিভুজের \(BC\) বাহুর মধ্যবিন্দু \(D\); \(P\) এবং \(Q\) যথাক্রমে \(BC\) ও \(BA\) বাহুর উপর এমনভাবে অবস্থিত যে, \(\triangle BPQ = \frac{1}{2} \triangle ABC\), প্রমাণ করতে হবে যে, \(DQ \parallel PA\)
অঙ্কন – \(A,D\) যুক্ত করা হল।
প্রমাণ – \(\triangle BPQ = \frac{1}{2} \triangle ABC = \triangle ABD\) [যেহেতু, \(AD\) মধ্যমা]
\(\therefore \triangle BDQ + \triangle DPQ = \triangle BDQ + \triangle ADQ\)অর্থাৎ, \(\triangle DPQ = \triangle ADQ\)
এখন, \(\triangle DPQ\) ও \(\triangle ADQ\)-এর একই ভূমি \(DQ\) এবং তাদের ক্ষেত্রফল সমান এবং তারা \(DQ\)-এর একই পার্শ্বে অবস্থিত।
\(\therefore DQ \parallel PA\) [প্রমাণিত]
19. \(ABCD\) সামান্তরিকের \(AB\), \(BC\), \(CD\) এবং \(DA\) বাহুর মধ্যবিন্দু যথাক্রমে \(E\), \(F\), \(G\) ও \(H\)।
প্রমাণ করি যে,
(i) \(EFGH\) একটি সামান্তরিক
(ii) \(EFGH\) সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল \(ABCD\) সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফলের অর্ধেক।
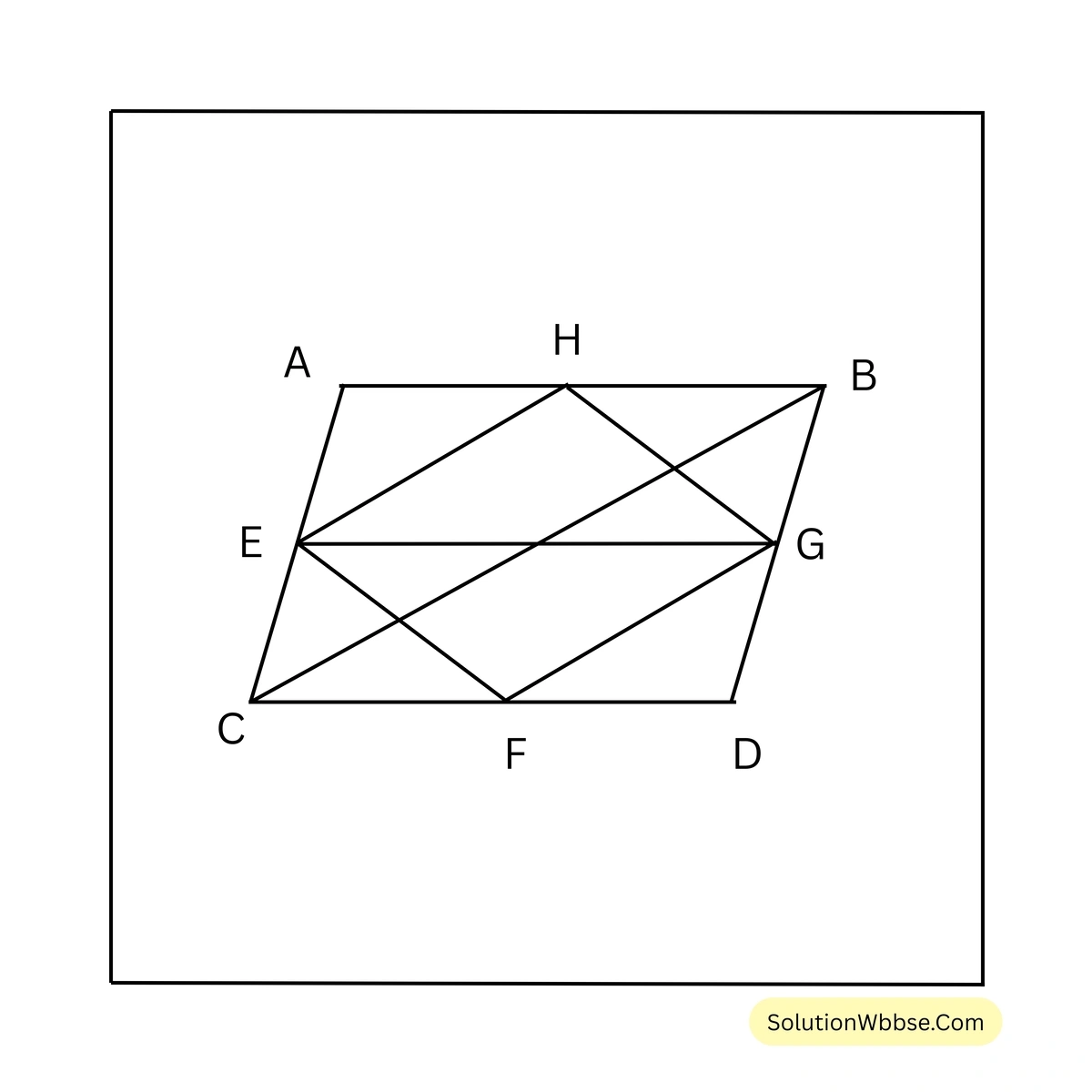
ধরি, \(ABCD\) সামান্তরিকের \(AB\), \(BC\), \(CD\) এবং \(DA\) বাহুর মধ্যবিন্দু যথাক্রমে \(E\), \(F\), \(G\) ও \(H\)।
প্রমাণ করতে হবে যে, (i) \(EFGH\) একটি সামান্তরিক (ii) \(EFGH\) সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল \(ABCD\) সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফলের অর্ধেক।
অঙ্কন – \(D,B\) ও \(E,G\) যুক্ত করা হল।
প্রমাণ – \(\triangle ABD\) এর \(AB\) এবং \(AD\) বাহুর মধ্যবিন্দু যথাক্রমে \(E\) এবং \(H\)
\(\therefore EH = \frac{1}{2} DB\) এবং \(EH \parallel BD\)
অনুরূপভাবে, \(\triangle BDC\) এর \(BC\) এবং \(CD\) বাহুর মধ্যবিন্দু যথাক্রমে \(F\) ও \(G\)
\(\therefore FG = \frac{1}{2} BD\) এবং \(FG \parallel BD\)
\(\therefore EH = FG\) এবং \(EH \parallel FG\)
\(\therefore EFGH\) একটি সামান্তরিক [(i) নং প্রমাণিত]
আবার, \(ABCD\) সামান্তরিকের \(AB\) ও \(DC\) বাহুর মধ্যবিন্দু যথাক্রমে \(E\) ও \(G\)
\(\therefore EG \parallel BC \parallel AD\)এখন, \(\triangle EFG\) ও সামান্তরিক \(BCGE\) এর একই ভূমি \(EG\) এবং তারা একই সমান্তরাল যুগল \(EG\) ও \(BC\) এর মধ্যে অবস্থিত।
\(\therefore \triangle EFG = \frac{1}{2}\) সামান্তরিক \(BCGE\)
একইভাবে, \(\triangle EHG\) ও সামান্তরিক \(AEGD\) এর একই ভূমি \(EG\) এবং তারা একই সমান্তরাল যুগল \(EG\) ও \(AD\) এর মধ্যে অবস্থিত।
\(\therefore \triangle EHG = \frac{1}{2}\) সামান্তরিক \(AEGD\)
\(\therefore \triangle EFG + \triangle EHG = \frac{1}{2}\) সামান্তরিক \(BCGE + \frac{1}{2}\) সামান্তরিক \(AEGD\)
\(\therefore\) সামান্তরিক \(EFGH = \frac{1}{2}\) (সামান্তরিক \(BCGE\) + সামান্তরিক \(AEGD\))
অর্থাৎ, সামান্তরিক \(EFGH = \frac{1}{2}\) সামান্তরিক \(ABCD\) [(ii) নং প্রমাণিত]
20. ABCD ট্রাপিজিয়ামের \( AB \parallel DC \) এবং \( BC \) বাহুর মধ্যবিন্দু \( E \); প্রমাণ করি যে, \( \triangle AED \) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল \( = \frac{1}{2} \times \) ABCD ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল।
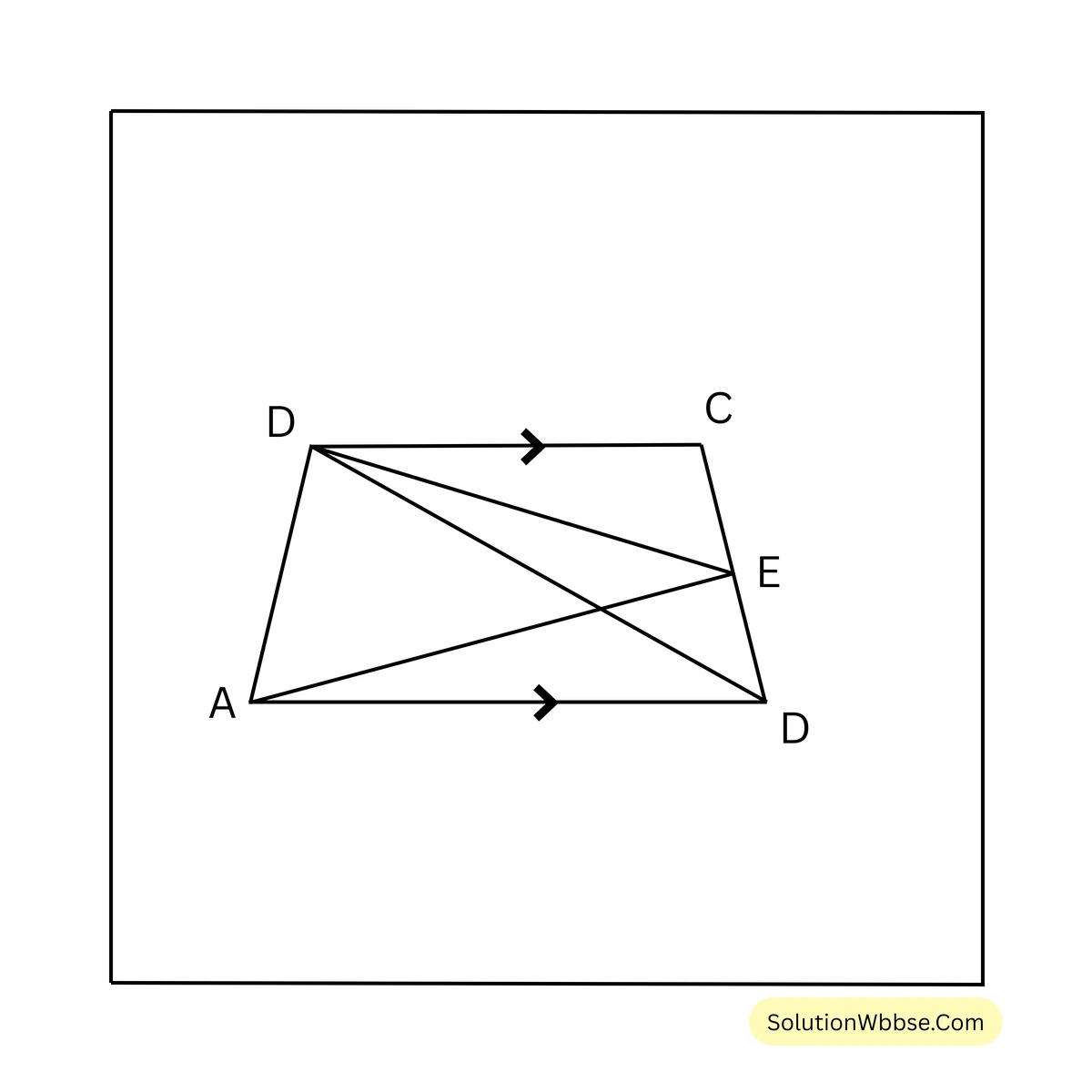
ধরি, ABCD ট্রাপিজিয়ামের \( AB \parallel DC \) এবং \( BC \) বাহুর মধ্যবিন্দু \( E \)।
প্রমাণ করতে হবে যে, \( \triangle AED \) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল \( = \frac{1}{2} \times \) ABCD ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল।
অঙ্কন – \( A,C \) এবং \( B,D \) যুক্ত করা হল।
প্রমাণ – \( \triangle ABC \) এর \( AE \) মধ্যমা
\( \therefore \triangle ABE = \triangle AEC = \frac{1}{2} \triangle ABC \)আবার, \( \triangle BDC \) এর \( DE \) মধ্যমা
\( \therefore \triangle CDE = \triangle BDE = \frac{1}{2} \triangle BDC \)এখন, \( \triangle BDC \) এবং \( \triangle ADC \) এর একই ভূমি \( DC \) এবং একই সমান্তরালযুগল \( DC \) ও \( AB \) এর মধ্যে অবস্থিত।
\( \therefore \triangle BDC = \triangle ADC \)\( \therefore \triangle CDE = \frac{1}{2} \triangle BDC = \frac{1}{2} \triangle ADC \)এখন, \( \triangle AED = \) ট্রাপিজিয়াম \( ABCD – (\triangle ABE + \triangle CDE) \)
বা, \( \triangle AED = \) ট্রাপিজিয়াম \( ABCD – \left( \frac{1}{2} \triangle ABC + \frac{1}{2} \triangle ADC \right) \)
বা, \( \triangle AED = \) ট্রাপিজিয়াম \( ABCD – \frac{1}{2} (\triangle ABC + \triangle ADC) \)
বা, \( \triangle AED = \) ট্রাপিজিয়াম \( ABCD – \frac{1}{2} \) ট্রাপিজিয়াম \( ABCD \)
বা, \( \triangle AED = \frac{1}{2} \) ট্রাপিজিয়াম \( ABCD \) [প্রমাণিত]
21. বহু বিকল্পীয় প্রশ্ন (M.C.Q)
(i) \( \Delta ABC \) এর BC, CA এবং AB বাহুর মধ্যবিন্দু যথাক্রমে D, E এবং F; যদি ABC = 16 বর্গ সেমি. হয় তাহলে FBCE ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল
(a) 40 বর্গ সেমি.
(b) 8 বর্গ সেমি.
(c) 12 বর্গ সেমি.
(d) 100 বর্গ সেমি.
Ans – (c) 12 বর্গ সেমি.
সমাধান –
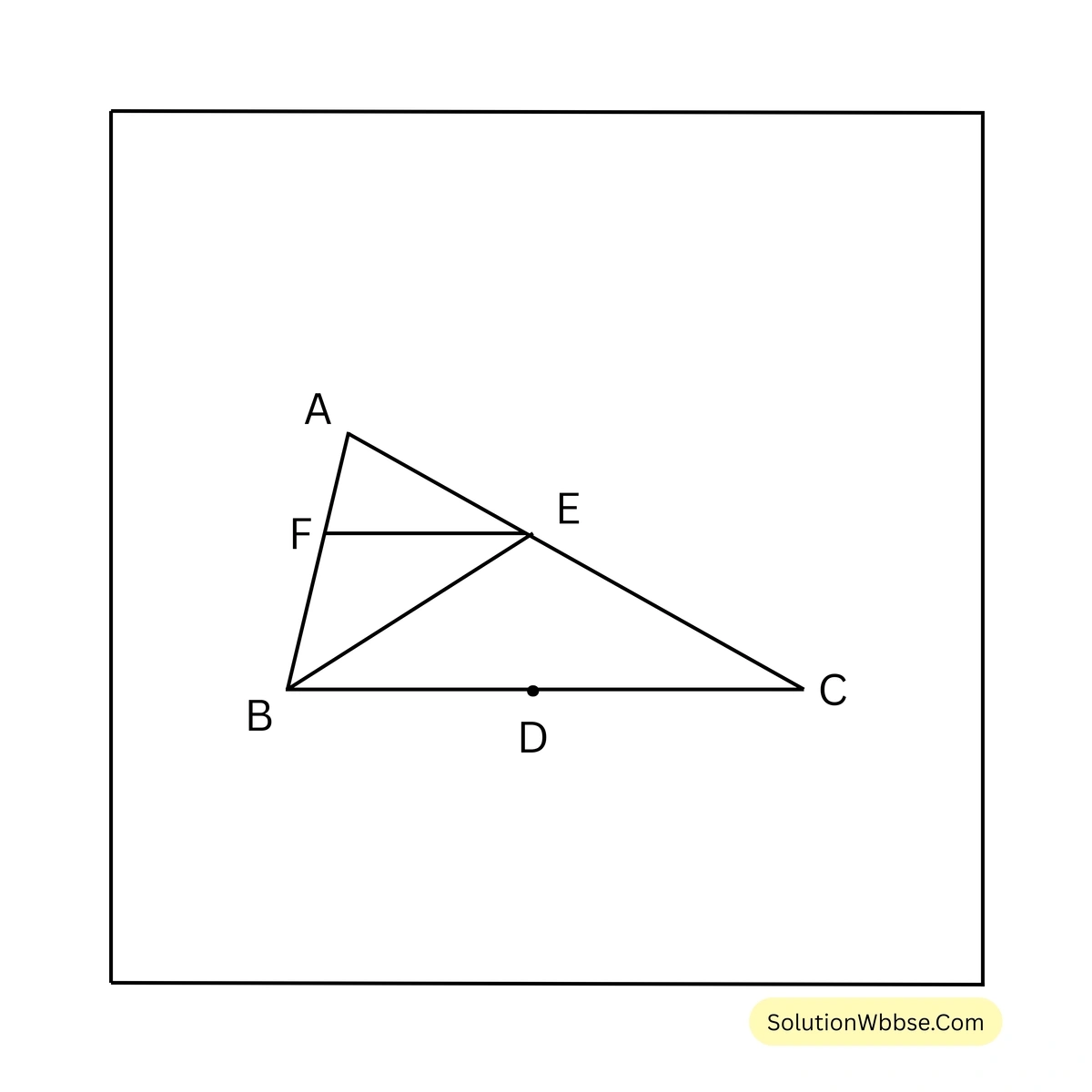
B, E যোগ করা হল।
\( \Delta ABC \) এর BE মধ্যমা।
\( \therefore \Delta ABE = \frac{1}{2} \Delta ABC = 16/2 \) বর্গসেমি. = 8 বর্গসেমি.
আবার, \( \Delta ABE \) এর EF মধ্যমা।
\( \therefore \Delta AEF = \frac{1}{2} \Delta ABE = 8/2 \) বর্গসেমি. = 4 বর্গসেমি.
\( \therefore \) ট্রাপিজিয়াম FBCE = \( \Delta ABC – \Delta AFE = (16 – 4) \) বর্গসেমি. = 12 বর্গসেমি.
(ii) A, B, C ও D যথাক্রমে PQRS সামান্তরিকের PQ, QR, RS, SP বাহুর মধ্যবিন্দু। PQRS সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল = 36 বর্গসেমি. হলে, ABCD ক্ষেত্রের ক্ষেত্রফল
(a) 24 বর্গসেমি.
(b) 18 বর্গসেমি.
(c) 30 বর্গসেমি.
(d) 36 বর্গসেমি.
Ans – (b) 18 বর্গসেমি.
সমাধান –
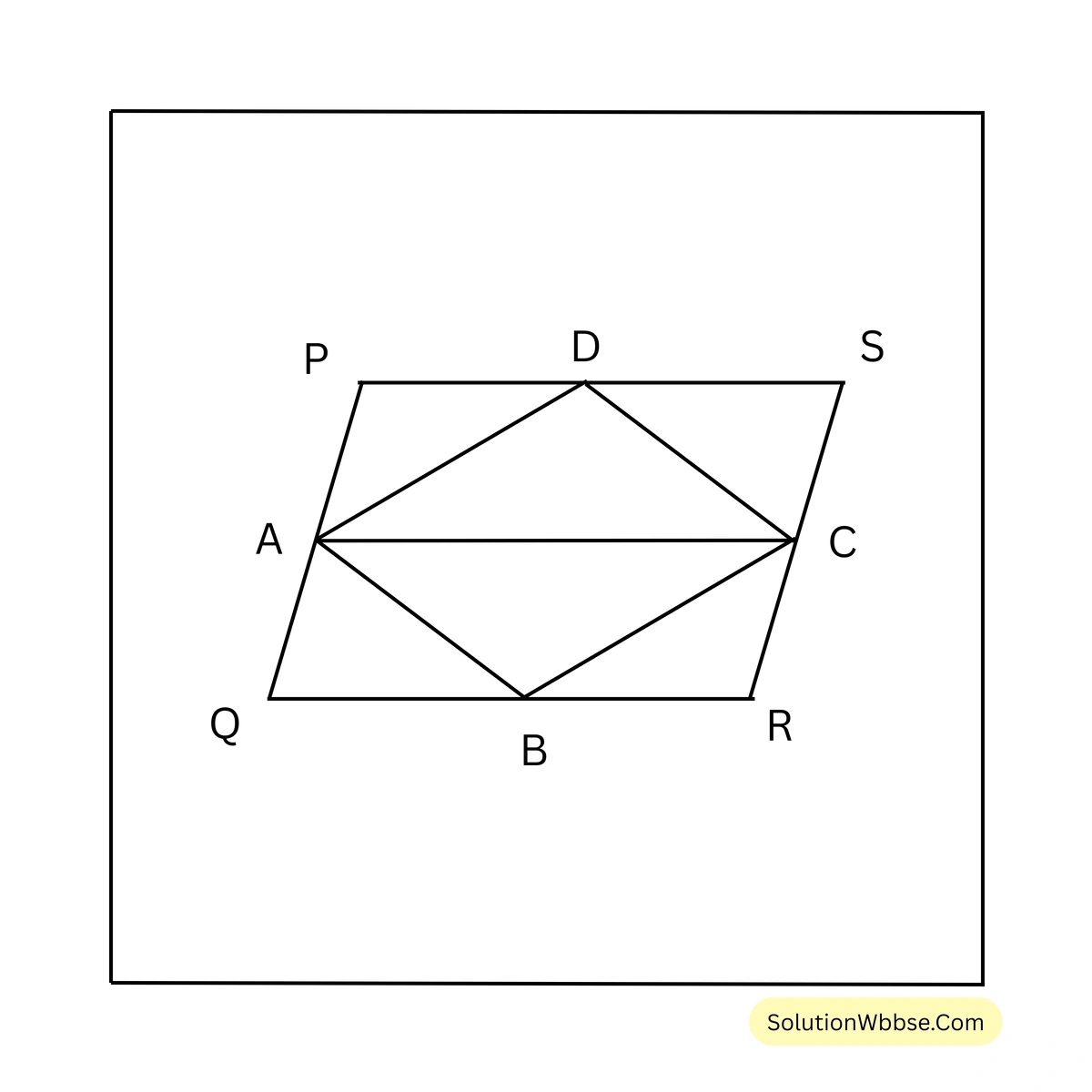
\( \therefore PACS \) এবং \( AQRC \) প্রত্যেকেই সামান্তরিক।
\( \therefore \Delta ABC = \frac{1}{2} \) সামান্তরিক \( AQRC \) এবং \( \Delta ADC = \frac{1}{2} \) সামান্তরিক \( APSC \) [যেহেতু, একই ভূমি ও একই সমান্তরালযুগলের মধ্যে অবস্থিত ত্রিভুজের ক্ষেত্রফল সামান্তরিকের ক্ষেত্রফলের অর্ধেক]
\( \therefore \Delta ABC + \Delta ADC = \frac{1}{2} \) সামান্তরিক \( AQRC + \frac{1}{2} \) সামান্তরিক \( APSC \)
বা, সামান্তরিক \( ABCD = \frac{1}{2} \) (সামান্তরিক \( AQRC + \) সামান্তরিক \( APSC \))
বা, সামান্তরিক \( ABCD = \frac{1}{2} \times \) সামান্তরিক \( PQRS \)
বা, সামান্তরিক \( ABCD = (\frac{1}{2} \times 36) \) বর্গসেমি. = 18 বর্গসেমি.
(iii) ABCD সামান্তরিকের ভিতর O যেকোনো একটি বিন্দু। \( \Delta AOB + \Delta COD = 16 \) বর্গসেমি. হলে, ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল
(a) 8 বর্গসেমি.
(b) 4 বর্গসেমি.
(c) 32 বর্গসেমি.
(d) 64 বর্গসেমি.
Ans – (c) 32 বর্গসেমি.
সমাধান –
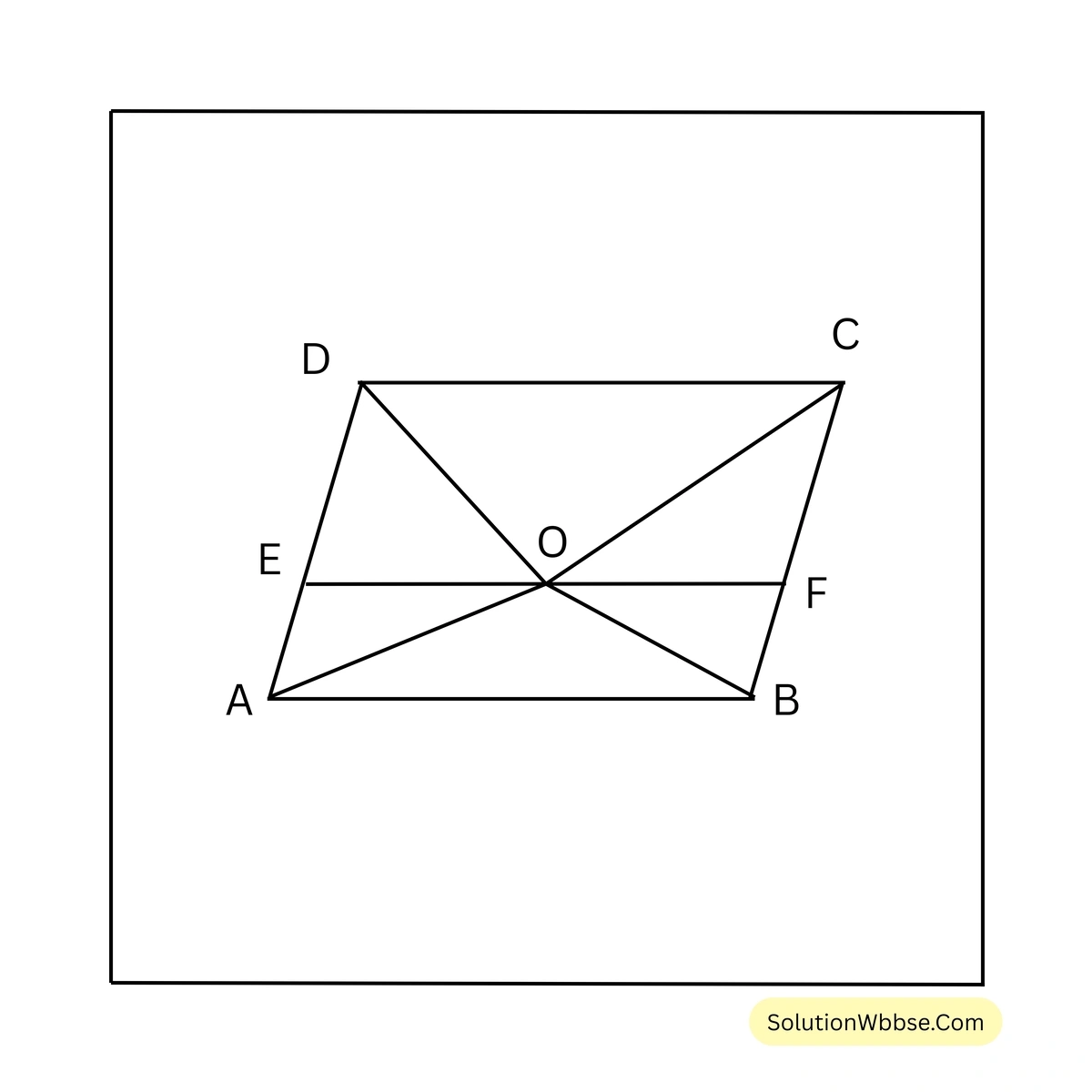
O বিন্দু দিয়ে AB ও CD বাহুর সমান্তরাল সরলরেখা টানা হল যা AD ও BC বাহুকে যথাক্রমে E ও F বিন্দুতে ছেদ করেছে।
\( \therefore AB \parallel EF \parallel DC \)\( \therefore CDEF \) এবং \( EABF \) প্রত্যেকেই সামান্তরিক
\( \therefore \Delta AOB = \frac{1}{2} \) সামান্তরিক \( EABF \) এবং \( \Delta COD = \frac{1}{2} \) সামান্তরিক \( CDEF \)
\( \therefore AOB + COD = \frac{1}{2} \) সামান্তরিক \( EABF + \frac{1}{2} \) সামান্তরিক \( CDEF \)
বা, \( 16 = \frac{1}{2} \) (সামান্তরিক \( EABF + \) সামান্তরিক \( CDEF \))
বা, (সামান্তরিক \( EABF + \) সামান্তরিক \( CDEF \)) \( = 32 \)
বা, সামান্তরিক \( ABCD \) এর ক্ষেত্রফল = 32 বর্গসেমি.
(iv) ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D, BD বাহুর মধ্যবিন্দু E এবং AE-এর মধ্যবিন্দু O; BOE ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(a) \( 1/3 \times ABC \) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(b) \( 1/4 \times ABC \) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(c) \( 1/6 \times ABC \) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(d) \( 1/8 \times ABC \) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
Ans – (d) \( 1/8 \times ABC \) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
সমাধান –
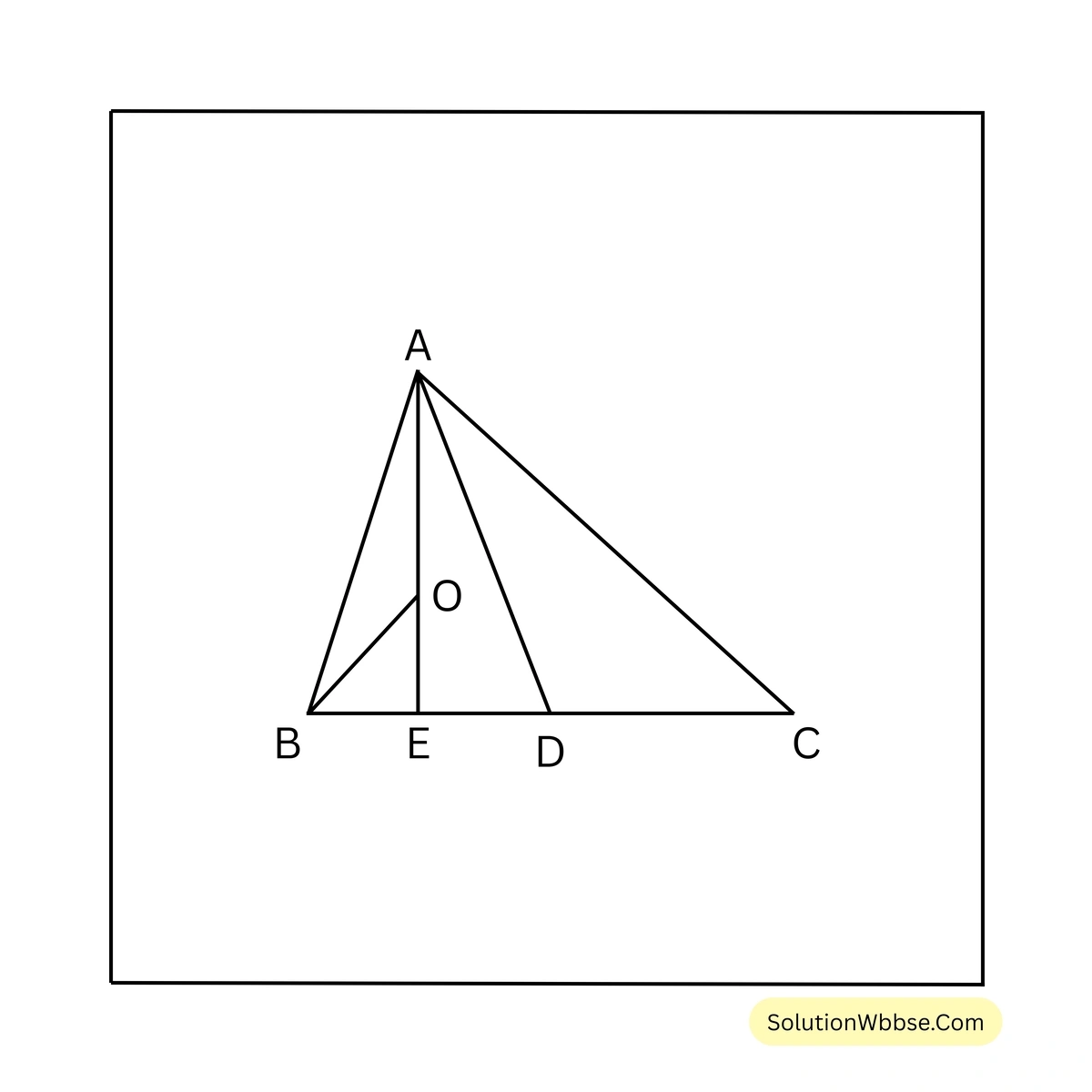
\( \Delta BOE = \frac{1}{2} \Delta ABE \) [যেহেতু, \( ABE \) ত্রিভুজের \( OB \) মধ্যমা]
বা, \( \Delta BOE = \frac{1}{2} \) (\( \frac{1}{2} \Delta ABD \)) [যেহেতু, \( ABD \) ত্রিভুজের \( AE \) মধ্যমা]
বা, \( \Delta BOE = \frac{1}{4} \Delta ABD \)
বা, \( \Delta BOE = \frac{1}{4} \) (\( \frac{1}{2} \Delta ABC \)) [যেহেতু, \( ABC \) ত্রিভুজের মধ্যমা \( AD \)]
বা, \( \Delta BOE = 1/8 \Delta ABC \)
(v) একটি সামান্তরিক আকারের ক্ষেত্র, একটি আয়তক্ষেত্র এবং একটি ত্রিভুজাকার ক্ষেত্র একই ভূমি ও একই সমান্তরালযুগলের মধ্যে অবস্থিত এবং তাদের ক্ষেত্রফল যথাক্রমে P, Q ও T হলে
(a) P = R = 2T
(b) P = R = T/2
(c) 2P = 2R = T
(d) P = R = T
Ans – (a) P = R = 2T
সমাধান –
একই ভূমি এবং একই সমান্তরালযুগলের মধ্যে অবস্থিত, একটি সামান্তরিক আকারের ক্ষেত্রফল = একটি আয়তক্ষেত্রের ক্ষেত্রফল = \( 2 \times \) একটি ত্রিভুজের ক্ষেত্রফল
বা, P = R = 2T
22. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন
(i) ABCD সামান্তরিকের D বিন্দু থেকে AB বাহুর উপর লম্ব DE এবং B বিন্দু থেকে AD বাহুর উপর লম্ব BF; AB = 10 সেমি., AD = 8 সেমি. এবং DE = 6 সেমি. হলে, BF-এর দৈর্ঘ্য কত তা লিখি।
সমাধান –
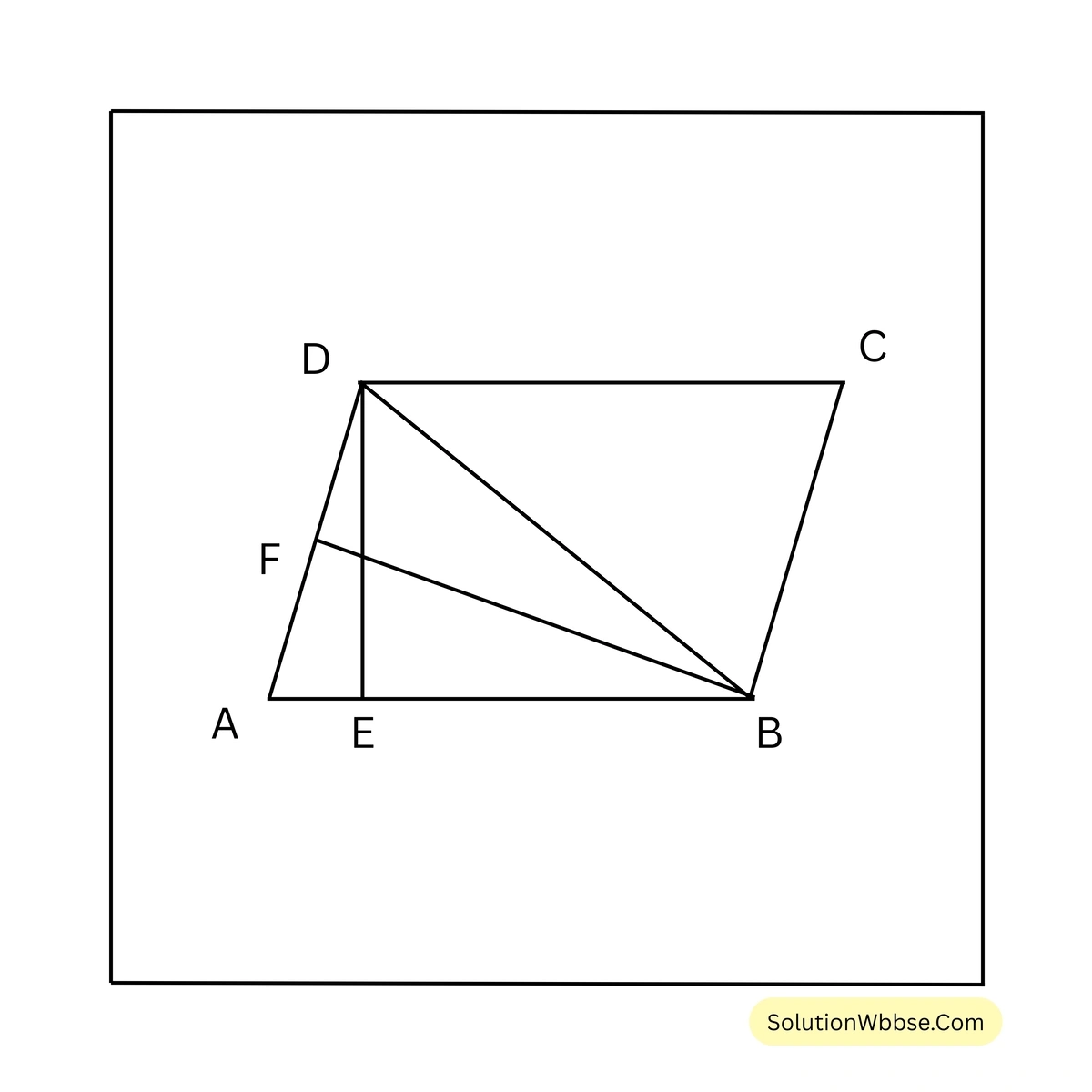
B, D যুক্ত করা হল।
AD কে ভূমি ধরে, \( \triangle ADB \) এর ক্ষেত্রফল \( = \frac{1}{2} \times AD \times BF \)
আবার, AB কে ভূমি ধরে, \( \triangle ADB \) এর ক্ষেত্রফল \( = \frac{1}{2} \times AB \times DE \)
∴ \( \frac{1}{2} \times AD \times BF = \frac{1}{2} \times AB \times DE \)
বা, \( \frac{1}{2} \times 8 \times BF = \frac{1}{2} \times 10 \times 6 \)
বা, \( 4 \times BF = 30 \)
বা, \( BF = \frac{30}{4} \)
বা, \( BF = 7.5 \)
∴ BF বাহুর দৈর্ঘ্য \( 7.5 \) সেমি.। [উত্তর]
(ii) ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল \( 100 \) বর্গএকক; BC বাহুর মধ্যবিন্দু P; ABP ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল কত তা লিখি।
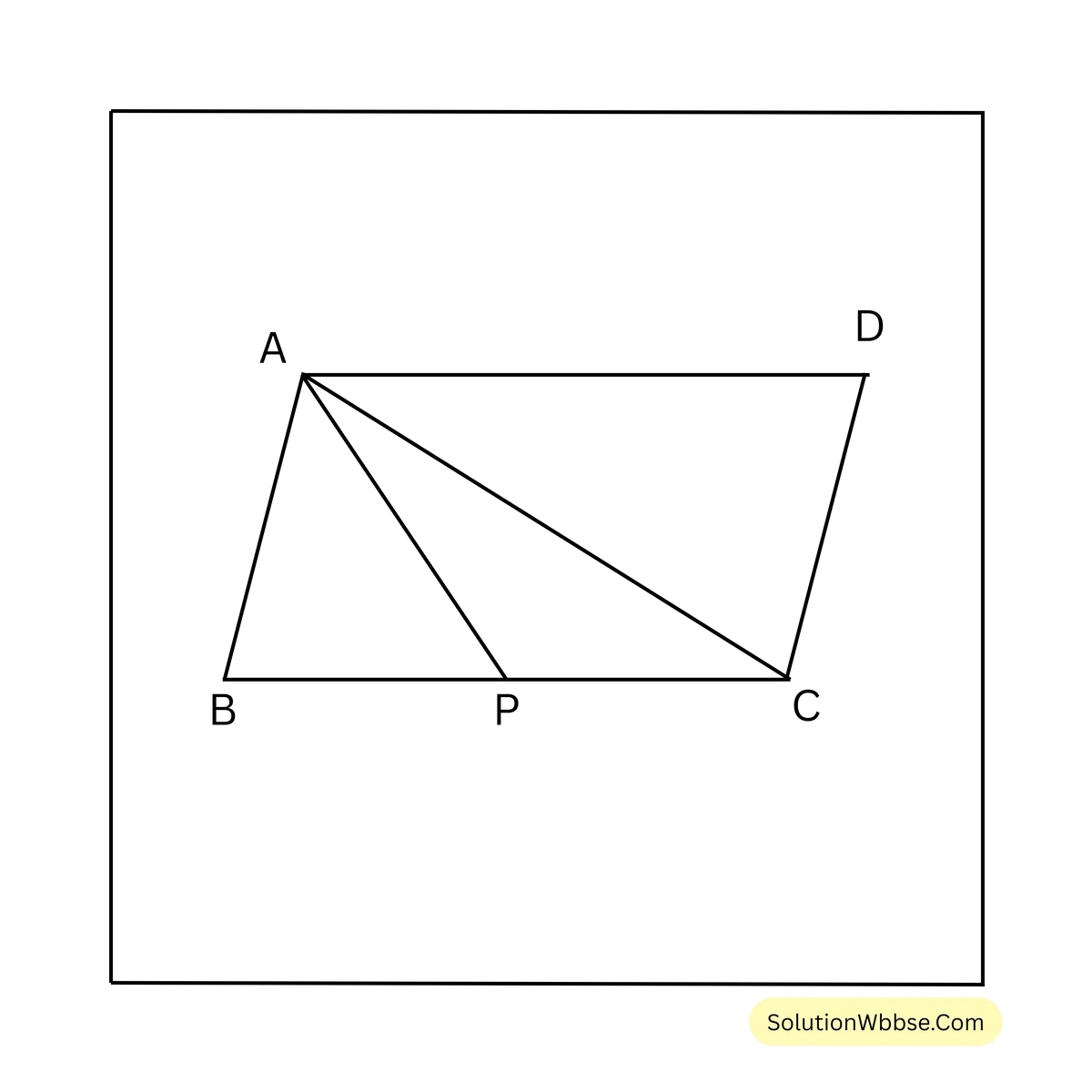
সমাধান –
AC কর্ণ টানা হল।
∴ \( \triangle ABC = \frac{1}{2} \times \) সামান্তরিক \( ABCD \)–এর ক্ষেত্রফল
আবার, \( \triangle ABP = \frac{1}{2} \triangle ABC \) [যেহেতু, \( AP \), \( \triangle ABC \) এর মধ্যমা]
∴ \( \triangle ABP = \frac{1}{2} \triangle ABC = \frac{1}{2} \left( \frac{1}{2} ABCD \right) = \frac{1}{4} ABCD \)
∴ ABP ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল ABCD সামান্তরিকের ক্ষেত্রফলের \( \frac{1}{4} \) অংশ।
∴ ABP ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল = \( \left( \frac{1}{4} \times 100 \right) \) বর্গসেমি. = \( 25 \) বর্গসেমি. [উত্তর]
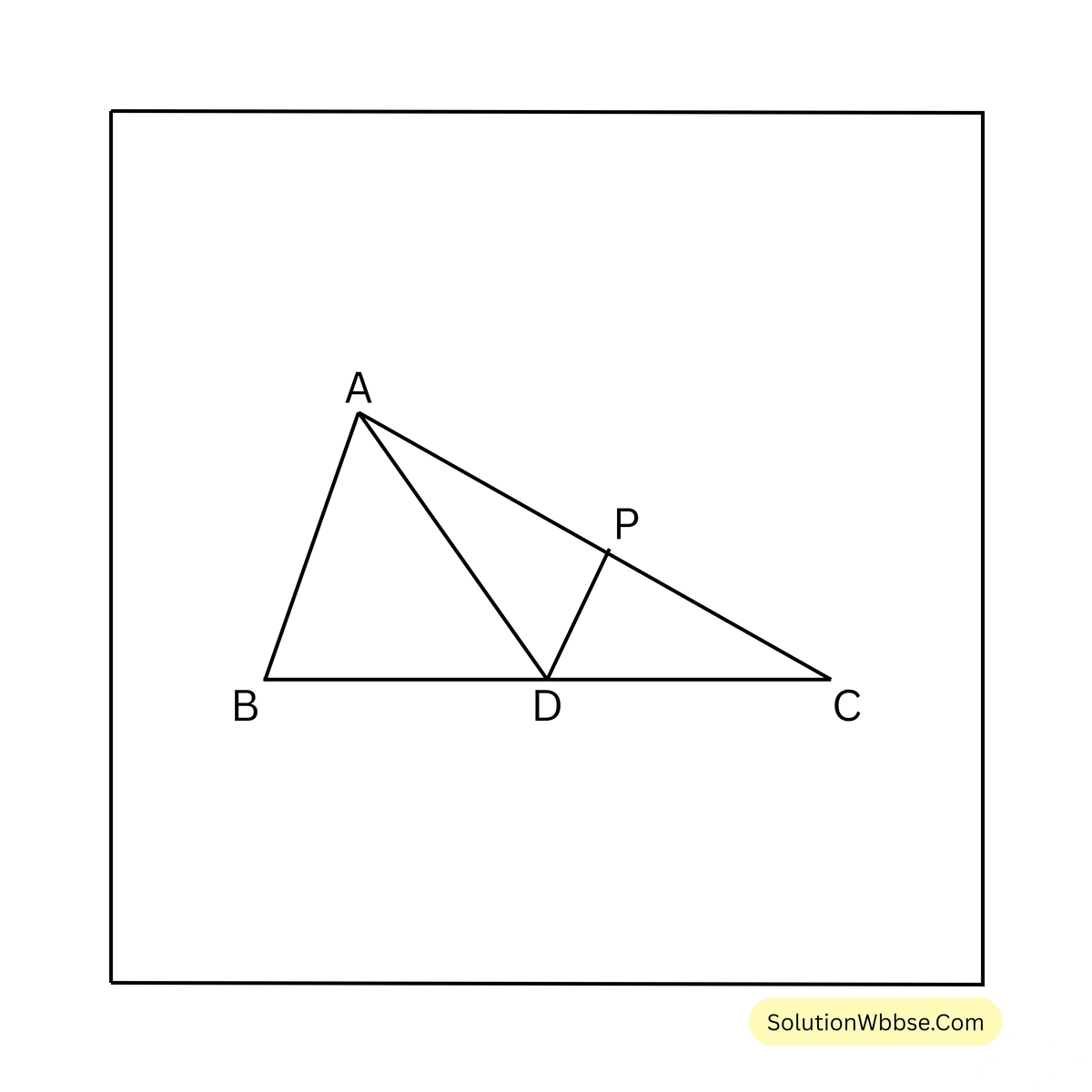
(iii) ABC ত্রিভুজের AD মধ্যমা এবং AC বাহুর উপর P এমন একটি বিন্দু যাতে ADP–এর ক্ষেত্রফল : ABD এর ক্ষেত্রফল = \( 2:3 \) হয়। PDC এর ক্ষেত্রফল : ABC এর ক্ষেত্রফল কত তা লিখি।
সমাধান –
যেহেতু, ABC ত্রিভুজের AD মধ্যমা।
∴ \( \triangle ABD = \triangle ADC \)
এবং \( \triangle ABC = 2 \triangle ADC \)
\( \triangle ADP \) এর ক্ষেত্রফল – \( \triangle ABD \)–এর ক্ষেত্রফল = \( 2:3 \)
∴ \( \triangle ADP \)–এর ক্ষেত্রফল = \( \frac{2}{3} \times \triangle ABD \) এর ক্ষেত্রফল = \( \frac{2}{3} \times \triangle ADC \) এর ক্ষেত্রফল
∴ \( \triangle PDC \)–এর ক্ষেত্রফল = \( \triangle ADC \) এর ক্ষেত্রফল – \( \triangle ADP \) এর ক্ষেত্রফল = \( \triangle ADC \) এর ক্ষেত্রফল – \( \frac{2}{3} \times \triangle ADC \) এর ক্ষেত্রফল
= \( \frac{1}{3} \triangle ADC \)–এর ক্ষেত্রফল
∴ \( \triangle PDC \) এর ক্ষেত্রফল : \( \triangle ABC \) এর ক্ষেত্রফল
= \( \frac{1}{3} \triangle ADC : 2 \triangle ADC \)
= \( \frac{1}{3} : 2 \)
= \( 1:6 \) [উত্তর]
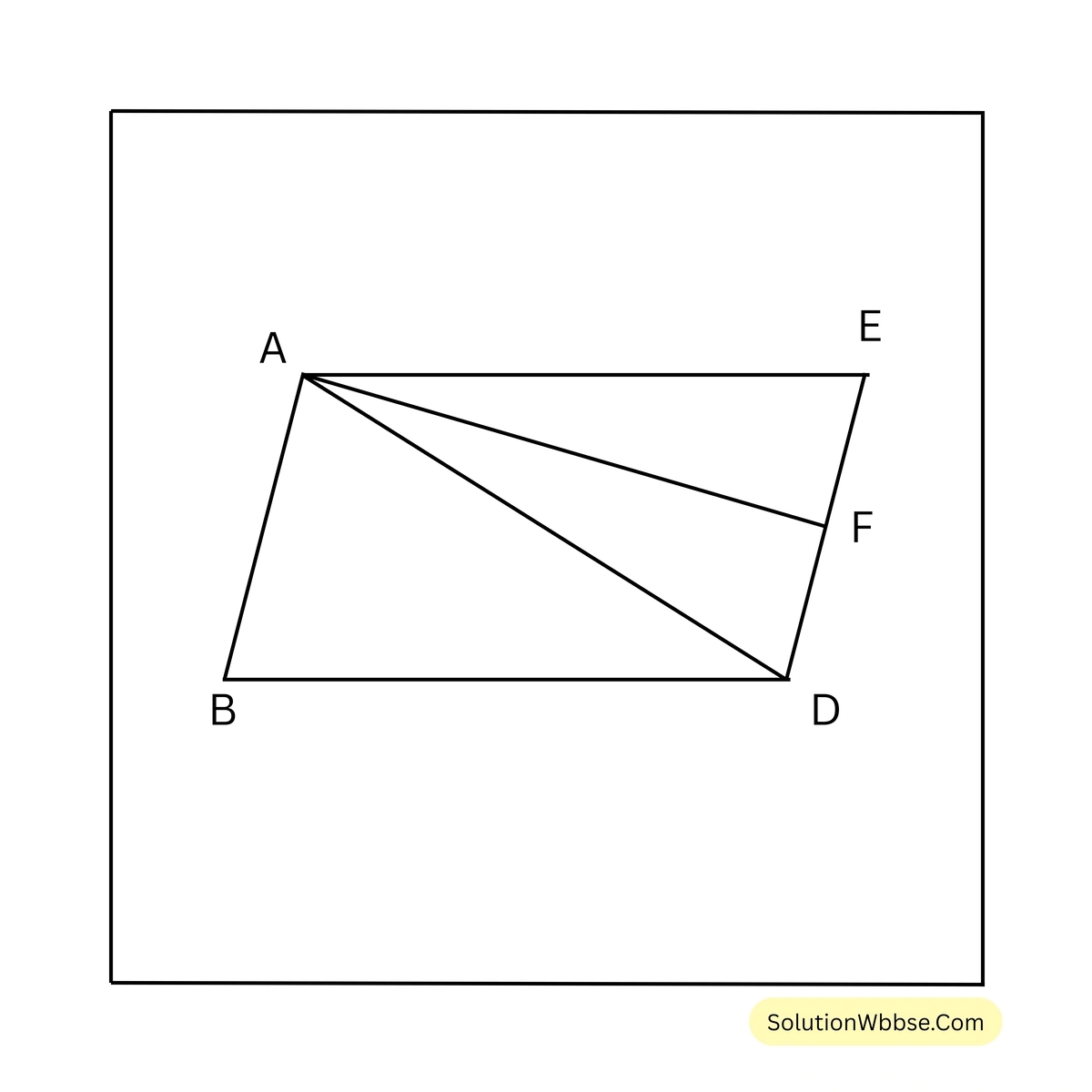
(iv) ABDE একটি সামান্তরিক। F, AD বাহুর মধ্যবিন্দু। ABD ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল \( 20 \) বর্গসেমি. হলে AEF ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল কত তা লিখি।
সমাধান –
ABDE সামান্তরিকের AD কর্ণ।
∴ \( \triangle ADE = \triangle ABD = 20 \) বর্গসেমি.
আবার, \( \triangle ADE \) এর AF মধ্যমা।
∴ \( \triangle AEF = \frac{1}{2} \triangle ADE = 10 \) বর্গসেমি. [উত্তর]
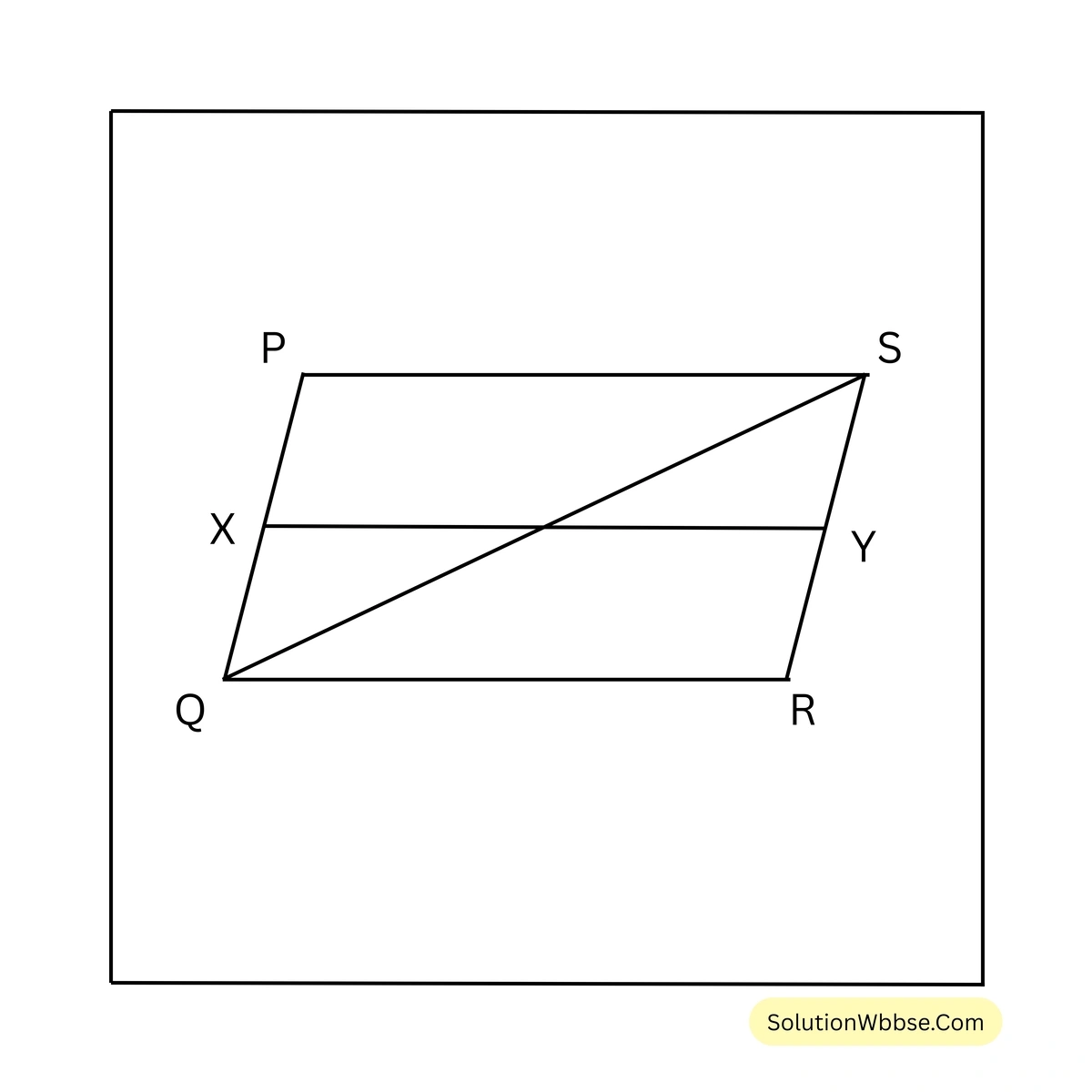
(v) PQRS একটি সামান্তরিক। X ও Y যথাক্রমে PQ ও SR বাহুর মধ্যবিন্দু। কর্ণ SQ যুক্ত করা হল। সামান্তরিক XQRY আকার ক্ষেত্রের ক্ষেত্রফল : QSR ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল কত তা লিখি।
সমাধান –
যেহেতু, X এবং Y যথাক্রমে PQ এবং RS বাহুর মধ্যবিন্দু
∴ \( XQRY \) আকার ক্ষেত্রের ক্ষেত্রফল = \( \frac{1}{2} PQRS \) সামান্তরিকের ক্ষেত্রফল
আবার, PQRS সামান্তরিকের কর্ণ \( SQ \)
∴ \( \triangle QSR \) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল = \( \frac{1}{2} PQRS \) সামান্তরিকের ক্ষেত্রফল
∴ \( XQRY \) আকার ক্ষেত্রের ক্ষেত্রফল = \( \triangle QSR \) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
∴ \( XQRY \) আকার ক্ষেত্রের ক্ষেত্রফল : \( \triangle QSR \) ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল = \( 1:1 \) [উত্তর]
এই আর্টিকেলে নবম শ্রেণির গণিতের ‘ক্ষেত্রফল সংক্রান্ত উপপাদ্য‘ অধ্যায়ের ‘কষে দেখি – 12’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।
কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন