আজকের আর্টিকেলে আমরা নবম শ্রেণীর ভৌতবিজ্ঞান বইয়ের দ্বিতীয় অধ্যায় “বল ও গতি” এর “নিউটনের দ্বিতীয় গতিসূত্র” থেকে সহজ ও সংক্ষিপ্ত প্রশ্ন-উত্তর শেয়ার করবো। এই প্রশ্নগুলো নবম শ্রেণির ইউনিট টেস্ট থেকে বার্ষিক পরীক্ষা এর জন্য যেমন গুরুত্বপূর্ণ, তেমনি চাকরি বা বিভিন্ন প্রতিযোগিতার পরীক্ষাতেও কাজে লাগবে। এই অধ্যায় থেকে স্কুল পরীক্ষা থেকে শুরু করে চাকরির পরীক্ষায় প্রায়ই প্রশ্ন আসে, তাই এই প্রশ্নোত্তরগুলো সবাইকে সাহায্য করবে। প্রতিটি প্রশ্নের উত্তর সহজ ভাষায় লেখা হয়েছে, যাতে সবাই বুঝতে পারেন। পড়ার শেষে এই অধ্যায়ের মুখ্য বিষয়গুলো আপনার আয়ত্তে চলে আসবে এবং যেকোনো পরীক্ষায় আত্মবিশ্বাসের সঙ্গে লিখতে পারবেন।

জ্ঞানমূলক প্রশ্নোত্তর
বস্তুর ভরবেগ বলতে কী বোঝায়? ভরবেগের মাত্রীয় সংকেত এবং CGS পদ্ধতি ও SI -তে এককগুলি লেখো।
ভরবেগ (Momentum) – ভর ও বেগের সমন্বয়ে কোনো গতিশীল বস্তুতে যে গতীয় ধর্মের সৃষ্টি হয়, তাকে ভরবেগ বলা হয়।
ভরবেগের মাত্রীয় সংকেত [MLT-1]।
CGS পদ্ধতিতে ভরবেগের একক গ্রাম-সেমি/সে এবং SI -তে কিগ্রা-মি/সে।
ভরবেগ স্কেলার না ভেক্টর রাশি?
ভরবেগ, একটি স্কেলার রাশি (ভর) ও একটি ভেক্টরের (বেগ) গুণফল হিসাবে প্রকাশিত হয় বলে এটি একটি ভেক্টর রাশি। বেগের অভিমুখই ভরবেগের ক্রিয়ার অভিমুখ।
একটি বাস্তব উদাহরণের সাহায্যে ভরবেগের ধারণা ও তার প্রয়োজনীয়তা ব্যাখ্যা করো।
বাস্তব উদাহরণের সাহায্যে ভরবেগের ধারণা – একটি মারবেলকে কাচের জানালায় স্পর্শ করিয়ে রাখলে দেয়ালের কোনো ক্ষতি হয় না, কিন্তু কিছু পরিমাণ বেগসহ সেটি জানালার দিকে নিক্ষেপ করলে জানালায় ফাটল ধরে বা জানালা ভেঙে যায়।
আবার একই বেগে গতিশীল একটি সাইকেল এবং একটি ভারী ট্রাক কোনো ব্যক্তিকে ধাক্কা দিলে দ্বিতীয়ক্ষেত্রে ধাক্কার অভিঘাত অনেক বেশি এবং বিপজ্জনক হয়।
এই দুটি উদাহরণ থেকে স্পষ্ট হয় যে, কোনো বস্তুর গতীয় আচরণ তার ভর ও বেগ এই দুই রাশির ওপরই সমানভাবে নির্ভরশীল। প্রথমক্ষেত্রে বেগ শূন্য অবস্থায় মারবেল জানালার উপর তার কোনো প্রভাব ফেলে না। কিন্তু, গতিশীল অবস্থায় পাথরটি ভরবেগ অর্জন করে এবং জানালার সঙ্গে সংঘাতে সেই ভরবেগের পরিবর্তন ঘটায় কাচের জানালায় তার প্রভাব পড়ে।
দ্বিতীয় উদাহরণটিতে বেগ অভিন্ন হলেও ট্রাকের ভর সাইকেল অপেক্ষা বহুগুণ বেশি বলে ট্রাকের সঙ্গে সংঘাতে ব্যক্তির উপর বেশি পরিমাণ ভরবেগ হস্তান্তরিত হয়, তাই আঘাতের তীব্রতাও এক্ষেত্রে বেশি (সাইকেলের তুলনায়) হয়ে থাকে।
সুতরাং, সচল বস্তুর গতীয় আচরণের সঠিক পরিমাণগত বর্ণনা একমাত্র ভর ও বেগ এই দুই ধরনের রাশির যৌথ প্রভাবে উৎপন্ন একটি নতুন রাশির দ্বারাই পাওয়া সম্ভব, একেই ভরবেগ (বিজ্ঞানী নিউটনের ভাষায় গতির পরিমাণ) বলা হয়।
বলের পরিমাপ সম্পর্কিত নিউটনের দ্বিতীয় গতিসূত্রটি বিবৃত করো। এই সূত্র থেকে কীভাবে বলের পরিমাপ করা যায় তা ব্যাখ্যা করো।
অথবা, বস্তুর ভরবেগ পরিবর্তনের সঙ্গে বলের সম্পর্ক কী?
নিউটনের দ্বিতীয় গতিসূত্র – বস্তুর ভরবেগ পরিবর্তনের হার বস্তুর উপর প্রযুক্ত বলের সমানুপাতিক এবং বল যেদিকে প্রযুক্ত হয়, ভরবেগের পরিবর্তনও সেই দিকে ঘটে।
দ্বিতীয় গতিসূত্র থেকে বলের পরিমাপ – ধরা যাক, m ভরসম্পন্ন কোনো বস্তুর উপর t সময় ধরে F বল ক্রিয়া করার ফলে বস্তুটি সরলরেখায় গতিশীল হয় এবং তার বেগ u থেকে সুষমভাবে বৃদ্ধি পেয়ে v হয়।
দ্বিতীয় সূত্র অনুসারে, বস্তুর ভরবেগ পরিবর্তনের হার তার উপর প্রযুক্ত বলের সমানুপাতিক।
এক্ষেত্রে, t সময়ে বস্তুর ভরবেগের পরিবর্তন
= চূড়ান্ত বা অন্তিম ভরবেগ – প্রাথমিক ভরবেগ
= mv – mu
∴ ভরবেগ পরিবর্তনের হার = একক সময়ে ভরবেগের পরিবর্তন
= \( m\frac{\left(v-u\right)}t \) [যখন m ধ্রুবক]
দ্বিতীয় গতিসূত্রের বিবৃতি অনুযায়ী লেখা যায়,
\( F\propto m\frac{\left(v-u\right)}t \\\)বা, \(F\propto ma\) [\( a=\frac{\left(v-u\right)}t\) যেহেতু সংজ্ঞানুসারে, বস্তুকণার ত্বরণ]
∴ F = kma [যেখানে, k একটি অশূন্য সমানুপাতিক ধ্রুবক]
এখন F = 1, m = 1 এবং a = 1 হলে k = 1 হয়, অর্থাৎ, একক ভরের বস্তুর উপর ক্রিয়া করে একক ত্বরণ সৃষ্টি করতে যে বল সক্ষম, তাকে একক ধরলে, সমানুপাতিক ধ্রুবকের মান 1 হয়।
∴ k = 1 ব্যবহার করে পাই,
F = ma
অর্থাৎ, প্রযুক্ত বল = বস্তুকণার ভর × ত্বরণ
এই সম্পর্ক থেকে বলের পরিমাপ পাওয়া যায়।
নিউটনের দ্বিতীয় সূত্রটি থেকে কোন কোন বিষয় জানা যায়?
নিউটনের দ্বিতীয় গতিসূত্র থেকে তিনটি বিষয় জানা যায় –
- ভরবেগের ধারণা
- বলের পরিমাপ
- বলের স্বাতন্ত্র্য বা নিরপেক্ষতার নীতি
- বলের একক
বাস্তব বল ও অলীক বল কাকে বলে?
দুই বা ততোধিক বস্তুর পারস্পরিক আন্তঃক্রিয়ার ফলে উদ্ভুত বলকে বাস্তব বল (Real force) বলে। ক্রিয়া-প্রতিক্রিয়া নীতির সাহায্যে এই বলের অস্তিত্বের ব্যাখ্যা দেওয়া সম্ভব। জড়ত্বীয় ও অজড়ত্বীয় যে-কোনো নির্দেশতন্ত্রে এই বল ক্রিয়া করতে পারে। অন্যদিকে ত্বরিত নির্দেশতন্ত্রে নিউটনের সূত্রগুলির কার্যকারিতা বজায় রাখার উদ্দেশ্যে বাস্তব বলের ক্রিয়ার অভিমুখের বিপরীতে যে বলের অস্তিত্ব আপাত সত্য বলে বিবেচনা করতে হয়, তাকে অলীক বল (Pseudo force) বলে। শুধুমাত্র অজড়ত্বীয় নির্দেশতন্ত্রেই এই বলের ধারণা কার্যকর হয়।
নিউটনের দ্বিতীয় গতিসূত্রকে কয়টি উপায়ে প্রকাশ করা যায়?
নিউটনের দ্বিতীয় গতিসূত্রকে দুটি ভিন্ন উপায়ে ভিন্ন গাণিতিক চেহারায় প্রকাশ করা যায় –
- ধ্রুবক ভরের ক্ষেত্রে,
- পরিবর্তনশীল ভরের ক্ষেত্রে।
বাস্তব উদাহরণের সাহায্যে প্রত্যেক ক্ষেত্রে নিউটনের গতিসূত্রকে কীভাবে প্রকাশ করা যায় তা আলোচনা করো এবং তাদের তাৎপর্য ব্যাখ্যা করো।
ধ্রুবক ভরের বস্তুর ক্ষেত্রে নিউটনের গতিসূত্র – সসীম মানবিশিষ্ট, ছোটো-বড়ো বিভিন্ন ভরের বস্তুর উপর পরীক্ষানিরীক্ষা করে নিউটন দুটি গুরুত্বপূর্ণ সিদ্ধান্তে পৌঁছোন।
- বিভিন্ন ভরের বস্তুতে একই পরিমাণ ত্বরণ সৃষ্টি করতে প্রয়োজনীয় বলের মান তাদের ভরের সমানুপাতিক অর্থাৎ, F ∝ m [যখন a ধ্রুবক]।
- |একটি নির্দিষ্ট ভরের ক্ষেত্রে বস্তুর উপর প্রযুক্ত বল বস্তুতে উৎপন্ন ত্বরণের সমানুপাতিক অর্থাৎ, F ∝ a [যখন m ধ্রুবক]
দুটি সমীকরণকে একত্রিত করে পাওয়া যায় F ∝ ma [যখন m ও a উভয়েই পরিবর্তনীয়]
বা, F = kma [k → সমানুপাতিক ধ্রুবক]
k -এর মান 1 বিবেচনা করে পাওয়া যায় F = ma।
এটিই ধ্রুবক ভরসম্পন্ন বস্তুর ক্ষেত্রে দ্বিতীয় সূত্রের গাণিতিক রূপ।
পরিবর্তনশীল ভরের ক্ষেত্রে নিউটনের গতিসূত্র – ধরা যাক, p ভরবেগসম্পন্ন কোনো গতিশীল বস্তুর ভরবেগ অতি ক্ষুদ্র ∆t সময় অবকাশে ∆p পরিমাণ পরিবর্তিত হল।
এক্ষেত্রে ভর পরিবর্তনশীল হওয়ায় সম্পর্কটিকে ∆p = m∆v আকারে লেখা যায় না। কারণ – ∆p = m∆v সম্পর্কটি শুধুমাত্র আলোর বেগের তুলনায় উপেক্ষণীয় বেগসম্পন্ন বস্তুর জন্যই প্রযোজ্য।
সুতরাং, বস্তুর ভরবেগ পরিবর্তনের হার \( \frac{\Delta p}{\Delta t}=\frac{\Delta\left(mv\right)}{\Delta t} \) সম্পর্ক দ্বারা নির্দেশিত হয়।
লক্ষণীয় যে, ∆p = ∆(mv) সম্পর্কটি শর্তনিরপেক্ষভাবে ছোটো, বড়ো যে-কোনো মানের বেগের জন্যই সত্য। m ধ্রুবক হলে
বা, \( \frac{\Delta p}{\Delta t}=\frac{m\Delta t}{\Delta t} \)
বা, \( \frac{\Delta p}{\Delta t}=F=ma \) চেহারায় পরিবর্তিত হয়।
পরিবর্তনশীল ভর বা বেগের ক্ষেত্রে, নিউটনের দ্বিতীয় গতিসূত্রের সাধারণ রূপ \( F=\frac{\Delta\left(mv\right)}{\Delta t} \)
উদাহরণ – ধ্রুবক ভরসম্পন্ন বস্তু ভর নির্দিষ্ট এমন যে-কোনো পার্থিব বস্তু যেমন – গতিশীল গাড়ি, চলমান ফুটবল ইত্যাদির ক্ষেত্রে প্রযুক্ত বলের পরিমাপ F = ma সম্পর্কের সাহায্যে পাওয়া যায়।
পরিবর্তনশীল ভরসম্পন্ন বস্তু – বেগ স্থির থেকে ভর পরিবর্তিত হলে (কয়লা বা বালি ভরতি হচ্ছে এমন ওয়াগান, পতনশীল বৃষ্টি বা শিশিরের ফোঁটা, ছিদ্র থেকে জল নির্গত হচ্ছে এমন জলপূর্ণ (বোতল) অথবা ভর ও বেগ দুই-ই পরিবর্তন হচ্ছে এমন বস্তুর (যেমন – রকেটের গতি) গতি বর্ণনায় \( F=\frac{\Delta p}{\Delta t} \) সম্পর্কটি প্রয়োগ করতে হয়।
তাৎপর্য – F = ma সম্পর্কটি নিউটনের দ্বিতীয় গতিসূত্রকে একটি বিশেষ দৃষ্টিকোণ থেকে ব্যাখ্যা করে। যেখানে বলকে কারণ এবং গতির পরিবর্তন বা ত্বরণকে তার ফল হিসেবে বর্ণনা করা হয়। এক্ষেত্রে ভরবেগের ধারণা ব্যবহারের প্রয়োজন হয় না।
পরিবর্তনশীল ভর বা পরিবর্তনশীল ভর ও বেগ দুইয়েরই ক্ষেত্রে ভরবেগের ধারণা ছাড়া নিউটনের দ্বিতীয় সূত্রকে বিবৃত করা সম্ভব নয় এবং বিবৃতিটি এক্ষেত্রে একটি সর্বজনীন চেহারায় প্রকাশযোগ্য হয়। তবে দুটি ক্ষেত্রেই দৈনন্দিন অভিজ্ঞতা এবং প্রয়োগজনিত সাফল্যের বিচারে F = ma বা \( F=\frac{\Delta p}{\Delta t} \) দুটি সম্পর্ককেই স্বীকার্যের সমতুল্য বলে ভাবা যায়।
ভর ধ্রুবক না থাকলে ভরবেগের পরিবর্তন বেগ স্থির থেকে শুধুমাত্র ভরের পরিবর্তনের জন্য বা ভর ও বেগ উভয়েরই পরিবর্তনের জন্য ঘটতে পারে। সেক্ষেত্রে কলনবিদ্যার (Calculus) সাহায্য নিয়ে কী দেখানো যায়?
ভর ধ্রুবক না থাকলে ভরবেগের পরিবর্তন বেগ স্থির থেকে শুধুমাত্র ভরের পরিবর্তনের জন্য বা ভর ও বেগ উভয়েরই পরিবর্তনের জন্য ঘটতে পারে। সেক্ষেত্রে কলনবিদ্যার (Calculus) সাহায্য নিয়ে দেখানো যায়, \(F=\frac{m\Delta v}{\Delta t}+v\frac{\Delta m}{\Delta t}\)।
বস্তুকণার বেগ শূন্য মাধ্যমে আলোর বেগের তুলনীয় (c = 3 × 108 m⋅s-1) হলে বস্তুর ভর আর ধ্রুবক থাকে না বরং তা বস্তুর বেগের সঙ্গে কী সম্পর্ক অনুসারে বৃদ্ধি পায়?
বস্তুকণার বেগ শূন্য মাধ্যমে আলোর বেগের তুলনীয় (c = 3 × 108 m⋅s-1) হলে বস্তুর ভর আর ধ্রুবক থাকে না বরং তা বস্তুর বেগের সঙ্গে \(m=\frac{m_0}{\sqrt{1-{\displaystyle\frac{v^2}{c^2}}}}\) সম্পর্ক অনুসারে বৃদ্ধি পায়। যেখানে m0 হল স্থির অবস্থায় বস্তুর ভর (Rest mass)।
F = ma সম্পর্কটি ব্যবহার করে কীভাবে বস্তুর সহজাত ধর্ম হিসেবে ভরের ধারণা পাওয়া যায়?
বস্তুর সহজাত ধর্ম হিসেবে ভরের ধারণা – বল = ভর × ত্বরণ সম্পর্কটি বস্তুর সহজাত ধর্মরূপে ভরকে বর্ণনা করে যাকে জড়জনিত বাধার সূচক বলে ভাবা যায়।
একটি নির্দিষ্ট বস্তুর উপর ভিন্ন ভিন্ন মানের বল এবং সেই বলের ক্রিয়ায় উৎপন্ন ত্বরণের মানের অনুপাত নির্ণয় করে পাওয়া যায় যে, প্রত্যেক ক্ষেত্রেই অনুপাতটির মান ধ্রুবক থাকছে। এই অনুপাতটি বস্তুর ভর, যা জড়তা বা জাড্যের পরিমাপ।
বলের মাত্রীয় সংকেত লেখো। বল পরিমাপের প্রচলিত একক কটি ও কী কী?
বলের মাত্রীয় সংকেত [F] = [ma] = [MLT-2]।
বল পরিমাপের প্রচলিত একক দুটি। সেগুলি হল –
- পরম একক ও
- অভিকর্ষীয় একক।
নিউটনের দ্বিতীয় গতিসূত্র থেকে একক বলের সংজ্ঞা দাও।
নিউটনের দ্বিতীয় গতিসূত্রানুযায়ী, F = ma। এখন m = 1, a = 1 হলে F = 1 হবে, অর্থাৎ, একক ভরের কোনো বস্তুর ওপর যে পরিমাণ বল প্রযুক্ত হলে বস্তুটিতে একক ত্বরণ উৎপন্ন হয়, তাকে একক বল বলে।
বলের পরম একক কাকে বলে? CGS ও SI -তে বলের পরম একক লেখো ও তাদের সংজ্ঞা দাও। তাদের মধ্যে সম্পর্ক প্রতিষ্ঠা করো।
একক ভরের বস্তুর উপর যে বল ক্রিয়া করে একক ত্বরণ সৃষ্টি করে, তাকে বলের পরম একক বলে।
CGS ও SI -তে বলের পরম একক দুটি হল ডাইন ও নিউটন।
ডাইন (dyne) – 1 গ্রাম ভরের বস্তুর উপর ক্রিয়া করে যে বল 1 সেমি/সে2 ত্বরণ সৃষ্টি করে, তাকে 1 ডাইন বলে।
নিউটন (newton) – 1 কিগ্রা ভরের বস্তুর উপর ক্রিয়া করে যে বল 1 মি/সে2 ত্বরণ সৃষ্টি করে, তাকে 1 নিউটন বলে।
সম্পর্ক – 1 নিউটন (N) = 1 kg × 1 m/s2
= (1000 × 100) gm-cm/s2 ।
অর্থাৎ, 1 N = 105 ডাইন।
CGS ও SI -তে বলের অভিকর্ষীয় একক দুটির সংজ্ঞা লেখো। সম্পর্ক নির্ণয় করো-
(a) কিগ্রা-ভার ও নিউটন;
(b) গ্রাম-ভার ও ডাইন।
CGS ও SI -তে বলের অভিকর্ষীয় একক দুটি হল গ্রাম-ভার (g-f) ও কিলোগ্রাম-ভার (kg-f)।
গ্রাম-ভার – 1 গ্রাম ভরের কোনো বস্তুকে পৃথিবী নিজ কেন্দ্র অভিমুখে যে বলে আকর্ষণ করে, তাকে 1 গ্রাম-ভার (g-f) বলে।
গ্রাম-ভার ও ডাইনের মাধ্য সম্পর্ক –
1 g-f = 1g × g = 981 dyn [∵ g = 981 cm/s2]
কিগ্রা-ভার – 1 কিগ্রা ভরের কোনো বস্তুকে পৃথিবী নিজ কেন্দ্র অভিমুখে যে বলে আকর্ষণ করে, তাকে 1 কিগ্রা-ভার বা 1 কিলোগ্রাম-ভার (kg-f) বলে।
কিগ্রা-ভার ও নিউটনের মধ্যে সম্পর্ক –
1 kg-f = 1 kg × g = 9.8 N [ ∵ g = 9.8 m/s2]
বলের সঙ্গে ত্বরণের পরিবর্তন, যখন ভর স্থির – লেখচিত্র অঙ্কন করো।
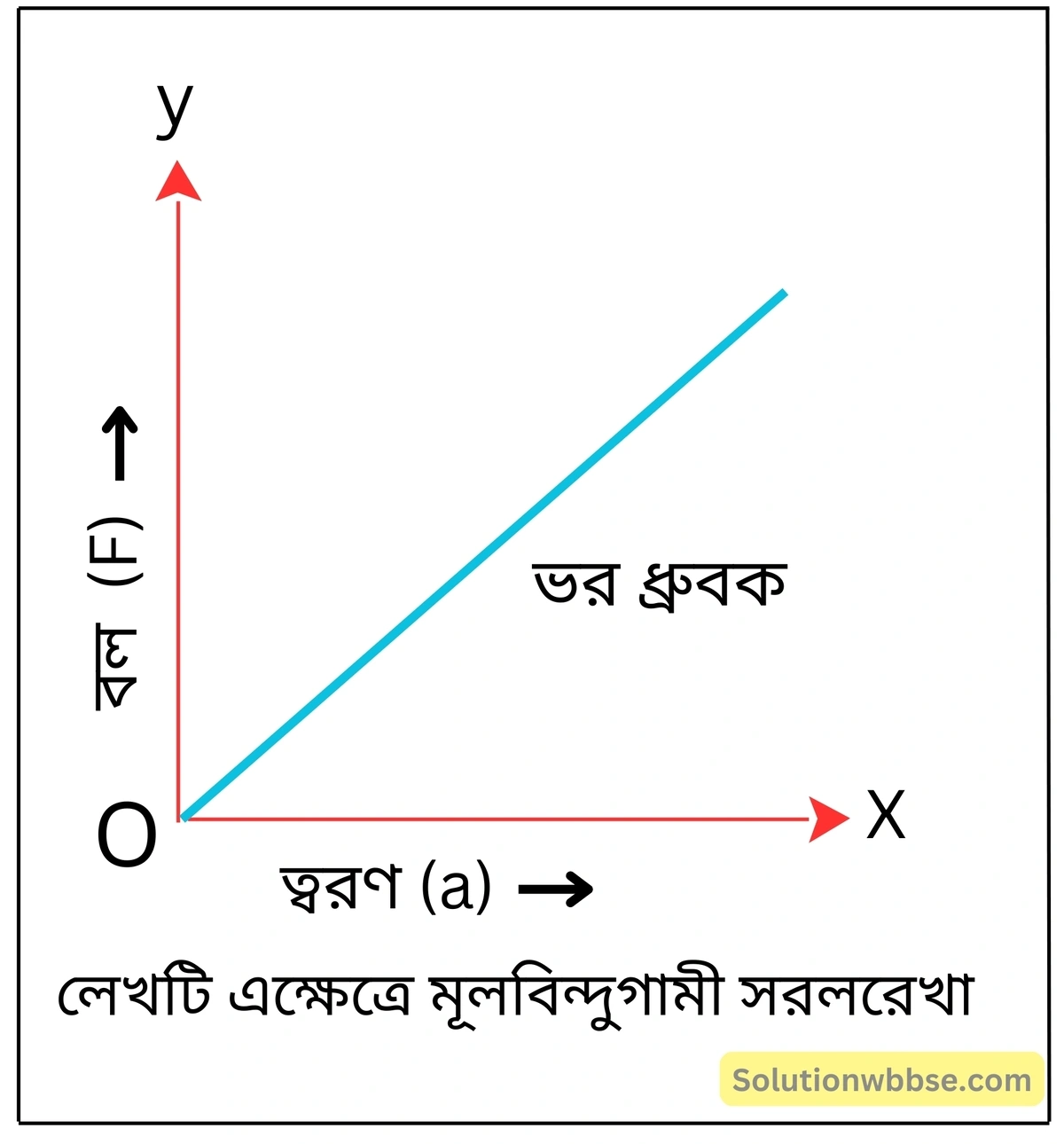
ভরের সঙ্গে বলের পরিবর্তন, যখন ত্বরণ ধ্রুবক – লেখচিত্র অঙ্কন করো।
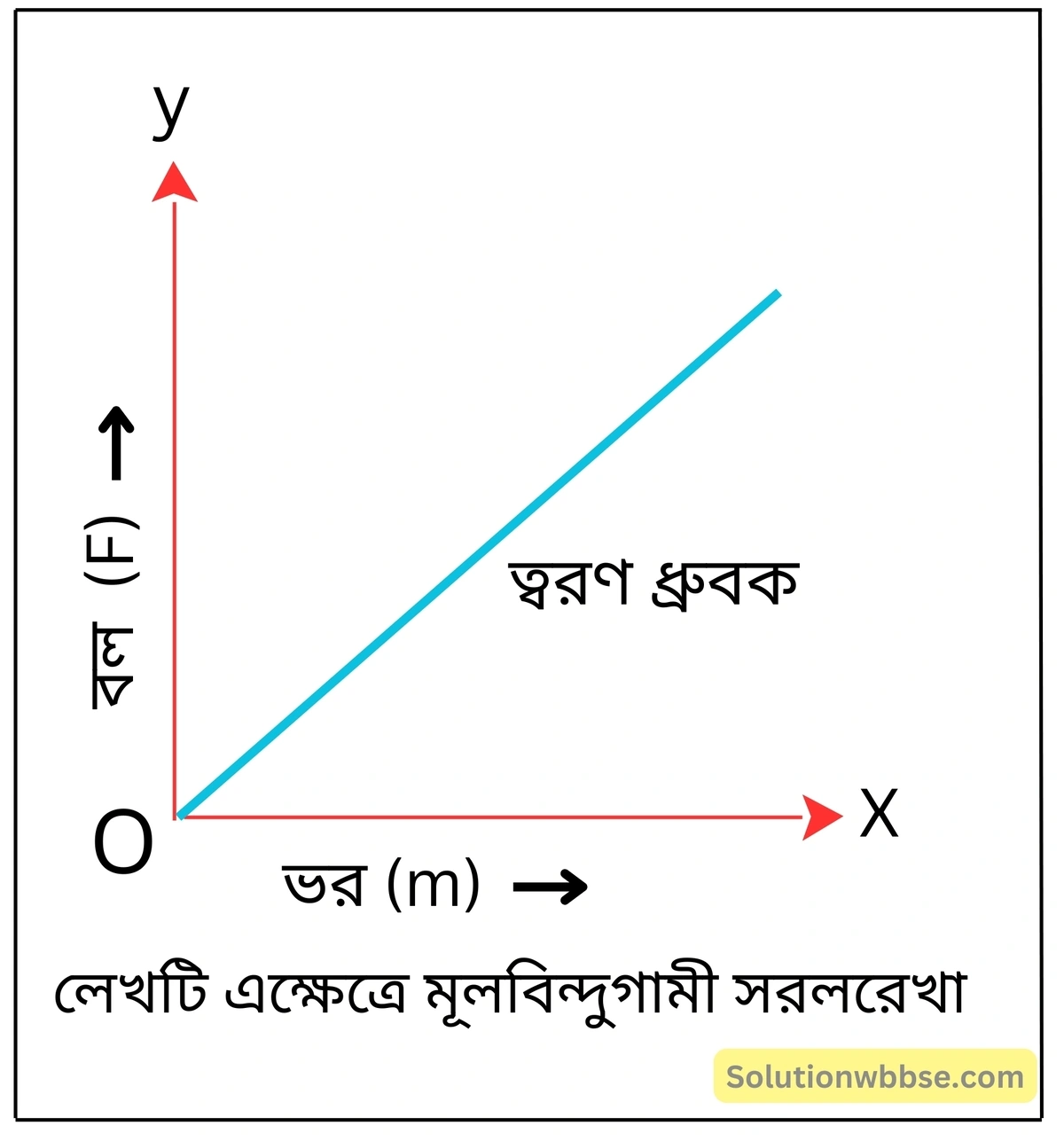
ভরের সঙ্গে ত্বরণের পরিবর্তন, যখন বল স্থির – লেখচিত্র অঙ্কন করো।
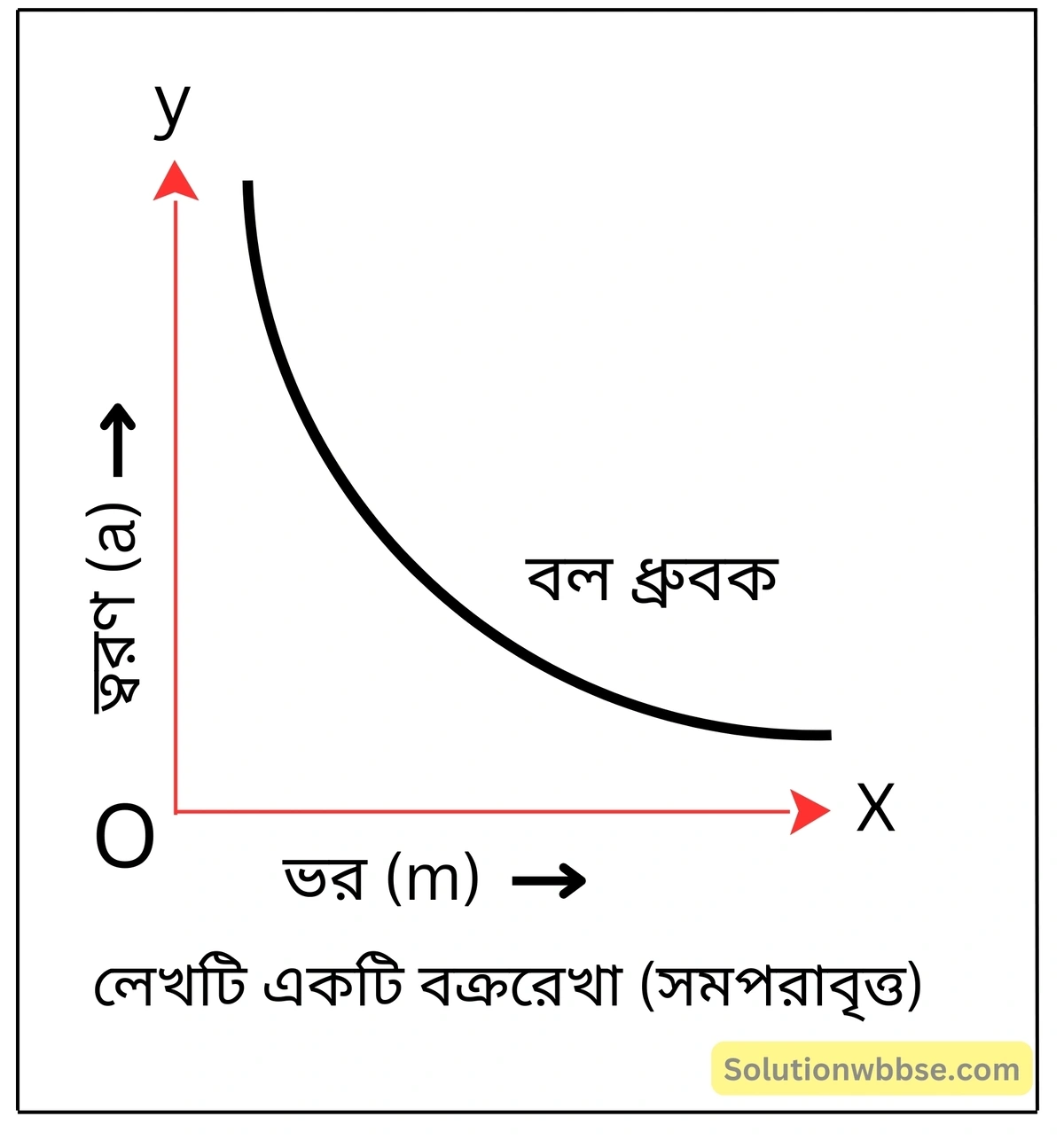
জড়ত্বীয় ভর কী? এর বৈশিষ্ট্যগুলি লেখো।
জড়স্বীয় ভর (Inertial mass) – কোনো বস্তুর উপর প্রযুক্ত বল ও ওই বস্তুতে সৃষ্ট ত্বরণের পরিমাণের অনুপাত সর্বদা একটি ধ্রুবক রাশি হয়। এই ধ্রুবককে বস্তুর জড়ত্বীয় ভর (mi) বলে।
∴
বৈশিষ্ট্য –
- জড়ত্বীয় ভর রৈখিক গতিতে সর্বদাই বস্তুর জাড্য বা জড়তার পরিমাপ দেয়।
- জড়ত্বীয় তুলা (Inertial balance) নামক বিশেষ ব্যবস্থা দ্বারা এই ভর মাপা যায়।
- জড়ত্বীয় ভরের মান সর্বদাই বস্তুর অভিকর্ষীয় ভরের সমান হয়ে থাকে।
- জড়ত্বীয় ভর বস্তুমধ্যস্থ পদার্থের পরিমাণের সঙ্গে সমানুপাতিক হয়।
- এর মান বস্তুর আকৃতি, আয়তন বা ভৌত অবস্থা, বাহ্যিক প্রভাব যেমন – উষ্ণতা, তড়িৎক্ষেত্র ইত্যাদি নিরপেক্ষ হয়।
বলের নিরপেক্ষতা নীতি কী?
বলের ‘নিরপেক্ষতা নীতি’ বা ‘প্রাকৃতিক স্বাধীনতা নীতি’ (Law of physical independence of force) – যে-কোনো অভিমুখে ক্রিয়াশীল বলকে সর্বদাই পরস্পর লম্ব অভিমুখে সক্রিয় দুটি বলের সমষ্টি বলে ভাবা যায়। এদের বলা হয় বলটির অনুভূমিক ও উল্লম্ব উপাংশ। এই দুটি উপাংশ সর্বদাই যুগপৎ পরস্পর নিরপেক্ষভাবে ক্রিয়া করে। যে-কোনো একটির মানের পরিবর্তনে ওদের লব্ধির মানের পরিবর্তন ঘটলেও অন্য উপাংশটি কোনোভাবেই প্রভাবিত হয় না। এই ধর্মটিকে বলা হয় বলের নিরপেক্ষতা নীতি। প্রকৃতপক্ষে এটি যে-কোনো ভেক্টরের বৈশিষ্ট্য।
বোধমূলক প্রশ্নোত্তর
নিউটনের দ্বিতীয় গতিসূত্র থেকে কীভাবে প্রথম গতিসূত্র পাওয়া যায়?
নিউটনের দ্বিতীয় গতিসূত্র অনুযায়ী, বল = ভর × ত্বরণ
অর্থাৎ, F = ma
বা, \( F=\frac{m\left(v-u\right)}t \) যেখানে, v = অন্তিম গতিবেগ, u = প্রাথমিক গতিবেগ।
যদি বাইরে থেকে বস্তুর ওপর কোনো বল ক্রিয়া না করে, তবে F = 0।
∴ \( \frac{m\left(v-u\right)}t=0 \)
বা, v – u = 0 (∵ m ≠ 0, t ≠ 0)
বা, v = u
অর্থাৎ, বস্তুটির বেগ পরিবর্তিত হবে না।
সুতরাং, বাইরে থেকে কোনো বল প্রযুক্ত না হলে বস্তুটি সমবেগে সরলরেখা বরাবর চলতে থাকবে।
আবার, u = 0 হলে v = 0 অর্থাৎ, স্থির বস্তু চিরকাল স্থির থাকবে।
এটিই নিউটনের প্রথম গতিসূত্র।
কেন নিউটনের দ্বিতীয় সূত্রটি প্রযোজ্য করার আগে প্রথম সূত্রের প্রযোজ্যতা নিশ্চিত করা জরুরি, এবং প্রথম সূত্রকে অনুমান করে প্রমাণের প্রয়াস কেন যৌক্তিক নয়?
নিউটনের দ্বিতীয় সূত্র F = ma আকারে কেবল জড়ত্বীয় নির্দেশতন্ত্রে প্রযোজ্য। আবার নির্দেশতন্ত্র জড়ত্বীয় হবে, যদি সেখানে প্রথম সূত্র প্রযোজ্য হয়। সুতরাং, নিউটনের দ্বিতীয় সূত্রটি ওই নির্দেশতন্ত্রে ব্যবহারের পূর্বে প্রথম সূত্র প্রযোজ্য কিনা তা নিশ্চিত করা আবশ্যক। এক্ষেত্রে প্রদত্ত যুক্তিটি কার্যত একটি Presupposition হয়ে দাঁড়ায়। প্রথম সূত্র, প্রমাণ করার পূর্বেই সেটির যথার্থ্য অনুমান করে নেওয়ার এহেন কৌশল যৌক্তিক বিচারে গ্রহণযোগ্য নয়।
ভরই বস্তুর জাড্যের পরিমাপ – ব্যাখ্যা করো।
নিউটনের দ্বিতীয় গতিসূত্র অনুসারে F = ma। এখন F ধ্রুবক হলে \(a\propto\frac1m\)।সুতরাং বলের মান ধ্রুবক হলে ত্বরণ ও বস্তুর ভর পরস্পর ব্যস্তানুপাতিক হয়। সুতরাং, ভিন্ন ভরের দুটি বস্তুর উপর একই মানের বল ক্রিয়া করলে যার ভর বেশি তার মধ্যে উৎপন্ন ত্বরণ কম হবে। ফলে বস্তুর জাড্যের পরিবর্তন (স্থিতি থেকে গতি বা গতি থেকে স্থিতি) অথবা গতির পরিবর্তন (বেগ বৃদ্ধি বা হ্রাস) ঘটানো এক্ষেত্রে বেশি কষ্টকর হয়। একারণেই বলা হয় ‘ভরই বস্তুর জাড্যের পরিমাপ’।
প্রযুক্ত বল কারণ হলে ভরবেগ হয় তার ফল – ব্যাখ্যা করো।
নিউটনের দ্বিতীয় গতিসূত্র অনুসারে বস্তুর ভরবেগ পরিবর্তনের হার ওর উপর প্রযুক্ত বলের সমানুপাতিক। যেহেতু বল প্রযুক্ত হলে তবেই বস্তুর ভরবেগ পরিবর্তন ঘটে, সুতরাং বলকে কারণ ও ভরবেগ পরিবর্তনকে তার ফল হিসেবে বিবেচনা করা যায়।
নিউটনের দ্বিতীয় গতিসূত্র কি যে-কোনো নির্দেশ- তন্ত্রেই প্রযোজ্য? – ব্যাখ্যা করো।
নিউটনের দ্বিতীয় গতিসূত্রের দুটি রূপই স্থির অথবা সমবেগে গতিশীল অর্থাৎ, জড়ত্বীয় নির্দেশতন্ত্রের ক্ষেত্রেই প্রযোজ্য। এই নির্দেশতন্ত্রে কোনো বস্তুর ভরকেন্দ্রে অপ্রতিমিত বা কার্যকর বল ক্রিয়াশীল হলেই বল = ভর × ত্বরণ সম্পর্কটি প্রয়োগ করা যায়।
একটি বাস্তব অভিজ্ঞতা বা উদাহরণ উল্লেখ করো যা থেকে ভরবেগের ধারণা পাওয়া যায়।
বন্দুক বা রাইফেল নিক্ষিপ্ত গুলির ভর কম কিন্তু গতিবেগ অনেক বেশি হওয়ায় ভরবেগ যথেষ্ট বেশি হয় ফলে আঘাতের পরিমাণও অনেক বেশি হয়ে থাকে। ফলে গুলির গতির অভিমুখে গুলিবিদ্ধ বস্তু ছিটকে পড়ে।
একটি গাড়ি অনুভূমিক রাস্তায় সমবেগে গতিশীল। গাড়িটির উপর কোনো বল কাজ করছে কি? গাড়িটির ত্বরণ কত?
গাড়িটি যদি মসৃণ অনুভূমিক রাস্তা বরাবর গতিশীল হয় তবে সমবেগযুক্ত হওয়ার কারণে ওর কোনো ত্বরণ থাকবে না। ফলে F = ma সম্পর্ক অনুযায়ী a = 0 হওয়ায় প্রযুক্ত বল (F) শূন্য হবে।
রাস্তাটি অমসৃণ হলে গাড়ির গতির বিরুদ্ধে ঘর্ষণ বল ক্রিয়া করে। সুতরাং, বেগ অপরিবর্তিত রাখতে হলে গাড়ির ইঞ্জিনকে ঘর্ষণজনিত বাধা অতিক্রম করার জন্য সমমানের বল সামনের দিকে প্রয়োগ করতে হবে। এক্ষেত্রেও গাড়ির উপর ক্রিয়াশীল লব্ধি বল শূন্য হওয়ায় ত্বরণ শূন্য হবে।
কোনো একটি বস্তুর ভরবেগের পরিবর্তন কখন ঘটতে পারে? ওই পরিবর্তনের দিক কীভাবে বোঝা যাবে?
যেহেতু বস্তুর ভরবেগ = বস্তুর ভর × বেগ। অতএব একটি বস্তুর ভরবেগের পরিবর্তন ঘটতে পারে যদি –
- বস্তুর ভর স্থির থাকে কিন্তু বস্তুর বেগের পরিবর্তন হয়,
- বস্তুর বেগ স্থির থাকে কিন্তু বস্তুর ভরের পরিবর্তন হয়,
- বস্তুর ভর ও বেগ উভয়েরই পরিবর্তন হয়।
কোনো বস্তুর ওপর বাইরে থেকে বল প্রযুক্ত হলে ওর ভরবেগের পরিবর্তন ঘটে।
প্রযুক্ত বলের অভিমুখ ও ভরবেগ পরিবর্তনের অভিমুখ নিউটনের দ্বিতীয় গতিসূত্র অনুসারে অভিন্ন হয়। তাই প্রযুক্ত বলের অভিমুখ থেকেই ভরবেগ পরিবর্তনের দিক বোঝা যাবে।
একই আয়তনবিশিষ্ট একটি নিরেট লোহার বল এবং একটি ফাঁপা বল একই বেগে গড়িয়ে যাচ্ছে। কোনটিকে থামাতে বেশি বল প্রয়োগ করতে হবে?
আয়তন ও উপাদান অভিন্ন হওয়ায় নিরেট বলটির ভর বেশি। দুটি বলই একই বেগে গতিশীল হওয়ায় নিরেট বলটির ভরবেগ বেশি। তাই প্রথম বলটিকে স্থিরাবস্থায় আনতে ভরবেগের পরিবর্তন দ্বিতীয়টির তুলনায় বেশি হয়। যেহেতু ভরবেগ পরিবর্তনের হারের সঙ্গে প্রযুক্ত বল সমানুপাতিক তাই প্রথম বলটিকে থামাতে বেশি বল প্রয়োগ করতে হবে।
একটি মালবাহী ট্রাক এবং একটি খালি ট্রাক একই দিকে চলছে। ট্রাক দুটির গঠন অবিকল এক। কোনটিকে ব্রেক কষে থামানো বেশি সহজ হবে?
মালবাহী ট্রাকের ভর বেশি হওয়ায় তার ভরবেগ খালি ট্রাক অপেক্ষা বেশি। সুতরাং, ব্রেক কষে থামাতে হলে মালবাহী ট্রাকের গতির বিরুদ্ধে বেশি বল প্রয়োগ করতে হবে। সুতরাং, খালি ট্রাকটিকে ব্রেক কষে থামানো সহজ হবে।
সমান ভরবেগবিশিষ্ট একটি হালকা ও ভারী বস্তুর মধ্যে কোনটির বেগ বেশি হয়?
ধরি, হালকা বস্তুর ভর = m1 এবং বেগ = v1
ভারী বস্তুর ভর = m2 এবং বেগ = V2
প্রশ্নানুযায়ী, বস্তু দুটির ভরবেগ সমান।
\(m_1v_1=m_2v_2\\\)বা, \(\frac{m_1}{m_2}=\frac{v_2}{v_1}\)
∵ \(\frac{m_1}{m_2}<1\), তাই \(\frac{v_2}{v_1}<1\)
∵ \(v_1>v_2\)
∴ হালকা বস্তুর বেগ তুলনামূলকভাবে বেশি হবে।
m ভরের একটি বস্তুর ওপর F মানের বল t সময় ধরে প্রযুক্ত হওয়ায় বস্তুটি ওই সময়ে x দূরত্ব অতিক্রম করে এবং বেগ অর্জন করে। দেখাও যে, \( v=\sqrt{\frac{2Fx}m} \) এবং \( t=\sqrt{\frac{2mx}F} \)
বস্তুর ভর = m; সময় = t; দূরত্ব = x; ধরি, ত্বরণ = a; প্রাথমিক বেগ (u) = 0; অন্তিম বেগ = v।
আমরা জানি, বল F = ma
বা, \( a=\frac Fm \)
আমরা জানি, \( s=ut+\frac12at^2 \)
বা, \( x=0\times t+\frac12\times\frac Fmt^2 \)
বা, \( x=\frac12\cdot\frac Fmt^2 \)
বা, \( \frac Fm=\frac{2x}{t^2} \)
বা, \( t^2=\frac{2mx}F \)
বা, \( t^2=\sqrt{\frac{2mx}F} \) (প্রমাণিত)
আমরা জানি, v = u + at
বা, \( v=0+\frac Fm\times\sqrt{\frac{2mx}F} \)
বা, \( v=\sqrt{\frac{2mxF^2}{Fm^2}} \)
∴ \( v=\sqrt{\frac{2Fx}m} \) (প্রমাণিত)
একটি চুম্বক আর কিছু লোহার টুকরোর সাহায্যে নিউটনের দ্বিতীয় গতিসূত্রের সত্যতা কীভাবে প্রমাণ করা যেতে পারে?
নিউটনের দ্বিতীয় গতিসূত্রের সত্যতা প্রমাণ করার পরীক্ষাটির জন্য কতকগুলি বিভিন্ন ভরের লোহা বা ইস্পাতের টুকরো এবং একটি চুম্বক নেওয়া হল। লোহা হল চৌম্বক পদার্থ। চুম্বক খুব সহজেই এই চৌম্বক পদার্থগুলিকে আকর্ষণ করতে পারে। চৌম্বক পদার্থ হিসেবে ধাতুর তৈরি ছোটো লেডিস ব্যাকক্লিপ, আলপিন, ছোটো-বড়ো বিভিন্ন আকারের পেরেক, স্কুড্রাইভার, 500 g -এর বাটখারা প্রভৃতি নেওয়া যেতে পারে।
প্রথমে কোনো মসৃণ অনুভূমিক সমতলের উপর চুম্বকটি রাখা হল। বেশ কিছুটা দূর থেকে আলপিনকে চুম্বকের যে-কোনো একটা মেরুর দিকে (ধরি, N মেরুর দিকে) আস্তে আস্তে সরিয়ে নিয়ে আসতে হবে। একটা সময় পর দেখা যাবে যে, আলপিনটি নিজে থেকেই চুম্বকের দিকে এগোতে শুরু করেছে। আলপিনটা যে অবস্থান থেকে নিজে থেকেই সরতে শুরু করেছে সেখানে পেনসিল দিয়ে একটা দাগ দেওয়া হল।
এরপর চুম্বকটির একবিন্দু যাতে সরণ না ঘটে সেজন্য চুম্বকটিকে একহাত দিয়ে শক্ত করে ধরে রাখা হল। তারপর এক এক করে পরপর ছোট্ট লেডিস ব্যাকক্লিপ, পেরেক, স্কুড্রাইভার, বাটখারা প্রভৃতিকে ওই দাগ দেওয়া জায়গায় রেখে পর্যবেক্ষণ করা হল। পর্যবেক্ষণ করে দেখা গেল যে, বস্তুর ভর যত বেশি নেওয়া হচ্ছে, চুম্বকের দিকে তার গতি তত কম হচ্ছে। অর্থাৎ বলা যায় যে, অপেক্ষাকৃত ভারী বস্তুর ত্বরণ কম হচ্ছে। কিন্তু চুম্বকের আকর্ষণ ক্ষমতা নির্দিষ্ট হওয়ায় চুম্বকটি সমান দূরত্বে রাখা ভারী বা হালকা প্রত্যেক বস্তুর উপর সমান বল প্রয়োগ করছে। কিন্তু বিভিন্ন বস্তুর ভর ভিন্ন ভিন্ন হওয়ার দরুন ওদের ত্বরণ বিভিন্ন হয়েছে। অর্থাৎ, ভরই হল বস্তুর জড়তা বা জাড্যের পরিমাপক।
সুতরাং, পরীক্ষাটি থেকে আমরা পেলাম,
প্রযুক্ত বল = ভর × ত্বরণ।
উপরিউক্ত সমীকরণটি হল নিউটনের দ্বিতীয় গতিসূত্রের গাণিতিক রূপ (স্থির ভরের বস্তুর ক্ষেত্রে)।
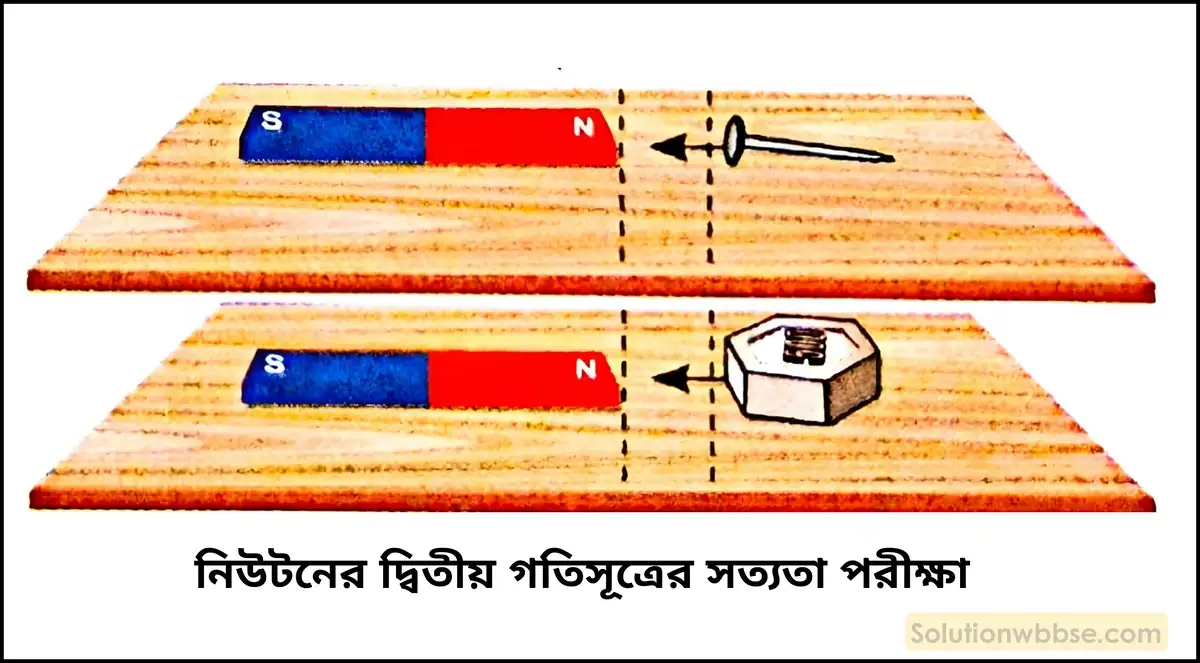
গাণিতিক প্রশ্নাবলি
প্রয়োজনীয় সূত্রাবলি
ভরবেগ = ভর × বেগ।
ভরবেগের পরিবর্তন = mv – mu
ভরবেগ পরিবর্তনের হার = বল = \(\frac{m\left(v-u\right)}t\)
বল (F) = বস্তুর ভর (m) × ত্বরণ (a)
একটি বস্তুর বেগ 20 cm/s এবং ভর 2 kg হলে, বস্তুটির ভরবেগ কত?
বস্তুর ভর = 2 kg এবং বেগ = 20 cm/s = 0.2 m/s
∴ বস্তুটির ভরবেগ = 2 × 0.2 = 0.4 kg.m.s-1
সূত্র – ভরবেগের পরিবর্তন = mv – mu
একটি 5 kg ভরের বস্তুর বেগ 20 m/s থেকে পরিবর্তিত হয়ে 10 m/s হল। বস্তুটির ভরবেগের পরিবর্তন নির্ণয় করো।
বস্তুটির প্রাথমিক ভরবেগ = ভর × প্রাথমিক বেগ
= 5 × 20 kg-m/s
= 100 kg-m/s
বস্তুটির অন্তিম ভরবেগ = ভর × অন্তিম বেগ
= 5 × 10 kg-m/s
= 50 kg-m/s
∴ ভরবেগের পরিবর্তন = (অন্তিম ভরবেগ – প্রাথমিক ভরবেগ)
= (50 – 100) kg-m/s
= – 50 kg-m/s
সুতরাং, বস্তুটির ভরবেগ 50 kg-m/s হ্রাস পেয়েছে।
2 kg ভরের একটি বস্তু 10 m/s বেগে চলছে। কত বল প্রয়োগে করলে 5s পর বস্তুর বেগ 25 m/s হবে?
এখানে m = 2 kg, u = 10 m/s, v = 25 m/s, t = 5 s
প্রযুক্ত বল \(\left(p\right)=\frac{m\left(v-u\right)}t\)
বা, প্রযুক্ত বল \(\left(p\right)=\frac{2\left(25-10\right)}5N\)
বা, প্রযুক্ত বল (P) = 6 N
একটি স্থির বস্তুর ওপর 200 N বল 20 s প্রয়োগ করায় বস্তুটির বেগ হয় 40 m/s। বস্তুর ভর কত?
প্রযুক্ত বল, F = 200 N, প্রাথমিক বেগ u = 0, অন্তিম বেগ, v = 40 m/s, সময় t = 20 s।
ধরা যাক, বস্তুর ভর = m
∴ \(\left(p\right)=\frac{m\left(v-u\right)}t\)
বা, \(200=\frac{m\left(40-0\right)}{20}\)
বা, m = 100 kg।
∴ বস্তুর ভর 100 kg।
একটি মেশিনগান থেকে প্রতি সেকেন্ডে n সংখ্যক বুলেট নির্গত হয়। প্রতিটি বুলেটের ভর m kg এবং এর বেগ v m/s হলে মেশিনগানের ওপর প্রযুক্ত বল (N এককে) কত হবে?
একটি বুলেটের ভরবেগ = mv
∴ nটি বুলেটের ভরবেগ = mnv
∴ প্রযুক্ত বল = ভরবেগের পরিবর্তনের হার
বা, প্রযুক্ত বল = \(\frac{mnv-0}1\) [∵ বুলেটের প্রাথমিক বেগ= 0 এবং সময় t = 1 s]
বা, প্রযুক্ত বল = mnv
প্রতিটি বুলেটের ভর m kg এবং এর বেগ v m/s হলে মেশিনগানের ওপর প্রযুক্ত বল (N এককে) mnv হবে।
3 kg ভরের একটি বস্তুতে 5 m/s2 ত্বরণ সৃষ্টি করতে না 4 kg ভরের বস্তুতে 5 m/s2 ত্বরণ সৃষ্টি করতে বেশি বল প্রয়োজন হবে? যুক্তি দাও।
প্রথম ক্ষেত্রে, বস্তুর ভর (m1) = 3 kg, বস্তুতে সৃষ্ট ত্বরণ (a1) = 5 m/s2
∴ বস্তুতে প্রযুক্ত বল (F1) = 3 × 5 = 15 N
দ্বিতীয় ক্ষেত্রে, বস্তুর ভর (m2) = 4 kg
বস্তুতে সৃষ্ট ত্বরণ (a2) = 5 m/s2
∴ বস্তুতে প্রযুক্ত বল (F2) = 4 × 5 = 20 N
সুতরাং, দ্বিতীয় বস্তুতে বেশি বল প্রযুক্ত হবে।
15 kg ভরবিশিষ্ট কোনো বস্তুতে 45 N বল প্রয়োগ করলে বস্তুটির ত্বরণ কত হবে?
এখানে F = 45 N, m = 15 kg
∴ বস্তুর ত্বরণ \(\left(a\right)=\frac Fm\)
বা, বস্তুর ত্বরণ \(\left(a\right)=\frac{45}{15}\)
বা, বস্তুর ত্বরণ \(\left(a\right)=3\) m/s2
A ও B ব্লক দুটির ভর যথাক্রমে 2 kg ও 3 kg। চিত্র অনুযায়ী একটি মসৃণ অনুভূমিক টেবিলের ওপর ব্লক দুটিকে পরস্পরের সংস্পর্শে রাখা হল। 10 N বল A ব্লকের ওপর অনুভূমিকভাবে প্রয়োগ করা হলে A ব্লক B ব্লকের ওপর কত বল প্রয়োগ করে?
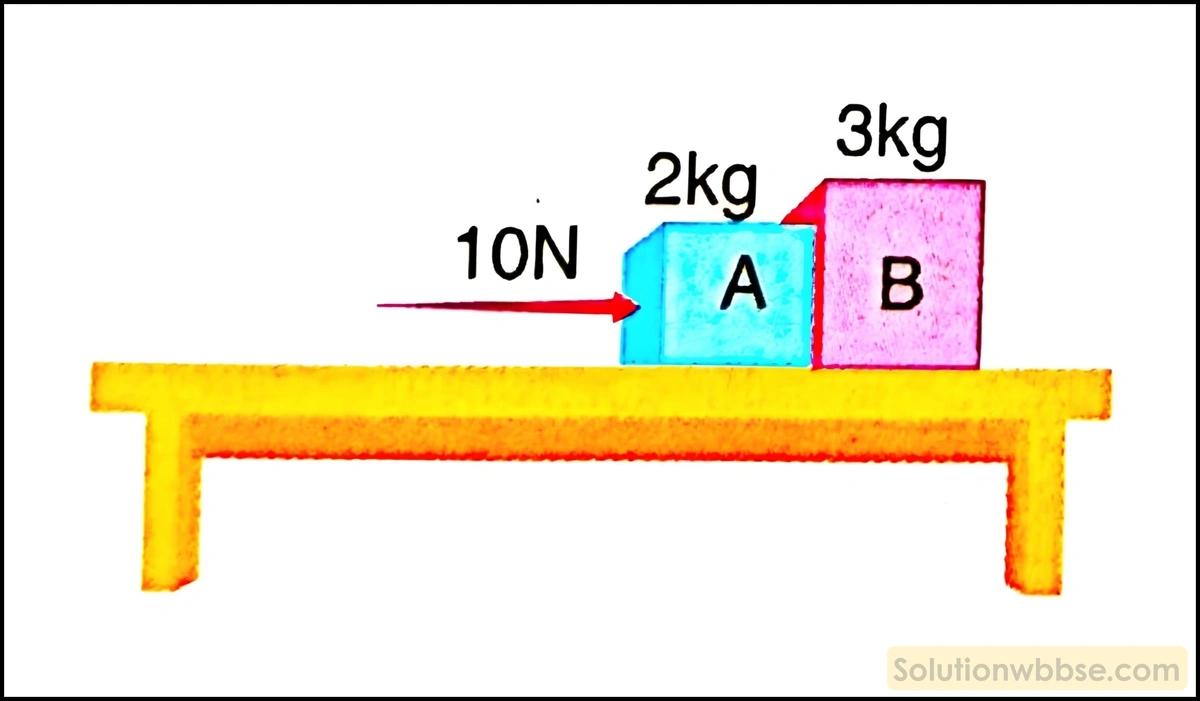
10 N বলে 2 kg ও 3 kg ভরবিশিষ্ট ব্লক দুটিকে ঠেলা হলে ব্লক দুটিতে সৃষ্ট ত্বরণ = [∵ বল = ভর × ত্বরণ]
= \(\frac{10N}{\left(2+3\right)kg}\)
= \(\frac{10}5\) m/s2
= 2 m/s2
আবার B ব্লক অর্থাৎ, 3 kg ভরবিশিষ্ট ব্লকটি এই 2 m/s2 ত্বরণসহ গতিশীল হওয়ায় তার ওপর A ব্লক অর্থাৎ, 2 kg ভরবিশিষ্ট ব্লক কর্তৃক প্রযুক্ত বল = ভর × ত্বরণ = (3 × 2) N = 6 N
50 g ভরের একটি বস্তুকণার উপর 100 N বল কিছু সময় ধরে প্রযুক্ত হওয়ায় বস্তুকণাটির বেগ ওই সময় অবকাশে 4 m/s থেকে বেড়ে 36 km/hr হল। ওই সময়ে কণার সরণ কত?
বস্তুকণার ভর (m) = 50 g = \(\frac{50}{1000}\) kg
প্রাথমিক বেগ (u) = 4 m/s
অন্তিম বেগ (v) = 36 km/hr = \(\frac{36000}{3600}\) m/s = 10 m/s
বল (F) = 100 N
আমরা জানি, F = ma,
বা, \(a=\frac Fm\)
বা, \(a=\frac{100\times1000}{50}\)
বা, \(a=2000\) m/s2
আবার সরণ = s হলে, v2 = u2 + 2aS থেকে পাই
বা, (10)2 = (4)2 + 2 × 2000 × S
বা, 100 = 16 + 4000 S
বা, 4000 S = 100 – 16
বা, 4000 S = 84
বা, \(S=\frac{84}{4000}=0.021\;m\)
∴ বস্তুকণাটির সরণ = 2.1 cm।
একটি গাড়ি 90 km/hr বেগে গতিশীল। গাড়িটি থামাবার জন্য ব্রেক প্রয়োগ করা হল। ব্রেক প্রয়োগ করার 4 s পর গাড়িটি স্থিরাবস্থায় এল। যদি চালক সমেত গাড়িটির ভর 1000 kg হয় তবে ব্রেকের সাহায্যে গাড়িটির ওপর কত বল প্রয়োগ করা হয়েছে?
গাড়ির প্রাথমিক বেগ (u) = 90 km/hr = \(\frac{90000}{3600}\) m/s = 25 m/s
সময় (t) = 4 sec,
অন্তিম বেগ (v) = 0,
ধরি, মন্দন = a
আমরা জানি, v = u – at
বা, 0 = 25 – a × 4
বা, 4a = 25
বা, a = \(\frac{25}4\)
চালকসমেত গাড়ির ভর (m) = 1000 kg
ব্রেকের সাহায্যে গাড়ির ওপর বল প্রয়োগ করা হয়েছে
= ma
= \(1000\times\frac{25}4\)
= 6250 N
∴ ব্রেকের সাহায্যে গাড়িটির ওপর 6250 N বল প্রয়োগ করা হয়েছে।
10 g ভরের একটি বুলেট 150 m/s বেগে অনুভূমিক দিকে গতিশীল হয়ে একটি স্থির কাঠের ব্লককে আঘাত করে 0.03 s -এ স্থির হল। বুলেটটি কাঠের মধ্যে কতটা দূরত্ব ভেদ করবে? কাঠের ব্লকটি বুলেটের ওপর কতটা বল প্রয়োগ করবে?
বুলেটের ভর (m) = 10 g = \(\frac{10}{1000}\) kg = 0.01 kg
বুলেটের প্রাথমিক বেগ (u) = 150 m/s
সময় (t) = 0.03 s,
অন্তিম বেগ (v) = 0,
ধরি, মন্দন = a,
আমরা জানি, v = u – at
বা, at = u – v
বা, \(a=\frac{u-v}t\)
বা, \(a=\frac{150-0}{0.03}\)
বা, \(a=\frac{150\times100}3\)
বা, \(a=5000\) m/s2
আবার, আমরা জানি, v2 = u2 – 2aS
বা, 2aS = u2 – v2
বা, \(S=\frac{u^2-v^2}{2a}\)
বা, \(S=\frac{\left(150\right)^2-\left(0\right)^2}{2\times5000}\)
বা, \(S=\frac{22500}{2\times5000}\)
বা, \(S=\frac94\)
বা, S = 2.25 m
∴ বুলেটটি কাঠের মধ্যে 2.25 m দূরত্ব ভেদ করবে।
∴ কাঠের ব্লকটি বুলেটের ওপর বল প্রয়োগ করবে,
= ma
= 0.01 × 5000
= 50 N
∴ কাঠের ব্লকটি বুলেটের ওপর 50 N বল প্রয়োগ করবে।
147 g ভরের একটি স্থির বস্তুর ওপর 15 gm-wt বল প্রয়োগ করা হল। বস্তুটির ত্বরণ কত? 2 sec পরে বস্তুটির বেগ কত হবে?
বস্তুর ভর (m) = 147 g,
প্রযুক্ত বল (P) = 15 gm-wt = 15 × 980 dyn
∴ বস্তুর ত্বরণ \(\left(a\right)=\frac Fm\)
বা, বস্তুর ত্বরণ \(\left(a\right)=\frac{15\times980}{147}[/latex
বা, বস্তুর ত্বরণ \(\)\left(a\right)=100\) cm/s2
2 s পরে বস্তুর বেগ v = u + at
এখানে u = 0, a = 100 cm/s2, t = 2 s
∴ v = 0 + 100 × 2
বা, v = 200 cm/s
∴ 2 sec পরে বস্তুটির বেগ 200 cm/s হবে।
10 g ভরের একটি বস্তুর ওপর একটি বল ক্রিয়া করায় 5 sec – এ বস্তুটি স্থির অবস্থা থেকে 15 cm/s বেগ লাভ করল। বস্তুটির ত্বরণ ও চরম ভরবেগ এবং বলটির মান নির্ণয় করো।
= \(\frac{15-0}5\)
= 3 cm/s2
চরম ভরবেগ = ভর × অন্তিম বেগ
= 10 × 15 g-cm/s
= 150 g-cm/s
প্রযুক্ত বল = ভর × ত্বরণ
= 10 × 3 dyn
= 30 dyn
∴ বলটির মান 30 dyn
Class 9 Physical Science – Notes for All Chapters
| Chapter Name | Tropics |
|---|---|
| পরিমাপ | পরিমাপ ও একক বিভিন্ন মাপের একক মাত্রা পরিমাপ |
| বল ও গতি | স্থিতি ও গতি গতির সমীকরণ নিউটনের প্রথম গতিসূত্র নিউটনের দ্বিতীয় গতি সূত্র নিউটনের তৃতীয় গতিসূত্র বিভিন্ন ধরনের বল রৈখিক ভরবেগ রৈখিক ভরবেগ সংরক্ষণ |
| পদার্থ : গঠন ও ধর্ম | তরল ও বায়ুর চাপ আর্কিমিডিসের নীতি পৃষ্ঠটান সান্দ্রতা বার্নোলির নীতি স্থিতিস্থাপকতা |
| পদার্থ : পরমাণুর গঠন ও পদার্থের ভৌত ও রাসায়নিক ধর্মসমূহ | পরমাণুর গঠন মোলের ধারণা দ্রবণ অ্যাসিড, ক্ষার, লবণ মিশ্রণের উপাদানের পৃথকীকরণ জল |
| শক্তির ক্রিয়া , কার্য, ক্ষমতা | শক্তির ক্রিয়া , কার্য, ক্ষমতা |
| তাপ | ক্যালোরিমিতি কার্য ও তাপের তুল্যতা লীনতাপ সম্পৃক্ত ও অসম্পৃক্ত বাষ্প জলের ব্যতিক্রান্ত প্রসারণ |
| শব্দ | শব্দের উৎস : কম্পন শব্দের বিস্তার : তরঙ্গ শব্দের কয়েকটি ধর্ম শব্দের বৈশিষ্ট্য মানুষের কান ও শব্দ শোনার কৌশল শব্দদূষণ |
আজকের আর্টিকেলে আমরা নবম শ্রেণির ভৌতবিজ্ঞান বইয়ের দ্বিতীয় অধ্যায় “বল ও গতি” এর “নিউটনের দ্বিতীয় গতিসূত্র” থেকে পরীক্ষায় আসা গুরুত্বপূর্ণ প্রশ্ন ও উত্তরগুলো আলোচনা করেছি। এই প্রশ্নোত্তরগুলো নবম শ্রেণির বার্ষিক পরীক্ষা, এমনকি চাকরি বা যেকোনো প্রতিযোগিতামূলক পরীক্ষার জন্যও উপযোগী। কারণ, এই অধ্যায়ের প্রশ্ন প্রায়ই বিভিন্ন পরীক্ষায় কমন আসে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সাহায্য করবে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন কিংবা টেলিগ্রামে যোগাযোগ করুন—আপনাদের প্রশ্নের উত্তর দিতে আমি সর্বদা প্রস্তুত।
ধন্যবাদ সবাইকে।






Leave a Comment