আজকের আর্টিকেলে আমরা নবম শ্রেণীর ভৌতবিজ্ঞান বইয়ের দ্বিতীয় অধ্যায় “বল ও গতি” এর “রৈখিক ভরবেগ” থেকে সহজ ও সংক্ষিপ্ত প্রশ্ন-উত্তর শেয়ার করবো। এই প্রশ্নগুলো নবম শ্রেণির ইউনিট টেস্ট থেকে বার্ষিক পরীক্ষা এর জন্য যেমন গুরুত্বপূর্ণ, তেমনি চাকরি বা বিভিন্ন প্রতিযোগিতার পরীক্ষাতেও কাজে লাগবে। এই অধ্যায় থেকে স্কুল পরীক্ষা থেকে শুরু করে চাকরির পরীক্ষায় প্রায়ই প্রশ্ন আসে, তাই এই প্রশ্নোত্তরগুলো সবাইকে সাহায্য করবে। প্রতিটি প্রশ্নের উত্তর সহজ ভাষায় লেখা হয়েছে, যাতে সবাই বুঝতে পারেন। পড়ার শেষে এই অধ্যায়ের মুখ্য বিষয়গুলো আপনার আয়ত্তে চলে আসবে এবং যেকোনো পরীক্ষায় আত্মবিশ্বাসের সঙ্গে লিখতে পারবেন।

জ্ঞানমূলক প্রশ্নোত্তর
রৈখিক ভরবেগ বলতে কী বোঝায়?
রৈখিক ভরবেগ (Linear momentum) – বক্র বা সরলরেখা বরাবর গতিশীল কোনো কণার ভর ও বেগের গুণফলই হল তার রৈখিক ভরবেগ। বক্র বা সরলরেখাটির যে-কোনো বিন্দুতে অঙ্কিত স্পর্শক বরাবর ওই বিন্দুতে রৈখিক ভরবেগের দিক নির্দেশিত হয়।
পরিবর্তনশীল ভরের বস্তুর ক্ষেত্রে নিউটনের দ্বিতীয় গতিসূত্র কীভাবে প্রযোজ্য হবে? এর থেকে ভরবেগের ধারণা দাও।
নিউটনের দ্বিতীয় গতিসূত্র অনুযায়ী, স্থির ভরের বস্তুর ক্ষেত্রে বল (F) = ভর (m) × ত্বরণ (a)।
এখন, ত্বরণ (a) =
∴ \(F=m\frac{\left(m-u\right)}t\)
বা, \(F=\frac{\left(mv-mu\right)}t\)
পরিবর্তনশীল বস্তুর ক্ষেত্রে যদি বস্তুটির প্রাথমিক ভর = m1 এবং অন্তিম ভর = m2 হয় তবে,
\(F=\frac{\left(m_2v-m_1u\right)}t\) [u ও v হল যথাক্রমে প্রাথমিক ও অন্তিম বেগ]
ভরবেগের ধারণা (Concept of momentum) – উপরোক্ত আলোচনা নির্দেশ করে বস্তুর ভর ও বেগের গুণফল হিসেবে প্রকাশিত একটি নতুন রাশি p -এর ধারণা বস্তুর গতীয় আচরণ বর্ণনার প্রশ্নে প্রাসঙ্গিক হয়, যার সময় সাপেক্ষে পরিবর্তনের হার কার্যত বস্তুর ওপর প্রযুক্ত বলের পরিমাপ নির্দেশ করে।
\( \Delta t\) ক্ষুদ্র সময় অবকাশে রাশিটির মানের ক্ষুদ্র পরিবর্তন, \( \Delta p\) = (m2v – m1u) হলে বস্তুর ওপর প্রযুক্ত বলের মান হয়, \( F=\frac{\Delta p}{\Delta t}\) এই রাশিটি (p) -কে বলা হয় বস্তুর ভরবেগ।
ভৌতরাশি হিসেবে রৈখিক ভরবেগের প্রয়োজনীয়তা লেখো।
মুখ্য গতি নিয়ন্ত্রক রাশি বা ‘গতির পরিমাণ’ হিসেবে ভরবেগের ধারণা অপরিহার্য হয়ে থাকে।
ভর কম হওয়া সত্ত্বেও বেগ বেশি থাকায় রাইফেল নিক্ষিপ্ত বুলেটের ভেদনশক্তি অনেক বেশি হয়। আবার অল্প বেগসহ গতিশীল হলেও ভর উচ্চমানের হওয়ায় ভারী ট্রাকের আঘাতে ক্ষয়ক্ষতির সম্ভাবনা বাড়ে। এই দুটি পরিচিত উদাহরণ থেকেই স্পষ্ট হয় যে, সংঘাতের মাধ্যমে কোনো গতিশীল বস্তু দ্বারা সৃষ্ট আঘাত এবং তার ফলে উৎপন্ন বল বস্তুর ভর ও বেগ দুটি রাশির ওপরই নির্ভর করে। তাই বস্তুর গতীয় আচরণের বর্ণনায় বা গতির পরিমাণ নির্ধারণে ভর ও বেগের সমন্বয়ে সৃষ্ট একটি নতুন রাশি ভরবেগের ধারণা প্রাসঙ্গিক হয়।
পরিবর্তনশীল ভর (যেমন – কয়লা ভরতি হওয়া অবস্থায় চলমান ওয়াগন) বা পরিবর্তনশীল ভর ও বেগযুক্ত বস্তু সংস্থায় (যেমন – রকেট) প্রযুক্ত বলের মান নির্ণয়ের ক্ষেত্রে F = ma সম্পর্কটি আদৌ কার্যকরী হয় না। এ ধরনের পরিস্থিতিতে প্রযুক্ত বলের পরিমাপ দ্বিতীয় গতিসূত্রের সাধারণ গাণিতিক রূপ \( F=\frac{\Delta p}{\Delta t} \) সম্পর্ক থেকেই পাওয়া সম্ভব। তাই ভর ধ্রুবক না থাকলে ভরবেগের ধারণা বলের পরিমাপ নির্ণয়ের ক্ষেত্রে অপরিহার্য হয়ে পড়ে।
রৈখিক ভরবেগের ধারণা ব্যবহার করে নিউটনের দ্বিতীয় গতিসূত্র বিবৃত করো। ওই বিবৃতি থেকে F = ma সূত্রটি প্রমাণ করো, যখন m ধ্রুবক।
রৈখিক ভরবেগের ধারণার ভিত্তিতে নিউটনের দ্বিতীয় গতিসূত্রের গাণিতিক রূপটি হল \( F=\frac{\Delta p}{\Delta t} \) যেখানে F প্রযুক্ত বল, \( \Delta p\) বস্তুর ভরবেগের পরিবর্তন ও \( \Delta t\) সময়ের পরিবর্তন চিহ্নিত করে।
F = ma রাশিমালা প্রতিষ্ঠা – ধরা যাক, F বাহ্যিক বল প্রযুক্ত হওয়ার ফলে m ভরসম্পন্ন (m -এর মান ধ্রুবক) একটি বস্তুর বেগ থেকে পরিবর্তিত হয়ে হয়। এই পরিবর্তন t সময়ে সংঘটিত হলে বস্তুর ভরবেগ পরিবর্তনের হার,
= \( \frac{\Delta p}{\Delta t} \)
= \(\frac{p_2-p_1}t \) [\(p_1\) ও \(p_2\) ভরবেগের প্রাথমিক ও চূড়ান্ত মান]
= \( \frac{mv-mu}t\)
= \( m\left(\frac{v-u}t\right)=ma \) [যেখানে বস্তুর ত্বরণ a = বেগ বৃদ্ধির হার = \( \frac{v-u}t \)]
∴ \( F=\frac{\Delta p}{\Delta t}=ma \)
বা, \( F=ma \)
ভরবেগ ও বলের মধ্যে সম্পর্ক কী?
অথবা, ভরবেগ পরিবর্তনের হার ও প্রযুক্ত বলের মধ্যে সম্পর্ক কী?
নিউটনের দ্বিতীয় গতিসূত্র অনুসারে বস্তুর ভরবেগ পরিবর্তনের হার ওর উপর প্রযুক্ত বলের সঙ্গে সমানুপাতিক হয়। সমানুপাতিক ধ্রুবকের মান গাণিতিক সুবিধার স্বার্থে 1 বিবেচনা করা হলে ভরবেগ পরিবর্তনের হারই বস্তুর ওপর বলের পরিমাপ হয়। ভরবেগ পরিবর্তনের অভিমুখ বলের ক্রিয়ার অভিমুখের সঙ্গে অভিন্ন হয়।
এমন কয়েকটি ক্ষেত্র উল্লেখ করো যেখানে নিউটনের দ্বিতীয় গতিসূত্রের গাণিতিক রূপ হিসেবে F = ma সম্পর্কটি প্রযোজ্য হয় না। সম্পর্কটি এক্ষেত্রে প্রাসঙ্গিক না হওয়ার কারণ কী?
F = ma সম্পর্কটির প্রাসঙ্গিকতা বজায় থাকে না এমন কতকগুলি গতির দৃষ্টান্ত হল –
- জলপূর্ণ বোতলের ছিদ্র দিয়ে জল নির্গমনরত অবস্থায় বোতলটির ঊর্ধ্ব বা নিম্নগতি,
- কয়লা ভরতি হওয়া অবস্থায় চলমান ওয়াগন বা গতিশীল বাহক বেল্ট যা বালি দ্বারা পূর্ণ করা হচ্ছে বা যার থেকে বালি নির্গত হচ্ছে তার গতি,
- রকেটের গতি,
- ঘনীভবনের ফলে ভরবৃদ্ধি হওয়া অবস্থায় শিশিরের ফোঁটার গতি ইত্যাদি।
উপরোক্ত প্রত্যেক উদাহরণের ক্ষেত্রেই বস্তু বা বস্তুসংস্থার ভর অথবা ভর ও বেগ উভয়েই পরিবর্তিত হওয়ায় F = ma সম্পর্কটি (যা শুধুমাত্র ধ্রুবক ভরের ক্ষেত্রেই সত্য) প্রযোজ্য হয় না।
পূর্বোক্ত ক্ষেত্র বা উদাহরণগুলির ক্ষেত্রে দ্বিতীয় গতিসূত্রকে ব্যবহার করতে হলে কোন্ ভৌতরাশির ধারণা অপরিহার্য হয়ে থাকে? সংশ্লিষ্ট পরিস্থিতিতে দ্বিতীয় গতিসূত্রের গাণিতিক রূপ কেমন হবে?
পূর্বোক্ত পরিস্থিতিতে দ্বিতীয় গতিসূত্রকে প্রয়োগ করতে হলে ভরবেগের ধারণা অপরিহার্য হয়ে থাকে। পরিবর্তনশীল ভর বা ভর ও বেগযুক্ত সংস্থায় নিউটনের দ্বিতীয় সূত্রের গাণিতিক রূপ – এক্ষেত্রে দ্বিতীয় গতিসূত্র তার সার্বজনীন চেহারা \( F=\frac{\Delta p}{\Delta t} \) আকারে প্রযোজ্য হয় যেখানে \( \Delta p\) ও \( \Delta t\) যথাক্রমে ভরবেগ ও সময়ের পরিবর্তন চিহ্নিত করে। যদি t সময় অবকাশে কোনো বস্তুকণার প্রাথমিক ভর m1 ও প্রাথমিক বেগ u মান থেকে যথাক্রমে m2 ও v মানে পরিবর্তিত হয় তবে, সময়ের পরিবর্তন \( \Delta t\) = (t – 0) = t।
ভরবেগের পরিবর্তন \( \left(\Delta t\right)\) = অন্তিম ভরবেগ (p2) – প্রাথমিক ভরবেগ (p1)
= m2v – m1u
∴ \( F=\frac{\Delta p}{\Delta t}=\frac{m_2v-m_1u}t \)
যদি বেগ ধ্রুবক থেকে সংস্থার ভর শুধুমাত্র পরিবর্তিত হয় তবে v = u। সেক্ষেত্রে, \( F=\frac{u\left(m_2-m_1\right)}t \)
একটি পড়ন্ত বোতল থেকে জল লিক্ করছে। এক্ষেত্রে নিউটনের দ্বিতীয় গতিসূত্র ব্যবহার করে বলের মান নির্ণয় করো।
মনে করি, একটি বোতল u গতিতে নীচে পড়ছে। সেই সময় বোতলটির ভর = m। যেহেতু বোতল থেকে জল লিক্ করছে তাই t সময় পরে তার ভর = m2 এবং বেগ v (m2 < m1)।
প্রাথমিক ভরবেগ = m1u, অন্তিম ভরবেগ = m2v
∴ ভরবেগের পরিবর্তন = m2v – m1u
∴ ভরবেগের পরিবর্তনের হার = \( \frac{m_2v-m_1u}t \)
∴ প্রযুক্ত বল (F) \( =\frac{m_2v-m_1u}t \)
একটি চলমান ওয়াগনে কয়লা ভরতি হচ্ছে। এক্ষেত্রে নিউটনের দ্বিতীয় গতিসূত্র ব্যবহার করে বলের মান নির্ণয় করো।
মনে করি, একটি চলমান ওয়াগনের বেগ = u এবং ভর m1। t সময় পরে বেগ এবং ভর m2, কারণ – ওয়াগনটি চলার সময় কয়লা ভরতি হচ্ছে। এখানে, m2 > m1।
চলার প্রাথমিক ভরবেগ = m1u, অন্তিম ভরবেগ = m2v
∴ ভরবেগের পরিবর্তন = m2v – m1u
∴ ভরবেগের পরিবর্তনের হার \( =\frac{m_2v-m_1u}t \)
∴ প্রযুক্ত বল \(\left(F\right)=\frac{m_2v-m_1u}t \)
যদি ওয়াগনটি স্থির বেগে চলে তবে \(v=u\),
∴ \( F=\frac{u(m_2-m_1)}t \)
চিত্রসহ রকেটের বর্ণনা দাও ও রকেটের ওপর ক্রিয়াশীল বল ও ত্বরণের মান হিসাব করো।
নীচের চিত্রে একটি রকেটের গঠন দেখানো হয়েছে।
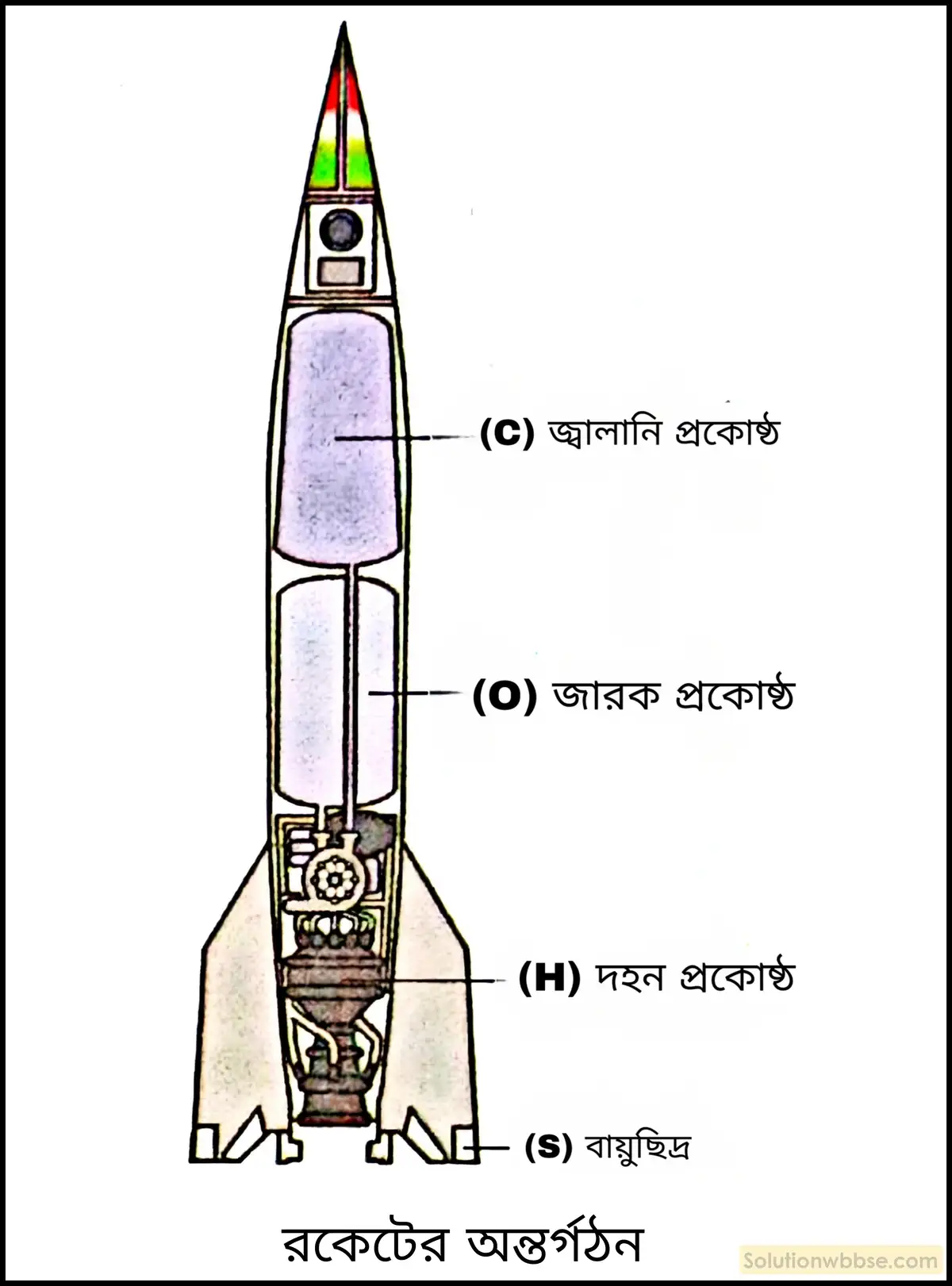
এখানে C = জ্বালানি প্রকোষ্ঠ। এই প্রকোষ্ঠে সাধারণত তরল হাইড্রোজেন, কেরোসিন ইত্যাদি জ্বালানি হিসেবে রাখা থাকে।
O = জারক প্রকোষ্ঠ। সাধারণত তরল অক্সিজেন, ওজোন, হাইড্রোজেন পারক্সাইড ইত্যাদি জারক পদার্থ হিসেবে ব্যবহৃত হয় ও এই প্রকোষ্ঠে রাখা থাকে।
H = দহন প্রকোষ্ঠ। পাম্পের সাহায্যে জ্বালানি ও জারক পদার্থকে এই প্রকোষ্ঠে নিয়ে গিয়ে জ্বালানো হয়। ফলে, সৃষ্ট গ্যাস প্রচণ্ড গতিতে রকেটের পিছনের ছিদ্র (S) দিয়ে বেরিয়ে আসে ও রকেটটি সামনের দিকে গতিশীল হয়।
বল ও ত্বরণের মান – ধরা যাক, রকেটের পিছনে নির্গত গ্যাসের বেগ = u। যেহেতু রকেটের অভ্যন্তরস্থ জ্বালানি ক্রমে পুড়ে নিঃশেষিত হতে থাকে তাই রকেটসহ জ্বালানির ভর ক্রমাগত পরিবর্তিত হতে থাকে।
ধরা যাক, t সময়ে ভর m1 থেকে পরিবর্তিত হয়ে m2 হয়।
∴ ভরের পরিবর্তন = (m1 – m2)
∴ প্রযুক্ত বল \(\left(F\right)=-u\left(\frac{m_1-m_2}t\right)\) [ঋণাত্মক কারণ গ্যাসের বেগ ও রকেটের গতির অভিমুখ পরস্পর বিপরীত]
রকেটটি a ত্বরণ লাভ করলে F = ma হয়।
∴ \( ma=-u\left(\frac{m_1-m_2}t\right) \) [m = রকেটের ভর]
∴ ত্বরণ \( \left(F\right)=-\frac um\left(\frac{m_1-m_2}t\right) \)
বোধমূলক প্রশ্নোত্তর
একটি জ্যোতিষ্ক ভূপৃষ্ঠে পড়ার আগেই ভস্মীভূত হয়ে গেল, তার ভরবেগের কী পরিণতি ঘটবে?
উল্কা বা জ্যোতিষ্কটি উচ্চবেগে পৃথিবীর বায়ুমণ্ডলে প্রবেশ করায় বায়ু কণাগুলির সঙ্গে ঘর্ষণে উৎপন্ন তাপ জ্যোতিষ্কটিকে জ্বালিয়ে দেয়। এক্ষেত্রে ওর ভরবেগ বায়ুমণ্ডলের ধূলিকণা, অন্যান্য উপাদান কণা ও দহনে উৎপন্ন গ্যাসীয় পদার্থে হস্তান্তরিত হয় এবং যে-কোনো মুহূর্তে মোট ভরবেগ সংরক্ষিত থাকে।
কোনো বস্তুর ওপর বল প্রযুক্ত না হলেও বস্তুর ভরবেগ থাকতে পারে কি?
মসৃণ তলে সমবেগে গতিশীল বস্তুর উপর কোনো বল ক্রিয়া করে না, যদিও বেগ থাকার ফলে বস্তুর ভরবেগ থাকে। সুতরাং, বল ছাড়াও ভরবেগের অস্তিত্ব থাকতে পারে।
m ভরসম্পন্ন একটি বস্তু v বেগসহ নির্দিষ্ট অভিমুখে গতিশীল। বাইরে থেকে সমভরের অপর একটি বস্তু প্রথম বস্তুটির সঙ্গে যুক্ত করা হলে বস্তুদুটি একত্রে পূর্বের এক-চতুর্থাংশ বেগসহ একই অভিমুখে গতিশীল হয়। কোন্ ক্ষেত্রে ভরবেগ বেশি হবে?
প্রথম ক্ষেত্রে বস্তুর ভরবেগ, \(p_1=mv\)
দ্বিতীয় ক্ষেত্রে সংযুক্ত বস্তুর ভরবেগ,
\(p_2=\left(m+m\right)\times\frac v4\\\)বা, \(p_2=\frac{mv}4\)
বা, \(p_2=\frac{p_1}2\)
∴ প্রথম ক্ষেত্রে ভরবেগ বেশি হবে।
একই উচ্চতা থেকে বালির উপর পড়লে কোনো ব্যক্তি যতটা আঘাত পায়, শক্ত মেঝের উপর পড়লে তার চেয়ে অনেক বেশি আঘাত পায় কেন?
যে-কোনো নির্দিষ্ট উচ্চতা থেকে কোনো ব্যক্তি বালির উপর পড়লে ব্যক্তি কিছুটা বালির মধ্যে ঢুকে গিয়ে তারপর স্থির অবস্থায় আসে অর্থাৎ, তার বেগের মান কম দ্রুততায় শূন্য হয়। ফলে ভরবেগের পরিবর্তনে কিছুটা সময় লাগে। কিন্তু একই উচ্চতা থেকে শক্ত মেঝের উপর পড়লে বেগ দ্রুত শূন্য হয়। ফলে ভরবেগের পরিবর্তন দ্রুত হয়। আবার বলের পরিমাপ করা হয় ভরবেগ পরিবর্তনের হার দ্বারা। এ কারণে প্রথম ক্ষেত্রে ব্যক্তির উপর প্রযুক্ত বাধা বল দ্বিতীয় ক্ষেত্রের তুলনায় অনেক কম হয়। তাই বালির উপর পড়লে কোনো ব্যক্তি যতটা আঘাত পায় শক্ত মেঝের উপর পড়লে তার চেয়ে অনেক বেশি আঘাত পায়।
তুমি তোমার বইখাতার ভারী ব্যাগটা সাইকেলের কেরিয়ারে বসিয়ে সমবেগে সাইকেল চালিয়ে স্কুলে যাচ্ছ। হঠাৎ ব্যাগটি কেরিয়ার থেকে পড়ে গেল।
1. এর ফলে ওই মুহূর্তে সাইকেলের গতীয় অবস্থার কী পরিবর্তন ঘটবে?
2. ব্যাগসমেত সাইকেল – এই সংস্থার কী পরিবর্তন ঘটবে?
3. এক্ষেত্রে ভরবেগের ধারণা দাও।
প্রথম ক্ষেত্রে
ব্যাগটি সাইকেল থেকে বিচ্ছিন্ন হওয়ার মুহূর্তে লক্ষ করলে দেখা যাবে যে, সাইকেলের বেগ তাৎক্ষণিকভাবে বৃদ্ধি পেয়েছে।
দ্বিতীয় ক্ষেত্রে –
সাইকেলের ভরবেগের অভিমুখ ও পিছনদিকে গতিপ্রাপ্ত ব্যাগটির ভরবেগের অভিমুখ পরস্পর বিপরীত হয়। উভয়ের ভরবেগের মান সঠিকভাবে পরিমাপ করা সম্ভব হলে দেখা যায় সামনের দিকে সাইকেলের বেগ ও সেই কারণে ভরবেগ যে পরিমাণ বৃদ্ধি পেয়েছে তার বিপরীতে ব্যাগটির ভরবেগ বৃদ্ধিও সমপরিমাণে ঘটেছে। সুতরাং ব্যাগসমেত – সাইকেল এই সংস্থার ভরবেগ ব্যাগ বিচ্ছিন্ন হওয়ার আগে ও পরে সমান বা অপরিবর্তিত থাকে।
তৃতীয় ক্ষেত্রে –
ব্যাগ বিচ্ছিন্ন হওয়ার পূর্বে সাইকেল সমবেগে গতিশীল থাকায় ওর উপর ক্রিয়াশীল লব্ধি বা কার্যকর বল শূন্য হয়। সুতরাং, ঘটনাটি নির্দেশ করে যে প্রযুক্ত বাহ্যিক বলের অনুপস্থিতিতে কোনো গতিশীল বস্তুর বা বস্তুসংস্থার ভর ও তাৎক্ষণিক বেগের গুণফল সর্বদাই ধ্রুবক বা অপরিবর্তনীয় থাকে। এই অপরিবর্তনীয় বা সংরক্ষিত রাশিটি বস্তুর গতির পরিমাণের সূচক। একেই বলা হয় বস্তুর ভরবেগ।
কোনো বস্তুর ভর বেশি হলেই ভরবেগ বেশি হয় কি? ব্যাখ্যা করো।
কোনো বস্তুর ভরবেগ ওই বস্তুর ভর ও বেগ উভয়ের ওপরই নির্ভরশীল। তাই কোনো বস্তুর ভর বেশি হলেও ভরবেগ বেশি নাও হতে পারে। যেমন – কোনো ভারী বস্তু স্থির অবস্থায় থাকলে তার ভরবেগ হয় শূন্য। আবার কোনো হালকা বস্তুর ভর কম হলেও যদি ওর বেগ থাকে, তাহলে বস্তুটির ভরবেগ থাকে। এক্ষেত্রে দ্বিতীয় (হালকা) বস্তুর ভরবেগ, প্রথম (ভারী) বস্তুর ভরবেগের তুলনায় বেশি হবে।
একটি ওয়াগান u সমবেগে মসৃণ তলের উপর দিয়ে গতিশীল। এই অবস্থায় ওয়াগানটি কয়লা দ্বারা পূর্ণ করা হতে থাকলে ওয়াগানটির উপর বল প্রযুক্ত হয় কেন?
ওয়াগানটি সমবেগে গতিশীল হলেও কয়লা ভরতি হওয়া শুরু হলে ওর ভর সময়ের সঙ্গে বৃদ্ধি পায়। সুতরাং বেগ অপরিবর্তিত থাকলেও ভর সময়ের সঙ্গে পরিবর্তিত হওয়ায় সংস্থার ভরবেগও সময়ের সঙ্গে পালটায়। যেহেতু নিউটনের দ্বিতীয় গতিসূত্র অনুসারে, বস্তু বা বস্তু সংস্থার ভরবেগ পরিবর্তনের হার ওর উপর প্রযুক্ত বলের সমানুপাতিক, তাই এক্ষেত্রে সমগতিতে চলা সত্ত্বেও ওয়াগানটির উপর বল প্রযুক্ত হতে থাকে।
একটি মালভরতি ট্রাক এবং একটি খালি ট্রাক একই বেগে গতিশীল। ট্রাক দুটির গঠন হুবহু এক। ব্রেক কষে কোনটিকে থামানো সহজ?
একটি মালভরতি ট্রাকের ভর অনুরূপ একটি খালি ট্রাকের ভরের চেয়ে বেশি হয়। দুটি ট্রাক একই বেগে গতিশীল হওয়ায় মালভরতি ট্রাকের ভরবেগ খালি ট্রাকের ভরবেগের চেয়ে বেশি হবে। এখন মালভরতি ট্রাকের ভরবেগ বেশি হওয়ায় ভরবেগের পরিবর্তন করতেও বেশি বল প্রয়োগ করতে হয়। অর্থাৎ, গতিশীল খালি ট্রাককে থামাতে যে বল প্রয়োগ করতে হয়, একই বেগে গতিশীল একটি মালভরতি ট্রাককে থামাতে তার চেয়ে বেশি বল প্রয়োগ করতে হয়। এই কারণে ব্রেক কষে খালি ট্রাকটিকে থামানো সহজতর হয়।
Class 9 Physical Science – Notes for All Chapters
| Chapter Name | Tropics |
|---|---|
| পরিমাপ | পরিমাপ ও একক বিভিন্ন মাপের একক মাত্রা পরিমাপ |
| বল ও গতি | স্থিতি ও গতি গতির সমীকরণ নিউটনের প্রথম গতিসূত্র নিউটনের দ্বিতীয় গতি সূত্র নিউটনের তৃতীয় গতিসূত্র বিভিন্ন ধরণের বল রৈখিক ভরবেগ রৈখিক ভরবেগ সংরক্ষণ |
| পদার্থ : গঠন ও ধর্ম | তরল ও বায়ুর চাপ আর্কিমিডিসের নীতি পৃষ্ঠটান সান্দ্রতা বার্নোলির নীতি স্থিতিস্থাপকতা |
| পদার্থ : পরমাণুর গঠন ও পদার্থের ভৌত ও রাসায়নিক ধর্মসমূহ | পরমাণুর গঠন মোলের ধারণা দ্রবণ অ্যাসিড, ক্ষার, লবণ মিশ্রণের উপাদানের পৃথকীকরণ জল |
| শক্তির ক্রিয়া , কার্য, ক্ষমতা | শক্তির ক্রিয়া , কার্য, ক্ষমতা |
| তাপ | ক্যালোরিমিতি কার্য ও তাপের তুল্যতা লীনতাপ সম্পৃক্ত ও অসম্পৃক্ত বাষ্প জলের ব্যতিক্রান্ত প্রসারণ |
| শব্দ | শব্দের উৎস : কম্পন শব্দের বিস্তার : তরঙ্গ শব্দের কয়েকটি ধর্ম শব্দের বৈশিষ্ট্য মানুষের কান ও শব্দ শোনার কৌশল শব্দদূষণ |
আজকের আর্টিকেলে আমরা নবম শ্রেণির ভৌতবিজ্ঞান বইয়ের দ্বিতীয় অধ্যায় “বল ও গতি” এর “রৈখিক ভরবেগ” থেকে পরীক্ষায় আসা গুরুত্বপূর্ণ প্রশ্ন ও উত্তরগুলো আলোচনা করেছি। এই প্রশ্নোত্তরগুলো নবম শ্রেণির বার্ষিক পরীক্ষা, এমনকি চাকরি বা যেকোনো প্রতিযোগিতামূলক পরীক্ষার জন্যও উপযোগী। কারণ, এই অধ্যায়ের প্রশ্ন প্রায়ই বিভিন্ন পরীক্ষায় কমন আসে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সাহায্য করবে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন কিংবা টেলিগ্রামে যোগাযোগ করতে পারেন—আপনাদের প্রশ্নের উত্তর দিতে আমি সর্বদা প্রস্তুত।
ধন্যবাদ সবাইকে।






মন্তব্য করুন