আজকের আর্টিকেলে আমরা নবম শ্রেণীর ভৌতবিজ্ঞান বইয়ের তৃতীয় অধ্যায় “পদার্থ : গঠন ও ধর্ম” এর “আর্কিমিডিসের নীতি” থেকে সহজ ও সংক্ষিপ্ত প্রশ্ন-উত্তর শেয়ার করবো। এই প্রশ্নগুলো নবম শ্রেণির ইউনিট টেস্ট থেকে বার্ষিক পরীক্ষা এর জন্য যেমন গুরুত্বপূর্ণ, তেমনি চাকরি বা বিভিন্ন প্রতিযোগিতার পরীক্ষাতেও কাজে লাগবে। এই অধ্যায় থেকে স্কুল পরীক্ষা থেকে শুরু করে চাকরির পরীক্ষায় প্রায়ই প্রশ্ন আসে, তাই এই প্রশ্নোত্তরগুলো সবাইকে সাহায্য করবে। প্রতিটি প্রশ্নের উত্তর সহজ ভাষায় লেখা হয়েছে, যাতে সবাই বুঝতে পারেন। পড়ার শেষে এই অধ্যায়ের মুখ্য বিষয়গুলো আপনার আয়ত্তে চলে আসবে এবং যেকোনো পরীক্ষায় আত্মবিশ্বাসের সঙ্গে লিখতে পারবেন।

জ্ঞানমূলক প্রশ্নোত্তর
আর্কিমিডিসের সূত্রটি উল্লেখ করো।
আর্কিমিডিসের নীতি – স্থির তরল বা গ্যাসীয় পদার্থে কোনো বস্তুকে আংশিক বা সম্পূর্ণ নিমজ্জিত করা হলে বস্তুটির কিছু পরিমাণ আপাত ওজন হ্রাস ঘটে, যা বস্তুর নিমজ্জিত অংশ দ্বারা অপসারিত তরল বা গ্যাসীয় পদার্থের ওজনের সমান।
একটি সহজ পরীক্ষা ব্যবস্থার সাহায্যে আর্কিমিডিসের নীতির সত্যতা প্রমাণ করো।
পরীক্ষার সাহায্যে আর্কিমিডিসের নীতির সত্যতা প্রমাণ –
আর্কিমিডিসের নীতির সত্যতা প্রমাণের পদ্ধতি –
- পার্শ্বনলযুক্ত বিকারের মধ্যে জল নিয়ে ওই নলের মুখ পর্যন্ত বিকারটি জলপূর্ণ করা হল।
- মুখে একটি ছোটো বিকার বা পার্শ্বনলটির গ্রাহকপাত্র রাখা হল।
- প্রমাণ ওজনের একটি বাটখারাকে একটি স্প্রিং তুলার হুক থেকে দড়ির সাহায্যে ঝুলিয়ে জলে সম্পূর্ণ নিমজ্জিত অবস্থায় বিকারের গায়ে বা তলদেশে না ঠেকিয়ে রাখা হল। এর ফলে কিছু পরিমাণ জল বেরিয়ে গ্রাহকপাত্রে জমা হল।
- এই অবস্থায় স্প্রিং তুলার সাহায্যে বাটখারাটির ওজনের পাঠ নেওয়া হল।
- গ্রাহকপাত্রে সংগৃহীত জলের ওজন পরিমাপ করা হল।
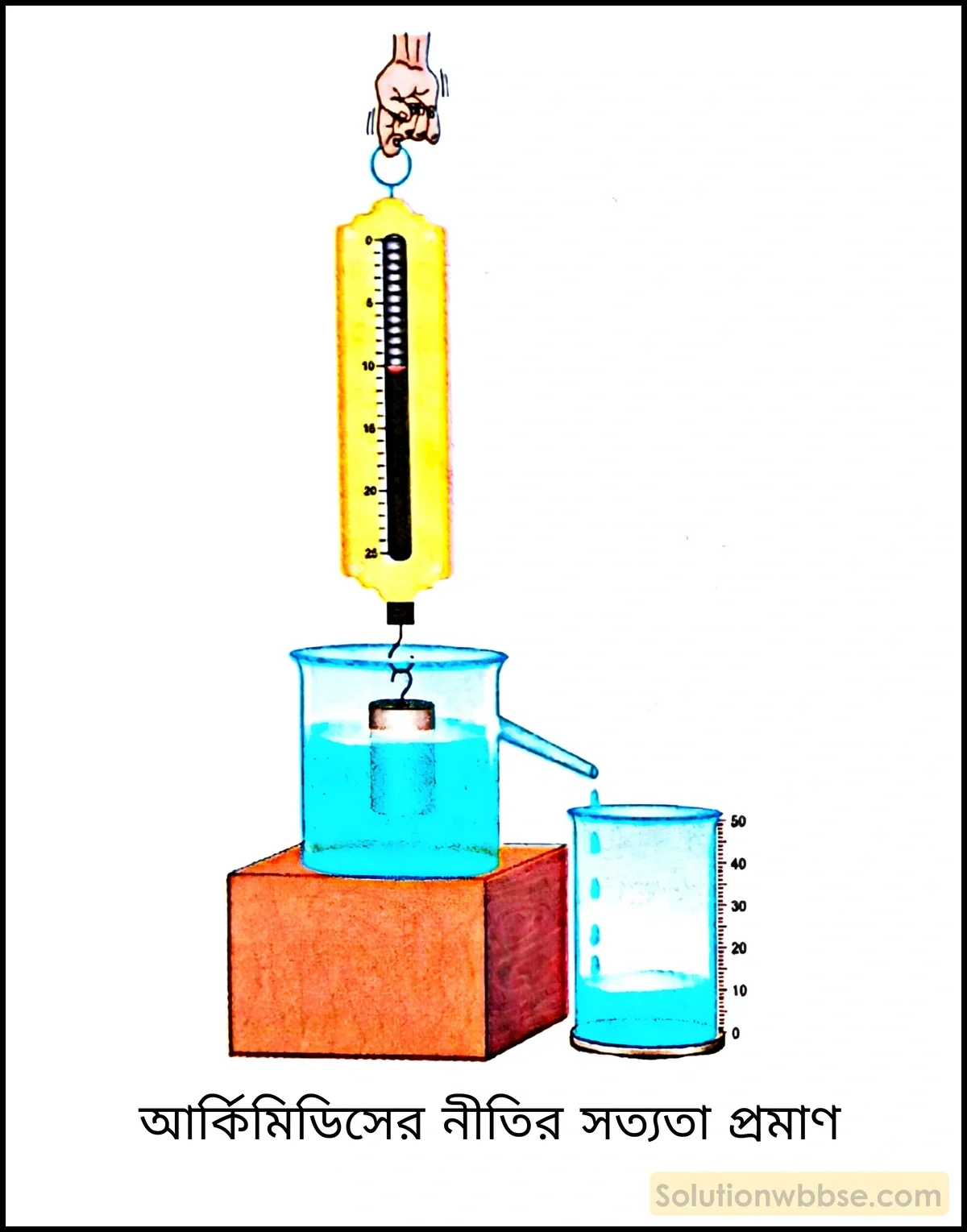
আর্কিমিডিসের নীতির সত্যতা প্রমাণের পর্যবেক্ষণ – দেখা গেল যে, জলে নিমজ্জিত অবস্থায় বাটখারার ওজন তার প্রকৃত ওজন (বায়ুতে ওজন) অপেক্ষা কিছুটা কম (মনে করি, a গ্রাম-ভার কম) এবং এই ওজন হ্রাস গ্রাহকপাত্রে সঞ্চিত হওয়া জলের ওজনের সমান। অর্থাৎ, বিকারে সংগৃহীত জলের ওজন a গ্রাম-ভার।
আর্কিমিডিসের নীতির সত্যতা প্রমাণের ব্যাখ্যা ও সিদ্ধান্ত – নিমজ্জিত অবস্থায় অপসারিত তরলের ওজনের সমান মানের বল বাটখারাটির উপর খাড়া ঊর্ধ্বমুখে ওজনের বিপরীতে, অর্থাৎ, প্লবতা বল হিসেবে কাজ করে এবং বস্তুর ওজনকে কমিয়ে দেয়। স্প্রিং তুলা থেকে প্রাপ্ত পাঠ নির্দেশ করে, তরলে নিমজ্জিত অবস্থায় বাটখারাটির ওজনের আপাত হ্রাস = বাটখারা দ্বারা অপসারিত জলের ওজন – এটিই আর্কিমিডিসের নীতির গাণিতিক রূপ।
কোন্ কোন্ শর্তে বা পরিস্থিতিতে আর্কিমিডিসের নীতিটি প্রযোজ্য হয় না?
আর্কিমিডিস নীতি প্রযোজ্য না হওয়ার শর্ত – আর্কিমিডিসের নীতিটি ওজনের ধারণার ওপর ভিত্তি করে প্রতিষ্ঠিত। যেক্ষেত্রে বস্তুর ওজন শূন্য হয়, সেরূপ পরিস্থিতিতে নীতিটি প্রয়োগ করা যায় না, যেমন –
- অবাধে পতনশীল বস্তুর ক্ষেত্রে,
- পৃথিবীর চারপাশে আবর্তনশীল কৃত্রিম উপগ্রহের অভ্যন্তরে,
- পৃথিবীর কেন্দ্রে।
আর্কিমিডিসের নীতি প্রয়োগ করে কীভাবে তরলে অদ্রাব্য কঠিন পদার্থের আয়তন ও ঘনত্ব নির্ণয় করা সম্ভব তা সংক্ষেপে আলোচনা করো।
আর্কিমিডিসের নীতির সাহায্যে কোনো কঠিন বস্তুর আয়তন ও ঘনত্ব নির্ণয় –
ধরা যাক, কোনো কঠিন বস্তুর ওজন W1 গ্রাম-ভার এবং ρ ঘনত্বের একটি তরলে সম্পূর্ণ নিমজ্জিত অবস্থায় ওই বস্তুর ওজন W2 গ্রাম-ভার। কঠিন বস্তুটি তার সমআয়তন তরল অপেক্ষা ভারী ও ওই তরলে অদ্রাব্য। আর্কিমিডিসের নীতি অনুযায়ী, বস্তুর আয়তন V ঘনসেমি হলে,
বস্তুটির আপাত ওজন হ্রাস = (W1 – W2) গ্রাম-ভার = বস্তু দ্বারা অপসারিত সমআয়তন তরলের ওজন (Vρ গ্রাম-ভার)।
যেহেতু, বস্তুটি নিজের আয়তনের সমান আয়তনের তরল অপসারণ করে, তাই Vρ = (W1 – W2)
∴ কঠিন বস্তুর আয়তন, \( V=\frac{W_1-W_2}\rho \) ঘনসেমি।
ব্যবহৃত তরলটি জল হলে, ρ = 1 গ্রাম/ঘনসেমি (CGS পদ্ধতি)।
∴ V = W1 – W2 ঘনসেমি
SI -তে জলের ঘনত্ব ρ = 1000 কিগ্রা/ঘনমি।
∴ \(V=\frac{W_1-W_2}{1000}\)
∴ বস্তুর উপাদানের ঘনত্ব (d) =
বা, \(d=\left(\frac{W_1}{W_1-W_2}\right)\times\rho\)
বস্তুটিকে জলে নিমজ্জিত করা হলে, CGS পদ্ধতিতে বস্তুর উপাদানের ঘনত্ব হয় \(d=\left(\frac{W_1}{W_1-W_2}\right)\) গ্রাম/ঘনসেমি।
SI -তে, \(d=\left(\frac{W_1}{W_1-W_2}\right)\times1000\) কিগ্রা/ঘনমি।
প্লবতার সংজ্ঞা দাও।
প্লবতা (Buoyancy) – স্থির তরল বা গ্যাসীয় পদার্থে কোনো বস্তুকে আংশিক বা সম্পূর্ণ নিমজ্জিত করলে ওই বস্তুর ওপর সংশ্লিষ্ট তরল একটি খাড়া ঊর্ধ্বমুখী বল প্রয়োগ করে, যা নিমজ্জিত বস্তুর ওজনকে আংশিক বা সম্পূর্ণ প্রতিমিত (balance) করতে চায়। তরলের দেওয়া এই খাড়া ঊর্ধ্বমুখী বলকেই প্লবতা বলে।
প্লবতার বৈশিষ্ট্যগুলি উল্লেখ করো।
প্লবতার বৈশিষ্ট্যসমূহ –
- প্লবতা বল সর্বদা ওজনের বিপরীতে অর্থাৎ, খাড়া ঊর্ধ্বাভিমুখে ক্রিয়া করে।
- প্লবতার মান বস্তু দ্বারা অপসারিত তরলের ওজনের সমান।
- তরলে নিমজ্জিত বস্তুর আয়তনের ওপর প্লবতার মান নির্ভর করে। বস্তুর নিমজ্জিত অংশের আয়তন বেশি হলে বস্তু দ্বারা অপসারিত প্রবাহীর (তরল/গ্যাস) ওজনও বেশি হয়। ফলে, প্লবতার মানও বাড়ে।
- তরলের ঘনত্ব বেশি হলে প্লবতার মানও বাড়ে, কারণ – ঘনত্ব বেশি হলে বস্তুর নিমজ্জিত অংশ দ্বারা অপসারিত প্রবাহীর ওজনও বাড়ে। ফলে, প্লবতার মানও বেড়ে যায়।
- প্লবতার মান তরলের মধ্যে নিমজ্জিত বস্তুর নিমজ্জনের গভীরতার ওপর নির্ভর করে না। স্থির তরলে বা গ্যাসে আংশিক বা সম্পূর্ণ নিমজ্জিত অবস্থায় ভাসমান কোনো বস্তুর ওজন তার ওপর ক্রিয়াশীল প্লবতা বলের সমান হয়।
বস্তুর প্রকৃত ও আপাত ওজন বলতে কী বোঝায়?
বস্তুর প্রকৃত ওজন (True weight) ও আপাত ওজন (Apparent weight) – ভূপৃষ্ঠে বায়ুমাধ্যমে (সঠিক অর্থে শূন্যস্থানে) রাখা কোনো বস্তুর ওজনের মানকে তার প্রকৃত ওজন (true weight) বলে।
জল বা অন্য কোনো তরল বা গ্যাসীয় পদার্থে আংশিক বা সম্পূর্ণ নিমজ্জিত অবস্থায় বস্তুটির ওজনের কিছু পরিমাণ আপাত হ্রাস হয়। সংশ্লিষ্ট মাধ্যমে নিমজ্জিত অবস্থায় বস্তুটির ওজনের যে মান পাওয়া যায়, তাকে বস্তুটির আপাত ওজন বলে।
প্লবতার রাশিমালা নির্ণয় করো।
প্লবতার রাশিমালা – আংশিক বা পূর্ণ নিমজ্জিত বস্তুর উপর তরল বা গ্যাস দ্বারা প্রযুক্ত ঊর্ধ্বমুখী ঘাতকেই বলা হয় ঊর্ধ্বঘাত বা প্লবতা।
ধরা যাক, একটি নিরেট আয়তাকার ঘনক লম্বভাবে কোনো তরলে পূর্ণ নিমজ্জিত অবস্থায় আছে। ঘনকটির AB ও CD প্রান্ত দুটি তরলের মুক্ত তলের সঙ্গে সমান্তরাল এবং তারা যথাক্রমে h1 ও h2 গভীরতায় অবস্থান করে।
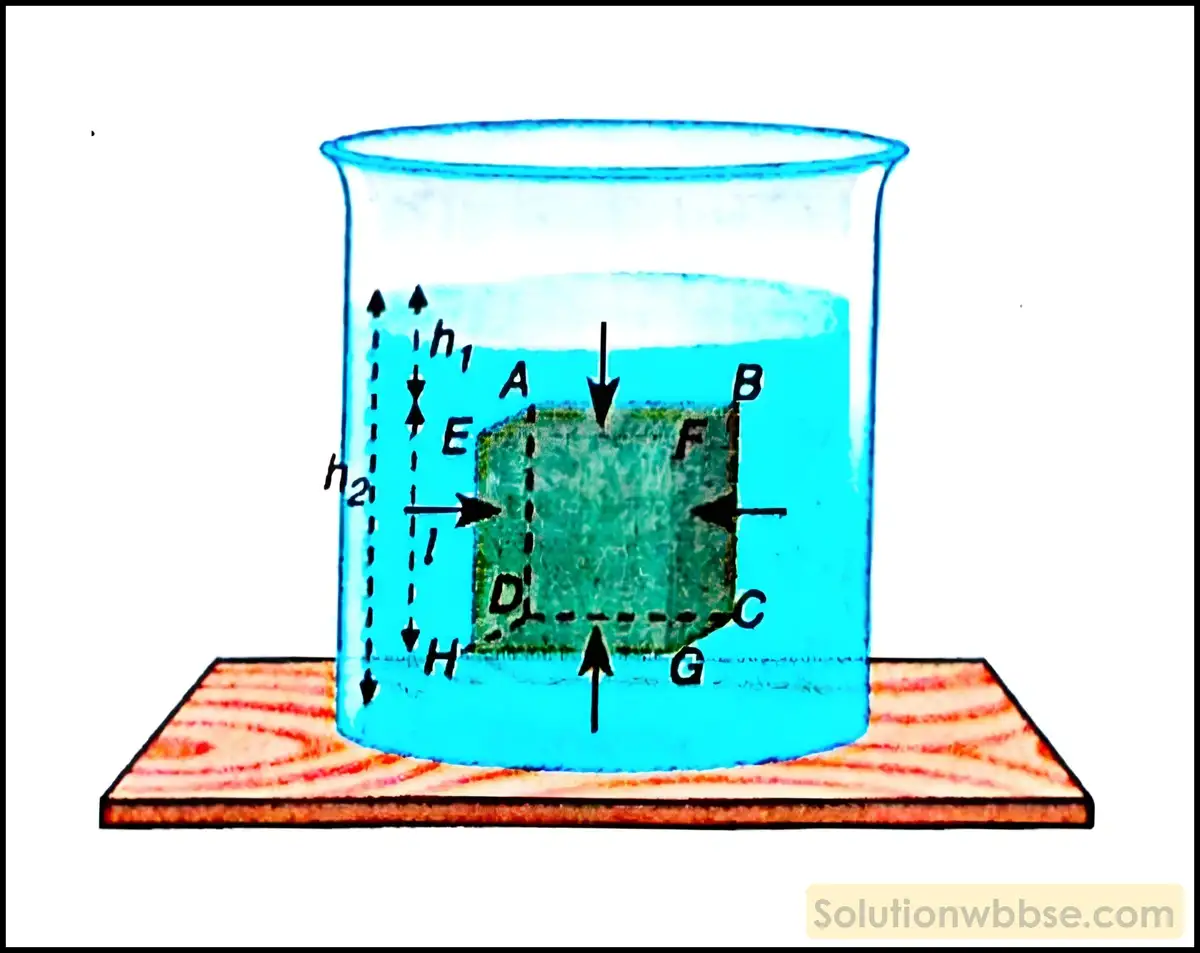
ঘনকটির প্রত্যেক প্রান্তের উপর তরল লম্ব অভিমুখে ঘাত প্রয়োগ করে। AD ও BC -এর উপর অনুভূমিক দিকে প্রযুক্ত পার্শ্বঘাত পরস্পর সমান ও বিপরীত হওয়ায় পরস্পরকে প্রতিমিত করে, কিন্তু ABFE এবং DCGH তলের গভীরতা ভিন্ন হওয়ায় তাদের উপর প্রযুক্ত ঘাত সমান হয় না।
ঘনকের প্রত্যেক তলের ক্ষেত্রফল a হলে, ABFE তলের উপর যে-কোনো বিন্দুতে তরলের দেওয়া নিম্নচাপ = h1ρg, যেখানে, ρ = তরলের ঘনত্ব।
∴ ABFE তলে প্রযুক্ত নিম্নঘাত = h1ρga
একইভাবে ঘনকের DCGH তলের প্রত্যেক বিন্দুতে তরল দ্বারা প্রযুক্ত ঊর্ধ্বচাপ h2ρg এবং ওই তলে প্রযুক্ত ঊর্ধ্বঘাত = h2ρga
∵ h2 > h1 সুতরাং, ঊর্ধ্বঘাতের মান নিম্নঘাত অপেক্ষা বেশি,
∴ ফলকটির উপর প্রযুক্ত মোট ঊর্ধ্বমুখী ঘাত
= (h2 – h1) ρga
= lgρa [(h2 – h1) = ঘনকের বাহুর দৈর্ঘ্য = l]
আবার, ঘনকের প্রত্যেক তলের ক্ষেত্রফল a = l2
∴ ঊর্ধ্বমুখী ঘাত বা প্লবতা = gρl2⋅l = ρgl3 = ঘনক দ্বারা অপসারিত সমআয়তন জলের ওজন।
অসম আকৃতির যে-কোনো বস্তুকেও এরূপ অসংখ্য ক্ষুদ্র ক্ষুদ্র ঘনকের সমষ্টি বলে কল্পনা করা যায়।
∴ সুষম বা অসম আকৃতির যে-কোনো ঘনবস্তুর উপর ক্রিয়াশীল প্লবতা বলের মান বস্তুটি দ্বারা অপসারিত সমআয়তন তরলের ওজনের সমান।
প্লবতা কেন্দ্র কাকে বলে? এটি কোথায় অবস্থান করে?
প্লবতা কেন্দ্র (Centre of buoyancy) – কোনো তরলে নিমজ্জিত বস্তুর উপর তরলের প্লবতা যে বিন্দুতে ক্রিয়া করে, তাকে প্লবতা কেন্দ্র বা ভাসন কেন্দ্র বলে।
প্লবতা কেন্দ্র নিমজ্জিত বস্তু দ্বারা অপসারিত তরলের ভারকেন্দ্রে অবস্থান করে।
স্প্রিং তুলার সাহায্যে তরলে আংশিক বা পূর্ণ নিমজ্জিত বস্তুর প্লবতা নির্ণয়ের পদ্ধতিটি সংক্ষেপে ব্যাখ্যা করো।
তরলে নিমজ্জিত বস্তুর প্লবতা নির্ণয় – ধরা যাক, একটি পাথরের টুকরো বা ধাতুখণ্ডের উপর ক্রিয়াশীল ঊর্ধ্বঘাত বা প্লবতা নির্ণয় করতে হবে।
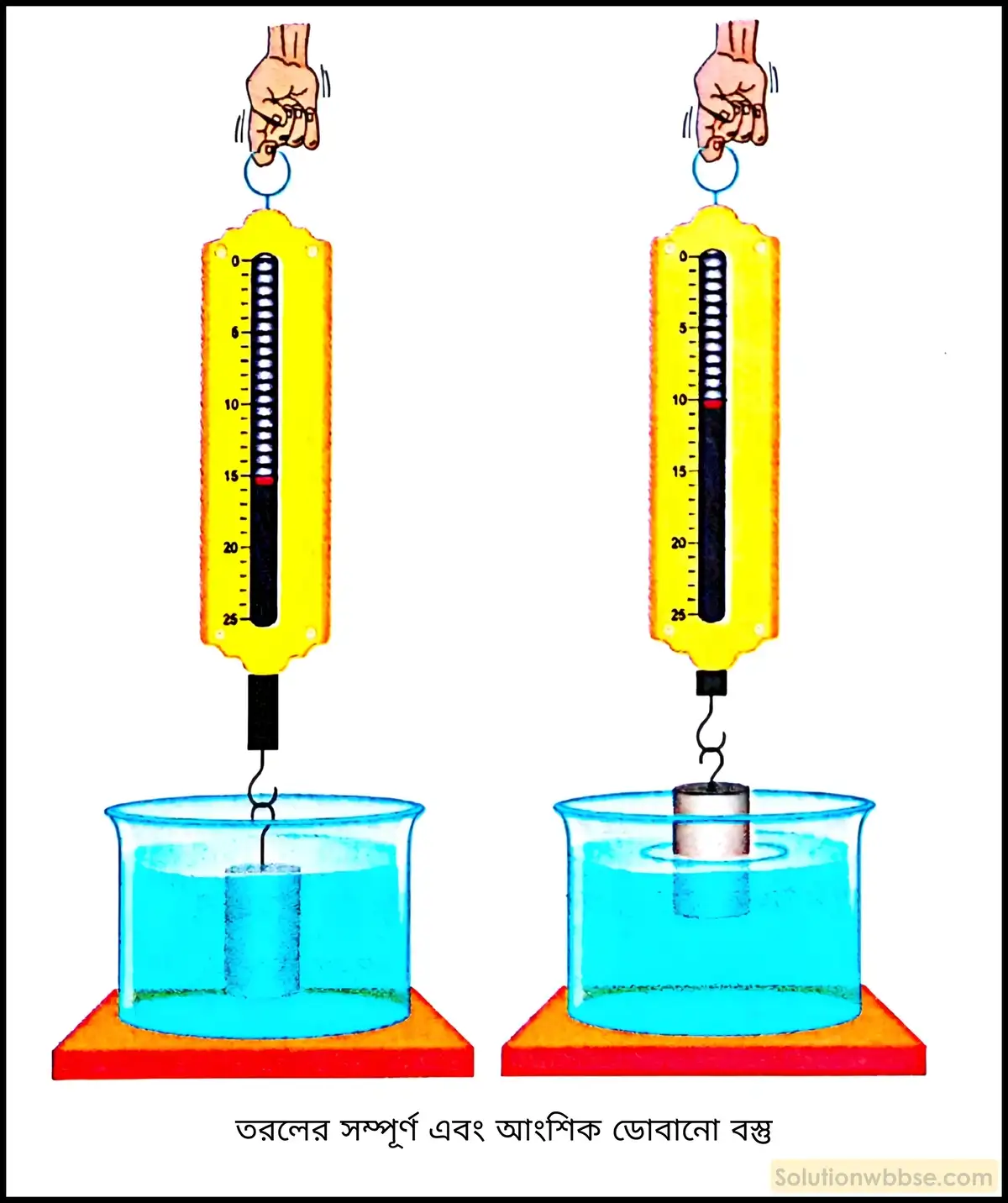
বস্তুটিকে একখণ্ড সুতোর সাহায্যে বেঁধে একটি স্প্রিং তুলার হুক থেকে বাধাহীনভাবে ঝুলিয়ে দেওয়া হল। এই অবস্থায় স্প্রিং তুলার পাঠ (ধরা যাক, W1 গ্রাম-ভার) বস্তুটির বায়ুতে ওজন নির্দেশ করে। এরপর সুতোয় বাঁধা বস্তুটিকে একটি তরলপূর্ণ বিকারের মধ্যে প্রথমে সম্পূর্ণ ও দ্বিতীয়ক্ষেত্রে আংশিক নিমজ্জিত অবস্থায় এমনভাবে রাখা হল যে, বস্তুটি যেন কোনোভাবেই বিকারের তলদেশ স্পর্শ না করে।
এই অবস্থায় দুইক্ষেত্রেই স্প্রিং তুলার পাঠ লক্ষ করা হল। ধরা যাক, পাঠ দুটি হয় যথাক্রমে W2 ও W3 গ্রাম-ভার (W3 < W2)।
তরলে সম্পূর্ণ নিমজ্জিত অবস্থায় বস্তুটির উপর ক্রিয়াশীল ঊর্ধ্বঘাত (B1) = বস্তুর বায়ুতে ওজন (W1) – বস্তুটির তরলে সম্পূর্ণ নিমজ্জিত অবস্থায় আপাত ওজন (W2)।
অর্থাৎ, B1 = (W1 – W2) গ্রাম-ভার।
একইভাবে, বস্তুটি তরলে আংশিক নিমজ্জিত অবস্থায় তার উপর ক্রিয়াশীল প্লবতা বা ঊর্ধ্বঘাত (B2) = বায়ুতে বস্তুর ওজন (W1) – তরলে আংশিক নিমজ্জিত অবস্থায় বস্তুর আপাত ওজন (W3)।
বা, B2 = (W1 – W3) গ্রাম-ভার।
প্লবতার প্রতিক্রিয়া বল কী এবং এটি কীভাবে নিউটনের তৃতীয় সূত্রের সাথে সম্পর্কিত?
অন্য যে-কোনো বাস্তব বলের মতোই প্লবতা বলেরও একটি সমান ও বিপরীত প্রতিক্রিয়া বল থাকে। তাই, বস্তুকে কোনো তরলে নিমজ্জিত করলে নিউটনের তৃতীয় সূত্র অনুসারে, বস্তুটি তরলের উপর এই সমান ও বিপরীতমুখী (নিম্নমুখী) প্রতিক্রিয়া প্রয়োগ করে। একে প্লবতার প্রতিক্রিয়া (Reaction of bouyancy) বলে।
যে-কোনো বিস্তৃত বস্তুর ওজন সর্বদা ওই বস্তু মধ্যস্থ একটি বিশেষ বিন্দুতে খাড়া নিম্নাভিমুখে ক্রিয়াশীল বলে কল্পনা করা হয়। এই বিন্দুটিকে বস্তুর ভারকেন্দ্র বলে। যে-কোনো বস্তুর ক্ষেত্রে এটি একটি অদ্বিতীয় (unique) বিন্দু হয়।
ভাসন ও নিমজ্জন কাকে বলে?
ভাসন (Floatation) – তরলে অদ্রবণীয় কোনো বস্তু তরলের মধ্যে পাত্রের তলদেশে না পৌঁছে যে-কোনো অবস্থানে স্থির হয়ে থাকার ঘটনাকে বলা হয় ভাসন।
ভাসন দুভাবে হতে পারে –
- তরলের মধ্যে বস্তুর কিছু অংশ ও বাকি অংশ তরলের বাইরে রেখে ভাসন অর্থাৎ, আংশিক নিমজ্জিত অবস্থায় ভাসন (যেমন – বরফ, কর্ক, শুকনো নারকেল ইত্যাদির জলে ভাসমান অবস্থা) এবং
- জলের মধ্যে বা তরলের মধ্যে না ডুবে পূর্ণ নিমজ্জিত অবস্থায় ভাসন (যেমন – ভেজা কাঠ, ডাব ইত্যাদির জলে ভাসমান থাকার ঘটনা)।
নিমজ্জন (Immersion) – তরলের মধ্যে প্রবেশ করে কোনো বস্তুর ওই তরলের তলদেশে পৌঁছে যাওয়ার এবং সেই অবস্থানে স্থির হয়ে থাকার ঘটনাকে বলা হয় নিমজ্জন।
ভাসন ও নিমজ্জনের শর্তগুলি বিবৃত করো।
ভাসনের শর্ত – বস্তুকে স্থির তরলে আংশিক বা সম্পূর্ণ নিমজ্জিত করলে বস্তুটির ওপর দুটি বল কাজ করে। একটি, বস্তুর ওজন (W1), যার অভিমুখ খাড়া নীচের দিকে ও অন্যটি, বস্তুর ওপর তরলের দেওয়া ঊর্ধ্বঘাত বা প্লবতা (W2), যা খাড়া উপরের দিকে ক্রিয়াশীল। এই দুই বলের মানের ওপর নির্ভর করে দুটি অবস্থা সৃষ্টি হতে পারে।
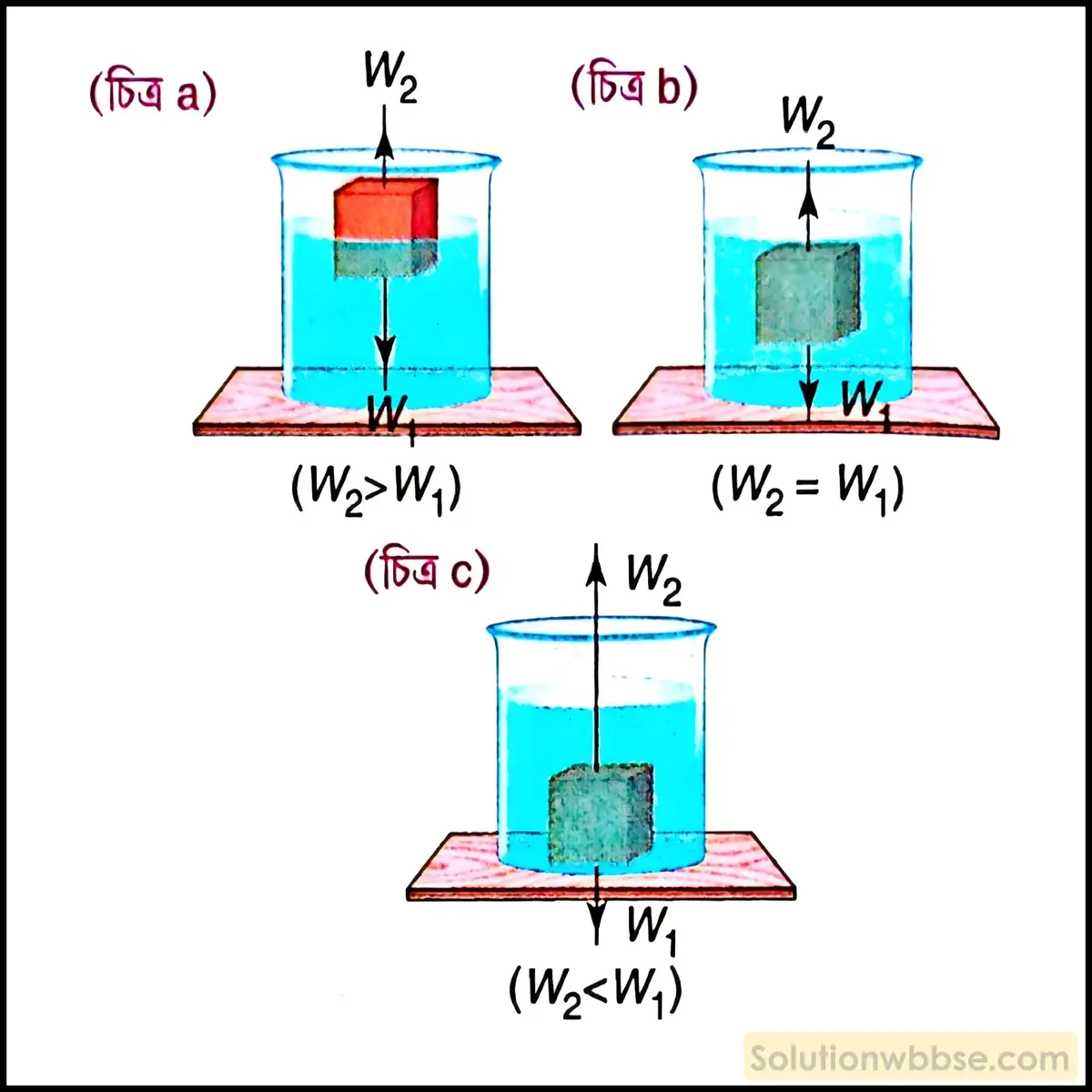
- আংশিক নিমজ্জিত অবস্থায় ভাসন – প্লবতার মান বস্তুর ওজন অপেক্ষা বেশি (W2 > W1) (চিত্র a)। বস্তু তার আয়তনের কিছু অংশ বাইরে রেখে ভাসে।
- পূর্ণ নিমজ্জিত অবস্থায় ভাসন – প্লবতার মান বস্তুর ওজনের সমান অর্থাৎ, W2 = W1 (চিত্র b)। বস্তু তরলের মধ্যে ডুবে থেকে ভাসে।
নিমজ্জনের শর্ত – প্লবতার মান বস্তুর ওজন অপেক্ষা কম (W2 < W1) (চিত্র c)। এই অবস্থায় বস্তু তরলের মধ্যে সম্পূর্ণ ডুবে যাবে।
ভাসমান বস্তুর সাম্যের শর্তগুলি বিবৃত ও ব্যাখ্যা করো।
ভাসমান বস্তুর সাম্যের শর্ত – ভাসমান বস্তুকে সাম্যে থাকতে হলে দুটি শর্ত পূরণ করতে হয় –
- ভাসনের শর্ত ও
- সাম্যের শর্ত।
ভাসনের শর্ত – ভাসমান বস্তুর ওজন অবশ্যই অপসারিত তরলের ওজনের সমান হবে।
সাম্যের শর্ত – বস্তুর ভারকেন্দ্র এবং প্লবতাকেন্দ্র অর্থাৎ, অপসারিত তরলের ভারকেন্দ্র অবশ্যই একই উল্লম্বরেখায় অবস্থান করবে।
ব্যাখ্যা – প্রথম শর্তটি মান্য হলে বস্তুটির ওপর কোনো লব্ধি বল ক্রিয়া করে না। ফলে, বস্তুটি ত্বরণহীন অবস্থায় অর্থাৎ, চলন সাম্যে অবস্থান করে।
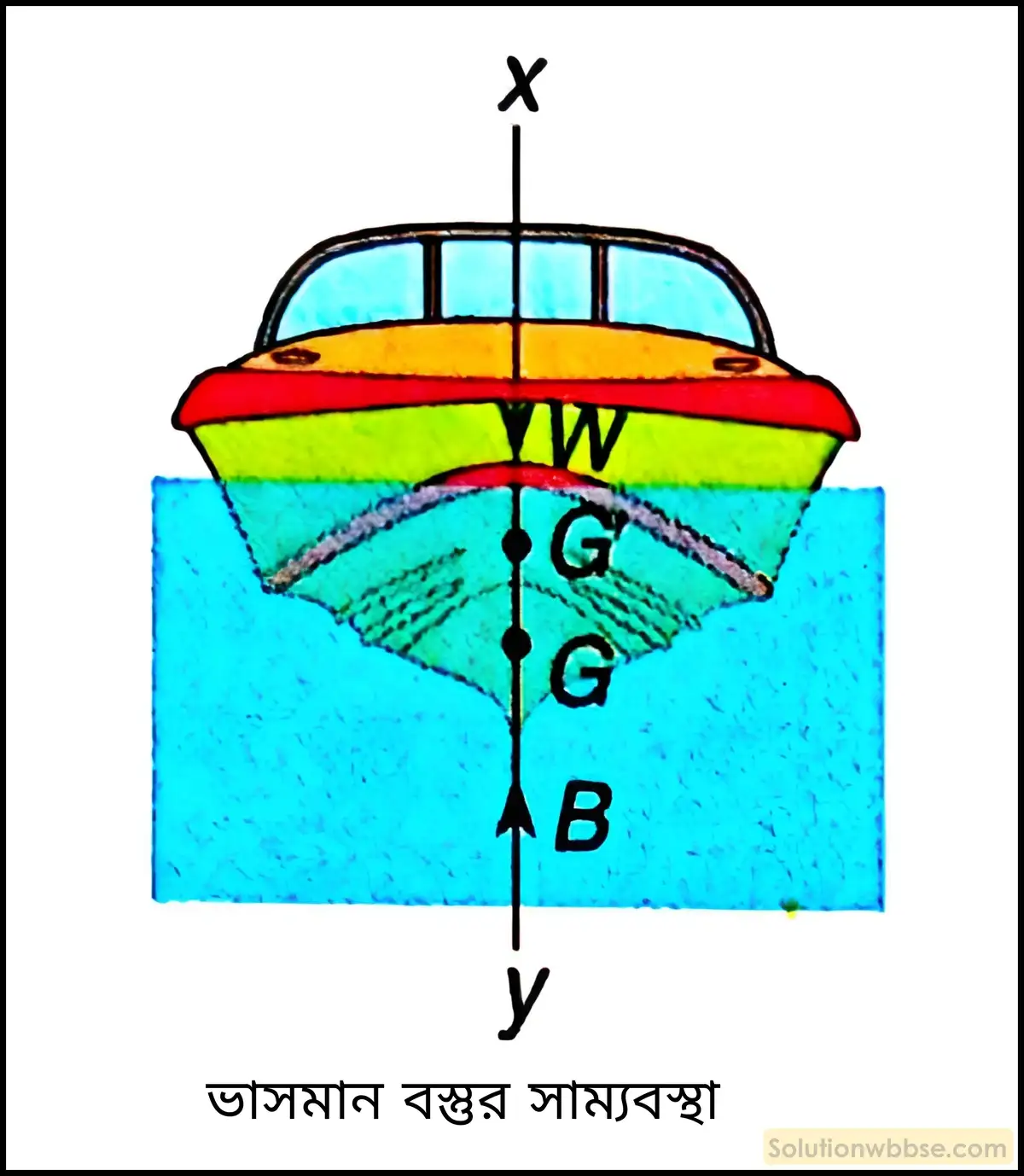
দ্বিতীয় শর্তটি পূরণ হলে বস্তুর মধ্যে কোনো আবর্ত গতি সৃষ্টি হয় না। একই রেখায় ক্রিয়াশীল দুটি বল বস্তুটির মধ্যে সমান কিন্তু বিপরীত ঘূর্ণন প্রবণতা সৃষ্টি করে, যার ফলে বস্তুটির মধ্যে কোনো কৌণিক ত্বরণ উৎপন্ন হয় না এবং সেটি ঘূর্ণন সাম্য বজায় রাখতে সক্ষম হয়।
যেমন চিত্রে দেখা যাচ্ছে, ভাসমান একটি বস্তু সাম্যাবস্থায় আছে। যেখানে xy → বস্তুর কেন্দ্রীয় রেখা, W → বস্তুর ওজন, B → প্লবতা বল, G → বস্তুর ভারকেন্দ্র, G’ → প্লবতা কেন্দ্র।
ভাসমান বস্তুর সাম্য ও প্লবতার শর্ত পরস্পরবিরোধী বলে মনে হলেও, বাস্তবে তারা কীভাবে সামঞ্জস্যপূর্ণ হয়? ব্যাখ্যা কর।
ভাসমান বস্তু সর্বদাই সাম্যে থাকে অর্থাৎ, ভাসমান অবস্থায় বস্তুর ওপর কোনো অপ্রতিমিত বল ক্রিয়া করে না। তাই আংশিক নিমজ্জিত অবস্থায় ভাসনের শর্ত [প্লবতা (W2) > বস্তুর ওজন (W1)] ও ভাসমান বস্তুর সাম্য একেবারেই পরস্পরবিরোধী বক্তব্য। এক্ষেত্রে মনে রাখা উচিত যে, W2 প্রকৃতপক্ষে পূর্ণ নিমজ্জিত অবস্থায় বস্তুর ওপর ক্রিয়াশীল প্লবতা নির্দেশ করে। বস্তুর উপাদান ঘনত্ব ও তরলের ঘনত্বের মানের ওপর নির্ভর করে বস্তু তার নিজের আয়তনের সেই ভগ্নাংশ এক্ষেত্রে তরলে নিমজ্জিত রাখে, যার জন্য ঊর্ধ্বঘাত বস্তুর ওজনকে সম্পূর্ণ প্রতিমিত করে বস্তুটিকে সাম্যে রাখতে সক্ষম হয়।
তরলে নিমজ্জিত বস্তুর নিমজ্জিত অংশ ও বস্তুর প্রকৃত আয়তনের সঙ্গে বস্তু ও ওই তরলের উপাদানের ঘনত্বের মধ্যে সম্পর্ক প্রতিষ্ঠা করো।
অথবা, দেখাও যে, তরলে ভাসমান কোনো বস্তুর আয়তনের যে ভগ্নাংশ নিমজ্জিত থাকে, তা কঠিনের ও তরলের ঘনত্বের অনুপাতের সমান।
ধরা যাক, V আয়তন ও ρ ঘনত্ববিশিষ্ট একটি বস্তু ρ1 ঘনত্বের একটি তরলে ভাসছে। বস্তুটির v আয়তন যদি তরলে নিমজ্জিত অবস্থায় থাকে, তবে নিমজ্জিত অংশ দ্বারা অপসারিত তরলের আয়তন হয় v।
এখন ভাসনের শর্ত অনুসারে, বস্তুর ওজন = অপসারিত তরলের ওজন।
বা, \(V\rho g=v\rho_1g\) অর্থাৎ, \(\frac vV=\frac\rho{\rho_1}\)
∴
বস্তুর আয়তনের n অংশ তরলে নিমজ্জিত থাকলে, \(\frac vV=n=\frac\rho{\rho_1}\)
বা, ρ = nρ1
ব্যবহৃত তরলটি জল হলে ρ1 = 1 অর্থাৎ, ρ = n
এক্ষেত্রে বলা যায় যে, বস্তুর আয়তনের যে ভগ্নাংশ জলে নিমজ্জিত থাকে সেটিই হল বস্তুটির ঘনত্বের পরিমাপ।
ঘনত্ব কাকে বলে? এর একক ও মাত্রীয় সংকেত লেখো।
ঘনত্ব (Density) – কোনো পদার্থের একক আয়তনের ভরকে ঘনত্ব বলে।
∴
∴ \(D=\frac MV\)
CGS পদ্ধতিতে ঘনত্বের একক গ্রাম/ঘনসেমি বা g/cc
SI -তে ঘনত্বের একক কিলোগ্রাম/ঘনমিটার বা kg/m3
FPS পদ্ধতিতে ঘনত্বের একক পাউন্ড/ঘনফুট বা Ib/cubic foot
ঘনত্বের ওপর চাপ ও উষ্ণতার প্রভাব লেখো।
ঘনত্বের ওপর চাপের প্রভাব – চাপ প্রয়োগে কঠিন বা তরল পদার্থের আয়তনের উল্লেখযোগ্য কোনো পরিবর্তন হয় না। তাই কঠিন বা তরল পদার্থের ঘনত্ব চাপের ওপর নির্ভর করে না। কিন্তু চাপ প্রয়োগে গ্যাসীয় পদার্থের আয়তন উল্লেখযোগ্যভাবে কমে যায়। তাই চাপ বাড়ালে গ্যাসীয় পদার্থের ঘনত্ব বাড়ে।
ঘনত্বের ওপর উষ্ণতার প্রভাব – উষ্ণতা বাড়ালে কঠিন, তরল, গ্যাসীয় ইত্যাদি সব পদার্থেরই আয়তন বাড়ে, অর্থাৎ, ঘনত্ব কমে যায়। গ্যাসের ক্ষেত্রে এই পরিবর্তন খুব বেশি হয়।
আপেক্ষিক ঘনত্ব বা আপেক্ষিক গুরুত্ব বলতে কী বোঝায়? এর একক ও মাত্রা লেখো।
আপেক্ষিক গুরুত্ব (Specific gravity) বা আপেক্ষিক ঘনত্ব (Relative density) – কোনো কঠিন বা তরল পদার্থের ঘনত্ব এবং 4°C উষ্ণতায় বিশুদ্ধ জলের ঘনত্বের অনুপাতকে ওই কঠিন বা তরল পদার্থের আপেক্ষিক গুরুত্ব বা আপেক্ষিক ঘনত্ব বলে।
∴
= [∵ ]
[∵ ভর ও ওজন সমানুপাতিক]
অর্থাৎ, আপেক্ষিক গুরুত্ব বা আপেক্ষিক ঘনত্বের দ্বিতীয় সংজ্ঞা হিসেবে বলা যায়, যে-কোনো আয়তনের পদার্থের ওজন ও 4°C উষ্ণতায় সমআয়তন জলের ওজনের অনুপাতকে ওই পদার্থের আপেক্ষিক গুরুত্ব বা আপেক্ষিক ঘনত্ব বলে।
আপেক্ষিক গুরুত্ব বা আপেক্ষিক ঘনত্ব দুটি ঘনত্বের বা দুটি ওজনের অনুপাত। তাই এটি একটি সংখ্যামাত্র। এর কোনো একক ও মাত্রা নেই। পরিমাপের সকল পদ্ধতিতেই আপেক্ষিক গুরুত্বের মান একই।
আপেক্ষিক ঘনত্ব নির্ণয়ে উষ্ণতা সংশোধন ব্যাখ্যা করো। পরিমাপের বিভিন্ন পদ্ধতিতে ঘনত্ব ও আপেক্ষিক ঘনত্বের মধ্যে সম্পর্ক নির্ণয় করো।
কোনো কঠিন বা তরল পদার্থের আপেক্ষিক গুরুত্ব নির্ণয়ের সময় জলের উষ্ণতা 4°C ধরা হয়। কারণ – 4°C উষ্ণতায় জলের ঘনত্ব সবচেয়ে বেশি যার মান 1 গ্রাম/ঘনসেমি। কিন্তু পরীক্ষাগারের উষ্ণতা 4°C বজায় রেখে আপেক্ষিক গুরুত্ব নির্ণয় করা প্রায় অসম্ভব। তাই নিম্নলিখিতভাবে আপেক্ষিক ঘনত্ব নির্ণয়ে উষ্ণতা সংশোধন করা হয়।
ধরা যাক, ব্যবহৃত জলের উষ্ণতা = t°C
∴
বা,
= নির্ণীত আপেক্ষিক গুরুত্ব × t°C -এ জলের আপেক্ষিক গুরুত্ব বিভিন্ন উষ্ণতায় জলের আপেক্ষিক গুরুত্ব কত হবে তার একটি তালিকা আছে। এই তালিকা থেকে t°C উষ্ণতায় জলের আপেক্ষিক গুরুত্বের মান জেনে তার সঙ্গে নির্ণীত আপেক্ষিক গুরুত্বের মান গুণ করলে পদার্থের সঠিক আপেক্ষিক গুরুত্ব জানা যায়। তবে খুব সূক্ষ্ম পরিমাপের প্রয়োজন না হলে এই সংশোধন উপেক্ষা করা হয়। কারণ – উষ্ণতা পরিবর্তনের সঙ্গে জলের ঘনত্বের পরিবর্তন খুবই নগণ্য।
CGS পদ্ধতিতে 4°C উষ্ণতায় জলের ঘনত্ব = 1 g/cm3
∴ CGS পদ্ধতিতে, পদার্থের ঘনত্ব = আপেক্ষিক ঘনত্ব
SI -তে 4°C উষ্ণতায় জলের ঘনত্ব = 1000 kg/m3
∴
বা, SI -তে পদার্থের ঘনত্ব = আপেক্ষিক ঘনত্ব × 1000
FPS পদ্ধতিতে 4°C উষ্ণতায় জলের ঘনত্ব = 62.5 lb/ft3
∴
বা, FPS পদ্ধতিতে পদার্থের ঘনত্ব = আপেক্ষিক ঘনত্ব × 62.5
ঘনত্বের তুলনায় আপেক্ষিক ঘনত্বের ধারণা বেশি সুবিধাজনক কেন?
আপেক্ষিক ঘনত্বের ধারণার উপযোগিতা –
এটি দুটি পদার্থের ঘনত্বের তুলনা ভাগ করে ব্যাখ্যা করা যায়। যেমন – সোনার ঘনত্ব (19.3 g/cc), রুপার ঘনত্বের (10.5 g/cc) 1.84 \(\left(=\frac{19.3}{10.5}\right)\) গুণ বেশি। কিন্তু বহুসংখ্যক পদার্থের ক্ষেত্রে এভাবে তুলনা করা ব্যাবহারিক দিক থেকে একান্তই অসুবিধাজনক। এই সমস্যা এড়াবার উদ্দেশ্যেই 4°C উষ্ণতায় জলের ঘনত্বকে মানক (Standard) বিবেচনা করে তার সাপেক্ষে অন্যান্য যে-কোনো পদার্থের ঘনত্বের তুলনা করা হয়। এই বিবেচনা থেকেই আপেক্ষিক গুরুত্বের ধারণার উদ্ভব। 4°C উষ্ণতায় জলের ঘনত্ব 1 g/cc হওয়ায় আপেক্ষিক গুরুত্ব বা আপেক্ষিক ঘনত্বের সাংখ্যমান CGS পদ্ধতিতে ঘনত্বের সমান, আবার মাত্রাহীন সংখ্যা হওয়ায় যে-কোনো পরিমাপ পদ্ধতিতে কোনো গাণিতিক রূপান্তর ছাড়াই এটি ব্যবহার করা যায়। তাই উদস্থিতিবিদ্যায় ঘনত্বের তুলনায় আপেক্ষিক ঘনত্বের ধারণা বেশি উপযোগী।
বোধমূলক প্রশ্নোত্তর
কৃত্রিম উপগ্রহে ঘনত্বের কি কোনো তাৎপর্য থাকে?
বস্তুর ভর ও আয়তনের অনুপাতকেই তার উপাদানের ঘনত্ব বলে। সুতরাং, ভর ও আয়তনের ধারণা প্রযোজ্য হলে ঘনত্বের ধারণাও অর্থপূর্ণ হয়। স্বকীয় বৈশিষ্ট্য হওয়ায় বস্তুর ভর এবং চাপ, উষ্ণতা ইত্যাদি নির্দিষ্ট শর্ত সাপেক্ষে কৃত্রিম উপগ্রহে বস্তুর আয়তন সর্বদাই ধ্রুবক হয়। তাই, কৃত্রিম উপগ্রহের মধ্যে বস্তু আপাত ভারহীন অবস্থায় থাকলেও ঘনত্বের ধারণার তাৎপর্য সর্বদাই বজায় থাকে।
মানুষবাহী বেলুন ভারী হওয়া সত্ত্বেও বায়ুর মধ্যে দিয়ে উপরে ওঠে কী করে?
মানুষবাহী বেলুনে বায়ু অপেক্ষা হালকা যে-কোনো গ্যাস, যেমন – হাইড্রোজেন বা হিলিয়াম ভরতি করে দিলে গ্যাসভরতি বেলুনের মোট ওজন অপসারিত বায়ুর ওজন অপেক্ষা কম হয়। ফলে, বায়ুর ঊর্ধ্বমুখী বল অর্থাৎ, প্লবতা বেশি হবার জন্য বেলুনটি ভারী হওয়া সত্ত্বেও বায়ুর মধ্যে দিয়ে উপরে উঠে যায়।
জলের সাপেক্ষে কোনো পদার্থের আপেক্ষিক ঘনত্বের মান 1 অপেক্ষা কম হলে, সেটি ডুবে যাবে না ভাসবে?
জলের সাপেক্ষে কোনো পদার্থের আপেক্ষিক ঘনত্বের মান 1 অপেক্ষা কম হলে পদার্থটির ঘনত্ব, জলের ঘনত্বের তুলনায় কম হয়। তাই, পদার্থটি জলে ভাসবে
কোনো বস্তুকে জলে ডোবালে হালকা বোধ হয় কেন?
কোনো বস্তুকে জলে ডোবালে বস্তুর ওজন লম্বভাবে নীচের দিকে ক্রিয়া করে এবং জল বস্তুর ওপর লম্বভাবে একটি ঊর্ধ্বমুখী বল (প্লবতা) প্রয়োগ করে। ফলে, প্লবতা বস্তুর ওজনের বিপরীত দিকে ক্রিয়া করে বস্তুর ওজনের আপাত হ্রাস ঘটায়। বস্তুর ওজনের এই আপাত হ্রাস, বস্তু যে আয়তনের জল অপসারিত করে তার ওজনের সমান হয়। তাই কোনো বস্তুকে জলে ডোবালে বস্তুটি হালকা হয়ে গেছে বলে মনে হয়।
সোনার আপেক্ষিক গুরুত্ব 19.3 বলতে কী বোঝায়?
বক্তব্যটির অর্থ হল – নির্দিষ্ট উষ্ণতায় নির্দিষ্ট আয়তনের সোনার ওজন, 4°C উষ্ণতায় সম আয়তন জলের ওজনের তুলনায় 19.3 গুণ ভারী।
জলে ভাসমান সম ওজনের লোহার বল ও লোহার কড়াই -এর মধ্যে কার ওপর প্লবতা বেশি ও কেন?
অথবা, লোহার তৈরি জাহাজ বা লোহার কড়াই জলে ভাসে কিন্তু একতাল লোহা জলে ডুবে যায় কেন?
লোহার তৈরি জাহাজের আয়তন, একই ওজনের একতাল লোহার আয়তনের চেয়ে অনেক বেশি এবং জাহাজের তলদেশ খুবই চওড়া ও ফাঁপা।

তাই, জাহাজ তার ওজনের চেয়ে অনেক বেশি পরিমাণ জল অপসারণ করতে পারে বলে প্লবতা বেশি হয়। ভাসনের শর্ত অনুযায়ী, প্লবতার মান বস্তুর ওজন অপেক্ষা বেশি হলে সেটি তরলে ভেসে থাকতে পারে। তাই, লোহার তৈরি জাহাজ বা কড়াই জলে ভাসে।
একতাল লোহার আয়তন অনেক কম হওয়ায় লোহার তাল কর্তৃক অপসারিত জলের ওজন অর্থাৎ, প্লবতার মান লোহার ওজন অপেক্ষা কম হয়। তাই, সেটি জলে ডুবে যায়।
বেলুনে হাইড্রোজেন গ্যাস ভরতি করে ছেড়ে দিলে তা কিছু উপরে উঠে যায়। আবার কিছুটা উপরে ওঠার পর আর ওঠে না। পর্যবেক্ষণগুলি আর্কিমিডিসের সূত্র অনুযায়ী ব্যাখ্যা করো।
হাইড্রোজেন গ্যাস দিয়ে পূর্ণ বেলুন বায়ুতে ছেড়ে দিলে প্রথমে খানিকটা উপরে ওঠে। গ্যাসপূর্ণ বেলুনের মোট ওজন বেলুন দ্বারা অপসারিত বায়ুর ওজন অপেক্ষা কম হয়। বেলুনের ওপর ক্রিয়াশীল উর্ধ্বমুখী ঘাত এই দুই ওজনের পার্থক্যের সমান। এই ঘাতের ক্রিয়ায় বেলুন উপরে ওঠে।
বেলুনের উচ্চতা যত বাড়ে, সংলগ্ন বায়ুস্তরের ঘনত্ব কমতে থাকে। ফলে, ঊর্ধ্বমুখী ঘাত বা প্লবতাও কম হয়। অবশেষে একটি নির্দিষ্ট উচ্চতায় বেলুন দ্বারা অপসারিত বায়ুর ওজন ওই বেলুনের আবরণ ও মধ্যবর্তী হাইড্রোজেন গ্যাসের ওজনের সমান হলে বেলুনটি ওই অবস্থানে স্থির হয়, আর উঠতে পারে না।
একটি ফাঁপা প্লাস্টিকের বল কেন জলে ভাসে তা ব্যাখ্যা করো।
জলে রাখা ফাঁপা প্লাস্টিকের বলের ওপর দুটি বল ক্রিয়া করে, যথা –
- তরলের ওজনজনিত বল,
- প্লবতাজনিত বল।
প্লাস্টিক বলের ওজন (W), যা নীচের দিকে ক্রিয়াশীল হওয়ায় প্লাস্টিকের বলটিকে জলে ডুবতে সাহায্য করে।
প্লবতাজনিত বল (B) -এর মান বস্তু দ্বারা অপসারিত জলের ওজনের সঙ্গে সমান এবং উপর দিকে ক্রিয়া করায় বস্তু (প্লাস্টিকের বল) -কে জলের ওপর ভাসিয়ে রাখতে সাহায্য করে।
এক্ষেত্রে, প্লাস্টিকের বালটি ফাঁপা হওয়ায় বলের ওজন (W) -এর মান প্লবতা বল (B) অপেক্ষা কম হয়। ফলে প্লাস্টিকের বলটি জলে ভেসে থাকে।
একটি কঠিন ও ভারী বস্তুকে জলে ও কেরোসিনে ডোবালে কোন্ ক্ষেত্রে প্লবতা বেশি হবে?
জলের ঘনত্ব কেরোসিন অপেক্ষা বেশি হওয়ায় বস্তু দ্বারা অপসারিত জলের ওজন সমআয়তন কেরোসিন অপেক্ষা বেশি হয়। সুতরাং, জলের প্লবতা বেশি হবে।
একটি ঘনক, একটি আয়তঘনক এবং একটি গোলকের উপাদান ও ভর অভিন্ন। ওদের জলে নিমজ্জিত করলে কোনটি সবচেয়ে বেশি প্লবতা অনুভব করবে?
প্রদত্ত বস্তু তিনটির আকৃতি আলাদা কিন্তু উপাদান অর্থাৎ, ঘনত্ব এবং ভর অভিন্ন। ফলে, বস্তু তিনটির আয়তনও অভিন্ন।
কারণ – আয়তন = ভর/ঘনত্ব।
তাই, ওদের জলে সম্পূর্ণ নিমজ্জিত করলে প্রত্যেক বস্তু দ্বারা অপসারিত জলের আয়তনও একই হবে। সুতরাং, প্রদত্ত তিনটি বস্তুর ক্ষেত্রে প্লবতার মান একই হবে।
একটি সোনার বালা তোমাকে দেওয়া হল। সোনার ঘনত্ব 19.3 গ্রাম/ঘনসেমি। বালাটিতে খাদ মেশানো আছে কি না তা কী করে বুঝবে?
প্রথমে সোনার বালার ভর ও পরে আয়তন নির্ণয় করা হল। ধরা যাক, এদের মান যথাক্রমে x গ্রাম এবং y ঘনসেমি।
তাই, সোনার ঘনত্ব = \(\frac xy\) গ্রাম/ঘনসেমি।
যদি \(\frac xy=19.3\) হয়, তবে বুঝতে হবে সোনা খাঁটি। কিন্তু \(\frac xy\neq19.3\) হলে সিদ্ধান্তে আসা যায় বালাটিতে খাদ মেশানো আছে।
একটি জলপূর্ণ পাত্রে একখণ্ড বরফ ভাসছে। বরফটি গলে গেলে জল কি উপচে পড়বে?
বরফ গলে গেলেও জল উপচে পড়বে না। কারণ – বরফটি যে আয়তনের জল অপসারণ করে ভাসছিল, বরফ গলনের ফলে উৎপন্ন জলের আয়তন তার সমান হয়। তাই, জলতলের উচ্চতার কোনো পরিবর্তন হবে না।
ডুবোজাহাজ বা সাবমেরিন কাজ করে কীভাবে?
ডুবোজাহাজে কপাটযুক্ত অনেকগুলি প্রকোষ্ঠ থাকে। এদের ওজন নিয়ন্ত্রণকারী প্রকোষ্ঠ বা ব্যালাস্ট ট্যাংক বলে। এই প্রকোষ্ঠগুলি যখন বায়ুপূর্ণ থাকে তখন ডুবোজাহাজের ওজন সমআয়তন জলের ওজন অপেক্ষা কম হয়। তখন এটি জলে ভেসে থাকে। আবার যান্ত্রিক উপায়ে প্রকোষ্ঠগুলি জলপূর্ণ করলে ডুবোজাহাজের ওজন সমআয়তন জলের ওজন অপেক্ষা বেশি হয়। ফলে, এটি জলে ডুবে যায়। আবার জলের উপর উঠতে হলে পাম্পের সাহায্যে প্রকোষ্ঠগুলি থেকে জল বের করে বায়ুপূর্ণ করা হয়। এভাবে ডুবোজাহাজ জলে ডুবে থাকতে পারে, আবার সাধারণ জাহাজের মতো ভেসেও থাকতে পারে।

বরফ জলে ভাসে কেন?
জল জমে বরফে পরিণত হলে আয়তনে বাড়ে। 0°C উষ্ণতায় 11 ঘনসেমি জল বরফে পরিণত হলে তার আয়তন হয় 12 ঘনসেমি। ফলে, 12 ঘনসেমি বরফের ওজন 11 ঘনসেমি আয়তনের জলের সমান হয়। তাই, একখণ্ড বরফ জলে ফেলে দিলে সেটি ডুবতে শুরু করে। বরফ টুকরোর \(\frac{11}{12}\) অংশ যখন জলে নিমজ্জিত হয় তখন অপসারিত জলের ওজন বরফের টুকরোর ওজনের সমান হয়। তাই বরফখণ্ডটি \(\left(1-\frac{11}{12}\right)\) অংশ = \(\frac1{12}\) অংশ জলের উপরে থাকা অবস্থায় ভাসতে থাকে।

মেরু অঞ্চলের সমুদ্রে ভাসমান বিশাল আকৃতির হিমশৈলের কত অংশ সাধারণত পানির ওপরে দেখা যায়, এবং উষ্ণতার পরিবর্তনের সাথে এটি কীভাবে প্রভাবিত হতে পারে?
মেরু অঞ্চলের সমুদ্রে প্রায়ই বিশাল আকৃতির হিমশৈল (Iceberg) ভাসতে দেখা যায়। সমুদ্রের জলে লবণ মিশ্রিত থাকায় তার ঘনত্ব অপেক্ষাকৃত বেশি (1.08 গ্রাম/সিসি) হয়। সুতরাং,
\(n=\frac{\rho_{ice}}{\rho_w}=\frac{0.917}{1.08}=0.85\)।
সুতরাং, হিমশৈলের আয়তনের (1 – 0.85) = 0.15 অংশ জলের বাইরে থাকে। অর্থাৎ, হিমশৈল তার মোট আয়তনের \(\frac17\) অংশ জলের উপর রেখে ভাসে। তবে, তবে, উষ্ণতার সঙ্গে ঘনত্বের তারতম্যের ওপর \(\frac17\) নির্ভর করে থেকে \(\frac19\) অংশের মধ্যে পরিবর্তিত হয়।
মানুষ সাঁতার কাটে কীভাবে?
মানুষের দেহ সমআয়তন জল অপেক্ষা হালকা, কিন্তু মাথা সমআয়তন জল অপেক্ষা ভারী। তাই মানুষের দেহ সহজেই জলে ভাসে, কিন্তু মাথা ডুবে যেতে চায়। জলের মধ্যে হাত ও পা নেড়ে মাথাকে ভাসিয়ে রাখতে শেখার নামই হল সাঁতার শেখা। এজন্য মানুষকে সাঁতার শিখতে হয়।

লাইফ জ্যাকেট কী?
লাইফ জ্যাকেট হল বায়ুপূর্ণ জ্যাকেট, যা দুর্ঘটনার ফলে জলে নিমজ্জিত ব্যক্তির জীবনরক্ষায় ব্যবহার করা হয়। বায়ু সমআয়তন জল অপেক্ষা হালকা। তাই লাইফজ্যাকেট পরিহিত কোনো ব্যক্তি জলে নিমজ্জিত হলে বায়ুপূর্ণ জ্যাকেট বেশি আয়তনের জল অপসারণ করে। ফলে, প্লবতার মান লাইফ জ্যাকেট পরা মানুষটির ওজনের সমান হয়ে যায়। ফলে ব্যক্তিটি ভেসে থাকতে পারে।

পশুরা কি স্বভাবগতভাবেই সাঁতার কাটতে সক্ষম? কেন?
পশুদের মাথার ওজন সমআয়তন জলের ওজন অপেক্ষা কম হয়ে থাকে। তাই পশুরা জলে সহজেই ভেসে থাকে। সুতরাং, বলা যায় সাঁতার কাটার কৌশল তাদের আলাদা করে রপ্ত করতে হয় না। এটি পশুদের স্বভাবজাত ধর্ম।
দুটি একই আয়তনের বেলুনকে একই চাপে দুটি ভিন্ন গ্যাস দিয়ে ভরতি করা হল, প্রথমটিকে হাইড্রোজেন এবং দ্বিতীয়টিকে হিলিয়াম দিয়ে। কোন্ বেলুনটির ক্ষেত্রে উর্ধ্বমুখী বল বেশি হবে?
দুটি সমান আয়তনের বেলুনকে বায়ু অপেক্ষা হালকা গ্যাস (H2 ও He) দিয়ে ভরতি করলে বেলুনের ওপর ক্রিয়াশীল বায়ুর প্লবতা, বেলুনের ওজনের থেকে বেশি হয়। ফলে বেলুন দুটির ওপর ঊর্ধ্বমুখী একটি লব্ধিবল ক্রিয়া করে। যে-কোনো একটি বেলুনের ওপর ঊর্ধ্বমুখী লব্ধিবল = বায়ুর প্লবতা – গ্যাসপূর্ণ বেলুনটির ওজন। এখন, বেলুন দুটির আয়তন সমান হওয়ায় দুটি বেলুনের ক্ষেত্রে বায়ুর প্লবতা সমান হয়। কিন্তু হাইড্রোজেন গ্যাসের ওজন, সমআয়তন হিলিয়াম গ্যাসের ওজনের তুলনায় কম হয়। ফলে, হাইড্রোজেন গ্যাসের ক্ষেত্রে উর্ধ্বমুখী লব্ধিবলের মান বেশি হয়। সুতরাং, হাইড্রোজেন গ্যাসপূর্ণ বেলুনটির ক্ষেত্রে উর্ধ্বমুখী বল বেশি হবে।
একটি বালক এক হাতে একটি জলের বালতি এবং অপর হাতে মাছ বইছে। মাছটিকে বালতির জলে ছেড়ে দিলে এবং ছাড়ার সময় কোনো জল ছিটকে না পড়লে বালকটি কি আগের চেয়ে কম ওজন বহন করবে?
এক্ষেত্রে মাছটিকে বালতির জলে ছেড়ে দিলে জলের প্লবতার কারণে মাছের ওজনের আপাত হ্রাস ঘটবে। আবার, তৃতীয় গতিসূত্র অনুসারে মাছও সমমানের প্রতিক্রিয়া বল (প্লবতার প্রতিক্রিয়া) জলের ওপর খাড়া লম্বভাবে প্রয়োগ করে। সুতরাং, প্লবতার ক্রিয়ায় মাছের ওজন যতখানি হ্রাস পায়, প্লবতার প্রতিক্রিয়া বালতির তলদেশে ঠিক সমপরিমাণে ক্রিয়াশীল হয়ে জলভরা বালতিসহ মাছ – এই সমগ্র ব্যবস্থার ওজন অপরিবর্তিত রাখে। সুতরাং, মোট ওজন একই থাকে বলে বালকটি আগের সমপরিমাণ ওজনই বহন করবে।
সমান ভর ও সমান ব্যাসার্ধের দুটি গোলকের একটি নিরেট ও অন্যটি ফাঁপা। একটি তরলের মধ্যে দুটি গোলককে নিমজ্জিত রাখলে কোনটি বেশি হালকা বোধ হবে?
ভর সমান হওয়ায় দুটি গোলকেরই ওজন সমান। আবার ব্যাসার্ধ সমান হওয়ায় উভয়ের আয়তন এবং সেই কারণে নিমজ্জিত অবস্থায় গোলক দ্বারা অপসারিত সম আয়তন জলের ওজন বা প্লবতা বলের মানও সমান। এখন নিমজ্জিত অবস্থায় বস্তুর আপাত ওজন = প্রকৃত ওজন – প্লবতা।
সুতরাং, প্রকৃত ওজন ও প্লবতা বল দুইয়েরই মান অভিন্ন হওয়ায় দুটি গোলকেরই আপাত ওজন সমান হবে। সুতরাং, উভয়েই সমান হালকা বা সমান ভারী বোধ হবে।
বায়ুপূর্ণ একটি বেলুনের সঙ্গে একটি লোহার টুকরো এমনভাবে জুড়ে দেওয়া হল যাতে বেলুনটি ঠিক জলে ডুবে ভাসতে পারে। এই ব্যবস্থাটিকে একটু চেপে জলের গভীরে ঠেলে দিলে দেখা যায় যে সেটি পাত্রের তলায় চলে যায়, আর ভেসে ওঠে না। কেন ব্যাখ্যা করো।
প্রথম ক্ষেত্রে, লোহার টুকরোসহ বেলুনের ওজন সমগ্র ব্যবস্থাটি দ্বারা অপসারিত জলের ওজন বা প্লবতার সমান হয় বলে ব্যবস্থাটি নিমজ্জিত অবস্থায় ভাসে।
ব্যবস্থাটিকে একটু চেপে জলের গভীরে ঠেলে দিলে, গভীরতা বৃদ্ধিতে জলের চাপ বাড়ে। এই বর্ধিত চাপে বেলুনের আয়তন সংকোচন হয় ফলে ব্যবস্থাটির ওপর ক্রিয়াশীল ঊর্ধ্বঘাতের মান ওজন অপেক্ষা কমে যায়। ফলে ব্যবস্থাটির আপাত ওজন বাড়ে এবং অপ্রতিমিত নিম্নমুখী বলের ক্রিয়ায় সেটি পাত্রের তলায় চলে যায়, আর ভেসে ওঠে না।
বায়ুর মধ্যে অঙ্গপ্রত্যঙ্গ নাড়াতে একটি মানুষকে যে বল প্রয়োগ করতে হয়, জলের মধ্যে অনুরূপভাবে নাড়াতে তার থেকে কম বল প্রয়োগ করতে হয় কেন?
আর্কিমিডিসের নীতি অনুসারে, কোনো বস্তুর ওজনের আপাত হ্রাস বস্তু কর্তৃক অপসারিত তরল বা বায়ুর ওজনের সমান। যেহেতু জলের ঘনত্ব বায়ু অপেক্ষা বেশি, মানুষের অঙ্গপ্রত্যঙ্গ কর্তৃক অপসারিত জলের ওজন, অঙ্গপ্রত্যঙ্গ কর্তৃক অপসারিত বায়ুর ওজন অপেক্ষা বেশি হয়। ফলে অঙ্গপ্রত্যঙ্গের ওজনের আপাত হ্রাস বায়ু অপেক্ষা জলে বেশি হয়। অর্থাৎ, বায়ু অপেক্ষা জলের মধ্যে মানুষের অঙ্গপ্রত্যঙ্গ বেশি হালকা বলে মনে হয়। এইজন্য বায়ুর মধ্যে অঙ্গপ্রত্যঙ্গ নাড়াতে মানুষকে যে বল প্রয়োগ করতে হয়, জলের মধ্যে অনুরূপভাবে নাড়াতে তার থেকে কম বল প্রয়োগ করতে হয়।
ধরা যাক, একটি আংশিক জলপূর্ণ বদ্ধ পাত্রে একটি ব্লক ভাসছে। যদি পাত্রে আরও কিছুটা বাতাস প্রবেশ করানো হয়, তবে ব্লকটির ভাসনের কী পরিবর্তন হবে?
এক্ষেত্রে, ব্লকটির ওজন = ব্লক দ্বারা অপসারিত জলের ওজন + ব্লক দ্বারা অপসারিত বায়ুর ওজন। তাই বন্ধ পাত্রে কিছুটা বায়ু প্রবেশ করালে পাত্রের মধ্যেকার বায়ুর ঘনত্ব বৃদ্ধি পায়। তাই ব্লক দ্বারা অপসারিত বায়ুর ওজনও বৃদ্ধি পায়। কিন্তু ব্লকের ওজন অপরিবর্তিত হওয়ায় ব্লক পূর্বের তুলনায় কম জল অপসারণ করবে। অর্থাৎ, ব্লকটি আরও একটু ভেসে উঠবে।
পাম্পের সাহায্যে আবদ্ধ পাত্র থেকে বায়ু নিষ্কাশন করা হলে ব্লকের সাম্য বজায় রাখতে অপসারিত জলের ওজন কেন বৃদ্ধি পায়?
পাম্পের সাহায্যে আবন্ধ পাত্র থেকে বায়ু নিষ্কাশন করা হলে অপসারিত বায়ুর ওজন শূন্য হবে ফলে, ব্লকের সাম্য অপরিবর্তিত রাখতে অপসারিত জলের ওজন বাড়বে। অর্থাৎ, ব্লকটি আরও কিছু পরিমাণ জলে ডুবে যাবে।
ডিম জলে ডুবে যায় কিন্তু লবণ মেশানো জলে ভাসে কীভাবে?
লবণমিশ্রিত জলের ঘনত্ব বিশুদ্ধ জলের তুলনায় বেশি। তাই বিশুদ্ধ জলের পরিবর্তে লবণ মেশানো জলে ডিম নিমজ্জিত থাকলে তার ওপর ক্রিয়াশীল প্লবতা বল বাড়ে। এই বলের মান ডিমের ওজনের সমান হলে ডিমটি পূর্ণ নিমজ্জিত হয় এবং ডিমের ওজনের তুলনায় বেশি হলে ডিম আংশিক নিমজ্জিত অবস্থায় ভাসে। অন্যদিকে স্বাভাবিক জলের ক্ষেত্রে ঘনত্ব কম হয় বলে প্লবতা সর্বদাই ডিমের ওজন অপেক্ষা কম হয়। তাই এক্ষেত্রে ডিম জলে ডুবে যায়।
1 কিগ্রা লোহা ও 1 কিগ্রা তুলার মধ্যে কোনটি বেশি ভারী ব্যাখ্যা করো।
কোনো বস্তুর ওজন বলতে সাধারণত বায়ুতে তার ওজন বোঝানো হয়। কিন্তু ঘনত্ব কম হওয়ায়, সামান্য হলেও বস্তু দ্বারা অপসারিত বায়ু ওই বস্তুর উপর ঊর্ধ্বঘাত বা প্লবতা প্রয়োগ করে, যা বস্তুটির ওজন অতি অল্প পরিমাণে হলেও কমিয়ে দেয়। তাই বায়ুতে বস্তুর যে ওজন পাওয়া যায়, তা তার আপাত ওজন, প্রকৃত ওজন নয়।
তুলার ঘনত্ব লোহার ঘনত্ব অপেক্ষা বহুগুণ কম বলে 1 কেজি তুলার আয়তন সমভরের লোহার আয়তন অপেক্ষা অনেক বেশি। তাই লোহা অপেক্ষা তুলার উপর বায়ু দ্বারা প্রযুক্ত ঊর্ধ্বঘাত অনেক বেশি হয়ে থাকে। স্বাভাবিকভাবেই তুলার ওজন হ্রাসও অনেক বেশি হয়। সাধারণভাবে যে-কোনো বস্তুকে বায়ু থেকে বায়ুশূন্য স্থানে নিয়ে গেলে প্লবতার মান শূন্য হয়ে যাওয়ার কারণে তার ওজন বৃদ্ধি হয়। বস্তুর আয়তন যত বেশি হয় তার ওজন বৃদ্ধিও তত বেশি হয়ে থাকে। তাই বায়ুতে ওজন করা (আপাত ওজন) 1 কেজি লোহা অপেক্ষা 1 কেজি তুলার আয়তন বেশি হওয়ায়, বায়ুশূন্য স্থানে মাপলে দেখা যায়, বায়ুতে ওজন করা 1 কেজি তুলা 1 কেজি লোহা অপেক্ষা ভারী।
ফোলানো বেলুনের ওজন বেশি হয় কি? তোমার উত্তরের স্বপক্ষে ব্যাখ্যা দাও।
একটি পাতলা রবারের বেলুনের ওজন ফোলানোর আগে ও পরে প্রায় সমানই থাকে। বায়ুপূর্ণ অবস্থায় বায়ুর ওজনের জন্য বেলুনের ওজন যতটা বৃদ্ধি পায়, বেলুনের আয়তন বৃদ্ধির জন্য অপসারিত বায়ুর ওজন বা প্লবতাও প্রায় একই পরিমাণে বাড়ে। এই কারণে ফোলাবার আগে ও পরে বেলুনের ওজনের উল্লেখযোগ্য পরিবর্তন দেখা যায় না।

উল্লেখ করা যায় যে, বেলুনের পরিবর্তে একটি ফাঁপা ধাতব গোলক নিয়ে পাম্পের সাহায্যে তার মধ্যে বায়ু প্রবেশ করালে দেখা যাবে, তার ওজন বৃদ্ধি পেয়েছে।
মেটাকেন্দ্র (Meta centre) কী এবং এটি ভাসমান বস্তুর স্থিতিশীলতার উপর কীভাবে প্রভাব ফেলে?
কোনো তরলের মধ্যে সাম্যে থাকা কোনো বস্তুকে তার সাম্যাবস্থান থেকে বিচ্যুত করলে বিচ্যুত অবস্থানে প্লবতাকেন্দ্রগামী উল্লম্ব রেখা বস্তুর কেন্দ্রীয় রেখাকে যে বিন্দুতে ছেদ করে, তাকে মেটাকেন্দ্র (Meta centre) বলে। মেটাকেন্দ্রের অবস্থান ভারকেন্দ্রের উপরে থাকলে ভাসমান বস্তু সুস্থির সাম্যে থাকে। এক্ষেত্রে বস্তুটি বিচ্যুত হলেও আবার তার পূর্বের অবস্থানে ফিরে আসতে চায়। অন্যদিকে মেটাকেন্দ্রের অবস্থান ভারকেন্দ্রের নীচে হলে সাম্যাবস্থার প্রকৃতি অস্থির হয়। অর্থাৎ, একবার বিচ্যুত হলে বস্তুটি আরও বেশি বিচ্যুত হতে চায়।
ভাসমান বস্তুর আপাত ওজন শূন্য হয় – ব্যাখ্যা করো।
তরলের আংশিক বা সম্পূর্ণ নিমজ্জিত যে-কোনো বস্তুর ক্ষেত্রেই বস্তুর উপর খাড়া ঊর্ধ্বমুখে ক্রিয়াশীল প্লবতা বল (B) সর্বদা বস্তুর ওজন (W) -এর সমান হয় এবং এই দুটি বল সর্বদা একই রেখায় পরস্পর বিপরীত অভিমুখে সক্রিয় হয়। সুতরাং, ভাসমান অবস্থায় বস্তুর কার্যকরী ওজন বা আপাত ওজন = (W – B) = 0। তাই বলা হয় যে, ভাসমান বস্তুর আপাত ওজন সর্বদা শূন্য হয়।
ভাসমান বস্তু সর্বদা সাম্যাবস্থায় থাকে। – ব্যাখ্যা করো।
তরলে আংশিক বা সম্পূর্ণ নিমজ্জিত বস্তুর উপর সমান ও বিপরীতমুখী দুটি বল ক্রিয়া করে –
- খাড়া নীচের দিকে ক্রিয়াশীল বস্তুর ওজন,
- খাড়া উল্লম্বদিকে ক্রিয়াশীল প্লবতা বল।
এই দুটি বল একই রেখা বরাবর বিপরীত অভিমুখে ক্রিয়া করায় একদিকে যেমন লব্ধি বল শূন্য হবার ফলে বস্তুটি চলন সাম্যে রৈখিক ত্বরণহীন থাকে, তেমনই বস্তুর মধ্যে কোনো আবর্তন গতিও সৃষ্টি হয় না। অর্থাৎ, বস্তুটি ঘূর্ণন সাম্যও বজায় রাখে। এই কারণে বলা হয় যে, ভাসমান বস্তু সর্বদা সাম্যে থাকে।
পার্থক্যধর্মী প্রশ্নোত্তর
কোনো পদার্থের ঘনত্ব (Density) ও আপেক্ষিক ঘনত্ব (Relative density) -এর মধ্যে পার্থক্য লেখো।
কোনো পদার্থের ঘনত্ব (Density) ও আপেক্ষিক ঘনত্ব (Relative density) -এর মধ্যে পার্থক্যগুলি হল –
| বিষয় | ঘনত্ব (Density) | আপেক্ষিক ঘনত্ব (Relative density) |
| সংজ্ঞা | পদার্থের একক আয়তনের ভরকে তার ঘনত্ব বলে। | কোনো পদার্থ তার সমআয়তন বিশিষ্ট 4°C উষ্ণতার জল অপেক্ষা যতগুণ ভারী, তাকে পদার্থটির আপেক্ষিক ঘনত্ব বলে। |
| একক | ঘনত্বের একটি নির্দিষ্ট একক আছে। SI ও CGS পদ্ধতিতে এর একক যথাক্রমে kg/m3 ও g/cm3। | আপেক্ষিক ঘনত্ব বা আপেক্ষিক গুরুত্বের কোনো একক নেই। |
| মাত্রীয় সংকেত | ঘনত্বের মাত্রীয় সংকেত [ML-3]। | আপেক্ষিক গুরুত্বের মাত্রীয় সংকেত নেই। |
| মান | পরিমাপের বিভিন্ন পদ্ধতিতে ঘনত্বের মান আলাদা। | পরিমাপের বিভিন্ন পদ্ধতিতে আপেক্ষিক গুরুত্বের মান সমান। |
গাণিতিক প্রশ্নাবলি
প্রয়োজনীয় সূত্রাবলি
প্লবতা = বস্তুর আপাত ওজন হ্রাস
বস্তুর প্রকৃত ওজন = জলে বস্তুর ওজন + বস্তুর ওজনের আপাত হ্রাস
একটি বস্তুর বায়ুতে ওজন 52 g-wt ও জলে নিমজ্জিত অবস্থায় ওজন 40g-wt। বস্তুটির ওপর ক্রিয়াশীল প্লবতা নির্ণয় করো।
বস্তুর বায়ুতে ওজন (W) = 52 g-wt।
আপাত ওজন বা জলে নিমজ্জিত অবস্থায় ওজন (W1) = 40 g-wt
∴ প্লবতা (B) = (W – W1)
= (52 – 40)
= 12 g-wt
= 12 × 1 × 980 dyn
= 11760 dyn
∴ বস্তুটির ওপর ক্রিয়াশীল প্লবতা 11760 dyn
জলে সম্পূর্ণ ডোবানো অবস্থায় একটি বস্তুর ওজন 50 g-wt। বস্তুটির আয়তন 15 cm3 হলে বস্তুটির প্রকৃত ওজন কত?
বস্তু দ্বারা অপসারিত জলের আয়তন = 15 cm3
ওই জলের ওজন = 15 × 1 = 15 g-wt (∵ জলের ঘনত্ব 1 g/cm3)
আর্কিমিডিসের সূত্রানুযায়ী,
বস্তু দ্বারা অপসারিত জলের ওজন = ওজনের আপাত হ্রাস = 15 g-wt
∴ বস্তুর প্রকৃত ওজন = জলে বস্তুর ওজন + বস্তুর ওজনের আপাত হ্রাস
= (50 + 15)
= 65 g-wt
∴ বস্তুটির প্রকৃত ওজন 65 g-wt
একটি কঠিন বস্তুর বায়ুতে ওজন 30 g-wt এবং আয়তন 10 cm3। বস্তুটিকে 1.75 g/cm3 ঘনত্বসম্পন্ন একটি তরলে সম্পূর্ণ ডোবানো হলে তরলে নিমজ্জিত অবস্থায় বস্তুটির ওজন কত হবে?
বস্তু কর্তৃক অপসারিত তরলের আয়তন = বস্তুর আয়তন
= 10 cm3
অপসারিত তরলের ওজন = বস্তুর উপর ক্রিয়াশীল প্লবতা বল
= (10 × 1.75)
= 17.5 g-wt
বস্তুটির আপাত ওজন হ্রাস = 17.5 g-wt
∴ বস্তুটির আপাত ওজন = (30 – 17.5) g-wt
= 12.5 g-wt
∴ তরলে নিমজ্জিত অবস্থায় বস্তুটির ওজন 12.5 g-wt
লোহার তৈরি একটি নিরেট গোলকের ব্যাস 21 cm। লোহার ঘনত্ব 7.8 g/cm3 হলে গোলকের ভর কত?
নির্ণেয় ভর = গোলকের আয়তন × ঘনত্ব
= \(\frac43\mathrm\pi\left(\frac{21}2\right)^3\times7.8\) g
= \(\frac43\times\frac{22}7\times\frac{21\times21\times21}{2\times2\times2}\times7.8\) g
= \(37837.8\) g
∴ গোলকের ভর \(37837.8\) g
D1 ও D2 ঘনত্বের দুটি পদার্থকে সমভরে মেশানো হলে মিশ্রণের ঘনত্ব কত হবে?
মনে করি পদার্থ দুটির ভর = m
∴ D1 ঘনত্ববিশিষ্ট পদার্থের আয়তন =\(\frac m{D_1}\)
∵
এবং D2 ঘনত্ববিশিষ্ট পদার্থের আয়তন = \(\frac m{D_2}\)
∴ মিশ্রণের ভর = m + m = 2 m
∴ মিশ্রণের আয়তন = \(\frac m{D_1}+\frac m{D_2}\)
∴
বা, মিশ্রণের ঘনত্ব = \(\frac{2m}{\left({\displaystyle\frac m{D_1}}+{\displaystyle\frac m{D_2}}\right)}\)
বা, মিশ্রণের ঘনত্ব = \(\frac{2m}{\left({\displaystyle\frac1{D_1}}+{\displaystyle\frac1{D_2}}\right)}\)
বা, মিশ্রণের ঘনত্ব = \(\frac{2D_1D_2}{D_1+D_2}\)
তিনটি তরলের ঘনত্বের অনুপাত 1 : 2 : 3। প্রথমটির ঘনত্ব 1 g/cm3 তরল তিনটিকে সম আয়তনে মেশালে মিশ্রণের ঘনত্ব কত হবে?
প্রশ্নানুযায়ী, প্রথম তরলের ঘনত্ব = 1 g/cm3 হলে দ্বিতীয়টির ঘনত্ব 2 g/cm3 এবং তৃতীয়টির ঘনত্ব 3 g/cm3।
মনে করি, প্রত্যেকটি তরলের V cm3 আয়তন নিয়ে মিশ্রণ তৈরি করা হল।
∴
বা, মিশ্রণের ঘনত্ব = \(\frac{V+2V+3V}{V+V+V}\)
বা, মিশ্রণের ঘনত্ব = \(\frac{6V}{3V}\)
বা, মিশ্রণের ঘনত্ব = 2 g/cm3।
একটি বস্তুর ভর 50 g। বস্তুটি জলে সম্পূর্ণ নিমজ্জিত অবস্থায় 100 cc জল অপসারণ করে। বস্তুটির ঘনত্ব কত?
বস্তুর ভর (m) = 50 g
বস্তুর আয়তন (V) = অপসারিত জলের আয়তন = 100 cc
∴ বস্তুর ঘনত্ব (d) = \(\frac mV\)
বা, বস্তুর ঘনত্ব (d) = \(\frac{50}{100}\)
বা, বস্তুর ঘনত্ব (d) = 0.05 g/cc
14°C তাপমাত্রায় 40 গ্রাম জলে একটি পাত্র পুরোপুরি ভরতি হয়। ওই পাত্রে 32 g কেরোসিন ধরলে কেরোসিনের ঘনত্ব কত?
বা, কেরোসিনের নির্ণেয় ঘনত্ব = \(\frac{32}{40}\) g/cc [∵ পাত্রের আয়তন = 40 g, জলের আয়তন = 40 cc]
বা, কেরোসিনের নির্ণেয় ঘনত্ব = 0.8 g/cc
1.5 g/cc ঘনত্বের 100 cc চিনির দ্রবণে আরও 100 cc জল মেশালে মিশ্রণটির ঘনত্ব কত হবে?
100 cc এবং 1.5 g/cc ঘনত্ববিশিষ্ট দ্রবণের ভর,
m1 = (100 × 1.5) g = 150 g
দ্রবণে মিশ্রিত জলের ভর,
m2 = (100 × 1) g = 100 g
∴ জলমিশ্রিত দ্রবণের ভর,
m = (m1 + m2) g = (150 + 100) g = 250 g
নতুন দ্রবণের আয়তন,
V = (100 + 100) cc = 200 cc
∴ মিশ্রণের ঘনত্ব, \(d=\frac mV\)
বা, মিশ্রণের ঘনত্ব, \(\frac{250}{200}\)
বা, মিশ্রণের ঘনত্ব, = \(\frac54\)
বা, মিশ্রণের ঘনত্ব, = 1.25 g/cc
∴ 100 cc জল মেশালে মিশ্রণটির ঘনত্ব 1.25 g/cc হবে।
259 g ভরের একটি ধাতব গোলককে 1.2 g/cc ঘনত্বযুক্ত তরলে সম্পূর্ণ নিমজ্জিত করা হলে নিমজ্জিত গোলকের ওজন হয় 19 g। এটির ঘনত্ব SI এককে নির্ণয় করো। গোলকটিকে আরও গভীরে নিমজ্জিত করলে ওর ওজন হ্রাস কি একই হবে?
নিমজ্জিত অবস্থায় গোলকের ওজন হ্রাস = সমআয়তন তরলের ওজন = (259 – 19) g = 240 g
∴ ওই তরলের আয়তন = গোলকের আয়তন
= \(\frac{240}{1.2}\) cc
= 200 cc
∴
= \(\frac{259}{200}\) g/cm3
= 1.295 g/cm3
গোলকটি আরও গভীরে নিমজ্জিত করলেও ওর ওজন হ্রাস একই হবে, কারণ – গোলকটি সব সময় সমআয়তন জল অপসরণ করবে। তাই ঊর্ধ্বমুখী বল বা প্লবতা একই থাকবে। তাই, ওজন হ্রাসও একই থাকবে।
লোহার আপেক্ষিক গুরুত্ব 7.8 এবং পারদের আপেক্ষিক গুরুত্ব 13.6। লোহা পারদে ভাসে। ভাসার সময় লোহার কত অংশ পারদে ডুবে থাকে?
কোনো বস্তুর আয়তনের n অংশ কোনো তরলে ডুবে থাকলে n = হবে।
যেখানে ρ = বস্তুর ঘনত্ব বা আপেক্ষিক গুরুত্ব
ρ1 = তরলের ঘনত্ব বা আপেক্ষিক গুরুত্ব
∴ \(n=\frac{7.8}{13.6}=0.573\)
∴ লোহার 0.573 অংশ পারদে ডুবে থাকে।
একটি স্প্রিং তুলা থেকে একটি ব্লককে বায়ুতে ঝুলিয়ে দেওয়া হলে সেটি 60 N পাঠ দেয়। ব্লকটি 4°C উষ্ণতার জলে নিমজ্জিত অবস্থায় থাকলে স্প্রিং তুলার পাঠ হয় 40 N। ব্লকটির আপেক্ষিক গুরুত্ব কত?
∴
বা, ব্লকটির আপেক্ষিক গুরুত্ব = \(\frac{60}{60-40}\)
বা, ব্লকটির আপেক্ষিক গুরুত্ব = \(\frac{60}{20}\)
বা, ব্লকটির আপেক্ষিক গুরুত্ব = 3
একটি নিরেট বস্তু জলে অংশ \(\frac45\) নিমজ্জিত রেখে ভাসে। বস্তুর ঘনত্ব SI এককে নির্ণয় করো।
ধরি, বস্তুর আয়তন = V, ঘনত্ব = d,
জলের ঘনত্ব (d1) = 1 g/cc
∴ বস্তুর ওজন = Vdg
বস্তু দ্বারা অপসারিত জলের আয়তন = \(\frac45\) V
বস্তু দ্বারা অপসারিত জলের ওজন = Vd1g
ভাসনের শর্তানুযায়ী,
Vdg = \(\frac45\) Vd1g
বা, d = \(\frac45\times1\) [∵ d1 = 1 g/cc]
বা, d = 0.8
∴ বস্তুর ঘনত্ব (SI এককে) = 0.8 × 1000= 800 kg/m3
একটি ফাঁপা গোলকের ভেতরের ও বাইরের ব্যাস যথাক্রমে 8 cm ও 10 cm। 1.5 g/cm3 ঘনত্বের তরলে গোলকটি ডোবেও না, ভাসেও না। গোলকটির উপাদানের ঘনত্ব কত?
ফাঁপা গোলকের বাইরের ব্যাস ও ভেতরের ব্যাস যথাক্রমে 10 cm ও 8 cm।
∴ ফাঁপা গোলকের বাইরের ব্যাসার্ধ ও ভেতরের ব্যাসার্ধ যথাক্রমে 5 cm ও 4 cm।
ফাঁপা গোলকের আয়তন (V) = \(\frac43\pi\left(5^3-4^3\right)\)
= \(\frac43\pi\left(125-64\right)\)
= \(\frac43\pi\times61\)
ধরি, গোলকটির উপাদানের ঘনত্ব = d
∴ গোলকটির ভর = \(\frac43\pi\times61\times d\)
যেহেতু গোলকটি তরলে ডোবেও না, ভাসেও না, সুতরাং গোলকের ভর = তরলে সম্পূর্ণ নিমজ্জিত অবস্থায় গোলকটির দ্বারা অপসারিত তরলের ভর।
∴ \(\frac43\pi\times61\times d=\frac43\pi\times5^3\times1.5\)
বা, \(d=\frac{125\times1.5}{61}=3.073\)
∴ গোলকটির উপাদানের ঘনত্ব = 3.073 g/cc
500 গ্রাম ভরের একটি কঠিনের আয়তন 350 cm3 1. কঠিনটির ঘনত্ব কত? 2. কঠিনটির আপেক্ষিক ঘনত্ব নির্ণয় করো। 3. কঠিনটিকে জলে ডোবালে তা কত ভরের জল অপসারণ করবে?
1.
= \(\frac{500}{350}\) g/cc
= 1.428 g/cc
2. যেহেতু CGS পদ্ধতিতে ঘনত্ব ও আপেক্ষিক ঘনত্বের মান সমান হয়, তাই কঠিনটির আপেক্ষিক ঘনত্ব = 1.428।
3. এখন কঠিনটিকে জলে ডোবালে তা নিজের সমআয়তন জল অর্থাৎ 350 cm3 জল অপসারণ করে। জলের ঘনত্ব 1 g/cm3 হওয়ায়, 350 cm3 জলের ভর 350 g।
∴ কঠিনটিকে জলে ডোবালে তা 350 g ভরের জল অপসারণ করবে।
একটি কঠিন বস্তুর বায়ুতে, জলে এবং কেরোসিনে ভর যথাক্রমে 5g, 3 g এবং 3.4 g। বস্তুটির উপাদানের এবং কেরোসিনের আপেক্ষিক ঘনত্ব নির্ণয় করো।
বস্তুটির বায়ুতে ওজন = 5 g-wt এবং জলে ওজন = 3 g-wt।
∴ জলে ওজনের আপাত হ্রাস = বস্তুর সমআয়তন জলের ওজন = (5 – 3) = 2 g-wt
∴ বস্তুর আয়তন = 2 cc [∵ জলের ঘনত্ব = 1 g/cc]
∴
= \(\frac52\) g/cc
= 2.5 g/cc
∴
= \(\frac{\left(5-3.4\right)}{\left(5-3\right)}\)
= \(\frac{1.6}2\)
= 0.8
একটি বস্তুর জলে নিমজ্জিত অবস্থায় ওজন 105 g-wt, কিন্তু বায়ুতে তার ওজন 120 g-wt। বস্তুটির আপেক্ষিক গুরুত্ব কত?
বায়ুতে বস্তুর ওজন বা প্রকৃত ওজন = 120 g-wt, জলে নিমজ্জিত অবস্থায় আপাত ওজন = 105 g-wt
∴ বস্তুর আপাত ওজন হ্রাস = (120 – 105) = 15 g-wt।
∴ বস্তুর আয়তন = 15 cc [∵ CGS পদ্ধতিতে জলের ঘনত্ব = 1 g/cc]
∴ বস্তুর ঘনত্ব = \(\frac{120}{15}=8\) g/cc
∴ আপেক্ষিক গুরুত্ব = 8
চিত্রে জলে নিমজ্জিত A বস্তুটির আয়তন ও ঘনত্ব নির্ণয় করো। বস্তুটির ভর 200 g।
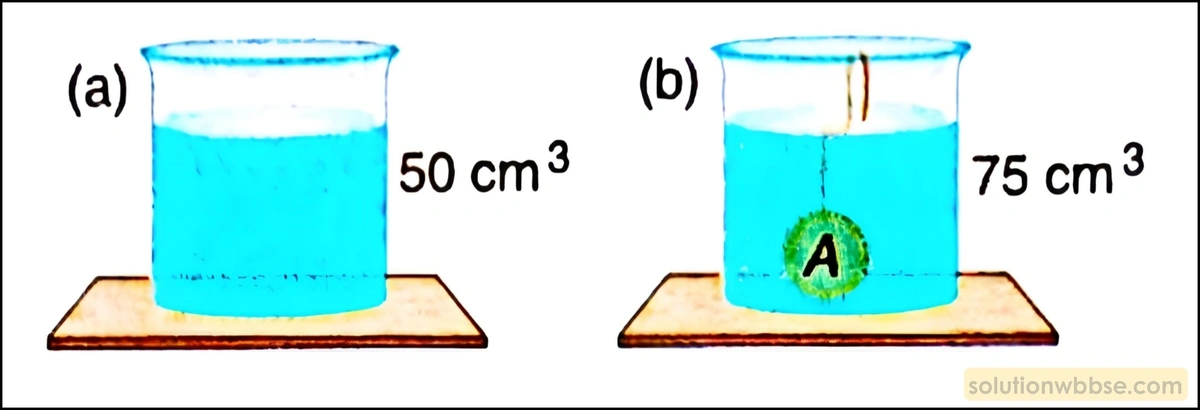
প্রথমে জলের আয়তন = 50 cm3
A বস্তুকে জলে নিমজ্জিত করলে জলের আয়তন = 75 cm3
∴ বস্তুর আয়তন = (75 – 50) = 25 cm3
∴
বা, বস্তুর ঘনত্ব = \(\frac{200}{25}=8\) g/cm3
বা, বস্তুর ঘনত্ব = = 8 g/cm3
500 g ভরের একটি প্লাস্টিকের বোতলের আয়তন 450 cc। বোতলটি জলের মধ্যে ডুবে যাবে না ভাসবে? জলের ঘনত্ব 1 g/cc। বোতল দ্বারা অপসারিত জলের ভর নির্ণয় করো।
প্লাস্টিক বোতলের ভর = 500 g
প্লাস্টিক বোতলের আয়তন (V) = 450 cc
∴ প্লাস্টিক বোতলের ওজন = 500 g-wt
জলের ঘনত্ব (d) = 1 g/cc
প্লাস্টিক বোতলের ওপর ক্রিয়াশীল প্লবতা = Vdg
= 450 × 1 × g
= 450 g
যেহেতু, প্লাস্টিক বোতলের ওজন, ওর ওপর ক্রিয়াশীল প্লবতা অপেক্ষা বেশি, তাই প্লাস্টিক বোতলটি জলের মধ্যে ডুবে যাবে।
∴ বোতল দ্বারা অপসারিত জলের আয়তন = 450 cc
∴ বোতল দ্বারা অপসারিত জলের ভর = Vd
= 450 × 1 g
= 450 g।
∴ বোতল দ্বারা অপসারিত জলের ভর 450 g
নৈর্ব্যক্তিক প্রশ্নোত্তর
সঠিক উত্তরটি নির্বাচন করো
যে উষ্ণতায় জলের ঘনত্ব সর্বাধিক তা হল –
- 32°F
- 42°F
- 4°F
- 39.2°F
উত্তর – 4. 39.2°F
দুটি তরলের ঘনত্ব যথাক্রমে d1 ও d2। তরল দুটিকে সমভরে মিশ্রিত করলে মিশ্রণের ঘনত্ব হবে –
- \(\frac{d_1+d_2}2\\\)
- \(\frac{2d_1d_2}{d_1+d_2}\\\)
- \(\frac{d_1+d_2}{2d_1d_2}\\\)
- \(\sqrt{d_1d_2}\)
উত্তর – 2. \(\frac{2d_1d_2}{d_1+d_2}\)
কোন্ উষ্ণতায় জলের ঘনত্ব সর্বাধিক? –
- 0°C
- 2°C
- 4°C
- 10°C
উত্তর – 3. 4°C
একটি স্টিমার নদী থেকে সাগরে প্রবেশ করলে –
- আরও ভেসে উঠবে
- ডুবে যাবে
- কিছুটা ডুবে যাবে
- কাত হয়ে পড়বে
উত্তর – 1. আরও ভেসে উঠবে
দুটি তরলের ঘনত্ব যথাক্রমে 1.6 g/cm3 এবং 2 g/cm3। তরল দুটি সমআয়তনে মিশ্রিত করলে মিশ্রণের ঘনত্ব হবে –
- 1.65 g/cm3
- 1.7 g/cm3
- 1.8 g/cm3
- 1.9 g/cm3
উত্তর – 3. 1.8 g/cm3
কোনো পদার্থের ঘনত্ব 8000 kg/m3 হলে, আপেক্ষিক গুরুত্ব কত হবে? –
- 6
- 10
- 16
- 8
উত্তর – 4. 8
W1 ওজনের একটি বস্তু W2 ওজনের জল অপসারিত করে। যদি বস্তুটি জলে ডুবে যায় তাহলে কোনটি সঠিক? –
- W1 = W2
- W1 > W2
- W1 < W2
- W1 ≥ W2
উত্তর – 2. W1 > W2
বায়ুতে কোনো বস্তুর ওজন W ও কোনো তরলে নিমজ্জিত অবস্থায় ওই তরল কর্তৃক বস্তুর ওপর প্রযুক্ত প্লবতা B হলে, ওই তরলের যে-কোনো বিন্দুতে বস্তুটির ভাসনের শর্ত হল –
- W > B
- W < B
- W = B
- W ≤ B
উত্তর – 4. W ≤ B
ঘনত্বের মাত্রীয় সংকেত হল –
- [ML2]
- [ML3]
- [ML-2]
- [ML-3]
উত্তর – 4. [ML-3]
ঘনত্বের মান উল্লেখ করার সময় কোন্ ক্ষেত্রে চাপের উল্লেখ অপরিহার্য? –
- কঠিন
- তরল
- গ্যাস
- উপরের তিন ক্ষেত্রেই
উত্তর – 3. গ্যাস
একটি নিরেট লোহার বলকে জলে ডোবালে লোহার বলের ওজন –
- একই থাকে
- কমে
- বাড়ে
- প্রথমে বাড়ে পরে কমে
উত্তর – 2. কমে
লবণমিশ্রিত জলের মধ্যে ডিম ডুবে ভাসে কারণ –
- ডিমের ওজন প্লবতার চেয়ে বেশি
- ডিমের ওজন প্লবতার চেয়ে কম
- ডিমের ওজন ও প্লবতা বলের মান সমান
- সবগুলিই সত্য।
উত্তর – 3. ডিমের ওজন ও প্লবতা বলের মান সমান
তরলে সম্পূর্ণ নিমজ্জিত বস্তুর গভীরতা বৃদ্ধির সঙ্গে এর ওপর –
- চাপ বৃদ্ধি পায় এবং প্লবতা হ্রাস পায়
- চাপ ও প্লবতা দুইই বৃদ্ধি পায়
- চাপ বৃদ্ধি পায় কিন্তু প্লবতা স্থির থাকে
- চাপ স্থির থাকে কিন্তু প্লবতা বৃদ্ধি পায়
উত্তর – 3. চাপ বৃদ্ধি পায় কিন্তু প্লবতা স্থির থাকে
একটি তরলপূর্ণ পাত্রে একখণ্ড কর্ক তার আয়তনেরও অংশ নিমজ্জিত রেখে ভাসে। এই অবস্থায় 4 তরলপূর্ণ পাত্রটিকে অবাধে পড়তে দিলে –
- কর্কটি তরল থেকে লাফিয়ে বাইরে চলে আসবে
- কর্কটি পুরোপুরি ডুবে যাবে
- কর্কটি পুরোপুরি ভেসে উঠবে
- কর্কটি তরল সাপেক্ষে একই অবস্থায় থাকবে
উত্তর – 4. কর্কটি তরল সাপেক্ষে একই অবস্থায় থাকবে
একটি জ্যান্ত মাছকে একটি জলের বালতিতে ছেড়ে দিলে বালতিসহ জলের ওজন –
- কমে যাবে
- বেড়ে যাবে
- একই থাকবে
- বলা সম্ভব নয়
উত্তর – 3. একই থাকবে
একটি বস্তু কোনো তরলে আংশিক নিমজ্জিত অবস্থায় আছে। বস্তু এবং তরলকে চাঁদে নিয়ে গেলে বস্তুটি –
- আগের মতো ভাসবে
- ডুবে যাবে
- কম অংশ নিমজ্জিত রেখে ভাসবে
- বেশি অংশ নিমজ্জিত রেখে ভাসবে
উত্তর – 1. আগের মতো ভাসবে
একটি বস্তু একটি তরলে ঠিক ডুবে ভাসছে, বস্তুটির ঘনত্ব ও তরলের ঘনত্ব সমান। বস্তুটিকে তরলের ভেতরে কিছুটা ঠেলে দেওয়া হল, বস্তুটির কী হবে? –
- এটি আস্তে আস্তে তার প্রাথমিক অবস্থানে ফিরে আসবে
- এটি ডুবে যাবে
- এটি নিমজ্জিত অবস্থাতেই থেকে যাবে
- এটি খুব দ্রুত উপরে উঠে আসবে
উত্তর – 3. এটি নিমজ্জিত অবস্থাতেই থেকে যাবে
প্লবতা নির্ভর করে না –
- অপসারিত তরলের আয়তন
- নিমজ্জিত বস্তুর ঘনত্ব
- তরলের ঘনত্ব
- অভিকর্ষজ ত্বরণের ওপর
উত্তর – 2. নিমজ্জিত বস্তুর ঘনত্ব
পারদের সমুদ্রে লোহার দণ্ড সর্বদা –
- ডুববে
- ডুবে ভাসবে
- ভাসবে
- ভাসতে পারে বা ডুবতে পারে
উত্তর – 3. ভাসবে
একটি বস্তুকে স্থির প্রবাহীতে নিমজ্জিত করলে বস্তুটির ওজন –
- একই থাকে
- বাড়ে
- কমে
- বাড়ে বা কমে
উত্তর – 3. কমে
শূন্যস্থান পূরণ করো
লোহা ___ -এ ডোবে কিন্তু ___ -এ ভাসে।
উত্তর লোহা জল -এ ডোবে কিন্তু পারদ -এ ভাসে।
আর্কিমিডিসের নীতি শুধু তরল নয়, ___ পদার্থের ক্ষেত্রেও প্রযোজ্য।
উত্তর – আর্কিমিডিসের নীতি শুধু তরল নয়, গ্যাসীয় পদার্থের ক্ষেত্রেও প্রযোজ্য।
SI এককে 4°C উষ্ণতায় জলের ঘনত্ব হল ___।
উত্তর – SI এককে 4°C উষ্ণতায় জলের ঘনত্ব হল 1000 কিগ্রা/ঘন মি।
আপেক্ষিক গুরুত্ব একটি ___ ভৌতরাশি।
উত্তর – আপেক্ষিক গুরুত্ব একটি মাত্রাহীন ভৌতরাশি।
___ এর জন্য তরলে নিমজ্জিত বস্তুর ওজন কমে যায়।
উত্তর – প্লবতা -এর জন্য তরলে নিমজ্জিত বস্তুর ওজন কমে যায়।
ভাসমান বস্তুর আপাত ওজন হয় ___।
উত্তর – ভাসমান বস্তুর আপাত ওজন হয় শূন্য।
কোনো বস্তুর বায়ুপূর্ণ স্থানে ওজন অপেক্ষা বায়ুশূন্য স্থানে ওজন ___ হয়।
উত্তর – কোনো বস্তুর বায়ুপূর্ণ স্থানে ওজন অপেক্ষা বায়ুশূন্য স্থানে ওজন বেশি হয়।
প্লবতার SI একক ___।
উত্তর – প্লবতার SI একক নিউটন।
SI -তে কোনো পদার্থের উপাদানের ঘনত্ব, CGS পদ্ধতিতে তার ঘনত্বের সাংখ্যমানের ___ গুণ।
উত্তর – SI -তে কোনো পদার্থের উপাদানের ঘনত্ব, CGS পদ্ধতিতে তার ঘনত্বের সাংখ্যমানের 1000 গুণ।
ঠিক বা ভুল নির্বাচন করো
ভাসমান বস্তু চলন সাম্য ও ঘূর্ণন সাম্যের শর্ত মেনে চলে।
উত্তর – ঠিক।
আর্কিমিডিসের সূত্রকে কাজে লাগিয়ে সংকর ধাতুতে তাদের উপাদানগুলির পরিমাণ নির্ণয় করা হয়।
উত্তর – ঠিক।
প্লবতার মান বস্তুর জ্যামিতিক আকৃতির ওপর নির্ভরশীল।
উত্তর – ভুল।
সঠিক উত্তর – আয়তনের ওপর।
জলের প্লবতার জন্য নৌকার তলার ছিদ্রের মধ্যে দিয়ে জল ঢোকে।
উত্তর – ঠিক।
পারদ জলের চেয়ে বেশি প্লবতা বল সৃষ্টি করতে পারে।
উত্তর – ঠিক।
নোঙর করা জাহাজ যাতে উলটে না যায়, সেজন্য তাকে একেবারে খালি রাখা হয়।
উত্তর – ভুল।
সঠিক উত্তর – কিছু পরিমাণ ভার চাপানো হয়।
বস্তুর ভাসন ও নিমজ্জন একান্তভাবেই বস্তু ও তরলের ঘনত্বের মানের ওপর নির্ভরশীল।
উত্তর – ঠিক।
উষ্ণতার সঙ্গে জলের ঘনত্ব পরিবর্তিত হয় বলে আপেক্ষিক গুরুত্বের পরীক্ষালব্ধ মানের উষ্ণতা সংশোধন প্রয়োজন হয়।
উত্তর – ঠিক।
বায়ুশূন্যস্থানে 1 কিগ্রা তুলা, 1 কিগ্রা লোহা অপেক্ষা ভারী হয়।
উত্তর – ঠিক।
দু-একটি শব্দে উত্তর দাও
প্লবতা কেন্দ্র কোথায় অবস্থিত?
বস্তু দ্বারা অপসারিত তরলের ভারকেন্দ্রে অবস্থিত।
উষ্ণতা বৃদ্ধিতে তরলের প্লবতার কী পরিবর্তন হবে? (যদি ধরে নেওয়া হয় বস্তুর তরলে নিমজ্জিত অংশের আয়তন অপরিবর্তিত)।
উষ্ণতা বৃদ্ধিতে তরলের প্লবতা কমে যাবে (কারণ, ঘনত্ব কমে যাবে)।
পরিমাপের কোন্ পদ্ধতিতে ঘনত্ব ও আপেক্ষিক গুরুত্বের মান সমান?
পরিমাপের CGS পদ্ধতিতে ঘনত্ব ও আপেক্ষিক গুরুত্বের মান সমান।
277K তাপমাত্রায় জলের ঘনত্ব SI এককে কত?
277K তাপমাত্রায় জলের ঘনত্ব SI এককে 277K তাপমাত্রায় জলের ঘনত্ব SI এককে কত? kg/m3।
অবাধে পতনশীল বস্তুর ক্ষেত্রে আর্কিমিডিসের নীতি প্রযোজ্য হবে কি?
অবাধে পতনশীল বস্তুর ক্ষেত্রে আর্কিমিডিসের নীতি প্রযোজ্য হবে না (কারণ অবাধে পতনশীল বস্তুর ওজন নেই)।
বায়ুতে কোনো বস্তুর ওজন W ও কোনো তরলে নিমজ্জিত অবস্থায় ওই তরল কর্তৃক বস্তুর ওপর প্লবতা B হলে, ওই তরলের যে-কোনো বিন্দুতে বস্তুটির ভাসনের শর্ত কী হবে?
বায়ুতে কোনো বস্তুর ওজন W ও কোনো তরলে নিমজ্জিত অবস্থায় ওই তরল কর্তৃক বস্তুর ওপর প্লবতা B হলে, ওই তরলের যে-কোনো বিন্দুতে বস্তুটির ভাসনের শর্ত W = B হবে।
মোমের ঘনত্ব 0.95 g/cm3। মোমের আপেক্ষিক গুরুত্ব কত?
মোমের ঘনত্ব 0.95 g/cm3। মোমের আপেক্ষিক গুরুত্ব 0.95।
প্লবতার মাত্রীয় সংকেত কী?
প্লবতার মাত্রীয় সংকেত [MLT-2] (কারণ- এটি একটি বল)।
প্লবতার SI একক কী?
প্লবতার SI একক নিউটন।
রুপোর আপেক্ষিক গুরুত্ব 10.8 হলে, SI -তে রুপোর ঘনত্ব কত হবে?
রুপোর আপেক্ষিক গুরুত্ব 10.8 হলে, SI -তে রুপোর ঘনত্ব (10.8 × 1000) kg/m3 = 10800 kg/m3 হবে।
4°C তাপমাত্রায় জলের ঘনত্ব SI -তে কত?
4°C তাপমাত্রায় জলের ঘনত্ব SI -তে 1000) kg/m3।
একক ও মাত্রাহীন একটি ভৌতরাশির নাম লেখো।
একক ও মাত্রাহীন একটি ভৌতরাশির নাম হল আপেক্ষিক গুরুত্ব (দুটি একই রাশির অনুপাত হওয়ায়)।
আর্কিমিডিসের সূত্রটি কি কৃত্রিম উপগ্রহের অভ্যন্তরে প্রযোজ্য?
না (কারণ এখানে বস্তুর ওজন শূন্য হয়)।
জল ও কেরোসিনের মধ্যে কার প্লবতা বেশি?
জল ও কেরোসিনের মধ্যে জলের প্লবতা বেশি (কারণ – জলের ঘনত্ব কেরোসিন অপেক্ষা বেশি) ।
চিত্রে A বস্তুটির আপাত ওজন কত হবে?
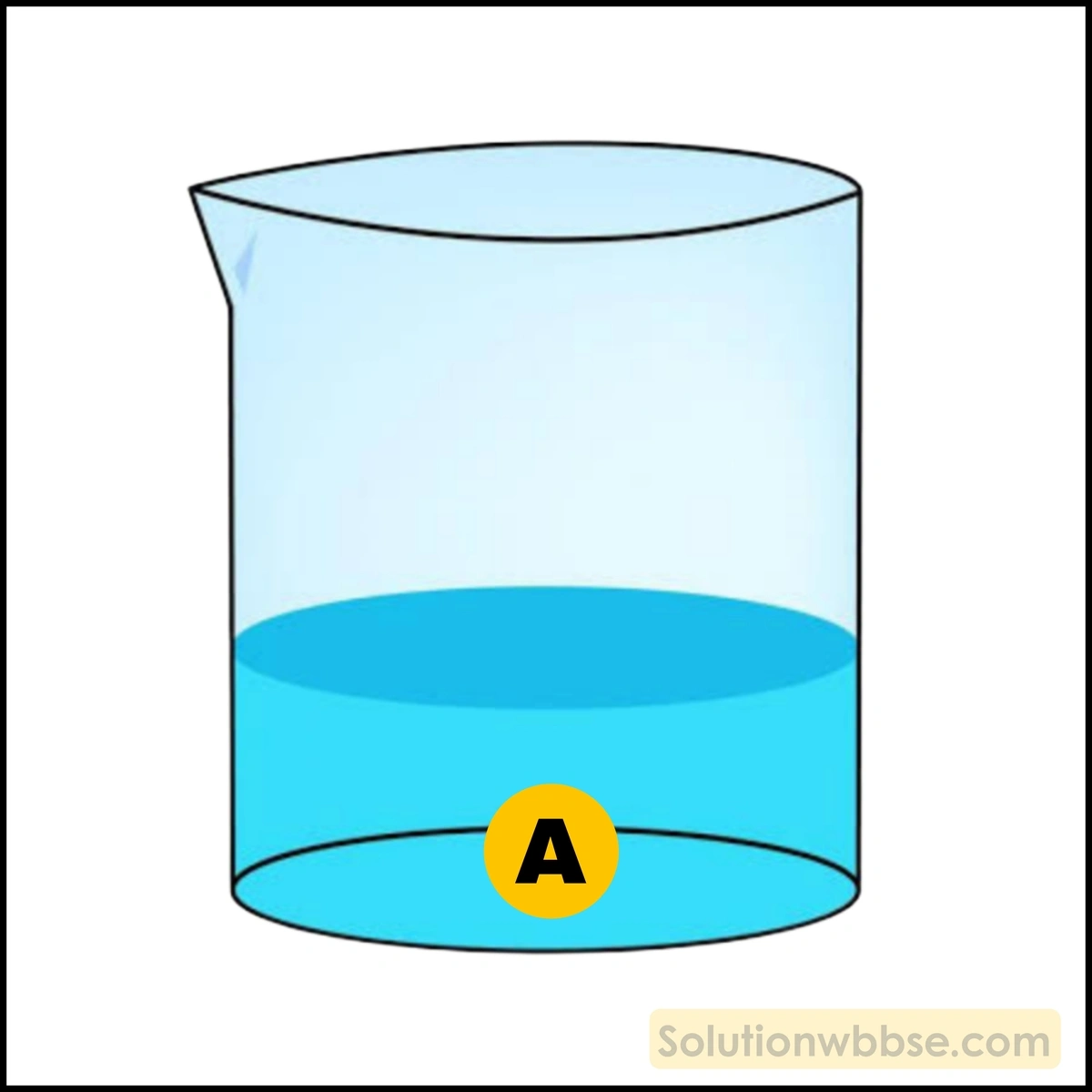
বস্তুটির আপাত ওজন শূন্য হবে (কারণ, এক্ষেত্রে বস্তুর ওজন ও প্লবতা সমান)।
আর্কিমিডিসের সূত্র কোন্ জাতীয় পদার্থের ক্ষেত্রে প্রযোজ্য?
আর্কিমিডিসের সূত্র স্থির প্রবাহী (তরল ও গ্যাস) -এর ক্ষেত্রে প্রযোজ্য।
আর্কিমিডিসের সূত্রকে কাজে লাগিয়ে কী কী নির্ণয় করা যায়?
আর্কিমিডিসের সূত্রকে কাজে লাগিয়ে যে-কোনো আকৃতির কঠিন বস্তুর আয়তন ও ঘনত্ব নির্ণয় করা যায়।
প্লবতা কোন্ অভিমুখে ক্রিয়া করে?
প্লবতা বস্তুর ওজনের বিপরীত দিকে ক্রিয়া করে।
একটি কর্ক জলে সম্পূর্ণ নিমজ্জিত অবস্থায় ভাসছে। ওর আপাত ওজন কত হবে?
একটি কর্ক জলে সম্পূর্ণ নিমজ্জিত অবস্থায় ভাসছে। ওর আপাত ওজন শূন্য হবে।
প্লবতা ক্রিয়া-প্রতিক্রিয়া নীতি মান্য করে কি?
হ্যাঁ, প্লবতা ক্রিয়া-প্রতিক্রিয়া নীতি মেনে চলে।
প্লিমসল রেখায় ব্যবহৃত TF, F, T, S, W চিহ্নগুলোর অর্থ কী এবং এগুলো জাহাজের ক্ষেত্রে কী নির্দেশ করে?
অনেক বেশি ভার বহনকারা জাহাজগুলি বাঁচাতে জাহাজের খোলের বাইরে প্লিমসল রেখা আঁকা থাকে। তাতে অক্ষরগুলি বিশেষ অর্থবহনকরে – TF = Tropical Fresh Water, F = Fresh Water, T = Tropical Sea Water, S = Summer Temperature Sea Water, W = Winter Sea Water.
দুটি একই মাপের গ্লাস জল দিয়ে কানায় কানায় ভরতি করা আছে। তবে একটিতে একখণ্ড বরফ ভাসছে। গ্লাস দুটির ওজন কি আলাদা হবে?
না, কারণ – যে গ্লাসটিতে বরফের টুকরো আছে সেখানে বরফখণ্ড যে আয়তনের জল অপসারণ করে আছে তার ওজন বরফের ওজনের সমান (ভাসনের শর্তানুসারে)। ফলে, বরফযুক্ত গ্লাসটিতে জলের পরিমাণ কম থাকলেও উভয় গ্লাসের ওজন সমান হবে।
একটি তুলাযন্ত্রের কোনো একটি তুলাপাত্রে জলপূর্ণ বিকার রেখে অপর পাত্রে উপযুক্ত বাটখারা চাপিয়ে তুলাদণ্ডটিকে অনুভূমিক করা আছে। এখন এক টুকরো লোহাকে সুতোয় বেঁধে বিকারের গায়ে না ঠেকিয়ে জলে ডুবিয়ে ধরা হল। এর ফলে তুলাদণ্ডের সাম্য নষ্ট হবে কি?
বিকারের জল লোহার টুকরোর উপর ঊর্ধ্বমুখী প্লবতা প্রয়োগ করে। নিউটনের তৃতীয় সূত্র অনুযায়ী, লোহার টুকরোটিও জলের উপর সমান ও বিপরীতমুখী প্রতিক্রিয়া বল (প্লবতার প্রতিক্রিয়া) প্রয়োগ করে। এই নিম্নমুখী প্রতিক্রিয়ার কারণেই বিকার বসানো তুলাপাত্রটি নীচে ঝুঁকে যায়। অর্থাৎ, তুলাদণ্ডের সাম্য নষ্ট হয়।
পরিভ্রমণরত মহাকাশযানের ভিতর একটি কর্ককে পারদে ডুবিয়ে ছেড়ে দিলে তা ভেসে উঠবে কি? যুক্তিসহ উত্তর দাও।
মহাশূন্যে অভিকর্ষজ ত্বরণের অস্তিত্ব না থাকায় পরিভ্রমণরত মহাকাশযানের ভিতরে সকল বস্তু ভারহীন অবস্থায় থাকে। তাই, সেখানে একটি কর্ককে পারদে ডোবালে, অপসারিত পারদের কোনো ওজন থাকবে না এবং পারদও কর্কের ওপর কোনো ঊর্ধ্বঘাত প্রয়োগ করবে না। অর্থাৎ, এই অবস্থায় প্লবতার ধারণারও কোনো অস্তিত্ব থাকে না। ফলে, কর্কটি পারদে ডুববে না বা ভাসবে না। যেখানে সেটিকে ছেড়ে দেওয়া হবে, কর্কটি সেখানেই স্থির থাকবে।
ρ1 ঘনত্ববিশিষ্ট একটি তরলের m1 ভরের সঙ্গে, ρ2 ঘনত্ববিশিষ্ট অপর একটি তরলের m2 ভর মিশ্রিত করা হল। যদি মিশ্রণের আয়তন অপরিবর্তিত থাকে তবে মিশ্রণের ঘনত্ব কত?
মিশ্রণের মোট ভর = (m1 + m2)
∴
= \(\frac{m_1}{\rho_1}\)
∴
= \(\frac{m_2}{\rho_2}\)
∴
= \(\frac{m_2}{\rho_2}\)
= \(\frac{m_1+m_2}{{\displaystyle\frac{m_1}{\rho_1}}+{\displaystyle\frac{m_2}{\rho_2}}}\)
= \(\frac{\rho_1\rho_2\left(m_1+m_2\right)}{m_1\rho_2+m_2\rho_1}\)
জাহাজের খোল খালি না রেখে তাতে কিছু ভার বা ব্যালাস্ট (Ballast) চাপানো হয় কেন?
ভরতি জাহাজ অপেক্ষা খালি জাহাজের ভারকেন্দ্র উপরে থাকে এবং মেটাকেন্দ্রিক উচ্চতা কম হয়। তাই, ভরতি জাহাজ অপেক্ষা খালি জাহাজ অস্থির সাম্যে থাকে এবং ঢেউ বা ঝড়ের দোলায় তার ডুবে যাওয়ার সম্ভাবনা বেশি হয়। এই কারণে, জাহাজ খালি না রেখে সুস্থিতি বৃদ্ধির জন্য তার খোলে কিছু ভার চাপিয়ে রাখা হয়।
পাথর বোঝাই একটি নৌকা পুকুরের জলে ভাসছে। পাথরগুলি জলে ফেলে দিলে পুকুরের জলতলের কী পরিবর্তন হবে?
ধরা যাক, পাথরগুলির মোট ভর m গ্রাম এবং পাথরের ঘনত্ব ρ গ্রাম/ঘনসেমি। পাথরগুলি নৌকার উপর থাকলে সেগুলি নিজ ওজনের সমান ওজনবিশিষ্ট জল নৌকার মাধ্যমে অপসারণ করে অর্থাৎ, অপসারিত জলের আয়তন হয় m ঘনসেমি।
কিন্তু পাথরগুলি জলে ফেলে দিলে সেগুলি নিজ আয়তনের \(\frac m\rho\) সমান অর্থাৎ, ঘনসেমি জল অপসারণ করে। এখন ρ > 1 হওয়ায় \(\frac m\rho<m\) ঘনসেমি। সুতরাং, দ্বিতীয় ক্ষেত্রে অপসারিত জলের আয়তন কম হবে। তাই, পুকুরের জলতল কিছুটা কমে যাবে।
আবদ্ধ খাঁচায় রাখা একটি পাখি তলায় না বসে খাঁচার মধ্যে উড়তে শুরু করল। খাঁচা একটি স্প্রিং তুলার হুক থেকে ঝোলানো হলে স্প্রিং তুলার পাঠে কী পরিবর্তন লক্ষ করা যাবে?
ওড়ার সময় পাখি নিজ ওজনের সমান নিম্নমুখী ঘাত বায়ুর উপর প্রয়োগ করে। আবদ্ধ খাঁচায় এই ঘাত খাঁচার তলদেশে সঞ্চালিত হয়। ফলে, পাখিসহ খাঁচার ওজন একই থাকে। অর্থাৎ, স্প্রিং তুলার পাঠের কোনো পরিবর্তন হয় না।
1.3 g/cc ঘনত্বের তরল দ্বারা কানায় কানায় পূর্ণ একটি বিকারের মধ্যে একখণ্ড বরফ ভাসছে। বরফটি সম্পূর্ণ গলে গেলে তরলতলের কোনো পরিবর্তন হবে কি?
ধরি, বরফখণ্ডের ভর = m গ্রাম।
সুতরাং, বরফখণ্ড কর্তৃক অপসারিত তরলের ভর = m গ্রাম।
∴ বরফখণ্ড কর্তৃক অপসারিত তরলের আয়তন = \(V_1=\frac m{1.3}\) cc।
এখন বরফটি সম্পূর্ণ গলে গেলে, বরফগলা জলের আয়তন হয় = \(V_2=\frac m1=m\) cc।
যেহেতু V2 > V1 এবং বিকারটি তরল দ্বারা কানায় কানায় পূর্ণ আছে। তাই, বরফটি সম্পূর্ণ গলে গেলে কিছু পরিমাণ তরল উপচে পড়বে।
দুটি তরল পদার্থ সমআয়তনে মেশালে মিশ্রণের আপেক্ষিক গুরুত্ব হয় 4। তাদের সমভরে মেশালে মিশ্রণের আপেক্ষিক গুরুত্ব হয় 3। তরল দুটির আপেক্ষিক গুরুত্ব নির্ণয় করো। ধরে নাও, মিশ্রণের ফলে আয়তনের কোনো পরিবর্তন হয় না।
ধরা যাক, তরল দুটির আপেক্ষিক গুরুত্ব S1 ও S2।
তরল দুটির প্রত্যেকটির আয়তন V হলে, মিশ্রণের মোট আয়তন হয় 2V যেহেতু ভর এক্ষেত্রে অপরিবর্তিত থাকে,
∴ VS1ρW + VS2ρW = 2V × 4ρw
বা, S1 + S2 = 8 ___(1) [পদার্থের ঘনত্ব = আপেক্ষিক গুরুত্ব × জলের ঘনত্ব (ρW)]
তরল দুটিকে সমভরে মেশালে মিশ্রণের মোট ভর হয় 2 m এবং আপেক্ষিক গুরুত্ব = 4।
এক্ষেত্রে আয়তন অপরিবর্তিত থাকায়,
\(\frac m{S_1\rho_W}+\frac m{S_2\rho_W}=\frac{2m}{3\rho_W}\\\)বা, \(\frac1{S_1}+\frac1{S_2}=\frac23\)
বা, \(\frac{S_1+S_2}{S_1S_2}=\frac23\) ___(2)
(1) ও (2) নং সমীকরণ সমাধান করে পাই,
\(\frac8{S_1S_2}=\frac23\\\)বা, S1S2 = 12 ___(3)
(1) ও (3) থেকে সমাধান করে পাওয়া যায়,
S1 = 6 এবং S2 = 2।
Class 9 Physical Science – Notes for All Chapters
| Chapter Name | Tropics |
|---|---|
| পরিমাপ | পরিমাপ ও একক বিভিন্ন মাপের একক মাত্রা পরিমাপ |
| বল ও গতি | স্থিতি ও গতি গতির সমীকরণ নিউটনের প্রথম গতিসূত্র নিউটনের দ্বিতীয় গতি সূত্র নিউটনের তৃতীয় গতিসূত্র বিভিন্ন ধরণের বল রৈখিক ভরবেগ রৈখিক ভরবেগ সংরক্ষণ |
| পদার্থ : গঠন ও ধর্ম | তরল ও বায়ুর চাপ আর্কিমিডিসের নীতি পৃষ্ঠটান সান্দ্রতা বার্নোলির নীতি স্থিতিস্থাপকতা |
| পদার্থ : পরমাণুর গঠন ও পদার্থের ভৌত ও রাসায়নিক ধর্মসমূহ | পরমাণুর গঠন মোলের ধারণা দ্রবণ অ্যাসিড, ক্ষার, লবণ মিশ্রণের উপাদানের পৃথকীকরণ জল |
| শক্তির ক্রিয়া , কার্য, ক্ষমতা | শক্তির ক্রিয়া , কার্য, ক্ষমতা |
| তাপ | ক্যালোরিমিতি কার্য ও তাপের তুল্যতা লীনতাপ সম্পৃক্ত ও অসম্পৃক্ত বাষ্প জলের ব্যতিক্রান্ত প্রসারণ |
| শব্দ | শব্দের উৎস : কম্পন শব্দের বিস্তার : তরঙ্গ শব্দের কয়েকটি ধর্ম শব্দের বৈশিষ্ট্য মানুষের কান ও শব্দ শোনার কৌশল শব্দদূষণ |
আজকের আর্টিকেলে আমরা নবম শ্রেণির ভৌতবিজ্ঞান বইয়ের তৃতীয় অধ্যায় “পদার্থ : গঠন ও ধর্ম” এর “আর্কিমিডিসের নীতি” থেকে পরীক্ষায় আসা গুরুত্বপূর্ণ প্রশ্ন ও উত্তরগুলো আলোচনা করেছি। এই প্রশ্নোত্তরগুলো নবম শ্রেণির বার্ষিক পরীক্ষা, এমনকি চাকরি বা যেকোনো প্রতিযোগিতামূলক পরীক্ষার জন্যও উপযোগী। কারণ, এই অধ্যায়ের প্রশ্ন প্রায়ই বিভিন্ন পরীক্ষায় কমন আসে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সাহায্য করবে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন কিংবা টেলিগ্রামে যোগাযোগ করতে পারেন—আপনাদের প্রশ্নের উত্তর দিতে আমি সর্বদা প্রস্তুত।
ধন্যবাদ সবাইকে।






মন্তব্য করুন