আজকের আর্টিকেলে আমরা নবম শ্রেণীর ভৌতবিজ্ঞান বইয়ের প্রথম অধ্যায় “পরিমাপ” এর “পরিমাপ” থেকে সহজ ও সংক্ষিপ্ত প্রশ্ন-উত্তর শেয়ার করবো। এই প্রশ্নগুলো নবম শ্রেণির ইউনিট টেস্ট থেকে বার্ষিক পরীক্ষা এর জন্য যেমন গুরুত্বপূর্ণ, তেমনি চাকরি বা বিভিন্ন প্রতিযোগিতার পরীক্ষাতেও কাজে লাগবে। এই অধ্যায় থেকে স্কুল পরীক্ষা থেকে শুরু করে চাকরির পরীক্ষায় প্রায়ই প্রশ্ন আসে, তাই এই প্রশ্নোত্তরগুলো সবাইকে সাহায্য করবে। প্রতিটি প্রশ্নের উত্তর সহজ ভাষায় লেখা হয়েছে, যাতে সবাই বুঝতে পারেন। পড়ার শেষে এই অধ্যায়ের মুখ্য বিষয়গুলো আপনার আয়ত্তে চলে আসবে এবং যেকোনো পরীক্ষায় আত্মবিশ্বাসের সঙ্গে লিখতে পারবেন।

জ্ঞানমূলক প্রশ্নোত্তর
মাপনী বা রুলার বা রৈখিক স্কেলের সাহায্যে কোনো বস্তুর দৈর্ঘ্য পরিমাপের পদ্ধতি সংক্ষেপে ব্যাখ্যা করো। রৈখিক স্কেলে পরিমাপের সীমা উল্লেখ করো।
রৈখিক স্কেলের সাহায্যে কোনো বস্তুর দৈর্ঘ্য পরিমাপ – ধরা যাক, পরীক্ষাধীন বস্তু একটি পেনসিল যার দৈর্ঘ্য মাপনী স্কেলের সাহায্যে নির্ণয় করতে হবে। এর জন্য প্রয়োজনীয় ধাপগুলি নীচে বর্ণনা করা হল।
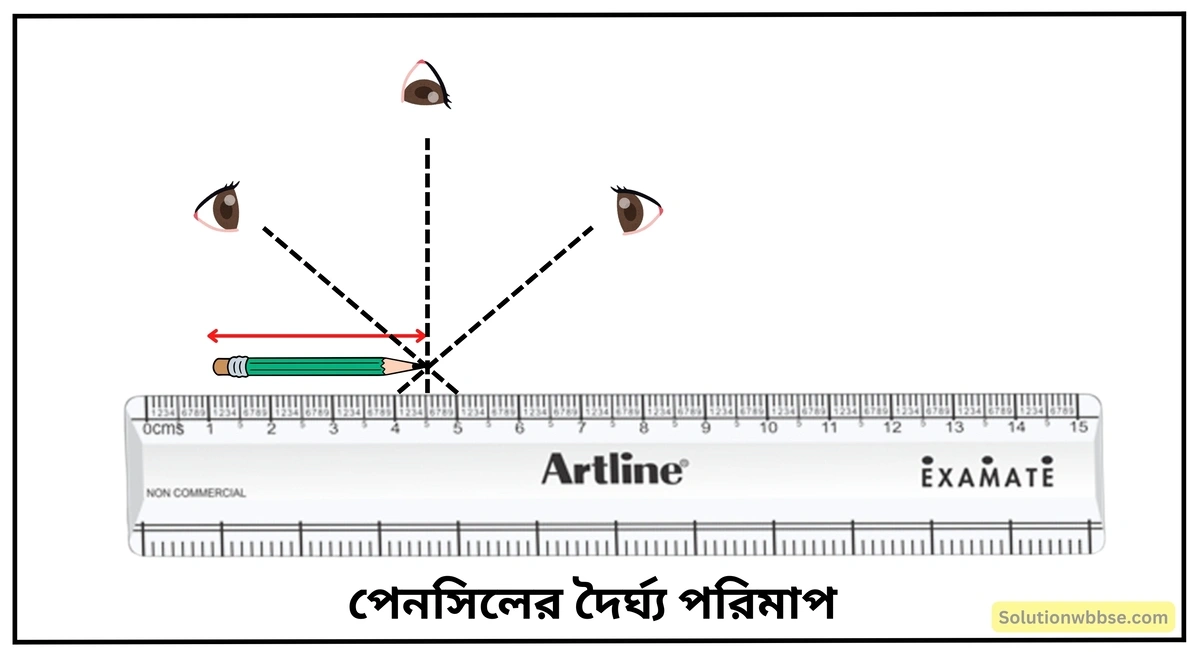
পদ্ধতি –
- পেনসিলকে প্রথমে রুলারের অংশাঙ্কিত প্রান্ত বরাবর স্থাপন করে পেনসিলের এক প্রান্ত মাপনীর একটি নির্দিষ্ট অংশাঙ্কনের (এক্ষেত্রে 1 cm) সঙ্গে মিলিয়ে চোখ খাড়া অর্থাৎ, লম্ব অবস্থানে রেখে পাঠ নেওয়া হল।
- এরপর পেনসিলের অপর প্রান্ত রৈখিক স্কেলের কোন্ অংশাঙ্কনের (দাগ) সঙ্গে মিলেছে, তা সতর্কভাবে আগের মতোই অভিলম্ব অবস্থানে চোখ রেখে নির্ণয় করা হল। ধরা যাক, এক্ষেত্রে প্রাপ্ত পাঠ হল 4.2 সেমি।
- সুতরাং, পেনসিলের দৈর্ঘ্যের নির্ণীত মান হল (4.2 – 1) সেমি = 3.2 সেমি।
- একাধিকবার এই পদ্ধতির পুনরাবৃত্তি করে প্রাপ্ত পাঠের গড় মান নেওয়া হয়। এই গড় মানই হল পেনসিলের দৈর্ঘ্য।
রৈখিক স্কেলের পরিমাপের সীমা – সাধারণ রৈখিক স্কেলের সাহায্যে সর্বোচ্চ 30 সেমি দৈর্ঘ্য মাপা যায়। প্রত্যেক দৈর্ঘ্য আবার সমান দশটি অংশে ভাগ করা থাকে। সুতরাং, এই স্কেলের সাহায্যে সর্বনিম্ন যে দৈর্ঘ্য মাপা যায়, তার মান 1 mm।
রৈখিক স্কেল ব্যবহারের অসুবিধাগুলি বিবৃত করো।
সাধারণ রৈখিক স্কেল ব্যবহারের অসুবিধা –
- সাধারণ স্কেলের সর্বনিম্ন অংশাঙ্কনের মান হল 1 mm। সুতরাং, 1 mm অপেক্ষা ছোটো দৈর্ঘ্য এর সাহায্যে মাপা যায় না।
- স্কেলের অংশাঙ্কন অনেকক্ষেত্রেই ত্রুটিপূর্ণ থাকে, তাই নির্ণীত পাঠ এক্ষেত্রে ত্রুটিপূর্ণ হয়। সেকারণে এই স্কেল ব্যবহার করলে গড় পাঠ নেওয়া অত্যন্ত জরুরি।
লম্বন ত্রুটি বা লম্বন দোষ কী?
লম্বন ত্রুটি (Parallax error) – সাধারণ স্কেলের সাহায্যে দৈর্ঘ্যের পাঠ নেওয়ার সময় চোখ ঠিক খাড়া অবস্থানের পরিবর্তে তির্যকভাবে অবস্থান করলে পাঠ নির্ণয়ে ত্রুটি আসে। চোখের অবস্থানজনিত কারণে পাঠ নির্ণয়ে যে ত্রুটি বা দোষের উদ্ভব হয়, তাকে লম্বন ত্রুটি বা লম্বন দোষ বলে।
সাধারণ রৈখিক স্কেল ব্যবহার করে নিম্নলিখিত বিষয়গুলি কীভাবে নির্ণয় করবে?
- বক্ররেখার (বাঁকানো দণ্ড বা তার) দৈর্ঘ্য।
- গোলকের ব্যাস।
- পাতলা কাগজ যেমন – বইয়ের পাতার বেধ।
স্কেল ও সুতোর সাহায্যে বক্ররেখার দৈর্ঘ্য নির্ণয় –
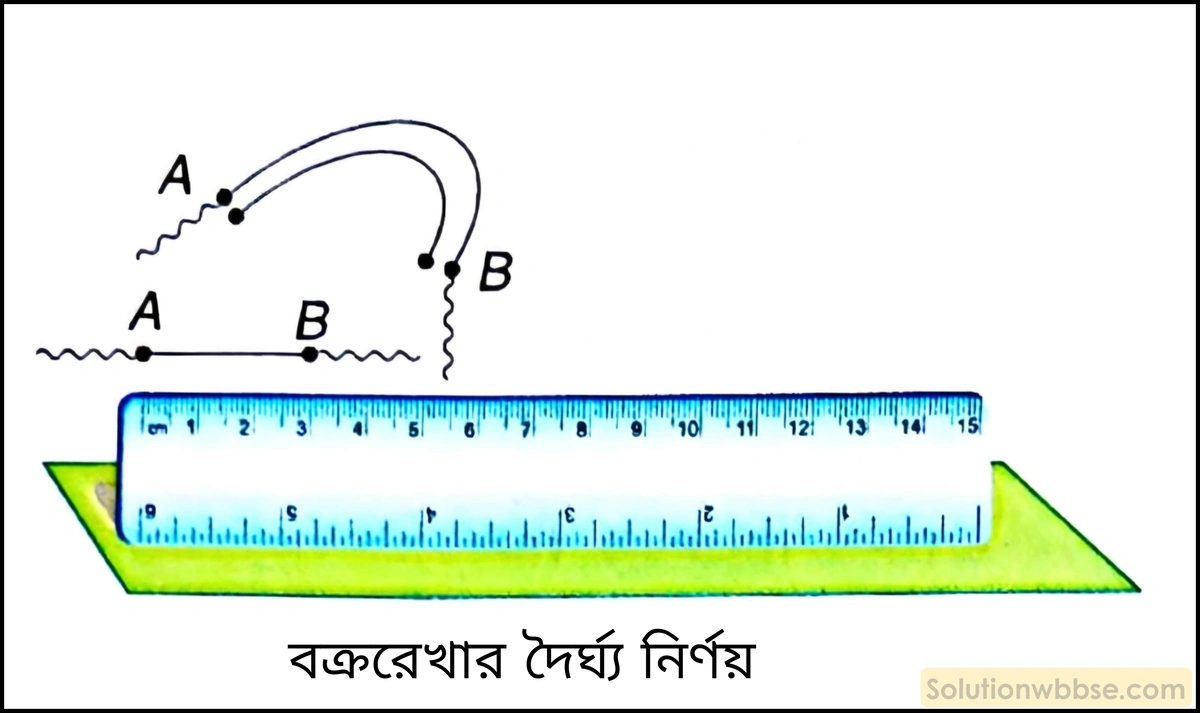
- বক্ররেখাটির আনুমানিক দৈর্ঘ্যের থেকে বেশি দৈর্ঘ্যের একটি সুতোর টুকরো নেওয়া হল।
- এবার সুতোর টুকরোটিকে বক্ররেখা বরাবর এমনভাবে রাখা হল, যাতে সুতোটি বক্ররেখার ওপর সব জায়গায় মিলে যায়।
- এই অবস্থায় সুতোটির যে স্থান দুটি বক্ররেখাটির দুই প্রান্তের সঙ্গে মিলেছে সেই স্থান দুটিতে সুতোর ওপর রং দিয়ে চিহ্নিত করা হল।
- এবার সুতোটিকে তুলে সোজা টান টান করে একটি সাধারণ স্কেলের সাহায্যে সুতোটির ওপর চিহ্নিত স্থান দুটির মধ্যবর্তী দৈর্ঘ্য নির্ণয় করা হল। সুতরাং, ওই দৈর্ঘ্যই হল বক্ররেখাটির প্রকৃত দৈর্ঘ্য।
গোলাকর ব্যাস নির্ণয় – যে-কোনো ছোটো গোলকসদৃশ বস্তু, যেমন – ক্রিকেট বল, ফুটবল, মুদ্রা ইত্যাদির ব্যাস নীচের পরীক্ষাব্যবস্থার দ্বারা শুধুমাত্র সাধারণ স্কেল ব্যবহার করে নির্ণয় করা যায়।
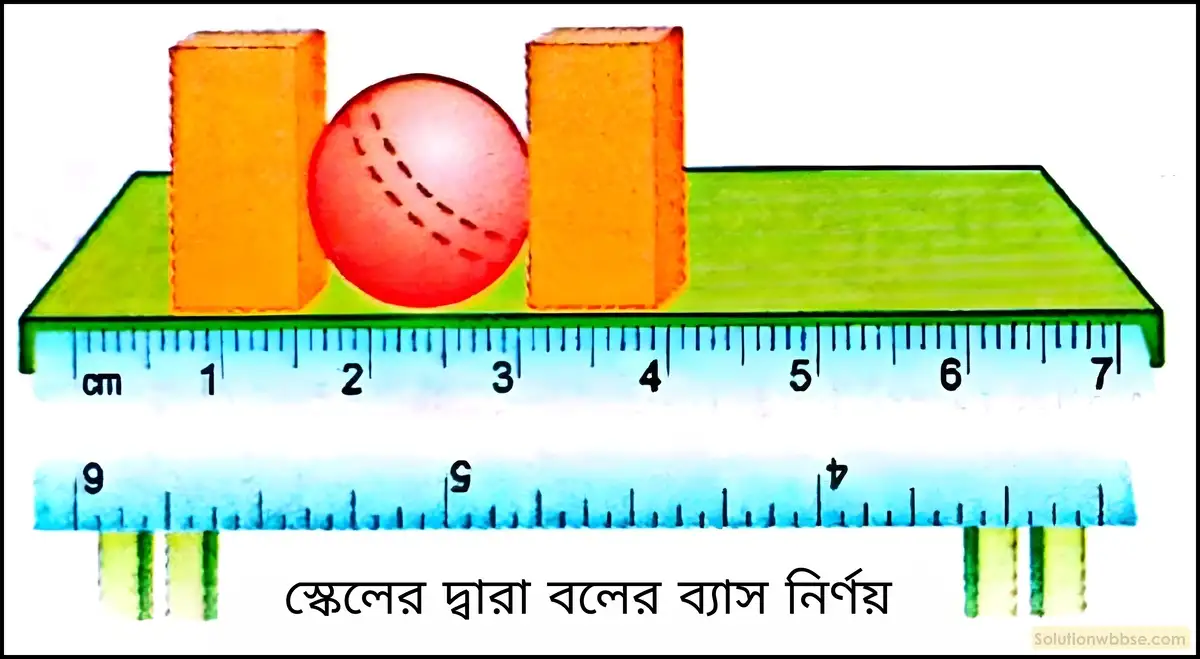
পদ্ধতি –
- পরীক্ষাধীন বস্তুটিকে একটি টেবিলের ওপর রাখা হল।
- দুটি কাঠের বা ধাতব ব্লককে ওই টেবিলের ওপর এমনভাবে বসানো হল যে তাদের পৃষ্ঠতল গোলকটির দুই বিপরীত প্রান্ত স্পর্শ করে থাকে। (চিত্র দ্রষ্টব্য)
- এই অবস্থায় ব্লক দুটির নীচের দুই প্রান্ত বরাবর রুলারটি রাখা হল।
- দুটি ব্লকের প্রত্যেকটির যে প্রান্ত গোলকের পৃষ্ঠতল স্পর্শ করে থাকে তাদের অবস্থানের পাঠ স্কেলের সাহায্যে নির্ণয় করা হল।
- নির্ণীত পাঠ দুটির পার্থক্যই হল গোলকের ব্যাসের পরিমাপ। যেমন – আলোচ্য ক্ষেত্রে, A ব্লকের অবস্থানের পাঠ 1.6 সেমি এবং B ব্লকের অবস্থানের পাঠ 3.1 সেমি।
∴ বলটির নির্ণেয় ব্যাস (d) = (3.1 – 1.6) সেমি = 1.5 সেমি।
পাতলা কাগজের বেধ নির্ণয় –
- অনেকগুলি অভিন্ন কাগজ একত্রিত করে বা বইয়ের ক্ষেত্রে সমগ্র বইটির বেধ সাধারণ স্কেলের সাহায্যে মাপা হল। ধরা যাক, এই পাঠ হল d সেমি।
- এই পাঠকে কাগজ বা বইয়ের পাতার সংখ্যা দিয়ে ভাগ করলে যে মান পাওয়া যায়, সেটিই একটি পাতার বেধ নির্দেশ করে।

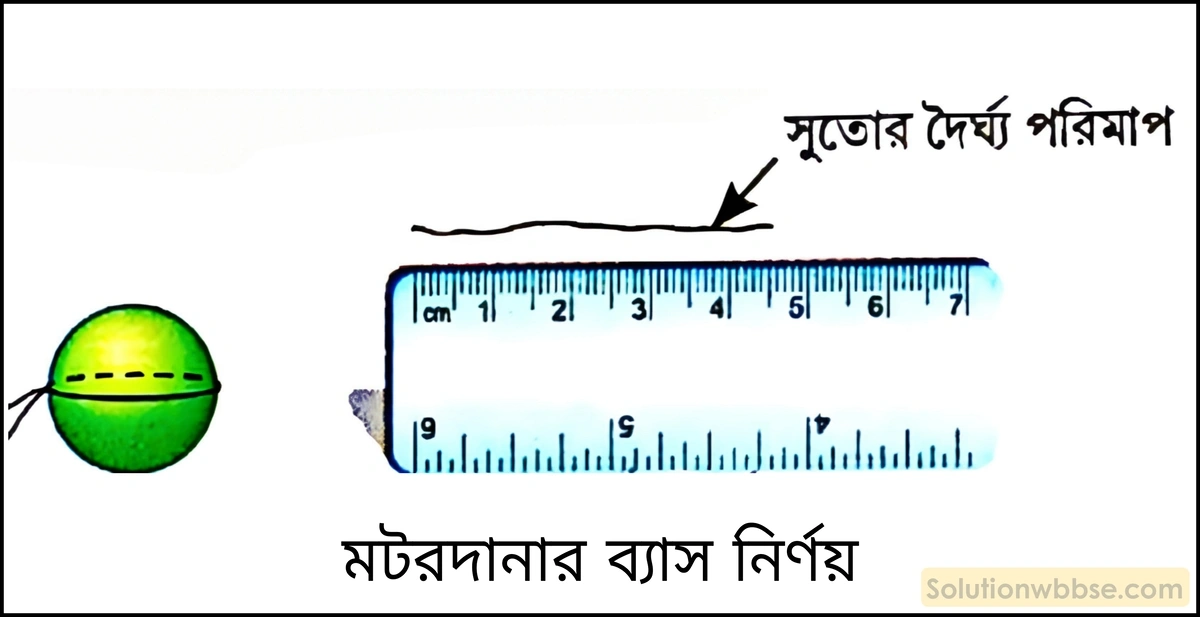
সাধারণ স্কেলের সাহায্যে কীভাবে একটি মটরদানার ব্যাস নির্ণয় করবে?
সাধারণ স্কেলের সাহ্যায্য মটরদানার ব্যাস নির্ণয় –
উপকরণ – সুতো, মটরদানা, সাধারণ স্কেল।
পদ্ধতি –
- একটি সুতো মটরদানার মাঝ বরাবর (অর্থাৎ, বৃহত্তম পরিধি বরাবর) বসিয়ে তার পরিধির মাপ নেওয়া হল।
- সুতোটি স্কেলের গা বরাবর বসিয়ে তার দৈর্ঘ্য পরিমাপ করা হল।
- এই পদ্ধতিতে বেশ কয়েকবার মটরদানাটিকে ঘুরিয়ে ফিরিয়ে তার মাঝ বরাবর দৈর্ঘ্য অর্থাৎ, পরিধি পরিমাপ করা হল।
- এরপর, প্রাপ্ত দৈর্ঘ্যগুলি যোগ করে ও পর্যবেক্ষণ সংখ্যা দিয়ে ভাগ করে তার গড় নির্ণয় করা হল। মনে করি, গড় দৈর্ঘ্য = x।
আমরা জানি,
পরিধি = 2 × π × ব্যাসার্ধ
= π × ব্যাস [∵ 2 × ব্যাসার্ধ = ব্যাস]
∴ π × ব্যাস = x
∴ ব্যাস =
সুতরাং, এই সূত্রের সাহায্যে মটরদানার ব্যাস নির্ণয় করা যাবে।
সাধারণ স্কেলের সাহায্যে কীভাবে তারের ব্যাস নির্ণয় করা যায়?
সাধারণ স্কেলের সাহ্যায্য ভারের ব্যাস নির্ণয় – সাধারণ স্কেলের সাহায্যে একটি সরু তারের ব্যাস প্রত্যক্ষভাবে নির্ণয় করা সম্ভব নয়, কারণ – তারের ব্যাস 1 mm অপেক্ষা কম হওয়ায় সাধারণ স্কেলের সাহায্যে তা অপ্রত্যক্ষভাবে পরিমাপ করা হয়।
পদ্ধতি –
- যে তারের ব্যাস নির্ণয় করতে হবে, সেই তারটিকে একটি সরু দণ্ড বা চোঙের ওপর পাক দিয়ে এমন ঘনসন্নিবিষ্টভাবে জড়ানো হল, যাতে পাকগুলির মধ্যে কোনো ফাঁক না থাকে।
- এবার একটি সাধারণ স্কেলের সাহায্যে পাকগুলির দ্বারা অধিকৃত দৈর্ঘ্য মাপা হল।
- এইভাবে কয়েকবার দৈর্ঘ্য পরিমাপ করে তার গড় মান নির্ণয় করা হল।
ধরি, পাকগুলির দ্বারা অধিকৃত গড় দৈর্ঘ্য = x cm।

∴ এই গড় দৈর্ঘ্যকে (x) তারের পাকসংখ্যা (ধরি, n) দিয়ে ভাগ করলে তারটির ব্যাস পাওয়া যাবে।
∴ তারের ব্যাস =
সময় কাকে বলে?
সময় (Time) – যে পরিমাপযোগ্য বিষয়ের সাহায্যে মানুষ তার পারিপার্শ্বিক বা মহাবিশ্বে সংঘটিত পরিবর্তনগুলি পর্যবেক্ষণ এবং তা লিপিবদ্ধ করার কাজ করে, তাকেই সময় বলে।
বৈজ্ঞানিক দৃষ্টিকোণ থেকে দেওয়া সময়ের সংজ্ঞা – দুটি ঘটনা সংঘটিত হওয়ার মধ্যে যে রাশির পার্থক্য বা অন্তর থাকে, তাকেই সময় বলে।
সময় পরিমাপক ব্যবস্থা বলতে কী বোঝায়? এর প্রকারভেদগুলি কী কী?
সময় পরিমাপক ব্যবস্থা – যে যন্ত্র বা ব্যবস্থার সাহায্যে সময়ের পরিমাপ করা হয়, তাকেই সময় পরিমাপক ব্যবস্থা বা চেনা নামে ঘড়ি বলা হয়।
প্রকারাভদ – সময় পরিমাপক ব্যবস্থা দুইরকম। যথা –
- প্রাচীন সময় পরিমাপক ব্যবস্থা – প্রাচীন মানুষ কোনো সহায়ক উপকরণ ছাড়া শুধুমাত্র পর্যবেক্ষণের সাহায্যেই যথেষ্ট উপযোগী সময় পরিমাপক ব্যবস্থা আবিষ্কার করেছিল। যেমন – বালিঘড়ি, সূর্যঘড়ি, জলঘড়ি ইত্যাদি।
- আধুনিক সময় পরিমাপক ব্যবস্থা – বিভিন্ন পর্যায়ে সময় পরিমাপক ধারণা বা ব্যবস্থাগুলি বিবর্তিত হয়ে আধুনিক সময় পরিমাপক যন্ত্র বা ঘড়ির চেহারা লাভ করেছে। যেমন – রিস্টওয়াচ, ডিজিট্যাল ঘড়ি, কোয়ার্জ ঘড়ি ইত্যাদি।
বালিঘড়ির সংক্ষিপ্ত টীকা লেখো।
বালিঘড়ি –

আওয়ার গ্লাস নামে পরিচিত এই যন্ত্রটি দুটি গোলকাকৃতি কাচের বাল্ব বা কুণ্ড দ্বারা নির্মিত। কুণ্ড দুটি আবার একটি সরু কাচের নল দ্বারা সংযুক্ত থাকে। উপরের কুণ্ডটিতে বালি থাকে, যার গতি এমনভাবে নিয়ন্ত্রণ করা হয় যে, একটি নির্দিষ্ট সময় অবকাশে ওই বালির একটি নির্দিষ্ট পরিমাণ নীচের কুণ্ডে এসে পৌঁছোয়। সম্পূর্ণ বালি নীচের কুণ্ডে জমা হলে ঘড়িটিকে আবার উলটে দেওয়া হয় এবং একই ঘটনার পুনরাবৃত্তি ঘটে।
সূর্যঘড়ির সংক্ষিপ্ত টীকা লেখো।
সূর্যঘড়ি –

সূর্যালোকের দ্বারা ছায়া গঠন এবং আকাশে সূর্যের অবস্থান পরিবর্তনের সঙ্গে ছায়ার দৈর্ঘ্য ও অবস্থান পরিবর্তন এই নীতির প্রয়োগে সূর্যঘড়ি নির্মিত হয়। ভারতবর্ষের রাজস্থানের জয়পুর, দিল্লির যন্তরমন্তর ইত্যাদি স্থানে এ ধরনের ঘড়ির নমুনা দেখতে পাওয়া যায়।
জলঘড়ির সংক্ষিপ্ত টীকা লেখো।
জলঘড়ি –

এটি বিশেষ একপ্রকার সময় নির্ণায়ক উপকরণ, যা জলের অন্তর্মুখী বা বহির্মুখী নিয়ন্ত্রিত প্রবাহের ওপর নির্ভর করে কাজ করে। অন্তর্মুখী নিয়ন্ত্রিত প্রবাহ ব্যবস্থায় রেখাঙ্কিত একটি পাত্রকে জল দ্বারা পূর্ণ করা হয়। ওই পাত্র থেকে নির্গত জলের হারকে নিয়ন্ত্রণ করে তা থেকে সময়ের পাঠ পাওয়া যায়। জল প্রবাহের হার লক্ষ করার কাজে রেখাগুলি ব্যবহার করা হয়।
আধুনিক সময় পরিমাপক যন্ত্র বলতে কী বোঝায়?
আধুনিক সময় পরিমাপক যন্ত্র – অতীত দিনে ব্যবহৃত ঘড়িগুলি থেকে প্রাপ্ত সময়ের পরিমাপ খুব নির্ভুল ছিল না। উন্নত প্রযুক্তির সহায়তায় বর্তমান সময়ে নিখুঁত ও নির্ভরযোগ্য সময় পরিমাপক ব্যবস্থার উদ্ভাবন ঘটানো সম্ভব হয়েছে। এগুলিই আধুনিক সময় পরিমাপক যন্ত্র বা আধুনিক ঘড়ি নামে পরিচিত।
দোলক ঘড়ির কার্যপদ্ধতি ও ব্যবহারের সংক্ষিপ্ত পরিচয় দাও।
দোলক ঘড়ি (Pendulum) – এটি বিজ্ঞানী গ্যালিলিয়ো দ্বারা উদ্ভাবিত প্রথম আধুনিক সময় মাপক যন্ত্র। এই যন্ত্রে দৃঢ় অবলম্বন থেকে ঝোলানো একটি ধাতব দণ্ডের শেষ প্রান্তে পিতলনির্মিত একটি ভারী ধাতব পিন্ড যুক্ত থাকে। পিণ্ডটি তার সাম্য বা মধ্য অবস্থান সাপেক্ষে পর্যাবৃত্ত দোলনগতি সম্পন্ন করে।

দোলকপিণ্ড যে-কোনো এক প্রান্ত থেকে যাত্রা শুরু করে অন্য প্রান্ত হয়ে আবার আগের অবস্থানে ফিরে আসতে যে সময় নেয় তার মান অর্থাৎ, দোলনের দোলনকাল বা পর্যায়কাল হয় 2 সেকেন্ড। বিশেষ যান্ত্রিক ব্যবস্থায় এই দোলনকাল অনুসারে ঘড়ির কাঁটা ঘুরে সময় নির্দেশ করে। এই ঘড়িতে দুটি কাঁটা থাকে। দীর্ঘতর কাঁটাটি মিনিট ও অপরটি ঘণ্টার পরিমাপ দেয়। কাঁটা দুটি একটি ডায়ালের উপর পর্যাবৃত্ত গতিতে আবর্তন করে।
দোলক ঘড়ি দ্বারা পরিমাপযোগ্য সর্বোচ্চ সময় 1 ঘণ্টা ও সর্বনিম্ন সময় 1 মিনিট। দিনের যে-কোনো মুহূর্তে সময় মাপার কাজে মূলত যন্ত্রটি ব্যবহার করা হয়ে থাকে।
রিস্টওয়াচের কার্যপদ্ধতি ও ব্যবহারের সংক্ষিপ্ত পরিচয় দাও।
রিস্টওয়াচ (Wrist watch) – যান্ত্রিক রিস্টওয়াচে একটি তুলনচক্র (Balance wheel) যুক্ত থাকে, যা দোলকের মতো আন্দোলিত হয় এবং সময়ের পরিমাপ দেয়। আধুনিক কোয়ার্জ ঘড়িতে তুলনচক্রের পরিবর্তে দ্রুত কম্পনশীল কোয়ার্জ কেলাস ব্যবহৃত হয়, যা একটি নির্দিষ্ট এবং নিখুঁত হারে কম্পিত হয় এবং সুবেদী সময় পরিমাপ দেয়। রিস্টওয়াচে ঘণ্টার ও মিনিটের কাঁটা ছাড়াও অতিরিক্ত একটি কাঁটা থাকে, যা সেকেন্ডের পরিমাপ নির্দেশ করে। সুতরাং, এই যন্ত্র দোলক ঘড়ি অপেক্ষা বেশি সুবেদী পরিমাপ দেয়। এই যন্ত্রে সময় পরিমাপের নিম্নসীমা হল সেকেন্ড এবং ঊর্ধ্বসীমা ঘণ্টা।

ব্যক্তিগত প্রয়োজনে কোনো মুহূর্তে সময়ের পাঠ নির্ণয়ের উদ্দেশ্যেই এটি ব্যবহার করা হয়। কবজির বা মণিবন্ধে বেল্ট বা ধাতব চেনের সঙ্গে যুক্ত থাকে বলে একে হাতঘড়ি বলা হয়।
ডিজিট্যাল ঘড়ির কার্যপদ্ধতি ও ব্যবহারের সংক্ষিপ্ত পরিচয় দাও।
ডিজিট্যাল ঘড়ি (Digital clock) – ডিজিট্যাল ঘড়িতে কোনো সেকেন্ড বা মিনিটের কাঁটা থাকে না, পরিবর্তে থাকে একটি ইলেকট্রনিক বর্তনী যা সময়কে সংখ্যার আকারে প্রদর্শন করে। এই ঘড়িতে সর্বোচ্চ যে সময়ের পাঠ পাওয়া যায় তা ঘণ্টা হলেও নিম্নসীমার পাল্লা এক্ষেত্রে যথেষ্ট বেশি। সাধারণ ডিজিট্যাল ঘড়ি সাধারণত সেকেন্ডের 100 ভাগের 1 ভাগ সময় পর্যন্ত নিখুঁতভাবে নির্দেশ করে। ন্যূনতম পরিমাপের সীমা এক্ষেত্রে 0.01 সেকেন্ড।

সাধারণ হাতঘড়ি হিসেবে ব্যবহার ছাড়াও এই যন্ত্রটি গবেষণাগারে বিভিন্ন পরীক্ষানিরীক্ষায় সময় নির্ণয়ের ক্ষেত্রেও ব্যবহার করা হয়ে থাকে। অনেক ক্ষেত্রে ডিজিট্যাল বর্তনী ব্যবহার করে বিরাম ঘড়ি বা ডিজিট্যাল স্টপওয়াচ নির্মাণ করা হয়। মাইক্রোওয়েভ উনুন বা অন্যান্য রান্নার উপকরণে অনেকসময় বিভিন্ন ধরনের টাইমার লাগানো থাকে, যা ডিজিট্যাল ঘড়িরই প্রকারভেদ।
পারমাণবিক ঘড়ির কার্যপদ্ধতি ও ব্যবহারের সংক্ষিপ্ত পরিচয় দাও।
পারমাণবিক ঘড়ি (Atomic clock) – গবেষণা ক্ষেত্রে সময় গণনার কাজে বিজ্ঞানীরা পারমাণবিক ঘড়ি ব্যবহার করে থাকেন। এ জাতীয় ঘড়িতে প্রমাণ চৌম্বকক্ষেত্রে পরমাণুর (যেমন – সিজিয়াম : 133Cs) কম্পনকে কাজে লাগিয়ে সময়ের হিসাব করা হয়। এই পরিমাপ এতই নির্ভুল যে একটি সিজিয়াম ঘড়ি প্রায় 6000 বছরে মাত্র 1 সেকেন্ড স্লো বা ফাস্ট যায়।
স্টপওয়াচের কার্যপদ্ধতি ও ব্যবহারের সংক্ষিপ্ত পরিচয় দাও।
স্টপওয়াচ ( watch) – অল্প সময়ের ব্যবধানে অনুষ্ঠিত বা সংঘটিত ঘটনার ক্ষেত্রে সময় পরিমাপক ব্যবস্থা হিসেবে স্টপওয়াচ ব্যবহার করা হয়। প্রয়োজনমতো চালানো বা বন্ধ করা যায় বলে একে বিরাম ঘড়িও বলা হয়। যন্ত্রটিতে দুটি কাঁটা থাকে-ছোটোটি মিনিট এবং বড়োটি সেকেন্ডের পরিমাপ দেয়। ঘড়িটি চালানো বা বন্ধ করার জন্য দুটি চাবি বা বোতাম থাকে। প্রথমবার চাবি টিপলে ঘড়ি চলতে শুরু করে এবং দ্বিতীয়বার প্রথম চাবি টিপলে ঘড়ি বন্ধ হয়। তখন কাঁটা দুটির অবস্থান লক্ষ করে সময় জানা যায়। তৃতীয়বার চাবি টিপলে উভয় কাঁটাই শূন্য বা প্রাথমিক অবস্থানে ফিরে আসে।
পরীক্ষাগারে, দৌড়, সাঁতার ও ক্যুইজ প্রতিযোগিতায় এই যন্ত্রের ব্যাপক ব্যবহার আছে।

বস্তুর ভর বলতে কী বোঝায়?
ভর (Mass) – কোনো বস্তুর মধ্যে থাকা জড় পদার্থের পরিমাণকে সেই বস্তুর ভর বলা হয়। অন্যভাবে বলা যায়, বস্তুর মধ্যে সঞ্চিত জড়তার পরিমাণকেই তার ভর বলে। এটি বস্তুর একটি স্বকীয় এবং অপরিবর্তনীয় ধর্ম।
সাধারণ তুলাযন্ত্রের সাহায্যে কোনো বস্তুর ভর পরিমাপের নীতিটি সংক্ষেপে বিবৃত করো।
সাধারণ তুলায় ভর পরিমাপের নীতি – সাধারণ তুলাযন্ত্রে কতগুলি প্রমাণ ওজনের বাটখারা ব্যবহার করা হয়। যন্ত্রটির সাহায্যে এই বাটখারাগুলির ভরের তুল্য কোনো পরীক্ষাধীন বস্তুর ভর সরাসরি নির্ণয় করা সম্ভব হয়। কার্যকরী অবস্থায় বাম তুলাপাত্রে বস্তু ও ডান তুলাপাত্রে প্রমাণ বাটখারা রেখে পরীক্ষানিরীক্ষা দ্বারা উপযুক্ত বাটখারাগুলি নির্বাচন করা হয়, যা স্থাপিত হলে তুলাদণ্ডটি সাম্যে অর্থাৎ, অনুভূমিক অবস্থায় আসে।
সাম্যাবস্থায়, বস্তুর ভর = তুলাপাত্রে রাখা বাটখারা বা বাটখারাগুলির মোট ভর।
চিহ্নিত চিত্র অঙ্কন করে সাধারণ তুলাযন্ত্রের বিভিন্ন অংশ ও তাদের গঠনের সংক্ষিপ্ত পরিচয় দাও।
সাধারণ তুলাযন্ত্রের গঠন – তুলাযন্ত্রের বিভিন্ন অংশের গঠন নীচে বর্ণনা করা হল –
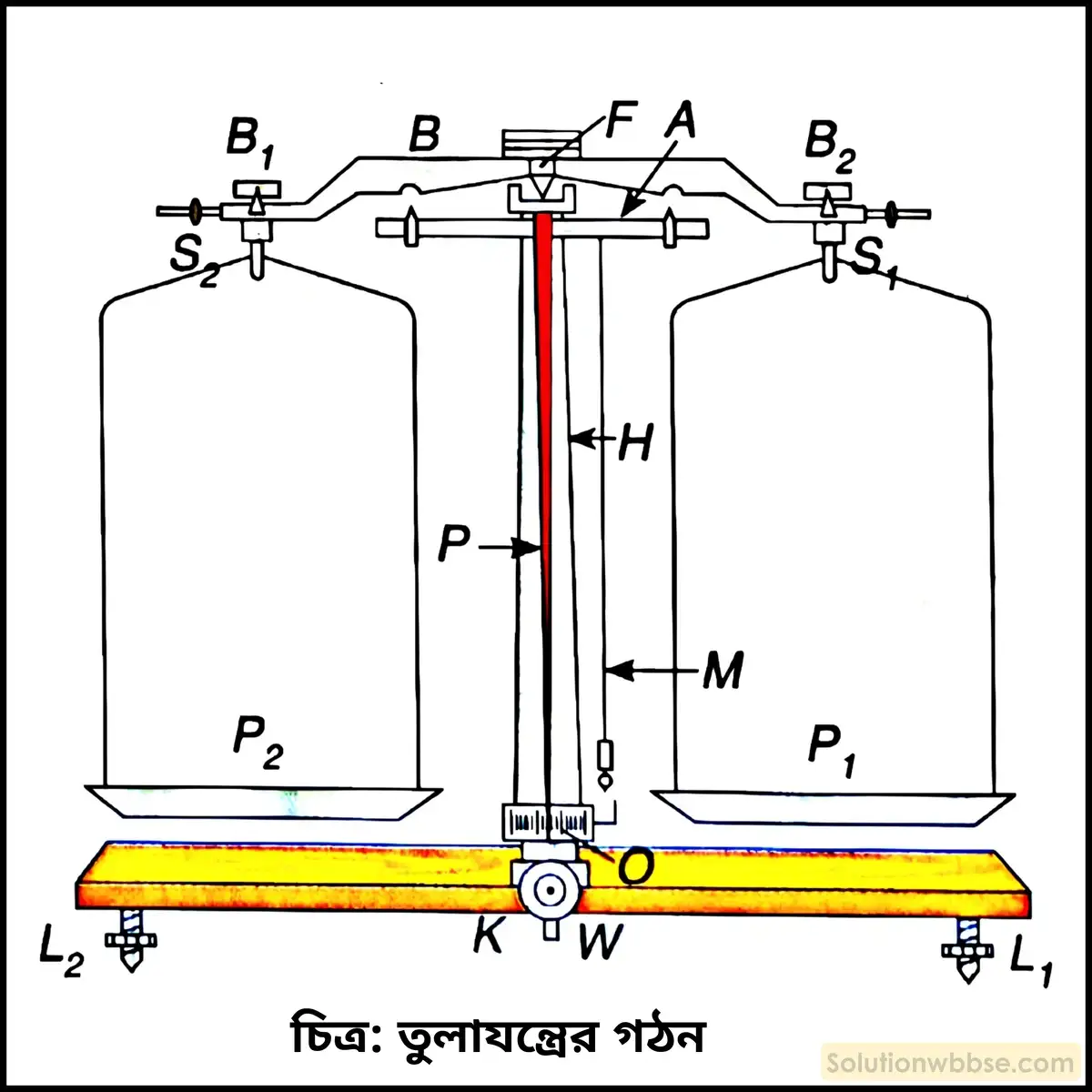
- তুলাদণ্ড – ধাতুনির্মিত দৃঢ় ধাতব দণ্ড (B)।
- অ্যাগেট – বিশেষ এক ধরনের সংকর ধাতু বা পাথরনির্মিত ত্রিভুজাকৃতি টুকরো (F)
- স্তম্ভ – এটি একটি ফাঁপা ধাতব থাম (H), এর ভিতর দিয়ে একটি দৃঢ় ধাতব দণ্ড ঢোকানো থাকে। দণ্ডের উপরের প্রান্তে যুক্ত একটি সমতল প্লেট (A) -এর উপর অ্যাগেট বসানো থাকে, যা ক্ষুরধার আলম্বের কাজ করে।
- সূচক ও স্কেল – স্তম্ভের সঙ্গে দৃঢ়ভাবে সংযুক্ত একটি ধাতব কাঁটা (P) লম্বভাবে অবস্থান করে, যা দণ্ডের সঙ্গে অনুভূমিকভাবে যুক্ত একটি রৈখিক স্কেল বরাবর আন্দোলিত হতে পারে। ধাতব কাঁটা (P) -টিকে বলা হয় সূচক।
- ওলনদড়ি – স্তম্ভের দৈর্ঘ্যের সমান্তরালে অবস্থিত একটি দড়ি (M), যার দুটি অর্ধ থাকে। এর সাহায্যে ব্যবস্থাটি অনুভূমিক আছে কি না তা যাচাই করা হয় বা না থাকলে তাকে অনুভূমিক করা হয়।
- তুলাপাত্র – দুটি অভিন্ন প্লেট বা বাটিসদৃশ পাত্র (P1, P2) যার একটিতে বস্তু ও অন্যটিতে বাটখারা রাখা হয়।
- স্টিরাপ – তুলাদণ্ডের দুই প্রান্তে রক্ষিত প্রিজমাকৃতি ক্ষুরধার থেকে ঝুলিয়ে দেওয়া সরু ধাতব আংটা বা শিকল যার সাহায্যে তুলাপাত্র দুটি ঝোলানো হয়।
- লেভেলিং স্কু – বিশেষ একজোড়া স্কু (L1, L2) যাদের সাহায্যে তুলাযন্ত্রকে প্রয়োজনে অনুভূমিক করা হয়।
- ব্যালান্সিং স্কু – তুলাদণ্ডের দুই প্রান্তে অবস্থানরত একজোড়া সরু স্কু (B1, B2)। তুলাপাত্র খালি থাকা অবস্থায় তুলাদণ্ড অনুভূমিক না থাকলে এদের সাহায্যে দণ্ডটি অনুভূমিক করা হয়।
- চাবি – এটি ধাতু বা শক্ত প্লাস্টিকনির্মিত একটি চাবি (K), যার সাহায্যে সমগ্র তুলাদণ্ডটিকে পাটাতনের সঙ্গে সংযোগ বিচ্ছিন্ন করে কার্যকরী অবস্থায় আনা হয়। সমগ্র যন্ত্রটি একটি কাঠের পাটাতন (W) – এর উপর বসানো থাকে, পাটাতনের ঠিক মাঝখানে K চাবিটি থাকে। সূক্ষ্ম পরিমাপে বাতাস যাতে বিঘ্ন না ঘটায় এবং ব্যবস্থাটি যাতে ধূলিমুক্ত থাকে তার জন্য যন্ত্রটিকে একটি কাচের বাক্সের মধ্যে রাখা হয়।
তুলাযন্ত্র ব্যবহার করার জন্য ওজন-বাক্সে কী কী ভরের প্রমাণ বাটখারা থাকে?
অথবা, ওজন-বাক্সের বাটখারাগুলির ভর 5 : 2 : 2 : 1 অনুপাতে থাকার কারণ কী?
তুলাযন্ত্রে ব্যবহারের জন্য 1 গ্রাম থেকে 100 গ্রাম পর্যন্ত এবং 10 মিলিগ্রাম থেকে 500 মিলিগ্রাম পর্যন্ত বিভিন্ন ভরের বাটখারা থাকে। গ্রাম বাটখারাগুলি সাধারণত পিতল বা স্টিল এবং মিলিগ্রাম বাটখারাগুলি অ্যালুমিনিয়াম নির্মিত হয়। এদের ভরের অনুপাত হয় 5 : 2 : 2 : 1।
একটি কাঠের বাক্সে বিভিন্ন ছোটো ছোটো খোপে বাটখারাগুলি রাখা হয়। নিখুঁত পরিমাপের জন্য বাটখারাগুলি তোলা বা রাখার সময়ে হাতের পরিবর্তে চিমটে ব্যবহার করা হয়ে থাকে।
তুলাযন্ত্রে পরিমাপযোগ্য সর্বোচ্চ ও সর্বনিম্ন ভর কত?
তুলাযন্ত্রের দ্বারা পরিমাপযোগ্য সর্বোচ্চ ভর হল 211.10 গ্রাম। যেহেতু, 10 mg -এর কম ভরের বাটখারা ওজন বাক্সে থাকে না, তাই পরিমাপযোগ্য সর্বনিম্ন ভরের মান এক্ষেত্রে 10 mg, তবে রসায়নাগারে ব্যবহৃত তুলাযন্ত্রে (Chemical balance) 10 mg অপেক্ষাও কম (1 – 10 পর্যন্ত) ভর মাপার জন্য একটি সরু বাঁকানো তার ব্যবহার করা হয়, তাকে রাইডার বলে।
সাধারণ তুলাযন্ত্রের সাহায্যে কোনো বস্তুর ভর নির্ণয়ের পদ্ধতিটি সংক্ষেপে ব্যাখ্যা করো।
সাধারণ তুলাযন্ত্রের সাহায্যে ভর নির্ণয়ের পদ্ধতি –
- লেভেলিং স্ক্রু ব্যবহার করে স্তম্ভকে উল্লম্ব অবস্থায় এনে যন্ত্রটিকে পরিমাপের জন্য প্রস্তুত করা হয়। সঠিক উল্লম্ব অবস্থানে স্তম্ভটি এলে ওলনদড়ির দুই অর্ধ একরেখায় অবস্থান করে এবং দড়িটি খাড়া হয়ে দাঁড়ায়।
- এই অবস্থায় চাবি ঘুরিয়ে তুলাদণ্ডটিকে পাটাতন W থেকে বিচ্ছিন্ন করে উপরে তুললে সূচক কাঁটা P তার মধ্য অবস্থান O -এর দুপাশে আন্দোলিত হয় এবং রৈখিক স্কেল বরাবর উভয় পার্শ্বেই সমদূরত্বে যায়। কোনো কারণে তা না হলে ব্যালান্সিং স্ক্রু -এর একটি বা প্রয়োজনে দুটিই ঘুরিয়ে সূচক কাঁটা যাতে সমান দূরত্ব অতিক্রম করে তা নিশ্চিত করা প্রয়োজন।
- এরপর বাম তুলাপাত্রে পরীক্ষাধীন বস্তু ও ডান তুলাপাত্রে উপযুক্ত ওজনের এমন বাটখারা চাপানো হয়, যাতে তুলাদণ্ডটি সম্পূর্ণ অনুভূমিক অবস্থায় আসে। সাম্য প্রতিষ্ঠিত হলে অর্থাৎ, সূচক কাঁটা বিন্দুতে স্থির অথবা O -এর দুপাশে সমান দূরত্বে আন্দোলিত হলে, পরীক্ষাধীন বস্তুর ভর = ব্যবহৃত বাটখারাগুলির মোট ভর।
সাধারণ তুলাযন্ত্র ব্যবহারের সময় কী কী সতর্কতা অবলম্বন করা উচিত?
সাধারণ তুলাযন্ত্র ব্যবহারে সতর্কতা –
- উপযুক্ত পদ্ধতি অবলম্বন করে তুলাদণ্ডকে সাম্য অবস্থানে আনতে হবে। তুলাদণ্ডটি সম্পূর্ণ অনুভূমিক হলে তবেই পাঠ নিতে হবে, না হলে পাঠ ত্রুটিপূর্ণ হওয়ার সম্ভাবনা থাকবে।
- সূচক কাঁটার দোলনকে বাইরের বায়ুর প্রভাব থেকে মুক্ত রাখতে পাঠগ্রহণের সময় কাচের বাক্সের দরজা বন্ধ রাখতে হবে।
- চাবি ঘুরিয়ে তুলাদণ্ডসহ সমগ্র ব্যবস্থাটি কাঠের পাটাতনের ওপর নামিয়ে এনে তবেই তুলাপাত্রে বস্তু ও বাটখারা চাপানো উচিত, অন্যথায় যন্ত্রটি ক্ষতিগ্রস্ত হওয়ার সম্ভাবনা থাকে।
- নির্ভুল ও সুবেদী পরিমাপ পেতে হলে বাটখারা বা বস্তুকে হাত দিয়ে স্পর্শ না করে চিমটের সাহায্যে তাদের তোলা বা নামানোর কাজ করা প্রয়োজন।
- পাঠগ্রহণের সময় চাবি ঘুরিয়ে তুলাদণ্ডকে সাবধানে ধীরে ধীরে তোলা বা নামানো দরকার, যাতে অনাবশ্যক ঝাঁকুনি না লাগে এবং যন্ত্রটি ক্ষতিগ্রস্ত না হয়।
- খুব গরম, খুব ঠান্ডা ও খুব ভারী বস্তুর ভর এই তুলাযন্ত্রের সাহায্যে পরিমাপ না করাই ভালো, কারণ – প্রত্যেক ক্ষেত্রেই যন্ত্রের সুবেদিতা ক্ষতিগ্রস্ত হতে পারে।
সাধারণ তুলার সুবেদিতা বলতে কী বোঝায়?
সাধারণ তুলার সুবেদিতা – সামান্য ভরের পার্থক্যও যে তুলাযন্ত্র সঠিকভাবে নির্দেশ করতে সক্ষম, তাকে সুবেদী তুলা (Sensitive balance) বলে। অতি ক্ষুদ্র ভরের পার্থক্যের কারণে তুলাদণ্ডের সাম্য বিনষ্ট হয় এবং তার ফলে দণ্ডের যে প্রান্ত বেশি ভারী সেই অভিমুখে দণ্ডটি হেলে যায়।
সামান্যতম ভরের পার্থক্য নিরূপণ করার এই সামর্থ্য তুলাযন্ত্রের একটি বিশেষ ধর্ম। একেই বলা হয় তুলাযন্ত্রের সুবেদিতা (Sensitivity of beam balance)।
একটি ভালো তুলাযন্ত্রের কী কী বৈশিষ্ট্য বা গুণ থাকা উচিত?
ভালো তুলাযন্ত্রের প্রয়োজনীয় গুণ বা বৈশিষ্ট্য –
- তুলাযন্ত্রটি নির্ভুল হওয়া প্রয়োজন। অর্থাৎ, দুই তুলাপাত্রই খালি অথবা উভয়পাত্রে সমান ভর থাকা অবস্থায় দণ্ডটি যেন অনুভূমিক হয়।
- তুলা সুবেদী হওয়া প্রয়োজন অর্থাৎ, দুই তুলাপাত্রে রাখা ভরের সামান্য পার্থক্যও যেন সে সঠিকভাবে চিহ্নিত করতে পারে।
- তুলা সুপ্রতিষ্ঠ (stable) হওয়া আবশ্যক অর্থাৎ, দোলনরত অবস্থা থেকে সূচক কাঁটা তথা তুলাদণ্ডটি যেন দ্রুত তার স্বাভাবিক অবস্থানে ফিরে আসে।
- তুলা দৃঢ় (rigid) হওয়া বাঞ্ছনীয় অর্থাৎ, তার বিভিন্ন অংশগুলি যেন মজবুত হয়।
সাধারণ তুলার সুবেদিতার শর্ত লেখো।
সাধারণ তুলার সুবেদিতার শর্ত –
- সুবেদী তুলা নির্মাণ করতে হলে তুলাদণ্ডের ভারকেন্দ্রকে আলম্বের যতদূর সম্ভব কাছাকাছি থাকতে হবে।
- তুলাদণ্ডের বাহু দুটি দীর্ঘ ও হালকা হওয়া আবশ্যক।
- তুলাপাত্র দুটি যথেষ্ট হালকা ও সূচক কাঁটার দৈর্ঘ্য যথেষ্ট বেশি হওয়া প্রয়োজন।
সাধারণ তুলাযন্ত্রের পরিমাপজনিত ত্রুটি ও তা সংশোধনের উপায় লেখো।
অথবা, তুলাযন্ত্রের বাহুর দৈর্ঘ্য অসমান হলে, বস্তুর প্রকৃত ভর কীভাবে নির্ণয় করবে?
সাধারণ তুলাযান্ত্র সাধারণত পরিমাপজনিত নিম্নলিখিত দুটি জুটি দেখা যায় –
অসম বাহুজনিত ত্রুটি – তুলাযন্ত্রের বাহুদুটির দৈর্ঘ্য সমান না হলে এই জাতীয় ত্রুটি দেখা যায়। এই ত্রুটি সংশোধনের জন্য বস্তুটিকে একবার বাম তুলাপাত্রে এবং একবার ডান তুলাপাত্রে রেখে ভর নির্ণয় করতে হয়। ধরা যাক, এক্ষেত্রে ভর দুটি যথাক্রমে m1 ও m2।
∴ বস্তুটির সঠিক ভর = \(\sqrt{m_1⋅m_2}\)
অসম ভরের তুলাপাত্রজনিত ত্রুটি – তুলাযন্ত্রের তুলাপাত্র দুটির ভর সমান না হলে এই জাতীয় ত্রুটি দেখা যায়। এই ত্রুটি সংশোধনের জন্য বস্তুটিকে একবার বাম তুলাপাত্রে আরেকবার ডান তুলাপাত্রে রেখে ভর নির্ণয় করতে হয়। ধরা যাক, নির্ণীত ভর দুটি যথাক্রমে m1 ও m2।
∴ বস্তুটির সঠিক ভর = \(\frac{m_1+m_2}2\)
গ্রাফ পেপারের সাহায্যে একটি অসম আকৃতির পাত বা ফলকের ক্ষেত্রফল নির্ণয় করবে কীভাবে?
অসম আকৃতির পাতটিকে গ্রাফ পেপারে বসিয়ে পেনসিলের সাহায্যে পাতটির প্রান্ত বরাবর দাগ টানা হল। এই দাগই হল পাতটির পরিধি। ওই অংশের ক্ষেত্রফল নির্ণয় করতে হলে প্রথমে দেখতে হবে এর মধ্যে কয়টি পূর্ণ বর্গক্ষেত্র আছে ও কতগুলি অসম্পূর্ণ বর্গক্ষেত্র আছে।
পাতটির ক্ষেত্রফল = পূর্ণ বর্গক্ষেত্রগুলির ক্ষেত্রফল + \(\frac12\) × অসম্পূর্ণ ক্ষেত্রগুলির ক্ষেত্রফল। (ধরে নেওয়া হয় অসম্পূর্ণ একটি বর্গক্ষেত্রের ক্ষেত্রফল = \(\frac12\) × একটি পূর্ণ বর্গক্ষেত্রের ক্ষেত্রফল)।
প্রদত্ত ছবিটি থেকে অসম আকৃতির ক্ষেত্রটির ক্ষেত্রফল নির্ণয় করো।
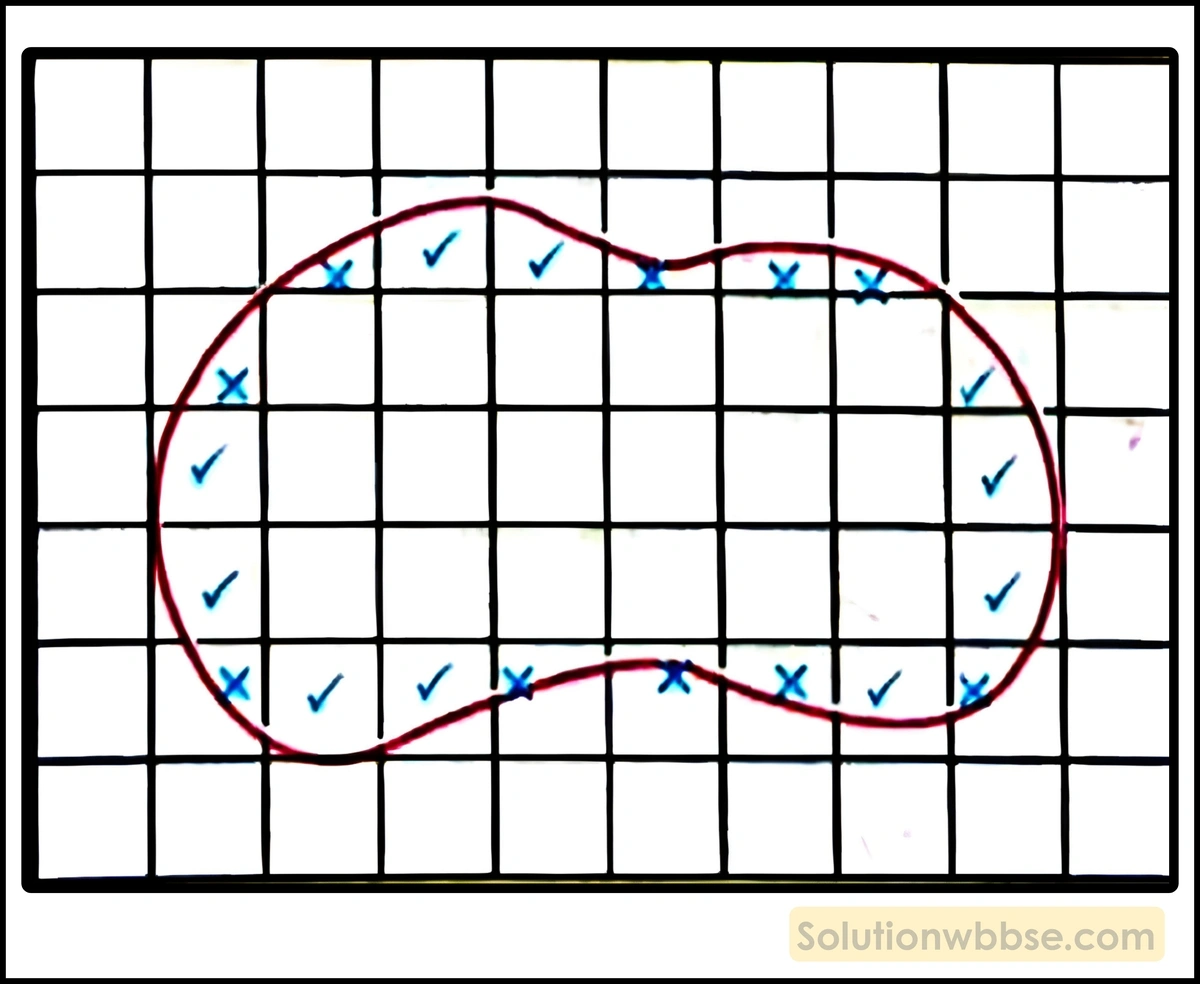
প্রদত্ত চিত্র থেকে পাই, সম্পূর্ণ বর্গের সংখ্যা = n1 = 18।
যেসব বর্গের অর্ধেকের বেশি অংশ (✓ চিহ্নিত) পেনসিলের রেখা দ্বারা আবদ্ধ তার সংখ্যা = n2 = 10।
যেসব বর্গের অর্ধেকের কম অংশ (× চিহ্নিত) পেনসিলের রেখা দ্বারা আবদ্ধ তার সংখ্যা = n3 = 10।
∴ অসম্পূর্ণ বর্গের গড় ক্ষেত্রফল = \(\frac{n_2+n_3}2\)
= \(\frac{10+10}2\)
= 10 বর্গএকক।
∴ পাতটির ক্ষেত্রফল = (18 +10) বর্গএকক = 28 বর্গএকক।
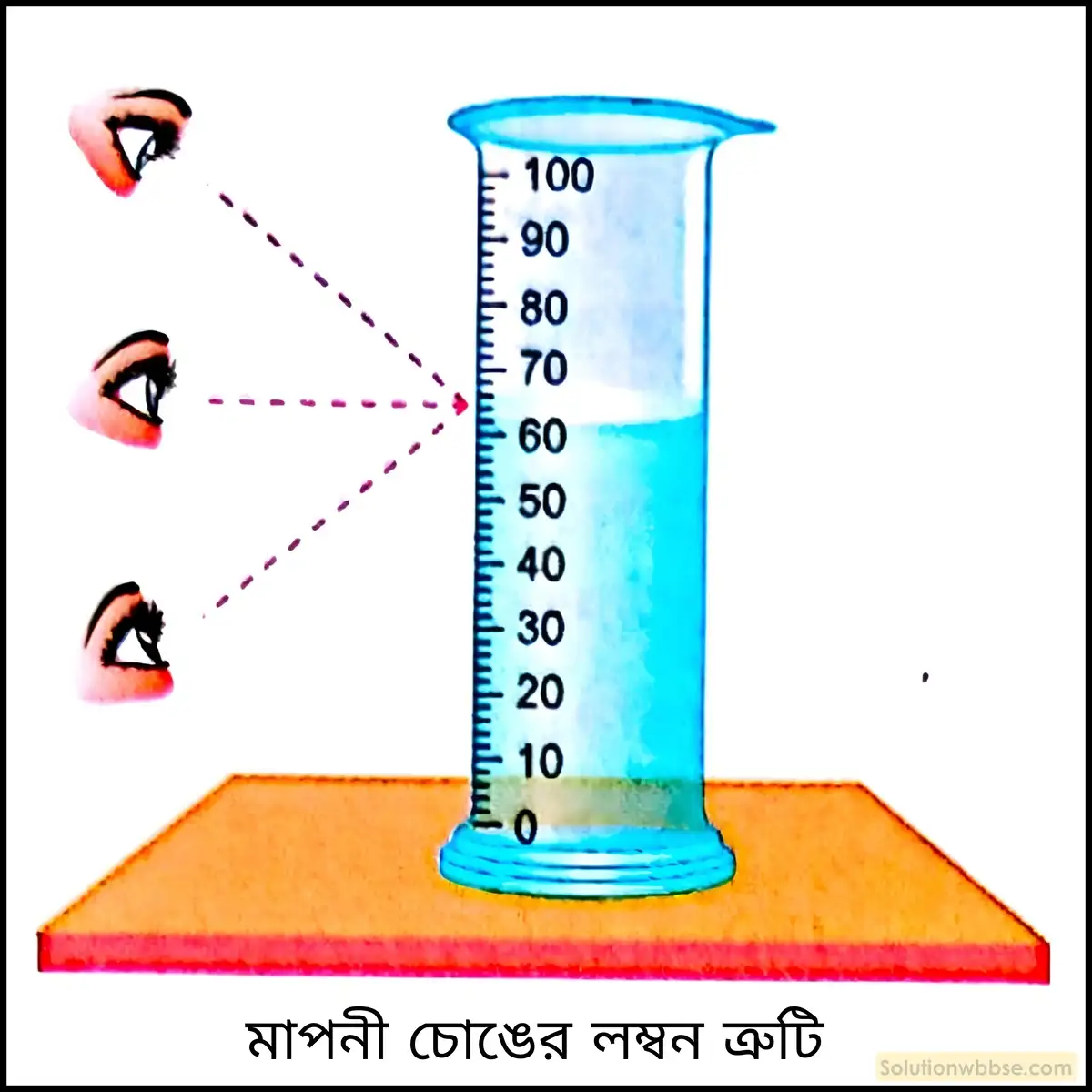
মাপনী চোঙ কাকে বলে?
মাপনী চোঙ (Measuring cylinder) – তরল পদার্থের আয়তন মাপার জন্য সম প্রস্থচ্ছেদবিশিষ্ট শক্ত কাচের তৈরি চোঙাকৃতি যে পাত্র ব্যবহার করা হয়, তাকে মাপনী চোঙ বা আয়তন মাপক চোঙ বলে। এর বাইরে নীচ থেকে ওপরের দিকে দৈর্ঘ্য বরাবর ঘন সেন্টিমিটারে (বা মিলিমিটারে) তার ভগ্নাংশের দাগ কাটা থাকে। পরীক্ষাগারে বিভিন্ন আয়তনের আয়তন মাপক চোঙ ব্যবহার করা হয়। যেমন – 1 L, 100 mL ইত্যাদি।
আয়তন মাপক চোঙের সাহায্যে কিছু পরিমাণ তরলের আয়তন কীভাবে নির্ণয় করবে? কী কী সতর্কতা সেই সময় অবলম্বন করবে?
মাপলী চোঙের সাহায্যে তরলের আয়তন নির্ণয় –
- একটি পরিষ্কার শুষ্ক মাপনী চোঙে সরাসরি পরীক্ষাধীন তরলটি ঢালা হয়,
- স্থির অবস্থায় অবতলাকৃতি (যেমন – জল) বা উত্তলাকৃতি (যেমন – পারদ) তরলতল অংশাঙ্কনের যে দাগ স্পর্শ করে তার পাঠ তরলতলের সমান্তরালে একই তলে চোখ রেখে নির্ণয় করা যায়।
- অবতল তরলতলের নিম্নপ্রান্ত অথবা, উত্তলাকৃতি তরলতলের উপরিঅংশ যে অংশাঙ্কন স্পর্শ করে সেটিই মাপনী চোঙে রাখা তরলের আয়তন নির্দেশ করে।

সতর্কতা – মাপনী চোঙের সাহায্যে তরল পদার্থের আয়তন নির্ণয় করার সময় নিম্নলিখিত সতর্কতাগুলি নেওয়া দরকার।
- পরীক্ষাধীন তরল চোঙে ঢালার সময় কোনো তরল যেন বাইরে ছিটকে না পড়ে।
- তরলের মধ্যে চোঙের গায়ে যেন বায়ুর বুদ্বুদ আটকে না থাকে।
- পাঠ নেওয়ার সময় চোখকে পাঠবিন্দুর সঙ্গে লম্বভাবে রাখতে হবে। এর ফলে লম্বন ত্রুটি হবে না।
- তরল-পৃষ্ঠের মাপ নেওয়ার সময় যেসব তরলের ওপরতল সামান্য অবতল (যেমন – জল) তাদের ক্ষেত্রে অবতল পৃষ্ঠের সবচেয়ে নীচের তলের পাঠ নিতে হবে। আবার যেসব তরলের ওপরতল সামান্য উত্তল (যেমন – পারদ) তাদের ক্ষেত্রে উত্তল পৃষ্ঠের সবচেয়ে উপরের তলের পাঠ নিতে হবে। এই কাজটি অত্যন্ত সতর্কতার সঙ্গে করা উচিত।
- কম পরিমাণ তরলের আয়তন মাপতে সরু চোঙ ব্যবহার করতে হবে যাতে ত্রুটির মাত্রা কম হয়।
- একই তরলের ক্ষেত্রে অন্তত দুবার পাঠ নিয়ে তার গড় নির্ণয় করতে হবে।
খুব কম পরিমাণ এবং বেশি পরিমাণ তরলের আয়তন পরিমাপের জন্য কী ধরনের আয়তন মাপক চোঙ ব্যবহার করা হয়?
উভয়ক্ষেত্রেই একই ধরনের আয়তন মাপক চোঙ ব্যবহার করা হয় না। খুব কম পরিমাণ তরলের ক্ষেত্রে সরু ও ছোটো আয়তন মাপক চোঙ ব্যবহার করতে হবে এবং বেশি পরিমাণ তরলের ক্ষেত্রে মোটা ও বড়ো আয়তন মাপক চোঙ ব্যবহার করতে হবে।
মাপনী চোঙের সাহায্যে জলে অদ্রাব্য জলের চেয়ে হালকা বস্তু বা একখণ্ড শোলার আয়তন কীভাবে নির্ণয় করবে?
শোলা জলের চেয়ে হালকা। তাই এর আয়তন নির্ণয় করতে শোলার সঙ্গে জানা আয়তনের (V1) একটি পাথরখণ্ড সুতো দিয়ে বেঁধে মাপনী চোঙে রাখা জলে ডোবাতে হবে। ফলে চোঙের জলতলের উচ্চতা বৃদ্ধি পাবে। উচ্চতা যতটুকু বৃদ্ধি পাবে সেটাই শোলা ও পাথরখণ্ডের মোট আয়তন (V2)। এর থেকে পাথরখণ্ডের আয়তন বাদ দিলেই শোলার আয়তন (V2 – V1) পাওয়া যাবে।
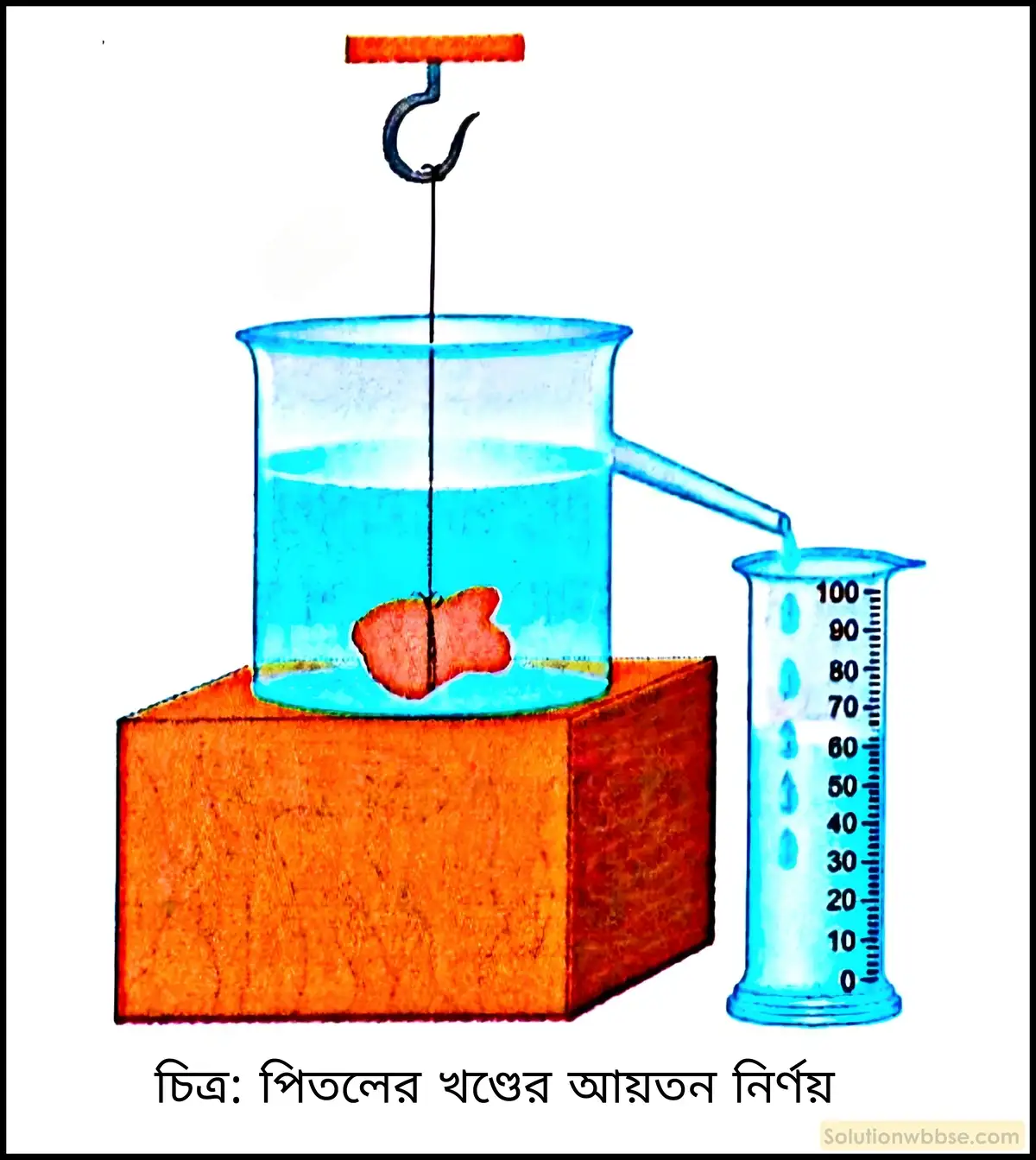
একটি পিতলের খণ্ড আয়তন মাপক চোঙের মধ্যে ঢুকছে না। এক্ষেত্রে তুমি খণ্ডটির আয়তন নির্ণয় করবে কীভাবে?
অথবা, মাপনী চোঙের মধ্যে ঢুকবে না এমন পাথরের টুকরোর আয়তন তুমি কীভাবে নির্ণয় করবে?
ছবির মতো পার্শ্বনলবিশিষ্ট একটি পাত্র নিয়ে তাতে পার্শ্বনলের তল পর্যন্ত জল ভরতি করা হল। এবার প্রদত্ত পিতলের খণ্ডটি বা পাথরটি মোমে ভেজানো সুতোয় বেঁধে পাত্রটির জলে ডুবিয়ে দেওয়া হল। তারপর পিতলের খণ্ডটি বা পাথরটি যতটুকু আয়তন পিতলের খণ্ডের আয়তন নির্ণয় জল অপসারণ করবে তা পার্শ্বনলের মাধ্যমে মাপনী চোঙে জমানো হল এবং তার পাঠ নেওয়া হল। মনে করি, মাপনী চোঙের পাঠ হল V cm3।
∴ পিতলের খণ্ডের বা পাথরের আয়তন = অপসারিত জলের আয়তন = Vcm3।
সাধারণ তুলাযন্ত্র ও মাপনী চোঙের সাহায্যে একটি অনিয়মিত আকারের কঠিন বস্তুর ঘনত্ব কীভাবে নির্ণয় করবে?
অথবা, জলে অদ্রাব্য কোনো অনিয়তাকার কঠিন বস্তুর ঘনত্ব আয়তনমাপক চোঙ ও সাধারণ তুলাযন্ত্রের সাহায্যে কীভাবে মাপবে?
সাধারণ তুলাযন্ত্র ও মাপনী চোঙের সাহায্যে কোনো অসম আকৃতির কঠিন বস্তুর ঘনত্ব নির্ণয় –
- প্রথমে সাধারণ তুলাযন্ত্রের সাহায্যে অসম আকৃতির কঠিন বস্তুর ভর পরিমাপ করা হল। ধরি, বস্তুটির ভর হল m একক।
- প্রথমে মাপনী চোঙটি ধুয়ে ভালোভাবে শুকিয়ে নেওয়া হল।
- এবার আয়তন মাপক চোঙে এমনভাবে জল ঢালা হল যাতে পরীক্ষাধীন বস্তুটি ওই জলে সম্পূর্ণ ডুবে যেতে পারে। এবার ওই জলতলের পাঠ নেওয়া হল। মনে করি, পাঠ V1 একক।
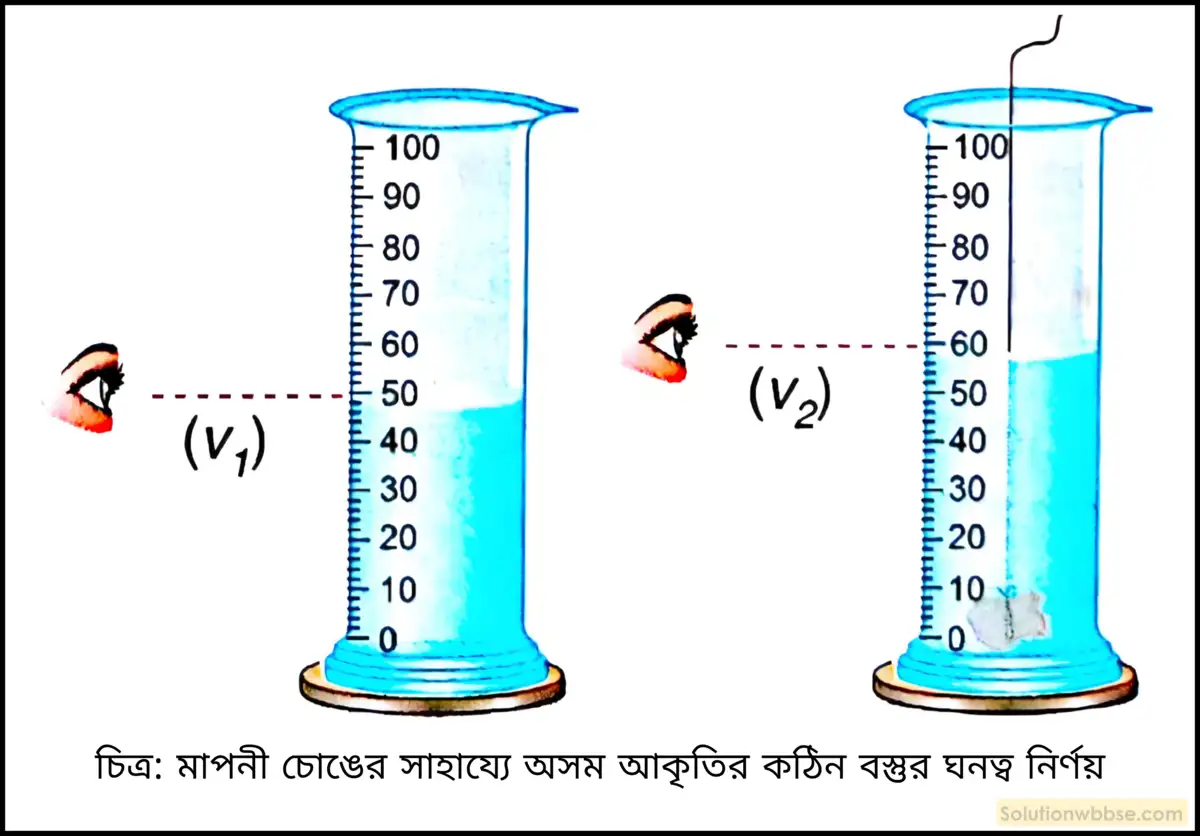
এবার বস্তুটিকে পরিষ্কার করে মোম মাখানো একটি সরু ও শক্ত সুতো দিয়ে বেঁধে ধীরে ধীরে তরলের মধ্যে ডোবানো হল। ফলে, জলতল কিছুটা উপরে উঠবে। এই অবস্থায় জলতলের পাঠ নেওয়া হল। মনে করি, এই পাঠ V2 ঘনএকক। [এক্ষেত্রে, মোম মাখালে সুতোটি ভেজে না। অর্থাৎ, জলশোষণ করে না, তাই পাঠে ত্রুটি আসে না।]
এখন বস্তুর প্রকৃত আয়তন পেতে গেলে (V2 – V1) পাঠ থেকে নিমজ্জিত সুতোর আয়তন বাদ দিতে হবে। এক্ষেত্রে পাঠ নেওয়ার সময় লম্বন ত্রুটি যাতে না আসে, সেদিকে লক্ষ রাখতে হবে।
∴ কঠিন বস্তুর ঘনত্ব (d) = একক।
∴ \(d=\frac m{V_1-V_2}\)
কঠিন বস্তুটি জলে দ্রাব্য হলে কেরোসিন ব্যবহার করা হয়কেন?
কঠিন বস্তুটি জলে দ্রাব্য (যেমন – তুঁতে, তালমিছরি, লবণ, চিনি ইত্যাদি) হলে জলের পরিবর্তে রাসায়নিকভাবে নিষ্ক্রিয় এমন তরল নির্বাচন করতে হবে যাতে বস্তুটি ওই তরলে অদ্রাব্য হয়। সাধারণত এক্ষেত্রে কেরোসিন ব্যবহার করা হয়।
পাত্র থেকে কোনো তরল যাতে ছিটকে বাইরে না পড়ে তা নিশ্চিত করার জন্য কঠিন বস্তুটি ধীরে ধীরে জলে বা উপযুক্ত তরলে ডোবানো উচিত। নির্ভুল পাঠ পাওয়ার জন্য সুতোয় মোমের প্রলেপ লাগানো বাঞ্ছনীয়।
একটি ড্রপারে একফোঁটা জলের আয়তন নির্ণয় করবো কিভাবে?
অথবা, একটি মাপনী চোঙের সাহায্যে তুমি কীভাবে একফোঁটা জলের আপাত আয়তন নির্ণয় করবে?
একটি সরু আকৃতির মাপনী চোঙে ড্রপারের সাহায্যে 100 ফোঁটা জল ফেলা হল। এই জলের আয়তন মাপনী চোঙের গায়ে কাটা দাগ থেকে জানা গেল। ধরি, এই আয়তন সিসি। সুতরাং, ড্রপারটির একফোঁটা জলের আয়তন \(\frac V{100}\) সিসি।
জলের ফোঁটার ব্যাস নির্ণয় করো।
জলের ফোঁটা গোলাকৃতি এবং তার ব্যাস d হলে,
\(\frac43\pi r^3=\frac V{100}\\\)বা, \(\frac43\pi\left(\frac d2\right)^3=\frac V{100}\)
বা, \( d=2\times\left(\frac{3V}{400\mathrm\pi}\right)^\frac13\)
∴ \(d=2\times\left(\frac{3V}{400\mathrm\pi}\right)^\frac13 \) এর থেকে জলের ফোঁটার ব্যাস নির্ণয় করা যায়।
একটি মাপনী চোঙ নাও, যাতে 100 cm3 পর্যন্ত দাগ কাটা আছে। এবার এতে প্রথমে জল, এরপর কেরোসিন তেল ও তারপর সরষের তেল নাও এবং প্রতিটি পদার্থের ঘনত্ব নির্ণয় করো।
প্রদত্ত মাপনী চোঙের সাহায্যে প্রত্যেক তরলের (অর্থাৎ, জল, কোরোসিন তেল ও সরষের তেলের) 100 cm3 আয়তন পরিমাপ করা হল। এরপর একটি সাধারণ তুলাযন্ত্রের সাহায্যে প্রত্যেক তরলের ভর পৃথকভাবে নির্ণয় করা হল। যদি তাদের ভর ও যথাক্রমে m1, m2 ও m3g হয় তবে, তাদের ঘনত্ব হবে যথাক্রমে \(\frac{m_1}{100}g/cm^3\), \(\frac{m_2}{100}g/cm^3\)ও \(\frac{m_3}{100}g/cm^3\)।
আয়তন মাপক চোঙ ও স্টপওয়াচের সাহায্যে কল থেকে জল পড়ার হার নির্ণয় করো।
আয়তন নাপক চোঙ ও স্টপওয়াচের সাহায্যে কল থোক জল পড়ার হার নির্ণয় –
- একটি শুকনো ও খালি মাপনী চোঙ নিয়ে কলের মুখে ধরা হল এবং সঙ্গে সঙ্গে স্টপওয়াচের চাবি প্রথমবার টিপে স্টপওয়াচ চালু করা হল।
- কিছুক্ষণ ধরে জল চোঙে সংগ্রহ করার পর চোঙটিকে কলের মুখ থেকে সরিয়ে নেওয়া হল এবং সঙ্গে সঙ্গে চাবি দ্বিতীয়বার টিপে স্টপওয়াচ বন্ধ করা হল।
স্টপওয়াচের সাহায্যে কত সময় ধরে জল নেওয়া হল তা পরিমাপ করা হল। মাপনী চোঙের সাহায্যে সংগৃহীত জলের আয়তন পরিমাপ করা হল।
ধরি, জলের আয়তন = V cc এবং t সেকেন্ড সময় ধরে জল নেওয়া হয়েছে।
∴ কল থেকে জল পড়ার হার = \(\frac Vtcc/s\)
একজন বালকের 100 মিটার দৌড়তে কত সময় লাগে তা কীভাবে পরিমাপ করা যায়?
নির্ণেয় সময় পরিমাপের জন্য স্টপওয়াচ ব্যবহার করতে হবে। এক্ষেত্রে বালকটি দৌড় শুরু করা মাত্র স্টপওয়াচ চালাতে হবে এবং 100 মিটারের দাগ অতিক্রম করার সঙ্গে সঙ্গে স্টপওয়াচ বন্ধ করতে হবে। স্টপওয়াচের পাঠ দেখে বলা যাবে বালকটির 100 মিটার দৌড়তে কত সময় লাগল।
কোনো পরিমাপক যন্ত্রের লঘিষ্ঠ ধ্রুবক বলতে কী বোঝায়?
লঘিষ্ঠ ধ্রুবক (Least count) – যে-কোনো পরিমাপক যন্ত্রের সঙ্গে একটি পরিমাপক স্কেল যুক্ত থাকে। এই স্কেলের একটি ক্ষুদ্রতম ঘর (division) -কে বলা হয় ওই যন্ত্রের লঘিষ্ঠ ধ্রুবক। সুতরাং, যে-কোনো যন্ত্র থেকে ন্যূনতম যে মানের পরিমাপ পাওয়া যায়, তাকে ওই যন্ত্রের লঘিষ্ঠ ধ্রুবক বলা হয়।
পরিমাপের ত্রুটি কাকে বলে? এটি কয়প্রকার ও কী কী?
যে-কোনো পরিমেয় ভৌতরাশির প্রকৃত মান এবং যন্ত্রের সাহায্যে প্রাপ্ত ওই রাশির পরীক্ষালব্ধ মানের পার্থক্যকে বলা হয় ওই রাশির পরিমাপের ত্রুটি।
কোনো যন্ত্র দ্বারা প্রাপ্ত পরিমাপে দুই প্রকার ত্রুটি বর্তমান –
- যান্ত্রিক ত্রুটি,
- অন্যান্য ত্রুটি।
যান্ত্রিক ত্রুটি হল সংশ্লিষ্ট যন্ত্রের পরিমাপের নিম্নসীমা। যেমন – সাধারণ রৈখিক স্কেলে লঘিষ্ঠ ধ্রুবক 0.1 cm। আবার ভার্নিয়ার স্কেলের লঘিষ্ঠ ধ্রুবক 0.01 cm।
অন্যান্য ত্রুটির উৎস হল পরিমাপে অসতর্কতা বা পাঠগ্রহণের সময় মনোযোগের অভাব বা অন্য কোনো সমস্যা। যথেষ্ট সংখ্যক সতর্কতার সঙ্গে গৃহীত পর্যবেক্ষণের দ্বারাই এই ত্রুটি কমানো সম্ভব।
পরিমাপের শতকরা বা শতাংশ ত্রুটি বলতে কী বোঝায়? উদাহরণসহ ব্যাখ্যা করো।
পরিমাপের শতাংশ ত্রুটি (Percentage error) – এই ত্রুটির গাণিতিক প্রকাশ হল –
উদাহরণ – ধরা যাক, একটি সাধারণ রৈখিক স্কেল দ্বারা পরিমাপে প্রাপ্ত কোনো পেনসিলের ব্যাসের মান 0.4 cm এবং ভার্নিয়ার স্কেল দ্বারা নির্ণীত মান 0.42 cm।
∴ সাধারণ স্কেল দ্বারা পরিমাপে প্রাপ্ত ত্রুটি = \(\left(\frac{0.1}{0.4}\times100\right)\%=25\%\)
ভার্নিয়ার স্কেল দ্বারা পরিমাপে প্রাপ্ত ত্রুটি = \(\left(\frac{0.01}{0.40}\times100\right)\%=2.5\%\)
সুতরাং, পরিমাপক যন্ত্রের লঘিষ্ঠ ধ্রুবক যত কম হয়, সেই যন্ত্র দ্বারা পরিমাপে শতাংশ ত্রুটিও তত কমে।
একটি স্টপওয়াচের চক্রাকার ডায়ালে 120টি ঘর আছে। ঘড়িটির লঘিষ্ঠ ধ্রুবক কত?
প্রশ্নানুযায়ী, 120টি ঘরের মান= 60 সেকেন্ড।
∴ 1টি ঘরের মান = \(\frac{60}{120}\) সেকেন্ড = 0.5 সেকেন্ড। [∴ কাঁটাটি একবার ঘুরলে 60 সেকেন্ড সময় যায়।]
∴ ঘড়িটির লঘিষ্ঠ ধ্রুবক = 0.5 সেকেন্ড।
বোধমূলক প্রশ্নোত্তর
রৈখিক স্কেল ধাতুর তৈরি না হয়ে সাধারণত প্লাস্টিক বা কাঠের হয় কেন?
উষ্ণতার পরিবর্তনে ধাতুর দৈর্ঘ্যর পরিবর্তন হয়। তাই উষ্ণতা বৃদ্ধিতে ধাতব স্কেলে ক্ষুদ্রতম ঘর দৈর্ঘ্যে বাড়ে এবং উষ্ণতা হ্রাসে কমে। উভয়ক্ষেত্রেই ওই স্কেলের সাহায্যে পরিমাপ ত্রুটিপূর্ণ হয়। সেকারণেই ধাতব স্কেল যে উষ্ণতায় অংশাঙ্কিত শুধুমাত্র সেই উষ্ণতায় সঠিক পাঠ দেয়।
অন্যদিকে কাঠ বা প্লাস্টিক কুপরিবাহী পদার্থ হওয়ায় উষ্ণতার পরিবর্তনে তাদের প্রসারণ বা সংকোচন উপেক্ষণীয় মানের হয়। ফলে যে-কোনো উষ্ণতায় কাঠ বা প্লাস্টিক স্কেল ধাতব স্কেলের তুলনায় নির্ভুল পাঠ দিতে পারে। একারণেই রৈখিক স্কেল প্লাস্টিক বা কাঠ দিয়ে তৈরি করা হয়। ধাতুর সাহায্যে নয়।
সাধারণ স্কেলের সাহায্যে কি 0.7 mm মাপ নেওয়া যায়?
সাধারণ স্কেলের সাহায্যে প্রত্যক্ষভাবে 0.7 mm মাপ নেওয়া সম্ভব নয়। কারণ সাধারণ স্কেলের সবচেয়ে ক্ষুদ্রতম ঘরের মান 1 mm। কিন্তু অপ্রত্যক্ষভাবে সাধারণ স্কেলের সাহায্যে 0.7 mm মাপ নেওয়া যায়। যেমন – বইয়ের একটি পাতার বেধ 1 mm অপেক্ষা কম হলেও সাধারণ স্কেলের সাহায্যে তা মাপা যায়। এক্ষেত্রে ব্যবহৃত সূত্রটি হল –
।
তবে 1 mm অপেক্ষা কম দৈর্ঘ্যের সঠিক পরিমাপ পেতে গেলে ভার্নিয়ার স্কেল ব্যবহার করা যেতে পারে।
কারণ – এই স্কেলের লঘিষ্ঠ ধ্রুবক 0.1 mm।
সাধারণ স্কেলে লম্বন ত্রুটি ছাড়া আর কী ত্রুটি থাকতে পারে?
সাধারণ স্কেলে লম্বন ত্রুটি ছাড়াও স্কেলের গঠনজনিত ত্রুটি থাকতে পারে। অর্থাৎ, স্কেলের দাগগুলির মধ্যে অনেকসময় সমান ব্যবধান থাকে না। এই ত্রুটির ফলে নিখুঁতভাবে দৈর্ঘ্য মাপা যায় না। এই ত্রুটি সংশোধনের জন্য স্কেলটির বিভিন্ন অংশ ব্যবহার করে কয়েকবার দৈর্ঘ্য মেপে তাদের গড় নিয়ে এই ধরনের ত্রুটি সংশোধন করা হয়।
একটি ধাতব স্কেলে 20°C উষ্ণতায় দাগ কাটা আছে। এই স্কেলটি দিয়ে 30°C উষ্ণতায় কোনো দৈর্ঘ্য পরিমাপ করলে কম না বেশি দৈর্ঘ্য পরিমিত হবে? ব্যাখ্যা করো।
স্কেলটি দিয়ে 30°C উষ্ণতায় কোনো দৈর্ঘ্য পরিমাপ করলে কম দৈর্ঘ্য পরিমিত হবে।
কারণ – 30°C উষ্ণতায় স্কেলটি নিজে দৈর্ঘ্যে বেড়ে যাওয়ায় ক্ষুদ্রতম ঘরগুলির ব্যবধান বেড়ে যাবে। তাই নির্ণীত দৈর্ঘ্য আসল দৈর্ঘ্য অপেক্ষা কম হবে।
দৌড় প্রতিযোগিতায় সাধারণ ঘড়ি ব্যবহার করা হয় না কেন?
সাধারণ ঘড়িকে ইচ্ছামতো চালানো বা বন্ধ করা যায় না। সে কারণে দৌড় প্রতিযোগিতার শুরু ও শেষের সময় সঠিকভাবে পরিমাপ করা যায় না। এছাড়া সাধারণ ঘড়ির সাহায্যে সেকেন্ডের ভগ্নাংশও পরিমাপ করা যায় না। তাই এক্ষেত্রে স্টপওয়াচ ব্যবহার করা হয়।
একটি টিভিতে চলচ্চিত্র দেখানোর জন্য প্রতি সেকেন্ডে 25টি ছবি (frame) দেখানো হয়। পরপর দুটি frame -এর মধ্যবর্তী সময়কাল কত?
প্রশ্নানুযায়ী, প্রতি সেকেন্ডে 25টি ছবি দেখানো হয়।
এই 25টি ছবি অর্থাৎ frame -এর মধ্যে সময়ের ব্যবধান আসে 24 বার।
∴ 24 বার ব্যবধান সৃষ্টি করতে সময় লাগে = 1 সেকেন্ড।
∴ 1 বার ব্যবধান সৃষ্টি করতে সময় লাগে = \(\frac1{24}\) সেকেন্ড।
অর্থাৎ, পরপর দুটি frame -এর মধ্যবর্তী সময়কাল = \(\frac1{24}\) সেকেন্ড।
25 g 19 mg ভরের কোনো বস্তুর ভর মাপতে তুমি কী কী ভরের বাটখারা ব্যবহার করবে?
25 g = 20 g + 5 g
19 mg = 10 mg + 5 mg + 2 mg + 2 mg
∴ 25 g 19 mg ভর মাপতে ন্যূনতম 5টি বাটখারা ব্যবহার করতে হবে। এদের ভর হবে (20, 5) g এবং (10, 5, 2) mg।
একটি বস্তুর ভর 8 g 20 mg। ওজন বাক্সে বাটখারাগুলির অনুপাত 1 : 2 : 2 : 5 হলে ন্যূনতম কয়টি ও কত ভরের বাটখারার সাহায্যে ওই ভর পরিমাপ করা যায়?
8 g 20 mg = (5 + 2 + 1) g (20) mg
[∴ ন্যূনতম চারটি বাটখারার সাহায্যে ওই ভর পরিমাপ করা যাবে যাদের ভর হল 5 g, 2 g, 1 g ও 20 mg
[∵ ওজন বাক্সে বাটখারাগুলির ভরের অনুপাত 1 : 2 : 2 : 5 তাই ওজন বাক্সে 1, 2, 2, 5 গ্রাম এবং 10, 20, 20, 50 মিলিগ্রাম বাটখারা আছে]
অতিমাত্রায় সুবেদী তুলাযন্ত্র সুস্থিত হতে পারে না কেন?
খুব সুবেদী তুলাযন্ত্র সুস্থিত হয় না। কারণ – খুব সুবেদী তুলাযন্ত্রের তুলাদণ্ডটি খুব হালকা হয়, সূচকটি খুব লম্বা হয় এবং দণ্ডের বাহুদুটিও লম্বা হয়। তাই তুলাপাত্র দুটির ভরের অর্থাৎ, বস্তুর ভর ও বাটখারার ভরের খুব সামান্য কম পার্থক্য হলেই তুলাদণ্ডটি বেশি ভরের দিকে হেলে যায় এবং বস্তুর ভর ও বাটখারার ভর সমান হলে তুলাদণ্ডটি ক্রমাগত স্কেলের শূন্য দাগের দুপাশে সমদূরত্ব যায় অর্থাৎ দুলতে থাকে। কিন্তু কখনোই শূন্য দাগে স্থির হয় না।
কোনো বস্তুকে কলকাতায় সাধারণ তুলাযন্ত্র ও স্প্রিং তুলাযন্ত্রে মাপা হল এবং দার্জিলিং -এ ওই বস্তুটিকে সাধারণ তুলাযন্ত্র ও স্প্রিং তুলাযন্ত্রে মাপা হল। কোন্ যন্ত্রে পাঠের পরিবর্তন হবে?
স্প্রিং তুলায় পাঠের পরিবর্তন হবে। কারণ – ভার, অভিকর্ষজ ত্বরণের ওপর নির্ভরশীল। কলকাতা ও দার্জিলিং -এ অভিকর্ষজ ত্বরণের মান সমান নয়। তাই ভারের পরিবর্তন হবে, কিন্তু ভরের পরিবর্তন হবে না। তাই সাধারণ তুলাযন্ত্রে পাঠের কোনো পরিবর্তন হয় না।
সাধারণ তুলাযন্ত্র কীসের পরিমাপ দেয়, ভর না ওজন? তোমার উত্তরের ব্যাখ্যা দাও।
সাধারণ তুলাযন্ত্রের দ্বারা ভর পরিমাপ করা হয়, ভার বা ওজন নয়।
ব্যাখ্যা – দণ্ড তুলাযন্ত্রে প্রমাণ ওজনের বাটখারাগুলির মোট ওজনের সঙ্গে পরীক্ষাধীন বস্তুর ওজনের তুলনা করে বাটখারার ভরের তুল্য ভর সরাসরি নির্ণয় করা হয়।
তুলাদণ্ডের সাম্য অবস্থানে,
∴ বাটখারাগুলির মোট ভার = পরীক্ষাধীন বস্তুর ভার
∴ বাটখারাগুলির ভর × g = পরীক্ষাধীন বস্তুর ভর × g
∴ বস্তুর ভর = বাটখারাগুলির ভর [যেহেতু, ওজন = ভর (m) × অভিকর্ষজ ত্বরণ (g)]
এটিই তুলাযন্ত্রের কার্যনীতি। যেহেতু, এই কার্যকর সম্পর্কের উভয়পক্ষেই অভিকর্ষজ ত্বরণ অনুপস্থিত। সুতরাং, সাধারণ তুলাযন্ত্র কেবল ভরের পরিমাপ দিতে সক্ষম, ভার বা ওজনের নয়।
অভিকর্ষহীন স্থানে সাধারণ তুলাযন্ত্র দিয়ে ভর মাপা যাবে কি?
সাধারণ তুলাযন্ত্রে বস্তুর ওজনের সঙ্গে বাটখারার ওজনের তুলনা করে বস্তুর ভর নির্ণয় করা হয়। অভিকর্ষহীন স্থানে বস্তুর ওজন শূন্য হয়। তাই এক্ষেত্রে বস্তুর ওজন = বাটখারার ওজন এই তুলনা করা যায় না। তাই ভর মাপা যাবে না।
প্রকৃত ভর মাপার জন্য কোনটি বেশি গুরুত্বপূর্ণ – তুলাযন্ত্র না বাটখারা?
প্রকৃত ভর মাপার জন্য বাটখারা বেশি গুরুত্বপূর্ণ। কারণ তুলাযন্ত্রে কোনো ত্রুটি থাকলে (যেমন – তুলাদণ্ড দুটির দৈর্ঘ্য অসমান হলে বা তুলাপাত্র দুটির ভর অসমান হলে) তা বিভিন্ন উপায়ে সংশোধন করা যায়। কিন্তু বাটখারায় ত্রুটি থাকলে তা সংশোধন করা যায় না।
দুটো স্বচ্ছ প্লাস্টিকের বোতল নাও। একটি বোতল কিছুটা শুকনো ও পরিষ্কার বালি দিয়ে ভরতি করা হল। ছিপি বন্ধ করে ছিপির ঠিক মাঝখানে একটি ছোটো ছিদ্র করো। অপর বোতলটির ছিপি খুলে প্রথম বোতলটির ওপর বসিয়ে দাও এবং সেলোটেপ দিয়ে শক্ত করে বোতল দুটিকে আটকে দাও। বোতল দুটিকে উলটে স্টপওয়াচের সাহায্যে বালি পড়ার সময় মাগো। এরকম কয়েকবার করে দ্যাখো প্রতি বারে একই সময় লাগছে কি না। তাহলে এটাকে কীভাবে একটি ঘড়ি হিসেবে ব্যবহার করবে?
দুটি স্বচ্ছ প্লাস্টিকের বোতল নিয়ে, তার মধ্যে একটি বোতল কিছুটা শুকনো ও পরিষ্কার বালি দিয়ে ভরতি করা হল। এখন ছিপি বন্ধ করে ছিপির ঠিক মাঝখানে একটি ছোটো ছিদ্র করা হল। এরপর অপর বোতলটির ছিপি খুলে প্রথম বোতলটির ওপর বসিয়ে দেওয়া হল এবং সেলোটেপ দিয়ে শক্ত করে বোতল দুটি আটকে দেবার পর বোতল দুটিকে উলটে স্টপওয়াচের সাহায্যে বালি পড়ার সময় মাপা হল। এরকমভাবে বেশ কয়েকবার করে দেখলে দেখা যাবে প্রতিবারে একই সময় লাগছে। ধরা যাক, বালি পড়ার সময় = 10 মিনিট। অর্থাৎ, এটি একটি ঘড়ি হিসেবে ব্যবহার করা যায়।
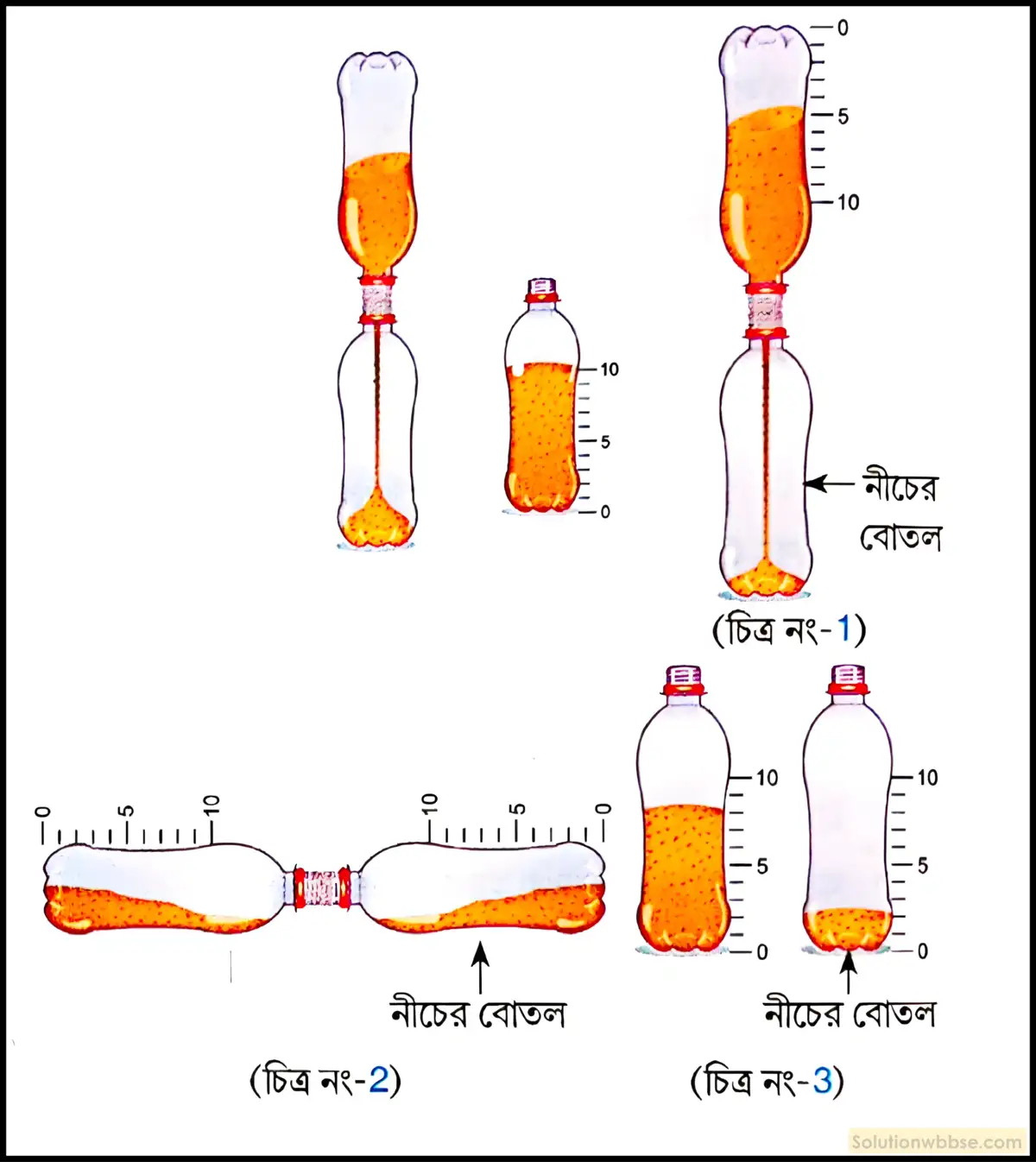
তার জন্য বোতলের গায়ে অংশাঙ্কন করতে হবে। যেহেতু বালি পড়তে 10 মিনিট সময় লাগছে তাই বোতলের বালির আয়তনকে 10 ভাগে ভাগ করলে প্রতি ভাগ 1 মিনিট নির্দেশ করবে। পাশের চিত্রটি লক্ষ করলে স্পষ্ট বোঝা যাবে।
এবার কোনো ঘটনা ঘটার সময় যদি ঘটনা শুরুর মুহূর্তে বোতল দুটিকে উলটে দেওয়া হয় এবং ঘটনা শেষের মুহূর্তে বোতল দুটি কাত করে রাখা হয় তবে নীচের বোতলে জমা হওয়া বালির আয়তন দেখে ঘটনাটি ঘটতে কত সময় লেগেছে তা বলা যাবে।
ধরি, টিভিতে কোনো বিজ্ঞাপন কত সময় ধরে হচ্ছে তা মাপতে চাই। এজন্য বিজ্ঞাপন শুরুর মুহূর্তে বোতল দুটিকে এমনভাবে ওলটাতে হবে যাতে সমস্ত বালি ওপরের বোতলে থাকে (চিত্র নং – 1)। এবার বিজ্ঞাপনটি শেষ হলেই বোতল দুটি কাত করে দিতে হবে (চিত্র নং – 2)। এবার সাবধানে ওপরের বোতলটি খুলে নেওয়া হল এবং নীচের বোতলের অংশাঙ্কন দেখে বিজ্ঞাপনটি ঘটার সময় পরিমাপ করতে পারি (চিত্র নং – 3)। চিত্রানুযায়ী বিজ্ঞাপনটি ঘটার সময় 2 মিনিট।
এই পদ্ধতিতে খুব সূক্ষ্ম পরিমাপ সম্ভব নয়। প্রয়োজনে বোতলের গায়ে বেশি অংশাঙ্কন করা যেতে পারে। যদি বালি পড়তে t মিনিট সময় লেগে থাকে এবং তুমি বোতলকে 10 ভাগে ভাগ করো তবে প্রতি ভাগ \(\frac t{10}\) মিনিট সময় নির্দেশ করবে। ব্যবস্থাটিকে ঘড়ি হিসেবে ব্যবহার করার জন্য খুব শুকনো ও পরিষ্কার বালি নিতে হবে এবং বোতল দুটির আয়তন সমান হতে হবে। এ ছাড়াও ছিদ্র দিয়ে সমহারে বালি পড়ছে কি না তাও লক্ষ রাখতে হবে।
গাণিতিক প্রশ্নাবলি
প্রয়োজনীয় সূত্রাবলি
কোনো পাত্রের জলের আয়তন = পাত্রটির আয়তন
পদার্থের ঘনত্ব,
তুলাযন্ত্রের বাহুর দৈর্ঘ্য আলাদা হলে, প্রকৃত ভর, \(m=\sqrt{m_1m_2}\) এবং তুলাপাত্রের ভর আলাদা হলে প্রকৃত ভর, \(m=\frac{m_1+m_2}2\) যেখানে, \(m_1\) = বাম তুলাপাত্রে রাখা বাটখারার ভর, \(m_2\) = ডান তুলাপাত্রে রাখা বাটখারার ভর।
একটি জলের ট্যাংকের ভিতরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 4 m, 3 m ও 2 m। 4°C উষ্ণতায় ওই ট্যাংকে কত জল ধরবে?
ট্যাংকের ভিতরের আয়তন = 4 m × 3 m × 2 m
= 400 × 300 × 200 cm3
= 24 × 106 cm3
= \(\frac{24\times10^6}{1000}L\)
= 24000 L
∴ ওই ট্যাংকে 24000 L জল ধরে।
একটি লোহার গোলকাকৃতি পাত্রের ব্যাস 20 cm হলে এর আয়তন কত? ওই পাত্রটিতে কত লিটার জল ধরবে?
গোলকের ব্যাসার্ধ = \(\frac{20}2\) = 10 cm
গোলকের আয়তন,
\(V=\frac43\pi r^3\\\)বা, \(V=\frac43\times\frac{22}7\times\left(10\right)^3\) cm3
বা, V = 4186.67 cm3
V ≈ 4.187 L [∵ 11 = 1000 cm3]
অর্থাৎ, ওই পাত্রটিতে 4.187 L জল ধরবে।
শঙ্কু আকৃতির একটি পাত্রের ভিতরের ব্যাস 6 cm এবং উচ্চতা 10 cm। ওই পাত্রটি জল দ্বারা পূর্ণ করা হলে জলের আয়তন কত হবে?
শঙ্কুর আয়তন = \(\frac13\pi r^2h\)
= \(\frac13\times\frac{22}7\times\left(\frac62\right)^2\times10\)
= 94.28 cm3
সুতরাং, জলের আয়তন = 94.28 cm3
= 94.28 × 10-3 L
= 0.0942 L
∴ জলের আয়তন 0.0942 L হবে।
একটি ধাতব চোঙাকৃতি পাত্রের ব্যাস 14 cm ও উচ্চতা 20 cm। চোঙটির আয়তন কত? ওই পাত্রটিতে জলের আয়তন কত?
চোঙের আয়তন = πr2h
= \(\frac{22}7\times\left(\frac{14}2\right)^2\times20\) cm3
= 3079.99 cm3
অর্থাৎ, পাত্রটিতে জলের আয়তন = 3.08 L
একখণ্ড লোহার ভর 760 g ও আয়তন 100 cc হলে লোহার ঘনত্ব কত?
নির্ণেয় লোহার ঘনত্ব =
= \(\frac{760}{100}\) g/cc
= 7.6 g/cc
= 7.6 g/cm3
লোহার ঘনত্ব 7.6 g/cm3 হবে।
একখণ্ড লোহার আয়তন 250 cc এবং ভর 2 kg হলে, এর ঘনত্ব কত হবে?
2 kg = 2000 g
নির্ণেয় লোহার ঘনত্ব =
= \(\frac{2000}{250}\) g/cc
= 8 g/cc
= 8 g/cm3
লোহার ঘনত্ব 8 g/cm3 হবে।
একটি মাপনী চোঙে 50 cc জল আছে। 9 গ্রাম ভরের একটি হালকা বস্তুকে 20 cc আয়তনের একটি লোহার টুকরোর সঙ্গে বেঁধে চোঙে ডোবানো হল। এর ফলে আয়তনের পাঠ পাওয়া গেল 80 cc। হালকা বস্তুর ঘনত্ব কত?
(জল + হালকা বস্তু + লোহার টুকরো) -এর আয়তন = 80 cc
জল ও লোহার টুকরোর আয়তন = (50 + 20) cc = 70 cc
হালকা বস্তুর আয়তন = (80 – 70) cc = 10 cc
হালকা বস্তুর ঘনত্ব \(\left(D\right)=\frac MV\)
= \(\frac9{10}\) g/cc
= 0.9 g/cc
∴ হালকা বস্তুর ঘনত্ব 0.9 g/cc
50 g ভরের একটি নিরেট ধাতব বলকে একটি মাপনী চোঙে থাকা 200 cc জলে পুরোপুরি ডুবিয়ে দিলে জলতলের পাঠ পাওয়া যায় 250 cc। ওই বলটির উপাদানের ঘনত্ব কত?
(জল + নিরেট ধাতব বল) -এর আয়তন = 250 cc
জলের আয়তন = 200 cc
নিরেট ধাতব বলের আয়তন = (250 – 200) cc = 50 cc
বলটির উপাদানের ঘনত্ব \(\left(D\right)=\frac MV\)
= \(\frac{50}{50}\) g/cc
= 1 g/cc
∴ বলটির উপাদানের ঘনত্ব 1 g/cc
একটি মাপনী চোঙে জলের প্রাথমিক লেভেল = 20 mL। একটি 15 g লোহার টুকরো জলে নিমজ্জিত করায় জলের লেভেল হয় 25 mL। আবার একটি কর্কের টুকরোকে লোহার টুকরোর সঙ্গে বেঁধে জলে নিমজ্জিত করলে জলের লেভেল হয় 35 mL। লোহার টুকরো ও কর্কের টুকরোর আয়তন নির্ণয় করো। লোহার ঘনত্ব নির্ণয় করো।
নির্ণেয় লোহার টুকরোর আয়তন = (25 – 20) = 5 mL
আবার, (কর্ক + লোহার) মোট আয়তন = 35 – 20 = 15 mL
∴ কর্কের টুকরোর আয়তন = (15 – 5) = 10 mL
সুতরাং, লোহার ঘনত্ব =
= \(\frac{15\;g}{5\;mL}\)
= 3 g/mL
= 3 g/cm3
∴ লোহার ঘনত্ব 3 g/cm3
4°C উষ্ণতায় 40 g জলে একটি পাত্র পুরোপুরি ভরতি হয়। ওই পাত্রে 32 g কেরোসিন ধরলে, কেরোসিনের ঘনত্ব কত?
4°C উষ্ণতায় জলের ঘনত্ব = 1 g/cc
∴ জলের আয়তন = \(\frac{40}1\) cc = 40 cc
ওই জল দিয়ে পাত্র ভরতি হয় বলে পাত্রের আয়তন 40 cc
∴ কেরোসিনের আয়তনও হবে 40 cc
∴ কেরোসিনের ঘনত্ব =
= \(\frac{32}{40}\) cc
= 0.8 g/cc
∴ কেরোসিনের ঘনত্ব 0.8 g/cc
লোহার ঘনত্ব 7.6 g/cm3 হলে, 38g লোহার আয়তন কত?
নির্ণেয় আয়তন =
= \(\frac{38\;g}{7.6\;g/cm^3}\)
= 5 cm3
∴ লোহার আয়তন 5 cm3
তরলের ঘনত্ব 8.4 একক হলে 100 cc তরলের ভর কত?
আমরা জানি,
ঘনত্ব =
∴ ভর = ঘনত্ব × আয়তন
= 8.4 × 100 g
= 840 g
∴ তরলের ভর 840 g
একটি পাত্রে 50 g জল ধরে। এই পাত্রে কত ভরের পারদ রাখা যাবে? দেওয়া আছে যে, জল ও পারদের ঘনত্ব যথাক্রমে 1 g/cm3 ও 13.6 g/cm3।
পাত্রে রাখা জলের আয়তন,
\(V=\frac md\\\)বা, \(V=\frac{50}1\) cc
বা, \(V=50\) cc
পাত্রের আয়তন = পাত্রে রাখা জলের আয়তন = 50 cc
ওই পাত্রকে পারদ দ্বারা পূর্ণ করলে পাত্রে থাকা পারদের ভর
∴ m1 = (V × dm)
বা, m1 = (50 × 13.6)
বা, m1 = 680 g
1.5 g/cc ঘনত্বের 100 cc চিনির দ্রবণে আরো 100 cc জল মেশালে মিশ্রণের ঘনত্ব কত হবে?
প্রশ্নানুযায়ী, প্রদত্ত দ্রবণের ঘনত্ব = 1.5 g/cc
এবং আয়তন = 100 cc
∴ দ্রবণের ভর = আয়তন × ঘনত্ব
= 100 × 1.5 g
= 150 g
দ্রবণে আরো 100 cc জল মেশালে, নতুন দ্রবণের আয়তন
= (100 + 100)
= 200 cc
নতুন দ্রবণের ভর
= (150 + 100)
= 250 g [∵ 100 cc জলের ভর = 100 g ]
নতুন দ্রবণের ঘনত্ব =
= \(\frac{250}{200}\) g/cc
= 1.25 g/cc
একটি সাধারণ তুলাযন্ত্রের বাহুগুলি অসমান। একবার বাম ও একবার ডান তুলাপাত্রে বস্তুটিকে চাপিয়ে ভর পাওয়া গেল যথাক্রমে 29 g এবং 31.03 g। বস্তুটির প্রকৃত ভর কত?
বাম তুলাপাত্রে ভর (m1) = 29 g, ডান তুলাপাত্রে ভর (m2) = 31.03 g
∴ প্রকৃত ভর \(\left(m\right)=\sqrt{m_1m_2}\)
বা, \(m=\sqrt{29\times31.03}\)
বা, \(m=\sqrt{899.87}\)
বা, \(m=29.99\;\approx\;30\;g\)
একটি সাধারণ তুলাযন্ত্রের তুলাপাত্র দুটির ভর আলাদা। এই তুলাযন্ত্রের দুটি তুলাপাত্রে বস্তুটিকে রেখে ভর পাওয়া গেল যথাক্রমে 25 g ও 25.4 g। বস্তুটির প্রকৃত ভর কত?
বাম ও ডান দুটি তুলাপাত্রে রাখা অবস্থায় ভর m1 ও m2 হলে প্রকৃত ভর \(\left(m\right)=\frac{m_1+m_2}2\)
∴ বস্তুটির প্রকৃত ভর = \(\frac12\left(25+25.4\right)\)
= 25.2 g
একটি সাধারণ তুলাদণ্ডের দুই বাহুর দৈর্ঘ্য সমান, কিন্তু তুলাপাত্র দুটির ভর আলাদা। কোনো বস্তুকে একবার বামদিকের ও পরেরবার ডানদিকের তুলাপাত্রে চাপালে ভর পাওয়া যায় যথাক্রমে 10 g ও 10.20 g। বস্তুর প্রকৃত ভর কত?
বাম ও ডান দুটি তুলাপাত্রে রাখা অবস্থায় ভর m1 ও m2 হলে প্রকৃত ভর \(\left(m\right)=\frac{m_1+m_2}2\)
∴ বস্তুটির প্রকৃত ভর = \(\frac12\left(10+10.20\right)\)
= 10.10 g
∴ বস্তুর প্রকৃত ভর 10.10 g
একটি কল থেকে সমহারে জল পড়ছে। মাপনী চোঙে জল ধরে দেখা গেল 20 s -এ 100 mL জল জমা হয়েছে। কল থেকে জল পড়ার হার কত?
আমরা জানি,
নির্ণেয় কল থেকে জল পড়ার হার = \(\frac{100}{20}\) mL/s
= 5 mL/s
∴ কল থেকে জল পড়ার হার 5 mL/s
একজন ছাত্রী একটি মাপনী চোঙে জল সংগ্রহ করছে। জল সংগ্রহের মধ্যবর্তী সময়ের ব্যবধান মাপার জন্য সে একটি ঘড়ি ব্যবহার করছে। দুটি আলাদা সময়ের জন্য মাপনী চোঙে জমা হওয়া জলের লেভেল চিত্রানুযায়ী বোঝা যাচ্ছে। এই দুই সময়ে সংগ্রহ করা জলের আয়তন এবং সময়ের ব্যবধান থেকে জল পড়ার হার নির্ণয় করো।
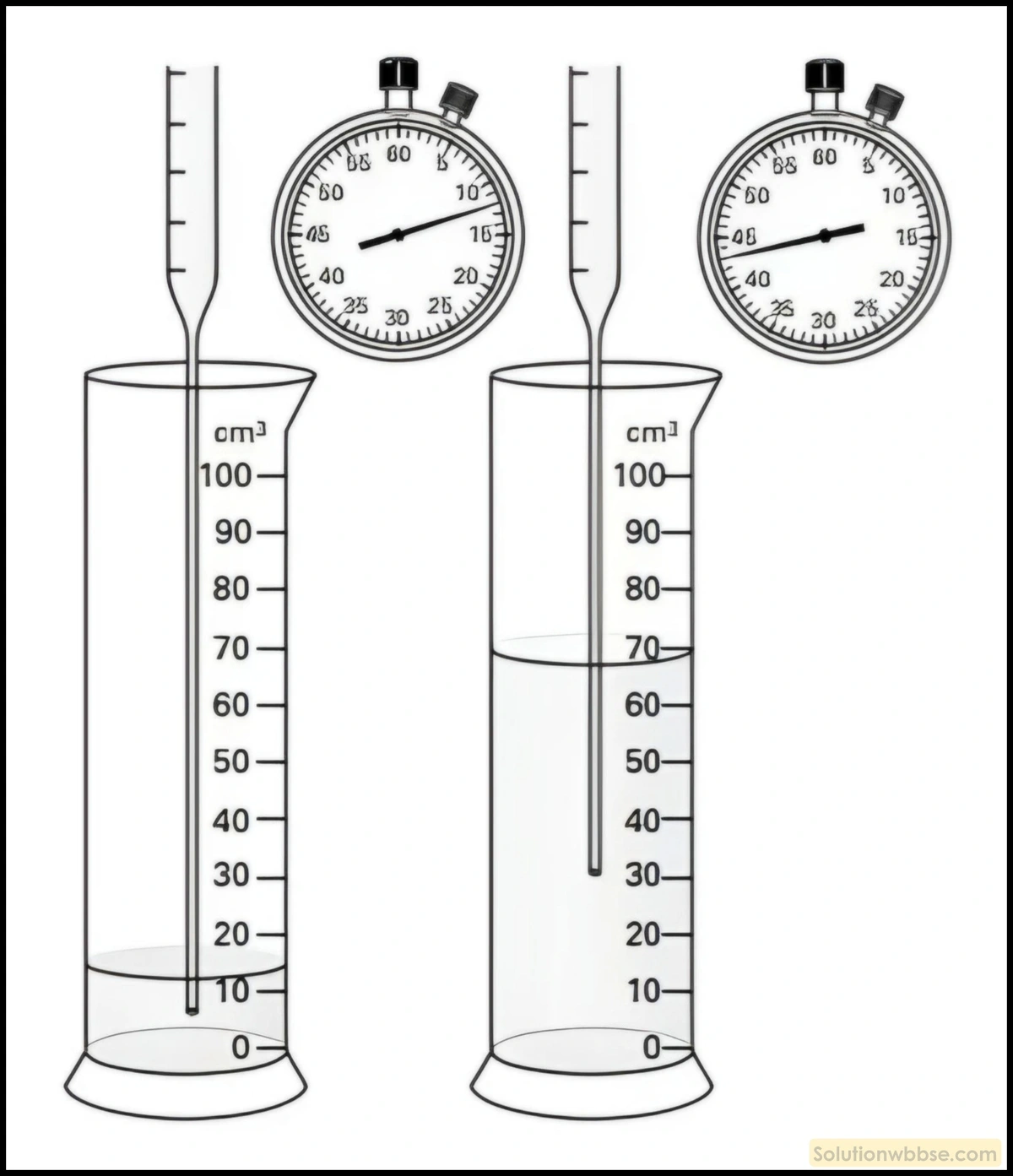
প্রথম ছবিতে 13 সেকেন্ডে জমা জলের আয়তন = 12 cc (চিত্রানুযায়ী)।
দ্বিতীয় ছবিতে 43 সেকেন্ডে জমা জলের আয়তন = 70 cc (চিত্রানুযায়ী)।
∴ (43 – 13) = 30 সেকেন্ডে সময়ের ব্যবধানে জমা জলের আয়তন (70 – 12) cc = 58 cc
∴
= \(\frac{58}{30}\) cc/s
= 1.93 cc/s
∴ এই দুই সময়ে সংগ্রহ করা জলের আয়তন এবং সময়ের ব্যবধান থেকে জল পড়ার হার 1.93 cc/s
কোনো বইয়ের পৃষ্ঠাসংখ্যা = 1000। সাধারণ স্কেলের সাহায্যে বইটির বেধ চারবার পরিমাপ করলে পাঠ হয় যথাক্রমে 5.6 cm, 5.7 cm, 5.5 cm ও 5.6 cm। বইটির একটি পাতার বেধ কত?
আমরা জানি,
সম্পূর্ণ বইটির গড় বেধ = \(\frac{5.6+5.7+5.5+5.6}4\) cm
= 5.6 cm
∴ বইটির একটি পাতার বেধ = \(\frac{5.6}{1000}\) cm
= 0.0056 cm
∴ বইটির একটি পাতার বেধ 0.0056 cm
তোমার ভৌতবিজ্ঞান বইয়ের প্রথম থেকে 46 পৃষ্ঠা পর্যন্ত পাতাগুলির মোট বেধ সাধারণ স্কেলের সাহায্যে মেপে পাওয়া গেল 8 mm। বইয়ের প্রত্যেক পাতার গড় বেধ নির্ণয় করো।
= \(\frac8{46}\) mm
= \(\frac8{46}\times10^{-3}\) µm
= 173 µm
∴ বইয়ের প্রত্যেক পাতার গড় বেধ 173 µm
400টি কাগজের একটি বান্ডিলের বেধ 2.4 cm। কাগজের বেধ মাইক্রন এককে প্রকাশ করো।
= \(\frac{2.4}{400}\) cm
= \(\frac{24}{400}\times10^3\) µm
= 60 µm
∴ কাগজের বেধ 60 µm মাইক্রন।
কোনো ভার্নিয়ার স্কেলের ভার্নিয়ার ধ্রুবক = 0.01 cm। এর সাহায্যে দৈর্ঘ্য পরিমাপ করে 10 cm পাঠ পাওয়া গেল। পাঠ -এর শতকরা কত ত্রুটি হবে?
= \(\frac{0.01}{10}\times100\%\)
= 0.1%
∴ পাঠ -এর শতকরা 0.1%
একটি আয়তন মাপক চোঙের ক্ষুদ্রতম ঘরের মান 2cc। ওই চোঙের সাহায্যে কিছু পরিমাণ তরলের আয়তন মেপে দেখা গেল 25cc। ওই পরিমাপে সম্ভাব্য শতকরা ত্রুটি কত?
= \(\frac2{25}\times100\%\)
= 8%
∴ সম্ভাব্য শতকরা ত্রুটি 8%
For High-Types
যদি x = a + bt + ct2 হয়, যেখানে x মিটারে এবং t সেকেন্ডে পরিমাপ করা হয়। a, b, c -এর একক ও মাত্রা নির্ণয় করো।
x = a + bt + ct2
সমীকরণটির বামপক্ষ -এর একক মিটার। সুতরাং, ডানপক্ষের প্রত্যেকটি পদের একক মিটার হবে।
ct2 = মিটার
বা, c =
∴ c = মিটার / সেকেন্ড2,
∴ c -এর মাত্রীয় সংকেত = [LT-2]
bt = মিটার
বা, b =
∴ b -এর একক = মিটার/সেকেন্ড,
∴ b -এর মাত্রীয় সংকেত = [LT-1]।
a = মিটার
∴ a -এর একক = মিটার,
∴ a -এর মাত্রা = [L]
mN ও Nm -এর মধ্যে কী পার্থক্য আছে?
mN -এর অর্থ মিলি নিউটন, যা বলের একক;
1 mN = 10-3 N
N⋅m -এর অর্থ নিউটন⋅মিটার, যা কার্যের একক।
অসাধু ব্যবসায়ীরা ক্রেতাদের ঠকানোর উদ্দেশ্যে কী জাতীয় অসদুপায় অবলম্বন করেন?
ক্রেতাদের ঠকাবার উদ্দেশ্যে অসাধু ব্যবসায়ীরা বিভিন্ন রকম বেআইনি ও অসৎ পদক্ষেপ গ্রহণ করেন। যেমন –
- দৈর্ঘ্য পরিমাপের জন্য ব্যবহৃত মিটার স্কেলের দৈর্ঘ্য মিটার অপেক্ষা কম থাকতে পারে। এক্ষেত্রে সংশ্লিষ্ট স্কেলে তিরচিহ্ন (Arrow mark) এবং সিলমোহর (stamp) আছে কি না তা যাচাই করা উচিত।
- ওজন করার কাজে ব্যবহৃত বাটখারাগুলি অনেক সময়ই প্রকৃত ওজন অপেক্ষা কম ওজনের হয়। নির্ভুল বাটখারাগুলি চিনতে হলে অবশ্যই বাটখারার গর্তের মধ্যে সিসা আছে কি না এবং তাতে উপযুক্ত সিলমোহর আছে কি না তা দেখা প্রয়োজন।
মাত্রা বিশ্লেষণের অসম্পূর্ণতাগুলি কী কী?
মাত্রা বিশ্লেষণের অসম্পূর্ণতাগুলি হল-
মাত্রা বিশ্লেষণের সাহায্যে কোনো সম্পর্কে থাকা ধ্রুবকের মান নির্ণয় করা যায় না। যেমন – মহাকর্ষ সূত্রানুযায়ী, \(F=G\frac{m_1\times m_2}{r^2}\)
যেখানে, F = আকর্ষণ বল; m1, m2 বস্তু দুটির ভর; r = বস্তু দুটির মধ্যে দূরত্ব এবং G = ধ্রুবক। এই G -এর মান মাত্রা বিশ্লেষণের সাহায্যে নির্ণয় করা যায় না।
কোনো সম্পর্কে যদি একটি মাত্রাহীন রাশি উপস্থিত থাকে তবে সম্পর্কটিতে উপস্থিত বাকি রাশিগুলির সঙ্গে মাত্রাহীন রাশিটি কীভাবে সম্পর্কযুক্ত তা মাত্রা বিশ্লেষণের সাহায্যে নির্ণয় করা যায় না। যেমন – W = FS cosθ যেখানে W = কৃতকার্য, F = প্রযুক্ত বল, S = সরণ এবং θ = F ও S -এর মধ্যবর্তী কোণ। যেহেতু θ একটি মাত্রাহীন রাশি তাই W = FS cosθ সম্পর্কটি মাত্রা বিশ্লেষণের সাহায্যে নির্ণয় করা যায় না।
কোনো সম্পর্কে তিনটির বেশি ভৌতরাশি থাকলে এই পদ্ধতি প্রয়োগ করা যায় না।
পারমাণবিক ভর এককের সাহায্যে একটি পূর্ণবয়স্ক হাতির ভর প্রকাশে অসুবিধা কোথায়?
1 পারমাণবিক ভর একক = 1.66054 × 10-27 kg
ধরা যাক, হাতিটির ভর = 5000 kg
= \(\frac{5000}{1.66054\times10^{-27}}\) amu
= 3011.069 × 1027 amu
এই সংখ্যাটি খুব বড়ো হওয়ায় ব্যাবহারিক ক্ষেত্রে কাজ করা প্রায় অসম্ভব। তাই পারমাণবিক ভর এককে একটি পূর্ণবয়স্ক হাতির ভর প্রকাশ করা হয় না।
চাল, গম, যব ইত্যাদির ভর কুইন্টাল এককে প্রকাশ করা হয়। অথচ মণি-মুক্তোর ভর ক্যারাট (Carat) এককে প্রকাশ করা হয় কেন?
মণি-মুস্তো খুবই মূল্যবান পদার্থ। তাই চাল, গম ইত্যাদির তুলনায় প্রকৃতিতে খুবই সামান্য পাওয়া যায়। সুতরাং, চাল, গম ইত্যাদি খাদ্যদ্রব্য হিসেবে যে বহুল পরিমাণে ব্যবহৃত হয়, মণি-মুস্তো ততটা বেশি পরিমাণে ব্যবহৃত হয় না। আবার, 1 কুইন্টাল = 100 কেজি এবং 1 ক্যারাট 200mg = 2 × 10-4 কেজি, তাই মূল্যবান পদার্থের (মণি-মুক্তো) ভর পরিমাপের ক্ষেত্রে কুইন্টালের তুলনায় ক্যারাট এককটি ব্যবহার করা অনেক বেশি সুবিধাজনক। অনুরূপে, খাদ্যদ্রব্যের ভর পরিমাপের ক্ষেত্রে কুইন্টাল এককটি ব্যবহার করা সুবিধাজনক।
এক বিক্রেতা দুজন ক্রেতাকে যথাক্রমে 30 টাকা/কেজি দরে 1 কেজি এবং 15 টাকা/পাউন্ড দরে 2 পাউন্ড চাল বিক্রয় করেন। কোন্ ক্ষেত্রে তাঁর লাভ হয়?
1 পাউন্ড = 453.6 গ্রাম (প্রায়)।
15 টাকা/পাউন্ড দরে 30 টাকায় বিক্রিত চালের ভর
= \(\frac{30}{15}\) পাউন্ড
= 2 পাউন্ড
= (453.6 × 2) g
= 907.2 g
= 0.9072 kg
∴ দ্বিতীয় ক্ষেত্রে বিক্রেতার লাভ হয়।
1 কিলোগ্রাম -এর আধুনিক সংজ্ঞা লেখো।
আধুনিকতম প্রস্তাবনা (20/05/2019) অনুসারে, নির্দিষ্ট সংখ্যক শক্তিকণা ফোটনের ভরের সাপেক্ষে SI -তে ভরের একক ‘কিলোগ্রাম’ -কে নতুন রূপে সংজ্ঞায়িত করা হয়েছে। নোবেলজয়ী পদার্থবিদ উলফ্গ্যাং কেটেলের গণনা অনুযায়ী, সিজিয়াম (Cs) পরমাণুর একটি নির্দিষ্ট তরঙ্গদৈর্ঘ্যের 1.4755214 × 1040 সংখ্যক ফোটনের ভরই হল 1 কিলোগ্রাম।
যথেষ্ট সাবধানতা অবলম্বন সত্ত্বেও পূর্বতন মানক ভরটি 130 বছরে 50 µg -এর মতো হ্রাস পেয়েছে। তাই, ধাতব উপাদানের ওপর নির্ভর না করে ফোটনের তরঙ্গদৈর্ঘ্যের সাপেক্ষে 1 কিলোগ্রামকে এমনভাবে সংজ্ঞায়িত করা হয়েছে, যাতে পরিমাপটি সর্বদা ধ্রুবক থাকে।
একটি সাধারণ তুলাযন্ত্রের তুলাদণ্ডের দুই বাহুর দৈর্ঘ্য অসমান, কিন্তু তুলাপাত্র দুটির ভর সমান। কোনো বস্তুর সঠিক ভর কীভাবে নির্ণয় করা যায়?
ধরা যাক, তুলাদণ্ডের বামবাহুর দৈর্ঘ্য= L1, এবং ডানবাহুর দৈর্ঘ্য = L এবং বস্তুর প্রকৃত ভর = m
বস্তুটিকে বাম তুলাপাত্রে রেখে, ডান তুলাপাত্রে m1 (ধরি) ভরের বাটখারা রাখলে তুলাদণ্ড অনুভূমিক হয়। ওই স্থানের অভিকর্ষজ ত্বরণ = g হলে, তুলাদণ্ডের অনুভূমিক অবস্থায়;
বস্তুর ভর × g × বামবাহুর দৈর্ঘ্য= বাটখারার ভর × g × ডানবাহুর দৈর্ঘ্য
বা, mgL1 = m1gL2 ___(1)
আবার, বস্তুটিতে ডান তুলাপাত্রে রেখে, বাম তুলাপাত্রে m2 (ধরি) ভরের বাটখারা রাখলে তুলাদণ্ড অনুভূমিক হয়। এই অবস্থায়,
বাটখারার ভর × g × বামবাহুর দৈর্ঘ্য = বস্তুর ভর × g × ডান বাহুর দৈর্ঘ্য
বা, m2gL1 = mgL2 ___(2)
(1) নং ÷ (2) নং করে পাই,
বা, \(\frac{mgL_1}{m_2gL_1}=\frac{m_2gL_2}{mgL_2}\)
বা, \(\frac m{m_2}=\frac{m_1}m\)
বা, \(m^2=m_1m_2\)
বা, \(m=\sqrt{m_1m_2}\) (∵ m > 0)
Class 9 Physical Science – Notes for All Chapters
| Chapter Name | Tropics |
|---|---|
| পরিমাপ | পরিমাপ ও একক বিভিন্ন মাপের একক মাত্রা পরিমাপ |
| বল ও গতি | স্থিতি ও গতি গতির সমীকরণ নিউটনের প্রথম গতিসূত্র নিউটনের দ্বিতীয় গতি সূত্র নিউটনের তৃতীয় গতিসূত্র বিভিন্ন ধরনের বল রৈখিক ভরবেগ রৈখিক ভরবেগ সংরক্ষণ |
| পদার্থ : গঠন ও ধর্ম | তরল ও বায়ুর চাপ আর্কিমিডিসের নীতি পৃষ্ঠটান সান্দ্রতা বার্নোলির নীতি স্থিতিস্থাপকতা |
| পদার্থ : পরমাণুর গঠন ও পদার্থের ভৌত ও রাসায়নিক ধর্মসমূহ | পরমাণুর গঠন মোলের ধারণা দ্রবণ অ্যাসিড, ক্ষার, লবণ মিশ্রণের উপাদানের পৃথকীকরণ জল |
| শক্তির ক্রিয়া , কার্য, ক্ষমতা | শক্তির ক্রিয়া , কার্য, ক্ষমতা |
| তাপ | ক্যালোরিমিতি কার্য ও তাপের তুল্যতা লীনতাপ সম্পৃক্ত ও অসম্পৃক্ত বাষ্প জলের ব্যতিক্রান্ত প্রসারণ |
| শব্দ | শব্দের উৎস : কম্পন শব্দের বিস্তার : তরঙ্গ শব্দের কয়েকটি ধর্ম শব্দের বৈশিষ্ট্য মানুষের কান ও শব্দ শোনার কৌশল শব্দদূষণ |
আজকের আর্টিকেলে আমরা নবম শ্রেণির ভৌতবিজ্ঞান বইয়ের প্রথম অধ্যায় “পরিমাপ” এর “পরিমাপ” থেকে পরীক্ষায় আসা গুরুত্বপূর্ণ প্রশ্ন ও উত্তরগুলো আলোচনা করেছি। এই প্রশ্নোত্তরগুলো নবম শ্রেণির বার্ষিক পরীক্ষা, এমনকি চাকরি বা যেকোনো প্রতিযোগিতামূলক পরীক্ষার জন্যও উপযোগী। কারণ, এই অধ্যায়ের প্রশ্ন প্রায়ই বিভিন্ন পরীক্ষায় কমন আসে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সাহায্য করবে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন কিংবা টেলিগ্রামে যোগাযোগ করুন—আপনাদের প্রশ্নের উত্তর দিতে আমি সর্বদা প্রস্তুত।
ধন্যবাদ সবাইকে।






Leave a Comment