নবম শ্রেণী – ভৌতবিজ্ঞান – শক্তির ক্রিয়া, কার্য, ক্ষমতা ও শক্তি – প্রশ্ন ও উত্তর

আজকের আর্টিকেলে আমরা নবম শ্রেণীর ভৌতবিজ্ঞান বইয়ের পঞ্চম অধ্যায় “শক্তির ক্রিয়া, কার্য, ক্ষমতা ও শক্তি” এর থেকে সহজ ও সংক্ষিপ্ত প্রশ্ন-উত্তর শেয়ার করবো। এই প্রশ্নগুলো নবম শ্রেণির ইউনিট টেস্ট থেকে বার্ষিক পরীক্ষা এর জন্য যেমন গুরুত্বপূর্ণ, তেমনি চাকরি বা বিভিন্ন প্রতিযোগিতার পরীক্ষাতেও কাজে লাগবে। এই অধ্যায় থেকে স্কুল পরীক্ষা থেকে শুরু করে চাকরির পরীক্ষায় প্রায়ই প্রশ্ন আসে, তাই এই প্রশ্নোত্তরগুলো সবাইকে সাহায্য করবে। প্রতিটি প্রশ্নের উত্তর সহজ ভাষায় লেখা হয়েছে, যাতে সবাই বুঝতে পারেন। পড়ার শেষে এই অধ্যায়ের মুখ্য বিষয়গুলো আপনার আয়ত্তে চলে আসবে এবং যেকোনো পরীক্ষায় আত্মবিশ্বাসের সঙ্গে লিখতে পারবেন।

জ্ঞানমূলক প্রশ্নোত্তর

কার্য কাকে বলে? উদাহরণ দাও। কার্যের পরিমাপ করা হয় কীভাবে?

কার্য (Work) – কোনো বস্তুর ওপর বল প্রয়োগ করলে যদি বলের প্রয়োগবিন্দুর সরণ হয়, তবে প্রযুক্ত বল কার্য করেছে বলা হয়।

কার্যের উদাহরণ – টেবিলের ওপর রাখা একটি বইকে ঠেললে সেটি সরে গেল। বইটির সরণ হওয়ায় বল কর্তৃক কৃতকার্য হয়েছে।

কার্যের পরিমাপ – বস্তুর ওপর প্রযুক্ত বল এবং ওই বলের অভিমুখে বলের প্রয়োগবিন্দুর সরণের গুণফল দ্বারা কৃতকার্যের পরিমাপ করা হয়। অর্থাৎ, কৃতকার্য = প্রযুক্ত বল × বলের প্রয়োগবিন্দুর সরণ।

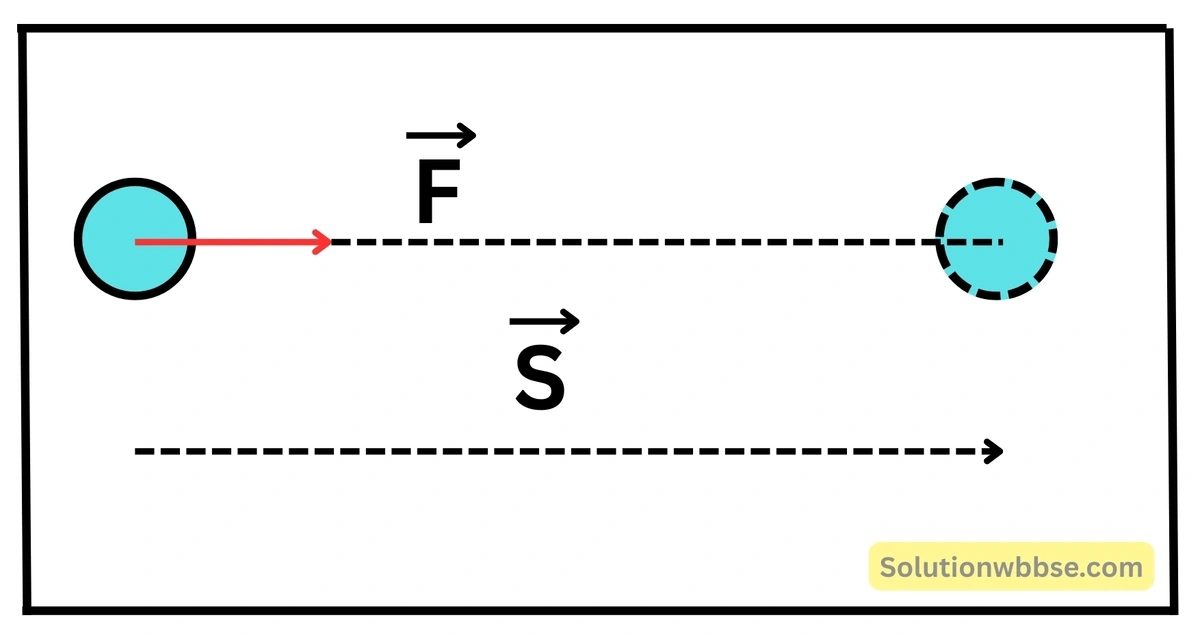
কোনো বস্তুর ওপর \(\vec{F}\) বল প্রয়োগ করা হলে, যদি বলের অভিমুখে বলের প্রয়োগবিন্দুর সরণ \(\vec{S}\) হয়, তবে কৃতকার্য \(\left(W\right)=\vec{F} \cdot \vec{S}\)।

যদি প্রযুক্ত বল \(\vec{F}\) অনুভূমিক তলের সঙ্গে \(θ\) কোণ করে কোনো বস্তুর ওপর ক্রিয়া করে এবং এর ফলে বস্তুর সরণ \(S\) হয়, তবে কৃতকার্য, \(\left(W\right)=FS\;Cos\theta\)।

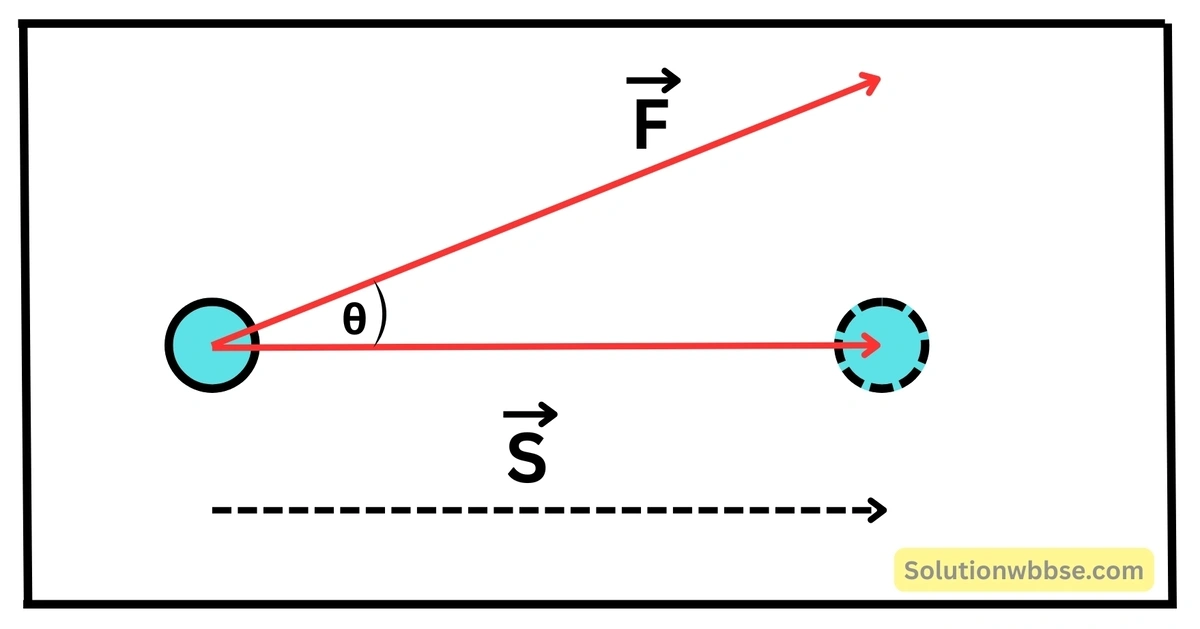
একটি স্কেলার গুণনের উদাহরণ দাও। 

কার্যের রাশিমালা \(W=FS\;\cos\theta=\vec{F} \cdot \vec{S}\)। \(\vec{F}\) ও \(\vec{S}\) উভয়েই ভেক্টর এবং \(W\) স্কেলার হওয়ায় এটি একটি স্কেলার গুণনের উদাহরণ।

CGS পদ্ধতি ও SI -তে কার্যের পরম এককগুলি লেখো। তাদের সংজ্ঞা দাও।

CGS পদ্ধতিতে কার্যের পরম একক আর্গ। SI -তে কার্যের পরম একক জুল।

আর্গ – কোনো বস্তুর ওপর এক ডাইন বল প্রয়োগ করলে যদি বলের অভিমুখে প্রয়োগবিন্দুর সরণ এক সেন্টিমিটার হয়, তবে কৃতকার্যের পরিমাণকে 1 আর্গ বলে। অর্থাৎ, 1 ডাইন × 1 সেমি = 1 আর্গ বা 1 আর্গ = 1 ডাইন-সেমি।

জুল – কোনো বস্তুর ওপর এক নিউটন বল প্রয়োগ করলে যদি বলের অভিমুখে প্রয়োগবিন্দুর সরণ এক মিটার হয়, তবে কৃতকার্যের পরিমাণকে 1 জুল বলে। অর্থাৎ, 1 জুল = 1 নিউটন × 1 মিটার = 1 নিউটন-মিটার।

CGS পদ্ধতি ও SI -তে কার্যের অভিকর্ষীয় এককগুলি লেখো। তাদের সংজ্ঞা দাও।

CGS পদ্ধতিতে কার্যের অভিকর্ষীয় একক গ্রাম-সেন্টিমিটার। SI -তে কার্যের অভিকর্ষীয় একক কিগ্রা-মিটার।

গ্রাম-সেন্টিমিটার – এক গ্রাম ভরের কোনো বস্তুকে অভিকর্ষের বিরুদ্ধে 1 সেমি উপরে তুলতে যে কার্য করা হয়, তাকে 1 গ্রাম-সেন্টিমিটার বলে।

কিলোগ্রাম-মিটার – এক কিলোগ্রাম ভরের কোনো বস্তুকে অভিকর্ষের বিরুদ্ধে 1 মিটার উপরে তুলতে যে কার্য করা হয়, তাকে 1 কিলোগ্রাম-মিটার বলে।

কার্যের মাত্রীয় সংকেত লেখো। কার্য একটি স্কেলার না ভেক্টর রাশি?

কার্যের মাত্রীয় সংকেত = বলের মাত্রা × সরণের মাত্রা

= [MLT^-2] × [L]

= [ML²T^-2]

বল ও সরণ উভয়ই ভেক্টর রাশি হলেও এদের গুণফল কার্য একটি স্কেলার রাশি। কার্যের কেবল মান আছে, অভিমুখ নেই।

জুল ও আর্গের সম্পর্ক নির্ণয় করো।

জুল ও আর্গের মধ্যে সম্পর্ক –

1 জুল = 1 নিউটন × 1 মিটার

বা, 1 জুল = 10⁵ ডাইন × 10² সেমি

বা, 1 জুল = 10⁷ ডাইন-সেমি

∴ 1 জুল = 10⁷ আর্গ।

গ্রাম-সেমি ও আর্গের সম্পর্ক নির্ণয় করো।

গ্রাম-সেমি ও আর্গের মধ্যে সম্পর্ক –

1 গ্রাম-সেমি = 1 গ্রাম-ভার × 1 সেমি

বা, 1 গ্রাম-সেমি = 981 ডাইন × 1 সেমি

বা, 1 গ্রাম-সেমি = 981 ডাইন-সেমি

∴ 1 গ্রাম-সেমি = 981 আর্গ।

কিলোগ্রাম-মিটার ও জুলের সম্পর্ক নির্ণয় করো।

কিলোগ্রাম-মিটার ও জুলের মধ্যে সম্পর্ক –

1 কিলোগ্রাম-মিটার = 1 কিগ্রা-ভার × 1 মিটার।

বা, 1 কিলোগ্রাম-মিটার = 9.81 নিউটন × 1 মিটার

বা, 1 কিলোগ্রাম-মিটার = 9.81 নিউটন-মিটার

∴ 1 কিলোগ্রাম-মিটার = 9.81 জুল।

কার্যের দুটি বৃহৎ একক কী কী এবং এদের মধ্যে পার্থক্য ব্যাখ্যা করো। 1 কিলোজুল (1 kJ) ও 1 মেগাজুল (1 MJ) এর মধ্যে সম্পর্ক কী? জুলের ব্যবহারিক প্রয়োগের পাশাপাশি কিলোজুল ও মেগাজুলের ব্যবহারের ক্ষেত্রগুলি উল্লেখ করো।

কার্যের দুটি বৃহৎ একক হল কিলো জুল ও মেগা জুল। 1 কিলো জুল (1 kJ) = 10³ জুল এবং 1 মেগা জুল (1 MJ) = 10⁶ জুল। জুল হল কার্যের ব্যাবহারিক একক। তবে প্রয়োজন অনুযায়ী, অন্যান্য এককও ব্যাবহারিক ক্ষেত্রে কাজে লাগে। যেমন – ব্যয়িত তড়িৎশক্তির পরিমাপে কিলো জুল, নিউক্লীয় বিক্রিয়ায় উৎপন্ন শক্তির পরিমাপে মেগা জুল ইত্যাদি।

অভিকর্ষ বলের দ্বারা কার্য এবং বলের বিরুদ্ধে কার্য উদাহরণসহ লেখো।

বলের দ্বারা কার্য (Work done by force) – কোনো বস্তুর ওপর বল প্রয়োগ করলে যদি বলের প্রয়োগবিন্দুর সরণ প্রযুক্ত বলের অভিমুখে হয় তবে বলা হয় যে, প্রযুক্ত বল দ্বারা কার্য করা হয়েছে। একে ধনাত্মক কার্যও বলে।

বলের দ্বারা কার্যের উদাহরণ –

• কোনো বস্তুকে ঠেলে দিলে বস্তুটি প্রযুক্ত বলের অভিমুখে সরে যায় অর্থাৎ, প্রযুক্ত বল দ্বারা কার্য হয়।
• কোনো বস্তুকে ওপর থেকে নীচে ফেলে দিলে বস্তুটি অভিকর্ষের টানে নীচে এসে পড়ে। অর্থাৎ, অভিকর্ষ বল দ্বারা কার্য হয়।

বলের বিরুদ্ধে কার্য (Work done against force) – কোনো বস্তুর ওপর বল প্রয়োগ করলে যদি বলের প্রয়োগবিন্দুর সরণ প্রযুক্ত বলের বিপরীত অভিমুখে হয় তবে বলা হয় যে, প্রযুক্ত বলের বিরুদ্ধে কার্য করা হয়েছে। একে ঋণাত্মক কার্যও বলে।

বলের বিরুদ্ধে কার্যের উদাহরণ –

• কোনো বস্তুকে ওপরের দিকে ছুড়ে দিলে বস্তুর সরণ হয় ওপরের দিকে, কিন্তু অভিকর্ষ বল কাজ করে নীচের দিকে। অর্থাৎ, বলের বিরুদ্ধে কাজ হয়।
• কোনো বস্তুকে টেবিলের উপর দিয়ে ঠেলে দিলে বস্তুর সরণ যেদিকে হয় তার বিপরীত দিকে ঘর্ষণ বল কাজ করে। অর্থাৎ, এক্ষেত্রে ঘর্ষণ বলের বিরুদ্ধে কাজ হয়।

কার্যহীন বল উদাহরণসহ লেখো।

কার্যহীন বল (No-work force) – বস্তুর ওপর প্রযুক্ত বল ও বলের প্রয়োগবিন্দুর সরণ যদি পরস্পর লম্ব হয়, তবে প্রযুক্ত বল কোনো কার্য করে না। ওই বলকে কার্যহীন বল বলে।

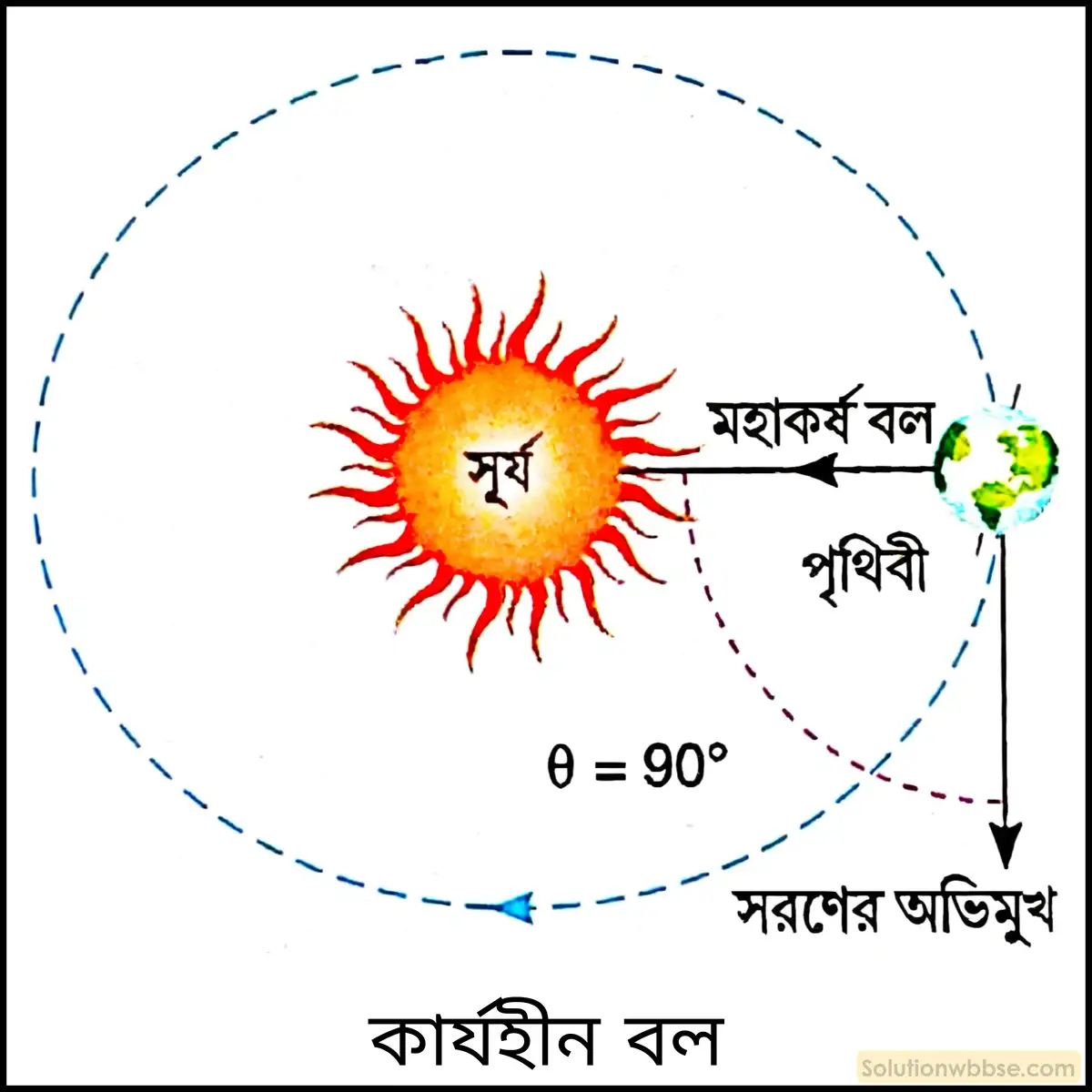
কার্যহীন বলের উদাহরণ – সূর্যের চারদিকে বৃত্তাকার পথে পৃথিবীর আবর্তনের সময় সূর্য ও পৃথিবীর মধ্যে মহাকর্ষ বলের অভিমুখ ও পৃথিবীর সরণের অভিমুখ পরস্পর লম্ব হওয়ায় সরণের অভিমুখে বলের কোনো উপাংশ থাকে না। ফলে, মহাকর্ষ বল দ্বারা কৃতকার্য এক্ষেত্রে শূন্য হয়।

বস্তুতে বল প্রযুক্ত হলেও কী কী অবস্থায় কার্য হয় না?

বস্তুতে বল প্রযুক্ত হলেও নিম্নলিখিত দুটি ক্ষেত্রে কার্য হয় না – কৃতকার্যের রাশিমালা W = FS cosθ যেখানে F প্রযুক্ত বল, S বস্তুর সরণ এবং θ হল F ও S -এর ক্রিয়ারেখার অন্তর্বর্তী কোণ। সুতরাং, বল প্রযুক্ত হলেও (অর্থাৎ, F ≠ 0) কৃতকার্য দুটি পরিস্থিতিতে শূন্য হতে পারে –

1. S = 0 অর্থাৎ বস্তুর সরণ যদি শূন্য হয়। দুটি উপায়ে এমন ঘটনা সম্ভব –

• বস্তু যদি আদৌ না সরে,
• বস্তুর প্রাথমিক ও অন্তিম অবস্থান একই হলে।

উদাহরণ –

• অনেক জোরে ঠেলা সত্ত্বেও ভারী আলমারির অবস্থান অপরিবর্তিত থাকলে অথবা,
• বৃত্তপথে গতিশীল বস্তু যখন তার প্রাথমিক অবস্থানে ফিরে আসে।

2. θ = 90° হলে, W = FS cos 90° = 0। এক্ষেত্রে বলটি কার্যহীন বল নামে চিহ্নিত হয়।

উদাহরণ – অনুভূমিক রাস্তায় হেঁটে যাওয়া ব্যক্তির ওজন একটি কার্যহীন বল কারণ – ওজন ও সরণের অভিমুখ পরস্পর লম্ব হয়। এ ছাড়াও, কোনো ব্যক্তি যদি অনুভূমিক তল বরাবর হেঁটে যায় তবে প্রযুক্ত বল অর্থাৎ, অভিকর্ষ বলের অভিমুখ ও ব্যক্তির সরণের অভিমুখ পরস্পর লম্বভাবে কাজ করে, তাই কোনো কার্য হয় না।

ধনাত্মক ও ঋণাত্মক কার্য কাকে বলে?

কার্য = \(\vec{F} \cdot \vec{S}=\left|F\right|\left|S\right|\cos\theta\)। \(\vec{F}\) ও \(\vec{S}\) -এর ক্রিয়ারেখা সমমুখী হওয়ায় θ = 0° হয়, অর্থাৎ W = FS cosθ বা W = FS হয়। সাধারণভাবে θ সুক্ষ্মকোণ হলে cosθ -এর মান ধনাত্মক অর্থাৎ, কার্যের রাশিমালা ধনাত্মক হয়। তাই, এই কৃতকার্যকে অনেক সময় ধনাত্মক কার্যও বলা হয়ে থাকে। সাধারণভাবে θ -এর মান 90° থেকে 180° -এর মধ্যে অর্থাৎ, স্থূলকোণ হলে বলের উপাংশ ও সরণ বিপরীত অভিমুখে ক্রিয়াশীল হয়। θ = 180° হলে উপাংশের পরিবর্তে সমগ্র বলই সরণের বিপরীতে ক্রিয়া করে এবং কৃতকার্য সর্বোচ্চ হয়। θ স্থূলকোণ হলে cosθ -এর মান ঋণাত্মক হওয়ায় কার্যের মানও ঋণাত্মক হয়ে থাকে। তাই, এই কার্যকে অনেক সময় ঋণাত্মক কার্যও বলা হয়।

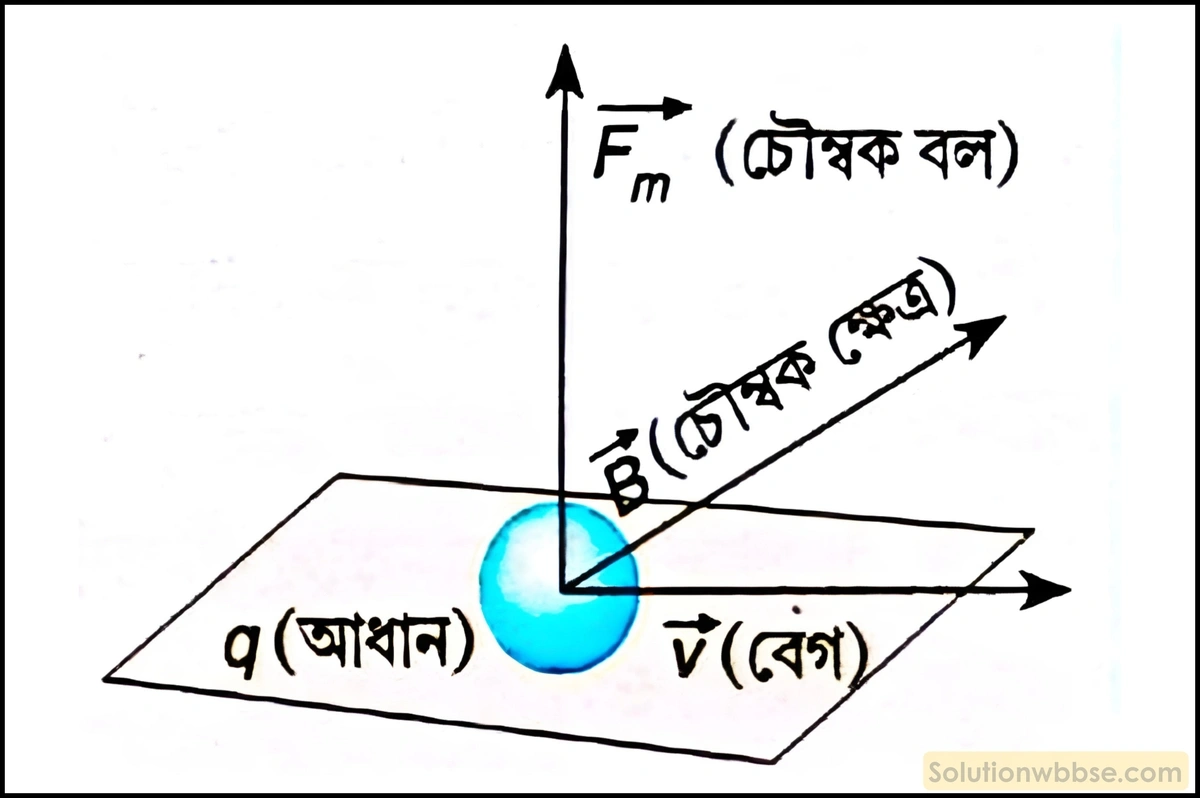
চৌম্বক বল কীভাবে কার্যহীন বলের বৈশিষ্ট্য প্রদর্শন করে?

চৌম্বকক্ষেত্রে কোনো আহিত কণার ওপর ক্রিয়ারত চৌম্বক বল, চৌম্বকক্ষেত্র ও কণার বেগ যে তলে অবস্থান করে তার লম্ব অভিমুখে কাজ করে। সুতরাং, চৌম্বক বলও একটি কার্যহীন বলের উদাহরণ। কার্যহীন বলের ক্রিয়ায় বস্তুর গতিশক্তির পরিবর্তন ঘটা সম্ভব নয়।

ক্ষমতা কাকে বলে? ক্ষমতার পরিমাপ করবে কীভাবে? ক্ষমতা ও বস্তুর বেগের মধ্যে সম্পর্ক প্রতিষ্ঠা করো।

ক্ষমতা (Power) – কোনো বস্তু বা সংস্থা দ্বারা একক সময়ে যে পরিমাণ কার্য করা হয়, তাকে ক্ষমতা বলে।

$\mathrm{t সময়ে\; সম্পাদিত\; কৃতকার্যের\; পরিমাণ\; W\; হলে,\; সংজ্ঞানুসারে,\; ক্ষমতা\; (P)}=\frac{\mathrm{কৃতকার্য\; (W)}}{\mathrm{সময়\; (t)}}$

∴ \(P=\frac Wt\)

ক্ষমতা ও বেগের সম্পর্ক – ধরা যাক, \(\vec{F}\) বলের ক্রিয়ায় কোন বস্তুকণার t সময়ে সরণ হয় \(\vec{S}\)। সংজ্ঞানুসারে, প্রযুক্ত বল দ্বারা কতকার্য \(W=\vec{F} \cdot \vec{S}\)।

∴ ব্যয়িত ক্ষমতা (P) = কৃতকার্যের হার = \(\frac Wt\)

= \(\frac{\overrightarrow F\cdot\overrightarrow S}t\)

= \(\overrightarrow F⋅\left(\frac{\overrightarrow S}t\right)\)

= \(\overrightarrow F⋅\overrightarrow v\)

যেখানে \(\overrightarrow v=\frac{\overrightarrow S}t=\) বস্তুকণার সরণের হার বা বেগ 

∴ ক্ষমতা \(=P=\overrightarrow F\cdot\overrightarrow v\)

\(\overrightarrow F\) ও \(\overrightarrow v\) সমমুখী হলে, \(P=Fv\)

অর্থাৎ, ক্ষমতা = বল × বেগ

ক্ষমতা কী ধরনের রাশি? কেন?

ক্ষমতা একটি স্কেলার রাশি।

ক্ষমতার মান আছে, কিন্তু অভিমুখ নেই। তাই এটি একটি স্কেলার রাশি।

CGS পদ্ধতি ও SI -তে ক্ষমতার পরম একক ও অভিকর্ষীয় একক লেখো। তাদের সংজ্ঞা দাও।

CGS পদ্ধতিতে ক্ষমতার পরম একক আর্গ/সেকেন্ড।

1 সেকেন্ডে 1 আর্গ কার্য করার ক্ষমতাকে 1 আর্গ/সেকেন্ড বলে।

SI -তে ক্ষমতার পরম একক ওয়াট (watt)। এটি ক্ষমতার ব্যাবহারিক একক।

1 সেকেন্ডে 1 জুল কার্য করার ক্ষমতাকে বলে 1 ওয়াট।

অর্থাৎ, 1 ওয়াট = 1 জুল/সেকেন্ড

= 10⁷ আর্গ/সেকেন্ড।

CGS পদ্ধতিতে ক্ষমতার অভিকর্ষীয় একক গ্রাম-সেন্টিমিটার/সেকেন্ড।

1 গ্রাম ভরের বস্তুকে অভিকর্ষের বিরুদ্ধে 1 সেকেন্ডে 1 সেন্টিমিটার ওপরে তুলতে যে ক্ষমতার প্রয়োজন হয়, তাকে 1 গ্রাম-সেমি/সেকেন্ড বলে।

∴ 1 গ্রাম-সেন্টিমিটার/সেকেন্ড

= 1 গ্রাম-ভার × 1 সেমি/সে

= 981 ডাইন × 1 সেমি/সে

= 981 আর্গ/সে। (∵ আর্গ = ডাইন × সেমি)

SI -তে ক্ষমতার অভিকর্ষীয় একক হল কিলোগ্রাম-মিটার/সেকেন্ড।

1 কিলোগ্রাম ভরের কোনো বস্তুকে অভিকর্ষের বিরুদ্ধে 1 সেকেন্ডে 1 মিটার ওপরে তুলতে যে ক্ষমতার প্রয়োজন হয়, তাকে 1 কিগ্রা-মি/ সেকেন্ড বলে।

∴ 1 কিগ্রা-মি/সেকেন্ড

= 1 কিগ্রা-ভার × 1 মি/সে

= 9.81 নিউটন × 1 মি/সে

= 9.81 জুল/সে (∵ জুল = নিউটন × মি)

= 9.81 ওয়াট।

অশ্বক্ষমতা কাকে বলে? অশ্বক্ষমতার সঙ্গে ওয়াট এবং কিলোওয়াটের কী সম্পর্ক?

অশ্বক্ষমতা – FPS পদ্ধতিতে অশ্বক্ষমতা হল ক্ষমতার ব্যাবহারিক একক। 550 পাউন্ড ভরের কোনো বস্তুকে অভিকর্ষের বিরুদ্ধে 1 সেকেন্ডে 1 ফুট ওপরে তুলতে যে ক্ষমতার প্রয়োজন হয়, তাকে 1 অশ্বক্ষমতা বা হর্স পাওয়ার বলে।

অশ্বক্ষমতা ও ওয়াটের সম্পর্ক –

1 অশ্বক্ষমতা = 550 ফুট-পাউন্ড/সেকেন্ড।

= 550 × 1 ফুট × 1 পাউন্ড/সেকেন্ড

= 550 × 30.48 cm × (453.6 × 1 × 981) ডাইন/সেকেন্ড (∵ 1 ফুট = 30.48 সেমি, 1 পাউন্ড = 453.6 গ্রাম)

= 746 × 10⁷ আর্গ/সেকেন্ড

= 746 জুল/সেকেন্ড

= 746 ওয়াট।

অশ্বক্ষমতা ও কিলোওয়াটের সম্পর্ক –

1 অশ্বক্ষমতা = 746 ওয়াট = 0.746 কিলোওয়াট।

1 কিলোওয়াট = 1000 ওয়াট

বা, 1 কিলোওয়াট = \(\frac{1000}{746}\) হর্স পাওয়ার। 

বা, 1 কিলোওয়াট = 1.34 হর্স পাওয়ার।

ক্ষমতার মাত্রীয় সংকেত নির্ণয় করো।

$\mathrm{ক্ষমতা}=\frac{\mathrm{কৃতকার্য}}{\mathrm{সময়}}$

$\mathrm{বা,\; ক্ষমতা}=\frac{\mathrm{প্রযুক্ত\; বল}\times \mathrm{সরণ}}{\mathrm{সময়}}$

∴ ক্ষমতার মাত্রীয় সংকেত = \(\frac{\left[MLT^{-2}\right]}{\left[L\right]}=\left[ML^2T^{-3}\right]\)

শক্তির সংজ্ঞা লেখো। শক্তি কীভাবে পরিমাপ করা হয়?

শক্তি (Energy) – কোনো বস্তু বা সংস্থার মধ্যে নিহিত বা সঞ্চিত কার্য করার মোট সামর্থ্যকে শক্তি বলে।

শক্তির পরিমাপ – শক্তির পরিমাপ করা হয় তার দ্বারা সম্পাদিত কৃতকার্যের মাধ্যমে। কার্য করার সামর্থ্য যত বেশি হয়, সেই বস্তু বা সংস্থার শক্তির সঞ্চয়ও তত বেশি হয়ে থাকে। তাই শক্তির পরিমাপ = কৃতকার্য = প্রযুক্ত বল × সরণ।

শক্তির বৈশিষ্ট্যগুলি বিবৃত করো। শক্তি স্কেলার না ভেক্টর রাশি?

শক্তির বৈশিষ্ট্যসমূহ –

• শক্তি বিভিন্ন রূপে প্রকৃতিতে আত্মপ্রকাশ করে। যেমন – যান্ত্রিক শক্তি, তাপশক্তি, আলোকশক্তি, বিদ্যুৎশক্তি ইত্যাদি।
• শক্তি মাত্রই অদৃশ্য, ভরহীন, আয়তনহীন কিন্তু ইন্দ্রিয়গ্রাহ্য।
• শক্তির অন্যতম গুরুত্বপূর্ণ বৈশিষ্ট্য হল তার রূপান্তরযোগ্যতা। যে-কোনো শক্তিকেই অন্য শক্তিতে এবং অন্য কোনো শক্তিকে সেই শক্তিতে রূপান্তরিত করা যায়। যেমন – হাতের তালু ঘর্ষণে গরম হয়ে ওঠে, এক্ষেত্রে যান্ত্রিকশক্তি তাপশক্তিতে রূপান্তরিত হয়। আবার, কয়লা পুড়িয়ে উৎপন্ন তাপশক্তিকে কাজে লাগিয়ে বাষ্পীয় ইঞ্জিন চালানো হয়। এটি তাপশক্তির যান্ত্রিকশক্তিতে রূপান্তরের উদাহরণ।
• কোনো বস্তু বা সংস্থা কাজ করলে তার শক্তি অন্য বস্তুতে হস্তান্তরিত হয়। সুতরাং, যে বস্তু কাজ করে তার শক্তির সঞ্চয় কমে এবং যার ওপর কার্য করা হয়, তার শক্তি বাড়ে।

শক্তির প্রকৃতি – কৃতকার্যের মাধ্যমেই শক্তির পরিমাপ করা হয়। যেহেতু কৃতকার্য স্কেলার রাশি, তাই শক্তিও একটি স্কেলার রাশি।

কার্য ও শক্তির মধ্যে সম্পর্ক কী? শক্তির বিভিন্ন পদ্ধতিতে এককগুলি উল্লেখ করো। শক্তির মাত্রীয় সংকেত লেখো।

কোনো বস্তু কার্য করতে সক্ষম হলে বলা হয় যে, ওই বস্তুটিতে শক্তি সঞ্চিত আছে। বস্তুটি যে পরিমাণ কার্য সম্পাদন করতে পারে তা দিয়েই তার শক্তির পরিমাপ করা হয়। বস্তু কার্য করলে তার মধ্যে নিহিত শক্তির পরিমাণ হ্রাস পায় এবং বস্তুর ওপর কার্য সংঘটিত হলে তার শক্তির সঞ্চয় বাড়ে। সুতরাং, কার্য ও শক্তি একই জাতীয় রাশি। তারা মাত্রাগতভাবে অভিন্ন এবং একই এককের সাহায্যে তাদের পরিমাপ করা হয়।

বিভিন্ন পদ্ধতিতে শক্তির একক –

পদ্ধতির নাম	পরম একক	অভিকর্ষীয় একক
CGS	আর্গ বা ডাইন-সেমি	গ্রাম-সেমি
SI	জুল বা নিউটন-মি	কিগ্রা-মি

শক্তির মাত্রীয় সংকেত –

[E] = [W] (যেখানে W হল কৃতকার্য)

বা, [E] = [ML²T^-2]।

যান্ত্রিক শক্তি কাকে বলে? এটি কয় প্রকার ও কী কী?

যান্ত্রিক শক্তি (Mechanical Energy) – কোনো বস্তু বা সংস্থা তার অবস্থান, আকৃতি, গতিশীল অবস্থা ইত্যাদির যে-কোনো একটির বা একাধিকের পরিবর্তনের কারণে যান্ত্রিক কার্য করার যে সামর্থ্য অর্জন করে, তাকেই ওই বস্তুর যান্ত্রিক শক্তি বলা হয়।

যান্ত্রিক শক্তির প্রকারভেদ – যান্ত্রিক শক্তি দু-প্রকার। যথা – স্থিতিশক্তি ও গতিশক্তি।

স্থিতিশক্তি ও গতিশক্তি কাকে বলে? উদাহরণ দাও।

স্থিতিশক্তি (Potential energy) –

কোনো বস্তু বা সংস্থা তার স্বাভাবিক অবস্থান বা আকৃতির পরিবর্তনের কারণে কার্য করার যে সামর্থ্য অর্জন করে, তাকেই ওই বস্তুর স্থিতিশক্তি বলা হয়।

স্থিতিশক্তির উদাহরণ – একটি লোহার ব্লককে হাত বা কপিকলের সাহায্যে কিছুটা ওপরে তুলে মাটিতে আংশিক প্রবিষ্ট কোনো ধাতব দণ্ডের উপর ফেলা হলে ব্লকের আঘাতে দণ্ডটির আরও বেশ কিছু অংশ মাটিতে প্রবেশ করে। ব্লকটিকে দণ্ডের সঙ্গে স্পর্শ করিয়ে রাখা হলে দেখা যায়, সেটি মাটিতে প্রবেশ করে না।

স্পষ্টতই বোঝা যায় উঁচুতে তোলা অর্থাৎ, অবস্থান পরিবর্তনের জন্যই লোহার ব্লকটিতে কার্য করার সামর্থ্য জন্মায়, যা দণ্ডটিতে সঞ্চারিত হয়ে তাকে মাটি ভেদ করতে সাহায্য করে।

গতিশক্তি (Kinetic energy) –

গতিশীল বস্তু তার ওই গতীয় অবস্থার কারণে কার্য করার যে সামর্থ্য অর্জন করে, তাকেই ওই বস্তুর গতিশক্তি বলে।

গতিশক্তির উদাহরণ –

• বায়ু প্রবাহিত হয় বলে বায়ুর গতিশক্তি আছে। বায়ুপ্রবাহের সাহায্যে পালতোলা নৌকা চালানো হয়। বায়ুচালিত যন্ত্রের (wind mill) সাহায্যে শস্য পেষাই করা হয়। এছাড়াও, বায়ুপ্রবাহের গতিশক্তি মরুভূমির বালিকে মরুঝড়ের সময় অতি দ্রুত একস্থান থেকে অন্যস্থানে স্থানান্তরিত করে।
• পাহাড়ের উপর থেকে নীচে নেমে আসা নদীর জলের গতিশক্তির প্রভাবেই ছোটো-বড়ো পাথর, বালি ইত্যাদি একস্থান থেকে অন্যত্র সরে যায়। আবার, নদীর স্রোতের গতিশক্তির সাহায্যে নৌকা চালানো যায় এবং এই গতিশক্তির সাহায্যে ডায়নামো চালিয়ে বিদ্যুৎশক্তি উৎপাদন করা হয়।

স্থিতিশক্তি কয় প্রকার ও কী কী? প্রত্যেকটির সংজ্ঞা দাও।

স্থিতিশক্তির প্রকারভেদ –

স্থিতিশক্তি দুই প্রকার –

• অবস্থানের জন্য স্থিতিশক্তি বা অভিকর্ষীয় স্থিতিশক্তি,
• আকৃতির জন্য স্থিতিশক্তি বা স্থিতিস্থাপক স্থিতিশক্তি।

অভিকর্ষীয় স্থিতিশক্তি (Gravitational potential energy) –

পৃথিবীর যে-কোনো বস্তুর স্বাভাবিক অবস্থান হল ভূপৃষ্ঠ। কোনো বস্তুকে পৃথিবীপৃষ্ঠ থেকে কিছু উচ্চতায় অভিকর্ষীয় বলের বিরুদ্ধে নিয়ে গেলে কার্য করার যে সামর্থ্য অর্জন করে, তাকে ওই বস্তুর অভিকর্ষীয় স্থিতিশক্তি বলে। বাঁধের উঁচু জলাধারে সঞ্চিত জল ভূপৃষ্ঠ থেকে অনেক উঁচুতে অবস্থানের জন্য স্থিতিশক্তি লাভ করে। তাই নীচে নামবার সময় তীব্রবেগে প্রবাহিত হয়। যা থেকে টারবাইন ঘুরিয়ে তড়িৎশক্তি উৎপন্ন করা যায়।

স্থিতিস্থাপক স্থিতিশক্তি (Elastic potential energy) –

কোনো বস্তুর স্বাভাবিক আকৃতির পরিবর্তন হলে বস্তুটির মধ্যে আকৃতি পরিবর্তনের জন্য কার্য করার যে সামর্থ্য অর্জিত হয়, তাকে স্থিতিস্থাপক স্থিতিশক্তি বলে। যেমন – ঘড়িতে দম দেওয়ার সময় ঘড়ির স্প্রিং সংকুচিত হয়। স্প্রিং -এর স্বাভাবিক আকৃতি পরিবর্তিত হওয়ার কারণে স্প্রিংটিতে স্থিতিশক্তি সঞ্চিত হয়। তাই, সংনমিত স্প্রিং তার স্বাভাবিক আকৃতিতে ফিরে আসার সময় কার্য করতে পারে, যা গতিশক্তিতে রূপান্তরিত হয়ে ঘড়ির কাঁটাকে সচল রাখে। এটি স্থিতিস্থাপক স্থিতিশক্তির উদাহরণ।

স্থির-তাড়িতিক স্থিতিশক্তি কী এবং এটি কীভাবে সৃষ্টি হয়?

এ ছাড়াও, আরেক ধরনের স্থিতিশক্তি হল স্থির-তাড়িতিক স্থিতিশক্তি। দুই বা ততোধিক আধানযুক্ত কণার পারস্পরিক আকর্ষণ বা বিকর্ষণের জন্য তাদের মধ্যে সৃষ্ট স্থিতিশক্তিই হল স্থির তাড়িতিক স্থিতিশক্তি (Electrostatic potential)।

স্থিতিশক্তির রাশিমালাটি লেখো। 

স্থিতিস্থাপক স্থিতিশক্তির সাধারণ রাশিমালা \(E_e=\frac12\) × প্রযুক্ত বল × দৈর্ঘ্যের পরিবর্তন। স্প্রিং -এ সঞ্চিত স্থিতিস্থাপক স্থিতিশক্তির রাশিমালা \(E_e=\frac12Kx^2\), যেখানে, K হল স্প্রিংয়ের বল ধ্রুবক, x হল স্প্রিংয়ের দৈর্ঘ্য সংকোচন বা প্রসারণ।

অভিকর্ষীয় স্থিতিশক্তির রাশিমালা নির্ণয় করো।

অভিকর্ষীয় স্থিতিশক্তির রাশিমালা – পৃথিবীকে নির্দেশতল হিসেবে বিবেচনা করে তার সাপেক্ষে কোনো নির্দিষ্ট উচ্চতায় কোনো বস্তুকে উত্তোলন করতে অভিকর্ষ বলের বিরুদ্ধে সম্পাদিত কার্যই হল ওই উচ্চতায় বস্তুটিতে সঞ্চিত অভিকর্ষীয় স্থিতিশক্তির পরিমাপ। ধরা যাক, m ভরের একটি বস্তুকে অভিকর্ষের বিরুদ্ধে খাড়া উল্লম্বরেখায় h উচ্চতায় তোলা হল।

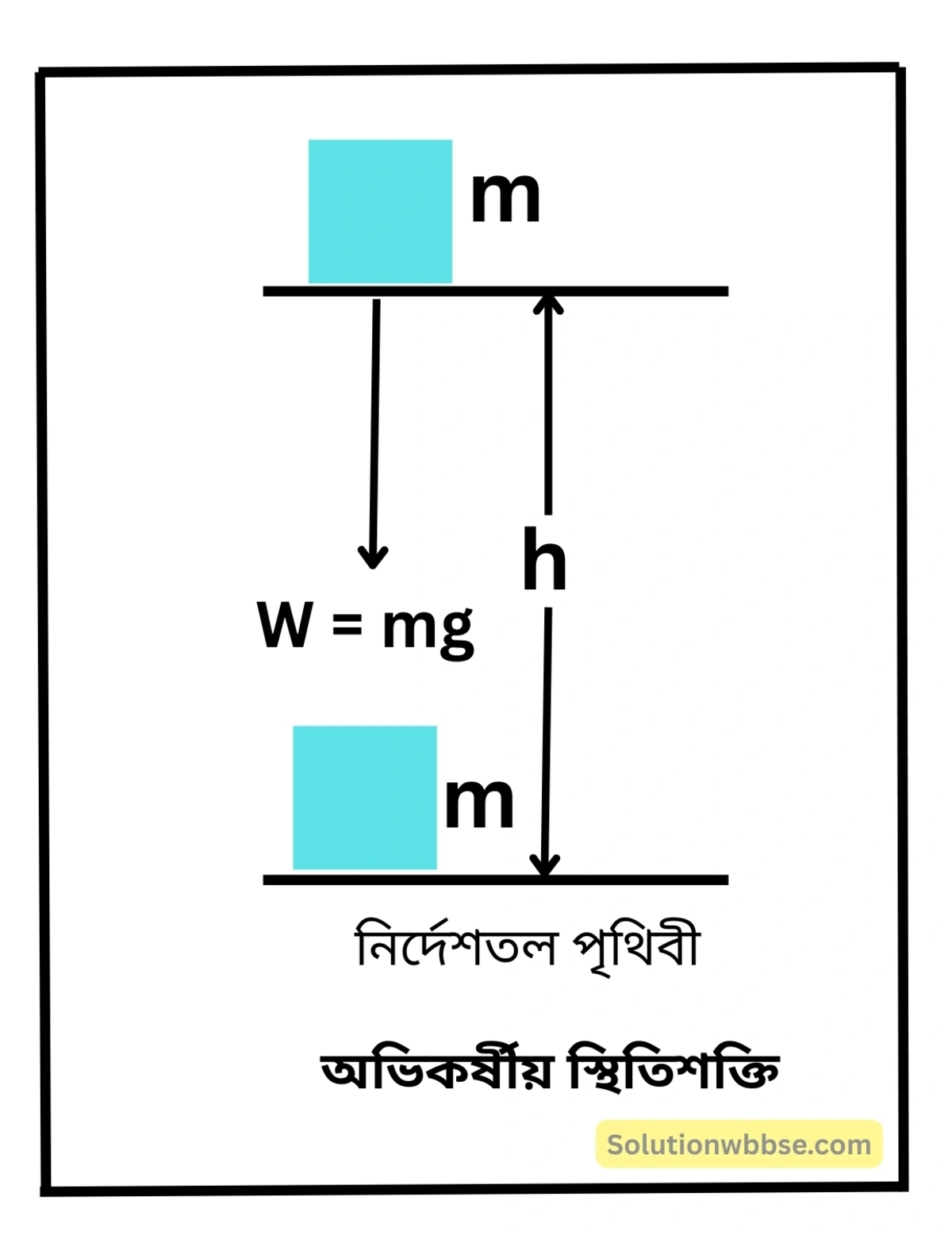
∴ বস্তুটির অবস্থান পরিবর্তনে অভিকর্ষ বলের বিরুদ্ধে কৃতকার্য = বস্তুটিতে অর্জিত স্থিতিশক্তি (E_p)।

অর্থাৎ, E_p = অভিকর্ষ বল × অভিকর্ষের বিরুদ্ধে বস্তুর সরণ

বা, E_p = বস্তুর ভার × সরণ

বা, Ep = W × h

বা, E_p = mgh [∵ W = বস্তুর ভার = mg, g → ওই স্থানের অভিকর্ষজ ত্বরণ]।

অর্থাৎ, অভিকর্ষীয় স্থিতিশক্তি = বস্তুর ভর (m) × অভিকর্ষজ ত্বরণ (g) × উল্লম্ব উচ্চতা (h)।

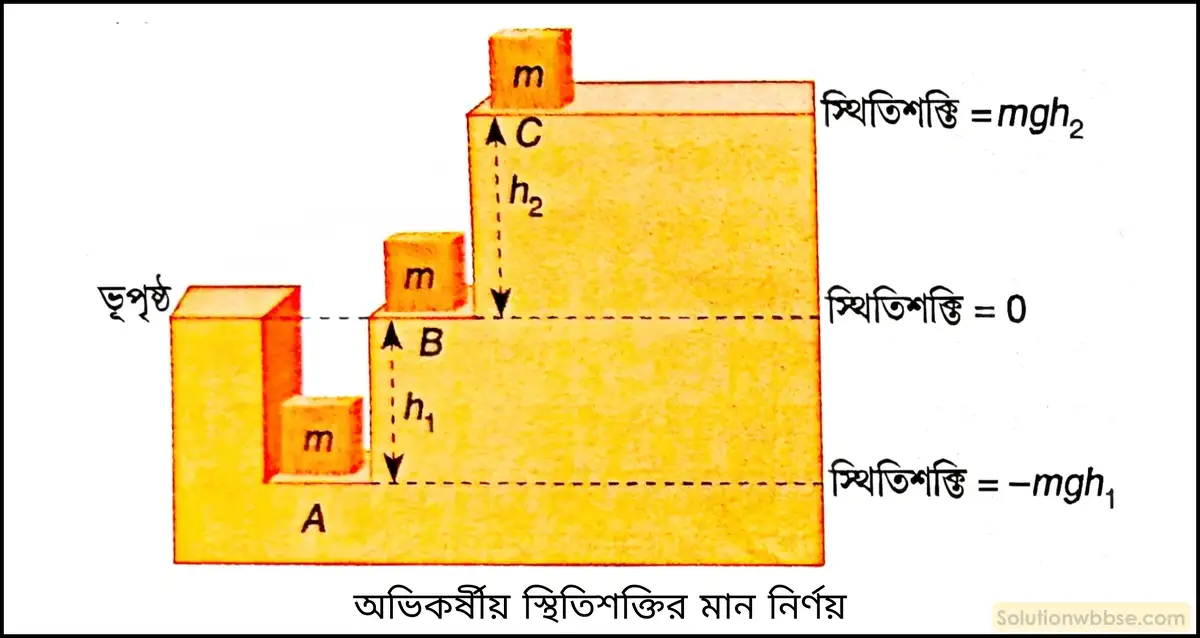
অভিকর্ষীয় স্থিতিশক্তির মান নির্দেশতলের ওপর কীভাবে নির্ভর করে?

অভিকর্ষীয় স্থিতিশক্তি সর্বদা কোনো পূর্বনির্দিষ্ট সুবিধাজনক তল বা পৃষ্ঠ (নির্দেশতল) (reference plane) সাপেক্ষে মাপা হয়। অন্য কিছু বলা না থাকলে সাধারণভাবে ভূপৃষ্ঠকেই নির্দেশতল বিবেচনা করা হয়।

নির্দেশতল প্রকৃতপক্ষে একটি শূন্যশক্তির অবস্থানকে চিহ্নিত করে থাকে। তাই, নির্দেশতলের সাপেক্ষে বস্তুর অবস্থানের ওপর নির্ভর করে বস্তুর স্থিতিশক্তির মান ধনাত্মক, ঋণাত্মক বা শূন্য হতে পারে। যেমন – কোনো বহুতল বাড়ির ছাদে অবস্থিত কোনো বস্তুর স্থিতিশক্তি ভূপৃষ্ঠ সাপেক্ষে ধনাত্মক। একইভাবে, খনিগর্ভে অবস্থিত কোনো বস্তুর স্থিতিশক্তি ভূপৃষ্ঠ সাপেক্ষে ঋণাত্মক এবং ভূপৃষ্ঠে অবস্থিত কোনো বস্তুর স্থিতিশক্তি শূন্য।

অবস্থানের জন্য স্থিতিশক্তি কীভাবে এবং কোন কোন বলের বিরুদ্ধে কার্য সম্পাদিত হওয়ার ফলে সৃষ্টি হতে পারে? কেলাসাকার গঠনযুক্ত পদার্থের ক্ষেত্রে এটি কীভাবে সংরক্ষিত থাকে?

অবস্থানের জন্য স্থিতিশক্তি, অভিকর্ষ ছাড়াও অন্য বলের বিরুদ্ধে কার্য সম্পাদিত হওয়ার কারণে সৃষ্টি হতে পারে। যেমন – কেলাসাকার গঠনযুক্ত পদার্থের ক্ষেত্রে অণুগুলি তাদের পারস্পরিক আন্তরাণবিক বলের বিরুদ্ধে কার্য করে একটি নির্দিষ্ট ব্যবধানে সজ্জিত হয়। এই কৃতকার্য ওই সংস্থার মধ্যে স্থিতিশক্তিরূপে সঞ্চিত হয়ে থাকে।

গতিশক্তি কয় প্রকার ও কী কী?

গতিশক্তি তিনপ্রকার। যথা –

• রৈখিক গতিশক্তি,
• আবর্ত গতিশক্তি,
• কম্পনজনিত গতিশক্তি।

রৈখিক গতিশক্তি (Translational kinetic energy) – যখন কোনো বস্তু সরলরেখায় চলে তখন তার মধ্যে সঞ্চারিত গতিশক্তিকে বলা হয় রৈখিক গতিশক্তি। যেমন – সরলরেখায় চলমান গাড়ি, কীটপতঙ্গ প্রভৃতির রৈখিক গতিশক্তি থাকে।

আবর্ত গতিশক্তি (Rotational kinetic energy) – যখন কোনো বস্তু নির্দিষ্ট কোনো অক্ষকে কেন্দ্র করে ঘূর্ণনরত হয়, তখন তার মধ্যে সঞ্চারিত গতিশক্তিকে বলা হয় আবর্ত গতিশক্তি। যেমন – ঘূর্ণায়মান লাট্টু, নাগরদোলা প্রভৃতির আবর্ত গতিশক্তি থাকে।

কম্পনজনিত গতিশক্তি (Vibrational kinetic energy) – যখন কোনো বস্তু এমনভাবে চলমান হয় যে, বস্তুটি বারবার একই বিন্দুতে ফিরে আসে তখন তার মধ্যে সঞ্চারিত গতিশক্তিকে বলা হয় কম্পনজনিত গতিশক্তি। যেমন – সরলদোলকের গতিশক্তি হল কম্পনজনিত গতিশক্তি।

প্রমাণ করো যে, গতিশক্তির রাশিমালা \(\frac12mv^2\), যেখানে চিহ্নগুলি প্রচলিত অর্থবহ।

গতিশক্তির রাশিমালা – কোনো গতিশীল বস্তু স্থিরাবস্থায় আসার আগে যে পরিমাণ কাজ করতে পারে তা দিয়েই তার গতিশক্তির পরিমাপ করা হয়।

ধরা যাক, m ভরের একটি বস্তু স্থিরাবস্থা থেকে F বলের ক্রিয়ায় সরলরেখা বরাবর সমত্বরণে S দূরত্ব অতিক্রম করে। বস্তুটির ত্বরণ a হলে,

গতি সমীকরণ v² = u² + 2aS ব্যবহার করে পাই,

v² = 0 + 2aS [∵ প্রাথমিক বেগ u = 0]

বা, S = \(\frac{v^2}{2a}\)

∴ বস্তুটির ওপর প্রযুক্ত বল দ্বারা কৃতকার্য,

W = F⋅S

বা, W = mas [F = ma সম্পর্ক ব্যবহার করে]

বা, W = \(ma\cdot\frac{v^2}{2a}\)

বা, W = \(\frac12mv^2\)

সংজ্ঞানুসারে, এই কৃতকার্যই বস্তুটির মধ্যে গতিশক্তি (E_k) রূপে সঞ্চিত হয়।

∴ বস্তুটির গতিশক্তি, E_k = \(\frac12mv^2\)

স্থিরাবস্থা থেকে m ভরের একটি বস্তু সমত্বরণে গতিশীল। t সময় পরে ওই বস্তুকণার গতিবেগ হল v। প্রমাণ করো যে, T সময়ে কৃতকার্য – \(W=\frac12\cdot\frac{mv^2T^2}{t^2}\)।

ধরা যাক, বস্তুকণাটির সমত্বরণ = \(a\), বস্তুকণাটি স্থিরাবস্থা থেকে যাত্রা শুরু করে বলে \(t\) সময় পরে গতিবেগ,

\(v=at\) [∵ কণাটির প্রাথমিক বেগ = 0]

বা, \(a=\frac vt\)

\(T\) সময় পরে ওই বস্তুকণার গতিবেগ = \(v_T\) হলে,

\(v_T=a_T\\\)

বা, \(v_T=\frac{vT}t\) [∵ \(a=\frac vt\)]

\(T\) সময় পরে বস্তুকণাটির দ্বারা কৃতকার্য \(W\) হলে,

\(W\) = গতিশক্তি বৃদ্ধি

বা, \(W\) = অন্তিম গতিশক্তি – প্রাথমিক গতিশক্তি

বা, \(W=\frac12mv_T^2-0\) [∵ বস্তুকণাটির প্রাথমিক বেগ = 0]

বা, \(W=\frac12mv_T^2\)

বা, \(W=\frac12m\left(\frac{vT}t\right)\) [∵ \(v_T=\frac{vT}t\)]

বা, \(W=\frac12mv_T^2\)

বা, \(W=\frac12\cdot\frac{mv^2T^2}{t^2}\) (প্রমাণিত)।

দেখাও যে, কৃতকার্য = গতিশক্তির বৃদ্ধি।

অথবা, কোনো বস্তুর ওপর বল দ্বারা কৃতকার্যই বস্তুর শক্তির পরিমাণ।

ধরা যাক, ধ্রুবক মানের বল F, m ভরসম্পন্ন একটি বস্তুর ওপর ক্রিয়া করায় বস্তুটির বেগ থেকে বৃদ্ধি পেয়ে হয়।

F বলের প্রভাবে বস্তুটিতে উৎপন্ন ত্বরণ a এবং বস্তু দ্বারা অতিক্রান্ত দূরত্ব S হলে v² = u² + 2aS

বা, v² – u² = 2aS ___(1)

এখন, বস্তুটির গতিশক্তির পরিবর্তন,

\(\Delta E=\frac12mv^2-\frac12mu^2\\\)

বা, \(\Delta E=\frac12m\left(v^2-u^2\right)\)

বা, \(\Delta E=\frac12m\times2aS\) [(1) নং সমীকরণ ব্যবহার করে]

বা, \(\Delta E=ma\times S\)

বা, \(\Delta E=F\times S\) [∵ \(F=ma\)]

∴ গতিশক্তির পরিবর্তন = বল × সরণ

বা, গতিশক্তির পরিবর্তন = কৃতকার্য

কোনো বস্তুর স্থিতিশক্তি থাকার শর্ত কী?

কোনো বলের বিরুদ্ধে কার্য করে কোনো বস্তুর আকৃতি বা আয়তন যদি প্রাথমিক মানের সাপেক্ষে পরিবর্তিত হয় অথবা, উপযুক্ত নির্দেশতল সাপেক্ষে তার অবস্থান যদি পালটায়, তখন সম্পাদিত কৃতকার্য ওই বস্তুটির মধ্যে স্থিতিশক্তি রূপে সঞ্চিত থাকে।

সুতরাং, কোনো বস্তুর স্থিতিশক্তি থাকার শর্ত হল বস্তুটিকে কোনো বলের ক্রিয়াক্ষেত্রে থাকতে হবে। যেমন – পৃথিবীর কেন্দ্রে বস্তুর অভিকর্ষীয় স্থিতিশক্তি থাকে না, কারণ পৃথিবীর কেন্দ্রে অভিকর্ষীয় বল শূন্য হয়।

দেখাও যে, স্থিরাবস্থা থেকে অবাধে পতনশীল m ভরের একটি বস্তুর t-তম সেকেন্ডে স্থিতিশক্তি হ্রাসের পরিমাণ \(\frac12mg^2\left(2t-1\right)\)।

স্থিরাবস্থা থেকে অবাধে পতনশীল বস্তু (t – 1) sec এবং t sec সময়ে যথাক্রমে \(h_1\) এবং \(h_2\) দূরত্ব নামলে,

\(h_1=\frac12g\left(t-1\right)^2\) [∵ স্থিরাবস্থা থেকে পতনশীল হওয়ায় বস্তুটির প্রাথমিক বেগ, u = 0]

এবং \(h_2=\frac12gt^2\)

∴ t-তম সেকেন্ডে বস্তুটি \(h\) দূরত্ব নামলে,

\(h=h_2-h_1\\\)

বা, \(h=\frac12gt^2-\frac12g\left(t-1\right)^2\)

বা, \(h=\frac12gt^2-\frac12g\left(t^2-2t+1\right)\)

বা, \(h=\frac12g\left(t^2-t^2+2t-1\right)\)

বা, \(h=\frac12g\left(2t-1\right)2\)

যেহেতু বস্তুটি অবাধে উল্লম্বভাবে পতনশীল, অতএব, বস্তুটির স্থিতিশক্তি হ্রাস পাবে।

∴ t-তম সেকেন্ডে m ভরের বস্তুটির স্থিতিশক্তি হ্রাস

= \(mgh\)

= \(mg\times\frac12g\left(2t-1\right)\)

= \(\frac12mg^2\left(2t-1\right)\) (প্রমাণিত)।

গতিশক্তির স্থিতিশক্তিতে এবং স্থিতিশক্তির গতিশক্তিতে রূপান্তরের উদাহরণ দাও।

গতিশক্তি ও স্থিতিশক্তির পারস্পরিক রূপান্তর – ভূপৃষ্ঠ থেকে কোনো বস্তুকে ওপর দিকে নির্দিষ্ট বেগসহ নিক্ষেপ করলে বস্তুটির গতিশক্তি ক্রমশ স্থিতিশক্তিতে রূপান্তরিত হয়। বস্তুটি নিক্ষিপ্ত হওয়ার মুহূর্তে তার শক্তি সম্পূর্ণ গতিশক্তি হয়। উচ্চতা বৃদ্ধির সঙ্গে সঙ্গে বস্তুর গতিশক্তি হ্রাস পায় এবং স্থিতিশক্তি বাড়ে। অবশেষে গতির সর্বোচ্চ বিন্দুতে পৌঁছালে প্রাথমিক গতিশক্তির সবটুকুই স্থিতিশক্তিতে পরিণত হয়। অর্থাৎ, এই অবস্থানে বস্তুর গতিশক্তি সর্বনিম্ন ও স্থিতিশক্তি সর্বোচ্চ হয়।

একইভাবে, বস্তুটি ওই উচ্চতা থেকে অবাধে পতনশীল হলে উচ্চতা হ্রাসের সঙ্গে সঙ্গে তার স্থিতিশক্তি কমে এবং প্রাথমিক (সর্বোচ্চ অবস্থানে) স্থিতিশক্তির একটি অংশ গতিশক্তিতে রূপান্তরিত হয়। বস্তুটি যত নীচে নামে গতিশক্তির মান তত বৃদ্ধি পেতে থাকে এবং ভূমি স্পর্শ করার পূর্ব মুহূর্তে তার স্থিতিশক্তি শূন্য হয় অর্থাৎ, প্রাথমিক স্থিতিশক্তির সবটুকুই গতিশক্তিতে রূপান্তরিত হয়।

সরল দোলন গতি নির্বাহকারী কোনো কণার গতিশক্তি ও স্থিতিশক্তির পরিবর্তনের ধরন ব্যাখ্যা করো।

সরল দোলগতি নির্বাহকারী কোনো কণা তার সাম্যাবস্থান থেকে প্রান্তীয় অবস্থানে গেলে গতিশক্তির মান সর্বোচ্চ থেকে ধীরে ধীরে কমে সর্বনিম্ন (শূন্য) হয়, কিন্তু স্থিতিশক্তি শূন্য থেকে বাড়তে বাড়তে সর্বোচ্চ হয়। কণা সাম্যাবস্থান অভিমুখে ফিরে আসার সময় বিপরীত ঘটনা ঘটে।

একটি বস্তুর ভর m এবং এর গতিশক্তি E। প্রমাণ করো, বস্তুটির ভরবেগ \(p=\sqrt{2mE}\)।

ধরা যাক, \(m\) ভরের বস্তুটির বেগ = \(v\)

∴ বস্তুটির ভরবেগ, \(p=mv\)

এবং বস্তুটির গতিশক্তি, \(E=\frac12mv^2\)

বা, \(E=\frac{m^2v^2}{2m}\)

∴ \(E=\frac{p^2}{2m}\) (∵ \(p=mv\))

বা, \(p^2=2mE\)

বা, \(p=\sqrt{2mE}\)

∴ বস্তুটির ভরবেগ, \(p=\sqrt{2mE}\) (প্রমাণিত)।

শক্তির নিত্যতা সূত্রটি লেখো।

শক্তির নিত্যতা সূত্র – শক্তি অবিনশ্বর, কোনো ভৌত বা রাসায়নিক প্রক্রিয়ায় শক্তিকে সৃষ্টি বা ধ্বংস করা যায় না। শক্তিকে কেবল এক রূপ থেকে অন্য (এক বা একাধিক) রূপে রূপান্তরিত করা যায়। মহাবিশ্বে মোট শক্তির পরিমাণ নির্দিষ্ট এবং অপরিবর্তনীয়।

অবাধে পতনশীল বস্তুর যান্ত্রিক শক্তির নিত্যতা সূত্রটি লেখো।

অবাধে পতনশীল বস্তুর ক্ষেত্রে যান্ত্রিকশক্তি সংরক্ষণ সূত্র – ঘর্ষণ বা অন্য কোনো শক্তিঅপচয়ী বল উপস্থিত না থাকলে, অবাধে পতনশীল বস্তুর গতির যে-কোনো অবস্থানে বস্তুটির মোট যান্ত্রিক শক্তি (স্থিতিশক্তি + গতিশক্তি) -এর পরিমাণ সর্বদাই সংরক্ষিত থাকে বা ধ্রুবক হয়।

প্রমাণ করো যে, অভিকর্ষের প্রভাবে অবাধে পতনশীল বস্তুর মোট যান্ত্রিক শক্তি সর্বদা ধ্রুবক।

ধরা যাক, m ভরের একটি বস্তুকণা শূন্যস্থানে h উচ্চতা থেকে বিনা বাধায় ছেড়ে দেওয়া হল। গতিপথের সর্বোচ্চ অবস্থানে অর্থাৎ, A বিন্দুতে কণার গতিশক্তি \(\left(E_K\right)=0\) (কারণ – A বিন্দুতে কণাটি স্থির) এবং স্থিতিশক্তি \(\left(E_K\right)=mgh\) [g → ওই স্থানে অভিকর্ষজ ত্বরণ]

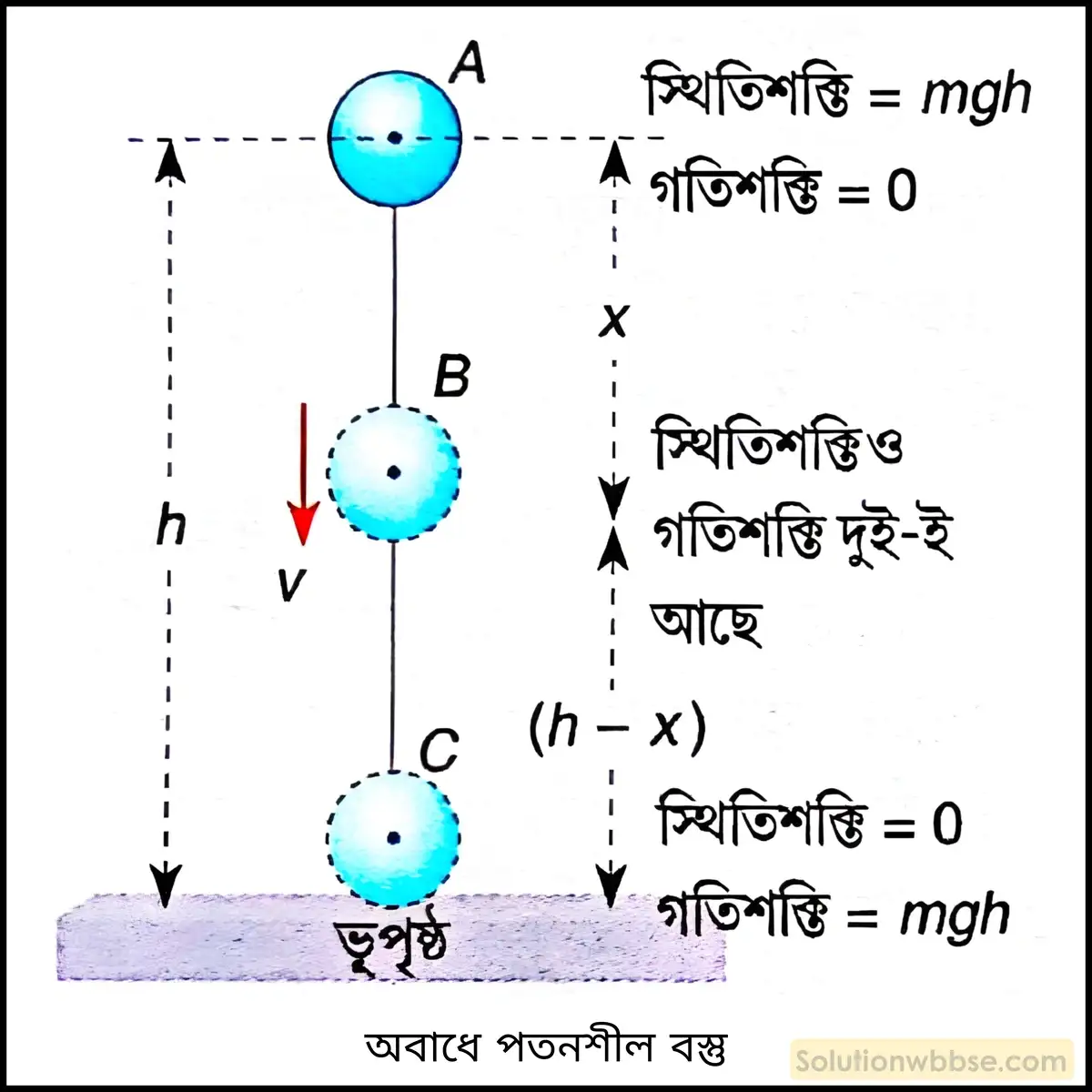
∴ A বিন্দুতে মোট যান্ত্রিক শক্তি, \(E_A=E_K+E_p\)

বা, \(E_A=0+mgh\)

বা, \(E_A=mgh\)

গতিপথের সর্বনিম্ন বিন্দু C -তে কণার বেগ \(v_C\) হলে,

 বা, \(v_C^2=0+2gh\) [∵ প্রাথমিক বেগ u = 0]

∴ C বিন্দুতে গতিশক্তি, \(E_k=\frac12mv_C^2\)

বা, \(E_k=\frac12m\times2gh\)

বা, \(E_k=mgh\)

ভূমি স্পর্শ করার মুহূর্তে \(h=0\),

∴ C বিন্দুতে \(E_p=mgh=0\)

∴ C বিন্দুতে মোট যান্ত্রিক শক্তি, \(E_C=E_p+E_K\)

বা, \(E_C=0+mgh\)

বা, \(E_C=mgh\)

মধ্যবর্তী যে-কোনো বিন্দুতে (যেমন – B বিন্দুতে) কণার স্থিতিশক্তি ও গতিশক্তি দুই-ই বর্তমান। এক্ষেত্রে, সর্বোচ্চ অবস্থান থেকে ভূপৃষ্ঠ অভিমুখে বস্তুকণার সরণ AB = x হলে, B বিন্দুতে নির্দেশতল (ভূপৃষ্ঠ) সাপেক্ষে ওর স্থিতিশক্তি, \(E_p=mg\left(h-x\right)\)।

∴ B বিন্দুতে কণার বেগ \(v_B\) হলে, \(v_B^2=0+2gx\) (∵ \(u=0\))

বা, \(v_B^2=2gx\)

∴ B বিন্দুতে গতিশক্তি \(E_K=\frac12mv_B^2\)

বা, \(E_K=\frac12m\times2gx\)

বা, \(E_K=mgx\)

∴ B বিন্দুতে মোট যান্ত্রিকশক্তি, \(E_B=E_p+E_K\)

বা, \(E_B=mg\left(h-x\right)+mgx\)

বা, \(E_B=mgh\)

সুতরাং, পতনশীল বস্তুর যে-কোনো অবস্থানে মোট যান্ত্রিক শক্তির মান সর্বদাই হয় \(mgh\)।

∴ অভিকর্ষের প্রভাবে অবাধে পতনশীল বস্তুর মোট যান্ত্রিক শক্তি ধ্রুবক থাকে (প্রমাণিত)।

ভূমি স্পর্শ করার পর বস্তুটির যান্ত্রিক শক্তি ভূপৃষ্ঠের সঙ্গে সংঘাতের ফলে শব্দশক্তি, তাপশক্তি ইত্যাদিতে রূপান্তরিত হয়ে যায়।

যান্ত্রিক শক্তি সংরক্ষণ নীতি কী? এটি কোন কোন পরিস্থিতিতে কঠোরভাবে প্রযোজ্য এবং বাস্তবে এর কতটুকু প্রভাব পরিলক্ষিত হয়?

যান্ত্রিক শক্তি সংরক্ষণ নীতিটি আদর্শ পরিস্থিতিতে অর্থাৎ, অবাধ পতনের ক্ষেত্রেই (যখন বায়ুর ঘর্ষণ অনুপস্থিত) সঠিকভাবে প্রযোজ্য। বাস্তবে বায়ুর ঘর্ষণজনিত বাধা অতিক্রম করার জন্য পতনশীল। বস্তুর শক্তির কিছু অংশ ব্যয়িত হয়। ফলে, নীতিটি কঠোরভাবে মান্য হয় না। তবে, অবাধে পতনশীল বস্তুর গতি ছাড়াও, মসৃণ নততল বরাবর গতিশীল বস্তুর ক্ষেত্রে তল বরাবর নিম্নাভিমুখে অভিকর্ষ বলের (পতনশীল বস্তুর ওজন) উপাংশ বিবেচনা করে প্রমাণ করা যায়, তলের ওপর যে-কোনো অবস্থানে পতনশীল বস্তুর মোট যান্ত্রিক শক্তির মান সর্বদা ধ্রুবক হয়।

বোধমূলক প্রশ্নোত্তর

একটি বালক কোনো বৃত্তাকার পথের একটি নির্দিষ্ট বিন্দু থেকে যাত্রা শুরু করে এক পাক ঘুরে এসে আবার সেই বিন্দুতে ফিরে এল। বালকটি দ্বারা সম্পাদিত কার্য কত?

একবার সম্পূর্ণ আবর্তনের পর বালক তার প্রারম্ভিক অবস্থান বিন্দুতে ফিরে এলে বালকটির সরণ শূন্য হয়। যেহেতু কৃতকার্য হল প্রযুক্ত বল ও সরণের গুণফল, তাই সরণ শূন্য হওয়ায় বালকটি দ্বারা সম্পাদিত কার্যের মানও শূন্য হবে।

এক ব্যক্তি স্রোতের বিরুদ্ধে সাঁতার কেটে তীরভূমি সাপেক্ষে নিজেকে স্থির রাখতে সক্ষম হলেন, ওই ব্যক্তি কোনো কার্য করছেন কি?

স্রোতের বিরুদ্ধে সাঁতার কেটে যদি ব্যক্তি তীরভূমি সাপেক্ষে নিজেকে স্থির রাখতে সমর্থ হন, তবে তীর সাপেক্ষে ব্যক্তির সরণ শূন্য হয়। তাই, বলের প্রয়োগবিন্দুর কোনো সরণ না হওয়ায় তীরের সাপেক্ষে লোকটি দ্বারা কৃতকার্য শূন্য হবে।

স্রোতের বেগে চলমান কোনো নির্দেশতন্ত্র থেকে দেখলে যদিও কৃতকার্য কখনোই শূন্য হবে না। এক্ষেত্রে, স্রোতের সাপেক্ষে ব্যক্তির বিপরীত অভিমুখে সরণ ঘটে, তাই কৃতকার্য শূন্য হয় না।

একটি বস্তুকে দুবার ভূমি থেকে একই উচ্চতায় তোলা হল – প্রথমবার দ্রুত ও দ্বিতীয়বার ধীরে ধীরে, উভয়ক্ষেত্রে কৃতকার্য সমান হবে কি?

নির্দিষ্ট উচ্চতায় উত্তোলনের ক্ষেত্রে কোনো বস্তু দ্বারা অর্জিত স্থিতিশক্তির রাশিমালা, E_p = mgh। যেখানে, m বস্তুর ভর, h উচ্চতা এবং g ওই স্থানের অভিকর্ষজ ত্বরণ নির্দেশ করে। সুতরাং, অর্জিত স্থিতিশক্তি কৃতকার্যে পরিণত হয় এবং এই কৃতকার্য সময় নিরপেক্ষ হওয়ায়, একই উচ্চতায় বস্তু তোলা হলে উভয়ক্ষেত্রে কৃতকার্যের পরিমাণ সমান হবে।

কোনো ভারোত্তলক একটি ওজন তার মাথার উপর তুলে দাঁড়িয়ে থাকলে তার কৃতকার্যের মান কত? যুক্তিসহ লেখো।

ওজনটিকে মাথার ওপর তোলার সময় ভার উত্তোলনকারীকে অভিকর্ষ বলের বিরুদ্ধে কার্য করতে হয়। কিন্তু ওজনটিকে মাথার উপর তুলে নিয়ে দাঁড়িয়ে থাকলে কোনো কার্য করা হয় না, কারণ ওই অবস্থায় ওজনটির কোনো সরণ হয় না।

সুতোয় বেঁধে একটি পাথরকে আঙুলের চারপাশে অনুভূমিকভাবে ঘোরাচ্ছ। পাথরটা ঘোরানোর জন্য এখানে কোন্ বল কোন্ দিকে কাজ করছে? যে-কোনো মুহূর্তে পাথরটির সরণ কোন্ দিকে? তোমার উত্তরের সপক্ষে যুক্তি দাও। পাথর ঘোরানোর ফলে তুমি কতখানি কার্য করছ তা বুঝিয়ে লেখো।

সুতোয় বেঁধে একটি পাথরকে আঙুলের চারপাশে অনুভূমিকভাবে ঘোরাবার সময় আঙুলে টান অনুভূত হয়। বৃত্তাকার পথের ব্যাসার্ধ বরাবর (এক্ষেত্রে সুতো বরাবর) ক্রিয়াশীল এই কেন্দ্রাভিমুখী টানের জন্যই পাথরটা ঘোরে। এই কেন্দ্রাভিমুখী টান বা বলকে বলা হয় অভিকেন্দ্র বল।

সুতোটি হঠাৎ ছিঁড়ে গেলে দেখা যায়, পাথরটা বৃত্তাকার পথের স্পর্শক বরাবর সোজা বেরিয়ে যায়। এর কারণ হল, বৃত্তাকার পথে ঘোরার সময় পাথরের সরণের অভিমুখ প্রতি মহর্তে বৃত্তাকার পথের স্পর্শক বরাবর থাকে।

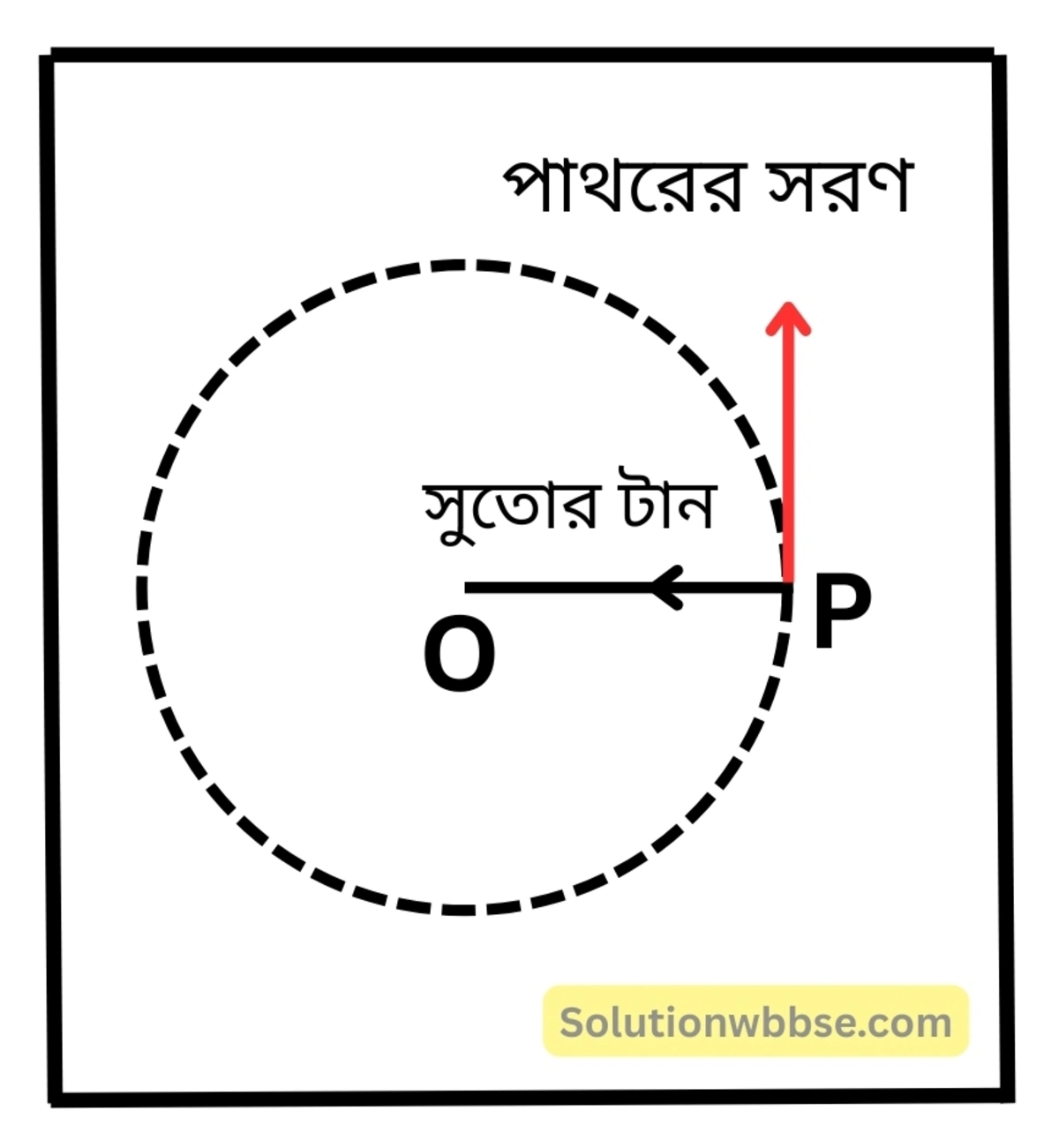
এক্ষেত্রে সুতোর টান বৃত্তাকার পথের ব্যাসার্ধ বরাবর এবং পাথরের সরণ বৃত্তপথের স্পর্শক বরাবর হওয়ায় এরা পরস্পরের উপর লম্ব। তাই পাথরের ওপর প্রযুক্ত বল দ্বারা কৃতকার্য শূন্য। অতএব, সুতোয় বেঁধে পাথর ঘোরানোর ফলে আমার কোনো কার্য করা হয় না।

কোনো অনুভূমিক রাস্তা বরাবর একটি মোটরগাড়ি সমবেগে চলছে। এ অবস্থায় গাড়ির ইঞ্জিন কোনো কার্য করছে কি?

এ অবস্থায় গাড়ির ইঞ্জিন অবশ্যই কার্য করবে। কারণ – সমবেগ বজায় রাখার জন্য গাড়ির ইঞ্জিন রাস্তার ঘর্ষণ বলের বিরুদ্ধে কার্য করবে এবং গাড়ির সরণও সেই দিকেই হবে। ঘর্ষণজনিত বাধা এবং গাড়ির সরণের গুণফল কৃতকার্যের পরিমাপ দেয়।

যখন কোনো বল কার্য করে তখন ওই বল অন্য কোনো বলের বিরুদ্ধে কার্য করে – ব্যাখ্যা করো।

প্রকৃতিতে বিচ্ছিন্ন বলের কোনো অস্তিত্ব নেই। কোনো বস্তুকে উপরে ছুড়ে দেওয়া হলে ওই বল অভিকর্ষ বলের বিরুদ্ধে কাজ করে। আবার, কোনো বস্তু যখন অবাধে অভিকর্ষ বলের অভিমুখে পড়তে থাকে তখন তা বায়ুর ঘর্ষণ বলের বিরুদ্ধে কার্য করে। কোনো বস্তুকে ভূমি বরাবর ঠেলে দিলে তা ভূমির ঘর্ষণ বলের বিরুদ্ধে কার্য করে।

সুতরাং, প্রকৃতিতে যে-কোনো বলই বৈশিষ্ট্যগতভাবে তার বিপরীতে সক্রিয় অপর একটি বলের বিরুদ্ধে কার্যকরী হয় এবং ওই বলের অভিমুখে প্রযুক্ত বল প্রয়োগবিন্দুর সরণ ঘটালে বাধাদানকারী বলের বিরুদ্ধে কার্য সম্পন্ন হয়ে থাকে।

A ও B দলের মধ্যে দড়ি টানাটানি খেলায় A দল 10 N বল প্রয়োগ করে এবং B দলের কাছে হেরে গেল। কারণ B দল 15 N বল প্রয়োগ করেছে। এক্ষেত্রে কোন্ দল ঋণাত্মক ও কোন্ দল ধনাত্মক কার্য করল?

দড়ি টানাটানি খেলায় A দল 10 N বল প্রয়োগ করে এবং B দলের কাছে হেরে গেল। অর্থাৎ, A দলের সরণ, B দলের দিকে ঘটল। এক্ষেত্রে, A দল নিজেদের দিকে 10 N বল B দলের ওপর প্রয়োগ করে ও বলের প্রয়োগবিন্দুর সরণ অর্থাৎ B দলের সরণ বলের গতির বিপরীত অভিমুখে ঘটে। ফলে A দল বলের বিরুদ্ধে কার্য করে। অর্থাৎ A দল ঋণাত্মক কার্য করে।

অপরপক্ষে, B দল A দলের ওপর নিজেদের দিকে 15 N বল প্রয়োগ করে। ফলে B দলের দিকেই A দলের সরণ ঘটে। অর্থাৎ, বলের প্রয়োগবিন্দুর (A দলের) সরণ, B দল দ্বারা প্রযুক্ত বলের অভিমুখেই ঘটে। ফলে, B দল বল দ্বারা কার্য সম্পন্ন করে। সুতরাং, B দল ধনাত্মক কার্য করে।

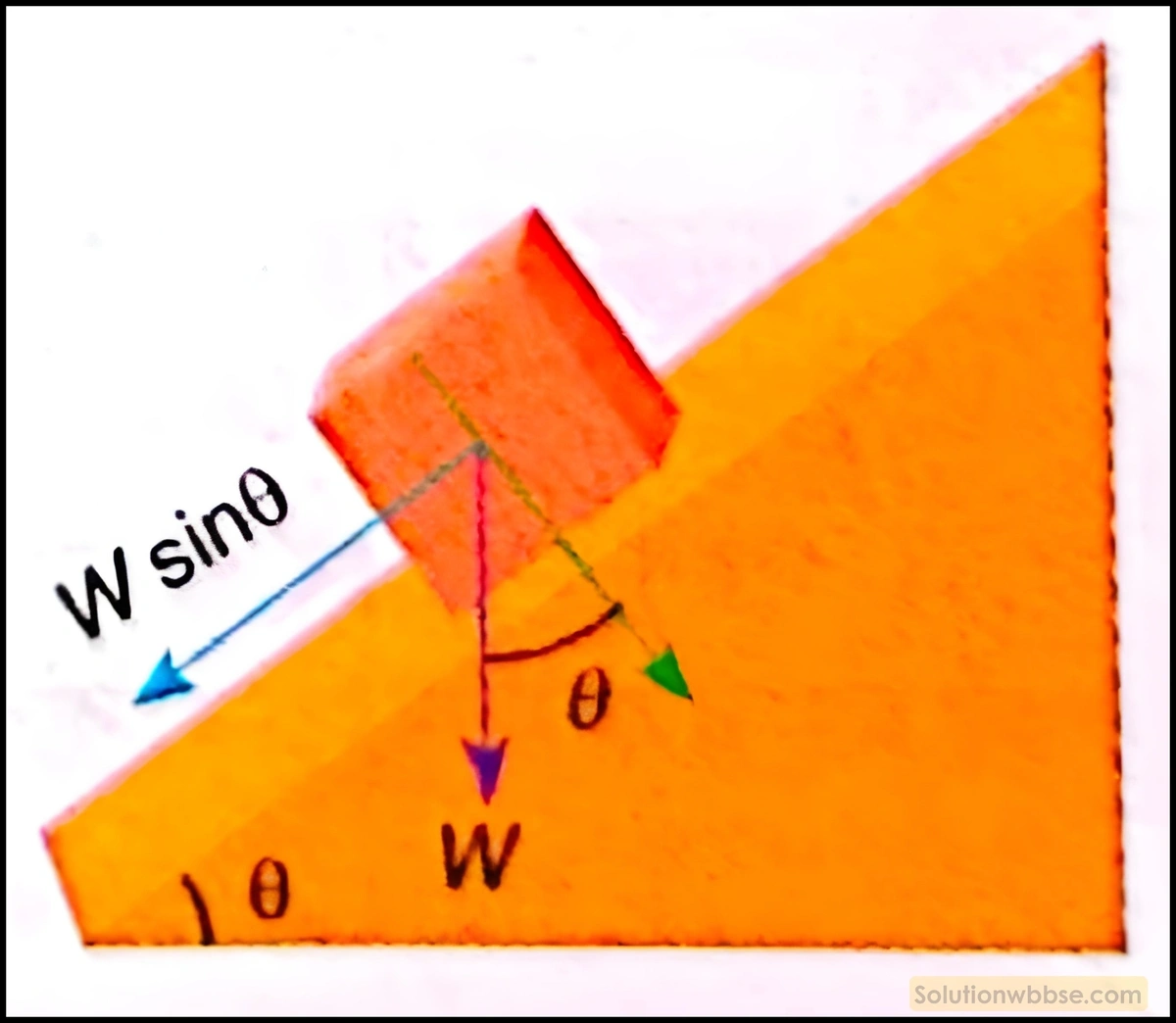
একটি বাক্সকে একটি নততল বরাবর উপরের দিকে তোলা হচ্ছে। অভিকর্ষ বল বাক্সের ওপর কোনো কার্য করছে কি?

বাক্সটির ওজন W হলে নততলের দৈর্ঘ্য বরাবর নীচের দিকে ক্রিয়াশীল এই ওজনের কার্যকরী অংশ বা উপাংশ হল W sinθ। তল বরাবর উপরের দিকে ওঠার সময় এই উপাংশের বিরুদ্ধে কার্য সম্পাদিত হয়ে থাকে। W sinθ সুতরাং, এক্ষেত্রে বাক্সের ওপর ক্রিয়াশীল অভিকর্ষ বলের উপাংশের বিরুদ্ধে কার্য করা হয়। তাই, অভিকর্ষ বল বাক্সের ওপর ঋণাত্মক কার্য করে।

দুর্বল দল শক্তিশালী দলের কাছে হেরে যায় – দড়ি টানাটানি খেলায় নিম্নোক্ত ক্ষেত্রগুলিতে কার দ্বারা কৃতকার্য কত হবে?

দড়ি টানাটানি খেলায় (Tug of war) বিজয়ী দলের অভিমুখে দড়ির বা আরও নির্দিষ্ট করে দড়িতে প্রযুক্ত বলের প্রয়োগবিন্দুর সরণ ঘটে। বিজয়ী ও বিজিত দল কর্তৃক প্রযুক্ত বল যথাক্রমে F₁ ও F₂ হলে কার্যকরী বা লব্ধি বল (F₁ – F₂) -এর অভিমুখে বিজয়ী দল দ্বারা কৃতকার্য = (F₁ – F₂) × S × cos 0°। যেখানে, S হল বিজয়ী দলের অভিমুখে দড়ির সরণ।

সুতরাং, বিজয়ী দল দ্বারা প্রযুক্ত বল কার্য করে এবং বিজিত দলের দ্বারা প্রদেয় বলের বিরুদ্ধে কার্য সংঘটিত হয়।

উভয়পক্ষই সমান জোরে দড়িতে টান দেয় – দড়ি টানাটানি খেলায় নিম্নোক্ত ক্ষেত্রগুলিতে কার দ্বারা কৃতকার্য কত হবে?

দুটি দলই সমশক্তিসম্পন্ন হলে দড়ির ওপর বিপরীত অভিমুখে সমান টান প্রযুক্ত হয়। এই অবস্থায় কোনো অভিমুখেই দড়ি বা বলের প্রয়োগবিন্দুর সরণ ঘটে না। সুতরাং, কৃতকার্য শূন্য হয়।

দীপিকা পুকুরে সাঁতার কাটছে – কার্যের ধারণা থেকে বলার চেষ্টা করো কোন্ ক্ষেত্রগুলিতে কার্য হচ্ছে ও কোন্ ক্ষেত্রগুলিতে কার্য হচ্ছে না?

দীপিকা পুকুরে সাঁতার কাটার সময় হাত-পা নেড়ে জলকে পিছনের দিকে ঠেলে সামনের দিকে এগিয়ে যায় অর্থাৎ, দীপিকার সরণ হওয়ায় সে জলের বাধার বিরুদ্ধে কার্য করে।

একটি গাধা তার পিঠে বোঝা বহন করে অনুভূমিক সমতল পথে চলছে – কার্যের ধারণা থেকে বলার চেষ্টা করো কোন্ ক্ষেত্রগুলিতে কার্য হচ্ছে ও কোন্ ক্ষেত্রগুলিতে কার্য হচ্ছে না?

যেহেতু, গাধার পিঠে থাকা বোঝার ওপর ক্রিয়াশীল অভিকর্ষ বল এবং বোঝার সরণ পরস্পর লম্ব। সুতরাং, গাধাটি অভিকর্ষ বলের বিরুদ্ধে বা পক্ষে কোনো কার্য করছে না। কিন্তু গাধাটি বোঝাসহ অনুভূমিক পথে চলায় পথের ঘর্ষণ বলের বিরুদ্ধে কার্য করছে।

বায়ুকলের সাহায্যে কুয়ো থেকে জল তোলা হচ্ছে – কার্যের ধারণা থেকে বলার চেষ্টা করো কোন্ ক্ষেত্রগুলিতে কার্য হচ্ছে ও কোন্ ক্ষেত্রগুলিতে কার্য হচ্ছে না?

বায়ুকলের সাহায্যে কুয়ো থেকে জল তোলার সময় অভিকর্ষ বলের বিরুদ্ধে কার্য করতে হয়।

একটি সবুজ উদ্ভিদ সালোকসংশ্লেষ প্রক্রিয়া সম্পন্ন করছে – কার্যের ধারণা থেকে বলার চেষ্টা করো কোন্ ক্ষেত্রগুলিতে কার্য হচ্ছে ও কোন্ ক্ষেত্রগুলিতে কার্য হচ্ছে না?

সালোকসংশ্লেষ প্রক্রিয়া সম্পন্ন হওয়ার সময় কোনো বল প্রযুক্ত হয় না বা সরণ হয় না বলে কোনো কার্য সম্পাদনও হয় না।

একটি ইঞ্জিন ট্রেনকে টানছে – কার্যের ধারণা থেকে বলার চেষ্টা করো কোন্ ক্ষেত্রগুলিতে কার্য হচ্ছে ও কোন্ ক্ষেত্রগুলিতে কার্য হচ্ছে না?

একটি ইঞ্জিন ট্রেনকে টানলে ট্রেনটির সরণ হওয়ায় ইঞ্জিন দ্বারা প্রযুক্ত বল কার্য করে।

সূর্যালোকে খাদ্যশস্য শুকানো হচ্ছে – কার্যের ধারণা থেকে বলার চেষ্টা করো কোন্ ক্ষেত্রগুলিতে কার্য হচ্ছে ও কোন্ ক্ষেত্রগুলিতে কার্য হচ্ছে না?

খাদ্যশস্য সূর্যালোকে শুকনো হওয়ার সময় কোনো বল প্রযুক্ত হচ্ছে না বা সরণও ঘটছে না। ফলে, কোনো কার্য হচ্ছে না।

বায়ুপ্রবাহের জন্য পালতোলা নৌকা চলছে – কার্যের ধারণা থেকে বলার চেষ্টা করো কোন্ ক্ষেত্রগুলিতে কার্য হচ্ছে ও কোন্ ক্ষেত্রগুলিতে কার্য হচ্ছে না?

বায়ুপ্রবাহের গতিশক্তি নৌকার পালে বল প্রয়োগ করায় প্রযুক্ত বলের অভিমুখে নৌকার সরণ ঘটে। এক্ষেত্রে, বায়ুপ্রবাহ কার্য করছে।

এক ব্যক্তি একটি স্যুটকেশ হাতে নিয়ে লিফ্টে উঠছেন। এই অবস্থায় – (1) স্যুটকেশের ওপর ওই ব্যক্তি কোনো কার্য করছেন কি? (2) স্যুটকেশটির শক্তির কোনো পরিবর্তন হবে কি?

এক ব্যক্তি একটি স্যুটকেশ হাতে নিয়ে লিফ্টে উঠছেন। এই অবস্থায় –

1. ওই ব্যক্তির সাপেক্ষে স্যুটকেশের কোনো সরণ হয় না। তাই ওই ব্যক্তি স্যুটকেশের ওপর কোনো কার্য করেন না।
2. ভূপৃষ্ঠ থেকে স্যুটকেশের উচ্চতা ক্রমশ বাড়ছে বলে স্থিতিশক্তি ক্রমশ বাড়তে থাকে। আর স্যুটকেশটির বেগ লিফ্টের বেগের সমান তাই স্যুটকেশটির গতিশক্তিও থাকবে। অর্থাৎ, মোট শক্তির পরিমাণ বৃদ্ধি পাবে।

একজন রোগা ও একজন মোটা লোক একই সময়ে সিঁড়ি বেয়ে একতলা থেকে দোতলায় উঠল। কার ক্ষমতা বেশি?

m ভরের এক ব্যক্তি অভিকর্ষের বিরুদ্ধে t সময়ে h উচ্চতায় আরোহণ করলে ব্যক্তি দ্বারা ব্যয়িত ক্ষমতা

$P=\frac{\mathrm{কৃতকার্য\; (W)}}{\mathrm{সময়\; (t)}}$

বা, \(P=\frac{mgh}t\)

এক্ষেত্রে দুই ব্যক্তিই একই উচ্চতা আরোহণ করায়, তাদের ব্যয়িত ক্ষমতার অনুপাত –

\(\frac{P_1}{P_2}=\frac{m_1\times t_2}{m_2\times t_2}\) (∵ h ধ্রুবক])।

তাদের ওজন ভিন্ন হওয়ায় ভরও ভিন্ন। সুতরাং, একই সময়ে তারা দোতলায় উঠলে অর্থাৎ, \(t_1=t_2\) হলে, \(\frac{P_1}{P_2}=\frac{m_1}{m_2}\)।

অর্থাৎ, সেক্ষেত্রে ব্যয়িত ক্ষমতা কখনোই সমান হবে না।

কিন্তু \(t_1\neq t_2\) হলে \(P_1=P_2\) হওয়া সম্ভব, যদি \(\left(m_1t_2\right)=\left(m_2t_1\right)\) হয়। এই শর্তে তাদের ক্ষমতা সমান হতে পারে।

একটি ইঞ্জিনের ক্ষমতা 5 HP বলতে কী বোঝায়?

ইঞ্জিনের ক্ষমতা 5 অশ্বক্ষমতা বা, 5 HP বলতে বোঝায় যে, ওই ইঞ্জিন 1 সেকেন্ডে (5 × 746) = 3730 জুল কাজ করতে পারে। [∵ 1 অশ্বক্ষমতা = 746 জুল/সেকেন্ড]।

এক বালতি জল হাতে ঝুলিয়ে তুমি 5 সেকেন্ডে অনুভূমিক পথে 3 মিটার পথ অতিক্রম করলে। এরপর ওই জলভরতি বালতিটি নিয়ে তুমি 5 সেকেন্ডে সিঁড়ি বেয়ে 3 মিটার উপরে উঠলে। কোন্ ক্ষেত্রে তোমার ক্ষমতা বেশি হবে তা বুঝিয়ে লেখো।

অনুভূমিক রাস্তায় চলনের ক্ষেত্রে আমার ওজন এবং জলপূর্ণ বালতির ওজন খাড়া লম্বভাবে নীচের দিকে ক্রিয়া করে এবং সরণের অভিমুখ, ওজনের ক্রিয়ার অভিমুখের সঙ্গে লম্ব হয়। সুতরাং, আমার ও জলপূর্ণ বালতির ওজন এক্ষেত্রে কার্যহীন বল হিসেবে কাজ করে, ফলে ওই বলের দ্বারা কৃতকার্য শূন্য হয় অর্থাৎ ব্যয়িত ক্ষমতাও শূন্য হয়।

সিঁড়ি বেয়ে উপরে ওঠার সময় আমার ওজন ও জলপূর্ণ বালতির ওজনের বিরুদ্ধে অর্থাৎ, অভিকর্ষ বলের বিরুদ্ধে কার্য সম্পাদিত হয় যা সংশ্লিষ্ট উচ্চতায় সংস্থার স্থিতিশক্তি হিসেবে সঞ্চিত হয়। সুতরাং, দ্বিতীয়ক্ষেত্রে কৃতকার্য ও ক্ষমতা দুই-ই থাকে।

∴ দ্বিতীয় ক্ষেত্রে ক্ষমতা বেশি হবে।

কোনো বস্তু উপর থেকে নীচে পড়ার সময় বস্তুটির বেগ কি বস্তুটির ভরের ওপর নির্ভর করে?

কোনো বস্তু উপর থেকে নীচে পড়ার সময় বস্তুটির বেগ বস্তুটির ভরের ওপর নির্ভর করে না। কারণ – পৃথিবী তার উপরিস্থ সমস্ত বস্তুকেই একই অভিকর্ষ বলে টানে।

ড্রাইভারদের শেখানো হয় যে, গাড়ির গতি দ্বিগুণ হলে থামানোর দূরত্ব চারগুণ হবে। ব্যাখ্যা করো।

গতিশক্তির রাশিমালা \(E_K=\frac12mv^2\), যা নির্দেশ করে \(E\propto v^2\) (যখন m ধ্রুবক)। স্পষ্টতই বেগ দ্বিগুণ হলে গতিশক্তির মান পূর্বের চারগুণ হয়। আবার, গতিশক্তির পরিবর্তন = কৃতকার্য = গাড়ির ব্রেক দ্বারা প্রযুক্ত বল × সরণ। সুতরাং, F -এর মান ধ্রুবক হলে দ্বিতীয়ক্ষেত্রে দূরত্ব প্রাথমিক মানের চারগুণ হবে।

একটি হালকা ও ভারী বস্তুর ভর যথাক্রমে m ও M। বস্তুগুলির ভরবেগ সমান হলে, কোল্টির গতিশক্তি বেশি হবে তা নির্ণয় করো।

m ভরবিশিষ্ট হালকা বস্তুটির গতিশক্তি, \(\left(E_1\right)=\frac12mv^2\) (যে-কোনো মুহূর্তে বস্তুটির বেগ \(v\))

এবং ওই মুহূর্তে বস্তুটির ভরবেগ \(\left(p\right)=mv\)

এখন, \(E_1=\frac12mv^2\)

বা, \( E_1=\frac{m^2v^2}{2m}\)

বা, \(E_1=\frac{\left(mv\right)^2}{2m} \)

বা, \(E_1=\frac{p^2}{2m} \) (∵ \(p=mv \) সম্পর্ক ব্যবহার করে)

সুতরাং, \(E_1\propto\frac1m \) অনুরূপভাবে, \(E_2\propto\frac1M \) (∵ \( p\) ধ্রুবক)

সুতরাং, \(\frac{E_1}{E_2}\propto\frac Mm>1\)

∴ \(E_1>E_2\) (∵ \( M>m\))

∴ একটি হালকা ও একটি ভারী বস্তুর ভরবেগ সমান হলে হালকা বস্তুর গতিশক্তি বেশি হবে।

একটি হালকা ও ভারী বস্তুর গতিশক্তি সমান। কোনটির ভরবেগ বেশি?

বস্তুর গতিশক্তি, \(E=\frac{p^2}{2m} \)। অর্থাৎ, \(p=\sqrt{2mE} \) (যেখানে চিহ্নগুলি প্রচলিত অর্থযুক্ত)

∴ \( p\propto\sqrt m\) (যখন \( E\) ধ্রুবক)

∴ একটি হালকা বস্তুর ভর \( m_1\) ও ভরবেগ \(p_1 \) এবং ভারী বস্তুর ভর \( m_2\) ও ভরবেগ \( p_2\) হলে, \(\frac{p_1}{p_2}=\sqrt{\frac{m_1}{m_2}}<1 \)।

∴ \(p_1<p_2 \)

সুতরাং, একটি হালকা ও একটি ভারী বস্তুর গতিশক্তি সমান হলে ভারী বস্তুর ভরবেগ বেশি হবে।

অসম ভরের দুটি বস্তু একই বেগে চলমান। কোনটি বেশি কার্য করতে পারে?

বস্তুর গতিবেগ বেশি হলে তার কার্য করার সামর্থ্যও বেশি হয়। গতিশক্তির রাশিমালা, \( E_K=\frac12mv^2\) সুতরাং, \( v\) ধ্রুবক হলে –

\( E_K\propto m\\\)

বা, \(\frac{E_2}{E_1}=\frac{m_2}{m_1}\)

এখানে \( m_2>m_1\)

অর্থাৎ, \( E_2>E_1\) হবে।

সুতরাং, ভারী বস্তুর গতিশক্তি বেশি হবে এবং সেটি বেশি কার্য করতে সক্ষম হবে।

বস্তুর গতিশক্তি ঋণাত্মক হতে পারে কি? যুক্তিসহ লেখো।

অথবা, কোন্ ধরনের যান্ত্রিক শক্তি ঋণাত্মক হতে পারে না? ব্যাখ্যা করো।

দুই প্রকার যান্ত্রিক শক্তির মধ্যে গতিশক্তি কখনোই ঋণাত্মক হতে পারে না, যদিও স্থিতিশক্তির মান ঋণাত্মক হওয়া সম্ভব।

গতিশক্তির রাশিমালা, \( E_K=\frac12mv^2\)। যেহেতু \(m\) এবং \( v^2\) (গতিবেগের বর্গ) সর্বদা ধনাত্মক, তাই গতিশক্তি সর্বদা ধনাত্মক রাশি। এটি কখনোই ঋণাত্মক হতে পারে না।

অন্যদিকে নির্দেশতল সাপেক্ষে নীচে অবস্থিত কোনো স্থানে রাখা বস্তুর ক্ষেত্রে নির্দেশতল থেকে ওই বস্তুর সরণের সময় অভিকর্ষ বল নিজে কার্য করে। ফলে তার স্থিতিশক্তি কমে। যেহেতু, নির্দেশতলের উচ্চতা \(h=0\) সুতরাং, স্থিতিশক্তি \( \left(E_p\right)=mgh=0\), তাই, স্বাভাবিকভাবেই ওই অবস্থানে বস্তুর স্থিতিশক্তি ঋণাত্মক।

জলপ্রপাতের জলের উষ্ণতা কোথায় বেশি হবে? শীর্ষদেশ না পাদদেশে?

জলপ্রপাতের জল শীর্ষ অবস্থান থেকে নীচে পতিত হলে জলের গতিশক্তির কিছু অংশ তাপশক্তিতে রূপান্তরিত হয়। ফলে, জলের উষ্ণতা বৃদ্ধি পায়। এই কারণে শীর্ষদেশ অপেক্ষা জলপ্রপাতের নীচের অংশে জল সামান্য হলেও বেশি উষ্ণ হয়।

একটি বালি ভরতি গতিশীল লরির তলদেশ দিয়ে বালি পড়ে যাচ্ছে। ইঞ্জিন দ্বারা ব্যয়িত ক্ষমতা অপরিবর্তিত থাকলে লরিটির গতিশক্তি কি পরিবর্তিত হবে?

বালিভরতি গতিশীল লরির তলদেশ দিয়ে ক্রমাগত বালি পড়ে গেলে লরিটির ভর ক্রমাগত কমে যেতে থাকে। যেহেতু ইঞ্জিন দ্বারা ব্যয়িত ক্ষমতা অপরিবর্তিত আছে, তাই এক্ষেত্রে ভরবেগের সংরক্ষণ সূত্র প্রযোজ্য হবে। অর্থাৎ, লরিটির ভরবেগ অপরিবর্তিত থাকবে। কিন্তু, লরিটির ভর ক্রমাগত কমে যাচ্ছে। তাই, ভরবেগ অপরিবর্তিত রাখার জন্য ওর বেগ ক্রমাগত বেড়ে যাবে। আবার, আমরা জানি, গতিশক্তি = \(\frac12\) × বস্তুর ভর × (বেগ)²। তাই, বেগ বেড়ে গেলে লরিটির গতিশক্তিও বেড়ে যাবে।

ওপরে ওঠার সময় গ্যাসবেলুনের গতিশক্তি ও স্থিতিশক্তি উভয়ই বৃদ্ধি পেলে শক্তির সংরক্ষণ সূত্র প্রযোজ্য হয় কি?

গ্যাসভরতি বেলুনের ওজন বেলুনের দ্বারা অপসারিত বায়ুর ওজন অপেক্ষা কম হওয়ায়, ঊর্ধ্বঘাত বা প্লবতার ক্রিয়ায় বেলুন ওপরে ওঠে। এক্ষেত্রে, বেলুনে আবদ্ধ গ্যাসের ঘনত্বের তুলনায় বায়ুর ঘনত্ব কম হয়। গ্যাসভরতি বেলুন ওপরে ওঠার সময় নীচে যে শূন্যতার সৃষ্টি হয়, ওপরের বায়ু নীচে এসে সেই স্থান দখল করে। এর ফলে বায়ুর স্থিতিশক্তি হ্রাস পায়, কিন্তু বেলুনের স্থিতিশক্তি বাড়ে। গ্যাসভরতি বেলুন ওপরে ওঠার ফলে যে পরিমাণ স্থিতিশক্তি লাভ করে, অধিক ঘনত্বের সম আয়তন বায়ু নীচে নামার ফলে তার থেকে অধিক স্থিতিশক্তি হারায়। অর্থাৎ, সংস্থার (বায়ু + বেলুন) মোট স্থিতিশক্তি হ্রাস পায়। এই স্থিতিশক্তি হ্রাসের বিনিময়েই বেলুনের গতিশক্তি বৃদ্ধি পেয়ে থাকে। সুতরাং, ঘটনাটিতে শক্তি সংরক্ষণ সূত্র লঙ্ঘিত হয় না।

এক ব্যক্তির বক্তব্য অনুযায়ী, আলমারিতে রাখা বই-এর স্থিতিশক্তি 20 J এবং অপর ব্যক্তির বক্তব্য অনুসারে ওই নির্দিষ্ট বইটির স্থিতিশক্তি 30 J। দুজনের বক্তব্য কি একই সঙ্গে সঠিক হতে পারে?

নির্দেশতল ভিন্ন হলে একই বস্তুর স্থিতিশক্তির মান ভিন্ন হতে পারে। এক্ষেত্রে ভূপৃষ্ঠ সাপেক্ষে আলমারিতে রাখা বইটির উচ্চতা যা হয়, ভূপৃষ্ঠের তুলনায় নীচে অবস্থিত কোনো বিন্দু সাপেক্ষে তার উচ্চতা বেশি হয়ে থাকে। যেহেতু স্থিতিশক্তির মান নির্দেশতল সাপেক্ষে বস্তুর উচ্চতার সঙ্গে সমানুপাতিক, তাই স্থিতিশক্তির মান প্রথমক্ষেত্রে 20 J ও দ্বিতীয়ক্ষেত্রে 30 J হওয়া সম্ভব।

সমপরিমাণ গতিশক্তিসহ গতিশীল একটি লরি ও একটি মোটরগাড়িকে ব্রেক চেপে স্থির অবস্থায় আনা হল। ব্রেক উভয় ক্ষেত্রে সমান মন্দন সৃষ্টি করলে কোন্ গাড়িটি কম দূরত্ব গিয়ে থামবে?

দুটি গাড়িরই প্রাথমিক গতিশক্তি একই হওয়ার জন্য স্থিরাবস্থায় আসার পূর্বে উভয়ের গতিশক্তির পরিবর্তন সমান হবে। যেহেতু, গতিশক্তির পরিবর্তন = কৃতকার্য, তাই দুটি গাড়িই সমান দূরত্ব অতিক্রম করে থামবে।

হাইজাম্প বা লংজাম্প দেওয়ার সময় প্রতিযোগীরা কিছুদূর থেকে দৌড়ে এসে লাফ দেয় কেন?

হাইজাম্প বা লংজাম্প দেওয়ার সময় প্রতিযোগীরা কিছুদুর থেকে দৌড়ে এসে লাফ দেয়, কারণ – দৌড়াবার সময় প্রতিযোগীরা যে গতিশক্তি অর্জন করে তার জন্য কিছু অতিরিক্ত কার্য করতে পারে। অর্থাৎ, সেই শক্তি ব্যয় করে প্রতিযোগীরা বেশি দূর পর্যন্ত লাফ দিতে পারে।

একটি বলকে বাড়ির ছাদ থেকে নীচে ছেড়ে দেওয়া হল। নিম্নলিখিত ক্ষেত্রে বলটিতে কী শক্তি আছে তা লেখো – (1) বলটি ছেড়ে দেওয়ার পূর্ব মুহূর্তে। (2) বলটি কিছুদূর নামার পর। (3) বলটি মাটি স্পর্শ করার পূর্ব মুহূর্তে। (4) বলটি মাটি স্পর্শ করার পর।

একটি বলকে বাড়ির ছাদ থেকে নীচে ছেড়ে বলটি –

1. বলটি ছাড়ার পূর্ব মুহূর্তে গতিবেগ শূন্য, অতএব গতিশক্তি শূন্য। তাই, কেবলমাত্র স্থিতিশক্তি থাকবে।
2. বলটি কিছুদূর নামার পর স্থিতিশক্তি কমবে, কিন্তু গতিশক্তি বাড়বে। অর্থাৎ, স্থিতিশক্তি ও গতিশক্তি দুই-ই থাকবে।
3. মাটি স্পর্শ করার পূর্ব মুহূর্তে স্থিতিশক্তি শূন্য হবে, কিন্তু গতিশক্তি সর্বোচ্চ হবে। অর্থাৎ, কেবলমাত্র গতিশক্তি থাকবে।
4. বলটি মাটি স্পর্শ করার পর তার গতিশক্তি শব্দশক্তি ও তাপশক্তিতে রূপান্তরিত হবে।

পেরেক পোঁতার সময় হাতুড়িকে খানিকটা উপরে তুলে পেরেককে আঘাত করা হয় কেন?

পেরেক পোঁতার সময় হাতুড়িকে খানিকটা উপরে তুললে হাতুড়িটির অবস্থানগত পরিবর্তনের জন্য তার মধ্যে স্থিতিশক্তি সঞ্চিত হয়। অর্থাৎ, হাতুড়িটি কার্য করার সামর্থ্য লাভ করে। যার ফলে পেরেক সহজেই কাঠের বাধা অতিক্রম করতে পারে।

কোনো গতিশীল বস্তুর ভর দ্বিগুণ করলে, বেগ দ্বিগুণ করলে গতিশক্তির কীরূপ পরিবর্তন ঘটবে?

\(m \) ভরের বস্তু \(v \) বেগে চললে তার গতিশক্তি, \(E=\frac12mv^2 \)।

ভর দ্বিগুণ করলে গতিশক্তি হবে, \( E_1=\frac12\cdot2m\cdot v^2\)

বা, \(E_1=2\cdot\frac{mv^2}2\)

বা, \( E_1=2E\)

অর্থাৎ, প্রাথমিক গতিশক্তির দ্বিগুণ।

বেগ দ্বিগুণ করলে গতিশক্তি হবে, \(E_2=\frac12m\left(2v\right)^2 \)

বা, \(E_2=4\cdot\frac12mv^2 \)

বা, \(E_2=4E \)

অর্থাৎ, প্রাথমিক গতিশক্তির চার গুণ।

সুতরাং, দেখা যাচ্ছে যে, ভরের তুলনায় বেগ দ্বিগুণ করলে তা বস্তুটির গতিশক্তির ওপর বেশি প্রভাব ফেলে।

একটি বস্তুকে অনুভূমিক পথে সরলরেখায় চালনা করা হল। বস্তুটি স্থিরাবস্থা থেকে গতিশীল হলে সময়ের সঙ্গে গতিশক্তি ও ক্ষমতার পরিবর্তন লেখচিত্রের সাহায্যে দেখাও।

স্থির মানের বল প্রযুক্ত হলে সৃষ্ট ত্বরণের মানও সময়ের সাপেক্ষে ধ্রুবক হয়। এই ত্বরণের মান \(a \) হলে। সময় পর বস্তুর বেগ \(v=at\)। এখন বস্তুর গতিশক্তি \( \left(E_K\right)=\frac12mv^2\)।

বা, \(\left(E_K\right)=\frac12ma^2t^2\)

∴ \(E_K\propto t^2\)।

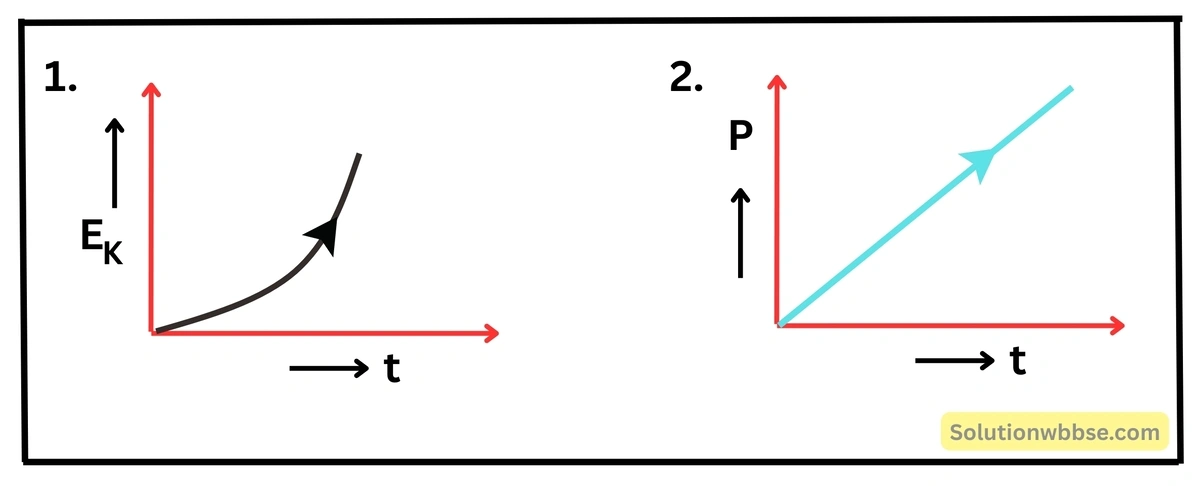
∴ \(t \) -এর সঙ্গে \(E_K\) -এর পরিবর্তনের লেখ বক্ররেখা (অধিবৃত্তীয়) হবে (1) নং চিত্র।

আবার, বস্তুর ক্ষমতা \(\left(P\right)=\frac{E_K}t\)।

বা, \(P=\frac12ma^2t\)

∴ \(P\propto t\)।

সুতরাং, \( t\) -এর সঙ্গে ক্ষমতা \( \left(P\right)\) পরিবর্তনের লেখচিত্র সরলরৈখিক হবে (2) নং চিত্র।

তুমি তোমার বাইসাইকেল নিয়ে একটি নততল বরাবর একটি নির্দিষ্ট উচ্চতায় উঠলে তোমার ও বাইসাইকেলের স্থিতিশক্তি বর্ধিত হল কি?

আমি আমার বাইসাইকেল নিয়ে একটি নততল বরাবর ওঠার সময় অভিকর্ষ বল আমাকে এবং সাইকেলটিকে উল্লম্বভাবে নীচের দিকে টানে। এর ফলে অভিকর্ষ বলের একটি উপাংশ নততলের

সঙ্গে সমকোণে ক্রিয়াশীল হয় এবং এই উপাংশটি আমার ও সাইকেলের সরণের সঙ্গে লম্বভাবে ক্রিয়া করায় কোনো কার্য করে না। কিন্তু, অভিকর্ষ বলের অপর উপাংশটি যা নততল বরাবর নীচের দিকে ক্রিয়া করে তার বিরুদ্ধে কার্য করে আমাকে সাইকেলসহ উপরে উঠতে হয়। এই সম্পাদিত কৃতকার্যই স্থিতিশক্তিরূপে সঞ্চিত হয়ে আমার ও সাইকেলের শক্তি বৃদ্ধি করে।

একটি বল h উচ্চতা থেকে নীচে পড়ছে। বলটির স্থিতিশক্তি, গতিশক্তি এবং মোট শক্তি উচ্চতার সঙ্গে কীভাবে পরিবর্তিত হবে তা একই লেখচিত্রে দেখাও।

মনে করি, বলটির স্থিতিশক্তি = E_p, গতিশক্তি = E_K এবং মোট শক্তি = E।

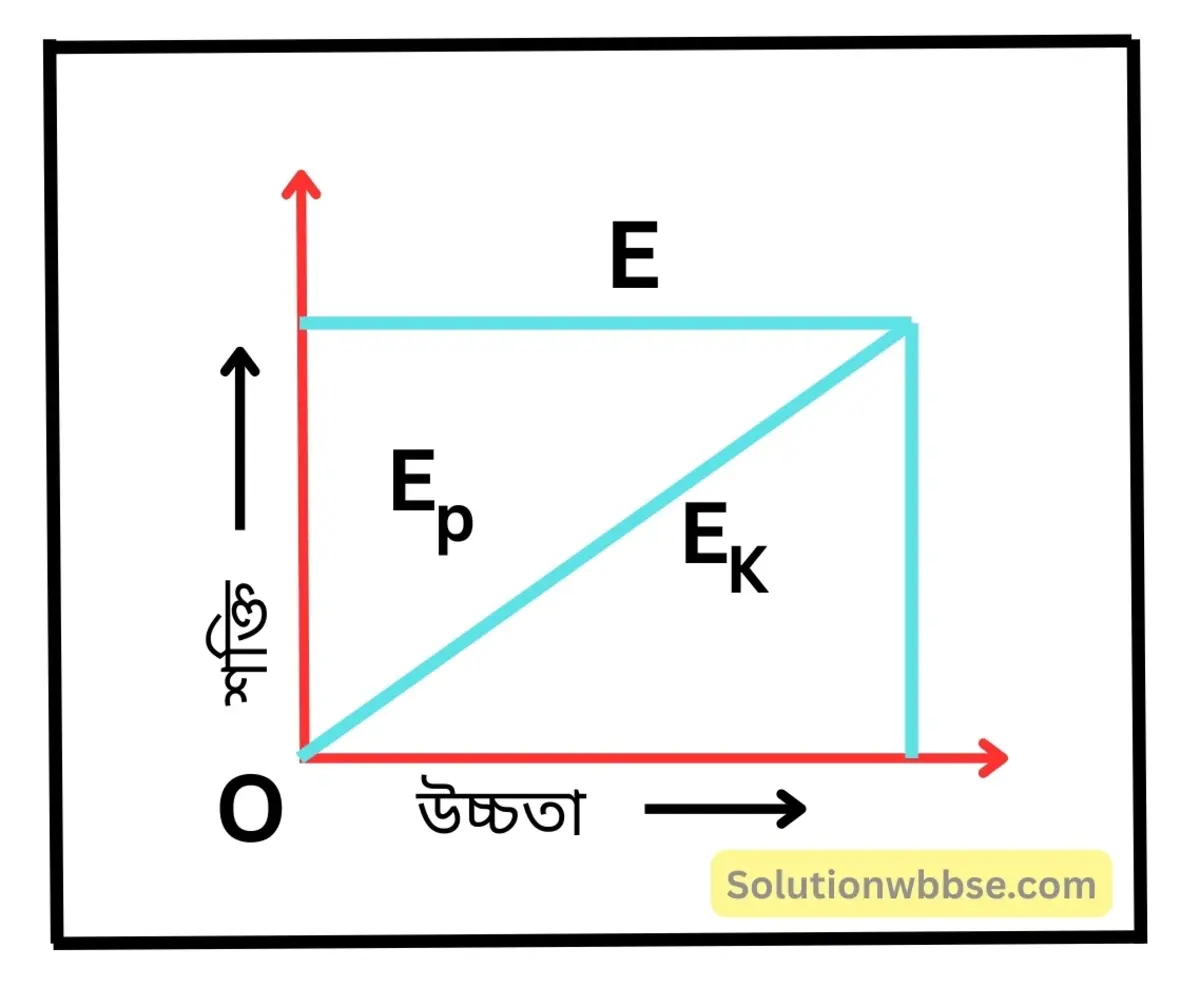
উচ্চতার সঙ্গে E_p, E_K এবং E -এর পরিবর্তন পাশের লেখচিত্রে দেখানো হল।

অর্থাৎ, উচ্চতার সঙ্গে মোট শক্তির কোনো পরিবর্তন হয় না যা সর্বদা ধ্রুবক থাকে। লেখ দুটির সরলরৈখিক প্রকৃতি নির্দেশ করে যে, E_p ও E_K -এর মান রৈখিক সমানুপাতিক হারে বাড়ে ও কমে।

একটি ধনুক নিয়ে তার ছিলার উপর একটি তিরকে স্থাপন করে, ছিলাটিকে টেনে ছেড়ে দাও। অর্থাৎ, তিরটিকে ছোড়ো। একবার ছিলাটিকে কম টেনে ও আর একবার ছিলাটিকে বেশি টেনে ছাড়লে দুই ক্ষেত্রে ঘটনার ফলাফল ও তার পার্থক্যের কারণ যুক্তিসহ আলোচনা করো।

একটি ধনুক নিয়ে তার ছিলার উপর একটি তিরকে স্থাপন করে ছিলাটিকে টেনে ধরলে, ধনুকটির স্বাভাবিক আকৃতির পরিবর্তন হয়। এই আকৃতিগত পরিবর্তনের দরুন ধনুকটির মধ্যে স্থিতিস্থাপক স্থিতিশক্তি সঞ্চিত হয় ও ছিলাটিকে ছেড়ে দিলে এই স্থিতিশক্তি তিরের গতিশক্তিতে রূপান্তরিত হয়।

এখন ছিলাটিকে কম টেনে ছেড়ে দিলে ছিলাটির মধ্যে সঞ্চিত স্থিতিশক্তির পরিমাণ কম হয়। এই স্থিতিশক্তিই গতিশক্তিতে রূপান্তরিত হয় বলে গতিশক্তির পরিমাণও কম হয়। সুতরাং, তিরটি কম বেগে গতিশীল হয়।

কিন্তু ছিলাটিকে বেশি টেনে ছেড়ে দিলে অর্থাৎ, ছিলাটির স্বাভাবিক আকৃতির বেশি পরিবর্তন ঘটালে ছিলাটির মধ্যে সঞ্চিত স্থিতিশক্তির পরিমাণ বেশি হয়। এই স্থিতিশক্তি সম্পূর্ণরূপে গতিশক্তিতে রূপান্তরিত হয়। ফলে তিরটির গতিবেগও খুব বেশি হয়।

পার্থক্যধর্মী প্রাশ্নাত্তর

স্থিতিশক্তি (Potential energy) ও গতিশক্তি (Kinetic energy)-এর মধ্যে সাদৃশ্য ও বৈসাদৃশ্যগুলি লেখো।

স্থিতিশক্তি (Potential energy) ও গতিশক্তি (Kinetic energy)-এর মধ্যে সাদৃশ্য ও বৈসাদৃশ্যগুলি হল –

সাদৃশ্য –

• প্রকৃতি – স্থিতিশক্তি ও গতিশক্তি উভয়ই স্কেলার রাশি।
• একক – উভয়েরই CGS ও SI -তে একক যথাক্রমে আর্গ ও জুল।
• নির্দেশতন্ত্র – উভয়েরই মান নির্দেশতল বা নির্দেশতন্ত্রের ওপর নির্ভরশীল।

বৈসাদৃশ্য –

বিষয়	স্থিতিশক্তি (Potential energy)	গতিশক্তি (Kinetic energy)
সংজ্ঞা	বস্তু তার স্বাভাবিক অবস্থান বা আকৃতির পরিবর্তনের জন্য কার্য করার যে সামর্থ্য লাভ করে, তাকে বস্তুটির স্থিতিশক্তি বলে।	বস্তু তার গতির জন্য কার্য করার যে সামর্থ্য লাভ করে, তাকে বস্তুটির গতিশক্তি বলে।
রাশিমালা	m ভরের বস্তুকে h উচ্চতায় তুললে বস্তুটির অভিকর্ষীয় স্থিতিশক্তি = mgh (g = অভিকর্ষজ ত্বরণ)।	m ভরের বস্তু বেগে গতিশীল হলে বস্তুটির গতিশক্তি = \(\frac12mv^2\)।
মান	এর মান ধনাত্মক, ঋণাত্মক বা শূন্যও হতে পারে।	গতিশক্তি সর্বদাই ধনাত্মক হয়। আবার এর মান শূন্যও হতে পারে।
‘g’ -এর ওপর নির্ভরশীলতা	কোনো স্থানে অভিকর্ষীয় স্থিতিশক্তির মান অভিকর্ষজ ত্বরণের ওপর নির্ভর করে।	গতিশক্তির মান অভিকর্ষজ ত্বরণের ওপর নির্ভর করে না।

কৃতকার্য (Work) ও ক্ষমতা (Power) -এর মধ্যে সাদৃশ্য ও বৈসাদৃশ্যগুলি লেখো।

কৃতকার্য (Work) ও ক্ষমতা (Power) -এর মধ্যে সাদৃশ্য ও বৈসাদৃশ্যগুলি হল –

সাদৃশ্য –

প্রকৃতি – কৃতকার্য ও ক্ষমতা উভয়েই স্কেলার রাশি এবং এরা স্কেলার গুণফলের উদাহরণ।

বৈসাদৃশ্য –

পার্থক্যের বিষয়	কৃতকার্য (Work)	ক্ষমতা (Power)
সংজ্ঞা	বলের প্রভাবে বস্তুর সরণ ঘটলে, প্রযুক্ত বল কার্য করেছে বলা হয়।	কোনো বস্তু বা সংস্থা দ্বারা একক সময়ে ব্যয়িত কার্য বা শক্তিই হল তার ক্ষমতা।
রাশিমালা	প্রযুক্ত বল \( \overrightarrow F\) ও সরণ \(\overrightarrow S \) হলে কৃতকার্য \(\left(W\right)=\overrightarrow F\cdot\overrightarrow S=FS\;cos\theta \) যেখানে θ হল \( \overrightarrow F\) ও \( \overrightarrow S\) -এর ক্রিয়ারেখার অন্তর্বর্তী কোণ।	ক্ষমতা \(\left(P\right)=\frac Wt \) যেখানে W হল সম্পাদিত কার্য এবং t ব্যয়িত সময় অথবা \( P=\overrightarrow F\cdot\overrightarrow v\) যেখানে, \( v\) বস্তু বা সংস্থার বেগ এবং \(F \) হল বস্তুর ওপর প্রযুক্ত বল।
সময় নির্ভরতা	কৃতকার্য সময় নিরপেক্ষ রাশি।	ক্ষমতার মান প্রত্যক্ষভাবে সময় নির্ভর। কার্যের পরিমাণ ধ্রুবক হলে ক্ষমতা সময়ের ব্যস্তানুপাতিক।
মাত্রীয় সংকেত ও একক	কার্যের মাত্রীয় সংকেত – [ML2T-2। একক CGS পদ্ধতি ও SI -তে একক যথাক্রমে আর্গ ও জুল।	ক্ষমতার মাত্রীয় সংকেত – [ML2T-3। CGS পদ্ধতি ও SI -তে একক যথাক্রমে আর্গ/সে ও জুল/সে বা ওয়াট।

শক্তি (Energy) ও ক্ষমতা (Power) -এর মধ্যে পার্থক্যগুলি লেখো।

শক্তি (Energy) ও ক্ষমতা (Power) -এর মধ্যে পার্থক্যগুলি হল –

পার্থক্যের বিষয়	শক্তি (Energy)	ক্ষমতা (Power)
সংজ্ঞা	কোনো বস্তু বা সংস্থার কার্য করার সামর্থ্যকে বলে শক্তি।	বস্তু বা সংস্থার কার্য করার হারকে তার ক্ষমতা বলা হয়।
সময় নির্ভরতা	মোট কৃতকার্য দ্বারা শক্তির পরিমাপ করা হয়। তাই, কার্য করতে ব্যয়িত সময়ের কোনো ভূমিকা নেই।	ক্ষমতা হল একক সময়ে কৃতকার্য। তাই, ক্ষমতার পরিমাপ প্রত্যক্ষভাবে সময়-নির্ভর।
একক	CGS পদ্ধতিতে শক্তির পরম একক ও অভিকর্ষীয় একক যথাক্রমে আর্গ ও গ্রাম-সেমি। SI -তে এগুলি হল যথাক্রমে জুল ও কিগ্রা-মি।	CGSপদ্ধতি ও SI -তে ক্ষমতার পরম একক যথাক্রমে আর্গ/সেকেন্ড ও জুল/সেকেন্ড বা ওয়াট। CGS পদ্ধতি ও SI -তে অভিকর্ষীয় এককগুলি হল গ্রাম-সেমি/সেকেন্ড ও কিগ্রা-মি/সেকেন্ড।
বিবর্ধন যোগ্যতা	শক্তি রূপান্তর প্রক্রিয়াতে অপচয়ী বলের বাধার কারণে সংস্থার চূড়ান্ত বা অন্তিম শক্তি, সর্বদা রূপান্তরের পূর্বে শক্তির পরিমাণ অপেক্ষা কম হয়। তাই শক্তির বিবর্ধন সম্ভব নয়।	উপযুক্ত শর্তে কোনো বস্তু বা সংস্থার ক্ষমতার বিবর্ধন ঘটানো সম্ভব।

গাণিতিক প্রশ্নাবলি

15 N বলের ক্রিয়ায় একটি বস্তুকে বলের অভিমুখে 1 cm সরাতে কত কাজ করতে হবে?

এক্ষেত্রে, প্রযুক্ত বল, F = 5 N

বলের অভিমুখে বস্তুর সরণ, S = 1 cm = 0.01 m

∴ কৃতকার্য, W = F × S

বা, W = 5 × 0.01 J

বা, W = 0.05 J

∴ একটি বস্তুকে বলের অভিমুখে 1 cm সরাতে 0.05 J কাজ করতে হবে।

একটি বস্তুকে 20 cm সরাতে 26.2 J কার্য করতে হয়। এক্ষেত্রে প্রযুক্ত বলের মান কত?

এখানে বস্তুর সরণ (S) = 20 cm = 0.2 m

এবং কৃতকার্য (W) = 26.2 J

∴ $\mathrm{প্রযুক্ত\; বল}=\frac{\mathrm{কৃতকার্য}}{\mathrm{সরণ}}$

বা, প্রযুক্ত বল = \(\frac{26.2}{0.2}\)

বা, প্রযুক্ত বল = 131 N

∴ এক্ষেত্রে প্রযুক্ত বলের মান 131 N

60 N বল বস্তুতে প্রযুক্ত হওয়ায় বলের অভিমুখের সঙ্গে লম্বদিকে বস্তুর 2.5 m সরণ হল। কৃতকার্য কত?

এখানে, প্রযুক্ত বল (F) = 60 N

সরণ (S) = 2.5 m

এবং বল ও সরণের মধ্যস্থ কোণ (θ) = 90°

∴ কৃতকার্য = FS cosθ

বা, কৃতকার্য = 60 × 2.5 × cos 90°

বা, কৃতকার্য = 60 × 2.5 × 0 [cos 90° = 0]

বা, কৃতকার্য = 0

∴ কৃতকার্য = 0

1 min -এ একটি যন্ত্র 1200 J কার্য করতে পারে। ওই যন্ত্রের ক্ষমতা কত?

$\mathrm{আমরা\; জানি,\; ক্ষমতা}=\frac{\mathrm{কৃতকার্য}}{\mathrm{সময়}}$

বা, ক্ষমতা = \(\frac{1200}{1\times60}\) J/s

বা, ক্ষমতা = 20 J/s

বা, ক্ষমতা = 20 W

∴ ওই যন্ত্রের ক্ষমতা = 20 W

500 W ক্ষমতাসম্পন্ন একটি বৈদ্যুতিক ইস্ত্রি দিয়ে 2 hr ধরে ইস্ত্রি করলে কী পরিমাণ তড়িৎশক্তি ব্যয় হবে?

$\mathrm{আমরা\; জানি,\; ক্ষমতা}=\frac{\mathrm{কৃতকার্য}}{\mathrm{সময়}}$

∴ কৃতকার্য = ক্ষমতা × সময়

∴ এক্ষেত্রে ব্যয়িত তড়িৎশক্তি = কৃতকার্য = 500 × 2 × 60 × 60 J [∵ সময় = 2 hr = 2 × 60 × 60 s]

 বা, তড়িৎশক্তি = 1000 × 3600 J

বা, তড়িৎশক্তি = 36 × 10⁵ J

 ∴ 2 hr ধরে ইস্ত্রি করলে 36 × 10⁵ J তড়িৎশক্তি ব্যয় হবে।

50 kg ভরের একজন বালক 5 s -এ সিঁড়ির 20টি ধাপ উঠল। প্রতিটি ধাপের উচ্চতা 30 cm হলে, বালকটি কত ক্ষমতা প্রয়োগ করল?

বালকের ভর, m = 50 kg

∴ বালকের ওজন = mg = 50 × 9.8 N

20টি সিঁড়ির ধাপের উচ্চতা = 20 × 30 cm

= 600 cm

= 6 m

বালকের দ্বারা কৃতকার্য, W = বল × সরণ

বা, কৃতকার্য, W = mg × S

বা, কৃতকার্য, W = 50 × 9.8 × 6 J

বালকটি এই পরিমাণ কার্য করতে সময় নেয় (t) = 5 s

∴ বালকটির ক্ষমতা, \(P=\frac Wt\)

বা, ক্ষমতা, \(P=\frac{50\times9.8\times6}5\;J/s\)

বা, ক্ষমতা, \(P=588\;Watt\)

∴ বালকটি কত ক্ষমতা \(588\;Watt\) প্রয়োগ করল।

60 kg ভরের এক ব্যক্তি 10 kg ভরের একটি ব্যাগ নিয়ে 2 min -এ 10 m উপরে উঠল। ওই ব্যক্তি কী পরিমাণ কার্য করল? ব্যক্তিটির ক্ষমতা কত? (g = 9.8 m/s²)

এখানে ব্যক্তি এবং ব্যাগের মোট ভর, m = (60 + 10) kg = 70 kg

ব্যক্তির সরণ, S = 10 m

∴ ব্যক্তি দ্বারা কৃতকার্য, W = বল × সরণ

বা, কৃতকার্য, W = mg × S

বা, কৃতকার্য, W = 70 × 9.8 × 10 J

বা, কৃতকার্য, W = 70 × 98 J

বা, কৃতকার্য, W = 6860 J

∴ $\mathrm{ব্যক্তিটির\; ক্ষমতা}=\frac{\mathrm{ব্যক্তি\; দ্বারা\; কৃতকার্য}}{\mathrm{সময়}}$

বা, ব্যক্তিটির ক্ষমতা \(\frac{6860}{2\times60}\) J/s [∵ সময় = 2 min = 2 × 60 s ]

বা, ব্যক্তিটির ক্ষমতা = 57.17 watt (প্রায়)।

∴ ব্যক্তিটির ক্ষমতা 57.17 watt (প্রায়)।

একটি পাম্পের সাহায্যে 50 m উঁচুতে জল তোলা হচ্ছে। যদি পাম্পের ক্ষমতা 3 kW হয় তবে প্রতি min -এ কত জল তোলা হচ্ছে? (g = 10 m/s²)

পাম্পের ক্ষমতা, P = 3 kW = 3000 watt

ধরা যাক, পাম্পের সাহায্যে প্রতি মিনিটে m kg জল তোলা হচ্ছে।

∴ m kg জলকে অভিকর্ষের বিরুদ্ধে, h = 50 m উচ্চতায় তুলতে কৃতকার্য, W = m × 10 × 50 J [∵ g = 10 m/s²]

এই কার্য সম্পাদন করতে সময় লাগে, t = 1 min = 60 s

∴ \(P=\frac Wt\)

বা, \(3000=\frac{m\times10\times50}{60}\)

বা, \(m=\frac{3000\times60}{10\times50}\)

বা, \(m=360\)

∴ প্রতি মিনিটে 360 kg জল তোলা হচ্ছে।

250 g ভরের একটি বস্তুকে ভূপৃষ্ঠ থেকে খাড়া 5 m উচ্চতায় তোলা হল। বস্তুটিতে সঞ্চিত স্থিতিশক্তির পরিমাণ আর্গ ও জুল এককে নির্ণয় করো। [g = 10 m/s²]

বস্তুর ভর \(\left(E_p\right)=250\;g=\frac{250}{1000}\;kg,\)

উচ্চতা \(\left(h\right)=5\;m\)

∴ অভিকর্ষীয় স্থিতিশক্তি \(\left(E_p\right)=mgh\)

বা, স্থিতিশক্তি \(\left(E_p\right)=\frac{250\times10\times5}{1000}J\)

বা, স্থিতিশক্তি \(\left(E_p\right)=12.5\;J\)

বা, স্থিতিশক্তি \(\left(E_p\right)=12.5\times10^7\;erg\)

150 kg ভরের একটি বস্তুকে কত উচ্চতায় তুলতে এর স্থিতিশক্তি 7350 J হবে?

আমরা জানি, বস্তুর অভিকর্ষীয় স্থিতিশক্তি, \(\left(E_p\right)=mgh\)

বা, \(h=\frac{E_p}{mg}\)

এখানে, \(E_p=7350\;J\), বস্তুর ভর \(m=150\;kg,\;g=9.8\;m/s^2\)

∴ \(h=\frac{7350}{150\times9.8}m\)

∴ নির্ণেয় উচ্চতা = \(5\;m\)

3 kg ভরের একটি বস্তুকে অভিকর্ষের বিরুদ্ধে খাড়া 10 m উচ্চতায় তোলা হল। এই অবস্থায় বস্তুটির গতিশক্তি 75 J হলে বস্তুটির ওপর প্রযুক্ত বল দ্বারা কৃতকার্য কত? (g = 9.8 m/s²)

10 m উচ্চতায় স্থিতিশক্তি = mgh

= 3 × 9.8 × 10 J

= 294 J

বস্তুটির গতিশক্তি = 75 J

∴ মোট শক্তি = (294 + 75) J = 369 J

∴ বস্তুটির ওপর প্রযুক্ত বল দ্বারা কৃতকার্য = বস্তুটির মোট শক্তি = 369 J

কোনো ব্যক্তি 5 m উঁচু গাছে আরোহণকালে যদি 2500 J পরিমাণ কার্য সম্পাদন করে তবে ওই ব্যক্তির ভর কত?

ধরা যাক, ব্যক্তির ভর m kg

অভিকর্ষজ ত্বরণ = g = 9.8 m/s²

∴ W = ওই ব্যক্তিটির স্থিতিশক্তি = m × 9.8 × 5 J

= 5 m উচ্চতায় উঠতে ব্যক্তি কর্তৃক সম্পাদিত কৃতকার্য আবার প্রশ্নানুসারে,

W = 2500 J

বা, m × 9.8 × 5 = 2500

বা, m = \(\frac{2500}{9.8\times5}\)

বা, m = 51.02 (প্রায়)

∴ ব্যক্তিটির ভর = 51.02 kg

একটি পাম্প প্রতি মিনিটে 54 L জল 100 m উচ্চতায় তুলতে পারে। পাম্পের ক্ষমতার 80% জল তোলার কাজে খরচ হলে পাম্পের ক্ষমতা কত?

\(54\;L\) জল \(100\;m\) উচ্চতায় তুলতে কৃতকার্য = \(mgh\)

= \(54\times1000\times100\times9.8\)

= \(52920000\;J\)

∴ ক্ষমতা = \(\frac{52920000}{60}\;watt=882000\;watt\)

প্রশ্নানুযায়ী, পাম্পের ক্ষমতার \(80\%=882000\;watt\)।

∴ পাম্পের ক্ষমতা = \(\frac{882000}{80}\times100=1102500\;watt\)।

500 g ভরের একটি বস্তু 10 m/s বেগে গতিশীল। বস্তুটির গতিশক্তি কত?

বস্তুর ভর, \(m=500\;g=\frac{500}{1000}\;kg=\frac12\;kg\) এবং বস্তুর বেগ, \(v=10\;m/s\)।

∴ বস্তুটির গতিশক্তি, \(E_K=\frac12mv^2\)

বা, গতিশক্তি, \(E_K=\frac12\times\frac12\times\left(10\right)^2\;J\)

বা, গতিশক্তি, \(E_K=\frac14\times100\;J\)

বা, গতিশক্তি, \(E_K=25\;J\)

∴ বস্তুটির গতিশক্তি \(25\;J\)

1 kg ভরের একটি বস্তু 1 m/s বেগে ধাবমান হলে, তার গতিশক্তি কত হবে নির্ণয় করো।

বস্তুর ভর \(\left(m\right)=1\;kg\), বেগ \(\left(v\right)=1\;m/s\)

∴ বস্তুটির গতিশক্তি, \(E_K=\frac12mv^2\)

বা, গতিশক্তি, \(E_K=\frac12\times1\times1^2\)

বা, গতিশক্তি, \(E_K=0.5\;J\)

60 km/h বেগে গতিশীল 18 kg ভরের একটি বস্তুকে থামাতে কত জুল কার্য করতে হবে?

বস্তুটির গতিশক্তি = \(\frac12mv^2\)

বা, গতিশক্তি, \(E_K=0.5\;J\)

বা, গতিশক্তি, \(E_K=\frac12\times18\times\frac{60000}{60\times60}\;J\)

বা, গতিশক্তি, \(E_K=150\;J\)

∴ বস্তুটিকে থামাতে \(150\;J\) কার্য করতে হবে। কারণ, বস্তুটিকে থামাতে হলে তার গতির বিপরীতে গতিশক্তির সমপরিমাণ কার্য করতে হবে।

80 g ভরের একটি বুলেটকে কত বেগে নিক্ষেপ করলে গতিশক্তি 400 J হবে?

আমরা জানি, গতিশক্তি, \(E_K=\frac12mv^2 \)

এক্ষেত্রে, \( E_K=400\;J\), বুলেটের ভর \(\left(m\right)=80\;g=\frac{80}{1000}\;kg \) এবং বুলেটের বেগ \( v=?\)

বা, \( E_K=\frac12mv^2\)

বা, \(v^2=\frac{2E_K}m \)

বা, \( v^2=2\times400\times\frac{1000}{80}\)

বা, \(v^2=10^4 \)

বা, \(v=\sqrt{10^4} \)

বা, \(v=10^2 \)

বা, \(v=100 \)

∴ বুলেটটির বেগ = \(100\;m/s\)

একটি 5 kg ভরের বস্তুকে 1000 J শক্তি দিয়ে সোজা উপরের দিকে ছোড়া হল। বস্তুটি যখন মাটি থেকে 5 m উপরে উঠবে তখন তার গতিশক্তি কত হবে? (g = 9.8 m/s²)

বস্তুটির প্রাথমিক গতিশক্তি, \(E_K=\frac12mv^2=1000\;J\)

∴ \(v^2=\frac{1000\times2}m \)

বা, \(v^2=\frac{1000\times2}5 \)

বা, \(v^2=400 \)

∴ \(v=\sqrt{400}=20 \;m/s\)

সুতরাং, বস্তুটির প্রাথমিক বেগ = \( 20 \;m/s\)।

ধরি, মাটি থেকে \(5 \) মিটার উপরে বেগ = \( v’ \)।

∴ \(v^2=u^2+2as \) সূত্র থেকে পাই

\(\left(v’\right)^2=\left(20\right)^2-2\times9.8\times5 \) (∵ \(u=20\;m/s,\;a=-g=-9.8\;m/s,\;S=5\;m \))

বা, \(\left(v’\right)^2=400-98\)

বা, \(\left(v’\right)^2=302\)

বা, \(v’ =\sqrt{302}=17.38\;m/s \)

∴ এখন গতিশক্তি \(E_K=\frac12\times5\times302\;J\)

বা, গতিশক্তি\(E_K=755\;J\)

m ও 2 m ভরের দুটি বস্তুর গতিশক্তির অনুপাত 1 : 2 হলে তাদের রৈখিক ভরবেগের অনুপাত কত?

ধরা যাক, প্রথম বস্তুর ভর = \(m \) ও বেগ = \(v \)

∴ প্রথম বস্তুর গতিশক্তি, \(E_1=\frac12mv_1^2 \) এবং ভরবেগ, \(p_1=mv_1 \) এবং দ্বিতীয় বস্তুর ভর = \(2\;m \) ও বেগ = \(v_2 \)

∴ দ্বিতীয় বস্তুর গতিশক্তি, \(E_2=\frac12\times2m\times v_2^2 \) এবং ভরবেগ \(p_2=2mv_2\)

বা, \(\frac{E_1}{E_2}=\frac{{\displaystyle\frac12}mv_1^2}{\frac12\times2m\times v_2^2}\)

বা, \(\frac{E_1}{E_2}=\frac{mv_1^2}{2mv_2^2}\)

বা, \( \frac{E_1}{E_2}=\frac{mv_1^2}{4mv_2^2}\times\frac{2m}m\)

বা, \( \frac{E_1}{E_2}=\frac{p_1^2}{p_2^2}\times2\) (∵ \(p_1=mv_1\) এবং \(p_2=mv_2\))

বা, \(\frac{E_1}{E_2}=\left(\frac{p_1}{p_2}\right)^2\times2 \)

বা, \( \left(\frac{p_1}{p_2}\right)^2\times2=\frac12\) (∵ \(E_1:E_2=1:2\))

বা, \( \left(\frac{p_1}{p_2}\right)^2=\frac14\)

বা, \( \frac{p_1}{p_2}=\frac12\)

বা, \( p_1:p_2=1:2\)

∴ বস্তু দুটির রৈখিক ভরবেগের অনুপাত হল \(1:2\)।

একটি গতিশীল বস্তুর রৈখিক ভরবেগ 30% বৃদ্ধি পেলে গতিশক্তির শতকরা পরিবর্তন কত হবে?

রৈখিক ভরবেগ = \(mv=p\)

গতিশক্তি = \(E=\frac12mv^2\)

বা, গতিশক্তি = \(\frac12\cdot\frac{\left(mv\right)^2}m \)

বা, গতিশক্তি = \( \frac12\cdot\frac{p^2}m\)

রৈখিক ভরবেগ 30% বাড়লে অন্তিম রৈখিক ভরবেগ হবে –

\(\left( p + \left( p \times \frac{30}{100} \right) \right) = \frac{13p}{10}\\\)

∴ এবং গতিশক্তি \( \frac1{2m}\cdot\left(\frac{13p}{10}\right)^2\)

= \(\frac12\cdot\frac{p^2}2\times\frac{169}{100} \)

= \(\frac{169}{100}E \)

গতিশক্তির পরিবর্তন = \( \frac{{\displaystyle\frac{169}{100}}E-E}E\times100\)

= \(\frac{69}{100}\times100\% \)

= \( 69\%\)

∴ গতিশক্তির শতকরা পরিবর্তন \( 69\%\) হবে।

একটি বস্তুর ভরবেগের সাংখ্যমান ওর গতিশক্তির সমান। বস্তুটির বেগ কত?

ধরা যাক, বস্তুটির ভর = \(m\) এবং বেগ = \( v\)

∴ বস্তুটির ভরবেগ, \(p=mv\) এবং গতিশক্তি, \(E_K=\frac12mv^2\)

প্রশ্নানুসারে, \(p=E_K \)

বা, \( mv=\frac12mv^2\)

বা, \( v^2=2v\) (∵ \( m\neq0\))

বা, \(v\left(v-2\right)=0 \) (∵ \( v\neq0\))

বা, \(v=2 \)

∴ বস্তুটির বেগ \(2 \) একক।

50 kg ভরের একটি বস্তুকে ভূমি থেকে 4 m উচ্চতায় তোলা হলে বস্তুটির স্থিতিশক্তি কত হবে? যদি বস্তুটি অভিকর্ষের অধীনে বিনা বাধায় নীচে পড়ে। ভূমি স্পর্শ করার মুহূর্তে বস্তুটির গতিবেগ কত হবে? (g = 10 m/s²)

এখানে, বস্তুর ভর = \(m=50\;kg\) ,

উচ্চতা = \(h=4\;m,\;g=10\;m/s^2\)

∴ বস্তুটির স্থিতিশক্তি, \(E_p=mgh\)

বা, স্থিতিশক্তি, \(E_p=50\times10\times4\)

বা, স্থিতিশক্তি, \(E_p=2000\;J\)

ওই উচ্চতা থেকে অভিকর্ষের অধীনে বিনা বাধায় পতনশীল প্রস্তুটির ভূমি স্পর্শ করার মুহূর্তে স্থিতিশক্তি = \(E’_p\) এবং গতিশক্তি = \(E’_K\) হলে, যান্ত্রিকশক্তির সংরক্ষণ নীতি অনুযায়ী,

\( E’_p+E’_K=E_p\\\)

বা, \(0+\frac12mv^2=mgh \) [∵ \( E’_p=0\), কারণ ভূমি স্পর্শ করার মুহূর্তে ভূমি থেকে বস্তুর উচ্চতা = \(0\)]

বা, \(\frac12mv^2=mgh \) [\(v \) = ভূমি স্পর্শ করার মুহূর্তে বস্তুর বেগ]

বা, \(v^2=2gh \)

বা, \( v^2=2\times10\times4\)

বা, \( v^2=80\)

বা, \( v=\sqrt{80}\)

বা, \(v=8.94 \)

∴ নির্ণেয় গতিবেগ = \(8.94\;m/s\) (প্রায়)।

বিকল্প পদ্ধতি

নির্ণেয় স্থিতিশক্তি = mgh = 50 × 10 × 4 = 2000 J

ধরি, ভূমি স্পর্শ করার মুহূর্তে বস্তুটির বেগ = v m/s

∴ v² = u² + 2aS সূত্র থেকে পাই –

v² = 0² + 2 × 10 × 4 [∵ u = 0, a = g = 10 m/s² এবং S = 4 m]

বা, v² = 80

বা, v = \(\sqrt{80}\)

বা, v = 8.94 m/s

∴ ভূমি স্পর্শ করার মুহূর্তে গতিবেগ 8.94 m/s

1 kg ভরের একটি বস্তুকে ভূপৃষ্ঠের 20 m উচ্চতা থেকে ছেড়ে দেওয়া হল। ছেড়ে দেওয়ার 1 sec পরে বস্তুটির স্থিতিশক্তি ও গতিশক্তি নির্ণয় করো।

বস্তুর ভর, \(m=1\;kg\)

ভূমি থেকে বস্তুর প্রাথমিক উচ্চতা, \(h=20\;m\)

অভিকর্ষজ ত্বরণ, \(g=9.8\;m/s^2\)

এই উচ্চতায়, স্থির অবস্থায় থাকাকালীন বস্তুটির মধ্যে সঞ্চিত স্থিতিশক্তি = \(E_p=mgh\)

বা, স্থিতিশক্তি \(E_p=1\times9.8\times20\;J\)

বা, স্থিতিশক্তি \(E_p=196\;J\)

এবং গতিশক্তি = \(E_K=0\)।

\(t=1\;s\) পরে বস্তুর বেগ \(v\) হলে,

\(v=gt\\\)

বা, \(v=9.8\times1\)

বা, \(v=9.8\;m/s\)

∴ \(1\;s\) পরে বস্তুর গতিশক্তি,

বা, গতিশক্তি, \(E′_K=\frac12mv^2\)

বা, গতিশক্তি, \(E′_K=\frac12\times1\times\left(9.8\right)^2\)

বা, গতিশক্তি, \(E′_K=48.02\;J\)

এবং স্থিতিশক্তি \(E′_p\) হলে, যান্ত্রিক শক্তির সংরক্ষণ নীতি অনুযায়ী,

\(E′_p+E′_K=E_p+E_K\\\)

বা, \(E′_p+48.02=196+0 \)

বা, \(E′_p=196-48.02 \)

বা, \( E′_p=147.98\;J\)

∴ \(1\;s\) পরে বস্তুটির স্থিতিশক্তি \(147.98\;J\) এবং গতিশক্তি \( 48.02\;J\)

একটি বস্তুকে 10 m/s বেগে উল্লম্বভাবে উপরের দিকে ছোড়া হল। বস্তুটি সর্বাধিক কত উচ্চতায় উঠবে তা শক্তির সংরক্ষণ সূত্র থেকে নির্ণয় করো। (g = 10 m/s²)

বস্তুটিকে উল্লম্বভাবে উপরের দিকে ছোড়ার মুহূর্তে বস্তুটির গতিশক্তি, \( E_K=\frac12mv^2\) [ \(v \) = বস্তুর বেগ ] এবং স্থিতিশক্তি, \(E_p=0 \)।

বস্তুটির সর্বোচ্চ অবস্থানে কোনো বেগ থাকে না। তাই, সর্বোচ্চ অবস্থানে বস্তুটির গতিশক্তি \(E′_K=0 \) এবং স্থিতিশক্তি = \(E′_p=mgh \) [ যেখানে \( h\) = বস্তুর সর্বাধিক উচ্চতা]

যান্ত্রিক শক্তির সংরক্ষণ সূত্রানুযায়ী,

\( E_p+E_K=E′_p+E′_K\\\)

বা, \(0+\frac12mv^2=mgh+0 \)

বা, \(v^2=2gh \)

বা, \(h=\frac{v^2}{2h} \)

বা, \(h=\frac{10^2}{2\times10} \)

বা, \(h=5\)

∴ বস্তুটি সর্বাধিক \( 5\;m\) উচ্চতা উঠবে।

100 g ভরের একটি বস্তুকে 20 m/s বেগে সোজা উপরের দিকে ছোড়া হল। বস্তুটির সর্বোচ্চ অবস্থানে গতিশক্তি ও স্থিতিশক্তি কত হবে? বস্তুটি পুনরায় ভূমি স্পর্শ করার মুহূর্তে কত গতিশক্তি লাভ করবে? (g = 10 m/s²)

ধরি, সর্বোচ্চ অবস্থানে বস্তুটির উচ্চতা = \(h\)

∴ \( v^2=u^2+2aS\) সমীকরণ থেকে পাই

\( 0^2=\left(20\right)^2-2\times10\times h\) [∵ \(v \) = সর্বোচ্চ অবস্থানে বেগ = \(0,\;a=-g=-10\;m/s^2,\;S=h\) এবং \(u=20\;m/s\)]

∴ \(h=\frac{20\times20}{2\times10}m \)

বা, \(h=20\;m\)

∴ সর্বোচ্চ অবস্থানে গতিশক্তি = \(\frac12mv^2=0 \) [∵ \(v=0 \)]

এবং স্থিতিশক্তি = \( mgh\)

বা, স্থিতিশক্তি = \( \frac{100}{1000}\times10\times20\;J\)

বা, স্থিতিশক্তি = \( 20\;J\)

বস্তুটি পুনরায় ভূমি স্পর্শ করার মুহূর্তে বেগ \(v\) হলে,

\( v^2=u^2+2aS\) সমীকরণ থেকে পাই –

\(v^2=0^2+2\cdot10\cdot20\) [∵ \( u=0,\;a=g=10\;m/s\) এবং \( S=h=20\;m\)]

বা, \( v^2=400\)

বা, \( v=\sqrt{400}\)

বা, \(v=20\;m/s\)

∴ ভূমি স্পর্শ করার মুহূর্তে গতিশক্তি,

= \(\frac12mv^2\)

= \( \frac12\times\frac{100}{1000}\times\left(20\right)^2\)

= \( 20\;J\)

∴ বস্তুটি পুনরায় ভূমি স্পর্শ করার মুহূর্তে \( 20\;J\) গতিশক্তি লাভ করবে।

চিত্র অনুযায়ী, 2 kg -র একটি বল প্রথমবার সরাসরি নীচে পড়ল এবং দ্বিতীয়বারে সিঁড়ি দিয়ে গড়িয়ে নীচে পড়ল। এখানে কোনো ঘর্ষণ বল কাজ করে না এবং অন্য কোনো শক্তি ক্ষয় হল না ধরে নিয়ে বিভিন্ন অবস্থানে বলটির গতিশক্তি (KE), স্থিতিশক্তি (PE) এবং বেগের মান (v) হিসাব করো (A₁, B₁, C₁, D₁, E₁, F₁, G₁, H₁, I₁, J₁, K₁ -এর মান কত?)

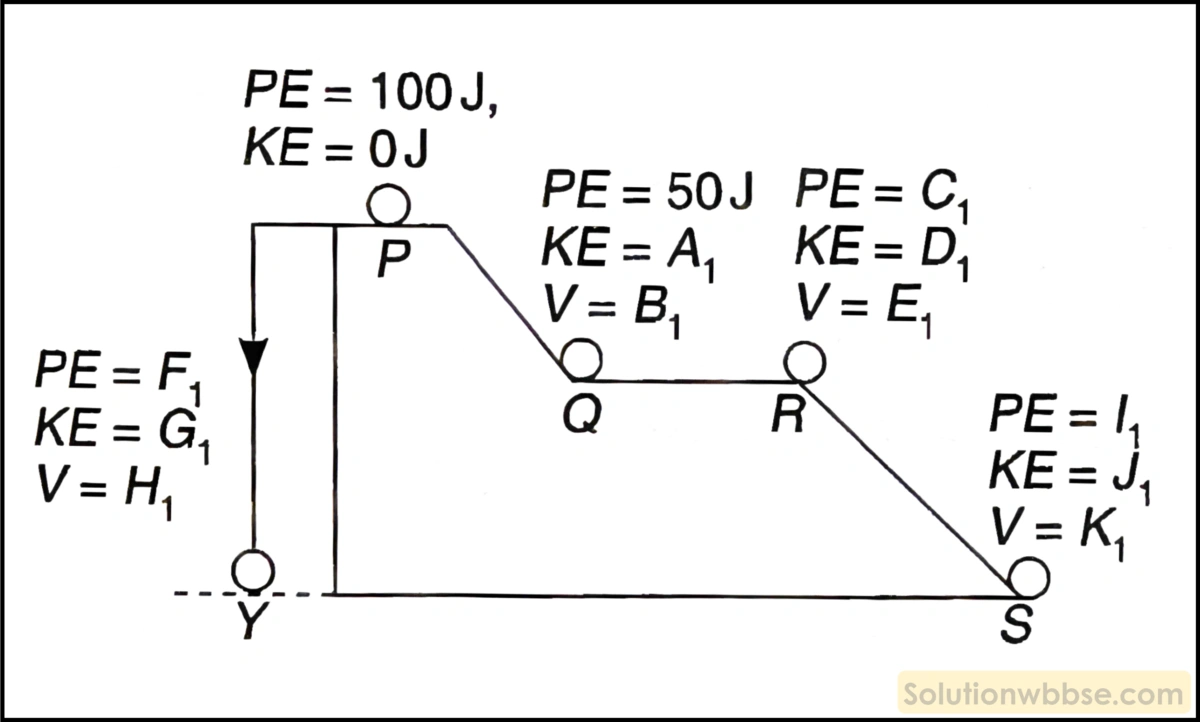
বলটির ভর \(m=2\;kg\)

চিত্রানুযায়ী, বলটি যখন \(P \) অবস্থানে স্থিরাবস্থায় থাকে, তখন বলটির স্থিতিশক্তি \(\left(PE\right)=100\;J\) এবং গতিশক্তি \(\left(KE\right)=0\;J\)।

সুতরাং, \(P \) অবস্থানে বলটির মোট যান্ত্রিক শক্তি

= \(100\;J+0\;J\)

= \(100\;J\)

1.

বলটি যখন অবস্থানে থেকে সরাসরি নীচে পড়ে, তখন ভূমিতে আঘাতের পূর্ব মুহূর্তে, \(Y\) অবস্থানে বলটির স্থিতিশক্তি

\(F_1=0\) এবং গতিশক্তি = \(G_1\) হলে যান্ত্রিক শক্তির সংরক্ষণ নীতি অনুযায়ী,

\(F_1+G_1=100\;J\\\)

বা, \(0+G_1=100\;J\)

বা, \(G_1=100\;J\)

ভূমি স্পর্শ করার মুহূর্তে বলটির বেগ \(\left(v\right)=H_1\) হলে,

\(\frac12mH_1^2=100\\ \)

বা, \( \frac12\times2\times H_1^2=100\)

বা, \( H_1^2=100\)

বা, \(H_1=10\;m/s\)

∴ \(F_1=0\;J,\;G_1=100\;J\) এবং \(H_1=10\;m/s\)

2.

বলটি যখন \(P\) অবস্থান থেকে গড়িয়ে \(Q\) স্থানে পৌঁছায় তখন বলটির স্থিতিশক্তি = \(50\;J\) (প্রদত্ত) এবং গতিশক্তি = \(A_1\)

∴ যান্ত্রিক শক্তির সংরক্ষণ নীতি অনুযায়ী,

\( 50+A_1=100\\\)

বা, \( A_1=50\;J\)

\(Q\) অবস্থানে বলটির অনুভূমিক বেগ \(\left(v\right)=B_1\) হলে,

\( \frac12\times m\times B_1^2=100\\\)

বা, \(\frac12\times2\times B_1^2=100\)

বা, \( B_1=5\sqrt2\)

∴ \( A_1=50\;J,\;B_1=5\sqrt2\;m/s\)।

3.

বলটি গতিশীল অবস্থায় \(Q \) থেকে \(R \) স্থানে পৌঁছালে বলটির ভূমি থেকে উচ্চতা একই থাকে।

∴ বলটির \(R\) অবস্থানে স্থিতিশক্তি = বলটির \(Q\) অবস্থানে স্থিতিশক্তি।

∴ \(C_1=50\;J\)

বলটির ওই অবস্থানে গতিশক্তি = \(D_1\)

∴ \(C_1+D_1=100 \)

বা, \(50+D_1=100\)

বা, \(D_1=50\;J \)

\(R \) অবস্থানে বলটির বেগ = \(E_1\) হলে

\(D_1=\frac12mE_1^2\\\)

বা, \(\frac12\times2\times E_1^2=50\)

বা, \(E_1=5\sqrt2\;m/s\)

∴ \( C_1=50\;J,\;D_1=50\;J,\;E_1=5\sqrt2\;m/s\)

4.

বলটি \(R\) অবস্থান থেকে গড়িয়ে ভূমি স্পর্শ করার মুহূর্তে যখন \(S\) অবস্থানে পৌঁছায়, তখন বলটির স্থিতিশক্তি \(I_1=0\) হয় এবং গতিশক্তি = \(J_1\) হয়।

∴ যান্ত্রিক শক্তির সংরক্ষণ নীতি অনুযায়ী,

\(I_1+J_1=100\;J\\\)

বা, \(0+J_1=100\;J\)

∴ \(J_1=100\;J\)

ভূমি স্পর্শ করার পূর্ব মুহূর্তে বলটির বেগ = \(K_1\)

∴ \(J_1=\frac12mK_1^2\)

বা, \(\frac12mK_1^2=100\)

বা, \(\frac12\times2\times K_1^2=100\)

∴ \(K_1=10\;m/s\)

∴ \(I_1=0\;J,\;J_1=100\;J,\;K_1=10\;m/s\)

সুতরাং, হিসাব করে পাওয়া যায়,

\(A_1=50\;J,\;B_1=5\sqrt2\;m/s,\;C_1=50\;J,\;D_1=10\;J,\\\)
\(E_1=5\sqrt2\;m/s,\;F_1=0\;J,\;G_1=100\;J,\;H_1=10\;m/s\\\)
\(I_1=0\;J,\;J_1=100\;J,\;K_1=10\;m/s\)

নৈর্ব্যক্তিক প্রশ্নোত্তর

সঠিক উত্তরটি নির্বাচন করো

কোনটি স্কেলার রাশি? –

1. বল
2. বেগ
3. সরণ
4. শক্তি

উত্তর – 4. শক্তি

1 kg ভরের কোনো বস্তুর গতিশক্তি 1 জুল হলে তার বেগ হবে –

1. 1 m/s
2. শূন্য
3. 0.5 m/s
4. 1cm/s

উত্তর – 1. 1 m/s

একটি পাথরের টুকরোকে খাড়া উপরের দিকে ছোঁড়া হল। পাথরটির এই ঊর্ধ্বমুখী যাত্রাপথের মধ্যবিন্দুতে পাথরটির –

1. গতিশক্তি সর্বাধিক
2. স্থিতিশক্তি সর্বাধিক
3. গতিশক্তি ও স্থিতিশক্তি উভয়ই সমান
4. গতিশক্তি অপেক্ষা স্থিতিশক্তি কম

উত্তর – 3. গতিশক্তি ও স্থিতিশক্তি উভয়ই সমান

একটি বলকে খাড়াভাবে উপরের দিকে ছোঁড়া হল। যাত্রাপথের সর্বোচ্চ বিন্দুতে কণাটির –

1. গতিশক্তি সর্বাধিক
2. গতিশক্তি ও স্থিতিশক্তির মান সমান
3. স্থিতিশক্তি সর্বাধিক
4. গতিশক্তি অপেক্ষা স্থিতিশক্তির মান কম

উত্তর – 3. স্থিতিশক্তি সর্বাধিক

শক্তির মাত্রীয় সংকেত হল –

1. [ML²T²]
2. [ML^-2T²]
3. [ML²T^-2]
4. [ML^-2T^-2]

উত্তর – 3. [ML²T^-2]

m ভরের কোনো স্থির কণার ওপর P বল t সময়ের জন্য প্রযুক্ত হলে, ওই সময়ের পর কণার গতিশক্তি হবে –

1. \(\frac{P^2t^2}m\\\)
2. \(\frac{P^2t^2}{2m}\\\)
3. \(\frac{2P^2t^2}m\\\)
4. \(\frac{Pt}{4m}\\\)

উত্তর – 2. \(\frac{P^2t^2}{2m}\)

m গ্রাম ভরের একটি বস্তুর গতিশক্তি E হলে ভরবেগ হবে –

1. \(\sqrt{2mE}\\\)
2. \(\sqrt{\frac m{2E}}\\\)
3. \(\sqrt{\frac{2E}m}\\\)
4. \(\sqrt{2m}E\\\)

উত্তর – 1. \(\sqrt{2mE}\)

ঋণাত্মক কার্যের ক্ষেত্রে প্রযুক্ত বল ও সরণের অভিমুখের মধ্যে কোণ হল –

1. 0°
2. 45°
3. 90°
4. 180°

উত্তর – 4. 180°

1 কিগ্রা-মিটার –

1. 9.81 J
2. 981 J
3. 9.81 erg
4. 981 erg

উত্তর – 1. 9.81 J

কার্যহীন বলের উদাহরণ –

1. ঘর্ষণ বল
2. অভিকেন্দ্র বল
3. পৃষ্ঠটানজনিত বল
4. কোনোটিই নয়

উত্তর – 2. অভিকেন্দ্র বল

জুল ও আর্গের মধ্যে সম্পর্কটি হল –

1. 1 J = 10⁷ erg
2. 1 J = 10⁵ erg
3. 1 J = 10 erg
4. 1 J = 10⁴ erg

উত্তর – 1. 1 J = 10⁷ erg

অশ্বক্ষমতা হল –

1. ক্ষমতার SI একক
2. কার্যের SI একক
3. ক্ষমতার FPS একক
4. কার্যের FPS একক

উত্তর – 3. ক্ষমতার FPS একক

একটি স্প্রিংকে সংকুচিত করলে স্থিতিস্থাপক স্থিতিশক্তি –

1. কমে যায়
2. বেড়ে যায়
3. একই থাকে
4. শূন্য হয়

উত্তর – 2. বেড়ে যায়

কোনো ব্যক্তির স্থিতিশক্তি সবচেয়ে কম হয় যদি ব্যক্তিটি –

1. দাঁড়িয়ে থাকে
2. চেয়ারে বসে থাকে
3. মেঝেতে বসে থাকে
4. মাটিতে শুয়ে থাকে

উত্তর – 4. মাটিতে শুয়ে থাকে

বাঁধের জলে সঞ্চিত থাকে –

1. স্থিতিশক্তি
2. গতিশক্তি
3. স্থিতিশক্তি ও গতিশক্তি উভয়ই
4. কোনোটিই নয়

উত্তর – 1. স্থিতিশক্তি

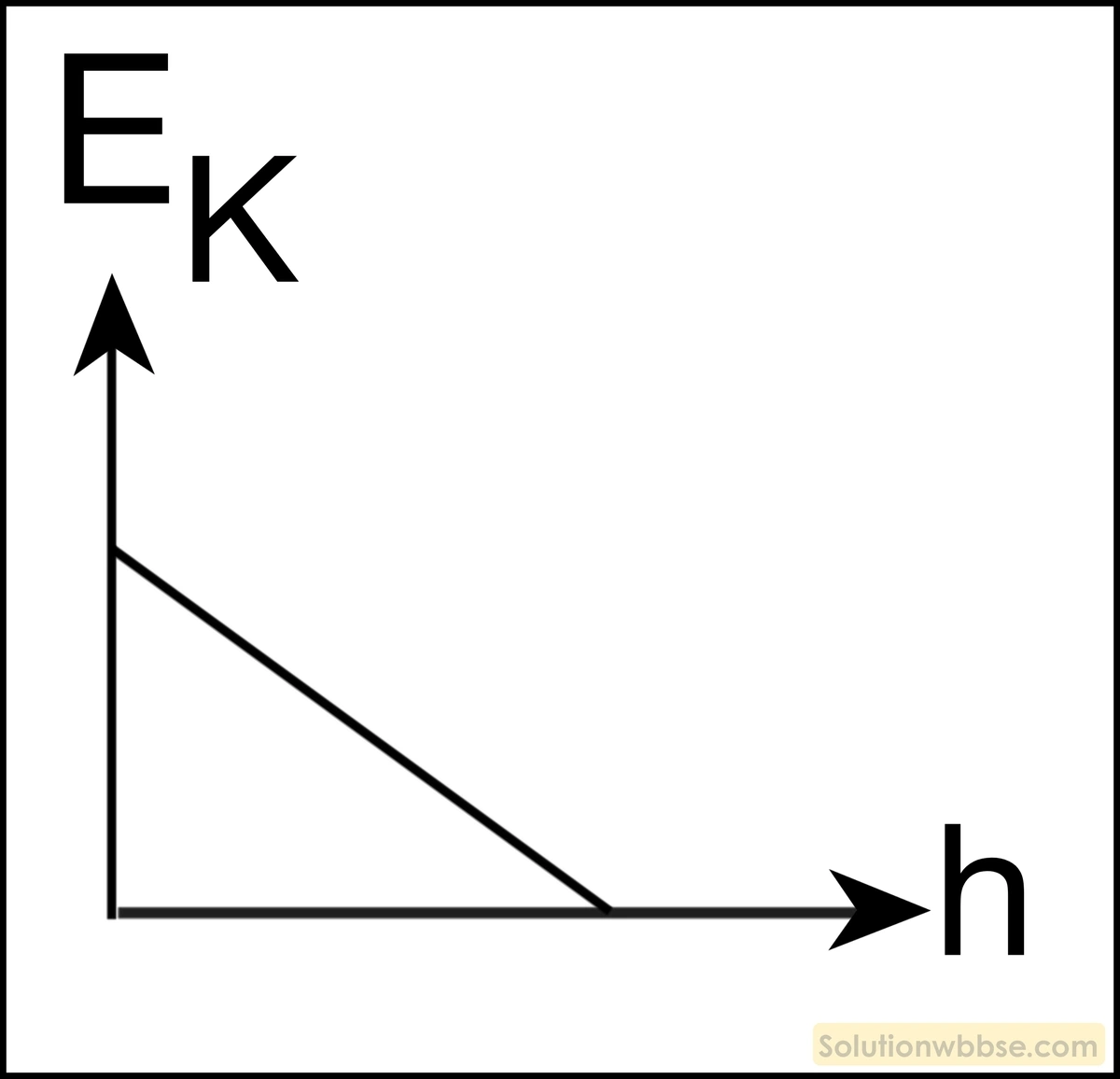
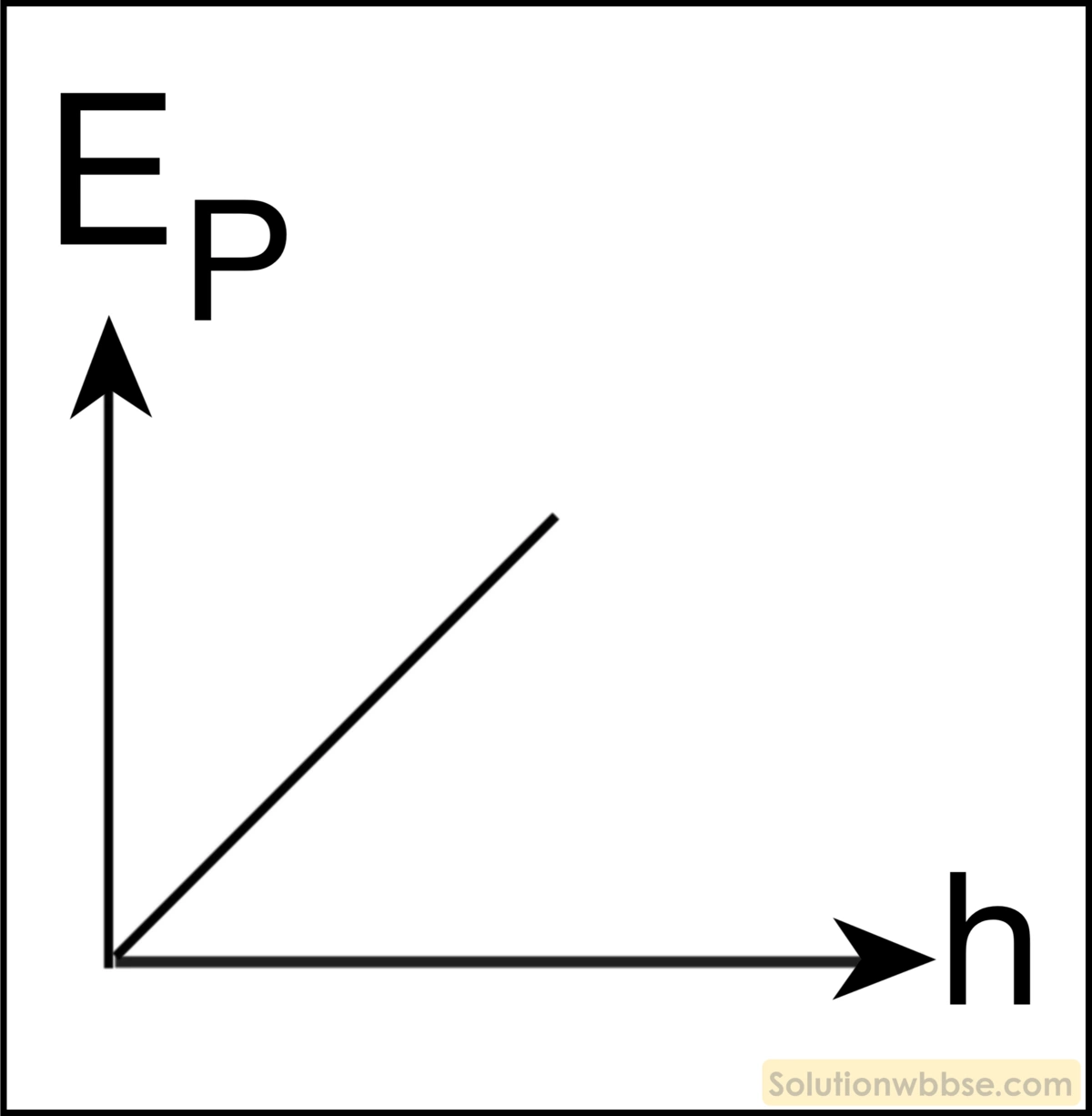
উচ্চতা সাপেক্ষে গতিশক্তির পরিবর্তনের লেখচিত্র হল –

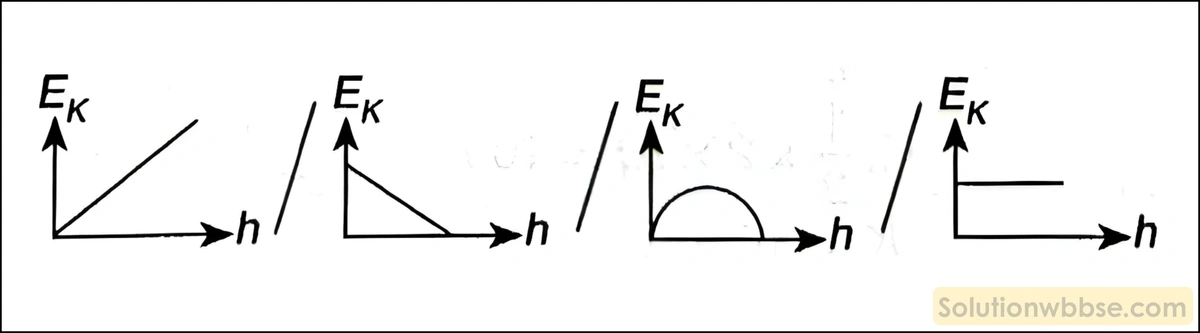
উত্তর – 3.

উচ্চতা সাপেক্ষে স্থিতিশক্তির পরিবর্তনের লেখচিত্র হল –

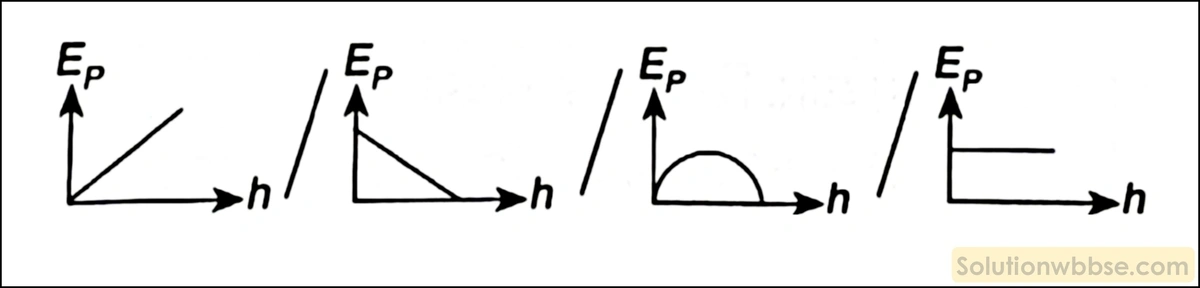
উত্তর – 1.

A ও B দুটি বস্তুর ভরের অনুপাত 1 : 4 এবং গতিশক্তির অনুপাত 4 : 1 হলে তাদের রৈখিক ভরবেগের অনুপাত হয় –

1. 1 : 4
2. 1 : 2
3. 1 : 1
4. 1 : 15

উত্তর – 3. 1 : 1

ভর স্থির রেখে একটি বস্তুর বেগ দ্বিগুণ করা হলে বস্তুটির গতিশক্তি –

1. সমান থাকে
2. দ্বিগুণ হয়
3. চারগুণ হয়
4. অর্ধেক হয়

উত্তর – 3. চারগুণ হয়

A 100 kg ভরের বস্তুকে 2 মিনিটে 100 m নিয়ে যেতে পারে। B 100 kg ভরের বস্তুকে 10 মিনিটে 300 m নিয়ে যেতে পারে। তবে কার শক্তি বেশি হবে? –

1. A -এর
2. B -এর
3. উভয়ের সমান হবে
4. এদের কোনোটিই নয়

উত্তর – 1. A -এর

2 kg ভরের একটি গতিশীল বস্তুর গতিশক্তি 16 J। বস্তুর ভরবেগ হল –

1. 2 kg⋅m⋅s^-1
2. 4 kg⋅m⋅s^-1
3. 8 kg⋅m⋅s^-1
4. 12 kg⋅m⋅s^-1

উত্তর – 3. 8 kg⋅m⋅s-1

কোনো বস্তুর গতিশক্তি পূর্বের 4 গুণ হলে অন্তিম ও প্রারম্ভিক ভরবেগের অনুপাত হবে –

1. 1 : 2
2. 4 : 1
3. 1 : 4
4. 2 : 1

উত্তর – 4. 2 : 1

কোনো জলাধারে সঞ্চিত জলের শক্তি হল –

1. তড়িৎশক্তি
2. গতিশক্তি
3. স্থিতিশক্তি
4. রাসায়নিক শক্তি

উত্তর – 3. স্থিতিশক্তি

1 watt –

1. 1 g-cm/s
2. 1 erg/s
3. 1 kg-m/s
4. 1 N-m/s

উত্তর – 4. 1 N-m/s

m ভরের একটি বস্তুকে ভূপৃষ্ঠ থেকে 2h গভীরতায় রাখা হলে ভূপৃষ্ঠের সাপেক্ষে বস্তুর স্থিতিশক্তি –

1. mgh
2. 2mgh
3. -mgh
4. -2mgh

উত্তর – 4. -2mgh

যে রাশির মান কখনোই ঋণাত্মক হওয়া সম্ভব নয়, তা হল –

• কার্য
• ক্ষমতা
• গতিশক্তি
• স্থিতিশক্তি

উত্তর – 3. গতিশক্তি

একটি বস্তুর ভর ও বেগ উভয়ই দ্বিগুণ হলে বস্তুটির গতিশক্তি হল –

1. পূর্বমানের অর্ধেক
2. চারগুণ
3. আটগুণ
4. দশগুণ

উত্তর – 3. আটগুণ

মোটর বাইকের ইঞ্জিনের ক্ষমতা সাধারণত কোন্ এককে প্রকাশ করা হয়ে থাকে?

1. HP
2. W
3. J/s
4. erg/s 

উত্তর – 1. HP

কোনো বস্তুকে ভূপৃষ্ঠ থেকে উঁচু স্থানে নিয়ে গেলে বস্তুটির স্থিতিশক্তি –

1. কমে
2. একই থাকে
3. বাড়ে
4. কোনোটিই নয়

উত্তর – 3. বাড়ে

কোনো বস্তুর ভরবেগ 10% বৃদ্ধি পেলে গতিশক্তি বৃদ্ধি পাবে –

1. 10%
2. 20%
3. 21%
4. 5%

উত্তর – 3. 21%

শূন্যস্থান পূরণ করো

বল ও সরণের মধ্যস্থ কোণ ___ হলে কৃতকার্য শূন্য হয়।

উত্তর – বল ও সরণের মধ্যস্থ কোণ 90° হলে কৃতকার্য শূন্য হয়।

ক্ষমতা = বল × ___।

উত্তর – ক্ষমতা = বল × বেগ।

শক্তি একটি ___ রাশি।

উত্তর – শক্তি একটি স্কেলার রাশি।

যখন একটি এরোপ্লেন উপরের দিকে উঠতে শুরু করে তখন ওর ওজনের দ্বারা কৃতকার্য ___।

উত্তর – যখন একটি এরোপ্লেন উপরের দিকে উঠতে শুরু করে তখন ওর ওজনের দ্বারা কৃতকার্য বেড়ে যায়।

SI -তে ক্ষমতার একক হল ___ ।

উত্তর – SI -তে ক্ষমতার একক হল ওয়াট।

গতিশক্তি = \(\frac12\) × বস্তুর ভর × ___।

উত্তর – গতিশক্তি = \(\frac12\) × বস্তুর ভর × (বস্তুর বেগ)²।

1 HP = ___ ওয়াট।

উত্তর – 1 HP = 746 ওয়াট।

অবাধে পতনশীল কোনো বস্তু নির্দিষ্ট উচ্চতা থেকে ভূমি স্পর্শ করার পূর্বমুহূর্তে যে বেগ অর্জন করে, তার মান বস্তুর ___ -এর ওপর নির্ভর করে না।

উত্তর – অবাধে পতনশীল কোনো বস্তু নির্দিষ্ট উচ্চতা থেকে ভূমি স্পর্শ করার পূর্বমুহূর্তে যে বেগ অর্জন করে, তার মান বস্তুর ভর -এর ওপর নির্ভর করে না।

ঠিক বা ভুল নির্বাচন করো

বলের ক্রিয়া ও সরণের অভিমুখের অন্তর্বর্তী কোণ 180° হলে কৃতকার্য ঋণাত্মক হয়।

উত্তর – ঠিক।

কার্য একটি ভেক্টর রাশি।

উত্তর – ভুল।

সঠিক উত্তর – স্কেলার রাশি।

অশ্বক্ষমতা ও ওয়াটের মধ্যে দ্বিতীয়টির মান বেশি।

উত্তর – ভুল।

সঠিক উত্তর – প্রথমটির।

1 lb ভরের কোনো বস্তুকে অভিকর্ষের বিরুদ্ধে 1 sec সময়ে 550 ft উল্লম্ব উচ্চতায় তোলা হলে ব্যয়িত ক্ষমতার মান হয় 1 HPI

উত্তর – ঠিক।

সূর্যের দেওয়া মহাকর্ষ বলের প্রভাবে বৃত্তাকার কক্ষপথে আবর্তনরত পৃথিবীর গতির অভিমুখ পরিবর্তিত হলেও গতিশক্তির কোনো পরিবর্তন হয় না।

উত্তর – ঠিক।

পতনশীল বস্তুর গতির যে-কোনো অবস্থানে তার মোট যান্ত্রিক শক্তি ধ্রুবক হয়।

উত্তর – ভুল।

সঠিক উত্তর – অবাধে পতনশীল বস্তুর।

ভূপৃষ্ঠ সাপেক্ষে যে-কোনো উচ্চতায় অভিকর্ষীয় স্থিতিশক্তির রাশিমালা হয় mgh।

উত্তর – ভুল।

সঠিক উত্তর – পৃথিবীর ব্যাসার্ধের তুলনায় উপেক্ষণীয় উচ্চতায় (h << R)।

কোনো বস্তুর উপর কার্য করলে তার শক্তির সঞ্চয় বাড়ে।

উত্তর – ঠিক।

দু-একটি শব্দে উত্তর দাও

For High-Types

কোনো বস্তুকে জলের মধ্যে h উচ্চতায় তুললে তার স্থিতিশক্তির কী পরিবর্তন হবে? যেখানে বস্তুর ঘনত্ব ρ, জলের ঘনত্ব ρ₀, এবং বস্তুর আয়তন V।

উত্তর বস্তুকে জলে ডোবালে বস্তুটির ওপর –

• ওজনজনিত নিম্নমুখী বল এবং
• ঊর্ধ্বমুখী জলের প্লবতা বল ক্রিয়া করে।

এখানে, ρ > ρ₀ হলে বস্তুর ওজন প্লবতা বল অপেক্ষা বড়ো হবে। অর্থাৎ, নিম্নমুখী লব্ধি বল= vρg – vρ₀g = vg(ρ – ρ₀)।

∴ বস্তুর স্থিতিশক্তি বৃদ্ধি = বস্তুটিকে ওই বলের বিরুদ্ধে h উচ্চতায় তুলতে কার্য = vg(ρ – ρ₀) × h = vgh(ρ – ρ₀)।

আবার, ρ < ρ₀ হলে, বস্তুর ওজন প্লবতা বল অপেক্ষা ছোটো হবে। অর্থাৎ, ঊর্ধ্বমুখী লব্ধিবল = vρ₀g – vρg = vg (ρ₀ – ρ)।

∴ এখন বস্তুর স্থিতিশক্তি হ্রাস = vgh(ρ₀ – ρ)।

লেখচিত্রের সাহায্যে কৃতকার্যকে কীভাবে বর্ণনা করা যায়?

বস্তুকণার সরণ (S) x অক্ষ বরাবর এবং তার ওপর প্রযুক্ত বল (F) -এর পরিবর্তন y অক্ষ বরাবর বিবেচনা করে যে লেখচিত্র পাওয়া যায়, সেই লেখচিত্র ও স্থানাঙ্ক অক্ষদ্বয় দ্বারা আবদ্ধ অংশের ক্ষেত্রফল ওই বল দ্বারা কৃতকার্যকে পরিমাপ করে। প্রযুক্ত বল সময়ের সঙ্গে ধ্রুবক বা পরিবর্তনশীল যাই হোক না কেন কার্যকে সর্বদা এজাতীয় (বল-সরণ) লেখ -এর সাহায্যে বর্ণনা করা যায়।

দুটি অবিকল একই রকমের স্প্রিংয়ের স্প্রিং ধ্রুবক 200 N/m। একটি স্প্রিংকে 10 cm সংকুচিত ও অন্যটিকে সমপরিমাণে প্রসারিত করা হল। স্প্রিং দুটিতে সঞ্চিত স্থিতিস্থাপক স্থিতিশক্তির পার্থক্য কী হবে?

সংকুচিত বা প্রসারিত স্প্রিংয়ের স্থিতিশক্তি \(\left(E_p\right)=\frac12kx^2\)। যেখানে, k স্প্রিংয়ের বলধ্রুবক এবং x তার দৈর্ঘ্যের সংকোচন বা প্রসারণ। উভয় স্প্রিংয়ের ক্ষেত্রে k ও x -এর মান অভিন্ন। সুতরাং, তাদের স্থিতিশক্তি সমান অথবা স্থিতিশক্তির পার্থক্য শূন্য।

একটি লাঠি মাটিতে শুইয়ে রাখলে তা সর্বদাই সাম্যে থাকে, কিন্তু খাড়া অবস্থায় মাটিতে দাঁড় করিয়ে দিলে তা সামান্য বিচ্যুতির ফলেই মাটিতে পড়ে যায়। ব্যাখ্যা করো।

অথবা, একটি পেনসিলকে মেঝের উপর উল্লম্বভাবে দাঁড় করিয়ে দিলে পেনসিলটি কাত হয়ে মেঝের উপর পড়ে যায় কেন?

ন্যূনতম স্থিতিশক্তির অবস্থান লাভ করতে চাওয়ার প্রবণতা যে-কোনো বস্তু বা বস্তু সমষ্টির স্বাভাবিক ধর্ম। স্থিতিশক্তি বৃদ্ধি পেলে বস্তুর সাম্য বিঘ্নিত হয়, তাই সুস্থির সাম্য বজায় রাখতে বস্তু সর্বদা চেষ্টা করে যাতে তার স্থিতিশক্তি ন্যূনতম হয়।

লাঠি মাটিতে শুইয়ে রাখলে তার স্থিতিশক্তি প্রায় শূন্য হয় এবং সেই সময় তার সাম্যও সুস্থির হয়। লাঠিকে খাড়া অবস্থায় মাটির উপর দাঁড় করালে তার স্থিতিশক্তি বৃদ্ধি পায় এবং সাম্যও বিঘ্নিত হয়। তাই, সুযোগ পেলেই লাঠি আবার মাটিতে পড়ে সুস্থিতি অর্জন করতে চায়।

দেখাও যে, m ভরের একটি বস্তুকে সরাসরি খাড়াভাবে h উচ্চতায় তুলতে যা কৃতকার্য হয় বস্তুটিকে একটি মসৃণ নততল বরাবর টেনে একই উচ্চতায় তুলতে একই পরিমাণ কৃতকার্যের প্রয়োজন হয়। এই ফলাফলের গুরুত্ব কী?

বস্তুটিকে খাড়া উচ্চতায় CB বরাবর C থেকে B বিন্দুতে অর্থাৎ, h উচ্চতায় তুলতে কৃতকার্য = বল × সরণ = mgh। নততলের দৈর্ঘ্য বরাবর নীচের দিকে ওজনের উপাংশ mg sinθ।

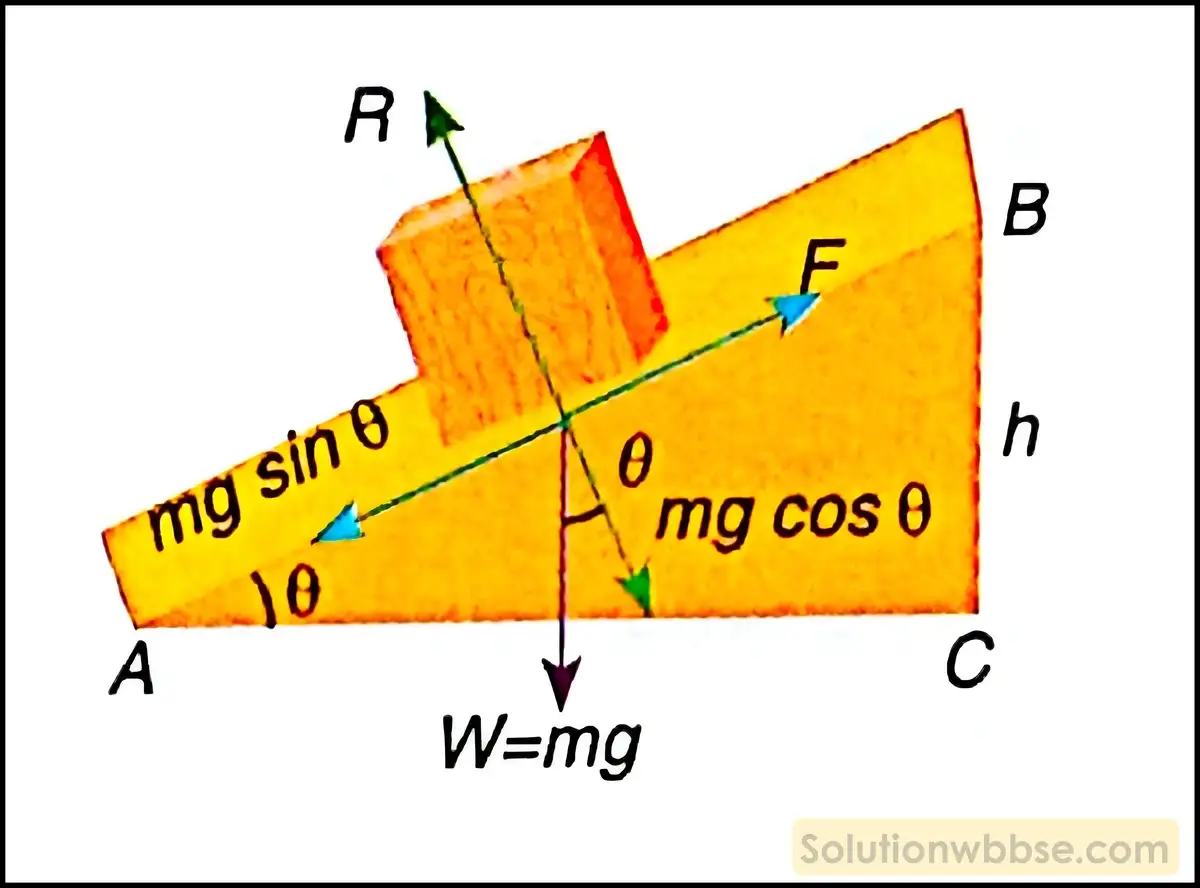
সুতরাং, বস্তুটিকে AB বরাবর A থেকে B বিন্দুতে উত্তোলন করতে ওজনের উপাংশের বিরুদ্ধে কৃতকার্য = mg sinθ × AB

= mg × AB sinθ

= mg × BC

= mgh

এই গণনা থেকে প্রমাণিত হয়, কৃতকার্য পথের ওপর নির্ভরশীল নয়। এই ফলাফল নির্দেশ করে যে, অভিকর্ষ একটি সংরক্ষী বল।

m ভরের একটি বস্তু স্থিরাবস্থা থেকে সমত্বরণে চলছে। n সময় পরে তার বেগ হল L। প্রমাণ করো, R সময় পরে তার কৃতকার্যের পরিমাণ \(\frac12m\frac{L^2R^2}{n^2}\)। 

ধরা যাক, বস্তুটির ত্বরণ = \(a\), বস্তুকণাটি স্থিরাবস্থা থেকে সমত্বরণে গতিশীল বলে \(n\) সময় পরে বেগ, \(L=an\)

∴ \(a=\frac Ln\)

\(R\) সময় পরে ওই বস্তুকণার বেগ হলে, \(v=aR \)

বা, \(v=\frac{LR}n \) [∵ \(a=\frac Ln\)]

\( R\) সময় পরে বস্তুটির দ্বারা কৃতকার্য

= বস্তুটির গতিশক্তি বৃদ্ধি

= অন্তিম গতিশক্তি – প্রাথিমিক গতিশক্তি

= \( \frac12mv^2-0\) [∵ বস্তুর প্রাথমিক বেগ = \(0\)]

= \(\frac12mv^2 \)

= \(\frac12m\cdot\left(\frac{LR}n\right)\) [∵ \(v=\frac{LR}n\)]

= \(\frac12m\frac{L^2R^2}{n^2}\) [প্রমাণিত]।

কখনো কখনো ক্রিকেট বলকে যে বেগে ছোড়া হয়, মাটিতে আঘাত করার পর তার গতিবেগ বেড়ে যায়। এটি কীভাবে সম্ভব?

বিশেষ এক ধরনের বল ছোড়ার পদ্ধতিতে (ক্রিকেটীয় পরিভাষায় আর্ম বল বা আর্মার) স্পিন বোলার এমনভাবে বল নিক্ষেপ করেন যে, বলের রৈখিক এবং আবর্ত দুই প্রকার গতিশক্তি থাকে। মাটিতে পড়ে লাফিয়ে ওঠার পর আবর্ত গতির আর অস্তিত্ব থাকে না। অর্থাৎ, বলটি শুধুমাত্র রৈখিক গতিসহ চলতে থাকে। কিন্তু শক্তি সর্বদা সংরক্ষিত থাকে বলে প্রাথমিক অবস্থায় বলটিতে যে আবর্ত গতিশক্তি ছিল তা রৈখিক গতিশক্তির সঙ্গে যুক্ত হয়ে যায়, ফলে বলটির বেগ বাড়ে।

A ও B দুটি যন্ত্রের সময় সাপেক্ষে যন্ত্র দ্বারা কৃতকার্যের লেখচিত্র দেখানো হল। ওই লেখচিত্র হতে যে বক্তব্যগুলি বলা হল তা ঠিক না ভুল উল্লেখ করো – A -এর ক্ষমতা 50 J ও B -এর ক্ষমতা 20 J/A -এর ক্ষমতা 4 W ও B -এর ক্ষমতা 2 W/A -এর ক্ষমতা B -এর ক্ষমতার 2.5 গুণ/B যে সময়ে 50 J কাজ করে সেই সময়ে A 100 J কাজ করে।

A -এর ক্ষমতা 4 W ও B -এর ক্ষমতা 2 W এবং B যে সময়ে 50 J কাজ করে, সেই সময়ে A 100 J কাজ করে।

Class 9 Physical Science – Notes for All Chapters

Chapter Name	Tropics
পরিমাপ	পরিমাপ ও একক বিভিন্ন মাপের একক মাত্রা পরিমাপ
বল ও গতি	স্থিতি ও গতি গতির সমীকরণ নিউটনের প্রথম গতিসূত্র নিউটনের দ্বিতীয় গতি সূত্র নিউটনের তৃতীয় গতিসূত্র বিভিন্ন ধরণের বল রৈখিক ভরবেগ রৈখিক ভরবেগ সংরক্ষণ
পদার্থ : গঠন ও ধর্ম	তরল ও বায়ুর চাপ আর্কিমিডিসের নীতি পৃষ্ঠটান সান্দ্রতা বার্নোলির নীতি স্থিতিস্থাপকতা
পদার্থ : পরমাণুর গঠন ও পদার্থের ভৌত ও রাসায়নিক ধর্মসমূহ	পরমাণুর গঠন মোলের ধারণা দ্রবণ অ্যাসিড, ক্ষার, লবণ মিশ্রণের উপাদানের পৃথকীকরণ জল
শক্তির ক্রিয়া , কার্য, ক্ষমতা	শক্তির ক্রিয়া , কার্য, ক্ষমতা
তাপ	ক্যালোরিমিতি কার্য ও তাপের তুল্যতা লীনতাপ সম্পৃক্ত ও অসম্পৃক্ত বাষ্প জলের ব্যতিক্রান্ত প্রসারণ
শব্দ	শব্দের উৎস : কম্পন শব্দের বিস্তার : তরঙ্গ শব্দের কয়েকটি ধর্ম শব্দের বৈশিষ্ট্য মানুষের কান ও শব্দ শোনার কৌশল শব্দদূষণ

---

আজকের আর্টিকেলে আমরা নবম শ্রেণির ভৌতবিজ্ঞান বইয়ের পঞ্চম অধ্যায় “শক্তির ক্রিয়া, কার্য, ক্ষমতা ও শক্তি” থেকে পরীক্ষায় আসা গুরুত্বপূর্ণ প্রশ্ন ও উত্তরগুলো আলোচনা করেছি। এই প্রশ্নোত্তরগুলো নবম শ্রেণির বার্ষিক পরীক্ষা, এমনকি চাকরি বা যেকোনো প্রতিযোগিতামূলক পরীক্ষার জন্যও উপযোগী। কারণ, এই অধ্যায়ের প্রশ্ন প্রায়ই বিভিন্ন পরীক্ষায় কমন আসে।

আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সাহায্য করবে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন কিংবা টেলিগ্রামে যোগাযোগ করতে পারেন—আপনাদের প্রশ্নের উত্তর দিতে আমি সর্বদা প্রস্তুত।

ধন্যবাদ সবাইকে।