Madhyamik 2018 Mathematics Question Paper With Answer

মাধ্যমিক পরীক্ষা শিক্ষার্থীদের জীবনের একটি গুরুত্বপূর্ণ মোড়। এই পরীক্ষার ফলাফল ভবিষ্যতের পথ নির্ধারণে গুরুত্বপূর্ণ ভূমিকা পালন করে। তাই পরীক্ষার জন্য ভালোভাবে প্রস্তুতি নেওয়া অত্যন্ত জরুরি।

এই আর্টিকেলটিতে, আমরা ২০১৮ সালের মাধ্যমিক গণিত পরীক্ষার প্রশ্ন ও উত্তর বিশ্লেষণ করবো। এই বিশ্লেষণ শিক্ষার্থীদের পরীক্ষার ধরন, গুরুত্বপূর্ণ বিষয় এবং প্রশ্নোত্তরের ধরণ সম্পর্কে ধারণা দেবে।

1. নিম্নলিখিত প্রশ্নগুলির প্রতিটি ক্ষেত্রে সঠিক উত্তরটি নির্বাচন করো।

(i) বার্ষিক 10% সরল সুদের হারে a টাকার b মাসের সুদ –

(a) \(\frac{ab}{100}\) টাকা

(b) \(\frac{ab}{120}\) টাকা

(c) \(\frac{ab}{1200}\) টাকা

(d) \(\frac{ab}{10}\) টাকা

উত্তর : (b) \(\frac{ab}{120}\) টাকা

(ii) যদি x ∝ y হয়, তাহলে –

(a) x² ∝ y³

(b) x³ ∝ y²

(c) x ∝ y²

(d) x² ∝ y²

উত্তর : (d) x² ∝ y²

(iii) ABCD বৃত্তস্থ চতুর্ভুজের ∠A মান = 100° হলে ∠C-এর মান –

(a) 50°

(b) 200°

(c) 80°

(d) 180°

উত্তর : (c) 80°

(iv) \(\frac{7\mathrm\pi}{12}\)-এর ষষ্টিক পদ্ধতিতে মানটি হল –

(a) 115°

(b) 150°

(c) 135°

(d) 105°

উত্তর : (d) 105°

(v) একটি ঘনকের একটি বাহুর দৈর্ঘ্য a একক এবং কর্ণের দৈর্ঘ্য d একক হলে a এবং d -এর সম্পর্ক হবে –

(a) \(\sqrt2\)a = d

(b) \(\sqrt3\)a = d

(c) a = \(\sqrt3\)d

(d) a = \(\sqrt2\)d

উত্তর : (b) \(\sqrt3\)a = d

(vi) 6, 7, x, 8, y, 16 সংখ্যাগুলির গড় 9 হলে –

(a) x + y = 21

(b) x + y = 17

(c) x – y = 21

(d) x – y = 19

উত্তর : (b) x + y = 17

2. শূন্যস্থান পূরণ করো (যে কোনো পাঁচটি)।

(i) বার্ষিক r% সরল সুদের হারে কোনো মূলধনের n বছরের সুদ \(\frac{pnr}{100}\) টাকা হলে মূলধনের পরিমাণ_______টাকা হবে।

উত্তর : 4P

(ii) (a – 2)x² + 3x + 5 = 0 সমীকরণটিতে a-এর মান_______এর জন্য দ্বিঘাত সমীকরণ হবে না।

উত্তর : 2

(iii) ABCD একটি বৃত্তস্থ সামান্তরিক হলে ∠A -এর মান হবে_______।

উত্তর : 90°

(iv) tan35° tan55° = sinθ হলে, θ-এর সর্বনিম্ন ধনাত্মক মান_______হবে।

উত্তর : 90°

(v) একমুখ কাটা একটি পেনসিলের আকার চোঙ ও_______র সমন্বয়।

 উত্তর : শঙ্কু।

(vi) মধ্যগামিতার মাপকগুলি হল গড়, মধ্যমা ও_______।

উত্তর : সংখ্যাগুরুমান।

3. সত্য বা মিথ্যা লেখো (যে কোনো পাঁচটি)।

(i) নির্দিষ্ট আসলের উপর সমান হারে সুদ হলে 2 বছরের সরল সুদ, চক্রবৃদ্ধি সুদের তুলনায় বেশী।

উত্তর : মিথ্যা।

(ii) x²y, x²y² এবং xy³ ক্রমিক সমানুপাতী।

উত্তর : সত্য।

(iii) অর্ধবৃত্তাংশস্থ অপেক্ষা ক্ষুদ্রতর বৃত্তাংশস্থ কোণ স্থূলকোণ।

উত্তর : মিথ্যা।

(iv) sec²27° – cot²63° -এর সরলতম মান 1.

উত্তর : সত্য।

(v) একটি গোলকের ব্যাসার্ধ দ্বিগুণ হলে গোলকটির আয়তন প্রথম গোলকের আয়তনের দ্বিগুণ হবে।

উত্তর : মিথ্যা।

(vi)

স্কোর	1	2	3	4	5
শিক্ষার্থীর সংখ্যা	3	6	4	7	5

বিভাজনটির সংখ্যাগুরু মান হল 3.

উত্তর : মিথ্যা।

4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাও (যে কোনো দশটি)।

(i) বার্ষিক সরল সুদের হার 4% থেকে \(3\frac34\)% হওয়ায় এক ব্যক্তির বার্ষিক আয় 60 টাকা কম হয়। ঐ ব্যক্তির মূলধন নির্ণয় করো।

উত্তর :

ধরি, ওই ব্যাক্তির মূলধন x টাকা।

∴ x টাকার 1 বছরের 4% হারে সুদ

= \(\frac{x\times1\times4}{100}\) টাকা

= \(\frac x{25}\) টাকা

আবার, x টাকার 1 বছরের \(3\frac34\)% হারে সুদ হারে সুদ

= \(\frac{x\times1\times3{\displaystyle\frac34}}{100}\) টাকা

= \(\frac{x\times15}{400}\) টাকা

= \(\frac{x\times15}{400}\) টাকা

শর্তানুসারে,

\(\frac x{25}-\frac{3x}{80}\) = 60

বা, \(\frac{16x-15x}{400}\) = 60

বা, \(\frac x{400}\) = 60

বা, x = 2400

∴ ওই ব্যাক্তির মূলধন 2400 টাকা।

(ii) A এবং B যথাক্রমে 15,000 টাকা ও 45,000 টাকা দিয়ে একটি ব্যবসা শুরু করল। 6 মাস পরে B লভ্যাংশ হিসাবে 3,030 টাকা পেল। A -এর লভ্যাংশ কত?

উত্তর :

ধরি, A এর লভ্যাংশ x টাকা।

∴ A এর মূলধন : B এর মূলধন = A এর লভ্যাংশ : B এর লভ্যাংশ

বা, 15000 : 45000 = x : 3030

বা, 1 : 3 = x : 3030

বা, \(\frac13=\frac x{3030}\)

বা, 3x = 3030

বা, x = \(\frac{3030}3\)

বা, x = 1010

∴ A এর লভ্যাংশ 1010 টাকা।

(iii) 2x + \(\frac1x\) = 2 হলে, \(\frac x{2x^2+x+1}\) -এর মান কত?

উত্তর :

2x + \(\frac1x\) = 2

বা, \(\frac{2x^2+1}x\) = 2

বা, 2x² + 1 = 2x

∴ \(\frac x{2x^2+x+1}\)

= \(\frac x{2x+x}\)

= \(\frac x{3x}\)

= \(\frac13\)

∴ \(\frac x{2x^2+x+1}=\frac13\)

(iv) কোনো দ্বিঘাত সমীকরণের বীজদ্বয় 2, -3 হলে সমীকরণটি লেখ।

উত্তর :

নির্ণেয় সমীকরণটি হবে

x² – (বীজদ্বয়ের যোগফল )x + (বীজদ্বয়ের গুনফল) = 0

বা, x² − {2 + (−3)}x + (2)(−3) = 0

বা, x² − (−x) − 6 = 0

বা, x² + x − 6 = 0

(v) ∆ABC-এর BC বাহুর সমান্তরাল সরলরেখা AB ও AC কে যথাক্রমে P ও Q বিন্দুতে ছেদ করে। যদি AP = 4 সেমি, QC = 9 সেমি এবং PB = AQ হয় তাহলে PB-এর দৈর্ঘ্য নির্ণয় করো।

উত্তর :

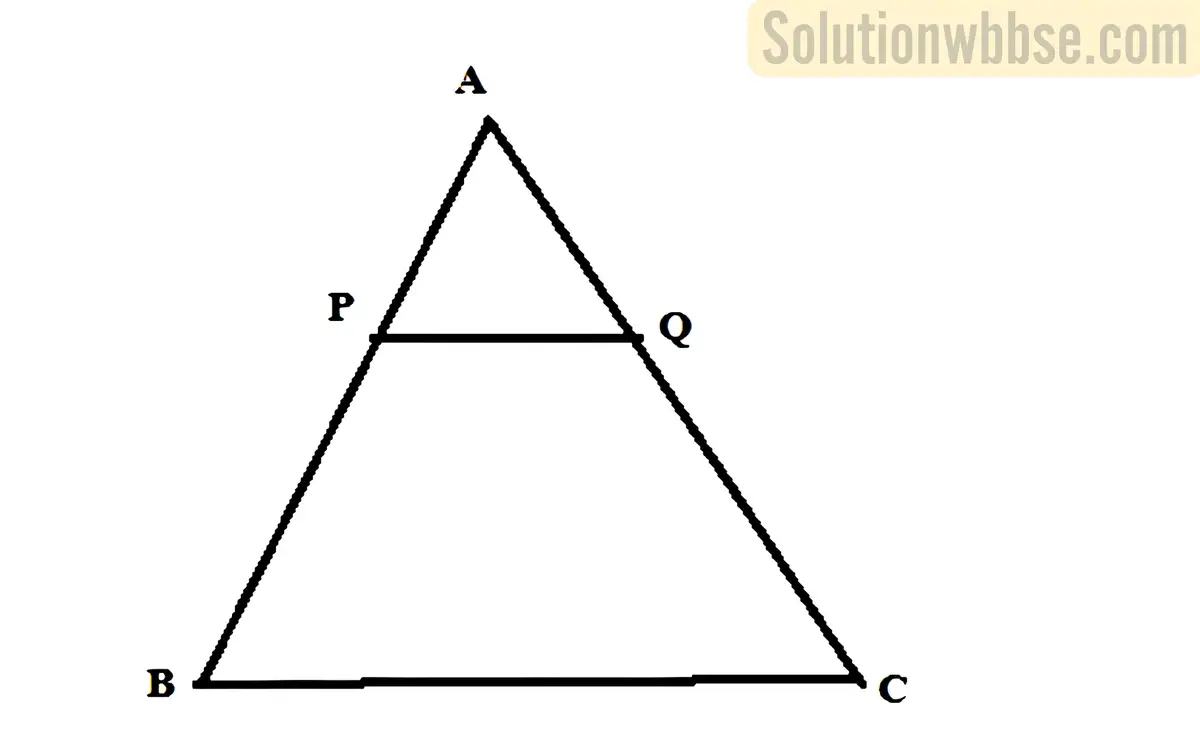
ABC ত্রিভুজের BC বাহুর সমান্তরাল সরলরেখা AB ও AC কে জথাক্রমে P ও Q বিন্দুতে ছেদ করে।

ধরি, PB = AQ = x সেমি.

∴ \(\frac{AP}{PB}=\frac{AQ}{QC}\)

বা, \(\frac{4}{x}=\frac{x}{9}\)

বা, x² = (6)²

বা, x = 6

∴ PB = 6 সেমি.

(vi) O কেন্দ্রীয় বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি। O বিন্দু থেকে 13 সেমি দূরত্বে P একটি বিন্দু। PQ এবং PR বৃত্তের দুটি স্পর্শক হলে PQOR চতুর্ভুজের ক্ষেত্রফল কত?

উত্তর :

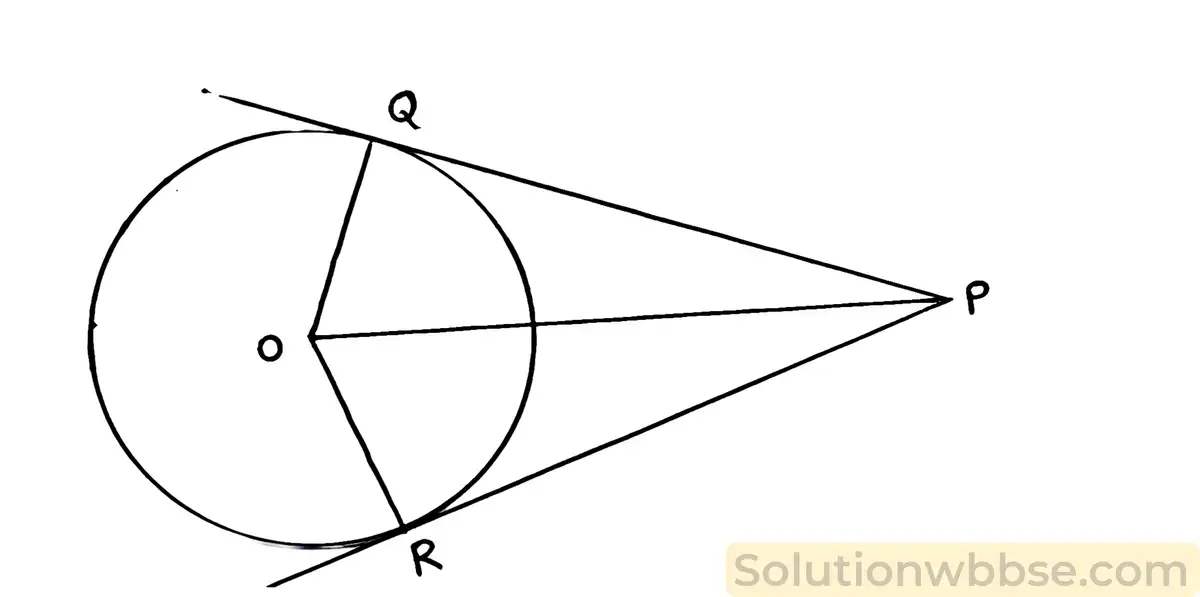
ΔOPR ত্রিভুজে OR = 5 সেমি. (বৃত্তের ব্যাসার্ধ), OP = 13 সেমি.

যেহেতু OR স্পর্শবিন্দুগামী ব্যাসার্ধ ∴ OR ⊥ PR

∴ সমকোণী ত্রিভুজ ΔOPR থেকে পাই,

OR² + PR² = OP²

বা, (5)² + PR² = (13)²

বা, PR² = 169 – 25

বা, PR² = 144

বা, PR² = (12)²

বা, PR = 12

যেহেতু, PR এবং PQ দুটি স্পর্শক এবং P বহিঃস্থ বিন্দু

∴ PR = PQ = 12 সেমি.

PQOR চতুর্ভুজের ক্ষেত্রফল = ত্রিভুজ ΔPOR এর ক্ষেত্রফল + ত্রিভুজ ΔPOQ এর ক্ষেত্রফল

= \(\frac12\) × 12 × 5 + \(\frac12\) × 12 × 5 বর্গ সেমি. [∵ সমকোণী ত্রিভুজের ক্ষেত্রফল = \(\frac12\) × ভুমি × উচ্চতা]

= (30 + 30) বর্গ সেমি.

= 60 বর্গ সেমি.

(vii) O কেন্দ্রীয় বৃত্তে AB ও CD জ্যা দুটি কেন্দ্র থেকে সমদূরবর্তী ∠AOB = 60° এবং CD = 6 সেমি হলে, বৃত্তটির ব্যাসার্ধের দৈর্ঘ্য কত?

উত্তর :

O কেন্দ্রীয় বৃত্তে AB ও CD জ্যা দুটি কেন্দ্র থেকে সমদূরবর্তী। ∴ AB = CD = 6 সেমি.।

ত্রিভুজ AOB এর, ∠AOB = 60°

আবার OA = OB [ একই বৃত্তের ব্যাসার্ধ]

∴ ∠OAB = ∠OBA

= \(\frac{(180^\circ-\angle AOB)}2\)

= \(\frac{(180^\circ-60^\circ)}2\)

= 60°

সুতরাং AOB সমবাহু ত্রিভুজ।

∴ OA = OB = AB = 6 সেমি.

∴ বৃত্তের ব্যাসার্ধ 6 সেমি.।

(viii) tanθ + cotθ = 2 হলে tan⁷θ + cot⁷θ = কত?

উত্তর :

tanθ + cotθ = 2

বা, tanθ + \(\frac1{\tan\theta}\) = 2

বা, \(\frac{\tan^2\theta+1}{\tan\theta}\) = 2

বা, tan²θ + 1 = 2tanθ

বা, tan²θ – 2tanθ + 1 = 0

বা, (tanθ – 1)² = 0

বা, (tanθ – 1) = 0

বা, tanθ = 1

∴ cotθ = \(\frac1{\tan\theta}\) = 1

∴ tan⁷θ + cot⁷θ

= (1)⁷ + (1)⁷

= 1 + 1

= 2

(ix) একটি স্তম্ভের ছায়ার দৈর্ঘ্য এবং স্তম্ভের উচ্চতার অনুপাত \(\sqrt3\) : 1 হলে, সূর্য্যের উন্নতি কোণ নির্ণয় করো।

উত্তর :

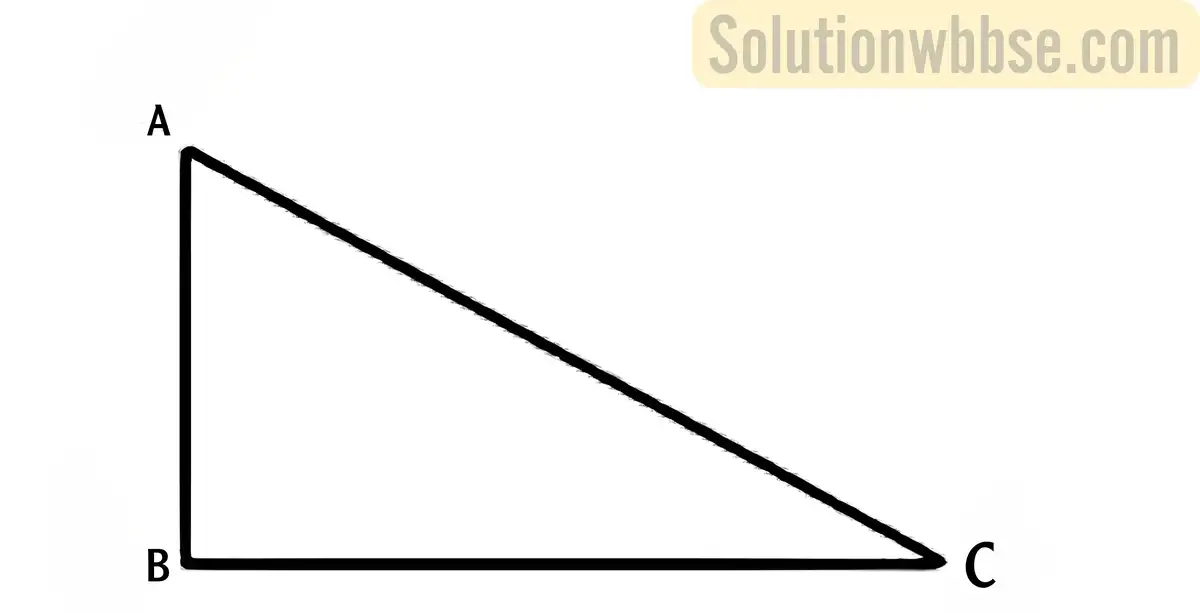
ধরাযাক, পোস্টটির উচ্চতা AB এবং পোস্টের ছায়ার দৈর্ঘ্য BC এবং সূর্যের উন্নতি কোণ θ

∴ \(\frac{AB}{BC}=\frac1{\sqrt3}\)

বা, tanθ = tan30°

বা, θ = 30°

(x) দুটি লম্ব বৃত্তাকার চোঙের আয়তন সমান ও তাদের উচ্চতার অনুপাত 1 : 2 হলে, চোঙদুটির ব্যাসার্ধের দৈর্ঘ্যর অনুপাত কত?

উত্তর :

ধরি, দুটি লম্ব বৃত্তাকার চোঙের উচ্চতা যথাক্রমে h1 একক এবং h2 একক এবং ব্যাসার্ধের দৈর্ঘ্য r1 একক এবং r2 একক।

∴ h₁ : h₂ = 1 : 2

যেহেতু লম্ববৃত্তাকার চোঙদুটির আয়তন সমান

∴ π(r₁)²h₁ = π(r₂)²h₂

বা, (r₁)²h₁ = (r₂)²h₂

বা, \(\left(\frac{r_1}{r_2}\right)^2=\frac{h_2}{h_1}\)

বা, \(\left(\frac{r_1}{r_2}\right)^2=\frac21\)

বা, \(\frac{r_1}{r_2}=\frac{\sqrt2}1\)

∴ চোঙ দুটির ব্যাসার্ধের অনুপাত \(\sqrt2\) : 1

(xi) একটি নিরেট অর্ধগোলকের আয়তন 144π ঘনসেমি হলে, গোলকটির ব্যাসের দৈর্ঘ্য কত?

উত্তর :

ধরি, অর্ধ গোলকটির ব্যাসার্ধের দৈর্ঘ্য r সেমি.।

∴ অর্ধগোলকের আয়তন = \(\frac23\mathrm{πr}^3\) ঘন সেমি.

শর্তানুসারে,

\(\frac23\mathrm{πr}^3\) = 144π

বা, \(\mathrm r^3=\frac{144\times3}2\)

বা, r³ = 216

বা, r³ = (6)³

∴ r = 6

∴ 2r = 12

∴ অর্ধ গোলকের ব্যাসের দৈর্ঘ্য 12 সেমি.।

(xii) একটি পরিসংখ্যা বিভাজনের গড় 8.1, Σf_ix_i = 132 + 5K এবং ∑f_i = 20 হলে K-এর মান কত?

উত্তর :

একটি পরিসংখ্যা বিভাজনের গড় 8.1

∴ \(\frac{\sum f_ix_i}{\sum f_i}=\frac{132+5k}{20}\)

বা, 8.1 = \(\frac{132+5k}{20}\)

বা, 162 = 132 + 5k

বা, 5k = 162 – 132

বা, 5k = 30

বা, k = \(\frac{30}5\)

বা, k = 6

∴ k এর মান 6

5. যে কোনো একটি প্রশ্নের উত্তর দাও।

(a) আমিনুর একটি ব্যাঙ্ক থেকে 64,000 টাকা ধার নিয়েছে। যদি ব্যাঙ্কের সুদের হার প্রতি বছরে প্রতি টাকায় 2.5 পয়সা হয়, তবে ঐ টাকার 2 বছরের চক্রবৃদ্ধি সুদ কত হবে?

উত্তর :

আসল (P) = 64000 টাকা।

সময় (n) = 2 বছর।

সুদের হার (r) = \(\frac{2.5}{100}\) × 100 = 2.5%

∴ 2 বছর পর সমূল চক্রবৃদ্ধি সুদ

= 6000 × \(\left(1+\frac{2.5}{100}\right)^2\) টাকা

= 6000 × \(\left(1+\frac{25}{1000}\right)^2\) টাকা

= 6000 × \(\left(1+\frac1{40}\right)^2\) টাকা

= 6000 × \(\frac{41}{40}\times\frac{41}{40}\) টাকা

= (40 × 41 × 41) টাকা

= 67240 টাকা

∴ চক্রবৃদ্ধি সুদ = 67240 টাকা – 64000 টাকা = 3240 টাকা।

∴ 2 বছর পর চক্রবৃদ্ধি সুদ হবে 3240 টাকা।

(b) A, B ও C যথাক্রমে 6,000 টাকা, 8,000 টাকা ও 9,000 টাকা মূলধন নিয়ে একত্রে ব্যবসা আরম্ভ করলো। কয়েক মাস পর A আরও 3,000 টাকা ব্যবসায় লগ্নী করলো। বছরের শেষে মোট 30,000 টাকা লাভ হল এবং C তার ভাগে 10,800 টাকা লভ্যাংশ পেল। A কখন আরও 3,000 টাকা লগ্নী করেছিল?

উত্তর :

ধরি, ব্যাবসা শুরু করার x মাস পরে A আরও 3000 টাকা লগ্নী করে।

∴ A,B ও C এর মূলধনের অনুপাত

= {(6000 × x) + (6000 + 3000)(12 – x)} : (8000 × 12) : (9000 × 12)

= (6000x – 9000x + 108000 ) : 96000 : 108000

= (108000 – 3000x) : 96000 : 108000

= 1000(108 – 3x) : 96000 : 108000

= (108-3x) : 96 : 108

= (36-x) : 32 : 36

প্রশ্নানুসারে,

\(\frac{36}{\left(36-x\right)+32+36}\) × 30000 = 10800

বা, \(\frac{36}{104-x}\) × 30000 = 10800

বা, \(\frac{36}{104-x}=\frac{10800}{30000}\)

বা, \(\frac{36}{104-x}=\frac9{25}\)

বা, 9(104 – x) = 900

বা, 936 – 9x = 900

বা, -9x = 900 – 936

বা, -9x = -36

বা, x = \(\frac{-36}{-9}\)

বা, x = 4

∴ ব্যাবসা শুরুর 4 মাস পর A ব্যাবসায় 3000 টাকা লগ্নী করে।

6. যে কোনো একটি প্রশ্নের উত্তর দাও।

(a) সমাধান করো – \(\left(\frac{x+4}{x-4}\right)^2-5\left(\frac{x+4}{x-4}\right)\) + 6 = 0 (x ≠ 0)

উত্তর :

ধরি, \(\left(\frac{x+4}{x-4}\right)\) = a

∴ প্রদত্ত দ্বিঘাত সমীকরণটি হল,

a² – 5a + 6 = 0

বা, a² – (3 + 2)a + 6 = 0

বা, a² – 3a – 2a + 6 = 0

বা, a(a – 3) -2(a – 3) = 0

বা, (a – 3)(a – 2) = 0

দুটি রাশির গুনফল শূন্য

∴ (a – 3) = 0

বা, a = 3

অথবা, (a – 2) =0

বা, a = 2

∴ a= 2 এবং a = 3

∴ \(\left(\frac{x+4}{x-4}\right)\) = 2

বা, x + 4 = 2x – 8

বা, x – 2x = -4 -8

বা, -x = -12

বা, x = 12

আবার, \(\left(\frac{x+4}{x-4}\right)\) = 3

বা, x + 4 = 3x – 12

বা, x – 3x = -4 -12

বা, -2x = -16

বা, x = \(\frac{-16}{-2}\)

বা, x = 8

∴ নির্ণেয় সমাধান x = 12 এবং x = 8

(b) দুই অঙ্কবিশিষ্ট একটি সংখ্যার একক স্থানীয় অঙ্কটি দশক স্থানীয় অঙ্ক অপেক্ষা 6 বেশী এবং অঙ্কদ্বয়ের গুণফল সংখ্যাটির চেয়ে 12 কম। সংখ্যাটির এককের অঙ্ক কী কী হতে পারে?

উত্তর :

ধরি, সংখ্যাটির দশক স্থানীয় অঙ্ক x

∴ সংখ্যাটির একক স্থানীয় অঙ্ক হবে (x + 6)

সুতরাং সংখ্যাটি হবে = 10x + (x + 6) = 11x + 6

শর্তানুসারে,

(11x + 6) -x(x + 6) = 12

বা, 11x + 6 – x² – 6x -12 = 0

বা, 5x – x² – 6 = 0

বা, – x² + 5x – 6 = 0

বা, -(x² – 5x + 6) = 0

বা, x² – 5x + 6 = 0

বা, x2 -(3 + 2)x + 6 = 0

বা, x² – 3x – 2x + 6 = 0

বা, x(x – 3)- 2(x – 3) = 0

বা, (x – 3)(x – 2) = 0

দুটি রাশির গুনফল শূন্য

∴ (x – 3) =0

বা, x = 3

অথবা

(x – 2) =0

বা, x = 2

∴ দশকের অঙ্কগুলি হল (2 + 6) = 8 বা (3 + 6) = 9

∴ সংখ্যাটির এককের ঘরের অঙ্কগুলি হবে 8 বা 9

7. যে কোনো একটি প্রশ্নের উত্তর দাও।

(a) সরলতম মান নির্ণয় করো \(\sqrt7\left(\sqrt5-\sqrt2\right)-\sqrt5\left(\sqrt7-\sqrt2\right)+\frac{2\sqrt2}{\sqrt5+\sqrt7}\)

উত্তর :

\(\sqrt7\left(\sqrt5-\sqrt2\right)-\sqrt5\left(\sqrt7-\sqrt2\right)+\frac{2\sqrt2}{\sqrt5+\sqrt7}\\\)

= \(\sqrt{35}-\sqrt{14}-\sqrt{35}\;+\sqrt{10}+\frac{2\sqrt2}{\sqrt5+\sqrt7}\times\frac{\sqrt5-\sqrt7}{\sqrt5-\sqrt7}\)

= \(\sqrt{35}-\sqrt{14}-\sqrt{35}\;+\sqrt{10}+\frac{2\sqrt2\left(\sqrt5-\sqrt7\right)}{\left(\sqrt5\right)^2-\left(\sqrt7\right)^2}\)

= \(\sqrt{35}-\sqrt{14}-\sqrt{35}\;+\sqrt{10}+\frac{2\sqrt2\left(\sqrt5-\sqrt7\right)}{\left(5-7\right)}\)

= \(\sqrt{35}-\sqrt{14}-\sqrt{35}\;+\sqrt{10}+\frac{2\sqrt2\left(\sqrt5-\sqrt7\right)}{-2}\)

= \(\sqrt{35}-\sqrt{14}-\sqrt{35}\;+\sqrt{10}-\sqrt2\left(\sqrt5-\sqrt7\right)\)

= \(\sqrt{35}-\sqrt{14}-\sqrt{35}\;+\sqrt{10}-\sqrt{10}+\sqrt{14}\)

= 0

(b) x ∝ y এবং y ∝ z হলে প্রমাণ করো (x² + y² + z²) ∝ (xy + yz + zx).

উত্তর :

x ∝ y

∴ x = Ay [A একটি অশূন্য ভেদ ধ্রুবক]

আবার y ∝ z

∴ y = Bz [B একটি অশূন্য ভেদ ধ্রুবক]

∴ x = Ay = A(Bz) = ABz = Cz [AB = C = অশূন্য ভেদ ধ্রুবক]

∴ x = Cz এবং y = Bz

∴ \(\frac{x^2+y^2+z^2}{xy+yz+zx}\)

= \(\frac{\left(Cz\right)^2+\left(Bz\right)^2+z^2}{\left(Cz)\left(Bz\right)\right)+\left(Bz\right)z+z\left(Cz\right)}\)

= \(\frac{C^2z^2+B^2z^2+z^2}{BCz^2+Bz^2+Cz^2}\)

= \(\frac{z^2\left(C^2+B^2+1\right)}{z^2\left(BC+B+C\right)}\)

= \(\frac{C^2+B^2+1}{BC+B+C}\)

= ধ্রুবক

(x² + y² + z²) ∝ (xy + yz + zx) (প্রমাণিত)

8. যে কোনো একটি প্রশ্নের উত্তর দাও।

(a) \(\frac{a+b-c}{a+b}=\frac{b+c-a}{b+a}=\frac{c+a-b}{c+a}\) এবং a + b + c ≠ 0 হলে প্রমাণ করো a = b = c.

উত্তর :

\(\frac{a+b-c}{a+b}=\frac{b+c-a}{b+a}=\frac{c+a-b}{c+a}\\\)

বা, \(\frac{a+b}{a+b}-\frac c{a+b}=\frac{b+c}{b+c}-\frac a{b+c}=\frac{c+a}{c+a}-\frac b{c+a}\)

বা, \(1-\frac c{a+b}=1-\frac a{b+c}=1-\frac b{c+a}\)

বা, \(\frac c{a+b}=\frac a{b+c}=\frac b{c+a}\) [প্রত্যেকটি পক্ষ থেকে 1বিয়োগ করে এবং প্রত্যেকটি পক্ষ কে-1 দ্বারা গুন করে পাই]

বা, \(\frac c{a+b}+1=\frac a{b+c}+1=\frac b{c+a}+1\)

বা, \(\frac{c+a+b}{a+b}=\frac{a+b+c}{b+c}=\frac{b+c+a}{c+a}\)

বা, \(\frac1{a+b}=\frac1{b+c}=\frac1{c+a}\) [প্রতিটি রাশিকে (a + b + c) দ্বারা ভাগ করে পাই, যেহেতু (a + b + c) ≠ 0]

এখন,

\(\frac1{a+b}=\frac1{b+c}\\\)

বা, b + c = a + b

বা, c = a_______(i)

আবার, \(\frac1{b+c}=\frac1{c+a}\)

বা, c + a = b + c

বা, a = b_______(ii)

 ∴ a = b = c (প্রমাণিত)

(b) x : a = y : b = z : c, হলে দেখাও (a² + b² + c²)(x² + y² + z²) = (ax + by + cz)² হবে।

ধরি, x : a = y : b = z : c = k [k (≠0) একটি আনুপাতিক ধ্রুবক]

∴ x = ak, y = bk, z = ck

বামপক্ষ –

(a² + b² + c²) (x² + y² + z²)

= (a² + b² + c²) {(ak)² + (bk)² + (ck)²}

= (a² + b² + c²) (a²k² + b²k² + c²k²)

= k²(a² + b² + c²) (a² + b² + c²)

= k²(a² + b² + c²)²

ডানপক্ষ –

(ax + by + cz)²

= {a(ak) + b(bk) + c(ck)}²

= (a²k + b²k + c²k)²

= k²(a² + b² + c²)²

∴ বামপক্ষ = ডানপক্ষ (প্রমানিত)

9. যে কোনো একটি প্রশ্নের উত্তর দাও।

(a) প্রমাণ করো একটি সমকোণী ত্রিভুজের সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে লম্বের দুপাশে যে দুটি ত্রিভুজ উৎপন্ন হয়, তারা মূল ত্রিভুজের সঙ্গে সদৃশ এবং পরস্পর সদৃশ।

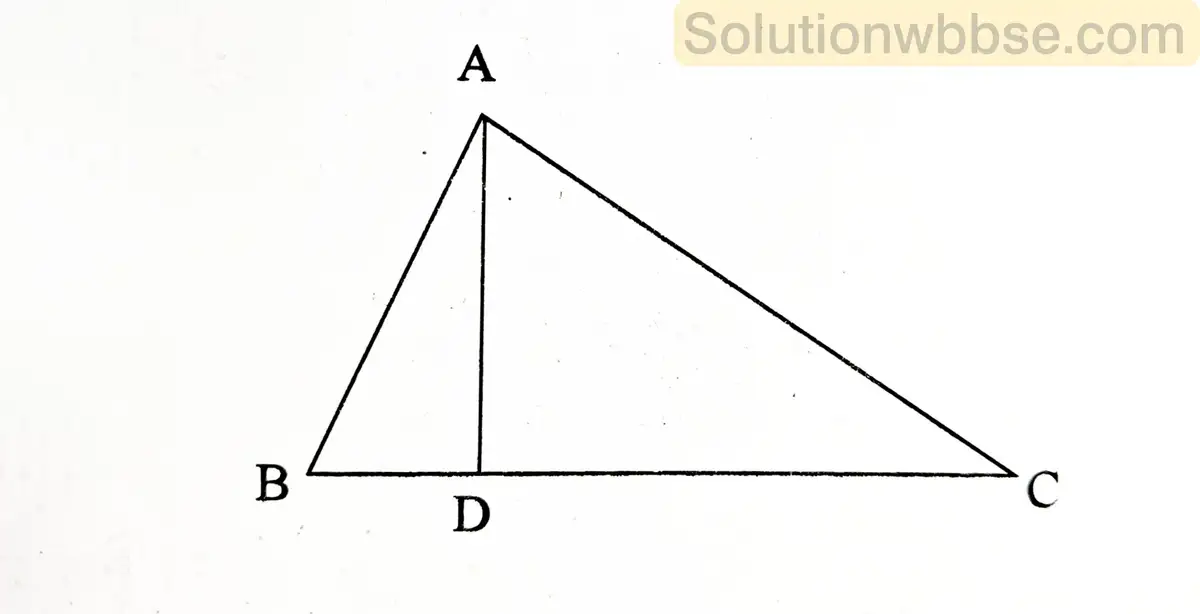
প্রদত্ত – ABC একটি সমকোণী ত্রিভুজ যার ∠A সমকোণ এবং সমকৌণিক বিন্দু A থেকে অতিভুজ BC-এর উপর AD লম্ব।

প্রমাণ করতে হবে – (i) ΔDBA ও ΔABC পরস্পর সদৃশ। (ii) ΔDAC ও ΔABC পরস্পর সদৃশ। (iii) ΔDBA ও ΔDAC পরস্পর সদৃশ।

প্রমাণ – ΔDBA ও ΔABC-এর মধ্যে,

∠BDA = ∠BAC = 90°

এবং∠ABD = ∠CBA. সুতরাং অবশিষ্ট ∠BAD = ∠BCA

∴ ΔDBA ও ΔABC সদৃশকোণী।

∴ ΔDBA ও ΔABC পরস্পর সদৃশ। [(ⅰ) প্রমাণিত]

আবার, ΔDAC ও ΔABC-এর মধ্যে,

∠ADC = ∠BAC = 90°

∠ACD = ∠BCA. সুতরাং অবশিষ্ট ∠CAD = ∠CBA

∴ ΔDAC ও ΔABC সদৃশকোণী।

∴ ΔDAC ও ΔABC সদৃশ। [(ii) প্রমাণিত]

ΔDBA ও ΔABC পরস্পর সদৃশ।

আবার, ΔDAC ও ΔABC পরস্পর সদৃশ।

সুতরাং ΔDBA ও ΔDAC পরস্পর সদৃশ। [(iii) প্রমাণিত]

(b) প্রমাণ করো কোনো বৃত্তের স্পর্শক ও স্পর্শ বিন্দুগামী ব্যাসার্ধ পরস্পর লম্ব।

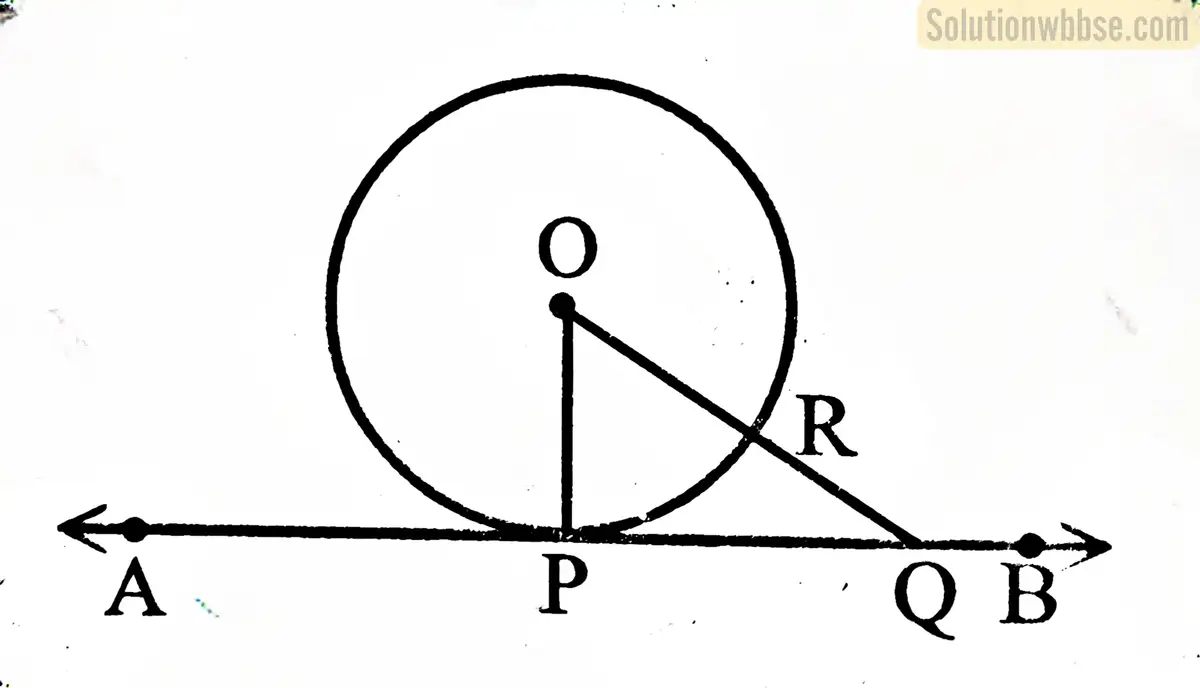
প্রদত্ত – O কেন্দ্রীয় বৃত্তের P বিন্দুতে AB স্পর্শক এবং OP, P বিন্দুগামী ব্যাসার্ধ।

প্রমাণ করতে হবে – OP ও AB স্পর্শক পরস্পর লম্ব। অর্থাৎ, OP ⊥ AB

অঙ্কন – AB স্পর্শকের উপর অপর যে-কোনো একটি বিন্দু Q নিলাম। O, Q বিন্দুদ্বয় যোগ করলাম।

প্রমাণ – স্পর্শক AB -এর উপর স্পর্শবিন্দু P ছাড়া অন্য যে-কোনো বিন্দু বৃত্তের বাইরে অবস্থিত। সুতরাং, OQ বৃত্তটিকে একটি বিন্দুতে ছেদ করবে।

মনে করি, ছেদবিন্দু R.

∴ OR < OQ [∵ R বিন্দু O, Q-এর মধ্যবর্তী]

আবার, OR = OP [∵ একই বৃত্তের ব্যাসার্ধ]

∴ OP < OQ

∵ Q বিন্দু A B স্পর্শকের উপর যে-কোনো বিন্দু, সুতরাং বৃত্তের কেন্দ্র O থেকে AB স্পর্শক পর্যন্ত যত সরলরেখাংশ অঙ্কন করা যায় OP তাদের মধ্যে ক্ষুদ্রতম। আবার ক্ষুদ্রতম দূরত্ব লম্ব দূরত্ব। সুতরাং, OP ⊥ AB (প্রমাণিত)

10. যে কোনো একটি প্রশ্নের উত্তর দাও।

(a) ABC ত্রিভুজের BC বাহুর উপর AD লম্ব এবং AD² = BD – DC; প্রমাণ করো ∠BAC একটি সমকোণ।

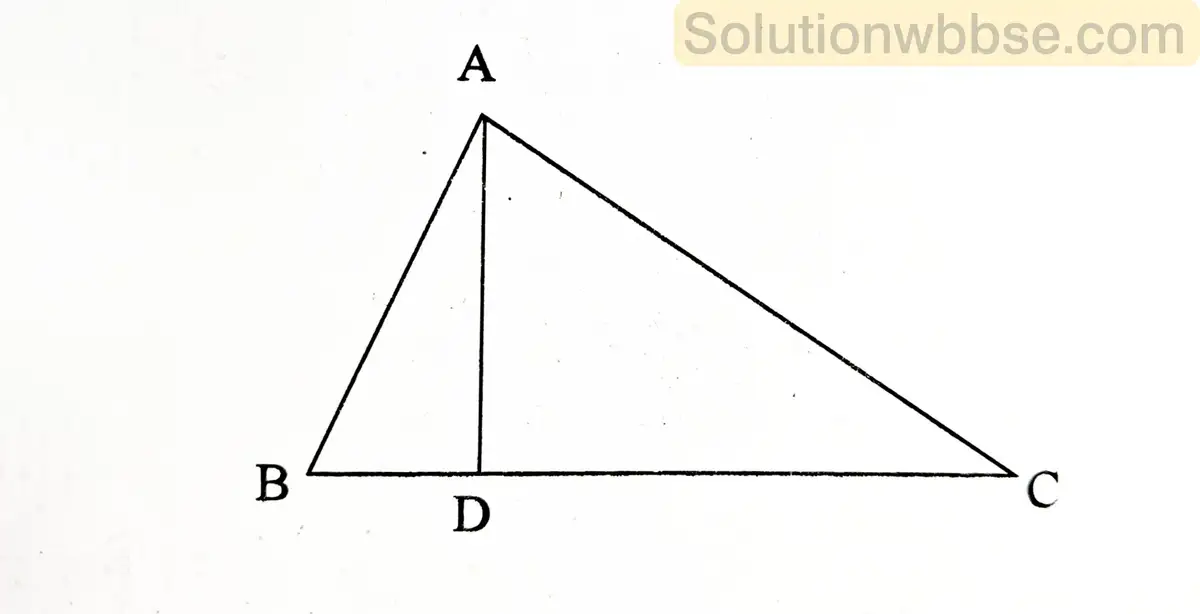
প্রমাণ – ΔBDA ও ΔADC-এর ∠BDA = ∠ADC = 90° [∵ AD ⊥ BC]

এবং AD2 = BD.DC

বা, \(\frac{AD}{BD}=\frac{DC}{AD}\)

∴ ΔBDA ও ΔADC সদৃশ। [যেহেতু দুটি ত্রিভুজের একটির একটি কোণ অপরটির একটি কোণের সমান হলে এবং কোণগুলির ধারক বাহুগুলি সমানুপাতী হলে, ত্রিভুজদ্বয় সদৃশ হয়]

সুতরাং, ∠ABD = ∠CAD এবং ∠BAD = ∠ACD

∴ ∠ABD + ∠ACD = ∠CAD + ∠BAD

বা, ∠B + ∠C = ∠A

বা, ∠A + ∠B+ ∠C = 2∠A

বা, 2∠A = 180°

∴ ∠A = 90°

∴ ∠BAC একটি সমকোণী ত্রিভুজ।

(b) একটি সরলরেখা দুটি এককেন্দ্রীয় বৃত্তের একটিকে A ও B বিন্দুতে এবং অপরটিকে C ও D বিন্দুতে ছেদ করেছে। প্রমাণ করো AC = BD.

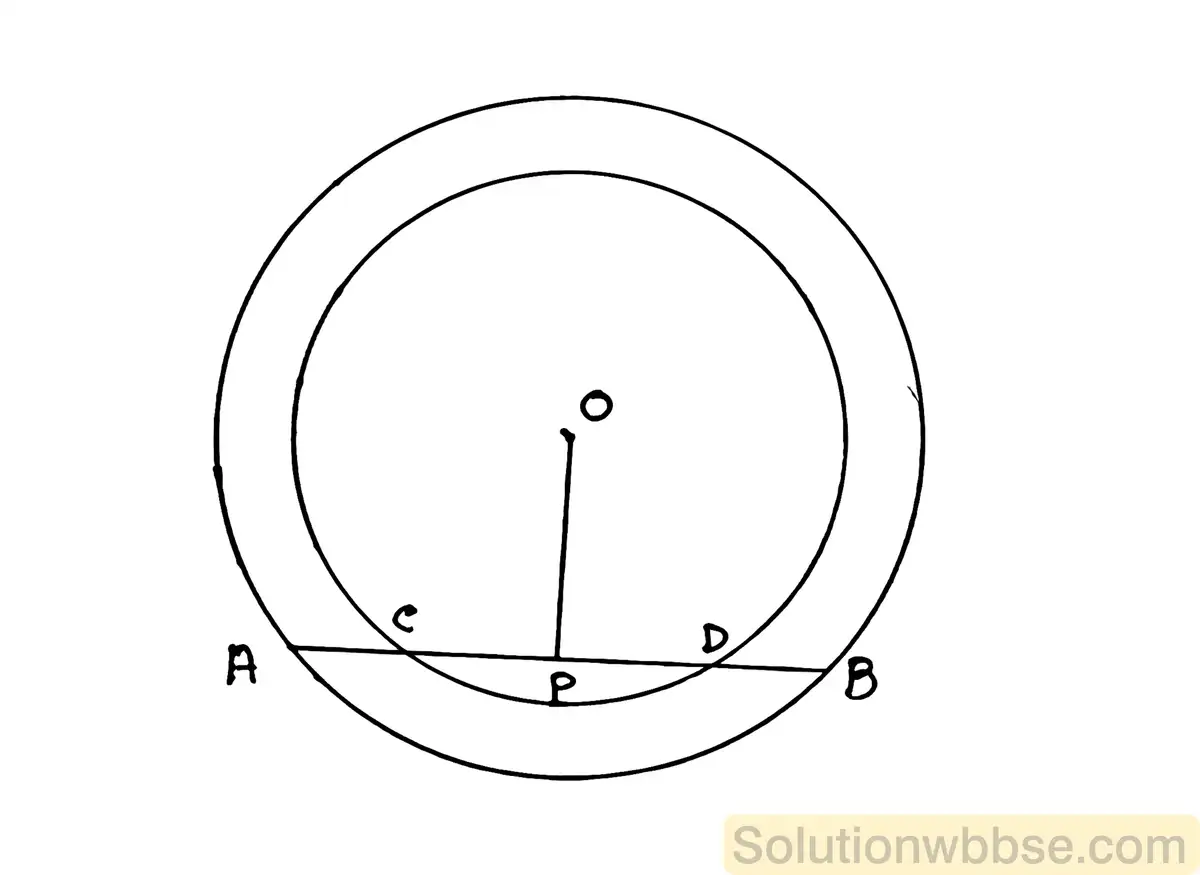
চিত্রে O কেন্দ্রীয় দুটি বৃত্তকে একটি সরলরেখা যথাক্রমে A,B এবং C,D বিন্দুতে ছেদ করেছে।

প্রমান করতে হবে যে – AB = CD

অঙ্কন – O থেকে AB এর ওপর একটি লম্ব OP অঙ্কন করা হল।

প্রমান – যেহেতু বৃত্তের কেন্দ্রগামী কোনও জ্যা এর ওপর অঙ্কিত লম্ব জ্যা টিকে সমদ্বিখন্ডিত করে। তাই P, AB এবং CD উভয়ের মধ্যবিন্দু।

∴ AP = PB এবং CP = PD

সুতরাং AP – CP = PB – PD

∴ AC = DB (প্রমানিত)

11. যে কোনো একটি প্রশ্নের উত্তর দাও।

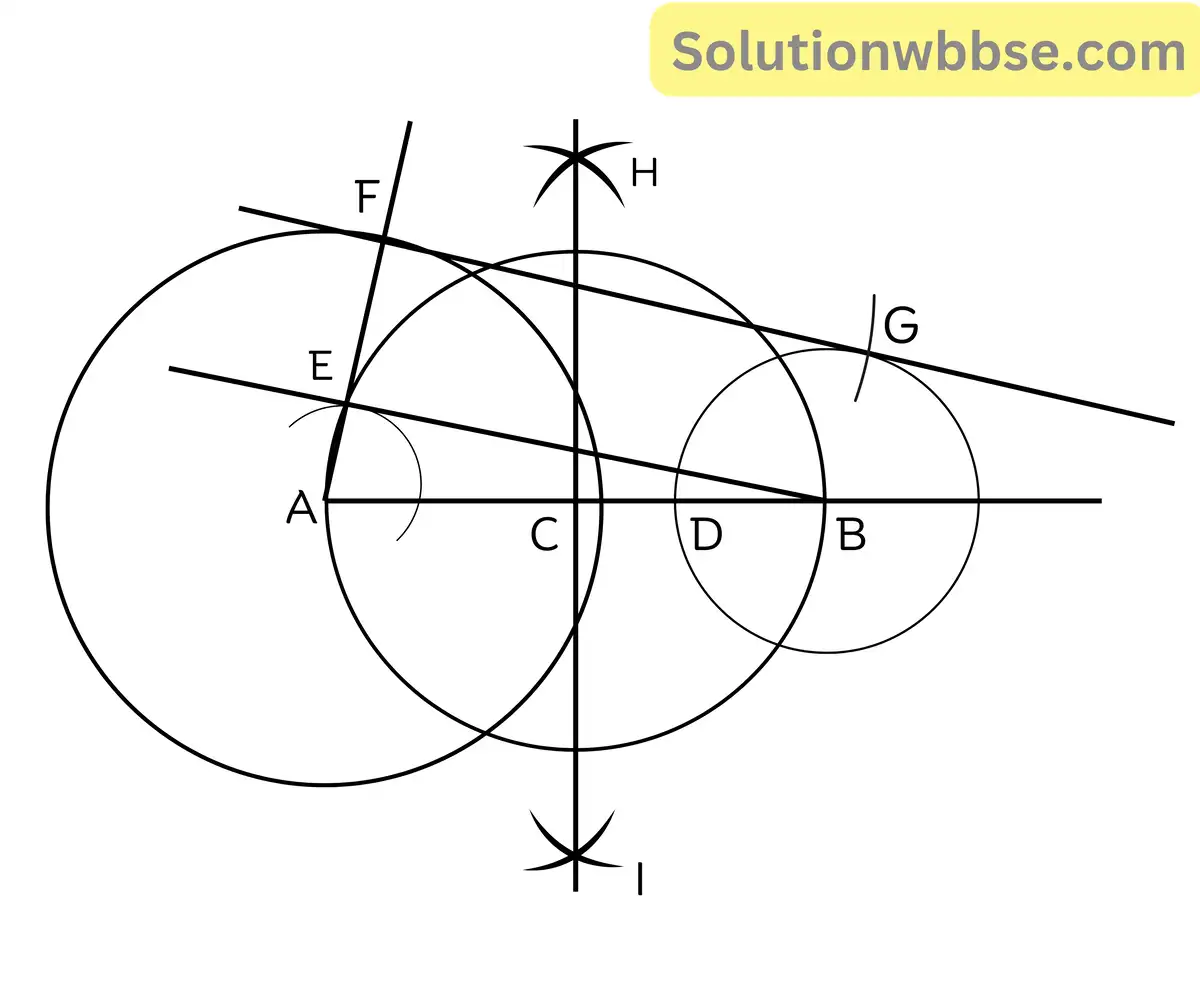
(a) 4 সেমি ও 2 সেমি ব্যাসার্ধবিশিষ্ট দুটি বৃত্ত অঙ্কন করো যাদের কেন্দ্রদ্বয়ের দূরত্ব 7 সেমি। ঐ বৃত্তদুটির একটি সরল সাধারণ স্পর্শক অঙ্কন করো। (কেবলমাত্র অঙ্কন চিহ্ন দিতে হবে।)

(b) একটি ত্রিভুজ অঙ্কন করো যার দুটি বাহুর দৈর্ঘ্য 9 সেমি 7 সেমি এবং তাদের অন্তর্ভুক্ত কোণ 60°; ত্রিভুজটির অন্তবৃত্ত অঙ্কন করো। (কেবলমাত্র অঙ্কন চিহ্ন দিতে হবে।)

12. যে কোনো দুটি প্রশ্নের উত্তর দাও।

(a) একটি বৃত্তের 220 সেমি দৈর্ঘ্যের বৃত্তচাপ বৃত্তের কেন্দ্রে 60° পরিমাপের কোণ উৎপন্ন করলে, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য নির্ণয় করো।

উত্তর :

60° = 60 × \(\frac{\mathrm\pi}{180^\circ}=\frac{\mathrm\pi}3\)

ধরি, বৃত্তের ব্যাসার্ধ r সেমি.

∴ \(\frac{220}r=\frac{\mathrm\pi}3\)

বা, πr = 660

বা, \(\frac{22}7\)r = 660

বা, r = \(\frac{660\times7}{22}\)

বা, r = 210

∴ বৃত্তের ব্যাসার্ধ 210 সেমি.।

(b) যদি, \(\cos^2\theta–\sin^2\theta=\frac12\) হয়, তাহলে \(\tan^2\theta\) -এর মান নির্ণয় কর।

উত্তর :

\(\cos^2\theta–\sin^2\theta=\frac12\\\)

বা, \(\cos^2\theta-\left(1-\cos^2\theta\right)=\frac12\)

বা, \(\cos^2\theta-1+\cos^2\theta=\frac12\)

বা, \(2\cos^2\theta-1=\frac12\)

বা, \(2\cos^2\theta=\frac12+1\)

বা, \(\cos^2\theta=\frac34\)

বা, \(sec^2\theta=\frac1{\cos^2\theta}=\frac1{\displaystyle\frac34}=\frac43\)

বা, \(1+\tan^2\theta=\frac43\)

বা, \(\tan^2\theta=\frac43-1\)

বা, \(\tan^2\theta=\frac13\)

∴ \(\tan^2\theta=\frac13\)

(c) মান নির্ণয় করো – \(\frac{sec17^\circ}{\cos ec73^\circ}+\frac{\tan68^\circ}{cot22^\circ}+\cos^244^\circ+\cos^246^\circ\)

উত্তর :

\(\frac{sec17^\circ}{\cos ec73^\circ}+\frac{\tan68^\circ}{cot22^\circ}+\cos^244^\circ+\cos^246^\circ\\\)

= \(\frac{sec17^\circ}{\cos ec\left(90^\circ-17^\circ\right)}+\frac{\tan68^\circ}{cot\left(90^\circ-68^\circ\right)}+\cos^244^\circ+\cos^246^\circ\)

= \(\frac{sec17^\circ}{\cos ec17^\circ}+\frac{\tan68^\circ}{cot68^\circ}+\cos^244^\circ+\cos^2\left(90^\circ-44^\circ\right)\)

= \(\frac{sec17^\circ}{\cos ec17^\circ}+\frac{\tan68^\circ}{cot68^\circ}+\cos^244^\circ+\sin^244^\circ\)

= 1 + 1 + 1

= 3

13. যে কোনো একটি প্রশ্নের উত্তর দাও।

(a) সূর্য্যের উন্নতি কোণ 45° থেকে বৃদ্ধি পেয়ে 60° হলে, একটি খুঁটির ছায়ার দৈর্ঘ্য 3 মিটার কমে যায়। খুঁটিটির উচ্চতা নির্ণয় করো।

উত্তর :

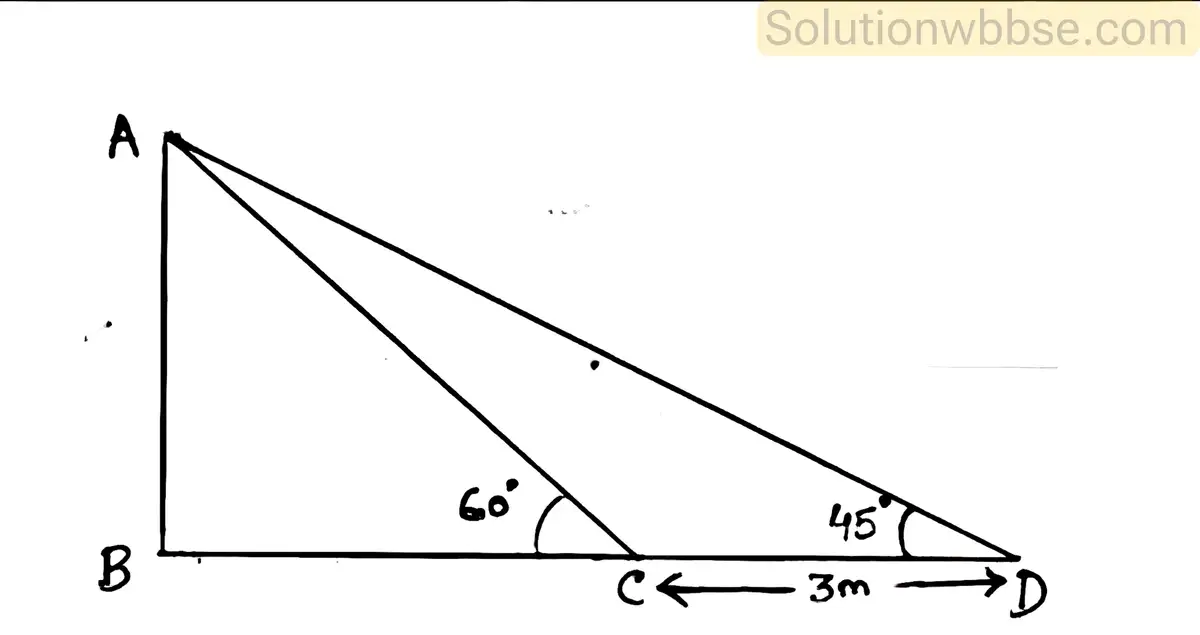
ধরাযাক, AB হল খুঁটির দৈর্ঘ্য। যখন সূর্যের উন্নতি কোণ 45° হলে খুঁটির ছায়ার দৈর্ঘ্য BD এবং সূর্যের উন্নতি কোণ 60° হলে খুঁটির ছায়ার দৈর্ঘ্য হয় BC, অর্থাৎ খুঁটির ছায়ার দৈর্ঘ্য CD কমে যায়।

∴ CD = 3 মিটার

ABC ত্রিভুজের ∠ABC = 90° এবং ∠ACB = 60°

এখন ABC সমকোণী ত্রিভুজ থেকে পাই,

tan∠ACB = tan 60° = $\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{AB}{BC}$

বা, \(\sqrt3=\frac{AB}{BC}\) [যেহেতু,tan 60° = \(\sqrt3\)]

বা, BC = \(\sqrt3\)_______(i)

আবার ABD ত্রিভুজের ∠ABD = 90° এবং ∠ADB = 30°

ABD সমকোণী ত্রিভুজ থেকে পাই,

tan∠ADB = tan 45° = $\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{AB}{BD}$

বা, 1 = \(\frac{AB}{BD}\) [যেহেতু, tan 45° = 1]

বা, AB = BD

বা, AB = BC + CD

বা, AB = \(\frac{AB}{\sqrt3}\) + 3 [যেহেতু, BC = \(\frac{AB}{\sqrt3}\) এবং CD = 3 মিটার]

বা, AB\(\sqrt3\) = AB + 3\(\sqrt3\)

বা, AB\(\sqrt3\) – AB = 3\(\sqrt3\)

বা, AB\(\left(\sqrt3-1\right)\) = 3\(\sqrt3\)

বা, AB = \(\frac{3\sqrt3}{\left(\sqrt3-1\right)}\)

বা, AB = \(\frac{3\sqrt3}{\left(\sqrt3-1\right)}\times\frac{\left(\sqrt3+1\right)}{\left(\sqrt3+1\right)}\)

বা, AB = \(\frac{3\sqrt3\left(\sqrt3+1\right)}{\left(\sqrt3\right)^2-1^2}\)

বা, AB = \(\frac{9+3\sqrt3}{3-1}\)

বা, AB = \(\frac{9+3\left(1.732\right)}2\) [[যেহেতু \(\sqrt3\) = 1.732]]

বা, AB = \(\frac{14.196}2\)

বা, AB = 7.098

∴ খুঁটিটির উচ্চতা 7.098 মিটার।

(b) 5 মিটার উঁচু একটি রেলওয়ে ওভারব্রিজে দাঁড়িয়ে এক ব্যক্তি প্রথমে একটি ট্রেনের ইঞ্জিনকে ব্রিজের এপারে 30° অবনতি কোণে দেখলেন। কিন্তু 2 সে. পরে ঐ ইঞ্জিনকে ব্রিজের ওপারে 45° অবনতি কোণে দেখলেন। ট্রেনটির গতিবেগ কত?

উত্তর :

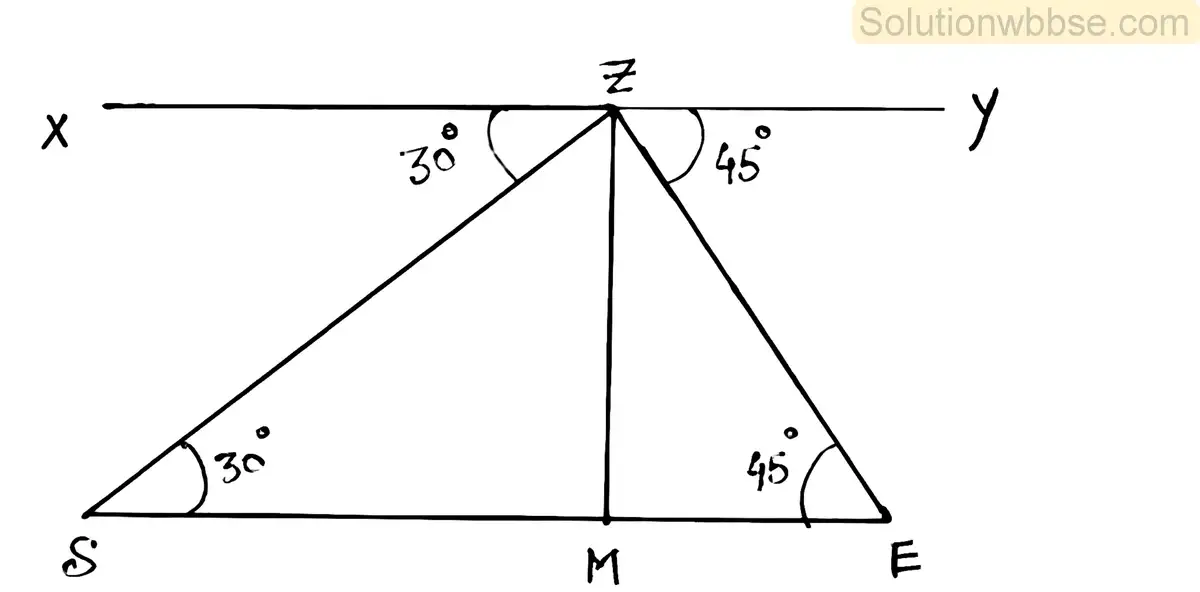
ধরি, ওই ব্যাক্তি XY রেলওয়ে ওভারব্রিজের Z বিন্দুতে দাঁড়িয়ে ট্রেনের ইঞ্জিনকে প্রথমে S বিন্দুতে এবং 2 সেকেন্ড পরে E বিন্দুতে দেখলেন । অবনতি কোণ ∠BAS =30° এবং ∠CAE = 45°

ZM = রেলওয়ে ওভারব্রিজের উচ্চতা = 5 মিটার

আবার যেহেতু XY∥SE

∴ ∠ZSM = একান্তর ∠XZS = 30°

এবং ∠ZEM = একান্তর ∠YZE = 45°

সমকোণী ত্রিভুজ ZSM থেকে পাই,

tan30° = $\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{ZM}{SM}=\frac{5\sqrt{3}}{SM}$

বা, \(\frac1{\sqrt3}=\frac{5\sqrt3}{SM}\)

বা, SM = 15

সমকোণী ত্রিভুজ ZEM থেকে পাই

tan45° = $\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{ZM}{ME}=\frac{5\sqrt{3}}{ME}$

বা, 1 = \(\frac{5\sqrt3}{ME}\)

বা, ME = \(5\sqrt3\)

∴ SE = SM + ME

= (15 + \(5\sqrt3\))

=15 + (5 × 1.732)

= 15 + 8.660

= 23.660

∴ 2 সেকেন্ডে ট্রেনটি অতিক্রম করে 23.660 মিটার।

∴ ট্রেনটির গতিবেগ = \(\frac{23.660}2\) মিটার/সেকেন্ড

= 11.83 মিটার/সেকেন্ড (প্রায়)

14. যে কোনো দুটি প্রশ্নের উত্তর দাও।

(a) একটি ঘনকের প্রতিটি বাহুকে 50% কমানো হল। মূল ঘনক ও পরিবর্তিত ঘনকের ঘনফলের অনুপাত কত?

উত্তর :

ধরি ঘনকের প্রতিটি বাহুর দৈর্ঘ্য a একক

∴ ঘনকটির ঘনফল = a³ ঘনএকক

প্রতিটি বাহুর দৈর্ঘ্য 50% কমানো হলে, পরিবর্তিত ঘনকের প্রতিটি বাহুর দৈর্ঘ্য

= \(\left\{a-\left(a\times\frac{50}{100}\right)\right\}\) একক

= \(\left(a-\frac a2\right)\) একক

= \(\frac a2\) একক

পরিবর্তিত ঘনকের ঘনফল

= \(\left(\frac a2\right)^3\) ঘন একক

= \(\frac{a^3}8\) ঘন একক

সুতরাং মূল ঘনক এবং পরিবর্তিত ঘনকের ঘনফলের অনুপাত

= \(a^3:\frac{a^3}8\)

= 8 : 1

∴ মূল ঘনক ও পরিবর্তিত ঘনকের অনুপাত 8 : 1

(b) ঢাকনাবিহীন একটি লম্ববৃত্তাকার চোঙাকৃতি পাত্রের সমগ্রতলের ক্ষেত্রফল 2002 বর্গসেমি। পাত্রটির ভূমির ব্যাসার্ধ্য 7 সেমি হলে, পাত্রটিতে কত লিটার জল ধরবে? (1 লিটার = 1 ঘন ডেসিমি)

উত্তর :

ঢাকনাবিহীন একটি লম্ব বৃত্তাকার পাত্রের ভূমির ব্যাসার্ধ (r) দৈর্ঘ্য 7 সেমি.

ধরি, লম্ব বৃত্তাকার পাত্রের উচ্চতা = h সেমি.

ঢাকনাবিহীন পাত্রটির সমগ্রতলের ক্ষেত্রফল

= 2rπh + πr² বর্গ সেমি.

= \(2\times\frac{22}7\times7\times h+\frac{22}7\times\left(7\right)^2\) বর্গ সেমি.

= 44h + 154 বর্গ সেমি.

শর্তানুসারে,

44h + 154 = 2002

বা, 44h = 2002 – 154

বা,44h = 1848

বা, h = 42

∴ পাত্রটির উচ্চতা 42 সেমি.।

∴ পাত্রটির আয়তন = πr²h

= \(\frac{22}7\times\left(7\right)^2\times42\) ঘন সেমি.

∴ পাত্রটিতে সংখ্যা জল ধরে 6468 লিটার।

(c) 21 ডেসিমি দীর্ঘ, 11 ডেসিমি প্রশস্ত ও 6 ডেসিমি গভীর একটি চৌবাচ্চার অর্ধেক জলপূর্ণ আছে। ঐ চৌবাচ্চায় যদি 21 সেমি ব্যাসের 100 টি নিরেট গোলক ডুবিয়ে দেওয়া যায়, তবে জলতল কত ডেসিমি উঠে আসবে?

উত্তর :

ধরি, 21 ডেসিমি. দীর্ঘ, 11 ডেসিমি. প্রশস্থ এবং 6 ডেসিমি. গভীর একটি চৌবাচ্চায় 21 সেমি. ব্যাসের 100 টি লোহার গোলক সম্পূর্ণ ডুবিয়ে দিলে জলতল h সেমি. উঠবে।

লোহার গোলকের ব্যাসের দৈর্ঘ্য 21 সেমি.

∴ লোহার গোলকের ব্যাসার্ধ (r) = \(\frac{21}2\) সেমি.

= \(\frac{21}{20}\) ডেসিমি.

এখন, h উচ্চতার জলস্তম্ভের আয়তন = 100 টি লোহার গোলকের আয়তন

∴ 21 × 11 × h = 100 × \(\frac43\mathrm\pi\left(\frac{21}{20}\right)^3\)

বা, 21 × 11 × h = 100 × \(\frac43\times\frac{22}7\times\frac{21}{20}\times\frac{21}{20}\times\frac{21}{20}\)

বা, h = 100 × \(\frac43\times\frac{22}7\times\frac{21}{20}\times\frac{21}{20}\times\frac{21}{20}\times\frac1{21}\times\frac1{11}\)

বা, h = 2.1 ডেসিমি.

∴ চৌবাচ্চার জলতল 2.1 ডেসিমি. উপরে উঠবে।

15. যে কোনো দুটি প্রশ্নের উত্তর দাও।

(a) নিম্নে প্রদত্ত প্রবেশিকা পরীক্ষায় পরীক্ষার্থীর বয়সের পরিসংখ্যা বিভাজন ছক থেকে সংখ্যাগুরু মান নির্ণয় করো।

বয়স (বছরে)	16-18	18-20	20-22	22-24	24-26
পরীক্ষার্থীর সংখ্যা	45	75	38	22	20

উত্তর :

প্রদত্ত পরিসংখ্যা বিভাজনের সংখ্যাগুরু মানের শ্রেণী = 18 – 20

সংখ্যাগুরু মান নির্ণয়ের সূত্রটি হলো = \(I+\left(\frac{f_1-f_0}{2f_1-f_0-f_2}\right)\times h\)

যেখানে,

I = হলো সংখ্যাগুরুমান সংবলিত শ্রেণীর নিম্ন শ্রেণী সীমানা।

h = সংখ্যাগুরু মান সংবলিত শ্রেণীর শ্রেণী দৈর্ঘ্য।

f₁ = সংখ্যাগুরুমান সংবলিত শ্রেণীর শ্রেণী পরিসংখ্যা।

f₀ = সংখ্যাগুরুমান সংবলিত শ্রেণীর ঠিক পূর্ববর্তী শ্রেণীর পরিসংখ্যা।

f₂ = সংখ্যাগুরুমান সংবলিত শ্রেণীর ঠিক পরবর্তী শ্রেণীর পরিসংখ্যা।

∴ \(I+\left(\frac{f_1-f_0}{2f_1-f_0-f_2}\right)\times h\)

= \(18+\left(\frac{75-45}{2\times75-45-38}\right)\times2\) [এখানে, I = 18, \(f_1\) = 75, \(f_0\) = 45. \(f_2\) = 38, h = 2]

= \(18+\frac{30}{67}\times2\)

= \(18+\frac{60}{67}\)

= 18 + 0.90

= 18.90 [ প্রায়]

(b) নীচের তথ্যের মধ্যমা নির্ণয় করো।

শ্রেণি সীমা	1-5	6-10	11-15	16-20	21-25	26-30	31-35
পরিসংখ্যা	2	3	6	7	5	4	3

উত্তর :

প্রদত্ত পরিসংখ্যা বিভাজনের ছকের শ্রেণীগুলি শ্রেণী অন্তর্ভুক্ত গথনে আছে।

শ্রেণী বহির্ভূত পরিসংখ্যা বিভাজনের তালিকা তৈরি করি,

শ্রেণী-সীমা	শ্রেণী সীমানা	পরিসংখ্যা	ক্রম-যৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক)
1-5	0.5 – 5.5	2	2
6-10	5.5 – 10.5	3	5
11-15	10.5 – 15.5	6	11
16-20	15.5 – 20.5	7	18
21-25	20.5 – 25.5	5	23
26-30	25.5 – 30.5	4	27
31-35	30.5 – 35.5	3	30 = n

এখানে n = 30

∴ \(\frac n2=\frac{30}2\) = 15

15 এর থেকে ঠিক বেশি পরিসংখ্যা বিশিষ্ট শ্রেণী টি হলো (15.5 – 20.5)

∴ মধ্যমা শ্রেণী টি হলো = 15.5 – 20.5

∴ মধ্যমা নির্ণয়ের সূত্র টি হলো

= \(I+\left[\frac{{\displaystyle\frac n2}-cf}f\right]\times h\)

I = মধ্যমা শ্রেণীর নিম্ন শ্রেণী সীমানা।

n = মোট পরিসংখ্যা।

f = মধ্যমা শ্রেণীর পরিসংখ্যা।

h = শ্রেণী দৈর্ঘ্য।

cf = মধ্যমা শ্রেণীর পূর্বের শ্রেণীর পরিসংখ্যা।

= \(I+\left[\frac{{\displaystyle\frac n2}-cf}f\right]\times h\)

= 15.5 + \(\left[\frac{15-11}7\right]\) × 5 [ এখানে, I = 15.5, n = 30, cf = 11, f = 7, h = 5]

= 15.5 + \(\frac47\) × 5

= 15.5 + \(\frac{20}7\)

= 15.5 + 2.86

= 18.36 [প্রায়]

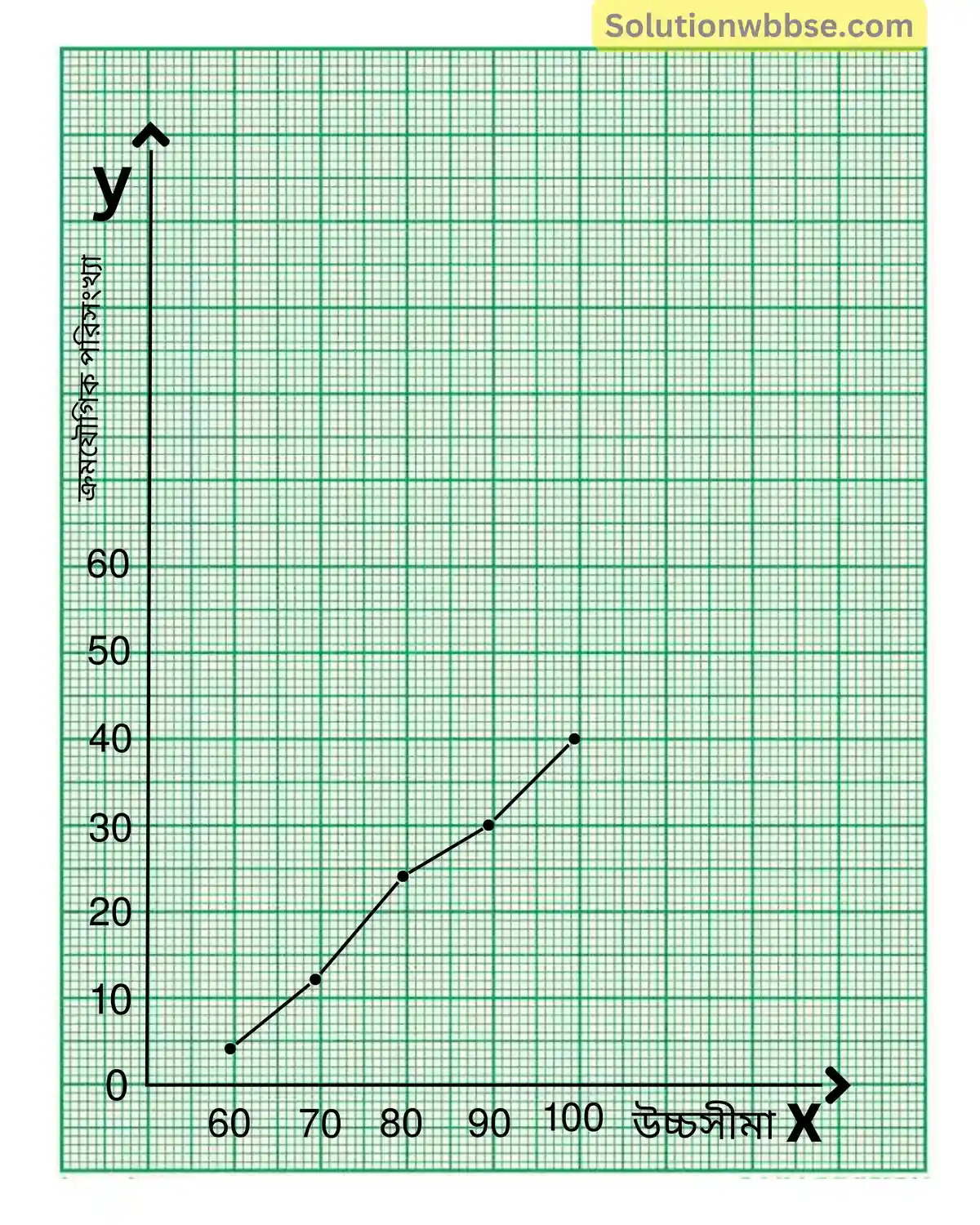
(c) নীচের পরিসংখ্যা বিভাজনের ক্ষুদ্রতর সূচক ওজাইভ অঙ্কন করো।

শ্রেণি সীমা	50-60	60-70	70-80	80-90	90-100
পরিসংখ্যা	4	8	12	6	10

উত্তর :

শ্রেণি	ক্ষুদ্রতর সূচক ক্রমযৌগিক পরিসংখ্যা
60 এর কম	4
70 এর কম	12
80 এর কম	24
90 এর কম	30
100 এর কম	40

X অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1 টি বাহুর দৈর্ঘ্য = 1 একক এবং y অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1 টি বাহুর দৈর্ঘ্য = 1 একক ধরে

(60,4), (70,12), (80,24), (90,30), (100,40) বিন্দুগুলি স্থাপন করে ও যুক্ত করে ক্ষুদ্রতর সুচক ওজাইভ অঙ্কন কর।

২০১৮ সালের মাধ্যমিক গণিত প্রশ্নপত্র ছিল সুষম এবং ভারসাম্যপূর্ণ। প্রশ্নগুলি বিভিন্ন বিষয় থেকে এসেছিল এবং বিভিন্ন ধরণের দক্ষতা পরীক্ষা করেছিল। পরবর্তী বছরের পরীক্ষার জন্য ভালোভাবে প্রস্তুতি নিতে হলে শিক্ষার্থীদের উচিত পাঠ্যপুস্তক ভালোভাবে পড়াশোনা করা, অনুশীলন করা এবং আগের বছরের প্রশ্নগুলি সমাধান করা।

এই ব্লগ পোস্টটি আপনাদের মাধ্যমিক গণিত পরীক্ষার প্রস্তুতি নেওয়ার ক্ষেত্রে সহায়ক হবে বলে আমরা আশা করি।