মাধ্যমিক ভৌতবিজ্ঞান – চলতড়িৎ – তড়িৎপ্রবাহ, ওহমের সূত্র ও রোধ

এই আর্টিকেলে আমরা মাধ্যমিক ভৌতবিজ্ঞানের একটি গুরুত্বপূর্ণ অংশ “তড়িৎপ্রবাহ, ওহমের সূত্র ও রোধ” নিয়ে আলোচনা করব। এই অংশটি মাধ্যমিক ভৌতবিজ্ঞান পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ। এই “তড়িৎপ্রবাহ, ওহমের সূত্র ও রোধ” অংশটি মাধ্যমিক ভৌতবিজ্ঞানের ষষ্ঠ অধ্যায় “চলতড়িৎ“ -এর একটি গুরুত্বপূর্ণ অংশ। এই “তড়িৎপ্রবাহ, ওহমের সূত্র ও রোধ” থেকে গুরুত্বপূর্ণ প্রশ্ন মাধ্যমিক পরীক্ষায় এবং চাকরির পরীক্ষায় প্রায়ই দেখা যায়।

মাধ্যমিক ভৌতবিজ্ঞান – চলতড়িৎ – তড়িৎপ্রবাহ, ওহমের সূত্র ও রোধ

তড়িৎপ্রবাহমাত্রা –

কোনো পরিবাহীর মধ্য দিয়ে তড়িৎগ্রস্ত কণার প্রবাহকে (যেমন – ইলেকট্রন) তড়িৎপ্রবাহ বলে। এক্ষেত্রে একক সময়ে পরিবাহীর যে-কোনো প্রস্থচ্ছেদের মধ্য দিয়ে যে পরিমাণ আধান প্রবাহিত হয় তাকে তড়িৎ প্রবাহমাত্রা বলে।

• প্রবাহমাত্রা \(I = \frac{Q}{t}\) [q = আধান] যদি n -সংখ্যক ইলেকট্রন প্রবাহিত হয় তাহলে Q = n⋅e সেক্ষেত্রে \(I = \frac{ne}{t}\)
• একক – SI একক হল কুলম্ব·সেকেন্ড⁻¹ বা অ্যাম্পিয়ার (A)
• প্রবাহমাত্রা হল স্কেলার রাশি।
• তড়িৎপ্রবাহ চলাকালীন তারের মধ্যে ইলেকট্রন প্রবাহিত হয় কিন্তু প্রবাহমাত্রার অভিমুখ ইলেকট্রন প্রবাহের অভিমুখের বিপরীতে ধরা হয়। অর্থাৎ, ইলেকট্রন -ve প্রান্ত থেকে +ve প্রান্তের দিকে যায় কিন্তু প্রবাহ +ve প্রান্ত থেকে -ve প্রান্তে যায়।
• প্রবাহমাত্রা প্রাথমিক রাশি। এর মাত্রা ‘A’।
• প্রবাহমাত্রা দুই প্রকার। যথা – সমমুখী প্রবাহ (DC current) ও পরিবর্তী প্রবাহ (AC current)। যে-কোনো কোশ থেকে সমমুখী প্রবাহ সৃষ্টি হয় যা সবসময় একই অভিমুখে যায় কিন্তু ডায়নামো থেকে AC প্রবাহ সৃষ্টি হয় যা নির্দিষ্ট সময় অন্তর দিকপরিবর্তন করে।

ওহমের সূত্র –

উষ্ণতা ও অন্যান্য ভৌত অবস্থা অপরিবর্তিত থাকলে কোনো পরিবাহীর দুই প্রান্তের বিভবপার্থক্য ওর মধ্য দিয়ে তড়িৎ প্রবাহমাত্রার সমানুপাতিক হয়।

• কোনো পরিবাহীর দুই প্রান্তের বিভবপার্থক্য V_A​ − V_B​ হলে এবং প্রবাহমাত্রা I হলে (V_A​ − V_B​​) ∝ I⋅R
• R হল পরিবাহীতে তড়িৎপ্রবাহের পথে বাধা, যাকে রোধ বলা হয়। রোধকে পরিবাহীর দুই প্রান্তের মধ্যে বিভবপার্থক্য ও পরিবাহীতে প্রবাহমাত্রার অনুপাতের সাহায্যে প্রকাশ করা হয়।

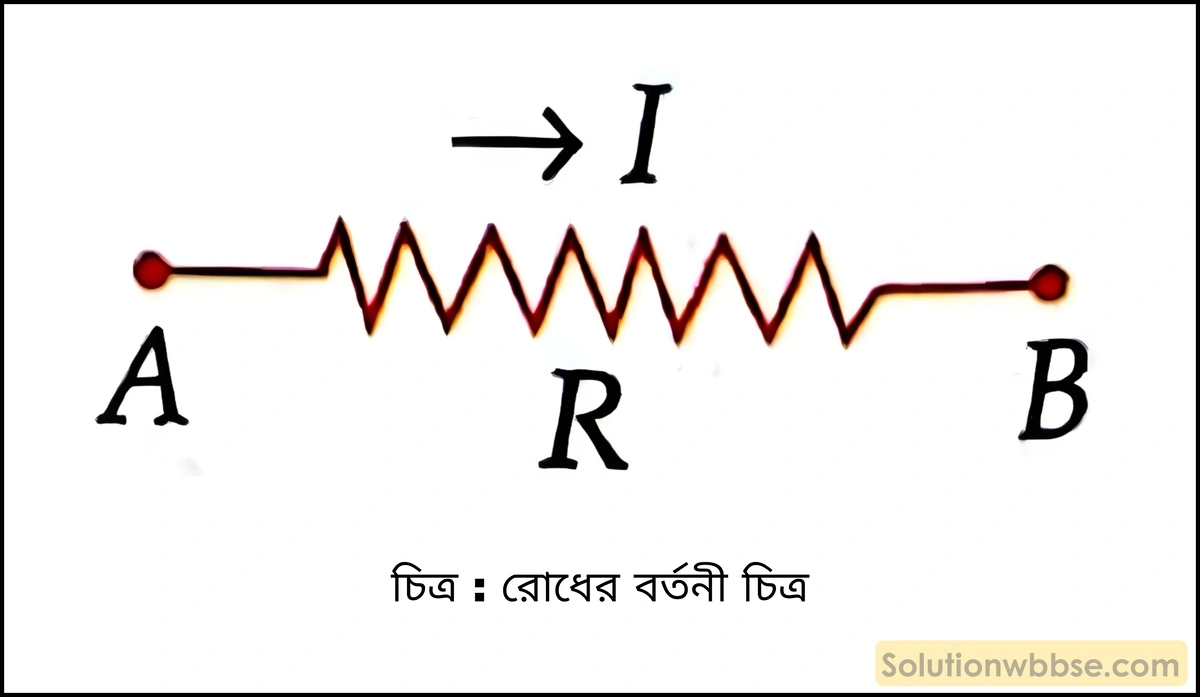
• রোধের একক হল ওহম (Ω) বা ভোল্ট-অ্যাম্পিয়ার⁻¹।
• রোধের মাত্রা হল ML²T⁻³A⁻²।
• রোধের অন্যোন্যক হল পরিবাহিতা। যারএকক হল ohm⁻¹ বা mho বা সিমেন্স (S)।
• পরিবাহিতার মাত্রা হল M⁻¹L⁻²T³A²।
• ওহমীয় পরিবাহীর ক্ষেত্রে V-I লেখচিত্র সরলরৈখিক। উদাহরণ – ধাতব পরিবাহী।

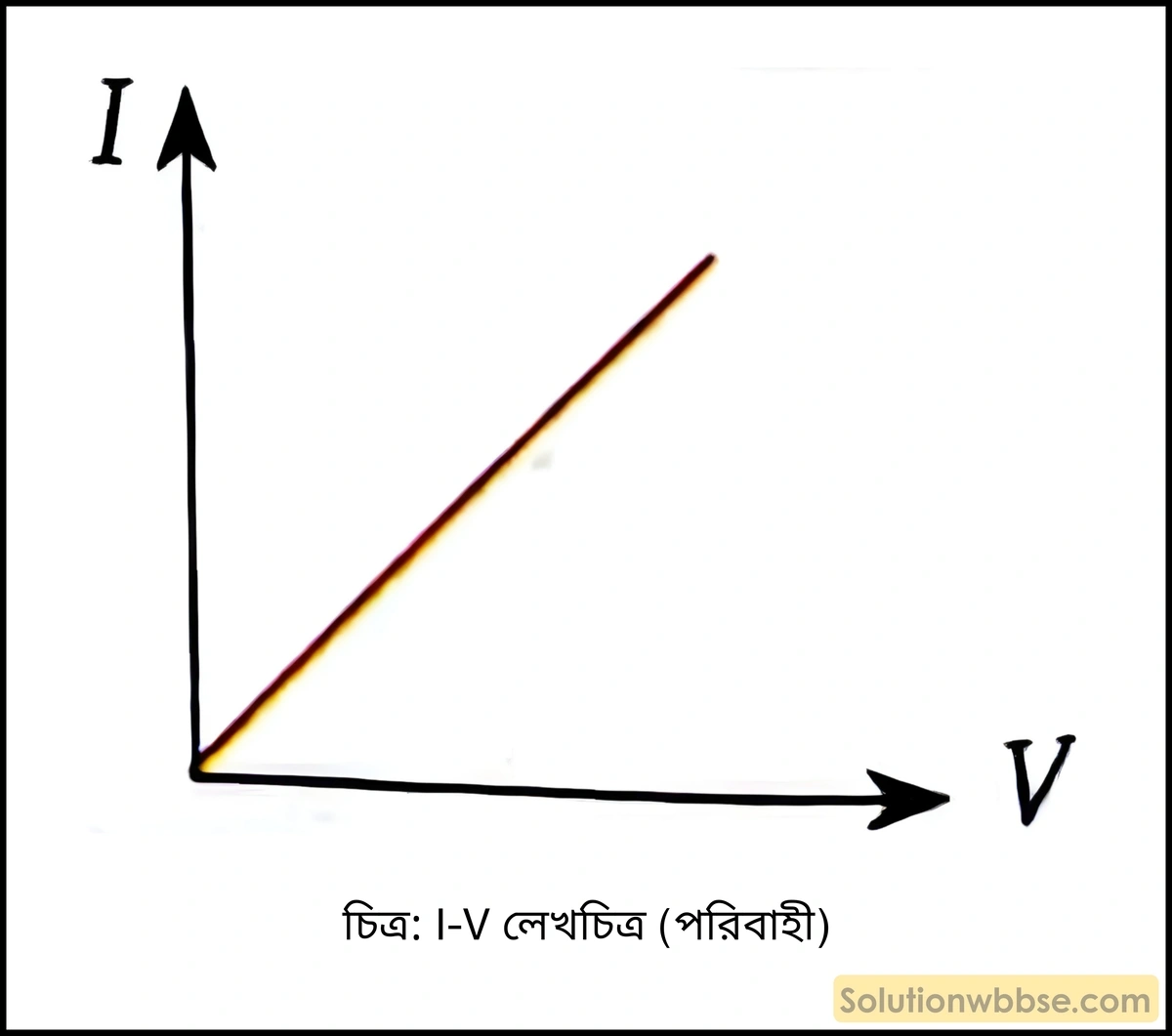
যে সমস্ত পরিবাহী ওহমের সূত্র মেনে চলে না তাদের অ-ওহমীয় পরিবাহী বলে। এদের ক্ষেত্রে V-I লেখচিত্র সরলরৈখিক হয় না। যেমন – অর্ধপরিবাহী Ge, Si।

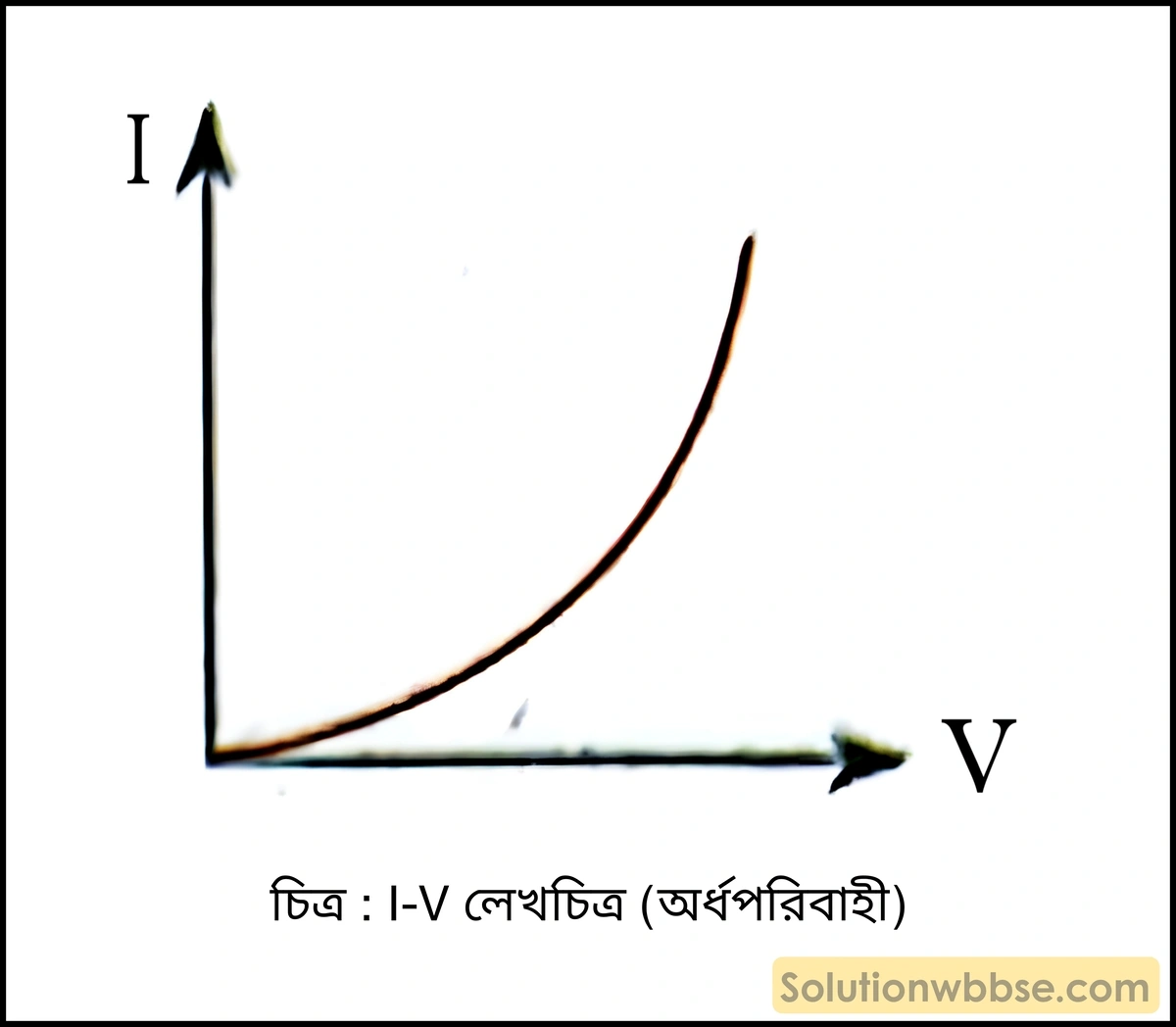
রোধের নির্ভরশীলতা –

কোনো পরিবাহীর রোধ নির্ভর করে –

• উষ্ণতার ওপর – উষ্ণতা বাড়লে পরিবাহীর রোধ বাড়ে। এক্ষেত্রে সম্পর্কটি হল R_t ​= R₀​(1 + αt),
  • দৈর্ঘ্যের ওপর R ∝ L,
  • প্রস্থচ্ছেদের ক্ষেত্রফলের ওপর \(R\propto\frac1A\),
  • উপাদানের ওপর।
• সমীকরণ হল \(R=\rho\cdot\frac1A\)​ [ρ হল রোধাঙ্ক]
• কোনো পরিবাহীর আয়তন স্থির রেখে দৈর্ঘ্য n গুণ বৃদ্ধি করা হলে তার রোধ হবে n² গুণ।

রোধাঙ্ক –

কোনো পরিবাহীর দৈর্ঘ্য ও প্রস্থচ্ছেদ একক হলে তার রোধকে রোধাঙ্ক বলে।

• রোধাঙ্কের একক Ω⋅m বা Ω⋅cm।
• এর মাত্রা হল ML³T⁻³A⁻²।
• রোধাঙ্ক নির্ভর করে উপাদানের ওপর এবং তাপমাত্রার ওপর।
• রোধাঙ্কের অন্যোন্যক হল পরিবাহিতাঙ্ক। এর একক মো⋅মিটার⁻¹ (Ω⋅m⁻¹)।

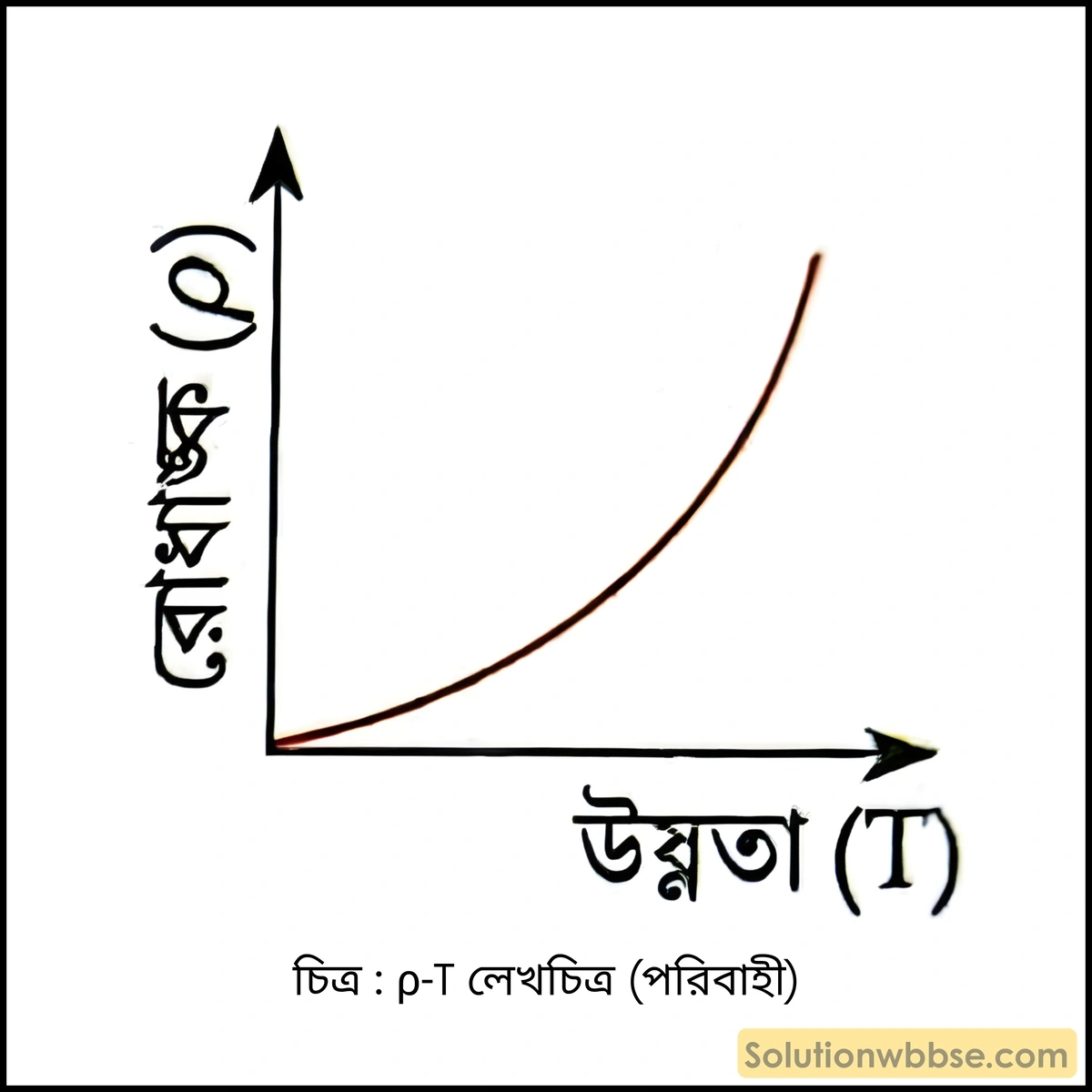
অর্ধপরিবাহী –

যে সমস্ত পদার্থের রোধ ও রোধাঙ্ক সুপরিবাহী ও অন্তরক পদার্থের অন্তবর্তী হয় তাদের অর্ধপরিবাহী বলে।

• উদাহরণ হল জারমেনিয়াম (Ge) ও সিলিকন (Si)।
• উষ্ণতা বাড়লে এদের রোধ ও রোধাঙ্ক কমে।
• এদের ক্ষেত্রে রোধের উষ্ণতা গুণাঙ্ক ঋণাত্মক হয়।

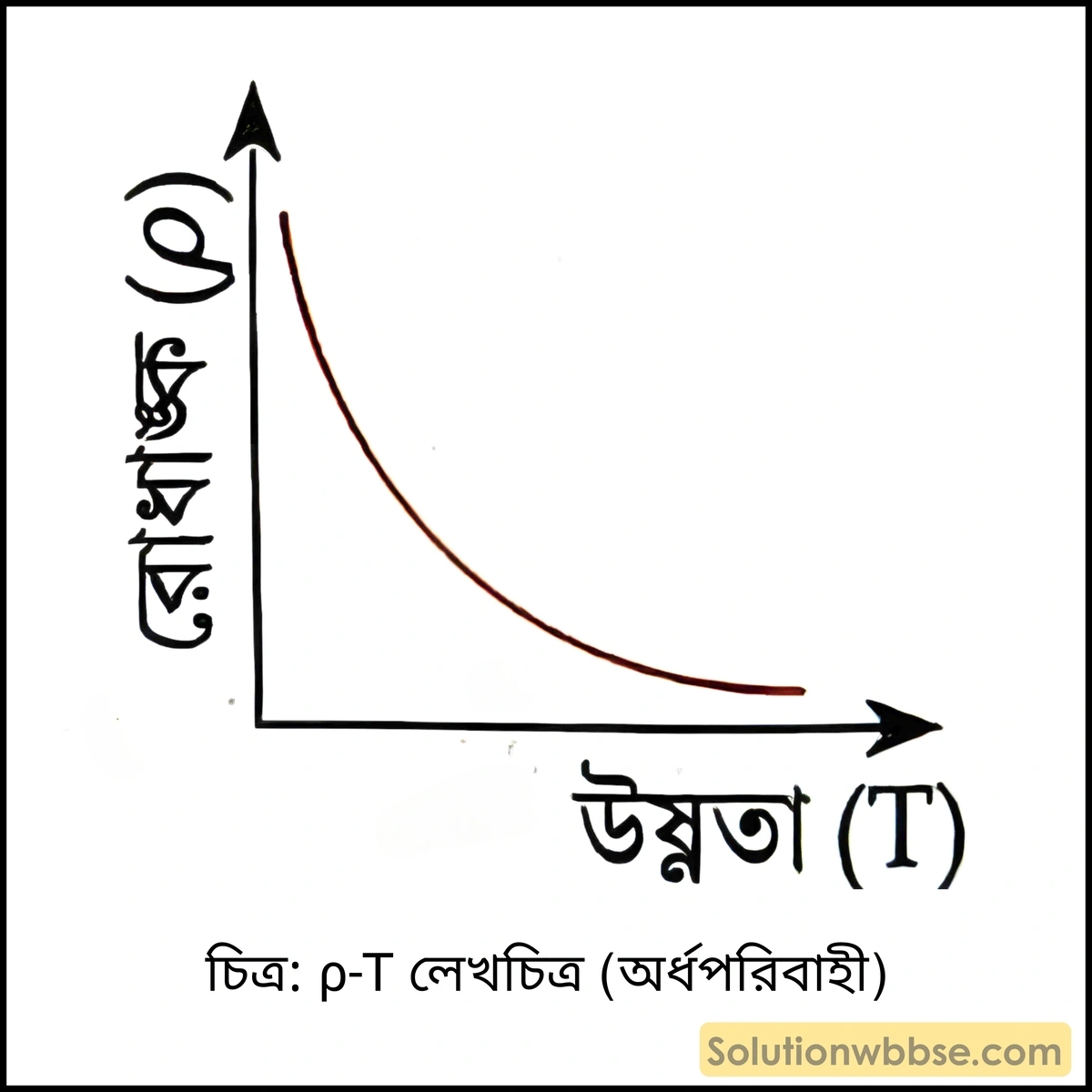
অতিপরিবাহী –

যে সমস্ত পরিবাহীর রোধ ও রোধাঙ্ক একটি নির্দিষ্ট তাপমাত্রায় শূন্য হয়ে যায় তাকে অতিপরিবাহী বলে।

সংকট তাপমাত্রায় রোধাঙ্ক শূন্য। উদাহরণ – 7K তাপমাত্রায় সিসা।

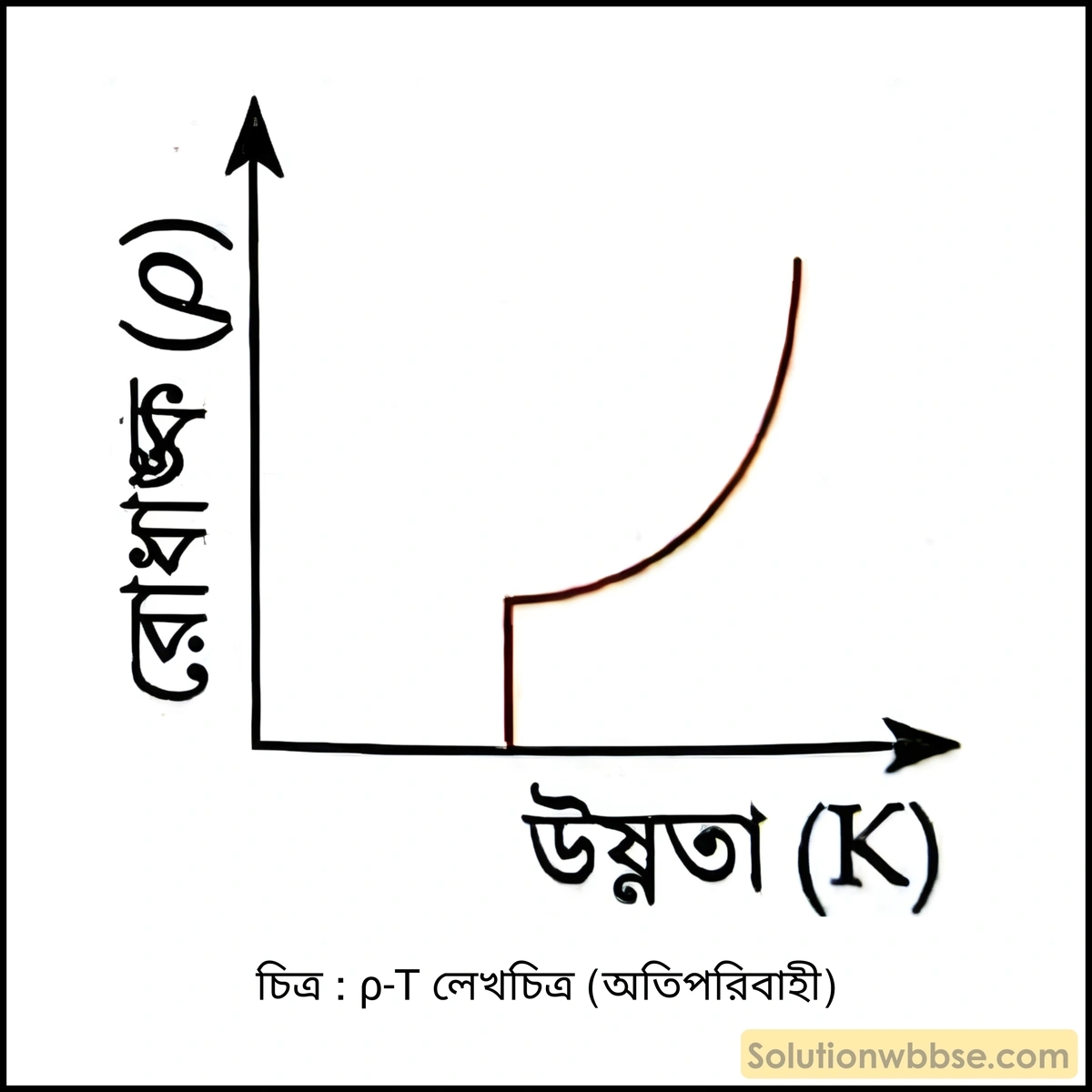
রোধের সমবায় –

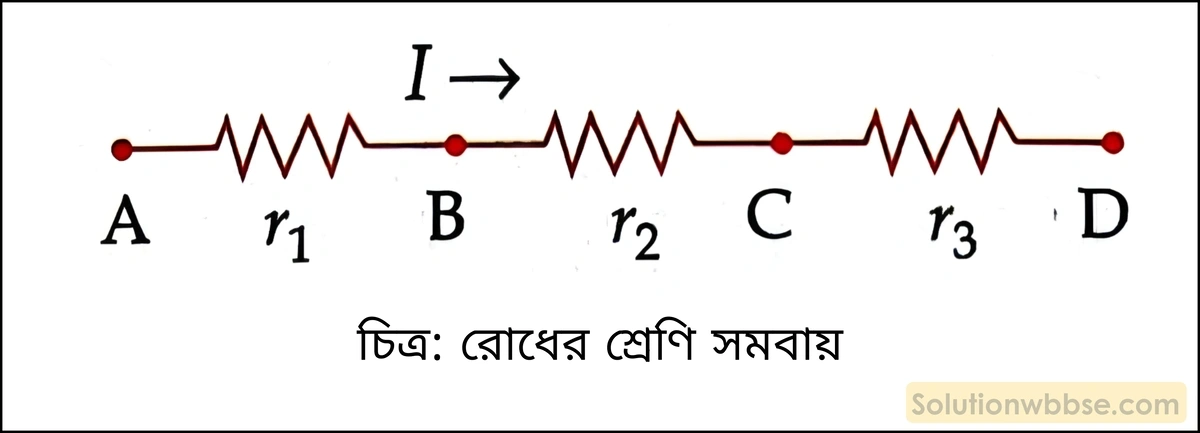
শ্রেণি সমবায় – একাধিক রোধকে শ্রেণি সমবায়ে যুক্ত করলে প্রতিটিতে প্রবাহ সমান হয় কিন্তু বিভব আলাদা হতে পারে।

• তুল্যরোধ R = R₁​ + R₂​ + R₃​
• তুল্যরোধের মান সমবায়ের সবচেয়ে বড়ো রোধের থেকেও বড়ো হয়।

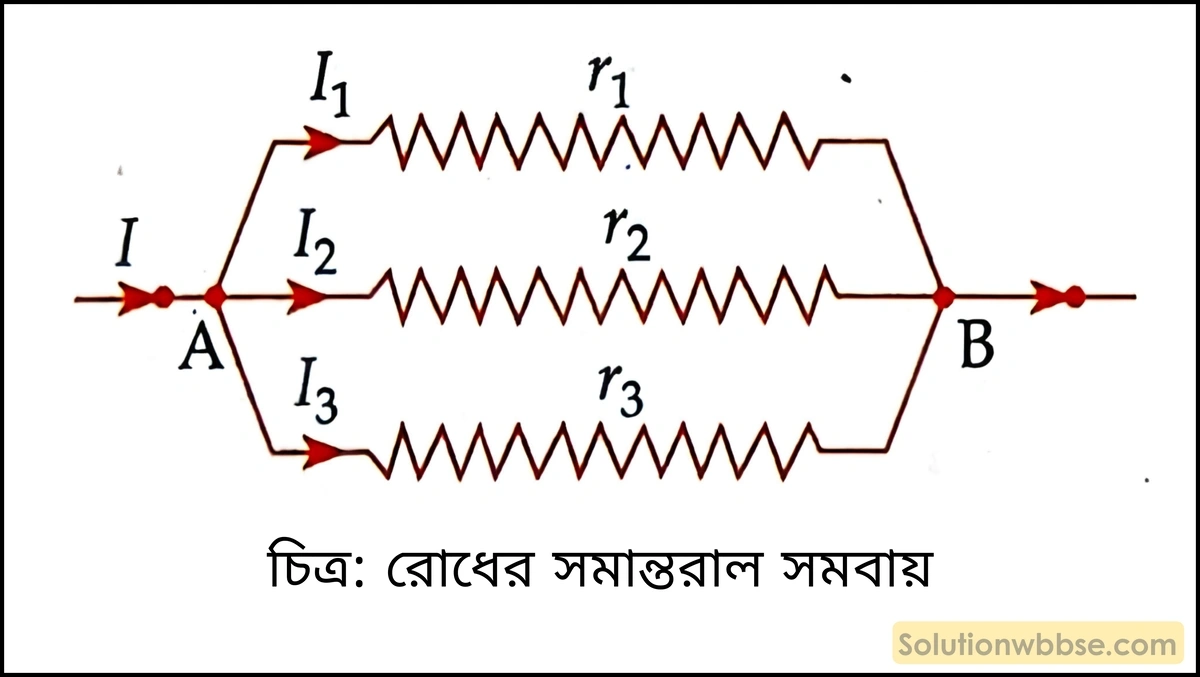
সমান্তরাল সমবায় – একাধিক রোধকে সমান্তরাল সমবায়ে যুক্ত করলে প্রতিটিতে প্রবাহ আলাদা হয় কিন্তু বিভব সমান থাকে।

• তুল্যরোধ R হলে, \(\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}\)
• তুল্যরোধের মান সমবায়ের ক্ষুদ্রতম রোধের থেকেও কম।
• সমান্তরাল সমবায়ের প্রতিটি অংশের রোধ ও প্রবাহমাত্রার গুণফল সমান।

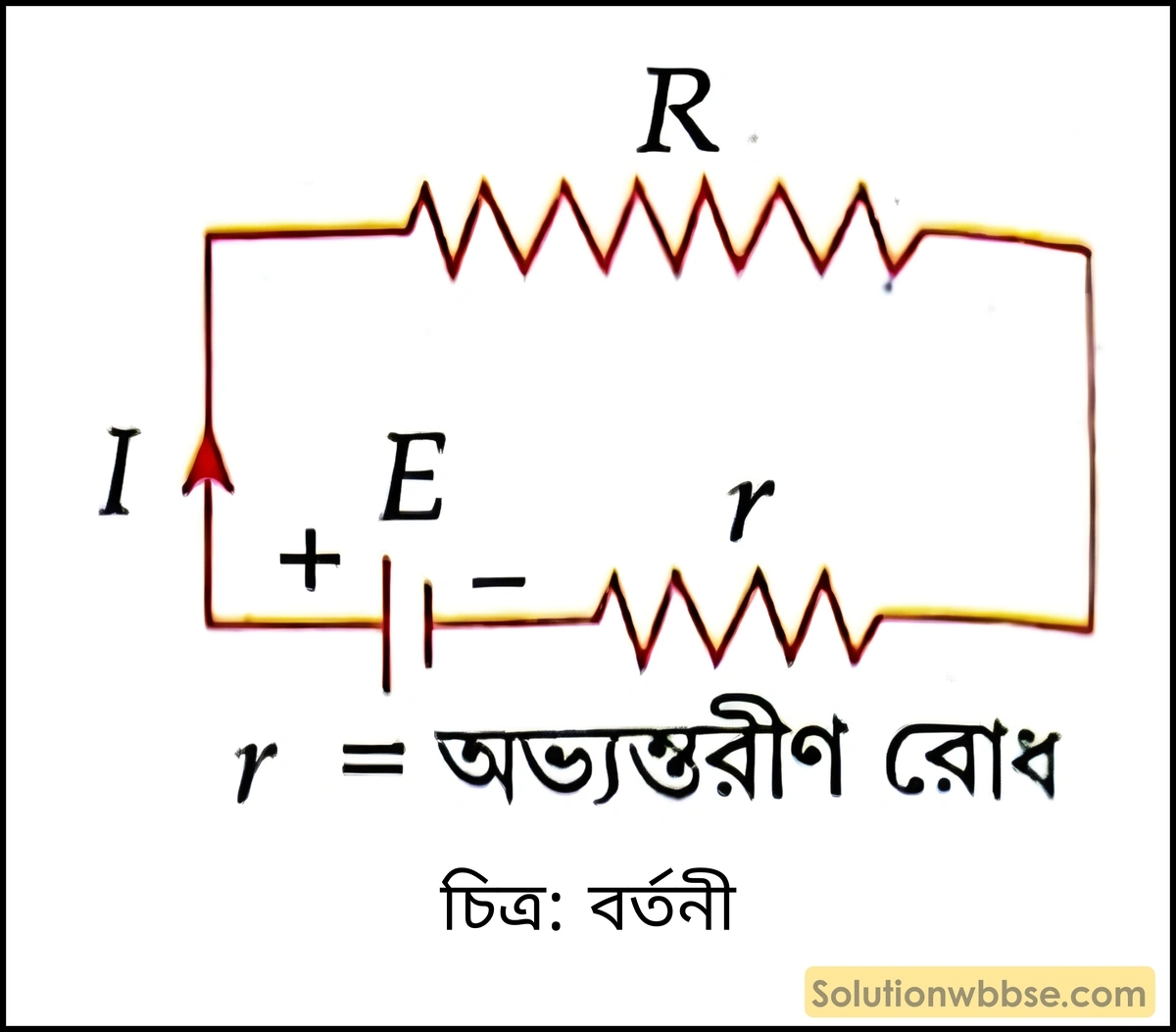
কোশ যুক্ত বর্তনী ও অভ্যন্তরীণ রোধ –

কোনো কোশের মধ্য দিয়ে প্রবাহ চলাকালীন কোশের ভিতরের উপাদানগুলি ওই প্রবাহে যে বাধা সৃষ্টি করে তাকে কোশের অভ্যন্তরীণ রোধ বলে।

• কোনো কোশের সঙ্গে তার দিয়ে কোনো রোধ যুক্ত করলে তাকে বর্তনী বলে।
• বর্তনীতে প্রবাহ অভ্যন্তরীণ রোধের মধ্য দিয়ে গেলে তার দুই প্রান্তে যে বিভব সৃষ্টি হয় তাকে নষ্ট ভোল্ট বলে। ∴ নষ্ট ভোল্ট = Ir
• E তড়িচ্চালক বলের খানিকটা R রোধের মধ্য দিয়ে প্রবাহ যাওয়ার ফলে বিভব হিসেবে সৃষ্টি হয় ও বাকিটা r রোধের মধ্যে নষ্ট ভোল্ট হিসেবে ব্যয় হয়। ∴ E = V + Ir

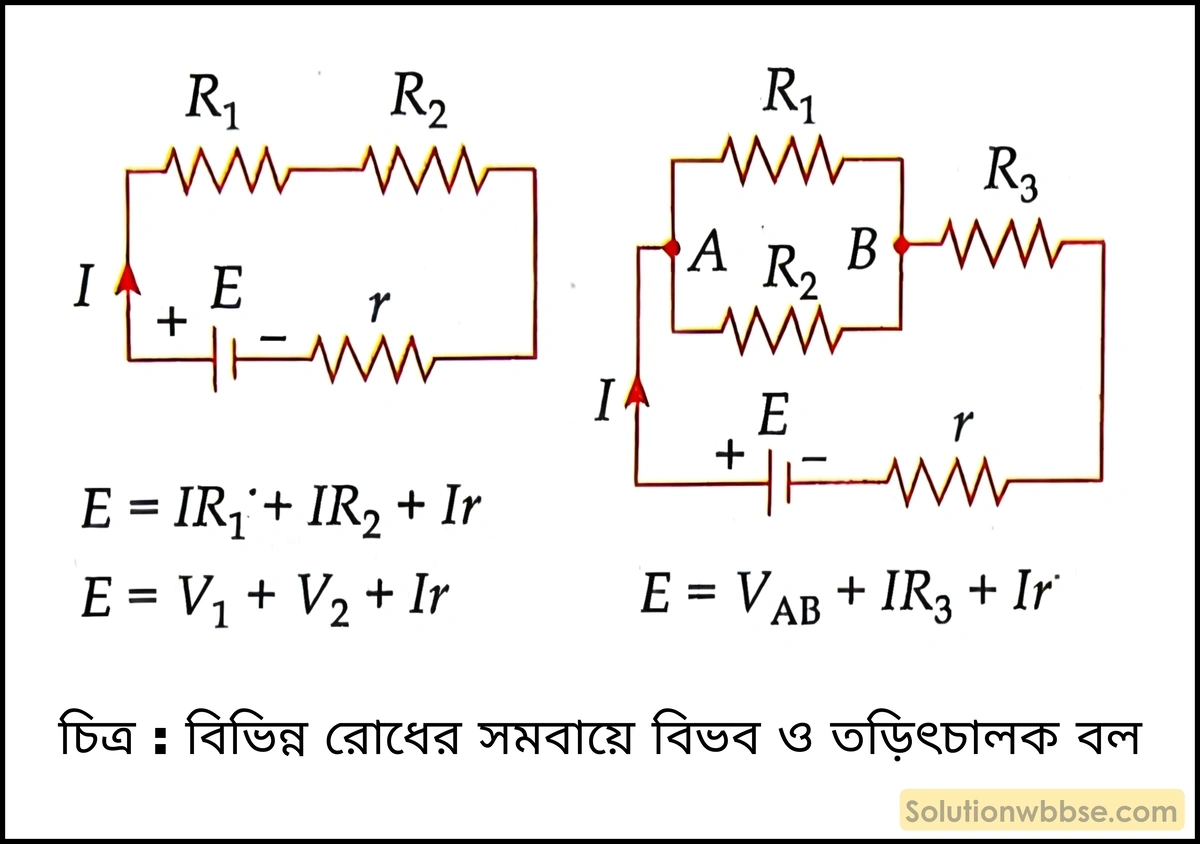
বিভিন্ন চিত্রে বিভব, তড়িচ্চালক বলের মধ্যে সম্পর্ক –

এই আর্টিকেলে আমরা মাধ্যমিক ভৌতবিজ্ঞানের একটি গুরুত্বপূর্ণ অংশ “তড়িৎপ্রবাহ, ওহমের সূত্র ও রোধ” নিয়ে আলোচনা করেছি। এই অংশটি মাধ্যমিক ভৌতবিজ্ঞান পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ। এই “তড়িৎপ্রবাহ, ওহমের সূত্র ও রোধ” অংশটি মাধ্যমিক ভৌতবিজ্ঞানের ষষ্ঠ অধ্যায় “চলতড়িৎ“ -এর একটি গুরুত্বপূর্ণ অংশ। এই “তড়িৎপ্রবাহ, ওহমের সূত্র ও রোধ” অংশটি মাধ্যমিক পরীক্ষায় এবং চাকরির পরীক্ষায় প্রায়ই দেখা যায়। আশা করি এই আর্টিকেলটি আপনাদের জন্য উপকারী হয়েছে। আপনাদের কোনো প্রশ্ন বা অসুবিধা থাকলে, আমাদের সাথে টেলিগ্রামে যোগাযোগ করুন।