মাধ্যমিক গণিত – বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য – প্রয়োগ

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের পঞ্চদশ অধ্যায়, ‘বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

প্রয়োগ 1. কোনো বৃত্তের কোনো ব্যাসার্ধের প্রান্তবিন্দু দিয়ে ব্যাসার্ধের উপর অঙ্কিত লম্ব সরলরেখা ওই বৃত্তের একটি স্পর্শক হবে।

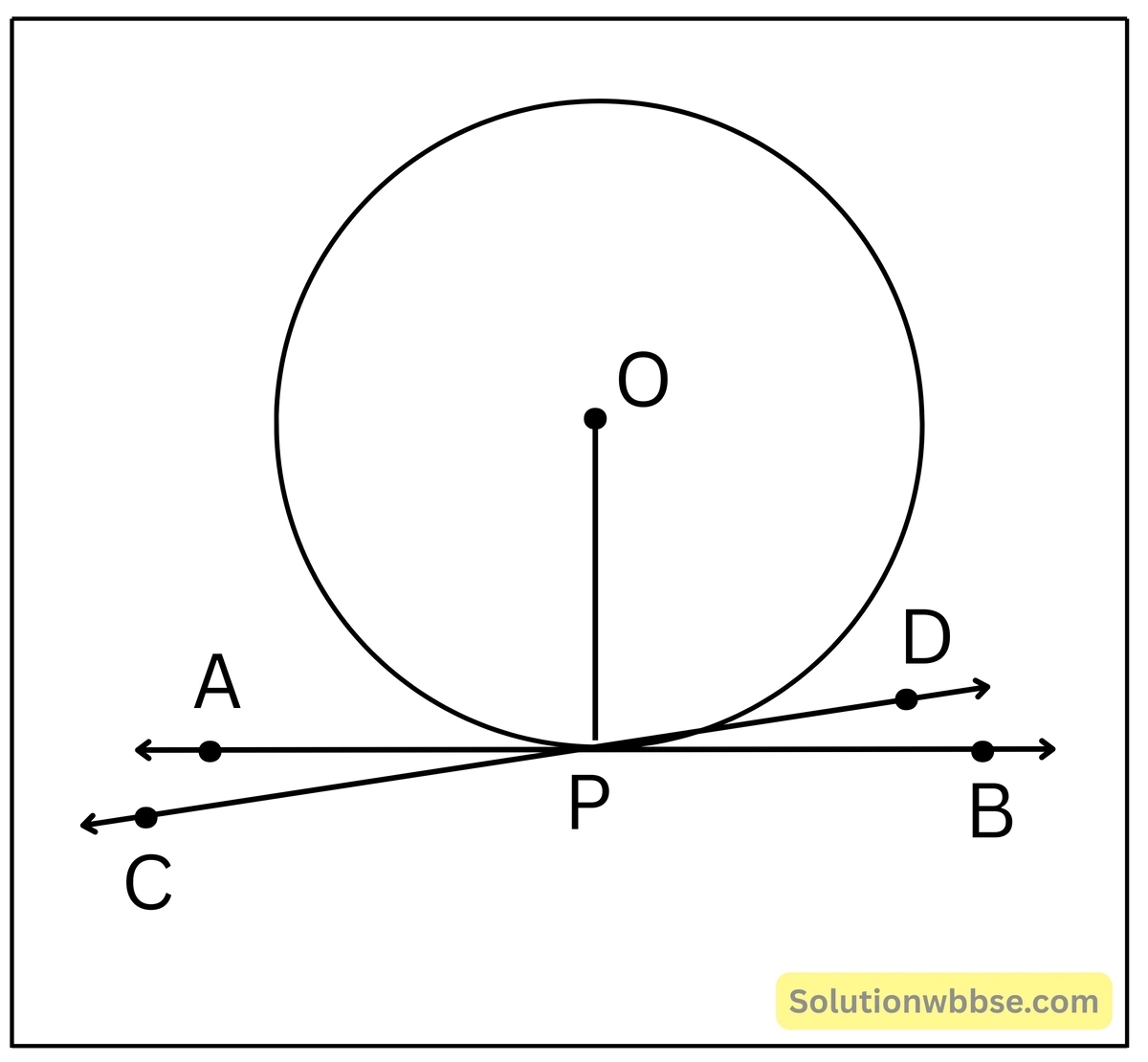
প্রদত্ত – O কেন্দ্রীয় বৃত্তে OP ব্যাসার্ধ এবং P বিন্দুতে OP ব্যাসার্ধের উপর AB সরলরেখা লম্ব।

প্রমাণ করতে হবে – সরলরেখা AB, P বিন্দুতে O কেন্দ্রীয় বৃত্তের স্পর্শক।

প্রমাণ – ধরি, AB সরলরেখা P বিন্দুতে O কেন্দ্রীয় বৃত্তের স্পর্শক নয়। O কেন্দ্রীয় বৃত্তের P বিন্দুতে একটি স্পর্শক CD অঙ্কন করি।

যেহেতু, O কেন্দ্রীয় বৃত্তের P বিন্দুতে CD স্পর্শক এবং OP, P বিন্দুগামী ব্যাসার্ধ,

সুতরাং OP, CD সরলরেখার উপর লম্ব। ∴∠OPD = 90°

আবার, ∠OPB = 90° (প্রদত্ত) [∵ OP, AB সরলরেখার উপর লম্ব]

∴∠OPD = ∠OPB অর্থাৎ CD সরলরেখা ও AB সরলরেখা পরস্পর সমাপতিত হবে।

∴ AB সরলরেখা O কেন্দ্রীয় বৃত্তের P বিন্দুতে স্পর্শক।

প্রয়োগ 2. প্রমাণ করি যে বৃত্তের উপর অবস্থিত কোনো বিন্দুতে একটি মাত্র স্পর্শক অঙ্কন করা যায়।

প্রমাণ –

ধরি, O কেন্দ্রীয় বৃত্তের পরিধির উপর P একটি বিন্দু। P বিন্দুতে AB ও CD দুটি স্পর্শক আঁকা হয়েছে। আমরা জানি, স্পর্শবিন্দুতে ব্যাসার্ধ স্পর্শকের উপর লম্ব হয়। সুতরাং, AB স্পর্শক P বিন্দুতে ব্যাসার্ধ OP-এর উপর লম্ব। অর্থাৎ, ∠OPB = 90°

আবার, CD স্পর্শকও P বিন্দুতে ব্যাসার্ধ OP-এর উপর লম্ব। অর্থাৎ, ∠OPD = 90°

যেহেতু, ∠OPB = ∠OPD = 90°, সেহেতু, AB ও CD দুটি ভিন্ন সরলরেখা হওয়া সত্ত্বেও একই সরলরেখা। কারণ, একটি নির্দিষ্ট বিন্দু থেকে একটি নির্দিষ্ট সরলরেখার উপর একটিই লম্ব আঁকা যায়। সুতরাং, বৃত্তের উপর অবস্থিত কোনো বিন্দুতে একটি মাত্র স্পর্শক আঁকা যায়। (প্রমাণিত)

প্রয়োগ 3. প্রমাণ করি যে, স্পর্শবিন্দুতে স্পর্শকের উপর অঙ্কিত লম্ব বৃত্তের কেন্দ্রগামী।

প্রমাণ –

ধরি, O কেন্দ্রীয় বৃত্তের AB একটি স্পর্শক যা বৃত্তটিকে P বিন্দুতে স্পর্শ করেছে।

আমরা জানি, স্পর্শবিন্দুতে ব্যাসার্ধ স্পর্শকের উপর লম্ব হয় (উপপাদ্য 40)।

সুতরাং, স্পর্শবিন্দু P তে ব্যাসার্ধ OP, স্পর্শক AB-এর উপর লম্ব।

এখন, P বিন্দুতে AB-এর উপর একটি লম্ব অঙ্কন করি।

আমরা জানি যে, একটি সরলরেখার উপর অবস্থিত একটি নির্দিষ্ট বিন্দুতে কেবলমাত্র একটিই লম্ব অঙ্কন করা যায়।

যেহেতু OP সরলরেখাটি P বিন্দুতে AB-এর উপর লম্ব, এবং P বিন্দুতে AB-এর উপর অঙ্কিত লম্বটি বৃত্তের কেন্দ্র দিয়ে যায়।

সুতরাং, স্পর্শবিন্দুতে স্পর্শকের উপর অঙ্কিত লম্ব অবশ্যই বৃত্তের কেন্দ্রগামী হবে। (প্রমাণিত)

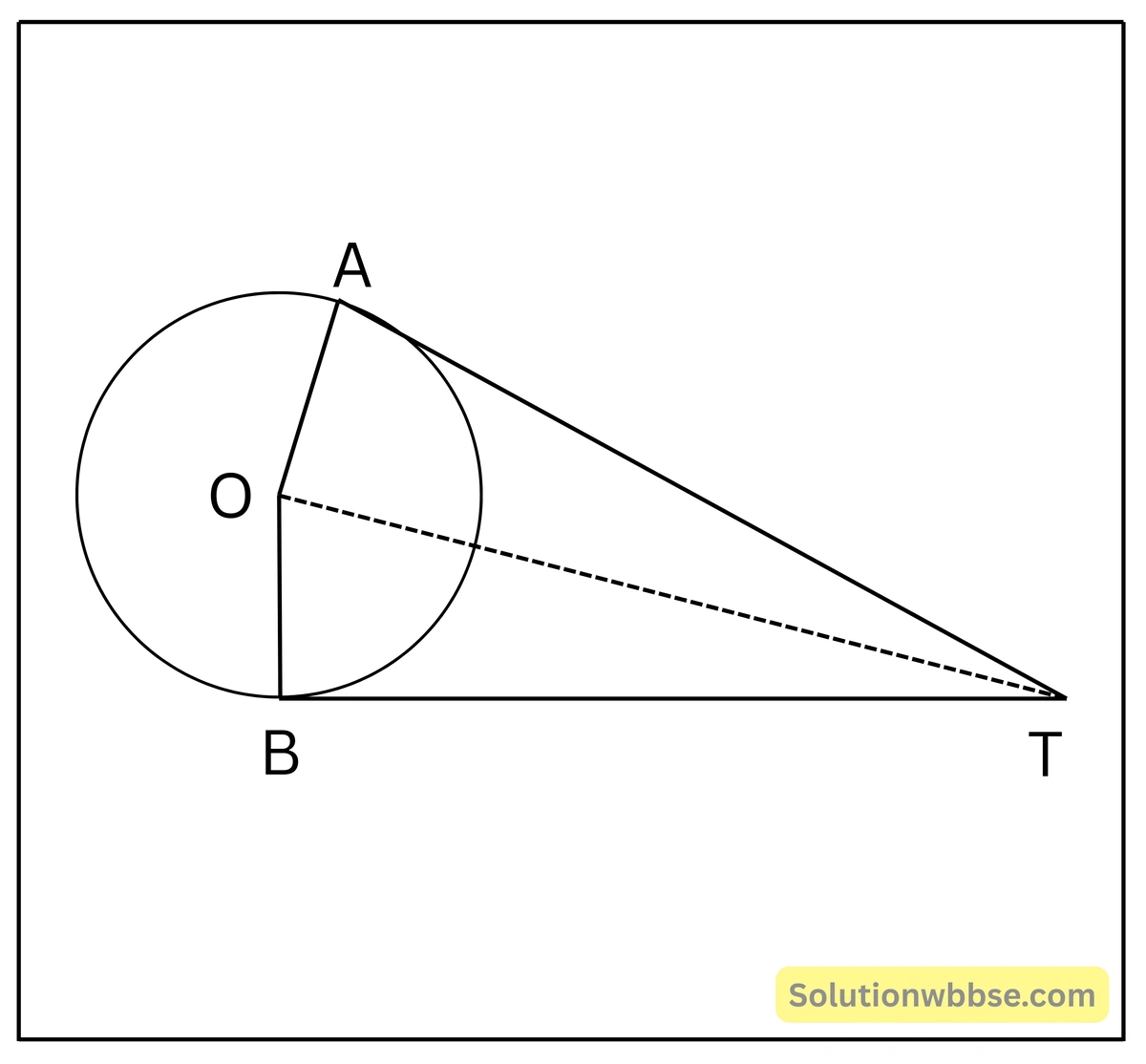
প্রয়োগ 4. পাশের চিত্রে O কেন্দ্রীয় বৃত্তে A বিন্দুতে AT একটি স্পর্শক। x কে y-এর সাহায্যে প্রকাশ করি।

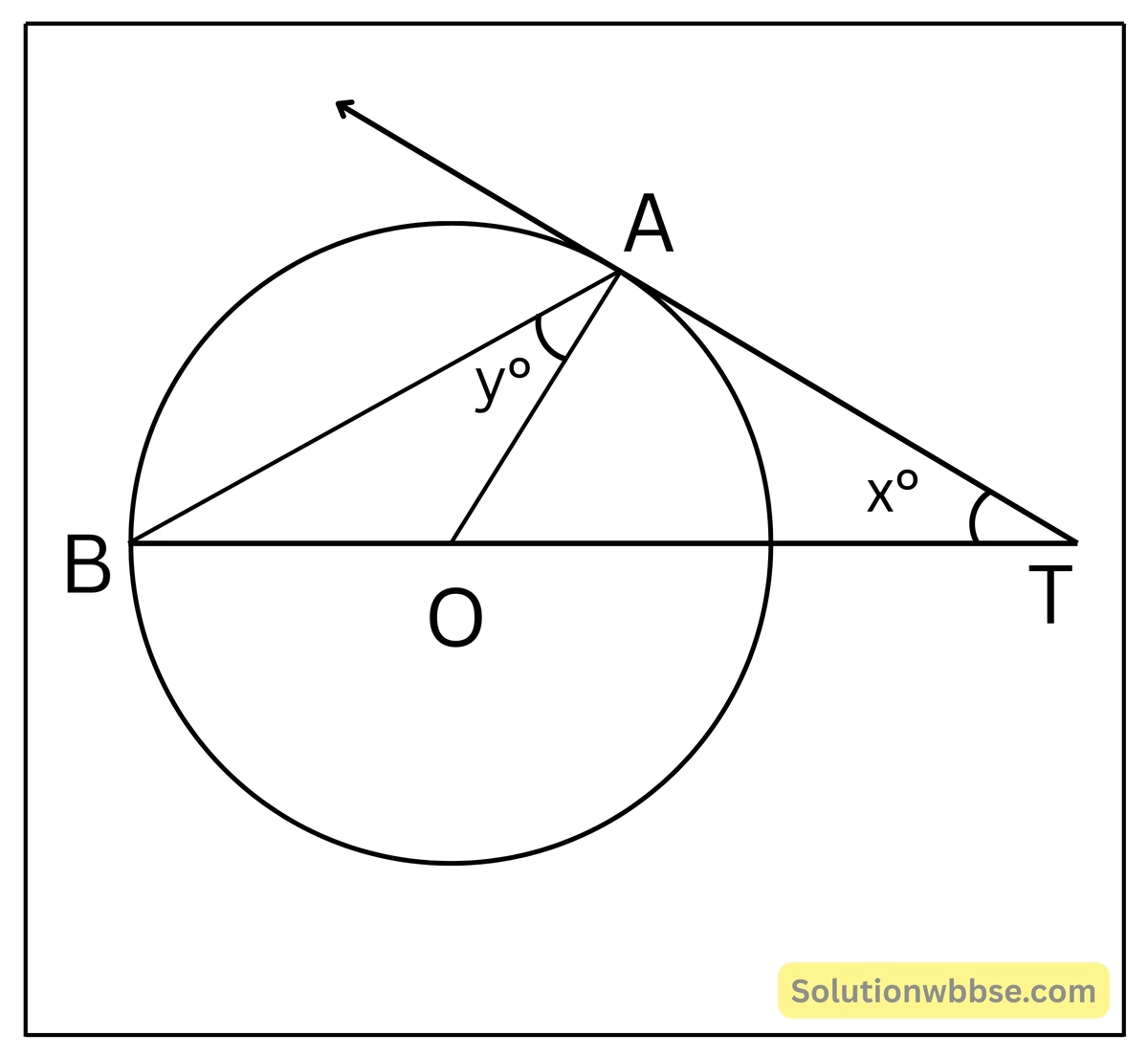
সমাধান –

চিত্র অনুযায়ী, O কেন্দ্রীয় বৃত্তে AT স্পর্শক এবং OA স্পর্শবিন্দুগামী ব্যাসার্ধ।

আমরা জানি, স্পর্শবিন্দুতে ব্যাসার্ধ স্পর্শকের উপর লম্ব হয়।

সুতরাং, ∠OAT = 90°

আবার, প্রদত্ত চিত্রে ∠ATO = x°

△AOT একটি সমকোণী ত্রিভুজ।

∠AOT = 180°−(∠OAT + ∠ATO)

∠AOT = 180°−(90° + x°)

∠AOT = 90° − x° —-(i)

আবার, △AOB -এ, OA এবং OB একই বৃত্তের ব্যাসার্ধ, তাই OA = OB।

সুতরাং, △AOB একটি সমদ্বিবাহু ত্রিভুজ।

অতএব, ∠OAB = ∠OBA = y°

△AOB -এ, বহিস্থ ∠AOT = ∠OAB + ∠OBA

∠AOT = y° + y°

∠AOT = 2y° —-(ii)

(i) এবং (ii) থেকে পাই,

90° − x° = 2y°

x° = 90° − 2y°

সুতরাং, x = 90 − 2y

প্রয়োগ 5. O কেন্দ্রীয় একটি বৃত্তে একটি ব্যাস AB এবং A বিন্দুতে বৃত্তের স্পর্শক PAQ; PAQ-এর সমান্তরাল জ্যা RS; যুক্তি দিয়ে প্রমাণ করি যে AB, RS-এর লম্বসমদ্বিখণ্ডক।

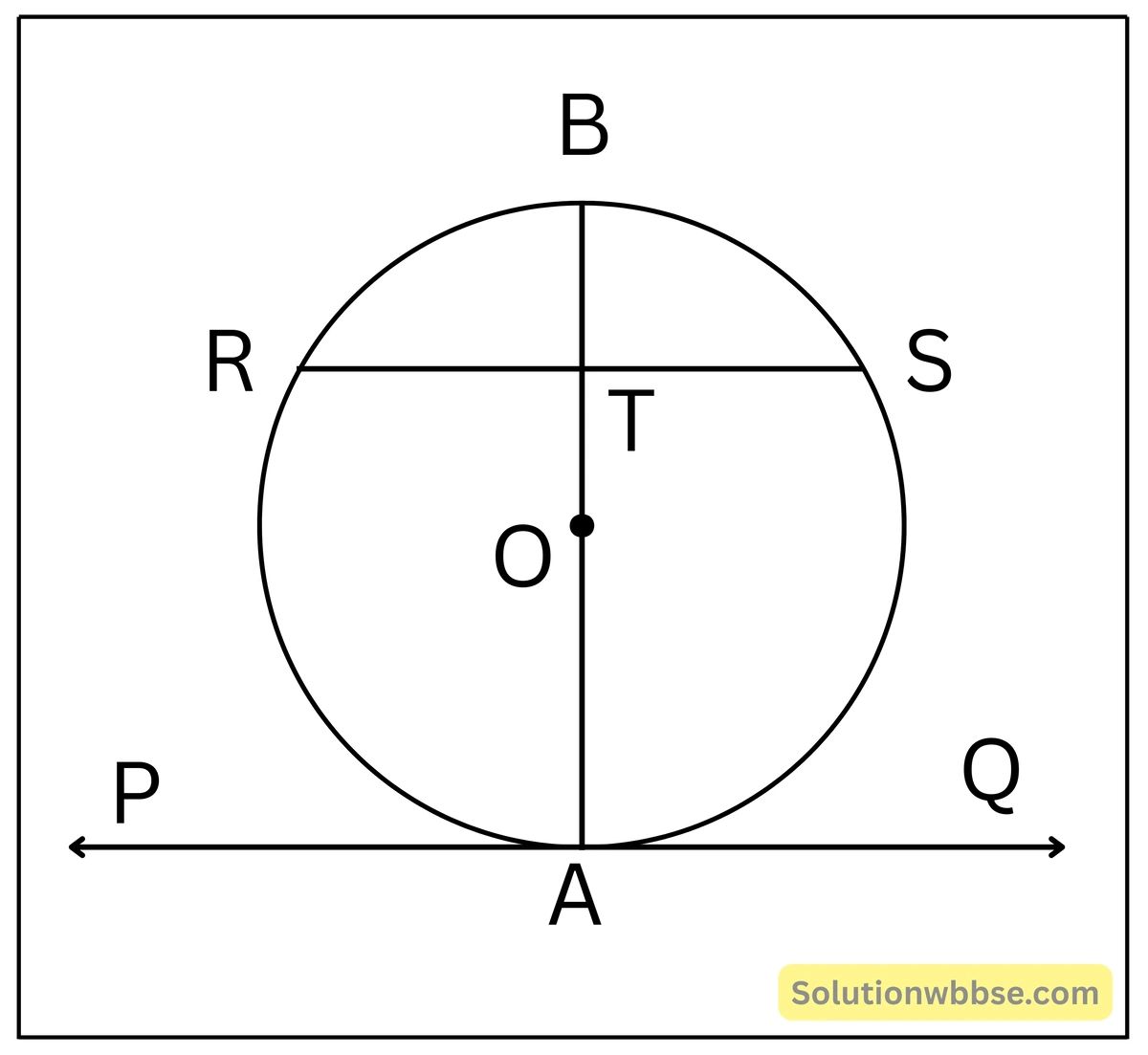
প্রমাণ –

ধরি, AB, RS-কে T বিন্দুতে ছেদ করেছে। O কেন্দ্রীয় বৃত্তের A বিন্দুতে PAQ স্পর্শক এবং AB ব্যাস।

আমরা জানি, স্পর্শবিন্দুগামী ব্যাসার্ধ বা ব্যাস স্পর্শকের উপর লম্ব হয়।

সুতরাং, AB ⊥ PQ।

আবার, PQ || RS (প্রদত্ত)

যেহেতু, AB সরলরেখাটি PQ-এর উপর লম্ব এবং PQ ও RS সমান্তরাল, তাই AB, RS -এর উপরও লম্ব হবে।

অর্থাৎ, AB ⊥ RS বা OT ⊥ RS

আমরা জানি, বৃত্তের কেন্দ্র থেকে কোনো জ্যা-এর উপর অঙ্কিত লম্ব সেই জ্যা-কে সমদ্বিখণ্ডিত করে।

যেহেতু OT, RS-এর উপর লম্ব এবং O বৃত্তের কেন্দ্র, তাই T বিন্দুটি RS -এর মধ্যবিন্দু।

সুতরাং, AB সরলরেখাটি RS -এর উপর লম্ব এবং RS-কে সমদ্বিখণ্ডিত করেছে।

অতএব, AB, RS -এর লম্বসমদ্বিখণ্ডক। (প্রমাণিত)

প্রয়োগ 6. প্রমাণ করো যে, কোনো বৃত্তের ব্যাসের প্রান্তবিন্দু দুটিতে অঙ্কিত স্পর্শকদুটি পরস্পর সমান্তরাল।

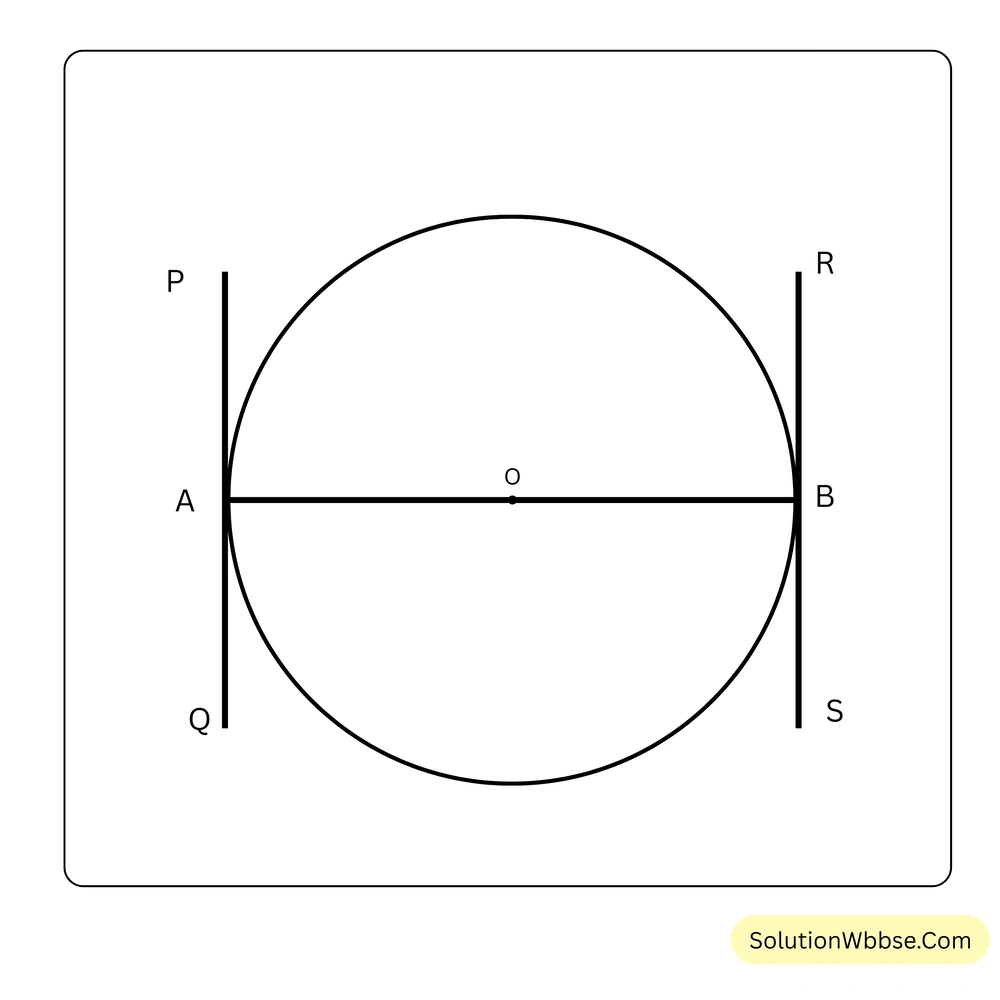
প্রদত্ত – একটি বৃত্ত যার কেন্দ্র O এবং ব্যাস AB। A বিন্দুতে PQ এবং B বিন্দুতে RS স্পর্শক।

প্রমাণ করতে হবে – PQ || RS (PQ সমান্তরাল RS)।

প্রমাণ –

আমরা জানি যে, বৃত্তের কোনো স্পর্শক এবং স্পর্শ বিন্দুগামী ব্যাসার্ধ পরস্পর লম্ব হয়।

সুতরাং, PQ স্পর্শকটি OA ব্যাসার্ধের ওপর লম্ব। অর্থাৎ, ∠OAQ=90° বা ∠BAQ=90°।

একইভাবে, RS স্পর্শকটি OB ব্যাসার্ধের ওপর লম্ব। অর্থাৎ, ∠OBR=90° বা ∠ABR=90°।

যেহেতু, ∠BAQ=90° এবং ∠ABR=90°, আমরা লিখতে পারি, ∠BAQ=∠ABR।

এখানে, AB একটি ছেদক যা PQ এবং RS দুটি সরলরেখাকে ছেদ করেছে। ∠BAQ এবং ∠ABR হলো একান্তর কোণ। যেহেতু একান্তর কোণ দুটি সমান, তাই সরলরেখা দুটি পরস্পর সমান্তরাল।

অতএব, PQ || RS। (প্রমাণিত)

প্রয়োগ 7. বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে ওই বৃত্তে দুটি স্পর্শক অঙ্কন করা যায়।

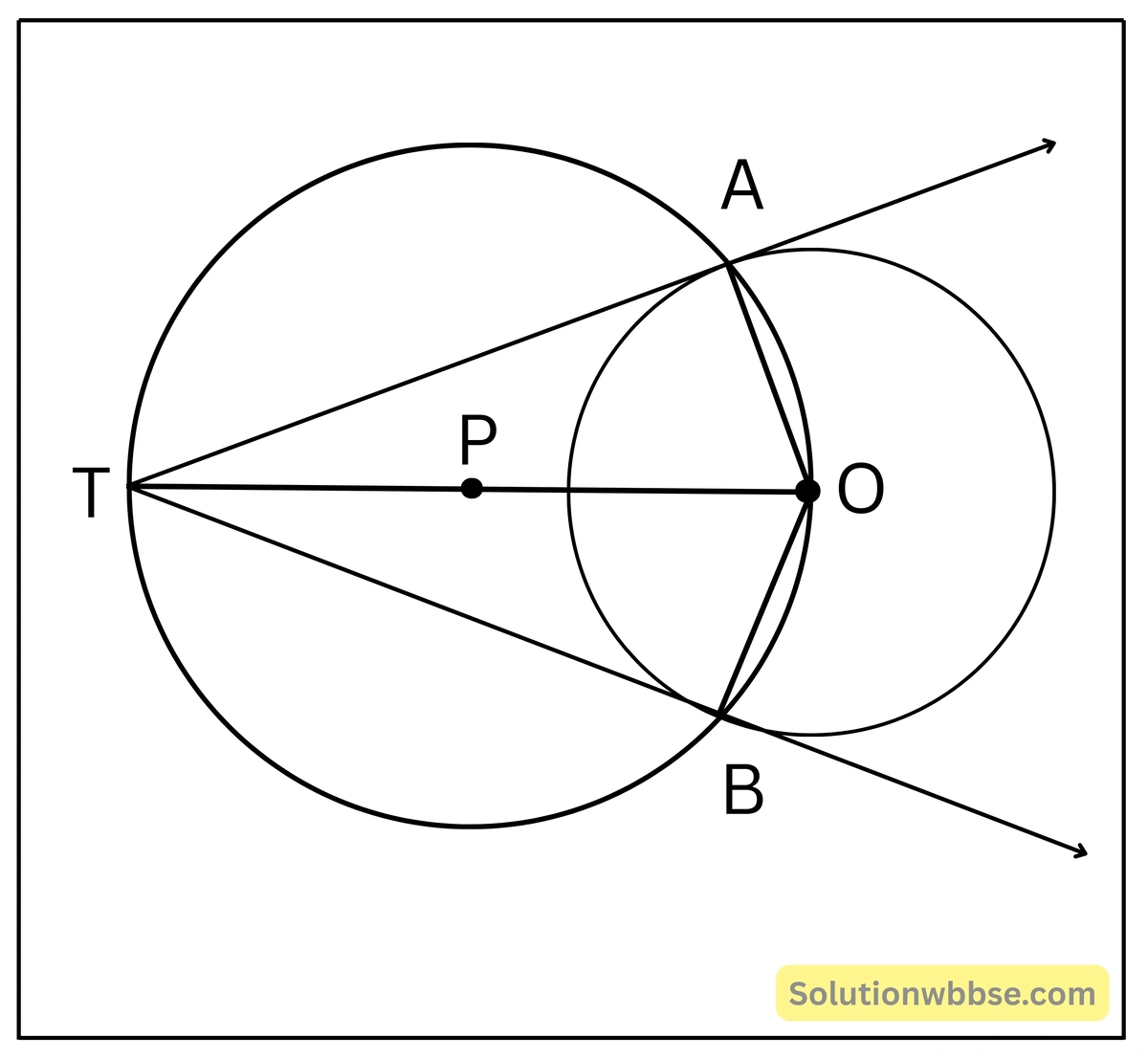
প্রদত্ত – O কেন্দ্রীয় বৃত্তের T যে-কোনো একটি বহিঃস্থ বিন্দু।

প্রমাণ করতে হবে – T বিন্দু থেকে O কেন্দ্রীয় বৃত্তের দুটি স্পর্শক অঙ্কন করা যায়।

অঙ্কন – T, O যুক্ত করলাম। T O -কে ব্যাস করে একটি বৃত্ত অঙ্কন করলাম।

যেহেতু T বিন্দুটি O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু এবং O অন্তঃস্থ বিন্দু। সুতরাং, TO-কে ব্যাস করে অঙ্কিত বৃত্তটি O কেন্দ্রীয় বৃত্তকে দুটি বিন্দুতে ছেদ করবে। ধরি, ছেদবিন্দু দুটি A এবং B; T, A; T, B; O, A; O, B যুক্ত করলাম।

প্রমাণ – ∠OAT এবং ∠OBT প্রত্যেকে অর্ধবৃত্তস্থ কোণ।

∴ ∠OAT = ∠OBT = 1 সমকোণ।

অর্থাৎ, OA ⊥ AT এবং OB ⊥ BT।

TA ও TB যথাক্রমে ব্যাসার্ধ OA এবং OB-এর উপর A ও B বিন্দুতে লম্ব।

∴ TA ও TB, O কেন্দ্রীয় বৃত্তে যথাক্রমে A ও B বিন্দুতে দুটি স্পর্শক। পেলাম, বহিঃস্থ বিন্দু থেকে একটি বৃত্তে দুটি স্পর্শক অঙ্কন করা যায়। [প্রমাণিত]

প্রয়োগ 8. প্রয়োগ 8 – আমি একটি O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু P থেকে দুটি স্পর্শক PA ও PB অঙ্কন করেছি যারা বৃত্তকে যথাক্রমে A ও B বিন্দুতে স্পর্শ করেছে। প্রমাণ করি যে, ∠APB + ∠AOB = 180°।

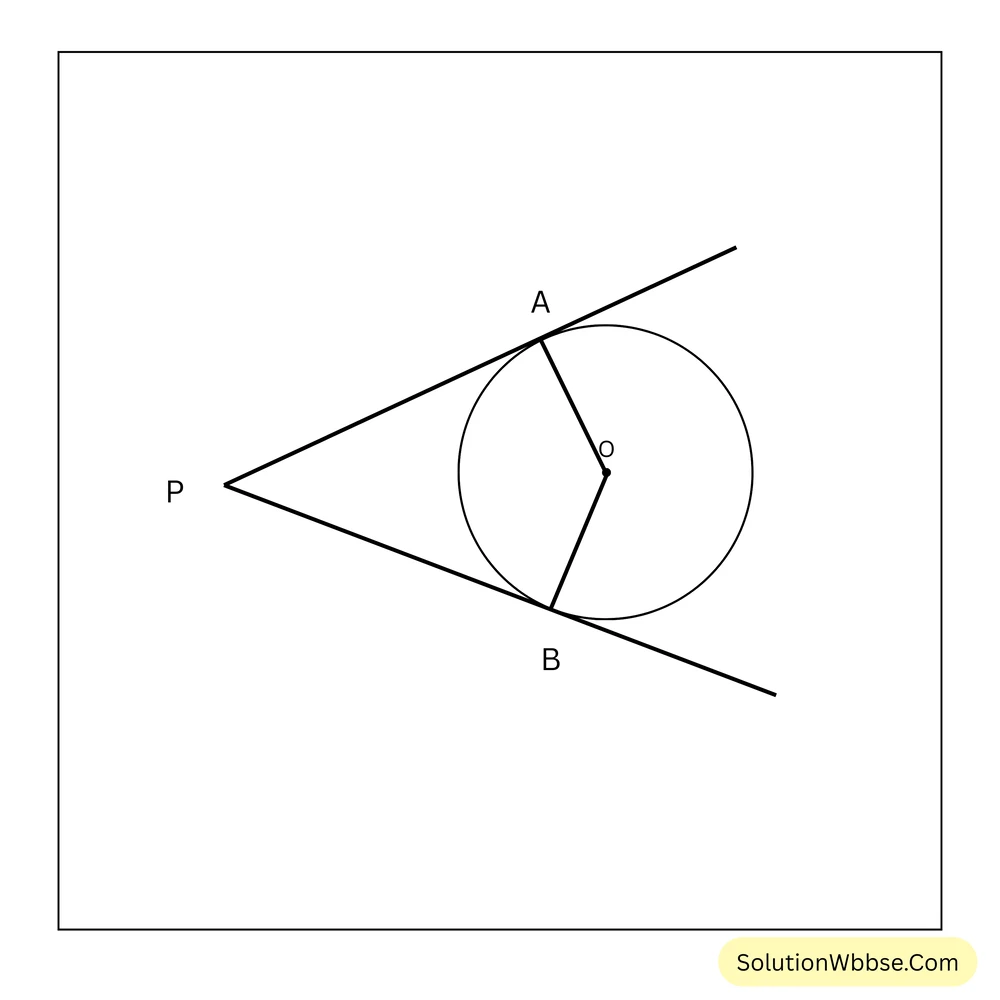
প্রদত্ত – একটি বৃত্ত যার কেন্দ্র O। P হলো বৃত্তের বাইরের একটি বিন্দু এবং PA ও PB হলো দুটি স্পর্শক যা A ও B বিন্দুতে বৃত্তকে স্পর্শ করে।

প্রমাণ করতে হবে – ∠APB + ∠AOB=180°।

প্রমাণ –

আমরা জানি যে, বৃত্তের কোনো স্পর্শক এবং স্পর্শবিন্দুগামী ব্যাসার্ধ পরস্পর লম্ব হয়।

অতএব, স্পর্শক PA, ব্যাসার্ধ OA এর উপর লম্ব। অর্থাৎ, ∠PAO=90°।

একইভাবে, স্পর্শক PB, ব্যাসার্ধ OB এর উপর লম্ব। অর্থাৎ, ∠PBO=90°।

এখন, P, A, O, B বিন্দু চারটি একটি চতুর্ভুজ গঠন করেছে।

আমরা জানি, চতুর্ভুজের চারটি কোণের যোগফল 360°।

সুতরাং, চতুর্ভুজ PAOB-এর ক্ষেত্রে: ∠APB+∠PAO+∠AOB+∠PBO=360°।

∠PAO এবং ∠PBO এর মান 90° বসিয়ে পাই:

∠APB + 90° + ∠AOB + 90° = 360°

∠APB + ∠AOB + 180° = 360°

∠APB + ∠AOB = 360° − 180°

∠APB + ∠AOB = 180°

প্রয়োগ 9. আমি একটি O কেন্দ্রীয় বৃত্ত অঙ্কন করেছি যার ব্যাসার্ধের দৈর্ঘ্য 6 সেমি। কেন্দ্র O থেকে 10 সেমি। দূরে অবস্থিত P বিন্দু থেকে PT স্পর্শক আঁকলাম। হিসাব করে PT স্পর্শকের দৈর্ঘ্য লিখি।

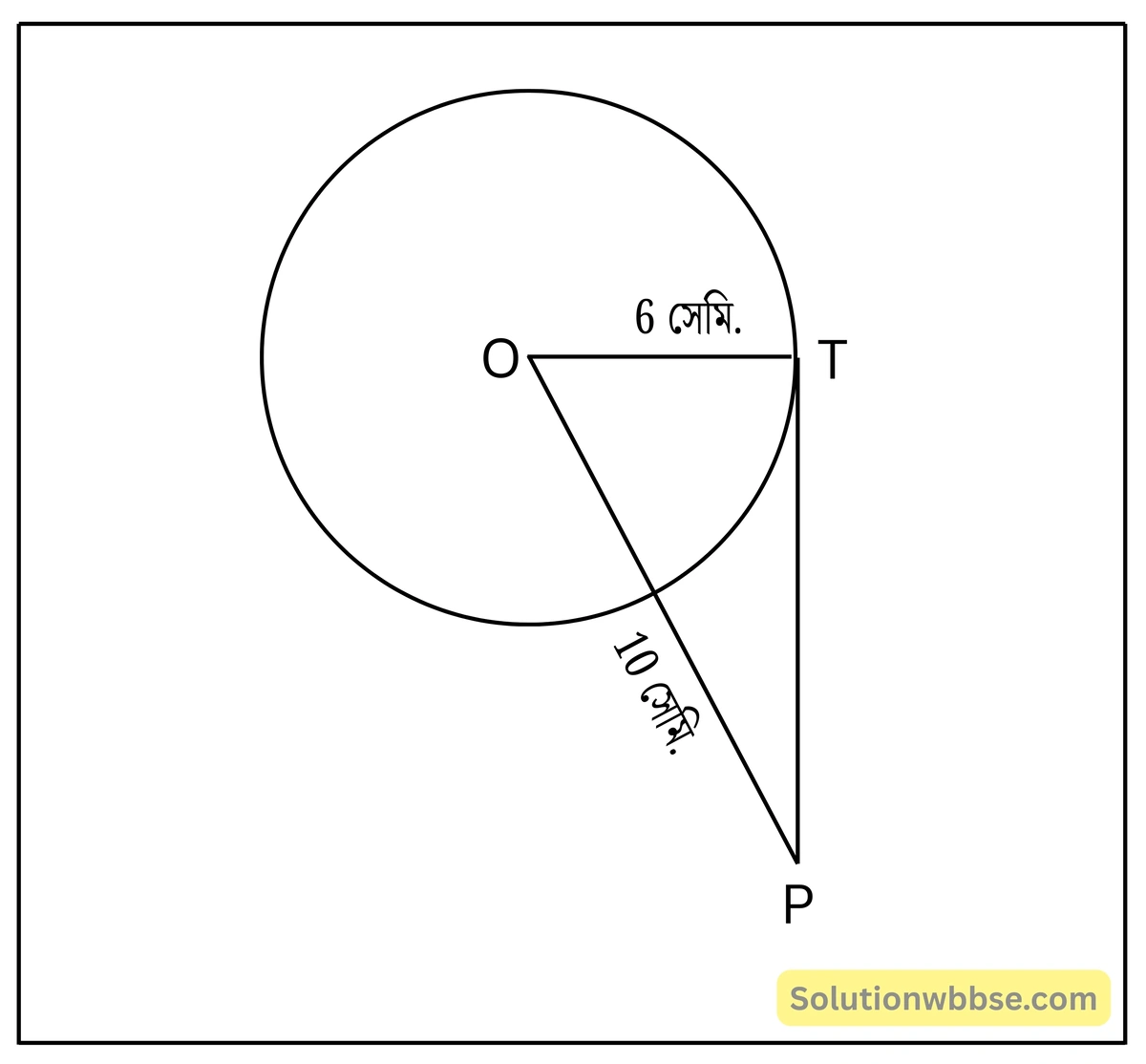
O কেন্দ্রীয় বৃত্তের OT ব্যাসার্ধ এবং PT স্পর্শক। . OT ⊥ PT

∴ সমকোণী ত্রিভুজ POT -তে, PT² = PO² – OT²

[পিথাগোরাসের উপপাদ্য থেকে পেলাম]

বা, PT² = (10)² – (6)² বর্গ সেমি।

বা, PT² = (100 – 36) বর্গ সেমি।

বা, PT² = 64 বর্গ সেমি।

∴ PT = √64​ সেমি।

= 8 সেমি।

∴ পেলাম PT স্পর্শকের দৈর্ঘ্য 8 সেমি।

প্রয়োগ 10. আমি যদি এমন একটি O কেন্দ্রীয় বৃত্ত আঁকি যার কেন্দ্র থেকে 26 সেমি. দূরত্বে অবস্থিত P বিন্দু থেকে অঙ্কিত বৃত্তের স্পর্শকের দৈর্ঘ্য 10 সেমি. হবে, তবে বৃত্তের ব্যাসার্ধের দৈর্ঘ্য কী হবে হিসাব করে লিখি।

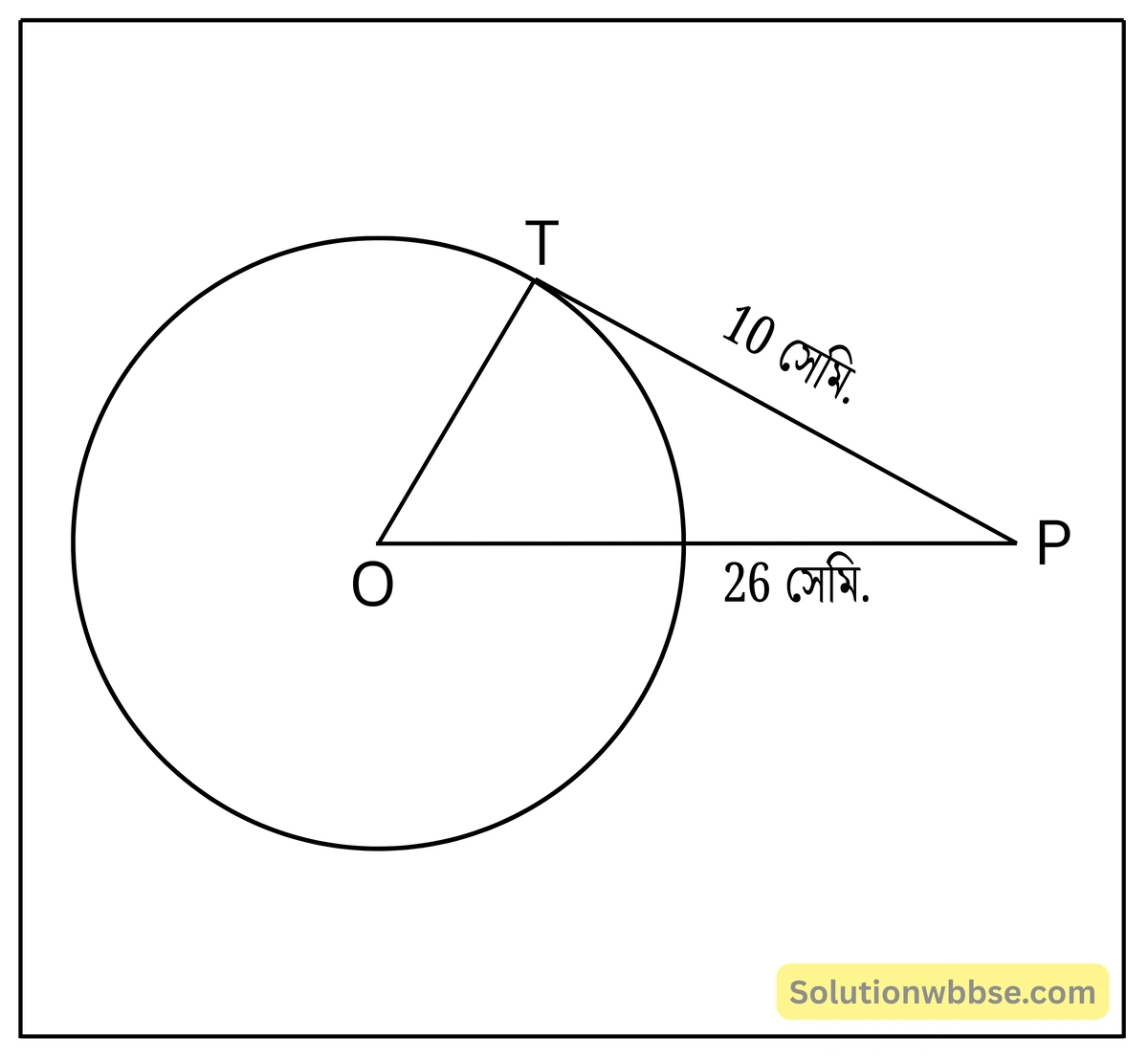
PT = 10 সেমি., PO = 26 সেমি.

সমকোণী △ POT থেকে পাই,

PO² = PT² + OT² [পিথাগোরাসের উপপাদ্য থেকে পাই]

∴ (26 সেমি.)² = (10 সেমি.)² + OT²

বা, OT² = (26 সেমি.)² – (10 সেমি.)²

বা, OT² = 576

∴ OT = 24 সেমি. [নিজে করি]

প্রয়োগ 11. পাশের চিত্রের O কেন্দ্রীয় বৃত্তের দুটি ব্যাসার্ধ OA ও OB-এর মধ্যবর্তী কোণ 130°; A ও B বিন্দুতে অঙ্কিত স্পর্শকদ্বয় T বিন্দুতে ছেদ করে। ∠ATB এবং ∠ATO-এর মান হিসাব করে লিখি।

A ও B বিন্দুতে অঙ্কিত বৃত্তের স্পর্শকদ্বয় পরস্পরকে T বিন্দুতে ছেদ করেছে।

∴ T বিন্দু থেকে অঙ্কিত দুটি স্পর্শক AT এবং BT এবং OA ও OB স্পর্শবিন্দুগামী ব্যাসার্ধ।

∴ OA ⊥ AT এবং

∴ ∠ATB + ∠AOB = 360° – (90° + 90°)

বা, ∠ATB + ∠AOB = 180°

∴ ∠ATB = 180° – 130° = 50°

আবার, যেহেতু OT, ∠ATB-কে সমদ্বিখণ্ডিত করে, সুতরাং ∠ATO = \(\frac{50^\circ}2\)​ = 25°

প্রয়োগ 12. O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু A থেকে দুটি স্পর্শক টানি যারা বৃত্তকে যথাক্রমে B ও C বিন্দুতে স্পর্শ করে। প্রমাণ করি যে, AO, BC-এর লম্বসমদ্বিখণ্ডক।

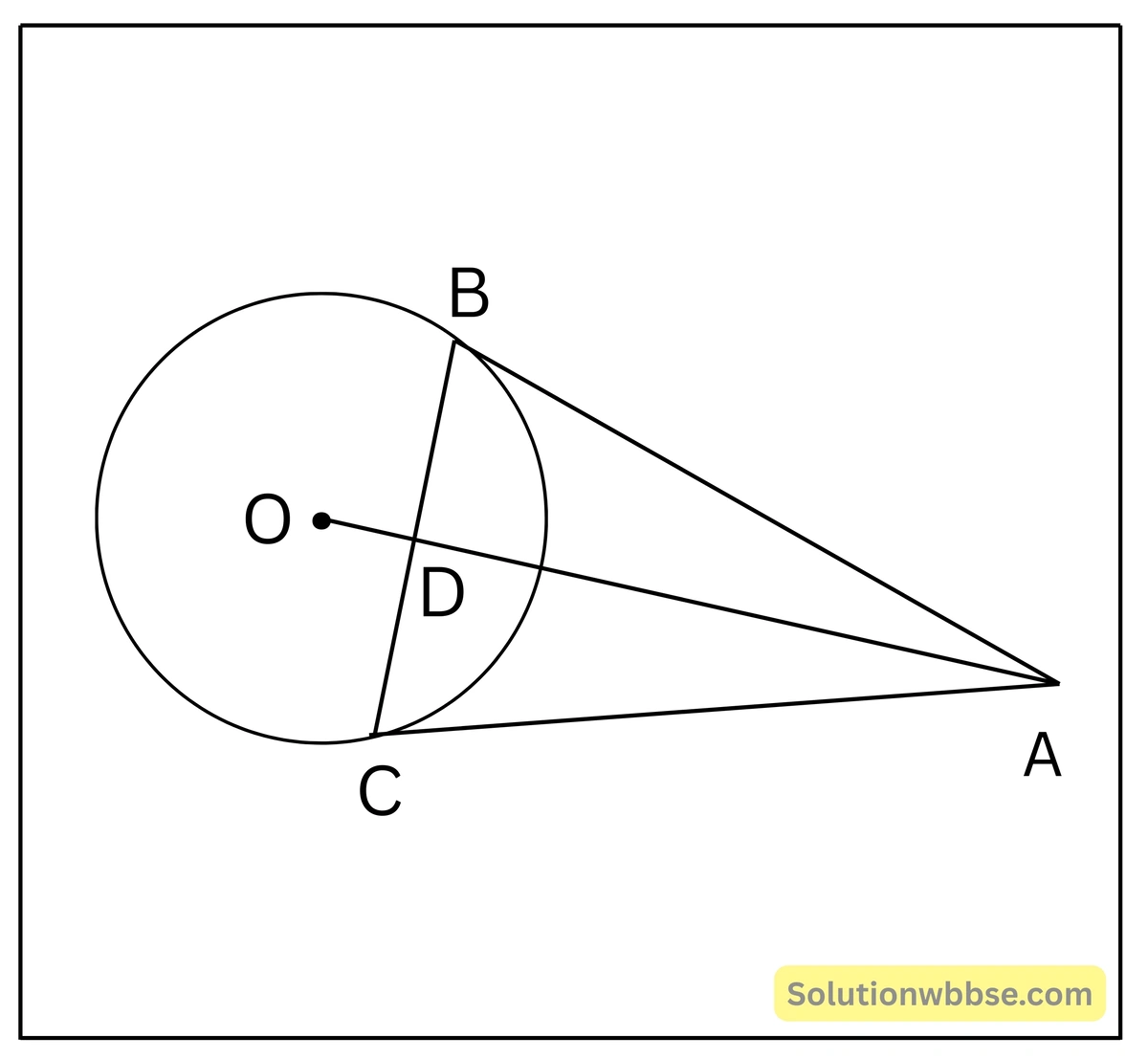
প্রদত্ত – O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু A থেকে দুটি স্পর্শক AB ও AC টানা হয়েছে যারা বৃত্তকে B ও C বিন্দুতে স্পর্শ করেছে। A, O বৃত্তের কেন্দ্র। AO, BC-কে D বিন্দুতে ছেদ করে।

প্রমাণ করতে হবে – AO, BC-এর লম্বসমদ্বিখণ্ডক।

প্রমাণ – O কেন্দ্রীয় বৃত্তের AB ও AC স্পর্শক। সুতরাং, AB = AC

এবং AO, ∠BAC-এর সমদ্বিখণ্ডক। অর্থাৎ, ∠BAD = ∠CAD

△ABD ও △ACD-তে, AB = AC

∠BAD = ∠CAD এবং AD সাধারণ বাহু

∴ △ABD ≅ △ACD (S-A-S সর্বসমতার শর্ত অনুসারে)

সুতরাং, BD = CD (সর্বসম ত্রিভুজের অনুরূপ বাহু)

এবং ∠BDA = ∠CDA (সর্বসম ত্রিভুজের অনুরূপ কোণ)

আবার, ∠BDA + ∠CDA = 180°
বা, 2 ∠BDA = 180° (∵ ∠BDA = ∠CDA)

∴ ∠BDA = 90° সুতরাং AD ⊥ BC

∴ AD, BC-এর লম্বসমদ্বিখণ্ডক। (প্রমাণিত)

প্রয়োগ 13. আমি O কেন্দ্রীয় একটি বৃত্ত অঙ্কন করেছি যার AB একটি ব্যাস। AB ব্যাসের A ও B বিন্দুতে বৃত্তের দুটি স্পর্শক অঙ্কন করেছি যা বৃত্তটির ওপর একটি বিন্দু T-তে অঙ্কিত স্পর্শককে যথাক্রমে P ও Q বিন্দুতে ছেদ করে। প্রমাণ করি, ∠POQ = 90°

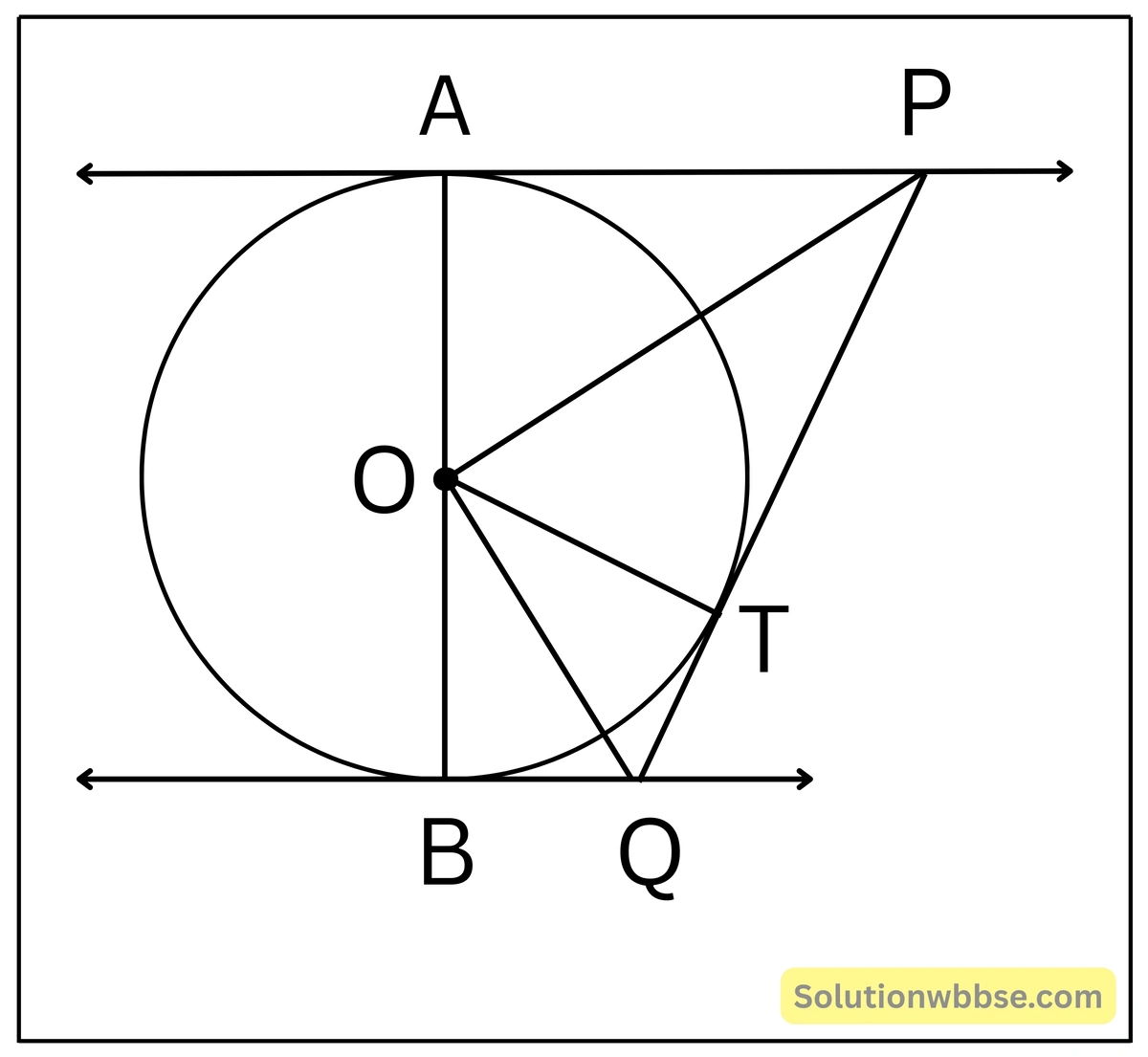
প্রদত্ত – O কেন্দ্রীয় বৃত্তের AB ব্যাস। A ও B বিন্দুতে দুটি স্পর্শক অঙ্কন করা হয়েছে। বৃত্তের ওপর একটি বিন্দু T -তে অঙ্কিত স্পর্শক A ও B বিন্দুতে অঙ্কিত স্পর্শককে যথাক্রমে P ও Q বিন্দুতে ছেদ করে।

প্রমাণ করতে হবে – ∠POQ = 90°

অঙ্কন – O, P; O, Q এবং O, T যুক্ত করি।

প্রমাণ – O কেন্দ্রীয় বৃত্তে A ও T বিন্দুতে অঙ্কিত স্পর্শক দুটি P বিন্দুতে ছেদ করেছে।

∴ PO, ∠APT -এর অন্তস্ধদ্বিখণ্ডক

∴ ∠TPO = \(\frac12\) ∠APT_________ (i)

অনুরূপে, T ও B বিন্দুতে অঙ্কিত স্পর্শকদুটি Q বিন্দুতে ছেদ করেছে।

∴ ∠TQO = \(\frac12\) ∠BQT_________ (ii)

আবার, AP ∥ BQ এবং PQ ছেদক।

∴ ∠APT + ∠BQT = 180°

∴ ∠TPO + ∠TQO =\(\frac12\) ∠APT + \(\frac12\) ∠BQT [i ও (ii) থেকে পেলাম]

= \(\frac12\) (∠APT + ∠BQT) = \(\frac12\)​ x 180° = 90°

∴ △POQ -এর অপর কোণটি অর্থাৎ ∠POQ = 90° [প্রমাণিত]

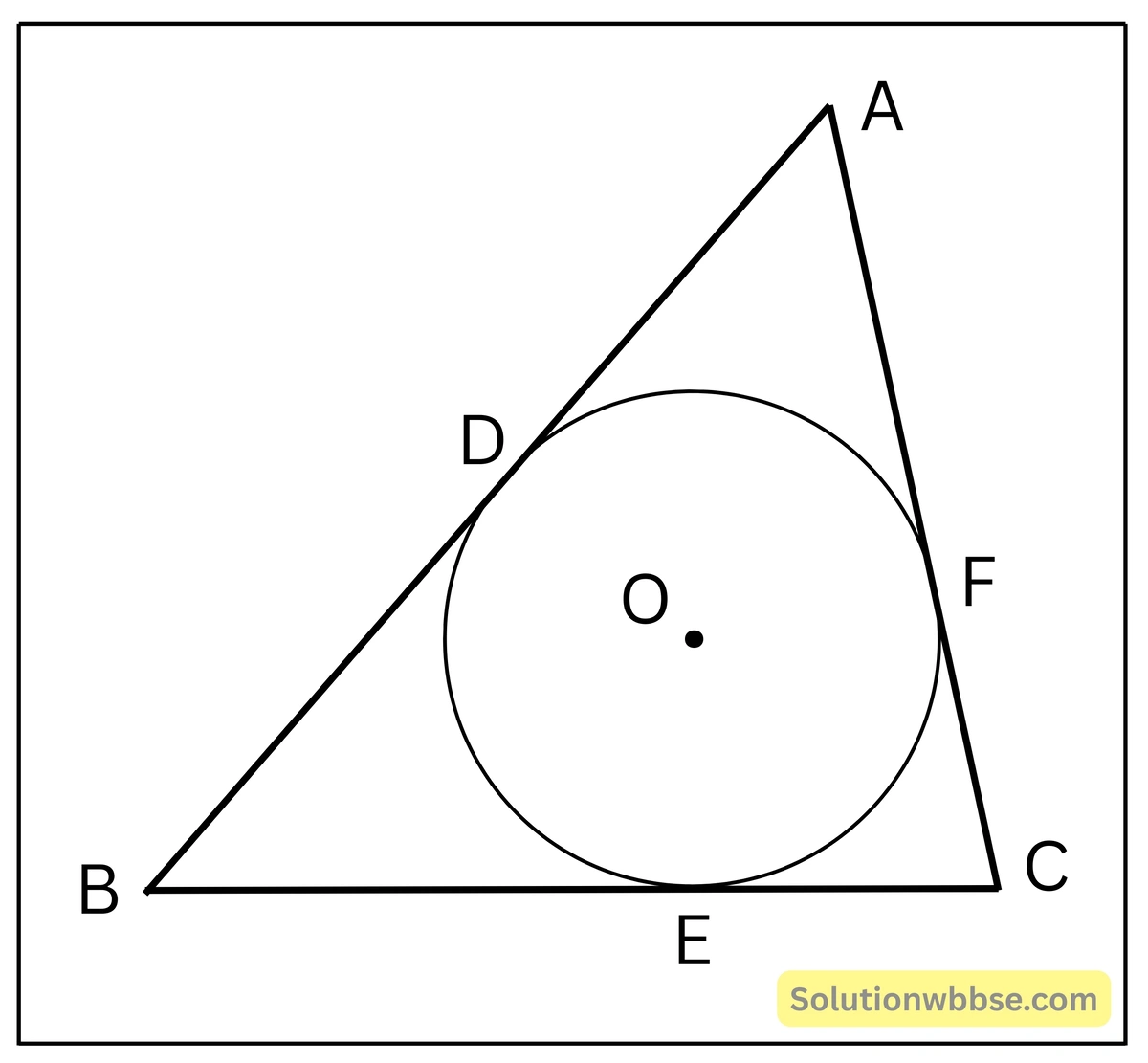
প্রয়োগ 14. O কেন্দ্রীয় বৃত্তের পরিলিখিত চতুর্ভুজ ABCD হলে প্রমাণ করি যে, AB + CD = BC + DA

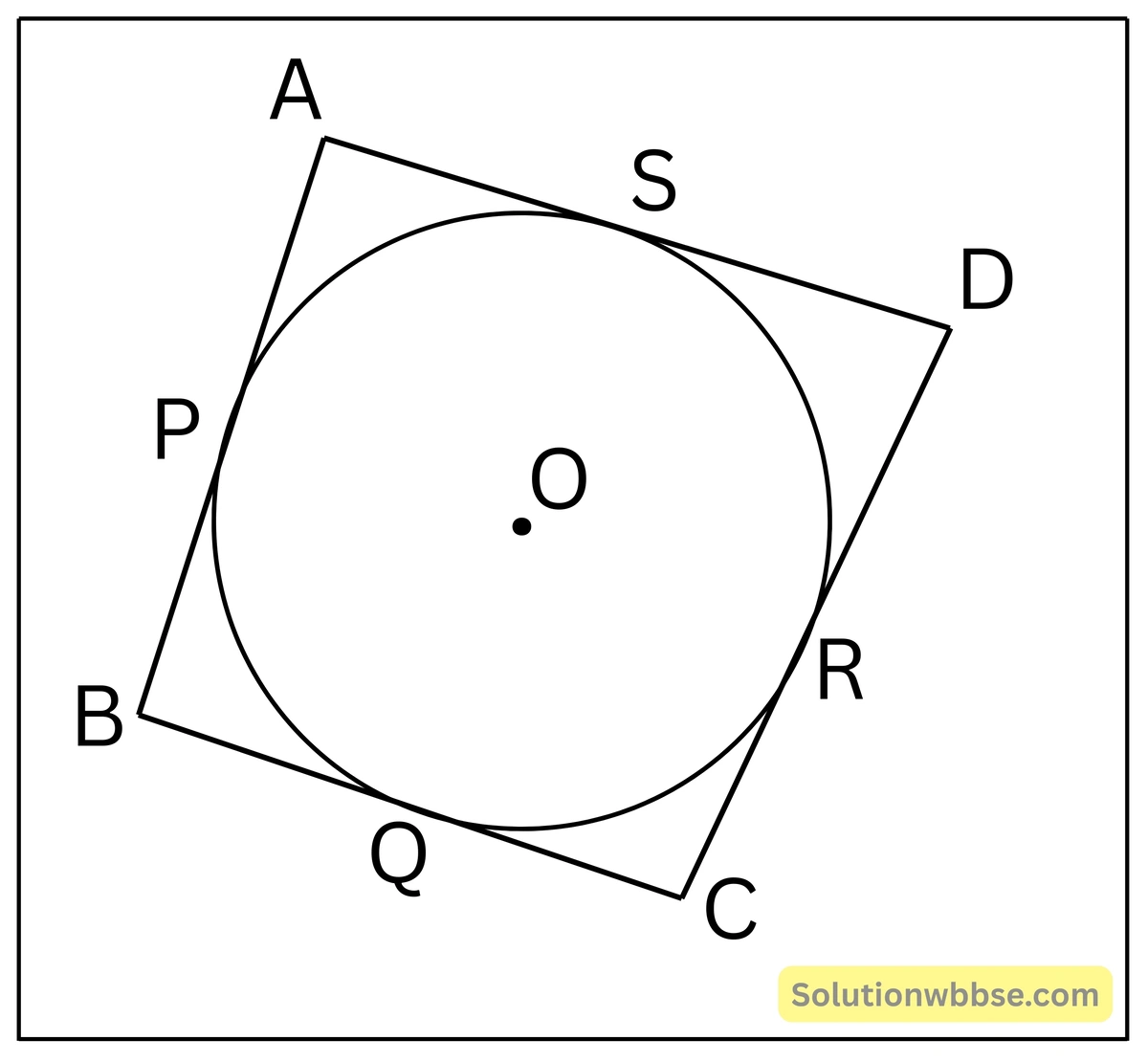
প্রদত্ত – ABCD চতুর্ভুজটি O কেন্দ্রীয় বৃত্তে পরিলিখিত।

ধরি, AB, BC, CD ও DA বৃত্তটিকে যথাক্রমে P, Q, R ও S বিন্দুতে স্পর্শ করেছে।

প্রমাণ করতে হবে – AB + CD = BC + DA

প্রমাণ – O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু A থেকে AS ও AP দুটি স্পর্শক

∴ AS = AP

অনুরূপে, BP = BQ, CQ = CR এবং DR = DS

AB + CD = AP + BP + CR + DR

AB + CD = AS + BQ + CQ + DS

AB + CD = (AS + DS) + (BQ + CQ)

AB + CD = AD + BC [প্রমাণিত]

প্রয়োগ 15. আমি একটি O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু P থেকে দুটি স্পর্শক PA ও PB অঙ্কন করেছি যারা যথাক্রমে A ও B বিন্দুতে স্পর্শ করেছে। প্রমাণ করো যে, ∠APB + ∠AOB = 180°

প্রদত্ত – একটি বৃত্ত যার কেন্দ্র O। P হলো বৃত্তের বাইরের একটি বিন্দু এবং PA ও PB হলো দুটি স্পর্শক যা A ও B বিন্দুতে বৃত্তকে স্পর্শ করে।

প্রমাণ করতে হবে -∠APB+∠AOB=180°।

প্রমাণ –

আমরা জানি যে, বৃত্তের কোনো স্পর্শক এবং স্পর্শবিন্দুগামী ব্যাসার্ধ পরস্পর লম্ব হয়।

অতএব, স্পর্শক PA, ব্যাসার্ধ OA এর উপর লম্ব। অর্থাৎ, ∠PAO=90°।

একইভাবে, স্পর্শক PB, ব্যাসার্ধ OB এর উপর লম্ব। অর্থাৎ, ∠PBO=90°।

এখন, P, A, O, B বিন্দু চারটি একটি চতুর্ভুজ গঠন করেছে।

আমরা জানি, চতুর্ভুজের চারটি কোণের যোগফল 360°।

সুতরাং, চতুর্ভুজ PAOB-এর ক্ষেত্রে – ∠APB+∠PAO+∠AOB+∠PBO=360°।

∠PAO এবং ∠PBO এর মান 90° বসিয়ে পাই –

∠APB + 90° + ∠AOB + 90° = 360°

∠APB + ∠AOB + 180° = 360°

∠APB + ∠AOB = 360° − 180°

∠APB + ∠AOB = 180° (প্রমাণিত)

প্রয়োগ 16. P ও Q কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পরকে A বিন্দুতে স্পর্শ করে। বৃত্ত দুটির একটি সরল সাধারণ স্পর্শক P-কেন্দ্রীয় বৃত্তকে R বিন্দুতে এবং Q-কেন্দ্রীয় বৃত্তকে S বিন্দুতে স্পর্শ করে। প্রমাণ করি যে,
(i) A বিন্দুতে অঙ্কিত সাধারণ স্পর্শক RS সরলরেখাকে সমদ্বিখণ্ডিত করে।
(ii) ∠RAS = 90°
(iii) যদি PT ও QT, যথাক্রমে AR ও AS-কে C ও B বিন্দুতে ছেদ করে, তবে ABTC একটি আয়তক্ষেত্র হবে।

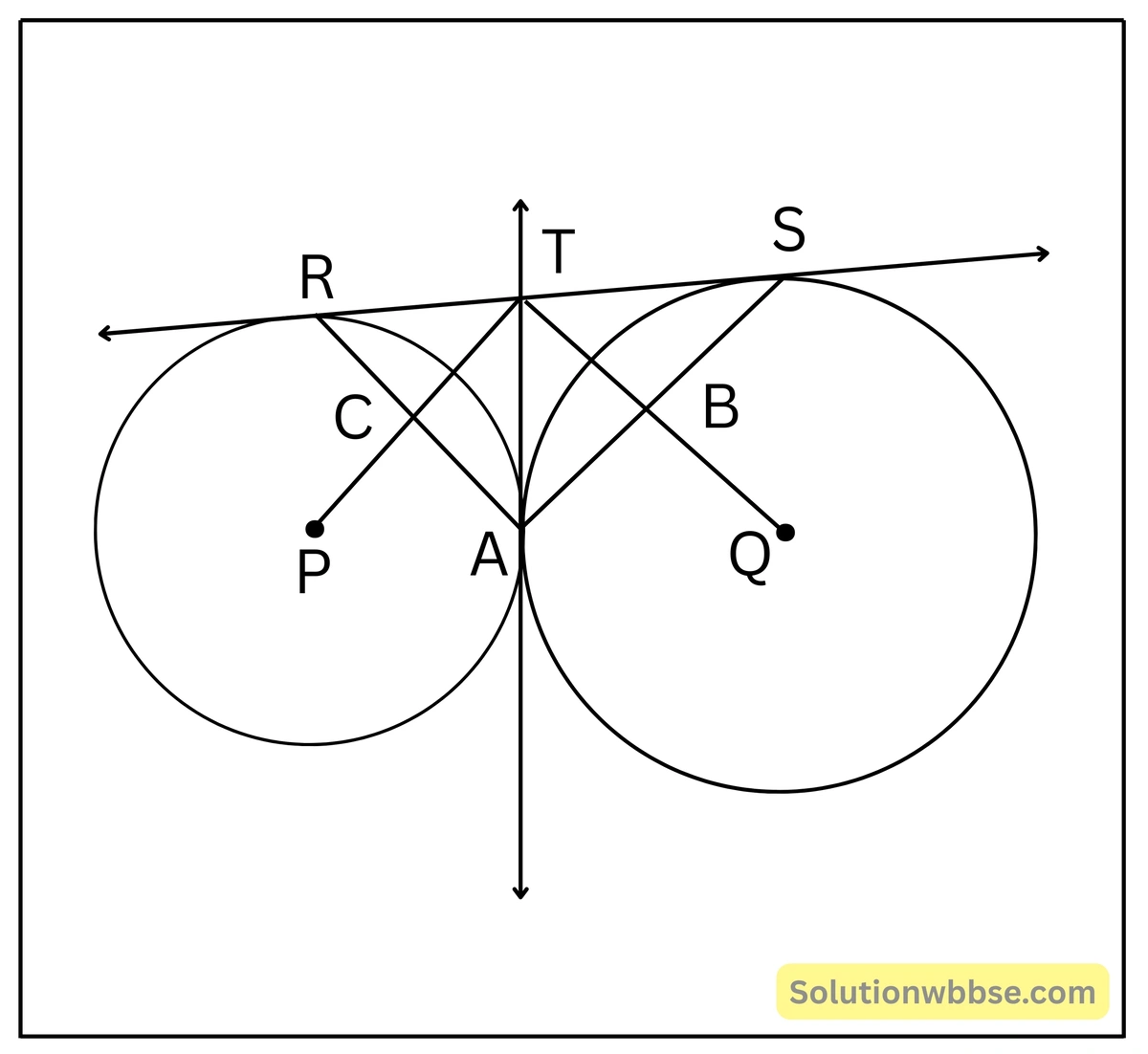
প্রদত্ত – P ও Q কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পরকে A বিন্দুতে বহিঃস্পর্শ করেছে। বৃত্ত দুটির একটি সরল সাধারণ স্পর্শক P ও Q কেন্দ্রীয় বৃত্ত দুটিকে যথাক্রমে R ও S বিন্দুতে স্পর্শ করে। A বিন্দুতে অঙ্কিত স্পর্শক RS-কে T বিন্দুতে ছেদ করে। PT, AR -কে C বিন্দুতে এবং QT, AS -কে B বিন্দুতে ছেদ করে।

প্রমাণ করতে হবে –

(i) AT, RS-কে সমদ্বিখণ্ডিত করে
(ii) ∠RAS = 1 সমকোণ
(iii) ABTC একটি আয়তাকার চিত্র।

প্রমাণ – A বিন্দুতে অঙ্কিত স্পর্শক RS-কে T বিন্দুতে ছেদ করেছে।

∴ T বিন্দু থেকে P-কেন্দ্রীয় বৃত্তে দুটি স্পর্শক TR ও TA

∴ TR = TA

অনুরূপে, TS = TA .. TR = TS

∴ AT, RS-কে T বিন্দুতে সমদ্বিখণ্ডিত করেছে। [(i) প্রমাণিত]

আবার ΔATR-এর TR = TA

∴ ∠TAR = ∠TRA

অনুরূপভাবে, ∠TAS = ∠TSA

∴ ∠RAS = ∠TAR + ∠TAS = 90°

[∵ ∠TRA + ∠TAR + ∠TAS + ∠TSA = 180°

∴ 2 (∠TAR + ∠TAS) = 180°; সুতরাং, ∠TAR + ∠TAS = 90°] [(ii) নং প্রমাণিত]

আবার, PT, ∠RTA-এর সমদ্বিখণ্ডক এবং QT, ∠ATS-এর সমদ্বিখণ্ডক

∴ PT ⊥ TQ অর্থাৎ, ∠PTQ = 1 সমকোণ। অনুরূপে, QT ⊥ SA

PT ⊥ RA এবং QT ⊥ SA, [কারণ ΔTRC ও ΔTAC -এর মধ্যে, TR = TA, ∠RTC = ∠ATC এবং TC উহাদের সাধারণ বাহু ∴ ΔTRC ≅ ΔTAC (S-A-S সর্বসমতার শর্তানুসারে) সুতরাং, ∠TCR = ∠TCA .. PT ⊥ RA]

∠ACT = ∠ABT = 1 সমকোণ

ABTC চতুর্ভুজের, ∠ACT = ∠ABT = 90°

এবং ∠CAB = 90° ∴ ∠CTB = 90°

∴ ABTC একটি সামান্তরিক (∵ চতুর্ভুজের বিপরীত কোণ সমান)

আবার, ABTC সামান্তরিকের একটি কোণ সমকোণ।

∴ ABTC একটি আয়তাকার চিত্র, [(iii) প্রমাণিত]

প্রয়োগ 17. সুমিতা দুটি বৃত্ত অঙ্কন করেছে যারা পরস্পরকে O বিন্দুতে বহিঃস্পর্শ করেছে। যদি PQ ও RS দুটি বৃত্তের ব্যাস হয় যারা পরস্পর সমান্তরাল, তবে প্রমাণ করি যে, P, O এবং S বিন্দু তিনটি সমরেখ।

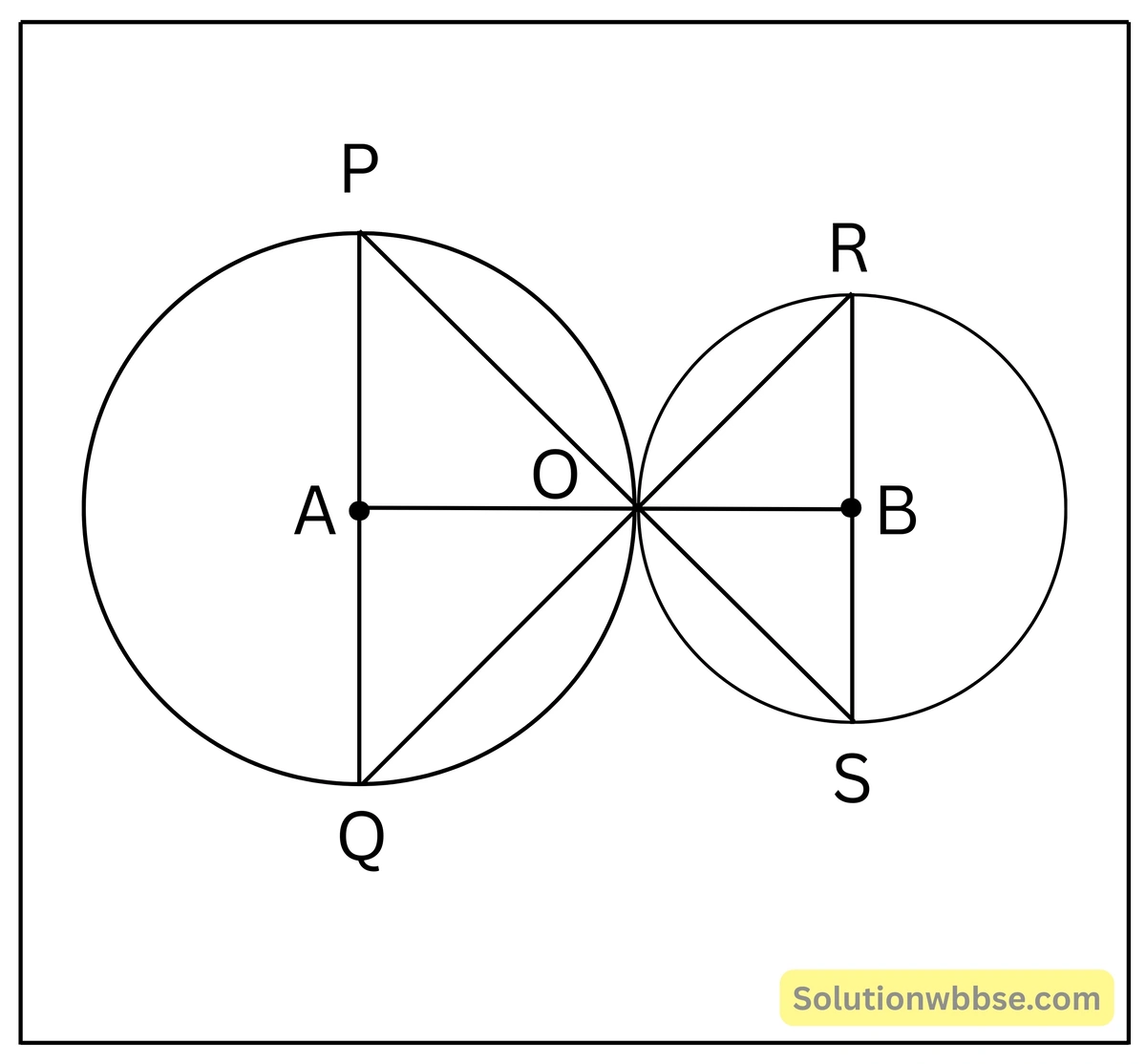
প্রদত্ত – দুটি বৃত্ত পরস্পরকে O বিন্দুতে বহিঃস্পর্শ করেছে। বৃত্ত দুটির ব্যাস PQ ও RS সমান্তরাল।

প্রমাণ করতে হবে – P, O, S বিন্দু তিনটি সমরেখ।

অঙ্কন – ধরি বৃত্ত দুটির কেন্দ্র A ও B; O, A; O, B; O, P; O, Q; O, R; O, S যুক্ত করি।

প্রমাণ – বৃত্তদুটির কেন্দ্র A ও B.

O বিন্দুতে বৃত্তদুটি পরস্পরকে বহিঃস্পর্শ করেছে।

∴ A, O ও B একই সরলরেখায় অবস্থিত।

∆AOP-এর AP = AO,

∴ ∠APO = ∠AOP

আবার ∠PAO + ∠APO + ∠AOP = 180°

∴ 2∠AOP = 180° − ∠PAO

অনুরূপভাবে, ∆BOR থেকে পাই 2∠ROB = 180° − ∠RBO

∴ 2∠AOP + 2∠ROB = 360° − (∠PAO + ∠RBO)

= 360° − 180° [∵ PQ || RS এবং AB ভেদক]

= 180°

∴ ∠AOP + ∠ROB = 90°

∴ ∠POR = 180° − (∠AOP + ∠ROB) = 180° − 90° = 90°

∠POR + ∠ROS = 90° + 90° = 180° (∵ ∠ROS অর্ধবৃত্তস্থ কোণ, সুতরাং ∠ROS = 90°)

∴ ∠POS = 180°

∴ P, O এবং S বিন্দু তিনটি সমরেখ। [প্রমাণিত]

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের পঞ্চদশ অধ্যায়, ‘বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।

আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।