এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের পঞ্চদশ অধ্যায়, ‘বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য’ -এর ‘কষে দেখি – 15.1’ বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

1. O কেন্দ্রীয় বৃত্তের AB একটি জ্যা। B বিন্দুতে অঙ্কিত স্পর্শক বর্ধিত AO-কে T বিন্দুতে ছেদ করে এবং ∠BAT = 21º।
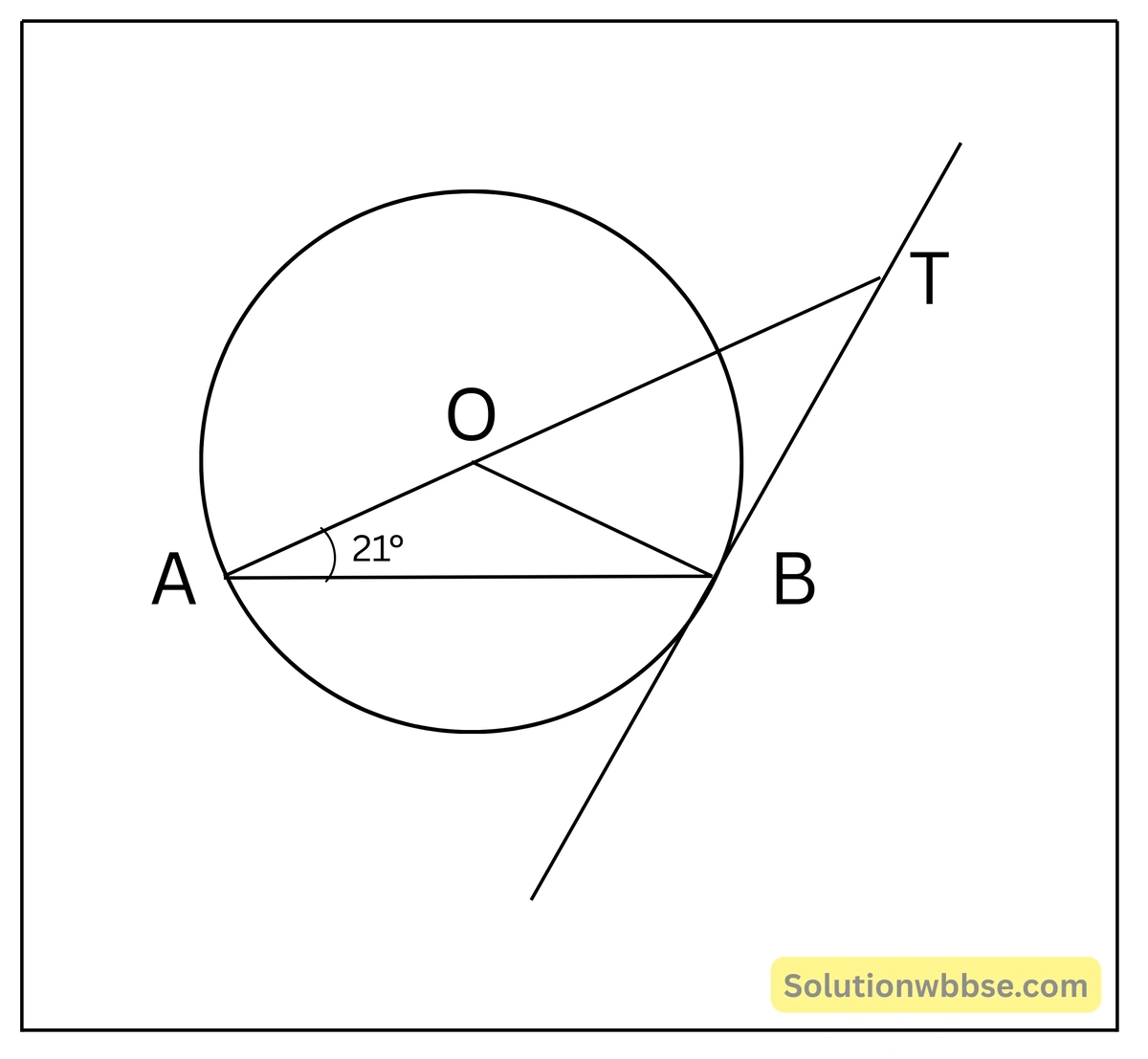
O কেন্দ্রীয় বৃত্তের AB একটি জ্যা। B বিন্দুতে অঙ্কিত স্পর্শক বর্ধিত AO-কে T বিন্দুতে ছেদ করে এবং ∠BAT = 21º।
∠BTA-এর মান নির্ণয় করতে হবে।
অঙ্কন – O, B যুক্ত করা হলো।
প্রমাণ –
যেহেতু ∠BAT = 21º, সুতরাং ∠OAB = 21º।
এখন, ∆OAB-এর মধ্যে,
OA = OB (কারণ তারা একই বৃত্তের ব্যাসার্ধ)
সুতরাং, ∆OAB একটি সমদ্বিবাহু ত্রিভুজ।
∴ ∠OBA = ∠OAB = 21º [∵ সমদ্বিবাহু ত্রিভুজের সমান বাহুর বিপরীত কোণগুলি সমান হয়]
আবার, আমরা জানি বৃত্তের কোনো বিন্দুতে অঙ্কিত স্পর্শক এবং ওই বিন্দুগামী ব্যাসার্ধ পরস্পর লম্বভাবে অবস্থান করে।
∴ OB ⊥ BT
সুতরাং, ∠OBT = 90º
এখন, ∆OAB-এর ক্ষেত্রে, বর্ধিত বাহু AO, T বিন্দু পর্যন্ত বিস্তৃত হওয়ায় বহিঃস্থ কোণ ∠BOT উৎপন্ন হয়েছে।
আমরা জানি, ত্রিভুজের বহিঃস্থ কোণ অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান।
∴ বহিঃস্থ ∠BOT = অন্তঃস্থ ∠OAB + অন্তঃস্থ ∠OBA
বা, ∠BOT = 21º + 21º = 42º
এবার, ∆OBT-এর তিনটি কোণের সমষ্টি 180º।
∴ ∠BTA + ∠OBT + ∠BOT = 180º
বা, ∠BTA + 90º + 42º = 180º
বা, ∠BTA + 132º = 180º
বা, ∠BTA = 180º – 132º
∴ ∠BTA = 48º
উত্তর – ∠BTA-এর মান হলো 48º।
2. কোনো বৃত্তের XY একটি ব্যাস। বৃত্তটির ওপর অবস্থিত A বিন্দুতে PAQ বৃত্তের স্পর্শক। X বিন্দু থেকে বৃত্তের স্পর্শকের ওপর অঙ্কিত লম্ব PAQ কে Z বিন্দুতে ছেদ করেছে। প্রমান করি যে XA, ∠YXZ এর সমদ্বিখন্ডক।
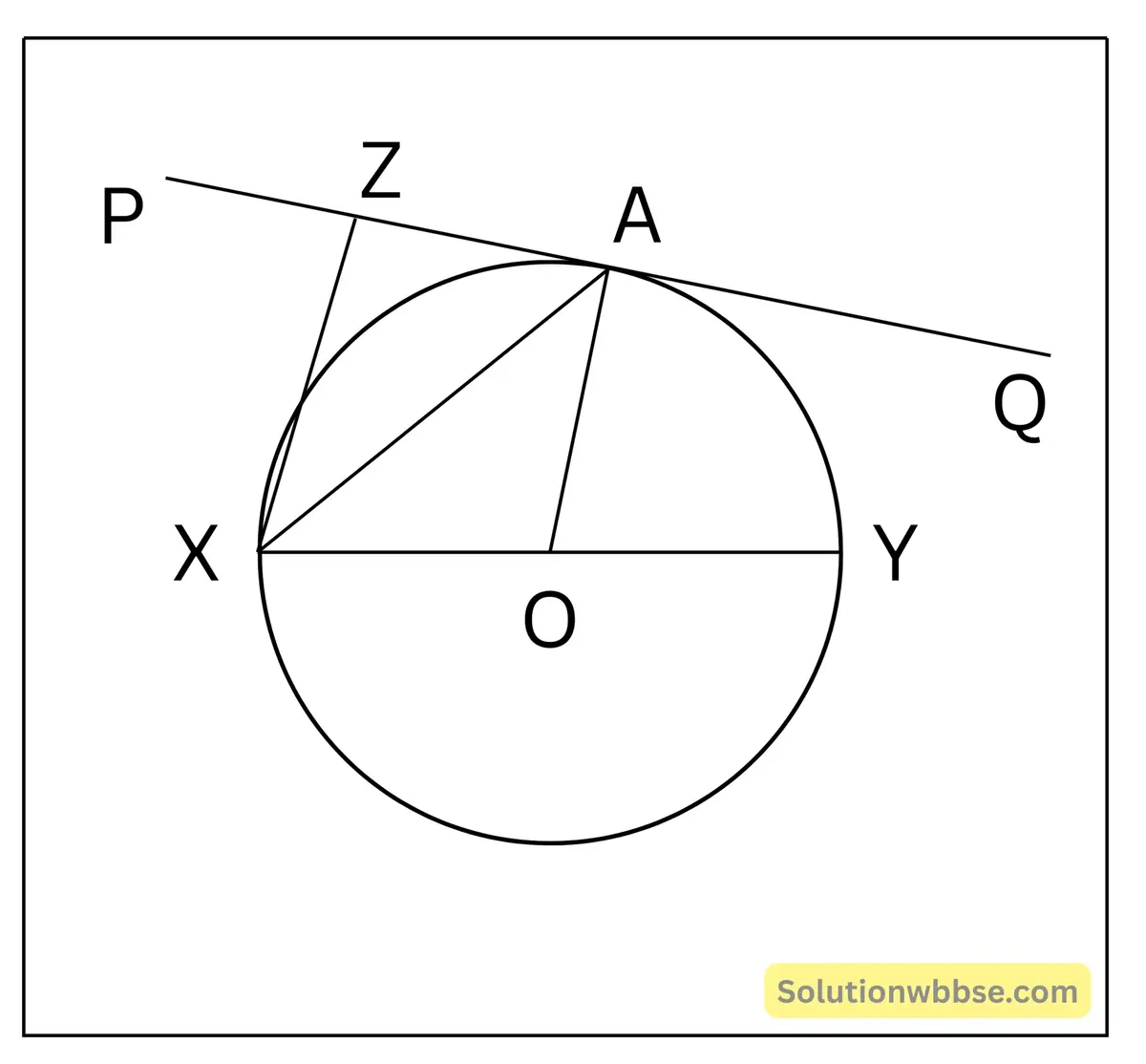
প্রদত্ত – O কেন্দ্রীয় একটি বৃত্তের XY একটি ব্যাস। বৃত্তটির উপর অবস্থিত A বিন্দুতে PAQ একটি স্পর্শক। X বিন্দু থেকে স্পর্শক PAQ -এর উপর XZ লম্ব অঙ্কন করা হয়েছে। XA যুক্ত করা হলো।
প্রামাণ্য বিষয় – XA, ∠YXZ-এর সমদ্বিখণ্ডক। অর্থাৎ, ∠YXA = ∠AXZ।
অঙ্কন – বৃত্তের কেন্দ্র O এবং A বিন্দু যুক্ত করা হলো (OA)।
প্রমাণ – যেহেতু বৃত্তের A বিন্দুতে PAQ একটি স্পর্শক এবং OA হলো ওই বিন্দুগামী ব্যাসার্ধ, ∴ OA ⊥ PAQ সুতরাং, ∠OAP = 90° বা, ∠OAX + ∠XAZ = 90° — (i)
আবার, প্রদত্ত আছে যে XZ ⊥ PAQ। সুতরাং, ∆AXZ একটি সমকোণী ত্রিভুজ, যার ∠AZX = 90°।
আমরা জানি, একটি ত্রিভুজের তিনটি কোণের সমষ্টি 180°।
∴ ∠AXZ + ∠XAZ + ∠AZX = 180°
বা, ∠AXZ + ∠XAZ + 90° = 180°
বা, ∠AXZ + ∠XAZ = 90° — (ii)
এখন, (i) ও (ii) নং সমীকরণ তুলনা করে পাই, ∠OAX + ∠XAZ = ∠AXZ + ∠XAZ
∴ ∠OAX = ∠AXZ — (iii)
আবার, ∆OAX-এর ক্ষেত্রে, OX = OA (কারণ উভয়েই একই বৃত্তের ব্যাসার্ধ) সুতরাং, ∆OAX একটি সমদ্বিবাহু ত্রিভুজ।
∴ ∠OXA = ∠OAX [∵ সমদ্বিবাহু ত্রিভুজের সমান বাহুর বিপরীত কোণগুলি সমান হয়] — (iv)
যেহেতু Y, O, X বিন্দু তিনটি একই সরলরেখায় অবস্থিত, তাই ∠OXA এবং ∠YXA একই কোণ। অর্থাৎ, ∠YXA = ∠OAX।
এখন, (iii) ও (iv) নং সমীকরণ থেকে আমরা পাই, ∠YXA = ∠AXZ
সুতরাং, XA সরলরেখাটি ∠YXZ-কে সমদ্বিখণ্ডিত করে। (প্রমাণিত)
3.
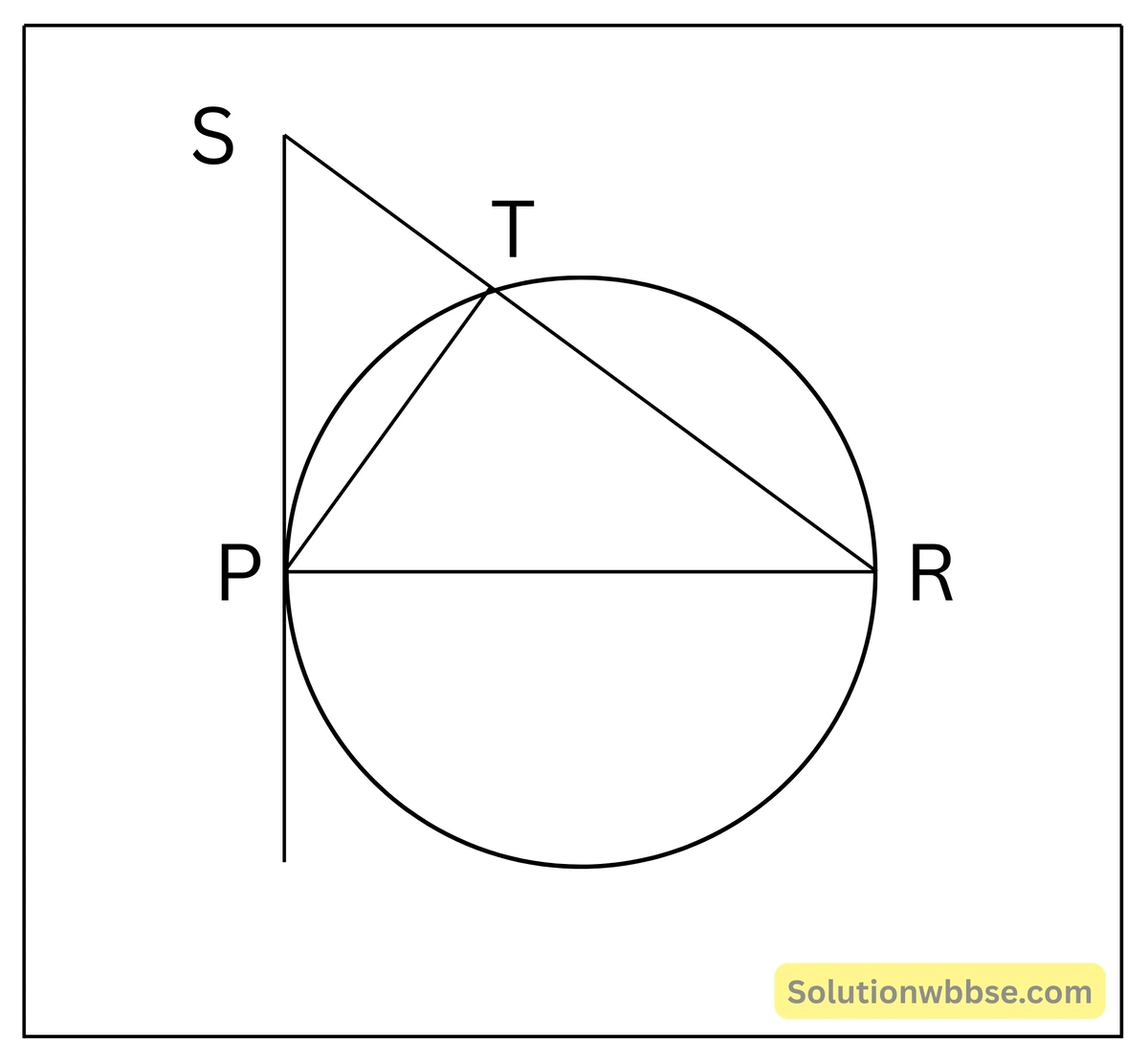
প্রদত্ত – একটি বৃত্ত অঙ্কন করা হয়েছে যার PR একটি ব্যাস। P বিন্দুতে একটি স্পর্শক অঙ্কন করা হয়েছে এবং ওই স্পর্শকের উপর S এমন একটি বিন্দু যে, PR = PS। RS সরলরেখা বৃত্তটিকে T বিন্দুতে ছেদ করে। P,T; R,T এবং P,S যুক্ত করা হলো।
প্রামাণ্য বিষয় – ST = RT = PT।
প্রমাণ – যেহেতু বৃত্তের P বিন্দুতে PS একটি স্পর্শক এবং PR হলো ব্যাস (যা P বিন্দুগামী ব্যাসার্ধ ধারণ করে),
∴ PR ⊥ PS
সুতরাং, ∆PRS একটি সমকোণী ত্রিভুজ, যার ∠SPR = 90°।
এখন, সমকোণী ত্রিভুজ ∆PRS-এর মধ্যে, প্রদত্ত আছে, PR = PS।
সুতরাং, এটি একটি সমদ্বিবাহু সমকোণী ত্রিভুজ।
∴ ∠PRS = ∠PSR [∵ সমান বাহুর বিপরীত কোণদ্বয় সমান]
আবার, ত্রিভুজের তিনটি কোণের সমষ্টি 180°।
∠SPR + ∠PRS + ∠PSR = 180°
বা, 90° + ∠PRS + ∠PRS = 180° [∵ ∠PRS = ∠PSR] বা, 2∠PRS = 180° – 90°
বা, 2∠PRS = 90°
∴ ∠PRS = 45° সুতরাং, ∠PRS = ∠PSR = 45°।
যেহেতু PR বৃত্তের ব্যাস এবং T বৃত্তের পরিধির উপর একটি বিন্দু,
∴ ∠PTR = 90° [∵ অর্ধবৃত্তস্থ কোণ সমকোণ]।
এখন, ∆PTR ত্রিভুজের ক্ষেত্রে –
∠PRT = ∠PRS = 45°
∠PTR = 90°
∴ ∠TPR = 180° – (∠PTR + ∠PRT)
বা, ∠TPR = 180° – (90° + 45°)
বা, ∠TPR = 180° – 135° = 45°।
যেহেতু ∆PTR -এর ∠TPR = ∠PRT = 45°,
∴ PT = RT — (i) [∵ সমান কোণের বিপরীত বাহুদ্বয় সমান]।
আবার, যেহেতু RTS একটি সরলরেখা, ∠PTS + ∠PTR = 180° [রৈখিক যুগ্ম কোণ]
বা, ∠PTS + 90° = 180°
∴ ∠PTS = 90°
এখন, ∆SPT ত্রিভুজের ক্ষেত্রে, ∠PST = ∠PSR = 45°
∠PTS = 90°
∴ ∠SPT = 180° – (∠PTS + ∠PST)
বা, ∠SPT = 180° – (90° + 45°)
বা, ∠SPT = 180° – 135° = 45°।
যেহেতু ∆SPT -এর ∠SPT = ∠PST = 45°,
∴ PT = ST — (ii) [∵ সমান কোণের বিপরীত বাহুদ্বয় সমান]।
এখন, (i) ও (ii) নং সমীকরণ থেকে পাই, ST = RT = PT। (প্রমাণিত)
4. একটি O কেন্দ্রীয় বৃত্ত অঙ্কন করি যার দুটি ব্যাসার্ধ OA ও OB পরস্পর লম্বভাবে অবস্থিত। A ও B বিন্দুতে অঙ্কিত স্পর্শকদ্বয় পরস্পরকে T বিন্দুতে ছেদ করলে, প্রমাণ করি যে, AB = OT এবং তারা পরস্পরকে লম্বভাবে সমদ্বিখন্ডিত করে।
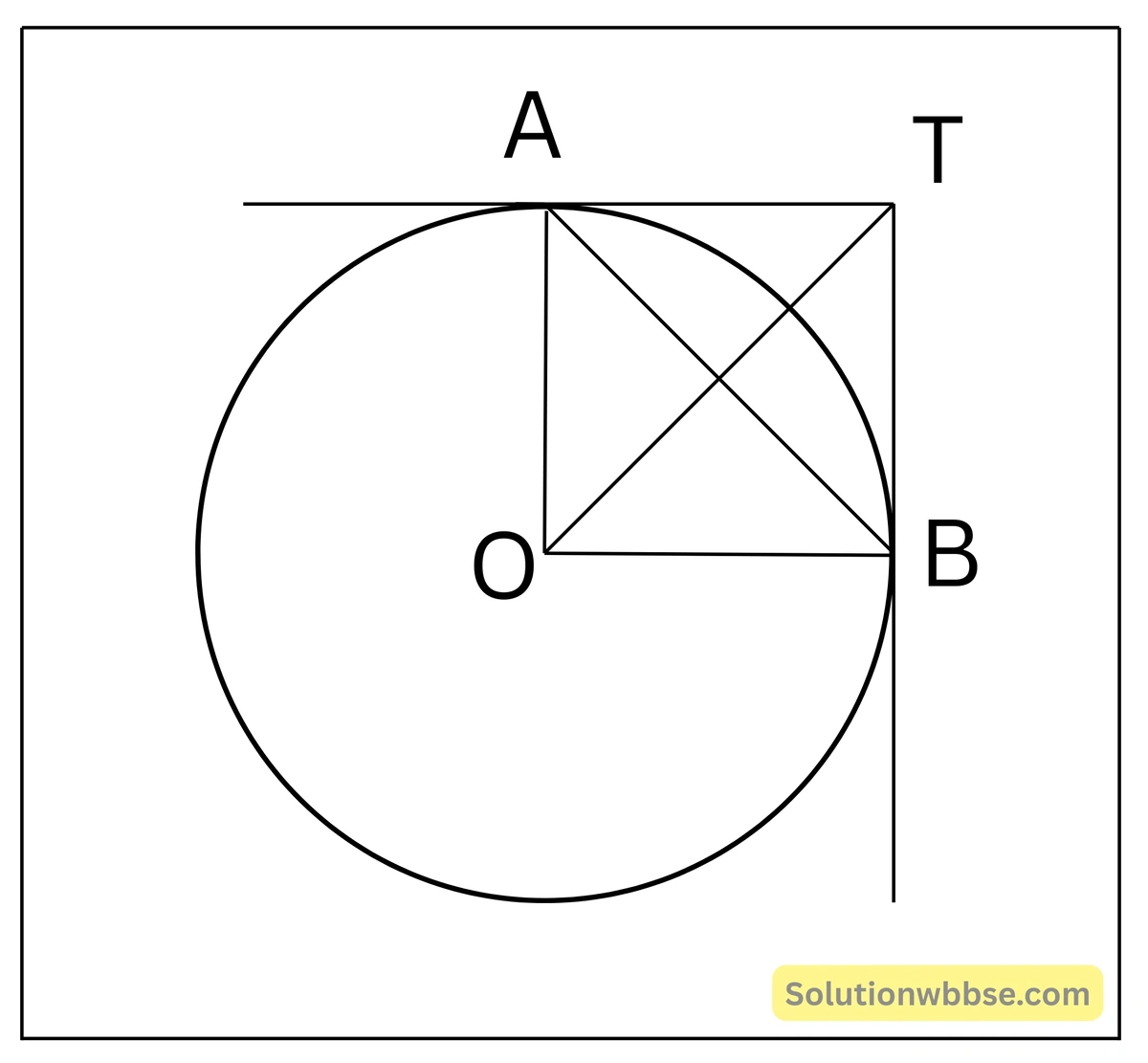
প্রদত্ত – O কেন্দ্রীয় বৃত্তের AB একটি জ্যা। B বিন্দুতে অঙ্কিত একটি স্পর্শক বর্ধিত AO -কে T বিন্দুতে ছেদ করে। ∠BAT = 21°।
নির্ণেয় – ∠BTA -এর মান নির্ণয় করতে হবে।
অঙ্কন – O, B যুক্ত করা হলো।
সমাধান – যেহেতু ∠BAT = 21°, সুতরাং ∠OAB = 21° (কারণ O, A, T একই সরলরেখায় অবস্থিত)।
এখন, ∆OAB -এর মধ্যে, OA = OB (একই বৃত্তের ব্যাসার্ধ) সুতরাং, ∆OAB একটি সমদ্বিবাহু ত্রিভুজ।
∴ ∠OBA = ∠OAB = 21° (সমদ্বিবাহু ত্রিভুজের সমান বাহুর বিপরীত কোণ দুটি সমান)
আবার, OB হলো B বিন্দুগামী ব্যাসার্ধ এবং BT হলো B বিন্দুতে অঙ্কিত স্পর্শক।
আমরা জানি, ব্যাসার্ধ ও স্পর্শক পরস্পর লম্ব হয়।
∴ ∠OBT = 90°
এখন, ∆OBT -তে, আমাদের ∠BTA -এর মান বের করতে হবে। এর জন্য আমাদের ∠BOT-এর মান জানা প্রয়োজন।
∆OAB -এর ক্ষেত্রে, AO বাহুকে T পর্যন্ত বর্ধিত করায় বহিঃস্থ কোণ ∠BOT উৎপন্ন হয়েছে। ত্রিভুজের বহিঃস্থ কোণ তার অন্তঃস্থ বিপরীত কোণ দুটির সমষ্টির সমান হয়।
∴ বহিঃস্থ ∠BOT = অন্তঃস্থ ∠OAB + অন্তঃস্থ ∠OBA
বা, ∠BOT = 21° + 21° = 42°
এখন, ত্রিভুজ ∆BOT -এর তিনটি কোণের সমষ্টি 180°।
∴ ∠BTA + ∠OBT + ∠BOT = 180°
বা, ∠BTA + 90° + 42° = 180°
বা, ∠BTA + 132° = 180°
বা, ∠BTA = 180° – 132°
∴ ∠BTA = 48°
সুতরাং, ∠BTA -এর নির্ণেয় মান হলো 48°।
5. দুটি এক কেন্দ্রীয় বৃত্তের বৃহত্তরটির AB ও AC জ্যা দুটি অপর বৃত্তকে যথাক্রমে P ও Q বিন্দুতে স্পর্শ করলে, প্রমাণ করি যে, PQ = ½ BC .
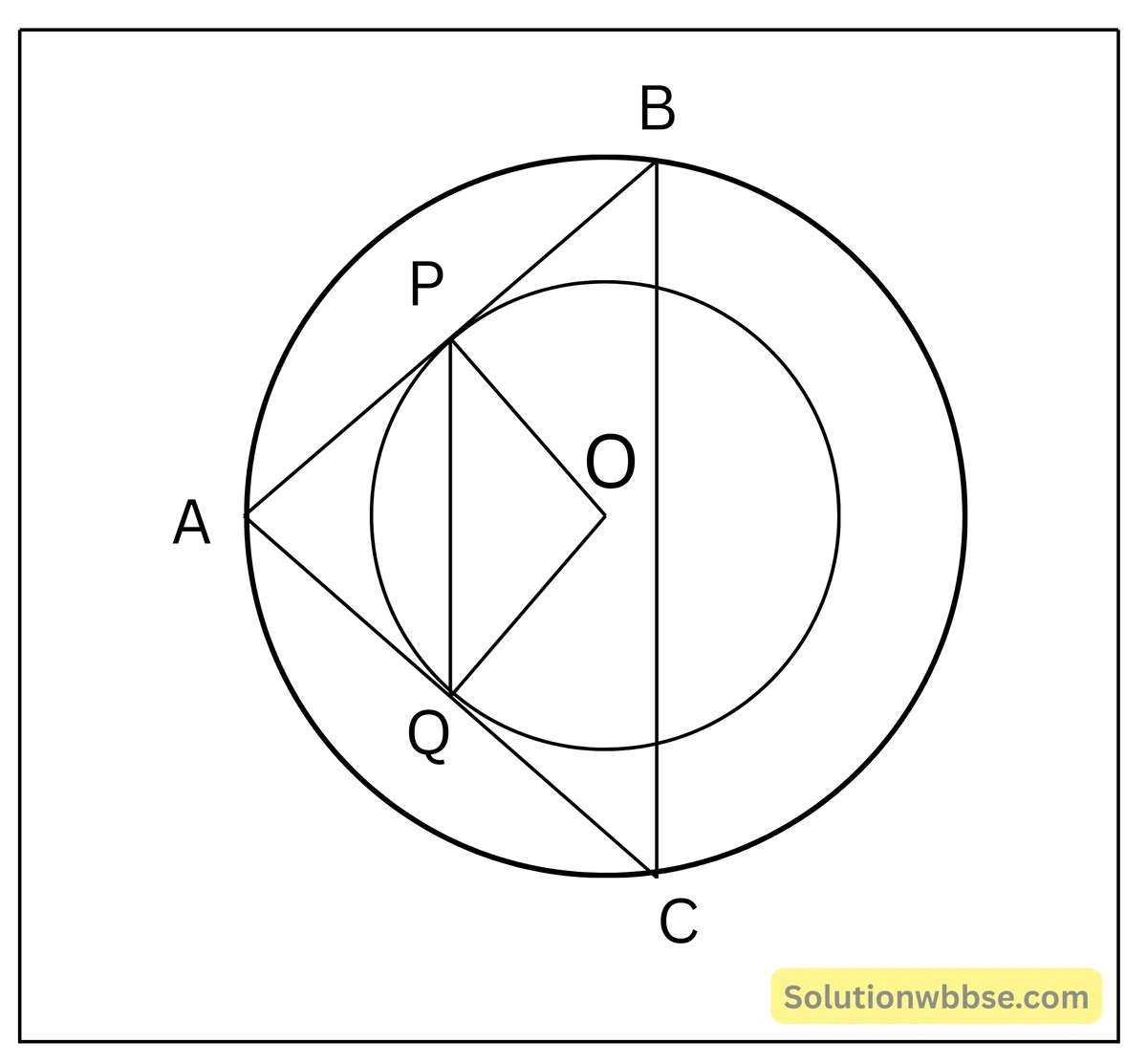
প্রদত্ত – O কেন্দ্রীয় দুটি এক কেন্দ্রীয় বৃত্তের ক্ষেত্রে, বৃহত্তর বৃত্তের দুটি জ্যা AB ও AC ছোট বৃত্তটিকে যথাক্রমে P ও Q বিন্দুতে স্পর্শ করেছে।
প্রামাণ্য বিষয় – PQ = ½ BC
অঙ্কন – O, P এবং O, Q যুক্ত করা হলো। B ও C যুক্ত করে ∆ABC গঠন করা হলো।
প্রমাণ – যেহেতু ছোট বৃত্তের P বিন্দুতে AB একটি স্পর্শক এবং OP হলো স্পর্শবিন্দুগামী ব্যাসার্ধ,
∴ OP ⊥ AB
এখন, বৃহত্তর বৃত্তের ক্ষেত্রে AB হলো একটি জ্যা এবং O হলো বৃত্তের কেন্দ্র।
যেহেতু কেন্দ্র O থেকে জ্যা AB-এর উপর OP লম্ব,
সুতরাং OP, জ্যা AB-কে সমদ্বিখণ্ডিত করে।
∴ P হলো AB-এর মধ্যবিন্দু।
একইভাবে, ছোট বৃত্তের Q বিন্দুতে AC একটি স্পর্শক এবং OQ হলো স্পর্শবিন্দুগামী ব্যাসার্ধ,
∴ OQ ⊥ AC
বৃহত্তর বৃত্তের ক্ষেত্রে AC হলো একটি জ্যা এবং কেন্দ্র O থেকে জ্যা AC-এর উপর OQ লম্ব।
∴ Q হলো AC-এর মধ্যবিন্দু।
এখন, ∆ABC-এর ক্ষেত্রে, P হলো AB বাহুর মধ্যবিন্দু এবং Q হলো AC বাহুর মধ্যবিন্দু।
আমরা জানি, মধ্যবিন্দু সংক্রান্ত উপপাদ্য অনুসারে, কোনো ত্রিভুজের দুটি বাহুর মধ্যবিন্দুর সংযোজক সরলরেখা তৃতীয় বাহুর সমান্তরাল ও অর্ধেক হয়।
∴ PQ ∥ BC এবং PQ = ½ BC
সুতরাং, PQ = ½ BC। (প্রমাণিত)
6. O কেন্দ্রীয় বৃত্তের উপর অবস্থিত A বিন্দুতে স্পর্শকের উপর X যেকোনো একটি বিন্দু। X বিন্দু থেকে অঙ্কিত একটি ছেদক বৃত্তকে Y ও Z বিন্দুতে ছেদ করে। YZ এর মধ্যবিন্দু P হলে, প্রমাণ করি যে XAPO বা XAOP একটি বৃত্তস্থ চতুর্ভুজ।
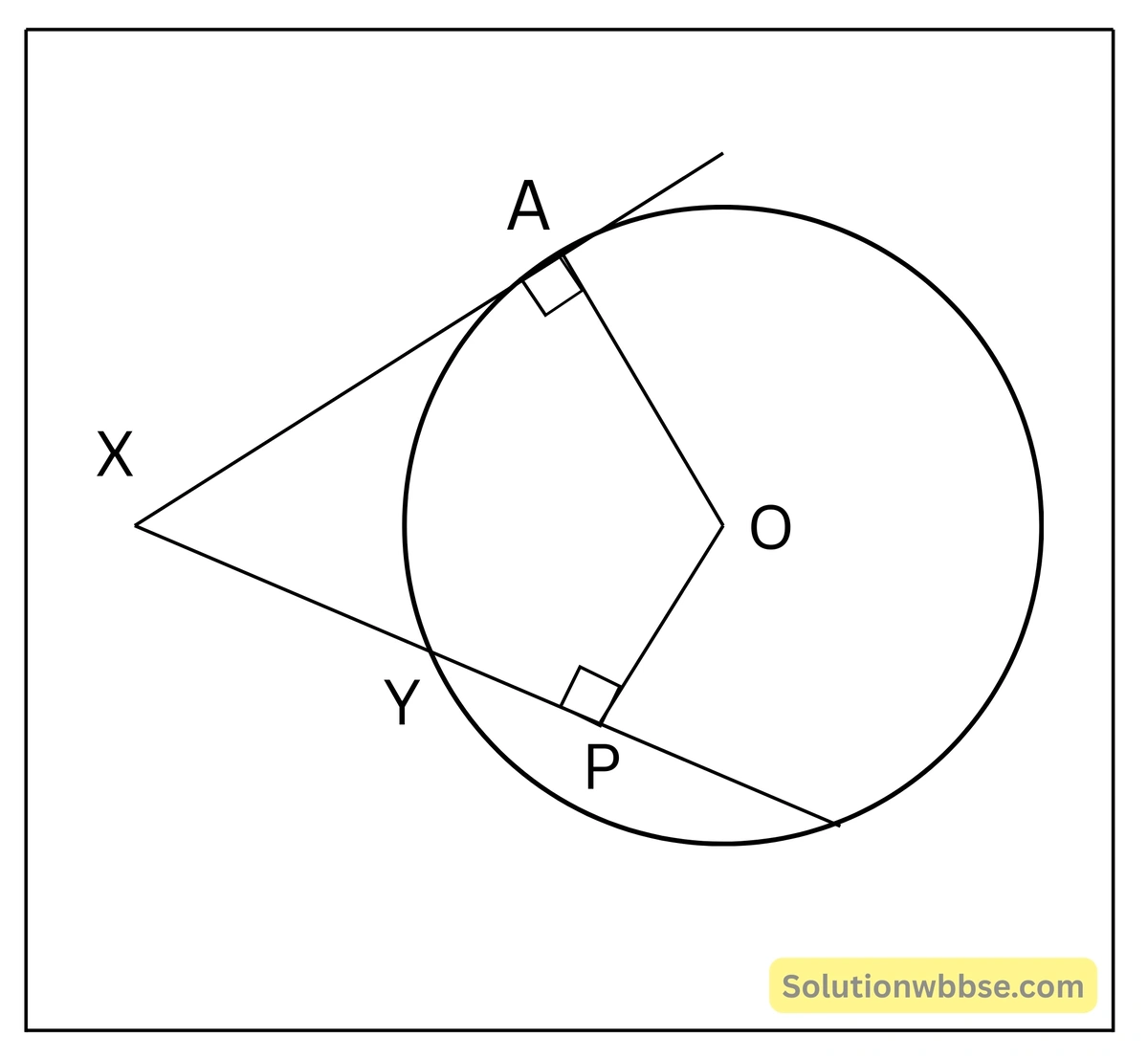
প্রদত্ত – O কেন্দ্রীয় একটি বৃত্তের উপর A একটি বিন্দু। A বিন্দুতে অঙ্কিত স্পর্শকের উপর X যেকোনো একটি বিন্দু। X বিন্দু দিয়ে অঙ্কিত একটি ছেদক বৃত্তটিকে Y ও Z বিন্দুতে ছেদ করে। YZ জ্যা-এর মধ্যবিন্দু হলো P।
প্রামাণ্য বিষয় – XAOP একটি বৃত্তস্থ চতুর্ভুজ।
অঙ্কন – O, A; O, P এবং A, P যুক্ত করা হলো।
প্রমাণ – যেহেতু বৃত্তের কেন্দ্র O এবং YZ জ্যা-এর মধ্যবিন্দু P, সুতরাং, কেন্দ্র ও জ্যা-এর মধ্যবিন্দুর সংযোজক সরলরেখা (OP) জ্যা-এর (YZ) উপর লম্ব হবে।
∴ OP ⊥ YZ
যেহেতু X, Y, P, Z বিন্দুগুলি একই সরলরেখায় (ছেদকের উপর) অবস্থিত,
∴ ∠OPX = 90°
আবার, বৃত্তের A বিন্দুতে AX হলো একটি স্পর্শক এবং OA হলো স্পর্শবিন্দুগামী ব্যাসার্ধ।
আমরা জানি, স্পর্শবিন্দুগামী ব্যাসার্ধ স্পর্শকের উপর লম্ব হয়।
∴ OA ⊥ AX
∴ ∠OAX = 90°
এখন, XAOP চতুর্ভুজটির ক্ষেত্রে, এর দুটি বিপরীত কোণ হলো ∠OAX এবং ∠OPX।
এই বিপরীত কোণ দুটির সমষ্টি = ∠OAX + ∠OPX = 90° + 90° = 180°
আমরা জানি, কোনো চতুর্ভুজের একজোড়া বিপরীত কোণের সমষ্টি 180° (বা দুই সমকোণ) হলে, চতুর্ভুজটি বৃত্তস্থ হয়।
সুতরাং, XAOP একটি বৃত্তস্থ চতুর্ভুজ। (প্রমাণিত)
7. O কেন্দ্রীয় কোন বৃত্তের একটি ব্যাসের উপর P যেকোনো একটি বিন্দু। ওই ব্যাসের ওপর O বিন্দুতে অঙ্কিত লম্ব বৃত্তকে Q বিন্দুতে ছেদ করে। বর্ধিত QP বৃত্তকে R বিন্দুতে ছেদ করে। R বিন্দুতে অঙ্কিত স্পর্শক বর্ধিত OP কে S বিন্দুতে ছেদ করে। প্রমাণ করি যে SP = SR।
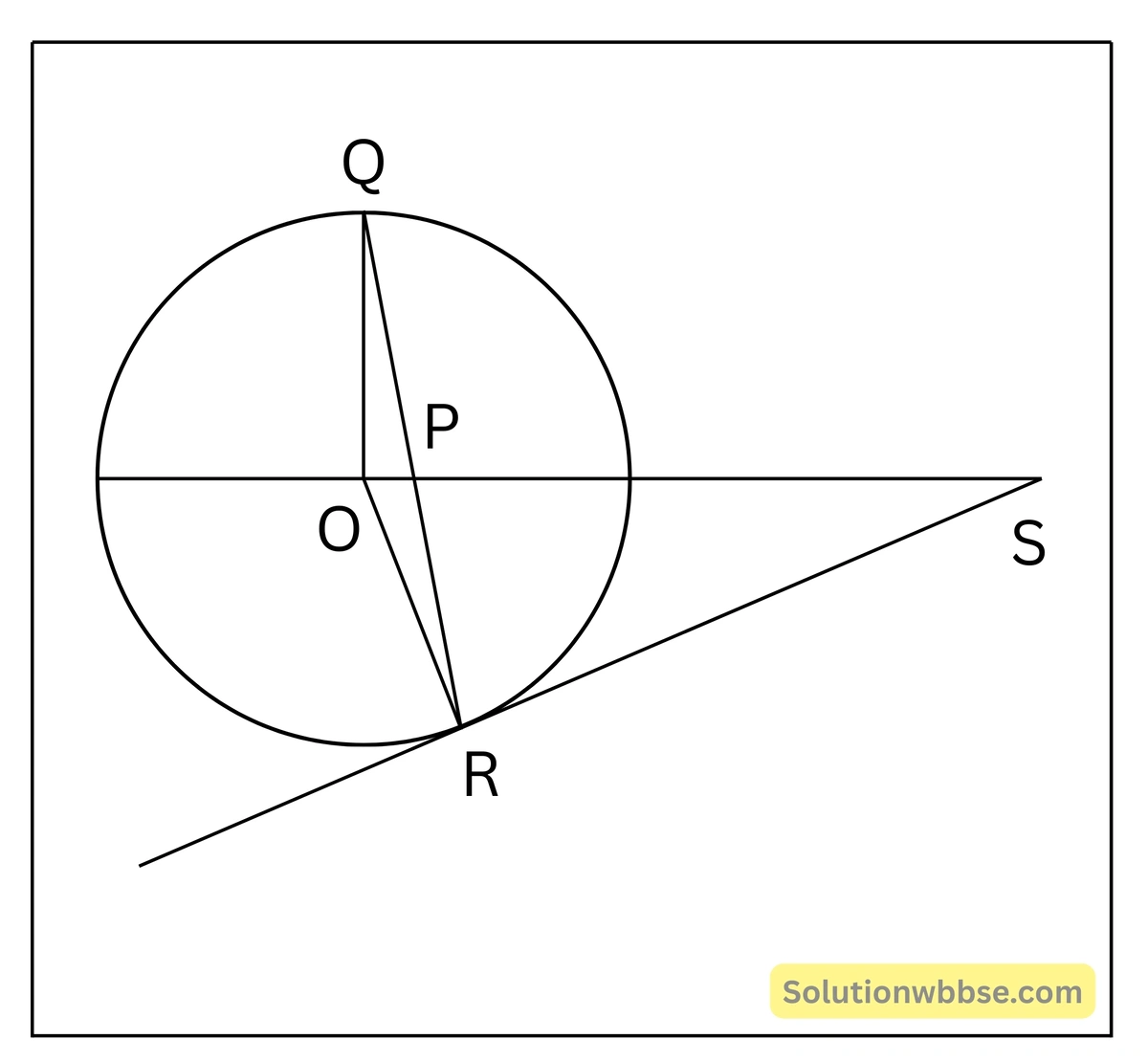
প্রদত্ত – O কেন্দ্রীয় একটি বৃত্তের কোনো একটি ব্যাসের উপর P যেকোনো একটি বিন্দু। ওই ব্যাসের উপর O বিন্দুতে অঙ্কিত লম্ব বৃত্তটিকে Q বিন্দুতে ছেদ করে। বর্ধিত QP সরলরেখা বৃত্তটিকে R বিন্দুতে ছেদ করে। R বিন্দুতে অঙ্কিত স্পর্শক বর্ধিত OP সরলরেখাকে S বিন্দুতে ছেদ করে।
প্রামাণ্য বিষয় – SP = SR
অঙ্কন – O, R যুক্ত করা হলো।
প্রমাণ – যেহেতু OQ, OP-এর উপর লম্ব, সুতরাং ∆OPQ একটি সমকোণী ত্রিভুজ, যার ∠POQ = 90°।
∴ ∠OPQ + ∠OQP = 90°
বা, ∠OPQ = 90° – ∠OQP — (i)
এখন, ∆OQR-এর ক্ষেত্রে, OQ = OR (একই বৃত্তের ব্যাসার্ধ) সুতরাং, ∆OQR একটি সমদ্বিবাহু ত্রিভুজ।
∴ ∠OQR = ∠ORQ (সমান বাহুর বিপরীত কোণ) অর্থাৎ, ∠OQP = ∠ORP (যেহেতু Q, P, R এবং Q, R বিন্দুগুলি যথাক্রমে একই সরলরেখায় অবস্থিত)
আবার, R বিন্দুতে RS একটি স্পর্শক এবং OR হলো স্পর্শবিন্দুগামী ব্যাসার্ধ।
∴ OR ⊥ RS সুতরাং, ∠ORS = 90°
বা, ∠ORP + ∠SRP = 90°
বা, ∠SRP = 90° – ∠ORP
বা, ∠SRP = 90° – ∠OQP [∵ ∠ORP = ∠OQP] — (ii)
এখন, (i) ও (ii) নং সমীকরণ তুলনা করে পাই, ∠OPQ = ∠SRP
আবার, QPR এবং OPS সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করায়, ∠SPR = ∠OPQ (বিপ্রতীপ কোণ)
সুতরাং, আমরা পাই, ∠SRP = ∠SPR
এখন, ∆SPR-এর ক্ষেত্রে, যেহেতু ∠SRP = ∠SPR, ∴ SP = SR (সমান কোণের বিপরীত বাহুদ্বয় সমান)
সুতরাং, SP = SR। (প্রমাণিত)
8. রুমেলা O কেন্দ্রীয় একটি বৃত্ত অঙ্কন করেছে যার QR একটি জ্যা। Q ও R বিন্দুতে দুটি স্পর্শক অঙ্কন করেছি যারা পরস্পরকে P বিন্দুতে ছেদ করেছে। QM বৃত্তের ব্যাস হলে, প্রমাণ করি যে, ∠QPR = 2∠RQM
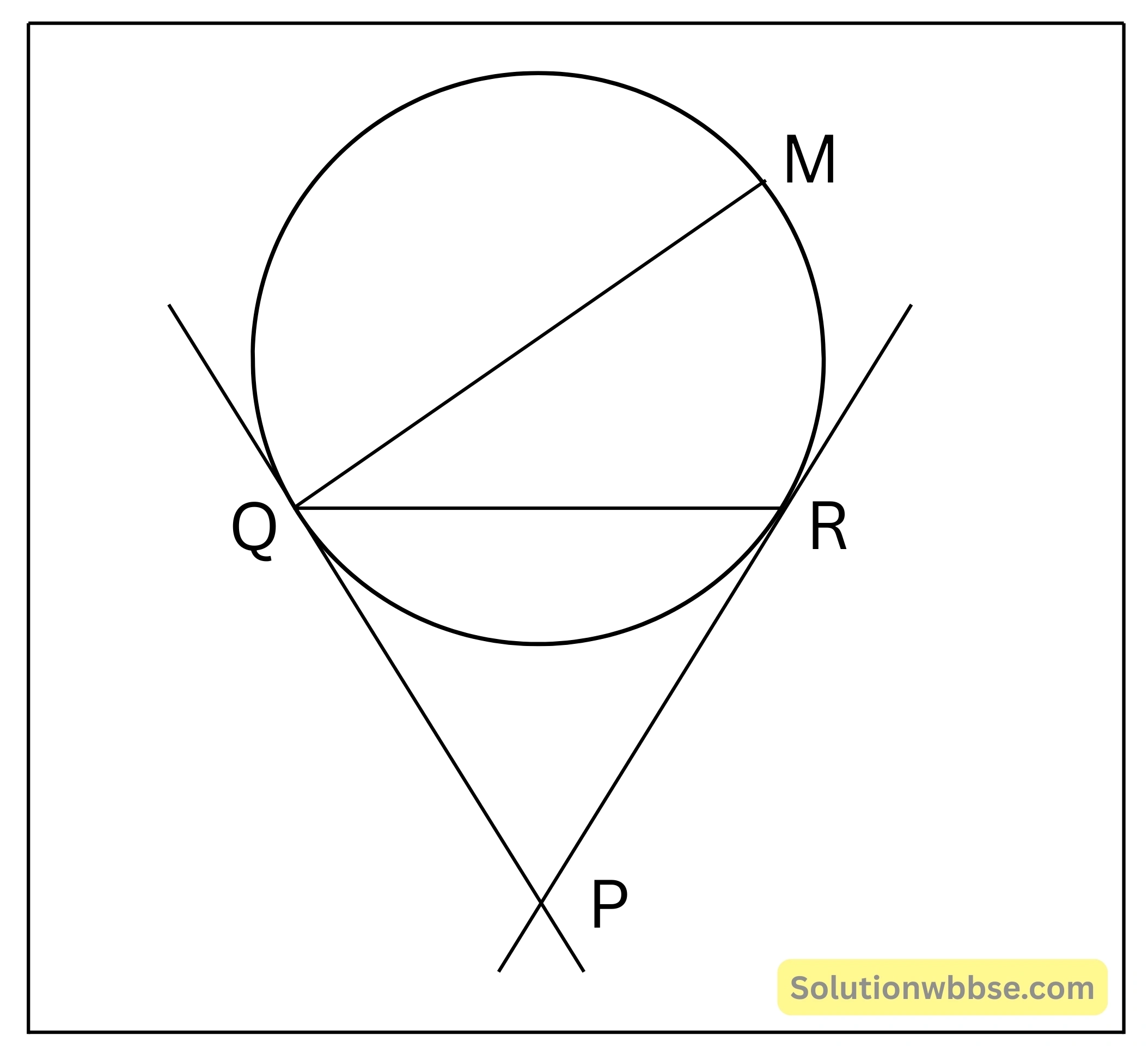
প্রদত্ত – O কেন্দ্রীয় একটি বৃত্তের QR একটি জ্যা। Q ও R বিন্দুতে অঙ্কিত দুটি স্পর্শক পরস্পরকে P বিন্দুতে ছেদ করে। QM বৃত্তটির একটি ব্যাস।
প্রামাণ্য বিষয় – ∠QPR = 2∠RQM
অঙ্কন – Q, R; P, Q; P, R এবং Q, M; R, M যুক্ত আছে।
প্রমাণ – যেহেতু বৃত্তের বহিঃস্থ বিন্দু P থেকে PQ এবং PR দুটি স্পর্শক অঙ্কন করা হয়েছে,
∴ PQ = PR (বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে অঙ্কিত স্পর্শকগুলির দৈর্ঘ্য সমান)
এখন, ∆PQR-এর মধ্যে, PQ = PR। সুতরাং, ∆PQR একটি সমদ্বিবাহু ত্রিভুজ।
∴ ∠PQR = ∠PRQ (সমান বাহুর বিপরীত কোণ)
∆PQR-এর তিনটি কোণের সমষ্টি 180°।
∴ ∠QPR + ∠PQR + ∠PRQ = 180°
বা, ∠QPR + ∠PQR + ∠PQR = 180° [∵ ∠PRQ = ∠PQR]
বা, ∠QPR + 2∠PQR = 180°
বা, ∠QPR = 180° – 2∠PQR — (i)
আবার, যেহেতু QM বৃত্তটির একটি ব্যাস এবং PQ হলো Q বিন্দুতে অঙ্কিত স্পর্শক,
∴ QM ⊥ PQ (স্পর্শবিন্দুগামী ব্যাস/ব্যাসার্ধ স্পর্শকের উপর লম্ব হয়) সুতরাং, ∠PQM = 90°
চিত্র থেকে দেখা যায়, ∠PQR + ∠RQM = ∠PQM = 90°
বা, ∠PQR = 90° – ∠RQM — (ii)
এখন, (i) নং সমীকরণে ∠PQR-এর মান বসিয়ে পাই, ∠QPR = 180° – 2(90° – ∠RQM)
বা, ∠QPR = 180° – 180° + 2∠RQM
বা, ∠QPR = 2∠RQM
সুতরাং, ∠QPR = 2∠RQM। (প্রমাণিত)
9. কোনো বৃত্তের AC ও BD জ্যা দুটি পরস্পরকে O বিন্দুতে ছেদ করেছে। A ও B বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে P বিন্দুতে এবং C ও D বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে Q বিন্দুতে ছেদ করলে, প্রমাণ করি যে, ∠P+∠Q = 2∠BOC.
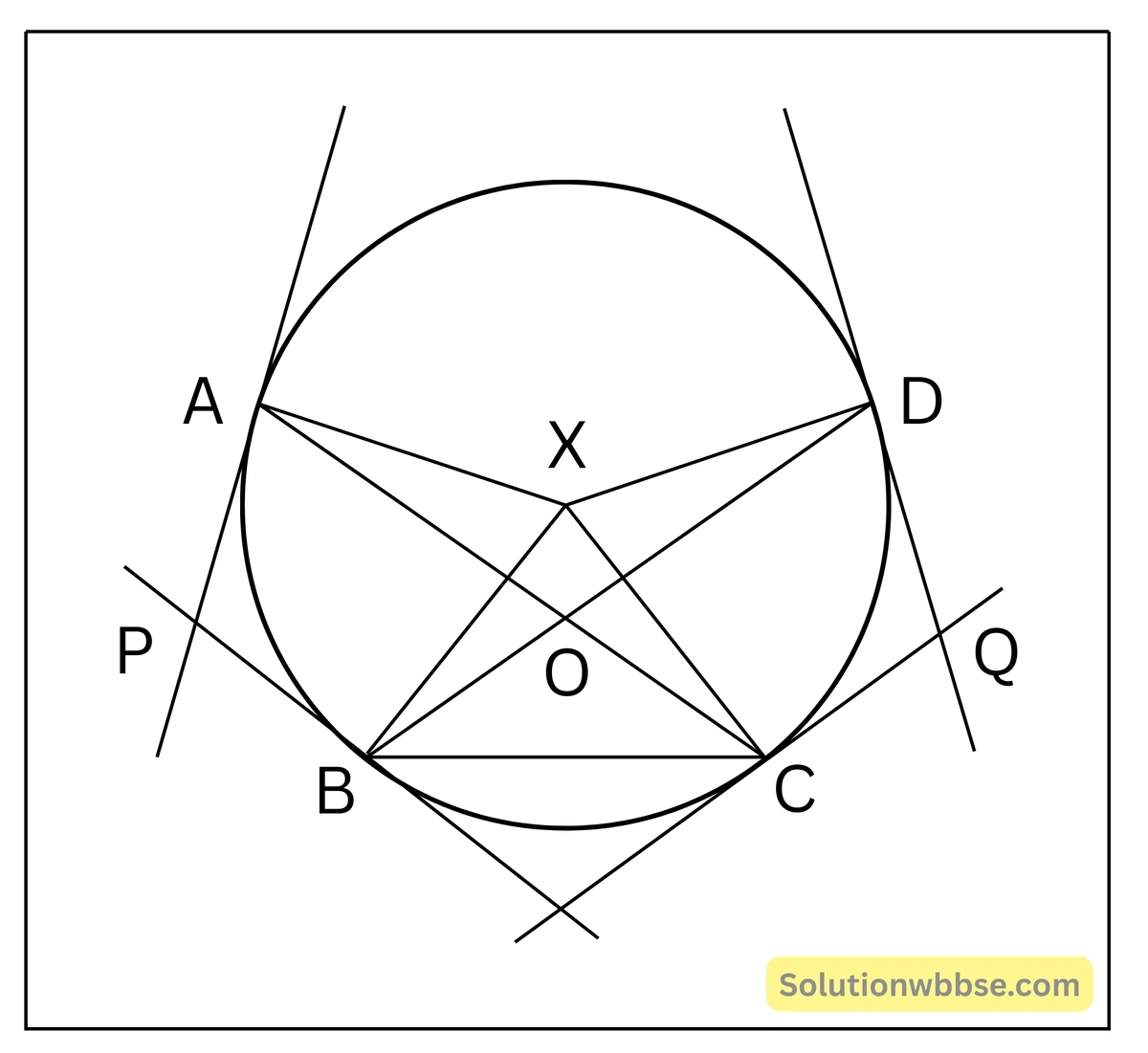
প্রদত্ত – একটি বৃত্তের AC ও BD জ্যা দুটি পরস্পরকে O বিন্দুতে ছেদ করেছে। A ও B বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে P বিন্দুতে এবং C ও D বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে Q বিন্দুতে ছেদ করে।
প্রামাণ্য বিষয় – ∠P + ∠Q = 2∠BOC
অঙ্কন – ধরা যাক, বৃত্তটির কেন্দ্র X। X,A; X,B; X,C এবং X,D যুক্ত করা হলো।
প্রমাণ – XAPB চতর্ভুজের ক্ষেত্রে, XA এবং XB হলো স্পর্শবিন্দুগামী ব্যাসার্ধ এবং PA ও PB হলো স্পর্শক।
∴ ∠XAP = 90° এবং ∠XBP = 90°
আমরা জানি, চতর্ভুজের চারটি কোণের সমষ্টি 360°।
∴ ∠P + ∠AXB + ∠XAP + ∠XBP = 360°
বা, ∠P + ∠AXB + 90° + 90° = 360°
বা, ∠P + ∠AXB = 360° – 180° = 180°
আবার, AB বৃত্তচাপের উপর কেন্দ্রস্থ কোণ হলো ∠AXB এবং পরিধিস্থ কোণ হলো ∠ACB। আমরা জানি, কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুণ।
∴ ∠AXB = 2∠ACB
সুতরাং, ∠P + 2∠ACB = 180°
বা, 2∠ACB = 180° – ∠P — (i)
একইভাবে, XCQD চতর্ভুজের ক্ষেত্রে প্রমাণ করা যায়, ∠Q + ∠CXD = 180° এবং CD বৃত্তচাপের উপর কেন্দ্রস্থ কোণ ∠CXD = 2 × পরিধিস্থ কোণ ∠CBD।
∴ ∠Q + 2∠CBD = 180°
বা, 2∠CBD = 180° – ∠Q — (ii)
এখন, (i) ও (ii) নং সমীকরণ যোগ করে পাই, 2∠ACB + 2∠CBD = (180° – ∠P) + (180° – ∠Q)
বা, 2(∠ACB + ∠CBD) = 360° – (∠P + ∠Q)
যেহেতু AC ও BD জ্যা দুটি O বিন্দুতে ছেদ করেছে, ∆BOC-এর ক্ষেত্রে, ∠OCB = ∠ACB এবং ∠OBC = ∠CBD।
∴ 2(∠OCB + ∠OBC) = 360° – (∠P + ∠Q)
এখন, ∆BOC-এর তিনটি কোণের সমষ্টি 180°।
∴ ∠OCB + ∠OBC + ∠BOC = 180°
বা, ∠OCB + ∠OBC = 180° – ∠BOC
এই মানটি উপরের সমীকরণে বসিয়ে পাই, 2(180° – ∠BOC) = 360° – (∠P + ∠Q)
বা, 360° – 2∠BOC = 360° – (∠P + ∠Q)
বা, -2∠BOC = – (∠P + ∠Q)
বা, 2∠BOC = ∠P + ∠Q
সুতরাং, ∠P + ∠Q = 2∠BOC (প্রমাণিত)
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের পঞ্চদশ অধ্যায়, ‘বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য’ -এর ‘কষে দেখি – 15.1’ বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment