মাধ্যমিক গণিত – লম্ব বৃত্তাকার চোঙ – প্রয়োগ

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের অষ্টম অধ্যায়, ‘লম্ব বৃত্তাকার চোঙ’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

প্রয়োগ 1. একটি লম্ব বৃত্তাকার চোঙের ভূমির ব্যাসের দৈর্ঘ্য 12 সেমি. এবং উচ্চতা 21 সেমি. হলে, চোঙের পার্শ্বতলের ক্ষেত্রফল কী হবে, হিসাব করে লিখি।

সমাধান –

লম্ব বৃত্তাকার চোঙের ব্যাসার্ধের দৈর্ঘ্য সেমি. = 6 সেমি.

∴ লম্ব বৃত্তাকার চোঙের পার্শ্বতলের ক্ষেত্রফল= 2 × π × 6 × 21 বর্গ সেমি.

= 2 × 27 × 6 × 21 বর্গ সেমি.

= \(2\times\frac{22}7\times6\times21\) বর্গ সেমি.

= \(\require{cancel}2\times\frac{22}{\cancel7}\times6\times\overset3{\cancel{21}}\) বর্গ সেমি.

= 792 বর্গ সেমি.

উত্তর – চোঙের পার্শ্বতলের ক্ষেত্রফল 792 বর্গ সেমি.

প্রয়োগ 2. যে চোঙের ভূমির পরিধি 44 মিটার এবং উচ্চতা 14 মিটার, তার পার্শ্বতলের ক্ষেত্রফল কী হবে, হিসাব করে লিখি। 

সমাধান –

চোঙটির পার্শ্বতলের ক্ষেত্রফল = ভূমির পরিধি × উচ্চতা

= (44 × 14) বর্গমিটার

= 616 বর্গমিটার

উত্তর – পার্শ্বতলের ক্ষেত্রফল 616 বর্গমিটার হবে।

প্রয়োগ 3. একটি ঢাকনাসমেত চোঙাকৃতি জলের ট্যাঙ্কের ভূমির ক্ষেত্রফল 616 বর্গ মিটার এবং উচ্চতা 21 মিটার। হিসাব করে ওই ট্যাঙ্কের সমগ্রতলের ক্ষেত্রফল লিখি।

সমাধান –

ধরি, জলের ট্যাঙ্কের বৃত্তাকার ভূমির ব্যাসার্ধের দৈর্ঘ্য = r মিটার

∴ ভূমির ক্ষেত্রফল = πr² বর্গ মিটার

শর্তানুসারে, πr² = 616

বা, \(\frac{22}7\times r^2=616\)

বা, \(r^2=616\times\frac7{22}\)

বা, \(r^2=\overset{28}{\cancel{616}}\times\frac7{\cancel{22}}\)

বা, r² = 196

বা, r² = (14)²

∴ r = 14

জলের ট্যাঙ্কের সমগ্রতলের ক্ষেত্রফল = (2πr² + 2πrh) বর্গ মিটার [যেখানে, চোঙের উচ্চতা = h মিটার]

= \(2\times\frac{22}7\times r\left(r+h\right)\) বর্গ মিটার

= \(2\times\frac{22}7\times14\left(14+21\right)\) বর্গ মিটার

= \(\require{cancel}2\times\frac{22}{\cancel7}\times\overset2{\cancel{14}}\left(14+21\right)\) বর্গ মিটার

= 2 × 22 × 70 বর্গ মিটার

= 3080 বর্গ মিটার

উত্তর – জলের ট্যাঙ্কের সমগ্রতলের ক্ষেত্রফল 3080 বর্গ মিটার।

প্রয়োগ 4. যদি কোনো ঢাকনাসমেত চোঙাকৃতি পাত্রের ভূমির পরিধি 22 ডেকামিটার এবং উচ্চতা 5 ডেকামিটার হয়, তবে ওই পাত্রের বাইরের সমগ্রতল রং করতে কতটা পরিমাণ জায়গা রং করতে হবে, হিসাব করে লিখি।

সমাধান –

মনে করি, পাত্রের ভূমির ব্যাসার্ধ = r ডেকামি ও উচ্চতা = h ডেকামি

এখানে 2πr = 22 ও h = 5

∴ \(2\times\frac{22}7r=22\)

বা, \(r=\frac72\) ডেকামি.

∴ পাত্রের সমগ্রতলের ক্ষেত্রফল = 2πr(r + h)

= \(2\times\frac{22}7\times\frac72\left(\frac72+5\right)\) বর্গ ডেকামি.

= \(\require{cancel}\cancel2\times\frac{22}{\cancel7}\times\frac{\cancel7}{\cancel2}\left(\frac72+5\right)\) বর্গ ডেকামি.

= \(22\left(\frac72+5\right)\) বর্গ ডেকামি.

= \(22\left(\frac{7+10}2\right)\) বর্গ ডেকামি.

= \(\overset{11}{\cancel{22}}\times\frac{17}{\cancel2}=187\) বর্গ ডেকামি.।

উত্তর – ওই পাত্রের বাইরের সমগ্রতল রং করতে 187 বর্গ ডেকামি. জায়গা রং করতে হবে।

প্রয়োগ 5. একটি একমুখ খোলা লম্ব বৃত্তাকার পাত্রের সমগ্রতলের ক্ষেত্রফল 1474 বর্গ সেমি.। পাত্রটির ভূমির ব্যাসের দৈর্ঘ্য 14 সেমি. হলে, উচ্চতা কত হবে, হিসাব করে লিখি।
আবার পাত্রটি যদি দুই মুখ বন্ধ হতো, তবে সমগ্রতলের ক্ষেত্রফল কত হতো হিসাব করে লিখি।

সমাধান –

লম্ব বৃত্তাকার পাত্রের ভূমির ব্যাসার্ধের দৈর্ঘ্য = \(\frac{14}2\) সেমি. = 7 সেমি.

ধরি, পাত্রটির উচ্চতা h সেমি.

পাত্রটির সমগ্রতলের ক্ষেত্রফল = ভূমির ক্ষেত্রফল + বক্রতলের ক্ষেত্রফল

= πr² + πrh

= \(\left(\frac{22}7\times7^2+\frac{22}7\times7\times h\right)\) বর্গ সেমি.

= (154 + 44h) বর্গ সেমি.

শর্তানুসারে, 154 + 44h = 1474

∴ 44h = 1474 – 154

বা, h = 1320

বা, h = \(\require{cancel}\frac{\displaystyle\overset{30}{\cancel{1320}}}{\cancel{44}}=30\)

∴ পাত্রটির উচ্চতা 30 সেমি.।

যদি পাত্রটির দুই মুখ বন্ধ হতো তখন ওই পাত্রের সমগ্রতলের ক্ষেত্রফল

= পাত্রের উপরিতলের ক্ষেত্রফল + 1474 বর্গ সেমি.

= \(\left(\frac{22}7\times7^2+1474\right)\) বর্গ সেমি.

= \(\frac{22}{\cancel7}\times\overset7{\cancel{49}}+1474\) বর্গ সেমি.

উত্তর – পাত্রটির উচ্চতা 30 সেমি.। পাত্রটির সমগ্রতলের ক্ষেত্রফল 1628 বর্গ সেমি.

প্রয়োগ 6. স্টিলের পাতলা চাদর দিয়ে তৈরি ঢাকনাসমেত একটি ড্রামের ভূমির ব্যাসের দৈর্ঘ্য 4.2 ডেসিমি.। যদি ড্রামটি তৈরি করতে 112.20 বর্গ ডেসিমি. চাদর লাগে, তবে ড্রামটির উচ্চতা কত হবে তা হিসাব করে লিখি। আবার 1 বর্গ মি. স্টিলের দাম 25 টাকা হলে, ড্রামটি তৈরি করতে কত খরচ হবে হিসাব করি।

সমাধান –

মনে করি, ড্রামটির উচ্চতা = h ডেসিমি.

ড্রামটির ভূমির ব্যাসার্ধ = \( \) = 2.1 ডেসিমি.

প্রশ্নানুসারে, 2π × 2.1(2.1 + h) = 112.20

বা, \(\require{cancel}2\times\frac{22}7\times\frac{21}{10}\left(2.1+h\right)=\frac{1122\cancel0}{10\cancel0}\)

বা, h = (8.5 – 2.1) = 6.4

∴ ড্রামটির উচ্চতা = 6.4 ডেসিমি.।

ড্রামটির সমগ্রতলের ক্ষেত্রফল = 112.20 বর্গ ডেসিমি = 1.1220 বর্গমি.।

1 বর্গমি. স্টিলের দাম 25 টাকা হলে ড্রামটি তৈরি করতে খরচ হবে

= (25 × 1.1220) টাকা

= 28.0500 টাকা

= 28.05 টাকা।

উত্তর – ড্রামটির উচ্চতা 6.4 ডেসিমি.। ড্রামটি তৈরি করতে খরচ হবে 28.05 টাকা।

প্রয়োগ 7. যদি গ্লাসের ভূমির ব্যাসের দৈর্ঘ্য 11.2 সেমি. এবং উচ্চতা 15 সেমি. হয়, তবে ওই গ্লাসে কত জল ধরবে, হিসাব করি।

সমাধান –

যদি গ্লাসের ভূমির ব্যাসের দৈর্ঘ্য 11.2 সেমি. এবং উচ্চতা 15 সেমি. হয়, তবে ওই গ্লাসে জল ধরবে

= \(\pi\times\left(\frac{11.2}2\right)^2\times15\) ঘন সেমি.

= \(\frac{22}7\times\frac{56}{10}\times\frac{56}{10}\times15\) ঘন সেমি.

= \(\require{cancel}\frac{22}{\cancel7}\times\frac{\displaystyle\overset8{\cancel{56}}}{10}\times\frac{56}{10}\times15\) ঘন সেমি.

= 1478.4 ঘন সেমি.।

উত্তর – ওই গ্লাসে 1478.4 ঘন সেমি. জল ধরবে।

ফাঁপা চোঙাকার ধাতব নলে কতটা পরিমাণ ধাতু আছে কীভাবে পাব?

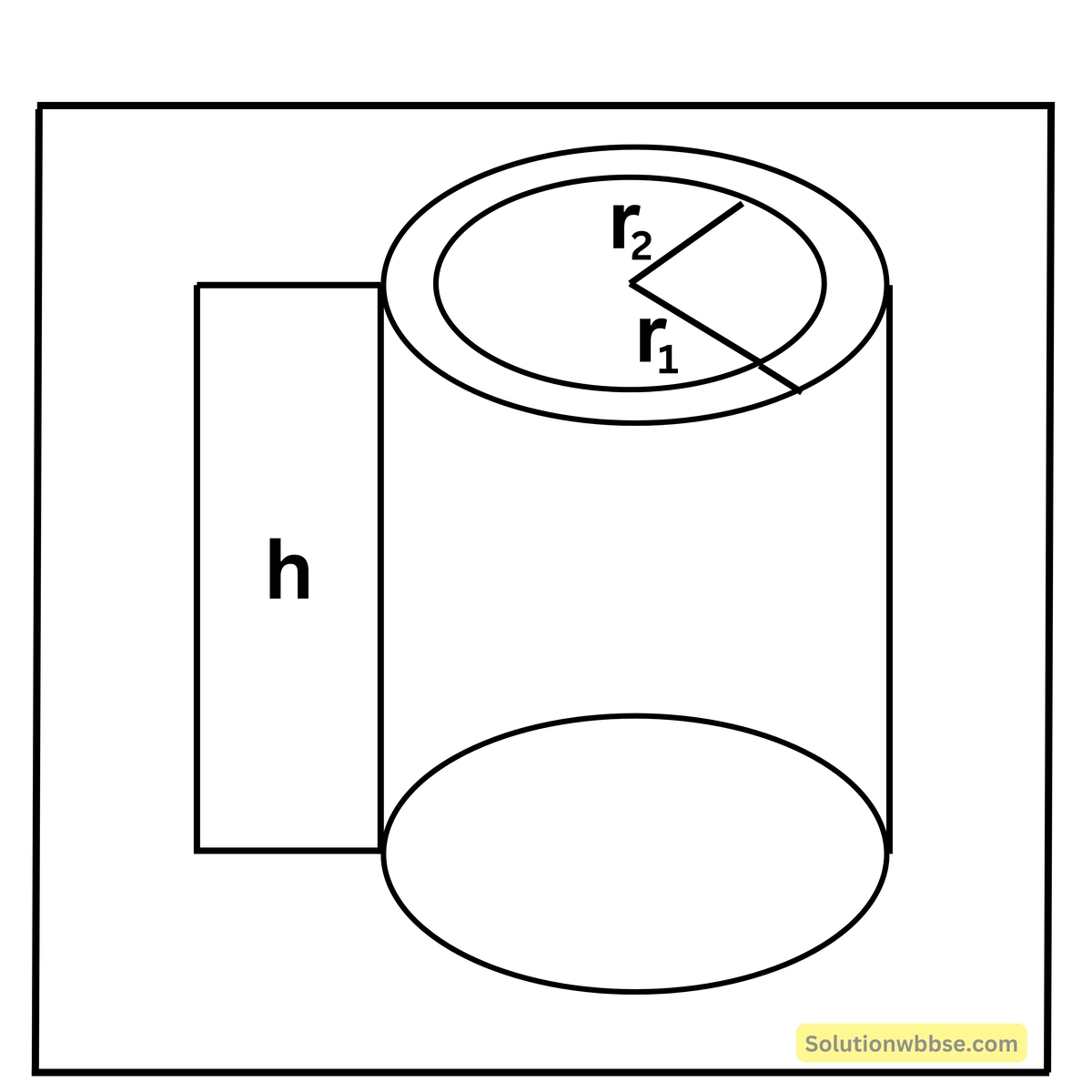
কোনো ফাঁপা চোঙের বাইরের ব্যাসার্ধের দৈর্ঘ্য r₁ একক, ভিতরের ব্যাসার্ধের দৈর্ঘ্য r₂, এবং উচ্চতা h একক হলে,

ফাঁপা চোঙটির আয়তন = \(\left(\pi r_1^2h-\pi r_2^2h\right)\) ঘন একক

= \(\pi\left(r_1^2-r_2^2\right)h\) ঘন সেমি.।

প্রয়োগ 8. দুই মুখ খোলা লোহার তৈরি একটি লম্ব বৃত্তাকার চোঙের উচ্চতা 42 সেমি.। চোঙটি 1 সেমি. পুরু এবং তার বহির্ব্যাসের দৈর্ঘ্য 10 সেমি. হলে, চোঙটি কত পরিমাণ লোহা দিয়ে তৈরি তা হিসাব করি।

সমাধান –

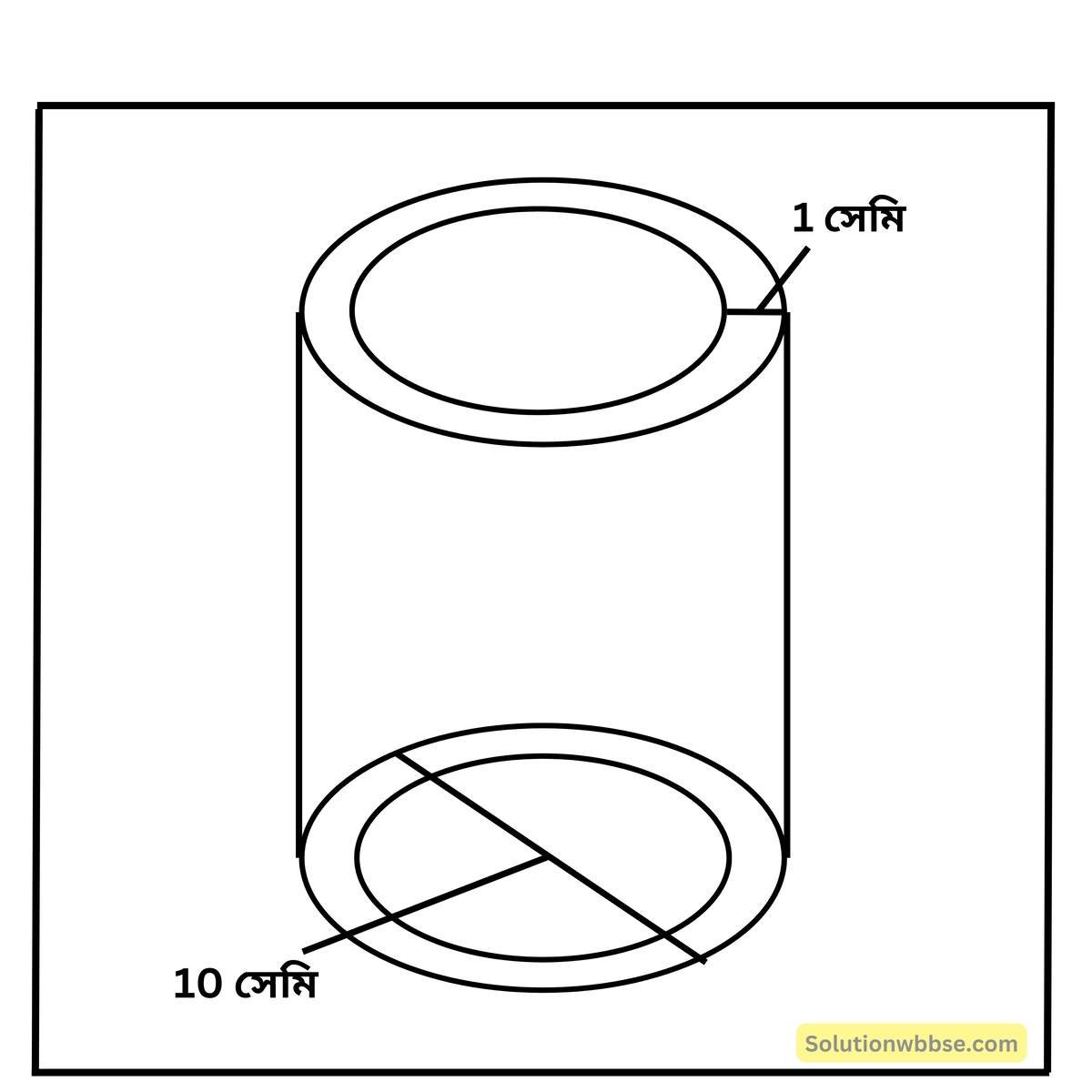
চোঙটির বাহিরের ব্যাসার্ধের দৈর্ঘ্য = \(\frac{10}2\) সেমি. = 5 সেমি.

∴ চোঙটি 1 সেমি. পুরু।

∴ চোঙটির ভিতরের ব্যাসার্ধের দৈর্ঘ্য = (5 – 1) সেমি. = 4 সেমি.

= \(\frac{22}7\times\left(5+4\right)\left(5-4\right)\times42\) ঘন সেমি. [∵ \(a^2-b^2=\left(a+b\right)\left(a-b\right)\)]

= \(\frac{22}7\times9\times1\times42\) ঘন সেমি.

= 22 × 9 × 6 ঘন সেমি.

= 1188 ঘন সেমি.।

উত্তর – চোঙটি 1188 ঘন সেমি. লোহা দিয়ে তৈরি।

প্রয়োগ 9. দুই মুখ খোলা ফাঁপা লম্ব বৃত্তাকার চোঙের ভিতর ও বাহিরে রং করলে কতটা পরিমাণ জায়গায় রং করতে হবে, হিসাব করে লিখি।

সমাধান –

এই দুই মুখ খোলা লম্ব বৃত্তাকার চোঙের ভিতর ও বাহিরের বক্রতলের মোট ক্ষেত্রফল

= (2 × π × 5 × 21 + 2 × π × 4 × 21) বর্গ সেমি.

= 2 × π × 21(5 + 4) বর্গ সেমি.

= \(2\times\frac{22}7\times21\times9\) বর্গ সেমি.

= \(\require{cancel}2\times\frac{22}{\cancel7}\times\overset3{\cancel{21}}\times9\) বর্গ সেমি.

= 1188 বর্গ সেমি.

উত্তর – দুই মুখ খোলা ফাঁপা লম্ব বৃত্তাকার চোঙের ভিতর ও বাহিরে রং করলে 1188 বর্গ সেমি. জায়গায় রং করতে হবে।

ফাঁপা চোঙের বাইরের ব্যাসার্ধের দৈর্ঘ্য r₁ একক এবং ভিতরের ব্যাসার্ধের দৈর্ঘ্য r₂ একক এবং উচ্চতা h একক হলে, ওই চোঙটির ভিতর ও বাহিরের বক্রতলের মোট ক্ষেত্রফল = 2π(r₁ + r₂)h বর্গ একক।

প্রয়োগ 10. একটি ফাঁপা লম্ব বৃত্তাকার চোঙাকৃতি লোহার নলের বহির্ব্যাসার্ধের দৈর্ঘ্য 5 সেমি. এবং অন্তর্ব্যাসার্ধের দৈর্ঘ্য 4 সেমি.। নলটির সমগ্রতলের ক্ষেত্রফল 1188 বর্গ সেমি. হলে, নলটির দৈর্ঘ্য কত হিসাব করি।

সমাধান –

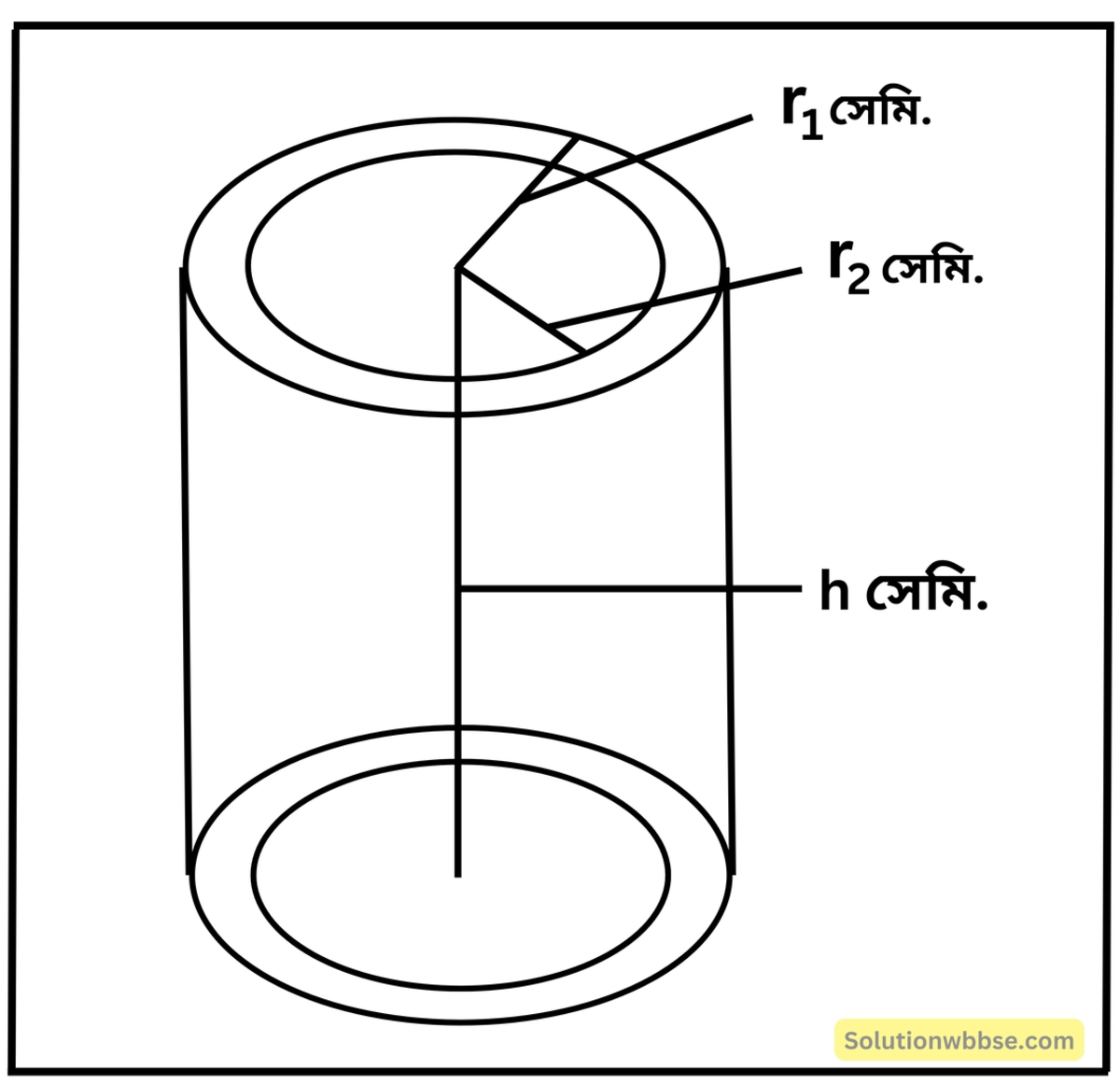
ফাঁপা চোঙের সমগ্রতলের ক্ষেত্রফল = \(2\mathrm\pi\left({\mathrm r}_1+{\mathrm r}_2\right)\mathrm h+2\mathrm\pi\left(\mathrm r_1^2-\mathrm r_2^2\right)\) বর্গসেমি.

যেখানে, বহির্ব্যাসার্ধের দৈর্ঘ্য r₁ সেমি, অন্তর্ব্যাসার্ধের দৈর্ঘ্য r₂ সেমি. এবং উচ্চতা = h সেমি.

শর্তানুসারে,

বা, π[(5 + 4)h + (5² – 4²)] = 594

বা, \(\frac{22}7\)[9h + 9] = 594

বা, 9h + 9 = 189 × \(\frac{22}7\)

বা, 9h = 189 – 9

বা, 9h = 180

বা, h = \(\frac{180}9\)

∴ h = 20

উত্তর – চোঙাকৃতি লোহার নলের দৈর্ঘ্য 20 সেমি.।

প্রয়োগ 11. 6 মিটার লম্বা একটি লম্ববৃত্তাকার চোঙাকৃতি লোহার ফাঁপা পাইপের ভিতরের ও বাইরের ব্যাসের দৈর্ঘ্য যথাক্রমে 3.5 সেমি. এবং 4.2 সেমি. হলে, পাইপটিতে কত লোহা আছে তা হিসাব করে লিখি।
এক ঘন ডেসিমি. লোহার ওজন 5 কিগ্রা., হলে, পাইপটির ওজন হিসাব করে লিখি।

সমাধান –

পাইপটির উচ্চতা = 6 মিটার = 60 ডেসিমি.

পাইপটির ভিতরের ব্যাসার্ধ = \(\frac{3.5}{20}\) = \(\frac{35}{200}\) ডেসিমি.

পাইপটির বাইরের ব্যাসার্ধ = \(\frac{4.2}{20}\) = \(\frac{42}{200}\) ডেসিমি.

পাইপটিতে লোহা আছে = \(\pi\left\{\left(\frac{42}{200}\right)^2-\left(\frac{35}{200}\right)^2\right\}\times60\) ঘন ডেসিমি.

= \(\pi\left\{\left(\frac{42+35}{200}\right)\times\left(\frac{42-35}{200}\right)\right\}\times60\) ঘন ডেসিমি.

= \(\require{cancel}\frac{\displaystyle\overset{11}{\cancel{22}}}{\cancel7}\times\frac{\displaystyle\overset{11}{\cancel{77}}}{200}\times\frac7{\displaystyle\underset{\underset5{\cancel{10}}}{\cancel{200}}}\times\overset3{\cancel{60}}\) ঘন ডেসিমি.

= \(\frac{121\times21}{1000}\) ঘন ডেসিমি.

= \(\frac{2541}{1000}\) ঘন ডেসিমি.

= 2.541 ঘন ডেসিমি.।

এখন 2.541 ঘন ডেসিমি. লোহার ওজন = (2.541 × 5) কিগ্রা. = 12.705 কিগ্রা.

উত্তর – পাইপটির ওজন = 12.705 কিগ্রা.।

প্রয়োগ 12. একটি চোঙের ভূমির ক্ষেত্রফল 13.86 বর্গ মিটার এবং উচ্চতা 8 মিটার হলে, চোঙের আয়তন হিসাব করি।

সমাধান –

ধরি, চোঙের ভূমির ব্যাসার্ধের দৈর্ঘ্য r মিটার।

শর্তানুসারে, πr² = 13.86

বা, \(\frac{22}7r^2=\frac{1386}{100}\)

বা, \(r^2=\frac{441}{100}\)

বা, \(r^2=\left(\frac{21}{10}\right)^2\)

∴ \(r=\frac{21}{10}\)

∴ চোঙের আয়তন = πr²h ঘন মিটার

∴ চোঙের আয়তন = \(\require{cancel}\frac{22}{\cancel7}\times\frac{\displaystyle\overset3{\cancel{21}}}{10}\times\frac{21}{10}\times8\) ঘন মিটার

= \(\frac{11088}{100}\) ঘন মিটার।

= 110.88 ঘন মিটার।

উত্তর – চোঙের আয়তন 110.88 ঘন মিটার।

প্রয়োগ 13. যে চোঙের ভূমির পরিধি 15.4 সেমি. এবং উচ্চতা 10 সেমি. তার আয়তন হিসাব করে লিখি।

সমাধান –

মনে করি, চোঙটির ভূমির ব্যাসার্ধ = r সেমি. ও উচ্চতা = h সেমি.

এখানে 2πr = 15.4 এবং h = 10

বা, \(2\times\frac{22}7\times r=15.4\)

বা, \(r=\frac{{\displaystyle\overset{\overset7{\cancel{14}}}{\cancel{154}}}\times7}{2\times{\displaystyle\underset{\cancel2}{\cancel{22}}}\times10}=\frac{49}{20}\) সেমি.

∴ চোঙটির আয়তন = πr²h ঘনসেমি.

= \(\mathrm\pi\left(\frac{49}{20}\right)^2\times10\) ঘনসেমি.

= \(\require{cancel}\frac{\displaystyle\overset{11}{\cancel{22}}}{\cancel7}\times\frac{\displaystyle\overset7{\cancel{49}}}{20}\times\frac{49}{\displaystyle\underset{\cancel2}{\cancel{20}}}\times\cancel{10}\) ঘনসেমি.

= \(\frac{3773}{20}\) ঘনসেমি.

= 188.65 ঘনসেমি।

উত্তর – চোঙের আয়তন 188.65 ঘনসেমি।

প্রয়োগ 14. 11 সেমি. বহিঃপরিধিবিশিষ্ট 105 সেমি. লম্বা টিউবলাইটের কাচ যদি 0.2 সেমি. পুরু হয়, তবে 5টি টিউবলাইট তৈরি করতে কত ঘন সেমি. কাচ লাগবে, হিসাব করে লিখি।

সমাধান –

ধরি, টিউবলাইটের বহিঃব্যাসার্ধের দৈর্ঘ্য = r₁ সেমি., অন্তঃব্যাসার্ধের দৈর্ঘ্য = r₂ সেমি. এবং উচ্চতা h সেমি.

শর্তানুসারে,

বহিঃপরিধি = 2πr₁ = 11

বা, \(r_1=\frac{11\times7}{2\times22}=\frac74\)

∴ বহিঃব্যাসার্ধের দৈর্ঘ্য = \(\frac74\) সেমি. = 1.75 সেমি.

টিউবলাইটের কাচ 0.2 সেমি. পরু।

∴ টিউবলাইটটির অন্তঃব্যাসার্ধের দৈর্ঘ্য = r₂ = (1.75 – 0.2) সেমি. = 1.55 সেমি.

প্রতিটি টিউবলাইটে কাচের আয়তন = \(\mathrm\pi\left(\mathrm r_1^2-\mathrm r_2^2\right)\mathrm h\)

= \(\frac{22}7\left\{\left(1.75\right)^2-\left(1.55\right)^2\right\}\times105\) ঘন সেমি.

= \(\frac{22}7\times\left(1.75+1.55\right)\left(1.75-1.55\right)\times105\) ঘন সেমি.

= \(\frac{22}7\times3.30\times0.2\times105\) ঘন সেমি.

= 217.8 ঘন সেমি.

উত্তর – 5টি টিউবলাইট তৈরি করতে কাচ লাগবে 5 × 217.8 ঘন সেমি. = 1089 ঘন সেমি.

প্রয়োগ 15. একটি ছিদ্র দিয়ে জাহাজের খোলে 110 কিলোলিটার জল ঢুকেছে। ছিদ্রটি বন্ধ করার পর জল নিকাশের জন্য একটি পাম্প লাগানো হয়েছে। পাম্পটির পাইপের ব্যাসের দৈর্ঘ্য 10 সেমি. এবং চালু অবস্থায় জলের গতিবেগ মিনিটে 350 মিটার হলে, সমস্ত জল নিকাশ করতে পাম্পটি কতক্ষণ চালু রাখতে হবে, হিসাব করে লিখি।

সমাধান –

এক মিনিটে পাম্পটি জল নিকাশ করতে পারে \(\frac{22}7\times\frac{10}2\times\frac{10}2\times\frac1{100}\times3500\) ঘন ডেসিমি.

= 2750 ঘন ডেসিমি. = 2750 লিটার [1 ঘন ডেসিমি. = 1 লিটার]

∴ 110 কিলোলিটার জল নিকাশ করতে সময় লাগবে = \(\frac{110000}{2750}\) মিনিট = 40 মিনিট

উত্তর – 40 মিনিটে পাম্পটি সমস্ত জল নিকাশ করতে পারবে।

প্রয়োগ 16. 5 মিটার উচ্চতাবিশিষ্ট একটি লম্ববৃত্তাকার চোঙাকৃতি ট্যাঙ্ক জলপূর্ণ আছে। 8 সেমি. দৈর্ঘ্যের ব্যাসের একটি পাইপ দিয়ে যদি মিনিটে 225 মিটার বেগে জল বের করা হয়, তাহলে 45 মিনিটে ট্যাঙ্কটির সমস্ত জল বেরিয়ে যায়। ট্যাঙ্কটির ব্যাসের দৈর্ঘ্য হিসাব করে লিখি।

সমাধান –

মনে করি, ট্যাংকটির ব্যাসার্ধ = r মিটার।

পাইপের ব্যাসার্ধ = \(\frac82\) সেমি = 4 সেমি = \(\frac4{100}\) = \(\frac1{25}\) মিটার।

প্রশ্নানুসারে, \(\mathrm{πr}^2\times5=45\times\mathrm\pi\left(\frac1{25}\right)^2\times225\)

বা, \(\require{cancel}5r^2=\overset9{\cancel{45}}\times\frac1{{\displaystyle\underset5{\cancel{25}}}\times\cancel{25}}\times\overset9{\cancel{225}}\)

বা, \(r^2=\frac{81}{25}\)

বা, \(r^2=\left(\frac95\right)^2\)

∴ \(r=\frac95\)

উত্তর – ট্যাঙ্কটির ব্যাস = \(\left(2\times\frac95\right)=\frac{18}5=3.6\) মিটার = 360 সেমি.।

প্রয়োগ 17. তামার তৈরি একটি আয়তঘনের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 11 সেমি., যথাক্রমে 9 সেমি. এবং 6 সেমি.। আয়তঘনটিকে গলিয়ে 3 সেমি. দৈর্ঘ্যের ব্যাসের এবং \(\frac14\) সেমি. পুরু কতগুলি মুদ্রা তৈরি করা যাবে হিসাব করি।

সমাধান –

আয়তঘনের আয়তন = 11 × 9 × 6 ঘন সেমি.

যেহেতু মুদ্রাগুলি লম্ব চোঙাকৃতি, সুতরাং চোঙের ব্যাসার্ধের দৈর্ঘ্য \(\frac32\) সেমি. এবং উচ্চতা \(\frac14\) সেমি.।

প্রতিটি মুদ্রার আয়তন = \(\frac{22}7\times\frac32\times\frac32\times\frac14\) ঘন সেমি.

সুতরাং মুদ্রার সংখ্যা = \(\frac{11\times9\times6}{\frac{22}7\times\frac32\times\frac32\times\frac14}\) টি

= \(\frac{\cancel{11}\times{\displaystyle\overset{\cancel3}{\cancel9}}\times6\times7\times\cancel2\times2\times4}{{\displaystyle\underset{\cancel2}{\cancel{22}}}\times\cancel3\times\cancel3}=336\) টি।

উত্তর – 336টি মুদ্রা তৈরি করা যাবে।

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের অষ্টম অধ্যায়, ‘লম্ব বৃত্তাকার চোঙ’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।

আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।