এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের দ্বাবিংশ অধ্যায়, ‘পিথাগোরাসের উপপাদ্য’ -এর ‘কষে দেখি – 22’ বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

1. যদি কোনো ত্রিভুজের বাহুর দৈর্ঘ্য নিম্নরূপ হয়, তবে কোন ক্ষেত্রে ত্রিভুজটি সমকোণী ত্রিভুজ হবে হিসাব করে লিখি
(i) 8 সেমি., 15 সেমি., 17 সেমি.
(ii) 9 সেমি., 11 সেমি., 6 সেমি.
(i) সমাধান – এক্ষেত্রে 82+152=17282+152=172 অর্থাৎ, 64+225=28964+225=289 এবং 172=289172=289। অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল, অপর বাহুগুলির উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের সমান। সুতরাং, ত্রিভুজটি নিশ্চিতভাবে একটি সমকোণী ত্রিভুজ।
(ii) সমাধান – এক্ষেত্রে 112≠92+62112=92+62 অর্থাৎ, 121≠81+36121=81+36 (যেহেতু 81+36=11781+36=117)। অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল, অপর বাহুগুলির উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের সমষ্টির সমান নয়। সুতরাং, 9 সেমি., 11 সেমি. এবং 6 সেমি. বাহু বিশিষ্ট ত্রিভুজটি সমকোণী ত্রিভুজ হবে না।
2. আমাদের পাড়ার রাস্তায় একটি 15 মিটার লম্বা মই এমনভাবে রাখা আছে যে মইটি ভূমি থেকে 9 মিটার উঁচুতে অবস্থিত বিল্ডিংয়ের জানালা স্পর্শ করেছে। এবার ওই রাস্তার একই বিন্দুতে মইটির পাদদেশ রেখে মইটিকে ঘুরিয়ে এমনভাবে রাখা হল যে মইটি রাস্তার অপর প্রান্তে অবস্থিত আমাদের জানালা স্পর্শ করল। আমাদের ওই জানালা যদি ভূমি থেকে 12 মিটার উপরে থাকে, তবে পাড়ার ওই রাস্তাটি কত চওড়া হিসাব করে লিখি।
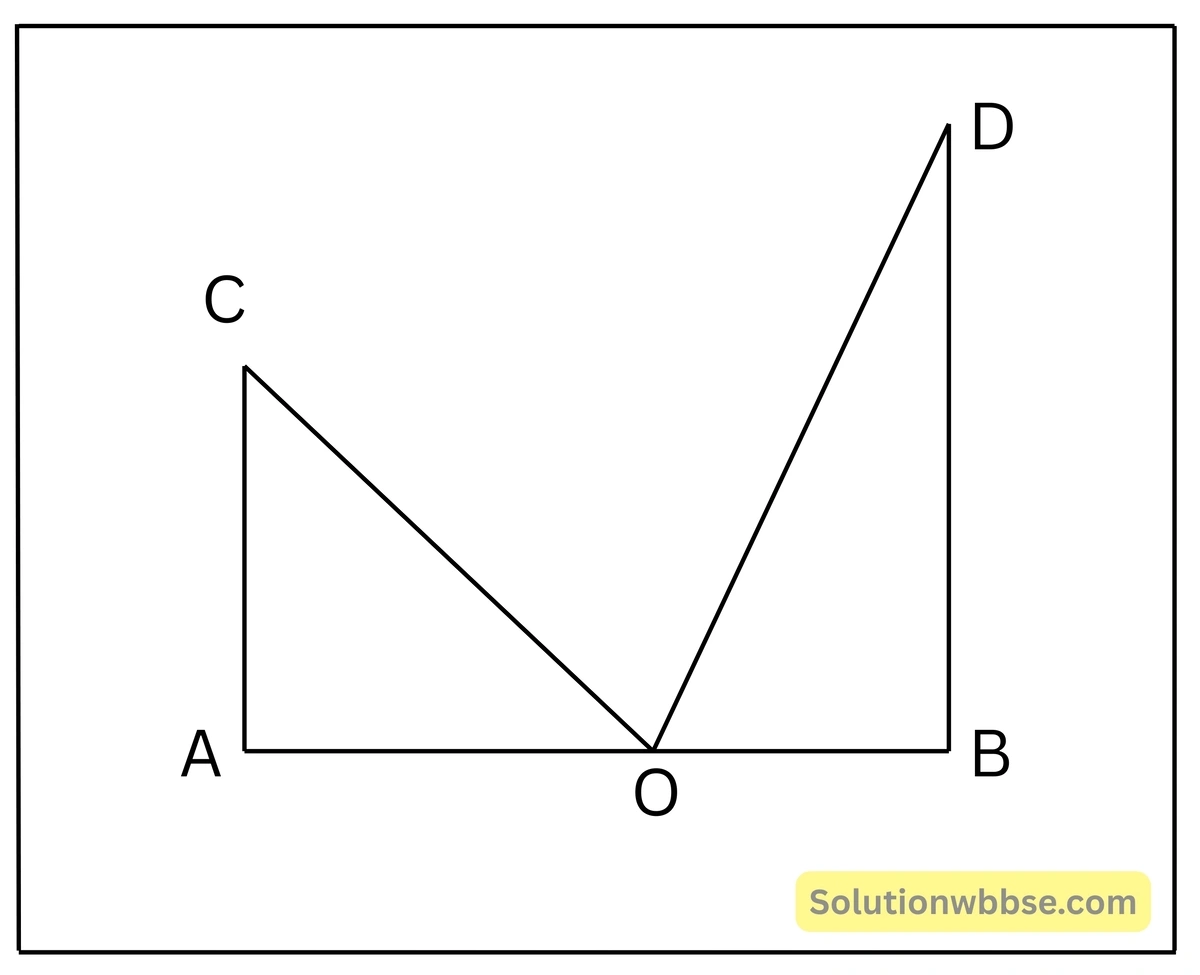
সমাধান – ধরা যাক, AB হল রাস্তাটির প্রস্থ, O হল মইয়ের পাদদেশ, C ও D হল যথাক্রমে বিল্ডিংয়ের এবং আমাদের জানালার অবস্থান।
∴ AC=9 মিটার, BD=12 মিটার এবং মইয়ের দৈর্ঘ্য OC=OD=15 মিটার।
এখন, ΔOAC এবং ΔOBD উভয়ই সমকোণী ত্রিভুজ।
∴ ΔOAC সমকোণী ত্রিভুজে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই,
OC²=OA²+AC²
বা, (15)² = OA² + (9)²
বা, OA² = (15)² – (9)²
বা, OA² = 225 – 81
বা, OA² = 144
বা, OA² = (12)²
বা, OA = 12
একইভাবে ΔOBD সমকোণী ত্রিভুজে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই,
OD²=OB²+BD²
বা, (15)² = OB² + (12)²
বা, 225 = OB² + 144
বা, OB² = 225 – 144
বা, OB² = 81
বা, OB² = (9)²
বা, OB = 9
∴ AB=AO+OB = (12+9)মিটার = 21 মিটার।
∴ রাস্তাটি 21 মিটার চওড়া।
3. 10 সেমি. বাহু বিশিষ্ট কোনো রম্বসের একটি কর্ণের দৈর্ঘ্য 12 সেমি. হলে, রম্বসটির অপর কর্ণের দৈর্ঘ্য হিসাব করে লিখি।
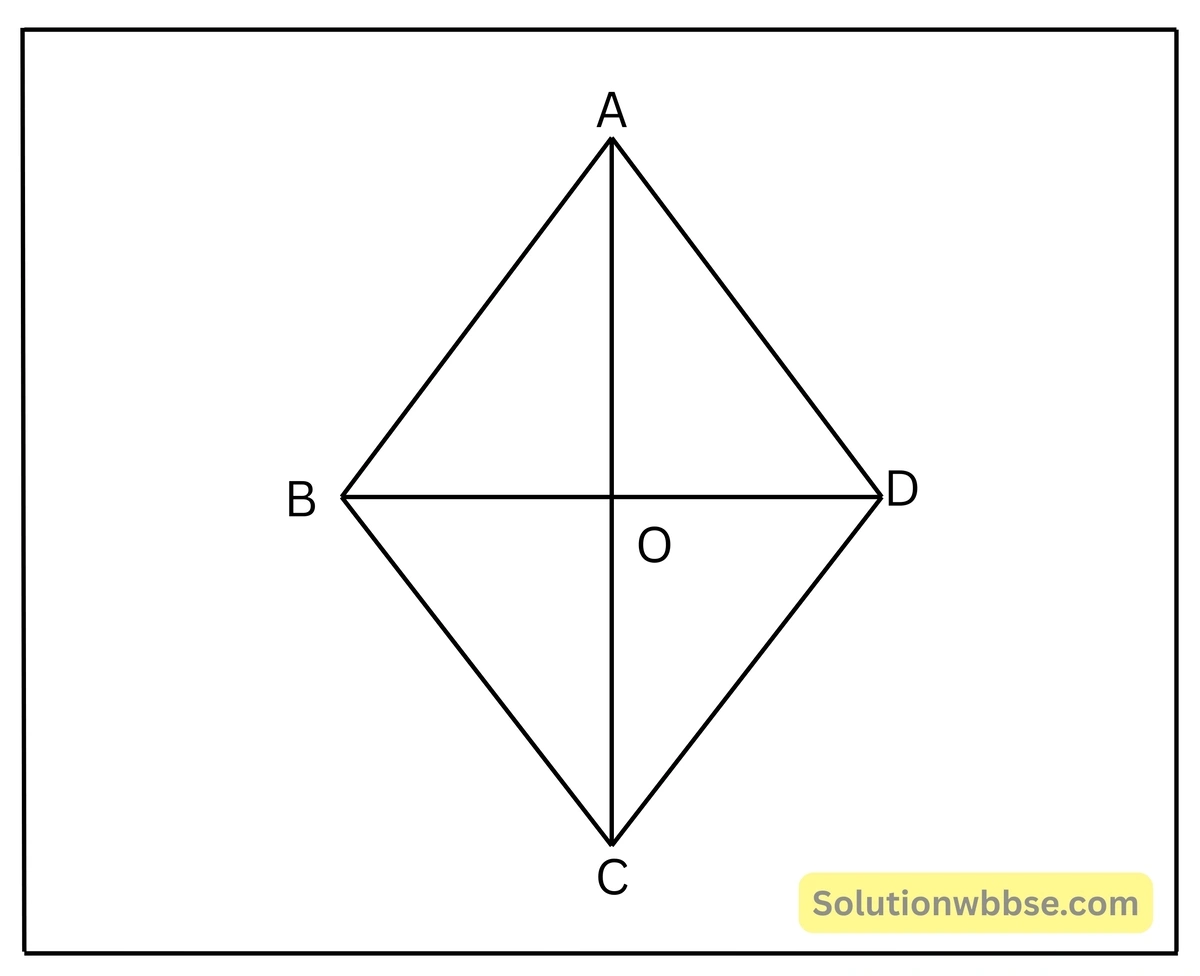
সমাধান –
ধরা যাক, ABCD একটি রম্বস যার দুটি কর্ণ AC এবং BD পরস্পরকে O বিন্দুতে ছেদ করেছে এবং BD = 12 সেমি.।
যেহেতু রম্বসের প্রতিটি বাহুর দৈর্ঘ্য 10 সেমি. ∴ AB = BC = CD = DA = 10 সেমি.।
যেহেতু, রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে,
∴ OD = 6 সেমি. এবং ∠AOD = 90°।
এখন, ΔAOD সমকোণী ত্রিভুজ থেকে পাই,
AD² = OA² + OD²
বা, (10)² = OA² + (6)²
বা, 100 = OA² + 36
বা, OA² = 100 – 36
বা, OA² = 64
বা, OA² = (8)²
বা, OA = 8
∴ AC = (2 × 8) সেমি. = 16 সেমি.
∴ অপর কর্ণের দৈর্ঘ্য 16 সেমি.।
4. একটি ত্রিভুজ ΔPQR অঙ্কন করেছি যার ∠Q সমকোণ। QR বাহুর উপর S যে-কোনো একটি বিন্দু হলে, প্রমাণ করি যে, PS²+QR² = PR²+QS²
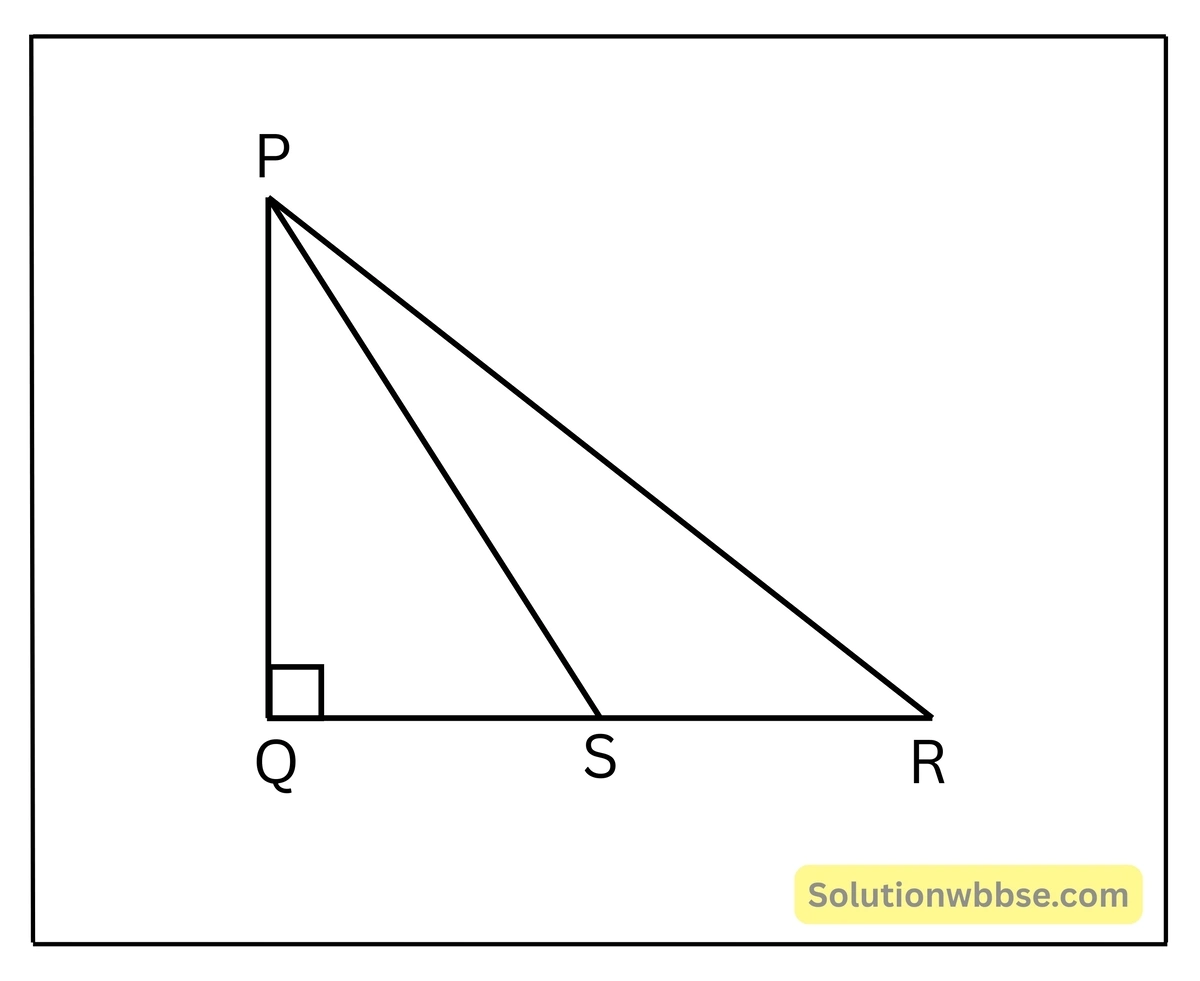
ধরি, ΔPQR একটি ত্রিভুজ যার ∠Q সমকোণ। QR বাহুর উপর S যেকোনো একটি বিন্দু হলে, প্রমাণ করতে হবে যে, PS²+QR² = PR²+QS²
প্রমাণ – যেহেতু, ∠Q সমকোণ,
∴ ∠PQS = ∠PQR = 90°
∴ ΔPQS এবং ΔPQR উভয়ই সমকোণী ত্রিভুজ।
ΔPQS সমকোণী ত্রিভুজ থেকে পাই,
PS² = PQ² + QS² — (i)
আবার ΔPQR সমকোণী ত্রিভুজ থেকে পাই,
PR² = PQ² + QR²
বা, QR² = PR² – PQ² — (ii)
(i) নং ও (ii) নং সমীকরণ যোগ করে পাই,
∴ PS² + QR² = PQ² + QS² + PR² – PQ²
বা, PS² + QR² = PR² + QS² [প্রমাণিত]
5. প্রমাণ করি, যে-কোনো রম্বসের বাহুগুলির উপর অঙ্কিত বর্গের সমষ্টি কর্ণ দুটির উপর অঙ্কিত বর্গ দুটির সমষ্টির সমান।

ধরি, \(ABCD\) একটি রম্বস, যার কর্ণদ্বয় হল \(AC\) এবং \(BD\)। প্রমাণ করতে হবে যে, \(AB^2+BC^2+CD^2+DA^2=AC^2+BD^2\)
প্রমাণ – যেহেতু \(ABCD\) একটি রম্বস, ∴ \(AC\) ও \(BD\) কর্ণদ্বয় পরস্পরকে \(O\) বিন্দুতে সমকোণে সমদ্বিখন্ডিত করে।
∴ \(OA=OC\) এবং \(OB=OD\) আবার \(OA = \frac{AC}{2}\) এবং \(OB= \frac{BD}{2}\)
∴ \(\triangle AOB\) সমকোণী ত্রিভুজ থেকে পাই \(AB^2=OB^2+OA^2\)
\(\triangle BOC\) সমকোণী ত্রিভুজ থেকে পাই \(BC^2=OB^2+OC^2\)
\(\triangle COD\) সমকোণী ত্রিভুজ থেকে পাই \(CD^2=OC^2+OD^2\)
\(\triangle AOD\) সমকোণী ত্রিভুজ থেকে পাই \(DA^2 = OA^2+OD^2\)
∴ \(AB^2+BC^2+CD^2+DA^2\)
= \( OB^2+OA^2+ OB^2+OC^2 +OC^2+OD^2 + OA^2+OD^2\)
= \( 2OA^2+2OB^2+2OC^2+2OD^2\)
= \( 4OA^2+4OB^2\) [যেহেতু, \(OA=OC\) এবং \(OB=OD\)]
= \( 4\left(\frac{AC}{2}\right)^2 + 4\left(\frac{BD}{2}\right)^2\) [যেহেতু, \(OA=\frac{AC}{2}\),
\(OB=\frac{BD}{2}\)]
= \( 4\times\frac{AC^2}{4} + 4\times\frac{BD^2}{4}\)
= \( AC^2+BD^2\)
∴ \(AB^2+BC^2+CD^2+DA^2 = AC^2+BD^2\) [প্রমাণিত]
6. ABC একটি সমবাহু ত্রিভুজ। AD , BC বাহুর উপর লম্ব হলে, প্রমাণ করি যে , \(AB^2+BC^2+CA^2=4AD^2\)
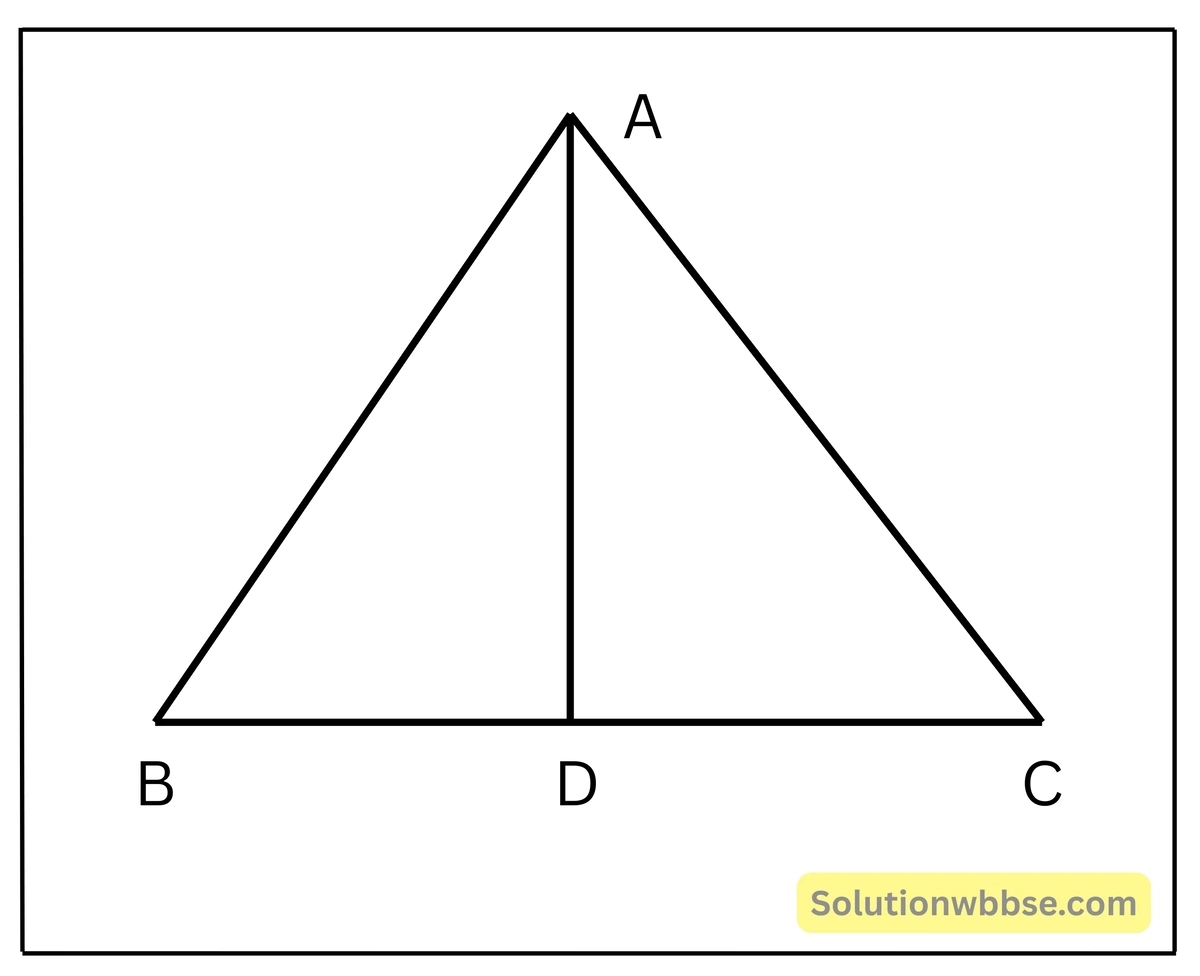
ধরি, ABC একটি সমবাহু ত্রিভুজ। A বিন্দু থেকে BC বাহুর উপরে AD লম্ব টানা হল, প্রমাণ করতে হবে যে, \(AB^2+BC^2+CA^2=4AD^2\)
প্রমাণ – ABC একটি সমবাহু ত্রিভুজ এবং A বিন্দু থেকে BC বাহুর উপর AD লম্ব ∴ AD একটি মধ্যমা, সুতরাং D, BC এর মধ্যবিন্দু।
যেহেতু AD, BC বাহুর উপর লম্ব সুতরাং ΔADB এবং ΔADC উভয়ই সমকোণী ত্রিভুজ।
∴ \(AB^2= AD^2+BD^2\)
বা, \(AB^2=AD^2+(\frac{BC}{2})^2\) [ যেহেতু, \(BD = \frac{1}{2}BC\) ]
বা, \(AB^2=AD^2+\frac{BC^2}{4}\)
বা, \(4AB^2 = 4AD^2+BC^2\)
বা, \(4AB^2-BC^2=4AD^2\)
বা, \(4AB^2-AB^2=4AD^2\) [ যেহেতু, \(AB=BC=CA\)]
বা, \(3AB^2 = 4AD^2\)
বা, \(AB^2+AB^2+AB^2=4AD^2\)
বা, \(AB^2+BC^2+CA^2 = 4AD^2\) [যেহেতু, \(AB=BC=CA\)]
∴ \(AB^2+BC^2+CA^2 = 4AD^2\) [প্রমাণিত]
7. একটি সমকোণী ত্রিভুজ \(\triangle ABC\) অঙ্কন করলাম যার \(\angle A\) সমকোণ। \(AB\) ও \(AC\) বাহুর উপর দুটি বিন্দু যথাক্রমে \(P\) ও \(Q\) নিলাম। \(P,Q; B,Q\) ও \(C,P\) যুক্ত করে, প্রমাণ করি যে, \(BQ^2+PC^2=BC^2+PQ^2\)
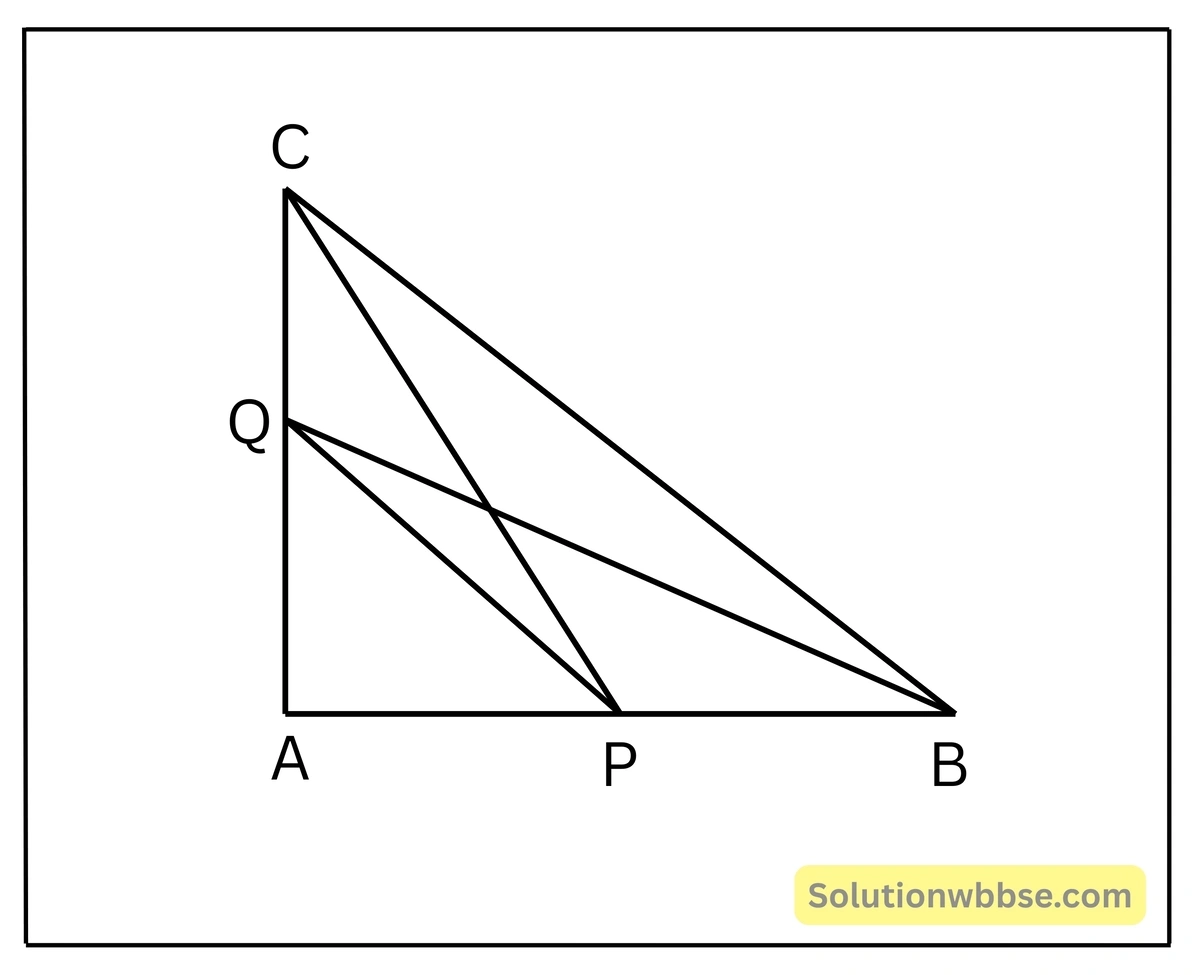
ধরি, \(\triangle ABC\) একটি সমকোণী ত্রিভুজ যার \(\angle A\) সমকোণ, \(AB\) ও
\(AC\) বাহুর উপর দুটি বিন্দু যথাক্রমে \(P\) ও \(Q\) নেওয়া হল। \(P, Q; B, Q\) ও
\(C, P\) যুক্ত করে, প্রমাণ করতে হবে যে, \(BQ^2+PC^2=BC^2+PQ^2\)
প্রমাণঃ যেহেতু \(\angle A\) সমকোণ,
∴ \(\triangle ABQ\), \(\triangle APC\), \(\triangle APQ\) এবং \(\triangle ABC\) প্রত্যেকে সমকোণী ত্রিভুজ।
\(\triangle ABQ\) সমকোণী ত্রিভুজ থেকে পাই \(BQ^2 = AQ^2+AB^2\) — (i)
\(\triangle APC\) সমকোণী ত্রিভুজ থেকে পাই \(PC^2 = AC^2+AP^2\) — (ii)
\(\triangle APQ\) সমকোণী ত্রিভুজ থেকে পাই \(PQ^2 = AP^2+AQ^2\) — (iii)
\(\triangle ABC\) সমকোণী ত্রিভুজ থেকে পাই \(BC^2 = AC^2+AB^2\) — (iv)
(i) নং ও (ii) নং সমীকরণ যোগ করে পাই,
\(BQ^2+PC^2\)= \( AQ^2+AB^2+AC^2+AP^2\)
= \( (AQ^2+AP^2) + (AC^2+AB^2)\)
= \( PQ^2+BC^2\) [(iii) ও (iv) নং সমীকরণ থেকে পাই]
∴ \(BQ^2+PC^2 = PQ^2+BC^2\) [প্রমাণিত]
8. ABCD চতুর্ভুজের দুটি কর্ণ পরস্পরকে লম্বভাবে ছেদ করলে, প্রমাণ করি যে, \(AB^2+CD^2=BC^2+DA^2\)
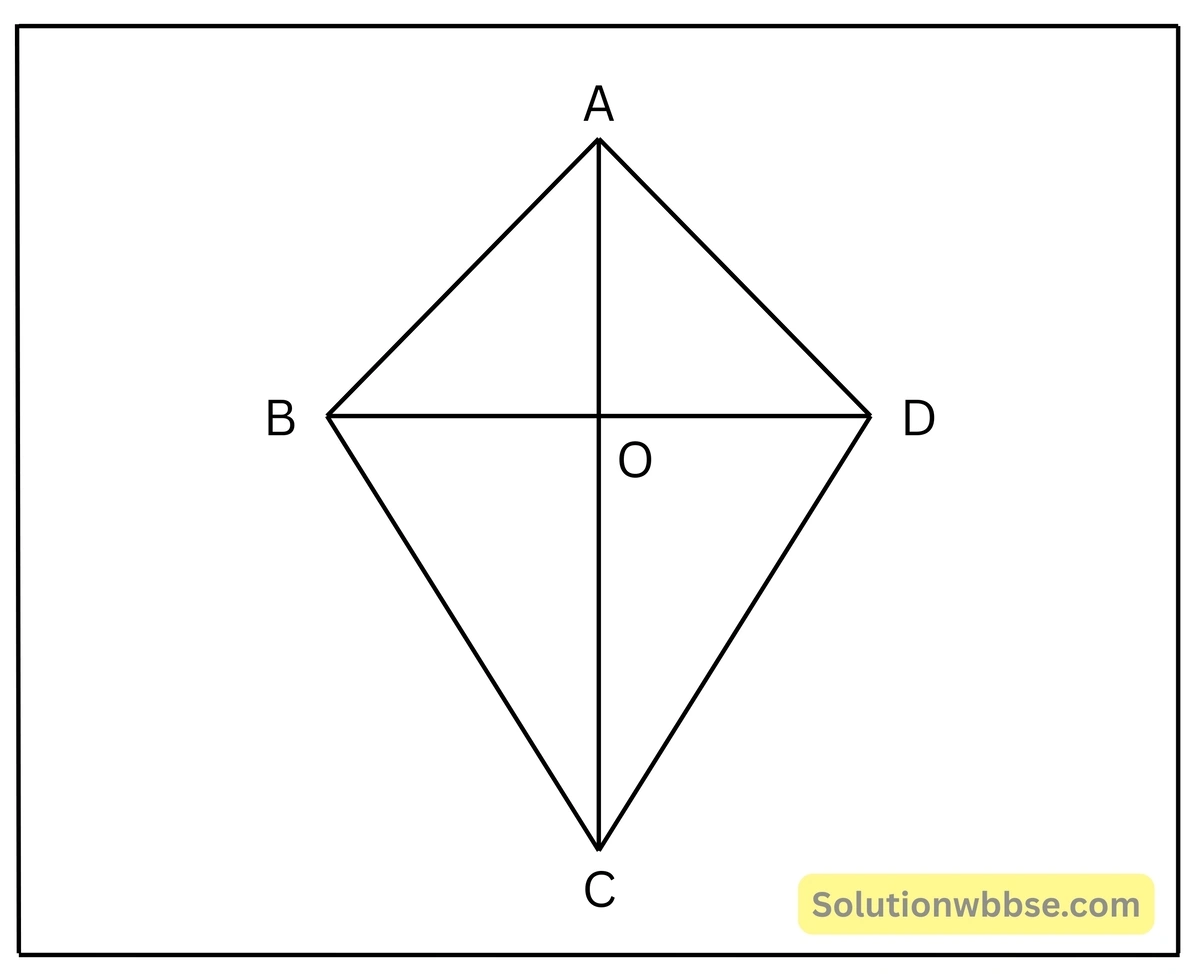
ধরি, ABCD চতুর্ভুজের কর্ণদ্বয় AC ও BD পরস্পরকে O বিন্দুতে লম্বভাবে ছেদ করেছে। প্রমাণ করতে হবে যে, \(AB^2+CD^2=BC^2+DA^2\)
প্রমাণ – যেহেতু, ABCD চতুর্ভুজের কর্ণদ্বয় পরস্পরকে O বিন্দুতে লম্বভাবে ছেদ করেছে,
\(\therefore \Delta AOB, \Delta BOC, \Delta COD\) এবং \(\Delta AOD\) প্রত্যেকে সমকোণী ত্রিভুজ।
\(\Delta AOB\) সমকোণী ত্রিভুজ থেকে পাই \(AB^2 = OA^2+OB^2\) —(i)
\(\Delta BOC\) সমকোণী ত্রিভুজ থেকে পাই \(BC^2 = OB^2+OC^2\) —(ii)
\(\Delta COD\) সমকোণী ত্রিভুজ থেকে পাই \(CD^2 = OC^2+OD^2\) —(iii)
\(\Delta DOA\) সমকোণী ত্রিভুজ থেকে পাই \(AD^2 = OA^2+OD^2\) —(iv)
(i) ও (iii) নং সমীকরণ যোগ করে পাই,
\(AB^2+CD^2\)= \(OA^2+OB^2+OC^2+OD^2\)
= \( (OA^2+OD^2)+(OB^2+OC^2)\)
= \( AD^2+BC^2\) [ (ii)ও(iv) নং সমীকরণ থেকে পাই ]
\(\therefore AB^2+CD^2=AD^2+BC^2\) [প্রমাণিত]
9. একটি ত্রিভুজ ABC অঙ্কন করেছি যার উচ্চতা AD; \(AB>AC\) হলে প্রমাণ করি যে \(AB^2-AC^2=BD^2-CD^2\)
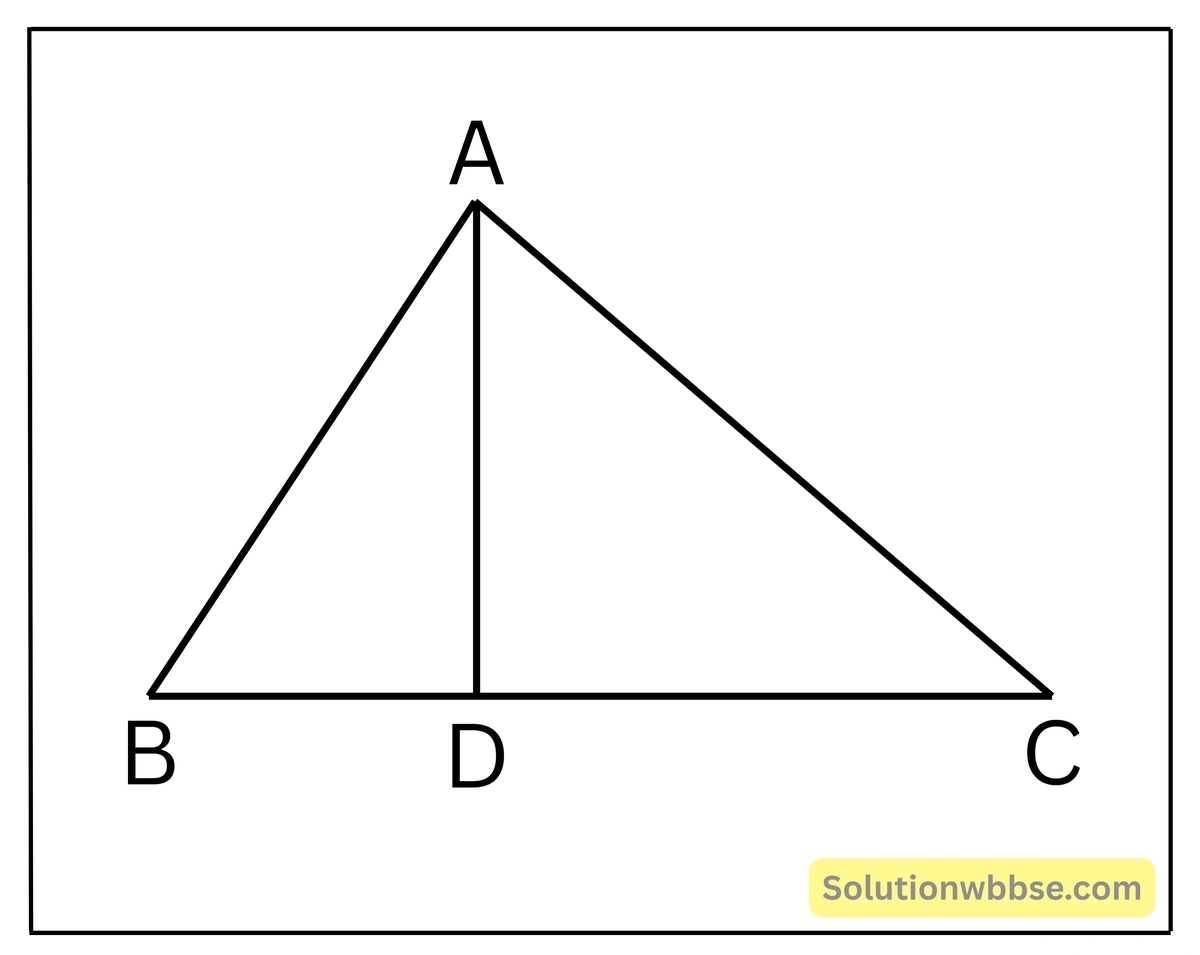
ধরি, ABC একটি সমকোণী ত্রিভুজ যার \(\angle A\) সমকোণ, AD হল ত্রিভুজটির উচ্চতা এবং \(AB>AC\), প্রমাণ করতে হবে যে, \(AB^2-AC^2=BD^2-CD^2\)
প্রমাণ – ABC সমকোণী ত্রিভুজে AD উচ্চতা।
∴ \(AD \perp BC\)
∴ \(\Delta ABD\) এবং \(\Delta ACD\) উভয়ই সমকোণী ত্রিভুজ।
\(\Delta ABD\) সমকোণী ত্রিভুজ থেকে পাই \(AB^2 = AD^2+BD^2\) —(i)
এবং \(\Delta ACD\) সমকোণী ত্রিভুজ থেকে পাই \(AC^2= AD^2+CD^2\) —(ii)
(i) ও (ii) নং সমীকরণ বিয়োগ করে পাই,
\(AB^2-AC^2\)= \( (AD^2+BD^2)-(AD^2+CD^2)\)
= \( AD^2+BD^2-AD^2-CD^2\)
= \( BD^2-CD^2\)
∴ \(AB^2-AC^2 = BD^2-CD^2\) [প্রমাণিত]
10. ABC এর শীর্ষবিন্দু B ও C থেকে AC ও AB (\(AC > AB\)) বাহু দুটির উপর দুটি লম্ব অঙ্কন করেছি যারা পরস্পরকে P বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, \(AC^2+BP^2=AB^2+CP^2\)
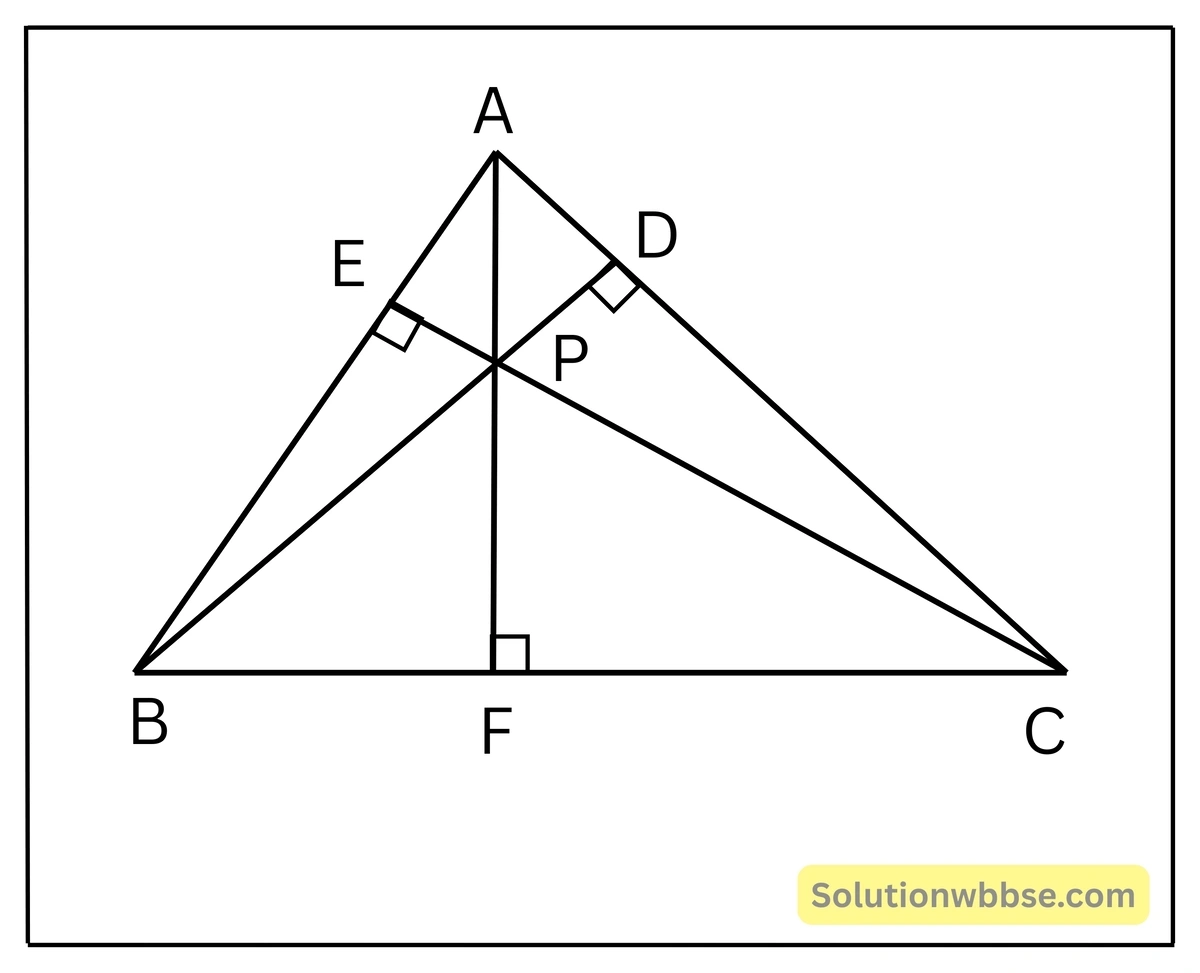
ABC একটি ত্রিভুজ যার B ও C বিন্দু থেকে AC ও AB বাহুর উপর দুটি লম্ব যথাক্রমে, BD ও CE অঙ্কন করেছি যারা পরস্পরকে P বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে, \(AC^2+BP^2=AB^2+CP^2\)
অঙ্কন – A,P যুক্ত করে বর্ধিত করা হল যা BC বাহুকে F বিন্দুতে ছেদ করেছে।
প্রমাণ – \(\Delta ABC\) এর \(AF \perp BC\) [যেহেতু, P লম্ববিন্দু]
সমকোণী ত্রিভুজ \(\Delta ACF\) থেকে পাই \(AC^2=AF^2+CF^2\) —(i)
সমকোণী ত্রিভুজ \(\Delta BPF\) থেকে পাই \(BP^2=BF^2+PF^2\) —(ii)
সমকোণী ত্রিভুজ \(\Delta ABF\) থেকে পাই \(AB^2=AF^2+BF^2\) —(iii)
সমকোণী ত্রিভুজ \(\Delta CPF\) থেকে পাই \(CP^2=PF^2+CF^2\) —(iv)
(i) ও (ii) নং সমীকরণ যোগ করে পাই,
\(AC^2 + BP^2=BF^2+PF^2 +AF^2+CF^2\)বা, \(AC^2 + BP^2 = AF^2+BF^2+PF^2+CF^2\)
বা, \(AC^2 + BP^2 = AB^2+CP^2\) [(iii) নং ও (iv) নং সমীকরণ থেকে পাই]
∴ \(AC^2 + BP^2 = AB^2+CP^2\) [প্রমাণিত]
11. \(\Delta ABC\) একটি সমদ্বিবাহু ত্রিভুজ যার \(C\) সমকোণ। \(D\), \(AB\) এর উপর যে-কোনো একটি বিন্দু হলে, প্রমাণ কর যে, \(AD^2+DB^2=2CD^2\)
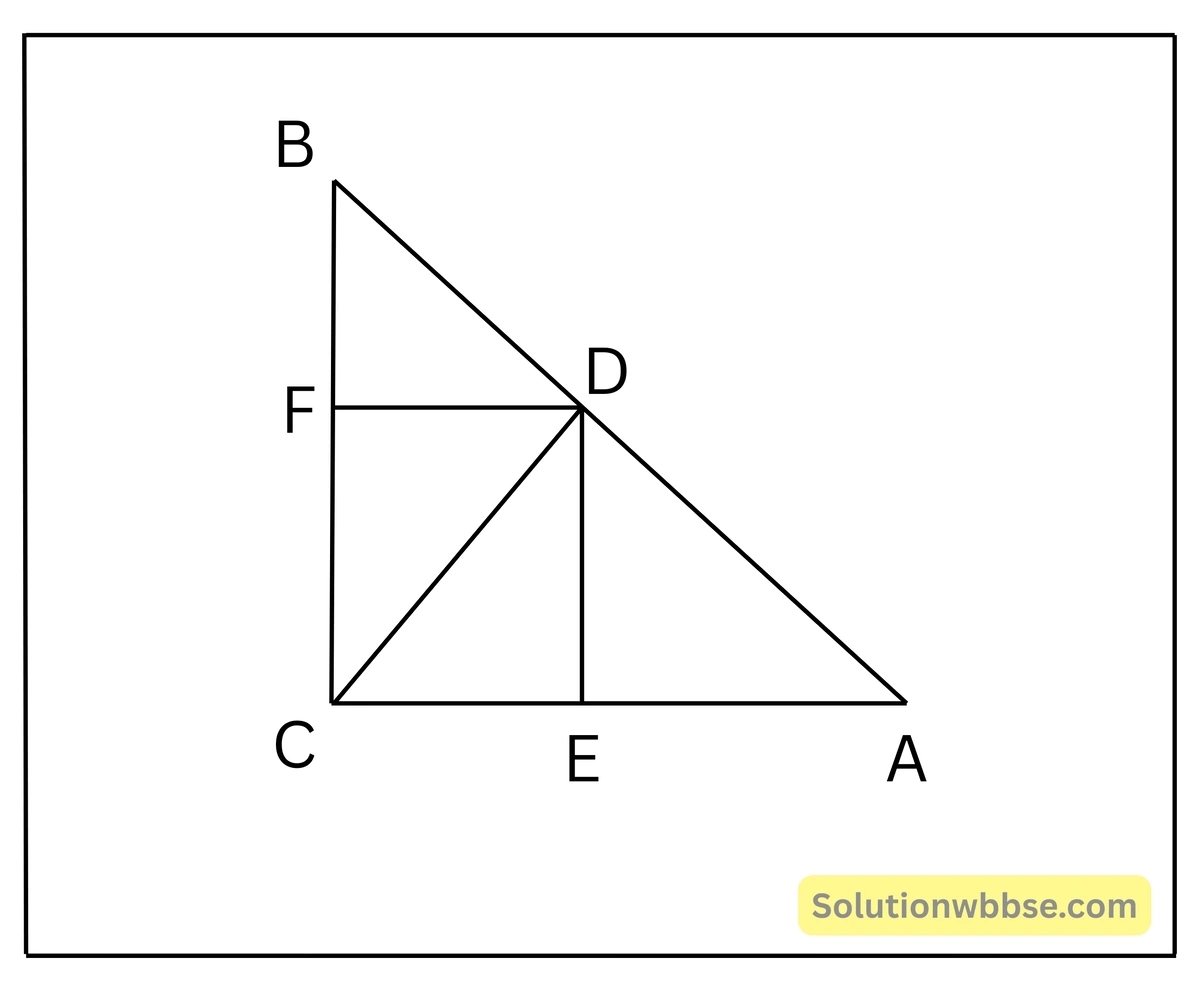
ধরাযাক, \(\Delta ABC\) একটি সমকোণী সমদ্বিবাহু ত্রিভুজ যার কোণ \(\angle C\) সমকোণ। \(D\), \(AB\) বাহুর উপর যেকোনো একটি বিন্দু, প্রমাণ করতে হবে যে, \(AD^2+DB^2= 2CD^2\)
অঙ্কন – \(D\) বিন্দু থেকে \(AC\) এবং \(BC\) এর উপর \(DE\) এবং \(DF\) লম্ব অঙ্কন করা হল।
প্রমাণ – \(\Delta ABC\) সমকোণী সমদ্বিবাহু ত্রিভুজ যার \(\angle C\) সমকোণ এবং \(AC = BC\)
∴ \(\angle CBA = \angle CAB = 45^\circ\)
আবার, \(\Delta ADE\) এর \(\angle AED = 90^\circ\) [যেহেতু, \(DE \perp AC\)] এবং
\(\angle EAD = 45^\circ\), ∴ \(\angle ADE = 45^\circ\)
∴ \(\Delta ADE\) এর \(\angle ADE=\angle EAD\)
∴ \(AE = DE\)
\(\Delta ADE\) ত্রিভুজের পিথাগোরাসের উপপাদ্য থেকে পাই,
\(AD^2 = AE^2 + DE^2\)= \( DE^2 + DE^2\)
= \( 2DE^2\) —(i)
আবার, \(\Delta DBF\) এর \(\angle BFD = 90^\circ\) এবং \(\angle FBD = 45^\circ\),
∴ \(\angle BDF = 45^\circ\)
∴ \(\Delta DBF\) এর \(\angle FBD=\angle BDF\), ∴ \(BF=FD\)
\(\Delta DBF\) সমকোণী ত্রিভুজে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই,
\(BD^2 = BF^2+FD^2\)= \( FD^2+FD^2\)
= \( 2FD^2\) —(ii)
(i) ও (ii) নং সমীকরণ যোগ করে পাই,
\(AD^2 +BD^2\)= \( 2DE^2 + 2FD^2\)
= \(2(DE^2+FD^2)\)
= \( 2(CF^2+FD^2)\) [ যেহেতু, \(CEDF\) চতুর্ভুজের \(\angle EDF\), \(\angle DEC\) এবং \(\angle DFC\) প্রত্যেকে \(90^\circ\), \(CEDF\) একটি আয়তক্ষেত্র, ∴
\(DE=CF\) এবং \(FD=CE\)]
= \( 2 CD^2\) [যেহেতু, \(\Delta CFD\) সমকোণী ত্রিভুজের ক্ষেত্রে \(CF^2+FD^2=CD^2\)]
∴ \(AD^2 +BD^2 =2CD^2\) [প্রমাণিত]
12. \(ABC\) ত্রিভুজে \(\angle A\) সমকোণ। \(CD\) মধ্যমা হলে, প্রমাণ করি যে, \(BC^2 = CD^2+3AD^2\)
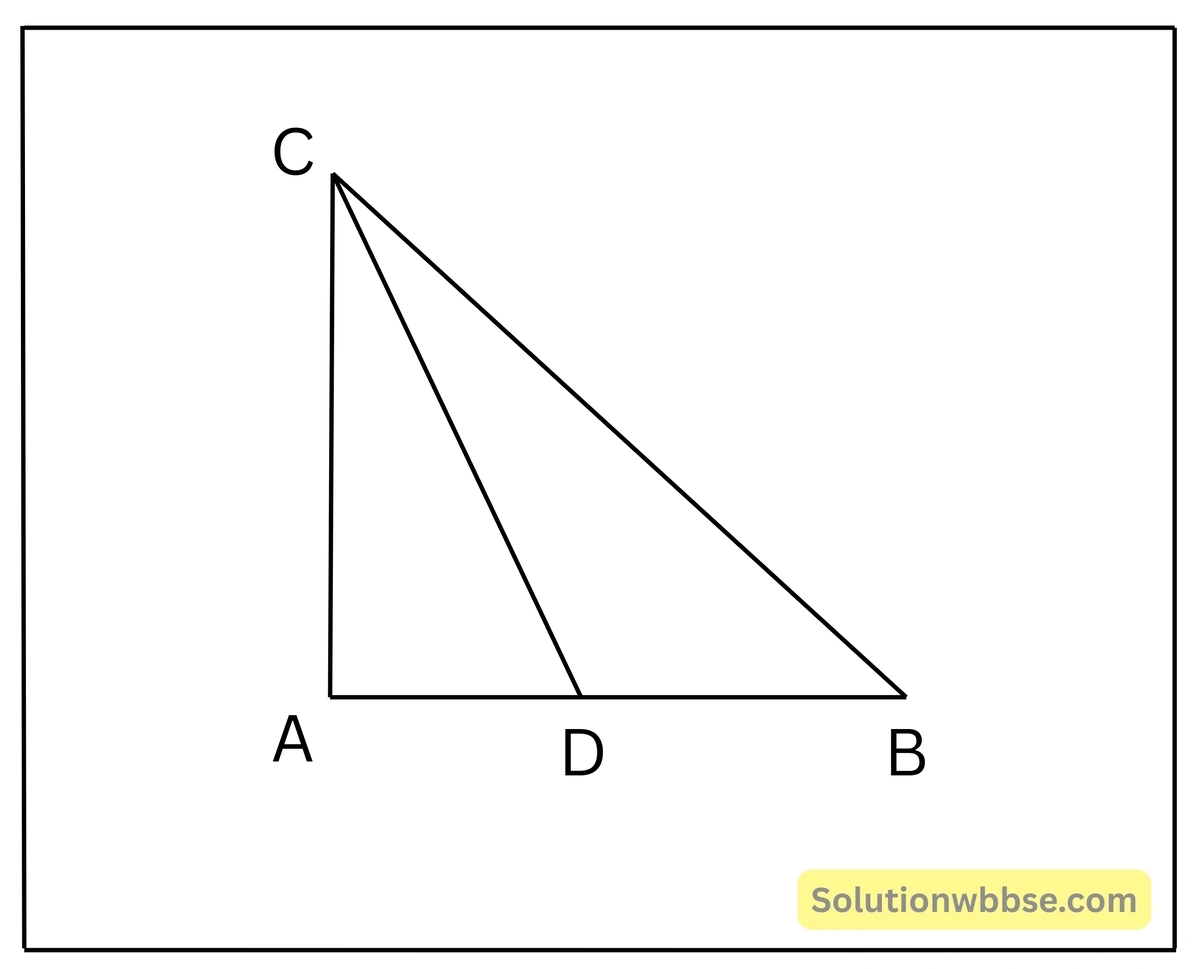
ধরাযাক, \(ABC\) সমকোণী ত্রিভুজ যার \(A\) সমকোণ। \(CD\) মধ্যমা, প্রমাণ করতে হবে যে, \(BC^2 = CD^2+3AD^2\)
প্রমাণ – \(\Delta ABC\) এবং \(\Delta ACD\) উভয়ই সমকোণী ত্রিভুজ যার \(A\) সমকোণ।
\(\Delta ABC\) সমকোণী ত্রিভুজ থেকে পাই \(AB^2+AC^2 = BC^2\)—(i)
\(\Delta ACD\) সমকোণী ত্রিভুজ থেকে পাই \(CD^2 = AD^2+AC^2\)—(ii)
∴ \(BC^2 = AB^2+AC^2\)
এখন \(D\), \(AC\) এর মধ্যবিন্দু।
∴ \(AC=2AD\)—(iii)
∴ \(BC^2 = (2AD)^2 + (CD^2-AD^2)\) [(ii) ও (iii) নং সমীকরণ থেকে পাই]
বা, \(BC^2 = 4AD^2+CD^2-AD^2\)
বা, \(BC^2 = CD^2+3AD^2\) [প্রমাণিত]
13. \(ABC\) ত্রিভুজের অভ্যন্তরস্থ একটি বিন্দু \(O\) থেকে \(BC\), \(CA\) ও \(AB\) বাহুর উপর যথাক্রমে \(OX\), \(OY\) ও \(OZ\) লম্ব অঙ্কন করেছি। প্রমাণ করি যে, \(AZ^2+BX^2+CY^2 = AY^2+CX^2+BZ^2\)
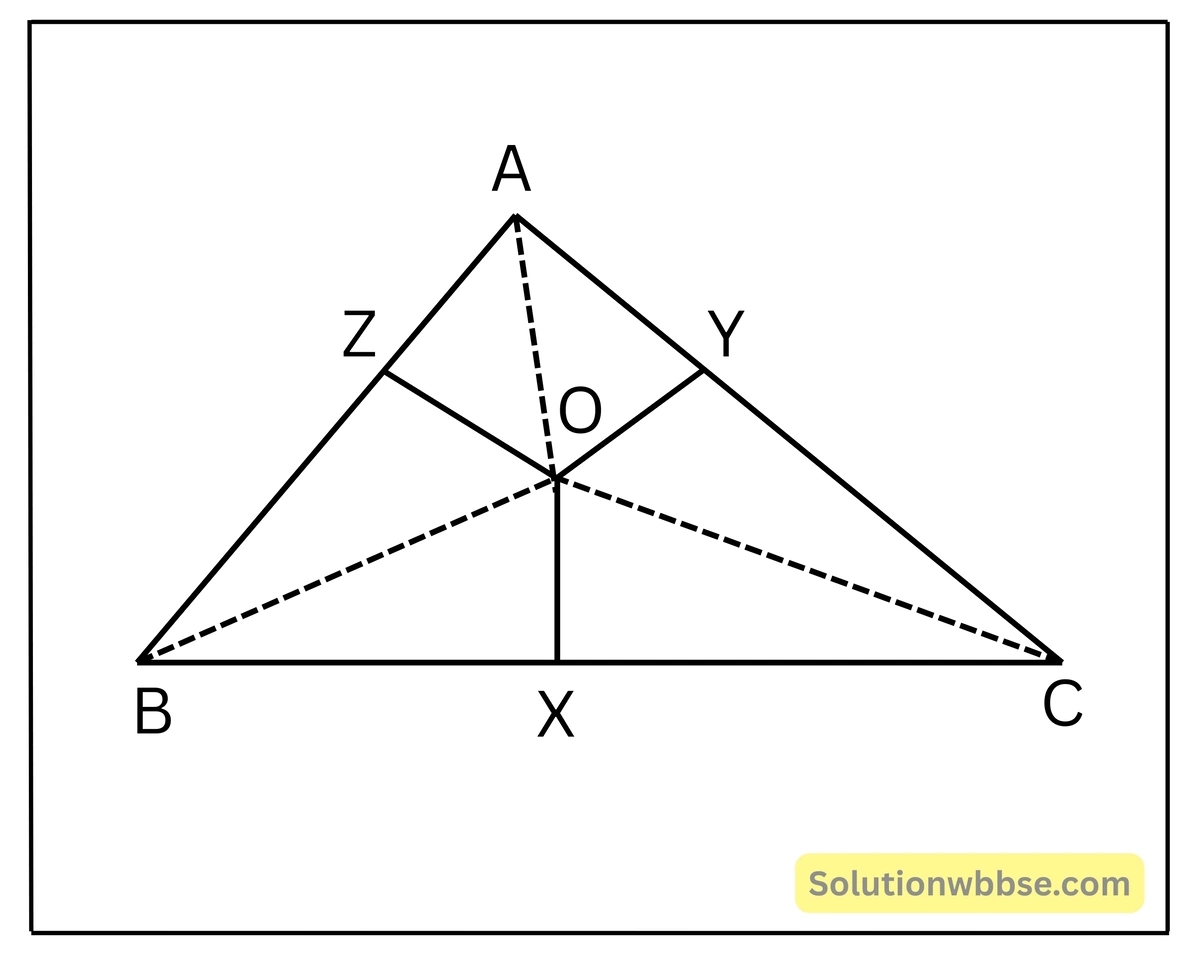
\(ABC\) একটি ত্রিভুজ যার অভ্যন্তরে \(O\) একটি বিন্দু এবং \(O\) বিন্দু থেকে \(BC\), \(CA\) এবং \(AB\) বাহুর উপরে যথাক্রমে \(OX\), \(OY\) এবং \(OZ\) লম্ব অঙ্কন করা হল।
প্রমাণ করতে হবে যে, \(AZ^2+BX^2+CY^2 = AY^2+CX^2+BZ^2\)
অঙ্কন – \(O,A\); \(O,B\) এবং \(O,C\) যুক্ত করা হল।
প্রমাণ – যেহেতু, \(OX\), \(OY\) এবং \(OZ\) যথাক্রমে \(BC\), \(CA\) এবং \(AB\) বাহুর উপর লম্ব।
∴ \(\Delta AOZ\), \(\Delta BOX\), \(\Delta COY\), \(\Delta AOY\),
\(\Delta COX\) এবং \(\Delta BOZ\) প্রত্যেকে সমকোণী ত্রিভুজ।
\(\Delta AOZ\) সমকোণী ত্রিভুজ থেকে পাই,
\(OA^2 = AZ^2+OZ^2\)বা, \(AZ^2 = OA^2 – OZ^2\) —(i)
\(\Delta BOX\) সমকোণী ত্রিভুজ থেকে পাই,
\(OB^2 = OX^2 +BX^2\)বা, \(BX^2 = OB^2 -OX^2\) —(ii)
\(\Delta COY\) সমকোণী ত্রিভুজ থেকে পাই,
\(OC^2 = OY^2+CY^2\)বা, \(CY^2 = OC^2 – OY^2\)—(iii)
\(\Delta AOY\) সমকোণী ত্রিভুজ থেকে পাই,
\(OA^2 = OY^2+AY^2\)বা, \(OA^2 – OY^2= AY^2\)—(iv)
\(\Delta COX\) সমকোণী ত্রিভুজ থেকে পাই,
\(OC^2 = OX^2+CX^2\)বা, \(CX^2 = OC^2-OX^2\) —(v)
\(\Delta BOZ\) সমকোণী ত্রিভুজ থেকে পাই,
\(OB^2 = OZ^2+BZ^2\)বা, \(BZ^2 = OB^2 -OZ^2\) —(vi)
∴ \(AZ^2+BX^2+CY^2 = OA^2 – OZ^2 + OB^2 -OX^2 +OC^2 – OY^2\)
বা, \(AZ^2+BX^2+CY^2 = OA^2-OY^2 + OC^2-OX^2 +OB^2-OZ^2\)
বা, \(AZ^2+BX^2+CY^2 = AY^2 +CX^2+BZ^2\) [ (iv), (v) এবং (vi) নং সমীকরণ থেকে পাই]
∴ \(AZ^2+BX^2+CY^2 = AY^2+CX^2+BZ^2\) [প্রমাণিত]
14. \(\Delta RST\) ত্রিভুজের \(\angle S\) সমকোণ। RS ও ST বাহুদ্বয়ের মধ্যবিন্দু যথাক্রমে X ও Y; প্রমাণ করি যে, \(RY^2+XT^2=5XY^2\)
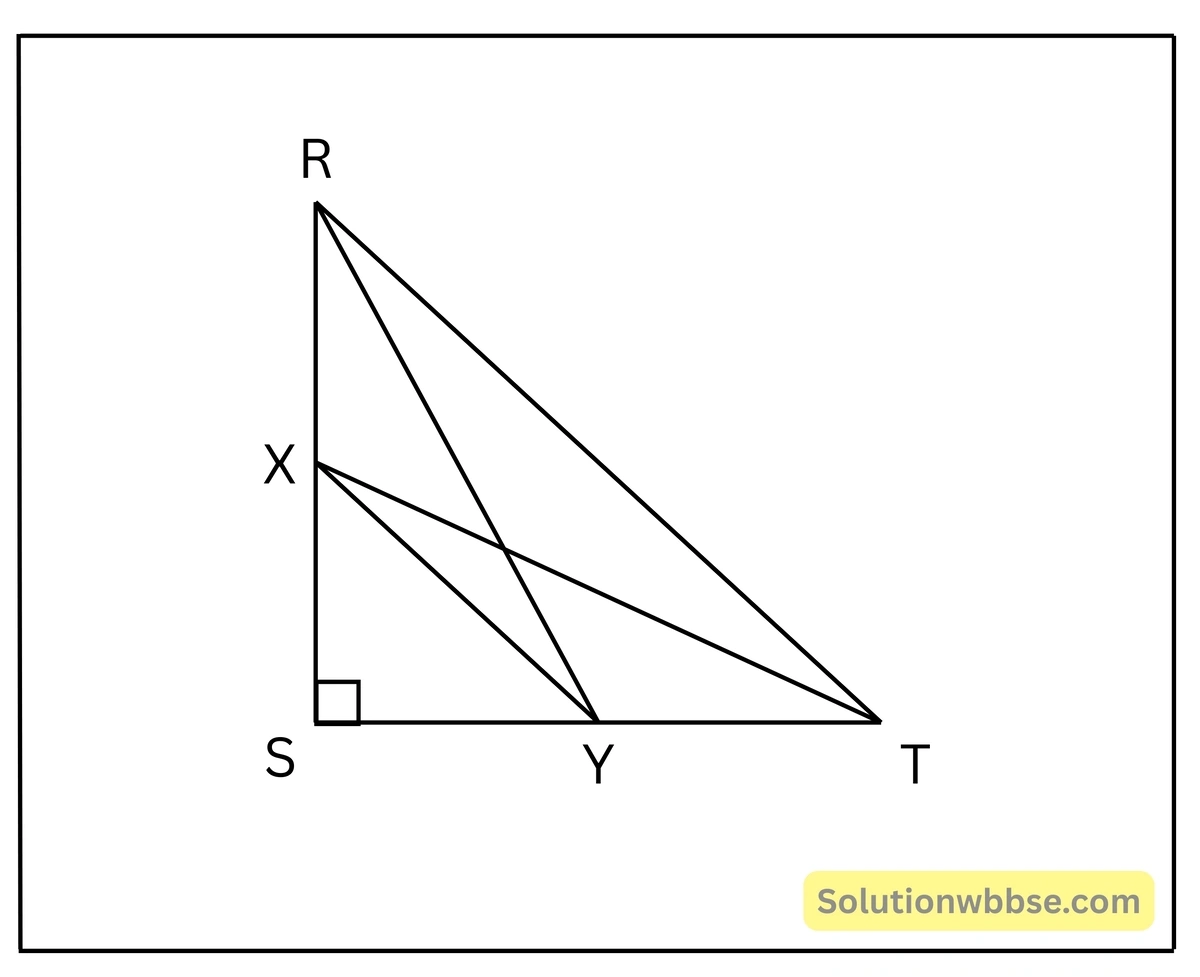
\(\Delta RST\) ত্রিভুজের \(\angle S\) সমকোণ। RS ও ST বাহুদ্বয়ের মধ্যবিন্দু যথাক্রমে X ও Y; প্রমাণ করতে হবে যে, \(RY^2+XT^2=5XY^2\)
প্রমাণ – \(\Delta RST\) ত্রিভুজে \(\angle S\) সমকোণ।
∴ \(\Delta RST\), \(\Delta RSY\), \(\Delta XST\), \(\Delta XSY\) প্রত্যেকে সমকোণী ত্রিভুজ।
∴ সমকোণী ত্রিভুজ \(\Delta RSY\) থেকে পাই \(RY^2 = RS^2+SY^2\) —(i)
সমকোণী ত্রিভুজ \(\Delta XST\) থেকে পাই \(XT^2 = XS^2+ST^2\) —(ii)
সমকোণী ত্রিভুজ \(\Delta XSY\) থেকে পাই \(XY^2 = XS^2+SY^2\) —(iii)
(i) নং ও (ii) নং সমীকরণ যোগ করে পাই,
\(RY^2 + XT^2 = RS^2+SY^2+ XS^2+ST^2\)বা, \(RY^2 + XT^2 = (2XS)^2+SY^2+XS^2+(2SY)^2\) [যেহেতু, RS ও ST বাহুদ্বয়ের মধ্যবিন্দু যথাক্রমে X ও Y]
বা, \(RY^2+XT^2 = 4XS^2+SY^2+XS^2+4SY^2\)
বা, \(RY^2+XT^2 = 5XS^2+5SY^2\)
বা, \(RY^2+XT^2 = 5(XS^2+SY^2)\)
বা, \(RY^2+XT^2 = 5XY^2\) [(iii) নং সমীকরণ থেকে পাই]
∴ \(RY^2+XT^2 = 5XY^2\) [প্রমাণিত]
15. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.)
(i) এক ব্যাক্তি একটি স্থান থেকে 24 মিটার পশ্চিমদিকে যাব এবং তারপর 10 মিটার উত্তরদিকে যাব। যাত্রাস্থল থেকে ব্যাক্তির দূরত্ব
(a) 34 মিটার
(b) 17 মিটার
(c) 26 মিটার
(d) 25 মিটার
Ans – (c) 26 মিটার
সমাধান –
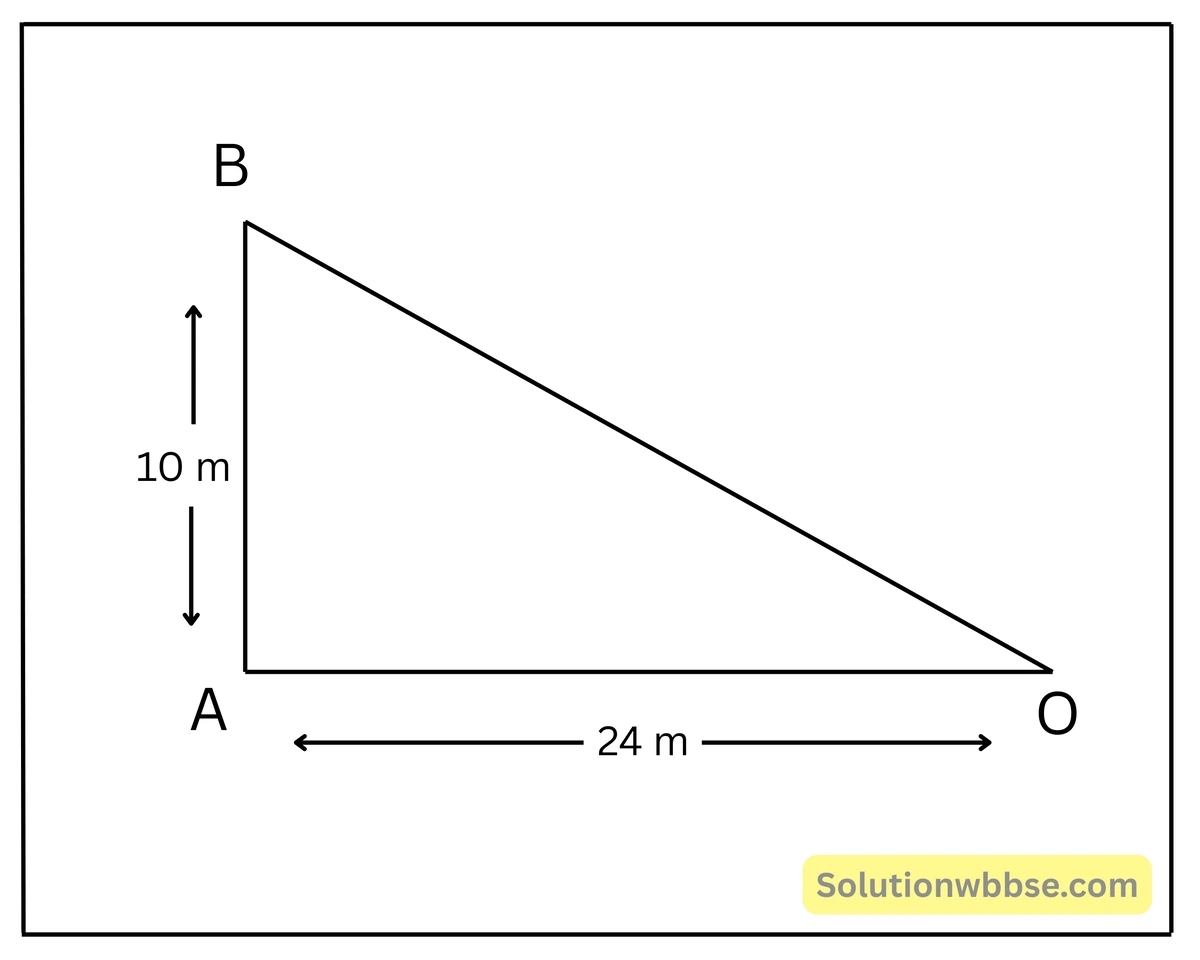
এক্ষেত্রে, \(OA = 24\) মিটার এবং \(AB = 10\) মিটার।
এখন স্পষ্টতই \(\Delta OAB\) সমকোণী ত্রিভুজ।
পিথাগোরাসের উপপাদ্য থেকে পাই,
\(OB^2 = OA^2+AB^2\)বা, \(OB^2 = (24)^2+(10)^2\)
বা, \(OB^2 = 576+100\)
বা, \(OB^2 = 676\)
বা, \(OB = \sqrt{676}\)
বা, \(OB = 26\)
(ii) ABC একটি সমবাহু ত্রিভুজ এবং AD লম্ব BC হলে, AD2 =
(a) \(\frac{3}{2} DC^2\)
(b) \(2 DC^2\)
(c) \(3DC^2\)
(d) \(4DC^2\)
Ans – (c) \(3DC^2\)

সমাধান –
ABC সমবাহু ত্রিভুজ যার AD লম্ব BC,
∴ AD মধ্যমা।
এখন, ADC সমকোণী ত্রিভুজ থেকে পাই,
\(AC^2= AD^2+CD^2\)বা, \(AD^2 = AC^2-CD^2\)
বা, \(AD^2 = BC^2-CD^2\) [যেহেতু, \(AB=BC=CA\)]
বা, \(AD^2 = (2CD)^2-CD^2\) [যেহেতু, AD মধ্যমা, ∴ \(BC=2CD\)]
বা, \(AD^2 = 4CD^2-CD^2\)
বা, \(AD^2 = 3CD^2\)
বা, \(AD^2 = 3DC^2\)
(iii) ABC সমদ্বিবাহু ত্রিভুজে \(AC = BC\) এবং \(AB^2 = 2AC^2\) হলে, \(\angle C\) এর পরিমাপ
(a) \(30^\circ\)
(b) \(90^\circ\)
(c) \(45^\circ\)
(d) \(60^\circ\)
Ans – (b) \(90^\circ\)
সমাধান –
\(AB^2 = 2AC^2\)বা, \(AB^2 = AC^2 + AC^2\)
বা, \(AB^2 = AC^2 + BC^2\) [ পিথাগোরাসের উপপাদ্য ]
∴ \(\angle C\) সমকোণ।
(iv) 13 মিটার ও 7 মিটার উচ্চ দুটি দণ্ড ভূমিরলে লম্বভাবে অবস্থিত এবং তাদের পাদদেশের মধ্যে দূরত্ব 8 মিটার। তাদের শীর্ষদেশের মধ্যে দূরত্ব
(a) 9 মিটার
(b) 10 মিটার
(c) 11 মিটার
(d) 12 মিটার
Ans – (b) 10 মিটার
সমাধান –
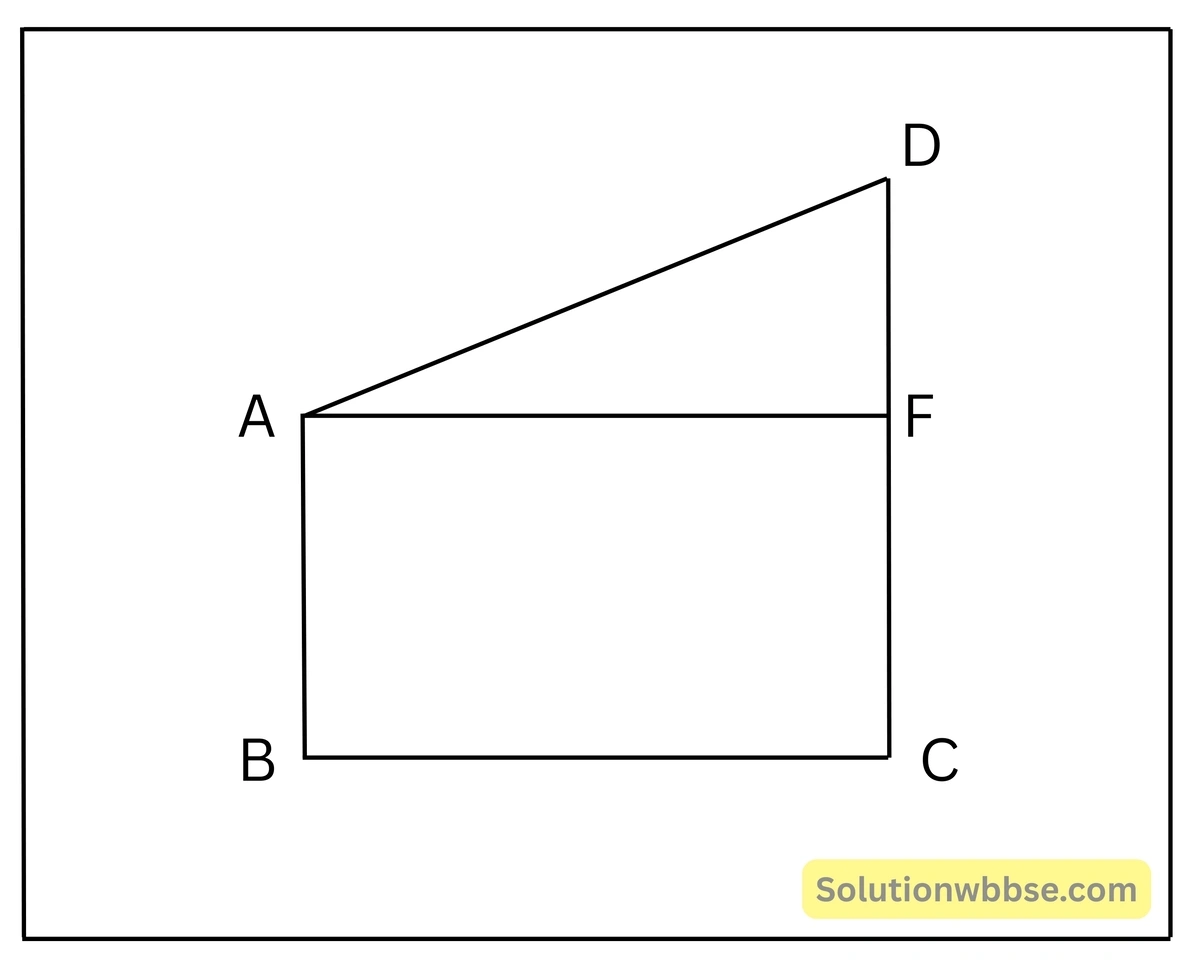
ধরাযাক, AB ও CD দুটি দণ্ড ভূমিরলে লম্বভাবে অবস্থিত।
∴ AB = 7মিটার, CD= 13মিটার এবং BC =8 মিটার
যেহেতু, AB এবং DC উভয়ই BC ভূমির উপর লম্ব সুতরাং AB || DC, আবার A থেকে DC এর উপর AF লম্ব সুতরাং AF || BC
আবার, ∠ABC = ∠BCF = 90°
∴ ABCF একটি আয়তক্ষেত্র।
∴ BC=AF = 8 মিটার এবং AB=FC =7 মিটার এবং AFD =90°
△AFD সমকোণী ত্রিভুজের ক্ষেত্রে AF = 8মিটার, DF=DC-FC=13-7=6মিটার
△AFD সমকোণী ত্রিভুজের ক্ষেত্রে পিথাগোরাসের উপপাদ্য অনুসারে পাই,
\(AD^2 = AF^2+DF^2\)বা, \(AD^2 = (8)^2+ (6)^2\)
বা, \(AD^2 =64+36\)
বা, \(AD^2 = 100\)
বা, \(AD^2 = (10)^2\)
বা, \(AD = 10\)
(v) একটি রম্বসের দুটি কর্ণের দৈর্ঘ্য 24 সেমি. এবং 10 সেমি. হলে, রম্বসটির পরিসীমা
(a) 13 সেমি.
(b) 26 সেমি.
(c) 52 সেমি.
(d) 25 সেমি.
Ans – (c) 52 সেমি.

সমাধান –
ধরাযাক, ABCD একটি রম্বস যার দুটি কর্ণ AC ও BD পরস্পরকে O বিন্দুতে ছেদ করেছে।
এখন △OAB সমকোণী ত্রিভুজ থেকে পাই,
\(OA^2+OB^2=AB^2\)বা, \((12)^2 + (5)^2 = AB^2\)
বা, \(144+25 = AB^2\)
বা, \(AB^2 = 169\)
বা, \(AB^2 = (13)^2\)
বা, AB= 13
∴ রম্বসের একটি বাহুর দৈর্ঘ্য 13 সেমি. সুতরাং রম্বসটির পরিসীমা = (13×4)সেমি. = 52 সেমি.।
B. নীচের বিবৃতি গুলি সত্য না মিথ্যা লিখিঃ
(i) একটি ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যের অনুপাত 3:4:5 হলে , ত্রিভুজটি সর্বদা সমকোণী ত্রিভুজ হবে।
উত্তর – সত্য
সমাধান – ধরি, ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য যথাক্রমে 3x একক, 4x একক এবং 5x একক।
এবং, \((5x)^2 = 25x^2 = 16x^2+9x^2 = (4x)^2+(3x)^2\)
∴ \((5x)^2 = (4x)^2+(3x)^2\)
∴ ত্রিভুজটির বাহুগুলি পিথাগোরাসের উপপাদ্যকে সমর্থন করে সুতরাং ত্রিভুজটি একটি সমকোণী ত্রিভুজ।
(ii) 10 সেমি. দৈর্ঘ্যের ব্যাসার্ধবিশিষ্ট একটি বৃত্তে কোনো জ্যা কেন্দ্রে সমকোণ উৎপন্ন করলে জ্যাটির দৈর্ঘ্য 5 সেমি. হবে।
উত্তর – মিথ্যা।
সমাধান –
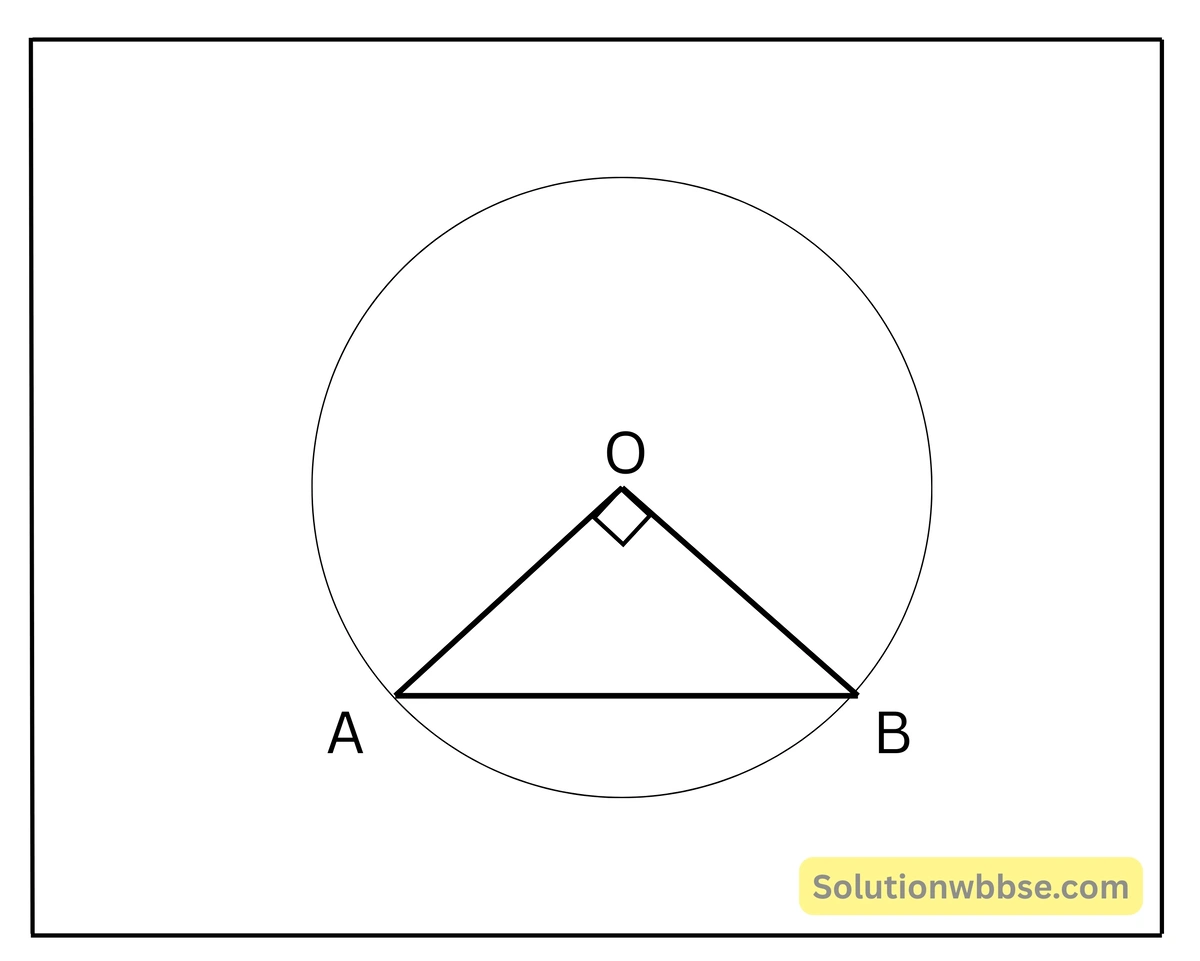
ধরা যাক, O কেন্দ্রীয় বৃত্তের AB জ্যা কেন্দ্রে সমকোণ উৎপন্ন করে। ∴ △AOB সমকোণী ত্রিভুজ।
এক্ষেত্রে, OA = OB = 10 সেমি.
এখন, △AOB সমকোণী ত্রিভুজ থেকে পাই,
\(AB^2 = OA^2+OB^2\)বা, \(AB^2 = (10)^2+(10)^2\)
বা, \(AB^2 = 100+100\)
বা, \(AB^2 = 200\)
বা, \(AB = \sqrt{200}\)
বা, \(AB = 10\sqrt{2}\)∴
AB জ্যা-এর দৈর্ঘ্য \(10\sqrt{2}\) সেমি.
(C) শুন্যস্থান পূরণ করি
(i) একটি সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুটি বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের _______ সমান।
উত্তর – সমষ্টির
(ii) একটি সমকোণী সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য \(4\sqrt{2}\) সেমি. হলে, অতিভুজের দৈর্ঘ্য _______ সেমি.।
উত্তর – 8 সেমি.
সমাধান – অতিভুজের দৈর্ঘ্য = \(\sqrt{(4\sqrt{2})^2 + (4\sqrt{2})^2} = \sqrt{32+32} = \sqrt{64} = 8\)
(iii) ABCD আয়তকার চিত্রের AC ও BD কর্ণদ্বয় পরস্পর O বিন্দুতে ছেদ করে। AB= 12 সেমি., AO = 6.5 সেমি. হলে, BC এর দৈর্ঘ্য ________ সেমি.।
উত্তর – 5 সেমি.
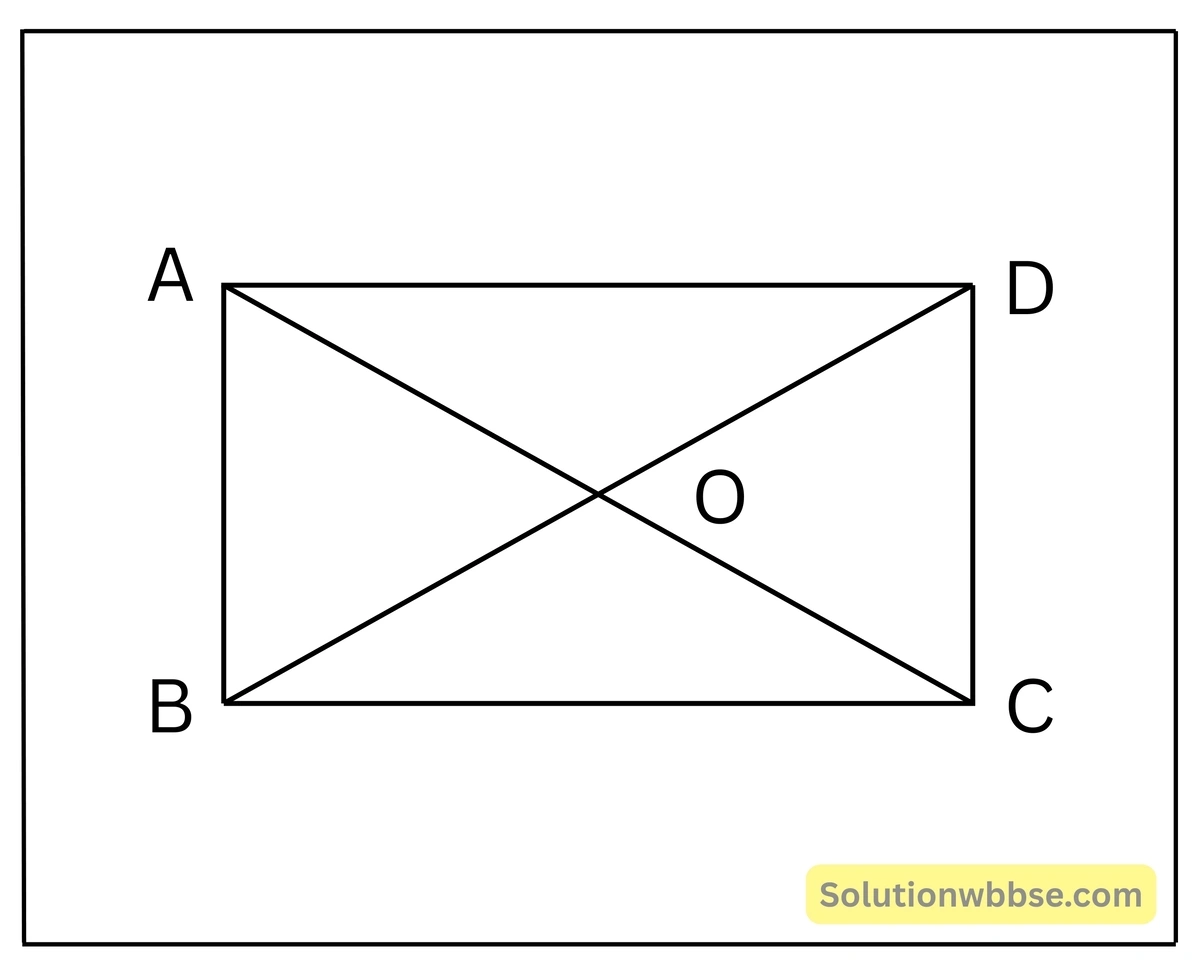
সমাধান –
যেহেতু, আয়তক্ষেত্রের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে, ∴ OA = OC= 6.5 সেমি.
∴ AC = (6.5×2)সেমি. = 13 সেমি.
এখন, △ABC সমকোণী ত্রিভুজের ক্ষেত্রে,
\(AC^2 = AB^2 + BC^2\)বা, \(BC^2 = AC^2 – AB^2\)
বা, \(BC^2 = (13)^2 – (12)^2\)
বা, \(BC^2 = 169-144\)
বা, \(BC^2 = 25\)
বা, \(BC^2 = (5)^2\)
বা, \(BC = 5\)
16. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
(i) \(\triangle ABC\) ত্রিভুজের \(AB=(2a-1)\) সেমি., \(AC= 2\sqrt{2a}\) সেমি. এবং \(BC=(2a+1)\) সেমি. হলে, \(\angle BAC\) এর মান হিসাব করে লিখি।
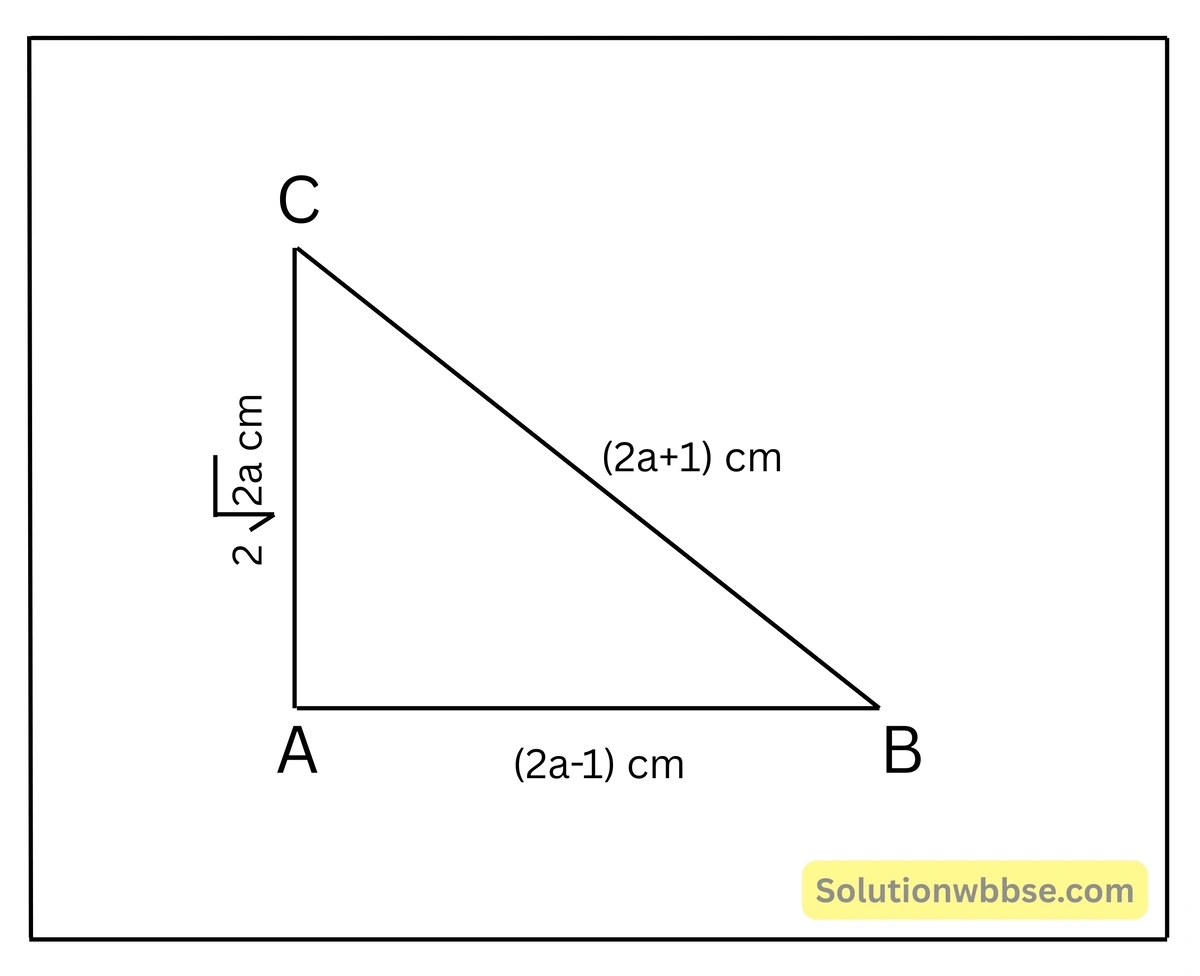
সমাধান –
\(AB^2+AC^2 = (2a-1)^2 + (2\sqrt{2a})^2 = 4a^2-4a+1+8a = 4a^2+4a+1=(2a+1)^2=BC^2\)∴ \(AB^2+AC^2 = BC^2\) [পিথাগোরাসের উপপাদ্য]
∴ \(\triangle ABC\) সমকোণী ত্রিভুজ যার \(\angle A\) সমকোণ।
∴ \(\angle A=90^\circ\)
(ii) পাশের চিত্রে \(△PQR\) ত্রিভুজের অভ্যন্তরে \(O\) বিন্দু এমনভাবে অবস্থিত যে, \(∠POQ=90°\), \(OP=6\) সেমি. এবং \(OQ=8\) সেমি.। যদি \(PR=24\)সেমি. এবং \(∠QPR=90°\) হয়, তাহলে \(QR\) বাহুর দৈর্ঘ্য কত তা লিখি।
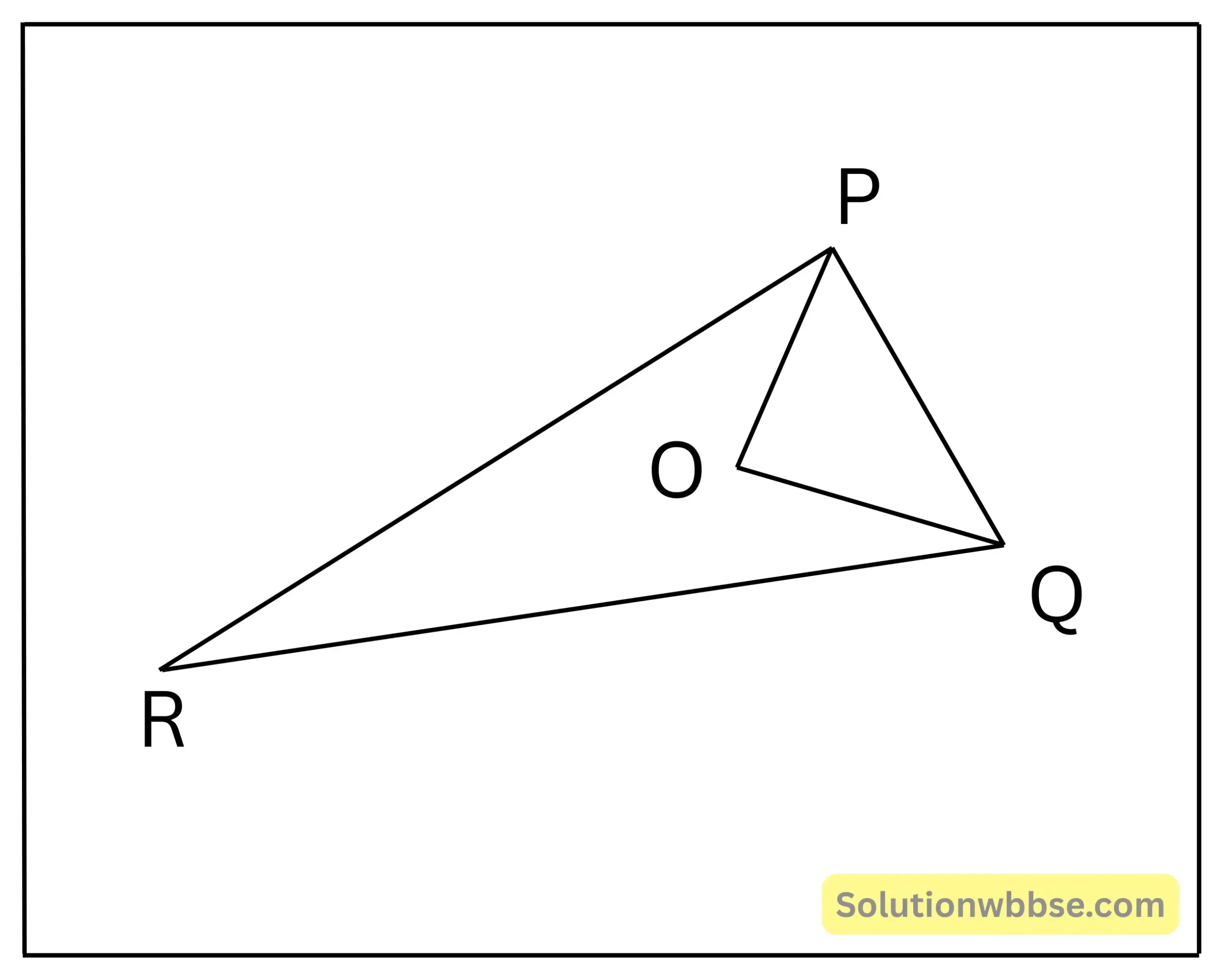
সমাধান –
\(△PQR\) ত্রিভুজে \(∠POQ=90°\), \(OP=6\) সেমি. এবং \(OQ=8\) সেমি.।
\(△PQR\) সমকোণী ত্রিভুজে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই,
\(PQ^2 = OP^2 + OQ^2\)বা, \(PQ^2 = (6)^2 + (8)^2\)
বা, \(PQ^2 = 36+64\)
বা, \(PQ^2 = 100\)
বা, \(PQ^2 = (10)^2\)
বা, \(PQ = 10\)
আবার \(△PQR\) সমকোণী ত্রিভুজ যার \(∠QPR=90°\)
\(∴\) \(PR^2+QP^2 = RQ^2\)
বা, \((24)^2+(10)^2 = QR^2\)
বা, \(576 + 100 = QR^2\)
বা, \(QR^2 = 676\)
বা, \(QR^2 = (26)^2\)
বা, \(QR = 26\)
\(∴\) \(QR\) বাহুর দৈর্ঘ্য \(26\) সেমি.।
(iii) \(ABCD\) আয়তকার চিত্রের অভ্যন্তরে \(O\) বিন্দু এমনভাবে অবস্থিত যে \(OB=6\) সেমি., \(OD=8\) সেমি. এবং \(OA=5\) সেমি.। \(OC\) এর দৈর্ঘ্য নির্ণয় কর।
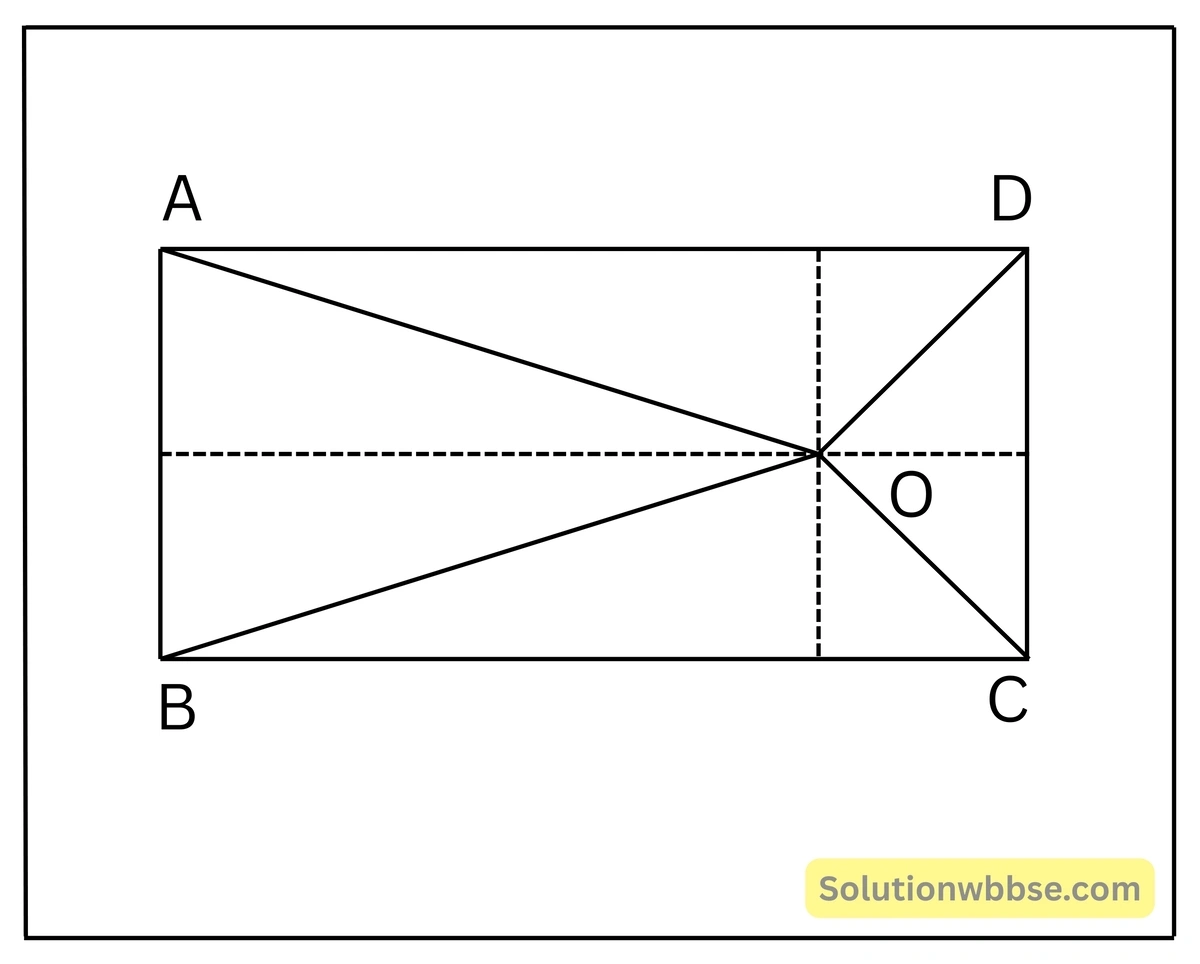
সমাধান –
\(ABCD\) আয়তকার চিত্রের অভ্যন্তরে \(O\) একটি বিন্দু হলে, \(OA^2+OC^2 = OB^2+OD^2\) হয়।
\(∴\) \(OA^2+OC^2 = OB^2+OD^2\)
বা, \((5)^2+OC^2 = (6)^2+(8)^2\)
বা, \(25+OC^2 = 36+64\)
বা, \(OC^2 = 100-25\)
বা, \(OC^2 = 75\)
বা, \(OC^2 = (5\sqrt{3})^2\)
বা, \(OC = 5\sqrt{3}\)
\(∴\) \(OC\) এর দৈর্ঘ্য \(5\sqrt{3}\) সেমি.।
(iv) \(\Delta ABC\) ত্রিভুজের \(A\) বিন্দু থেকে \(BC\) বাহুর উপর \(AD\) লম্ব \(BC\) বাহুর সঙ্গে \(D\) বিন্দুতে মিলিত হয়। যদি \(BD=8\) সেমি., \(DC=2\) সেমি. এবং \(AD=4\) সেমি. হয়, তাহলে \(\angle BAC\) এর পরিমাপ কত তা লিখি।
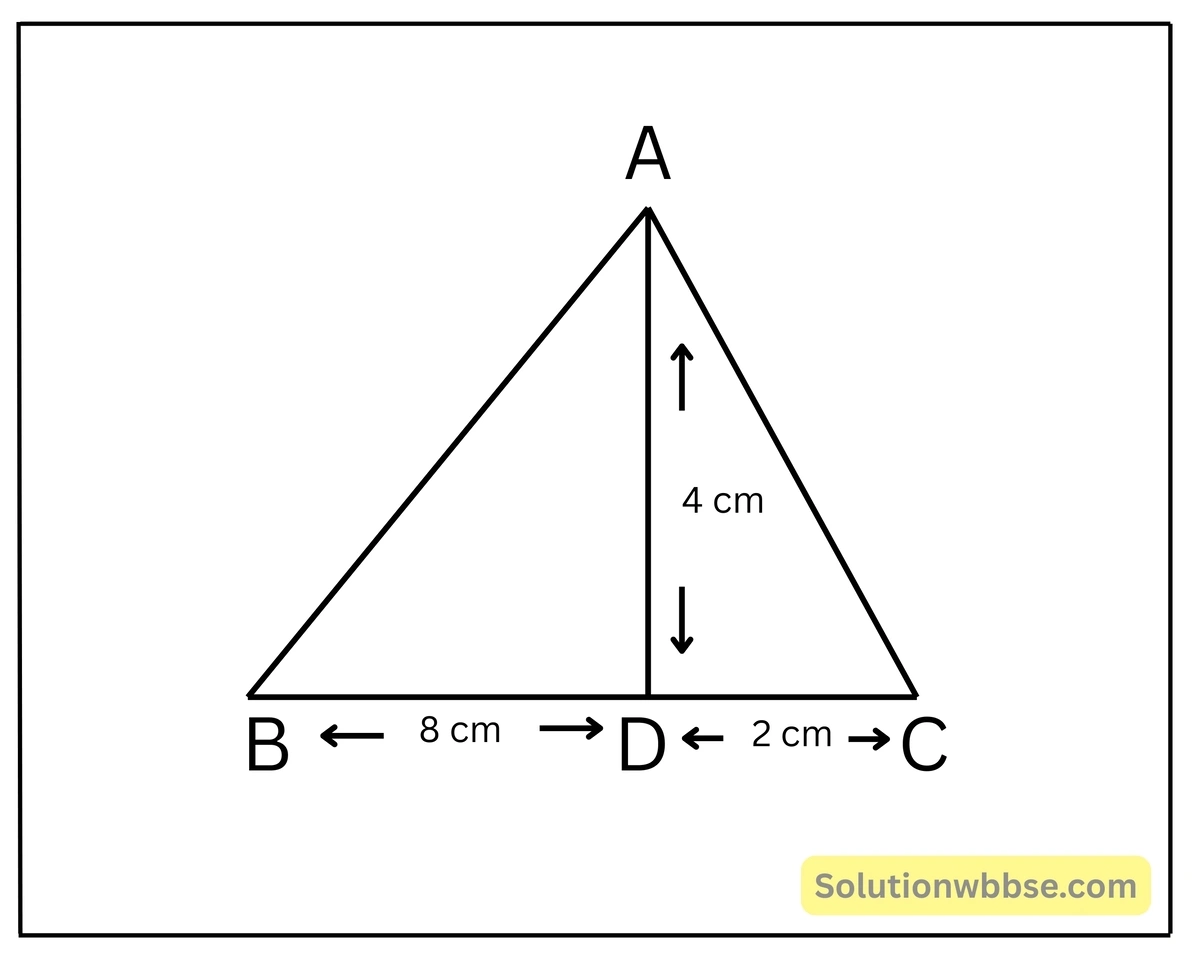
সমাধান –
\(\Delta ABC\) ত্রিভুজের \(A\) বিন্দু থেকে \(BC\) বাহুর উপর \(AD\) লম্ব যা \(BC\) বাহুর সঙ্গে \(D\) বিন্দুতে মিলিত হয়।
\(∴\) \(\Delta ABD\) এবং \(\Delta ACD\) উভয়ই সমকোণী ত্রিভুজ।
এখন, \(\Delta ABD\) সমকোণী ত্রিভুজ থেকে পাই,
\(AB^2 = AD^2+BD^2\)বা, \(AB^2 = (4)^2+(8)^2\)
বা, \(AB^2 = 16+64\)
বা, \(AB^2 = 80\)
আবার, \(\Delta ACD\) সমকোণী ত্রিভুজ থেকে পাই,
\(AC^2 = AD^2+CD^2\)বা, \(AC^2 = (4)^2+(2)^2\)
বা, \(AC^2 = 16+4\)
বা, \(AC^2 = 20\)
\(BC= BD+CD = 8+2 =10\) সেমি.
আবার, \(\Delta ABC\) ত্রিভুজের ক্ষেত্রে,
\(AB^2 +AC^2 = 80+20=100=(10)^2=BC^2\)\(∴\) \(AB^2+AC^2 = BC^2\)
\(∴\) \(\Delta ABC\) সমকোণী ত্রিভুজ
\(∴\) \(\angle BAC = 90°\)
(v) \(\Delta ABC\) সমকোণী ত্রিভুজের \(\angle ABC = 90^\circ\), \(AB = 3\) সেমি., \(BC=4\) সেমি. এবং \(B\) বিন্দু থেকে \(AC\) বাহুর উপর লম্ব \(BD\) যা \(AC\) বাহুর সঙ্গে \(D\) বিন্দুতে মিলিত হয়। \(BD\) এর দৈর্ঘ্য নির্ণয় কর।
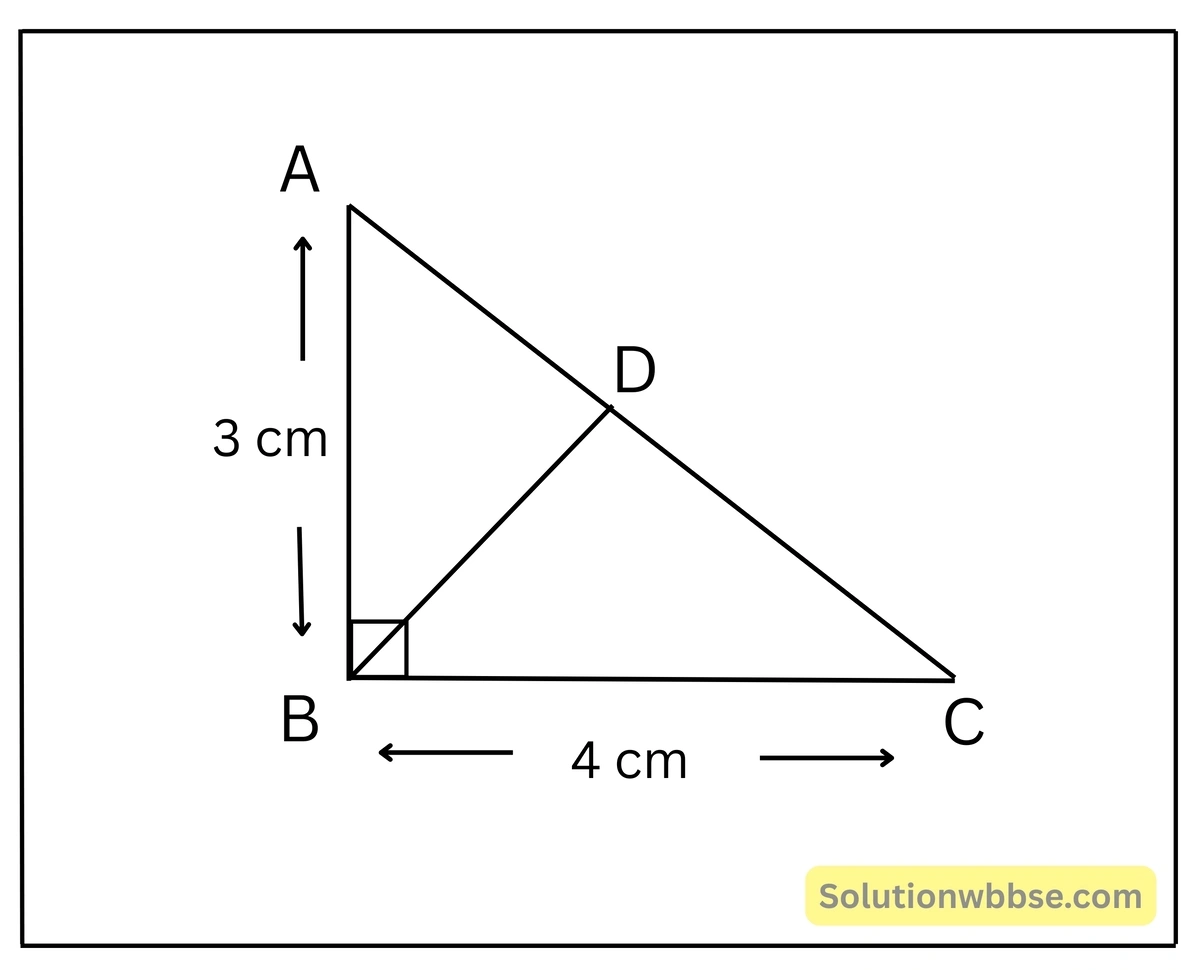
সমাধান –
\(\Delta ABC\) সমকোণী ত্রিভুজের ক্ষেত্রে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই,
\(AC^2 = AB^2+BC^2\)বা, \(AC^2 = (3)^2+(4)^2\)
বা, \(AC^2 = 9+16\)
বা, \(AC^2 = 25\)
বা, \(AC^2 = (5)^2\)
বা, \(AC = 5\)
এখন, \(\Delta ABC\) সমকোণী ত্রিভুজের \(BC\) ভূমি হলে \(AB\) উচ্চতা এবং \(AC\) ভূমি হলে \(BD\) উচ্চতা।
\(\therefore ABC\) ত্রিভুজের ক্ষেত্রফল = \(\frac{1}{2} \times 4 \times 3\) বর্গসেমি = \(\frac{1}{2} \times 5 \times BD\) বর্গসেমি
\(\therefore \frac{1}{2} \times 4 \times 3 = \frac{1}{2} \times 5 \times BD\)বা, \(6 = \frac{5BD}{2}\)
বা, \(BD = \frac{12}{5}\)
বা, \(BD = 2.4\)
\(\therefore BD\) এর দৈর্ঘ্য \(2.4\) সেমি.।
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের দ্বাবিংশ অধ্যায়, ‘পিথাগোরাসের উপপাদ্য’ -এর ‘কষে দেখি – 22’ বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment