এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের দ্বাবিংশ অধ্যায়, ‘পিথাগোরাসের উপপাদ্য’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

প্রয়োগ 1. m ও n -এর বিভিন্ন উপযুক্ত মান ধরে 2টি সমকোণী ত্রিভুজের বাহুগুলির দৈর্ঘ্যগুলি লিখি। [নিজে করি]
মনেকরি, m = 3, n = 2
∴ m² + n² = 3² + 2² = 9 + 4 = 13
2mn = 2 × 3 ×2 = 12
m² – n² = 3² – 2² = 9 – 4 = 5
∴ বাহুগুলির দৈর্ঘ্য যথাক্রমে 13, 12, 5
আবার মনেকরি m = 4, n = 3
∴ m² + n² = 4² + 3² = 16 + 9 = 25
2mn = 2 × 4 × 3 = 24
m² – n² = 4² – 3² = 16 – 9 = 7
∴ বাহুগুলির দৈর্ঘ্য যথাক্রমে 25, 24, 7
প্রয়োগ 2. আমাদের বাগানে একটি 25 মিটার লম্বা মই পাঁচিলে হেলান দিয়ে এমনভাবে রাখা আছে যে মইটি ভূমি থেকে 24 মিটার উঁচুতে পাঁচিল স্পর্শ করে আছে। মই-এর পাদদেশটি পাঁচিল থেকে কত দূরে আছে হিসাব করে লিখি।
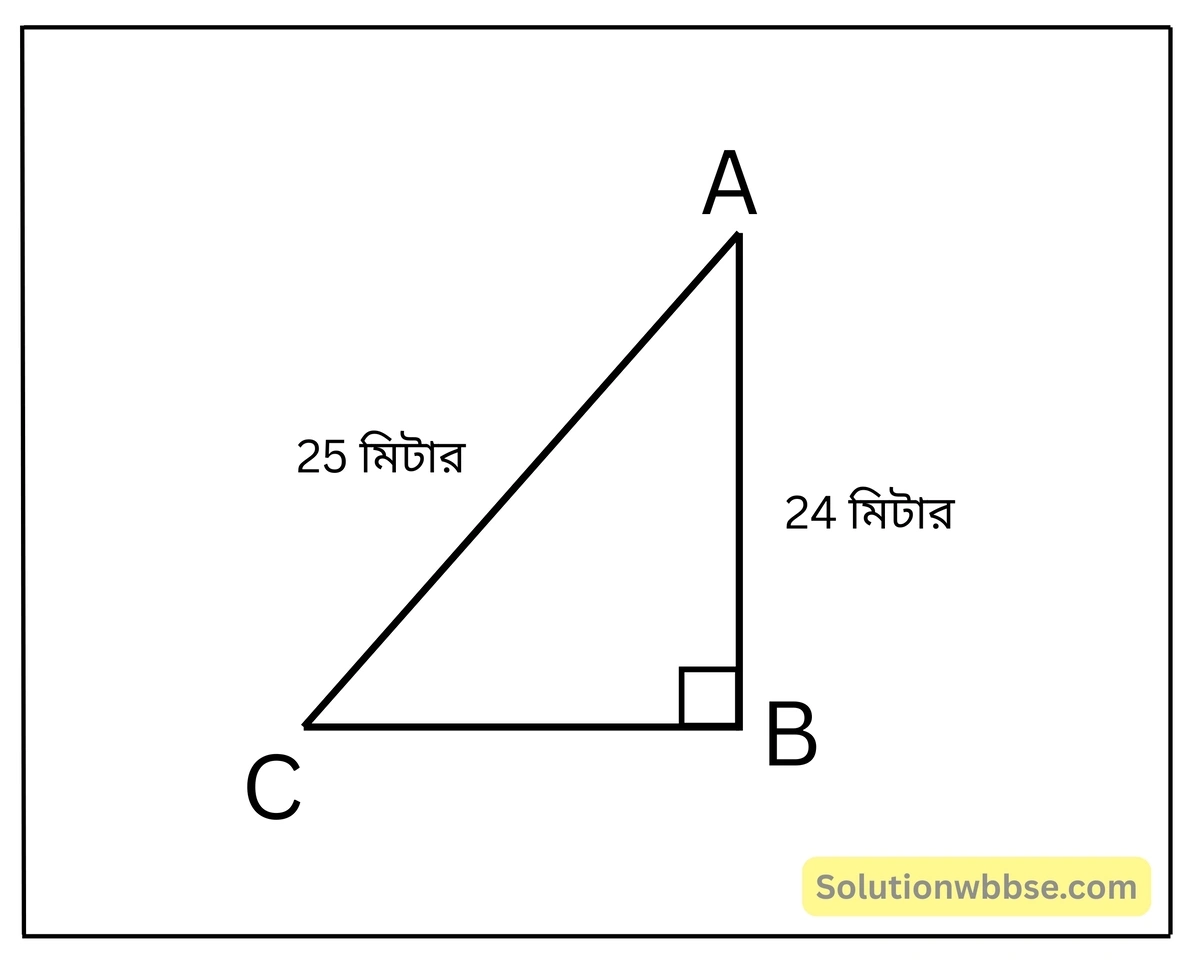
ধরি, AC মই-এর দৈর্ঘ্য = 25 মিটার, AB = 24 মিটার;
ABC সমকোণী ত্রিভুজে পিথাগোরাসের সূত্র থেকে পাই, AB² + BC² = AC²
বা, (24 মিটার)² + (BC)² = (25 মিটার)²
বা, BC² = (25 মিটার)² – (24 মিটার)²
∴ BC = 7 মিটার
∴ মই-এর পাদদেশটি পাঁচিল থেকে 7 মিটার দূরে আছে।
প্রয়োগ 3. কোনো রম্বসের কর্ণদ্বয়ের দৈর্ঘ্য যথাক্রমে 12 সেমি ও 16 সেমি হলে, রম্বসের একটি বাহুর দৈর্ঘ্য হিসাব করে লিখি। [নিজে করি]
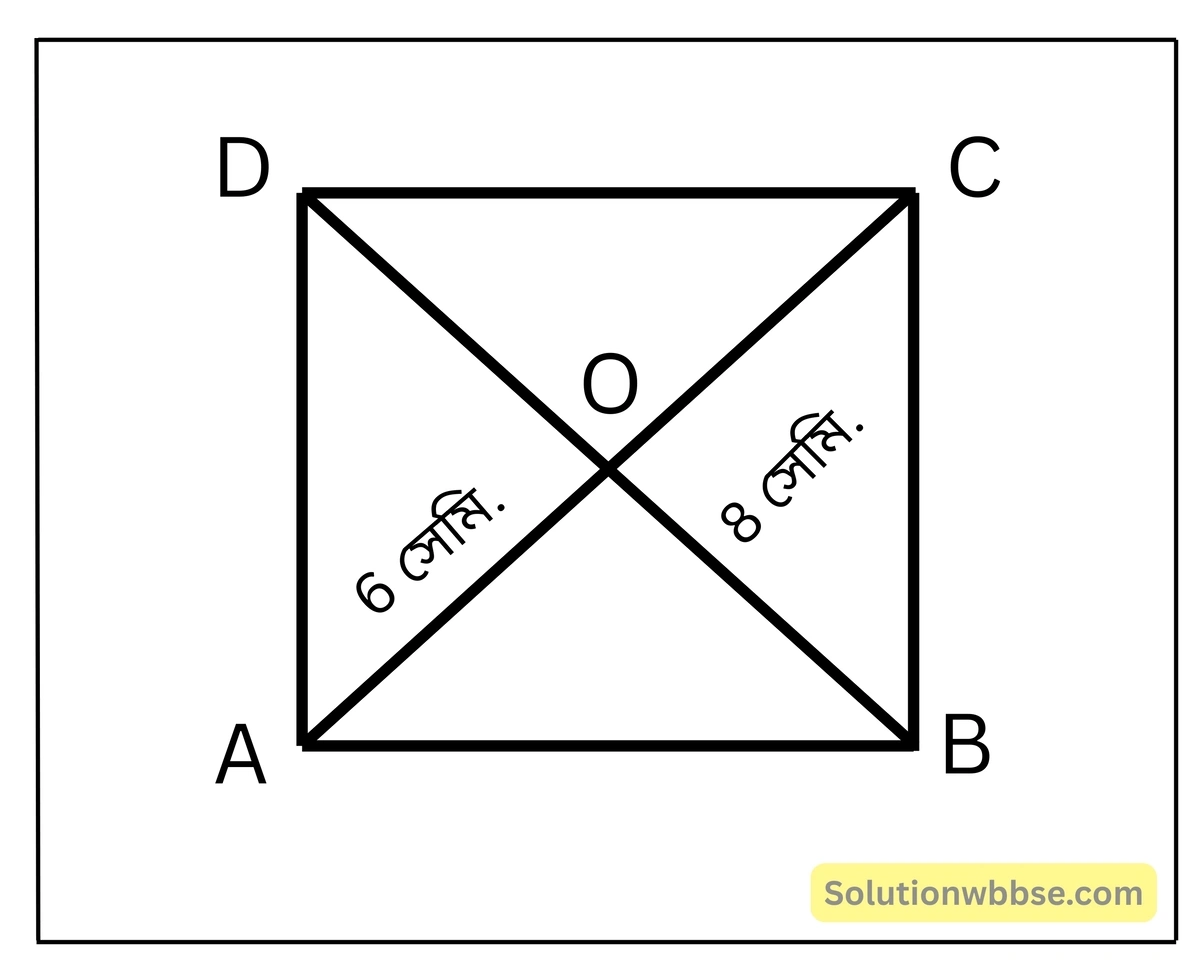
উত্তর সংকেত –
রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।
∴ OA = \(\frac{12}{2} \) সেমি. = 6 সেমি, OB = 8 সেমি
AOB সমকোণী ত্রিভুজ।
∴ পিথাগোরাসের সূত্র থেকে পাই, AB² = OA² + OB
ধরি, BD = 16 cm. AC = 12 cm.
∴ আমরা জানি, রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।
∴ BO = OD = 8 সেমি ∴ AO = OC = 6 সেমি
∴ ∠BOC = ∠COD = ∠DOA = ∠AOB = 90°.
∴ △BOC একটি সমকোণী ত্রিভুজ।
∴ BC = \(\sqrt{BO^2 + OC^2} = \sqrt{8^2+6^2} = \sqrt{64+36}$\) সেমি
= \(\sqrt{100}\) সেমি = 10 সেমি (Ans.)
প্রয়োগ 4. একটি সমদ্বিবাহু ত্রিভুজ ABC অঙ্কন করেছি যার \(\angle B\) সমকোণ। \(\angle BAC\)-এর সমদ্বিখণ্ডক অঙ্কন করেছি যা BC বাহুকে D বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, \(CD^2 = 2BD^2\)
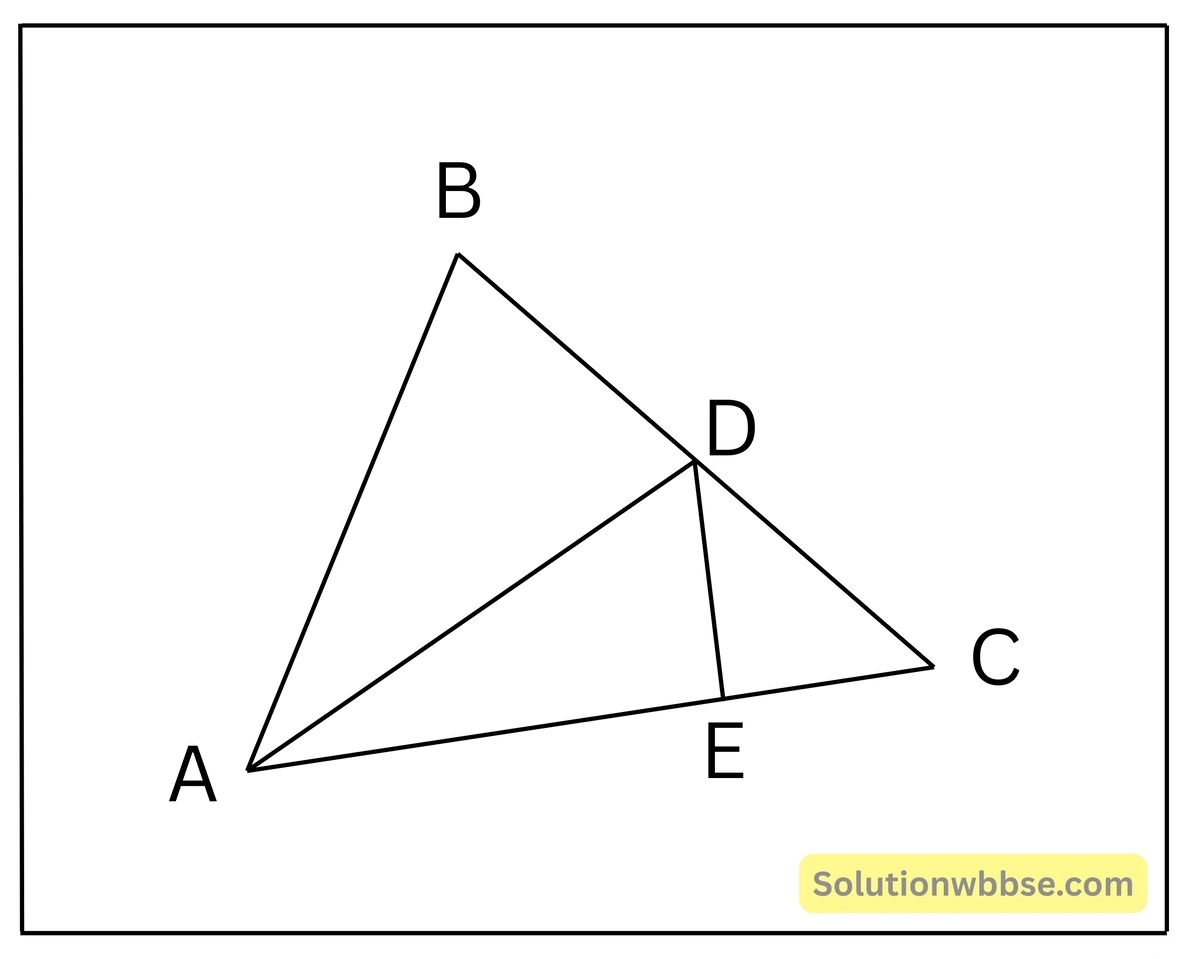
প্রদত্ত – ABC সমদ্বিবাহু ত্রিভুজের \(\angle B = 1\) সমকোণ। \(\angle BAC\)-এর সমদ্বিখণ্ডক AD, BC বাহুকে D বিন্দুতে ছেদ করে।
প্রমাণ করতে হবে – \(CD^2 = 2BD^2\)
অঙ্কন – D বিন্দু থেকে AC-এর উপর DE লম্ব অঙ্কন করলাম যা AC বাহুকে E বিন্দুতে ছেদ করল।
প্রমাণ – ABC সমকোণী সমদ্বিবাহু ত্রিভুজ। ∴ \(\angle ACB = 45^\circ\)
∴ DEC সমকোণী ত্রিভুজে, \(\angle DCE = 45^\circ\) (∵ \(\angle ACB = 45^\circ\));
আবার, ∴ \(\angle DEC = 90^\circ\), সুতরাং, \(\angle EDC = 45^\circ\);
∴ \(\triangle DEC\)-তে, DE = EC
\(\triangle ABD\) ও \(\triangle AED\)-এর মধ্যে, \(\angle BAD = \angle EAD\) [∵ AD, \(\angle BAE\)-এর সমদ্বিখণ্ডক]
\(\angle ABD = \angle AED\) (প্রত্যেকে 1 সমকোণ) এবং AD উহাদের সাধারণ বাহু।
∴ \(\triangle ABD \cong \triangle AED\) (A-A-S সর্বসমতার শর্তানুসারে)
সুতরাং, BD = DE (সর্বসম ত্রিভুজের অনুরূপ বাহু)
DEC সমকোণী ত্রিভুজে, \(DC^2 = DE^2 + CE^2 = 2DE^2\) (∵ CE = DE)
= \(2BD^2\) (∵ DE = BD) [প্রমাণিত]
প্রয়োগ 5. ত্রিভুজ ABCD এর AD লম্ব BC হলে প্রমাণ করি যে, \(AB^2+CD^2=AC^2+BD^2\)
ABC ত্রিভুজের AD লম্ব BC
∴ ABD এবং ADC প্রত্যেকেই সমকোণী ত্রিভুজ। এখন সমকোণী ত্রিভুজ ABD থেকে পাই,
বা, \(AB^2-BD^2=AD^2\) —(i)
আবার, সমকোণী ত্রিভুজ ADC থেকে পাই,
\(AD^2+CD^2=AC^2\)বা, \(AD^2 = AC^2-CD^2\)—(ii)
সুতরাং, (i) ও (ii) থেকে পাই,
\(AB^2 -BD^2 = AC^2 -CD^2\)বা, \(AB^2+CD^2=AC^2+BD^2\) [প্রমাণিত]
প্রয়োগ 6. \(\triangle ABC\)-এর \(\angle A\) সমকোণ এবং BP ও CQ দুটি মধ্যমা হলে, প্রমাণ করি যে, \(5BC^2 = 4(BP^2 + CQ^2)\)
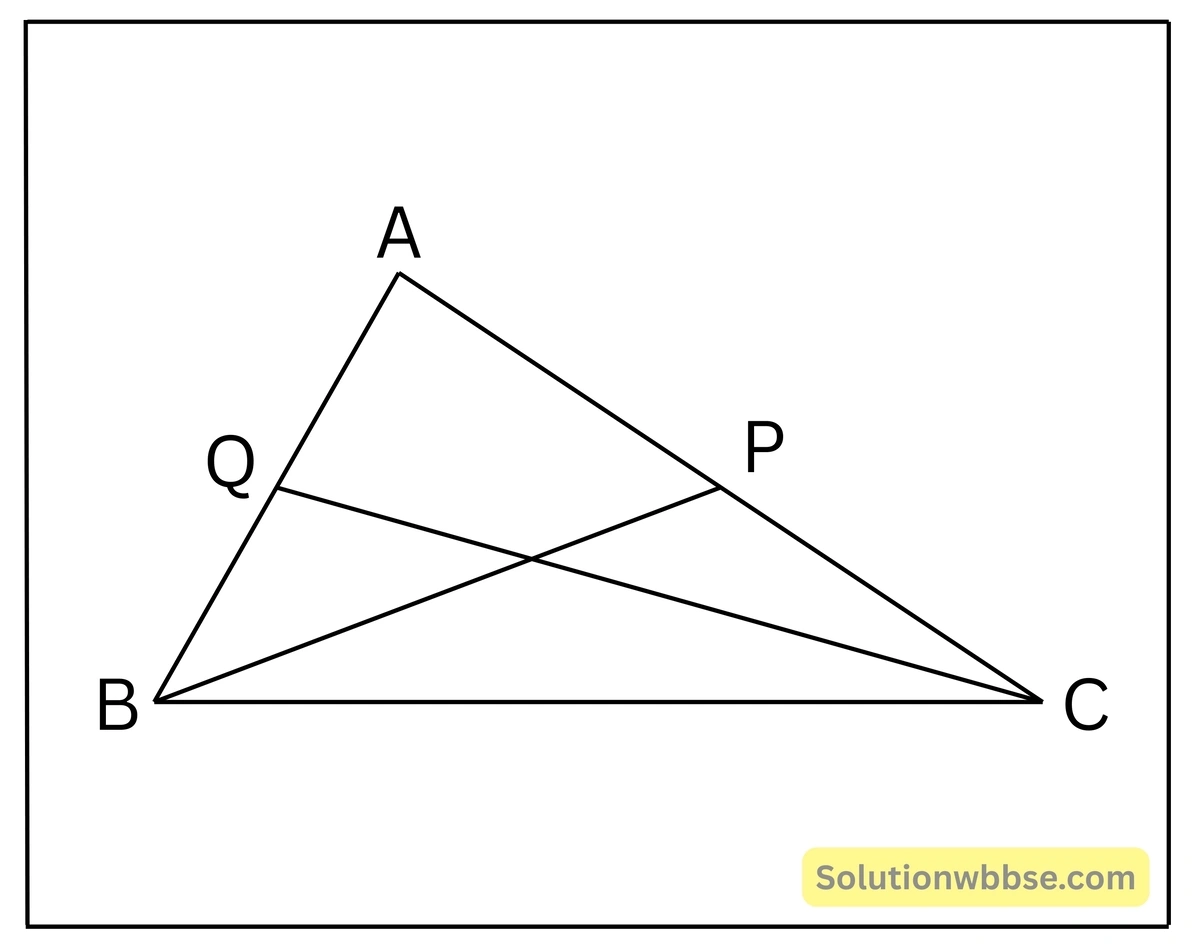
প্রদত্ত – \(\triangle ABC\)-এর \(\angle BAC = 1\) সমকোণ। BP ও CQ ত্রিভুজটির দুটি মধ্যমা।
প্রমাণ করতে হবে – \(5BC^2 = 4(BP^2 + CQ^2)\)
প্রমাণ – \(\triangle ABC\)-এর \(\angle A\) সমকোণ।
∴ \(BC^2 = AB^2 + AC^2\)
= \((2AQ)^2 + (2AP)^2\) [∵ P ও Q যথাক্রমে AC ও AB বাহুদ্বয়ের মধ্যবিন্দু]
∴ \(BC^2 = 4(AQ^2 + AP^2)\) …………… (i)
আবার, \(\triangle BAP\) ও \(\triangle CAQ\) সমকোণী ত্রিভুজ।
∴ \(BP^2 = AB^2 + AP^2 \)
= \((2AQ)^2 + AP^2 \)
= \(4AQ^2 + AP^2\)
\(CQ^2 = AC^2 + AQ^2 = (2AP)^2 + AQ^2 = 4AP^2 + AQ^2\)∴ \(BP^2 + CQ^2 = 4AQ^2 + AP^2 + 4AP^2 + AQ^2 \)
= \(5AQ^2 + 5AP^2 \)
= \(5(AQ^2 + AP^2)\) ……(ii)
\(5BC^2 = 5 \cdot 4 (AQ^2 + AP^2)\) [(i) হইতে পাই]
= \(4 \cdot 5 (AQ^2 + AP^2) = 4 (BP^2 + CQ^2)\) [(ii) হইতে পাই] [প্রমাণিত]
প্রয়োগ 7. ΔABC-এর শীর্ষবিন্দু A থেকে BC বাহুর উপর AD লম্ব অঙ্কন করেছি যা BC বাহুকে D বিন্দুতে ছেদ করেছে এবং AD² = BD.CD হলে, প্রমাণ করি যে, ABC একটি সমকোণী ত্রিভুজ এবং ∠A = 90°
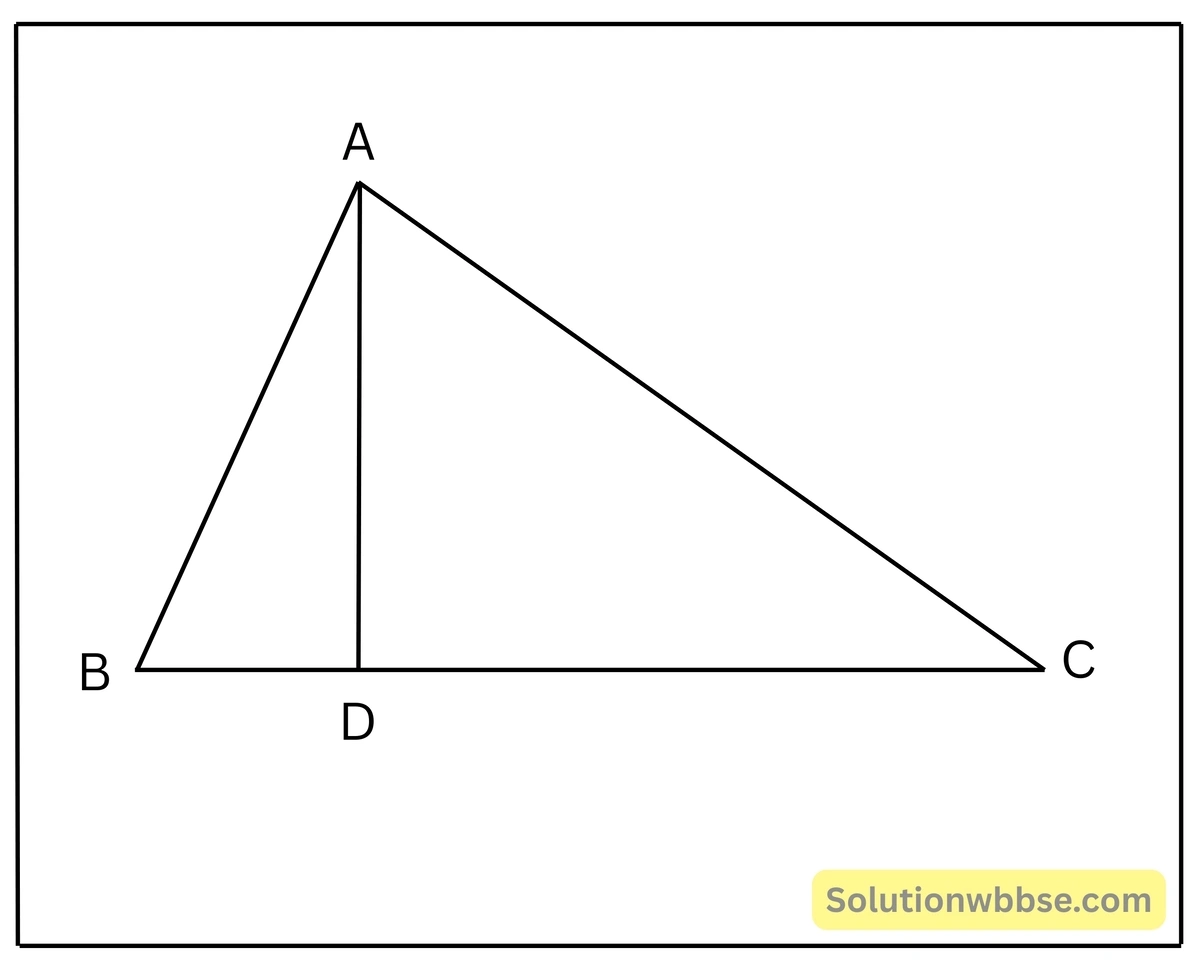
প্রদত্ত – ΔABC-এর AD ⊥ BC এবং AD² = BD.DC
প্রমাণ করতে হবে – ∠BAC = 90°
প্রমাণ – ADB একটি সমকোণী ত্রিভুজ যার ∠ADB = 90° ∴ AB² = AD² + BD² ………. (i) [পিথাগোরাসের উপপাদ্য থেকে পাই]
আবার, ADC সমকোণী ত্রিভুজের ∠ADC = 90° ∴ AC² = AD² + CD² ………. (ii) [পিথাগোরাসের উপপাদ্য থেকে পাই]
(i) ও (ii) যোগ করে পাই,
AB² + AC² = BD² + CD² + 2AD²
= BD² + CD² + 2BD.CD [∵ AD² = BD.CD]
= (BD + CD)² = BC²
∴ AB² + AC² = BC²
∴ পিথাগোরাসের বিপরীত উপপাদ্য থেকে পাই ABC একটি সমকোণী ত্রিভুজ যার ∠BAC = 90° [প্রমাণিত]
প্রয়োগ 8 – প্রমাণ করি যেকোনো বর্গক্ষেত্রের কর্ণের ওপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল ওই বর্গক্ষেত্রের ক্ষেত্রফলের দ্বিগুণ।
সমাধান –
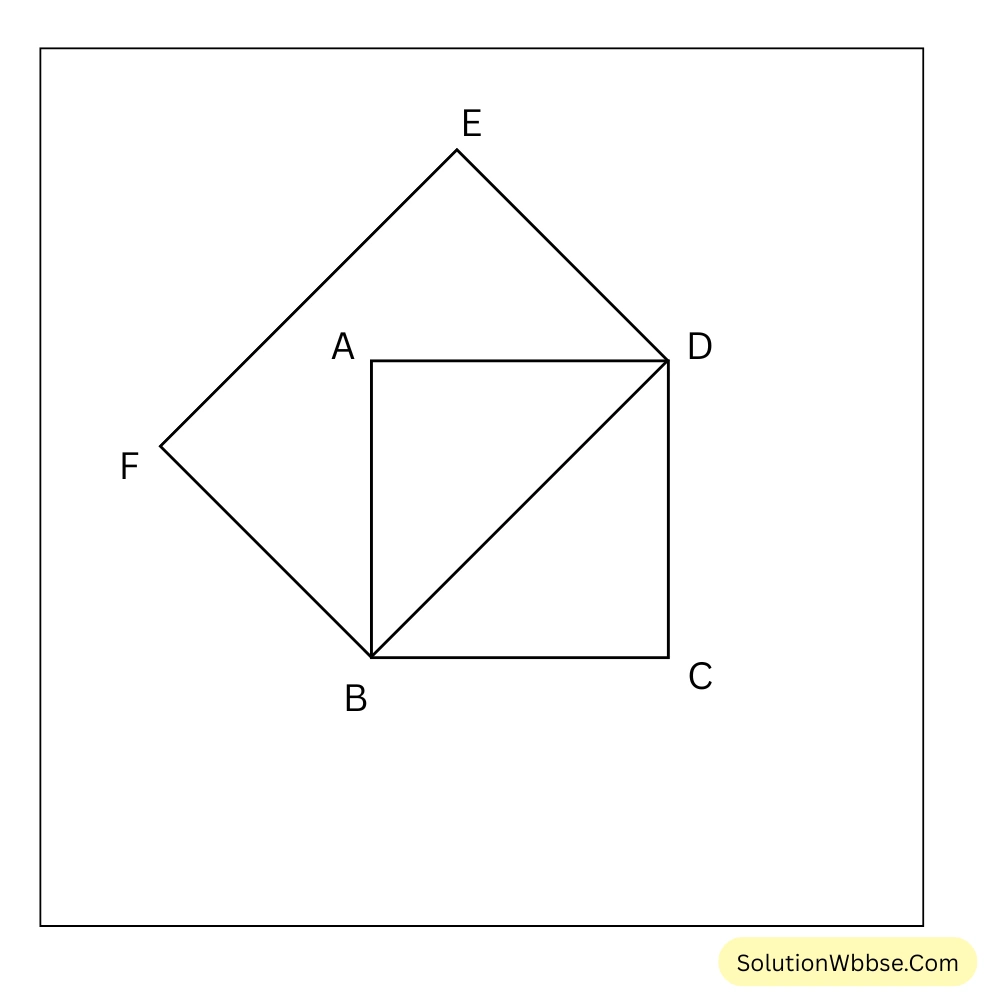
ধরি, ABCD একটি বর্গক্ষেত্র এবং ABCD বর্গক্ষেত্রের BD কর্ণের ওপর অঙ্কিত বর্গক্ষেত্রটি হল BDEF। প্রমাণ করতে হবে BDEF বর্গক্ষেত্রের ক্ষেত্রফল = 2 × ABCD বর্গক্ষেত্রের ক্ষেত্রফল
প্রমাণ – ABCD বর্গক্ষেত্রের BCD সমকোণী ত্রিভুজ
∴ BC²+CD²= BD² [পিথাগোরাসের উপপাদ্য]
বা , BC² +BC² = BD² [∵ BC =CD]
বা, 2BC² = BD²
∴ 2 × ABCD বর্গক্ষেত্রের ক্ষেত্রফল = BDEF বর্গক্ষেত্রের ক্ষেত্রফল।
প্রয়োগ 9. ABCD একটি আয়তাকার চিত্র অঙ্কন করেছি। O আয়তাকার চিত্রের অভ্যন্তরে যে-কোনো একটি বিন্দু হলে, প্রমাণ করি যে, OA² + OC² = OB² + OD²
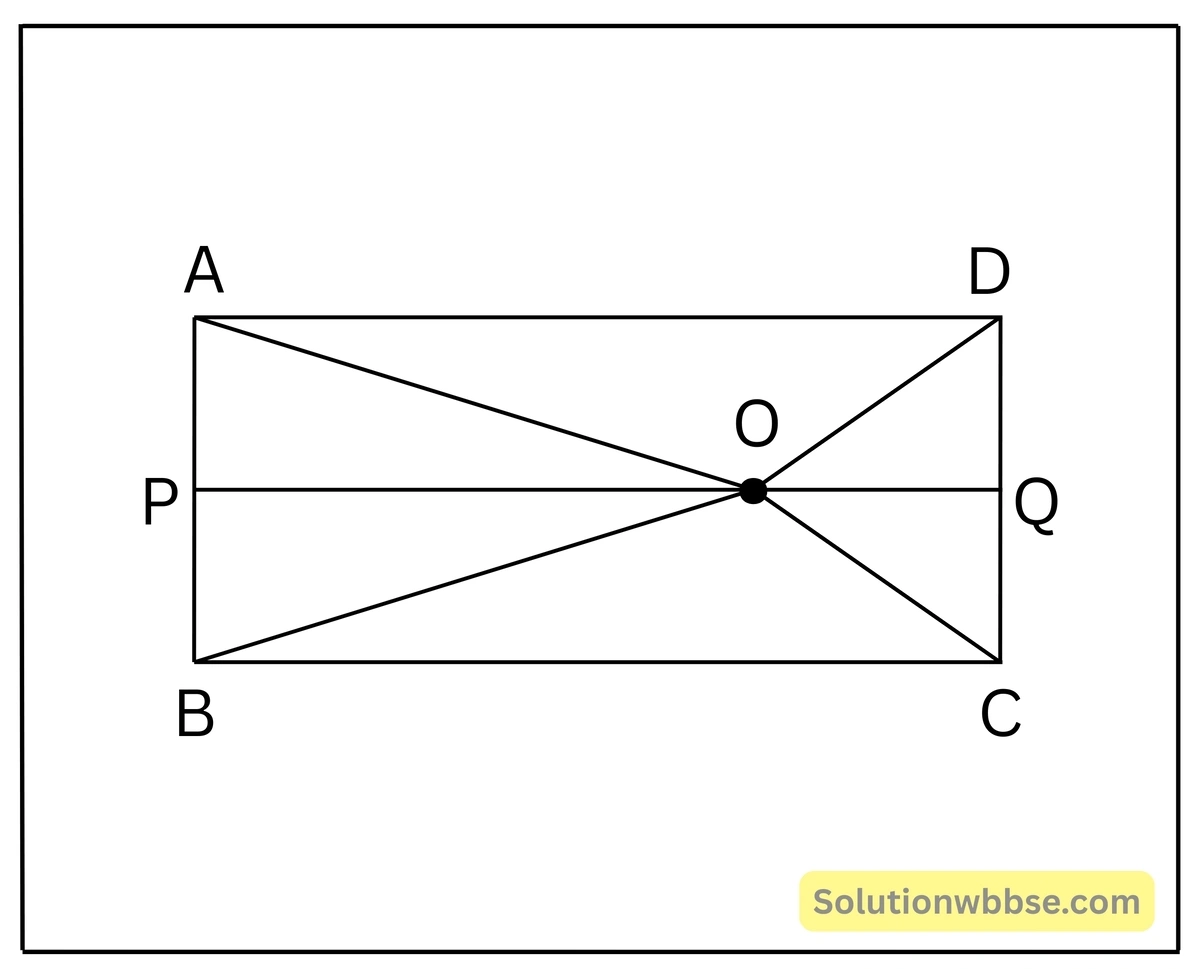
প্রদত্ত – ABCD আয়তাকার চিত্রের অভ্যন্তরে O যে-কোনো একটি বিন্দু।
প্রমাণ করতে হবে – OA² + OC² = OB² + OD²
অঙ্কন – O বিন্দু দিয়ে BC-এর সমান্তরাল সরলরেখা অঙ্কন করলাম যা AB ও DC বাহুদ্বয়কে যথাক্রমে P ও Q বিন্দুতে ছেদ করল।
প্রমাণ – অঙ্কনানুসারে PQ || BC
∴ PQ ⊥ AB এবং PQ ⊥ DC (∵ ∠B = 90° এবং ∠C = 90°)
∴ ΔAPO, ΔBPO, ΔCQO এবং ΔDQO প্রত্যেকে সমকোণী ত্রিভুজ।
∴ OA² = AP² + OP² OB²
= BP² + OP² OC²
= CQ² + OQ² OD²
= DQ² + OQ²
∴ OA² + OC² = AP² + OP² + CQ² + OQ² ………….. (i)
কিন্তু অঙ্কন অনুসারে, APQD ও BPQC এরা প্রত্যেকে আয়তাকার চিত্র। সুতরাং, AP = DQ এবং CQ = BP
(i) থেকে পাই,
OA² + OC² = DQ² + OP² + BP² + OQ²
= (DQ² + OQ²) + (BP² + OP²)
= OD² + OB²
= OB² + OD² [প্রমাণিত]
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের দ্বাবিংশ অধ্যায়, ‘পিথাগোরাসের উপপাদ্য’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন