এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের ষট্বিংশ অধ্যায়, ‘রাশিবিজ্ঞান: গড়, মধ্যমা, ওজাইভ, সংখ্যাগুরুমান’ -এর ‘কষে দেখি – 26.3’ বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

1. আমাদের গ্রামের 100 টি দোকানের দৈনিক লাভের (টাকায়) পরিমাণের ছকটি হলো,
| প্রতি দোকানের লাভ (টাকায়) | 0-50 | 50-100 | 100-150 | 150-200 | 200-250 | 250-300 |
| দোকানের সংখ্যা | 10 | 16 | 28 | 22 | 18 | 6 |
প্রদত্ত তথ্যের ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক) তালিকা তৈরি করে ছক কাগজে ওজাইভ (ogive) অঙ্কন করি।
সমাধান –
প্রথমে ক্ষুদ্রতর সূচক ক্রমযৌগিক পরিসংখ্যার ছক তৈরি করা যাক,
| শ্রেণী (ঊর্ধ্ব সীমানা) | ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক) |
| 50 | 10 |
| 100 | 26 |
| 150 | 54 |
| 200 | 76 |
| 250 | 94 |
| 300 | 100 |
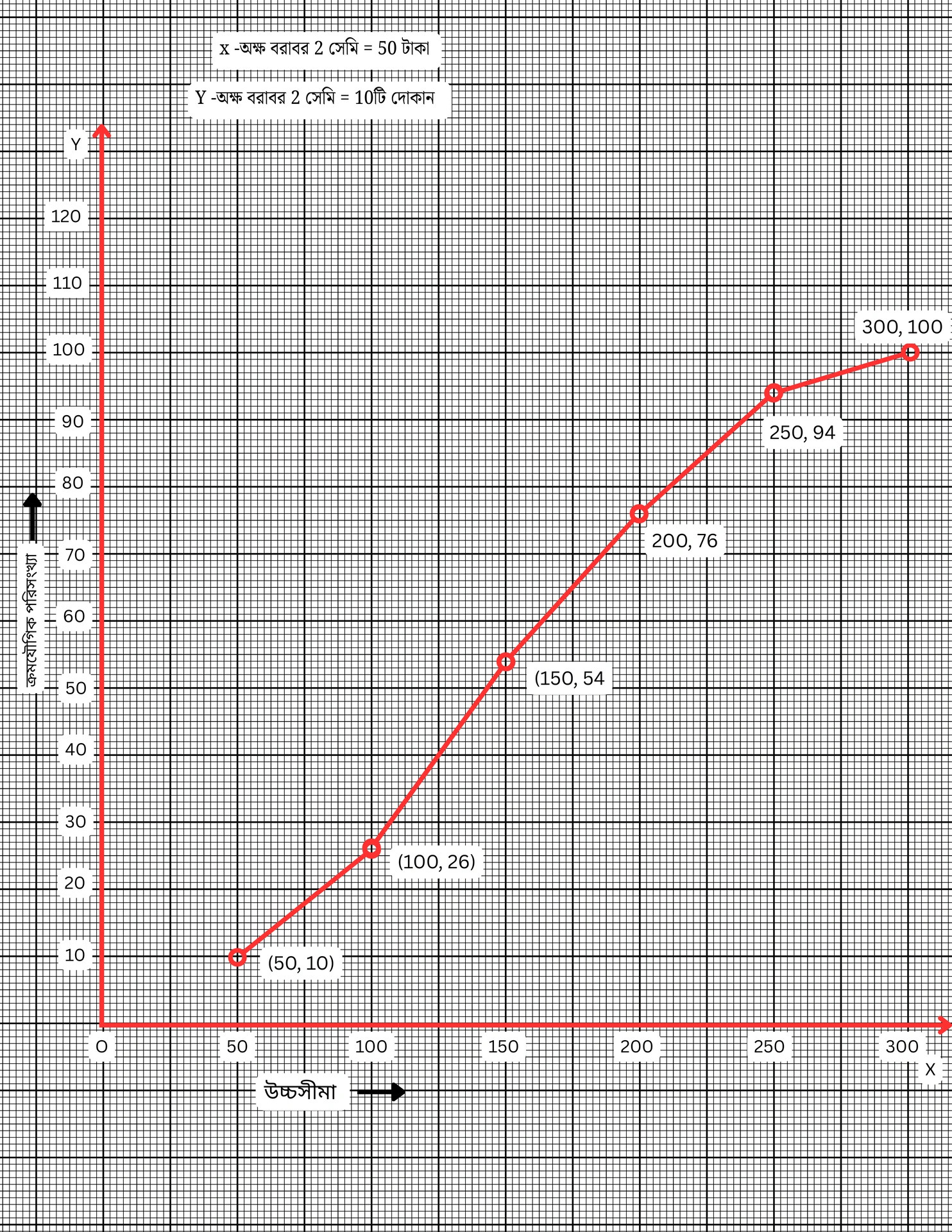
∴ বিন্দুগুলি হলো (50, 10), (100, 26), (150, 54), (200, 76), (250, 94), (300, 100)।
এখন x-অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 1 টি বাহুর দৈর্ঘ্য = 2.5 একক এবং y-অক্ষ বরাবর 1 টি বাহুর দৈর্ঘ্য = 0.5 একক ধরে উপরের বিন্দুগুলি স্থাপন করা হলো এবং বিন্দুগুলি যুক্ত করে ক্ষুদ্রতর সূচক ওজাইভ (ogive) অঙ্কন করা হলো।
2. নিবেদিতার ক্লাসের 35 জন শিক্ষার্থীর ওজনের তথ্য হলো,
| ওজন (কিলোগ্রাম) | 38-এর কম | 40-এর কম | 42-এর কম | 44-এর কম | 46-এর কম | 48-এর কম | 50-এর কম | 52-এর কম |
| শিক্ষার্থীর সংখ্যা | 0 | 4 | 6 | 9 | 12 | 28 | 32 | 35 |
প্রদত্ত তথ্যের ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক) তালিকা তৈরি করে ছক কাগজে ওজাইভ অঙ্কন করি এবং লেখচিত্র থেকে মধ্যমা নির্ণয় করি। সূত্রের সাহায্যে মধ্যমা নির্ণয় করে যাচাই করি।
সমাধান –
প্রদত্ত তথ্য থেকে লেখচিত্র অঙ্কনের জন্য যে বিন্দুগুলো পাওয়া যায়, সেগুলি হলো –
(38, 0), (40, 4), (42, 6), (44, 9), (46, 12), (48, 28), (50, 32), (52, 35)
X -অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহুর দৈর্ঘ্য = 1 একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহুর দৈর্ঘ্য = 0.5 একক ধরে বিন্দুগুলো স্থাপন করা হলো ও বিন্দুগুলো যুক্ত করে ওজাইভ পাওয়া গেল।
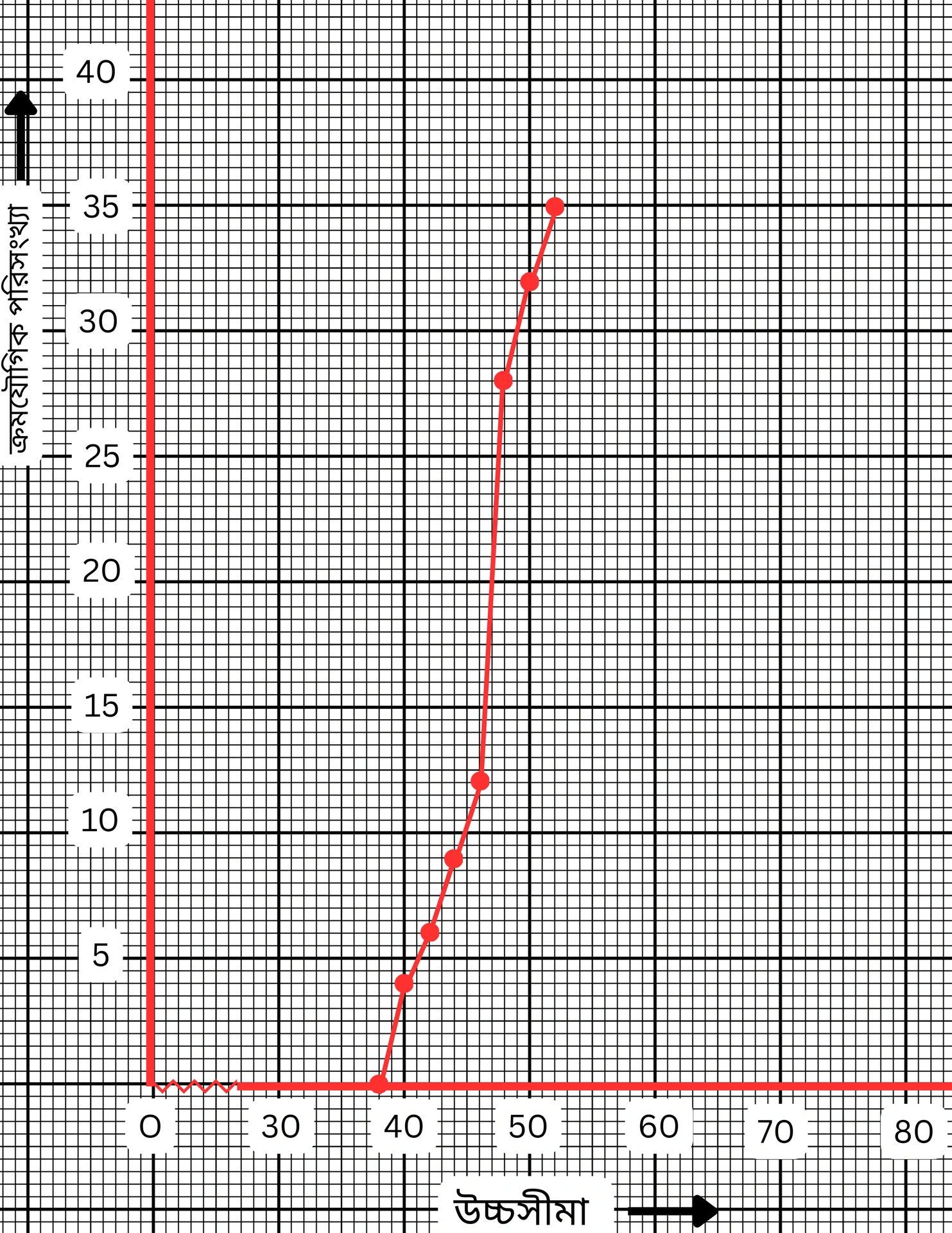
এক্ষেত্রে মোট শিক্ষার্থীর সংখ্যা (n) = 35 জন
∴ \(\frac{n}{2} = \frac{35}{2} = 17.5\)
(0, 17.5) বিন্দু দিয়ে x অক্ষের সমান্তরাল সরলরেখা ওজাইভকে P বিন্দুতে ছেদ করল। P বিন্দু দিয়ে x অক্ষের ওপর লম্ব টানা হল যা x অক্ষ কে M বিন্দুতে ছেদ করে। M বিন্দুর স্থানাঙ্ক (46.69, 0)
∴ মধ্যমা = 46.69 ( প্রায় )
সূত্রের সাহায্যে মধ্যমা নির্ণয় –
প্রদত্ত তথ্য থেকে পরিসংখ্যা বিভাজন তালিকা তৈরি করি,
| শ্রেণি – সীমানা | পরিসংখ্যা | ক্রমযৌগিক পরিসংখ্যা ( ক্ষুদ্রতর সূচক ) |
| 0-38 | 0 | 0 |
| 38-40 | 4 | 4 |
| 40-42 | 2 | 6 |
| 42-44 | 3 | 9 |
| 44-46 | 3 | 12 |
| 46-48 | 16 | 28 |
| 48-50 | 4 | 32 |
| 50-52 | 3 | 35 = n |
17.5 এর ঠিক বেশি ক্রমযৌগিক পরিসংখ্যা 46-48 এই শ্রেণীর মধ্যে আছে।
সুতরাং মধ্যমা শ্রেণীটি হলো (46-48)
মধ্যমা নির্ণয়ের সূত্রটি হলো
l = মধ্যমা শ্রেণীর নিম্ন শ্রেণী সীমানা।
n = মোট পরিসংখ্যা।
f = মধ্যমা শ্রেণীর পরিসংখ্যা।
h = শ্রেণী দৈর্ঘ্য।
cf = মধ্যমা শ্রেণীর পূর্বের শ্রেণীর ক্রমযৌগিক পরিসংখ্যা।
∴ নির্ণেয় মধ্যমা = \( l + \left[\frac{\frac{n}{2}-cf}{f}\right] \times h\)
= \( 46 + \left[\frac{17.5-12}{16}\right] \times 2\)
[এক্ষেত্রে, l=46, n=35, cf=12, f=16, h=2]
= \( 46 + \frac{5.5}{16} \times 2\)
= \( 46 + \frac{11}{16}\)
= \(46+0.69\)
= \( 46.69\) [প্রায়]
অর্থাৎ ওজাইভ থেকে প্রাপ্ত মধ্যমা এবং সূত্রের সাহায্যে প্রাপ্ত মধ্যমা দুটি সমান।
3.
| শ্রেণি | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 |
| পরিসংখ্যা | 4 | 10 | 15 | 8 | 3 | 5 |
প্রদত্ত তথ্যের ক্রমযৌগিক পরিসংখ্যা ( বৃহত্তর সূচক ) তালিকা তৈরি করে ছক কাগজে ওজাইভ অঙ্কন করি।
সমাধান –
প্রদত্ত তথ্য থেকে ক্রমযৌগিক পরিসংখ্যা বিভাজন তা লিকা তৈরি করি,
| শ্রেণি | ক্রমযৌগিক পরিসংখ্যা বৃহত্তর সূচক |
| 0 বা 0 এর বেশি | 45 |
| 5 বা 5 এর বেশি | 41 |
| 10 বা 10 এর বেশি | 31 |
| 15 বা 15 এর বেশি | 16 |
| 20 বা 20 এর বেশি | 8 |
| 25 বা 25 এর বেশি | 5 |
X অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের প্রতিটি বাহুর দৈর্ঘ্য 0.5 একক ও Y অক্ষ বরাবর প্রতিটি বাহুর দৈর্ঘ্য 0.5 একক ধরে (0,45), (5,41), (10,31), (15,16), (20,8), (25,5) বিন্দুগুলি স্থাপন করে ও যুক্ত করে ও জাইভ অঙ্কন করা হলো।
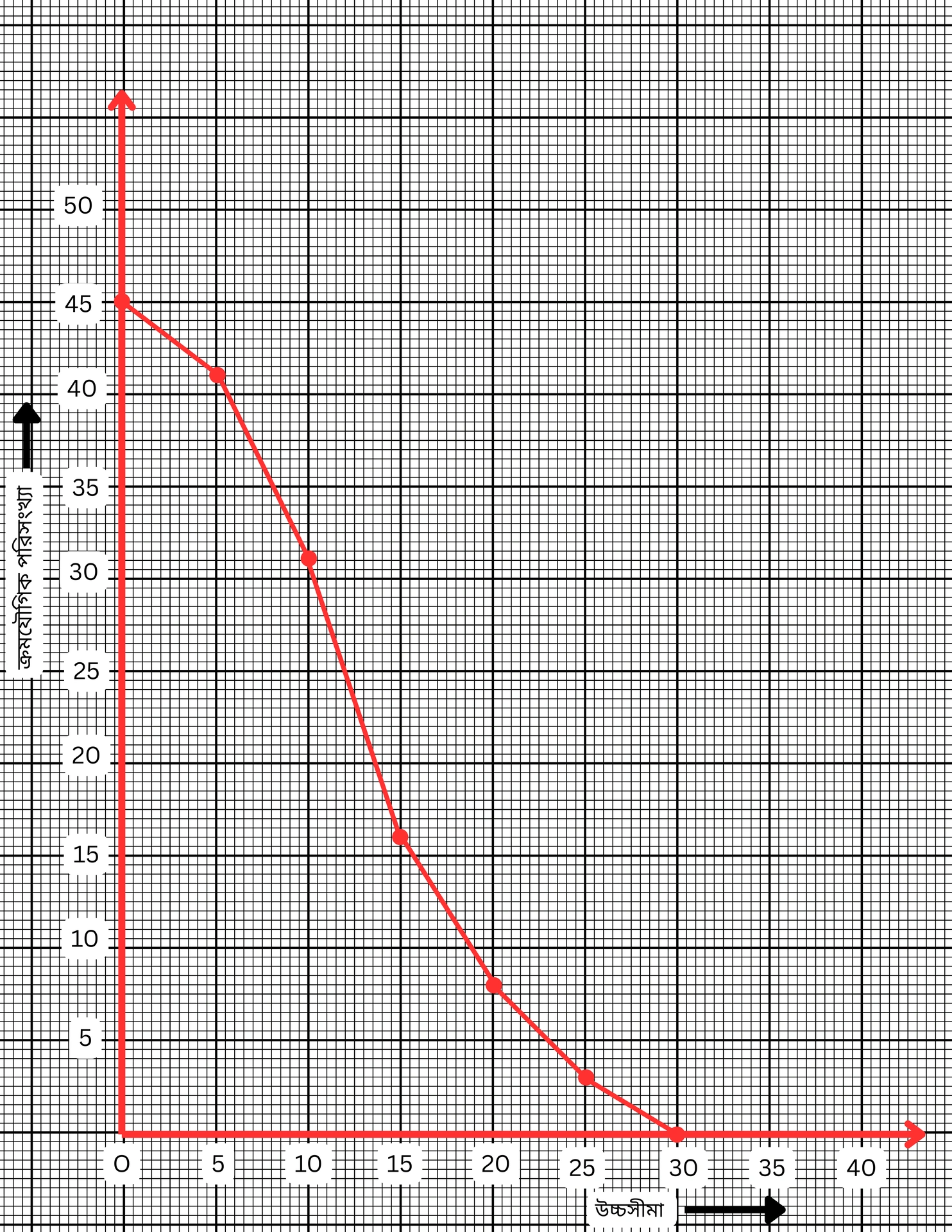
4.
| শ্রেণি | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 |
| পরিসংখ্যা | 12 | 14 | 8 | 6 | 10 |
প্রদত্ত তথ্যের একই অক্ষ বরাবর ক্ষুদ্রতর সূচক ওজাইভ ও বৃহত্তর সূচক ওজাইভ ছক কাগজে অঙ্কন করে মধ্যমা নির্ণয় করি।
সমাধান –
| শ্রেণি | ক্রমযৌগিক পরিসংখ্যা (বৃহত্তর সূচক) |
| 100 বা 100 এর বেশি | 50 |
| 120 বা 120 এর বেশি | 38 |
| 140 বা 140 এর বেশি | 24 |
| 160 বা 160 এর বেশি | 16 |
| 180 বা 180 এর বেশি | 10 |
| শ্রেণি | ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক) |
| 120 এর কম | 12 |
| 140 এর কম | 26 |
| 160 এর কম | 46 |
| 180 এর কম | 52 |
| 200 এর কম | 62 |
X অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1 টি বাহু = 2.5 একক ধরে ও y অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1 টি বাহু = 0.5 একক ধরে (100, 50), (120, 38), (140, 24), (160, 16), (180, 10) বিন্দুগুলি স্থাপন করে ও যুক্ত করে বৃহত্তর সূচক ওজাইভ অঙ্কন করা হলো, আবার (120, 12), (140, 26), (160, 46), (180, 52), (200, 62) বিন্দুগুলি স্থাপন করে ও যুক্ত করে ক্ষুদ্রতর সূচক ওজাইভ অঙ্কন করা হলো।
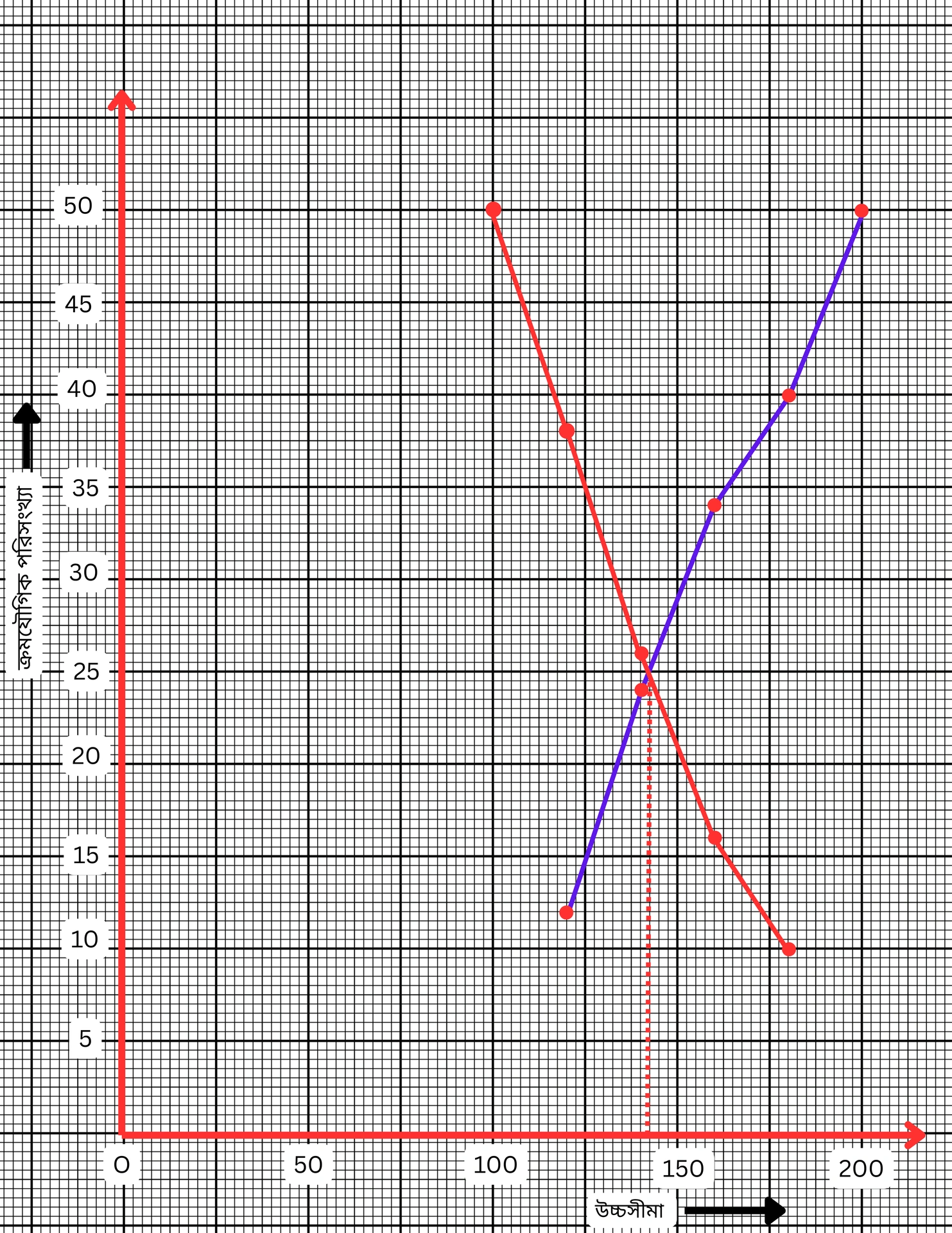
ক্ষুদ্রতর সূচক ওজাইভ এবং বৃহত্তর সূচক ওজাইভ পরস্পর কে P বিন্দুতে ছেদ করেছে। P বিন্দু থেকে x অক্ষের ওপর লম্ব অঙ্কন করা হলো যা x অক্ষ কে M বিন্দুতে ছেদ করেছে।
M বিন্দুর স্থানাঙ্ক (138.57,0)
∴ নির্ণেয় মধ্যমা = 138.57
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের ষট্বিংশ অধ্যায়, ‘রাশিবিজ্ঞান: গড়, মধ্যমা, ওজাইভ, সংখ্যাগুরুমান’ -এর ‘কষে দেখি – 26.3’ বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment