এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের ষট্বিংশ অধ্যায়, ‘রাশিবিজ্ঞান: গড়, মধ্যমা, ওজাইভ, সংখ্যাগুরুমান’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

প্রয়োগ 1. আমাদের গ্রামের উচ্চমাধ্যমিক বিদ্যালয়ে নবম শ্রেণির 40 জন শিক্ষার্থীর উচ্চতার তালিকা তৈরি করেছি। ওদের গড় উচ্চতা নির্ণয় করি।
| শিক্ষার্থীর সংখ্যা | 2 | 6 | 8 | 12 | 7 | 3 | 2 |
|---|---|---|---|---|---|---|---|
| শিক্ষার্থীর উচ্চতা (সেমি.) | 90 | 97 | 110 | 125 | 134 | 140 | 148 |
| শিক্ষার্থীর উচ্চতা (সেমি.) \(x_i\) | শিক্ষার্থীর সংখ্যা \(f_i\) | \(x_i f_i\) |
|---|---|---|
| 90 | 2 | \(90 \times 2 = 180\) |
| 97 | 6 | \(97 \times 6 = 582\) |
| 110 | 8 | \(110 \times 8 = 880\) |
| 125 | 12 | \(125 \times 12 = 1500\) |
| 134 | 7 | \(134 \times 7 = 938\) |
| 140 | 3 | \(140 \times 3 = 420\) |
| 148 | 2 | \(148 \times 2 = 296\) |
| মোট | \(\sum f_i = 40\) | \(\sum f_i x_i = 4796\) |
∴ শিক্ষার্থীর গড় উচ্চতা = \(\frac{\sum f_i x_i}{\sum f_i} = \frac{4796}{40}\) সেমি. = 119.9 সেমি.
প্রয়োগ 2. বিশাখের শ্রেণির 30 জন ছাত্রের ভূগোল পরীক্ষায় প্রাপ্ত নম্বর হলো, 61, 78, 80, 77, 80, 69, 73, 61, 82, 78, 79, 72, 78, 62, 80, 71, 82, 73, 66, 73, 62, 80, 74, 78, 62, 80, 66, 70, 79, 75 ভূগোল পরীক্ষায় প্রাপ্ত নম্বরের যৌগিক গড় নির্ণয় করি। [নিজে করি]
উত্তর –
| ভূগোলে প্রাপ্ত নম্বর (\(x_i\)) | ছাত্র সংখ্যা (\(f_i\)) | \(x_i f_i\) |
|---|---|---|
| 61 | 2 | 122 |
| 62 | 3 | 186 |
| 66 | 2 | 132 |
| 69 | 1 | 69 |
| 70 | 1 | 70 |
| 71 | 1 | 71 |
| 72 | 1 | 72 |
| 73 | 3 | 219 |
| 74 | 1 | 74 |
| 75 | 1 | 75 |
| 77 | 1 | 77 |
| 78 | 4 | 312 |
| 79 | 2 | 158 |
| 80 | 5 | 400 |
| 82 | 2 | 164 |
| \(\Sigma f_i = 30\) | \(\Sigma f_i x_i = 2201\) |
ভূগোলে প্রাপ্ত গড় নম্বর = \(\frac{\Sigma f_i x_i}{\Sigma f_i} = \frac{2201}{30} = 73.36 \approx 73.4\)।
প্রয়োগ 3. আমি Table-2 থেকে গতমাসে আশাকাকিমার দোকানের লাভের যৌগিক গড় নির্ণয় করি ও কী পাই দেখি।
সারণি-2 (Table – 2)
| লাভের পরিমাণ (টাকা) | দিনসংখ্যা (\(f_i\)) |
|---|---|
| 300 – 350 | 2 |
| 350 – 400 | 5 |
| 400 – 450 | 7 |
| 450 – 500 | 7 |
| 500 – 550 | 5 |
| 550 – 600 | 4 |
| মোট | 30 |
সারণি-3 (Table – 3)
| লাভের পরিমাণ (টাকা) | দিনসংখ্যা (পরিসংখ্যা \(f_i\)) | শ্রেণি মধ্যক (\(x_i\)) | \(x_i f_i\) |
|---|---|---|---|
| 300 – 350 | 2 | 325 | 650 |
| 350 – 400 | 5 | 375 | 1875 |
| 400 – 450 | 7 | 425 | 2975 |
| 450 – 500 | 7 | 475 | 3325 |
| 500 – 550 | 5 | 525 | 2625 |
| 550 – 600 | 4 | 575 | 2300 |
| মোট | \(\Sigma f_i = 30\) | \(\Sigma f_i x_i = 13750\) |
∴ লাভের যৌগিক গড় = \(\frac{\Sigma f_i x_i}{\Sigma f_i} = \frac{13750}{30}\) টাকা = 458.33 টাকা (প্রায়)
প্রয়োগ 4. আমি a=425 ধরে, di=xi−a=xi−425 লিখে Table – 1 থেকে প্রাপ্ত তথ্যের যৌগিক গড় নির্ণয় করি।
সারণি-4 (Table – 4)
| লাভের পরিমাণ (টাকা) | দিনসংখ্যা (পরিসংখ্যা fi) | শ্রেণি মধ্যক (xi) | (di=xi−a) di=(xi−425) | difi |
| 300 – 350 | 2 | 325 | –100 | –200 |
| 350 – 400 | 5 | 375 | –50 | –250 |
| 400 – 450 | 7 | 425 = a | 0 | 0 |
| 450 – 500 | 7 | 475 | 50 | 350 |
| 500 – 550 | 5 | 525 | 100 | 500 |
| 550 – 600 | 4 | 575 | 150 | 600 |
| মোট | Σfi=30 | Σfidi=1000 |
∴ উপরের ছক থেকে পাই, d=ΣfiΣfidi=301000=33.33 (প্রায়)
প্রয়োগ 4. Table-4 থেকে \(\overline{u} = \frac{\Sigma f_i u_i}{\Sigma f_i}\) নির্ণয় করি যেখানে \(u_i = \frac{x_i-a}{h}\), এখানে a=425 এবং h=50
সারণি-1 (Table – 1)
| লাভের পরিমাণ (টাকা) | দিনসংখ্যা (পরিসংখ্যা \(f_i\)) | শ্রেণি মধ্যক (\(x_i\)) | (\(d_i = x_i – a\)) \(d_i = x_i – 425\) | \(u_i = \frac{x_i – a}{50}\) | \(f_i u_i\) |
|---|---|---|---|---|---|
| 300 – 350 | 2 | 325 | –100 | –2 | –4 |
| 350 – 400 | 5 | 375 | –50 | –1 | –5 |
| 400 – 450 | 7 | 425 | 0 | 0 | 0 |
| 450 – 500 | 7 | 475 | 50 | 1 | 7 |
| 500 – 550 | 5 | 525 | 100 | 2 | 10 |
| 550 – 600 | 4 | 575 | 150 | 3 | 12 |
| মোট | \(\Sigma f_i = 30\) | \(\Sigma f_i u_i = 20\) |
∴ পেলাম, \(\overline{u} = \frac{\Sigma f_i u_i}{\Sigma f_i} = \frac{20}{30} = \frac{2}{3}\)
প্রয়োগ 5. আমি ও সতীশ আমাদের পাড়ার 50 টি পরিবারের এক সপ্তাহে বিদ্যুৎ খরচের তথ্যটি একটি ছকে লিখেছি, সেই ছকটি হলো—
| বিদ্যুৎ খরচের পরিমাণ (ইউনিট) | 85–105 | 105–125 | 125–145 | 145–165 | 165–185 | 185–205 |
|---|---|---|---|---|---|---|
| পরিবারের সংখ্যা | 3 | 12 | 18 | 10 | 5 | 2 |
আমি যৌগিক গড় নির্ণয়ের তিনটি পদ্ধতিতে 50 টি পরিবারের এক সপ্তাহের বিদ্যুৎ খরচের যৌগিক গড় নির্ণয় করি।
প্রথমে শ্রেণি মধ্যক নির্ণয় করে প্রদত্ত তথ্যটি লিখি,
| বিদ্যুৎ খরচের পরিমাণ (ইউনিট) | পরিবারের সংখ্যা (পরিসংখ্যা \(f_i\)) | শ্রেণি মধ্যক (\(x_i\)) |
|---|---|---|
| 85 – 105 | 3 | 95 |
| 105 – 125 | 12 | 115 |
| 125 – 145 | 18 | 135 |
| 145 – 165 | 10 | 155 |
| 165 – 185 | 5 | 175 |
| 185 – 205 | 2 | 195 |
| মোট | \(\Sigma f_i = 50\) |
ধরি, \(a = 155\) এবং এখানে শ্রেণি দৈর্ঘ্য \(h = 20\)
∴ \(d_i = x_i – 155\) এবং \(u_i = \frac{x_i – 155}{20}\) ধরে নীচের ছকে লিখি।
| বিদ্যুৎ খরচের পরিমাণ (ইউনিট) | পরিবারের সংখ্যা (\(f_i\)) | শ্রেণি মধ্যক (\(x_i\)) | \(d_i = x_i – 155\) | \(u_i = \frac{x_i – 155}{20}\) | \(f_i x_i\) | \(f_i d_i\) | \(f_i u_i\) |
|---|---|---|---|---|---|---|---|
| 85 – 105 | 3 | 95 | –60 | –3 | 285 | –180 | –9 |
| 105 – 125 | 12 | 115 | –40 | –2 | 1380 | –480 | –24 |
| 125 – 145 | 18 | 135 | –20 | –1 | 2430 | –360 | –18 |
| 145 – 165 | 10 | 155 | 0 | 0 | 1550 | 0 | 0 |
| 165 – 185 | 5 | 175 | 20 | 1 | 875 | 100 | 5 |
| 185 – 205 | 2 | 195 | 40 | 2 | 390 | 80 | 4 |
| মোট | 50 | 6910 | –840 | –42 |
∴ উপরের ছক থেকে পেলাম, \(\Sigma f_i = 50\), \(\Sigma f_i x_i = 6910\), \(\Sigma f_i d_i = –840\) এবং \(\Sigma f_i u_i = –42\)
∴ প্রত্যক্ষ পদ্ধতি থেকে পাই, যৌগিক গড় = \(\frac{\Sigma f_i x_i}{\Sigma f_i} = \frac{6910}{50}\) ইউনিট = 138.2 ইউনিট
কল্পিত গড় পদ্ধতি থেকে পাই, যৌগিক গড় = \(a + \frac{\Sigma f_i d_i}{\Sigma f_i} = 155 + \frac{(-840)}{50}\) ইউনিট
= \(155 – 16.8 = 138.2\) ইউনিট
আবার, ক্রম-বিচ্যুতি পদ্ধতি থেকে পাই, যৌগিক গড় = \(a + \frac{\Sigma f_i u_i}{\Sigma f_i} \times h\)
= \(155 + (\frac{-42}{50}) \times 20\) ইউনিট
= \(155 – 16.8 = 138.2\) ইউনিট
∴ তিনটি পদ্ধতির সাহায্যে দেখছি, পাড়ার 50 টি পরিবারের এক সপ্তাহের বিদ্যুৎ খরচের যৌগিক গড় 138.2 ইউনিট।
প্রয়োগ 6. রমেশ তাঁতির অনেকগুলি তাঁত আছে। সেখানে 35 জন তাঁতির সাপ্তাহিক আয়ের (টাকায়) পরিমাণের তথ্যটি নীচের ছকে লিখেছি।
| আয় (টাকায়) | 2500 – 3000 | 3000 – 3500 | 3500 – 4000 | 4000 – 4500 | 4500 – 5000 |
|---|---|---|---|---|---|
| পরিসংখ্যা | 3 | 6 | 9 | 12 | 5 |
আয়ের যৌগিক গড় নির্ণয় করি।
\(a=3750\) এবং \(h=500\) ধরে ক্রম-বিচ্যুতি [Step-deviation] পদ্ধতিতে যৌগিক গড় নির্ণয় করি।
| আয় (টাকায়) (শ্রেণি অন্তর) | পরিসংখ্যা (\(f_i\)) | শ্রেণি মধ্যক (\(x_i\)) | \(u_i = \frac{x_i – 3750}{500}\) | \(f_i u_i\) |
|---|---|---|---|---|
| 2500 – 3000 | 3 | 2750 | –2 | –6 |
| 3000 – 3500 | 6 | 3250 | –1 | –6 |
| 3500 – 4000 | 9 | 3750 | 0 | 0 |
| 4000 – 4500 | 12 | 4250 | 1 | 12 |
| 4500 – 5000 | 5 | 4750 | 2 | 10 |
| মোট | \(\Sigma f_i = 35\) | \(\Sigma f_i u_i = 10\) |
∴ আয়ের যৌগিক গড় = \(3750\) টাকা + \(500 \times \frac{\Sigma f_i u_i}{\Sigma f_i}\) টাকা
= \(3750\) টাকা + \(500 \times \frac{10}{35}\) টাকা = \(3892.86\) টাকা
প্রয়োগ 7. যে-কোনো পদ্ধতির সাহায্যে নীচের তথ্যের যৌগিক গড় নির্ণয় করি। [নিজে করি]
| শ্রেণি | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 |
| পরিসংখ্যা | 7 | 5 | 6 | 12 | 8 | 2 |
| শ্রেণি | পরিসংখ্যা (\(f_i\)) | শ্রেণি মধ্যক (\(x_i\)) | \(f_i x_i\) |
|---|---|---|---|
| 0 – 10 | 7 | 5 | \(35\) |
| 10 – 20 | 5 | 15 | \(75\) |
| 20 – 30 | 6 | 25 | \(150\) |
| 30 – 40 | 12 | 35 | \(420\) |
| 40 – 50 | 8 | 45 | \(360\) |
| 50 – 60 | 2 | 55 | \(110\) |
| মোট | \(\Sigma f_i = 40\) | \(\Sigma f_i x_i = 1150\) |
∴ যৌগিক গড় = \(\frac{\Sigma f_i x_i}{\Sigma f_i} = \frac{1150}{40} = 28.75\)
প্রয়োগ 8. যদি নীচের পরিসংখ্যা বিভাজন তালিকার যৌগিক গড় 54 হয়, তবে k-এর মান নির্ণয় করি।
| শ্রেণি | 0 – 20 | 20 – 40 | 40 – 60 | 60 – 80 | 80 – 100 |
|---|---|---|---|---|---|
| পরিসংখ্যা | 7 | 11 | k | 9 | 13 |
| শ্রেণি অন্তর | পরিসংখ্যা (\(f_i\)) | শ্রেণি মধ্যক (\(x_i\)) | \(f_i x_i\) | \(u_i = \frac{x_i – 50}{20}\) | \(f_i u_i\) |
|---|---|---|---|---|---|
| 0 – 20 | 7 | 10 | 70 | –2 | –14 |
| 20 – 40 | 11 | 30 | 330 | –1 | –11 |
| 40 – 60 | k | 50 = a | 50k | 0 | 0 |
| 60 – 80 | 9 | 70 | 630 | 1 | 9 |
| 80 – 100 | 13 | 90 | 1170 | 2 | 26 |
| মোট | \(\Sigma f_i = 40+k\) | \(\Sigma f_i x_i = 2200+50k\) | \(\Sigma f_i u_i = 10\) |
∴ নির্ণেয় যৌগিক গড় = \(\frac{\Sigma f_i x_i}{\Sigma f_i} = \frac{2200+50k}{40+k}\)
শর্তানুসারে, \(\frac{2200+50k}{40+k} = 54\)
বা, \(2200+50k = 2160+54k\)
বা, \(50k-54k = 2160-2200\)
বা, \(-4k = -40\)
∴ \(k = 10\)
অন্যভাবে,
যৌগিক গড় = \(a + \frac{\Sigma f_i u_i}{\Sigma f_i} \times h\)
\(54 = 50 + \frac{10}{40+k} \times 20\)বা, \(4 = \frac{200}{40+k}\)
বা, \(40+k = 50\)
∴ \(k=10\)
Here is the text extracted from the image:
প্রয়োগ 9. যদি নীচের পরিসংখ্যা বিভাজন তালিকার যৌগিক গড় 25 হয়, তবে k-এর মান নির্ণয় করি। [নিজে করি]
| শ্রেণি | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
|---|---|---|---|---|---|
| পরিসংখ্যা | 5 | k | 15 | 16 | 6 |
উঃ
| শ্রেণি অন্তর | পরিসংখ্যা (\(f_i\)) | শ্রেণি মধ্যক | \(f_i x_i\) |
|---|---|---|---|
| 0-10 | 5 | 5 | 25 |
| 10-20 | k | 15 | 15k |
| 20-30 | 15 | 25 | 375 |
| 30-40 | 16 | 35 | 560 |
| 40-50 | 6 | 45 | 270 |
| মোট | \(\Sigma f_i = 42 + k\) | \(\Sigma f_i x_i = 1230 + 15k\) |
∴ নির্ণেয় যৌগিক গড় = \(\frac{\Sigma f_i x_i}{\Sigma f_i} = \frac{1230+15k}{42+k}\)
শর্তানুসারে, \(\frac{1230+15k}{42+k} = 25\)
বা, \(1230 + 15k = 1050 + 25k\)
বা, \(15k – 25k = 1050 – 1230\)
বা, \(-10k = -180\)
বা, \(k = \frac{180}{10} = 18\)
প্রয়োগ 10. মারিয়া তাদের গ্রামের একজন প্রতিযোগিতায় কে কত নম্বর পেয়েছে তার একটি ক্রমযৌগিক পরিসংখ্যা বিভাজন তালিকা তৈরি করেছে। তালিকাটি হলো –
| নম্বর | 0 অথবা 0-এর বেশি | 10 অথবা 10-এর বেশি | 20 অথবা 20-এর বেশি | 30 অথবা 30-এর বেশি | 40 অথবা 40-এর বেশি | 50 অথবা 50-এর বেশি |
|---|---|---|---|---|---|---|
| প্রতিযোগীর সংখ্যা | 40 | 36 | 22 | 11 | 2 | 0 |
আমি একজন প্রতিযোগিতায় প্রাপ্ত নম্বরের যৌগিক গড় নির্ণয় করি।
প্রথমে বৃহত্তর সূচক ক্রম যৌগিক পরিসংখ্যা বিভাজন তালিকাটিকে সাধারণ বিভাজন তালিকায় প্রকাশ করি।
দেখছি, 40 জন শিক্ষার্থী 0 বা 0-এর বেশি নম্বর পেয়েছে,
এবং 36 জন শিক্ষার্থী 10 বা 10-এর বেশি নম্বর পেয়েছে।
∴ 0 থেকে 10 -এর মধ্যে নম্বর পেয়েছে \(40-36\) জন = 4 জন শিক্ষার্থী
একইভাবে 10 থেকে 20 -এর মধ্যে নম্বর পেয়েছে \(36-22\) জন = 14 জন শিক্ষার্থী
∴ পরিসংখ্যা বিভাজন তালিকাটি হলো –
| নম্বর | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
|---|---|---|---|---|---|
| প্রতিযোগীর সংখ্যা | 4 | 14 | 11 | 9 | 2 |
কল্পিত গড় 25 ধরে ক্রম বিচ্যুতি পদ্ধতিতে যৌগিক গড় নির্ণয় করি—
| শ্রেণি-সীমানা (নম্বর) | প্রতিযোগীর সংখ্যা (\(f_i\)) | শ্রেণি মধ্যক (\(x_i\)) | \(u_i = \frac{x_i – 25}{10}\) | \(f_i u_i\) |
|---|---|---|---|---|
| 0 – 10 | 4 | 5 | -2 | -8 |
| 10 – 20 | 14 | 15 | -1 | -14 |
| 20 – 30 | 11 | 25 | 0 | 0 |
| 30 – 40 | 9 | 35 | 1 | 9 |
| 40 – 50 | 2 | 45 | 2 | 4 |
| মোট | \(\sum f_i = 40\) | \(\sum f_i u_i = -9\) |
নির্ণেয় যৌগিক গড়
= \(25 + 10 \times \frac{\sum f_i u_i}{\sum f_i} = 25 + 10 \left(\frac{-9}{40}\right) = 25 – 2.25 = 22.75\)
∴ 40 জন প্রতিযোগীর প্রাপ্ত নম্বরের গড় \(22.75\)
প্রয়োগ 11. আমি নীচের পরিসংখ্যা বিভাজন তালিকার যৌগিক গড় নির্ণয় করি :
| শ্রেণি-সীমা | 20 – 29 | 30 – 39 | 40 – 49 | 50 – 59 | 60 – 69 | 70 – 79 |
|---|---|---|---|---|---|---|
| পরিসংখ্যা | 12 | 20 | 14 | 6 | 5 | 3 |
প্রদত্ত পরিসংখ্যা বিভাজন তালিকার শ্রেণিগুলি শ্রেণি-অন্তর্ভুক্ত।
তাই প্রথমে পরিসংখ্যা বিভাজন তালিকার শ্রেণি-অন্তর্ভুক্ত শ্রেণিগুলি শ্রেণি-বহির্ভূত আকারে লিখে যৌগিক গড় নির্ণয় করি।
কল্পিত গড় \(44.5\) ধরি। এখানে শ্রেণি দৈর্ঘ্য \(h = 10\)
| শ্রেণি-সীমা | শ্রেণি-সীমানা | পরিসংখ্যা \(f_i\) | শ্রেণি মধ্যক \(x_i\) | \(u_i = \frac{x_i-a}{h}\) \(u_i = \frac{x_i-44.5}{10}\) | \(f_i u_i\) |
|---|---|---|---|---|---|
| 20 – 29 | 19.5 – 29.5 | 12 | 24.5 | -2 | -24 |
| 30 – 39 | 29.5 – 39.5 | 20 | 34.5 | -1 | -20 |
| 40 – 49 | 39.5 – 49.5 | 14 | 44.5 | 0 | 0 |
| 50 – 59 | 49.5 – 59.5 | 6 | 54.5 | 1 | 6 |
| 60 – 69 | 59.5 – 69.5 | 5 | 64.5 | 2 | 10 |
| 70 – 79 | 69.5 – 79.5 | 3 | 74.5 | 3 | 9 |
| মোট | \(\sum f_i = 60\) | \(\sum f_i u_i = -19\) |
∴ নির্ণেয় যৌগিক গড় = \(44.5 + h \times \frac{\sum f_i u_i}{\sum f_i} = 44.5 + \left(10 \times \frac{-19}{60}\right) = \boxed{41.33}\)
প্রয়োগ 11. আমি নীচের পরিসংখ্যা বিভাজন তালিকার যৌগিক গড় নির্ণয় করি
| শ্রেণি-সীমা | 20 – 29 | 30 – 39 | 40 – 49 | 50 – 59 | 60 – 69 | 70 – 79 |
|---|---|---|---|---|---|---|
| পরিসংখ্যা | 12 | 20 | 14 | 6 | 5 | 3 |
প্রদত্ত পরিসংখ্যা বিভাজন তালিকার শ্রেণিগুলি শ্রেণি-অন্তর্ভুক্ত।
তাই প্রথমে পরিসংখ্যা বিভাজন তালিকার শ্রেণি-অন্তর্ভুক্ত শ্রেণিগুলি শ্রেণি-বহির্ভূত আকারে লিখে যৌগিক গড় নির্ণয় করি।
কল্পিত গড় \(44.5\) ধরি। এখানে শ্রেণি দৈর্ঘ্য \(h = 10\)
| শ্রেণি-সীমা | শ্রেণি-সীমানা | পরিসংখ্যা (\(f_i\)) | শ্রেণি মধ্যক (\(x_i\)) | \(u_i = \frac{x_i-a}{h}\) \(u_i = \frac{x_i-44.5}{10}\) | \(f_i u_i\) |
|---|---|---|---|---|---|
| 20 – 29 | 19.5 – 29.5 | 12 | 24.5 | -2 | -24 |
| 30 – 39 | 29.5 – 39.5 | 20 | 34.5 | -1 | -20 |
| 40 – 49 | 39.5 – 49.5 | 14 | 44.5 | 0 | 0 |
| 50 – 59 | 49.5 – 59.5 | 6 | 54.5 | 1 | 6 |
| 60 – 69 | 59.5 – 69.5 | 5 | 64.5 | 2 | 10 |
| 70 – 79 | 69.5 – 79.5 | 3 | 74.5 | 3 | 9 |
| মোট | \(\sum f_i = 60\) | \(\sum f_i u_i = -19\) |
∴ নির্ণেয় যৌগিক গড় = \(44.5 + h \times \frac{\sum f_i u_i}{\sum f_i} = 44.5 + \left(10 \times \frac{-19}{60}\right) = 41.33\)
প্রয়োগ 12. নীচের পরিসংখ্যা বিভাজন তালিকার যৌগিক গড় নির্ণয় করি। [নিজে করি]
| শ্রেণি-সীমা | পরিসংখ্যা \(f_i\) | শ্রেণিমধ্যক \(x_i\) | \(d_i = x_i – 37\) | \(f_i d_i\) |
|---|---|---|---|---|
| 25-29 | 10 | 27 | -10 | -100 |
| 30-34 | 12 | 32 | -5 | -60 |
| 35-39 | 15 | 37 = a | 0 | 0 |
| 40-44 | 5 | 42 | 5 | 25 |
| 45-49 | 3 | 47 | 10 | 30 |
| 50-54 | 5 | 52 | 15 | 75 |
| মোট | \(\sum f_i = 50\) | \(\sum f_i d_i = -30\) |
∴ \(\bar{d} = \frac{\sum f_i d_i}{\sum f_i} = \frac{-30}{50} = -0.6\)
∴ \(\bar{x} = a + \bar{d} = 37 + (-0.6) = 36.4\)
প্রয়োগ 13. নীচের তালিকা থেকে একটি বিদ্যালয়ের দশম শ্রেণির 52 জন ছাত্রের গড় নম্বর প্রত্যক্ষ পদ্ধতি ও কল্পিত গড় পদ্ধতিতে নির্ণয় করি।
| ছাত্র সংখ্যা | 4 | 7 | 10 | 15 | 8 | 5 | 3 |
| নম্বর | 30 | 33 | 35 | 40 | 43 | 45 | 48 |
ধরি, কল্পিত গড় (a) = 40
| নম্বর (xi) | ছাত্র সংখ্যা (fi) | fixi | (di = xi−a) di=(xi−40) | fidi |
| 30 | 4 | 120 | −10 | −40 |
| 33 | 7 | 231 | −7 | −49 |
| 35 | 10 | 350 | −5 | −50 |
| 40=a | 15 | 600 | 0 | 0 |
| 43 | 8 | 344 | 3 | 24 |
| 45 | 5 | 225 | 5 | 25 |
| 48 | 3 | 144 | 8 | 24 |
| মোট | ∑fi = 52 | ∑fixi = 2014 | ∑fidi = −66 |
প্রত্যক্ষ পদ্ধতিতে গড় নম্বর = \(\frac{2014}{52} = 38.73\) (প্রায়)
কল্পিত গড় পদ্ধতিতে, গড় নম্বর = \(a + \frac{\sum f_i d_i}{\sum f_i}\)
= \(40 + \frac{-66}{52}\)
= \(40 – \frac{66}{52}\)
= \((40 – 1.27)\) (প্রায়)
= \(38.73\) (প্রায়)
প্রয়োগ 14. আমি আমার কিছু বন্ধুর ওজন নীচে লিখেছি, তাদের ওজনের মধ্যমা নির্ণয় করি।
32 কিগ্রা., 30 কিগ্রা., 38 কিগ্রা., 40 কিগ্রা., 36 কিগ্রা., 45 কিগ্রা., 50 কিগ্রা., 52 কিগ্রা., 40 কিগ্রা., 65 কিগ্রা., 54 কিগ্রা.
বন্ধুদের ওজন মানের ঊর্ধ্বক্রমে সাজিয়ে পাই,
30 কিগ্রা., 32 কিগ্রা., 36 কিগ্রা., 38 কিগ্রা., 40 কিগ্রা., 40 কিগ্রা., 45 কিগ্রা., 50 কিগ্রা., 52 কিগ্রা., 54 কিগ্রা., 65 কিগ্রা.
এখানে, n=11 অর্থাৎ n অযুগ্ম।
ওজনের মধ্যমা = \((\frac{n+1}{2})\)-তম মান = \((\frac{11+1}{2})\)-তম মান = 6-তম মান = 40 কিগ্রা.
প্রয়োগ 15. আমি আমার কিছু বন্ধুদের এই মাসে স্কুলে উপস্থিতির দিনসংখ্যা লিখেছি। যেমন, 20 দিন, 25 দিন, 10 দিন, 18 দিন, 21 দিন, 18 দিন, 16 দিন, 22 দিন। আমি বন্ধুদের উপস্থিতির দিনসংখ্যার মধ্যমা নির্ণয় করি।
এই মাসে স্কুলে বন্ধুদের উপস্থিতির দিনসংখ্যা ঊর্ধ্বক্রমে সাজিয়ে পাই, 10 দিন, 16 দিন, 18 দিন, 18 দিন, 20 দিন, 21 দিন, 22 দিন, 25 দিন
এখানে, n=8 অর্থাৎ n যুগ্ম।
∴ নির্ণেয় মধ্যমা = \(\frac{1}{2}\{(\frac{8}{2})\)-তম মান + \((\frac{8}{2}+1)\)-তম মান\(\}\)
= \(\frac{1}{2}\)(চতুর্থ মান + পঞ্চম মান)
= \(\frac{1}{2}[18\text{দিন} + 20\text{দিন}] = 19\text{দিন}\)
প্রয়োগ 16. দুটি কবাডি দলের বিভিন্ন ম্যাচে প্রাপ্ত পয়েন্ট নীচে দেওয়া হলো। এদের মধ্যমা নির্ণয় করি।
(i) 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
সমাধান – 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15-এর ক্ষেত্রে পদের সংখ্যা = 11
যেহেতু, 11 একটি অযুগ্ম। সুতরাং এক্ষেত্রে মধ্যমা \((\frac{11+1}{2}) = \frac{12}{2} = 6\) তম পদ। ∴ মধ্যমা = 10।
(ii) 6, 7, 8, 9, 10, 15, 16, 17, 19, 25 [নিজে করি]
সমাধান : 6, 7, 8, 9, 10, 15, 16, 17, 19, 25-এর ক্ষেত্রে পদের সংখ্যা 12
∴ এক্ষেত্রে মধ্যমা \((\frac{12}{2})\) তম ও \((\frac{12}{2}+1)\) তম পদের গড়। ∴ নির্ণেয় মধ্যমা =
\(\frac{10+15}{2} = 12.51\)প্রয়োগ 17. নিয়ামতচাচার দোকানে ছয়রকম দৈর্ঘ্যের ব্যাসবিশিষ্ট 100 টি বল আছে। ওই বলগুলির ব্যাসের দৈর্ঘ্যের পরিসংখ্যা বিভাজন নিম্নরূপ, আমি এই 100 টি বলের ব্যাসের দৈর্ঘ্যের মধ্যমা নির্ণয় করি।
| ব্যাস (মিমি.) | 44 | 45 | 46 | 47 | 48 | 49 |
| পরিসংখ্যা (বলের সংখ্যা) | 12 | 15 | 23 | 20 | 15 | 15 |
এখানে, n = 100 অর্থাৎ n যুগ্ম।
∴ মধ্যমা = \((\frac{n}{2})\)-তম ও \((\frac{n}{2}+1)\)-তম পর্যবেক্ষণের গড়
= 50-তম ও 51-তম পর্যবেক্ষণের গড়
বলের ব্যাসের দৈর্ঘ্যের মধ্যমা নির্ণয়ের জন্য প্রথমে প্রদত্ত পরিসংখ্যা বিভাজন তালিকার ক্ষুদ্রতর সূচক ক্রমযৌগিক পরিসংখ্যা বিভাজন তালিকা তৈরি করি।
| ব্যাসের দৈর্ঘ্য (মিমি.) | বলের সংখ্যা |
| 44 পর্যন্ত | 12 |
| 45 পর্যন্ত | 12 + 15= 27 |
| 46 পর্যন্ত | 27 + 23 = 50 |
| 47 পর্যন্ত | 50 + 20 = 70 |
| 48 পর্যন্ত | 70 + 15 = 85 |
| 49 পর্যন্ত | 85 + 15 = 100 |
∴ প্রদত্ত পরিসংখ্যা বিভাজন ছকে ক্রমযৌগিক পরিসংখ্যার স্তম্ভ যোগ করে পাই,
| ব্যাসের দৈর্ঘ্য (মিমি.) | পরিসংখ্যা | ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক) |
| 44 | 12 | 12 |
| 45 | 15 | 27 |
| 46 | 23 | 50 |
| 47 | 20 | 70 |
| 48 | 15 | 85 |
| 49 | 15 | 100 = n |
উপরের ছক থেকে দেখছি, 50 -তম পর্যবেক্ষণ 46
এবং 51-তম পর্যবেক্ষণ 47
∴ মধ্যমা = 246+47=46.5
∴ নিয়ামতচাচার দোকানের 100 টি বলের ব্যাসের দৈর্ঘ্যের মধ্যমা 46.5 মিমি.।
বুঝেছি, নিয়ামত চাচার দোকানের 50% বলের ব্যাসের দৈর্ঘ্য 46.5 মিলিমিটারের কম এবং 50% বলের ব্যাসের দৈর্ঘ্য 46.5 মিলিমিটারের বেশি।
প্রয়োগ 18. আমি নীচের পরিসংখ্যা বিভাজন তালিকা থেকে তথ্যটির মধ্যমা নির্ণয় করি।
| চল (xi) | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
| পরিসংখ্যা (fi) | 4 | 2 | 4 | 7 | 6 | 5 | 5 | 4 | 2 |
প্রথমে প্রদত্ত পরিসংখ্যা বিভাজন তালিকার একটি ক্ষুদ্রতর সূচক ক্রমযৌগিক পরিসংখ্যা বিভাজন তালিকা তৈরি করি –
| চল (xi) | পরিসংখ্যা (fi) | ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক) |
| 25 | 4 | 4 |
| 26 | 2 | 6 |
| 27 | 4 | 10 |
| 28 | 7 | 17 |
| 29 | 6 | 23 |
| 30 | 5 | 28 |
| 31 | 5 | 33 |
| 32 | 4 | 37 |
| 33 | 2 | 39 = n |
এখানে, n = 39 অর্থাৎ n অযুগ্ম।
∴ মধ্যমা = \((\frac{n+1}{2})\)-তম পর্যবেক্ষণ
= \(\frac{39+1}{2}\)-তম পর্যবেক্ষণ = 20-তম পর্যবেক্ষণ
উপরের ছক থেকে দেখছি, 18-তম থেকে 23-তম সব পর্যবেক্ষণের একই মান 29.
∴ নির্ণেয় মধ্যমা = 20 -তম পদ = 29
প্রয়োগ 19. আমি নীচের পরিসংখ্যা বিভাজন থেকে তথ্যটির মধ্যমা নির্ণয় করি: [নিজে করি]
| চল (xi) | 1 | 2 | 3 | 4 | 5 | 6 |
| পরিসংখ্যা (fi) | 8 | 12 | 16 | 19 | 21 | 24 |
প্রদত্ত পরিসংখ্যা বিভাজন তালিকার একটি ক্ষুদ্রতর সূচক ক্রমযৌগিক পরিসংখ্যা বিভাজন তালিকা তৈরি করি।
| চল (xi) | পরিসংখ্যা (fi) | ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক) |
| 1 | 8 | 8 |
| 2 | 12 | 8 + 12 = 20 |
| 3 | 16 | 20 + 16 = 36 |
| 4 | 19 | 36 + 19 = 55 |
| 5 | 21 | 55 + 21 = 76 |
| 6 | 24 | 76 + 24 = 100 = ? |
এখানে, n = 100, উপরের ছক থেকে দেখছি, 50তম পর্যবেক্ষণ 4 এবং 51 তম পর্যবেক্ষণ 4।
∴ নির্ণেয় মধ্যমা = \( \frac{4+4}2=4\)
প্রয়োগ 20. আমাদের গ্রামের 45 জন ছাত্রীদের হাতের কাজের উপরে কিছু নম্বর দেওয়া হয়েছে। সেই নম্বরের তালিকাটি নীচের ছকে লিখলাম।
| নম্বর (xi) | 0-4 | 5-9 | 10-14 | 15-19 | 20-24 | 25-29 | 30-34 | 35-39 |
| ছাত্রী সংখ্যা (fi) | 4 | 5 | 7 | 8 | 7 | 5 | 6 | 3 |
উপরের পরিসংখ্যা বিভাজনের মধ্যমা নির্ণয় করি।
প্রদত্ত পরিসংখ্যা বিভাজন ছকের শ্রেণিগুলি শ্রেণি অন্তর্ভুক্ত গঠনে আছে।
∴ প্রথমে ছকটি শ্রেণি বহির্ভূত গঠনে লিখি এবং ক্ষুদ্রতর সূচক ক্রমযৌগিক পরিসংখ্যা লিখি।
| নম্বর (xi) | -0.5-4.5 | 4.5-9.5 | 9.5-14.5 | 14.5-19.5 | 19.5-24.5 | 24.5-29.5 | 29.5-34.5 | 34.5-39.5 |
| ছাত্রী সংখ্যা (fi) | 4 | 5 | 7 | 8 | 7 | 5 | 6 | 3 |
| ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক) | 4 | 9 | 16 | 24 | 31 | 36 | 42 | 45=n |
এখানে n=45, ∴ \(\frac{n}{2} = 22.5\)
22.5 -এর থেকে ঠিক বেশি ক্রমযৌগিক পরিসংখ্যা 24 এবং অনুরূপ শ্রেণি (14.5 -19.5)
∴ মধ্যমা শ্রেণি (Median class) = (14.5 – 19.5)
∴ নির্ণেয় মধ্যমা = \(l + \left[ \frac{\frac{n}{2} – cf}{f} \right] \times h\) [এখানে, \(l=14.5, n=45, f=8, cf=16, h=5\)]
= \(14.5 + \left[ \frac{\frac{45}{2} – 16}{8} \right] \times 5\)
= \(14.5 + 4.06\)
= \(18.56\)
∴ অর্ধেক সংখ্যক ছাত্রী 18.56-এর কম নম্বর পেয়েছে এবং অর্ধেক সংখ্যক ছাত্রী 18.56-এর বেশি নম্বর পেয়েছে।
প্রয়োগ 21. নীচের পরিসংখ্যা বিভাজন ছক দেখি এবং মধ্যমা নির্ণয় করি : [নিজে করি]
| শ্রেণি অন্তর | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| পরিসংখ্যা | 8 | 10 | 24 | 16 | 15 | 7 |
| শ্রেণি অন্তর | পরিসংখ্যা (fi) | ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক) |
| 0-10 | 8 | 8 |
| 10-20 | 10 | 18 |
| 20-30 | 24 | 42 |
| 30-40 | 16 | 58 |
| 40-50 | 15 | 73 |
| 50-60 | 7 | 80 = x |
x = 80. ∴ 2x=40.
40-এর থেকে ঠিক বেশি ক্রমযৌগিক পরিসংখ্যা (20-30) শ্রেণির মধ্যে আছে। ∴ মধ্যমা শ্রেণিটি হলো (20-30)
∴ নির্ণেয় মধ্যমা = l+[f2n−cf]×h=20+[2440−18]×10=20+9.16=29.16≈29.17
∴ নির্ণেয় মধ্যমা = 29.17 (প্রায়)।
প্রয়োগ 22. নীচের পরিসংখ্যা বিভাজন থেকে তথ্যটির মধ্যমা নির্ণয় করি
| প্রাপ্ত নম্বর | 10-এর কম | 20-এর কম | 30-এর কম | 40-এর কম | 50-এর কম | 60-এর কম |
| শিক্ষার্থী সংখ্যা | 8 | 15 | 29 | 42 | 60 | 70 |
প্রদত্ত ক্রমযৌগিক পরিসংখ্যা ছক থেকে পরিসংখ্যা বিভাজন ছকটি পাই,
| প্রাপ্ত নম্বর (xi) | পরিসংখ্যা (fi) [শিক্ষার্থীর সংখ্যা] | ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক) |
| 10-এর কম | 8 | 8 |
| 10 – 20 | 7 | 15 |
| 20 – 30 | 14 | 29 |
| 30 – 40 | 13 | 42 |
| 40 – 50 | 18 | 60 |
| 50 – 60 | 10 | 70 = n |
n = 70, ∴ \(\frac{n}{2} = 35\)
35-এর থেকে ঠিক বেশি ক্রমযৌগিক পরিসংখ্যা (30-40) শ্রেণির মধ্যে আছে।
সুতরাং, মধ্যমা শ্রেণিটি হলো (30-40)
∴ নির্ণেয় মধ্যমা = \(l + \left[ \frac{\frac{n}{2} – cf}{f} \right] \times h\) [এখানে, \(l=30, n=70, cf=29, f=13, h=10\)]
= \(30 + \left[ \frac{35 – 29}{13} \right] \times 10 \)
= \(30 + \frac{6}{13} \times 10 \)
= \(30 + \frac{60}{13} = 30 + 4.615…\)
= \(34.6\)
∴ নির্ণেয় মধ্যমা 34.6
প্রয়োগ 23. নীচের তথ্যের মধ্যমা 525 হলে, x ও y-এর মান নির্ণয় করি, যখন পরিসংখ্যার সমষ্টি 100
| শ্রেণি অন্তর | পরিসংখ্যা |
| 0 – 100 | 2 |
| 100 – 200 | 5 |
| 200 – 300 | x |
| 300 – 400 | 12 |
| 400 – 500 | 17 |
| 500 – 600 | 20 |
| 600 – 700 | y |
| 700 – 800 | 9 |
| 800 – 900 | 7 |
| 900 – 1000 | 4 |
প্রদত্ত তথ্যের ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক) বিভাজন তালিকা তৈরি করি—
| শ্রেণি অন্তর | পরিসংখ্যা (fi) | ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক) |
| 0 – 100 | 2 | 2 |
| 100 – 200 | 5 | 7 |
| 200 – 300 | x | 7 + x |
| 300 – 400 | 12 | 19 + x |
| 400 – 500 | 17 | 36 + x |
| 500 – 600 | 20 | 56 + x |
| 600 – 700 | y | 56 + x + y |
| 700 – 800 | 9 | 65 + x + y |
| 800 – 900 | 7 | 72 + x + y |
| 900 – 1000 | 4 | 76 + x + y = n |
যেহেতু \(n = 100\), সুতরাং \(76+x+y = 100\) ∴ \(x+y = 24\) __ (i)
আবার , মধ্যমা \(= 525\)
∴ মধ্যমার শ্রেণিটি \(500-600\)
∴ \(525 = l + \left[ \frac{\frac{n}{2} – cf}{f} \right] \times h\) \(l=500, n=100, cf=36+x, f=20, h=100\)
বা, \(525 = 500 + \left[ \frac{50 – (36+x)}{20} \right] \times 100\)
বা, \(525 – 500 = (14-x)5\)
বা, \(5(14-x) = 25\)
বা, \(14-x = 5\) ∴ \(x = 9\)
(i) থেকে পাই, \(x+y = 24\)
বা, \(y = 24 – x = 24 – 9 = 15\) ∴ \(x = 9\) এবং \(y = 15\)
প্রয়োগ 24. যদি নীচের তথ্যের মধ্যমা 28.5 হয়, এবং পরিসংখ্যার সমষ্টি 60 হয়, তাহলে x ও y-এর মান নির্ণয় করি। [নিজে করি]
| শ্রেণি অন্তর | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| পরিসংখ্যা | 5 | x | 20 | 15 | y | 5 |
| শ্রেণি অন্তর | পরিসংখ্যা (fi) | ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক) |
| 0-10 | 5 | 5 |
| 10-20 | x | 5 + x |
| 20-30 | 20 | 25 + x |
| 30-40 | 15 | 40 + x |
| 40-50 | y | 40 + x + y |
| 50-60 | 5 | 45 + x + y |
যেহেতু \(x = 60\). ∴ \(45 + x + y = 60\) বা, \(x + y = 15\)………..(i)
আবার মধ্যমা \(28.5\). ∴ মধ্যমা শ্রেণিটি \(20 – 30\).
∴ \(28.5 = 20 + \left[ \frac{30 – (5+x)}{20} \right] \times 10 \)
= \(20 + \frac{25-x}{20} \times 10 \)
= \(20 + \frac{25-x}{2} \)
= \(\frac{40+25-x}{2}\)
বা, \(57 = 65 – x\)
বা, \(x = 65 – 57\)
বা, \(x = 8\)
(i) থেকে পাই \(x + y = 15\)
বা, \(8 + y = 15\) বা, \(y = 15 – 8\) বা, \(y = 7\)
∴ \(x = 8\) এবং \(y = 7\).
প্রয়োগ 25. নীচের পরিসংখ্যা বিভাজনের মধ্যমা নির্ণয় করি।
| প্রাপ্ত নম্বর | 0-10 | 10-30 | 30-60 | 60-70 | 70-90 |
| ছাত্র-ছাত্রীর সংখ্যা | 15 | 25 | 30 | 4 | 10 |
| প্রাপ্ত নম্বর (xi) | ছাত্র-ছাত্রীর সংখ্যা | ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক) |
| 0 – 10 | 15 | 15 |
| 10 – 30 | 25 | 15+25 = 40 |
| 30 – 60 | 30 | 40+30 = 70 |
| 60 – 70 | 4 | 70+4 = 74 |
| 70 – 90 | 10 | 74+10 = 84 = n |
\(n=84\), ∴ \(\frac{n}{2}=42\)
42-এর থেকে ঠিক বেশি ক্রমযৌগিক পরিসংখ্যা (30-60) শ্রেণির মধ্যে আছে।
কিন্তু এখানে দেখছি সব শ্রেণির শ্রেণি দৈর্ঘ্য সমান নয়। তাহলে শ্রেণি দৈর্ঘ্য কত নেব?
যেহেতু, \(h\) = মধ্যমা শ্রেণির দৈর্ঘ্য, তাই সব শ্রেণির শ্রেণি দৈর্ঘ্য সমান না হলেও মধ্যমা শ্রেণির দৈর্ঘ্য নেব।
∴ মধ্যমা = \(l + \left[ \frac{\frac{n}{2} – cf}{f} \right] \times h\) \(l=30, \frac{n}{2}=42, cf=40, f=30, h=30\)
\(= 30 + \left[ \frac{42-40}{30} \right] \times 30 = 30+2 = 32\) নম্বর
অর্থাৎ, অর্ধেক সংখ্যক ছাত্র-ছাত্রী 32-এর কম নম্বর পেয়েছে এবং অর্ধেক সংখ্যক ছাত্র-ছাত্রী 32-এর বেশি নম্বর পেয়েছে।
প্রয়োগ 26. নীচের পরিসংখ্যা বিভাজনের ওজাইভ অঙ্কন করি এবং সেই ওজাইভ থেকে মধ্যমা নির্ণয় করি।
| শ্রেণি | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| পরিসংখ্যা | 7 | 10 | 23 | 50 | 6 | 4 |
প্রথমে ক্ষুদ্রতর সূচক ক্রমযৌগিক পরিসংখ্যার ছক তৈরি করি।
| শ্রেণি | 10-এর কম | 20-এর কম | 30-এর কম | 40-এর কম | 50-এর কম | 60-এর কম |
| ক্ষুদ্রতর সূচক ক্রমযৌগিক পরিসংখ্যা | 7 | 17 | 40 | 90 | 96 | 100 |
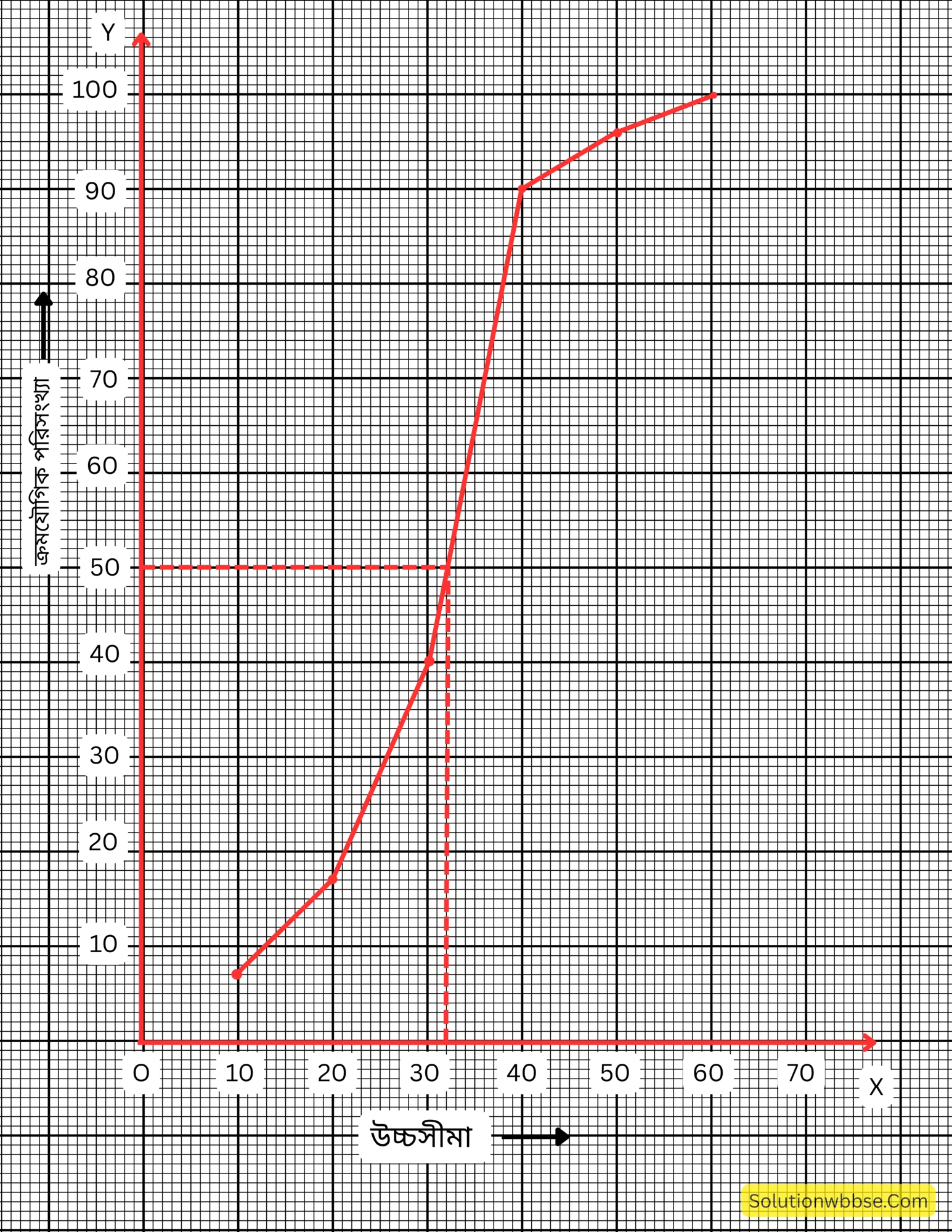
ছক কাগজের x অক্ষের ক্ষুদ্রতম বর্গক্ষেত্রের 1 টি বাহুর দৈর্ঘ্য \(= 1\) একক এবং y-অক্ষের ক্ষুদ্রতম বর্গক্ষেত্রের 1 টি বাহুর দৈর্ঘ্য \(= 1\) একক ধরে \((10, 7)\), \((20, 17)\), \((30, 40)\), \((40, 90)\) \((50, 96)\) এবং \((60, 100)\) বিন্দুগুলি স্থাপন করে যুক্ত করলাম এবং নিম্নেয় ওজাইভ (ক্ষুদ্রতর সূচক) পেলাম। এখানে মোট পরিসংখ্যা \((n) = 100\)
∴ \( n/2 = 50 \)
y-অক্ষের \((0, 50)\) বিন্দু দিয়ে x-অক্ষের সমান্তরাল সরলরেখা ওজাইভকে P বিন্দুতে ছেদ করল। P বিন্দু থেকে x-অক্ষের উপর PM লম্ব টানলাম যা x-অক্ষকে M বিন্দুতে ছেদ করল। দেখছি, M বিন্দুর স্থানাঙ্ক \((32, 0)\)
∴ ওজাইভ থেকে পেলাম, মধ্যমা \(= 32\)
প্রয়োগ 27. একটি মেডিকেলের প্রবেশিকা পরীক্ষায় 200 জন পরীক্ষার্থীর প্রাপ্ত নম্বরের পরিসংখ্যা বিভাজন ছকটি হলো,
| প্রাপ্ত নম্বর | 400-450 | 450-500 | 500-550 | 550-600 | 600-650 | 650-700 | 700-750 | 750-800 |
| পরীক্ষার্থীর সংখ্যা | 20 | 30 | 28 | 26 | 24 | 22 | 18 | 32 |
ওজাইভ অঙ্কন করি ও তার সাহায্যে মধ্যমা নির্ণয় করি। সূত্রের সাহায্যে মধ্যমা নির্ণয় করে যাচাই করি।
প্রথমে প্রদত্ত তথ্যের ক্ষুদ্রতর সূচক ক্রমযৌগিক পরিসংখ্যা বিভাজন ছকটি নির্ণয় করি।
| প্রাপ্ত নম্বর | 450-এর কম | 500-এর কম | 550-এর কম | 600-এর কম | 650-এর কম | 700-এর কম | 750-এর কম | 800-এর কম |
| ক্ষুদ্রতর সূচক ক্রমযৌগিক পরিসংখ্যা | 20 | 50 | 78 | 104 | 128 | 150 | 168 | 200 |
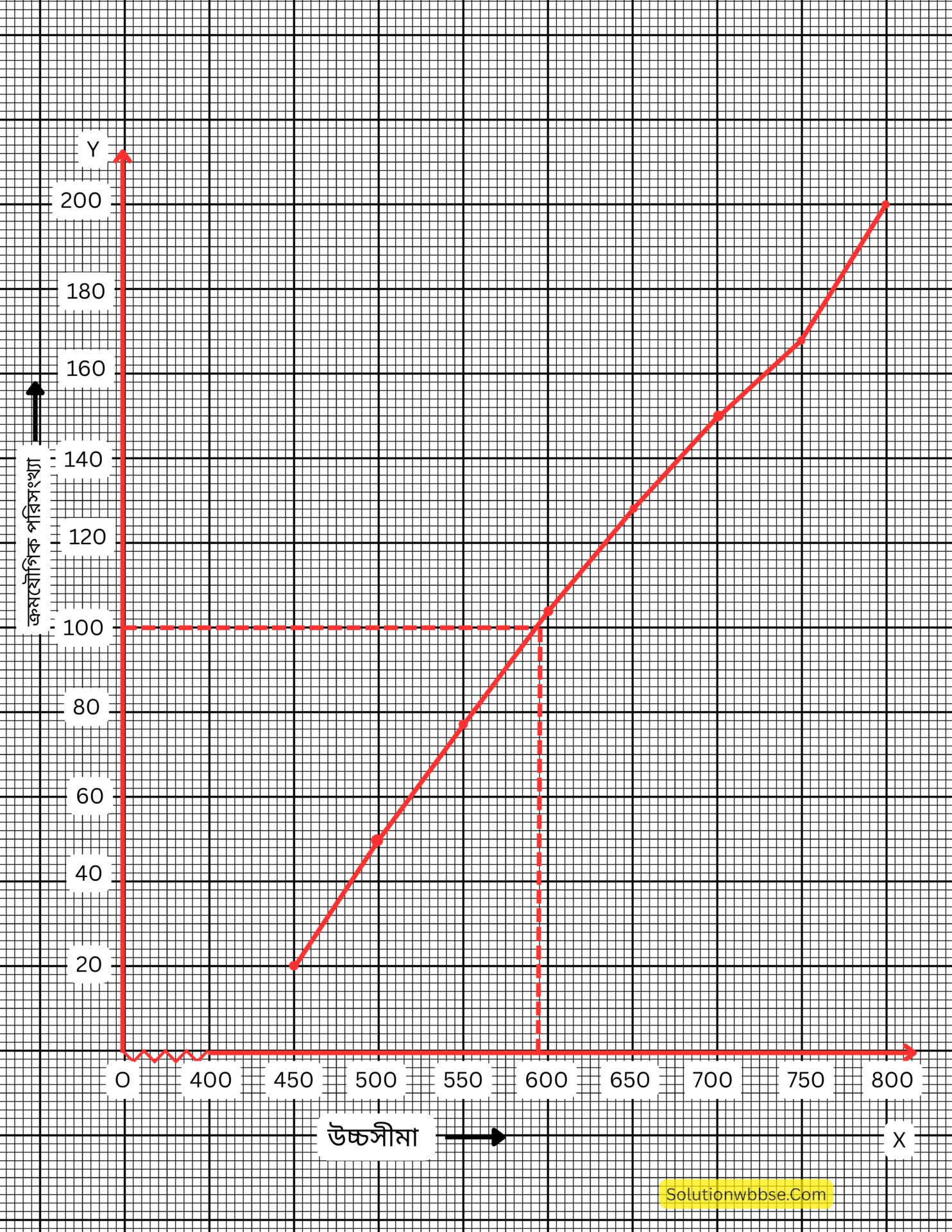
x-অক্ষের ক্ষুদ্রতম বর্গক্ষেত্রের 1 টি বাহুর দৈর্ঘ্য = 5 নম্বর এবং y অক্ষের ক্ষুদ্রতম বর্গক্ষেত্রের 1 টি বাহুর দৈর্ঘ্য = 2 জন পরীক্ষার্থী ধরে (450, 20), (500, 50), (550,78), (600,104), (650,128),(700,150), (750, 168) ও (800,200) বিন্দুগুলি স্থাপন করে ও যুক্ত করে ওজাইভ (ক্ষুদ্রতর সূচক) পেলাম।
এখানে মোট পরীক্ষার্থী (n) = 200 জন
∴ n/2 = 100
∴ (0, 100) বিন্দু দিয়ে x -অক্ষের সমান্তরাল সরলরেখা ওজাইভকে P বিন্দুতে ছেদ করল। P বিন্দু থেকে OX -এর উপর PM লম্ব টানি যা x -অক্ষকে M বিন্দুতে ছেদ করে। M বিন্দুর স্থানাঙ্ক (592.3)
∴ মধ্যমা = 592.3
প্রয়োগ 28. নীচের পরিসংখ্যা বিভাজন তালিকার বৃহত্তর সূচক ও ক্ষুদ্রতর সূচক ওজাইভ অঙ্কন করি ও মধ্যমা নির্ণয় করি। [নিজে করি]
| শ্রেণি | 50-55 | 55-60 | 60-65 | 65-70 | 70-75 | 75-80 | 80-85 |
| পরিসংখ্যা | 2 | 8 | 12 | 24 | 34 | 16 | 4 |
বৃহত্তর সূচক (More than type)
| শ্রেণি ক্রমযৌগিক পরিসংখ্যা | মান |
| 50 বা 50-এর বেশি | 100 |
| 55 বা 55-এর বেশি | 98 |
| 60 বা 60-এর বেশি | 90 |
| 65 বা 65-এর বেশি | 78 |
| 70 বা 70-এর বেশি | 54 |
| 75 বা 75-এর বেশি | 20 |
| 80 বা 80-এর বেশি | 4 |
ক্ষুদ্রতর সূচক (Less than type)
| শ্রেণি ক্রমযৌগিক পরিসংখ্যা | মান |
| 55-এর কম | 2 |
| 60-এর কম | 10 |
| 65-এর কম | 22 |
| 70-এর কম | 46 |
| 75-এর কম | 80 |
| 80-এর কম | 96 |
| 85-এর কম | 100 |
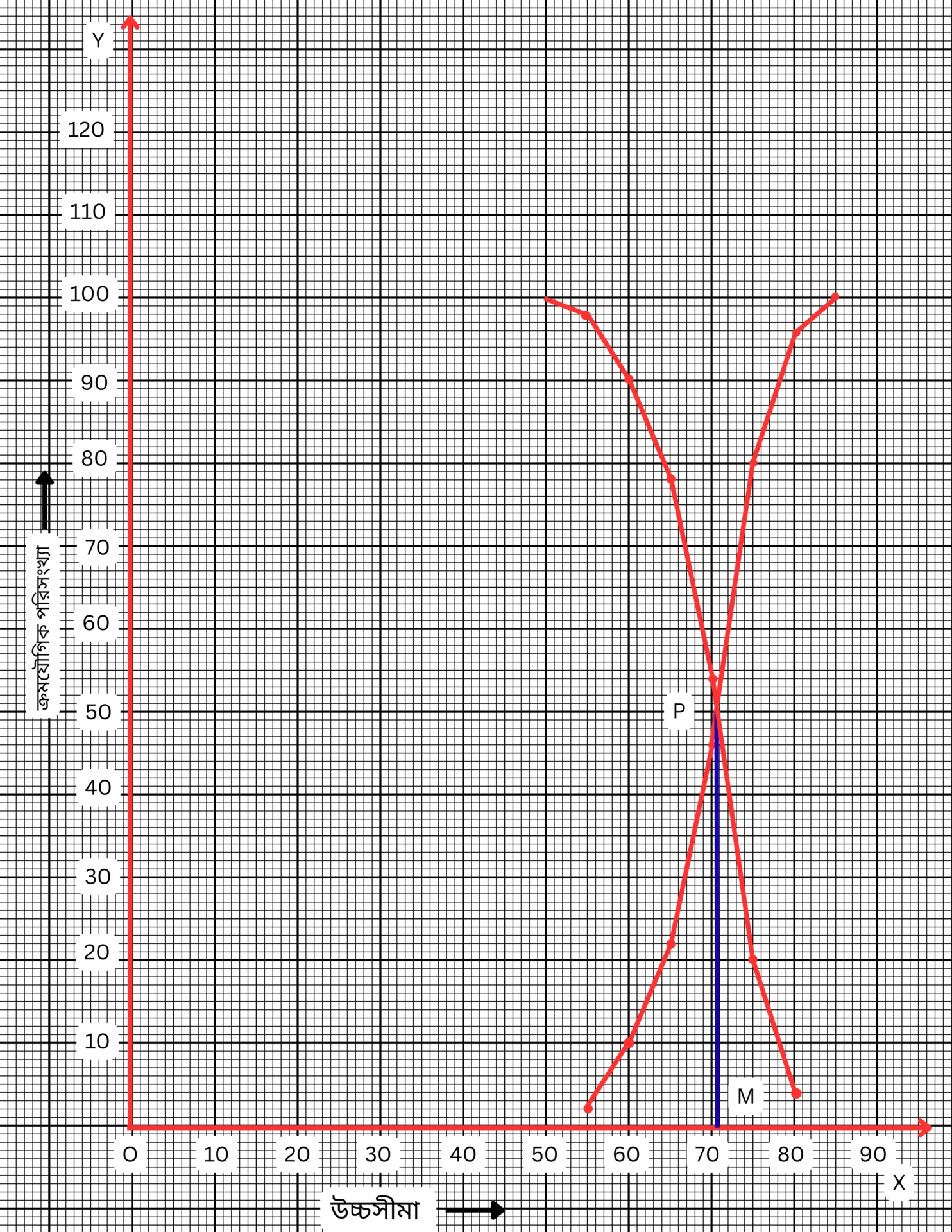
X-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহুর দৈর্ঘ্য \(= 1\) একক এবং Y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহুর দৈর্ঘ্য \(= 1\) একক ধরে ওজাইভ অঙ্কন করতে হবে।
বৃহত্তর সূচক ওজাইভ এর বিন্দুগুলি – \((50, 100)\), \((55, 98)\), \((60, 90)\), \((65, 78)\), \((70, 54)\), \((75, 20)\), \((80, 4)\), \((85, 0)\)
ক্ষুদ্রতর সূচক ওজাইভ এর বিন্দুগুলি – \((55, 2)\), \((60, 10)\), \((65, 22)\), \((70, 46)\), \((75, 80)\), \((80, 96)\), \((85, 100)\)
এই বিন্দুগুলি স্থাপন করে যুক্ত করলে দুটি ওজাইভ obtained হবে। তারা পরস্পরকে P বিন্দুতে ছেদ করবে। P বিন্দু থেকে X-অক্ষের উপর PM লম্ব টানলে, যা X-অক্ষকে M বিন্দুতে ছেদ করে।
গ্রাফ থেকে, M বিন্দুর স্থানাঙ্ক approximately \((70.59, 0)\) হবে। তাই মধ্যমা \(= 70.59\)।
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের ষট্বিংশ অধ্যায়, ‘রাশিবিজ্ঞান: গড়, মধ্যমা, ওজাইভ, সংখ্যাগুরুমান’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment