এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের ত্রয়োবিংশ অধ্যায়, ‘ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি’ -এর ‘কষে দেখি – 23.2’ বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

1. আমাদের বাড়ির জানালায় একটি মই ভূমির সঙ্গে \(60^\circ\) কোণে রাখা আছে। মইটি \(2\sqrt{3}\) মিটার লম্বা হলে আমাদের জানালাটি ওই ভূমি থেকে কত উপরে আছে ছবি এঁকে হিসাব করে লিখি।
সমাধান –
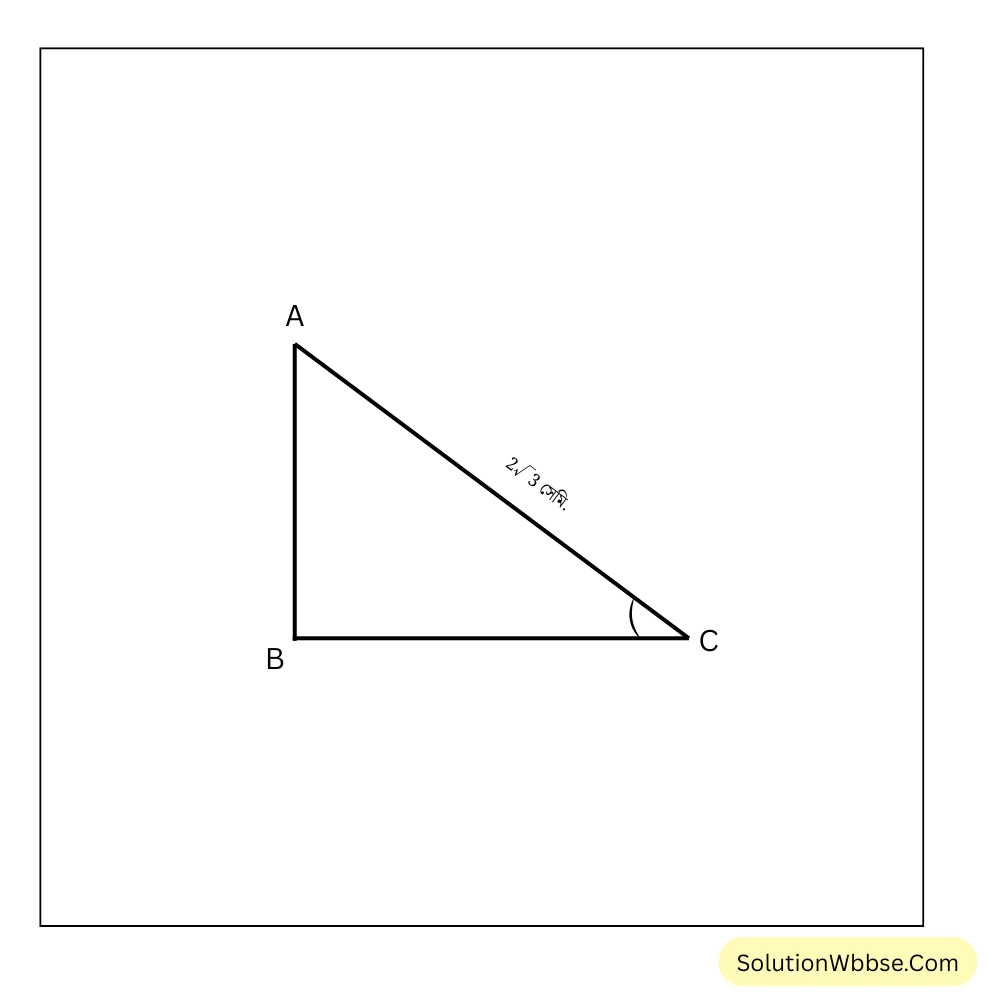
ধরাযাক \(AB\) হল ভূমি থেকে আমাদের বাড়ির জানালার উচ্চতা। \(AC\) হল মইয়ের উচ্চতা। \(\therefore AC = 2\sqrt{3}\) মিটার। মইটি ভূমির সাথে \(60^\circ\) কোণ করেছে।
\(\therefore \angle ACB = 60^\circ\)
এখন সমকোণী ত্রিভুজ \(ABC\) থেকে পাই –
বা, \(\frac{\sqrt{3}}{2} = \frac{AB}{AC}\)
বা, \(\frac{\sqrt{3}}{2} = \frac{AB}{2\sqrt{3}}\)
বা, \(2AB= 6\)
বা, \(AB = 6/2\)
বা, \(AB = 3\)
\(\therefore\) ভূমি থেকে আমাদের বাড়ির জানালার উচ্চতা \(3\) মিটার।
2. ABC সমকোণী ত্রিভুজের B সমকোণ। AB = \(8\sqrt{3}\) সেমি. এবং BC=\(8\) সেমি. হলে, \(\angle ACB\) ও \(\angle BAC\) –এর মান হিসাব করে লিখি।
সমাধান –
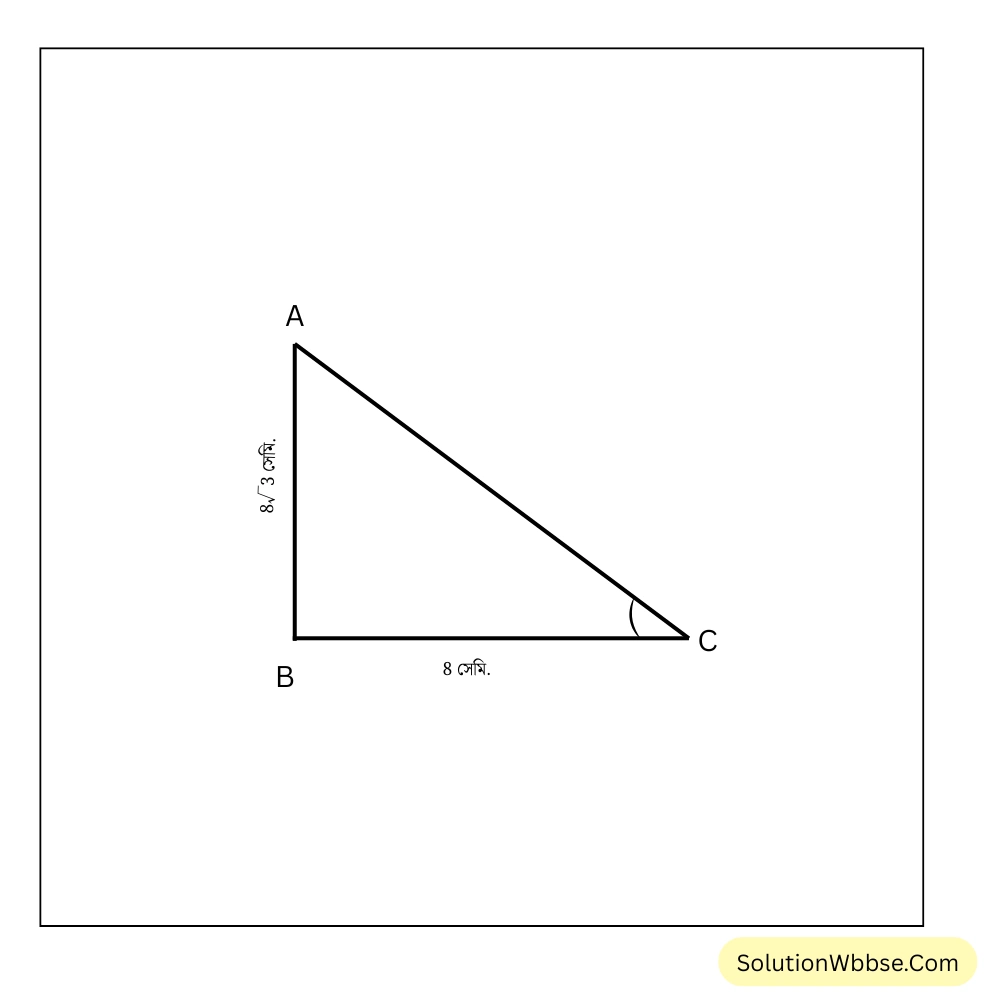
ABC সমকোণী ত্রিভুজের B সমকোণ। AB = \(8\sqrt{3}\) সেমি. এবং BC=\(8\) সেমি.। \(\angle ACB\) এর সাপেক্ষে AB উচ্চতা এবং BC ভূমি এবং AC অতিভুজ। আবার \(\angle BAC\) এর সাপেক্ষে AB ভূমি এবং BC উচ্চতা এবং AC অতিভুজ।
∴ \(\therefore \angle ACB=60^\circ\)আবার, \(\therefore \angle BAC=30^\circ\)3. ABC সমকোণী ত্রিভুজের \(\angle B =90^\circ\), \(\angle A=30^\circ\) এবং \(AC =20\) সেমি.। \(BC\) এবং \(AB\) বাহুদ্বয়ের দৈর্ঘ্য হিসাব করে লিখি।
সমাধান –
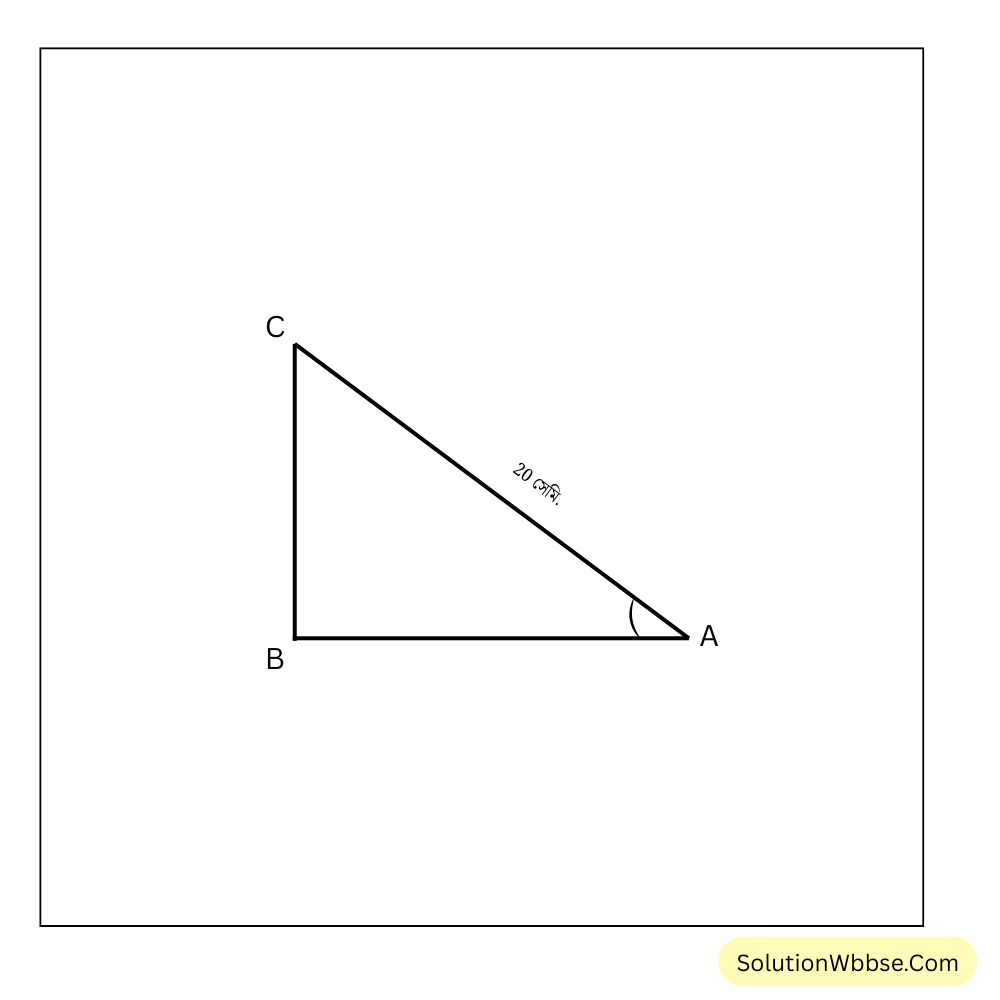
ABC সমকোণী ত্রিভুজে \(B =90^\circ\) এবং \(A=30^\circ\) এবং \(AC =20\) সেমি.
বা, \(\sin 30^\circ = \frac{BC}{20}\)
বা, \(\frac{1}{2} = \frac{BC}{20}\) [যেহেতু \(\sin 30^\circ = \frac{1}{2}\)]
বা, \(2BC = 20\)
বা, \(BC = 20/2\)
বা, \(BC = 10\)
\(\therefore\)BC বাহুর দৈর্ঘ্য \(10\) সেমি.।
বা, \(\cos 30^\circ = \frac{AB}{20}\)
বা, \(\frac{\sqrt{3}}{2} = \frac{AB}{20}\)
বা, \(2AB = 20\sqrt{3}\)
বা, \(AB = \frac{20\sqrt{3}}{2}\)
বা, \(AB = 10\sqrt{3}\)
\(\therefore\) AB বাহুর দৈর্ঘ্য \(10\sqrt{3}\) সেমি.।
4. PQR সমকোণী ত্রিভুজের \(\angle Q = 90^{\circ}\), \(\angle R = 45^{\circ}\) ; যদি \(PR = 3\sqrt{2}\) মিটার হয়,তাহলে PQ ও QR বাহুদ্বয়ের দৈর্ঘ্য হিসাব করে লিখি।
সমাধান –
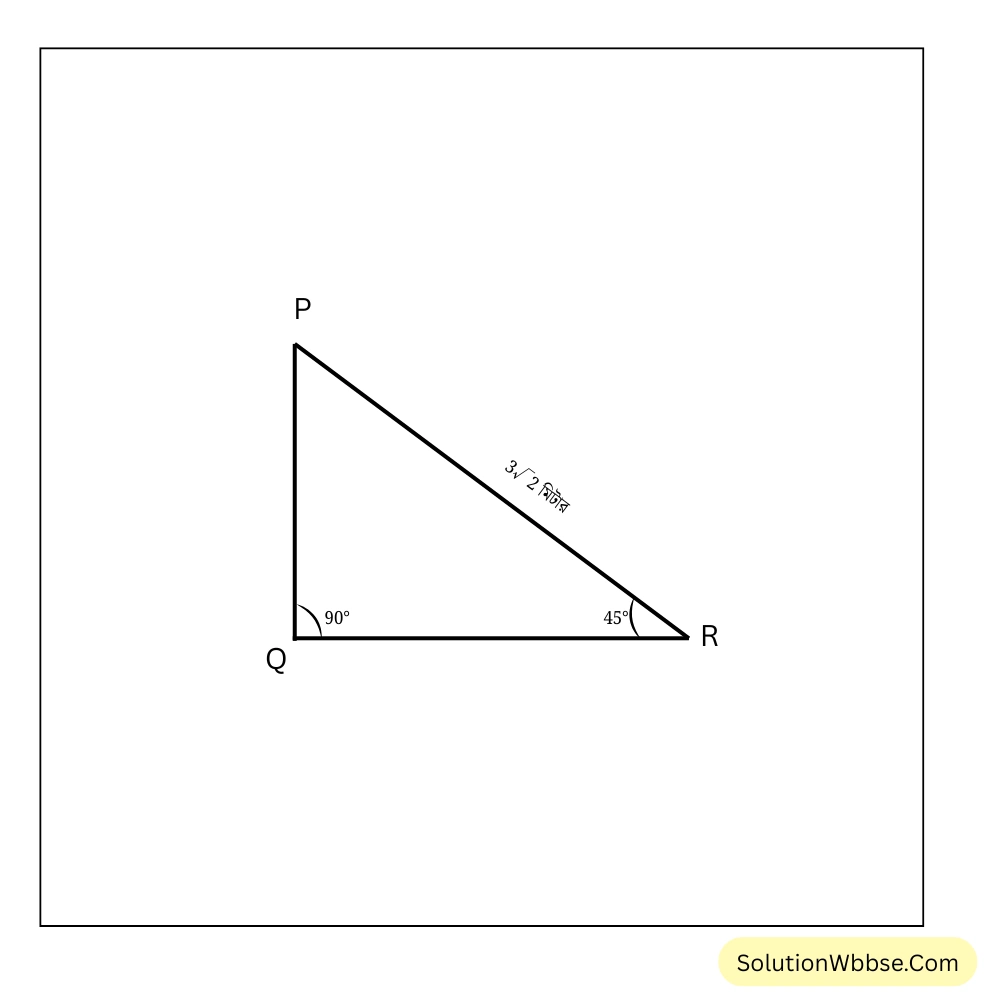
PQR সমকোণী ত্রিভুজের \(\angle Q = 90^{\circ}\), \(\angle R = 45^{\circ}\) এবং \(PR = 3\sqrt{2}\) মিটার
PQR ত্রিভুজের \(\angle R\)-এর সাপেক্ষে –
বা, \(sin45^{\circ} = \frac{PQ}{3\sqrt{2}}\)
বা, \(\frac{1}{\sqrt{2}} = \frac{PQ}{3\sqrt{2}}\)
বা, \(PQ = 3\)
∴ PQ বাহুর দৈর্ঘ্য 3 মিটার।
আবার,বা, \(cos45^{\circ} = \frac{QR}{3\sqrt{2}}\)
বা, \(\frac{1}{\sqrt{2}} = \frac{QR}{3\sqrt{2}}\)
বা, \(QR = 3\)
∴ QR বাহুর দৈর্ঘ্য 3 মিটার।
5. মান নির্ণয় করি
(i) \(sin^2 45^{\circ} – cosec^2 60^{\circ} + sec^2 30^{\circ}\)
(ii) \(sec^2 45^{\circ} – cot^2 45^{\circ} – sin^2 30^{\circ} – sin^2 60^{\circ}\)
(iii) \(3tan^2 45^{\circ} – sin^2 60^{\circ} – \frac{1}{3}cot^2 30^{\circ} – \frac{1}{8}sec^2 45^{\circ}\)
(iv) \(\frac{4}{3}cot^2 30^{\circ} + 3sin^2 60^{\circ} – 2cosec^2 60^{\circ} – \frac{3}{4}tan^2 30^{\circ}\)
(v) \(\frac{\frac{1}{3}\text{cos}30^\circ}{\frac{1}{2}\text{sin}45^\circ} + \frac{\text{tan}60^\circ}{\text{cos}30^\circ}\)
(vi) cot²30° -2cos²60° – \(\frac{3}{4}\)sec²45° -4sin²30°
(vii) \(\sec^2 60^\circ – \cot^2 30^\circ – \frac{2\tan 30^\circ \csc 60^\circ}{1+\tan^2 30^\circ}\)
(viii) \(\frac{\tan 60^\circ-\tan 30^\circ}{1+\tan 60^\circ \tan 30^\circ} + \cos 60^\circ \cos 30^\circ + \sin 60^\circ \sin 30^\circ\)
(ix) \( \frac{1-\text{sin}^2 30^\circ}{1+\text{sin}^2 45^\circ} \times \frac{\text{cos}^2 60^\circ + \text{cos}^2 30^\circ}{\text{cosec}^2 90^\circ – \text{cot}^2 90^\circ} \div (\text{sin}60^\circ \text{tan}30^\circ) \)
(i) \(sin^2 45^{\circ} – cosec^2 60^{\circ} + sec^2 30^{\circ}\)
সমাধান –
\(sin^2 45^{\circ} – cosec^2 60^{\circ} + sec^2 30^{\circ}\)= \(\frac{1}{\sqrt{2}}^2 – (\frac{2}{\sqrt{3}})^2 + (\frac{2}{\sqrt{3}})^2\)
= \(\frac{1}{2} – \frac{4}{3} + \frac{4}{3}\)
= \(\frac{3-8+8}{6}\)
= \(\frac{3}{6}\)
= \(\frac{1}{2}\)
∴ \(sin^2 45^{\circ} – cosec^2 60^{\circ} + sec^2 30^{\circ} = \frac{1}{2}\)
(ii) \(sec^2 45^{\circ} – cot^2 45^{\circ} – sin^2 30^{\circ} – sin^2 60^{\circ}\)
সমাধান –
\(sec^2 45^{\circ} – cot^2 45^{\circ} – sin^2 30^{\circ} – sin^2 60^{\circ}\)= \(\sqrt{2}^2 – (1)^2 – (\frac{1}{2})^2 – (\frac{\sqrt{3}}{2})^2\)
= \(2-1-\frac{1}{4} – \frac{3}{4}\)
= \(\frac{8-4-1-3}{4}\)
= \(\frac{8-8}{8}\)
= \(0\)
∴ \(sec^2 45^{\circ} – cot^2 45^{\circ} – sin^2 30^{\circ} – sin^2 60^{\circ} = 0\)
(iii) \(3tan^2 45^{\circ} – sin^2 60^{\circ} – \frac{1}{3}cot^2 30^{\circ} – \frac{1}{8}sec^2 45^{\circ}\)
সমাধান –
\(3tan^2 45^{\circ} – sin^2 60^{\circ} – \frac{1}{3}cot^2 30^{\circ} – \frac{1}{8}sec^2 45^{\circ}\)= \(3(1)^2 – (\frac{\sqrt{3}}{2})^2 – \frac{1}{3}(\sqrt{3})^2 – \frac{1}{8}(\sqrt{2})^2\)
= \(3 – \frac{3}{4} – \frac{1}{3} \times 3 – \frac{1}{8} \times 2\)
= \(3 – \frac{3}{4} – 1 – \frac{1}{4}\)
= \(\frac{12-3-4-1}{4}\)
= \(\frac{4}{4}\)
= \(1\)
∴ \(3tan^2 45^{\circ} – sin^2 60^{\circ} – \frac{1}{3}cot^2 30^{\circ} – \frac{1}{8}sec^2 45^{\circ} = 1\)
(iv) \(\frac{4}{3}cot^2 30^{\circ} + 3sin^2 60^{\circ} – 2cosec^2 60^{\circ} – \frac{3}{4}tan^2 30^{\circ}\)
সমাধান –
\(\frac{4}{3}cot^2 30^{\circ} + 3sin^2 60^{\circ} – 2cosec^2 60^{\circ} – \frac{3}{4}tan^2 30^{\circ}\)= \(\frac{4}{3} \times (\sqrt{3})^2 + 3 \times (\frac{\sqrt{3}}{2})^2 – 2 \times (\frac{2}{\sqrt{3}})^2 – \frac{3}{4} \times (\frac{1}{\sqrt{3}})^2\)
= \(\frac{4}{3} \times 3 + 3 \times \frac{3}{4} – 2 \times \frac{4}{3} – \frac{3}{4} \times \frac{1}{3}\)
= \(4 + \frac{9}{4} – \frac{8}{3} – \frac{1}{4}\)
= \(\frac{48+27-32-3}{12}\)
= \(\frac{40}{12}\)
= \(\frac{10}{3}\)
= \(3\frac{1}{3}\)
∴ \(\frac{4}{3}cot^2 30^{\circ} + 3sin^2 60^{\circ} – 2cosec^2 60^{\circ} – \frac{3}{4}tan^2 30^{\circ} = 3\frac{1}{3}\)
(v) \(\frac{\frac{1}{3}\text{cos}30^\circ}{\frac{1}{2}\text{sin}45^\circ} + \frac{\text{tan}60^\circ}{\text{cos}30^\circ}\)
সমাধান –
\(\frac{\frac{1}{3}\text{cos}30^\circ}{\frac{1}{2}\text{sin}45^\circ} + \frac{\text{tan}60^\circ}{\text{cos}30^\circ}\)= \(\frac{\frac{1}{3}\times\frac{\sqrt{3}}{2}}{\frac{1}{2}\times\frac{1}{\sqrt{2}}} + \frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}\)
= \(\frac{\frac{\sqrt{3}}{6}}{\frac{1}{2\sqrt{2}}} + 2\)
= \(\frac{\sqrt{3}}{6}\times2\sqrt{2} + 2\)
= \(\frac{\sqrt{6}}{3} + 2\)
= \(\frac{\sqrt{6}+6}{3}\)
উত্তর – \((\sqrt{6}+6)/3\)
(vi) cot²30° -2cos²60° – \(\frac{3}{4}\)sec²45° -4sin²30°
সমাধান –
cot²30° -2cos²60° – \(\frac{3}{4}\)sec²45° -4sin²30°
= \((\sqrt{3})^2 – 2(\frac{1}{2})^2 – \frac{3}{4}(\sqrt{2})^2 – 4(\frac{1}{2})^2\)
= 3 – 2×\(\frac{1}{4}\) – \(\frac{3}{4}\)×2 – 4×\(\frac{1}{4}\)
= 3 – \(\frac{1}{2}\) – \(\frac{3}{2}\) – 1
= \(\frac{6-1-3-2}{2}\)
= \(\frac{6-6}{2}\)
= 0
উত্তর – 0
(vii) \(\sec^2 60^\circ – \cot^2 30^\circ – \frac{2\tan 30^\circ \csc 60^\circ}{1+\tan^2 30^\circ}\)
সমাধান –
\(\sec^2 60^\circ – \cot^2 30^\circ – \frac{2\tan 30^\circ \csc 60^\circ}{1+\tan^2 30^\circ}\)= \((2)^2 – (\sqrt{3})^2 – \frac{2 \times \frac{1}{\sqrt{3}} \times \frac{2}{\sqrt{3}}}{1 + (\frac{1}{\sqrt{3}})^2}\)
= \(4 – 3 – \frac{\frac{4}{3}}{1+\frac{1}{3}}\)
= \(1 – \frac{\frac{4}{3}}{\frac{4}{3}}\)
= \(1 – 1\)
= \(0\)
উত্তর – \(0\)
(viii) \(\frac{\tan 60^\circ-\tan 30^\circ}{1+\tan 60^\circ \tan 30^\circ} + \cos 60^\circ \cos 30^\circ + \sin 60^\circ \sin 30^\circ\)
সমাধান –
\(\frac{\tan 60^\circ-\tan 30^\circ}{1+\tan 60^\circ \tan 30^\circ} + \cos 60^\circ \cos 30^\circ + \sin 60^\circ \sin 30^\circ\)= \(\frac{\sqrt{3}-\frac{1}{\sqrt{3}}}{1+\sqrt{3}\times\frac{1}{\sqrt{3}}} + \frac{1}{2}\times\frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{2}\times\frac{1}{2}\)
= \(\frac{\frac{2}{\sqrt{3}}}{2} + \frac{\sqrt{3}}{4} + \frac{\sqrt{3}}{4}\)
= \(\frac{1}{\sqrt{3}} + \frac{\sqrt{3}}{4} + \frac{\sqrt{3}}{4}\)
= \(\frac{4+3+3}{4\sqrt{3}}\)
= \(\frac{10}{4\sqrt{3}}\)
= \(\frac{5}{2\sqrt{3}}\)
উত্তর – \(\frac{5}{2\sqrt{3}}\)
(ix) \( \frac{1-\text{sin}^2 30^\circ}{1+\text{sin}^2 45^\circ} \times \frac{\text{cos}^2 60^\circ + \text{cos}^2 30^\circ}{\text{cosec}^2 90^\circ – \text{cot}^2 90^\circ} \div (\text{sin}60^\circ \text{tan}30^\circ) \)
সমাধান –
\( \frac{1-\text{sin}^2 30^\circ}{1+\text{sin}^2 45^\circ} \times \frac{\text{cos}^2 60^\circ + \text{cos}^2 30^\circ}{\text{cosec}^2 90^\circ – \text{cot}^2 90^\circ} \div (\text{sin}60^\circ \text{tan}30^\circ) \)= \( \frac{1-(\frac{1}{2})^2}{1+(\frac{1}{\sqrt{2}})^2} \times \frac{(\frac{1}{2})^2+(\frac{\sqrt{3}}{2})^2}{1-0} \div \frac{\sqrt{3}}{2} \times \frac{1}{\sqrt{3}} \)
= \( \frac{1-\frac{1}{4}}{1+\frac{1}{2}} \times \frac{\frac{1}{4}+\frac{3}{4}}{1} \div \frac{1}{2} \)
= \( \frac{\frac{3}{4}}{\frac{3}{2}} \times 1 \times 2 \)
= \( \frac{3}{4} \times \frac{2}{3} \times 2 \)
= \( \frac{1}{2} \times 2 \)
= \( 1 \)
উত্তর – 1
6. দেখাই যে,
(i) \( \sin^2 45^\circ + \cos^2 45^\circ = 1 \)
(ii) \( \cos 60^\circ = \cos^2 30^\circ – \sin^2 30^\circ \)
(iii) \( \frac{2\text{tan}30^\circ}{1-\text{tan}^2 30^\circ} = \sqrt{3} \)
(iv) \( \sqrt{\frac{1+\text{cos}30^\circ}{1-\text{cos}30^\circ}} = \text{sec}60^\circ + \text{tan}60^\circ \)
(v) \( \frac{2\text{tan}^2 30^\circ}{1-\text{tan}^2 30^\circ} + \text{sec}^2 45^\circ – \text{cot}^2 45^\circ = \text{sec}60^\circ \)
(vi) \( \tan^2\frac{\pi}{4} \sin\frac{\pi}{3} \tan\frac{\pi}{6} \tan^2\frac{\pi}{3} = 1\frac{1}{2} \)
(vii) \( \sin\frac{\pi}{3} \tan\frac{\pi}{6} + \sin\frac{\pi}{2} \cos\frac{\pi}{3} = 2 \sin^2\frac{\pi}{4} \)
(i) \( \sin^2 45^\circ + \cos^2 45^\circ = 1 \)
সমাধান –
\( \sin^2 45^\circ + \cos^2 45^\circ \)= \( \left(\frac{1}{\sqrt{2}}\right)^2 + \left(\frac{1}{\sqrt{2}}\right)^2 \)
= \( \frac{1}{2} + \frac{1}{2} \)
= \( 1 \)
∴ \( \sin^2 45^\circ + \cos^2 45^\circ = 1 \) [প্রমাণিত]
(ii) \( \cos 60^\circ = \cos^2 30^\circ – \sin^2 30^\circ \)
সমাধান –
বামপক্ষ –
\( \cos 60^\circ = \frac{1}{2} \)ডানপক্ষ –
\( \cos^2 30^\circ – \sin^2 30^\circ = \left(\frac{\sqrt{3}}{2}\right)^2 – \left(\frac{1}{2}\right)^2 = \frac{3}{4} – \frac{1}{4} = \frac{2}{4} = \frac{1}{2} \)∴ \( \cos 60^\circ = \cos^2 30^\circ – \sin^2 30^\circ \) [প্রমাণিত]
(iii) \( \frac{2\text{tan}30^\circ}{1-\text{tan}^2 30^\circ} = \sqrt{3} \)
সমাধান –
\( \frac{2\text{tan}30^\circ}{1-\text{tan}^2 30^\circ} \)= \( \frac{2\times\frac{1}{\sqrt{3}}}{1-(\frac{1}{\sqrt{3}})^2} \)
= \( \frac{\frac{2}{\sqrt{3}}}{1-\frac{1}{3}} \)
= \( \frac{\frac{2}{\sqrt{3}}}{\frac{2}{3}} \)
= \( \frac{2}{\sqrt{3}}\times\frac{3}{2} \)
= \( \sqrt{3} \)
∴ \( \frac{2\text{tan}30^\circ}{1-\text{tan}^2 30^\circ} = \sqrt{3} \) [প্রমাণিত]
(iv) \( \sqrt{\frac{1+\text{cos}30^\circ}{1-\text{cos}30^\circ}} = \text{sec}60^\circ + \text{tan}60^\circ \)
সমাধান –
বামপক্ষ –
\( \sqrt{\frac{1+\text{cos}30^\circ}{1-\text{cos}30^\circ}} \)= \( \sqrt{\frac{1+\frac{\sqrt{3}}{2}}{1-\frac{\sqrt{3}}{2}}} \)
= \( \sqrt{\frac{\frac{2+\sqrt{3}}{2}}{\frac{2-\sqrt{3}}{2}}} \)
= \( \sqrt{\frac{2+\sqrt{3}}{2-\sqrt{3}}} \)
= \( \sqrt{\frac{(2+\sqrt{3})(2+\sqrt{3})}{(2-\sqrt{3})(2+\sqrt{3})}} \)
= \( \sqrt{\frac{(2+\sqrt{3})^2}{4-3}} \)
= \( (2+\sqrt{3}) \)
ডানপক্ষ –
\( \text{sec}60^\circ + \text{tan}60^\circ = 2 + \sqrt{3} \)∴ বামপক্ষ = ডানপক্ষ [প্রমাণিত]
(v) \( \frac{2\text{tan}^2 30^\circ}{1-\text{tan}^2 30^\circ} + \text{sec}^2 45^\circ – \text{cot}^2 45^\circ = \text{sec}60^\circ \)
সমাধান –
বামপক্ষ –
\( \frac{2\text{tan}^2 30^\circ}{1-\text{tan}^2 30^\circ} + \text{sec}^2 45^\circ – \text{cot}^2 45^\circ \)= \( \frac{2(\frac{1}{\sqrt{3}})^2}{1-(\frac{1}{\sqrt{3}})^2} + (\sqrt{2})^2 – (1)^2 \)
= \( \frac{\frac{2}{3}}{1-\frac{1}{3}} + 2 – 1 \)
= \( \frac{\frac{2}{3}}{\frac{2}{3}} + 1 \)
= \( 1+1 \)
= \( 2 \)
ডানপক্ষ –
\( \text{sec}60^\circ = 2 \)∴ বামপক্ষ = ডানপক্ষ [প্রমাণিত]
(vi) \( \tan^2\frac{\pi}{4} \sin\frac{\pi}{3} \tan\frac{\pi}{6} \tan^2\frac{\pi}{3} = 1\frac{1}{2} \)
সমাধান –
\( \tan^2\frac{\pi}{4} \sin\frac{\pi}{3} \tan\frac{\pi}{6} \tan^2\frac{\pi}{3} \)= \((1)^2 \times \frac{\sqrt{3}}{2} \times \frac{1}{\sqrt{3}} \times (\sqrt{3})^2 \)
= \(\frac{3}{2} \)
= \(1\frac{1}{2} \)
∴ \( \tan^2\frac{\pi}{4} \sin\frac{\pi}{3} \tan\frac{\pi}{6} \tan^2\frac{\pi}{3} = 1\frac{1}{2} \) [প্রমাণিত]
(vii) \( \sin\frac{\pi}{3} \tan\frac{\pi}{6} + \sin\frac{\pi}{2} \cos\frac{\pi}{3} = 2 \sin^2\frac{\pi}{4} \)
সমাধান –
বামপক্ষ –
\( \sin\frac{\pi}{3} \tan\frac{\pi}{6} + \sin\frac{\pi}{2} \cos\frac{\pi}{3} \)= \( \frac{\sqrt{3}}{2}\times\frac{1}{\sqrt{3}} + 1\times\frac{1}{2} \)
= \( \frac{1}{2} + \frac{1}{2} \)
= \( 1 \)
ডানপক্ষ –
\( 2 \sin^2\frac{\pi}{4} \)= \( 2 \times (\frac{1}{\sqrt{2}})^2 \)
= \( 2 \times \frac{1}{2} \)
= \( 1 \)
বামপক্ষ = ডানপক্ষ [প্রমাণিত]
7. (i) \( x \sin45^\circ \cos45^\circ \tan60^\circ = \tan45^\circ – \cos60^\circ \) হলে, x-এর মান নির্ণয় করি।
সমাধান –
\( x \sin45^\circ \cos45^\circ \tan60^\circ = \tan45^\circ – \cos60^\circ \)বা, \( x \times \frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}} \times \sqrt{3} = 1 – \frac{1}{2} \)
বা, \( \frac{x\sqrt{3}}{2} = \frac{1}{2} \)
বা, \( x = \frac{1}{\sqrt{3}} \)
∴ \( x = \frac{1}{\sqrt{3}} \)
7. (ii) \( x \sin60^\circ \cos^2 30^\circ = \frac{\tan^2 45^\circ \sec60^\circ}{cosec60^\circ} \)
সমাধান –
\( x \sin60^\circ \cos^2 30^\circ = \frac{\tan^2 45^\circ \sec60^\circ}{cosec60^\circ} \)বা, \( x \times \frac{\sqrt{3}}{2} \times \left(\frac{\sqrt{3}}{2}\right)^2 = \frac{1 \times 2}{\frac{2}{\sqrt{3}}} \)
বা, \( x \times \frac{\sqrt{3}}{2} \times \frac{3}{4} = \sqrt{3} \)
বা, \( x = \frac{8\sqrt{3}}{3\sqrt{3}} \)
বা, \( x = \frac{8}{3} \)
বা, \( x = 2\frac{2}{3} \)
∴ x এর মান \( 2\frac{2}{3} \)
7. (iii) \( x^2 = \sin^2 30^\circ + 4 \cot^2 45^\circ – \sec^2 60^\circ \) হলে, x এর মান নির্ণয় করি।
সমাধান –
\( x^2 = \sin^2 30^\circ + 4 \cot^2 45^\circ – \sec^2 60^\circ \)বা, \( x^2 = \left(\frac{1}{2}\right)^2 + 4(1)^2 – (2)^2 \)
বা, \( x^2 = \frac{1}{4} + 4 – 4 \)
বা, \( x^2 = \frac{1}{4} \)
বা, \( x = \pm \frac{1}{2} \)
∴ x এর মান \( \pm \frac{1}{2} \)
8. \(x \tan 30^\circ + y \cot 60^\circ = 0\) এবং \(2x – y \tan 45^\circ = 1\) হলে, x ও y –এর মান হিসাব করে লিখি।
সমাধান –
প্রদত্ত সমীকরণ দুটি হল,
\(x \tan 30^\circ + y \cot 60^\circ = 0\)বা, \(x \times \frac{1}{\sqrt{3}} + y \times \frac{1}{\sqrt{3}} = 0\)
বা, \(\frac{1}{\sqrt{3}} (x+y)=0\)
বা, \(x + y = 0\) — (i)
এবং \(2x – y \tan 45^\circ = 1\)
বা, \(2x – y(1) = 1\)
বা, \(2x – y = 1\)—(ii)
(i) ও (ii) নং সমীকরণ যোগ করে পাই,
\(x+y + 2x – y = 1\)বা, \(3x = 1\)
বা, \(x = \frac{1}{3}\)
X এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই,
\(x + y = 0\)বা, \(\frac{1}{3} + y = 0\)
বা, \(y = -\frac{1}{3}\)
∴ নির্ণেয় সমাধান \(x = \frac{1}{3}\) এবং \(y = -\frac{1}{3}\)।
9. যদি A=B =45° হয়,তবে যাচাই করি যে,
(i) \(\sin(A+B) = \sin A \cos B + \cos A \sin B\)
(ii) \(\cos(A+B) = \cos A \cos B – \sin A \sin B\)
সমাধান –
(i) \(\sin(A+B) = \sin A \cos B + \cos A \sin B\)
বামপক্ষ –
\(\sin(A+B)\)= \( \sin(45^\circ+45^\circ)\)
= \( \sin 90^\circ\)
= \( 1\)
ডানপক্ষ –
\(\sin A \cos B + \cos A \sin B\)= \( \sin 45^\circ \cos 45^\circ + \cos 45^\circ \sin 45^\circ\)
= \( \left(\frac{1}{\sqrt{2}}\right) \times \left(\frac{1}{\sqrt{2}}\right) + \left(\frac{1}{\sqrt{2}}\right) \times \left(\frac{1}{\sqrt{2}}\right)\)
= \( \frac{1}{2} + \frac{1}{2}\)
= \( 1\)
∴ \(\sin(A+B) = \sin A \cos B + \cos A \sin B\) [প্রমাণিত]
(ii) \(\cos(A+B) = \cos A \cos B – \sin A \sin B\)
বামপক্ষ –
\(\cos(A+B)\)= \( \cos(45^\circ+45^\circ)\)
= \( \cos 90^\circ\)
= \( 0\)
ডানপক্ষ –
\(\cos A \cos B – \sin A \sin B\)= \( \cos 45^\circ \cos 45^\circ – \sin 45^\circ \sin 45^\circ\)
= \( \left(\frac{1}{\sqrt{2}}\right) \times \left(\frac{1}{\sqrt{2}}\right) – \left(\frac{1}{\sqrt{2}}\right) \times\left(\frac{1}{\sqrt{2}}\right)\)
= \( \frac{1}{2} – \frac{1}{2}\)
= \( 0\)
∴ \(\cos(A+B) = \cos A \cos B – \sin A \sin B\) [প্রমাণিত]
10 (i). ABC সমবাহু ত্রিভুজের BD মধ্যমা। প্রমাণ করি যে, tan∠ABD = cot∠BAD
সমাধান –
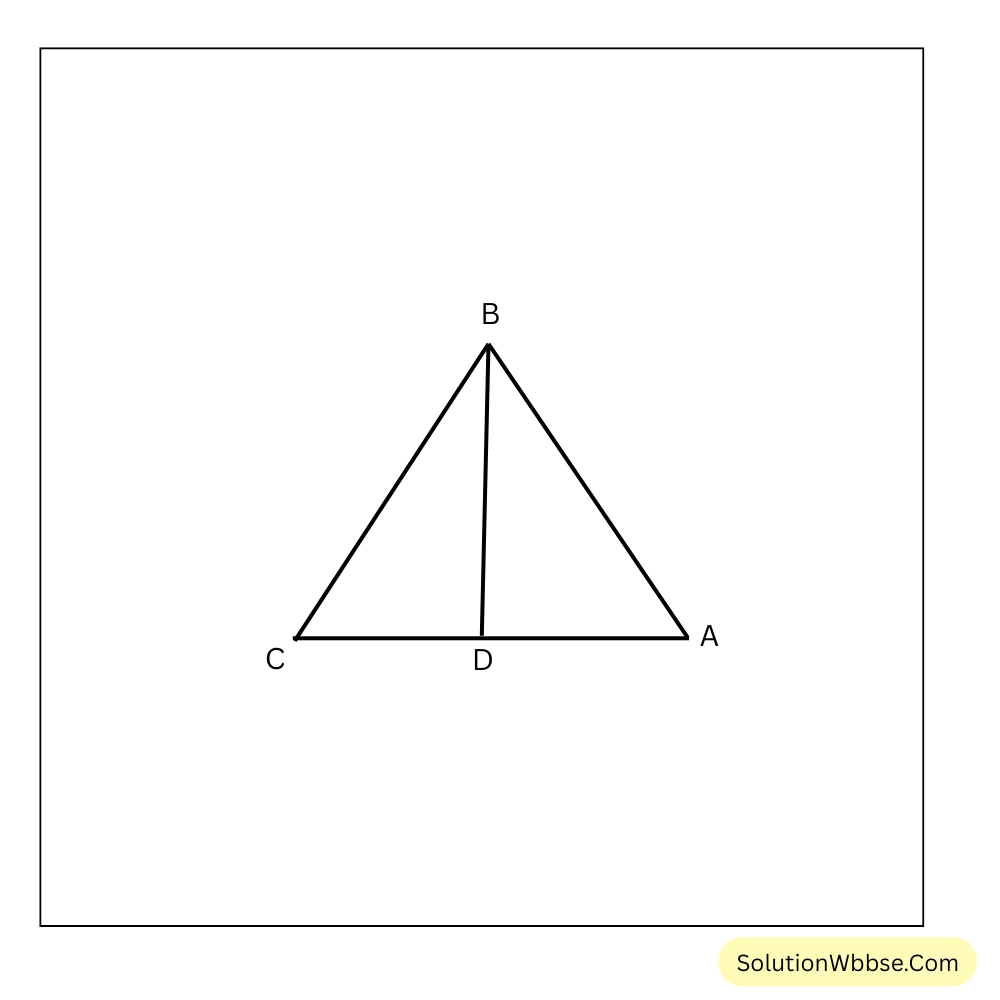
ABC সমবাহু ত্রিভুজের BD মধ্যমা।
∴ BD ⊥ AC
∴ ABD সমকোণী ত্রিভুজ যার ∠ADB সমকোণ।
∠ABD এর সাপেক্ষে,
tan ∠ABD = লম্ব/ভূমি = AD/BD
∠BAD এর সাপেক্ষে,
cot ∠BAD = ভূমি/লম্ব = AD/BD
∴ tan ∠ABD = cot ∠BAD [প্রমাণিত]
10 (ii). \(\triangle ABC\) সমদ্বিবাহু ত্রিভুজের \(AB = AC\) এবং \(\angle BAC = 90^\circ\) ; \(\angle BAC\) এর সমদ্বিখণ্ডক \(BC\) বাহুকে \(D\) বিন্দুতে ছেদ করে। প্রমাণ করি যে, \(\dfrac{sec \angle ACD}{sin \angle CAD} = cosec^2 \angle CAD\)
সমাধান –
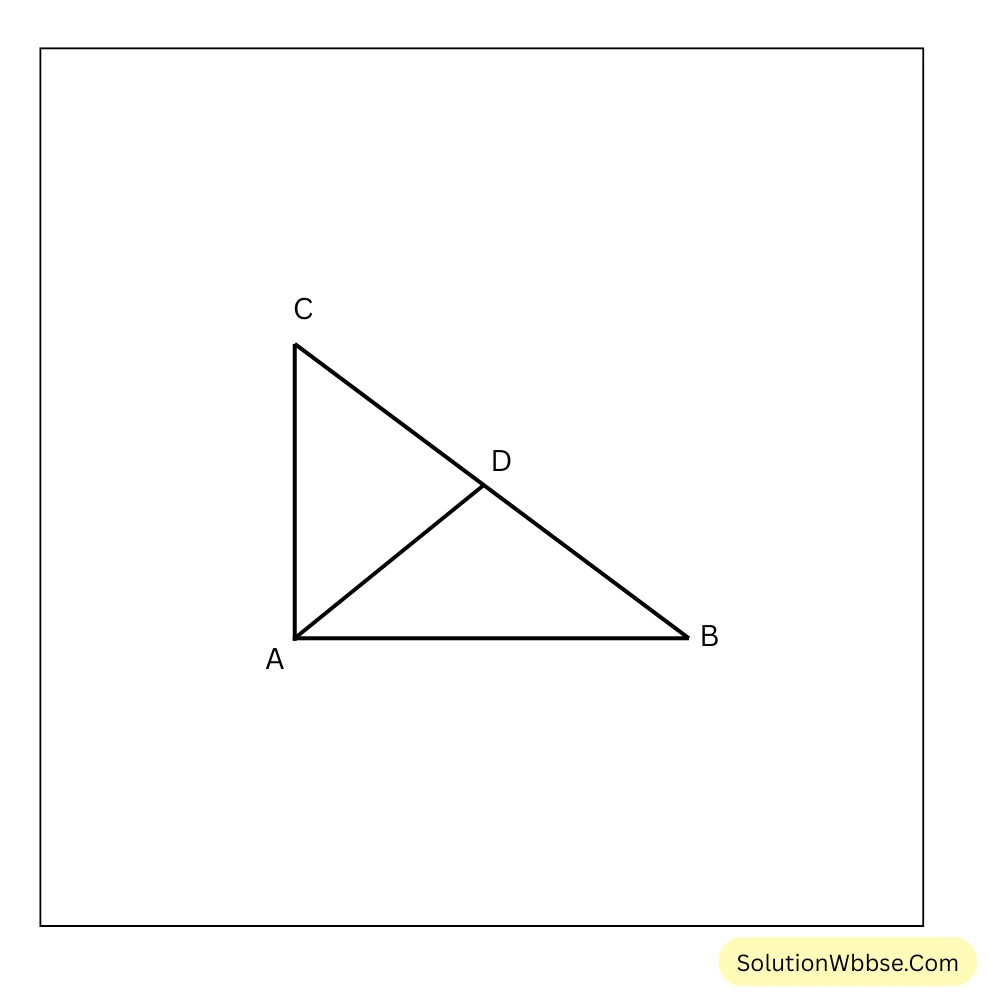
\(\triangle ABC\) সমদ্বিবাহু ত্রিভুজের \(AB = AC\) এবং \(\angle BAC = 90^\circ\) ; \(\angle BAC\) -এর সমদ্বিখণ্ডক \(AD\) \(BC\) বাহুকে \(D\) বিন্দুতে ছেদ করে।
প্রমাণ করতে হবে \(\dfrac{sec \angle ACD}{sin \angle CAD} = cosec^2 \angle CAD\)
প্রমাণ – \(\triangle ABC\) -এর \(\angle BAC = 90^\circ\) এবং \(\angle BAC\) -এর সমদ্বিখণ্ডক \(AD\)
\(\therefore \angle BAD = \angle CAD = 45^\circ\)আবার \(\triangle ABC\) ত্রিভুজের \(\angle BAC = 90^\circ\) এবং \(AB = AC\)
\(\therefore \angle ACB = \angle ABC = 45^\circ\)বা, \(\angle ACD = \angle ABD = 45^\circ\)
\(\therefore \dfrac{sec \angle ACD}{sin \angle CAD} = \dfrac{sec 45^\circ}{sin 45^\circ} = \dfrac{\sqrt{2}}{1/\sqrt{2}} = 2\)এবং \(cosec^2 \angle CAD = cosec^2 45^\circ = (\sqrt{2})^2 = 2\)
\(\therefore \dfrac{sec \angle ACD}{sin \angle CAD} = cosec^2 \angle CAD\) [প্রমাণিত]
11. \(\theta\) (\(0^\circ \leq \theta \leq 90^\circ\)) –এর কোন মান /মানগুলির জন্য \(2\cos^2\theta – 3\cos\theta + 1 = 0\) সত্য হবে নির্ণয় করি।
সমাধান –
\(2\cos^2\theta – 3\cos\theta + 1 = 0\)বা, \(2\cos^2\theta – (2+1)\cos\theta + 1 = 0\)
বা, \(2\cos^2\theta – 2\cos\theta – \cos\theta + 1 = 0\)
বা, \(2\cos\theta (\cos\theta – 1) – 1(\cos\theta – 1) = 0\)
বা, \((\cos\theta – 1)(2\cos\theta – 1) = 0\)
দুটি রাশির গুণফল শূন্য,
হয় \((\cos\theta – 1) = 0\)
বা, \(\cos\theta = 1\)
বা, \(\cos\theta = \cos 0^\circ\)
বা, \(\theta = 0^\circ\)
অথবা \((2\cos\theta – 1) = 0\)
বা, \(\cos\theta = \frac{1}{2}\)
বা, \(\cos\theta = \cos 60^\circ\)
বা, \(\theta = 60^\circ\)
∴ \(\theta\) -এর মান \(0^\circ\) বা \(60^\circ\)
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের ত্রয়োবিংশ অধ্যায়, ‘ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি’ -এর ‘কষে দেখি – 23.2’ বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment