এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের দ্বাবিংশ অধ্যায়, ‘পিথাগোরাসের উপপাদ্য’ -এর উপপাদ্যমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

উপপাদ্য 49. পিথাগোরাসের উপপাদ্য: যে কোনো সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের সমষ্টির সমান।
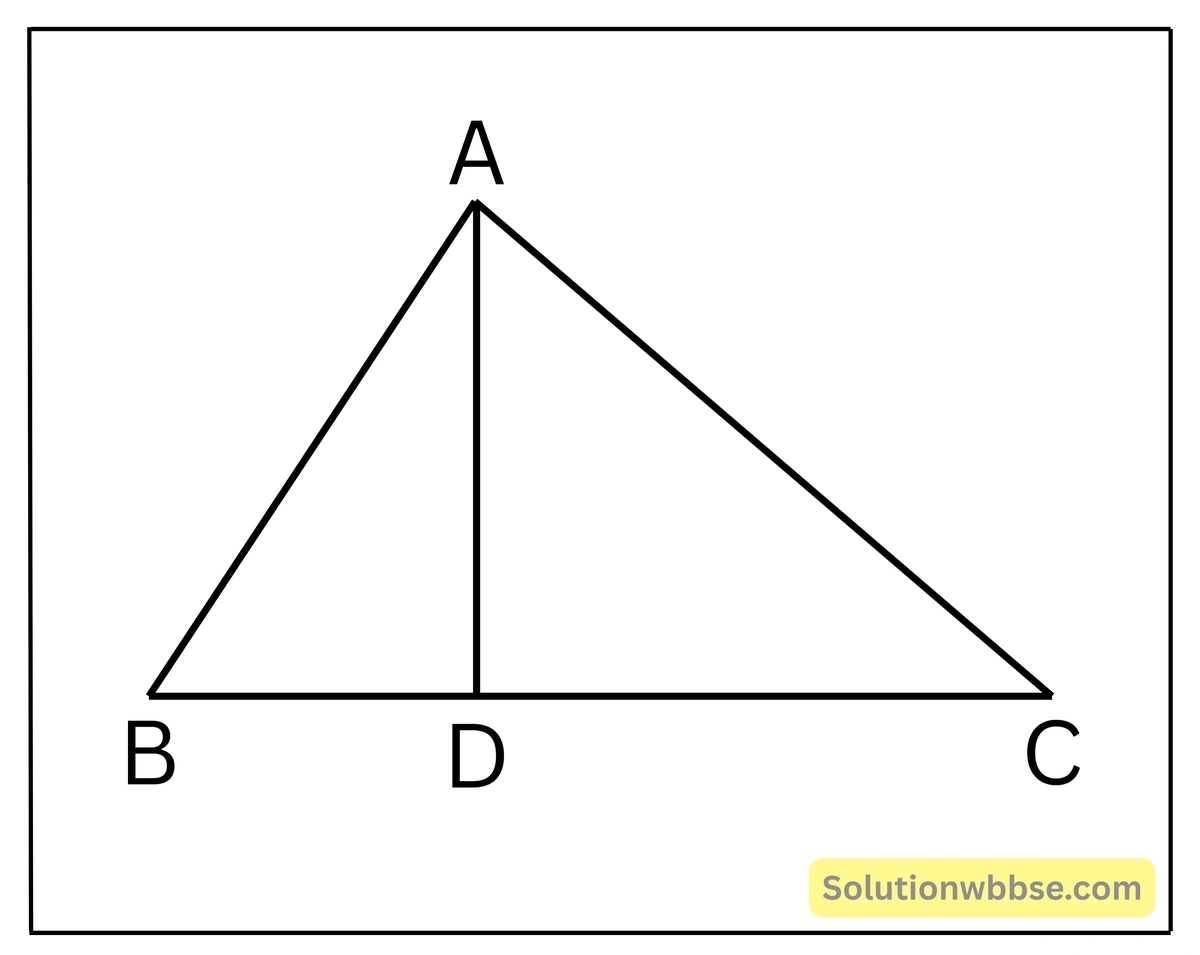
প্রদত্ত – ABC একটি সমকোণী ত্রিভুজ যার ∠A সমকোণ।
প্রমাণ করতে হবে – BC² = AB² + AC²
অঙ্কন – সমকৌণিক বিন্দু A থেকে অতিভুজ BC-এর উপর AD লম্ব অঙ্কন করলাম যা BC বাহুকে D বিন্দুতে ছেদ করে।
প্রমাণ – সমকোণী ত্রিভুজ ABC-এর অতিভুজ BC-এর উপর AD লম্ব।
∴ ΔABD ও ΔCBA সদৃশ। সুতরাং, \(\frac{AB}{BC} = \frac{BD}{AB}\)
∴ AB² = BC.BD …………….(I)
আবার, ΔCAD ও ΔCBA সদৃশ। সুতরাং, \(\frac{AC}{BC} = \frac{DC}{AC}\)
∴ AC² = BC.DC …………….(II)
সুতরাং (I) ও (II) যোগ করে পাই, AB² + AC² = BC.BD + BC.DC = BC (BD + DC) = BC.BC = BC²
∴ BC² = AB² + AC² [প্রমাণিত]
উপপাদ্য 50. পিথাগোরাসের উপপাদ্যের বিপরীত উপপাদ্য যে-কোনো ত্রিভুজের একটি বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান হলে প্রথম বাহুর বিপরীত কোণটি সমকোণ হবে।
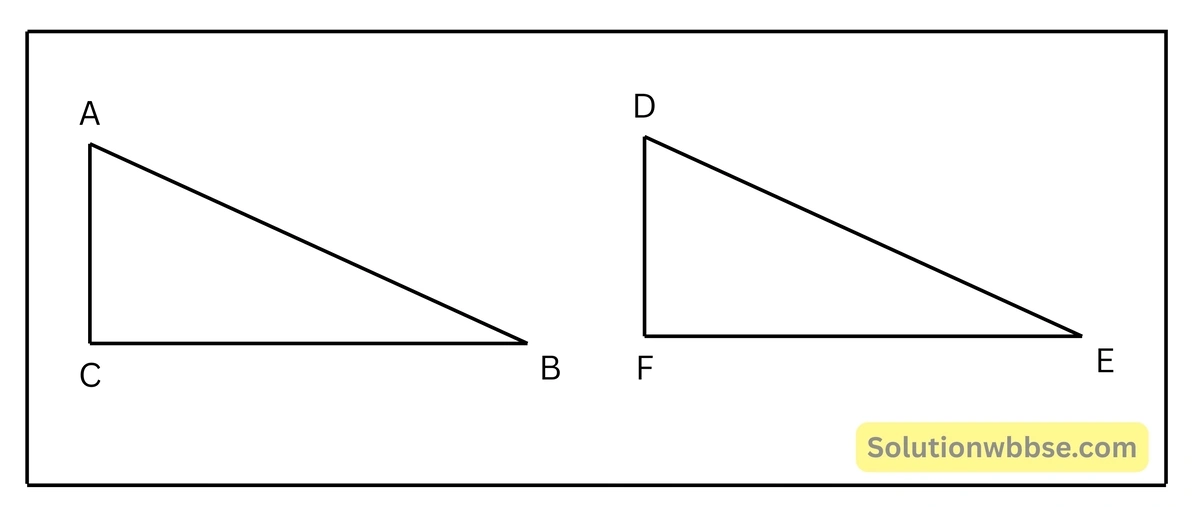
প্রদত্ত – ΔABC-এর AB বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল BC ও AC বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান। অর্থাৎ, \(AB^2 = AC^2 + BC^2\)
প্রমাণ করতে হবে – ∠ACB = 1 সমকোণ
অঙ্কন – CB-এর সমান করে FE সরলরেখাংশ অঙ্কন করলাম। FE বাহুর উপর F বিন্দুতে লম্ব অঙ্কন করলাম এবং সেই লম্ব থেকে CA বাহুর সমান করে FD অংশ কেটে নিলাম এবং D ও E বিন্দুদ্বয় যোগ করলাম।
প্রমাণ – \(AB^2 = BC^2 + AC^2\) [প্রদত্ত]
\(= EF^2 + DF^2\) [∵ অঙ্কনানুসারে, EF = BC এবং AC = DF]
\(= DE^2\) [∵ ∠DFE = 1 সমকোণ]
∴ AB = DE
এখন ΔABC ও ΔDEF -তে, AB = DE, BC = EF এবং AC = DF
∴ ΔABC ≅ ΔDEF (S-S-S সর্বসমতার শর্তানুসারে)
∴ ∠ACB = ∠DFE = 1 সমকোণ [∵ DF ⊥ EF অঙ্কনানুসারে]
∴ ∠ACB = 1 সমকোণ [প্রমাণিত]
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের দ্বাবিংশ অধ্যায়, ‘পিথাগোরাসের উপপাদ্য’ -এর উপপাদ্যমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন