মাধ্যমিক পরীক্ষা শিক্ষার্থীদের জীবনে একটি গুরুত্বপূর্ণ পর্ব। এই পরীক্ষার ফলাফল ভবিষ্যতের পথ নির্ধারণে গুরুত্বপূর্ণ ভূমিকা পালন করে। তাই, পরীক্ষার জন্য ভালোভাবে প্রস্তুতি নেওয়া অত্যন্ত জরুরি। পুরাতন বছরের প্রশ্ন ও উত্তর বিশ্লেষণ করাই এর একটি কার্যকর উপায়। এই আর্টিকেলে আমরা মাধ্যমিক গণিত পরীক্ষা ২০১৯ সালের প্রশ্ন ও উত্তর নিয়ে আলোচনা করব। এই প্রশ্নগুলো শিক্ষার্থীদের জন্য বিশেষ গুরুত্বপূর্ণ কারণ এগুলো পরীক্ষার ধরন, প্রশ্নের মান এবং বিষয়বস্তুর গভীরতা সম্পর্কে ধারণা দেয়। আশা করি, এই আর্টিকেলটি মাধ্যমিক গণিত পরীক্ষার জন্য প্রস্তুতি নেওয়ায় শিক্ষার্থীদের সাহায্য করবে।

1. নিম্নলিখিত প্রশ্নগুলির প্রতিটি ক্ষেত্রে সঠিক উত্তরটি নির্বাচন করো।
(i) কোনো অংশীদারী ব্যবসায়ে দুই বন্ধুর প্রাপ্ত লভ্যাংশের অনুপাত \(\frac12:\frac13\) হলে, তাদের মূলধনের অনুপাত –
(a) 2 : 3
(b) 3 : 2
(c) 1 : 1
(d) 5 : 3
Ans. (b) 3 : 2
সমাধান,
আমরা জানি কোনো অংশীদারি ব্যাবসায় মূলধনের অনুপাত এবং লভ্যাংশের অনুপাত সমান হয়।
∴ এক্ষেত্রে মূলধনের অনুপাত হবে
= \(\frac12:\frac13\)
= 3 : 2
(ii) যদি p + q = \(\sqrt3\) এবং p – q = \(\sqrt5\) হয়, তাহলে pq-এর মান –
(a) 2
(b) 18
(c) 9
(d) 8
Ans. (a) 2
সমাধান,
\(pq=\left(\frac{p+q}2\right)^2-\left(\frac{p-q}2\right)^2\)= \(\left(\frac{\sqrt{13}}2\right)^2-\left(\frac{\sqrt5}2\right)^2\)
= \(\frac{13}4-\frac54\)
= \(\frac84\)
= 2
(iii) কোনো বৃত্তের কেন্দ্র O এবং ব্যাস AB। ABCD বৃত্তস্থ চতুর্ভুজ। ∠ABC = 65°, ∠DAC = 40° হলে ∠BCD-এর মান –
(a) 75°
(b) 105°
(c) 115°
(d) 80°
Ans. (c) 115°
সমাধান,
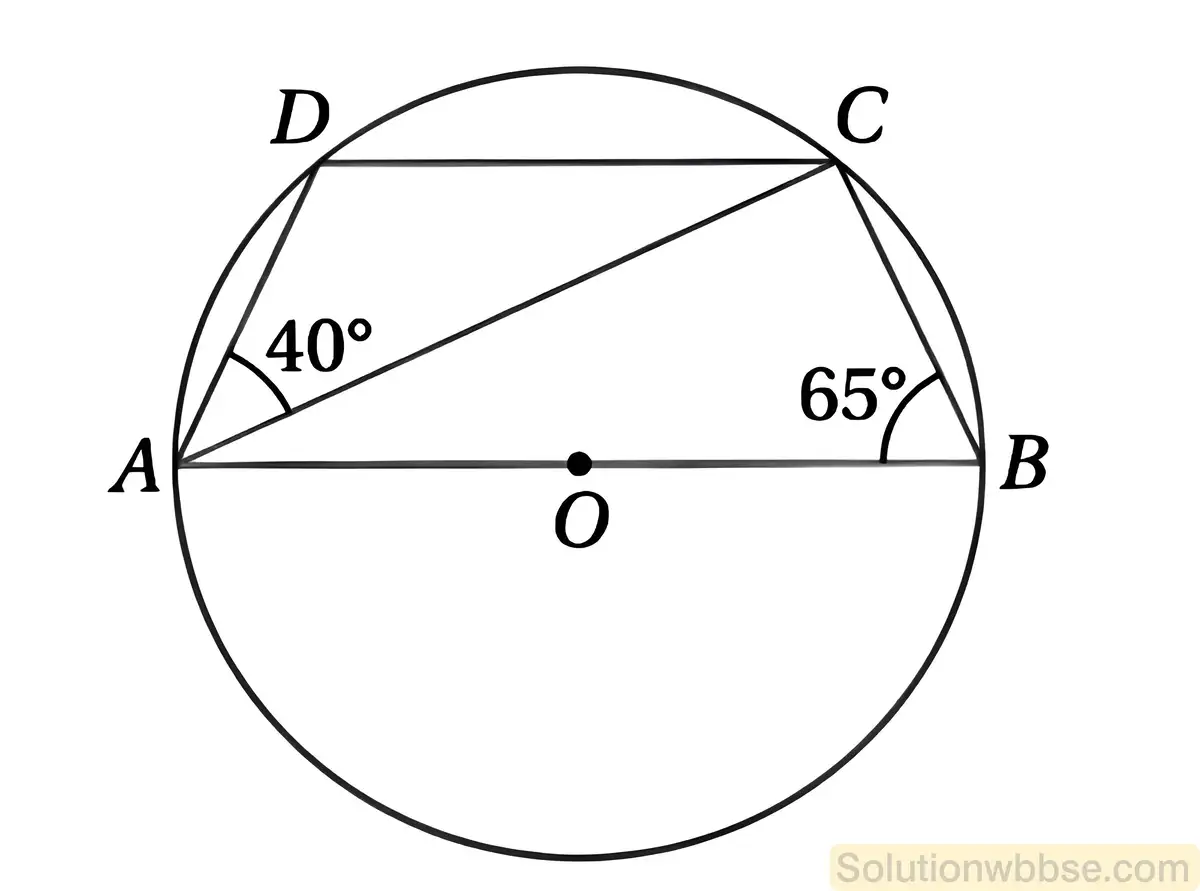
∠ACB অর্ধ বৃত্তস্থ কোণ
∴ ∠ACB = 90°
∴ ∠BAC = 180° – (∠ACB + ∠ABC)
= 180° – (90° + 65°)
= 180° – 155°
= 25°
∴ ∠DAB = ∠DAC + ∠BAC
= 40° + 25°
= 65°
আমরা জানি বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক
∴∠DAB + ∠BCD =180°
বা, 65° + ∠BCD = 180°
বা, ∠BCD = 180° – 65°
বা, ∠BCD = 115°
(iv) tanα + cotα = 2 হলে tan13α + cot13α-এর মান –
(a) 13
(b) 2
(c) 1
(d) 0
Ans. (b) 2
সমাধান,
tanα + cotα = 2
বা, \(\tan\alpha+\frac1{\tan\alpha}=2\)
বা, \(\frac{\tan^2\alpha+1}{\tan\alpha}=2\)
বা, tan²α + 1 = 2tanα =2
বা, tan²α – 2tanα + 1 = 0
বা, (tanα – 1)² = 0
বা, (tana – 1) =0
বা, tanα =1
∴ \(cot\alpha=\frac1{\tan\alpha}=1\)
∴ tan13α + cot13α
= (1)13 + (1)13
= 1 + 1
= 2 [Ans.]
(v) \(2\sqrt6\) সেমি বাহুবিশিষ্ট দুটি ঘনক পাশাপাশি রাখলে উৎপন্ন আয়তঘনকটির কর্ণের দৈর্ঘ্য হবে –
(a) 10 সেমি
(b) 6 সেমি
(c) 2 সেমি
(d) 12 সেমি
Ans. (d) 12 সেমি
সমাধান,
\(2\sqrt6 \) সেমি বাহু বিশিষ্ট দুটি ঘনক পাশাপাশি রাখলে উৎপন্ন আয়তঘনকটির দৈর্ঘ্য (I) = \(2\sqrt6+2\sqrt6=4\sqrt6\)
প্রস্থ (b) = \(2\sqrt6\) সেমি
উচ্চতা (h) = \(2\sqrt6\) সেমি
∴ আয়তঘনকটির কর্ণের দৈর্ঘ্য হবে
= \(\sqrt{\left(I\right)^2+{(b)}^2+{(h)}^2}\)
= \(\sqrt{\left(4\sqrt6\right)^2+{(2\sqrt6)}^2+{(2\sqrt6)}^2}\)
= \(\sqrt{96+24+24}\)
= \(\sqrt{144}\)
= 12 cm.
(vi) x1, x2, x3 …., x10 রাশিগুলির গড় 20 হলে x1 + 43 x2 + 43 x3 + 4, …., x10 + 4 রাশিগুলির গড় হবে –
(a) 20
(b) 24
(c) 40
(d) 10
Ans. (b) 24
সমাধান,
x1, x2,x3 ……, x10 রাশিগুলির গড় 20
∴ \(\frac{x_1+x_2+x_3+ ……+x_{10}}{10}=20\)
বা, x1 + x2 + x3 +……+ x10 = 200
∴ X1 + 4, X2 + 4 +…….+ X10 + 4 রাশিগুলির গড় হবে –
= \(\frac{x_1+4+x_2+4+x_3+4+…….+x_{10}+4}{10}\)
= \(\frac{x_1+x_2+x_3+…….+x_{10}+40}{10}\)
= \(\frac{200+40}{10}\)
= \(\frac{240}{10}\)
= 24
2. শূন্যস্থান পূরণ করো (যে-কোনো পাঁচটি)
(i) এক ব্যক্তি ব্যাংকে 100 টাকা জমা রেখে, 2 বছর পর সমূল চক্রবৃদ্ধি পেলেন 121 টাকা। বার্ষিক সুদের হার ছিল_______%।
Ans. 10%
সমাধান,
ধরি, বার্ষিক সুদের হার r %
∴ \(100\left(1+\frac r{100}\right)^2=121\)
বা, \(\left(1+\frac r{100}\right)^2=\frac{121}{100}\)
বা, \(\left(1+\frac r{100}\right)^2=\frac{121}{100}\)
বা, \(\left(1+\frac r{100}\right)^2=\left(\frac{11}{10}\right)^2\)
বা, \(\left(1+\frac r{100}\right)=\frac{11}{10}\)
বা, \(\frac r{100}=\frac{11}{10}-1\)
বা, \(\frac r{100}=\frac1{10}\)
বা, \(r=\frac{100}{10}\)
বা, r = 10
∴ বার্ষিক সুদের হার 10%
(ii) দুটি দ্বিঘাত করণীর যোগফল ও গুণফল একটি মূলদ সংখ্যা হলে করণীদ্বয়_______করণী।
Ans. অনুবন্ধী করণী
(iii) দুটি ত্রিভুজের ভূমি একই সরলরেখায় অবস্থিত এবং ত্রিভুজ দুটির অপর শীর্ষবিন্দুটি সাধারণ হলে, ত্রিভুজ দুটির ক্ষেত্রফলের অনুপাত ভূমির দৈর্ঘ্যের অনুপাতের_______।
Ans. সমান
(iv) \(\frac{\cos53^\circ}{\sin37^\circ}\)-এর সরলতম মান_______।
সমাধান,
\(\frac{\cos53^\circ}{\sin37^\circ}\)= \(\frac{\cos53^\circ}{\sin\left(90^\circ-53^\circ\right)}\)
= \(\frac{\cos53^\circ}{\sin53^\circ}\)
= 1
(v) একটি লম্ব বৃত্তাকার চোঙের তলসংখ্যা_______।
Ans. 3টি।
(vi) x1, x2,…., X100 চলগুলি ঊর্ধ্বক্রমে থাকলে, এদের মধ্যমা_______।
Ans. \(\frac{x_{50}+x_{51}}2\)
সমাধান,
= = == \(\frac{x_{50}+x_{51}}2\)
3. সত্য বা মিথ্যা লেখো (যে-কোনো পাঁচটি)
(i) বার্ষিক 10% হারে 100 টাকার 1 বছরের সরল সুদ ও চক্রবৃদ্ধি সুদের পার্থক্য 1 টাকা।
Ans. মিথ্যা।
[এক বছরের চক্রবৃদ্ধি সুদ ও সরল সুদ সমান হয়।]
(ii) ab : c2, bc : a2 এবং ca : b2-এর যৌগিক অনুপাত 1 : 1।
Ans. সত্য।
সমাধান,
ab : c², bc : a², ca : b² -এর যৌগিক অনুপাত
=ab × bc × ca : c² × a² × b²
= a² b²c² : a² b²c²
= 1:1
(iii) তিনটি অসমরেখ বিন্দু দিয়ে একটি মাত্র বৃত্ত আঁকা যায়।
Ans. সত্য।
(iv) sin 30° + sin 60° > sin 90°।
Ans. সত্য।
সমাধান,
sin30° + sin60°
= \(\frac12+\frac{\sqrt3}2\)
= \(\frac{1+\sqrt3}2\)
= \(\frac{1+1.732}2\)
= \(\frac{2.732}2\)
= 1.366 > 1 = sin90°
(v) একই ভূমি ও একই উচ্চতা বিশিষ্ট একটি লম্ব বৃত্তাকার শঙ্কু ও একটি লম্ব বৃত্তাকার চোঙের আয়তনের অনুপাত 1 : 3 হবে।
Ans. সত্য।
সমাধান,
ধরি, লম্ব বৃত্তাকার শঙ্কু ও লম্ব বৃত্তাকার চোঙের ব্যাসার্ধ r একক এবং উচ্চতা h একক।
∴ এদের আয়তনের অনুপাত
= \(\frac13\mathrm{πr}^2\mathrm h:\mathrm{πr}^2\mathrm h\)
= 1: 3
(vi) 2, 3, 9, 10, 9, 3, 9 তথ্যের মধ্যমার মান 10।
Ans. মিথ্যা।
সমাধান,
সংখ্যা গুলিকে মানের উর্দ্ধক্রমে সাজিয়ে পাই,
2, 3, 3, 9, 9, 9, 10
এক্ষেত্রে n = 7
∴ মধ্যমা = \(\frac{\left(n+1\right)}2\)তম মান
= \(\frac82\)তম মান
= 4
∴ 4 তম মান = 9
4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাও (যে-কোনো দশটি)
(i) বার্ষিক 5% সরল সুদের হারে কত টাকার মাসিক সুদ 1 টাকা হবে তা নির্ণয় করো।
সমাধান
ধরি আসল = x টাকা
শর্তানুসারে,
বা, \(I=x\times\frac1{12}\times\frac5{100}\)
বা, x = \(\frac{12\times100}5\)
বা, x = 12 × 20
বা, x = 240
∴ মাসিক সুদ 240 টাকা।
(ii) এক অংশীদারী ব্যবসায় তিনজনের মূলধনের অনুপাত 3 : 5 : 8, প্রথম ব্যক্তির লাভ তৃতীয় ব্যক্তির লাভের থেকে 60 টাকা কম হলে ব্যবসায় মোট কত লাভ হয়েছিল?
সমাধান,
ধরি, বাবসায় মোেট লাভ হয়েছিল x টাকা।
প্রথম ব্যাক্তির লাভ = \(\frac3{3+5+8}\times x\) টাকা
= \(\frac{3x}{16}\) টাকা
প্রথম ব্যাক্তির লাভ = \(\frac8{3+5+8}\times x\) টাকা
= \(\frac{8x}{16}\) টাকা
∴ \(\frac{8x}{16}-\frac{3x}{16}=60\)
বা, \(\frac{8x-3x}{16}=60\)
বা, \(\frac{5x}{16}=60\)
বা, 5x = 60 × 16
বা, x = \(\frac{60\times16}5\)
বা, x = 192
∴ ব্যাবসায় মোট লাভ 192 টাকা।
(iii) \(\frac a2=\frac b3=\frac c4=\frac{2a-3b+4c}p\) হলে, p-এর মান কত?
সমাধান,
ধরি, \(\frac a2=\frac b3=\frac c4=\frac{2a-3b+4c}p=k \) [k(≠0)একটি আনুপাতিক ধ্রুবক]
∴ a = 2k, b = 3k, c = 4k
এবং \(\frac{2a-3b+4c}p=k\)
বা, \(\frac{2(2k)-3\left(3k\right)+4\left(4k\right)}p=k\)
বা, \(\frac{4k-9k+16k}p=k\)
বা, \(\frac{11k}p=k\)
বা, p = 11
(iv) x ∝ y2 এবং y = 2a, x = a হলে দেখাও যে y2 = 4ax।
সমাধান,
x ∝ y2
বা, x = ky2
বা, a = k(2a)2
বা, a = k(4a)2
বা, k = \(\frac a{4a^2}\)
বা, k = \(\frac 1{4a^2}\)
∴ x = ky2
বা, x = \(\frac{y^2}{4a}\)
বা, y2 = 4ax [প্রমাণিত]
(v) ABCD ট্রাপিজিয়ামের BC||AD এবং AD = 4 সেমি। AC ও BD কর্ণদ্বয় এমনভাবে O বিন্দুতে ছেদ করে যে \(\frac{AO}{OC}=\frac{DO}{OB}=\frac12\) হয়। BC-এর দৈর্ঘ্য কত?
সমাধান,
ABCD ট্রাপিজিয়ামের BC||AD এবং AD = 4 সেমি.। AC ও BD কর্ণদ্বয় এমনভাবে O বিন্দুতে ছেদ করে যে, \( \frac{AO}{OC}=\frac{DO}{OB}=\frac12\) হয়
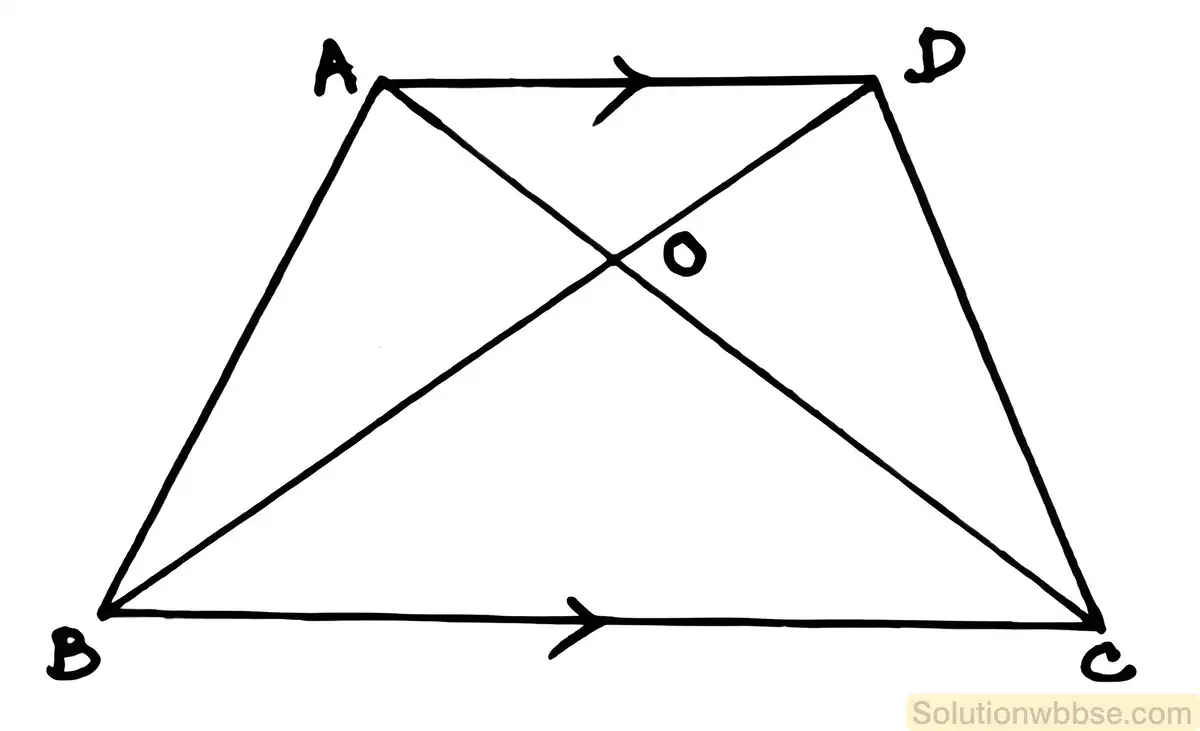
ΔAOD ও ΔCOB এর ক্ষেত্রে,
∠OAD = ∠OCD [ একান্তর কোণ, যেহেতু, AD||BC এবং AC ভেদক]
আবার, ∠ODA = ∠OCB [একান্তর কোণ, যেহেতু, AD||BC এবং DB ভেদক]
∠AOD = ∠BOC [বিপ্রতীপ কোন]
∴ ΔAOD এবং ΔCOB সদৃশকোণী। যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী,
∴ \(\frac{AO}{CO}=\frac{DO}{OB}=\frac{AD}{BC}\)
আবার, \(\frac{AO}{OC}=\frac{DO}{OB}=\frac12\)[প্রদত্ত]
∴ \(\frac{AD}{BC}=\frac12\)
বা, \(\frac4{BC}=\frac12\) [যেহেতু, AD = 4সেমি.]]
বা, BC = 8
∴ BC এর দৈর্ঘ্য 8 সেমি.।
(vi) একটি বৃত্তে দুটি জ্যা AB এবং AC পরস্পর লম্ব। AB = 4 সেমি এবং AC = 3 সেমি হলে; বৃত্তটির ব্যাসার্ধের দৈর্ঘ্য নির্ণয় করো।
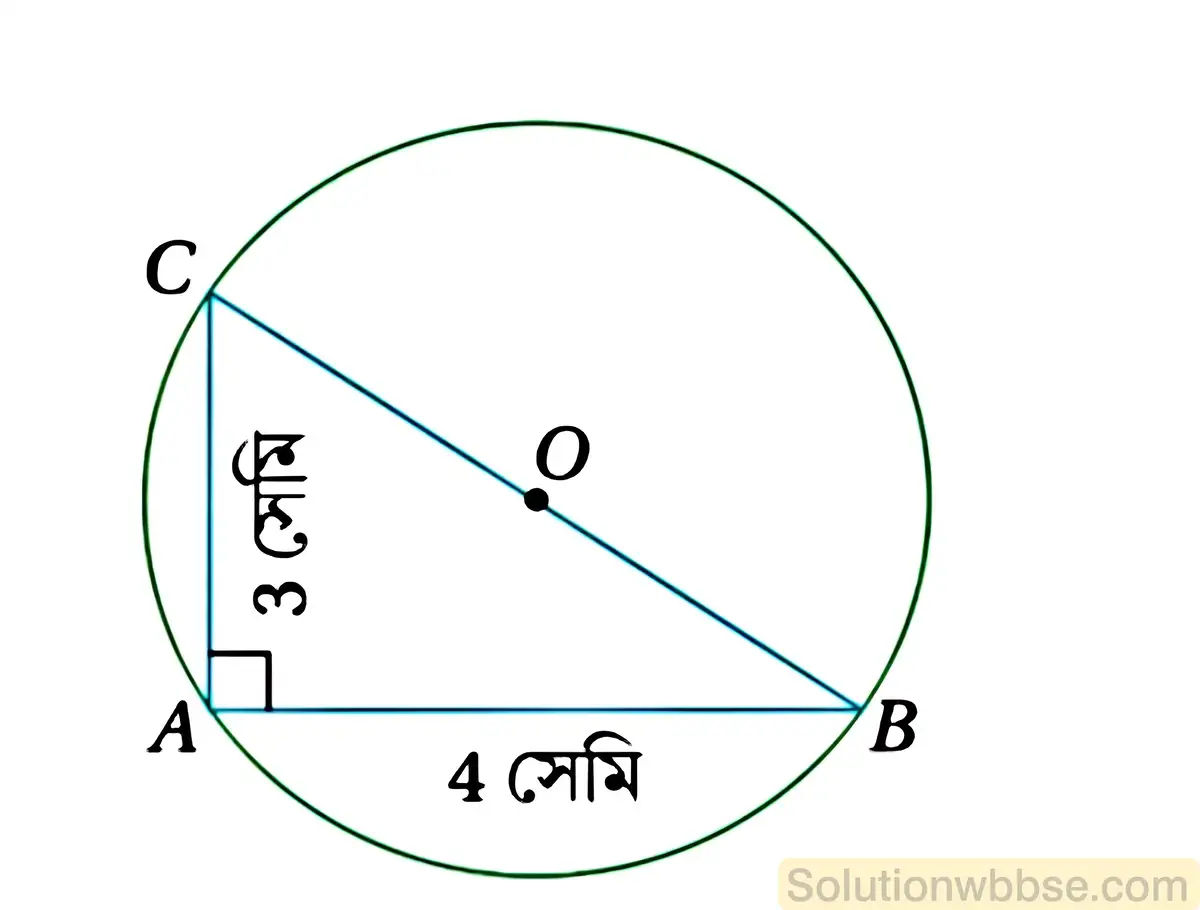
সমাধান,
যেহেতু, AB এবং AC জ্যা দুটি পরস্পর লম্ব সুতরাং ACB সমকোণী ত্রিভুজ। AB = 4 সেমি. ও AC = 3 সেমি.
∴ অতিভুজ BC = \(\sqrt{\left(AB\right)^2+\left(AC\right)^2}\)
= \(\sqrt{\left(4\right)^2+\left(3\right)^2}\)
= \(\sqrt{16+9}\)
= \(\sqrt{25}\)
= 5
যেহেতু ∠BAC = 90°
∴ BC হল ব্যাস
∴ ব্যাসার্ধ = \(\frac{BC}2 \) সেমি.
= \(\frac{5}2 \) সেমি.
= 2.5 সেমি.
(vii) ∆ABC এর ∠ABC = 90° এবং BD ⊥ AC, যদি AB = 5 সেমি এবং BC = 12 সেমি হয়, তবে BD-এর দৈর্ঘ্য কত?
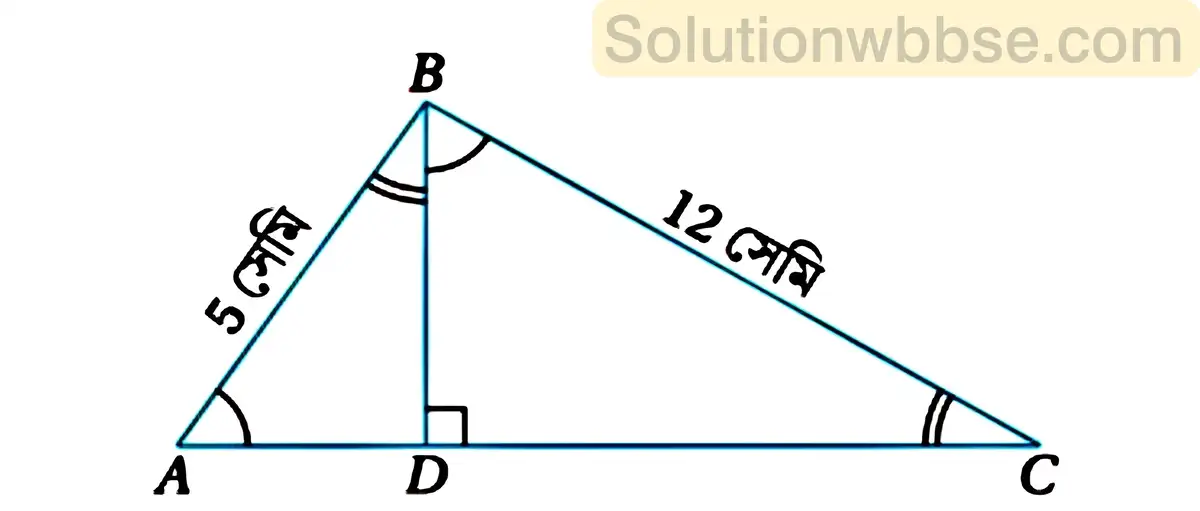
সমাধান,
ABC সমকোণী ত্রিভুজে,
\(AC=\sqrt{\left(AB\right)^2+\left(BC\right)^2}\)= \(\sqrt{\left(5\right)^2+\left(12\right)^2}\)
= \(\sqrt{25+144}\)
= \(\sqrt{169}\)
= 13
আবার ABC ত্রিভুজের ∠ABC = 90° এবং সমকৌণিক বিন্দু B থেকে অতিভুজ AC এর উপর BD লম্ব। যেহেতু সমকোণী ত্রিভুজের সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা মূল ত্রিভুজের সঙ্গে সদৃশ।
∴ ΔАВС ~ ΔADB
∴ \(\frac{AC}{AB}=\frac{BC}{BD}\)
বা, \(BD=\frac{AB\times BC}{AC}\)
= \(\frac{5\times 12}{13}\) সেমি
= \(\frac{60}{13}\)
= \(4\frac8{13}\)
∴ BD = \(4\frac8{13}\) সেমি.
(viii) θ (0° ≤ θ ≤ 90°)-এর কোন্ মান/মানগুলির জন্য 2sinθcosθ = cosθ হবে?
সমাধান,
2sinθcosθ = cosθ
বা, 2sinθcosθ – cosθ = 0
বা, cosθ (2sinθ – 1) = 0
হয়, cosθ = 0
বা, cosθ = cos90°
বা, θ = 90°
অথবা, (2sinθ – 1) = 0
বা, sinθ = \(\frac12\)
বা, sinθ = sin30°
∴ θ = 30°
∴ θ = 90° অথবা θ = 30° হলে 2sinθcosθ = cosθ হবে।
(ix) sín10θ cos8θ এবং 10θ ধনাত্মক সূক্ষ্মকোণ হলে, tan9θ-এর মান নির্ণয় করো।
সমাধান,
sín10θcos8θ
sin10θ = cos8θ
বা, cos(90° – 10θ) = cos8θ
বা, 90° – 10θ = 8θ
বা, – 10θ – 8θ = – 90°
বা, – 18θ = – 90°
বা, 18θ = 90°
বা, θ = \(\frac{90^\circ}{18}\)
বা, θ = 5°
∴ tan9θ
= tan(9×5°)
= tan45°
= 1
(x) একটি আয়তঘনাকৃতি ঘরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে a, b এবং c একক এবং a + b + c = 25, ab + bc + ca = 240.5 হলে ঘরটির মধ্যে যে বৃহত্তম দণ্ডটি রাখা যাবে তার দৈর্ঘ্য কত হবে?
সমাধান,
a + b + c = 25 এবং ab + bc + ca = 240.5
এখন, a² + b² + c² = (a + b + c)² – 2(ab + bc + ca)
বা, a² + b² + c² = (25)² – 2(240.5)
= 625 – 481
= 144
বা, \(\sqrt{a^2+b^2+c^2}=\sqrt{144}\)
বা, \(\sqrt{a^2+b^2+c^2}=12\)
∴ আয়তঘনাকৃতি ঘরের কর্ণের দৈর্ঘ্য 12 একক অর্থাৎ ওই ঘরে সর্বাপেক্ষা যে লম্বা দণ্ডটি রাখা যাবে তার মান 12 একক।
(xi) একটি লম্ব বৃত্তাকার শঙ্কুর পার্শ্বতলের ক্ষেত্রফল ভূমির ক্ষেত্রফলের \(\sqrt5\) গুণ। শঙ্কুটির উচ্চতা ও ভূমির ব্যাসার্ধের অনুপাত কত?
সমাধান,
ধরি, লম্ব বৃত্তাকার শঙ্কুর ব্যাসার্ধ r একক, উচ্চতা h একক এবং তির্যক উচ্চতা l একক।
∴ লম্ব বৃত্তাকার শঙ্কুর পার্শ্বতলের ক্ষেত্রফল = πrl বর্গ একক এবং ভূমিতলের ক্ষেত্রফল πr² বর্গ একক
শর্তানুসারে,
πrl = \(\sqrt5\times\pi rl\)
বা, l = \(r\sqrt5\)
বা, l2 = 5r2 [উভয়পক্ষে বর্গ করে পাই]
বা, h2 + r2 = 5r2 [l2 = h2 + r2]
বা, h2 = 4r2
বা, \(\frac hr=\frac21\)
বা, h : r = 2 : 1
∴ শঙ্কুটির উচ্চতা ও ব্যাসার্ধের অনুপাত 2 : 1
(xii) প্রথম (2n + 1) সংখ্যক ক্রমিক স্বাভাবিক সংখ্যার মধ্যবর্তী সংখ্যা \(\frac{n+103}3\) হলে, n-এর মান নির্ণয় করো।
সমাধান,
প্রথম (2n + 1) সংখ্যক ক্রমিক স্বাভাবিক সংখ্যার মধ্যবর্তী সংখ্যা = (n + 1) তম সংখ্যা =(n + 1)
∴ (n + 1) = \(\frac{n+103}3\)
বা, 3n + 3 = n + 103
বা, 3n – n = 103 – 3
বা, 2n = 100
বা, n = \(\frac{100}2\)
বা, n = 50
∴ n = 50
5. যে-কোনো একটি প্রশ্নের উত্তর দাও।
(i) যদি 6 মাস অন্তর সুদ আসলের সঙ্গে যুক্ত হয় তাহলে বার্ষিক 10% চক্রবৃদ্ধি হার সুদে 8,000 টাকার \(1\frac12\) বছরের সমূল চক্রবৃদ্ধি ও চক্রবৃদ্ধি সুদ কত হবে?
সমাধান,
আসল (P) = 8000 টাকা
সুদের হার (r) = 10%
6 মাস অন্তর সুদ আসলের সঙ্গে যুক্ত হয় সুতরাং চক্রবৃদ্ধি সুদের পর্ব = 2
সময় (t) = \(1\frac12\) বছর
= \(\frac32\)
∴ \(1\frac12\) বছরের সমূল চক্রবৃদ্ধি
= \(P\left(1+\frac r{100}\right)^{2n}\) টাকা
= \(P\left(1+\frac5{100}\right)^{2\times\frac32}\) টাকা
= \(8000\left(1+\frac1{20}\right)^3\) টাকা
= \(8000\times\frac{21}{20}\times\frac{21}{20}\times\frac{21}{20}\) টাকা
= 9261 টাকা।
∴ সমূল চক্রবৃদ্ধি 9261 টাকা।
এবং চক্রবৃদ্ধি সুদ = সমূল চক্রবৃদ্ধি – আসল
= (9261 – 8000) টাকা
= 1261 টাকা।
(ii) দুই বন্ধু যথাক্রমে 40,000 টাকা ও 50,000 টাকা দিয়ে একটি অংশীদারী ব্যবসা শুরু করে। তাদের মধ্যে একটি চুক্তি হয় যে, লাভের 50% নিজেদের মধ্যে সমান ভাগে এবং লাভের অবশিষ্টাংশ মূলধনের অনুপাতে ভাগ হবে। প্রথম বন্ধুর লভ্যাংশ যদি দ্বিতীয় বন্ধুর লভ্যাংশ অপেক্ষা 800 টাকা কম হয়, তবে প্রথম বন্ধুর লভ্যাংশ কত?
সমাধান,
দুই বন্ধুর মুলধনের অনুপাত = 40000 : 50000
= 4 : 5
ধরি, মোট লাভ = x টাকা।
এখন, তাদের মধ্যে চুক্তি অনুযায়ী লাভের 50% তাদের মধ্যে সমান ভাগে ভাগ হয় এবং বাকি অংশ মূলধনের অনুপাতে ভাগ হয়।
লাভের 50% = \(x\times\frac{50}{100}\) টাকা
= \(\frac x2\) টাকা
এই \(\frac x2\) টাকা তাদের মধ্যে সমান ভাগে ভাগ হয়
∴ প্রত্যেকে পাবে \(\frac12\times\frac x2\) টাকা
= \(\frac x4\) টাকা করে।
∴ লাভের বাকি অংশ =\(\left(x-\frac x2\right)\)।
= \(\frac x2\) টাকা
এই \(\frac x2\) টাকা তাদের মধ্যে মূলধনের অনুপাতে ভাগ হয়
∴ প্রথম বন্ধু পাবে = \(\frac4{4+5}\times\frac x2\) টাকা
= \(\frac{4x}{18}\) টাকা
এবং দ্বিতীয় বন্ধু পাবে = \(\frac5{4+5}\times\frac x2\) টাকা
= \(\frac{5x}{18}\) টাকা
∴ প্রথম বন্ধুর মোট লাভ =\(\left(\frac x4+\frac{4x}{18}\right)\) টাকা
= \(\frac{9x+8x}{36}\) টাকা
= \(\frac{17x}{36}\) টাকা
এবং দ্বিতীয় বন্ধুর মোট লাভ = \(\left(\frac x4+\frac{5x}{18}\right)\) টাকা
= \(\frac{9x+10x}{36}\) টাকা
= \(\frac{19x}{36}\) টাকা
শর্তানুসারে,
\(\frac{19x}{36}-\frac{17x}{36}=800\\\)বা, \(\frac{19x-17x}{36}=800\)
বা, \(\frac{2x}{36}=800\)
বা, \(\frac x{18}=800\)
বা, x = 800 × 18
বা, x = 14400
∴ মোট লাভ = 14400 টাকা
এবং প্রথম বন্ধুর লাভ = \(\frac{17x}{36}\) টাকা
= \(\frac{17}{36}\times14400\) টাকা
= 6800 টাকা
∴ প্রথম বন্ধুর লাভের পরিমান 6800 টাকা।
6. যে-কোনো একটি প্রশ্নের উত্তর দাও।
(i) x2 + x + 1 = 0 সমীকরণটির বীজগুলির বর্গ যে সমীকরণের বীজ, সেই সমীকরণটি নির্ণয় করো।
সমাধান,
ধরি, x2 + x + 1 = 0 সমীকরনের বীজগুলি হল a এবং b আমাদের যে সমীকরণটি নির্ণয় করতে হবে তার বীজগুলি প্রদত্ত সমীকরণের বীজগুলির বর্গ হবে অর্থাৎ a2 এবং b2 বীজ বিশিষ্ট দ্বিঘাতসমীকরণ নির্ণয় করতে হবে
x2 + x + 1 = 0 সমীকরনের বীজগুলি হল a এবং b
যেহেতু, দ্বিঘাত সমীকরণের বীজদ্বয়ের যোগফল = – এবং দ্বিঘাত সমীকরণের বীজদ্বয়ের গুনফল =
∴ a + b = -1 এবং ab = 1
এখন, a2 + b2 = (a + b)2 – 2ab
= (-1)2 – 2(1) [যেহেতু, a + b = -1 এবং ab = 1]
= 1 – 2
= -1
এবং a2b2 = (ab)2
=(1)2 [∵ ab = 1]
= 1
নির্ণেয় সমীকরণটি হল,
x2 – (a2 + b2)x + a2b2 = 0
বা, x2 – (-1)x + 1 = 0
বা, x2 + x + 1 = 0
∴ x2 + x + 1 = 0 এই সমীকরণটি হল সেই সমীকরণ যার বীজগুলি প্রদত্ত দ্বিঘাত সমীকরণের বীজগুলির বর্গ।
(ii) কলমের মূল্য প্রতি ডজনে 6 টাকা কম হলে 30 টাকায় আরও তিনটি বেশী কলম পাওয়া যাবে। কমার পূর্বে প্রতি ডজন কলমের মূল্য নির্ণয় করো।
সমাধান,
ধরি প্রতি ডজন কলমের মূল্য x টাকা।
∴ x টাকায় পাওয়া যাবে 12 টি কলম
1 টাকায় পাওয়া যাবে \(\frac{12}x\) টি কলম
30 টাকায় পাওয়া যাবে \(\frac{\left(30\times12\right)}x\) টি কলম =\(\frac{360}x\) টি কলম।
এখন প্রতি ডজন কলমের মূল্য (x – 6) টাকা
∴ (x – 6) টাকায় পাওয়া যায় 12 টি কলম
1 টাকায় পাওয়া যায় \(\frac{12}{\left(x-6\right)}\) টি কলম
30 টাকায় পাওয়া যায় \(\frac{\left(30\times12\right)}{\left(x-6\right)}\)টি কলম = \(\frac{360}{\left(x-6\right)}\) টি কলম।
শর্তানুসারে,
\(\left(\frac{360}{x-6}-\frac{360}x\right)=3\)বা, \(360\left(\frac1{x-6}-\frac1x\right)=3\)
বা, \(\frac1{x-6}-\frac1x=\frac3{360}\)
বা, \(\frac{x-\left(x-6\right)}{x\left(x-6\right)}=\frac1{120}\)
বা, \(\frac6{x\left(x-6\right)}=\frac1{120}\)
বা, 720 = x(x – 6)
বা x2 – 6x = 720
বা, x2 – 6x – 720 = 0
বা, x2 – (30 – 24)x – 720 = 0
বা, x2 – 30x + 24x – 720 = 0
বা, x(x – 30) + 24(x – 30) = 0
বা, (x – 30) (x + 24) = 0
দুটি রাশির গুনফল শূন্য
∴ হয় (x – 30) = 0
বা, x = 30
অথবা, (x + 24) = 0
বা, x = -24
কলমের মূল্য ঋণাত্মক হতে পারেনা, সুতরাং x = 30
অর্থাৎ প্রতি ডজন কলমের মূল্য 30 টাকা।
7. যে-কোনো একটি প্রশ্নের উত্তর দাও।
(i)সরল করো:\(\frac{4\sqrt3}{2-\sqrt3}-\frac{30}{4\sqrt3-\sqrt{18}}-\frac{\sqrt{18}}{3-\sqrt{12}}\)
সমাধান,
\(\frac{4\sqrt3}{2-\sqrt3}-\frac{30}{4\sqrt3-\sqrt{18}}-\frac{\sqrt{18}}{3-\sqrt{12}}\\\)= \(\frac{4\sqrt3}{2-\sqrt2}-\frac{30}{4\sqrt3-\sqrt{3\times3\times2}}-\frac{\sqrt{3\times3\times2}}{3-\sqrt{2\times2\times3}}\)
= \(\frac{4\sqrt3}{2-\sqrt2}-\frac{30}{4\sqrt3-3\sqrt2}-\frac{3\sqrt2}{3-2\sqrt3}\)
হরের করণী নিরসন করে পাই,
= \(\frac{4\sqrt3}{2-\sqrt2}\times\frac{2+\sqrt2}{2+\sqrt2}-\frac{30}{4\sqrt3-3\sqrt2}\times\frac{4\sqrt3+3\sqrt2}{4\sqrt3+3\sqrt2}-\frac{3\sqrt2}{3-2\sqrt3}\times\frac{3+2\sqrt3}{3+2\sqrt3}\)
= \(\frac{4\left(2\sqrt3+\sqrt6\right)}{\left\{\left(2\right)^2-\left(\sqrt2\right)^2\right\}}-\frac{30\left(4\sqrt3+3\sqrt2\right)}{\left\{\left(4\sqrt3\right)^2-\left(3\sqrt2\right)^2\right\}}-\frac{3\left(3\sqrt2+2\sqrt6\right)}{\left\{\left(3\right)^2-\left(2\sqrt3\right)^2\right\}}\) [যেহেতু, \( a^2-b^2=\left(a+b\right)\left(a-b\right)\)]
= \(\frac{4\left(2\sqrt3+\sqrt6\right)}{4-2}-\frac{30\left(4\sqrt3+3\sqrt2\right)}{48-18}-\frac{3\left(3\sqrt2+2\sqrt6\right)}{9-12}\)
= \(\frac{4\left(2\sqrt3+\sqrt6\right)}2-\frac{30\left(4\sqrt3+3\sqrt2\right)}{30}-\frac{3\left(3\sqrt2+2\sqrt6\right)}{-3}\)
= \(2\left(2\sqrt3+\sqrt6\right)-\left(4\sqrt3+3\sqrt2\right)+\left(3\sqrt2+2\sqrt6\right)\)
= \(4\sqrt3+2\sqrt6-4\sqrt3-3\sqrt2+3\sqrt2+2\sqrt6\)
= \(4\sqrt6\)
(ii) যদি \(\left(\frac1x-\frac1y\right)\propto\frac1{x-y}\) হয় তবে দেখাও যে, (x² + y²) ∝ xy।
সমাধান,
\(\left(\frac1x-\frac1y\right)\propto\frac1{x-y}\\\)বা, \(\left(\frac1x-\frac1y\right)=\frac k{x-y}\) [k = (≠0) একটি সমানুপাতিক ধ্রুবক]
বা, \(\frac{\left(y-x\right)}{xy}=\frac k{x-y}\)
বা, (y – x)(x – y) = kxy
বা, -(x – y)² = kxy
বা, (x – y)² = -kxy
বা, x² – 2xy + y² = -kxy
বা, x² + y² = 2xy – kxy
বা, x² + y² = xy(2 – k)
বা, \(\frac{x^2+y^2}{xy}\) = (2 – k) = ধ্রুবক [যেহেতু k ধ্রুবক]
∴ (x² + y²) ∝ xy [প্রমাণিত]
8. যে-কোনো একটি প্রশ্নের উত্তর দাও।
(i) (3x – 2y) : (x + 3y) = 5 : 6 হলে, (2x + 5y) : (3x + 4y) নির্ণয় করো।
সমাধান,
(3x – 2y) : (x + 3y) = 5 : 6
বা, \(\frac{\left(3x+2y\right)}{\left(x+3y\right)}=\frac56\)
বা, 6(3x – 2y) = 5(x + 3y)
বা, 18x – 12y = 5x + 15y
বা, 18x – 5x = 12y + 15y
বা, 13x = 27y
বা, \(\frac xy=\frac{27}{13}\)
বা, \(\frac x{27}=\frac{2y}{13}=k\) (ধরি) [k (≠0) একটি সমানুপাতিক ধ্রুবক]
∴ x = 27k এবং y = 13k
∴ (2x + 5y) : (3x + 4y)
= {2(27k) + 5(13k)} : {3(27k) + 4(13k)}
= (54k + 65k) : (81k + 52k)
= 119k : 133k
= 119 : 133
= 17 : 19
∴ (2x + 5y) : (3x + 4y) = 17 : 19
(ii) যদি \(\frac{b+c-a}{y+z-x}=\frac{c+a-b}{z+x-y}=\frac{a+b-c}{x+y-z}\) হয়, তবে প্রমাণ করো যে, \(\frac ax=\frac by=\frac cz\)।
সমাধান,
\(\frac{b+c-a}{y+z-x}=\frac{c+a-b}{z+x-y}=\frac{a+b-c}{x+y-z}\\\)∴ প্রতিটি অনুপাতের মান
= \(\frac{b+c-a+c+a-b+a+b-c}{y+z-x+z+x-y+x+y-z}\) [সংযোজন প্রক্রিয়া]
= \(\frac{a+b+c}{x+y+z}\)
∴ \(\frac{b+c-a}{y+z-x}=\frac{a+b+c}{x+y+z}\)
বা, \(\frac{-\left(b+c-a\right)}{-\left(y+z-x\right)}=\frac{a+b+c}{x+y+z}=\frac{-b-c+a+a+b+c}{-y-z+x+x+y+z}\) [সংযোজন প্রক্রিয়া]
= \(\frac{2a}{2x}\)
= \(\frac ax\)
∴ প্রতিটি অনুপাত = \(\frac ax\)
আবার, \(\frac{c+a-b}{z+x-y}=\frac{a+b+c}{x+y+z}\)
বা, \(\frac{-\left(c+a-b\right)}{-\left(z+x-y\right)}=\frac{a+b+c}{x+y+z}=\frac{-c-a+b+a+b+c}{-z-x+y+x+y+z}\) [সংযোজন প্রক্রিয়া]
= \(\frac{2b}{2y}\)
= \(\frac by\)
∴ প্রতিটি অনুপাত = \(\frac by\)
এবং \(\frac{a+b-c}{x+y-z}=\frac{a+b+c}{x+y+z}\)
বা, \(\frac{-\left(a+b-c\right)}{-\left(x+y-z\right)}=\frac{a+b+c}{x+y+z}=\frac{-a-b+c+a+b+c}{-x-y+z+x+y+z}\) [সংযোজন প্রক্রিয়া]
= \(\frac{2c}{2z}\)
= \(\frac cz\)
∴ প্রতিটি অনুপাত = \(\frac cz\)
∴ \(\frac ax=\frac by=\frac cz\) [প্রমাণিত]
9. যে-কোনো একটি প্রশ্নের উত্তর দাও।
(i) অর্ধবৃত্তস্থ কোণ সমকোণ-প্রমাণ করো।
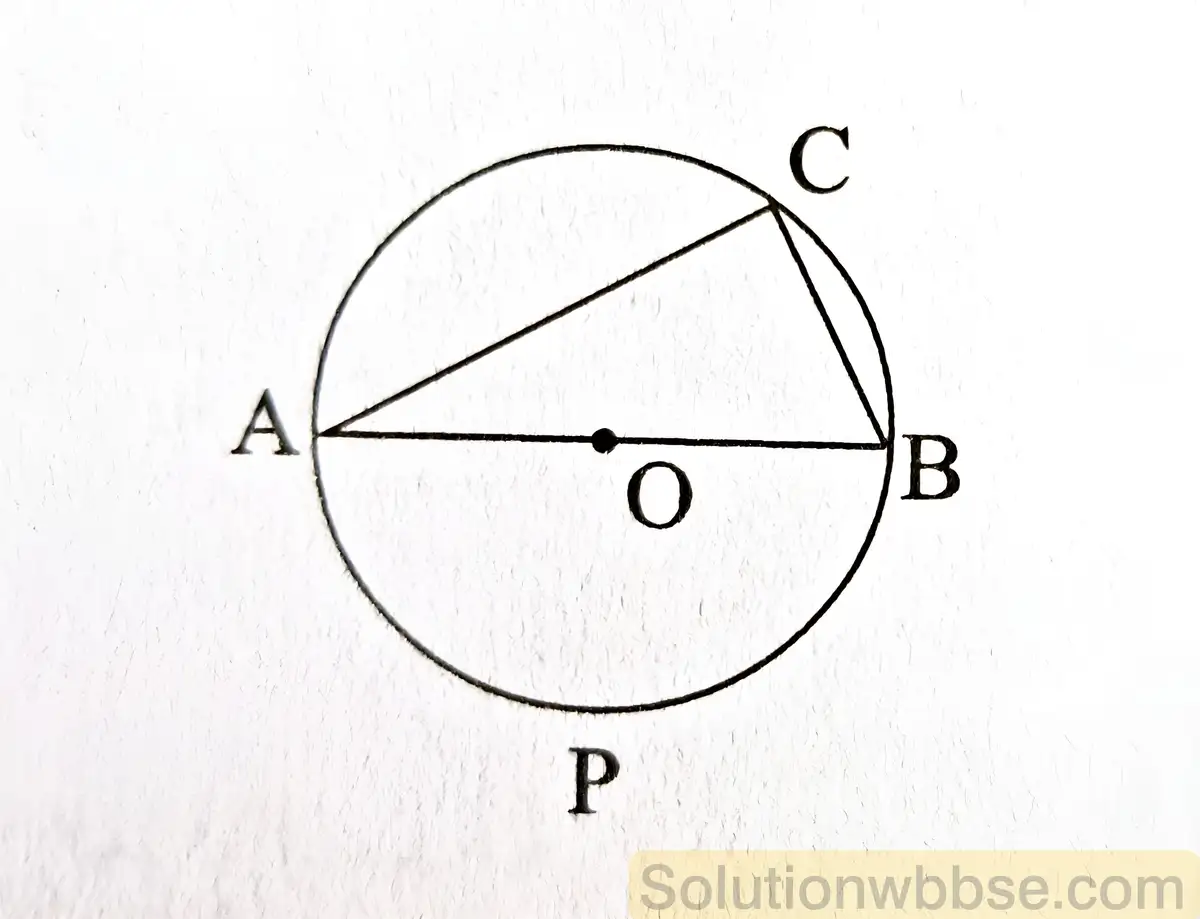
প্রদত্ত – O কেন্দ্রীয় বৃত্তের ∠ACB যে-কোনো একটি অর্ধবৃত্তস্থ কোণ।
প্রমাণ করতে হবে যে – ∠ACB = 1 সমকোণ।
প্রমাণ – O কেন্দ্রীয় বৃত্তের বৃত্তচাপের দ্বারা গঠিত সম্মুখ কেন্দ্রস্থ কোণটি ∠AOB এবং ∠ACB ওই বৃত্তচাপের দ্বারা গঠিত সম্মুখ বৃত্তস্থ কোণ।∴ ∠AOB = 2∠ACB_______(i)
যেহেতু AB একটি সরলরেখাংশ, সুতরাং ∠AOB একটি সরলকোণ।
∴ ∠AOB = 2 সমকোণ সুতরাং, 2∠ACB = 2 সমকোণ [(i) থেকে পেলাম]
∴ ∠ACB = 1 সমকোণ [প্রমাণিত]
(ii) প্রমাণ করো যে, যদি দুটি বৃত্ত পরস্পরকে বহিঃস্পর্শ করে, তাহলে স্পর্শ বিন্দুটি কেন্দ্র দুটির সংযোগ সরলরেখাংশের উপর অবস্থিত হবে।
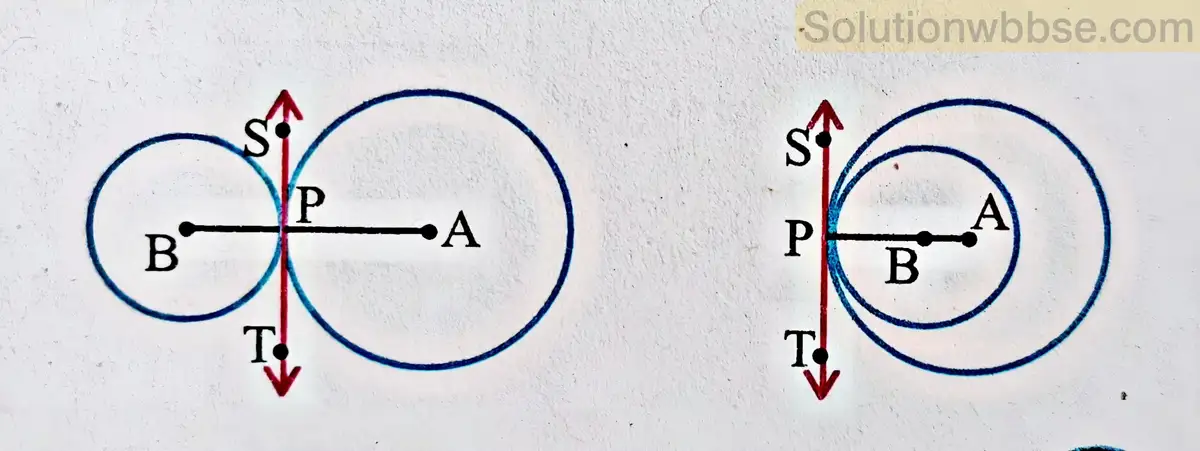
প্রদত্ত – A ও B কেন্দ্রীয় দুটি বৃত্ত পরস্পরকে P বিন্দুতে স্পর্শ করেছে।
প্রমাণ করতে হবে – A, P ও B সমরেখ।
অঙ্কন – A, P ও B, P যোগ করলাম।
প্রমাণ – A কেন্দ্রীয় ও B কেন্দ্রীয় বৃত্তদুটি পরস্পরকে P বিন্দুতে স্পর্শ করেছে।
∴ P বিন্দুতে বৃত্তদুটির একটি সাধারণ স্পর্শক আছে।
ধরি, ST হলো সাধারণ স্পর্শক যা দুটি বৃত্তকেই P বিন্দুতে স্পর্শ করেছে।
∵ A কেন্দ্রীয় বৃত্তের ST স্পর্শক এবং AP স্পর্শবিন্দুগামী ব্যাসার্ধ,
∴ AP ⊥ ST
আবার, যেহেতু B কেন্দ্রীয় বৃত্তের ST স্পর্শক এবং BP স্পর্শবিন্দুগামী ব্যাসার্ধ,
∴ BP ⊥ ST
∴ AP ও BP একই P বিন্দুতে ST সরলরেখার উপর লম্ব।
∴ AP ও BP একই সরলরেখায় অবস্থিত অর্থাৎ A, P ও B সমরেখ। [প্রমাণিত]
10. যে-কোনো একটি প্রশ্নের উত্তর দাও।
(i) O কেন্দ্রীয় বৃত্তে পরিলিখিত চতুর্ভুজ ABCD হলে প্রমাণ করো যে, AB + CD = BC + DA।
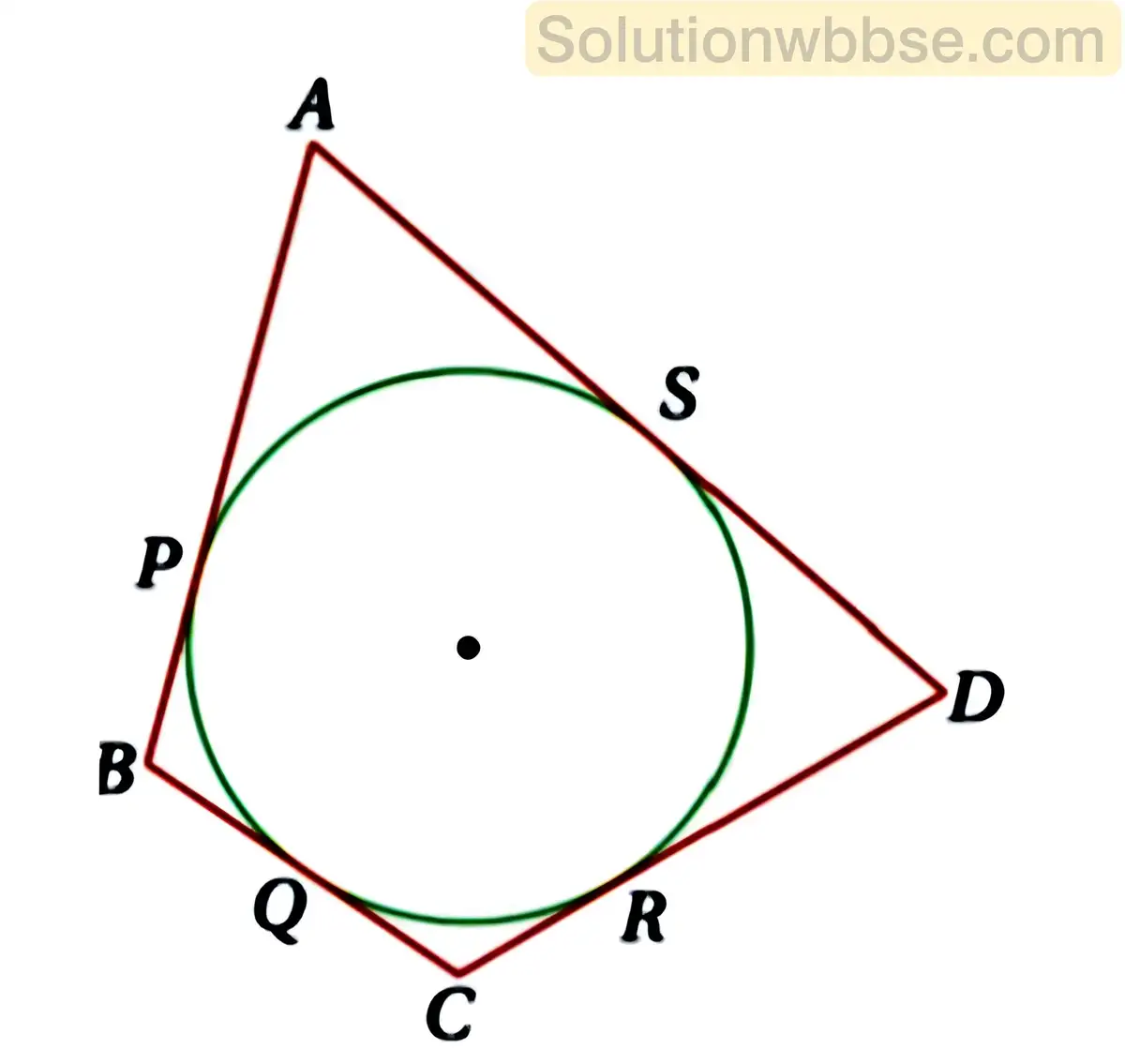
ধরাযাক, ABCD চতুর্ভুজটির AB, BC, CD এবং DA বাহুগুলি বৃত্তটিকে যথাক্রমে P,Q,R এবং S বিন্দুতে স্পর্শ করেছে।
প্রমাণ করতে হবে যে – AB + CD = BC + DA
A বিন্দু থেকে দুটি স্পর্শক AP ও AS টানা হয়েছে।
∴ AP = AS_______(i)
B বিন্দু থেকে দুটি স্পর্শক BP ও BQ অঙ্কন করা হয়েছে
∴ BP = BQ_______(ii)
আবার, C বিন্দু থেকে দুটি স্পর্শক CQ ও CR অঙ্কন করা হয়েছে।
∴ CQ = CR_______(iii)
এবং D বিন্দু থেকে দুটি স্পর্শক DS ও DR অঙ্কন অরা হয়েছে
∴ DS = DR_______(iv)
এখন AB + CD
= AP + PB + CR + RD
= AS + BQ + CQ + DS [(i), (ii), (iii) ও (iv) থেকে পাই]
= (AS + DS) + (BQ + CQ)
= AD + BC [প্রমাণিত]
(ii) ∆ABC এর ∠A সমকোণ এবং BP ও CQ দুটি মধ্যমা হলে, প্রমাণ করো যে; 5BC2 = 4(BP)2 + CQ2)।
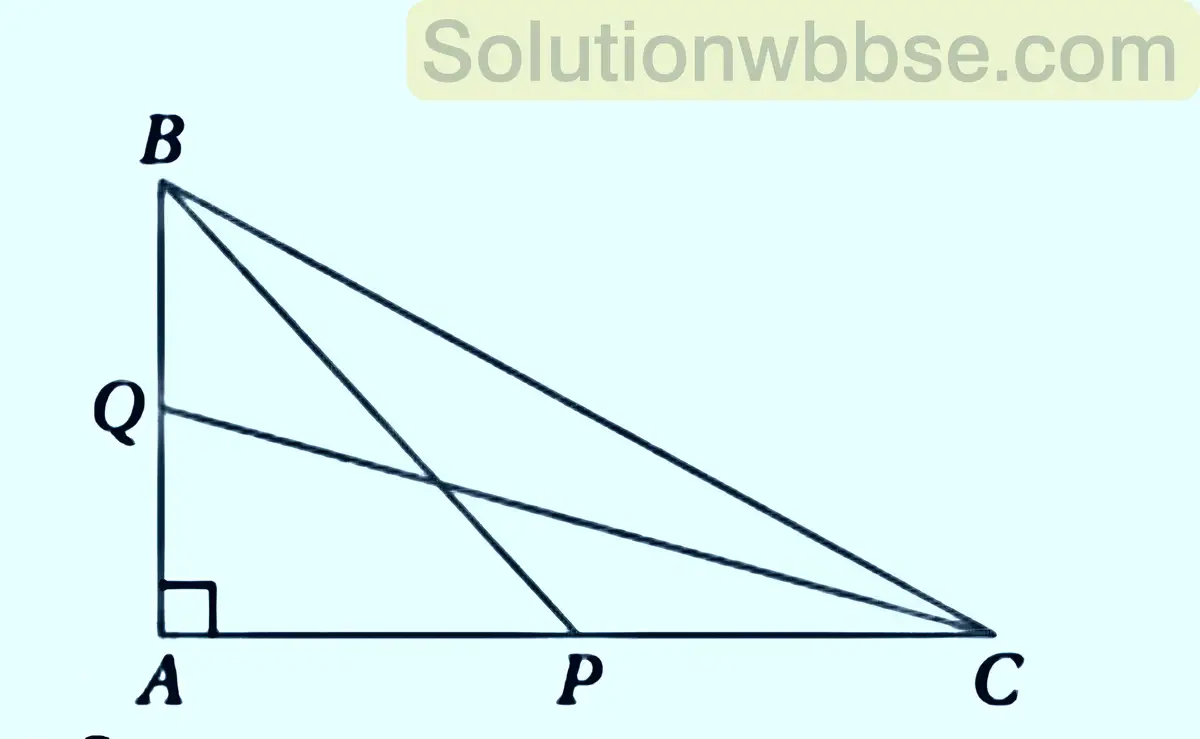
ত্রিভুজ ABC-এর ∠A সমকোণ এবং BP ও CQ দুটি মধ্যমা, প্রমাণ করতে হবে যে 5BC2 = 4(BP2 + CQ2)
প্রমাণ – ABC একটি সমকোণী ত্রিভুজ যার ∠A সমকোণ
∴ BC2 = AB2 + AC2
= (2AQ)2 + (2AP)2 [ যেহেতু P ও Q যথাক্রমে AC ও AB এর মধ্যবিন্দু]
∴ BC2 = 4AQ2 + 4AP2_______(i)
আবার সমকোণী ত্রিভুজ BAP ও CAQ থেকে পাওয়া যায়,
BP2 = AP2 + AB2
বা, BP2 = AP2 + (2AQ)2
বা, BP2 = AP2 + 4AQ2
এবং CQ2 = AC2 + AQ2
বা, CQ2 = (2AP)2 + AQ2
বা, CQ2 = 4AP2 + AQ2
∴ BP2 + CQ2
= AP2 + 4AQ2 + 4AP2 +AQ2
= 5AP2 + 5AQ2
= 5(AP2 + AQ2)_______(ii)
∴ 5BC2
= 5(4AQ2 + 4AP2) [(i) থেকে পাই]
= 4.{5(AQ2 + AP2)}
= 4 (BP2 + CQ2) [(ii) থেকে পাই ] [ প্রমাণিত]
11. যে-কোনো একটি প্রশ্নের উত্তর দাও।
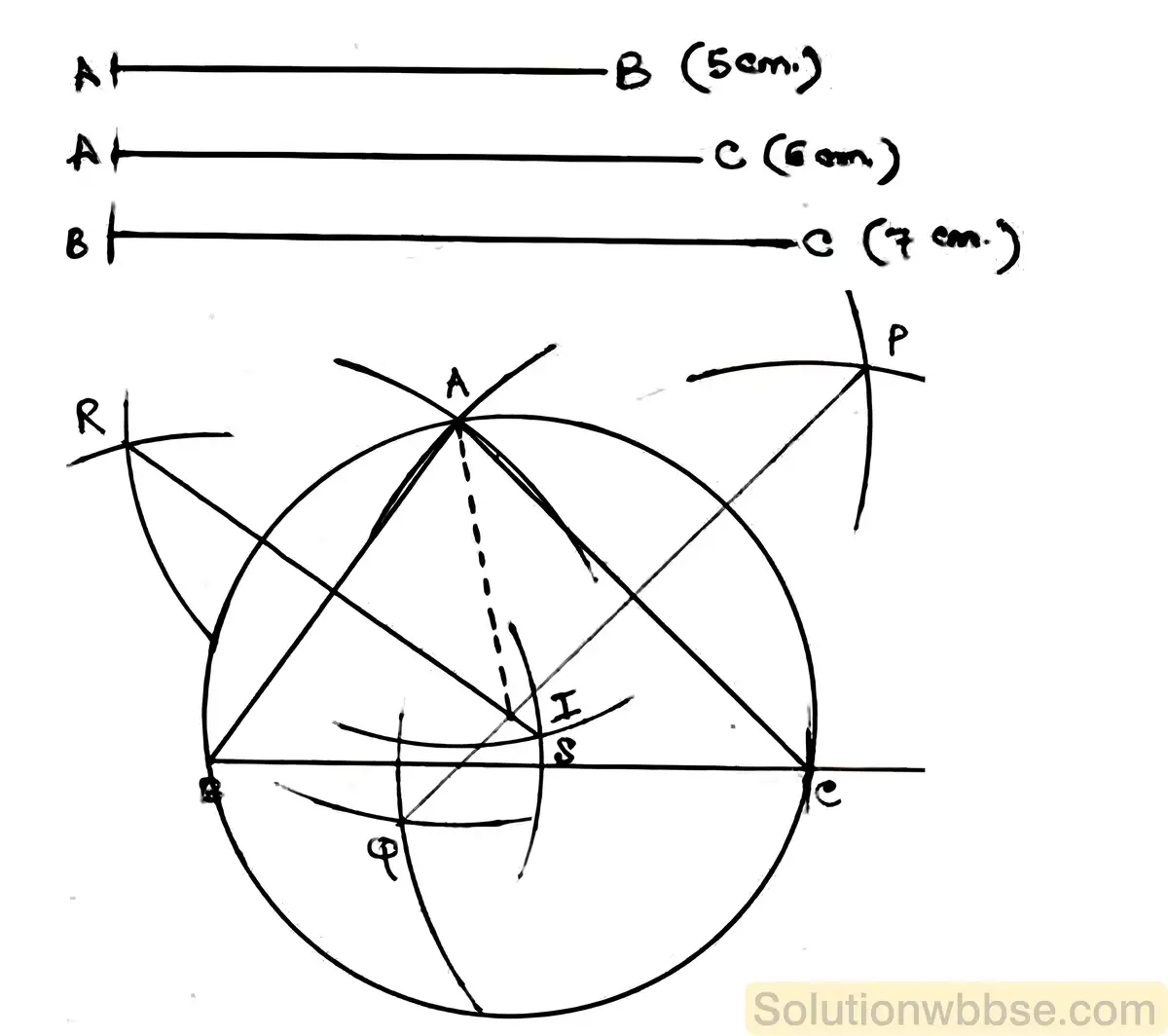
(i) ABC একটি ত্রিভুজ অঙ্কন করো যার BC = 7 সেমি, AB = 5 সেমি এবং AC = 6 সেমি। ABC ত্রিভুজটির পরিবৃত্ত অঙ্কন করো। (কেবলমাত্র অঙ্কন চিহ্ন দিতে হবে)।
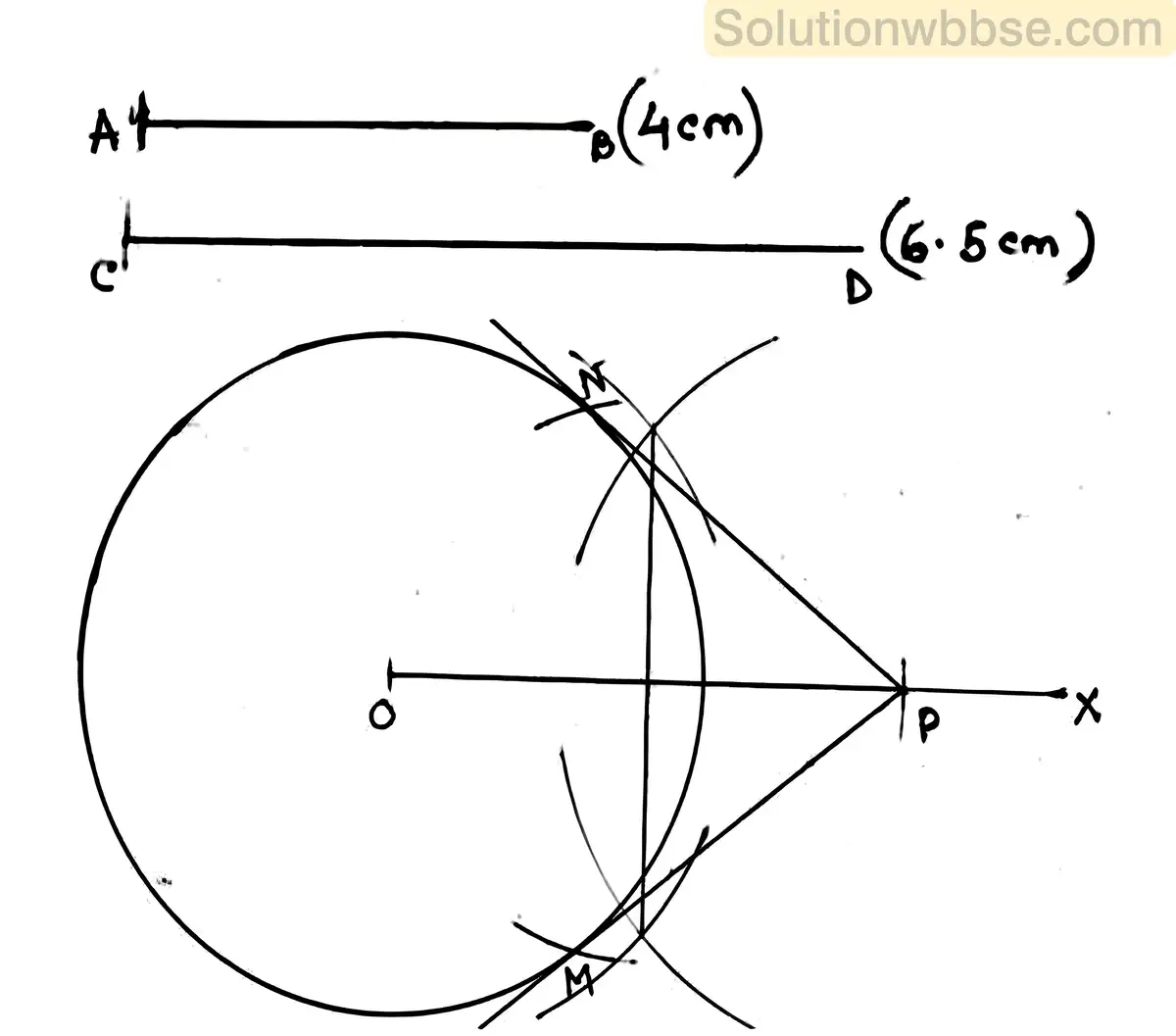
(ii) 4 সেমি ব্যাসার্ধ বিশিষ্ট একটি বৃত্ত অঙ্কন করো। বৃত্তের কেন্দ্র থেকে 6.5 সেমি দূরে কোনো বহিঃস্থ বিন্দু থেকে ঐ বৃত্তের দুটি স্পর্শক অঙ্কন করো।
12. যে-কোনো দুটি প্রশ্নের উত্তর দাও।
(i) ΔABC এর ∠C = 90°, যদি BC = m এবং AC = n হয় তবে দেখাও যে, msinA + nsinB = \(\sqrt{m^2+n^2}\)
সমাধান,
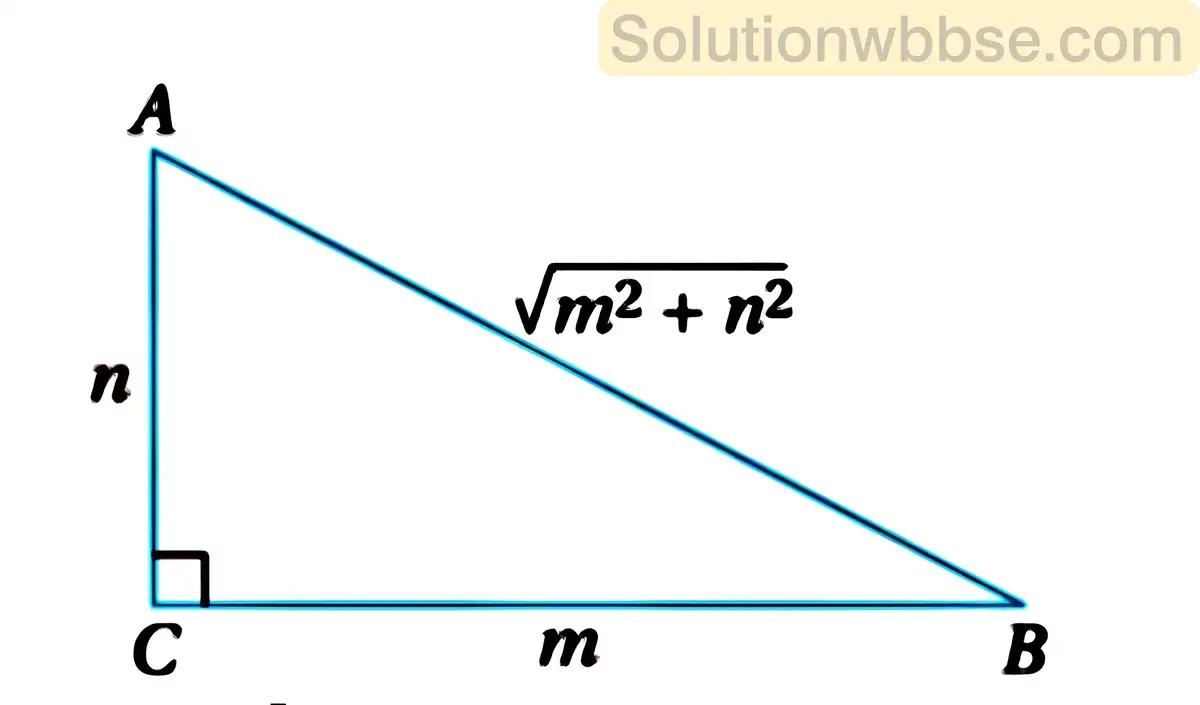
ABC ত্রিভুজের C =90° এবং BC= m একক এবং AC = n একক
∴ \(AB=\sqrt{AC^2+BC^2}=\sqrt{m^2+n^2}\)
∴ ∠A এর সাপেক্ষে BC লম্ব এবং AB অতিভুজ
∴ sinA = \(\frac{BC}{AB}\)
বা, sinA = \(\frac m{\sqrt{m^2+n^2}}\)
আবার∠B এর সাপেক্ষে AC লম্ব এবং BC ভূমি
∴ sinB = \(\frac{AC}{AB}\)
বা, sinB = \(\frac n{\sqrt{m^2+n^2}}\)
∴ msinA + nsinB
= \(m\times\frac m{\sqrt{m^2+n^2}}+n\times\frac n{\sqrt{m^2+n^2}}\)
= \(\frac{m^2}{\sqrt{m^2+n^2}}+\frac{n^2}{\sqrt{m^2+n^2}}\)
= \(\frac{m^2+n^2}{\sqrt{m^2+n^2}}\)
= \(\sqrt{m^2+n^2}\) [প্রমাণিত]
(ii) মান নির্ণয় করো – \(\frac43cot^230^\circ+3\sin^260^\circ-2\cos ec^260^\circ-\frac34\tan^230^\circ\)
সমাধান,
= \(\frac43\left(\sqrt3\right)^2+3\left(\frac{\sqrt3}2\right)^2-2\left(\frac2{\sqrt3}\right)^2-\frac34\left(\frac1{\sqrt3}\right)^2\)
= \(\frac43\times3+3\times\frac34-2\times\frac43-\frac34\times\frac14\)
= \(4+\frac94-\frac83-\frac14\)
= \(\frac{16+9}4-\left(\frac{32+3}{12}\right)\)
= \(\frac{25}4-\frac{35}{12}\)
= \(\frac{75-35}{12}\)
= \(\frac{40}{12}\)
= \(\frac{10}{3}\)
= \(3\frac13\)
(iii) যদি ∠P + ∠Q = 90° হয়, তবে দেখাও যে, \(\sqrt{\frac{\sin P}{\cos Q}}-\sin PCosQ=\cos^2P\)
সমাধান,
P + Q = 90°
∴ Q = 90° – P
∴ \(\sqrt{\frac{\sin P}{\cos Q}}-\sin PcosQ\)
= \(\sqrt{\frac{\sin P}{\cos(90^\circ-P)}}-\sin Pcos(90^\circ-P)\)
= \(\sqrt{\frac{\sin P}{\cos P}}-\sin P.\sin Q\)
= 1 – sin2P
= cos2P
∴ \(\sqrt{\frac{\sin P}{\cos Q}}-\sin P\cos Q=\cos^2P\) [প্রমাণিত]
13. যে-কোনো একটি প্রশ্নের উত্তর দাও।
(i) 600 মিটার চওড়া কোনো নদীর একটি ঘাট থেকে দুটি নৌকা দুটি ভিন্ন অভিমুখে নদীর ওপারে যাওয়ার জন্য রওনা দিল। যদি প্রথম নৌকাটি নদীর এপারের সঙ্গে 30° কোণ এবং দ্বিতীয় নৌকাটি প্রথম নৌকার গতিপথের সঙ্গে 90° কোণ করে চলে ওপারে পৌঁছায় তাহলে ওপারে পৌঁছানোর পরে নৌকাদুটির মধ্যে দূরত্ব কত হবে?
সমাধান,
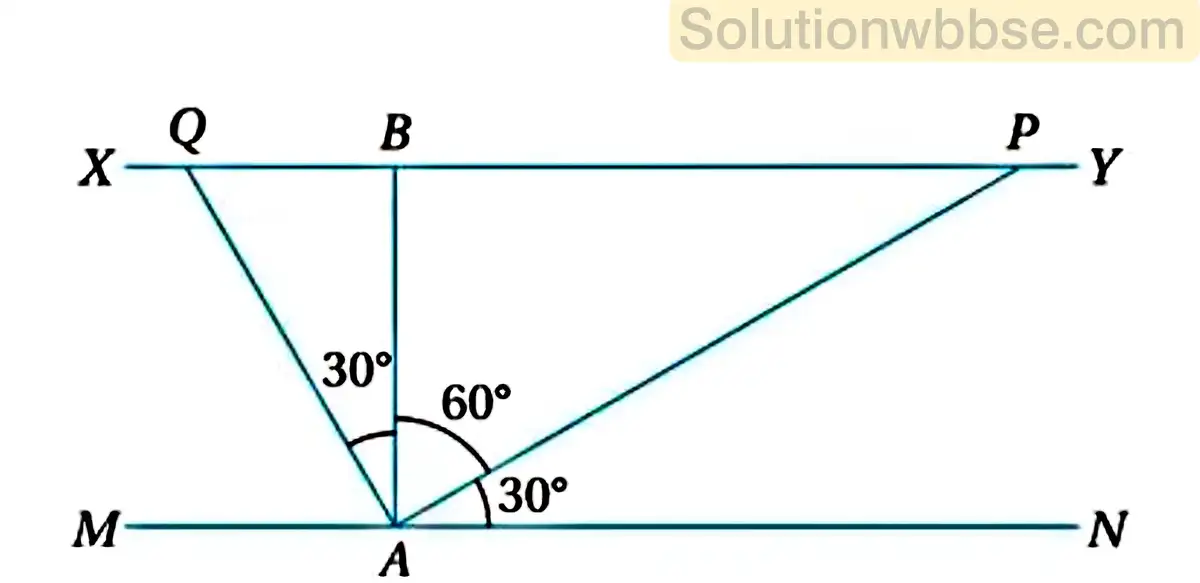
ধরা যাক, MN পাড়ের A বিন্দুস্থ ঘাট থেকে প্রথম নৌকা AP পথে গিয়ে নদীর অপর পাড় XY -এর P বিন্দুতে এবং দ্বিতীয় নৌকা AQ পথে গিয়ে Q বিন্দুতে ওপারে পৌঁছায়।
AB = নদীর চওড়া = 600 মিটার।
সুতরাং, ∠PAN = 30°, ∠PAQ = 90°
∴ ∠PAB = 60° এবং ∠BAQ = 30°
PQ = নৌকা দুটির দূরত্ব
সমকোণী ত্রিভুজ PAB থেকে পাওয়া যায়, \(\frac{BP}{AB}=\tan60^\circ=\sqrt3\)
বা, BP = \(\sqrt3\)
বা, BP = 600\(\sqrt3\) [∵ AB = 600]
আবার সমকোণী ত্রিভুজ BAQ থেকে পাওয়া যায়, \(\frac{QB}{AB}=\tan30^\circ=\frac13\)
বা, QB = \(\frac{600}{\sqrt3}\) মিটার = \(\frac{600\sqrt3}3\) মিটার = \(200\sqrt3\)
∴ PQ = BP + QB
= \(600\sqrt3+200\sqrt3\) মিটার
= \(800\sqrt3\) মিটার
∴ নৌকা দুটির দূরত্ব \(800\sqrt3\) মিটার।
(ii) একটি তিনতলা বাড়ির ছাদে 3.6 মিটার দৈর্ঘ্যের কেটি পতাকা দণ্ড আছে। রাস্তার কোনো একস্থান থেকে দেখলে পতাকা দণ্ডটির চূড়া ও পাদদেশের উন্নতি কোণ যথাক্রমে 50° ও 45° হয়। বাড়িটির উচ্চতা কত? [ধরে নাও tan50° = 1.2]
সমাধান,
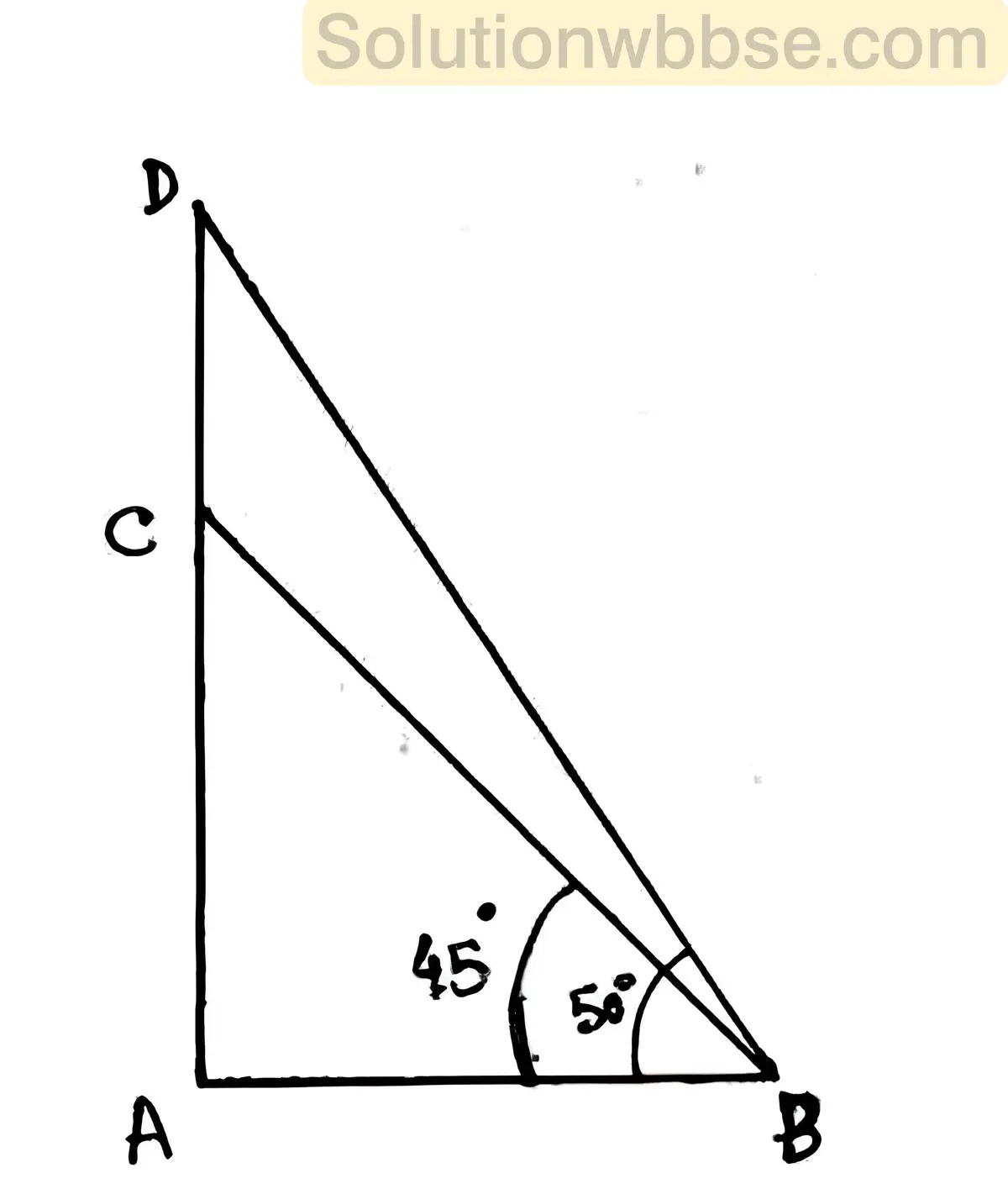
AC হল তিনতলা বাড়ির উচ্চতা এবং CD হল পতাকার দৈর্ঘ্য। রাস্তার উপর একটি বিন্দু B থেকে পতাকার পাদদেশের অর্থাৎ C বিন্দুর উন্নতি কোণ 45° এবং B বিন্দু থেকে পতাকার চূড়া অর্থাৎ D বিন্দুর উন্নতি কোণ 50°।
∴ CD = 3.6 এবং ∠ABC = 45° এবং ∠ABD = 50°
এখন, ABC ত্রিভুজে ∠BAC = 90° এবং ∠ABC = 45°
বা, 1 = \(\frac{AC}{AB}\)
বা, AB = AC_______(i)
আবার, ABD ত্রিভুজে ∠BAD = 90° এবং ∠ABD = 50°
বা, tan50° = \(\frac{AD}{AB}\)
বা, 1.2 = \(\frac{AD}{AB}\) [যেহেতু tan50° = 1.2]
বা, 1.2 = \(\frac{AC+CD}{AC}\) [(i)থেকে পাই AB = AC]
বা, 1.2 = \(\frac{AC+3.6}{AC}\) [যেহেতু CD = 3.6 মিটার]
বা, 1.2AC = AC + 3.6
বা, 1.2AC – AC = 3.6
বা, 0.2AC = 3.6
বা, AC = \(\frac{3.6}{0.2}\)
বা, AC = 18
∴ তিনতলা বাড়ির উচ্চতা 18 মিটার।
14. যে-কোনো দুটি প্রশ্নের উত্তর দাও।
(i) ঘনকাকৃতি একটি জলপূর্ণ চৌবাচ্চা থেকে সমান মাপের 64 বালতি জল তুলে নিলে চৌবাচ্চাটির \( \frac13\) অংশ জলপূর্ণ থাকে। চৌবাচ্চাটির বাহুর দৈর্ঘ্য যদি 1.2 মিটার হয়, তবে প্রতিটি বালতিতে কত লিটার জল ধরে? (1 ঘন ডেসিমিটার = 1 লিটার)
সমাধান,
ঘনকাকৃতি জলপূর্ণ চৌবাচ্চাটির আয়তন
= 1.2 × 1.2 × 1.2 ঘন মিটার
= 1.728 ঘন মিটার
= 1728 ঘন ডেসিমি
= 1728 লিটার
সমগ্র চৌবাচ্চাটির \( \frac13\) অংশ
= \(\frac13\times1.728\) ঘনমিটার
= 0.576 ঘন মিটার
= 576 ঘন ডেসিমি
= 576 লিটার
চৌবাচ্চাটি থেকে তুলে নেওয়া জলের পরিমান
= 1728 – 576
= 1152 লিটার
ধরি প্রতিটি বালতিতে জলধরে = x লিটার
∴ 64বালতিতে জল ধরে 64x লিটার
শর্তানুসারে,
64x = 1152
বা, x = \(\frac{1152}{64}\)
বা, x = 18
∴ প্রতিটি বালতিতে 18 লিটার জল ধরে।
(ii) একটি তারের প্রস্থচ্ছেদের ব্যাস 50% কমনো হল। আয়তন অপরিবর্তিত রাখতে হলে তারটির দৈর্ঘ্য কত শতাংশ বাড়াতে হবে?
সমাধান,
ধরি, তারের প্রস্থচ্ছেদের ব্যাসার্ধ r একক এবং দৈর্ঘ্য h একক।
∴ ব্যাস = 2r একক
তারের প্রস্থচ্ছেদের ব্যাস 50% কমানো হলে, পরিবর্তিত ব্যাস হবে
= \(\left(2r-2r\times\frac{50}{100}\right)\) একক
= (2r – r)একক
= r একক
∴ পরিবর্তিত ব্যাসার্ধ = \(\frac r2\) একক
পূর্বে তারটির আয়তন ছিল = πr²h ঘন একক
ধরা যাক, আয়তন অপরিবর্তিত রাখতে হলে তারটির দৈর্ঘ্য হবে H একক
∴ πr²h = π\(\left(\frac r2\right)^2\)H
বা, H = 4h
∴ তারটির দৈর্ঘ্য শতকরা বাড়বে
= একক
= \(\left(\frac{H-h}h\times100\right)\) একক
= \(\left(\frac{4h-h}h\times100\right)\) একক
= \(\left(\frac{3h}h\times100\right)\) একক
= 300 একক
∴ তারটির দৈর্ঘ্য 300% বৃদ্ধি করতে হবে।
(iii) লম্ব বৃত্তাকার শঙ্কু আকৃতির একটি তাঁবু তৈরি করতে 77 বর্গমিটার ত্রিপল লেগেছে। তাঁবুটির তির্যক উচ্চতা যদি 7 মিটার হয়, তবে তাঁবুটির ভূমিতলের ক্ষেত্রফল কত?
সমাধান,
লম্ব বৃত্তাকার শঙ্কু আকৃতির একটি তাঁবু তৈরি করতে 77 বর্গ মিটার ত্রিপল লেগেছে।
অর্থাৎ তাঁবুটির পার্শ্ব তলের ক্ষেত্রফল 77 বর্গ মিটার।
তাঁবুটির তির্যক উচ্চতা (I) = 7 মিটার।
ধরি, তাঁবুটির ভূমিতলের ব্যাসার্ধ r মিটার।
শর্তানুসারে,
πrl = 77
বা, \(\frac{22}7\times r\times7\) = 77
বা, r = \(\frac{77\times7}{22\times7}\)
বা, r = \(\frac72\)
বা, r = 3.5
∴ শঙ্কুর ভূমিতলের ব্যাসার্ধ 3.5 মি.।
∴ তাঁবুটির ভূমিতলের ক্ষেত্রফল
= πr² বর্গ মি.
= \(\frac{22}7\times\left(3.5\right)^2\) বর্গ মি.
= \(\frac{22}7\times3.5\times3.5\) বর্গ মি.
= 22 × 0.5 × 3.5 বর্গ মি.
= 38.5 বর্গ মি.
∴ তাঁবুটির ভূমিতলের ক্ষেত্রফল 38.5 বর্গ সেমি.।
15. যে কোনো দুটি প্রশ্নের উত্তর দাও।
(i) যদি নীচের পরিসংখ্যা বিভাজন তালিকার যৌগিক গড় 54 হয়, তবে K-এর মান নির্ণয় করো –
| শ্রেণী | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
| পরিসংখ্যা | 7 | 11 | K | 9 | 13 |
সমাধান,
| শ্রেণী | পরিসংখ্যা (fi) | শ্রেণী মধ্যক (xi) | fixi |
| 0-20 | 7 | 10 | 70 |
| 20-40 | 11 | 30 | 330 |
| 40-60 | K | 50 | 50k |
| 60-80 | 9 | 70 | 630 |
| 80-100 | 13 | 90 | 1170 |
| মোট | ∑fi = 40 + k | ∑fixi = 2200 + 50k |
∴ যৌগিক গড় = \(\frac{\sum f_ix_i}{\sum f_i}\)
= \(\frac{2200+50k}{40+k}\)
প্রশ্নানুসারে,
\(\frac{2200+50k}{40+k}\) = 54
বা, 2160 + 54k = 2200 + 50k
বা, 54k – 50k = 2200 – 2160
বা, 4k = 40
বা, k = \(\frac{40}4\)
বা, k = 10
∴ k = 10
(ii) নীচের প্রদত্ত ক্রমযৌগিক পরিসংখ্যা বিভাজন ছকটি থেকে পরিসংখ্যা বিভাজন ছক তৈরি করে তথ্যটির সংখ্যাগুরু মান নির্ণয় করো –
| শ্রেণী | 10 এর কম | 20 এর কম | 30 এর কম | 40 এর কম | 50 এর কম | 60 এর কম | 70 এর কম | 80 এর কম |
| পরিসংখ্যা | 4 | 16 | 40 | 76 | 96 | 112 | 120 | 125 |
সমাধান,
প্রদত্ত ক্রমযৌগিক পরিসংখ্যা থেকে পরিসংখ্যা বিভাজন ছক তৈরি করা হল –
| শ্রেণি সীমানা | পরিসংখ্যা |
| 0-10 | 4 |
| 10-20 | 16 – 4 = 12 |
| 20-30 | 40 – 16 = 24 |
| 30-40 | 76 – 40 = 36 |
| 40-50 | 96 – 76 = 20 |
| 50-60 | 112 – 96 = 16 |
| 60-70 | 120 – 112 = 8 |
| 70-80 | 125 – 120 = 5 |
সংখ্যাগুরু মান সম্বলিত শ্রেণীটি হল (30 – 40)।
∴ সংখ্যাগুরুমান = I +\(\left(\frac{f_1-f_0}{2f_1-f_0-f_2}\right)\)× h
যেখানে, I = সংখ্যাগুরু শ্রেণীর নিম্নসীমানা = 30
f1 = সংখ্যাগুরু শ্রেণীর পরিসংখ্যা = 36
f0 = সংখ্যাগুরু শ্রেণীর ঠিক পূর্ববর্তী শ্রেণীর পরিসংখ্যা = 24
f2 = সংখ্যাগুরু শ্রেনির ঠিক পরবর্তী শ্রেণীর পরিসংখ্যা = 20
h = শ্রেণী দৈর্ঘ্য = 10
∴ সংখ্যাগুরুমান
= 30 +\(\left(\frac{36-24}{2\times36-24-20}\right)\) × 10
= 30 +\(\left(\frac{12}{72-44}\right)\) × 10
= 30 + \(\frac{12}{28}\) × 10
= 30 + \(\frac{30}{7}\)
= 30 + 4.29 (প্রায়)
= 34.29 (প্রায়)
(iii) নীচের তালিকা থেকে একটি বিদ্যালয়ের দশম শ্রেণীর 52 জন ছাত্রের গড় নম্বর প্রত্যক্ষ পদ্ধতি ও কল্পিত গড় পদ্ধতিতে নির্ণয় করো –
| শ্রেণী | 4 | 7 | 10 | 15 | 8 | 5 | 3 |
| পরিসংখ্যা | 30 | 33 | 35 | 40 | 43 | 45 | 48 |
সমাধান,
| বছর (xi) | ছাত্র সংখ্যা (fi) | fixi | D1 = xi – a = xi – 40 | fidi |
| 30 | 4 | 120 | -10 | -40 |
| 33 | 7 | 231 | -7 | -49 |
| 35 | 10 | 350 | -5 | -50 |
| 40 = a | 15 | 600 | 0 | 0 |
| 43 | 8 | 344 | 3 | 24 |
| 45 | 5 | 225 | 5 | 25 |
| 48 | 3 | 144 | 8 | 24 |
| মোট | ∑fi = 52 | ∑fixi = 2014 | ∑fidi = -66 |
প্রত্যক্ষ পদ্ধিতিতে, গড় নম্বর = \(\frac{2014}{52}\)
= 78.73 (প্রায়)
কল্পিত গড় (a) = 40 (ধরা হল)
∴ কল্পিত গড় পদ্ধতিতে, গড় নম্বর = a + \(\frac{\sum f_id_i}{\sum f_i}\)
= 40 + \(\left(\frac{-66}{52}\right)\)
= 40 – 1.27 (প্রায়)
= 38.73 (প্রায়)
মাধ্যমিক পরীক্ষা, বিশেষ করে গণিত, অনেক শিক্ষার্থীর জন্য চ্যালেঞ্জিং। ভালো ফলাফল করতে কী দরকার? ২০২৯ সালের মাধ্যমিক গণিত পরীক্ষার প্রশ্ন বিশ্লেষণ করে আমরা জানতে পারি শুধু মুখস্থ জ্ঞানই যথেষ্ট নয়। গণিতে সফল হতে হলে ধারণা বুঝতে হবে। সংখ্যা, চিহ্ন, আর সূত্র মুখস্থ করে কোন লাভ নেই, যদি না সেগুলোর কার্যক্রম এবং কেন-কারণটা আপনি বুঝতে না পারেন। ধারণা বুঝলে যেকোনো সমস্যার সমাধান আপনি নিজেই খুঁজে বের করতে পারবেন। এছাড়াও, গণিতে সফল হওয়ার জন্য সমস্যা সমাধানের দক্ষতা এবং বিশ্লেষণাত্মক চিন্তাভাবনা জরুরি। কঠিন সমস্যার সমাধানের জন্য একাধিক পদ্ধতি থাকতে পারে। কোন পদ্ধতি সবচেয়ে কার্যকর, তা নির্বাচন করতে হবে। এর জন্য প্রয়োজন বিশ্লেষণ করে সমস্যার গভীরে যাওয়ার ক্ষমতা। মাধ্যমিক গণিতে ভালো ফলাফল করার জন্য নিয়মিত অনুশীলন এবং পুরাতন বছরের প্রশ্ন সমাধান করা খুবই জরুরি। নিয়মিত অনুশীলনের ফলে আপনার গতি বাড়বে এবং আत्मবিশ্বাস জন্ম নেবে। পুরাতন বছরের প্রশ্ন সমাধান করার ফলে আপনি আগামী পরীক্ষার ধরণ, প্রশ্নের মান এবং বিষয়বস্তু সম্পর্কে ধারণা পাবেন। এছাড়াও, বিভিন্ন ধরণের প্রশ্নের সাথে পরিচিতি থাকা গুরুত্বপূর্ণ। মাধ্যমিক গণিতে নানা ধরনের প্রশ্ন আসতে পারে, যেমন বহু-নির্বাচন, সত্য-মিথ্যা, সংক্ষিপ্ত উত্তর, বিশদ উত্তর এবং সমস্যা সমাধান। বিভিন্ন ধরণের প্রশ্নের মোকাবিলা করার জন্য নিয়মিত অনুশীলন এবং বিভিন্ন ধরনের প্রশ্নের সংগ্রহের সঙ্গে অনুশীলন করুন। এই টিপস গুলো মেনে চললে আপনিও পারবেন মাধ্যমিক গণিতে ভালো ফলাফল করতে। শুধু মুখস্থ না করে, ধারণা বুঝে এবং নিয়মিত অনুশীলন করুন। বিশ্লেষণ করে সমস্যা সমাধান করুন এবং বিভিন্ন ধরণের প্রশ্নের সঙ্গে নিজেকে মানিয়ে নিন। শুভকামনা!






মন্তব্য করুন