এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের দশম অধ্যায়, ‘বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য’ -এর ‘কষে দেখি – 10’ বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

1. পাশের ছবির PQRS বৃত্তস্থ চতুর্ভুজের কর্ণদ্বয় পরস্পরকে X বিন্দুতে এমনভাবে ছেদ করেছে যে ∠PRS = 65° এবং ∠RQS = 45°; ∠SQP ও ∠RSP-এর মান হিসাব করে লিখি।
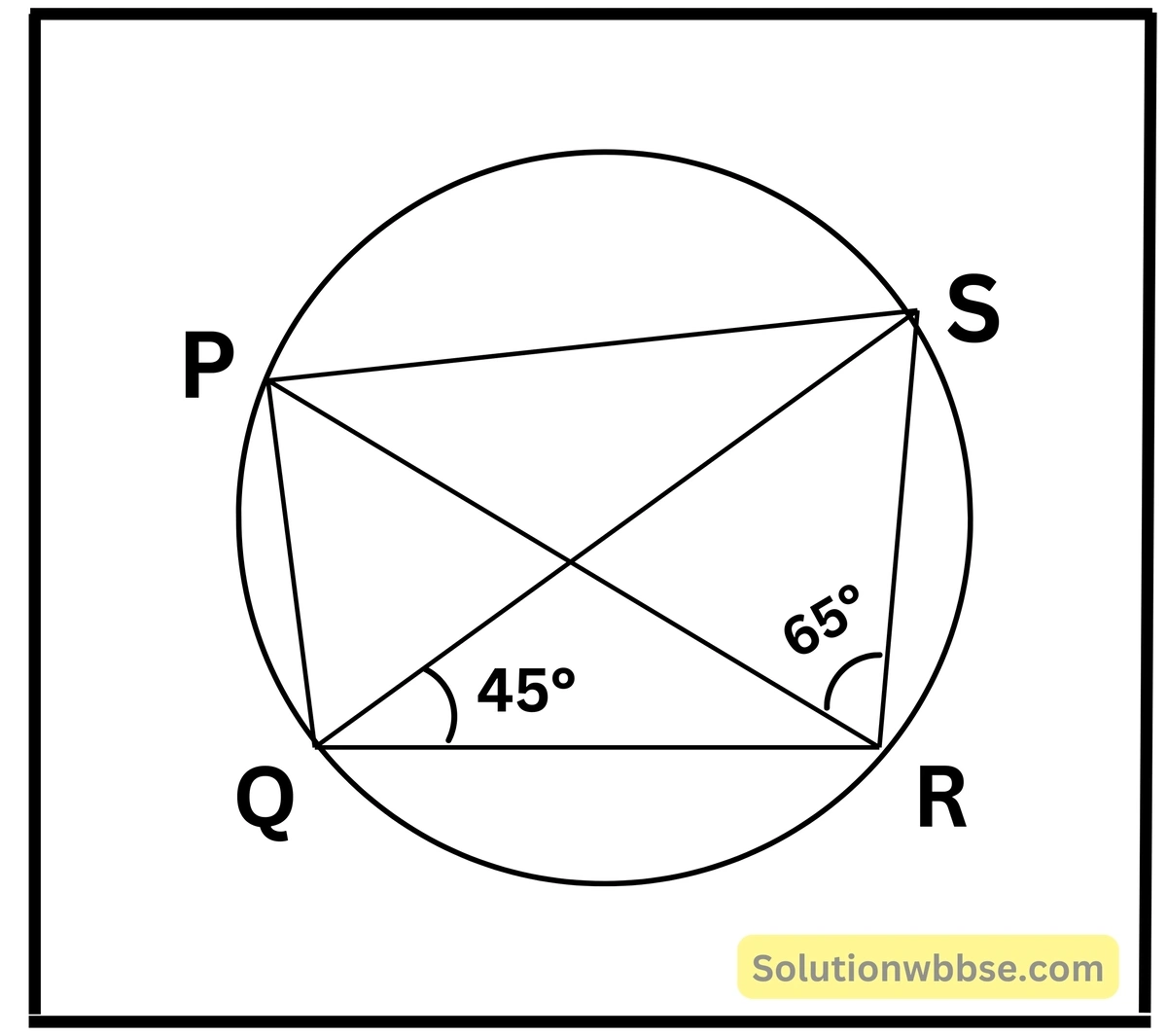
∠SQP = ∠PRS [একই বৃত্তাংশস্থ সকল কোণের মান সমান।
∴ ∠SQP = 65°
∠SQR = ∠SPR [একই বৃত্তাংশস্থ সকল কোণের মান সমান]
∴ ∠SPR = 45°
∴ ΔSPR এর ক্ষেত্রে,
∠PSR = 180° – (∠SPR + ∠SRP)
= 180° – (45° + 65°)
= 180° – 110°
= 70°
∴ ∠RSP = 70°
2. ABCD বৃত্তস্থ চতুর্ভুজের AB বাহুকে X বিন্দু পর্যন্ত বর্ধিত করলাম এবং মেপে দেখছি ∠XBC = 82° এবং ∠ADB = 47°; ∠BAC-এর মান হিসাব করে লিখি।
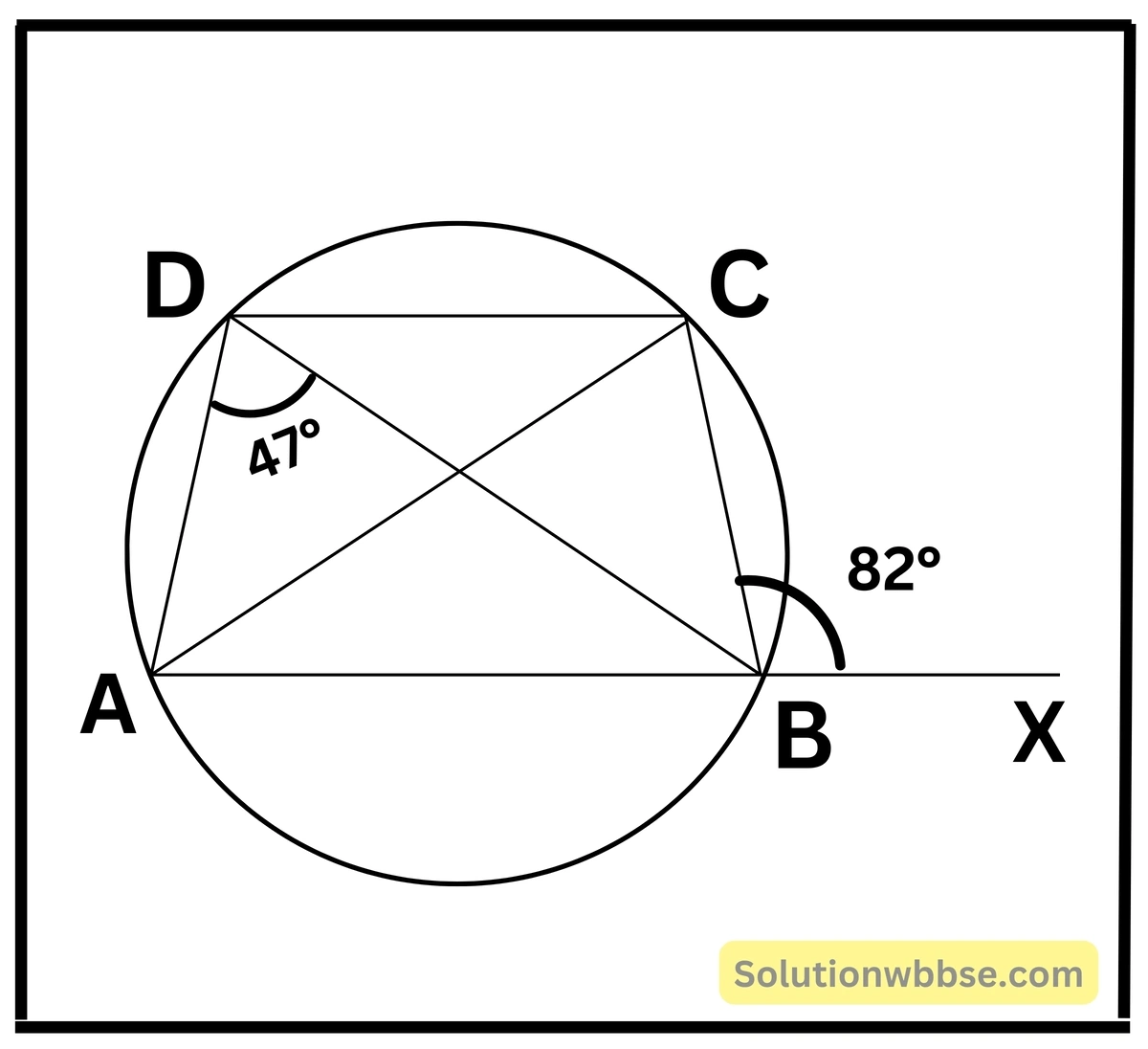
∠XBC = 82°
∴ ∠ABC = 180° – 82° = 98°
∴ ∠ADC = 180° – 98° = 82°[∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক]
∴ ∠ADB + ∠BDC = 82°
বা, 47° + ∠BDC = 82°
বা, ∠BDC = 82° – 47°
বা, ∠BDC = 35°
∴ ∠BAC = 35° [একই বৃত্তাংশস্থ সকল কোণের মান সমান]
3. PQRS বৃত্তস্থ চতুর্ভুজের PQ, SR বাহু দুটি বর্ধিত করায় T বিন্দুতে মিলিত হলো। বৃত্তের কেন্দ্র O, ∠POQ = 110°, ∠QOR = 60°, ∠ROS = 80° হলে ∠RQS ও ∠QTR -এর মান হিসাব করে লিখি।
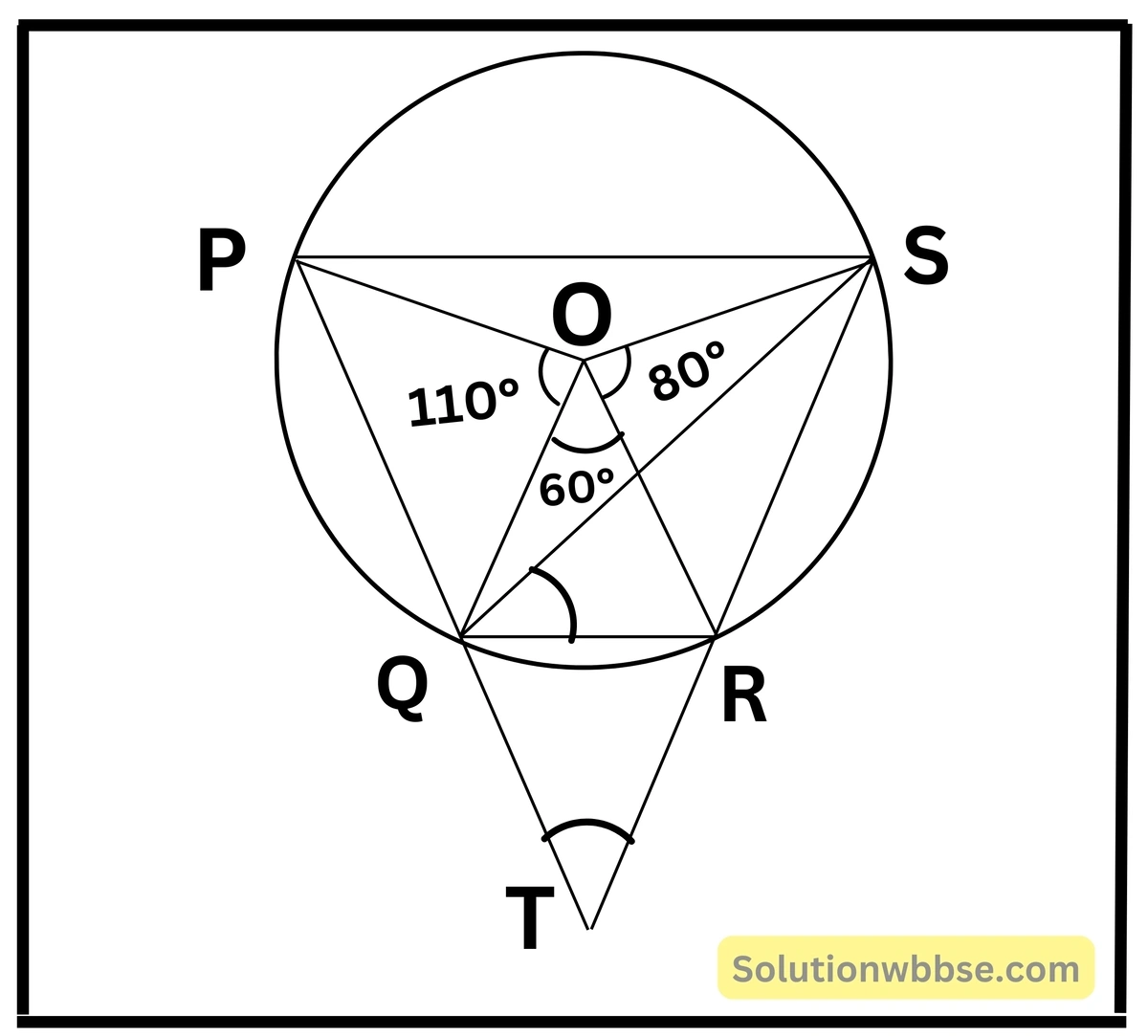
RS বৃত্তচাপের ওপর ∠ROS কেন্দ্রস্থ কোণ এবং ∠RQS পরিধিস্থ কোণ।
\(\angle RQS=\frac12\angle ROS\) [∵ একই বৃত্তচাপের ওপর অবস্থিত কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন।]
= \(\frac12\times80^\circ\)
∴ ∠RQS = 40°
\(\angle OSR=\frac12\times\angle QOR\) [∵ QR বৃত্তচাপের ওপর কেন্দ্রস্থ কোণ ∠QOR এবং পরিধিস্থ কোণ ∠QSR, একই বৃত্তচাপের ওপর অবস্থিত কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন]
\(\angle OSR=\frac12\times60^\circ\)বা, ∠QSR = 30°
বা, ∠POS = 360° – (∠POQ + ∠QOR + ∠ROS)
বা, ∠POS = 360° – (110° + 60° + 80°)
বা, ∠POS = 360° – 250°
বা, ∠POS = 110°
PS বৃত্তচাপের ওপর ∠POS কেন্দ্রস্থ কোণ এবং ∠PQS পরিধিস্থ কোণ।
\(\angle PQS=\frac12\times\angle POS\) [∵ একই বৃত্তচাপের ওপর অবস্থিত কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন।
\(\angle PQS=\frac12\times110^\circ\)∠PQS = 55°
আবার ΔSQT এর বহিঃস্থ কোণ ∠PQS = ∠QST + ∠QTS [∵ ত্রিভুজের কোনো একটি বাহুকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণ অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান]
55° = 30° + ∠QTS
বা, ∠QTS = 55° – 30°
বা, ∠QTS = 25°
∴ ∠QTS = 25° [∵ ∠QTR – ∠QTS]
4. দুটি বৃত্ত পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে। P ও Q বিন্দুগামী দুটি সরলরেখা একটি বৃত্তকে যথাক্রমে A ও C এবং অপর বৃত্তকে যথাক্রমে B ও D বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, AC || BD
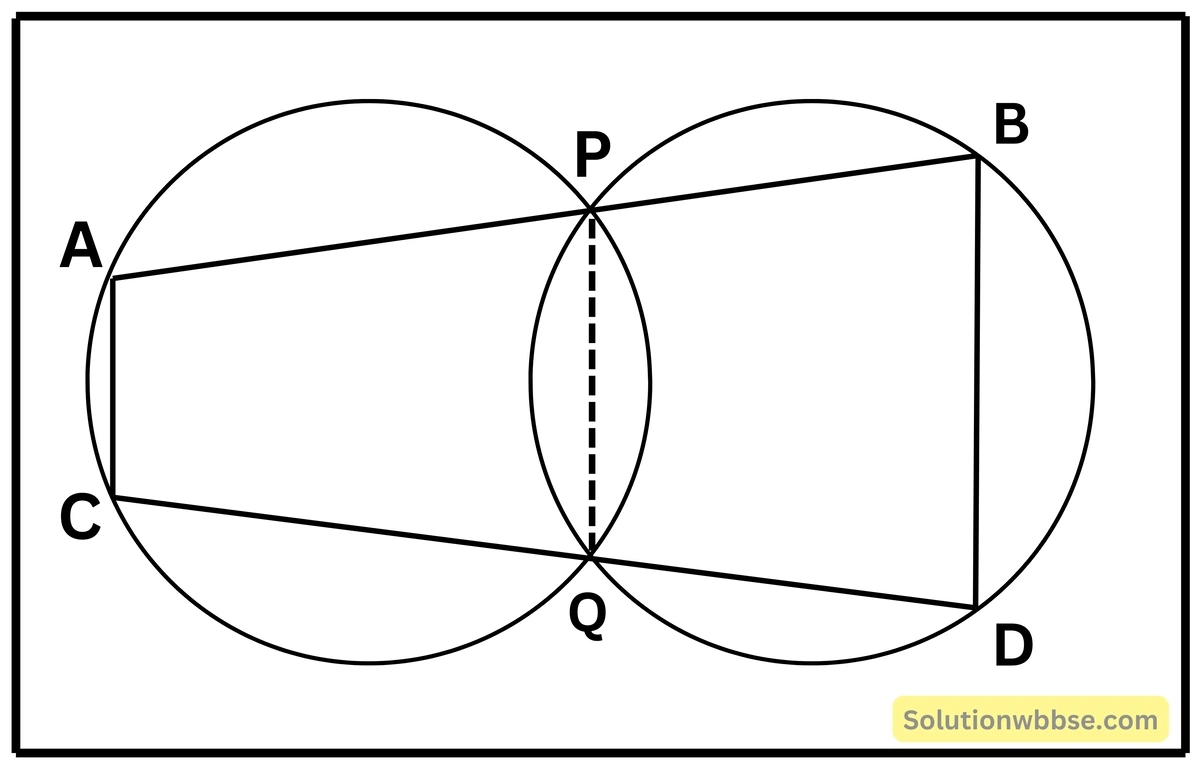
দুটি বৃত্ত পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে। P এবং Q বিন্দু দিয়ে অঙ্কিত দুটি সরলরেখা বৃত্তদুটিকে যথাক্রমে AC ও BD বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে যে, AC ∥ BD
অঙ্কন – P ও Q যুক্ত করা হল।
প্রমাণ – ACQP বৃত্তস্থ চতুর্ভুজ।
∴ ∠ACQ + ∠APQ = 180° [∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক]
আবার, AB সরলরেখার ওপর P বিন্দুতে PQ সরলরেখা দণ্ডায়মান, তাই,
∠APQ + ∠BPQ = 180° [এক সরল কোণ]
∠ACQ + ∠APQ = ∠APQ + ∠BPQ
∠ACQ = ∠BPQ
আবার, PQDB বৃত্তস্থ চতুর্ভুজের ক্ষেত্রে,
∠BDQ + ∠BPQ = 180° [∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক]
∠BDQ + ∠ACQ = 180° [∵ ∠BPQ = ∠ACQ]
এখন, AC ও BD সরলরেখাকে, CD ভেদক ছেদ করায় একই পার্শ্বস্থ অন্তঃকোণ ∠BDQ ও ∠BCQ উৎপন্ন হয় এবং এদের সমষ্টি 2 সমকোণ।
∴ AC ∥ BD [প্রমাণিত]
5. ABCD একটি বৃত্তস্থ চতুর্ভুজ অঙ্কন করেছি এবং এর BC বাহুকে E বিন্দু পর্যন্ত বর্ধিত করলাম। প্রমাণ করি যে, ∠BAD ও ∠DCE -এর সমদ্বিখণ্ডকদ্বয় বৃত্তের উপর মিলিত হবে।
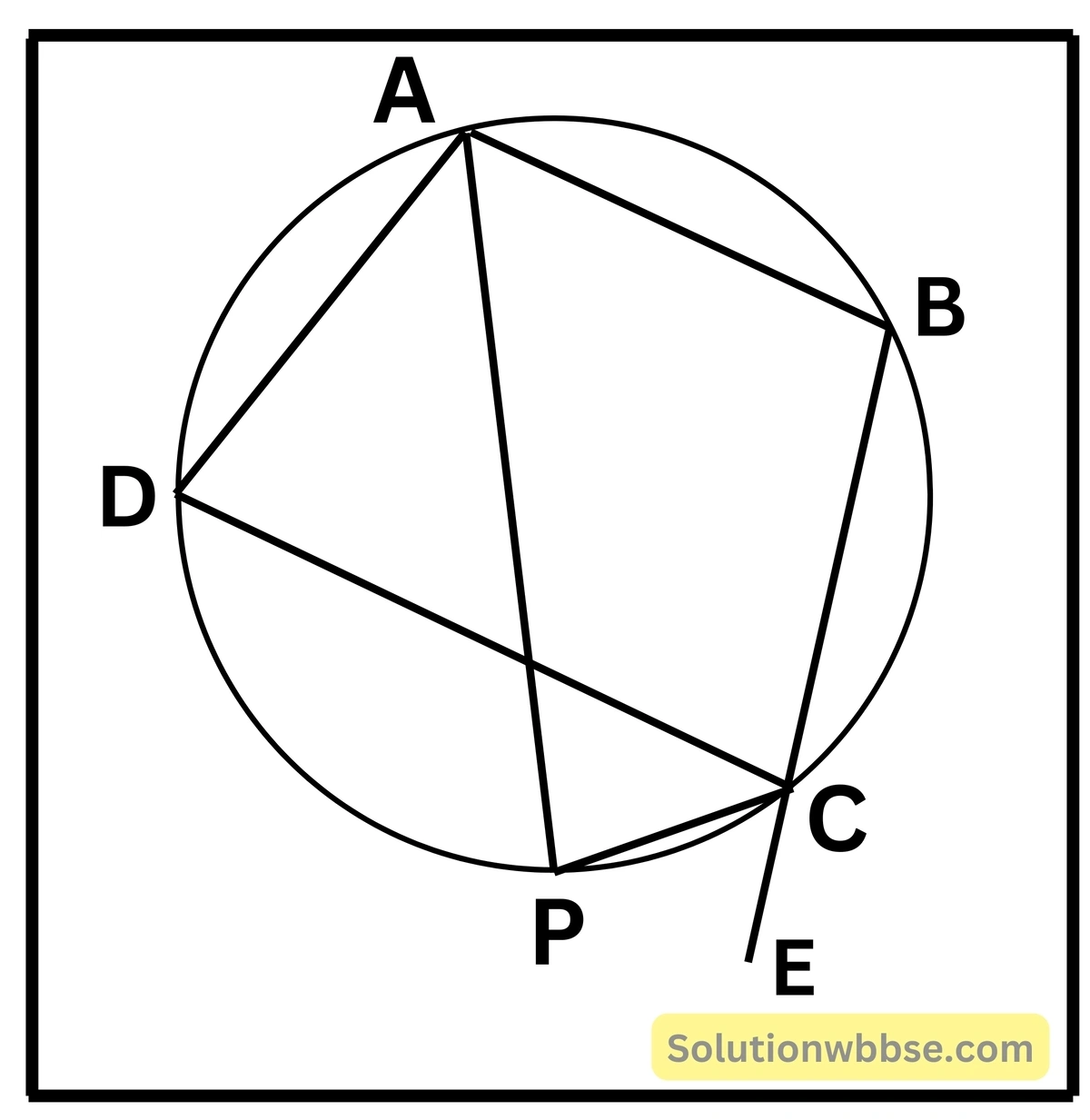
ABCD বৃত্তস্থ চতুর্ভুজের BC বাহুকে E পর্যন্ত বর্ধিত করা হল। ∠BAD -এর সমদ্বিখণ্ডক AP বৃত্তটিকে P বিন্দুতে ছেদ করে। CP অঙ্কন করা হল।
প্রমাণ করতে হবে যে, CP, ∠DCE -এর সমদ্বিখণ্ডক।
প্রমাণ – এখানে ABCD চতুর্ভুজের ∠DAB -এর সমদ্বিখণ্ডক AP
∴ ∠DAP = ∠BAP
আবার, ∠DAP = ∠DCP (একই বৃত্তাংশস্থ কোণ)
∴ ∠BAP = ∠DCP
এখন ABCP বৃত্তস্থ চতুর্ভুজ।
∴ ∠BAP + ∠BCP = 2 সমকোণ।
কিন্তু ∠BCP + ∠ECP = 2 সমকোণ।
∴ ∠BAP + ∠BCP = ∠BCP + ∠ECP
∴ ∠BAP – ∠ECP
∴ ∠DCP = ∠ECP
∴ CP, ∠DCE -এর সমদ্বিখণ্ডক।
6. মোহিত একটি বৃত্তের বহিঃস্থ কোনো বিন্দু X দিয়ে দুটি সরলরেখা অঙ্কন করেছে যারা বৃত্তটিকে যথাক্রমে A, B বিন্দু ও C, D বিন্দুতে ছেদ করেছে। যুক্তি দিয়ে প্রমাণ করি যে, ΔXAC ও ΔXBD -এর দুটি করে কোণ সমান।
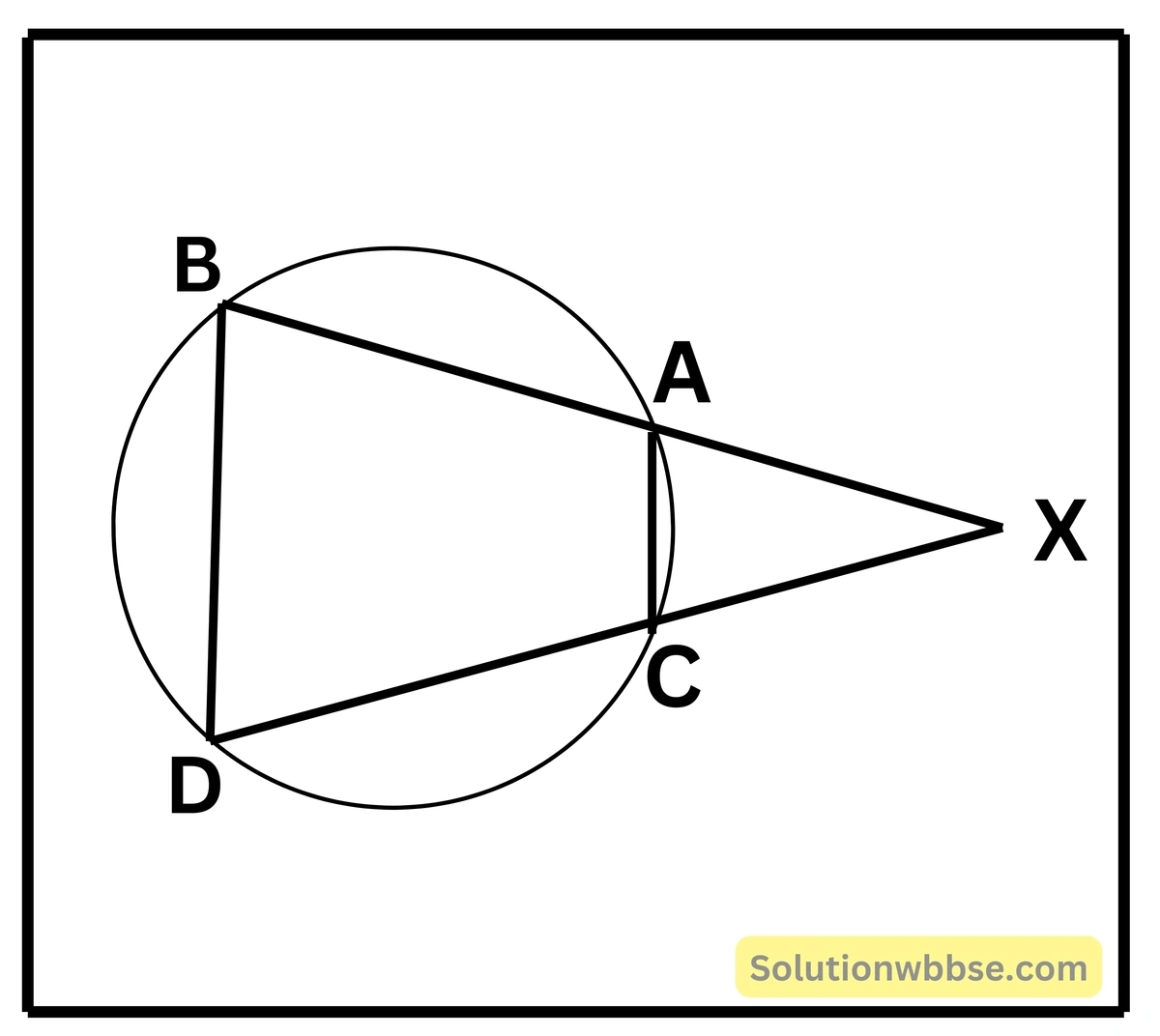
বৃত্তের বহিঃস্থ বিন্দু X দিয়ে দুটি সরলরেখা টানা হয়েছে, যারা বৃত্তটিকে যথাক্রমে A, B বিন্দু এবং C, D বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে যে, ∠XAC = ∠XBD
অঙ্কন – B, D ও A, C যুক্ত করা হল।
প্রমাণ – ABDC একটি বৃত্তস্থ চতুর্ভুজ।
∴ ∠BDC + ∠BAC = 180° [∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক]
আবার, ∠BAC + ∠XAC = 180° [এক সরলকোণ = 180°]
∠BDC + ∠BAC = ∠BAC + ∠XAC
বা, ∠BDC = ∠XAC
∴ ΔXAC ও ΔXBD এর দুটি করে কোণ সমান [প্রমাণিত]।
7. দুটি বৃত্ত অঙ্কন করেছি যারা পরস্পরকে G ও H বিন্দুতে ছেদ করেছে। এবার G বিন্দুগামী একটি সরলরেখা অঙ্কন করলাম যেটি বৃত্ত দুটিকে P ও Q বিন্দুতে এবং H বিন্দুগামী PQ -এর সমান্তরাল অপর একটি সরলরেখা অঙ্কন করলাম যা বৃত্তদুটিকে R ও S বিন্দুতে ছেদ করল। প্রমাণ করি যে PQ = RS
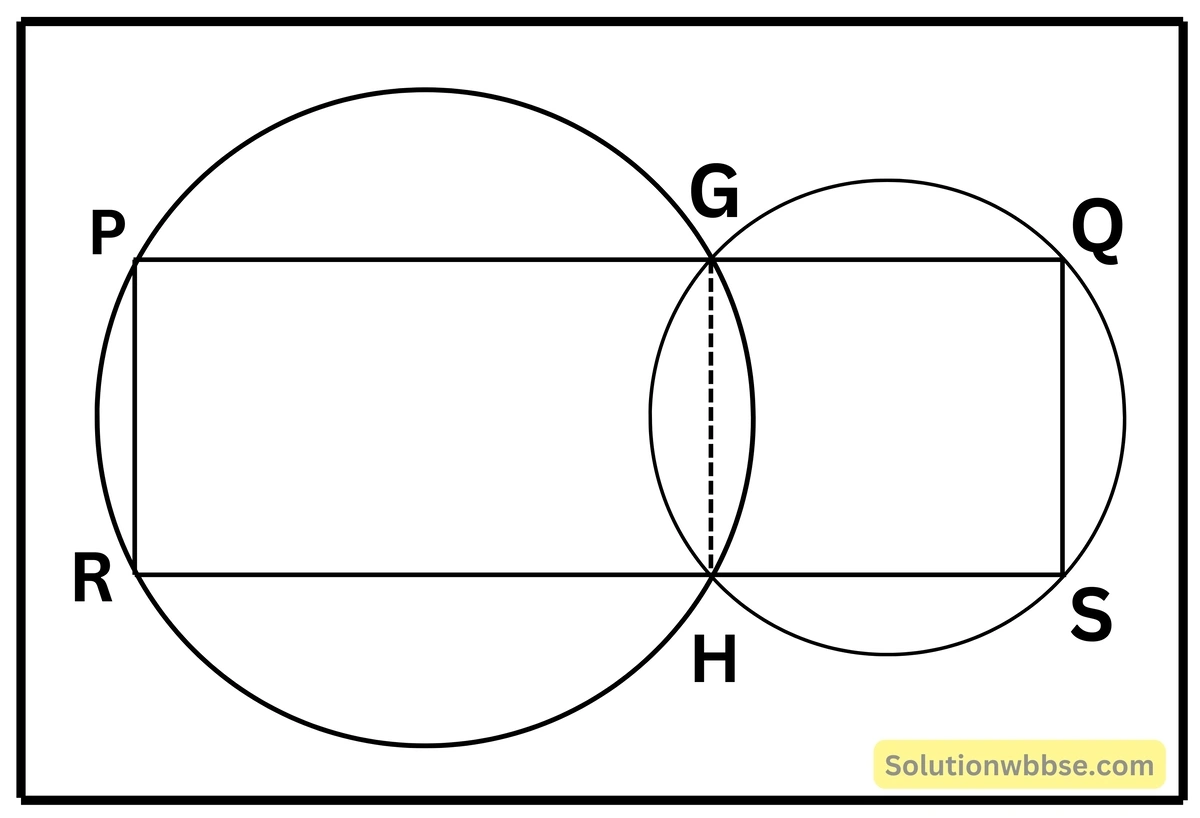
অঙ্কন – P, R; G, H এবং Q,S যুক্ত করা হল।
প্রমাণ – GHSQ বৃত্তস্থ চতুর্ভুজের ক্ষেত্রে,
∠HSQ + ∠HGQ = 180°
আবার, PS সরলরেখার ওপর ও বিন্দুতে, GH দণ্ডায়মান,
∴ ∠PGH + ∠ HGQ = 180°
বা, ∠HSQ + ∠HGQ = ∠PGH + ∠HGQ
বা, ∠HSQ = ∠PGH
আবার, PRHG বৃত্তস্থ চতুর্ভুজের ক্ষেত্রে,
∠PRH + ∠PGH = 180°
∠PRH + ∠HSQ = 180° [∵ ∠PGH = ∠HSQ]
∴ PR ও QS বাহুদ্বয়ের ভেদক RS এর একই পার্শ্বস্থ অন্তঃকোণের সমষ্টি 180°
∴ PR ∥ QS
আবার, PQ ∥ RS
∴ PRSQ একটি সামান্তরিক।
∴ PQ = RS [প্রমাণিত]
8. ABC একটি ত্রিভুজ অঙ্কন করেছি যার AB = AC এবং বর্ধিত BC -এর উপর E যে-কোনো একটি। বিন্দু। ΔABC -এর পরিবৃত্ত AE -কে D বিন্দুতে ছেদ করলে প্রমাণ করি যে, ∠ACD = ∠AEC
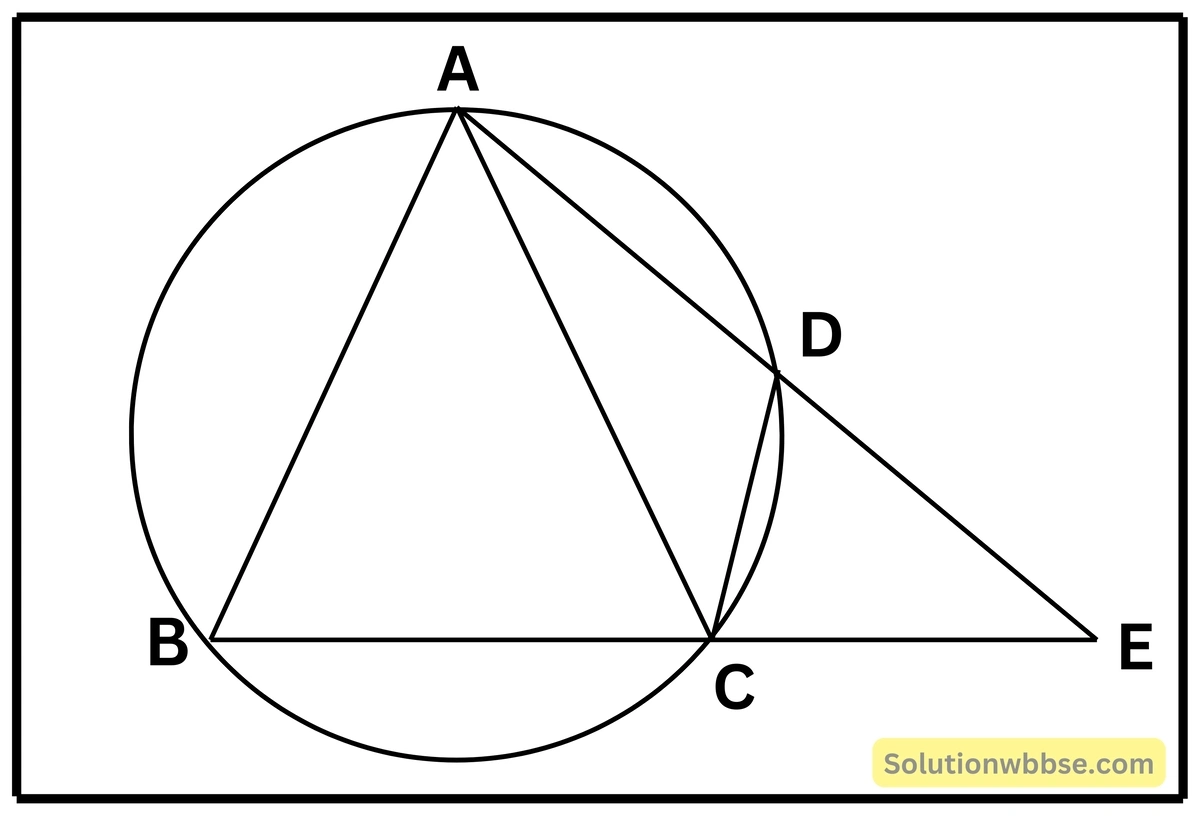
প্রমাণ – ABCD একটি বৃত্তস্থ চতুর্ভুজ।
∠ABC + ADC = 180° [∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক]
আবার, ∠ADC + ∠EDC = 180° [∵ CD সরলরেখা, AE সরলরেখার ওপর দণ্ডায়মান]
∴ ∠ABC + ∠ADC = ∠ADC + ∠EDC
∠ABC = ∠EDC
∠ABC = ∠CDE —(i)
আবার, ΔABC এর AB = AC
∴ ∠ABC = ∠ACB —(ii)
CDE এর EC বাহু B পর্যন্ত বর্ধিত,
∴ ∠DCB = ∠CDE + ∠CED [∵ ত্রিভুজের কোনো একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয় তা অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান]
∠ACD + ∠ACB = ∠ABC + ∠CED [∵ (i) থেকে পাই ∠ABC = ∠CDE]
∠ACD = ∠CED [∵ (ii) থেকে পাই, ∠ACB = ∠ABC]
∴ ∠ACD = ∠AEC [প্রমাণিত]
9. ABCD একটি বৃত্তস্থ চতুর্ভুজ। DE জ্যা ∠BDC -এর বহির্দ্বিখণ্ডক। প্রমাণ করি যে, AE (বা বর্ধিত AE) ∠BAC -এর বহির্দ্বিখণ্ডক।
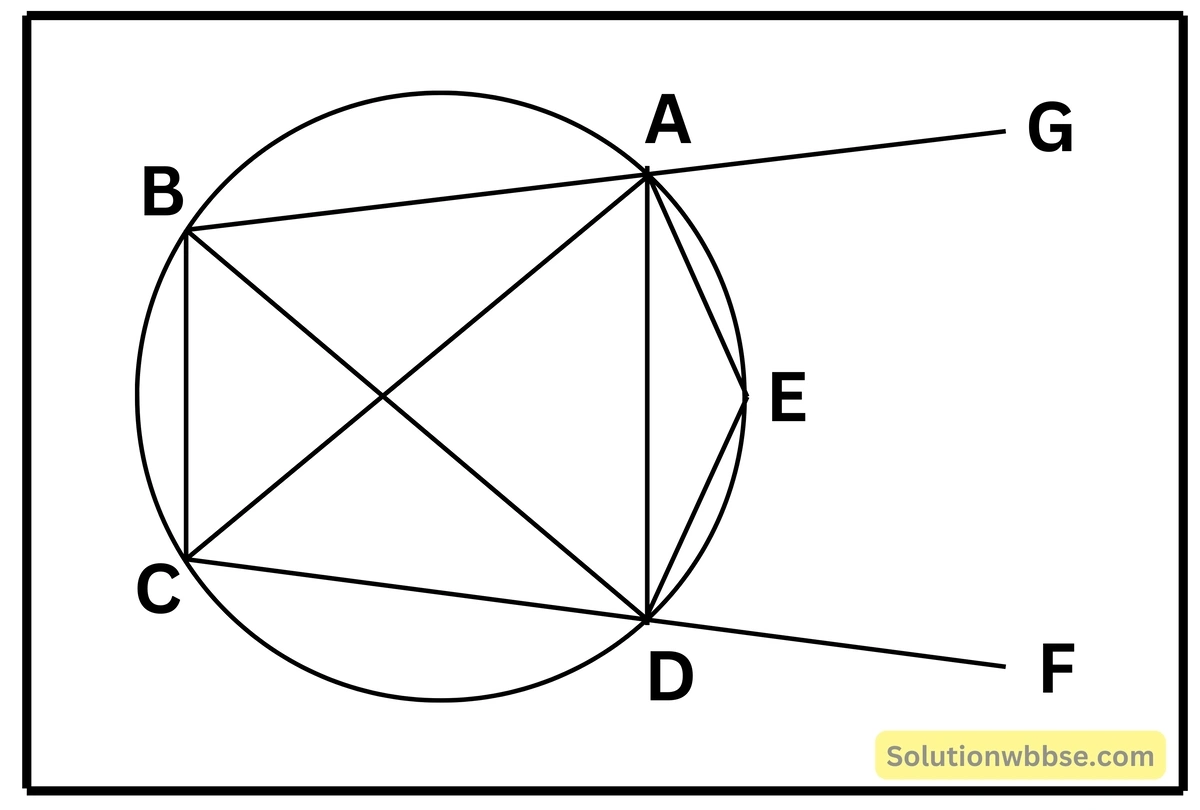
বৃত্তস্থ চতুর্ভুজ ABCD এর BDC এর বহির্দ্বিখণ্ডক DE জ্যা।
প্রমাণ করতে হবে যে, AE, ∠BAC -এর বহির্দ্বিখণ্ডক।
অঙ্কন – CD কে F পর্যন্ত এবং BA কে G পর্যন্ত বর্ধিত করা হল।
প্রমাণ – বৃত্তস্থ চতুর্ভুজ AEDB থেকে পাই,
যেহেতু বৃত্তস্থ চতুর্ভুজের বহিঃস্থ কোণ বিপরীত কোণের সমান
∴ ∠EAG = ∠EDB
আবার যেহেতু ED, ∠BAC এর বহির্দ্বিখণ্ডক তাই,
∠EDB = ∠EDF
∴ ∠EAG = ∠EDF —(i)
আবার, বৃত্তস্থ চতুর্ভুজ ACDE থেকে পাই,
∠EDF = ∠EAC —(ii) [∵ বৃত্তস্থ চতুর্ভুজের বহিঃস্থ কোণ বিপরীত অন্তঃস্থ কোণের সমান]
(i) ও (ii) নং সমীকরণ থেকে পাই,
∠EAG = ∠EAC
∴ EA, ∠BAC এর বহির্দ্বিখণ্ডক [প্রমাণিত]।
10. ABC ত্রিভুজের AC ও AB বাহুর উপর BE ও CF যথাক্রমে লম্ব। প্রমাণ করি যে, B, C, E, F বিন্দু চারটি সমবৃত্তস্থ। এর থেকে প্রমাণ করি যে, ∆AEF ও ∆ABC এর দুটি করে কোণ সমান।
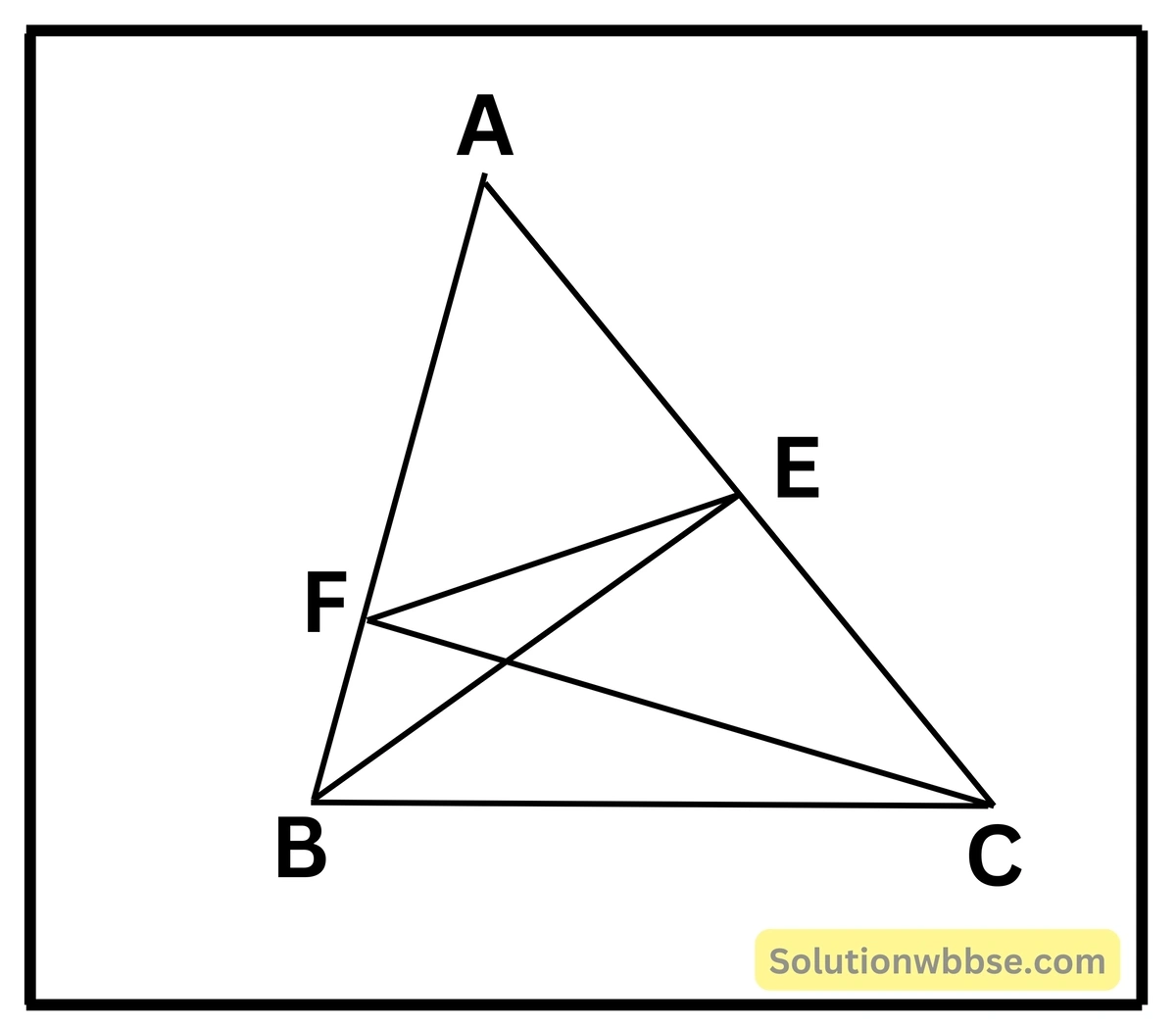
ABC এর AC এবং AB বাহুর ওপর যথাক্রমে BE ও CF লম্ব।
প্রমান করতে হবে যে, B, C, E, F বিন্দু চারটি সমবৃত্তস্থ।
অঙ্কন – E, F যোগ করা হল।
প্রমাণ – ∠CEB = 1 সমকোণ
এবং ∠BFC = 1 সমকোণ
∴ একই রেখাংশ BC এর ওপর অবস্থিত দুটি কোণ ∠CEB = ∠BFC = 1 সমকোণ
∴ B, C, E, F বিন্দু চারটি সমবৃত্তস্থ [প্রমাণিত]
ΔAEF এবং ΔABC থেকে পাই,
যেহেতু B, C, E, F বিন্দু চারটি সমবৃত্তস্থ
∴ বৃত্তস্থ চতুর্ভুজ BCEF -এর
বহিঃস্থ কোণ ∠AEF = বিপরীত অন্তঃস্থ কোণ ∠FBC
এবং বহিঃস্থ কোণ ∠AFE = বিপরীত অন্তঃস্থ কোণ ∠ECB
ΔAEF এবং ΔABC থেকে পাই,
∠AEF = ∠ABC [∵ ∠FBC = ∠ABC]
∠AFE = ∠ACB [∵ ECB = ∠ACB]
∴ ΔAEF ও ABC এর দুটি করে কোণ সমান [প্রমাণিত]।
11. ABCD একটি সামান্তরিক। A ও B বিন্দুগামী একটি বৃত্ত AD ও BC -কে যথাক্রমে E ও F বিন্দুতে ছেদ করে। প্রমাণ করি যে, E, F, C, D বিন্দু চারটি সমবৃত্তস্থ।
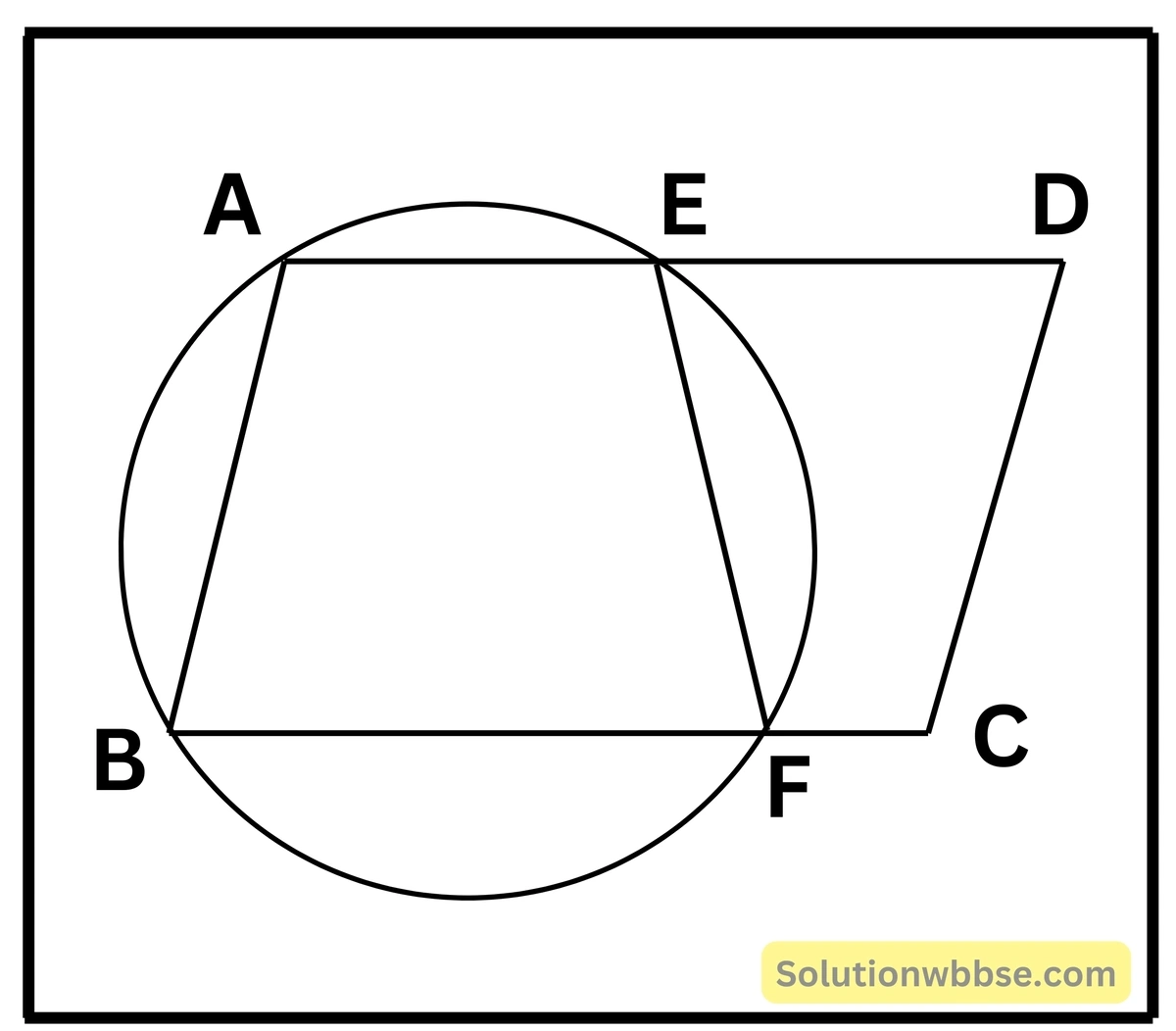
দেওয়া আছে – ABCD একটি সামান্তরিক। A ও B বিন্দুগামী একটি বৃত্ত AD ও BC কে E ও F বিন্দুতে ছেদ করে।
প্রমাণ করতে হবে – E, F, C, D বিন্দু চারটি সমবৃত্তস্থ।
অঙ্কন – E, F যোগ করা হল।
প্রমাণ –
∵ ABCD একটি সামন্তরিক।
∴ ∠BAD + ∠ADC = 2 সমকোণ।
আবার, ABEF একটি বৃত্তস্থ চতুর্ভুজ।
∴ ∠BAE + ∠BFE = 2 সমকোণ,
কিন্তু ∠BFF + ∠EFC = 2 সমকোণ
∴ ∠EFC = ∠BAE
∴ ∠EFC = ∠BAD
∴ ∠EFC = ∠ADC = 2 সমকোণ।
∴ ∠EFC = ∠EDC = 2 সমকোণ।
∴ EFCD একটি বৃত্তস্থ চতুর্ভুজ।
∴ E, F, C, D সমবৃত্তস্থ।
12. ABCD একটি বৃত্তস্থ চতুর্ভুজ। AB ও DC বাহুদ্বয়কে বর্ধিত করলে P বিন্দুতে এবং AD ও BC বাহুদ্বয়কে বর্ধিত করলে R বিন্দুতে মিলিত হয়। ∆BCP এবং ∆CDR -এর পরিবৃত্তদ্বয় T বিন্দুতে ছেদ করে। প্রমাণ করি যে, P, T, R সমরেখ।
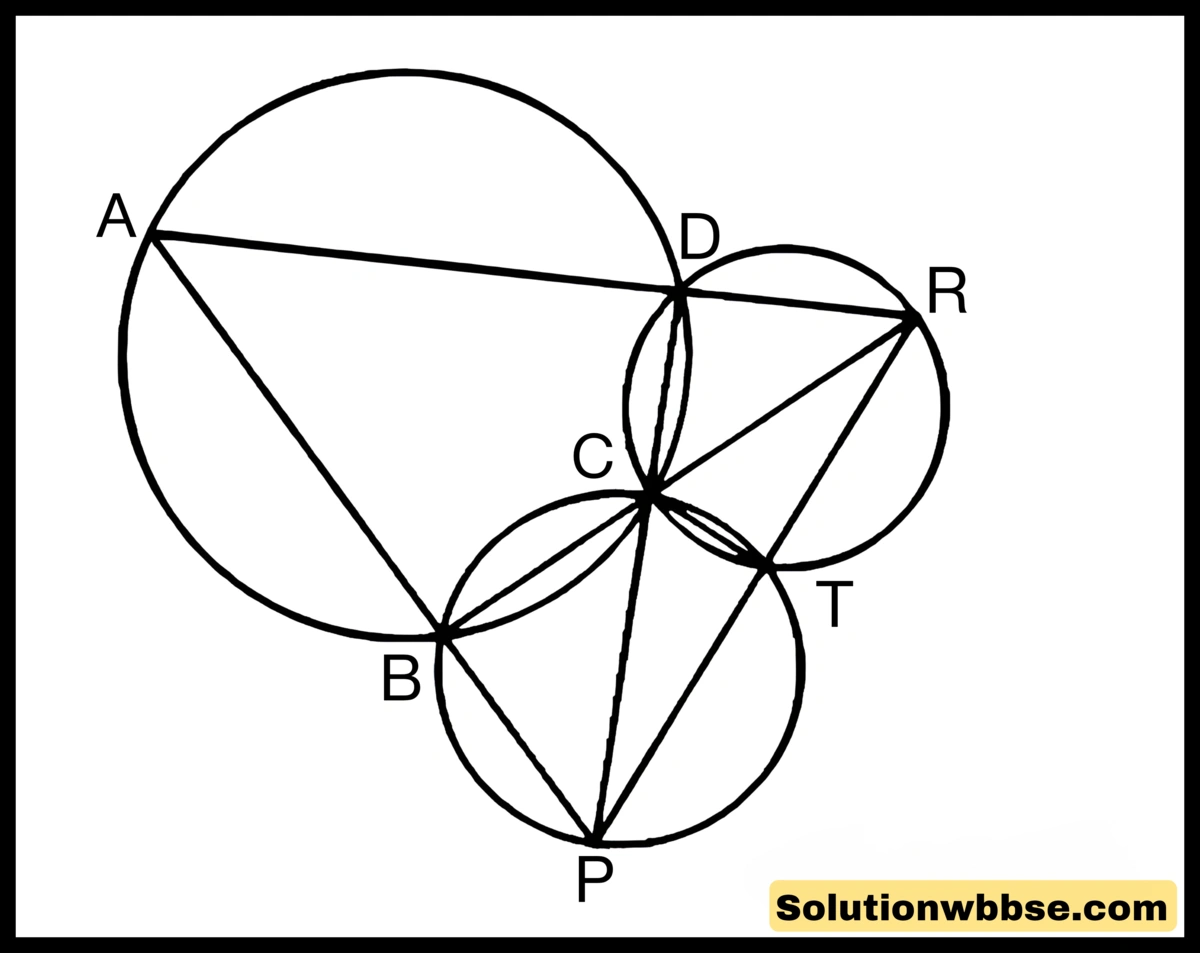
দেওয়া আছে – ABCD একটি বৃত্তস্থ চতুর্ভুজ। AB ও DC বাহুদুটিকে বর্ধিত করায় P বিন্দুতে এবং AD ও BC বাহুদুটিকে বর্ধিত করায় R বিন্দুতে মিলিত হয়েছে এবং ΔBCP এবং ΔCDR -এর পরিবৃত্তদ্বয় T বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে – P, T, R সমরেখ।
অঙ্কন – P, T; T, R ও C, T যোগ করা হল।
ΔBCP ও ΔADP এর ∠BPC = ∠APD
বা, ∠PBC = ∠ADP
∴ ∠BCP = ∠PAD
ΔBCP ও ΔAPD সদৃশকোণী অর্থাৎ সদৃশ
অনুরূপে ΔABR ও ΔDCR সদৃশকোণী অর্থাৎ সদৃশ
এখন ΔPCT ও ΔRCT এর ∠PCT = ∠CRT
CT সাধারণ বাহু
∠RCT = ∠TPC
∴ ΔPCT ≅ ΔRCT
∴ ∠PTC = ∠RTC (অনুরূপ কোণ)
∴ CT, ∠PTC ও ∠RTC এর সাধারণ বাহু
∴ TR ও TP একই সরলরেখায় অবস্থিত হবে।
∴ P, T, R বিন্দু তিনটি সমরেখ।
13. ABC ত্রিভুজের লম্ববিন্দু O; প্রমাণ করি যে বিন্দুটি পাদত্রিভুজের অন্তঃকেন্দ্র।
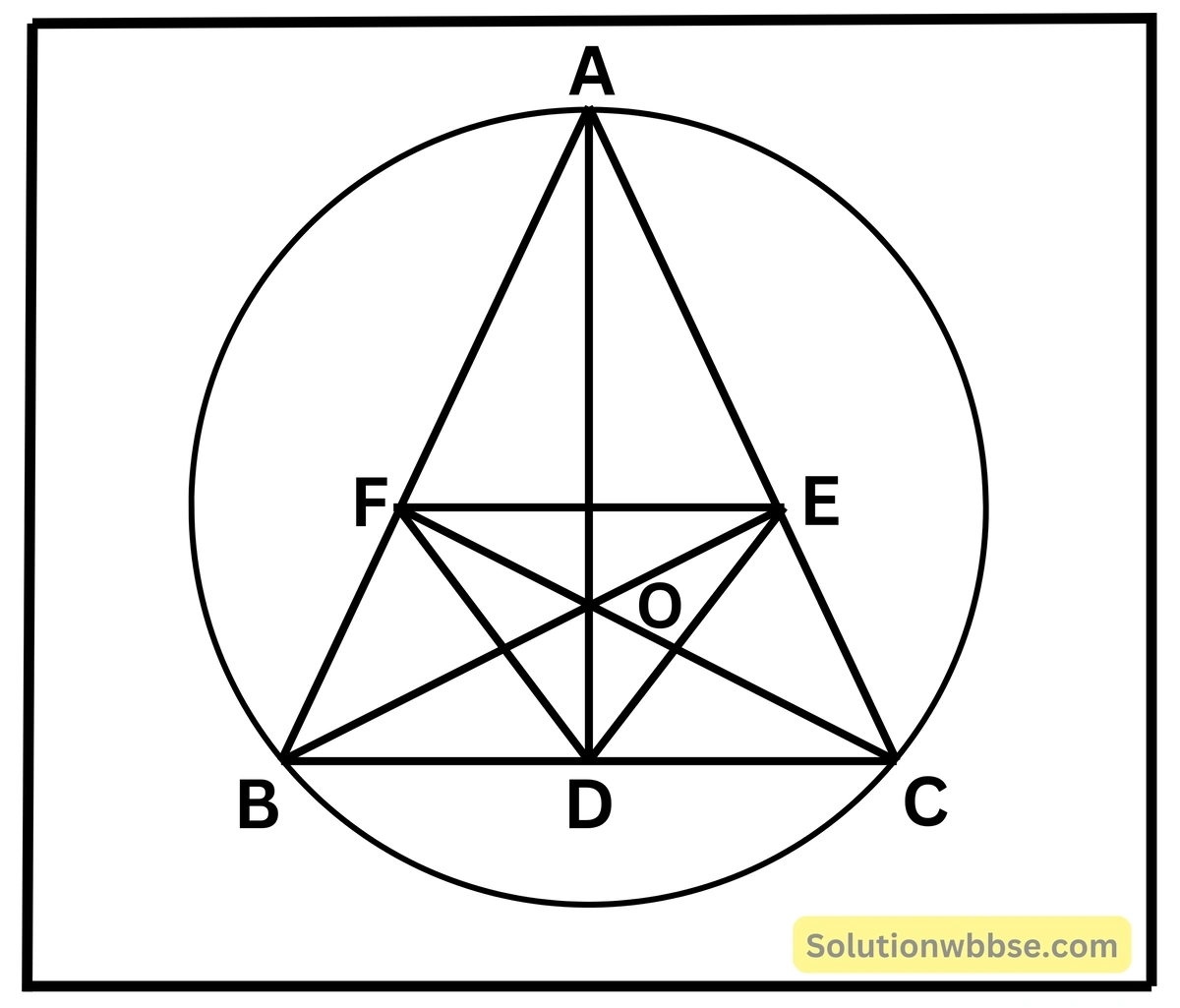
মনে করি, ΔABC -এর লম্ব বিন্দু O; A, B, C শীর্ষবিন্দু তিনটি থেকে বিপরীত বাহুর উপর অঙ্কিত লম্ব তিনটি যথাক্রমে D, E ও F বিন্দুতে ছেদ করেছে। D, E; E, F ও F, D যোগ করা হল।
প্রমাণ করতে হবে যে, DEF ত্রিভুজের অন্তঃকেন্দ্র O।
প্রমাণ – ΔBDO ও ΔΑΕΟ এর ∠BOD = ∠AOE, ∠BDO = ∠AEO = 90°
অবশিষ্ট ∠DBO = অবশিষ্ট ∠EAO
∴ ΔBDO ≅ ΔΑΕΟ
∴ OD = OE
অনুরূপে ΔBOD ≅ ΔAFO ∴ OD = OF
OD = OE = OF
O, ΔDEF এর অন্তঃকেন্দ্র।
14. ABCD এমন একটি বৃত্তস্থ চতুর্ভুজ এঁকেছি যে, AC, ∠BAD -কে সমদ্বিখণ্ডিত করেছে, এবার AD কে E পর্যন্ত এমনভাবে বর্ধিত করলাম যেন DE = AB হয়। প্রমাণ করি যে, CE = CA
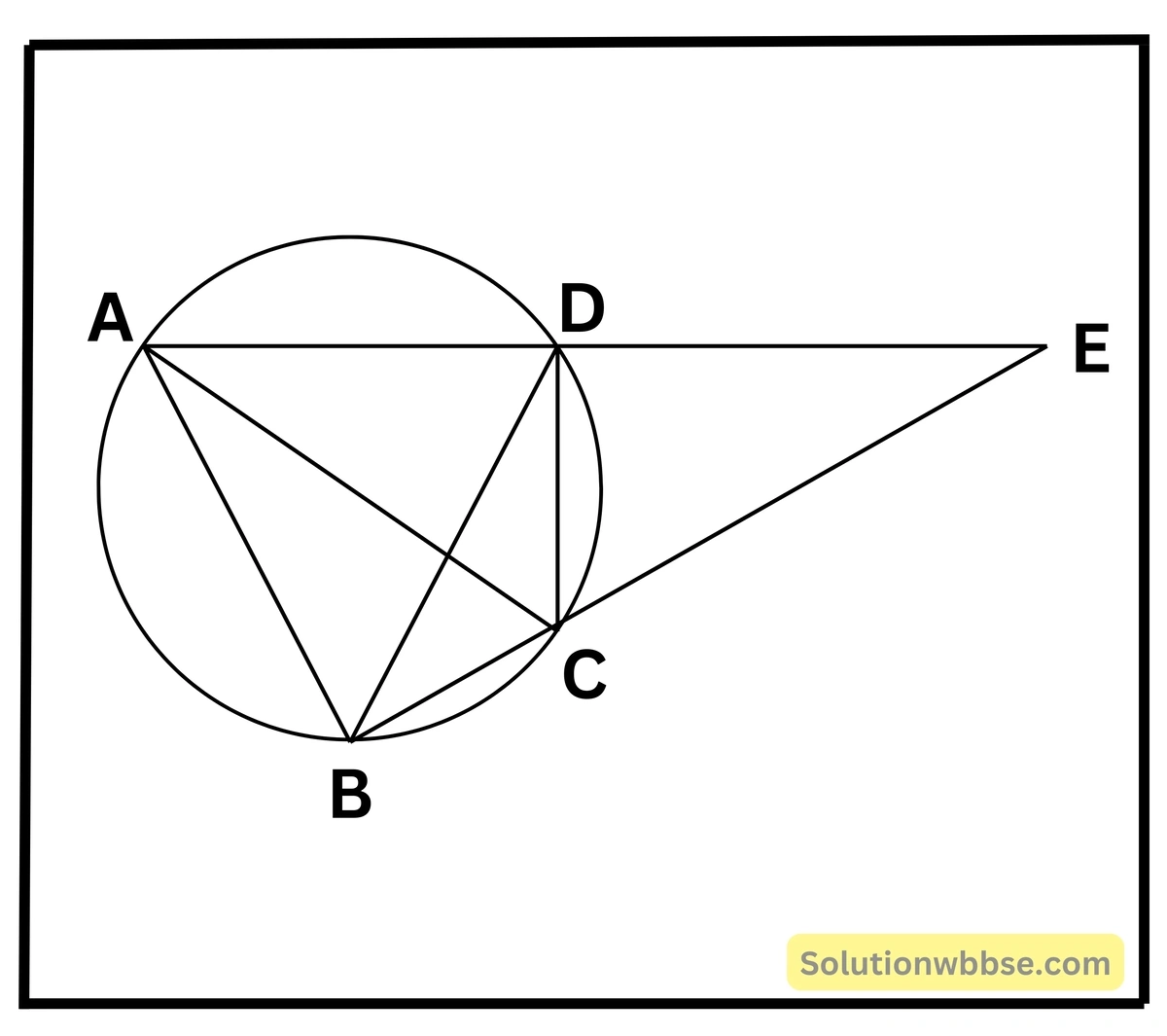
দেওয়া আছে – ABCD একটি বৃত্তস্থ চতুর্ভুজ। AC, ∠BAD কে সমদ্বিখণ্ডিত করেছে।
প্রমাণ করতে হবে যে – CE = CA
অঙ্কন – B ও D যোগ করা হল।
প্রমাণ – ∵ AC কর্ণ ∠BAD কে সমদ্বিখণ্ডিত করেছে।
∠BAC = ∠DAC
একই বৃত্তচাপ DC -এর উপর অবস্থিত ∠DBC = ∠DAC
আবার একই বৃত্তচাপ BC এর উপর অবস্থিত ∠BDC = ∠BAC
∴ ∠DBC = ∠BDC
∴ BC = DC
একই বৃত্তচাপ AD এর উপর অবস্থিত ∠ACD = ∠ABD
∴ ∠ABC = ∠ABD + ∠DBC
∠CDE = ∠DAC + ∠ACD
∴ ∠ABC = ∠CDE
এখন ΔABC ও ΔCED -এর মধ্যে AB = DE (প্রদত্ত)।
BC = DC (পূর্বে প্রমাণিত) এর ∠ABC = ∠CDE (পূর্বে প্রমাণিত)
ΔABC ≅ ΔCED (S-A-S সর্বসমতা অনুসারে)
∴ AC = CE (অনুরূপ বাহু) [প্রমাণিত]
15. দুটি বৃত্তের একটি অপরটির কেন্দ্র O বিন্দুগামী এবং বৃত্ত দুটি পরস্পরকে A ও B বিন্দুতে ছেদ করেছে। A বিন্দুগামী একটি সরলরেখা বিন্দুগামী বৃত্তকে P বিন্দুতে এবং O কেন্দ্রীয় বৃত্তকে R বিন্দুতে ছেদ করেছে। P, B ও R, B যুক্ত করে প্রমাণ করি যে PR = PB
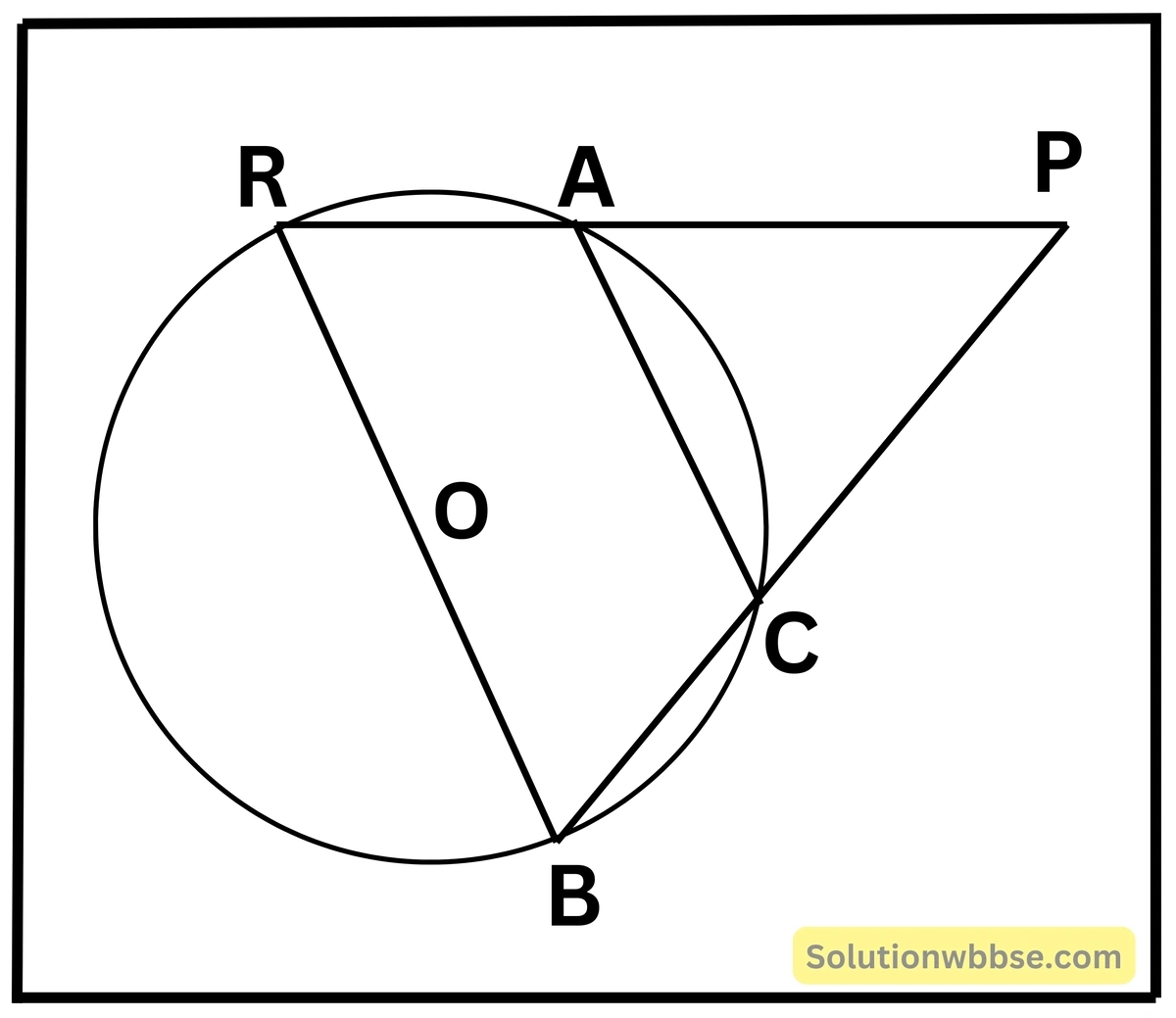
মনে করি, PB সরলরেখা O কেন্দ্রীয় বৃত্তকে C বিন্দুতে ছেদ করে। A, C যোগ করা হল।
প্রমাণ – ΔPRB ও ΔACP এর ∠BPR = ∠APC (একই কোণ)
∠PBR = ∠CAP (∵ ARBC বৃত্তস্থ চতুর্ভুজ)
সুতরাং ∠PBR + ∠RAC = 2 সমকোণ
= ∠RAC + ∠CAP
ΔPRB ও ΔACP স্থূলকোণী অর্থাৎ সদৃশ
∴ ∠PRB = ∠PBR
∴ PB = PR [প্রমাণিত]।
16. প্রমাণ করি যে, একটি সুষম পঞ্চভুজের যে কোন চারটি শীর্ষবিন্দু সমবৃত্তস্থ।
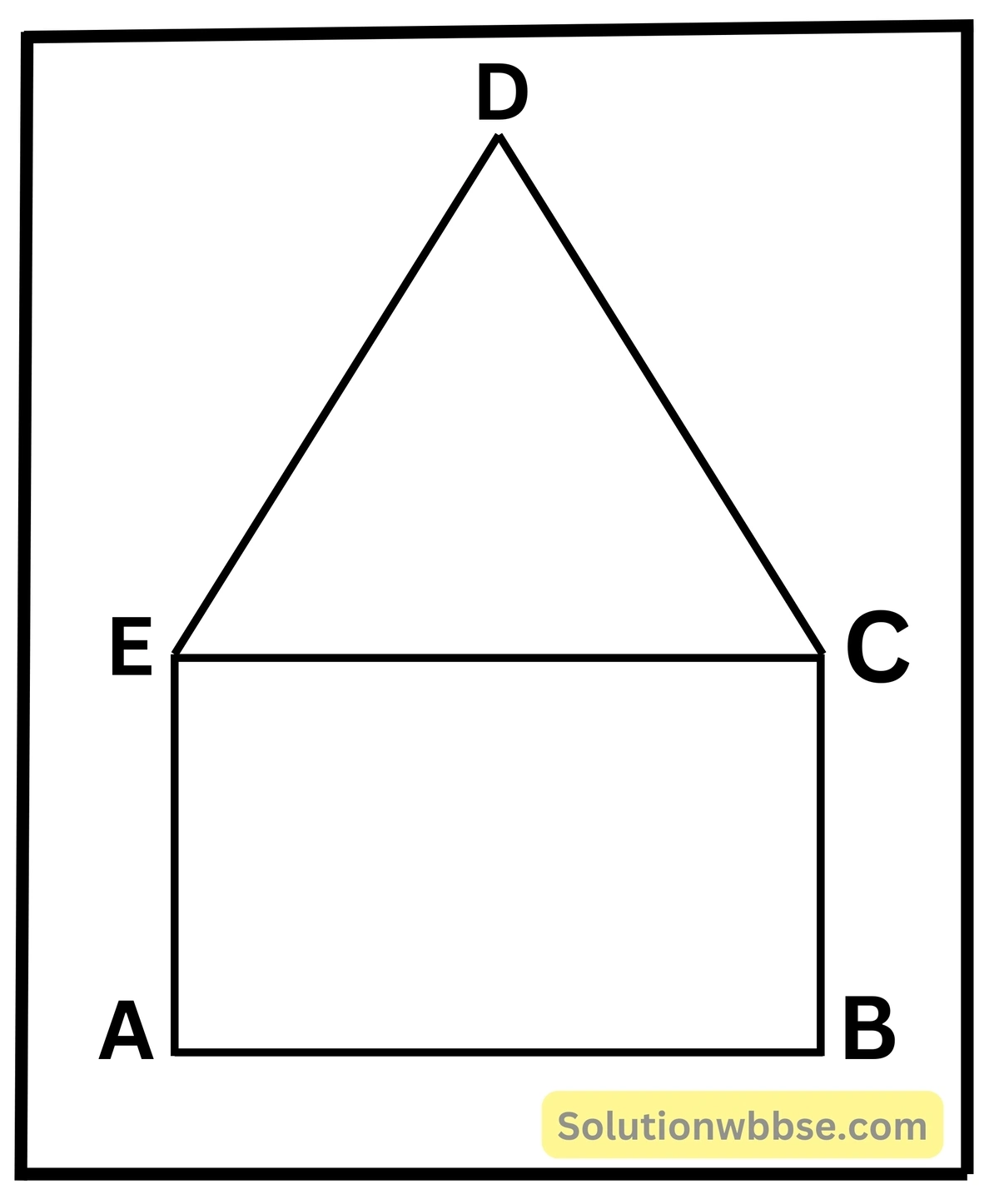
মনে করি, ABCDE একটি পঞ্চভুজ।
প্রমাণ করতে হবে যে, A, B, C, E বিন্দু চারটি অর্থাৎ শীর্ষবিন্দু চারটি সমবৃত্তস্থ।
অঙ্কন – AB এর সমান্তরাল সরলরেখা C, E যোগ করা হল।
প্রমাণ – AB || CE
∠AEC + ∠EAB = 2 সমকোণ
আবার ∠ABC + ∠BCE = 2 সমকোণ
∴ AB সরলরেখার উপরিস্থিত বিন্দু বিপরীত কোণদ্বয় পরস্পর সম্পূরক।
∴ A, B, C, E বিন্দু চারটি সমবৃত্তস্থ।
17. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V. S. A.)
(A) বহুবিকল্লীষ প্রশ্ন (ML. C. Q.) –
(i) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস। ABCD বৃত্তস্থ চতুর্ভুজ। ∠ADC = 120° হলে, ∠BAC -এর মান
(a) 50°
(b) 60°
(c) 30°
(d) 40°
উত্তর – (c) 30°
সমাধান,
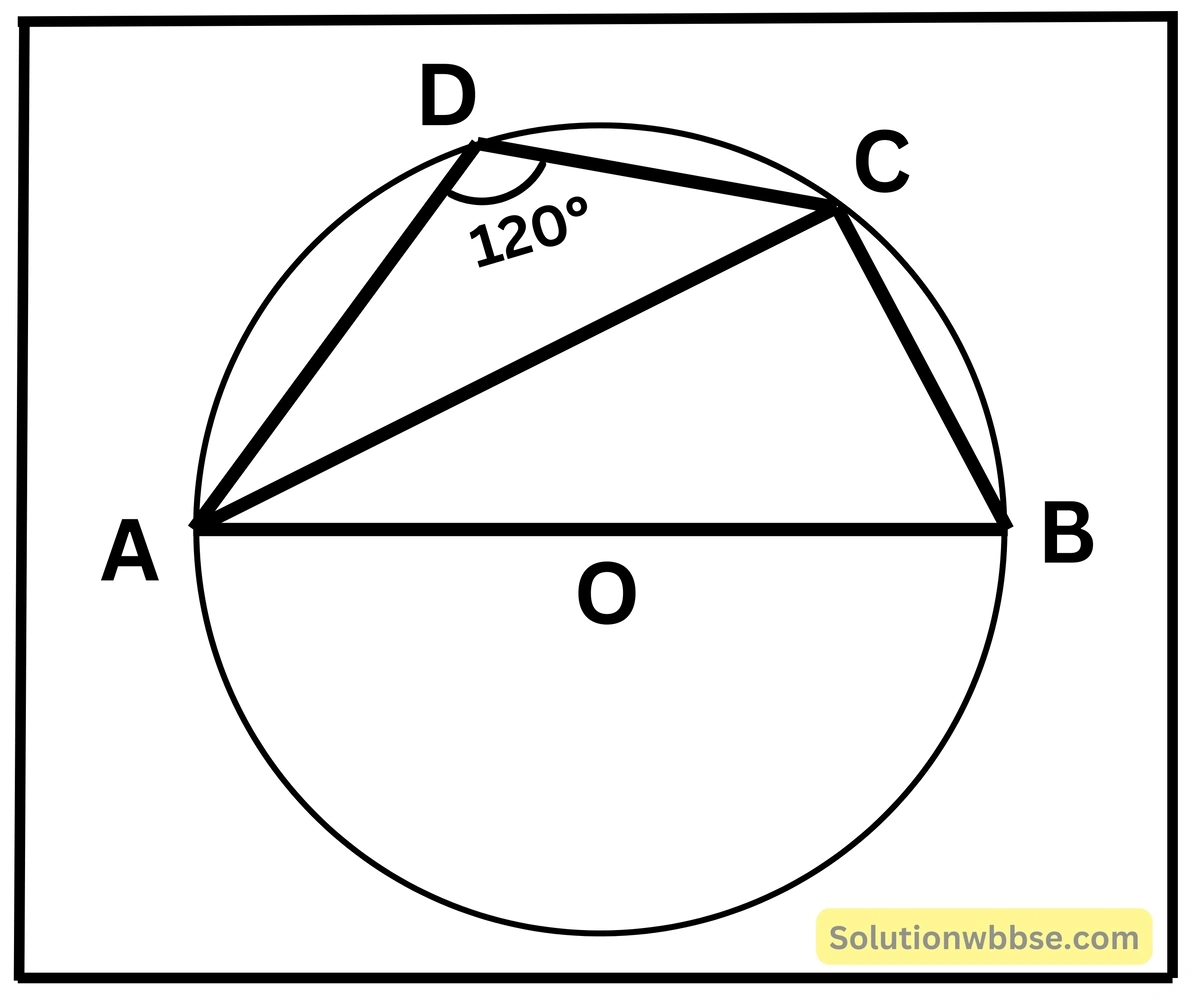
ABCD বৃত্তস্থ চতুর্ভুজ।
∴ ∠ADC + ∠ABC = 180° [∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক]
∴ ∠ABC = 180° – ∠ADC
বা, ∠ABC = 180° – 120°
বা, ∠ABC = 60°
আবার, ∠ACB = 90° [∵ অর্ধবৃত্তস্থ কোণ সমকোণ]
এখন, ΔABC থেকে পাই,
∠ABC + ∠ACB + ∠BAC = 180°
বা, 60° + 90° + ∠BAC = 180°
বা, ∠BAC = 30°
(ii) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস। ABCD বৃত্তস্থ চতুর্ভুজ। ∠ABC = 65°, ∠DAC = 40° হলে, ∠BCD -এর মান
(a) 75°
(b) 105°
(c) 115°
(d) 80°
উত্তর – (c) 115°
সমাধান,
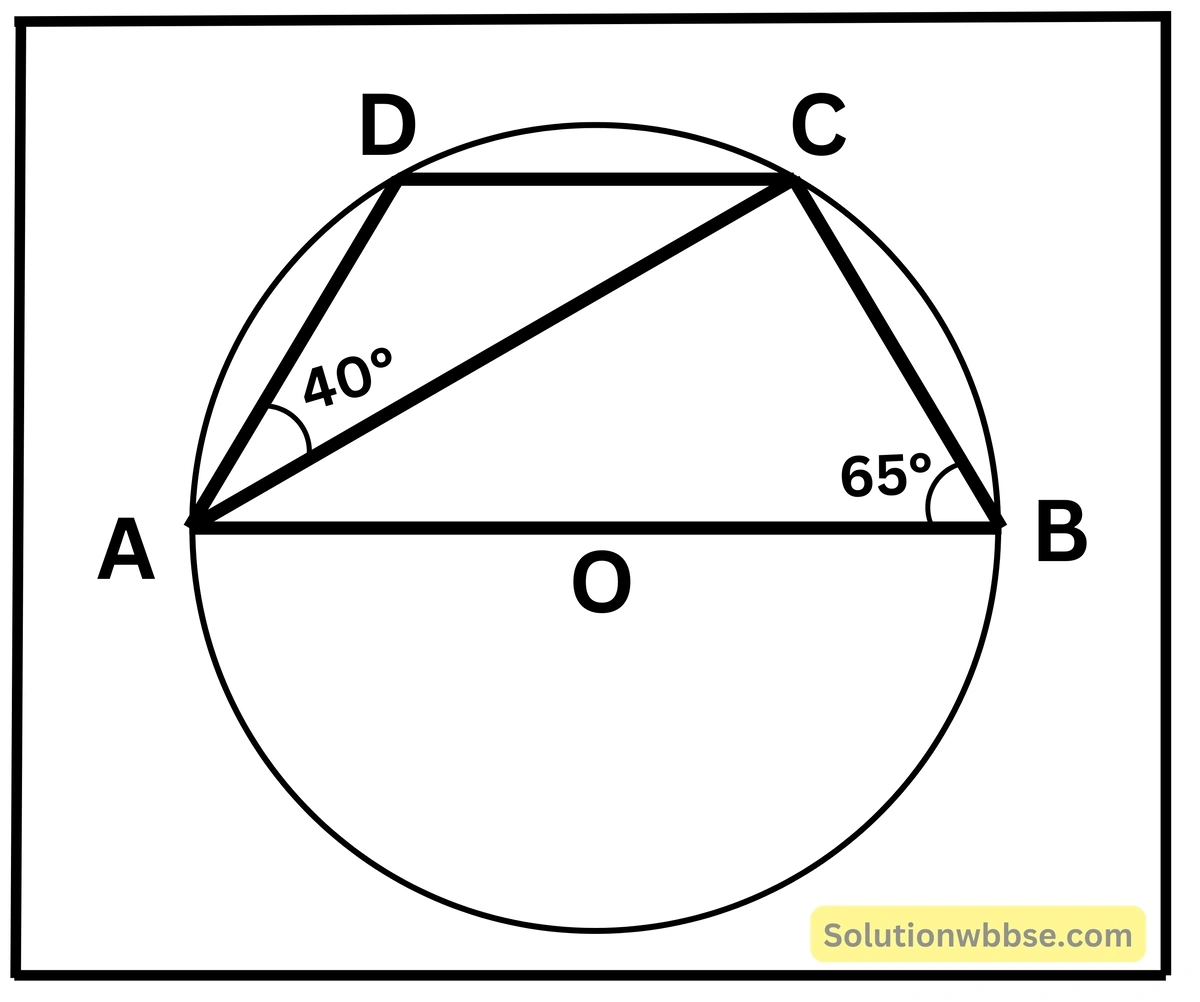
ABCD একটি বৃত্তস্থ চতুর্ভুজ।
∴ ∠ABC + ∠ADC = 180° [∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক]
∴ ∠ADC = 180° – ABC
= 180° – 65°
= 115°
∴ ∠ADC = 115°
∠ACD = 180° – (∠ADC + ∠DAC)
= 180° – (115° + 40°)
= 180° – 155°
= 25°
∴ ∠ACD = 25°
∠ACB = 90° [অর্ধবৃত্তস্থ কোণ]
∴ ∠BCD = ∠ACB + ∠ACD
= 90° + 25°
= 115°
∴ ∠BCD = 115°
(iii) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB বৃত্তের ব্যাস। ABCD বৃত্তস্থ চতুর্ভুজ যার AB || DC এবং ∠BAC = 25° হলে ∠DAC -এর মান
(a) 50°
(b) 25°
(c) 130°
(d) 40°
উত্তর – (d) 40°
সমাধান,
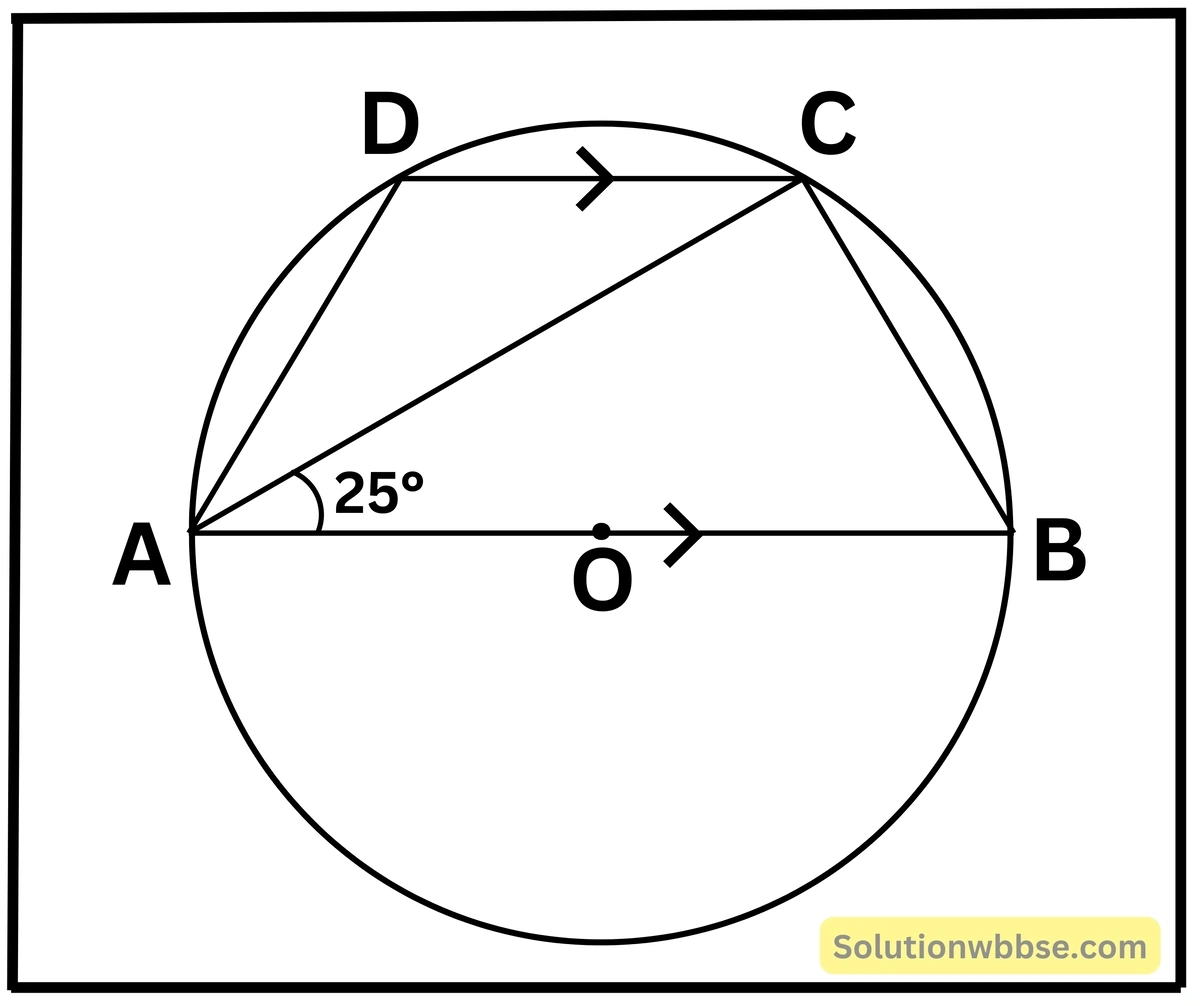
∠BAC = ∠ACD [একান্তর কোণ, AB || DC, AC ভেদক]
∴ ∠ACD = 25°
∠ACB = 90° [অর্ধবৃত্তস্থ কোণ সমকোণ]
∠ABC = 180° – (∠ACB + ∠BAC)
বা, ∠ABC = 180° – (90° + 25°)
বা, ∠ABC = 180° – 115°
বা, ∠ABC = 65°
∴ ∠ADC = 180° – 65° = 115° [বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক]
∴ ∠DAC = 180° – (∠ADC + ∠ACD)
= 180° – (115° + 25°)
= 180° – 140°
= 40°
(iv) পাশের চিত্রে ABCD বৃত্তস্থ চতুর্ভুজ। BA -কে F বিন্দু পর্যন্ত বর্ধিত করা হলো। AE || CD, ∠ABC = 92° এবং ∠FAE = 20° হলে, ∠BCD -এর মান
(a) 20°
(b) 88°
(c) 108°
(d) 72°
উত্তর – (c) 108°
সমাধান,
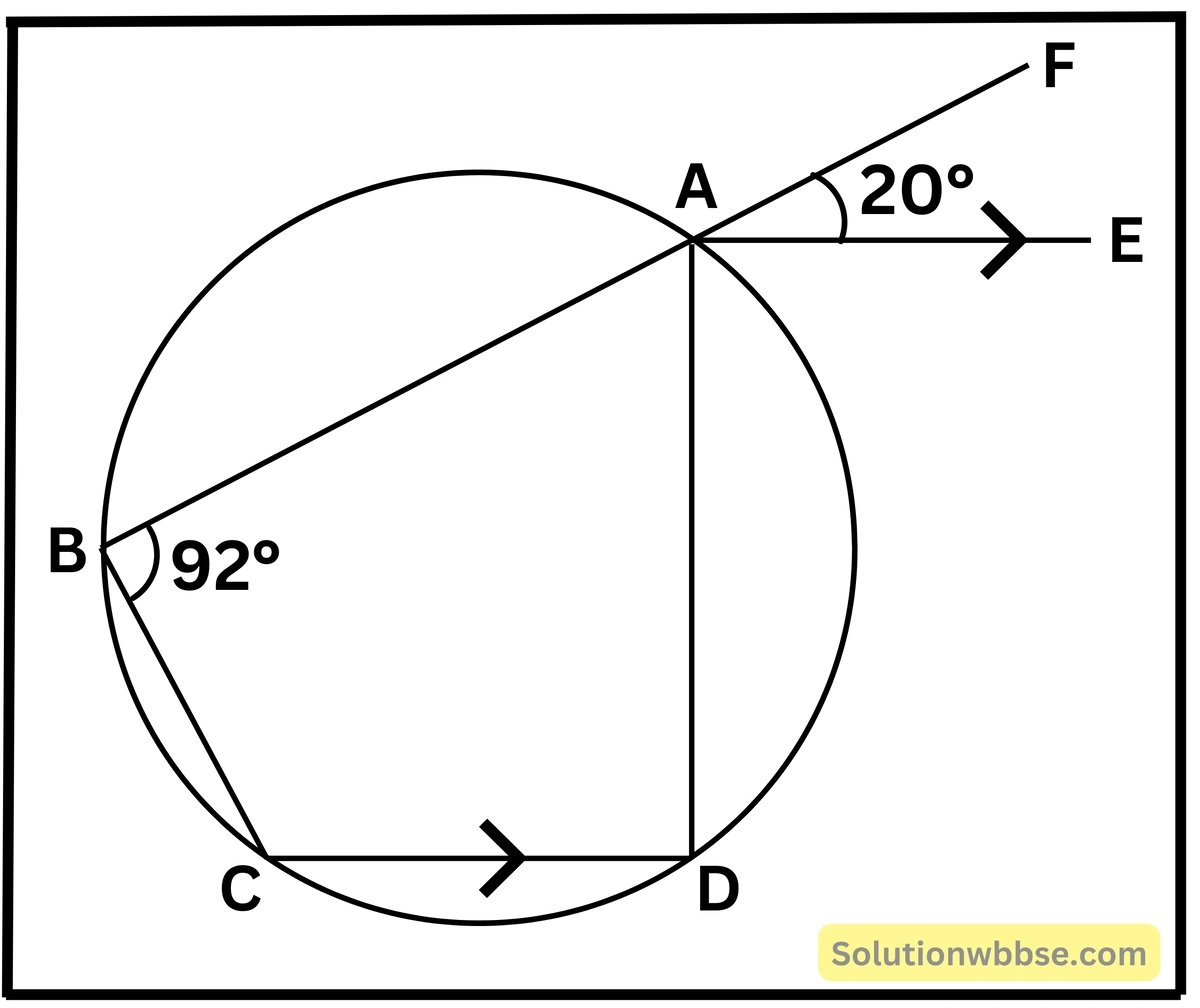
ABCD বৃত্তস্থ চতুর্ভুজের ∠ABC = 92°
∠ADC = 180° – 92° = 88° [বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক]
∠ADC = ∠DAE [একান্তর কোণ, AE || CD, AD ভেদক]
∠DAE = 88°
∠DAF = 88° + 20° = 108°
∴ ∠BCD = 108° [∵ বৃত্তস্থ চতুর্ভুজের বহিঃস্থ কোণ, অন্তঃস্থ বিপরীত কোণের সমান]
(v) পাশের চিত্রে দুটি বৃত্ত পরস্পরকে C ও D বিন্দুতে ছেদ করে। D ও C বিন্দুগামী দুটি সরলরেখা একটি বৃত্তকে যথাক্রমে A ও B বিন্দুতে এবং অপর বৃত্তকে E ও F বিন্দুতে ছেদ করে। ∠DAB = 75° হলে, ∠DEF -এর মান
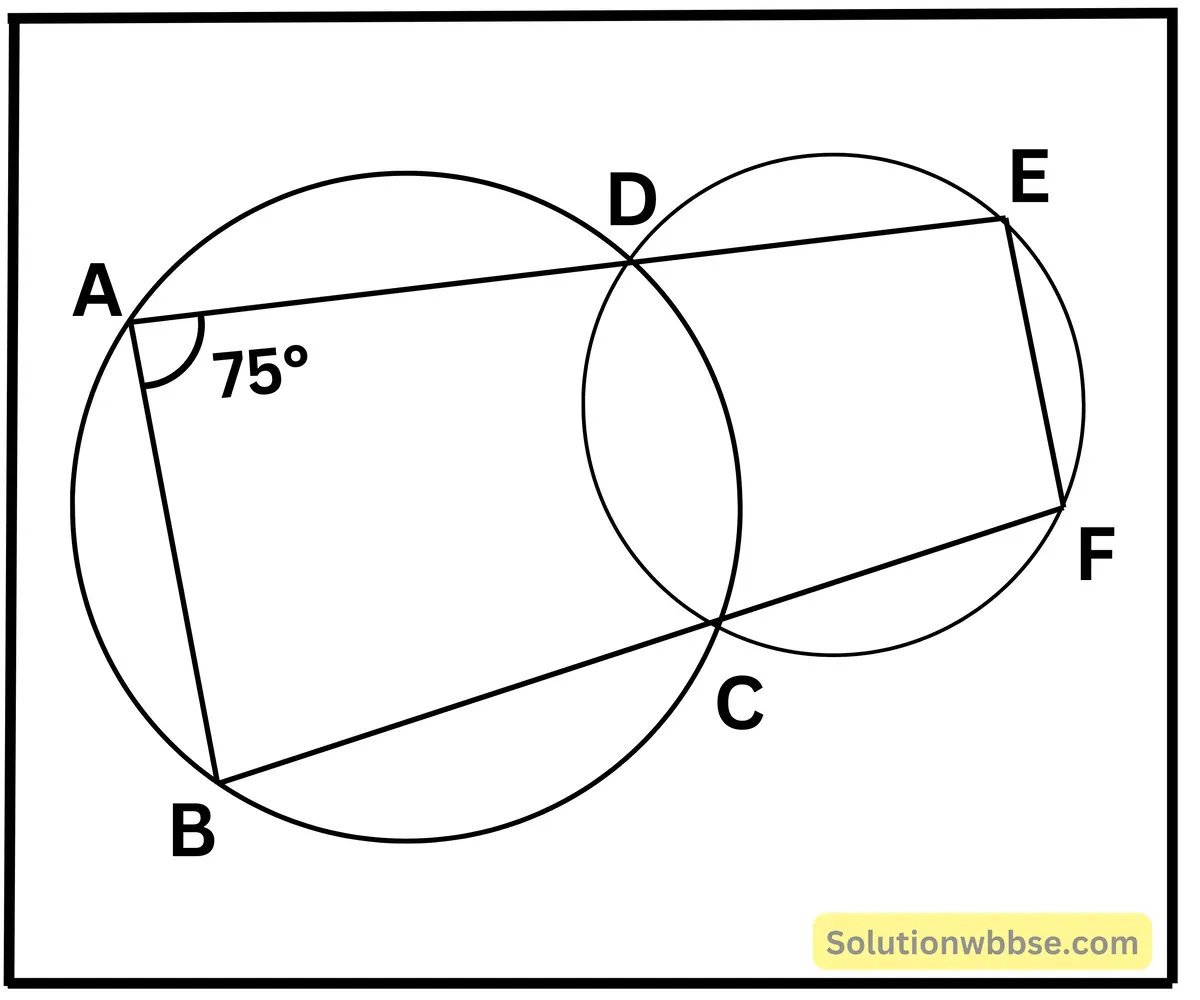
(a) 75°
(b) 70°
(c) 60°
(d) 105°
উত্তর – (d) 105°
সমাধান,
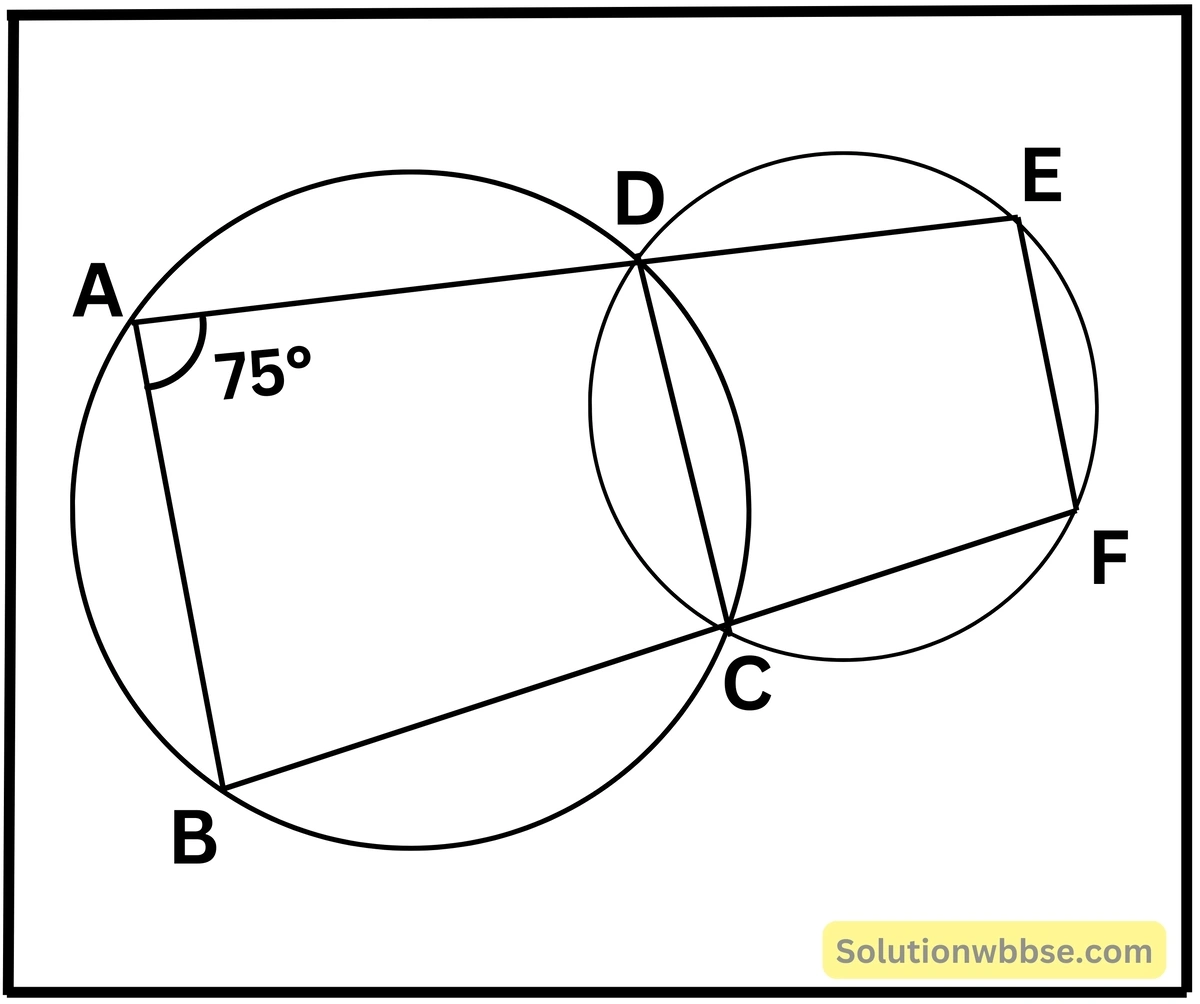
ABCD বৃত্তস্থ চতুর্ভুজ।
এবং ∠BAC = 75°
∠BCD = 180° – 75° = 105° [∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক]
∠DCF = 180° – 105°=75° [∵ BF সরলরেখার ওপর বিন্দুতে, CD দণ্ডায়মান]
আবার, DCFE বৃত্তস্থ চতুর্ভুজ
∠DEF = 180° – 75° = 105° [∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক]
(B) সত্য/মিথ্যা লিখি –
(i) একটি বৃত্তস্থ চতুর্ভুজের বিপরীত কোণ পরস্পর পূরক।
উত্তর – বিবৃতিটি মিথ্যা।
(ii) একটি বৃত্তস্থ চতুর্ভুজের একটি বাহুকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণ বিপরীত অন্তঃস্থ কোণের সমান হয়।
উত্তর – বিবৃতিটি সত্য।
(C) শূন্যস্থান পূরণ করি –
(i) একটি চতুর্ভুজের বিপরীত কোণদ্বয় পরস্পর সম্পূরক হলে চতুর্ভুজের শীর্ষবিন্দুগুলি ___।
উত্তর – সমবৃত্তস্থ।
(ii) একটি বৃত্তস্থ সামান্তরিক একটি ___ চিত্র।
উত্তর – আয়তকার।
(iii) একটি বর্গাকার চিত্রের শীর্ষবিন্দুগুলি ___।
উত্তর – সমবৃত্তস্থ।
18. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S. A.) –
(i) পাশের চিত্রে P ও Q কেন্দ্রবিশিষ্ট বৃত্তদুটি B ও C বিন্দুতে ছেদ করেছে। ACD একটি সরলরেখাংশ। ∠ARB = 150°, ∠BQD = x° হলে, x -এর মান নির্ণয় করি।
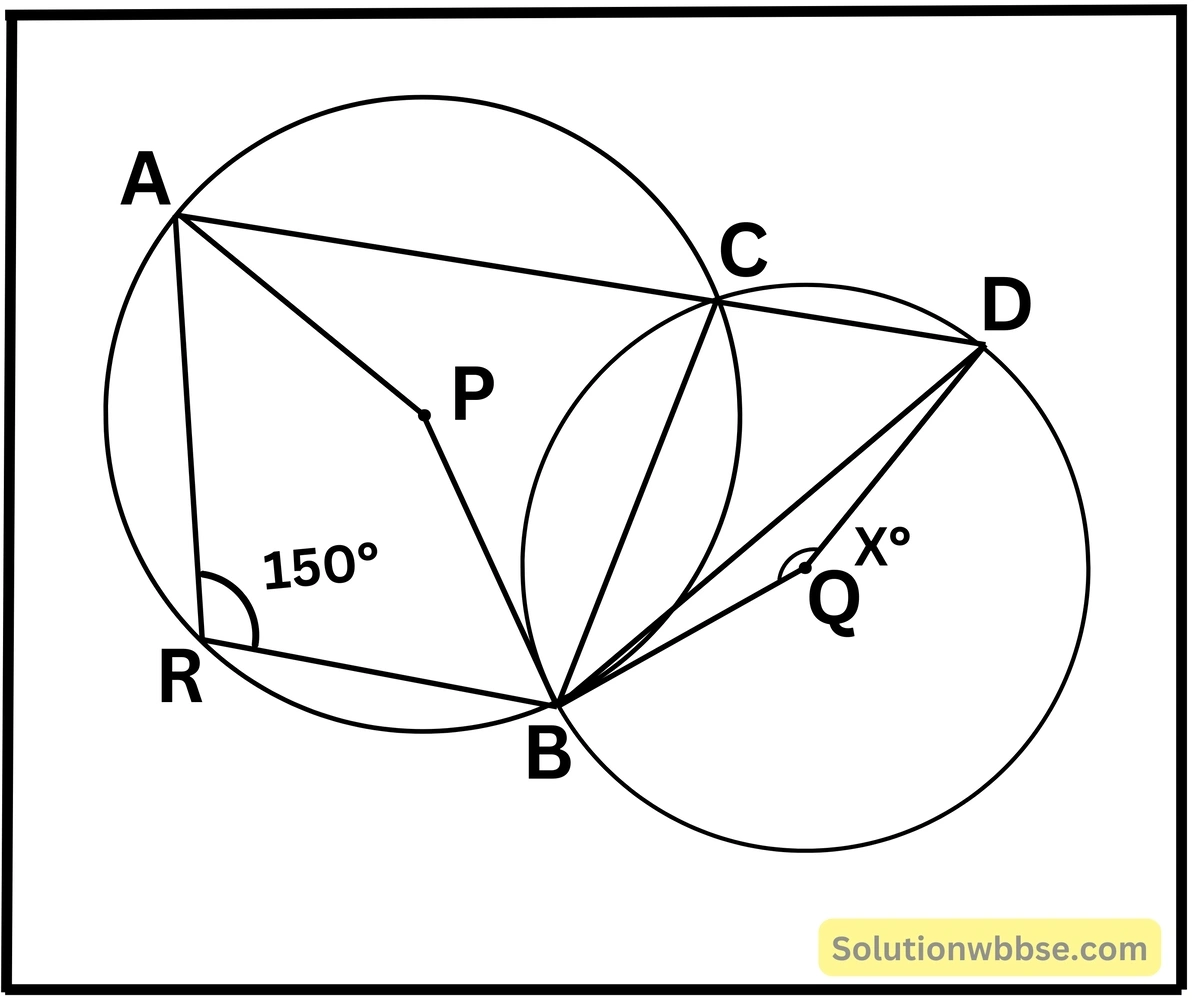
∠ARB = 150°
ARBC বৃত্তস্থ চতুর্ভুজ এবং বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক।
∠ACB + ∠ARB = 180°
বা, ∠ACB = 180° – 150° = 30°
আবার, ∠ACD = 180°
∠BCD = 180° – ∠ACB
বা, ∠BCD = 180° – 30°
বা, ∠BCD = 150°
প্রবিদ্ধ কোণ ∠BQD = 2 × ∠BCD [∵ একই বৃত্তচাপের ওপর অবস্থিত কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন]
∴ প্রবিদ্ধ ∠BQD = 2 ×150° = 300°
বা, ∠BQD = 360° – প্রবিদ্ধ ∠BQD
বা, ∠BQD= 360° – 300°
বা, ∠BQD = 60°
∴ x° = 60°
(ii) পাশের চিত্রে দুটি বৃত্ত পরস্পর P ও Q বিন্দুতে ছেদ করে। ∠QAD = 80° এবং ∠PDA = 84° হলে, ∠QBC ও ∠BCP -এর মান নির্ণয় করি।
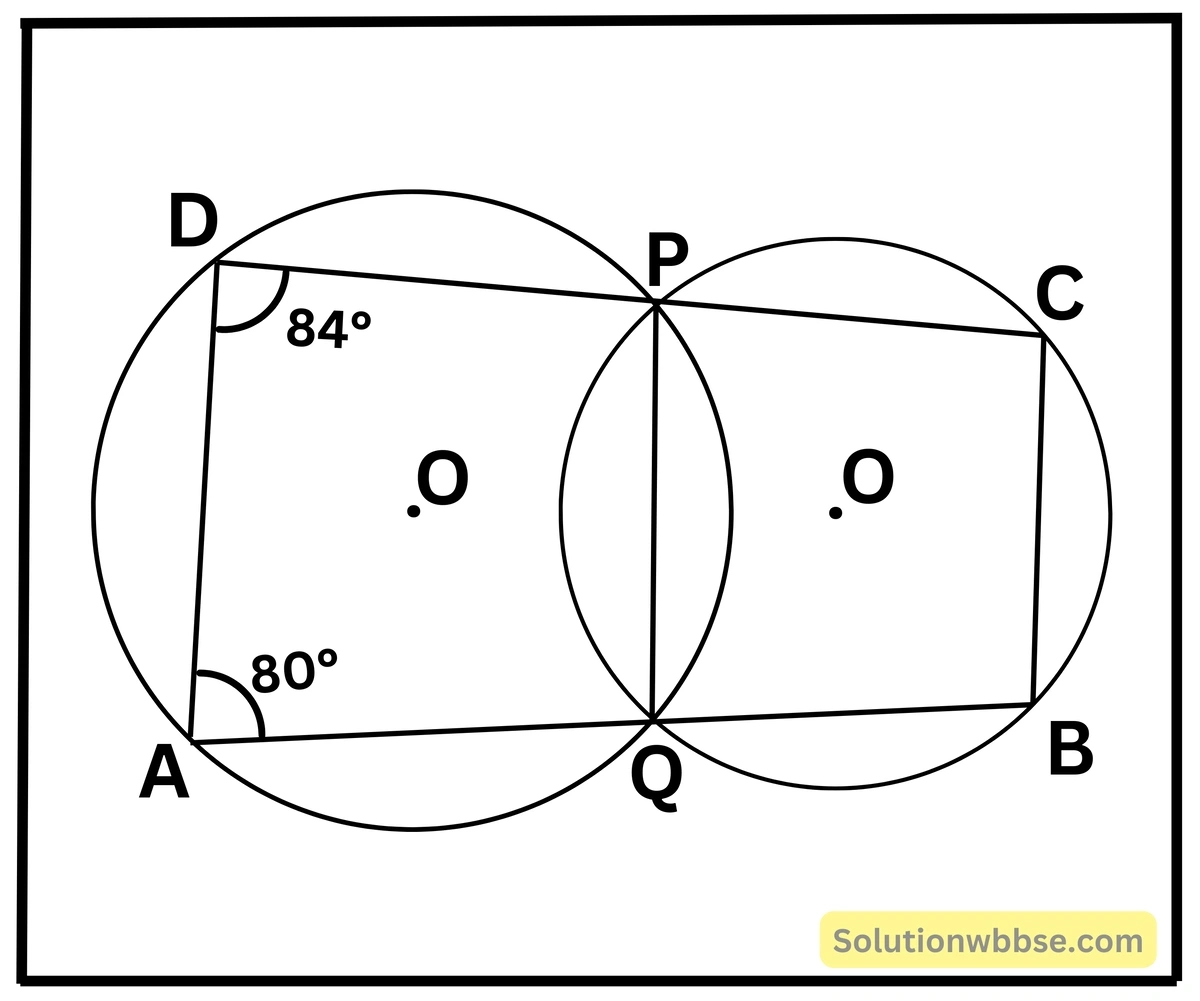
∠QAD = 80°
ADPQ বৃত্তস্থ চতুর্ভুজ।
∴ ∠QAD + ∠QPD = 180° [∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক]
বা, ∠QPD = 180° – ∠QAD
বা, ∠QPD = 180° – 80°
বা, ∠QPD = 100°
আবার, DC একটি সরলরেখা
∴ ∠QPC = 180° – 100° = 80°
আবার, PQBC বৃত্তস্থ চতুর্ভুজ
∴ ∠QPC + ∠QBC = 180° [যেহেতু, বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক]
বা, ∠QBC = 180° – ∠QPC
বা, ∠QBC = 180° – 80°
বা, ∠QBC = 100°
একিইভাবে, ∠PDA = 84° হলে, বহিঃস্থ কোণ∠PQB = 84°
∴ ∠PCB = 180° – 84° = 96° [যেহেতু, ∠PQB এবং ∠PCB বৃত্তস্থ চতুর্ভুজের বিপরীত কোণ অতএব তারা সম্পূরক]
∴ ∠PCB = 96°
(iii) পাশের চিত্রে ∠BAD = 60°, ∠ABC = 80° হলে, ∠DPC এবং ∠BQC -এর মান নির্ণয় করি।
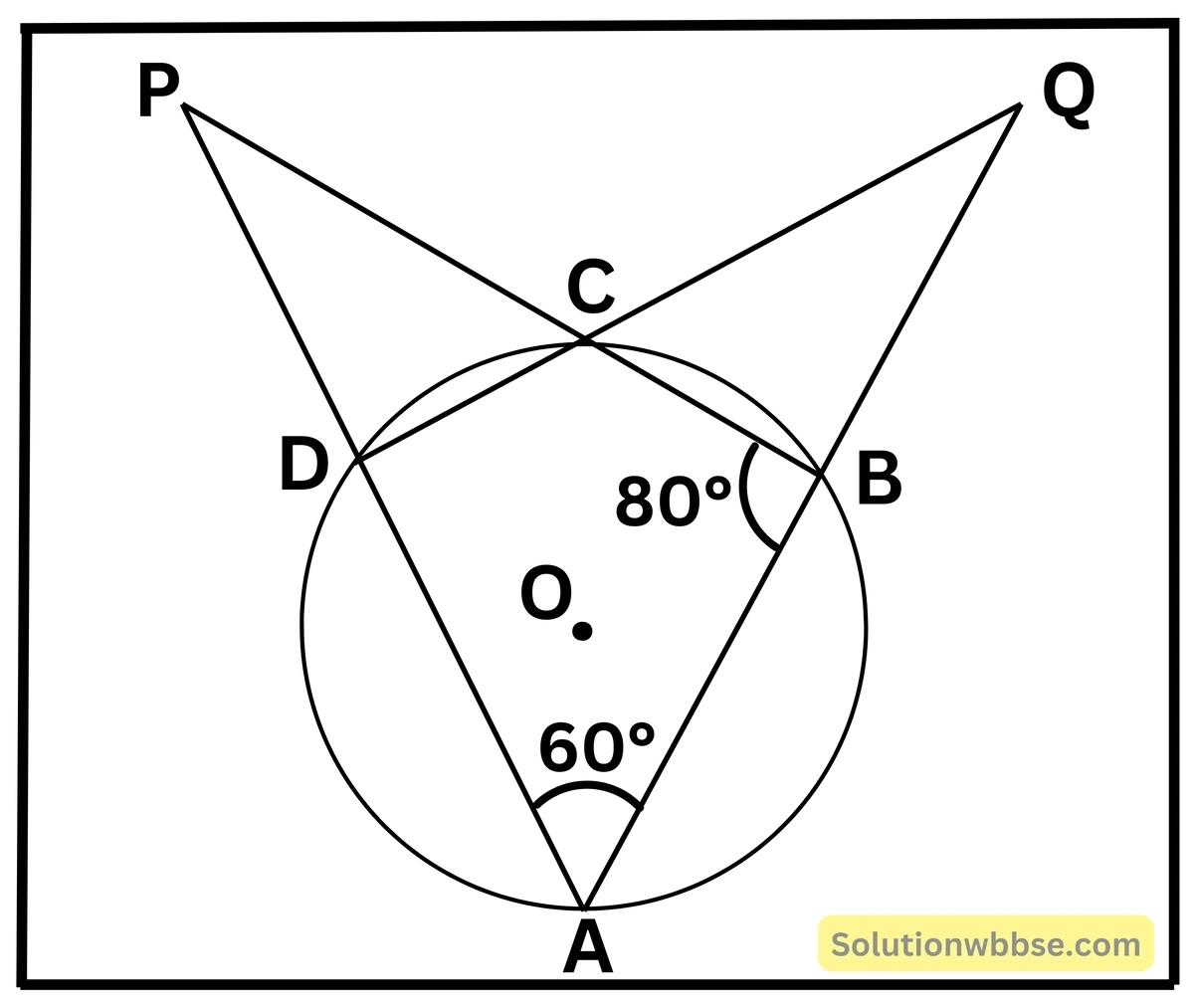
ABCD একটি বৃত্তস্থ চতুর্ভুজ।
∠BAD = 60° (প্রদত্ত)
∴ ∠DCP = 60° [যেহেতু, বৃত্তস্থ চতুর্ভুজের কোনো একটি বহিঃস্থ কোণের মান অন্তঃস্থ বিপরীত কোণের সমান]
আবার, ∠ABC = 80°
∴ ∠CDP = 80° [ যেহেতু, বৃত্তস্থ চতুর্ভুজের কোনো একটি বহিঃস্থ কোণের মান অন্তঃস্থ বিপরীত কোণের সমান্]
∆CPD ত্রিভুজ থেকে পাই,
∠CPD = 180° – (∠CDP + ∠DCP)
বা, ∠CPD =180° – (80° + 60°)
বা, ∠CPD = 180° – 140°
বা, ∠CPD = 40°
∴ ∠DPC = 40°
আবার, ∠BCQ = ∠BAD = 60° [ যেহেতু, বৃত্তস্থ চতুর্ভুজের কোনো একটি বহিঃস্থ কোণের মান অন্তঃস্থ বিপরীত কোণের সমান]
∠CBQ = 180° – ∠ABC = 180° – 80° = 100°
∆CQB থেকে পাই,
∠BQC =180° – (∠BCQ + ∠CBQ)
∠BQC = 180° – (60° + 100°)
বা, ∠BQC = 180° – 160°
বা, ∠BQC = 20°
∴ ∠BQC = 20°
(iv) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AC ব্যাস। ∠AOB = 80° এবং ∠ACE = 10° হলে, ∠BED -এর মান নির্ণয় করি।
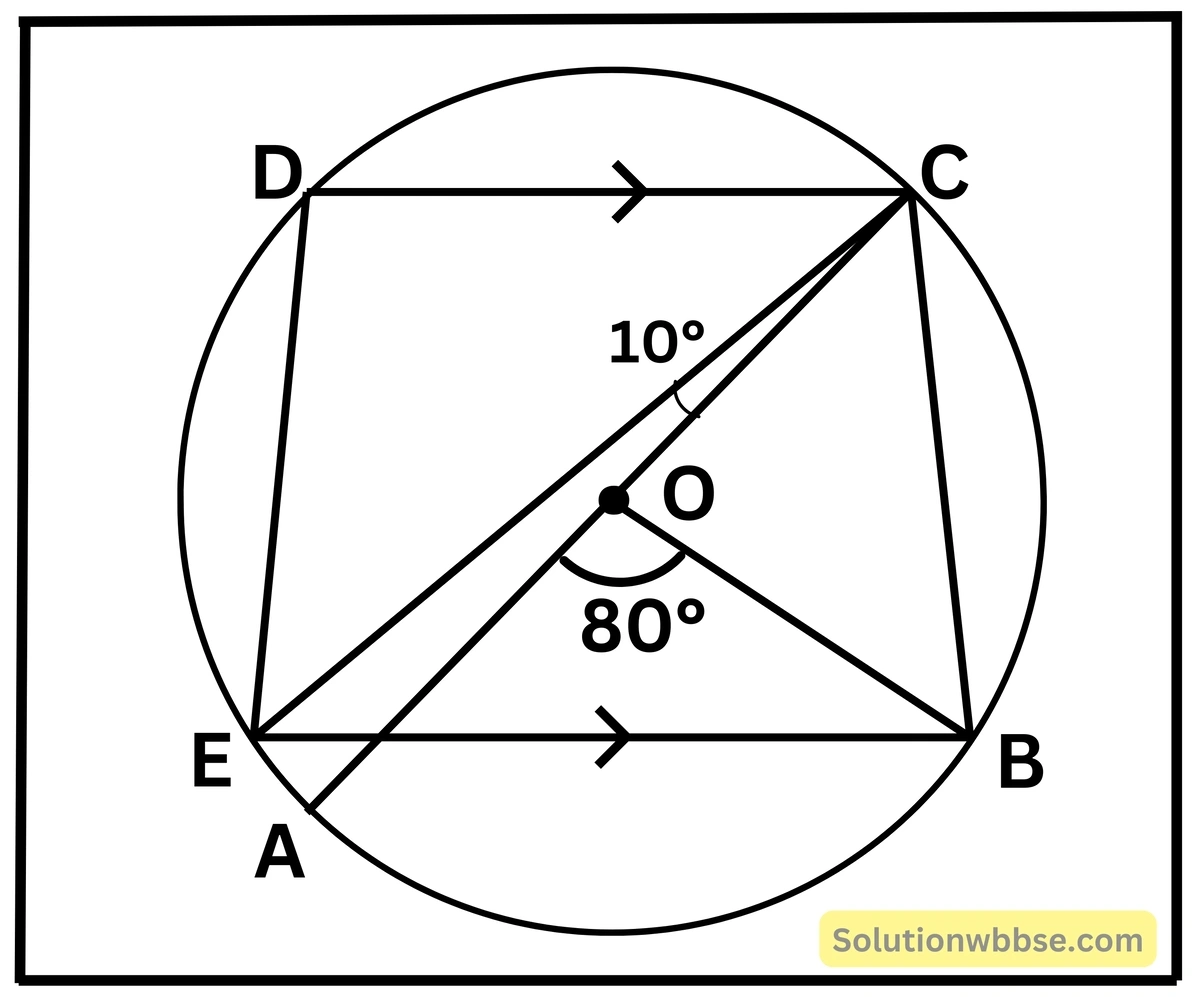
∠AOB = 80°
এখন, ∠ACB = \(\frac12\) × ∠AOB [যেহেতু AB বৃত্তচাপের ওপর ∠AOB কেন্দ্রস্থ কোণ এবং ∠ACB পরিধিস্থ কোণ]
∴ ∠ACB = \(\frac12\times80^\circ\) = 40°
আবার, ∠ECB= ∠ACE + ∠ACB
∴ ∠ECB = 10° + 40°
বা, ∠ECB = 50°
আবার, ∠BOC = 180° – ∠AOB
বা, ∠BOC = 180° – 80°
বা, ∠BOC = 100°
আবার, BC বৃত্তচাপের ওপর ∠BOC কেন্দ্রস্থ কোণ এবং BEC পরিধিস্থ কোণ
∴ ∠BEC = \(\frac12\) × ∠BOC [ যেহেতু কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন]
বা, ∠BEC = \(\frac12\times100^\circ\)
বা, ∠BEC = 50°
আবার, ∠BEC = ∠DCE = 50° [একান্তর কোণ, কারণ EB || DC এবং EC ভেদক]
∴ ∠DCE = 50°
∴ ∠DCB = ∠DCE + ∠ECB
= 50° + 50°
= 100°
এখন, ∠BED = 180° – ∠DCB [যেহেতু, DEBC একটি বৃত্তস্থ চতুর্ভুজ এবং বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক]
বা, ∠BED =180° – 100°
বা, ∠BED = 80°
∴ ∠BED = 80°
(v) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB বৃত্তের ব্যাস। ∠AOD = 140° এবং ∠CAB = 50° হলে, ∠BED -এর মান নির্ণয় করি।
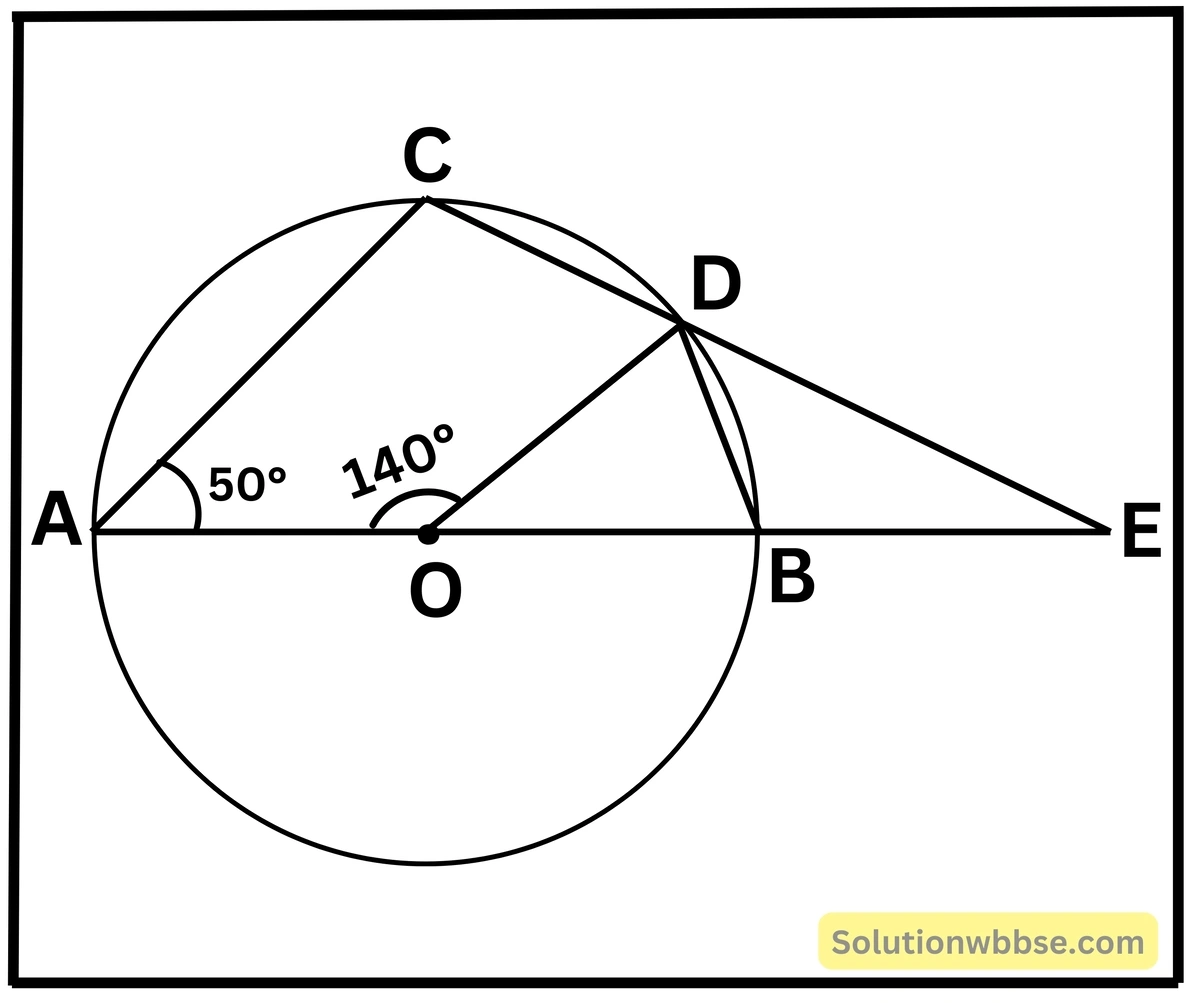
ABDC একটি বৃত্তস্থ চতুর্ভুজ।
∴ ∠CAB + ∠BDC = 180°
বা, 50° + ∠BDC = 180°
বা, ∠BDC = 180° – 50°
বা, ∠BDC = 130°
এবং ∠BDE = 180° – 130° = 50° [∵ ∠CDE = 180°]
আবার, ∠BOD = 180° – 140° = 40°
OBD ত্রিভুজের ক্ষেত্রে,
OB = OD [একই বৃত্তের ব্যাসার্ধ।
∠OBD = ∠ODB
বা, \(\angle OBD=\frac{\left(180^\circ-\angle BOD\right)}2\)
বা, \(\angle OBD=\frac{\left(180^\circ-40^\circ\right)}2\) [∵ ∠BOD = 40°]
বা, ∠ODB = 70°
এখন, BED ত্রিভুজের বহিঃস্থ কোণ ∠OBD = ∠BDE + ∠BED (অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টি)
∴ 70° – 50° + ∠BED
বা, ∠BED = 70° – 50°
∴ ∠BED = 20°
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের দশম অধ্যায়, ‘বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য’ -এর ‘কষে দেখি – 10’ বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন