আজকের আর্টিকেলে আমরা নবম শ্রেণীর ভৌতবিজ্ঞান বইয়ের দ্বিতীয় অধ্যায় “বল ও গতি” এর “নিউটনের প্রথম গতিসূত্র” থেকে সহজ ও সংক্ষিপ্ত প্রশ্ন-উত্তর শেয়ার করবো। এই প্রশ্নগুলো নবম শ্রেণির ইউনিট টেস্ট থেকে বার্ষিক পরীক্ষা এর জন্য যেমন গুরুত্বপূর্ণ, তেমনি চাকরি বা বিভিন্ন প্রতিযোগিতার পরীক্ষাতেও কাজে লাগবে। এই অধ্যায় থেকে স্কুল পরীক্ষা থেকে শুরু করে চাকরির পরীক্ষায় প্রায়ই প্রশ্ন আসে, তাই এই প্রশ্নোত্তরগুলো সবাইকে সাহায্য করবে। প্রতিটি প্রশ্নের উত্তর সহজ ভাষায় লেখা হয়েছে, যাতে সবাই বুঝতে পারেন। পড়ার শেষে এই অধ্যায়ের মুখ্য বিষয়গুলো আপনার আয়ত্তে চলে আসবে এবং যেকোনো পরীক্ষায় আত্মবিশ্বাসের সঙ্গে লিখতে পারবেন।

জ্ঞানমূলক প্রশ্নোত্তর
কার্যকর বা অপ্রতিমিত বল ও প্রতিমিত বল কাকে বলে?
কার্যকর বল (Effective force) বা অপ্রতিমিত বল (Unbalanced force) – কোনো বস্তুর ওপর এক বা একাধিক বল যদি এমনভাবে ক্রিয়া করে, যে ওই বলটির বা বলগুলির ক্রিয়ায় স্থির বস্তুর অবস্থানের পরিবর্তন হয়, অথবা সমবেগে গতিশীল বস্তুটিতে ত্বরণ সৃষ্টি হয়, তবে সংশ্লিষ্ট বলসমূহকে কার্যকর বা অপ্রতিমিত বল বলে।
কার্যকর বলের উদাহরণ – একটি বইকে ঠেললে বইটি সরে যায়। অর্থাৎ, বলের ক্রিয়ায় বস্তুর অবস্থানের পরিবর্তন হয়। তাই একে কার্যকর বল বা অপ্রতিমিত বল বলে।
প্রতিমিত বল (Balanced force) – কোনো বস্তুর ওপর ক্রিয়াশীল দুই বা ততোধিক বল যদি এমনভাবে ক্রিয়া করে যে বলগুলির ক্রিয়ায় বস্তুর জড়ত্বীয় অবস্থার (স্থিতি বা গতীয় অবস্থার) পরিবর্তন হয় না অর্থাৎ, বস্তুটিতে কোনো ত্বরণ সৃষ্টি হয় না, তবে সেই বলকে প্রতিমিত বল বলে। এই বল বস্তুর গতীয় অবস্থার পরিবর্তন ঘটাতে পারে না।
প্রতিমিত বলের উদাহরণ – একটি খুব ভারী আলমারিকে ঠেলে সরানো সম্ভব নয়, কারণ – এক্ষেত্রে আলমারিতে যে বল প্রযুক্ত হয়, সেটি হল প্রতিমিত বল, যার ফলে আলমারিতে কোনো ত্বরণ সৃষ্টি হয় না।
কোনো বস্তুর ওপর কার্যকর ও প্রতিমিত বলের প্রভাব কী?
কোনো বস্তুর ওপর কার্যকর বল ক্রিয়া করলে বস্তুর স্থিতিশীল বা গতিশীল অবস্থার পরিবর্তন হয়। অতএব, কার্যকর বলের প্রভাবে –
- স্থির বস্তুকে গতিশীল করা যায়।
- গতিশীল বস্তুর বেগের মান পরিবর্তন করা যায়।
- গতিশীল বস্তুর বেগের অভিমুখ পরিবর্তন করা যায়।
- গতিশীল বস্তুর বেগের মান ও অভিমুখ উভয়েই পরিবর্তন করা যায়।
কোনো বস্তুর ওপর প্রতিমিত বল প্রয়োগ করলে –
- বস্তুর স্থিতিশীল বা গতিশীল অবস্থার কোনো পরিবর্তন হবে না, কিন্তু
- নমনীয় বস্তুর আকার বা আকৃতির পরিবর্তন হয়।
লব্ধি কাকে বলে? গতি সম্পর্কিত আলোচনায় লব্ধির ধারণার গুরুত্ব কী?
লব্ধি বল (Resultant force) – দুই বা তার বেশি সংখ্যক বলকে সংযুক্ত করে সর্বদা একটি নির্দিষ্ট মানের বল পাওয়া যায় যার একক ক্রিয়ার ফলাফল সংযোজিত বলগুলির সম্মিলিত ক্রিয়ার ফলাফলের সমান। এই নির্দিষ্ট মানের বলটিকে বলা হয় লব্ধি বল।
গতিবিদ্যার আলোচনায় লব্ধি বলের ধারণা বিশেষ গুরুত্বপূর্ণ। লব্ধি বলের মান শূন্য হলে বস্তু বা কণা স্থির অবস্থায় বা সমবেগে গতিশীল হয়। একে সাম্যাবস্থা (equilibrium) বলে। অন্যদিকে লব্ধি অশূন্য হলে বস্তু ত্বরণ লাভ করে। সুতরাং কার্যকর বল ও লব্ধি বলের ধারণা বস্তুত সমতুল্য। নিউটনের প্রথম সূত্রে উল্লিখিত ‘বল’ বলতে প্রকৃতপক্ষে এই লব্ধি বা কার্যকর বলকেই বোঝানো হয়।
অভ্যন্তরীণ বল ও বাহ্যিক বল কাকে বলে?
অথবা, বল কাকে বলে, তা ব্যাখ্যা করো।
অভ্যন্তরীণ বল (Internal force) – দুই বা ততোধিক বস্তু পরস্পর প্রত্যক্ষ বা পরোক্ষ (সংযোজী উপকরণ তার, দড়ি ইত্যাদির মাধ্যমে) সংযোগে থেকে যে সংহতি গঠন করে, তাকে বস্তুসংস্থা (system of bodies) বলে। একই বস্তুসংস্থার অন্তর্গত বিভিন্ন বস্তুগুলি একে অন্যের উপর যে বল প্রয়োগ করে তাদের অভ্যন্তরীণ বল বলা হয়। এ জাতীয় বলের ক্রিয়ায় বস্তু সর্বদাই সাম্যে থাকে।
অভ্যন্তরীণ বলের উদাহরণ – টানটান অবস্থায় থাকা দড়ি বা তারের অভ্যন্তরে যে-কোনো অংশে ক্রিয়াশীল টান (Tension)।
বাহ্যিক বল (External force) – কোনো বস্তুর ওপর বল প্রয়োগ করার সময় যদি বল প্রয়োগকারী এবং বস্তু পৃথক সংস্থা হয় তাহলে প্রযুক্ত বল বস্তুর স্থিতিশীল বা গতিশীল অবস্থার পরিবর্তন করে বা পরিবর্তনের চেষ্টা করে। এই বলকে বাহ্যিক বল বলা হয়।
বাহ্যিক বলের উদাহরণ – ত্বরণসহ গতিশীল গাড়ির উপর ইঞ্জিন দ্বারা প্রযুক্ত বল।
বলের সংযোজন বলতে কী বোঝায়? উদাহরণসহ ব্যাখ্যা করো। কীভাবে বলের সংযোজন হয়?
বলের সংযোজন (Composition of forces) – দুই বা ততোধিক বল কোনো বস্তুর ওপর একই সঙ্গে ক্রিয়া করলে ওই বলগুলির ক্রিয়ার ফলাফল জানার জন্য লব্ধি বল নির্ণয় করতে হয়। এই লব্ধি বল নির্ণয়ের পদ্ধতিকেই বলা হয় বলের সংযোজন।
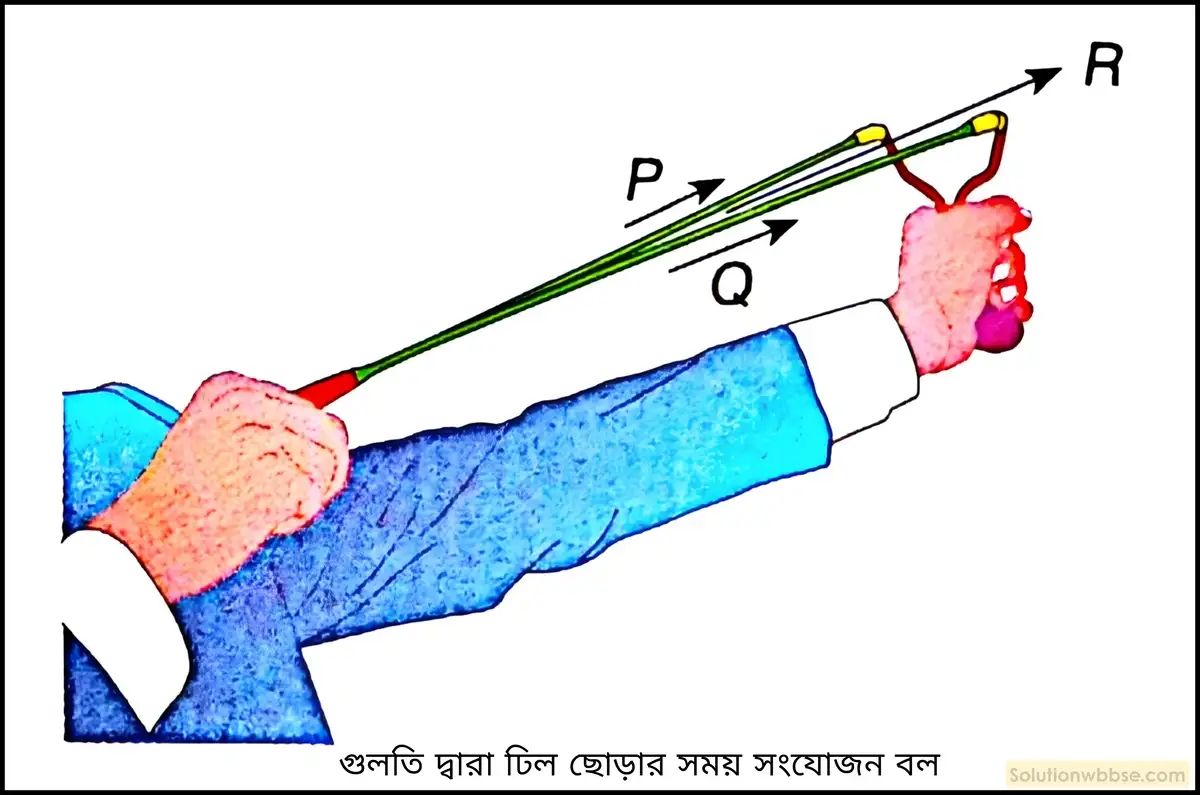
বলের সংযোজনের উদাহরণ – গুলতি দিয়ে ঢিল ছোড়ার সময় ঢিলসহ রবারের ফিতে দুটিকে পেছনে টানা হয়। ফলে, ঢিলের উপর দুটি ফিতে বরাবর \(\overrightarrow P\) ও \(\overrightarrow Q\) বল ক্রিয়া করে। কিন্তু ছেড়ে দিলে ঢিলটি \(\overrightarrow P\) বা \(\overrightarrow Q\) অভিমুখে না গিয়ে ওদের লব্ধি বল \(\overrightarrow R\) অভিমুখে ছিটকে যায়। ∴ \(\overrightarrow R=\overrightarrow P+\overrightarrow Q\)
বাতাস না থাকলে মাঝিরা যখন গুন টেনে নৌকা চালিয়ে নিয়ে যায় তখন দু-পাড় থেকে মাঝিরা দড়ি দিয়ে \(\overrightarrow P\) ও \(\overrightarrow Q\) বল প্রয়োগ করে। তখন নৌকাটি \(\overrightarrow P\) ও \(\overrightarrow Q\) -এর লব্ধি বল \(\overrightarrow R\) অভিমুখে এগিয়ে যায়। এক্ষেত্রেও \(\overrightarrow R=\overrightarrow P+\overrightarrow Q\) হয়।

বলের সংযোজনের পদ্ধতি – বল ভেক্টর রাশি হওয়ায় একাধিক বলের ক্ষেত্রে বীজগাণিতিক প্রক্রিয়াগুলি (যোগ, বিয়োগ গুণ ইত্যাদি) সম্পাদন করতে হলে মানের পাশাপাশি বলের ক্রিয়ার অভিমুখও বিবেচনা করতে হয়। তাই বীজগাণিতিক যোগফল অর্থাৎ শুধুমাত্র সাংখ্যমানের যোগফল গণনা করে বলের সংযোজন করা যায় না।
সুনির্দিষ্ট কিছু জ্যামিতিক নিয়ম (সংযোজন উপপাদ্য যেমন – সামান্তরিক সূত্র, ত্রিভুজ সূত্র ইত্যাদি) প্রয়োগ করেই বলের সংযোজন অর্থাৎ লব্ধি নির্ণয় সম্ভব হয়ে থাকে।
বলের সংযোজন সম্পর্কিত সামন্তরিক সূত্রটি বিবৃত করো। উপযুক্ত উদাহরণসহ সূত্রটির ব্যাখ্যা দাও।
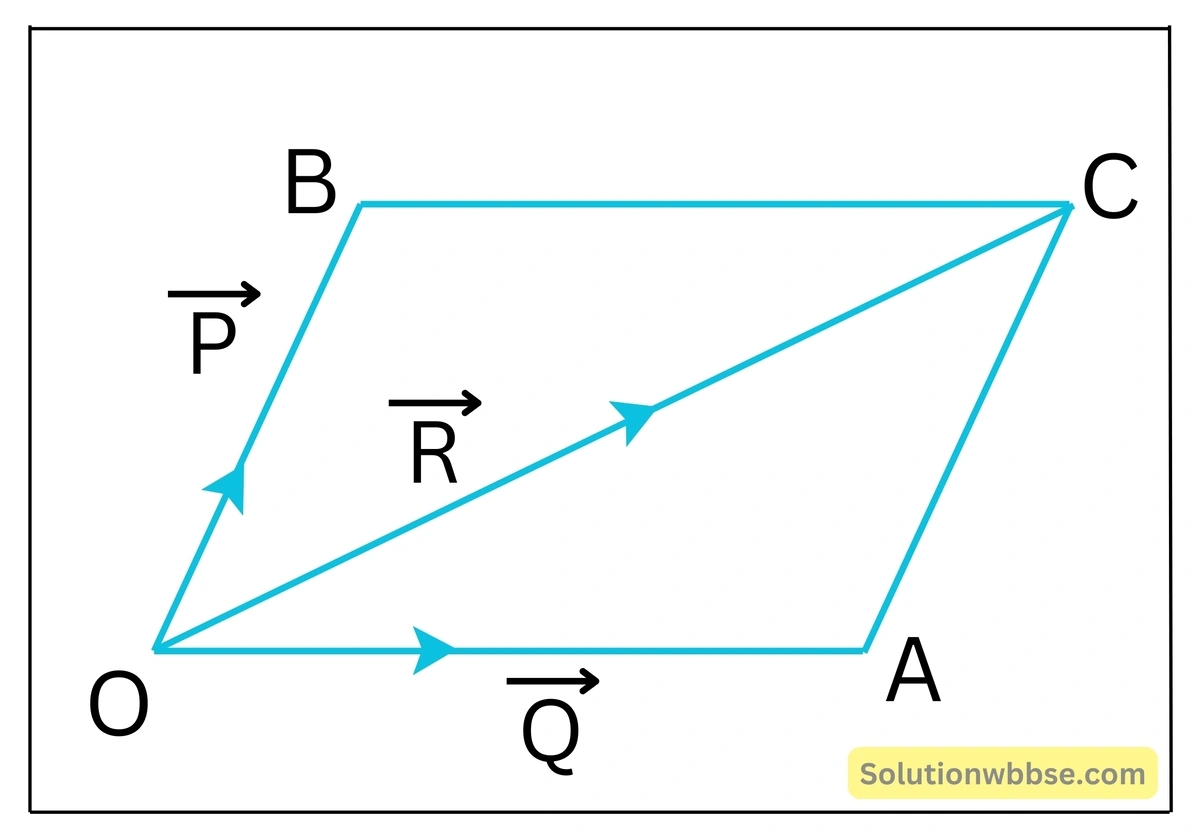
বলের সংযোজন সম্পর্কিত সামান্তরিক সূত্র – এক বিন্দুতে ক্রিয়াশীল দুটি একতলীয় বলকে যদি একটি সামান্তরিকের দুটি সন্নিহিত বা পাশাপাশি বাহু দ্বারা দিক ও মানে প্রকাশ করা যায় তবে ওই বিন্দু দিয়ে অঙ্কিত ওই সামান্তরিকের কর্ণ বলদুটির লব্ধিকে দিক ও মানে প্রকাশ করে।
যেমন – চিত্রে \(OACB\) সামান্তরিকের দুটি সন্নিহিত বাহু \(\overline{OB}\) এবং \(\overline{OA}\) যথাক্রমে \(\overrightarrow R=\overrightarrow P+\overrightarrow Q\) দুটি একতলীয় বল ভেক্টরকে দিকে ও মানে প্রকাশ করলে \(O\) বিন্দু দিয়ে অঙ্কিত \(OACB\) সামান্তরিকের কর্ণ \(\overrightarrow{OC}\) ভেক্টর দুটির লব্ধি \(\overrightarrow R\) -কে দিকে ও মানে সূচিত করে।
উদাহরণ – গুন টেনে নৌকা চালানোর উদাহরণটিতে দেখা যায়, \(\overrightarrow R=\overrightarrow P+\overrightarrow Q\) বল নির্দেশক ভেক্টর দুটিকে সন্নিহিত বাহু বিবেচনা করে যে সামান্তরিক আঁকা হয়েছে তার যে কর্ণটি বল দুটির ক্রিয়ারেখার ছেদবিন্দুগামী, সেই কর্ণ বরাবরই লব্ধি বল \(\overrightarrow R\) সক্রিয় হয়েছে।
সমজাতীয় দুটি একতলীয় ভেক্টরের লব্ধির মান ও অভিমুখ জ্যামিতিক পদ্ধতিতে সামান্তরিক সূত্রের সাহায্যে নির্ণয় করো।
সমজাতীয় দুটি একতলীয় ভেক্টরের লব্ধির মান ও অভিমুখ জ্যামিতিক পদ্ধতিতে সামান্তরিক সূত্রের সাহায্যে নির্ণয় করা সম্ভব।
বল, ভরবেগ ইত্যাদি যে-কোনো ভেক্টর রাশিকেই উপযুক্ত স্কেলে অঙ্কিত একটি তিরচিহ্নযুক্ত সরলরেখা দ্বারা প্রকাশ করা হয়। এক্ষেত্রে রেখাটির দৈর্ঘ্য ভেক্টরটির মান। রেখাটি নিজে তার ক্রিয়ার দিক এবং আরোপিত তিরচিহ্নটি ক্রিয়ার অভিমুখ নির্দেশ করে থাকে।
যেমন – 5 cm দীর্ঘ একটি সরলরেখা দ্বারা নির্দিষ্ট অভিমুখে ক্রিয়াশীল 10 N বলকে দেখানো হয়েছে, এক্ষেত্রে প্রতি 1 cm দৈর্ঘ্য 2 N বলের মানের সমান।
বলের বিভাজন কাকে বলে?
বলের বিভাজন (Resolution of force) – নির্দিষ্ট মানের একটি বল বা যে-কোনো ভেক্টরকে যদি দুই বা তার বেশি সংখ্যক অংশে এমনভাবে খন্ডিত করা যায় যে, খণ্ডিত অংশগুলির ভেক্টর যোগফল ওই নির্দিষ্ট মানের বল বা ভেক্টরটির সঙ্গে সমান হয়, তবে এই বিশ্লেষণ প্রক্রিয়াকে বলা হয় বলের বিভাজন বা সাধারণভাবে ভেক্টর বিভাজন।
উপাংশ কাকে বলে? উদাহরণসহ ব্যাখ্যা দাও।
উপাংশ (Component) – নির্দিষ্ট মানের বল বা কোনো ভেক্টরকে ভেক্টর বিভাজন প্রক্রিয়ায় বিভাজিত করলে প্রাপ্ত খণ্ড বা অংশগুলির প্রত্যেকটিকে বলা হয় ওই বল বা ভেক্টরটির উপাংশ।
ব্যাখ্যা – নিচের ছবিতে \(\overline{OC}\) একটি নির্দিষ্ট ভেক্টর বা বল \(\overrightarrow R\) -কে দিকে ও মানে প্রকাশ করে। \(\overline{OC}\) -কে কর্ণ বিবেচনা করে অঙ্কিত সামান্তরিকের \(\left(OACB\right)\) \(\overline{OB}\) ও \(\overline{OA}\) বাহু দুটি যথাক্রমে \(\overrightarrow P\) ও \(\overrightarrow Q\) বলকে দিকে ও মানে চিহ্নিত করে, যেগুলি হল \(\overrightarrow R\) ভেক্টর বা বলের উপাংশ।

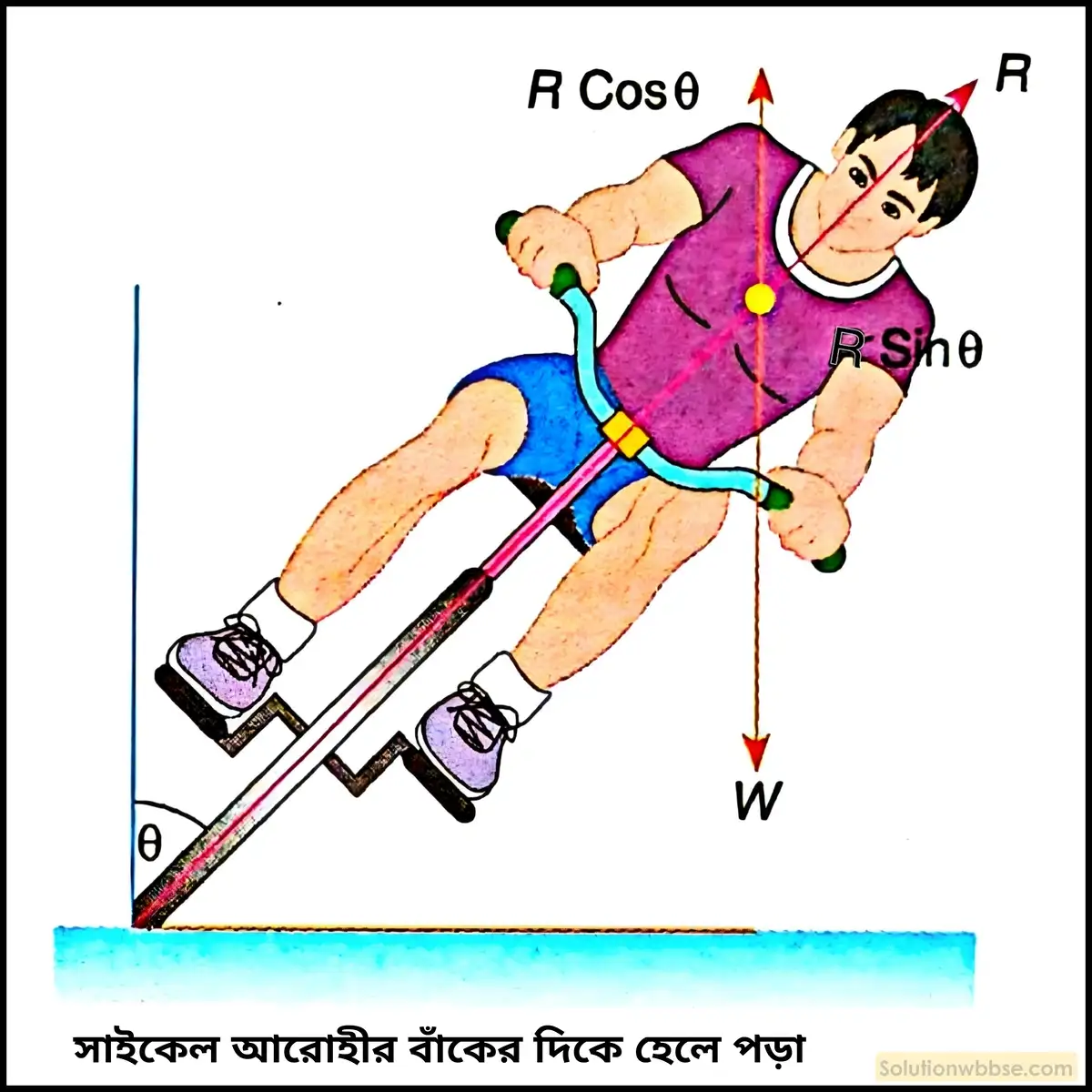
ভেক্টর বিশ্লেষণ ও উপাংশের উদাহরণ – বৃত্তাকার পথে বাঁক নেওয়ার মুহূর্তে সাইকেল আরোহীর ভিতরের দিকে (বাঁকের কেন্দ্র যেদিকে থাকে সেই দিকে) হেলে যাওয়ার ঘটনা বলের উপাংশ বিভাজনের একটি পরিচিত উদাহরণ। এখানে সাইকেলসহ আরোহী আনতভাবে রাস্তার ওপর চাপ দেয়, ফলে রাস্তার প্রতিক্রিয়া \(\overrightarrow R\) অনুভূমিক তলের সঙ্গে আনতভাবে সাইকেলের উপর ক্রিয়া করে। এই প্রতিক্রিয়ার একটি উপাংশ (R sinθ) আরোহীকে বৃত্তপথে বাঁক নেওয়ার জন্য প্রয়োজনীয় অভিকেন্দ্র বল সরবরাহ করে এবং অপর উপাংশ (R cosθ) আরোহীসহ সাইকেলের ওজনকে প্রতিমিত করে।
উপাংশগুলি স্কেলার রাশি না ভেক্টর রাশি? যুক্তিসহ ব্যাখ্যা করো।
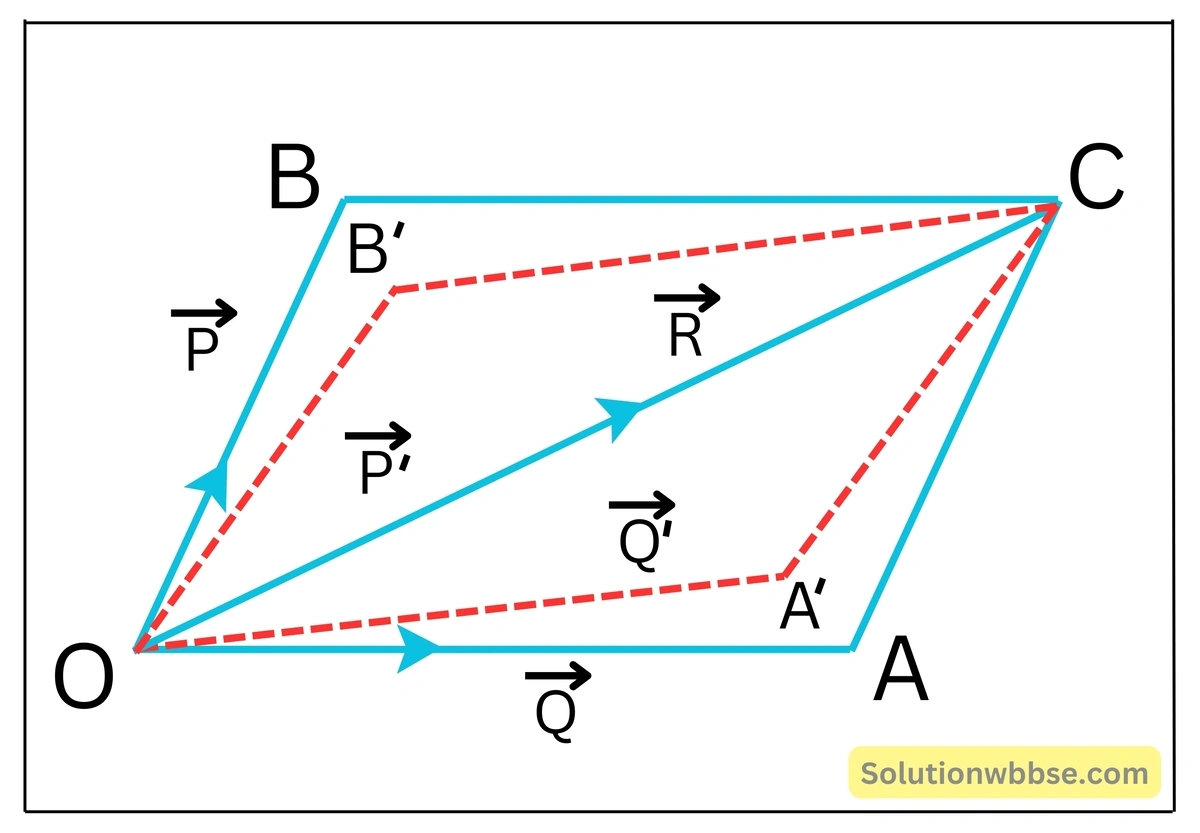
একটি নির্দিষ্ট বল বা ভেক্টরকে কর্ণ হিসেবে বিবেচনা করে বহু সংখ্যক সামান্তরিক (যেমন – ছবিতে OACB OA’CB’ ইত্যাদি) অঙ্কন করা সম্ভব যাদের প্রত্যেকের সন্নিহিত বাহু দুটি ওই বল বা ভেক্টরকে দুটি নির্দিষ্ট উপাংশকে চিহ্নিত করে। সুতরাং, উপাংশগুলির কোনো নির্দিষ্ট মান বা অভিমুখ নেই, তবে কোনো নির্দিষ্ট অভিমুখে ভেক্টর বা বলকে বিশ্লেষিত করা হলে তার মান ও অভিমুখ দুই-ই নির্দিষ্ট হয়ে যায়। সুতরাং, নির্দিষ্ট অভিমুখে বল বা ভেক্টরের বিশ্লেষণে প্রাপ্ত উপাংশগুলি ভেক্টরের মতো আচরণ করে অর্থাৎ, নির্দিষ্ট অভিমুখে বিভাজিত উপাংশ ভেক্টর রাশি।
উপাংশের রাশিমালা কাকে বলে?
উপাংশের রাশিমালা – কোনো সামতলিক ভেক্টর বা বলকে যে-কোনো দুটি বা তার বেশি সংখ্যক অভিমুখে নির্দিষ্ট সংখ্যক উপাংশে বিশ্লেষণ করা যায়। যদি কোনো নির্দিষ্ট ভেক্টর বা বলকে এমন দুটি উপাংশে বিভক্ত করা যায় যে উপাংশ দুটি নিজেরা পরস্পর লম্ব তবে সেই বিভাজন প্রক্রিয়াকে বলা হয় লম্ব উপাংশে বিভাজন বা লম্ব বিভাজন (Resolution in cartesian components)। সংশ্লিষ্ট উপাংশ দুটিকে বলা হয় লম্ব উপাংশ বা বিভক্তাংশ (cartesian components)। অন্যান্য ক্ষেত্রগুলির তুলনায় লম্ব উপাংশে ভেক্টরের বিভাজন ব্যবহারিক দিক থেকে অনেক সুবিধাজনক, কারণ – উপাংশ দুটিকে এক্ষেত্রে সংক্ষিপ্ত ও সহজ গাণিতিক চেহারায় প্রকাশ করা যায়।
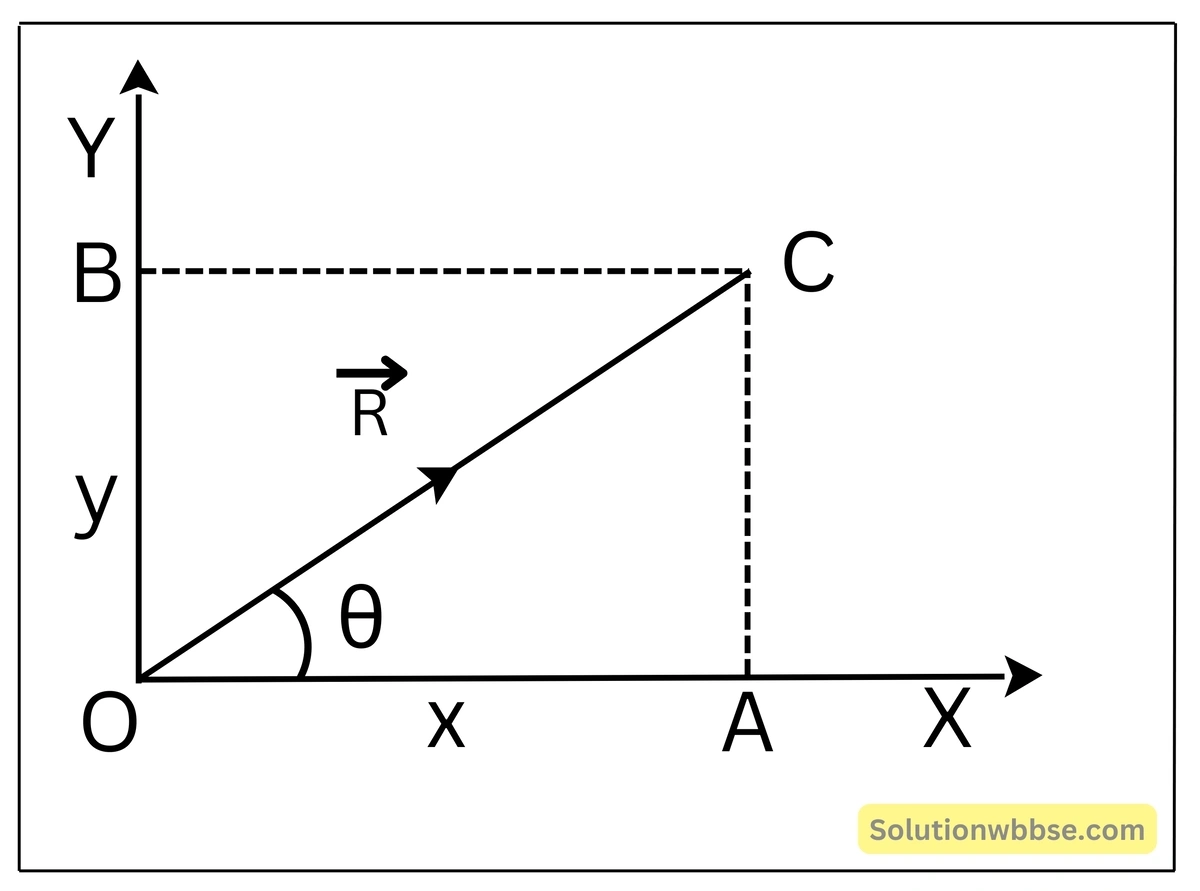
যদি কোনো বল বা ভেক্টর \(\overrightarrow R\) -কে পরস্পর লম্ব দুটি অভিমুখ OX ও OY বরাবর দুটি উপাংশে (যথাক্রমে, OA ও OB) বিশ্লেষণ করা হলে △OAC সমকোণী ত্রিভুজে, \(\cos\theta=\frac{OA}{OC}=\frac XR\) এবং \(\sin\theta=\frac{AC}{OC}=\frac YR\) যেখানে, x ও y হল উপাংশদুটির মান এবং θ, OA অভিমুখের সঙ্গে \(\overrightarrow R\) ভেক্টরের ক্রিয়ারেখা দ্বারা উৎপন্ন কোণ।
x = R cosθ এবং y = R sinθ; x ও y -কে বলা হয় \(\overrightarrow R\) ভেক্টরের যথাক্রমে অনুভূমিক ও উল্লম্ব উপাংশ।
ত্রিমাত্রিক স্থানাঙ্কতন্ত্রে অবস্থান ভেক্টর নির্ণয় করো?
কোনো নির্দিষ্ট অভিমুখে সক্রিয় কোনো ভেক্টরকে তার মান দিয়ে ভাগ করলে ওই অভিমুখে ক্রিয়াশীল এমন একটি ভেক্টর পাওয়া যায়, যার মান একক (1)। এই ভেক্টরটিকে বলা হয় ওই অভিমুখের বৈশিষ্ট্যসূচক একক ভেক্টর।
একক ভেক্টরের সাহায্যে কোনো দূরত্বকে নির্দিষ্ট অভিমুখে একটি সরণ ভেক্টরে রূপান্তরিত করা যায়। ত্রিমাত্রিক কার্টেজীয় স্থানাঙ্ক তন্ত্রে X অক্ষ, Y অক্ষ ও Z অক্ষ বরাবর ক্রিয়াশীল তিনটি একক ভেক্টর যথাক্রমে, \(\widehat i,\;\widehat j\) ও \(\widehat k\) কল্পনা করা হলে একটি ত্রিমাত্রিক বিন্দু P (X, Y, Z) -এর অবস্থান স্থানাঙ্কতন্ত্রের মূলবিন্দু O -এর সাপেক্ষে একটি নির্দিষ্ট ভেক্টর \(\left(\overrightarrow{OP}\right)\) এর সাহায্যে প্রকাশ করা যায়। এই বিশেষ ভেক্টরকে বলা হয় ওই বিন্দুর অবস্থান ভেক্টর \(\left(\overrightarrow r\right)\)। এক্ষেত্রে প্রমাণ করা যায় P বিন্দুর অবস্থান ভেক্টর।
\(\overrightarrow{OP}=\overrightarrow r=x\widehat i+y\widehat j+z\widehat k\\\)ত্রিমাত্রিক বিন্দুর পরিবর্তে P একটি সামতলিক বিন্দু হলে, সামান্তরিক সূত্রের সাহায্যে সহজেই প্রমাণ করা যায়
\(\overrightarrow{OP}=\overrightarrow r=x\widehat i+y\widehat j\left[\overrightarrow{OP}=\overrightarrow{OC}+\overrightarrow{PC}\right]\\\)(x, y, z) বা (x, y) হল অবস্থান ভেক্টরের X, Y ও Z অক্ষ বরাবর অথবা X ও Y অক্ষ বরাবর উপাংশ।
কৃতকার্যের ক্ষেত্রে বলের সামান্তরিক সূত্রটিকে কীভাবে প্রয়োগ করবে তা উদাহরণের সাহায্যে বোঝাও।
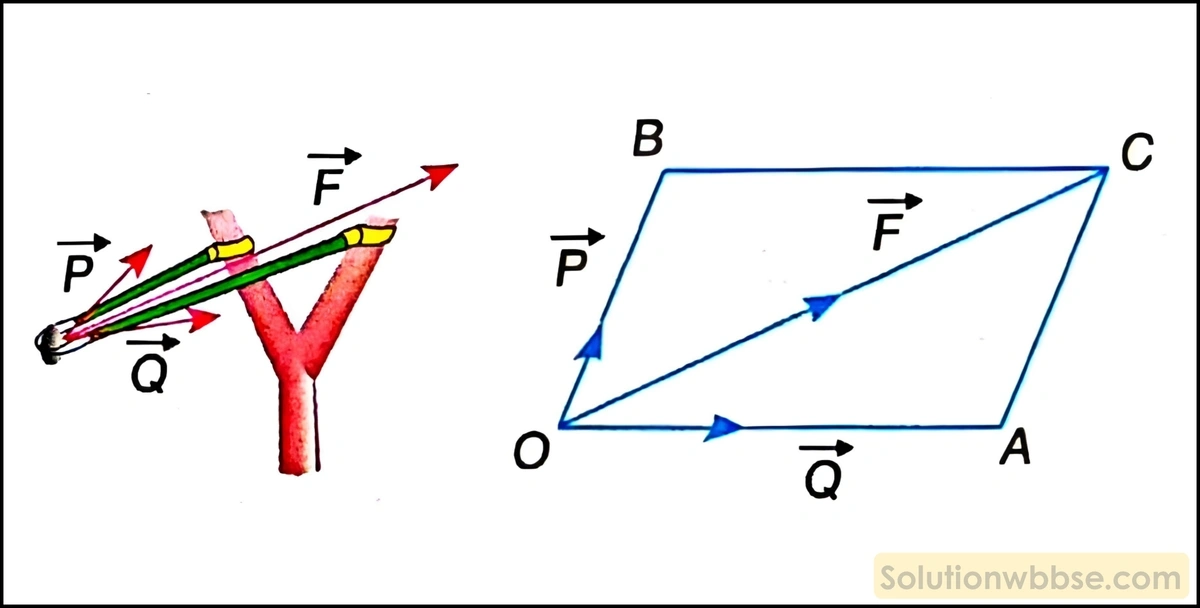
গুলতি দিয়ে ঢিল ছোঁড়ার সময় ঢিলসহ রবারের ফিতেটাকে পিছনদিকে টানা হয়। ফলে, ঢিলের ওপর ফিতের দুই অর্ধাংশ বরাবর \(\overrightarrow P\) ও \(\overrightarrow Q\) বল (ধরি) ক্রিয়া করে। এই অবস্থায় ফিতে ছেড়ে দিলে ঢিলটি \(\overrightarrow P\) বা \(\overrightarrow Q\) অভিমুখে না গিয়ে ওদের লব্ধি বল \(\overrightarrow F\) অভিমুখে ছিটকে যায়।
এক্ষেত্রে ঢিলটির উপর ক্রিয়াশীল দুটি বলের লব্ধি বলের সামান্তরিক সূত্রের সাহায্যে নির্ণয় করা যায়। \(2\) নং চিত্রানুযায়ী, ঢিলটির উপর ক্রিয়াশীল দুটি বল \(\overrightarrow P\) ও \(\overrightarrow Q\) -কে \(OACB\) সামান্তরিকের দুটি সন্নিহিত বাহু \(OB\) ও \(OA\) দ্বারা মানে ও দিকে প্রকাশ করা হয়েছে।
অতএব ওই দুটি বাহুর ছেদবিন্দু \(O\) -এর মধ্য দিয়ে অঙ্কিত \(OACB\) সামান্তরিকের কর্ণ \(\overrightarrow{OC}\) বল দুটির লব্ধি বল \(\overrightarrow F\) -কে মানে ও দিকে প্রকাশ করে।
∴ \(\overrightarrow F=\overrightarrow P+\overrightarrow Q\)
যেহেতু, লব্ধি বল \(\overrightarrow F\) -এর ক্রিয়ায় লব্ধি বলের অভিমুখেই ঢিলটির সরণ হয়। সুতরাং, এক্ষেত্রে লব্ধি বলই হল কার্যকর বল \(\left(\overrightarrow F\right)\) ঢিলটির সরণ \(\left(\overrightarrow s\right)\) হলে,
∴ কৃতকার্য \(\left(W\right)\) = কার্যকর বল বলের \(\left(\overrightarrow F\right)\) × অভিমুখে ঢিলটির সরণ \(\left(\overrightarrow s\right)\)
বা, \(W=\overrightarrow F⋅\overrightarrow s\)
কৃতকার্যের ক্ষেত্রে বলের বিভাজনকে কীভাবে প্রয়োগ করবে তা উল্লেখ করো।
কৃতকার্যের পরিমাণ নির্ণয়ের ক্ষেত্রে যখন বস্তুর সরণ প্রযুক্ত বলের অভিমুখে হয় না, সেক্ষেত্রে প্রযুক্ত বলকে পরস্পরের সমকোণে দুটি উপাংশে বিভাজন করা হয়। প্রযুক্ত বলের বিভাজিত লম্ব উপাংশ দুটির মধ্যে যে উপাংশটি বস্তুর সরণের অভিমুখে ক্রিয়াশীল হয়, শুধুমাত্র সেই উপাংশের সঙ্গে বস্তুর সরণের গুণফল দ্বারা কৃতকার্যের পরিমাপ করা হয়।
সুতরাং, কৃতকার্য = সরণের অভিমুখে প্রযুক্ত বলের উপাংশ × সরণ।
চিত্রানুযায়ী A অবস্থানে থাকা বস্তুর ওপর AB অভিমুখে F বল প্রয়োগ করায় বস্তুর অনুভূমিক দিকে \(\overrightarrow{AC}=\overrightarrow s\) (ধরি) পরিমাণ সরণ হল। এখানে যেহেতু F -এর অভিমুখে সরণ হয়নি তাই F -কে দুটি সমকৌণিক উপাংশ Fx ও Fy -তে বিভাজন করা হয়েছে। যেহেতু, কেবলমাত্র F -এর অনুভূমিক উপাংশ Fx -এর জন্য এই AC পরিমাণ সরণ ঘটেছে।
সুতরাং, এক্ষেত্রে কৃতকার্য W = Fx × s
গতিসূত্র কাকে বলে? এদের তাৎপর্য কী?
গতিসূত্র (Law of motion) – বস্তুর গতি সম্পর্কিত বিভিন্ন ঘটনাবলির পরীক্ষানিরীক্ষা ও তার বিশ্লেষণের মাধ্যমে মহাবিজ্ঞানী স্যার আইজ্যাক নিউটন তাঁর বিখ্যাত ‘প্রিন্সিপিয়া’ গ্রন্থে তিনটি সূত্রের উপস্থাপনা করেন। এগুলিই সাধারণভাবে ‘গতিসূত্র’ নামে পরিচিত।
গতিসূত্রের তাৎপর্য – নিউটন প্রস্তাবিত এই তিনটি সূত্রের ধারণা প্রকৃত অর্থেই মৌলিক। পদার্থবিদ্যার কোনো পুরানো ধারণা থেকে সূত্রগুলির ব্যাখ্যা বা প্রমাণ করা যায় না। এই তিনটি সূত্রকে সনাতনী বলবিদ্যার (Classical mechanics) স্তম্ভ হিসেবে বিবেচনা করা হয়। এই শাখায় ক্ষুদ্র বা বিস্তৃত বস্তুর উপর প্রযুক্ত বল ও তাদের প্রভাবে বস্তুর আচরণকে গুণগত বা পরিমাণগতভাবে বর্ণনা করা হয়ে থাকে।
নিউটনের প্রথম গতিসূত্রটি বিবৃত করো।
প্রথম গতিসূত্র – বাইরে থেকে প্রযুক্ত বল দ্বারা অবস্থার পরিবর্তনে বাধ্য না করলে স্থির বস্তু চিরকাল স্থির থাকে, গতিশীল বস্তু চিরকাল সমগতিতে সরলরেখায় চলতে থাকবে।
নিউটনের প্রথম গতিসূত্র থেকে কী কী বিষয় জানা যায়?
প্রথম গতিসূত্র থেকে দুটি গুরুত্বপূর্ণ বিষয়ের ধারণা পাওয়া যায় –
- জাড্য ধর্ম (Property of inertia)
- বলের গুণগত সংজ্ঞা (Qualitative definition of force)
জাড্য কাকে বলে? এটি কয় প্রকার ও কী কী? উদাহরণসহ ব্যাখ্যা করো।
অথবা, প্রাত্যহিক জীবনে ঘটা কোনো ঘটনার উল্লেখ করে স্থিতিজাড্যের ব্যাখ্যা করো।
জাড্য (Inertia) – পদার্থের যে মৌলিক ধর্মের জন্য স্থির বস্তু চিরকাল তার স্থিতিশীল অবস্থা বা গতিশীল বস্তু তার সমবেগযুক্ত গতি বজায় রাখে বা রাখার চেষ্টা করে, তাকেই জাড্য বলে। জাড্য দুই প্রকার –
- স্থিতিজাড্য (Inertia of rest) ও
- গতিজাড্য (Inertia of motion)।
স্থিতিজাড্য (Inertia of rest) – স্থির বস্তুর স্থির অবস্থা বজায় রাখা বা রাখার প্রবণতাকে বলা হয় স্থিতিজাড্য।
স্থিতিজাড্যের উদাহরণ – গাছের কাণ্ড বা ডাল ধরে জোরে নাড়া দিলে ডালগুলিতে গতির সৃষ্টি হয় অথচ স্থিতিজাড্যের জন্য ফলগুলি তাদের অবস্থান বজায় রাখার চেষ্টা করে। এই কারণে ফলগুলি বৃন্তচ্যুত হয় এবং অভিকর্ষের ক্রিয়ায় নীচে পড়ে।
গতিজাড্য (Inertia of motion) – সচল বস্তুর সমবেগে গতিশীল থাকার প্রবণতাকে বলা হয় গতিজাড্য।
স্থিতিজাড্যের উদাহরণ – বৈদ্যুতিক পাখার সুইচ ‘অফ’ করে দিলেও গতিজাড্যের জন্য পাখাটি আরও কিছু সময় ঘুরতে থাকে। একই কারণে সাইকেলের প্যাডেল করা বন্ধ করলেও সাইকেল বেশ কিছু দূরত্ব এগিয়ে যাওয়ার পর গতিহীন হয়।
স্থিতিজাড্য ও গতিজাড্যের ধারণা পরীক্ষার দ্বারা ব্যাখ্যা করো।
স্থিতিজাড্যের পরীক্ষা – নীচের ছবিতে দেখানো পরীক্ষা ব্যবস্থার সাহায্যে স্থিতিজাড্যের ধারণা সহজে ব্যাখ্যা করা সম্ভব। এই ব্যবস্থায় একটি খাড়া দণ্ডের উপরের প্রান্তে একটি বাটি বসানো থাকে। বাটির উপরে একটি কার্ডবোর্ড রেখে তার ঠিক মাঝখানে একটি ছোটো বল রাখা হয়। এটি ধাতব স্প্রিংকে ক্ল্যাম্পের সাহায্যে (নীচের ছবিতে যেমন দেখানো হয়েছে) একপাশে টেনে রাখা হয়।
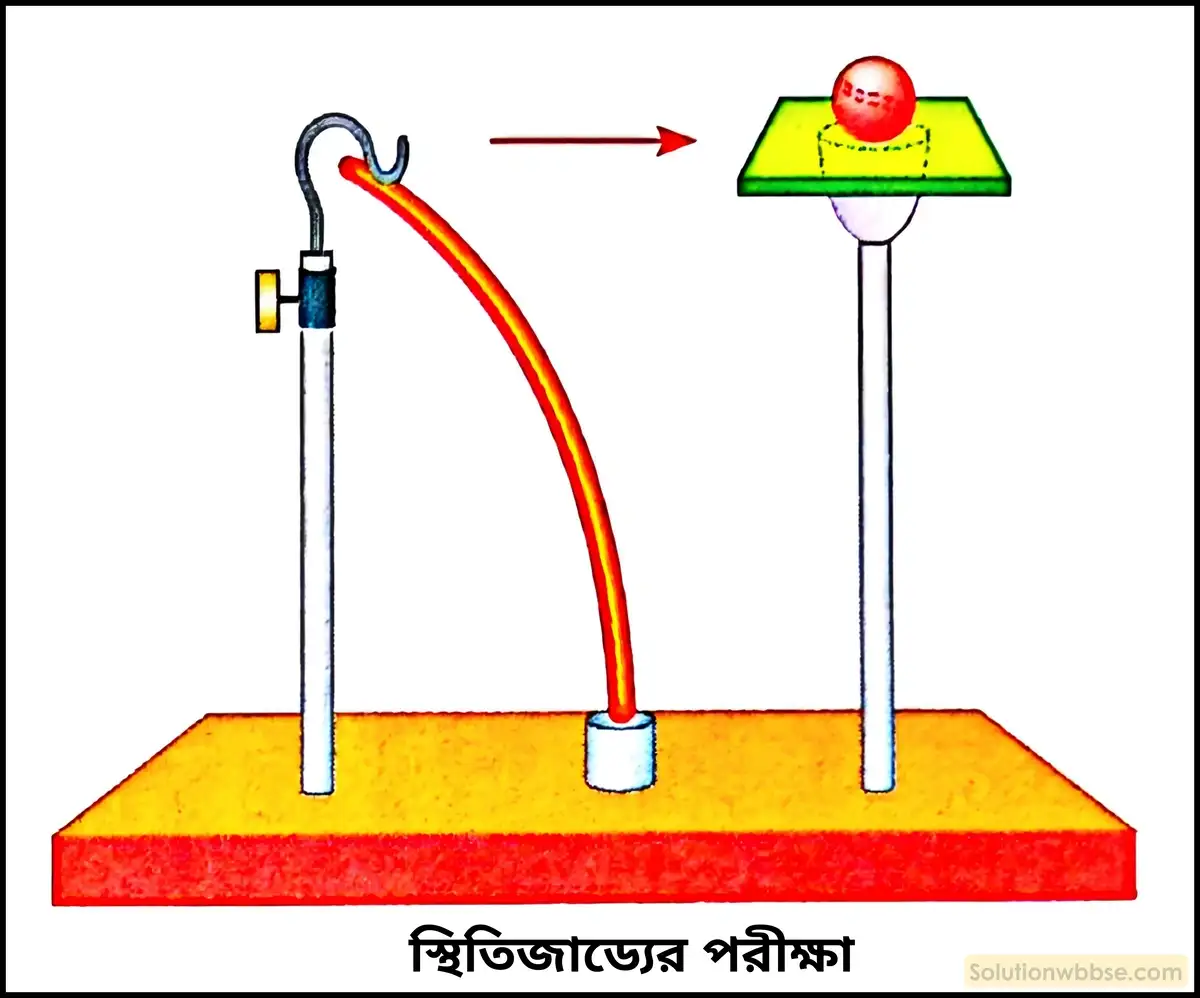
স্প্রিংটিকে হঠাৎ ছেড়ে দিলে সেটি কার্ডবোর্ডে আঘাত করা মাত্রই কার্ডবোর্ডটি ছিটকে যায়, কিন্তু স্থিতিজাড্যের জন্য ধাতব বলটি তার প্রাথমিক অবস্থান বজায় রাখতে চায় ও বাটির ভিতরে পড়ে যায়।
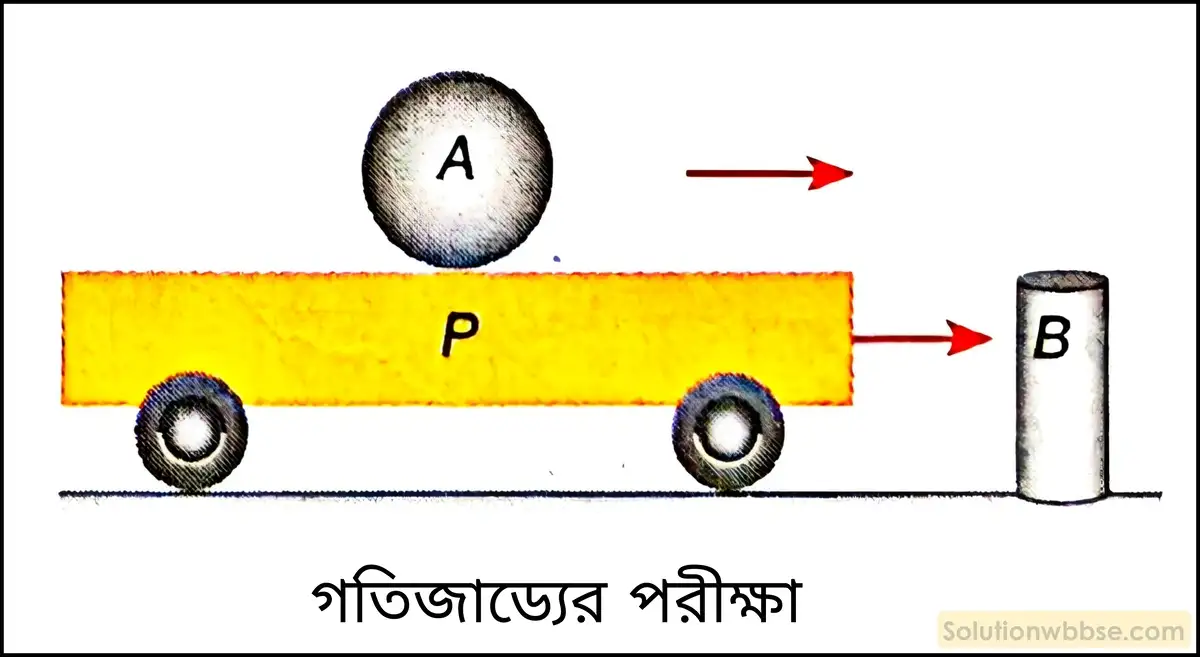
গতিজাড্যের পরীক্ষা – নীচে বর্ণিত সহজ পরীক্ষা ব্যবস্থাটি গতিজাড্যের ধারণা দেয়। ব্যবস্থাটিতে একটি ছোটো লোহার গোলক (A) একটি চাকাযুক্ত কাঠের পাটাতন (P) বা খেলনা গাড়ির পাটাতন সদৃশ অংশের উপর বসানো থাকে। পাটাতন থেকে একটি নির্দিষ্ট দূরত্বে একটি ধাতব ব্লক (B) রাখা থাকে যার উচ্চতা পাটাতনের সমান। পাটাতনটিকে ব্লক B অভিমুখে গতিশীল করা হলে A গোলকটি গতিজাড্যের জন্য পাটাতনের সমান বেগ লাভ করে। এই অবস্থায় ব্লকের সঙ্গে সংঘাত ঘটলে পাটাতনটি থেমে গেলেও গোলকটি তার গতি বজায় রাখতে চায় এবং ব্লকের বাধা অতিক্রম করে সামনের দিকে ছিটকে পড়ে।
নিউটনের প্রথম সূত্র থেকে কীভাবে বলের সংজ্ঞা পাওয়া যায় তা ব্যাখ্যা করো।
প্রথম সূত্র থেকে বলের সংজ্ঞা – প্রথম সূত্রের ধারণা অনুসারে, বাইরে থেকে প্রযুক্ত যে বাহ্যিক কারণ (External cause) বা ভৌত কারণ (Physical cause) স্থির বস্তুর স্থিতিশীল অথবা গতিশীল বস্তুর সমবেগে গতিশীল বস্তুর গতীয় অবস্থার পরিবর্তন অর্থাৎ বস্তুর জাড্য ধর্মের পরিবর্তন ঘটায় বা ঘটানোর চেষ্টা করে, তাকে বল (Force) বলা হয়।
এই বর্ণনায় বলকে কারণ এবং বস্তুর জাড্যের পরিবর্তনকে তার ফল হিসেবে প্রকাশ করা হয় মাত্র। কোনো গাণিতিক তাৎপর্য বা রাশিমালার সাহায্য এই ব্যাখ্যায় জড়িত না থাকায় এই সংজ্ঞাকে গুণগত আখ্যা দেওয়া হয়।
অভিমুখের জড়তা বলতে কী বোঝায়?
অভিমুখের জড়তা (Intertia of Direction) – কোনো বাহ্যিক বল বা প্রভাব ছাড়া নিজে থেকেই কোনো নির্দিষ্ট অভিমুখে গতিশীল বস্তুর পক্ষে তার গতির অভিমুখ পরিবর্তন করা সম্ভব নয়। এই বিশেষ ধর্মটি অভিমুখের জড়তা নামে পরিচিত।
বোধমূলক প্রশ্নোত্তর
ঘোড়া গাড়িকে যে বলে টানে, গাড়িও ঘোড়াকে সেই সমান বলে বিপরীত দিকে টানে। তবুও গাড়ি চলে। – বলের সংযোজন বা বিভাজন উপাংশের ঘটনাটি ব্যাখ্যা করো।
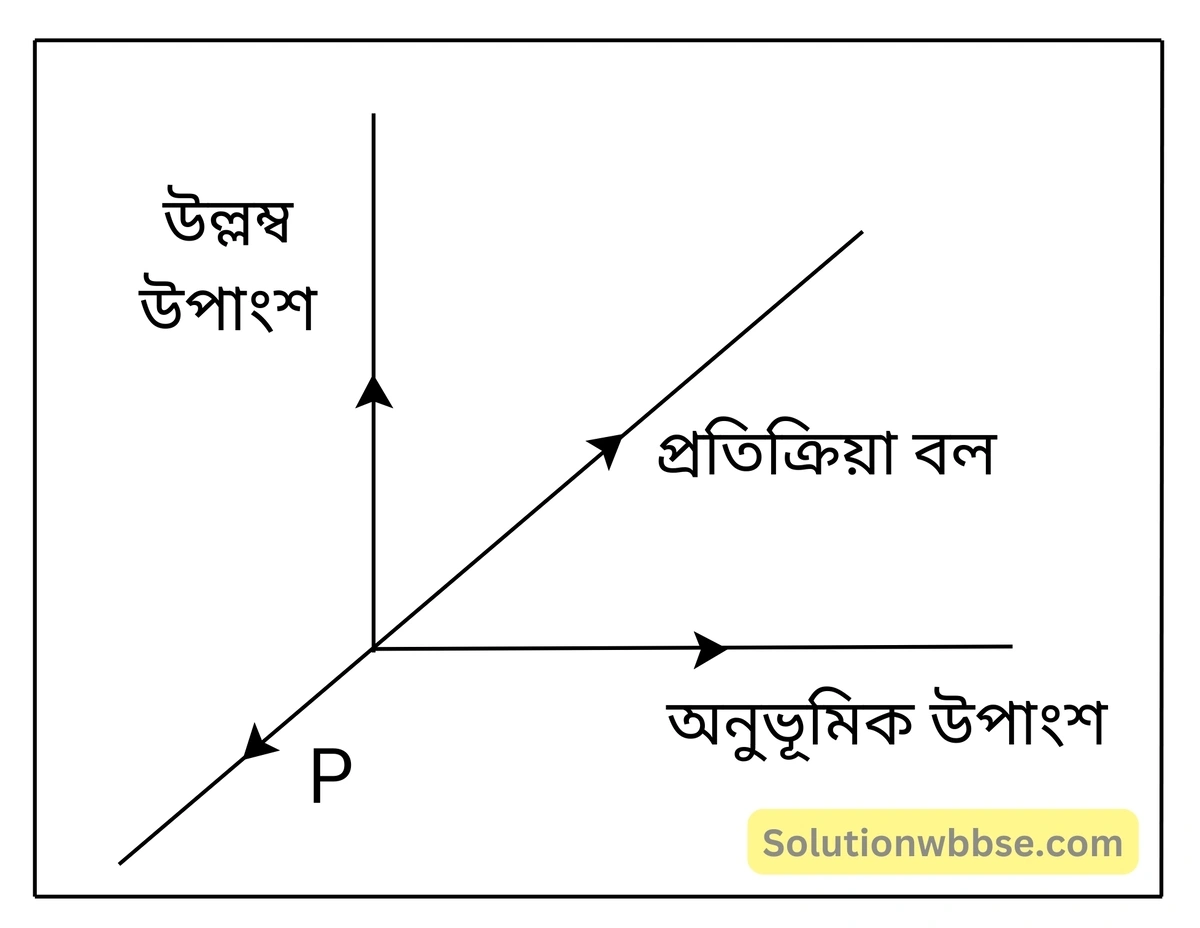
ঘোড়া গাড়িকে যে বলে টানে, গাড়িও ঘোড়াকে সেই বলে বিপরীত দিকে টানে। ঘোড়া মাটিতে তির্যকভাবে পা রেখে গাড়ি টানে। অর্থাৎ, মাটিতে তির্যকভাবে একটি বল (P) প্রয়োগ করে। মাটি ও পা বরাবর একটি সমান ও বিপরীতমুখী প্রতিক্রিয়া বল দেয়। এই প্রতিক্রিয়া বলকে দুটি লম্ব উপাংশে ভাগ করা যায়। অনুভূমিক উপাংশটি, গাড়ি ঘোড়াকে যে বলে বিপরীত দিকে টানে সেই বল এবং গাড়ি ও রাস্তার মধ্যে ঘর্ষণ বলের চেয়ে বেশি হলে গাড়ি সামনের দিকে চলবে।
বৃষ্টির দিনে চলন্ত ট্রেনে বসে কোনো যাত্রীর কাছে উল্লম্বভাবে পতনশীল বৃষ্টির জলবিন্দুগুলি তির্যকভাবে পড়ছে বলে মনে হয়। – বলের সংযোজন বা বিভাজন উপাংশের ঘটনাটি ব্যাখ্যা করো।
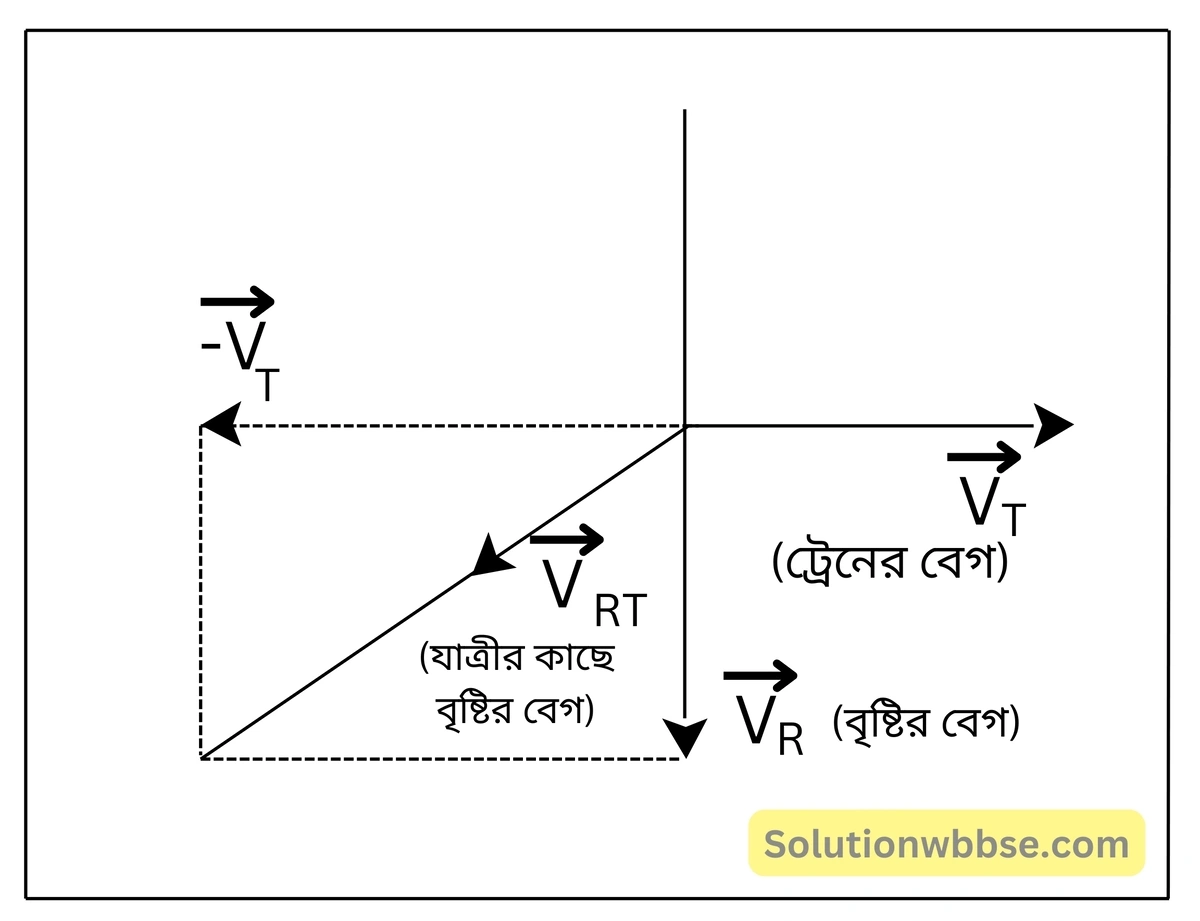
ধরি, ট্রেনটি \(v_T\) গতিবেগ নিয়ে চলছে এবং বৃষ্টির ফোঁটাগুলি \(v_R\) গতিবেগে নীচে পড়ছে। এক্ষেত্রে যাত্রীর কাছে বৃষ্টির বেগের আপাত মান, ট্রেন সাপেক্ষে বৃষ্টির আপেক্ষিক বেগ অর্থাৎ \(\overrightarrow{v_{RT}}=\overrightarrow{v_R}-\overrightarrow{v_T}\) দ্বারা নির্দেশিত হয়। চিত্র থেকে সহজেই বোঝা যায়, \(\overrightarrow{v_T}\) ও \(\overrightarrow{v_R}\) -কে একটি সামান্তরিকের সন্নিহিত দুটি বাহু হিসেবে ধরলে ওই সামান্তরিকের কর্ণ হবে লব্ধি এবং যাত্রীর মনে হবে বৃষ্টির ফোঁটাগুলি ওই লব্ধি বরাবর পড়ছে। অর্থাৎ, ট্রেন চলতে থাকলে কোনো যাত্রীর কাছে উল্লম্বভাবে পতনশীল বৃষ্টিকে তির্যকভাবে পড়ছে বলে মনে হবে।
সমবেগে সরলরেখায় চলমান একটি ট্রেনের মধ্যে থাকা এক ব্যক্তি ট্রেনের বাইরে একটি মুদ্রা ফেললে অন্য ব্যাক্তি মুদ্রাটিকে কোন পথে পড়তে দেখবে?
সমবেগে সরলরেখায় চলমান একটি ট্রেনের মধ্যে থাকা এক ব্যক্তি ট্রেনের বাইরে একটি মুদ্রা ফেললে প্ল্যাটফর্মে দাঁড়িয়ে থাকা কোনো ব্যক্তি মুদ্রাটিকে অধিবৃত্তাকার পথে পড়তে দেখবে।
প্রতিমিত বল বস্তুতে কোনো ধরনের পরিবর্তন বা প্রভাব সৃষ্টি করতে পারে কি?
প্রতিমিত বলের ক্রিয়ায় বস্তুর গতীয় ধর্ম বা স্থিতিশীল অবস্থার কোনো পরিবর্তন না ঘটলেও নমনীয় বস্তুর ক্ষেত্রে এ জাতীয় বলের প্রভাবে বস্তুর আকৃতি বা আয়তনের পরিবর্তন হতে পারে। যেমন – স্থির অবস্থায় থাকা একটি স্প্রিংকে দুটি বিপরীত দিক থেকে সমান বল দিয়ে টানলে স্প্রিংয়ের সরণ ঘটে না তবে সেটি দৈর্ঘ্যে প্রসারিত হয়।
একটি খেলনা গাড়ি মসৃণ মেঝের উপর দিয়ে সমবেগে গতিশীল। গাড়িটির উপর সামনে ও পিছনে ঠিক বিপরীত অভিমুখে 5N মানের বল প্রযুক্ত হলে গাড়ির গতির কী পরিবর্তন হবে?
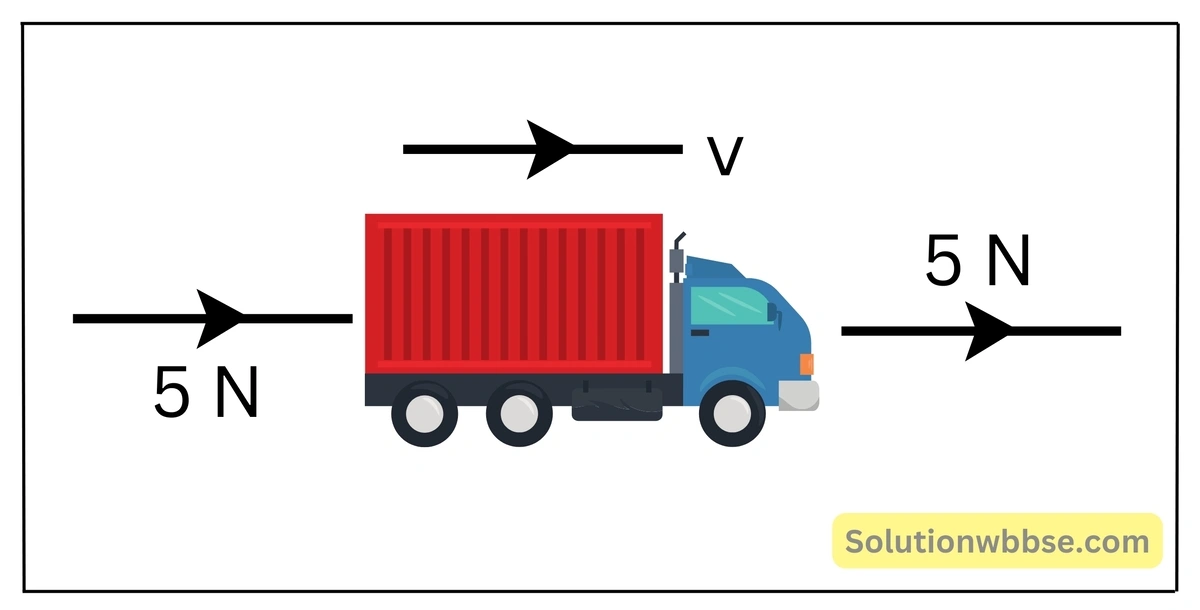
গাড়িটির উপর সমান ও বিপরীতমুখী দুটি বল ক্রিয়া করায় বল দুটির লব্ধি R = (5 – 5) = 0 N। সুতরাং ক্রিয়াশীল বলদুটি এক্ষেত্রে প্রতিমিত বল হিসেবে কাজ করে। তাই এদের যৌথ ক্রিয়ায় গাড়ির জাড্যের কোনো পরিবর্তন ঘটে না। অর্থাৎ গাড়িটি তার সমগতি বজায় রাখবে।
নিউটনের প্রথম গতিসূত্রকে জাড্যের সূত্র বলা হয় কেন?
নিউটনের প্রথম সূত্র থেকে জানা যায় যে, স্থির বস্তু নিজে থেকে সচল হতে পারে না কিংবা সচল বস্তু নিজে থেকে তার গতিশীল অবস্থার পরিবর্তন করতে পারে না। স্থির বস্তুর ধর্ম চিরকাল স্থির থাকা এবং গতিশীল বস্তুর ধর্ম সমবেগে একই সরলরেখায় চলতে থাকা। এটি জড় পদার্থের একটি মৌলিক ধর্ম। এই ধর্মের জন্যই বস্তু তার স্থিতি বা গতির অবস্থা পরিবর্তনের যে-কোনো চেষ্টাকে বাধা দেয়। পদার্থের এই ধর্মের নাম জাড্য বা জড়তা (Inertia)। এজন্য নিউটনের প্রথম সূত্রকে জাড্যের সূত্র বা জড়তার সূত্র বলে।
2 ডাইন + 5 ডাইন = ? তোমার উত্তরের সপক্ষে যুক্তি দাও।
এক্ষেত্রে যোগফলের মান নির্দিষ্ট নয়। বল ভেক্টর রাশি হওয়ায় দুটি বলের সংযোজনের সময় বলদ্বয়ের মান ও অভিমুখ দুই-ই সমান গুরুত্বসহ বিবেচনা করতে হয়, কারণ দুটি বলের সংযোজনের ফলাফল বা লব্ধি বলের মান প্রত্যক্ষভাবে বলের ক্রিয়ারেখা দুটির অন্তর্বর্তী কোণের ওপর নির্ভর করে। গাণিতিকভাবে প্রমাণ করা যায় যে, \(\overrightarrow P\) ও \(\overrightarrow Q\) দুটি বলের লব্ধি R -এর সর্বোচ্চ মান
Rmax = (P + Q) (যখন অন্তর্বর্তী কোণ θ = 0°) এবং ন্যূনতম মান
(R)min = (P – Q), P > Q (যখন θ = 180°)।
∴ (P – Q) ≤ R ≤ (P + Q)
সুতরাং লব্ধি বলের মান θ -এর ওপর নির্ভর করে (5 – 2) = 3 ডাইন থেকে (5 + 2) = 7 ডাইন পর্যন্ত যে-কোনো সম্ভাব্য মান হতে পারে।
জাড্য সূত্র সর্বত্রভাবে প্রযোজ্য হয় কি?
নিউটনের প্রথম গতিসূত্রই জাড্যের সূত্র বা জড়তার সূত্র নামে পরিচিত। এই সূত্রটি বা অন্য দুটি গতিসূত্রও শুধুমাত্র জড়ত্বীয় (পৃথিবী সাপেক্ষে স্থির বা সমবেগে গতিশীল) নির্দেশতন্ত্রেই কঠোরভাবে প্রযোজ্য। ত্বরিত বা অজড়ত্বীয় নির্দেশতন্ত্রে সূত্রগুলি তাদের মূল (নিউটন প্রস্তাবিত) চেহারায় আদৌ প্রযোজ্য নয়। তবে অজড়ত্বীয় নির্দেশতন্ত্রে তার বৈশিষ্ট্যসূচক অলীক বলের অস্তিত্ব আপাত সত্য বলে বিবেচনা করে সূত্রগুলি পরিমার্জিত চেহারায় ব্যবহার করা যেতে পারে।
স্থিতিজাড্য ও গতিজাড্যের পরিবর্তন কীভাবে বোঝা যায়?
স্থিতিশীল বস্তুর গতিপ্রাপ্ত হওয়া অথবা গতিশীল বস্তুর গতির পরিবর্তন (গতিবেগ বৃদ্ধি, হ্রাস বা একসময় স্থিরবস্থায় আসা) সরাসরি পর্যবেক্ষণ করে জাড্যের পরিবর্তন উপলব্ধি করা যায়। আবার বলের প্রভাবই যেহেতু জাড্যের পরিবর্তনের কারণ, তাই স্থির বা গতিশীল বস্তুর উপর বাহ্যিক বল প্রযুক্ত হলে তা থেকে নিশ্চিত সিদ্ধান্তে আসা যায় যে জাড্যের পরিবর্তন ঘটেছে।
একটি ঝুলন্ত বালির বস্তা বা একটি দোলকপিণ্ড – কোনটিকে টেনে একই দূরত্ব সরাতে বেশি বল প্রয়োগ করতে হয় এবং কেন?
একটি ঝুলন্ত বালির বস্তা ও একটি দোলকপিণ্ডের মধ্যে বালির বস্তাটিকে টেনে একই দূরত্ব সরাতে অনেক বেশি বল প্রয়োগ করতে হয়।
ধরি, প্রথমে বালির বস্তা ও দোলকপিণ্ড স্থির অবস্থায় ছিল। দোলকপিণ্ডের তুলনায় বালির বস্তার ভর অনেক বেশি। তাই বালির বস্তার জাড্যও তুলনামূলকভাবে বেশি। আমরা জানি, যে বস্তুর জাড্য যত বেশি, সেই বস্তুর ত্বরণ অর্থাৎ বেগ পরিবর্তন করা তত বেশি কষ্টকর। এক্ষেত্রে বালির বস্তার জাড্য বেশি, তাই বালির বস্তার বেগ পরিবর্তন করতে তুলনামূলকভাবে বেশি বল প্রয়োগ করতে হবে। তাই বালির বস্তাটিকে টেনে একই দূরত্ব সরাতে দোলকপিণ্ড অপেক্ষা বেশি বল প্রয়োগ করতে হয়।
বাসের ছাদে রাখা কোনো মালপত্র দড়ি দিয়ে বেঁধে রাখতে পরামর্শ দেওয়া হয় কেন?
ছাদে মালপত্র থাকা অবস্থায় বাস হঠাৎ গতিশীল হলে মালপত্রগুলি স্থিতিজাড্যের কারণে তাদের পূর্বের অবস্থান বজায় রাখতে চায়। ফলে বাস সামনের দিকে এগোতে থাকলেও মালপত্রগুলি পিছনে সরে যাওয়ার প্রবণতা দেখায়। আবার গতিশীল অবস্থায় থাকা বাস প্রয়োজনে হঠাৎ ব্রেক কষে থামতে চাইলে গতিজাড্যের কারণে মালপত্রগুলি তাদের সম্মুখ গতি বজায় রাখার চেষ্টা করে ও ছাদ থেকে পড়ে যাওয়ার সম্ভাবনা দেখা দেয়। একারণেই বাসের ছাদে রাখা মালপত্র দড়ি দিয়ে বেঁধে রাখার পরামর্শ দেওয়া হয়।
একটি জলপূর্ণ বালতিকে হঠাৎ করে ঠেললে জল কোনদিকে চলকে পড়বে?
একটি জলপূর্ণ বালতিকে হঠাৎ সামনের দিকে গতিশীল করলে বালতি থেকে কিছুটা জল পিছনদিকে চলকিয়ে পড়ে। স্থিতিজাড্য বজায় রাখতে চাওয়ার কারণে বালতিতে সামনের দিকে বল প্রয়োগ করলে জল নিজ স্থানে স্থির থাকতে চাইবে এবং ফলস্বরূপ পিছনের দিকে পড়তে চাইবে।
কার্পেটের ধুলো ঝাড়ার সময় কার্পেটটি লাঠি দিয়ে পেটানো হয় কেন?
লাঠি দিয়ে আঘাত করলে কার্পেটে গতীয় অবস্থা সৃষ্টি হয়। কিন্তু কার্পেটের মধ্যে থাকা ধূলিকণাগুলি স্থিতিজাড্যের জন্য আগের অবস্থানেই থাকতে চায়। তাই কোনো অবলম্বন না পাওয়ায় ধূলিকণাগুলি নীচে পড়ে যায়।
কাচের জানালা পাথর ছুঁড়ে মারলে সমগ্র কাচে ফাটল সৃষ্টি হয় কিন্তু বন্দুকের গুলি ছুড়লে একটি গোল গর্ত সৃষ্টি হয় কেন?
নিক্ষিপ্ত পাথরের বেগ অনেক কম হওয়ায় জানালার কাচের সঙ্গে পাথরের সংঘাতকালীন সময় যথেষ্ট বেশি হয়। এরফলে কাচের জানালায় প্রায় সর্বত্র অসম বল সৃষ্টি হয়ে কাচে ফাটল তৈরি করে। বৃহৎ অংশ জুড়ে কাচের বিভিন্ন বিন্দুতে স্থিতিজাড্য বিঘ্নিত হয় এবং কিছু কাচের টুকরো আলাদা হয়ে গিয়ে সমগ্র জানালাটিকেও টুকরো টুকরো করে দিতে পারে।
অন্যদিকে বন্দুক থেকে নিক্ষিপ্ত গুলির বেগ পাথরের তুলনায় বহুগুণ বেশি বলে সংঘাতকালীন সময় অত্যন্ত কম হয়। এর ফলে অসম বল সৃষ্টি হয় না এবং তার মাধ্যমে জানালার সর্বত্র স্থিতিজাড্য বিনষ্ট হয় না, শুধুমাত্র আঘাতপ্রাপ্ত অংশে থাকা কাচ অণুগুলি গুলির আঘাতে স্থানচ্যুত হয় এবং গুলির আকারের ছিদ্র তৈরি হয়।
মালবোঝাই করা ভারী মালগাড়ির চালক মালগাড়িকে গতিশীল করার জন্য প্রথমে সামান্য পিছনদিকে চালিয়ে পরে সামনের দিকে চালায় কেন?
মালবোঝাই গাড়িকে গতির শুরুতে সামান্য পিছনদিকে চালনা করলে মালগাড়ির বিভিন্ন কামরাগুলির মাঝের শিকলের সংযোগ (coupling) শিথিল হয় ও তাদের মধ্যে ব্যবধান অপেক্ষাকৃত বেড়ে যায়। এই অবস্থায় ইঞ্জিনকে সামনের দিকে চালনা করলে মালগাড়ির সামনের অংশই শুধু গতিপ্রাপ্ত হয়। গতিজাড্যের ক্রিয়ায় এই গতিশীলতা ধর্ম ক্রমে পিছনে থাকা কামরাগুলিতে সেই গতি হস্তান্তরিত হয়। ফলে সহজে, অপেক্ষাকৃত কম বল প্রয়োগেই গাড়িটি সামনে অগ্রসর হতে পারে।
এর পরিবর্তে গাড়িটি প্রথমেই সামনের দিকে চালাতে চাইলে সংযোজী শিকলগুলির মাধ্যমে মালগাড়ির কামরাগুলি দৃঢ়ভাবে আবদ্ধ থাকায় সমগ্র গাড়িটি একসঙ্গে গতিশীল হতে চায়। তাই কাঙ্ক্ষিত গতি সৃষ্টি করতে প্রথমোক্ত ক্ষেত্রের তুলনায় অনেক বেশি বল প্রয়োজন হয়।
বর্তমানে সমস্ত গাড়িতে সিটবেল্ট লাগানো থাকে কেন?
আপৎকালীন পরিস্থিতিতে ব্রেক কষে চলন্ত মোটরগাড়িকে থামানোর প্রয়োজন হলে গতিজাড্যের কারণে গাড়ির ভিতরে বসে থাকা আরোহীর দেহের ঊর্ধ্বাংশ তখনও সচল থাকে এবং সম্মুখগতি বজায় রাখতে চায়। ফলে আরোহী সামনে হুমড়ি খেয়ে পড়ে চোট পেতে পারেন। এই বিপদ এড়াবার উদ্দেশ্যেই গাড়ি চালানোর সময় চালক ও আরোহীদের সিটবেল্ট ব্যবহারের পরামর্শ দেওয়া হয়।
চলন্ত গাড়ি থেকে নামার সময় কোনো ব্যক্তিকে পিছনে হেলে নামতে হয় কেন?
চলন্ত গাড়ি থেকে নামার সময় যাত্রীর সমস্ত দেহ গতিশীল থাকে। গাড়ি থেকে নামার সঙ্গে সঙ্গে যাত্রীর পা মাটির সংস্পর্শে এসে স্থির হয়। কিন্তু দেহের ঊর্ধ্বাংশ গতিজাড্যের জন্য সামনের দিকে এগিয়ে যায়। তাই হুমড়ি খেয়ে পড়ার ভয় থাকে। কিন্তু পিছন দিকে হেলে নামলে দেহের ঊর্ধ্বাংশ কিছুদূর এগিয়ে স্থির অবস্থায় আসে। তাই হুমড়ি খেয়ে পড়ার ভয় থাকে না। তাই চলন্ত গাড়ি থেকে নামার সময় যাত্রীকে পিছনদিকে হেলে নামতে হয়।
যাত্রীবাহী গাড়ি হঠাৎ চলতে শুরু করলে যাত্রীরা পিছন দিকে হেলে পড়ে কেন?
গাড়ি যখন স্থির থাকে তখন যাত্রীরাও স্থির থাকে। গাড়ি হঠাৎ চলতে শুরু করলে যাত্রীর দেহের নিম্নাংশ গাড়ির সংস্পর্শে থাকায় হঠাৎ চলতে শুরু করে। কিন্তু যাত্রীর দেহের ঊর্ধ্বাংশ স্থিতিজাড্যের জন্য স্থির অবস্থাতেই থাকতে চায়। তাই যাত্রীবাহী গাড়ি হঠাৎ চলতে শুরু করলে যাত্রীরা পিছনদিকে হেলে পড়ে।
বৈদ্যুতিক পাখার সুইচ বন্ধ করলেও পাখাটি ঘুরতে থাকে কেন?
বৈদ্যুতিক পাখার সুইচ বন্ধ করলেও গতিজাড্যের জন্য পাখাটি তার গতি বজায় রাখতে চায়। তাই সুইচ বন্ধ করলেও গতিজাড্যের জন্য পাখাটি ঘুরতে থাকে ও কিছুক্ষণ পর পাখার ভিতরের যন্ত্রাংশের মধ্যে সৃষ্ট ঘর্ষণ বল ও বায়ুর বাধায় তা স্থির হয়।
চলন্ত ট্রাম থেকে নেমে সামনের দিকে কিছুটা ছুটে যেতে হয় কেন?
ট্রামের ভিতরে অবস্থানকালে ব্যক্তির দেহের সমগ্র অংশ ট্রামের সমান গতি লাভ করে। চলন্ত ট্রাম থেকে নামার সময় ভূমি স্পর্শ করার সঙ্গে সঙ্গে ব্যক্তির পা স্থিরাবস্থায় আসে যদিও দেহের ঊর্ধ্বাংশ গতিজাড্যের কারণে সম্মুখ গতি বজায় রাখার চেষ্টা করে। তাই ব্যক্তি সামনে মুখ থুবড়ে পড়ে যান।
এক্ষেত্রে ভূমি স্পর্শ করার সঙ্গে সঙ্গে ব্যক্তি আবার পা তুলে নিয়ে সামনের দিকে দেহকে খানিকটা এগিয়ে নিতে সক্ষম হন অর্থাৎ ট্রামের গতির অভিমুখে কিছুটা জোরে ছুটতে থাকেন। তবে দেহের ঊর্ধ্বাংশ ও নিম্নাংশের গতিজাড্যের পার্থক্য কমে এবং ব্যক্তির দেহের ভারসাম্য বজায় থাকে। এর ফলে সামনের দিকে ব্যক্তির হুমড়ি খেয়ে পড়ার সম্ভাবনা প্রতিহত হয় এবং অল্প সময়ের মধ্যেই দেহ গতিজাড্যের প্রভাব থেকে মুক্ত হয়ে স্থিরাবস্থায় আসে।
লং জাম্প দেওয়ার সময় প্রতিযোগী অনেকটা দূর থেকে দৌড়ে আসেন কেন?
দূর থেকে দৌড়ে এলে প্রতিযোগীর শরীরে গতিজাড্য সৃষ্টি হয় এবং তা ব্যবহার করে প্রতিযোগী দীর্ঘ দূরত্ব লাফাতে সক্ষম হয়ে থাকেন। এই কারণে লং জাম্প বা দীর্ঘ লম্ফন দেওয়ার সময় প্রতিযোগীকে অনেকটা দূর থেকে দৌড়ে আসতে হয়।
কোনো স্থির গাড়িতে বসে থাকা আরোহী কি ভিতর থেকে ঠেলে গাড়িকে গাতিশীল করতে পারে?
নিউটনের প্রথম গতিসূত্র অনুযায়ী, বাইরে থেকে বল প্রযুক্ত না হলে গতির সৃষ্টি সম্ভব নয়। কারণ গাড়ি ও আরোহী মিলে গঠিত সংস্থার সাপেক্ষে গাড়ির ভিতরে বসে থাকা আরোহী যে বল প্রয়োগ করেন, তা অভ্যন্তরীণ বল। এই বল গাড়িটিকে গতিশীল করতে পারে না।
চলন্ত গাড়ির কামরায় কোনো আরোহী একটি বলকে উল্লম্বভাবে ছুঁড়লে তা আবার তার হাতেই এসে পড়ে কেন?
চলন্ত বাসে বসে থাকা যাত্রী গাড়ির ভিতরে একটি বলকে খাড়া উপরদিকে নিক্ষেপ করলে গতিজাড্যের কারণে বলটি শূন্যে থাকা অবস্থায় বাসের সমান সম্মুখ বেগ লাভ করে। বলটি যতক্ষণ ভাসমান থাকে সেই সময়কালে বাসের বেগ যদি পরিবর্তিত না হয় তবে উৎক্ষিপ্ত বলটি মাটিতে ফিরে আসতে যে সময় নেয় সেই অবকাশে বাস ও বল একই অভিমুখে একই দূরত্ব অতিক্রম করে। ফলে বলটি এক্ষেত্রে যাত্রীর হাতে এসে পৌঁছোয়।
চলন্ত অবস্থায় গাড়ির ভিতরের যাত্রী একটি বলকে উপরদিকে ছুঁড়লে বলটি সোজা হাতে না এসে আগে বা পিছনে পড়লে গাড়িটির গতি সম্পর্কে কী সিদ্ধান্তে আসবে?
চলন্ত গাড়ির ভিতরের যাত্রী একটি বলকে উপরদিকে ছোড়ার সময় গাড়িটি ত্বরণপ্রাপ্ত হলে গাড়ির সরণ বলের সরণ অপেক্ষা বেশি হয়। তাই বলটি এক্ষেত্রে যাত্রীর পিছনে পড়ে। একইভাবে গাড়িটিতে মন্দন সৃষ্টি হলে একই যুক্তিতে বলা যায় যে বলটি যাত্রীর সামনে পড়বে।
সুতরাং বলটি আগে পড়লে বুঝতে হবে গাড়িটিতে মন্দন সৃষ্টি হয়েছে এবং সেটি পিছনে পড়লে সিদ্ধান্তে আসা যাবে গাড়ির গতি ত্বরণযুক্ত।
দৌড় প্রতিযোগিতায় প্রতিযোগী সীমারেখায় পৌঁছে থেমে যেতে পারে না কেন?
দৌড় প্রতিযোগিতায় প্রতিযোগী যখন দৌড়ায় তখন গতির জন্য তার মধ্যে গতিজাড্যের সৃষ্টি হয়। দৌড় প্রতিযোগিতার শেষ সীমারেখায় পৌঁছে প্রতিযোগী হঠাৎ থেমে যেতে চাইলে তার দেহের নিম্নাংশ স্থির হয়ে যায়, কিন্তু দেহের ঊর্ধ্বাংশ গতিজাড্যের দরুন সামনের দিকে এগিয়ে যায়। ফলে প্রতিযোগীর সামনের দিকে হুমড়ি খেয়ে পড়ে আঘাত লাগার সম্ভাবনা থাকে। এই আঘাত যাতে না লাগে সেজন্য প্রতিযোগী শেষ সীমারেখায় পৌঁছেও থামে না। বরং সে তার গতিকে কমিয়ে থামার জন্য আরও কিছুটা দূরত্ব অতিক্রম করে।
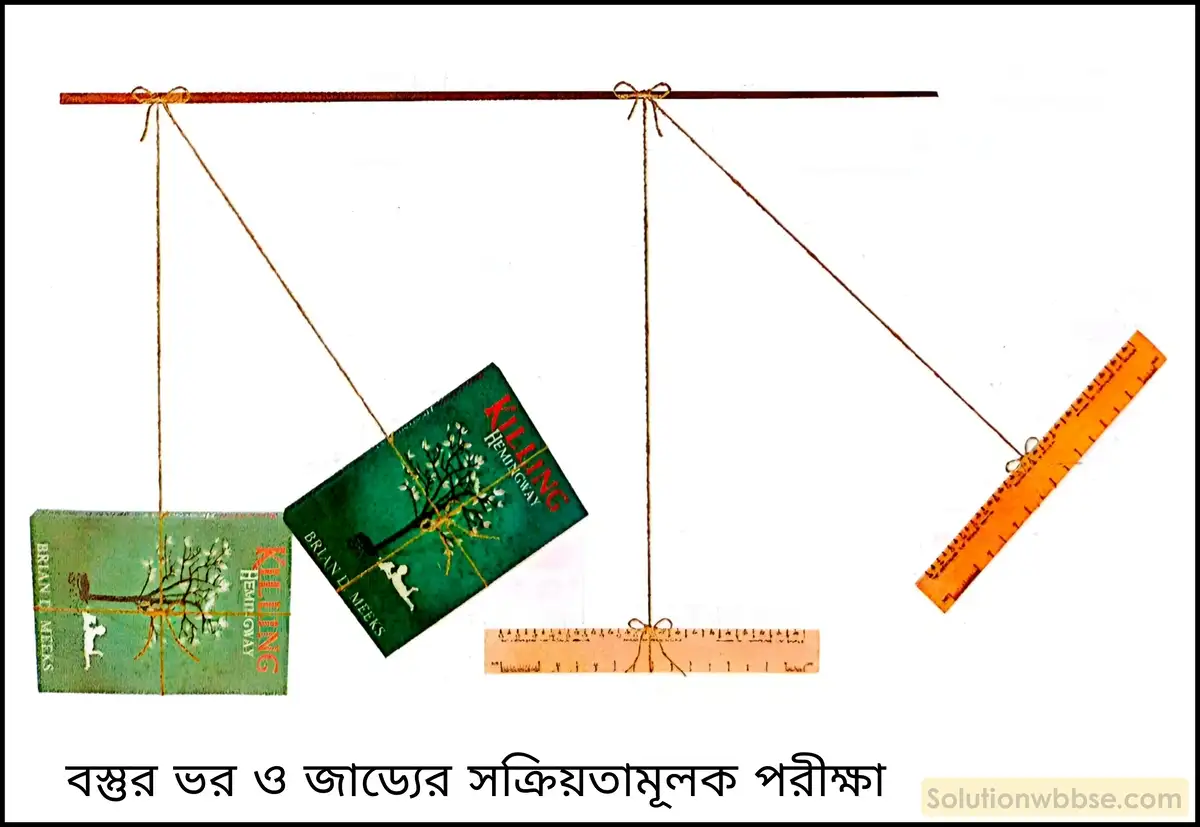
একটি মোটা বই, একটি স্কেল এবং দুটি শক্ত দড়ি দিয়ে বস্তুর ভর ও জাড্যের সম্পর্ক কীভাবে জানা যেতে পারে?
একটি মোটা বই, একটি স্কেল ও দুটি শক্ত দড়ি নেওয়া হল। এরপর ওই দুটি শক্ত দড়ির সাহায্যে মোটা বইটিকে ও স্কেলকে পৃথকভাবে বাঁধা হল। তারপর বই ও স্কেলটিকে এমনভাবে ঝোলানো হল যাতে ওগুলি জোরে দুললেও একে অপরের সঙ্গে ধাক্কা না লাগে।
স্থির অবস্থায় থাকার সময় স্কেল ও বইটিতে একই পরিমাণ বল প্রয়োগ করার পর দেখা গেল, স্কেলের তুলনায় মোটা বইটি কম গতিশীল হল। অর্থাৎ মোটা বইটির বেগের পরিবর্তন কম হল। এক্ষেত্রে মোটা বইটির ভর বেশি হওয়ায় ওর বেগের পরিবর্তন করা কষ্টকর হয়। আবার আমরা জানি, যে বস্তুর বেগের পরিবর্তন করা যত কঠিন, তার জাড্যধর্মও তত বেশি। সুতরাং মোটা বইটির ভর তুলনামূলকভাবে বেশি হওয়ায় ওর জাড্যধর্মও তুলনামূলকভাবে বেশি হয়। এর থেকে বোঝা যায় যে, বস্তুর ভর ও জাড্যের মধ্যে সম্পর্কটি হল ‘সরল’ সম্পর্ক।
পার্থক্যধর্মী প্রশ্নোত্তর
প্রতিমিত (Balanced force) ও অপ্রতিমিত বল (Unbalanced force) -এর মধ্যে পার্থক্য লেখো।
প্রতিমিত (Balanced force) ও অপ্রতিমিত বল (Unbalanced force) -এর মধ্যে পার্থক্যগুলি হল –
| বিষয় | প্রতিমিত বল (Balanced force) | অপ্রতিমিত বল (Unbalance force) |
| সংজ্ঞা | কোনো বস্তুর ওপর বাইরে থেকে ক্রিয়াশীল একাধিক বল যদি বস্তুর ত্বরণ সৃষ্টি করতে না পারে, কেবল বস্তুর বিকৃতি ঘটায়, তাহলে ওই বলগুলিকে প্রতিমিত বল বলে। | যে বল বা বলসমূহ কোনো বস্তুর ওপর বাইরে থেকে প্রযুক্ত হয়ে বস্তুটির স্থিতিশীল বা গতিশীল অবস্থার পরিবর্তন ঘটায় তাকে বা তাদের কার্যকর বা অপ্রতিমিত বল বলে। |
| লব্ধিবলের মান | প্রতিমিত বলের ক্ষেত্রে বস্তুর ওপর ক্রিয়াশীল বলগুলির লব্ধি শূন্য হয়। | অপ্রতিমিত বলের ক্ষেত্রে বস্তুর ওপর ক্রিয়াশীল বলগুলির লব্ধি শূন্য হয় না। লব্ধিবল একটি নির্দিষ্ট অভিমুখে ক্রিয়া করে। |
| প্রভাব | প্রতিমিত বলের প্রভাবে কোনো বস্তুর স্থির বা গতিশীল অবস্থার কোনো পরিবর্তন ঘটে না। প্রতিমিত বলের প্রভাবে বস্তুর বিকৃতি ঘটে। | কোনো বস্তুর ওপর অপ্রতিমিত বল ক্রিয়া করলে বস্তুর স্থির অবস্থা বা সমবেগযুক্ত গতির পরিবর্তন ঘটে। |
Class 9 Physical Science – Notes for All Chapters
| Chapter Name | Tropics |
|---|---|
| পরিমাপ | পরিমাপ ও একক বিভিন্ন মাপের একক মাত্রা পরিমাপ |
| বল ও গতি | স্থিতি ও গতি গতির সমীকরণ নিউটনের প্রথম গতিসূত্র নিউটনের দ্বিতীয় গতি সূত্র নিউটনের তৃতীয় গতিসূত্র বিভিন্ন ধরনের বল রৈখিক ভরবেগ রৈখিক ভরবেগ সংরক্ষণ |
| পদার্থ : গঠন ও ধর্ম | তরল ও বায়ুর চাপ আর্কিমিডিসের নীতি পৃষ্ঠটান সান্দ্রতা বার্নোলির নীতি স্থিতিস্থাপকতা |
| পদার্থ : পরমাণুর গঠন ও পদার্থের ভৌত ও রাসায়নিক ধর্মসমূহ | পরমাণুর গঠন মোলের ধারণা দ্রবণ অ্যাসিড, ক্ষার, লবণ মিশ্রণের উপাদানের পৃথকীকরণ জল |
| শক্তির ক্রিয়া , কার্য, ক্ষমতা | শক্তির ক্রিয়া , কার্য, ক্ষমতা |
| তাপ | ক্যালোরিমিতি কার্য ও তাপের তুল্যতা লীনতাপ সম্পৃক্ত ও অসম্পৃক্ত বাষ্প জলের ব্যতিক্রান্ত প্রসারণ |
| শব্দ | শব্দের উৎস : কম্পন শব্দের বিস্তার : তরঙ্গ শব্দের কয়েকটি ধর্ম শব্দের বৈশিষ্ট্য মানুষের কান ও শব্দ শোনার কৌশল শব্দদূষণ |
আজকের আর্টিকেলে আমরা নবম শ্রেণির ভৌতবিজ্ঞান বইয়ের দ্বিতীয় অধ্যায় “বল ও গতি” এর “নিউটনের প্রথম গতিসূত্র” থেকে পরীক্ষায় আসা গুরুত্বপূর্ণ প্রশ্ন ও উত্তরগুলো আলোচনা করেছি। এই প্রশ্নোত্তরগুলো নবম শ্রেণির বার্ষিক পরীক্ষা, এমনকি চাকরি বা যেকোনো প্রতিযোগিতামূলক পরীক্ষার জন্যও উপযোগী। কারণ, এই অধ্যায়ের প্রশ্ন প্রায়ই বিভিন্ন পরীক্ষায় কমন আসে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সাহায্য করবে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন কিংবা টেলিগ্রামে যোগাযোগ করুন—আপনাদের প্রশ্নের উত্তর দিতে আমি সর্বদা প্রস্তুত।
ধন্যবাদ সবাইকে।






Leave a Comment