আজকের আর্টিকেলে আমরা নবম শ্রেণীর ভৌতবিজ্ঞান বইয়ের তৃতীয় অধ্যায় “পদার্থ : গঠন ও ধর্ম” এর “বার্নোলির নীতি” থেকে সহজ ও সংক্ষিপ্ত প্রশ্ন-উত্তর শেয়ার করবো। এই প্রশ্নগুলো নবম শ্রেণির ইউনিট টেস্ট থেকে বার্ষিক পরীক্ষা এর জন্য যেমন গুরুত্বপূর্ণ, তেমনি চাকরি বা বিভিন্ন প্রতিযোগিতার পরীক্ষাতেও কাজে লাগবে। এই অধ্যায় থেকে স্কুল পরীক্ষা থেকে শুরু করে চাকরির পরীক্ষায় প্রায়ই প্রশ্ন আসে, তাই এই প্রশ্নোত্তরগুলো সবাইকে সাহায্য করবে। প্রতিটি প্রশ্নের উত্তর সহজ ভাষায় লেখা হয়েছে, যাতে সবাই বুঝতে পারেন। পড়ার শেষে এই অধ্যায়ের মুখ্য বিষয়গুলো আপনার আয়ত্তে চলে আসবে এবং যেকোনো পরীক্ষায় আত্মবিশ্বাসের সঙ্গে লিখতে পারবেন।

জ্ঞানমূলক প্রশ্নোত্তর
প্রবহমান তরলের কয় প্রকার শক্তি থাকে তা আলোচনা করো।
প্রবহমান তরল বা গ্যাসীয় পদার্থের তিনপ্রকার শক্তি থাকে। যেমন – গতিশক্তি, স্থিতিশক্তি এবং চাপশক্তি।
গতিশক্তি (Kinetic energy) – প্রবাহীর আয়তন V ,ভর m, ঘনত্ব ρ এবং গতিবেগ v হলে, ওই প্রবাহীর গতিশক্তি, \(E_K=\frac12mv^2\)।
সুতরাং, প্রবাহীর একক আয়তনে গতিশক্তি = \(\frac{\frac12mv^2}V\)
= \(\frac12\left(\frac mV\right)v^2\)
= \(\frac12\rho v^2\)।
একক ভরে গতিশক্তি = \(\frac12\frac{mv^2}m=\frac{v^2}2\)।
স্থিতিশক্তি (Potential energy) – m ভরসম্পন্ন প্রবাহী কোনো অনুভূমিক তল (নির্দেশতল) থেকে h উচ্চতায় অবস্থান করলে ওই প্রবাহীর স্থিতিশক্তি = mgh।
প্রবাহীর একক আয়তনে স্থিতিশক্তি = \(\frac{mgh}V=\rho gh\) একক ভরে স্থিতিশক্তি = \(\frac{mgh}m=gh\)।
চাপশক্তি (Pressure energy) – কোনো তরল তার নিজস্ব চাপের জন্য কার্য করার যে সামর্থ্য অর্জন করে, তাকে ওই তরলের চাপশক্তি বলে।
প্রবহমান তরলের প্রস্থচ্ছেদের ক্ষেত্রফল A, ওই প্রস্থচ্ছেদের ওপর ক্রিয়াশীল চাপ P এবং তরলের বেগ হলে A প্রস্থচ্ছেদে প্রযুক্ত বল = PA। যেহেতু, তরলের বেগ = v একক সময়ে তরল দ্বারা অতিক্রান্ত রৈখিক দূরত্ব,
∴ প্রতি সেকেন্ডে তরল দ্বারা কৃতকার্য = PA × v
আবার, A প্রস্থচ্ছেদের মধ্য দিয়ে প্রতি সেকেন্ডে প্রবাহিত তরলের আয়তন = A × v।
∴ Av আয়তনের তরলে এই প্রক্রিয়ায় সঞ্চিত শক্তি = PAv, যা চাপশক্তি নামে পরিচিত।
∴ একক আয়তনে তরলের চাপশক্তি = \(\frac{PAv}{Av}=P\) ও
∴ একক ভরে চাপশক্তি = \(\frac{PAv}m=\frac{PAv}{Av\rho}=\frac P\rho\)।
প্রবহমান তরলের গতি সম্পর্কিত বার্নোলির উপপাদ্যটি বিবৃত ও ব্যাখ্যা করো।
অথবা, বার্নোলির নীতির গাণিতিক রূপটি লিখে দেখাও যে, ধারারেখ প্রবাহের ক্ষেত্রে আদর্শ তরলের যে-কোনো বিন্দুতে বেগশীর্ষ, উচ্চতাশীর্ষ ও চাপশীর্ষের সমষ্টি ধ্রুবক।
বার্নোলির উপপাদ্য (Bernouli’s theorem) – তরল বা গ্যাসীয় পদার্থের গতির ক্ষেত্রে শক্তির সংরক্ষণ সূত্রের পরিমার্জিত রু পই হল বার্নোলির তত্ত্ব বা বার্নোলির উপপাদ্য। এর বিবৃতিটি হল – “আদর্শ তরলের ধারারেখ প্রবাহের ক্ষেত্রে, প্রবাহরেখার যে-কোনো বিন্দুতে একক আয়তনে (বা একক ভরে) তরলের গতিশক্তি, স্থিতিশক্তি ও চাপশক্তির সমষ্টি ধ্রুবক।”
বার্নোলির উপপাদ্যের ব্যাখ্যা – ধরা যাক, অসম প্রস্থচ্ছেদবিশিষ্ট একটি প্রবাহ নলের মধ্যে দিয়ে শান্ত প্রবাহে গতিশীল কোনো তরলের দুটি অভিলম্ব ছেদ A ও B -তে তরলের চাপ যথাক্রমে P1 ও P2 এবং তরলের বেগ যথাক্রমে v1 ও v2। নির্দেশতল নির্দেশতল সাপেক্ষে A ও B -এর উচ্চতা যথাক্রমে h1 ও h2 হলে, বার্নোলির উপপাদ্য বা নীতি অনুযায়ী,
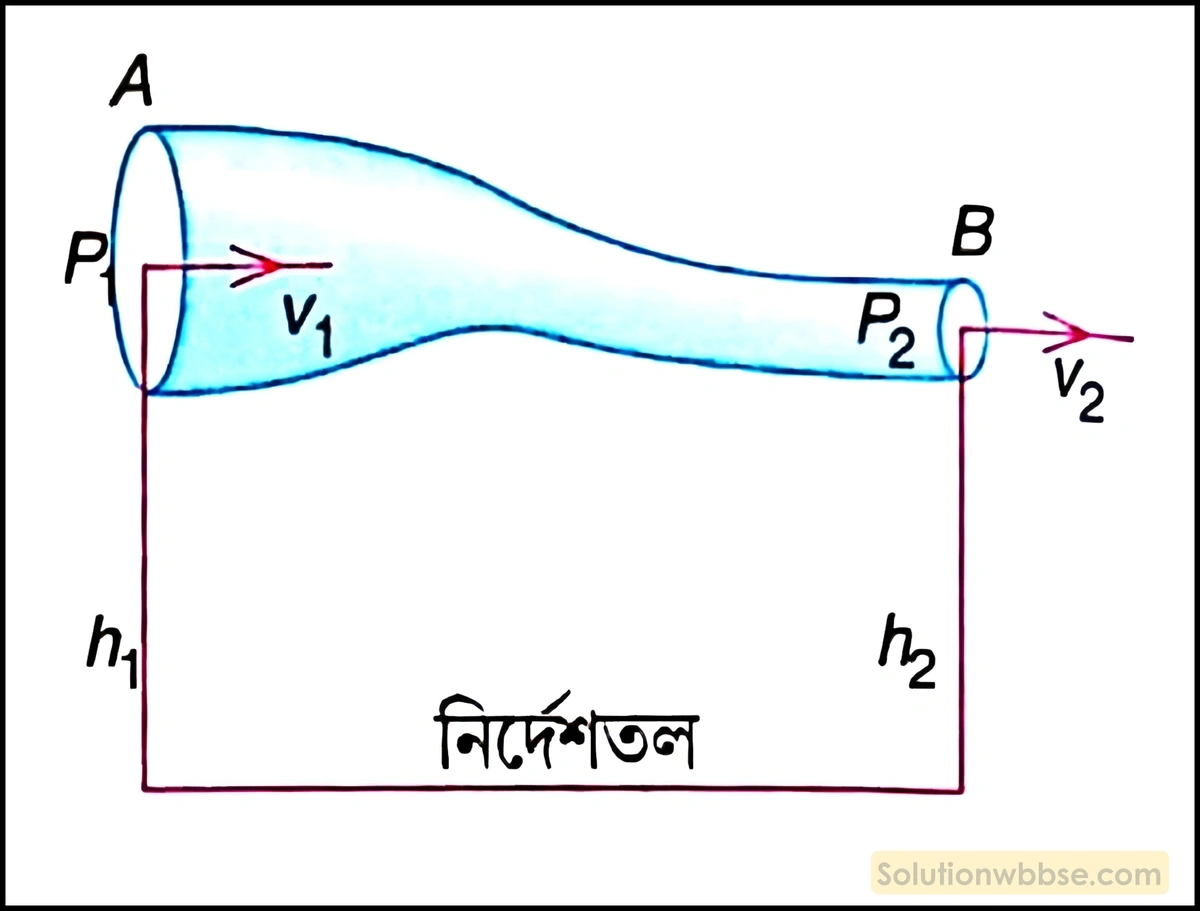
বা, \(\frac12\rho v_1^2+\rho gh+P\) = ধ্রুবক (একক আয়তনের ক্ষেত্রে) ___(1)
অথবা, \(\frac{P_1}\rho+gh_1+\frac12v_1^2=\frac{P_2}\rho+gh_2+\frac12v_2^2\) (একক ভরের ক্ষেত্রে) ___(2)
বা, \(\frac P\rho+gh+\frac{v^2}2\) = ধ্রুবক।
তরলের প্রবাহ অনুভূমিক তল বরাবর হলে h ধ্রুবক হয় এবং (1) নং সমীকরণকে লেখা যায়, \(P+\frac12\rho v^2\) = ধ্রুবক। এই সমীকরণে P ও \(\frac12\rho v^2\) রাশি দুটিকে যথাক্রমে স্থৈতিক চাপ ও গতীয় চাপ বলে। (2) নং সমীকরণের প্রত্যেকটি পদকে g দ্বারা ভাগ করে পাওয়া যায়, \(\frac P{\rho g}+h+\frac{v^2}{2g}\) = ধ্রুবক। সমীকরণের বামপক্ষে উপস্থিত প্রতিটি পদ উচ্চতা (দৈর্ঘ্য) বোঝায়। এদের বলা হয় যথাক্রমে চাপশীর্ষ (Pressure head), উচ্চতাশীর্ষ (Elevation head) ও বেগশীর্ষ (Kinetic head)।
বার্নোলির নীতি প্রযোজ্য হবার শর্তগুলি কী কী?
বার্নোলির উপপাদ্য প্রযোজ্য হওয়ার শর্ত –
নিম্নোক্ত শর্তসাপেক্ষে এটি প্রযোজ্য হয়ে থাকে –
- যদি বিবেচনাধীন তরলটি আদর্শ অর্থাৎ, অসংনম্য ও অসান্দ্র হয়,
- প্রবাহনলটি খুবই সরু অর্থাৎ, তার যে-কোনো ছেদে যে-কোনো বিন্দুতে প্রবাহীর বেগ একই থাকে,
- তরল প্রবাহিত হওয়ার সময় শক্তির কোনোরকম অপচয় না হয়, অর্থাৎ, ঘর্ষণ বা অন্যান্য বাধাদানকারী বলের ক্রিয়া এক্ষেত্রে উপেক্ষণীয়।
ফরাসি গণিতজ্ঞ ও পদার্থবিদ ড্যানিয়েল বার্নোলি কোন সালে তার সূত্রটি গাণিতিকভাবে প্রতিষ্ঠা করেন, এবং এটি কোন বিষয়ের গুরুত্বপূর্ণ নীতি?
ফরাসি গণিতজ্ঞ ও পদার্থবিদ ড্যানিয়েল বার্নোলি 1738 খ্রিস্টাব্দে সূত্রটি গাণিতিকভাবে প্রতিষ্ঠা করেন। এটি উদ্গতিবিদ্যার (Hydrodynamics) একটি বিশেষ গুরুত্বপূর্ণ নীতি।
স্থির তরলের কোনো বিন্দুতে চাপের রাশিমালা, – বার্নোলির নীতি প্রয়োগ করে প্রতিষ্ঠা করো।
বার্নোলির উপপাদ্যের প্রয়োগ –
চাপের রাশিমালা নির্ণয় – স্থির তরলের যে-কোনো বিন্দুতে তরলের বেগ শূন্য। তরলপৃষ্ঠে যে-কোনো বিন্দু A এবং h গভীরতায় অপর একটি বিন্দু B বিবেচনা করা হল,
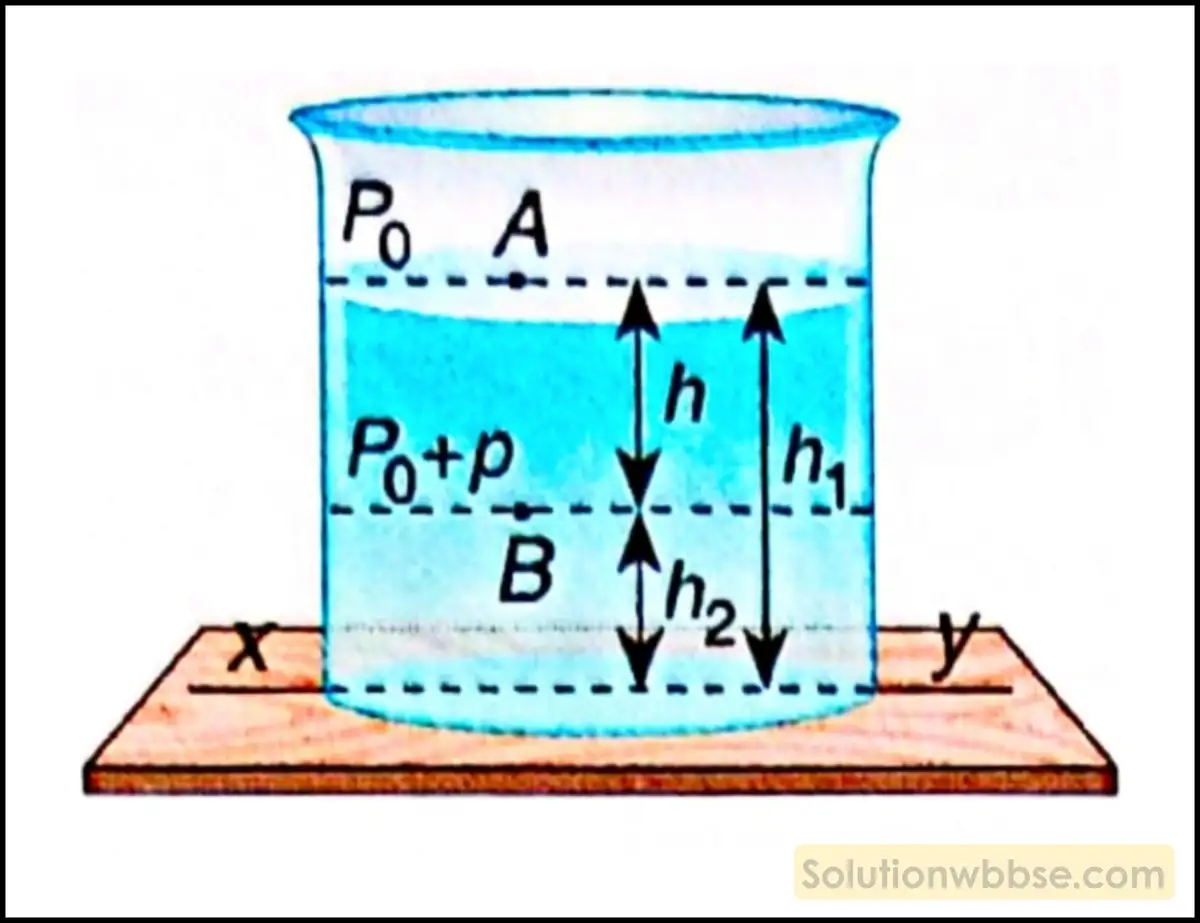
A বিন্দুতে চাপ = বায়ুমণ্ডলীয় চাপ (P0)
B বিন্দুতে চাপ = বায়ুমণ্ডলীয় চাপ (P0) + h উচ্চতার তরলস্তম্ভের চাপ (P)
নির্দেশতল XY সাপেক্ষে A ও B বিন্দুর উচ্চতা যথাক্রমে h1 ও h2 হলে বার্নোলির নীতি অনুযায়ী,
0 + ρgh1 + P0 = 0 + ρgh2 + (P0 + P)
বা, P = ρg (h1 – h2)
বা, P = hρg [h = h1 – h2]
∴ P = hρg
আবদ্ধ পাত্রের গায়ে থাকা কোনো ছিদ্রের মধ্য দিয়ে তরলের নির্গমন বেগের রাশিমালা বার্নোলির নীতি প্রতিষ্ঠা করো।
নির্গমন বেগের রাশিমালা – কোনো তরলপূর্ণ পাত্রের দেয়ালে অবস্থিত কোনো ছিদ্রের মধ্য দিয়ে তরল যে বেগে নির্গত হয়, তাকে ওই তরলের নির্গমন বেগ বলা হয়।

ধরা যাক, পাত্রের তলদেশ থেকে তরলের মুক্তপৃষ্ঠ ও ছিদ্রের উচ্চতা যথাক্রমে h1 ও h2। পাত্রের প্রস্থচ্ছেদের তুলনায় ছিদ্রের প্রস্থচ্ছেদ উপেক্ষণীয় হলে তরলের উপরিপৃষ্ঠে যে-কোনো বিন্দুতে তরলের বেগ প্রায় শূন্য বলে বিবেচনা করা যায়। A ও O বিন্দু উভয়ই উন্মুক্ত বলে উভয় বিন্দুতে চাপ বায়ুমণ্ডলীয় চাপের (P0) সমান। সুতরাং, O বিন্দুতে তরলের নির্গমন বেগ হলে, বার্নোলির নীতি প্রয়োগ করে লেখা যায়,
বা, \(0+\rho gh_1+P_0=\frac12\rho v^2+\rho gh_2+P_0\)
বা, \(\frac12\rho v^2=\rho g\left(h_1-h_2\right)=\rho gh\) [যেখানে, h = h1 – h2 অর্থাৎ, মুক্তপৃষ্ঠ থেকে ‘O’ বিন্দুর গভীরতা]
বা, \(v=\rho gh\)
বা, \(v=\sqrt{2gh}\)
সুতরাং, কোনো ছিদ্র দিয়ে তরলের নির্গমন বেগ, ওই তরলের মুক্তপৃষ্ঠ থেকে ছিদ্রের তল পর্যন্ত কোনো বস্তু অবাধে পতনশীল হলে যে বেগ অর্জন করে তার সমান হয়।
ফলাফলটির আবিষ্কারক ইভান জেলিস্টা টরিসেলির নামে এটি টরিসেলির সূত্র বলে পরিচিত।
প্রবাহীর অনুভূমিক প্রবাহের ক্ষেত্রে বার্নোলির উপপাদ্য থেকে দেখাও যে, কোনো বিন্দুতে চাপ বৃদ্ধি পেলে সেই বিন্দুতে প্রবাহীর বেগ হ্রাস পাবে এবং অপরপক্ষে চাপ হ্রাস পেলে বেগ বৃদ্ধি পাবে।
বার্নোলির উপপাদ্য অনুসারে, আদর্শ প্রবাহীর ধারারেখ প্রবাহের ক্ষেত্রে, ধারারেখর প্রতিটি বিন্দুতে প্রবাহীর একক আয়তনের স্থিতিশক্তি, গতিশক্তি ও চাপশক্তির সমষ্টি ধ্রুবক হয়।
ধরি, ধারারেখর উপর কোনো বিন্দুতে তরলের বেগ = v,
একটি নির্দিষ্ট নির্দেশতল থেকে ওই বিন্দুর উচ্চতা h এবং
তরলের ঘনত্ব = ρ হলে,
একক আয়তনের তরলের গতিশক্তি = \(\frac12\rho v^2\)
স্থিতিশক্তি = ρgh [g = ওই স্থানে অভিকর্ষজ ত্বরণ]
চাপশক্তি = P হলে,
বার্নোলির উপপাদ্য অনুযায়ী,
\(\frac12\rho v^2+\rho gh+P\) = ধ্রুবক ___(1)
যদি প্রবাহীর প্রবাহ অনুভূমিক তল বরাবর হয়, তবে নির্দেশতল থেকে ওর সর্বস্থানের উচ্চতা সমান থাকে অর্থাৎ, h = ধ্রুবক হয়।
∴ (1) নং সমীকরণ থেকে লেখা যায়,
\(\frac12\rho v^2+P\) = ধ্রুবক
অর্থাৎ, গতিশক্তি ও চাপশক্তির মধ্যে যে-কোনো একটির মান বাড়লে বা কমলে ধ্রুবকটির মান অপরিবর্তিত রাখার জন্য অপরটির মানও যথাক্রমে কমবে বা বাড়বে। ফলে, যে-কোনো বিন্দুতে চাপ বৃদ্ধি পেলে সেই বিন্দুতে প্রবাহীর বেগ হ্রাস পাবে এবং অপরপক্ষে, চাপ হ্রাস পেলে বেগ বৃদ্ধি পাবে।
বার্নোলির নীতির প্রয়োগগুলি উল্লেখ করো।
বার্নোলির নীতির প্রায়াগগুলি হল –
- কোনো নলের মধ্যে দিয়ে প্রতি সেকেন্ডে কতটা তরল প্রবাহিত হচ্ছে তা মাপার জন্য ভেঞ্চুরিমিটার যন্ত্র ব্যবহৃত হয়। এই যন্ত্রের ক্রিয়া বার্নোলির নীতির ওপর প্রতিষ্ঠিত।
- কোনো নলে তরলের প্রবাহের হার মাপার জন্য পিটোট নল ব্যবহৃত হয়। বার্নোলির নীতির ওপর ভিত্তি করেই এই যন্ত্রটি তৈরি করা হয়েছে।
- জল, কীটনাশক, সুগন্ধি প্রভৃতি ছড়িয়ে দেওয়ার কাজে যে স্প্রেয়ার ব্যবহার করা হয় তার ক্রিয়াও বার্নোলির নীতির ওপর নির্ভর করে।
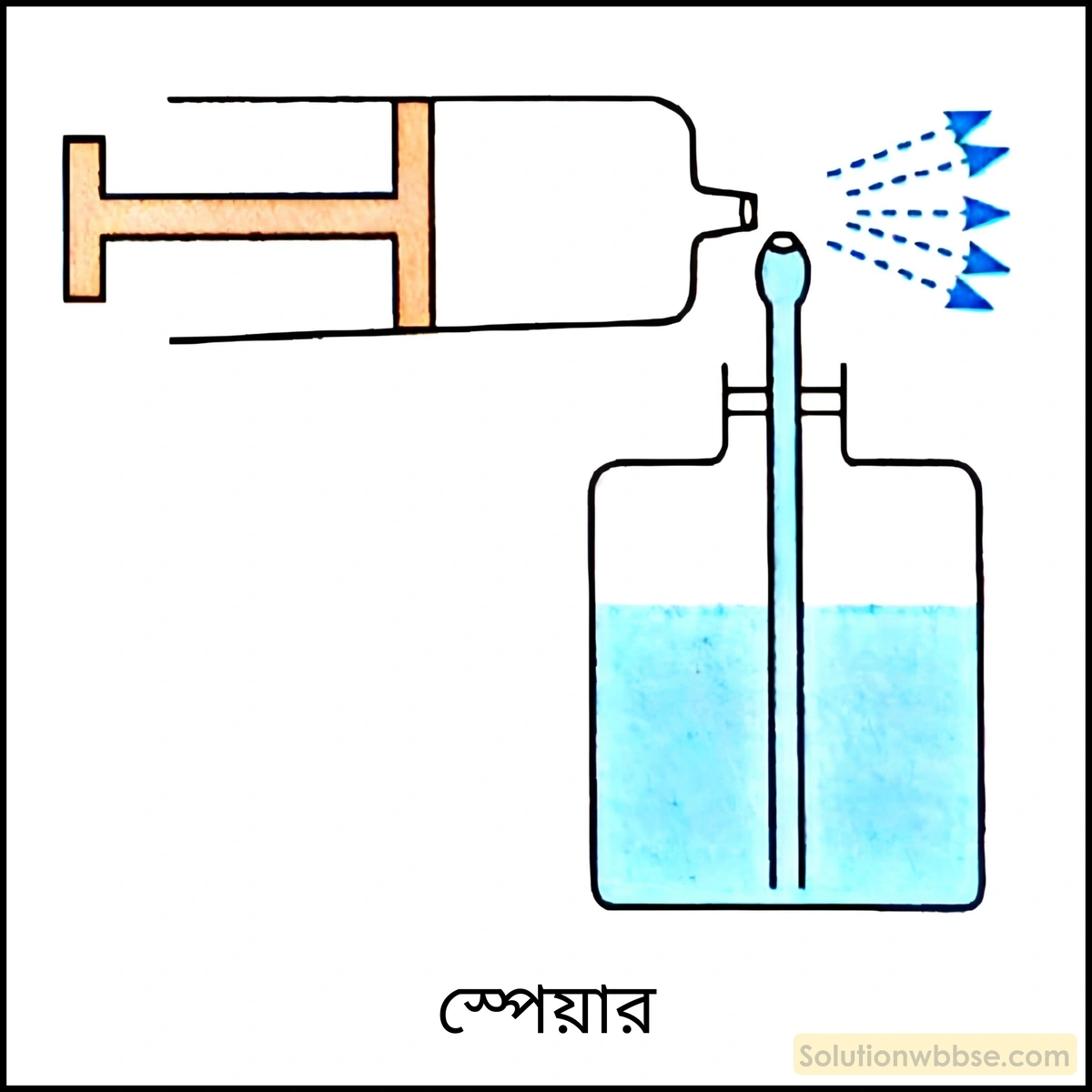
বার্নোলির নীতি প্রয়োগ করে স্প্রেয়ার বা অ্যাটোমাইজারের কার্যনীতি ব্যাখ্যা করো।
সুগন্ধি তরল, সেন্ট, কীটনাশক ইত্যাদি ছড়ানোর কাজে স্প্রেয়ার বা অ্যাটোমাইজার (Sprayer or Atomizer) যন্ত্র ব্যবহার করা হয়। যন্ত্রটি আসলে একটি চোঙাকৃতি পাত্র, যা সংশ্লিষ্ট তরল দ্বারা পূর্ণ রাখা হয়। একটি সরু নল ওই পাত্রে রাখা তরলের নীচ পর্যন্ত ডোবানো থাকে। একটি পিস্টন ব্যবস্থার সাহায্যে নলের খোলা মুখের উপর দিয়ে প্রচণ্ড বেগে বায়ুর চালনা করা হয়। বার্নোলির নীতি অনুসারে, এর ফলে নলের মুখে বায়ুচাপ কমে যায় এবং পাত্রের ভিতরে তরলতলের উপরে থাকা বায়ুর দেওয়া চাপে সরু নলের মধ্য দিয়ে তরল উপরে উঠে আসে এবং বায়ুপ্রবাহের সঙ্গে মিশে সূক্ষ্ম কণার আকারে ছড়িয়ে পড়ে।
বোধমূলক প্রশ্নোত্তর
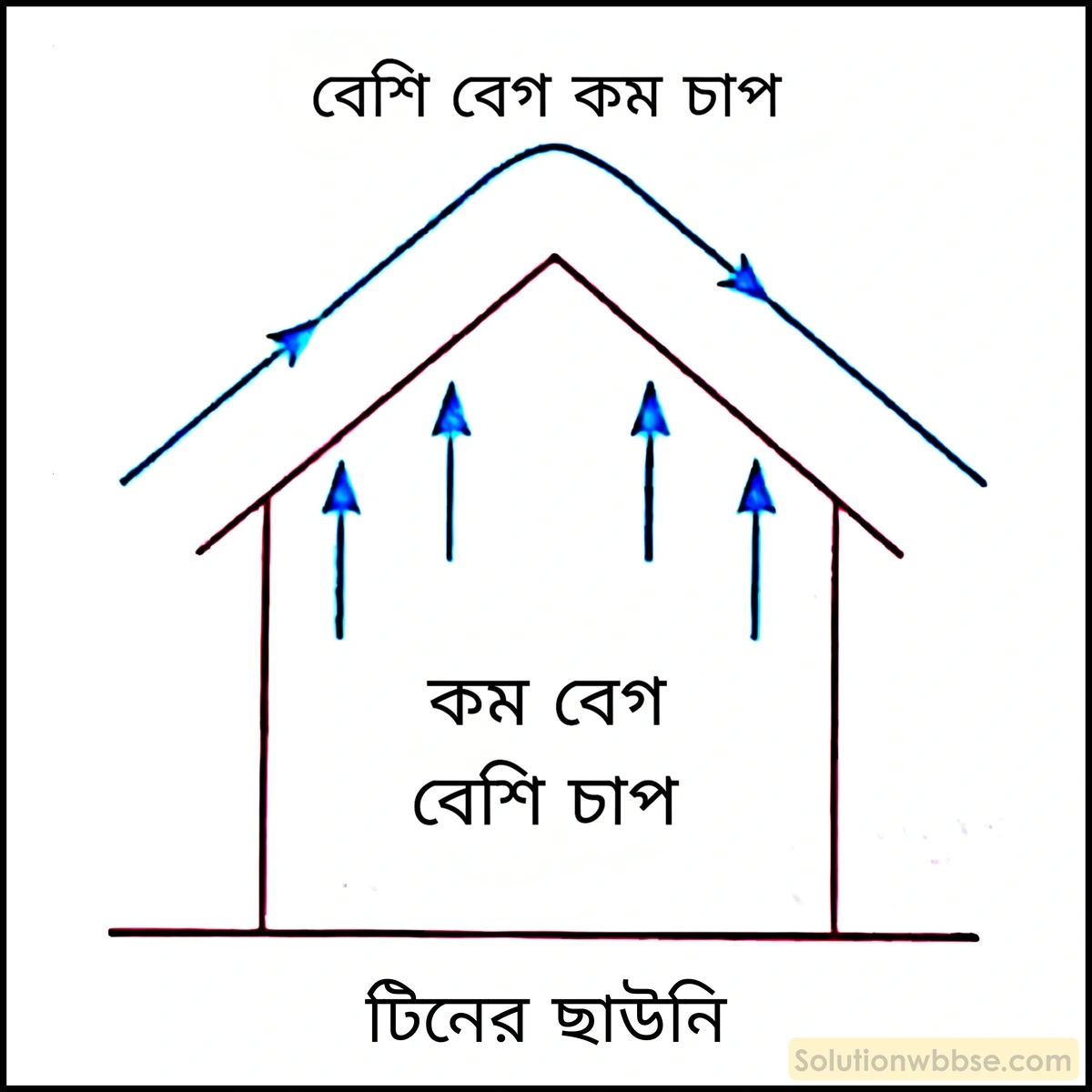
ঝড় হলে অনেক সময় ঘরের চাল উড়ে যায়। – বার্নোলির নীতি প্রয়োগ করে নীচের ঘটনাটির ব্যাখ্যা দাও।
প্রচণ্ড ঝড়ের সময় কুঁড়েঘরের খড়ের বা টিনের ছাউনি উড়ে যেতে দেখা যায়। কুঁড়েঘরের ছাউনির উপরের অংশে বায়ুর বেগ বেশি বলে বার্নোলির নীতি অনুযায়ী, ওই অংশের বায়ু ছাউনির ওপর যে নিম্নচাপ দেয় তা ঘরের মধ্যে থাকা স্থির বায়ু বা ছাউনির নীচে অপেক্ষাকৃত কম বেগে গতিশীল বায়ু দ্বারা প্রযুক্ত ঊর্ধ্বচাপ অপেক্ষা কম। এই চাপের পার্থক্যই ছাউনিকে উড়িয়ে নিয়ে যায়।
দ্রুতগামী ট্রেনের কাছে দাঁড়িয়ে থাকা বিপজ্জনক। – বার্নোলির নীতি প্রয়োগ করে নীচের ঘটনাটির ব্যাখ্যা দাও।
দ্রুতগামী ট্রেনের কাছাকাছি দাঁড়ানো বিপজ্জনক হয়। ট্রেন চলার ফলে ট্রেনের আশপাশের বায়ুর গতিবেগ বেশি এবং বার্নোলির নীতি অনুযায়ী, চাপ কম হয়। রেললাইন সংলগ্ন অঞ্চল থেকে অপেক্ষাকৃত দূরে থাকা বায়ুর বেগ কম ও চাপ বেশি। এই চাপের পার্থক্যই দর্শককে ট্রেনের দিকে ঠেলে দেয়, ফলে দুর্ঘটনা ঘটার সম্ভাবনা থাকে।

বায়ুপ্রবাহের সময় পতাকা পতপত করে ওড়ে। – বার্নোলির নীতি প্রয়োগ করে নীচের ঘটনাটির ব্যাখ্যা দাও।
পতাকার দুপাশে বায়ু বিভিন্ন বেগে প্রবাহিত হয়। বার্নোলির নীতি অনুযায়ী, পতাকার যেদিকে বায়ুপ্রবাহের বেগ অপেক্ষাকৃত বেশি, সেদিকে বায়ুর চাপ অপর দিকের তুলনায় কম হয়। এর ফলে, পতাকার দু’পাশের বায়ুচাপের পার্থক্য দেখা যায়। চাপের এই পার্থক্যের জন্য বায়ুপ্রবাহের সময় পতাকা পতপত করে উড়তে থাকে।

একটি ফানেলের সরু নল বরাবর ফুঁ দিয়ে ওর মধ্যে থাকা ফিলটার কাগজকে সরানো যায় না কেন?
ফানেলের সরু নল বরাবর ফুঁ দেওয়া হলে ফানেল ও ফিলটার কাগজের মধ্যে থাকা সরু নালি পথে বায়ুপ্রবাহ ঘটে। বার্নোলির নীতি অনুসারে, এর জন্য ওই অংশে বায়ুর চাপ কমে। বিপরীতক্রমে ফানেলের শঙ্কুসদৃশ অংশের প্রস্থচ্ছেদের ক্ষেত্রফল নালি পথটির তুলনায় বেশি বলে ওই অংশে বায়ুর বেগ কম ও চাপ বেশি হয়ে থাকে। এই বর্ধিত চাপ, ওই অংশে রাখা ফিলটার কাগজটিকে ফানেলের গায়ে আটকে রাখে।

ফোয়ারার শীর্ষে বা সামান্য নীচে যে-কোনো পাশে একটি পিংপং বল রাখলে তা আটকে থাকে কীভাবে?
ফোয়ারার শীর্ষে বা ঊর্ধ্বমুখী জলপ্রবাহের একপাশে পিংপং বল রাখলে তা আটকে থাকে। বার্নোলির নীতি থেকে ঘটনাটির ব্যাখ্যা পাওয়া যায়। এক্ষেত্রে, জলপ্রবাহের জন্য বলের যে পাশে জলধারার অবস্থান সেই অংশে চাপ হ্রাস পায়। যদিও তার বিপরীত দিকে বায়ু প্রায় স্থির থাকায় ওই বায়ুর দেওয়া পার্শ্বচাপ বেশি হয়। এই অতিরিক্ত চাপেই বলটি জলপ্রবাহের গায়ে আটকে থাকে।
জলপ্রবাহের বেগের তারতম্য হওয়ার কারণে, বলের দুপাশে চাপের পার্থক্যেরও অনবরত পরিবর্তন হয়। এই কারণে, ক্ষেত্রবিশেষে বলটি ঘুরতে থাকে বা সামান্য উপরে ও নীচে ওঠা-নামা করে।
হার্ট অ্যাটাকের কারণ বার্নোলির নীতি অনুসারে কীভাবে ব্যাখ্যা করা যায়?
ধমনি প্রাচীরের অভ্যন্তরে ফ্যাট, কোলেস্টেরল ইত্যাদি পদার্থ দীর্ঘদিন ধরে সঞ্চিত হওয়ার ফলে ধমনির মধ্যে প্রবাহ ছেদের ক্ষেত্রফল কমে যায়। ধারাবাহিকতার সমীকরণ অনুযায়ী, এর ফলে ওই ছেদে রক্ত চলাচলের বেগ বাড়ে। এই প্রবাহ প্রায় ধারারেখ বিবেচনা করে বলা যায় যে, বার্নোলির নীতি অনুসারে ধমনির ভিতরে রক্তচাপ হ্রাস পায়। এমতাবস্থায় বাইরের অধিক চাপে ধমনি বুদ্ধ হয়ে রক্তপ্রবাহ বন্ধ হওয়ার উপক্রম হয়। এর ফলে ‘হার্ট অ্যাটাক’ হয়ে থাকে।
বই বা খাতার দুটি পাতার মধ্যে ফুঁ দিলে অনেক সময় পাতাগুলি না খুলে পরস্পরের সঙ্গে আটকে যায়। ব্যাখ্যা করো।
দুটি পাতার মধ্যে ফুঁ দিলে পাতা দুটির মধ্যবর্তী ওই অংশে বায়ুপ্রবাহ হয়। ফলে, ওই স্থানে বার্নৌলির নীতি অনুযায়ী বায়ুচাপ হ্রাস পায়। কিন্তু পাতা দুটির দুই পাশে বায়ুর চাপ তুলনামূলকভাবে বেশি থাকায়, বাইরের বায়ুর পার্শ্বচাপ পাতাগুলিকে আটকে রেখে দেয়।
সমুদ্রে চলমান দুটি জাহাজ কখনোই পরস্পরের খুব কাছাকাছি আসে না কেন?
দুই জাহাজের মধ্যবর্তী অংশে জলের বেগ বেশি হওয়ায় ওই অংশের চাপ যথেষ্ট কমে যায়। এই অবস্থায় দুটি জাহাজের বিপরীত পাশে অপেক্ষাকৃত কম বেগে গতিশীল জলের দেওয়া পার্শ্বচাপের মান বেশি হয়। ফলে, জাহাজ দুটি পরস্পরের দিকে আরও বেশি সরে আসে এবং ধাক্কা লাগার সম্ভাবনা থাকে। তাই, জাহাজ দুটি কখনোই পরস্পরের কাছাকাছি আসে না।
রাস্তায় বোমা ফাটলে জানালার কাচের ভাঙা টুকরো রাস্তায় ছড়িয়ে পড়ে, কিন্তু ঘরের ভিতরে আসে না – ব্যাখ্যা করো।
বোমা বিস্ফোরণের মুহূর্তে জানালা সংলগ্ন বাইরের বায়ু তীব্র বেগে প্রবাহিত হয়। ফলে, ওই অংশে বায়ুচাপ কমে যায়। ঘরের ভিতরে আবদ্ধ বায়ু স্থির থাকে বলে ওই স্থানে বায়ুচাপও তুলনামূলকভাবে বেশি হয়। বিস্ফোরণের অভিঘাতে জানালার কাঁচ ভেঙে টুকরো হলে ওই টুকরোগুলির ওপর কার্যকরী চাপ ঘরের ভিতর থেকে বাইরের দিকে ক্রিয়া করে। তাই, কাচের টুকরোগুলি ঘরের ভিতরে না গিয়ে রাস্তায় বিভিন্ন অভিমুখে ছড়িয়ে পড়ে।
বার্নোলির নীতি অনুসারে ঘূর্ণি ঝড়ের কেন্দ্রের বাতাসের চাপ কেন কমে যায় এবং এর ফলে চারপাশের হালকা বস্তুগুলোর কী ধরনের গতি লক্ষ্য করা যায়?
ঘূর্ণি ঝড়ের সময় ঘূর্ণির কেন্দ্র অভিমুখে বায়ুর বেগ বেশি হওয়ায় বার্নোলির নীতি অনুসারে এই স্থানে বাতাসের চাপ কমে যায়। এর ফলে ঘূর্ণির বাইরের উচ্চচাপযুক্ত অংশ থেকে ছেঁড়া কাগজ, গাছের পাতা, ছোটো বোতল, কাঠের টুকরো ইত্যাদি ঘূর্ণির কেন্দ্রে প্রবেশ করে এবং বায়ুপ্রবাহ দ্বারা তাড়িত হয়ে ঘুরতে ঘুরতে উপরে উঠতে থাকে।
গাণিতিক প্রশ্নাবলি
প্রয়োজনীয় সূত্রাবলি
\(\frac12\rho v^2+\rho gh+P\\\)বা, \(\frac{v^2}{2g}+h+\frac P{\rho g}\)
বার্নৌলির উপপাদ্য অনুযায়ী,
যেখানে, \(\frac{v^2}{2g}\) = বেগশীর্ষ, h = উচ্চতাশীর্ষ ও \(\frac P{\rho g}\) = চাপশীর্ষ।
অসমপ্রস্থচ্ছেদ যুক্ত একটি অনুভূমিক নল দিয়ে জল প্রবাহিত হচ্ছে। নলের ভিতর একটি বিন্দুতে চাপ = 5 mm পারদস্তম্ভ এবং বেগ = 0.5 m/s। যে বিন্দুতে বেগ = 0.25 m/s সেখানে চাপ কত? পারদের আপেক্ষিক গুরুত্ব = 13.6।
অনুভূমিক নলের ক্ষেত্রে h1 = h2
বার্নোলির সূত্র প্রয়োগ করে পাই,
\(\frac12\rho v_1^2+P_1=\frac12\rho v_2^2+P_2\) (∵ ρ ও ধ্রুবক রাশি)
∴ \(P_2-P_1=\frac12\rho\left(v_1^2-v_2^2\right)\)
বা, \(P_2-P_1=\frac12\times1000\left(0.5^2-0.25^2\right)\) [জলের ঘনত্ব ρ = 1000 kg/m3]
বা, \(P_2-P_1=\frac{93.75}{13.6\times1000\times9.8}\) m পারদস্তম্ভের চাপ
∴ \(P_2-P_1=0.7\) mm পারদস্তম্ভের চাপ।
এক্ষেত্রে, P1 = 5 mm পারদস্তম্ভের চাপ
∴ P2 = (5 + 0.7) mm পারদস্তম্ভের চাপ
বা, P2 = 5.7 mm পারদস্তম্ভের চাপ।
কোনো নলের মধ্যে জলের বেগ 40 cm/s হলে বেগশীর্ষ কত? [g = 10 m/s2]
জলপ্রবাহের বেগশীর্ষের মান = \(\frac{v^2}{2g}\)
= \(\frac{40\times40}{2\times1000}\) cm [ g = 10 m/s2 = 1000 cm/s2 ]
= \(\frac{800}{1000}\)
= 0.8 cm
∴ বেগশীর্ষ 0.8 cm
একটি উড়োজাহাজের ডানার উপরিতলে ও নীচের তলে বায়ুপ্রবাহের বেগ যথাক্রমে 60 m/s এবং 50 m/s। ডানার ক্ষেত্রফল 3 m2 এবং বায়ুর ঘনত্ব 1.3 kg/m3 হলে ডানার উপরে ও নীচে চাপের পার্থক্য কত হবে? উড়োজাহাজের উপর ঊর্ধ্বমুখী যে বল ক্রিয়া করবে তার মান কত?
ডানার উপর ও নীচের তলে চাপ যথাক্রমে P1 ও P2 এবং বায়ুপ্রবাহের বেগ যথাক্রমে v1 ও v2 হলে,
\(\frac12\rho v_1^2+P_1=\frac12\rho v_2^2+P_2\\\)বা, \(P_2-P_1=\frac12\rho\left(v_2^2-v_2^1\right)\)
∴ নির্ণেয় চাপের পার্থক্য, \(\Delta P=\left(P_2-P_1\right)=715\) N/m2
উড়োজাহাজের ওপর ক্রিয়াশীল উত্থানকারী বল
F = ΔP × ডানার ক্ষেত্রফল (A)
বা, F = (715 × 3) N
বা, F = 2145 N
∴ উড়োজাহাজের উপর ঊর্ধ্বমুখী যে বল ক্রিয়া করবে তার মান 2145 N
নৈর্ব্যক্তিক প্রশ্নোত্তর
সঠিক উত্তরটি নির্বাচন করো
বার্নোলির উপপাদ্য যে নীতির ওপর প্রতিষ্ঠিত তা হল –
- শক্তির সংরক্ষণ
- ভরের সংরক্ষণ
- ভরবেগ সংরক্ষণ
- এদের কোনোটিই নয়
উত্তর – 1. শক্তির সংরক্ষণ
বার্নোলির উপপাদ্য অনুযায়ী = ধ্রুবক হলে, ধ্রুবকটির মাত্রীয় সংকেত কী? (P = চাপ, ρ = ঘনত্ব, h = উচ্চতা, v = বেগ, g = অভিকর্ষজ ত্বরণ) –
- [M0L0T0]
- [M0LT0]
- [ML2T-2]
- [M0L2T-4]
উত্তর – 4. [M0L2T-4]
বিমানের ওপর প্রযুক্ত উত্থান বল নির্ভর করে –
- আর্কিমিডিসের সূত্র
- বার্নোলির সূত্র
- হুকের সূত্র
- স্টোক্সের সূত্র-এর ওপর
উত্তর – 2. বার্নোলির সূত্র
একটি ধারারেখীয় প্রবাহে অভিকর্ষীয় শীর্ষ h হলে বেগশীর্ষ ও চাপশীর্ষ হয় –
- \(\frac{v^2}g\) ও \(\frac\rho P\)
- \(\frac{v^2}2\) ও \(\frac\rho P\)
- \(\frac{v^2}{2g}\) ও \(\frac P{\rho g}\)
- \(\frac{v^2}2\) ও \(\frac\rho{Pg}\)
উত্তর – 3. \(\frac{v^2}{2g}\) ও \(\frac P{\rho g}\)
বডি স্প্রের জন্য ব্যবহৃত অটোমাইজারে প্রয়োগ করা হয় –
- আর্কিমিডিসের নীতি
- বার্নোলির নীতি
- পৃষ্ঠটান
- স্টোকসের সূত্র
উত্তর – 2. বার্নোলির নীতি
যে ঘটনাগুলি বার্নোলির উপপাদ্য দ্বারা ব্যাখ্যা করা যায় না তা হল –
- বেশ উঁচু আকাশ হতে পড়া বৃষ্টিবিন্দুর সমবেগসম্পন্ন গতি
- ভেঞ্চুরিমিটারের উল্লম্ব নলে তরলের উচ্চতার পার্থক্য
- তরল বিন্দুর গোলক আকার
- প্রদীপের পলতে বেয়ে তেলের উঠে আসা
উত্তর – 4. প্রদীপের পলতে বেয়ে তেলের উঠে আসা
A ও C নলের ব্যাসার্ধ একই, কিন্তু B নলের ব্যাসার্ধ কম। তরল স্তম্ভের উচ্চতা –
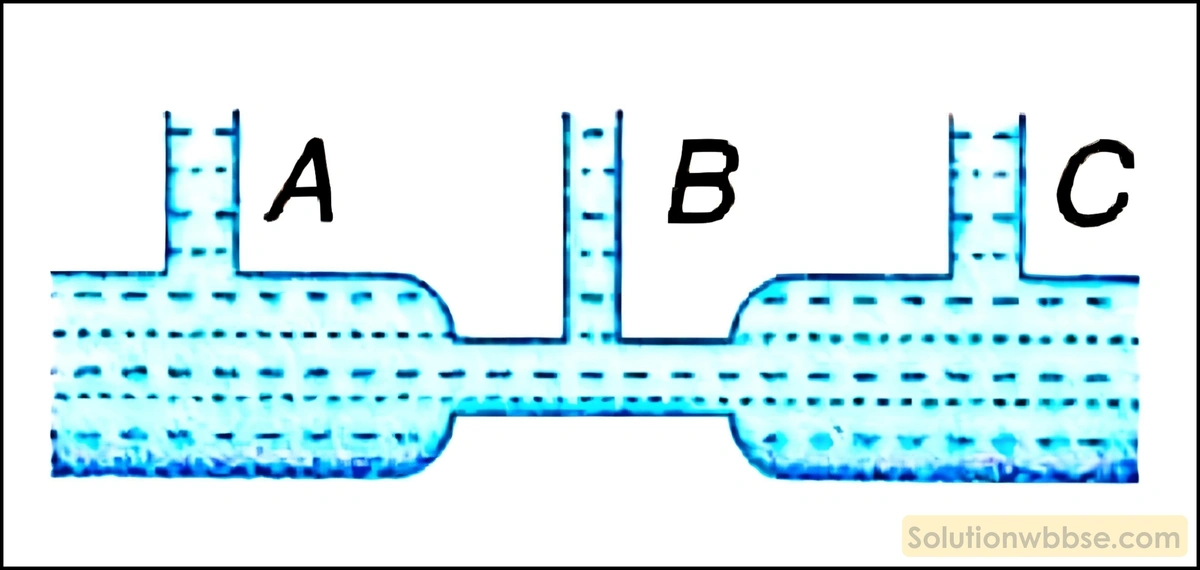
- A -তে বেশি
- B -তে বেশি
- তিনটিতেই সমান
- Aও C -তে সমান
উত্তর – 3. তিনটিতেই সমান
শূন্যস্থান পূরণ করো
বার্নোলির নীতি অনুযায়ী প্রবাহীর বেগ কম হলে চাপ ___ হয়।
উত্তর – বার্নোলির নীতি অনুযায়ী প্রবাহীর বেগ কম হলে চাপ বেশি হয়।
বার্নোলির উপপাদ্যের একটি রূপ হল – স্থিতীয় চাপ + ___ = ধ্রুবক।
উত্তর – বার্নোলির উপপাদ্যের একটি রূপ হল – স্থিতীয় চাপ + গতীয় চাপ = ধ্রুবক।
কোনো নলরে মধ্যে দিয়ে জলের বেগ 2 m/s হলে, বেগশীর্ষ হয় ___।
উত্তর – কোনো নলরে মধ্যে দিয়ে জলের বেগ 2 m/s হলে, বেগশীর্ষ হয় 0.2 m প্রায়।
ঝড় হলে ঘরের চাল উড়ে যায়, ___ নীতির সাহায্যে এই ঘটনা ব্যাখ্যা করা যায়।
উত্তর – ঝড় হলে ঘরের চাল উড়ে যায় বার্নোলি নীতির সাহায্যে এই ঘটনা ব্যাখ্যা করা যায়।
___ খ্রিস্টাব্দে পৃথিবীর সর্ববৃহৎ flying boat Hughes H-4 Hercules নির্মিত হয়েছিল।
উত্তর – 1947 খ্রিস্টাব্দে পৃথিবীর সর্ববৃহৎ flying boat Hughes H-4 Hercules নির্মিত হয়েছিল।
ঠিক বা ভুল নির্বাচন করো
বার্নোলির নীতিটি স্থির বা গতিশীল উভয় প্রবাহীর জন্যই প্রযোজ্য।
উত্তর – ভুল।
সঠিক উত্তর – শুধুমাত্র গতিশীল।
জলভরতি একটি পাত্রের উপরিতল থেকে h গভীরতায় পাত্রের দেয়ালে একটি ছিদ্র করলে, ছিদ্র থেকে নির্গত তরল প্রবাহের হার হবে \(\sqrt{2gh\alpha}\) (যেখানে, α ছিদ্রের প্রস্থচ্ছেদ)।
উত্তর – ঠিক।
উড়োজাহাজের মধ্যে তরল প্রবাহের হার নির্ণয় করতে পিটোট নল ব্যবহৃত হয়।
উত্তর – ঠিক।
দু-একটি শব্দে উত্তর দাও
উদ্গতিবিদ্যায় শক্তি সংরক্ষণ সূত্রের পরিবর্তিত রূপটি কী?
উদ্গতিবিদ্যায় শক্তি সংরক্ষণ সূত্রের পরিবর্তিত রূপটি বার্নোলির নীতি।
গতিশীল বায়ুর দেওয়া চাপ, স্থির বায়ুর দ্বারা প্রযুক্ত চাপ অপেক্ষা কম। – এই ধারণা কে আবিষ্কার করেন?
গতিশীল বায়ুর দেওয়া চাপ, স্থির বায়ুর দ্বারা প্রযুক্ত চাপ অপেক্ষা কম। – এই ধারণা ড্যানিয়েল বার্নোলি আবিষ্কার করেন।
প্রবহমান তরলের কত রকমের শক্তি থাকে?
প্রবহমান তরলের স্থিতিশক্তি, গতি শক্তি ও চাপশক্তি রকমের শক্তি থাকে।
বার্নোলির নীতিটি কোন্ ধরনের প্রবাহীর ক্ষেত্রে যথাযথ ভাবে প্রযোজ্য?
বার্নোলির নীতিটি অসংনম্য ও অসান্দ্র প্রবাহীর ধারারেখ প্রবাহের ক্ষেত্রে ধরনের প্রবাহীর ক্ষেত্রে যথাযথ ভাবে প্রযোজ্য।
উড়োজাহাজের ডানার বিশেষ আকৃতি কার সঙ্গে সাদৃশ্যযুক্ত হয়?
উড়োজাহাজের ডানার বিশেষ আকৃতি বায়ুপাতের (Aerofoil) মতো সঙ্গে সাদৃশ্যযুক্ত হয়।
উড়োজাহাজের উপরে ওঠার জন্য কোন বল দায়ী এবং এটি কীভাবে উৎপন্ন হয়?
উড়োজাহাজের ডানার গঠন অনেকটা পাখির ডানার মতো। সামনের দিকটা মোটা ও পিছনের অংশ অপেক্ষাকৃত পাতলা এবং উপরের পৃষ্ঠ নীচের পৃষ্ঠ অপেক্ষা বেশি বক্র। উড়োজাহাজের ডানার এই বিশেষ আকৃতির জন্য এটি একটি বায়ুপাত (Aerofoil) -এর মতো দেখতে হয়। ডানার দুই অংশে চাপের পার্থক্যের জন্য সৃষ্ট ঊর্ধ্বমুখী ঘাতের ক্রিয়ায় উড়োজাহাজের উপরে ওঠার ঘটনাকে বলা হয় Dynamic lift এবং অনেকসময় ঘাতটিকেও গতীয় উত্থানকারী বল (Dynamic lifting force) বলা হয়।
For High-Types
বার্নোলির উপপাদ্য অনুযায়ী সুষম প্রস্থচ্ছেদের অনুভূমিক নলের মধ্য দিয়ে গতিশীল জলের চাপ সর্বদা সমান থাকার কথা, কিন্তু বাস্তবে তা ধীরে ধীরে কমতে থাকে। কেন?
বার্নোলির উপপাদ্যে বিবেচনাধীন তরলটি অসান্দ্র ধরা হয়। বাস্তবে যে-কোনো তরলের জন্যই সান্দ্রতার অস্তিত্ব বর্তমান, যা তরলের প্রবাহকে বাধাদান করে। সুতরাং, সময়ের সঙ্গে প্রবহমান তরলের চাপশক্তি হ্রাস পায়। তাই, বাস্তবে চাপ ধীরে ধীরে কমতে থাকে।
ম্যাগনাস ক্রিয়া (Magnus effect) কী?
ক্রিকেট খেলায় কোনো বোলার যখন স্পিন করে, অর্থাৎ, ঘুরিয়ে বল ছাড়ে তখন বলের গতিপথ ওর আবর্তনের অভিমুখে বেঁকে যায়। এর কারণ হল ঘূর্ণনের ফলে বলের দুই পাশে বল সাপেক্ষে বায়ুর বেগ আলাদা হয়ে যায়। সুতরাং, বার্নোলির নীতি অনুসারে ক্রিকেট বলের দুপাশে বায়ুচাপের তারতম্য ঘটে এবং বলের গতিপথ বেঁকে যায়। ঊনবিংশ শতাব্দীর মধ্যভাগে জার্মান বিজ্ঞানী HG Magnus ঘটনাটি লক্ষ করেন। তাঁর নামেই এটি ‘ম্যাগনাস ক্রিয়া’ বলে চিহ্নিত করা হয়।
ভেঞ্চুরিমিটার ও পিটোট নল কী?
ভেঞ্চুরিমিটার ও পিটোট নল হল দুটি বিশেষ যন্ত্র বা ব্যবস্থা, যাদের কোনো নলের মধ্যে দিয়ে তরলপ্রবাহের হার পরিমাপের কাজে ব্যবহার করা হয়। উভয়েরই কার্যনীতি বার্নোলির নীতির ওপর প্রতিষ্ঠিত।

Class 9 Physical Science – Notes for All Chapters
| Chapter Name | Tropics |
|---|---|
| পরিমাপ | পরিমাপ ও একক বিভিন্ন মাপের একক মাত্রা পরিমাপ |
| বল ও গতি | স্থিতি ও গতি গতির সমীকরণ নিউটনের প্রথম গতিসূত্র নিউটনের দ্বিতীয় গতি সূত্র নিউটনের তৃতীয় গতিসূত্র বিভিন্ন ধরনের বল রৈখিক ভরবেগ রৈখিক ভরবেগ সংরক্ষণ |
| পদার্থ : গঠন ও ধর্ম | তরল ও বায়ুর চাপ আর্কিমিডিসের নীতি পৃষ্ঠটান সান্দ্রতা বার্নোলির নীতি স্থিতিস্থাপকতা |
| পদার্থ : পরমাণুর গঠন ও পদার্থের ভৌত ও রাসায়নিক ধর্মসমূহ | পরমাণুর গঠন মোলের ধারণা দ্রবণ অ্যাসিড, ক্ষার, লবণ মিশ্রণের উপাদানের পৃথকীকরণ জল |
| শক্তির ক্রিয়া , কার্য, ক্ষমতা | শক্তির ক্রিয়া , কার্য, ক্ষমতা |
| তাপ | ক্যালোরিমিতি কার্য ও তাপের তুল্যতা লীনতাপ সম্পৃক্ত ও অসম্পৃক্ত বাষ্প জলের ব্যতিক্রান্ত প্রসারণ |
| শব্দ | শব্দের উৎস : কম্পন শব্দের বিস্তার : তরঙ্গ শব্দের কয়েকটি ধর্ম শব্দের বৈশিষ্ট্য মানুষের কান ও শব্দ শোনার কৌশল শব্দদূষণ |
আজকের আর্টিকেলে আমরা নবম শ্রেণির ভৌতবিজ্ঞান বইয়ের তৃতীয় অধ্যায় “পদার্থ : গঠন ও ধর্ম” এর “বার্নোলির নীতি” থেকে পরীক্ষায় আসা গুরুত্বপূর্ণ প্রশ্ন ও উত্তরগুলো আলোচনা করেছি। এই প্রশ্নোত্তরগুলো নবম শ্রেণির বার্ষিক পরীক্ষা, এমনকি চাকরি বা যেকোনো প্রতিযোগিতামূলক পরীক্ষার জন্যও উপযোগী। কারণ, এই অধ্যায়ের প্রশ্ন প্রায়ই বিভিন্ন পরীক্ষায় কমন আসে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সাহায্য করবে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন কিংবা টেলিগ্রামে যোগাযোগ করুন—আপনাদের প্রশ্নের উত্তর দিতে আমি সর্বদা প্রস্তুত।
ধন্যবাদ সবাইকে।






Leave a Comment