আজকের আর্টিকেলে আমরা নবম শ্রেণীর ভৌতবিজ্ঞান বইয়ের তৃতীয় অধ্যায় “পদার্থ : গঠন ও ধর্ম” এর “স্থিতিস্থাপকতা” থেকে সহজ ও সংক্ষিপ্ত প্রশ্ন-উত্তর শেয়ার করবো। এই প্রশ্নগুলো নবম শ্রেণির ইউনিট টেস্ট থেকে বার্ষিক পরীক্ষা এর জন্য যেমন গুরুত্বপূর্ণ, তেমনি চাকরি বা বিভিন্ন প্রতিযোগিতার পরীক্ষাতেও কাজে লাগবে। এই অধ্যায় থেকে স্কুল পরীক্ষা থেকে শুরু করে চাকরির পরীক্ষায় প্রায়ই প্রশ্ন আসে, তাই এই প্রশ্নোত্তরগুলো সবাইকে সাহায্য করবে। প্রতিটি প্রশ্নের উত্তর সহজ ভাষায় লেখা হয়েছে, যাতে সবাই বুঝতে পারেন। পড়ার শেষে এই অধ্যায়ের মুখ্য বিষয়গুলো আপনার আয়ত্তে চলে আসবে এবং যেকোনো পরীক্ষায় আত্মবিশ্বাসের সঙ্গে লিখতে পারবেন।

জ্ঞানমূলক প্রশ্নোত্তর
স্থিতিস্থাপকতা বলতে কী বোঝায়? উদাহরণ দাও।
স্থিতিস্থাপকতা (Elasticity) – যে সহজাত ধর্মের জন্য কোনো পদার্থ বাইরে থেকে প্রযুক্ত বল বা দ্বন্দ্বের ক্রিয়ায় তার আকার ও আয়তনের বা উভয়েরই পরিবর্তনের প্রচেষ্টাকে বাধা দেয় এবং ওই প্রযুক্ত বাহ্যিক বল অপসারিত হলে বস্তু তার পূর্বের আকার ও আয়তন ফিরে পায়, তাকে স্থিতিস্থাপকতা বলে।
স্থিতিস্থাপকতার উদাহরণ – একটি রবারের বলকে হাতে রেখে সুষমভাবে চাপ দিলে সেটি আকৃতিতে গোলাকার থাকলেও আয়তনে সংকুচিত হয়। চাপ সরিয়ে নিলে বলটি তার পূর্বের আয়তন ফিরে পায়।
দ্বন্দ্ব (Couple) কী? এর ফলে কোনো বস্তুর কী ধরনের গতি সৃষ্টি হয়?
কোনো বস্তুর ওপর দুটি ভিন্ন বিন্দুতে একজোড়া সমান বল বিপরীত অভিমুখে ক্রিয়াশীল হলে ওই বল দুটির যৌথ প্রভাবে বস্তুটির মধ্যে কোনো রৈখিক গতি সৃষ্টি না হয়ে বিশুদ্ধ ঘূর্ণন গতি উৎপন্ন হয়। এই বল জোড়াকে দ্বন্দ্ব (Couple) বলা হয়।
স্থিতিস্থাপকতা কোন্ কোন্ বিষয়ের ওপর কীভাবে নির্ভর করে?
স্থিতিস্থাপকতা নিম্নলিখিত বিষয়গুলির ওপর নির্ভর করে –
- অপদ্রব্যের প্রভাব – কোনো ধাতুর সঙ্গে অপদ্রব্য মিশিয়ে দিলে ধাতুটির স্থিতিস্থাপকতা পরিবর্তিত হয়।
- প্রযুক্ত বলের প্রভাব – কোনো ধাতুকে বল প্রয়োগ করে বারবার বিকৃত করলে ধাতুটির স্থিতিস্থাপকতা কমে যায়।
- উষ্ণতার প্রভাব – সাধারণত উষ্ণতা বাড়লে কোনো পদার্থের স্থিতিস্থাপকতা কমে যায় এবং উষ্ণতা কমলে স্থিতিস্থাপকতা বেড়ে যায় (ব্যতিক্রম – ইনভার, এর স্থিতিস্থাপকতা উষ্ণতার সঙ্গে পরিবর্তিত হয় না)।
- পদার্থের অবস্থা – পদার্থের ভৌত অবস্থার ওপর তার স্থিতিস্থাপক আচরণ প্রদর্শনের সামর্থ্য সরাসরি নির্ভর করে। কঠিন পদার্থের ক্ষেত্রে এই সামর্থ্য সব থেকে বেশি। কারণ – দৈর্ঘ্য, আকৃতি, আয়তন ইত্যাদি বিভিন্ন বৈশিষ্ট্যের মান এই অবস্থায় নির্দিষ্ট থাকে। তরল বা গ্যাসের স্থিতিস্থাপকতা তুলনামূলকভাবে কম।
একটি সক্রিয়তামূলক কাজের মাধ্যমে স্থিতিস্থাপকতার ধারণা ব্যাখ্যা করো।
সক্রিয়তামূলক কাজের মাধ্যমে স্থিতিস্থাপকতার ধারণা – দৃঢ় অবলম্বনের সঙ্গে যুক্ত একটি স্প্রিংয়ের মুক্ত প্রান্ত হাত দিয়ে টেনে F বল প্রয়োগ করলে মনে হয় স্প্রিংটিও যেন হাতকে বিপরীত দিকে সমান বলে টানছে।
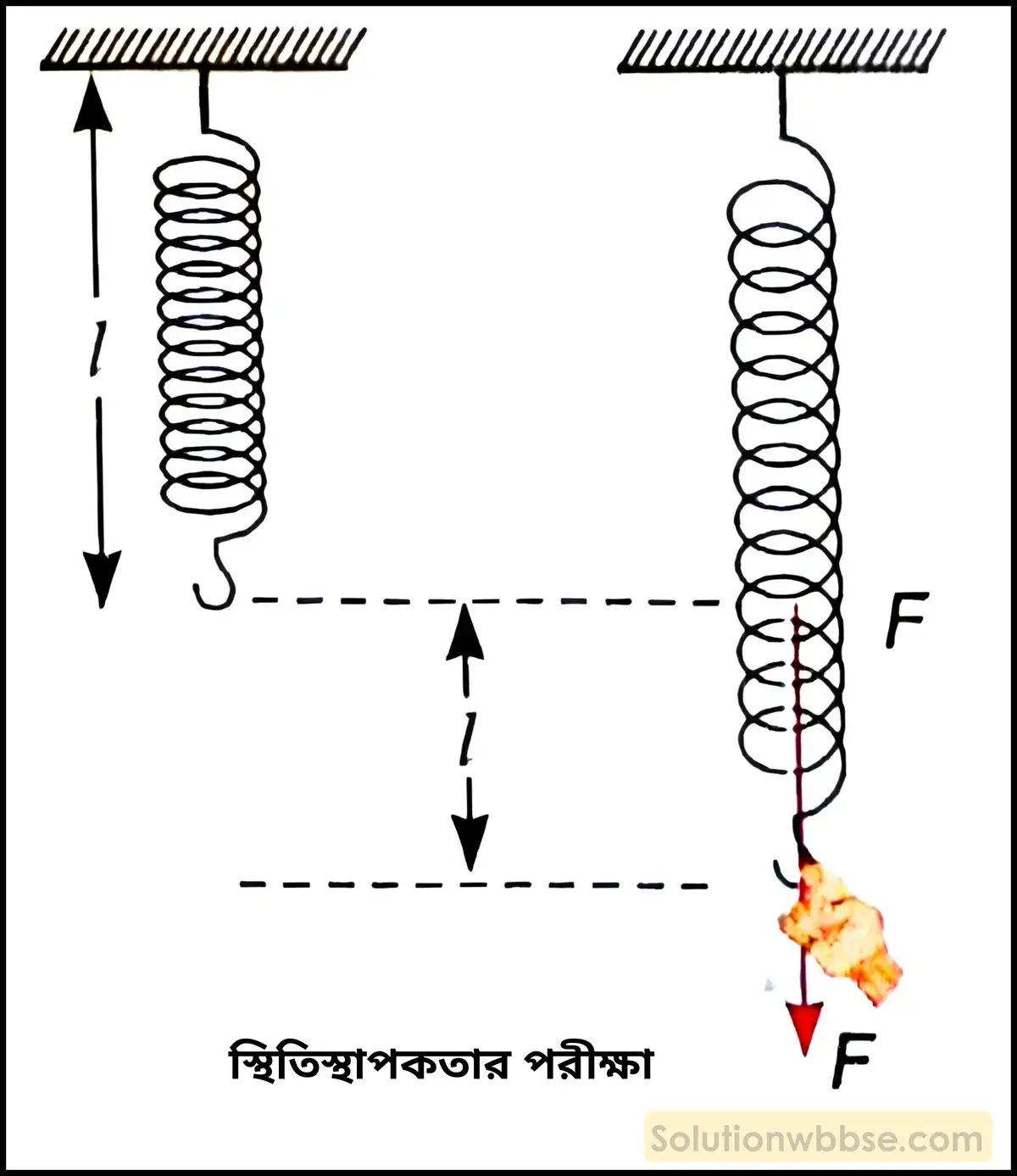
বল প্রয়োগের সঙ্গে সঙ্গে সেই বলের প্রতিক্রিয়া হিসেবে অবলম্বন হাতের উপর সমমানের বল বিপরীত অভিমুখে প্রয়োগ করে, যার ফলে হাতসহ স্প্রিংয়ের কোনো কার্যকরী সরণ হয় না। কিন্তু প্রযুক্ত বলের ক্রিয়ায় স্প্রিংয়ের বিভিন্ন অংশের আপেক্ষিক সরণ ঘটে এবং দৈর্ঘ্য বৃদ্ধি পায়, যা প্রতিহত করার চেষ্টায় স্প্রিংয়ের মধ্যে একটি অভ্যন্তরীণ প্রতিক্রিয়া উৎপন্ন হয়। এই প্রতিক্রিয়া স্প্রিংকে আরও বিকৃত বা প্রসারিত হতে বাধা দেয়। আকার বা আয়তনের পরিবর্তনকে রোধ করতে চাওয়ার এই প্রবণতা সমস্ত বস্তুর সাধারণ বৈশিষ্ট্য। একে স্থিতিস্থাপকতা বলে।
পূর্ণ স্থিতিস্থাপক বস্তু – সংজ্ঞা দাও।
পূর্ণ স্থিতিস্থাপক বস্তু (Perfectly elastic body) – প্রযুক্ত বাহ্যিক বলের বা দ্বন্দ্বের যে-কোনো মানের জন্য বস্তুটি বিকৃত হলেও বিকৃতি উৎপাদনকারী বলের অপসারণের সঙ্গে সঙ্গেই যদি বস্তুটি তার পূর্বের আকার বা আয়তন সম্পূর্ণ ফিরে পায়, তবে ওই বস্তুকে পূর্ণ স্থিতিস্থাপক বস্তু বলা হয়।
পূর্ণ স্থিতিস্থাপক বস্তুর উদাহরণ – বাস্তবে এরকম কোনো বস্তুর অস্তিত্ব নেই।
পূর্ণ অস্থিতিস্থাপক বস্তু – সংজ্ঞা দাও।
পূর্ণ অস্থিতিস্থাপক বস্তু (Perfectly inelastic body) – প্রযুক্ত বাহ্যিক বল বা দ্বন্দ্বের যে-কোনো মানের জন্যই কোনো বস্তু যদি বিকৃত হয় এবং ওই বাহ্যিক বল অপসারিত হওয়ার পরও সেটি বিকৃত অবস্থাতেই থেকে যায়, তাকে পূর্ণ অস্থিতিস্থাপক বা সম্পূর্ণ নমনীয় বস্তু বলা হয়।
পূর্ণ অস্থিতিস্থাপক বস্তুর উদাহরণ – বাস্তবে এরকম বস্তুও পাওয়া যায় না, তবে মাখন, কাদামাটিকে সম্পূর্ণ অস্থিতিস্থাপক বস্তু বলা যায়।
আংশিক স্থিতিস্থাপক বস্তু – সংজ্ঞা দাও।
আংশিক স্থিতিস্থাপক বস্তু (Partly elastic body) – বাহ্যিক বল বা দ্বন্দ্ব অপসারণের পর বিকৃত বস্তু যদি তার পূর্বের আকৃতি বা আয়তন আংশিক ফিরে পেতে সমর্থ হয়, তবে ওই বস্তুকে আংশিক স্থিতিস্থাপক বস্তু বলে।
আংশিক স্থিতিস্থাপকর উদাহরণ – দৈনন্দিন জীবনে ব্যবহৃত সমস্ত বস্তুই আংশিক স্থিতিস্থাপক।
একান্ত দৃঢ় বস্তু – সংজ্ঞা দাও।
একান্ত দৃঢ় বস্তু (Perfectly rigid body) – প্রযুক্ত বাহ্যিক বল বা দ্বন্দ্বের যে-কোনো মানের জন্যই যদি কোনো বস্তুর বিভিন্ন অংশের কোনো আপেক্ষিক সরণ না ঘটে অর্থাৎ, বস্তুটির আকার বা আয়তনের কোনো পরিবর্তন হয় না, তবে ওই বস্তুকে একান্ত দৃঢ় বা পূর্ণ দৃঢ় বস্তু বলে অভিহিত করা হয়।
একান্ত দৃঢ় বস্তুর উদাহরণ – আদর্শ পূর্ণ দৃঢ় বস্তুর ধারণাও কাল্পনিক, তবে কাচকে প্রায় পূর্ণ দৃঢ় বস্তু বলে গণ্য করা যায়।
স্থিতিস্থাপক সীমা – সংজ্ঞা দাও।
স্থিতিস্থাপক সীমা (Elastic limit) – দৈনন্দিন অভিজ্ঞতায় দেখা যায় যে, প্রযুক্ত বাহ্যিক বলের একটি নির্দিষ্ট ঊর্ধ্বসীমা পর্যন্ত প্রতিটি বস্তু পূর্ণ স্থিতিস্থাপক বস্তুর তুল্য আচরণ করে। অর্থাৎ, বিকৃতি উৎপাদনকারী বল অপসারিত হলে বস্তুটি তার নিজস্ব আকার ও আয়তন পূর্ণমাত্রায় ফিরে পেতে সমর্থ হয়। প্রযুক্ত বলের এই সীমাস্থ মানকে বস্তুর উপাদানের স্থিতিস্থাপক সীমা বলে।
বিকৃতি বলতে কী বোঝায়?
বিকৃতি (Strain) – বাহ্যিক বল বা দ্বন্দ্বের ক্রিয়ায় কোনো বস্তুর বিভিন্ন অংশের মধ্যে আপেক্ষিক সরণ ঘটে। ফলে, বস্তুটির আকার বা আয়তনের পরিবর্তন হয়। প্রাথমিক মানের তুলনায় বস্তুর দৈর্ঘ্য, আয়তন বা আকৃতির যে আনুপাতিক পরিবর্তন ঘটে, তাকে বিকৃতি বলা হয়।
বিকৃতির বিভিন্ন পদ্ধতিতে একক ও মাত্রীয় সংকেত লেখো।
সমজাতীয় রাশির অনুপাত হওয়ায় বিকৃতি সর্বদা মাত্রাশূন্য তথা এককবিহীন রাশি।
বিকৃতির মাত্রীয় সংকেত – [M0L0T0]।
বিকৃতির বিভিন্ন প্রকারভেদগুলির সংক্ষিপ্ত পরিচয় দাও।
বিভিন্ন ধরার বিকৃতি – দৈর্ঘ্য, আয়তন বা আকৃতির পরিবর্তনের ভিন্নতা অনুযায়ী বিকৃতি তিনপ্রকার হয়ে থাকে – অনুদৈর্ঘ্য বিকৃতি, আয়তন বিকৃতি, কৃন্তন বিকৃতি।
অনুদৈর্ঘ্য বিকৃতি (Longitudinal strain) – বাহ্যিক বল বা টানের প্রভাবে কোনো বস্তুর একক দৈর্ঘ্যে যে দৈর্ঘ্য পরিবর্তন সংঘটিত হয়, তাকে অনুদৈর্ঘ্য বিকৃতি বলে।
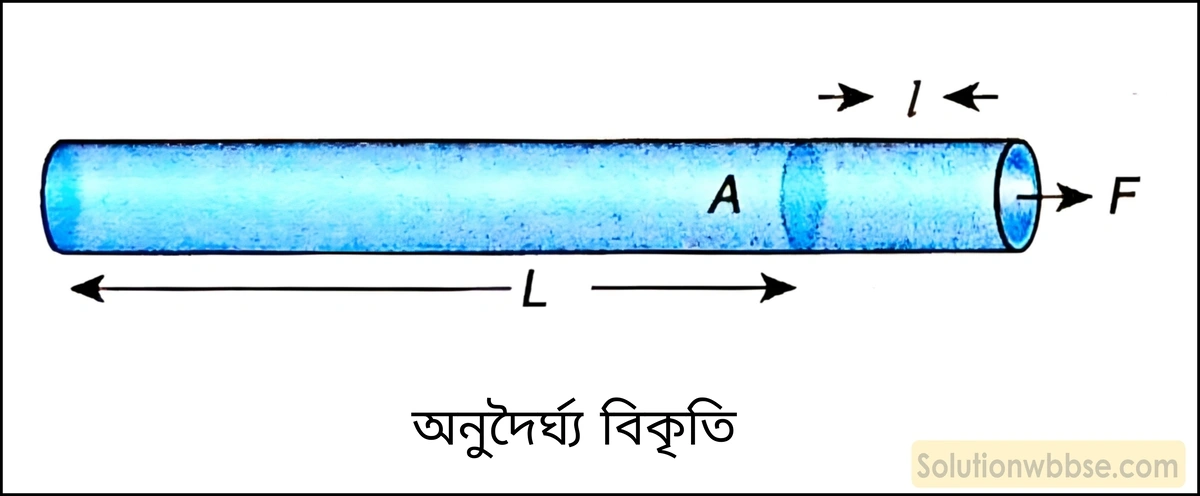
L দৈর্ঘ্যবিশিষ্ট একটি দণ্ডের উপর প্রসারক বা সংনমক বলের ক্রিয়ায় দৈর্ঘ্য পরিবর্তন l হলে দণ্ডটির অনুদৈর্ঘ্য বিকৃতি = \(\frac lL\)
আয়তন বিকৃতি (Volume strain) – বাহ্যিক বলের ক্রিয়ায় কোনো বস্তুর একক আয়তনে সৃষ্ট আয়তন পরিবর্তনকে আয়তন বিকৃতি বলা হয়। প্রাথমিক আয়তন ও আয়তন পরিবর্তন যথাক্রমে V ও v দ্বারা নির্দেশিত হলে,
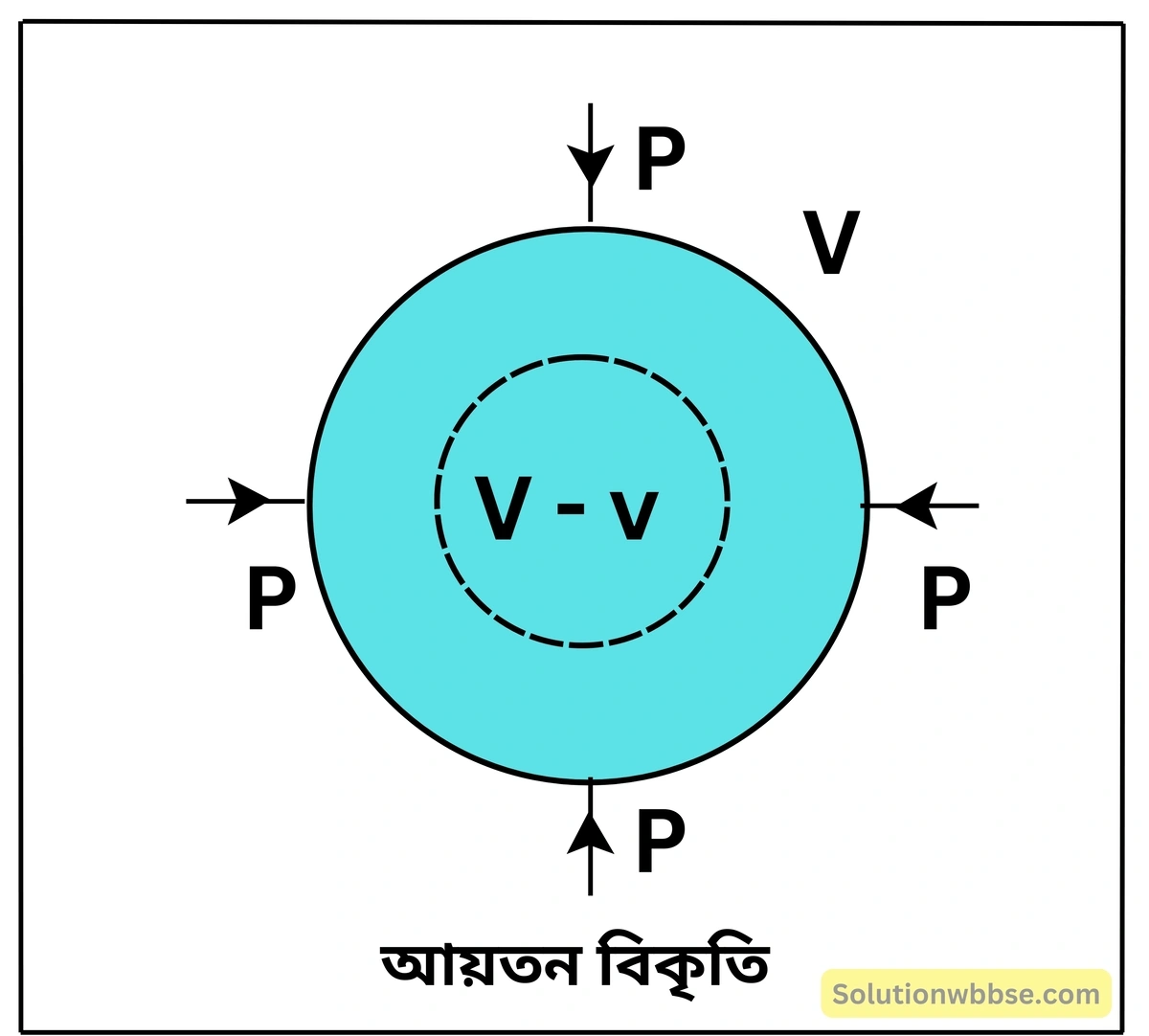
আয়তন বিকৃতি = \(\frac vV\)
কৃন্তন বিকৃতি (Shearing strain) – বাহ্যিক বলের ক্রিয়ায় আয়তন অপরিবর্তিত থেকে বস্তুর শুধুমাত্র আকৃতির পরিবর্তন ঘটলে সংশ্লিষ্ট পরিবর্তনকে মোচড় বা কৃন্তন বিকৃতি বলা হয়।
মোচড়ের ফলে প্রযুক্ত বলের অভিমুখের সঙ্গে লম্বভাবে অবস্থিত কোনো রেখা যে কোণে হেলে যায়, তাকে কৃন্তন বিকৃতি বলে।
মোচড়ের পরিমাণ যথেষ্ট কম হলে পরবর্তী চিত্র থেকে পাওয়া যায়, কৃন্তন বা মোচড় বিকৃতি \(\left(h\right)=\theta\approx\tan\theta=\frac{AA’}{AD}\)
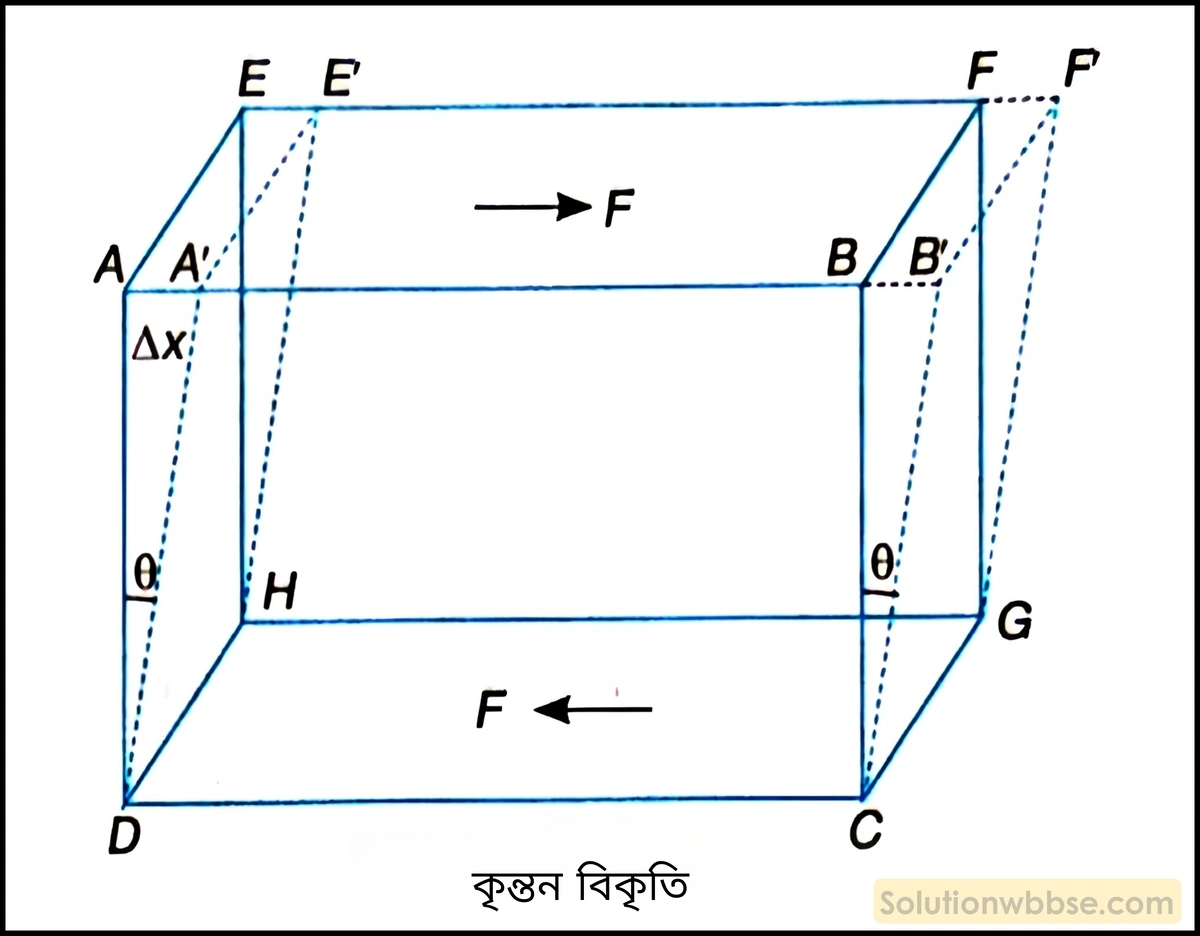
একক দূরত্বে অবস্থিত দুটি তলের আপেক্ষিক সরণই হল কৃন্তন বিকৃতির পরিমাপ।
কোণ (θ) খুবই ক্ষুদ্র হওয়ায় এবং দুই তলের আপেক্ষিক সরণও খুবই ক্ষুদ্র হওয়ায় একে কী ধরা হয়?
কোণ (θ) খুবই ক্ষুদ্র হওয়ায় tanθ ≈ θ ধরা হয়েছে এবং দুই তলের আপেক্ষিক সরণও খুবই ক্ষুদ্র হওয়ায় একে Δx ধরা হয়।
পীড়ন বলতে কী বোঝায়?
পীড়ন (Stress) – প্রতিমিত বাহ্যিক বলের ক্রিয়ায় কোনো বস্তু বিকৃত হলে স্থিতিস্থাপকতা ধর্মের কারণে বস্তুটির মধ্যে একটি অভ্যন্তরীণ প্রতিক্রিয়া বল উদ্ভূত হয়, যা বিকৃতি উৎপাদনের চেষ্টাকে প্রতিহত করতে চায়। বস্তুর প্রস্থচ্ছেদের প্রতি একক ক্ষেত্রফলে সৃষ্ট অভ্যন্তরীণ প্রতিক্রিয়া বলকেই পীড়ন বলা হয়।
পীড়ন [S] = একক ক্ষেত্রফলে প্রযুক্ত বল = \(\frac FA\)
প্রক্রিয়া-প্রতিক্রিয়া সূত্র অনুযায়ী, বস্তুর অভ্যন্তরে সৃষ্ট এই প্রতিক্রিয়া বল মানগতভাবে প্রযুক্ত বাহ্যিক বলের সমান। তাই একক ক্ষেত্রফলে ক্রিয়াশীল বাহ্যিক বলের সাহায্যেই সাধারণত পীড়নের পরিমাপ করা হয়ে থাকে।
পীড়নের বিভিন্ন পদ্ধতিতে একক – CGS পদ্ধতিতে পীড়নের একক – ডাইন/সেমি2। SI -তে পীড়নের – একক নিউটন/মি2।
পীড়নের মাত্রীয় সংকেত –
[পীড়ন] = \(\left[\frac FA\right]=\left[\frac{MLT^{-2}}{L^2}\right]=\left[ML^{-1}T^{-2}\right]\)
পীড়নের প্রকারভেদ – বিকৃতির মতো পীড়নের তিনটি প্রকারভেদ বর্তমান, যেমন – অনুদৈর্ঘ্য পীড়ন, আয়তন পীড়ন, কৃন্তন পীড়ন।
অনুদৈর্ঘ্য পীড়ন (Longitudinal stress) – অনুদৈর্ঘ্য বিকৃতির কারণে কোনো বস্তুর প্রস্থচ্ছেদের প্রতি একক ক্ষেত্রফলে সৃষ্ট অভ্যন্তরীণ প্রতিক্রিয়া বলকে অনুদৈর্ঘ্য পীড়ন বলে।
A প্রস্থচ্ছেদযুক্ত একটি তারের উপর প্রযুক্ত বল F হলে উদ্ভূত অনুদৈর্ঘ্য পীড়ন = \(\frac FA\) হয়।
আয়তন পীড়ন (Volume stress) – আয়তন বিকৃতি ঘটেছে এমন কোনো বস্তুর প্রতি একক ক্ষেত্রফলে ক্রিয়াশীল পীড়নকেই বলা হয় আয়তন পীড়ন।
কোনো বস্তুর পৃষ্ঠের প্রত্যেক বিন্দুতে প্রতি একক ক্ষেত্রফলে লম্বভাবে প্রযুক্ত বল অর্থাৎ চাপ (P) হল আয়তন পীড়নের পরিমাপ।
কৃন্তন পীড়ন (Shearing stress) – মোচড় বা কৃন্তন বিকৃতি সংঘটিত হওয়ার ফলে বস্তুর তলের স্পর্শক বরাবর প্রতি একক ক্ষেত্রফলে যে প্রতিক্রিয়া বল কার্যকরী হয়, তাকেই মোচড় পীড়ন বা কৃন্তন পীড়ন বলে।
∴ কৃন্তন পীড়ন =
অভিলম্ব পীড়ন এবং স্পর্শর্কীয় পীড়ন কীভাবে বাহ্যিক বলের প্রতিক্রিয়ার উপর নির্ভরশীল? বস্তুর অনুদৈর্ঘ্য বা আয়তন বিকৃতির ক্ষেত্রে এই পীড়নগুলির ভূমিকা কী?
অভিলম্ব পীড়ন (Normal stress) ও স্পর্শর্কীয় পীড়ন (Tangential stress) – প্রযুক্ত বাহ্যিক বল সংশ্লিষ্ট বস্তুর তলের সঙ্গে আনতভাবে ক্রিয়া করলে ওই বাহ্যিক বল বা তার প্রতিক্রিয়াকে পরস্পর লম্বভাবে অবস্থিত দুটি অভিমুখ বরাবর উপাংশে (অর্থাৎ, সমকৌণিক উপাংশে) বিভাজিত করা যায়।
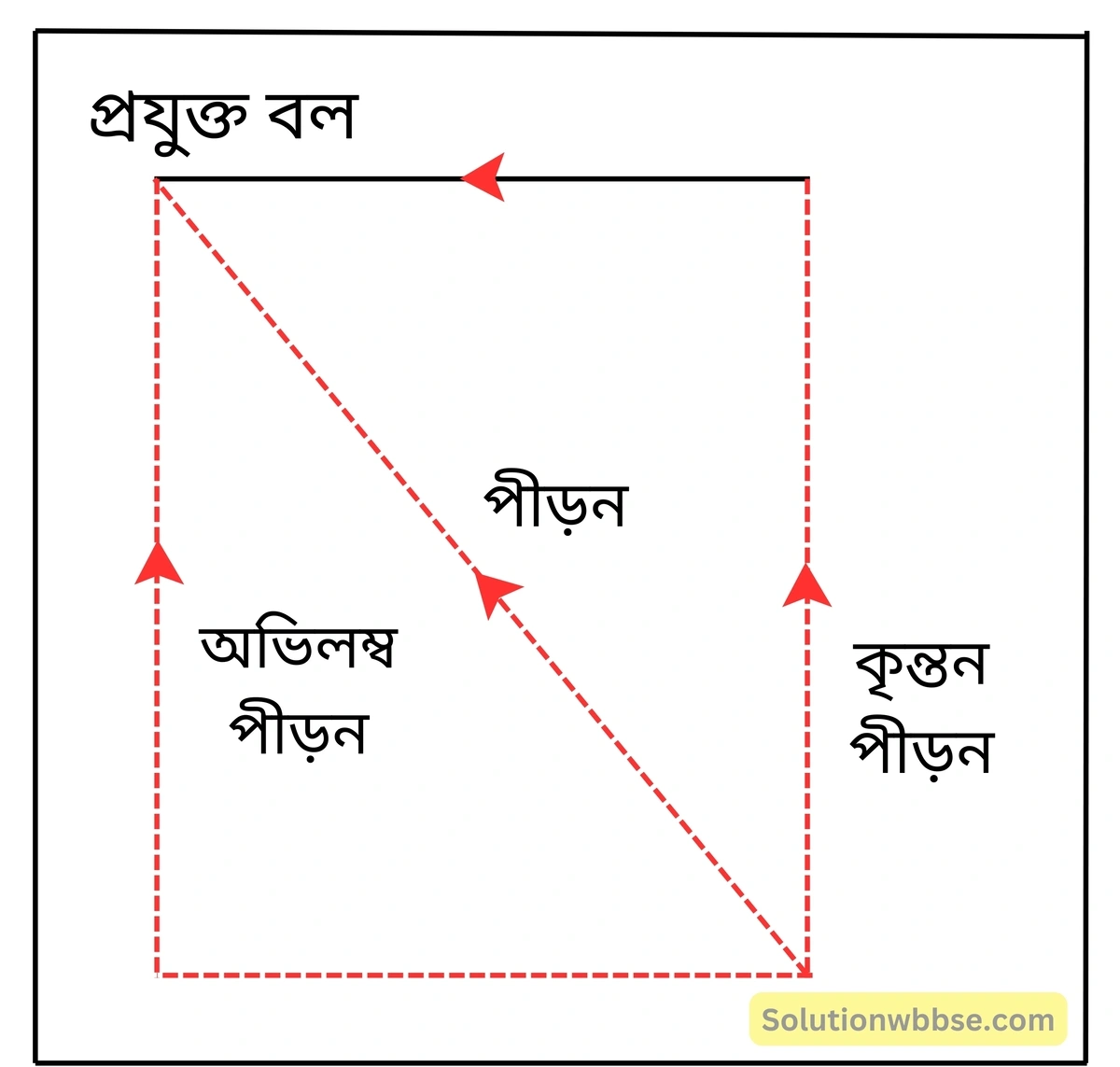
এক্ষেত্রে, একক ক্ষেত্রফলে সক্রিয় ওই বলের অভিলম্ব উপাংশকে বল অভিলম্ব পীড়ন ও তলের সমান্তরালে ক্রিয়ারত উপাংশকে স্পর্শর্কীয় পীড়ন অভিলম্ব বা কৃন্তন পীড়ন বলা হয়।
বস্তুর অনুদৈর্ঘ্য বা আয়তন বিকৃতি ঘটলে অভিলম্ব পীড়ন এবং আকৃতির পরিবর্তনকে প্রতিহত করার প্রচেষ্টারূপে স্পর্শকীয় বা কৃন্তন পীড়নের উদ্ভব হয়ে থাকে।
হুকের সূত্রটি বিবৃত করো। সূত্রটি লেখচিত্রের আকারে প্রকাশ করো।
হুকের সূত্র (Hooke’s law) – স্থিতিস্থাপক সীমার মধ্যে পীড়ন ও বিকৃতি পরস্পর সমানুপাতিক হয়।
অর্থাৎ, পীড়ন ∝ বিকৃতি।
বা, ।
এই সমানুপাতিক ধ্রুবকটিকে বস্তুর উপাদানের স্থিতিস্থাপক গুণাঙ্ক (Modulus of elasticity) বলে।
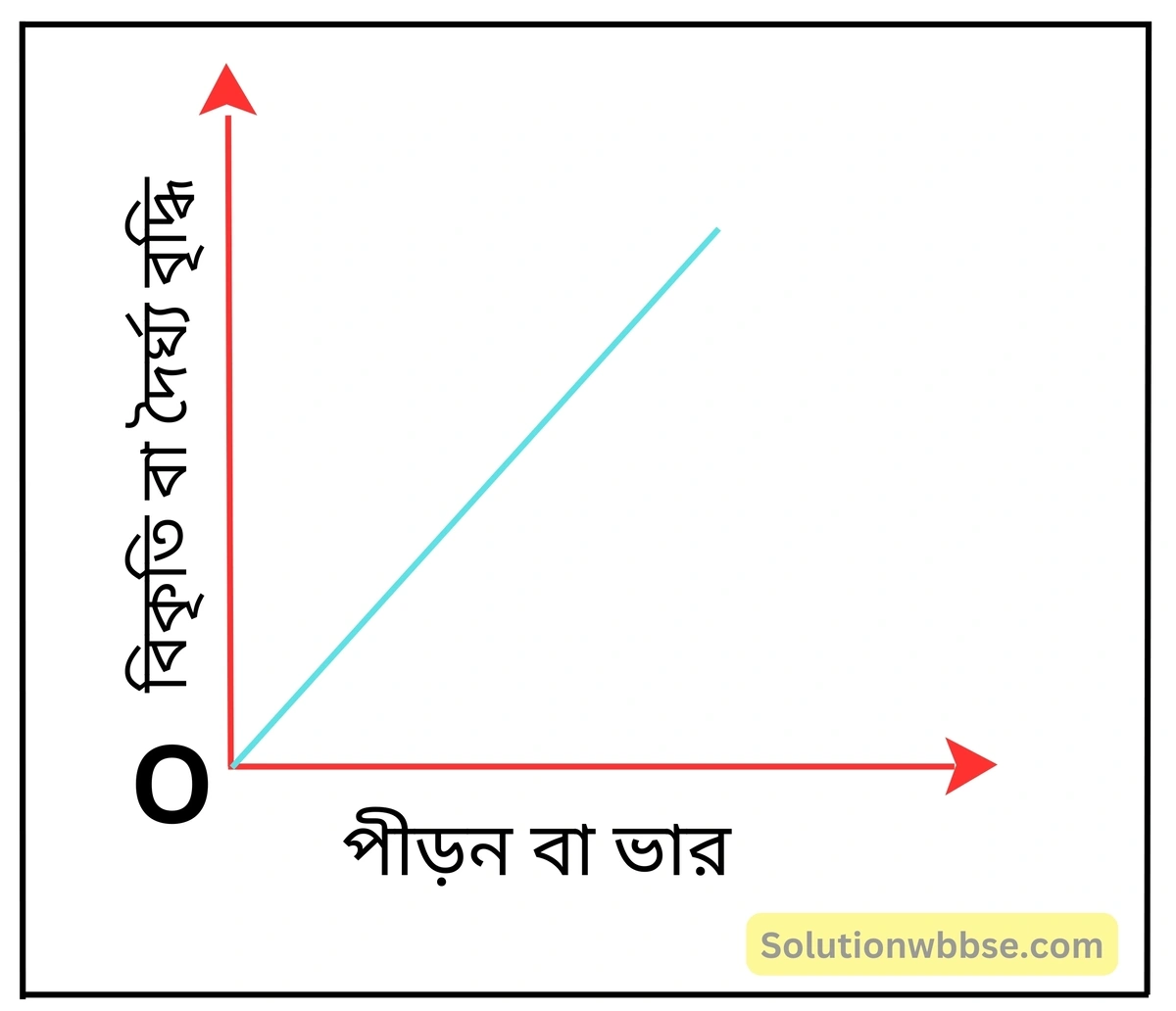
হুকের সূত্রানুযায়ী, পীড়ন ∝ বিকৃতি। অর্থাৎ, x -অক্ষ বরাবর পীড়ন বা প্রযুক্ত ভার এবং y -অক্ষ বরাবর বিকৃতি বা দৈর্ঘ্য বৃদ্ধির মান বসিয়ে লেখচিত্র অঙ্কন করলে তা একটি সরলরেখা হবে এবং মূলবিন্দু দিয়ে যাবে।
বিজ্ঞানী রবার্ট হুক 1676 খ্রিস্টাব্দে স্থিতিস্থাপকতার মূল সূত্রটি উপস্থাপন করেন। তাঁর সূত্রের মূল বক্তব্য কী? এবং পরবর্তীকালে টমাস ইয়ং কীভাবে হুকের সূত্রটি পরিমার্জিত করেন?
বিজ্ঞানী রবার্ট হুক 1676 খ্রিস্টাব্দে স্থিতিস্থাপকতার মূল সূত্রটি উপস্থাপন করেন। তাঁর মূল সূত্রটি হল – ‘স্থিতিস্থাপক সীমার মধ্যে প্রযুক্ত বাহ্যিক বল এবং বস্তুতে উৎপন্ন বিকার (বস্তুর আকৃতি বা আয়তনের পরিবর্তন) পরস্পর সমানুপাতিক হয়।’
পরবর্তীকালে টমাস ইয়ং বল ও বিকারের পরিবর্তে পীড়ন ও বিকৃতির ধারণা ব্যবহার করে হুকের সূত্রকে পরিমার্জিত ও সাধারণ চেহারায় প্রকাশ করেন।
এ ছাড়াও হুকের সূত্রটি পদার্থবিজ্ঞানের ইতিহাসে আবিষ্কৃত প্রথম পরীক্ষামূলক সূত্র বলে মনে করা হয়।
স্থিতিস্থাপক গুণাঙ্ক কাকে বলে? এর একক ও মাত্রীয় সংকেত লেখো।
স্থিতিস্থাপক গুণাঙ্ক (Modulus of elasticity) –
হুকের সাধারণ সূত্র অনুসারে, = ধ্রুবক = স্থিতিস্থাপক গুণাঙ্ক।
সুতরাং, কোনো বস্তুতে একক বিকৃতি উৎপন্ন হওয়ার ফলে সৃষ্ট পীড়নকেই ওই বস্তুর উপাদানের স্থিতিস্থাপক গুণাঙ্ক বলে।
স্থিতিস্থাপক গুণাঙ্কের একক – যেহেতু, বিকৃতির একক ও মাত্রীয় সংকেত নেই তাই স্থিতিস্থাপক গুণাঙ্কের একক ও মাত্রীয় সংকেত যথাক্রমে পীড়নের একক ও মাত্রীয় সংকেতের সমান। স্থিতিস্থাপক গুণাঙ্কের এককগুলি হল –
SI -তে – নিউটন/মিটার2।
CGS পদ্ধতিতে – ডাইন/সেমি2।
FPS পদ্ধতিতে – পাউন্ডাল/ফুট2।
স্থিতিস্থাপক গুণাঙ্কের মাত্রীয় সংকেত – [ML-1T-2]।
স্থিতিস্থাপক গুণাঙ্কের প্রকারভেদগুলি লেখো।
স্থিতিস্থাপক গুণাঙ্কের প্রকারভেদ – প্রযুক্ত বাহ্যিক বল বা দ্বন্দ্বের ক্রিয়ায় বস্তুর বৈশিষ্ট্যের পরিবর্তন (দৈর্ঘ্য, আয়তন, আকৃতি) ঘটে, এর ওপর নির্ভর করে স্থিতিস্থাপক গুণাঙ্ক তিনপ্রকার হতে পারে। যেমন – ইয়ং গুণাঙ্ক (Y), আয়তন বিকৃতি গুণাঙ্ক (K) ও দৃঢ়তা গুণাঙ্ক (n)।
ইয়ং গুণাঙ্কের সংজ্ঞা দাও। এর রাশিমালা নির্ণয় করো।
ইয়ং গুণাঙ্ক (Young’s modulus) – স্থিতিস্থাপক সীমার মধ্যে দৈর্ঘ্য বরাবর প্রসারিত বা সংকুচিত কোনো দণ্ড বা তারের অনুদৈর্ঘ্য পীড়ন ও অনুদৈর্ঘ্য বিকৃতির অনুপাতকে বলা হয় ওই দণ্ড বা তারের ইয়ং গুণাঙ্ক।
ইয়ং গুণাঙ্ক -এর রাশিমালা – L দৈর্ঘ্য এবং A প্রস্থচ্ছেদবিশিষ্ট একটি তারের এক প্রান্ত একটি দৃঢ় অবলম্বন থেকে ঝুলিয়ে তারটির অপর প্রান্তে একটি ভর m ঝোলানো হল। এই ভরের জন্য তারটির দৈর্ঘ্য বরাবর নীচের দিকে mg (g = অভিকর্ষজ ত্বরণ) বল কাজ করে। ধরি, এই বলের জন্য তারটির দৈর্ঘ্য বৃদ্ধি হয় = l
∴
∴ ইয়ং গুণাঙ্ক \(\left(Y\right)=\frac{mgL}{Al}\)
বা, \(Y=\frac{mgL}{Al}\)
ধাতব তারের পীড়ন ও বিকৃতি লেখচিত্র সম্পর্কে লিখ।
নীচের চিত্রে একটি ধাতব তারের পীড়ন-বিকৃতি পীড়ন লেখচিত্র দেখানো হয়েছে। এর বিভিন্ন অংশগুলি নীচে ব্যাখ্যা করা হল।
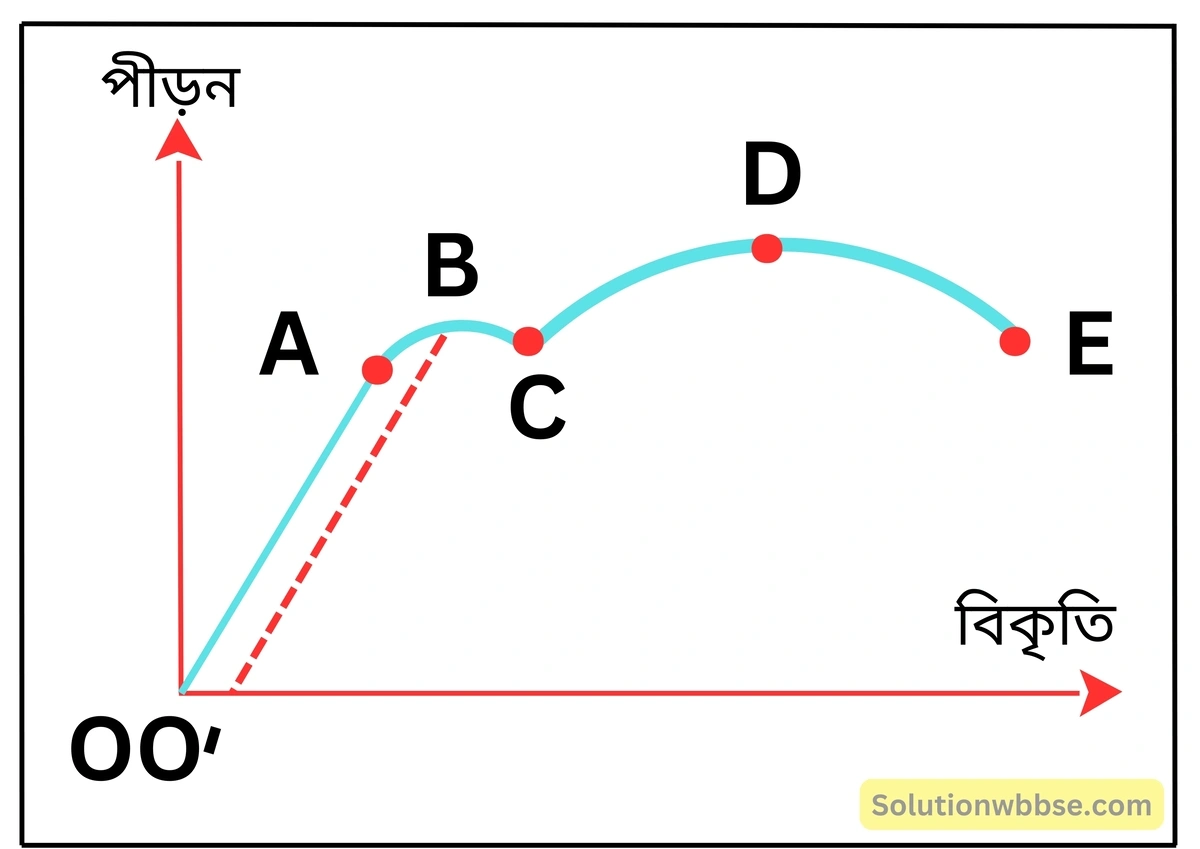
- OA সরলরেখা – এই অংশে ধাতুটি হুকের সূত্র মেনে চলে। অর্থাৎ, পীড়ন ও বিকৃতি পরস্পর বিকৃতি সমানুপাতিক হয়। এই অংশে পীড়ন অর্থাৎ, প্রযুক্ত বল সরিয়ে নিলে বস্তুটি আবার আগের অবস্থায় ফিরে আসে অর্থাৎ বিকৃতি শূন্য হয়। A বিন্দু পদার্থের স্থিতিস্থাপক সীমা নির্দেশ করে।
- AB রেখাংশ – এই অংশে পীড়ন/বিকৃতি অনুপাত ক্রমশ কমতে থাকে এবং ধাতুটি স্থিতিস্থাপক ধর্ম হারাতে থাকে। এই অংশে পীড়ন অর্থাৎ, প্রযুক্ত বল সরিয়ে নিলে বস্তুটি আর আগের অবস্থায় ফিরে আসে না। অর্থাৎ, তারটিতে স্থায়ী বিকৃতি (OO’) সৃষ্টি হয়। B বিন্দুটিকে বলা হয় নতিবিন্দু (Yield point)।
- BC রেখাংশ – এই অংশে পীড়ন অর্থাৎ, প্রযুক্ত বল সরিয়ে নিলেও বস্তুটির বিকৃতি বেড়ে যায়। এই অঞ্চলে পদার্থ নমনীয় আচরণ দেখায়।
- CD রেখাংশ – এই অংশে পীড়ন/বিকৃতি অনুপাত সবচেয়ে কম হয় এবং তারটির বিকৃতি খুব বেশি হয়। ফলে, তারটির কোনো কোনো জায়গা খুব সরু হয়ে যায়।
- DE রেখাংশ – এই অংশে তারটির বিকৃতি আরও বাড়ে এবং E বিন্দুতে তারটি ছিঁড়ে যায়। E বিন্দুকে বলা হয় অসহ বিন্দু (Breaking Point)।
অসহ ভার ও অসহ পীড়ন বলতে কী বোঝায়?
অসহ ভার (Breaking load) – কোনো বস্তুর ওপর যে পরিমাণ বল প্রয়োগ করলে বস্তুটি ছিঁড়ে যায় বা ভেঙে যায়, তাকে অসহ ভার বলে।
অসহ পীড়ন (Breaking stress) – কোনো বস্তুর ওপর অসহ ভার প্রযুক্ত হলে বস্তুটির অভ্যন্তরে সৃষ্ট প্রতিক্রিয়া বলকে অসহ পীড়ন বলে।
স্থিতিস্থাপক ক্লান্তি বলতে কী বোঝায়?
স্থিতিস্থাপক ক্লান্তি (Elastic fatigue) – কোনো বস্তুকে বারবার বিকৃত করতে থাকলে বস্তুটির স্থিতিস্থাপকতা ধর্মের অবনতি ঘটে। ফলে, কিছুক্ষণের মধ্যেই বস্তুটি স্থিতিস্থাপক সীমার মধ্যেই ছিঁড়ে বা ভেঙে যায়। বস্তুর এই অবস্থাকে স্থিতিস্থাপক ক্লান্তি বা অবসাদ বলে। এই কারণে বহু পুরোনো লোহার ব্রিজকে বিপজ্জনক আখ্যা দেওয়া হয়। কারণ – বারবার বিকৃতির ফলে ব্রিজের স্থিতিস্থাপকতা ধর্মের অবনতি ঘটে।
কোন বিজ্ঞানী স্থিতিস্থাপক অবসাদের ধারণাটি পরীক্ষামূলকভাবে আবিষ্কার করেছিলেন এবং এটি কী ধরনের অবস্থাকে বর্ণনা করে?
বিকৃতি উৎপাদনকারী বল অপসারিত হওয়া সত্ত্বেও প্রাথমিক আকৃতি বা আয়তন ফিরে পেতে বস্তুর ব্যর্থতাকে বলা হয় স্থিতিস্থাপক শৈথিল্য (Elastic hysterisis)। ঢালাই করা যন্ত্রাংশের বিভিন্ন স্থানে সূক্ষ্ম ফাটল আছে কিনা তা x-রশ্মির সাহায্যে পরীক্ষা করা হয়। সাধারণত এই ফ্যাটলগুলিতেই স্থিতিস্থাপক অবসাদ দেখা দেয় এবং সেগুলি দুর্বল হয়ে ভেঙে পড়ার সম্ভাবনা থাকে। স্থিতিস্থাপক অবসাদের ধারণা পরীক্ষামূলকভাবে আবিষ্কার করেন লর্ড কেলভিন।
স্থিতিস্থাপক সুরক্ষাগুণক কাকে বলে?
স্থিতিস্থাপক সুরক্ষাগুণক – নিরাপত্তা নিশ্চিত করার স্বার্থে ধাতব যন্ত্রাংশে, ঢালাই করা নির্মাণ ইত্যাদিতে স্থিতিস্থাপক সীমার মধ্যে যে সর্বোচ্চ পীড়ন উৎপাদনকারী বল প্রয়োগ করা সম্ভব বাস্তবে প্রযুক্ত বলের মান তার থেকে অনেকটাই কম হয়। সেতু, বাড়ি ইত্যাদি নির্মাণের সময় ভারবাহী অংশগুলির নকশা এমন রাখা হয়, যাতে সম্ভাব্য প্রযুক্ত বল অপেক্ষা তাতে প্রযুক্ত বলের সহনসীমা বা অসহ বলের মান যেন বেশ কয়েকগুণ বেশি থাকে।
যন্ত্রাংশ, ঢালাই করা নির্মাণ ইত্যাদির ক্ষেত্রে উৎপাদনযোগ্য সর্বোচ্চ পীড়ন এবং অনুমোদিত কার্যকরী পীড়নের অনুপাতকে স্থিতিস্থাপক সুরক্ষাগুণক (Factor of elastic safety) বলে।
দৈনন্দিন জীবনে স্থিতিস্থাপকতার প্রয়োগগুলি আলোচনা করো।
দৈনন্দিন জীবনে স্থিতিস্থাপকতার প্রায়াগ – দৈনন্দিন জীবনের বিভিন্ন কাজে আমরা বিভিন্ন ধরনের পদার্থ ব্যবহার করি। কোন্ কাজে কী ধরনের পদার্থ ব্যবহার করব তা কাজটির ওপর নির্ভর করে। যেমন –
- গহনা তৈরি করার সময় এমন পদার্থ নিতে হবে যা প্রসার্যশীল। তাই এক্ষেত্রে সোনা বা রুপো ব্যবহৃত হয়।
- বাসনপত্র বা যন্ত্রপাতি তৈরি করার সময় এমন পদার্থ নিতে হবে যা বল প্রয়োগে সহজে বিকৃত না হয়, অর্থাৎ যার স্থিতিস্থাপক সীমা বেশি। এজন্য অ্যালুমিনিয়াম, স্টিল, ইস্পাত ইত্যাদি ব্যবহৃত হয়।
- ক্রেনে ব্যবহৃত লোহার চেন কতটা মোটা (thick) রাখা হবে তা লোহার উপাদানের স্থিতিস্থাপক সীমার মানকে কাজে লাগিয়ে নির্ণয় করা হয়।
- সেতু নির্মাণের সময় বা গৃহ নির্মাণের ক্ষেত্রে নিজ ওজনের জন্য দণ্ড (beam) বা স্তম্ভের (column) বেঁকে যাওয়া (buckling) একটি পরিচিত সমস্যা। এই সমস্যার সমাধানে এবং নির্মাণগুলি স্থায়িত্ব বৃদ্ধির জন্য দণ্ড বা স্তম্ভগুলির মধ্যভাগের তুলনায় প্রান্তীয় অংশগুলি বেশি চওড়া অর্থাৎ ‘I’ গঠনযুক্ত করা হয়। এর ফলে উপাদানের অপচয় না ঘটিয়েও দণ্ডের দৃঢ়তা যথেষ্ট বেশি রাখা যায় এবং তা সংশ্লিষ্ট ভারবহনের উপযোগী হতে পারে।
- আসবাবপত্র তৈরি করার জন্য এমন পদার্থ নিতে হয় যার স্থিতিস্থাপক সীমা বেশি অথচ হালকা। এজন্য কাঠ, শক্ত প্লাস্টিক ইত্যাদি ব্যবহৃত হয়।
- কাচ ভঙ্গুর পদার্থ হলেও বিভিন্ন কাজে আমরা কাচ ব্যবহার করি। কারণ, কাচ ভঙ্গুর হলেও দৃঢ়। যে-কোনো মানের বল প্রযুক্ত হলেও কাচে বিকৃতি খুব কম হয়। তাই নানান কাজে কাচ ব্যবহার করা হয়।
স্থিতিস্থাপকতার ধারণা থেকে ভঙ্গুরতা, প্রসার্যতা ও নমনীয়তা ব্যাখ্যা করো।
আমরা জানি, কোনো বস্তুতে বল প্রয়োগ করলে বস্তুটিতে বিকৃতি সৃষ্টি হয়। যদি এই বিকৃতি খুব কম হয় এবং প্রযুক্ত বল সরিয়ে নিলে বস্তুটি তার পূর্বের আকার, আকৃতি পুরোপুরি ফিরে পায় তবে বস্তুটিকে স্থিতিস্থাপক বস্তু বলে। প্রযুক্ত বাহ্যিক বলের একটি নির্দিষ্ট সীমা পর্যন্ত প্রত্যেক বস্তুই স্থিতিস্থাপক। এই সীমাকে বস্তুর উপাদানের স্থিতিস্থাপক সীমা বলে। এই স্থিতিস্থাপক সীমার ধারণা থেকে ভঙ্গুরতা, প্রসার্যতা ও নমনীয়তা ব্যাখ্যা করা যায়।
ভঙ্গুরতা (Brittleness) – যদি প্রযুক্ত বল স্থিতিস্থাপক সীমা ছাড়িয়ে গেলে বস্তুটি খুব তাড়াতাড়ি ভেঙে যায়, তবে বস্তুটিকে ভঙ্গুর (Brittle) বলে। বস্তুটির এই ধর্মকে ভঙ্গুরতা বলে। যেমন – কাচ হল ভঙ্গুর পদার্থ।

প্রসার্যতা (Ductility) – যদি প্রযুক্ত বল স্থিতিস্থাপক সীমা ছাড়িয়ে গেলেও বস্তুটি না ভাঙে এবং ক্রমাগত এর দৈর্ঘ্য বৃদ্ধি ঘটে, তবে বস্তুটিকে প্রসার্যশীল (Ductile) বলা হয়। বস্তুটির এই ধর্মকে প্রসার্যতা বলে। যেমন – সোনা, তামা ইত্যাদি হল প্রসার্যশীল পদার্থ।

নমনীয়তা (Malleability) – যদি যে-কোনো মানের প্রযুক্ত বলের (খুব কম বা বেশি) জন্যই বস্তুটিতে বিকৃতি সৃষ্টি হয় এবং প্রযুক্ত বল সরিয়ে নিলেও বস্তুটি বিকৃত অবস্থাতেই থেকে যায়, তবে বস্তুটিকে নমনীয় (Malleable) বলে। বস্তুটির এই ধর্মকে নমনীয়তা বলে। যেমন – মাখন, কাদামাটি ইত্যাদি নমনীয় পদার্থ।

স্প্রিং -এর বলধ্রুবক কাকে বলে? এর একক ও মাত্রীয় সংকেত কী?
স্প্রিং -এর বল ধ্রুবক (Force constant of spring) – একটি স্প্রিং -এর এক প্রান্ত কোনো দৃঢ় অবলম্বনে আটকে অপরপ্রান্তে প্রসারক বল বা টানা বল প্রয়োগ করলে স্প্রিংটির দৈর্ঘ্য বৃদ্ধি পায়। যে প্রযুক্ত বলের জন্য স্প্রিংটির একক পরিমাণ দৈর্ঘ্য বৃদ্ধি হয়, সেই পরিমাণ বলকেই স্প্রিংটির বলধ্রুবক বলে।
।
স্প্রিং -এর বলধ্রুবকের এককগুলি হল – SI -তে N/m, CGS পদ্ধতিতে dyn/cm এবং FPS পদ্ধতিতে poundal/ft।
এর মাত্রীয় সংকেত = \(\left[k\right]=\left[\frac F{\Delta l}\right]=\frac{\left[MLT^{-2}\right]}{\left[L\right]}=\left[MT^{-2}\right]\)।
সহজ পরীক্ষার সাহায্যে হাতেকলমে স্প্রিং-এর বলধ্রুবক নির্ণয়ের পদ্ধতি সংক্ষেপে আলোচনা করো।
স্প্রিং -এর বলধ্রুবক নির্ণয়ের পরীক্ষা –
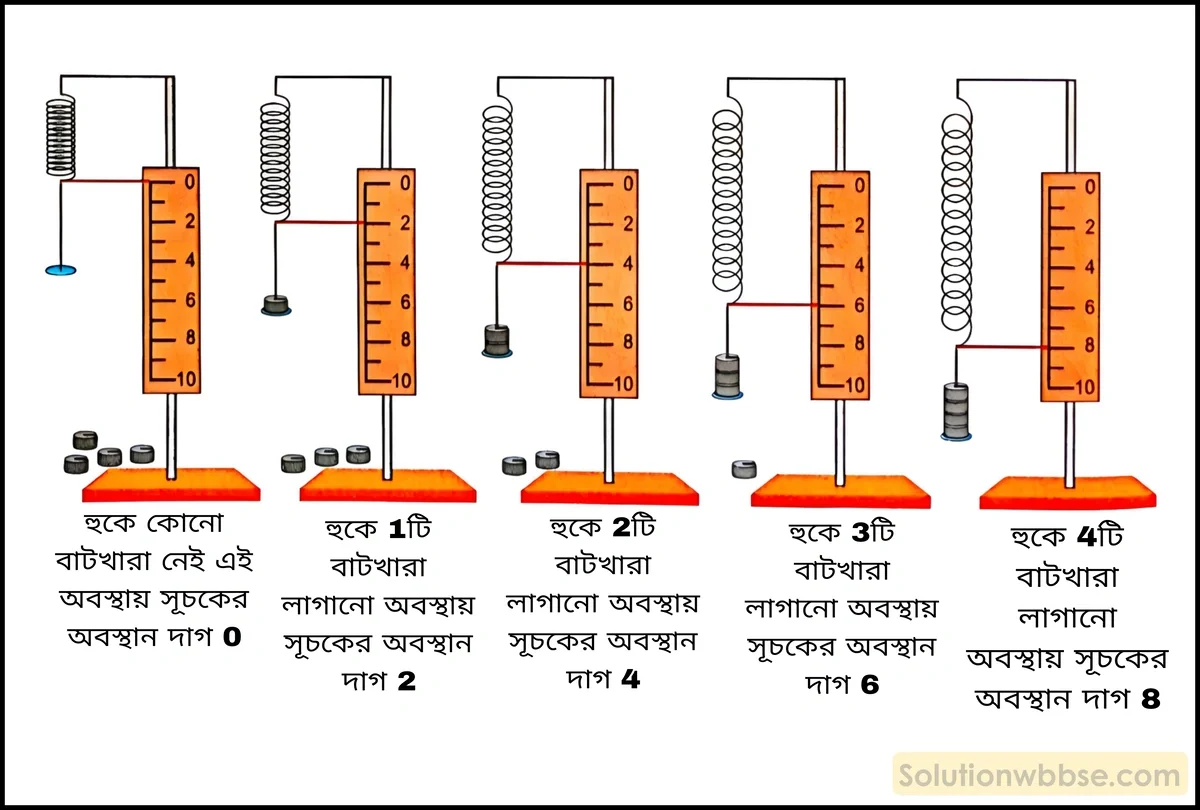
স্প্রিং -এর বলধ্রুবক পরীক্ষা পদ্ধতি – চিত্রে প্রদর্শিত ব্যবস্থা অনুযায়ী একপ্রান্তে আবদ্ধ একটি স্প্রিং -এর মুক্ত প্রান্তে একটি বাটখারা ঝোলানোর হুক লাগিয়ে প্রথমে বাটখারার অনুপস্থিতিতে সূচক কাঁটার অবস্থান (রৈখিক স্কেলের 0 চিহ্নিত পাঠ) নির্ণয় করা হল।
এরপর কতকগুলি নির্দিষ্ট ওজনের বাটখারা (50 g-wt) ওই হুকের ওপর একটি একটি করে চাপানো হল এবং প্রত্যেক ক্ষেত্রে সেমি এককে অংশাঙ্কিত রৈখিক স্কেলের কোন্ দাগে স্প্রিং -এর সূচক কাঁটা স্পর্শ করেছে তা সতর্কতার সঙ্গে নির্ণয় করা হল।
স্প্রিং -এর বলধ্রুবক -এর ফলাফল –
| বাটখারার সংখ্যা | স্প্রিংয়ে প্রযুক্ত বল বা ভার (g-wt) | দৈর্ঘ্য বৃদ্ধি (cm) | ভার/ দৈর্ঘ্যবৃদ্ধি (g-wt/cm) |
| 0 | 0 | 0 | – |
| 1 | 50 | 2 | 25 |
| 2 | 100 | 4 | 25 |
| 3 | 150 | 6 | 25 |
| 4 | 200 | 8 | 25 |
পরীক্ষালব্ধ ফলাফল থেকে পাওয়া যায়, প্রত্যেক ক্ষেত্রে স্প্রিং -এ চাপানো ভার এবং তার দৈর্ঘ্যবৃদ্ধির অনুপাত ধ্রুবক। সুতরাং, এক্ষেত্রে হুকের সূত্রটি প্রযোজ্য হয়। g-wt/cm এককে প্রকাশিত ধ্রুবকটির মানই হল স্প্রিংয়ের বলধ্রুবক।
পোয়াসোঁ অনুপাত কী এবং এটি কিভাবে প্রমাণিত হয় যে, স্থিতিস্থাপক সীমার মধ্যে পার্শ্বীয় বিকৃতি অনুদৈর্ঘ্য বিকৃতির সমানুপাতিক হয়?
প্রসারক বলের ক্রিয়ায় কোনো তার বা বেলনাকার দণ্ডের দৈর্ঘ্য প্রসারণ ঘটানো হলে তা ব্যাস বরাবর সংকুচিত হয়ে থাকে। সুতরাং, অনুদৈর্ঘ্য বিকৃতির ফলে সংশ্লিষ্ট অভিমুখের অভিলম্বভাবে পার্শ্বীয় বিকৃতিও ঘটে থাকে।
প্রসারক বা সংনমক পীড়নের কারণে কোনো দণ্ড বা তারের পার্শ্বীয় দৈর্ঘ্যের (ব্যাসের) প্রতি একক দৈর্ঘ্যে দৈর্ঘ্য পরিবর্তনকেই পার্শ্বীয় বিকৃতি (Lateral strain) বলা হয়। বিভিন্ন উপাদাননির্মিত বস্তু নিয়ে পরীক্ষানিরীক্ষা করে ফরাসি বিজ্ঞানী পোয়াসোঁ (Poisson) দেখান যে, স্থিতিস্থাপক সীমার মধ্যে পার্শ্বীয় বিকৃতি অনুদৈর্ঘ্য বিকৃতির সমানুপাতিক হয়। অর্থাৎ,
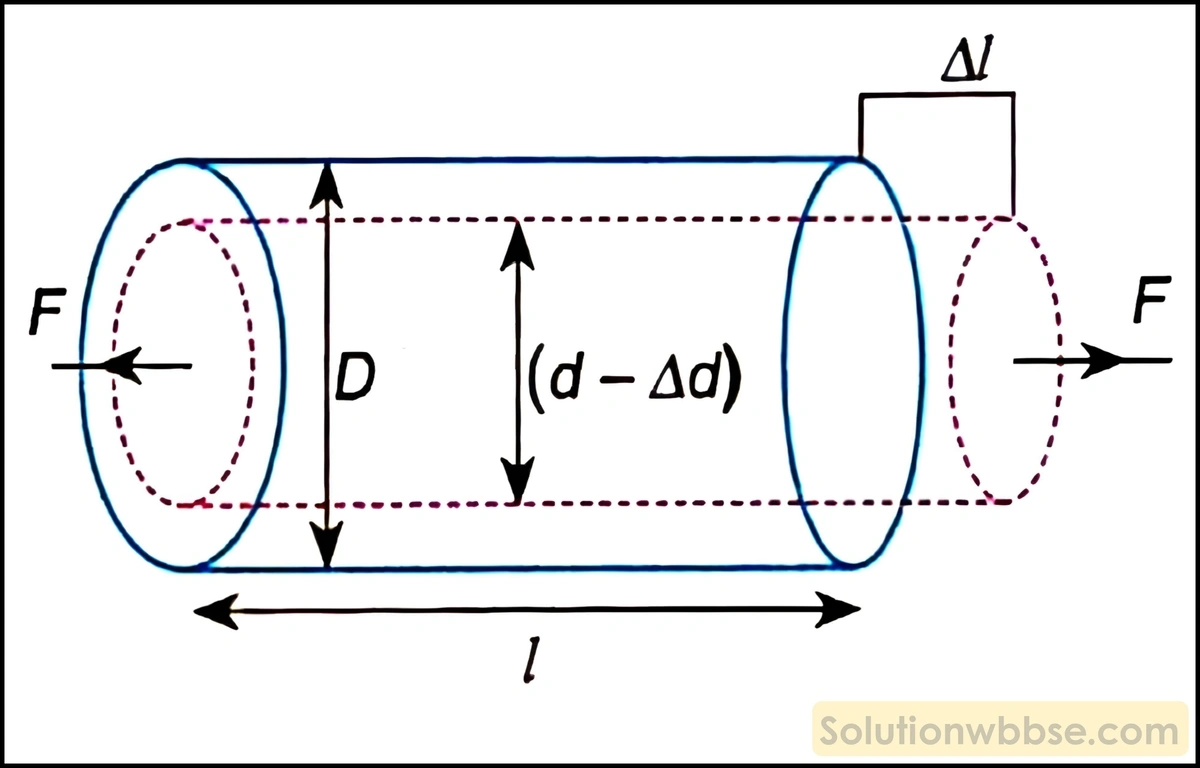
(ধ্রুবক) [D → তারের ব্যাস, d → ব্যাসের পরিবর্তন]
সমানুপাতিক ধ্রুবক σ -কে বলা হয় পোয়াসোঁ অনুপাত। ‘-‘ চিহ্ন নির্দেশ করে দৈর্ঘ্য প্রসারণের ফলে ব্যাস বরাবর সংকোচন হয়।
দুটি বিকৃতির অনুপাত হওয়ায় পোয়াসোঁ অনুপাত মাত্রাহীন, যা একটি বিশুদ্ধ সংখ্যামাত্র। পীড়ন ও বিকৃতির অনুপাত হিসেবে প্রকাশযোগ্য না হওয়ায় একে স্থিতিস্থাপক গুণাঙ্ক বলা যায় না। তবে এটি কঠিন পদার্থের স্থিতিস্থাপক বৈশিষ্ট্যকে প্রকাশ করে এবং সেকারণেই একে স্থিতিস্থাপক ধ্রুবক (Elastic constant) বলা হয়।
তাত্ত্বিকভাবে প্রমাণ করা যায়, σ -এর মান -1 থেকে \(\frac12\) -এর মধ্যে থাকে, যদিও বাস্তব উপাদানের ক্ষেত্রে এটি 0 এবং \(\frac12\) -এর মধ্যবর্তী হয়। অধিকাংশ ধাতুর ক্ষেত্রে σ -এর মান 0.3 -এর কাছাকাছি হয়ে থাকে।
বলধ্রুবকের মাধ্যমে স্প্রিংয়ের কোন্ ধর্ম পরিমাপ করা হয়?
বলধ্রুবক রাশিটির সাহায্যে স্প্রিংয়ের অনমনীয়তা ধর্মের পরিমাপ করা হয়। এর মান যত বেশি হয়, স্প্রিংটির অনমনীয়তাও তত বাড়ে।
স্পষ্টতই নির্দিষ্ট স্প্রিংয়ের জন্য বলধ্রুবক (k) -এর মান নির্দিষ্ট। তাই বলধ্রুবকের মান যত বাড়ে, Δl -এর মানও তত কমে। অর্থাৎ, স্প্রিং তত অনমনীয় হয়।
k1 ও k2 বলধ্রুবকবিশিষ্ট দুটি স্প্রিংয়ের এক প্রান্তের সঙ্গে অপরটি যুক্ত করলে যুগ্ম স্প্রিংটির কার্যকর বলধ্রুবক কত হবে?
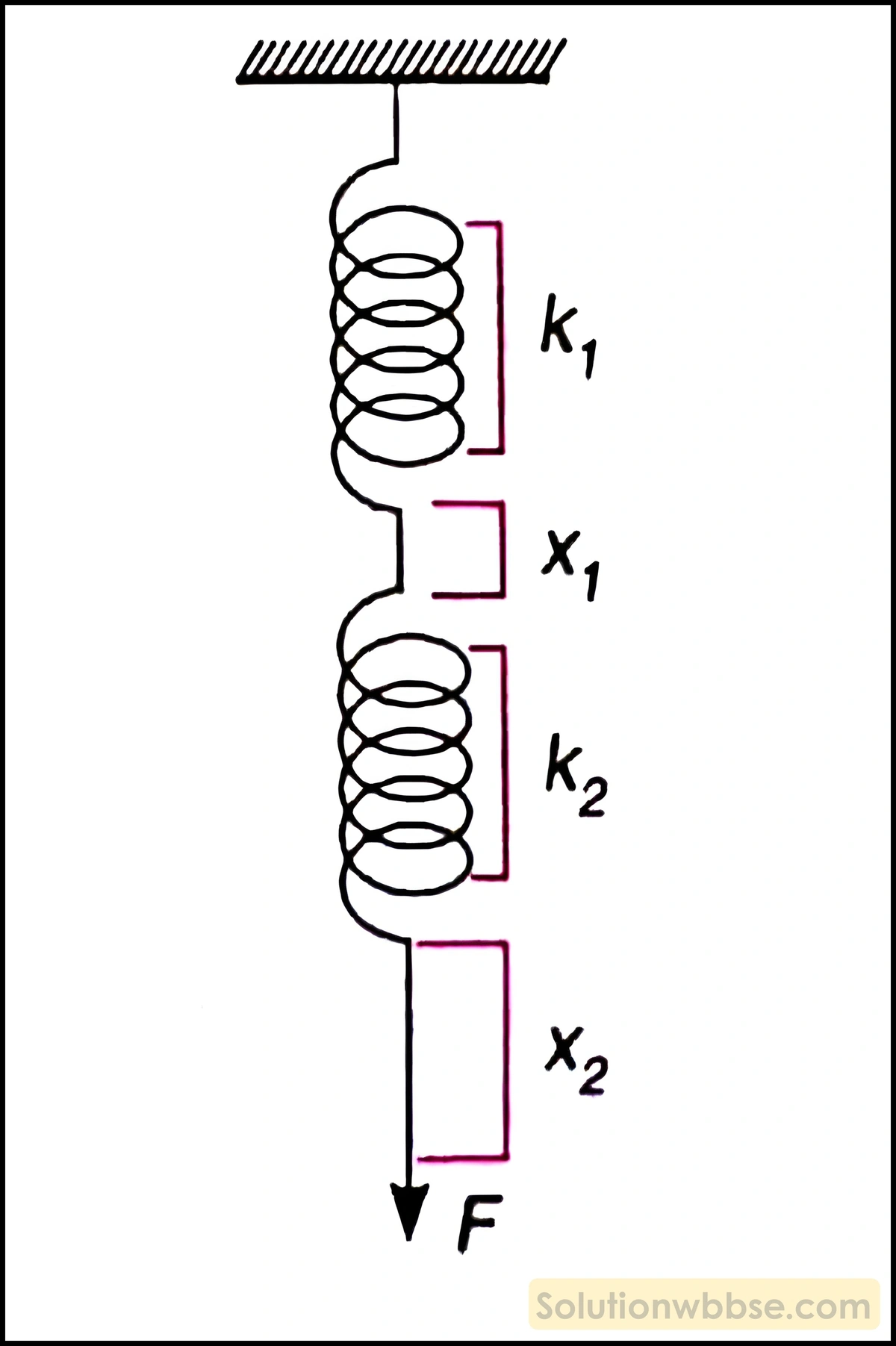
দুটি স্প্রিং -এর বলধ্রুবক k1 ও k2।
ধরি, ওদের প্রান্তে ‘F’ বল প্রয়োগ করলে ওদের দৈর্ঘ্য বৃদ্ধি হয় যথাক্রমে x1 ও x2।
সুতরাং, বলধ্রুবকের সংজ্ঞানুযায়ী, F = k1x1 = k2x2।
∴ \(x_1=\frac F{k_1}\) এবং \(x_2=\frac F{k_2}\)
\(F=\frac{x_1}{\left({\displaystyle\frac1{k_1}}\right)}=\frac{x_2}{\left({\displaystyle\frac1{k_2}}\right)}=\frac{x_1+x_2}{\left({\displaystyle\frac1{k_1}}+{\displaystyle\frac1{k_2}}\right)}\) ___(1)
ধরি, যুগ্ম স্প্রিং -এর বলধ্রুবক k এবং স্প্রিং -এর মোট দৈর্ঘ্য বৃদ্ধি হয় = (x1 + x2)
∴ \(F=k\left(x_1+x_2\right)\)
∴ \(F=\frac{\left(x_1+x_2\right)}{\left({\displaystyle\frac1k}\right)}\) ___(2)
(1) নং সমীকরণ ও (2) নং সমীকরণ তুলনা করে পাই,
\(\frac{x_1+x_2}{\displaystyle\frac1k}=\frac{x_1+x_2}{\displaystyle\frac1{k_1}+\frac1{k_2}}\\\)∴ \(\frac1k=\frac1{k_1}+\frac1{k_2}\)
বা, \(\frac1k=\frac{k_2+k_1}{k_1k_2}\)
বা, \(\frac1k=\frac{k_1k_2}{k_1+k_2}\)
∴ \(k=\frac{k_1k_2}{k_1+k_2}\)
স্থিতিস্থাপক বস্তুর ক্ষেত্রে পীড়ন ও বিকৃতির মধ্যে কোনটি মৌলিক এবং কেন?
বাহ্যিক বলের প্রয়োগে কোনো বস্তুকে বিকৃত করা হলে বস্তুটির মধ্যে স্থিতিস্থাপকতা ধর্মের কারণে একটি অভ্যন্তরীণ প্রতিক্রিয়া বলের উদ্ভব হয়। একক ক্ষেত্রফলে সৃষ্ট এই অভ্যন্তরীণ প্রতিক্রিয়াকেই পীড়ন বলে। সুতরাং, বিকৃত বস্তুতেই কেবল পীড়নের অস্তিত্ব থাকে। অর্থাৎ, পীড়নের উৎপত্তির কারণই হল বিকৃতি। সুতরাং, বিকৃতি পীড়ন অপেক্ষা বেশি মৌলিক।
একটি ধাতুর ইয়ং গুণাঙ্ক 9.8 × 10 ডাইন/সেমি2। – এই কথাটির অর্থ ব্যাখ্যা করো।
পিতলের ইয়ং গুণাঙ্কের মান 9.8 × 1011 ডাইন/সেমি2 – এই বক্তব্যের অর্থ হল একটি পিতলের দণ্ড বা তারে একক অনুদৈর্ঘ্য বিকৃতি উৎপাদন করতে ওই দণ্ডের প্রস্থচ্ছেদের প্রতি বর্গসেমি ক্ষেত্রফলে 9.8 × 1011 ডাইন বল প্রয়োগ করতে হবে।
স্প্রিং সাধারণত তামার তৈরি না হয়ে ইস্পাতের তৈরি হয় কেন?
তামার তুলনায় ইস্পাতের স্থিতিস্থাপক সীমা বেশি। তাই একই দৈর্ঘ্যের দুটি স্প্রিংয়ের একটির উপাদান তামা ও অন্যটি লোহা হলে দ্বিতীয়টি অপেক্ষাকৃত বেশি মানের বলের ক্রিয়াতেও অবিকৃত থাকে। তাই স্প্রিং -এর উপাদান হিসেবে সাধারণভাবে ইস্পাতকেই নির্বাচন করা হয়। তাছাড়াও ইস্পাতের স্প্রিংয়ের বলধ্রুবকের মানও তুলনামূলকভাবে বেশি হয়ে থাকে।
যেসব ক্ষেত্রে বেশি মানের বল প্রযুক্ত হওয়ার সম্ভাবনা নেই, সেক্ষেত্রে তামার তৈরি স্প্রিং ব্যবহার করার ক্ষেত্রে অসুবিধা না থাকলেও তামা ইস্পাতের চেয়ে দামি বলে সাধারণত তামার স্প্রিং -এর ব্যবহার খুব বেশি দেখা যায় না।
রবার অপেক্ষা ইস্পাত বেশি স্থিতিস্থাপক – ব্যাখ্যা করো।
সাধারণ ধারণায় যে বস্তুকে যত সহজে বিকৃত করা যায় তার স্থিতিস্থাপকতা বেশি বলে মনে করা হলেও বৈজ্ঞানিক ধারণা এর বিপরীত। পদার্থবিদ্যার মতে, যে পদার্থের স্থিতিস্থাপক সীমা যত বেশি সেটি তত বেশি স্থিতিস্থাপক।
ইস্পাতের স্থিতিস্থাপক সীমা রবার অপেক্ষা বেশি। তাই যে বলের ক্রিয়ায় রবারের মধ্যে স্থায়ী বিকৃতি সৃষ্টি হয় সেই একই বল প্রযুক্ত হলেও ইস্পাত সম্পূর্ণ অবিকৃত থাকে। একারণেই রবার অপেক্ষা ইস্পাত অধিক স্থিতিস্থাপক।
রবারকে শক্ শোষক হিসেবে ব্যবহার করা হয় কেন?
রবারকে দুটি কম্পনশীল বস্তুর মাঝে রাখলে রবার বারবার সংকুচিত ও প্রসারিত হয় এবং কম্পনশক্তির বেশিরভাগ অংশ শোষণ করে নেয়। তাই কম্পনশীল বস্তু দুটি কম্পনজনিত ক্ষতি থেকে রক্ষা পায়। একারণে রবারকে শক্ শোষক হিসেবে ব্যবহার করা হয়।
ফোল্ডিং ছাতায় ব্যবহৃত স্প্রিং এবং টিপ্ পেনে ব্যবহৃত স্প্রিং -এর মধ্যে কোনটি বেশি অনমনীয়? কোনটির স্প্রিং ধ্রুবক বেশি? কারণসহ লেখো।
ফোল্ডিং ছাতা খুলতে যে মানের বল প্রয়োগ করতে হয় আঙুলে চাপ দিয়ে টিপ পেন খুলতে সেই তুলনায় অনেক কম বল প্রয়োজন হয়ে থাকে।
তাই বলা যায় যে, ফোল্ডিং ছাতায় ব্যবহৃত স্প্রিংয়ের অনমনীয়তা বেশি। আবার স্প্রিং -এর অনমনীয়তা বেশি হলে তার বলধ্রুবকও বেশি হয়ে থাকে, সুতরাং ফোল্ডিং ছাতায় ব্যবহৃত স্প্রিং -এর বলধ্রুবক বেশি হয়।
সরু চেন তৈরির জন্য লোহা, তামা, সোনা বা রুপোর মতো পদার্থ নেওয়া হয়, কিন্তু সিসার মতো পদার্থ ব্যবহার করা হয় না কেন?
লোহা, তামা, সোনা বা রূপার প্রসার্যতা অনেক বেশি। অর্থাৎ, স্থিতিস্থাপক সীমা ছাড়িয়ে গেলেও ধাতুগুলি ভেঙে যায় না এবং বল প্রয়োগে উক্ত ধাতুগুলির দৈর্ঘ্য বাড়তে থাকে। ফলে এইসব পদার্থগুলিকে ইচ্ছেমতো টেনে সরু তারের আকৃতি দেওয়া সম্ভব হয়।
তবে সোনা বা রূপোর প্রসার্যতা ও নমনীয়তা লোহা বা তামার তুলনায় অনেক বেশি হওয়ায় অল্প বল প্রয়োগেই সোনা বা রুপো প্রসারিত হয়। তাই অতি অল্প পরিমাণ সোনা বা রুপোর সাহায্যে নানা আকৃতির সূক্ষ্ম ও পাতলা গয়না বানানো সম্ভব হয়।
কিন্তু সিসা একটি ভঙ্গুর পদার্থ। অর্থাৎ, অল্প বল প্রয়োগেই সিসা ভেঙে যায়। আবার সিসার প্রসার্যতা প্রায় নেই বললেই চলে। তাই সরু চেন তৈরির জন্য সিসা ব্যবহার করা হয় না।
সেতু অনেকদিন ধরে ব্যবহারের পর বিপজ্জনক বলে ঘোষণা করা হয় কেন?
দীর্ঘদিন ধরে ব্যবহৃত লোহার সেতু, কাঠামো বা অন্য নির্মাণকার্যে দীর্ঘ সময় ধরে ক্রমাগতভাবে বাহ্যিক পীড়নের হ্রাস-বৃদ্ধি ঘটে। এর ফলে সেতু বা নির্মাণে স্থিতিস্থাপক অবসাদ উৎপন্ন হয় এবং সেটির ভার বহনের সামর্থ্য কমে যায়। তার বিভিন্ন অংশগুলি দুর্বল হয়ে পড়ে এবং সেগুলিতে সৃষ্ট বিকৃতিও যথেষ্ট বেশি হয়। এর ফলে যে-কোনো সময় কাঠামো তার দুর্বলতম অংশ থেকে ভেঙে যেতে পারে। একারণেই সেতু অনেকদিন ধরে ব্যবহার হওয়ার পর বিপজ্জনক বলে ঘোষণা করা হয়।
স্প্রিং তুলা অনেকদিন ব্যবহার করলে ভুল পাঠ দেখায় কেন?
অনেকদিন ধরে স্প্রিং তুলা ব্যবহার করলে স্প্রিং তুলার স্থিতিস্থাপক ধর্মের অবনতি ঘটে। অর্থাৎ, স্প্রিং তুলাটির স্থিতিস্থাপক অবসাদ ঘটে এবং স্প্রিং -এর শক্তি হ্রাস পায়। এই ধরনের স্প্রিং তুলার সাহায্যে কোনো বস্তুর ভার পরিমাপ করার সময় ভারের জন্য স্প্রিং -এর প্রসারণ যা হওয়া উচিত, স্প্রিং তার থেকে বেশি প্রসারিত হয়। ফলে স্প্রিং তুলা বস্তুটির সঠিক ভার নির্দেশ করে না অর্থাৎ, ভুল পাঠ দেয়। এইজন্য স্প্রিং তুলা অনেকদিন ধরে ব্যবহার করলে ভুল পাঠ দেখায়।
ইয়ং গুণাঙ্ক কেবলমাত্র কঠিন পদার্থরই বৈশিষ্ট্য কেন?
যেহেতু, কঠিন পদার্থের ক্ষেত্রেই একমাত্র দৈর্ঘ্য বৈশিষ্ট্যটির অস্তিত্ব আছে। তাই ইয়ং গুণাঙ্ক কেবলমাত্র কঠিন পদার্থের বৈশিষ্ট্য।
একটি গাছ নির্দিষ্ট উচ্চতার পর আর বাড়তে পারে না কেন?
যে-কোনো গাছের বৃদ্ধি একটি নির্দিষ্ট উচ্চতা পর্যন্ত হয়ে থাকে। ওই নির্দিষ্ট উচ্চতার পর গাছটি আর বাড়তে পারে না। এর কারণ হল অসহ পীড়ন। গাছে উদ্ভূত এই অসহ পীড়নের থেকে বেশি পীড়ন গাছের মধ্যে সৃষ্টি হলে গাছটি নিজের ওজনের জন্যই ভেঙে পড়ে। এই কারণে কোনো গাছ একটি নির্দিষ্ট উচ্চতার পর আর বাড়তে পারে না।
ধরি, চোঙাকৃতি গুঁড়ির একটি গাছের সর্বোচ্চ উচ্চতা = h
গুঁড়ির প্রস্থচ্ছেদের ক্ষেত্রফল = A
জীবিত গাছের গড় ঘনত্ব = ρ, অভিকর্ষজ ত্বরণ = g
যদি গাছের অসহ পীড়ন = F হয়,
তাহলে \(F=\frac{Ah\rho g}A=h\rho g\)
বা, \(h=\frac F{\rho g}\)
গাছটির সর্বাধিক উচ্চতা হবে \(\left(h\right)=\frac F{\rho g}\)
ভিন্ন দৈর্ঘ্যের একটি সরু লোহার তার এবং একটি মোটা লোহার তারের ইয়ং গুণাঙ্কের মান কি একই হবে?
ইয়ং গুণাঙ্কের মান পদার্থের উপাদানের বৈশিষ্ট্য। নির্দিষ্ট পদার্থের জন্য এটি সর্বদা ধ্রুবক এবং এর মান পদার্থের দৈর্ঘ্য, প্রস্থচ্ছেদ ইত্যাদি বৈশিষ্ট্যের ওপর নির্ভর করে না। সুতরাং, ভিন্ন দৈর্ঘ্যের সরু বা মোটা যে-কোনো লোহার তারের ক্ষেত্রে ইয়ং গুণাঙ্কের মান সমান হয়।
দুটি স্প্রিং A ও B -এর বলধ্রুবক যথাক্রমে KA ও KB, KA > KB। এছাড়া স্প্রিং দুটি সর্বত্র একই প্রকৃতির।
স্প্রিং দুটি সমান প্রসারিত করলে,
সমান বলে প্রসারিত করলে কোন্ স্প্রিং -এর ক্ষেত্রে বেশি কার্য করতে হবে?
প্রথমত, kA > kB বলতে বোঝায় যে, স্প্রিং দুটিকে সমান প্রসারিত করতে A স্প্রিং -এর ক্ষেত্রে বেশি বল প্রয়োগ করতে হবে। সুতরাং, এক্ষেত্রে A স্প্রিং -এর বেলায় বেশি কাজ করতে হবে।
দ্বিতীয়ত, KA > kB হওয়ায় দুটি স্প্রিং -এর উপর সমান বল প্রয়োগ করলে A স্প্রিংয়ের প্রসারণ, B স্প্রিং -এর প্রসারণ অপেক্ষা কম হবে। সুতরাং, এক্ষেত্রে B স্প্রিং -এর ক্ষেত্রে কৃতকার্য বেশি হবে।
পার্থক্যধর্মী প্রশ্নোত্তর
পীড়ন (Stress) ও বিকৃতি (Strain) -এর মধ্যে পার্থক্য লেখো।
পীড়ন (Stress) ও বিকৃতি (Strain) -এর মধ্যে পার্থক্যগুলি হল –
| পার্থক্যের বিষয় | পীড়ন (Stress) | বিকৃতি (Strain) |
| সংজ্ঞা | পদার্থের অভ্যন্তরে একক ক্ষেত্রফলে সৃষ্ট অভ্যন্তরীণ প্রতিক্রিয়াকে পীড়ন বলে। | প্রাথমিক মানের সাপেক্ষে বস্তুর দৈর্ঘ্য, আয়তন ও আকৃতির যে আনুপাতিক পরিবর্তন ঘটে, তাকেই বিকৃতি বলে। |
| মাত্রীয় সংকেত ও একক | পীড়ন মাত্রাযুক্ত রাশি, এর মাত্রীয় সংকেত [ML-1T-2]। এর CGS ও SI একক যথাক্রমে ডাইন/সেমি2 ও নিউটন/মি2। | বিকৃতি মাত্রাহীন তথা এককবিহীন রাশি। এর মাত্রীয় সংকেত [M0L0T0]। |
| বৈশিষ্ট্য | বস্তু বিকৃত হলে তবেই তার মধ্যে পীড়ন সৃষ্টি হয়। সুতরাং, পীড়ন হল বিকৃতির ফল। | বিকৃতির ধারণা পীড়নের তুলনায় অধিকতর মৌলিক। বিকৃতিকে পীড়নের কারণ বলে বিবেচনা করা যায়। |
গাণিতিক প্রশ্নাবলি
প্রয়োজনীয় সূত্রাবলি
3 m দীর্ঘ তামার তারে 150 kg ওজন ঝোলালে তারের দৈর্ঘ্য 2.7 mm বাড়ে। তারটির অনুদৈর্ঘ্য বিকৃতি কত হবে?
L = 3 m
দৈর্ঘ্য বৃদ্ধি \(\left(l\right)=\frac{2.7}{1000}\;m=0.0027\;m\)
∴ অনুদৈর্ঘ্য বিকৃতি = \(\frac lL\)
বা, অনুদৈর্ঘ্য বিকৃতি = \(\frac{0.0027}3=0.0009\)
∴ তারটির অনুদৈর্ঘ্য বিকৃতি 0.0009 হবে।
একটি তারের বিকৃতি 0.1 -এর 2% হলে, 10 m দীর্ঘ তারের দৈর্ঘ্য পরিবর্তন কত হবে?
∴ \(\frac lL=0.1\) -এর 2% \(=\frac{0.1\times2}{100}=\frac2{1000}\)
এখন তারের দৈর্ঘ্য, L = 10 m = 10 × 100 = 1000 cm
দৈর্ঘ্য বৃদ্ধি,
\(l=L\times\frac2{1000}\\\)বা, \(l=1000\times\frac2{1000}\)
বা, \(l=2\)
∴ তারের দৈর্ঘ্য পরিবর্তন 2 cm হবে।
1 L আয়তনের একটি তরলের উপর চাপ ক্রিয়া করায় তরলের আয়তন 0.245 mL কমে গেল। এই তরলের আয়তন বিকৃতি কত হবে?
= \(\frac{0.245}{1000}\)
= \(0.245\times10^{-3}\)।
∴ তরলের আয়তন বিকৃতি \(0.245\times10^{-3}\) হবে।
3.5 mm ব্যাসার্ধবিশিষ্ট একটি স্থিতিস্থাপক দড়ির দৈর্ঘ্য স্থিতিস্থাপক সীমার মধ্যে \(\frac1{20}\) দ্রুত অংশ বৃদ্ধি করতে। 10 N বল প্রয়োজন হয়। দড়ির উপাদানের ইয়ং গুণাঙ্ক কত?
এক্ষেত্রে, \(\frac lL=\frac1{20}\), F = 10 N = 106 dyn এবং r = 3.5 mm = 0.35 cm
∴ \(Y=\frac F{\pi r^2l/L}\)
বা, \(Y=\frac{10^6}{{\displaystyle\frac{22}7}\times\left(0.35\right)^2\times{\displaystyle\frac1{20}}}\)
বা, \(Y=\frac{7\times10^7}{11\times\left(0.35\right)^2}\)
বা, \(Y=5.2\times10^7\) dyn/cm2
∴ দড়ির উপাদানের ইয়ং গুণাঙ্ক \(Y=5.2\times10^7\) dyn/cm2
1 mm ব্যাসের একটি তারের নীচে 15 kg-wt ঝুলিয়ে দিলে তারের দৈর্ঘ্য দাঁড়ায় 700.5 cm। ভর সরিয়ে নিলে তারের দৈর্ঘ্য 5 mm কমে যায়। তারের উপাদানের ইয়ং গুণাঙ্ক নির্ণয় কর।
ভারহীন অবস্থায় তারের দৈর্ঘ্য = (700.5 – 0.5) cm = 700 cm
তারের ব্যাস = 1 mm, ব্যাসার্ধ (r) = 0.5 mm = 0.05 cm
তারের প্রস্থচ্ছেদের ক্ষেত্রফল (A) = πr2 = 3.14 × (0.05)2
F = mg = 15 × 1000 × 980
ইয়ং গুণাঙ্ক, \(Y=\frac{F/A}{l/F}=\frac{FL}{Al}\)
বা, \(Y=\frac{15\times1000\times980\times700}{3.14\times\left(0.05\right)^2\times0.05}\)
সুতরাং, \(Y=26.21\times10^{11}\) dyn/cm2
2 mm ও 3 mm ব্যাসবিশিষ্ট দুটি ভিন্ন উপাদানের তারের প্রত্যেকটির দৈর্ঘ্য 4 m। প্রত্যেক তারে 5 kg ভরের বস্তু ঝুলিয়ে দেখা গেল একটি তারের প্রসারণ অপরটির দ্বিগুণ। তার দুটির উপাদানের ইয়ং গুণাঙ্কের অনুপাত নির্ণয় করো।
\(r_1=\frac22\;mm=10^{-1}\;cm,\;r_2=\frac32\;mm=1.5\times10^{-1}\;cm\\\)\(L_1=L_2=4\;m=400\;cm\\\)\(F_1=F_2=5\times10^3\times980\) ডাইন, \(l_1=2l_2\)
∴ \(\frac{Y_1}{Y_2}=\frac{{\displaystyle\frac{F_1}{\pi r_1^2}}\div{\displaystyle\frac{l_1}{l_2}}}{{\displaystyle\frac{F_2}{\mathrm{πr}_2^2}}\div{\displaystyle\frac{l_2}{L_2}}}\)
বা, \(\frac{Y_1}{Y_2}=\frac{F_1}{F_2}⋅\left(\frac{r_2}{r_1}\right)^2⋅\frac{l_2}{l_1}⋅\frac{L_1}{L_2}\)
বা, \(\frac{Y_1}{Y_2}=\frac{F_1}{F_2}\times\frac{\left({\displaystyle\frac32}\right)^2}{\left({\displaystyle\frac32}\right)^2}\times\frac{L_1}{L_2}\times\frac12\)
বা, \(\frac{Y_1}{Y_2}=\left(\frac32\right)^2\times\frac12\)
বা, \(\frac{Y_1}{Y_2}=\frac98\)
বা, \(\frac{Y_1}{Y_2}=\frac98\) (∵ \(F_1=F_2\))
∴ দুটির উপাদানের ইয়ং গুণাঙ্কের অনুপাত 9 : 8।
বিভিন্ন উপাদানে দুটি সমান দৈর্ঘ্যবিশিষ্ট তারের একটির ব্যাস 1 mm ও অপরটির ব্যাস 3 mm। তার দুটিকে একই বলে টানলে একটির দৈর্ঘ্য বৃদ্ধি অপরটির তিনগুণ হয়। দেখাও যে, এদের ইয়ং গুণাঙ্কের অনুপাত= 3 : 1।
প্রথম তারের ইয়ং গুণাঙ্ক \(\left(Y_1\right)=\frac F{\mathrm\pi\left({\displaystyle\frac{0.1}2}\right)^2}⋅\frac L{3l}\)
দ্বিতীয় তারের ইয়ং গুণাঙ্ক \(\left(Y_2\right)=\frac F{\mathrm\pi\left({\displaystyle\frac{0.3}2}\right)^2}⋅\frac Ll\) [ ∵ একটির দৈর্ঘ্য বৃদ্ধি l হলে, অপরটি 3l ]
∴ \(Y_1:Y_2=\frac{FL}{\mathrm\pi\left({\displaystyle\frac{0.1}2}\right)^2\times3\mathrm l}:\frac{FL}{\mathrm\pi\left({\displaystyle\frac{0.3}2}\right)^2\times\mathrm l}\)
বা, \(Y_1:Y_2=\frac1{\left(0.1\right)^2\times3}:\frac1{\left(0.3\right)^2\times1}\)
বা, \(Y_1:Y_2=\frac13:\frac19\)
বা, \(Y_1:Y_2=3:1\) (প্রমাণিত)
একই দৈর্ঘ্য ও প্রস্থচ্ছেদের দুটি দণ্ডের উপাদানের ইয়ং গুণাঙ্ক যথাক্রমে Y1 ও Y2। দণ্ড দুটির একটিকে অপরটির একপ্রান্তে যুক্ত করা হলে দেখাও যে যুগ্ম দণ্ড দুটির তুল্য ইয়ং গুণাঙ্ক = \(\frac{2Y_1Y_2}{Y_1+Y_2}\)
\(Y_1=\frac FA⋅\frac L{l_1}\) এবং \(Y_2=\frac FA⋅\frac L{l_2}\)
∴ \(l_1=\frac FA⋅\frac L{Y_1}\)
∴ \(l_2=\frac FA⋅\frac L{Y_2}\)
∴ তুল্য ইয়ং গুণাঙ্ক \(Y=\frac FA⋅\frac{2L}{\left(l_1+l_2\right)}\)
বা, \(Y=\frac FA⋅\frac{2L}{\left({\displaystyle\frac FA}⋅{\displaystyle\frac L{Y_1}}+{\displaystyle\frac FA}⋅{\displaystyle\frac L{Y_2}}\right)}\)
বা, \(Y=\frac FA⋅\frac{2L}{{\displaystyle\frac FA}⋅L\left({\displaystyle\frac1{Y_1}}+{\displaystyle\frac1{Y_2}}\right)}\)
∴ \(Y=\frac{2Y_1Y_2}{Y_1+Y_2}\) (প্রমাণিত)।
250 cm দীর্ঘ ও 1 mm ব্যাসের একটি লোহার তারের এক প্রান্ত দড়ির সঙ্গে দৃঢ়ভাবে যুক্ত অন্য প্রান্তে 8 kg ভরের একটি বস্তু রাখা হলে তারের দৈর্ঘ্য বৃদ্ধি কত হবে? [লোহার ইয়ং গুণাঙ্ক = 20 × 1011 dyn/cm2]
এখানে, L = 250 cm, r = 0.5 mm = 0.05 cm, g = 980 cm/s2
F= 8 kg-wt = 8 × 103 × 980 dyn
Y = 20 × 1011 dyn/cm2, g = 980 cm/s2
\(Y=\frac{F/\pi r^2}{l/L}=\frac{FL}{\mathrm{πr}^2\mathrm l}\\\)বা, \(\frac{8\times10^3\times980\times250}{3.14\times\left(0.05\right)^2\times l}=20\times10^{11}\)
বা, \(l=\frac{8\times10^3\times980\times250}{3.14\times\left(0.05\right)^2\times20\times10^{11}}\)
বা, \(l=0.125\;cm\)
ইস্পাতের ইয়ং গুণাঙ্ক 2 × 1011 dyn/cm2। 1 m লম্বা এবং 0.1 cm2 প্রস্থচ্ছেদ বিশিষ্ট একটি ইস্পাতের তারে 2 kg ভার ঝোলালে দৈর্ঘ্য বৃদ্ধি কত হবে?
ইস্পাতের ইয়ং গুণাঙ্ক (Y) = 2 × 1011 dyn/cm2
ইস্পাতের তারের প্রাথমিক দৈর্ঘ্য (L) = 1 m = 100 cm
ইস্পাতের প্রস্থচ্ছেদের ক্ষেত্রফল (A) = 0.1 cm2
ধরি, দৈর্ঘ্য বৃদ্ধি = l
F = mg = 2 × 1000 × 980 dyn
আমরা জানি, \(Y=\frac{F/L}{l/L}\)
বা, \(Y=\frac{FL}{Al}\)
বা, \(l=\frac{FL}{AY}\)
বা, \(l=\frac{2\times1000\times980\times100}{0.1\times2\times10^{11}}\)
বা, \(l=0.0098\;cm\)
বা, \(l=0.098\;mm\)
একটি তারে 9.8 × 106 N⋅m-2 পীড়ন প্রয়োগ করলে দৈর্ঘ্য বৃদ্ধির শতকরা হার কত? দেওয়া আছে, তারের উপাদানের ইয়ং গুণাঙ্ক Y = 10 × 1011 N⋅m-2।
তারের পীড়ন = 9.8 × 106 N⋅m-2
তারের উপাদানের ইয়ং গুণাঙ্ক (Y) = 10 × 1011 N⋅m-2
ধরি, দৈর্ঘ্য বৃদ্ধি = l, প্রাথমিক দৈর্ঘ্য = L
বা,
বা, \(\frac lL=\frac{9.8\times10^6}{10\times10^{11}}\)
বা, \(\frac lL\times100=\frac{9.8\times10^6\times100}{10\times10^{11}}\)
বা, \(\frac lL\times100=9.8\times10^{-3}\)
∴ দৈর্ঘ্য বৃদ্ধির শতকরা হার \(9.8\times10^{-3}\)।
A ও B দুটি একই ধাতুনির্মিত তারের দৈর্ঘ্যের অনুপাত 1 : 2 এবং ব্যাসের অনুপাত 2 : 1। যদি তার দুটিকে একই বল দ্বারা টান দেওয়া হয় তবে A ও B -এর দৈর্ঘ্য বৃদ্ধির অনুপাত কত হবে?
প্রশ্নানুযায়ী, প্রথম তারের ইয়ং গুণাঙ্ক \(\left(Y_A\right)=\frac F{\pi\left({\displaystyle\frac{2r}2}\right)^2}\times\frac L{l_A}\)
দ্বিতীয় তারের ইয়ং গুণাঙ্ক \(\left(Y_B\right)=\frac F{\pi\left({\displaystyle\frac r2}\right)^2}\times\frac{2L}{l_B}\)
[ যেখানে একটির দৈর্ঘ্য বৃদ্ধি lA ও অপরটির lB ]
তার দুটি একই ধাতুনির্মিত বলে YA = YB
∴ \(\frac F{\pi\left({\displaystyle\frac{2r}2}\right)^2}\times\frac L{l_A}=\frac F{\pi\left({\displaystyle\frac r2}\right)^2}\times\frac{2L}{l_B}\)
∴ \(\frac{l_A}{l_B}=1:8\)
∴ A ও B -এর দৈর্ঘ্য বৃদ্ধির অনুপাত = 1 : 8।
2 m লম্বা একটি তারের দৈর্ঘ্য 5 mm বাড়ানো হল। তারের উপাদানের ইয়ং গুণাঙ্ক Y = 2 × 1011 N⋅m-2 হলে তারে উৎপন্ন পীড়ন নির্ণয় করো।
তারের প্রাথমিক দৈর্ঘ্য (L) = 2 m;
তারের দৈর্ঘ্য বৃদ্ধি (l) = 5 mm = 5 × 10-3 m
তারের উপাদানের ইয়ং গুণাঙ্ক (Y) = 2 × 1011 N⋅m-2
বা, পীড়ন = \(Y\times\frac lL\)
বা, পীড়ন = \(2\times10^{11}\times\frac{5\times10^{-3}}2\)
বা, পীড়ন = 5 × 108 N⋅m-2।
একটি তারের ইয়ং গুণাঙ্ক Y। প্রস্থচ্ছেদের ক্ষেত্রফল 1 একক হলে তারের দৈর্ঘ্য দ্বিগুণ করতে কত বল লাগবে?
তারের ইয়ং গুণাঙ্ক = Y;
তারের প্রস্থচ্ছেদের ক্ষেত্রফল (A) = 1 একক
ধরি, তারের প্রাথমিক দৈর্ঘ্য = L একক
দৈর্ঘ্য দ্বিগুণ করলে দৈর্ঘ্য বৃদ্ধি (l) = 2L – L = L একক
ধরি, বল = \(F\)
বা, \(Y=\frac{F/A}{l/L}\)
বা, \(\frac FA\times\frac Ll=Y\)
বা, \(F=\frac{YAl}L\)
বা, \(F=\frac{Y\times1\times L}L\)
বা, F = Y
∴ তারের দৈর্ঘ্য দ্বিগুণ করতে Y একক বল লাগবে।
একটি বস্তুর পীড়ন-বিকৃতি লেখচিত্র নীচে দেওয়া হল। নীচের লেখচিত্র থেকে বস্তুটির ইয়ং গুণাঙ্কের মান নির্ণয় করো।
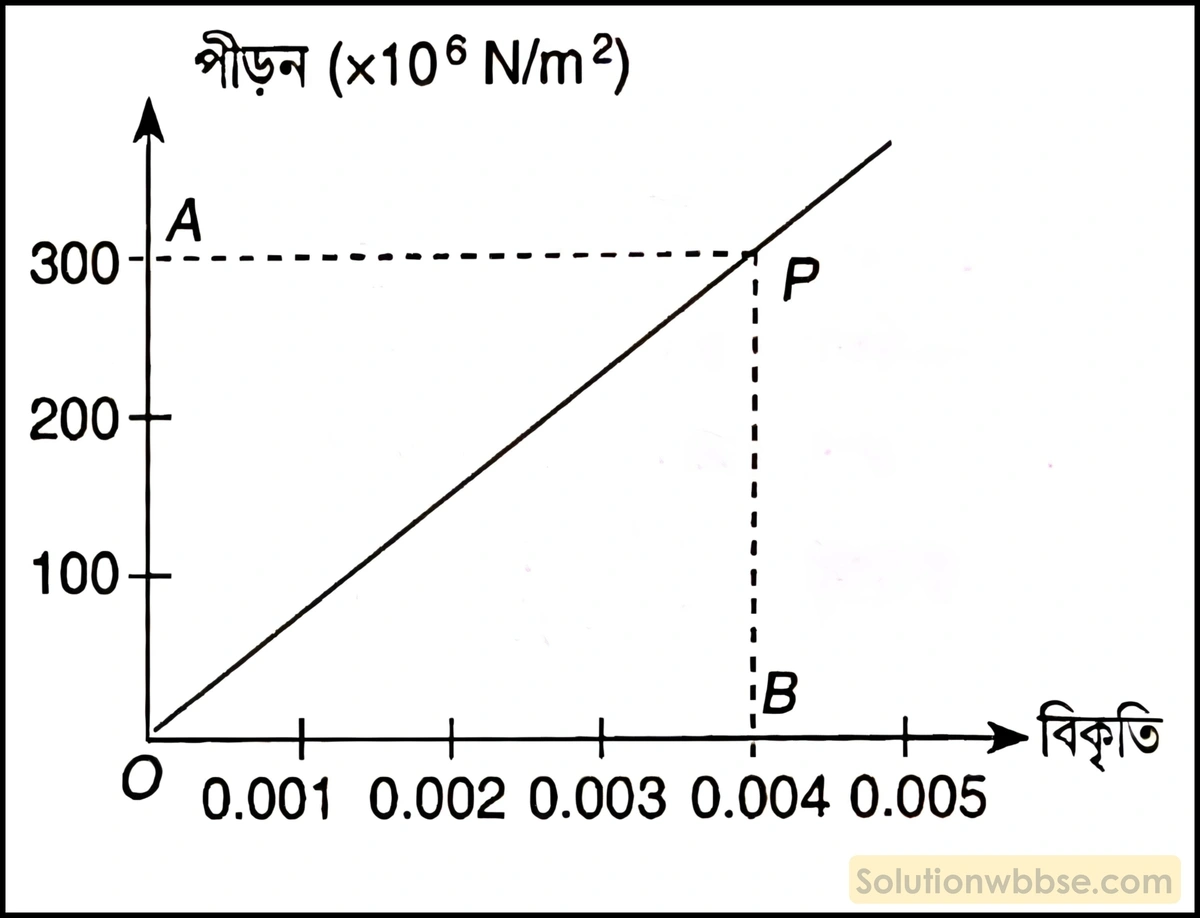
লেখচিত্র থেকে বোঝা যায়, পীড়ন = 300 × 106 N/m2 হলে বিকৃতি = 0.004।
∴
বা, বস্তুটির ইয়ং গুণাঙ্ক = \(\frac{300\times10^6}{0.004}\) N/m2
বা, বস্তুটির ইয়ং গুণাঙ্ক = 75 × 109 N/m2
1 m দীর্ঘ একটি তারের এক প্রান্ত সিলিং-এ দৃঢ়ভাবে আকন্দ রেখে অপর প্রান্তে W ভার চাপানো হল। তারটির ভার-বিস্তৃতি লেখচিত্র নিম্নরূপ। তারটির প্রস্থচ্ছেদের ক্ষেত্রফল 10-6 m2 হলে ইয়ং গুণাঙ্ক কত?
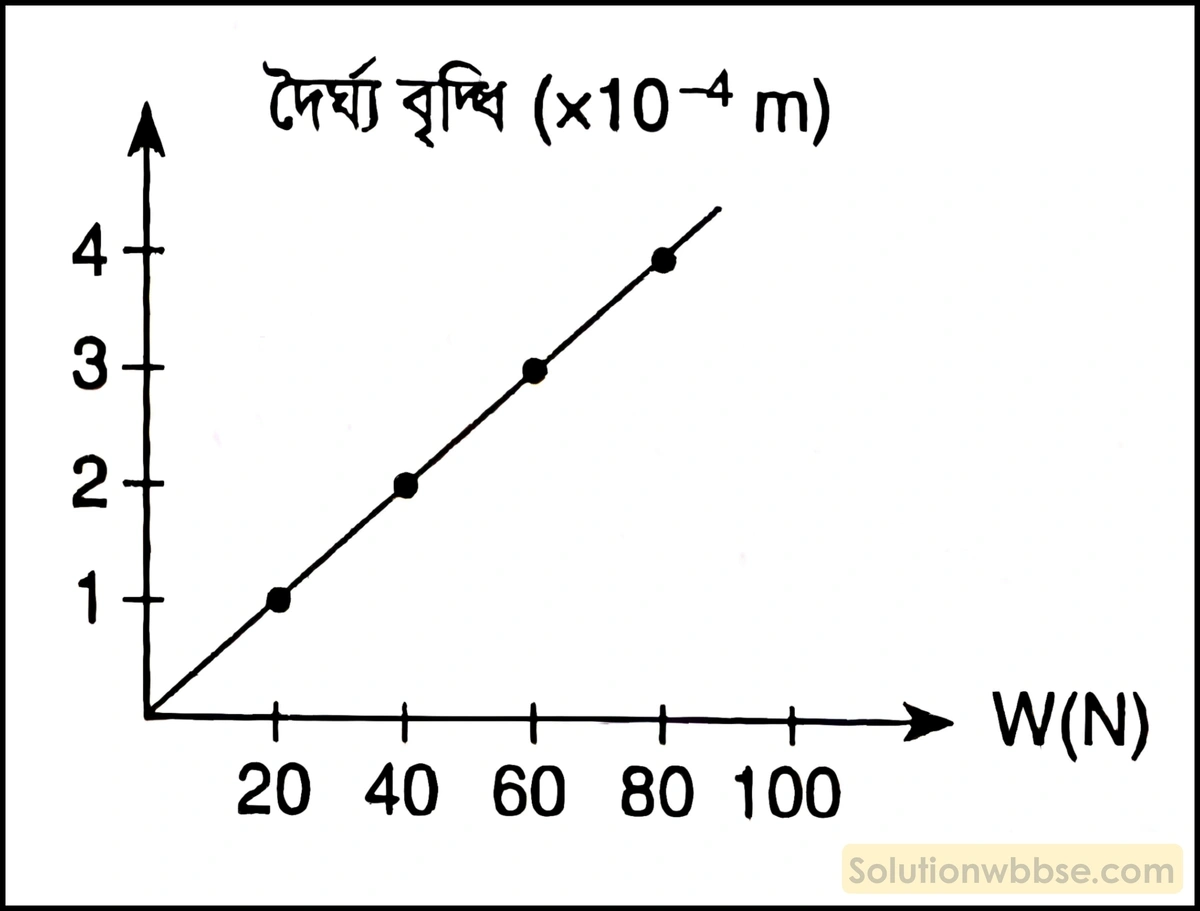
বা, ইয়ং গুণাঙ্ক = \(\frac{80}{10^{-6}}\div\frac{4\times10^{-4}}1\;N/m^2\)
বা, ইয়ং গুণাঙ্ক = \(\frac{80}{10^{-6}\times4\times10^{-4}}\;N/m^2\)
বা, ইয়ং গুণাঙ্ক = \(20\times10^{10}\;N/m^2\)
∴ তারটির ইয়ং গুণাঙ্ক = \(20\times10^{10}\;N/m^2\)।
30 m দীর্ঘ এবং 2 × 10-6 m2 প্রস্থচ্ছেদের একটি তারের এক প্রান্তে 5 kg ওজন ঝোলালে তারের দৈর্ঘ্য 0.49 × 10-2 m বাড়ে। তারটির অনুদৈর্ঘ্য পীড়ন, অনুদৈর্ঘ্য বিকৃতি এবং ইয়ং গুণাঙ্ক নির্ণয় করো।
বা, অনুদৈর্ঘ্য পীড়ন = \(\frac{5\times9.8}{2\times10^{-6}}\;N/m^2\)
বা, অনুদৈর্ঘ্য পীড়ন = \(2.45\times10^7\;N/m^2\)
বা, অনুদৈর্ঘ্য বিকৃতি = \(\frac{0.49\times10^{-2}}{30}\;N/m^2\)
বা, অনুদৈর্ঘ্য বিকৃতি = \(1.63\times10^{-4}\;N/m^2\)
বা, ইয়ং গুণাঙ্ক = \(\frac{2.45\times10^7}{1.63\times10^{-4}}\;N/m^2\)
বা, ইয়ং গুণাঙ্ক = \(1.5\times10^{11}\;N/m^2\)
2 mm ব্যাসার্ধের একটি ঝুলন্ত তামার তারের মুক্ত প্রান্ত থেকে 5 kg ভর ঝোলানো হল। তারটিতে অদ্ভূত অনুদৈর্ঘ্য পীড়ন কত হবে? এক্ষেত্রে তারটির অনুদৈর্ঘ্য বিকৃতি = 0.02 হলে তামার ইয়ং গুণাঙ্ক কত?
বা, অনুদৈর্ঘ্য পীড়ন = \(\frac{5\times1000\times980}{\mathrm\pi\times\left(0.2\right)^2}\;dyn/cm^2\)
বা, অনুদৈর্ঘ্য পীড়ন = \(3.9\times10^7\;dyn/cm^2\)
বা, তামার ইয়ং গুণাঙ্ক = \(\frac{3.9\times10^7}{0.02}\;dyn/cm^2\)
বা, তামার ইয়ং গুণাঙ্ক = \(1.95\times10^9\;dyn/cm^2\)
একটি স্প্রিংয়ের নিম্নপ্রান্ত থেকে 4 kg ওজন ঝুলিয়ে দিলে স্প্রিংয়ের 2 cm দৈর্ঘ্য বৃদ্ধি হয়। স্প্রিংটির বলধ্রুবক কত?
আমরা জানি, F = kx
এখানে, F = 4 × 9.8 N, x = 2 cm = 0.02 m
∴ \(k=\frac Fx\)
বা, \(k=\frac{4\times9.8}{0.02}\)
বা, \(k=1960\) N/m
∴ স্প্রিংটির বলধ্রুবক 1960 N/m।
একটি স্প্রিংয়ের দৈর্ঘ্য 2 cm বৃদ্ধি করার জন্য 50 N বলের প্রয়োজন হয়। স্প্রিংটির বলধ্রুবক কত?
বল (F) = 50 N; দৈর্ঘ্যবৃদ্ধি (x) = 2 cm = \(\frac2{100}\) m
∴ স্প্রিংটির বলধ্রুবক \(\left(k\right)=\frac Fx\)
বা, \(k=\frac{50}{\displaystyle\frac2{100}}\)
বা, \(k=\frac{50}1\times\frac{100}2\)
বা, \(k=2500\) N/M
একটি স্প্রিংয়ের বলধ্রুবক 2 N/m হলে, স্প্রিংটির 0.5 mm দৈর্ঘ্য বৃদ্ধি করতে কত বল প্রয়োগ করতে হবে?
স্প্রিংয়ের বলধ্রুবক (k) = 2 N/m
স্প্রিংয়ের দৈর্ঘ্য বৃদ্ধি (x) = 0.5 mm = 0.5 × 10-3 m
∴ F = kx
বা, F = 2 × 0.5 × 10-3
বা, F = 1 × 10-3 N
বা, F = 0.001 N।
∴ স্প্রিংটির 0.5 mm দৈর্ঘ্য বৃদ্ধি করতে 0.001 N বল প্রয়োগ করতে হবে।
একটি স্প্রিংকে তিনটি সমান ভাগে কাটলে, স্প্রিং -এর টুকরোগুলির প্রতিটির বলধ্রুবকের মানের কী পরিবর্তন হবে?
ধরা যাক, স্প্রিং-এর প্রাথমিক দৈর্ঘ্য x এবং তা থেকে সর্বোচ্চ যে ভার ঝোলানো হয়েছে তার মান F।
∴ ওই স্প্রিংয়ের বলধুবক \(\left(k\right)=\frac Fx\)
স্প্রিংটিকে তিনটি সমান খণ্ডে বিভক্ত করলে প্রত্যেক খণ্ডের দৈর্ঘ্য হয়, \(x_1=\frac x3\)
∴ প্রত্যেক টুকরোর বলধ্রুবক \(\left(k_1\right)=\frac F{x_1}\)
বা, \(k_1=\frac F{\displaystyle\frac x3}\)
বা, \(k_1=\frac{3F}x\)
বা, \(k_1=3k\)
একটি স্প্রিংকে কেটে দু-টুকরো করলে প্রতিটি অংশের বলধ্রুবক কত হবে?
ধরা যাক, বল প্রয়োগে মূল স্প্রিংয়ের দৈর্ঘ্য বৃদ্ধি = \(x\)
∴ মূল স্প্রিংয়ের বলধ্রুবক \(\left(k\right)=\frac Fx\)
এবার মূল স্প্রিংকে কেটে দু-টুকরো করে প্রতিটি অংশে বল প্রয়োগ করলে স্প্রিংটির দৈর্ঘ্য বৃদ্ধি = \(\frac x2\)
∴ প্রতিটি অংশের বলধ্রুবক \(\left(k’\right)=\frac F{\displaystyle\frac x2}\)
বা, \(\left(k’\right)=2\times\frac Fx\)
বা, \(\left(k’\right)=2k\)
বা, \(\left(k’\right)=2\) × মূল স্প্রিংয়ের বলধ্রুবক।
একটি স্প্রিংয়ের একপ্রান্ত কোনো দৃঢ় অবলম্বনের সঙ্গে আটকে অপর প্রান্ত থেকে 4 kg ওজন ঝোলালে স্প্রিংটির দৈর্ঘ্য 1 cm বাড়ে। স্প্রিংটির বলধ্রুবক কত? যদি 2 kg ওজন ঝোলানো হত, তবে স্প্রিংটির দৈর্ঘ্য বৃদ্ধি কত হত?
প্রদত্ত স্প্রিংয়ের বলধ্রুবক = \(\frac{4\times9.8}{0.01}\)
= \(3920\;N/m\)।
= \(\frac{2\times9.8}{3920}\)
= 0.005 m
= 0.5 cm
∴ স্প্রিংটির দৈর্ঘ্য বৃদ্ধি 0.5 cm হত।
নৈর্ব্যক্তিক প্রশ্নোত্তর
সঠিক উত্তরটি নির্বাচন করো
ন্যূনতম স্থিতিস্থাপক সামর্থ্য দেখায় –
- কঠিন
- তরল
- গ্যাস
- কোনোটিই নয়
উত্তর – 3. গ্যাস
রবারের স্থিতিস্থাপকতা লোহা অপেক্ষা –
- বেশি
- কম
- সমান
- স্থিতিস্থাপক নয়
উত্তর – 2. কম
স্থিতিস্থাপক ধ্রুবক মাত্রাগতভাবে তুল্য –
- পীড়ন -এর সঙ্গে
- বিকৃতি -এর সঙ্গে
- পৃষ্ঠটান -এর সঙ্গে
- ত্বরণ -এর সঙ্গে
উত্তর – 1. পীড়ন -এর সঙ্গে
ধাতুর যে ধর্মের জন্য ধাতুটিকে খুব সরু তারে পরিণত করা যায়, তা হল –
- সান্দ্রতা
- নমনীয়তা
- স্থিতিস্থাপকতা
- প্রসারণশীলতা
উত্তর – 4. প্রসারণশীলতা
পীড়ন ও বিকৃতির ধারণা ব্যবহার করে যে সূত্রটি প্রকাশ করা হয়, তা হল –
- ইয়ং -এর সূত্র
- হুকের সূত্র
- নিউটনের সূত্র
- টরিসেলির সূত্র
উত্তর – 1. ইয়ং -এর সূত্র
কোনো তারের অনুদৈর্ঘ্য বিকৃতি মাপার জন্য তারটি কী আকারের হওয়া উচিত? –
- লম্বা সরু তার
- ক্ষুদ্র সরু তার
- আয়তাকার ব্লক
- মোটা তার
উত্তর – 1. লম্বা সরু তার
বল প্রয়োগে কোনো তার হঠাৎ ছিঁড়ে গেলে তারের উষ্ণতা –
- কমবে
- একই থাকবে
- বাড়বে
- প্রথমে কমবে, পরে বাড়বে
উত্তর – 3. বাড়বে
পদার্থের কোন্ বৈশিষ্ট্যটি ঝালাইয়ের কাজে লাগে? –
- সান্দ্রতা
- ঘর্ষণ
- পৃষ্ঠটান
- স্থিতিস্থাপকতা
উত্তর – 4. স্থিতিস্থাপকতা
k বলধ্রুবক বিশিষ্ট স্প্রিংকে দুটি সমান অংশে কাটলে প্রতি অংশের বলধ্রুবক হয় –
- 4k
- 2k
- k
- \(\frac K2\)
উত্তর – 2. 2k
যে পদার্থগুলির ক্ষেত্রে স্থিতিস্থাপক সীমা অতিক্রম করে পীড়ন বৃদ্ধি করার সঙ্গে সঙ্গে পদার্থগুলি ভেঙে যায়, তারা –
- নমনীয়
- ভঙ্গুর
- প্রসার্য
- প্লাস্টিক
উত্তর – 2. ভঙ্গুর
কোনো পদার্থের ইয়ং গুণাঙ্ক CGS ও SI -তে যথাক্রমে Y1 ও Y2 হল –
- Y1 = Y2
- Y1 = 10 Y2
- Y2 = 10 Y1
- কোনোটিই নয়।
উত্তর – 2. Y1 = 10 Y2
স্থিতিস্থাপক সীমার মধ্যে পীড়ন ও বিকৃতির পরিবর্তনের লেখচিত্রটি হয় –
- অধিবৃত্ত
- বৃত্ত
- সরলরেখা
- পরাবৃত্ত
উত্তর – 3. সরলরেখা
দুটি স্প্রিংয়ের বলধ্রুবক k1 ও k2 (k1 > k2)। একই বল F -এর ক্রিয়ায় তাদের দৈর্ঘ্যবৃদ্ধি x1 ও x2 হলে, যা সম্ভব, তা হল –
- \(k_1x_1=k_2x_2\\\)
- \(\frac{k_1}{x_1}=\frac{k_2}{x_2}\\\)
- \(\frac{k_1^2}{x_1}=\frac{k_2^2}{x_2}\\\)
- \(\left(\frac{k_1}{x_1}\right)^2=\left(\frac{k_2}{x_2}\right)^2\\\)
উত্তর – 1. \(k_1x_1=k_2x_2\)
শূন্যস্থান পূরণ করো
SI -তে পীড়ন ও ___ রাশির একক অভিন্ন।
উত্তর – SI -তে পীড়ন ও চাপ রাশির একক অভিন্ন।
দুটি ___ অনুপাত হওয়ায় বিকৃতি একটি মাত্রাহীন রাশি।
উত্তর – দুটি দৈর্ঘ্যের অনুপাত হওয়ায় বিকৃতি একটি মাত্রাহীন রাশি।
স্প্রিং সাধারণত ___ তৈরি হয়।
উত্তর – স্প্রিং সাধারণত ইস্পাতের তৈরি হয়।
বলধ্রুবকের মান যত বেশি হবে, স্প্রিং তত ___ হবে।
উত্তর – বলধ্রুবকের মান যত বেশি হবে, স্প্রিং তত নমনীয় হবে।
একটি ভঙ্গুর পদার্থের উদাহরণ হল ___।
উত্তর – একটি ভঙ্গুর পদার্থের উদাহরণ হল কাচ।
তোমার বইয়ের পার্শ্বতলটি আয়তাকার থেকে সামান্তরিক আকার হলে ___ বিকৃতি হবে।
উত্তর – তোমার বইয়ের পার্শ্বতলটি আয়তাকার থেকে সামান্তরিক আকার হলে কৃন্তন বিকৃতি হবে।
বিকৃত বস্তুতে সৃষ্টি ___ হয়।
উত্তর – বিকৃত বস্তুতে পীড়ন সৃষ্টি হয়।
নিকেল, টিটেনিয়ামের তৈরি ধাতব উপাদানগুলির ___ ক্ষমতা সর্বোচ্চ।
উত্তর – নিকেল, টিটেনিয়ামের তৈরি ধাতব উপাদানগুলির স্থিতিস্থাপক ক্ষমতা সর্বোচ্চ।
সর্বপ্রথম আধুনিক ঝুলন্ত সেতু নর্থ ওয়ালস-এর মিনাই ব্রিজ (Menai Bridge), যা শক্ত ___ পদার্থ দ্বারা তৈরি।
উত্তর – সর্বপ্রথম আধুনিক ঝুলন্ত সেতু নর্থ ওয়ালস-এর মিনাই ব্রিজ (Menai Bridge), যা শক্ত স্থিতিস্থাপক পদার্থ দ্বারা তৈরি।
ঠিক বা ভুল নির্বাচন করো
আন্তরাণবিক দূরত্ব অপরিবর্তিত রাখতে চাওয়ার প্রবণতা থেকেই স্থিতিস্থাপক ধর্মের উৎপত্তি।
উত্তর – ঠিক।
পীড়ন একটি মাত্রাহীন রাশি।
উত্তর – ভুল।
সঠিক উত্তর – মাত্রীয় সংকেত [ML-1T-2]।
যে-কোনো স্থিতিস্থাপক গুণাঙ্ককেই পীড়ন ও বিকৃতির অনুপাত হিসেবে প্রকাশ করা যায়।
উত্তর – ঠিক।
একটি তারের অসহভার W1 তারটিকে কেটে দুটি সমান টুকরো করলে প্রত্যেক খণ্ডের অসহভার \(\frac W2\) হবে।
উত্তর – ভুল।
সঠিক উত্তর – একই থাকবে।
বলধ্রুবকের মান যত বেশি হয় স্প্রিংকে বল প্রয়োগে সংকুচিত করা তত সহজ হয়।
উত্তর – ভুল।
সঠিক উত্তর – তত কঠিন হয়।
দু-একটি শব্দে উত্তর দাও
পীড়নের মাত্রীয় সংকেত কী?
পীড়নের মাত্রীয় সংকেত [ML-1T-2]।
পীড়নের SI এককটি লেখো।
পীড়নের SI একক নিউটন/মি2।
কোনটি বেশি স্থিতিস্থাপক – হিরে না ইস্পাত?
হিরে বেশি স্থিতিস্থাপক।
ইয়ং গুণাঙ্কের মাত্রীয় সংকেত কী?
ইয়ং গুণাঙ্কের মাত্রীয় সংকেত [ML-1T-2]।
জলের কি ইয়ং গুণাঙ্ক আছে?
না, ইয়ং গুণাঙ্ক কঠিনের বৈশিষ্ট্য।
একটি পূর্ণ স্থিতিস্থাপক বস্তুর ইয়ং গুণাঙ্কের মান কত?
একটি পূর্ণ স্থিতিস্থাপক বস্তুর ইয়ং গুণাঙ্কের মান অসীম।
তামার কোন্ ধর্মকে কাজে লাগিয়ে ইলেকট্রিকের সরু তার তৈরি হয়?
তামার প্রসারণশীলতা ধর্মকে কাজে লাগিয়ে ইলেকট্রিকের সরু তার তৈরি হয়।
একটি তারকে সমান দুভাগে ভাগ করলে প্রতি ভাগের ইয়ং গুণাঙ্কের কী পরিবর্তন হবে?
একটি তারকে সমান দুভাগে ভাগ করলে প্রতি ভাগের ইয়ং গুণাঙ্কের কোনো পরিবর্তন হবে না।
একটি প্রসার্যশীল পদার্থের উদাহরণ দাও।
একটি প্রসার্যশীল পদার্থের উদাহরণ হল সোনা।
রবার ও ইস্পাতের মধ্যে কোনটির ইয়ং গুণাঙ্কের মান বেশি হবে?
রবার ও ইস্পাতের মধ্যে ইস্পাতের ইয়ং গুণাঙ্কের মান বেশি হবে।
হুকের সূত্রের ধ্রুবকের নাম কী?
হুকের সূত্রের ধ্রুবকের নাম বল ধ্রুবক।
একই উপাদানে তৈরি দুটি তারের ইয়ং গুণাঙ্ক তাদের প্রস্থচ্ছেদের ওপর কীভাবে নির্ভর করে?
অপরিবর্তিত থাকবে।
বলধ্রুবক স্প্রিং -এর কোন্ ধর্ম প্রকাশ করে?
বলধ্রুবক স্প্রিং -এর অনমনীয়তা ধর্ম প্রকাশ করে।
পূর্ণ নমনীয় বস্তুর ক্ষেত্রে ইয়ং গুণাঙ্কের মান কত?
পূর্ণ নমনীয় বস্তুর ক্ষেত্রে ইয়ং গুণাঙ্কের মান শূন্য।
তামার ইয়ং গুণাঙ্ক কত?
তামার ইয়ং গুণাঙ্ক 1.26 × 1010 N/m2 (প্রায়)।
লোহা ও অ্যালুমিনিয়ামের মধ্যে কোনটির ইয়ং গুণাঙ্ক বেশি?
লোহা ও অ্যালুমিনিয়ামের মধ্যে লোহার ইয়ং গুণাঙ্ক বেশি।
10 m দীর্ঘ তারে টান প্রয়োগে দৈর্ঘ্য বৃদ্ধি 1 cm হলে অনুদৈর্ঘ্য বিকৃতির মান কত?
10 m দীর্ঘ তারে টান প্রয়োগে দৈর্ঘ্য বৃদ্ধি 1 cm হলে অনুদৈর্ঘ্য বিকৃতির মান \(\frac lL=\frac1{10\times100}=0.001\)।
For High-Types
একটি ইস্পাতের তার থেকে ভার ঝুলিয়ে এর দৈর্ঘ্য দ্বিগুণ করা যায় কি?
ইস্পাতের তার থেকে ভার ঝুলিয়ে এর দৈর্ঘ্য দ্বিগুণ করা সম্ভব নয়। কারণ দৈর্ঘ্য দ্বিগুণ হতে হলে দৈর্ঘ্য বৃদ্ধি প্রাথমিক দৈর্ঘ্যের সমান হওয়া প্রয়োজন। কিন্তু দৈর্ঘ্য বৃদ্ধির মান প্রাথমিক দৈর্ঘ্যের সমান হওয়ার বহু পূর্বেই অসহভার অতিক্রম করে তারটি ছিঁড়ে যায়।
এলিনভার কী?
নিকেল এবং ইনভার দ্বারা নির্মিত বিশেষ কিছু সংকর ধাতুর ক্ষেত্রে ওই উপাদানের স্থিতিস্থাপকতা ধর্ম উষ্ণতা নিরপেক্ষ হয়। এদের এলিনভার বলে।
[Elinver : El, (Elastic) + invar (invariable)
স্থিতিস্থাপক গুণাঙ্কগুলির মান উষ্ণতা ও চাপের দ্বারা কীভাবে প্রভাবিত হয়?
উষ্ণতা বৃদ্ধিতে সাধারণত পদার্থের স্থিতিস্থাপকতা কমে (ব্যতিক্রম রবার)। তবে বিভিন্ন স্থিতিস্থাপক গুণাঙ্কগুলির মানের পরিবর্তন কোনো নির্দিষ্ট নিয়ম অনুযায়ী ঘটে না।
150°C উষ্ণতা পর্যন্ত ইয়ং গুণাঙ্ক (Y) পরম উষ্ণতার (T) সঙ্গে সূচকীয়ভাবে হ্রাস পায়। 15°C থেকে 100°C উষ্ণতার পাল্লায় কৃন্তন গুণাঙ্ক উষ্ণতার সঙ্গে কমে। তবে তরলের আয়তন বিকৃতি গুণাঙ্ক উষ্ণতার সঙ্গে বাড়ে।
চাপ বৃদ্ধিতে গ্যাসীয় ও তরল পদার্থের সংনম্যতা হ্রাস পায়। তরলের ক্ষেত্রে এই পরিবর্তন প্রথম দিকে দ্রুত ও পরে ধীর গতিতে হয়। প্রচণ্ড চাপে কৃন্তন গুণাঙ্ক সামান্য বৃদ্ধি পেয়ে থাকে (ব্যতিক্রম – কাচ)। ইয়ং গুণাঙ্কও অত্যধিক চাপে সামান্য বাড়ে।
একটি টান করা তার হঠাৎ ছিঁড়ে গেলে তার উষ্ণতার পরিবর্তন হয় কেন?
টান করা তারটির দৈর্ঘ্য বৃদ্ধি করতে যে পরিমাণ কার্য করতে হয়, তা তারের মধ্যে স্থিতিশক্তি হিসেবে সঞ্চিত থাকে। তারটি হঠাৎ ছিঁড়ে গেলে ওই স্থিতিশক্তি, তাপশক্তিতে রূপান্তরিত হয়। ফলে টান করা তারটির উষ্ণতা বৃদ্ধি পায়।
স্থিতিস্থাপক সীমা ছাড়িয়ে গেলে কোনো তারের কেমন পরিবর্তন হবে উল্লেখ করো।
স্থিতিস্থাপক সীমা ছাড়িয়ে গেলে পীড়নের মাত্রা বাড়ালে বিকৃতি পূর্বের অনুপাতের তুলনায় আরও বেশি বাড়বে। পীড়ন আরও বাড়ালে বিকৃতি খুব দ্রুত হারে বাড়বে এবং অবশেষে তারটির কোনো অংশ অন্যান্য অংশের তুলনায় সরু হবে এবং শেষ পর্যন্ত তারটির ওই অংশ ছিঁড়ে যাবে।
একটি তারকে কেটে তার দৈর্ঘ্য অর্ধেক করলে ওই তারটি যে সর্বাধিক ভার বহন করবে, তার কোনো পরিবর্তন হবে কি?
তারটি সর্বাধিক যে ভার বহনে সক্ষম, অর্থাৎ, অসহ ভারের মান তারটিতে সৃষ্ট অসহ পীড়নের ওপর নির্ভর করে, তার প্রাথমিক দৈর্ঘ্য বা দৈর্ঘ্য পরিবর্তনের ওপর নয়। বিকৃত অবস্থায় তারের অভ্যন্তরে যে পীড়ন সৃষ্টি হয়, সেটি তারের প্রস্থচ্ছেদের ক্ষেত্রফলের ব্যস্তানুপাতিক, তাই তারটি কেটে দৈর্ঘ্য অর্ধেক করলেও প্রস্থচ্ছেদ অপরিবর্তিত থাকায়, অসহ ভারের মানের কোনো পরিবর্তন হবে না।
Class 9 Physical Science – Notes for All Chapters
| Chapter Name | Tropics |
|---|---|
| পরিমাপ | পরিমাপ ও একক বিভিন্ন মাপের একক মাত্রা পরিমাপ |
| বল ও গতি | স্থিতি ও গতি গতির সমীকরণ নিউটনের প্রথম গতিসূত্র নিউটনের দ্বিতীয় গতি সূত্র নিউটনের তৃতীয় গতিসূত্র বিভিন্ন ধরনের বল রৈখিক ভরবেগ রৈখিক ভরবেগ সংরক্ষণ |
| পদার্থ : গঠন ও ধর্ম | তরল ও বায়ুর চাপ আর্কিমিডিসের নীতি পৃষ্ঠটান সান্দ্রতা বার্নোলির নীতি স্থিতিস্থাপকতা |
| পদার্থ : পরমাণুর গঠন ও পদার্থের ভৌত ও রাসায়নিক ধর্মসমূহ | পরমাণুর গঠন মোলের ধারণা দ্রবণ অ্যাসিড, ক্ষার, লবণ মিশ্রণের উপাদানের পৃথকীকরণ জল |
| শক্তির ক্রিয়া , কার্য, ক্ষমতা | শক্তির ক্রিয়া , কার্য, ক্ষমতা |
| তাপ | ক্যালোরিমিতি কার্য ও তাপের তুল্যতা লীনতাপ সম্পৃক্ত ও অসম্পৃক্ত বাষ্প জলের ব্যতিক্রান্ত প্রসারণ |
| শব্দ | শব্দের উৎস : কম্পন শব্দের বিস্তার : তরঙ্গ শব্দের কয়েকটি ধর্ম শব্দের বৈশিষ্ট্য মানুষের কান ও শব্দ শোনার কৌশল শব্দদূষণ |
আজকের আর্টিকেলে আমরা নবম শ্রেণির ভৌতবিজ্ঞান বইয়ের তৃতীয় অধ্যায় “পদার্থ : গঠন ও ধর্ম” এর “স্থিতিস্থাপকতা” থেকে পরীক্ষায় আসা গুরুত্বপূর্ণ প্রশ্ন ও উত্তরগুলো আলোচনা করেছি। এই প্রশ্নোত্তরগুলো নবম শ্রেণির বার্ষিক পরীক্ষা, এমনকি চাকরি বা যেকোনো প্রতিযোগিতামূলক পরীক্ষার জন্যও উপযোগী। কারণ, এই অধ্যায়ের প্রশ্ন প্রায়ই বিভিন্ন পরীক্ষায় কমন আসে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সাহায্য করবে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন কিংবা টেলিগ্রামে যোগাযোগ করুন—আপনাদের প্রশ্নের উত্তর দিতে আমি সর্বদা প্রস্তুত।
ধন্যবাদ সবাইকে।






মন্তব্য করুন