পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) দশম শ্রেণির গণিত পাঠ্যবইয়ের একবিংশতম অধ্যায় হলো ‘লগারিদম’। এই পোস্টে ‘কষে দেখি – 21‘-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. মান নির্ণয় করি
(i) \(\log_4 \left(\frac{1}{64}\right)\)
সমাধান –
ধরি, \(\log_4 \left(\frac{1}{64}\right) = x\)
বা, \(4^x = \frac{1}{64}\)
বা, \(4^x = \left(\frac{1}{4}\right)^3\)
বা, \(4^x = 4^{-3}\)
বা, \(x = -3\)
\(\therefore \log_4 \left(\frac{1}{64}\right) = -3\)(ii) \(\log_{0.01} 0.000001\)
সমাধান –
ধরি, \(\log_{0.01} 0.000001 = x\)
বা, \((0.01)^x = 0.000001\)
বা, \((0.01)^x = (0.01)^3\)
বা, \(x = 3\)
\(\therefore \log_{0.01} 0.000001 = 3\)(iii) \(\log_{\sqrt{6}} 216\)
সমাধান –
ধরি, \(\log_{\sqrt{6}} 216 = x\)
বা, \((\sqrt{6})^x = 216\)
বা, \((\sqrt{6})^x = (6)^3\)
বা, \((\sqrt{6})^x = \{(\sqrt{6})^2\}^3\)
বা, \((\sqrt{6})^x = (\sqrt{6})^6\)
বা, \(x = 6\)
\(\therefore \log_{\sqrt{6}} 216 = 6\)(iv) \(\log_{2\sqrt{3}} 1728\)
সমাধান –
ধরি, \(\log_{2\sqrt{3}} 1728 = x\)
বা, \((2\sqrt{3})^x = 1728\)
বা, \((2\sqrt{3})^x = 2^6 \times 3^3\)
বা, \((2\sqrt{3})^x = 2^6 \times \{(\sqrt{3})^2\}^3\)
বা, \((2\sqrt{3})^x = 2^6 \times (\sqrt{3})^6\)
বা, \((2\sqrt{3})^x = (2\sqrt{3})^6\)
বা, \(x = 6\)
\(\therefore \log_{2\sqrt{3}} 1728 = 6\)2. (a) 625-এর লগারিদম 4 হলে, নিধান কী হবে হিসাব করে লিখি।
সমাধান –
ধরি, নিধান \(x\)।
\(\therefore \log_x 625 = 4\)বা, \(x^4 = 625\)
বা, \(x^4 = 5^4\)
বা, \(x = 5\)
\(\therefore\) নিধান \(5\)।
2. (b) 5832-এর লগারিদম 6 হলে, নিধান কী হবে হিসাব করে লিখি।
সমাধান –
ধরি, নিধান = \( x\)
\(\therefore \log_x 5832 = 6\)বা, \(x^6 = 5832\)
বা, \(x^6 = 2^3 \times 3^6\)
বা, \(x^6 = (\sqrt{2})^6 \times 3^6\)
বা, \(x^6 = (3\sqrt{2})^6\)
বা, \(x = 3\sqrt{2}\)
\(\therefore\) নিধান = \( 3\sqrt{2}\)
3. (a) \(1 + \log_{10} a = 2 \log_{10} b\) হলে, a কে b দ্বারা প্রকাশ করি।
সমাধান –
\(1 + \log_{10} a = 2 \log_{10} b\)বা, \(\log_{10} 10 + \log_{10} a = \log_{10} b^2\) [যেহেতু, \(\log_a a = 1\) এবং \(N \log_a M = \log_a M^N\)]
বা, \(\log_{10} (10a) = \log_{10} b^2\) [যেহেতু, \(\log_a M + \log_a N = \log_a (MN)\)]
বা, \(10a = b^2\) [যেহেতু, \(\log_a M = \log_a N \Rightarrow M = N\)]
বা, \(a = \frac{b^2}{10}\) [উত্তর]
3. (b) \(3 + \log_{10} x = 2 \log_{10} y\) হলে, x কে y দ্বারা প্রকাশ করো।
সমাধান –
বা, \(3 \log_{10} 10 + \log_{10} x = 2 \log_{10} y\) [যেহেতু, \(\log_{10} 10 = 1\)]
বা, \(\log_{10} 10^3 + \log_{10} x = \log_{10} y^2\) [যেহেতু, \(N \log_a M = \log_a M^N\)]
বা, \(\log_{10} 1000 + \log_{10} x = \log_{10} y^2\)
বা, \(\log_{10} (1000x) = \log_{10} y^2\)
বা, \(1000x = y^2\)
বা, \(x = \frac{y^2}{1000}\) [উত্তর]
4. মান নির্ণয় করি
(a) \(\log_2 [\log_2 \{\log_3 (\log_3 27^3)\}]\)
সমাধান –
\(\log_2 [\log_2 \{\log_3 (\log_3 27^3)\}]\)= \( \log_2 [\log_2 \{\log_3 (3 \log_3 27)\}]\) [যেহেতু, \(N \log_a M = \log_a M^N\)]
= \( \log_2 [\log_2 \{\log_3 (3 \log_3 3^3)\}]\)
= \( \log_2 [\log_2 \{\log_3 (9 \log_3 3)\}]\) [যেহেতু, \(3 \log_3 3^3 = 9\)]
= \( \log_2 [\log_2 \{\log_3 9\}]\) [যেহেতু, \(\log_a a = 1\)]
= \( \log_2 [\log_2 \{\log_3 3^2\}]\)
= \( \log_2 [\log_2 \{2 \log_3 3\}]\) [যেহেতু, \(N \log_a M = \log_a M^N\)]
= \( \log_2 [\log_2 2]\) [যেহেতু, \(\log_a a = 1\)]
= \( \log_2 1\) [যেহেতু, \(\log_a a = 1\)]
= \( 0\) [যেহেতু, \(\log_a 1 = 0\)] [উত্তর]
(b) \(\frac{\log \sqrt{27} + \log 8 – \log \sqrt{1000}}{\log 1.2}\)
সমাধান –
\(\frac{\log \sqrt{27} + \log 8 – \log \sqrt{1000}}{\log 1.2}\)= \( \frac{\log 3^{\frac{3}{2}} + \log 2^3 – \log 10^{\frac{3}{2}}}{\log \frac{12}{10}}\)
= \( \frac{\frac{3}{2} \log 3 + 3 \log 2 – \frac{3}{2} \log 10}{\log 12 – \log 10}\) [যেহেতু, \(N \log_a M = \log_a M^N\) এবং \(\log_p \frac{A}{B} = \log_p A – \log_p B\)]
= \( \frac{\frac{3}{2} (\log 3 + 2 \log 2 – \log 10)}{\log (3 \times 4) – \log 10}\)
= \( \frac{\frac{3}{2} (\log 3 + 2 \log 2 – \log 10)}{\log 3 + \log 4 – \log 10}\) [যেহেতু, \(\log_p (AB) = \log_p A + \log_p B\)]
= \( \frac{\frac{3}{2} (\log 3 + 2 \log 2 – \log 10)}{\log 3 + \log 2^2 – \log 10}\)
= \( \frac{\frac{3}{2} (\log 3 + 2 \log 2 – \log 10)}{\log 3 + 2 \log 2 – \log 10}\) [যেহেতু, \(N \log_a M = \log_a M^N\)]
= \( \frac{3}{2}\) [উত্তর]
(c) \(\log_3 4 \times \log_4 5 \times \log_5 6 \times \log_6 7 \times \log_7 3\)
সমাধান –
\(\log_3 4 \times \log_4 5 \times \log_5 6 \times \log_6 7 \times \log_7 3\)= \( \frac{\log 4}{\log 3} \times \frac{\log 5}{\log 4} \times \frac{\log 6}{\log 5} \times \frac{\log 7}{\log 6} \times \frac{\log 3}{\log 7}\)
= \( 1\) [উত্তর]
(d) \(\log_{10} \frac{384}{5} + \log_{10} \frac{81}{32} + 3 \log_{10} \frac{5}{3} + \log_{10} \frac{1}{9}\)
সমাধান –
\(\log_{10} \frac{384}{5} + \log_{10} \frac{81}{32} + 3 \log_{10} \frac{5}{3} + \log_{10} \frac{1}{9}\)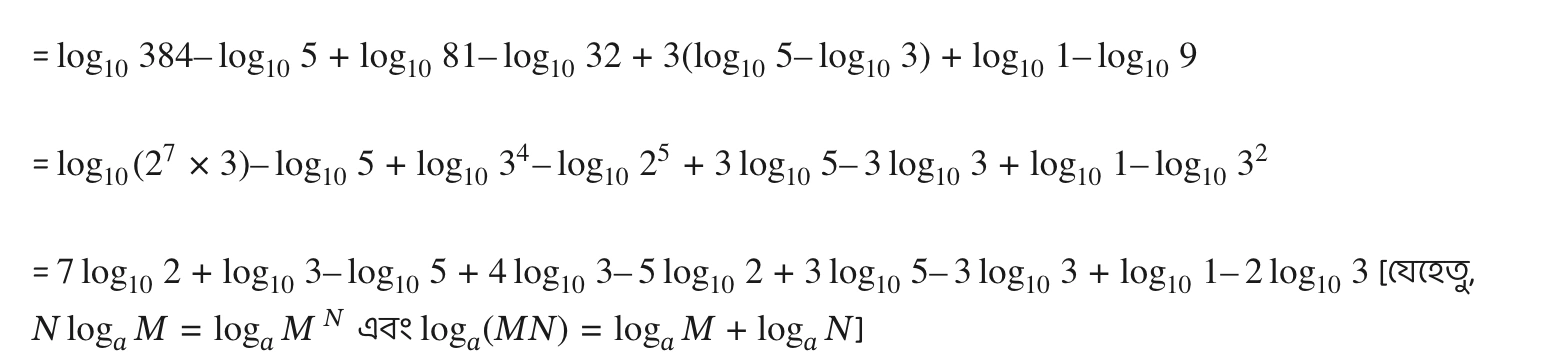
= \( 2 \log_{10} 2 + 5 \log_{10} 3 – 5 \log_{10} 3 + 2 \log_{10} 5 + \log_{10} 1\)
= \( 2(\log_{10} 2 + \log_{10} 5)\) [যেহেতু, \(\log_a 1 = 0\)]
= \( 2 \log_{10} (2 \times 5)\) [যেহেতু, \(\log_a (MN) = \log_a M + \log_a N\)]
= \( 2 \log_{10} 10\)
= \( 2\) [যেহেতু, \(\log_a a = 1\)] [উত্তর]
5. প্রমাণ করি
(i) \(\log \frac{75}{16} – 2\log \frac{5}{9} + \log \frac{32}{243} = \log 2\)
সমাধান –
\(\log \frac{75}{16} – 2\log \frac{5}{9} + \log \frac{32}{243}\)= \( \log 75 – \log 16 – 2(\log 5 – \log 9) + \log 32 – \log 243\) [যেহেতু, \(\log_a (M/N) = \log_a M – \log_a N\) এবং \(N\log_a M = \log_a M^N\)]
= \( \log 75 – \log 16 – 2\log 5 + 2\log 9 + \log 32 – \log 243\)
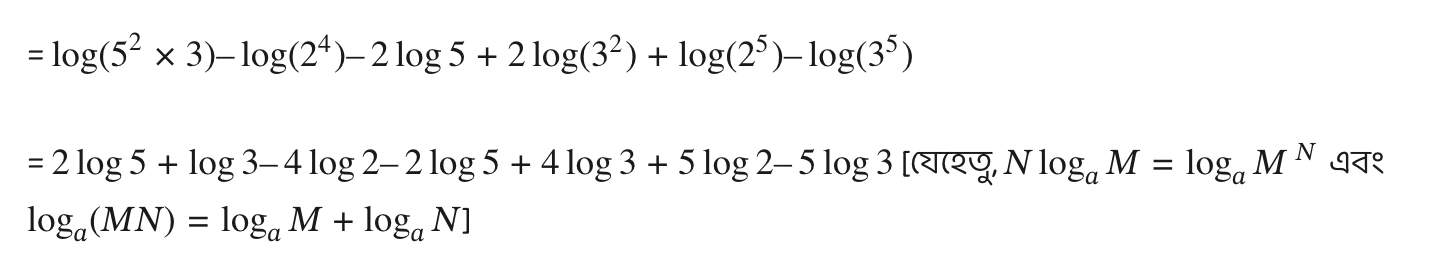
= \( \log 2\) [প্রমাণিত]

(iii) \(\log_2\log_2\log_4 256 + 2\log_{\sqrt{2}} 2 = 5\)
সমাধান –
\(\log_2\log_2\log_4 256 + 2\log_{\sqrt{2}} 2\)= \( \log_2\log_2\log_4 256 + 2\log_{\sqrt{2}} (\sqrt{2})^2\)
= \( \log_2\log_2\log_4 256 + 4 \log_{\sqrt{2}} \sqrt{2}\) [যেহেতু, \(N\log_a M = \log_a M^N\)]
= \( \log_2\log_2\log_4 256 + 4\) [যেহেতু, \(\log_a a = 1\)]
= \( \log_2\log_2\log_4 4^4 + 4\)
= \( \log_2\log_2 (4 \log_4 4) + 4\) [যেহেতু, \(N\log_a M = \log_a M^N\)]
= \( \log_2\log_2 4 + 4\) [যেহেতু, \(\log_a a = 1\)]
= \( \log_2\log_2 2^2 + 4\)
= \( \log_2 (2\log_2 2) + 4\) [যেহেতু, \(N\log_a M = \log_a M^N\)]
= \( \log_2 2 + 4\) [যেহেতু, \(\log_a a = 1\)]
= \( 1 + 4\) [যেহেতু, \(\log_a a = 1\)]
= \( 5\) [প্রমাণিত]
(iv) \(\log_{x^2} x \times \log_{y^2} y \times \log_{z^2} z = \frac{1}{8}\)
সমাধান –
\(\log_{x^2} x \times \log_{y^2} y \times \log_{z^2} z\)= \( \frac{\log x}{\log x^2} \times \frac{\log y}{\log y^2} \times \frac{\log z}{\log z^2}\) [যেহেতু, \(\log_a M = \frac{\log M}{\log a}\)]
= \( \frac{\log x}{2\log x} \times \frac{\log y}{2\log y} \times \frac{\log z}{2\log z}\) [যেহেতু, \(\log a^n = n\log a\)]
= \( \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}\)
= \( \frac{1}{8}\) [প্রমাণিত]
(v) \(\log_{b^3} a \times \log_{c^3} b \times \log_{a^3} c = \frac{1}{27}\)
সমাধান –
\(\log_{b^3} a \times \log_{c^3} b \times \log_{a^3} c\)= \( \frac{\log a}{\log b^3} \times \frac{\log b}{\log c^3} \times \frac{\log c}{\log a^3}\) [যেহেতু, \(\log_a x = \frac{\log x}{\log a}\)]
= \( \frac{\log a}{3\log b} \times \frac{\log b}{3\log c} \times \frac{\log c}{3\log a}\) [যেহেতু, \(\log a^n = n\log a\)]
= \( \frac{1}{3} \times \frac{1}{3} \times \frac{1}{3}\)
= \( \frac{1}{27}\) [প্রমাণিত]
(vi) \(\frac{1}{\log_{xy} (xyz)} + \frac{1}{\log_{yz} (xyz)} + \frac{1}{\log_{zx} (xyz)} = 2\)
সমাধান –
\(\frac{1}{\log_{xy} (xyz)} + \frac{1}{\log_{yz} (xyz)} + \frac{1}{\log_{zx} (xyz)}\)= \( \frac{1}{\frac{1}{\log_{xyz} (xy)}} + \frac{1}{\frac{1}{\log_{xyz} (yz)}} + \frac{1}{\frac{1}{\log_{xyz} (zx)}}\) [যেহেতু, \(\log_b a = \frac{1}{\log_a b}\)]
= \( \log_{xyz} xy + \log_{xyz} yz + \log_{xyz} zx\)
= \( \log_{xyz} (xy \times yz \times zx)\) [যেহেতু, \(\log_a (MN) = \log_a M + \log_a N\)]
= \( \log_{xyz} (x^2 y^2 z^2)\)
= \( \log_{xyz} (xyz)^2\)
= \( 2 \log_{xyz} xyz\) [যেহেতু, \(N\log_a M = \log_a M^N\)]
= \( 2\) [প্রমাণিত] [যেহেতু, \(\log_a a = 1\)]
(vii) \(\log\frac{a^2}{bc} + \log\frac{b^2}{ca} + \log\frac{c^2}{ab} = 0\)
সমাধান –
\(\log \frac{a^2}{bc} + \log \frac{b^2}{ca} + \log \frac{c^2}{ab}\)= \( \log a^2 – \log bc + \log b^2 – \log ca + \log c^2 – \log ab\) [যেহেতু, \(\log_a (M/N) = \log_a M – \log_a N\)]
= \( \log a^2 + \log b^2 + \log c^2 – \log bc – \log ca – \log ab\)
= \( \log(a^2 b^2 c^2) – \log(bc \times ca \times ab)\) [যেহেতু, \(\log_a M + \log_a N = \log_a (MN)\)]
= \( \log(abc)^2 – \log(abc)^2\)
= \( 0\) [প্রমাণিত]
(viii) \(x^{\log y – \log z} \times y^{\log z – \log x} \times z^{\log x – \log y} = 1\)
সমাধান –
\(x^{\log y – \log z} \times y^{\log z – \log x} \times z^{\log x – \log y}\)ধরি, \(P = x^{\log y – \log z} \times y^{\log z – \log x} \times z^{\log x – \log y}\)
উভয়পক্ষে লগ নিয়ে পাই,
\(\log P = \log(x^{\log y – \log z} \times y^{\log z – \log x} \times z^{\log x – \log y})\)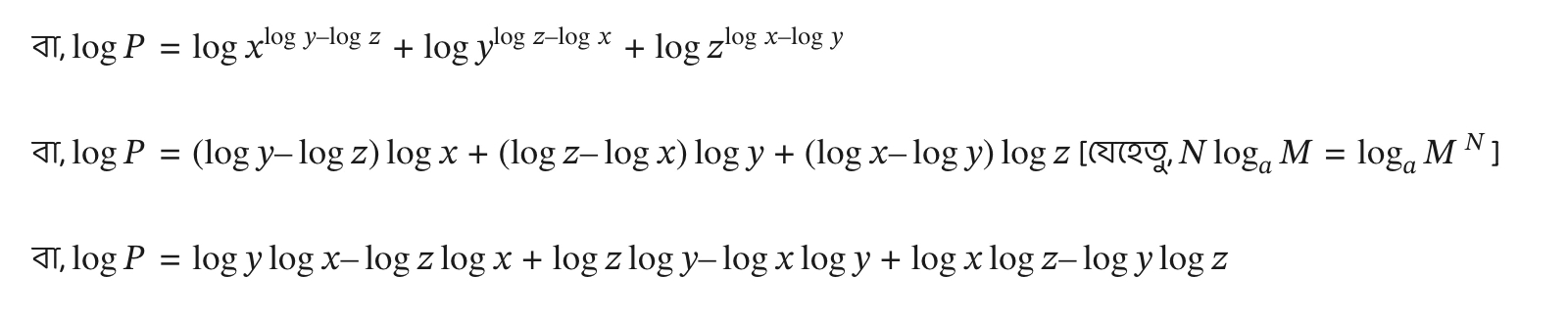
বা, \(\log P = 0\)
বা, \(\log P = \log 1\) [যেহেতু, \(\log 1 = 0\)]
বা, \(P = 1\)
\(\therefore x^{\log y – \log z} \times y^{\log z – \log x} \times z^{\log x – \log y} = 1\) [প্রমাণিত]
8. যদি, \( \frac{\log x}{b-c} = \frac{\log y}{c-a} = \frac{\log z}{a-b} \) হয়, তাহলে প্রমাণ করি যে
(a) \( x^{b+c} \cdot y^{c+a} \cdot z^{a+b} = 1 \)
(b) \( x^{b^2+bc+c^2} \cdot y^{c^2+ca+a^2} \cdot z^{a^2+ab+b^2} = 1 \)
সমাধান –
(a) \( x^{b+c} \cdot y^{c+a} \cdot z^{a+b} = 1 \)
ধরি, \( \frac{\log x}{b-c} = \frac{\log y}{c-a} = \frac{\log z}{a-b} = k \)
[যেখানে \( K(\neq 0) \) একটি সমানুপাতিক ধ্রুবক]
\( \therefore \log x = k(b-c) \)বা, \( (b+c) \log x = k(b-c)(b+c) \)
বা, \( (b+c) \log x = k(b^2-c^2) \dots (i) \)
এবং, \( \log y = k(c-a) \)
বা, \( (c+a) \log y = k(c+a)(c-a) \)
বা, \( (c+a) \log y = k(c^2-a^2) \dots (ii) \)
এবং \( \log z = k(a-b) \)
বা, \( (a+b) \log z = k(a-b)(a+b) \)
বা, \( (a+b) \log z = k(a^2-b^2) \dots (iii) \)
\( \therefore \log (x^{b+c} \cdot y^{c+a} \cdot z^{a+b}) \)= \( \log x^{b+c} + \log y^{c+a} + \log z^{a+b} \)
= \( (b+c) \log x + (c+a) \log y + (a+b) \log z \) [যেহেতু \( N\log M=\log M^N \)]
= \( k(b^2-c^2) + k(c^2-a^2) + k(a^2-b^2) \) [(i), (ii) ও (iii) থেকে পাই]
= \( k(b^2-c^2+c^2-a^2+a^2-b^2) \)
= \( k \cdot 0 \)
= \( 0 \)
= \( \log 1 \)
\( \therefore \log (x^{b+c} \cdot y^{c+a} \cdot z^{a+b}) = \log 1 \)বা, \( (x^{b+c} \cdot y^{c+a} \cdot z^{a+b}) = 1 \) [প্রমাণিত]
(b) \( x^{b^2+bc+c^2} \cdot y^{c^2+ca+a^2} \cdot z^{a^2+ab+b^2} = 1 \)
ধরি, \( \frac{\log x}{b-c} = \frac{\log y}{c-a} = \frac{\log z}{a-b} = k \)
[যেখানে \( K(\neq 0) \) একটি সমানুপাতিক ধ্রুবক]
\( \therefore \log x = k(b-c) \)বা, \( (b^2+bc+c^2)\log x = k(b-c)(b^2+bc+c^2) \)
বা, \( (b^2+bc+c^2)\log x = k(b^3-c^3) \dots (i) \)
\( \log y = k(c-a) \)বা, \( (c^2+ca+a^2) \log y = k(c-a)(c^2+ca+a^2) \)
বা, \( (c^2+ca+a^2) \log y = k(c^3-a^3) \dots (ii) \)
এবং \( \log z = k(a-b) \)
বা, \( (a^2+ab+b^2) \log z = k(a-b)(a^2+ab+b^2) \)
বা, \( (a^2+ab+b^2) \log z = k(a^3-b^3) \dots (iii) \)
\( \therefore \log \left(x^{b^2+bc+c^2} \cdot y^{c^2+ca+a^2} \cdot z^{a^2+ab+b^2}\right) \)= \( \log x^{b^2+bc+c^2} + \log y^{c^2+ca+a^2} + \log z^{a^2+ab+b^2} \)
= \( (b^2+bc+c^2) \log x + (c^2+ca+a^2) \log y + (a^2+ab+b^2) \log z \)
= \( k(b^3-c^3) + k(c^3-a^3) + k(a^3-b^3) \) [(i), (ii) ও (iii) থেকে পাই]
= \( k(b^3-c^3+c^3-a^3+a^3-b^3) \)
= \( k \cdot 0 \)
= \( 0 \)
\( \therefore \log \left(x^{b^2+bc+c^2} \cdot y^{c^2+ca+a^2} \cdot z^{a^2+ab+b^2}\right) = 0 \)\( \Rightarrow \log \left(x^{b^2+bc+c^2} \cdot y^{c^2+ca+a^2} \cdot z^{a^2+ab+b^2}\right) = \log 1 \)\( \therefore \left(x^{b^2+bc+c^2} \cdot y^{c^2+ca+a^2} \cdot z^{a^2+ab+b^2}\right) = 1 \) [প্রমাণিত]
9. যদি, \( a^{3-x} \cdot b^{5x} = a^{5+x} \cdot b^{3x} \) হয়, তাহলে দেখাই যে, \( x \log (b/a) = \log a \)
সমাধান –
\( a^{3-x} \cdot b^{5x} = a^{5+x} \cdot b^{3x} \)বা, \( \frac{a^{3-x}}{a^{5+x}} = \frac{b^{3x}}{b^{5x}} \)
বা, \( a^{3-x-5-x} = b^{3x-5x} \)
বা, \( a^{-2-2x} = b^{-2x} \)
বা, \( a^{-2} \cdot a^{-2x} = b^{-2x} \)
বা, \( a^{-2} = (b/a)^{-2x} \)
উভয়পক্ষে \( \log \) নিয়ে পাই,
\( \log a^{-2} = \log (b/a)^{-2x} \)বা, \( -2 \log a = -2x \log (b/a) \) [যেহেতু, \( N \log M = \log M^N \)]
বা, \( \log a = x \log(b/a) \) [প্রমাণিত]
10. সমাধান করি
(a) \( \log_{8} [\log_{2}\{\log_{3} (4^x+17)\}] = 1/3 \)
সমাধান –
\( \log_{8} [\log_{2}\{\log_{3} (4^x+17)\}] = 1/3 \)বা, \( (8)^{1/3} = \log_{2}\{\log_{3}(4^x+17)\} \)
বা, \( (2)^{3 \times 1/3} = \log_{2}\{\log_{3}(4^x+17)\} \)
বা, \( 2 = \log_{2}\{\log_{3}(4^x+17)\} \)
বা, \( \log_{3}(4^x+17) = 2^2 \)
বা, \( \log_{3}(4^x+17) = 4 \)
বা, \( (4^x+17) = (3)^4 \)
বা, \( 4^x+17 = 81 \)
বা, \( 4^x = 81-17 \)
বা, \( 4^x = 64 \)
বা, \( 4^x = (4)^3 \)
বা, \( x = 3 \)
\( \therefore \) নির্ণেয় সমাধান \( x = 3 \) ।
(b) \( \log_{8}x + \log_{4}x + \log_{2}x = 11 \)
সমাধান –
\( \log_{8}x + \log_{4}x + \log_{2}x = 11 \)বা, \( \frac{1}{\log_x 8} + \frac{1}{\log_x 4} + \frac{1}{\log_x 2} = 11 \) [যেহেতু, \( \log_a M = \frac{1}{\log_M a} \) ]
বা, \( \frac{1}{\log_x 2^3} + \frac{1}{\log_x 2^2} + \frac{1}{\log_x 2} = 11 \)
বা, \( \frac{1}{3\log_x 2} + \frac{1}{2\log_x 2} + \frac{1}{\log_x 2} = 11 \)
বা, \( \frac{2+3+6}{6\log_x 2} = 11 \)
বা, \( \frac{11}{6\log_x 2} = 11 \)
বা, \( 11 \times \log_x 2 = 11 \times 6 \)
বা, \( \log_2 x = 6 \) [যেহেতু, \( \log_a M = 1/ \log_M a \) ]
বা, \( 2^6 = x \)
বা, \( x = 64 \)
\( \therefore \) নির্ণেয় সমাধান \( x = 64 \) ।
11. দেখাই \( \log_{10}2 \) –এর মান \( 1/4 \) এবং \( 1/3 \) এর মধ্যে অবস্থিত ।
সমাধান –
ধরি, \( \log_{10}2 = x \)
\( \therefore (10)^x = 2 \)বা, \( (10)^{12x} = 2^{12} = 4096 \)
আবার, \( 1000 < 4096 < 10000 \)
বা, \( 10^3 < 2^{12} < 10^4 \)
বা, \( 10^3 < 10^{12x} < 10^4 \)
বা, \( 3 < 12x < 4 \)
বা, \( \frac{3}{12} < x < \frac{4}{12} \)
বা, \( \frac{1}{4} < x < \frac{1}{3} \) [প্রমাণিত]
12. বহু বিকল্পীয় প্রশ্ন (M.C.Q.)
(i) যদি, \( \log_{\sqrt{x}} 0.25 = 4 \) হয়, তাহলে x এর মান
(a) 0.5
(b) 0.25
(c) 4
(d) 16
Ans – (a) 0.5
সমাধান –
\( \log_{\sqrt{x}} 0.25 = 4 \)বা, \( (\sqrt{x})^4 = 0.25 \)
বা, \( x^2 = 0.25 \)
বা, \( x^2 = (0.5)^2 \)
বা, \( x = 0.5 \)
(ii) \( \log_{10} (7x-5) = 2 \) হলে, x –এর মান
(a) 10
(b) 12
(c) 15
(d) 18
Ans – (c) 15
সমাধান –
\( \log_{10} (7x-5) = 2 \)বা, \( 10^2 = 7x-5 \)
বা, \( 7x-5 = 100 \)
বা, \( 7x = 105 \)
বা, \( x = \frac{105}{7} \)
বা, \( x = 15 \)
(iii) \( \log_2 3 = a \) হলে, \( \log_8 27 \) হবে
(a) 3a
(b) \( \frac{1}{a} \)
(c) 2a
(d) a
Ans – (d) a
সমাধান –
\( \log_2 3 = a \)বা, \( 2^a = 3 \)
\( \therefore \log_8 27 \)= \( \log_8 (3)^3 \)
= \( 3\log_8 3 \)
= \( 3\log_8 (2^a) \)
= \( 3a \log_8 2 \)
= \( 3a \cdot \frac{1}{\log_2 8} \)
= \( 3a \cdot \frac{1}{\log_2 2^3} \)
= \( 3a \cdot \frac{1}{3\log_2 2} \)
= \( a \) [যেহেতু, \( \log_a a = 1 \)]
(iv) \( \log_{\sqrt{2}} x = a \) হলে, \( \log_{2\sqrt{2}} x \) হবে
(a) \( \frac{a}{3} \)
(b) a
(c) 2a
(d) 3a
Ans – (a) \( \frac{a}{3} \)
সমাধান –
\( \log_{\sqrt{2}} x = a \)\( \therefore (\sqrt{2})^a = x \)\( \therefore \log_{2\sqrt{2}} x \)= \( \log_{2\sqrt{2}} (\sqrt{2})^a \)
= \( a \log_{2\sqrt{2}} (\sqrt{2}) \)
= \( a \cdot \frac{1}{\log_{\sqrt{2}} (2\sqrt{2})} \) [যেহেতু, \( \log_a M = \frac{1}{\log_M a} \)]
= \( a \cdot \frac{1}{\log_{\sqrt{2}} ((\sqrt{2})^3)} \)
= \( a \cdot \frac{1}{3 \log_{\sqrt{2}} \sqrt{2}} \)
= \( \frac{a}{3} \) [যেহেতু, \( \log_a a = 1 \)]
(v) \( \log_x \frac{1}{3} = -\frac{1}{3} \) হলে, x-এর মান হবে
(a) 27
(b) 9
(c) 3
(d) \( \frac{1}{27} \)
Ans – (a) 27
সমাধান –
\( \log_x \frac{1}{3} = -\frac{1}{3} \)বা, \( x^{-\frac{1}{3}} = \frac{1}{3} \)
বা, \( x^{-1} = \left(\frac{1}{3}\right)^3 \) [উভয়পক্ষে ঘন করে পাই]
বা, \( x^{-1} = \frac{1}{27} \)
বা, \( x^{-1} = 27^{-1} \)
বা, \( x = 27 \)
13. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন
(i) \( \log_4\log_4 \log_4 256 \)-এর মান কত হবে হিসাব করে লিখি।
সমাধান –
\( \log_4\log_4 \log_4 256 \)= \( \log_4\log_4 \log_4 (4^4) \)
= \( \log_4\log_4 (4 \cdot \log_4 4) \)
= \( \log_4\log_4 (4 \cdot 1) \) [যেহেতু, \( \log_a a = 1 \)]
= \( \log_4 (\log_4 4) \)
= \( \log_4 (1) \) [যেহেতু, \( \log_4 4 = 1 \)]
= \( 0 \) [যেহেতু, \( \log_a 1 = 0 \)] [উত্তর]
(ii) \( \log \left(\frac{a^n}{b^n}\right) + \log \left(\frac{b^n}{c^n}\right) + \log \left(\frac{c^n}{a^n}\right) \) –এর মান কত হবে হিসাব করে লিখি।
সমাধান –
\( \log \left(\frac{a^n}{b^n}\right) + \log \left(\frac{b^n}{c^n}\right) + \log \left(\frac{c^n}{a^n}\right) \)= \( \log (a^n) – \log (b^n) + \log (b^n) – \log (c^n) + \log (c^n) – \log (a^n) \)
= \( 0 \) [উত্তর]
(iii) দেখাই যে, \( a^{\log_a x} = x \)।
সমাধান –
ধরি, \( \log_a x = u \)।
\( \therefore a^u = x \)।
\( \therefore a^{\log_a x} \)= \( a^u \)
= \( x \)
\( \therefore a^{\log_a x} = x \) [প্রমাণিত]
(iv) \( \log_e 2 \cdot \log_x 25 = \log_{10} 16 \cdot \log_e 10 \) হলে \( x \) –এর মান কত?
সমাধান –
\( \log_e 2 \cdot \log_x 25 = \log_{10} 16 \cdot \log_e 10 \)বা, \( \log_e 2 \cdot \log_x 25 = \log_e (16) \)
বা, \( \log_e 2 \cdot \log_x 25 = \log_e (2^4) \)
বা, \( \log_e 2 \cdot \log_x 25 = 4 \log_e (2) \) [যেহেতু, \( N \log_a M = \log_a M^N \)]
বা, \( \log_x 25 = \frac{4 \log_e 2}{\log_e 2} \)
বা, \( \log_x 25 = 4 \)
বা, \( x^4 = 25 \)
বা, \( x^4 = (\sqrt{5})^4 \)
বা, \( x = \sqrt{5} \)
\( \therefore x = \sqrt{5} \) [উত্তর]
এই আর্টিকেলে নবম শ্রেণির গণিতের ‘লগারিদম‘ অধ্যায়ের ‘কষে দেখি – 21’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।
কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন