আজকের আর্টিকেলে আমরা নবম শ্রেণীর ভৌতবিজ্ঞান বইয়ের দ্বিতীয় অধ্যায় “বল ও গতি” এর “রৈখিক ভরবেগ সংরক্ষণ” থেকে সহজ ও সংক্ষিপ্ত প্রশ্ন-উত্তর শেয়ার করবো। এই প্রশ্নগুলো নবম শ্রেণির ইউনিট টেস্ট থেকে বার্ষিক পরীক্ষা এর জন্য যেমন গুরুত্বপূর্ণ, তেমনি চাকরি বা বিভিন্ন প্রতিযোগিতার পরীক্ষাতেও কাজে লাগবে। এই অধ্যায় থেকে স্কুল পরীক্ষা থেকে শুরু করে চাকরির পরীক্ষায় প্রায়ই প্রশ্ন আসে, তাই এই প্রশ্নোত্তরগুলো সবাইকে সাহায্য করবে। প্রতিটি প্রশ্নের উত্তর সহজ ভাষায় লেখা হয়েছে, যাতে সবাই বুঝতে পারেন। পড়ার শেষে এই অধ্যায়ের মুখ্য বিষয়গুলো আপনার আয়ত্তে চলে আসবে এবং যেকোনো পরীক্ষায় আত্মবিশ্বাসের সঙ্গে লিখতে পারবেন।

জ্ঞানমূলক প্রশ্নোত্তর
রৈখিক ভরবেগ সংরক্ষণ সূত্রটি বিবৃত ও ব্যাখ্যা করো।
রৈখিক ভরবেগের সংরক্ষণ সূত্র (Law of conservation of linear momentum) – কোনো বস্তু বা বস্তু সংস্থার উপর বাহ্যিক বল ক্রিয়া না করলে ওই বস্তু বা বস্তু সংস্থার মোট রৈখিক ভরবেগ (মানে ও দিকে) ধ্রুবক থাকে। অর্থাৎ, একাধিক বস্তু পরস্পরের ওপর বল প্রয়োগ করে সচল হতে পারে, কিন্তু বাইরে থেকে কোনো বল প্রয়োগ না করলে ওদের মোট ভরবেগ সবসময় অপরিবর্তিত থাকে।
রৈখিক ভরবেগের সংরক্ষণ সূত্রের ব্যাখ্যা – ধরা যাক, m1 ও m2 ভরের দুটি বস্তুকণা যথাক্রমে u1 ও u2 (u1 > u2) বেগে একই সরলরেখায় গতিশীল হয়ে পরস্পর সংঘাত ঘটায়। সংঘাতের পর বস্তুকণা দুটির বেগ যথাক্রমে v1 ও v2 এবং সংঘাতটি একরেখীয় হলে রৈখিক ভরবেগ সংরক্ষণ সূত্র অনুযায়ী,
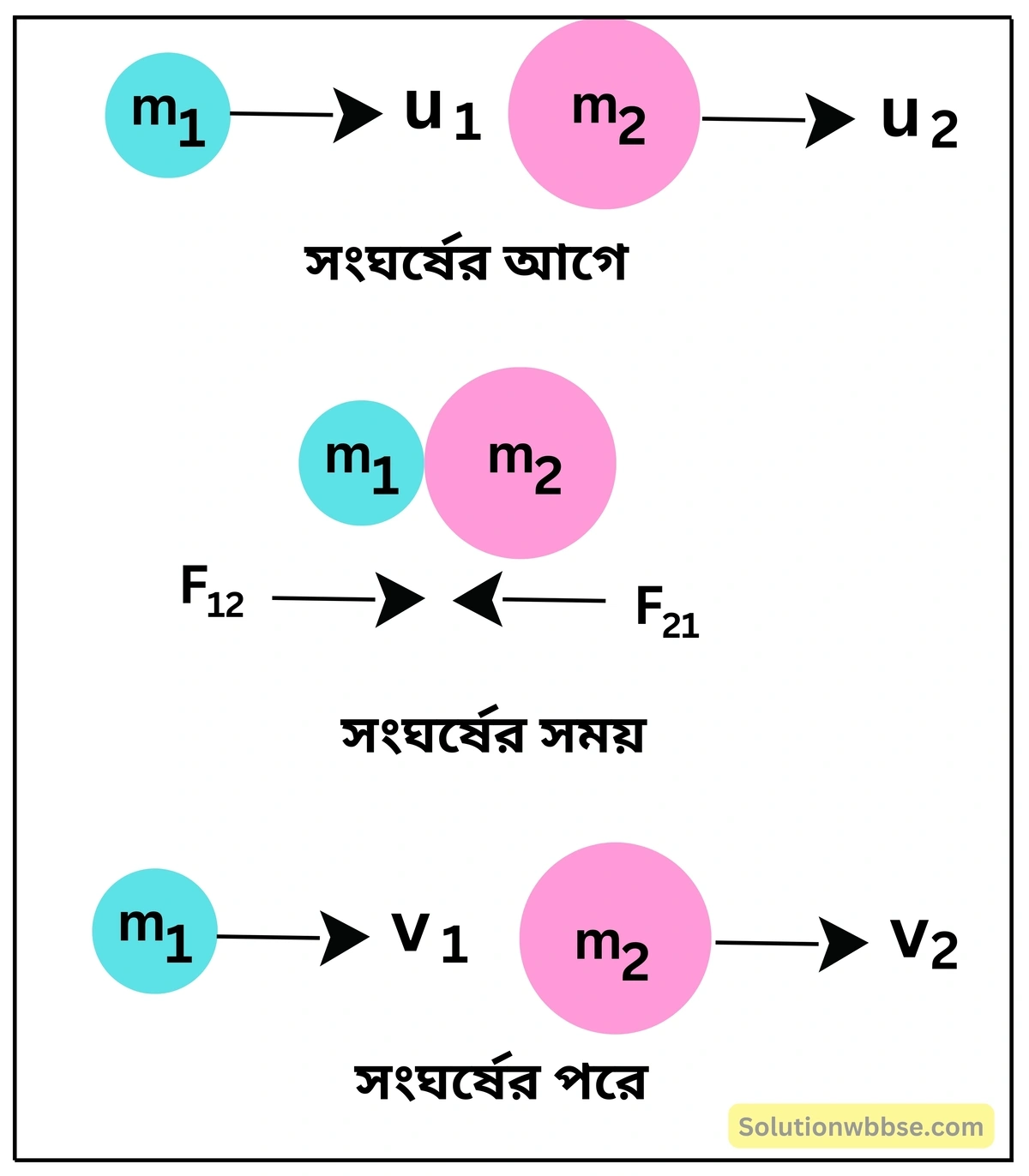
[m1 < m2, u1 > u2, v1 < v2]
সংঘাতের পূর্বে কণা দুটির মোট ভরবেগ = সংঘাতের পর কণা দুটির মোট ভরবেগ
বা, m1u1 + m2u2 = m1v1 + m2v2
ভরবেগ সংরক্ষণ নীতির যথার্থতা কীভাবে আলোর বেগের তুলনীয় বেগসহ গতিশীল বস্তু বা উপপারমাণবিক কণা সংস্থার ক্ষেত্রে বজায় থাকে, যেখানে নিউটনের গতিসূত্রগুলি প্রযোজ্য নয়?
ভরবেগ সংরক্ষণ নীতিটিকে পদার্থবিজ্ঞানের অন্যতম মৌলিক নীতি (fundamental principle) বলে গণ্য করা হয়। আলোর বেগের তুলনীয় বেগসহ গতিশীল বস্তু, উপপারমাণবিক কণা সংস্থা (sub-atomic particle system) যেখানে নিউটনের গতিসূত্রগুলি প্রযোজ্য নয় এরূপ পরিস্থিতিতেও নীতিটির যথার্থতা বজায় থাকে।
রৈখিক ভরবেগের সংরক্ষণ সূত্রটি প্রযোজ্য হওয়ার শর্ত কী?
রৈখিক ভরবেগের সংরক্ষণ সূত্রটি প্রযোজ্য হওয়ার শর্ত হল – বস্তুটির ওপর প্রযুক্ত লব্ধি বাহ্যিক বল শূন্য হতে হবে।
নিউটনের তৃতীয় গতিসূত্র ব্যবহার করে কীভাবে ভরবেগ সংরক্ষণ সূত্রটি প্রমাণ করা যায়?
মনে করি, m1 ভরবিশিষ্ট কোনো বস্তু u1 বেগে যাচ্ছে এবং t সময় ধরে বস্তুটি দ্বিতীয় কোনো বস্তুর সঙ্গে সংঘর্ষ ঘটাল। ফলে বস্তুর বেগ পরিবর্তিত হয়ে হল v1।
বস্তুতে উৎপন্ন ত্বরণ \( \left(a_1\right)=\frac{v_1-u_1}t \)
এবং প্রযুক্ত বল \( F_{12}=m_1a_1 \)
এক্ষেত্রে, দ্বিতীয় বস্তুটির বেগ \( =u_2 \) এবং ভর \( =m_2 \)।
সংঘর্ষের পর বেগ \( =v_2 \)।
বস্তুতে উৎপন্ন ত্বরণ \( \left(a_2\right)=\frac{v_2-u_2}t \)
এবং প্রযুক্ত বল = \(F_{21}=m_2a_2 \)
নিউটনের তৃতীয় গতিসূত্র অনুযায়ী, ক্রিয়া বল ও প্রতিক্রিয়া বল পরস্পরের সমান ও বিপরীত।
∴ \( F_{12}=–F_{21} \)
বা, \( m_1a_1=-m_2a_2 \)
বা, \( m_1\left(\frac{v_1-u_1}t\right)=-m_2\left(\frac{v_2-u_2}t\right) \)
বা, \( m_1v_1-m_1u_1=-m_2v_2+m_2u_2\)
বা, \( m_1v_1+m_2v_2=m_1u_1+m_2u_2\)
বা, মোট অন্তিম ভরবেগ = মোট প্রাথমিক ভরবেগ।
অর্থাৎ, সংঘর্ষের আগে ও পরে বস্তু দুটির মোট ভরবেগ সংরক্ষিত থাকে। এটিই ভরবেগের সংরক্ষণ সূত্র।
এভাবে নিউটনের তৃতীয় গতিসূত্র থেকে ভরবেগের সংরক্ষণ সূত্র পাওয়া যায়।
সংঘাত বা সংঘর্ষ কাকে বলে?
সংঘাত বা সংঘর্ষ – দুই বা ততোধিক বস্তুর মধ্যে প্রত্যক্ষ বা পরোক্ষ সংযোগের মাধ্যমে সংঘটিত যে আন্তঃক্রিয়ার ফলে বস্তুগুলির ভরবেগের নির্দিষ্ট পরিবর্তন ঘটে, যদিও সংস্থার ভরবেগ সংরক্ষিত হয়, তাকেই সংঘাত বা সংঘর্ষ বলে।
বস্তুগুলি ক্ষেত্র বলের অধীনে থাকলে, প্রত্যক্ষ স্পর্শ ছাড়াও কীভাবে সংঘর্ষ ঘটতে পারে?
বস্তুগুলি ক্ষেত্র বলের অধীনে থাকলে প্রত্যক্ষ স্পর্শ ছাড়াও সংঘর্ষ ঘটতে পারে যেমন ব্যবধানে থাকা দুটি চুম্বকের মেরুর মধ্যে আকর্ষণ বা বিকর্ষণের ঘটনা, রাদারফোর্ডের α-কণা পরীক্ষায় নিউক্লিয়াসের বিকর্ষণে α-রশ্মির প্রতিক্ষেপ ইত্যাদি।
সংঘাতের প্রকারভেদগুলি উদাহরণসহ আলোচনা করো।
সংঘর্ষের প্রকারভেদ –
সংঘাতের পূর্বে ও পরে বস্তুগুলির গতীয় আচরণের তারতম্যের ভিত্তিতে দুটি বস্তুর মধ্যে সংঘর্ষকে প্রধানত তিনটি শ্রেণিতে ভাগ করা যায় –
- পূর্ণ স্থিতিস্থাপক সংঘর্ষ (Perfectly elastic collision)
- পূর্ণ অস্থিতিস্থাপক সংঘর্ষ (Perfectly inelastic collision)
- আংশিক স্থিতিস্থাপক সংঘর্ষ (Partly elastic collision)
পূর্ণ স্থিতিস্থাপক সংঘর্ষ (Perfectly elastic collision) –
দুটি বস্তুর মধ্যে আপেক্ষিক বেগ সংঘর্ষের আগে ও পরে অপরিবর্তিত থাকলে সংঘর্ষটিকে পূর্ণ স্থিতিস্থাপক সংঘর্ষ বলে।
এই ধরনের সংঘর্ষে মোট গতিশক্তি সংরক্ষিত থাকে। অর্থাৎ, সংঘর্ষের আগে মোট গতিশক্তি ও সংঘর্ষের পর মোট গতিশক্তি একই থাকে।
পূর্ণ স্থিতিস্থাপক সংঘর্ষের উদাহরণ – বাস্তবে এই ধরনের সংঘর্ষ দেখতে পাওয়া যায় না। অণু বা পরমাণুর মধ্যে সংঘর্ষ এবং ইলেকট্রন, প্রোটন, নিউট্রন ইত্যাদি কণার মধ্যে সংঘর্ষকে পূর্ণ স্থিতিস্থাপক সংঘর্ষ বলে মনে করা যায়।
পূর্ণ অস্থিতিস্থাপক সংঘর্ষ (Perfectly inelastic collision) –
দুটি বস্তুর মধ্যে সংঘর্ষের পর আপেক্ষিক বেগ শূন্য হলে সংঘর্ষটিকে পূর্ণ অস্থিতিস্থাপক সংঘর্ষ বলে।
এই ধরনের সংঘর্ষে মোট গতিশক্তি সংরক্ষিত হয় না এবং গতিশক্তির নির্দিষ্ট অংশের অপচয় ঘটে সংঘর্ষের পর বস্তু দুটি যুক্ত হয়ে একটি বস্তুরুপে চলতে থাকে।
পূর্ণ অস্থিতিস্থাপক সংঘর্ষের উদাহরণ – দুটি কাদামাটির তালের সংঘর্ষকে প্রায় পূর্ণ অস্থিতিস্থাপক সংঘর্ষ বলে ধরা যায়।
আংশিক স্থিতিস্থাপক সংঘর্ষ (Partly elastic collision) –
দুটি বস্তুর মধ্যে আপেক্ষিক বেগ সংঘর্ষের পর কমে গেলে, সংঘর্ষটিকে আংশিক স্থিতিস্থাপক সংঘর্ষ বলে। এই ধরনের সংঘর্ষের মোট গতিশক্তি সংরক্ষিত হয় না। বাস্তবে এই ধরনের সংঘর্ষই সাধারণত ঘটে।
আংশিক স্থিতিস্থাপক সংঘর্ষের উদাহরণ – বাস্তবে সংঘটিত যে-কোনো সংঘর্ষ। যেমন- ব্যাট ও বলের সংঘর্ষ।
সংঘাত গুণাঙ্ক (coefficient of restitution) কাকে বলে বর্ণনা করো।
দুটি বস্তুর মধ্যে সংঘর্ষকে গাণিতিকভাবে বর্ণনার ক্ষেত্রে সংঘাত গুণাঙ্ক (coefficient of restitution) বলে একটি রাশির ধারণা অর্থপূর্ণ হয়। সংজ্ঞানুসারে, সংঘাত গুণাঙ্ক e হলে,
বা, \( e=\frac{v_2-v_1}{u_1-u_2} \) স্পষ্টতই পূর্ণ স্থিতিস্থাপক সংঘাতের ক্ষেত্রে,
(u1 – u2) = (v2 – v1) অর্থাৎ e = 1
পূর্ণ অস্থিতিস্থাপক সংঘাতে v1 = v2 অর্থাৎ v1 – v2 = 0
∴ e = 0
আংশিক স্থিতিস্থাপক সংঘাতের ক্ষেত্রে,
(V2 – V1) < (u1 – u2) অর্থাৎ 0 < e < 1।
একটি সহজ পরীক্ষার সাহায্যে ভরবেগ সংরক্ষণ সূত্রের সত্যতা কীভাবে যাচাই করা যায় তা ব্যাখ্যা করো।
সমান ভরের দুটি খেলনা গাড়ি A ও B -কে একটি অনুভূমিক রেলের উপর বসানো হল। সংনমিত অবস্থায় একটি স্প্রিংকে মাঝখানে রেখে গাড়ি দুটি শক্ত করে সুতোর সাহায্যে বাঁধা হল।
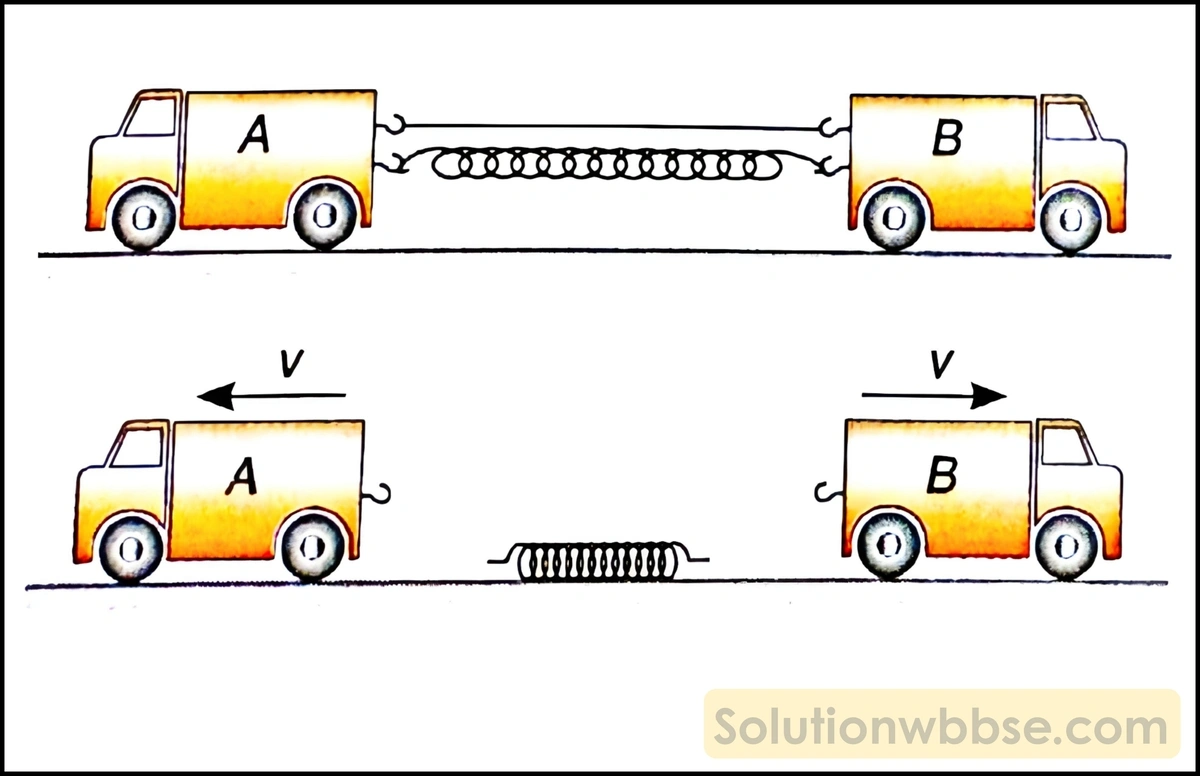
এই অবস্থায় দেশলাই কাঠি জ্বেলে সুতোটি পুড়িয়ে দিলে দেখা যাবে গাড়ি দুটি পরস্পর বিপরীত অভিমুখে সমবেগে অগ্রসর হয়েছে।
ব্যাখ্যা – এই ফলাফল ভরবেগ সংরক্ষণের সত্যতা সমর্থন করে, প্রাথমিক অবস্থায় দুই গাড়ি দ্বারা গঠিত সংস্থার ভরবেগ (গাড়ি দুটি স্থির থাকায়) শূন্য ছিল।
সচল অবস্থায় সংস্থার মোট ভরবেগ = mv – mv [∵ গাড়ি দুটি সমবেগে বিপরীত অভিমুখে গতিপ্রাপ্ত হয়]
∴ সংস্থার প্রাথমিক ভরবেগ = সংস্থার চূড়ান্ত ভরবেগ – যা ভরবেগ সংরক্ষণ নীতির বক্তব্য।
ভরবেগ সংরক্ষণ সূত্রের সাহায্যে নিউটনের তৃতীয় গতিসূত্রটি প্রমাণ করো।
রৈখিক ভরবেগের সংরক্ষণ সূত্রটি থোক নিউটনের তৃতীয় গতিসূত্র প্রতিষ্ঠা –
মনে করি, m1 ও m2 ভরের দুটি বস্তু একই সরলরেখায় একই দিকে যথাক্রমে u1 ও u2 বেগে যাচ্ছে।
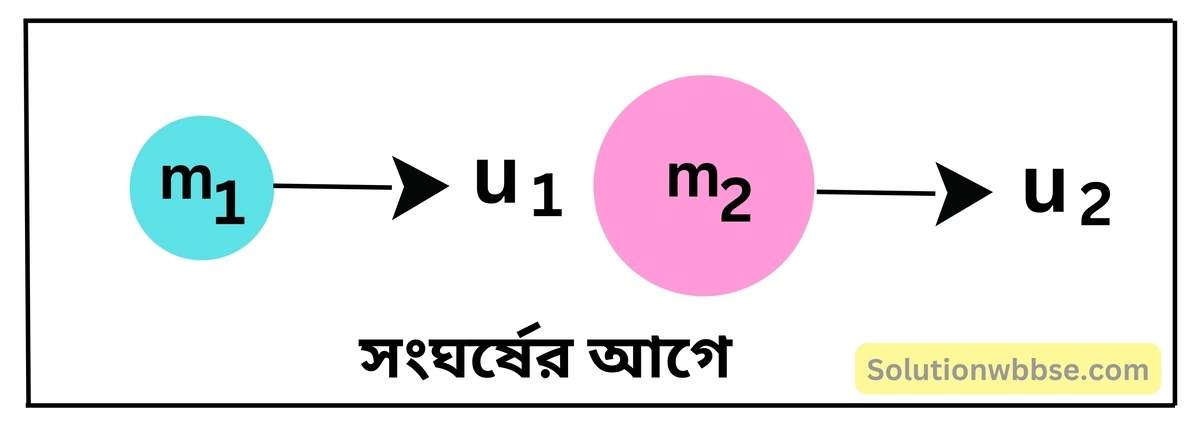
∴ তাদের মোট ভরবেগ = m1u1 + m2u2
বস্তু দুটির মধ্যে t সময় ধরে সংঘর্ষ হয় এবং তারা পরস্পরের উপর ক্রিয়া প্রতিক্রিয়া বল F12 ও F21 প্রয়োগ করে
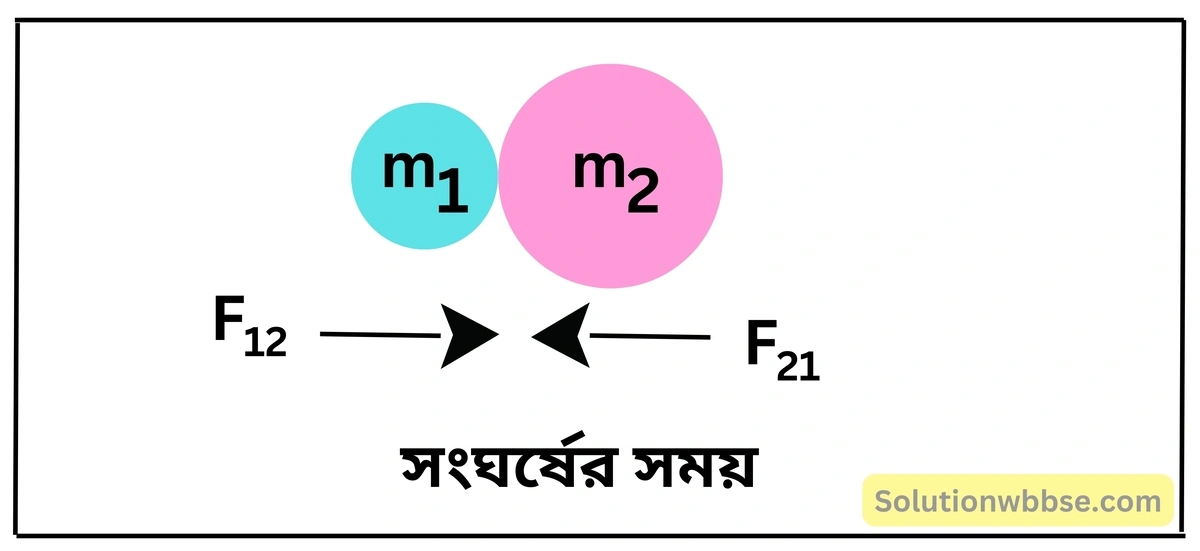
সংঘর্ষের পরও তারা একই সরলরেখায় একই দিকে চলে। এক্ষেত্রে প্রথম বস্তুর বেগ v1 ও দ্বিতীয় বস্তুর বেগ v2।
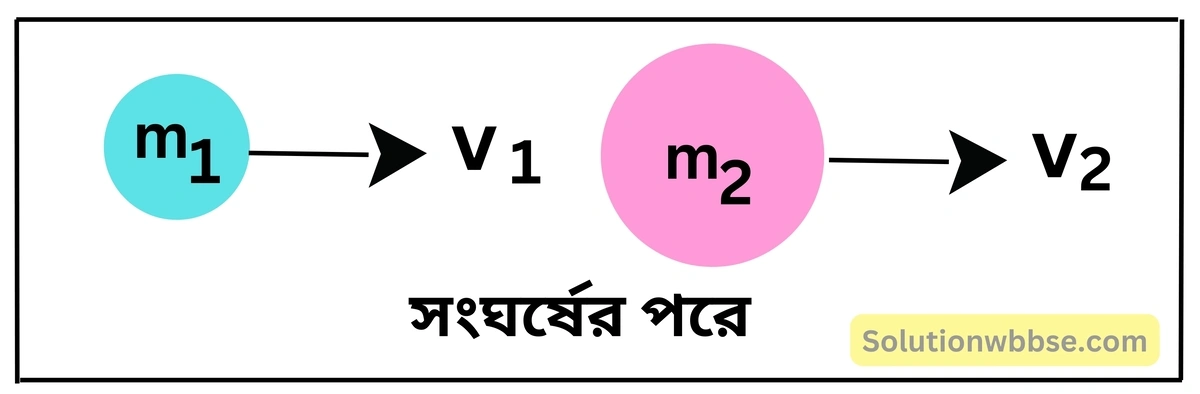
∴ তাদের মোট ভরবেগ = m1v1 + m2v2
রৈখিক ভরবেগের সংরক্ষণ সূত্রানুযায়ী,
প্রাথমিক ভরবেগ = অন্তিম ভরবেগ
বা, m1u1 + m2u2 = m1v1 + m2v2
বা, m1u1 – m1v1 = m2v2 – m2u2
বা, m1 (u1 – v1) = m2 (v2 – u2)
বা, – m1 (v1 – u1) = m2 (v2 – u2)
বা, \( -m_1\left(\frac{v_1-u_1}t\right)=m_2\left(\frac{v_2-u_2}t\right) \) [t দিয়ে ভাগ করে]
বা, \( -m_1a_1=m_2a_2 \) [\( \frac{v_1-u_1}t=a_1 \) = প্রথম বস্তুর ত্বরণ এবং \( \frac{v_2-u_2}t=a_2 \) দ্বিতীয় বস্তুর ত্বরণ]
বা, -F12 = F21 [ক্রিয়া বল = F12 = m1a1, প্রতিক্রিয়া বল = F21 = m2a2]
বা, – ক্রিয়া বল = প্রতিক্রিয়া বল।
∴ ক্রিয়া ও প্রতিক্রিয়া বল পরস্পর সমান ও বিপরীত – এটিই নিউটনের তৃতীয় গতিসূত্র।
জেট ও রকেটের কার্যনীতির সংক্ষেপে বর্ণনা দাও।
জেট ও রকেটের কার্যনীতি ভরবেগ সংরক্ষণ সূত্রের ওপর প্রতিষ্ঠিত।
জেটের কার্যনীতি – বর্তমানে বহুল ব্যবহৃত টার্বোজেটের গঠন একটি লম্বা নলের মতো। এর সামনের দিকে থাকে সংনমক যার কাজ হল সামনের দিক থেকে বায়ুশোষণ করে উচ্চচাপে দহন কক্ষে পাঠানো। দহন কক্ষে জ্বালানির দহনে উচ্চচাপযুক্ত দগ্ধ গ্যাস উৎপন্ন হয়। এই গ্যাস টারবাইনের মধ্য দিয়ে গিয়ে পিছনের দিক দিযে বাইরে বেরিয়ে যায়। ভরবেগ সংরক্ষণ নীতি অনুসারে সংস্থার মোট রৈখিক ভরবেগ অপরিবর্তিত রাখার উদ্দেশ্যে জ্বালানিসহ বায়ুযানটির অবশিষ্ট অংশ দগ্ধ গ্যাসের গতির বিপরীতে সমপরিমাণ ভরবেগ লাভ করে। এর ফলে জেট সামনের দিকে গতিপ্রাপ্ত হয়। জ্বালানির দহনে উৎপন্ন গ্যাসের ওপর রকেট যে বলপ্রয়োগ করে তার প্রতিক্রিয়ায় জেট সামনের দিকে ত্বরণসহ এগিয়ে যায়।
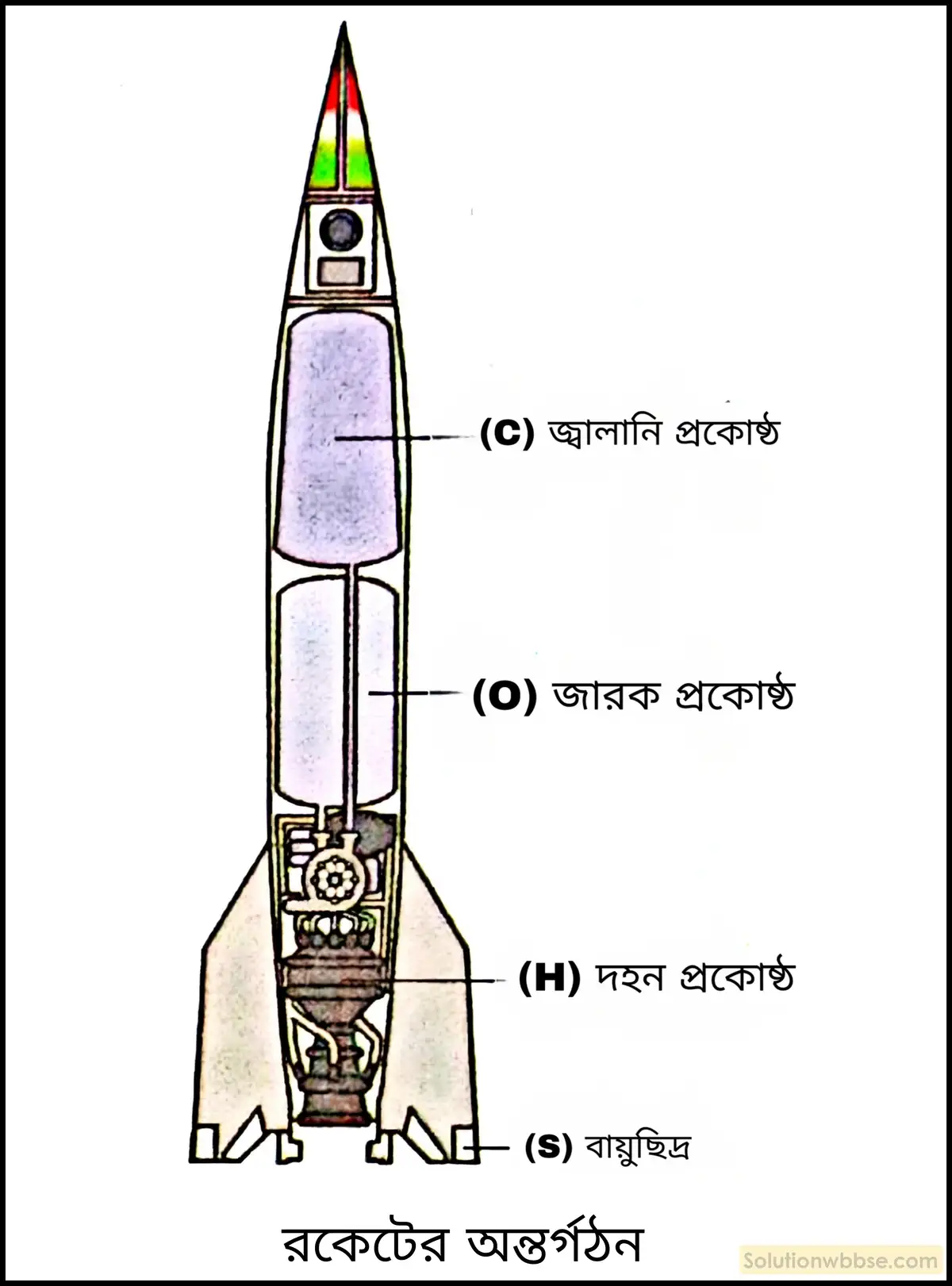
রকেটের কার্যনীতি – রকেটের সাধারণত চারটি প্রকোষ্ঠ বা কক্ষ থাকে – বহন প্রকোষ্ঠ, জ্বালানি প্রকোষ্ঠ, জারক প্রকোষ্ঠ, দহন প্রকোষ্ঠ। জ্বালানিরূপে সাধারণত তরল হাইড্রোজেন, কোরোসিন, ইথাইল অ্যালকোহল ইত্যাদি এবং জারক দ্রব্য (দহন সহায়ক পদার্থ) হিসেবে তরল অক্সিজেন, ওজোন, হাইড্রোজেন পার অক্সাইড ব্যবহৃত হয়ে থাকে। রকেটকে সাধারণত বোমা, কৃত্রিম উপগ্রহ ইত্যাদি বহন করার কাজে ব্যবহার করা হয় যা বহন প্রকোষ্ঠে রাখা থাকে। জ্বালানি এবং জারক দ্রব্যকে পাম্পের সাহায্যে নিয়ন্ত্রিত মাত্রায় দহন কক্ষে নিয়ে এসে সূক্ষ্ম ধারায় স্প্রে করা হয়। এই মিশ্রণে আগুন দিলে উৎপন্ন গ্যাস তীব্রবেগে পিছনে অবস্থিত সরু নির্গম নল দিয়ে বেরিয়ে যায়। এর ফলে সৃষ্ট প্রতিক্রিয়া রকেটকে সামনে চালায়।
বোধমূলক প্রশ্নোত্তর
বন্দুক থেকে বুলেট ছোড়া – উদাহরণের সাহায্যে রৈখিক ভরবেগের সংরক্ষণ সূত্রটি ব্যাখ্যা করো।
ধরা যাক, M ভরের একটি বন্দুক থেকে m ভরের একটি গুলি ছোড়া হল। গুলি নিক্ষেপের আগে বন্দুক ও গুলি দুই-ই স্থির থাকে।
∴ মোট প্রাথমিক ভরবেগ = M⋅0 + m⋅0 = 0
মনে করি, বুলেট ছোড়ার পর বন্দুকের বেগ V এবং বুলেটের বেগ v।
∴ মোট অন্তিম ভরবেগ = MV + mv
ভরবেগের সংরক্ষণ সূত্রানুযায়ী,
মোট প্রাথমিক ভরবেগ = মোট অন্তিম ভরবেগ।
বা, 0 = MV + mv
বা, MV = -mv [∵ M >> m তাই V << v]
অর্থাৎ, বন্দুকের বেগ অনেক কম কিন্তু বুলেটের বেগ অনেক বেশি। ঋণাত্মক চিহ্ন থেকে বোঝা যায় উভয়ের বেগ পরস্পর বিপরীত। বন্দুকের এই বেগকে বলে প্রতিক্ষিপ্ত বেগ।
অর্থাৎ, রৈখিক ভরবেগের সংরক্ষণ সূত্র থেকে বোঝা যায়, বন্দুক থেকে বুলেট ছুঁড়লে বুলেটটি তীব্রবেগে সামনের দিকে ছুটে যায় এবং বন্দুকটি অনেক কম বেগে পিছন দিকে সরে আসে। ফলে, বন্দুকধারী ব্যক্তিও কিছুটা পিছন দিকে সরে আসে।
হোসপাইপের মধ্যে দিয়ে জল প্রবাহিত হওয়া – উদাহরণের সাহায্যে রৈখিক ভরবেগের সংরক্ষণ সূত্রটি ব্যাখ্যা করো।
হোসপাইপের মধ্যে দিয়ে জল প্রবাহিত হওয়ার সময় প্রথমে হোসপাইপ ও জল উভয়েই স্থির থাকে। অর্থাৎ, উভয়েরই প্রাথমিক ভরবেগ = শূন্য।
মনে করি, হোসপাইপের মধ্যে দিয়ে জল প্রবাহিত হলে নির্গত জলের বেগ = v এবং জলের ভর = m, হোসপাইপটির ভর = M এবং গতিবেগ = V।
মোট অন্তিম ভরবেগ = mv + MV
রৈখিক ভরবেগ সংরক্ষণ সূত্রানুযায়ী, mv + MV = 0
বা, MV = – mv
∴ M ≈ m এবং V ≈ v তাই হোসপাইপ দিয়ে যে গতিবেগে জল বেরোয় প্রায় একই গতিবেগে পাইপটিও পিছনে সরে আসে। তাই হোসপাইপের মধ্যে দিয়ে জল প্রবাহিত হওয়ার সময় পাইপটিকে হাতে রাখা অসুবিধাজনক হয়ে পড়ে।
চলমান রকেট – উদাহরণের সাহায্যে রৈখিক ভরবেগের সংরক্ষণ সূত্রটি ব্যাখ্যা করো।
ধরা যাক, চলমান রকেটের ক্ষেত্রে ছাড়ার আগের মুহূর্তে জ্বালানিসহ রকেটের মোট ভর = M এবং বেগ = 0
∴ প্রাথমিক ভরবেগ = M⋅0 = 0
রকেট ছাড়ার পর জ্বালানির ভর m1 এবং বেগ u
রকেটের ভর m2 এবং বেগ V
∴ অন্তিম ভরবেগ = m1u + m2V
রৈখিক ভরবেগের সংরক্ষণ সূত্রানুযায়ী, m1u + m2V = 0
∴ m1u = -m2V
অর্থাৎ, নির্গত গ্যাসের বিপরীত দিকে রকেট সমান মানের ভরবেগ লাভ করে ও প্রচণ্ড বেগে সামনের দিকে এগোতে থাকে।
একটি বলকে উপরে ছুঁড়ে দিলে প্রথমে ওর ভরবেগ কমে এবং পরে বাড়ে। এই ঘটনায় ভরবেগ সংরক্ষণ সূত্র লঙ্ঘিত হয় কি?
ভরবেগ সংরক্ষণ সূত্র মান্য হওয়ার অপরিহার্য শর্ত হল বাহ্যিক বলের অনুপস্থিতি। এক্ষেত্রে নিক্ষিপ্ত বলটির উপর বাহ্যিক বল অভিকর্ষের ক্রিয়া সর্বদাই বজায় থাকে। তাই ভরবেগ সংরক্ষণ সূত্র এক্ষেত্রে প্রযোজ্যই হয় না, তাই লঙ্ঘিত হওয়ার কোনো প্রশ্ন আসে না।
বলটি উপরে ওঠার সময় অভিকর্ষ ওর গতির বিপরীতে ক্রিয়া করে ফলে ভরবেগ কমে আবার নিম্নাভিমুখী গতির ক্ষেত্রে অভিকর্ষ সক্রিয় হয় বলে ভরবেগ বাড়ে।
একটি ট্রাক থেকে চলন্ত অবস্থায় কিছু মাল ফেলে দিলে ট্রাকের গতিবেগ কীরকমভাবে পরিবর্তিত হবে?
অথবা, কোনো চলমান তেলের ট্যাঙ্কের একটি ছিদ্র থেকে অনবরত তেল নির্গত হচ্ছে। ট্যাঙ্কটির ভরবেগ অটুট রাখতে কী করতে হবে?
মনে করি, চলন্ত অবস্থায় ট্রাকটির প্রাথমিক ভর = M এবং প্রাথমিক গতিবেগ = V। ট্রাকটি থেকে কিছু মাল ফেলে দিলে ট্রাকটির অন্তিম ভর = m এবং অন্তিম গতিবেগ = V।
∴ ট্রাকটির প্রাথমিক ভরবেগ = MV এবং অন্তিম ভরবেগ = mv
যদি ট্রাকটি অসমবেগে চলতে থাকে তবে রৈখিক ভরবেগের সংরক্ষণ সূত্র অনুযায়ী, MV = mv
∴ v = \(\frac Mm⋅V\)
যেহেতু M> m ∴ v> V
অর্থাৎ, ট্রাকটির বেগ বেড়ে যাবে।
যদি ট্রাকটি সমবেগে চলতে চায় তবে ওর ওপর বল ক্রিয়া করতে হবে। এই বল ইঞ্জিন কর্তৃক প্রযুক্ত হবে।
যদি t সময় ধরে মাল ফেলা হয়।
প্রযুক্ত বল = ভরবেগের পরিবর্তনের হার = \(\frac{MV-mv}t\)
যদি সমবেগে চলে V = v।
∴ বল = \(\frac{M-m}t⋅V\)।
জেট বিমান সাধারণত অনেক উঁচুতে ওড়ে, কিন্তু প্রপেলার বিমান অপেক্ষাকৃত কম উচ্চতায় ওড়ে। – ব্যাখ্যা করো।
জেট বিমানের কার্যনীতি ভরবেগ সংরক্ষণ নীতির ওপর প্রতিষ্ঠিত। জ্বালানি দহনের জন্য প্রয়োজনীয় অক্সিজেন জেট বায়ু থেকে সংগ্রহ করলেও বায়ুর ঘনত্বের ওপর জেট বিমানের চলাচল নির্ভর করে না। বায়ুর সঙ্গে ঘর্ষণে উৎপন্ন তাপ উৎপাদন এড়ানোর জন্য এই বিমান অনেক উঁচুতে ওড়ে, যেখানে বায়ুর ঘনত্ব কম, যা জ্বালানির দহনের জন্য যথেষ্ট।
প্রপেলার বিমান তার ব্লেড বায়ুতে ঘোরায় এবং বায়ুকে তীব্রবেগে পিছনে ঠেলে ফেলে পিছনের বায়ুর দেওয়া প্রতিক্রিয়া তাকে সামনে এগিয়ে নিয়ে যায়। অর্থাৎ, বায়ুর ঘনত্ব বেশি হলে প্রতিক্রিয়া বলও বেশি হয় এবং বিমান অপেক্ষাকৃত দ্রুত এগোতে পারে। তাই প্রপেলার বিমান অনেক নীচুতে ওড়ে, যেখানে বায়ুর ঘনত্ব বেশি।
রকেট বায়ুমণ্ডলের উপর উঠতে পারে। কিন্তু জেটবিমান পারে না কেন?
রকেটের মধ্যস্থ জ্বালানির দহনের জন্য প্রয়োজনীয় অক্সিজেন রকেট নিজেই বহন করে। তাই রকেট বায়ুমণ্ডলের ওপর উঠতে পারে। কিন্তু জেটবিমানকে তার জ্বালানির দহনের জন্য বায়ুমণ্ডল থেকে অক্সিজেন সংগ্রহ করতে হয়। তাই জেটবিমান বায়ুমণ্ডলের ওপর উঠতে পারে না।
m ভরের একটি পাথরের টুকরো v বেগে মসৃণ বরফের তলের ওপর দিয়ে গড়িয়ে আসছে। ওই তলের ওপর দাঁড়ানো M ভরের একজন বালক পাথরটিকে কুড়িয়ে নিল। বরফের তলের ওপর দাঁড়ানো বালকটি কত প্রাথমিক বেগ অর্জন করবে?
সংঘর্ষের পূর্বে মোট ভরবেগ
= বালকের ভরবেগ + পাথরের ভরবেগ
= 0 + mv [∵ সংঘর্ষের পূর্বে বালকের বেগ = 0]
= mv
যেখানে, m ও v যথাক্রমে পাথরের ভর ও বেগ।
ধরা যাক, সংঘর্ষের পর অর্থাৎ বালকটি পাথর কুড়িয়ে নেওয়ার পর বালকের প্রাথমিক বেগ = u এবং বালকের ভর = M (প্রশ্নানুযায়ী)
সুতরাং, সংঘর্ষের পর মোট ভরবেগ = বালকের ভরবেগ + পাথরের ভরবেগ
= Mu + mu [∵ সংঘর্ষের পর পাথরের বেগ = u]
= (M + m)u
∴ রৈখিক ভরবেগ সংরক্ষণ সূত্রানুযায়ী, (M + m) u = mv
∴ u = \(\frac{Mv}{M+m}\)
∴ u << v
গাণিতিক প্রশ্নাবলি
প্রয়োজনীয় সূত্র
m1 ও m2 ভরের দুটি বস্তুকণা u1 ও u2 বেগে গতিশীল। সংঘাতের পর বেগ v1 ও v2 হলে, রৈখিক ভরবেগের সংরক্ষণ নীতি অনুযায়ী, m1u1 + m2u2 = m1v1 + m2v2
6 kg ভরের একটি বন্দুক থেকে 10 g ভরের একটি বুলেট ছোড়া হল। বুলেটের বেগ 300 m/s হলে বন্দুকের প্রতিক্ষেপ বেগ কত?
বুলেটের ভর (m) = 10 g = \(\frac{10}{1000}\) kg = 0.01 kg
বুলেটের বেগ (v) = 300 m/s
বন্দুকের ভর (M) = 6 kg
বন্দুকের প্রতিক্ষেপ বেগ (V) = ?
ভরবেগ সংরক্ষণ সূত্রানুযায়ী mv + MV = 0
(যেহেতু, প্রাথমিক ভরবেগ = 0)
বা, 0.01 × 300 + 6V = 0
বা, 6V = -3
বা, V = \(-\frac36\) = -0.5 m/s
ঋণাত্মক চিহ্নের অর্থ বন্দুকের গতি বুলেটের গতির বিপরীত দিকে।
M ও m ভরের দুটি বল পরস্পরের দিকে যথাক্রমে u এবং v বেগ নিয়ে চলে। ধাক্কার ফলে তারা পরস্পরের সঙ্গে সংযুক্ত হল। সংঘর্ষের পর তাদের বেগ কত হবে?
M ভরের বলটির বেগ = u এবং m ভরের বলটির বেগ = v
ধরি ধাক্কার ফলে সংযুক্ত অবস্থায় তাদের বেগ = V
রৈখিক ভরবেগের সংরক্ষণ সূত্রানুযায়ী,
Mu – mv = (M + m)V
বা, V = \(\frac{Mu-mv}{M+m}\)
∴ সংঘর্ষের পর তাদের বেগ হবে = \(\frac{Mu-mv}{M+m}\)
1.5 kg ভরের দুটি বস্তু একই রেখা বরাবর কিন্তু বিপরীত অভিমুখে গতিশীল। সংঘর্ষের সময় তারা পরস্পরের সঙ্গে জুড়ে যাওয়ার পূর্বে তাদের প্রত্যেকের বেগ ছিল 2.5 m/s। সংঘর্ষের পর সংযুক্ত অবস্থায় বস্তুদ্বয়ের বেগ কত হবে?
বস্তুদুটির প্রত্যেকের ভর (m) = 1.5 kg
বস্তুদুটির প্রত্যেকের বেগ (v) = 2.5 m/s
ধরি, সংঘর্ষের পর সংযুক্ত অবস্থায় বস্তুদ্বয়ের বেগ = V
∴ রৈখিক ভরবেগের সংরক্ষণ নীতি অনুযায়ী,
mv – mv (m + m)V
বা, (1.5 + 1.5)V = 0
বা, V = 0
∴ সংঘর্ষের পর সংযুক্ত অবস্থায় বস্তুদ্বয়ের বেগ শূন্য হবে।
1500 কেজি ভরের একটি গাড়ি 25 মি/সে বেগে চলতে চলতে 1000 কেজি ভরের ও 15 মি/সে বেগে চলতে থাকা অন্য একটি গাড়ির সঙ্গে সংঘর্ষ ঘটাল। সংঘর্ষের পর প্রথম গাড়ির বেগ 20 মি/সে হলে দ্বিতীয় গাড়ির বেগ কত?
সংঘর্ষের আগে প্রথম গাড়ির ভরবেগ
= 1500 × 25
= 37500 kg⋅m/s
সংঘর্ষের আগে দ্বিতীয় গাড়ির ভরবেগ
= 1000 × 15
= 15000 kg⋅m/s
∴ সংঘর্ষের আগে দুটি গাড়ির মোট ভরবেগ
= 37500 + 15000
= 52500 kg⋅m
ধরি, সংঘর্ষের পর দ্বিতীয় গাড়ির বেগ v m/s
∴ সংঘর্ষের পর দুটি গাড়ির মোট ভরবেগ
= (1500 × 20 + 1000 × v) kg⋅m/s
রৈখিক ভরবেগ সংরক্ষণ সূত্রানুযায়ী,
সংঘর্ষের পূর্বে মোট ভরবেগ = সংঘর্ষের পরে মোট ভরবেগ
অর্থাৎ, 52500 = 30000 + 1000 v
বা, 1000v = 52500 – 30000
বা, 1000v = 22500
বা, v = \(\frac{22500}{1000}\)
বা, v = 22.5 m/s
∴ সংঘর্ষের পর দ্বিতীয় গাড়িটির বেগ 22.5 m/s।
একটি বোমা খাড়াভাবে নীচের দিকে পড়ার সময় যে মুহূর্তে তার বেগ u তখন বিস্ফোরণ ঘটল এবং 2 : 1 ভরের অনুপাতে দুটি খণ্ডে বিভক্ত হল। ভারী খণ্ডটি 2u বেগে খাড়া নীচের দিকে যাত্রা শুরু করলে সেই মুহূর্তে হালকা খণ্ডটির বেগের মান ও অভিমুখ নির্ণয় করো।
ধরা যাক, বোমাটির প্রাথমিক ভর = 3m
∴ বিস্ফোরণে সৃষ্ট খণ্ড দুটির ভর = 2m ও m
বিস্ফোরণের পর হালকা খণ্ডটির বেগ হলে ভরবেগের সংরক্ষণ সূত্রানুযায়ী,
3m × u = 2m × 2u + m × v
বা, 3mu = 4mu + mv
বা, mv = -mu
বা, v = -u
∴ বিস্ফোরণের পর হালকা খণ্ডটি খাড়া উপরের দিকে u বেগে গতিশীল হবে।
100 g ভরের একটি বস্তু ও 400 g ভরের একটি বস্তু পরস্পরের দিকে যথাক্রমে 90 cm/s ও 10 cm/s বেগে অগ্রসর হচ্ছে। যদি সংঘাতের পর বস্তুদুটি পরস্পর যুক্ত হয় তবে সংঘাতের পর যুগ্মভরের বেগ কত হবে? 10 s সময়ে যুগ্ম ভরটি কত দূরত্ব যাবে?
100 g ভরের বস্তুর বেগ = 90 cm/s
এবং 400 g ভরের বস্তুর বেগ = 10 cm/s
ধরা যাক, সংঘাতের পর যুগ্ম বস্তুদ্বয়ের বেগ = v
∴ ভরবেগের সংরক্ষণ সূত্রানুযায়ী,
100 × 90 – 400 × 10 = (100 + 400)v
বা, v = \(\frac{9000-4000}{500}\)
বা, v = 10
∴ সংঘাতের পর যুগ্মভরের বেগ 10 হবে।
সংঘাতের পর যুগ্মভরটি প্রথম বস্তুর গতির অভিমুখে 10 cm/s বেগে অগ্রসর হবে।
10 sec সময়ে যুগ্ম ভরটির সরণ হবে,
S = vt
বা, S = 10 × 10
বা, S = 100 cm
∴ 10 s সময়ে যুগ্ম ভরটি 100 cm দূরত্ব যাবে।
For High-Types
5 N এবং 3 N বল দুটি পরস্পরের সঙ্গে 30° কোণে ক্রিয়াশীল। জ্যামিতিক পদ্ধতিতে বলদুটির লব্ধি বল নির্ণয় করো।
1 cm দৈর্ঘ্যকে 1 N ধরলে 5 N ও 3 N বল দুটিকে যথাক্রমে 5 cm ও 3 cm দৈর্ঘ্য দ্বারা প্রকাশ করা যাবে। এখন, খাতায় স্কেলের সাহায্যে AB = 5 cm, AD = 3 cm দৈর্ঘ্যের দুটি রেখাংশ আঁকা হল এবং এদের মধ্যবর্তী কোণ ∠BAD = 30° আঁকা হল। এরপর এই তথ্যগুলির সাহায্যে ABCD সামান্তরিকটি আঁকা হল।
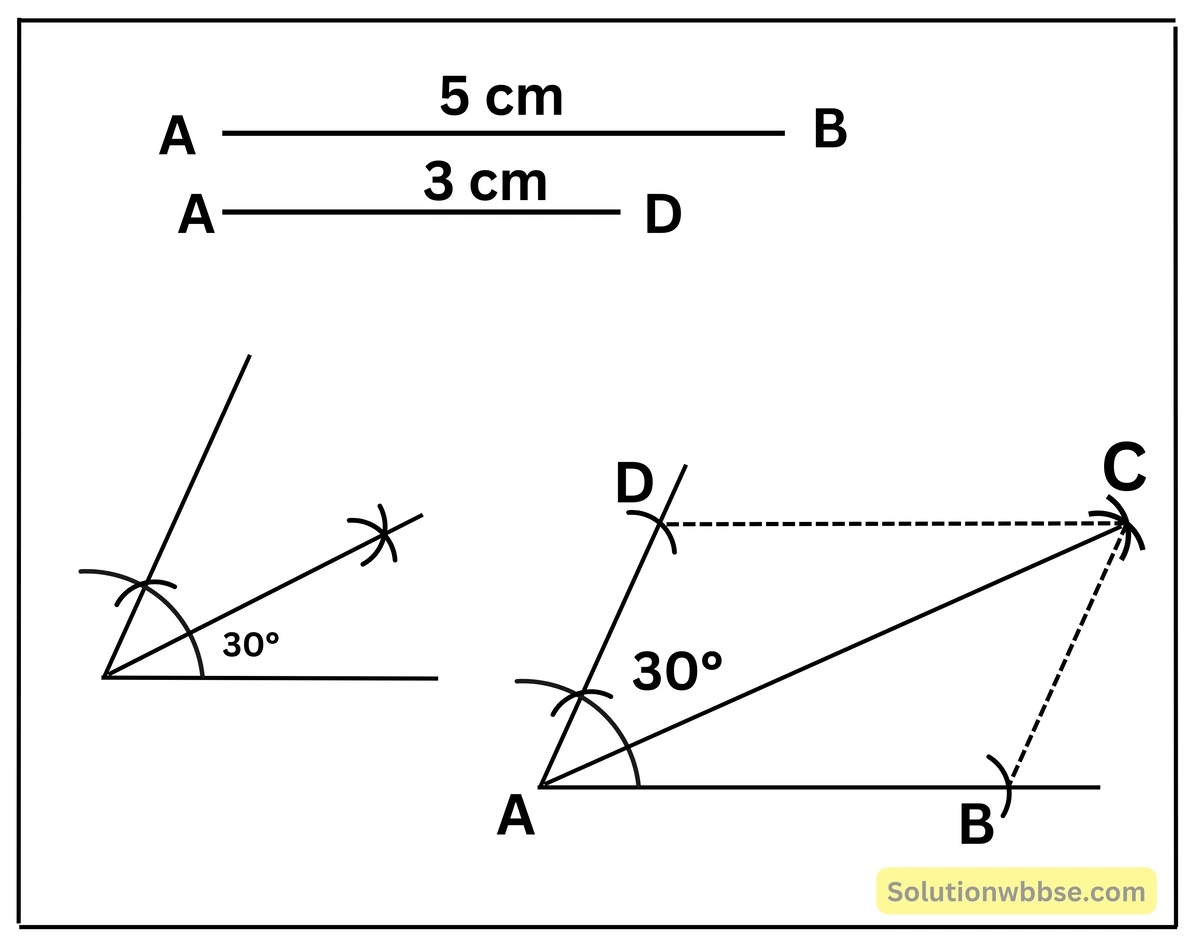
বলের সংযোজনের সামান্তরিক সূত্র অনুযায়ী এক্ষেত্রে AC কর্ণের দৈর্ঘ্য থেকে পরোক্ষভাবে বল দুটির লব্ধি নির্ণয় করতে পারব। স্কেলের সাহায্যে AC কর্ণের দৈর্ঘ্য মেপে পাওয়া গেল 7.7 cm।
∴ 7.7 cm দৈর্ঘ্য 7.7 × 1 N = 7.7N বলকে প্রকাশ করে।
অতএব, বল দুটির লব্ধি বলের মান হল 7.7 N।
চাঁদার সাহায্যে মেপে দেখা গেল ∠BAC = 11°
অতএব, 5 N ও 3 N মানের দুটি বল পরস্পরের সঙ্গে 30° কোণে ক্রিয়াশীল হলে লব্ধির মান হয় 7.7 N এবং লব্ধি বল 5 N মানের বলের সঙ্গে 11° কোণে আনত থাকে।
প্রদত্ত চিত্রে \(\overrightarrow F\) বলের অনুভূমিক ও উল্লম্ব উপাংশগুলি নির্ণয় করো।
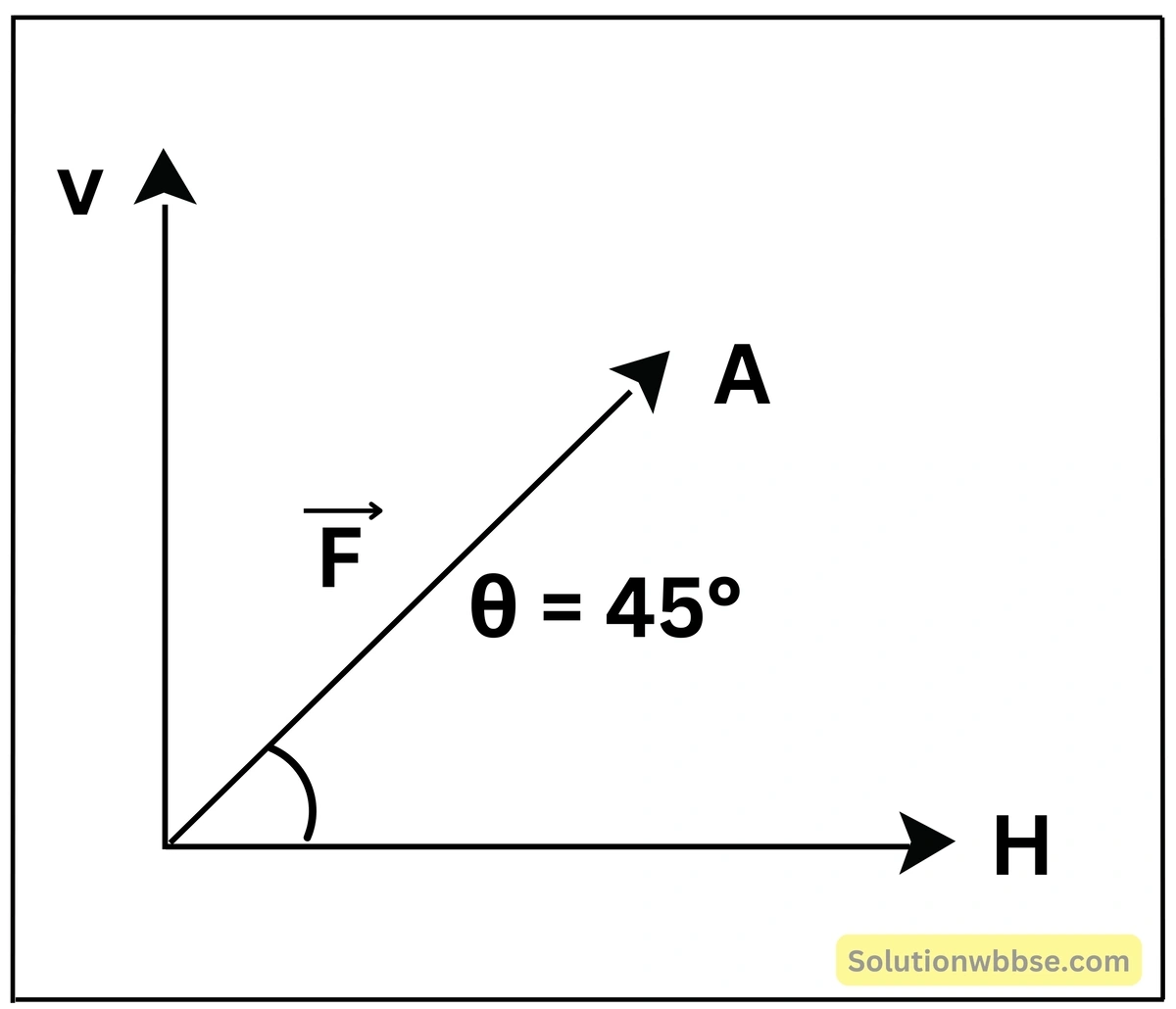
F বলের অনুভূমিক উপাংশ,
\(\left(H\right)=F\cos45^\circ=F\times\frac1{\sqrt2}=\frac F{\sqrt2}\\\)F বলের উল্লম্ব উপাংশ,
\(\left(v\right)=F\sin45^\circ=F\times\frac1{\sqrt2}=\frac F{\sqrt2}\\\)দৃঢ় অনুভূমিক তলে Q ওজনের একটি মানুষ মাথার খানিক ওপরে দৃঢ়বদ্ধ একটি পুলির সাহায্যে ভারহীন অপ্রসার্য দড়ির একপ্রান্ত ধরে দাঁড়িয়ে আছে, যাতে দড়ির অন্য প্রান্তে যুক্ত P ওজনের একটি বস্তুর পতন রোধ হয়। মানুষটি কী পরিমাণ বল অনুভূমিক তলে প্রয়োগ করছে?
ধরা যাক, দড়ির দুই অর্ধে টান T। দড়ির দুই অর্ধে থাকা ওজন ও ব্যক্তির সাম্যের শর্ত বিবেচনা করে পাই –
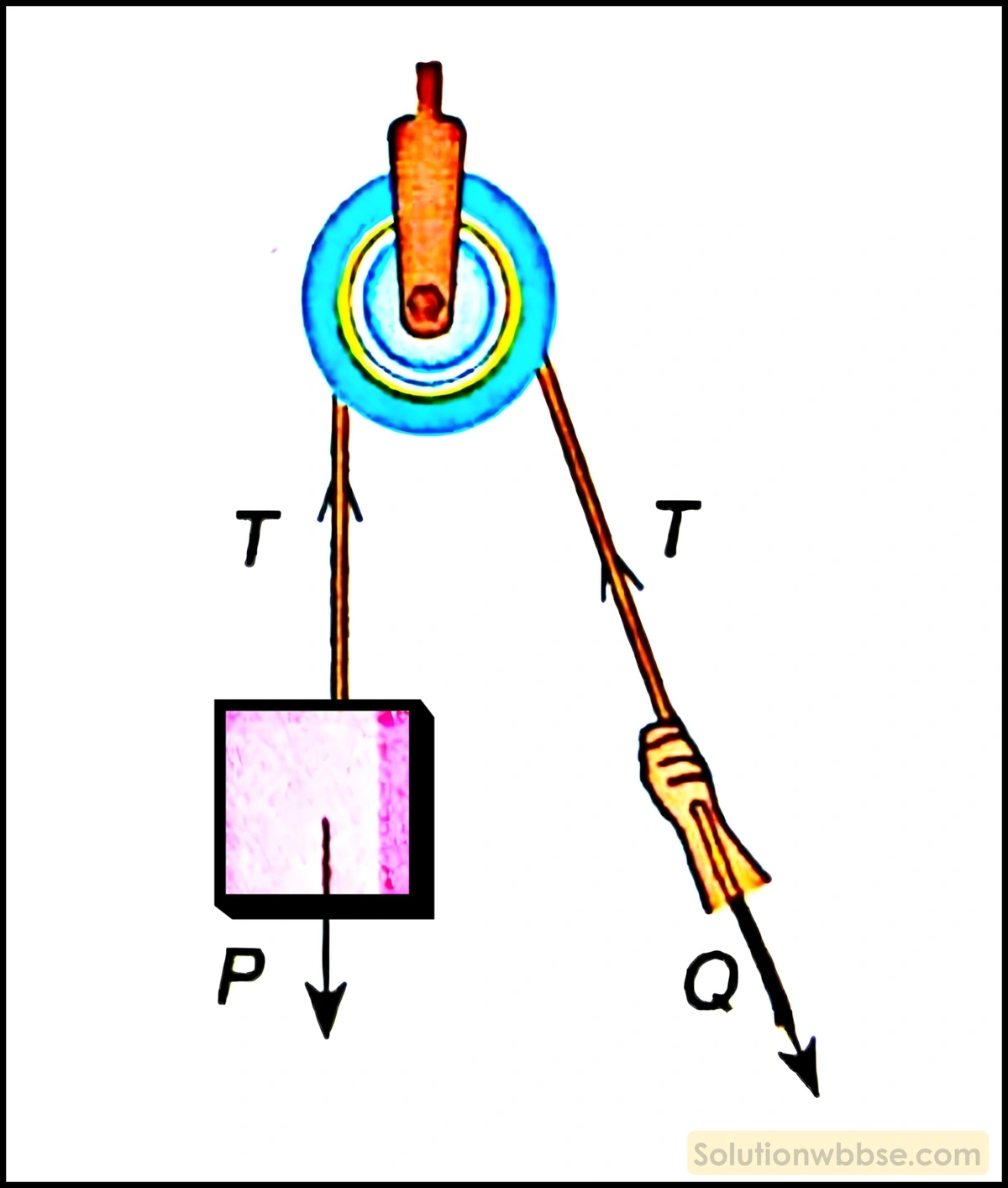
বা, \(T=\frac{P+Q}2\)
∴ অনুভূমিক তলে মানুষটি যে বল প্রয়োগ করে তা হল –
\(Q-T=Q-\frac{P+Q}2\\\)বা, \(Q-T=\frac{Q-P}2\)
একটি পাথরখণ্ড ওপরের দিকে ছুঁড়ে দিলে পাথরখণ্ড পৃথিবীর দিকে আসে কিন্তু পৃথিবী পাথরখণ্ডের দিকে এগিয়ে যায় না কেন?
নিউটনের তৃতীয় গতিসূত্রানুযায়ী, পৃথিবী ও পাথরখণ্ড পরস্পরকে সমান বল দ্বারা আকর্ষণ করবে। ধরি, সেই আকর্ষণ বলের মান F। পৃথিবীর ভর Me এবং পাথরের ভর Ms। পৃথিবীর ত্বরণ \(a_e=\frac F{M_e}\) পাথরের ত্বরণ \(a_s=\frac F{M_s}\)
সুতরাং, \(\frac{a_e}{a_s}=\frac{\displaystyle\frac F{M_e}}{\displaystyle\frac F{M_s}}\)
বা, \(\frac{a_e}{a_s}=\frac{M_s}{M_e}\)
বা, \(\frac{a_e}{a_s}<<1\)
∵ Me >> Ms
সুতরাং, পাথরখণ্ডের ত্বরণ পৃথিবীর ত্বরণ অপেক্ষা অনেক বেশি। এই কারণে পৃথিবী পাথরখণ্ডের দিকে যায় না।
একটি মসৃণ তলের উপর L দৈর্ঘ্যবিশিষ্ট একটি সুষম দড়ি রয়েছে। এর এক প্রান্তকে F বল দিয়ে টানা হল। ওই প্রান্ত থেকে x দূরত্বে দড়ির টান কত?
ধরা যাক, দড়ির সমগ্র ভর M ও ত্বরণ a এবং দড়ির ওপর C বিন্দুতে টান T হলে, AC ও BC অংশের জন্য লেখা যায়,
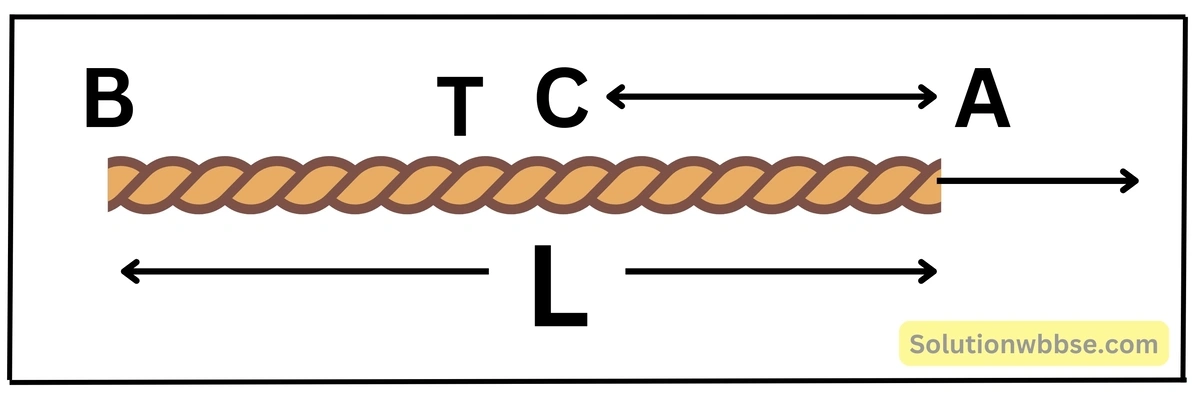
\(F-T=\frac ML⋅x⋅a\) এবং \(T=\frac ML\left(L-x\right)a\)
যোগ করে পাই, \(T=\frac{Ma}L\left(x-x+L\right)=Ma\)
∴ \(F=\frac{Ma}L\left(L-x\right)=\frac Fa\left(L-x\right)\)
একই সরলরেখায় থাকা ছয়টি সমভরের বল পরস্পরের সংস্পর্শে আছে। বলগুলি পৃথক সুতোর সাহায্যে ঝোলানো আছে। এবার বাঁদিকের শেষ প্রান্তের বলটিকে একটু সরিয়ে ছেড়ে দিলে দেখা যায় যে, বলটি এসে পাশের বলটিকে আঘাত করলে অন্যপ্রান্তের একটি বলই ছিটকে যায়, আবার বাঁদিকের দুটি বল নিয়ে আঘাত করতে দুটি বল ছিটকে যায় – কারণ কী?
এক বা একাধিক বলের সঙ্গে সংস্পর্শে থাকা অবশিষ্ট স্থির বলগুলির সংঘাত একটি বিশেষ ধরনের আন্তঃক্রিয়া যেখানে সংঘাতে লিপ্ত বলগুলির রৈখিক ভরবেগ ও গতিশক্তি উভয়ই সংরক্ষিত থাকে। এ ধরনের সংঘাত বা সংঘর্ষকে স্থিতিস্থাপক সংঘর্ষ বলে। সুতরাং, রৈখিক ভরবেগ ও গতিশক্তি এই দুই রাশির মান সংরক্ষিত হওয়ার শর্ত দ্বারাই সংঘাতের পর কতগুলি বল ছিটকে যাবে তা নির্ধারিত হয়।
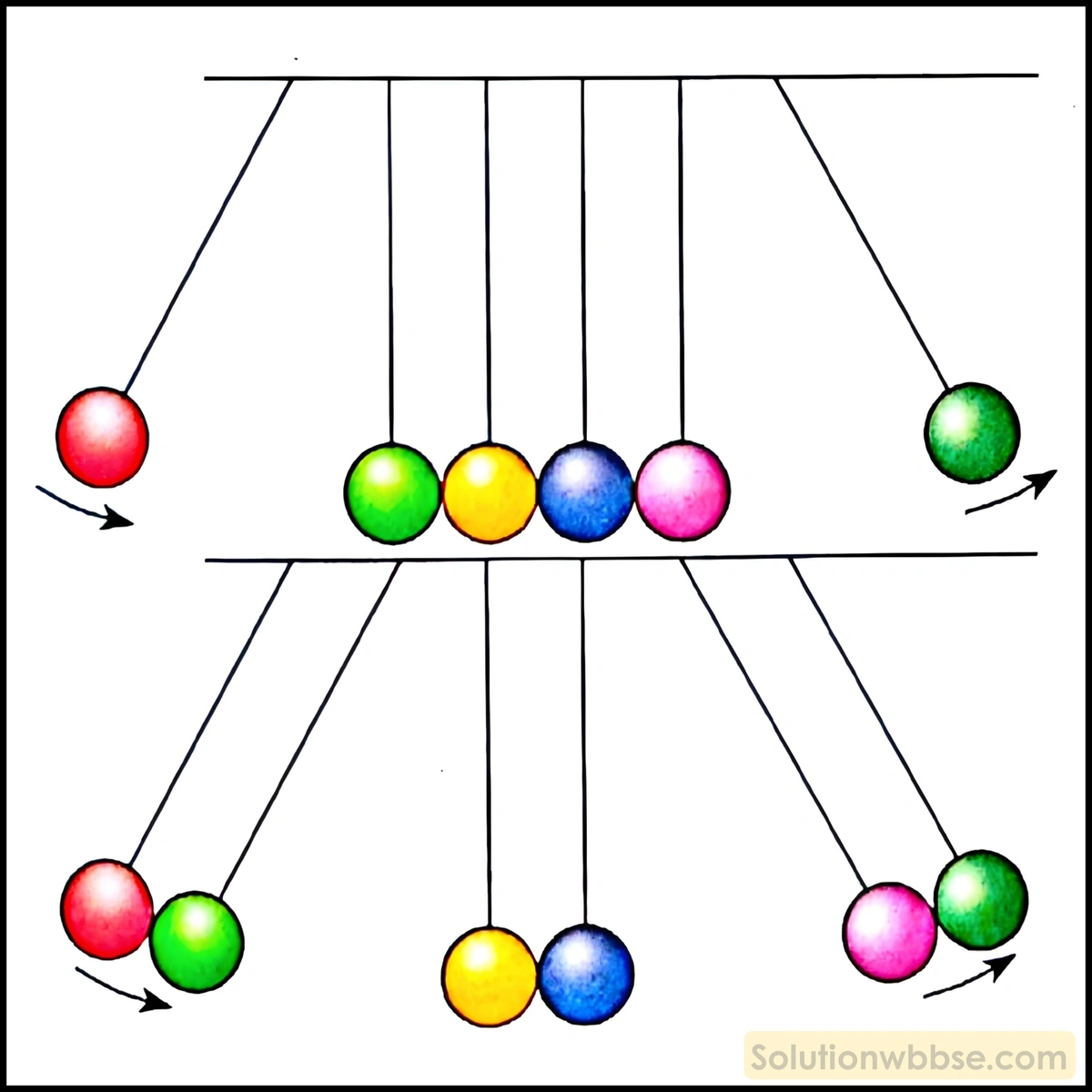
একটি বল দ্বারা আঘাতের ক্ষেত্রে দেখা যায় যে এই শর্ত প্রতিফলিত হয় যদি বিপরীত প্রান্ত থেকে একটি বল ছিটকে যায়। আবার দুটি বলের ক্ষেত্রে সংশ্লিষ্ট শর্তদ্বয় মান্য হয়, যদি দুটি বল অপর প্রান্ত থেকে ছিটকে যায়।
ঘটনাটিকে গাণিতিকভাবেও ব্যাখ্যা করা সম্ভব –
প্রথমক্ষেত্রে একটি বল (ভর m) u বেগে অপর পাঁচটি বলকে আঘাত করলে সংঘাতের পূর্বে ভরবেগ = mu, গতিশক্তি = \(\frac12mu^2\) সংঘাতের পর একটিই বল বিচ্যুত হলে, সংস্থার চূড়ান্ত ভরবেগ = mu ও চূড়ান্ত ও গতিশক্তি \(\frac12mu^2\) হয়। অর্থাৎ ভরবেগ ও গতিশক্তির নিত্যতা মান্য হয়।
দুটি অভিন্ন বলের দ্বারা সংঘাতের ক্ষেত্রে –
সংঘাতের পূর্বে সংস্থার মোট ভরবেগ = mu + mu = 2mu
সংস্থার মোট গতিশক্তি = \(\frac12mu^2\times2=mu^2\)
সংঘাতের পর একটি বল নির্গত হলে,
চূড়ান্ত বেগ \(v=\frac{2mu}m=2u\) এবং
চূড়ান্ত গতিশক্তি = \(\frac12m\times\left(2u\right)^2=2mu^2\neq mu^2\) (প্রাথমিক গতিশক্তি)
∴ গতিশক্তির সংরক্ষণ এক্ষেত্রে লঙ্ঘিত হয়।
দুটি বল একসঙ্গে বেগে গতিশীল হলে,
ভরবেগের সংরক্ষণ নীতি অনুযায়ী, mv + mv = 2mu
বা, 2mv = 2mu
বা, v = u
সংঘাতের পর গতিশক্তি = \(\frac12mv^2+\frac12mv^2\)
= \(=mv^2\)
= \(mu^2\) (প্রাথমিক গতিশক্তি)
∴ সংঘাতের পর অপর প্রান্ত থেকে দুটি মার্বেল একই বেগে গতিশীল হবে।
একই পদ্ধতি অবলম্বনে দেখানো যায় যে, তিন বা ততোধিক বল গতিশীল হলে ভরবেগ ও যান্ত্রিক শক্তি একইসঙ্গে মান্য হয় না। ফলে তিন বা ততোধিক বল বিচ্যুত হওয়া সম্ভব নয়।
পৃথিবী ও চাঁদ পরস্পরকে আকর্ষণ করে, কিন্তু তারা একে অপরের ওপর পড়ে যায় না কেন?
পৃথিবী ও চাঁদ পরস্পরকে মহাকর্ষীয় বল দ্বারা আকর্ষণ করে, কিন্তু চাঁদ বা পৃথিবী পরস্পরের কাছে এগিয়ে আসে না। কারণ চাঁদ ও পৃথিবীর মধ্যে ক্রিয়াশীল মহাকর্ষ বল চাঁদকে পৃথিবীর চারপাশে বৃত্তাকার পথে আবর্তনের জন্য প্রয়োজনীয় অভিকেন্দ্র বল সরবরাহ করে, যার প্রভাবে প্রতি মুহূর্তে চাঁদের গতির অভিমুখ বদলায় ও চাঁদ বৃত্তাকার কক্ষপথে আবন্ধ থাকে। আবর্তনরত অবস্থায় চন্দ্রপৃষ্ঠে অবস্থিত কোনো ব্যক্তিকে নিজের আপাত স্থিতিশীল অবস্থা ব্যাখ্যা করার জন্য মহাকর্ষ বলের বিপরীতে সমমানের একটি বলের ক্রিয়া আপাত সত্য বলে বিবেচনা করতে হয়। এই বল (অপকেন্দ্র বল) মহাকর্ষের প্রভাব প্রতিমিত করে চন্দ্রকে আপাত সাম্যে রাখে।
Class 9 Physical Science – Notes for All Chapters
| Chapter Name | Tropics |
|---|---|
| পরিমাপ | পরিমাপ ও একক বিভিন্ন মাপের একক মাত্রা পরিমাপ |
| বল ও গতি | স্থিতি ও গতি গতির সমীকরণ নিউটনের প্রথম গতিসূত্র নিউটনের দ্বিতীয় গতি সূত্র নিউটনের তৃতীয় গতিসূত্র বিভিন্ন ধরণের বল রৈখিক ভরবেগ রৈখিক ভরবেগ সংরক্ষণ |
| পদার্থ : গঠন ও ধর্ম | তরল ও বায়ুর চাপ আর্কিমিডিসের নীতি পৃষ্ঠটান সান্দ্রতা বার্নোলির নীতি স্থিতিস্থাপকতা |
| পদার্থ : পরমাণুর গঠন ও পদার্থের ভৌত ও রাসায়নিক ধর্মসমূহ | পরমাণুর গঠন মোলের ধারণা দ্রবণ অ্যাসিড, ক্ষার, লবণ মিশ্রণের উপাদানের পৃথকীকরণ জল |
| শক্তির ক্রিয়া , কার্য, ক্ষমতা | শক্তির ক্রিয়া , কার্য, ক্ষমতা |
| তাপ | ক্যালোরিমিতি কার্য ও তাপের তুল্যতা লীনতাপ সম্পৃক্ত ও অসম্পৃক্ত বাষ্প জলের ব্যতিক্রান্ত প্রসারণ |
| শব্দ | শব্দের উৎস : কম্পন শব্দের বিস্তার : তরঙ্গ শব্দের কয়েকটি ধর্ম শব্দের বৈশিষ্ট্য মানুষের কান ও শব্দ শোনার কৌশল শব্দদূষণ |
আজকের আর্টিকেলে আমরা নবম শ্রেণির ভৌতবিজ্ঞান বইয়ের দ্বিতীয় অধ্যায় “রৈখিক ভরবেগ সংরক্ষণ” এর “রৈখিক ভরবেগ সংরক্ষণ” থেকে পরীক্ষায় আসা গুরুত্বপূর্ণ প্রশ্ন ও উত্তরগুলো আলোচনা করেছি। এই প্রশ্নোত্তরগুলো নবম শ্রেণির বার্ষিক পরীক্ষা, এমনকি চাকরি বা যেকোনো প্রতিযোগিতামূলক পরীক্ষার জন্যও উপযোগী। কারণ, এই অধ্যায়ের প্রশ্ন প্রায়ই বিভিন্ন পরীক্ষায় কমন আসে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সাহায্য করবে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন কিংবা টেলিগ্রামে যোগাযোগ করতে পারেন—আপনাদের প্রশ্নের উত্তর দিতে আমি সর্বদা প্রস্তুত।
ধন্যবাদ সবাইকে।






মন্তব্য করুন