আজকের আর্টিকেলে আমরা নবম শ্রেণীর ভৌতবিজ্ঞান বইয়ের তৃতীয় অধ্যায় “পদার্থ : গঠন ও ধর্ম” এর “সান্দ্রতা” থেকে সহজ ও সংক্ষিপ্ত প্রশ্ন-উত্তর শেয়ার করবো। এই প্রশ্নগুলো নবম শ্রেণির ইউনিট টেস্ট থেকে বার্ষিক পরীক্ষা এর জন্য যেমন গুরুত্বপূর্ণ, তেমনি চাকরি বা বিভিন্ন প্রতিযোগিতার পরীক্ষাতেও কাজে লাগবে। এই অধ্যায় থেকে স্কুল পরীক্ষা থেকে শুরু করে চাকরির পরীক্ষায় প্রায়ই প্রশ্ন আসে, তাই এই প্রশ্নোত্তরগুলো সবাইকে সাহায্য করবে। প্রতিটি প্রশ্নের উত্তর সহজ ভাষায় লেখা হয়েছে, যাতে সবাই বুঝতে পারেন। পড়ার শেষে এই অধ্যায়ের মুখ্য বিষয়গুলো আপনার আয়ত্তে চলে আসবে এবং যেকোনো পরীক্ষায় আত্মবিশ্বাসের সঙ্গে লিখতে পারবেন।

জ্ঞানমূলক প্রশ্নোত্তর
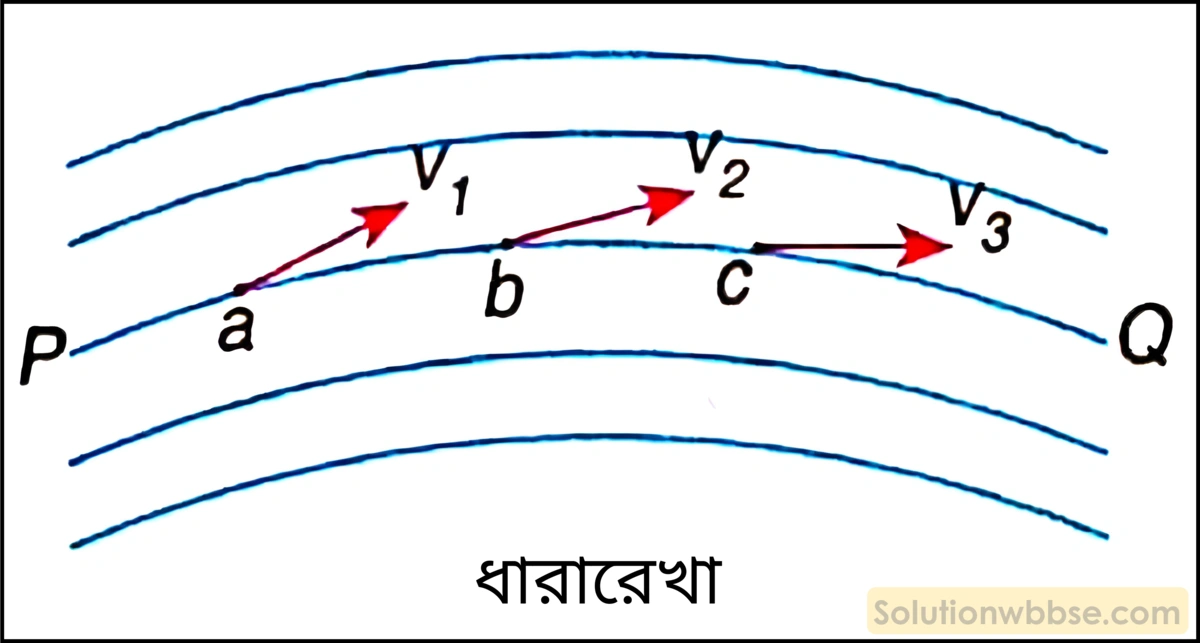
ধারারেখ প্রবাহ বা শান্ত প্রবাহ কাকে বলে?
ধারারেখ প্রবাহ (Streamline flow) – যদি কোনো প্রবাহী এমনভাবে প্রবাহিত হয় যে প্রবাহ পথের প্রত্যেক বিন্দুতে প্রবাহের বেগের মান ও অভিমুখ সর্বদা অপরিবর্তিত থাকে, তবে সেই প্রবাহকে বলা হয় ধারারেখ প্রবাহ।
চিত্রে তরলের ধারারেখ প্রবাহ দেখানো হয়েছে। তরল প্রবাহের সময় যে-কোনো কণা A বিন্দুতে এলে তার গতিবেগ হবে v, B বিন্দুতে v, C বিন্দুতে v ইত্যাদি। অর্থাৎ, প্রত্যেক বিন্দুতে প্রবাহের বেগের মান ও অভিমুখ অপরিবর্তিত।
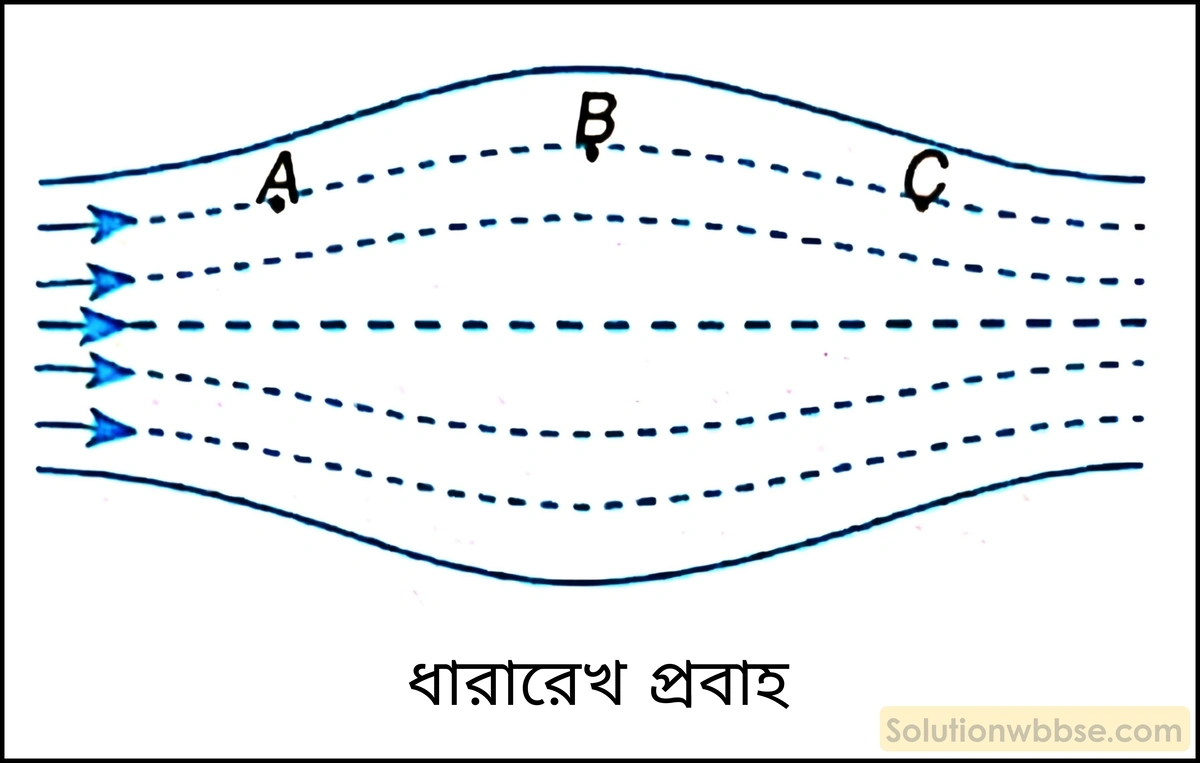
ধারারেখ প্রবাহের উদাহরণ – কম গতিবেগসহ গতিশীল যে-কোনো তরলের গতি সাধারণভাবে ধারারেখ হয়ে থাকে।
ধারারেখা বা প্রবাহরেখা কী?
ধারারেখা (Streamlines) – ধারারেখ প্রবাহের ক্ষেত্রে যে-কোনো বিন্দুতে কোনো তরলকণা তার পূর্ববর্তী কণার গতিপথকে একই বেগসহ অবিকৃতভাবে অনুসরণ করে। এরূপ প্রবাহে তরল পদার্থের কণা যে পথ বরাবর গতিশীল হয়, তাকেই ধারারেখা বা প্রবাহরেখা বলে। এটি সরল বা বক্র যে-কোনো রেখা হতে পারে।
ধারারেখার বৈশিষ্ট্যগুলি আলোচনা করো।
ধরোরেখার বৈশিষ্ট্যসমূহ –
- ধারারেখার যে-কোনো নির্দিষ্ট বিন্দুতে কোনো কণার বেগ নির্দিষ্ট থাকে, যদিও বেগের মান বিভিন্ন বিন্দুতে ভিন্ন ভিন্ন হয়।
- ধারারেখার যে-কোনো বিন্দুতে অঙ্কিত স্পর্শক ওই বিন্দুতে প্রবাহীর বেগের অভিমুখ নির্দেশ করে।
- দুটি ধারারেখা কখনোই পরস্পরকে ছেদ করতে পারে না।
- প্রবাহীর বেগ যেখানে বেশি সেখানে ধারারেখাগুলি পরস্পরের থেকে ঘনসন্নিবিশিষ্ট এবং যেখানে কম সেখানে তারা পরস্পরের থেকে দূরে অবস্থান করে।
অশান্ত বা বিক্ষুদ্ধ প্রবাহ বলতে কী বোঝায়?
অশান্ত বা বিক্ষুদ্ধ প্রবাহ (Turbulent or Disorderly flow) – যে ধরনের গতির ক্ষেত্রে কোনো নির্দিষ্ট বিন্দুতে প্রবাহী কণার বেগের মান ও অভিমুখ কোনোটিই নির্দিষ্ট থাকে না, বরং সময়ের সঙ্গে এলোমেলোভাবে পরিবর্তিত হয়, তাকেই অশান্ত বা বিক্ষুদ্ধ প্রবাহ বলে। প্রবাহী কণার গতিপথ এক্ষেত্রে চূড়ান্ত বিশৃঙ্খল ও অবিন্যস্ত হয়ে থাকে।
অশান্ত বা বিক্ষুদ্ধ প্রবাহের উদাহরণ – পাহাড়ি খরস্রোতা নদীতে জলের প্রবাহ, দ্রুতগামী স্টিমার বা জাহাজের গতিপথের পাশের জলতলে তৈরি হওয়া ঘূর্ণি, পতাকার পতপত করে ওড়া (flutterring), দ্রুতগামী ট্রেন সংলগ্ন অঞ্চলে বয়ে যাওয়া বায়ুপ্রবাহ ইত্যাদি অশান্ত প্রবাহের উদাহরণ।
সন্ধিবেগ বা সংকট বেগ কাকে বলে?
সন্ধিবেগ (Critical velocity) – প্রবাহীর গতিবেগের যে সর্বোচ্চ মান পর্যন্ত তার গতির প্রকৃতি ধারারেখ থাকে অর্থাৎ, যে ঊর্ধ্বসীমা অতিক্রান্ত হলে গতির প্রকৃতি অশান্ত বা বিক্ষুব্ধ হয়, তাবেই বলা হয় সন্ধিবেগ বা সংকট বেগ (vc)।
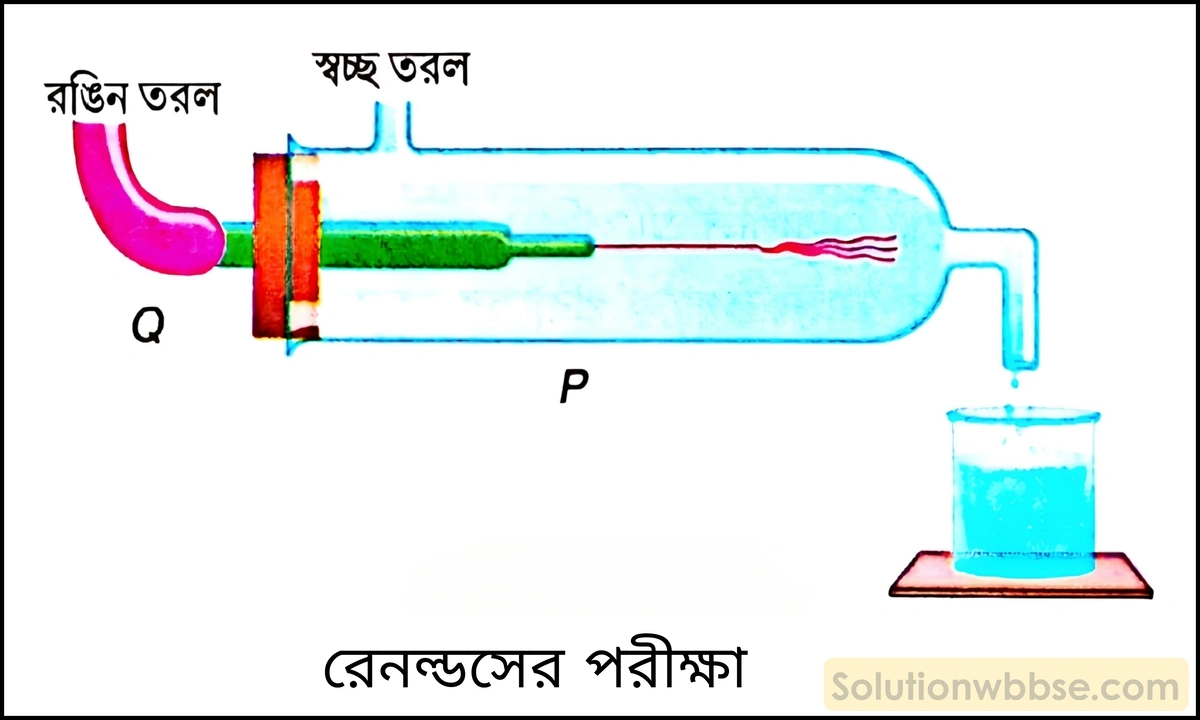
একটি সহজ পরীক্ষার সাহায্যে ধারারেখ ও অশান্ত প্রবাহের পার্থক্য বোঝাও।
বিজ্ঞানী রেনল্ডস্ একটি সহজ পরীক্ষার মাধ্যমে ধারারেখ ও অশান্ত প্রবাহের পার্থক্য দেখিয়েছেন। নীচের চিত্রে একটি মোটা নল P -এর মধ্যে দিয়ে একটি স্বচ্ছ তরল প্রবাহিত হচ্ছে। নলটিকে উঠিয়ে বা নামিয়ে তরলের বেগ বাড়ানো বা কমানো যেতে পারে। অন্য আর একটি পাত্রে ওই তরলের সঙ্গে গোলাপি রং মিশিয়ে একটি সরু নল Q -এর সাহায্যে P -এর অক্ষ বরাবর ওই রঙিন তরলকে সরু সুতোর মতো করে ছাড়া যায়। স্বচ্ছ তরলের বেগ কম হলে রঙিন তরল সুতোর মতো অবিচ্ছিন্নভাবে প্রবাহিত হয়। অর্থাৎ, প্রবাহ ধারারেখ। এবার স্বচ্ছ তরলের বেগ বাড়তে থাকলে রঙিন তরলের ধারাটি কাঁপতে থাকে। পরে ধারাটি এলোমেলোভাবে চলতে থাকে বা ছিন্ন হয়ে আবর্তের সৃষ্টি করে। ক্রমান্বয়ে নলের সমস্ত জলটাই রঙিন হয়ে যায়। এঘটনা প্রমাণ করে, জলের প্রবাহ আর স্থির বা ধারারেখ নেই – প্রবাহ অশান্ত হয়ে পড়েছে।
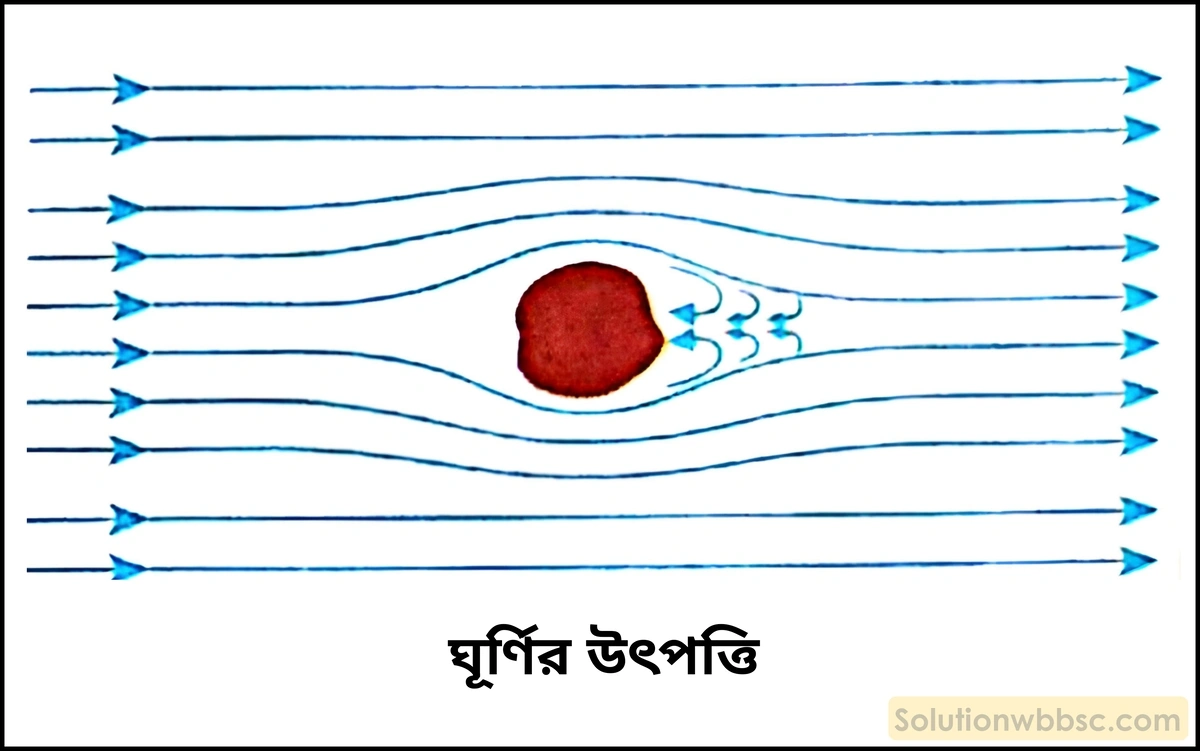
পাহাড়ি খরস্রোতা নদীর উচ্চ প্রবাহে কেন অসংখ্য ঘূর্ণি দেখা যায়?
কোনো প্রবাহীর গতি অশান্ত হলে এবং ওর গতিপথে কোনো বস্তু থাকলে বস্তুর ঠিক পিছনে অবস্থিত অঞ্চলে আবর্ত ও ঘূর্ণির সৃষ্টি হয়। এর ফলে বিপুল পরিমাণ শক্তি অপচয় হয়। পাহাড়ি খরস্রোতা নদীর গতি অশান্ত হয় এবং ওর গতিপথে অনেক সময় প্রস্তরখণ্ড থাকে। এর ফলে প্রস্তরখণ্ডের ঠিক পিছনে আবর্ত ও ঘূর্ণির সৃষ্টি হয়। এইসব নদীর উচ্চ প্রবাহে সাধারণত অসংখ্য ঘূর্ণি দেখা যায়।
ধারানল (Stream tube) বা প্রবাহনল (tube of flow) কী এবং এটি কীভাবে তরল প্রবাহের সীমা নির্ধারণ করে?
তরলের অভ্যন্তরে যদি অতি ক্ষুদ্র একটি ক্ষেত্রের অস্তিত্ব কল্পনা করা হয়, তবে ওই কল্পিত ক্ষেত্রের সীমাতলের প্রত্যেক বিন্দু দিয়ে নির্গত ধারারেখাগুলি একটি কাল্পনিক নল গঠন করে, যাকে ধারানল (Stream tube) বা প্রবাহনল (tube of flow) বলে।
তরল কণাগুলির কোনোটিরই বেগের কোনো উপাংশ এই নলের বাইরে থাকতে পারে না বলে এই নল থেকে তরল বা কোনো প্রবাহীর বাইরে বেরিয়ে আসা সম্ভব হয় না।
বিজ্ঞানী অসবর্ণ রেনল্ডস্ এই দুই প্রকার গতি নিয়ে দীর্ঘ পরীক্ষানিরীক্ষা করেন এবং সিদ্ধান্তে আসেন যে, বেগের মান কম থাকলে প্রবাহের প্রকৃতি ধারারেখ হয় এবং তা বৃদ্ধি পেয়ে একটি নির্দিষ্ট সীমা অতিক্রম করলে প্রবাহের প্রকৃতি বিক্ষুদ্ধ বা অশান্ত হয়।
উল্লেখ করা যায় যে, বেগের মানের বৃদ্ধির সঙ্গে প্রবাহের প্রকৃতির এই পরিবর্তন হঠাৎ না হয়ে ক্রমিক (Gradual) হয়ে থাকে।
সান্দ্রতা কাকে বলে?
সান্দ্রতা (Viscosity) – কোনো প্রবহমান তরল বা গ্যাসের দুটি পাশাপাশি স্তরের মধ্যে বেগের পার্থক্য থাকলে প্রবাহী এদের আপেক্ষিক বেগ কমাতে চায় অর্থাৎ, দ্রুতগামী স্তর অপেক্ষাকৃত ধীরগতিসম্পন্ন স্তরের বেগ বৃদ্ধি করতে চায় এবং ধীরগতিসম্পন্ন স্তর দ্রুতগামী স্তরটির বেগ কমাতে সচেষ্ট হয়। প্রবাহীর এই বিশেষ ধর্মকে সান্দ্রতা বলা হয়।
বিকল্প সংজ্ঞা
যে নিজস্ব ধর্মের জন্য কোনো প্রবাহী তার অভ্যন্তরস্থ বিভিন্ন স্তরগুলির আপেক্ষিক গতির বিরুদ্ধে বাধা সৃষ্টি করে, তাকে প্রবাহীর সান্দ্রতা বলে।
সান্দ্রবল বলতে কী বোঝায়?
সান্দ্রবল (Viscous force) – সান্দ্রতা ধর্মের দরুন তরলের দুই স্তরের মধ্যে স্পর্শীয়ভাবে ক্রিয়াশীল যে বল স্তর দুটির আপেক্ষিক বেগ কমাতে চেষ্টা করে, তাকেই সান্দ্রবল বা সান্দ্রতাজনিত বল বলা হয়।
সান্দ্রতার উৎপত্তি হয় কীভাবে?
সান্দ্রতার উৎপত্তি – কোনো দৃঢ় অনুভূমিক তলের ওপর দিয়ে তরল ধারারেখ প্রবাহে গতিশীল হলে আসঞ্জন বলের ক্রিয়ায় তলের সঙ্গে সংযোগে থাকা তরলস্তর স্থির থাকলেও প্রবাহের লম্ব অভিমুখে দূরত্ব বৃদ্ধির সঙ্গে সঙ্গে তরল স্তরগুলির বেগ ক্রমশ বৃদ্ধি পায়।
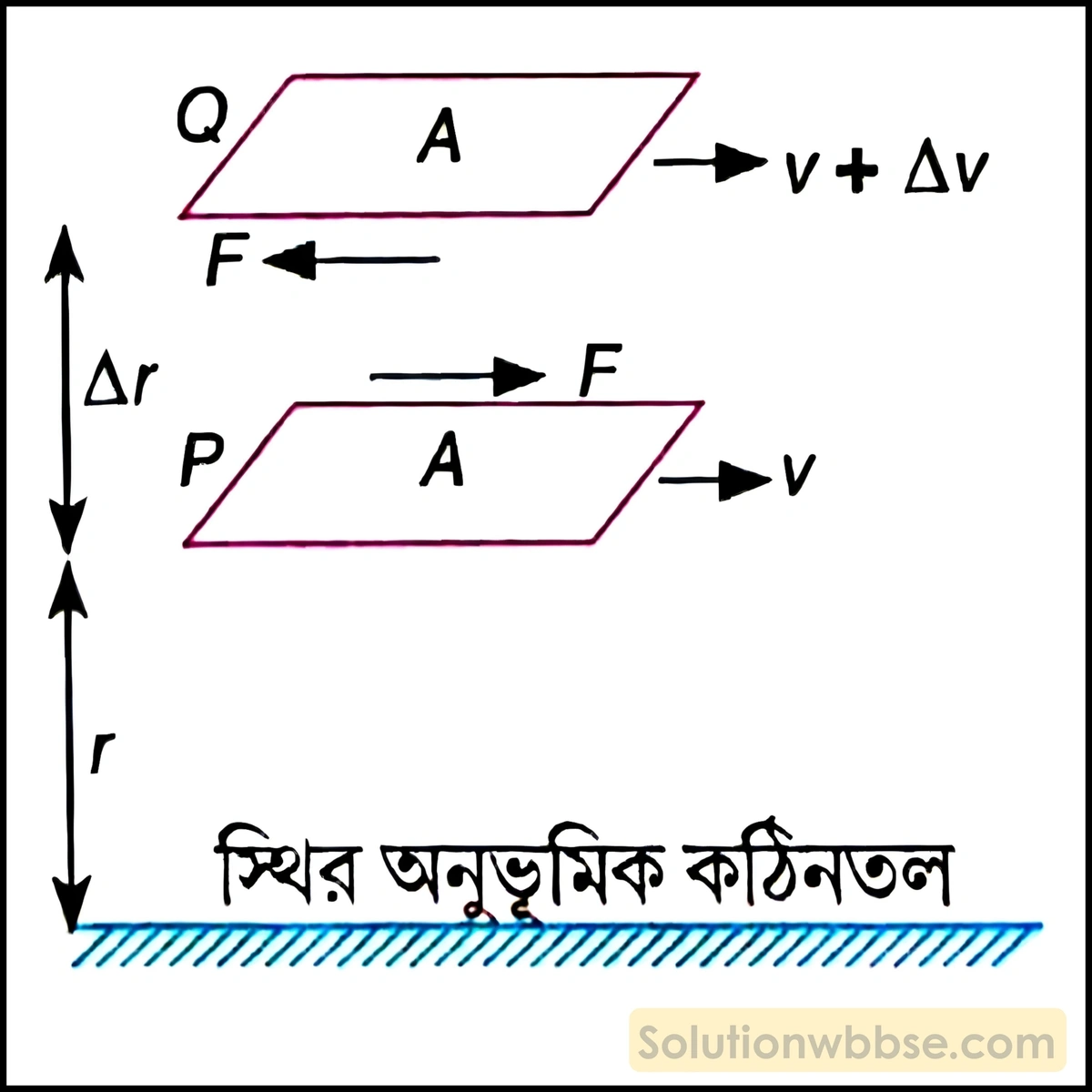
পরপর অবস্থিত এমন দুটি তরলস্তর (যেমন – P ও Q) -এর ক্ষেত্রে উপরের স্তরটি নীচের স্তরের বেগ বৃদ্ধি এবং নীচের স্তরটি উপরের স্তরটির বেগ হ্রাস করতে সচেষ্ট হয়। এর ফলে স্তর দুটি তাদের মধ্যে ক্রিয়াশীল আপেক্ষিক গতিকে বিনষ্ট করতে চায়। এই পারস্পরিক আন্তঃক্রিয়াকে প্রবাহের বিরুদ্ধে স্তর দুটির সঙ্গে স্পর্শকীয়ভাবে গতিকে বাধাদানকারী একটি বল হিসেবে গণ্য করা যায়, যা প্রবাহকে বাধা দেয় এবং কিছু সময় পরে ওই প্রবাহ বন্ধ হয়। এই বলকেই সান্দ্র বল বলা হয়। বাইরে থেকে বল প্রয়োগ করে সান্দ্রতাকে প্রতিমিত করা হলে তবেই প্রবাহ বজায় থাকে।
সান্দ্রতা কোন্ কোন্ বিষয়ের ওপর নির্ভর করে?
তরলের সান্দ্রতা প্রদত্ত তিনটি বিষয়ের ওপর নির্ভর করে –
- তরলের প্রকৃতি,
- স্পর্শতলের ক্ষেত্রফল,
- প্রবাহের লম্বদিকে দূরত্বের সঙ্গে বেগ পরিবর্তনের হার।
সান্দ্রবল সম্পর্কিত নিউটনের সূত্রটি লেখো।
সান্দ্রবল সম্পর্কিত নিউটনের সূত্র – শান্ত প্রবাহে গতিশীল কোনো তরলের ক্ষেত্রে পরীক্ষালব্ধ ফলাফল বিশ্লেষণ করে বিজ্ঞানী আইজ্যাক নিউটন দেখান যে, গতির বিরুদ্ধে ক্রিয়াশীল সান্দ্রতাজনিত বাধা তরলের প্রকৃতি, স্পর্শতলের ক্ষেত্রফল এবং প্রবাহের লম্ব অভিমুখে দূরত্বের সঙ্গে বেগের পরিবর্তন – এই তিনটি রাশির ওপর নির্ভর করে।
তরলতলের ক্ষেত্রফল \(A\), তরলপ্রবাহের লম্ব অভিমুখে দূরত্ব বৃদ্ধির সাপেক্ষে তরলের স্তরের বেগ বৃদ্ধির হার বা বেগের নতিমাত্রা \(\left(\frac{\Delta v}{\Delta r}\right)\) হলে নিউটনের সূত্রানুসারে, সান্দ্রতাজনিত বাধা বা সান্দ্রবল \(F\propto A\) [যখন \(\frac{\Delta v}{\Delta r}\) ধ্রুবক] এবং \(F\propto\frac{\Delta v}{\Delta r}\) [যখন \(A\) ধ্রুবক]
∴ যৌগিক ভেদের সূত্র অবলম্বনে পাওয়া যায়, \(F\propto A\frac{\Delta v}{\Delta r}\) [যখন, \(A\) ও \(F\propto\frac{\Delta v}{\Delta r}\) উভয়েই পরিবর্তনীয়]
বা, \(F=-\eta A\frac{\Delta v}{\Delta r}\) [যখন, \(\eta\) সমানুপাতিক ধ্রুবক]
সমানুপাতিক ধ্রুবক \(\eta\) -এর মান নির্দিষ্ট তরলের জন্য ধ্রুবক হয়ে থাকে। একে বলা হয় সংশ্লিষ্ট তরলের সান্দ্রতাঙ্ক।
[‘-‘ চিহ্ন নির্দেশ করে সান্দ্রতাজনিত বল প্রবাহের বিরুদ্ধে ক্রিয়া করে।]
সান্দ্রতাঙ্ক কাকে বলে?
সান্দ্রতাঙ্ক (Coefficient of viscosity) – \(F=-\eta A\frac{\Delta v}{\Delta r}\) [চিহ্ন উপেক্ষা করে] সম্পর্ক অনুযায়ী \(A=1\), \(\frac{\Delta v}{\Delta r}=1\) হলে, \(F=\eta\) হয়। অর্থাৎ, একক দূরত্বে অবস্থিত দুটি প্রবাহী স্তরের মধ্যে একক আপেক্ষিক বেগ বজায় রাখতে প্রবাহীর যে-কোনো স্তরের সঙ্গে স্পর্শকীয়ভাবে একক ক্ষেত্রফলে যে বল প্রয়োগ করতে হয়, তাকেই ওই প্রবাহীর সান্দ্রতাঙ্ক বলা হয়।
সান্দ্রতাঙ্কের CGS পদ্ধতিতে ও SI -তে একক লেখো। এর মাত্রীয় সংকেত লেখো।
CGS পদ্ধতি ও SI -তে সান্দ্রতাঙ্কের একক যথাক্রমে পয়েজ (Poise), পাস্কাল⋅সেকেন্ড (Pa⋅s)।
CGS পদ্ধতিতে –
1 poise = \(\frac{1\;dyn\times1\;cm}{1\;cm^2\times1\;cm/s}\)
বা, 1 poise = 1 dyn⋅s⋅cm-2
SI পদ্ধতিতে –
1 Pa⋅s = \(\frac{1N\times1\;m}{1\;m^2\times1\;m/s}\)
বা, 1 Pa⋅s = 1 N⋅s⋅m-2
মাত্রীয় সংকেত – \(\left[\eta\right]=\left[\frac F{A{\displaystyle\frac{\Delta v}{\Delta r}}}\right]\)
বা, \(\left[\eta\right]=\left[\frac{MLT^{-2}}{L^2{\displaystyle\frac{LT^{-1}}L}}\right]\)
বা, \(\left[\eta\right]=\left[ML^{-1}T^{-1}\right]\)
গতিবেগের নতিমাত্রা বলতে কী বোঝায়? এর একক ও মাত্রীয় সংকেত লেখো।
কোনো তরল অনুভূমিক তলের উপর দিয়ে চলার সময় যখন তরলটির শান্ত প্রবাহ হয়, তখন তরল প্রবাহের অভিমুখের সমকোণে একক দূরত্বে তরল প্রবাহের বেগের যে পরিবর্তন ঘটে, তাকে গতিবেগের নতিমাত্রা বলে।
গতিবেগের নতিমাত্রার একক s-1। এর মাত্রীয় সংকেত [T-1]।
একটি ব্যাবহারিক উদাহরণের সাহায্যে তরলের সান্দ্রতার ধারণা ব্যাখ্যা করো। সান্দ্রতার প্রাকৃতিক ও ব্যাবহারিক দৃষ্টান্ত উল্লেখ করো।
জলপূর্ণ বালতির মধ্যে হাত ঢুকিয়ে ঘোরালে দেখা যায় বালতির জলও আবর্তিত হচ্ছে। ভালো করে লক্ষ করলে দেখা যায়, আবর্তনের বেগ বালতির দেয়ালসংলগ্ন অংশের জলে কম এবং মাঝখানে সবথেকে বেশি। জলের উপরে কাঠের গুঁড়ো ছড়িয়ে দিলে পার্থক্য স্পষ্ট বোঝা যায়। এ থেকে বোঝা যায় যে, জলের বিভিন্ন স্তরের মধ্যে আপেক্ষিক গতি বর্তমান। বাইরে থেকে বল প্রয়োগ করা না হলেও দেখা যায়, কিছুক্ষণ পরে বালতির জলের এই আবর্তন নিজে থেকেই থেমে যায়।
বলবিদ্যার প্রাথমিক ধারণা থেকে আমরা জানতে পারি, যে-কোনো সচল বস্তুকে স্থিরাবস্থায় আনতে তার গতির বিরুদ্ধে বল প্রয়োগ করা আবশ্যক। বাহ্যিক বলের অনুপস্থিতিতেও জল গতিহীন হওয়ার ঘটনা প্রমাণ করে যে, তরলের অভ্যন্তরে নিশ্চয়ই কোনো বল সৃষ্টি হয়েছে, যা তরলের ভিতরে বিভিন্ন স্তরের মধ্যে আপেক্ষিক গতিকে বাধা দেয়। এটিই সান্দ্রতা বল।
সান্দ্রতার প্রাকৃতিক ও ব্যাবহারিক উদাহরণ –
- বাতাসের সান্দ্রতাজনিত বাধার কারণে মেখে ভাসমান জলকণা অত্যন্ত ধীরগতিতে নীচের দিকে নামতে থাকে যাতে মনে হয় যেন মেঘ আকাশে ভেসে বেড়াচ্ছে।
- আমরা বাতাসের মধ্যে দিয়ে দ্রুত হাঁটতে সক্ষম হলেও জলের মধ্যে অত দ্রুত হেঁটে বা সাঁতরে যেতে পারি না। কারণ – বাতাসের তুলনায় জলের সান্দ্রতার মান বেশি।
সান্দ্রতার দুটি ব্যাবহারিক উপযোগিতা লেখো।
সান্দ্রতার ব্যাবহারিক উপাযাগিতাগুলি হল –
- সান্দ্রতার ধারণা এবং উষ্ণতার সঙ্গে সান্দ্রতাঙ্কের মানের পরিবর্তনের প্রকৃতি জানা থাকলে বিভিন্ন ঋতুতে কোনো মেশিনের যন্ত্রাংশে ব্যবহারের উপযোগী উপযুক্ত পিচ্ছিলকারক (lubricants) নির্বাচন সহজ হয়।
- মানবশরীরের বিভিন্ন অংশে শিরা ও ধমনির মাধ্যমে রক্তসংবহন প্রক্রিয়ায় সান্দ্রতা সম্পর্কিত ঘটনাবলি বিভিন্ন গুরুত্বপূর্ণ ভূমিকা পালন করে।
সান্দ্রতাঙ্কের ওপর উষ্ণতা ও চাপের প্রভাব লেখো।
সান্দ্রতাঙ্কের ওপর উষ্ণতার প্রভাব – উত্তপ্ত করলে তরলের উষ্ণতা বৃদ্ধি পায়, ফলে অণুগুলির গতিশক্তি বাড়ে এবং আণবিক আকর্ষণ দুর্বল হয়ে পড়ে। তাই উষ্ণতা বৃদ্ধিতে তরলের সান্দ্রতাঙ্ক সাধারণভাবে হ্রাস পায়।
গ্যাসের ক্ষেত্রে সান্দ্রবল এক স্তর থেকে অন্য স্তরে ব্যাপনের মাধ্যমে ভরবেগ স্থানান্তরের ফলে সৃষ্টি হয়। প্রমাণ করা যায় যে, গ্যাসের ব্যাপন হার উষ্ণতার বর্গমূলের সঙ্গে সমানুপাতিক। সুতরাং, গ্যাসের সান্দ্রতাক্ষের মান \(\eta\propto\sqrt T\) হয়, যেখানে \(T\) পরম স্কেলে গ্যাসের উষ্ণতা।
সান্দ্রতাঙ্কের ওপর চাপের প্রভাব – জল ছাড়া যে-কোনো তরলের ক্ষেত্রে সান্দ্রতাঙ্কের মান চাপ বৃদ্ধির সঙ্গে সমানুপাতে বাড়ে। জলের ক্ষেত্রে কয়েকশো বায়ুমণ্ডলীয় চাপ বৃদ্ধির সঙ্গে সান্দ্রতাঙ্ক হ্রাস পায়।
বিস্তীর্ণ পাল্লার মধ্যে গ্যাসের সান্দ্রতাঙ্কের মান চাপের পরিবর্তনে নিরপেক্ষ হয়ে থাকে।
ধারারেখীয় গঠন বলতে কী বোঝায়? উদাহরণ দাও।
ধারারেখীয় গঠন (Streamlined shape) – প্রবাহীর মধ্যে দিয়ে দ্রুতবেগে গতিশীল বস্তুর বিরুদ্ধে সান্দ্রতাজনিত বাধা কমাক্ষ্মেনার উদ্দেশ্যে সংশ্লিষ্ট বস্তুর গঠন এমন করা হয় যে, তার প্রস্থচ্ছেদের ক্ষেত্রফল পিছনদিকে ক্রমশ সরু হতে থাকে। তার পৃষ্ঠতল যথাসম্ভব মসৃণ হয় এবং আকারে কোথাও কোনো অনিয়মিত ভাঁজ বা খাঁজ থাকে না। এই বিশেষ আকার বা অবয়বকে ধারারেখীয় গঠন বলে।
ধারারেখীয় গঠনের উদাহরণ – মাছ, টর্পেডো, বিমান, দ্রুতগামী জলযান, ইত্যাদির মাকুসদৃশ (দুই প্রান্ত সরু এবং মধ্যভাগ মোটা ও চ্যাপটা) গঠন।
সান্দ্রতা এবং সীমান্ত বেগের ধারণা কীভাবে বিজ্ঞানী মিলিক্যানের তৈলবিন্দু পরীক্ষায় ইলেকট্রনের আধান নির্ণয়ে সহায়তা করেছে?
সান্দ্রতার ধারণাকে বেশ কিছু জৈব তরল যেমন – প্রোটিন, সেলুলোজ ইত্যাদির আকৃতি ও আণবিক ওজন নির্ণয়ের কাজে ব্যবহার করা হয়। সান্দ্রতা এবং সীমান্ত বেগের ধারণাকে সফলভাবে কাজে লাগিয়ে বিজ্ঞানী মিলিক্যান তাঁর বিখ্যাত তৈলবিন্দু পরীক্ষার (Oil drop experiment) পরিকল্পনা করেন, যার মাধ্যমে ইলেকট্রনের আধান নির্ণয় করা সম্ভব হয়।
উষ্ণতার সঙ্গে সান্দ্রতাঙ্কের পরিবর্তন স্লটের স্থূল সূত্রটি লেখো।
উষ্ণতার সঙ্গে সান্দ্রতাঙ্কের পরিবর্তন স্লটের স্থূল সূত্রের (Slote’s empirical formula) সাহায্যে আনুমানিক চেহারায় প্রকাশকরাহয় – যেখানে ηt, ও η0 যথাক্রমে t°C ও 0°C উষ্ণতায় সান্দ্রতাঙ্গ, উষ্ণতা বৃদ্ধি, α ও β ধ্রুবক।
বিভিন্ন তরলের সান্দ্রতা বিভিন্ন হয় – একটি সহজ পরীক্ষার সাহায্যে প্রমাণ করো।
নিম্নলিখিত পরীক্ষার সাহায্যে প্রমাণ করা যায় – বিভিন্ন তরলের সান্দ্রতা বিভিন্ন হয়।
উপকরণ –
- তিনটি সমান আকারের পাত্র,
- সামান্য পরিমাণ জল, মধু ও আলকাতরা।

পরীক্ষা – তিনটি সমান আকারের পাত্রে সমপরিমাণ জল, মধু ও আলকাতরা নিয়ে পাত্রগুলিকে একইভাবে নাড়িয়ে দেওয়া হল।
পর্যবেক্ষণ – দেখা গেল, আলকাতরা সবার আগে স্থির হল। তারপর মধু ও সবশেষে জল স্থির হল।
সিদ্ধান্ত ও ব্যাখ্যা – উপরের পরীক্ষাটি থেকে বোঝা গেল, জলের সচলতা সবচেয়ে বেশি, তারপর মধু ও সবচেয়ে কম সচলতা আলকাতরার। যে তরলের সান্দ্রতা যত বেশি, সেই তরলের সচলতা তত কম। তাই বলা যায়, জল অপেক্ষা মধুর সান্দ্রতা বেশি। আবার মধু অপেক্ষা আলকাতরার সান্দ্রতা বেশি। অর্থাৎ, বিভিন্ন তরলের সান্দ্রতা বিভিন্ন।
সান্দ্রতার সঙ্গে প্রবাহীর সচলতা কীভাবে সম্পর্কযুক্ত?
সান্দ্রতার ধারণা প্রবাহীর সচলতা তথা গতিশীলতা (mobility) ধর্মের সঙ্গে সরাসরি সম্পর্কযুক্ত। সান্দ্রতা তথা সান্দ্রতাক্ষের মান বৃদ্ধি পেলে অপরিবর্তিত শর্তে প্রবাহীর বিভিন্ন স্তরের মধ্যে আপেক্ষিক গতির বিরুদ্ধে ক্রিয়াশীল বাধা বা সান্দ্রবলের (viscous drag) মানও বাড়ে, ফলে প্রবাহীর গতি মন্থর হয় এবং তা দ্রুত স্থিরাবস্থায় আসে।
যেমন – তেলের সান্দ্রতা অ্যালকোহলের তুলনায় বেশি হওয়ায় দুটি অনুরূপ পাত্রে একই পরিমাণ তেল ও অ্যালকোহল নিয়ে তাদের একই মাত্রায় নাড়িয়ে দিলে দেখা যায় তেল অ্যালকোহলের তুলনায় অনেক তাড়াতাড়ি থেমে যায়।
প্রান্তীয় বেগ কাকে বলে? সান্দ্র মাধ্যমে গতিশীল বস্তু কীভাবে প্রান্তীয় বেগ অর্জন করে?
প্রান্তীয় বেগ (Terminal Velocity) – কোনো সান্দ্র প্রবাহী মাধ্যমে গতিশীল কোনো বস্তু যে সর্বোচ্চ মানের স্থির বেগসহ খাড়া নীচে বা উপরের দিকে গতিশীল হয়, তাকে ওই বস্তুর প্রান্তীয় বা সীমান্ত বেগ বলে।
প্রান্তীয় বেগ অর্জিত হওয়ার ব্যাখ্যা – সান্দ্র প্রবাহী মাধ্যমে কোনো বস্তু অভিকর্ষের ক্রিয়ায় খাড়া নীচের দিকে গতিশীল হলে বস্তু সংলগ্ন প্রবাহী স্তরও বস্তুটির সঙ্গে একই বেগে একই অভিমুখে গতিশীল হতে চায়। বস্তুটি থেকে যথেষ্ট দূরত্বে অবস্থিত স্তরগুলি যদিও প্রায় স্থির থাকে।
এর ফলে প্রবাহীর বিভিন্ন স্তরের মধ্যে আপেক্ষিক গতির উদ্ভব হয়, যার ফলে গতিশীল বস্তুর বিরুদ্ধে প্রবাহী একটি সান্দ্র বাধা বল (viscous force) প্রয়োগ করে। পতনশীল বস্তুর বেগ বৃদ্ধি পেলে ঊর্ধ্বমুখী এই সান্দ্রতাজনিত বলের মানও সমানুপাতিক হারে বাড়ে এবং একসময় বস্তুর ওপর খাড়া ঊর্ধ্বমুখে ক্রিয়াশীল সান্দ্রতা ও প্লবতা বলের লব্ধির মান অভিকর্ষ বলের সমান হয়। এই মুহূর্ত থেকে বস্তুর ওপর কার্যকরী বা লব্ধি বল শূন্য হয় এবং বস্তু স্থির মানের বেগসহ নীচের দিকে পড়তে থাকে। একেই বস্তুর প্রান্তীয় বা সীমান্ত বেগ বলা হয়।
স্টোকসের সূত্রটি বিবৃত করো। সূত্রটি প্রযোজ্য হওয়ার শর্তগুলি লেখো। এই সূত্র ব্যবহার করে সান্দ্র মাধ্যমে গতিশীল বস্তু দ্বারা অর্জিত প্রান্তীয় বেগের রাশিমালা প্রতিষ্ঠা করো।
স্টোকসের সূত্র – η সান্দ্রতাঙ্কবিশিষ্ট কোনো বিস্তৃত প্রবাহীর মধ্য দিয়ে r ব্যাসার্ধযুক্ত কোনো ক্ষুদ্র গোলক ν সুষম বেগসহ (প্রান্তীয় বেগ) গতিশীল হলে বিজ্ঞানী স্টোকসের সূত্র অনুসারে, গতির বিরুদ্ধে ক্রিয়াশীল সান্দ্রতাজনিত বলের মান (F) প্রদত্ত সম্পর্ক দ্বারা প্রকাশিত হয় – F = 6πηrν।
স্টোকসের সূত্র নিম্নবর্ণিত শর্তসাপেক্ষ প্রাযাজ্য হয় –
- প্রবাহী মাধ্যমটি সমসত্ত্ব ও অসীম বিস্তৃতিসম্পন্ন।
- পতনশীল গোলকটির পাশ দিয়ে প্রবাহীর গতি ধারারেখ।
- গোলকটি আকারে ক্ষুদ্র হলেও প্রবাহী মাধ্যমের অণুগুলির আন্তরাণবিক দূরত্বের তুলনায় তা আকারে বড়ো।
- গোলকটি সম্পূর্ণ দৃঢ় এবং তার পৃষ্ঠতল সম্পূর্ণ মসৃণ।
- মাধ্যমটির মধ্য দিয়ে পতনকালে গোলকটি কোনোভাবেই পিছলে যায় না।
প্রান্তীয় বেগের রাশিমালা – ধরা যাক, r ব্যাসার্ধের একটি ক্ষুদ্র গোলক σ ঘনত্ব ও η সান্দ্রতাঙ্ক বিশিষ্ট একটি বিস্তৃত সান্দ্র মাধ্যমের মধ্যে দিয়ে নীচে পড়ছে। গতির যে-কোনো মুহূর্তে গোলকটির ওপর ক্রিয়াশীল বিভিন্ন বলগুলি হল –
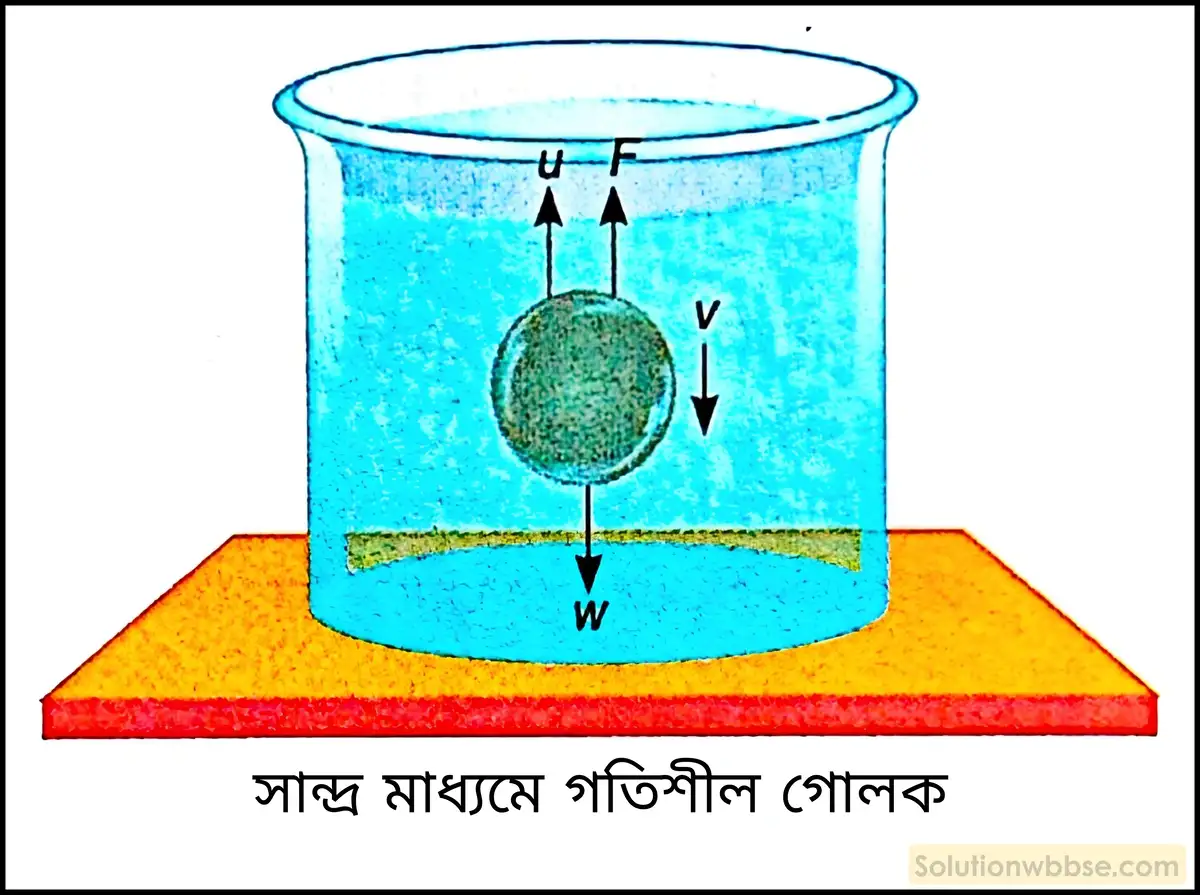
- বস্তুর ওজন \(\mathrm W=\mathrm{mg}=\frac43\mathrm{πr}^3\mathrm{ρg}\) বস্তুর ঘনত্ব → ρ।
- প্রবাহীর দেওয়া উর্ধ্বঘাত বা প্লবতা \(\left(\mathrm u\right)=\frac43\mathrm{πr}^3\mathrm{σg}\)।
- খাড়া উপরের দিকে ক্রিয়াশীল সান্দ্র বাধা বল, F = 6πησg।
বস্তুর গতিবেগ বৃদ্ধির সঙ্গে F -এর মানও সমানুপাতিক হারে বাড়ে। যে মুহূর্তে ও F -এর লব্ধি (u + F), W -কে প্রতিমিত করে সেই মুহূর্ত থেকে বস্তুর ওপর ক্রিয়াশীল লব্ধি বল শূন্য হয়। এই অবস্থায় বস্তু ওই মুহূর্তে অর্জিত স্থির মানের বেগ বা সীমান্ত বেগসহ নীচে পড়ে।
∴ সীমান্ত বেগ অর্জিত হওয়ার শর্ত –
u + F = W
বা, F= W – u
বা, \(6\mathrm{πηrv}=\frac43\mathrm{πr}^3\left(\mathrm\rho-\mathrm\sigma\right)\mathrm g\)
বা, \(\mathrm v=\frac{2\mathrm r^2\left(\mathrm\rho-\mathrm\sigma\right)\mathrm g}{9\mathrm\eta}\)
বস্তুর ঘনত্ব (ρ) ও গোলকের ঘনত্বের (σ) মধ্যে সম্পর্ক লেখো।
- ρ > σ হলে সীমান্ত বেগের অভিমুখ খাড়া নীচের দিকে হয়।
- ρ < σ হলে v -এর মান হয় ঋণাত্মক, যা নির্দেশ করে যে বস্তুর গতির অভিমুখ খাড়া ওপর দিকে হয়ে থাকে। উদাহরণ – জলের গভীরে ছেড়ে দেওয়া তেলের ফোঁটা বা সৃষ্টি হওয়া বায়ু বুদবুদের ঊর্ধ্বগতি। একই কারণে আকাশে ভাসমান মেঘকে ঊর্ধ্বগামী দেখতে পাওয়া যায়।
- ρ = σ হলে বস্তুটি ওই প্রবাহীতে স্থির হয়ে বা ঝুলে থাকে।
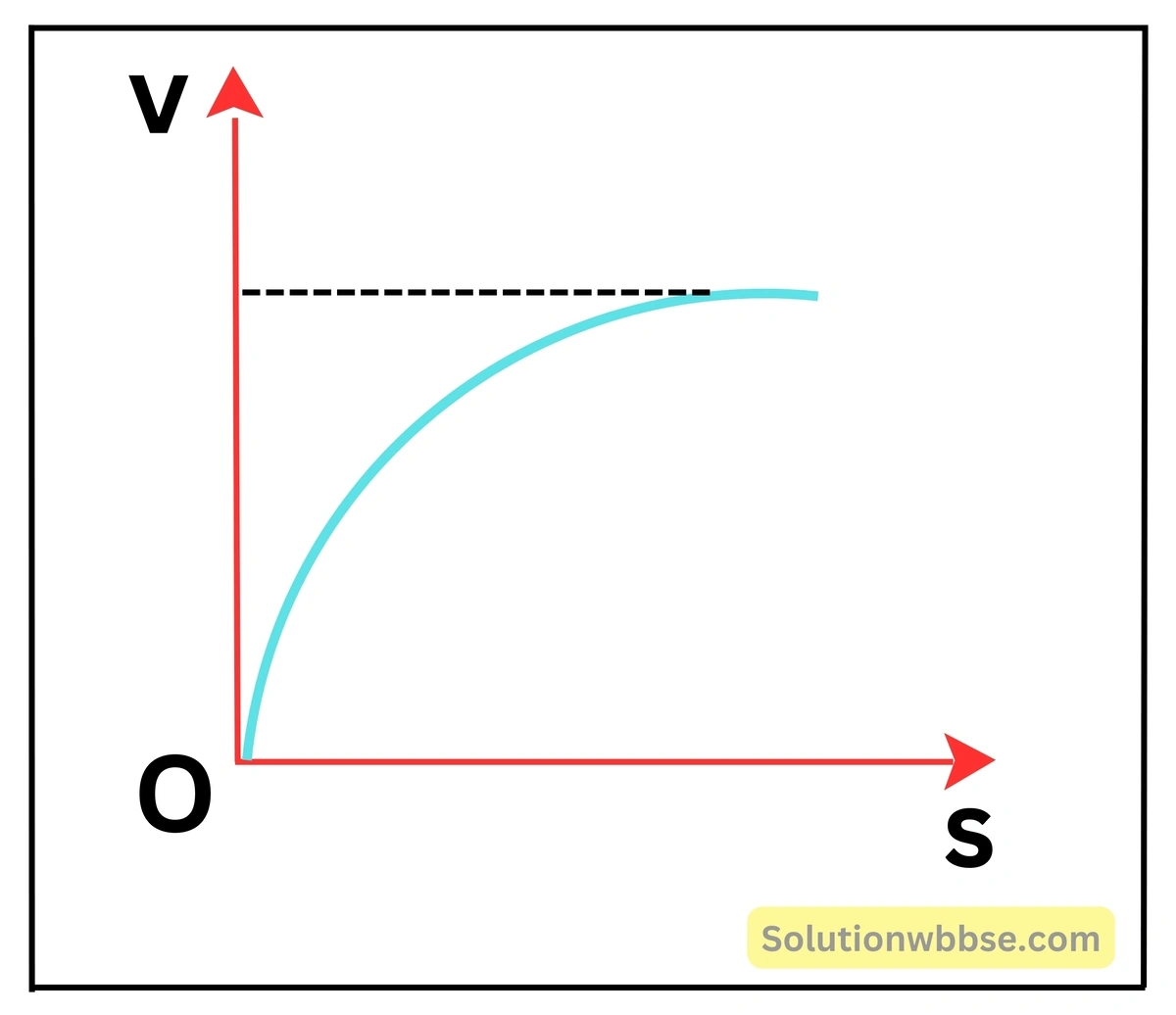
একটি বিস্তৃত সান্দ্র মাধ্যমে পতনশীল কোনো বস্তুর বেগ সময়ের সঙ্গে কীভাবে পরিবর্তিত হয়, তা লেখচিত্রের সাহায্যে দেখাও। লেখটি ব্যাখ্যা করো।
বেগ-সময় লেখচিত্রে প্রান্তীয় বেগ –
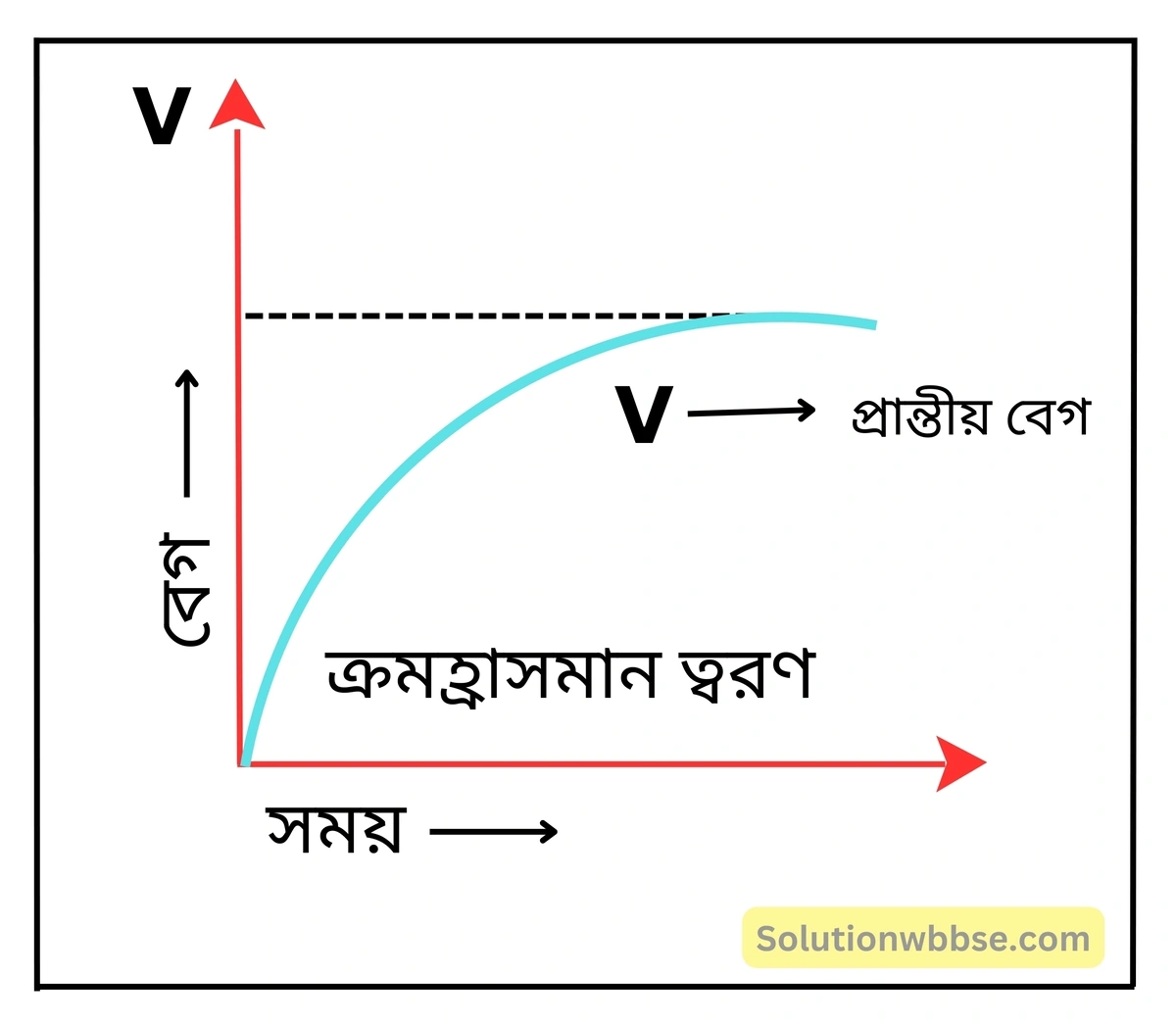
লেখচিত্রের ব্যাখ্যা – এক্ষেত্রে বেগ প্রথমে সময়ের সঙ্গে বৃদ্ধি পেলেও বেগ বৃদ্ধির হার ধীরে ধীরে কমে এবং সীমান্ত বেগ অর্জিত হলে লেখচিত্রটি সময় অক্ষের সমান্তরাল হওয়ার উপক্রম করে।
তরল প্রবাহের হার কাকে বলে? এর রাশিমালা প্রতিষ্ঠা করো। এটি কোন্ কোন্ বিষয়ের উপর নির্ভরশীল?
তরল প্রবাহের হার (Rate of flow of liquid) – প্রবাহ নলের যে-কোনো প্রস্থচ্ছেদের মধ্যে দিয়ে একক সময়ে প্রবাহিত তরলের আয়তনকে বলা হয় তরল প্রবাহের হার।
তরল প্রবাহের রাশিমালা – ধরা যাক, α প্রস্থচ্ছেদবিশিষ্ট একটি নলের মধ্যে দিয়ে v মানের স্থির গতিবেগসহ একটি তরল প্রবাহিত হচ্ছে। এই নলের মধ্য দিয়ে প্রতি সেকেন্ডে প্রবহমান তরলের আয়তন হল α প্রস্থচ্ছেদ ও v দৈর্ঘ্যবিশিষ্ট একটি চোঙে আবদ্ধ তরলের আয়তনের সমান।
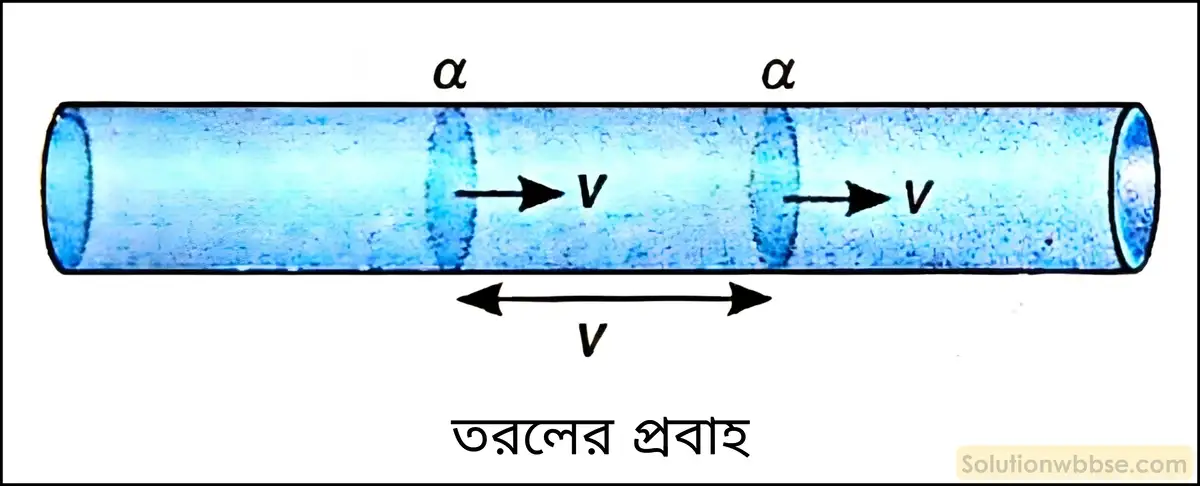
∴ তরল প্রবাহের হার = প্রতি সেকেন্ডে প্রবাহিত তরলের আয়তন = vα ঘনএকক। তরলের ঘনত্ব (ρ) চোঙের সর্বত্র সমান থাকলে, প্রতি সেকেন্ডে প্রবাহিত তরলের ভর = প্রতি সেকেন্ডে প্রবাহিত তরলের আয়তন × তরলের ঘনত্ব = vαρ।
তরল প্রবাহের হার প্রদত্ত দুটি বিষয়ের ওপর নির্ভর করে –
- তরলের প্রবাহের বেগ বাড়লে তরলের প্রবাহের হার বাড়ে ও তরলের প্রবাহের বেগ কমলে তরলের প্রবাহের হার কমে যায়।
- নলের প্রস্থচ্ছেদ বাড়লে তরলের প্রবাহের হার বাড়ে ও নলের প্রস্থচ্ছেদ কমলে তরলের প্রবাহের হার কমে যায়।
CGS পদ্ধতি ও SI -তে রাশিটির একক কী?
একক – তরল প্রবাহের হারের CGS একক cm3/s, SI একক m3/s এবং ব্যাবহারিক একক L/s।
ব্যাবহারিক ক্ষেত্রে বা হাতেকলমে তরল প্রবাহের হার কীভাবে পরিমাপ করা যায়?
হাতেকলমে তরল প্রবাহের হার নির্ণয় – স্থির হারে তরল প্রবাহ ঘটছে এমন কোনো সরবরাহ নলের একটি খোলা মুখের ঠিক নীচে একটি বড়ো পাত্র রেখে নির্দিষ্ট সময়ের জন্য ওই পাত্রে তরল সংগ্রহ করা হয়। সরবরাহ নলের কোনো অংশে প্যাঁচকল থাকলে তার ঠিক নীচে পাত্রটি বসিয়ে কল খুলে একইভাবে তরল সংগ্রহ করা যেতে পারে। তরল সংগ্রহের সময় একটি স্টপওয়াচের সাহায্যে এবং সংগৃহীত তরলের আয়তন মাপনী চোঙ ব্যবহার করে নির্ভুলভাবে পরিমাপ করা যায়। নির্ণীত সময় ও আয়তনের পাঠ যথাক্রমে \(t\) সেকেন্ড ও \(v\;mL\) হলে তরল প্রবাহের হারের পরিমাপ হবে \(\frac vtmL/s\)।
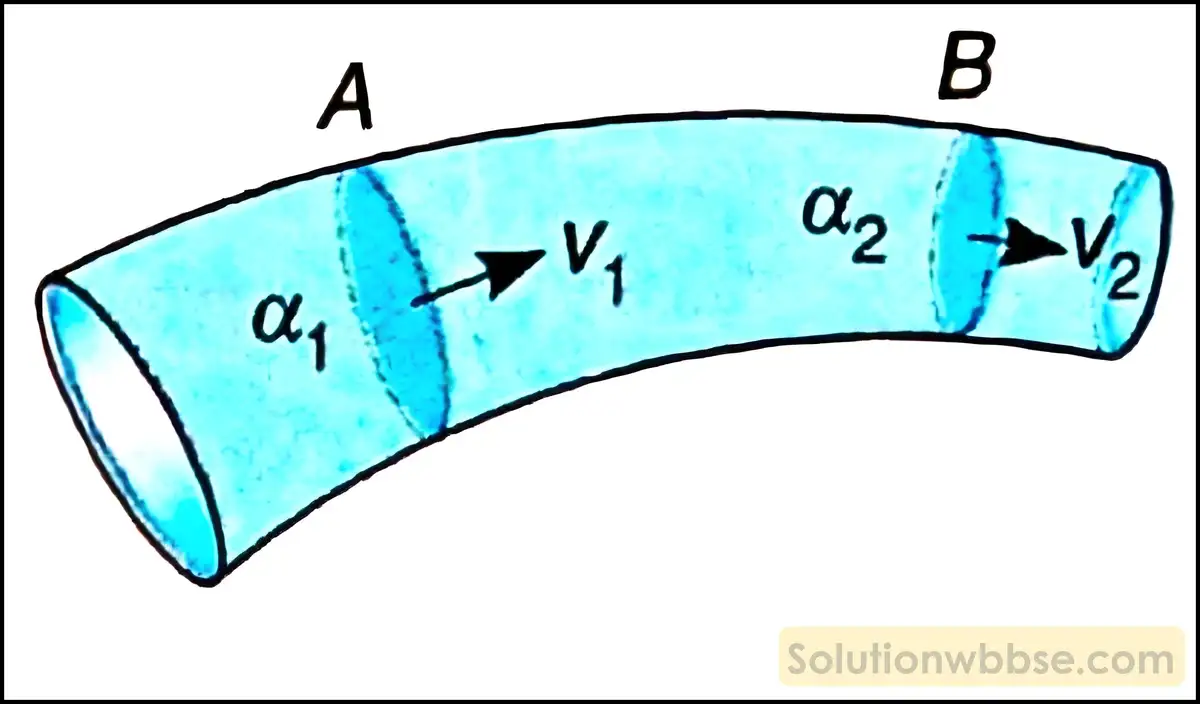
ধারাবাহিকতার সমীকরণ সম্পর্কে ব্যাখ্যা করে উপরের বিবৃতি অনুসারে সঠিক প্রশ্নটি কী হতে পারে?
অসংনম্য ও অসান্দ্র তরলের ধারারেখ প্রবাহের ক্ষেত্রে প্রবাহনলে প্রবিষ্ট নল থেকে বহির্গত তরলের ভর সর্বদা সমান থাকে, কারণ এক্ষেত্রে প্রবাহনলের ভিতর থেকে প্রবাহী কখনো বাইরে যেতে পারে না বা প্রবাহী নলের কোথাও জমে থাকে না। তাই অসম প্রস্থচ্ছেদযুক্ত প্রবাহীর ক্ষেত্রেও, vαρ = ধ্রুবক বা αv = ধ্রুবক (অসংনম্য তরলের ক্ষেত্রে ρ ধ্রুবক)। নলের যে-কোনো দুটি ছেদ A ও B -এর প্রস্থচ্ছেদের ক্ষেত্রফল α1 ও α2 এবং ছেদ দুটির লম্ব অভিমুখে প্রবাহীর তাৎক্ষণিক বেগ v1 ও v2 হলে αv = ধ্রুবক বা, α1v1 = α2v2। ফলাফলটি ধারাবাহিকতার সমীকরণ নামে পরিচিত।
বোধমূলক প্রশ্নোত্তর
সান্দ্রতাকে তরলের অভ্যন্তরীণ ঘর্ষণ বলে কেন?
সান্দ্রতাকে তরলের অভ্যন্তরীণ ঘর্ষণ বলা হয়, কারণ – ঘর্ষণের সঙ্গে সান্দ্রতার বেশ কতকগুলি ঘনিষ্ঠ সাদৃশ্য বর্তমান –
- দুটি বলই আণবিক আকর্ষণের ক্রিয়ায় সৃষ্টি হয়।
- ক্ষেত্রে সান্দ্রতা এবং কঠিন দুটি স্পর্শতলের ক্ষেত্রে ঘর্ষণ উভয়ই গতির বিরুদ্ধে ক্রিয়া করে অর্থাৎ, এরা বাধাদানকারী বল। দুটি বলেরই অস্তিত্ব উপলব্ধি করা যায় যখন সংস্পর্শে থাকা স্তরগুলির মধ্যে আপেক্ষিক গতি বজায় থাকে।
ঘনত্ব ও সান্দ্রতা দুটি আলাদা রাশি – ব্যাখ্যা করো।
সান্দ্রতা ও ঘনত্ব উভয়েই পদার্থের গুরুত্বপূর্ণ সাধারণ ধর্মগুলির অন্যতম হলেও এরা সম্পূর্ণ ভিন্ন রাশি। এই বক্তব্যের সমর্থনে যুক্তিগুলি হল –
- প্রবাহীর প্রবাহ চলাকালে অথবা প্রবাহীর মধ্যে অন্য কোনো বস্তু গতিশীল থাকলে সান্দ্রতার ধারণা অর্থপূর্ণ হয়। অন্যদিকে ঘনত্ব স্থির বা গতিশীল যে-কোনো অবস্থায় থাকা কঠিন, তরল বা গ্যাসের বৈশিষ্ট্য।
- পদার্থের একক আয়তনে ভরই হল তার ঘনত্বের পরিমাপ, অন্যদিকে সান্দ্রতা হল প্রবাহীর অভ্যন্তরস্থ বিভিন্ন স্তরের মধ্যে আপেক্ষিক গতিকে বাধাদান করার ধর্ম। সান্দ্রতাজনিত বাধা বা সান্দ্র বলের (viscous drag) সাহায্যে এই ধর্মের পরিমাপ করা হয়।
- উষ্ণতা বৃদ্ধিতে যে-কোনো পদার্থের ঘনত্ব হ্রাস পায়। অন্যদিকে উষ্ণতা বৃদ্ধিতে তরলের সান্দ্রতা হ্রাস পেলেও গ্যাসের সান্দ্রতা বাড়ে।
- বেশি ঘনত্বযুক্ত পদার্থ বেশি সান্দ্রতাযুক্ত হতে পারে আবার নাও পারে, যেমন – পারদের ঘনত্ব আলকাতরার তুলনায় বেশি হলেও দ্বিতীয়টি বেশি সান্দ্র। আবার, মধুর ঘনত্ব ও সান্দ্রতা উভয়ই জলের তুলনায় বেশি।
কোনো কোনো ক্ষেত্রে ঘনত্ব বৃদ্ধির সঙ্গে তরলের সান্দ্রতা হ্রাস বা বৃদ্ধি পেলেও তা কোনো সাধারণ নিয়ম হিসেবে স্বীকার করা যায় না—এটি কীভাবে প্রমাণ করা যায়? অ্যালকোহল ও জলের সান্দ্রতা ও ঘনত্বের তুলনামূলক বিশ্লেষণ থেকে কী বোঝা যায়?
কোনো কোনো ক্ষেত্রে ঘনত্ব বৃদ্ধির সঙ্গে তরলের সান্দ্রতা হ্রাস বা বৃদ্ধি পেলেও তা কোনো সাধারণ নিয়ম হিসেবে স্বীকার করা যায় না, যেমন – অ্যালকোহলের ঘনত্ব (0.81 g/cm3) জলের তুলনায় কম হলেও 30°C উষ্ণতায় অ্যালকোহলের সান্দ্রতাঙ্ক (0.00989 poise) সম উষ্ণতায় জলের সান্দ্রতাঙ্ক (0.000789) অপেক্ষা বেশি। তবে, প্রবাহীর গতীয় সান্দ্রতার (সান্দ্রতাঙ্ক ও ঘনত্বের অনুপাতের) মান সর্বদাই তার ঘনত্বের ব্যস্তানুপাতিক।
তরলের ঘনত্ব ও সান্দ্রতা বৃদ্ধি পেলে প্রান্তীয় বেগের মান কীরূপে পরিবর্তিত হয়?
η সান্দ্রতাঙ্কবিশিষ্ট সান্দ্র মাধ্যমে গতিশীল r ব্যাসার্ধ ও ρ ঘনত্ববিশিষ্ট একটি গোলক দ্বারা অর্জিত প্রান্তীয় বেগের রাশিমালা \(\mathrm v=\frac{2\mathrm r^2\left(\mathrm\rho-\mathrm\sigma\right)\mathrm g}{9\mathrm\eta}\); যেখানে, σ → মাধ্যমের ঘনত্ব, g → অভিকর্ষজ ত্বরণ।
উপরের সম্পর্কটি নির্দেশ করে যে, v ∝ (ρ – σ); যখন r, g, η ধ্রুবক; অর্থাৎ, σ ধ্রুবক থাকলে v ∝ ρ, অর্থাৎ ঘনত্ব বৃদ্ধি পেলে প্রান্তীয় বেগ বৃদ্ধি পায় এবং \(v\propto\frac1\eta\), যখন r, g, ρ ধ্রুবক। সুতরাং, মাধ্যমের সান্দ্রতাঙ্ক বৃদ্ধি পেলে প্রান্তীয় বেগ হ্রাস পায়।
দুটি ধারারেখ কখনোই পরস্পরকে ছেদ করে না কেন?
দুটি ধারারেখা কখনোই পরস্পরকে ছেদ করতে পারে না, কারণ – ছেদবিন্দুতে দুটি রেখার উপর দুটি ভিন্ন স্পর্শক অঙ্কন করা হত, যার অর্থ সংশ্লিষ্ট বিন্দুতে কণার বেগের সম্ভাব্য দুটি অভিমুখ থাকত। স্পষ্টতই এটি অবাস্তব। কারণ – বেগ একটি ভেক্টর রাশি হওয়ায় তার মান ও অভিমুখ দুইই নির্দিষ্ট।
তরলের সন্ধিবেগ শূন্য হওয়ার অর্থ কী?
সন্ধিবেগের মান কোনো তরল প্রবাহের বেগ কোন সর্বোচ্চ সীমা পর্যন্ত ধারারেখ থাকে তা নির্দেশ করে। সুতরাং, সন্ধিবেগ শূন্য হওয়ার অর্থ হল, বেগের যে-কোনো মানে ওই তরলের প্রবাহ অশান্ত বা বিক্ষুব্ধ হয়।
দুটি ফ্লাস্কের একটিতে জল অন্যটিতে গ্লিসারিন নিয়ে পাত্র দুটি ভালোভাবে নাড়িয়ে টেবিলের ওপর রাখা হল। কোন্ ফ্লাস্কের তরল আগে স্থির হবে?
যে মাধ্যমের সান্দ্রতা যত বেশি, তার সচলতা তত কম হয়। অর্থাৎ, সেই তরলটিকে গতিশীল করতে তত বেশি বল প্রয়োগ করতে হয়। গ্লিসারিন জলের তুলনায় বেশি সান্দ্র হওয়ায়, তার বিভিন্ন স্তরের মধ্যে আপেক্ষিক গতি জলের তুলনায় বেশি মাত্রায় বাধাপ্রাপ্ত হয়। তাই, জলের তুলনায় গ্লিসারিনের সচলতা তুলনামূলকভাবে কম। ফলে, দুটি ফ্লাস্ককে একই মাত্রায় নাড়িয়ে দিলে গ্লিসারিনপূর্ণ ফ্লাস্কের তরল আগে স্থির হবে।
শিশি থেকে তেল বা জল ঢাললে তা সঙ্গে সঙ্গে পড়তে থাকলেও টম্যাটো সস্ বা মধু ঢালতে গেলে সময় লাগে কেন?
যে-কোনো তরল পদার্থের অণুগুলির মধ্যে পারস্পরিক আকর্ষণ বল অর্থাৎ, সংসক্তি বল ক্রিয়া করে। তরলের ঘনত্ব যত বেশি হয়, সংসক্তি বলের মানও তত বেশি হয়। তাই তেল বা জলের তুলনায় টম্যাটো সস্ বা মধুর ক্ষেত্রে সংসক্তি বলের মান বেশি হয়। কারণ টম্যাটো সস্ বা মধুর ঘনত্ব অনেক বেশি। ফলে শিশি থেকে তাদের ঢালতে গেলে তরল অণুদুটির মধ্যস্থ আকর্ষণ ওদের পরস্পর থেকে বিচ্ছিন্ন করতে বেশি বাধা দেয়। তাই বেশি সময় লাগে।

কেন বিভিন্ন ঋতুতে ভিন্ন ভিন্ন সান্দ্রতাযুক্ত তেল ব্যবহৃত হয়?
গ্রীষ্মকালে বাতাসের উষ্ণতা যথেষ্ট বেশি থাকে। ওই বর্ধিত উষ্ণতায় তরলের সান্দ্রতাঙ্ক কমে যায়। ফলে তরলের গতির বিরুদ্ধে বাধা কম ক্রিয়া করে, অর্থাৎ, তরলের সচলতা বাড়ে। তাই, শীতকালের তুলনায় গ্রীষ্মকালে বেশি সান্দ্র তেল ব্যবহৃত হয়।
শীতকালে যন্ত্রের চলনক্ষম অংশগুলি আটকে যায় বলে মনে হয় কেন?
শীতকালে উষ্ণতা অপেক্ষাকৃত কম হওয়ায় যন্ত্রে ব্যবহৃত পিচ্ছিলকারক তেলের সান্দ্রতা বৃদ্ধি পায়। ফলে, তরলটির সচলতা হ্রাস পায় এবং যন্ত্রের চলনক্ষম অংশগুলি সহজে গতিশীল হয় না এবং আটকে যায় বলে বোধ হয়।
আগুন নেভানোর জন্য দমকল কর্মীরা যে জলের পাইপ ব্যবহার করেন তার মুখে পিতলের শঙ্কু লাগানো থাকে কেন?
জল ছেটানো পাইপের সম্মুখপ্রান্তে পিতলের শঙ্কু লাগানো থাকে। শঙ্কুর প্রস্থচ্ছেদের ক্ষেত্রফল কম হওয়ায় মূল পাইপের তুলনায় পাইপের মুখ অপেক্ষাকৃত সরু থাকে। যেহেতু জলপ্রবাহের হার পাইপের সর্বত্র সমান, পাইপের যে-কোনো ছেদের ক্ষেত্রফল ও ওই ছেদের সঙ্গে লম্বভাবে নির্গত তরলের বেগের গুণফল ধ্রুবক হয়। তাই পাইপের মুখ সরু (শঙ্কু আকৃতিযুক্ত হলে) হওয়ায় ওই মুখ দিয়ে জল তীব্রবেগে বেরিয়ে আসে ও দীর্ঘদূরত্ব অতিক্রম করতে পারে।

দ্রুত গতিসম্পন্ন কোনো বস্তুর অবয়বকে ধারারেখ গঠন দেওয়া হয় – ব্যাখ্যা করো।
ধারারেখ প্রবাহের ক্ষেত্রে প্রবাহীর কোনো কণা যে পথ বরাবর চলে, তাকে ধারারেখা বলে। ধারারেখ আকারের বৈশিষ্ট্য হল, এর আকারে কোথাও কোনো অনিয়মিত ভাঁজ থাকে না এবং পিছন দিকটা ক্রমশ সরু হয়ে যায়। দ্রুতগতিসম্পন্ন কোনো বস্তুর অবয়বকে ধারারেখ আকার দিলে, বস্তুটি বায়ুর মধ্যে দিয়ে অগ্রসর হওয়ার সময় বায়ুর স্তরগুলি বস্তুর গা বরাবর ধারারেখার আকারে পিছনের দিকে তীব্রবেগে গতিশীল হয়। এজন্য বায়ুর মধ্যে দিয়ে যাওয়ার সময় বায়ু, বস্তুর ওপর কম বাধা প্রয়োগ করে। ফলে, বস্তুটি সামনের দিকে দ্রুতগতিতে অগ্রসর হতে পারে। তাই, দ্রুতগতিসম্পন্ন কোনো বস্তুর অবয়বকে ধারারেখ আকার দেওয়া হয়। একই কারণে রকেট, বিমান, দ্রুতগামী ট্রেনের গঠন ধারারেখ করা হয়।
একটি ছোটো নিরেট গোলক বায়ুর মধ্যে দিয়ে উল্লম্বভাবে পড়ার সময় 0.2 m/s প্রান্তীয় বেগ অর্জন করে, কিন্তু গোলকটি যদি শূন্য মাধ্যমের ভিতর দিয়ে পড়ত, তবে কোনো প্রান্তীয় বেগ থাকত না, এর কারণ কী?
অথবা, সান্দ্র তরলের মধ্যে একটি বস্তুকে ছেড়ে দিলে সমবেগ লাভ করে কি?
পতনশীল গোলকের ওপর তিনটি বল কাজ করে – নিম্নাভিমুখে গোলকের ওজন (W) এবং খাড়া উর্ধ্বদিকে বায়ুর দেওয়া প্লবতা (u) এবং গোলকের গতির বিরুদ্ধে বায়ুমাধ্যমের দেওয়া সান্দ্রতাজনিত বাধা (F)। সময়ের সঙ্গে গোলকের বেগ বৃদ্ধি পেলে F -এর মানও বাড়ে এবং একসময় (u + F) -এর মান W -এর সঙ্গে সমান হয়। এই মুহূর্ত থেকে গোলকের ওপর খাড়া নীচের দিকে ক্রিয়াশীল কার্যকর লব্ধিবল শূন্য হয়ে যায় অর্থাৎ, গোলকটির ত্বরণ শূন্য হয়। তাই নিউটনের প্রথম গতিসূত্র অনুযায়ী ওই মুহূর্তে অর্জিত বেগসহ গোলকটি সমবেগে অর্থাৎ, প্রান্তীয় বেগ (এক্ষেত্রে মান 0.2 m/s) নিয়ে নীচে নামতে থাকে।
শূন্য মাধ্যমে প্লবতা ও সান্দ্রাতাজনিত বাধা উভয়ই অনুপস্থিত থাকায় নিম্নমুখী গতি কোনোভাবেই বাধাপ্রাপ্ত হয় না। ফলে সর্বদাই গোলকটির ওপর অপ্রতিমিত বল ক্রিয়া করায় এটি কখনওই ক্রান্তীয় বেগ অর্জনের সমর্থ হয় না।
ছোটো বৃষ্টির ফোঁটার চেয়ে বড়ো বৃষ্টির ফোঁটা বায়ুতে দ্রুততর বেগে পড়তে থাকে কেন?
বায়ুমণ্ডলীয় ঘনীভবনের ফলে সৃষ্ট ক্ষুদ্র জলবিন্দুগুলির ব্যাসার্ধ অত্যন্ত কম বলে অর্জিত প্রান্তীয় বেগের মানও অত্যন্ত কম হয়। তাই, এরা ধীরগতিতে চলাচল করে আকাশে ভেসে থাকে। ভাসমান অবস্থায় একাধিক জলবিন্দু পরস্পর যুক্ত হয়ে বৃহৎ জলবিন্দু গঠন করলে বর্ধিত ওজনের কারণে তারা ভূপৃষ্ঠের দিকে নামতে থাকে। অভিকর্ষ বলের প্রভাবে তাদের বেগ যত বাড়ে স্টোকসের সূত্র অনুযায়ী গতির বিরুদ্ধে সান্দ্রতাজনিত বাধাও সমানুপাতিক হারে বৃদ্ধি পায়। অবশেষে বেগের একটি নির্দিষ্ট মানে সান্দ্র বাধা ও প্লবতা বলের সমষ্টি ওজনের সমান হলে জলবিন্দু সীমান্ত বেগ অর্জন করে এবং বৃষ্টির ফোঁটারূপে সমবেগে ভূপৃষ্ঠে এসে পৌঁছোয়।
দীর্ঘ সময় ধরে বাতাসের মধ্যে ধূলিকণাগুলি ভেসে থাকে কেন?
বায়ুর মধ্যে দিয়ে পতনশীল কোনো কণার প্রান্তীয় বেগ কণার ব্যাসার্ধের বর্গের সমানুপাতিক হয়। ধূলিকণার আকার খুব ছোটো বলে ধূলিকণার প্রান্তীয় বেগও খুব কম হয়। পতনশীল ধূলিকণার ওজন নীচের দিকে ক্রিয়া করে এবং বায়ুর প্লবতা ও সান্দ্রতাজনিত বল ঊর্ধ্বমুখে ক্রিয়া করে। একসময় বায়ুর প্লবতা ও ঊর্ধ্বমুখী সান্দ্রতাজনিত বল, ধূলিকণার ওজনকে প্রশমিত করে দেয়। ফলে, নিম্নমুখী লব্ধিবল শূন্য হয়ে যায় এবং ধূলিকণাগুলি আর নীচের দিকে নামতে পারে না। তাই, দীর্ঘ সময় ধরে ধূলিকণাগুলি বাতাসে ভেসে থাকে।
কোনো ব্যক্তি বিমান থেকে প্যারাসুট নিয়ে অবতরণ করার সময় কেন কম বেগ নিয়ে নীচে নামেন?
আকৃতিতে বৃহৎ প্যারাসুট তার ওজনের বিরুদ্ধে বেশি প্লবতা ও নিম্নমুখী গতির বিরুদ্ধে বেশি পরিমাণ সান্দ্র বল অর্জন করে। তাই কোনো ব্যক্তি যখন বিমান থেকে প্যারাসুট নিয়ে জরুরি অবতরণ করেন তখন বায়ুর সান্দ্রতাজনিত বাধার কারণে ব্যক্তিটি পতনের অল্প সময়ের মধ্যে প্রান্তীয় বেগ অর্জন করে ফেলেন এবং ওই স্থির মানের বেগসহ ভূপৃষ্ঠে পৌঁছান। নিম্নগতি শুরুর প্রায় সঙ্গে সঙ্গেই প্রান্তীয় বেগ লাভ করার ফলে ওই বেগের মান যথেষ্ট কম থাকে। ফলে, ব্যক্তির পক্ষে নিরাপদে অবতরণ করা সম্ভব হয়।

বায়ুর বাধা না থাকলে ব্যক্তি অভিকর্ষের টানে ত্বরণসহ পতিত হয়ে প্রচণ্ড বেগে ভূপৃষ্ঠে পৌঁছোতেন, ফলে আঘাত পাওয়ার সম্ভাবনা থাকত।
পার্থক্যধর্মী প্রশ্নোত্তর
ধারারেখ (Streamline flow) ও অশান্ত প্রবাহ (Tarbulent flow) -এর মধ্যে পার্থক্য লেখো।
ধারারেখ (Streamline flow) ও অশান্ত প্রবাহ (Tarbulent flow) -এর মধ্যে পার্থক্যগুলি হল –
| বিষয় | ধারারেখ প্রবাহ (Streamline flow) | অশান্ত প্রবাহ (Turbulent flow) |
| সংজ্ঞা | প্রবাহীর গতিপথের যে-কোনো বিন্দুতে প্রবাহীর বেগের মান ও অভিমুখ সময় সাপেক্ষে অপরিবর্তিত থাকলে ওই প্রবাহকে ধারারেখ প্রবাহ বলা হয়। | প্রবাহীর গতিপথের যে-কোনো বিন্দুতে প্রবাহীর বেগের মান ও অভিমুখ দুই-ই সময়ের সাপেক্ষে এলোমেলোভাবে পরিবর্তিত হলে সেই প্রবাহকে অশান্ত বা বিক্ষুব্ধ প্রবাহ বলা হয়। |
| বেগের মান | এই প্রবাহে প্রবাহীর বেগের মান সর্বদাই সংশ্লিষ্ট প্রবাহের সন্ধিবেগের মান অপেক্ষা কম হয়। | প্রবাহীর বেগ এক্ষেত্রে সর্বদাই সন্ধিবেগ অপেক্ষা বেশি হয়ে থাকে। |
| শক্তি ব্যয় | তরল বা গ্যাসকে চালনা করার জন্য প্রযুক্ত শক্তির শুধু সান্দ্রতাজনিত বাধা অতিক্রম করতে ব্যয়িত হয়। | প্রযুক্ত শক্তির অধিকাংশই প্রবাহীতে ঘূর্ণি বা আবর্ত সৃষ্টির প্রয়োজনে ব্যয়িত হয়ে থাকে। |
সান্দ্র বল ও ঘর্ষণ বলের মধ্যে পার্থক্য লেখো।
সান্দ্র বল ও ঘর্ষণ বলের মধ্যে পার্থক্যগুলি হল –
| বিষয় | সান্দ্র বল (Viscous force) | ঘর্ষণ বল (Frictional force) |
| ক্ষেত্রফল নির্ভরতা | সান্দ্র বলের মান সংস্পর্শে থাকা তরল স্তরগুলির ক্ষেত্রফলের সমানুপাতিক। | সংস্পর্শে থাকা স্তরগুলির ক্ষেত্রফলের ওপর ঘর্ষণ বল আদৌ নির্ভর করে না। |
| বেগের ওপর নির্ভরশীলতা | সান্দ্র বলের মান স্তর দুটির আপেক্ষিক বেগের পার্থক্যের সমানুপাতিক। | ঘর্ষণ বল স্পর্শতল দুটির আপেক্ষিক বেগের মান নিরপেক্ষ হয়। |
| লম্ব প্রতিক্রিয়ার প্রভাব | এই বলের মান স্পর্শে থাকা তরলস্তর দুটির পারস্পরিক লম্ব প্রতিক্রিয়া নিরপেক্ষ হয়। | ঘর্ষণ বলের মান স্পর্শতলদ্বয়ের পারস্পরিক লম্ব প্রতিক্রিয়ার সঙ্গে সমানুপাতিক। |
| বৈশিষ্ট্য | একই তরল বা গ্যাসের দুটি স্তরের মধ্যে ক্রিয়া করে। | সংস্পর্শে থাকা দুটি সমজাতীয় বা ভিন্ন প্রকার কঠিন পদার্থের দুটি স্তরের মধ্যে সক্রিয় হয়। |
সন্ধিবেগ (Critical velocity) ও প্রান্তীয় বেগ (Terminal velocity) -এর মধ্যে পার্থক্য লেখো।
সন্ধিবেগ (Critical velocity) ও প্রান্তীয় বেগ (Terminal velocity) -এর মধ্যে পার্থক্যগুলি হল –
| বিষয় | সন্ধিবেগ (Critical velocity) | প্রান্তীয় বেগ (Terminal velocity) |
| সংজ্ঞা | বেগের যে সর্বোচ্চ মান পর্যন্ত কোনো প্রবাহীর গতি ধারারেখ থাকে, তাকেই সন্ধিবেগ বলে। | অসীম বিস্তৃত কোনো প্রবাহীর মধ্যে দিয়ে বস্তু যে ধ্রুবক মানের সর্বোচ্চ বেগসহ গতিশীল হয়, তাকেই প্রান্তীয় বেগ বলে। |
| বৈশিষ্ট্য | সন্ধিবেগের মান তরলের প্রকৃতি, নলের প্রস্থচ্ছেদ ও দেয়ালের মসৃণতার মাত্রার ওপর নির্ভর করে। | প্রান্তীয় বেগের মান প্রবাহীর সান্দ্রতাঙ্কের মান, বস্তুর আকার, বস্তুটির ব্যাসার্ধ এবং বস্তু ও প্রবাহীর উপাদানের ঘনত্বের ওপর নির্ভরশীল হয়ে থাকে। |
| সান্দ্রতাঙ্কের ওপর নির্ভরতা | অন্যান্য শর্ত অপরিবর্তিত থাকলে এই বেগের মান প্রবহমান তরল বা গ্যাসের সান্দ্রতাঙ্কের সঙ্গে সমানুপাতিক হয়। | অপরিবর্তিত শর্তে এই বেগ প্রবাহীর সান্দ্রতাঙ্কের সঙ্গে ব্যস্তানুপাতিক হয়ে থাকে। |
গাণিতিক প্রশ্নাবলি
প্রয়োজনীয় সূত্রাবলি
\(F=\eta A\frac{\Delta v}{\Delta r}\\\)\(\mathrm v=\frac{2\mathrm r^2\left(\mathrm\rho-\mathrm d\right)\mathrm g}{9\mathrm\eta}\\\)αv = α1ν1 + α2ν2
F = 6πηrν
1 mm ব্যাসার্ধবিশিষ্ট গ্লিসারিন স্তরের উপর 100 cm2 ক্ষেত্রফলের একটি প্লেট স্থাপন করা হল। প্লেটটিকে অনুভূমিকভাবে 3 cm/s বেগে চালনা করতে কত অনুভূমিক বল প্রয়োজন হবে? [গ্লিসারিনের সান্দ্রতাঙ্ক = 10 poise]
সান্দ্রতাজনিত বাধা অতিক্রম করতে প্রয়োজনীয় অনুভূমিক বল, \(F=\eta A\frac{\Delta v}{\Delta r}\)
এক্ষেত্রে η = 10 poise, A = 100 cm2, Δv = 3 cm/s,
Δr =1 mm = 0.1 cm
∴ \(F=\eta A\frac{\Delta v}{\Delta r}\)
বা, \(F=10\times100\times\frac3{0.1}\)
বা, \(F=3\times10^4\) dyn
∴ প্লেটটিকে অনুভূমিকভাবে 3 cm/s বেগে চালনা করতে \(F=3\times10^4\) dyn অনুভূমিক বল প্রয়োজন হবে।
2 mm ব্যাসার্ধের একটি ইস্পাতনির্মিত গোলক গ্লিসারিনের ভিতর দিয়ে পড়ছে, গোলকটির প্রান্তীয় বেগ নির্ণয় করো। ইস্পাত ও গ্লিসারিনের আপেক্ষিক গুরুত্ব যথাক্রমে 8 এবং 1.3, গ্লিসারিনের সান্দ্রতাঙ্ক = 8.3 CGS একক।
স্টোকসের সূত্রানুযায়ী প্রান্তীয় বেগ
এক্ষেত্রে r = 2 mm = 0.2 cm, ρ = 8 g/cm3, d = 1.3 g/cm3, η = 8.3 CGS একক, g = 980 cm/s2।
∴ \({\mathrm v}_0=\frac{2\mathrm r^2\left(\mathrm\rho-\mathrm d\right)\mathrm g}{9\mathrm\eta}\)
বা, \({\mathrm v}_0=\frac{2\times\left(0.2\right)^2\times\left(8-1.3\right)\times980}{9\times8.3}\)
বা, \({\mathrm v}_0=7.03\) cm/s
∴ গোলকটির প্রান্তীয় বেগ = 7.03 cm/s
8টি সমান আকারের জলবিন্দু বায়ুর ভিতর দিয়ে 10 m/s স্থির বেগে পড়ে, জলবিন্দু আটটি মিশে একটি জলবিন্দুতে পরিণত হলে ওই জলবিন্দুর প্রান্তীয় বেগ কত হবে?
মনে করি, ক্ষুদ্র জলবিন্দুটির ব্যাসার্ধ r এবং বৃহৎ জলবিন্দুর ব্যাসার্ধ R।
∴ \(8\times\frac43\pi r^3=\frac43\pi R^3\)
বা, \(\frac Rr=\left(8\right)^\frac13=2\)
∴ \(R=2r\)
এখন, ক্ষুদ্র ও বৃহৎ জলবিন্দু দুটির প্রান্তীয় বেগ যথাক্রমে v1 ও v2 হলে, স্টোকসের সূত্রানুসারে,
∴ \(\frac{v_2}{v_1}=\left(\frac Rr\right)^2\)
বা, \(\frac{v_2}{10}=\left(\frac Rr\right)^2=\left(2\right)^2\)
বা, v2 = 4 × 10 m/s = 40 m/s
∴ জলবিন্দুটির প্রান্তীয় বেগ 40 m/s
নীচের চিত্রে প্রদর্শিত শাখাযুক্ত নলের মধ্যে দিয়ে তরলের প্রবাহ ঘটছে। নলের নীচের শাখার মধ্যে দিয়ে তরলের বেগ নির্ণয় করো।
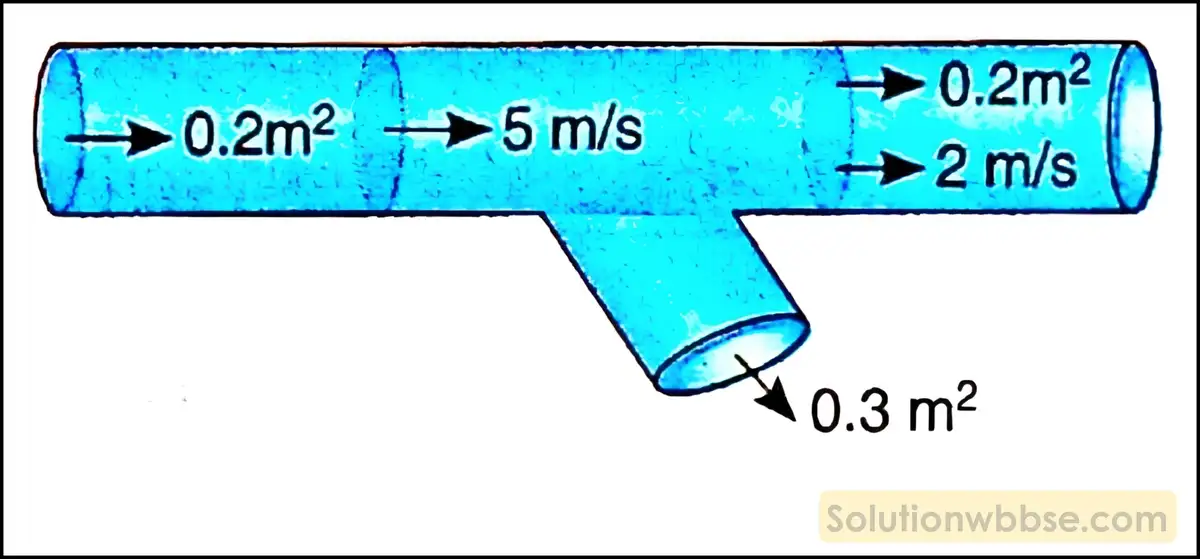
ধারাবাহিকতার সমীকরণ অনুসারে, αv = α1ν1 + α2ν2।
অর্থাৎ, 0.2 × 5 = 0.2 × 2 + 0.3 × v
বা, \(v=\frac{1-0.4}{0.3}\)
বা, \(v=\frac{0.6}{0.3}=2\)
∴ \(v=2\) m/s
∴ তরলের বেগ \(v=2\) m/s
1 mm ব্যাসার্ধের একটি সিসার গোলক একটি 10 m উচ্চতাসম্পন্ন গ্লিসারিন স্তম্ভের মধ্যে দিয়ে পড়ছে। গোলকটির প্রান্তীয় বেগ 1 m/s হলে ওর ওপর ক্রিয়াশীল সান্দ্রতাজনিত বাধার মান নির্ণয় করো। [দেওয়া আছে, গ্লিসারিনের সান্দ্রতাঙ্ক = 10 Poise]
স্টোকসের সূত্র অনুযায়ী গোলকটির ওপর ক্রিয়াশীল সান্দ্র বল, F = 6 π ηrν
[r = 1 mm = \(\frac1{10}\) cm, v = 1 m/s = 100 cm/s, = η = 10 poise]
বা, F = \(6\mathrm\pi\times10\times\left(\frac1{10}\right)\times100\)
বা, F = 600 π dyn
∴ সান্দ্রতাজনিত বাধার মান 600 π dyn
নৈর্ব্যক্তিক প্রশ্নোত্তর
সঠিক উত্তরটি নির্বাচন করো
সান্দ্রতা হল –
- তরলের ধর্ম
- গ্যাসের ধর্ম
- তরল ও কঠিনের ধর্ম
- তরল ও গ্যাসের ধর্ম
উত্তর – 4. তরল ও গ্যাসের ধর্ম
একটি গ্লাসে থাকা জলকে একটি চামচ দিয়ে নাড়িয়ে দিলে কিছুক্ষণ পরে জল স্থির অবস্থায় আসার কারণ –
- পৃষ্ঠটান
- সান্দ্রতা
- স্থিতিস্থাপকতা
- প্লবতা
উত্তর – 2. সান্দ্রতা
জলের গতিশীলতা তেল অপেক্ষা বেশি, কারণ –
- পৃষ্ঠটান
- সংসক্তি
- আসঞ্জন
- সান্দ্রতা
উত্তর – 4. সান্দ্রতা
পড়ন্ত বৃষ্টির ফোঁটার প্রান্তীয় বেগ লাভ করার কারণ হল –
- বায়ুর সান্দ্রতা
- বায়ুর ঊর্ধ্বঘাত
- বায়ুপ্রবাহ
- পৃষ্ঠটান
উত্তর – 2. বায়ুর সান্দ্রতা
গ্যাসের উষ্ণতা বাড়লে সান্দ্রতা –
- কমে
- বাড়ে
- অপরিবর্তিত থাকে
- প্রথমে বাড়ে ও পরে কমে
উত্তর – 2. বাড়ে
তরলের উষ্ণতা বাড়লে সান্দ্রতা –
- বাড়ে
- কমে
- প্রথমে বাড়ে ও পরে কমে
- অপরিবর্তিত থাকে
উত্তর – 2. কমে
তরলগুলির মধ্যে সর্বোচ্চ সান্দ্র হল –
- জল
- অ্যালকোহল
- গ্লিসারিন
- তেল
উত্তর – 3. গ্লিসারিন
একটি তরলে দুটি স্তরের মধ্যে ক্রিয়াশীল সান্দ্র বল স্তর দুটির আপেক্ষিক বেগ –
- বৃদ্ধি করে
- হ্রাস করে
- অপরিবর্তিত রাখে
- হ্রাস-বৃদ্ধি করে
উত্তর – 2. হ্রাস করে
প্রবাহীর গতি শান্ত না অশান্ত, তা নির্ণয় করে –
- প্রবাহীর বেগ
- প্রবাহীর ঘনত্ব
- নলের ব্যাসার্ধ
- সান্দ্রতা
উত্তর – 4. সান্দ্রতা
প্রবাহীর মধ্যে দিয়ে পড়ার সময় কোনো বস্তু 10 m⋅s-1 সীমান্ত বেগে পড়ছে। শূন্যস্থানে পড়লে সীমান্ত বেগ হবে –
- 10 m⋅s-1 অপেক্ষা বেশি
- 10 m⋅s-1
- 10 m⋅s-1 অপেক্ষা কম
- শূন্য
উত্তর – 4. শূন্য
শূন্যস্থান পূরণ করো
সান্দ্রতা হল বেগের একক নতিমাত্রা বজায় রাখতে একক ক্ষেত্রফলে ক্রিয়াশীল ___।
উত্তর – সান্দ্রতা হল বেগের একক নতিমাত্রা বজায় রাখতে একক ক্ষেত্রফলে ক্রিয়াশীল বল।
সান্দ্র বল তরলের ___ ওপর নির্ভর করে।
উত্তর – সান্দ্র বল তরলের ক্ষেত্রফলের ওপর নির্ভর করে।
সান্দ্রতাকে তরলের ___ বলে।
উত্তর – সান্দ্রতাকে তরলের অভ্যন্তরীণ ঘর্ষণ বলে।
চাপ বাড়লে জলের সান্দ্রতা ___।
উত্তর – চাপ বাড়লে জলের সান্দ্রতা কমে।
প্রবাহীর ক্ষেত্রে সান্দ্রতা কঠিনের ক্ষেত্রে ___ -এর সমতুল্য।
উত্তর – প্রবাহীর ক্ষেত্রে সান্দ্রতা কঠিনের ক্ষেত্রে ঘর্ষণ -এর সমতুল্য।
নলের প্রস্থচ্ছেদ বেশি হলে প্রবাহের বেগ ___ যায়।
উত্তর – নলের প্রস্থচ্ছেদ বেশি হলে প্রবাহের বেগ কমে যায়।
সর্বোচ্চ যে বেগে প্রবাহী কোনো নলের মধ্যে দিয়ে ধারারেখ প্রবাহে প্রবাহিত হয়, তা হল প্রবাহীর ___।
উত্তর – সর্বোচ্চ যে বেগে প্রবাহী কোনো নলের মধ্যে দিয়ে ধারারেখ প্রবাহে প্রবাহিত হয়, তা হল প্রবাহীর সন্ধিবেগ।
কুইন্সল্যান্ডের বিশ্ববিদ্যালয়ের অধ্যাপক ___ 1990 খ্রিস্টাব্দে ___ দ্বারা সান্দ্রতার মাত্রা নির্ণয় করেন।
উত্তর – কুইন্সল্যান্ডের বিশ্ববিদ্যালয়ের অধ্যাপক জন মেইনস্টোন 1990 খ্রিস্টাব্দে Pitch drop experiment দ্বারা সান্দ্রতার মাত্রা নির্ণয় করেন।
ঠিক বা ভুল নির্বাচন করো
সান্দ্রতা শুধুমাত্র তরলের বৈশিষ্ট্য।
উত্তর – ভুল।
সঠিক উত্তর – তরল ও গ্যাস উভয়েরই।
সান্দ্রতা ও ঘর্ষণ বলের মধ্যে পার্থক্য ও সাদৃশ্য দুই আছে।
উত্তর – ঠিক।
সান্দ্রতা বৃদ্ধিতে প্রবাহীর সচলতা বৃদ্ধি পায়।
উত্তর – ভুল।
সঠিক উত্তর – হ্রাস পায়।
একটি সান্দ্র তরলের মধ্য দিয়ে গতিশীল কোনো ক্ষুদ্র বস্তুর বেগ-সময় লেখচিত্র একটি বক্ররেখা হয়।
উত্তর – ঠিক।
শুধুমাত্র পতনশীল বস্তুর পক্ষেই সান্দ্র মাধ্যমে সীমান্ত বেগ অর্জন সম্ভব।
উত্তর – ভুল।
সঠিক উত্তর – উল্লম্বরেখায় গতিশীল যে-কোনো বস্তুর।
দু-একটি শব্দে উত্তর দাও
ধারারেখার যে-কোনো বিন্দুতে স্পর্শক কী নির্দেশ করে?
ধারারেখার যে-কোনো বিন্দুতে স্পর্শক ওই বিন্দুতে প্রবাহীর বেগের অভিমুখ নির্দেশ করে।
জলে গ্লিসারিন যোগ করলে পাত্রের তলার দিকে কে থাকবে?
জলে গ্লিসারিন যোগ করলে পাত্রের তলার দিকে গ্লিসারিন থাকবে।
প্রবাহীর সন্ধিবেগের SI একক কী?
প্রবাহীর সন্ধিবেগের SI একক m/s।
সুদীর্ঘ সান্দ্র মাধ্যমে কোনো বস্তু সমবেগে পতনশীল হয়, সেই বেগকে কী বলে?
সুদীর্ঘ সান্দ্র মাধ্যমে কোনো বস্তু সমবেগে পতনশীল হয়, সেই বেগকে প্রান্তীয় বেগ বলে।
তরল প্রবাহের ধারাবাহিকতা কোন্ সংরক্ষণ সূত্রকে প্রকাশ করে?
তরল প্রবাহের ধারাবাহিকতা ভরের সংরক্ষণ সূত্রকে প্রকাশ করে।
প্রান্তীয় বেগে গতিশীল বস্তুর আপাত ওজন কত?
প্রান্তীয় বেগে গতিশীল বস্তুর আপাত ওজন শূন্য।
সীমান্ত বা প্রান্তীয় বেগসহ কোনো গতিশীল বস্তুর ওপর কার্যকর বল কত হবে?
সীমান্ত বা প্রান্তীয় বেগসহ কোনো গতিশীল বস্তুর ওপর কার্যকর বল শূন্য হবে।
আদর্শ তরলের সান্দ্রতাঙ্কের মান কত?
আদর্শ তরলের সান্দ্রতাঙ্কের মান শূন্য।
প্রবাহীর গতির বিরুদ্ধে বাধা কোনো প্রবাহে বেশি অশান্ত না ধারারেখ?
প্রবাহীর গতির বিরুদ্ধে বাধা কোনো প্রবাহে বেশি ধারারেখ।
For High-Types
গতীয় সান্দ্রতা বলতে কী বোঝায়?
গতীয় সান্দ্রতা (Kinematic viscosity) – কোনো প্রবাহীর সান্দ্রতাঙ্ক ও ঘনত্বের অনুপাতকে বলা হয় ওই প্রবাহীর গতীয় সান্দ্রতা। অর্থাৎ, গতীয় সান্দ্রতা \(\eta_K=\frac\eta\rho\)।
এর মাত্রীয় সংকেত হল [L2T-1] এবং CGS একক হল স্টোকস (Stokes)।
\(1\;stokes=\frac{1\;poise}{1\;g/cm^3}\\\)বা, \(1\;stokes=1\;cm^2/s\)
একটি সিসার বল গ্লিসারিনের দীর্ঘ স্তম্ভের মধ্য দিয়ে পড়ে। সিসার বলের বেগের সঙ্গে অতিক্রান্ত দূরত্বের লেখচিত্র কীরূপ হবে?
গ্লিসারিন হল একটি সান্দ্র তরল। সিসার বলটি সান্দ্র তরলের মধ্য দিয়ে যাবার সময় প্রথমে বলটির বেগ বৃদ্ধি পায় এবং একসময় বলটি প্রান্তীয় বেগ লাভকরে। তখন বলটি সমবেগে গতিশীল হয়। পাশের বেগ-অতিক্রান্ত দূরত্ব লেখচিত্র দ্বারা গ্লিসারিনের মধ্যে সিসার বলটির বেগ দেখানো হল।
Class 9 Physical Science – Notes for All Chapters
| Chapter Name | Tropics |
|---|---|
| পরিমাপ | পরিমাপ ও একক বিভিন্ন মাপের একক মাত্রা পরিমাপ |
| বল ও গতি | স্থিতি ও গতি গতির সমীকরণ নিউটনের প্রথম গতিসূত্র নিউটনের দ্বিতীয় গতি সূত্র নিউটনের তৃতীয় গতিসূত্র বিভিন্ন ধরণের বল রৈখিক ভরবেগ রৈখিক ভরবেগ সংরক্ষণ |
| পদার্থ : গঠন ও ধর্ম | তরল ও বায়ুর চাপ আর্কিমিডিসের নীতি পৃষ্ঠটান সান্দ্রতা বার্নোলির নীতি স্থিতিস্থাপকতা |
| পদার্থ : পরমাণুর গঠন ও পদার্থের ভৌত ও রাসায়নিক ধর্মসমূহ | পরমাণুর গঠন মোলের ধারণা দ্রবণ অ্যাসিড, ক্ষার, লবণ মিশ্রণের উপাদানের পৃথকীকরণ জল |
| শক্তির ক্রিয়া , কার্য, ক্ষমতা | শক্তির ক্রিয়া , কার্য, ক্ষমতা |
| তাপ | ক্যালোরিমিতি কার্য ও তাপের তুল্যতা লীনতাপ সম্পৃক্ত ও অসম্পৃক্ত বাষ্প জলের ব্যতিক্রান্ত প্রসারণ |
| শব্দ | শব্দের উৎস : কম্পন শব্দের বিস্তার : তরঙ্গ শব্দের কয়েকটি ধর্ম শব্দের বৈশিষ্ট্য মানুষের কান ও শব্দ শোনার কৌশল শব্দদূষণ |
আজকের আর্টিকেলে আমরা নবম শ্রেণির ভৌতবিজ্ঞান বইয়ের তৃতীয় অধ্যায় “পদার্থ : গঠন ও ধর্ম” এর “সান্দ্রতা” থেকে পরীক্ষায় আসা গুরুত্বপূর্ণ প্রশ্ন ও উত্তরগুলো আলোচনা করেছি। এই প্রশ্নোত্তরগুলো নবম শ্রেণির বার্ষিক পরীক্ষা, এমনকি চাকরি বা যেকোনো প্রতিযোগিতামূলক পরীক্ষার জন্যও উপযোগী। কারণ, এই অধ্যায়ের প্রশ্ন প্রায়ই বিভিন্ন পরীক্ষায় কমন আসে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সাহায্য করবে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন কিংবা টেলিগ্রামে যোগাযোগ করতে পারেন—আপনাদের প্রশ্নের উত্তর দিতে আমি সর্বদা প্রস্তুত।
ধন্যবাদ সবাইকে।






মন্তব্য করুন