আজকে আমরা এই আর্টিকেলে মাধ্যমিক পরীক্ষার পুরাতন বছরের প্রশ্ন ও তাদের উত্তর নিয়ে আলোচনা করবো। এই আর্টিকেলের সাহায্যে শিক্ষার্থীরা মাধ্যমিক পরীক্ষায় আগের বছর কী প্রশ্ন এসেছিল তা সম্পর্কে একটি স্পষ্ট ধারণা পাবে। এই আর্টিকেলে আমরা Madhyamik Math Question Paper ২০২০ With Answer নিয়ে আলোচনা করবো। মাধ্যমিক ২০২০ এর প্রশ্নগুলি শিক্ষার্থীদের পরের বছরের জন্য অনেক গুরুত্বপূর্ণ। আশা করি তোমরা মাধ্যমিক গণিত পরীক্ষা দিতে যাওয়ার আগে Madhyamik Math Question Paper ২০২০ With Answer টি দেখে পরীক্ষা দিতে যাবে।

1. নিম্নলিখিত প্রশ্নগুলির প্রতিটি ক্ষেত্রে সঠিক উত্তর নির্বাচন করো
(i) কোনো মূলধন 10 বছরে দ্বিগুন হলে, বার্ষিক সরল সুদের হার –
(a) 5%
(b) 10%
(c) 15%
(d) 20%
Ans. (b) 10%
সমাধান,
ধরি, মূলধনের পরিমাণ x টাকা এবং বার্ষিক সরল সুদের হার r%
শর্তানুসারে,
\(x+\frac{x\times10\times r}{100}=2x\\\)বা, \(\frac{x\times10\times r}{100}=x\)
বা, \(r=\frac{x\times100}{10x}\)
বা, r = 10%
∴ বার্ষিক সরল সুদের হার 10%
(ii) x2 – 7x + 3 = 0 সমীকরণের বীজদ্বয়ের গুনফল
(a) 7
(b) -7
(c) 3
(d) -3
Ans. (c) 3
সমাধান,
x2 – 7x + 3 = 0 সমীকরণের বীজদ্বয়ের গুনফল
=
(iii) O কেন্দ্রীয় বৃত্তের AB ও CD জ্যা দুটির দৈর্ঘ্য সমান, ∠AOB = 60° হলে, ∠COD এর মান কত হবে –
(a) 30°
(b) 60°
(c) 120°
(d) 180°
Ans. (b) 60°
সমাধান,
আমরা জানি সমান জ্যা বৃত্তের কেন্দ্রে সমান কোন উৎপন্ন করে।
∴ ∠AOB = ∠COD = 60°
(iv) দুটি লম্ব বৃত্তাকার শঙ্কুর আয়তনের অনুপাত 1 : 4 এবং তাদের ভূমিতলের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত 4 : 5 হলে তাদের উচ্চতার অনুপাত –
(a) 1 : 5
(b) 5 : 4
(c) 25 : 16
(d) 25 : 64
Ans. (d) 25 : 64
\(\frac{v_1}{v_2}=\frac14\\\)সমাধান,
ধরি, শঙ্কু দুটির ভূমিতলের ব্যাসার্ধ যথাক্রমে r1 একক এবং r2 একক
শঙ্কু দুটির উচ্চতা যথাক্রমে h1 একক এবং h2 একক
শঙ্কু দুটির আয়তন যথাক্রমে V1 ঘন একক ও V2 ঘন একক
∴ r1 : r2 = 4 : 5
এবং V1 : V2 = 1 : 4
\(\frac{v_1}{v_2}=\frac14\\\)বা, \(\frac{{\displaystyle\frac13}\pi\left(r_1\right)^2h_1}{{\displaystyle\frac13}\pi\left(r_2\right)^2h_2}=\frac14\)
বা, \(\left(\frac{r_1}{r_2}\right)^2\times\frac{h_1}{h_2}=\frac14\)
বা, \(\left(\frac45\right)^2\times\frac{h_1}{h_2}=\frac14\)
বা, \(\frac{16}{25}\times\frac{h_1}{h_2}=\frac14\)
বা, \(\frac{h_1}{h_2}=\frac{25}{64}\)
∴ h1 : h2 = 25 : 64
(v) যদি, sinθ – cosθ = 0, (0° ≤ θ ≤ 90°) এবং secθ + cosecθ = x, হয় তাহলে x এর মান –
(a) 1
(b) 2
(c) \(\sqrt2\)
(d) \(2\sqrt2\)
Ans. (d) \(2\sqrt2\)
সমাধান,
sinθ – cosθ = 0
বা, sinθ = cosθ
বা, \(\frac{\sin\theta}{\cos\theta}=1\)
বা, tanθ = 1
বা, tanθ = tan45°
বা, θ = 45°
∴ secθ + cosecθ = x
বা, sec45° + cosec45° = x
বা, \(\sqrt2+\sqrt2=x\)
বা, \(2\sqrt2=x\)
বা, \(x=2\sqrt2\)
(vi) 1, 3, 2, 8, 10, 8, 3, 2, 8, 8 এর সংখ্যাগুরু মান –
(a) 2
(b) 3
(c) 8
(d) 10
Ans. (c) 8
2. শূন্যস্থান পূরণ কর
(i) আনিসূর 500 টাকা 9 মাসের জন্য এবং ডেভিড 600 টাকা 5 মাসের জন্য একটি যৌথ ব্যাবসা শুরু করে। তাদের লভ্যাংশের অনুপাত হবে_______।
Ans. আনিসূর 500 টাকা 9 মাসের জন্য এবং ডেভিড 600 টাকা 5 মাসের জন্য একটি যৌথ ব্যাবসা শুরু করে। তাদের লভ্যাংশের অনুপাত হবে 3 : 2
সমাধান,
আনিসূর 500 টাকা 9 মাসের জন্য এবং ডেভিড 600 টাকা 5 মাসের জন্য একটি যৌথ ব্যাবসা শুরু করে।
∵ তাদের লভ্যাংশের অনুপাত = তাদের মূলধনের অনুপাত
= (500✕9) : (600✕5)
= 4500:3000
= 3:2
(ii) ax2 + 2bx + c = 0 (a≠0), দ্বিঘাত সমীকরণের বীজদ্বয় বাস্তব ও সমান হলে b2 =_____হবে।
Ans. ax2 + 2bx + c = 0 (a ≠ 0), দ্বিঘাত সমীকরণের বীজদ্বয় বাস্তব ও সমান হলে b2 = 4bc হবে।
(iii) দুটি কোণের সমষ্টি _______ হলে তাদেরকে পরস্পরের সম্পূরক বলা হয়।
Ans. দুটি কোণের সমষ্টি 180° হলে তাদেরকে পরস্পরের সম্পূরক বলা হয়।
(iv) sin3θ এর সর্বচ্চ মান _____।
Ans. sin3θ এর সর্বচ্চ মান 1
(v) একটি নিরেট গোলক গলিয়ে একটি নিরেট লম্ব বৃত্তাকার চোঙ তৈরি করা হলে গোলক ও চোঙের ______সমান হবে।
Ans. একটি নিরেট গোলক গলিয়ে একটি নিরেট লম্ব বৃত্তাকার চোঙ তৈরি করা হলে গোলক ও চোঙের আয়তন সমান হবে।
(vi) কিছু ছাত্রের বয়স হলো (বছরে) 10, 11, 9, 7, 13, 8, 14 এদের বয়সের মধ্যমা হল______বছর।
Ans. কিছু ছাত্রের বয়স হলো (বছরে) 10, 11, 9, 7, 13, 8, 14 এদের বয়সের মধ্যমা হল 10 বছর।
সমাধান,
∴ মধ্যমা = \(\frac{\left(n+1\right)}2\) তম মান।
= \(\frac{\left(7+1\right)}2\) তম মান।
= 4 তম মান
= 10 বছর
3. সত্য বা মিথ্যা লেখো
বার্ষিক \(\frac r2\%\) সরল সুদের হারে 2p টাকার t বছরের সুদে আসলে হলো \(\left(2p+\frac{ptr}{100}\right)\)টাকা।
Ans. সত্য
সমাধান,
বার্ষিক \(\frac r2\%\) সরল সুদের হারে 2p টাকার t বছরের সুদে আসলে হলো \(\left(2p+\frac{2p\times t\times r}{2\times100}\right)\) টাকা = \(\left(2p+\frac{ptr}{100}\right)\)টাকা।
(ii) 2a = 3b = 4c হলে a : b : c = 2 : 3 : 4
Ans. মিথ্যা
(iii) একটি ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যের অনুপাত 5 : 12 : 13 হলে ত্রিভুজটি সমকোণী ত্রিভুজ হবে।
Ans. সত্য
(iv) একটি রশ্মির প্রান্তবিন্দুকে কেন্দ্র করে, রশ্মিটিকে ঘড়ির কাঁটার বিপরীত দিকে ঘোরার জন্য উৎপন্ন কোণটি ধনাত্মক হবে।
Ans. সত্য
(v) n যদি যুগ্ম সংখ্যা হয়, তবে মধ্যমা হবে \(\left(\frac n2\right)\) তম ও \(\left(\frac n2-1\right)\) তম পর্যবেক্ষণের গড়।
Ans. সত্য।
(vi) একটি লম্ব বৃত্তাকার শঙ্কুর ভূমিতলের ব্যাসার্ধের দৈর্ঘ্য অর্ধেক এবং উচ্চতা দ্বিগুন করা হলে শঙ্কুর আয়তন একই থাকে।
Ans. মিথ্যা
4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাও
(i) কোনো আসল ও তার 5 বছরের সবৃদ্ধি মূলের অনুপাত 5 : 6 হলে, বার্ষিক সরল সুদের হার নির্ণয় কর।
সমাধান,
ধরি, আসলের পরিমাণ P টাকা এবং বার্ষিক সরল সুদের হার r%
এখন p টাকার 5 বছরের সবৃদ্ধি মূল = \(p+\frac{p\times5\times r}{100}\) টাকা = \(p\left(1+\frac r{20}\right)\) টাকা।
শর্তানুসারে,
\(p:p\left(1+\frac r{20}\right)=5:6\\\)বা, \(1:1\left(1+\frac r{20}\right)=5:6\)
বা, \(\frac1{\left(1+{\displaystyle\frac r{100}}\right)}=\frac56\)
বা, \(5\left(1+\frac r{100}\right)=6\)
বা, \(5+\frac{5r}{20}=6\)
বা, \(\frac{5r}{20}=1\)
বা, r = 4
∴ বার্ষিক সরল সুদের হার 4%
(ii) A ও B কোনো ব্যাবসায় 1050 টাকা লাভ করে। A এর মূলধন 900 টাকা এবং লভ্যাংশ 630 টাকা হলে B এর মূলধন কত?
সমাধান,
ধরি, B এর মূলধন x টাকা।
∴ A ও B এর মূলধনের অনুপাত 900 : x
শর্তানুসারে,
\(\frac{900}{900+x}\times1050=630\\\)বা, \(\frac{900}{900+x}=\frac{630}{1050}\)
বা, \(\frac{900}{900+x}=\frac35\)
বা, 4500 = 2700 + 3x
বা, 3x = 4500 – 2700
বা, 3x = 18010
বা, \(x=\frac{1800}3\)
বা, x = 600
∴ B এর মূলধন 600 টাকা।
(iii) x ∝ y, y ∝ z এবং z ∝ x হলে, ভেদ ধ্রুবক তিনটির গুনফল নির্ণয় কর।
সমাধান,
x ∝ y
∴ x = k1y [k1 একটি অশূন্য ভেদ ধ্রুবক]______(i)
এবং, y ∝ z
∴ y = k2z [k2 একটি অশূন্য ভেদ ধ্রুবক]______(ii)
আবার, z ∝ x
∴ z = k3x [k3 একটি অশূন্য ভেদ ধ্রুবক]______(iii)
(i), (ii) ও (iii) নং সমীকরণকে গুন করে পাই,
xyz = k1k2k3 xyz
বা, k1k2k3 = xyz/xyz
বা, k1k2k3 = 1
∴ ভেদ ধ্রুবক তিনটির গুণফল 1 [এটাই ভেদধ্রুবক তিনটির মধ্যে সম্পর্ক]
(iv) \(5x^2-2x+3=0\) দ্বিঘাত সমীকরণের বীজদ্বয় α ও β হলে \(\frac1\alpha+\frac1\beta\) এর মান নির্ণয় করো।
সমাধান,
5x2 – 2x + 3 = 0 দ্বিঘাত সমীকরণের বীজদ্বয় α ও β
∴
= \(\frac{-\left(-2\right)}5=\frac25\)
এবং
∴ \(\frac1\alpha=\frac1\beta\)
= \(\frac{\alpha+\beta}{\alpha\beta}\)
= \(\frac{\displaystyle\frac25}{\displaystyle\frac35}\)
= \(\frac25\times\frac53\)
= \(\frac23\)
(iv) ABCD আয়তকার চিত্রের অভ্যন্তরে O বিন্দু এমনভাবে অবস্থিত যে OB = 6 সেমি, OD = 8 সেমি. এবং OA = 5 সেমি.। OC এর দৈর্ঘ্য নির্ণয় কর।
সমাধান,
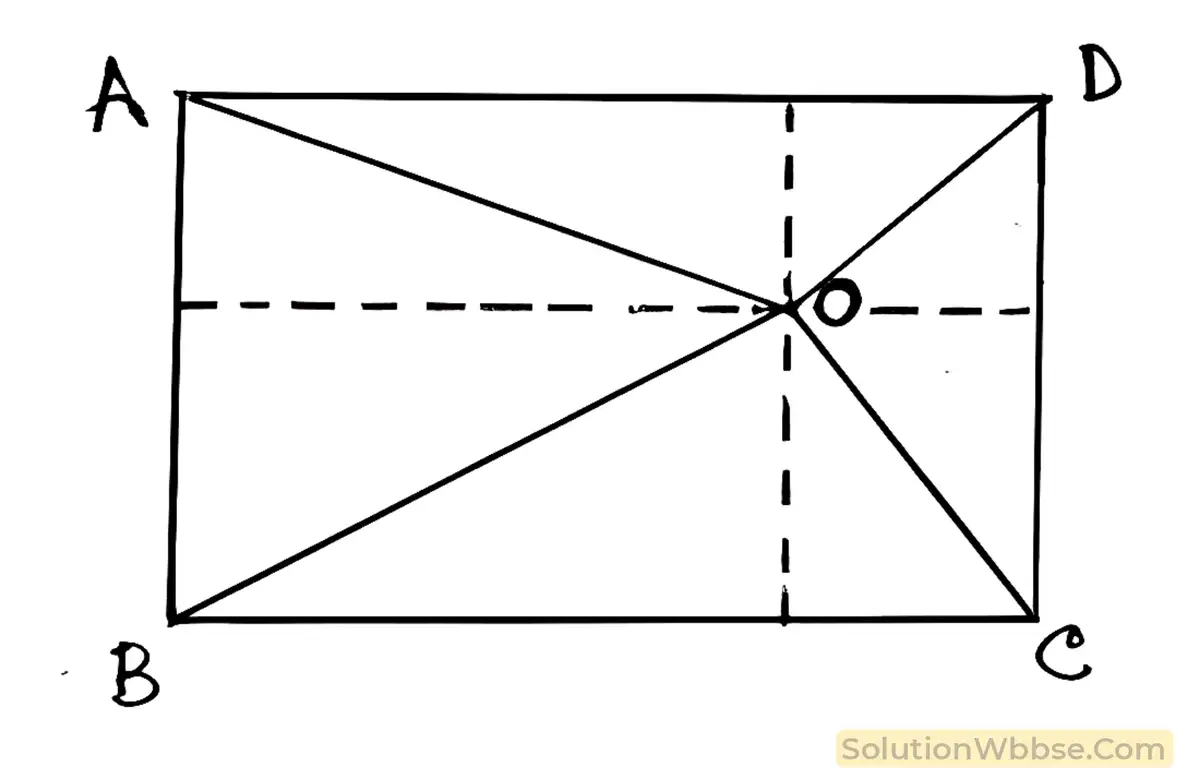
ABCD আয়তকার চিত্রের অভ্যন্তরে O একটি বিন্দু হলে, OA2 + OC2 = OB2 + OD2 হয়।
∴ OA2 + OC2 = OB2 + OD2
বা, (5)2 +OC2 = (6)2 +(8)2
বা, 25 + OC2 = 36 + 64
বা, OC2 = 100 – 25
বা, OC2 = 75
বা, \(OC^2=\;\left(5\sqrt3\right)^2\)
বা, \(OC=\;5\sqrt3\)
∴ OC এর দৈর্ঘ্য = \(5\sqrt3\) সেমি
(vi) ABC একটি সমকোণী ত্রিভুজের ∠ABC = 90°, AB = 3 সেমি, এবং BC = 4 সেমি, এবং B বিন্দু থেকে AC বাহুর উপর লম্ব BD যা AC বাহুর সঙ্গে D বিন্দুতে মিলিত হয়। BD এর দৈর্ঘ্য নির্ণয় কর।
সমাধান,
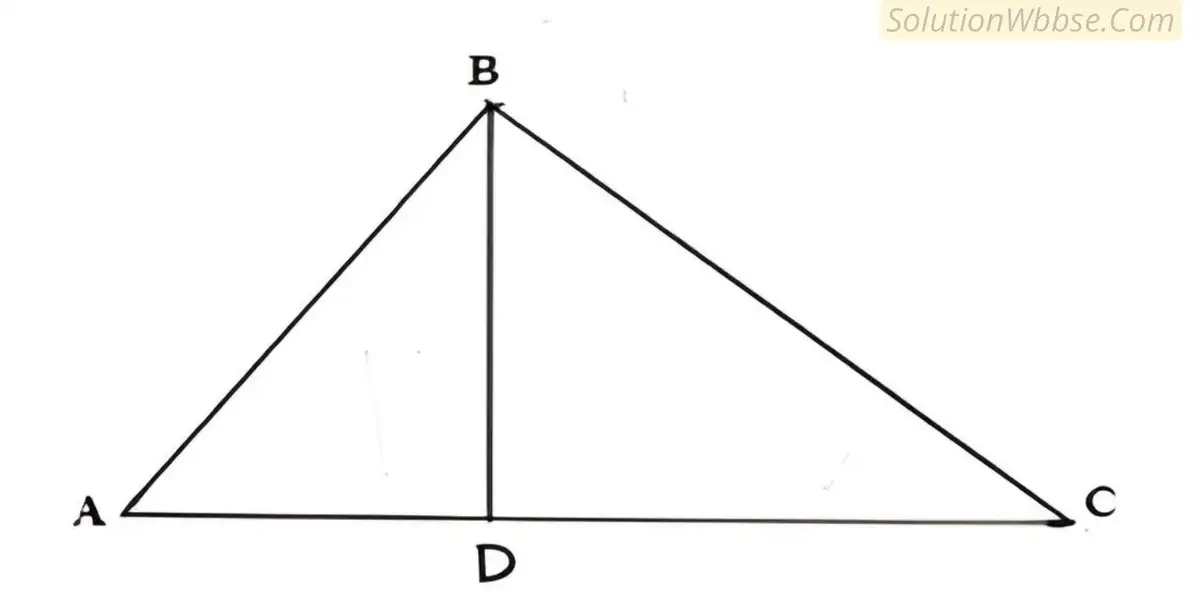
ABC ত্রিভুজের ∠ABC = 90° এবং সমকৌণিক বিন্দু B থেকে অতিভুজ AC এর উপর BD লম্ব। যেহেতু সমকোণী ত্রিভুজের সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে লম্বের উভয়পার্শ্বে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা পরস্পর সদৃশ।
∴ ΔBDC এবং ΔADB পরস্পর সদৃশ।
∴ \(\frac{BD}{AD}=\frac{DC}{BD}=\frac{BC}{AD}\) [যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক]
∴ \(\frac{BD}{AD}=\frac{BC}{AD}\)
বা, \(\frac{BD}{AD}=\frac43\)[যেহেতু AB = 3 সেমি, এবং BC = 4 সেমি]
বা, \(\frac{AD}{BD}=\frac34\)
আবার,
\(\frac{DC}{BD}=\frac{BC}{AB}\\\)বা, \(\frac{DC}{BD}=\frac43\) [যেহেতু AB = 3 সেমি, এবং BC = 4 সেমি]
∴ \(\frac{AD}{BD}+\frac{DC}{BD}=\frac34+\frac43\)
বা, \(\frac{AD+DC}{BD}=\frac{9+16}{12}=\frac{25}{12}\)
বা, \(\frac{AC}{BD}=\frac{25}{12}\)
বা, \(\frac{\sqrt{\left(AB\right)^2+\left(BC\right)^2}}{BD}=\frac{25}{12}\) [ΔABC সমকোণী ত্রিভুজের পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই।সমকোণী ত্রিভুজের পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই।]
বা, \(\frac{\sqrt{\left(3\right)^2+\left(4\right)^2}}{BD}=\frac{25}{12}\)
বা, \(\frac5{BD}=\frac{25}{12}\)
বা, \(BD=\frac{60}{25}\)
বা, \(BD=\frac{12}5\)
বা, \(BD=2\frac25\)
∴ BD এর দৈর্ঘ্য \(2\frac25\) সেমি।
(vii) দুটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 8 সেমি. ও 3 সেমি.। তাদের কেন্দ্রদ্বয়ের দূরত্ব 13 সেমি.। বৃত্ত দুটির সরল সাধারণ স্পর্শকের দৈর্ঘ্য কত?
সমাধান,
দুটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 8সেমি, ও 3 সেমি। তাদের কেন্দ্রদ্বয়ের মধ্যে দূরত্ব 13 সেমি।
∴ r1 = 8 সেমি, r2 = 3 সেমি, এবং d = 13 সেমি
∴ বৃত্ত দুটের সরল সাধারণ স্পর্শকের দৈর্ঘ্য = \(\sqrt{d^2-\left(r_1-r_2\right)^2}\) সেমি
= \(\sqrt{13^2-\left(8-3\right)^2}\) সেমি
= \(\sqrt{169-25}\) সেমি
= \(\sqrt{144}\) সেমি
= 12 সেমি
∴ বৃত্ত দুটের সরল সাধারণ স্পর্শকের দৈর্ঘ্য = 12 সেমি
(viii) একটি ঘড়ির ঘণ্টার কাঁটা 1 ঘণ্টায় যে কোণ আবর্তন করে তার বৃত্তীয় মান কত?
সমাধান,
একটি ঘড়ির ঘণ্টার কাঁটা 12 ঘণ্টায় আবর্তন করে 360°
∴ ঘড়ির ঘন্টার কাঁটা 1 ঘন্টায় অতিক্রম করে \(\frac{360^\circ}{12}=30^\circ=\frac{30\times\pi^c}{180}=\frac{\pi^c}6\)
যেহেতু ঘড়ির কাঁটা ঘুরলে ঋণাত্মক কোন উৎপন্ন করে
∴ 1 ঘন্টায় ঘড়ির ঘন্টার কাঁটায় যে কোন উৎপন্ন করে তার বৃত্তীয়মান \(\frac{\pi^c}6\)
(ix) tan4θ tan6θ =1 এবং 6θ ধনাত্মক সূক্ষ্মকোণ হলে, θ -এর মান নির্ণয় কর।
সমাধান,
tan4θ tan6θ = 1
বা, \(\tan4\theta=\frac1{\tan6\theta}\)
বা, tan4θ = cot6θ
বা, tan4θ = tan(90° – 6θ )
বা, 4θ =90° – 6θ
বা, 10θ = 90°
বা, \(\theta=\frac{90^\circ}{10}\)
বা, θ = 9°
∴ θ – এর মান 9°
(x) কোনো লম্ব বৃত্তাকার শঙ্কুর উচ্চতা 12 সেমি এবং আয়তন 100 π ঘন সেমি.। শঙ্কুর তির্যক উচ্চতা নির্ণয় কর।
সমাধান,
ধরি,
শঙ্কুর ভূমিতলের ব্যাসার্ধ r সেমি.
শঙ্কুর উচ্চতা (h) = 12 সেমি.
শঙ্কুর আয়তন = 100 π ঘন সেমি.
ধরি,শঙ্কুর ব্যাসার্ধ r সেমি.
∴ \(\frac13\times\pi\times r^2\times h=100\pi\)
বা, \(\frac13\times\pi\times r^2\times12=100\pi\)
বা, 4 × π × r2 = 100π
বা, 4r2 = 100
বা, r2 = 25
বা, r2 = (5)2
বা, r = 5
শঙ্কুর তির্যক উচ্চতা I হলে,
I2=h2+r2
বা, I2 = (12)2+(5)2
বা, I2 = 144+25
বা, I2 = 169
বা, I2 = (13)2
বা, I = 13
∴ শঙ্কুর তির্যক উচ্চতা 13 সেমি.।
(xi) দুটি গোলকের বক্রতলের ক্ষেত্রফলের অনুপাত 1 : 4 হলে, তাদের আয়তনের অনুপাত নির্ণয় কর।
সমাধান,
দুটি গোলকের বক্রতলের ক্ষেত্রফলের অনুপাত 1 : 4
ধরি, গোলকটির ব্যাসার্ধ r1 একক এবং r2 একক।
∴ 4πr12 : 4πr22 = 1 : 4
বা, \(\frac{4\pi r_1^2}{4\pi r_2^2}=\frac14\)
বা, \(\left(\frac{r_1}{r_2}\right)^2=\frac14\)
বা, \(\frac{r_1}{r_2}=\frac14\)
বা, r1 : r2 = 1 : 2
∴ গোলক দুটির আয়তনের অনুপাত
= \(\frac43\pi r_1^3:\frac43\pi r_2^3\)
= \(r_1^3:r_2^3\)
= \(\left(\frac{r_1}{r_2}\right)^3\)
= \(\left(\frac12\right)^3\)
= \(\frac18\)
= 1 : 8
(xii) যদি \(u_i=\frac{x_i-35}{10},\sum f_iu_i=30\) এবং \(\sum f_i=60\) হয় তাহলে \(\overline x\) এর মান নির্ণয় করো।
সমাধান,
এখানে, a = 35 এবং h = 10
∴ \(\overline x=a+\frac{\sum f_iu_i}{\sum f_i}\times h\)
= \(35+\frac{30}{60}\times10\)
= 35 + 5
= 40 [উত্তর]
5. যে কোনো একটি প্রশ্নের উত্তর দাও
(i) তোমার কাকার কারখানার একটি মেশিনের মূল্য প্রতি বছর 10 % হারে হ্রাস প্রাপ্ত হয়। মেশিনটির মূল্য 6000 টাকা হলে 3 বছর পরে ওই মেশিনের মূল্য কত হবে?
সমাধান,
বর্তমানে মেশিনের মূল্য (P) = 6000 টাকা।
মেশিনের মূল্য হ্রাসের হার (r) = 10%
সময় (n) = 3 বছর
ধরি, মেশিনটির 3 বছর পর মূল্য হবে A টাকা
∴ \(p\left(1-\frac r{100}\right)^3=A\)
বা,\(6000\left(1-\frac{10}{100}\right)^3=A\)
বা,\(6000\left(1-\frac1{10}\right)^3=A\)
বা,\(6000\left(\frac9{10}\right)^3=A\)
বা,\(A=6000\left(\frac9{10}\right)^3\)
বা,\(A=6000\times\frac9{10}\times\frac9{10}\times\frac9{10}\)
বা, A = 4374
∴ মেশিনটির মূল্য 3 বছর পর হবে 4374 টাকা।
(ii) তিন বন্ধু যথাক্রমে 1,20,000 টাকা, 1,50,000 টাকা ও 1,10,000 টাকা মূলধন নিয়ে একটি বাস ক্রয় করেন। প্রথমজন ড্রাইভার ও বাকি দুজন কন্ডাক্টরের কাজ করেন। তারা ঠিক করেন যে মোট আয়ের \(\frac25\) অংশ তারা কাজের জন্য 3:2:2 অনুপাতে ভাগ করবেন এবং বাকি টাকা মূলধনের অনুপাতে ভাগ করে নেবেন। কোনো একমাসে যদি 29260 টাকা আয় হয়, তবে কে কত টাকা পাবে হিসাব করে লিখি।
সমাধান,
তিন বন্ধুর মূলধনের পরিমানের অনুপাত
= 1,20,000 : 1,50,000 : 1,10,000
= 12 : 15 : 11
তাদের মাসিক আয় = 29260 টাকা
এই লাভের \(\frac25\) অংশ তারা নিজেদের মধ্যে 3 : 2 : 2 অনুপাতে ভাগ করে এবং বাকি অংশ মূলধনের অনুপাতে ভাগ করেন।
লাভের = \(\frac25\) অংশ = \(\frac25\times29260\) টাকা = 11704 টাকা
এখন এই টাকা থেকে পাবে,
ড্রাইভার পাবে = \(\frac3{3+2+2}\times11704\) টাকা = \(\frac37\times11704\) টাকা = 5016 টাকা
প্রথম কন্ডাক্টার পাবে = \(\frac2{3+2+2}\times11704\) টাকা = \(\frac27\times11704\) টাকা = 3344 টাকা
দ্বিতীয় কন্ডাক্টার পাবে = \(\frac2{3+2+2}\times11704\) টাকা = \(\frac27\times11704\) টাকা = 3344 টাকা
এই টাকা তারা মূলধনের অনুপাতে ভাগ করবেন,
ড্রাইভার পাবে = \(\frac{12}{12+15+11}\times17556\) টাকা = 5016 টাকা
প্রথম কন্ডাক্টার পাবে = \(\frac{15}{12+15+11}\times17556\) টাকা = 6930 টাকা
দ্বিতীয় কন্ডাক্টার পাবে = \(\frac{11}{12+15+11}\times17556\) টাকা = 5082 টাকা
∴ ড্রাইভার মোট পাবে = (5016+5544) টাকা = 10560 টাকা
প্রথম কন্ডাক্টর মোট পাবে = (3344+6930) টাকা = 10274 টাকা
দ্বিতীয় কন্ডাক্টর মোট পাবে = (3344+5082 ) টাকা = 8426 টাকা
6.যে কোনো একটি সমাধান কর
(i) \(\frac1{\left(x-3\right)}-\frac1{\left(x+5\right)}=\frac16\)
সমাধান,
\(\frac1{\left(x-3\right)}-\frac1{\left(x+5\right)}=\frac16\\\)বা, \(\frac{\left(x+5\right)-\left(x-3\right)}{\left(x-3\right)\left(x+5\right)}=\frac16\)
বা, \(\frac{x+5-x+3}{\left(x-3\right)\left(x+5\right)}=\frac16\)
বা, \(\frac8{\left(x-3\right)\left(x+5\right)}=\frac16\)
বা, (x-3)(x+5) = 48
বা, x2 – 3x + 5x – 15 – 48 = 0
বা, x2 + 2x – 63 =0
বা, x2 – ( 9 – 7)x – 63=0
বা, x2 – 9x + 7x – 63 = 0
বা, x(x-9) + 7 (x – 9) = 0
বা, (x-9) (x+7) = 0
দুটি রাশির গুনফল শূন্য
∴ (x – 9) = 0
বা, x = 9
এবং (x + 7) = 0
বা, x = -7
∴ নির্ণেয় সমাধান 9 এবং -7
(ii) দুটি ক্রমিক ধনাত্মক অযুগ্ম সংখ্যার গুনফল 143 হলে সমীকরণটি গঠন করো এবং শ্রীধর আচার্যের সূত্র প্রয়োগ করে সংখ্যা দুটি নির্ণয় কর।
সমাধান,
ধরি, দুটি ক্রমিক অযুগ্ম সংখ্যা হল x এবং x + 2
শর্তানুসারে,
x (x + 2) = 143
বা, x2 + 2x – 143 = 0
সমীকরণটিকে ax2 + bx + c = 0 সমীকরণের সাথে তুলনা করে পাই,
a = 1, b = 2 এবং c = -143
∴ b2 – 4ac = (2)2 – 4(1)(-143) = 4 + 572 = 576 > 0
∴ সমীকরণটির বীজদ্বয় বাস্তব।
শ্রীধর আচার্যের সূত্র প্রয়োগ করে পাই,
\(x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\\)বা, \(x=\frac{-2\pm\sqrt{\left(2\right)^2-4\left(1\right)\left(-143\right)}}{2\left(1\right)}\)
বা, \(x=\frac{-2\pm\sqrt{576}}2\)
বা, \(x=\frac{-2\pm24}2\)
∴ \(x=\frac{-2+24}2\)
বা, \(x=\frac{22}2\)
বা, \(x=11\)
আবার, \(x=\frac{-2-24}2\)
বা, \(x=\frac{-26}2\)
বা, \(x=-13\)
∴ x = 11 এবং x = 13
∴ সংখ্যা দুটি হল 11 এবং 13
7. যে কোনো একটি প্রশ্নের উত্তর দাও
(i) \(x=2+\sqrt3\) এবং \(\left(x+y\right)=4\) হলে \(xy=\frac1{xy}\) এর সরলতম মান নির্ণয় করো।
সমাধান,
\(x=2+\sqrt3\\\)এবং (x+y) = 4
∴ y = 4 – x
বা, \(y=4-\left(2+\sqrt3\right)\)
বা, \(y=\left(2+\sqrt3\right)\)
∴ \(xy=\left(2+\sqrt3\right)\left(2-\sqrt3\right)=\left(2\right)^2-\left(3\right)^2=4-3=1\)
∴ \(xy+\frac1{xy}\)
= 1+1
= 2
(ii) a ∝ b এবং b ∝ c হলে, প্রমাণ কর যে, a3+b3+c3 ∝ 3abc
সমাধান,
A ∝ b
∴ a = pb [যেখানে p একটি অশূন্য ভেদ ধ্রুবক]
আবার, b ∝ c
∴ b = qc [যেখানে q একটি অশূন্য ভেদ ধ্রুবক]
∴ a = pb = p(qc) = pqc = rc [যেখানে pq = r = অশূন্য ভেদ ধ্রুবক]
∴ \(\frac{a^3+b^3+c^3}{3abc}\)
= \(\frac{\left(rc\right)^3+\left(qc\right)^3+c^3}{3\left(rc\right)\left(qc\right)c}\)
= \(\frac{r^3c^3+q^3c^3+c^3}{3qrc^3}\)
= \(\frac{c^3\left(r^3+q^3+1\right)}{3qrc^3}\)
= \(\frac{\left(r^3+q^3+1\right)}{3qr}\)
= ধ্রুবক
∴ a3 + b3 + c3 ∝ 3abc [প্রমাণিত ]
8. যে কোনো একটি প্রশ্নের উত্তর দাও
(i) \(x:a=y:b=z:c\) হলে দেখাও যে \(\frac{x^3}{a^3}+\frac{y^3}{b^3}+\frac{z^3}{c^3}=\frac{3xyz}{abc}\)
সমাধান,
ধরি, x : a = y : b = z : c = k [k(≠0) একটি সমানুপাতিক ধ্রুবক]
∴ x = ak, y = bk এবং z = ck
বামপক্ষ,
\(\frac{x^3}{a^3}+\frac{y^3}{b^3}+\frac{z^3}{c^3}\\\)= \(\frac{\left(ak\right)^3}{a^3}+\frac{\left(bk\right)^3}{b^3}+\frac{\left(ck\right)^3}{c^3}\)
= \(\frac{a^3k^3}{a^3}+\frac{b^3k^3}{b^3}+\frac{c^3k^3}{c^3}\)
= k3k3k3
=3k3
ডানপক্ষ,
\(\frac{3xyz}{abc}\\\)= \(\frac{3\left(ak\right)\left(bk\right)\left(ck\right)}{abc}\)
= \(\frac{3abck^3}{abc}\)
= 3k3
∴ বামপক্ষ = ডানপক্ষ [ প্রমাণিত ]
(ii)যদি \(\frac{ay-bx}c=\frac{cx-az}b=\frac{bz-cy}a\) হয়, তবে প্রমাণ করো যে \(\frac xa=\frac yb=\frac zc\)
সমাধান,
\(\frac{ay-bx}c=\frac{cx-az}b=\frac{bz-cy}a\\\)বা, \(\frac{ayz-bxz}{cz}=\frac{cxy-azy}{by}=\frac{xbz-cyx}{ax}\)
বা, \(=\frac{ayz-bxz+cxy-azy+xbz-cyx}{\left(cz+by+ax\right)}=0\) [সংযোজন প্রক্রিয়া]
∴ প্রতিটি অনুপাতের মান শূন্য
∴ \(\frac{ay-bx}c=0\)
বা, ay = bx
বা, \(\frac yb=\frac xa\)—- (i)
আবার, \(\frac{cx-az}b=0\)
বা, cx = az
বা, \(\frac xa=\frac zc\)—- (ii)
(i)ও (ii) নং সমীকরণ থেকে পাই,
\(\frac xa=\frac yb=\frac zc\)(প্রমাণিত)
9. যে কোনো একটি প্রশ্নের উত্তর দাও
(i) প্রমাণ করো, একই বৃত্তাংশস্থ সকল কোনই সমান।
প্রদত্ত: মনে করি O কেন্দ্রীয় বৃত্তের ∠ACB ও ∠ADB যে-কোনো দুটি কোণ ABDC বৃত্তাংশে অবস্থিত।
প্রমাণ করতে হবে: ACDB বৃত্তাংশস্থ সকল বৃত্তস্থ কোণই সমান।
যেহেতু ∠ACB ও ∠ADB ওই বৃত্তাংশস্থ যে-কোনো দুটি বৃত্তস্থ কোণ, সুতরাং ∠ACB ও ∠ADB পরস্পর সমান প্রমাণ করলেই উপপাদ্যটি প্রমাণিত হবে।
অঙ্কন: O, A বিন্দুদ্বয় ও O, B বিন্দুদ্বয় সরলরেখাংশ দ্বারা যুক্ত করলাম।
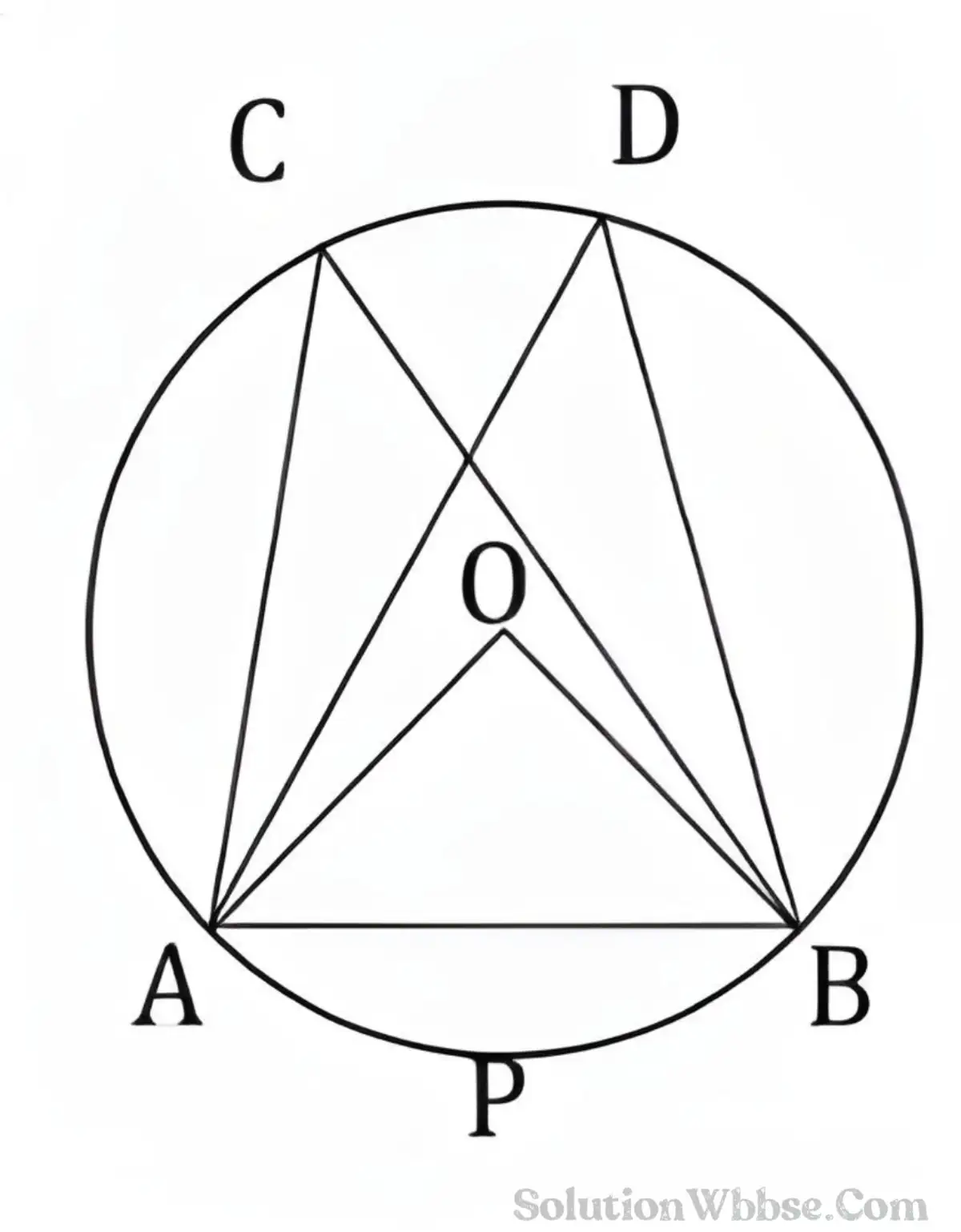
প্রমাণ: APB বৃত্তচাপের দ্বারা গঠিত ∠AOB কেন্দ্রস্থ কোণ এবং ∠ACB ও ∠ADB বৃত্তস্থ কোণ।
∴ AOB = 2∠ACB
এবং ∠AOB = 2∠ADB
সুতরাং, 2∠ACB = 2∠ADB
∴ ∠ACB = ∠ADB [প্রমাণিত]
(ii) প্রমাণ কর, বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে যে দুটি স্পর্শক অঙ্কন করা যায় তাদের স্পর্শবিন্দু দুটির সঙ্গে বহিঃস্থ বিন্দুর সংযোজক সরলরেখাংশ দৈর্ঘ্য দুটির সমান।
প্রদত্ত – O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু P থেকে PA ও PB দুটি স্পর্শক যাদের স্পর্শবিন্দু যথাক্রমে A ও B, O, A; O, B; O, P যুক্ত করায় PA ও PB সরলরেখাংশ দুটি কেন্দ্রে যথাক্রমে ∠POA ও ∠POB দুটি কোণ উৎপন্ন করেছে।
প্রমাণ করতে হবে – (i) PA = PB (ii) ∠POA = ∠PОВ
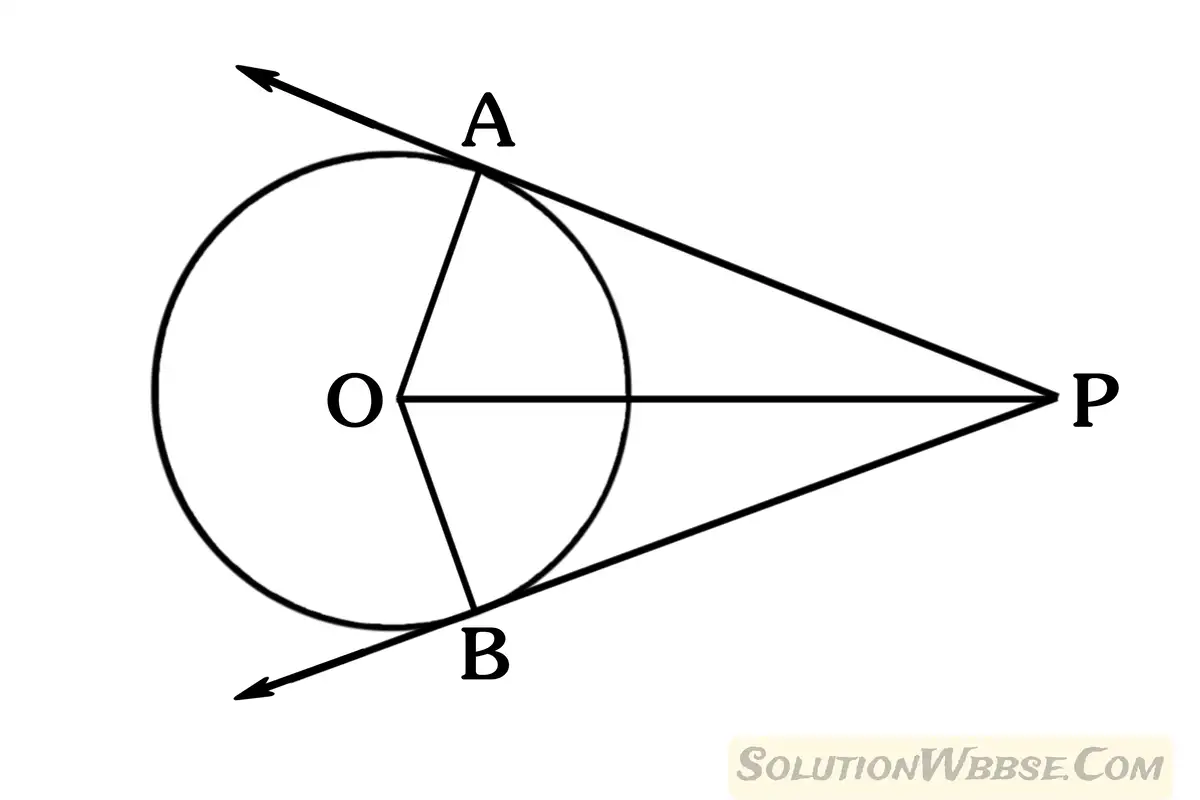
প্রমাণ – PA ও PB স্পর্শক এবং OA ও OB স্পর্শবিন্দুগামী ব্যাসার্ধ।
∴ OA ⊥ PA এবং OB ⊥ PB
POA ও POB সমকোণী ত্রিভুজদ্বয়ের মধ্যে, ∠OAP = ∠OBP (প্রত্যেকে 1 সমকোণ) অতিভুজ OP সাধারণ বাহু এবং OA = OB (একই বৃত্তের ব্যাসার্ধ)
ΔΡΑΟ ≅ ΔΡΒΟ [সর্বসমতার R-H-S শর্তানুসারে]
∴ PA = PB (সর্বসম ত্রিভুজের অনুরূপ বাহু) —- [(i) প্রমাণিত]
এবং ∠POA = ∠POB (সর্বসম ত্রিভুজের অনুরূপ কোণ) —- [(ii) প্রমাণিত]
10. যে কোনো একটি প্রশ্নের উত্তর দাও
(i) দুটি বৃত্ত পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে। PA ও PB যথাক্রমে দুটি বৃত্তের ব্যাস হলে, প্রমান কর A, Q ও B বিন্দুত্রয় সমরেখ।
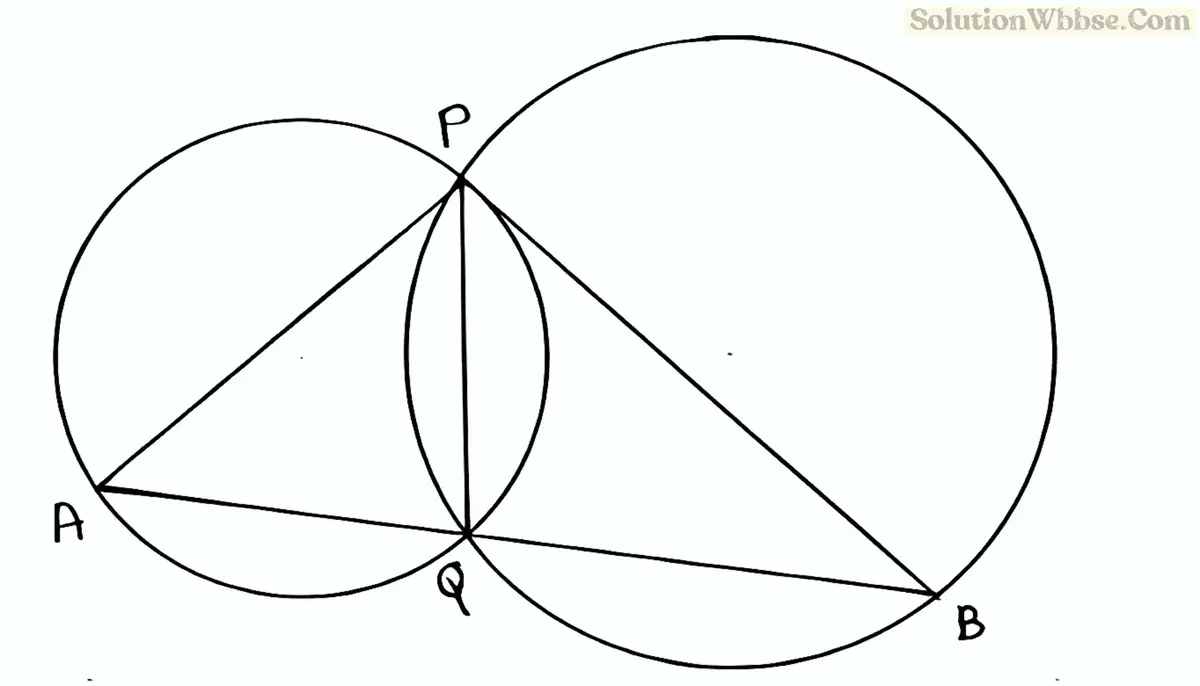
দুটি বৃত্ত পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে, PA ও PB যথাক্রমে দুটি বৃত্তের ব্যাস প্রমান করেতে হবে যে A, Q ও B বিন্দুত্রয় সমরেখ।
অঙ্কন: P,Q যুক্ত করা হল।
প্রমাণ: APQ ত্রিভুজে, AP ব্যাস।
∴ ∠AQP = 90° [যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ]
আবার, ∆BQP ত্রিভুজে, PB ব্যাস
∴ ∠PQB = 90° [যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ]
এখন, ∠AQB
= ∠AQP+∠PQB
= 90°+90°
= 180°
∴ A,Q ও B একই সরলরেখায় অবস্থিত।
∴ A,Q ও B সমরেখ।
(ii)সমকোণী ত্রিভুজ ABC এর ∠A = 90°, BC এর উপর AD লম্ব, প্রমাণ করো,
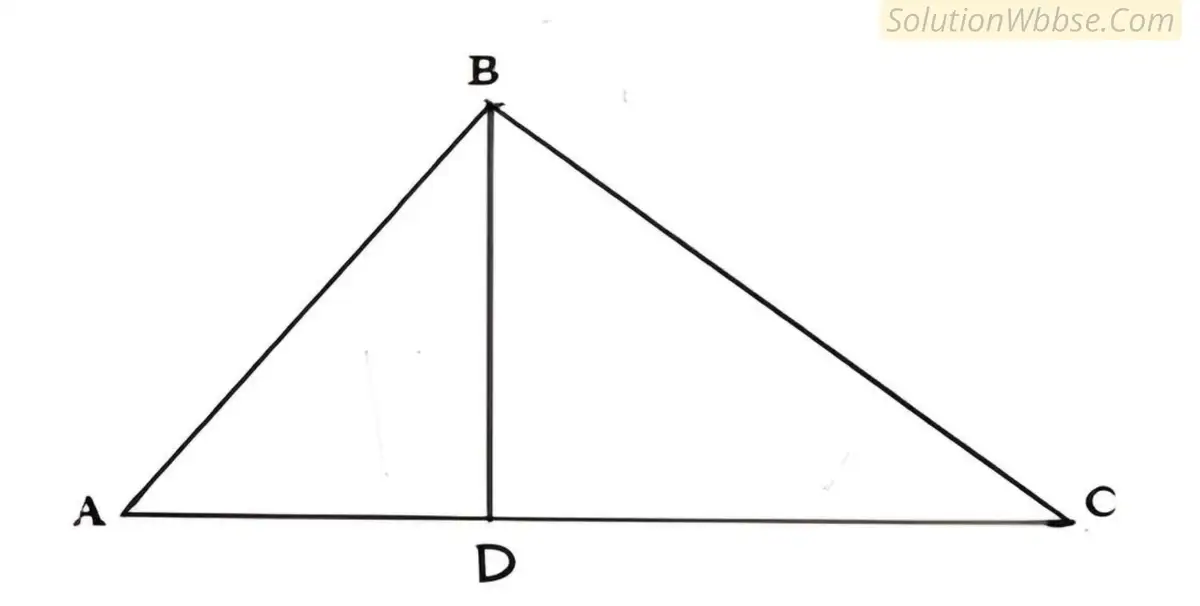
ABC সমকোণী ত্রিভুজের ∠BAC সমকোণ, অতিভুজ BC -এর উপর AD লম্ব হলে, প্রমাণ করি যে,
প্রমাণ: ABC সমকোণী ত্রিভুজের ∠BAC সমকোণ এবং সমকৌণিক বিন্দু A থেকে BC এর উপর AD লম্ব। যেহেতু সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে লম্বের উভয়পার্শ্বে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা পরস্পর সদৃশ এবং প্রত্যেকটি ত্রিভুজ মূল ত্রিভুজের সাথে সদৃশ।
∴ ∆ABC এবং ∆DAC পরস্পর সদৃশ
∴∴ ]
বা,
বা, [যেহেতু, ]
বা,
∴ [প্রমাণিত]
11. যে কোনো একটি প্রশ্নের উত্তর দাও
(i) 4 সেমি. ও 3 সেমি. দৈর্ঘ্যের সরলরেখাংশ দুটির মধ্য সমানুপাতী অঙ্কন কর।
সমাধান,
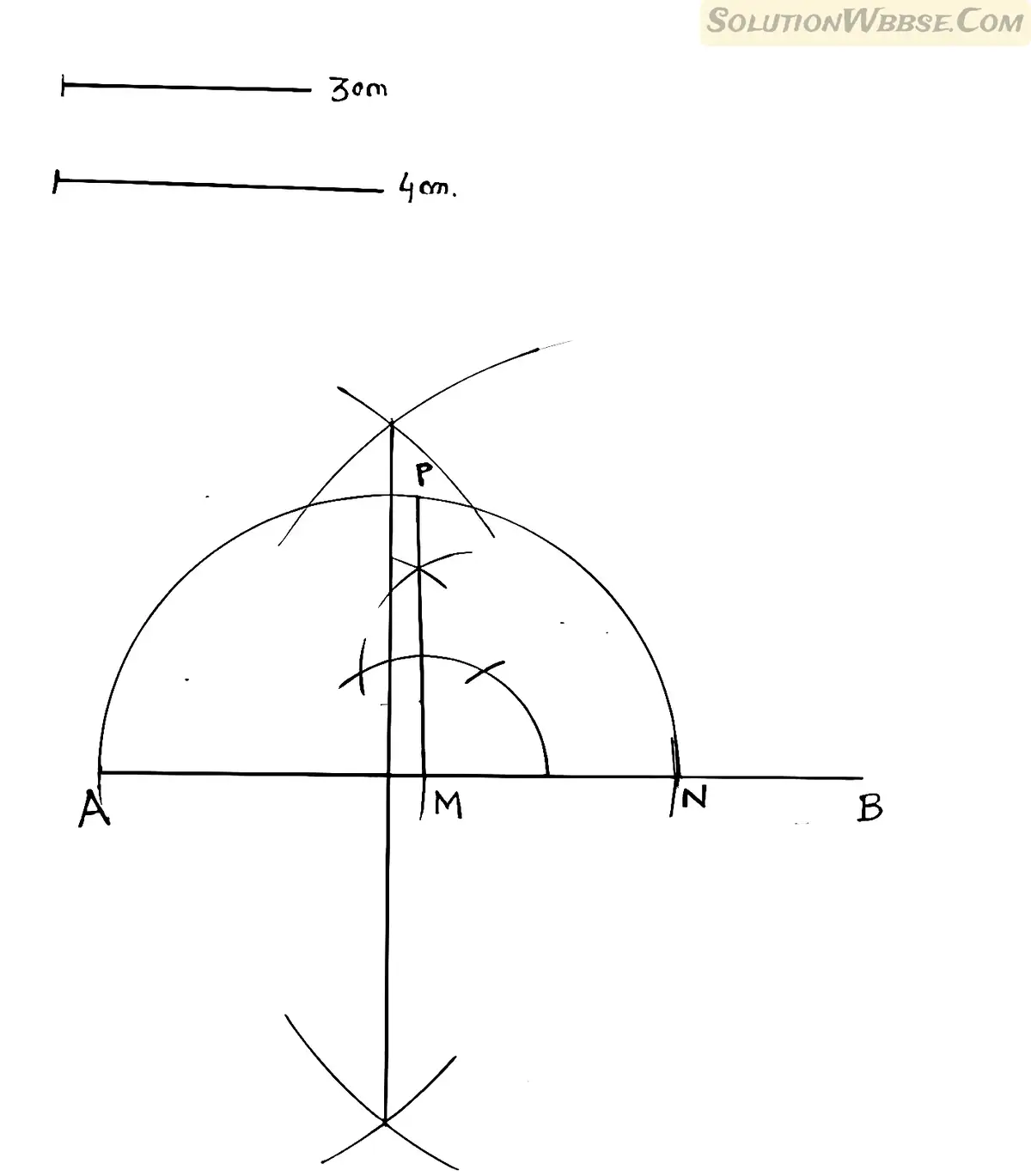
∴ নির্ণেয় মধ্যসমানুপাতীটি হল PM যার দৈর্ঘ্য 3.5সেমি।
(ii) 3 সেমি ব্যাসার্ধের একটি বৃত্ত অঙ্কন কর। বৃত্তের উপর A বিন্দুতে স্পর্শক অঙ্কন কর।
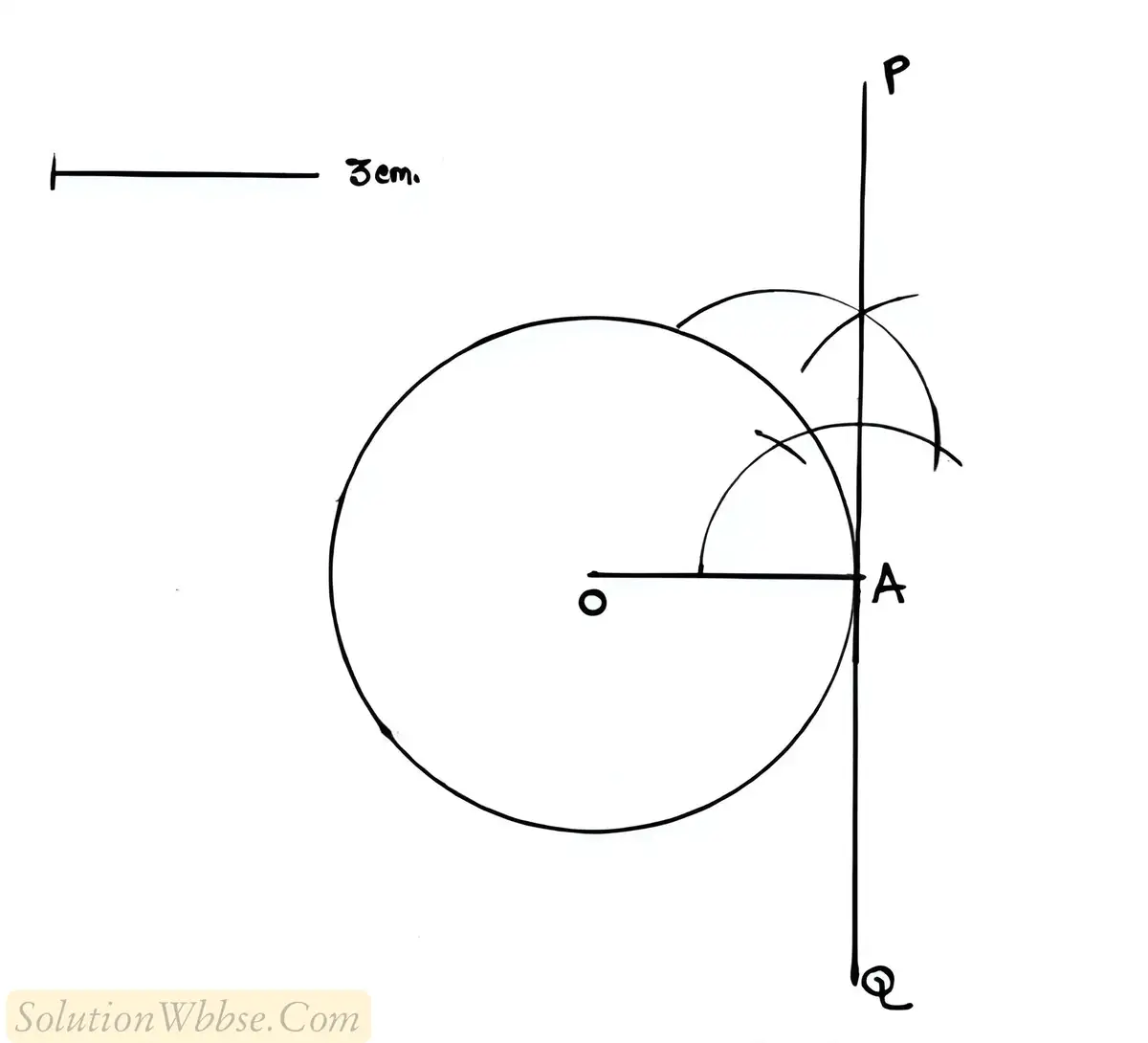
12. যে কোনো দুটি প্রশ্নের উত্তর দাও
(i) যদি \(\sin17^\circ=\frac xy\) হয়, তাহলে দেখাও \(\sin17^\circ-\sin73^\circ=\frac{x^2}{y\sqrt{y^2-x^2}}\)
সমাধান,
\(\sin17^\circ=\frac xy\\\)∴ cos17°
= \(\sqrt{1-\sin^217^\circ}\)
= \(\sqrt{1-\left(\frac xy\right)^2}\)
= \(\sqrt{1-\frac{x^2}{y^2}}\)
= \(\sqrt{\frac{y^2-x^2}{y^2}}\)
= \(\frac{\sqrt{y^2-x^2}}y\)
∴ sec17° – sin73°
= \(\frac1{\cos17^\circ}-\sin\left(90^\circ-17^\circ\right)\)
= \(\frac1{\cos17^\circ}-\cos17^\circ\)[যেহেতু, sin(90° – θ) = cosθ]
= \(\frac{1-\cos^217^\circ}{\cos17^\circ}\)
= \(\frac{\sin^217^\circ}{\cos17^\circ}\)
= \(\frac{\left({\displaystyle\frac xy}\right)^2}{\displaystyle\frac{\sqrt{y^2-x^2}}y}\)
= \(\frac{x^2}{y^2}\div\frac{\sqrt{y^2-x^2}}y\)
= \(\frac{x^2}{y^2}\times\frac y{\sqrt{y^2-x^2}}\)
= \(\frac{x^2}{y\sqrt{y^2-x^2}}\)
∴ \(sec17^\circ-\sin73^\circ=\frac{x^2}{y\sqrt{y^2-x^2}}\)
(ii) দুটি কোণের সমষ্টি 135° এবং তাদের অন্তর\(\frac{\mathrm\pi}{12}\)হলে, কোণ দুটির ষষ্টিক ও বৃত্তীয় মান লিখো
সমাধান,
ধরি, কোণ দুটি হল A এবং B
∴ A + B = 135°______(i)
এবং A – B = \(\frac{\mathrm\pi}{12}\)
বা, A – B = 15°______(ii)
(i) ও (ii) নং সমীকরণ যোগ করে পাই,
A + B + A – B = 135°+15°
বা, 2A = 150°
বা, \(A=\frac{150^\circ}2\)
বা, A = 75°
A এর প্রাপ্ত মান (i) নং সমীকরনে বসিয়ে পাই,
75° + B = 135°
বা, B = 135° – 75°
বা, B = 60°
∴ A ও B কোণের ষষ্টিক মান যথাক্রমে 75° এবং 60°
∴ A এর বৃত্তীয়মান = \(\frac{75\mathrm\pi}{180}\) রেডিয়ান = \(\frac{5\mathrm\pi}{12}\) রেডিয়ান
এবং B এর বৃত্তীয়মান = \(\frac{60\mathrm\pi}{180}\) রেডিয়ান = \(\frac{\mathrm\pi}3\) রেডিয়ান
(iii) মান নির্ণয় করো \(\frac{5\cos^2{\displaystyle\frac{\mathrm\pi}3}+4sec^2{\displaystyle\frac{\mathrm\pi}6}-\tan^2{\displaystyle\frac{\mathrm\pi}4}}{\sin^2{\displaystyle\frac{\mathrm\pi}6}+\cos^2{\displaystyle\frac{\mathrm\pi}6}}\)
সমাধান,
\(\frac{5\cos^2{\displaystyle\frac{\mathrm\pi}3}+4sec^2{\displaystyle\frac{\mathrm\pi}6}-\tan^2{\displaystyle\frac{\mathrm\pi}4}}{\sin^2{\displaystyle\frac{\mathrm\pi}6}+\cos^2{\displaystyle\frac{\mathrm\pi}6}}\\\)= \(\frac{5\left({\displaystyle\frac12}\right)^2+ 4\left({\displaystyle\frac2{\sqrt3}}\right)^2-\left(1\right)^2}{\left({\displaystyle\frac12}\right)^2+\left({\displaystyle\frac2{\sqrt3}}\right)^2}\)
= \(\frac{5\times{\displaystyle\frac14}+4\times{\displaystyle\frac43}-1}{{\displaystyle\frac14}+{\displaystyle\frac34}}\)
= \(\frac{{\displaystyle\frac54}+{\displaystyle\frac{16}3}-1}{\displaystyle\frac44}\)
= \(\frac{\displaystyle\frac{15+64-12}{12}}1\)
= \(\frac{67}{12}\)
= \(5\frac7{12}\)[উত্তর]
13. যে কোনো একটি প্রশ্নের উত্তর দাও
(i) একটি হ্রদের h মিটার ওপর একটি বিন্দু থেকে কোনো মেঘের উন্নতি কোণ α এবং হ্রদের উপর ওই প্রতিবিম্বের অবনতি কোণ β। প্রমাণ করো, যে বিন্দু থেকে মেঘ দেখা যাচ্ছে সেখান থেকে মেঘের দূরত্ব\(\frac{2h\;sec\alpha}{\tan\beta-\tan\alpha}\)
সমাধান,
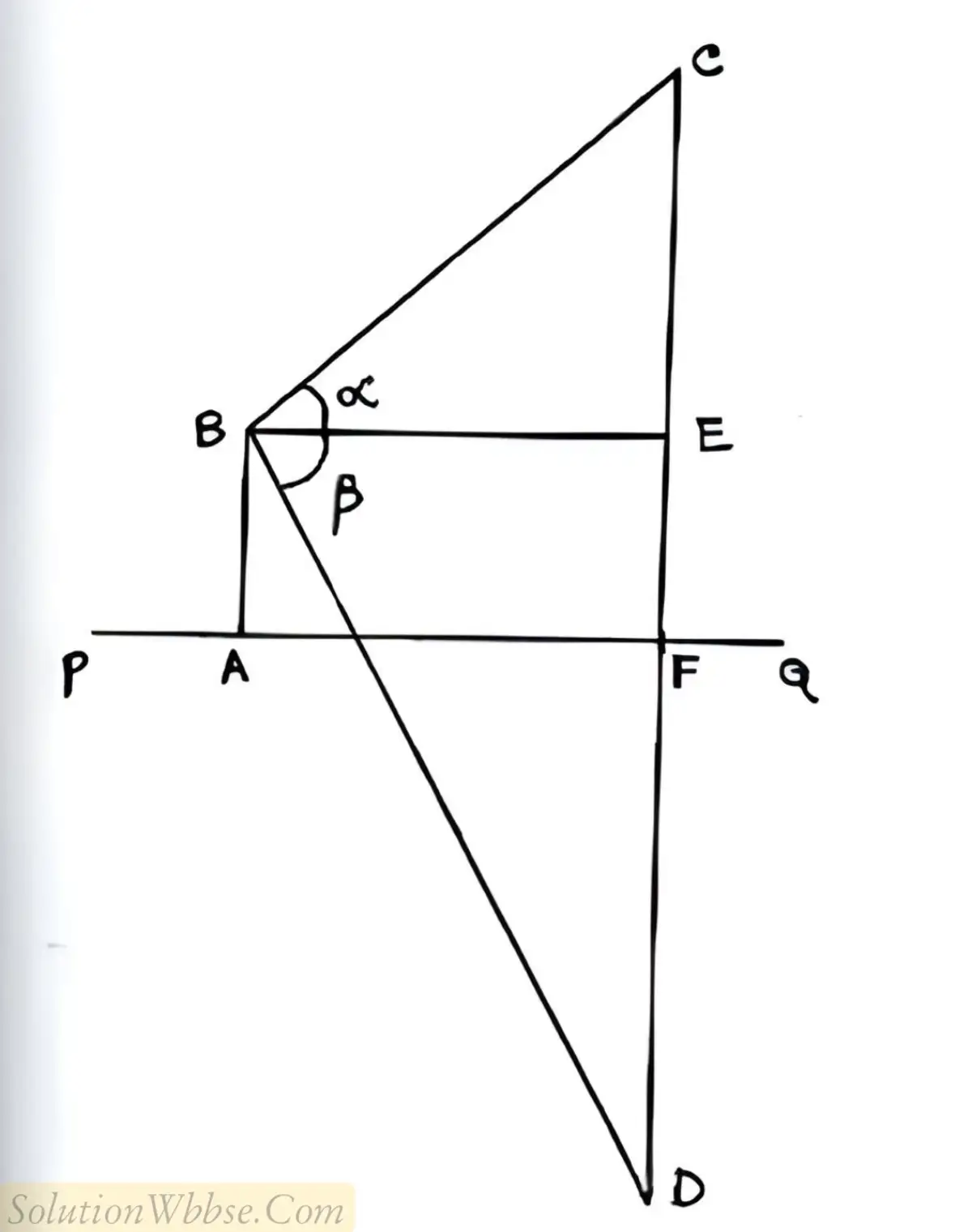
ধরা যাক, PQ হ্রদের A বিন্দু থেকে h উচ্চতায় B বিন্দু থেকে c বিন্দুতে অবস্থিত মেঘের উন্নতি কোণ α আবার B বিন্দু থেকে মেঘের প্রতিবিম্বের অবনতি কোণ β
∴ ∠CBE = α এবং ∠EBD = β
B বিন্দু থেকে PQ এর সমান্তরাল সরলরেখা টানা হল যা CD বাহুকে E বিন্দুতে ছেদ করে।
BEC সমকোণী ত্রিভুজ থেকে পাই,
\(\tan\beta=\frac{DE}{BE}\\\)বা, DE = BE tanβ
বা, DF + FE = BE tanβ
বা, CF + AB = BE tanβ [যেহেতু হ্রদ থেকে মেঘের দূরত্ব এবং হ্রদ থেকে প্রতিবিম্বের দূরত্ব সমান ∴ CF = FD এবং AB = EF = h মিটার।]
বা, CE + EF + AB = BE tanβ
বা, CE + h + h = BE tanβ
বা, CE + 2h = BE tanβ
বা, BE tanα +2h = BE tanβ
বা, 2h = BE tanβ – BE tanα
বা, 2h = BE (tanβ – tanα)
বা, \(BE=\frac{2h}{\left(\tan\beta-\tan\alpha\right)}\)
সমকোণী ত্রিভুজ BEC থেকে পাই
\(\cos\alpha=\frac{BE}{BC}\\\)বা, BE = BC cosα
∴ \(BC\;\cos\alpha=\frac{2h}{\left(\tan\beta-\tan\alpha\right)}\)
বা, \(BC=\frac{2h}{\left(\tan\beta-\tan\alpha\right)\cos\alpha}\)
বা, \(BC=\frac{sec\alpha2h}{\left(\tan\beta-\tan\alpha\right)}\)
∴ যেখান থেকে মেঘ দেখা যায় সেখান থেকে মেঘের দূরত্ব \(\frac{sec\alpha2h}{\left(\tan\beta-\tan\alpha\right)}\) মিটার।
(ii) দুটি স্তম্ভের উচ্চতা যথাক্রমে 180 মিটারও 60 মিটার।দ্বিতীয় স্তম্ভটির গোড়া থেকে প্রথম চূড়ার উন্নতি কোণ 60°হলে, প্রথমটির গোড়া থেকে দ্বিতীয় চূড়ার উন্নতি কোণ নির্ণয় কর।
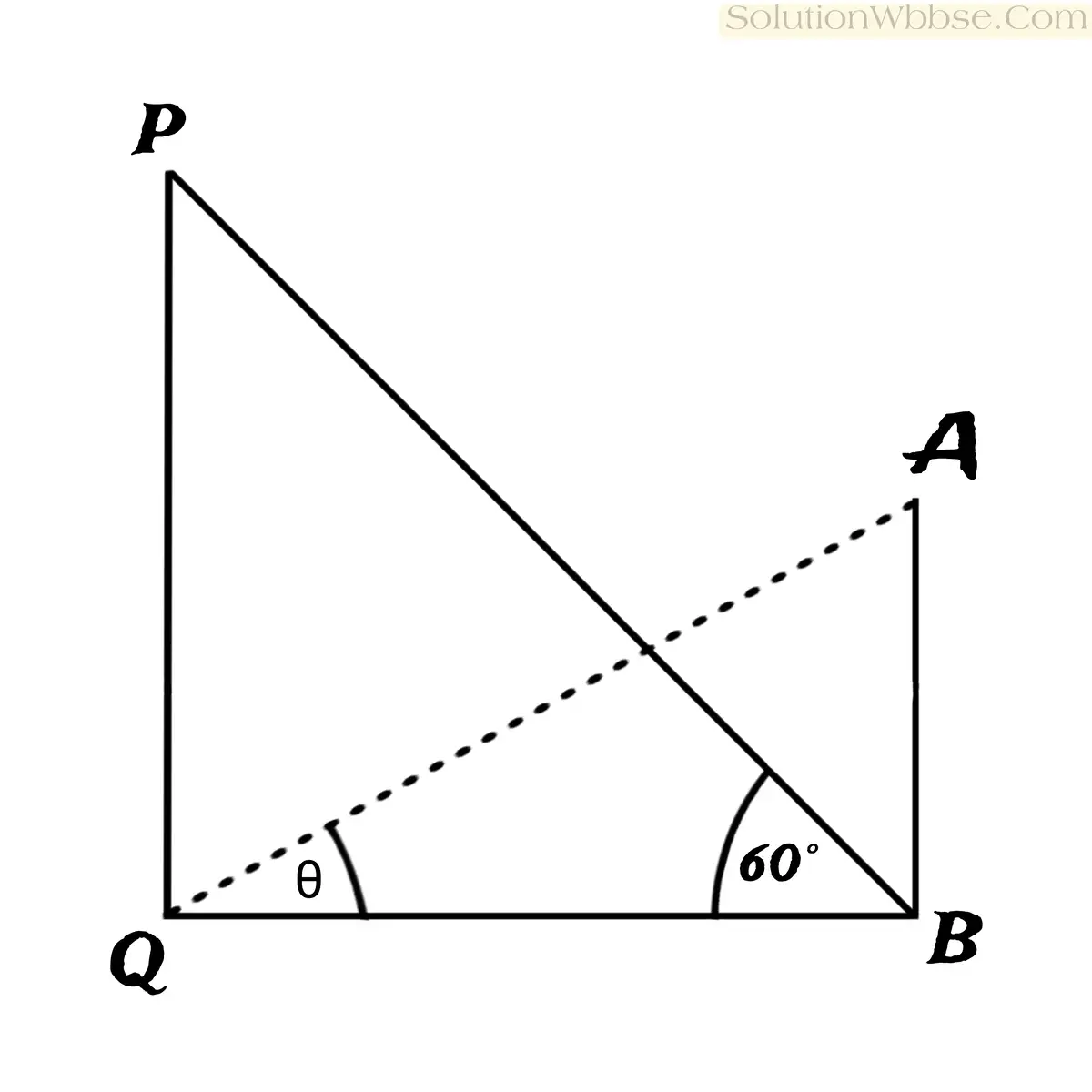
14. যে কোনো দুটি প্রশ্নের উত্তর দাও
(i) একটি লম্ব বৃত্তাকার চোঙাকৃতি নলের বহির্ব্যাসার্ধের দৈর্ঘ্য 5 সেমি. এবং অন্তর্ব্যাসার্ধের দৈর্ঘ্য 4 সেমি। নলটির সমগ্রতলের ক্ষেত্রফল 1188 বর্গসেমি হলে, নলটির দৈর্ঘ্য নির্ণয় করো।
সমাধান,
ধরি, নলটির দৈর্ঘ্য h সেমি
নলটির বহির্ব্যাসার্ধ (R) = 5 সেমি.
নলটির অন্তর্ব্যাসার্ধ (r) = 4 সেমি.
নলটির সমগ্রতলের ক্ষেত্রফল
= {2πRh + 2πrh + π(R2-r2)h} বর্গসেমি.
= \(\left[2\times\frac{22}7\times5\times h+2\times\frac{22}7\times4\times h+\frac{22}7\times\left\{\left(5\right)^2-\left(4\right)^2\right\}h\right]\) বর্গসেমি
= \(\left[\frac{220h}7+\frac{176h}7+\frac{396}7\right]\) বর্গসেমি
শর্তানুসারে,
\(\frac{220h}7+\frac{176h}7+\frac{396}7 = 1188\\\)বা, \(\frac{2220h+176h+396}7=1188\)
বা, 396h + 396 = 8316
বা, 396h = 8316 – 396
বা, 396h = 7920
বা, \(h=\frac{7920}{396}\)
বা, h = 20
∴ নলটির দৈর্ঘ্য 20 সেমি.।
(ii) 9 সেমি. অন্তর্ব্যাসার্ধ বিশিষ্ট একটি অর্ধ গোলাকার পাত্র সম্পূর্ণ জলপূর্ণ আছে। এই জল 3 সেমি. ব্যাস এবং 4 সেমি. উচ্চতা বিশিষ্ট চোঙাকৃতি বোতলে ভর্তি করে রাখা হবে। পাত্রটি খালি করতে কতগুলি এইরূপ বোতল দরকার তা নির্ণয় কর।
সমাধান,
অর্ধ গোলকের ব্যাসার্ধ (R) = 9 সেমি.
∴ অর্ধ গোলাকৃতি পাত্রের আয়তন
= \(\frac23\mathrm{πR}^3\)
= \(\frac23\mathrm\pi\left(9\right)^3\)
চোঙাকৃতি বোতলের ব্যাস 3 সেমি. ।
∴ বোতলের ব্যাসার্ধ (r) = 3/2 সেমি.
∴ বোতলের ব্যাসার্ধ \(\left(r\right)=\frac32\) সেমি
বোতলের উচ্চতা (h) = 4 সেমি.
∴ চোঙাকৃতি বোতলের আয়তন
= πr2h ঘন সেমি.
= \(\mathrm\pi\times\left(\frac32\right)^2\times4\)
ধরি, পাত্রটি খালি করতে x টি বোতলের প্রয়োজন হবে।
∴ পাত্রের পাত্রের জলের আয়তন = x টি বোতলের জলের আয়তন
∴ \(\frac23\mathrm\pi\left(9\right)^3=\mathrm x\times\mathrm\pi\times\left(\frac32\right)^2\times4\)
বা, \(\frac23\times729=\mathrm x\times\frac94\times4\)
বা, 486 = 9x
বা, \(x=\frac{486}9\)
বা, x = 54
∴ পাত্রটি খালি করতে 54 টি বোতলের প্রয়োজন হবে।
(iii) একটি লম্ব বৃত্তাকার শঙ্কুর ভূমিতলের ব্যাস 21 মিটার এবং উচ্চতা 14 মিটার। প্রতিও বর্গ মিটার 1.50 টাকা হিসাবে পার্শ্বতল রঙ করতে কত খরচ পড়বে?
সমাধান,
লম্ব বৃত্তাকার শঙ্কুর ব্যাস 21 মিটার।
∴ লম্ব বৃত্তাকার শঙ্কুর ব্যাসার্ধ \(\left(r\right)=\frac{21}2\) সেমি.
লম্ব বৃত্তাকার শঙ্কুর উচ্চতা (h) = 14 মিটার ।
ধরি , লম্ব বৃত্তাকার শঙ্কুর তির্যক উচ্চতা I সেমি.
∴ I2 = h2+r2
বা, \(I^2=\left(14\right)^2+\left(\frac{21}2\right)^2\)
বা, \(I^2=196+\frac{441}4\)
বা, \(I^2=\frac{784+441}4\)
বা, \(I^2=\frac{1225}4\)
বা, \(I^2=\left(\frac{35}2\right)^2\)
বা, \(I=\frac{35}2\)
∴ শঙ্কুর পার্শ্বতলের ক্ষেত্রফল
= \(\mathrm{πrI}\) বর্গসেমি
= \(\frac{22}7\times\frac{21}2\times\frac{35}2\) বর্গসেমি
= \(\frac{1155}2\) বর্গসেমি
∴ পার্শ্বতল 1.50 টাকা হিসেবে রং করতে মোট খরচ পড়বে = \(\left(\frac{1155}2\times1.50\right)\) টাকা
15. যে কোনো দুটি প্রশ্নের উত্তর দাও
(i) ছাত্রীদের প্রাপ্ত নম্বরের গড় নির্ণয় কর যদি তাদের প্রাপ্ত নম্বরের ক্রমযৌগিক পরিসংখ্যা নিম্নরূপ হয় –
| নম্বর | ছাত্রী সংখ্যা |
| 10 এর কম | 6 |
| 20 এর কম | 10 |
| 30 এর কম | 18 |
| 40 এর কম | 30 |
| 50 এর কম | 46 |
সমাধান,
এখানে দেখা যাচ্ছে যে 6 জন 10 এর কম পেয়েছে , অর্থাৎ 0-10 এর মধ্যে পেয়েছে 6 জন। আবার 10 জন 20 এর কম পেয়েছে, সুতরাং 10-20 এর মধ্যে পেয়েছে (10-6) জন = 4 জন। এভাবে পরিসংখ্যা তালিকাটি তৈরি করলে তা হবে।
| নম্বর | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| ছাত্রী সংখ্যা | 6 | 4 | 89 | 12 | 16 |
এক্ষেত্রে a = 25 এবং h = 10 ধরে পাই ,
| শ্রেণী সীমানা | পরিসংখ্যা (fi) | শ্রেণী মধ্যক (xi) | ui = (xi-a)/10 | fiui |
| 0 – 10 | 6 | 5 | -2 | -12 |
| 10 – 20 | 4 | 15 | -1 | -4 |
| 20 – 30 | 8 | 25 = a | 0 | 0 |
| 30 – 40 | 12 | 35 | 1 | 12 |
| 40 – 50 | 16 | 45 | 2 | 32 |
| মোট | ∑fi = 46 | ∑fiui = 28 |
ছাত্রীদের প্রাপ্ত নম্বরের গড়
= \(a+10\times\frac{\sum f_iu_i}{\sum f_i}\)
= \(25+10\times\frac{28}{46}\)
= 25 + 6.09
= 31.09 (প্রায়) [উত্তর]
(ii) নীচের পরিসংখ্যা বিভাজন থেকে তথ্যটির মধ্যমা নির্ণয় করি।
| শ্রেণী সীমানা | পরিসংখ্যা |
| 0 – 10 | 4 |
| 10 – 20 | 7 |
| 20 – 30 | 10 |
| 30 – 40 | 15 |
| 40 – 50 | 10 |
| 50 – 60 | 8 |
| 60 – 70 | 5 |
সমাধান,
পরিসংখ্যা বিভাজন তালিকাটি হল
| শ্রেণি সীমানা | পরিসংখ্যা | ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক ) |
| 0-10 | 4 | 4 |
| 10-20 | 7 | 11 |
| 20-30 | 10 | 21 |
| 30-40 | 15 | 36 |
| 40-50 | 10 | 46 |
| 50-60 | 8 | 54 |
| 60-70 | 5 | 59 = n |
এখানে n = 59
∴ \(\frac n2=\frac{59}2=29.5\)
29.5 এর থেকে ঠিক বেশি ক্রমযৌগিক পরিসংখ্যা (30-40) শ্রেণীর মধ্যে আছে ।
সুতরাং মধ্যমা শ্রেণীটি হল (30-40)
∴ নির্ণেয় মধ্যামা
= \(I+\left[\frac{{\displaystyle\frac n2}-cf}f\right]\times h\)
[এখানে, I = 30, n = 59, cf = 21, f = 15, h = 10]
= \(30+\left[\frac{{\displaystyle\frac{59}2}-21}{15}\right]\times10\)
= \(30+\frac{8.5}{15}\times10\)
= \(30+\frac{85}{15}\)
= 30 + 5.67
= 35.67 (প্রায়)
(iii) নীচের শ্রেণী –বিন্যাসিত পরিসংখ্যা বিভাজনের সংখ্যাগুরু মান নির্ণয় কর।
| শ্রেণী সীমানা | পরিসংখ্যা |
| 1-6 | 2 |
| 6-9 | 6 |
| 9-12 | 12 |
| 12-15 | 24 |
| 15-18 | 21 |
| 18-21 | 12 |
| 21-24 | 3 |
সমাধান,
উপরের পরিসংখ্যা বিভাজনের সংখাগুরুমান শ্রেণীটি হল 12-15
∴ নির্ণেয় সংখ্যাগুরুমান
= \(I+\left[\frac{f_1-f_0}{2f_1-f_0-f_2}\right]\times h\)
= \(12+\left[\frac{24-12}{2\times24-12-21}\right]\times3\) \(\left[I=12,\;f_1=24,\;f_0=12,\;f_2=21,\;h=3\right]\)
= \(12+\frac{12}{15}\times5\)
= 12 + 4
= 16 [উত্তর]
এই আর্টিকেলের মাধ্যমে আমরা মাধ্যমিক পরীক্ষার পুরাতন বছরের প্রশ্ন ও তাদের উত্তর নিয়ে বিস্তারিত আলোচনা করেছি। আশা করি, আমাদের এই প্রচেষ্টা আপনাদের জন্য অত্যন্ত সহায়ক হবে এবং আগের বছরের প্রশ্নপত্রের মাধ্যমে পরবর্তী পরীক্ষার জন্য একটি স্পষ্ট ধারণা পাবেন। বিশেষ করে, মাধ্যমিক ২০২০ সালের গণিত প্রশ্নপত্র ও তার উত্তরগুলি পর্যালোচনা করে আপনারা প্রস্তুতিকে আরও সুদৃঢ় করতে পারবেন।
আমাদের আন্তরিক অনুরোধ, আপনারা পরীক্ষার আগে অবশ্যই Madhyamik Math Question Paper ২০২০ With Answer ভালোভাবে দেখে প্রস্তুতি নেবেন। সবার জন্য শুভকামনা রইল!




মন্তব্য করুন