মাধ্যমিক গণিত – ত্রিকোণমিতিক অনুপাত এবং অভেদাবলী – কষে দেখি 23.1

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের ত্রয়োবিংশ অধ্যায়, ‘ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি’ -এর ‘কষে দেখি – 23.1’ বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

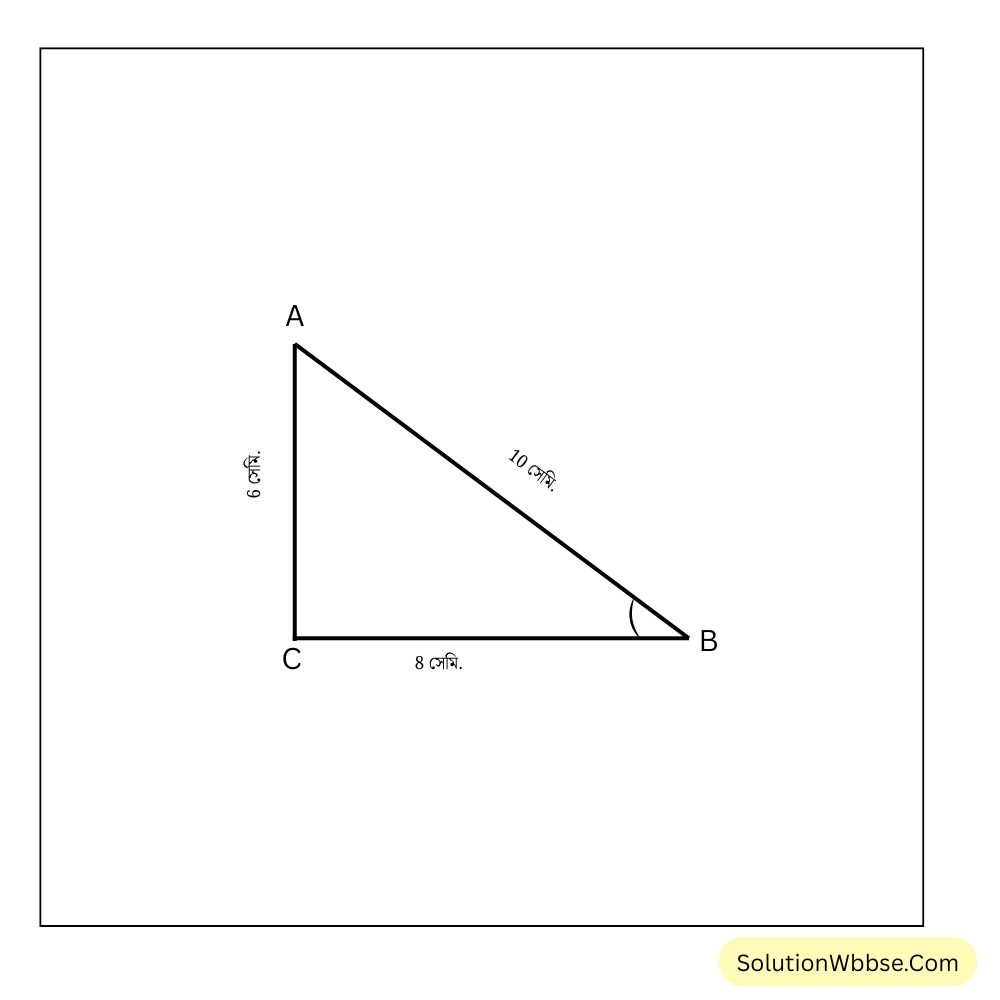
1. একটি সমকোণী ত্রিভুজ এঁকেছি যার অতিভুজ AB=10 সেমি., ভূমি BC=8 সেমি. এবং লম্ব AC=6 সেমি.। ∠ ABC –এর sine এবং tangent এর মান নির্ণয় করি।

সমাধান –

সমকোণী ত্রিভুজ ABC-তে ∠ ABC এর সাপেক্ষে, অতিভুজ AB=10 সেমি., ভূমি BC=8 সেমি. এবং লম্ব AC=6 সেমি.।

∴ sin ∠ABC = লম্ব / অতিভুজ = \(\frac{AC}{AB} = \frac{6}{10} = \frac{3}{5}\)

এবং tan ∠ABC = লম্ব / ভূমি = \(\frac{AC}{BC} = \frac{6}{8} = \frac{3}{4}\)

2. সোমা একটি সমকোণী ত্রিভুজ ABC এঁকেছে যার ∠ABC=90°, AB=24 সেমি. এবং BC=7 সেমি.। হিসাব করে sinA, cosA, tanA ও cosecA-এর মান লিখি।

সমাধান –

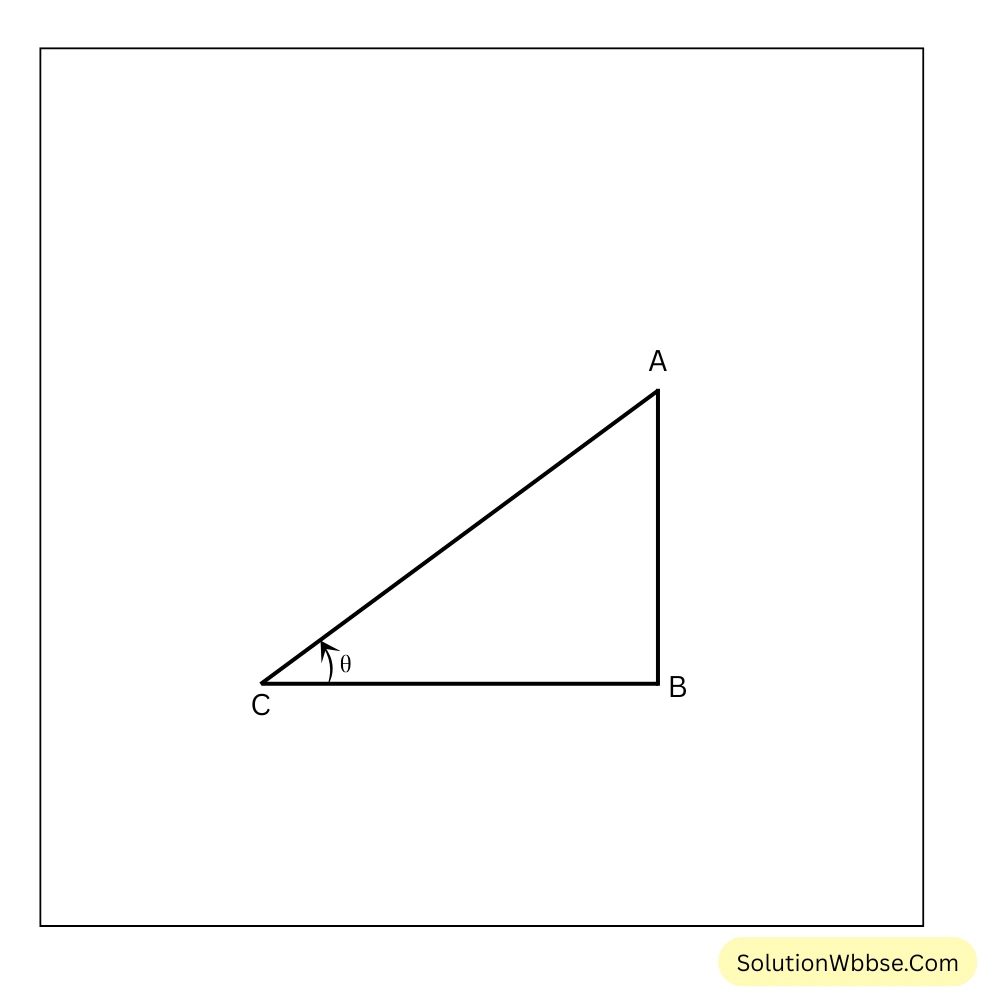
সমকোণী ত্রিভুজ ABC এর কোণ ∠A এর সাপেক্ষে ভূমি AB=24 সেমি. এবং লম্ব BC=7 সেমি. এবং অতিভুজ AC।

পিথাগোরাসের উপপাদ্য থেকে পাই,

(অতিভুজ)² = (লম্ব)² + (ভূমি)²

বা, (AC)² = (BC)² + (AB)²

বা, (AC)² = 49 + 576

বা, (AC)² = 625

বা, (AC)² = (25)²

বা, AC = 25

∴ অতিভুজ AC = 25 সেমি.

∴ sinA = লম্ব / অতিভুজ = \(\frac{BC}{AC} = \frac{7}{25}\)

cosA = ভূমি / অতিভুজ = \(\frac{AB}{AC} = \frac{24}{25}\)

tanA = লম্ব / ভূমি = \( \frac{BC}{AB} = \frac{7}{24} \)

cosecA = অতিভুজ / লম্ব = \(\frac{AC}{BC} = \frac{25}{7}\)

3. যদি ABC একটি সমকোণী ত্রিভুজের ∠C = 90°, BC = 21 একক এবং AB = 29 একক হয়, তাহলে Sin A, Cos A, Sin B ও Cos B এর মান নির্ণয় করি।

সমাধান –

ABC সমকোণী ত্রিভুজের ∠C = 90°, BC = 21 একক এবং AB = 29 একক।

∴ AC = \(\sqrt{AB^2 – BC^2}\)

= \(\sqrt{(29)^2 – (21)^2}\)

= \(\sqrt{841 – 441}\)

= \(\sqrt{400}\)

= \(20\) একক।

∠A এর সাপেক্ষে ভূমি AC এবং লম্ব BC এবং অতিভুজ AB আবার B কোণের সাপেক্ষে লম্ব AC এবং ভূমি BC এবং অতিভুজ AB

∴ $\sin A=\frac{\mathrm{লম্ব}}{\mathrm{অতিভুজ}}=\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{21}{29}$

∴ $\cos A=\frac{\mathrm{ভূমি}}{\mathrm{অতিভুজ}}=\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{20}{29}$

∴ $\sin B=\frac{\mathrm{লম্ব}}{\mathrm{অতিভুজ}}=\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{20}{29}$

∴ $\cos B=\frac{\mathrm{ভূমি}}{\mathrm{অতিভুজ}}=\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{21}{29}$

4. যদি cos θ = 7/25 হয়, তাহলে θ কোণের সকল ত্রিকোণমিতিক অনুপাত নির্ণয় করি।

সমাধানঃ

$\cos \theta =\frac{\mathrm{ভূমি}}{\mathrm{অতিভুজ}}=\frac{7}{25}$

ধরি, ভূমি = \(7k\) এবং অতিভুজ = \(25k\) [\(k(\neq 0)\) একটি আনুপাতিক ধ্রুবক]।

পিথাগোরাসের উপপাদ্য থেকে পাই,

${\left(\mathrm{অতিভুজ}\right)}^2={\left(\mathrm{লম্ব}\right)}^2+{\left(\mathrm{ভূমি}\right)}^2$

বা, ${\left(25k\right)}^2={\left(\mathrm{লম্ব}\right)}^2+{\left(7k\right)}^2$

বা, ${\left(\mathrm{লম্ব}\right)}^2=625k^2–49k^2$

বা, ${\left(\mathrm{লম্ব}\right)}^2=576k^2$

বা, ${\left(\mathrm{লম্ব}\right)}^2={\left(24k\right)}^2$

বা, $\mathrm{লম্ব}=24k$

$\tan \theta =\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{24k}{7k}=\frac{24}{7}$

$\sec \theta =\frac{\mathrm{অতিভুজ}}{\mathrm{ভূমি}}=\frac{25k}{7k}=\frac{25}{7}$

$\mathrm{cosec}\theta =\frac{\mathrm{অতিভুজ}}{\mathrm{লম্ব}}=\frac{25k}{24k}=\frac{25}{24}$

$\cot \theta =\frac{\mathrm{ভূমি}}{\mathrm{লম্ব}}=\frac{7k}{24k}=\frac{7}{24}$

5. যদি cotθ = 2 হয়, তাহলে tanθ ও secθ -এর মান নির্ণয় করি এবং দেখাই যে, 1+tan²θ=sec²θ

সমাধান –

$\cot \theta =2=\frac{\mathrm{ভূমি}}{\mathrm{লম্ব}}$

ধরি, ভূমি = \(2k\) এবং লম্ব = \(k\) [\(k (\neq 0)\) একটি আনুপাতিক ধ্রুবক]।

$\therefore \mathrm{অতিভুজ}=\sqrt{{\left(\mathrm{লম্ব}\right)}^2+{\left(\mathrm{ভূমি}\right)}^2}$

$=\sqrt{k^2+{\left(2k\right)}^2}$

$=\sqrt{k^2+4k^2}$

$=\sqrt{5k^2}$

$=k\sqrt{5}$

∴ $\sec \theta =\frac{\mathrm{অতিভুজ}}{\mathrm{ভূমি}}=\frac{k\sqrt{5}}{2k}=\frac{\sqrt{5}}{2}$

এবং $\tan \theta =\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{k}{2k}=\frac{1}{2}$

∴ \(1+\tan^2\theta = 1+\left(\frac{1}{2}\right)^2\)

= \(1+\frac{1}{4}\)

= \(\frac{5}{4}\)

= \(\left(\frac{\sqrt{5}}{2}\right)^2\)

= \(\sec^2\theta\)

∴ \(1+\tan^2\theta = \sec^2\theta\) [প্রমাণিত]

6. যদি cosθ = 0.6 হয়, তাহলে দেখাই যে, (5sinθ – 3tanθ) = 0

সমাধান –

$\cos \theta =\frac{6}{10}=\frac{3}{5}=\frac{\mathrm{ভূমি}}{\mathrm{অতিভুজ}}$

ধরি, ভূমি = \(3k\) এবং অতিভুজ = \(5k\) [\(k(\neq 0)\) একটি আনুপাতিক ধ্রুবক]

∴ লম্ব = \(\sqrt{(5k)^2 – (3k)^2} = \sqrt{25k^2 – 9k^2} = \sqrt{16k^2} = 4k\)

∴ $\sin \theta =\frac{\mathrm{লম্ব}}{\mathrm{অতিভুজ}}=\frac{4k}{5k}=\frac{4}{5}$

∴ $\tan \theta =\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{4k}{3k}=\frac{4}{3}$

∴ \((5\sin\theta-3\tan\theta) = 5 \times \frac{4}{5} – 3 \times \frac{4}{3} = 4 – 4 = 0\)

∴ \((5\sin\theta-3\tan\theta)=0\) [প্রমাণিত]

7. যদি cotA = 4/7.5 হয়, তাহলে cosA এবং cosecA -এর মান নির্ণয় করি এবং দেখাই যে, 1+cot²A = cosec²A

সমাধানঃ

cotA=47.5=4075=815=ভূমিলম্ব

ধরি, ভূমি = \(8k\) এবং লম্ব = \(15k\) [\(k(\neq 0)\) একটি আনুপাতিক ধ্রুবক]

∴ অতিভুজ = \(\sqrt{(15k)^2 + (8k)^2}\)

= \(\sqrt{225k^2 + 64k^2}\)

= \(\sqrt{289k^2}\)

= \(17k\)

∴ $\cos A=\frac{\mathrm{ভূমি}}{\mathrm{অতিভুজ}}=\frac{8k}{17k}=\frac{8}{17}$

∴ $\mathrm{cosec}A=\frac{\mathrm{অতিভুজ}}{\mathrm{লম্ব}}=\frac{17k}{15k}=\frac{17}{15}$

∴ \(1+\cot^2 A = 1 + \left(\frac{8}{15}\right)^2\)

= \(1 + \frac{64}{225}\)

= \(\frac{225+64}{225}\)

= \(\frac{289}{225}\)

= \(\left(\frac{17}{15}\right)^2\)

= \(cosec^2 A\)

∴ \(1+\cot^2 A=cosec^2 A\) [প্রমাণিত]

8. যদি sinC = 2/3 হয়, তবে cosC × cosecC –এর মান হিসাব করে লিখি।

সমাধান –

$\sin C=\frac{2}{3}=\frac{\mathrm{লম্ব}}{\mathrm{অতিভুজ}}$

ধরি, লম্ব = \(2k\) এবং অতিভুজ = \(3k\) [\(k(\neq 0)\) একটি আনুপাতিক ধ্রুবক]

∴ ভূমি = \(\sqrt{(3k)^2 – (2k)^2} = \sqrt{9k^2 – 4k^2} = \sqrt{5k^2} = \sqrt{5}k\)

∴ $\cos C=\frac{\mathrm{ভূমি}}{\mathrm{অতিভুজ}}=\frac{\sqrt{5}k}{3k}=\frac{\sqrt{5}}{3}$

∴ \(\cos C \times cosec C = \frac{\sqrt{5}}{3} \times \frac{3}{2} = \frac{\sqrt{5}}{2}\)

9. নীচের বিবৃতিগুলি সত্য না মিথ্যা তা যুক্তি সহকারে লিখি।

(i) tanA এর মান সর্বদা 1 অপেক্ষা বড়।

উত্তর – মিথ্যা।

সমাধান – tanA = লম্ব / ভূমি

এখন লম্ব < ভূমি হলে tanA<1 হবে সুতরাং বিবৃতিটি মিথ্যা।

(ii) cotA এর মান 1 অপেক্ষা ছোট।

উত্তর – মিথ্যা।

সমাধান –

cotA = ভূমি/লম্ব

এখন ভূমি > লম্ব হলে cotA > 1 হবে সুতরাং বিবৃতিটি মিথ্যা।

(iii) একটি কোণ θ-এর জন্য sinθ = 4/3 হতে পারে।

উত্তর – মিথ্যা।

সমাধান –

sinθ = লম্ব/অতিভুজ = 4/3

একক্ষেত্রে লম্ব 4 একক হলে অতিভুজ 3 একক কিন্তু কোনো একটি সমকোণী ত্রিভুজে লম্ব অপেক্ষা অতিভুজ ছোট হতে পারে না।

∴ sinθ = 4/3 হতে পারে না।

(iv) একটি কোণ α –এর জন্য seca=12/5 হতে পারে না।

উত্তর – মিথ্যা।

সমাধান – secα= অতিভুজ/ভূমি = 12/5

একটি সমকোণী ত্রিভুজের অতিভুজ 12 একক হলে ভূমি 5 একক হওয়া সম্ভব।

সুতরাং বিবৃতিটি মিথ্যা।

(V) একটি কোণ β (Beta) –এর জন্য cosecβ=5/13 হতে পারে।

উত্তর – মিথ্যা।

সমাধান –

cosec β = অতিভুজ/লম্ব = 5/13

অর্থাৎ অতিভুজ 5 একক হলে লম্ব 13 একক যা অসম্ভব কারণ সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য সর্বাধিক।

∴ cosec β =5/13 হতে পারে না।

(vi) একটি কোণ θ-এর জন্য cosθ =3/5 হতে পারে।

উত্তর – সত্য।

সমাধান – cosθ = ভূমি/অতিভুজ = 3/5

∴ ভূমি 3 একক হলে অতিভুজ 5 একক হতে পারে।

সুতরাং cosθ =3/5 হতে পারে।

---

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের ত্রয়োবিংশ অধ্যায়, ‘ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি’ -এর ‘কষে দেখি – 23.1’ বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।

আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।