মাধ্যমিক পরীক্ষা শিক্ষার্থীদের জীবনে একটি গুরুত্বপূর্ণ পর্ব। এই পরীক্ষার ফলাফল ভবিষ্যতের পথ নির্ধারণে গুরুত্বপূর্ণ ভূমিকা পালন করে।
এই আর্টিকেলটিতে, আমরা ২০১৭ সালের মাধ্যমিক গণিত পরীক্ষার প্রশ্নপত্র বিশ্লেষণ করব। শিক্ষার্থীরা এই প্রশ্নপত্রটি পর্যালোচনা করে আগের বছরের পরীক্ষার ধরন, গুরুত্বপূর্ণ বিষয় এবং প্রশ্নের ধরণ সম্পর্কে ধারণা পেতে পারবে।

1. নিম্নলিখিত প্রশ্নগুলির প্রতিটি ক্ষেত্রে সঠিক উত্তরটি নির্বাচিত, করো।
(i) কোনো আসল ও তার বার্ষিক সবৃদ্ধিমূলের অনুপাত 25 : 28 হলে বার্ষিক’ সুদের হার –
(a) 3%
(b) 12%
(c) \(10\frac57\) %
(d) 8%
উত্তর : (b) 12%
উত্তর :
ধরি আসল x টাকা এবং বার্ষিক সুদের হার r%।
সরল সুদ = \(\frac{x\times1\times r}{100}\) টাকা
∴ সবৃদ্ধি মূল = সুদ + আসল
= \(\left(\frac{x\times1\times r}{100}+x\right)\)
প্রশ্নানুসারে,
x : \(\left(\frac{x\times1\times r}{100}+x\right)\) = 25 : 28
বা, x : x\(\left(\frac r{100}+1\right)\) = 25 : 28
বা, 1 : \(\left(\frac r{100}+1\right)\) = 25 : 28
বা, \(\frac1{\left(\frac r{100}+1\right)}=\frac{25}{28}\)
বা, \(\left(\frac r{100}+1\right)\) × 25 = 28
বা, \(\frac r4\) + 25 = 28
বা, \(\frac r4\) = 3
বা, r = 12
∴ বার্ষিক সরল সুদের হার 12%।
(ii) কোন শর্তে ax² + bx + c = 0 দ্বিঘাত সমীকরণটির একটি বীজ শূন্য হবে?
(a) a = 0
(b) b = 0
(c) c = 0
(d) এদের কোনটিই নয়।
উত্তর : (c) c = 0
উত্তর :
ax² + bx + c = 0 দ্বিঘাত সমীকরণের একটি বীজ শূন্য
∴ a.0 + b.0 + c = 0
বা, c = 0
∴ দ্বিঘাত সমীকরণের একটি বীজ শূন্য হওয়ার শর্ত হল c = 0
(iii) দুটি বৃত্ত পরস্পরকে স্পর্শ বা ছেদ না করলে বৃত্তদুটির সাধারণ স্পর্শক সংখ্যা –
(a) 2টি
(b) 1টি
(c) 3টি
(d) 4টি
উত্তর : (d) 4টি
(iv) sinθ = cosθ হলে 2θ-এর মান হবে –
(a) 30°
(b) 60°
(c) 45
(d) 90°
উত্তর : (d) 90°
উত্তর :
sinθ = cosθ
বা, \(\frac{\sin\theta}{\cos\theta}\) = 1
বা, tanθ = 1 = tan45°
বা, θ = 45°
∴ 2θ = 2 × 45° = 90°
(v) একটি শঙ্কুর ভূমির ব্যাসার্ধের দৈর্ঘ্য এবং উচ্চতা প্রত্যেকটি দ্বিগুণ হলে শঙ্কুটির আয়তন হয় পূর্বের শঙ্কুর আয়তনের –
(a) 3 গুণ
(b) 4 গুণ
(c) 6 গুণ
(d) 8 গুণ
উত্তর : (d) 8 গুণ
ধরি, শঙ্কুর ব্যাসার্ধ r একক এবং উচ্চতা h একক।
∴ শঙ্কুর আয়তন = \(\frac13\mathrm{πr}^2\mathrm h\) ঘনএকক
আবার শঙ্কুটির ব্যাসার্ধ এবং উচ্চতা প্রত্যেকে দ্বিগুন হলে পরিবর্তিত ব্যাসার্ধ হবে 2r একক এবং পরিবর্তিত উচ্চতা হবে 2h একক
এখন শঙ্কুটির আয়তন = \(\frac13\mathrm\pi\left(2\mathrm r\right)^2\left(2\mathrm h\right)\) ঘনএকক
= 8 × \(\left(\frac13\mathrm{πr}^2\mathrm h\right)\) ঘনএকক
∴ এখন শঙ্কুটির আয়তন পূর্বের শঙ্কুর আয়তনের তুলনায় 8 গুন বৃদ্ধি পাবে।
(vi) 2, 8, 2, 3, 8, 3, 9, 5, 6 সংখ্যাগুলির মধ্যমা –
(a) 8
(b) 6.5
(c) 5.5
(d) 5
উত্তর : (d) 5
উত্তর :
2, 8, 2, 3, 8, 5, 9, 5, 6 সংখ্যাগুলিকে ছোট থেকে বড় হিসেবে সাজিয়ে পাই,
2, 2, 3, 5, 5, 6, 8, 8, 9
এক্ষেত্রে n = 9 (বিজোড় সংখ্যা)
∴ নির্ণেয় মধ্যমা
= \(\frac{n+1}2\) তম মান
= \(\frac{9+1}2\) তম মান
= 5 তম মান
= 5
2. শূন্যস্থান পূরণ কর (যে কোনো পাঁচটি)
(i) কোনো মূলধনের বার্ষিক শতকরা একই সুদের হারে _______ বছরের সরলসুদ ও চক্রবৃদ্ধি সুদের পরিমাণ সমান।
উত্তর : এক।
(ii) ax2 + bx + c = 0 (a ≠ 0) দ্বিঘাত সমীকরণের b2 = 4ac হলে ধীজদ্বয় বাস্তব ও _______ হবে।
উত্তর : সমান।
(iii) দুটি ত্রিভুজের বাহুগুলির দৈর্ঘ্যের পরিমাপ সমানুপাতে থাকলে ত্রিভুজ দুটি _______ হবে।
উত্তর : সদৃশ।
(iv) \(\cos^2\theta-\sin^2\theta=\frac1x\) (x > 1), হলে \(\cos^4\theta-\sin^4\theta\) _______।
উত্তর : \(\frac1x\)
উত্তর :
\(\cos^4\theta-\sin^4\theta=\left(\cos^2\theta+sin^2\theta\right)\left(\cos^2\theta-\sin^2\theta\right)=\frac1x\\\)(v) একটি নিরেট অর্ধগোলকের সমতল সংখ্যা _______।
উত্তর : একটি।
(vi) \(x_1,x_2,x_3,….,x_n\)এই n সংখ্যক সংখ্যার গড় \(\overline x\) হলে \(Kx_1,Kx_2,Kx_3,….,Kx_n\) এর গড়) _______ (K≠ 0)
উত্তর :
∴ \(x_1,x_2,x_3,….,x_n\)এই n সংখ্যক সংখ্যার গড় \(\overline x\)
\(\frac{x_1,x_2,x_3,….,x_n}n=\overline x\\\)∴ Kx1, Kx2, Kx3,….,Kxn এর গড়
\(\frac{Kx_1,Kx_2,Kx_3,….,Kx_n}n\)= \(\frac{K\left(x_1,x_2,x_3,….,x_n\right)}n=K\overline x\)
3. সত্য বা ‘মিথ্যা লেখ (যে কোনো পাঁচটি)
(i) A 10,000 টাকা দিয়ে ব্যবসা শুরু করার 6 মাস পরে B 20,000 টাকা দিল। বৎসরান্তে তাদের লভ্যাংশের পরিমাণ সমান হবে।
উত্তর : সত্য।
উত্তর :
A ও B এর মূলধনের অনুপাত
= (10000 × 12) : (20000 × 6)
= 120000 : 120000
= 1 : 1
এখন যেহেতু মূলধনের অনুপাত = লভ্যাংশের অনুপাত
∴ A ও B এর লভ্যাংশের অনুপাতও হবে 1 : 1 । সুতরাং A ও B এর লভ্যাংশের পরিমাণ সমান হবে।
(ii) x = 2 + \(2\sqrt3\) হলে x + \(\frac1x\)এর মান হবে \(2\sqrt3\)
উত্তর : মিথ্যা।
উত্তর :
x = 2 + \(\sqrt3\)
বা, \(\frac1x=\frac1{2+\sqrt3}\)
বা, \(\frac1x=\frac1{2+\sqrt3}\times\frac{2-\sqrt3}{2-\sqrt3}\)
বা, \(\frac1x=\frac{2-\sqrt3}{\left(2\right)^2-\left(\sqrt3\right)^2}\)
বা, \(\frac1x=\frac{2-\sqrt3}{4-3}\)
বা, \(\frac1x=\left(2-\sqrt3\right)\)
∴ x + \(\frac1x\) = \(2+\sqrt3+2-\sqrt3\)
= 4
(iii) 7 সেমি ও ও সেমি ব্যাসার্ধবিশিষ্ট দুটি বৃত্ত বহিঃস্পর্শ করলে তাদের কেন্দ্রদ্বয়ের মধ্যে দূরত্ব 4 সেমি হবে।
উত্তর : মিথ্যা।
(iv) 0° < θ < 90° হলে sinθ > sin2θ হবে।
উত্তর : সত্য।
(v) একটি অর্ধগোলকের সমগ্রতলের ক্ষেত্রফল 36π বর্গ সেমি হলে উহার ব্যাসার্ধ 3 সেমি হবে।
উত্তর : মিথ্যা।
উত্তর :
একটি অর্ধগোলোকের সমগ্রতলের ক্ষেত্রফল 36π
∴ 3πr² = 36π
বা, r² = 12
বা, r = \(\sqrt{12}\) সেমি।
(vi) ওজাইভ দুটির ছেদবিন্দু থেকে x অক্ষের উপর লম্ব টানলে, x অক্ষ ও লম্বের ছেদবিন্দুর ভুজ়ই হল মধ্যমা।
উত্তর : মিথ্যা।
4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাও (যে কোনো দশটি)
(i) r% হার চক্রবৃদ্ধি সুদে কোনো মূলধন 8 বছরে দ্বিগুণ হলে চারগুণ হবে কত বছরে?
উত্তর :
ধরি, মূলধনের পরিমাণ x টাকা।
এখন x টাকা r% চক্রবৃদ্ধি হার সুদে 8 বছরে দ্বিগুন হয়।
∴ \(x\left(1+\frac r{100}\right)^8\) = 2x
বা, \(\left(1+\frac r{100}\right)^8\) = 2_______(i)
ধরি, x টাকা n বছরে 4 গুন হবে।
∴ \(x\left(1+\frac r{100}\right)^n\) = 4x
বা, \(\left(1+\frac r{100}\right)^n\) = 4
বা, \(\left(1+\frac r{100}\right)^n=\left(2\right)^2\)
বা, \(\left(1+\frac r{100}\right)^n=\left\{\left(1\times\frac r{100}\right)^8\right\}^2\) [(i) নং সমীকরণ থেকে পাই]
বা, \(\left(1+\frac r{100}\right)^n=\left(1\times\frac r{100}\right)^{16}\)
বা, n = 16
∴ 16 বছরে ওই মূলধন 4 গুন হবে।
(ii) কোনো এক ব্যবসায় A-এর মূলধন B-এর মূলধনের দেড়গুণ। ওই ব্যবসায় বৎসরান্তে B 1,500 টাকা লভ্যাংশ পেলে, A কত টাকা পাবে?
উত্তর :
ধরি, B এর মূলধন x টাকা।
∴ A এর মূলধন \(1\frac12x\) টাকা।
∴ A ও B এর মূলধনের অনুপাত \(1\frac12x:x\)
= \(\frac32:1\)
= 3 : 2
ধরি, A এর লভ্যাংশ y টাকা।
যেহেতু মূলধনের অনুপাত এবং লভ্যাংশের অনুপাত সমান
∴ 3 : 2 = y : 1500
বা, \(\frac32=\frac y{1500}\)
বা, 2y = 4500
বা, y = \(\frac{4500}2\)
বা, y = 2250
∴ A 2250 টাকা লভ্যাংশ পাবে।
(iii) সমাধান না করে ‘p’ এর যে সকল মানের জন্য x² + (p – 3) x + p = 0 সমীকরণের বাস্তব ও সমান বীজ আছে তা নির্ণয় করো।
উত্তর :
প্রদত্ত দ্বিঘাত সমীকরণকে ax2 + bx + c =0 সমীকরণের সাথে তুলনা করে পাই, a = 1, b = (p – 3) এবং c = p
যেহেতু দ্বিঘাত সমীকরণের বীজদ্বয় বাস্তব ও সমান
∴ b2 – 4ac = 0
বা, (p – 3)2 – 4(1)(p) = 0
বা, p2 – 6p + 9 – 4p = 0
বা, p2 – 10p + 9 = 0
বা, p2 – 9p – p + 9 = 0
বা, p(p – 9) – 1(p – 9) = 0
বা, (p – 9)(p – 1) = 0
দুটি রাশির গুনফল শূন্য
∴ হয়, (p – 9) = 0
বা, p = 9
অথবা, (p – 1) = 0
বা, p = 1
∴ p = 1 এবং p = 9
∴ P এর মান 1 বা 9 হলে প্রদত্ত দ্বিঘাত সমীকরণের বীজদ্বয় বাস্তব ও সমান হবে।
(iv) x ∝ yz এবং y ∝ zx হলে, দেখাও যে, z (≠ 0) একটি ধ্রুবক।
উত্তর :
x ∝ yz
∴ x = Ayz [ A একটি অশূন্য ভেদ ধ্রুবক]
আবার, x ∝ zy
∴ y = Bzx [ B একটি অশূন্য ভেদ ধ্রুবক]
∴ y = Bz (Ayz) [যেহেতু x = Ayz]
বা, y = ABz2y
বা, ABz2 = 1
বা, \(z=\frac1{\sqrt{AB}}\) = ধ্রুবক
∴ z = ধ্রুবক (প্রমাণিত)
(v) একটি সদৃশ ত্রিভুজের পরিসীমা যথাক্রমে 20 সেমি ও 16 সেমি, প্রথম ত্রিভুজের একটি বাহুর দৈর্ঘ্য 9 সেমি হলে, দ্বিতীয় ত্রিভুজের অনুরূপ বাহুর দৈর্ঘ্য কত?
উত্তর :
ধরা যাক, ত্রিভুজ ABC এবং ত্রিভুজ DEF পরস্পর সদৃশ।
∴ \(\frac{AB}{DE}=\frac{BC}{BF}=\frac{AC}{DF}=k\) [k ≠ 0 একটি আনুপাতিক ধ্রুবক]_______(i)
∴ AB = kDE, BC = kEF এবং AC = kDF
∴ AB + BC + AC = k(DE + EF + DF)
বা, 20 = k(16) [যেহেতু ত্রিভুজ ABC এবং ত্রিভুজ DEF এর পরিসীমা যথাক্রমে 20 সেমি. এবং 16 সেমি.]
বা, k = \(\frac{20}{16}\)
বা, k = \(\frac{5}{4}\)
(i) নং সমীকরণ থেকে পাই,
আবার, \(\frac{BC}{EF}\) = k
বা, \(\frac9{EF}=\frac54\) [ধরি, BC = 9 সেমি. এবং k = \(\frac54\)]
বা, 5EF = 36
বা, EF = \(\frac{36}5\)
বা, EF = 7.2
∴ দ্বিতীয় ত্রিভুজের অনুরূপ বাহুর দৈর্ঘ্য 7.2 সেমি.।
(vi) ΔABC-এর ∠ABC = 90°, AB = 5 সেমি, BC = 12 সেমি. হলে ওই ত্রিভুজটির পরিব্যাসার্ধের দৈর্ঘ্য কত?
উত্তর :
ত্রিভুজ ABC-এর অতিভুজ AC = \(\sqrt{{(AB)}^2+\left(BC\right)^2}\)
ত্রিভুজ ABC-এর অতিভুজ AC = \(\sqrt{{(AB)}^2+\left(BC\right)^2}\)
= \(\sqrt{{(5)}^2+\left(12\right)^2}\)
= \(\sqrt{{(5)}^2+\left(12\right)^2}\)
= \(\sqrt{25+144}\)
= \(\sqrt{169}\)
= 13
∴ ওই ত্রিভুজটির পরিব্যাসার্ধের দৈর্ঘ্য = \(\frac{13}2\) সেমি.
= 6.5 সেমি.।
(vii) ABC ত্রিভুজের AB = (2a – 1) সেমি, AC = \(2\sqrt{2a}\) সেমি এবং BC = (2a + 1) সেমি হলে ∠BAC এর মান লেখো।
উত্তর :
AB2 + AC2
= \(\left(2a-1\right)^2+\left\{2\sqrt{\left(2a\right)}\right\}^2\)
= 4a2 – 4a + 1 + 8a
= 4a2 + 4a + 1
= (2a + 1)2
= BC2
∴ AB2 + AC2 = BC2 [পিথাগোরাসের উপপাদ্য]
∴ ABC সমকোণী ত্রিভুজ যার A সমকোণ।
∴ ∠BAC = 90°
(viii) x = asecθ, y = btanθ হলে এবং এর θ বর্জিত সম্পর্ক নির্ণয় করো।
উত্তর :
x = asecθ
∴ \(\frac xa=sec\theta\)
y = btanθ
∴ \(\frac yb=sec\theta\)
যেহেতু, sec2θ – tan2θ = 1
∴ \(\left(\frac xa\right)^2-\left(\frac yb\right)^2=1\)
বা, \(\frac{x^2}{a^2}-\frac y{b^2}^2=1\)
∴ বর্জিত সম্পর্কটি হল = \(\frac{x^2}{a^2}-\frac y{b^2}^2=1\)
(ix) tan(θ + 15°) = \(\sqrt3\) হলে sinθ + cosθ-এর মান নির্ণয় করো।
উত্তর :
tan(θ + 15°) = \(\sqrt3\)
বা, tan(θ + 15°) = tan60°
বা, (θ + 15°) = 60°
বা, θ = 60° – 15°
বা, θ = 45°
∴ sinθ + cosθ
= sin45° + cos45°
= \(\frac1{\sqrt2}+\frac1{\sqrt2}\)
= \(\frac2{\sqrt2}\)
= \(\sqrt2\)
∴ sinθ + cosθ = \(\sqrt2\)
(x) একটি গোলকের ব্যাস অপর একটি গোলকের ব্যাসের দ্বিগুণ। যদি বড় গোলকটির সমগ্রতলের ক্ষেত্রফলের সাংখ্যমান ছোট গোলকটির আয়তনের সাংখ্যমানের সমান হয়, তবে ছোট গোলকটির ব্যাসার্ধ কত?
উত্তর :
ধরি, বড় গোলোকটির ব্যাস 2R একক এবং ছোট গোলোকটির ব্যাস 2r একক।
∴ 2R = 2(2r)
বা, R = 2r
বড় গোলোকের সমগ্রতলের ক্ষেত্রফল = 4πR2 বর্গ একক।
ছোট গোলোকের আয়তন \(\frac43\pi r^3\) ঘন একক।
শর্তানুসারে,
4π\(R^2=\frac43\pi r^3\)
বা, 4π\(\left(2r\right)^2=\frac43\pi r^3\)
বা, 16π\(r^2=\frac43\pi r^3\)
বা, 48πr2 = 4πr3
বা, \(\frac{r^3}{r^2}=\frac{48}4\)
বা, r =12
∴ ছোট গোলোকের ব্যাসার্ধের দৈর্ঘ্য 12 একক।
(xi) একটি আয়তঘনকের তলসংখ্যা x, ধার সংখ্যা y, শীর্ষবিন্দুর সংখ্যা z এবং কর্ণের সংখ্যা P হলে x – y + z + P এর মান কত?
উত্তর :
একটি আয়তঘনকের তলসংখ্যা x, ধার সংখ্যা y, শীর্ষবিন্দুর সংখ্যা z এবং কর্ণের সংখ্যা P।
∴ x = 6, y = 8, z = 4 এবং p = 4
∴ x – y + z + p = 6 – 8 + 4 + 4
= 6
(xii) 11, 12, 14, x – 2, x + 4, x + 9, 32, 38, 47 রাশিগুলি ঊর্ধ্বক্রমানুসারে সাজানো এবং তাদের মধ্যমা 24 হলে x এর মান নির্ণয় কর।
উত্তর :
রাশিগুলির সংখ্যা (n) = 9
∴ নির্ণেয় মধ্যমা = \(\frac{n+1}2\) তম মান
= \(\frac{9+1}2\) তম মান
= 5 তম মান
= x + 4
∴ x + 4 = 24
বা, x = 24 – 4
বা, x = 20
∴ x = 20
5. যে কোনো একটি প্রশ্নের উত্তর দাও।
(i) বার্ষিক 4% হার সুদে কত টাকার 2 বছরের সরল সুদ ও চক্রবৃদ্ধি সুদের অন্তর 80 টাকা হবে?
উত্তর :
ধরি, বার্ষিক 4% হার সুদে x টাকার 2 বছরের সরল সুদ ও চক্রবৃদ্ধি সুদের অন্তর 80 টাকা হবে।
বার্ষিক 4% হার সুদে x টাকার 2 বছরের চক্রবৃদ্ধি সুদ
= \(\left\{x\left(1+\frac4{100}\right)^2-x\right\}\) টাকা
= \(x\left\{\left(1+\frac4{100}\right)^2-1\right\}\) টাকা
= \(x\left(1+\frac4{100}+1\right)\left(1+\frac4{100}-1\right)\) টাকা
= \(x\times\left(2+\frac4{100}\right)\;\times\frac4{100}\) টাকা
= \(x\times\left(2+\frac1{25}\right)\;\times\left(\frac1{25}\right) \) টাকা
= \(x\times\frac{51}{25}\;\times\frac1{25}\) টাকা
= \(\frac{51x}{625}\) টাকা
বার্ষিক 4% হার সুদে x টাকার 2 বছরের সরল সুদ
= \(\frac{x\times2\times4}{100}\) টাকা
= \(\frac{2x}{25}\) টাকা
শর্তানুসারে,
\(\frac{51x}{625}-\frac{2x}{25}\) = 80
বা, \(\frac{51x-50x}{625}\)
বা, x = 80 × 625
বা, x = 50000
∴ আসল 50000 টাকা
∴ বার্ষিক 4% হার সুদে 50000 টাকার 2 বছরের সরল সুদ ও চক্রবৃদ্ধি সুদের অন্তর 50000 টাকা।
(ii) A, B, C যৌথভাবে 1,90,000 টাকা দিয়ে একটি ব্যবসা শুরু করল। A, B এর থেকে 20,000 টাকা বেশি এবং B, C এর থেকে 20,000 টাকা বেশি দিল। লাভের পরিমাণ 10,800 টাকা তাদের মধ্যে ভাগ করে দাও।
উত্তর :
ধরি, C এর মূলধনের পরিমাণ x টাকা
∴ B এর মূলধনের পরিমাণ = (x + 20000) টাকা এবং A এর মূলধনের পরিমাণ = (x + 20000 + 20000) টাকা = (x + 40000) টাকা।
∴ x + x + 20000 + x + 40000 = 180000
বা, 3x + 60000 = 180000
বা, 3x = 180000 – 60000
বা, 3x = 120000
বা, x = \(\frac{120000}3\)
বা, x = 40000
∴ A, B ও C এর মূলধনের অনুপাত
= (40000 + 40000) : (40000 + 20000) : 40000
= 80000 : 60000 : 40000
= 4 : 3 : 2
∴ A এর লভ্যাংশ = \(\frac4{4+3+2}\) × 10800 টাকা
= \(\frac49\) × 10800 টাকা
= 4800 টাকা
∴ B এর লভ্যাংশ = \(\frac3{4+3+2}\) × 10800 টাকা
= \(\frac39\) × 10800 টাকা
= 3600 টাকা
∴ C এর লভ্যাংশ = \(\frac2{4+3+2}\) × 10800 টাকা
= \(\frac29\) × 10800 টাকা
= 2400 টাকা
∴ A এর লাভের পরিমাণ 4800 টাকা, B এর লাভের পরিমাণ 3600 টাকা এবং C এর লাভের পরিমাণ 2400 টাকা।
6. যে কোনো একটি সমাধান কর
(i) \(\frac1{a+b+x}=\frac1a+\frac1b+\frac1x\), [x ≠ 0, -(a + b)]
উত্তর :
\(\frac1{a+b+x}=\frac1a+\frac1b+\frac1x\\\)বা, \(\frac1{a+b+x}-\frac1x=\frac1a+\frac1b\)
বা, \(\frac{x-\left(a+b+x\right)}{x\left(a+b+x\right)}=\frac{b+a}{ab}\)
বা, \(\frac{x-a-b-x}{x\left(a+b+x\right)}=\frac{b+a}{ab}\)
বা, \(\frac{-\left(a+b\right)}{x\left(a+b+x\right)}=\frac{a+b}{ab}\)
বা, \(\frac{-1}{x\left(a+b+x\right)}=\frac1{ab}\)
বা, -ab = x(a + b + x)
বা, x(a + b + x) + ab = 0
বা, ax + bx + x2 + ab = 0
বা, x2 + ax + bx + ab = 0
বা, x(x + a) + b(x + b) = 0
বা, (x + a)(x + b) = 0
দুটি রাশির গুনফল শূন্য
∴ হয় (x + a)=0
বা, x = -a
অথবা (x + b)=0
বা, x = -b
∴ নির্ণেয় সমাধান x = -a এবং x = -b
(ii) একটি অখণ্ড ধনাত্মক সংখ্যার পাঁচগুণ, তার বর্গের দ্বিগুণ অপেক্ষা 3 কম হলে সংখ্যাটি কত?
উত্তর :
ধরি, ধনাত্মক অখণ্ড সংখ্যাটি হল x।
শর্তানুসারে,
5x = 2x2 – 3
বা, 2x2 – 5x – 3 = 0
বা, 2x2 – (6 – 1)x – 3 = 0
বা, 2x2 – 6x + x – 3 = 0
বা, 2x(x – 3) + 1(x – 3) = 0
বা, (x – 3) (2x + 1) = 0
দুটি রাশির গুনফল শূন্য
∴ (x – 3) = 0
বা, x = 3
অথবা, (2x + 1) = 0
বা, 2x = -1
বা, x = –\(\frac12\)
যেহেতু সংখ্যাটি ধনাত্মক অখণ্ড সংখ্যা
∴ x = 3
সুতরাং সংখ্যাটি হল 3।
7. যে কোনো একটি প্রশ্নের উত্তর দাও।
\(\frac1{\sqrt2+\sqrt3}-\frac{\sqrt3+1}{2+\sqrt3}+\frac{\sqrt2+1}{3+2\sqrt2}\)
= \(\frac1{\sqrt2+\sqrt3}-\frac{\sqrt3+1}{2+\sqrt3}+\frac{\sqrt2+1}{3+2\sqrt2}\)
হরের করণী নিরসন করে পাই,
= \(\frac1{\sqrt2+\sqrt3}\times\frac{\sqrt2-\sqrt3}{\sqrt2-\sqrt3}-\frac{\sqrt3+1}{2+\sqrt3}\times\frac{2-\sqrt3}{2-\sqrt3}+\frac{\sqrt2+1}{3+2\sqrt2}\times\frac{3-2\sqrt2}{3-2\sqrt2}\)
= \(\frac{\sqrt2-\sqrt3}{\left\{\left(\sqrt2\right)^2-\left(\sqrt3\right)^2\right\}}-\frac{\left(\sqrt3+1\right)\left(2-\sqrt3\right)}{\left\{\left(2\right)^2-\left(\sqrt3\right)^2\right\}}+\frac{\left(\sqrt2+1\right)\left(3-2\sqrt2\right)}{\left\{\left(3\right)^2-\left(2\sqrt2\right)^2\right\}}\)
= \(\frac{\sqrt2-\sqrt3}{\left(2-3\right)}-\frac{\left(\sqrt3+1\right)\left(2-\sqrt3\right)}{\left(4-3\right)}+\frac{\left(\sqrt2+1\right)\left(3-2\sqrt2\right)}{\left(9-8\right)}\)
= \(\frac{\sqrt2-\sqrt3}{-1}-\frac{\left(\sqrt3+1\right)\left(2-\sqrt3\right)}1+\frac{\left(\sqrt2+1\right)\left(3-2\sqrt2\right)}1\)
= \(\sqrt3-\sqrt2-\left(2\sqrt3+2-3-\sqrt3\right)+\left(3\sqrt2+3-4-2\sqrt2\right)\)
= \(\sqrt3-\sqrt2-\left(\sqrt3-1\right)+\left(\sqrt2-1\right)\)
= \(\sqrt3-\sqrt2-\sqrt3+1+\sqrt2-1\)
= 0
ii) একটি হোস্টেলের ব্যয় আংশিক ধ্রুবক ও আংশিক ঐ হোস্টেলের আবাসিকদের সংখ্যার সঙ্গে সরলভেদে আছে। আবাসিক সংখ্যা 120 হলে ব্যয়। 2000 টাকা এবং আবাসিক সংখ্যা 100 হলে ব্যয় 1700 টাকা হয়। ব্যয় 1880 টাকা হলে হোস্টেলের আবাসিক সংখ্যা কত হবে?
উত্তর :
ধরি, হোস্টেলের আবাসিকদের সংখ্যা x জন এবং ধ্রুবক অংশের পরিমাণ K টাকা এবং ব্যায়ের বাকি অংশ y টাকা এবং মোট খরচ A টাকা।
এখন যেহেতু আংশিক ব্যায় হোস্টেলের আবাসিকদের সংখ্যার সঙ্গে সরলভেদে আছে
∴ y ∝ x
বা, y = px [ যেখানে p একটি অশূন্য ভেদ ধ্রুবক ]
∴ মোট খরচ A = K + px_______(i)
এখন x = 120 হলে A = 2000 টাকা।
.∴ 2000 = K + 120p_______(ii)
আবার, x = 100 হলে A = 1700 টাকা
∴ 1700 = K + 100p_______(iii)
(ii) ও (iii) নং সমীকরণ বিয়োগ করে পাই,
20p = 300
বা, p = \(\frac{300}{20}\)
বা, p = 15
P এর প্রাপ্ত মান (ii) নং সমীকরনে বসিয়ে পাই,
K + 120(15) = 2000
বা, K + 1800 = 2000
বা, K = 2000 – 1800
বা, K = 200
∴ (i) নং সমীকরন থেকে পাই,
A = 200 + 15x
এখন মোট খরচ A = 1880 টাকা হলে,
1880 = 200 + 15x
বা, 15x = 1680
বা, x = \(\frac{1680}{15}\)
বা, x = 112
∴ নির্ণেয় আবাসিক সংখ্যা 112 জন।
8. যে কোনো একটি প্রশ্নের উত্তর দাও।
(i) \(\frac a{b+c}=\frac b{c+a}=\frac c{a+b}\) যদি হয়, তবে প্রমাণ কর যে, প্রত্যেকটি অনুপাতের মান \(\frac12\) হয় অথবা -1.
∴ \(\frac a{b+c}=\frac b{c+a}\)
বা, a(c + a) = b(b + c)
বা, ac + a2 = b2 + bc
বা, a2 – b2 + ac – bc = 0
বা, (a + b)(a – b) + c(a – b) = 0
বা, (a – b)(a + b + c) = 0
∴ হয় (a + b + c) = 0
অথবা (a – b) = 0
বা, a = b_______(i)
আবার, \(\frac b{c+a}=\frac c{a+b}\)
বা, b(a + b) = c(c + a)
বা, ba + b2 = c2 + ca
বা, b2 – c2 + ba – ca = 0
বা, (b + c)(b – c) + a(b – c) = 0
বা, (b – a)(b + c + a) = 0
∴ হয় (a + b + c) = 0
অথবা (b – c) = 0
বা, b = c_______(ii)
(i) ও (ii) নং সমীকরণ থেকে পাই, a = b =c
এখন, \(\frac a{\left(b+c\right)}=\frac a{\left(a+a\right)}=\frac a{2a}=\frac12\)
এবং, \(\frac b{\left(c+a\right)}=\frac b{\left(b+b\right)}=\frac b{2b}=\frac12\)
এবং, \(\frac c{\left(a+b\right)}=\frac c{\left(c+c\right)}=\frac c{2c}=\frac12\)
∴ \(\frac a{b+c}=\frac b{c+a}=\frac c{a+b}=\frac12\)
আবার, (a + b + c) = 0 হলে,
(a + b) = -c, (b + c) = -a এবং (c + a) = -b হয়।
∴ \(\frac a{b+c}=\frac b{c+a}=\frac c{a+b}=\frac12\)
সুতরাং প্রতিটি অনুপাতের মান \(\frac12\) অথবা -1 (প্রমাণিত)।
(ii) যদি (b + c – a)x = (c + a – b)y = (a + b – c)z = 2, হয়, তবে দেখাও যে \(\left(\frac1x+\frac1y\right)\left(\frac1y+\frac1z\right)\left(\frac1z+\frac1x\right)=abc\).
উত্তর :
(b + c – a)x = (c + a – b)y = (a + b – c)z = 2
∴ (b + c – a)x = 2
বা, (b + c – a) = \(\frac2x\)
বা, \(\frac{b+c-a}2=\frac1x\)
এবং (c + a – b)y = 2
বা, (c + a – b) = \(\frac2y\)
বা, \(\frac{c+a-b}2=\frac1y\)
এবং (a + b – c)z = 2
বা, (a + b – c) = \(\frac2z\)
বা, \(\frac{a+b-c}2=\frac1z\)
∴ \(\left(\frac1x+\frac1y\right)\left(\frac1y+\frac1z\right)\left(\frac1z+\frac1x\right)\)
= \(\left(\frac{b+c-a}2+\frac{c+a-b}2\right)\left(\frac{c+a-b}2+\frac{a+b-c}2\right)\left(\frac{a+b-c}2+\frac{b+c-a}2\right)\)
= \(\left(\frac{b+c-a+c+a-b}2\right)\left(\frac{c+a-b+a+b-c}2\right)\left(\frac{a+b-c+b+c-a}2\right)\)
= \(\left(\frac{2c}2\right)\left(\frac{2a}2\right)\left(\frac{2b}2\right)\)
= abc (প্রমাণিত)
9. যে কোনো একটি প্রশ্নের উত্তর দাও।
(i) যে কোনো ত্রিভুজের একটি বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান হলে প্রমাণ কর প্রথম বাহুর বিপরীত কোণটি সমকোণ হবে।
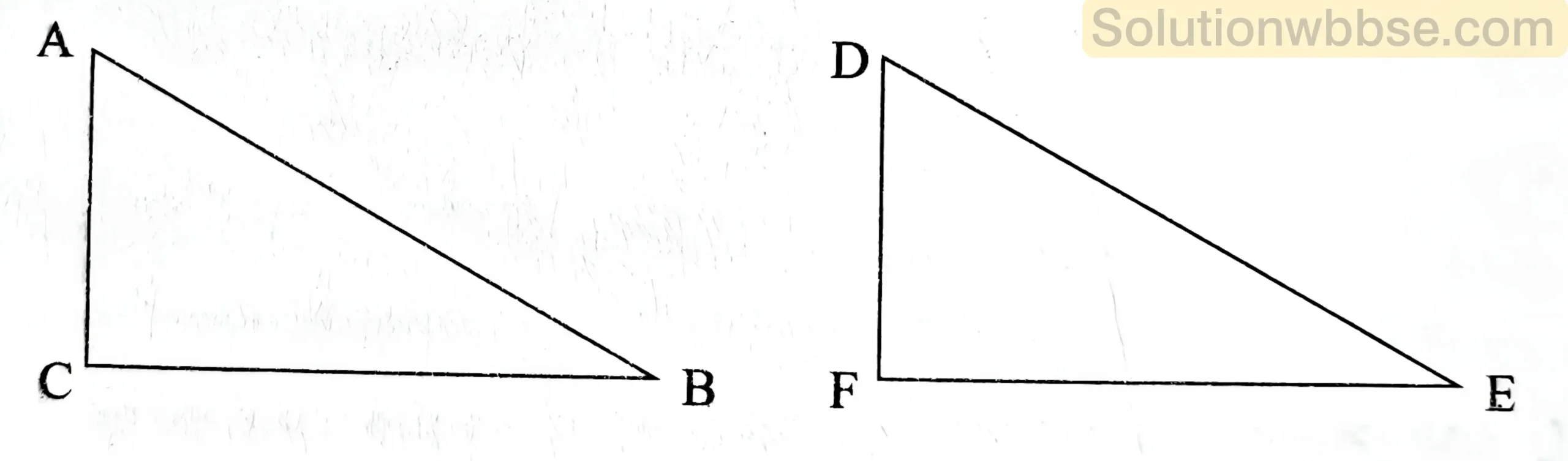
প্রদত্ত – ΔABC-এর AB বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল BC ও AC বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান। অর্থাৎ, AB2 = AC2 + BC2
প্রমাণ করতে হবে – ∠ACB = 1 সমকোণ
অঙ্কন – CB-এর সমান করে FE সরলরেখাংশ অঙ্কন করলাম। FE বাহুর উপর F বিন্দুতে লম্ব অঙ্কন করলাম এবং সেই লম্ব থেকে CA বাহুর সমান করে FD অংশ কেটে নিলাম এবং D ও E বিন্দুদ্বয় যোগ করলাম।
প্রমাণ – AB2 = BC2 + AC2 [প্রদত্ত]
= EF2 + DF2 [∵ অঙ্কনানুসারে, EF = BC এবং AC = DF]
= DE2 [ ∵ ∠DFE = 1 সমকোণ]
∴ AB = DE
এখন ΔABC ও ΔDEF-তে, AB = DE, BC = EF এবং AC = DF
∴ ΔABC ≅ ΔDEF (S-S-S সর্বসমতার শর্তানুসারে)
∴ ∠ACB = ∠DFE = 1 সমকোণ [∵ DF ⊥ EF অঙ্কনানুসারে]
∴ ∠ACB = 1 সমকোণ (প্রমাণিত)
(ii) কোনো বৃত্তের বহিঃস্থ কোন বিন্দু থেকে যে দুটি স্পর্শক অঙ্কন করা যায় তাদের স্পর্শবিন্দু দুটির সঙ্গে বহিঃস্থ বিন্দুর সংযোগক সরলরেখাংশ দুটির দৈর্ঘ্য সমান।
প্রদত্ত – O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু P থেকে PA ও PB দুটি স্পর্শক যাদের স্পর্শবিন্দু যথাক্রমে A ও B, O, A; O, B; O, P যুক্ত করায় PA ও PB সরলরেখাংশ দুটি কেন্দ্রে যথাক্রমে ∠POA ও ∠POB দুটি কোণ উৎপন্ন করেছে।
প্রমাণ করতে হবে – (i) PA = PB (ii) ∠POA = ∠PОВ
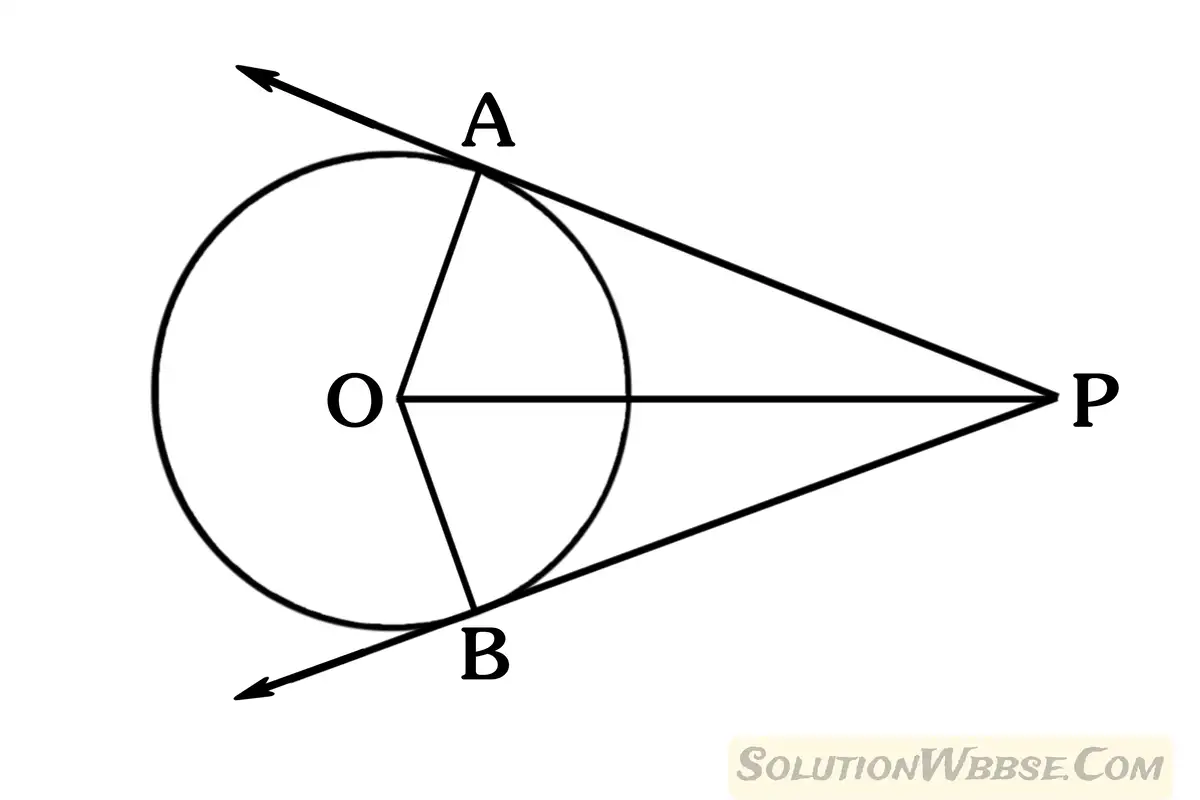
প্রমাণ – PA ও PB স্পর্শক এবং OA ও OB স্পর্শবিন্দুগামী ব্যাসার্ধ।
∴ OA ⊥ PA এবং OB ⊥ PB
POA ও POB সমকোণী ত্রিভুজদ্বয়ের মধ্যে, ∠OAP = ∠OBP (প্রত্যেকে 1 সমকোণ) অতিভুজ OP সাধারণ বাহু এবং OA = OB (একই বৃত্তের ব্যাসার্ধ)
ΔΡΑΟ ≅ ΔΡΒΟ [সর্বসমতার R-H-S শর্তানুসারে]
∴ PA = PB (সর্বসম ত্রিভুজের অনুরূপ বাহু)_______ (i) প্রমাণিত
এবং ∠POA = ∠POB (সর্বসম ত্রিভুজের অনুরূপ কোণ)_______ (ii) প্রমাণিত
10. যে কোনো একটি প্রশ্নের উত্তর দাও।
(i) প্রমাণ কর যে, কোনো চতুর্ভুজের কোণ চারটির সমদ্বিখণ্ডকগুলি পরস্পর মিলিত হয়ে যে চতুর্ভুজ গঠন করে, সেটি বৃত্তঃস্থ চতুর্ভুজ।
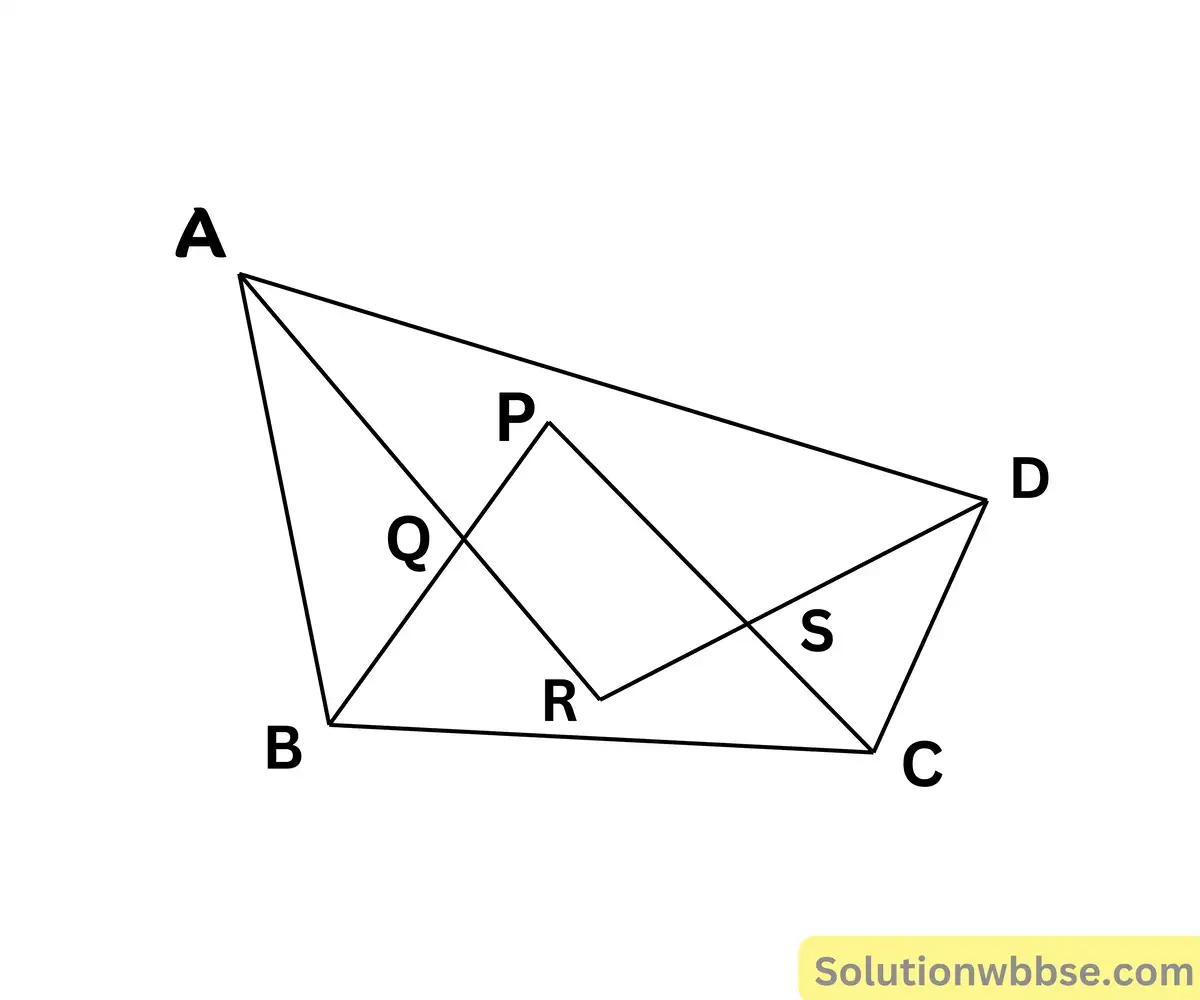
প্রদত্ত – ABCD একটি চতুর্ভুজের AR, BP,CP ও DR যথাক্রমে ∠A, ∠B, ∠C ও ∠D এর সমদ্বিখন্ডক পরস্পর মিলিত হয়ে PQRS চতুর্ভুজ উৎপন্ন করেছে।
প্রমাণ করতে হবে যে – PQRS একটি বৃত্তস্থ চতুর্ভুজ।
প্রমান – ΔARD এর, ∠ARD + ∠RDA + ∠DAR = 180°
বা, ∠ARD + \(\frac{\angle A}2+\frac{\angle D}2\) = 180°_______(i)
আবার, ΔBPC-এর, ∠BPC + ∠PCB + ∠CBP = 180°
বা, ∠BPC + \(\frac{\angle C}2+\frac{\angle B}2\) = 180°_______(ii)
(i) ও (ii) যোগ করে পাই,
∠ARD + \(\frac{\angle A}2+\frac{\angle D}2\) + ∠BPC + \(\frac{\angle C}2+\frac{\angle B}2\) = 180° + 180°
∠ARD + ∠BPC + \(\frac12\)(∠A + ∠B + ∠C + ∠D) = 360°
বা, ∠ARD + ∠BPC
= 360° – 180°
= 180°
∴ ∠QRS + ∠QPS = 180°
∴ PQRS চতুর্ভুজের একজোড়া বিপরীত কোণ সম্পূরক
∴ PQRS একটি বৃত্তস্থ চতুর্ভুজ (প্রমাণিত)।
(ii) ∆ABC-এর পরিকেন্দ্র O এবং OD ⊥ BC; প্রমাণ করো যে, ∠BOD = ∠BAC
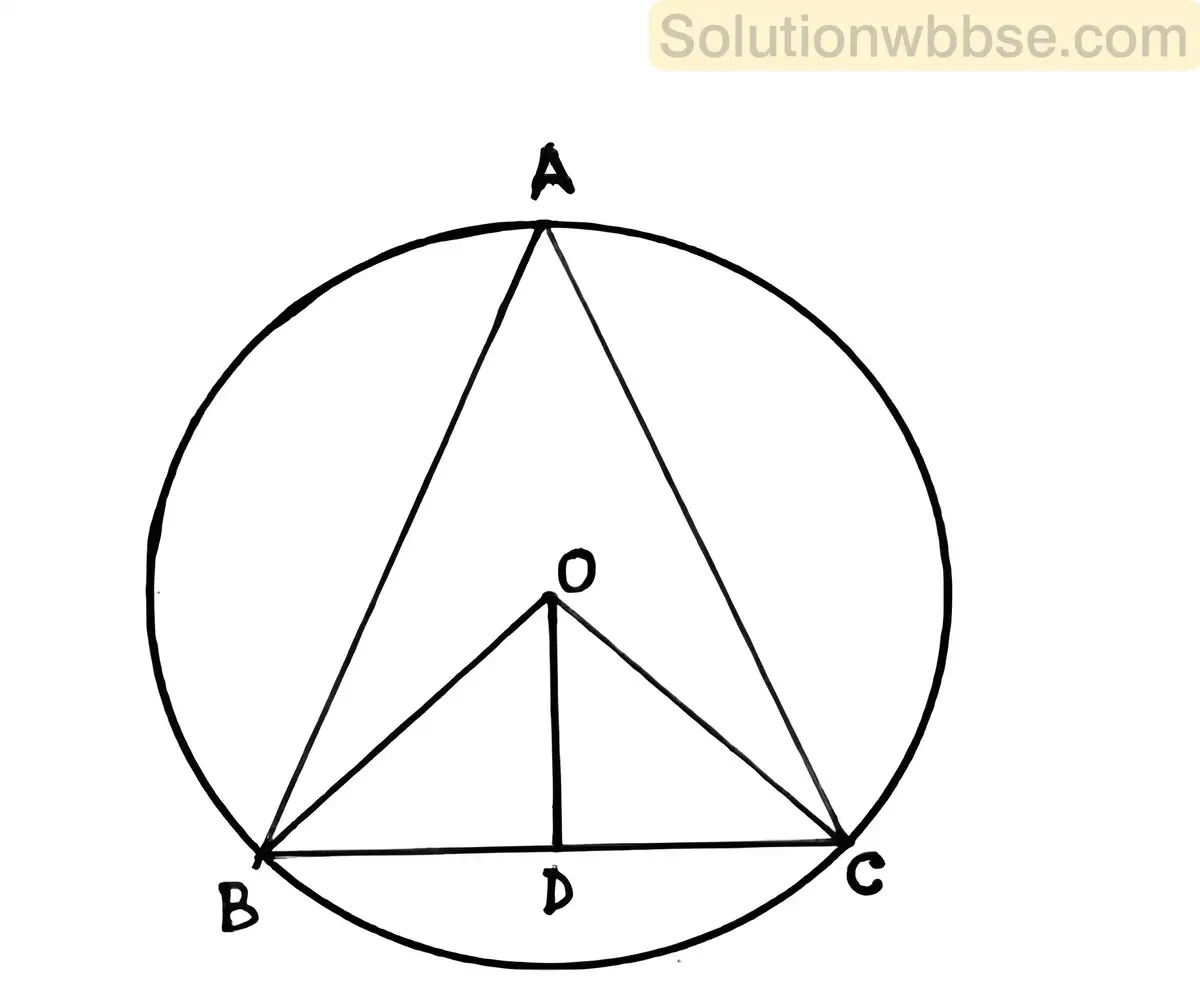
ধরি, ত্রিভুজ ABC এর পরিকেন্দ্র O এবং OD ⊥ BC, প্রমাণ করতে হবে যে, ∠BOD = ∠BAC
অঙ্কন – B,O এবং C,O যুক্ত করা হল।
প্রমাণ – BC চাপের ওপর অবস্থিত কেন্দ্রস্থ কোণ ∠BOC এবং পরিধিস্থ কোণ ∠BAC
∴ ∠BOC = 2∠BAC_______(i)
এখন ΔBOD ও ΔCOD এর মধ্যে
OB = OC = বৃত্তের ব্যাসার্ধ
∠ODB = ∠ODC [উভয়ই সমকোণ]
এবং OD সাধারণ বাহু।
∴ ΔBOD ≅ ΔCOD
∴ ∠BOD = ∠COD = \(frac12\)
∠BOC = \(frac12\).2∠BAC [(i) নং থেকে]
= ∠BAC
∴ ∠BOD = ∠BAC (প্রমাণিত)
11. যে কোনো একটি প্রশ্নের উত্তর দাও।
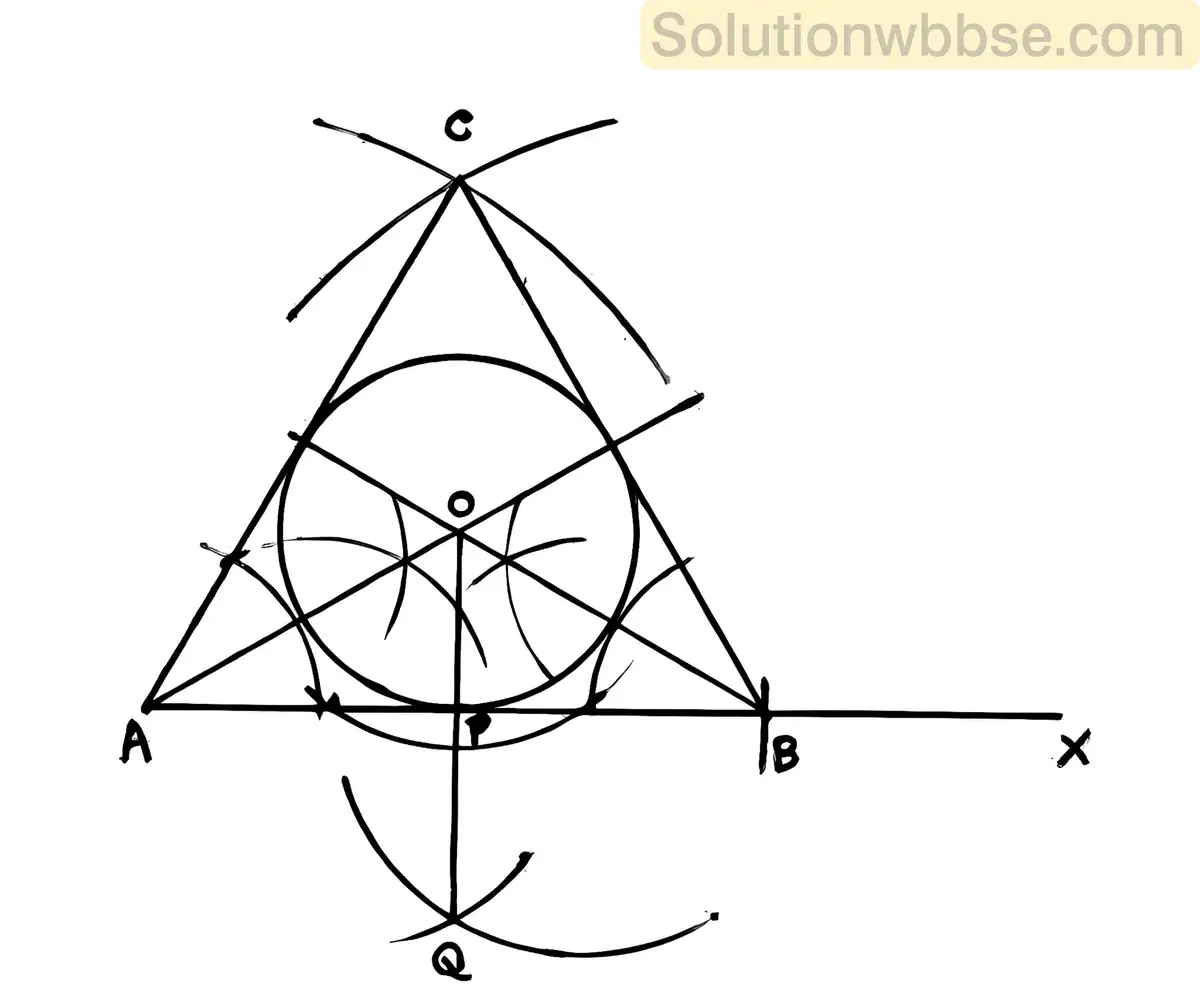
(i) 6 সেমি বাহুবিশিষ্ট একটি সমবাহু ত্রিভুজ অঙ্কন কর এবং ঐ ত্রিভুজটির অন্তর্বৃত্ত অঙ্কন কর। (কেবলমাত্র অঙ্কন চিহ্ন দিতে হবে।)
(ii) 8 সেমি ও 6 সেমি বাহুবিশিষ্ট একটি আয়তক্ষেত্র অঙ্কন কর এবং ঐ আয়তক্ষেত্রের সমান ক্ষেত্রফলবিশিষ্ট একটি বর্গক্ষেত্র অঙ্কন কর। (কেবলমাত্র অঙ্কন চিহ্ন দিতে হবে।)
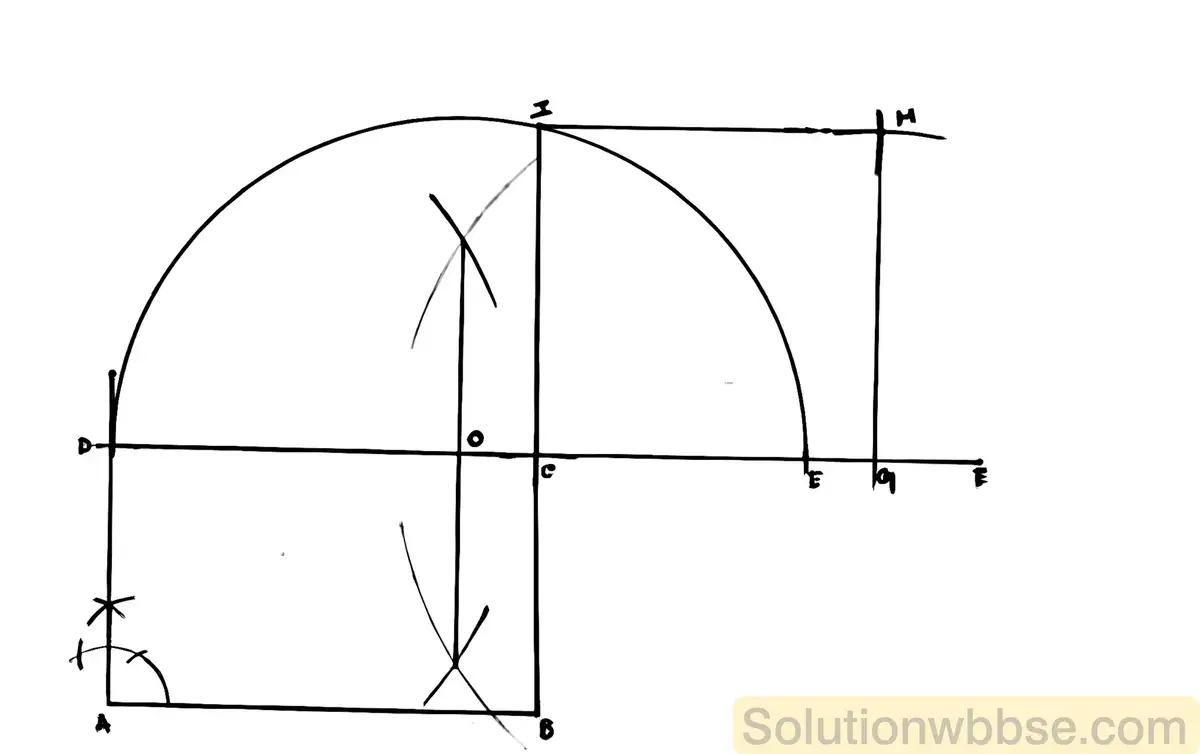
ABCD আয়তক্ষেত্রের সমান ক্ষেত্রফল বিশিষ্ট বর্গক্ষেত্রটি হল CGHI।
12. যে কোনো দুটি প্রশ্নের উত্তর দাও।
(i) কোনো চতুর্ভুজের তিনটি কোণের পরিমাপ \(\frac{\mathrm\pi}3,\frac{5\mathrm\pi}6\), 90° হলে চতুর্থ কোণটির ষষ্ঠিক ও বৃত্তীয় মান লেখো।
উত্তর :
কোনো চতুর্ভুজের তিনটি কোণের পরিমাপ যথাক্রমে
\(\frac{\mathrm\pi}3,\frac{5\mathrm\pi}6\), ও 90°
90° = \(\frac{\mathrm\pi}{180}\times90^\circ=\frac{\mathrm\pi}2\)
∴ চতুর্থ কোণটির বৃত্তীয় মান
2π – \(\left(\frac{\mathrm\pi}3+\frac{5\mathrm\pi}6+\frac{\mathrm\pi}2\right)\) [যেহেতু চতুর্ভুজের চারটি কোণের সমষ্টি 360° = 2π]
= 2π – \(\frac{2\mathrm\pi+5\mathrm\pi+3\mathrm\pi}6\)
= 2π – \(\frac{10\mathrm\pi}6\)
= \(\frac{12\mathrm\pi-10\mathrm\pi}6\)
= \(\frac{2\mathrm\pi}6\)
= \(\frac{\mathrm\pi}3\)
∴ চতুর্থ কোণটির বৃত্তীয় মান \(\frac{\mathrm\pi}3\)
এবং চতুর্থ কোণটির ষষ্টিক মান = \(\frac{\mathrm\pi}3=\frac{180^\circ}3=60^\circ\)
(ii) \(\frac{\sin\theta}x=\frac{\cos\theta}y\) হলে প্রমাণ কর যে, sinθ – cosθ = \(\frac{x-y}{\sqrt{x^2+y^2}}\)
উত্তর :
\(\frac{\sin\theta}x=\frac{\cos\theta}y\)বা, \(\frac{\sin\theta}{\cos\theta}=\frac xy\)
বা, \(\tan\theta=\frac xy\)
আমরা জানি, sec2θ – tan2θ = 1
∴ \(sec\theta=\sqrt{1+\tan^2\theta}\)
= \(\sqrt{1+\left(\frac xy\right)^2}\)
= \(\sqrt{\frac{y^2+x^2}{y^2}}\)
= \(\frac{\sqrt{y^2+x^2}}y\)
∴ \(\cos\theta=\frac1{sec\theta}\)
= \(\frac1{\displaystyle\frac{\sqrt{y^2+x^2}}y}\)
= \(\frac y{\sqrt{x^2+y^2}}\)
আমরা জানি, sin2θ + cos2θ = 1
∴ \(\sin\theta=\sqrt{1-\cos^2\theta}\)
= \(\sqrt{1-\left(\frac y{\sqrt{x^2+y^2}}\right)^2}\)
= \(\sqrt{\frac{x^2+y^2-y^2}{x^2+y^2}}\)
= \(\sqrt{\frac{x^2}{x^2+y^2}}\)
= \(\frac x{\sqrt{x^2+y^2}}\)
∴ sinθ – cosθ
= \(\frac x{\sqrt{x^2+y^2}}-\frac y{\sqrt{x^2+y^2}}\)
= \(\frac{x-y}{\sqrt{x^2+y^2}}\)
∴ sinθ – cosθ = \(\frac{x-y}{\sqrt{x^2+y^2}}\) (প্রমাণিত)
(iii) যদি tan 9° = \(\frac ab\) হয় তবে প্রমাণ কর যে, \(\frac{sec^281^\circ}{1+cot^281^\circ}=\frac{b^2}{a^2}\)
উত্তর :
tan 9° = \(\frac ab\)
বা, tan (90° – 81°) = \(\frac ab\)
বা, cot81° = \(\frac ab\) [যেহেতু tan (90° – θ) = cotθ]
বা, \(cot^281^\circ=\frac{a^2}{b^2}\) [উভয়পক্ষে বর্গ করে পাই]
বা, \(\frac1{cot^281^\circ}=\frac1{\frac{a^2}{b^2}}\)
বা, \(tan^281^\circ=\frac{b^2}{a^2}\) [যেহেতু tanθ = \(\frac1{cot\theta}\)]
বা, \(1+\tan^281^\circ=1+\frac{b^2}{a^2}\)
বা, \(sec^281^\circ=\frac{a^2+b^2}{a^2}\) [যেহেতু \(sec^2\theta-\tan^2\theta=1\)]
∴ \(\frac{sec^281^\circ}{1+cot^281^\circ}=\frac{b^2}{a^2}\)
= \(\frac{\displaystyle\frac{a^2+b^2}{a^2}}{1+{\displaystyle\frac{a^2}{b^2}}}\)
= \(\frac{\displaystyle\frac{a^2+b^2}{a^2}}{\displaystyle\frac{b^2+a^2}{b^2}}\)
= \(\frac{a^2+b^2}{a^2}\div\frac{b^2+a^2}{b^2}\)
= \(\frac{a^2+b^2}{a^2}\times\frac{b^2}{b^2+a^2}\)
= \(\frac{b^2}{a^2}\) (প্রমাণিত)
13. যে কোনো দুটি প্রশ্নের উত্তর দাও।
(i) দুটি স্তম্ভের দূরত্ব 150 মি.। একটির উচ্চতা অন্যটির তিনগুণ। স্তম্ভদ্বয়ের পাদদেশ সংযোগকারী রেখাংশের মধ্যবিন্দু থেকে তাদের শীর্ষের উন্নতি কোণদ্বয় পরস্পর পূরক। ছোট স্তম্ভটির উচ্চতা নির্ণয় কর।
উত্তর :
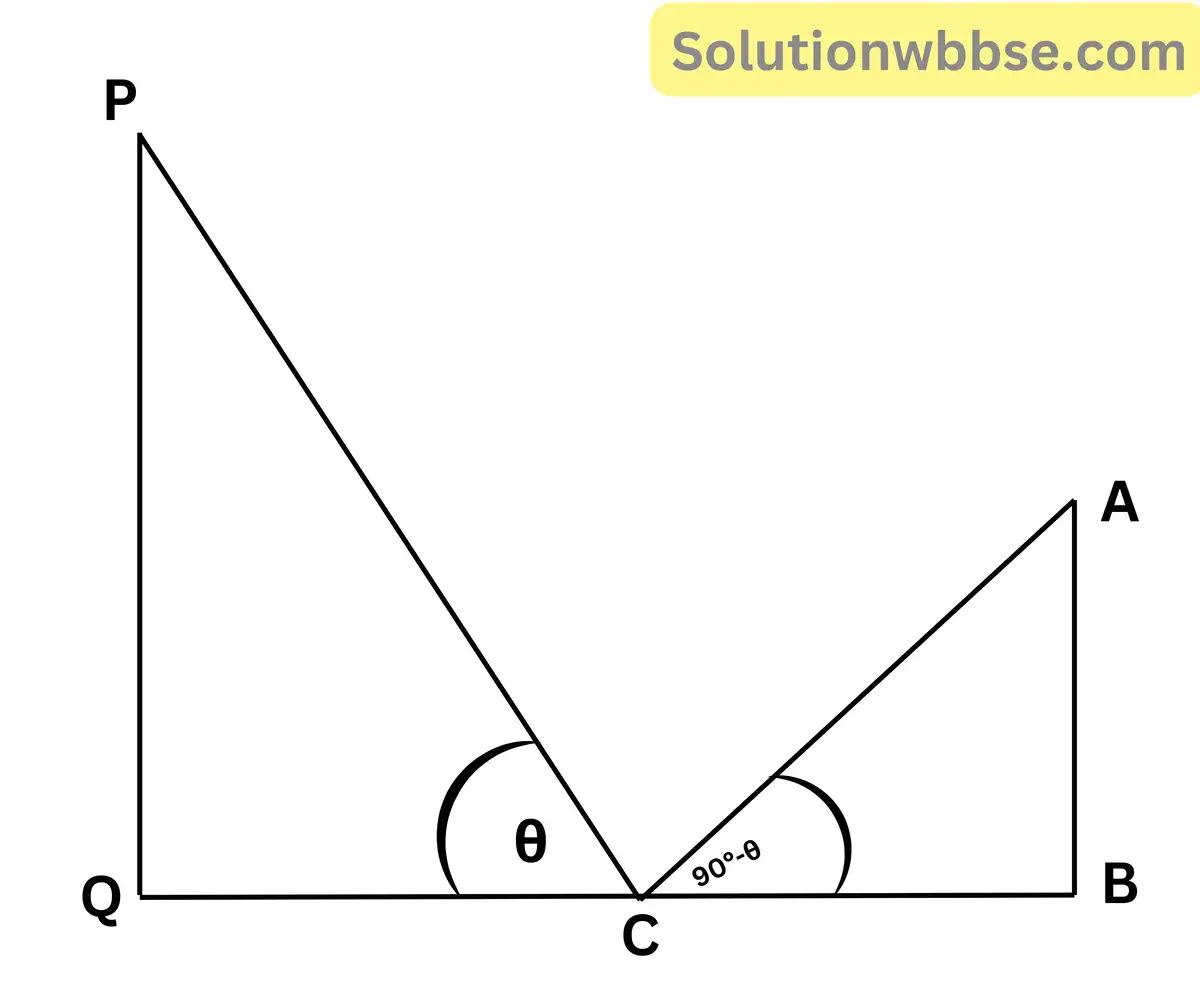
মনে করি, বৃহত্তম স্তম্ভটি PQ এবং অপর স্তম্ভটি AB.
এখানে PQ ও AB পাদদেশের সংযোজক রেখাংশ BQ -এর মধ্যবিন্দু C তে স্তম্ভ দুটির শীর্ষের উন্নতি কোণ যথাক্রমে θ এবং (90° – θ).
অর্থাৎ ∠PCQ = θ এবং ∠ACB = (90° – θ). আবার BQ = 150 মিটার।
∴ BC = QC= 75 মিটার।
এখন ΔPCQ এর ∠PQC = 90° এবং ∠PCQ = θ
∴ tanθ = \(\frac{PQ}{QC}\)
বা, PQ = QCtanθ
বা, 3AB = 75 tanθ [ যেহেতু PQ = 3AB ]
বা, AB = 25tanθ_______(i)
আবার, ∆ABC -এর ∠ABC = 90° এবং ∠ACB =(90° – θ)
∴ tan(90° – θ) = \(\frac{AB}{BC}\)
বা, cotθ = \(\frac{AB}{BC}\)
বা, AB = BCcotθ
বা, AB = 75cotθ_______(ii)
এখন (i) ও (ii) নং সমীকরণ গুন করে পাই,
AB2 = 25tanθ × 75cotθ
বা, AB2 = 25 × 25 × 3
বা, AB = 25\(\sqrt3\)
∴ PQ = 3AB
= 3 × 25\(\sqrt3\)
= 75\(\sqrt3\)
সুতরাং বড় স্তভের উচ্চতা 75\(\sqrt3\) মিটার এবং ছোট স্তম্ভের উচ্চতা 25\(\sqrt3\) মিটার।
(ii) একটি লাইটহাউস থেকে তার সঙ্গে একই সরলরেখায় অবস্থিত দুটি জাহাজের অবনতি কোণ যদি 60° এবং 30° হয় এবং কাছের জাহাজটি যদি লাইটহাউস থেকে 150 মি. দূরে থাকে তবে লাটিহাউস থেকে দূরের জাহাজটির দূরত্ব কত?
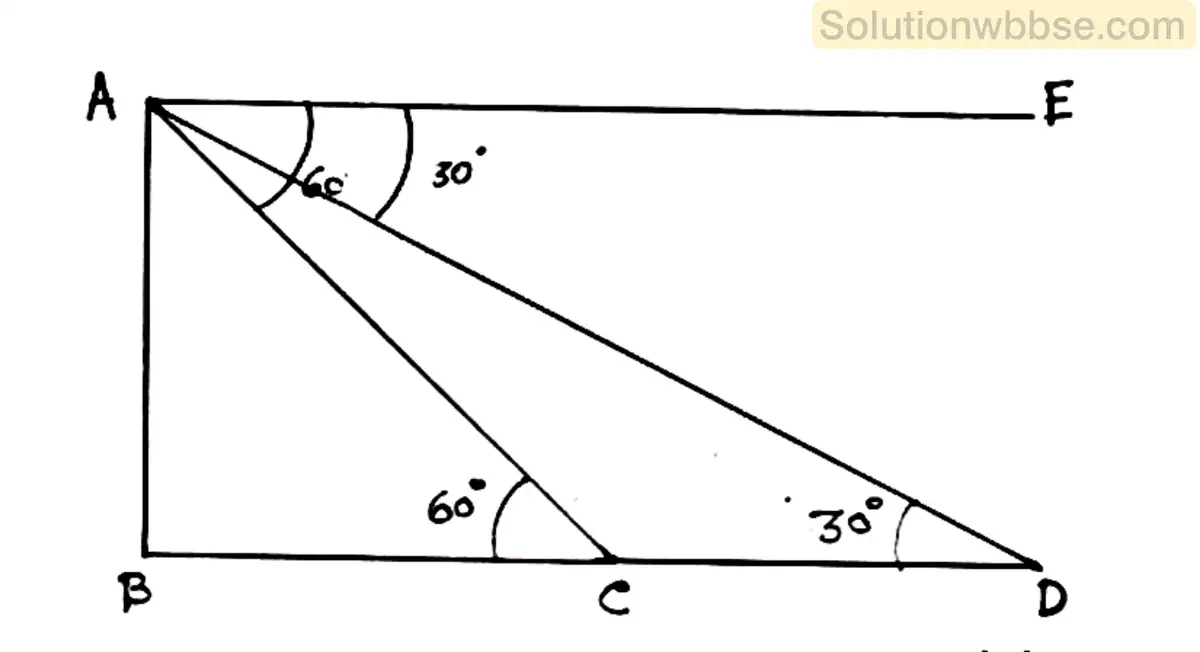
উত্তর :
ধরাযাক, AB হল লাইট হাউসের উচ্চতা। A বিন্দু থেকে C বিন্দুতে এবং D বিন্দুতে অবস্থিত জাহাজের মাস্তুলের অবনতি কোণ যথাক্রমে 60° ও 30°। আবার লাইট হাউস থেকে কাছের জাহাজের দূরত্ব 150 মিটার।
∴ BC = 150 মিটার।
AE || BD অঙ্কন করা হল
∴ ∠EAC = 60°এবং ∠EAD = 30°
আবার, ∠ACB = ∠EAC [একান্তর কোণ] এবং ∠EAD = ∠ADB [একান্তর কোণ]
∴ ∠ACB = 60° এবং ∠ADB = 30°
ABC ত্রিভুজে ∠ACB = 60° এবং ∠ABC = 90°
∴ tan∠ACB = tan 60° =
বা, \(\sqrt3=\frac{AB}{BC}\) [যেহেতু, tan 60° = \(\sqrt3\)]
বা, \(\sqrt3=\frac{AB}{150}\)
বা, AB = 150\(\sqrt3\)_______(i)
আবার, ABD ত্রিভুজে ∠ABD = 90° এবং ∠ADB = 30°
∴ tan∠ADB =
বা, tan30° = \(\frac{AB}{BC+CD}\)
বা, \(\frac1{\sqrt3}=\frac{150\sqrt3}{150+CD}\) [যেহেতু, AB = 150 \(\sqrt3\) এবং tan 30° = \(\frac1{\sqrt3}\)]
বা, 150 + CD = 450
বা, CD = 300
∴ BD = BC + CD
= 150 + 300
= 450 মিটার
∴ লাইট হাউস থেকে দূরের জাহাজের দূরত্ব 450 মিটার।
14. যে কোনো দুটি প্রশ্নের উত্তর দাও।
(i) 4.2 ডেসি মি দৈর্ঘ্যের ধারবিশিষ্ট একটি নিরেট কাঠের ঘনক থেকে সবথেকে কম কাঠ নষ্ট করে যে নিরেট লম্ববৃত্তাকার শঙ্কু পাওয়া যাবে তার আয়তন নির্ণয় কর।
উত্তর :
4.2 ডেসিমি. দৈর্ঘ্যের ধারবিশিষ্ট একটি নিরেট ঘনক থেকে সবচেয়ে কম কাঠ নষ্ট করে যে নিরেট লম্ব বৃত্তাকার শঙ্কু পাওয়া যাবে তার ভূমিতলের ব্যাসের দৈর্ঘ্য = ঘনকের বাহুর দৈর্ঘ্য = 4.2 ডেসিমি.
∴ শঙ্কুটির ব্যাসার্ধ (r) = \(\frac{4.2}2\) ডেসিমি.
= 2.1 ডেসিমি.
আবার, শঙ্কুর উচ্চতা, ঘনকের বাহুর দৈর্ঘ্যের সাথে সমান
∴ শঙ্কুরটির উচ্চতা (h) = 4.2 ডেসিমি.
∴ শঙ্কুটির আয়তন
= \(\frac13\times\mathrm\pi\times\mathrm r^2\times\mathrm h\) ঘন ডেসিমি.
= \(\frac13\times\frac{22}7\times\left(2.1\right)^2\times4.2\) ঘন ডেসিমি.
= \(\frac13\times\frac{22}7\times2.1\times2.1\times4.2\) ঘন ডেসিমি.
= 22 × 0.1 × 2.1 × 4.2 ঘন ডেসিমি.
= 19.404 ঘন ডেসিমি.
∴ লম্ব বৃত্তাকার শঙ্কুর আয়তন 19.404 ঘন ডেসিমি.।
(ii) 9 সেমি দৈর্ঘ্যের ব্যাসার্ধ বিশিষ্ট একটি অর্ধগোলাকার পাত্র সম্পূর্ণ জলপূর্ণ আছে। এই জল 3 সেমি দৈর্ঘ্যের ব্যাস এবং 4 সেমি উচ্চবিশিষ্ট চোঙাকৃতি বোতলে ভর্তি করে রাখা হবে। পাত্রটি খালি করতে কতগুলি বোতল দরকার হবে?
উত্তর :
অর্ধ গোলকের ব্যাসার্ধ (R) = 9 সেমি.
∴ পাত্রের আয়তন
= \(\frac23\mathrm{πR}^3\) ঘনসেমি
= \(\frac23\mathrm\pi\left(9\right)^3\) ঘনসেমি.
চোঙাকৃতি বোতলের ব্যাস 3 সেমি.।
∴ বোতলের ব্যাসার্ধ (r) = \(\frac32\) সেমি.
বোতলের উচ্চতা (h) = 4 সেমি.
∴ চোঙাকৃতি বোতলের আয়তন = πr2h ঘন সেমি.
= \(\mathrm\pi\times\left(\frac32\right)^2\times4\) ঘনসেমি.
ধরি, পাত্রটি খালি করতে x টি বোতলের প্রয়োজন হবে।
∴ পাত্রের পাত্রের জলের আয়তন = x টি বোতলের জলের
∴ \(\frac23\mathrm\pi\left(9\right)^3=\mathrm x\times\left(\frac32\right)^2\times4\)
বা, \(\frac23\times729=\mathrm x\times\frac94\times4\)
বা, 486 = 9x
বা, x = \(\frac{486}9\)
বা, x = 54
∴ পাত্রটি খালি করতে 54 টি বোতলের প্রয়োজন হবে।
(iii) একটি ঢাকনা সমেত চোঙাকৃতি জলের ট্যাঙ্কের ভূমির ক্ষেত্রফল 616 বর্গমিটার এবং উচ্চতা 21 মিটার। ঐ ট্যাঙ্কের সমগ্রতলের ক্ষেত্রফল নির্ণয় কর।
উত্তর :
ধরি, চোঙাকৃতি জলের ট্যাঙ্কের ভূমির ব্যাসার্ধ r মিটার
∴ ভূমির ক্ষেত্রফল = πr2 বর্গ একক
∴ πr2 = 616
বা, \(\frac{22}7\times r^2\) = 616
বা, \(r^2=\frac{616\times7}{22}\)
বা, r2 = 196
বা, r2 = (14)2
বা, r = 14
∴ চোঙাকৃতি জলের ট্যাঙ্কের ব্যাসার্ধ 14 মিটার।
চোঙাকৃতি জলের ট্যাঙ্কের উচ্চতা (h) = 21 মিটার।
∴ সমগ্রতলের ক্ষেত্রফল
= (2πr2 + 2πrh) বর্গ মিটার
= (2 x 616 + \(\frac{22}7\) × 14 × 21 ) বর্গ মিটার
= (1232 + 1848) বর্গ মিটার
= 3080 বর্গ মিটার।
∴ ঢাকনা সহ চোঙাকৃতি ট্যাঙ্কের সমগ্র তলের ক্ষেত্রফল 3080 বর্গ মিটার।
15. যে কোনো দুটি প্রশ্নের উত্তর দাও
(i) নীচের তথ্যের মধ্যমা 32 হলে, x ও y-এর মান নির্ণয় কর যখন পরিসংখ্যার সমষ্টি 100
| শ্রেণী-সীমা | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| পরিসংখ্যা | 10 | x | 25 | 30 | y | 10 |
উত্তর :
শ্রেণিটির পরিসংখ্যা বিভাজন তালিকাটি হল
| শ্রেণি-সীমানা | পরিসংখ্যা | ক্রম যৌগিক পরিসংখ্যা |
| 0-10 | 10 | 10 |
| 10-20 | X | 10 + x |
| 20-30 | 25 | 35 + x |
| 30-40 | 30 | 65 + x |
| 40-50 | Y | 65 + x + y |
| 50-60 | 10 | 75 + x + y = n |
এখানে n = 100 (প্রদত্ত) শর্তানুসারে,
75 + x + y = 100
বা, x + y = 25_______(i)
আবার যেহেতু মধ্যমা = 32
সুতরাং মধ্যমা শ্রেণিটি হল (30-40)
∴ নির্ণেয় মধ্যমা = \(I+\left[\frac{{\displaystyle\frac n2}-cf}f\right]\times h\) [এখানে, I = 30,n = 100, cf = 35 + x, f = 30, h = 10]
= 30 + \(\left[\frac{50-\left(35+x\right)}{30}\right]\) × 10
= 30 + \(\frac{15-x}{30}\) × 10
= 30 + \(\frac{15-x}3\)
শর্তানুসারে,
30 \(\frac{15-x}3\) + = 32
বা, \(\frac{15-x}3\) = 2
বা, 15 – x = 6
বা, x = 9
(i) নং সমীকরণে x এর মান বসিয় পাই,
9 + y = 25
বা, y = 25 – 9
বা, y = 16
∴ x = 9 এবং y = 16
(ii) নীচের পরিসংখ্যা বিভাজনের সংখ্যাগুরুমান নির্ণয় কর –
| শ্রেণী-সীমা | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 | 35-35 |
| পরিসংখ্যা | 5 | 12 | 18 | 28 | 17 | 12 | 8 |
উত্তর :
উপরের পরিসংখ্যা বিভাজনের সংখ্যাগুরু শ্রেণি (15 – 20)
∴ নির্ণেয় সংখ্যাগুরু মান = \(I+\left(\frac{f_1-f_0}{2f_1-f_0-f_2}\right)\times h\) [এখানে, \(I=15,f_1=28,f_0=18,f_2=17,h=5\)]
= 15 + \(\left(\frac{28-18}{2\times28-18-17}\right)\) × 5
= 15 + \(\frac{10}{21}\) × 5
= 15 + \(\frac{50}{21}\)
= 15 + 2.38 (প্রায়)
= 17.38 (প্রায়)
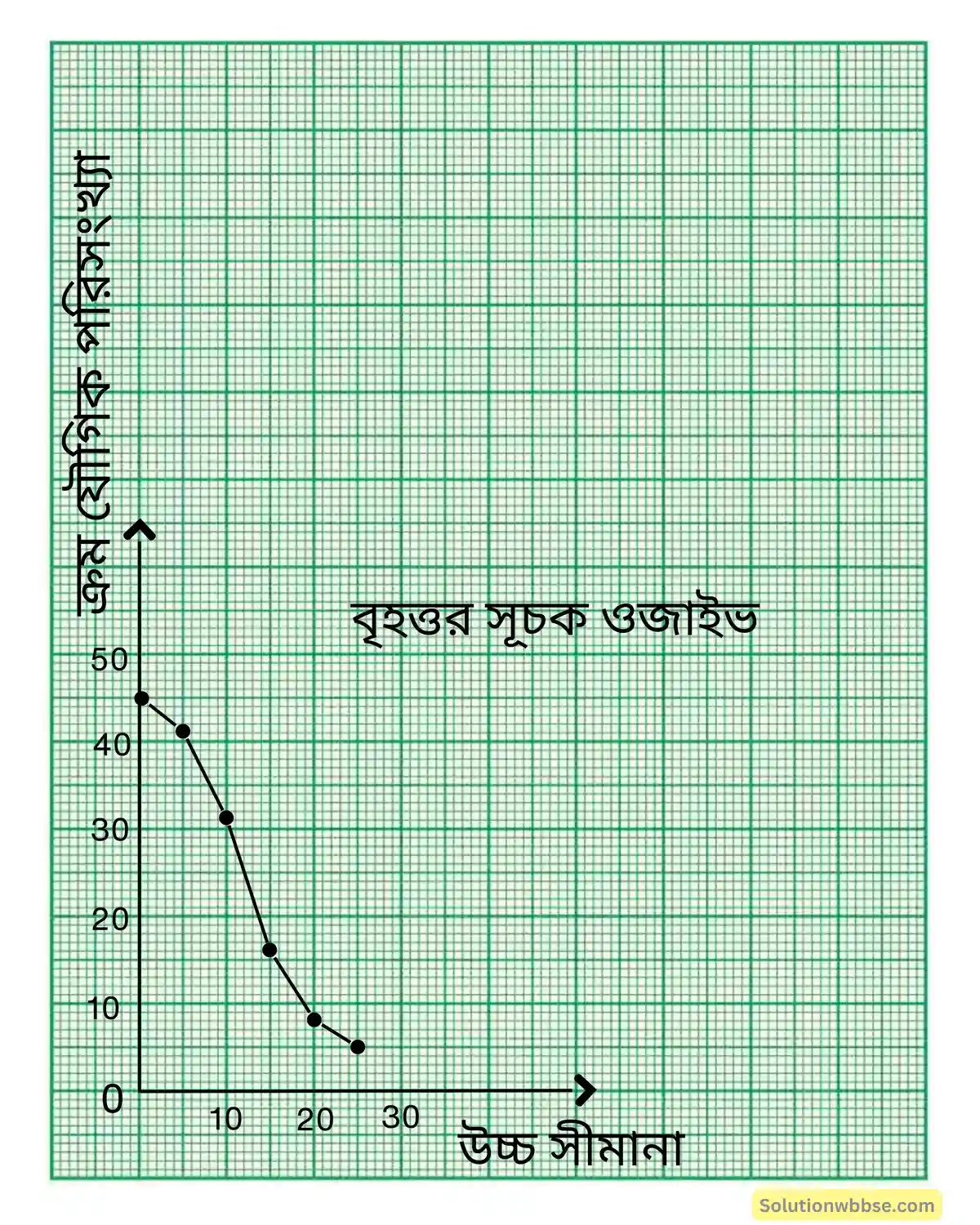
(iii) নীচের তথ্যের ক্রমযৌগিক পরিসংখ্যা (বৃহত্তর সূচক) তালিকা তৈরি করে ছক কাগজে ওজাইভ অঙ্কন কর।
| শ্রেণী-সীমা | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 |
| পরিসংখ্যা | 4 | 10 | 15 | 8 | 3 | 5 |
উত্তর :
| শ্রেণি | বৃহত্তর সূচক ক্রমযৌগিক পরিসংখ্যা |
| 0 বা 0 এর বেশী | 45 |
| 5 বা 5 এর বেশী | 41 |
| 10 বা 10 এর বেশী | 31 |
| 15 বা 15 এর বেশী | 16 |
| 20 বা 20 এর বেশী | 8 |
| 25 বা 25 এর বেশী | 5 |
X অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1 টি বাহুর দৈর্ঘ্য = 1 একক এবং y অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1 টি বাহুর দৈর্ঘ্য = 1 একক ধরে (0, 45), (5, 41), (10, 31),(15, 16), (20, 8), (25, 5) বিন্দুগুলি স্থাপন করে ও যুক্ত করে বৃহত্তর সূচক ওজাইভ পাওয়া গেল।
এই আর্টিকেলের মাধ্যমে আমরা মাধ্যমিক পরীক্ষার পূর্ববর্তী বছরের প্রশ্ন ও উত্তর বিশ্লেষণ করেছি। এই আলোচনার মাধ্যমে শিক্ষার্থীরা আগের বছরের প্রশ্নের ধরণ এবং গুরুত্বপূর্ণ বিষয় সম্পর্কে স্পষ্ট ধারণা লাভ করেছেন। বিশেষ করে, মাধ্যমিক গণিত প্রশ্নপত্র ২০১৭ আলোচনা করা হয়েছে। এই বছরের প্রশ্নপত্র পরবর্তী বছরের পরীক্ষার্থীদের জন্য বেশ গুরুত্বপূর্ণ কারণ এটি প্রশ্ন নির্বাচনের ধরণ এবং বিষয়ের গভীরতা সম্পর্কে ধারণা দেয়। মাধ্যমিক গণিত পরীক্ষার জন্য প্রস্তুতি নেওয়ার সময়, শিক্ষার্থীদের এই প্রশ্নপত্রটি অবশ্যই মনোযোগ সহকারে অনুশীলন করা উচিত। এটি তাদের পরীক্ষার ধরনের সাথে পরিচিত হতে এবং সময় ব্যবস্থাপনা দক্ষতা উন্নত করতে সাহায্য করবে। আশা করি এই আর্টিকেলটি মাধ্যমিক গণিত পরীক্ষার জন্য প্রস্তুতি নেওয়ার ক্ষেত্রে শিক্ষার্থীদের জন্য সহায়ক হবে। মনে রাখবেন, নিয়মিত অনুশীলন এবং ধৈর্যের মাধ্যমে আপনি পরীক্ষায় সফল হতে পারবেন।






মন্তব্য করুন