মাধ্যমিক ভৌতবিজ্ঞান – তাপের ঘটনাসমূহ – সংক্ষিপ্ত ও দীর্ঘ প্রশ্নোত্তর

এই আর্টিকেলে আমরা মাধ্যমিক ভৌতবিজ্ঞান বইয়ের তাপের ঘটনাসমূহ অধ্যায়ের সংক্ষিপ্ত ও দীর্ঘ প্রশ্নোত্তর নিয়ে আলোচনা করব। যেগুলি মাধ্যমিক পরীক্ষার জন্য খুবই গুরুত্বপূর্ণ। তাপের ঘটনাসমূহ অধ্যায়ের সংক্ষিপ্ত ও দীর্ঘ প্রশ্নোত্তর গুলি আপনি যদি ভালো করে দেখে মুখস্ত করে যান, তাহলে মাধ্যমিক পরীক্ষায় তাপের ঘটনাসমূহ অধ্যায়ের সংক্ষিপ্ত ও দীর্ঘ প্রশ্নোত্তর থেকে যা প্রশ্ন আসবে না কেন আপনি সঠিক উত্তর দিতে পারবেন।

কঠিনের তাপীয় প্রসারণ কাকে বলে?

কোনো কঠিন পদার্থের তাপমাত্রা বৃদ্ধি পেলে, পদার্থটির আকার ও আয়তন বৃদ্ধি পায়। তাপমাত্রা বৃদ্ধির কারণে কঠিন পদার্থের যে আকার ও আয়তনের বৃদ্ধি ঘটে, তাকে কঠিনের তাপীয় প্রসারণ বলা হয়।

গ্যাসের আয়তন গুণাঙ্কের মান কত?

গ্যাসের আয়তন গুণাঙ্কের মান হল,
\( \gamma_p = 1273^\circ C^{-1} \)

কঠিনের তাপীয় সংকোচন কাকে বলে?

কোনো কঠিন পদার্থের তাপমাত্রা হ্রাস পেলে, পদার্থটির আকার ও আয়তনে সংকুচিত হয়। তাপমাত্রা হ্রাসের কারণে কঠিন পদার্থের যে আকার ও আয়তনের সংকোচন ঘটে, তাকে কঠিনের তাপীয় সংকোচন বলা হয়।

একটি পরীক্ষার সাহায্যে দেখাও উষ্ণতা বৃদ্ধি করলে কঠিন পদার্থের প্রসারণ হয়।

পরীক্ষা: একটি স্ট্যান্ড (S), একটি হুক (H), একটি বল (B) এবং একটি আংটা (R) নেওয়া হলো। আংটা (R) হুকের (H) নিচে স্ট্যান্ডের মাঝখানে ভালোভাবে স্থাপন করা হলো। এরপর সুতোর সাহায্যে বলটিকে (B) হুক (H) থেকে ঝুলিয়ে দেওয়া হলো। বল এবং আংটা আলাদা ধাতুর তৈরি। আংটার মাপ এমনভাবে নেওয়া হলো যাতে সাধারণ তাপমাত্রায় বলটি আংটার মধ্যে কোনো রকমে গলে যায়। এবার বলটিকে কিছুক্ষণ গরম করে আংটার মধ্যে গলানোর চেষ্টা করা হলে দেখা গেল, বলটি আংটার মধ্যে দিয়ে আর গলছে না। বলটিকে আবার ঠান্ডা করে আংটার মধ্যে গলানোর চেষ্টা করলে দেখা গেল, বলটি সহজেই আংটার মধ্যে গলে যাচ্ছে।

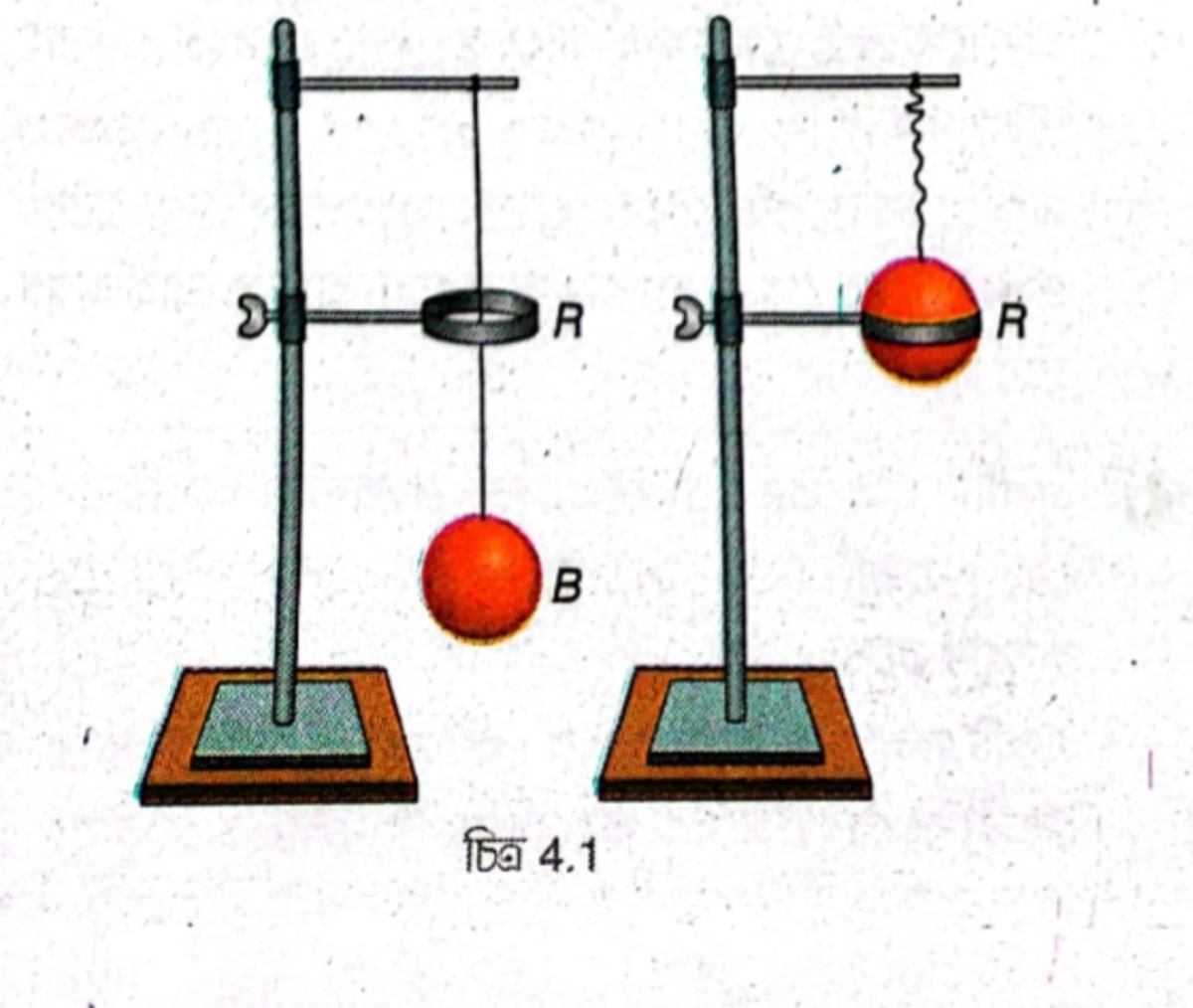
সিদ্ধান্ত: এই পরীক্ষা থেকে প্রমাণিত হয় যে, তাপমাত্রা বৃদ্ধির ফলে কঠিন পদার্থ প্রসারিত হয় এবং তাপমাত্রা হ্রাসের ফলে সংকুচিত হয়। এখানে বলটিকে উত্তপ্ত করার ফলে বলের আয়তন বেড়ে গেছে, কিন্তু আংটার তাপমাত্রা অপরিবর্তিত থাকায় আংটার কোনো রকম প্রসারণ হয়নি। ফলে উত্তপ্ত অবস্থায় বলটি আংটার মধ্যে দিয়ে গলতে পারেনি। বলটিকে ঠান্ডা করে ঘরের তাপমাত্রায় আনলে, বলটি সংকুচিত হয়ে পূর্বের আকার ফিরে পায় এবং তখন বলটি আংটার মধ্যে দিয়ে সহজেই গলে যায়।

কঠিনের তাপীয় প্রসারণ কয় প্রকার ও কী কী?

কঠিনের তাপীয় প্রসারণ তিন প্রকার –
১. দৈর্ঘ্য প্রসারণ।
২. ক্ষেত্র প্রসারণ।
৩. আয়তন প্রসারণ।

কঠিনের সমদৈশিক প্রসারণ কাকে বলে?

তাপ প্রয়োগে বেশিরভাগ কঠিন পদার্থের সবদিকে সুষমভাবে প্রসারণ ঘটে। এই ধরনের প্রসারণকে সমদৈশিক প্রসারণ বলা হয়।

কঠিনের অসমদৈশিক প্রসারণ কাকে বলে?

তাপ প্রয়োগে কিছু কঠিন পদার্থের সবদিকে সুষমভাবে প্রসারণ ঘটে না। এই ধরনের প্রসারণকে অসমদৈশিক প্রসারণ বলা হয়।

কঠিনের দৈর্ঘ্য প্রসারণ গুণাঙ্ক কাকে বলে?

কোনো কঠিন পদার্থের প্রতি একক তাপমাত্রা বৃদ্ধিতে প্রতি একক দৈর্ঘ্যে যে পরিমাণ দৈর্ঘ্য প্রসারণ ঘটে, তাকে ওই কঠিন পদার্থের দৈর্ঘ্য প্রসারণ গুণাঙ্ক বলা হয়।

কঠিনের দৈর্ঘ্য প্রসারণ গুণাঙ্কের রাশিমালাটি লেখো।

মনে করা যাক, \( t_1 \) তাপমাত্রায় কোনো কঠিন পদার্থের দৈর্ঘ্য \( l_1 \) এবং তাপমাত্রা বৃদ্ধি করে \( t_2 \) করা হলে দৈর্ঘ্য হয় \( l_2 \); কঠিন পদার্থটির দৈর্ঘ্য প্রসারণ গুণাঙ্ক \( \alpha \) হলে, \( \alpha \)-এর সংজ্ঞানুসারে লেখা যায়, \( \alpha = \frac{l_2 – l_1}{l_1 (t_2 – t_1)} \)

কঠিন পদার্থের দৈর্ঘ্য প্রসারণ গুণাঙ্ক কিভাবে নির্ণয় করা হয়?

মনে করি, \( t_1 \) তাপমাত্রায় কোনো কঠিন দণ্ডের দৈর্ঘ্য \( l_1 \) এবং তাপমাত্রা বৃদ্ধি করে \( t_2 \) করা হলে, দণ্ডটির দৈর্ঘ্য হয় \( l_2 \)।

∴ দণ্ডটির দৈর্ঘ্য প্রসারণ = \( l_2 – l_1 \), তাপমাত্রা বৃদ্ধি = \( t_2 – t_1 \)

দৈর্ঘ্য প্রসারণ দণ্ডের প্রাথমিক দৈর্ঘ্য ও তাপমাত্রা বৃদ্ধির সমানুপাতিক, অর্থাৎ,
\( (l_2 – l_1) \propto l_1 \) যখন (t_2 – t_1) স্থির

এবং \( (l_2 – l_1) \propto (t_2 – t_1) \) যখন \( l_1 \) স্থির

∴ \( (l_2 – l_1) \propto l_1 (t_2 – t_1) \) যখন \( l_1 \) এবং \( (t_2 – t_1) \) উভয়ই পরিবর্তনশীল

বা, \( (l_2 – l_1) = \alpha l_1 (t_2 – t_1) \)

যেখানে \( \alpha \) একটি ধ্রুবক, একে পদার্থের দৈর্ঘ্য প্রসারণ গুণাঙ্ক বলা হয়।

বা, \( \alpha = \frac{l_2 – l_1}{l_1 (t_2 – t_1)} \)
বা, \( l_2 – l_1 = l_1 \alpha (t_2 – t_1) \)

এখানে, দৈর্ঘ্য প্রসারণ = প্রাথমিক দৈর্ঘ্য × দৈর্ঘ্য প্রসারণ গুণাঙ্ক × তাপমাত্রা বৃদ্ধি
অথবা, \( l_2 = l_1 \left[ 1 + \alpha (t_2 – t_1) \right] \)

বিভিন্ন কঠিন পদার্থের দৈর্ঘ্য প্রসারণ গুণাঙ্কের তালিকা

বিভিন্ন কঠিন পদার্থের দৈর্ঘ্য প্রসারণ গুণাঙ্কের তালিকা

পদার্থ	α (°C⁻¹ এককে)	পদার্থ	α (°C⁻¹ এককে)	পদার্থ	α (°C⁻¹ এককে)
কোয়ার্টস	\( 0.5 \times 10^{-6} \)	ক্লাউন কাচ	\( 9 \times 10^{-6} \)	রূপো	\( 18.8 \times 10^{-6} \)
ইনভার	\( 0.7 \times 10^{-6} \)	ইস্পাত	\( 11 \times 10^{-6} \)	পিতল	\( 19 \times 10^{-6} \)
হিরে	\( 8.9 \times 10^{-6} \)	লোহা	\( 12 \times 10^{-6} \)	অ্যালুমিনিয়াম	\( 22.9 \times 10^{-6} \)
পাইরেক্স কাচ	\( 3.2 \times 10^{-6} \)	সোনা	\( 14 \times 10^{-6} \)	দস্তা	\( 26.8 \times 10^{-6} \)
প্ল্যাটিনাম	\( 8.9 \times 10^{-6} \)	তামা	\( 16.7 \times 10^{-6} \)	সিসা	\( 29 \times 10^{-6} \)

দেখাও যে, দৈর্ঘ্য প্রসারণ গুণাঙ্কের একক দৈর্ঘ্যের এককের ওপর নির্ভর করে না, শুধুমাত্র তাপমাত্রার এককের ওপর নির্ভরশীল।

মনে করি, \( l_1 \) দৈর্ঘ্যের কোনো দণ্ডের তাপমাত্রা \( t_1 \) থেকে বৃদ্ধি করে \( t_2 \) করা হলে দণ্ডটির অন্তিম দৈর্ঘ্য হয় \( l_2 \)।

∴ দৈর্ঘ্য প্রসারণ গুণাঙ্ক,

\( \alpha = \frac{l_2 – l_1}{l_1 (t_2 – t_1)} \) ;
\( \alpha = \frac{l_2 – l_1}{l_1} \)

দৈর্ঘ্য প্রসারণ গুণাঙ্ক হল দুটি সমজাতীয় রাশির অনুপাত, তাই এককহীন। সুতরাং, দৈর্ঘ্য প্রসারণ গুণাঙ্কের একক শুধুমাত্র \( (t_2 – t_1) \) -এর একক বা উষ্ণতার এককের ওপর নির্ভরশীল।

লোহারের দৈর্ঘ্য প্রসারণ গুণাঙ্ক 12 × 10⁻⁶/°C বলতে কী বোঝ?

লোহারের দৈর্ঘ্য প্রসারণ গুণাঙ্ক 12 × 10⁻⁶/°C বলতে বোঝায়, কোনো লৌহদণ্ডের উষ্ণতা 1°C বৃদ্ধি করলে দণ্ডটির প্রাথমিক দৈর্ঘ্যের 12 × 10⁻⁶ অংশ দৈর্ঘ্য বৃদ্ধি হয়।

সেলসিয়াস ও ফারেনহাইট স্কেলে দৈর্ঘ্য প্রসারণ গুণাঙ্কের মধ্যে সম্পর্ক স্থাপন করো।

মনে করি, কোনো কঠিন পদার্থের দৈর্ঘ্য প্রসারণ গুণাঙ্ক,
\( \alpha = \frac{x}{°C} \)

আবার, 1°C -এর পরিবর্তন = \( \frac{9}{5} \)°F -এর পরিবর্তন

∴ \( \alpha = \frac{x}{\frac{9}{5} , °F} = \frac{5}{9} \cdot x / °F \)

∴ সেলসিয়াস ও ফারেনহাইট স্কেলে দৈর্ঘ্য প্রসারণ গুণাঙ্ক যথাক্রমে \( \alpha_C \) ও \( \alpha_F \) হলে,
\( \alpha_F = \frac{5}{9} \cdot \alpha_C \)

ইস্পাতের তৈরি একটি ছিপি পিতলের তৈরি একটি বোতলে আটকে গেছে। ছিপিটি খোলার জন্য কী করবে?

পিতলের দৈর্ঘ্য প্রসারণ গুণাঙ্ক ইস্পাতের তুলনায় বেশি। সংস্থাটিকে উত্তপ্ত করলে পিতলের প্রসারণ ইস্পাতের তুলনায় বেশি হবে, ফলে ছিপিটি আরও আটকে যাবে। কিন্তু সংস্থাটিকে ঠান্ডা করলে পিতলের সংকোচন ইস্পাতের তুলনায় বেশি হবে, ফলে ছিপিটি আলগা হয়ে খুলে যাবে। সুতরাং, এক্ষেত্রে ছিপি খোলার জন্য সংস্থাটিকে ঠান্ডা করতে হবে।

দুটি দণ্ডের দৈর্ঘ্যের পার্থক্য সকল উষ্ণতায় সমান থাকার শর্ত নির্ণয় করো।

মনে করি, \( t_1 \) উষ্ণতায় দুটি দণ্ডের দৈর্ঘ্য যথাক্রমে \( l_1 \) ও \( l_2 \) (\( l_1 > l_2 \)) এবং উষ্ণতা বৃদ্ধি করে \( t_2 \) করা হলে দণ্ড দুটির দৈর্ঘ্য হবে যথাক্রমে \( l’_1 \) ও \( l’_2 \); দণ্ড দুটির দৈর্ঘ্য প্রসারণ গুণাঙ্ক যথাক্রমে \( \alpha_1 \) ও \( \alpha_2 \) হলে,

শর্তানুসারে,

\( l_1 – l_2 = l’_1 – l’_2 \)

বা, \( l’_1 – l_1 = l’_2 – l_2 \)

বা, \( l_1 \alpha_1 (t_2 – t_1) = l_2 \alpha_2 (t_2 – t_1) \)

বা, \( l_1 \alpha_1 = l_2 \alpha_2 \)

বা, \( \frac{l_1}{l_2} = \frac{\alpha_2}{\alpha_1} \)

অর্থাৎ, দণ্ড দুটির দৈর্ঘ্য, তাদের দৈর্ঘ্য প্রসারণ গুণাঙ্কের ব্যস্তানুপাতে থাকলে যে-কোনো উষ্ণতায় দণ্ড দুটির দৈর্ঘ্যের পার্থক্য একই থাকবে।

একটি লোহার দণ্ড একটি বৃত্তাকার লোহার বলয়ের ব্যাস বরাবর যুক্ত। সংস্থাটিকে সমভাবে উত্তপ্ত করলে বলয়টি বৃত্তাকার থাকবে কি? ব্যাখ্যা করো।

মনে করি, লোহার দণ্ডের দৈর্ঘ্য, \( l_1 = l \)

∴ বৃত্তের ব্যাস = \( l \) এবং লোহার বলয়ের দৈর্ঘ্য,
\( l_2 = \pi l \)

∴ \( \frac{l_2}{l_1} = \frac{\pi l}{l} = \pi \)

মনে করি, সংস্থাটির উষ্ণতা বৃদ্ধি = \( t \)

এখন লোহার দণ্ডের দৈর্ঘ্য, \( l’_1 = (1 + \alpha t) \) (যেখানে \( \alpha \) হল লোহার দৈর্ঘ্য প্রসারণ গুণাঙ্ক)

এবং লোহার বলয়ের দৈর্ঘ্য, \( l’_2 = \pi l(1 + \alpha t) \)

∴ \( \frac{l’_2}{l’_1} = \frac{\pi l(1 + \alpha t)}{l(1 + \alpha t)} = \pi \)

যেহেতু উভয়ক্ষেত্রেই বৃত্তের পরিধি ও ব্যাসের অনুপাত অপরিবর্তিত থাকে, তাই বলয়টি বৃত্তাকারই থাকবে।

জেনে রাখো – কঠিন পদার্থের দৈর্ঘ্য প্রসারণ গুণাঙ্ক পরিমাপের সময় যে-কোনো উষ্ণতাকে প্রাথমিক উষ্ণতা ধরা যেতে পারে, তবে সূক্ষ্ম পরিমাপের ক্ষেত্রে ০°C উষ্ণতাকে প্রাথমিক উষ্ণতা ধরা হয়। যে সমস্ত কঠিন পদার্থের গলনাঙ্ক কম তাদের দৈর্ঘ্য প্রসারণ গুণাঙ্কের মান কম।

একই তাপমাত্রা বৃদ্ধিতে একই দৈর্ঘ্যের সকল কঠিন পদার্থের কি একই প্রসারণ হয়? একটি পরীক্ষার সাহায্যে দেখাও।

একই তাপমাত্রা বৃদ্ধিতে একই দৈর্ঘ্যের সকল কঠিন পদার্থের একই প্রসারণ হয় না, সমদৈর্ঘ্যের বিভিন্ন কঠিন পদার্থের একই তাপমাত্রা বৃদ্ধিতে বিভিন্ন প্রসারণ হয়।

পরীক্ষা: একই দৈর্ঘ্যের লোহা, তামা ও পিতলের দণ্ড নেওয়া হলো। একটি দৈর্ঘ্য পরিমাপক যন্ত্রের সাহায্যে তিনটি দণ্ডের প্রাথমিক দৈর্ঘ্য মাপা হলো এবং দেখা গেল যে, তিনটি দণ্ডের দৈর্ঘ্য সমান। এরপর দণ্ড তিনটির তাপমাত্রা একই পরিমাণে বৃদ্ধি করা হলো। মনে করা যাক, প্রতিটি দণ্ডের তাপমাত্রা 100°C বৃদ্ধি করা হলো। এরপর প্রতিটি দণ্ডের অন্তিম দৈর্ঘ্য পরিমাপ করা হলো। অন্তিম দৈর্ঘ্য থেকে প্রাথমিক দৈর্ঘ্য বিয়োগ করে দেখা গেল যে, তামার চেয়ে পিতলের প্রসারণ বেশি হয়েছে, কিন্তু লোহার দৈর্ঘ্য প্রসারণ কম।

সিদ্ধান্ত – এই পরীক্ষা থেকে বোঝা যায় যে, সমদৈর্ঘ্যের বিভিন্ন কঠিন পদার্থের তাপমাত্রা একই পরিমাণ বৃদ্ধি করলে দৈর্ঘ্য প্রসারণ বিভিন্ন হয়।

দৈর্ঘ্য প্রসারণ গুণাঙ্কের মাত্রীয় সংকেত নির্ণয় করো ও মাত্রা লেখো।

দৈর্ঘ্য প্রসারণ গুণাঙ্ক, $\alpha =\frac{\text{দৈর্ঘ্য বৃদ্ধি}}{\text{প্রাথমিক দৈর্ঘ্য}\times \text{তাপমাত্রা বৃদ্ধি}}$

কঠিনের ক্ষেত্র প্রসারণ গুণাঙ্ক কাকে বলে?

কোনো কঠিন পদার্থের একক উষ্ণতা বৃদ্ধিতে, প্রতি একক ক্ষেত্রফলে যে ক্ষেত্র প্রসারণ হয় তাকে ওই কঠিন পদার্থের ক্ষেত্র প্রসারণ গুণাঙ্ক বলা হয়।

কঠিনের ক্ষেত্র প্রসারণ গুণাঙ্কের রাশিমালাটি লেখো।

মনে করা যাক, \( t_1 \) উষ্ণতায় কোনো কঠিন পদার্থে পৃষ্ঠতলের ক্ষেত্রফল \( S_1 \) এবং উষ্ণতা বৃদ্ধি করে \( t_2 \) করা হলে পৃষ্ঠতলের ক্ষেত্রফল হয় \( S_2 \); কঠিন পদার্থটির ক্ষেত্র প্রসারণ গুণাঙ্ক \( \beta \) হলে, \( \beta \) -এর সংজ্ঞানুসারে লেখা যায়,

\( \beta = \frac{S_2 – S_1}{S_1 (t_2 – t_1)} \)

কঠিন পদার্থের ক্ষেত্র প্রসারণ গুণাঙ্ক কিভাবে নির্ণয় করবে?

মনে করি, \( t_1 \) উষ্ণতায় কোনো কঠিন পদার্থের পৃষ্ঠতলের ক্ষেত্রফল \( S_1 \) এবং উষ্ণতা বৃদ্ধি করে \( t_2 \) করা হলে ক্ষেত্রফল হয় \( S_2 \);

∴ পদার্থটির ক্ষেত্র প্রসারণ = \( S_2 – S_1 \) এবং তাপমাত্রা বৃদ্ধি = \( (t_2 – t_1) \)

ক্ষেত্র প্রসারণ কঠিনের প্রাথমিক ক্ষেত্রফল ও উষ্ণতা বৃদ্ধির সমানুপাতিক।

\( (S_2 – S_1) \propto S_1 \) [\(যখন (t_2 – t_1) \)স্থির]

এবং \( (S_2 – S_1) \propto (t_2 – t_1) \quad \ \)[যখন \(S_1 \)স্থির]

∴ \( S_2 – S_1 = S_1 (t_2 – t_1) \quad \) যখন \([ S_1 ও (t_2 – t_1)\) উভয়েই পরিবর্তনশীল]

বা, \( S_2 – S_1 = S_1 \beta (t_2 – t_1) \) [যেখানে β একটি ধ্রুবক, যাকে কঠিন পদার্থটির ক্ষেত্র প্রসারণ গুণাঙ্ক বলে।]

বা, \( S_2 = S_1 \left(1 + \beta (t_2 – t_1)\right) \)

দেখাও যে, ক্ষেত্র প্রসারণ গুণাঙ্কের একক ক্ষেত্রফলের এককের ওপর নির্ভর করে না, শুধুমাত্র উষ্ণতার এককের ওপর নির্ভরশীল।

মনে করি, \( t_1 \) উষ্ণতায় কোনো কঠিন পদার্থের পৃষ্ঠতলের ক্ষেত্রফল \( S_1 \) এবং উষ্ণতা বৃদ্ধি করে \( t_2 \) করা হলে ক্ষেত্রফল হয় \( S_2 \)

∴ ক্ষেত্র প্রসারণ গুণাঙ্ক, \( \beta = \frac{S_2 – S_1}{S_1 (t_2 – t_1)} \) এবং, \( \beta = \frac{S_2 – S_1}{S_1} \) হল দুটি সমজাতীয় রাশির অনুপাত, তাই এককহীন। সুতরাং, ক্ষেত্র প্রসারণ গুণাঙ্কের একক শুধুমাত্র \( (t_2 – t_1) \) -এর একক বা উষ্ণতার এককের ওপর নির্ভরশীল।

ক্ষেত্র প্রসারণ গুণাঙ্কের মাত্রীয় সংকেত নির্ণয় করো ও মাত্রা লেখো।

ক্ষেত্র প্রসারণ গুণাঙ্ক, $\beta =\frac{\text{ক্ষেত্র প্রসারণ}}{\text{প্রাথমিক ক্ষেত্রফল}\times \text{তাপমাত্রা বৃদ্ধি}}$

∴ \( \beta \) -এর মাত্রীয় সংকেত = \( \frac{L^2}{L^2} \times \Theta = \Theta^{-1} \)

∴ ক্ষেত্র প্রসারণ গুণাঙ্কের মাত্রা হল তাপমাত্রায় –1।

কঠিন পদার্থের আয়তন প্রসারণ গুণাঙ্ক কাকে বলে?

কোনো কঠিন পদার্থের প্রতি একক উষ্ণতা বৃদ্ধিতে, প্রতি একক আয়তনে যে আয়তন প্রসারণ হয়, তাকে ওই পদার্থের আয়তন প্রসারণ গুণাঙ্ক বলা হয়।

জেনে রাখো – বিশুদ্ধ সিলিকনের তাপমাত্রা 18 K থেকে 120 K পর্যন্ত বৃদ্ধি করলে আয়তন কমে যায়।

কঠিনের আয়তন প্রসারণ গুণাঙ্কের রাশিমালাটি লেখো।

মনে করা যাক, $t_1$ উষ্ণতায় কোনো কঠিন পদার্থের আয়তন $V_1$ এবং উষ্ণতা বৃদ্ধি করে $t_2$ করা হলে আয়তন হয় $V_2$। কঠিন পদার্থটির আয়তন প্রসারণ গুণাঙ্ক $\gamma$ হলে, $\gamma$ -এর সংজ্ঞানুসারে লেখা যায়,

$\gamma =\frac{V_2–V_1}{V_1{\mathrm{(t}}_2–t_{\mathrm{1)}}}$

দেখাও যে, আয়তন প্রসারণ গুণাঙ্কের একক আয়তনের এককের ওপর নির্ভর করে না, শুধুমাত্র তাপমাত্রার এককের ওপর নির্ভরশীল।

মনে করি, V₁ আয়তনের কোনো কঠিন পদার্থের তাপমাত্রা t₁ থেকে বৃদ্ধি করে t₂ করা হলে অন্তিম আয়তন হয় V₂।

∴ আয়তন প্রসারণ গুণাঙ্ক, $\gamma =\frac{\mathrm{আয়তন\; প্রসারণ}}{\mathrm{প্রাথমিক\; আয়তন}\times \mathrm{উষ্ণতা\; বৃদ্ধি}}$

∴ আয়তন প্রসারণ গুণাঙ্কের একক$=\frac{\mathrm{আয়তনের\; একক}}{\mathrm{আয়তনের\; একক}\times \mathrm{উষ্ণতার\; একক}}=\frac{1}{\mathrm{উষ্ণতার\; একক}}$

∴ আয়তন প্রসারণ গুণাঙ্কের একক শুধুমাত্র উষ্ণতার এককের ওপর নির্ভরশীল।

আয়তন প্রসারণ গুণাঙ্কের মাত্রীয় সংকেত নির্ণয় করো ও মাত্রা লেখো।

আয়তন প্রসারণ গুণাঙ্ক, $\gamma =\frac{\mathrm{আয়তন\; প্রসারণ}}{\mathrm{প্রাথমিক\; আয়তন}\times \mathrm{উষ্ণতা\; বৃদ্ধি}}$

∴ γ এর মাত্রীয় সংকেত =$\frac{L^3}{L^3\times \Theta }={\Theta }^{–1}$

∴ আয়তন প্রসারণ গুণাঙ্কের মাত্রা হল তাপমাত্রায় –1।

লোহার আয়তন প্রসারণ গুণাঙ্ক 36 × 10⁻⁶/°C বলতে কী বোঝা যায়?

লোহার আয়তন প্রসারণ গুণাঙ্ক 36 × 10⁻⁶/°C বলতে বোঝায়, লোহার তাপমাত্রা ১°C বৃদ্ধি করলে প্রাথমিক আয়তনের 36 × 10⁻⁶ অংশ বৃদ্ধি পায়।

বিকল্প উত্তর: লোহার আয়তন প্রসারণ গুণাঙ্ক 36 × 10^-6/°C বলতে বোঝায়, 1 cm³ বা 1 m³ লোহার তাপমাত্রা 1°C বৃদ্ধি করলে লোহার আয়তন যথাক্রমে 36 × 10^-6 cm³ বা 36 × 10^-6 m³ বৃদ্ধি পাবে।

ধাতব স্কেল যে উষ্ণতায় তৈরি, সেই উষ্ণতা ছাড়া সঠিক পাঠ দেয় না কেন?

একটি ধাতব স্কেলের উষ্ণতা বৃদ্ধি বা হ্রাস পেলে স্কেলের দৈর্ঘ্য পরিবর্তিত হয়, অর্থাৎ, স্কেল প্রসারিত বা সংকুচিত হয়। এর ফলে অংশাঙ্কিত দাগগুলোর মধ্যবর্তী দূরত্বও বৃদ্ধি বা হ্রাস পায়। এজন্য ধাতব স্কেলটি যে উষ্ণতায় অংশাঙ্কিত, শুধুমাত্র সেই উষ্ণতাতেই এটি সঠিক পাঠ দেয়। যখন উষ্ণতা বৃদ্ধি পায়, স্কেল প্রদর্শিত পাঠ অপেক্ষা প্রকৃত পাঠ বেশি হয়, এবং উষ্ণতা হ্রাস পেলে স্কেল প্রদর্শিত পাঠ অপেক্ষা প্রকৃত পাঠ কম হয়।

ঢালাইয়ের সময় কেন লোহার রডই ব্যবহার করা হয়, অন্য ধাতুর রড নেওয়া হয় না কেন?

ঢালাইয়ের সময় লোহাকে কংক্রিটের মধ্যে প্রবেশ করিয়ে দেওয়া হয়। গ্রীষ্মকালে তাপমাত্রা বেশি থাকায়, কংক্রিট এবং রড উভয়েরই তাপীয় প্রসারণ ঘটে। শীতকালে তাপমাত্রা কম হলে উভয়ই সংকুচিত হয়। লোহা ও কংক্রিটের প্রসারণ গুণাঙ্ক প্রায় সমান হওয়ায়, লোহার রডই কংক্রিটের সঙ্গে সামঞ্জস্যপূর্ণ হয়। যদি অন্য ধাতুর রড ব্যবহার করা হয়, তবে সেই ধাতুর প্রসারণ ও সংকোচন কংক্রিটের চেয়ে আলাদা হবে, ফলে ঢালাই ফেটে যেতে পারে।

অভিন্ন আকারের একটি তামার পাত এবং একটি লোহার পাতকে রিভেট করে যুক্ত করা হলো। এই সংস্থাটিকে উত্তপ্ত করলে কী ঘটবে?

তামার দৈর্ঘ্য প্রসারণ গুণাঙ্ক লোহার চেয়ে বেশি। ফলে একই তাপমাত্রায় উত্তপ্ত করলে তামার প্রসারণ লোহার চেয়ে বেশি হবে। যেহেতু দুটি পাত রিভেট করে যুক্ত করা হয়েছে, উত্তপ্ত হলে সংস্থাটি বেঁকে যাবে। তামার প্রসারণ বেশি হওয়ায় এটি বাঁকের বাইরের দিকে থাকবে।

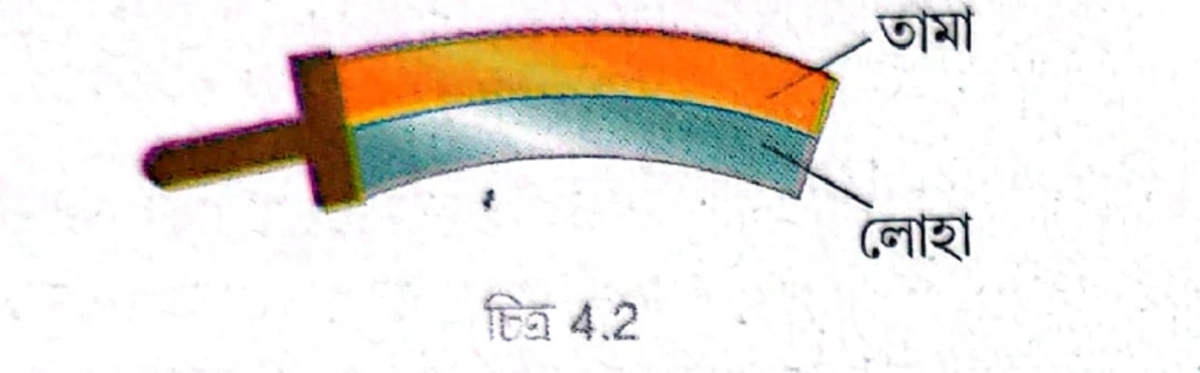
অভিন্ন আকারের একটি তামার পাত এবং একটি লোহার পাতকে রিভেট করে যুক্ত করা হলো। এই সংস্থাটির তাপমাত্রা হ্রাস করলে কী ঘটবে?

তামার দৈর্ঘ্য প্রসারণ গুণাঙ্ক লোহার চেয়ে বেশি, তাই একই তাপমাত্রা হ্রাস করলে তামার দৈর্ঘ্য সংকোচন লোহার চেয়ে বেশি হবে। যেহেতু দুটি পাত রিভেট করে যুক্ত করা হয়েছে, তাপমাত্রা হ্রাসে সংস্থাটি বেঁকে যাবে। তামার সংকোচন বেশি হওয়ায় এটি বাঁকের ভেতরের দিকে থাকবে।

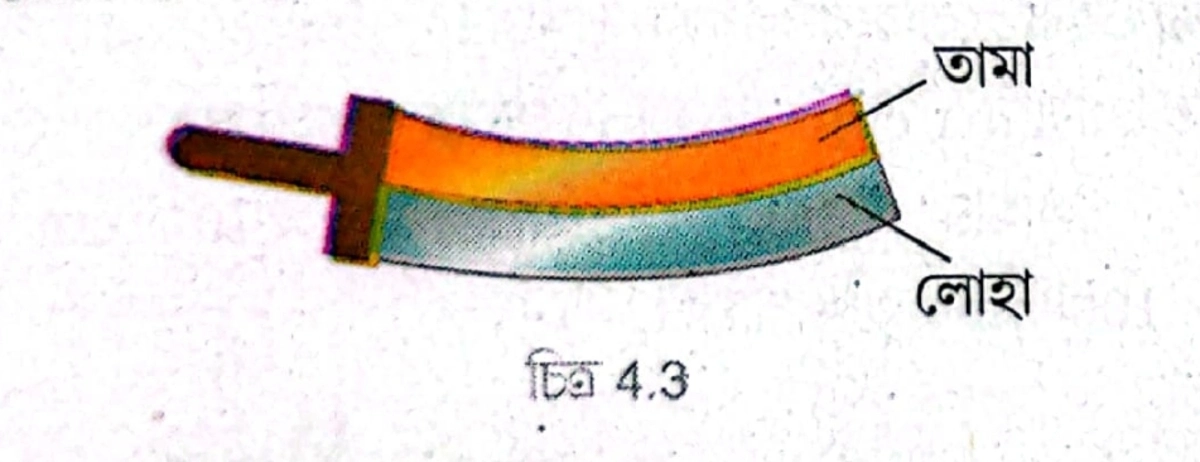
একটি সহজ পরীক্ষার সাহায্যে তরলের আপাত প্রসারণ ও প্রকৃত প্রসারণ বোঝাও।

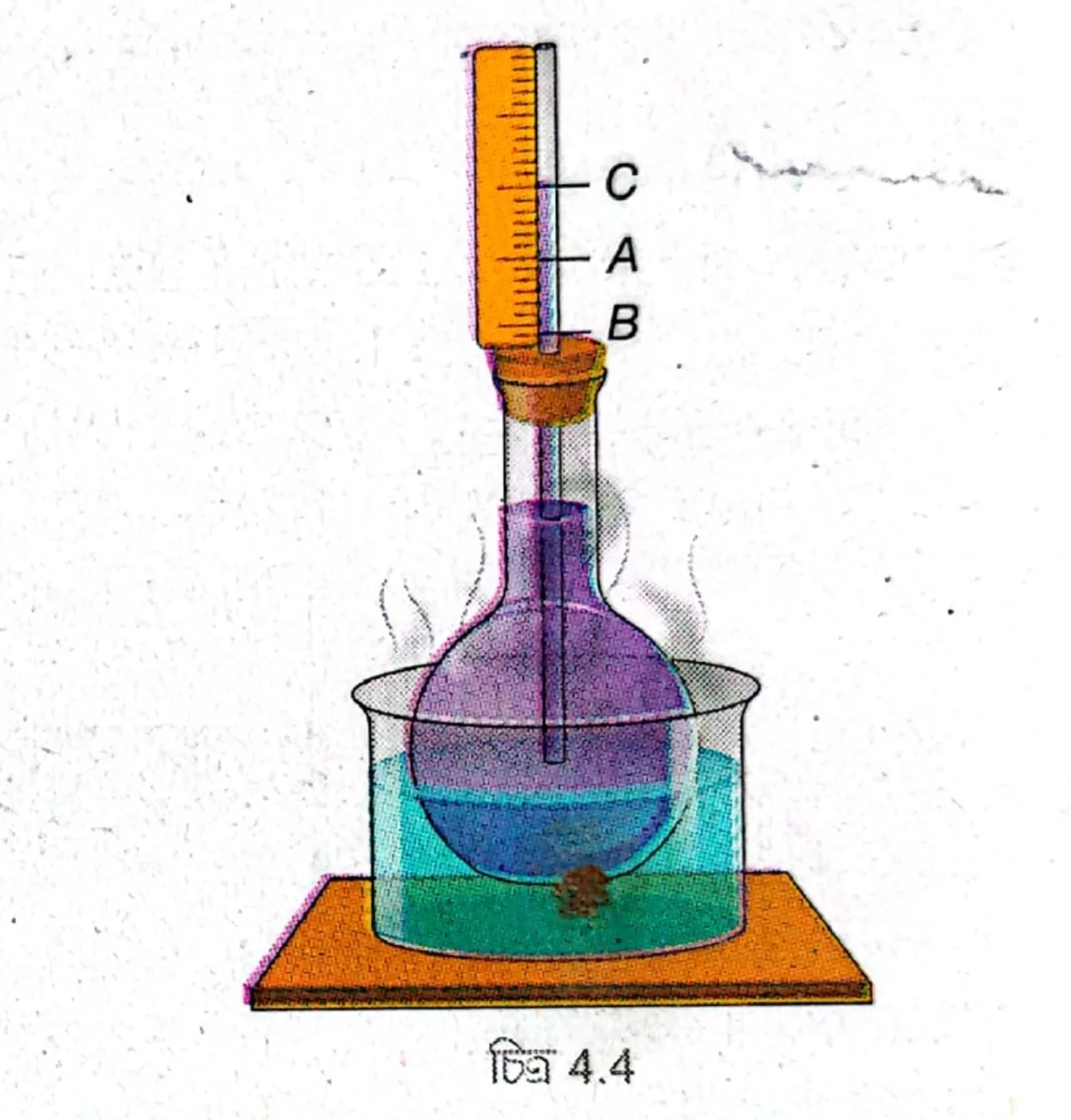
পরীক্ষা: প্রথমে ছিপিযুক্ত একটি কাচের ফ্লাস্ক নেওয়া হলো। ছিপির মধ্য দিয়ে একটি সরু কাচের নল প্রবেশ করানো হলো এবং নলের গায়ে একটি স্কেল যুক্ত করা হলো। কাচের ফ্লাস্ক ও নলের কিছুটা অংশ পর্যন্ত রঙিন তরল দিয়ে পূর্ণ করা হলো। নলে তরলের প্রাথমিক স্তর হলো A। এখন ফ্লাস্কটিকে গরম জলে পূর্ণ একটি পাত্রে ডোবানো হলো। দেখা যাবে, নলে তরলের স্তর A থেকে নেমে B-তে এলো। এরপর তরলের স্তর ধীরে ধীরে উঠতে থাকল এবং কিছুক্ষণ পর C-তে এসে স্থির হলো।

সিদ্ধান্ত: ফ্লাস্কটিকে গরম জলে ডোবানোর ফলে কাচ গরম জল থেকে তাপ সংগ্রহ করে প্রসারিত হয়, তাই নলে তরলের স্তর A থেকে নেমে B-তে আসে। এরপর, কাচের মাধ্যমে তাপ তরলে সঞ্চালিত হয় এবং তরল প্রসারিত হতে শুরু করে। তাই নলে তরলের স্তর আবার ওপরে উঠতে থাকে। যেহেতু কাচ তাপের কুপরিবাহী, তাই প্রথমে কাচের পাত্র প্রসারিত হয় এবং পরে তরল প্রসারিত হয়। ফলে প্রথমে তরলের স্তর নিচে নামে এবং পরে ওপরে উঠতে শুরু করে। অবশেষে তরল একটি স্থির তাপমাত্রায় উপনীত হলে নলে তরলের স্তর C-তে স্থির হয়।

এই পরীক্ষা থেকে বোঝা যায় যে, AB দৈর্ঘ্যের আয়তন হলো পাত্রের প্রসারণ এবং BC দৈর্ঘ্যের আয়তন হলো তরলের প্রকৃত প্রসারণ। পাত্রের প্রসারণকে অগ্রাহ্য করলে তরলের যে প্রসারণ হয়, তা হলো আপাত প্রসারণ। নলের AC দৈর্ঘ্যের আয়তন তরলের আপাত প্রসারণ বোঝায়।

যেহেতু BC = AB + AC

∴ তরলের প্রকৃত প্রসারণ = পাত্রের আয়তন প্রসারণ + তরলের আপাত প্রসারণ

তরলের আপাত প্রসারণ ও প্রকৃত প্রসারণ কাকে বলে?

তরলের আপাত প্রসারণ: কোনো তরল পদার্থকে যে পাত্রে রেখে উত্তপ্ত করা হয়, সেই পাত্রের প্রসারণকে অগ্রাহ্য করলে, তরলের যে প্রসারণ পাওয়া যায়, তাকে ওই তরলের আপাত প্রসারণ বলা হয়।

তরলের প্রকৃত প্রসারণ: কোনো তরল পদার্থকে যে পাত্রে রেখে উত্তপ্ত করা হয়, সেই পাত্রের প্রসারণকে তরলের আপাত প্রসারণের সাথে যুক্ত করলে তরলের যে প্রসারণ পাওয়া যায়, তাকে ওই তরলের প্রকৃত প্রসারণ বলা হয়।

তরলের আপাত প্রসারণ গুণাঙ্ক ও প্রকৃত প্রসারণ গুণাঙ্ক কাকে বলে?

তরলের আপাত প্রসারণ গুণাঙ্ক: কোনো তরলের প্রতি একক তাপমাত্রা বৃদ্ধিতে, প্রতি একক আয়তনে যে আপাত প্রসারণ ঘটে, তাকে তরলের আপাত প্রসারণ গুণাঙ্ক বলে।

তরলের প্রকৃত প্রসারণ গুণাঙ্ক: কোনো তরলের প্রতি একক তাপমাত্রা বৃদ্ধিতে, প্রতি একক আয়তনে যে প্রকৃত প্রসারণ ঘটে, তাকে তরলের প্রকৃত প্রসারণ গুণাঙ্ক বলে।

তরলের আপাত প্রসারণ গুণাঙ্কের রাশিমালাটি লেখো

মনে করি, \(t_1\)​ উষ্ণতায় নির্দিষ্ট ভরের কোনো তরল পদার্থের আয়তন \(V_1\)​ এবং উষ্ণতা বৃদ্ধি করে \(t_2\)​ করা হলে তরলটির আপাত আয়তন হয় \(V’_2​\)।

তাহলে, তরলের আপাত প্রসারণ গুণাঙ্ক,\(
\gamma_{\alpha} = \frac{V’_2 – V_1}{V_1 (t_2 – t_1)}
\)

তরলের প্রকৃত প্রসারণ গুণাঙ্কের রাশিমালাটি লেখো।

মনে করি, \(t_1\) উষ্ণতায় নির্দিষ্ট ভরের কোনো তরল পদার্থের আয়তন \(V_1\)​ এবং উষ্ণতা বৃদ্ধি করে \(t_2\) করা হলে তরলটির প্রকৃত আয়তন হয় \(V_2​[latex]।

তাহলে, তরলের প্রকৃত প্রসারণ গুণাঙ্ক,[latex]
\gamma_r = \frac{V_2 – V_1}{V_1 (t_2 – t_1)}
\)

জেনে রাখো, সাধারণত তরলের প্রসারণ গুণাঙ্ক উষ্ণতার বিভিন্ন পাল্লায় একই ধরে নেওয়া হয়, কিন্তু বাস্তবে বিভিন্ন উষ্ণতায় তরলের প্রসারণ গুণাঙ্ক একই হয় না। তাই সূক্ষ্ম পরিমাপের ক্ষেত্রে, 0°C উষ্ণতার আয়তনকে প্রাথমিক আয়তন ধরে নেওয়া হয়।

তরলের প্রকৃত প্রসারণ কোন্ কোন্ বিষয়ের ওপর নির্ভরশীল?

তরলের প্রকৃত প্রসারণ নিম্নলিখিত বিষয়গুলির ওপর নির্ভরশীল –

• তরলের প্রাথমিক আয়তন।
• উষ্ণতা বৃদ্ধি।
• তরলের প্রকৃতি।

তরলের আপাত প্রসারণ কোন্ কোন্ বিষয়ের ওপর নির্ভরশীল?

তরলের আপাত প্রসারণ নিম্নলিখিত বিষয়গুলির ওপর নির্ভরশীল –

• তরলের প্রাথমিক আয়তন।
• উষ্ণতা বৃদ্ধি।
• তরলের প্রকৃতি।
• পাত্রের উপাদান।

কোনো তরলের আপাত ও প্রকৃত প্রসারণ গুণাঙ্কের মধ্যে কোনটি তরলের নিজস্ব ধর্ম?

কোনো তরলের প্রকৃত প্রসারণ গুণাঙ্ক তার নিজস্ব ধর্ম। আপাত প্রসারণ গুণাঙ্ক পাত্রের আয়তন প্রসারণ গুণাঙ্কের ওপর নির্ভরশীল। নির্দিষ্ট তরলকে বিভিন্ন উপাদানের পাত্রে রাখলে আপাত প্রসারণ গুণাঙ্ক বিভিন্ন হয়, কিন্তু প্রকৃত প্রসারণ গুণাঙ্ক অপরিবর্তিত থাকে। তাই, প্রকৃত প্রসারণ গুণাঙ্ক হলো তরলের নিজস্ব ধর্ম।

লম্ব-বৃত্তাকার চোঙাকৃতি একটি পাত্রে তরল আছে। পাত্রটিকে উত্তপ্ত করলে পাত্রে তরলের স্তরের কোনো পরিবর্তন হয় না। এটি কীভাবে সম্ভব?

নির্দিষ্ট উষ্ণতা বৃদ্ধিতে পাত্র ও তরল উভয়েরই আয়তন প্রসারণ যদি একই হয় তাহলে পাত্রে তরলের স্তরের কোনো পরিবর্তন হয় না। এক্ষেত্রে তরলের আপাত প্রসারণ গুণাঙ্ক শূন্য হয়।

জেনে রাখো – কোনো তরলের আপাত ও প্রকৃত প্রসারণ গুণাঙ্ক যথাক্রমে γ_a ও γ_r এবং তরলকে যে পাত্রে রাখা হয়েছে তার আয়তন প্রসারণ গুণাঙ্ক γ_g হলে, γ_r = γ_a + γ_g

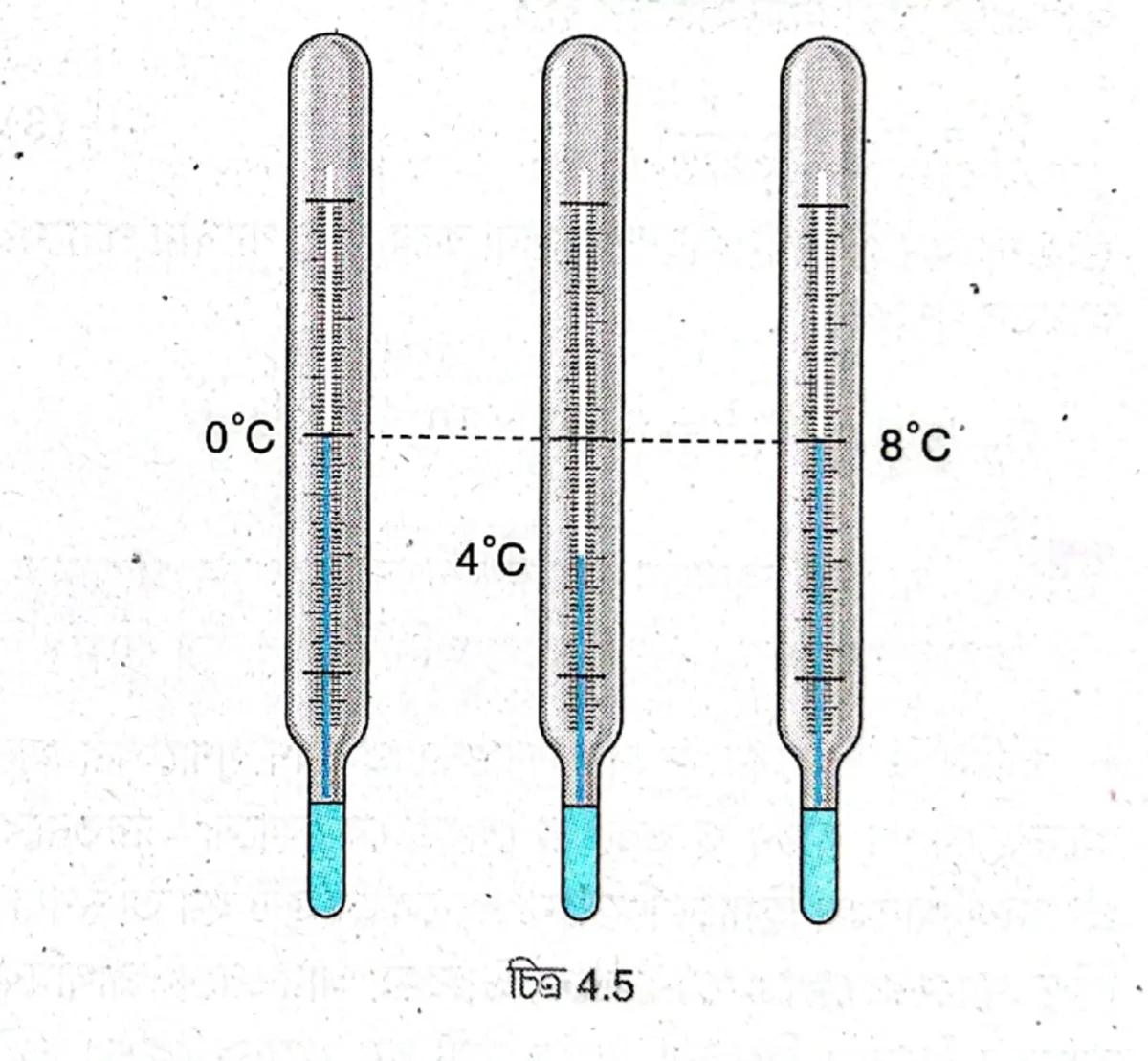
একটি থার্মোমিটারেএ ভুল করে পারদের পরিবর্তে জল দেওয়া হয়েছে। 0°C থেকে ৪°C পর্যন্ত উষ্ণতা বৃদ্ধির ক্ষেত্রে কী লক্ষ্য করবে?

0°C থেকে উষ্ণতা বৃদ্ধি করতে থাকলে দেখা যাবে থার্মোমিটাররের নলে জলের স্তর কমছে এবং 4°C তে সেটি সর্বনিম্ন হবে। এরপর পাঠ বাড়তে থাকলে এবং 8°C উষ্ণতায় পাঠ 0°C উষ্ণতায় পাঠের প্রায় সমান হবে। এর কারণ হলো জলের ব্যতিক্রমী প্রসারণ। নির্দিষ্ট ভরের জলের উষ্ণতা 0°C থেকে বৃদ্ধি করতে থাকলে 4°C পর্যন্ত জলের আয়তন হ্রাস পায়, এরপর অন্যান্য তরলের মতো উষ্ণতা বৃদ্ধি করলে আয়তন বাড়ে। 8°C উষ্ণতায় জলের আয়তন 0°C উষ্ণতায় আয়তনের প্রায় সমান হয়।

গ্যাসের তাপীয় প্রসারণের কয়েকটি উদাহরণ দাও।

গ্রীষ্মকালে প্রখর রোদে দাঁড়িয়ে থাকা সাইকেলের টায়ার অনেক সময় ফেটে যায়। কারণ, উচ্চ তাপমাত্রায় টায়ারের ভিতরে থাকা বায়ু প্রসারিত হয়। সাইকেলের টায়ার যদি সম্পূর্ণ বায়ুতে পূর্ণ থাকে, তবে বায়ু প্রসারণের ফলে সেটি ফেটে যায়। আবার, একটি বেলুন ফুলিয়ে জ্বলন্ত উনুনের ওপরে ধরলে বেলুনটি একই কারণে ফেটে যায়।

গ্যাসের আয়তন গুণাঙ্ক (${\gamma }_p$) কাকে বলে?

চাপ স্থির রেখে নির্দিষ্ট ভরের কোনো গ্যাসের উষ্ণতা 0°C থেকে 1°C বৃদ্ধি করলে গ্যাসের প্রতি একক আয়তনে যে আয়তন প্রসারণ হয়, তাকে ওই গ্যাসের আয়তন গুণাঙ্ক বলা হয়।

গ্যাসের আয়তন গুণাঙ্কের রাশিমালাটি লেখো এবং চার্লসের সূত্রের সাহায্যে এর মান নির্ণয় করো।

মনে করা যাক, স্থির চাপে নির্দিষ্ট ভরের কোনো গ্যাসের 0°C উষ্ণতায় আয়তন \(V_0\)​ এবং উষ্ণতা বৃদ্ধি করে t°C করা হলে গ্যাসের আয়তন হয় \(V_t\)​। আয়তন গুণাঙ্কের সংজ্ঞানুসারে লেখা যায়,

\(
\gamma_p = \frac{V_t – V_0}{V_0 t} \quad \text{——(1)}
\)

(1) নং সমীকরণ থেকে পাই,
\( V_t – V_0 = V_0 \gamma_p \cdot t \)

বা, \( V_t = V_0 + V_0 \gamma_p t \)

বা, \( V_t = V_0 (1 + \gamma_p t) \quad \text{——(2)} \)

আবার, চার্লসের সূত্র থেকে পাই, স্থির চাপে নির্দিষ্ট ভরের কোনো গ্যাসের ০°C উষ্ণতায় আয়তন V0V_0V0​ এবং উষ্ণতা বৃদ্ধি করে ১°C করা হলে আয়তন হবে,

\(
V_t = V_0 \left( 1 + \frac{t}{273} \right) \quad \text{——(3)}
\)

(2) নং ও (3) নং সমীকরণ তুলনা করে পাই, গ্যাসীয় পদার্থের আয়তন গুণাঙ্ক, \( \gamma_p = \frac{1}{273^\circ C} – 1 = 3.663 \times 10^{-3} , \text{°C}^{-1} \)

গ্যাসের আয়তন প্রসারণ গণনার ক্ষেত্রে প্রাথমিক আয়তনের জন্য 0°C উষ্ণতাকে নির্দিষ্ট ধরা হয় কেন?

কঠিন ও তরলের তুলনায় গ্যাসের প্রসারণ গুণাঙ্কের মান অনেক বেশি। কঠিন ও তরলের ক্ষেত্রে যে-কোনো আয়তনকে প্রাথমিক আয়তন হিসেবে বিবেচনা করলে যে ত্রুটি হয় তা নগণ্য। কিন্তু গ্যাসের ক্ষেত্রে যে-কোনো উষ্ণতার আয়তনকে প্রাথমিক আয়তন হিসেবে বিবেচনা করলে ত্রুটি হয় অনেক বেশি। তাই গ্যাসের ক্ষেত্রে প্রাথমিক আয়তনের জন্য 0°C উষ্ণতাকে নির্দিষ্ট উষ্ণতা হিসেবে ধরা হয়।

তরলের আপাত প্রসারণ গুণাঙ্ক আছে, কিন্তু গ্যাসের ক্ষেত্রে আপাত প্রসারণ গুণাঙ্ক ধরা হয় না কেন?

তরল বা গ্যাস উভয় পদার্থকে কোনো পাত্রে রেখে উত্তপ্ত করতে হয়, ফলে তরল বা গ্যাসের প্রসারণের সঙ্গেই পাত্রেরও প্রসারণ হয়। তরলের প্রসারণের তুলনায় কঠিনের প্রসারণ কম হলেও উপেক্ষা করা যায় না। কিন্তু গ্যাসের প্রসারণের তুলনায় কঠিনের প্রসারণ প্রায় 1000 অংশ, তাই এক্ষেত্রে পাত্রের প্রসারণ বিবেচনা করা হয় না। এই কারণে তরলের আপাত প্রসারণ আছে কিন্তু গ্যাসের ক্ষেত্রে আপাত প্রসারণ গুণাঙ্ক ধরা হয় না।

পরিবহণ কাকে বলে?

তাপ সঞ্চালনের যে পদ্ধতিতে কোনো পদার্থের উষ্ণতর স্থান থেকে শীতলতর স্থানে অণুগুলির কম্পনের দ্বারা তাপ সঞ্চালিত হয় কিন্তু অণুগুলির কোনো স্থানচ্যুতি হয় না তাকে পরিবহণ বলা হয়।

পরিবহণ পদ্ধতিতে তাপ সঞ্চালনের বৈশিষ্ট্যগুলি লেখো।

পরিবহণ পদ্ধতিতে তাপ সঞ্চালনের বৈশিষ্ট্য –

• পরিবহণ পদ্ধতিতে তাপ পদার্থের উষ্ণতর স্থান থেকে শীতলতর স্থানে অণুগুলির কম্পনের দ্বারা সঞ্চালিত হয়।
• পরিবহণ পদ্ধতিতে তাপ সঞ্চালনের জন্য জড় মাধ্যমের প্রয়োজন।
• পরিবহণ মন্থর পদ্ধতি।
• পরিবহণ পদ্ধতিতে তাপ সঞ্চালনের সময় মাধ্যম উত্তপ্ত হয়।
• পরিবহণ পদ্ধতিতে তাপ সঞ্চালনের সময় সেই মাধ্যমের অণুগুলির স্থানচ্যুতি হয় না।
• পরিবহণ পদ্ধতিতে তাপ সরল বা বক্রপথে সঞ্চালিত হতে পারে।

তাপ পরিবহণের ক্ষেত্রে স্থিতপূর্ব অবস্থা ও স্থিতাবস্থা কাকে বলে?

স্থিতপূর্ব অবস্থা: কোনো দণ্ডের মধ্য দিয়ে যখন তাপের পরিবহণ হয় তখন দণ্ডের বিভিন্ন স্তরে যদি তাপের পরিবহণ ও শোষণ একই সঙ্গে চলতে থাকে, তাহলে দণ্ডের এই তাপীয় অবস্থাকে স্থিতপূর্ব অবস্থা বলা হয়।

স্থিতাবস্থা: কোনো দণ্ডের মধ্য দিয়ে যখন তাপের পরিবহণ হয় তখন দণ্ডের বিভিন্ন স্তরে যদি তাপের শুধুমাত্র পরিবহণ হয়, কোনো রকম শোষণ না হয়, ফলে প্রতিটি স্তরের উষ্ণতা স্থির থাকে, তাহলে দণ্ডের এই তাপীয় অবস্থাকে স্থিতাবস্থা বলা হয়।

তাপের সুপরিবাহী ও কুপরিবাহী পদার্থ কাকে বলে?

তাপের সুপরিবাহী পদার্থ: যেসব পদার্থের মধ্য দিয়ে তাপ সহজে পরিবাহিত হয়, তাদের তাপের সুপরিবাহী পদার্থ বলা হয়।

তাপের কুপরিবাহী পদার্থ: যেসব পদার্থের মধ্য দিয়ে তাপ সহজে পরিবাহিত হয় না, তাদের তাপের কুপরিবাহী পদার্থ বলা হয়।

একটি পরীক্ষার সাহায্যে দেখাও যে, বিভিন্ন পদার্থের তাপ পরিবহণ ক্ষমতা বিভিন্ন।

পরীক্ষা: একটি আয়তক্ষেত্রাকার ধাতব পাত্রের একটি বৃহত্তর উল্লম্ব তলে তিনটি ছিদ্র করে একই দৈর্ঘ্য ও প্রস্থচ্ছেদের তিনটি ভিন্ন ধাতব দণ্ড যেমন – তামা, অ্যালুমিনিয়াম, ও লোহাকে রবারের ছিপির সাহায্যে ছিদ্রের মধ্য দিয়ে সমান দূরত্ব পর্যন্ত প্রবেশ করিয়ে দণ্ডগুলির বাইরের অংশে সমান বেধের মোমের প্রলেপ লাগানো হল। এবার ধাতব পাত্রে জল নিয়ে বুনসেন বার্নারের সাহায্যে পাত্রটিকে উত্তপ্ত করা হল যাতে জল ফুটতে শুরু করে। এই অবস্থায় দণ্ড বরাবর তাপের পরিবহণ হবে। কোনো নির্দিষ্ট দণ্ডের যে অংশের উষ্ণতা মোমের গলনাঙ্কের সমান বা বেশি হবে, সেখানে মোম গলে যাবে। কিছুক্ষণ পর দেখা যাবে, বিভিন্ন দণ্ডে বিভিন্ন দৈর্ঘ্য পর্যন্ত মোম গলেছে।

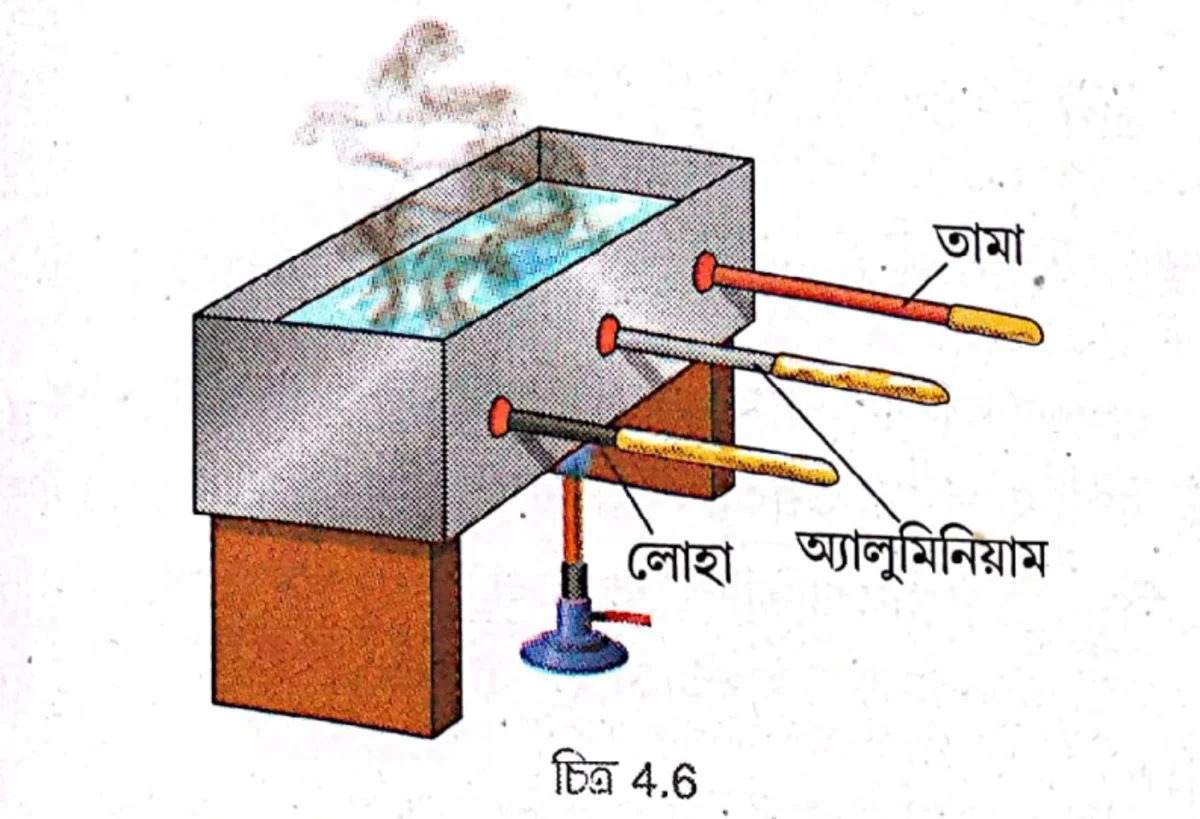
সিদ্ধান্ত: এই পরীক্ষা থেকে বোঝা যায় যে, বিভিন্ন পদার্থের তাপ পরিবহণ ক্ষমতা বিভিন্ন। তামা, অ্যালুমিনিয়াম ও লোহার দণ্ডে যথাক্রমে l₁, l₂ ও l₃ দূরত্ব পর্যন্ত মোম গললে দেখা যায় l₁ > l₂ > l₃।

কোনো আয়তাকার ফলকের বেধ, ক্ষেত্রফল ও দুই পৃষ্ঠের উষ্ণতার পার্থক্য দ্বারা তাপ পরিবাহিতাঙ্কের রাশিমালাটি প্রতিষ্ঠা করো।

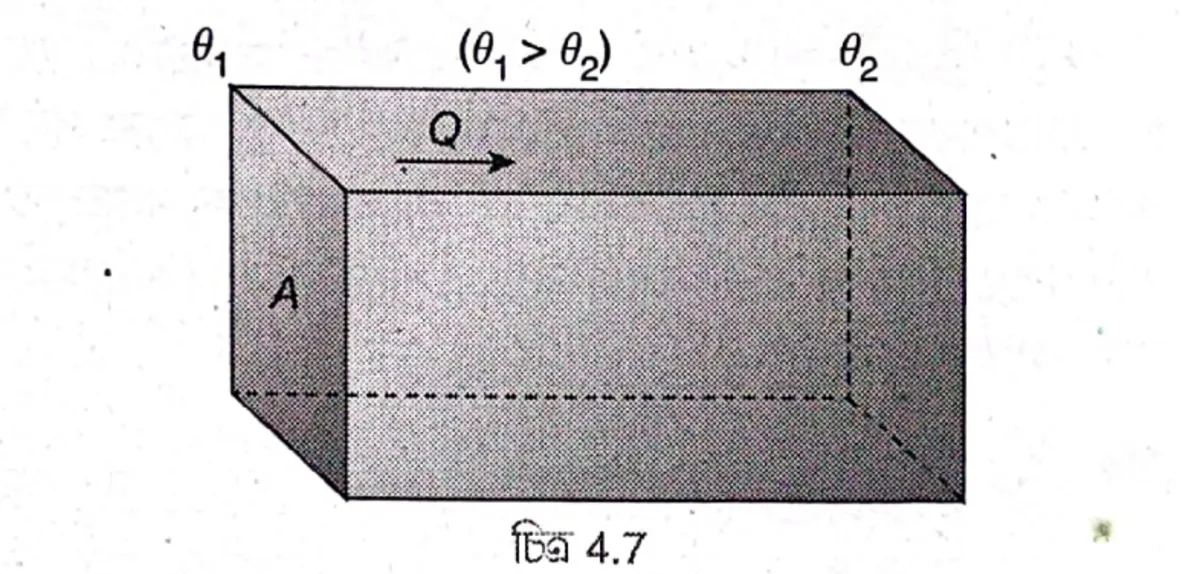
মনে করি, কোনো পদার্থের একটি আয়তাকার ফলকের বেধ d, প্রস্থচ্ছেদের ক্ষেত্রফল A এবং দুই বিপরীত পৃষ্ঠের উষ্ণতা যথাক্রমে \( \theta_1\) ​ ও \( \theta_2\) ​ (যেখানে \( \theta_1 > \theta_2\) ​)।

স্থিতাবস্থায় t সময়ে উষ্ণতর পৃষ্ঠ থেকে শীতলতর পৃষ্ঠের দিকে লম্বভাবে Q পরিমাণ তাপ পরিবাহিত হলে,

(i) \( Q \propto A \)

(ii) \( Q \propto \theta_1 – \theta_2 \)

(iii) \( Q \propto \frac{1}{d} \)

(iv) \( Q \propto t \)

যৌগিক ভেদের সূত্র থেকে পাই,

\( k \propto A (\theta_1 – \theta_2) \frac{t}{d} \)

বা, \( Q = kA (\theta_1 – \theta_2) \frac{t}{d} \)

∴ \( k = \frac{Q \cdot d}{A (\theta_1 – \theta_2) t} \)

যেখানে k একটি ধ্রুবক, যাকে ওই পদার্থের তাপ পরিবাহিতাঙ্ক বলা হয়।

তাপ পরিবাহিতাঙ্ক কাকে বলে?

একক বেধ ও একক প্রস্থচ্ছেদের ক্ষেত্রফলযুক্ত কোনো পদার্থের দুই বিপরীত পৃষ্ঠের উষ্ণতার পার্থক্য একক হলে তলের সঙ্গে লম্বভাবে একক সময়ে যে তাপ পরিবাহিত হয় তাকে ওই পদার্থের তাপ পরিবাহিতাঙ্ক বলা হয়।

তাপ পরিবাহিতাঙ্কের মাত্রীয় সংকেত নির্ণয় করো।

কোনো পদার্থের একটি আয়তাকার ফলকের বেধ d, প্রস্থচ্ছেদের ক্ষেত্রফল A ও দুই বিপরীত পৃষ্ঠের উষ্ণতা যথাক্রমে ${\theta }_1$ ও ${\theta }_2$(${\theta }_1>{\theta }_2$) হলে যদি স্থিতাবস্থায় t সময়ে তলের সঙ্গে লম্বভাবে Q পরিমাণ তাপ পরিবাহিত হয় তাহলে,

$Q=\frac{k\mathrm{A(}{\theta }_1–{\theta }_2\mathrm{)t}}{d}$
বা, $k=\frac{Qd}{\mathrm{A(}{\theta }_1–{\theta }_2)·t}$

তাপ পরিবাহিতাঙ্কের মাত্রীয় সংকেত

= \(\frac{\left[Q\right]\cdot\left[d\right]}{\left[A\right]\cdot\left[\left(\theta_1-\theta_2\right)\right]\cdot t}\)

= \(\frac{ML^2T^{-2}\times L}{L^2\times\Theta\times T}\)

= \(MLT^{-3}\Theta^{-1}\)

তাপ পরিবাহিতাঙ্কের CGS পদ্ধতি ও SI -তে এককের মধ্যে সম্পর্ক স্থাপন করো।

তাপ পরিবাহিতাঙ্কের CGS পদ্ধতি ও SI -তে একক হল যথাক্রমে cal⋅cm^-1⋅°C^-1⋅s^-1 ও W⋅m^-1⋅K^-1

∴ 1 cal⋅cm^-1⋅C^-1⋅s^-1

= 4.2 J⋅(10^-2 m)^-1⋅K^-1⋅s^-1

= 420 W⋅m^-1⋅K^-1 [∵ 1 J⋅s^-1 = 1 W]

বিভিন্ন পদার্থের তাপ পরিবাহিতাঙ্কের তালিকা

বিভিন্ন পদার্থের তাপ পরিবাহিতাঙ্কের তালিকা [18 °C তাপমাত্রার]

পদার্থ	তাপ পরিবাহিতাঙ্ক k(cal⋅cm-1⋅°C-1⋅s-1)	পদার্থ	তাপ পরিবাহিতাঙ্ক k(cal⋅cm-1⋅°C-1⋅s-1)	পদার্থ	তাপ পরিবাহিতাঙ্ক k(cal⋅cm-1⋅°C-1⋅s-1)
হিরে	2.13	অ্যালুমিনিয়াম	0.48	কাঠ	0.0003
রুপো	0.97	পিতল	0.26	কর্ক	0.0001
তামা	0.92	লোহা	0.16	জল	0.0015
সোনা	0.72	কাচ	0.0025	বায়ু	0.00006

যে কাঠ থেকে কাঠের গুঁড়ো নির্গত হয়, সেই কাঠ অপেক্ষা কাঠের গুঁড়োর তাপ পরিবাহিতা কম কেন?

কাঠ থেকে নির্গত কাঠের গুঁড়োর মধ্যে বায়ু আবদ্ধ থাকে। কাঠের তাপ পরিবাহিতা কম এবং কাঠ অপেক্ষা বায়ুর তাপ পরিবাহিতা অনেক কম। ফলে কাঠের গুঁড়োর তাপ পরিবাহিতা কাঠ অপেক্ষা কম হয়।

বায়ুর তাপ পরিবাহিতাঙ্ক ফেল্ট অপেক্ষা কম হওয়া সত্ত্বেও তাপ অন্তরক হিসেবে বায়ু অপেক্ষা ফেল্টের ব্যবহার বেশি। কারণ কী?

বায়ুর তাপ পরিবাহিতাঙ্ক ফেল্ট অপেক্ষা কম, কিন্তু উত্তপ্ত বস্তুর সংস্পর্শে বায়ু থাকলে বায়ুতে পরিচলন স্রোতের সৃষ্টি হয়, ফলে উত্তপ্ত বস্তু থেকে তাপক্ষয় হতে থাকে এবং কিছুক্ষণের মধ্যে উত্তপ্ত বস্তুর তাপমাত্রা ঘরের উষ্ণতার সমান হয়। কিন্তু বস্তুটিকে ফেল্ট দিয়ে ঢেকে রাখলে ফেল্টের তাপ পরিবাহিতাঙ্ক কম হওয়ার জন্য পরিবহণ পদ্ধতিতে তাপক্ষয় হয় না এবং উত্তপ্ত বস্তু বায়ুতে উন্মুক্ত না হওয়ায় পরিচলন পদ্ধতিতেও তাপক্ষয় হয় না। এই কারণে বায়ুর তাপ পরিবাহিতাঙ্ক ফেল্ট অপেক্ষা কম হওয়া সত্ত্বেও তাপ অন্তরক হিসেবে বায়ু অপেক্ষা ফেল্টের ব্যবহার বেশি।

তাপীয় রোধ কাকে বলে?

যে ধর্মের জন্য কোনো পদার্থ তার মধ্য দিয়ে তাপের পরিবহণকে বাধা দেয়, তাকে তাপীয় রোধ বলা হয়।

তড়িত্ রোধের সঙ্গে সাদৃশ্য দেখিয়ে তাপীয় রোধের রাশিমালাটি প্রতিষ্ঠা করো।

মনে করা যাক, কোনো কঠিন পদার্থের তৈরি একটি আয়তাকার ফলকের বেধ ( d ), দুই বিপরীত পৃষ্ঠের উষ্ণতা যথাক্রমে \( ( \theta_1 ) ও ( \theta_2 ) (( \theta_1 > \theta_2 ))\) এবং প্রস্থচ্ছেদের ক্ষেত্রফল ( A ), স্থিতাবস্থায় ( t ) সময়ে তলের সঙ্গে লম্বভাবে ( Q ) পরিমাণ তাপ পরিবাহিত হলে, তাপ প্রবাহের হার,

\( Q_t = \frac{kA(\theta_1 – \theta_2)}{d} \) \( \\Q_t=\frac{kA(\theta_1-\theta_2)}d\;\text{——(1)}\)

আবার, কোনো পরিবাহীর দুটি বিন্দুতে তড়িত্ বিভব যথাক্রমে \(( V_1 ) ও ( V_2 ) (( V_1 > V_2 ))\) হলে যদি পরিবাহীতে তড়িত্ প্রবাহ হয়, তাহলে ওহমের সূত্র থেকে পাই,

\( I = \frac{(V_1 – V_2)}{R} \)

সুতরাং, আধান প্রবাহের হার,\( q_t = \frac{(V_1 – V_2)}{R} \quad \text{——(2)} \)

যেখানে ( R ) হল পরিবাহীর রোধ। কোনো পরিবাহীর দুই প্রান্তে বিভবপ্রভেদ না থাকলে যেমন তড়িত্ প্রবাহ হয় না, তেমনই কোনো ফলকের দুই বিপরীত পৃষ্ঠের মধ্যে তাপমাত্রার পার্থক্য না থাকলে তাপের পরিবহণ হয় না। তাই (1) ও (2) নং সমীকরণ তুলনা করে পাই, \( \frac{d}{kA} \) রাশিটি পরিবাহীর রোধের সমতুল্য। এই কারণে \( \frac{d}{kA} \) রাশিটিকে তাপীয় রোধ বলা হয়।

∴ তাপীয় রোধ, \( R_T = \frac{d}{kA} \)

তাপীয় রোধের মাত্রিক সংকেত নির্ণয় করো।

কোনো কঠিন পদার্থের একটি আয়তাকার ফলকের বেধ (d), দুই বিপরীত পৃষ্ঠের উষ্ণতা যথাক্রমে \((\theta_1) ও (\theta_2) ((\theta_1 > \theta_2))\) এবং দুই বিপরীত পৃষ্ঠের প্রতিটির ক্ষেত্রফল (A) হলে যদি স্থিতাবস্থায় (t) সময়ে তলের সঙ্গে লম্বভাবে (Q) পরিমাণ তাপ পরিবাহিত হয় তাহলে,

\(
Q = kA(\theta_1 – \theta_2)\frac{t}{d}
\)

অথবা, \(
d = \frac{kA(\theta_1 – \theta_2)t}{Q}
\)

∴ তাপীয় রোধ, \(
R_T = \frac{d}{kA} = \frac{(\theta_1 – \theta_2)t}{Q}
\)

∴ তাপীয় রোধের মাত্রিক সংকেত = \(([(\theta_1 – \theta_2)]\cdot[t]\cdot[Q])\)

\(
=\frac{\Theta\cdot T}{ML^2T^{-2}}\) \(\\
= M^{-1} L^{-2} T^{-3} \Theta
\)

কেটলির হাতলে বেত জড়ানো থাকে কেন?

কেটলি সাধারণত অ্যালুমিনিয়ামের তৈরি হয়, যা তাপের সুপরিবাহী। কেটলিতে জল বা অন্য কোনো তরল গরম করার সময় কেটলির শরীরও উত্তপ্ত হয়ে ওঠে। এই অবস্থায় কেটলির হাতল ধরা কঠিন হয়ে যায়, কারণ তাপ সরাসরি হাতের মাধ্যমে শরীরে পৌঁছাতে পারে। বেত তাপের কুপরিবাহী, অর্থাৎ তাপ সঞ্চালন করতে পারে না। তাই কেটলির হাতলে বেত জড়িয়ে দিলে হাতের মাধ্যমে তাপ সঞ্চালিত হয় না, ফলে সহজে হাতল ধরা যায়। এই কারণেই কেটলির হাতলে বেত জড়ানো থাকে।

শীতকালে পাখিরা পালক ফুলিয়ে রাখে কেন?

শীতকালে পাখিরা তাদের পালক ফুলিয়ে রাখে, যার ফলে পালকের ফাঁকে বায়ু আটকে যায়। বায়ু তাপের কুপরিবাহী, অর্থাৎ তাপ পরিবহন করতে পারে না। এই আবদ্ধ বায়ু পাখির শরীরের তাপ বাইরের ঠান্ডা পরিবেশে চলে যেতে বাধা দেয়, ফলে পাখির শরীর উষ্ণ থাকে। এই কারণেই শীতকালে পাখিরা পালক ফুলিয়ে রাখে।

বরফকে কাঠের গুঁড়ো দিয়ে ঢেকে রাখলে সহজে গলে যায় না কেন?

কাঠ এবং কাঠের গুঁড়ো তাপের কুপরিবাহী, অর্থাৎ তাপ সঞ্চালন করতে পারে না। কাঠের গুঁড়োর মধ্যে বায়ু আবদ্ধ থাকে, যা তাপ পরিবাহিতা আরও কমিয়ে দেয়। ফলে বাইরের তাপ বরফের মধ্যে সঞ্চালিত হতে পারে না, এবং বরফ সহজে গলে না।

শীতকালে একই উষ্ণতায় থাকা একটি কাঠের চেয়ার এবং একটি লোহার চেয়ারে হাত দিলে লোহার চেয়ারটি বেশি ঠান্ডা মনে হয় কেন?

শীতকালে আমাদের শরীরের তাপমাত্রা সাধারণত চেয়ারের তাপমাত্রার চেয়ে বেশি থাকে। লোহা তাপের সুপরিবাহী, অর্থাৎ তাপ দ্রুত সঞ্চালিত হয়, এবং কাঠ তাপের কুপরিবাহী, অর্থাৎ তাপ সঞ্চালন করতে পারে না। লোহার চেয়ারে হাত দিলে শরীরের তাপ দ্রুত চেয়ারের মাধ্যমে পরিবাহিত হয়, তাই এটি বেশি ঠান্ডা মনে হয়। অন্যদিকে, কাঠের চেয়ারে তাপ সঞ্চালন ধীরে হয়, ফলে তা তুলনামূলক কম ঠান্ডা অনুভূত হয়।

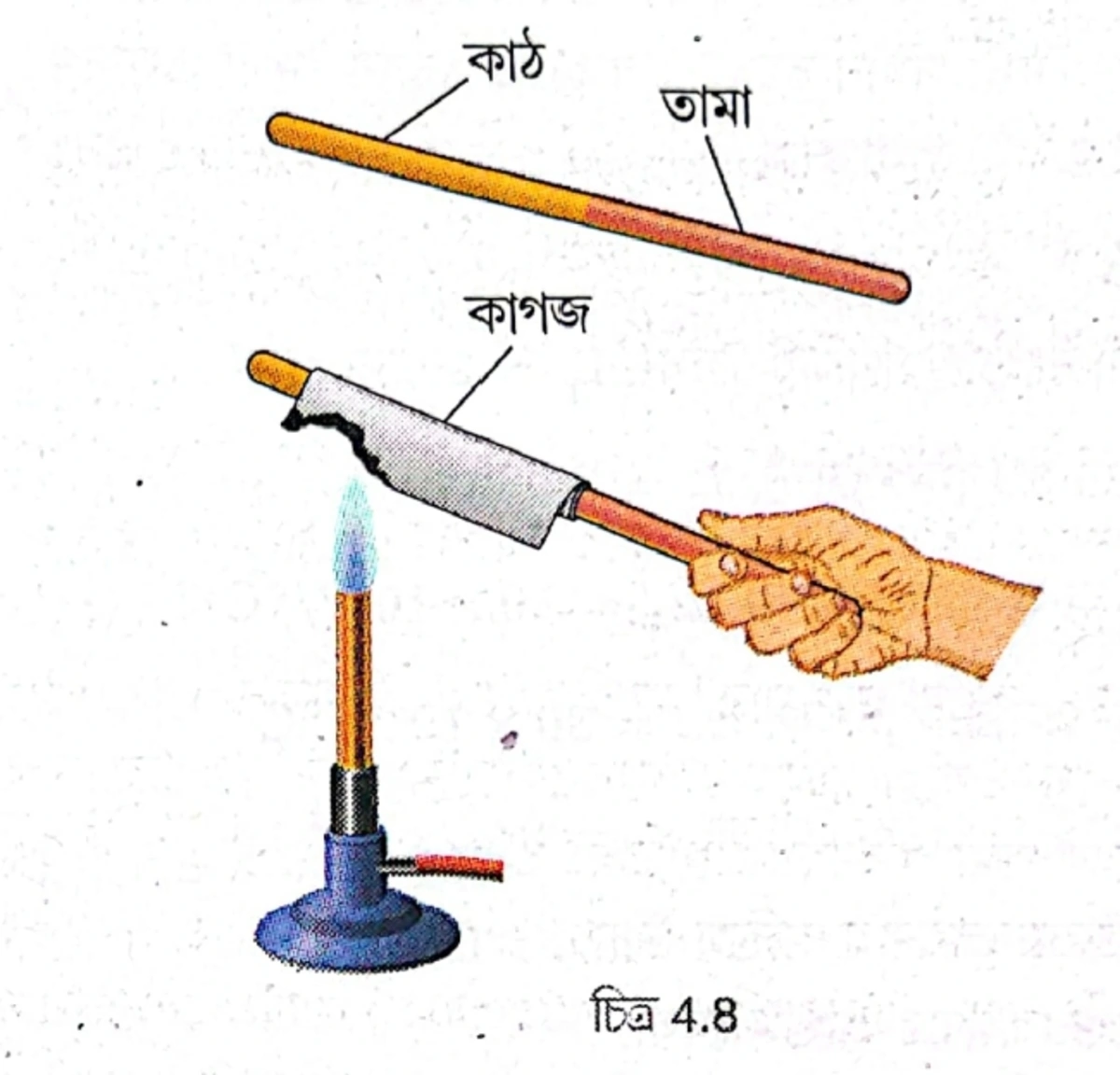
একটি যুগ্মদণ্ডের অর্ধেক তামার ও অর্ধেক কাঠের। একটি পাতলা কাগজকে ওই দণ্ডে একপাক জড়িয়ে বার্নারের শিখার কাছে ধরলে কী দেখা যাবে তা উপযুক্ত কারণসহ লেখো।

যুগ্ম দণ্ডটি বার্নারের শিখায় ধরলে দেখা যাবে, তামার অংশের ওপরের কাগজ পুড়ে না গেলেও কাঠের অংশের কাগজ পুড়ে যাবে। কারণ তামা তাপের সুপরিবাহী, ফলে বার্নারের তাপ তামার মধ্য দিয়ে সঞ্চালিত হয়ে যায় এবং কাগজের তাপমাত্রা জ্বলনাঙ্কে পৌঁছায় না। কিন্তু কাঠ তাপের কুপরিবাহী হওয়ায় তাপ সঞ্চালিত করতে পারে না, ফলে কাঠের অংশের কাগজের তাপমাত্রা জ্বলনাঙ্কে পৌঁছে পুড়ে যায়। তবে দীর্ঘ সময় ধরে বার্নারের শিখায় ধরলে তামার ওপরের কাগজও পুড়ে যাবে।

সিলিকনের আয়তন কখন কমে যায়?

সিলিকনের তাপমাত্রা 18 K থেকে 20 K পর্যন্ত বৃদ্ধি করলে আয়তন কমে যায়।

আজকে আমরা আমাদের আর্টিকেলে মাধ্যমিক ভৌতবিজ্ঞান বইয়ের তাপের ঘটনাসমূহ অধ্যায়ের কিছু সংক্ষিপ্ত ও দীর্ঘ প্রশ্নোত্তর নিয়ে আলোচনা করেছি। এই প্রশ্নগুলো মাধ্যমিক পরীক্ষার জন্য বা আপনি যদি প্রতিযোগিতামূলক পরীক্ষার প্রস্তুতি নেন তাহলে আপনার জন্য খুবই গুরুত্বপূর্ণ। কারণ এই প্রশ্নগুলি মাধ্যমিক পরীক্ষা বা চাকরির পরীক্ষায় প্রায়ই দেখা যায়। আশা করি এই আর্টিকেলটি আপনাদের জন্য উপকারী হয়েছে। আপনাদের কোনো প্রশ্ন বা অসুবিধা হলে আপনারা আমাকে টেলিগ্রামে যোগাযোগ করতে পারেন, আমি উত্তর দেওয়ার চেষ্টা করব। এছাড়া, নিচে আমাদের এই পোস্টটি আপনার প্রিয়জন, যার এটি প্রয়োজন হবে তার সাথে শেয়ার করুন। ধন্যবাদ।